第三章 运输问题1
管理运筹学第3章-运输规划1

6
9 u2=-2
5
9
10
6
3
-11
-3
6
13 u3=6
v1=10
v2=6
v3=4
v4=0
c32 - z32= c32 – (u3+v2)= 9 – 6-6=-3
3.3 迭代规则 运算方法—闭回路调整法
调整的步骤如下: (1)先确定最小检验数:; (2)找出以空格为一个顶点,其余顶点全是数字
-----退化解出现
3.3 迭代规则 运算方法—闭回路调整法
1
2
3
4
6
7
1
14
5
5
3
5
u1=-4
7
8
4
2
7
2
8
13
6
9 u2=-2
5
9
10
6
3
-11
-3
6
13 u3=6
v1=10
v2=6
v3=4
v4=0
x31进基, min{x21,x33}=min{8,6}=6, x33离基
转轴运算,重新计算检验数,确定进基、离基变量
第三章 运输问题
运输问题及其数学模型 运输问题表上作业法
3.1 运输问题及其数学模型
一、一般运输问题
设某种货物有m个产地A1,A2,…,Am,产量分 别为a1,a2,…,am,有n个销地B1,B2,…,Bn,销量分 别为b1,b2,…,bn,而且从Ai到Bj的单位运价为 Cij。若产销平衡( ai= bj),问如何制定调 运方案,可以使总运费最小?
v3=4
4 3
u1
7 u2=-2
6
13 u3=6
运筹学胡运权第三版第三章运输问题

§1运 输 问 题 及 其 数 学 模 型
二、运输问题数学模型的特点: 运输问题一定有最优解;基变量的个数=m+n-1 运输问题约束条件的系数矩阵:
x1m
x2m
xm1
xmm
x11
x12
…
x21
x22
…
xm2
…
…
m行
n行
§1运 输 问 题 及 其 数 学 模 型
解 的 最 优 性 检 验
运输问题及其数学模型
用表上作业法求解运输问题
运输问题的进一步讨论
应用问题举例
本章内容
3运输问题进一步讨论
01.
产销不平衡的运输问题 有转运的运输问题
02.
1.当产大于销时,即 产销不平衡问题 平衡后的数学模型为: 加入假想销地(假想仓库),销量为 ,由于实际并不运 送,它们的运费为 = 0;
解 的 最 优 性 检 验
解 的 最 优 性 检 验
销地产地
B1
B2
B3
B4
产量
ui
A1
16
u1(1)
A2
10
u2(0)
A3
22
u3(-4)
销量
8
14
12
14
48
vj
v1(2)
v2(9)
v3(3)
v4(10)
4
2
8
12
5
4
10
11
3
9
6
11
表3-9
1.增加一位势列和位势行并计算位势
其中
8
10
2
6
8
产量
A1
第三章--运输问题

A1 A2 A3 销量
B1 B2 B3 B4 产量
3 11 3 10
7
1928
4
7 4 10 5
9
3
6
5
6
20
A1 A2 A3 A1 0 1 3 A2 1 0 M A3 3 M 0
B1
B2
B3
B4
B1
0142
B2
1021
B3
4203
B4
2130
A1 A2 A3 T1 T2 T3 T4 B1 B2 B3 B4 T1 2 3 1 0 1 3 2 2 8 4 6 T2 1 5 M 1 0 1 1 4 5 2 7 T3 4 M 2 3 1 0 2 1 8 2 4 T4 3 2 3 2 1 2 0 1 M 2 6
A1 A2 A3 T1 T2 T3 T4 B1 B2 B3 B4 产量 A1 0 1 3 2 1 4 3 3 1 3 10 27
1
A2 1 0 M 3 5 M 2 1 9 2 8 24 A3 3 M 0 1 M 2 3 7 4 10 5 29 T1 2 3 1 0 1 3 2 2 8 4 6 20 T2 1 5 M 1 0 1 1 4 5 2 7 20 T3 4 M 2 3 1 0 2 1 8 2 4 20 T4 3 2 3 2 1 2 0 1 M 2 6 20 B1 3 1 7 2 4 1 1 0 1 4 2 20 B2 11 9 4 8 5 8 M 1 0 2 1 20 B3 3 2 10 4 2 2 2 4 2 0 3 20 B4 10 8 5 6 7 4 6 2 1 3 0 20 销量 20 20 20 20 20 20 20 23 2 25 26
– 产地和销地之间虽有直达路线,但直达运输的费用或 运输距离分别比经过某些中转站还要高或远。
运筹学(胡运权版)第三章运输问题课后习题答案
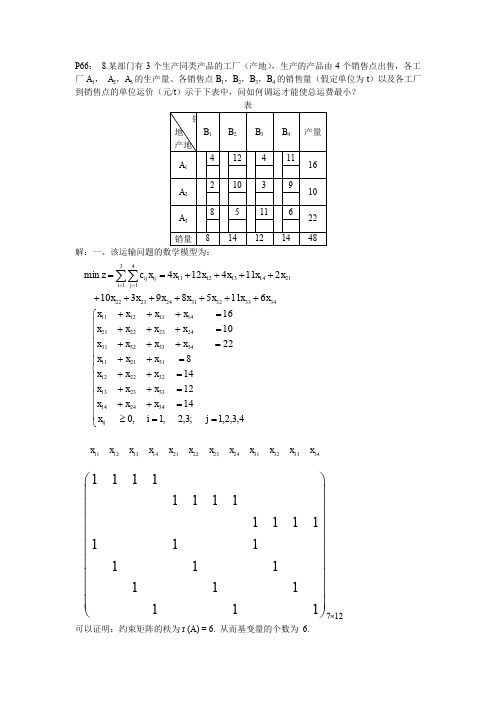
P66: 8.某部门有3个生产同类产品的工厂(产地),生产的产品由4个销售点出售,各工厂A 1, A 2,A 3的生产量、各销售点B 1,B 2,B 3,B 4的销售量(假定单位为t )以及各工厂到销售点的单位运价(元/t )示于下表中,问如何调运才能使总运费最小?表解:一、该运输问题的数学模型为:可以证明:约束矩阵的秩为r (A) = 6. 从而基变量的个数为 6.34333231242322213141141312116115893102114124min x x x x x x x x x x x x x c z i j ij ij +++++++++++==∑∑==⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧==≥=++=++=++=++=+++=+++=+++4,3,2,1;3,2,1,01412148221016342414332313322212312111343332312423222114131211j i x x x x x x x x x x x x x x x x x x x x x x x x x ij 111213142122232431323334x x x x x x x x x x x x 712111111111111111111111111⨯⎛⎫ ⎪⎪⎪ ⎪⎪⎪ ⎪⎪ ⎪⎝⎭二、给出运输问题的初始可行解(初始调运方案)1. 最小元素法思想:优先满足运价(或运距)最小的供销业务。
其余(非基)变量全等于零。
此解满足所有约束条件,且基变量(非零变量)的个数为6(等于m+n-1=3+4-1=6).总运费为(目标函数值) ,1013=x ,821=x ,223=x ,1432=x ,834=x ,614=x ∑∑===3141i j ijij x c Z2. 伏格尔(Vogel)法伏格尔法的基本思想:运输表中各行各列的最小运价与次小运价之差值(罚数)应尽可能地小。
或者说:优先供应罚数最大行(或列)中最小运费的方格,以避免将运量分配到该行(或该列)次小运距的方格中。
运筹学第三章 运输问题

销地 产地 A1
A2
B1
B2
B3
B4
产量
6
5 3
3 1
4
4
2
A3
销量 2
4 7
1 3
4
4 6
3
7 5
3
5
6
8
4 3 13
σ11=-3, σ12=-2,σ23=-4, σ31=-1,σ33=1, σ34=-1
销地 产地 A1
A2
B1
B2
B3
B4
产量
6
5 0
3 4
4
4
2
A3
销量 2
4 7
4
4 6
3
4 3
5
3
4
3
4 7
1
5
4 6
A3 销量 2
7
0
4
6
3
5
3
4
8
3 13
x11检验数为 6-4+8-6+4-4=4
销地 产地 A1
A2
B1
B2
B3
B4
产量
6 4 2 4
5
3
4
3
4 7
1
5
4 6
A3 销量 2
7
0
4
6
3
5
3
4
8
3 13
x12检验数为 5-4+8-6=3
销地 产地 A1
A2
B1
B2
B3
B4
产量
2、位势法 当运输问题变量的格数较多时,用闭 回路法计算检验数比较麻烦,而位势法比 较简便。 对于运输问题 minf=CX AX=b X≥0 设B为其一个可行基,则xij的检验数为 σ ij=CBB-1Pij-Cij
运输问题——精选推荐

运输问题第三章运输问题⼀、选择1. 运输问题在⽤表上作业法计算的时候,⽤闭回路法进⾏调整检验时,通过任⼀空格可以找到()闭回路A、惟⼀B、多个C、零个D 不能确定2. 在产销不平衡的运输问题中,如果产⼤于销,我们(B )把他变成⼀个产销平衡的运输问题A 假想⼀个产地B 假想⼀个销地C 去掉⼀个产地D 没有办法3.最⼩元素法的基本思想就是(D)。
A依次供应B全⾯供应C 选择供应D就近供应4.运输问题中在闭回路调整中,使⽅案中有数字的格为(C )。
A mB nC m+nD m+n-15. 在表上作业法中,调运⽅案中有数字的格为(C )A m+nB m-nC m+n-1D m*n6.运输问题的数学模型中,包含有(D)变量。
A m+nB m-nC m+n-1D m*n7. 运输问题的数学模型中,包含有(A)个约束条件。
A m+nB m-nC m+n-1D m*n8. 运输问题的数学模型中,系数矩阵中线性独⽴的列向量的最⼤个数为(C )A m+nB m-nC m+n-1D m*n9. 运输问题的解中的基变量数⼀般为(C )A m+nB m-nC m+n-1D m*n10.运输问题中,在检验数表上所有检验数都(C ),此时运输表中给出的⽅案就是最优⽅案。
A⼤于零B等于零C⼤于等于零D⼩于零11.在产销不平衡的运输问题中,如果销⼤于产时,可以在产销平衡表上(A),把他变成⼀个产销平衡的运输问题A 假想⼀个产地B 假想⼀个销地C 去掉⼀个产地D 没有办法12. 运输问题数学模型的特点之⼀是()A ⼀定有最优解B 不⼀定有最优解C ⼀定有基可⾏解D 不⼀定有基可⾏解13.运输问题的数学模型的约束条件的系数矩阵的元素由()组成。
A 0B1C0,1D 不确定14.⼆、填空1. 求解不平衡的运输问题的基本思想是(设⽴虚供地或虚需求点,化为供求平衡的标准形式) 。
2.运输问题中求初始基本可⾏解的⽅法通常有 (最⼩元素法 )、 (伏格尔法 ) 两种⽅法。
运筹学基础-运输问题(1)

xij≥0 (i=1,2,3;j=1,2,3,4)
4
运输问题
运输问题举例 (续)
【例2】某公司下属三个工厂(甲厂、乙厂、丙厂)生产同类 产品,供应不同地区的3个城市(A城、B城、C城),工厂的 供应量、城市的需求量及工厂到不同城市的单件运费如表,写 出本例数学模型 产销大于销
销地 产地 甲厂 乙厂 丙厂 需求量 A城 8元 4元 7元 5000 B城 6元 3元 4元 7500 C城 7元 5元 6元 7500
56
16 66
36
41
16
运输问题
西北角法图示
初始基可行解:x11=56,x21=16,x22=66,x32=36,x33=41
此时运费 Z=31240
销地 产地 W厂 X厂 A段
5656 40
B段
C段
供应量
0 70
66 36
0 140 0 110
41
56 82
16
16 120 0 80
72
66 240 36 130
运输问题
【另例】
销地
产地
B1 6
7
2
B2
2
B3 3
5
1
B4 2
8
2
2
产量 5
4
行差额
产量
j 1 m
ij
ai , bj ,
i 1,2,...,m j 1,2,...,n
a1 a2 … am
x
i 1
ij
xij 0
11
运输问题
产小于销
a b
i 1 i j 1
m
n
j
min Z cij xij
运筹学第3章:运输问题

5
B3
B4
产量
B1
B2
B3
B4
A1
A2 A3 销量
15 5
25 18 3 5 45
20
22 12
11
17 24
30
19 16
21
30 28
对应的目标函数值为: z=10×20+5×11+7×17+15×19+30×3+5×28=889(元) 3、伏格尔法 ⑴在运价表中分别增加一行(列差额)和一列(行差额),并分 别计算出各行和各列次最小运价和最小运价的差额。 ⑵从行差额或列差额中选出最大者,选择它所在的行或列中 的最小运价优先安排运量。
第三章 运输问题
(Transportation Problem)
运输问题及其数学模型 表上作业法 运输问题的进一步讨论
WinQSB软件应用
第一节 运输问题及其数学模型
一、运输问题的数学模型
【例1】已知某产品有A1、A2、A3三个生产地,其可供应的产量分别为15、 25、5吨;有B1、B2、B3、B4四个销售地可以销售该产品,其对该产品的需求 量分别为10、12、15、8吨。从Ai运往Bj单位产品的运价如下表所示。
⑴在运价表中找到最小运价cLk; ⑵将AL的产品给B k;
①若aL>b k,则将aL改写为aL-bk,划掉bk,同时将运价表中 K列的运价划掉; ②若aL<b k,则将bk改写为bk-aL,划掉aL,同时将运价表中 L行的运价划掉。
如此重复⑴、⑵,直到分配完毕。
【例3-2】以例3-1为例进行说明。
二、运输问题的特点
1、平衡运输问题必有可行解,也必有最优解; 2、运输问题的基本可行解中应包括 m+n-1个基变量。
运筹学第三章 运输问题

8
1.运输问题模型及有关概念
表4-3 运输问题数据表
销地
产地
A1 A2
┇
Am
销量
B1 B2 … Bn
c11
c12 … c1n
c21
c22 … c2n
┇ ┇ ┇┇
cm1
cm2 … cmn
b1
b2 … bn
产量
a1 a2
┇
am
设 xij 为从产地 Ai 运往销地 Bj 的运
式(4-8)中的变量称为这个闭回路的顶点。
22
1.运输问题模型及有关概念
例如,x13, x16, x36, x34, x24, x23 ; x23, x53, x55, x45, x41, x21 ; x11, x14, x34, x31等都是闭回路。
若把闭回路的各变量格看作节点, 在表中可以画出如下形式的闭回路:
得到下列运输量表:
4
1.运输问题模型及有关概念
Min Z s.t.
= 6x11+4x12+6x13+6x21+5x22+5x23 x11+ x12 + x13 = 200
x21 + x22+ x23 = 300
x11 + x21 = 150
x12 + x22 = 150
x13 + x23 = 200
2.每列只有两个 1,其余为 0,分别 表示只有一个产地和一个销地被使用。
7
1.运输问题模型及有关概念
一般运输问题的线性规划模型及求解思路
一般运输问题的提法:
假设 A1, A2,…,Am 表示某物资的m个 产地;B1,B2,…,Bn 表示某物资的n个销地; ai表示产地 Ai 的产量;bj 表示销地 Bj 的 销量;cij 表示把物资从产地 Ai 运往销地 Bj 的单位运价(表4-3)。如果 a1 + a2 + … + am = b1 + b2 + … + bn
《运筹学》第三章 运输问题
销量 3 6 5 6
A1 A2 A3
销量
B1 B1 B3 B4
2 1
6
5
3 3
3656
产量
7 4 9
精品课件
24
例:
B1 B2 B3 B4 产量
A1 (1) (2) 4 2 6 A2 3 (1) 2 (-1) 5 A3 (10) 6 (12) 3 9 销量 3 6 6 5
B1 B2 B3 B4 产量
(3) 在进行调运方案改进时,若沿闭合回路出现多个可作为 调出变量的数字格(即闭回路上的数字格最小值有多 个),此时,任选一个为调出变量,其余的填0,保证调 整后的调运方案中仍有m+n-1个数字格。
精品课件
23
例:
B1 B1 B3 B4 产量
A1 (0) (2) 5 2 7 A2 3 (2) (1) 1 4 A3 (9) 6 (12) 3 9
产 销 平 衡 表
单 位 运 价 表
精品课件
7
一般模 型表示 (ai=bj)
精品课件
8
三、模型的特点
1.变量数:mn个 2.约束方程数:m+n个
最大独立方程数:m+n-1 3.系数列向量结构:
0
Pij= 1 ——第i个分量
1 ——第m+j个分量 0
…… …
精品课件
9
······
······
x11 x12 ······ x1n x21 x22 ······ x2n ,············, xm1 xm2 ······ xmn
第3章 运输问题
精品课件
1
3.1 运输问题的典例和数学模型 3.2 运输问题的求解方法:表上作业 法 3.3 几类特殊的运输问题
运筹学第三版之第三章运输问题

在第一章线性规划模型的应用中,我们介绍了运输问 题,建立了其数学模型,这类问题属线性规划问题, 当然可以使用单纯形法进行求解,但是,由于运输问 题的约束系数矩阵有其特殊的结构和性质,因而有比 单纯形法更有效的方法来求解。
此法是纯粹的人为的规定,没有理论依据和实际背 景,但它易操作,特别适合在计算机上编程计算,因 而备受欢迎。
1、求初始调运方案:
例1 设有某物资共有3个产地A1,A2,A3,其产量分别为 9,5,7个单位,另有4个销地B1,B2,B3,B4,其销量分别为 3,8,4,6,已知由产地Ai运往销地Bj的单位运价见下表, 问应如何调运,才能使总运费最省?
集合,若用一条封闭折线将它们连接起来形成的图形称 为一个闭回路,其中诸变量称为闭回路的顶点,连接相 邻两个顶点及最后一个顶点与第一个顶点的线段称为闭 回路的边。 x11 , x14 , x44 , x45 , x35 , x32 , x22 , x21
B1 B2 B3 B4 B5
A1 x11
A2 x21
i 1
j1
当产大于销时,其模型是:
mn
min Z cij xij i1 j1
n
j1
xij
ai
, i
1,2,...,m
s
.t
.
m
xij
bj
,
j
1,2,...,n
i1
xij 0 i 1,...,m , j 1,...,n
(3.2)
m
n
ai bj
大学运筹学[第三章运输问题]山东大学期末考试知识点复习
![大学运筹学[第三章运输问题]山东大学期末考试知识点复习](https://img.taocdn.com/s3/m/f86d790576eeaeaad0f33063.png)
20XX年复习资料大学复习资料专业:班级:科目老师:日期:第三章运输问题1.运输问题的特点一般运输问题是要把某种产品(或物资)从若干个产地调运到若干个销地,每个产地的产量、每个销地的销量和产销各地之间的单位运价(或运距)已知,要求确定出使总运输费用最小的运输方案。
这类问题可以用以下数学语言描述。
已知有m个产地Ai ,其产量分别为ai,i=1,2,…,m;有n个销地Bi,其销量分别为bi ,i=1,2,…,n;从Ai到Bj的运输的单价为cij。
这些已知数据可以归纳为表3—1。
设z玎表示从Ai 到Bj的运量,求解表3—2中的xij的值,使总运费最小。
上述这种形式,可称为表格形式的运输问题模型。
2.产销平衡问题与表上作业法(1)产销平衡问题的数学模型。
它包含m×n个变量,(m+n)个约束方程,其系数矩阵的结构比较松散,且特殊。
其系数矩阵为:该系数矩阵中对应于变量xij 的系数列向量Pij,其分量中除第i个和第m+j个为1以外,其余的都为,即故最多只有m+n-1个独立的约束方程,即系数矩阵的秩≤m+n-1产销平衡问题的基可行解中只有m+n-1个基变量,有(m×72)-(m+n-1)个非基变量。
(2)表上作业法。
表上作业法是单纯形法在求解运输问题的一种简化方法。
其计算步聚如下:①列出产销平衡表。
②确定初始基可行解,即在产销平衡平面表上给出m+n-1个数字格,确定初始基可行解一般用最小元素法和伏格尔法。
③求各非基变量的检验数,即在表上计算空格的检验数,判别是否达到最优解。
如已是最优解,则停止计算,否则转入下一步。
④确定换人变量的空格。
⑤确定换出变量的空格。
⑥沿闭回路调整运输数量θ。
⑦重复步骤③~⑥,直至所有空格的检验数“均为非负为止,此时便可得到最优方案。
3.产销不平衡运输问题的求解法对于总产量不等于总需求量的运输问题,不能直接采用表上作业法求最优调运方案,而是将产销不平衡问题转化为产销平衡运输问题,然后再采用表上作业法进行求解。
运筹学第3章运输问题

运筹学第3章运输问题第1节运输问题的数学模型第2节表上作业法钱颂迪制作运筹学(第三版)《运筹学》教材编写组第3章运输问题清华大学出版社第3章运输问题第1节运输问题的数学模型第2节表上作业法第3节产销不平衡的运输问题及其求解方法第4节应用举例第1节运输问题的数学模型已知有m个生产地点Ai,i=1,2,…,m。
可供应某种物资,其供应量(产量)分别为ai,i=1,2,…,m,有n个销地Bj,j=1,2,…,n,其需要量分别为bj,j=1,2,…,n,从Ai到Bj运输单位物资的运价(单价)为cij,这些数据可汇总于产销平衡表和单位运价表中,见表3-1,表3-2。
有时可把这两表合二为一。
表3-1销地产地1 2 ┉ n产量12┆mA 1A2┆Am销量B1 B2 ┈ BNn表3-2若用xij表示从Ai到Bj的运量,那么在产销平衡的条件下,要求得总运费最小的调运方案,数学模型这就是运输问题的数学模型。
它包含m×n个变量,(m+n)个约束方程。
其系数矩阵的结构比较松散,且特殊。
该系数矩阵中对应于变量xij的系数向量Pij,其分量中除第i个和第m+j个为1以外,其余的都为零。
即Pij=(0,… ,1,0,…,0,1,0,…,0)T=ei+em+j对产销平衡的运输问题,由于有以下关系式存在:第2节表上作业法表上作业法是单纯形法在求解运输问题时的一种简化方法,其实质是单纯形法。
但具体计算和术语有所不同。
可归纳为:(1) 找出初始基可行解。
即在(m×n)产销平衡表上用西北角法或最小元素法,Vogel法给出m+n-1个数字,称为数字格。
它们就是初始基变量的取值。
(2) 求各非基变量的检验数,即在表上计算空格的检验数,判别是否达到最优解。
如已是最优解,则停止计算,否则转到下一步。
(3) 确定换入变量和换出变量,找出新的基可行解。
在表上用闭回路法调整。
(4) 重复(2),(3)直到得到最优解为止。
例 1 某公司经销甲产品。
管理运筹学讲义第3章运输问题

• 可以证明,如果对闭回路的方向不加区别, 对每一个非基变量可以找到而且只能找到唯一的 一个闭回路。
•38
•所谓闭回路法,就是对于代表非基变量的 空格(其调运量为零),把它的调运量调 整为1,由于产销平衡的要求,我们必须对 这个空格的闭回路的顶点的调运量加上或 减少1。最后我们计算出由这些变化给整个 运输方案的总运输费带来的变化。如果所 有代表非基变量的空格的检验数也即非基 变量的检验数都大于等于零,则已求得最 优解,否则继续迭代找出最优解。
•39
•方法:对每个非基变量 xij 其检验数为 • ij = (闭回路上的奇数次顶点单位运费之和
) - (闭回路上的偶数次顶点单位运费之和)
销
产
B1 B2 B3 B4 产量 B1 B2 B3 B4
A1
4 3 7 3 11 3 10
A2 3
1
4 19 2 8
A3
6
3 9 7 4 10 5
需求 3 6 5 6 20
•
xij ≥ 0 ( i = 1、2、3;j = 1、2、3
•6
•其系数矩阵为 :
•共有 m+n 行,分别表示产地和销地;有 mn 列分别 表示各变量;每列只有两个 1,其余为 0 。
•7
运输问题的一般提法是:设某种物资有m个产地和n个
销地。产地Ai的产量为
;
销地Bj的销量为
。从第i个产地向
第j个销地运输每单位物资的运价为Cij,这就是由多个
上从一个代表非基变量的空格出发,沿水平或垂 直方向前进,只有遇到代表基变量的填入数字的 格才能向左或右转90度(当然也可以不改变方向 )继续前进,这样继续下去,直至回到出发的那 个空格,由此形成的封闭折线叫做闭回路。一个 空格存在唯一的闭回路。
《运筹学》第三章运输问题

Vogel近似法
考虑运输成本差异, 进行逼近最优解。
运输问题的扩展和变体
1
生产产能约束
考虑生产能力限制,同时优化货物的运输方案。
2
供需不平衡
存在供需不平衡时如何有效分配货物,避免浪费和延误。
3
多目标运输问题
同时考虑多个目标,如最小化成本和最大化利润。
运输问题的应用实例和案例分析
物流领域的应用
通过运输问题的优化,提升物流效率,降低成本。
运输问题的基本模型
运输方案的表示
常用的表示方法包括运输矩阵和网络图。
目标函数和约束条件
目标函数通常是最小化运输成本,约束条件包 括供需平衡和容量限制。
运输问题的解决方法
最小成本法
逐步分配货物,直至 达到最小总成本。
北北角法
按照最小单位运输成 本进行分配,直至l's Approximation Method)法为基础, 逐步分配货物。
《运筹学》第三章运输问 题
运输问题是运筹学中重要的问题之一,涉及到各种场景下的货物运输优化。 本章将介绍运输问题的定义、基本模型、解决方法,以及其在物流和生产调 度中的应用实例。
运输问题的概念和应用领域
• 运输问题是一种优化问题,旨在找到使运输成本最小的货物运输方案。 • 运输问题广泛应用于物流管理、供应链优化以及交通规划等领域。
生产调度中的应用
合理安排生产计划,提高生产线的利用率。
总结和展望
运输问题是优化领域的重要研究方向,未来随着物流技术的发展将有更多的应用场景和解决方法出现。
运筹学课件:第三章 运输问题[1]
![运筹学课件:第三章 运输问题[1]](https://img.taocdn.com/s3/m/2704103ce009581b6ad9eb1f.png)
某公司下属两个工厂,生产同一种产品。产品均可运往三个中心 仓库去销售。已知每个工厂的产量,各仓库的销量及各工厂到每 个仓库的运输单价如下表所示。问如何组织调运可使生产与运输 的总费用最少?
Operation Research
运输问题的数学模型(2)
建立模型
第七讲
Operation Research
运输问题检验数的计算公式
第七讲
求解检验数的关键在于如何确定ui和vj
Operation Research 求解ui和vj
第七讲
Operation Research
表上作业法(8)
第七讲
运输问题解的讨论
有无穷多最优解
空格(非基变量)的检验数全部大于等于0,并且某个空格(非基变量) 的检验数为0。
Operation Research
运输问题的数学模型(4)
建立模型
第七讲
Operation Research
第七讲
运输问题的数学模型(5)
Operation Research
运输问题的特征(1)
产销平衡的运输问题必有可行解也必有最优解 运输问题的约束条件矩阵属于大型稀疏矩阵
第七讲
Operation Research
Operation Research
表上作业法(4)
第七讲
确定初始基可行解——伏格尔(Vogel)法
基本思路:元素差额法,在一行(或一列)中,算出最小元素和 次小元素的差额,如果差额很大,则优先用最小元素所对应的供 应关系供应。
方法:
(1)分别计算各行和各列的最小运费和次小运费差额,并填入表中;
在整个运输系统内部,各类点之间的运输关系为:
Q
管理学第三章运输问题

该公司应如何调运产品,在满足各销售点
的需要量的前提下,使总运费最少.
表3-5信息表
第三章 运输问题
B 1 B 2 B 3 B 4 产量
A1
3 11
3 10 7
A2
19
基于此,采用伏格尔法确定初始基本可行解,仍以例2为例 第一步:在运价表中计算出各行最小运费和次最小运费的差额, 行差额记为ui,i=1,2,…,m;同时求出每列次小运价与最小运价 之差,记为vj,j=1,2,…,n;填入表中的最右列和最下行
第三章 运输问题
第二步:从行或列差额中选出最大者,选择它所在行或列中 的最小运价.即L=max{ui,vi},差额L对应行或列的最小运
……
m
cm1 cm2 … cmn
第三章 运输问题
【解】设xij为从产地Ai运往销地Bj的物资数 量(i=1,…m;j=1,…n),由于从Ai 运出的物资总量应等于Ai的产量ai,因此 xij应满足:
n
xij ai
j 1
i 1,2, , m
第三章 运输问题
同理,运到Bj的物资总量应该等于Bj的销量bj,所以xij还 应满足:
(4)粮食的运量应大于或等于零(非负要求),即
有些问题表面上与运输问题没有多大关系,其模型的数学 结构与例1运输问题模型形式相同,我们把这类模型都称为 运输模型。
不失一般性.
第三章 运输问题
设有m个产点Ai, i=1,2,…,m. 可供应某种物资, 其供应量(产量)分别为ai , i=1,2,…,m. 有n个 销地Bj , j=1,2,…,n. 其需要量分别为bj, j=1,2,…,n. 从Ai到Bj运输单位物资的运价为
运筹学学习(自制笔记)第3章 运输问题
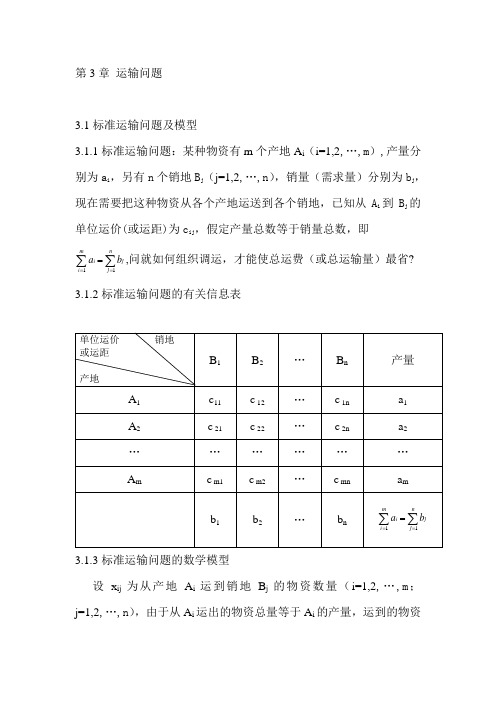
第3章 运输问题3.1标准运输问题及模型3.1.1标准运输问题:某种物资有m 个产地A i (i=1,2,…,m ),产量分别为a i ,另有n 个销地B j (j=1,2,…,n ),销量(需求量)分别为b j ,现在需要把这种物资从各个产地运送到各个销地,已知从A i 到B j 的单位运价(或运距)为c ij ,假定产量总数等于销量总数,即11m niji j a b ===∑∑,问就如何组织调运,才能使总运费(或总运输量)最省?3.1.2标准运输问题的有关信息表3.1.3标准运输问题的数学模型设x ij 为从产地A i 运到销地B j 的物资数量(i=1,2,…,m ;j=1,2,…,n ),由于从A i 运出的物资总量等于A i 的产量,运到的物资总量等于的销量,得模型如下: mi Z=11mnij iji j c x==∑∑s.t.1nijij xa ==∑1mijj i xb ==∑0ij x ≥且有11m niji j a b Q ====∑∑即满足产销平衡条件,故此模型描述的是产销平衡运输问题。
3.1.4标准运输问题的特点⑴平衡条件下的运输问题必有最优解此问题是一个有m ×n 个变量,m+n 个等型约束条件的线性规划最小化问题,由于目标函数不可能为负,故有下界存在,而/ij i j x a b Q =是问题的一组可行解,因此一定有最优解。
既是线性规划问题,无疑可用单纯形法求解,但其数学模型自身结构有其特殊性,可以利用更简便的表上作业法求解。
⑵标准运输问题约束方程组的系数矩阵运输问题是一个具有m ×n 个变量,m+n 个等型约束条件的线性规划问题,问题的约束方程组的系数矩阵A 是一个只有0和1两个数值的稀疏矩阵,ij x 对应的列ij P 只有第i 行和第m+j 行为1,其余各行皆为0。
⑶标准运输问题的基变量总数为m+n-1。
可以证明系数矩阵A 和增广矩阵A ′的秩为m+n-1。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例:
二、表上作业法
B1
4
1 2
第三章
销地 产地 A1
A2 A3 销量
B2
12
B3
4 10
B4
11 6
产量 16
10 22 48
2
8
1
10
2
3
-1
9 6
8 14
8
10
5
14 14
12
11
12
8
二、表上作业法
例: 销地 产地 B1 4 0 2 8 8 9 8 14 14 2 5 12 12 2 10 1 11 8 14 B2 12 12 3 2 6 B3 4 4 9 B4 11 产量
第三章
A1
A2
16
10
A3
销量
22
48
由于所有非基变量的检验数全非负,故这个解为最优解。 又由于非基变量有零检验数,所以有无穷多最优解。
练习题
练习题
销地 产地 A1 A2 A3 销量 22
二、表上作业法
第三章
B1
6 14 8 8 5
B2
7 4 13 9 6 13 6
B3
5 2 10
B4
3 7 6 13 13
)
三、运输问题的进一步讨论
第三章
上一节讲述的运输问题的算法,是以总产量 等于总销量(产销平衡)为前提的。实际上,在很
多运输问题中,总产量不等于总销量。
三、运输问题的进一步讨论
1、产销不平衡的运输问题
第三章
表上作业法 —— 以产销平衡 为前提。 ai b j
min z
C x
i 1 j 1 n
2、再对现行解作最优性判别; 3、若这个解不是最优解,就在运输表上对它进行调整 改进,得出—个新解; 4、再判别,再改进; 5、直至得到运输问题的最优解为止。 迭代过程中得出的所有解都要求是运输问题的基可行解。
二、表上作业法
例1 :
销地 产地 A1 A2 A3 销量 8
第三章
B1
4 2 8
B2
12 10 5 14
B3
4 3 11 12
B4
11 9 6 14
产量
16 10 22 48
二、表上作业法
1、初始基可行解--最小元素法 销地 产地 A1 A2 A3 销量 8 B1 4 2 B2 12 B3 4 B4 11 产量 16 10 22 48
第三章
10
10 3
6
9
8
8 5
2
11 6
14
14 12
8
14
所以,初始基可行解为:……目标函数值Z=246
二、表上作业法
1、初始基可行解--沃格尔法 沃格尔法计算步骤: 1) 分别算出各行、各列的罚数。
第三章
2) 从行、列中选出差额最大者,选择它所在行、 列中的最小元素,进行运量调整。 3) 对剩余行、列再分别计算各行、列的差额。返 回1)、2)。
二、表上作业法
销地 产地 A1 A2 A3 销量 8 B1 4 B2 12 B3 B4 4 产量 16 10 22 48
一、运输问题及其数学模型
3.运输问题的解 (1)解x必须满足模型中的所有约束条件;
第三章
(2)基变量对应的约束方程组的系数列向量线性无关; (3)解中非零变量xij的个数不能大于(m+n-1)个,原因是 运输问题中虽有(m+n)个结构约束条件,但由于总产量等 于总销量,故只有(m+n-1)个结构约束条件是线性独立的; (4)为使迭代顺利进行,基变量的个数在迭代过程中保 持为 (m+n-1)个。 运输问题解的每一个分量,都唯一对应其运输表中的 一个格 填有数字的格 或 空格
第三章
12
4 2
11
2
10
5
3
11
9
6
8
8
14
14 12
8
14
所以,初始基可行解为:……目标函数值Z=244
二、表上作业法
2、解的最优性检验--闭回路法
第三章
某空格的检验数是以该空格为第一个 顶点,某回路的奇数顶点运价和减去 其偶数顶点运价和。
销地 产地 A1 A2 A3 销量
B1
B2
B3
B4
产量 16 10 22 48
运输问题数学模型的特点:
第三章
1.运输问题有有限最优解
是一个可行解。同时,目标函数有下界,且不会趋
于负无穷。所以,必存在有限最优解。
一、运输问题及其数学模型
2.运输问题约束条件的系数矩阵
第三章
m 行
A =
n 行
第i个 第m+ j个
系数列向量:
一、运输问题及其数学模型
由此可知,运输问题具有下述特点:
第三章
(1)约束条件系数矩阵的元素等于0或1; (2)约束条件系数矩阵的每一列有两个非零元素,这 对应于每一个变量在前m个约束方程中出现一次,在后n 个约束方程中也出现一次;
对产销平衡运输问题,除上述两个特点外,还有以 下特点: (3)所有结构约束条件都是等式约束; (4)各产地产量之和等于各销地销量之和。 秩 ( A) =m+n-1 运输问题的基可行解中应包含m+n-1个基变量.
运价
6 7 5
需求地 1 d1=22
1
s2=27 s3 =19 3=24
2 3
3 8 4 2 7 5 9 10 6
2
d2=13
3
d3=12 d4=13
需 求 量
+5
000
4
5
d5=5 假想销地
三、运输问题的进一步讨论
产销不平衡
产大于销 模型:
i
第三章
产销平衡
a b
m n
j
min z
C
4
12 9 11 12
2
2 10 4 13
7
6
二、表上作业法
4、需要说明的几个问题
第三章
1)若运输问题的某一基可行解有几个非基变量的 检验数均为负,在继续进行迭代时,取它们中的任一 变量为换入变量均可使目标函数值得到改善,但通常 取小于零的检验数中最小者对应的变量为换入变量。
2)当迭代到运输问题的最优解时,如果有某非 基变量的检验数等于零,则说明该运输问题有多重(无 穷多)最优解。
4
1 2
12
10 10
1
4
6 3
11
9
-1
2 8 8
10
2
5 11
12
6
8
14 14
8
14
12
二、表上作业法
2、解的最优性检验--对偶变量法
第三章
原问题
设其对偶变量为:
二、表上作业法
对偶问题:
第三章
考虑原问题变量xj的检验数为:
二、表上作业法
则运输问题变量xij的检验数为:
第三章
假设已得到一个基可行解,其基变量为:
i 1 j 1 n
ij
xij i 1,2,...m j 1,2,...n
x
j 1 m i 1
ij
ai bj
x
ij
0
一、运输问题及其数学模型
运输问题的描述:
第三章
设某种物品有m个产地A1,A2,...,Am,各产地的产量 分别是a1,a2,...,am;有n个销地B1,B2,...,Bn,各销地的销
量分别为b1,b2,....bn。假定从产地Ai(i=1,2,…,m)向销地
出Bj(j=l,2,….n)运输单位物品的运价是cij,问怎样调运
第三章
min z 6x 11 7x 12 5x 13 3x 14 8x 21 4x 22 2x 23 7x 24 5x 31 9x 32 10x 33 6x 34 14 供 27 地 19 约 22
束 需 13 求 12 地 约 13 束 应
二、表上作业法
B2 7 5 5 B3 5 -4 B4 3 产量 14 27 19
第三章
8
2 5 13
4
12 9
2
-2 10
7
6
6
22
8
13
11
12
13
13
答案
二、表上作业法
第三章
销地 产地 A1 A2 A3 销量 1
B1 6 5
B2 7 5
B3 5
B4 3 13
产量 14 27 19
8
2 5 19 22 8 13 13
需 求 量
运输问题网络图
4
一、运输问题及其数学模型
s.t. x 11 x 12 x 13 x 14 x 21 x 22 x 23 x 24 x 31 x 32 x 33 x 34 x 11 x 12 x 13 x 14 x 11 x 12 x 13 x 14 x 21 x 22 x 23 x 21 x 22 x 23 x 24 x 24 x 31 x 32 x 33 x 31 x 32 x 33 x 34 x 34
量,以得到另一个更好的基可行解。
二、表上作业法
解改进的具体步骤
第三章
(1)以xij为换入变量,找出它在运输表中的闭回路; (2)以空格(Ai,Bj)为第一个奇数顶点,沿闭回路的顺(或逆) 时针方向前进,对闭回路上的顶点依次编号; (3)在闭回路上的所有偶数顶点中,找出运输量最小的顶 点(格子),以该格中的变量为换出变量; (4)以换出变量的运输量为调整量,将该闭回路上所有奇 数顶点处的运输量都增加这一数值,所有偶数顶点处的运输 量都减去这一数值,从而得出一新的运输方案。该运输方案 的总运费比原运输方案减少,改变量等于换出变量的检验数。 然后,再对得到的新解进行最优性检验,加不是最优 解,就重复以上步骤继续进行调整,一直到得出最优解为止。
