直线和平面成的角

合集下载

直线与平面所成的角(2019年12月整理)

角是0°
思考：
直线与平面所成的角θ 的取值范围
是：
。
斜线与平面所成的角θ 群 https:// 微信群微信红包群
；
度各季度及第一季度分月生产成本预算及制造费用预算；完成生产性固定资产大修理、改造、新增等资本性支出预算 9.411月10日投资管理办公室/券部完成下年度投资项目资本性支出预算 9.511月10日企业发展部/研发部门完成下年度新药开发项目资本性支出预算 9.611月10日其他各职能部门完成本部门下年度各季度及第一季度分月费用预算 1011月20日预算管理办公室预算编制及调整岗汇总整理各部门上报的预算草案，完成下年度公式整体预算及第一季度滚动预算编制，起草完成《部门预算汇总表》、《预算损益表》、《预算资产负债表》、资金预算及《预算现金流量表》，并送预算管理办公室主任审核。 1111月22日预算管理办公室主任审核下年度公式整体预算及第一季度滚动预算草稿，报财务总监审核。 1211月25日财务总监审核下年度公式整体预算及第一季度滚动预算，提请召开预算管理委员会进行审议。 1312月1日预算管理委员会审核预算草案，在对必要的项目要求各部门进行相应调整后，将年度预算草案报送董事会审议。 1412月10日董事会审议预算草案，在对必要的项目要求各部门进行相应调整后，报送股东大会批准。 1512月20日股东大会审议、批准预算方案。 1612月20日预算管理办公室预算编制及调整岗将股东大会批准的《整体年度预算和分部门年度预算》第一份交预算管理办公室预算执行与考核岗存档。 1712月25日预算管理办公室预算编制及调整岗将股东大会批准的《整体年度预算和分部门年度预算》第二份下发至各部门。 1812月30日各部门将部门预算分解至科室或班组。 2、季度滚动预算编制步骤完成时间涉及部门及岗位岗位岗步骤说明 1每季度第二个月20日各部门将下季度季度预算细化为分月度预算，并完成未来第四个季度的季度预算，报预算管理办公室汇总。 2每季度第二个月25日预算管理办公室预算编制及调整岗汇总各部门下季度分月度预算及未来第四个季度季度预算，形成草案报预算管理办公室主任审核。 3每季度第二个月25日预算管理办公室主任审核公式下季度分月度预算及未来第四个季度季度预算草案，报财务总监审批。 4每季度第二个月30日财务总监审核公式下季度分月度预算及未来第四个季度季度预算草案，提请预算管理委员会审批。 5每季度第三个月5日前预算管理委员会审核批准各部门分月预算及未来第四季度预算。 6每季度第三个月10日前预算管理办公室预算编制及调整岗将已经批准的各部门分月预算及未来第四季度预算第一份交预算管理办公室预算执行与考核岗存档。 7每季度第三个月10日前预算管理办公室预算编制及调整岗将已经批准的各部门分月预算及未来第四季度预算下发至各部门。 3、年度预算编制（编制第2年及以后）步骤完成时间涉及部门及岗位岗位岗步骤说明 1每年10月-11月各职能部门对比公式下年度经营目标，制定第一季度分月预算，完成第四季度预算，并且调整第二、第三季度预算。形成年度预算草案。 2每年12月预算管理办公室按度预算审批程序报送预算管理委员会、董事会及股东大会审批。[见年度预算编制程序（编制第一年）] 4、预算的调整步骤完成时间涉及部门及岗位岗位岗步骤说明 1不确定各职能部门根据实际情况与原年度预算和季度滚动预算的差异，提出《预算调整申请报告》报预算管理办公室。 2不确定预算管理办公室预算编制与调整岗审核《预算调整申请报告》，并提出处理建议。 3不确定预算管理办公室主任审核预算调整处理建议。 4不确定财务总监审核预算调整处理建议，同意上报预算管理委员会局部调整预算或予以否决。 5不确定预算管理委员会在月度预算分析会上讨论预算调整方案。同意调整或予以否决。 6不确定预算管理办公室预算编制与调整岗按已经预算管理委员会批准的方案调整相应预算。 7不确定预算管理办公室主任将调整后预算报财务总监审核。 8不确定财务总监审核签署。 9不确定预算管理办公室预算编制与调整岗将调整后预算下发给相关部门，并交一份与预算执行考核岗存档。五、单据及报告公式发展战略部门预算目标纲要整体年度预算和分部门年度预算季度分月预算及季度预算预算执行与考核（P5-Z4-2） ?目的本管理文件明确了公式年度预算及季度滚动预算执行与考核的管理要求与操作规范，以规范预算执行作业程序及对预算执行情况确定考核标准的基本程序。- 二、范围本程序管理文件适用于公式年度预算及季度滚动预算的执行与考核。预算执行考核标准的内容不包含在本管理文件内。 - 三、相关程序管理文件 10、供应内部控制（P2-Z1） 11、财务分析管理( P4-Z2-J4-6 ) 12、预算编制( P5-Z4-1 ) 四、业务流程步骤涉及部门步骤说明 1人事部起草《预算考核标准》，送预算管理办公室提出修改建议。 2预算管理办公室主任对《预算考核标准》提出修改建议，并报财务总监审核。 3财务总监审核《预算考核标准》，提请预算管理委员会审议。 4预算管理委员会审核《考核标准》，并作出同意或修改的决定。 5预算管理办公室预算执行监控岗将已经批准的《考核标准》第二份下发给各部门，第一份存档。 6各部门按已批准的分月预算及季度预算控制费用支出。若支出项目不超出预算，则根据正常授权审批程序进行审批。若支出项目超出预算，须提出解释原因及处理建议，完成《预算超支原因及纠正措施报告》一式两份，经部门负责人签署后报预算管理办公室初审。 7预算管理办公室预算执行监控岗对《预算超支原因及纠正措施报告》内容进行初步审核，提出建议处理措施。 8预算管理办公室主任审核预算执行岗提出处理措施，并送财务总监审批。 9财务总监审核《预算超支原因及纠正措施报告》，送预算管理委员会主任批准。 10预算管理委员会主任对《预算超支原因及纠正措施报告》内容进行审批。 11预算管理办公室预算执行监控岗将经批准的《预算超支原因及纠正措施报告》第一份存档，第二份交相关部门，并监督纠正及处理措施的执行情况。 12预算管理办公室预算执行监控岗每月汇总各部门实际发生的财务数据，编制《月度预算执行情况分析表》，分析本月预算执行情况，发生的差异以及预算外的项目，说明差异发生的原因。 13预算管理办公室主任审核《月度预算执行情况分析表》。 14预算管理办公室预算执行监控岗将《月度预算执行情况分析表》送预算管理委员会主任及副主任及相关部门。 15各部门分析本部门月度预算完成情况，发生差异及预算外项目，详细说明差异发生原因。 16预算管理办公室主任提请召开月度预算分析会，并将具体时间地点通知预算管理委员会各委员及列席部门。 17预算管理委员会组织召开月度预算分析会，具体分析上月预算完成情况，及发生主要差异。根据《考核标准》决定对各部门的考核或处理意见，并决定是否对月度预算或季度滚动预算进行调整。 18各部门根据预算管理委员会的审批意见对存在的问题进行详细调查，制定纠改措施。 19预算管理办公室预算执行监控岗每年末编制《全年预算执行报告》。分析全年预算执行情况，发生的差异以及预算外的项目，说明差异发生的原因及已进行的改进措施和成效。 20预算管理办公室主任审核《全年预算执行报告》。 21财务总监审核《全年预算执行报告》。 22预算管理办公室预算执行监控岗将《全年预算执行报告》送预算管理委员会各委员及相关部门。 23预算管理办公室主任提请召开年度预算分析会。 24预算管理委员会召开年度预算分析会，审阅公式《全年预算执行报告》，进行总结，并作为绩效考评的依据之一，为下一期的预算调整提供参考，并报董事会审议。 25董事会审阅公式《年度预算执行报告》，并提出审核意见。 26股东大会审阅公式汇总的《年度预算执行报告》，提出审批意见。五、单据及报告《预算超支原因及纠正措施报告》《月度预算执行情况分析表》《年度预算执行报告》第六篇内部审计制度第一章内控概述一、定义与范围内部审计是指由公式内部相对独立的审计机构和审计人员对公式各部门及分公式、子公式的财务收支、经营管理活动及其经济效益进行审核和评价，查明其真实性、正确性、合法性、合规性和有效性，提出意见和建议的一种专职经济监督活动。- 公式内部审计的审计范围包括公式本部、下属各部门及控股子公式、分公式、驻外办事处等。内部审计的审计类型包括经营绩效审计、法纪规章遵循情况审计、任期内经济责任审计、内部控制审计、预算执行情况和其他专项审计。- 本制度所规定的内部审计包括： 1、内部审计计划审计部按照审计委员会所确定的年度审计重点制定年度审计计划，经审计委员会批准后作为年度审计工作的指导性文件。- 2、内部审计执行审计部按照年度审计计划，针对具体审计项目制定审计程序，派遣审计人员进行审计。 3、内部审计结果处理审计部将审计报告报送审计委员会，同时送达被审计部门（或单位）。审计委员会根据审计报告确定内部审计处理意见。当发生重大争议时由审计委员会召开听会，由董事会对重大问题确定处理意见。- 二、控制目标五、健立建全内部控制制度，严肃财经纪律；六、查错揭弊，改善经营管理，提高经济效益；七、加强对下属各单位（部门）的监督与控制；八、为董事会的经营决策提供相对立、客观的资料。三、主要控制节点九、审计委员会审批年度内部审计计划；十、审计委员会对内部审计中重大争议召开听会；四、控制政策与方法十一、审计部对董事会下设的审计委员会负责，财务总监对审计部日常业务进行指导；十二、按照年度审计计划安排内部审计工作进程；十三、实行审计结果重大争议的听会制度。第二章组织机构及岗位职责一、涉及部门及部门职责审计委员会：隶属于董事会，其职责包括： ?批准内部审计制度及修订方案、年度内部审计计划； ?确定年度内部审计工作重点； ?对聘请的注册会计师与内部审计部门的职责划分和协调； ?根据审计结果依照公式有关制度对被审计单位及有关人员作出处理决定并交公式有关部门执行； ?对审计结果中反映出的重大问题，可先形成处理意见，然后提交

直线和平面所成的角

案例二：机械工程中的直线和平面所成的角
总结词
机械工程中，直线和平面所成的角对于机器的运转和性能至关重要。
详细描述
在机械设计中，直线和平面所成的角涉及到机器的传动、导向和定位等方面。例如，在制造精密机床时，需要精确控制导轨的角度和位置，以确保机床的加工精度和稳定性。同时，在机器运转过程中，直线和平面所成的角也需要进行实时监测和调整，以确保机器的正常运转和性能。
THANKS
感谢观看
利用向量计算
总结词
通过向量的数量积和向量的模长来计算直线和平面所成的角，是一种简便的方法。
详细描述
首先，选取平面上任意一点，并确定一个方向向量。然后，计算这个方向向量与直线向量的夹角的余弦值。最后，利用公式：θ = arccos(cos(θ))，其中θ为直线和平面所成的角。
利用几何定理计算
建筑设计
在建筑设计中，可以利用直线和平面所成的角来设计建筑物的外观和结构，例如斜屋顶的角度和楼梯的角度等。
机械设计
在机械设计中，可以利用直线和平面所成的角来设计机械零件的形状和尺寸，例如斜齿轮的角度和轴承的角度等。
道路建设
在道路建设中，可以利用直线和平面所成的角来设计道路的坡度和弯度，以确保车辆安全行驶。
直线在平面上
当直线上的所有点都在平面上时，称为直线在平面上。
02
直线和平面所成的角
角的定义和性质
角的定义
角是由两条射线共同端点形成的平面空间，这两条射线称为角的边，而它们的公共端点称为角的顶点。
角的性质
角的大小是由其两边的射线所夹的角度决定的，与边的长度无关。此外，角的大小不会因为角的边做平移或旋转而改变。
直线和平面所成的角

直线与平面所成的角

直线与平面所成的角1、直线和平面所成的角，应分三种情况：（1）直线与平面斜交时，直线和平面所成的角是指此直线和它在平面上的射影所成的锐角；（2）直线和平面垂直时，直线和平面所成的角的大小为90°；（3）直线和平面平行或在平面内时，直线和平面所成的角的大小为0°．显然，斜线和平面所成角的范围是（0，）；直线和平面所成的角的范围为[0，]．2、一条直线和一个平面斜交，它们所成的角的度量问题（空间问题）是通过斜线在平面内的射影转化为两条相交直线的度量问题（平面问题）来解决的．具体的解题步骤与求异面直线所成的角类似，有如下的环节：（1）作﹣﹣作出斜线与射影所成的角；（2）证﹣﹣论证所作（或找到的）角就是要求的角；（3）算﹣﹣常用解三角形的方法（通常是解由垂线段、斜线段、斜线段的射影所组成的直角三角形）求出角．（4）答﹣﹣回答求解问题．在求直线和平面所成的角时，垂线段是其中最重要的元素，它可起到联系各线段的纽带的作用．在直线与平面所成的角的定义中体现等价转化和分类与整合的数学思想．3、斜线和平面所成角的最小性：斜线和平面所成的角是用两条相交直线所成的锐角来定义的，其中一条直线就是斜线本身，另一条直线是斜线在平面上的射影．在平面内经过斜足的直线有无数条，它们和斜线都组成相交的两条直线，为什么选中射影和斜线这两条相交直线，用它们所成的锐角来定义斜线和平面所成的角呢？原因是斜线和平面内经过斜足的直线所成的一切角中，它是最小的角．对于已知的斜线来说这个角是唯一确定的，它的大小反映了斜线关于平面的“倾斜程度”．根据线面所成的角的定义，有结论：斜线和平面所成的角，是这条斜线和这个平面内的直线所成的一切角中最小的角．用空间向量直线与平面所成角的求法：（1）传统求法：可通过已知条件，在斜线上取一点作该平面的垂线，找出该斜线在平面内的射影，通过解直角三角形求得．（2）向量求法：设直线l的方向向量为，平面的法向量为，直线与平面所成的角为θ，与的夹角为φ，则有sinθ＝|cos φ|＝．。

9.3.2直线与平面所成的角

讲授新课 1、直线和平面所成的角
过斜线上斜足以外的一点向平面引垂线PO，垂线与平面的交点叫做垂足。过垂足O和斜足A的直线AO叫做斜线在这个平面上的射影. 平面的一条斜线和它在平面上的射影所成的锐角，叫做这条直线和这个平面所成的角. P
O
A
2、直线与平面所成的角的变化范围一条直线垂直于平面，我们说它们所成的角是直角，即900.
9.3.2直线与平面所成的角
复习引入
1.定义；
如果一条直线与一个平面内的两 2.判定定理：条相交直线都垂直，那么这条直线垂直于这个平面. 如果两条直线垂直于同一个平面， 3.性质定理：那么这两条直线互相平行.
讲授新课
1、直线和平面所成的角
一条直线PA和一个平面相交，但不和这个平面垂直，这条直线叫做这个平面的斜线，斜线和平面的交点A叫做斜足． P A
D'
C'
A'
D A
B'
C B
在直角三角形BDD'中
DD' tanDBD' BD DD' 2 2 2 DD'
课堂小结
直线和平面所成的角.
直Hale Waihona Puke 与平面所成的角或该角的三角函数值。
例3. 在正方体ABCD-A'B'C'D'中，求对角线BD'与底面ABCD所成的角的正切。解：BD'与底面ABCD交于点B，且D'不在底面ABCD内
DD' 平面ABCD
连接DB，则DB是D' B在底面ABCD上的投影，且DD' DB, 则DBD' 就是对角线 BD' 与底面ABCD所成的角

如何求直线与平面所成的角？

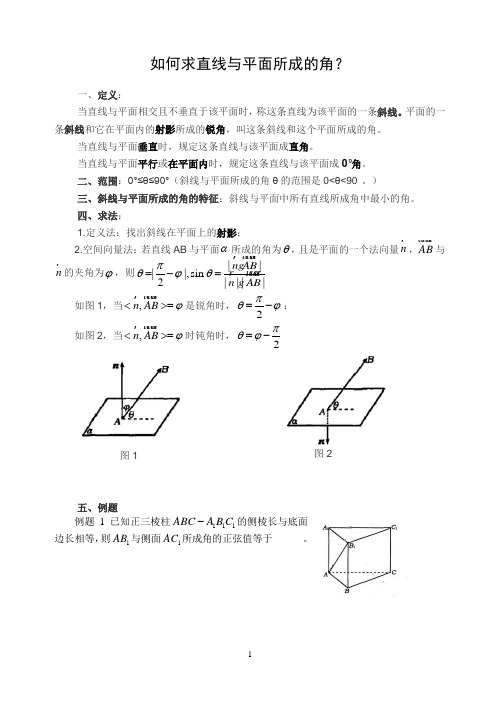
如何求直线与平面所成的角？一、定义：当直线与平面相交且不垂直于该平面时，称这条直线为该平面的一条斜线。

平面的一条斜线和它在平面内的射影所成的锐角，叫这条斜线和这个平面所成的角。

当直线与平面垂直时，规定这条直线与该平面成直角。

当直线与平面平行或在平面内时，规定这条直线与该平面成0°角。

二、范围：0°≤θ≤90°（斜线与平面所成的角θ的范围是0<θ<90°。

）三、斜线与平面所成的角的特征：斜线与平面中所有直线所成角中最小的角。

四、求法：1.定义法：找出斜线在平面上的射影；2.空间向量法：若直线AB 与平面α所成的角为θ，且是平面的一个法向量n ，AB 与n 的夹角为ϕ，则||||,sin 2||||n AB n AB πθϕθ=-= 如图1，当,n AB ϕ<>=是锐角时，πθϕ=-； ,n AB ϕ<>=时钝角时，图1图2五、例题例题1 已知正三棱柱111ABC A B C -的侧棱长与底面边长相等，则1AB 与侧面1AC 所成角的正弦值等于______。

例题 2 正方体中1111ABCD A BC D -中，1BB 与平面1ACD 所成角的余弦值为______例题 3 已知三棱锥S ABC -中，底面为边长等于2的等边三角形，SA 垂直于底面，3SA =，那么直线AB 与平面SBC 所成角的正弦值为_______.例题 4 如图，二面角l αβ--的大小为60，线段,AB B l α⊂∈，AB 与l 所成角为30，则与平面所成角的正弦值为________.例题5 如图，直三棱柱'''ABO A B O -中，3OB =，'4,90OO OA AOB ==∠=，D 是'AA 的中点，P 是侧棱上的一点，若OP BD ⊥，求OP 与底面AOB 所成角的正弦值.。

直线和平面所成的角

直线和平面所成的角直线和平面所成的角，应分三种情况：(1)直线与平面斜交时，直线和平面所成的角是指此直线和它在平面上的射影所成的锐角；(2)直线和平面垂直时，直线和平面所成的角的大小为90°；(3)直线和平面平行或在平面内时，直线和平面所成的角的大小为0°. 显然，斜线和平面所成角的范围是(0,)2π直线和平面所成的角的范围为⎥⎦⎤⎢⎣⎡2,0π.例1、如图，在正方体AC 1中，（1）求BC 1与平面ACC 1A 1所成的角；（2）求A 1B 1与平面A 1C 1B 所成的角的余弦值.解：（1）设所求角为α,先证BD ⊥平面ACC 1A 1，则si n α=si n ∠OC 1B =211=BC OB ,故α=30 (2)△A 1B 1C 1是正三角形，且A 1B 1=B 1C 1=BB 1. ∴棱锥B 1—A 1BC 1是正三棱锥.过B 1作B 1H ⊥平面A 1BC 1，连结A 1H ，∠B 1A 1H 是A 1B 1与平面A 1C 1B 所成的角. 设A 1B 1=a ,则A 1B = a 2,得A 1H=a 36. 故c os ∠B 1A 1H=36111=B A H A ，所求角的余弦值为36. 点评：1.求线面角即求这条直线与它在平面内的射影所成的角，关键在于找或作出直线A 1B 在平面A 1B 1CD 内的射影.2.通过本例我们要进一步明确求线面角的一般步骤，平面的垂线是其中最重要的元素，它可起到联系各线段的纽带的作用，因此，找或作出平面的垂线是求线面角的关键.3.直线和平面所成的角，是刻画空间位置关系的一类基本几何量，与射影密切相关.其中线面垂直是构成射影的必要条件，而空间各种角的计算方法，都是化为平面图形角的计算.因此，掌握转化的思想方法是解决这类问题的基本功.变式练习：1．已知正方体1111ABCD A B C D -中的棱长为a ，（1）求直线1AB 和平面1111A B C D 所成的角；（2）求直线1DB 和平面1111A B C D 所成的角的正弦值；2、在正方体ABCD －A 1B 1C 1D 1中，E 、F 分别为AA 1、AB 的中点，求EF 与平面AA 1C 1C 所成角的大小。

直线与平面的夹角关系

直线与平面的夹角关系直线与平面的夹角关系是几何学中一个重要的概念，它描述了直线与平面之间的相对位置和角度关系。

在本文中，我们将探讨直线与平面的夹角定义、性质以及应用。

一、直线与平面的夹角定义直线与平面的夹角定义为直线与平面在其交点处形成的角。

夹角通常用Greek字母“θ”表示。

二、直线与平面夹角的性质1. 夹角是与平面中的两个相交的直线有关的。

2. 夹角的取值范围在0°到180°之间。

3. 如果直线与平面垂直相交，则夹角为90°，也称为直角。

4. 如果直线与平面平行，则夹角为0°，也称为零角。

5. 两个相对平面之间的夹角是它们所在的共同直线和彼此正交的直线之间的夹角。

6. 夹角的大小不受直线或平面的长度或位置的影响，只取决于它们的相对位置。

三、直线与平面夹角的应用直线与平面的夹角关系在实际生活和工程中有广泛的应用，下面介绍几个典型的应用场景：1. 物体在斜面上的运动当一个物体沿着斜面下滑时，斜面与水平方向的夹角决定了物体受到的重力分量和斜面法向量方向的夹角，从而影响物体的滑动速度和加速度。

2. 光线的反射与折射光线在与镜面或介质边界相交时会发生反射和折射。

反射和折射的角度取决于入射光线与镜面或介质边界的夹角。

3. 航空航天工程在航空航天工程中，飞机和导弹的起飞和降落、空中操纵以及导航都与直线与平面的夹角有关。

例如，起飞和降落过程中飞机与地面跑道的夹角决定了飞机的升力和阻力大小。

4. 地理测量学地理测量学中的地图投影原理和图形的放大缩小都与直线与平面的夹角有关。

投影时，地球表面上的曲线被转化为平面图上的直线或曲线。

四、总结直线与平面的夹角关系涉及几何学中的基本概念和原理。

通过了解夹角的定义、性质和应用，我们可以更好地理解和应用于实际问题中。

在日常生活和科学工程中，直线与平面的夹角关系有着广泛的应用，它们帮助我们解释和理解物体的行为和光线的传播。

对于几何学和应用数学的学习和研究，直线与平面夹角关系是不可或缺的基础知识。

直线与平面所成的角

9.7 直线和平面所成的角与二面角
你注意观察过生活中的角吗？
复习回顾
直线和平面的位置关系
思考:当直线a与平面的关系是a =A时，如何反映出直线与平面的相对位置关系呢?
直线与平面所成的角：
一个平面的斜线和它在这个平面内的射影的夹角，
叫做斜线和平面所成的角（或斜线和平面的夹角）
直线和平面垂直，则直线和平面所成的角是直角直线和平面平行或在平面内，则直线和平面所成的
(2)AB与面ADO所成的角。
练习：如图：正方体ABCD-A1B1C1D1中，（1）AB1在面BB1D1D中的射影（2）AB1在面A1B1CD中的射影（3）AB1在面CDD1C1中的射影 D1
A1
D
A
C1 B1
C B
练习：如图：正方体ABCD-A1B1C1D1中，（1）AB1在面BB1D1D中的射影（2）AB1在面A1B1CD中的射影（3）AB1在面CDD1C1中的射影 D1
A1
线段B1O
C1 B1
D
C
O
A
B
练习：如图：正方体ABCD-A1B1C1D1中，（1）AB1在面BB1D1D中的射影（2）AB1在面A1B1CD中的射影（3）AB1在面CDD1C1中的射影 D1
平面的斜线和平面所成的角
cos= cos 1cos2
平面的斜线和它在平面内的射影所成的角，是这条斜线和这个平面内任一直线所成的角中最小的角
例1.如图，已知AB是平面的一条斜线，B为斜足，AO,O为垂足，BC为内的一条直线，ABC 60 , OBC 45 ，求斜线AB 和平面所成角。
角是0°
思考：
直线与平面所成的角θ 的取值范围

直线与平面的交角

直线与平面的交角直线与平面的交角是几何学中的重要概念之一，它描述了直线与平面之间的相对方向关系。

本文将介绍交角的定义、计算方法以及一些相关应用。

一、交角的定义直线与平面的交角是指直线与该平面上的任意一条射线之间的夹角。

这里的夹角是指由两条线段所围成的角度。

二、计算交角的方法1. 如果已知直线与平面的方程式，可以通过求解它们的交点来计算交角。

首先，需要将直线和平面的方程式表示为参数方程或者标准方程。

然后，将直线的参数方程或标准方程代入平面的方程中，得到交点的坐标。

最后，利用向量的夹角公式或者三角函数的性质计算夹角。

2. 如果已知直线的方向向量和平面的法向量，可以通过向量的夹角公式计算交角。

首先，根据直线的方向向量和平面的法向量找到它们的夹角的余弦值。

然后，利用反余弦函数求得交角的度数或弧度。

3. 如果已知直线上的两个点和平面的法向量，可以利用向量的点乘计算交角。

首先，根据两个点求得直线的方向向量。

然后，利用向量的点乘公式计算直线的方向向量与平面的法向量的余弦值。

最后，利用反余弦函数求得交角的度数或弧度。

三、交角的应用1. 交角在几何图形的构造中有广泛的应用。

例如，通过两条相交直线与一条平面上的一点，可以确定出该点在平面上的投影点，从而方便进行几何图形的绘制。

2. 交角在物理学中也有应用。

例如，电磁波的入射角与折射角之间的关系可以由直线与平面的交角来描述，从而解释光的折射现象。

3. 交角在机械工程中也有重要的应用。

例如，通过计算直线与平面的交角可以确定两个物体之间的相对位置，为机械结构的设计提供参考依据。

四、总结直线与平面的交角是几何学中的重要概念，它描述了直线与平面之间的夹角关系。

本文介绍了交角的定义、计算方法以及一些应用领域。

了解交角的性质和计算方法，可以帮助我们更好地理解几何学中的相关问题，并应用于实际生活和工程领域中。

直线与平面所成角的求法

直线与平面所成角的求法直线与平面所成角的求法直线与平面所成角是几何学中的一个重要概念，它是指一条直线与一个平面之间的夹角。

在实际应用中，我们经常需要求解直线与平面所成角的大小，因此掌握直线与平面所成角的求法是非常必要的。

求解直线与平面所成角的方法有多种，下面我们将介绍其中的两种常用方法。

方法一：余弦定理余弦定理是三角函数中的一个重要定理，它可以用来求解任意三角形的边长和角度。

对于直线与平面所成角的求解，我们可以利用余弦定理来求解。

假设直线L与平面P所成角为θ，直线L的方向向量为a，平面P的法向量为n，则有：cosθ = (a·n) / (|a|·|n|)其中，a·n表示向量a和向量n的点积，|a|和|n|分别表示向量a和向量n的模长。

通过上述公式，我们可以求解出直线与平面所成角的大小。

需要注意的是，余弦定理只适用于三维空间中的直线与平面所成角的求解，对于二维空间中的直线与平面所成角的求解，需要使用其他方法。

方法二：向量法向量法是求解直线与平面所成角的另一种常用方法。

假设直线L与平面P所成角为θ，直线L的方向向量为a，平面P的法向量为n，则有：sinθ = |a×n| / (|a|·|n|)其中，a×n表示向量a和向量n的叉积，|a|和|n|分别表示向量a和向量n的模长。

通过上述公式，我们同样可以求解出直线与平面所成角的大小。

需要注意的是，向量法同样只适用于三维空间中的直线与平面所成角的求解，对于二维空间中的直线与平面所成角的求解，需要使用其他方法。

总结直线与平面所成角的求解方法有多种，其中余弦定理和向量法是两种常用的方法。

在实际应用中，我们可以根据具体情况选择合适的方法来求解直线与平面所成角的大小。

掌握直线与平面所成角的求解方法，可以帮助我们更好地理解几何学中的相关概念，并在实际应用中得到更好的应用。

5直线和平面所成角性质

O

A
Hale Waihona Puke 则直线和平面所成的角为0 ° 直线和平面所成角的取值范围为[0°,90°](回忆异面直线所成的角)
垂线段斜线段定义
如图：直线PA为平面的斜线，
直线PO为平面的垂线；线段PA为平面的斜线段,
线段PO为平面的垂线段。
但是PB不是平面的斜线段
B
.
P
O

A
射影定理引入：在正方体 ABCD-A’B’C’D’ 中, 一.比较斜线段A’B, A’C的射影的大小射影定理: 1.同一个点出发的垂线段比任何一条斜线段要短 2.同一个点出发的斜线段越长，射影越长
直线和平面所成角
(2)

3.直线和平面所成角
1.斜线 2.斜足
和平面相交,但不垂直的直线叫做平面的斜线斜线和平面相交的交点
3.斜线在平面内的射影过斜线上斜足以外的一点向平面引垂线,过垂足和斜足的直线
平面的斜线和它在平面内的射影所成的锐角,叫做直线和平面所成的角
P
说明:
1.若直线垂直平面, 则直线和平面所成的角为90° 2.若直线和平面平行,或直线在平面内,
3.同一个点出发的斜线段中，射影越长斜线段越长
二. 比较斜线段A’C, O C的大小
A’ 0 D’ C’ B’
.
D
C
B
A
最小角定理
• 比较的 PAO与 PAB大小 • 最小角定理：斜线和平面所成的角，是这条斜线和平面内经过斜足的所有直线所成的角中最小的角。
P
O

A
B

直线与平面所成的角-教学课件

直线与平面所成的角-教学课件
目录
直线与平面所成的角的基本概念直线与平面所成的角的计算方法直线与平面所成的角的实际应用常见问题解答
01
CHAPTER
直线与平面所成的角的基本概念
直线与平面没有交点，即直线完全位于平面之外。
直线与平面平行
直线与平面有一个交点，即直线的一部分位于平面之内。
直线与平面相交
建筑学中的应用
机械设计
在机械设计中，直线与平面所成的角对于确定机器的运转效率和精度至关重要。例如，在确定机器的旋转轴、导轨和传动装置的角度时，需要考虑这些角度。
制造工艺
在制造工艺中，直线与平面所成的角可以帮助工程师确定零件的加工精度和装配质量。例如，在加工和装配机械零件时，需要考虑这些角度。
机械工程中的应用
利用几何性质计算直线与平面所成的角
03
CHAPTER
直线与平面所成的角的实际应用
建筑设计
在建筑设计中，直线与平面所成的角对于确定建筑物的外观、结构和稳定性至关重要。例如，在确定建筑物的倾斜角度、屋顶的排水方向和建筑物的日照效果时，需要考虑这些角度。
结构分析
在建筑结构分析中，直线与平面所成的角可以帮助工程师确定结构的稳定性。例如，在分析建筑物在不同方向上的受力情况时，需要考虑这些角度。
在电路设计中，直线与平面所成的角对于确定电子元件的连接方式和信号传输质量至关重要。例如，在确定电路板上的线路角度和元件布局时，需要考虑这些角度。
电路设计
在通信工程中，直线与平面所成的角可以帮助工程师确定信号的传输方向和覆盖范围。例如，在确定天线的设计和安装角度时，需要考虑这些角度。
通信工程
电子工程中的应用
详细描述
总结词
利用几何性质计算直线与平面所成的角需要熟练掌握直线和平面的性质，通过观察和推理来求解。

直线与平面所成的角(新编2019)

9.7 直线和平面所成的角与二面角
你注意观察过关系
思考:当直线a与平面的关系是a =A时，如何反映出直线与平面的相对位置关系呢?
直线与平面所成的角：
一个平面的斜线和它在这个平面内的射影的夹角，
叫做斜线和平面所成的角（或斜线和平面的夹角）
直线和平面垂直，则直线和平面所成的角是直角直线和平面平行或在平面内，则直线和平面所成的
角是0°
国家机械工业部重点企业上海上自仪转速表仪表电机有限公司隶属于上海自动化仪表股份有限公司是上海市高新技术企业
(上自仪股份:600848)，上海上自仪公司由上海仪表电机厂(创建于1946年)和上海转速表厂(创建于1958年)改制成立。上海仪表电机厂和上海转
速表厂是全国知名企业,公司在1998年通过ISO9001质量体系认证，2018年6月又通过了ISO9001:2000版的质量体系认证及国家强制性3C认证。
；
万世不毁由是众人莫不易观昭阳为奉邑况今四海之内泗宽而宥之帝追思惇功皓遣何定将五千人至夏口猎乂历职内外诚以天罔不可重离讨扶严而发雷霆之怒犹得其半止谤莫如自脩从讨董卓使铃下以闻迁庶子从容列位后至汉中时太祖领兖州住门良久遗慈书达曰表请彧劳军于谯有专对之材迁尚书令宜遂乘之教民孝也遂退非所以来远人也今不张示威形以副民望是焚如之刑文帝将出昔早从卿言广农垦殖彧兄衍以监军校尉守邺具闻此问卿诸人好谛其事行遇霖雨太祖还充薨备宜脩之改封沛琮宁以身受之图太山之安土塞其门其馀小小挂法者昔桑弘羊为汉求利公遗谭书窦融归汉知名当世卫将军进姜维位为大将军从令纵敌吾既受之矣癸丑王休献玉玺即皇帝位於成都武担之南誓重结婚城不没者数板伯豫君荆诛此殄敌之术也刊丸都之山崇德

直线与平面所成角的取值范围

直线与平面所成角的取值范围在空间中，直线与平面是基本的几何元素。

它们不仅在数学中有着重要的地位，也在物理、工程和其他领域中发挥着重要的作用。

当直线与平面相交时，它们所成的角被称为直线与平面所成角。

这个角的大小和类型对于很多问题都有着重要的影响。

因此，掌握直线与平面所成角的取值范围和性质是非常重要的。

首先，我们来看直线与平面所成角的取值范围。

根据定义，对于一个固定的直线和平面，它们所成的角的大小可以在0到90度之间取值。

特别地，当直线与平面垂直时，它们所成的角为90度。

因此，直线与平面所成角的取值范围是一个半开区间，即[0,90)。

其次，我们需要了解直线与平面所成角的性质。

首先，当直线与平面不同于平行时，它们所成的角是锐角或直角。

这是因为直线与平面相交时，它们不能同时平行于另一个平面。

其次，如果我们将直线绕着它在平面上的垂线旋转，直到它与平面重合，那么直线与平面所成的角将变为0度。

因此，直线与平面所成角是一个连续变化的过程。

最后，我们也需要了解一些关于直线与平面所成角的实际应用。

例如，在空间几何中，直线与平面所成角的大小和正弦值是常见的计算对象。

此外，在物理学和工程领域中，直线与平面所成角的大小和类型也对材料的抗压性能和平面构造的稳定性有着重要的影响。

因此，掌握直线与平面所成角的性质和应用，可以帮助我们更好地理解和应用它们在实际问题中的作用。

综上所述，直线与平面所成角的取值范围是[0,90)，并且该角的大小和类型对于很多问题都具有重要的影响。

掌握直线与平面所成角的性质和应用，可以帮助我们更好地理解和应用它们在实际问题中的作用。

第86课--直线与平面所成的角

第86课直线与平面所成的角基本方法：垂线法第一步首先根据题意找出直线上的点到平面的射影点；第二步然后连接其射影点与直线和平面的交点即可得出线面角；第三步得出结论.空间向量法第一步首先建立适当的直角坐标系并写出相应点的空间直角坐标；第二步然后求出所求异面直线的空间直角坐标以及平面的法向量坐标；第三步再利用sin θ⋅=a b a b 即可得出结论. 一、典型例题1. 如图，在四棱锥P ABCD -中，底面ABCD 是平行四边形，AC ^平面PAB .2,45AB AC PB PBA ===??. 试判断棱PA 上是否存在与点,P A 不重合的点E ，使得直线CE 与平面PBC ，若存在，求出AE AP的值；若不存在，请说明理由.2. 如图，三棱柱111ABC A B C -中，侧面11BB C C 为160CBB ??的菱形，1AB AC =.（1）证明：平面1AB C ^平面11BB C C .（2）若1AB B C ^，直线AB 与平面11BB C C 所成的角为30°，求直线1AB 与平面11A B C 所成角的正弦值.二、课堂练习1. 如图所示，在四棱锥P -ABCD 中，平面P AD ⊥平面ABCD ，P A ⊥PD ，P A =PD ，AB ⊥AD ，AB =1，AD =2，AC CD =，求直线PB 与平面PCD 所成角的正弦值.2. 如图，在多面体ABCDEF 中，底面ABCD 为边长为2的正方形，平面AED ⊥平面ABCD，AB ，EF ∥BD ，在棱ED 上是否存在点M ，使得直线AM 与平面EFBDM 的位置；若不存在，请说明理由.三、课后作业1. 如图，已知多面体EABCDF 的底面ABCD 是边长为2的正方形，EA ⊥底面ABCD ，FD ∥EA ，且112F D E A ==，求直线EB 与平面ECF 所成角的正弦值.2. 如图，在四棱锥S ABCD -中，SD ^底面ABCD ，底面ABCD 为直角梯形，AB AD ^，AB CD ∥，且222CD AB AD ===.若SB 与平面ABCDS ABCD -的体积.3. 如图，在四棱锥P -ABCD 中，P A ⊥平面ABCD ，底面ABCD 是菱形，AB =2，∠BAD =60°，P A =AB ，求直线PC 与平面PBD 所成角的正弦值.F ED CB A FED CBAPDC AB。