利率风险计量概论

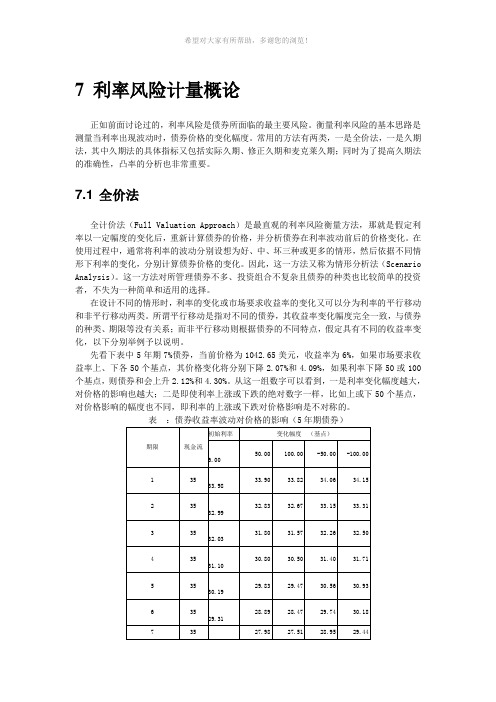
7利率风险计量概论正如前面讨论过的，利率风险是债券所面临的最主要风险。

衡量利率风险的基本思路是测量当利率出现波动时，债券价格的变化幅度。

常用的方法有两类，一是全价法，一是久期法，其中久期法的具体指标又包括实际久期、修正久期和麦克莱久期；同时为了提高久期法的准确性，凸率的分析也非常重要。

7.1 全价法全计价法（Full V aluation Approach）是最直观的利率风险衡量方法，那就是假定利率以一定幅度的变化后，重新计算债券的价格，并分析债券在利率波动前后的价格变化。

在使用过程中，通常将利率的波动分别设想为好、中、坏三种或更多的情形，然后依据不同情形下利率的变化，分别计算债券价格的变化。

因此，这一方法又称为情形分析法（Scenario Analysis）。

这一方法对所管理债券不多、投资组合不复杂且债券的种类也比较简单的投资者，不失为一种简单和适用的选择。

在设计不同的情形时，利率的变化或市场要求收益率的变化又可以分为利率的平行移动和非平行移动两类。

所谓平行移动是指对不同的债券，其收益率变化幅度完全一致，与债券的种类、期限等没有关系；而非平行移动则根据债券的不同特点，假定具有不同的收益率变化，以下分别举例予以说明。

先看下表中5年期7%债券，当前价格为1042.65美元，收益率为6%，如果市场要求收益率上、下各50个基点，其价格变化将分别下降2.07%和4.09%，如果利率下降50或100个基点，则债券和会上升2.12%和4.30%。

从这一组数字可以看到，一是利率变化幅度越大，对价格的影响也越大；二是即使利率上涨或下跌的绝对数字一样，比如上或下50个基点，对价格影响的幅度也不同，即利率的上涨或下跌对价格影响是不对称的。

表：债券收益率波动对价格的影响（5年期债券）另一方面，针对不同期限的债券，利率的上涨或下跌对价格影响也是不同的，如果上面的债券期限不是5年，而是10年，则其结果将如下表：表：债券收益率变化对债券价格的影响（10年期债券）可以看到，对于10年期债券，利率上、下浮动50个基点，其价格分别下降3.54%和上升3.71%，上涨的幅度大于下跌的幅度；利率上、下浮动100个基点时，价格分别下降6.92%和上升7.59%，同样上涨的幅度大于下跌的幅度。

这一幅度远大于5年期债券，且同样表现出非对称性和随利率波动幅度增大而增大的特点。

对于利率的非平行波动，即对不同期限或不同种类的债券，利率波动幅度不同时的情况，与上述的平行波动相似，这里不再赘述。

7.2 债券价格波动特征债券价格主要随期限、息票利率、嵌入期权及市场要求收益率等因素的影响而波动。

对于无期权的固定利率债券，其债券价格波动主要有以下几个特征：一是债券价格波动方向与市场要求收益率相反，即市场要求收益率越高、债券价格越低，否则越高。

但债券价格随要求收益率变化的幅度并不对称，即收益率的同等反向波动，其价格波动方向相反，但幅度不等。

二是如果收益率的变化足够小，债券价格的波动幅度可以认为保持不变。

不过要特别注意，这里指的是当收益率变化非常小的时候，如果收益率变化太大，这一特征将不再成立。

三是对幅度相同、方向相反的收益率变化，债券价格上升的幅度大于价格下跌的幅度。

关于这几个特点，在上一小节的表格分析中已经可以清楚地看到，为了更直观地了解这几个特征，可以参看下图：上图是一10年期债券的价格与不同市场要求收益率的关系图。

图中，Y1-Y o=Y0-Y2 =4.5%，但Po-P1=589.66-422.12＝167.54美元≠P2－Po=844.11-589.66＝254.45美元，二者相差86.92美元。

市场要求收益率上、下浮动的幅度一致，但导致的价格变化却不同。

显然，这与价格－收益率曲线的凸性有关，即价格－收益率曲线不是直线，而是凸向原点的。

不同债券，其价格－收益曲线凸向原点的幅度，即曲线的凸率是不同的，凸率越大，则上述差值更大；反之，如果凸率较小，差值也越小。

上图中曲线是凸向原点的，也有债券的价格－收益曲线是凸出的方向是远离原点的，这时曲线的凸率为负（Negative Convexity ）。

对于具有负凸率的价格－收益曲线的债券，同样的收益率上、下波动，债券价格下跌的幅度将大于价格上涨的幅度，如图所示：图 ：债券－收益曲线凸率为负的情形与前面凸率为正的曲线不同，这里同样幅度的收益率上涨或下跌，所造成的债券价格下跌或上涨的幅度刚好相反，下跌的幅度超过上涨。

图中，Y1-Y o=Y o-Y2，但Po-P1>P2-Po 。

这种情况在有赎回权的债券价格波动中，表现得很明显。

对嵌有期权的债券，其价格波动与上述无期权债券的价格有所不同。

例如，对嵌有赎回权的债券，当市场利率下降到一定程度，使赎回债券进行再融资对发行人有利时，债券就极有可能被赎回。

这时债券价格随着市场要求收益率下降而上升的幅度就会小于同等条件没有赎回期权的债券。

嵌有赎回权的债券，其价格随市场收益率波动而变化的情形如下图所示。

图中，CC ’是嵌赎回期权债券的价格－收益曲线，而CC ’’则是无赎回权普通债券的价格－收益曲线。

在收益率y*之上，两曲线没有差异。

当收益率降到y*之下后，两曲线出现了明显P0-P1P2-PoP2 P1Po Y1Y oY2的差异，即有赎回权的债券价格将低于无期权债券的价格，且对收益率的弹性也较无期权债券的小，即增长幅度更小。

同时，嵌赎回权债券的价格－收益曲线的凸率由无期权债券的正凸率变成了有期权债券的负凸率。

CC’与CC’’两线之间的差异，则是赎回权的价格。

前面介绍的负凸率曲线，在嵌赎回权的债券中，当市场收益率低于某个临界值（如债券的息票利率）后可以看得很清楚。

因此，对嵌赎回期权的债券，在计算其收益率时，要分两种情况，一是如果市场要求收益率高于y*时，与普通无期权债券一样，直接计算其到期收益率；如果市场要求收益率低于y*时，则应计算其赎回收益率，即假定债券会按赎回规划被赎回时的收益率。

与赎回权不同的，回卖权是属于投资者的选择权，当市场利率较高时，投资者有权按既定条件将债券回卖给发行人，并取得资金用于再投资。

嵌回卖权的债券，其价格－收益曲线则如下图所示：图：嵌回卖权债券的价格－收益曲线图中PP’是嵌回卖权债券的价格－收益曲线，而PP’’则是普通无期权债券的价格－收益曲线。

可以看到，在y*之下，两种债券的之间并无差异，但当市场要求收益上升到y*之上时，债券的持有人就可能选择将债券回卖给发行人取得资金用于再投资。

两线之间的差异，表示在不同收益率时，回卖权的价值。

可以看到，当市场要求收益率上升到y*以上后，有回卖权的债券，价格将高于无期权债券。

前面对债券价格随利率或收益波动而变化的分析，都是定性的。

作为对债券价值的分析，只定性是不够的，下面介绍久期和凸率等常用的债券利率风险分析工具。

7.3 久期久期（Duration ），也有将其译为持续期，无论怎么译，仅从文字意义上很难理解这一概念的准确含义， 这与英文原文的含义相关。

之所以会这样，与麦考雷久期算法中，以债券现金流现值为权重，对获得各现金流的时间作加权平均后所得的值，这个值从计量单位上讲有时间的含义。

但这里要特别说明的是，虽然上述方法计算的值的确在计量单位上有时间的含义，但并不表示久期真是一个时间概念。

如果非要从时间含义上去理解，可以理解为收到债券现值的平均时间，例如某一债券的久期为5年，可以理解为收到该债券现值的平均时间约为5年，但绝对不表示债券将于5年后到期。

总之，从时间含义上理解久期是很令人费解的，不如直接将其理解为价格弹性更直接。

另有一种说法，即将久其理解为价格－收益曲线的一阶导数。

从本节中以后内容中可以看到，久期预测价格的直线的确是价格－收益曲线的切点，从数学推导中，这种说法的确不错。

但这种说法与其说有助于理解债券的价格－收益关系，不如说其说明了久期与价格－收益关系间的数理联系。

久期的本质含义是对债券价格相对于利率的弹性的测度，比如，利率每100个基点的变化，债券价格会变化多少个百分点。

引入久期这一工具的原因，是为了给投资者提供一个简便的分析债券价格变化的方法，特别是对于大型投资公司等持有多种债券的投资者。

利用久期可以简单和快捷地估算出利率的变动对持有债券价值的影响幅度。

在具体使用久期分析债券价格时，通常也同时运用凸率分析以提高分析的准确性。

所以这一分析法也常称为久期－凸率分析法（Duration-Convexity Approach ）。

按上面弹性的定义，则久期的计算公式为：002D P P D P yP y P y P -+-+-=⨯⨯∆∆∆其中：：久期：当利率下跌后的债券价格：当利率上升后的债券价格：当利率未改变时债券的价格比如前面图中的债券，当收益率为10%时，债券价格为589.66美元，当收益率下降或上升波动50个基点后，其价格分别为612.91美元和567.46美元，则该债券在收益率为10%时，其久期为：612.91567.467.70782589.660.005D -=⨯⨯＝这一计算的结果表明，对于该债券，在收益率为10%时，利率每波动100个基点，债券的价格会逆向波动约770.78个基点，或7.7078个百分点。

当然，这只是一种粗略的估计。

同时，上例中利率波动幅度较大，可能会影响这一方法的准确性。

根据久期的含义，我们也可以使用久期对债券价格的变化加以分析，即：D y 100⨯∆⨯债券价格波动的百分比＝－用于上例的分析，当利率为10%时，债券的价格为589.66美元，如果利率分别上、下波动10，50，100，200，450个基点，其真实价格与按久期预测的价格分别如下表：表 ：全价法与久期法预测债券价格的差异值接近计算久期时所设定的利率波动值时，差异最小，仅差0.53美元，在图中表现为利率在10%时最低；二是当估计价格使用的利率波动值偏离计算久期使用的利率波动值时，差异扩大，无论是从波动幅度扩大的方向，还是从缩小的方向，这种差异都扩大，在图中表现为曲线两端上翘；三是久期法预测的准确性，与计算久期时所使用的利率波动值有关，且也与所选择的点有关，例如，不选择利率为10%的点，而选择利率为5%或其它值的点作基础计算，则上表又会不同。

四是与全价法相比，久期法倾向于低估债券的价格，无论是对涨价还是跌价时，都会低估债券的价格，在凸性的图中表现为久期预测的直线总是处于抛物线的下方；五是在利率上涨或下跌时，对债券价格预测的偏差的不对称的，即图中以利率为10%（无利率差）为中心，则曲线两边不对称。

之所以出现这些特征，与价格－收益曲线的凸性有关。

麦考雷久期（Macaulay Duration ），是1938年由弗雷德里克·麦考雷提出的，其计算公式为：1122n nf f n n t PV C F t PV C F +...+t PV C F D =k PD t n k:y:PV C F n ⨯+⨯⨯⨯其中： ：麦考雷久期 ：时间阶段值， 每年中付息次数 收益率 ：第时间阶段现金流的现值这就是前面提到过的，以现金流现值为权重计算加权平均时间的久期。