2020届高考文数复习常考题型大通关(全国卷): 推理与证明
考点48 推理与证明-2020年高考数学(文)考点一遍过

专题48 推理与证明(十八)推理与证明1.合情推理与演绎推理(1)了解合情推理的含义,能利用归纳和类比等进行简单的推理,了解合情推理在数学发现中的作用. (2)了解演绎推理的重要性,掌握演绎推理的基本模式,并能运用它们进行一些简单推理. (3)了解合情推理和演绎推理之间的联系和差异. 2.直接证明与间接证明(1)了解直接证明的两种基本方法——分析法和综合法;了解分析法和综合法的思考过程、特点. (2)了解间接证明的一种基本方法——反证法;了解反证法的思考过程、特点.一、推理 1.推理(1)定义:根据一个或几个已知的判断来确定一个新的判断的思维过程就是推理.推理一般包含两个部分:一是前提,是指已知的事实(或假设);二是结论,是由已知判断推出的新的判断,即推理的形式为“前提⇒结论”.(2)分类:推理⎩⎪⎨⎪⎧合情推理演绎推理.2.合情推理(1)定义:根据已有的事实,经过观察、分析、比较、联想,再进行归纳类比,然后提出猜想的推理叫做合情推理. (2)特点:①合情推理的结论是猜想,不一定正确; ②合情推理是发现结论的推理. (3)分类:合情推理⎧⎨⎩归纳推理类比推理.(4)归纳推理和类比推理的定义、特征及步骤3.演绎推理(1)定义:从一般性的原理出发,推出某个特殊情况下的结论,我们把这种推理称为演绎推理,简言之,演绎推理是由一般到特殊的推理.(2)特点:①演绎推理在大前提、小前提和推理形式都正确时,得到的结论一定正确;若大前提、小前提、推理形式三者中有一个是错误的,所得的结论就是错误的.②演绎推理是证明结论的推理.(3)模式:三段论是演绎推理的一般模式,即①大前提——已知一般的原理;②小前提——所研究的特殊情况;③结论——根据一般原理,对特殊情况作出的判断.【注】三段论常用的格式为:大前提:M是P.小前提:S是M.结论:S是P.二、证明1.直接证明——综合法与分析法(1)综合法①定义:利用已知条件和某些数学定义、定理、公理等,经过一系列的推理论证,最后推导出所要证明的结论成立,这种证明方法叫做综合法.②框图表示:(其中P表示已知条件、已有的定义、定理、公理等,Q表示要证的结论)③思维过程:由因导果.(2)分析法①定义:从要证明的结论出发,逐步寻求使它成立的充分条件,直到最后,把要证明的结论归结为判定一个明显成立的条件(已知条件、定理、定义、公理等)为止,这种证明方法叫做分析法.②框图表示:(其中P表示要证明的结论)③思维过程:执果索因.2.间接证明——反证法(1)定义:一般地,假设原命题不成立(即在原命题的条件下,结论不成立),经过正确的推理,最后得出矛盾,因此说明假设错误,从而证明了原命题成立,这样的证明方法叫做反证法.(2)反证法中的矛盾主要是指以下几方面:①与已知条件矛盾;②与假设矛盾;③与定义、公理、定理矛盾;④与公认的简单事实矛盾;⑤自相矛盾.考向一合情推理常见的类比、归纳推理及求解策略:(1)在进行类比推理时,不仅要注意形式的类比,还要注意方法的类比,且要注意以下两点:①找两类对象的对应元素,如:三角形对应三棱锥,圆对应球,面积对应体积等等;②找对应元素的对应关系,如:两条边(直线)垂直对应线面垂直或面面垂直,边相等对应面积相等.(2)归纳推理是由部分到整体、由特殊到一般的推理,由归纳推理所得的结论不一定正确,通常归纳的个体数目越多,越具有代表性,那么推广的一般性命题也会越可靠,它是一种发现一般性规律的重要方法.典例1 在等差数列{}n a 中,若100a =,则有等式121219n n a a a a a a -+++=+++L L ()*19,n n <∈N 成立.类比上述性质,相应地在等比数列{}n b 中,若81b =,则成立的等式是 A .()*12121515,n n b b b b b b n n -+++=+++<∈N L L B .()*12121616,n n b b b b b b n n -+++=+++<∈N L LC .()*12121515,n n b b b b b b n n -⋅=⋅<∈N L L D .()*12121616,n n b b b b b b n n -⋅=⋅<∈N L L【答案】C【解析】在等差数列{}n a 中,若100a =,则有等式121219n n a a a a a a -+++=+++L L ()*19,n n <∈N 成立∴在等比数列{}n b 中,若81b =,则有()*12121515,n n b b b b b b n n -⋅=⋅<∈N L L 等式成立.故选C .【名师点睛】类比推理应用的类型及相应方法:(1)类比定义:在求解由某种熟悉的定义产生的类比推理型试题时,可以借助原定义来求解;(2)类比性质:从一个特殊式子的性质、一个特殊图形的性质入手,提出类比推理型问题,求解时要认真分析两者之间的联系与区别,深入思考两者的转化过程是求解的关键;(3)类比方法:有一些处理问题的方法具有类比性,可以把这种方法类比应用到其他问题的求解中,注意知识的迁移.典例2 观察下列式子:3211=,332123+=,33321236++=,33332123410+++=,…,根据以上式子可归纳:3333123n ++++=L ________________.【答案】()212n n +⎡⎤⎢⎥⎣⎦【解析】因为33321=11+2=12+,(),33321+2+3=123()++,333321+2+3+4=1234+++(),所以()233331+2+3+123n n =++++L L =()2214n n +【技巧点拨】解决此类问题时,通常利用归纳推理,其步骤如下: ①分别归纳各式左、右两边的规律; ②明确各式左、右两边之间的关系;③按归纳出的规律写出即可.解决此类问题一般需要转化为求数列的通项公式或前n 项和等.1.在《九章算术》方田章圆田术(刘徽注)中指出,“割之弥细,所失弥少,制之又割,以至于不可割,则与圆周合体而无所失矣.”注述中所用的割圆术是一种无限与有限的转化过程,比如在“…”即代表无限次重复,但原式却是个定值x x =确定出来2x =,类比上述结论可得222log 2log (2log ()[]2)+++L 的正值为A .1BC .2D .42.古希腊毕达哥拉斯学派研究了“多边形数”,人们把多边形数推广到空间,研究了“四面体数”,下图是第一至第四个四面体数.(已知()()22221211236n n n n +++++⋅⋅⋅+=)观察上图,由此得出第5个四面体数为______(用数字作答);第n 个四面体数为______.考向二 演绎推理(1)演绎推理是从一般到特殊的推理;其一般形式是三段论,应用三段论解决问题时,应当首先明确什么是大前提和小前提,如果前提是显然的,则可以省略.(2)演绎推理的结论是否正确,取决于该推理的大前提、小前提和推理形式是否全部正确,因此,分析推理中的错因实质就是判断大前提、小前提和推理形式是否正确.典例3 有一段“三段论”,推理是这样的:对于可导函数()f x ,如果0()0f x '=,那么0x x =是函数()f x 的极值点.因为3()f x x =在0x =处的导数值(0)0f '=,所以0x =是函数3()f x x =的极值点.以上推理中A .大前提错误B .小前提错误C .推理形式错误D .结论正确【答案】A【解析】因为对于可导函数)(x f ,如果0()0f x '=,那么0x x =不一定是函数)(x f 的极值点,所以大前提错误. 故选A .典例4 甲、乙、丙三人中,一人是教师、一人是记者、一人是医生.已知:丙的年龄比医生大;甲的年龄和记者不同;记者的年龄比乙小.根据以上情况,下列判断正确的是 A .甲是教师,乙是医生,丙是记者 B .甲是医生,乙是记者,丙是教师 C .甲是医生,乙是教师,丙是记者D .甲是记者,乙是医生,丙是教师【答案】C【解析】由甲的年龄和记者不同和记者的年龄比乙小可以推得丙是记者,再由丙的年龄比医生大,可知甲是医生,故乙是教师. 故选C.3.“四边形是矩形,四边形的对角线相等”补充以上推理的大前提是 A .正方形都是对角线相等的四边形 B .矩形都是对角线相等的四边形 C .等腰梯形都是对角线相等的四边形D .矩形都是对边平行且相等的四边形4.某市为了缓解交通压力,实行机动车限行政策,每辆机动车每周一到周五都要限行一天,周末(周六和周日)不限行.某公司有A ,B ,C ,D ,E 五辆车,每天至少有四辆车可以上路行驶.已知E 车周四限行,B 车昨天限行,从今天算起,A ,C 两车连续四天都能上路行驶,E 车明天可以上路,由此可知下列推测一定正确的是 A .今天是周四B .今天是周六C .A 车周三限行D .C 车周五限行考向三 直接证明利用综合法、分析法证明问题的策略: (1)综合法的证明步骤如下:①分析条件,选择方向:确定已知条件和结论间的联系,合理选择相关定义、定理等;②转化条件,组织过程:将条件合理转化,书写出严密的证明过程.特别地,根据题目特点选取合适的证法可以简化解题过程.(2)分析法的证明过程是:确定结论与已知条件间的联系,合理选择相关定义、定理对结论进行转化,直到获得一个显而易见的命题即可.(3)实际解题时,用分析法思考问题,寻找解题途径,用综合法书写解题过程,或者联合使用分析法与综合法,即从“欲知”想“已知”(分析),从“已知”推“可知”(综合),双管齐下,两面夹击,找到沟通已知条件和结论的途径.典例5 已知0a >12a a+-. 【答案】见解析.12a a≥+-,12a a≥++. ∵0a >,∴只需要证2212)(a a ≥++,即222211142)2a a a a a a ++≥+++++,从而只需要证1)a a≥+, ∴只需要证2222114()2(2)a a a a+≥++, 即2212a a+≥,而上述不等式显然成立, 故原不等式成立.【名师点睛】①逆向思考是用分析法证明的主要思想,通过反推,逐步寻找使结论成立的充分条件.正确把握转化方向是使问题顺利获解的关键.②证明较复杂的问题时,可以采用两头凑的办法,即通过分析法找出某个与结论等价(或充分)的中间结论,然后通过综合法证明这个中间结论,从而使原命题得证.5.在各项均为正数的数列{}n a 中,1a a =,且122n n na a a +=+. (1)当32a =时,求a 的值;(2)求证:当2n ≥时,1n n a a +≤. 考向四 间接证明1.用反证法证明不等式要把握的三点(1)必须先否定结论,即肯定结论的反面.(2)必须从否定结论进行推理,即应把结论的反面作为条件,且必须依据这一条件进行推证.(3)推导出的矛盾可能多种多样,有的与已知矛盾,有的与假设矛盾,有的与已知事实矛盾等,且推导出的矛盾必须是明显的. 2.反证法的一般步骤用反证法证明命题时,要从否定结论开始,经过正确的推理,导出逻辑矛盾,从而达到新的否定(即肯定原命题)的过程.这个过程包括下面三个步骤:(1)反设——假设命题的结论不成立,即假设原结论的反面为真; (2)归谬——由“反设”作为条件,经过一系列正确的推理,得出矛盾; (3)存真——由矛盾结果断定反设错误,从而肯定原结论成立. 即反证法的证明过程可以概括为:反设——归谬——存真.典例6 用反证法证明某命题时,对结论“自然数a ,b ,c 中恰有一个偶数”正确的反设是 A .自然数a ,b ,c 中至少有两个偶数B .自然数a ,b ,c 中至少有两个偶数或都是奇数C .自然数a ,b ,c 都是奇数D .自然数a ,b ,c 都是偶数 【答案】B【解析】“恰有一个偶数”的反面应是“至少有两个偶数或都是奇数”,故选B.【名师点睛】反证法证明含“至少”、“至多”型命题时,可减少讨论情况,目标明确.否定结论时需弄清楚结论的否定是什么,避免出现错误.需注意“至少有一个”的否定为“一个都没有”,“至多有一个”的否定为“至少有两个”.典例7 若a ,b ,c 均为实数,2π22a x x =-+,24πb y y =-+,2π22c z z =-+.求证:a ,b ,c 中至少有一个大于0. 【答案】见解析.【解析】设a 、b 、c 都小于或等于0,即a ≤0,b ≤0,c ≤0, ∴a +b +c ≤0,而a +b +c =(x 2-2x )+(y 2-4y )+(z 2-2z )+2π=(x -1)2+(y -2)2+(z -1)2+2π-6>0, 这与假设矛盾,即原命题成立.【名师点睛】用反证法,假设,,a b c 都小于或等于0,推出a b c ++的值大于0,出现矛盾,从而得到假设不正确,命题得证.反证法的适用范围: (1)否定性命题;(2)结论涉及“至多”、“至少”、“无限”、“唯一”等词语的命题;(3)命题成立非常明显,直接证明所用的理论较少,且不容易证明,而其逆否命题非常容易证明; (4)要讨论的情况很复杂,而反面情况较少.6.已知数列{a n }的前n 项和为S n ,且满足a n +S n =2. (1)求数列{a n }的通项公式;(2)求证:数列{a n }中不存在三项按原来顺序成等差数列.1.有一段演绎推理是这样的:“直线平行于平面,则平行于平面内所有直线;已知直线b ⊄平面α,直线a ⊂平面α,直线b ∥平面α,则直线b ∥直线a ”的结论显然是错误的,这是因为A .大前提错误B .小前提错误C .推理形式错误D .非以上错误2.用反证法证明命题:“三角形的内角中至少有一个不大于60度”时,反设正确的是 A .假设三内角都不大于60度 B .假设三内角至多有两个大于60度 C .假设三内角至多有一个大于60度D .假设三内角都大于60度3.用演绎法证明函数3y x =是增函数时的小前提是 A .函数3y x =满足增函数的定义 B .增函数的定义C .若12x x <,则12()()f x f x <D .若12x x >,则12()()f x f x >4.现有一个关于平面图形的命题:如图所示,同一平面内有两个边长都是a 的正方形,其中一个正方形的某顶点在另一个正方形的中心,则这两个正方形重叠部分的面积恒为24a ,类比到空间,有两个棱长均为a 的正方体,其中一个的某顶点在另一个的中心,则这两个正方体重叠部分的体积恒为A .32aB .34aC .38aD .316a5.有一个奇数列1,3,5,7,9,…,现进行如下分组:第1组为{}1,第2组为{}3,5;第3组为{}7,9,11;…试观察每组内各数之和n S 与该组的编号数n 的关系为A .2n S n = B .3n S n =C .4n S n =D .()1n S n n =+6.沈老师告知高三文数周考的附加题只有6名同学A ,B ,C ,D ,E ,F 尝试做了,并且这6人中只有1人答对了.同学甲猜测:D 或E 答对了;同学乙猜测:C 不可能答对;同学丙猜测:A ,B ,F 当中必有1人答对了;同学丁猜测:D ,E ,F 都不可能答对.若甲、乙、丙、丁中只有1人猜对,则此人是 A .甲B .乙C.丙D.丁7.设F为椭圆的左焦点,A为椭圆的右顶点,B为椭圆短轴上的一个顶点,当AB=时,该椭圆的离心率为12,将此结论类比到双曲线,得到的正确结论为A.设F为双曲线的左焦点,A为双曲线的右顶点,B为双曲线虚轴上的一个顶点,当AB=时,该双曲线的离心率为2B.设F为双曲线的左焦点,A为双曲线的右顶点,B为双曲线虚轴上的一个顶点,当AB=时,该双曲线的离心率为4C.设F为双曲线的左焦点,A为双曲线的右顶点,B为双曲线虚轴上的一个顶点,当FB=时,该双曲线的离心率为2D.设F为双曲线的左焦点,A为双曲线的右顶点,B为双曲线虚轴上的一个顶点,当FB=时,该双曲线的离心率为48.A4纸是生活中最常用的纸规格.A系列的纸张规格特色在于:①A0、A1、A2、…、A5,所有尺寸的纸张长宽比都相同.②在A系列纸中,前一个序号的纸张以两条长边中点连线为折线对折裁剪分开后,可以得到两张后面序号大小的纸,比如1张A0纸对裁后可以得到2张A1纸,1张A1纸对裁可以得到2张A2纸,依此类推.这是因为A:1这一特殊比例,所以具备这种特性.已知A0纸规格为84.1厘米×118.9厘米,那么A4纸的长度约为A.14.8厘米B.21.0厘米C.29.7厘米D.42.0厘米9.甲、乙、丙、丁四名同学组成一个4⨯100米接力队,老师要安排他们四人的出场顺序,以下是他们四人的要求.甲:我不跑第一棒和第二棒;乙:我不跑第一棒和第四棒;丙:我也不跑第一棒和第四棒;丁:如果乙不跑第二棒,我就不跑第一棒.老师听了他们四人的对话,安排了一种合理的出场顺序,满足了他们的所有要求,据此我们可以断定在老师安排的出场顺序中跑第三棒的人是 A .丁 B .乙 C .丙D .甲10.我国南宋数学家杨辉1261年所著的《详解九章算法》一书里出现了如图所示的表,即杨辉三角,这是数学史上的一个伟大成就.在“杨辉三角”中,第n 行的所有数字之和为12n -,若去除所有为1的项,依次构成数列2,3,3,4,6,4,5,10,10,5,L ,则此数列的前55项和为A .4072B .2026C .4096D .204811.若a ,b 都是正整数,且a b ¹,则由下列不等式:①3322a b a b ab +>+;②664224a b a b a b +>+;③996336a b a b a b +>+.归纳推广出一个一般不等式为______.12.求“5=的解”有如下解题思路:设()f x =,则()f x 在R 上单调递增,且(4)5f =,所以原方程有唯一解4x =.类比上述解题思路,方程623(2)2x x x x +=+++的解集为______.13.已知ABC △的内角A ,B ,C 对应的边分别为a ,b ,c ,三边互不相等,且满足2b ac <.(1 (2)求证:B 不可能是钝角.14.已知函数()311f x x x =++,[]0,1x ∈. (1)用分析法证明:()21f x x x ≥-+; (2)证明:()34f x >.1.【2019年高考全国I 卷文数】古希腊时期,人们认为最美人体的头顶至肚脐的长度与肚脐至足底的长度之比是12(12≈0.618,称为黄金分割比例),著名的“断臂维纳斯”便是如此.此外,最美人体的头顶至咽喉的长度与咽喉至肚脐的长度之比也是12.若某人满足上述两个黄金分割比例,且腿长为105 cm,头顶至脖子下端的长度为26 cm,则其身高可能是A.165 cm B.175 cmC.185 cm D.190 cm2.【2019年高考北京卷文数】在天文学中,天体的明暗程度可以用星等或亮度来描述.两颗星的星等与亮度满足m2−m1=52lg21EE,其中星等为m k的星的亮度为E k(k=1,2).已知太阳的星等是−26.7,天狼星的星等是−1.45,则太阳与天狼星的亮度的比值为A.1010.1B.10.1C.lg10.1 D.10–10.13.【2017年高考全国II卷文数】甲、乙、丙、丁四位同学一起去向老师询问成语竞赛的成绩.老师说:你们四人中有2位优秀,2位良好,我现在给甲看乙、丙的成绩,给乙看丙的成绩,给丁看甲的成绩.看后甲对大家说:我还是不知道我的成绩.根据以上信息,则A.乙可以知道四人的成绩B.丁可以知道四人的成绩C.乙、丁可以知道对方的成绩D.乙、丁可以知道自己的成绩4.【2016年高考北京卷文】某学校运动会的立定跳远和30秒跳绳两个单项比赛分成预赛和决赛两个阶段.下表为10名学生的预赛成绩,其中有三个数据模糊.在这10名学生中,进入立定跳远决赛的有8人,同时进入立定跳远决赛和30秒跳绳决赛的有6人,则A.2号学生进入30秒跳绳决赛B.5号学生进入30秒跳绳决赛C .8号学生进入30秒跳绳决赛D .9号学生进入30秒跳绳决赛5.【2016年高考新课标II 卷文】有三张卡片,分别写有1和2,1和3,2和3.甲,乙,丙三人各取走一张卡片,甲看了乙的卡片后说:“我与乙的卡片上相同的数字不是2”,乙看了丙的卡片后说:“我与丙的卡片上相同的数字不是1”,丙说:“我的卡片上的数字之和不是5”,则甲的卡片上的数字是 . 6.【2017年高考北京卷文数】某学习小组由学生和教师组成,人员构成同时满足以下三个条件: (ⅰ)男学生人数多于女学生人数; (ⅱ)女学生人数多于教师人数; (ⅲ)教师人数的两倍多于男学生人数.①若教师人数为4,则女学生人数的最大值为_________. ②该小组人数的最小值为_________.7.【2019年高考全国II 卷文数】中国有悠久的金石文化,印信是金石文化的代表之一.印信的形状多为长方体、正方体或圆柱体,但南北朝时期的官员独孤信的印信形状是“半正多面体”(图1).半正多面体是由两种或两种以上的正多边形围成的多面体.半正多面体体现了数学的对称美.图2是一个棱数为48的半正多面体,它的所有顶点都在同一个正方体的表面上,且此正方体的棱长为1.则该半正多面体共有________个面,其棱长为_________.(本题第一空2分,第二空3分.)1.【答案】C【解析】由题意可得2log (2)x x =+,0x >,∴22x x =+,解得2x =.故选C .【名师点睛】本题考查了推理与证明中的类比推理,属中档题.2.【答案】35;()()1126n n n ++【解析】观察可得, 第一个四面体数为1; 第二个四面体数为()112++;第三个四面体数为()()112123+++++;第四个四面体数为()()()11+2+1+2+3+1+2+3+4+; ……由此可归纳,第n 个四面体数为()()()112123123n +++++++++++L L ,即为()11362n n +++++L , 设该式中的每个数从左至右的排列为数列{}n a ,即{}n a 为1,3,6,10,…… 得到递推关系为212a a -=,323a a -=,…,1n n a a n --=,相加后得()()()21211222n n n a a n n +--==+-,()212n a n n ∴=+, 故数列{}n a 的和()()()()()()22222222111112233123123222n S n n n n ⎡⎤=++++++++=+++++++++⎣⎦L L L ()()()()()1211111=1226226n n n n n n n n +++=⋅+⋅++, ∴当5n =时,1567356n S =⨯⨯⨯=.故答案为:35;()()1126n n n ++.【名师点睛】本题考查归纳推理,累加法求通项,分组法数列求和,考查图形分析能力,逻辑推理能力,找到数字的演变规律是解题关键.求解时,通过观察图形,先将图形的规律转化为数字规律,通过观察发现,相邻的数字差分别是3,6,10,……,即第n 项应为13610++++L ,那么就把问题转化为求数列{}n a 的和,{}n a 为1,3,6,10,……,根据这些数字可以发现,21312a a -=-=, 323a a -=,……, 1n n a a n --=,利用累加法可以得到()212n a n n =+,再利用题目所给已知,求出前n 项和,即为第n 个四面体数,当5n =时,即为第5个四面体数. 3.【答案】B【解析】根据题意,用演绎推理即三段论形式推导一个结论成立,大前提应该是结论成立的依据, ∵由四边形是矩形,得到四边形的对角线相等的结论, ∴大前提一定是矩形都是对角线相等的四边形,故选B .【名师点睛】本题考查演绎推理的定义,关键是掌握演绎推理的形式,属于基础题.根据题意,用三段论的形式分析即可得答案. 4.【答案】A【解析】首先考查选项A :若今天是周四,A ,B ,C ,D ,E 五辆车分别在周一、周三、周二、周五、周四,满足题意, 据此可排除B ,C ,D ,故选A .【名师点睛】本题主要考查推理案例的处理方法,特殊值法处理选择题等知识,意在考查学生的转化能力和计算求解能力.5.【答案】(1)2a =;(2)证明见解析. 【解析】(1)∵32a =, ∴232222a a a +==, ∴22244a a +=,解得22a =,同理解得12a =,即2a =.(2)要证2n ≥时,+1(0)n n n a a a >≤,只需证11n na a +≤,只需证221n n na a a +≤,只需证21212n a +≤,只需证24n a ≥,只需证2n a ≥,根据基本不等式得11222n n n a a a --=+≥=,当且仅当1122n n a a --=,即12n a -=时等号成立.所以原不等式成立.【名师点睛】本题考查实数值的求法,考查数列的递推公式、递推思想等基础知识,考查运算求解能力,是中档题.求解时,(1)推导出232222a a a +==,解得22a =,从而121222a a a +==,由此能求出a 的值;(2)利用分析法,只需证21212na +≤,只需证24n a ≥,只需证2n a ≥,根据基本不等式即可得到结果.6.【答案】(1)112n n a -=;(2)见证明. 【解析】(1)当n =1时,a 1+S 1=2a 1=2,则a 1=1. 又a n +S n =2,所以a n +1+S n +1=2,两式相减得112n n a a +=, 所以{a n }是首项为1,公比为12的等比数列, 所以112n n a -=. (2)(反证法)假设存在三项按原来顺序成等差数列,记为a p +1,a q +1,a r +1(p <q <r ,且p ,q ,r ∈N *),则2a q +1=a p +1+a r +1,即1112222q p r ⋅=+, 所以2·2r -q =2r -p +1.①又因为p <q <r ,r ∈N *, 所以r -q ,r -p ∈N *.所以①式左边是偶数,右边是奇数,等式不成立. 所以假设不成立,原命题得证.【名师点睛】本题主要考查数列通项的求法,考查反证法,意在考查学生对这些知识的理解掌握水平,属于中档题.求解时,(1)利用项和公式求数列{a n }的通项公式;(2)利用反证法证明.1.【答案】A【解析】在推理过程“直线平行于平面,则平行于平面内所有直线;已知直线b ⊄平面α,直线a ⊂平面α,直线b ∥平面α,则直线b ∥直线a ”中,直线平行于平面,则平行于平面内所有直线为大前提,由线面平行的性质易得直线平行于平面,则直线可与平面内的直线可能平行、也可能异面,这是一个假命题,故这个推理过程错误的原因是:大前提错误. 故选A .【名师点睛】由三段论的一般模式,可得结论.三段论是演绎推理的一般模式: (1)大前提——已知的一般原理; (2)小前提——所研究的特殊情况;(3)结论——根据一般原理,对特殊情况作出的判断. 2.【答案】D【解析】根据反证法的步骤可知,假设是对原命题结论的否定,“至少有一个”的否定为“一个也没有”即“三角形三个内角都大于60度”,故选D .【名师点睛】本题主要考查了反证法的概念,以及命题的否定的应用,着重考查了逻辑推理能力,属于基础题.求解时,根据反证法的定义,假设是对原命题结论的否定,即可求得,得到答案. 3.【答案】A【解析】证明函数3y x =是增函数,依据的原理是增函数的定义,因此,用演绎法证明函数3y x =是增函数时,大前提是:增函数的定义;小前提是函数3y x =满足增函数的定义.故选A.【名师点睛】本题主要考查演绎推理,熟记概念即可,属于基础题型.大前提提供了一个一般性的原理,小前提提出了一个特殊的对象,两者联系,即可得出结果.【名师点睛】(1)归纳推理和演绎推理会出现错误的原因是由合情推理的性质决定的,但演绎推理出现错误,有三种可能,一种是大前提错误,第二种是小前提错误,第三种是逻辑结构错误.(2)在使用三段论推理证明中,如果命题是错误的,则可能是“大前提”错误,也可能是“小前提”错误,也可能是逻辑错误.仔细分析“直线平行于平面,则平行于平面内所有直线;已知直线b ⊄平面α,直线a ⊂平面α,直线b ∥平面α,则直线b ∥直线a ”的推理过程,不难得到结论.4.【答案】C【解析】由题意,因为同一个平面内有两个边长都是a 的正方形,其中一个的某顶点在另一个的中心,则这两个正方形重叠的部分的面积恒为24a ,类比到空间中由两个棱长均为a 的正方体,其中一个的某顶点在另一个的中心,则这两个正方体的重叠部分的体积为38a ,故选C.。
2020高考数学知识考点精析22 推理与证明 精品

第二十二讲推理与证明1、 合情推理最常见的是归纳和类比。
由某类事物的部分对象具有某些特征推出该类事物的全部对象具有这些特征的推理。
或者由个别事实概括出一般结论的推理,称为归纳推理,简言之是从部分到整体,从个别到一般的推理。
由两类对象具有某些类似特征和其中一类对象具有的某些已知特征推出另一类对象也具有这些特征的推理称为类比推理。
类比推理是从特殊到特殊的推理。
练习:(1)、观察下图中各正方形图案,每条边上有(2)n n ≥个圆圈,每个图案中圆圈的总数是n S ,按此规律推出:当2n ≥时,n S 与n 的关系式 .key :22(2)n n --24n S == 38n S == 412n S ==(2)、观察下式:1=12,2+3+4=32,3+4+5+6+7=52,4+5+6+7+8+9+10=72,…,则可得出一般结论: .key :2*(1)(32)(21),n n n n n N +-++-=-∈L(3)类比平面内的直角三角形的性质猜想空间中的类似定理。
2、 演绎推理:从一般性的原理,推出某个特殊情况下的结论。
是从一般到特殊的推理。
“三段论”是演绎推理的一般模式,它包括:(1)大前提___已知的一般原理。
(2)小前提___所研究的特殊情况。
(3)结论__根据一般原理对特殊情况做出的判断。
演绎推理是一个必然性的推理,演绎推理产前提与结论之间有蕴涵关系,只要大前提、小前提都是真实的,推理的形式是正确的,那么结论必是真实的。
但错误的前提可能导致错误的结论,推理的形式不对也会导致错误的结论。
3、 综合法:利用已知条件和某些数学定义、公理、定理等,经过一系的推理论证,最后推导出所要证明的结论成立。
又叫由因导果法或顺推证法。
4、 分析法:从要证明的结论出发,逐步寻求使它成立的充分条件,直至最后,把要证明的结论归结为判定一个明显成立的条件(已知条件、定理、定义、公理等)为止。
又叫逆推证法或执因索果法。
5、 反证法:假设原命题不成立,经过正确的推理,最后得出矛盾,因此说明假设错误,从而证明了原命题成立。
2020版高考文科数学大一轮复习人教A版文档:第十二章 推理与证明、算法、复数12.2 Word版含答案.docx

§12.2直接证明与间接证明1.直接证明(1)综合法①定义:一般地,利用已知条件和某些数学定义、公理、定理等,经过一系列的推理论证,最后推导出所要证明的结论成立,这种证明方法叫做综合法.②框图表示:P⇒Q1―→Q1⇒Q2―→Q2⇒Q3―→…―→Q n⇒Q(其中P表示已知条件、已有的定义、公理、定理等,Q表示所要证明的结论).③思维过程:由因导果.(2)分析法①定义:一般地,从要证明的结论出发,逐步寻求使它成立的充分条件,直至最后,把要证明的结论归结为判定一个明显成立的条件(已知条件、定理、定义、公理等)为止,这种证明方法叫做分析法.②框图表示:Q⇐P1―→P1⇐P2―→P2⇐P3―→…―→得到一个明显成立的条件(其中Q表示要证明的结论).③思维过程:执果索因.2.间接证明反证法:一般地,假设原命题不成立(即在原命题的条件下,结论不成立),经过正确的推理,最后得出矛盾,因此说明假设错误,从而证明原命题成立的证明方法.题组一 思考辨析1.判断下列结论是否正确(请在括号中打“√”或“×”) (1)综合法是直接证明,分析法是间接证明.( × )(2)分析法是从要证明的结论出发,逐步寻找使结论成立的充要条件.( × ) (3)用反证法证明结论“a >b ”时,应假设“a <b ”.( × ) (4)反证法是指将结论和条件同时否定,推出矛盾.( × )(5)在解决问题时,常常用分析法寻找解题的思路与方法,再用综合法展现解决问题的过程.( √ )(6)证明不等式2+7<3+6最合适的方法是分析法.( √ )题组二 教材改编2.[P89T2]若P =a +6+a +7,Q =a +8+a +5(a ≥0),则P ,Q 的大小关系是( ) A .P >Q B .P =QC .P <QD .由a 的取值确定答案 A解析 P 2=2a +13+2a 2+13a +42, Q 2=2a +13+2a 2+13a +40, ∴P 2>Q 2,又∵P >0,Q >0,∴P >Q .3.[P91B 组T2]设实数a ,b ,c 成等比数列,非零实数x ,y 分别为a 与b ,b 与c 的等差中项,则a x +cy 等于( )A .1B .2C .4D .6 答案 B解析 由题意,得x =a +b 2,y =b +c 2,b 2=ac ,∴xy =(a +b )(b +c )4,a x +c y =ay +cxxy =a ·b +c 2+c ·a +b 2xy =a (b +c )+c (a +b )2xy =ab +bc +2ac2xy=ab +bc +ac +b 22xy =(a +b )(b +c )2xy =(a +b )(b +c )2×(a +b )(b +c )4=2.题组三 易错自纠4.若a ,b ,c 为实数,且a <b <0,则下列命题正确的是( ) A .ac 2<bc 2 B .a 2>ab >b 2 C.1a <1b D.b a >a b答案 B解析 a 2-ab =a (a -b ),∵a <b <0,∴a -b <0,∴a 2-ab >0, ∴a 2>ab .①又ab -b 2=b (a -b )>0,∴ab >b 2,② 由①②得a 2>ab >b 2.5.用反证法证明命题:“设a ,b 为实数,则方程x 3+ax +b =0至少有一个实根”时,要作的假设是( )A .方程x 3+ax +b =0没有实根B .方程x 3+ax +b =0至多有一个实根C .方程x 3+ax +b =0至多有两个实根D .方程x 3+ax +b =0恰好有两个实根 答案 A解析 方程x 3+ax +b =0至少有一个实根的反面是方程x 3+ax +b =0没有实根,故选A. 6.在△ABC 中,三个内角A ,B ,C 的对边分别为a ,b ,c ,且A ,B ,C 成等差数列,a ,b ,c 成等比数列,则△ABC 的形状为________三角形. 答案 等边解析 由题意得2B =A +C , ∵A +B +C =π,∴B =π3,又b 2=ac ,由余弦定理得b 2=a 2+c 2-2ac cos B =a 2+c 2-ac , ∴a 2+c 2-2ac =0,即(a -c )2=0,∴a =c , ∴A =C ,∴A =B =C =π3,∴△ABC 为等边三角形.题型一 综合法的应用1.已知m >1,a =m +1-m ,b =m -m -1,则以下结论正确的是( )A .a >bB .a <bC .a =bD .a ,b 大小不定答案 B解析 ∵a =m +1-m =1m +1+m ,b =m -m -1=1m +m -1.而m +1+m >m +m -1>0(m >1), ∴1m +1+m <1m +m -1,即a <b .2.(2018·大庆质检)如果a a +b b >a b +b a 成立,则a ,b 应满足的条件是__________________________. 答案 a ≥0,b ≥0且a ≠b 解析 ∵a a +b b -(a b +b a ) =a (a -b )+b (b -a ) =(a -b )(a -b ) =(a -b )2(a +b ).∴当a ≥0,b ≥0且a ≠b 时,(a -b )2(a +b )>0. ∴a a +b b >a b +b a 成立的条件是a ≥0,b ≥0且a ≠b . 3.(2018·武汉月考)若a ,b ,c 是不全相等的正数,求证: lga +b 2+lg b +c 2+lg c +a2>lg a +lg b +lg c . 证明 ∵a ,b ,c ∈(0,+∞), ∴a +b 2≥ab >0,b +c 2≥bc >0,a +c 2≥ac >0. 由于a ,b ,c 是不全相等的正数, ∴上述三个不等式中等号不能同时成立, ∴a +b 2·b +c 2·c +a2>abc >0成立. 上式两边同时取常用对数,得 lg ⎝⎛⎭⎫a +b 2·b +c 2·c +a 2>lg abc ,∴lg a +b 2+lg b +c 2+lg c +a 2>lg a +lg b +lg c .思维升华 (1)综合法是“由因导果”的证明方法,它是一种从已知到未知(从题设到结论)的逻辑推理方法,即从题设中的已知条件或已证的真实判断(命题)出发,经过一系列中间推理,最后导出所要求证结论的真实性.(2)综合法的逻辑依据是三段论式的演绎推理.题型二 分析法的应用典例 (2018·长沙模拟)已知函数f (x )=tan x ,x ∈⎝⎛⎭⎫0,π2,若x 1,x 2∈⎝⎛⎭⎫0,π2,且x 1≠x 2,求证:12[f (x 1)+f (x 2)]>f ⎝⎛⎭⎫x 1+x 22.证明 要证12[f (x 1)+f (x 2)]>f ⎝⎛⎭⎫x 1+x 22, 即证明12(tan x 1+tan x 2)>tan x 1+x 22,只需证明12⎝⎛⎭⎫sin x 1cos x 1+sin x 2cos x 2>tan x 1+x 22,只需证明sin (x 1+x 2)2cos x 1cos x 2>sin (x 1+x 2)1+cos (x 1+x 2).由于x 1,x 2∈⎝⎛⎭⎫0,π2,故x 1+x 2∈(0,π). 所以cos x 1cos x 2>0,sin(x 1+x 2)>0,1+cos(x 1+x 2)>0, 故只需证明1+cos(x 1+x 2)>2cos x 1cos x 2, 即证1+cos x 1cos x 2-sin x 1sin x 2>2cos x 1cos x 2, 即证cos(x 1-x 2)<1.由x 1,x 2∈⎝⎛⎭⎫0,π2,x 1≠x 2知上式显然成立, 因此12[f (x 1)+f (x 2)]>f ⎝⎛⎭⎫x 1+x 22. 引申探究若本例中f (x )变为f (x )=3x -2x ,试证:对于任意的x 1,x 2∈R ,均有f (x 1)+f (x 2)2≥f⎝⎛⎭⎫x 1+x 22. 证明 要证明f (x 1)+f (x 2)2≥f⎝⎛⎭⎫x 1+x 22,即证明121212122(32)(32)3222x x x x x x x x+-+-+-⋅,≥因此只要证明12122121233()3(),2x x x x x x x x ++-+-+≥ 即证明12122333,2x x x x ++≥因此只要证明12332x x + 由于当x 1,x 2∈R 时,1230,30xx>>,由基本不等式知12332x x +x 1=x 2时,等号成立.故原结论成立.思维升华 (1)逆向思考是用分析法证题的主要思想,通过反推,逐步寻找使结论成立的充分条件.正确把握转化方向是使问题顺利解决的关键.(2)证明较复杂的问题时,可以采用两头凑的办法,即通过分析法找出某个与结论等价(或充分)的中间结论,然后通过综合法证明这个中间结论,从而使原命题得证. 跟踪训练 已知非零向量a ,b ,且a ⊥b ,求证:|a |+|b ||a +b |≤ 2.证明 由a ⊥b 得,a·b =0,要证|a |+|b ||a +b |≤2,只需证|a |+|b |≤2|a +b |,只需证|a |2+2|a ||b |+|b |2≤2(a 2+2a·b +b 2), 只需证|a |2+2|a||b |+|b |2≤2a 2+2b 2, 只需证|a |2+|b |2-2|a||b |≥0, 即(|a |-|b |)2≥0,上式显然成立,故原不等式得证.题型三 反证法的应用命题点1 证明否定性命题典例 设{a n }是公比为q 的等比数列. (1)推导{a n }的前n 项和公式;(2)设q ≠1,证明:数列{a n +1}不是等比数列. (1)解 设{a n }的前n 项和为S n ,则 当q =1时,S n =a 1+a 1+…+a 1=na 1; 当q ≠1时,S n =a 1+a 1q +a 1q 2+…+a 1q n -1,①qS n =a 1q +a 1q 2+…+a 1q n ,② ①-②得,(1-q )S n =a 1-a 1q n , ∴S n =a 1(1-q n )1-q,∴S n =⎩⎪⎨⎪⎧na 1,q =1,a 1(1-q n )1-q,q ≠1.(2)证明 假设{a n +1}是等比数列,则对任意的k ∈N *, (a k +1+1)2=(a k +1)(a k +2+1), a 2k +1+2a k +1+1=a k a k +2+a k +a k +2+1,a 21q 2k +2a 1q k =a 1qk -1·a 1q k +1+a 1q k -1+a 1q k +1, ∵a 1≠0,∴2q k =q k -1+q k +1.∵q ≠0,∴q 2-2q +1=0, ∴q =1,这与已知矛盾.∴假设不成立,故{a n +1}不是等比数列.命题点2 证明存在性命题典例 已知四棱锥S -ABCD 中,底面是边长为1的正方形,又SB =SD =2,SA =1. (1)求证:SA ⊥平面ABCD ;(2)在棱SC 上是否存在异于S ,C 的点F ,使得BF ∥平面SAD ?若存在,确定F 点的位置;若不存在,请说明理由.(1)证明 由已知得SA 2+AD 2=SD 2,∴SA ⊥AD . 同理SA ⊥AB .又AB ∩AD =A ,AB ⊂平面ABCD ,AD ⊂平面ABCD , ∴SA ⊥平面ABCD .(2)解 假设在棱SC 上存在异于S ,C 的点F ,使得BF ∥平面SAD . ∵BC ∥AD ,BC ⊄平面SAD . ∴BC ∥平面SAD .而BC ∩BF =B , ∴平面FBC ∥平面SAD .这与平面SBC 和平面SAD 有公共点S 矛盾, ∴假设不成立.∴不存在这样的点F ,使得BF ∥平面SAD .命题点3 证明唯一性命题典例 (2018·宜昌模拟)已知M 是由满足下列条件的函数构成的集合:对任意f (x )∈M ,①方程f (x )-x =0有实数根;②函数f (x )的导数f ′(x )满足0<f ′(x )<1.(1)判断函数f (x )=x 2+sin x 4是不是集合M 中的元素,并说明理由;(2)集合M 中的元素f (x )具有下面的性质:若f (x )的定义域为D ,则对于任意[m ,n ]⊆D ,都存在x 0∈(m ,n ),使得等式f (n )-f (m )=(n -m )f ′(x 0)成立.试用这一性质证明:方程f (x )-x =0有且只有一个实数根.(1)解 ①当x =0时,f (0)=0,所以方程f (x )-x =0有实数根0; ②f ′(x )=12+cos x4,所以f ′(x )∈⎣⎡⎦⎤14,34,满足条件0<f ′(x )<1. 由①②可得,函数f (x )=x 2+sin x 4是集合M 中的元素.(2)证明 假设方程f (x )-x =0存在两个实数根α,β (α≠β),则f (α)-α=0,f (β)-β=0. 不妨设α<β,根据题意存在c ∈(α,β), 满足f (β)-f (α)=(β-α)f ′(c ).因为f (α)=α,f (β)=β,且α≠β,所以f ′(c )=1. 与已知0<f ′(x )<1矛盾. 又f (x )-x =0有实数根,所以方程f (x )-x =0有且只有一个实数根.思维升华 应用反证法证明数学命题,一般有以下几个步骤: 第一步:分清命题“p ⇒q ”的条件和结论; 第二步:作出与命题结论q 相反的假设綈q ;第三步:由p 和綈q 出发,应用正确的推理方法,推出矛盾结果;第四步:断定产生矛盾结果的原因在于开始所作的假设綈q 不真,于是原结论q 成立,从而间接地证明了命题p ⇒q 为真.所说的矛盾结果,通常是指推出的结果与已知公理、已知定义、已知定理或已知事实矛盾,与临时假设矛盾以及自相矛盾等都是矛盾结果.跟踪训练 若f (x )的定义域为[a ,b ],值域为[a ,b ](a <b ),则称函数f (x )是[a ,b ]上的“四维光军”函数.(1)设g (x )=12x 2-x +32是[1,b ]上的“四维光军”函数,求常数b 的值;(2)是否存在常数a ,b (a >-2),使函数h (x )=1x +2是区间[a ,b ]上的“四维光军”函数?若存在,求出a ,b 的值;若不存在,请说明理由.解 (1)由题设得g (x )=12(x -1)2+1,其图象的对称轴为x =1,区间[1,b ]在对称轴的右边,所以函数在区间[1,b ]上单调递增.由“四维光军”函数的定义可知,g (1)=1,g (b )=b , 即12b 2-b +32=b ,解得b =1或b =3. 因为b >1,所以b =3.(2)假设存在常数a ,b (a >-2),使函数h (x )=1x +2是区间[a ,b ] 上的“四维光军”函数, 因为h (x )=1x +2在区间(-2,+∞)上单调递减,所以有⎩⎪⎨⎪⎧h (a )=b ,h (b )=a ,即⎩⎨⎧1a +2=b ,1b +2=a ,解得a =b ,这与已知矛盾.故不存在.反证法在证明题中的应用典例 (12分)直线y =kx +m (m ≠0)与椭圆W :x 24+y 2=1相交于A ,C 两点,O 是坐标原点.(1)当点B 的坐标为(0,1),且四边形OABC 为菱形时,求AC 的长; (2)当点B 在W 上且不是W 的顶点时,证明:四边形OABC 不可能为菱形.思想方法指导 在证明否定性命题,存在性命题,唯一性命题时常考虑用反证法证明,应用反证法需注意:(1)掌握反证法的证明思路及证题步骤,正确作出假设是反证法的基础,应用假设是反证法的基本手段,得到矛盾是反证法的目的.(2)当证明的结论和条件联系不明显、直接证明不清晰或正面证明分类较多、而反面情况只有一种或较少时,常采用反证法.(3)利用反证法证明时,一定要回到结论上去. 规范解答(1)解 因为四边形OABC 为菱形,则AC 与OB 相互垂直平分.由于O (0,0),B (0,1), 所以设点A ⎝⎛⎭⎫t ,12,代入椭圆方程得t 24+14=1, 则t =±3,故|AC |=2 3.[4分] (2)证明 假设四边形OABC 为菱形,因为点B 不是W 的顶点,且AC ⊥OB ,所以k ≠0.由⎩⎪⎨⎪⎧x 2+4y 2=4,y =kx +m , 消y 并整理得(1+4k 2)x 2+8kmx +4m 2-4=0.[6分] 设A (x 1,y 1),C (x 2,y 2),则x 1+x 22=-4km 1+4k 2,y 1+y 22=k ·x 1+x 22+m =m1+4k 2. 所以AC 的中点为M ⎝ ⎛⎭⎪⎫-4km 1+4k 2,m 1+4k 2.[8分] 因为M 为AC 和OB 的交点,且m ≠0,k ≠0, 所以直线OB 的斜率为-14k,因为k ·⎝⎛⎭⎫-14k =-14≠-1, 所以AC 与OB 不垂直.[10分]所以四边形OABC 不是菱形,与假设矛盾.所以当点B 在W 上且不是W 的顶点时,四边形OABC 不可能是菱形.[12分]1.(2017·绵阳周测)设t =a +2b ,s =a +b 2+1,则下列关于t 和s 的大小关系中正确的是( ) A .t >s B .t ≥s C .t <s D .t ≤s 答案 D解析 s -t =b 2-2b +1=(b -1)2≥0, ∴s ≥t ,故选D.2.分析法又称执果索因法,若用分析法证明:“设a >b >c ,且a +b +c =0,求证b 2-ac <3a ”索的因应是( ) A .a -b >0 B .a -c >0 C .(a -b )(a -c )>0 D .(a -b )(a -c )<0答案 C解析 由题意知b 2-ac <3a ⇐b 2-ac <3a 2 ⇐(a +c )2-ac <3a 2 ⇐a 2+2ac +c 2-ac -3a 2<0 ⇐-2a 2+ac +c 2<0 ⇐2a 2-ac -c 2>0⇐(a -c )(2a +c )>0⇐(a -c )(a -b )>0.3.(2018·太原模拟)设f (x )是定义在R 上的奇函数,且当x ≥0时,f (x )单调递减,若x 1+x 2>0,则f (x 1)+f (x 2)的值( ) A .恒为负值B .恒等于零C .恒为正值D .无法确定正负答案 A 解析 由f (x )是定义在R 上的奇函数,且当x ≥0时,f (x )单调递减,可知f (x )是R 上的单调递减函数,由x 1+x 2>0,可知x 1>-x 2,f (x 1)<f (-x 2)=-f (x 2),则f (x 1)+f (x 2)<0.4.①已知p 3+q 3=2,证明:p +q ≤2.用反证法证明时,可假设p +q ≥2;②若a ,b ∈R ,|a |+|b |<1,求证:方程x 2+ax +b =0的两根的绝对值都小于1.用反证法证明时可假设方程有一根x 1的绝对值大于或等于1,即假设|x 1|≥1.以下结论正确的是( )A .①与②的假设都错误B .①的假设正确;②的假设错误C .①与②的假设都正确D .①的假设错误;②的假设正确答案 D解析 对于①,结论的否定是p +q >2,故①中的假设错误;对于②,其假设正确,故选D.5.(2017·上饶质检)设x ,y ,z >0,则三个数y x +y z ,z x +z y ,x z +x y( ) A .都大于2B .至少有一个大于2C .至少有一个不小于2D .至少有一个不大于2答案 C解析 因为⎝⎛⎭⎫y x +y z +⎝⎛⎭⎫z x +z y +⎝⎛⎭⎫x z +x y=⎝⎛⎭⎫y x +x y +⎝⎛⎭⎫y z +z y +⎝⎛⎭⎫z x +x z ≥6,当且仅当x =y =z 时等号成立.所以三个数中至少有一个不小于2,故选C.6.(2018·济宁模拟)设a ,b 是两个实数,给出下列条件:①a +b >1;②a +b =2;③a +b >2;④a 2+b 2>2;⑤ab >1.其中能推出:“a ,b 中至少有一个大于1”的条件是( )A .②③B .①②③C .③D .③④⑤答案 C解析 若a =12,b =23,则a +b >1, 但a <1,b <1,故①推不出;若a =b =1,则a +b =2,故②推不出;若a =-2,b =-3,则a 2+b 2>2,故④推不出;若a =-2,b =-3,则ab >1,故⑤推不出;对于③,即a +b >2,则a ,b 中至少有一个大于1,下面用反证法证明:假设a ≤1且b ≤1,则a +b ≤2与a +b >2矛盾,因此假设不成立,a ,b 中至少有一个大于1.7.(2018届湖南益阳桃江一中月考)用反证法证明“若x +y ≤0,则x ≤0或y ≤0”时,应假设______________.答案 x >0且y >08.(2018·邢台调研)6+7与22+5的大小关系为______________.答案 6+7>22+ 5解析 要比较6+7与22+5的大小,只需比较(6+7)2与(22+5)2的大小,只需比较6+7+242与8+5+410的大小, 只需比较42与210的大小,只需比较42与40的大小,∵42>40,∴6+7>22+ 5.9.已知点A n (n ,a n )为函数y =x 2+1图象上的点,B n (n ,b n )为函数y =x 图象上的点,其中n ∈N *,设c n =a n -b n ,则c n 与c n +1的大小关系____________.答案 c n +1<c n解析 由条件得c n =a n -b n =n 2+1-n =1n 2+1+n, 则c n 随n 的增大而减小,∴c n +1<c n .10.(2017·武汉联考)已知直线l ⊥平面α,直线m ⊂平面β,有下列命题:①α∥β⇒l ⊥m ;②α⊥β⇒l ∥m ;③l ∥m ⇒α⊥β;④l ⊥m ⇒α∥β.其中正确命题的序号是________.答案 ①③解析 ① ⎭⎪⎬⎪⎫l ⊥αα∥β⇒l ⊥β, 又∵m ⊂β,∴l ⊥m ,①正确;②⎭⎪⎬⎪⎫l ⊥αα⊥β⇒l ∥β或l ⊂β, ∴l ,m 平行、相交、异面都有可能,故②错误;③ ⎭⎪⎬⎪⎫l ∥m l ⊥α⇒m ⊥α, 又m ⊂β,∴β⊥α,故③正确;④ ⎭⎪⎬⎪⎫l ⊥αl ⊥m ⇒m ⊂α或m ∥α. 又m ⊂β,∴α,β可能相交或平行,故④错误.11.(2017·东北三省三校模拟)已知a ,b ,c >0,a +b +c =1.求证: (1)a +b +c ≤3;(2)13a +1+13b +1+13c +1≥32. 证明 (1)∵(a +b +c )2=(a +b +c )+2ab +2bc +2ca ≤(a +b +c )+(a +b )+(b +c )+(c +a )=3, ∴a +b +c ≤3(当且仅当a =b =c 时取等号).(2)∵a >0,∴3a +1>0,∴43a +1+(3a +1)≥243a +1(3a +1)=4, ∴43a +1≥3-3a ⎝⎛⎭⎫当且仅当a =13时,取等号, 同理得43b +1≥3-3b ,43c +1≥3-3c , 以上三式相加得4⎝⎛⎭⎫13a +1+13b +1+13c +1≥9-3(a +b +c )=6, ∴13a +1+13b +1+13c +1≥32(当且仅当a =b =c =13时取等号). 12.(2017·北京)设{a n }和{b n }是两个等差数列,记c n =max{b 1-a 1n ,b 2-a 2n ,…,b n -a n n }(n =1,2,3,…),其中max{x 1,x 2,…,x s }表示x 1,x 2,…,x s 这s 个数中最大的数.(1)若a n =n ,b n =2n -1,求c 1,c 2,c 3的值,并证明{c n }是等差数列;(2)证明:或者对任意正数M ,存在正整数m ,当n ≥m 时,c n n>M ;或者存在正整数m ,使得c m ,c m +1,c m +2,…是等差数列.(1)解 c 1=b 1-a 1=1-1=0,c 2=max{b 1-2a 1,b 2-2a 2}=max{1-2×1,3-2×2}=-1,c 3=max{b 1-3a 1,b 2-3a 2,b 3-3a 3}=max{1-3×1,3-3×2,5-3×3}=-2.当n ≥3时,(b k +1-na k +1)-(b k -na k )=(b k +1-b k )-n (a k +1-a k )=2-n <0,所以b k -na k 在k ∈N *上单调递减.所以c n =max{b 1-a 1n ,b 2-a 2n ,…,b n -a n n }=b 1-a 1n =1-n .所以对任意n ≥1,c n =1-n ,于是c n +1-c n =-1,所以{c n }是等差数列.(2)证明 设数列{a n }和{b n }的公差分别为d 1,d 2,则b k -na k =b 1+(k -1)d 2-[a 1+(k -1)d 1]n=b 1-a 1n +(d 2-nd 1)(k -1).所以c n =⎩⎪⎨⎪⎧b 1-a 1n +(n -1)(d 2-nd 1),d 2>nd 1,b 1-a 1n ,d 2≤nd 1. ①当d 1>0时,取正整数m >d 2d 1,则当n ≥m 时,nd 1>d 2, 因此,c n =b 1-a 1n ,此时,c m ,c m +1,c m +2,…是等差数列.②当d 1=0时,对任意n ≥1,c n =b 1-a 1n +(n -1)max{d 2,0}=b 1-a 1+(n -1)(max{d 2,0}-a 1).此时,c 1,c 2,c 3,…,c n ,…是等差数列.③当d 1<0时,当n >d 2d 1时,有nd 1<d 2, 所以c n n =b 1-a 1n +(n -1)(d 2-nd 1)n=n (-d 1)+d 1-a 1+d 2+b 1-d 2n≥n (-d 1)+d 1-a 1+d 2-|b 1-d 2|.对任意正数M ,取正整数m >max ⎩⎨⎧⎭⎬⎫M +|b 1-d 2|+a 1-d 1-d 2-d 1,d 2d 1, 故当n ≥m 时,c n n>M .13.(2018·长春模拟)若二次函数f (x )=4x 2-2(p -2)x -2p 2-p +1,在区间[-1,1]内至少存在一点c ,使f (c )>0,则实数p 的取值范围是____________.答案 ⎝⎛⎭⎫-3,32 解析 若二次函数f (x )≤0在区间[-1,1]内恒成立,则⎩⎪⎨⎪⎧f (-1)=-2p 2+p +1≤0,f (1)=-2p 2-3p +9≤0, 解得p ≤-3或p ≥32, 故满足题干要求的p 的取值范围为⎝⎛⎭⎫-3,32. 14.设x ≥1,y ≥1,证明x +y +1xy ≤1x +1y+xy . 证明 由于x ≥1,y ≥1,所以要证明x +y +1xy ≤1x +1y+xy , 只需证xy (x +y )+1≤y +x +(xy )2.将上式中的右式减左式,得[y +x +(xy )2]-[xy (x +y )+1]=[(xy )2-1]-[xy (x +y )-(x +y )]=(xy +1)(xy -1)-(x +y )(xy -1)=(xy -1)(xy -x -y +1)=(xy -1)(x -1)(y -1).因为x ≥1,y ≥1,所以(xy -1)(x -1)(y -1)≥0,从而所要证明的不等式成立.15.(2018·海口调研)已知函数f (x )=a x +x -2x +1(a >1). (1)证明:函数f (x )在(-1,+∞)上为增函数;(2)用反证法证明方程f (x )=0没有负数根. 证明 (1)任取x 1,x 2∈(-1,+∞),不妨设x 1<x 2,则x 2-x 1>0.∵a >1,∴211x x a >-且10x a >,21121(1)0.x x x x x a a a a ∴>--=-又∵x 1+1>0,x 2+1>0,∴x 2-2x 2+1-x 1-2x 1+1=(x 2-2)(x 1+1)-(x 1-2)(x 2+1)(x 1+1)(x 2+1) =3(x 2-x 1)(x 1+1)(x 2+1)>0. 于是f (x 2)-f (x 1)=21x x a a -+x 2-2x 2+1-x 1-2x 1+1>0, 故函数f (x )在(-1,+∞)上为增函数.(2)假设存在x 0<0(x 0≠-1)满足f (x 0)=0,则0x a =-x 0-2x 0+1. ∵a >1,∴0<0x a <1,∴0<-x 0-2x 0+1<1, 即12<x 0<2,与假设x 0<0相矛盾, 故方程f (x )=0没有负数根.16.(2017·江苏)对于给定的正整数k ,若数列{a n }满足a n -k +a n -k +1+…+a n -1+a n +1+…+a n +k -1+a n +k =2ka n 对任意正整数n (n >k )总成立,则称数列{a n }是“P (k )数列”.(1)证明:等差数列{a n }是“P (3)数列”;(2)若数列{a n }既是“P (2)数列”,又是“P (3)数列”,证明:{a n }是等差数列. 证明 (1)因为{a n }是等差数列,设其公差为d , 则a n =a 1+(n -1)d ,从而,当n ≥4时,a n -k +a n +k =a 1+(n -k -1)d +a 1+(n +k -1)d =2a 1+2(n -1)d =2a n ,k =1,2,3,所以a n -3+a n -2+a n -1+a n +1+a n +2+a n +3=6a n , 因此等差数列{a n }是“P (3)数列”.(2)数列{a n }既是“P (2)数列”,又是“P (3)数列”,因此, 当n ≥3时,a n -2+a n -1+a n +1+a n +2=4a n ,① 当n ≥4时,a n -3+a n -2+a n -1+a n +1+a n +2+a n +3 =6a n .②由①知,a n -3+a n -2=4a n -1-(a n +a n +1),③ a n +2+a n +3=4a n +1-(a n -1+a n ).④将③④代入②,得a n -1+a n +1=2a n ,其中n ≥4, 所以a 3,a 4,a 5,…是等差数列,设其公差为d ′. 在①中,取n =4,则a 2+a 3+a 5+a 6=4a 4, 所以a 2=a 3-d ′,在①中,取n=3,则a1+a2+a4+a5=4a3,所以a1=a3-2d′,所以数列{a n}是等差数列.。
2020年高考数学三轮题型突破 2 填空题突破 题型16 副题07 推理与证明(教师版含解析)

第二篇副题7 推理与证明【副题考法】本副题考题类型为选择填空题,并与平面几何、立体几何、解析几何、三角函数、数列等相结合考查归纳推理、类比推理合情推理思想与演绎推理思想,考查分析法、综合法、反证法等分析问题解决问题的思想方法的,考查对新概念的理解和新概念的应用,考查推理论证能力、运算求解能力、阅读理解新概念及应用新概念解决问题能力、转化与化归思想,其难度较多是中等题,分值为5分.【主题考前回扣】1.推理推理分为合情推理与演绎推理,合情推理包括归纳推理和类比推理;演绎推理的一般模式是三段论.合情推理的思维过程(1)归纳推理的思维过程实验、观察―→概括、推广→猜测一般性结论(2)类比推理的思维过程实验、观察―→联想、类推→猜测新的结论2.证明方法(1)分析法的特点:从未知看需知,逐步靠拢已知.推理模式:框图表示Q⇐P1→P1⇐P2→P2⇐P3→…→得到一个明显成立的条件(2)综合法的特点:从已知看可知,逐步推出未知.推理模式框图表示:P⇒Q1→Q1⇒Q2→Q2⇒Q3→…→Q n⇒Q(其中P表示已知条件、已有的定义、公理、定理等,Q表示要证明的结论).学-科网(3)反证法一般地,假设原命题不成立(即在原命题的条件下,结论不成立),经过正确的推理,最后得出矛盾,因此说明假设错误,从而证明了原命题成立,这样的证明方法叫做反证法.【易错点提醒】1.应用合情推理应注意的问题:(1)在进行归纳推理时,要先根据已知的部分个体,把它们适当变形,找出它们之间的联系,从而归纳出一般结论.(2)在进行类比推理时,要充分考虑已知对象性质的推理过程,然后类比推导类比对象的性质. 注意:归纳推理关键是找规律,类比推理关键是看共性.2. 应用分析法时,忽视①每一步要找的是上一步成立的充分条件,②要注意书写格式这两点致错.3. 应用反证法是要假设结论的反面成立,将结论的反面作为条件进行推理导出矛盾,因结论反面考虑不全致错. 【副题考向】考向一 归纳推理【解决法宝】 归纳推理是由部分到整体、由个别到一般的推理.在进行归纳时,要先把已知的部分个体适当变形,再通过对这些个体的观察、分析、比较,发现它们的相同性质或变化规律,找出它们之间的联系,从这些相同性质或变化规律推出一个明确表述的一般命题,从而归纳出一般结论,对所得的一般性命题进行检验,归纳推理关键是找规律.学科=网例1【2020•邯郸模拟】公元前四世纪,毕达哥拉斯学派对数和形的关系进行了研究.他们借助几何图形(或格点)来表示数,称为形数.形数是联系算数和几何的纽带)图为五角形数的前4个,则第10个五角形数为()A .120B .145C .270D .285【分析】记第n 个五角形数为n a ,由11130a ==+⨯,214131a a -==+⨯,327132a a -==+⨯,推导出113(1)n n a a n --=+-,由累加法能求出结果.【解析】记第n 个五角形数为n a ,由题意知:11130a ==+⨯,214131a a -==+⨯,327132a a -==+⨯,4310133a a -==+⨯,⋯,113(1)n n a a n -∴-=+-,由累加法得:1213243541n n n a a a a a a a a a a a a -=+-+-+-+-+⋯+-1(131)(132)(133)[13(1)]n =++⨯++⨯++⨯+⋯++-13[123(1)]n n =⨯++++⋯+-(1)32n n n -=+⨯g(31)2n n -=,∴10(3101)101452a ⨯-⨯==,故选B . 考向二 类比推理【解题法宝】类比推理是由特殊到特殊的推理,是两类类似的对象之间的推理,其中一个对象具有某个性质,则另一个对象也具有类似的结论,在进行类比推理时,要充分考虑已知对象性质的推理过程,然后通过类比,推导出类比对象的性质,类比推理关键是看共性.例 2 【2020山东模拟】设ABC ∆的三边长分别为a 、b 、c ,ABC ∆的面积为S ,内切圆半径为r ,则2Sr a b c=++;类比这个结论可知:四面体P ABC -的四个面的面积分别为1S 、2S 、3S 、4S ,内切球的半径为r ,四面体P ABC -的体积为V ,则r = .【分析】根据平面与空间之间的类比推理,由点类比点或直线,由直线 类比 直线或平面,由内切圆类比内切球,由平面图形面积类比立体图形的体积,结合求三角形的面积的方法类比求四面体的体积即可. 【解析】设四面体的内切球的球心为O ,则球心O 到四个面的距离都是R ,所以四面体的体积等于以O 为顶点,分别以四个面为底面的4个三棱锥体积的和,则四面体的体积为12341()3S S S S r +++,12343Vr S S S S ∴=+++.考向三 演绎推理【解题法宝】演绎推理是由一般到特殊的推理.数学的证明过程主要是通过演绎推理进行的,只要采用的演绎推理的大前提、小前提和推理形式是正确的,其结论一定是正确的,一定要注意推理过程的正确性与完备性. 例3【2020•齐齐哈尔一模】已知甲、乙、丙三人恰好都去过北京、上海中的某一个城市,三人分别给出了以下说法:甲说:我去过北京,乙去过上海,丙去过北京; 乙说:我去过上海,甲说的不完全对; 丙说:我去过北京,乙说的对.若甲、乙、丙三人中恰好有1人说得不对,则去过北京的是 .【分析】若甲说得不对,则乙、丙说得对,若乙或丙说得不对,则得出与”甲、乙、丙三人中恰有1人说得不对“矛盾,从而得到去过北京的是丙.【解析】若甲说得不对,则乙、丙说得对,即乙一定去过上海,丙一定去过北京,甲只去过上海,若乙或丙说得不对,则得出与”甲、乙、丙三人中恰有1人说得不对“矛盾,故去过北京的是丙.考向四 间接证明【解决法宝】用反证法证明数学命题步骤如下: 第一步,分清命题“q p ⇒”的条件和结论; 第二步,作出与结论q 相反的假设q ⌝;学-科网第三步,由p 和q ⌝出发,应用正确的推理方法,推出矛盾结果;第四步,断定矛盾结果的原因在于开始所作的假设q ⌝不真,于是结论q 成立,从而证明了命题q p ⇒为真.所说的矛盾结果,通常是指推出的结果和已知公理、已知定义、已知定理、已知条件矛盾,与临时假设矛盾以及自相矛盾等都是矛盾结果.例4 【2020四川广安期末】用反证法证明命题:“三角形三个内角至少有一个不大于60︒”时,应假设( ) A .三个内角都不大于60︒ B .三个内角至多有一个大于60︒C .三个内角都大于60︒D .三个内角至多有两个大于60︒【分析】熟记反证法的步骤,从命题的反面出发假设出结论,直接得出答案即可.【解析】Q 用反证法证明在一个三角形中,至少有一个内角不大于60︒,∴第一步应假设结论不成立,即假设三个内角都大于60︒,故选C考向五 新定义【解决法宝】一般是以新课标教材内容为背景,给出某种新概念、新运算(符号)、新法则(公式)等,学生在理解相关新概念、新运算(符号)、新法则(公式)之后,运用新课标学过的知识,结合已掌握的技能,通过推理、运算等寻求问题解决.结合高等数学的题目通常是以高等数学符号、概念直接出现或以高等数学概念、定理作为依托融于初等数学知识中.此类问题的设计虽来源于高等数学,但一般是起点高,落点低,它的解决的方法还是运用中学数学的基本知识和基本技能.这要求学生认真阅读相关定义或方法,在充分理解题意的基础上,结合已有的知识进行解题.学*科网结合其他学科的题目,主要是介绍数学知识在其他学科或领域的运用,一般都会介绍运用时的知识背景、数学模型,因而题中文字、信息较多.学生必须准确地把握题意、理顺线索、分析相应数学模型与数学知识的内在联系,结合学生已有的知识和能力进行推理、运算.“新定义”型的问题,通常是选取合适的数学背景,把新定义、新运算、新符号等巧妙的融入高考试题中来,虽然它的构思巧妙、题意新颖、隐蔽性强,到处都体现出新意,但是,它考查的还是基本知识和基本技能,解题的关键在于全面准确理解题意,科学合理的推理运算.因此,“新题”不一定是“难题”,只有夯实基础,掌握好双基,以不变应万变才是我们取胜的法宝.例5【2019届湖南省长沙市长郡中学五调】定义两个实数间的一种新运算:,,.对任意实数、、,给出如下结论:①;②;③,其中正确的是( )【分析】首先根据题中所给的条件,利用新定义运算法则,分别求相应的量,逐个验证是否正确,从而选出正确的结果.【解析】根据运算法则,可知,,所以,故①正确;结合相应式子的运算律,可知,故②正确;,,所以,故③正确;所以正确的是①②③,故选D. 【主题集训】1.【2020河北石家庄期末】观察下列各式:553125=,6515625=,7578125=,⋯,则20195的末四位数字为( ) A .3125 B .5625C .0625D .8125【答案】D【解析】由553125=,6515625=,7578125=,85390625=,951953125=,1059765625=⋯,可归纳出5(5)n n …的最后四位数为3125,5625,8125,0625,且以4为周期,又201950347=⨯+,即20195的末四位数字与75的末四位数字相同,即20195的末四位数字为8125,故选D . 2.【2019届安徽亳州一中2模】三角形的面积为,其中,,为三角形的边长,为三角形内切圆的半径,则利用类比推理,可得出四面体的体积为( )A.B.C.,(为四面体的高)D.,(,,,分别为四面体的四个面的面积,为四面体内切球的半径) 【答案】D【解析】设四面体的内切球的球心为O,则球心O到四个面的距离都是r,根据三角形的面积的求解方法:分割法,将O与四顶点连起来,可得四面体的体积等于以O为顶点,分别以四个面为底面的4个三棱锥体积的和,∴V(S1+S2+S3+S4)r,故选D.3.【2020•山东模拟】甲,乙,丙,丁四名学生,仅有一人阅读了语文老师推荐的一篇文章.当它们被问到谁阅读了该篇文章时,甲说:“丙或丁阅读了”;乙说:“丙阅读了”;丙说:“甲和丁都没有阅读”;丁说:“乙阅读了”.假设这四名学生中只有两人说的是对的,那么读了该篇文章的学生是() A.甲B.乙C.丙D.丁【答案】B【解析】①当读了该篇文章的学生是甲,则四位同学都错了,与题设矛盾,故读了该篇文章的学生不是甲,②当读了该篇文章的学生是乙,则丙,丁说的是对的,与题设相符,故读了该篇文章的学生是乙,③当读了该篇文章的学生是丙,则甲,乙,丙说的是对的,与题设矛盾,故读了该篇文章的学生不是丙,④当读了该篇文章的学生是丁,则甲说的是对的,与题设矛盾,故读了该篇文章的学生不是丁,综合①②③④得:读了该篇文章的学生是乙,故选B.4.【2019届河北省衡水十三中质检(四)】利用反证法证明:若,则,假设为( ) A.,都不为0 B.,不都为0C.,都不为0,且D.,至少有一个为0【答案】B【解析】的否定为,即,不都为0,选B.5.【2020届江西省南昌市第一次模拟】《聊斋志异》中有:“挑水砍柴不堪苦,请归但求穿墙术”.在数学中,我们称形如以下形式的等式具有“穿墙术”:22334422,33,4,33881515===则按照以上规律,若m mmm n n=具有“穿墙术”,则m ,n 满足的关系式为( ) A .n =2m -1 B .n =2(m -1)C .n =(m -1)2D .n =m 2 -1【答案】D【解析】由题可知:22222223321==-,23333338831==-,2444444151541==-,则可归纳:21m m mmm m n n m ==-,所以21n m =-,故选D 6.【2019届新疆第一次诊断】对于任意实数x ,y ,把代数运算的值叫做x 与y 的“加乘和谐数”,记作符号“”,其中a ,b ,c 是常数,若已知,,若恒成立,则当且仅当非零实数m 的值为 A .2 B .4C .6D .8【答案】B【解析】根据题意,若已知,,则有,变形可得,,又由对于任意实数x 恒成立,则有,∵m 为非零实数,则,又由,则有,又由,解可得,故选B .7.【2020届四川省攀枝花第二次统考】中国古代用算筹来进行记数,算筹的摆放形式有纵横两种形式(如图所示),表示一个多位数时,像阿拉伯记数一样,把各个数位的数码从左到右排列,但各位数码的筹式需要纵横相间,其中个位、百位、方位……用纵式表示,十位、千位、十万位……用横式表示,则56846可用算筹表示为( )A .B .C .D .【答案】B【解析】根据题意可得,各个数码的筹式需要纵横相间,个位,百位,万位用纵式表示;十位,千位,十万位用横式表示,56846∴用算筹表示应为:纵5横6纵8横4纵6,从题目中所给出的信息找出对应算筹表示为B 中的,故选B .8.【2019届四川省南充市第一次适应性考试】在实数的原有运算法则(“” “”仍为通常的乘法和减法)中,我们补充定义新运算 “如下:当时,;当时,,则当时,函数的最大值等于A .-1B .1C .6D .12 【答案】C【解析】由已知得所以,可求出:当时,函数最大值是-1;当时,函数最大值是6;当时,函数不存在最大值是;所以函数的最大值等于6,选C9.【2020届湖北省宜昌市3月线上统一调研】已知数列{}n a 满足132n n a -=⨯,*n N ∈,现将该数列按下图规律排成蛇形数阵(第i 行有i 个数,*i N ∈),从左至右第i 行第j 个数记为(),i j a (*,i j N ∈且j i ≤),则()21,20a =( )A .20932⨯B .21032⨯C .21132⨯D .21232⨯【答案】C【解析】由题可知,第i 行有i 个数,当i 为奇数时,该行由右至左i 逐渐增大,()21,20a 表示第21行第20个数,即为第21行倒数第2个数,则前20行共有()1+2020=2102⨯个数,即第21行倒数第1个数为211a,所以()21121221,2032a a ==⨯,故选C10.【2020届安徽省皖江名校联盟第五次联考】在数学中,泰勒级数用无限项连加式——级数来表示一个函数,包括正弦,余弦,正切三角函数等等,其中泰勒级数是以于1715年发表了泰勒公式的英国数学家布鲁克•泰勒(Sir Brook Taylor )的名字来命名的.1715年,泰勒提出了一个常用的方法来构建这一系列级数并适用于所有函数,这就是后来被人们所熟知的泰勒级数,并建立了如下指数函数公式:01230!0!1!2!3!!n nxn x x x x x x e n n ∞===+++++∑L ,其中x ∈R ,*n N ∈,!1234n n =⨯⨯⨯⨯⨯L ,例如:0!1=,1!1=,2!2=,3!6=.试用上述公式估计12e 的近似值为(精确到0.001)( )A .1.601B .1.642C .1.648D .1.647【答案】C【解析】由题意,只需要精确到0.001即可,令0.5,4x n ==,代入可得,()012340.50.50.50.50.50.50.5 1.648434 1.6484!0!1!2!3!4!nn e∞===++++=≈∑,所以12e 的近似值为1.648,故选C.11.【2020届福建厦门第一次质量检测】中国古代近似计算方法源远流长,早在八世纪,我国著名数学家、天文学家张隧(法号:一行)为编制《大衍历》发明了一种近似计算的方法——二次插值算法(又称一行算法,牛顿也创造了此算法,但是比我国张隧晚了上千年):对于函数()y f x =在()123123,,x x x x x x <<处的函数值分别为()()()112233,,y f x y f x y f x ===,则在区间[]13,x x 上()f x 可以用二次函数()()()111212()f x y k x x k x x x x =+-+--来近似代替,其中3221112213231,,y y y y k k k k k x x x x x x ---===---.若令10x =,2π2x =,3πx =,请依据上述算法,估算2πsin 5的近似值是( ) A .2425B .1725 C .1625 D .35【答案】A【解析】函数()sin y f x x ==在0x =,π2x =,πx =处的函数值分别为 1(0)0y f ==,2π()12y f ==,3(π)0y f ==,故211212y y k x x π-==-,32322y y k x x π-==--,122314k k k x x π-==--,故2222444()()2f x x x x x x πππππ=--=-+,即2244sin x x x ππ≈-+,∴222424224sin()55525πππππ≈-⨯+⨯=,故选A . 12.【2019届江西省南昌市一模】杨辉三角,是二项式系数在三角形中的一种几何排列.在欧洲,这个表叫做帕斯卡三角形,帕斯卡(1623-1662)是在1654年发现这一规律的.我国南宋数学家杨辉1261年所著的《详解九章算法》一书里出现了如图所示的表,这是我国数学史上的一个伟大成就.如图所示,在“杨辉三角”中,去除所有为1的项,依次构成数列,则此数列前135项的和为( )A .B .C .D .【答案】A【解析】n 次二项式系数对应杨辉三角形的第n+1行,例如(x+1)2=x 2+2x+1,系数分别为1,2,1,对应杨辉三角形的第3行,令x =1,就可以求出该行的系数之和,第1行为20,第2行为21,第3行为22,以此类推即每一行数字和为首项为1,公比为2的等比数列,则杨辉三角形的前n 项和为S n2n ﹣1,若去除所有的为1的项,则剩下的每一行的个数为1,2,3,4,……,可以看成一个首项为1,公差为1的等差数列,则T n,可得当n =15,在加上第16行的前15项时,所有项的个数和为135,由于最右侧为2,3,4,5,……,为首项是2公差为1的等差数列,则第16行的第16项为17,则杨辉三角形的前18项的和为S 18=218﹣1,则此数列前135项的和为S 18﹣35﹣17=218﹣53,故选A . 13.【2020湖南株洲一中期末】若数列{}n a 是等差数列,则数列12nn a a a b n++⋯+=也为等差数列.类比这一性质可知,若正项数列{}n c 是等比数列,且n d 也是等比数列,则n d 的表达式应为( ) A .12n n c c c d n++⋯+=B .12nn c c c d n ⋅⋅⋯⋅=C .12n n nnnn c c c d n++⋯+= D .12n n n d c c c =⋅⋅⋯⋅【答案】D【解析】Q 数列{}n a 是等差数列,则()12112n n na a a a d n -++⋯++=,∴数列12112n n a a a n b a d n ++⋯+-==+也为等差数列,Q 正项数列{}n c 是等比数列,设首项为1c ,公比为q ,则()112121111nn nn n c c c c c q c qc q--⋅⋅⋯⋅⋅⋅⋯==⋅,∴112121111n n n n n n d c c c c c q c q c q--=⋅⋅⋯⋅=⋅⋅⋯⋅=,∴12n n n d c c c =⋅⋅⋯⋅是等比数列,故选D .14.【2019届黑龙江省齐齐哈尔市二模】德国大数学家高斯年少成名,被誉为数学届的王子,19岁的高斯得到了一个数学史上非常重要的结论,就是《正十七边形尺规作图之理论与方法》,在其年幼时,对的求和运算中,提出了倒序相加法的原理,该原理基于所给数据前后对应项的和呈现一定的规律生成,因此,此方法也称之为高斯算法.现有函数,则等于( )A .B .C .D .【答案】A 【解析】,又,两式相加可得,故选A 项.15.【2020辽宁锦州一中期中】设△ABC 的三边长分别为a ,b ,c ,△ABC 的面积为S ,则△ABC 的内切圆半径为2Sb cr a =++.将此结论类比到空间四面体:设四面体S ABC -的四个面的面积分别为S 1,S 2,S 3,S 4,体积为V ,则四面体的内切球半径为r =( ) A .1234VS S S S +++B .12342VS S S S +++C .12343VS S S S +++D .12344VS S S S +++【答案】C【解析】设四面体的内切球的球心为O ,则球心O 到四个面的距离都是r ,所以四面体的体积等于以O 为顶点,分别以四个面为底面的4个三棱锥体积的和.则四面体的体积为:()123413V S S S S r =+++,所以12343VS S S S r =+++,故选C16.【2019河南洛阳二高2模】如图所示,将若干个点摆成三角形图案,每条边(包括两个端点)有个点,相应的图案中总的点数记为,则等于( )A .B .C .D .【答案】C 【解析】时,;时,;时,;时所以是3为公差的等差数列,所以。
2020年高考课标版高考文科数学 第十二章 推理与证明

第十二章 推理与证明挖命题【真题典例】【考情探究】5年考情考点内容解读考题示例考向关联考点预测热度2017课标全国Ⅱ,9,5分合情推理逻辑推理2016课标全国Ⅱ,16,5分合情推理逻辑推理合情推理与演绎推理①了解合情推理的含义,能利用归纳和类比等进行简单的推理,了解合情推理在数学发现中的作用;②了解演绎推理的重要性,掌握演绎推理的基本模式,并能运用它们进行简单的推理;③了解合情推理和演绎推理之间的联系和差异2014课标Ⅰ,14,5分合情推理逻辑推理★★☆2018江苏,20,16分直接证明转化,推理直接证明与间接证明①了解直接证明的两种基本方法:分析法与综合法,并了解分析法和综合法的思考过程、特点;②了解间接证明的一种基本方法:反证法,并了解反证法的思考过程、特点2014天津,20,14分直接证明转化,推理★★☆分析解读 本部分在高考中主要考查以下几个方面:1.归纳推理与类比推理以选择题、填空题的形式出现,考查学生的逻辑推理能力,而演绎推理多出现在立体几何的证明中;2.直接证明与间接证明作为证明和推理数学命题的方法,常以不等式、立体几何、解析几何、函数为载体,考查综合法、分析法及反证法.本节内容在高考中的分值分配:①归纳推理与类比推理分值为5分左右,属于中档题;②证明问题以解答题形式出现,分值为12分左右,属于中高档题.【考点集训】考点一 合情推理与演绎推理1.(2018安徽安庆二模,11)对于大于1的自然数的三次幂可以分解成几个奇数的和,比如23=3+5,33=7+9+11,43=13+15+17+19,……,以此规律,453的分解和式中一定不含有( ) A.2 069B.2 039C.2 009D.1 979答案 D2.(2017江西鹰潭一模,2)用三段论推理:“任何实数的绝对值大于0,因为a 是实数,所以a 的绝对值大于0”,你认为这个推理( )A.大前提错误B.小前提错误C.推理形式错误D.是正确的答案 A3.(2017陕西渭南一模,4)古希腊人常用小石子在沙滩上摆成各种形状来研究数,例如:他们研究过图中的1,3,6,10,…,由于这些数能够表示成三角形,故将其称为三角形数,由以上规律,知这些三角形数从小到大形成一个数列{a n },那么a 10的值为( )A.45 B.55 C.65 D.66答案 B 考点二 直接证明与间接证明1.(2018湖北普通高中联考,7)分析法又叫执果索因法,若使用分析法证明:设a<b<c,且a+b+c=0,求证:b 2-ac<3c 2,则证明的依据应是( )A.c-b>0 B.c-a>0C.(c-b)(c-a)>0D.(c-b)(c-a)<0答案 C 2.(2017山西大学附中第二次模拟,17)在等比数列{a n }中,a 3=,S 3=.3292(1)求数列{a n }的通项公式;(2)设b n =log 2,且{b n }为递增数列,若c n =,求证:c 1+c 2+c 3+…+c n <.6a2n +11b n ·b n +114解析 (1)设{a n }的公比为q(q ≠0).∵a 3=,S 3=,3292∴⇒或{S 3-a 3=a 1+a 2=a 1(1+q)=3,a 3=a 1·q 2=32{q =1,a 1=32{q =-12,a 1=6,∴a n =或a n =6.32(-12)n -1(2)证明:由题意知b n =log 2=log 2=log 222n =2n,6a2n +166(-12)2n∴c n ===,1b n ·b n +114n (n +1)14(1n -1n +1)∴c 1+c 2+c 3+…+c n ===-<.14(1-12+12-13+…+1n -1n +1)14(1-1n +1)1414(n +1)14【方法集训】方法 归纳推理与类比推理的应用1.(2018广东肇庆一模,14)观察下列不等式:1+<,1++<,1+++<,……,照此规律,第五个不等式122321221325312213214274为 . 答案 1+++++<1221321421521621162.(2017上海浦东期中联考,12)在Rt △ABC 中,两直角边长分别为a 、b,设h 为斜边上的高,则=+,由此类比:三棱锥P-ABC 中1ℎ21a21b2的三条侧棱PA 、PB 、PC 两两垂直,且长度分别为a 、b 、c,设棱锥底面△ABC 上的高为h,则 . 答案 =++1ℎ21a21b 21c2过专题【五年高考】A 组 统一命题·课标卷题组1.(2016课标全国Ⅱ,16,5分)有三张卡片,分别写有1和2,1和3,2和3.甲,乙,丙三人各取走一张卡片,甲看了乙的卡片后说:“我与乙的卡片上相同的数字不是2”,乙看了丙的卡片后说:“我与丙的卡片上相同的数字不是1”,丙说:“我的卡片上的数字之和不是5”,则甲的卡片上的数字是 . 答案 1和32.(2014课标Ⅰ,14,5分)甲、乙、丙三位同学被问到是否去过A,B,C 三个城市时,甲说:我去过的城市比乙多,但没去过B 城市;乙说:我没去过C 城市;丙说:我们三人去过同一城市.由此可判断乙去过的城市为 . 答案 AB 组 自主命题·省(区、市)卷题组考点一 合情推理与演绎推理1.(2015陕西,16,5分)观察下列等式1-=12121-+-=+12131413141-+-+-=++1213141516141516……据此规律,第n 个等式可为 . 答案 1-+-+…+-=++…+12131412n -112n 1n +11n +212n2.(2016山东,12,5分)观察下列等式:+=×1×2;(sin π3)-2(sin 2π3)-243+++=×2×3;(sin π5)-2(sin 2π5)-2(sin 3π5)-2(sin 4π5)-243+++…+=×3×4;(sin π7)-2(sin 2π7)-2(sin 3π7)-2(sin 6π7)-243+++…+=×4×5;(sin π9)-2(sin 2π9)-2(sin 3π9)-2(sin 8π9)-243……照此规律,+++…+= . (sin π2n +1)-2(sin 2π2n +1)-2(sin 3π2n +1)-2(sin 2nπ2n +1)-2答案 4n (n +1)33.(2017北京,14,5分)某学习小组由学生和教师组成,人员构成同时满足以下三个条件:(i)男学生人数多于女学生人数;(ii)女学生人数多于教师人数;(iii)教师人数的两倍多于男学生人数.①若教师人数为4,则女学生人数的最大值为 ; ②该小组人数的最小值为 . 答案 ①6 ②12考点二 直接证明与间接证明1.(2018江苏,20,16分)设{a n }是首项为a 1,公差为d 的等差数列,{b n }是首项为b 1,公比为q 的等比数列.(1)设a 1=0,b 1=1,q=2,若|a n -b n |≤b 1对n=1,2,3,4均成立,求d 的取值范围;(2)若a 1=b 1>0,m ∈N *,q ∈(1,],证明:存在d ∈R ,使得|a n -b n |≤b 1对n=2,3,…,m+1均成立,并求d 的取值范围(用b 1,m,q 表示).m2解析 (1)由条件知a n =(n-1)d,b n =2n-1.因为|a n -b n |≤b 1对n=1,2,3,4均成立,即|(n-1)d-2n-1|≤1对n=1,2,3,4均成立.即1≤1,1≤d ≤3,3≤2d ≤5,7≤3d ≤9,得≤d ≤.7352因此,d 的取值范围为.[73,52](2)由条件知:a n =b 1+(n-1)d,b n =b 1q n-1.若存在d ∈R ,使得|a n -b n |≤b 1(n=2,3,…,m+1)均成立,即|b 1+(n-1)d-b 1q n-1|≤b 1(n=2,3,…,m+1).即当n=2,3,…,m+1时,d 满足b 1≤d ≤b 1.qn -1-2n -1qn -1n -1因为q ∈(1,],m2所以1<q n-1≤q m ≤2,从而b 1≤0,b 1>0,对n=2,3,…,m+1均成立.qn -1-2n -1qn -1n -1因此,取d=0时,|a n -b n |≤b 1对n=2,3,…,m+1均成立.下面讨论数列的最大值和数列的最小值(n=2,3,…,m+1).{qn -1-2n -1}{qn -1n -1}①当2≤n ≤m 时,-==,q n-2n q n -1-2n -1nq n-q n-n q n -1+2n (n -1)n (q n-q n -1)-q n+2n (n -1)当1<q ≤时,有q n ≤q m ≤2,21m从而n(q n -q n-1)-q n +2>0.因此,当2≤n ≤m+1时, 数列单调递增,{qn -1-2n -1}故数列的最大值为.{qn -1-2n -1}q m-2m ②设f(x)=2x (1-x),当x>0时,f '(x)=(ln 2-1-xln 2)2x <0.所以f(x)单调递减,从而f(x)<f(0)=1.当2≤n ≤m 时,=≤=f <1.q n nqn -1n -1q (n -1)n 21n(1-1n )(1n )因此,当2≤n ≤m+1时,数列单调递减,{qn -1n -1}故数列的最小值为.{qn -1n -1}q mm 因此,d 的取值范围为.[b 1(q m -2)m,b 1qmm ]2.(2014天津,20,14分)已知q 和n 均为给定的大于1的自然数.设集合M={0,1,2,…,q-1},集合A={x|x=x 1+x 2q+…+x n q n-1,x i ∈M,i=1,2,…,n}.(1)当q=2,n=3时,用列举法表示集合A;(2)设s,t ∈A,s=a 1+a 2q+…+a n q n-1,t=b 1+b 2q+…+b n q n-1,其中a i ,b i ∈M,i=1,2,…,n.证明:若a n <b n ,则s<t.解析 (1)当q=2,n=3时,M={0,1},A={x|x=x 1+x 2·2+x 3·22,x i ∈M,i=1,2,3}.可得,A={0,1,2,3,4,5,6,7}.(2)证明:由s,t ∈A,s=a 1+a 2q+…+a n q n-1,t=b 1+b 2q+…+b n q n-1,a i ,b i ∈M,i=1,2,…,n 及a n <b n ,可得s-t=(a 1-b 1)+(a 2-b 2)q+…+(a n-1-b n-1)q n-2+(a n -b n )q n-1≤(q-1)+(q-1)q+…+(q-1)q n-2-q n-1=-q n-1(q -1)(1-q n -1)1-q=-1<0.所以,s<t.C 组 教师专用题组考点一 合情推理与演绎推理1.(2016北京,8,5分)某学校运动会的立定跳远和30秒跳绳两个单项比赛分成预赛和决赛两个阶段.下表为10名学生的预赛成绩,其中有三个数据模糊.学生序号12345678910立定跳远(单位:米) 1.96 1.92 1.82 1.80 1.78 1.76 1.74 1.72 1.68 1.6030秒跳绳(单位:次)63a 7560637270a-1b65在这10名学生中,进入立定跳远决赛的有8人,同时进入立定跳远决赛和30秒跳绳决赛的有6人,则( )A.2号学生进入30秒跳绳决赛B.5号学生进入30秒跳绳决赛C.8号学生进入30秒跳绳决赛D.9号学生进入30秒跳绳决赛答案 B 2.(2014陕西,14,5分)已知f(x)=,x ≥0,若f 1(x)=f(x), f n+1(x)=f(f n (x)),n ∈N +,则f 2 014(x)的表达式x1+x 为 . 答案 f 2 014(x)=x1+2 014x3.(2014福建,16,4分)已知集合{a,b,c}={0,1,2},且下列三个关系:①a≠2;②b=2;③c≠0有且只有一个正确,则100a+10b+c 等于 . 答案 2014.(2014江西,21,14分)将连续正整数1,2,…,n(n ∈N *)从小到大排列构成一个数,F(n)为这个数的位数(如n=12时,此数123…n 为123 456 789 101 112,共有15个数字,F(12)=15),现从这个数中随机取一个数字,p(n)为恰好取到0的概率.(1)求p(100);(2)当n ≤2 014时,求F(n)的表达式;(3)令g(n)为这个数中数字0的个数, f(n)为这个数中数字9的个数,h(n)=f(n)-g(n),S={n|h(n)=1,n ≤100,n ∈N *},求当n ∈S 时p(n)的最大值.解析 (1)当n=100时,这个数中总共有192个数字,其中数字0的个数为11,所以恰好取到0的概率为p(100)=.11192(2)F(n)={n , 1≤n ≤9,2n -9,10≤n ≤99,3n -108,100≤n ≤999,4n -1 107,1 000≤n ≤2 014.(3)当n=b(1≤b ≤9,b ∈N *)时,g(n)=0;当n=10k+b(1≤k ≤9,0≤b ≤9,k ∈N *,b ∈N )时,g(n)=k;当n=100时,g(n)=11,即g(n)={0, 1≤n ≤9,k ,n =10k +b,1≤k ≤9,0≤b ≤9,k ∈N *,b ∈N ,11,n =100.同理有f(n)=1≤k ≤8,0≤b ≤9,k ∈N *,b ∈N ,{0, 1≤n ≤8,k ,n =10k +b -1,n -80,89≤n ≤98,20,n =99,100.由h(n)=f(n)-g(n)=1,可知n=9,19,29,39,49,59,69,79,89,90.所以当n ≤100时,S={9,19,29,39,49,59,69,79,89,90}.当n=9时,p(9)=0;当n=90时,p(90)===;g (90)F (90)9171119当n=10k+9(1≤k ≤8,k ∈N *)时,p(n)===,由于y=关于k 单调递增,故当n=10k+9(1≤k ≤8,k ∈N *)时,p(n)的g (n )F (n )k2n -9k20k +9k20k +9最大值为p(89)=.8169又<,所以当n ∈S 时,p(n)的最大值为.8169119119考点二 直接证明与间接证明1.(2016浙江,20,15分)设函数f(x)=x 3+,x ∈[0,1].证明:11+x (1)f(x)≥1-x+x 2;(2)< f(x)≤.3432证明 (1)因为1-x+x 2-x 3==,1-(-x )41-(-x )1-x 41+x 由于x ∈[0,1],有≤,1-x41+x 1x +1即1-x+x 2-x 3≤,1x +1所以f(x)≥1-x+x 2.(2)由0≤x ≤1得x 3≤x,故f(x)=x 3+≤x+=x+-+=+≤,1x +11x +11x +13232(x -1)(2x +1)2(x +1)3232所以f(x)≤.32由(1)得f(x)≥1-x+x 2=+≥,(x -12)23434又因为f =>,(12)192434所以f(x)>.34综上,<f(x)≤.3432疑难突破 (1)将证明f(x)≥1-x+x 2转化为证明1-x+x 2-x 3≤成立,而左边==≤=右边,从而问题得1x +1(1-x +x 2-x 3)(1+x)1+x 1-x41+x 11+x 证.(2)运用放缩思想,由0≤x ≤1⇒x 3≤x,从而f(x)=x 3+≤x+,而x+=x+-+=+≤,由(1)及f =>1x +11x +11x +11x +13232(x -1)(2x +1)2(x +1)3232(12)192434得f(x)>,从而问题得证.342.(2016江苏,20,16分)记U={1,2,…,100}.对数列{a n }(n ∈N *)和U 的子集T,若T=⌀,定义S T =0;若T={t 1,t 2,…,t k },定义S T =a t 1++…+.例如:T={1,3,66}时,S T =a 1+a 3+a 66.现设{a n }(n ∈N *)是公比为3的等比数列,且当T={2,4}时,S T =30.a t 2a t k(1)求数列{a n }的通项公式;(2)对任意正整数k(1≤k ≤100),若T ⊆{1,2,…,k},求证:S T <a k+1;(3)设C ⊆U,D ⊆U,S C ≥S D ,求证:S C +S C ∩D ≥2S D .解析 (1)由已知得a n =a 1·3n-1,n ∈N *.于是当T={2,4}时,S T =a 2+a 4=3a 1+27a 1=30a 1.又S T =30,故30a 1=30,即a 1=1.所以数列{a n }的通项公式为a n =3n-1,n ∈N *.(2)因为T ⊆{1,2,…,k},a n =3n-1>0,n ∈N *,所以S T ≤a 1+a 2+…+a k =1+3+…+3k-1=(3k -1)<3k .12因此,S T <a k+1.(3)下面分三种情况证明.①若D 是C 的子集,则S C +S C ∩D =S C +S D ≥S D +S D =2S D .②若C 是D 的子集,则S C +S C ∩D =S C +S C =2S C ≥2S D .③若D 不是C 的子集,且C 不是D 的子集.令E=C ∩∁U D,F=D ∩∁U C,则E ≠⌀,F ≠⌀,E ∩F=⌀.于是S C =S E +S C ∩D ,S D =S F +S C ∩D ,进而由S C ≥S D 得S E ≥S F .设k 为E 中的最大数,l 为F 中的最大数,则k ≥1,l ≥1,k ≠l.由(2)知,S E <a k+1.于是3l-1=a l ≤S F ≤S E <a k+1=3k ,所以l-1<k,即l ≤k.又k ≠l,故l ≤k-1.从而S F ≤a 1+a 2+…+a l =1+3+…+3l-1=≤=≤,3l -123k -1-12a k -12S E -12故S E ≥2S F +1,所以S C -S C ∩D ≥2(S D -S C ∩D )+1,即S C +S C ∩D ≥2S D +1.综合①②③得,S C +S C ∩D ≥2S D .【三年模拟】时间:45分钟 分值:55分一、选择题(每小题5分,共35分)1.(2018广东六校第三次联考,10)自主招生联盟成形于2009年清华大学等五校联考,主要包括“北约”联盟,“华约”联盟,“卓越”联盟和“京派”联盟.调查某高中学校学生自主招生报考的情况,得到如下结果:①报考“北约”联盟的学生,都没报考“华约”联盟;②报考“华约”联盟的学生,也报考了“京派”联盟;③报考“卓越”联盟的学生,都没报考“京派”联盟;④不报考“卓越”联盟的学生,就报考“华约”联盟.根据上述调查结果,下列结论错误的是( )A.没有同时报考“华约”和“卓越”联盟的学生B.报考“华约”和“京派”联盟的考生一样多C.报考“北约”联盟的考生也报考了“卓越”联盟D.报考“京派”联盟的考生也报考了“北约”联盟答案 D 2.(2017山东青岛一模,4)中国有句名言“运筹帷幄之中,决胜千里之外”,其中的“筹”原意是指《孙子算经》中记载的算筹,古代是用算筹来进行计算的,算筹是将几寸长的小竹棍摆在平面上进行运算,算筹的摆放有纵横两种形式,如图,当表示一个多位数时,像阿拉伯计数一样,把各个数位的数码从左到右排列,但各位数码的筹式需要纵横相间,个位,百位,万位数用纵式表示,十位,千位,十万位用横式表示,以此类推.例如6 613用算筹表示就是,则8 335用算筹可表示为( )中国古代的算筹数码答案 B 3.(2017江西南昌调研,11)设等比数列{a n }的公比为q,其前n 项和为S n ,前n 项之积为T n ,并且满足条件:a 1>1,a 2 016a 2 017>1,<0,下列结论中正确的是( )a 2 016-1a 2 017-1A.q<0B.a 2 016a 2 018-1>0C.T 2 016是数列{T n }中的最大项D.S 2 016>S 2 017答案 C4.(2019届福建龙岩期中,6)如图,第n 行首尾两数均为n,图中的递推关系类似于杨辉三角,则第19行(n ≥2)第2个数是( )A.170B.172C.174D.176答案 B5.(2019届福建福州期中,6)某次数学考试成绩公布后,甲、乙、丙、丁四人谈论成绩的情况.甲说:“我们四个人的分数都不一样,但我和乙的成绩之和等于丙、丁两人的成绩之和.”乙说:“丙、丁两人中一人分数比我高,一人分数比我低.”丙说:“我的分数不是最高的.”丁说:“我的分数不是最低的.”则四人中成绩最高的是( )A.甲B.乙C.丙D.丁答案 D6.(2019届湖北孝感期中,5)因为余弦函数是偶函数,而f(x)=cos(x 2+1)是余弦函数,所以f(x)=cos(x 2+1)是偶函数,以上推理( )A.结论不正确B.大前提不正确C.小前提不正确D.全不正确答案 C7.(2019届北京朝阳期中,8)将正奇数数列1,3,5,7,9,…依次按两项、三项分组,得到分组序列如下:(1,3),(5,7,9),(11,13),(15,17,19),……,若称(1,3)为第1组,(5,7,9)为第2组,……,依此类推,则原数列中的2 019位于分组序列中的( )A.第404组 B.第405组C.第808组 D.第809组答案 A 二、填空题(每小题5分,共20分)8.(2018江西上饶第二次模拟,13)二维空间中,圆的一维测度(周长)l=2πr,二维测度(面积)S=πr 2;三维空间中,球的二维测度(表面积)S=4πr 2,三维测度(体积)V=πr 3.应用合情推理,若四维空间中,“特级球”的三维测度V=12πr 3,则其四维测度43W= . 答案 3πr 49.(2018河北衡水中学第十次模拟考试,16)观察下列各式:13=1;23=3+5;33=7+9+11;43=13+15+17+19;……若m 3(m ∈N *)按上述规律展开后,发现等式右边含有“2 017”这个数,则m 的值为 . 答案 4510.(2018河北衡水中学模拟,16)数列{a n }满足a n+1=已知a 7=2,{a n }的前7项和的最大值为S,把a 1的所有可{12a n ,a n 是正偶数,3a n +1,a n 是正奇数,能取值按从小到大排成一个新数列{b n },{b n }所有项的和为T,则S-T= . 答案 6411.(2018豫南九校第六次质量考评,15)已知函数f(x)=++,由f(x-1)=++是奇函数,可得函数f(x)的图象关于1x 1x +11x +21x -11x 1x +1点(-1,0)对称,类比这一结论,可得函数g(x)=++…+的图象关于点 对称. x +2x +1x +3x +2x +7x +6答案 (-72,6)。
2020版高考文科数学大一轮复习人教A版文档:第十二章 推理与证明、算法、复数12.3 Word版含答案.docx
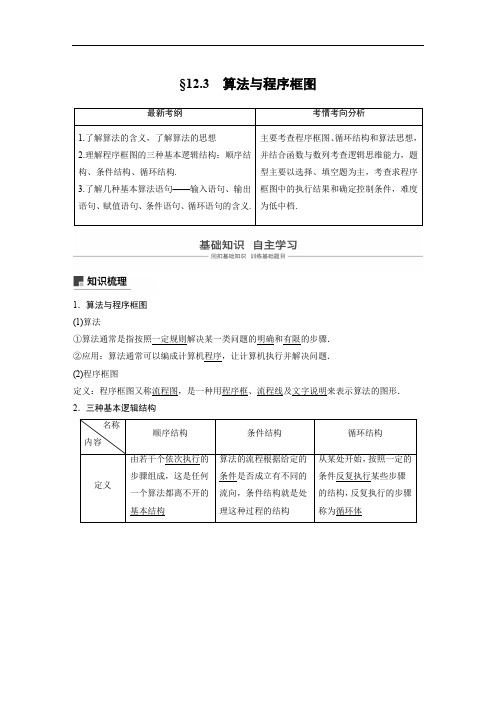
§12.3算法与程序框图1.算法与程序框图(1)算法①算法通常是指按照一定规则解决某一类问题的明确和有限的步骤.②应用:算法通常可以编成计算机程序,让计算机执行并解决问题.(2)程序框图定义:程序框图又称流程图,是一种用程序框、流程线及文字说明来表示算法的图形.2.三种基本逻辑结构3.算法语句(1)输入语句、输出语句、赋值语句的格式与功能(2)条件语句①程序框图中的条件结构与条件语句相对应.②条件语句的格式a.IF—THEN格式b.IF—THEN—ELSE格式(3)循环语句①程序框图中的循环结构与循环语句相对应.②循环语句的格式a .UNTIL 语句b .WHILE 语句题组一 思考辨析1.判断下列结论是否正确(请在括号中打“√”或“×”) (1)算法只能解决一个问题,不能重复使用.( × ) (2)程序框图中的图形符号可以由个人来确定.( × ) (3)输入框只能紧接开始框,输出框只能紧接结束框.( × )(4)条件结构的出口有两个,但在执行时,只有一个出口是有效的.( √ ) (5)5=x 是赋值语句.( × )(6)输入语句可以同时给多个变量赋值.( √ )题组二 教材改编2.[P30例8]执行如图所示的程序框图,则输出S 的值为( )A .-32 B.32 C .-12 D.12答案 D解析 按照程序框图依次循环运算,当k =5时,停止循环,当k =5时,S =sin5π6=12.3.[P25例5]如图为计算y=|x|函数值的程序框图,则此程序框图中的判断框内应填.答案x<0?解析输入x应判断x是否大于等于零,由图知判断框应填x<0?.题组三易错自纠4.(2016·全国Ⅱ)中国古代有计算多项式值的秦九韶算法,如图是实现该算法的程序框图,执行该程序框图,若输入的x=2,n=2,依次输入的a为2,2,5,则输出的s等于()A.7 B.12 C.17 D.34答案 C解析由框图可知,输入x=2,n=2,a=2,s=2,k=1,不满足条件;a=2,s=4+2=6,k=2,不满足条件;a=5,s=12+5=17,k=3,满足条件,输出s=17,故选C.5.执行如图所示的程序框图,若输出k的值为8,则判断框内可填入的条件是()A .s ≤34?B .s ≤56?C .s ≤1112?D .s ≤2524?答案 C解析 由s =0,k =0满足条件,则k =2,s =12,满足条件;k =4,s =12+14=34,满足条件;k =6,s =34+16=1112,满足条件;k =8,s =1112+18=2524,不满足条件,输出k =8,所以应填“s ≤1112?”.6.运行如图所示的程序框图,若输出的y 值的范围是[0,10],则输入的x 值的范围是 .答案 [-7,9]解析 该程序的功能是计算分段函数的值, y =⎩⎪⎨⎪⎧3-x ,x <-1,x 2,-1≤x ≤1,x +1,x >1.当x <-1时,由0≤3-x ≤10可得-7≤x <-1; 当-1≤x ≤1时,0≤x 2≤10恒成立; 当x >1时,由0≤x +1≤10可得1<x ≤9. 综上,输入的x 值的范围是[-7,9].题型一 算法的基本结构1.(2017·厦门质检)阅读如图所示的程序框图,运行相应的程序.若输入x 的值为1,则输出y 的值为( )A .2B .7C .8D .128 答案 C解析 由程序框图知,y =⎩⎪⎨⎪⎧2x ,x ≥2,9-x ,x <2.∵输入x 的值为1,比2小,∴执行的程序要实现的功能为9-1=8,故输出y 的值为8.2.(2017·全国Ⅲ)执行下面的程序框图,为使输出S 的值小于91,则输入的正整数N 的最小值为( )A .5B .4C .3D .2 答案 D解析 假设N =2,程序执行过程如下: t =1,M =100,S =0,1≤2,S =0+100=100,M =-10010=-10,t =2,2≤2,S =100-10=90,M =--1010=1,t =3,3>2,输出S =90<91.符合题意. ∴N =2成立.显然2是N 的最小值. 故选D.3.(2016·全国Ⅰ)执行下面的程序框图,如果输入的x =0,y =1,n =1,则输出x ,y 的值满足( )A .y =2xB .y =3xC .y =4xD .y =5x答案 C解析 执行题中的程序框图,知 第一次进入循环体:x =0+1-12=0,y =1×1=1, x 2+y 2<36;第二次执行循环体:n =1+1=2,x =0+2-12=12,y =2×1=2,x 2+y 2<36;第三次执行循环体:n =2+1=3,x =12+3-12=32,y =3×2=6,满足x 2+y 2≥36,故退出循环,输出x =32,y =6,满足y =4x ,故选C.思维升华 (1)高考对算法初步的考查主要是对程序框图含义的理解与运用,重点应放在读懂框图上,尤其是条件结构、循环结构.特别要注意条件结构的条件,对于循环结构要搞清进入或退出循环的条件、循环的次数,是解题的关键. (2)解决程序框图问题要注意几个常用变量:①计数变量:用来记录某个事件发生的次数,如i =i +1. ②累加变量:用来计算数据之和,如S =S +i . ③累乘变量:用来计算数据之积,如p =p ×i .题型二 程序框图的识别与完善命题点1 由程序框图求输出结果典例 (1)(2017·全国Ⅱ)执行如图所示的程序框图,如果输入的a =-1,则输出的S 等于( )A.2 B.3 C.4 D.5答案 B解析当K=1时,S=0+(-1)×1=-1,a=1,执行K=K+1后,K=2;当K=2时,S=-1+1×2=1,a=-1,执行K=K+1后,K=3;当K=3时,S=1+(-1)×3=-2,a=1,执行K=K+1后,K=4;当K=4时,S=-2+1×4=2,a=-1,执行K=K+1后,K=5;当K=5时,S=2+(-1)×5=-3,a=1,执行K=K+1后,K=6;当K=6时,S=-3+1×6=3,执行K=K+1后,K=7>6,输出S=3.结束循环.故选B.(2)(2017·山东)执行两次如图所示的程序框图,若第一次输入的x的值为7,第二次输入的x 的值为9,则第一次、第二次输出的a的值分别为()A.0,0 B.1,1 C.0,1 D.1,0答案 D解析当x=7时,∵b=2,∴b2=4<7=x.又7不能被2整除,∴b=2+1=3.此时b2=9>7=x,∴退出循环,a=1,∴输出a=1.当x=9时,∵b=2,∴b2=4<9=x.又9不能被2整除,∴b=2+1=3.此时b2=9=x,又9能被3整除,∴退出循环,a=0.∴输出a=0.故选D.命题点2完善程序框图典例(2017·全国Ⅰ)如图所示的程序框图是为了求出满足3n-2n>1 000的最小偶数n,那么在◇和▭两个空白框中,可以分别填入()A.A>1 000?和n=n+1B.A>1 000?和n=n+2C.A≤1 000?和n=n+1D.A≤1 000?和n=n+2答案 D解析因为题目要求的是“满足3n-2n>1 000的最小偶数n”,所以n的叠加值为2,所以▭内填入“n=n+2”.由程序框图知,当◇内的条件不满足时,输出n,所以◇内填入“A≤1 000?”.故选D.命题点3辨析程序框图的功能典例如果执行如图的程序框图,输入正整数N(N≥2)和实数a1,a2,…,a N,输出A,B,则()A .A +B 为a 1,a 2,…,a N 的和 B.A +B 2为a 1,a 2,…,a N 的算术平均数C .A 和B 分别是a 1,a 2,…,a N 中最大的数和最小的数D .A 和B 分别是a 1,a 2,…,a N 中最小的数和最大的数 答案 C解析 不妨令N =3,a 1<a 2<a 3, 则有k =1,x =a 1,A =a 1,B =a 1; k =2,x =a 2,A =a 2; k =3,x =a 3,A =a 3, 故输出A =a 3,B =a 1,故选C.思维升华 (1)已知程序框图,求输出的结果,可按程序框图的流程依次执行,最后得出结果. (2)完善程序框图问题,结合初始条件和输出结果,分析控制循环的变量应满足的条件或累加、累乘的变量的表达式.(3)对于辨析程序框图功能问题,可将程序执行几次,即可根据结果作出判断.跟踪训练 (2018·唐山模拟)根据下面的程序框图,对大于2的整数N ,输出的数列的通项公式是( )A .a n =2nB .a n =2(n -1)C .a n =2nD .a n =2n -1答案 C解析 由程序框图可知,第一次运行:i =1,a 1=2,S =2; 第二次运行:i =2,a 2=4,S =4; 第三次运行:i =3,a 3=8,S =8; 第四次运行:i =4,a 4=16,S =16. 故选C.题型三 基本算法语句典例 (2017·宜春模拟)如图是根据所输入的x 值计算y 值的一个算法程序,若x 依次取数列⎩⎨⎧⎭⎬⎫n 2+4n (n ∈N *)的项,则所得y 值的最小值为( )A .4B .9C .16D .20答案 C解析 由条件语句,知y =⎩⎪⎨⎪⎧x 2,x <5,5x ,x ≥5.又n 2+4n =n +4n ≥4(当且仅当n =2时等号成立),所以当x =4时,y 有最小值42=16.思维升华 解决算法语句有三个步骤:首先通读全部语句,把它翻译成数学问题;其次领悟该语句的功能;最后根据语句的功能运行程序,解决问题.跟踪训练 (2018·保定模拟)根据如图所示的语句,可知输出的结果S = .答案 7解析 I =1,S =1;S =1+2=3,I =1+3=4<8; S =3+2=5,I =4+3=7<8; S =5+2=7,I =7+3=10>8. 退出循环,故输出S =7.程序框图中变量的取值典例 执行如图所示的程序框图所表示的程序,则输出的A 等于( )A.2 047 B.2 049 C.1 023 D.1 025现场纠错解析本题计算的是递推数列a0=1,a n+1=2a n+1(n=0,1,2,…)的第11项,{a n+1}是首项为2,公比为2的等比数列,故a10+1=211,故a10=2 047.答案 A纠错心得程序框图对计数变量及求和变量取值时,要注意两个变量的先后顺序.1.(2016·全国Ⅲ)执行如图的程序框图,如果输入的a=4,b=6,那么输出的n等于()A.3 B.4 C.5 D.6答案 B解析第一次循环a=6-4=2,b=6-2=4,a=4+2=6,s=6,n=1;第二次循环a=4-6=-2,b=4-(-2)=6,a=6-2=4,s=10,n=2;第三次循环a=6-4=2,b=6-2=4,a=4+2=6,s=16,n=3;第四次循环a=4-6=-2,b=4-(-2)=6,a=6-2=4,s=20,n=4,满足题意,结束循环.2.(2016·四川)秦九韶是我国南宋时期的数学家,普州(现四川省安岳县)人,他在所著的《数书九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法.如图所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例,若输入n,x的值分别为3,2,则输出v 的值为()A.9 B.18 C.20 D.35答案 B解析初始值n=3,x=2,程序运行过程如下:v=1i=2v=1×2+2=4i=1v=4×2+1=9i=0v=9×2+0=18i=-1跳出循环,输出v=18,故选B.3.(2017·天津)阅读下面的程序框图,运行相应的程序,若输入N的值为24,则输出N的值为()A.0 B.1 C.2 D.3答案 C解析 第一次循环执行条件语句,此时N =24,24能被3整除,则N =24÷3=8. ∵8≤3不成立,∴进入第二次循环执行条件语句,此时N =8,8不能被3整除,则N =8-1=7. ∵7≤3不成立,∴进入第三次循环执行条件语句,此时N =7,7不能被3整除,则N =7-1=6. ∵6≤3不成立,∴进入第四次循环执行条件语句,此时N =6,6能被3整除,则N =6÷3=2. ∵2≤3成立,∴此时输出N =2. 故选C.4.(2017·北京)执行如图所示的程序框图,输出的s 值为( )A .2 B.32 C.53 D.85答案 C解析 开始:k =0,s =1; 第一次循环:k =1,s =2; 第二次循环:k =2,s =32;第三次循环:k =3,s =53,此时不满足循环条件,输出s ,故输出的s 值为53.故选C.5.(2018·南宁质检)已知实数x ∈{1,2,3,4,5,6,7,8},执行如图所示的程序框图,则输出的x 不小于121的概率为( )A.34B.58C.78D.12 答案 B解析 由题意可知,当输入x =1时,进入循环体,输出x =40;当输入x =2时,进入循环体,输出x =67;当输入x =3时,进入循环体,输出x =94;当输入x ≥4时,输出的x 均不小于121,因此输出的x 不小于121的概率为58.6.(2018·佛山模拟)如图,若依次输入的x 分别为5π6,π6,相应输出的y 分别为y 1,y 2,则y 1,y 2的大小关系是( )A .y 1=y 2B .y 1>y 2C .y 1<y 2D .无法确定答案 C解析 由程序框图可知,当输入的x 为5π6时,sin 5π6>cos 5π6成立,所以输出的y 1=sin 5π6=12; 当输入的x 为π6时,sin π6>cos π6不成立,所以输出的y 2=cos π6=32,所以y 1<y 2.7.阅读程序框图,运行相应的程序,则程序运行后输出的结果为( )A .7B .9C .10D .11 答案 B解析 i =1,S =0,第一次循环:S =0+lg 13=-lg 3>-1;第二次循环:i =3,S =lg 13+lg 35=lg 15=-lg 5>-1;第三次循环:i =5,S =lg 15+lg 57=lg 17=-lg 7>-1;第四次循环:i =7,S =lg 17+lg 79=lg 19=-lg 9>-1;第五次循环:i =9,S =lg 19+lg 911=lg 111=-lg 11<-1.故输出i =9.8.公元263年左右,我国数学家刘徽发现当圆内接正多边形的边数无限增加时,多边形面积可无限逼近圆的面积,并创立了“割圆术”,利用“割圆术”刘徽得到了圆周率精确到小数点后两位的近似值3.14,这就是著名的“徽率”.如图是利用刘徽的“割圆术”思想设计的一个程序框图,则输出n 的值为 .(参考数据:sin 15°≈0.258 8,sin 7.5°≈0.130 5)答案 24解析 n =6,S =12×6×sin 60°=332≈2.598<3.1,不满足条件,进入循环;n =12,S =12×12×sin 30°=3<3.1,不满足条件,继续循环;n =24,S =12×24×sin 15°≈12×0.258 8=3.105 6>3.1,满足条件,退出循环,输出n 的值为24.9.(2017·江苏)如图是一个程序框图,若输入x 的值为116,则输出y 的值是 .答案 -2解析 输入x =116,116≥1不成立,执行y =2+log 2116=2-4=-2.故输出y 的值为-2.10.(2017·安徽江南名校联考)某程序框图如图所示,判断框内为“k ≥n ?”,n 为正整数,若输出的S =26,则判断框内的n = .答案 4解析 依题意,执行题中的程序框图,进行第一次循环时,k =1+1=2,S =2×1+2=4;进行第二次循环时,k =2+1=3,S =2×4+3=11;进行第三次循环时,k =3+1=4,S =2×11+4=26.因此当输出的S =26时,判断框内的条件n =4.11.如图所示的程序框图,若输入的x 的值为1,则输出的n 的值为 .答案 3解析 由x 2-4x +3≤0,解得1≤x ≤3.当x =1时,满足1≤x ≤3,所以x =1+1=2,n =0+1=1; 当x =2时,满足1≤x ≤3,所以x =2+1=3,n =1+1=2; 当x =3时,满足1≤x ≤3,所以x =3+1=4,n =2+1=3; 当x =4时,不满足1≤x ≤3,所以输出n =3.12.(2017·西安模拟)执行如图所示的程序框图,如果输出S =3,那么判断框内应填入的条件是 .答案 k ≤7?解析 首次进入循环体,S =1×log 23,k =3;第二次进入循环体,S =lg 3lg 2×lg 4lg 3=2,k =4;依次循环,第六次进入循环体,S =3,k =8, 此时结束循环,则判断框内填k ≤7?.13.(2018·泉州模拟)下面程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图,若输入的a ,b 分别为14,18,则输出的a 等于( )A .0B .2C .4D .14 答案 B解析 由题知,若输入a =14,b =18,则 第一次执行循环结构时,由a <b 知,a =14,b =b -a =18-14=4; 第二次执行循环结构时,由a >b 知, a =a -b =14-4=10,b =4; 第三次执行循环结构时,由a >b 知, a =a -b =10-4=6,b =4; 第四次执行循环结构时,由a >b 知, a =a -b =6-4=2,b =4;第五次执行循环结构时,由a <b 知, a =2,b =b -a =4-2=2;第六次执行循环结构时,由a =b 知,输出a =2,结束. 故选B.14.阅读下面的程序,当分别输入实数x =3和x =0时,其输出的结果是 .答案3-2和0解析 由程序可知,它解决的是求分段函数y =⎩⎪⎨⎪⎧x -2,x >1,2x ,x ≤1的函数值问题,显然,当x =3时,y =3-2;当x =0时,y =0.故输出的结果是3-2和0.15.(2016·山东)执行如图所示的程序框图,若输入的a ,b 的值分别为0和9,则输出的i 的值为 .答案 3解析 第1次循环:i =1,a =1,b =8,a <b ;第2次循环:i =2,a =3,b =6,a <b ;第3次循环:i =3,a =6,b =3,a >b ,输出i 的值为3.16.设a 是一个各位数字都不是0且没有重复数字的三位数.将组成a 的3个数字按从小到大排成的三位数记为I (a ),按从大到小排成的三位数记为D (a )(例如a =815,则I (a )=158,D (a )=851).阅读如图所示的程序框图,运行相应的程序,任意输入一个a ,输出的结果b = .答案 495解析 取a 1=815,则b 1=851-158=693≠815,则a 2=693;由a 2=693知b 2=963-369=594≠693,则a 3=594;由a 3=594知b 3=954-459=495≠594,则a 4=495;由a 4=495知b 4=954-459=495=a 4,则输出b =495.17.(2018·太原模拟)关于函数f (x )=⎩⎪⎨⎪⎧-x ,1<x ≤4,cos x ,-1≤x ≤1的程序框图如图所示,现输入区间[a ,b ],则输出的区间是 .答案 [0,1]解析 由程序框图的第一个判断条件为f (x )>0,当f (x )=cos x ,x ∈[-1,1]时满足.然后进入第二个判断框,需要解不等式f ′(x )=-sin x ≤0,即0≤x ≤1.故输出区间为[0,1].18.执行如图所示的程序框图,如果输入的x ,y ∈R ,那么输出的S 的最大值为 .答案 2解析 当条件x ≥0,y ≥0,x +y ≤1不成立时输出S 的值为1;当条件x ≥0,y ≥0,x +y ≤1成立时S =2x +y ,下面用线性规划的方法求此时S 的最大值.作出不等式组⎩⎪⎨⎪⎧ x ≥0,y ≥0,x +y ≤1表示的平面区域如图中阴影部分(含边界),由图可知当直线S =2x +y 经过点M (1,0)时S 最大,其最大值为2×1+0=2,故输出S 的最大值为2.19.(2018·沈阳质检)以下给出了一个程序,根据该程序回答:(1)若输入4,则输出的结果是 ;(2)该程序的功能所表达的函数解析式为 .答案 (1)15 (2)y =⎩⎪⎨⎪⎧ 2x ,x <3,2,x =3,x 2-1,x >3解析 (1)x =4不满足x <3,∴y =x 2-1=42-1=15.输出15.(2)当x <3时,y =2x ,当x >3时,y =x 2-1;否则,即x =3,y =2.∴y =⎩⎪⎨⎪⎧ 2x ,x <3,2,x =3,x 2-1,x >3.20.(2018·长沙模拟)已知函数f (x )=ax 3+12x 2在x =-1处取得极大值,记g (x )=1f ′(x ).程序框图如图所示,若输出的结果S >2 0172 018,则判断框中可以填入的关于n 的判断条件是 .(填序号)①n ≤2 017?②n ≤2 018? ③n >2 017?④n >2 018?答案 ②解析 由题意得f ′(x )=3ax 2+x ,由f ′(-1)=0,得a =13,∴f ′(x )=x 2+x , 即g (x )=1x 2+x =1x (x +1)=1x -1x +1. 由程序框图可知S =0+g (1)+g (2)+…+g (n )=0+1-12+12-13+…+1n -1n +1=1-1n +1, 由1-1n +1>2 0172 018,得n >2 017. 故可填入②.。
2020年高考数学《新高考创新题型》之11:推理与证明(含精析)

2020年高考数学(新高考创新题型)之11.推理与证明(含精析)一、选择题。
1.下列推理中属于归纳推理且结论正确的是( )A .由a n =2n ﹣1,求出S 1=12,S 2=22,S 3=32,…,推断:数列{a n }的前n 项和S n =n 2B .由f (x )=xcosx 满足f (﹣x )=﹣f (x )对R x ∈∀都成立,推断:f (x )=xcosx 为奇函数C .由圆x 2+y 2=r 2的面积S=πr 2,推断:椭圆=1的面积S=πabD .由3222122)13(,2)12(,2)11(>+>+>+,…,推断:对一切*N n ∈,(n+1)2>2n2.已知111()123f n n=++++(n N *∈),计算得3(2)2f =,(4)2f >,5(8)2f >,(16)3f >,7(32)2f >,由此推算:当2n ≥时,有( )A.21(2)2n f n +>(n N *∈)B.2(1)1(2)2n f n +->(n N *∈)C.21(2)2n n f +>(n N *∈)D.2(2)2n n f +>(n N *∈)3.将2n 个正整数1、2、3、 、2n (2n ≥)任意排成n 行n 列的数表.对于某一个数表,计算各行和各列中的任意两个数a 、b (a b >)的比值ab,称这些比值中的最小值为这个数表的“特征值”.当2n =时,数表的所有可能的“特征值”最大值为( ) A .3 B .2 C .43D .324.六个面都是平行四边形的四棱柱称为平行六面体。
如,在平行四边形ABCD 中,有)(22222AD AB BD AC +=+,那么在图(2)的平行六面体1111D C B A ABCD -中有21212121DB CA BD AC +++等于( )A .22212()AB AD AA ++ B .22213()AB AD AA ++C .22214()AB AD AA ++ D .223()AB AD +5.对于任意正整数n ,定义“!!n ”如下: 当n 是偶数时,!!(2)(4)642n n n n =⋅-⋅-⋅⋅⋅⋅,当n 是奇数时,!!(2)(4)531n n n n =⋅-⋅-⋅⋅⋅⋅现在有如下四个命题:①(2003!!)(2002!!)20032002321⋅=⨯⨯⨯⨯⨯;②10012002!!210011000321=⨯⨯⨯⨯⨯⨯;③2002!!的个位数是0 ④2003!!的个位数是5。
2020年高考试题:推理证明

2020 年高考试题:推理证明(2020北京21)已知{}n a 是无穷数列.给出两个性质:①对于{}n a 中任意两项,()i j a a i j >,在{}n a 中都存在一项m a ,使2i m ja a a =; ②对于{}n a 中任意项(3)n a n ,在{}n a 中都存在两项,()k l a a k l >.使得2kn la a a =.(Ⅰ)若(1,2,)n a n n ==,判断数列{}n a 是否满足性质①,说明理由;(Ⅱ)若12(1,2,)n n a n -==,判断数列{}n a 是否同时满足性质①和性质②,说明理由;(Ⅲ)若{}n a 是递增数列,且同时满足性质①和性质②,证明:{}n a 为等比数列. 【解析】(Ⅰ){}2323292,3,2n a a a a Z a ===∉∴不具有性质①;(Ⅱ){}22*(2)1*2,,,2,2i j i i i j n j ja a i j N i j i j N a a a a ---∀∈>=-∈∴=∴具有性质①;{}2*(2)11,3,1,2,22,k l n k n n la n N n k n l a n a a ---∀∈≥∃=-=-===∴具有性质②;(Ⅲ)【解法一】首先,证明数列中的项数同号,不妨设恒为正数:显然()0*n a n N ≠∉,假设数列中存在负项,设{}0max |0n N n a =<, 第一种情况:若01N =,即01230a a a a <<<<<,由①可知:存在1m ,满足12210m a a a =<,存在2m ,满足22310m a a a =<,由01N =可知223211a a a a =,从而23a a =,与数列的单调性矛盾,假设不成立.第二种情况:若02N ≥,由①知存在实数m ,满足0210Nm a a a =<,由0N 的定义可知:0m N ≤,另一方面,000221NNm N N a a a a a a =>=,由数列单调性可知:0m N >,这与0N 的定义矛盾,假设不成立. 同理可证得数列中的项数恒为负数. 综上可得,数列中的项数同号.其次,证明2231a a a =:利用性质②:取3n =,此时()23kla a k l a =>,由数列的单调性可知0k l a a >>, 而3kk k la a a a a =⋅>,故3k <, 此时必有2,1k l ==,即2231a a a =,最后,用数学归纳法证明数列为等比数列:假设数列{}n a 的前()3k k ≥项成等比数列,不妨设()111s s a a q s k -=≤≤,其中10,1a q >>,(10,01a q <<<情况类似)由①可得:存在整数m ,满足211k km k k a a a q a a -==>,且11k m k a a q a +=≥ (*)由②得:存在s t >,满足:21s s k s s t ta aa a a a a +==⋅>,由数列的单调性可知:1t s k <≤+,由()111s s a a qs k -=≤≤可得:2211111s t k s k k ta a a q a a q a ---+==>= (**)由(**)和(*)式可得:211111k s t k a q a q a q ---≥>, 结合数列的单调性有:211k s t k ≥-->-, 注意到,,s t k 均为整数,故21k s t =--, 代入(**)式,从而11kk a a q +=.总上可得,数列{}n a 的通项公式为:11n n a a q -=. 即数列{}n a 为等比数列.的【解法二】假设数列中的项数均为正数:首先利用性质②:取3n =,此时()23kla a k l a =>,由数列的单调性可知0k l a a >>, 而3kk k la a a a a =⋅>,故3k <, 此时必有2,1k l ==,即2231a a a =,即123,,a a a 成等比数列,不妨设()22131,1a a q a a qq ==>,然后利用性质①:取3,2i j ==,则224331121m a a q a a q a a q===,即数列中必然存在一项的值为31a q ,下面我们来证明341a a q =, 否则,由数列的单调性可知341a a q <,在性质②中,取4n =,则24k k k k l l a aa a a a a ==>,从而4k <,与前面类似的可知则存在{}{}(),1,2,3k l k l ⊆>,满足24kl a a a =,若3,2k l ==,则:2341kla a a q a ==,与假设矛盾;若3,1k l ==,则:243411kla a a q a q a ==>,与假设矛盾;若2,1k l ==,则:22413kla a a q a a ===,与数列的单调性矛盾;即不存在满足题意的正整数,k l ,可见341a a q <不成立,从而341a a q =, 同理可得:455161,,a a q a a q ==,从而数列{}n a 为等比数列,同理,当数列中的项数均为负数时亦可证得数列为等比数列.由推理过程易知数列中的项要么恒正要么恒负,不会同时出现正数和负数.从而题中的结论得证,数列{}n a为等比数列.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
常考题型大通关:第11题 推理与证明
1、现有甲、乙、丙、丁四人参加数学竞赛,其中只有一位获奖. 有人走访了四人,甲说:“乙、丁都未获奖”,乙说:“是甲或丙获奖”,丙说:“是甲获奖”,丁说:“是乙获奖”,四人所说话中只有一位是真话,则获奖的人是( ) A .甲
B .乙
C .丙
D .丁
2、要证: 2
2
22
10a b a b +--≤,只要证明( ) A.22
20ab a b -≥ B.2
2
(1)(1)0a b --≥
C.
2
22()102a b a b +--≥ D.44
2
2
102
a b a b ++--≤ 3、用数学归纳法证明()()()()()
*1221321N n n n n n n n +++=⨯⨯⨯⨯+∈L L 时,从n k =到
1n k =+,等式左边增乘的代数式为( ).
A .2(21)k +
B .21k +
C .
21
1
k k ++ D .
23
1
k k ++ 4、用数学归纳法证明42
2
1232
n n n +++++=L ,则当1n k =+时,左端应在n k =的基础上加
上( ) A.21k +
B.2(1)k +
C.2
2
2
(1)(2)(1)k k k ++++++L
D.42(1)(1)2
k k +++
5、用数学归纳法证明()2
2
2
2
2
2
2
21211(21)
(1)()3
2n n n n n ++++++=--+时,由n k =时的假
设到证明1n k =+时,等式左边应添加的式子是( )
A.22(1)2k k ++
B. 22(1)k k ++
C. 2(1)k +
D.
21
(1)[2(1)1]3
k k +++ 6、用数学归纳法证明“52n n
-能被3整除”的第二步中,当1n k =+时,为了使用假设,应
将1
15
2k k ++-变形为( )
A .(52)452k k k k
-+⨯-
B .5(52)32k k k
-+⨯
C .(52)(52)k k
--
D .2(52)35k k k
--⨯
7、用数学归纳法证明63
3
123...,N 2
n n n n *+++++=∈,则当1n k =+时应当在n k =时对应的
等式的左边加上( ) A.31k + B.()
()333(1)2...1k k k ++++++ C.()31k +
D.54
8、用数学归纳法证明:2121n n x y --+(N n *∈)能被x y +整除.从假设n k =成立到1n k =+成立时,被整除式应为( ) A.2323k k x y +++
B.2222k k x y +++
C.2121k k x y +++
D.22k k x y +
9、用反证法证明命题:",,R,0,0,0,a b c a b c ab bc ca abc ∈++>++>>则0,0,0a b c >>>"时应假设为( ) A.a ,b ,c 均不为正数 B.a ,b ,c 至少有一个正数 C.a ,b ,c 不全为正数
D.a ,b ,c 至多有一个正数
10、用反证法证明命题“三角形三个内角至少有一个不大于60︒”时,应假设( ) A. 三个内角都不大于60︒ B. 三个内角都大于60︒
C. 三个内角至多有一个大于60︒
D. 三个内角至多有两个大于60︒
11、用反证法证明命题“已知*,N a b ∈,如果ab 可被5整除,那么,a b 中至少有一个能被5整除”时,假设的内容应为( ) A.,a b 都能被5整除
B.,a b 都不能被5整除
C.,a b 不都能被5整除 D .a 不能被5整除
12、用反证法证明命题“三角形的内角至多有一个钝角”时,假设的内容应为( ) A.假设至少有一个钝角 B.假设至少有两个钝角
C.假设没有一个钝角
D.假设没有一个钝角或至少有两个钝角 13、用反证法证明命题 “自然数a b c 、、中恰有一个偶数”时,需假设原命题不成立,下列假设正确的是( )
A .a b c 、、都是奇数
B .a b c 、、都是偶数
C .a b c 、、中或都是奇数或至少有两个偶数
D .a b c 、、中至少有两个偶数
14、用反证法证明命题“三角形的内角中至多有一个钝角”时,反设正确的是( ) A.三个内角中至少有一个钝角 B.三个内角中至少有两个钝角 C.三个内角都不是钝角
D.三个内角都不是钝角或至少有两个钝角
15、用反证法证明“R,20x
x ∀∈>”,应假设为( )
A. 0R,20x
x ∀∈≤ B. 00R,20x x ∃∈≤ C. 00R,20x x ∀∈< D.
00R,20x x ∃∈>
答案以及解析
1答案及解析: 答案:B
解析:若甲是获奖的,则三句说假话,不合题意。
若丙是获奖的,则丁、乙、丙都说真话,甲 说假话,不符合题意。
若丁是获奖的,则都说假话,不符合题意。
故答案为:乙
2答案及解析: 答案:B
解析:要证:2222
10a b a b +--≤,只要证明2
2
(1)(1)0a b --≤,
只要证明22(1)(1)0a b --≥. 故选:B
3答案及解析: 答案:A 解析:
4答案及解析: 答案:C
解析:当n k =时,等式左端212k =+++L ,
当1n k =+时,等式左端22221212(1)k k k k =++++++++++L L ,增加了项2222(1)(2)(3)(1)k k k k ++++++++L .
故选:C .
5答案及解析:
答案:B 解析:
6答案及解析: 答案:B
解析:115255225(52)52225(52)32k k k k k k k k k k k ++-=⋅-⋅=-+⨯-⨯=-+⨯
7答案及解析:
答案:B
解析:
8答案及解析:
答案:C
解析:
9答案及解析:
答案:C
解析:用反证法证明某命题时,应先假设命题的否定成立,而000
,,的否定为
>>>
a b c
a,b,c不全为正数,故选C
10答案及解析:
答案:A
解析:
11答案及解析:
答案:B
解析:
12答案及解析:
答案:B
解析:试题分析:反证明法的证明步骤:1.假设命题不成立
2.由假设出发,经过推理论证,得出矛盾
3.由矛盾得出假设不成立,从而证明原命题正确
本题中至多有一个钝角的反面是至少有两个是钝角。
13答案及解析:
答案:C
解析:
14答案及解析:
答案:B
解析:
15答案及解析:答案:B
解析:。
