动点问题中的平行四边形

合集下载

初二数学经典动点问题

初二数学经典动点问题1、在直角梯形ABCD中，AD∥BC，∠B=90°，AD=24cm，AB=8cm，BC=26cm。

动点P从A开始沿AD边向D以1cm/s的速度运动，动点Q从点C开始沿CB边向B 以3cm/s的速度运动。

P、Q分别从点A、C同时出发，当其中一点到达端点时，另外一点也随之停止运动，设运动时间为t秒。

1）当t为何值时，四边形PQCD为平行四边形？2）当t为何值时，四边形PQCD为等腰梯形？3）当t为何值时，四边形PQCD为直角梯形？2、在△ABC中，点O为AC边上的一个动点，过点O作直线MN∥BC，设MN交∠BCA的外角平分线CF于点F，交∠ACB内角平分线CE于点E。

1）试说明EO=FO；2）当点O运动到何处时，四边形AECF是矩形并证明你的结论；3）若AC边上存在点O，使四边形AECF是正方形，猜想△XXX的形状并证明你的结论。

3、在梯形ABCD中，AD∥BC，∠B=90°，AB=14cm，AD=15cm，BC=21cm。

点M从点A开始，沿边AD向点D运动，速度为1cm/s；点N从点C开始，沿边CB向点B运动，速度为2cm/s。

点M、N分别从点A、C出发，当其中一点到达端点时，另一点也随之停止运动，设运动时间为t秒。

1）当t为何值时，四边形MNCD是平行四边形？2）当t为何值时，四边形MNCD是等腰梯形？4、在矩形ABCD中，BC=20cm，P，Q，M，N分别从A，B，C，D出发沿AD，BC，CB，DA方向在矩形的边上同时运动。

当有一个点先到达所在运动边的另一个端点时，运动即停止。

已知在相同时间内，若BQ=xcm（x≠0），则AP=2xcm，CM=3xcm，DN=x/2 cm。

1）当x为何值时，以PQ，MN为两边，以矩形的边（AD或BC）的一部分为第三边构成一个三角形；2）当x为何值时，以P，Q，M，N为顶点的四边形是平行四边形；3）以P，Q，M，N为顶点的四边形能否为等腰梯形？如果能，求x的值；如果不能，请说明理由。

动点问题（四边形动点专题）

动态几何问题--------动点问题（四边形动点专题）【动态几何问题的特点】动态几何是以几何知识和几何图形为背景，渗透运动变化观点的一类试题；用运动的观点研究几何图形中图形的位置、角与角、线段与线段之间的位置及大小关系。

几何图形按一定的条件进行运动，有的几何量是随之而有规律地变化的，形成了轨迹和极值；而有的量是始终保持不变，也就是我们常说的定值。

动态几何就是研究在几何图形的运动中，伴随着出现一定的图形位置、数量关系的 “变”与“不变”性；动态几何问题常常集几何、代数知识于一体，数形结合，有较强的综合性，题目灵活、多变，动中有静，动静结合，能够在运动变化中发展空间想象能力，综合分析能力，是近几年中命题的热点。

【动态几何问题的解决方法】解决动态几何题，通过观察，对几何图形运动变化规律的探索，发现其中的“变量”和“定量”。

动中求静，即在运动变化中探索问题中的不变性；动静互化，抓住“静”的瞬间，使一般情形转化为特殊问题，从而找到“动与静”的关系；这需要有极敏锐的观察力和多种情况的分析能力，加以想象、结合推理，得出结论。

解决这类问题，要善于探索图形的运动特点和规律，抓住变化中图形的性质与特征，化动为静，以静制动。

解决运动型试题需要用运动与变化的眼光去观察和研究图形，把握图形运动与变化的全过程，抓住其中的等量关系和变量关系，并特别关注一些不变量和不变关系或特殊关系.【动态几何问题的分类】动态几何问题是以几何图形为背景的，几何图形有直线型和曲线型两种，那么动态几何也有直线型的和曲线型的两类，即全等三角形、相似三角形中的动态几何问题，也有圆中的动态问题。

有点动、线动、面动，就其运动形式而言，有平移、旋转、翻折、滚动等。

根据其运动的特点，又可分为：（1）动点类（点在线段或弧线上运动）也包括一个动点或两个动点；（2）动直线类；（3）动图形问题。

【典型例题】例1.如图，在梯形中，ABCD 动点从点出发沿线段3545AD BC AD DC AB B ====︒∥，，，，∠．M B 以每秒2个单位长度的速度向终点运动；动点同时从点出发沿线段BC C N C 以每秒1个单位长度的速度向终点运动．设运动的时间为秒．CD D t （1）求的长；BC （2）当时，求的值；MN AB ∥t （3）试探究：为何值时，t MNC △CB例2. 已知：等边三角形的边长为4厘米，长为1厘米的线段在ABC MN 的边上沿方向以1厘米/秒的速度向点运动（运动开始时，点ABC △AB AB B 与点重合，点到达点时运动终止），过点分别作边的垂线，M A N B M N 、AB 与的其它边交于两点，线段运动的时间为秒．ABC △P Q 、MN t （1）线段在运动的过程中，为何值时，四边形恰为矩形？并求出MN t MNQP 该矩形的面积；（2）线段在运动的过程中，四边形的面积为，运动的时间MN MNQP S 为．求四边形的面积随运动时间变化的函数关系式，并写出自变量t MNQP S t 的取值范围．t 例3.如图，在等腰梯形中，∥，,AB =12 ABCD AB DC cm BC AD 5==cm,CD =6cm , 点从开始沿边向以每秒3cm 的速度移动，点从开P A AB B Q C 始沿CD 边向D 以每秒1cm 的速度移动，如果点P 、Q 分别从A 、C 同时出发，当其中一点到达终点时运动停止。

中考数学动点问题归纳总结5.因动点产生的平行四边形问题

5.因动点产生的平行四边形问题1.如图，抛物线214y x bx c =++与x 轴交于()5,0A 、()1,0B -两点，过点A 作直线AC x ⊥轴，交直线2y x =于点C ．（1）求该抛物线的解析式；（2）求点A 关于直线2yx =的对称点A '的坐标，判定点A '是否在该抛物线上，并说明理由；（3）点P 是抛物线上一动点，过点P 作y 轴的平行线，交线段CA '于点M ，是否存在这样的点P ，使四边形PACM 是平行四边形？若存在，求出点P 的坐标；若不存在，请说明理由．解析：（1）∵抛物线214y x bx c =++与x 轴交于()5,0A 、()1,0B -两点 ∴25504104b c b c ⎧++=⎪⎪⎨⎪-+=⎪⎩解得154b c =-⎧⎪⎨=-⎪⎩ ∴抛物线的解析式为21544yx x =-- （2）过点A '作A E x '⊥轴于E ，AA '与OC 交于点D∵点C 在直线2y x =上，()5,10C ∴∵点A 和A '关于直线2yx =对称，OC AA '∴⊥，A D AD '= 5,10,OA AC ==OC ∴===1122OAC S OA AC OC AD ∆=⋅=⋅，AD AA '∴=∴=在Rt A EA '∆和Rt OAC ∆中90A AE A AC ''∠+∠=︒，90ACD A AC '∠+∠=︒A AE ACD '∴∠=∠又90A EA OAC '∠=∠=︒，A EA OAC '∆∆∽A E AE AA OA AC OC''∴==，即510A E AE '==4,8,3A E AE OE AE OA '∴===-=∴点A '的坐标为()3,4-当3x =-时，()21533444y =⨯-+-=∴点A '在该抛物线上（3）存在理由：设直线CA '的解析式为y kx b =+则51034k b k b +=⎧⎨-+=⎩解得34254k b ⎧=⎪⎪⎨⎪=⎪⎩ ∴直线CA '的解析式为32544y x =+ 设215,44P x x x ⎛⎫-- ⎪⎝⎭，则325,44M x x ⎛⎫+ ⎪⎝⎭ PM AC ∥∴要使四边形PACM 是平行四边形，只需PMAC = 又点M 在点P 的上方，232515104444x x x ⎛⎫∴+---= ⎪⎝⎭ 解得122,5x x ==（不合题意，舍去）当2x =时，94y =-∴当点P 运动到92,4⎛⎫- ⎪⎝⎭时，四边形PACM 是平行四边形 2.如图，抛物线()20y ax bx c a =++≠与y 轴交于点()0,4C ，与x 轴交于点A 和点B ，其中点A 的坐标为()2,0-，抛物线的对称轴1x =与抛物线交于点D ，与直线BC 交于点E ．（1）求抛物线的解析式；（2）在直线BC 上方的抛物线上是否存在点F ，使四边形ABFC 的面积为17，若存在，求出点F 的坐标；若不存在，请说明理由；（3）平行于DE 的动直线l 与直线BC 相交于点P ，与抛物线相交于点Q ，若以D 、E 、P 、Q 为顶点的四边形是平行四边形，求点P 的坐标．解析：（1）由抛物线经过点()0,4C可得4c = ① ∵对称轴1,22b x b a a =-=∴=- ② 又抛物线过点()2,0A -，042a b c ∴=-+③ 由①②③解得：1,1,42a b c =-== ∴抛物线的解析式为2142yx x =-++ （2）假设存在满足条件的点F ，连接BC 、CF 、OF ，作FHx ⊥轴于H ，FG y ⊥轴于G设点F 的坐标为21,42t t t ⎛⎫-++ ⎪⎝⎭，其中04t << 则2142FH t t =-++，FG t =221114428222OBF S OB FH t t t t ∆⎛⎫∴=⋅=⨯⨯-++=-++ ⎪⎝⎭ 114222OCF S OC FG t t ∆=⋅=⨯⨯= 224282412AOC OBF OFC ABFC S S S S t t t t t ∆∆∆∴=++=-+++=-++四边形令241217t t -++=，即2450t t -+=则()244540∆=--⨯=-<，方程无解故不存在满足条件的点F（3）设直线BC 的解析式为()0y kx bk =+≠，又过点()4,0B ，()0,4C044k b b =+⎧∴⎨=⎩解得14k b =-⎧⎨=⎩ ∴直线BC 的解析式为4yx =-+ 由()2211941222y x x x =-++=--+，得91,2D ⎛⎫ ⎪⎝⎭又点E 在直线BC 上，则点()1,3E于是93322DE =-= 由于DE PQ ∥，若以D 、E 、P 、Q 为顶点的四边形是平行四边形，只需DE PQ =设点(),4P m m -+，则21,42Q m m m ⎛⎫-++ ⎪⎝⎭①当04m <<时，()221144222PQ m m m m m =-++--+=-+ 由213222m m -+=，解得1m =或3m = 当1m =时，线段PQ 与DE 重合，1m =舍去3m ∴=，此时()13,1P②当0m <或4m >时，221144222PQ m m m m m ⎛⎫=-+--++=- ⎪⎝⎭由213222m m -=，解得2m =±此时，((232,2P P +--+综上所述，满足条件的点P 有三个，分别是()13,1P ，((232,2P P +--+. 3.如图，抛物线222y x x m=-与x 轴负半轴交于点A ，顶点为B ，且对称轴与x 轴交于点C ．（1）求点B 的坐标（用含m 的代数式表示）；（2）D 为BO 中点，直线AD 交y 轴于E ，若点E 的坐标为()0,2，求抛物线的解析式；（3）在（2）的条件下，点M 在直线BO 上，且使得AMC ∆的周长最小，P 在抛物线上，Q 在直线BC 上，若以A 、M 、P 、Q 为顶点的四边形是平行四边形，求点P 的坐标．解析：（1）222211222y x x x m m m m ⎛⎫=-=-- ⎪⎝⎭ ∴抛物线的顶点B 的坐标为11,22m m ⎛⎫- ⎪⎝⎭ （2）令2220x x m-=，解得10x =，2x m = ∵抛物线222y x x m=-与x 轴负半轴交于点A (),0A m ∴且0m <.过点D 作DF x ⊥轴于F由D 为BO 中点，DF BC ∥，可得12CF FO CO == 12DF BC ∴= 由抛物线的对称性得3,4AF AC OC AO =∴=DF EO ∥，ADF AEO ∴∆∆∽，DF AF EO AO∴= 由()0,2E ，11,22B m m ⎛⎫- ⎪⎝⎭，得12,4OE DF m ==- 13424m -∴=，6m ∴=- ∴抛物线的解析式为2123yx x =-- （3）依题意，得()6,0A -，()3,3B -，()3,0C -可得直线OB 的解析式为y x =-，直线BC 为3x =-作点C 关于直线BO 的对称点()10,3C ，连接1AC 交BO 于M ，则M 即为所求由()6,0A -，()10,3C ，可得直线1AC 的解析式为132y x =+ 由132y x y x⎧=+⎪⎨⎪=-⎩解得22x y =-⎧⎨=⎩ ∴点M 的坐标为()2,2-由点P 在抛物线2123yx x =--上，设21,23P t t t ⎛⎫-- ⎪⎝⎭①当AM 为平行四边形的一边时如图，过M 作MG x ⊥轴于G ，过P 作PHBC ⊥于H 则2,3G M H B x x x x ==-==-可证AMG PQH ∆∆≌，得4PH AG ==()34t ∴--=，1t ∴=171,3P ⎛⎫∴- ⎪⎝⎭如图，同理可4PH AG ==34,7t t ∴--=∴=-277,3P ⎛⎫∴-- ⎪⎝⎭ ②当AM 为平行四边形的对角线时如右图，过M 作MHBC ⊥于H ，过P 作PG x ⊥轴于G 则3,H B G P x x x x t ==-==可证APG MQH ∆∆≌，得1AG MH ==()61,5t t ∴--=∴=-35:5,3P ⎛⎫∴- ⎪⎝⎭ 综上，点P 的坐标为171,3P ⎛⎫∴- ⎪⎝⎭，277,3P ⎛⎫-- ⎪⎝⎭，355,3P ⎛⎫- ⎪⎝⎭4.已知正方形OABC 的边OC 、OA 分别在x 、y 轴的正半轴上，点B 坐标为()4,4，点(),0P t 是x 轴上一动点，过点O 作OH AP ⊥于点H ，直线OH 交直线BC 于点D ，连接AD ．（1）如图1，当点P 在线段OC 上时，求证：OP CD =；（2）在点P 运动过程中，AOP ∆与以A 、B 、D 为顶点的三角形相似时，求t 的值；（3）如图2，抛物线212463y x x =-++上是否存在点Q ，使得以P 、D 、Q 、C 为顶点的四边形为平行四边形？若存在，求出t 的值；若不存在，请说明理由．解析：（1）证明：正方形OABC ，OA OC ∴=，90AOP OCD ∠=∠=︒90OAP APO ∴∠+∠=︒OH AP ⊥，90COD APO ∴∠+∠=︒OAP COD ∴∠+∠，AOP OCD ∴∆∆≌OP CD ∴=（2）解：当点P 在线段OC 上时若AOP ABD ∆∆∽，AO AB =，AOP ABD ∴∆∆≌ ,2,2OP CD OP BD CD t ∴=∴===∴=当点P 在OC 延长线上时，如图1ADB ODC APO ∠>∠=∠∴若AOP DBA ∆∆∽，则AO OP DB AB= 可证AOP OCD ∆∆≌，OP CD ∴=，4DB PC t ∴==-444t t ∴=-，解得2t =-（舍去）或2t =+ 当点P 在CO 延长线上时，如图290COD ODC ∠+∠=︒，90HOP APO ∠+∠=︒又COD HOP ∠=∠，ODC APO ∴∠=∠ODC ADB ∠>∠，APO ADB ∴∠>∠∴若AOP DBA ∆∆∽，则AO OP DB AB= 可证AOP OCD ∆∆≌，OP CD ∴=,4DB PC t ∴==-444t t -∴=-，解得2t =+（舍去）或2t =-∴当AOP ∆与以A 、B 、D 为顶点的三角形相似时，2t=或2+或2- （3）①若CD 为平行四边形的对角线则,DQ PC DQ PC =∥（i ）当点P 在线段OC 上时，如图3,,4OP t DC OP t DQ PC t =∴====-()8,Q t t ∴-，代入212463y x x =-++，得 ()()21288463t t t --+-+=，解得2t =或4t =（舍去）（ii ）当点P 在CO 延长线上时，如图OP t =-，DC OP t ∴==-，4DQ PC t ==-()8,Q t t ∴-，代入212463y x x =-++，得 ()()21288463t t t --+-+=，解得2t =（舍去）或4t =（舍去） ②若CD 为平行四边形的边则,PQ DC PQ DC =∥（i ）当点P 在OC 延长线上时，如图5,OP t PQ DC OP t =∴===(),Q t t ∴-，代入212463y x x =-++，得 212463t t t -++=-，解得2t =-（舍去）或12t = （ii ）当点P 在CO 延长线上时，如图6、图7OP t =-，PQ DC OP t ∴===-(),Q t t ∴或(),Q t t -把(),Q t t 代入212463y x x =-++，得 212463t t t -++=，解得6t =-或4t =（舍去）把(),Q t t -代入212463y x x =-++，得 212463t t t -++=-，解得2t =-或12t =（舍去）综上所述，抛物上存在点Q ，使得以P 、D 、Q 、C 为顶点的四边形为平行四边形， t 的值为：12t =，212t =，36t =-，42t =-5.如图，在平面直角坐标系中，O 是坐标原点，矩形OABC 的顶点)A ，()0,1C ，将AOC ∆沿AC 翻折得APC ∆．（1）求点P 的坐标；（2）若抛物线243yx bx c =-++经过P 、A 两点，试判断点C 是否在该抛物线上，并说明理由；（3）设（2）中的抛物线与矩形OABC 的边BC 交于点D ，与x 轴交于另一点E ，点M 在x 轴上运动，N 在y 轴上运动，若以点E 、M 、D 、N 为顶点的四边形是平行四边形，试求点M 、N 的坐标．解析：（1）在Rt OAC ∆中，OA =1OC =，30,OAC ∴∠=︒过P 作PQ OA ⊥于Q ，如图1⑦在Rt PAQ ∆中，60,PAQ AP ∠=︒=2OQ AQ ∴==，32PQ =，322P ⎛⎫∴ ⎪⎝⎭（2）将P 、A 两点坐标代入抛物线的解析式中，得：312240c c ⎧-++=⎪⎨⎪-++=⎩解得1b c ⎧=⎪⎨=⎪⎩∴抛物线的解析式为2413yx =-++ 当0x =时，1y =，∴点()0,1C 在该抛物线上（3）①若DE 是平行四边形的对角线，如图2点C 在y 轴上，CD x ∥轴，∴过点D 作DM CE ∥交x 轴于M ，则四边形EMDC 为平行四边形把1y =代入抛物线解析式，得点D的坐标为4⎛⎫ ⎪⎝⎭把0y =代入抛物线解析式，得点E的坐标为4⎛⎫- ⎪⎝⎭2M ⎛⎫∴ ⎪⎝⎭，N 点即为C 点，坐标是()0,1②若DE 是平行四边形的边，如图3、图4过点A 作AN DE ∥交y 轴于N ，四边形DANE 是平行四边形2DE AN ∴====3ON OA =，30EAN ∴∠=︒ ,30AN DE DEA EAN ∴∠=∠=︒∥)(),0,1M N ∴- 同理过点C 作CM DE ∥交x 轴于M ，四边形CMED 是平行四边形()(),0,1M N ∴6.如图，已知抛物线211:4C y x bx c =-++与x 轴交于点A 、B （A 在B 的左侧），与y 轴交于点C ，抛物线2C 与抛物线1C 关于y 轴对称，点A 、B 的对称点分别是E 、D ，连接CD 、CB ，设AD m =．（1）当2m =时，求b 的值；（2）若点P 是抛物线1C 上的一个动点（P 不与点A 、B 重合），试判断点P 关于原点的对称点Q 是否在抛物线2C 上，请说明理由；（3）将CDB ∆沿直线BC 折叠，点D 的对应点为G ．是否存在实数m ，使得四边形CDBG 为平行四边形，且点G 恰好落在抛物线2C 上，若存在，求出m 的值；若不存在，请说明理由．解析：（1）∵抛物线211:4C y x bx c =-++的对称轴为直线2x b = 抛物线2C 与抛物线1C 关于y 轴对称∴抛物线2C 的对称轴为直线2x b =-12,222,2m b b b =∴--=∴=- （2）∵抛物线211:4C y x bx c =-++，抛物线2C 与抛物线1C 关于y 轴对称 ∴抛物线221:4C y x bx c =--+ 设(),P x y 是抛物线1C 上任意一点(0)y ≠则点P 关于原点的对称点()11,Qx y --，且21114y x bx c =-++ 将点Q 的横坐标代入抛物线2C 的解析式得2111114Q y x bx c y y =-++=≠- ∴点Q 不在抛物线2C 上（3）存在B 、D 关于y 轴对称，点C 在y 轴上，CD CB ∴=由折叠知CG CD =∵四边形CDBG 是平行四边形，CD BG ∴=CB CG BG ∴==，CGB ∴∆是等边三角形CDB ∴∆是等边三角形假设点G 恰好落在抛物线2C 上由抛物线和等边三角形的对称性可知B 点一定在抛物线2C 的对称轴上BD BE AD m ∴===1,2OD OB m ∴==31,0,,022A m B m ⎛⎫⎛⎫∴- ⎪ ⎪⎝⎭⎝⎭CDB ∆为等边三角形，2c CO m ∴=== 对于抛物线211:4C y x bx c =-++，根据根与系数的关系，有31422m m c -⋅=-314222m m m ∴-⋅=-⨯0,3m m ≠∴=∴存在实数3m =，使得四边形CDBG 为平行四边形，且点G 恰好落在抛物线2C 上 7.已知抛物线212y x c =+经过点()3,5A -，顶点为Q ，点P 是y 轴上位于点Q 上方的一个动点，连接AP 并延长，交抛物线于点B ，分别过点A 、B 作x 轴的垂线，垂足为C 、D ，连接AQ 、BQ ．（1）求抛物线的解析式；（1）当A 、Q 、B 三点构成直角三角形时，求点P 的坐标；（2）当AC 、AP 、BD 、BP 四条线段构成平行四边形时，求点P 的坐标．解析：（1）∵抛物线212y x c =+经过点()3,5A - ()21532c ∴=⨯-+，12c ∴= ∴抛物线的解析式为21122y x =+（2）21122y x =+，10,2Q ⎛⎫∴ ⎪⎝⎭①若90AQB ∠=︒过点Q 作EF x ∥轴，分别交AC 、BD 于E 、F 则195,322AE AC EC EQ =-=-== 易证AEQ QFB ∆∆∽，AE EQ QF FB ∴= 32AE FQ QE FB ∴== 设13,22B m m ⎛⎫+ ⎪⎝⎭，代入抛物线解析式，得49m = 425,318B ⎛⎫∴ ⎪⎝⎭可得直线AB 的解析式为5562y x =-+ 50,2P ⎛⎫∴ ⎪⎝⎭ ②若90QAB ∠=︒过点Q 作QE x ∥轴，交AC 于E()13,5,0,,22A Q AQ ⎛⎫-∴= ⎪⎝⎭易证AEQ QAP ∆∆∽，PQ AQ AQ AE ∴=，2132AQ PQ AE ∴== ()0,7P ∴③若90ABQ ∠=︒过点A 、Q 分别作x 轴的平行线，交BD 于E 、F 设211,22B n n ⎛⎫+ ⎪⎝⎭，则3,AE n QF n =+= 22119152222BE n n =--=-，2211112222BF n n =+-= 可证ABE BQF ∆∆∽，AE BE BF QF∴= 229132212n n n n -+∴=，即()()23340n n n +-+= 30n ∴+=，得3n =-（舍去）或2340n n -+=，方程无实数解∴当ABQ ∆为直角三角形时，点P 的坐标为50,2⎛⎫ ⎪⎝⎭或()0,7 （3）①若AC BD =，AP BP =，此时点A 与点B 关于y 轴对称()5,0,5OP AC P ∴==∴②若ACAP =，设()0,P y ，则()29525y +-= 解得1y=或9y = 当1y =时，则()0,1P此时直线AP 解析式为413yx =-+ 与抛物线的交点B 为19()35，59BP BD ∴=== 此时AC 、AP 、BD 、BP 四条线段能构成平行四边形()0,1P ∴符合题意当9y =时，则()0,9P此时直线AP 解析式为493y x =+ 与抛物线的交点B 为17149()39，过P 作PE BD ⊥于E ，则1731739PE ⨯==， 149684179999BE ⨯=-== 51785149999BP ⨯∴==<，即BP BD < 此时AC 、AP 、BD 、BP 四条线段不能构成平行四边形()0,9P ∴不符合题意 ③若AC BP =，则点P 必在点A 上方，AP BD ≠此时AC 、AP 、BD 、BP 四条线段不能构成平行四边形∴满足条件的点P 的坐标为()0,5或()0,1 8.如图，抛物线2y x bx c =-++与直线122y x =+交于C 、D 两点，其中点C 在y 轴上，点D 的坐标为7(3)2，．点P 是y 轴右侧的抛物线上一动点，过点P 作PE x ⊥轴于点E ，交CD 于点F ．（1）求抛物线的解析式；（2）若点P 的横坐标为m ，当m 为何值时，以O 、C 、P 、F 为顶点的四边形是平行四边形？请说明理由．（3）若存在点P ，使45PCF ∠=︒，请直接写出相应的点P 的坐标．解析：（1）在直线解析式122y x =+中，令0x =，得2y =， (02)C ∴，．∵点(02)C ，、7D(3)2，在抛物线2y x bx c =-++上， 27932c b c =⎧⎪∴⎨-++=⎪⎩，解得722b c ⎧=⎪⎨⎪=⎩， ∴抛物线的解析式为：2722yx x =-++．（2）PF OC ∥，且以O 、C 、P 、F 为顶点的四边形是平行四边形，2PF OC ∴==， ∴将直线122y x =+沿y 轴向上、下平移2个单位之后得到的直线，与抛物线y 轴右侧的交点，即为所求之交点．由答图1可以直观地看出，这样的交点有3个．将直线122y x =+沿y 轴向上平移2个单位，得到直线142y x =+，联立2142722y x y x x ⎧=+⎪⎪⎨⎪=-++⎪⎩，解得121,2x x ==，121,2m m ∴==；将直线122y x =+沿y 轴向下平移2个单位，得到直线12y x =，联立212722y x y x x ⎧=⎪⎪⎨⎪=-++⎪⎩，解得3433,22x x +-==（在y 轴左侧，不合题意，舍去），32m +∴=． ∴当m 为值为12，或2时，以O 、C 、P 、F 为顶点的四边形是平行四边形．（3）存在．理由：设点P 的横坐标为m ，则271,2,,222P m m m F m m ⎛⎫⎛⎫-+++ ⎪ ⎪⎝⎭⎝⎭．由答图2所示，过点C 作CM PE ⊥于点M ，则,2CM m EM ==，12F FM y EM m ∴=-=， tan 2CFM ∴∠=．在Rt CFM ∆中，由勾股定理得：2CF m =．过点P 作PN CD ⊥于点N ，则tan tan 2PN FN PEN FN CFMFN =⋅∠=⋅∠∠=45PCF ∠=︒，PN CN ∴=，而2PN FN =，,22FN CF m PN FN ∴====，在Rt PFN ∆中，由勾股定理得：52PF m ==． 227122322P F PF y y m m m m m ⎛⎫⎛⎫=-=-++-+=-+ ⎪ ⎪⎝⎭⎝⎭， 2532m m m ∴-+=，整理得：2102m m -=，解得0m =（舍去）或12m =， 17()22P ∴，；同理求得，另一点为2313()618P ，． ∴符合条件的点P 的坐标为17()22，或2313()618，．9.如图，抛物线22y x x c =-+的顶点A 在直线:5l y x =-上．（1）求抛物线顶点A 的坐标；（2）设抛物线与y 轴交于点B ，与x 轴交于点C 、D （C 点在D 点的左侧），试判断ABD ∆的形状；（3）在直线l 上是否存在一点P ，使以点P 、A 、B 、D 为顶点的四边形是平行四边形，若存在，求点P 的坐标；若不存在，请说明理由．解析：（1）∵顶点A 的横坐标为212x-=-=，且顶点A 在5y x =-上 ∴当1x =时，154y =-=-()1,4A ∴-（2）ABD ∆是直角三角形将(14)A -，代入22y x x c =-+，得124c -+=-，3c ∴=-223y x x ∴=--，(03)B ∴-，当0y =时，2230x x --=，121,3x x ∴=-=(10)C ∴-，，(30)D ，22218BD OB OD =+=，()2224312AB =-+=，()22231420AD =-+= 222BD AB AD +=，90ABD ∴∠=︒即ABD ∆是直角三角形（3）存在．由题意知：直线5yx =-交y 轴于点(05)E -，，交x 轴于点(50)F ，5OE OF ∴==，又3OB OD ==OEF ∴∆与OBD ∆都是等腰直角三角形BD l ∴∥，即PA BD ∥则构成平行四边形只能是PADB 或PABD ，如图,过点P 作y 轴的垂线，过点A 作x 轴的垂线并交于点G设11(5)P x x -，，则1(15)G x -，则11PG x =-，11541AG x x =--=-PA BD ==由勾股定理得：()()22111118x x -+-=，12x ∴=-或24x =(27)P ∴--，或(41)P -，∴存在点(27)P --，或(41)P -，使以点P 、A 、B 、D 为顶点的四边形是平行四边形10.抛物线2y axbx c =++与x 轴交于(20)A -，、(40)B ，两点，与y 轴负半轴交于点C ，且12ABC S ∆=．（1）求此抛物线的解析式；（2）如图1，P 为直线BC 上一点，若以O 、P 、B 为顶点的三角形与ABC ∆相似，求点P 的坐标；（3）如图2，过点A 作AM AC ⊥交抛物线于点M ，交y 轴于点D ，直线x m =与抛物线交于点Q ，与直线AM 交于点R ．问是否存在这样的m ，使C 、D 、Q 、R 四点构成平行四边形？若存在，求出m 的值，若不存在；说明理由．解析：（1）(20)A -，、(40)B ，2,46OA OB AB ∴===，1161222ABC S AB OC CO ∆=⋅=⨯⋅=，4OC ∴= ∵点C 在y 轴负半轴上，(04)C ∴-，42016404a b c a b c c -+=⎧⎪∴++=⎨⎪=-⎩解得1214a b c ⎧=⎪⎪=-⎨⎪=-⎪⎩∴抛物线的解析式为2142y x x =-- （2）易知ABC ∆为锐角三角形∴若以O 、P 、B 为顶点的三角形与ABC ∆相似，点P 只能在线段BC 上过P 作PE OB ⊥于E ，设PE t = 当OP AC ∥时，OBP ABC ∆∆∽ 则EP OB OC AB =，446t ∴=，83t ∴= 4OB OC ==，45OBC ∴∠=︒BE PE t ∴==， 84433OE OB BE ∴=-=-= 148()33P ∴-，当BPO BAC ∠=∠时，PBO ABC ∆∆∽过A 作AH BC ⊥于H，则2AH AB ==EP OB AH BC ∴=，=，3t ∴=431OE ∴=-=2(13)P ∴-，（3）,AD AC ODA OAC ⊥∴∆∆∽OD OA OA OC∴=，224OD ∴= 1OD ∴=，5CD ∴=，(01)D ，，设直线AM 的解析式为y kx b =+则201k b b -+=⎧⎨=⎩解得121k b ⎧=⎪⎨⎪=⎩ ∴直线AM 的解析式为112y x =+ 设21(4)2Q m m m --，，则1(1)2R m m +，QR CD ∥，∴当QR CD =时，C 、D 、Q 、R 四点构成平行四边形 2114(1)522m m m ∴---+=解得32m ±= 或2111(4)522m m m +---= 解得0m =（舍去）或3m =∴当32m ±=或3m =时，C 、D 、Q 、R 四点构成平行四边形。

专题03 特殊平行四边形中的三种几何动点问题(解析版)-2024年常考压轴题攻略(9年级上册人教版)

专题03特殊平行四边形中的三种几何动点问题类型一、面积问题(1)直接写出CD的长（cm）(2)当四边形PBQD为平行四边形时，直接写出四边形(3)在点P、点Q的运动过程中，是否存在某一时刻，使得条件的t的值；若不存在，请说明理由．【答案】(1)16(2)8+813(3)存在，满足条件的t的值为【分析】（1）过点A作AM性质以及勾股定理可得结果；（2）当四边形PBQD是平行四边形，则点-=四边形的性质可得103t（3）分两种情况进行讨论：计算即可．∠︒，BCD⊥，=90AM CD∥，∴AM CB由运动知，103BP t =-，DQ 1032t t ∴-=，2t ∴=，此时，4BP DQ ==，12CQ =∴四边形PBQD 的周长为(2BP （3）①当点P 在线段AB 上时，即：如图2，()1110322BPQ S PB BC t =⋅=- 2512t ∴=；②当点P 在线段BC 上时，即：310BP t =-，162CQ t =-，(1131022BPQ S PB CQ t ∴=⋅=- 5t ∴=或193t =（舍），即：满足条件的t 的值为2512秒或【点睛】本题考查了四边形的动点问题，平行四边形的判定与性质，勾股定理，读懂题意，根据相应图形的性质列出方程是解本题的关键．【变式训练1】如图，在四边形点P 自点A 沿折线AD DC -以同时出发，其中一个点到达终点，另一个点也停止运动．设运动时间为(1)当P 在AD 边上，点Q 在BC ①用含t 的代数式表示：DP类型二、几何图形存在性问题，的长；(1)求AB AC(2)求证：AE DF=；(3)当t为何值时，DEF为直角三角形？请说明理由．【答案】(1)AB=5，AC=10；(2)证明见解析5②∠DEF=90°时，∵AB⊥BC，DF⊥BC，．∴AE DF又∵AE=DF，∴四边形AEFD为平行四边形，，∴AD EF③∠EFD=90°时，此种情况不存在．(1)连接PD 、PQ 、DQ ，求当t 为何值时，PQD △的面积为(2)当点P 在BC 上运动时，是否存在这样的t 使得PQD △合条件的t 的值；若不存在，请说明理由．【答案】(1)1秒或94秒(2)存在，43t =秒或(424)-秒【分析】（1）根据正方形的性质和面积公式，利用割补法即可求解；（2）根据勾股定理、等腰三角形的性质得出一元二次方程，分情况讨论以【详解】（1）解：当P 在BC 上时如图：根据题意，得4AB BC CD AD ====AQ t =，4QB t =-，2BP t =，42PC t =-，7PQD ADQ BPQ DPC ABCD S S S S S =---=△△△△正方形，1111642(4)4(42)7222t t t t -⨯⨯-⨯--⨯⨯-= 整理，得2210t t -+=，4(24)8DP t =--=-1(82)42PQD S t ∴=-⨯△94t ∴=答：当t 为1秒或94（2）①当PD DQ =解得143t =，24t =（不符合题意，舍去）②当PD PQ =时，根据勾股定理，得216(42)(4t +-=-解得1424t =-，2t 答：存在这样的t =【点睛】本题考查了正方形、一元二次方程、等腰三角形的相关知识，解决本题的关键是分类讨论思想的运用．例3．如图，在四边形由；(3)从运动开始，当t 取何值时，四边形PQBA 是矩形？(4)在整个运动过程中是否存在t 值，使得四边形PQBA 是正方形？若存在，请求出t 值；若不存在，请说明理由．【答案】(1)4(2)不存在，理由见解析(3)6(4)不存在，理由见解析【分析】（1）利用平行四边形的判定和性质进行求解即可；（2）利用菱形的判定和性质进行求解即可；（3）利用矩形的判定和性质进行求解即可；（4）利用正方形的判定和性质进行求解即可．（1）解：由运动知，AP ＝t cm ，CQ ＝2t cm ，∴DP ＝AD ﹣AP ＝（12﹣t ）cm ，∵AD BC ∥，要PQ CD ∥，∴四边形CDPQ 为平行四边形，∴DP ＝CQ ，∴12﹣t ＝2t ，∴t ＝4，即t ＝4时，PQ ∥CD ；（2）不存在，理由：∵四边形PQCD 是菱形，∴CQ ＝CD ，∴2t ＝10，∴t ＝5，此时，DP ＝AD ﹣AP ＝12﹣5＝7（cm ），而DP ≠CD ，∴四边形PQCD 不可能是菱形；（3）如图4，∵∠B ＝90°，AD ∥BC ，∴当AP ＝BQ 时，四边形ABQP 是矩形，即t ＝18﹣2t ，解得：t ＝6，∴当t ＝6时，四边形PQBA 是矩形；（4）由当t ＝6时，四边形PQBA 是矩形，∴AP ＝6cm ，∵AB ＝8cm ，∴AP ≠AB ，∴矩形PQBA 不能是正方形，即不存在时间t ，使四边形PQBA 是正方形．【点睛】本题考查四边形中的动点问题．解题的关键是熟练掌握平行四边形、菱形、矩形和正方形的判定和性质，确定动点的位置．例4．如图，在菱形ABCD 中，对角线AC 与BD 交于点O ，且8AC =，6BD =，现有两动点M ，N 分别从A ，C 同时出发，点M 沿线段AB 向终点B 运动，点N 沿折线C D A --向终点A 运动，当其中一点到达终点时，另一点也随之停止运动，设运动时间为t （秒）．2③如图4，AEMN为菱形，EN交AM ∴==-=，BT NS523∴=，， 1.4CSBS=4.8∴=+=+=，CN NS CS1.43 4.4∴=÷=÷=；4 4.44 1.1a CN综上所述，a的取值有1.5或1.94或1.4．【点睛】本题主要考查了菱形的性质、三角函数、勾股定理、面积计算，分类讨论等重要知识点，综合性和技巧性很强，计算量也较大，对学生的能力要求较高，因此综合应用所学知识成为解答本题的关键．类型三、直线位置关系问题(1)直接写出AB的长．(2)当点Q落在AB边上时，用含t的代数式表示10PQDM (1)分别求BD和BE的长度；(2)连接PQ，当95t=时，判断PQ与AD是否垂直，并说明理由；(3)试判断是否存在t的值，使得以P，Q，C，D 存在，请说明理由；动点P从点D出发沿DA以1/scm的速度向终点运动，60∴∠=∠=︒，ADQ QDC∴∠=∠=︒，60QDC BCD∴ 是等边三角形，CDQ120CDA ∠=︒ ，60PDP '∴∠=︒，点P 的对称点在线段CD 的延长线上，CDQ ∴∠BCD CDQ CQD ∠=∠+∠ ，30CDQ CQD ∴∠=∠=︒，6CD CQ ∴==，12618BQ ∴=+=，418t ∴=，92t ∴=，过点P 作PH BC ⊥于H ，则33PH DE cm ==，60BCD ∠=︒ ，6CD AB cm ==，DE BC ⊥，∴272QH CQ EH CE cm ∴=++=，(1)t 为何值时，四边形DPQA (2)t 为何值时，四边形PQBC 【答案】(1)当132t =秒时，四边形(2)当6t =秒时，四边形PQBC 【分析】（1）根据AB CD ∥（2）根据平行四边形的判定和性质，得【详解】（1）∵AB CD ∥，∴AQ DP ∥，当AQ DP =时，四边形DPQA ∵90A ∠=︒，∴平行四边形DPQA 为矩形，∵动点P 从D 开始沿DC 边向动，∴cm DP t =，3cm BQ t =，∴263AQ AB BQ t =-=-，发现：(1)在点O 的运动过程中，OE 与OF 的关系是(2)当=2t 时，=EF ______cm ．探究：当=t ______时，四边形AECF 拓展：若点O 在运动过程中，能使四边形【答案】(1)OE OF =，详见解析(2)8cm ，探究：3，拓展：=AB 10cm【分析】()1根据角平分线的定义、平行线的性质分别得到角形的判定定理得到OE OC =，OF ()2根据直角三角形斜边上的中线的性质解答；探究：根据矩形的判定定理得到=OA OC 时，四边形AECF 是矩形，进而求出OA ，求出t ；拓展：根据正方形的对角线平分一组对角得到45ACE ∠=︒，进而得到90ACB ∠=︒，根据勾股定理计算，得到答案．【详解】（1）解：OE OF =，理由如下：CE 平分ACB ∠，BCE ACE ∴∠=∠，EF BC ∥ ，BCE OEC ∴∠=∠，OEC ACE ∴∠=∠，OE OC ∴=，同理可得，ACF OFC ∠=∠，OF OC ∴=，OE OF ∴=，故答案为：OE OF =；（2）由题意得，当=2t 时，2cm OA =，则4cm OC AC OA =-=，BCE ACE ∠=∠ ，GCF ACF ∠=∠，90ECF ∴∠=︒，OE OF = ，()28cm EF OC ∴==，故答案为：8；探究：当=3t 时，四边形AECF 是矩形，理由如下：90ECF ∠=︒ ，OE OF =，∴当=OA OC 时，四边形AECF 是矩形，此时，3cm OA OC ==，3t ∴=时，四边形AECF 是矩形，故答案为：3；拓展：当四边形AECF 是正方形时，45ACE ∠=︒，CE 平分ACB ∠，(1)当运动时间为秒时，点P与点Q相遇；∥时，求线段DQ的长度；(2)当BQ PD全等时，求t的值．(3)连接PA，当PAB和QAD【答案】(1)3.2(2)3.2(3)t为0.8或83【分析】（1）先判断出点P，Q相遇时，必在正方形的边BC上，利用运动路程之和为正方形的正常建立方程即可；=，进而表示出（2）先判断出四边形BQDP是平行四边形，得出BP DQ求解即可；（3）分点Q在正方形的边AB，AD，CD，BC上，建立方程求解即可得出结论；BC=，【详解】（1）解：点P的运动速度为2，8∴点P运动到点C的时间为4，点Q的运动速度为8，∴点Q从点B出发沿BA AD DC CB---方向顺时针作折线运动到点相遇时在边BC上，∴+=⨯=，t t2848323.2t ∴=，故答案为3.2；（2）解：如图1，//BQ PD ，∴点Q 只能在边AD 上，四边形ABCD 是正方形，//AD BC ∴，∴四边形BQDP 是平行四边形，BP DQ ∴=，2288t t ∴=⨯-，1.6t ∴=，288 3.2DQ t ∴=⨯-=；（3）解：①当点Q 在边AB 上时，如图2，AB AD = ，ABP DAQ ∠=∠，要使PAB ∆和ΔQAD 全等，只能是PAB QDA ≅ ，BP AQ ∴=，88AQ t =- ，2BP t =，882t t ∴-=，0.8t ∴=，同①的方法得，要使∴=，BP DQt t∴=-，28168t∴=，3④当点Q在边BC时，即：当PAB和QAD【点睛】本题考查四边形综合题、正方形的性质、平行四边形的判定和性质、全等三角形的判定和性质等知识，解题的关键是学会分类讨论．Y4．如图，在ABCD运动，同时点Q从点设点P运动的时间为(1)CB的长为______．(2)用含t的代数式表示线段QB的长．(3)连接PQ，若PQ 与AC 互相平分，则四边形APCQ 是平行四边形，∴AP CQ =，∵4AP t CQ t ==，，若PQ 与AB 互相平分，则四边形APBQ 是平行四边形，∴AP BQ =，∴45t t =-，由对称得，PAQ P AQ '∠=∠，∵AD BC ∥，∴PAQ AQB ∠=∠，由对称得，12∠=∠，∵AD BC ∥，∴13∠=∠，∵24∠∠==；(1)求证：PE DQ(1)=a______cm，b=______cm；(2)t为何值时，EP把四边形BCDE的周长平分？(1)当2t =时，BP =___________cm ；(2)当t 为何值时，连接,,CP DP CDP △是等腰三角形；(3)Q 为AD 边上的点，且6DQ =，P 与Q 不重合，当角形与DCQ 全等．【答案】(1)1(2)54t =或4或232∴PD CP =，在长方形ABCD 中，∴DAP CBP ≌∴AP BP =，∴1522AP AB ==∵动点P 的速度是∴54t =；②当点P 在BC ∵90C ∠=︒，∴5CD CP ==，∵90D Ð=°，∴5DP CD ==，∴2AB CB t ++=综上所述，54t =（3）解：根据题意，如图，连接∵5,AB CD ==∠∴要使一个三角形与①当点P 运动到∴点P 的路程为：∴72 3.5t =÷=；②当点P 运动到∴点P 的路程为：∴112 5.5t =÷=③当点P 运动到∴点P 的路程为：3585220AB BC CD DP +++=+++=，∴20210t =÷=，④当点P 运动到4P 时，即P 与Q 重合时，46DP DQ ==，此时4CDQ CDP △≌△，∴点P 的路程为：4585624AB BC CD DP +++=+++=∴24212t =÷=，此结果舍去，不符合题意，综上所述，t 的值可以是： 3.5t =，5.5或10．【点睛】本题考查了动点问题，灵活运用分类讨论思想是解题关键．。

中考数学二次函数动点问题-因动点产生的平行四边形问题

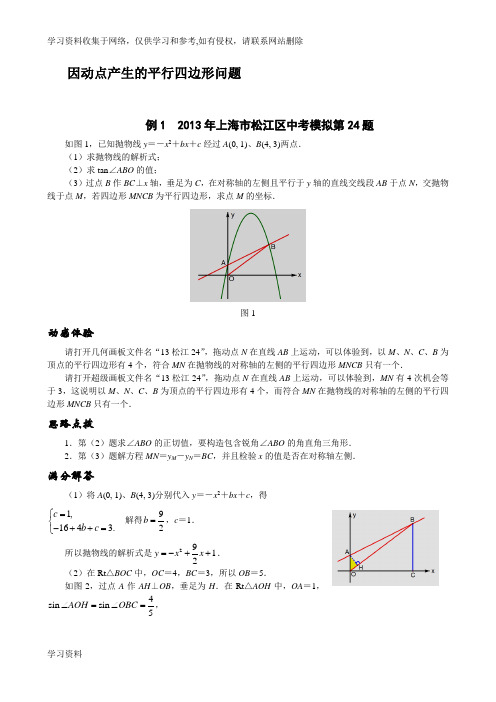
因动点产生的平行四边形问题例1 2013年上海市松江区中考模拟第24题如图1，已知抛物线y ＝－x 2＋bx ＋c 经过A (0, 1)、B (4, 3)两点．（1）求抛物线的解析式；（2）求tan ∠ABO 的值；（3）过点B 作BC ⊥x 轴，垂足为C ，在对称轴的左侧且平行于y 轴的直线交线段AB 于点N ，交抛物线于点M ，若四边形MNCB 为平行四边形，求点M 的坐标．图1动感体验请打开几何画板文件名“13松江24”，拖动点N 在直线AB 上运动，可以体验到，以M 、N 、C 、B 为顶点的平行四边形有4个，符合MN 在抛物线的对称轴的左侧的平行四边形MNCB 只有一个．请打开超级画板文件名“13松江24”，拖动点N 在直线AB 上运动，可以体验到，MN 有4次机会等于3，这说明以M 、N 、C 、B 为顶点的平行四边形有4个，而符合MN 在抛物线的对称轴的左侧的平行四边形MNCB 只有一个．思路点拨1．第（2）题求∠ABO 的正切值，要构造包含锐角∠ABO 的角直角三角形． 2．第（3）题解方程MN ＝y M －y N ＝BC ，并且检验x 的值是否在对称轴左侧．满分解答（1）将A (0, 1)、B (4, 3)分别代入y ＝－x 2＋bx ＋c ，得1,164 3.c b c =⎧⎨-++=⎩ 解得92b =，c ＝1．所以抛物线的解析式是2912y x x =-++．（2）在Rt △BOC 中，OC ＝4，BC ＝3，所以OB ＝5．如图2，过点A 作AH ⊥OB ，垂足为H ．在Rt △AOH 中，OA ＝1，4sin sin 5AOH OBC ∠=∠=，所以4sin 5AH OA AOH =⋅∠=．图2 所以35OH =，225BH OB OH =-=．在Rt △ABH 中，4222tan 5511AH ABO BH ∠==÷=．（3）直线AB 的解析式为112y x =+．设点M 的坐标为29(,1)2x x x -++，点N 的坐标为1(,1)2x x +，那么2291(1)(1)422MN x x x x x =-++-+=-+．当四边形MNCB 是平行四边形时，MN ＝BC ＝3．解方程－x 2＋4x ＝3，得x ＝1或x ＝3．因为x ＝3在对称轴的右侧（如图4），所以符合题意的点M 的坐标为9(1,)2（如图3）．图3 图4考点伸展第（3）题如果改为：点M 是抛物线上的一个点，直线MN 平行于y 轴交直线AB 于N ，如果M 、N 、B 、C 为顶点的四边形是平行四边形，求点M 的坐标．那么求点M 的坐标要考虑两种情况：MN ＝y M －y N 或MN ＝y N －y M ．由y N －y M ＝4x －x 2，解方程x 2－4x ＝3，得27x =±（如图5）．所以符合题意的点M 有4个：9(1,)2，11(3,)2，57(27,)2--，57(27,)2++．图5例2 2012年福州市中考第21题如图1，在Rt△ABC中，∠C＝90°，AC＝6，BC＝8，动点P从点A开始沿边AC向点C以每秒1个单位长度的速度运动，动点Q从点C开始沿边CB向点B以每秒2个单位长度的速度运动，过点P作PD//BC，交AB于点D，联结PQ．点P、Q分别从点A、C同时出发，当其中一点到达端点时，另一点也随之停止运动，设运动的时间为t秒（t≥0）．（1）直接用含t的代数式分别表示：QB＝_______，PD＝_______；（2）是否存在t的值，使四边形PDBQ为菱形？若存在，求出t的值；若不存在，说明理由，并探究如何改变点Q的速度（匀速运动），使四边形PDBQ在某一时刻为菱形，求点Q的速度；（3）如图2，在整个运动过程中，求出线段PQ的中点M所经过的路径长．图1 图2动感体验请打开几何画板文件名“12福州21”，拖动左图中的点P运动，可以体验到，PQ的中点M的运动路径是一条线段．拖动右图中的点Q运动，可以体验到，当PQ//AB时，四边形PDBQ为菱形．请打开超级画板文件名“12福州21”，拖动点Q向上运动，可以体验到，PQ的中点M的运动路径是一条线段．点击动画按钮的左部，Q的速度变成1.07，可以体验到，当PQ//AB时，四边形PDBQ为菱形．点击动画按钮的中部，Q的速度变成1.思路点拨1．菱形PDBQ必须符合两个条件，点P在∠ABC的平分线上，PQ//AB．先求出点P运动的时间t，再根据PQ//AB，对应线段成比例求CQ的长，从而求出点Q的速度．2．探究点M的路径，可以先取两个极端值画线段，再验证这条线段是不是点M的路径．满分解答（1）QB＝8－2t，PD＝43t．（2）如图3，作∠ABC的平分线交CA于P ，过点P作PQ//AB交BC于Q，那么四边形PDBQ是菱形．过点P作PE⊥AB，垂足为E，那么BE＝BC＝8．在Rt△ABC中，AC＝6，BC＝8，所以AB＝10．图3在Rt△APE中，23cos5AEAAP t===，所以103t=．当PQ//AB时，CQ CPCB CA=，即106386CQ-=．解得329CQ=．所以点Q的运动速度为3210169315÷=．（3）以C为原点建立直角坐标系．如图4，当t＝0时，PQ的中点就是AC的中点E(3，0)．如图5，当t＝4时，PQ的中点就是PB的中点F(1，4)．直线EF的解析式是y＝－2x＋6．如图6，PQ的中点M的坐标可以表示为（62t-，t）．经验证，点M（62t-，t）在直线EF上．所以PQ的中点M的运动路径长就是线段EF的长，EF＝25．图4 图5 图6考点伸展第（3）题求点M的运动路径还有一种通用的方法是设二次函数：当t＝2时，PQ的中点为(2，2)．设点M的运动路径的解析式为y＝ax2＋bx＋c，代入E(3，0)、F(1，4)和(2，2)，得930,4,42 2.a b ca b ca b c++=⎧⎪++=⎨⎪++=⎩解得a＝0，b＝－2，c＝6．所以点M的运动路径的解析式为y＝－2x＋6．例3 2012年烟台市中考第26题如图1，在平面直角坐标系中，已知矩形ABCD的三个顶点B(1, 0)、C(3, 0)、D(3, 4)．以A为顶点的抛物线y＝ax2＋bx＋c过点C．动点P从点A出发，沿线段AB向点B运动，同时动点Q从点C出发，沿线段CD向点D运动．点P、Q的运动速度均为每秒1个单位，运动时间为t秒．过点P作PE⊥AB交AC 于点E．（1）直接写出点A的坐标，并求出抛物线的解析式；（2）过点E作EF⊥AD于F，交抛物线于点G，当t为何值时，△ACG的面积最大？最大值为多少？（3）在动点P、Q运动的过程中，当t为何值时，在矩形ABCD内（包括边界）存在点H，使以C、Q、E、H为顶点的四边形为菱形？请直接写出t的值．图1动感体验请打开几何画板文件名“12烟台26”，拖动点P在AB上运动，可以体验到，当P在AB的中点时，△ACG的面积最大．观察右图，我们构造了和△CEQ中心对称的△FQE和△ECH′，可以体验到，线段EQ 的垂直平分线可以经过点C和F，线段CE的垂直平分线可以经过点Q和H′，因此以C、Q、E、H为顶点的菱形有2个．请打开超级画板文件名“12烟台26”，拖动点P在AB上运动，可以体验到，当P在AB 的中点时，即t=2，△ACG的面积取得最大值1．观察CQ，EQ，EC的值，发现以C、Q、E、H为顶点的菱形有2个．点击动画按钮的左部和中部，可得菱形的两种准确位置。

中考数学专题17 函数动点问题中平行四边形存在性(解析版)

专题17 函数动点问题中平行四边形存在性类型一、平行四边形存在性结论：A C B DA CB Dx x x xy y y y+=+⎧⎨+=+⎩类型二、特殊平行四边形存在性1. 矩形存在性常用解题思路：构造一线三直角（借助相似或三角函数求解）；利用矩形对角线相等（直角三角形斜边的中线等于斜边的一半）借助勾股定理求解等.2. 菱形存在性常用解题思路：利用菱形四条边相等，对角线互相垂直，借助勾股定理等求解.3. 正方形存在性常用解题思路：兼具矩形和菱形二者.【例1】（2018·郑州预测卷）如图，直线y=334x-+与x轴交于点C，与y轴交于点B，抛物线y= 234ax x c++经过B、C两点.（1）求抛物线的解析式；（2）如图，点E是直线BC上方抛物线上的一个动点，当△BEC的面积最大时，求出点E的坐标和最大值；（3）在（2）条件下，过点E作y轴的平行线交直线BC于点M，连接AM，点Q是抛物线对称轴上的动点，在抛物线上是否存在点P，使以点P、Q、A、M为顶点的四边形是平行四边形？若存在，请直接写出点P的坐标；若不存在，请说明理由.【答案】见解析.【解析】解：（1）∵直线y =334x -+与x 轴交于点C ，与y 轴交于点B ，∴B (0,3)，C (4,0)，将B (0,3)，C (4,0)代入y = 234ax x c ++得： 16303a c c ++=⎧⎨=⎩，解得：383a c ⎧=-⎪⎨⎪=⎩， ∴抛物线的解析式为：233384y x x =-++.（2）过点E 作EF ⊥x 轴于F ，交BC 于M ，设E （x ，233384x x -++），则M （x ，334x -+），∴ME =233384x x -++－（334x -+）=23382x x -+∴S △BEC =12×EM ×OC =2EM=2(23382x x -+)=()23234x --+,∴当x =2时，△BEC 的面积取最大值3，此时E (2，3).（3）由题意得：M (2，32)，抛物线对称轴为：x =1，A (－2,0),设P (m ，y )，y =233384m m -++，Q (1，n )①当四边形APQM 为平行四边形时，有：212m -+=+，解得：m =－3，即P (－3，218-)； ②当四边形AMPQ 为平行四边形时，有：－2+m =2+1，即m =5 即P (5, 218-)； ③当四边形AQMP 为平行四边形时，有：2－2=1+m ，得：m =－1，即P (－1，158)；综上所述，抛物线上存在点P ，使以点P 、Q 、A 、M 为顶点的四边形是平行四边形，点P 的坐标为：(－3，218-)，(5, 218-)，(－1，158).【变式1-1】（2018·河师大附中模拟）如图，抛物线y =ax 2+bx +c （a ≠0）与x 轴交于点A (－1，0)、B (3，0)两点，与y 轴交于点C (0，－3).（1）求抛物线的解析式与顶点M 的坐标；（2）求△BCM 的面积与△ABC 面积的比；（3）若P 是x 轴上一个动点，过P 作射线PQ ∥AC 交抛物线于点Q ，随着P 点的运动，在x 轴上是否存在这样的点P ，使以点A 、P 、Q 、C 为顶点的四边形为平行四边形？若存在请直接写出点P 的坐标；若不存在，请说明理由.【答案】见解析.【解析】解：（1）将A (－1，0)，B (3，0)， C (0，－3)代入y =ax 2+bx +c ，得：9303a b c a b c c -+=⎧⎪++=⎨⎪=-⎩，解得：a =1，b =－2，c =－3，即抛物线的解析式为：y=x2－2x－3，顶点M的坐标为：（1，－4）；（2）连接BC，BM，CM，过M作MD⊥x轴于D，如图所示，S△BCM=S梯形ODMC+S△BDM－S△BOC=3，S△ACB=6，∴S△BCM：S△ACB=1：2；（3）存在.①当点Q在x轴上方时，过Q作QF⊥x轴于F，如图所示，∵四边形ACPQ为平行四边形，∴QP∥AC，QP=AC∴△PFQ≌△AOC，∴FQ=OC=3，∴3=x2﹣2x﹣3，解得x或x=1，∴Q，3)或(1，3)；②当点Q在x轴下方时，过Q作QE⊥x轴于E，如图所示，同理，得：△PEQ≌△AOC，∴EQ=OC=3，∴﹣3=x2﹣2x﹣3，解得：x=2或x=0(与C点重合，舍去)，∴Q(2，﹣3)；综上所述，点Q的坐标为：，3)或(1，3)或(2，﹣3).【例2】（2018·郑州三模）如图所示，在平面直角坐标系中，已知抛物线y=ax2+bx－5与x轴交于A(-1,0),B(5,0)两点，与y轴交于点C.（1）求抛物线的解析式；（2）如图2所示，CE∥x轴与抛物线相交于点E，点H是直线CE下方抛物线上的动点，过点H且与y轴平行的直线与BC、CE分别交于点F、G，试探究当点H运动到何处时，四边形CHEF的面积最大，求点H的坐标及最大面积；（3）点M是（1）中所求抛物线对称轴上一动点，点N是反比例函数y=kx图象上一点，若以点B、C、M、N为动点的四边形是矩形，请直接写出满足条件的k的值.【答案】见解析.【解析】解：（1）将A (-1,0),B (5,0)代入y =ax 2+bx －5得：5025550a b a b --=⎧⎨+-=⎩，解得：14a b =⎧⎨=-⎩，即抛物线的解析式为：y =x 2－4x －5.（2）在y =x 2－4x －5中，当x =0时，y =－5，即C (0，－5), ∵CE ∥x 轴，则C 、E 关于直线x =2对称， ∴E (4，－5), CE =4，由B （5,0）, C (0，－5)得直线BC 的解析式为：y =x －5，设H (m ，m 2－4m －5)， ∵FH ⊥CE ， ∴F (m ，m －5)，∴FH = m －5－（m 2－4m －5)= －m 2+5m ， S 四边形CHEF =12·FH ·CE =12（－m 2+5m ）×4 =－2（m －52）2+252，当m =52时，四边形CHEF 的面积取最大值252，此时H (52，354-).（3）设M （2，m ），N (n ，kn)，B (5,0)，C (0，－5)， ①当BC 为矩形对角线时，此时：2+n =5+0，m +kn=0－5，即n =3，设BC 与MN 交于点H ，则H (52，52-)，MH =12BC =2，∴222552222m ⎛⎛⎫⎛⎫-++= ⎪ ⎪ ⎝⎭⎝⎭⎝⎭，解得：m =1或m =－6，当m =1时，k =－18；m =－6时，k =3， ②当BC 为矩形边时，分两种情况讨论：（i ）当点M 在直线BC 下方时，即四边形BCMN 为矩形，则∠BCM=90°，2+5=n+0，m=kn－5，过M作MH⊥y轴于H，则由OB=OC知，∠OCB=45°，∴∠MCH=∠CMH=45°，即CH=MH，∴－5－m=2，解得：m=－7，n=7，k=－14；（ii）当点M在直线BC上方时，即四边形BCNM为矩形，则∠CBM=90°，n+5=2，kn=m－5，设对称轴与x轴交于点H，同理可得：BH=MH，∴3=m，n=－3，k=6；综上所述，k的值为：－18，3，－14或6.【变式2-1】（2019·驻马店二模）如图，抛物线y=-x2+bx+c经过A(-1，0)，B(3，0)两点，且与y轴交于点C，点D是抛物线的顶点，抛物线的对称轴DE交x轴于点E，连接BD．（1）求经过A，B，C三点的抛物线的函数表达式．（2）点P是线段BD上一点，当PE=PC时，求点P的坐标．（3）在（2）的条件下，过点P作PF⊥x轴于点F，G为抛物线上一动点，M为x轴上一动点，N 为直线 PF 上一动点，当以 F ，M ，G ，N 为顶点的四边形是正方形时，请求出点 M 的坐标．【答案】见解析.【解析】解：（1）∵抛物线 y =-x 2+bx +c 经过 A (-1，0)，B (3，0)两点，∴10930b c b c --+=⎧⎨-++=⎩，解得：23b c =⎧⎨=⎩，即抛物线的解析式为：y =-x 2+2x +3.（2）由y =-x 2+2x +3知，C (0，3)，E (1，0)，D (1,4)，可得直线BD 的解析式为：y =-2x +6，设P （m ，-2m +6），由勾股定理得：PE 2=()()22126m m -+-+，PC 2=()22263m m +-+-，由PE =PC ，得：()()22126m m -+-+=()22263m m +-+-，解得：m =2，即P (2，2).（3）∵M 在x 轴上，N 在直线PF 上， ∴∠NFM =90°，由四边形MFNG 是正方形，知MF =MG ，设M (n ，0)，则G (n ，-n 2+2n +3)， MG =|-n 2+2n +3|，MF =|n -2|， ∴|-n 2+2n +3|=|n -2|，解得：n n n n ，故点M 的坐标为：0），0），（12，0），（12-，0）.【变式2-2】（2019·大联考）如图1，抛物线y =ax 2+bx +c 经过点A (-4,0)，B (1,0)，C （0,3），点P 在抛物线上，且在x 轴的上方，点P 的横坐标记为t .（1）求抛物线的解析式；（2）如图2，过点P 作y 轴的平行线交直线AC 于点M ，交x 轴于点N ，若MC 平分∠PMO ，求t 的值.（3）点D 在直线AC 上，点E 在y 轴上，且位于点C 的上方，那么在抛物线上是否存在点P ，使得以点C 、D 、E 、P 为顶点的四边形是菱形？若存在，请直接写出菱形的面积.图1 图2【答案】见解析.【解析】解：（1）∵抛物线y =ax 2+bx +c 经过点A (-4,0)，B (1,0)，C （0,3），∴301640c a b c a b c =⎧⎪++=⎨⎪-+=⎩，解得：39434c b a ⎧⎪=⎪⎪=-⎨⎪⎪=-⎪⎩，即抛物线的解析式为：y =34-x 294-x +3. （2）由A (-4,0)，C (0,3)得直线AC 的解析式为：y =334x +， ∵点P 的横坐标为t ， ∴M (t ,334t +)， ∵PN ∥y 轴， ∴∠PMC =∠MCO ， ∵MC 平分∠PMO ， ∴∠PMC =∠OMC ， ∴∠MCO =∠OMC ，即OM =OC =3，∴OM 2=9，即223394t t ⎛⎫++= ⎪⎝⎭，解得：t =0（舍）或t =7225，∴当MC 平分∠PMO 时，t =7225. （3）设P (t , 34-t 294-t +3)， ①当CE 为菱形的边时，四边形CEPD 为菱形，则PD ∥y 轴，CD =PD ，则D (t ，334t +),∴PD =34-t 294-t +3－（334t +）=34-t 23-t ，由勾股定理得：CD =54t -，∴34-t 23-t =54t -，解得：t =0（舍）或t =73-，即PD =3512，菱形面积为：3512×73=24536； ②当CE 为菱形的对角线时，此时P 与D 点关于y 轴对称，则D (-t , 34-t 294-t +3)，将D 点坐标代入y =334x +，得： 34-t 294-t +3=()334t -+，解得：t =0（舍）或t =－2， PD =4，CE =3，菱形的面积为：12×4×3=6；综上所述，菱形的面积为：24536或6.1.（2019·南阳毕业测试）如图1，抛物线y ＝ax 2+bx +2与x 轴交于A ，B 两点，与y 轴交于点C ，AB ＝4，矩形OBDC 的边CD ＝1，延长DC 交抛物线于点E ．（1）求抛物线的解析式；（2）如果点N 是抛物线对称轴上的一点，抛物线上是否存在点M ，使得以M ，A ，C ，N 为顶点的四边形是平行四边形？若存在，直接写出所有满足条件的点M 的坐标；若不存在，请说明理由．【答案】见解析．【解析】解：（1）∵矩形OBDC 的边CD ＝1， ∴OB ＝1，由AB ＝4，得OA ＝3， ∴A （﹣3，0），B （1，0），∵抛物线y ＝ax 2+bx +2与x 轴交于A ，B 两点， ∴a +b +2=0，9a －3b +2=0，解得：a =23-，b =43-， ∴抛物线解析式为y ＝23-x 243-x +2；（2）以AC 为边或对角线分类讨论： A （﹣3，0），C （0，2），抛物线y ＝23-x 243-x +2的对称轴为x ＝﹣1，设M (m , y M )，N (－1，n )，y M =23-m 243-m +2 ①当四边形ACMN 为平行四边形时，有：312Mm y n -+=-⎧⎨=+⎩，解得：m =2，y M =103-，即M (2，103-)； ②当四边形ACNM 为平行四边形时，有：312Mmy n --=⎧⎨+=⎩，解得：m =－4，y M =103-，即M (－4，103-)； ③当四边形AMCN 为平行四边形时，有：312Mm y n -=-⎧⎨=+⎩，解得：m =－2，y M =2，即M (－2，2)；综上所述，点M 的坐标为（2，103-）或（﹣4，103-）或（﹣2，2）． 2.（2019·开封模拟）如图，直线y ＝﹣x +4与抛物线y ＝﹣12x 2+bx +c 交于A ，B 两点，点A 在y 轴上，点B 在x 轴上．（1）求抛物线的解析式；（2）在x 轴下方的抛物线上存在一点P ，使得∠ABP ＝90°，求出点P 坐标；（3）点E 是抛物线对称轴上一点，点F 是抛物线上一点，是否存在点E 和点F 使得以点E ，F ，B ，O 为顶点的四边形是平行四边形？若存在，求出点F 的坐标；若不存在，请说明理由．【答案】见解析.【解析】解：（1）在y＝﹣x+4中，当x＝0时，y＝4，当y＝0时，x＝4，即点A、B的坐标分别为（0，4）、（4，0），将（0，4）、（4，0），代入二次函数表达式，并解得：b=1，c=4，抛物线的解析式为：y＝﹣12x2+x+4；（2）∵OA＝OB＝4，∴∠ABO＝45°，∵∠ABP＝90°，则∠PBO=45°，若直线PB交y轴于点M，则OM=OB=4，可得直线BP的解析式为：y=x－4，联立：y=x－4，y＝﹣12x2+x+4，得：x=4，y=0(即B点)；x=－4，y=－8，即P(－4，－8).（3）存在；由y＝﹣12x2+x+4知抛物线的对称轴为：x=1，设E(1，m)，F(n，﹣12n2+n+4)，O(0,0)，B(4,0)，①当四边形OBEF是平行四边形时，有：EF=4，∴n-1=-4，即n=-3，F点坐标为（-3，72 -）；②当四边形OBFE是平行四边形时，有：EF=4，n-1=4，即n=5，F点坐标为（5，72 -）；③当四边形OFBE 是平行四边形时，有：410Fn m y =+⎧⎨=+⎩,即n =3，F 点坐标为（3，52）；综上所述：点F 的坐标为（5，72-），（﹣3，72-），（3，52）． 3.（2019·开封二模）如图，抛物线y ＝ax 2+bx +2与直线y ＝﹣x 交第二象限于点E ，与x 轴交于A （﹣3，0），B 两点，与y 轴交于点C ，EC ∥x 轴．（1）求抛物线的解析式；（2）如果点N 是抛物线对称轴上的一个动点，抛物线上存在一动点M ，若以M ，A ，C ，N 为顶点的四边形是平行四边形，请直接写出所有满足条件的点M 的坐标．【答案】见解析.【解析】解：（1）由题意知：A （﹣3，0），C （0，2），EC ∥x 轴 ∴点E 的纵坐标为2， ∵点E 在直线y ＝﹣x 上， ∴点E （﹣2，2），∵将A （﹣3，0）、E （﹣2，2）代入y ＝ax 2+bx +2，得：93204222a b a b -+=⎧⎨-+=⎩，解得：2343a b ⎧=-⎪⎪⎨⎪=-⎪⎩抛物线的解析式为：224233y x x =--+；（2）由224233y x x =--+知，抛物线的对称轴为x =－1，设N (－1，n )，M (m ，224233m m --+)，∵A （﹣3，0），C （0，2），（1）当四边形ACNM 是平行四边形时，有：312Mm n y --=⎧⎨=+⎩，得：m =－4，y M = 103-；即M (－4，103-). （2）当四边形ACMN 是平行四边形时，有：312Mm n y -+=-⎧⎨+=⎩，得：m =2，y M = 103-；即M (2，103-). （3）当四边形ANCM 是平行四边形时，有：312Mmn y -=-+⎧⎨=+⎩，得：m =－2，y M = 2；即M (－2，2).综上所述，M 点的坐标是(－4，103-)，(2，103-)，(－2，2). 4.（2019·名校模考）如图，抛物线y ＝ax 2+bx ﹣1（a ≠0）交x 轴于A ，B （1，0）两点，交y 轴于点C ，一次函数y ＝x +3的图象交坐标轴于A ，D 两点，E 为直线AD 上一点，作EF ⊥x 轴，交抛物线于点F（1）求抛物线的解析式；（2）在平面直角坐标系内存在点G ，使得G ，E ，D ，C 为顶点的四边形为菱形，请直接写出点G 的坐标．【答案】见解析．【解析】解：（1）将y ＝0代入y ＝x +3，得x ＝﹣3．∴A（﹣3，0）．∵抛物线y＝ax2+bx﹣1交x轴于A（﹣3，0），B（1，0）两点，∴109310a ba b+-=⎧⎨--=⎩，解得：1323ab⎧=⎪⎪⎨⎪=⎪⎩抛物线的解析式为y＝13x2+23x﹣1；（2）点G的坐标为（2，1），（﹣，﹣1），（﹣1），（﹣4，3）．①当四边形DCEG是菱形时，CD=CE=EG=4，设E(m，m+3)，则G（m，m+7），由C(0，－1)，E(m，m+3)，得：CE2=m2+(m+4)2=16，解得：m=0（舍）或m=－4，此时G(－4,3)；②当四边形DCGE是菱形时，CG2=16,设E(m，m+3)，则G（m，m－1），即m2+ m2=16，解得：m=m=－此时，G(1)或G(－－1)；③当四边形DGCE是菱形时，设E(m，m+3)，则G（－m，－m－1），此时E在CD的垂直平分线上，即m+3=1，m=－2，此时G(2，1);综上所述，点G的坐标为：(－4,3)、(1)、(－－1)、(2，1).5.（2019·枫杨外国语三模）（2019·枫杨外国语三模）如图，抛物线y＝﹣x2+bx+c与x轴交于A、B两点，与y轴交于点C，点A的坐标为(-1，0)，点C的坐标为(0，3)，点D和点C关于抛物线的对称轴对称，直线AD与y轴交于点E．（1）求抛物线的解析式；（2）点M是抛物线的顶点，点P是y轴上一点，点Q是坐标平面内一点，以A，M，P，Q为顶点的四边形是以AM为边的矩形．若点T和点Q关于AM所在直线对称，求点T的坐标．【答案】见解析.【解析】解：（1）将(-1，0)，(0，3)代入y＝﹣x2+bx+c，得：－1－b+c=0，c=3，解得：b=2，c=3，即抛物线的解析式为：y＝﹣x2+2x+3.（2）由y＝﹣x2+2x+3知，点M(1，4)，分两种情况讨论，①当四边形MAPQ是矩形时，过M作MH⊥x轴于H，则MH=4，AH=2，易证得：∠APO=∠MAH，∴tan∠APO= tan∠MAH，即OA MHOP AH=2，∴OP=12，即P（0，－12），由A(-1，0)、M(1，4)，P（0，－12）得：点Q坐标为（2，72），∵点T和点Q关于AM所在直线对称，即点Q与点T关于点M(1，4)对称，∴T(0，92 )；②当四边形AMPQ是矩形时，同理可得：T(0，12 -)；综上所述，点T的坐标为(0，92)，(0，12-).6.（2019·焦作二模）如图，在平面直角坐标系中，一次函数y=x+b的图象经过点A(-2，0)，与反比例函数kyx=（x>0）的图象交于点B(a，4).（1）求一次函数和反比例函数的表达式；（2）设M是直线AB上一点，过M作MN∥x轴，交反比例函数kyx=（x>0）的图象于点N，若以A，O，M，N为顶点的四边形是平行四边形，求点M的横坐标.【答案】见解析.【解析】解：（1）将A(-2,0)代入y=x+b，得：b=2，即一次函数的解析式为：y=x+2，将B(a，4)代入y=x+2，得：a=2，即B(2，4),将B(2，4)代入kyx=得：x=8，即反比例函数的解析式为：8 yx =.（2）设M(m，m+2)，则N(82m+，m+2)，由题意知，MN∥OA，则需MN=OA=2时，以A，O，M，N为顶点的四边形是平行四边形，∴82mm-+=2，解得：m=2或m=－2（舍）或m=m=－（舍），∴点M的坐标为：（2，+2）.7.（2019·许昌月考）如图1，二次函数y=43x2+bx+c的图象与x轴交于A（3，0），B（﹣1，0）两点，与y轴交于点C．（1）求该二次函数的解析式；（2）设该抛物线的顶点为D，求△ACD的面积（请在图1中探索）；（3）若点P，Q同时从A点出发，都以每秒1个单位长度的速度分别沿AB，AC边运动，其中一点到达端点时，另一点也随之停止运动，当P，Q运动到t秒时，△APQ沿PQ所在的直线翻折，点A恰好落在抛物线上E点处，请直接判定此时四边形APEQ的形状，并求出E点坐标（请在图2中探索）．图1 图2【答案】见解析．【解析】解：（1）∵二次函数y=43x2+bx+c的图象与x轴交于A（3，0），B（﹣1，0），∴493034103b cb c⎧⨯++=⎪⎪⎨⎪⨯-+=⎪⎩，解得：834bc⎧=-⎪⎨⎪=-⎩，即抛物线的解析式为：y=43x2﹣83x﹣4；（2）过点D作DM⊥y轴于点M，y =43x 2﹣83x ﹣4 =43（x ﹣1）2﹣163， ∴点D （1，﹣163）、点C （0，﹣4）， S △ACD =S 梯形AOMD ﹣S △CDM ﹣S △AOC=12×（1+3）×163﹣12×（163﹣4）×1﹣12×3×4 =4；（3）四边形APEQ 为菱形，理由如下：E 点关于PQ 与A 点对称，过点Q 作QF ⊥AP 于F ，由折叠性质知： AP =EP ，AQ =EQ ∵AP =AQ =t ， ∴AP =AQ =QE =EP ， ∴四边形AQEP 为菱形， ∵FQ ∥OC ，∴AF FQ AQOA OC AC ==， ∴345AF FQ t ==∴AF =35t ，FQ =45t ，Q （3﹣35t ，﹣45t ），E （3﹣35t ﹣t ，﹣45t ），∵E 在二次函数y =43x 2﹣83x ﹣4上，∴﹣45t =43（3﹣85t ）2﹣83（3﹣85t ）﹣4，∴t =14564或t =0（舍去）， ∴E （﹣58，﹣2916）．8.（2018·新乡一模）如图，一次函数122y x =-+分别交y 、x 轴于A 、B 两点，抛物线2y x bx c=-++过A ，B 两点.（1）求这个抛物线的解析式；（2）作垂直于x 轴的直线x ＝t ，在第一象限交直线AB 于M ，交这个抛物线于N . 求当t 取何值时，MN 有最大值？最大值是多少？（3）在(2)的情况下，以A ，M 、N 、D 为顶点作平行四边形，直接写出第四个顶点D 的坐标.【答案】见解析【解析】解：（1）在122y x =-+得，当x =0时，y =2；y =0时，x =4，即A （0，2），B （4，0），把A (0，2)，B (4，0)代入2y x bx c =-++，得： 21640c b c =⎧⎨++=⎩-，解得722b c ⎧=⎪⎨⎪=⎩， ∴抛物线解析式为2722y x x =-++. （2）由题意知，1(,2)2M t t -+，27(,2)2N t t t -++，∴MN =2712(2)22t t t -++--+=2(2)4t --+， ∴当t =2时，MN 有最大值4.（3）根据平行四边形的性质，得：D 点坐标为：（0，6），（0，-2）或（4，4）.9.（2019·周口二模）如图，在平面直角坐标系中，抛物线y =ax 2+bx +4与x 轴交于A (-1，0)，B (4，0)两点，与y 轴交于点C ．（1）求这个抛物线的解析式；（2）设E 是该抛物线上位于对称轴右侧的一个动点，过点E 作x 轴的平行线交抛物线于另一点F ，过点E 作EH ⊥x 轴于点H ，再过点F 作FG ⊥x 轴于点G ，得到矩形EFGH ．在点E 的运动过程中，当矩形EFGH 为正方形时，直接写出该正方形的边长．【答案】见解析.【解析】解：（1）∵抛物线y =ax 2+bx +4与x 轴交于A (-1，0)，B (4，0)两点，∴4016440a b a b -+=⎧⎨++=⎩，解得：13a b =-⎧⎨=⎩，即抛物线的解析式为：y =－x 2+3x +4. （2）∵四边形EFGH 是矩形，∴当EF =EH 时，四边形EFGH 是正方形，设E(m, －m2+3m+4)，则F(3－m，－m2+3m+4)，m>32，∴EF=2m－3，EH=|－m2+3m+4|，∴2m－3=|－m2+3m+4|，解得：m或m（舍）或m或m（舍）∴正方形的边长EF2，综上所述，正方形EFGH的边长为：2.10.（2019·郑州一中模拟）如图所示，平面直角坐标系中直线y=x+1交坐标轴于点A、D两点，抛物线y=ax2+bx－3经过A、C两点，点C坐标为（a，5）. 点M为直线AC上一点，过点M作x轴的垂线，垂足为F，交抛物线于点N.（1）求抛物线解析式；（2）是否存在点M，使得以点D、E、M、N为顶点的四边形为平行四边形，如果有，求点M的坐标，如果没有，请说明理由.【解析】解：∵直线y =x +1交坐标轴于点A 、D 两点， ∴A (－1,0)，D (0，1)，∵点C （a ，5）在直线y =x +1上， ∴a =4，即C (4,5)，将A (－1,0)，C (4,5)代入y =ax 2+bx －3得：3016435a b a b --=⎧⎨+-=⎩，解得：12a b =⎧⎨=-⎩， ∴抛物线的解析式为：y =x 2－2x －3. （2）存在，E （0，－3），∴DE =4，由题意知：DE ∥MN ，∴当DE =MN =4时，四边形DENM 是平行四边形，设N (m , m 2－2m －3)，则M (m , m +1)， ∴| m +1-（m 2－2m －3）|=4，解得：m =0（舍）或m =3或m =或m = ，综上所述，点M 的坐标为：（3,4），，）.11.（2019·郑州模拟）如图，已知二次函数23234y ax a x ⎛⎫=--+ ⎪⎝⎭的图象经过点A (4,0),与y 轴交于点B ，在x 轴上有一动点C (m ,0) （0<m <4），过点C 作x 轴的垂线交直线AB 于点E ，交该二次函数图象于点D .（1）求a 的值和直线AB 的解析式；（2）过点D 作DF ⊥AB 于点F ，设△ACE ，△DEF 的面积分别为S 1，S 2，若S 1=4S 2，求m 的值；（3）点H 是该二次函数图象上第一象限内的动点，点G 是线段AB 上的动点，当四边形DEGH 是平行四边形，且平行四边形DEGH 的周长取最大值时，求点G 的坐标.【答案】见解析.【解析】解：（1）将A (4,0)代入23234y ax a x ⎛⎫=--+ ⎪⎝⎭得：a =34-，∴抛物线的解析式为：239344y x x =-++，设直线AB 的解析式为：y =kx +b ， ∴4k +b =0，b =3，即k =34-，b =3， ∴直线AB 的解析式为：y =34-x +3. （2）∵点C 的横坐标为m ，∴D (m , 239344m m -++)，E (m , 34-m +3)，AC =4－m ，DE =239344m m -++－(34-m +3)= 2334m m -+，∵BC ∥y 轴， ∴43AC OA CE OB ==，即443m CE -=， ∴CE =()344m -，AE =()544m -， ∵∠DF A =∠DCA =90°，∠DBF =∠AEC ， ∴△DFE ∽△ACE ， ∵S 1=4S 2， ∴AE =2DE ，即()544m -=2（2334m m -+），解得：m =4（舍）或m =56，即m 的值为56.（3）如图，过点G 作GM ⊥DC 于M ，设G 、H 点横坐标为n ，由DE =2334m m -+，得GH =2334n n -+，2334m m -+=2334n n -+，得：m =n （舍）或n =4－m ，∴MG =4-2m ，由45MG EG =得：EG =()5424m -, ∴C 四边形DEGH =2()25342344m m m ⎡⎤--+⎢⎥⎣⎦=23102m m -++=23161236m ⎛⎫--+ ⎪⎝⎭，∴当m =13时，C 最大，此时n =113，即G (113，14)，E (13，114), 由图象可知当E 、G 互换位置时满足题意，即G (13，114),E (113，14)，综上所述，G 点坐标为：(13，114)，(113，14).13.（2018·郑州模拟）如图，抛物线y ＝﹣x 2+bx +c 与x 轴交于点A 和点B （3，0），与y 轴交于点C （0，3），点D 是抛物线的顶点，过点D 作x 轴的垂线，垂足为E ，连接DB ．（1）求此抛物线的解析式及顶点D 的坐标；（2）点M 是抛物线上的动点，设点M 的横坐标为m ． ①当∠MBA ＝∠BDE 时，求点M 的坐标；②过点M 作MN ∥x 轴，与抛物线交于点N ，P 为x 轴上一点，连接PM ，PN ，将△PMN 沿着MN 翻折，得△QMN ，若四边形MPNQ 恰好为正方形，直接写出m 的值．【答案】见解析.【解析】解：（1）将点B（3，0），C（0，3）代入y＝﹣x2+bx+c，并解得：b=2，c=3，∴抛物线的解析式为y＝﹣x2+2x+3．顶点D（1，4）．（2）①过点M作MG⊥x轴于G，连接BM．则∠MGB＝90°，设M（m，﹣m2+2m+3），∴MG＝|﹣m2+2m+3|，BG＝3﹣m，∵DE⊥x轴，D（1，4），B（3，0），∴∠DEB＝90°，DE＝4，OE＝1，BE＝2，∵∠MBA＝∠BDE，∴tan∠MBA＝tan∠BDE＝12，∴2233m mm-++-＝12解得：m=12-或m=32-或m=3（舍）∴满足条件的点M坐标（12-，74）或（32-，94-）；②∵MN∥x轴，∴点M、N关于抛物线的对称轴对称，∵四边形MPNQ是正方形，∴OP＝1，由∠QPM=∠MPO=45°，得：GM＝GP，即|﹣m2+2m+3|＝|1﹣m|，解得：m或m或m或m即满足条件的m.14.（2017·信阳二模）如图，抛物线y=ax2+bx﹣4与x轴交于A（﹣2，0）、B（8，0）两点，与y轴交于点C，连接BC，以BC为一边，点O为对称中心做菱形BDEC，点P是x轴上的一个动点，设点P的坐标为（m，0），过点P作x轴的垂线l交抛物线于点Q．（1）求抛物线的解析式；（2）当点P在线段OB上运动时，直线l分别交BD、BC于点M、N，试探究m为何值时，四边形CQMD 是平行四边形，此时，请判断四边形CQBM的形状，并说明理由．【答案】见解析.【解析】解：（1）将A（﹣2，0）、B（8，0）代入y=ax2+bx﹣4并解得：a=14，b=32-，即抛物线的解析式为：y=14x232-x－4.（2）由y=14x232-x－4知，C(0，－4),由菱形的性质可知：D（0，4），设直线BD的解析式为：y=kx+n，将点B（8,0）、D（0，4）代入得：k=12-,n=4，即直线BD的解析式为：y=12-x+4,由M（m，12-m+4），Q（m，14m232-m－4）．当MQ=DC时，四边形CQMD为平行四边形．∴12-m+4﹣（14m232-m－4）=8，解得m=4或m=0（舍去）．∴MD∥CQ，MD=CQ，M（4，2），∴M为BD的中点，∴MD=MB．∴CQ=MB，又∵MB∥CQ，∴四边形CQBM为平行四边形．。

专题：二次函数中的动点问题(平行四边形存在性问题)

二次函数中的动点问题（二）平行四边形的存在性问题一.技巧提炼如图1,点人（召,开）、3（忑,儿）、C（X3Os）是坐标平面内不在同一直线上的三点。

平面直角坐标系中是否存在点D,使得以A、B、C、D四点为顶点的四边形为平行四边形，如果存在，请求出点D的坐标。

如图2,过A、B、C分别作BC、AC、AB的平行线，则以不在同一直线上的三点为顶点的平行四边形有三个。

由已知的三点坐标可根据图形平移的坐标性质，直接写出第四个顶点的坐标。

3、平面直角坐标系中直线和直线12:当h时k尸k2；当h丄I2时ki-k2=-14、二次函数中平行四边形的存在性问题：解题思路：（1）先分类（2）再画图（3）后计算二、精讲精练1、已知抛物线y=ax-+bx+c与x轴相交于A、E两点（A、B分别在原点的左右两侧），与y轴正半轴相交于C点，且OA：OB：OC=1：3：3,AABC的面积为6,（如图1）（1）求抛物线的解析式：（2）坐标平面内是否存在点M,使得以点M、A、B、C为顶点四边形是平行四边形？若存在，请求出点M的坐标；若不存在，请说明理由；（3）如图2,在直线BC±方的抛物线上是否存在一动点P,ABCP面枳最大？如果存在，求出最人面积,2、如图，己知抛物线经过A(-2,0),B(・3,3)及原点6顶点为C(1)求抛物线的函数解析式：(2)设点D在抛物线上，点E在抛物线的对称轴上，且以AO为边的四边形AODE是平行四边形，求点D的坐标。

【变式练习】7如图，对称轴为直线x二一的抛物线经过点A(6,0)和B(0,4)・2(1)求抛物线解析式及顶点坐标；(2)设点E(x,y)是抛物线上一动点，且位于第四彖限，四边形0EAF是以0A为对角线的平行四边形, 求平行四边形OEAF的面积S与x之间的函数关系式，并写出自变量x的取值范围；①当平行四边形OEAF的面积为24时，请判断平行四边形0EAF是否为菱形？②是否存在点E,使平行四边形0EAF为正方形？若存在，求出点E的坐标；若不存在，请说明理由.、方法规律1、平行四边形模型探究如图1，点&（內,开）、3（七,儿）、C（X3，”）是坐标平面内不在同一直线上的三点。

初中数学_二次函数专题复习—平行四边形存在性问题教学设计学情分析教材分析课后反思

《平行四边形存在性问题》教学设计执教者学情分析本节课是在已经进行过一轮复习，也适当做了一些往年的中考试卷，对于基础知识学生掌握的还是不错的，但对于综合性的题目却感觉困难，特别是动点问题。

对于这类问题存在以下几种情况：1、这类问题无论教师做了多大的努力,对学生来说都比较困难,所以一部分学生放弃作答。

2、一部分学生对动点问题从根本上不理解,勉强照猫画虎,写了不少但不得分。

3、学生对动点问题有一定认识,对分类能进行简单尝试, 但不完整。

针对以上情况，我希望通过本节课的学习，一方面帮助学生树立信心，让他们明白所谓的综合题都是由诸多小知识点组成的，所谓的动态问题可以变为“静”来解决，通过代数解决几何问题另一方面通过例题讲解让学生掌握解决这类题目的解题策略。

效果分析针对学生面临的困难：首先，我在教学时注意层次性，讲究循序渐进，由浅入深，由易到难，不要一步到位，逐步过渡。

其次，注意所选例题的典型性，选了最具代表性的两类动点问题产生的平行四边形形存在性问题，一类一个例题，这样就可由一题推及一类，让学生可触类旁通，达到举一反三的效果。

教学时注重这几个方面：1、利用几何画板动态画图，让学生体会点在运动过程中，图形会跟着发生变化。

在变化的过程中抓住某一瞬间，化“动”为“静”，使其构成平行四边形，再利用所学知识解决问题。

2、注重板书。

通过清晰的板书让学生一目明了如何分析平行四边形存在性问题。

3、注重数学思想方法的渗透。

数学思想方法是数学学科的精髓，是数学素养的重要内容之一，在数学教学和探究活动中始终体现这些数学思想方法，动点问题也不例外，因此，在数学教学中应特别注重这些思想方法的渗透，因为只有让学生充分掌握领会这种思维，才能更有效地运用所学知识，形成求解动点问题的能力。

动点问题中主要体现方程思想，数形结合思想，分类讨论思想等。

方程思想，大多数动点问题到最后都转化为方程形式，然后利用方程来求解。

数形结合思想，动点问题中，所研究的量的几何特征与数量特征紧密结合，体现了数形结合的特征与方法。

平行四边形的应用动点问题

Q
C
合作交流，探索新知
变式1：在四边形ABCD中，AD∥BC,AB⊥AD,
AD=12cm,BC=21cm,,点P从点A以1cm/s的速度向点D
运动，同时点Q从点C以1.5cm/s的速度向点B运动.设运
动时间为t秒．问当t为何值时，以P、D、C、Q为顶点
的四边形是平行四边形？
AP
D
解：依题意得．AP=t，CQ=1.5t.
本节课重点来探究平行四边形的应用之动点问题
动点问题常见的类型有: 单动点型、双动点型及多动点型
如何解动点型问题？
知识回顾
（1）平行四边形的性质：
文字叙述
对称性平行四边形是中心对称图形，对称中心是对角线的交点
边
平行四边形的对边平行且相等
角
平行四边形的对角相等、邻角互补
对角线平行四边形的对角线互相平分（2）平行四边形的判定：
当PD=CQ时，四边形PQCD是平行四边形 B 则 12-t=1.5t，解得 t=4.8
QC
图①
2）若P在BC上，Q在AD上时，如图②
A
依题意得QD=45-1.5t，PC=t-27
QD
当QD=PC时，四边形QPCD是平行四边形
则 45-1.5t=t-27，解得 t=28.8
B
综上所述，存在以P、D、C、Q为顶点的四边
A
P
D
A
QD
B
Q
C
B
PC
图①
图②
探究动点关键：化动为静，分类讨论，关注全过程
合作交流，探索新知
解：（3）存在.
∵tp=(12+15+21) ÷1=48(秒)， tQ=(21+12+12) ÷1.5=30(秒)

初二数学《平行四边形中的动点问题》(附练习及答案)

四边形中的动点问题所谓“动点型问题”是指题设图形中存在一个或多个动点,它们在线段、射线或直线上运动的一类开放性题目。

解决这类问题关键是动中求静,灵活运用有关数学知识。

数学思想：分类思想、函数思想、方程思想、数形结合思想、转化思想，其注重对几何图形运动变化能力的考查。

这类类问题从变换的角度和运动变化来研究三角形、四边形、函数图像等图形，通过“对称、动点的运动”等研究手段和方法，来探索与发现图形性质及图形变化，在解题过程中渗透空间观念和合情推理。

选择基本的几何图形，让学生经历探索的过程，以能力立意，考查自主探究能力，促进培养学生解决问题的能力。

解决这类问题首先要在动点的运动过程中观察图形的变化情况，需要画出图形在不同位置的情况，才能做好计算推理的过程；其次在变化中找到不变量的性质是解决数学“动点”探究题的基本思路,这也是动态几何数学问题中最核心的数学本质。

动点问题题型方法归纳：动态几何特点----问题背景是特殊图形，考查问题也是特殊图形，所以要把握好一般与特殊的关系；分析过程中，特别要关注图形的特性（特殊角、特殊图形的性质、图形的特殊位置。

）动点问题一直是中考热点，近几年考查探究运动中的特殊性：等腰三角形、直角三角形、相似三角形、平行四边形、梯形、特殊角或其三角函数、线段或面积的最值。

下面就四边形中的动点问题的常见题型作简单介绍，解题方法、关键给以点拨。

1、如图，把矩形ABCD沿EF翻折，点B恰好落在AD边的B′处，若AE＝2，DE＝6，∠EFB ＝60°，则矩形ABCD的面积是_____________2、如图，在四边形ABCD中，对角线AC⊥BD，垂足为O，点E，F，G，H分别为边AD，AB，BC，CD的中点．若AC＝8，BD＝6，则四边形EFGH 的面积为________（第1题）（第2题）（第3题）3、如图，正方形ABCD的边长为4，点P在DC边上，且DP＝1，点Q是AC上一动点，则DQ＋PQ的最小值为____________4、如图，在Rt△ABC中，∠B＝90°，AC＝60 cm，∠A＝60°，点D从点C出发沿CA方向以4 cm/s的速度向点A匀速运动，同时点E从点A出发沿AB方向以2 cm/s的速度向点B匀速运动，当其中一个点到达终点时，另一个点也随之停止运动．设点D，E运动的时间是t s(0 < t ≤15)．过点D作DF⊥BC于点F，连接DE，EF.(1)求证：AE＝DF；(2)四边形AEFD能够成为菱形吗？如果能，求出相应的t值；如果不能，请说明理由；(3)当t为何值时，△DEF为直角三角形？请说明理由5、如图，在等边三角形ABC中，BC=6cm．射线AG∥BC，点E从点A出发沿射线AG以1cm/s 的速度运动，同时点F从点B出发沿射线BC以2cm/s的速度运动，设运动时间为t（s）；（1）连接EF，当EF经过AC边的中点D时，求证：△ADE≌△CDF；（2）求当t为何值时，四边形ACFE是菱形；（3）是否存在某一时刻t，使以A、F、C、E为顶点的四边形内角出现直角？若存在，求出t的值；若不存在，请说明理由．6、在菱形ABCD中，∠B=60°，点E在射线BC上运动，∠EAF=60°，点F在射线CD上（1）当点E在线段BC上时（如图1），（1）求证：EC+CF=AB；（2）当点E在BC的延长线上时（如图2），线段EC、CF、AB有怎样的相等关系？写出你的猜想，不需证明7、如图，在菱形ABCD中，AB=2，∠DAB=60°，点E是AD边的中点．点M是AB边上一动点（不与点A重合），延长ME交射线CD于点N，连接MD、AN．（1）求证：四边形AMDN是平行四边形；（2）填空：①当AM的值为______时，四边形AMDN是矩形；②当AM的值为______时，四边形AMDN是菱形．8、如图，△ABC中，点O是边AC上一个动点，过O作直线MN∥BC，设MN交∠BCA的平分线于点E，交∠BCA的外角平分线于点F．（1）探究：线段OE与OF的数量关系并加以证明；（2）当点O运动到何处，且△ABC满足什么条件时，四边形AECF是正方形？（3）当点O在边AC上运动时，四边形BCFE会是菱形吗？若是，请证明，若不是，则说明理由．9、如图，已知菱形ABCD中，∠ABC=60°，AB=8，过线段BD上的一个动点P（不与B、D重合）分别向直线AB、AD作垂线，垂足分别为E、F．（1）BD的长是______；（2）连接PC，当PE+PF+PC取得最小值时，此时PB的长是______（第9题）（第10题）10、如图，∠MON=90°，矩形ABCD的顶点A、B分别在边OM，ON上，当B在边ON上运动时，A随之在OM上运动，矩形ABCD的形状保持不变，其中AB=2，BC=1，运动过程中，点D到点O的最大距离为______．11、如图，已知矩形ABCD，AD=4，CD=10，P是AB上一动点，M、N、E分别是PD、PC、CD 的中点．（1）求证：四边形PMEN是平行四边形；（2）请直接写出当AP为何值时，四边形PMEN是菱形；（3）四边形PMEN有可能是矩形吗？若有可能，求AP的长；若不可能，请说明理由．12、如图，在平行四边形ABCD中，对角线BD=12cm，AC=16cm，AC，BD相交于点O，若E，F 是AC上两动点，分别从A，C两点以相同的速度向C、A运动，其速度为0.5cm／s。

特殊平行四边形动点问题

特殊四边形：动点问题题型一：1．已知直角梯形ABCD 中,AD ∥BC ,AB ⊥BC ,AD =2,BC =DC =5,点P 在BC 上移动,则当PA +PD 取最小值时,△APD 中边AP 上的高为A 、17172B 、17174C 、 17178D 、3 2.如图4,在梯形ABCD 中,AD ∥BC ,AD ＝6,BC ＝16,E 是BC 的中点.点P 以每秒1个单位长度的速度从点A 出发,沿AD 向点D 运动；点Q 同时以每秒2个单位长度的速度从点C 出发,沿CB 向点B 运动.点P 停止运动时,点Q 也随之停止运动.当运动时间t ＝秒时,以点P ,Q ,E ,D 为顶点的四边形是平行四边形.3．如图,在梯形ABCD 中,AD ∥BC,E 是BC 的中点,AD=5,BC=12,CD=42,∠C=045,点P 是BC 边上一动点,设PB 长为x.1当x 的值为时,以点P 、A 、D 、E 为顶点的四边形为直角梯形. 2当x 的值为时,以点P 、A 、D 、E 为顶点的四边形为平行四边形.3点P 在BC 边上运动的过程中,以点P 、A 、D 、E 为顶点的四边形能否构成菱形试说明理由.4.在一个等腰梯形ABCD 中,AD1.t 为何值时,四边形ABQP 为平行四边形2.四边形ABQP 能为等腰梯形吗如果能,求出t 的值,如果不能,请说明理由;6.梯形ABCD 中,AD ∥BC,∠B=90°,AD=24cm,AB=8cm,BC=26cm,动点P 从点A 开始,沿AD 边,以1厘米/秒的速度向点D 运动；动点Q 从点C 开始,沿CB 边,以3厘米/秒的速度向B 点运动;已知P 、Q 两点分别从A 、C 同时出发,,当其中一点到达端点时,另一点也随之停止运动;假设运动时间为t 秒,问：1t 为何值时,四边形PQCD 是平行四边形2在某个时刻,四边形PQCD 可能是菱形吗为什么3t 为何值时,四边形PQCD 是直角梯形4t 为何值时,四边形PQCD 是等腰梯形5 t 为何值时, APQ 是等腰三角形7．如图,在直角梯形ABCD 中,∠B=90°,AD ‖BC,且AD=4cm,AB=8cm,DC=10cm;若动点P 从点A 出发,以每秒4cm 的速度沿线段AD 、DC 向C 点运动；动点Q 从C 点以每秒5cm 的速度沿CB 向B 点运动;当Q 点到达B 点时,动点P 、Q 同时停止运动;设P 、Q 同时出发,并运动了t 秒; 1直角梯形ABCD 的面积为__________cm 的平方.2当t=________秒时,四边形PQCD 为平行四边形;3当t=________秒时,PQ=DC4是否存在t,使得P 点在线段DC 上,且PQ ⊥DC 如图2所示若存在,列出方程求出此时的t ；若不存在,请说明理由;8．如图,在直角梯形ABCD 中,∠B=90°,AB ‖CD,且AB=4cm,BC=8cm,DC=10cm;若动点P 从点A 出发,以每秒1cm 的速度沿线段AB 、BC 向C 点运动；动点Q 从C 点以每秒1cm 的速度沿CB 向B 点运动;当Q 点到达B 点时,动点P 、Q 同时停止运动;设P 、Q 同时出发,并运动了t 秒; 1直角梯形ABCD 的面积为__________cm 的平方.2当t=________秒时,四边形PBCQ 为平行四边形;3当t=________秒时,PQ=BC.10. 如图,在等腰梯形ABCD 中,AB ∥CD,其中AB=12 cm,CD=6cm ,梯形的高为4,点P 从开始沿AB 边向点B 以每秒3cm 的速度移动,点Q 从开始沿CD 边向点D 以每秒1cm 的速度移动,如果点P 、Q 分别从A 、C 同时出发,当其中一点到达终点时运动停止;设运动时间为t 秒; 1求证：当t 为何值时,四边形APQD 是平行四边形；2PQ 是否可能平分对角线BD 若能,求出当t 为何值时PQ 平分BD ；若不能,请说明理由； 3若△DPQ 是以PQ 为腰的等腰三角形,求t 的值;11.如图,在直角梯形ABCD 中,AB1求CD 的长;2当四边形PBQD 为平行四边形时,求四边形PBQD 的周长；3在点P,点Q 的运动过程中,是否存在某一时刻,使得ΔBPQ 的面积为20cm 2若存在,请求出所有满足条件的t 的值；若不存在,请说明理由;13. 已知,矩形ABCD 中,4AB cm =,8BC cm =,AC 的垂直平分线EF 分别交AD 、BC 于点E 、F ,垂足为O .1如图10-1,连接AF 、CE .求证四边形AFCE 为菱形,并求AF 的长；2如图10-2,动点P 、Q 分别从A 、C 两点同时出发,沿AFB ∆和CDE ∆各边匀速运动一周.即点P 自A →F →B →A 停止,点Q 自C →D →E →C 停止.在运动过程中,①已知点P 的速度为每秒5cm ,点Q 的速度为每秒4cm ,运动时间为t 秒,当A 、C 、P 、Q 四点为顶点的四边形是平行四边形时,求t 的值.②若点P 、Q 的运动路程分别为a 、b 单位:cm ,0ab ≠,已知A 、C 、P 、Q 四点为顶点的四边形是平行四边形,求a 与b 满足的数量关系式.14.已知：如图,在梯形ABCD 中,AB ∥DC,∠B=90°,BC=8cm,CD=24cm,AB=26Cm,点P 从C 出发,以1cm/s 的速度向D 运动,点Q 从A 出发,以3cm/s 的速度向B 运动,其中一动点达到端点时,另一动点随之停止运动．从运动开始．1经过多少时间,四边形AQPD 是平行四边形2经过多少时间,四边形AQPD 成为等腰梯形3在运动过程中,P 、Q 、B 、C 四点有可能构成正方形吗为什么A BC D EF 图10-1 O 图10-2 备用图如图,在梯形ABCD 中,AD ∥BC,∠B=90°,AD=16cm,AB=12cm,BC=21cm,动点P 从点B 出发,沿射线BC 的方向以每秒2cm 的速度运动,动点Q 从点A 出发,在线段AD 上以每秒1cm 的速度向点D 运动,点P,Q 分别从点B,A 同时出发,当点Q 运动到点D 时,点P 随之停止运动,设运动的时间为t 秒．①当t 为何值时,四边形PQDC 是平行四边形；②当t 为何值时,以C,D,Q,P 为顶点的梯形面积等于60cm 2 ③是否存在点P,使△PQD 是等腰三角形若存在,请求出所有满足要求的t 的值,若不存在,请说明理由． 15.如图,在梯形ABCD 中,AD ∥BC,AD=6,DC=10,AB=65,∠B=45°．动点M 从B 点出发沿线段BC 以每秒2个单位长度的速度向终点C 运动；动点N 同时从C 点出发沿线段CD 以每秒1个单位长度的速度向终点D 运动．设运动的时间为t 秒．16.1求BC 的长．17.2当MN ∥AB 时,求t 的值．18.3△MNC 可能为等腰三角形吗若能,请求出t 的值；若不能,请说明理由．（4）△MNC 可能为直角三角形吗若能,请求出t 的值；若不能,请说明理由．（5）△MNC 为20时,请求出t 的值．如图,直角梯形ABCD 中,AB ∥CD,∠A=90°,AB=34,AD=4,DC=234 ,点P 从点A 出发沿折线段AD-DC-CB 以每秒3个单位长的速度向点B 匀速运动,同时,点Q 从点A 出发沿射线AB 方向以每秒2个单位长的速度匀速运动,当点P 与点B 重合时停止运动,点Q 也随之停止,设点P,Q 的运动时间是t 秒t ＞0．1当点P 到达终点B 时,求t 的值；2设△APQ 的面积为S,分别求出点P 运动到AD 、CD 上时,S 与t 的函数关系式；3当t 为何值时,能使PQ ∥DB ；4当t 为何值时,能使P 、Q 、D 、B 四点构成的四边形是平行四边形;16.如图,在等腰梯形ABCD 中,AD ∥BC,AB=DC=60,AD=75,BC=135．点P 从点B 出发沿折线段BA-AD-DC 以每秒5个单位长的速度向点C 匀速运动；点Q 从点C 出发沿线段CB 方向以每秒3个单位长的速度匀速运动,过点Q 向上作射线QK ⊥BC,交折线段CD-DA-AB 于点E ．点P 、Q 同时开始运动,当点P 与点C 重合时停止运动,点Q 也随之停止．设点P 、Q 运动的时间是t 秒t ＞0．1当点P 到达终点C 时,求t 的值,并指出此时BQ 的长；2当点P 运动到AD 上时,t 为何值能使PQ ∥DC ；3设射线QK 扫过梯形ABCD 的面积为S,分别求出点E 运动到CD 、DA 上时,S 与t 的函数关系式；不必写出t 的取值范围4△PQE 能否成为直角三角形若能,写出t 的取值范围；若不能,请说明理由．17.如图,直角梯形ABCD 中,AD ∥BC,∠ABC=90°,已知AD=AB=3,BC=33,动点P 从B 点出发,沿线段BC 向点C 作匀速运动；动点Q 从点D 出发,沿线段DA 向点A 作匀速运动．过Q 点垂直于AD 的射线交AC 于点M,交BC 于点N ．P 、Q 两点同时出发,速度都为每秒1个单位长度．当Q 点运动到A 点,P 、Q 两点同时停止运动．设点Q 运动的时间为t 秒．1求NC,MC 的长用t 的代数式表示；2当t 为何值时,四边形PCDQ 构成平行四边形3当t 为何值时,射线QN 恰好将△ABC 的面积平分并判断此时△ABC 的周长是否也被射线QN 平分．19.如图,已知直角梯形ABCD 中,AD ∥BC,AB ⊥BC,AD=2,AB=8,CD=10．1求梯形ABCD 的面积S ；2动点P 从点B 出发,以2cm/s 的速度、沿B →A →D →C 方向,向点C 运动；动点Q 从点C 出发,以2cm/s 的速度、沿C →D →A 方向,向点A 运动．若P 、Q 两点同时出发,当其中一点到达目的地时整个运动随之结束,设运动时间为t 秒．问：①当点P 在B →A 上运动时,是否存在这样的t,使得直线PQ 将梯形ABCD 的周长平分若存在,请求出t 的值,并判断此时PQ 是否平分梯形ABCD 的面积；若不存在,请说明理由；②在运动过程中,是否存在这样的t,使得以P 、D 、Q 为顶点的三角形恰好是以DQ 为一腰的等腰三角形若存在,请求出所有符合条件的t 的值；若不存在,请说明理由．20.在直角梯形ABCD 中,∠C=90°,高CD=6cm,底BC=10cm 如图1．动点Q 从点B 出发,沿BC 运动到点C 停止,运动的速度都是1cm/s ．同时,动点P 也从B 点出发,沿BA →AD 运动到点D 停止,且PQ 始终垂直BC ．设P,Q 同时从点B 出发,运动的时间为ts,点P 运动的路程为ycm ．分别以t,y 为横、纵坐标建立直角坐标系如图2,已知如图中线段为y 与t 的函数的部分图象．经测量点M 与N 的坐标分别为4,5和2, 25．1求M,N 所在直线的解析式；2求梯形ABCD 中边AB 与AD 的长；3写出点P 在AD 边上运动时,y 与t 的函数关系式注明自变量的取值范围,并在图2中补全整运动中y 关于t 的函数关系的大致图象．22.如图,在直角梯形ABCD中,AD∥BC,∠B=90°,AD=6,BC=8,AB=3 3,点M是BC的中点．点P从点M出发沿MB以每秒1个单位长的速度向点B匀速运动,到达点B后立刻以原速度沿BM 返回；点Q从点M出发以每秒1个单位长的速度在射线MC上匀速运动．在点P,Q的运动过程中,以PQ为边作等边三角形EPQ,使它与梯形ABCD在射线BC的同侧．点P,Q同时出发,当点P返回到点M时停止运动,点Q也随之停止．设点P,Q运动的时间是t秒t＞0．23.1设PQ的长为y,在点P从点M向点B运动的过程中,写出y与t之间的函数关系式不必写t的取值范围；24.2当BP=1时,求△EPQ与梯形ABCD重叠部分的面积；已知：如图,在直角梯形COAB中,OC∥AB,∠AOC=90°,AB=4,AO=8,OC=10,以O为原点建立平面直角坐标系,点D为线段BC的中点,动点P从点A出发,以每秒4个单位的速度,沿折线AOCD 向终点C运动,运动时间是t秒．1D点的坐标为；2当t为何值时,△APD是直角三角形；3如果另有一动点Q,从C点出发,沿折线CBA向终点A以每秒5个单位的速度与P点同时运动,当一点到达终点时,两点均停止运动,问：P、C、Q、A四点围成的四边形的面积能否为28如果可能,求出对应的t；如果不可能,请说明理由．在梯形ABCO中,OC∥AB,以O为原点建立平面直角坐标系,A、B、C三点的坐标分别是A8,0,B8,10,C0,4．点D4,7为线段BC的中点,动点P从O点出发,以每秒1个单位的速度,沿折线OAB的路线运动,运动时间为t秒．1求直线BC的解析式；2设△OPD的面积为s,求出s与t的函数关系式,并指出自变量t的取值范围；33当t为何值时,△OPD的面积是梯形OABC的面积的8如图,在直角梯形COAB中,CB∥OA,以O为原点建立直角坐标系,A、C的坐标分别为A10,0、C0,8,CB=4,D为OA中点,动点P自A点出发沿A→B→C→O的线路移动,速度为1个单位/秒,移动时间为t秒．1求AB的长,并求当PD将梯形COAB的周长平分时t的值,并指出此时点P在哪条边上；2动点P在从A到B的移动过程中,设△APD的面积为S,试写出S与t的函数关系式,并指出t的取值范围；3几秒后线段PD将梯形COAB的面积分成1：3的两部分求出此时点P的坐标已知直角梯形OABC在如图所示的平面直角坐标系中,AB∥OC,AB=10,OC=22,BC=15,动点M从A点出发,以每秒一个单位长度的速度沿AB向点B运动,同时动点N从C点出发,以每秒2个单位长度的速度沿CO向O点运动．当其中一个动点运动到终点时,两个动点都停止运动．1求B点坐标；2设运动时间为t秒；①当t为何值时,四边形OAMN的面积是梯形OABC面积的一半；②当t为何值时,四边形OAMN的面积最小,并求出最小面积；③若另有一动点P,在点M、N运动的同时,也从点A出发沿AO运动．在②的条件下,PM+PN 的长度也刚好最小,求动点P的速度．如图1,以梯形OABC的顶点O为原点,底边OA所在的直线为轴建立直角坐标系．梯形其它三个顶点坐标分别为：A14,0,B11,4,C3,4,点E以每秒2个单位的速度从O点出发沿射线OA 向A点运动,同时点F以每秒3个单位的速度,从O点出发沿折线OCB向B运动,设运动时间为t．1当t=4秒时,判断四边形COEB是什么样的四边形2当t为何值时,四边形COEF是直角梯形3在运动过程中,四边形COEF能否成为一个菱形若能,请求出t的值；若不能,请简要说明理由,并改变E、F两点中任一个点的运动速度,使E、F运动到某时刻时,四边形COEF 是菱形,并写出改变后的速度及t的值如图,在平面直角坐标系中,四边形OABC为直角梯形,OA∥BC,BC=14,A16,0,C0,2．1如图①,若点P、Q分别从点C、A同时出发,点P以每秒2个单位的速度由C向B运动,点Q以每秒4个单位的速度由A向O运动,当点Q停止运动时,点P也停止运动．设运动时间为t秒0≤t≤4．①求当t为多少时,四边形PQAB为平行四边形②求当t为多少时,直线PQ将梯形OABC分成左右两部分的比为1：2,并求出此时直线PQ 的解析式．2如图②,若点P、Q分别是线段BC、AO上的任意两点不与线段BC、AO的端点重合,且四边形OQPC面积为10,试说明直线PQ一定经过一定点,并求出该定点的坐标．如图,在平面直角坐标系中,直角梯形ABCO的变OC落在x轴的正半轴上,且AB方形ODEF 的两边分别坐落在坐标轴上,且它的面积等于直角梯形ABCO面积,将正方形ODEF沿x轴的正半轴平行移动,设它与直角梯形ABCO的重叠部分面积为S;（1）求正方形ODEF的边长;（2）求OA所在直线的解析式（3）当正方形ODEF移动到顶点O与C重合时,求S的值（4）设正方形ODEF顶点O向右移动的距离为x,当正方形ODEF的边ED与y轴重合时,停止移动,求重叠部分面积S与x的函数关系式;如图,在△ABC中,∠ACB=90°,AC=BC=6cm,等腰RT△DEF中,∠D=90°,EF=在BC所在直线L上,开始时点F与点C重合,让等腰RT△DEF沿直线L向右以每秒1cm的速度做匀速运动,最后点E和点B重合;（1）请直接写出等腰RT△DEF运动6S时与△ABC重叠部分面积（2）设运动时间为xS,运动过程中,等腰RT△DEF与△ABC重叠部分面积为ycm2①在等腰RT△DEF运动6S后至运动停止前这段时间内,求y与x之间的函数关系式②在RT△DEF整个运动过程中,求当x为何值时,y=1/2.题型二：1.如图,正方形ABCD的边长为4cm,两动点P、Q分别同时从D、A出发,以1cm/秒的速度各自沿着DA、AB边向A、B运动;试解答下列各题：1当P出发后多少秒时,三角形PDO为等腰三角形；2当P、Q出发后多少秒,四边形APOQ为正方形；3当P、Q出发后多少秒时,ABCD PQDSS正方形325=∆.2.如图所示,有四个动点P 、Q 、E 、F 分别从正方形ABCD 的四个顶点出发,沿着AB 、BC 、CD 、DA 以同样的速度向B 、C 、D 、A 各点移动;1试判断四边形PQEF 是正方形并证明;2PE 是否总过某一定点,并说明理由;（3）四边形PQEF 的顶点位于何处时,其面积最小,最大各是多少（4）3.已知：如图,边长为a 的菱形ABCD 中,∠DAB=60°,E 是异于A 、D 两点的动点,F 是CD 上的动点;请你判断：无论E 、F 怎样移动,当满足：AE+CF=a 时,△BEF 是什么三角形并说明你的结论;4.如图,四边形ABCD 是正方形,△ABE 是等边三角形,M 为对角线BD 不含B 点上任意一点,将BM 绕点B 逆时针旋转60°得到BN,连接EN 、AM 、CM.⑴ 求证：△AMB ≌△ENB ；⑵ ①当M 点在何处时,AM ＋CM 的值最小；②当M 点在何处时,AM ＋BM ＋CM 的值最小,并说明理由；⑶ 当AM ＋BM ＋CM 的最小值为13 时,求正方形的边长.题型三：1.如图,在直角梯形ABCD 中,AD//BC,∠C ＝90°,BC ＝16,DC ＝12,AD ＝21;动点P 从点D 出发,沿射线DA 的方向以每秒2两个单位长的速度运动,动点Q 从点C 出发,在线段CB 上以每秒1个单位长的速度向点B 运动,点P,Q 分别从点D,C 同时出发,当点Q 运动到点B 时,点P 随之停止运动;设运动的时间为t 秒;（1）设▲BPQ 的面积为S,求S 与t 之间的函数关系式;（2）当t 为何值时,四边形ABPQ 平行四边形3当t 为何值时,以B 、P 、Q 三点为顶点的三角形是等腰三角形4是否存在时刻t,使得PQ ⊥BD 若存在,求出t 的值；若不存在,请说明理由;E A DB C N M2.如图①,在等腰梯形ABCD中,AD边长为6的菱形ABCD中,动点M从点A出发,沿A→B→C向终点C运动,连接DM交AC于点N．1如图25－1,当点M在AB边上时,连接BN．△≌△；①求证：ABN ADN②若∠ABC = 60°,AM = 4,∠ABN =α,求点M到AD的距离及tanα的值；2如图25－2,若∠ABC = 90°,记点M运动所经过的路程为x6≤x≤12．试问：x为何值时,△ADN为等腰三角形．4．在正方形ABCD中,M是边BC中点,E是边AB上的一个动点,MF⊥ME,MF交射线CD于点F,AB=4,BE=x,CF=y1求y关于x的解析式及定义域2当点F在边CD上时,四边形AEFD的周长是否随点E的运动而发生变化请说明理由3当DF=1时,求点A到直线EF的距离;5.如图1,在等腰梯形ABCD中,AD‖BC,E是AB的中点,过点E作EF‖BC交CD于点F;AB=4,BC=6,∠B=60°1求点E到BC的距离;2点P为线段EF上的一个动点,过点P作PM⊥EF交BC于点M,过M作MN‖AB交折线ADC于点N,连接PN,设EP=x.①当点N在线段AD上时,△PMN的形状是否发生改变若不变,求出△PMN的周长,若改变,说明理由.②当点N在线段DC上时,是否存在点P,使△PMN为等腰三角形若存在,请求出所有满足要求的x的值,若不存在,说明理由.6.在平行四边形ABCD中,AD=4cm,∠A=60°,BD⊥AD;一动点P从A出发以每秒1cm的速度沿A-B-C的路线做匀速运动,过点P做直线PM,使PM⊥AD;当点P运动2秒时,另一动点Q也从A 出发沿A-B-C的路线运动,且在AB上以每秒1cm的速度匀速运动,在BC上以每秒2cm的速度匀速运动;过Q做直线QN,使QN∥PM;设点Q的运动时间为t秒0≤t≤10,直线PM与QN截平cm行四边形所得图形的面积为S2①求S关于t的函数关系式；②求S的最大值;7.菱形ABCD中∠A=60°,边长为4CM,动点P从A出发,以1CM/秒的速度沿A-B-C的路线运动,在点P出发1秒后,点Q以同样的速度,沿同样的路径运动,过点P、Q的直线L1、L2互相平行,且都与AB边所在的直线成60°角,设点P运动的时间是X1≤X≤8秒,直线L1、L2在菱形上截出的图形周长为Y厘米1求Y与X的函数关系;2当X取何值时,Y的值最大最大值是多少8．如图,在矩形ABCD中,AB＝12cm,BC＝8cm,点E、F、G分别从点A、B、C三点同时出发,沿矩形的边按逆时针方向移动,点E、G的速度均为2cm/s,点F的速度为4cm/s,当点F追上点G即点F与点G重合时,三个点随之停止移动．设移动开始后第t秒时,△EF G的面积为Scm2．1当t＝1秒时,S的值是多少2写出S和t之间的函数解析式,并指出自变量t的取值范围．。

有关平行四边形的动点问题

有关平行四边形的动点问题
平行四边形是由两组相邻的平行线和它们之间的四条线段组成的四边形。

在平行四边形中，我们可以考虑一个点在它沿着一个方向移动的同时，沿着另一个方向的轨迹。

这个点被称为“动点”。

如果动点沿着平行四边形的一条边上移动，那么它所相应的高度和底边也会相应地改变。

因此，如果我们将平行四边形分成许多小长方形，并在这些小长方形的顶点处放置动点，则可以形成一条光滑的曲线。

这个曲线被称为平行四边形的“径线”。

如果动点同时沿着两个方向移动，则可以得到一个新的曲线，称为“余弦曲线”。

这个曲线看起来像是一个上下波动的曲线，与平行四边形的一条对角线平行。

有趣的是，这两个曲线都是周期性的，其周期等于平行四边形的面积除以它沿着这个方向的速度。

因此，我们可以通过这些曲线来计算平行四边形的面积和周长。

通过研究这些平行四边形的动点问题，我们能够深入了解其内在的几何性质和性质之间的相互关系。

这不仅有助于帮助我们更好地理解平行四边形，还可以为其他更复杂的几何形状和问题提供有用的洞见和启示。

平行四边形的动点问题

平行四边形的动点问题1. 平行四边形是指具有两对相对平行的边的四边形。

在这个问题中，我们关注一个动点在平行四边形内移动的情况。

2. 首先，让我们定义平行四边形的四个顶点为A、B、C和D，并假设它们按顺时针方向排列。

我们还假设动点记为P，并且它可以在平行四边形内的任意位置移动。

3. 问题的第一部分是，如果动点P从A点出发，按一定路径移动，最后回到A点，那么它经过的路径会是什么样子4. 要回答这个问题，我们需要注意到平行四边形的两对相对边分别是AB和CD，以及AD和BC。

因此，如果动点P从A点出发并回到A 点，它必定会经过平行四边形的另外两个顶点，即C和B。

5. 为了更具体地描述动点P的路径，我们可以进一步假设动点P沿着直线AC移动到顶点C，然后沿着直线CB移动到顶点B，最后沿着直线BA移动回到顶点A。

这样，动点P所经过的路径形成了一个三角形ABC。

6. 需要注意的是，这个路径并不是唯一的。

动点P可以按任意方式从A到C，再从C到B，最后从B到A。

但无论路径如何，最终的路径都是一个三角形ABC。

7. 接下来，让我们来看问题的第二部分。

如果动点P从一个顶点出发，按一定路径移动，最后回到另一个顶点，那么它经过的路径会是什么样子8. 在这种情况下，我们可以假设动点P从顶点A出发，并沿着直线AC移动到顶点C。

然后，它会继续按照平行四边形的形状，沿着直线CB移动到顶点B，并最终沿着直线BA返回到顶点A。

9. 与第一部分类似，这个路径也不是唯一的。

动点P可以从任意顶点出发，按照相应的顺序经过其他两个顶点，最后回到初始的顶点。

10. 总结起来，平行四边形的动点问题涉及动点在平行四边形内移动的路径问题。

无论是从一个顶点出发回到同一个顶点，还是从一个顶点出发回到另一个顶点，最终路径都可以看作是一个三角形。

11. 这个问题的解答可以帮助我们更好地理解平行四边形的形状和特性，以及动点在平行四边形内移动时的可能路径。

它也为我们提供了一种思考和探索几何问题的方式。

平行四边形动点问题方法总结

平行四边形动点问题方法总结1. 引言：为什么我们要关注平行四边形动点问题？嘿，朋友们！今天我们来聊聊一个看似枯燥却又很有趣的数学话题——平行四边形动点问题。

别急着打哈欠，咱们慢慢来，这可是个让你从头到脚都充满成就感的数学冒险哦。

平行四边形动点问题，听名字就知道，讲的是在平行四边形里，某个点在移动时，会发生什么奇妙的事情。

这不仅仅是数学题，更像是一场迷人的舞蹈。

你知道吗？这些问题其实很接地气，因为它们涉及到很多我们生活中常见的现象，比如房子四角是直角的，家具摆放的角度等等。

2. 方法一：坐标法——从数学角度看平行四边形的奇妙。

2.1 说到解决这类问题，坐标法可是个不可或缺的好帮手。

咱们首先给平行四边形的四个顶点分配坐标，比如A、B、C、D分别是(0, 0)、(a, 0)、(b, c)、(d, e)。

坐标法就是把平行四边形里的每个点都用坐标表示出来，这样一来，不管点怎么动，我们都能通过数学公式来搞定。

2.2 你可以把平行四边形当成一个平面上的大布景，点A、B、C、D就是布景上的关键位置。

然后，动点就是在这个布景上游走的小演员。

比如，如果你要找出某个点P 的轨迹，只需要把P的坐标带入公式，就能知道P跑到哪儿去了。

坐标法简直是数学里的瑞士军刀，万能又省事。

3. 方法二：向量法——用矢量的眼光看世界。

3.1 向量法是另一个很酷的方法。

想象一下，向量就像是一把利刃，把复杂的数学问题一刀切成简单易懂的形状。

比如，平行四边形的对角线是彼此平行的，那么它们之间的向量关系就能告诉我们很多有用的秘密。

如果我们把动点P的运动看作一个向量变化，我们就能用向量运算来分析它的行为。

3.2 向量法的好处在于，它能帮我们迅速搞清楚平行四边形中各个点的相对位置和移动规律。

用这个方法，你可以非常方便地计算出点P在平行四边形内的各种可能位置，也能找到一些隐含的规律，比如点P可能会在平行四边形的对角线附近来回移动。

数学就像个魔术师，向量法让我们能透过表面看到更多的奥秘。

二次函数中的动点问题之平行四边形教学设计

广东省中考数学疑难问题教学设计：二次函数中的动点问题之平行四边形一、教学内容的确定及前期思考：二次函数中的动点问题无疑会成为压轴题三位主角中的一个，而动点产生平行四边形的问题也经常出现，本人发现：无论是各种复习资料对这类题给出的解答方法，还是我听公开课时发现很多老师给出的解决方式都将简单问题复杂化了，而我们数学老师的任务应该是化繁为简，找出各个知识点之间的联系，充分利用我们熟悉的数学方法和数学思想去解决压轴题中的疑难问题，由此产生了将此类问题形成一篇教学设计的想法，并已长达两年之久。

二、教学目标分析：（一）通性通法：1、通过知识转化、类比、迁移的方式学会观察分析并找出线段的平移和点的坐标之间的关系，再利用形成平行四边形的动点的位置的特殊性（在抛物线上或在抛物线的对称轴上等），求出动点的坐标。

2、熟练掌握和应用函数模型、数形结合、分类讨论与整合、化归与转化等数学思想和方法。

（二）情感教育：能通过本节课化繁为简、化难为易的学习过程克服对压轴题的恐惧心理，增强学生解决压轴题的信心和勇气。

三、教学重点与难点分析：重点：掌握根据平移与点的坐标之间的关系规律来解决二次函数中动点产生平行四边形的问题。

1难点：首先是能利用平移画出大致图形，其次是能充分利用隐含的条件（如点在对称轴上就意味着已知横坐标等）来求出动点的坐标。

四、教学过程设计总流程如下：具体教学过程如下：（一）观看旧解，提出问题：环节一：展示疑难题图，引出课题设计意图：展示三道平行四边形和二次函数结合的题图，冲击学生的视觉，让学生的注意力一下子就集中到本节课要学习的题目类型上。

开场白设计：在压轴题中，我们经常会见到平行四边形和二次函数相依相伴的身影，这节课我们就一起来研究二次函数和平行四边形的那些事儿。

环节二：探讨平行四边形中暗含的平移知识（聊天引入）让我们先把平行四边形请过来做客吧！下面，给你们展示一道题以及这道题的解题过程，你知道答案是怎么做的吗？辅例 1、（选自练习册中的练习题）在直角坐标系中,已知: A（-1，0），B（3，0），C（0，2）．以A、B、C、D 为顶点的四边形是平行四边形,求 D 点的坐标。

第十八章平行四边形四边形中的动点问题(教案)人教版八年级数学下册

3.成果分享：每个小组将选择一名代表来分享他们的讨论成果。这些成果将被记录在黑板上或投影仪上，以便全班都能看到。
（五）总结回顾（用时5分钟）
今天的学习，我们了解了平行四边形中动点问题的基本概念、重要性和应用。同时，我们也通过实践活动和小组讨论加深了对动点问题的理解。我希望大家能够掌握这些知识点，并在日常生活中灵活运用。最后，如果有任何疑问或不明白的地方，请随时向我提问。
五、教学反思
在今天的教学中，我发现同学们对平行四边形内动点问题的探究表现得非常积极。他们对于动点的运动规律和性质有了初步的认识，也尝试着将这些知识应用到实际问题中。我觉得这是一个很好的开始，但也发现了一些需要改进的地方。
首先，理论讲授部分，我发现有些同学对动点问题的基本概念掌握不够扎实。可能是我讲解得不够细致，也可能是同学们对这些概念还不够熟悉。在以后的教学中，我需要更加注意这一点，尽量用简单易懂的语言和丰富的例子来帮助他们理解。
3.重点难点解析：在讲授过程中，我会特别强调动点的运动规律和利用平行四边形性质解题这两个重点。对于难点部分，我会通过举例和比较来帮助大家理解。
（三）实践活动（用时10分钟）
1.分组讨论：学生们将分成若干小组，每组讨论一个与动点问题相关的实际问题。
2.实行四边形中的运动规律和性质。
-难点二：在实际问题中，学生可能不知道如何选择合适的定理和性质来解决动点问题。教师应指导学生通过分析问题结构，识别关键信息，进而选择恰当的几何定理进行求解。
-难点三：针对不同动点问题，如路径最短、面积最大等，学生可能不知如何下手。教师应教授学生分类讨论和优化的方法，帮助学生理清思路，找到解题突破口。
4.培养合作意识和团队精神，在小组讨论和探究过程中，学会倾听、交流、表达和协作，共同解决问题。

动点问题(学生用)

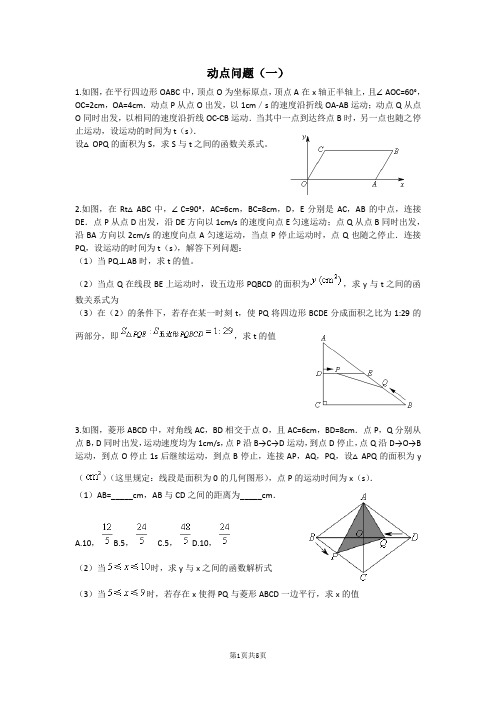
动点问题（一）1.如图，在平行四边形OABC中，顶点O为坐标原点，顶点A在x轴正半轴上，且∠AOC=60°，OC=2cm，OA=4cm．动点P从点O出发，以1cm／s的速度沿折线OA-AB运动；动点Q从点O同时出发，以相同的速度沿折线OC-CB运动．当其中一点到达终点B时，另一点也随之停止运动，设运动的时间为t（s）．设△OPQ的面积为S，求S与t之间的函数关系式。

2.如图，在Rt△ABC中，∠C=90°，AC=6cm，BC=8cm，D，E分别是AC，AB的中点，连接DE．点P从点D出发，沿DE方向以1cm/s的速度向点E匀速运动；点Q从点B同时出发，沿BA方向以2cm/s的速度向点A匀速运动，当点P停止运动时，点Q也随之停止．连接PQ，设运动的时间为t（s），解答下列问题：（1）当PQ⊥AB时，求t的值。

（2）当点Q在线段BE上运动时，设五边形PQBCD的面积为，求y与t之间的函数关系式为（3）在（2）的条件下，若存在某一时刻t，使PQ将四边形BCDE分成面积之比为1:29的两部分，即，求t的值3.如图，菱形ABCD中，对角线AC，BD相交于点O，且AC=6cm，BD=8cm．点P，Q分别从点B，D同时出发，运动速度均为1cm/s，点P沿B→C→D运动，到点D停止，点Q沿D→O→B 运动，到点O停止1s后继续运动，到点B停止，连接AP，AQ，PQ，设△APQ的面积为y（）（这里规定：线段是面积为0的几何图形），点P的运动时间为x（s）．（1）AB=_____cm，AB与CD之间的距离为_____cm．A.10，B.5，C.5，D.10，（2）当时，求y与x之间的函数解析式（3）当时，若存在x使得PQ与菱形ABCD一边平行，求x的值4.如图，在梯形ABCD中，AB∥CD，AD⊥AB，AD=4cm，DC=6cm，CB=5cm．点P从点B出发，以1cm/s的速度沿线段BA向点A匀速运动；与此同时，点Q从点A出发，以2cm/s 的速度沿折线AD-DC匀速运动，过点P作PM⊥AB交折线BC-CD于点M，连接QM，PQ，当其中一点到达终点时，另一点也停止运动．设运动时间为t秒，△PQM的面积为S（）．（1）Q，M两点相遇时t的值为( )（2）当时，求S与t的函数关系式。

二次函数中动点问题——平行四边形

2018年04月28日187****6232 的初中数学组卷一•解答题(共5小题)1 •如图，已知抛物线y=ax2+bx+c经过点A (- 1, 0),点B (3, 0)和点C (0, 3).(1)求抛物线的解析式和顶点E的坐标；(2)点C是否在以BE为直径的圆上请说明理由；(3)点Q是抛物线对称轴上一动点，点R是抛物线上一动点，是否存在点Q、R,使以Q、R、C、B为顶点的四边形是平行四边形若存在，直接写出点Q、R2•如图，已知抛物线y=af+bx+c过点A (- 3, 0)，B (-2, 3)，C (0, 3)，其顶点为D.(1)求抛物线的解析式；(2)设点M (1, m),当MB+MD的值最小时，求m的值；(3)若P是抛物线上位于直线AC上方的一个动点，求△ APC的面积的最大值；(4)若抛物线的对称轴与直线AC相交于点N, E为直线AC上任意一点，过点E 作EF// ND交抛物线于点F,以N, D, E, F为顶点的四边形能否为平行四边形若能，求点E的坐标；若不能，请说明理由.3•如图，抛物线y=X2 - 2x- 3与x轴交于A、B两点（点A在点B的左侧），直线I与抛物线交于A, C两点，其中点C的横坐标为2 .（1）求A，B两点的坐标及直线AC的函数表达式；（2）P是线段AC上的一个动点（P与A，C不重合），过P点作y轴的平行线交抛物线于点丘，求厶ACE H积的最大值；（3）若直线PE为抛物线的对称轴，抛物线与y轴交于点D,直线AC与y轴交于点Q,点M为直线PE上一动点，则在x轴上是否存在一点N,使四边形DMNQ 的周长最小若存在，求出这个最小值及点M ,N的坐标；若不存在，请说明理由.（4）点H是抛物线上的动点，在x轴上是否存在点F,使A、C、F、H四个点为顶点的四边形是平行四边形如果存在，请直接写出所有满足条件的F点坐标；如4. 如图，在平面直角坐标系中，直线y=-3x-3与x轴交于点A,与y轴交于点C.抛物线y=x2+bx+c经过A, C两点，且与x轴交于另一点B （点B在点A右侧）. （1）求抛物线的解析式及点B坐标；(2)若点M是线段BC上一动点，过点M的直线EF平行y轴交x轴于点F,交抛物线于点E.求ME长的最大值；(3)试探究当ME取最大值时，在x轴下方抛物线上是否存在点P,使以M， F，B，P为顶点的四边形是平行四边形若存在，请求出点P的坐标；若不存在，试说明理由.5. 如图，矩形OABC在平面直角坐标系中，点A在x轴正半轴，点C在y轴正半轴，OA=4, OC=3抛物线经过O，A两点且顶点在BC边上，与直线AC交于点D.(1)求抛物线的解析式；(2)求点D的坐标；(3)若点M在抛物线上，点N在x轴上，是否存在以A，D，M，N为顶点的2018年04月28日187****6232 的初中数学组卷参考答案与试题解析一•解答题(共5小题)1 •如图，已知抛物线y=ax2+bx+c经过点A (- 1, 0),点B (3, 0)和点C (0, 3).(1)求抛物线的解析式和顶点E的坐标；(2)点C是否在以BE为直径的圆上请说明理由；(3)点Q是抛物线对称轴上一动点，点R是抛物线上一动点，是否存在点Q、R,使以Q、R、C、B为顶点的四边形是平行四边形若存在，直接写出点Q、R【分析】(1)将A(- 1, 0)、B(3, 0)、C(0, 3)三点坐标代入抛物线y=af+bx+c 中，列方程组求a、b、c的值即可；(2) 根据勾股定理的逆定理可得：/ BCE=90,可得结论；(3) 分两种情况：①以BC为边时，如图1, R在对称轴的右侧时，BC// RQ四边形CQRB是平行四边形，根据平移规律先得R的横坐标为4,代入抛物线的解析式可得R (4,- 5),由平移规律可得Q (1,- 2)；如图2, R在对称轴的左侧，RC// BQ,四边形CRQB是平行四边形，同理可得点Q、R的坐标.②以BC为对角线时，如图3,同理根据平移规律可得结论.r a-b>+e=O【解答】解：(1)由题意，得：二0,c=3 kTt解得：，22 ,3i匸二故这个抛物线的解析式为y= - X2+2X+3,y= -X2+2X+3=-(X- 1) 2+4,•••顶点 E (1, 4);(2) 点C在以BE为直径的圆上，理由是：•- C( 0, 3), B (3, 0), E( 1 , 4),••• BG=32+32=18, C底=12+12=2, B民(3- 1) 2+42=20,••• B G+C E=B W,•••/ BCE=90,•••点C在以BE为直径的圆上；(3) 存在，分两种情况：①以BC为边时，如图1, R在对称轴的右侧时，BC// RQ,四边形CQRB是平行四边形, 由C到B的平移规律可知：Q的横坐标为1,则R的横坐标为4,当X=4时，y=-X2+2X+3=- 42+2X 4+3= - 16+8+3=- 5,•- R( 4 , - 5),•- Q (1 , - 2);如图2, R在对称轴的左侧,RC// BQ ,四边形CRQB是平行四边形, 由C到B的平移规律可知：Q的横坐标为1,则R的横坐标为-2 ,当X=- 2 时，y=-X2+2X+3=- 4+2X( - 2) +3=-5 ,•- R(-2, - 5),•- Q (1, - 8);②以BC为对角线时，如图3 ,由C和Q的平移规律可得：R的横坐标为2 ,当X=2时，y=- 4+4+3=3,•- R( 2 , 3),根据R到B的平移规律可得：Q (1, 0);综上所述，R (4,- 5), Q (1,- 2)或R (-2, - 5), Q (1,- 8)或R (2, 3), Q (1, 0).【点评】本题是二次函数的综合题，考查了待定系数法求解析式，圆周角定理, 勾股定理的应用，平行四边形的判定等，分类讨论的思想是( 3)的关键.2•如图，已知抛物线y=af+bx+c过点A (- 3, 0), B (-2, 3), C (0, 3),其顶点为D.(1)求抛物线的解析式；(2)设点M (1, m),当MB+MD的值最小时，求m的值；(3)若P是抛物线上位于直线AC上方的一个动点，求△ APC的面积的最大值；(4)若抛物线的对称轴与直线AC相交于点N, E为直线AC上任意一点，过点E 作EF// ND交抛物线于点F,以N, D, E, F为顶点的四边形能否为平行四边形若能，求点E的坐标；若不能，请说明理由.【分析】(1)根据待定系数法，可得答案;(2)利用轴对称求最短路径的知识，找到 B 点关于直线x=1的对称点B',连接 B'D, B'D 与直线x=1的交点即是点M 的位置，继而求出m 的值.(3) 根据平行于y 轴的直线上两点间的距离是较大的纵坐标减去较小的纵坐标，可得PE 的长，根据三角形的面积，可得二次函数，根据二次函数的性质，可得答案；(4) 设出点E 的，分情况讨论，①当点E 在线段AC 上时，点F 在点E 上方，② 当点E 在线段AC (或CA )延长线上时，点F 在点E 下方，根据平行四边形的性质，可得关于x 的方程，继而求出点E 的坐标.【解答】解：(1)将A ，B, C 点的坐标代入解析式，得9a-3b+c — 0I ■- ■ - ■ 1， c=3解得心-2，t c=3抛物线的解析式为y=- x 2 - 2x+3(2) 配方，得y=-(x+1) 2+4,顶点D 的坐标为(-1, 4)作B 点关于直线x=1的对称点B',则 B' (4, 3)，由(1)得 D (- 1 可求出直线DB 的函数关系式为y 当M (1, m )在直线DB 上时，MN+MD 的值最小, 贝U m=-£x 1 + 严=¥ .5 5 5(圍1(3)作PE±x轴交AC于E点，如图2AC的解析式为y=x+3,设P (m, - m2- 2m+3), E (m, m+3),PE=- m2- 2m+3-( m+3) =- m2- 3m& APC^PE|X A|=—(-m2- 3m) x 3=-当口=-3时，厶APC的面积的最大值是2(4)由(1)、(2)得 D (- 1, 4), N(-1, 2)点E在直线AC上，设E (x, x+3),①当点E在线段AC上时，点F在点E上方，则F(x，- x2-2x+3)，•••EF=DN•••- x2- 2x+3-( x+3) =4 - 2=2,解得，x=- 2或x=- 1 (舍去)，则点E的坐标为：(-2, 1).②当点E在线段AC(或CA)延长线上时，点F在点E下方，则F(x，- x2- 2x+3), •••EF=DN• ( x+3)- (- x2- 2x+3) =2,解得x= 或x=~2即点E的坐标为：(2 2综上可得满足条件的点E为E (-2, 1)或：(I", ；)或(2 ).【点评】本题考查了二次函数的综合题，解(1)的关键是待定系数法，解(2) 利用轴对称求最短路径；解(3)的关键是利用三角形的面积得出二次函数；解(4) 的关键是平行四边形的性质得出关于x的方程，要分类讨论，以防遗漏.3•如图，抛物线y=x2- 2x-3与x轴交于A、B两点(点A在点B的左侧)，直线I 与抛物线交于A，C两点，其中点C的横坐标为2 .(1)求A，B两点的坐标及直线AC的函数表达式；(2)P是线段AC上的一个动点(P与A，C不重合)，过P点作y轴的平行线交抛物线于点丘，求厶ACE H积的最大值；(3)若直线PE为抛物线的对称轴，抛物线与y轴交于点D,直线AC与y轴交于点Q,点M为直线PE上一动点，则在x轴上是否存在一点N,使四边形DMNQ 的周长最小若存在，求出这个最小值及点M ,N的坐标；若不存在，请说明理由.(4)点H是抛物线上的动点，在x轴上是否存在点F,使A、C、F、H四个点为顶点的四边形是平行四边形如果存在，请直接写出所有满足条件的F点坐标；如【分析】(1)令抛物线y=x2- 2x- 3=0，求出x的值，即可求A，B两点的坐标，根据两点式求出直线AC的函数表达式；(2)设P点的横坐标为x (- Kx<2)，求出P、E的坐标，用x表示出线段PE 的长，求出PE的最大值，进而求出△ ACE的面积最大值；(3)根据D点关于PE的对称点为点C (2，- 3)，点Q (0，- 1)点关于x轴的对称点为M (0，1)，则四边形DMNQ的周长最小，求出直线CM的解析式为y=-2x+1,进而求出最小值和点M， N的坐标；(4)结合图形，分两类进行讨论，① CF平行x轴，如图1,此时可以求出F点两个坐标；②CF不平行x轴，如题中的图2，此时可以求出F点的两个坐标. 【解答】解：(1)令y=0，解得x i = - 1或X2=3,••• A (- 1, 0), B (3, 0);将C点的横坐标x=2代入y=x2- 2x- 3得y=- 3,•-C( 2,- 3),•••直线AC的函数解析式是y=-x- 1,(2)设P点的横坐标为x (- Kx<2),则P、E 的坐标分别为：P (x,- x- 1), E (x, x2-2x- 3),I P 点在E点的上方，PE= (- x- 1)-( x2-2x- 3) =- X2+X+2,.••当x丄时，PE 的最大值」,2 4△ ACE的面积最大值丄PE[2-( - 1) ]—PE」,2 2 8(3) D点关于PE的对称点为点C( 2, - 3),点Q (0, - 1)点关于x轴的对称点为K (0 , 1),连接CK交直线PE于M点,交x轴于N点,可求直线CK的解析式为y=- 2x+1 , 此时四边形DMNQ的周长最小,最小值=|CM|+QD=2 !,+2,求得M (1, - 1) , N (订,0).(4) 存在如图1,若AF// CH,此时的D和H点重合,CD=2,则AF=2,再根据 |HA|=|CF| ,求出 F 4 （4—衙，0）, Q ）.综上所述，满足条件的F 点坐标为F i (1, 0), F 2 (- 3, 0) , F3如护,°), F 4 (4-一 , 0).【点评】本题主要考查二次函数的综合题的知识点，解答本题的关键是熟练掌握对称的知识和分类讨论解决问题的思路，此题难度较大.4. 如图，在平面直角坐标系中，直线 y=-3x -3与x 轴交于点A ,与y 轴交于点C .抛物线y=x 2+bx+c 经过A , C 两点，且与x 轴交于另一点B (点B 在点A 右侧).(1) 求抛物线的解析式及点B 坐标；(2) 若点M 是线段BC 上一动点，过点M 的直线EF 平行y 轴交x 轴于点F ,交抛物如图2,根据点A 和F 的坐标中点和点 C 和点H 的坐标中点相同,线于点E.求ME长的最大值；(3)试探究当ME取最大值时，在x轴下方抛物线上是否存在点P,使以M， F，B，P为顶点的四边形是平行四边形若存在，请求出点P的坐标；若不存在，试说明理由.【分析】(1)先根据直线的解析式求出A、C两点的坐标，然后将A、C的坐标代入抛物线中即可求出二次函数的解析式.进而可根据抛物线的解析式求出B 点的坐标.(2)ME的长实际是直线BC的函数值与抛物线的函数值的差，据此可得出一个关于ME的长和F点横坐标的函数关系式，可根据函数的性质来求出ME的最大值.(3)根据(2)的结果可确定出F，M的坐标，要使以M， F，B，P为顶点的四边形是平行四边形，必须满足的条件是MP// =BF,那么只需将M点的坐标向左或向右平移BF长个单位即可得出P点的坐标，然后将得出的P点坐标代入抛物线的解析式中，即可判断出是否存在符合条件的P点.【解答】解：(1)当y=0时，-3x- 3=0, x=- 1•-A (- 1, 0)当x=0 时，y=- 3,•-C( 0,- 3),抛物线的解析式是：y=f - 2x- 3.当y=0 时，x2- 2x- 3=0,解得：X1=— 1 , x2=3••• B (3, 0).(2)由(1)知 B (3, 0), C (0,- 3)直线 BC 的解析式是：y=x -3, 设 M (x , x -3) (0<x < 3),贝U E (x , x 2- 2x - 3)••• ME= (x - 3)-( x 2- 2x - 3) =- x 2+3x=-( x -丄)2丄；.••当x 』时，ME 的最大值为—. 2 4(3)答：不存在.•皿亡，BF =O B- OFj 设在抛物线x 轴下方存在点P ,使以P 、M 、F 、B 为顶点的四边形是平行四边形, 贝U BP// MF , BF// PM .• P i (0,- 一)或 P 2 (3,• P 2不在抛物线上.综上所述：在x 轴下方抛物线上不存在点P ,使以P 、M 、F 、B 为顶点的四边形是平行四边形.【点评】本题着重考查了待定系数法求二次函数解析式、平行四边形的判定和性质等知识点，综合性强，考查学生分类讨论，数形结合的数学思想方法. (2)中弄清线段ME 长度的函数意义是解题的关键. 5. 如图，矩形OABC 在平面直角坐标系中，点 A 在x 轴正半轴，点C 在y 轴正半轴，OA=4, OC=3抛物线经过O , A 两点且顶点在BC 边上，与直线AC 交于点D .(1) 求抛物线的解析式；由(2)知ME 取最大值时ME J , E4 15T 当 P i (0, 2 • P i 不在抛物线上. )时，由(1)知 y=“ - 2x - 3=- 3工-当 P 2 (3, )时，由(1)知 y=« - 2x - 3=0工-(2) 求点D的坐标；(3) 若点M在抛物线上，点N在x轴上，是否存在以A, D, M , N为顶点的-2)2+3,将A(4, 0)坐标代入q求出a即可解决问题；(2)求出直线AC的解析式，利用方程组确定交点坐标即可;(3) 分两种情况考虑：①当点M在x轴上方时，如答图1所示；②当点M在x轴下方时，如答图2所示；分别利用待定系数法即可解决问题；【解答】解：(1)设抛物线顶点为E,根据题意OA=4, OC=3得：E (2，3)，设抛物线解析式为y=a (x- 2) 2+3,将A (4, 0)坐标代入得：0=4a+3,即a=-二，4则抛物线解析式为y=-[ (x-2) 2+3二-二/+3x;(2)设直线AC解析式为y=kx+b (〜0), 将A (4, 0)与C (0, 3)代入得: f 4Hb=0仏犬，解得：4,故直线AC解析式为y=-[x+3,与抛物线解析式联立得:3y=〒+3y=a (x（3）存在，分两种情况考虑：①当点M 在x 轴上方时，如答图1所示: B/ o M 3 —h四边形ADMN 为平行四边形，DM // AN, DM=AN,由对称性得到 M （3,号），即DM=2，故AN=2,•-N i （2，0），N 2 （6，0）;②当点M 在x 轴下方时，如答图2所示:/o\「 ■ 1 迟A 、\过点D 作DQ 丄x 轴于点Q ,过点M 作MP 丄x 轴于点P ,可得△ ADQ ^^ NMP ， ••• MP=DQ 卑,NP=AQ=34将y M =-寸代入抛物线解析式得：-亍=-亍x 2+3x ,解得：X M =2 -.厂或 X M =2+：：厂 i ,X N =X M - 3=-F F - 1 或曲 i — 1, K=1则点D 坐标为（二N3 (-屮1, o), N4( -1, o).综上所述，满足条件的点N有四个：N i (2, 0), N2 (6, 0), N3 (-W - 1, 0), N4 (衙-1, 0).【点评】此题考查了二次函数综合题、待定系数法确定抛物线解析式，一次函数与二次函数的交点，平行四边形的性质等知识，解题的关键是熟练掌握待定系数法解决问题，学会用分类讨论的思想思考问题，属于中考压轴题.。