离散数学6-5
离散数学作业6_集合与关系答案

离散数学作业作业6 ——等价关系1. 设R和S均为A上的等价关系,确定下列各式,哪些是A上的等价关系?如果是,证明之;否则,举反例说明。
(1)R∩S (2)R∪S (3)r (R-S)(4)R- S (5)R◦S (6)R2解:(1),(6)正确,其余错误。
2. R是集合A上的二元关系, a,b,c ,若aRb,且bRc,有cRb,则称R 是循环关系。
证明R是自反和循环的,当且仅当R是一等价关系。
分析: 需要证明两部分:(1)已知R是自反和循环的,证明:R是一等价关系(2)已知R是一等价关系, 证明R是自反和循环的.证明:(1)先证必要性。
只需要证明R是对陈的和传递的。
任取(x,y)∈R。
因为R是自反的,所以(y,y)∈R。
由R是循环的可得(y,x)∈R,即R是对陈的。
任取(x,y),(y,z)∈R。
因R是循环的,所以(z,x)∈R。
由R对称性得(x,z)∈R,即R是传递的。
(2)证充分性。
只需要证明R是循环的。
任取(x,y),(y,z)∈R,下证(z,x)∈R。
由于R是传递的,所以(x,z)∈R。
又由R是对称的得(z,x)∈R。
所以R是循环的。
3. 设|A|=n ,在A 上可以确定多少个不同的等价关系?解:2n!/((n+1)n!n!)4. 给定集合S={ 1 , 2 , 3, 4, 5 },找出S 上的等价关系R ,此关系R 能够产生划分{{1,2},{3},{4,5}},并画出关系图。
解:{(1,2),(2,1),(4,5),(5,4)}S R I =⋃5. 设A={1,2,3,4,5}。
R 是集合A 上的二元关系,其关系矩阵如下图所示。
求包含R 的最小等价关系和该等价关系所确定的划分。
⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=0010001000000000101000001RM 分析: 可以证明tsr(R)是包含R 的最小等价关系.解:包含R 的最小等价关系的矩阵表示如下:1000001010001010101000101⎛⎫ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭上述等价关系确定的划分为{{1},{2,4},{3,5}}.6. 自学华氏(WalShall)算法,写出算法的基本概念、基本步骤和一个求解传递闭包的具体实例,并可清晰讲解算法整体实现过程。
《离散数学》第六章 集合代数

例3: 4个x ,3个y,2个z的全排列中,求不出现xxxx,yyy ,zz图象的排列。
设x不具有性质P1,P2,…,Pm ,那么x∉Ai,i= 1,2,…m。则它对等式左边计数的贡献为1,对 等式右边的计数的贡献也是1。
根据牛顿二项式定理不难得到上面式子的结果是0.而 由于x具有n个性质,它对等式左边的贡献也为0。
4.3 几个例子
例1:求1-1000之间(包括1和1000)不能被5,也不能被6, 还不能被8整除的整数有多少个?
总体上还是多采用命题逻辑中的等值式,但在叙述
上采用半形式化的方法。
例6.6 证明A-(B∪C)=(A-B)∩(A-C).
证明: 对于∀x
x ∈ A-(B∪C) Ù x ∈ A ∧ x ∉(B∪C) Ù x ∈ A ∧ ⎤ (x∈B ∨ x∈C) Ù x ∈ A ∧ (⎤x∈B ∧ ⎤x∈C) Ù x ∈ A ∧ (x ∉ B ∧ x ∉ C) Ù x∈A∧x∉B∧x∉C Ù (x ∈ A ∧ x ∉ B) ∧ (x ∈ A ∧ x ∉ C) Ù x ∈ A- B ∧ x ∈ A- C Ù x ∈( A- B) ∩(A- C)
全排列的个数为:9!/(4!3!2!)=1260; 所以要求的排列数为
1260-(60+105+280)+(12+20+30)-6 =871.
4.4 三个练习
练习1:求由a,b,c,d构成的n位符号串中,a,b,c,d都至 少出现一次的符号串的数目。
离散数学习题

第1章命题逻辑一、单项选择题1. 下列命题公式等值的是( )BBAAQPQQPQB AABAAQPQP),()D(),()C() (),()B(,)A(∧∨⌝∨∨⌝∨→→→⌝→→∨⌝∧⌝2. 设命题公式G:)(RQP∧→⌝,则使公式G取真值为1的P,Q,R赋值分别是( )0,0,1)D(0,1,0)C(1,0,0)B(0,0,0)A(3. 命题公式QQP→∨)(为( )(A) 矛盾式(B) 仅可满足式(C) 重言式(D) 合取范式4 命题公式)(QP→⌝的主析取范式是( ).(A) QP⌝∧(B) QP∧⌝(C) QP∨⌝(D) QP⌝∨5. 前提条件PQP,⌝→的有效结论是( ).(A) P(B) ⌝P(C) Q(D)⌝Q6. 设P:我将去市里,Q:我有时间.命题“我将去市里,仅当我有时间时”符号化为( )QPQPQPPQ⌝∨⌝↔→→)D()C()B()A(二、填空题1. 设命题公式G:P→⌝(Q→P),则使公式G为假的真值指派是2. 设P:我们划船,G:我们跑步,那么命题“我们不能既划船,又跑步”可符号化为3. 含有三个命题变项P,Q,R的命题公式P∧Q的主析取范式是4. 若命题变元P,Q,R赋值为(1,0,1),则命题公式G=)())((QPRQP∨⌝↔→∧的真值是5. 命题公式P→⌝(P∧Q)的类型是.6. 设A,B为任意命题公式,C为重言式,若C⇔∧,那么A∧CBA↔是式(重言式、矛盾式或可满B足式)三、解答化简计算题1.判别下列语句是否命题?如果是命题,指出其真值.(1) 中国是一个人口众多的国家. (2) 存在最大的质数.(3) 这座楼可真高啊!(4) 请你跟我走! (5) 火星上也有人.2.作命题公式)P∨∧→→的真值表,并判断该公式的类Q)((P)(PQ型.3. 试作以下二题:(1) 求命题公式(P∨⌝Q)→(P∧Q)的成真赋值.(2) 设命题变元P,Q,R的真值指派为(0,1,1),求命题公式∨P→R→⌝↔的真值.∧P⌝(()Q)((QR))4. 化简下式命题公式)⌝∧P∧∨Q⌝∧(P))Q((P5. 求命题公式))⌝∧→的主合取范式.Q→P∧P)(P((Q6. 求命题公式R→∧⌝⌝)((的真值.→(∧))QP∨PRQ∨↔RP7. 求命题公式)→∧→⌝的主析取范式,并求该命题公P⌝(Q)(PQ式的成假赋值.8. 将命题公式)⌝∧⌝化为只含∨和⌝的尽可能简单的⌝∧RQP→(P等值式.9. 求命题公式)∨⌝∧的真值表.P⌝∧)((QPQ四、证明题1. 证明S∧∧→)∨⌝)⌝(()(RQRS∧QP⌝P⌝∨⇒2. 构造推理证明:QR→→())((⇒S→)RPSQ→P∧∧3. 证明命题公式(P→(Q∨⌝R))∧⌝P∧Q与⌝(P∨⌝Q)等值.4. 证明命题公式)R→与QP→∧)(有相同的主析取范∨)((QRP→Q式.命题逻辑习题参考答案一、1. C 2. D 3. B 4. A 5. D 6. B二、1. 1,0;1,1 2. )(Q P ∧⌝或Q P ⌝∨⌝ 3. (P ∧Q ∧R )∨(P ∧Q ∧⌝R )4. 05. 非永真式的可满足式6. 重言三、1. (1) 是命题,真值为1. (2) 是命题,真值为0. (3), (4)不是命题. (5)是命题.1. 判别下列语句是否命题?如果是命题,指出其真值.(1) 中国是一个人口众多的国家. (2) 存在最大的质数.(3) 这座楼可真高啊! (4) 请你跟我走! (5) 火星上也有人.2. 命题公式))(()(P Q P Q P ∨∧→→的真值表 P Q P →Q Q P ∧ P Q P ∨∧)())(()(P Q P Q P ∨∧→→ 0 0 1 0 0 00 1 1 0 0 01 0 0 0 1 11 1 1 1 1 1原式为可满足式.3. (1) (P ∨⌝Q )→(P ∧Q )⇔(⌝P ∧Q )∨(P ∧Q )⇔(⌝P ∨P )∧Q ⇔Q可见(P ∨⌝Q )→(P ∧Q )的成真赋值为(0,1),(1,1).(2) ))()(()(Q R Q P R P →⌝∨⌝→⌝∧↔0))10()01(()10(⇔→∨→∧↔⇔4. ))()((P Q P Q P ∧⌝∧⌝∨∧P Q P Q P ∧⌝∧⌝∨∧⇔)()()()(P P Q P Q P ∧⌝∧⌝∨∧∧⇔0)(∨∧⇔Q PQ P ∧⇔5. ))()((Q P P Q P ∧⌝∧→→))()((Q P P Q P ∧⌝∧∨⌝∨⌝⇔)())(Q P P Q P Q P ∧⌝∧∨∧⌝∧⌝∨⌝⇔)00(∧∨⌝⇔P)(Q Q P ⌝∧∨⌝⇔)()(Q P Q P ⌝∨⌝∧∨⌝⇔6. R P R Q P P R Q ∨↔∨→⌝∧→⌝∧)())((R P R Q P P R Q ∨↔∨∨∧∨∨⌝⇔)()(R P Q Q R P ∨↔∧⌝∨∨⇔)(1⇔7. Q P Q P Q P Q P Q P ⌝∧⇔⌝∨⌝∧⌝∧⇔⌝→∧→⌝)()()()(因为成真赋值是(1,0),故成假赋值为(0,0),(0,1),(1,1)8. ))()()(R P Q P P R Q P ∨∧∨⌝⇔→⌝∧⌝∧⌝))()((R P Q P ∨⌝∨∨⌝⇔不唯一.9. 作真值表P Q P∧Q⌝P⌝Q⌝P∨⌝Q (P∧Q)∧(⌝P∨⌝Q)0 0 0 1 1 1 00 1 0 1 0 1 01 0 0 0 1 1 01 1 1 0 0 0 0四、证明题1.①⌝Q∨R P②⌝R P③⌝Q①,②析取三段论④P→Q P⑤P⌝③,④拒取式⑥P∨⌝S P⑦⌝S⑤,⑥析取三段论2.前提:QPRSQP,)),((→→→结论:SR→证明:①R附加前提②R→P前提引入③P①,②假言推理④P→(Q→S) 前提引入⑤Q→S③,④假言推理⑥Q前提引入⑦S⑤,⑥假言推理3. (P→(Q∨⌝R))∧⌝P∧Q⇔(⌝P∨(Q∨⌝R))∧⌝P∧Q⇔(⌝P∧⌝P∧Q)∨(Q∧⌝P∧Q)∨(⌝R∧⌝P∧Q)⇔(⌝P∧Q)∨(⌝P∧Q)∨(⌝P∧Q∧⌝R)⇔⌝P∧Q⇔⌝(P∨⌝Q)4.方法1.)()(QRQP→∨→⇔)()(QRQP∨⌝∨∨⌝⇔∨∧⌝⇔QRP)(QRP→∧)(因为两命题公式等值,由主合取范式的惟一性,可知两命题公式的主合取范式是相同.方法2.)()(QRQP→∨→⇔)()(QRQP∨⌝∨∨⌝RQPQRP⌝∨∨⌝⇔∨⌝∨⌝⇔RQPQRPQRP⌝∨∨⌝⇔∨⌝∨⌝⇔→∧)(因为它们的主合取范式相同,可知它们的主析取范式也相同.第2章谓词逻辑习题一、 单项选择题1. 谓词公式)())()((x Q y yR x P x →∃∨∀中量词∀x 的辖域是( )(A) ))()((y yR x P x ∃∨∀ (B) P (x ) (C) )()(y yR x P ∃∨ (D) )(x Q2. 谓词公式∃xA (x )∧⌝∃xA (x )的类型是( )(A) 永真式 (B) 矛盾式(C) 非永真式的可满足式 (D) 不属于(A ),(B ),(C )任何类型3 设个体域为整数集,下列公式中其真值为1的是( )(A) )0(=+∃∀y x y x(B) )0(=+∀∃y x x y (C))0(=+∀∀y x y x (D) )0(=+∃⌝∃y x y x 4 设L (x ):x 是演员,J (x ):x 是老师,A (x ,y ):x 佩服y. 那么命题“所有演员都佩服某些老师”符号化为( )(A) ),()(y x A x xL →∀ (B) ))),()(()((y x A y J y x L x ∧∃→∀(C) )),()()((y x A y J x L y x ∧∧∃∀ (D) )),()()((y x A y J x L y x →∧∃∀ 5. 设个体域是整数集合,P 代表∀x ∃y ((x <y )→(x -y <0)),下面4个命题中为真的是( )(A) P 是真命题 (B) P 是谓词逻辑公式,但不是命题(C) P 是假命题 (D) P 不是谓词逻辑公式6. 表达式))(),(())(),((z zQ y x R y z Q y x P x ∀→∃∧∨∀中x ∀的辖域是( )(A) P (x ,y ) (B)R (x ,y ) (C)P (x ,y )∧R (x ,y ) (D) P (x ,y )∨Q (z )二、 填空题1. 设个体域D ={1,2},那么谓词公式)()(y yB x xA ∀∨∃消去量词后的等值式为.2. 设个体域D={a,b},公式))Gx→∀消去量词化为yHx∃(y,()(x3. 设N(x):x是自然数,Z(y);y是整数,则命题“每个自然数都是整数,而有些整数不是自然数”符号化为4. 谓词公式∀x(F(x)→G(x))∧⌝∀y(F(y)→G(y))的类型是.5. 设个体域{1,2},谓词P(1)=1,P(2)=0,Q(1)=0,Q(2)=1,则∀x(P(x)∨Q(x))的真值是三、解答化简计算题1. 判别谓词公式),(x∃yF∀→∃的类型.∀x,)yx(yyxF2. 指出谓词公式)(xQyPx∀中∀x和∃x的辖xR→∧∃x∧(,))x))(S)((x(域,并指出该公式的约束变元和自由变元以及约束出现次数和自由出现次数.3. 求谓词公式))PQx∧→x∀的真值.(R(())f(a其中P:4>3,Q(x):x>1,R(x):x≤2.f(-3)=1,f(1)=5,f(5)= -3.a:5.个体域D=(-3,1,5).4.说明公式))xP∀xyG→(∀是逻辑有效式(永真式).→x∃()y(,)(xxP5. 通过等值演算说明下列等值式成立:PxxxPQ∃→⇔∀→x∃)()()))(xQ(x(x6. 求谓词公式),,(xyyGxxF∃∧∀的前束范式.→∀yzH)(,,(xy(z))四、证明题1. 试利用代换实例证明谓词公式xyzGxF∀∃∀→∀x→,)())((xF(x)z是逻辑有效式(永真式).2. 构造推理证明))xxQxxP∀∃.→∀⇒xP→(()()(Q(x)x(提示:))xA∨xxBx∀x∨∀⇒∀.))(()(()xB(xA谓词逻辑习题参考答案一、1. C ;2.. B ;3 A ;4. B ;5. A 6. D二、1. A (1)∨A (2)∨(B (1)∧B (2)) 2. (G (a )→(H (a ,a )∨H (a ,b )))∧ (G (b )→(H (b ,a )∨H (b ,b )))3.))()(())()((x N x Z x x Z x N x ⌝∧∃∧→∀ 4. 永假式 5. 1三、1.设I 为任意一个解释,D 为I 的个体域. 若在解释I 下,该公式的前件为0,无论),(y x xF y ∃∀如何取值,),(),(y x xF y y x yF x ∃∀→∀∃为1; 若在解释I 下,该公式的前件为1,则,0D x ∈∃使得),(y x yF ∀为1,它蕴含着),(,0y x F D y '∈'∀为1),(y x xF '∃⇒为1,由y '的任意性,必有),(y x xF y ∃∀为1,于是),(),(y x xF y y x yF x ∃∀→∀∃为1. 所以,),(),(y x xF y y x yF x ∃∀→∀∃是永真式.2. ∀x 的辖域为:P (x )→Q (x ,y )∧∃xR (x )∃x 的辖域为:R (x )x 既是约束变元,也是自由变元,约束出现3次,自由出现1次.y是自由变元,自由出现1次. 3. ))(())((a f R x Q P x ∧→∀=))5(())5(())1(())3((f R Q P Q P Q P ∧→∧→∧-→=)3()11()01()01(-∧→∧→∧→R01100=∧∧∧=4. 已知1)()(⇔∨⌝∨⌝⇔∨⌝∨⌝⇔→→P Q P P Q P P Q P因为))(),(()(x xP y x yG x xP ∀→∃→∀是)(P Q P →→的代换实例,可知))(),(()(x xP y x yG x xP ∀→∃→∀是逻辑有效式.或))(),(()(x xP y x yG x xP ∀∨⌝∃∨⌝∀1)(),()(⇔∨⌝∃∨⌝∀⇔x P y x yG x xP5. ⇔→∃))()((x Q x P x )()((x Q x P x ∨⌝∃))()(x xQ x P x ∃∨⌝∃⇔)()(x xQ x xP ∃∨⌝∀⇔)()(x xQ x xP ∃→∀⇔6. ),,()),(),((z y x zH y x yG y x xF ∃∧∀→∀),,()),(),((z y x zH y x yG y x xF ∃∧∀∨⌝∀⇔),,()),(),((z y x zH v u vG y u F u ∃∧∀∨⌝∃⇔)),,()),(),((z y x zH v u vG y u F u ∃∧∀∨⌝∃⇔)),,()),(),(((z y x H v u Q y u F z v u ∧∨⌝∃∀∃⇔(或)),,()),(),(((z y x H v u Q y u F z v u ∧→∃∀∃⇔)四、1.谓词公式))(),(()(x xF z x zG y x xF ∀→∃∀→∀ 是命题公式)(P Q P →→的代换实例.因为命题公式⇔∨⌝∨⌝⇔→→P Q P P Q P )(1是永真式, 故))(),(()(x xF z x zG y x xF ∀→∃∀→∀是逻辑有效式.2.前提:)()(x xQ x xP ∀→∃.结论:)()(x xQ x xP ∀→∃.证 ① )()(x xQ x xP ∀→∃ 前提引入② )()(x xQ x xP ∀∨⌝∃ T ①,蕴含等值式③ )()(x xQ x P x ∀∨⌝∀ T ②,量词否定④ ))()((x Q x P x ∨⌝∀⑤ ))()((x Q x P x →∀ T ④,蕴含等值式第3章 集合及其运算一、 单项选择题1. 设a 是集合A 的元素,则以下正确的是( )A a A a A a a a ∈⊆⊆⊆}){D ()C (}){B (}){A (2. 设集合A ={1,2,3,4},B ={2,4,6,9},那么集合A ,B 的对称差A ⊕B=( )(A) {1,3} (B) {2,4,6} (C) {1,3,6,9} (D) {1,2,3,4,6,9}3. 设集合A ={{1,2,3},{4,5},{6,7,8}},则下列各式为真的是( )(A) 1∈A (B) {{4,5}}⊂A(C) {1,2,3}⊆A (D) ∅∈A4. 设A , B , C 都是集合,如果A ⋂C =B ⋂C ,则有( ) (A) A =B (B) A ≠B (C) 当A -C =B -C 时,有A =B(D) 当C =U 时, 有A ≠B5. 设集合A ={∅,a },则P (A )= ( )}},{},{},{,){D (}}}},{,{},{},{,){C (}},{},{},){{B (}},{},{,){A (a a A a a a a a a ∅∅∅∅∅∅∅∅∅∅6. 设A ={1,2,3},B ={2,3,4,5},C ={2,3},则(A ∪B )⊕C 为( )(A) {1,2} (B) {2,3} (C) {1,4,5} (D) {1,2,3}二、 填空题1.设A , B 代表集合,命题A -B =∅⇔A=B 的真值为 .2. 设A , B 为任意集合,命题A -B =∅⇔A⊆B 的真值为 .3. 设集合A ={∅,{a }},则A 的幂集P (A )=4. 设集合A ={{a ,b },c }, B ={c ,d }, 那么A -B =5. 设集合A ={1,2,3,4},B ={a ,b ,c },则∣A ×B ∣=三、解答化简计算题1. 试作以下二题:(1) 设有序对<2x +y ,6>=<5,x +y >,求x ,y ;(2)设集合A ={1,2},求A ×P (A ).2. 设集合A ={a ,b ,c },B ={b ,d ,e },求B ⋂A ,A ⋃B ,A -B ,B ⊕A .3. 化简集合表达式:((A ⋃B ⋃C )⋂(A ⋃B ))-((B ⋃(B -C ))-A )4. 判断下列哪些运算结果是对的?哪些是错的?请将错误的运算结果更正过来.(1) ∅=∅⋂∅}{ (2) ∅=∅⋃∅}{(3) }{}}{,{}{∅=∅∅⋂∅ (4) }}{,{}{}}{,{∅∅=∅-∅∅(5)A B B A =⋃-)( (6)A B B A =-⋃)((7)A A A =⊕ (8)∅=-⋂A B A )(5.易,0.5,8,掌握,2-2 设全集E =(a ,b ,c ,d ,e ,f ), A ={a ,d },B ={a ,b ,e },C ={b ,d },求下列集合:(1) C B A ~)(⋃⋂; (2))()(A P A A ⋃⊕.6. 设},{},,,{},,{},,,,,{42=521=41=54321=C B A E求 (A ⋂B )⋃~C ,P (A )-P (B ),A ⊕B .四、证明题1. 设A ,B ,C 为三个集合,证明若C ⊆A .则(A ⋂B )⋃C ⊆A ⋂(B ⋃C )2. 试证明对任意集合A ,B ,C ,如果B A ⊆且D C ⊆,则C BD A -⊆- 3. 设A ,B ,C 为任意集合,证明:)()()(C B C A C B A ---=--集合练习题参考答案一、1. B 2. C 3. B 4. C 5. D 6. C 二、1. 0 2. 1 3. }}}{,{}},{{},{,{a a ∅∅∅ 4. {{a ,b }} 5.12三、解答化简题1. (1) 由有序对定义,解方程⎩⎨⎧=+=+652y x y x 解得x=-1,y=7.(4分)(2)P (A )={∅,{1},{2}{1,2}}A ⨯P (A )={<1,∅>,<2,∅>,<1,{1}>,<2,{1}>,<1,{2}>,<2,{2}>,<1,{1,2}>,<2,{1,2}>}2. B ⋂A ={b } A ⋃B ={a ,b ,c ,d ,e } A -B ={a ,c } B ⊕A ={a ,b ,c ,d ,e }-{b }={a ,c ,d ,e }3. ((A ⋃B ⋃C )⋂(A ⋃B ))-((B ⋃(B -C ))-A )=(A ⋃B )-(B -A ) =(A ⋃B )⋂(~B ⋃A ) =A ⋃(B ⋂~B )=A ⋃∅=A4. (1) 对. (2) 错.应为}{∅. (3) 对. (4) 错.应为{}{∅}(5)错.应为B A ⋃ (6)错.应为B A -(或B A ~⋂或A -AB )(7)错.应为∅,即∅=⋂-⋃=⊕A A A A A A (8)对. 5. (1) },,,{},,,{}{~)(f e c a f e c a a C B A =⋃=⋃⋂ (2)∅=⋂-⋃=⊕)()()(A A A A A A . }},{},{},{,{)(d a d a A P ∅=.故)()(A P A A ⋃⊕=}},{},{},{,{d a d a ∅ 6. (A ⋂B )⋃~C ={1}⋃}5,3,1{}5,3,1{=}},{},{{}},{},{},{,{}},{},{},{,{)()(411=4242-4141=-φφC P A PA⊕B =(A⋃B)-(A⋂B)=}5,4,2{}5,4,2,1{=-}1{四、证明题1. 已知xC∀⊆,A∈⋂∨⇔⋃(∈)x∈⋂CAxABxBC∈∧(⇔)∈∨Cx∈BxAx∨∈x∈∧⇔A∈∨∈x(C)(x)BCx∈∈x⋃∨⋂∧A⇒∈∈⇔B(C(xA)BxC)即)⋂A⋃⊆⋂B⋃(CC)(AB2. 由于C⇔~⊆⊆,DC~D又有BA⊆,所以⊆⋂~⋂DCA~B即C-.⊆A-DB3. )A⋂CC⋂B---A=⋂~)~(~C(B(C))(⋂A⋃C=⋂~B(~))(CA⋂CB⋂⋂A⋂⋃=(~))~(C~C=C)~~(⋂⋂⋂=⋂= C)(BBAC~A~(-)BA-第3章 二元关系练习题一、 单项选择题1. 设集合A ={0,b },B ={1,b ,3},则A ⋃B 上的恒等关系是 ( ).(A) {<0,0>,<1,1>,<3,3>} (B){<0,0>,<1,1>,<b ,b >,<3,3>}(C) {<1,1>,<b ,b >,<3,3>} (D) {<0,1>,<1,b ><b ,3>,<3,0>} 2. 已知集合A ={a ,b ,c }上的二元关系R 的关系矩阵M R =⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡001011010,那么R =( ),(A) {<a ,b >,<b ,a >,<b ,b >,<a ,c >} (B) {<a ,b >,<b ,a >,<b ,b >,<c ,b >} (C) {<a ,b >,<a ,a >,<b ,b >,<c ,a >} (D) {<a ,b >,<b ,a >,<b ,b >,<c ,a >} 3. 设集合A ={1,2,3,4}, A 上的二元关系R 的关系矩阵为M R =⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡00000001011001则关系R 的表达式是( )(A) {<1,1>,<1,4>,<2,1>,<2,3>} (B) {<1,1>,<1,2>,<1,4>,<2,3>} (C) {<1,1>,<2,1>,<3,2>,<1,4>} (D) {<1,1>,<2,1>,<3,2>,<4,1>}4. 设A ={a ,b ,c },R ={<a ,a >,<b ,b >},则R 具有性质( ) (A) 自反的 (B) 反自反的 (C) 反对称的 (D) 等价的5. 设R 是集合A 上的二元关系,I A 是A 上的恒等关系,如果R ⊂I A ,则下面四个命题中为真的是( )(A) R 不是自反的 (B) R 不是传递的 (C) R 不是对称的 (D) R不是反对称的 二、填空题1. 设R ,S 都是集合A 上的等价关系,则对称闭包s (R ⋂S )=2. 如果关系R 是传递的,则R ∙R ⊆ .3. 设集合A ={1,2,3,4 }, B ={6,8,12}, A 到B 的关系R =},,2,{B y A x x y y x ∈∈=><,那么R -1=4. 设X ={a ,b ,c },R 是X 上的二元关系,其关系矩阵为 M R=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡001001101,那么R 的关系图为 .5. 设A ={1,2,3,4},A 上的二元关系}3,{Z ∈-><=y x y x R ,其中Z 是整数集合.试用列举法那么R= . 三、解答化简计算题1. 设集合A ={a ,b ,c ,d },在A 上定义二元关系R ={<a ,a >,<a ,d >,<b ,b >,<b ,c >,<c ,b >,<c ,c >,<d ,a >,<d ,d >} R 是否为等价关系,说明理由.2. 设R 是实数集,R 上的二元关系S 为 S ={<x ,y >∣x ,y ∈R ∧x =y }试问二元关系S 具有哪些性质?简单说明理由.3. 设A ={1,2},B ={a ,b },试问从A 到B 的二元关系有多少个?4. 设集合A ={0,1,2,3,4,5,6}上的偏序关系R 如下: R={<0,1>,<0,2>,<0,3>,<0,4>,<0,5>,<0,6>,<4,6>,<2,5>,<3,5>}⋃I A 做偏序集<A ,R >的哈斯图,并求B ={0,2,3}的极大元、极小元、最大元和最小元.5. 设集合A ={0,1,2,3,4},定义A 上的二元关系R 为: R ={<x ,y >⎪x ,y ∈A ∧(x =y ∨x +y ∈A )}试写出二元关系R 的集合表达式,并指出R 具有的性质.6. 已知集合A 上的二元关系R 的关系图如图4-1,试写出R 的集合表达式和R 的关系矩阵.并指出R 所有的性质.7. 设集合A ={1,2,3,4}, B ={2,4,6} 从A 到B 的二元关系R 定义为R =},{N k k xy B y A x y x ∈∧=∧∈∧∈><试求R 的集合表达式和关系矩阵M R .8. 设R 1是A 1={1,2}到A 2=(a ,b ,c )的二元关系,R 2是A 2到A 3={βα,}的二元关系,R 1= {<1,a >,<1,b >,<2,c >}, R 2={<a ,β>,<b ,β>} 试用关系矩阵求R 1∙R 2的集合表达式.9. 设集合X ={a ,b ,c ,d },X 上的二元关系R 的关系图如图4-2所示.试写出R 的表达式和关系矩阵.10. 设集合S ={1,2,3,4},定义S 上的二元关系 })(,,{2y x S y x S y x y x R >∧∈-∧∈><=},,{是素数yx S y x y x T ∧∈><=试求R ,T 的元素表达式,并计算R ∙T . 四、证明题1. 证明如果非空集合A 上的二元关系R 和S 是偏序关系,则S R ⋂也是A 上的偏序关系.2. 设R 是集合A 上的二元关系,试证明R 是自反的当且仅当R I A ⊆.3. 假设R 是非空集合A 上的等价关系,证明R 的逆关系R -1也是A 上的等价关系.0 ∙ ∙2 1∙ 图4- 1a db c图4-2二元关系习题参考答案一、1. B 2. D 3. A 4. C 5. A二、1. R ⋂S 2. R 3. {<6,3>,<8,4> }4. 如图4-3.5. }1,4,4,1{><><⋃A I三、1. R 含有<a ,a >,<b ,b >,<c ,c >,<d ,d >, 是自反的;R 含有<a ,a >,<b ,b >,<c ,c >,<d ,d >,<a ,d >,<d ,a >,<b ,c >,<c ,b >, 是对称的; 对R z x R z y R y x >∈⇒<>∈<>∈<∀,,,,,是传递的.故R 是A 上的等价关系.2. S 具有自反性,显然<x ,x >∈S ; S 具有对称性,∀<x ,y >∈S ,有x =y ,则<y ,x >∈S ; S 具有反对称性,∀<x ,y >,<y ,x >∈S ,有x =y ; S 具有传递性,∀<x ,y >,<y ,z >∈S ,因为x =y =z ,故<x ,z >∈S .3. 二元关系共有16个.4. A ={0,1,2,3,4,5,6}, B ={0,2,3}, 哈斯图如图4-4.B 的极大元:2,3, B 的极小元:0 B 的最大元:无 B 的最小元:05. 由题设,R =I A ⋃{<0,1>,<1,0>,<0,2>,<2,0>,<0,3>,<3,0>,<0,4>,<4,0>,<1,2>,<2,1>,<1,3>,<3,1>}易知,R 具有自反性和对称性.6. }0,2,2,0,2,2,0,0{><><><><=R⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=101000101RMR 有对称性和传递性.7. R ={<1,2>,<1,4>,<1,6>,<2,2>,<2,4>,<2,6>,<3,6>,<4,4>}M R =⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡01100111111 a c b 图4-3 6∙ 5∙∙4 3∙ 2∙ ∙10∙ 图4-48. ,100111⎥⎦⎤⎢⎣⎡=R M⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=0010102R M ⎥⎦⎤⎢⎣⎡=∙10001121R R M ⎥⎦⎤⎢⎣⎡=⎥⎥⎦⎤⎢⎢⎣⎡0010001010 },1{21><=∙βR R9. R ={<a ,a >,<a ,c >,<b ,c >,<d ,d >}⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=1000000001000101R M 10. }2,4,3,4,2,3,1,2{><><><><=R}2,4,1,3,1,2{><><><=T }1,4,1,3{><><=⋅T R四、证明题1. .① S R x x S x x R x x A x ⋂>∈⇒<>∈<>∈<∈∀,,,,,,所以S R ⋂有自反性;②,,A y x ∈∀因为R ,S 是反对称的,yx x y y x S x y S y x R x y R y x S x y R x y S y x R y x S R x y S R y x =⇔=∧=⇒>∈<∧>∈<∧>∈<∧>∈<⇔>∈<∧>∈<∧>∈<∧>∈<⇔⋂><∧⋂><),,(),,(),,(),,(,, 所以,R ⋂S 有反对称性.③ A z y x ∈∀,,,因为R ,S 是传递的, S R z y S R y x ⋂>∈<∧⋂>∈<,,S z y R z y S y x R y x >∈<∧>∈<∧>∈<∧>∈⇔<,,,, S z y S y x R z y R y x >∈<∧>∈<∧>∈<∧>∈⇔<,,,, S R z x S z x R z x ⋂>∈⇔<>∈<∧>∈⇒<,,,所以,S R ⋂有传递性. 总之,R 是偏序关系. 2. 先证必要性.假设R I A ⊆/,则必存在x ∈A ,使得<x ,x >∈I A ,且<x ,x >∉R ,这与R 是自反的相矛盾.所以R I A ⊆.再证充分性.设R I A ⊆,则对,,,A I x x A x >∈<∈∀因为R I A ⊆,所以R x x >∈<,.因此R 是自反的.3. (1) ∀x ∈A ,则<x ,x >∈R ,显然<x ,x >∈R -1,R -1具有自反性. (2) ∀x ,y ∈A , 如果<x ,y >∈R -1⇔<y ,x >∈R⇒<x ,y >∈R (R 是对称的)⇔<y ,x >∈R -1, R -1具有对称性.(3) ∀x ,y ,z ∈A ,如果<x ,y >∈R -1∧<y ,z >∈R 1⇔<y ,x >∈R ∧<z ,y >∈R ⇔<z ,y >∈R ∧<y ,x >∈R ⇒<z ,x >∈R (R 是传递的)⇔<x ,z >R -1,R 具有传递性.总之,R 是等价关系.第5章 群练习题一、单项选择题1. 设A =Q ×Q ,其中Q 是有理数集,定义A 上的二元运算*为:),,(b a ∀,A y x ∈),(,),(),(),(b ay ax y x b a +=*,则(1,2)*(3,4)=())6,3)(D ()8,6)(C ()1,5)(B ()10,3)(A (-2. 下列集合和运算能构成群的是 ( ).(A) (M n (R ),+),其中M n (R )是定义在实数集上的n 阶矩阵,+是普通加法 (B)(A ,+),其中A ={0,±1,±2,…,±n },+是普通加法 (C)({21,0,2},+),其中+是普通加法(D) ({0,1,2,3},⊗),其中运算⊗是模4乘法3. 在自然数集N 上定义的二元运算*,满足结合律的是( )ba b a b a b a b a b a b a b a -=*=*2+=*-=*)D (},max{)C ()B ()A (4. 以下代数系统中,只是半群的为( ). (A) (Z ,︒),其中Z 是整数集,∀a ,b ∈Z ,a ︒b =a +b -2 (B) (Z ,︒),其中Z 是整数集,∀a ,b ∈Z ,a ︒b =b (C) (Z ,︒),其中Z 是整数集,∀a ,b ∈Z ,a ︒b =a +b -ab(D) (R -{0},︒),其中R 是实数集,∀a ,b ∈R ,a ︒b =ab 5. 以下群中,是循环群的为( ). (A) (Z ,+),其中Z 是整数集,+是数的加法 (B) (Q +,×),其中Q +是正有理数集,×是数的乘法 (C) (Q ,+),其中Q 是有理数集,+是数的加法(D) (P (A),⊕),其中A ={a ,b },P (A)是A 的幂集,⊕是集合的对称差运算 二、填空题 1. 设R 是实数集,∀a ,b ∈R ,定义二元运算*:a *b =a +b +ab ,已知0∈R 是其单位元,那么∀a ∈R ,但a ≠-1,则a 的逆元是 .2. 设(R *, )是代数系统,其中R *=R -{0},二元运算 定义为abb a R b a =∈∀ ,,*,那么,a R a ,*∈∀的逆元是3. 设集合A ={1,2,3},在A 上定义二元运算︒为:,,A b a ∈∀a ︒b =},min{b a ,则︒的运算表为︒ 1 2 3 1 2 34. 设S 是非空有限集合,P (S )是S 的幂集,则代数系统<P (S ),⋃ >存在单位元是 三、解答化简计算题1. 设代数系统(R *, ︒),其中R *是非0实数集,二元运算︒为:∀a ,b ∈R , a ︒b =ab. 试问︒是否满足交换律、结合律,并求单位元以及可逆元素的逆元.2. 验证H 2={e ,a 3}是6阶循环群G ={ e ,a 1,a 2,a 3,a 4, a 5}的子群.3. 验证代数系统(Z ,+)与(2Z ,+)同构.4. 设集合A ={1,2,3},P (A )是A 的幂集合,⊕是集合的对称差运算.求运算⊕在P (A )上的单位元.∀x ∈P (A ),求x 关于运算⊕的逆元.并解方程{1,2}⊕y ={1}.四、证明题1. 设群(G ,*), 若∀a ∈G ,都有a 的逆元a -1=a ,则G 是交换群.2. 设R *=R -{0},集合S 定义为},00{*R b a b a S ∈⎥⎦⎤⎢⎣⎡= 证明代数系统(S ,*)是群,其中*是矩阵的乘法运算.3. 在整数集合Z 上定义二元运算︒:∀x ,y ∈Z , x ︒y =x +y -2,已知<Z , ︒>是半群,证明<Z ,︒>是群.4. 证明群(R ,+)与(R +,∙)同构,其中+和∙分别是数的加法和乘法.(提示:考虑函数f (x )=e x )群练习题参考答案一、1. D 2. A 3. C 4. B 5. A 二、1. 1+-a a 2.a1 3.4. ∅三、1. ∀a ,b ,c ∈R *, a ︒b =ab =ba =b ︒a ,可交换; (a ︒b )︒c =ab ︒c =abc =a (bc )=a ︒(bc )=a ︒(b ︒c ),可结合. 易见,单位元为1.对∀a ∈R *, a ︒a -1=aa -1=1=a -1a =a -1︒a ,故a 的逆元:aa 11=-2. (1) H 2⊂G .易验证∀x ,y ∈H 2,有xy ∈H 2.且在H 2上满足结合律. e 是其单位元,(e )-1=e ,(a 3)-1=a 3. 故H 2是G 的子群.3. ∀z ∈Z ,f (z )=2z ,有f :Z →2Z .∀z 1,z 2∈Z ,f (z 1+z 2)=2(z 1+z 2)= 2z 1+2z 2= f (z 1)+f (z 2) 所以,(Z ,+)与(2Z ,+)同态.又因为f (z )=2z 是双射函数,故(Z ,+)与(2Z ,+)同构. 4. ∀S ∈P (A),S ⊕∅=∅⊕S =S ,故∅是单位元. ∀x ∈P (A),x ⊕x =∅,故x 的逆元是它自己. 因为(1,2)的逆元是{1,2},故y ={1,2}⊕{1}={2}. 四、1. 111,,)(,,,---==*=*∈*∈∀b b a a b a b a G b a G b a 由题设(3分) 于是有a b a b b a b a b a *====--------11111111)(*)()*()*(* 所以G 是一个交换群.2. 任取S 中的元素⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡d c y x b a00,00,00,其中a ,b ,x ,y ,c ,d ∈R *,有⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡byd axc yd xcb a dc y x b a byd axc d c by ax d c y x b a 0000*00)00*00(*000000*0000*)00*00(︒1 2 3 1 1 1 1 21 2 2 3123可见,*满足结合律,故(S ,*)是半群. 取E =S ∈⎥⎦⎤⎢⎣⎡1001,∀A ∈S ,有AE =EA =A .E 为S 的单位元.∀X ∈S ,X =⎥⎦⎤⎢⎣⎡y x0,x ,y ∈R *,则存在⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡y x 1001∈S ,则有⎥⎦⎤⎢⎣⎡y x0*⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡y x 1001=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡y x 1001*⎥⎦⎤⎢⎣⎡y x 00=E ,即X -1=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡y x 1001.S 的每个元素都有逆元.故(S , *)是群. 3. 因为<Z ,︒>是半群,易见二元运算︒满足交换律.设幺元为e , ∀x ∈Z ,有x ︒e =x +e -2=x ,得到e =2∈Z ,幺元存在惟一;∀x ∈Z , x 的逆元记作x -1, x ︒x -1=x +x -1-2=2, 即x -1=4-x ∈Z ,即x 的逆元存在且惟一.所以,<Z ,︒>是群. 4.设f (x )=e x ,可知f :R →R +.(1) ∈∀21,x x R ,)()(e e e )(21212121x f x f x x f x x x x ∙===++∈R +. 0和1分别是(R ,+)和(R +,∙)的单位元,有 f (0)=e 0=1对任意x ∈R ,x 关于+的逆元为-x ,而f (-x )=e -x =)(11x f ex=.(2) f :R →R +是双射函数.所以,(R ,+)与(R +,∙)同构.第6章 格与布尔代数及环、域练习题一、 单项选择题1.下列偏序集中是格的为( )2. 设布尔代数式c b a f ⋅+=,则f 的对偶式f *=( )(A) c b a ⋅+ (B) c b a ⋅+ (C) c b a +⋅ (D) c b a +⋅ 3. ( )是布尔代数. (A) 有余有界格 (B) 有余分配格 (C) 有界分配格 (D) 有余代数格 4. 设G 是非空集合,G 上二元运算︒和*,*对︒有左、右分配律,又满足( ),则(G ,︒,*)称为环.(A) (G ,*)是交换群,(G ,︒)是交换群 (B) (G ,*)是半群,(G ,︒)是半群(C) (G ,*)是群,(G ,︒)是群 (D) (G ,*)是半群,(G ,︒)是交换群二、 填空题1. 设代数系统(L ,︒,*),若(L ,︒)是 ,(L ,*)是半群,又二元运算*对︒满足分配律,则(L ,︒,*)是环.2. 布尔代数式))(()1(c a b a +⋅+⋅的对偶式是3.在布尔代数中,有b a b a a +=⋅+)(成立,则其对偶式 一定成立.4. 若<G ,+,∙>是环,那么∀a ,b ∈G ,有 则称<G ,+,∙>是交换环. 三、解答化简计算题1. 设代数系统(Z ,+,×),已知(Z ,×)是半群,验证(Z ,+,×)是环.2. 设(L ,*,︒)是有补格,∀a ,b ∈L ,化简表达式 (a *b )*(a '︒b ')(其中a ',b '分别是元素a ,b 的补元)3. 已知(L ,*,︒)是格,且二元运算*和︒满足分配律,∀a ,b ,c ∈L ,化简表达式 ((a *b )︒(a *c ))* ((a *b )︒(b *c ))4. 试作以下二题:(1)已知A ≠∅,则(P (A ),⋃,⋂,~,∅,A )是布尔代数,∀S ∈P (A ),求S 的补元,说明理由.(2)布尔代数(),,,+∙B ,其中}1,0{=B ,若B 上的三个变元的表达式c b c b a c b a E ++∙+=),,(求)1,1,0(E 的真值.四、证明题1. 设R 为实数集,证明(R ,+)是交换群,(R ,×)是半群,且×对+满足左、右分配律,即(R ,+,×)是环.其中+,×是普通加法和乘法.2. 设<S ,+,∙,,0,1>为一布尔代数,证明∀a ,b ∈S ,有b a b a a +=∙+)(;b a b a a ∙=+∙)((A)(B) (C) (D)格等代数系统习题参考答案一、 1. B 2. C 3. B 4. D二、1.交换群 2. ))(()0(c a b a ⋅+⋅+ 3. b a b a a ⋅=+⋅)( 4. a ∙b =b ∙a 三、1.只需验证(Z ,+)是交换群. 易验证整数具有结合律,交换律. 0是加法的单位元.(4分)∀k ∈Z ,∃-k ∈Z ,有 k +(―k )=(―k )+k =0Z 中每个元素有逆元.故(Z ,+)是交换群. 所以(Z ,+,×)是环.(8分)2. (a *b )*(a '︒b ')=(a *b )* (a *b ) '=13. ((a *b )︒(a *c ))*((a *b )︒(b *c ))=(a *b )︒ ( (a *c )* (b *c ))(分配律) =(a *b ) ︒((a *b )*c ) (幂等律) =a *b (吸收律)4. (1) 对任意S , 因为S ⋃(A -S )=(S ⋃A )⋂(S ⋃~S )=A ,S ⋂(A -S )=S ⋂(A ⋂~S )=∅故S 的补元为A -S .(2) 因为c b c b a c b a E ++∙+=),,(所以, E (0,1,1) =11110++∙+=1110++∙=0+1=1四、1. (1)∀x ,y ,z ∈R ,有(x +y )+z =x +(y +z ),满足加法 R 上满足加法结合律. (2) ∀x ,y ∈R ,有x +y =y +x ,满足加法R 上满足加法交换律.(3)R 中存在元素0,使得∀x ∈R ,有x +0 =0+x , 加法单位元存在,为0. (4) ∀x ∈R , 存在-x ∈R ,使得x +(-x )=0,加法逆元存在,x -1=-x . 可见(R ,+)是交换群; (5) ∀x ,y ,z ∈R ,有(x ×y )×z =x ×(y ×z ),满足乘法结合律. 可见(R ,×)是半群; (6) ∀x ,y ,z ∈R ,有(x +y )×z =x ×z +(y ×z ), z ×(x +y )=z ×x +z ×y , 满足左、右分配律.二元运算×对+满足左右分配律.总之,(R ,+,×>是环. 2. b a b a b a a a b a a +=+∙=+∙+=∙+)(1)()()( b a b a b a a a b a a ∙=∙+=∙+∙=+∙0)()(第7章 图的基本概念一、 单项选择题1. 设V ={a ,b ,c ,d },与V 能构成强连通图的边集E =( )(A) {<a ,b >,<a ,c >,<d ,a >,<b ,d >,<c ,d >} (B) {<a ,d >,<b ,a >,<b ,c >,<b ,d >,<d ,c >} (C) {<a ,c >,<b ,a >,<b ,c >,<d ,a >,<d ,c >} (D) {<a ,d >,<b ,a >,<b ,d >,<c ,d >,<d ,c >} 2. 有向完全图D =<V ,E >, 则图D 的边数是( )(A)2)1(-E E (B)2)1(-V V (C) ∣E ∣(∣E ∣-1) (D) ∣V ∣(∣V ∣-1)3. n 阶无向完全图K n 中的边数为( ) (A)2)1(-n n (B)2)1(+n n (C) n (D)n (n +1)4. 给定无向图G 图5-1所示,下面给出的顶点集子集中,不是点割集的为( )(A) {b ,d } (B) {d } (C) {a ,c } (D) {g ,e } 5. 下列数组中,不能构成无向图的度数列的数组是( )(A) (1,1,1,2,3) (B) (1,2,3,4,5) (C) (2,2,2,2,2) (D) (1,3,3,3)二、 填空题1.设有向图D =<V ,E >的邻接矩阵为A (D )=0110101000010110⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦,那么∣E ∣= . 2. 无向图G (如图5-2)的关联矩阵M (G )=3. 数列{2,3,3,4}不能构成无向简单图的度数列,此命题的真值为4. 在有向图的邻接矩阵中,第i 行元素之和与第j 列元素之和分别为 .5. 图G 如图5-3,那么图G 的割点是6. 有16条边,每个顶点都是2度顶点的无向图有个顶点.三、解答化简计算题 1. 设图G 如图5-4所示.已知通路(1) v 1e 5 v 5e 7 v 2e 2 v 3(2) v 5e 6 v 2e 2 v 3e 3 v 4e 8 v 2e 7 v 5 (3) v 2e 7 v 5e 6 v 2(4) v 1e 1 v 2e 2 v 3e 3 v 4e 8 v 2e 6 v 5试回答它们各是简单通路、简单回路、 初级通路还是初级回路.a gb d fc e 图5- 1 v 2e 2 v 3 e 1 e 3 v 1 e 4 v 4 图5-2a bf ce d图5-3 v 1 e 1 e 5 v 2 e 6 v 5 e 2 e 7 e 4 e 8v 3 e 3 v 4 图5-42. 指出有向图D(如图5-5)中各图是强连通,单侧连通还是弱连通?3. 找出无向图G(如图5-6所示)中的一个点割集,三条边和四条边的边割集各一个.4. 已知有向图D(如图5-7)的邻接矩阵为A(D)=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡111111111求从v2到v4长度为2和从v3到v3长度为2的通路条数,并将它们具体写出.5. 设图G=<V,E>,其中V={a,b,c,d,e}, E={(a,b),(b,c),(c,d), (a,e)}试作出图G的图形,并指出图G是简单图还是多重图?是连通图吗?说明理由.6. 设简单连通无向图G有12条边,G中有2个1度结点,2个2度结点,3个4度结点,其余结点度数为3.求G中有多少个结点.试作一个满足该条件的简单无向图.四、证明题1. 若无向图G中只有两个奇数度结点,则这两个结点一定是连通的.2 证明在任何有向完全图中,所有结点的入度平方之和等于所有结点的出度平方之和.(1)(2)(3)(4)(5)图5-5a bce d图5-6v4 v3v1 v2图5-7图的基本概念习题参考答案一、1. A 2. D 3. A 4. A 5. B二、1. 7 2. ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡11001101101001 3. 1 4.结点v i 的出度与结点v j 的入度 5. a , f 6. 16 三、1. (1) 初级通路; (2) 简单回路; (3) 初级回路; (4) 简单通路.2. 强连通图为:图5-5的(1),(4),(5);单侧连通图为:如图5-5的(1),(2),(4),(5),或图5-5的(2); 弱连通图为:图5-5(1)~(5),或图5-5的(3)..3. 点割集:{a ,c ,d }(不惟一) 三条边的边割集:{(b ,c ),(c ,e ),(c ,d )}(不惟一) 四条边的边割集:{(a ,b ),(a ,d ),(d ,e ),(c ,e )}(不惟一)4.. A 2(D )=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡2120020221201212从矩阵A 2(D )中a 24=2,a 33=2可知,从v 2到v 4长度为2的通路有2条. 它们是: v 2v 3v 4,和v 2v 1v 4, 从v 3到v 3长度为2的通路有2条. 它们是: v 3v 4v 3,和v 3v 2v 3,5. 图G 如图5-8.图G 中既无环,也无平行边,是简单图.图G 是连通图. G 中任意两点都连通. 6. 设图G 有x 个结点,有握手定理 2⨯1+2⨯2+3⨯4+3⨯(x -2-2-3)=12⨯2271821243=-+=xx =9 图G 有9个结点. 作图如图5-10四、1. 用反证法.设G 中的两个奇数度结点分别为u 和v .假若u 和v 不连通. 即它们之间无任何通路,则G 至少有两个连通分支G 1,G 2,且u 和v 分别属于G 1和G 2,于是G 1和G 2各含有一个奇数度结点.这与握手定理的推论矛盾.因而u 和v 一定是连通的.ab ec d图5-8 图5-10第七章几种特殊图练习题一、 单项选择题1. 以下命题真值为1的是( )(A) 无向完全图都是欧拉图 (B) 有n 个结点n -1条边的无向图都是树 (B) 无向完全图都是平面图 (D) 树的每条边都是割边 2. 有4个结点的非同构的无向树有 ( )个. (A) 2 (B) 3 (C) 4 (D) 5 3. 无向完全图K 4是( )(A )欧拉图 (B )哈密顿图 (C )树 (D )非平面图 4. 以下各图中存在哈密顿回路的图是 ( )5. 设G 是连通平面图,有v 个结点,e 条边,r 个面,则r = ( ). (A) e -v +2 (B)v +e -2 (C)e -v -2 (D) e +v +26. 无向图G 是欧拉图,当且仅当( )(A) G 中所有结点的度数全为偶数 (B) G 中所有结点的度数全为奇数 (C) G 连通且所有结点的度数全为偶数 (D) G 连通且所有结点的度数全为奇数 7. 设G 是有6个结点的无向完全图,从G 中删去( )条边,则得到树. (A) 6 (B) 9 (C) 10 (D) 15二、填空题1. 无向连通图G 含有欧拉回路的充分必要条件是2. 设图G =<V ,E >,其中|V |=n ,|E |=m .则图G 是树当且仅当G 是连通的,且m = .3. 图G (如图6-1所示)带权图中最小生成树的权是4.在平面图>=<E V G ,中,则∑=ri i r 1)deg(= ,其中r i (i =1,2,…,r )是图G 的面.5. 设图>=<E V G ,是简单图,若图中每对结点的度数之和 ,则G 一定是哈密顿图.6. 设G 是连通平面图,v ,e ,r 分别表示G 的结点数,边数和面数,则v ,e 和r 满足的关系式是三、解答化简计算题1. 设无向图G =<V ,E >, 那么图G 中∣V ∣与∣E ∣满足什么条件,图G 一定是树.2. 图G (如图6-2)能否一笔画出?说明理由. 若能画出,请写出一条通路或回路.3. 给定三个图如图6-3所示,试判断它们是否 为欧拉图、哈密顿图、或平面图?并说明理由.(A) (B) (C) (D)∙2 2 3∙ 1 ∙7 9 2∙ 8 ∙ 6 图6-1v 5 d v 4 v 1 v 2 v 3 图6-2 e f n c a h g b。
离散数学ch2.二元关系(5、6、7节)

VS
详细描述
关系的对称差运算可以用符号表示为 R△S,其中 R 和 S 是两个关系。它包括 属于 R 但不属于 S,以及属于 S 但不属 于 R 的所有有序对。如果 (a, b) 在 R△S 中,那么 (a, b) 或者只属于 R,或者只属 于 S。
04
CATALOGUE
关系的闭包
闭包的定义
1 2
关系的交运算可以用符号表示为 R ∩ S,其中 R 和 S 是两个关系 。它包括同时属于 R 和 S 的所有 有序对。如果 (a, b) 在 R ∩ S 中 ,那么 (a, b) 同时是 R 和 S 的差是一种集合差集操作,它从第一个 关系中去除与第二个关系共有的元素。
中可以推导出的新事实。
数据完整性
03
在数据库设计中,闭包的概念用于确保数据的完整性和准确性
,防止出现冗余和不一致的情况。
05
CATALOGUE
关系的类型
函数关系
总结词
函数关系是一种特殊的二元关系,它满足每 个自变量都有唯一的因变量与之对应。
详细描述
在函数关系中,对于定义域中的每一个元素 ,在值域中都有唯一一个元素与之对应。这 种关系具有明确性、确定性和无重复性。常 见的函数关系有数学函数、映射函数等。
离散数学ch2.二元 关系(5、6、7节)
contents
目录
• 引言 • 二元关系的性质 • 关系的运算 • 关系的闭包 • 关系的类型 • 关系在数据库中的应用 • 关系在人工智能中的应用
01
CATALOGUE
引言
定义与概念
定义
二元关系是集合论中的一个基本概念 ,它描述了两个元素之间的联系。
在设计关系型数据库时,需要考虑数据结构、数据完整性、数据冗余和数 据安全性等方面。
离散数学结构第6章集合代数

离散数学结构第6章集合代数第六章集合代数1. 集合,相等,(真)包含,⼦集,空集,全集,幂集2. 交,并,(相对和绝对)补,对称差,⼴义交,⼴义并3. ⽂⽒图,有穷集计数问题4. 集合恒等式(等幂律,交换律,结合律,分配律,德·摩根律,吸收律,零律,同⼀律,排中律,⽭盾律,余补律,双重否定律,补交转换律等)学习要求1. 熟练掌握集合的⼦集、相等、空集、全集、幂集等概念及其符号化表⽰2. 熟练掌握集合的交、并、(相对和绝对)补、对称差、⼴义交、⼴义并的定义及其性质3. 掌握集合的⽂⽒图的画法及利⽤⽂⽒图解决有限集的计数问题的⽅法4. 牢记基本的集合恒等式(等幂律、交换律、结合律、分配律、德·摩根律、收律、零律、同⼀律、排中律、⽭盾律、余补律、双重否定律、补交转换律)5. 准确地⽤逻辑演算或利⽤已知的集合恒等式或包含式证明新的等式或包含式6.1 集合的基本概念⼀.集合的表⽰集合是不能精确定义的基本概念。
直观地说,把⼀些事物汇集到⼀起组成⼀个整体就叫集合,⽽这些事物就是这个集合的元素或成员。
例如:⽅程x2-1=0的实数解集合;26个英⽂字母的集合;坐标平⾯上所有点的集合;……集合通常⽤⼤写的英⽂字母来标记,例如⾃然数集合N(在离散数学中认为0也是⾃然数),整数集合Z,有理数集合Q,实数集合R,复数集合C等。
表⽰⼀个集合的⽅法有两种:列元素法和谓词表⽰法,前⼀种⽅法是列出集合的所有元素,元素之间⽤逗号隔开,并把它们⽤花括号括起来。
例如A={a,b,c,…,z}Z={0,±1,±2,…}都是合法的表⽰。
谓词表⽰法是⽤谓词来概括集合中元素的属性,例如集合B={x|x∈R∧x2-1=0}表⽰⽅程x2-1=0的实数解集。
许多集合可以⽤两种⽅法来表⽰,如B也可以写成{-1,1}。
但是有些集合不可以⽤列元素法表⽰,如实数集合。
集合的元素是彼此不同的,如果同⼀个元素在集合中多次出现应该认为是⼀个元素,如{1,1,2,2,3}={1,2,3}集合的元素是⽆序的,如{1,2,3}={3,1,2}在本书所采⽤的体系中规定集合的元素都是集合。
离散数学结构试题集5-6

第5章一.填空题1. 群中有唯一的()。
2. 如果群运算是可交换的,则群为()。
3. 设*是定义在集合A上的二元运算,如果对于A中任意的两个元素x,y,都有x*y∈A,则称二元运算*在A上是()。
4. 设*是定义在集合A上的二元运算,如果对于A中任意的两个元素x,y,都有x*y=y*x,则称二元运算*在A上是()。
5. 设★是定义在有理数集合Q上的二元运算,如果对于Q中任意的两个元素x,y,都有x★y=x+y-x*y,其中*表示普通乘法元算,则二元运算★在Q上是()。
(填写可交互/不可交换)6. 设*是定义在集合A上的二元运算,如果对于A中任意的元素x,y,z,都有(x*y)*z=x*(y*z) ,则称二元运算*在A上是()。
7. 设★是定义在非空集合A上的二元运算,如果对于A中任意的两个元素x,y,都有x*y=y,则二元运算★在A上是()。
(填写可结合/不可结合)8. 设*,★是定义在集合A上的两个二元运算,如果对于A中任意的元素x,y,z,都有(x*y) ★z=(x★z)*(y★z),z★(x*y)=(z★x)*(z★y),则称二元运算★对于*在A上是()。
9. 设*,★是定义在集合A上的两个可交换的二元运算,如果对于A中任意的元素x,y,都有x*(x★y)=x, x★(x*y)=x,则称二元运算*对于★在A上满足()。
10. 设*是定义在集合A上的二元运算,如果对于A中任意的元素x,都有x*x=x,则称二元运算*是()。
11. 设*是定义在集合A上的二元运算,如果在A中存在元素el,对于A中任意的元素x,都有el*x=x,则称el为A中关于运算*的()。
12. 设*是定义在集合A上的二元运算,如果在A中存在元素ol,对于A中任意的元素x,都有ol*x=x,则称ol为A中关于运算*的()。
13. 设*是定义在集合A上的二元运算,如果在A中存在元素er,对于A中任意的元素x,都有x*erl =x,则称er为A中关于运算*的()。
《离散数学》第6章 图的基本概念

E ' E )。
生成子图—— G ' G 且 V ' V 。
导出子图 ——非空 V ' V ,以 V ' 为顶点集, 以两端均在 V ' 中的边的全体为边集的 G 的 子图,称 V ' 的导出子图。 ——非空 E ' E ,以 E ' 为边集,以
E ' 中边关联的顶点的全体为顶点集的 G 的子
0 vi与ek 不关联 无向图关联的次数 1 vi与ek 关联1次 2 v 与e 关联2次(e 为环) i k k
1 vi为ek的始点 有向图关联的次数 0 vi与ek 不关联 1 v 为e 的终点 (无环) i k
点的相邻——两点间有边,称此两点相邻 相邻 边的相邻——两边有公共端点,称此两边相邻
孤立点——无边关联的点。 环——一条边关联的两个顶点重合,称此边 为环 (即两顶点重合的边)。 悬挂点——只有一条边与其关联的点,所
对应的边叫悬挂边。
(3) 平行边——关联于同一对顶点的若干条边 称为平行边。平行边的条数称为重数。 多重图——含有平行边的图。
简单图——不含平行边和环的图。
如例1的(1)中,
第六章 图的基本概念 第一节 无向图及有向图
内容:有向图,无向图的基本概念。
重点:1、有向图,无向图的定义, 2、图中顶点,边,关联与相邻,顶点 度数等基本概念,
3、各顶点度数与边数的关系
d (v ) 2m 及推论,
i 1 i
n
4、简单图,完全图,子图, 补图的概念, 5、图的同构的定义。
一、图的概念。 1、定义。 无序积 A & B (a, b) a A b B 无向图 G V , E E V & V , E 中元素为无向边,简称边。 有向图 D V , E E V V , E 中元素为有向边,简称边。
离散数学讲义(第6章)

18
6-2 分配格(续)
定理:如果在一个格中交运算对并运算可分配,则并运算 对交运算一定可分配。反之亦然。
定理:每个链是分配格。
定理:设〈A, ≤ 〉为一个分配格,则对任意的a,b,c A,如果有a b = a c且a b = a c,则b=c。
19
6-2 分配格(续)
定义:设〈A,,〉是由格〈A, ≤ 〉所诱导的代数系统。 如果对任意的a,b,cA,当b ≤ a时,有: a (b c) = b (a c) 则称〈A, ≤ 〉是模格。
5
6-1 格的概念(续)
偏序集但不是格
e d f
格
c a b
6
6-1 格的概念(续)
代数系统
设〈A, ≤ 〉是一个格,如果在A上定义两个二元运 算和,使得对于任意的a,bA,ab等于a和b的最小 上界,ab等于a和b的最大下界,那么就称〈A, , 〉 为由格〈A, ≤ 〉所诱导的代数系统。二元运算, 分 别称为并运算和交运算。
定理:分配格一定是模格。
21
6-3 有补格
定义:设〈A, ≤ 〉是一个格,如果存在元素aA,对 任意的xA,都有a ≤ x, 则称a为格〈A, ≤ 〉的全下界。记作 0。 定义:设〈A, ≤ 〉是一个格,如果存在元素bA,对 任意的xA,都有x ≤ b, 则称b为格〈A, ≤ 〉的全上界。记作 1。
{a,b} {a,b} {a,b} {a,b} {a,b}
{b} {a,b}
6-4 布尔代数(续)
定理:对布尔代数中的任意两个元素a,b,有
(a ) a
ab a b
a b ab
定义:具有有限个元素的布尔代数称为有限布尔代数。
26
离散数学6(共15张PPT)
1
a
bc
0
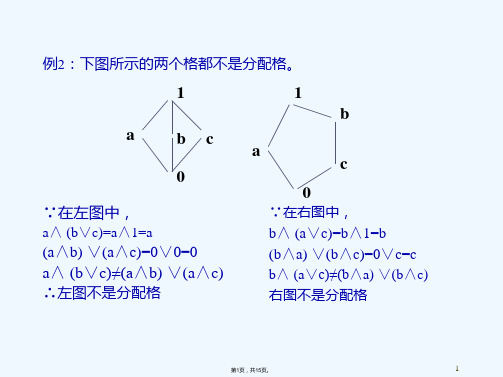
∵在左图中,
a∧ (b∨c)=a∧1=a
(a∧b) ∨(a∧c)=0∨0=0 a∧ (b∨c)≠(a∧b) ∨(a∧c) ∴左图不是分配格
1 b
a c∧1=b (b∧a) ∨(b∧c)=0∨c=c
b∧ (a∨c)≠(b∧a) ∨(b∧c) 右图不是分配格
第1页,共15页。
1
注意:按照定义证明某个格是分配格不容易,但要证明一个格 不是分配格,只要找出一组元素不满足某一分配式即可。上例 中的两个五元格可用来判断某格是否是分配格。
定理1:一个格是分配格的充要条件是在该格中没有任何子格与这
两个五元格中的任一个同构。
例3:右图所示的两个格都不是分配格
第2页,共15页。
(1) 设 b≤a且c≤a,∴a∧b = b,a∧c = c ∴ (a∧b)∨(a∧c) = b∨c 又∵ b∨c≤a,∴ a∧(b∨c) = b∨c
∴ a∧(b∨c) = (a∧b)∨(a∧c)
(2) 设 a≤b或a≤c,不论b≤c还是c≤b ,都有a≤b∨c
∴ a ∧( b∨c) = a,(a∧b)∨(a∧c)=a
∴ a∧(b∨c) = (a∧b)∨(a∧c) 由定理1,有a∨ (b∧c) = (a ∨ b) ∧(a∨c)
因此<A, ≤>是分配格。
第4页,共15页。
4
定理4:设<A, ≤>是分配格,则对a,b,cA, 若有 a∧b = a∧c且a∨b = a∨c ,则必有b = c 。
证明:∵a∧b≤b b = b∨(a∧b) = b∨(a∧c) = (b∨a)∧(b∨c) = (a∨c)∧(b∨c)
离散数学第六章

6.1.6 循环群和置换群
§循环群 在循环群G=<a>中, 生成元a的阶与群G的阶是一样 的. 如果a是有限阶元, |a|=n, 则称G为n阶循环群. 如 果a是无限阶元, 则称G为无限阶循环群. 例如: <Z,+>是无限阶循环群; <Z6,>是n阶循环群. 注意:(1) 对9 无限阶循环群G=<a>, G的生成元是a和a-1; (2) 对n阶循环群G=<a>=<e,a,…,an-1>,G的生成元是at 当且仅当t与n互素, 如12阶循环群中, 与12互素的数 有1、5、7、11. 那么G的生成元有a1=a、a5、a7、 a11. (3) N阶循环群G=<a>, 对于n的每个正因子d, G恰好有 一个d阶子群H=<an/d>.
6.1.3 子群
例如, 群<Z6,>中由2生成的子群包含2的各次 幂, 20=e=0, 21=2, 22=22=4, 23=222=0, 所 以由2生成的子群:<2>={0,2,4}.
对于Klein四元群G={e,a,b,c}来说, 由它的每个 元素生成的子群是 <e>={e}, <a>={e,a}, <b>={e,b}, <c>={e,c}
6.1.6 循环群和置换群
§循环群
定义6.7 在群G中, 如果存在aG使得 G={ak|kZ} 则称G为循环群, 记作G=<a>,称a为G的生成元. ☆ 循环群必定是阿贝尔群, 但阿贝尔群不一定 是循环群. 证明: 设<G,*>是一个循环群, 它的生成元是a, 那么,对于任意x,yG, 必有r,sZ, 使得 x=as,y=at, 而且x*y=as*at=as+t=at*as=y*x 由此可见<G,*>是一个阿贝尔群. 例如,<Z,+>是一个循环群, 其生成元是1或-1.
离散数学第六章

第六章几个典型的代数系统6.1 半群与群引言:简略介绍群论产生的背景1. 图形的对称性如正三角形、正方形(一般地正n 边形)、长方形、 等腰三角形、等腰梯形等;三维空间中的正四面体、 正方体、长方体等都各有自己的对称性。
画图解释:2.用根式求解代数方程的根(1)一元二次方程:20x bx c ++=⇒122b x -±=,。
注:①约公元前2000年即出现二次方程求根问题; ②约公元9世纪时,阿拉伯人花拉子米首次得到上述求根公式。
(2)三次及四次方程的求根公式一般三次方程: 320x ax bx c +++=。
先作变换:用3a x -代替x 后可化成 3x mx n +=(不含二次项), (*)其中 332,3327a ab a m b n c =-=--。
利用恒等式:333()3()u v uv u v u v -+-=-,把它与(*)比较得:33,3,x u v uv m u v n =-=-=。
由后面两个关于33,u v 的方程可得u x u v v ⎫⎪=⎪⇒=-= (即*方程的解) 以上求解三次方程的公式叫做卡丹公式, 出现在公元1545年出版的著作《大书》中。
关于四次方程的求根公式这里从略,可以肯定的是, 四次一般方程也有求根公式,并且也叫卡丹公式。
(3从1545年之后的近300年间,人们都没能找到五次(当然,这并不排除对 某些特殊的五次及五次以上的方程可以求出它们的根)。
直到1830年由法国人Galois (伽珞瓦)解决,证明出:五次及五次以上的一般方程不存在用加、减、乘、除及开方表示的求根公式,所用方法就是现在已广为接受的群的思想。
可是在当时,很多同时代的大数学家都无法理解和接受他的思想方法。
3.群在其它方面的应用:如编码理论、计算机等。
一.群的定义及简单性质1定义:设,G ⋅是一个具有二元运算⋅的代数系统,如果⋅同时满足(1)结合律:即,,a b c G ∀∈,()()a b c a b c ⋅⋅=⋅⋅总成立;(2)存在单位元(也称为幺元,记为e ),即 ,;a e e a a a G ⋅=⋅=∀∈(3)中每个元素a 都有逆元(记为1a -):即存在1a G -∈,使得11a a a a e --⋅=⋅=,则称G 关于运算⋅构成一个群。
离散数学模拟试题(05年6月)

离散数学模拟试题(一)一、选择题1、由集合运算的定义,下列各式中,正确的是( )。
(A) A ∪E = A; (B) A ∩∅ = A; (C) A ⊕ ∅ = A; (D) A ⊕ A = A.2、设G 如右图:那么G 不是( ). (A)平面图; (B)完全图;(C)欧拉图; (D)哈密顿图.3、设个体域为整数,下列公式中真值为1的是( )。
(A)∀x ∀y(x + y = 1); (B)∀x ∃y(x + y = 1); (C)∃x ∀y(x + y = 1); (D) ⌝ ∃x ∃y(x + y = 1)。
4、下列命题为假的是( )。
(A) {∅}∈ρ(∅); (B) ∅ ⊆ρ({∅});(C) {∅} ⊇ρ(∅); (D)ρ(∅) ∈ρ({∅})。
5、设集合A = {1,2,3,4},A 上的关系R = {(1,1),(2,3),(2,4),(3,4)},则R 具有( ). (A)自反性; (B)传递性; (C)对称性; (D)以上都不是.6、谓词公式)())()((x Q y yR x P x →∃∨∀中量词∀x 的辖域是( )(A) ))()((y yR x P x ∃∨∀ (B) P (x ) (C) )()(y yR x P ∃∨ (D) )(x Q7、谓词公式∃xA (x )∧⌝∃xA (x )的类型是( )(A) 永真式 (B) 矛盾式(C) 非永真式的可满足式 (D) 不属于(A),(B),(C)任何类型8、设L (x ):x 是演员,J (x ):x 是老师,A (x ,y ):x 佩服y. 那么命题“所有演员都佩服某些老师”符号化为( ) (A) ),()(y x A x xL →∀ (B) )),()(()((y x A y J y x L x ∧∃→∀(C) )),()()((y x A y J x L y x ∧∧∃∀ (D) )),()()((y x A y J x L y x →∧∃∀9、设命题公式⌝(P ∧(Q →⌝P )),记作G ,则使G 的真值指派为0的P ,Q 的取值是( ) (A) (0,0) (B) (0,1) (C) (1,0) (D) (1,1) 10、与命题公式P →(Q →R )等值的公式是( )(A) (P ∨Q )→R (B)(P ∧Q )→R (C) (P →Q )→R (D) P →(Q ∨R ) 二、填空题1、命题: ∅ ⊆ {{a }} ⊆ {{a },3,4,1} 的真值 = ____ .2、 设A= {a,b}, B = {x | x 2-(a+b) x+ab = 0}, 则两个集合的关系为:A____B.3、设集合A ={a ,b ,c },B ={a ,b }, 那么 ρ(B )-ρ(A )=______ .4、无孤立点的有限有向图有欧拉路的充分必要条件为: _______________________________________________.5、公式))(),(()),()((x S z y R z y x Q x P x →∃∨→∀的自由变元是 , 约束变元是 .6、设个体域D ={1,2},那么谓词公式)()(y yB x xA ∀∨∃消去量词后的等值式为 .7、设N (x ):x 是自然数,Z (y );y 是整数,则命题“每个自然数都是整数,而有些整数不是自然数”符号化为 8、设G 是n 个结点的简单图,若G 中每对结点的度数之和 ,则G 一定是哈密顿图. 9、设全集合E ={1,2,3,4,5},A ={1,2,3},B ={2,5},~A ⋃~B = .10、设集合A ={a ,b ,c },B ={a ,b },那么P (A )-P (B )= 三、计算题1、求公式 G = (P ∧Q)→R 的主析取范式和主合取范式。
离散数学 第五-六章

例 题4
设集合A={ ,}, A上定义的二元运算如表所示. 对*可分配吗? * 对 ?
代数结构 >运算性质
定义5-2.6 设,△是定义在集合A上的两个二元运 算,如果对 x y∈A,都有 x (x△y) = x x△(x y) =x 则称运算和运算△满足吸收律。
代数系统 >代数系统的引入
二元运算的例子 • N上 +, 是N上二元运算,而-, 不是. • 整数集I上 +,-, 是I上的二元运算, 而 不是. • R-{0}上的 , 是R-{0}上的二元运算,而+,-不是. • 矩阵的 +, 是N阶实矩阵集合上的二元运算,但不是 全体实矩阵集合上的二元运算. • ,,, 是真值集合{0,1}上 的二元运算. • ,, 是幂集P(A)上的二元运算. 一元运算的例子 • R上的 求绝对值|X|运算. • 整数 I上求负运算是一元运算,但不是N上的一元运算.
n 例如 实数集上的+, ; 集合上的运算, ;,命题 集合P上的,都是可结合的.
例题3
A为非空集合,*定义为:对任意的a,bA,有 a*b=b. 证*可结合的.
代数结构 >运算性质
定义5-2.4 设是定义在集合A上的一个二元运算, x∈A,若xx=x,称x是等幂元; 若对x∈A,都有
2 独异点(monoid)
定义5-3.3 含有幺元的半群称为独异点。 独异点的判定: 对给定集合S 及运算*, 1)是封闭的, 即对x,y∈S, 有 xy∈S (是代数系统) 2)是可结合的,即对x,y,z∈S, 有(x y) z= x (y z) 3) 有幺元,即e∈S, 对x∈S,有ex=xe=x. 例如 <R, +>是独异点,幺元为0, <I+,+ >不是. <R, * >, <I, * >都是独异点,幺元为1 <{0,1}, > , <{0,1}, >都是独异点,幺元分别为0和1. < P(S), >和 < P(S), >是独异点?
离散数学

第二章
關係式 (Relations)
2-0 簡介
• 若有元素a與b,兩者間存在某種關係R,即可以 式 “aRb” 表示之,此為關係式(Relations)。我們 曾熟悉的如 “等於(=)”、“大於(>)”、“因此(→)” 等均屬之。 • 關係式中也談集合(Sets),於第一章 {a, b} = {b, a},元素的先後次序並不影響集合的含義;但於 關係式中的集合 {a, b}≠{b, a},除非 a = b,因其 先後次序代表著不同的含義。
• 設有一集合A = {O, P, Q, R},其元素是由 集合O, P, Q, R組成。此時A是謂 “群集合 (Class of Sets)”;B = {O, P}是謂 “子群集 合 (SubClass或Subcollection)”。
1-9 含意 (Arguments) 與 范氐圖 (Venn Digrams)
1-1 集合與元素 (Sets and Elements)
• 所謂集合(Set)是謂 “有一定義完善的範圍 (well-defined List/Collection),在範圍內包 涵適當數量之元素(Elements)”。 習慣上、 集合(Set) 以大寫字母表示(如A、B、 C、…);元素(Elements) 以小寫字母表示 (如a、b、c、…) 。
3-2函數圖形(Graph of Function)
• 函數(Function) “f:A → B” 在函數圖形 (Graph of Function) 定義為:每一A的元素 a A、必配屬一組 序對(Ordered Pair) 關 係元(Relation) 如 (a, b),且該關係元是唯 一的(Unique)。
2-1 積集合 (Product Sets)
离散数学要点

1.1 命题1-1-1 命题命题是一个能表达判断并具有确定真值的陈述句。
1-1-2 真值作为命题的陈述句所表达的判断结果称为命题的真值。
真值只有真和假两种,通常记为T和F。
真值为真的命题称为真命题,真值为假的命题称为假命题。
真命题表达的判断正确,假命题表达的判断错误。
任何命题的真值都是唯一的。
1-1-3 命题变项用命题标识符(大写字母)来表示任意命题时,该命题标识符称为命题变项。
1-1-4 简单命题无法继续分解的简单陈述句称为简单命题或原子命题。
(不包含任何与、或、非一类联结词的命题)1-1-5 复合命题由一个或几个简单命题通过联结词复合所构成的新的命题,称为复合命题,也称分子命题。
1.2 命题联结词及真值表1-2-1 命题联结词命题联结词可将命题联结起来构成复杂的命题,是由已有命题定义新命题的基本方法。
命题联结词又可分为一元命题联结词、二元命题联结词和多元命题联结词。
常用的命题联结词包括否定词、合取词、析取词、蕴涵词和双条件词。
其它联结词还包括异或(不可兼或)、与非和或非等。
1-2-2 否定词否定词是一元命题联结词。
设P为一命题,P的否定是一个新的命题,记作P,读作非P。
若P为T,P为T;若P为F,P为T。
1-2-3 合取词合取词是二元命题联结词。
两个命题P和Q的合取构成一个新的命题,记作P∧Q。
读作P、Q的合取(或读作P与Q,P且Q)。
当且仅当P、Q 同时为T时,P∧Q为T。
否则,P∧Q的真值为F。
1-2-4 析取词析取词是二元命题联结词。
两个命题P和Q的析取构成一个新的命题,记作P∨Q。
读作P、Q的析取(也读作P或Q)。
当且仅当P、Q同时为F 时,P∨Q的真值为F。
否则,P∨Q的真值为T。
1-2-5 蕴涵词蕴涵词是二元命题联结词。
两个命题P和Q用蕴涵词“→”联结起来,构成一个新的命题,记作P→Q。
读作如果P则Q,或读作P蕴涵Q。
当且仅当P 的真值为T,Q的真值为F时,P→Q的真值为F,否则P∨Q的真值为T。
《离散数学》(左孝凌李为鉴刘永才编著)课后习题集标准答案上海科学技术文献出版社

1-1,1-2(1)解:a)是命题,真值为T。
b)不是命题。
c)是命题,真值要根据具体情况确定。
d)不是命题。
e)是命题,真值为T。
f)是命题,真值为T。
g)是命题,真值为F。
h)不是命题。
i)不是命题。
(2)解:原子命题:我爱北京天安门。
复合命题:如果不是练健美操,我就出外旅游拉。
(3)解:a)(┓P ∧R)→Qb)Q→Rc)┓Pd)P→┓Q(4)解:a)设Q:我将去参加舞会。
R:我有时间。
P:天下雨。
Q↔ (R∧┓P):我将去参加舞会当且仅当我有时间和天不下雨。
b)设R:我在看电视。
Q:我在吃苹果。
R∧Q:我在看电视边吃苹果。
c) 设Q:一个数是奇数。
R:一个数不能被2除。
(Q→R)∧(R→Q):一个数是奇数,则它不能被2整除并且一个数不能被2整除,则它是奇数。
(5) 解:a)设P:王强身体很好。
Q:王强成绩很好。
P∧Qb)设P:小李看书。
Q:小李听音乐。
P∧Qc)设P:气候很好。
Q:气候很热。
P∨Qd)设P: a和b是偶数。
Q:a+b是偶数。
P→Qe)设P:四边形ABCD是平行四边形。
Q :四边形ABCD的对边平行。
P↔Qf)设P:语法错误。
Q:程序错误。
R:停机。
(P∨ Q)→ R(6) 解:a)P:天气炎热。
Q:正在下雨。
P∧Qb)P:天气炎热。
R:湿度较低。
P∧Rc)R:天正在下雨。
S:湿度很高。
R∨Sd)A:刘英上山。
B:李进上山。
A∧Be)M:老王是革新者。
N:小李是革新者。
M∨Nf)L:你看电影。
M:我看电影。
┓L→┓Mg)P:我不看电视。
Q:我不外出。
R:我在睡觉。
P∧Q∧Rh)P:控制台打字机作输入设备。
Q:控制台打字机作输出设备。
P∧Q1-3(1)解:a)不是合式公式,没有规定运算符次序(若规定运算符次序后亦可作为合式公式)b)是合式公式c)不是合式公式(括弧不配对)d)不是合式公式(R和S之间缺少联结词)e)是合式公式。
(2)解:a)A是合式公式,(A∨B)是合式公式,(A→(A∨B))是合式公式。
离散数学(第二版)课后习题答案详解(完整版)

离散数学(第⼆版)课后习题答案详解(完整版)习题⼀1.下列句⼦中,哪些是命题?在是命题的句⼦中,哪些是简单命题?哪些是真命题?哪些命题的真值现在还不知道?(1)中国有四⼤发明.答:此命题是简单命题,其真值为 1.(2)5 是⽆理数.答:此命题是简单命题,其真值为 1.(3)3 是素数或 4 是素数.答:是命题,但不是简单命题,其真值为1.(4)2x+ <3 5 答:不是命题.(5)你去图书馆吗?答:不是命题.(6)2 与3 是偶数.答:是命题,但不是简单命题,其真值为0.(7)刘红与魏新是同学.答:此命题是简单命题,其真值还不知道.(8)这朵玫瑰花多美丽呀!答:不是命题.(9)吸烟请到吸烟室去!答:不是命题.(10)圆的⾯积等于半径的平⽅乘以π.答:此命题是简单命题,其真值为 1.(11)只有6 是偶数,3 才能是2 的倍数.答:是命题,但不是简单命题,其真值为0.(12)8 是偶数的充分必要条件是8 能被3 整除.答:是命题,但不是简单命题,其真值为0.(13)2008 年元旦下⼤雪.答:此命题是简单命题,其真值还不知道.2.将上题中是简单命题的命题符号化.解:(1)p:中国有四⼤发明.(2)p: 是⽆理数.(7)p:刘红与魏新是同学.(10)p:圆的⾯积等于半径的平⽅乘以π.(13)p:2008 年元旦下⼤雪.3.写出下列各命题的否定式,并将原命题及其否定式都符号化,最后指出各否定式的真值.(1)5 是有理数.答:否定式:5 是⽆理数. p:5 是有理数.q:5 是⽆理数.其否定式q 的真值为1.(2)25 不是⽆理数.答:否定式:25 是有理数. p:25 不是⽆理数. q:25 是有理数. 其否定式q 的真值为1.(3)2.5 是⾃然数.答:否定式:2.5 不是⾃然数. p:2.5 是⾃然数. q:2.5 不是⾃然数. 其否定式q 的真值为1.(4)ln1 是整数.答:否定式:ln1 不是整数. p:ln1 是整数. q:ln1 不是整数. 其否定式q 的真值为1.4.将下列命题符号化,并指出真值.(1)2 与5 都是素数答:p:2 是素数,q:5 是素数,符号化为p q∧,其真值为 1.(2)不但π是⽆理数,⽽且⾃然对数的底e 也是⽆理数.答:p:π是⽆理数,q:⾃然对数的底e 是⽆理数,符号化为p q∧,其真值为1.(3)虽然2 是最⼩的素数,但2 不是最⼩的⾃然数.答:p:2 是最⼩的素数,q:2 是最⼩的⾃然数,符号化为p q∧? ,其真值为1.(4)3 是偶素数.答:p:3 是素数,q:3 是偶数,符号化为p q∧,其真值为0.(5)4 既不是素数,也不是偶数.答:p:4 是素数,q:4 是偶数,符号化为? ∧?p q,其真值为0.5.将下列命题符号化,并指出真值.(1)2 或3 是偶数.(2)2 或4 是偶数.(3)3 或5 是偶数.(4)3 不是偶数或4 不是偶数.(5)3 不是素数或4 不是偶数.答: p:2 是偶数,q:3 是偶数,r:3 是素数,s:4 是偶数, t:5 是偶数(1)符号化: p q∨,其真值为1.(2)符号化:p r∨,其真值为1.(3)符号化:r t∨,其真值为0.(4)符号化:? ∨?q s,其真值为1.(5)符号化:? ∨?r s,其真值为0.6.将下列命题符号化.(1)⼩丽只能从筐⾥拿⼀个苹果或⼀个梨.答:p:⼩丽从筐⾥拿⼀个苹果,q:⼩丽从筐⾥拿⼀个梨,符号化为: p q∨ .(2)这学期,刘晓⽉只能选学英语或⽇语中的⼀门外语课.答:p:刘晓⽉选学英语,q:刘晓⽉选学⽇语,符号化为: (? ∧∨∧?p q)(p q) .7.设p:王冬⽣于1971 年,q:王冬⽣于1972 年,说明命题“王冬⽣于1971 年或1972年”既可以化答:列出两种符号化的真值表:合命题可以发现,p 与q 不可能同时为真,故上述命题有两种符号化⽅式.8.将下列命题符号化,并指出真值., 就有;(1)只要, 则;, 才有;(3)只有, 才有;(4)除⾮, 否则;(5)除⾮(6)仅当.答:设p: , 则: ; 设q: , 则: .(1);(2);;(3);(4);(5);(6);(7).答:根据题意,p 为假命题,q 为真命题.(1);(2);(3);(4).答:根据题意,p 为真命题,q 为假命题.(1)若2+2=4,则地球是静⽌不动的;(2)若2+2=4,则地球是运动不⽌的;(3)若地球上没有树⽊,则⼈类不能⽣存;(4)若地球上没有⽔,则是⽆理数.12.将下列命题符号化,并给出各命题的真值:(1)2+2=4 当且仅当3+3=6;(2)2+2=4 的充要条件是3+3 6;(3)2+2 4 与3+3=6 互为充要条件;(4)若2+2 4,则3+3 6,反之亦然.答:设p:2+2=4,q:3+3=6.(1)若今天是星期⼀,则明天是星期⼆;(2)只有今天是星期⼀,明天才是星期⼆;(3)今天是星期⼀当且仅当明天是星期⼆;(4)若今天是星期⼀,则明天是星期三.答:设p:今天是星期⼀,q:明天是星期⼆,r:明天是星期三.(1)刘晓⽉跑得快,跳得⾼;(2)⽼王是⼭东⼈或者河北⼈;(3)因为天⽓冷,所以我穿了⽻绒服;(4)王欢与李乐组成⼀个⼩组;(5)李欣与李末是兄弟;(6)王强与刘威都学过法语;(7)他⼀⾯吃饭,⼀⾯听⾳乐;(8)如果天下⼤⾬,他就乘班车上班;(9)只有天下⼤⾬,他才乘班车上班;(10)除⾮天下⼤⾬,否则他不乘班车上班;(11)下雪路滑,他迟到了;(12)2 与4 都是素数,这是不对的;(13)“2 或 4 是素数,这是不对的”是不对的.答:q:⼤熊猫产在中国.r:太阳从西⽅升起. 求下列符合命题的真值:(1)(2)(3)(4)解:p真值为1,q 真值为1,r 真值为0.(1)0,(2)0,(3)0,(4)116.当p,q 的真值为0,r,s 的真值为1 时,求下列各命题公式的真值:(1)(2)(3)(4)解:(1)0,(2)0,(3)0,(4)117.判断下⾯⼀段论述是否为真:“ 是⽆理数.并且,如果3 是⽆理数,则也是⽆理数.另外,只有6 能被2 整除,6 才能被4 整除.”解:p: 是⽆理数q: 3 是⽆理数r:是⽆理数s: 6 能被2 整除t:6 能被 4 整除符号化为: ,该式为重⾔式,所以论述为真。
离散数学第二版答案(6-7章)

第七章
6.1
1.画出图 的图示,指出其中哪些图是简单图。
(1)
不是简单图。
(2)
不是简单图。
(3)
是简单图。
2.写出图7-8的抽象数学定义。
(1)解: ,其中 , , (2)解: ,其中 , ,
3.证明:在n阶简单有向图中,完全有向图的边数最多,其边数为 。
证明:简单有向图是没有自环,没有平行边的有向图,只要两个不同的结点之间才能有边。完全有向图是每个结点的出度和入度都是n-1的简单有向图,也就是每个结点都有到其他所有结点的边,因此,完全有向图的边数最多。
任取 ,分情况讨论:
(1)x和y都可以表示成 ,设 ,
那么 ,
(2)x和y都不能表示成 ,那么 也不能表示成
,
(3)x可以表示成 ,y不能表示成 ,那么 也不能表示成
,
(4)x不可以表示成 ,y能表示成 ,那么 也不能表示成
,
可知,无论x和y如何取值,都能够保证 。
综上所述, 是U到V的同态映射。
5.
两个图的结点和边的数目都相同。假设函数 ,左图中相邻的结点是1和4,1和5,1和6,2和4,2和5,2和6,3和4,3和5,3和6,对应的像点1’和4’,1’和2’,1’和6’,5’和4’,5’和2’,5’和6’,3’和5’,3’和2’,3’和6’在右图中也相邻,因此,两图同构。
7.证明:在任意六个人中,若没有三个人彼此认识,则必有三个人彼此都不认识。
, ,此时
故二元运算*是不可结合的。
不存在这样 使得任意的 都有 ,
因此,二元运算*不含幺元。
②
对于任意的 都有 ,故二元运算*是可交换的。
故二元运算*是不可结合的。
离散数学(屈婉玲版)第六章部分答案

可见 , 存在幺元,幺元为 2。 对 x∈Z 有 4-x∈Z,使 x ° (4-x)= (4-x) °x=2
所以 x-¹= 4-x 所以 Z 与运算 ° 能构成群 。
6.7 下列各集合对于整除关系都构成偏序集,判断哪些偏序集是格? (1)L={1,2,3,4,5}. (2)L={1,2,3,6,12}. (3)L={1,2,3,4,6,9,12,18,36}. (4)L={1,2,2(2),…,2(n)}.
答:满足封闭性,因为矩阵加法可结合所以为半群,且幺元为 e=0 的矩阵,故为 独异点。又因为以任一 n 阶矩阵的逆元存在是它的负矩阵,所以是群。 评语:答案太简单
6.2 (1)因为可结合,交换,幺元为 1,但不存在逆元 所以是半群 (2)因为可交换,结合,幺元为 0,是有限阶群并且是循环群,G 中的 2 阶元是 2,4 阶元 是1和3
设 a={1,3} b={3,4,5} ∴a,b∈p(A) ∵<p(A), >构成群 a x=b ∴a-1 a x= a-1b
e x= a-1b x= a-1b
e= a-1=a ∴x=ab={1,3}{3,4,5}={1,4,5} (2)由 B 生成的循环子群<B>为 {,{1,4,5}}
6.10
答案太简单621因为可结合交换幺元为1但不存在逆元所以是半群2因为可交换结合幺元为0是有限阶群并且是循环群gz为正数集合在z上定义二元运算yxy2那么z与运算c2abc4bc22abc44x4x4x所以67下列各集合对于整除关系都构成偏序集判断哪些偏序集是格
6.1(5) S5 = Mn (R),+为矩阵加法,则 S 是(群)
110
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1 2 3 4 5
用偏序集定义的格
用代数系统定义的格
特殊格 布尔代数 布尔表达式
1
设<A,∨,∧, - >是布尔代数,考虑一个从An到A的函数, 例如设A={0,1},则下表表示了一个A3到A的函数 f
< x1, x2 , x3 > < 0, 0, 0 > < 0, 0, 1 > f 1 0
(1) 命题逻辑可用布尔代数<{F,T},∨,∧, ┒>描述。 一个原子命题就是一个变元,其取值为 F 或 T ;
任一复合命题可以用代数系统<{F,T},∨,∧, ┒>上的一个布 尔函数来表示。
(2) 开关代数可用布尔代数<{断开,闭合},并联,串联,反向>描述。 一个开关就是一个变元,其取值为“断开”或“闭合”; 任一开关线路可以用代数系统<{断开,闭合},并联,串联,反向> 上的一},∨,∧, - >上两个布尔表达式 E1 (x1,x2,x3) = ( x1∧x2 )∨(x1∧x3 )
E2 (x1,x2,x3) = x1∧(x2 ∨x3 ) 求证 E1 = E2
证明:(1)按照布尔表达式相等的定义证明
< x1, x2 , x3 > E1 E2
< 0, 0, 0 >
< 0, 0, 1 > < 0, 1, 0 > < 0, 1, 1 > < 1, 0, 0 > < 1, 0, 1 > < 1, 1, 0 > < 1, 1, 1 >
0
0 0 0 1 0 0 1
0
0 0 0 1 0 0 1
(2) 利用分配律,得
E2 = x1∧(x2 ∨x3 ) = ( x1∧x2 )∨(x1∧x3 ) = E1
E (x1,x2,x3) = ( x1∨x2 )∧( x1∨x2 )∧( x2∨x3 )
若给定变元赋值 x1=1, x2=0, x3=1,
则可求出布尔表达式的值: E ( 1, 0, 1) = ( 1∨0 )∧( 1∨0 )∧( 0∨1 )
= 1∧1∧0 = 0
4
定义4:布尔代数<A,∨,∧, - >上的两个n元的布尔表达式为 E1(x1,x2,…,xn)和E2(x1,x2,…,xn),如果对n个变元的任 意赋值 xi = xi*, xi*A 时都有 E1(x1*,x2*,…,xn*) = E2(x1*,x2*,…,xn*) 则称这两个布尔表达式是等价的(相等的)。 记为 E1(x1,x2,…,xn) = E2(x1,x2,…,xn)
6
定义5:<A,∨,∧, - >是一个布尔代数,一个从An到A上的函 数,如果它能够用<A,∨,∧, - >上的n元布尔表达式 来表示,则称该函数为布尔函数。
定理:对于两个元素的布尔代数<{0,1},∨,∧, - > ,任何
一个从 {0,1} n 到 {0,1} 的函数都是布尔函数。
7
布尔代数的应用:
< 0, 1, 0 >
< 0, 1, 1 > < 1, 0, 0 > < 1, 0, 1 > < 1, 1, 0 > < 1, 1, 1 >
1
0 1 1 0 1
2
定义1:设<A,∨,∧, - >是一个布尔代数,并在这个布尔代数上 定义布尔表达式如下: 1、A中任何元素是一个布尔表达式 2、任何变元是一个布尔表达式 3、如果e1和e2是布尔表达式,则e1、(e1∨e2)和 (e1∧e2)也都是布尔表达式。 4、只有有限次使用规则2和3所得到的符号串是 布尔表达式。
8
定义2:一个含有n个相异变元的布尔表达式,称为 含有n元的布尔表达式。 记为E(x1,x2,…,xn),其中x1,x2,……,xn为变元。
3
定义3:布尔代数<A,∨,∧, - >上的一个含有n元的布尔表达式 E(x1,x2,…,xn)的值是指:将A中的元素作为变元xi (i=1,2,…,n)的值来代替表达式中相应的变元(即对变 元赋值),从而计算出表达式的值。 例:布尔代数<{0,1},∨,∧, - >上布尔表达式
