2011届高考数学三角函数的图象与性质1

合集下载

高考数学10年真题解析— 三角函数图象与性质

三角函数图象与性质年份题号考点考查内容2011课标理11三角函数性质三角函数的周期性、奇偶性、单调性课标文11三角函数性质三角公式、诱导公式、三角函数的性质及分析处理问题能力．2012课标理9三角函数性质三角函数的单调性课标文9三角函数性质三角函数的对称轴等性质2013卷2文16三角函数图像变换三角函数图像平移变换2014卷1文7三角函数图像本三角函数的周期性．2015卷1理8文8三角函数图像已知三角函数图像求解析式及三角函数的单调性．2016卷3理14三角函数图像变换两角和与差的三角公式及图像平移变换．卷1文6三角函数图像变换三角函数周期、三角函数的平移变换．卷2文3三角函数图像已知三角函数图像求解析式卷3文14三角函数图像辅助角公式及三角函数平移变换．2017卷1理9三角函数图像变换诱导公式、三角函数图像变换，化归与转化思想卷3理6三角函数性质三角函数周期、对称性、零点与单调性．卷2文3三角函数性质三角函数周期性2018卷2理10三角函数性质辅助角公式、三角函数的单调性，运算求解能力与化归与转化思想．卷3理15三角函数性质三角函数的零点、转化与化归思想与运算求解能力卷2文10三角函数性质辅助角公式、三角函数的单调性，运算求解能力与化归与转化思想．卷3文6同角三角函数基本关系三角函数性质同角三角函数基本关系与三角函数的周期，运算求解能力与化归与转化思想．2019卷2理9三角函数性质含绝对值的三角函数的周期性与单调性，转化与化归思想．卷3理12三角函数性质含绝对值的三角函数的周期性、单调性、极值与零点，转化与化归思想．卷1文15三角函数性质诱导公式、三角函数的最值，转化与化归思想．卷2文8三角函数性质三角函数的极值、周期等性质．2020卷1理7三角函数图象及其性质三角函数的图象，三角函数的周期性文7三角函数图象及其性质三角函数的图象，三角函数的周期性卷3理16三角函数图象及其性质三角函数最值，三角函数图象的对称性文12三角函数图象及其性质三角函数最值，三角函数图象的对称性考点39三角函数性质1．(2020全国Ⅲ文12理16)已知函数()1sin sin f x x x=+，则()A ．()f x 的最小值为2B ．()f x 的图像关于y 轴对称C ．()f x 的图像关于直线x =π对称D ．()f x 的图像关于直线2x π=对称【答案】D【思路导引】根据基本不等式使用条件可判断A ；根据奇偶性可判断B ；根据对称性判断C ，D ．【解析】sin x 可以为负，所以A 错；()()()1sin 0,,sin sin x x k k f x x f x xπ≠∴≠∈-=--=-Z Q Q ，()f x ∴关于原点对称；11(2)sin (),()sin (),sin sin f x x f x f x x f x x xππ-=--≠-=+=Q 故B 错；()f x ∴关于直线2x π=对称，故C 错，D 对，故选D ．2．(2019•新课标Ⅱ，理9)下列函数中，以2π为周期且在区间(4π，2π单调递增的是()A ．()|cos 2|f x x =B ．()|sin 2|f x x =C ．()cos ||f x x =D ．()sin ||f x x =【答案】A【解析】()sin ||f x x =不是周期函数，可排除D 选项；()cos ||f x x =的周期为2π，可排除C 选项；()|sin 2|f x x =在4π处取得最大值，不可能在区间(4π，)2π单调递增，可排除B ．故选A ．3．(2019•新课标Ⅲ，理12)设函数()sin(0)5f x x πωω=+>，已知()f x 在[0，2]π有且仅有5个零点．下述四个结论：①()f x 在(0,2)π有且仅有3个极大值点②()f x 在(0,2)π有且仅有2个极小值点③()f x 在(0,)10π单调递增④ω的取值范围是12[5，29)10其中所有正确结论的编号是()A ．①④B ．②③C ．①②③D ．①③④【答案】D【解析】当[0x ∈，2]π时，[55x ππω+∈，25ππω+，()f x 在[0，2]π有且仅有5个零点，5265πππωπ∴+< ，∴1229510ω<，故④正确，因此由选项可知只需判断③是否正确即可得到答案，下面判断③是否正确，当(0,)10x π∈时，[55x ππω+∈，(2)]10ωπ+，若()f x 在(0,10π单调递增，则(2)102ωππ+<，即3ω<，1229510ω<，故③正确，故选D ．4．(2019•新课标Ⅱ，文8)若14x π=，234x π=是函数()sin (0)f x x ωω=>两个相邻的极值点，则(ω=)A ．2B ．32C ．1D ．12【答案】A 【解析】14x π= ，234x π=是函数()sin (0)f x x ωω=>两个相邻的极值点，322()44T ππππω∴=-==，2ω∴=，故选A ．5．(2018•新课标Ⅱ，理10)若()cos sin f x x x =-在[a -，]a 是减函数，则a 的最大值是()A ．4πB ．2πC ．34πD ．π【答案】A【解析】()cos sin (sin cos )2sin()4f x x x x x x π=-=--=--，由ππk 22+-≤πππk x 224+≤-，k Z ∈，得ππππk x k 24324+≤≤+-，k Z ∈，取0k =，得()f x 的一个减区间为[4π-，3]4π，由()f x 在[a -，]a 是减函数，得⎪⎪⎩⎪⎪⎨⎧≤-≥-434ππa a ，∴4π≤a ，则a 的最大值是4π，故选A ．6．(2018•新课标Ⅱ，文10)若()cos sin f x x x =-在[0，]a 是减函数，则a 的最大值是()A ．4πB ．2πC ．34πD ．π【答案】C【解析】()cos sin (sin cos )2sin()4f x x x x x x π=-=--=--，由22422πππππ+≤-≤+-k x k ，k Z ∈，得43224ππππ+≤≤+-k x k ，k Z ∈，取0k =，得()f x 的一个减区间为[4π-，3]4π，由()f x 在[0，]a 是减函数，得43π≤a ，则a 的最大值是34π，故选C ．7．(2018•新课标Ⅲ，文6)函数2tan ()1xf x tan x=+的最小正周期为()A ．4πB ．2πC ．πD ．2π【答案】C【解析】函数222tan sin cos 1()sin 21cos sin 2x x x f x x tan x x x ===++的最小正周期为22ππ=，故选C ．8．(2017新课标卷3，理6)设函数π()cos()3f x x =+，则下列结论错误的是()A ．()f x 的一个周期为2π-B ．()y f x =的图像关于直线8π3x =对称C ．()f x π+的一个零点为π6x =D ．()f x 在π(,π)2单调递减【答案】D【解析】函数()πcos 3f x x ⎛⎫=+ ⎪⎝⎭的图象可由cos y x =向左平移π3个单位得到，如图可知，()f x 在π,π2⎛⎫⎪⎝⎭上先递减后递增，D 选项错误，故选D ．9．(2017新课标卷2，文3)函数()f x =πs i n （2x +）3的最小正周期为A ．4πB ．2πC ．πD ．2π【答案】C【解析】由题意22T ππ==，故选C ．10．(2014新课标I ，文7)在函数①|2|cos x y =，②|cos |x y =，③)62cos(π+=x y ，④42tan(π-=x y 中，最小正周期为π的所有函数为A ．②④B ．①③④C ．①②③D ．①③【答案】C【解析】∵|2|cos x y ==cos 2x ，∴T =22π=π；由|cos |x y =图像知其周期为π，由周期公式知，62cos(π+=x y 为π，)42tan(π-=x y 为2π，故选C ．11．(2012全国新课标，理9)已知ω＞0，函数()f x =sin()4x πω+在(2π，π)单调递减，则ω的取值范围是()A ．[12，54]B ．[12，34]C ．(0，12]D ．(0，2]【答案】A【解析】∵ω＞0，x ∈(2π，π)，∴4x πω+∈(24ωππ+，4πωπ+)，∵()f x =sin()4x πω+在(2π，π)单调递减，∴(24ωππ+，4πωπ+)⊂(2π，32π)，∴2π≤24ωππ+且4πωπ+≤32π，解得12≤ω≤54，故选A ．12．(2012全国新课标，文9)已知ω>0，0ϕπ<<，直线x =4π和x =54π是函数()sin()f x x ωϕ=+图像的两条相邻的对称轴，则ϕ=()(A)π4(B)π3(C)π2(D)3π4【答案】A【解析】由题设知，πω=544ππ-，∴ω=1，∴4πϕ+=2k ππ+(k Z ∈)，∴ϕ=4k ππ+(k Z ∈)，∵0ϕπ<<，∴ϕ=4π，故选A ．13．(2011全国课标，理11)设函数()f x =sin()cos()x x ωϕωϕ+++(ω＞0，||ϕ＜2π)的最小正周期为π，且()f x -=()f x ，则()f x (A)在(0，2π)单调递减(B)在(4π，34π)单调递减(C)在(0，2π)单调递增(D)在(4π，34π)单调递增【答案】A【解析】∵()f x +4x πωϕ+，由题意知2πω=π且+4πϕ=2k ππ+，解得ω=2，ϕ=4k ππ+，又∵||ϕ＜2π，∴ϕ=4π，∴()f x +)2x π2x ，当x ∈(0，2π)时，2x ∈(0，π)，故()f x 在(0，2π)单调递减，故选A ．14．设函数()f x =sin(2cos(244x x ππ+++，则y =()f x (A)在(0，2π)单调递增，其图像关于直线x =4π对称(B)在(0，2π)单调递增，其图像关于直线x =2π对称(C)在(0，2π)单调递减，其图像关于直线x =4π对称(D)在(0，2π)单调递减，其图像关于直线x =2π对称【答案】D【解析】()f x =sin(2cos(2)44x x ππ+++2x π+2x ，∵2u x =在(0，2π)上是增函数，值域为(0,)π，y u =在(0,)π是减函数，∴()f x 在(0，2π)是减函数，又∵(4f π)4π⨯=0，不是最值，()2f π2π⨯）=是最小值，∴()f x 图像关于直线x =2π对称，故选D ．15．(2017天津)设函数()2sin()f x x ωϕ=+，x ∈R ，其中0ω>，||ϕ<π．若5()28f π=，()08f 11π=，且()f x 的最小正周期大于2π，则A ．23ω=，12ϕπ=B ．23ω=，12ϕ11π=-C ．13ω=，24ϕ11π=-D ．13ω=，24ϕ7π=【答案】A 【解析】由题意5π8x =取最大值，11π8x =与x 相交，设()f x 周期为T ，所以11538844T πππ-==或34T，所以3T π=或T π=，又()f x 的最小正周期大于2π，所以3T π=，所以223T πω==，排除C 、D ；由5π()28f =，即252sin()238πϕ⨯+=，102242k ππϕπ+=+，即212k πϕπ=+，令0k =，12πϕ=．选A ．16．(2015四川)下列函数中，最小正周期为π且图象关于原点对称的函数是A ．cos(22y x π=+B ．sin(2)2y x π=+C ．sin 2cos 2y x x =+D ．sin cos y x x=+【答案】A【解析】由cos(2sin 22y x x π=+=-，可知该函数的最小正周期为π且为奇函数，故选A ．17．(2015安徽)已知函数()()sin f x Αx ωϕ=+(Α，ω，ϕ均为正的常数)的最小正周期为π，当23x π=时，函数()f x 取得最小值，则下列结论正确的是A ．()()()220f f f <-<B ．()()()022f f f <<-C ．()()()202f f f -<<D ．()()()202f f f <<-【答案】A【解析】∵()sin()f x A x ωϕ=+的最小正周期为π，且23x π=是经过函数()f x 最小值点的一条对称轴，∴2326x πππ=-=是经过函数()f x 最大值的一条对称轴．∵12|2|66ππ--=，512|(2)|66πππ---=，|0|66ππ-=，∴|2||(2)||0|666ππππ->-->-，且2233ππ-<<，2233πππ-<-<，2033ππ-<<，∴(2)(2)(0)f f f π<-<，即(2)(2)(0)f f f <-<，故选A ．18．(2011山东)若函数()sin f x x ω=(ω>0)在区间0,3π⎡⎤⎢⎥⎣⎦上单调递增，在区间,32ππ⎡⎤⎢⎥⎣⎦上单调递减，则ω=A ．23B ．32C ．2D ．3【答案】B【解析】由于()sin f x x ω=的图象经过坐标原点，根据已知并结合函数图象可知，3π为函数()f x 的四分之一周期，故243ππω=，解得32ω=．19．(2011安徽)已知函数()sin(2)f x x ϕ=+，其中ϕ为实数，若()()6f x f π≤对x R ∈恒成立，且(()2f f ππ>，则()f x 的单调递增区间是A ．,()36k k k Z ππππ⎡⎤-+∈⎢⎥⎣⎦B ．,()2k k k Z πππ⎡⎤+∈⎢⎥⎣⎦C ．2,()63k k k Z ππππ⎡⎤++∈⎢⎥⎣⎦D ．,()2k k k Z πππ⎡⎤-∈⎢⎥⎣⎦【答案】C【解析】因为当x R ∈时，()|(|6f x f π≤恒成立，所以()sin()163f ππϕ=+=±，可得26k πϕπ=+或526k πϕπ=-，k Z ∈，因为()sin()sin ()sin(2)sin 2f f ππϕϕππϕϕ=+=->=+=，故sin 0ϕ<，所以526k πϕπ=-，所以5()sin(26f x x π=-，由5222262k x k πππππ-+-+≤≤(k Z ∈)，得263k x k ππππ++≤≤(k Z ∈)，故选C ．20．(2019•新课标Ⅰ，文15)函数3()sin(23cos 2f x x x π=+-的最小值为．【答案】4-【解析】3()sin(23cos 2f x x x π=+- 2cos 23cos 2cos 3cos 1x x x x =--=--+，令cos t x =，则11≤≤-t ，2()231f t t t =--+ 的开口向上，对称轴34t =-，在[1-，1]上先增后减，故当1t =即cos 1x =时，函数有最小值4-．21．(2018•新课标Ⅲ，理15)函数()cos(36f x x π=+在[0，]π的零点个数为．【答案】3【解析】()cos(3)06f x x π=+= ，362x k πππ∴+=+，k Z ∈，193x k ππ∴=+，k Z ∈，当0k =时，9x π=，当1k =时，49x π=，当2k =时，79x π=，当3k =时，109x π=，[0x ∈ ，]π，9x π∴=，或49x π=，或79x π=，故零点的个数为3．22．(2018北京)设函数π()cos(0)6f x x ωω=->，若π()()4f x f ≤对任意的实数x 都成立，则ω的最小值为___．【答案】23【解析】由于对任意的实数都有π()(4f x f ≤成立，故当4x π=时，函数()f x 有最大值，故(14f π=，246k πωππ-=(k ∈Z )，∴283k ω=+(k ∈Z )，又0ω>，∴min 23ω=．23．(2018江苏)已知函数sin(2)()22y x ϕϕππ=+-<<的图象关于直线3x π=对称，则ϕ的值是．【答案】π6-【解析】由函数sin(2)(22y x ϕϕππ=+-<<的图象关于直线3x π=对称，得2sin()13πϕ+=±，因为22ϕππ-<<，所以27636πππϕ<+<，则232ππϕ+=，6πϕ=-．24．(2011安徽)设()f x =sin 2cos 2a x b x +，其中,a b ∈R ，0ab ≠，若()()6f x f π≤对一切则x ∈R 恒成立，则①11()012f π=②7()10f π＜()5f π③()f x 既不是奇函数也不是偶函数④()f x 的单调递增区间是2,()63k k k Z ππππ⎡⎤++∈⎢⎥⎣⎦⑤存在经过点(,)a b 的直线与函数()f x 的图像不相交以上结论正确的是(写出所有正确结论的编号)．【答案】①③【解析】()sin 2cos 2)f x a x b x x ϕ=+=+(其中tan baϕ=)，因此对一切x R ∈，()|()|6f x f π≤恒成立，所以sin()13πϕ+=±，可得()6k k Z πϕπ=+∈，故())6f x x π=+．而1111(012126f πππ=⨯+=，所以①正确；74717|()||||123030f πππ==，17|()||530f ππ=，所以7|()||()|105f f ππ=，故②错；③明显正确；④错误：由函数())6f x x π=+和()6f x x π=+的图象(图略)可知，不存在经过点(,)a b 的直线与函数()f x 的图象不相交，故⑤错误．25．(2017浙江)已知函数22()sin cos cos f x x x x x =--()x ∈R ．(Ⅰ)求2(3f π的值；(Ⅱ)求()f x 的最小正周期及单调递增区间．【解析】(Ⅰ)由2sin32π=，21cos 32π=-，2()3f π223131(()2222=---⨯-得2()23f π=．(Ⅱ)由22cos 2cos sin x x x =-与sin 22sin cos x x x =得()cos 222sin(26f x x x x π=-=-+所以()f x 的最小正周期是π由正弦函数的性质得3222262k x k πππππ+++≤≤，k ∈Z 解得263k x k ππππ++≤≤，k ∈Z 所以()f x 的单调递增区间是2[,]63k k ππππ++(k ∈Z )．26．(2013北京)已知函数21()(2cos 1)sin 2cos 42f x x x x =-+(1)求()f x 的最小正周期及最大值；(2)若(,)2παπ∈，且2()2f α=，求α的值．【解析】：(1)21()(2cos 1)sin 2cos 42f x x x x =-+1cos 2sin 2cos 42x x x =+11sin 4cos 422x x=+2sin(424x π=+所以，最小正周期242T ππ==当4242x k πππ+=+(k Z ∈)，即216k x ππ=+(k Z ∈)时，max 2()2f x =．(2)因为22()sin(4242f παα=+=，所以sin(4)14πα+=，因为2παπ<<，所以9174444πππα<+<，所以5442ππα+=，即916πα=．27．(2012广东)已知函数()2cos()6f x x πω=+，(其中0ω>，x R ∈)的最小正周期为10π．(1)求ω的值；(2)设,[0,2παβ∈，56(5)35f απ+=-，516(5)617f βπ-=，求cos()αβ+的值．【解析】(1)21105T ππωω==⇔=．(2)56334(5)cos(sin ,cos 352555f ππαααα+=-⇔+=-⇔==516815(5)cos ,sin 6171717f πβββ-=⇔==．4831513cos()cos cos sin sin 51751785αβαβαβ+=-=⨯-⨯=-．28．(2018上海)设常数a R ∈，函数2()sin 22cos f x a x x =+．(1)若()f x 为偶函数，求a 的值；(2)若(14f π=+，求方程()1f x =-ππ-［，］上的解．【解析】(1)若()f x 为偶函数，则对任意∈R x ，均有()()=-f x f x ；即22sin 22cos sin 2()2cos ()+=-+-a x x a x x ，化简得方程sin 20=a x 对任意∈R x 成立，故0=a ；(2)2()sin(22cos (11444πππ=⨯+=+=+f a a ，所以=a故2()22cos =+f x x x ．则方程()1=f x 222cos 1+=x x ，222cos 1+-=x x ，化简即为2sin(26π+=x ，即2sin(2)62π+=-x ，解得1124ππ=-+x k 或524ππ'=-+x k ，,'∈Zk k 若求该方程在[,]ππ-上有解，则1335[,2424∈-k ，1929[,]2424'∈-k ，即0=k 或1；0'=k 或1，对应的x 的值分别为：1124π-、1324π、524π-、1924π．考点40三角函数图像1．(2020全国Ⅰ文理7)设函数()cos π6f x x ω=+⎛⎫⎪⎝⎭在[],-ππ的图像大致如下图，则()f x 的最小正周期为()A ．10π9B ．7π6C ．4π3D ．3π2【答案】C【思路导引】由图可得：函数图像过点4,09π⎛⎫-⎪⎝⎭，即可得到4cos 096ππω⎛⎫-⋅+= ⎪⎝⎭，结合4,09π⎛⎫- ⎪⎝⎭是函数()f x 图像与x 轴负半轴的第一个交点即可得到4962πππω-⋅+=-，即可求得32ω=，再利用三角函数周期公式即可得解．【解析】由图可得：函数图像过点4,09π⎛⎫-⎪⎝⎭，将它代入函数()f x 可得：4cos 096ππω⎛⎫-⋅+= ⎪⎝⎭，又4,09π⎛⎫-⎪⎝⎭是函数()f x 图像与x 轴负半轴的第一个交点，∴4962πππω-⋅+=-，解得：32ω=，∴函数()f x 的最小正周期为224332T πππω===，故选C ．2．(2020浙江4)函数cos sin y x x x =+在区间[],-ππ的图像大致为()A ．B ．C ．D．【答案】A【思路导引】首先确定函数的奇偶性，然后结合函数在x π=处的函数值排除错误选项即可确定函数的图像．【解析】()()()()()()cos sin cos sin f x x x x x x x f x -=--+-=-+=-，[],x ππ∈-，∴函数是奇函数，故排除C ，D ，当0,2x π⎛⎫∈ ⎪⎝⎭时，cos sin 0x x x +>，∴排除B ，故选A ．3．(2020山东10)右图是函数sin()y x ωϕ=+的部分图像，则sin()=x ωϕ+()A ．πsin()3x +B ．πsin(2)3x -C ．πcos(2)6x +D ．5πcos(2)6x -【答案】BC【思路导引】首先利用周期确定ω的值，然后确定ϕ的值即可确定函数的解析式，最后利用诱导公式可得正确结果．【解析】由函数图像可知：22362T πππ=-=，则222T ππωπ===，所以不选A ，当2536212x πππ+==时，1y =-∴()5322122k k Z ππϕπ⨯+=+∈，解得：()223k k ϕππ=+∈Z ，即函数的解析式为：2sin 22sin 2cos 2sin 236263y x k x x x ππππππ⎛⎫⎛⎫⎛⎫⎛⎫=++=++=+=- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭，而5cos 2cos(2)66x x ππ⎛⎫+=-- ⎪⎝⎭，故选BC ．4．(2016全国新课标卷2，文3)函数=sin()y A x ωϕ+的部分图像如图所示，则(A)2sin(2)6y x π=-(B)2sin(2)3y x π=-(C)2sin(+)6y x π=(D)2sin(+)3y x π=【答案】A5．(2015新课标Ⅰ，理8)函数()f x =cos()x ωϕ+的部分图像如图所示，则()f x 的单调递减区间为()(A)(kπ−14，kπ+34，)，k ∈ (B)(2kπ−14，2kπ+34)，k ∈ (C)(k −14，k +34)，k ∈(D)(2k −14，2k +34)，k ∈【答案】D【解析】由五点作图知，1+4253+42πωϕπωϕ⎧=⎪⎪⎨⎪=⎪⎩，解得=ωπ，=4πϕ，所以()cos()4f x x ππ=+，令22,4k x k k Z πππππ<+<+∈，解得124k -＜x ＜324k +，k Z ∈，故单调减区间为(124k -，324k +)，k Z ∈，故选D ．6．(2011辽宁)已知函数)(x f =A tan(ωx +ϕ)(2||,0πϕω<>)，y =)(x f 的部分图像如下图，则=)24(πf A ．3B 3C ．33D ．23-【答案】B【解析】半周期为3884πππ-=，即最小正周期为2π，所以2ω=．由题意可知，图象过定点3(,0)8π，所以30tan(2)8A πϕ=⨯+，即34k πϕπ+=()k Z ∈，所以3()4k k Z πϕπ=-∈，又||2πϕ<，所以4πϕ=，又图象过定点(0,1)，所以1A =．综上可知()tan(2)4f x x π=+，故有(tan(2)tan242443f ππππ=⨯+==7．(2014江苏)已知函数x y cos =与)2sin(ϕ+=x y (0≤πϕ<)，它们的图象有一个横坐标为3π的交点，则ϕ的值是．【答案】6π【解析】由题意交点为1(,)32π，所以21sin()32πϕ+=，又0ϕπ<≤，解得6πϕ=．8．(2011江苏)函数()sin(),(,,f x A x A w ωϕϕ=+是常数，0,0)A ω>>的部分图象如图所示，则(0)f =．【答案】62【解析】由图可知：A =，741234T πππ=-=，所以T π=，22T πω==，又函数图象经过点(,0)3π，所以23πϕπ⨯+=，则3πϕ=，故())3f x x π=+，所以6(0)32f π==．9．(2012湖南)函数()sin()f x x ωϕ=+的导函数()y f x '=的部分图像如图4所示，其中，P 为图像与y轴的交点，A ，C 为图像与x 轴的两个交点，B 为图像的最低点．(1)若6πϕ=，点P 的坐标为(0，332)，则ω=；(2)若在曲线段ABC 与x 轴所围成的区域内随机取一点，则该点在△ABC 内的概率为．【答案】(1)3；(2)4π【解析】(1)()y f x '=cos()x ωωϕ=+，当6πϕ=，点P 的坐标为(0，332)时33cos ,362πωω=∴=；10．(2016江苏省)定义在区间[]0,3π上的函数sin 2y x =的图象与cos y x =的图象的交点个数是．【答案】7【解析】画出函数图象草图，共7个交点．11．(2012湖南)已知函数()sin()f x A x ωϕ=+(,x R ∈0ω>，0)2πϕ<<的部分图像如图所示．(Ⅰ)求函数()f x 的解析式；(Ⅱ)求函数()(()1212g x f x f x ππ=--+的单调递增区间．【解析】(Ⅰ)由题设图像知，周期11522(),21212T Tππππω=-=∴==．因为点5(,0)12π在函数图像上，所以55sin(2)0,sin()0126A ππϕϕ⨯+=+=即．又55450,,=26636πππππϕϕϕπ<<∴<+<+ 从而，即=6πϕ．又点0,1（）在函数图像上，所以sin1,26A A π==，故函数()f x 的解析式为()2sin(26f x x π=+(Ⅱ)()2sin[2()2sin[2()]126126g x x x ππππ=-+-++2sin 22sin(23x x π=-+132sin 22(sin 2cos 2)22x x x =-+sin 232x x =-2sin(23x π=-由222,232k x k πππππ-≤-≤+得5,.1212k x k k z ππππ-≤≤+∈()g x ∴的单调递增区间是5,,.1212k k k z ππππ⎡⎤-+∈⎢⎥⎣⎦考点41三角函数图像变换1．(2020天津8)已知函数()sin 3f x x π⎛⎫=+ ⎪⎝⎭．给出下列结论：①()f x 的最小正周期为2π；②2f π⎛⎫⎪⎝⎭是()f x 的最大值；③把函数sin y x =的图象上所有点向左平移3π个单位长度，可得到函数()y f x =的图象．其中所有正确结论的序号是A ．①B ．①③C ．②③D ．①②③【答案】B【思路导引】对所给选项结合正弦型函数的性质逐一判断即可．【解析】因为()sin()3f x x π=+，所以周期22T ππω==，故①正确；51()sin()sin 122362f ππππ=+==≠，故②不正确；将函数sin y x =的图象上所有点向左平移3π个单位长度，得到sin(3y x π=+的图象，故③正确．故选B ．2．(2017课标卷1，理9)已知曲线1:cos C y x =，22π:sin 23C y x ⎛⎫=+ ⎪⎝⎭，则下面结论正确的是()A ．把1C 上各点的横坐标伸长到原来的2倍，纵坐标不变，再把得到的曲线向右平移π6个单位长度，得到曲线2C B ．把1C 上各点的横坐标伸长到原来的2倍，纵坐标不变，再把得到的曲线向左平移π12个单位长度，得到曲线2C C ．把1C 上各点的横坐标缩短到原来的12倍，纵坐标不变，再把得到的曲线向右平移π6个单位长度，得到曲线2C D ．把1C 上各点的横坐标缩短到原来的2倍，纵坐标不变，再把得到的曲线向左平移π12个单位长度，得到曲线2C 【答案】D【解析】1:cos C y x =，22π:sin 23⎛⎫=+ ⎪⎝⎭C y x ，首先曲线1C 、2C 统一为一三角函数名，可将1:cos C y x =用诱导公式处理，πππcos cos sin 222⎛⎫⎛⎫==+-=+ ⎪ ⎪⎝⎭⎝⎭y x x x ．横坐标变换需将1=ω变成2=ω，即112πππsin sin 2sin 2224⎛⎫⎛⎫⎛⎫=+−−−−−−−−−→=+=+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭C 上各坐短它原y x y x x 点横标缩来2ππsin 2sin 233⎛⎫⎛⎫−−→=+=+ ⎪ ⎪⎝⎭⎝⎭y x x ，注意ω的系数，在右平移需将2=ω提到括号外面，这时π4+x 平移至π3+x ，根据“左加右减”原则，“π4+x ”到“π3+x ”需加上π12，即再向左平移π12．3．(2016•新课标Ⅰ，文6)将函数2sin(26y x π=+的图象向右平移14个周期后，所得图象对应的函数为()A ．2sin(2)4y x π=+B ．2sin(2)3y x π=+C ．2sin(2)4y x π=-D ．2sin(23y x π=-【答案】D【解析】函数2sin(26y x π=+的周期为22T ππ==，由题意即为函数2sin(2)6y x π=+的图象向右平移4π个单位，可得图象对应的函数为2sin[2()]46y x ππ=-+，即有2sin(2)3y x π=-，故选D ．4．(2016北京)将函数sin(23y x π=-图像上的点(,)4P t π向左平移s (0s >)个单位长度得到点P '．若P '位于函数sin 2y x =的图像上，则A ．12t =，s 的最小值为6πB ．32t =，s 的最小值为6πC ．12t =，s 的最小值为3πD ．32t =，s 的最小值为3π【答案】A 【解析】因为点(,)4P t π在函数sin(23y x π=-的图象上，所以sin(2)43t ππ=⨯-=1sin 62π=，又1(,42P s π'-在函数sin 2y x =的图象上，所以1sin 2()24s π=-，则2()246s k πππ-=+或52()246s k πππ-=+，k Z ∈，得6s k ππ=-+或6s k ππ=--，k Z ∈．又0s >，故s 的最小值为6π，故选A ．5．(2019天津理7)已知函数()sin()(0,0,||)f x A x A ωϕωϕπ=+>><是奇函数，将()y f x =的图像上所有点的横坐标伸长到原来的2倍(纵坐标不变)，所得图像对应的函数为()g x ．若()g x 的最小正周期为2π，且π4g ⎛⎫=⎪⎝⎭，则3π8f ⎛⎫= ⎪⎝⎭A ．2-B ．CD ．2【答案】C【解析】因为()f x 是奇函数，所以0ϕ=，()sin f x A x ω=．将()y f x =的图像上所有点的横坐标伸长到原来的2倍(纵坐标不变)，所得图像对应的函数为()g x ，即()1sin 2g x A x ω⎛⎫=⎪⎝⎭，因为()g x 的最小正周期为2π，所以2212ωπ=π，得2ω=，所以()sin g x A x =，()sin 2f x A x =．若24g π⎛⎫= ⎪⎝⎭，即2sin 2442g A A ππ⎛⎫=== ⎪⎝⎭，即2A =，所以()2sin 2f x x =，3322sin 22sin 228842f ππ3π⎛⎫⎛⎫=⨯==⨯ ⎪ ⎪⎝⎭⎝⎭C ．6．(2015山东)要得到函数4sin(4)3y x π=-的图像，只需要将函数sin 4y x =的图像A ．向左平移12π个单位B ．向右平移12π个单位C ．向左平移3π个单位D ．向右平移3π个单位【答案】B【解析】sin 4(12y x π=-，只需将函数sin 4y x =的图像向右平移12π个单位，故选B ．7．(2014浙江)为了得到函数x x y 3cos 3sin +=的图象，可以将函数2y x =的图像A ．向右平移12π个单位B ．向右平移4π个单位C ．向左平移12π个单位D ．向左平移4π个单位【答案】A 【解析】因为sin 3cos32)2)412y x x x x ππ=+=-=-，所以将函数2y x =的图象向右平移12π个单位后，可得到24y x π=-的图象，故选A ．8．(2013福建)将函数)22)(2sin()(πθπθ<<-+=x x f 的图象向右平移)0(>ϕϕ个单位长度后得到函数)(x g 的图象，若)(),(x g x f 的图象都经过点23,0(P ，则ϕ的值可以是A ．35πB ．65πC ．2πD ．6π【答案】B【解析】把23,0(P 代入22)(2sin()(πθπθ<<-+=x x f ，解得3πθ=，所以)232sin()(ϕπ-+=x x g ，把)23,0(P 代入得，πϕk =或6ππϕ-=k ，故选B 9．(2012安徽)要得到函数)12cos(+=x y 的图象，只要将函数x y 2cos =的图象A ．向左平移1个单位B ．向右平移1个单位C ．向左平移12个单位D ．向右平移12个单位【答案】C【解析】cos 2y x =向左平移12→1cos 2(cos(21)2y x x =+=+，故选C ．10．(2012浙江)把函数cos 21y x =+的图像上所有点的横坐标伸长到原来的2倍(纵坐标不变)，然后向左平移1个单位长度，再向下平移1个单位长度，得到的图像是【答案】A【解析】cos 21cos 1cos(1)1cos(1)y x y x y x y x =+⇒=+⇒=++⇒=+，故选A ．11．(2012天津)将函数()sin f x x ω=(其中ω>0)的图像向右平移4π个单位长度，所得图像经过点3(,0)4π，则ω的最小值是A ．13B ．1C ．53D ．2【答案】D 【解析】函数向右平移4π得到函数4sin(4(sin 4()(ωπωπωπ-=-=-=x x x f x g ，因为此时函数过点)0,43(π，所以0443(sin =-ππω，即,2)443(πωπππωk ==-所以Z k k ∈=,2ω，所以ω的最小值为2，选D ．12．(2020江苏10)将函数3sin(24y x π=+的图象向右平移6π个单位长度，则平移后的图象中与y 轴最近的对称轴的方程是．【答案】524x π=-【解析】∵()3sin(24f x x π=+，将函数()3sin(2)4f x x π=+的图象向右平移6π个单位长度得()()3sin(2)3sin(263412g x f x x x ππππ=-=-+=-，则()y g x =的对称轴为2122x k πππ-=+，k Z ∈，即7242k x ππ=+，k Z ∈，0k =时，724x π=，1k =-时，524x π=-，∴平移后的图象中与y 轴最近的对称轴的方程是524x π=-．13．(2016新课标卷3，理14)函数sin y x x =的图像可由函数sin y x x =+的图像至少向右平移_____________个单位长度得到．【答案】32π【解析】因为sin 2sin(3y x x x π=+=+，sin 2sin()3y x x x π=-=-＝2sin[(]33x π2π+-，所以函数sin y x x =-的图像可由函数sin y x x =+的图像至少向右平移32π个单位长度得到．14．(2016全国新课标卷3，文14)函数sin y x x =-的图像可由函数2sin y x =的图像至少向右平移_____________个单位长度得到．【答案】3π【解析】因为sin 2sin()3y x x x π=-=-，所以函数sin y x x =-的的图像可由函数2sin y x =的图像至少向右平移3π个单位长度得到．15．(2013新课标Ⅱ，文16)函数cos(2)()y x ϕπϕπ=+-≤≤的图象向右单位后，与函数的图象重合，则ϕ=_________．【解析】因为cos(2)y x ϕ=+=cos(2)x ϕ--=16．(2014重庆)将函数()()⎪⎭⎫ ⎝⎛<≤->+=220sin πϕπωϕω，x x f 图象上每一点的横坐标缩短为原来的一半，纵坐标不变，再向右平移6π个单位长度得到x y sin =的图像，则=⎪⎭⎫ ⎝⎛6πf ______．【答案】22【解析】把函数sin y x =图象向左平移6π个单位长度得到sin()y x ωϕ=+的图象，再把函数sin()6y x π=+图象上每一点的横坐标伸长为原来的2倍，纵坐标不变，得到函数1()sin(26f x x π=+的图象，所以=⎪⎭⎫ ⎝⎛6πf 1sin()sin 26642πππ⨯+==．。

2011年高考数学重点难点讲解十五：三角函数的图象和性质(学生版)

难点15 三角函数的图象和性质三角函数的图象和性质是高考的热点，在复习时要充分运用数形结合的思想，把图象和性质结合起来.本节主要帮助考生掌握图象和性质并会灵活运用.●难点磁场(★★★★)已知α、β为锐角，且x (α+β－2π)＞0,试证不等式f (x )=)sin cos ()sin cos (αββα+x x ＜2对一切非零实数都成立.●案例探究［例1］设z 1=m +(2－m 2)i ,z 2=cos θ+(λ+sin θ)i ,其中m ,λ,θ∈R ，已知z 1=2z 2，求λ的取值范围.命题意图：本题主要考查三角函数的性质，考查考生的综合分析问题的能力和等价转化思想的运用，属★★★★★级题目.［例2］如右图，一滑雪运动员自h =50m 高处A 点滑至O 点，由于运动员的技巧(不计阻力)，在O 点保持速率v 0不为，并以倾角θ起跳，落至B 点，令OB =L ，试问，α=30°时，L 的最大值为多少？当L 取最大值时，θ为多大？命题意图：本题是一道综合性题目，主要考查考生运用数学知识来解决物理问题的能力.属★★★★★级题目.［例3］如下图，某地一天从6时到14时的温度变化曲线近似满足函数y =A sin(ωx +φ)+b .(1)求这段时间的最大温差.(2)写出这段曲线的函数解析式.命题意图：本题以应用题的形式考查备考中的热点题型，要求考生把所学的三角函数知识与实际问题结合起来分析、思考，充分体现了“以能力立意”的命题原则.属★★★★级题目.●锦囊妙计本难点所涉及的问题及解决的方法主要有：1.考查三角函数的图象和性质的基础题目，此类题目要求考生在熟练掌握三角函数图象的基础上要对三角函数的性质灵活运用.2.三角函数与其他知识相结合的综合题目，此类题目要求考生具有较强的分析能力和逻辑思维能力.在今后的命题趋势中综合性题型仍会成为热点和重点，并可以逐渐加强.3.三角函数与实际问题的综合应用.此类题目要求考生具有较强的知识迁移能力和数学建模能力，要注意数形结合思想在解题中的应用.●歼灭难点训练一、选择题1.(★★★★)函数y =－x ·cos x 的部分图象是( )2.(★★★★)函数f (x )=cos2x +sin(2π+x )是( )A.非奇非偶函数B.仅有最小值的奇函数C.仅有最大值的偶函数D.既有最大值又有最小值的偶函数二、填空题3.(★★★★)函数f (x )=(31)｜cos x ｜在［－π，π］上的单调减区间为_________. 4.(★★★★★)设ω＞0，若函数f (x )=2sin ωx 在［－4,3ππ，］上单调递增，则ω的取值范围是_________.三、解答题5.(★★★★)设二次函数f (x )=x 2+bx +c (b ,c ∈R ),已知不论α、β为何实数恒有f (sin α)≥0和f (2+cos β)≤0.(1)求证：b +c =－1；(2)求证c ≥3；(3)若函数f (sin α)的最大值为8，求b ，c 的值.6.(★★★★★)用一块长为a ，宽为b (a ＞b )的矩形木板，在二面角为α的墙角处围出一个直三棱柱的谷仓，试问应怎样围才能使谷仓的容积最大？并求出谷仓容积的最大值.7.(★★★★★)有一块半径为R ，中心角为45°的扇形铁皮材料，为了获取面积最大的矩形铁皮，工人师傅常让矩形的一边在扇形的半径上，然后作其最大内接矩形，试问：工人师傅是怎样选择矩形的四点的？并求出最大面积值.8.(★★★★)设－6π≤x ≤4π，求函数y =log 2(1+sin x )+log 2(1－sin x )的最大值和最小值.9.(★★★★★)是否存在实数a ，使得函数y =sin 2x +a ·cos x +85a －23在闭区间［0，2π］上的最大值是1？若存在，求出对应的a 值；若不存在，试说明理由.。

全稿--2011高考数学之三角函数精品

三角函数任意角的三角函数一、角的概念的推广1．与角α终边相同的角的集合为．2．与角α终边互为反向延长线的角的集合为．3．轴线角（终边在坐标轴上的角）终边在x轴上的角的集合为，终边在y轴上的角的集合为，终边在坐标轴上的角的集合为．4．象限角是指：．5．区间角是指：．6．弧度制的意义：圆周上弧长等于半径长的弧所对的圆心角的大小为1弧度的角，它将任意角的集合与实数集合之间建立了一一对应关系．7．弧度与角度互化：180º＝弧度，1º＝弧度，1弧度＝≈º．8．弧长公式：l ＝；扇形面积公式：S＝.二、任意角的三角函数9．定义：设P(x, y)是角α终边上任意一点，且|PO| ＝r，则sinα＝；cosα＝；tanα＝；10．三角函数的符号与角所在象限的关系：1213．三角函数线：在图中作出角α的正弦线、余弦线、正切线．1．同角公式：(1) 平方关系：sin 2α＋cos 2α＝1，1＋tan 2α＝，1＋cot 2α＝ (2) 商数关系：tanα＝，cotα＝(3) 倒数关系：tanα ＝1，sinα ＝1，cotα ＝1 2．诱导公式：规律：奇变偶不变，符号看象限－＋－+cos x , ＋＋－－ sin x ,－＋＋－tan x ,x y O xyO x y O3．同角三角函数的关系式的基本用途：根据一个角的某一个三角函数值，求出该角的其他三角函数值；化简同角三角函数式；证明同角的三角恒等式． 4．诱导公式的作用：0°~90º角的三角函数值．例1. 已知f(α)=)sin()tan()tan()2cos()sin(αππαπααπαπ-----+---;（1）化简f(α);（2）若α是第三象限角，且cos 5123=⎪⎭⎫ ⎝⎛-πα，求f(α)的值.例2．求值：(1) 已知53)7cos(,2-=-<<παπαπ，求)2cos(απ+的值．2) 已知11tan tan -=-αα，求下列各式的值．①ααααcos sin cos 3sin +-；②2cos sin sin 2++ααα例3. 已知－02<<x π，sin x ＋cos x ＝51．（1）求sin x －cos x 的值．（2）求xx x tan 1sin 22sin 2-+的值．1．基本公式sin(α±β)＝sinα cosβ±cosα sinβ cos(α±β)＝ ; tan(α±β)＝ . 2．公式的变式tan α＋tan β＝tan (α＋β)(1－tan α tan β) 1－tan α tan β＝)tan(tan tan βαβα++3．常见的角的变换： 2α＝(α＋β)＋(α－β)；α＝2βα+＋2βα- α＝(α＋β)－β ＝(α－β)＋β2βα+＝(α－2β)－(2α－β)； )4()4(x x ++-ππ＝2π例1．求［2sin50°+sin10°(1+3tan10°)］· 80sin 22的值.变式训练1：(1)已知α∈(2π,π)，sin α=53,则tan(4πα+)等于（）A.71B.7C.－ 71D.－7例2. 已知α∈(4π，43π)，β∈(0，4π),cos (α－4π)＝53，sin(43π＋β)＝135，求sin(α＋β)的值．变式训练2：设cos （α－2β）=－91，sin （2α－β）=32，且2π＜α＜π，0＜β＜2π，求cos （α+β）.1．基本公式：sin2α＝；cos2α＝＝＝；tan2α＝ . 2．公式的变用：1＋cos2α＝；1－cos2α＝．例1. 求值：140cos 40cos 2)40cos 21(40sin 2-︒+︒︒+︒变式训练1：)12sin12(cos ππ-(cos12π＋sin 12π)＝（）A ．－23 B ．－21 C ． 21 D ．23例2．已知α为锐角，且21tan =α，求ααααα2cos 2sin sin cos 2sin -的例3．已知x x x x f cos sin sin 3)(2+-=；(1) 求)625(πf 的值； (2) 设2341)2(),,0(-=∈απαf ，求sinα的值．变式训练3：已知sin(απ-6)＝31，求cos(απ232+)的值．三角函数的化简和求值例1. （1）化简：40cos 170sin )10tan 31(50sin 40cos +++ （2）化简：xx x x 4466cos sin 1cos sin 1----例2. 已知0cos 2cos sin sin 622=-+αααα，α∈[2π，π]，求sin （2α＋3π）的值．例3. 已知tan(α－β)＝21，tan β＝-71，且α、β∈（0，π），求2α－β的值.三角函数的图象与性质例1已知函数y=3sin )421(π-x（1）说明此图象是由y=sinx 的图象经过怎么样的变化得到的；（2）求此函数的振幅、周期和初相；（3）求此函数图象的对称轴方程、对称中心.例2：已知函数23cos sin 3)(2+-=x x xcox x f ϖϖϖ ),(R x R ∈∈ϖ的最小正周期为π且图象关于6π=x 对称；(1) 求f(x)的解析式；(2) 若函数y ＝1－f(x)的图象与直线y ＝a 在]2,0[π上中有一个交点，求实数a 的范围．例3：函数y=Asin(ωx+ϕ)(ω＞0,|ϕ|＜2π,x ∈R )的部分图象如图，则函数表达式为( )A. y=-4sin )48(ππ-x B. y=-4sin )48(ππ+xC. y=4sin )48(ππ-x D. y=4sin )48(ππ+x例4．设关于x 的方程cos2x ＋3sin2x ＝k ＋1在[0，2π]内有两不同根α，β，求α＋β的值及k 的取值范围．变式训练4.已知函数f (x)＝sin(ωx ＋ϕ)(ω>0，0≤ϕ≤π)是R 上的偶函数，其图象关于点M(43π，0)对称，且在区间[0，2π]上是单调函数，求ϕ和ω的值．三角函数的性质1．函数y ＝sinx 的对称性与周期性的关系．⑴ 若相邻两条对称轴为x ＝a 和x ＝b ，则T ＝． ⑵ 若相邻两对称点(a ，0)和(b ，0) ，则T ＝．⑶ 若有一个对称点(a ，0)和它相邻的一条对称轴x ＝b ，则T ＝．注：该结论可以推广到其它任一函数．例1. 化简f (x)＝cos(x k 2316++π)＋cos(x k 2316--π)＋23sin(3π＋2x)(x ∈R ，k ∈Z)．并求f (x)的值域和最小正周期．变式训练1：已知函数)12(sin 2)62sin(3)(2ππ-+-=x x x f )(R x ∈；（1）求函数f(x)的最小正周期；（2）求使函数f(x)取得最大值的x 的集合．例2已知函数f (x)＝xx 2cos 1sin 2+⑴ 求f (x)的定义域．⑵ 用定义判断f (x)的奇偶性．⑶ 在[－π，π]上作出函数f (x)的图象．⑷ 指出f (x)的最小正周期及单调递增区间．例3设函数)10(cos 3sin )(<<+=a ax ax x f ，)10()6tan()(<<+=m mx x g π，已知f(x)、g(x)的最小正周期相同，且2(g)＝f(1)；（1）试确定f(x)、g(x)的解的式；（2）求函数f(x)的单调递增区间．变式训练3：已知函数f (x)＝21log (sinx －cosx)⑴ 求它的定义域和值域；⑵ 求它的单调区间；⑶ 判断它的奇偶性；⑷ 判定它的周期性，如果是周期函数，求出它的最小正周期．例4.已知函数y ＝acosx ＋b 的最大值为1，最小值是－3，试确定)(x f ＝b sin(ax ＋3π)的单调性三角函数的最值一、求值问题例一若tan α=3x ，tan β=3-x , 且α-β=6π，求x 的值。

2011高考数学重点知识归纳+3.三角函数

五．三角函数一、终边相同的角的表示方法：凡是与终边α相同的角，都可以表示成k ·3600+α的形式，特例，终边在x 轴上的角集合{α|α=k ·1800，k ∈Z}，终边在y 轴上的角集合{α|α=k ·1800+900，k ∈Z}，终边在坐标轴上的角的集合{α|α=k ·900，k ∈Z}。

在已知三角函数值的大小求角的大小时，通常先确定角的终边位置，然后再确定大小。

理解弧度的意义，并能正确进行弧度和角度的换算；⑴角度制与弧度制的互化：π弧度 180=，1801π=弧度，1弧度 )180(π='1857 ≈⑵弧长公式：||l R α=；扇形面积公式：211||22S lR R α==。

例：已知扇形AOB 的周长是6cm ，该扇形的中心角是1弧度，求该扇形的面积。

（答：22cm ）二、任意角的三角函数的定义、三角函数的符号规律、特殊角的三角函数值、同角三角函数的关系式、诱导公式：（1）三角函数定义：角α中边上任意一点P 为),(y x ，设r OP =||则：,cos ,sin r x r y ==ααxy =αtan （2）三角函数符号规律：一全正，二正弦，三正切，四余弦；（4）同角三角函数的基本关系：x xx x tan cos ;1cos sin 22==+ （5）诱导公式（奇变偶不变，符号看象限．．．．．．．．．．．）: (注意：公式中始终视．．．α．为锐角．．．)． sin(πα-)＝sin α,cos(πα-)＝－cos α,tan(πα-)＝－tan α sin(πα+)＝－sin α,cos(πα+)＝－cos α,tan(πα+)＝tan α sin(α-)＝－sin α,cos(α-)＝cos α,tan(α-)＝－tan αsin(2πα-)＝－sin α,cos(2πα-)＝cos α,tan(2πα-)＝－tan αsin(2k πα+)＝sin α,cos(2k πα+)＝cos α,tan(2k πα+)＝tan α，()k Z ∈ sin(2πα-)＝cos α,cos(2πα-)＝sin α ， sin(2πα+)＝cos α,cos(2πα+)＝-sin α例：若角α的终边经过点P (1,-2),则tan 2α的值为 .（答： 34）例：已知11tan tan -=-αα，则ααααc os sin c os 3sin +-＝____；2cos sin sin 2++ααα＝_________（答：35-；513）；齐次分式弦化切,一般问题切化弦。

2011年高考数学理科试卷分类解析——三角函数

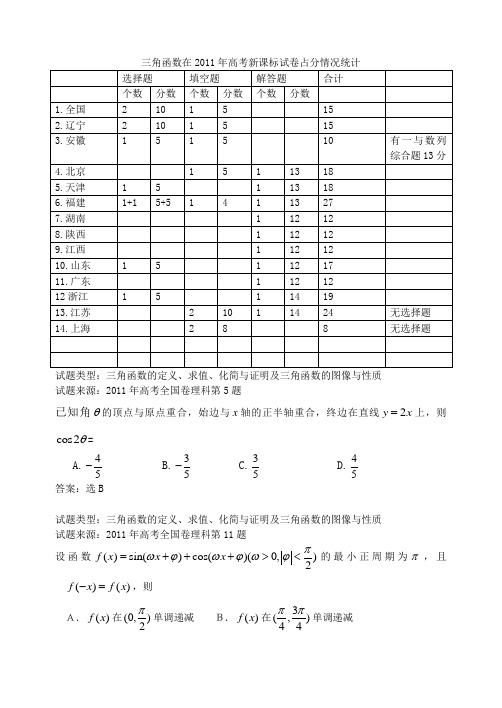
三角函数在2011年高考新课标试卷占分情况统计试题类型：三角函数的定义、求值、化简与证明及三角函数的图像与性质试题来源：2011年高考全国卷理科第5题已知角θ的顶点与原点重合，始边与x 轴的正半轴重合，终边在直线2y x =上，则cos 2θ=A.45-B.35-C.35D.45答案：选B试题类型：三角函数的定义、求值、化简与证明及三角函数的图像与性质试题来源：2011年高考全国卷理科第11题设函数()s i n ()c o s ()(0,)2f x x x πωϕωϕωϕ=+++><的最小正周期为π，且()()f x f x -=，则Ａ．()f x 在(0,)2π单调递减Ｂ．()f x 在3(,)44ππ单调递减Ｃ．()f x 在(0,)2π单调递增Ｄ．()f x 在3(,)44ππ单调递增答案：选A析：()sin()cos())4f x x x x πωϕωϕωϕ=+++=++．由()()f x f x -=知，()f x 为偶函数，所以2,42k k Z ππϕπ+=+∈，又2πϕ<，则4πϕ=∴()f x x =.有余弦函数的性质（或图像）知()f x 在(0,)2π单调递减.说明：本题主要考查三角函数的恒等变形（sin cos )y a x b x x ϕ=+=+）及性质（())4f x x πϕ=++为偶函数，而()sin f x A x ω=为奇函数，所以函数要变名，令2,42k k Z ππϕπ+=+∈即可）.试题类型：三角函数的定义、求值、化简与证明及三角函数的图像与性质试题来源：2011年高考辽宁卷理科第7题设1+=43πθsin(），则sin 2θ= A.79- B.19- C.19 D.79答案：选A试题类型：三角函数的定义、求值、化简与证明及三角函数的图像与性质试题来源：2011年高考辽宁卷理科第16题已知函数()tan()(0,)2f x A x πωϕωϕ=+><，()y f x =的部分图像如右图，则()24f =π____________.试题类型：三角函数的定义、求值、化简与证明及三角函数的图像与性质试题来源：2011年高考安徽卷理科第9题已知函数()sin(2)f x x ϕ=+，其中ϕ为实数，若()()6f x f π≤对x R ∈恒成立，且()()2f f ππ>，则()f x 的单调递增区间是A.,()36k k k Z ππππ⎡⎤-+∈⎢⎥⎣⎦ B.,()2k k k Z πππ⎡⎤+∈⎢⎥⎣⎦C.2,()63k k k Z ππππ⎡⎤++∈⎢⎥⎣⎦ D.,()2k k k Z πππ⎡⎤-∈⎢⎥⎣⎦答案：选C【解析】若()()6f x f π≤对x R ∈恒成立，则()sin()163f ππϕ=+=，所以,32k k Z ππϕπ+=+∈，,6k k Z πϕπ=+∈.由()()2f f ππ>，（k Z ∈），可知sin()sin(2)πϕπϕ+>+，即s i n 0ϕ<，所以(21),6k k Z πϕπ=++∈，代入()s i n (2f x x ϕ=+，得()sin(2)6f x x π=-+，由3222262k x k πππππ+++剟，得263k x k ππππ++剟，故选C.【命题意图】本题考查正弦函数的有界性，考查正弦函数的单调性.属中等偏难题.试题类型：三角函数的定义、求值、化简与证明及三角函数的图像与性质试题来源：2011年高考北京卷理科第15题已知函数()4cos sin()16f x x x π=+-。

2011高考数学二轮复习专题二第1讲三角函数的图象与性质课件理大纲人教版

变式训练 1 已知点 P(sin34π，cos34π)落在角 θ 的终边上，
且 θ∈[0,2π)，则 θ 的值为
(D )
π
3π
A.4
B. 4
5π
7π
C. 4
D. 4
解析
tan θ＝cos343π＝－coπsπ4＝－1， sin4π sin4
又 sin34π>0，cos34π<0，
∴θ 为第四象限角且 θ∈[0,2π)，∴θ＝74π，故选 D.
高点、最低点或特殊点求 A；由函数的周期确定 ω；由图象上的关键点确定 φ. (2)求函数的周期时，注意以下规律：相邻的最高点与最低点的横坐标之差的绝对值为半个周期，最高点(或最低点)的横坐标与相邻零点差的绝对值为41个周期．
变式训练 2 (2010·天津)右图是函数 y＝ Asin(ωx＋φ)(x∈R)在区间[－π6，56π]上的图象．为了得到这个函数的图象，只要将 y＝sin x(x∈R)的图象上所有的点 ( ) A．向左平移π3个单位长度，再把所得各点的横坐标缩短到原来的12倍，纵坐标不变 B．向左平移π3个单位长度，再把所得各点的横坐标伸长到原来的 2 倍，纵坐标不变 C．向左平移π6个单位长度，再把所得各点的横坐标缩短到原来的12倍，纵坐标不变 D．向左平移π6个单位长度，再把所得各点的横坐标伸长到原来的 2 倍，纵坐标不变
探究提高 (1)求三角函数的周期、单调区间、最值及判断三角函数的奇偶性，往往是在定义域内，先化简三角函数式，尽量化为 y＝Asin(ωx＋φ)＋B 的形式，然后再求解． (2)对于形如 y＝asin ωx＋bcos ωx 型的三角函数，要通过引入辅助角化为 y ＝ a2＋b2 sin(ωx ＋ φ)(cos φ ＝

2011年高考数学第四章第三节三角函数的图像

同步检测训练一、选择题 1．(2009·某某皖北联考一)定义一种运算(a ，b )(c ，d )＝ad －bc ，将函数f (x )＝(1，sin x )(3，cos x )的图象向左平移φ(φ>0)个单位，所得图象对应的函数为偶函数，则φ的最小值是()A.π6B.π3C.2π3D.5π6 答案：C解析：f (x )＝(1，sin x )(3，cos x )＝cos x －3sin x ＝2cos(x ＋π3)，向左平移φ(φ>0)个单位得y ＝2cos(x ＋π3＋φ)，由于它是偶函数，则φ的最小值是2π3，故选C.2．(2009·某某质检)关于函数y ＝sin2x －3cos2x 图象的对称性，下列说法正确的是()A ．关于直线x ＝π3对称B ．关于直线x ＝π6对称C ．关于点(π3，0)对称D ．关于点(π6，0)对称答案：D解析：y ＝sin2x －3cos2x ＝2sin(2x －π3)，经验证函数图象关于(π6，0)对称，故选D.3．(2009·某某六市一模)已知f ′(x )是函数f (x )＝sin x 的导数，要得到y ＝f ′(2x ＋π3)的图象，只需将y ＝f (2x )的图象()A ．向左平移个π6个单位B ．向右平移5π6个单位C ．向左平移π3个单位D ．向左平移5π12个单位答案：D解析：f ′(x )＝cos x ，f ′(2x ＋π3)＝cos(2x ＋π3)＝cos2(x ＋π6)，f (2x )＝sin2x ＝cos2(x －π4)，则要得到y ＝f ′(2x ＋π3)的图象，只需将y ＝f (2x )的图象向左平移5π12个单位，故选D.4．(2007·某某)如下图，函数y ＝sin ⎝⎛⎭⎫2x －π3在区间⎣⎡⎦⎤－π2，π的简图是()答案：A解析：当x ＝0时，y ＝sin ⎝⎛⎭⎫－π3＝－32，排除B 、D. 而x ＝－π6时，y ＝sin ⎝⎛⎭⎫－2π3＝－12，排除C ，故选A. 5．(2007·某某)已知函数f (x )＝sin(ωx ＋π3)(ω>0)的最小正周期为π，则该函数的图象()A ．关于点(π3，0)对称B ．关于直线x ＝π4对称C ．关于点(π4，0)对称D ．关于直线x ＝π3对称答案：A解析：T ＝π⇒ω＝2⇒f (π3)＝sin(2π3＋π3)＝0∴f (x )关于(π3，0)对称，故选A.6．下列函数中，图象的一部分如下图所示的是()A ．y =sin(x +π6)B ．y =sin(2x -π6)C ．y =cos(4x -π3)D ．y =cos(2x -π6)答案：D解析：本题考查三角函数的图象．当x ＝π12时y ＝1由此可排除A 、B.由图可知，此函数的周期T ＝4(π12＋π6)＝π∴ω＝2ππ＝2故选D.7．要得到函数y ＝2cos x 的图象，只需将函数y ＝2sin(2x ＋π4)的图象上所有的点的()A ．横坐标缩短到原来的12倍(纵坐标不变)，再向左平行移动π8个单位长度B ．横坐标缩短到原来的12倍(纵坐标不变)，再向右平行移动π4个单位长度C ．横坐标伸长到原来的2倍(纵坐标不变)，再向左平行移动π4个单位长度D ．横坐标伸长到原来的2倍(纵坐标不变)，再向右平行移动π8个单位长度答案：C解析：y ＝2cos x ＝2sin(x ＋π2)，y ＝2sin(2x ＋π4)图象上所有点的纵坐标不变，横坐标伸长为原来的2倍，得到y ＝2sin(x ＋π4)的图象，再向左平移π4个单位得到y ＝2sin(x ＋π2)的图象．故选C.8．(2009·市东城区)已知函数f (x )＝2sin(ωx ＋π6)(ω>0)的最小正周期为4π，则该函数的图象()A ．关于点(π3，0)对称B ．关于点(5π3，0)对称C ．关于直线x ＝π3对称D ．关于直线x ＝5π3对称答案：B解析：∵函数f (x )＝2sin(ωx ＋π6)(ω>0)的最小正周期是4π，而T ＝2πω＝4π，∴ω＝12；∴f (x )＝2sin(12x ＋π6)．而f (x )＝sin x 的图象关于点(kπ，0)(k ∈Z )对称，∴12x ＋π6＝kπ⇒x ＝2kπ－π3(k ∈Z )；即函数f (x )＝2sin(12x ＋π6)的图象关于点(2kπ－π3，0)(k ∈Z )对称；又f (x )＝sin x 的图象关于直线x ＝kπ＋π2(k ∈Z )对称，∴12x ＋π6＝kπ＋π2⇒x ＝2kπ＋23π(k ∈Z )；即函数f (x )＝2sin(12x ＋π6)的图象关于直线x ＝2kπ＋23π(k ∈Z )对称，结合选项，故选B.二、填空题9．(2009·市西城区)对于函数f (x )＝sin x ，g (x )＝cos x ，h (x )＝x ＋π3，有如下四个命题：①f (x )－g (x )的最大值为2；②f [h (x )]在区间[－π2，0]上是增函数；③g [f (x )]是最小正周期为2π的周期函数；④将f (x )的图象向右平移π2个单位可得g (x )的图象．其中真命题的序号是________．答案：①②解析：f (x )－g (x )＝sin x －cos x ＝2sin(x －π4)≤2，故①正确；当x ∈[－π2，0]时，x ＋π3∈[－π6，π3]，函数f [h (x )]＝sin(x ＋π3)为增函数，故②正确；函数g [f (x )]＝cos(sin x )的最小正周期为π，故③错误；将f (x )的图象向左平移π2个单位可得g (x )的图象，故④错误．10．(2009·东城3月·12)关于函数f (x )＝sin x (cos x －sin x )＋12给出下列三个命题：(1)函数f (x )在区间[π2，5π8]上是减函数；(2)直线x ＝π8是函数f (x )的图象的一条对称轴；(3)函数f (x )的图象可以由函数y ＝22sin2x 的图象向左平移π4而得到．其中正确的正确序号是________．(将你认为正确命题序号都填上) 答案：(1)(2)解析：f (x )＝sin x (cos x －sin x )＋12＝12sin2x －12(1－cos2x )＋12＝ 22sin(2x ＋π4)．对于(1)，x ∈[π2，5π8]，2x ＋π4∈[5π4，3π2]，则函数f (x )在区间[π2，5π8]上是减函数，(1)正确；对于(2)，验证直线x＝π8是函数f (x )的图象的一条对称轴，则(2)正确；对于(3)，函数f (x )的图象可以由函数y ＝22sin2x 的图象向左平移π8而得到，则(3)不正确；故填(1)(2)．11．(2009·某某丹阳高级中学一模)给出下列四个命题，其中不正确命题的序号是________．①若cos α＝cos β，则α－β＝2kπ，k ∈Z ；②函数y ＝2cos(2x ＋π3)的图象关于x ＝π12对称；③函数y ＝cos(sin x )(x ∈R )为偶函数；④函数y ＝sin|x |是周期函数，且周期为2π.答案：①②④ 解析：对于①，若cos α＝cos β，则α－β＝2kπ或α＋β＝2kπ或k ∈Z ，①不正确；对于②，函数y ＝2cos(2x ＋π3)的图象关于点(π12，0)对称，则②不正确；对于③，经验证函数y ＝cos(sin x )(x ∈R )为偶函数，则③正确；对于④，函数y ＝sin|x |不是周期函数，则④不正确；综上所述，应填①②④.三、解答题 12．(2009·某某市二调)已知向量a ＝(sin x,23cos x )，b ＝(2sin x ，sin x )，设f (x )＝a ·b －1.(1)若x ∈[0，π2]，求f (x )的值域；(2)(理)若函数y ＝f (x )的图象按向量m ＝(t,0)作长度最短的平移后，其图象关于原点对称，求向量m 的坐标．(文)若函数y ＝f (x )的图象关于直线x ＝α(α>0)对称，求α的最小值．解：(1)f (x )＝a ·b －1＝2sin2x ＋23sin x cos x －1＝3sin2x －cos2x ＝2sin(2x －π6)．x ∈[0，π2]⇒2x －π6∈[－π6，5π6]⇒sin(2x －π6)∈[－12，1]⇒f (x )的值域y ∈[－1,2]．(2)(理)由(1)可设平移后的函数解析式为y ＝2sin[2(x ＋φ)－π6]，即y ＝2sin[2x ＋(2φ－π6)]，∵其图象关于原点对称，∴2φ－π6＝kπ，k ∈Z .即φ＝π12＋kπ2，k ∈Z .令k ＝0得所求的φ＝π12.因此所求的m ＝(－π12，0)．(文)由题设，2α－π6＝kπ＋π2(k ∈Z )，即α＝kπ2＋π3(k ∈Z )．∵α>0，∴当k ＝0时，αmin ＝π3.13．(2009·某某六市一模)已知函数f (x )＝sin(ωx ＋φ)(ω>0,0≤φ≤π)是R 上的偶函数，其图象关于点(3π4，0)对称，且在区间[0，π2]上是单调函数，求φ和ω的值．解：∵f (x )是R 上的偶函数，且0≤φ≤π，∴φ＝π2，∴f (x )＝sin(ωx ＋π2)＝cos ωx .又∵图象关于点(3π4，0)对称，∴f (3π4)＝0.即cos 3π4ω＝0，3π4ω＝kπ＋π2，k ∈Z ，∴ω＝43k ＋23，k ∈Z .又f (x )在[0，π2]上是单调函数，∴π2ω≤π，∵ω>0，∴0<ω≤2，即0<43k ＋23≤2，∴－12<k ≤1，k ∈Z .∴k ＝0或k ＝1，∴ω＝23或ω＝2.14．(2008·某某一中)已知函数f (x )＝12cos2x －sin x cos x －12sin2x .(1)求f (x )的最小正周期和函数f (x )图象的对称轴的方程； (2)求f (x )的单调增区间；(3)函数y ＝cos2x 的图象可以由函数f (x )的图象经过怎样的变换得到？解：(1)f (x )＝22cos ⎝⎛⎭⎫2x ＋π4. f (x )的最小正周期为T ＝π，函数f (x )图象的对称轴的方程为x ＝kπ2－π8(k ∈Z )．(2)f (x )的单调增区间为⎣⎡⎦⎤kπ－5π8，kπ－π8(k ∈Z )． (3)先将f (x )＝22cos ⎝⎛⎭⎫2x ＋π4的图象向右平移π8个单位，再将图象上所有点的横坐标不变纵坐标变为原来的2倍．15．已知函数f (x )＝A sin 2(ωx ＋φ)(A >0，ω>0,0<φ<π2)，且y ＝f (x )的最大值为2，其图象相邻两对称轴间的距离为2，并过点(1,2)．(1)求φ；(2)计算f (1)＋f (2)＋…＋f (2008)．解：(1)y ＝A sin2(ωx ＋φ) ＝A 2－A2cos(2ωx ＋2φ)． ∵y ＝f (x )的最大值为2，A >0， ∴A 2＋A2＝2，A ＝2. 又∵其图象相邻两对称轴间的距离为2，ω>0， ∴12×2π2ω＝2，ω＝π4. ∴f (x )＝22－22cos(π2x ＋2φ)＝1－cos(π2x ＋2φ)．∵y ＝f (x )过(1,2)点，∴cos(π2＋2φ)＝－1.∴π2＋2φ＝2kπ＋π，k ∈Z ， ∴2φ＝2kπ＋π2，k ∈Z ，∴φ＝kx ＋π4，k ∈Z .又∵0<φ<π2，∴φ＝π4.(2)解法一：∵φ＝π4，∴y ＝1－cos(π2x ＋π2)＝1＋sin π2x .∴f (1)＋f (2)＋f (3)＋f (4)＝2＋1＋0＋1＝4. 又∵y ＝f (x )的周期为4,2008＝4×502. ∴f (1)＋f (2)＋…＋f (2008)＝4×502＝2008.解法二：∵f (x )＝2sin2(π4x ＋φ)，∴f (1)＋f (3)＝2sin2(π4＋φ)＋2sin2(3π4＋φ)＝2，f (2)＋f (4)＝2sin2(π2＋φ)＋2sin2(π＋φ)＝2，∴f (1)＋f (2)＋f (3)＋f (4)＝4. 又y ＝f (x )的周期为4,2008＝4×502. ∴f (1)＋f (2)＋…＋f (2008)＝4×502＝2008.。

高三数学三角函数的图象和性质(1)

2. 由图象求解析式时,”第一零点”的确定很重要,尽量使A取正值. 3. 由图象求解析式 y A sin(x ) k 或由代数条件确定解析式时,应注意:
1 (1) 振幅 A= ( y max y min ) 2
2
(2) 相邻两个最值对应的横坐标之差,或一个单 1 调区间的长度为 T ,由此推出的值. 3)确定值,一般用给定特殊点坐标代入解析式来确定.
热点题型4 (备选) 对数函数与三角函数复合而成的复合函数的性质
例4 已知函数 f ( x) log1 (sin x cos x) ，（ 1 ）求它的定义域和值域；（ 2 ）求它的单调区间；（3）判断它的奇偶性；（4）判断它的周期性，如果是周期函数，求出它的最小正周期。
2
； / 项目运营及偿债能力综合评级报告
(|m|< 2 )平移后得到函数y=f(x)的图象，求实数 m、n的值.

b 例2．设函数f(x)=a ·
a
启示：向量的平移与图象的左右上下的平移有紧密的联系.如沿向量 a =( 3,2) 平移,实质上就是右移3个单位,下移2个单位. 变式2：已知向量 a = ( 3 ，2) ，向量 2 sin 2 x , cos x) , ( 0) = ( b
y
- - 2
1 o -1
2
3 2 2 5 2
y
7 3 2
4
x
y
y=tanx
y=cotx
3 2
-
-
2
o
2

3 2
x
-
-
2
o
2

3 2
2
x
2 三角函数与其他知识相结合的综合题目，此类题目要求考生具有较强的分析能力和逻辑思维能力在今后的命题趋势中综合性题型仍会成为热点和重点，并可以逐渐加强

2011年高考试题分类考点13 三角函数的图象与性质

考点13 三角函数的图象与性质一、选择题1.（2011·安徽高考理科·Ｔ9）已知函数()sin(2)f x x ϕ=+，其中ϕ为实数，若()()6f x f π≤对x R∈恒成立，且()()2f f ππ>，则()f x 的单调递增区间是( )（A ）,()36k k k Z ππππ⎡⎤-+∈⎢⎥⎣⎦ （B ）,()2k k k Z πππ⎡⎤+∈⎢⎥⎣⎦ （C ）2,()63k k k Z ππππ⎡⎤++∈⎢⎥⎣⎦ （D ）,()2k k k Z πππ⎡⎤-∈⎢⎥⎣⎦【思路点拨】由()()6f x f π≤对x R ∈恒成立，知)(x f 在6π=x 处取得最大值或最小值，从而得到ϕ的两组取值，再利用()()2f f ππ>排除一组，从而得到ϕ的取值,利用整体代换思想求出()f x 的单调递增区间.【精讲精析】选C. 由()()6f x f π≤对x R ∈恒成立知，2262ππϕπ±=+⨯k ()∈k Z ，得到65-262ππϕππϕk k =+=或，代入)(x f 并由()()2f f ππ>检验得，ϕ的取值为65-π，所以2265222πππππ+≤-≤-k x k ，计算得单调递增区间是2,()63k k k Z ππππ⎡⎤++∈⎢⎥⎣⎦. 2.（2011·新课标全国高考理科·Ｔ11）设函数()sin()cos()(0,)2f x x x πωϕωϕωϕ=+++><的最小正周期为π，且()()f x f x -=，则( )（A ）()f x 在0,2π⎛⎫ ⎪⎝⎭单调递减（B ）()f x 在3,44ππ⎛⎫⎪⎝⎭单调递减（C ）()f x 在0,2π⎛⎫⎪⎝⎭单调递增（D ）()f x 在3,44ππ⎛⎫⎪⎝⎭单调递增【思路点拨】先将()f x 化为()+)4f x x πωϕ=+，然后根据已知条件确定ω和ϕ的值，最后求单调区间.【精讲精析】选A.()sin()cos()f x x x ωϕωϕ=+++ +)4x πωϕ+，又 ()f x 的最小正周期为π，∴2ππω=，即2ω=，又()()f x f x -=，这说明()f x 是偶函数，即4πϕ+为2π的奇数倍才行，考虑到||2πϕ<，所以ϕ取4π，从而()2f x x =，容易确定其在(0,)2π上单调递减.3.（2011·新课标全国高考文科·Ｔ11）设函数()sin(2)cos(2)44f x x x ππ=+++，则( )（A ）()y f x =在0,2π⎛⎫⎪⎝⎭内单调递增，其图象关于直线4x π=对称（B ）()y f x =在0,2π⎛⎫⎪⎝⎭内单调递增，其图象关于直线2x π=对称（C ）()y f x =在0,2π⎛⎫⎪⎝⎭内单调递减，其图象关于直线4x π=对称（D ）()y f x =在0,2π⎛⎫⎪⎝⎭内单调递减，其图象关于直线2x π=对称【思路点拨】()f x sin(2)cos 2)44x x ππ=+++（)44x ππ=++，然后求函数()f x 的单调递增区间和对称轴.【精讲精析】选D. ()f x sin(2)cos 2)44x x ππ=+++（)44x ππ=++2x =，∴()f x 在0,2π⎛⎫⎪⎝⎭内单调递减，且图象关于2x π=对称.二、填空题4.（2011·安徽高考文科·Ｔ15）设()sin 2cos 2f x a x b x =+，其中,,0a b R ab ∈≠，若()()6f x f π≤对一切x R ∈恒成立，则①11()012f π= ②7()10f π＜()5f π③()f x 既不是奇函数也不是偶函数④()f x 的单调递增区间是2,()63k k k z ππππ⎡⎤++∈⎢⎥⎣⎦⑤存在经过点（a,b ）的直线与函数()f x 的图象不相交.以上结论正确的是 _____________________________(写出正确结论的编号). 【思路点拨】先将()sin 2cos2,,,0f x a x b x a b R ab =+∈≠’变形为)2sin()(22ϕ++=x b a x f ，再由()6f x f π≤f ()π对一切x R ∈恒成立得a,b 之间关系，然后顺次判断命题真假.【精讲精析】),2sin(2cos 2sin )(22ϕ++=+=x b a x b x a x f由()()6f x f π≤对一切x R ∈恒成立知22)6(b a f +=π，求得03>=b a 。

2011届高考数学三角函数

三角函数必修4 第1章三角函数§1.1任意角的概念、弧度制重难点：理解任意角的概念，掌握角的概念的推广方法,能在直角坐标系讨论任意角，判断象限角、轴线角，掌握终边相同角的集合．掌握弧长公式、扇形面积公式并能灵活运用．考纲要求：①了解任意角的概念．②了解弧度制概念，能进行弧度与角度的互化．经典例题：写出与下列各角终边相同的角的集合S，并把S中适合不等式-3600≤β<7200的元素β写出来：（1）600；（2）-210；（3），当堂练习：1．已知A={第一象限角}，B={锐角}，C={小于90°的角}，那么A、B、C关系是（）A．B=A∩C B．B∪C=C C．A C D．A=B=C2 下列各组角中，终边相同的角是（）A．与B．C．D．3．已知弧度数为2的圆心角所对的弦长也是2，则这个圆心角所对的弧长是（）A．2 B．C．D．4．设角的终边上一点P的坐标是，则等于（）A．B．C．D．5．将分针拨慢10分钟，则分钟转过的弧度数是（）A．B．－C．D．－6．设角和的终边关于轴对称，则有（）A．B．C．D．7．集合A={ ，B={ ，则A、B之间关系为（）A．B．C．B A D．A B8．某扇形的面积为1 ，它的周长为4 ，那么该扇形圆心角的度数为（）A．2°B．2 C．4°D．49．下列说法正确的是（）A．1弧度角的大小与圆的半径无关B．大圆中1弧度角比小圆中1弧度角大C．圆心角为1弧度的扇形的弧长都相等D．用弧度表示的角都是正角10．中心角为60°的扇形，它的弧长为2 ，则它的内切圆半径为（）A．2 B．C．1 D．11．一个半径为R的扇形，它的周长为4R，则这个扇形所含弓形的面积为（）A．B．C．D．12．若角的终边落在第三或第四象限，则的终边落在（）A．第一或第三象限B．第二或第四象限C．第一或第四象限D．第三或第四象限13．，且是第二象限角，则是第象限角.14．已知的取值范围是.15．已知是第二象限角，且则的范围是.16．已知扇形的半径为R，所对圆心角为，该扇形的周长为定值c，则该扇形最大面积为.17．写出角的终边在下图中阴影区域内角的集合（这括边界）（1）（2）（318．一个视力正常的人，欲看清一定距离的文字，其视角不得小于5′.试问：（1）离人10米处能阅读的方形文字的大小如何？（2）欲看清长、宽约0.4米的方形文字，人离开字牌的最大距离为多少？19．一扇形周长为20cm，当扇形的圆心角等于多少弧度时，这个扇形的面积最大？并求此扇形的最大面积？20．绳子绕在半径为50cm的轮圈上，绳子的下端B处悬挂着物体W，如果轮子按逆时针方向每分钟匀速旋转4圈，那么需要多少秒钟才能把物体W的位置向上提升100cm? 21．已知集合A={求与A∩B中角终边相同角的集合S.必修4 第1章三角函数考纲总要求：①理解任意角三角函数（正弦、余弦、正切）的定义．②能利用单位圆中的三角函数线推导出，的正弦、余弦、正切的诱导公式，能画出，，的图像，了解三角函数的周期性．③理解正弦函数、余弦函数在区间的性质（单调性、最大和最小值与轴交点等），理解正切函数在区间的单调性．④理解同角三角函数的基本关系式．⑤了解函数的物理意义；能画出的图像，了解参数对函数图像变化的影响．⑥了解三角函数是描述周期变化现象的重要函数模型，会用三角函数解决一些简单实际问题．§1.2.1-2任意角的三角函数值、同角三角函数的关系重难点：任意角的正弦、余弦、正切的定义（包括这三种三角函数的定义域和函数值在各象限的符号），以及这三种函数的第一组诱导公式；能利用与单位圆有关的有向线段，将任意角α的正弦、余弦、正切函数值分别用他们的集合形式表示出来；掌握同角三角函数的基本关系式，三角函数值的符号的确定，同角三角函数的基本关系式的变式应用以及对三角式进行化简和证明．经典例题：已知为第三象限角，问是否存在这样的实数m，使得、是关于的方程的两个根，若存在，求出实数m，若不存在，请说明理由.当堂练习：1．已知的正弦线与余弦线相等，且符号相同，那么的值为（）A．B．C．D．2．若为第二象限角，那么的值为（）A．正值B．负值C．零D．为能确定3．已知的值为（）A．－2 B．2 C．D．－4．函数的值域是（）A．{－1，1，3} B．{－1，1，－3} C．{－1，3} D．{－3，1}5．已知锐角终边上一点的坐标为（则=（）A．B．3 C．3－D．－36．已知角的终边在函数的图象上，则的值为（）A．B．－C．或－D．7．若那么2 的终边所在象限为（）A．第一象限B．第二象限C．第三象限D．第四象限8．、、的大小关系为（）A．B．C．D．9．已知是三角形的一个内角，且，那么这个三角形的形状为（）一切为了学生的发展一切为了家长的心愿A．锐角三角形B．钝角三角形C．不等腰的直角三角形D．等腰直角三角形10．若是第一象限角，则中能确定为正值的有（）A．0个B．1个C．2个D．2个以上11．化简（是第三象限角）的值等于（）A．0 B．－1 C．2 D．－212．已知，那么的值为（）A．B．－C．或－D．以上全错13．已知则.14．函数的定义域是_________.15．已知，则=______.16．化简.17．已知求证：.18．若,求角的取值范围.19．角的终边上的点P和点A（）关于轴对称（）角的终边上的点Q与A关于直线对称. 求的值.20．已知是恒等式. 求a、b、c的值.21．已知、是方程的两根，且、终边互相垂直. 求的值.必修4 第1章三角函数§1.2.3三角函数的诱导公式重难点：能借助于单位圆，推导出正弦、余弦的诱导公式；能正确运用诱导公式将任意角的三角函数化为锐角的三角函数，并解决求值、化简和恒等式证明问题；能通过公式的运用，了解未知到已知、复杂到简单的转化过程．经典例题：已知数列的通项公式为记求当堂练习：1．若那么的值为（）A．0 B．1 C．－1 D．2．已知那么（）一切为了学生的发展一切为了家长的心愿A．B．C．D．3．已知函数，满足则的值为（）A．5 B．－5 C．6 D．－64．设角的值等于（）A．B．－C．D．－5．在△ABC中，若，则△ABC必是（）A．等腰三角形B．直角三角形C．等腰或直角三角形D．等腰直角三角形6．当时，的值为（）A．－1 B．1 C．±1 D．与取值有关7．设为常数），且那么（）A．1 B．3 C．5 D．78．如果则的取值范围是（）A．B．C．D．9．在△ABC中，下列各表达式中为常数的是（）A．B．C．D．10．下列不等式上正确的是（）A．B．C．D．11．设那么的值为（）A．B．－C．D．12．若，则的取值集合为（）A．B．C．D．13．已知则.14．已知则.15．若则.16．设，其中m、n、、都是非零实数，若则.17．设和求的值.18．已知求证：19．已知、是关于的方程的两实根，且求的值.20．已知（1）求的表达式；（2）求的值.21．设满足,（1）求的表达式；（2）求的最大值．一切为了学生的发展一切为了家长的心愿必修4 第1章三角函数§1.3.1-2三角函数的周期性、三角函数的图象和性质重难点：理解周期函数的概念．能利用单位圆中的正弦线作正弦函数的图象；对正、余弦函数奇、偶性和单调性的理解与应用，能灵活应用正切函数的性质解决相关问题．经典例题：设（1）令表示P；（2）求t的取值范围，并分别求出P的最大值、最小值.当堂练习：1．若，则（）A．α<βB．α>βC．α+β>3πD．α+β<2π2．函数的单调减区间为（）A．B．C．D．3．已知有意义的角x等于（）A．B．C．D．4．函数的图象的一条对称轴方程是（）A．B．C．D．5．直线y=a（a为常数）与y=tanωx（ω>0）的相邻两支的交点距离为（）A．πB．C．D．与a有关的值6．下列函数中，以π为周期的偶函数是（）A．B．C．D．7．在区间（－，）内，函数y=tanx与函数y=sinx图象交点的个数为（）A．1 B．2 C．3 D．48．下列四个函数中为周期函数的是（）A．y=3 B．C．D．9．在△ABC中，A>B是tanA>tanB的（）A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件10．函数的定义域是（）A．B．C．D．11．方程的解集为（）A．B．C．D．12．函数上为减函数，则函数上（）A．可以取得最大值M B．是减函数C．是增函数D．可以取得最小值－M13．.14．若= .15．函数y=2arccos（x－2）的反函数是. 16．函数的定义域为.17．求函数上的反函数.18．如图，某地一天从6时到11时的温度变化曲线近似满足函数(1) 求这段时间最大温差；(2) 写出这段曲线的函数解析式．19．若，求函数的最值及相应的x值.20．已知函数的最大值为1，最小值为－3，试确定的单调区间.一切为了学生的发展一切为了家长的心愿21．设函数当在任意两个连续整数间（包括整数本身）变化时至少有两次失去意义，求k 的最小正整数值.必修4 第1章三角函数§1.3.3函数的图象和性质重难点：函数的图像的画法和设图像与函数y=sinx图像的关系，以及对各种变换内在联系的揭示．经典例题：如图，表示电流强度I与时间t的关系式在一个周期内的图象.（１）试根据图象写出的解析式；（２）为了使中t在任意一段秒的时间内I能同时取最大值|A|和最小值－|A|，那么正整数的最小值为多少？当堂练习：1．函数的图象（）A．关于原点对称B．关于点（－，0）对称C．关于y轴对称D．关于直线x= 对称2．要得到的图象只需将y=3sin2x的图象（）A．向左平移个单位B．向右平移个单位C．向左平移个单位D．向右平移个单位3．如图，曲线对应的函数是（）A．y=|sinx|B．y=sin|x|C．y=－sin|x|D．y=－|sinx|4．已知f(1+cosx)=cos2x,则f(x)的图象是下图中的（）5．如果函数y=sin2x+αcos2x的图象关于直线x=－对称，那么α的值为（）A．B．－C．1 D．－16．已知函数在同一周期内，时取得最大值，时取得最小值－，则该函数解析式为（）A．B．C．D．7．方程的解的个数为（）A．0 B．无数个C．不超过3 D．大于38．已知函数那么函数y=y1+y2振幅的值为（）A．5 B．7 C．13 D．9．已知的图象可以看做是把的图象上所有点的横坐标压缩到原来的1/3倍（纵坐标不变）得到的，则= （）A．B．2 C．3 D．10．函数y=－x•cosx的部分图象是（）11．函数的单调减区间是（）A．B．C．D．一切为了学生的发展一切为了家长的心愿12．函数的最小正周期为（）A．πB．C．2πD．4π13．若函数的周期在内，则k的一切可取的正整数值是. 14．函数的最小值是．15．振动量的初相和频率分别为，则它的相位是．16．函数的最大值为．17．已知函数（１）求的最小正周期;（２）求的单调区间;（３）求图象的对称轴，对称中心.18．函数的最小值为－2,其图象相邻的最高点与最低点横坐标差是3π，又图象过点（0，1）求这个函数的解析式.19．已知函数=sin2x+acos2x在下列条件下分别求a的值.（１）函数图象关于原点对称;（２）函数图象关于对称.20．已知函数的定义域为，值域为[－5，1]求常数a、b的值．21．已知α、β为关于x的二次方程的实根，且，求θ的范围．必修4 第1章三角函数§1.3.4三角函数的应用重难点：掌握三角函数模型应用基本步骤:(1)根据图象建立解析式; (2)根据解析式作出图象;(3)将实际问题抽象为与三角函数有关的简单函数模型；利用收集到的数据作出散点图，并根据散点图进行函数拟合，从而得到函数模型．经典例题：已知某海滨浴场的海浪高度是时间( ,单位:小时)的函数,记作.下表是某日各时的浪高数据:经长期观察, 的曲线可近似地看成是函数的图象.(1)根据以上数据,求出函数的最小正周期,振幅及函数表达式;(2)依据规定,当海浪高度高于时才对冲浪爱好者开放,请依据(1)的结论,判断一天内的上午到晚上之间,有多少时间可供冲浪者进行活动?当堂练习：1.若A、B是锐角△ABC的两个内角,则点P(cosB-sinA,sinB-cosA)在( )A.第一象限B.第二象限C.第三象限D.第四象限2.(2004北京西城一模)设0＜|α|＜,则下列不等式中一定成立的是( )A.sin2α＞sinαB.cos2α＜cosαC.tan2α＞tanαD.cot2α＜cotα3.已知实数x、y、m、n满足m2+n2=a,x2+y2=b(a≠b),则mx+ny的最大值为( )A. B. C. D.4. 初速度v0，发射角为，则炮弹上升的高度y与v0之间的关系式为（）A. B. C. D.5. 当两人提重为的书包时，夹角为，用力为，则为____时，最小（）A． B. C. D.6.某人向正东方向走x千米后向右转，然后朝新的方向走3千米，结果他离出发点恰好千米，那么x的值为（）A． B. C. D.7. 甲、乙两楼相距60米，从乙楼底望甲楼顶仰角为，从甲楼顶望乙楼顶俯角为，则甲、乙两楼的高度分别为____________________.8.一树干被台风吹断折成角，树干底部与树尖着地处相距20米，树干原来的高度是________.9.(2006北京海淀模拟)在△ABC中,∠A=60°,BC=2,则△ABC的面积的最大值为_________.10.在高出地面30 m的小山顶上建造一座电视塔CD(如右图),今在距离B点60 m的地面上取一切为了学生的发展一切为了家长的心愿一点A,若测得C、D所张的角为45°,则这个电视塔的高度为_______________.11.已知函数的最小正周期为,最小值为,图象经过点,求该函数的解析式.12．如图，某地一天从时到时的温度变化曲线近似满足函数,(I)求这段时间的最大温差;(II)写出这段曲线的函数解析式.13.若x满足,为使满足条件的的值(1)存在;(2)有且只有一个;(3)有两个不同的值;(4)有三个不同的值,分别求的取值范围.14.如图,化工厂的主控制表盘高1米,表盘底边距地面2米,问值班人员坐在什么位置上表盘看得最清楚?(设值班人员坐在椅子上时,眼睛距地面1.2米)必修4 第1章三角函数§1.4三角函数单元测试1. 化简等于（）A. B. C. 3 D. 12. 在ABCD中，设, ，, ,则下列等式中不正确的是（）A．B．C．D．3. 在中，①sin(A+B)+sinC；②cos(B+C)+cosA；③；④，其中恒为定值的是（）A、①②B、②③C、②④D、③④4. 已知函数f(x)=sin(x+ )，g(x)=cos(x－)，则下列结论中正确的是（）A．函数y=f(x)•g(x)的最小正周期为2B．函数y=f(x)•g(x)的最大值为1C．将函数y=f(x)的图象向左平移单位后得g(x)的图象D．将函数y=f(x)的图象向右平移单位后得g(x)的图象5. 下列函数中，最小正周期为，且图象关于直线对称的是（）A．B．C．D．6. 函数的值域是（）A、B、C、D、7. 设则有（）A． B. C. D.8. 已知sin , 是第二象限的角，且tan( )=1,则tan 的值为（）A．－7 B．7 C．－D．9. 定义在R上的函数既是偶函数又是周期函数，若的最小正周期是，且当时，，则的值为（）一切为了学生的发展一切为了家长的心愿A. B C D10. 函数的周期是（）A．B．C．D．11. 2002年8月，在北京召开的国际数学家大会会标如图所示，它是由4个相同的直角三角形与中间的小正方形拼成的一大正方形，若直角三角形中较小的锐角为，大正方形的面积是1，小正方形的面积是的值等于（）A．1 B．C．D．12. 使函数f(x)=sin(2x+ )+ 是奇函数，且在[0，上是减函数的的一（）A．B．C．D．13、函数的最大值是3，则它的最小值______________________14、若，则、的关系是____________________15、若函数f(χ)是偶函数，且当χ＜0时，有f(χ)=cos3χ+sin2χ，则当χ＞0时，f(χ)的表达式为.16、给出下列命题：(1)存在实数x，使sinx+cosx＝; (2)若是锐角△的内角，则> ; (3)函数y＝sin( x- )是偶函数；(4)函数y＝sin2x的图象向右平移个单位，得到y＝sin(2x+ )的图象.其中正确的命题的序号是.17、求值:18、已知π2 <α<π,0<β<π2 ,tanα=－34 ,cos(β－α)= 513 ,求sinβ的值.19、已知函数（1）求它的定义域、值域以及在什么区间上是增函数；（2）判断它的奇偶性；（3）判断它的周期性。

2011高考数学真题考点分类新编考点13三角函数的图象与性质(新课标地区)

考点13三角函数的图象与性质一、选择题1.（2011·安徽高考理科·Ｔ9）已知函数()sin(2)f x x ϕ=+，其中ϕ为实数，若()()6f x f π≤对x R ∈恒成立，且()()2f f ππ>，则()f x 的单调递增区间是（A ）,()36k k k Z ππππ⎡⎤-+∈⎢⎥⎣⎦（B ）,()2k k k Z πππ⎡⎤+∈⎢⎥⎣⎦（C ）2,()63k k k Z ππππ⎡⎤++∈⎢⎥⎣⎦ （D ）,()2k k k Z πππ⎡⎤-∈⎢⎥⎣⎦【思路点拨】由()()6f x f π≤对x R ∈恒成立知)(x f 在6π=x 处取得最大值或最小值，从而得到ϕ的两组取值，再利用()()2f f ππ>排除一组，从而得到ϕ的取值,利用整体代换思想求出()f x 的单调递增区间.【精讲精析】选C. 由()()6f x f π≤对x R ∈恒成立知，2262ππϕπ±=+⨯k ()K Z ∈，得到65-262ππϕππϕk k =+=或，代入)(x f 并由()()2f f ππ>检验得，ϕ的取值为65-π，所以2265222πππππ+≤-≤-k x k ，计算得单调递增区间是2,()63k k k Z ππππ⎡⎤++∈⎢⎥⎣⎦. 2.（2011·新课标全国高考理科·Ｔ11）设函数()sin()cos()(0,)2f x x x πωϕωϕωϕ=+++><的最小正周期为π，且()()f x f x -=，则A.()f x 在0,2π⎛⎫ ⎪⎝⎭单调递减 B.()f x 在3,44ππ⎛⎫⎪⎝⎭单调递减C.()f x 在0,2π⎛⎫⎪⎝⎭单调递增D.()f x 在3,44ππ⎛⎫⎪⎝⎭单调递增【思路点拨】先将()f x 化为()+)4f x x πωϕ=+，然后根据已知条件确定ω和ϕ的值，最后求单调减区间.【精讲精析】选A ()sin()cos()f x x x ωϕωϕ=++++)4x πωϕ+，又()f x 的最小正周期为π，∴2ππω=，即2ω=，又()()f x f x -=，这说明()f x 是偶函数，即4πϕ+为2π的奇数倍才行，考虑到||2πϕ<，所以ϕ取4π，从而()f x x =，容易确定其在(0,)2π上单调递减.3.（2011·新课标全国高考文科·Ｔ11）设函数()sin(2)cos(2)44f x x x ππ=+++，则( )A. ()y f x =在0,2π⎛⎫⎪⎝⎭单调递增，其图像关于直线4x π=对称 B ．()y f x =在0,2π⎛⎫⎪⎝⎭单调递增，其图像关于直线2x π=对称 C ．()y f x =在0,2π⎛⎫⎪⎝⎭单调递减，其图像关于直线4x π=对称 D ．()y f x =在0,2π⎛⎫⎪⎝⎭单调递减，其图像关于直线2x π=对称【思路点拨】()f x sin(2)cos2)44x x ππ=+++（)44x ππ=++，然后求函数 ()f x 的单调递增区间和对称轴方程.【精讲精析】选D()f x sin(2)cos2)44x x ππ=+++（)44x ππ=++2x =，∴()f x 在0,2π⎛⎫⎪⎝⎭内单调递减，且图像关于2x π=对称.二、填空题4.（2011·安徽高考文科·Ｔ15）设()sin 2cos 2f x a x b x =+，其中,,0a b R ab ∈≠，若()()6f x f π≤对一切x R ∈恒成立，则①11()012f π= ②7()10f π＜()5f π③()f x 既不是奇函数也不是偶函数 ④()f x 的单调递增区间是2,()63k k k z ππππ⎡⎤++∈⎢⎥⎣⎦⑤存在经过点（a,b ）的直线与函数()f x 的图象不相交.以上结论正确的是 _____________________________(写出正确结论的编号).【思路点拨】先将()sin 2cos 2,,,0f x a x b x a b R ab =+∈≠’变形为)2sin()(22ϕ++=x b a x f ，再由()6f x fπ≤对一切x R ∈恒成立得a,b 之间关系，然后顺次判断命题真假.【精讲精析】答案:①③.),2sin(2cos 2sin )(22ϕ++=+=x b a x b x a x f由()()6f x f π≤对一切x R ∈恒成立知22)6(b a f +=π，求得03>=b a 。

2011届山东新课标高考数学权威预测三角函数的图象与性质

2011届山东新课标高考数学权威预测：三角函数的图象与性质一．【课标要求】1．能画出y =sin x , y =c os x , y =t a n x 的图像，了解三角函数的周期性；2．借助图像理解正弦函数、余弦函数在[0，2π]，正切函数在（－π/2，π/2）上的性质（如单调性、最大和最小值、图像与x 轴交点等）；3．结合具体实例，了解y =A sin （w x +φ）的实际意义；能借助计算器或计算机画出y =A sin （w x +φ）的图像，观察参数A ，w ，φ对函数图像变化的影响二．【命题走向】近几年高考降低了对三角变换的考查要求，而加强了对三角函数的图象与性质的考查，因为函数的性质是研究函数的一个重要内容，是学习高等数学和应用技术学科的基础，又是解决生产实际问题的工具，因此三角函数的性质是本章复习的重点。

在复习时要充分运用数形结合的思想，把图象与性质结合起来，即利用图象的直观性得出函数的性质，或由单位圆上线段表示的三角函数值来获得函数的性质，同时也要能利用函数的性质来描绘函数的图象，这样既有利于掌握函数的图象与性质，又能熟练地运用数形结合的思想方法预测2011年高考对本讲内容的考察为： 1．题型为1道选择题（求值或图象变换），1道解答题（求值或图像变换）；2．热点问题是三角函数的图象和性质，特别是y =A sin （w x +φ）的图象及其变换；三．【要点精讲】1．正弦函数、余弦函数、正切函数的图像2．三角函数的单调区间：x y sin =的递增区间是⎥⎦⎤⎢⎣⎡+-2222ππππk k ，)(Z k ∈，递减区间是⎥⎦⎤⎢⎣⎡++23222ππππk k ，)(Z k ∈；x y cos =的递增区间是[]πππk k 22，-)(Z k ∈，递减区间是[]πππ+k k 22，)(Z k ∈， x y tan =的递增区间是⎪⎭⎫ ⎝⎛+-22ππππk k ，)(Z k ∈，3．函数B x A y ++=)sin(ϕω），（其中00>>ωA最大值是B A +，最小值是A B -，周期是ωπ2=T ，频率是πω2=f ，相位是ϕω+x ，初相是ϕ；其图象的对称轴是直线)(2Z k k x ∈+=+ππϕω，凡是该图象与直线B y =的交点都是该图象的对称中心4．由y ＝sin x 的图象变换出y ＝sin(ωx ＋ϕ)的图象一般有两个途径，只有区别开这两个途径，才能灵活进行图象变换。

2011届高考数学三角函数的图象与性质6

学案9 三角函数的图象与性质（1）【课前预习,听课有针对性】（5m ）1.用“五点法”作出函数sinx y =在cosx y =][0,2π内的图像。

2.用“五点法”作出函数sinx y =、)6-sin(x y π=、sin2x y =及2sinx y =的图像。

3．用“五点法”作出函数sinx y =及1)6-x 21sin(y +=π的图像。

【及时巩固,牢固掌握知识】（20——30m ）A 组夯实基础，运用知识4.将函数5sin(3)y x =-的周期扩大到原来的2倍，再将函数图象左移3π，得到图象对应解析式是（ A ）()A 335sin()22x y π=- ()B 735sin()102x y π=- ()C 5sin(6)6y x π=- ()D 35cos 2xy =5.若函数()f x 图象上每一个点的纵坐标保持不变，横坐标伸长到原来的两倍，然后再将整个图象沿x 轴向右平移2π个单位，向下平移3个单位，恰好得到1sin 2y x =的图象，则()f x =11sin(2)3cos 23222x x π++=+．6.（2010全国卷2理数7）为了得到函数sin(2)3y x π=-的图像，只需把函数sin(2)6y x π=+的图像( B )A.向左平移4π个长度单位 B.向右平移4π个长度单位 C.向左平移2π个长度单位 D.向右平移2π个长度单位【命题意图】本试题主要考查三角函数图像的平移. 【解析】sin(2)6y x π=+=sin 2()12x π+，sin(2)3y x π=-=sin 2()6x π=-，所以将sin(2)6y x π=+的图像向右平移4π个长度单位得到sin(2)3y x π=-的图像，故选B.7. （2010重庆理数6）已知函数)20,( )x sin(y πϕωϕω<>+=的部分图象如题（6）图所示，则( D )A. ω=1,ϕ=6π B.ω=1,ϕ=- 6πC.ω=2,ϕ=6πD.ω=2,ϕ=-6π解析：2=∴=ϖπT 由五点作图法知232πϕπ=+⨯，ϕ=-6π8.（2010天津文数8）5y Asin x x R 66ππωϕ⎡⎤=∈⎢⎥⎣⎦右图是函数（+）（）在区间-，上的图象，为了得到这个函数的图象，只要将y sin x x R =∈（）的图象上所有的点( A ) A.向左平移3π个单位长度，再把所得各点的横坐标缩短到原来的12倍，纵坐标不变 B.向左平移3π个单位长度，再把所得各点的横坐标伸长到原来的2倍，纵坐标不变C.向左平移6π个单位长度，再把所得各点的横坐标缩短到原来的12倍，纵坐标不变D.向左平移6π个单位长度，再把所得各点的横坐标伸长到原来的2倍，纵坐标不变【解析】本题主要考查三角函数的图像与图像变换的基础知识，属于中等题。