高考数学一轮复习模拟试题集
2023年新高考数学一轮复习4-4 导数的综合应用(真题测试)含详解

专题4.4 导数的综合应用(真题测试)一、单选题1.(2017·全国·高考真题(理))已知函数211()2()x x f x x x a e e --+=-++有唯一零点,则=a ( ) A .12-B .13C .12D .12.(2015·陕西·高考真题(理))对二次函数(为非零整数),四位同学分别给出下列结论,其中有且仅有一个结 论是错误的,则错误的结论是 A .是的零点 B .1是的极值点 C .3是的极值D .点在曲线上3.(2022·青海·海东市第一中学模拟预测(理))已知函数()2e 2xx f x a x =-+,若有且仅有两个正整数,使得()0f x <成立,则实数a 的取值范围是( ) A .211,3e e ⎡⎫⎪⎢⎣⎭B .3291,5e e ⎡⎫⎪⎢⎣⎭C .391,5e 3e ⎡⎫⎪⎢⎣⎭D .212,2e e ⎡⎫⎪⎢⎣⎭4.(2014·全国·高考真题(文))已知函数,若存在唯一的零点,且,则的取值范围是( ) A .B .C .D .5.(2022·青海·海东市第一中学模拟预测(理))若函数()()22e e x x f x x ax a a R =+-∈有三个不同的零点,则实数a 的取值范围是( ) A .1,e ⎛⎫+∞ ⎪⎝⎭B .1,1e ⎛⎫ ⎪⎝⎭C .2110,,1e e e ⎛⎫⎛⎫⋃ ⎪ ⎪-⎝⎭⎝⎭D .210,e e ⎛⎫ ⎪-⎝⎭6.(2022·河南·开封市东信学校模拟预测(理))对任意0x >,不等式e ln()(1)0x ax a x -+-≥恒成立,则正数a 的最大值为( ) ABC .1eD .e7.(2015·全国·高考真题(理))设函数()(21)xf x e x ax a =--+,其中1a < ,若存在唯一的整数0x ,使得2()f x ax bx c =++a 1-()f x ()f x ()f x (2,8)()y f x =32()31f x ax x =-+()f x 0x 00x >a ()2,+∞()1,+∞(),2-∞-(),1-∞-0()0f x <,则a 的取值范围是( )A .3,12e ⎡⎫-⎪⎢⎣⎭B .33,2e 4⎡⎫-⎪⎢⎣⎭ C .33,2e 4⎡⎫⎪⎢⎣⎭ D .3,12e ⎡⎫⎪⎢⎣⎭8.(2022·内蒙古·海拉尔第二中学模拟预测(理))已知函数()()e ln e (0)xf x a a a =+>,若对任意实数1x >,不等式()()ln 1f x x ≥-总成立,则实数a 的取值范围为( ) A .210,e ⎛⎫ ⎪⎝⎭B .221,e e ⎛⎤⎥⎝⎦C .21,e ⎛⎫+∞ ⎪⎝⎭D .21,e ⎡⎫+∞⎪⎢⎣⎭二、多选题9.(2022·辽宁实验中学模拟预测)我们把形如(),,0f x y y '=的方程称为微分方程,符合方程的函数()y f x =称为微分方程的解,下列函数为微分方程0xy y xy +-'=的解的是( ) A .e x y = B .e x y x =C .e 1x y x =+D .e (R)x y c x c =⋅∈⋅10.(2022·河北沧州·二模)已知实数,a b 满足e e e a b a b ++=,则( ) A .0ab < B .1a b +> C .e e 4a b +D .e 1a b >11.(2022·湖南·模拟预测)已知1x >,1y >,且()()1e 11e y xx y ++=+,则下列结论一定正确的是( )A .()ln 0x y ->B .122x y +<C .226x y +>D .()ln ln3x y +<12.(2022·全国·高考真题)已知函数,则( )A .有两个极值点B .有三个零点C .点是曲线的对称中心D .直线是曲线的切线三、填空题13.(2020·河南高三其他(理))函数()2222ln x f x x e x ax =--,若0a =,则()f x 在[]1,2的最小值为_______;当0x >时,()1f x ≥恒成立,则a 的取值范围是_____. 14.(2022·全国·模拟预测(理))若曲线ln x y x =与212y kx =-仅有1个公共点,则k 的取值范围是3()1f x x x =-+()f x ()f x (0,1)()y f x =2y x =()y f x =___________.15.(2012·福建·高考真题(理))对于实数a 和b ,定义运算“*”: 设f (x )=(2x -1)*(x -1),且关于x 的方程为f (x )=m (m ∈R )恰有三个互不相等的实数根x 1,x 2,x 3,则x 1x 2x 3的取值范围是_________________16.(2022·江苏·常州高级中学模拟预测)已知函数22()ln 2e f x x x mx =-+,若()0f x ≥的解集中恰有一个整数,则m 的取值范围为________. 四、解答题17.(2018·全国·高考真题(文))已知函数.(1)求曲线在点处的切线方程; (2)证明:当时,.18.(2017·全国·高考真题(理))已知函数(1)讨论的单调性;(2)若有两个零点,求的取值范围.19.(2017·全国·高考真题(文))已知函数.(1)讨论的单调性; (2)当时,证明. 20.(2016·全国·高考真题(文))设函数. (Ⅰ)讨论的单调性; (Ⅱ)证明当时,; (Ⅲ)设,证明当时,.21.(2015·全国·高考真题(理))设函数.(1)证明:在单调递减,在单调递增;(2)若对于任意,都有,求m 的取值范围.22.(2014·四川·高考真题(理))已知函数,其中,为自然对数的底数.(Ⅰ)设是函数的导函数,求函数在区间上的最小值;22,,a ab a ba b b ab a b ⎧-≠=⎨->⎩()21x ax x f x e +-=()y f x =()0,1-1a ≥()0f x e +≥()()2e 2e x xf x a a x =+--()f x ()f x a 2()ln (21)f x x ax a x =+++()f x 0a <3()24f x a≤--()ln 1f x x x =-+()f x (1,)x ∈+∞11ln x x x-<<1c >(0,1)x ∈1(1)xc x c +->2()e mx f x x mx =+-()f x (,0)-∞(0,)+∞12,[1,1]x x ∈-12|()()|1f x f x e -≤-2()1x f x e ax bx =---,a b R ∈ 2.71828e =()g x ()f x ()g x [0,1](Ⅱ)若,函数在区间内有零点,求的取值范围(1)0f ()f x (0,1)a专题4.4 导数的综合应用(真题测试)一、单选题1.(2017·全国·高考真题(理))已知函数211()2()x x f x x x a e e --+=-++有唯一零点,则=a ( ) A .12-B .13C .12D .1【答案】C 【解析】 【分析】 【详解】因为()221111()2()1()1x x x x f x x x a e e x a e e --+--+=-++=-++-,设1t x =-,则()()()21t t f x g t t a e e -==++-,因为()()g t g t =-,所以函数()g t 为偶函数,若函数()f x 有唯一零点,则函数()g t 有唯一零点,根据偶函数的性质可知,只有当0=t 时,()0g t =才满足题意,即1x =是函数()f x 的唯一零点,所以210a -=,解得12a =.故选:C. 2.(2015·陕西·高考真题(理))对二次函数(为非零整数),四位同学分别给出下列结论,其中有且仅有一个结 论是错误的,则错误的结论是 A .是的零点 B .1是的极值点 C .3是的极值 D .点在曲线上【答案】A 【解析】 【详解】若选项A 错误时,选项B 、C 、D 正确,,因为是的极值点,是的极值,所以,即,解得:,因为点在曲线上,所以,即,解得:,所以,,所以,因为,所以不是的零点,所以选项A 错误,选项B 、C 、D 正确,故选A .3.(2022·青海·海东市第一中学模拟预测(理))已知函数()2e 2xx f x a x =-+,若有且仅有两个正整2()f x ax bx c =++a 1-()f x ()f x ()f x (2,8)()y f x =()2f x ax b ='+1()f x 3()f x ()()10{13f f '==203a b a b c +=⎧⎨++=⎩2{3b a c a =-=+()2,8()y f x =()42238a a a +⨯-++=5a =10b =-8c =()25108f x x x =-+()()()21511018230f -=⨯--⨯-+=≠1-()f x数,使得()0f x <成立,则实数a 的取值范围是( ) A .211,3e e ⎡⎫⎪⎢⎣⎭B .3291,5e e ⎡⎫⎪⎢⎣⎭C .391,5e 3e ⎡⎫⎪⎢⎣⎭D .212,2e e ⎡⎫⎪⎢⎣⎭【答案】C 【解析】 【分析】将()0f x <转化为2(2)exx a x +<,再分别求导分析2()e x x g x =和()(2)h x a x =+的图象,再分别求得1,1g ,()()2,2g ,()()3,3g 到()20-,的斜率,分析临界情况即可 【详解】由()0f x <且0x >,得2(2)exx a x +<,设2()e x x g x =,()(2)h x a x =+, 22()exx x g x '-=,已知函数()g x 在(0,2)上单调递增,在(2,)+∞上单调递减, 函数()(2)h x a x =+的图象过点(2,0)-,(1)11(2)3e g =--,2(2)12(2)e g =--,3(3)93(2)5e g =--,结合图象,因为329115e 3e e <<,所以3915e 3ea ≤<. 故选:C4.(2014·全国·高考真题(文))已知函数,若存在唯一的零点,且,则的取值范围是( ) A . B . C . D .【答案】C 【解析】 【详解】试题分析:当时,,函数和,不满足题意,舍去;当时,,令,得或.时,;时,;时,,且,此时在必有零点,故不满足题意,舍去;当时,时,32()31f x ax x =-+()f x 0x 00x >a ()2,+∞()1,+∞(),2-∞-(),1-∞-0a =2()31f x x =-+()f x 0a >2()36f x ax x '=-()0f x '=0x =2x a =(,0)x ∈-∞()0f x '>2(0,)x a ∈()0f x '<2(,)x a∈+∞()0f x '>(0)0f >(,0)x ∈-∞0a <2(,)x a∈-∞;时,;时,,且,要使得存在唯一的零点,且,只需,即,则,选C .5.(2022·青海·海东市第一中学模拟预测(理))若函数()()22e e x xf x x ax a a R =+-∈有三个不同的零点,则实数a 的取值范围是( ) A .1,e ⎛⎫+∞ ⎪⎝⎭B .1,1e ⎛⎫ ⎪⎝⎭C .2110,,1e e e ⎛⎫⎛⎫⋃ ⎪ ⎪-⎝⎭⎝⎭D .210,e e ⎛⎫ ⎪-⎝⎭【答案】D 【解析】 【分析】令()0f x =得20e e x xx xa a ⎛⎫⎛⎫+-= ⎪ ⎪⎝⎭⎝⎭,利用导数研究()e x x g x =的图像,由函数()f x 有三个零点可知,若令1e e xxt t ⎛⎫=≤ ⎪⎝⎭,则可知方程20t at a +-=的一根1t 必在10,e ⎛⎫ ⎪⎝⎭内,另一根21e t =或20t =或()2,0t ∈-∞上,分类讨论即可求解. 【详解】由22e e 0xxx ax a +-=得20e ex xx xa a ⎛⎫⎛⎫+-= ⎪ ⎪⎝⎭⎝⎭,令()e x x g x =, 由()10e xxg x -'==,得1x =,因此函数()g x 在(),1-∞上单调递增,在()1,+∞上单调递减,且()00g =,当0x >时,()0e x x g x =>,则()ex xg x =的图像如图所示: 即函数()g x 的最大值为()11eg =,令1e e xx t t ⎛⎫=≤ ⎪⎝⎭,则()20h t t at a =+-=,由二次函数的图像可知,二次方程的一根1t 必在10,e ⎛⎫ ⎪⎝⎭内,另一根21e t =或20t =或()2,0t ∈-∞上,当21e t =时,21e ea =-,则另一根111e t =-,不满足题意,当20t =时,a =0,则另一根10t =,不满足题意,()0f x '<2(,0)x a ∈()0f x '>(0,)x ∈+∞()0f x '<(0)0f >()f x 0x 00x >2()0f a>24a >2a <-当()2,0t ∈-∞时,由二次函数()20h t t at a =+-=的图像可知22000110e e a a a a ⎧+⋅-<⎪⎨⎛⎫+⋅->⎪ ⎪⎝⎭⎩, 解得210e ea <<-, 则实数a 的取值范围是210,e e ⎛⎫ ⎪-⎝⎭,故选:D.6.(2022·河南·开封市东信学校模拟预测(理))对任意0x >,不等式e ln()(1)0x ax a x -+-≥恒成立,则正数a 的最大值为( ) ABC .1eD .e【答案】D 【解析】 【分析】将不等式化为ln()e ln()e x ax x ax +≥+,构造()e x f x x =+有()(ln())f x f ax ≥,利用函数的单调性及参变分离法有e xa x ≤在0x >上恒成立,应用导数求右侧最小值,即可得结果.【详解】∵e ln()(1)0x ax a x -+-≥,∴ln()e ln()ln()e x ax x ax ax ax +≥+=+.令()e x f x x =+,则不等式化为()(ln())f x f ax ≥. ∵()e (0)x f x x x =+>为增函数,∴ln()x ax ≥,即e xa x≤.令e ()=x g x x ,则2(1)e ()x x g x x '-=,当01x <<时,()0g x '<,即()g x 递减;当1x >时,()0g x '>,即()g x 递增; 所以()()min 1e e g x g a ⇒≤==. ∴实数a 的最大值为e . 故选:D7.(2015·全国·高考真题(理))设函数()(21)xf x e x ax a =--+,其中1a < ,若存在唯一的整数0x ,使得0()0f x <,则a 的取值范围是( )A .3,12e ⎡⎫-⎪⎢⎣⎭B .33,2e 4⎡⎫-⎪⎢⎣⎭C .33,2e 4⎡⎫⎪⎢⎣⎭D .3,12e ⎡⎫⎪⎢⎣⎭【答案】D 【解析】 【分析】设()()21xg x e x =-,()1y a x =-,问题转化为存在唯一的整数0x 使得满足()()01g x a x <-,求导可得出函数()y g x =的极值,数形结合可得()01a g ->=-且()312g a e-=-≥-,由此可得出实数a 的取值范围.【详解】设()()21xg x e x =-,()1y a x =-,由题意知,函数()y g x =在直线y ax a =-下方的图象中只有一个点的横坐标为整数,()()21x g x e x '=+,当12x <-时,()0g x '<;当12x >-时,()0g x '>.所以,函数()y g x =的最小值为12122g e -⎛⎫-=- ⎪⎝⎭.又()01g =-,()10g e =>.直线y ax a =-恒过定点()1,0且斜率为a , 故()01a g ->=-且()31g a a e -=-≥--,解得312a e≤<,故选D.8.(2022·内蒙古·海拉尔第二中学模拟预测(理))已知函数()()e ln e (0)xf x a a a =+>,若对任意实数1x >,不等式()()ln 1f x x ≥-总成立,则实数a 的取值范围为( )A .210,e ⎛⎫ ⎪⎝⎭B .221,e e ⎛⎤⎥⎝⎦C .21,e ⎛⎫+∞ ⎪⎝⎭D .21,e ⎡⎫+∞⎪⎢⎣⎭【答案】D 【解析】 【分析】将所求不等式变形为()()ln 1ln eln eln 1x x ax a x -+++≥+-,构造函数()e xg x x =+,可知该函数在R 上为增函数,由此可得出()ln ln 1a x x ≥--,其中1x >,利用导数求出()()ln 1h x x x =--的最大值,即可求得实数a 的取值范围. 【详解】当1x >时,由()()ln 1f x x ≥-可得()ln eln 1ln 1x aa x +++≥-, 即()()()ln 1ln eln 1ln 1eln 1x x ax a x x x -+++≥-+-=+-,构造函数()e xg x x =+,其中x ∈R ,则()e 10x g x '=+>,所以,函数()g x 在R 上为增函数, 由()()ln 1ln eln eln 1x x ax a x -+++≥+-可得()()ln ln 1g x a g x +≥-⎡⎤⎣⎦,所以,()ln ln 1x a x +≥-,即()ln ln 1a x x ≥--,其中1x >, 令()()ln 1h x x x =--,其中1x >,则()12111xh x x x -'=-=--. 当12x <<时,()0h x '>,函数()h x 单调递增, 当2x >时,()0h x '<,函数()h x 单调递减, 所以,()()max ln 22a h x h ≥==-,21e a ∴≥. 故选:D.二、多选题9.(2022·辽宁实验中学模拟预测)我们把形如(),,0f x y y '=的方程称为微分方程,符合方程的函数()y f x =称为微分方程的解,下列函数为微分方程0xy y xy +-'=的解的是( ) A .e x y = B .e x y x =C .e 1x y x =+D .e (R)x y c x c =⋅∈⋅【答案】CD 【解析】 【分析】根据导数的运算求得导函数y ',代入微分方程检验即可. 【详解】选项A ,e x y =,则e x y '=,e e e e 0x x x x xy y xy x x '+-=+-=≠,不是解;选项B ,e x y x =,e e x x y x '=+,22e e e e 0x x x x xy y xy x x x x '+-=+--=,是方程的解;选项C ,e 1x y x =+,e e x x y x '=+,22e e 1e e 10x x x x xy y xy x x x x x x '+-=+++--=+≠,不是方程的解; 选项D ,e (R)x y c x c =⋅∈⋅,e e x x y c cx '=+,22e e e e 0x x x x xy y xy cx cx cx cx '+-=+--=,是方程的解. 故选:CD .10.(2022·河北沧州·二模)已知实数,a b 满足e e e a b a b ++=,则( ) A .0ab < B .1a b +> C .e e 4a b + D .e 1a b >【答案】BCD 【解析】 【分析】A.由e e e a b a b ++=得到111e ea b +=判断;BC.由e e e 2e e a b a b a b ++==2b 判断;D. 由111e e a b +=,得到e e e 1e 11e 1e 1b b b ab b b b b -+-=-=--,令()e e 1,0b b f b b b =-+>,用导数法判断. 【详解】 由e e e a b a b ++=得111e ea b +=,又e 0,e 0a b >>,所以e 1,e 1a b >>,所以0,0a b >>,所以0ab >,选项A 错误;因为e e e 2e e a b a b a b ++==2b ,即e e e 4a b a b ++=,所以ln41a b +>,选项B C ,正确,因为111e e a b +=,所以e e e 1b ab =-,所以e e e 1e 11e 1e 1b b b a bbb b b -+-=-=--.令()e e 1,0b b f b b b =-+>,则()e 0b f b b '=>,所以f b 在区间()0,∞+上单调递增,所以()()00f b f >=,即e e 10b b b -+>,又e 10b ->,所以e 10a b ->,即e 1a b >,选项D 正确. 故选:BCD11.(2022·湖南·模拟预测)已知1x >,1y >,且()()1e 11e y xx y ++=+,则下列结论一定正确的是( )A .()ln 0x y ->B .122x y +<C .226x y +>D .()ln ln3x y +<【答案】AC 【解析】 【分析】构造函数()e xf x x=,利用导数判断函数的单调性,得出1x y >+,结合不等式以及指、对数函数的性质逐一判断即可. 【详解】令()e x f x x=,则()()2e 1e e xx x x x f x x x --'==, 所以当1x >时,()0f x '>,所以()f x 在()1,+∞上单调递增; 由()()1e 11e yxx y ++=+得1e e 111x y x y y +=+++,即1e e 111x y x y y +-=++,∵1y >,∴11012y <<+, ∴1e e 1012x y x y +<-<+,即()()1012f x f y <-+<, ∴1x y >+,即1->x y ,∴()ln 0x y ->,A 正确;由1x y >+知12x y +>+,所以12222x y y ++>>,所以选项B 错误; 由1x y >+知12222326x y y y y ++>+=⋅>,所以选项C 正确.由1x y >+,1y >知213x y y +>+>,所以()()ln ln 21ln3x y y +>+>, 所以D 错误,故选:AC .12.(2022·全国·高考真题)已知函数,则( )A .有两个极值点B .有三个零点C .点是曲线的对称中心D .直线是曲线的切线【答案】AC 【解析】 【分析】利用极值点的定义可判断A ,结合的单调性、极值可判断B ,利用平移可判断C ;利用导数的几何意义3()1f x x x =-+()f x ()f x (0,1)()y f x =2y x =()y f x =()f x判断D. 【详解】由题,,令得或令得, 所以在上单调递减,在,上单调递增, 所以是极值点,故A 正确;因,,, 所以,函数在上有一个零点, 当时,,即函数在上无零点, 综上所述,函数有一个零点,故B 错误;令,该函数的定义域为,,则是奇函数,是的对称中心, 将的图象向上移动一个单位得到的图象, 所以点是曲线的对称中心,故C 正确;令,可得,又,当切点为时,切线方程为,当切点为时,切线方程为, 故D 错误.故选:AC.三、填空题13.(2020·河南高三其他(理))函数()2222ln x f x x e x ax =--,若0a =,则()f x 在[]1,2的最小值为_______;当0x >时,()1fx ≥恒成立,则a 的取值范围是_____.【答案】e (],1-∞ 【解析】当0a =时,∵()222ln x f x x ex =-,∴()222222x x f x xe x xe x'=+⋅-. 当1x >时,()0f x '>恒成立,()231f x x '=-()0fx '>x >x <()0f x '<x <()f x ((,-∞)+∞x =(10f =+>10f =>()250f -=-<()f x ,⎛-∞ ⎝⎭x ≥()0f x f ≥>⎝⎭()f x ⎫∞⎪⎪⎝⎭()f x 3()h x x x =-R ()()()()33h x x x x x h x -=---=-+=-()h x (0,0)()h x ()h x ()f x (0,1)()y f x =()2312f x x '=-=1x =±()(1)11f f =-=(1,1)21y x =-(1,1)-23y x =+∴()f x 在[]1,2上单调递增.∴()f x 在[]1,2上最小值为()1f e =.又0x >时,()1f x ≥恒成立,令 ()1xg x e x =--,()()100xg x e g ''=->=,所以()g x 在()0,∞+ 递增,()()00g x g >= 所以1x e x >+ ∴()22222ln 22ln 2ln x x x f x x e x ax e x ax +=--=--()2222ln 12ln 111x x x ax a x ≥++--=-+≥恒成立,∴1a ≤.故答案为e ;(],1-∞.14.(2022·全国·模拟预测(理))若曲线ln x y x =与212y kx =-仅有1个公共点,则k 的取值范围是___________. 【答案】(]1,02⎧⎫-∞⋃⎨⎬⎩⎭##1|02k k k ⎧⎫≤=⎨⎬⎩⎭或【解析】 【分析】将原问题转化为32ln 12x k x x =+只有一个解,令()()32ln 102x g x x x x =+>,利用导数求出()g x 的单调性及最值即可得答案. 【详解】 由题意可得:2ln 12x kx x =-只有一个解()0x >, 即32ln 12x k x x=+只有一个解. 令()32ln 12x g x x x=+, ()0x >原问题等价于y k =与()y g x =只有一个交点. 因为()43413ln 113ln x x xg x x x x '---=-= 因为13ln y x x =--在()0,∞+上单调递减, 且在1x =处的值为0 ,所以当()0,1x ∈时, ()()0,g x g x '>单调递增,当()1,x ∈+∞时, ()()0,g x g x '<单调递减且恒为正, 所以()()max 112g x g ==, 又因为y k =与()y g x =只有一个交点, 所以(]1,02k ⎧⎫∈-∞⎨⎬⎩⎭.故答案为: (]1,02⎧⎫-∞⋃⎨⎬⎩⎭.15.(2012·福建·高考真题(理))对于实数a 和b ,定义运算“*”: 设f (x )=(2x -1)*(x -1),且关于x 的方程为f (x )=m (m ∈R )恰有三个互不相等的实数根x 1,x 2,x 3,则x 1x 2x 3的取值范围是_________________ 【答案】【解析】 【详解】由定义运算“*”可知 即,该函数图像如下:由,假设当关于x 的方程为f (x )=m (m ∈R )恰有三个互不相等的实数根时, m 的取值范围是,且满足方程,所以令则, 所以令22,,a ab a ba b b ab a b ⎧-≠=⎨->⎩⎫⎪⎪⎝⎭22(21)(21)(1)0()?(1)(21)(1)0x x x x f x x x x x ⎧----=⎨---->⎩2220()0x x x f x x x x ⎧-=⎨-+>⎩1124f ⎛⎫= ⎪⎝⎭1230x x x <<<10,4⎛⎫⎪⎝⎭23,x x 2-+=x x m 23=x x m 22-=x x m 1=x 123==x x x m 10,4⎛⎫=∈ ⎪⎝⎭y m所以, 又在递增的函数, 所以,所以,所以在递减, 则当时,;当时,所以.16.(2022·江苏·常州高级中学模拟预测)已知函数22()ln 2e f x x x mx =-+,若()0f x ≥的解集中恰有一个整数,则m 的取值范围为________.【答案】22ln 22e ,4e 2⎡⎫-⎪⎢⎣⎭【解析】【分析】由()0f x ≥且0x >,得出2ln 2e x x m x -+≥-,构造函数()ln =-xg x x,利用导数研究()g x 的单调性,画出()ln =-x g x x 和22e y x =-的大致图象,由图可知0m >,设0x 为()ln =-xg x x和22e y x m =-+的交点的横坐标,结合题意可知该整数为1,即012x ≤<,当直线22e y x m =-+过1,0A 和ln 22,2B ⎛⎫- ⎪⎝⎭时,即可求出求出m 的值,从而得出m 的取值范围.【详解】由题可知,22()ln 2e f x x x mx =-+,0x >, 由于()0f x ≥的解集中恰有一个整数,即22ln 2e 0x x mx -+≥,即222e ln x mx x -+≥-,因为0x >,所以2ln 2e xx m x-+≥-的解集中恰有一个整数, 令()ln =-x g x x ,则()2ln 1-'=x g x x , 当1e x <<时,()0g x '<;当e x >时,()0g x '>, 所以()g x 在()1,e 上单调递减,在()e,+∞上单调递增, 画出()ln xy xg x ==-和22e y x =-的大致图象,如图所示: 要使得2ln 2e xx m x-+≥-,可知0m >, 114'⎛= ⎝y ()=h m 10,4⎛⎫⎪⎝⎭()()01>=h m h 0y '<=y 10,4⎛⎫ ⎪⎝⎭0m =0y =14m ==y 123⎫∈⎪⎪⎝⎭x x x设0x 为()ln =-xg x x和22e y x m =-+的交点的横坐标, 而2ln 2e xx m x-+≥-的解集中恰有一个整数,可知该整数为1,即012x ≤<, 当01x =时,得()10g =;当02x =时,得()ln 222g =-, 即1,0A ,ln 22,2B ⎛⎫- ⎪⎝⎭,当直线22e y x m =-+过点1,0A 时,得22e m =,当直线22e y x m =-+过点ln 22,2B ⎛⎫- ⎪⎝⎭时,得2ln 24e 2m =-, 所以m 的取值范围为22ln 22e ,4e 2⎡⎫-⎪⎢⎣⎭.故答案为:22ln 22e ,4e 2⎡⎫-⎪⎢⎣⎭四、解答题17.(2018·全国·高考真题(文))已知函数.(1)求曲线在点处的切线方程; (2)证明:当时,.【答案】(1)切线方程是(2)证明见解析 【解析】 【分析】(1)求导,由导数的几何意义求出切线方程.(2)当时,,令,只需证明即可.【详解】()21x ax x f x e +-=()y f x =()0,1-1a ≥()0f x e +≥210x y --=a 1≥()12f x e 1x x e x x e +-+≥++-()12gx 1x e x x +=++-gx 0≥(1),.因此曲线在点处的切线方程是.(2)当时,.令,则,当时,,单调递减;当时,,单调递增; 所以 .因此.18.(2017·全国·高考真题(理))已知函数(1)讨论的单调性;(2)若有两个零点,求的取值范围. 【答案】(1)见解析;(2). 【解析】 【详解】试题分析:(1)讨论单调性,首先进行求导,发现式子特点后要及时进行因式分解,再对按,进行讨论,写出单调区间;(2)根据第(1)问,若,至多有一个零点.若,当时,取得最小值,求出最小值,根据,,进行讨论,可知当时有2个零点.易知在有一个零点;设正整数满足,则.由于,因此在有一个零点.从而可得的取值范围为.试题解析:(1)的定义域为,,(ⅰ)若,则,所以在单调递减. (ⅱ)若,则由得.当时,;当时,,所以在单调递减,在单调递增.(2)(ⅰ)若,由(1)知,至多有一个零点.(ⅱ)若,由(1)知,当时,取得最小值,最小值为. ()()2212xax a x f x e-++'-=()02f '=()y f x =()0,1-210x y --=1a ≥()()211x xf x e x x e e +-+≥+-+()211xg x x x e +=+-+()121x g x x e +=++'()120x g x e +''=+>1x <-()()10g x g '-'<=()g x 1x >-()()10g x g '-'>=()g x ()g x ()1=0g ≥-()0f x e +≥()()2e 2e x xf x a a x =+--()f x ()f x a (0,1)()f x a 0a ≤0a >0a ≤()f x 0a >ln x a =-()f x 1(ln )1ln f a a a-=-+1a =(1,)∈+∞a (0,1)a ∈(0,1)a ∈()f x (,ln )a -∞-0n 03ln(1)n a>-00000000()e (e 2)e 20n n n n f n a a n n n =+-->->->3ln(1)ln a a->-()f x (ln ,)a -+∞a (0,1)()f x (),-∞+∞()()()()2221121x x x xf x ae a e ae e =+---'=+0a ≤()0f x '<()f x (),-∞+∞0a >()0f x '=ln x a =-(),ln x a ∈-∞-()0f x '<()ln ,x a ∈-+∞()0f x '>()f x (),ln a -∞-()ln ,a -+∞0a ≤()f x 0a >ln x a =-()f x ()1ln 1ln f a a a-=-+①当时,由于,故只有一个零点; ②当时,由于,即,故没有零点; ③当时,,即. 又,故在有一个零点.设正整数满足,则.由于,因此在有一个零点. 综上,的取值范围为.19.(2017·全国·高考真题(文))已知函数.(1)讨论的单调性; (2)当时,证明. 【答案】(1)见解析;(2)见解析. 【解析】 【分析】(1)先求函数导数,再根据导函数符号的变化情况讨论单调性:当时,,则在单调递增;当时,在单调递增,在单调递减. (2)证明,即证,而,所以需证,设g (x )=ln x -x +1 ,利用导数易得,即得证. 【详解】(1) 的定义域为(0,+),. 若a ≥0,则当x ∈(0,+)时,,故f (x )在(0,+)单调递增.若a <0,则当时,时;当x ∈时,. 故f (x )在单调递增,在单调递减. (2)由(1)知,当a <0时,f (x )在取得最大值,最大值为. 1a =()ln 0f a -=()f x ()1,a ∈+∞11ln 0a a-+>()ln 0f a ->()f x ()0,1a ∈11ln 0a a-+<()ln 0f a -<()()4222e 2e 22e 20f a a ----=+-+>-+>()f x (),ln a -∞-0n 03ln 1n a ⎛⎫>- ⎪⎝⎭()()00000000e e 2e 20n n n nf n a a n n n =+-->->->3ln 1ln a a ⎛⎫->- ⎪⎝⎭()f x ()ln ,a -+∞a ()0,12()ln (21)f x x ax a x =+++()f x 0a <3()24f x a≤--(21)(1)'()(0)ax x f x x x++=>0a ≥'()0f x >()f x (0,)+∞0a <()f x 1(0,)2a -1(,)2a-+∞3()24f x a ≤--max 3()24f x a ≤--max 1()()2f x f a=-11ln()1022a a -++≤max ()(1)0g x g ==()f x ∞()()‘1211)22(1x ax f x ax a x x++=+++=∞’)(0f x >∞10,2x a ⎛⎫∈- ⎪⎝⎭()0f x '>1()2a ∞-+,’)(0f x <’)(0f x >1()2a∞-+,12x a=-111()ln()1224f a a a -=---所以等价于,即. 设g (x )=ln x -x +1,则. 当x ∈(0,1)时,;当x ∈(1,+)时,.所以g (x )在(0,1)单调递增,在(1,+)单调递减.故当x =1时,g (x )取得最大值,最大值为g (1)=0.所以当x >0时,g (x )≤0.从而当a <0时,,即. 20.(2016·全国·高考真题(文))设函数.(Ⅰ)讨论的单调性; (Ⅱ)证明当时,; (Ⅲ)设,证明当时,.【答案】(Ⅰ)当时,单调递增;当时,单调递减;(Ⅱ)见解析;(Ⅲ)见解析. 【解析】 【详解】试题分析:(Ⅰ)首先求出导函数,然后通过解不等式或可确定函数的单调性;(Ⅱ)左端不等式可利用(Ⅰ)的结论证明,右端将左端的换为即可证明;(Ⅲ)变形所证不等式,构造新函数,然后通过利用导数研究函数的单调性来处理. 试题解析:(Ⅰ)由题设,的定义域为,,令,解得. 当时,,单调递增;当时,,单调递减. (Ⅱ)由(Ⅰ)知,在处取得最大值,最大值为. 所以当时,. 故当时,,,即. (Ⅲ)由题设,设,则,令,解得.当时,,单调递增;当时,,单调递减. 由(Ⅱ)知,,故,又,故当时,. 所以当时,.3()24f x a≤--113ln()12244a a a ---≤--11ln()1022a a -++≤’1(1)g x x=-()0g x '>∞()0g x '<∞11ln()1022a a -++≤3()24f x a≤--()ln 1f x x x =-+()f x (1,)x ∈+∞11ln x x x-<<1c >(0,1)x ∈1(1)xc x c +->01x <<()f x 1x >()f x ()f x '()0f x '>()0f x '<()f x x 1x()f x (0,)+∞1()1f x x=-'()0f x '=1x =01x <<()0f x '>()f x 1x >()0f x '<()f x ()f x 1x =(1)0f =1x ≠ln 1x x <-(1,)x ∈+∞ln 1x x <-11ln1x x <-11ln x x x-<<1c >()1(1)x g x c x c =+--'()1ln xg x c c c =--'()0g x =01lnln ln c c x c-=0x x <'()0g x >()g x 0x x >'()0g x <()g x 11ln c c c-<<001x <<(0)(1)0g g ==01x <<()0g x >(0,1)x ∈1(1)xc x c +->21.(2015·全国·高考真题(理))设函数.(1)证明:在单调递减,在单调递增;(2)若对于任意,都有,求m 的取值范围.【答案】(1)在单调递减,在单调递增;(2).【解析】【详解】(Ⅰ).若,则当时,,;当时,,.若,则当时,,;当时,,.所以,在单调递减,在单调递增.(Ⅱ)由(Ⅰ)知,对任意的,在单调递减,在单调递增,故在处取得最小值.所以对于任意,的充要条件是:即①,设函数,则.当时,;当时,.故在单调递减,在单调递增.又,,故当时,.当时,,,即①式成立.当时,由的单调性,,即;当时,,即.综上,的取值范围是.22.(2014·四川·高考真题(理))已知函数,其中,为自然对数的底数.(Ⅰ)设是函数的导函数,求函数在区间上的最小值;(Ⅱ)若,函数在区间内有零点,求的取值范围【答案】(Ⅰ)当时, ;当 时, ; 当时, .(Ⅱ) 的范围为. 【解析】【详解】试题分析:(Ⅰ)易得,再对分情况确定的单调区间,根据在上的单调性即可得在上的最小值.(Ⅱ)设为在区间内的一个零点,注意到2()e mx f x x mx =+-()f x (,0)-∞(0,)+∞12,[1,1]x x ∈-12|()()|1f x f x e -≤-()f x (,0)-∞(0,)+∞[1,1]-()(1)2mx f x m e x -'=+0m ≥(,0)x ∈-∞10mx e -≤()0f x '<(0,)x ∈+∞10mx e -≥()0f x '>0m <(,0)x ∈-∞10mx e ->()0f x '<(0,)x ∈+∞10mx e -<()0f x '>()f x (,0)-∞(0,)+∞m ()f x [1,0]-[0,1]()f x 0x =12,[1,1]x x ∈-12()()1f x f x e -≤-(1)(0)1,{(1)(0)1,f f e f f e -≤---≤-1,{1,m m e m e e m e --≤-+≤-()1t g t e t e =--+()1t g t e =-'0t <()0g t '<0t >()0g t '>()g t (,0)-∞(0,)+∞(1)0g =1(1)20g e e --=+-<[1,1]t ∈-()0g t ≤[1,1]m ∈-()0g m ≤()0g m -≤1m >()g t ()0g m >1m e m e ->-1m <-()0g m ->1m e m e -+>-m [1,1]-2()1x f x e ax bx =---,a b R ∈ 2.71828e =()g x ()f x ()g x [0,1](1)0f =()f x (0,1)a 12a ≤()(0)1g x g b ≥=-122e a <≤()22ln(2)g x a a a b ≥--2e a >()2g x e a b ≥--a ()2,1e -()2,()2x x g x e ax b g x e a -='=--a ()g x ()g x [0,1]()g x [0,1]0x ()f x (0,1).联系到函数的图象可知,导函数在区间内存在零点,在区间内存在零点,即在区间内至少有两个零点. 由(Ⅰ)可知,当及时,在内都不可能有两个零点.所以.此时,在上单调递减,在上单调递增,因此,且必有.由得:,代入这两个不等式即可得的取值范围.试题解答:(Ⅰ)①当时,,所以.②当时,由得.若,则;若,则. 所以当时,在上单调递增,所以. 当时,在上单调递减,在上单调递增,所以. 当时,在上单调递减,所以. (Ⅱ)设为在区间内的一个零点,则由可知,在区间上不可能单调递增,也不可能单调递减.则不可能恒为正,也不可能恒为负.故在区间内存在零点.同理在区间内存在零点.所以在区间内至少有两个零点.由(Ⅰ)知,当时,在上单调递增,故在内至多有一个零点. 当时,在上单调递减,故在内至多有一个零点. 所以. 此时,在上单调递减,在上单调递增,因此,必有.由得:,有(0)0,(1)0f f ==()g x 0(0,)x 1x ()g x 0(),1x 2x ()g x (0,1)12a ≤2e a ≥()g x (0,1)122e a <<()g x [0,ln 2]a [ln 2,1]a 12(0,ln(2)],(ln(2),1)x a x a ∈∈(0)10,(1)20g b g e a b =->=-->(1)10f e a b =---=1b e a =--a ()2,()2x xg x e ax b g x e a -='=--0a ≤()20x g x e a -'=>()(0)1g x g b ≥=-0a >()20x g x e a -'=>2,ln(2)x e a x a >>12a >ln(2)0a >2e a >ln(2)1a >102a <≤()g x [0,1]()(0)1g x g b ≥=-122e a <≤()g x [0,ln 2]a [ln 2,1]a ()(ln 2)22ln 2g x g a a a a b ≥=--2e a >()g x [0,1]()(1)2g x g e a b ≥=--0x ()f x (0,1)0(0)()0f f x ==()f x 0(0,)x ()g x ()g x 0(0,)x 1x ()g x 0(),1x 2x ()g x (0,1)12a ≤()g x [0,1]()g x (0,1)2e a ≥()g x [0,1]()g x (0,1)122e a <<()g x [0,ln 2]a [ln 2,1]a 12(0,ln(2)],(ln(2),1)x a x a ∈∈(0)10,(1)20g b g e a b =->=-->(1)10f e a b =---=12a b e +=-<.解得.当时,在区间内有最小值.若,则,从而在区间上单调递增,这与矛盾,所以.又,故此时在和内各只有一个零点和.由此可知在上单调递增,在上单调递减,在上单调递增.所以,,故在内有零点.综上可知,的取值范围是. (0)120,(1)210g b a e g e a b a =-=-+>=--=->21e a -<<21e a -<<()g x [0,1](ln(2))g a (ln(2))0g a ≥()0([0,1])g x x ≥∈()f x [0,1](0)(1)0f f ==(ln(2))0g a <(0)20,(1)10g a e g a =-+>=->()g x (0,ln(2))a (ln(2),1)a 1x 2x ()f x 1[0,]x 1(,x 2)x 2[,1]x 1()(0)0f x f >=2()(1)0f x f <=()f x 1(,x 2)x a (2,1)e -。
世纪金榜高三理科数学一轮复习全套试题含答案:课时提能演练(三) 1.3

课时提能演练(三)(45分钟 100分)一、选择题(每小题6分,共36分)1.(2012·福州模拟)已知命题“∃x∈R,x2+2ax+1<0”是真命题,则实数a的取值范围是()(A)(-∞,-1)(B)(1,+∞)(C)(-∞,-1)∪(1,+∞) (D)(-1,1)2.如果命题“⌝(p∨q)”是假命题,则下列说法正确的是( )(A)p、q均为真命题(B)p、q中至少有一个为真命题(C)p、q均为假命题(D)p、q至少有一个为假命题3.(预测题)下列命题是假命题的为( )(A)∃x0∈R,0xlge=0(B)∃x0∈R,0tanx=x0π),sinx<1(C)∀x∈(0,2(D)∀x∈R,e x>x+14.已知命题p:存在x0∈(-∞,0),00x x<;命题q:△ABC中,若sinA>sinB,23则A>B,则下列命题为真命题的是( )(A)p∧q (B)p∨(⌝q)(C)(⌝p)∧q (D)p ∧(⌝q)5.(2012·厦门模拟)命题:(1)⌝x ∈R,2x-1>0,(2) ∀x ∈N *,(x-1)2>0, (3)∃x 0∈R,lgx 0<1,(4)若p:1x 1- >0,则⌝p:1x 1-≤0,(5)∃x 0∈R,sinx 0≥1其中真命题个数是( )(A)1 (B)2 (C)3 (D)46.(2012·南昌模拟)已知命题p:“∀x ∈[0,1],a ≥e x ”,命题q :“∃x 0∈R ,20x +4x 0+a=0”,若命题“p ∧q ”是假命题,则实数a 的取值范围是( ) (A)(-∞,4] (B)(-∞,1)∪(4,+∞) (C)(-∞,e)∪(4,+∞) (D)(1,+∞) 二、填空题(每小题6分,共18分)7.已知命题p: ∃x 0∈R ,3200x x -+1≤0,则命题⌝p 是_________. 8.(2012·江南十校联考)命题“∃x 0∈R ,220x -3ax 0+9<0”为假命题,则实数a 的取值范围是_______.9.若∀a ∈(0,+∞), ∃θ∈R ,使asin θ≥a 成立,则cos(θ- 6π)的值为________.三、解答题(每小题15分,共30分)10.(易错题)写出下列命题的否定,并判断真假. (1)q: ∀x ∈R ,x 不是5x-12=0的根; (2)r:有些素数是奇数; (3)s: ∃x 0∈R ,|x 0|>0.11.(2012·南平模拟)已知命题p:A={x|x2-2x-3<0,x∈R},q:B={x|x2-2mx+m2-9<0, x∈R,m∈R}.(1)若A∩B=(1,3),求实数m的值;(2)若﹁p是﹁q的必要不充分条件,求实数m的取值范围.【探究创新】(16分)已知命题p:方程2x2+ax-a2=0在[-1,1]上有解;命题q:只有一个实数x0满足不等式2x+2ax0+2a≤0,若命题“p∨q”是假命题,求a的取值范围.答案解析1.【解析】选C.“∃x∈R,x2+2ax+1<0”是真命题,即不等式x2+2ax+1<0有解,∴Δ=(2a)2-4>0,得a2>1即a>1或a<-1.2.【解析】选B.因为“⌝(p∨q)”是假命题,则“p∨q”是真命题,所以p、q中至少有一个为真命题.3.【解析】选D.当x=0时,e x=x+1,故选D.)x>1,即2x>3x,所以命题p为假,4.【解析】选C.因为当x<0时,(23从而⌝p为真.△ABC中,由sinA>sinB⇒a>b⇒A>B,所以命题q为真.故选C.5.【解析】选C.(1)根据指数函数的性质,正确;(2)当x=1时,不成≤0立,故错误;(3)x=1时,lgx=0<1,故正确;(4)⌝p应为:“1-x1π使sinx≥1成立,故真命题有3个.或x=1”,故错误;(5)存在x=26.【解题指南】“p∧q”为假命题是“p∧q”为真命题的否定,故可先求出“p∧q”为真命题时a的取值范围,再根据补集的思想求“p∧q”为假命题时a的取值范围.【解析】选C.当p为真命题时,a≥e;当q为真命题时,x2+4x+a=0有解,则Δ=16-4a≥0,∴a≤4.∴“p∧q”为真命题时,e≤a≤4.∴“p∧q”为假命题时,a<e或a>4.7.【解析】命题p是特称命题,其否定为全称命题.答案:∀x∈R,x3-x2+1>08.【解析】因为命题“∃x0∈R,22x-3ax0+9<0”为假命题,所以“∀x∈R,2x2-3ax+9≥0”为真命题.a≤∴Δ=9a2-4×2×9≤0⇒答案:【误区警示】本题易出现不知利用命题及其否定的关系来求解,而使用直接法求a 的取值范围,导致结果错误或计算繁杂的情况. 9.【解析】∵∀a ∈(0,+∞),asin θ≥a, ∴sin θ≥1,又sin θ≤1,∴sin θ=1,∴θ=2k π+2π(k ∈Z),∴cos(θ- 6π)=sin 6π= 12. 答案:1210.【解析】(1)⌝q: ∃x 0∈R ,x 0是5x-12=0的根,真命题. (2)⌝r:每一个素数都不是奇数,假命题. (3)⌝s:∀x ∈R ,|x|≤0,假命题.11.【解析】(1)A={x|-1<x<3,x ∈R},B={x|m-3<x<m+3,x ∈R,m ∈R}, ∵A ∩B=(1,3),∴m=4.(2)∵﹁p 是﹁q 的必要不充分条件, ∴﹁q ⇒﹁p, ﹁p ﹁q, ∴﹁p ⇒﹁q, ﹁q﹁p,∴AB,1m 3,0m 2.3m 3-≥-⎧∴∴≤≤⎨≤+⎩【探究创新】【解析】由2x 2+ax-a 2=0,得(2x-a)(x+a)=0, ∴x=a2或x=-a,∴当命题p 为真命题时,|a 2|≤1或|-a|≤1, ∴|a|≤2.又“只有一个实数x 0满足不等式20x +2ax 0+2a ≤0”,即抛物线y=x2+2ax+2a与x轴只有一个交点, ∴Δ=4a2-8a=0,∴a=0或a=2.∴当命题q为真命题时,a=0或a=2.∴命题“p∨q”为真命题时,|a|≤2.∵命题“p∨q”为假命题,∴a>2或a<-2. 即a的取值范围为a>2或a<-2.。
高考理科数学第一轮复习测试题6

(时间:40分钟 满分:60分)一、填空题(每小题5分,共40分)1.如图所示,AB 是⊙O 的直径,MN 与⊙O 切于点C ,AC =12BC ,则sin ∠MCA =________.解析 由弦切角定理得, ∠MCA =∠ABC ,sin ∠ABC =AC AB =AC AC 2+BC 2=AC 5AC =55.答案552.如图所示,已知AB 是⊙O 的直径,CD 与AB 相交于点E ,∠ACD =60°,∠ADC =45°,则∠AEC =________.解析 如图,连接BC ,由圆周角定理推论2知,∠ACB =90°. ∵∠ACD =60°,∴∠DCB =30°, 的度数=60°.∴∠ADC =45°,∴ 的度数=90°. ∴∠AEC =12( )的度数=75°.答案 75°3.如图,AB 为⊙O 的直径,C 为⊙O 上一点.AD 和过C 点的切线互相垂直,垂足为D ,∠DAB =80°,则∠ACO =________.解析 ∵CD 是⊙O 的切线,∴OC ⊥CD ,又∵AD ⊥CD ,∴OC ∥AD . 由此得,∠ACO =∠CAD ,∵OC =OA ,∴∠CAO =∠ACO ,∴∠CAD =∠CAO ,故AC 平分∠DAB .∴∠CAO =40°, 又∵∠ACO =∠CAO ,∴∠ACO =40°. 答案 40°4.如右图所示,已知⊙O 的直径与弦AC 的夹角为30°,过C 点的切线PC 与AB 的延长线交于P ,PC =5, 则⊙O 的半径为________.解析 如图,连接OC ,则有∠COP =60°, OC ⊥PC ,可求OC =53 3.答案533 5.(2011·深圳模拟)如图,P 是等边三角形ABC 外接圆 上任一点,AP 交BC 于点D ,AP =4,AD =2,则AC =________.解析 如图,连接PC 、PB ,在等边三角形A BC 中,有∠ABC =∠ACB =60°, 又∠ABC =∠APC ,所以∠ACB =∠APC . 而∠P AC 是公共角,所以△APC 和△ACD 相似, 所以AC AP =AD AC,即AC 2=AP ·AD =4×2=8, 即AC =2 2. 答案 2 26.(2011·东莞调研)如图,P A 、PB 是圆O 的切线 ,切点分别为A 、B ,点C 在圆O 上,如果∠P =50°,那么∠ACB =________.解析 连接OA 、OB ,因为P A 、PB 是圆O 的切线,所以∠OBP =∠OAP =90°,又因为∠P =50°,所以∠AOB =130°,所以∠ACB =65°. 答案 65°7.(2011·汕头调研)如图,已知P A 是圆O (O 为圆心)的切线,切点为A ,PO 交圆O 于B ,C 两点,AC =3,∠P AB =30°,则圆O 的面积为________.解析 连接OA ,由∠P AB =30°,得∠OCA =∠OAC =30°, 由余弦定理得,AC 2=OA 2+OC 2-2OA ·OC cos 120°=3OA 2, OA =13AC =1,因此圆O 的面积等于π×12=π. 另解 由∠P AB =30°,∴∠ACB =30°,在Rt △ABC 中, AC =3,∴CB =2,∴OC =1,因此圆O 的面积等于π×12=π. 答案 π8.(2011·韶关调研)如图所示,CA 和CB 都是⊙O 的切线,切点分别是A 、B ,如果⊙O 的半径为23,且AB =6,则∠ACB =________.解析 如图,连接OC 交于AB 于点D .∵CA 、CB 分别是 ⊙O 的切线,∴CA =CB ,OC 平分∠ACB ,故OC ⊥AB . 由AB =6,可知BD =3,在Rt △OBD 中,OB =23,故sin ∠BOD =BD OB =323=32,所以∠BOD =60°,又因为B 是切点,故OB ⊥BC ,所以∠OCB =30°.故∠ACB =60°. 答案 60°二、解答题(共20分)9.(10分)如右图所示,AB 为圆O 的直径,BC ,CD 为圆O 的切线,B 、D 为切点. (1)求证:AD ∥OC ;(2)若圆O 的半径为1,求AD ·OC 的值. (1)证明 如图所示,连接OD ,BD , ∵BC ,CD 为⊙O 的切线,∴BD ⊥OC , ∴又AB 为圆O 的直径,∴AD ⊥DB , ∴AD ∥OC .(2)解 因为AO =OD ,则∠1=∠A =∠3,Rt △BAD ∽Rt △COD ,∴AD OD =ABOC ,即AD ·OC=AB ·OD =2.10.(10分)如图,△ABC 的角平分线AD 的延长线交它的外接圆于点E .(1)证明:△ABE ∽△ADC ;(2)若△ABC 的面积S =12AD ·AE ,求∠BAC 的大小.(1)证明 由已知条件,可得∠BAE =∠CAD . 因为∠AEB 与∠ACB 是同弧上的圆周角, 所以∠AEB =∠ACD . 故△ABE ∽△ADC .(2)解 因为△ABE ∽△ADC , 所以AB AD =AE AC ,即AB ·AC =AD ·AE .又S =12AB ·AC sin ∠BAC ,且S =12AD ·AE .故AB ·AC sin ∠BAC =AD ·AE .则sin ∠BAC =1,又∠BAC 为三角形内角, 所以∠BAC =90°.。
2023年高考数学一轮复习提升专练(新高考地区用)3-5 幂函数与一元二次函数(精讲)(解析版)

3.5 幂函数与一元二次函数(精讲)(提升版)思维导图考点呈现考点一 幂函数及性质【例1-1】(2022·全国·高三专题练习)幂函数223()(55)()m mf x m m x m Z -=+-∈是偶函数,且在(0,+∞)上是减函数,则m 的值为( ) A .﹣6 B .1 C .6 D .1或﹣6【答案】B【解析】∵幂函数223()(55)()mmf x m m x m Z -=+-∈是偶函数,且在(0,+∞)上是减函数,∵2255130m m m m ⎧+-=⎨-<⎩,且23m m -为偶数1m ∴=或6m =- 当1m =时,232m m -=-满足条件;当6m =-时,2354m m -=,舍去因此:m =1故选:B【例1-2】(2022·全国·高三专题练习)幂函数2232m m y x --=是偶函数,在()0,∞+上是减函数,则整数m 的值为( ) A .0 B .1 C .0或1 D .2【答案】A【解析】因为幂函数2232m m y x --=在()0,∞+上是减函数,所以22320m m --<,解得122m -<<,又m Z ∈,所以0m =或1m =, 当0m =时,221yxx 定义域为()(),00,-∞⋃+∞,且()2211x x =-,所以2y x 是偶函数,满足题意;当1m =时,331y x x -==定义域为()(),00,-∞⋃+∞,而()3311x x =--,所以3y x -=是奇函数,不满足题意,舍去;综上,0m =.故选:A 【一隅三反】1.(2022·全国·高三专题练习)(多选)已知幂函数()f x x α=的图象经过点(16,4),则下列说法正确的有( )例题剖析A .函数是偶函数B .函数是增函数C .当1x >时,()1f x >D .当120x x <<时,1212()()22f x f x x x f ++⎛⎫< ⎪⎝⎭【答案】BCD【解析】因为幂函数()f x x α=的图象经过点(16,4),所以164α=,则12α=, 所以12()f x x ==[)0,+∞,不关于原点对称,所以该函数是非奇非偶函数,故A 错; 又102>,所以12()f x x =是增函数,故B 正确; 因此当1x >时,()(1)1f x f >=,故C 正确;当120x x <<时,因为12()()2f x f x +122x x f +⎛⎫ ⎪⎝⎭则22121212()()222f x f x x x x x f +⎡+⎤+⎡⎤⎛⎫-=-= ⎪⎢⎥⎢⎥⎣⎦⎝⎭⎣⎦20=-<⎝⎭,所以1212()()22f x f x x x f ++⎛⎫< ⎪⎝⎭,故D 正确.故选:BCD. 2.(2022·全国·高三专题练习)(多选)已知函数()()2231mm f x m m x+-=--是幂函数,对任意1x ,()20,x ∈+∞,且12x x ≠,满足()()12120f x f x x x ->-.若a ,b R ∈,且()()f a f b +的值为负值,则下列结论可能成立的有( )A .0a b +>,0ab <B .0a b +<,0ab >C .0a b +<,0ab <D .0a b +>,0ab >【答案】BC【解析】由于函数()f x 为幂函数,故211m m --=,即220m m --=,解得1,2m m =-=.当1m =-时,()21f x x =,当2m =时,()3f x x =.由于“对任意()12,0,,x x ∈+∞,且12x x ≠,满足()()12120f x f x x x ->-”知,函数在()0,∞+上为增函数,故()3f x x =.易见()()f x f x -=-,故函数()3f x x =是单调递增的奇函数.由于()()0f a f b +<,即()()()f a f b f b <-=-,得a b <-,所以0a b +<,此时,若当0a =时,0b <,故0ab =;当0a >时,0a b <<-,故0b <,故0ab <;当0a <时,由a b <-知,b a <-,故0b <或0b =或0b >,即0ab >或0ab =或0ab <.综上可知,0a b +<,且0ab >或0ab =或0ab <.故选:BC. 3.(2022·全国·高三专题练习(理))已知幂函数()223()mm f x x m Z --=∈的图像关于y 轴对称,与x 轴及y 轴均无交点,则由m 的值构成的集合是__________. 【答案】{}1,1,3-【解析】由幂函数()f x 与x 轴及y 轴均无交点,得2230m m -≤-,解得13m -≤≤, 又m Z ∈,即{}1,0,1,2,3m ∈-,()223()mm f x x m Z --=∈的图像关于y 轴对称,即函数为偶函数,故223m m --为偶数,所以{}1,1,3m ∈-,故答案为:{}1,1,3-.4.(2022·上海·高三专题练习)已知函数()22()1a f x a a x +=-+为幂函数,且为奇函数,则实数a 的值_____.【答案】1【解析】因为函数()22()1a f x a a x +=-+为幂函数,所以2211,0,1a a a a a -+=∴-=∴=或0a =.当0a =时,()2f x x =为偶函数,不符合题意,所以舍去;当1a =时,()3f x x =为奇函数,符合题意.故答案为:1考点二 一元二次函数【例2-1】(2021·重庆市清华中学校高三阶段练习)若函数234y x x =--的定义域为[]0,m ,值域为25,44⎡⎤--⎢⎥⎣⎦,则实数m 的取值范围是( ) A .(]0,4 B .25,44⎡⎤--⎢⎥⎣⎦C .3,32⎡⎤⎢⎥⎣⎦D .3,2⎡⎫+∞⎪⎢⎣⎭【答案】C【解析】函数234y x x =--的图象如图所示,因为223253424y x x x ⎛⎫=--=-- ⎪⎝⎭当0x =或3x =时,4y =-;当32x =时,254y =-,因为函数的定义域为[]0,m ,所以3,32m ⎡⎤∈⎢⎥⎣⎦.故选:C .【例2-2】(2022·宁夏·平罗中学模拟预测(理))已知,(0,1)a b ∈,则函数2()41f x ax bx =-+在[1,)+∞上是增函数的概率为( )A .45B .34C .25D .14【答案】D【解析】由题设()f x 对称轴为2bx a=,而,(0,1)a b ∈,函数开口向上, 所以()f x 的增区间为2[,)b a +∞,故在[1,)+∞上是增函数有201b a <≤,综上,01012a b b a<<⎧⎪<<⎨⎪≤⎩对应可行域如下阴影部分:所以阴影部分面积为14,而,(0,1)a b ∈的面积为1,故在[1,)+∞上是增函数的概率为14.故选:D 【例2-3】(2022·全国·高三专题练习)(多选)若函数244y x x =--的定义域为[)0,a ,值域为[]8,4--,则正整数a 的值可能是( ) A .2B .3C .4D .5【答案】BC 【解析】函数244y x x =--的图象如图所示:因为函数在[)0,a 上的值域为[]8,4--,结合图象可得24a <≤,结合a 是正整数,所以BC 正确.故选: BC. 【一隅三反】1.(2022·全国·高三专题练习)若a ,b ,c 成等差数列,则二次函数22y ax bx c =-+的图象与x 轴的交点个数为( ) A .0 B .1 C .2 D .1或2【答案】D【解析】由a ,b ,c 成等差数列,可得2b a c =+, 所以()()2224440b ac a c ac a c ∆=-=+-=-≥,所以二次函数22y ax bx c =-+的图象与x 轴交点的个数为1或2.故选:D.2.(2022·天津·南开中学二模)已知函数()21,14log 1,1a ax x x f x x x ⎧--≤⎪=⎨⎪->⎩是R 上的单调函数,则实数a 的取值范围为( ) A .11,42⎡⎫⎪⎢⎣⎭B .11,42⎡⎤⎢⎥⎣⎦C .10,2⎛⎤ ⎥⎝⎦D .1,12⎛⎫ ⎪⎝⎭【答案】B 【解析】当函数()21,14log 1,1a ax x x f x x x ⎧--≤⎪=⎨⎪->⎩是R 上的单调递减函数,所以01112514a a a ⎧⎪<<⎪⎪≥⎨⎪⎪-≥-⎪⎩,解得1142a ≤≤,因为0a >且1a ≠,所以当1x ≤时,()f x 不可能是增函数,所以函数()f x 在R 上不可能是增函数, 综上:实数a 的取值范围为11,42⎡⎤⎢⎥⎣⎦,故选:B3(2022·重庆·模拟预测)已知二次函数24y x x a =-+的两个零点都在区间()1,+∞内,则a 的取值范围是( ) A .(),4-∞ B .()3,+∞C .()3,4D .(),3-∞【答案】C【解析】二次函数24y x x a =-+,对称轴为2x =,开口向上,在(),2-∞上单调递减,在()2,+∞上单调递增,要使二次函数2()4f x x x a =-+的两个零点都在区间()1,+∞内,需(1)140(2)480f a f a =-+>⎧⎨=-+<⎩,解得34a <<故实数a 的取值范围是()3,4故选:C4.(2022·全国·高三专题练习(理))若集合2{|(2)20,}A x x a x a x Z =-++-<∈中有且只有一个元素,则正实数a 的取值范围是___________ 【答案】12(,]23【解析】由题意,不等式2(2)20x a x a -++-<且0a >,即222(1)x x a x -+<+,令()()222,(1)f x x x g x a x =-+=+,所以()(){|,}A x f x g x x Z =<∈,所以()y f x =是一个二次函数,图象是确定的一条抛物线, 而()y g x =一次函数,图象是过一定点(1,0)-的动直线,作出函数()222f x x x =-+和()(1)g x a x =+的图象,如图所示,其中()()11,22f f ==,又因为,0x Z a ∈>,结合图象,要使得集合2{|(2)20,}A x x a x a x Z =-++-<∈中有且只有一个元素,可得()(1)122g g >⎧⎨≤⎩,即2132a a >⎧⎨≤⎩,解得1223a <≤.即正实数a 的取值范围是12(,]23.故答案为:12(,]23.考点三 一元二次函数与其他知识综合【例3】(2022·山东济宁·三模)已知二次函数()()22f x ax x c x =++∈R 的值域为[)1,+∞,则14a c+的最小值为( ) A .3- B .3 C .4- D .4【答案】B【解析】若0a =,则函数()f x 的值域为R ,不合乎题意,因为二次函数()()22f x ax x c x =++∈R 的值域为[)1,+∞,则0a >,且()min 44114ac ac f x a a --===,所以,1ac a -=,可得101a c =>-,则1c >,所以,144113c a c c +=+-≥=,当且仅当2c =时,等号成立,因此,14a c +的最小值为3.故选:B.【一隅三反】1.(2021·广东·湛江二十一中)若函数()25log 212a f x x ax a ⎛⎫=-+- ⎪⎝⎭有最大值,则a 的取值范围为( ) A .10,2⎛⎫⎪⎝⎭B .1,12⎛⎫ ⎪⎝⎭C .21,52⎛⎫ ⎪⎝⎭D .()1,2【答案】B【解析】令25212t x ax a =-+-,要使函数()25log 212a f x x ax a ⎛⎫=-+- ⎪⎝⎭有最大值,则内层函数25212t x ax a =-+-要有最小正值,且外层函数()log a f t t =为减函数,可知0<a <1.要使内层函数25212t x ax a =-+-要有最小正值,则2544(1)02a a ∆=--<,解得122a <<.综合得a 的取值范围为1,12⎛⎫⎪⎝⎭.故选:B.2.(2022·黑龙江)若关于x 的方程19310x x m ++-+=有解,则实数m 的取值范围是( ) A .()1,+∞ B .5,4⎡⎫-+∞⎪⎢⎣⎭C .(],3-∞D .(]1,3【答案】A【解析】方程19310x x m ++-+=有解,2(3)3310x x m ∴+⨯-+=有解, 令30x t =>,则可化为2310t t m +-+=有正根,则231t t m +=-在()0,∞+有解,又当()0,t ∈+∞时,230t t +>所以101m m ->⇒>,故选:A .3.(2022·全国·高三专题练习)函数y =R ,则实数a 的取值范围是( ) A .(][),22,-∞-+∞ B .[)()1,00,-⋃+∞ C .(,1)-∞-D .[)1,1-【答案】A【解析】因为函数y =R ,可得真数部分y = 即函数21y x ax =++取到所有的正数,所以(0,)+∞是函数21y x ax =++的值域的子集, 所以240a ∆=-≥解得:2a ≤-或2a ≥,所以实数a 的取值范围是:(][),22,-∞-+∞.故选:A.考点四 图像问题【例4-1】(2022·全国·高三专题练习)函数x y a =(0a >且1a ≠)与函数()2121y a x x =---(0a >且1a ≠)在同一个坐标系内的图象可能是( )A .B .C .D .【答案】C【解析】两个函数分别为指数函数和二次函数,其中二次函数图象过点(0,-1),故排除A ,D ; 二次函数图象的对称轴为直线11x a =-,当01a <<时,指数函数递减,101a <-,C 符合题意; 当1a >时,指数函数递增,101a >-,B 不符合题意.故选:C . 【例4-2】(陕西省部分地市学校2022届高三下学期高考全真模拟考试理科数学试题)函数2ln x y x=的图象大致是( )A .B .C .D .【答案】C【解析】由题意,函数()2ln x f x x=的定义域为(,1)(1,0)(0,1)(1,)-∞--+∞,关于原点对称,且满足()()22()ln ln x x f x f x x x--===-, 所以函数()f x 为偶函数,其图象关于y 轴对称,排除B 选项;当1x >时,可得()2ln x f x x=,则()()()222ln (2ln 1)ln ln x x x x x f x x x --'==,当x ∈时,()0f x '<,()f x 单调递减;排除A 选项当)x ∈+∞时,()0f x '>,()f x 单调递增,所以排除D 选项,选项C 符合.故选:C.【一隅三反】1.(2021·山东·新泰市第一中学高三阶段练习)若不等式20ax x c -->的解集为1{|1}2x x -<<,则函数2y cx x a =--的图象可以为( )A .B .C .D .【答案】C【解析】由题可得1-和12是方程20ax x c --=的两个根,且0a <, 1112112a ca ⎧-+=⎪⎪∴⎨⎪-⨯=-⎪⎩,解得2,1a c =-=-,则()()22221y cx x a x x x x =--=--+=-+-, 则函数图象开口向下,与x 轴交于()()2,01,0,-.故选:C.2.(2022·全国·高三专题练习)已知函数2y ax bx c =++,如果a b c >>且0a b c ++=,则它的图象可能是( ) A . B . C . D .【答案】A【解析】由题意,函数2y ax bx c =++,因为0a b c ++=,令1x =,可得0y a b c =++=,即函数图象过点(1,0), 又由a b c >>,可得0,0a c ><,所以抛物线的开口向上,可排除D 项, 令0x =,可得0y c =<,可排除B 、C 项;故选:A.3.(2022·全国·高三专题练习)函数43y x =的图象是( )A .B .C .D .【答案】A【解析】函数443()y f x x ===,满足()()f x f x -=,即函数是偶函数,图象关于y 轴对称,D 错误;该函数是幂函数y x α=,413α=>,故该函数是增函数,且增长得越来越快,故A 正确,BC 错误. 故选:A.4.(江西省2022届高三5月高考适应性大练兵联考数学(理)试题)函数()f x 的部分图象大致为( )A .B .C .D .【答案】C【解析】由题得()()f x f x -===,则f (x )为偶函数,排除A ;又()01f =,排除B ;当2,0x π⎛∈⎫ ⎪⎝⎭时()0f x >,当3(,)22x ππ∈时,()1f x =所以()11f x -<<排除D , 故选:C . 5.(安徽省十校联盟2022届高三下学期最后一卷文科数学试题)函数()3e 2x f x x x =-在R 上的图象大致为( )A . B . C . D .【答案】A【解析】由题意得,()()()33e 2e 2x x f x x x x x f x --=---=-+=-, 故函数()f x 为奇函数,图象关于原点对称,排除D ;()2322e 220f =-⨯<,排除B ;()()()30.10.10.10.1e 20.10.1e 0.020f =-⨯=->,排除C , 故选:A.。
高考数学(理)一轮复习模拟题汇练:考点21数列的概念与简单表示法 (1)

2020高考复习模拟试题荟萃 考点21数列的概念与简单表示法一、选择题1.(2019·西宁模拟)数列{a n }满足a 1=2,a n +1=a 2n (a n >0),则a n =( ) A .10n -2B .10n -1C .102n -4D .22n -12.(2019·武昌区调研考试)已知数列{a n }的前n 项和S n =n 2-1,则a 1+a 3+a 5+a 7+a 9=( )A .40B .44C .45D .493.(2019·翼州中学联考)若数列{a n }的通项公式是a n =(-1)n (3n -2),则a 1+a 2+…+a 10等于( )A .15B .12C .-12D .-154.(2019·山西师大附中月考)定义:称n P 1+P 2+…+P n为n 个正数P 1,P 2,…,P n 的“均倒数”.若数列{a n }的前n 项的“均倒数”为12n -1,则数列{a n }的通项公式为( )A .a n =2n -1B .a n =4n -1C .a n =4n -3D .a n =4n -55.(2018·湖南六校联考)已知数列{a n }满足:∀m ,n ∈N *,都有a n ·a m =a n +m ,且a 1=12,那么a 5=( )A .132B .116C .14D .126.(2018·南昌模拟)在数列{a n }中,a 1=1,a n a n -1=a n -1+(-1)n (n ≥2,n ∈N *),则a 3a 5的值是( )A .1516B .158C .34D .387.(2019·黄冈质检)已知数列{x n }满足x n +2=|x n +1-x n |(n ∈N *),若x 1=1,x 2=a (a ≤1,a ≠0),且x n +3=x n 对于任意的正整数n 均成立,则数列{x n }的前2020项和S 2020=( )A .673B .674C .1345D .1347 8.(2018·河南郑州一中考前冲刺)数列{a n }满足:a 1=1,且对任意的m ,n ∈N *,都有a m +n =a m +a n +mn ,则1a 1+1a 2+1a 3+…+1a 2018=( )A .20172018B .20182019C .40342018D .40362019二、填空题9.(2019·山东重点中学联考)传说古希腊毕达哥拉斯学派的数学家经常在沙滩上面画点或用小石子表示数.他们研究过如图所示的三角形数:将三角形数1,3,6,10,…记为数列{a n },则数列{a n }的通项公式为________.10.(2018·福建晋江季延中学月考)已知数列{a n }满足a 1+2a 2+3a 3+…+na n =n +1(n ∈N *),则数列{a n }的通项公式为________.11.(2018·北京海淀区模拟)数列{a n }的通项为a n =⎩⎪⎨⎪⎧2n -1,n ≤4,-n 2+(a -1)n ,n ≥5(n ∈N *),若a 5是{a n }中的最大值,则a 的取值范围是________.12.(2018·佛山模拟)若数列{a n }满足12a 1+122a 2+123a 3+…+12n a n =2n +1,则数列{a n }的通项公式a n =________.13.(2019·湖南永州模拟)已知数列{a n }中,a 1=a ,a 2=2-a ,a n +2-a n =2,若数列{a n }单调递增,则实数a 的取值范围为________.14.(2019·长春模拟)已知数列{a n }满足a n ≠0,2a n (1-a n +1)-2a n +1(1-a n )=a n -a n +1+a n ·a n +1,且a 1=13,则数列{a n }的通项公式a n =________.三、解答题15.(2019·云南昆明一模)已知数列{a n }的前n 项和S n =n 2+1,数列{b n }满足b n =2a n +1,且前n 项和为T n .设c n =T 2n +1-T n .(1)求数列{b n }的通项公式; (2)判断数列{c n }的增减性.16.(2019·开封模拟)已知数列{a n }中,a n =1+1a +2(n -1)(n ∈N *,a ∈R 且a ≠0).(1)若a =-7,求数列{a n }中的最大项和最小项的值;(2)若对任意的n∈N*,都有a n≤a6成立,求a的取值范围.17.(2018·湖南联考)已知数列{a n}的前n项和为S n,a1=1,a n≠0,a n a n+1=4S n-1(n∈N*).(1)证明:a n+2-a n=4;(2)求数列{a n}的通项公式.参考答案1. 答案:D解析:因为数列{a n }满足a 1=2,a n +1=a 2n (a n >0),所以log 2a n +1=2log 2a n ⇒log 2a n +1log 2a n=2,所以{log 2a n }是公比为2的等比数列,所以log 2a n =log 2a 1·2n -1⇒a n =22n -1.2. 答案:B解析:法一:因为S n =n 2-1,所以当n ≥2时,a n =S n -S n -1=n 2-1-(n -1)2+1=2n -1,又a 1=S 1=0,所以a n =⎩⎪⎨⎪⎧0,n =12n -1,n ≥2,所以a 1+a 3+a 5+a 7+a 9=0+5+9+13+17=44.故选B.法二:因为S n =n 2-1,所以当n ≥2时,a n =S n -S n -1=n 2-1-(n -1)2+1=2n -1,又a 1=S 1=0,所以a n =⎩⎪⎨⎪⎧0,n =12n -1,n ≥2,所以{a n }从第二项起是等差数列,a 2=3,公差d =2,所以a 1+a 3+a 5+a 7+a 9=0+4a 6=4×(2×6-1)=44,故选B.3. 答案:A解析: 由题意知a 1+a 2+…+a 10=-1+4-7+10-…+(-1)10×(3×10-2)=(-1+4)+(-7+10)+…+[(-1)9×(3×9-2)+(-1)10×(3×10-2)]=3×5=15.4. 答案:C解析: 因为n a 1+a 2+…+a n =12n -1,所以a 1+a 2+…+a n n =2n -1,所以a 1+a 2+a 3…+a n =(2n -1)n ,a 1+a 2+…+a n -1=(2n -3)·(n -1)(n ≥2),当n ≥2时,a n =(2n -1)n -(2n -3)(n -1)=4n -3;a 1=1也适合此等式,所以a n =4n -3.5. 答案: A解析: ∵数列{a n }满足:∀m ,n ∈N *,都有a n ·a m =a n +m ,且a 1=12,∴a 2=a 1a 1=14,a 3=a 1·a 2=18.那么a 5=a 3·a 2=132.故选A .6. 答案: C解析: 由已知得a 2=1+(-1)2=2,∴2a 3=2+(-1)3,a 3=12,∴12a 4=12+(-1)4,a 4=3, ∴3a 5=3+(-1)5,∴a 5=23,∴a 3a 5=12×32=34.故选C .7. 答案: D解析: ∵x 1=1,x 2=a (a ≤1,a ≠0),∴x 3=|x 2-x 1|=|a -1|=1-a ,∴x 1+x 2+x 3=1+a +(1-a )=2,又x n +3=x n 对于任意的正整数n 均成立,∴数列{x n }的周期为3,∴数列{x n }的前2020项和S 2020=S 673×3+1=673×2+1=1347.故选D .8. 答案: D解析: ∵a 1=1,且对任意的m ,n ∈N *都有a m +n =a m +a n +mn ,∴a n +1=a n +n +1,即a n +1-a n =n +1,用累加法可得a n =a 1+(n -1)(n +2)2=n (n +1)2,∴1a n =2n (n +1)=21n -1n +1,∴1a 1+1a 2+1a 3+…+1a 2018=21-12+12-13+…+12018-12019=40362019,故选D . 9. 答案: a n =n (n +1)2解析: 由图可知a n +1-a n =n +1,a 1=1,由累加法可得a n =n (n +1)2.10. 答案: a n =⎩⎪⎨⎪⎧2,n =1,1n ,n ≥2解析: 已知a 1+2a 2+3a 3+…+na n =n +1,将n =1代入,得a 1=2;当n ≥2时,将n -1代入得a 1+2a 2+3a 3+…+(n -1)a n -1=n ,两式相减得na n =(n +1)-n =1,∴a n =1n,∴a n =⎩⎪⎨⎪⎧2,n =1,1n ,n ≥2.11. 答案: [9,12]解析: 当n ≤4时,a n =2n -1单调递增,因此n =4时取最大值,a 4=24-1=15.当n ≥5时,a n =-n 2+(a -1)n =-(n -a -12)2+(a -1)24.∵a 5是{a n }中的最大值,∴⎩⎪⎨⎪⎧a -12≤5.5,-25+5(a -1)≥15,解得9≤a ≤12.∴a 的取值范围是[9,12]. 12. 答案:⎩⎪⎨⎪⎧6,n =1,2n +1,n ≥2解析:因为12a 1+122a 2+123a 3+…+12n a n =2n +1,所以12a 1+122a 2+123a 3+…+12n a n +12n +1a n +1=2(n +1)+1,两式相减得12n +1a n +1=2,即a n =2n +1,n ≥2.又12a 1=3,所以a 1=6,因此a n =⎩⎪⎨⎪⎧6,n =1,2n +1,n ≥2.13. 答案:(0,1)解析:由a n +2-a n =2可知数列{a n }的奇数项、偶数项分别递增,若数列{a n }单调递增,则必有a 2-a 1=(2-a )-a >0且a 2-a 1=(2-a )-a <a n +2-a n =2,可得0<a <1,故实数a 的取值范围为(0,1).14. 解析:因为a n ≠0,2a n (1-a n +1)-2a n +1(1-a n )=a n -a n +1+a n ·a n +1, 所以两边同除以a n ·a n +1,得2(1-a n +1)a n +1-2(1-a n )a n =1a n +1-1a n+1,整理,得1a n +1-1a n =1,即{1a n }是以3为首项,1为公差的等差数列,所以1a n =3+(n -1)×1=n +2,即a n =1n +2.答案:1n +215. 解析: (1)a 1=S 1=2,a n =S n -S n -1=2n -1(n ≥2),所以b n=⎩⎨⎧23,n =1,1n ,n ≥2.(2)因为c n =b n +1+b n +2+…+b 2n +1=1n +1+1n +2+…+12n +1,所以c n +1-c n =12n +2+12n +3-1n +1=-1(2n +2)(2n +3)<0,即c n +1<c n ,所以数列{c n }是递减数列.16. 解析: (1)因为a n =1+1a +2(n -1)(n ∈N *,a ∈R ,且a ≠0),又a =-7,所以a n =1+12n -9(n ∈N *).结合函数f (x )=1+12x -9的单调性,可知1>a 1>a 2>a 3>a 4,a 5>a 6>a 7>…>a n >1(n ∈N *).所以数列{a n }中的最大项为a 5=2,最小项为a 4=0.(2)a n =1+1a +2(n -1)=1+12n -2-a2,已知对任意的n ∈N *,都有a n ≤a 6 成立,结合函数f (x )=1+12x -2-a2的单调性,可知5<2-a2<6,即-10<a <-8.17. 解析: (1)证明:∵a n a n +1=4S n -1, ∴a n +1a n +2=4S n +1-1, ∴a n +1(a n +2-a n )=4a n +1. 又a n ≠0,∴a n +2-a n =4.(2)由a n a n +1=4S n -1,a 1=1,得a 2=3.由a n+2-a n=4知数列{a2n}和{a2n-1}都是公差为4的等差数列,∴a2n=3+4(n-1)=2(2n)-1,a2n-1=1+4(n-1)=2(2n-1)-1,∴a n=2n-1.。
2021版高考数学一轮复习 滚动评估检测(四)(含解析)新人教B版-新人教B版高三全册数学试题

滚动评估检测(四)(120分钟150分)一、单项选择题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.集合A={y=,0≤x≤4},B=,则A∩B=( )A.∪B.∪C.D.【解析】选D.因为A=[0,2],B=,所以A∩B=(1,2].2.已知i为虚数单位,复数z满足=2+i,则= ( )A.1B.C.D.5【解析】选A.由题可得1-i=(2+i)(1+z),整理得z=--i,==1.3.已知x∈R,则“x>2”是“x2-3x+2>0”成立的( )A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件【解析】选A.由x2-3x+2>0得x<1或x>2,所以“x>2”是“x2-3x+2>0”成立的充分不必要条件.4.已知是等差数列,其前n项和为S n,若a3=6,S3=12,则公差d等于( ) A.1B. C.2D.3【解析】选C.因为a3=a1+2d=6,S3=3a1+3d=12,所以a1=2,d=2.5.在△ABC中,M是BC的中点,AM=1,点P在AM上且满足=2,则·(+)等于( )A.-B.-C.D.【解析】选A.如图,因为=2,所以=+,所以·(+)=-,因为AM=1且=2,所以||=,所以·(+)=-.6.某调查机构对全国互联网行业进行调查统计,得到整个互联网行业从业者年龄分布饼状图、90后从事互联网行业岗位分布条形图,则下列结论中不正确的是( ) 注:90后指1990-1999年之间出生,80后指1980-1989年之间出生,80前指1979年及以前出生.A.互联网行业从业人员中90后占一半以上B.互联网行业中从事技术岗位的人数超过总人数的20%C.互联网行业中90后从事运营岗位的人数比从事产品岗位的人数多D.互联网行业中从事技术岗位的人数90后比80后多【解析】选D.A.由互联网行业从业者年龄分布饼状图可知,90后占了56%,故A选项结论正确;B.互联网行业中,从事技术的90后占56%×39.6%>20%,仅90后就超过20%,故B选项结论正确;C.由90后从事互联网行业岗位分布条形图可知C选项结论正确;D.在互联网行业从业者中90后与80后的比例相差不大,故无法判断其技术岗位的人数是谁多,故D选项结论不一定正确.7.(2020·某某模拟)已知函数f(x)=,则y=f(x)的图象大致为( )【解析】选A.令g(x)=x-lnx-1,则x>0,因为g′(x)=1-=,由g′(x)>0,得x>1,即函数g(x)在(1,+∞)上单调递增,由g′(x)<0,得0<x<1,即函数g(x)在(0,1)上单调递减,所以当x=1时,函数g(x)有最小值,g(x)min=g(1)=0,于是对任意的x∈(0,1)∪(1,+∞),有g(x)>0,则f(x)>0,故排除B、D.8.(2019·全国卷Ⅱ)设函数f(x)的定义域为R,满足f(x+1)=2f(x),且当x∈(0,1]时,f(x)=x(x-1).若对任意x∈(-∞,m],都有f(x)≥-,则m的取值X围是世纪金榜导学号( )A. B.C. D.【解析】选B.如图,令f(x)=-,结合图象可得f(x-1)=-,则f(x-2)=-,当x∈(0,1]时,f(x)=x(x-1)=-,解得x=或,当f(x)=-时,x=或,即若f(x)≥-,对任意x∈(-∞,m]都成立,则m≤.二、多项选择题(本题共4小题,每小题5分,共20分,多选题全部选对得5分,选对但不全对的得3分,有选错的得0分)9.已知sinx=,则sin2x= ( )A.-B.-C.D.【解析】选BD.因为sinx=,所以cosx=±=±=±,所以sin2x=2sinxcosx=2××=±.10.(2020·某某新高考模拟)函数f(x)的定义域为R,且f(x+1)与f(x+2)都为奇函数,则( )A.f(x)为奇函数B.f(x)为周期函数C.f(x+3)为奇函数D.f(x+4)为偶函数【解析】选ABC.由f(x+1)与f(x+2)都为奇函数知函数f(x)的图象关于点(-1,0),(-2,0)对称,所以f(x)+f(-2-x)=0,f(x)+f(-4-x)=0,所以f(-2-x)=f(-4-x),所以f(x)是以2为周期的函数.所以f(x),f(x+3)均为奇函数.11.(2020·某某新高考模拟)如图为某地区2006年~2018年地方财政预算内收入、城乡居民储蓄年末余额折线图.根据该折线图可知,关于该地区2006年~2018年的说法正确的是( )A.财政预算内收入、城乡居民储蓄年末余额均呈增长趋势B.财政预算内收入、城乡居民储蓄年末余额的逐年增长速度相同C.财政预算内收入年平均增长量高于城乡居民储蓄年末余额年平均增长量D.城乡居民储蓄年末余额与财政预算内收入的差额逐年增大【解析】选AD.由图可以看出两条曲线均在上升,从而选项A正确;图中两曲线间隔越来越大,说明年增长速度不同,差额逐年增大,故选项B错误,选项D正确;又从图中可以看出财政预算内收入年平均增长量应该小于城乡居民储蓄年末余额年平均增长量,所以选项C错误.12.(2020·某某新高考模拟)正方体ABCD-A1B1C1D1的棱长为1,E,F,G分别为BC,CC1,BB1的中点.则( )A.直线D1D与直线AF垂直B.直线A1G与平面AEF平行C.平面AEF截正方体所得的截面面积为D.点C与点G到平面AEF的距离相等【解析】选BC.对选项A:方法一:以D点为坐标原点,DA,DC,DD1所在的直线分别为x,y,z轴,建立空间直角坐标系,则D(0,0,0),D1(0,0,1),A(1,0,0),A1(1,0,1),E,F,G.从而=(0,0,1),=,从而·=≠0,所以D1D与直线AF不垂直,选项A错误;方法二:取DD1的中点N,连接AN,则AN为直线AF在平面ADD1A1内的射影,AN与DD1不垂直,从而AF与DD1也不垂直,选项A错误;取B1C1的中点为M,连接A1M、GM,则A1M∥AE,GM∥EF,A1M∩GM=M,AE∩EF=E,所以平面A1MG∥平面AEF,从而A1G∥平面AEF,选项B正确;对于选项C,连接AD1,D1F,易知四边形AEFD1为平面AEF截正方体所得的截面四边形(如图所示),且D1H=AH=,AD1=,所以=×=,而==,从而选项C正确;对于选项D:方法一:由于S△GEF=S梯形BEFG-S△EBG=×-××=,而S△ECF=××=,而V A-GEF=S△EFG·AB,V A-ECF=S△ECF·AB,所以V A-GEF=2V A-ECF,即V G-AEF=2V C-AEF,点G到平面AEF的距离为点C到平面AEF的距离的二倍.从而D错误. 方法二:假设点C与点G到平面AEF的距离相等,即平面AEF将CG平分,则平面AEF必过CG的中点,连接CG交EF于点O,易知O不是CG的中点,故假设不成立,从而选项D错误.三、填空题(本大题共4小题,每小题5分,共20分.请把正确答案填在题中横线上)13.的展开式中x2y3的系数为________.【解析】由二项式定理可知,展开式的通项为T r+1=(-2y)r,要求的展开式中含x2y3的项,则r=3,所求系数为(-2)3=-20.答案:-2014.(2018·全国卷Ⅰ)记S n为数列的前n项和.若S n=2a n+1,则S6=________. 世纪金榜导学号【解析】依题意,作差得a n+1=2a n,所以数列{a n}是公比为2的等比数列,又因为a1=S1=2a1+1,所以a1=-1,所以a n=-2n-1,所以S6==-63.答案:-6315.双曲线-=1的离心率为__________,渐近线方程为__________.【解析】双曲线-=1中,a=2,b=,c==,所以e==,渐近线方程为y=±x=±x.答案:y=±x16.圆O的半径为1,P为圆周上一点,现将如图放置的边长为1的正方形(实线所示,正方形的顶点A与点P重合)沿圆周逆时针滚动,点A第一次回到点P的位置,则点A走过的路径的长度为________. 世纪金榜导学号【解析】每次转动一个边长时,圆心角转过60°,正方形有4边,所以需要转动11次,回到起点.在这11次中,半径为1的6次,半径为的3次,半径为0的2次,点A走过的路径的长度=×2π×1×6+×2π××3=.答案:四、解答题(本大题共6小题,共70分.解答时应写出必要的文字说明、证明过程或演算步骤)17.(10分)(2020·某某新高考模拟)在①b1+b3=a2,②a4=b4,③S5=-25这三个条件中任选一个,补充在下面问题中,若问题中的k存在,求k的值,若k不存在,请说明理由.设等差数列{a n}的前n项和为S n,{b n}是等比数列,____________,b1=a5,b2=3,b5=-81,是否存在k,使得S k>S k+1且S k+1<S k+2?注:如果选择多个条件分别解答,按第一个解答计分.【解析】因为在等比数列{b n}中,b2=3,b5=-81,所以其公比q=-3, 从而b n=b2(-3)n-2=3×(-3)n-2,从而a5=b1=-1.若存在k,使得S k>S k+1,即S k>S k+a k+1,从而a k+1<0;同理,若使S k+1<S k+2,即S k+1<S k+1+a k+2,从而a k+2>0.方法一:若选①:由b1+b3=a2,得a2=-1-9=-10,所以a n=3n-16,当k=4时满足a5<0,且a6>0成立;若选②:由a4=b4=27,且a5=-1,所以数列{a n}为递减数列,故不存在a k+1<0,且a k+2>0;若选③:由S5=-25==5a3,解得a3=-5,从而a n=2n-11,所以当k=4时,能使a5<0,a6>0成立.方法二:若选①:由b1+b3=a2,得a2=-1-9=-10,所以公差d==3,a1=a2-d=-13,从而S n=-13n+×d=(3n2-29n);⇔解得<k<,又k∈N*,从而k=4满足题意.若选②与若选③(仿上可解决,略).18.(12分)(2020·黄冈模拟)在△ABC中,设内角A,B,C所对的边分别为a,b,c,且=.(1)求角B的大小.(2)求cos2-sin cos的取值X围.【解析】(1)由=得到=,即2sinAcosB=sin(B+C),即2sinAcosB=sinA.又因为A为三角形内角,所以sinA≠0,所以cosB=,从而B=.(2)cos2-sin cos=(cosC+1)-sinA=cosC-sin+=cosC-sinC+=cos(C+)+,因为0<C<,所以<C+<,所以-<cos(C+)<,所以<cos(C+)+<.所以cos2-sin cos的取值X围为.19.(12分)如图,在四棱锥P-ABCD中,AB∥CD,AB⊥AD,平面ABCD⊥平面PAD,E是PB的中点,F 是DC上一点,G是PC上一点,且PD=AD,AB=2DF=6.(1)求证:平面EFG⊥平面PAB.(2)若PA=4,PD=3,求直线PB与平面ABCD所成角的正弦值.【解析】(1)如图,取PA的中点M,连接MD,ME,则ME∥AB,ME=AB,又DF∥AB,DF=AB,所以ME∥DF,ME=DF,所以四边形MDFE是平行四边形,所以EF∥MD,因为PD=AD,所以MD⊥PA,因为平面ABCD⊥平面PAD,平面ABCD∩平面PAD=AD,AB⊥AD,所以AB⊥平面PAD,因为MD⊂平面PAD,所以MD⊥AB,因为PA∩AB=A,所以MD⊥平面PAB,所以EF⊥平面PAB,又EF⊂平面EFG,所以平面EFG⊥平面PAB.(2)过点P作PH⊥AD于点H,则PH⊥平面ABCD,以H为坐标原点,HA所在直线为x轴,过点H 且平行于AB的直线为y轴,PH所在直线为z轴,建立如图所示的空间直角坐标系H-xyz,在等腰三角形PAD中,PD=AD=3,PA=4,因为PH·AD=MD·PA,所以3PH=4×,解得PH=,则AH=,所以P,B,所以=,易知平面ABCD的一个法向量为n=(0,0,1),所以cos<,n>==-,所以直线PB与平面ABCD所成角的正弦值为.20.(12分)已知F1,F2是椭圆C:+=1(a>b>0)的左、右焦点,圆O:x2+y2=c2(|F1F2|=2c)与椭圆有且仅有两个交点,点在椭圆上.(1)求椭圆的标准方程.(2)过y轴正半轴上一点P的直线l与圆O相切,与椭圆C交于点A,B,若=,求直线l的方程.【解析】(1)依题意,得c=b,所以a==b,所以椭圆C为+=1,将点代入,解得b=1,则a=,所以椭圆的标准方程为+y2=1.(2)由题意知直线l的斜率存在,设l斜率为k,P(0,m)(m>1),则直线l的方程为y=kx+m,设A(x1,y1),B(x2,y2),直线l与圆O相切,则=1,即m2=1+k2,联立直线与椭圆方程,消元得(1+2k2)x2+4kmx+2m2-2=0,Δ>0⇒k≠0,x1+x2=-,x1x2==,因为=,所以x2=2x1,即x1=-,=,所以=1,解得k2=,即k=±,m=,故所求直线方程为y=±x+.21.(12分)(2018·某某高考)已知某单位甲、乙、丙三个部门的员工人数分别为24,16,16. 现采用分层抽样的方法从中抽取7人,进行睡眠时间的调查.(1)应从甲、乙、丙三个部门的员工中分别抽取多少人?(2)若抽出的7人中有4人睡眠不足,3人睡眠充足,现从这7人中随机抽取3人做进一步的身体检查.①用X表示抽取的3人中睡眠不足的员工人数,求随机变量X的分布列与数学期望;②设A为事件“抽取的3人中,既有睡眠充足的员工,也有睡眠不足的员工”,求事件A发生的概率.【解析】(1)由已知,得甲、乙、丙三个部门的员工人数之比为3∶2∶2,由于采用分层抽样的方法从中抽取7人,因此应从甲、乙、丙三个部门的员工中分别抽取3人,2人,2人.(2)①随机变量X的所有可能取值为0,1,2,3.P(X=k)=(k=0,1,2,3).所以,随机变量X的分布列为X 0 1 2 3P所以随机变量X的数学期望E(X)=0×+1×+2×+3×=.②设事件B为“抽取的3人中,睡眠充足的员工有1人,睡眠不足的员工有2人”;事件C为“抽取的3人中,睡眠充足的员工有2人,睡眠不足的员工有1人”,则A=B∪C,且B与C互斥,由①知,P(B)=P(X=2)=,P(C)=P(X=1)=,故P(A)=P(B∪C)=P(X=2)+P(X=1)=.所以,事件A发生的概率为.22.(12分)已知函数f=cos,g=e x·f′,其中e为自然对数的底数.世纪金榜导学号(1)求曲线y=g在点处的切线方程.(2)若对任意x∈不等式g≥x·f+m恒成立,某某数m的取值X围.(3)试探究当x∈时,方程g=x·f的解的个数,并说明理由.【解析】(1)依题意得f=si n x,g=e x·cosx.g=e0cos0=1,g′=e x cosx-e x si n x,g′(0)=1,所以曲线y=g在点(0,g(0))处的切线方程为y=x+1.(2)原题等价于对任意x∈,m≤[g-x·f]mi n.设h(x)=g-x·f,x∈.则h′=e x cosx-e x si n x-si n x-xcosx=cosx-si n x,因为x∈,所以cosx≥0,si n x≤0,所以h′≥0,故h(x)在上单调递增,因此当x=-时函数h(x)取得最小值, h=-;所以m≤-,即实数m的取值X围是. (3)设H(x)=g-x·f,x∈.当x∈时,H′(x)=e x(cosx-si n x)-si n x-xcosx<0,所以函数H(x)在上单调递减,故函数H(x)在上至多只有一个零点,又H=(-)>0,H=-<0,而且函数H(x)在上是连续不断的, 因此,函数H(x)在上有且只有一个零点.即方程g(x)=x·f(x)只有一个解.。
2023-2024学年新高考卷高三一轮复习模拟考试检测试题含参考答案

2023—2024学年新高考卷高三一轮复习模拟考试检测试题含参考答案一、非连续性文本阅读阅读下面的文字,完成下面小题。
材料一:我国优秀的古典长篇小说,除《红楼梦》外,尚有《三国演义》《水许传》《西游记》《儒林外史》等,为什么《红楼梦》又独独高居于其他名著之上而被推崇为最伟大、艺术成就最高的巨著呢?在《红楼梦》之前,我国的长篇小说,总是在述说前人的故事,或取材于史书,或据传说演绎,即便有取自当代社会的,也多为奇闻轶事之类,仍属不相干者在说他人的故事。
所以小说是小说,作者是作者,读者、评论者也只看小说写得如何,却没有人去关心小说的作者,因为谁都知道那些作者,不论是罗贯中、施耐庵或吴承恩,都与诸葛亮、宋江、孙悟空等拉不上任何关系。
所以,当时人索隐《红楼梦》写的是谁的故事时,总从顺治皇帝与董鄂妃、纳兰明珠与纳兰性德、张侯家事或康熙间的一批名人名臣的事去比附,再也想不到作者在取材上会有全然不同于传统观念的新思路,开始用现实题材进行创作。
《红楼梦》一反从前只取古人或他人故事来编写小说的旧方法,它是在作者亲见亲闻、亲身经历和自己最熟悉的、感受最深切的生活素材基础上创作的。
但《红楼梦》写的不是一家一事一人,它不是自传体小说,也不是小说化了的曹氏一门的兴衰史,虽则在小说中毫无疑问地融入了大量作者自身见闻、经历和自己家庭荣枯变化的种种可供其创作构思的素材。
只是作者搜罗并加以提炼的素材的来源和范围都要更广泛得多,其目光和思想,更是从几个家庭扩展到整个现实社会和人生。
《红楼梦》一出来,传统的写人的手法都打破了,不再是好人都好,坏人都坏了。
作者如实描写,从无讳饰;因而,每个人物形象都是活生生的,有血有肉的。
这一看法,是鲁迅先生首先提出来的。
诸葛亮在小说中是一个十足理想化的甚至神化了的人物,成了智慧的化身,你很难从他身上找出什么缺点来;高俅先是流氓无赖,后成奸邪权臣,你也找不到他还有哪一点可以肯定的,除了踢得一脚好球;倒是神话人物孙悟空、猪八戒还复杂一点。
2023年新高考数学一轮复习5-5 函数y=Asin(ωx+φ)的图象及其应用(真题测试)含详解
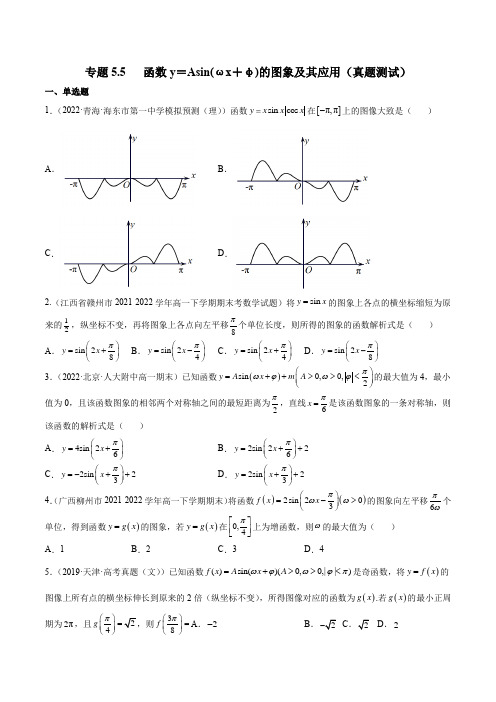
专题5.5 函数y =Asin(ωx +φ)的图象及其应用(真题测试)一、单选题1.(2022·青海·海东市第一中学模拟预测(理))函数sin cos yx x x 在[]π,π-上的图像大致是( )A .B .C .D .2.(江西省赣州市2021-2022学年高一下学期期末考数学试题)将sin y x =的图象上各点的横坐标缩短为原来的12,纵坐标不变,再将图象上各点向左平移8π个单位长度,则所得的图象的函数解析式是( ) A .sin 28y x π⎛⎫=+ ⎪⎝⎭ B .sin 24y x π⎛⎫=- ⎪⎝⎭C .sin 24y x π⎛⎫=+ ⎪⎝⎭D .sin 28y x π⎛⎫=- ⎪⎝⎭3.(2022·北京·人大附中高一期末)已知函数()sin 0,0,2y A x m A πωϕωϕ⎛⎫=++>>< ⎪⎝⎭的最大值为4,最小值为0,且该函数图象的相邻两个对称轴之间的最短距离为2π,直线6x π=是该函数图象的一条对称轴,则该函数的解析式是( )A .4sin 26y x π⎛⎫=+ ⎪⎝⎭B .2sin 226y x π⎛⎫=++ ⎪⎝⎭C .2sin 23y x π⎛⎫=-++ ⎪⎝⎭D .2sin 23y x π⎛⎫=++ ⎪⎝⎭4.(广西柳州市2021-2022学年高一下学期期末)将函数()()2sin 203f x x πωω⎛⎫=-> ⎪⎝⎭的图象向左平移6πω个单位,得到函数()y g x =的图象,若()y g x =在0,4⎡⎤⎢⎥⎣⎦π上为增函数,则ω的最大值为( )A .1B .2C .3D .45.(2019·天津·高考真题(文))已知函数()sin()(0,0,||)f x A x A ωϕωϕπ=+>><是奇函数,将()y f x =的图像上所有点的横坐标伸长到原来的2倍(纵坐标不变),所得图像对应的函数为()g x .若()g x 的最小正周期为2π,且4g π⎛⎫= ⎪⎝⎭38f π⎛⎫= ⎪⎝⎭A .2-B .CD .26.(2017·全国·高考真题(理))已知曲线C 1:y =cos x ,C 2:y =sin (2x +2π3),则下面结论正确的是 A .把C 1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移π6个单位长度,得到曲线C 2B .把C 1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向左平移π12个单位长度,得到曲线C 2C .把C 1上各点的横坐标缩短到原来的12倍,纵坐标不变,再把得到的曲线向右平移π6个单位长度,得到曲线C 2D .把C 1上各点的横坐标缩短到原来的12倍,纵坐标不变,再把得到的曲线向左平移π12个单位长度,得到曲线C 27.(2018·天津·高考真题(文))将函数sin 25y x π⎛⎫=+ ⎪⎝⎭的图象向右平移10π个单位长度,所得图象对应的函数A .在区间,44ππ⎡⎤-⎢⎥⎣⎦ 上单调递增B .在区间,04π⎡⎤-⎢⎥⎣⎦ 上单调递减C .在区间,42ππ⎡⎤⎢⎥⎣⎦上单调递增D .在区间,2ππ⎡⎤⎢⎥⎣⎦上单调递减8.(2019·全国·高考真题(理))关于函数()sin |||sin |f x x x =+有下述四个结论: ①f (x )是偶函数 ②f (x )在区间(2π,π)单调递增 ③f (x )在[,]-ππ有4个零点 ④f (x )的最大值为2 其中所有正确结论的编号是 A .①②④ B .②④ C .①④ D .①③二、多选题9.(2022·河北承德·高一阶段练习)将函数()sin 1f x x =-图像上所有点的纵坐标伸长为原来的3倍,横坐标缩短为原来的13,再将所得的图像向右平移12π个单位长度,得到函数()g x 的图像,则( )A .()3sin 3312g x x π⎛⎫=-- ⎪⎝⎭B .()g x 的图像关于直线4x π=对称C .()g x 的图像关于点5,312π⎛⎫- ⎪⎝⎭对称D .()g x 在0,3π⎡⎤⎢⎥⎣⎦上单调递增10.(2022·全国·模拟预测)将函数()()sin 0f x x x ωωω=>的图象向右平移π3个单位,得到的图象关于y 轴对称,则下列说法正确的是( )A .()f x 最小正周期的最大值为4π5B .()f x 最小正周期的最大值为4π11C .当()f x 的最小正周期取最大值时,平移后的函数在π0,5⎡⎤⎢⎥⎣⎦上单调递增D .当()f x 的最小正周期取最大值时,平移后的函数在π0,11⎡⎤⎢⎥⎣⎦上单调递减11.(2022·贵州·六盘水市第二中学高一阶段练习)已知函数()()πsin ,0,0,2f x A x x A ωϕωϕ⎛⎫=+∈>>< ⎪⎝⎭R 的部分图像如图所示,则下列说法正确的是( )A .()f x 的图像关于点1,06⎛⎫- ⎪⎝⎭对称B .()f x 的图像关于直线43x =对称 C .()f x 在11,23⎡⎤--⎢⎥⎣⎦上为增函数D .把()f x 的图像向右平移23个单位长度,得到一个奇函数的图像12.(2022·全国·南京外国语学校模拟预测)若函数()2cos f x x x x =的是( )A .函数()y f x =的图象可由函数sin 2y x =的图象向右平移π4个单位长度得到B .函数()y f x =的图象关于直线3π8x =-对称 C .函数()y f x =的图象关于点3π,08⎛⎫- ⎪⎝⎭对称D .函数()y x f x =+在π0,8⎛⎫⎪⎝⎭上为增函数三、填空题13.(2020·江苏·高考真题)将函数y =πsin(2)43x﹢的图象向右平移π6个单位长度,则平移后的图象中与y 轴最近的对称轴的方程是____.14.(2021·长岭县第二中学高三三模)函数22sin cos 2()2cos x x x xf x x x +++=+的图象关于点_______成中心对称,记函数的最大值为M ,最小值为N ,则M N +=_______. 15.(2014·重庆·高考真题(文))将函数图像上每一点的横坐标缩短为原来的一半,纵坐标不变,再向右平移个单位长度得到的图像,则______.16.(2021·山东高三月考)已知定义在R 上函数()()sin f x A x =+ωϕ(0>ω)振幅为2,满足212x x -=,且()()21f x f x =()0,102上()f x 零点个数最少为______. 四、解答题17.(2022·上海市嘉定区第二中学高一期末)已知函数()()(sin 0,0,)f x A x A ωϕωϕπ=+>><的部分图像如图所示.(1)求()f x 的解析式及对称中心;(2)先将()f x 的图像纵坐标缩短到原来的12倍,再向右平移π12个单位后得到()g x 的图像,求函数()y g x =在π3π,124x ⎡⎤∈⎢⎥⎣⎦上的单调减区间和最值.18.(2021·天津·静海一中高三月考)已知函数2())2sin 1(0,0)2x f x x πωϕωϕωϕ+⎛⎫++-><< ⎪⎝⎭为奇函数,且()f x 图象的相邻两对称轴间的距离为π2.(1)求()f x 的解析式.(2)求()()sin cos h x f x x x =++的最大值.(3)将函数()f x 的图象向右平移12π个单位长度,再把横坐标缩小为原来的12(纵坐标变),得到函数()y g x =的图象,求()y g x =的解析式.19.(2022·上海市新场中学高一期末)已知函数2()cos 2cos 1f x x x x =+-, (1)求函数()f x 的最小正周期; (2)若0,2x π⎡⎤∈⎢⎥⎣⎦求()f x 的值域;(3)将函数()f x 图象向右平移6π个单位后,得到函数()y g x =的图象,求函数()1y g x =-的零点.20.(2022·北京·北师大实验中学高一期中)某游乐场的摩天轮示意图如图.已知该摩天轮的半径为30米,轮上最低点与地面的距离为2米,沿逆时针方向匀速旋转,旋转一周所需时间为24T =分钟.在圆周上均匀分布12个座舱,标号分别为1~12(可视为点),现从图示位置,即1号座舱位于圆周最右端时开始计时,旋转时间为t 分钟.(1)当6t =时,求1号座舱与地面的距离;(2)在前24分钟内,求1号座舱与地面的距离为17米时t 的值;(3)记1号座舱与5号座舱高度之差的绝对值为H 米,若在00t t ≤≤这段时间内,H 恰有三次取得最大值,求0t 的取值范围.21.(2015·福建·高考真题(文))已知函数()2cos 10cos 222x x x f x =+.(1)求函数()f x 的最小正周期;(2)将函数()f x 的图象向右平移6π个单位长度,再向下平移a (0a >)个单位长度后得到函数()g x 的图象,且函数()g x 的最大值为2.(ⅰ)求函数()g x 的解析式; (ⅱ)证明:存在无穷多个互不相同的正整数0x ,使得()00g x >. 22.(2022·上海市嘉定区第一中学高一期末)某小区拟用一块半圆形地块(如图所示)建造一个居民活动区和绿化区.已知半圆形地块的直径4AB =千米,点O 是半圆的圆心,在圆弧上取点C 、D ,使得BC DC =,把四边形ABCD 建为居民活动区,并且在居民活动区周围铺上一条由线段AB ,BC ,CD 和DA 组成的塑胶跑道,其它部分建为绿化区.设COB θ∠=,且62ππθ≤<;(1)当6πθ=时,求四边形ABCD 的面积;(2)求塑胶跑道的总长l 关于θ的函数关系式;(3)当θ为何值时,塑胶跑道的总长l 最短,并求出l 的最小值.(答案保留2位小数)专题5.5 函数y =Asin(ωx +φ)的图象及其应用(真题测试)一、单选题1.(2022·青海·海东市第一中学模拟预测(理))函数sin cos yx x x 在[]π,π-上的图像大致是( )A .B .C .D .【答案】D 【解析】 【分析】利用函数的单调性,奇偶性和特值点等性质来判断图像. 【详解】易知f (x )是偶函数,排除B ,C 项;当0πx ≤≤时,sin 0x ≥,所以sin cos 0y x x x =≥,排除A 项. 故选:D2.(江西省赣州市2021-2022学年高一下学期期末考数学试题)将sin y x =的图象上各点的横坐标缩短为原来的12,纵坐标不变,再将图象上各点向左平移8π个单位长度,则所得的图象的函数解析式是( ) A .sin 28y x π⎛⎫=+ ⎪⎝⎭ B .sin 24y x π⎛⎫=- ⎪⎝⎭C .sin 24y x π⎛⎫=+ ⎪⎝⎭D .sin 28y x π⎛⎫=- ⎪⎝⎭【答案】C 【解析】 【分析】直接利用三角函数的图象的平移变换和伸缩变换的应用求出结果.【详解】将sin y x =的图象上各点的横坐标缩短为原来的12,纵坐标不变,可得sin 2y x =;再将图象上各点向左平移8π个单位长度,可得sin 2sin 284y x x ππ⎛⎫⎛⎫=+=+ ⎪ ⎪⎝⎭⎝⎭.故选:C3.(2022·北京·人大附中高一期末)已知函数()sin 0,0,2y A x m A πωϕωϕ⎛⎫=++>>< ⎪⎝⎭的最大值为4,最小值为0,且该函数图象的相邻两个对称轴之间的最短距离为2π,直线6x π=是该函数图象的一条对称轴,则该函数的解析式是( )A .4sin 26y x π⎛⎫=+ ⎪⎝⎭B .2sin 226y x π⎛⎫=++ ⎪⎝⎭C .2sin 23y x π⎛⎫=-++ ⎪⎝⎭D .2sin 23y x π⎛⎫=++ ⎪⎝⎭【答案】B 【解析】 【分析】由题意可得40A m A m +=⎧⎨-+=⎩,求出22A m =⎧⎨=⎩,再由该函数图象的相邻两个对称轴之间的最短距离为2π,可求出2ω=,由直线6x π=是该函数图象的一条对称轴,可得2,Z 62k k ππϕπ⨯+=+∈,从而线结合已知条件可求出ϕ,进而可求得函数的解析式 【详解】因为函数()sin 0,0,2y A x m A πωϕωϕ⎛⎫=++>>< ⎪⎝⎭的最大值为4,最小值为0,所以40A m A m +=⎧⎨-+=⎩,解得22A m =⎧⎨=⎩,因为该函数图象的相邻两个对称轴之间的最短距离为2π, 所以22T π=,所以T π=, 所以2ππω=,得2ω=,所以()2sin 22y x ϕ=++, 因为直线6x π=是该函数图象的一条对称轴,所以2,Z 62k k ππϕπ⨯+=+∈,得,Z 6k k πϕπ=+∈,因为2πϕ<,所以6π=ϕ, 所以2sin 226y x π⎛⎫=++ ⎪⎝⎭,故选:B4.(广西柳州市2021-2022学年高一下学期期末)将函数()()2sin 203f x x πωω⎛⎫=-> ⎪⎝⎭的图象向左平移6πω个单位,得到函数()y g x =的图象,若()y g x =在0,4⎡⎤⎢⎥⎣⎦π上为增函数,则ω的最大值为( )A .1B .2C .3D .4【答案】A 【解析】 【分析】函数()()2sin 203f x x πωω⎛⎫=-> ⎪⎝⎭的图象向左平移6πω个单位,得到函数()y g x =的表达式,然后利用在0,4⎡⎤⎢⎥⎣⎦π上为增函数,说明44T π≥,利用周期公式,求出1ω≤,得到ω的最大值. 【详解】函数()()2sin 203f x x πωω⎛⎫=-> ⎪⎝⎭的图象向左平移6πω个单位,得到函数()2sin 22sin 263y g x x x πϖϖπω⎡⎤⎛⎫==+-= ⎪⎢⎥⎝⎭⎣⎦,()y g x =在0,4⎡⎤⎢⎥⎣⎦π上为增函数,所以44T π≥,即2244ππω≥,即1ω≤,所以ω的最大值为1. 故选:A.5.(2019·天津·高考真题(文))已知函数()sin()(0,0,||)f x A x A ωϕωϕπ=+>><是奇函数,将()y f x =的图像上所有点的横坐标伸长到原来的2倍(纵坐标不变),所得图像对应的函数为()g x .若()g x 的最小正周期为2π,且4g π⎛⎫= ⎪⎝⎭38f π⎛⎫=⎪⎝⎭A .2- B.CD .2【答案】C 【解析】只需根据函数性质逐步得出,,A ωϕ值即可.【详解】因为()f x 为奇函数,∴(0)sin 0=,0,f A k k ϕϕπ==∴=,0ϕ=; 又12()sin ,2,122g x A x T πωπω=∴==2ω=,2A =,又()4g π∴()2sin 2f x x =,3()8f π= 故选C .6.(2017·全国·高考真题(理))已知曲线C 1:y =cos x ,C 2:y =sin (2x +2π3),则下面结论正确的是 A .把C 1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移π6个单位长度,得到曲线C 2B .把C 1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向左平移π12个单位长度,得到曲线C 2C .把C 1上各点的横坐标缩短到原来的12倍,纵坐标不变,再把得到的曲线向右平移π6个单位长度,得到曲线C 2D .把C 1上各点的横坐标缩短到原来的12倍,纵坐标不变,再把得到的曲线向左平移π12个单位长度,得到曲线C 2 【答案】D 【解析】 【详解】把C 1上各点的横坐标缩短到原来的12倍,纵坐标不变,得到函数y=cos2x 图象,再把得到的曲线向左平移π12个单位长度,得到函数y=cos2(x+π12)=cos (2x+π6)=sin (2x+2π3)的图象,即曲线C 2,故选D .点睛:三角函数的图象变换,提倡“先平移,后伸缩”,但“先伸缩,后平移”也常出现在题目中,所以也必须熟练掌握.无论是哪种变形,切记每一个变换总是对字母x 而言. 函数sin()()y A x x R ωϕ=+∈是奇函数π()k k Z ϕ⇔=∈;函数sin()()y A x x R ωϕ=+∈是偶函数ππ+()2k k Z ϕ⇔=∈;函数cos()()y A x x R ωϕ=+∈是奇函数ππ+()2k k Z ϕ⇔=∈;函数cos()()y A x x R ωϕ=+∈是偶函数π()k k Z ϕ⇔=∈.7.(2018·天津·高考真题(文))将函数sin 25y x π⎛⎫=+ ⎪⎝⎭的图象向右平移10π个单位长度,所得图象对应的函数A .在区间,44ππ⎡⎤-⎢⎥⎣⎦上单调递增 B .在区间,04π⎡⎤-⎢⎥⎣⎦ 上单调递减C .在区间,42ππ⎡⎤⎢⎥⎣⎦上单调递增D .在区间,2ππ⎡⎤⎢⎥⎣⎦上单调递减【答案】A 【解析】 【详解】分析:首先确定平移之后的对应函数的解析式,然后逐一考查所给的选项是否符合题意即可.详解:由函数25y sin x π⎛⎫=+ ⎪⎝⎭的图象平移变换的性质可知:将sin 25y x π⎛⎫=+ ⎪⎝⎭的图象向右平移10π个单位长度之后的解析式为:sin 2sin 2105y x x ππ⎡⎤⎛⎫=-+= ⎪⎢⎥⎝⎭⎣⎦.则函数的单调递增区间满足:()22222k x k k Z ππππ-≤≤+∈,即()44k x k k Z ππππ-≤≤+∈,令0k =可得函数的一个单调递增区间为,44ππ⎡⎤-⎢⎥⎣⎦,选项A 正确,B 错误;函数的单调递减区间满足:()322222k x k k Z ππππ+≤≤+∈,即()344k x k k Z ππππ+≤≤+∈, 令0k =可得函数的一个单调递减区间为3,44ππ⎡⎤⎢⎥⎣⎦,选项C ,D 错误;本题选择A 选项.8.(2019·全国·高考真题(理))关于函数()sin |||sin |f x x x =+有下述四个结论: ①f (x )是偶函数 ②f (x )在区间(2π,π)单调递增 ③f (x )在[,]-ππ有4个零点 ④f (x )的最大值为2 其中所有正确结论的编号是 A .①②④ B .②④C .①④D .①③【答案】C 【解析】【分析】化简函数()sin sin f x x x =+,研究它的性质从而得出正确答案. 【详解】()()()()sin sin sin sin ,f x x x x x f x f x -=-+-=+=∴为偶函数,故①正确.当2x ππ<<时,()2sin f x x =,它在区间,2π⎛⎫π ⎪⎝⎭单调递减,故②错误.当0x π≤≤时,()2sin f x x =,它有两个零点:0,π;当0x π-≤<时,()()sin sin 2sin f x x x x =--=-,它有一个零点:π-,故()f x 在[],-ππ有3个零点:0-π,,π,故③错误.当[]()2,2x k k k *∈ππ+π∈N 时,()2sin f x x =;当[]()2,22x k k k *∈π+ππ+π∈N 时,()sin sin 0f x x x =-=,又()f x 为偶函数,()f x ∴的最大值为2,故④正确.综上所述,①④ 正确,故选C . 【点睛】画出函数()sin sin f x x x =+的图象,由图象可得①④正确,故选C .二、多选题9.(2022·河北承德·高一阶段练习)将函数()sin 1f x x =-图像上所有点的纵坐标伸长为原来的3倍,横坐标缩短为原来的13,再将所得的图像向右平移12π个单位长度,得到函数()g x 的图像,则( )A .()3sin 3312g x x π⎛⎫=-- ⎪⎝⎭B .()g x 的图像关于直线4x π=对称C .()g x 的图像关于点5,312π⎛⎫- ⎪⎝⎭对称D .()g x 在0,3π⎡⎤⎢⎥⎣⎦上单调递增【答案】BC 【解析】 【分析】由平移和伸缩变换判断A ;采用代入法判断BC ;由正弦函数的单调性判断D.【详解】由题意得,()3sin 333sin 33124g x x x ππ⎡⎤⎛⎫⎛⎫=--=-- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦,A 错误.3442πππ⨯-=,B 正确.因为53124πππ⨯-=,所以()g x 的图像关于点5,312π⎛⎫- ⎪⎝⎭对称,C 正确.由0,3x π⎡⎤∈⎢⎥⎣⎦,得33,444x πππ⎡⎤-∈-⎢⎥⎣⎦,所以()g x 在0,3π⎡⎤⎢⎥⎣⎦上不单调递增,D 错误.故选:BC10.(2022·全国·模拟预测)将函数()()sin 0f x x x ωωω=>的图象向右平移π3个单位,得到的图象关于y 轴对称,则下列说法正确的是( )A .()f x 最小正周期的最大值为4π5B .()f x 最小正周期的最大值为4π11C .当()f x 的最小正周期取最大值时,平移后的函数在π0,5⎡⎤⎢⎥⎣⎦上单调递增D .当()f x 的最小正周期取最大值时,平移后的函数在π0,11⎡⎤⎢⎥⎣⎦上单调递减【答案】AC 【解析】 【分析】先化简()π2sin 3f x x ω⎛⎫=+ ⎪⎝⎭,再根据平移法则可得π3f x ⎛⎫- ⎪⎝⎭的图象关于y 轴对称,即可得到132k ω=--,k ∈Z ,0>ω,从而可以判断各选项的真假.【详解】因为()πsin 2sin 3f x x x x ωωω⎛⎫==+ ⎪⎝⎭,所以其图象向右平移π3个单位后得到函数()1ππππ2sin 2sin 3333y f x x x ωωω-⎡⎤⎡⎤⎛⎫⎛⎫=-=-+=+⎢⎥ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦⎣⎦的图象,因为其函数图象关于y 轴对称,所以()1ππ32k ωπ-=+,k ∈Z ,所以132k ω=--,k ∈Z ,0>ω,所以min15322ω=-=,所以max min2π4π5T ω==.又因为5π52sin 2cos 222x y x ⎛⎫-=- ⎪⎝⎭=,令52π2ππ2k x k ≤≤+,k ∈Z ,所以442πππ555k x k ≤≤+,k ∈Z ,当0k =时,2π0,5x ⎡⎤∈⎢⎥⎣⎦,所以52cos 2y x =-在π0,5⎡⎤⎢⎥⎣⎦上单调递增.故选:AC .11.(2022·贵州·六盘水市第二中学高一阶段练习)已知函数()()πsin ,0,0,2f x A x x A ωϕωϕ⎛⎫=+∈>>< ⎪⎝⎭R 的部分图像如图所示,则下列说法正确的是( )A .()f x 的图像关于点1,06⎛⎫- ⎪⎝⎭对称B .()f x 的图像关于直线43x =对称 C .()f x 在11,23⎡⎤--⎢⎥⎣⎦上为增函数D .把()f x 的图像向右平移23个单位长度,得到一个奇函数的图像【答案】ABC 【解析】 【分析】根据函数图像求出函数解析式()π2sin π6f x x ⎛⎫=+ ⎪⎝⎭,然后利用三角函数的性质逐一判断即可.【详解】解:由已知2A =,514263T ⎛⎫=⨯-= ⎪⎝⎭,2ππ2ω==,π2sin 23ϕ⎛⎫+= ⎪⎝⎭, ππ2π32k ϕ+=+,k ∈Z , 又π2ϕ<,π6ϕ∴=,()π2sin π6f x x ⎛⎫∴=+ ⎪⎝⎭,对于A ,1ππ2sin 0666f ⎛⎫⎛⎫-=-+= ⎪ ⎪⎝⎭⎝⎭,故A 正确;对于B ,令ππππ62x k +=+,得13x k =+,k ∈Z ,1k =时,43x =,故B 正确;对于C ,11,23x ⎡⎤∈-⎢⎥⎣⎦时,令ππππ,632t x ⎡⎤=+∈-⎢⎥⎣⎦,sin y t =在ππ,32⎡⎤-⎢⎥⎣⎦上递增,故C 正确;对于D ,把()f x 的图像向右平移23个单位长度,得函数表达式为()2ππ2sin π2sin π2cos π362g x x x x ⎡⎤⎛⎫⎛⎫=-+=-=- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦,它是偶函数,故D 错误.故选:ABC.12.(2022·全国·南京外国语学校模拟预测)若函数()2cos f x x x x =的是( )A .函数()y f x =的图象可由函数sin 2y x =的图象向右平移π4个单位长度得到 B .函数()y f x =的图象关于直线3π8x =-对称 C .函数()y f x =的图象关于点3π,08⎛⎫- ⎪⎝⎭对称D .函数()y x f x =+在π0,8⎛⎫⎪⎝⎭上为增函数【答案】BD 【解析】 【分析】由三角函数的恒等变换化简()πsin 24f x x ⎛⎫=+ ⎪⎝⎭,再由三角函数的平移变换可判断A ;求出3π18f ⎛⎫-=- ⎪⎝⎭可判断B 、C ;先判断()y f x =在π0,8⎛⎫ ⎪⎝⎭上为增函数,即可判断()y x f x =+在π0,8⎛⎫⎪⎝⎭的单调性.【详解】由题意,()2πcos 22sin 24f x x x x x x x ⎛⎫=+ ⎪⎝⎭. 函数sin 2y x =的图象向右平移π4个单位长度可得到()ππsin 2sin 2cos 242f x x x x ⎛⎫⎛⎫=-=-=- ⎪ ⎪⎝⎭⎝⎭,故A 错误;3π3ππsin 21884f ⎡⎤⎛⎫⎛⎫-=⨯-+=- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦,所以函数()y f x =的图象关于直线3π8x =-对称,故B 正确,C 错误;函数y x =在π0,8⎛⎫ ⎪⎝⎭上为增函数,π0,8x ⎛⎫∈ ⎪⎝⎭时,πππ2,442x ⎛⎫+∈ ⎪⎝⎭,故函数()f x 在π0,8⎛⎫⎪⎝⎭上单调递增,所以函数()y x f x =+在π0,8⎛⎫⎪⎝⎭上为增函数,故D 正确.故选:BD . 三、填空题13.(2020·江苏·高考真题)将函数y =πsin(2)43x﹢的图象向右平移π6个单位长度,则平移后的图象中与y 轴最近的对称轴的方程是____. 【答案】524x π=- 【解析】 【分析】先根据图象变换得解析式,再求对称轴方程,最后确定结果.【详解】3sin[2()]3sin(2)6412y x x πππ=-+=-72()()122242k x k k Z x k Z πππππ-=+∈∴=+∈当1k =-时524x π=- 故答案为:524x π=-14.(2021·长岭县第二中学高三三模)函数22sin cos 2()2cos x x x xf x x x +++=+的图象关于点_______成中心对称,记函数的最大值为M ,最小值为N ,则M N +=_______. 【答案】(0,1) 2 【分析】先将()f x 分离常数,找到与奇函数的关系,再利用平移求出对称中心及最大值与最小值之和. 【详解】2sin ()12cos x xf x x x +=++,记2sin ()2cos x x g x x x+=+, 22sin()sin ()()2()cos()2cos x x x xg x g x x x x x--+-==-=--+-+∴()g x 是奇函数,其图象关于坐标原点(0,0)中心对称. 则()g x 的最大值和最小值之和为0,把()g x 的图象向上平移一个单位得到()()1f x g x =+的图象,即()f x 的图象关于点(0,1)对称,且0112M N +=++=.故答案为:(0,1);2.15.(2014·重庆·高考真题(文))将函数图像上每一点的横坐标缩短为原来的一半,纵坐标不变,再向右平移个单位长度得到的图像,则______.【解析】 【详解】试题分析:由题意,6sin sin 6y x y x ππ⎛⎫=→=+ ⎪⎝⎭个单位向左平移()21sin 26f x x π⎛⎫→=+ ⎪⎝⎭纵坐标不变每个点的横坐标都伸长到原来的倍所以1sin sin 62664f ππππ⎛⎫⎛⎫=⨯+= ⎪ ⎪⎝⎭⎝⎭所以答案应填:2. 16.(2021·山东高三月考)已知定义在R 上函数()()sin f x A x =+ωϕ(0>ω)振幅为2,满足212x x -=,且()()21f x f x =()0,102上()f x 零点个数最少为______. 【答案】16 【分析】根据题意可得2A =,要使零点个数最少,周期需最大,12,x x 应为()y f x =与y =求出6π=ω,进而求出周期212T ωπ==,为了使区间零点最少,将第一个零点放在原点,得出11021282T T ÷=+,即可求解.【详解】振幅为2,2A ∴=,212x x -=,()()21f x f x =要使零点个数最少,周期需最大,12,x x 应为()y f x =与y =()()12sin sin x x ωϕωϕ⎧+=⎪⎪∴⎨⎪+=⎪⎩()212333x x πππω⇒-=-=,212x x -=,6πω∴=, 由212T ωπ==,为了使区间零点最少,将第一个零点放在原点,11021282T T ∴÷=+,最后1个零点恰好在102x =处不在区间()0,102中,2816∴⨯=,所以()0,102上()f x 零点个数最少为16. 故答案为:16四、解答题17.(2022·上海市嘉定区第二中学高一期末)已知函数()()(sin 0,0,)f x A x A ωϕωϕπ=+>><的部分图像如图所示.(1)求()f x 的解析式及对称中心;(2)先将()f x 的图像纵坐标缩短到原来的12倍,再向右平移π12个单位后得到()g x 的图像,求函数()y g x =在π3π,124x ⎡⎤∈⎢⎥⎣⎦上的单调减区间和最值. 【答案】(1)()2sin 23f x x π⎛⎫=- ⎪⎝⎭,对称中心为,03k ππ⎛⎫- ⎪⎝⎭,k Z ∈.(2)单调递减区间为423,ππ⎡⎤⎢⎥⎣⎦;max ()1g x =,min ()g x =【解析】【分析】(1)由函数的图像的顶点坐标求出A ,由周期求出ω,由五点法作图求出ϕ的值,可得()f x 的解析式,再利用三角函数的图像的对称性,得出结论.(2)由题意利用函数sin()y A x ωϕ=+的图像变换规律,求得()g x 的解析式,再利用余弦函数的单调性、余弦函数的定义域和值域,得出结论. (1)解:根据函数()sin()(0f x A x A ωϕ=+>,0>ω,||)ϕπ<的部分图像, 可得2A =,3254123πππω⋅=+,2ω∴=. 再根据五点法作图,52122ππϕ⨯+=,3ϕπ∴=-,故有()2sin 23f x x π⎛⎫=- ⎪⎝⎭.根据图像可得,,03π⎛-⎫⎪⎝⎭是()f x 的图像的一个对称中心,故函数的对称中心为,03k ππ⎛⎫- ⎪⎝⎭,k Z ∈.(2)解:先将()f x 的图像纵坐标缩短到原来的12,可得sin 23y x π⎛⎫=- ⎪⎝⎭的图像,再向右平移12π个单位,得到sin 2sin(2)cos 21232y x x x πππ⎡⎤⎛⎫=--=-=- ⎪⎢⎥⎝⎭⎣⎦的图像, 即()cos 2g x x =-,令222k x k πππ-≤≤,k Z ∈,解得2k x k πππ-≤≤,k Z ∈,可得()g x 的减区间为,2k k πππ⎡⎤-⎢⎥⎣⎦,k Z ∈,结合3,124x ππ⎡⎤∈⎢⎥⎣⎦,可得()g x 在3,124ππ⎡⎤⎢⎥⎣⎦上的单调递减区间为423,ππ⎡⎤⎢⎥⎣⎦.又32,62x ππ⎡⎤∈⎢⎥⎣⎦,故当2x π=,2x π=时,()g x 取得最大值,即max ()1g x =;当26x π=,12x π=时,()g x 取得最小值,即min ()g x =18.(2021·天津·静海一中高三月考)已知函数2())2sin 1(0,0)2x f x x πωϕωϕωϕ+⎛⎫++-><< ⎪⎝⎭为奇函数,且()f x 图象的相邻两对称轴间的距离为π2.(1)求()f x 的解析式.(2)求()()sin cos h x f x x x =++的最大值.(3)将函数()f x 的图象向右平移12π个单位长度,再把横坐标缩小为原来的12(纵坐标变),得到函数()y g x =的图象,求()y g x =的解析式.【答案】(1)()2sin 2f x x =,(2)2(3)()2sin 46g x x π⎛⎫=- ⎪⎝⎭【分析】(1)结合二倍角公式和辅助角公式将函数化简为()2sin 6f x x πωϕ⎛⎫=+- ⎪⎝⎭,再根据正弦函数的周期性奇偶性,分别求出ω和ϕ,从而可求得()f x 的解析式(2)令sin cos [4t x x x π⎛⎫=+=+∈ ⎪⎝⎭,则利用换元法可得222y t t =+-,从而可求出其最大值,(3)利用三角函数图象变换规律可求出函数解析式 【详解】(1)()()22sin 12x f x x ωϕωϕ+⎛⎫++- ⎪⎝⎭)cos()2sin 6x x x πωϕωϕωϕ⎛⎫=+-+=+- ⎪⎝⎭,因为()f x 图象的相邻两对称轴间的距离为π2所以222T πππω=⨯==,得2ω=,因为()f x 为奇函数, 所以,6k k Z πϕπ-=∈,即6,k k Z πϕπ=+∈,因为0ϕπ<<,所以6π=ϕ, 所以()2sin 2f x x =,(2)()()sin cos 2sin 2sin cos h x f x x x x x x =++=++,令sin cos [4t x x x π⎛⎫=+=+∈ ⎪⎝⎭,则222y t t =+-,因为对称轴为14t =-,所以当t =时,y 取得最大值2222⨯=(3)将函数()f x 的图象向右平移12π个单位长度,可得2sin 22sin 2126y x x ππ⎛⎫⎛⎫=-=- ⎪ ⎪⎝⎭⎝⎭,再把横坐标缩小为原来的12(纵坐标变),得到函数()2sin 46y g x x π⎛⎫==- ⎪⎝⎭19.(2022·上海市新场中学高一期末)已知函数2()cos 2cos 1f x x x x =+-, (1)求函数()f x 的最小正周期; (2)若0,2x π⎡⎤∈⎢⎥⎣⎦求()f x 的值域;(3)将函数()f x 图象向右平移6π个单位后,得到函数()y g x =的图象,求函数()1y g x =-的零点.【答案】(1)π; (2)[1,2]-; (3)6x k ππ=+或2x k ππ=+,Z k ∈.【解析】 【分析】(1)应用降幂公式化简()2sin(2)6f x x π=+,由正弦函数性质求最小正周期;(2)根据正弦型函数的性质求()f x 的区间值域;(3)由图象平移得()2sin(2)6g x x π=-,令()10y g x =-=结合三角函数的性质求零点即可.(1)由()2cos22sin(2)6f x x x x π=+=+,所以()f x 的最小正周期22T ππ==. (2)由0,2x π⎡⎤∈⎢⎥⎣⎦,则72[,]666x πππ+∈,即1sin(2)[,1]62x π+∈-,所以()[1,2]f x ∈-. (3)由题设()()2sin(2)66g x f x x ππ=-=-, 令()10y g x =-=,即2sin(2)16x π-=,可得1sin(2)62x π-=,所以2266x k πππ-=+或52266x k πππ-=+,Z k ∈, 即6x k ππ=+或2x k ππ=+,Z k ∈.故()1y g x =-的零点为6x k ππ=+或2x k ππ=+,Z k ∈.20.(2022·北京·北师大实验中学高一期中)某游乐场的摩天轮示意图如图.已知该摩天轮的半径为30米,轮上最低点与地面的距离为2米,沿逆时针方向匀速旋转,旋转一周所需时间为24T =分钟.在圆周上均匀分布12个座舱,标号分别为1~12(可视为点),现从图示位置,即1号座舱位于圆周最右端时开始计时,旋转时间为t 分钟.(1)当6t =时,求1号座舱与地面的距离;(2)在前24分钟内,求1号座舱与地面的距离为17米时t 的值;(3)记1号座舱与5号座舱高度之差的绝对值为H 米,若在00t t ≤≤这段时间内,H 恰有三次取得最大值,求0t 的取值范围. 【答案】(1)62m(2)16t =或20t =(3)03244t ≤< 【解析】 【分析】(1)设1号座舱与地面的距离h 与时间t 的函数关系的解析式为()sin()(0h t A t b A ωϕ=++>,0)ω>,根据所给条件求出A 、b 、ω、ϕ,即可得到函数解析式,再令6t =代入计算可得; (2)由(1)中的解析式()17h t =,结合正弦函数的性质计算可得;(3)依题意可得1h ,5h ,从而得到高度差函数()30sin 3230sin 2128123H t t ππ⎛⎫⎡⎤=- ⎪⎢⎥⎝⎭⎣++⎦+,利用两角和差的正弦公式化简,再结合正弦函数的性质求出函数取得最大值时t 的值,即可得解; (1)解:设1号座舱与地面的距离h 与时间t 的函数关系的解析式为()sin()(0h t A t b A ωϕ=++>,0>ω,0)t ≥, 则30A =,32b =,所以()30sin()32(0)h t t ωϕω=++> 依题意24min T =,所以2(/min)12rad T ππω==, 当0=t 时()32h t =,所以0ϕ=,故()30sin 3212h t t π=+()0t ≥,所以()630sin 6326212h π⎛⎫=⨯+=⎪⎝⎭, 即当6t =时,求1号座舱与地面的距离为62m ; (2)解:令()17h t =,即71230sin 321t π+=,所以1sin122t π=-, 又024t ≤≤,所以0212t ππ≤≤,所以4123t ππ=或5123t ππ=,解得16t =或20t =, 即16t =或20t =时1号座舱与地面的距离为17米; (3)解:依题意130sin3212h t π+=,()530sin83212h t π++=,所以()30sin 3230sin 2128123H t t ππ⎛⎫⎡⎤=- ⎪⎢⎥⎝⎭⎣++⎦+()30sin 30sin 81212t t ππ=+-2301sinsi 2123n t t πππ⎛⎫+ ⎪⎝-⎭=s 3013sin 2122t t ππ=6n 12t ππ⎛⎫=- ⎪⎝⎭令,1262k k N t ππππ-=+∈,解812,k k N t =+∈,所以当812,k k N t =+∈时H 取得最大值, 依题意可得03244t ≤<21.(2015·福建·高考真题(文))已知函数()2cos 10cos 222x x x f x =+.(1)求函数()f x 的最小正周期;(2)将函数()f x 的图象向右平移6π个单位长度,再向下平移a (0a >)个单位长度后得到函数()g x 的图象,且函数()g x 的最大值为2.(ⅰ)求函数()g x 的解析式; (ⅱ)证明:存在无穷多个互不相同的正整数0x ,使得()00g x >. 【答案】(1)2π;(2)(ⅰ)()10sin 8g x x =-; (ⅱ)证明见解析. 【解析】 【详解】(Ⅰ)因为()2cos 10cos 222x x xf x =+5cos 5x x =++10sin 56x π⎛⎫=++ ⎪⎝⎭.所以函数()f x 的最小正周期2πT =.(Ⅱ)(Ⅰ)将()f x 的图象向右平移6π个单位长度后得到10sin 5y x =+的图象,再向下平移a (0a >)个单位长度后得到()10sin 5g x x a =+-的图象.又已知函数()g x 的最大值为2,所以1052a +-=,解得13a =. 所以()10sin 8g x x =-.(Ⅱ)要证明存在无穷多个互不相同的正整数0x ,使得()00g x >, 就是要证明存在无穷多个互不相同的正整数0x , 使得010sin 80x ->,即04sin 5x >.由45<知,存在003πα<<,使得04sin 5α=. 由正弦函数的性质可知,当()00,x απα∈-时,均有4sin 5x >. 因为sin y x =的周期为2π,所以当()002,2x k k παππα∈++-(k ∈Z )时,均有4sin 5x >. 因为对任意的整数k ,()()00022213k k πππαπαπα+--+=->>,所以对任意的正整数k ,都存在正整数()002,2k x k k παππα∈++-,使得4sin 5k x >. 亦即存在无穷多个互不相同的正整数0x ,使得()00g x >.22.(2022·上海市嘉定区第一中学高一期末)某小区拟用一块半圆形地块(如图所示)建造一个居民活动区和绿化区.已知半圆形地块的直径4AB =千米,点O 是半圆的圆心,在圆弧上取点C 、D ,使得BC DC =,把四边形ABCD 建为居民活动区,并且在居民活动区周围铺上一条由线段AB ,BC ,CD 和DA 组成的塑胶跑道,其它部分建为绿化区.设COB θ∠=,且62ππθ≤<;(1)当6πθ=时,求四边形ABCD 的面积;(2)求塑胶跑道的总长l 关于θ的函数关系式;(3)当θ为何值时,塑胶跑道的总长l 最短,并求出l 的最小值.(答案保留2位小数)【答案】(1)2+(2)48sin4cos 2l θθ=++(3)6πθ=时,塑胶跑道的总长l 最短,最小值9.53千米.【解析】 【分析】 (1)6COD πθ∠==,23DOA π∠=,由三角形面积公式求得三个三角形面积后可得四边形面积; (2)COD θ∠=,2DOA πθ∠=-,利用等腰三角形的性质求得底边长,从而得l 的表达式;(3)利用二倍角公式化简函数式为关于sin 2θ的二次函数,结合二次函数性质、正弦函数性质得最小值.(1)连接OD ,因为6πθ=,又BC CD =,则6COD πθ∠==,所以23DOA π∠=,212sin 126BOCCODSSπ==⨯⨯=,2122sin 23AODS π=⨯⨯=所以112ABCD BOCCODDCAS SSS=++=+=; (2)由(1)知2sin4sin22BC CD OB θθ===,2AOD πθ∠=-,2sin4sin()4cos 22AOD AD OA πθθ∠==-=, 所以48sin 4cos ,622l AB BC CD DA θππθθ=+++≤+<=+(千米).(3) 2248sin4cos 48sin4(12sin )8sin 8sin 822222l θθθθθθ=++=++-=-++218(sin )1022θ=--+, 62ππθ≤<,1224πθπ≤<,所以1sin22θ=,即3πθ=时,max 10l =.6πθ=时,sinsin()sin cos cos sin 12343434πππππππ=-=-=218)109.532l =-⨯+≈,2πθ=时,218)109.662l =-⨯+≈,所以6πθ=时,l 取得最小值9.53千米.。
2023年新高考数学一轮复习9-3 椭圆(真题测试)含详解

专题9.3 椭圆(真题测试)一、单选题1.(2023·全国·高三专题练习(文))已知椭圆22214x y C a +=:的一个焦点为(2,0),则C 的离心率为( )A .13B .12C .2D .32.(2017·浙江·高考真题)椭圆22194x y +=的离心率是( )A B C .23D .593.(全国·高考真题(文))已知椭圆C :22221(0)x y a b a b +=>>的左右焦点为F 1,F 2F 2的直线l 交C 与A,B 两点,若△AF 1B 的周长为C 的方程为( )A .22132x y +=B .2213x y +=C .221128x y +=D .221124x y +=4.(2020·山东·高考真题)已知椭圆的长轴长为10,焦距为8,则该椭圆的短轴长等于( ) A .3B .6C .8D .125.(2019·北京·高考真题(理))已知椭圆2222 1x y a b+=(a >b >0)的离心率为12,则( )A .a 2=2b 2B .3a 2=4b 2C .a =2bD .3a =4b6.(2018·全国·高考真题(文))已知1F ,2F 是椭圆C 的两个焦点,P 是C 上的一点,若12PF PF ⊥,且2160PF F ∠=︒,则C 的离心率为( )A .1B .2CD 17.(2018·全国·高考真题(理))已知1F ,2F 是椭圆22221(0)x y C a b ab+=>>:的左,右焦点,A 是C 的左顶点,点P 在过A 12PF F △为等腰三角形,12120F F P ∠=︒,则C 的离心率为( ) A .23B .12 C .13 D .148.(2021·全国·高考真题(理))设B 是椭圆2222:1(0)x y C a b a b+=>>的上顶点,若C 上的任意一点P 都满足||2PB b ≤,则C 的离心率的取值范围是( )A .⎫⎪⎪⎣⎭B .1,12⎡⎫⎪⎢⎣⎭C .⎛ ⎝⎦D .10,2⎛⎤⎥⎝⎦二、多选题9.(2023·全国·高三专题练习)设圆锥曲线C 的两个焦点分别为12,F F ,若曲线C 上存在点P 满足1122::4:3:2PF F F PF =,则曲线C 的离心率可以是( ) A .12B .23C .32D .210.(2022·广东·高三开学考试)已知椭圆C :2212516x y +=,1F 、2F 是椭圆C 的两个焦点,M 、N 是椭圆C 上两点,且M 、N 分别在x 轴两侧,则( ) A .若直线MN 经过原点,则四边形12MF NF 为矩形 B .四边形12MF NF 的周长为20 C .12MF F △的面积的最大值为12D .若直线MN 经过2F ,则1F 到直线MN 的最大距离为811.(2022·江苏南通·模拟预测)在平面直角坐标系xOy 中,已知F 1,F 2分别是椭圆22:142x y C +=的左,右焦点,点A ,B 是椭圆C 上异于长轴端点的两点,且满足11AF F B λ=,则( ) A .△ABF 2的周长为定值 B .AB 的长度最小值为1 C .若AB ⊥AF 2,则λ=3D .λ的取值范围是[1,5]12.(2022·山东·济南市历城第二中学模拟预测)设1F ,F 为椭圆221204x y +=的左、右焦点,P 为椭圆上的动点,且椭圆上至少有17个不同的点(1,2,3)i P i =,1FP ,2FP ,3FP ,…组成公差为d 的递增等差数列,则( )A .FP 的最大值为4B .1F PF △的面积最大时,14tan 3F PF ∠=-C .d 的取值范围为10,2⎛⎤⎥⎝⎦D .椭圆上存在点P ,使134F PF π∠= 三、填空题13.(2021·山东高考真题)已知椭圆的中心在坐标原点,右焦点与圆22670x my m +--=的圆心重合,长轴长等于圆的直径,那么短轴长等于______.14.(2022·全国·南宁二中高三期末(文))椭圆C :22221x y a b +=(a >b >0)的焦距为2c ,O 为坐标原点,A 为椭圆的右顶点,以OA 为直径的圆与圆222x y c +=交于P ,Q 两点,若|PQ |=|OA |,则椭圆C 的离心率为______.15.(2019·全国·高考真题(理))设12F F ,为椭圆22:+13620x yC =的两个焦点,M 为C 上一点且在第一象限.若12MF F △为等腰三角形,则M 的坐标为___________.16.(2022·全国·高考真题)已知椭圆2222:1(0)x y C a b a b +=>>,C 的上顶点为A ,两个焦点为1F ,2F ,离心率为12.过1F 且垂直于2AF 的直线与C 交于D ,E 两点,||6DE =,则ADE 的周长是________________. 四、解答题17. (2022·全国·高三专题练习)已知椭圆()222210x y a b a b +=>>,过椭圆的左焦点F l与椭圆交于A 、B 两点(A 点在B 点的上方),若有2AF FB =,求椭圆的离心率.18.(陕西·高考真题(理))已知椭圆:E 22221x y a b+=(0a b >>)的半焦距为c ,原点O 到经过两点(),0c ,()0,b 的直线的距离为12c .(Ⅰ)求椭圆E 的离心率;(Ⅱ)如图,AB 是圆:M ()()225212x y ++-=的一条直径,若椭圆E 经过A ,B 两点,求椭圆E 的方程. 19.(2019·天津·高考真题(理))设椭圆22221(0)x y a b a b+=>>的左焦点为F ,上顶点为B .已知椭圆的短轴长为4,离心率为55. (Ⅰ)求椭圆的方程;(Ⅱ)设点P 在椭圆上,且异于椭圆的上、下顶点,点M 为直线PB 与x 轴的交点,点N 在y 轴的负半轴上.若||||ON OF =(O 为原点),且OP MN ⊥,求直线PB 的斜率.20.(2019·江苏·高考真题)如图,在平面直角坐标系xOy 中,椭圆C :22221(0)x y a b a b +=>>的焦点为F 1(–1、0),F 2(1,0).过F 2作x 轴的垂线l ,在x 轴的上方,l 与圆F 2:222(1)4x y a -+=交于点A ,与椭圆C 交于点D .连结AF 1并延长交圆F 2于点B ,连结BF 2交椭圆C 于点E ,连结DF 1.已知DF 1=52.(1)求椭圆C 的标准方程;(2)求点E 的坐标.21.(2021·天津·高考真题)已知椭圆()222210x y a b a b+=>>的右焦点为F ,上顶点为B ,且BF =(1)求椭圆的方程;(2)直线l 与椭圆有唯一的公共点M ,与y 轴的正半轴交于点N ,过N 与BF 垂直的直线交x 轴于点P .若//MP BF ,求直线l 的方程.22.(2018·天津·高考真题(文))设椭圆22221(0)x y a b a b +=>>的右顶点为A ,上顶点为B .已知椭圆的离心AB = (1)求椭圆的方程;(2)设直线:(0)l y kx k =<与椭圆交于P ,Q 两点,l 与直线AB 交于点M ,且点P ,M 均在第四象限.若BPM△的面积是BPQ 面积的2倍,求k 的值.专题9.3 椭圆(真题测试)一、单选题1.(2023·全国·高三专题练习(文))已知椭圆22214x y C a +=:的一个焦点为(2,0),则C 的离心率为( )A .13B .12C .2D .32.(2017·浙江·高考真题)椭圆22194x y +=的离心率是( )A B C .23D .593.(全国·高考真题(文))已知椭圆C :22221(0)x y a b a b +=>>的左右焦点为F 1,F 2F 2的直线l 交C 与A,B 两点,若△AF 1B 的周长为C 的方程为( )A .22132x y +=B .2213x y +=C .221128x y +=D .221124x y +=c e a ==22b ∴=,所以方程为4.(2020·山东·高考真题)已知椭圆的长轴长为10,焦距为8,则该椭圆的短轴长等于( ) A .3 B .6 C .8 D .12【答案】B【分析】根据椭圆中,,a b c 的关系即可求解. 【详解】椭圆的长轴长为10,焦距为8, 所以210a =,28c =,可得5a =,4c =, 所以22225169b a c =-=-=,可得3b =, 所以该椭圆的短轴长26b =, 故选:B.5.(2019·北京·高考真题(理))已知椭圆2222 1x y a b+=(a >b >0)的离心率为12,则( )A .a 2=2b 2B .3a 2=4b 2C .a =2bD .3a =4b6.(2018·全国·高考真题(文))已知1F ,2F 是椭圆C 的两个焦点,P 是C 上的一点,若12PF PF ⊥,且2160PF F ∠=︒,则C 的离心率为( )A .1B .2CD 1290,PF ∠1,||PF =故选D.7.(2018·全国·高考真题(理))已知1F ,2F 是椭圆22221(0)x y C a b a b+=>>:的左,右焦点,A 是C 的左顶点,点P在过A12PF F△为等腰三角形,12120F F P∠=︒,则C的离心率为()A.23B.12C.13D.148.(2021·全国·高考真题(理))设B是椭圆2222:1(0)x yC a ba b+=>>的上顶点,若C上的任意一点P都满足||2PB b≤,则C的离心率的取值范围是()A.⎫⎪⎪⎣⎭B.1,12⎡⎫⎪⎢⎣⎭C.⎛⎝⎦D.10,2⎛⎤⎥⎝⎦二、多选题9.(2023·全国·高三专题练习)设圆锥曲线C 的两个焦点分别为12,F F ,若曲线C 上存在点P 满足1122::4:3:2PF F F PF =,则曲线C 的离心率可以是( )A .12 B .23C .32D .210.(2022·广东·高三开学考试)已知椭圆C :2212516x y +=,1F 、2F 是椭圆C 的两个焦点,M 、N 是椭圆C 上两点,且M 、N 分别在x 轴两侧,则( ) A .若直线MN 经过原点,则四边形12MF NF 为矩形 B .四边形12MF NF 的周长为20 C .12MF F △的面积的最大值为12D .若直线MN 经过2F ,则1F 到直线MN 的最大距离为811.(2022·江苏南通·模拟预测)在平面直角坐标系xOy 中,已知F 1,F 2分别是椭圆22:142x y C +=的左,右焦点,点A ,B 是椭圆C 上异于长轴端点的两点,且满足11AF F B λ=,则( )A .△ABF 2的周长为定值B .AB 的长度最小值为1C .若AB ⊥AF 2,则λ=3D .λ的取值范围是[1,5]【详解】因为11AF F B λ=,则A 三点共线,2ABF 周长21=≠,B 错.,则12AF AF ⊥,A 在上、下顶点处,不妨设A解得0x =⎧⎪⎨或,422,-12.(2022·山东·济南市历城第二中学模拟预测)设1F ,F 为椭圆221204x y +=的左、右焦点,P 为椭圆上的动点,且椭圆上至少有17个不同的点(1,2,3)i P i =,1FP ,2FP ,3FP ,…组成公差为d 的递增等差数列,则( )A .FP 的最大值为4B .1F PF △的面积最大时,14tan 3F PF ∠=-C .d 的取值范围为10,2⎛⎤ ⎥⎝⎦D .椭圆上存在点P ,使134F PF π∠=三、填空题13.(2021·山东高考真题)已知椭圆的中心在坐标原点,右焦点与圆22670x my m+--=的圆心重合,长轴长等于圆的直径,那么短轴长等于______.【答案】【分析】由于22670x my m +--=是圆,可得1m =,通过圆心和半径计算,,a b c ,即得解 【详解】由于22670x my m +--=是圆,1m ∴= 即:圆22670x y x +--= 其中圆心为()3,0,半径为4那么椭圆的长轴长为8,即3c =,4a =,b ==那么短轴长为故答案为:14.(2022·全国·南宁二中高三期末(文))椭圆C :22221x y a b +=(a >b >0)的焦距为2c ,O 为坐标原点,A 为椭圆的右顶点,以OA 为直径的圆与圆222x y c +=交于P ,Q 两点,若|PQ |=|OA |,则椭圆C 的离心率为______.15.(2019·全国·高考真题(理))设12F F ,为椭圆22:+13620x yC =的两个焦点,M 为C 上一点且在第一象限.若12MF F △为等腰三角形,则M 的坐标为___________.16.(2022·全国·高考真题)已知椭圆2222:1(0)x y C a b a b +=>>,C 的上顶点为A ,两个焦点为1F ,2F ,离心率为12.过1F 且垂直于2AF 的直线与C 交于D ,E 两点,||6DE =,则ADE 的周长是________________. 称性将ADE 的周长转化为【详解】∵椭圆的离心率为2213y c =,即2a OF c =,两点,DE 为线段∴ADE 的周长等于24a a a +=四、解答题17. (2022·全国·高三专题练习)已知椭圆()222210x y a b a b +=>>,过椭圆的左焦点F l与椭圆交于A 、B 两点(A 点在B 点的上方),若有2AF FB =,求椭圆的离心率.【答案】23由2AF FB =可得x 的坐标代入椭圆方程中化简可求出离心率 【详解】因为2AF FB =,设A 4⋅⋅⋅⋅⋅⋅①②①-②得:,1220y y +=,18.(陕西·高考真题(理))已知椭圆:E 22221x y a b+=(0a b >>)的半焦距为c ,原点O 到经过两点(),0c ,()0,b 的直线的距离为12c .(Ⅰ)求椭圆E 的离心率;(Ⅱ)如图,AB 是圆:M ()()225212x y ++-=的一条直径,若椭圆E 经过A ,B 两点,求椭圆E 的方程. 【答案】(Ⅰ)32;(Ⅱ)221123x y +=.19.(2019·天津·高考真题(理))设椭圆22221(0)x y a b a b +=>>的左焦点为F ,上顶点为B .已知椭圆的短轴长为4 (Ⅰ)求椭圆的方程;(Ⅱ)设点P 在椭圆上,且异于椭圆的上、下顶点,点M 为直线PB 与x 轴的交点,点N 在y 轴的负半轴上.若||||ON OF =(O 为原点),且OP MN ⊥,求直线PB 的斜率.5520.(2019·江苏·高考真题)如图,在平面直角坐标系xOy中,椭圆C:22221(0)x ya ba b+=>>的焦点为F1(–1、0),F2(1,0).过F2作x轴的垂线l,在x轴的上方,l与圆F2:222(1)4x y a-+=交于点A,与椭圆C交于点D.连结AF1并延长交圆F2于点B,连结BF2交椭圆C于点E,连结DF1.已知DF1=52.(1)求椭圆C的标准方程;(2)求点E的坐标.43因为BF2=2a,EF1+EF2=2a,所以EF1=EB,21.(2021·天津·高考真题)已知椭圆()222210x y a b a b+=>>的右焦点为F ,上顶点为B ,且BF =(1)求椭圆的方程;(2)直线l 与椭圆有唯一的公共点M ,与y 轴的正半轴交于点N ,过N 与BF 垂直的直线交x 轴于点P .若//MP BF ,求直线l 的方程.因此,椭圆2215x y +=在点()00,M x y 处的切线方程为0015x x y y +=.22.(2018·天津·高考真题(文))设椭圆22221(0)x y a b a b +=>>的右顶点为A ,上顶点为B .已知椭圆的离心AB = (1)求椭圆的方程;(2)设直线:(0)l y kx k =<与椭圆交于P ,Q 两点,l 与直线AB 交于点M ,且点P ,M 均在第四象限.若BPM△的面积是BPQ 面积的2倍,求k 的值.的面积是BPQ 面积的23,x y y kx +=⎧⎨=⎩所以,k 的值为12-.。
备战2023数学高考一轮复习真题演练(2021-22年真题) 一元二次不等式与其他常见不等式解法

专题05 一元二次不等式与其他常见不等式解法【考点预测】 1、一元二次不等式一元二次不等式20(0)ax bx c a ++>≠,其中24b ac ∆=-,12,x x 是方程20(0)ax bx c a ++>≠的两个根,且12x x <(1)当0a >时,二次函数图象开口向上. (2)①若0∆>,解集为{}21|x x x x x ><或. ②若0∆=,解集为|2b x x R x a ⎧⎫∈≠-⎨⎬⎩⎭且. ③若0∆<,解集为R .(2) 当0a <时,二次函数图象开口向下. ①若0∆>,解集为{}12|x x x x << ②若0∆≤,解集为∅ 2、分式不等式 (1)()0()()0()f x f xg x g x >⇔> (2)()0()()0()f x f xg x g x <⇔< (3)()()0()0()0()f x g x f x g x g x ≥⎧≥⇔⎨≠⎩ (4)()()0()0()0()f x g x f x g x g x ≤⎧≤⇔⎨≠⎩ 3、绝对值不等式(1)22()()[()][()]f x g x f x g x >⇔>(2)()()(()0)()()()()f x g x g x f x g x f x g x >>⇔><-或;()()(()0)()()()f x g x g x g x f x g x <>⇔-<<;(3)含有两个或两个以上绝对值符号的不等式,可用零点分段法和图象法求解 【方法技巧与总结】1.已知关于x 的不等式02>++c bx ax 的解集为)(n m ,(其中0>mn ),解关于x 的不等式02>++a bx cx .由02>++c bx ax 的解集为)(n m ,,得:01)1(2>++c x b x a 的解集为)11(m n ,,即关于x 的不等式02>++a bx cx 的解集为)11(mn ,.已知关于x 的不等式02>++c bx ax 的解集为)(n m ,,解关于x 的不等式02≤++a bx cx .由02>++c bx ax 的解集为)(n m ,,得:01)1(2≤++c x b x a 的解集为)1[]1(∞+-∞,,m n 即关于x 的不等式02≤++a bx cx 的解集为)1[]1(∞+-∞,,mn .2.已知关于x 的不等式02>++c bx ax 的解集为)(n m ,(其中0>>m n ),解关于x 的不等式02>+-a bx cx .由02>++c bx ax 的解集为)(n m ,,得:01)1(2>+-c x b x a 的解集为)11(n m --,即关于x 的不等式02>+-a bx cx 的解集为)11(nm --,. 3.已知关于x 的不等式02>++c bx ax 的解集为)(n m ,,解关于x 的不等式02≤+-a bx cx .由02>++c bx ax 的解集为)(n m ,,得:01)1(2≤+-c x b x a 的解集为)1[]1(∞+---∞,,n m 即关于x 的不等式02≤+-a bx cx 的解集为)1[]1(∞+---∞,,nm ,以此类推. 4.已知关于x 的一元二次不等式02>++c bx ax 的解集为R ,则一定满足⎩⎨⎧<∆>00a ;5.已知关于x 的一元二次不等式02>++c bx ax 的解集为φ,则一定满足⎩⎨⎧≤∆<00a ;6.已知关于x 的一元二次不等式02<++c bx ax 的解集为R ,则一定满足⎩⎨⎧<∆<00a ;7.已知关于x 的一元二次不等式02<++c bx ax 的解集为φ,则一定满足⎩⎨⎧≤∆>00a .【题型归纳目录】题型一:不含参数一元二次不等式的解法 题型二:含参数一元二次不等式的解法 题型三:一元二次不等式与韦达定理及判别式 题型四:其他不等式解法 题型五:二次函数根的分布问题【典例例题】题型一:不含参数一元二次不等式的解法例1.(2022·新疆乌鲁木齐·二模(理))不等式(2)(1)0x x +->的解集为( ) A .{2}xx <-∣ B .{1}x x >∣ C .{21}x x -<<∣ D .{2∣<-xx 或1}x > 【答案】D 【解析】 【分析】结合一元二次不等式的解法求得正确答案即可. 【详解】由(2)(1)0x x +->解得2x <-,或1x >,所以不等式(2)(1)0x x +->的解集为{2∣<-x x 或1}x >, 故选:D.例2.(2022·全国·高三专题练习(文))已知函数()25x f x a -=-(0a >且1a ≠)的图象过定点(),m n ,则不等式210x mx n +++<的解集为( ) A .()1,3 B .()3,1-- C .()(),31,-∞-⋃+∞ D .()3,1-【答案】D 【解析】 【分析】根据指数型函数的定点求解,m n ,代入后再求解一元二次不等式. 【详解】当2x =时,()220255154f aa -=-=-=-=-,故2,4m n ==-,所以不等式为2230x x +-<,解得31x -<<,所以不等式的解集为()3,1-. 故选:D例3.(2022·全国·高三专题练习)已知函数()f x =()21,02,0ln x x x x ⎧+≥⎨-<⎩,则不等式()2f x +<()22f x x +的解集是( ) A .(﹣2,1) B .(0,1)C .(﹣∞,﹣2)∪(1,+∞)D .(1,+∞)【答案】C 【解析】 【分析】根据()f x 解析式,可得()f x 的单调性,根据条件,可得x +2<x 2+2x ,根据一元二次不等式的解法,即可得答案.【详解】函数()f x =()21,02,0ln x x x x ⎧+≥⎨-<⎩,可得x ≥0,()f x 递增; 当x <0时,()f x 递增;且x =0时函数连续,所以()f x 在R 上递增,不等式()2f x +<()22f x x +,可化为x +2<x 2+2x ,即x 2+x ﹣2>0,解得x >1或x <﹣2, 则原不等式的解集为(﹣∞,﹣2)∪(1,+∞). 故选:C例4.(2022·全国·高三专题练习)关于x 的不等式()2210m m x m x -+++>的解集为R ,则实数m 的范围是( )A .m <B .m >C .0m >D .m >m <【答案】B 【解析】 【分析】根据该不等式是否为二次不等式,分情况讨论. 【详解】当0m =时,该不等式为210x -+>,解集为12x <,不成立; 当0m ≠时,由不等式的解集为R ,得()()2Δ2410m m m m >⎧⎪⎨=+-+<⎪⎩,解得m >故选:B.例5.(2022·全国·高三专题练习)若函数()23x f x x =+,则不等式()()124f x f x +≥-的解集为( )A .[)3,+∞B .(],2-∞C .[]2,3D .[]1,5【答案】D 【解析】 【分析】根据奇偶性定义可知()f x 为偶函数,并根据指数函数和二次函数单调性确定()f x 的单调性,从而将所求不等式转化为124x x +≥-,解不等式可求得结果.【详解】()f x 定义域为R ,()()()2233x x f x x x f x --=+-=+=,()f x ∴为定义在R 上的偶函数,图象关于y 轴对称;当0x ≥时,()23x f x x =+,又3x y =,2yx 在[)0,∞+上均为增函数,()f x ∴在[)0,∞+上为增函数,则()f x 在(],0-∞上为减函数;由()()124f x f x +≥-可得:124x x +≥-,即()()22124x x +≥-,解得:15x ≤≤,即不等式()()124f x f x +≥-的解集为[]1,5. 故选:D.【方法技巧与总结】解一元二次不等式不等式的思路是:先求出其相应方程根,将根标在x 轴上,结合图象,写出其解集 题型二:含参数一元二次不等式的解法例6.(2022·浙江·高三专题练习)不等式()()22200ax a x a -++≥<的解集为( )A .2,1a ⎡⎤⎢⎥⎣⎦B .11,a ⎡⎤⎢⎥⎣⎦C .2,[1,)a ⎛⎤-∞⋃+∞ ⎥⎝⎦D .2(,1],a ⎫⎡-∞⋃+∞⎪⎢⎣⎭【答案】A 【解析】 【分析】根据一元二次不等式的解法即可求解. 【详解】解:原不等式可以转化为:()()120x ax --≥,当0a <时,可知2()(1)0x x a --≤,对应的方程的两根为1,2a,根据一元二次不等式的解集的特点,可知不等式的解集为:2[,1]a. 故选:A.例7.(2022·全国·高三专题练习)设1a <-,则关于x 的不等式1()0a x a x a ⎛⎫--< ⎪⎝⎭的解集为( )A .{|x x a <或1x a ⎫>⎬⎭B .{x |x >a }C .{x x a 或1x a ⎫<⎬⎭D .1|x x a ⎧⎫<⎨⎬⎩⎭【答案】A 【解析】 【分析】当1a <-时,根据开口方向及根的大小关系确定不等式的解集. 【详解】因为1a <-,所以1()0a x a x a ⎛⎫--< ⎪⎝⎭等价于1()0x a x a ⎛⎫--> ⎪⎝⎭,又因为当1a <-时,1a a >,所以不等式1()0x a x a ⎛⎫--> ⎪⎝⎭的解集为:{|x x a <或1x a ⎫>⎬⎭. 故选:A . 【点睛】本题考查含参一元二次不等式的解法,较简单,解答时,注意根的大小关系比较.例8.(2022·全国·高三专题练习)已知定义在R 上的函数()f x 满足()()()f x y f x f y -=-,且当0x <时,()0f x >,则关于x 的不等式()()()()2222f mx f m f m x f x +>+(其中0m < )A .2x m x m ⎧⎫<<⎨⎬⎩⎭B .{|x x m <或2}x m >C .2x x m m ⎧⎫<<⎨⎬⎩⎭D .{|x x m >或2}x m<【答案】A 【解析】 【分析】先判断函数()f x 单调递减,再利用已知条件和函数的单调性得()()20mx x m --<,解不等式即得解. 【详解】任取12x x <,由已知得()120f x x ->,即()()120f x f x ->,所以函数()f x 单调递减.由()()()()2222f mx f m f m x f x +>+可得()()()()2222f mx f x f m x f m ->-,即()22f mx x f ->()22m x m -,所以2222mx x m x m -<-,即()22220mx m x m -++<,即()()20mx x m --<,又因为0m << 所以2m m >,此时原不等式解集为2x m x m ⎧⎫<<⎨⎬⎩⎭.故选:A 【点睛】方法点睛:解抽象函数不等式一般先要判断函数的单调性,再利用单调性化抽象函数不等式为具体的函数不等式解答.例9.(2022·全国·高三专题练习)在关于x 的不等式2(1)0x a x a -++<的解集中至多包含2个整数,则a 的取值范围是 A .(3,5)-B .(2,4)-C .[3,5]-D .[2,4]-【解析】 【详解】因为关于x 的不等式2(1)0x a x a -++<可化为(1)()0x x a --<, 当1a >时,不等式的解集为1x a <<, 当1a <时,不等式的解集为1<<a x ,要使得解集中至多包含2个整数,则4a ≤且2a ≥-,所以实数a 的取值范围是[2,4]a ∈-,故选D.点睛:本题主要考查了不等式解集中整数解的存在性问题,其中解答中涉及到一元二次不等式的求解,元素与集合的关系等知识点的综合应用,试题比较基础,属于基础题,同时着重考查了分类讨论思想的应用,解答中正确求解不等式的解集是解答的关键.例10.(2022·浙江·高三专题练习)设R a ∈,关于x 的二次不等式2220ax x a -->的解集为A ,集合{}12B x x =<<,满足A B ⋂≠∅,求实数a 的取值范围. 【答案】()(),22,∞∞--⋃+ 【解析】 【分析】由题意0a ≠,求出方程2220ax x a --=的两根,讨论a 的正负,确定二次不等式的解集A 的形式,然后结合数轴列出不等式求解即可得答案. 【详解】解:由题意0a ≠,令2220ax x a --=,解得两根为1211x x aa ==由此可知120,0x x <>, 当0a >时,解集{}{}12||A x x x x x x =<>,因为120,1x x <>,所以A B ⋂≠∅的充要条件是22x<,即12a ,解得2a >;当0a <时,解集{}12|A x x x x =<<,因为120,2x x <<,所以A B ⋂≠∅的充要条件是21>x ,即11a>,解得2a <-;综上,实数a 的取值范围为()(),22,∞∞--⋃+.例11.(2022·全国·高三专题练习)已知关于x 的不等式(kx -k 2-4)(x -4)>0,其中k ∈R. (1)当k 变化时,试求不等式的解集A ;(2)对于不等式的解集A ,若满足A ∩Z =B (其中Z 为整数集).试探究集合B 能否为有限集?若能,求出使得集合B 中元素个数最少的k 的所有取值,并用列举法表示集合B ;若不能,请说明理由. 【答案】(1)答案见解析(2)能;2k =-,B ={-3,-2,-1,0,1,2,3} 【解析】(1)对k 进行分类讨论,结合一元二次不等式的解法求得不等式的解集A . (2)结合(1)的结论进行分类讨论,结合基本不等式求得和正确答案. (1)当k =0时,A ={x |x <4};当k >0且k ≠2时,A ={x |x <4或4x k k>+}; 当k =2时,A ={x |x ≠4};当k <0时,A ={x |4k k+<x <4}. (2)由(1)知:当k ≥0时,集合B 中的元素的个数有无限个;当k <0时,集合B 中的元素的个数有限,此时集合B 为有限集. 因为4k k+=-[(-k )+()4k -]≤-4,当且仅当k =-2时取等号, 所以当k =-2时,集合B 中的元素个数最少,此时A ={x |-4<x <4},故集合B ={-3,-2,-1,0,1,2,3}.例12.(2022·全国·高三专题练习)已知关于x 的不等式21ln 02x mx x m ---<的解集为(,)a b ,其中0a >,若该不等式在(,)a b 中有且只有一个整数解,求实数m 的取值范围 【答案】12ln2(,]43-【解析】 【分析】将不等式转化为22ln 2(1)x x m x ->+,构造函数22ln ()=2(1)x xf x x -+,利用导数判断单调性,结合题意即可求解.【详解】关于x 的不等式21ln 02x mx x m ---<化为:22ln 2(1)x x m x ->+,令22ln ()=2(1)x xf x x -+,0x >,则3222222ln ()2(1)x x x x xf x x x +--+'=+.令32()2222ln u x x x x x x =+--+,2()342ln u x x x x '=++在(0,)+∞上单调递增,因此存在0(0,1)x ∈,使得20000()342ln 0u x x x x '=++=,20002ln 34x x x =--, 3232232200000000000000000()2222ln 222(34)22222(1)(1)0u x x x x x x x x x x x x x x x x x =+--+=+--+--=----=-++<,u (1)10=-<,u (2)104ln20=+>.因此存在1(1,2)x ∈,使得1()0u x =,因此函数()f x 在1(0,)x 内单调递减,在1(x ,)∞+单调递增.f (1)14=,f (2)2ln23-=.关于x 的不等式21ln 02x mx x m ---<的解集为(,)a b ,其中0a >, 该不等式在(,)a b 中有且只有一个整数解,∴实数m 的取值范围是12ln2(,]43-.【方法技巧与总结】 1.数形结合处理.2.含参时注意分类讨论.题型三:一元二次不等式与韦达定理及判别式例13.(2022·湖南岳阳·二模)已知关于x 的不等式2240ax bx ++<的解集为4,m m ⎛⎫⎪⎝⎭,其中0m <,则44b a b +的最小值为( ) A .2- B .1 C .2 D .8【答案】C 【解析】 【分析】由一元二次不等式的解与方程根的关系求出系数1a =,确定2b ≥,然后结合基本不等式得最小值. 【详解】2240ax bx ++<的解集为4,m m ⎛⎫ ⎪⎝⎭,则2240ax bx ++=的两根为m ,4m ,∴44m m a ⋅=,∴1a =,42m b m +=-,则424b m m=-+≥-,即2b ≥,44244b b a b b +=+≥,当且仅当4b =时取“=”, 故选:C.例14.(2022·江苏南京·模拟预测)已知关于x 的不等式22430(0)x ax a a -+<<的解集为()12x x ,,则1212ax x x x ++的最大值是( ) AB.CD. 【答案】D 【解析】 【分析】一元二次不等式解集转化为一元二次方程的解,根据韦达定理求出124x x a +=,2123x x a =,再用基本不等式求出最值【详解】22430(0)x ax a a -+<<的解集为()12x x ,,则12x x ,是方程22430-+=x ax a 的两个根,故124x x a +=,2123x x a =,故1212143a x x a x x a++=+ 因为0a <,所以有基本不等式得:114433a a a a ⎡⎤⎛⎫+=--+-≤-= ⎪⎢⎥⎝⎭⎣⎦,当且仅当143a a -=-即a =1212a x x x x ++的最大值为 故选:D(多选题)例15.(2022·全国·高三专题练习)已知关于x 的不等式20ax bx c ++>的解集为(,2)(3,)-∞-⋃+∞,则( ) A .0a >B .不等式0bx c +>的解集是{}|6x x <-C .0a b c ++>D .不等式20cx bx a -+<的解集为11(,)(,)32-∞-⋃+∞【答案】ABD 【解析】 【分析】根据不等式20ax bx c ++>的解集判断出0a >,结合根与系数关系、一元二次不等式的解法判断BCD 选项的正确性.【详解】关于x 的不等式20ax bx c ++>的解集为()(),23,,0,A a ∞∞--⋃+∴>选项正确; 且-2和3是关于x 的方程20ax bx c ++=的两根,由韦达定理得2323b a c a ⎧-+=-⎪⎪⎨⎪-⨯=⎪⎩,则,6b a c a =-=-,则60a b c a ++=-<,C 选项错误; 不等式0bx c +>即为60ax a -->,解得6,B x <-选项正确;不等式20cx bx a -+<即为260ax ax a -++<,即2610x x -->,解得13x <-或1,D 2x >选项正确. 故选:ABD .例16.(2022·全国·高三专题练习)若不等式2510ax x ++≤的解集为1123x x ⎧⎫-≤≤-⎨⎬⎩⎭,则不等式303x ax -<-的解集为___________. 【答案】{}23x x <<【解析】 【分析】由不等式2510ax x ++≤的解集为1123x x ⎧⎫-≤≤-⎨⎬⎩⎭可得参数a 的值,则不等式303x ax -<-也具体化了,按分式不等式解之即可. 【详解】由不等式2510ax x ++≤的解集为1123x x ⎧⎫-≤≤-⎨⎬⎩⎭,可知方程251=0ax x ++有两根121123x x =-=-,,故6a =,则不等式303x ax -<-即3603x x -<-等价于3(2)(3)0x x --<, 不等式3(2)(3)0x x --<的解集为{}23x x <<, 则不等式303x ax -<-的解集为{}23x x <<, 故答案为:{}23x x <<.例17.(2022·全国·高三专题练习)已知不等式210ax bx --≥的解集是11|23⎧⎫-≤≤-⎨⎬⎩⎭x x ,则不等式20x bx a --< 的解集是________.【答案】{|23}x x << 【解析】【分析】根据给定的解集求出a ,b 的值,再代入解不等式即可作答. 【详解】依题意,12-,13-是方程210ax bx --=的两个根,且0a <,于是得11()()23111()()23b aa ⎧-+-=⎪⎪⎨⎪-⨯-=-⎪⎩,解得:6,5ab =-=,因此,不等式20x bx a --<为:2560x x -+<,解得23x <<, 所以不等式20x bx a --< 的解集是{|23}x x <<. 故答案为:{|23}x x <<【方法技巧与总结】1.一定要牢记二次函数的基本性质.2.含参的注意利用根与系数的关系找关系进行代换. 题型四:其他不等式解法例18.(2022·上海市青浦高级中学高三阶段练习)不等式是12x>的解集为______. 【答案】10,2⎛⎫ ⎪⎝⎭【解析】 【分析】 由12x>可得120x ->,结合分式不等式的解法即可求解.【详解】 由12x >可得120x ->,整理可得:120xx ->,则()210x x -<,解可得:102x <<. 所以不等式是12x >的解集为: 10,2⎛⎫ ⎪⎝⎭. 故答案为:10,2⎛⎫⎪⎝⎭.例19.(2022·全国·高三专题练习)不等式111x >+的解集为___________. 【答案】()1,0- 【解析】【分析】根据分式不等式的解法进行求解. 【详解】1111000101111x x x x x x x ->⇒->⇒>⇒<⇒-<<++++, 故答案为:()1,0-.例20.(2022·全国·高三专题练习)写出一个解集为()0,2的分式不等式___________. 【答案】02xx <- 【解析】 【分析】由题意根据分式不等式的解法,得出结论. 【详解】一个解集为()0,2的分式不等式可以是02xx <-, 故答案为:02xx <-.(答案不唯一) 例21.(2022·上海·高三专题练习)关于x 230≥的解集为_________.【答案】[4,5) 【解析】 【分析】通过2330x x -+>0≥恒成立,将不等式最终转化为405010x x x -≥⎧⎪->⎨⎪+≠⎩,解出即可.【详解】解:对于233x x -+,有23340∆=-⨯<,则2330x x -+>恒成立,0≥恒成立,2323(34)00150x x x x ⎧--≥⎪≥⇔+⎨⎪->⎩又2333(34)(4)(1)11x x x x x x ---+=++, 23(34)0150x x x x ⎧--≥⎪∴+⎨⎪->⎩, 2333(34)(4)(1)x x x x --=-+405010x x x -≥⎧⎪∴->⎨⎪+≠⎩解得不等式的解集为[4,5).故答案为:[4,5). 【点睛】本题考查分式不等式的求解,发现部分因式恒大于零,以及分母不为零是解题的关键,是中档题. 例22.(2022·四川德阳·三模(文))对于问题:“已知关于x 的不等式20ax bx c ++>的解集为()1,2-,解关于x 的不等式20ax bx c -+>”,给出如下一种解法: 解析:由20ax bx c ++>的解集()1,2-,得()()20a x b x c -+-+>的解集为()2,1-,即关于x 的不等式20ax bx c -+>的解集为()2,1-. 参考上述解法,若关于x 的不等式0k x b x a x c ++<++的解集为111,,1,32⎛⎫⎛⎫--⋃ ⎪ ⎪⎝⎭⎝⎭关于x 的不等式1011kx bx ax cx ++<++的解集为____. 【答案】()()3,11,2--.【解析】 【分析】 关于x 的不等式1011kx bx ax cx ++<++可看成前者不等式中的x 用1x 代入可得不等式1011kx bx ax cx ++<++的解集.【详解】 若关于x 的不等式0k x b x a x c ++<++的解集为111,,1,32⎛⎫⎛⎫--⋃ ⎪ ⎪⎝⎭⎝⎭则关于x 的不等式1011kx bx ax cx ++<++可看成前者不等式中的x 用1x 代入可得,则1111,,132x ⎛⎫⎛⎫∈--⋃ ⎪ ⎪⎝⎭⎝⎭,则()()3,11,2x ∈--⋃. 故解集为:()()3,11,2--.【点睛】本题考查不等式的解法,考查方法的类比,正确理解题意是关键.【方法技巧与总结】1.分式不等式化为二次或高次不等式处理. 2.根式不等式绝对值不等式平方处理. 题型五:二次函数根的分布问题例23.(2022·浙江·高三专题练习)若关于x 的方程2210ax ax -+=有两个不同的正根,则实数a 的取值范围是( ) A .()0,1 B .()0,∞+C .()1,+∞D .(),0-∞【答案】C 【解析】 【分析】由0a ≠,判别式0∆>及根与系数关系列出不等式组,即可求出实数a 的取值范围. 【详解】因为关于x 的方程2210ax ax -+=有两个不同的正根,所以2044010a a a a ⎧⎪≠⎪∆=->⎨⎪⎪>⎩,解得1a >,故实数a 的取值范围是()1,+∞.故选:C例24.(2022·全国·高三专题练习)已知函数321()13f x x ax x =+++在(,0)-∞,(3,)+∞上为增函数,在()1,2上为减函数,则实数a 的取值范围为( ) A .(,1]-∞- B .55,34⎡⎤--⎢⎥⎣⎦C .5,13⎛⎤-- ⎥⎝⎦D .55,34⎛⎫-- ⎪⎝⎭【答案】B 【解析】求导得到2()21'=++f x x ax ,然后根据()f x 在(,0)-∞,(3,)+∞上为增函数,在()1,2上为减函数,由(0)0(1)0(2)0(3)0f f f f ''≥⎧⎪≤⎪⎨''≤⎪⎪≥⎩求解. 【详解】已知函数321()13f x x ax x =+++,则2()21'=++f x x ax ,因为()f x 在(,0)-∞,(3,)+∞上为增函数,在()1,2上为减函数,所以(0)0(1)0(2)0(3)0f f f f ''≥⎧⎪≤⎪⎨''≤⎪⎪≥⎩,即10121044109610a a a ≥⎧⎪++≤⎪⎨++≤⎪⎪++≥⎩,解得 5534a -≤≤-, 所以实数a 的取值范围为55,34⎡⎤--⎢⎥⎣⎦故选:B 【点睛】本题主要考查导数与函数的单调性以及二次函数与根的分布,还考查了逻辑推理和运算求解的能力,属于中档题.例25.(2022·全国·高三专题练习)若函数()()()1cos 23sin cos 212f x x a x x a x =+++-在0,2π⎡⎤⎢⎥⎣⎦上单调递减,则实数a 的取值范围为A .11,5⎡⎤-⎢⎥⎣⎦B .1,15⎡⎤-⎢⎥⎣⎦C .[)1,1,5⎛⎤-∞-⋃+∞ ⎥⎝⎦D .(]1,1,5⎡⎫-∞-⋃+∞⎪⎢⎣⎭【答案】A 【解析】化简函数f (x ),根据f (x )在区间0,2π⎡⎤⎢⎥⎣⎦上单调递减,f ′(x )≤0恒成立,由此解不等式求出a 的取值范围.【详解】由函数()()()1cos 23sin cos 212f x x a x x a x =+++-,且f (x )在区间0,2π⎡⎤⎢⎥⎣⎦上单调递减,∴在区间0,2π⎡⎤⎢⎥⎣⎦上,f ′(x )=−sin 2x +3a (cosx −sinx )+2a −1≤0恒成立,∵设4t cosx sinx x π=⎛⎫ ⎪⎝-⎭-,∴当x ∈0,2π⎡⎤⎢⎥⎣⎦时,444x πππ-⎥∈-⎡⎤⎢⎣⎦,,t ∈[−1,1],即−1≤cosx −sinx ≤1,令t ∈[−1,1],sin 2x =1−t 2∈[0,1],原式等价于t 2+3at +2a −2≤0,当t ∈[−1,1]时恒成立,令g (t )=t 2+3at +2a −2,只需满足312(1)510a g a ⎧-≤-⎪⎨⎪=-≤⎩或312(1)10ag a ⎧-≥⎪⎨⎪-=--≤⎩或3112(1)510(1)10a g a g a ⎧-<-<⎪⎪=-≤⎨⎪-=--≤⎪⎩,解得∅或213a -≤≤-或2135a -<≤,综上,可得实数a 的取值范围是11,5⎡⎤-⎢⎥⎣⎦,故选:A . 【点睛】本题考查三角函数的公式及导数的应用,解题的关键是利用换元将不等式恒成立问题转化为一元二次不等式恒成立问题,属于较难题.例26.(2022·全国·高三专题练习)已知曲线322()13f x x x ax =-+-上存在两条斜率为3的不同切线,且切点的横坐标都大于零,则实数a 可能的取值( ) A .196B .3C .103 D .92【答案】AC 【解析】 【分析】本题先求导函数并根据题意建立关于m 的方程,再根据根的分布求a 的取值范围,最后判断得到答案即可. 【详解】 解:∵ 322()13f x x x ax =-+-, ∴ 2()22f x x x a '=-+,可令切点的横坐标为m ,且0m >,可得切线斜率2223k m m a =-+=即22230m m a -+-=,由题意,可得关于m 的方程22230m m a -+-=有两个不等的正根,且可知1210m m +=>,则1200m m ∆>⎧⎨⋅>⎩,即2242(3)0302a a ⎧-⨯⨯->⎪⎨->⎪⎩, 解得:732a <<,所以a 的取值可能为196,103. 故选:AC. 【点睛】本题考查求导函数,导数的几何意义,根的分布,是中档题.例27.(2022·全国·高三专题练习)若一元二次方程2(1)30mx m x -++=的两个实根都大于1-,则m 的取值范围____【答案】2m <-或5m ≥+ 【解析】根据一元二次方程根的分布建立不等式组,解之可得答案. 【详解】由题意得应满足0,11,20,(1)0m m m mf ≠⎧⎪+⎪>-⎪⎨⎪∆≥⎪->⎪⎩解得:2m <-或5m ≥+.故答案为:2m <-或5m ≥+.例28.(2022·全国·高三专题练习)设2()32f x ax bx c =++,若0,(0)0,(1)0a b c f f ++=>>,求证: (Ⅰ) 0a >且21ba-<<-; (Ⅰ)方程()0f x =在(0,1)内有两个实根. 【答案】(Ⅰ)见解析;(Ⅰ)见解析. 【解析】 【分析】(Ⅰ)先由条件求得,a c 的符号,结合条件可得; (Ⅰ)根据(0),(1)()3bf f f a-的符号可得. 【详解】(Ⅰ)因为(0)0,(1)0f f >>,所以0,320c a b c >++>. 由条件0a b c ++=,消去b ,得0a c ;由条件0a b c ++=,消去c ,得0a b +<,20a b +>.故21ba-<<-. (Ⅰ)函数2()32f x ax bx c =++的顶点坐标为23(,)33b ac b a a--,在21b a -<<-的两边乘以13-,得12333b a <-<.又因为(0)0,(1)0,f f >>而22()0,33b a c acf a a+--=-<又因为2()32f x ax bx c =++在(0,)3ba -上单调递减,在(,1)3b a-上单调递增, 所以方程()0f x =在区间(0,)3ba -与(,1)3b a-内分别各有一实根. 【方法技巧与总结】解决一元二次方程的根的分布时,常常需考虑:判别式,对称轴,特殊点的函数值的正负,所对应的二次函数图象的开口方向.【过关测试】 一、单选题1.(2022·河南·南阳中学高三阶段练习(文))已知集合{}2280A x x x =--≤,203x B xx ⎧⎫-=≤⎨⎬+⎩⎭,则A B ⋃=( ) A .{}22x x -≤≤ B .{}42,3x x x -≤≤≠- C .{}34x x ≤≤ D .{}34x x -<≤【答案】D 【解析】 【分析】由一元二次不等式的解法和简单分式不等式的解法求出集合,A B ,然后根据并集的定义即可求解. 【详解】解:因为集合{}{}228024A x x x x x =--≤=-≤≤,()(){}2302032330x x x B x x x x x x ⎧⎫⎧-+≤⎧⎫-⎪⎪=≤==-<≤⎨⎬⎨⎨⎬++≠⎩⎭⎩⎪⎪⎩⎭,所以{}34A B x x ⋃=-<≤, 故选:D.2.(2022·河北·模拟预测)“11a <”是“2,20x x x a ∃∈-+<R ”的( ) A .充分不必要条件 B .必要不充分条件 C .充要条件 D .既不充分也不必要条件【答案】B 【解析】【分析】2,20x x x a ∃∈-+<R ,列出不等式,求出1a <,从而判断出答案. 【详解】2,20x x x a ∃∈-+<R ,则要满足440a ∆=->,解得:1a <,因为11a <⇒1a <,但111a a <⇒<故“11a <”是“2,20x x x a ∃∈-+<R ”的必要不充分条件. 故选:B3.(2022·陕西·模拟预测(理))已知集合234|0A x x x ,{}2|B x a x a =<<,若A B =∅,则实数a 的取值范围是( ) A .(],1-∞- B .[)4,+∞ C .()(),12,4-∞-⋃ D .[][)1,24,-⋃+∞【答案】D 【解析】 【分析】由题知{}1,4A =-,进而分B =∅和B ≠∅空集两种情况讨论求解即可. 【详解】解:由题知{}{}2|3401,4A x x x =--==-,因为A B =∅, 所以,当{}2|B x a x a=<<=∅时,2a a≥,解得01a ≤≤,当{}2|B x a x a =<<≠∅时,2241a a a a ⎧≤⎪≥-⎨⎪>⎩或24a a a ≥⎧⎨>⎩,解得[)(][)1,01,24,a ∈-+∞,综上,实数a 的取值范围是[][)1,24,-⋃+∞. 故选:D4.(2022·重庆南开中学模拟预测)已知函数()()ln ln 2cos 2f x x x x π=---,则关于t 的不等式()()20f t f t +<的解集为( )A .()2,1- B.(-C .()0,1D.(【答案】C 【解析】 【分析】根据函数解析式判断函数关于点(1,0)成中心对称,再由基本初等函数判断函数单调性,转化原不等式后求解即可. 【详解】()()ππln ln 2cosln 2ln cos(π)0)2()(22f x f x x x x x x x ----+----=+=, ()f x ∴图象关于点(1,0)成中心对称,又()()ln ln 2cos2f x x x x π=---的定义域为(0,2),由πln ,ln(2),cos 2y x y x y x ==--=-在(0,2)上单调递增知, ()()ln ln 2cos2f x x x x π=---在(0,2)上递增,()()20f t f t +<,()20(2)f f t t ∴+-<-,即()2(2)f t f t <-,22t t ∴<-,解得21t -<<,又20202t t <<⎧⎨<<⎩,解得0t << 所以01t <<. 故选:C5.(2022·山西·二模(理))已知集合{}23A x x =∈<Z ,32B x a x a ⎧⎫=<<+⎨⎬⎩⎭,若A B 有2个元素,则实数a 的取值范围是( ) A .3,12⎛⎫-- ⎪⎝⎭B .3,02⎛⎫- ⎪⎝⎭C .()3,01,2⎛⎫-⋃+∞ ⎪⎝⎭D .31,1,022⎛⎫⎛⎫--⋃- ⎪ ⎪⎝⎭⎝⎭【答案】D 【解析】 【分析】由题知{}1,0,1A =-,进而根据题意求解即可. 【详解】解:因为{}{}231,0,1A x Z x =∈<=-,32B x a x a ⎧⎫=<<+⎨⎬⎩⎭,若A B 有2个元素,则13012a a <-⎧⎪⎨<+≤⎪⎩或10312a a -≤<⎧⎪⎨+>⎪⎩,解得312a -<<-或102a -<<, 所以,实数a 的取值范围是31,1,022⎛⎫⎛⎫--⋃- ⎪ ⎪⎝⎭⎝⎭.故选:D .6.(2022·重庆·高三阶段练习)若关于x 的不等式sin |sin |2x x k -≤对任意5,66x ππ⎡⎤∈⎢⎥⎣⎦恒成立,则实数k 的取值范围为( )A .[1,3]- B .75,22⎡⎤-⎢⎥⎣⎦C.[1,- D.[1,【答案】A 【解析】【分析】令1sin ,[,1]2t x t =∈,则||2t t k -≤.对k 进行讨论,即可求出答案.【详解】令1sin ,[,1]2t x t =∈,则||2t t k -≤.(1)当12k <时,则2()220t t k t kt -≤⇒--≤, 令2()2g t t kt =--,max ()(1)101g t g k k ==--≤⇒≥-.故112k -≤<. (2)当1k >时,则2()220t k t t kt -≤⇒-+≥, 令2()2g t t kt =-+ ①当12k<时,212k k <⇒<<,则22min ()()201242k k k g t g k ==-+≥⇒<≤②当12k≥时,2k ≥, 则min ()(1)120323g x g k k k ==-+≥⇒≤⇒≤≤ 故13k << (3)当112k ≤≤时,则||2t t k -≤在1[,1]2t ∈上恒成立, 故112k ≤≤. 综上所述:[1,3]k ∈- 故选:A.7.(2022·江苏无锡·模拟预测)已知实数a ,b 满足如下两个条件:(1)关于x 的方程2320x x ab --=有两个异号的实根;(2)211a b+=,若对于上述的一切实数a ,b ,不等式222a b m m +>+恒成立,则实数m 的取值范围是( ) A .()4,2- B .()2,4-C .][(),42,-∞-⋃+∞ D .][(),24,-∞-⋃+∞【答案】A 【解析】 【分析】首先判断0,0a b >>,再化简()214224a b a b a b a b b a ⎛⎫+=++=++ ⎪⎝⎭,利用基本不等式求解.【详解】解:设方程2320x x ab --=的两个异号的实根分别为1x ,2x ,则1203abx x =-<,0ab ∴>. 又211a b+=,0a ∴>,0b >,则()21422448a b a b a b a b b a ⎛⎫+=++=++≥+= ⎪⎝⎭(当且仅当4a =,2b =时取“=”), 由不等式222a b m m +>+恒成立,得228m m +<,解得42m -<<.∴实数m 的取值范围是()4,2-. 故选:A .8.(2022·全国·高三专题练习)已知[1a ∈-,1],不等式2(4)420x a x a +-+->恒成立,则x 的取值范围为()A .(-∞,2)(3⋃,)∞+B .(-∞,1)(2⋃,)∞+C .(-∞,1)(3⋃,)∞+D .(1,3)【答案】C 【解析】 【分析】把不等式看作是关于a 的一元一次不等式,然后构造函数()2(2)44f a x a x x =-+-+,由不等式在[1-,1]上恒成立,得到(1)0(1)0f f ->⎧⎨>⎩,求解关于a 的不等式组得x 得取值范围.【详解】解:令()2(2)44f a x a x x =-+-+,则不等式2(4)420x a x a +-+->恒成立转化为()0f a >在[1,1]a ∈-上恒成立.∴有(1)0(1)0f f ->⎧⎨>⎩,即22(2)4402440x x x x x x ⎧--+-+>⎨-+-+>⎩, 整理得:22560320x x x x ⎧-+>⎨-+>⎩,解得:1x <或3x >.x 的取值范围为()(),13,-∞⋃+∞. 故选:C . 二、多选题9.(2022·全国·高三专题练习)若不等式2sin sin 20x a x -+≥对任意的0,2x π⎛⎤∈ ⎥⎝⎦恒成立,则实数a 可能是A .1B .2C .3D .4【答案】ABC 【解析】 【分析】利用换元法令sin t x =,不等式可整理为220t at -+≥在(]0,1t ∈上恒成立,即2a t t ≤+,即min 2a t t ⎛⎫≤+ ⎪⎝⎭,求函数的最小值即可得解. 【详解】设sin t x =,0,2x π⎛⎤∈ ⎥⎝⎦,(]0,1t ∴∈则不等式2sin sin 20x a x -+≥对任意0,2x π⎛⎤∈ ⎥⎝⎦恒成立,即转化为不等式220t at -+≥在(]0,1t ∈上恒成立, 即转化为222t a t t t+≤=+在(]0,1t ∈上恒成立, 由对勾函数知2y t t=+在(]0,1t ∈上单减,min 2131y =+=,3a ∴≤故选:ABC 【点睛】关键点点睛:本题主要考查不等式恒成立问题,利用换元法结合对勾函数的单调性求出函数的最值是解题的关键,考查学生的转化与化归能力,属于一般题.10.(2022·江苏·高三专题练习)已知不等式20ax bx c ++>的解集为{}x m x n <<,其中0m >,则以下选项正确的有( ) A .0a <B .0c >C .20cx bx a ++>的解集为11x x nm ⎧⎫<<⎨⎬⎩⎭D .20cx bx a ++>的解集为{1x x n<或}1x m >【答案】AC 【解析】由一元二次不等式的解法,再结合根与系数的关系逐个分析判断可得答案 【详解】解:因为不等式20ax bx c ++>的解集为{}x m x n <<,其中0m >, 所以0a <,,m n 是方程20ax bx c ++=的两个根,所以A 正确; 所以b m n a c mn a ⎧+=-⎪⎪⎨⎪=⎪⎩,解得()b m n a c mna =-+⎧⎨=⎩,因为0m >,m n <,所以0n >,又由于0a <,所以0c mna =<,所以B 错误; 所以20cx bx a ++>可化为2()0mnax m n ax a -++>, 即2()10mnx m n x -++<,即(1)(1)0mx nx --<, 因为0n m >>,所以11n m<, 所以不等式20cx bx a ++>的解集为11x x nm ⎧⎫<<⎨⎬⎩⎭,所以C 正确,D 错误, 故选:AC 【点睛】关键点点睛:此题考查一元二次不等式的解法的应用,解题的关键由一元二次不等式的解法可知0a <,且,m n 是方程20ax bx c ++=的两个根,再利用根与系数的关系得b m n a c mn a ⎧+=-⎪⎪⎨⎪=⎪⎩,再求得()b m n a c mna =-+⎧⎨=⎩,从而可求解不等式20cx bx a ++>,考查转化思想,属于中档题11.(2022·全国·高三专题练习)已知函数()222f x x mx m =--,则下列命题正确的有( )A .当0m ≠时,()0f x <的解集为2mx x m ⎧⎫-<<⎨⎬⎩⎭B .当1m =时,[)12,1,x x ∀∈+∞时,()()()12120x x f x f x -->⎡⎤⎣⎦C .121,,4x x m ⎛⎤∀∈-∞ ⎥⎝⎦且12x x ≠时,()()121222f x f x x x f ++⎛⎫> ⎪⎝⎭D .当0m <时,若120x x <<,则()()2112>x f x x f x 【答案】BC 【解析】对于A ,分0m >和0m <时求解不等式; 对于B ,根据函数的单调性可判断;对于C ,根据函数的单调性,任取两点,根据数形结合的方式可判断;对于D ,构造函数()()(0)f x g x x x=>,看作()y f x =在y 轴右侧图象上的点与原点所在直线的斜率, 数形结合可判断单调性,即可得出结果. 【详解】对于A ,由2220x mx m --<得()(2)0x m x m -+<,当0m >时,原不等式的解集为|2m x x m ⎧⎫-<<⎨⎬⎩⎭;当0m <时,原不等式的解集为|2m x m x ⎧⎫<<-⎨⎬⎩⎭,故A 错误;对于B ,1m =时,2219()212()48f x x x x =--=--在[)1+∞,上是增函数,则1212()()0f x f x x x ->-,即()[]1212()()0x x f x f x -->,故B 正确;对于C. ()f x 在1,4⎛⎤-∞ ⎥⎝⎦m 上单调递减,当121,4x x m ⎛⎤∈-∞ ⎥⎝⎦,时,设11(,())A x f x 、()22,()B x f x ,则AB 的中点C1212()(),22x x f x f x ++⎛⎫⎪⎝⎭,又设1212,22x x x D f x ⎛⎫⎛++⎫ ⎪ ⎪⎝⎭⎝⎭, 数形结合可知,点D 位于点C 的下方,即1212()()22x x f x f x f ++⎛⎫< ⎪⎝⎭,故C 正确;对于D ,设()()(0)f x g x x x=>,则()g x 表示()y f x =在y 轴右侧图象上的点与原点所在直线的斜率, 数形结合可知,()g x 是增函数,当120x x <<时,12()()<g x g x ,则1212()()f x f x x x <,即2112()()x f x x f x <,故D 错误.故选:BC. 【点睛】关键点睛:本题考查二次函数性质的综合应用,对于CD 选项的判断,关键是根据函数的单调性,利用数形结合的方法进行判断.12.(2022·重庆巴蜀中学高三阶段练习)已知两个变量x ,y 的关系式(,)(1)f x y x y =-,则以下说法正确的是( )A .(1,3)(3,1)0f f ==B .对任意实数a ,都有1(,)4f a a ≤成立 C .若对任意实数x ,不等式(,)4f x a x a -≤-+恒成立,则实数a 的取值范围是[5,3]- D .若对任意正实数a ,不等式(,)4f x a x a -≤-+恒成立,则实数x 的取值范围是(,0)-∞ 【答案】BC 【解析】 【分析】(1,3)f 和(3,1)f 的值直接代入即可求得,1(,)4f a a ≤转化为求二次函数最大值的问题,若对任意实数x ,不等式(,)4f x a x a -≤-+恒成立转化为关于x 的二次函数与x 轴至多有一个交点的问题,若对任意正实数a ,不等式(,)4f x a x a -≤-+恒成立转化为关于a 的一次函数在0a >内恒大于等于零恒成立的问题.【详解】对于选项A ,()(1,3)1132f =⨯-=-,()(3,1)3110f =⨯-=,即(1,3)(3,1)f f ≠,则A 选项错误;对于选项B ,()22211111(,)144244f a a a a a a a a a ⎛⎫⎛⎫=-=-=--++=--+≤ ⎪ ⎪⎝⎭⎝⎭,则B 选项正确;对于选项C , ()()()2(,)114f x a x x a x x a x a a -=--=-++-≤-+ 恒成立,即()2140x a x -++≥ 恒成立,则()21160a ∆=+-≤,解得53a -≤≤,即实数a 的取值范围是[5,3]-,则C选项正确;对于选项D ,()2140x a x -++≥ 恒成立,令()24 0y ax x x a =-+-+>,当0x >时,该函数看成关于a 的一次函数,函数单调递减,不可能恒大于0,当0x =时,40y =≥成立,当0x <时,该函数看成关于a 的一次函数,函数单调递增,当0a =时,24y x x =-+211544x x =-++2115024x ⎛⎫=-+> ⎪⎝⎭,则实数x 的取值范围是(],0-∞,则D 选项错误;故选:BC . 三、填空题13.(2022·全国·高三专题练习)不等式210ax x c a++>的解集为{|21}x x -<<,则函数y =递增区间是_______ 【答案】[0,1] 【解析】根据不等式的解集可知一元二次不等式所对应的一元二次方程的根,利用韦达定理可求出a ,c 的值,再根据复合函数求单调区间的方法,得出单调递增区间. 【详解】由题知-2和1是210ax x c a++=的两根, 由根与系数的关系知-2+1=21a -,−2×1=c a , 由不等式的解集为{|21}x x -<<,可知0a <, 12a c ∴=-=,,则y因为函数y []0,2x ∈,令()22g x x x =-+则该函数的增区间为(],1-∞所以y =[]0,1 故答案为:[]0,1.14.(2022·浙江·高三专题练习)若不等式2(3)16x b -<的解集中的整数有且仅有1,2,3,则实数b 的取值范围是___________. 【答案】()5,7 【解析】 【分析】首先解一元二次不等式,求出不等式的解集,再根据解集中整数的情况,得到不等式组,解得即可;【详解】 解:因为2(3)16x b -<,所以()()34340x b x b -+--<,解得4433b b x -+<<,所以原不等式的解集为44|33b b x x -+⎧⎫<<⎨⎬⎩⎭,又解集中的整数有且仅有1,2,3, 所以40134343b b -⎧<⎪⎪⎨+⎪<⎪⎩解得:57b <<,即()5,7b ∈,故答案为:()5,7.15.(2022·全国·高三专题练习)若关于x 的不等式()2220x a x a -++->恰有1个正整数解,则a 的取值范围是___________. 【答案】()(],13,4-∞【解析】 【分析】先解带有参数的一元二次不等式,再对a 进行分类讨论,使得恰有1个正整数解,最后求出a 的取值范围 【详解】不等式()2220x a x a -++->等价于()2220x a x a -++<.令()2220x a x a -++=,解得2x =或x a =.当2a >时,不等式()2220x a x a -++<的解集为()2,a ,要想恰有1个正整数解,则34a <; 当2a =时,不等式()2220x a x a -++<无解,所以2a =不符合题意; 当2a <时,不等式()2220x a x a -++<的解集为(),2a ,则1a <.综上,a 的取值范围是()(],13,4-∞.故答案为:()(],13,4-∞16.(2022·全国·高三专题练习)设a ,b ,c R ∈,对任意满足1x 的实数x ,都有21ax bx c ++,则a b c++的最大可能值为__. 【答案】3 【解析】 【分析】可先通过赋值0x =,判断1c ≤,再令1,0c b =-=,结合二次函数最值,可得所求最大值. 【详解】任意满足1x 的实数x ,都有21ax bx c ++,若0x =,则1c ,可取1c =-,0b =,可得211ax -,即22ax ≤恒成立,由于201x ,可得a 最大取2, 可得3a b c ++,即有a b c ++的最大可能值为3. 故答案为:3. 四、解答题17.(2022·北京·高三学业考试)已知函数2()1f x x mx =++(m 是常数)的图象过点(1,2). (1)求()f x 的解析式;(2)求不等式()21f x x <+的解集. 【答案】(1)2()1f x x =+; (2)(0,2). 【解析】 【分析】(1)把点代入解析式可得0m =,即得; (2)利用一元二次不等式的解法即得. (1)由题意,(1)22f m =+=, 所以0m =.。
(浙江专用)高考数学一轮复习 专题十 计数原理 10.1 计数原理与排列、组合试题(含解析)-人教版

专题十计数原理【考情探究】课标解读考情分析备考指导主题内容一、计数原理、排列、组合1.分类加法计数原理,分步乘法计数原理(1)理解分类加法计数原理和分步乘法计数原理.(2)会用两个原理分析和解决一些简单的实际问题.2.排列与组合(1)理解排列、组合的概念.(2)能利用计数原理推导排列数公式、组合数公式.(3)能解决简单的实际问题.从近几年高考命题情况来看,这一部分主要考查分类加法、分步乘法计数原理以及排列、组合的简单应用.题型以选择题、填空题为主,在解答题中一般将排列、组合知识综合起来,有时也与求事件概率,分布列问题相结合考查.1.求特定项系数问题可以分两步完成:第一步是根据所给出的条件(特定项)和通项公式建立方程来确定指数(求解时要注意二项式系数中n和r的隐含条件,即n,r均为非负整数,且n≥r);第二步是根据所求的指数求解所求的项.2.有理项是字母指数为整数的项.解此类问题必须合并通项公式中同一字母的指数,根据具体要求,令其为整数,再根据数的整除性来求解.1.用排列、组合知识解决计数问题时,如果遇到的情况较为复杂,即分类较多,标准也较多,同时所求计数的结果不太容易计算时,往往利用表格法、树状图法将其所有的可能一一列举出来,这样会更容易得出结果.2.求解二项展开式的特定项时,即求展开式中的某一项,如第n项,常数项、有理项、字母指数为某些特殊值的项,先准确写出通项T r+1=r a n-r b r,再把系数与字母分离出来(注意符号),最后根据题目中所指定的字母的指数所具有的特征,列出关系式求解即可.二、二项式定理1.能用计数原理证明二项式定理.2.会用二项式定理解决与二项展开式有关的简单问题.【真题探秘】§10.1计数原理与排列、组合基础篇固本夯基【基础集训】考点计数原理、排列、组合1.甲、乙、丙、丁、戊、己6名同学站成一排照毕业相,要求甲不站在两侧,而且乙和丙相邻、丁和戊相邻,则不同的站法种数为( )A.60B.96C.48D.72答案 C2.在我国第一艘航空母舰“某某舰”的某次舰载机起降飞行训练中,有5架“歼-15”飞机甲、乙、丙、丁、戊准备着舰,规定乙机不能最先着舰,且丙机必须在甲机之前着舰(不一定相邻),那么不同的着舰方法种数为( )A.24B.36C.48D.96答案 C3.中国国家队在2018俄罗斯世界杯亚洲区预选赛12强小组赛中以1比0力克韩国国家队,赛后有六名队员打算排成一排照相,其中队长主动要求排在排头或排尾,甲、乙两人必须相邻,则满足要求的排法有( )A.34种B.48种C.96种D.144种答案 C4.某医院拟派2名内科医生、3名外科医生和3名护士共8人组成两个医疗分队,平均分到甲、乙两个村进行义务巡诊,其中每个分队都必须有内科医生、外科医生和护士,则不同的分配方案有( )A.72种B.36种C.24种D.18种答案 B5.将5个不同的球放入4个不同的盒子中,每个盒子至少放一个球,则不同放法共有( )A.480种B.360种C.240种D.120种答案 C6.高考结束后6名同学游览某市包括日月湖在内的6个景区,每名同学任选一个景区游览,则有且只有两名同学选择日月湖景区的方案有( )A.A62×A54种B.A62×54种C.C62×A54种D.C62×54种答案 D7.如图所示,用五种不同的颜色分别给A、B、C、D四个区域涂色,相邻区域必须涂不同颜色,若允许同一种颜色多次使用,则不同的涂色方法共有种.答案1808.有3女2男共5名志愿者要全部分到3个社区去参加志愿服务,每个社区1到2人,甲、乙两名女志愿者需到同一社区,男志愿者到不同社区,则不同的分法种数为.答案12综合篇知能转换【综合集训】考法一排列、组合问题的解题方法1.(2019某某万州二模,6)某中学某班主任要从7名同学(其中3男4女)中选出两名同学,其中一名担任班长,另一名担任学习委员,且这两名同学中既有男生又有女生,则不同的安排方法有( )A.42种B.14种C.12种D.24种答案 D2.(2018某某某某调研性检测,9)用数字0,1,2,3,4组成没有重复数字且大于3 000的四位数,这样的四位数有( )A.250个B.249个C.48个D.24个答案 C3.(2018豫北名校联考,9)2018年元旦假期,高三的8名同学准备拼车去旅游,其中(1)班、(2)班、(3)班、(4)班每班各两名,分乘甲乙两辆汽车,每车限坐4名同学(乘同一辆车的4名同学不考虑位置),其中(1)班两位同学是孪生姐妹,需乘同一辆车,则乘坐甲车的4名同学中恰有2名同学是来自同一个班的乘坐方式共有( )A.18种B.24种C.48种D.36种答案 B4.(2019某某嘉峪关一中模拟)在高三某班进行的演讲比赛中,共有5位选手参加,其中3位女生,2位男生,如果2位男生不能连续出场,且女生甲不能排第一个,那么出场顺序的排法种数为.答案605.(2020届某某某某执信中学10月月考,14)有6X卡片分别写有数字1,1,1,2,2,2,从中任取4X,可排出的四位数有个.答案14考法二分组分配问题的解题方法6.(2018某某某某二模,8)某某西湖公园花展期间,安排6位志愿者到4个展区提供服务,要求甲、乙两个展区各安排一个人,剩下两个展区各安排两个人,不同的安排方案共有( )A.90种B.180种C.270种D.360种答案 B7.(2019某某某某第一次统测,11)将甲、乙、丙、丁、戊共5人分配到A、B、C、D共4所学校,每所学校至少一人,且甲不去A学校,则不同的分配方法有( )A.72种B.108种C.180种D.360种答案 C8.(2018某某某某一模,5)某学校为了更好地培养尖子生,使其全面发展,决定由3名教师对5个尖子生进行“包教”,要求每名教师的“包教”学生不超过2人,则不同的“包教”方案有( )A.60种B.90种C.150种D.120种答案 B9.(2020届某某某某一中10月月考,7)小明和小红都计划在国庆节的7天假期中,到某某“两日游”,若他们不同一天出现在某某,则他们出游的不同方案共有( )A.16种B.18种C.20种D.24种答案 C【五年高考】考点计数原理、排列、组合1.(2017课标Ⅱ,6,5分)安排3名志愿者完成4项工作,每人至少完成1项,每项工作由1人完成,则不同的安排方式共有( )A.12种B.18种C.24种D.36种答案 D2.(2016课标Ⅱ,5,5分)如图,小明从街道的E处出发,先到F处与小红会合,再一起到位于G 处的老年公寓参加志愿者活动,则小明到老年公寓可以选择的最短路径条数为( )A.24B.18C.12D.9答案 B3.(2015某某,6,5分)用数字0,1,2,3,4,5组成没有重复数字的五位数,其中比40 000大的偶数共有( )A.144个B.120个C.96个D.72个答案 B4.(2016课标Ⅲ,12,5分)定义“规X01数列”{a n}如下:{a n}共有2m项,其中m项为0,m项为1,且对任意k≤2m,a1,a2,…,a k中0的个数不少于1的个数,若m=4,则不同的“规X01数列”共有( )A.18个B.16个C.14个D.12个答案 C5.(2018课标Ⅰ,15,5分)从2位女生,4位男生中选3人参加科技比赛,且至少有1位女生入选,则不同的选法共有种.(用数字填写答案)答案166.(2017某某,14,5分)用数字1,2,3,4,5,6,7,8,9组成没有重复数字,且至多有一个数字是偶数的四位数,这样的四位数一共有个.(用数字作答)答案 1 0807.(2017某某,16,4分)从6男2女共8名学生中选出队长1人,副队长1人,普通队员2人组成4人服务队,要求服务队中至少有1名女生,共有种不同的选法.(用数字作答)答案6608.(2015某某,12,5分)某高三毕业班有40人,同学之间两两彼此给对方仅写一条毕业留言,那么全班共写了条毕业留言.(用数字作答)答案 1 560教师专用题组考点计数原理、排列、组合1.(2014大纲全国,5,5分)有6名男医生、5名女医生,从中选出2名男医生、1名女医生组成一个医疗小组.则不同的选法共有( )A.60种B.70种C.75种D.150种答案 C2.(2014某某,9,5分)某次联欢会要安排3个歌舞类节目、2个小品类节目和1个相声类节目的演出顺序,则同类节目不相邻的排法种数是( )A.72B.120C.144D.168答案 B3.(2014某某,8,5分)从正方体六个面的对角线中任取两条作为一对,其中所成的角为60°的共有( )A.24对B.30对C.48对D.60对答案 C4.(2014某某,8,5分)设集合A={(x1,x2,x3,x4,x5)|x i∈{-1,0,1},i=1,2,3,4,5},那么集合A中满足条件“1≤|x1|+|x2|+|x3|+|x4|+|x5|≤3”的元素个数为( )A.60B.90C.120D.130答案 D5.(2014某某,6,5分)6把椅子摆成一排,3人随机就座,任何两人不相邻的坐法种数为( )A.144B.120C.72D.24答案 D6.(2014某某,6,5分)六个人从左至右排成一行,最左端只能排甲或乙,最右端不能排甲,则不同的排法共有( )A.192种B.216种C.240种D.288种答案 B7.(2014某某,14,4分)在8X奖券中有一、二、三等奖各1X,其余5X无奖.将这8X奖券分配给4个人,每人2X,不同的获奖情况有种(用数字作答).答案608.(2014,13,5分)把5件不同产品摆成一排.若产品A与产品B相邻,且产品A与产品C不相邻,则不同的摆法有种.答案369.(2018某某,23,10分)设n∈N*,对1,2,…,n的一个排列i1i2…i n,如果当s<t时,有i s>i t,则称(i s,i t)是排列i1i2…i n的一个逆序,排列i1i2…i n的所有逆序的总个数称为其逆序数,例如:对1,2,3的一个排列231,只有两个逆序(2,1),(3,1),则排列231的逆序数为2.记f n(k)为1,2,…,n的所有排列中逆序数为k的全部排列的个数.(1)求f3(2), f4(2)的值;(2)求f n(2)(n≥5)的表达式(用n表示).解析本题主要考查计数原理、排列等基础知识,考查运算求解能力和推理论证能力.(1)记τ(abc)为排列abc的逆序数,对1,2,3的所有排列,有τ(123)=0,τ(132)=1,τ(213)=1,τ(231)=2,τ(312)=2,τ(321)=3,所以f3(0)=1,f3(1)=f3(2)=2.对1,2,3,4的排列,利用已有的1,2,3的排列,将数字4添加进去,4在新排列中的位置只能是最后三个位置.因此f4(2)=f3(2)+f3(1)+f3(0)=5.(2)对一般的n(n≥4)的情形,逆序数为0的排列只有一个:12…n,所以f n(0)=1.逆序数为1的排列只能是将排列12…n中的任意相邻两个数字调换位置得到的排列,所以f n(1)=n-1.为计算f n+1(2),当1,2,…,n的排列及其逆序数确定后,将n+1添加进原排列,n+1在新排列中的位置只能是最后三个位置.因此, f n+1(2)=f n(2)+f n(1)+f n(0)=f n(2)+n.当n≥5时,f n(2)=[f n(2)-f n-1(2)]+[f n-1(2)-f n-2(2)]+…+[f5(2)-f4(2)]+f4(2)=(n-1)+(n-2)+…+4+f4(2)=n2-n-22.因此,当n≥5时, f n(2)=n 2-n-22.疑难突破要做好本题,关键是理解“逆序”“逆序数”“f n(k)”的含义,不妨从比较小的1,2,3入手去理解这几个概念,这样就能得到f3(2). f4(2)是指1,2,3,4这4个数中逆序数为2的全部排列的个数,可以通过与f3(2), f3(1),f3(0)联系得到,4分别添加在f3(2)的排列中最后一个位置、f3(1)的排列中的倒数第2个位置、f3(0)的排列中的倒数第3个位置.有了上述的理解就能得到f n+1(2)与f n(2),f n(1), f n(0)的关系:f n+1(2)=f n(2)+f n(1)+f n(0)=f n(2)+n,从而得到f n(2)(n≥5)的表达式.【三年模拟】一、单项选择题(每题5分,共50分)1.(2020届九师联盟9月质量检测,8)从1,3,5,7,9中任取两个数,从0,2,4,6,8中任取2个数,则组成没有重复数字的四位数的个数为( )A.2 100B.2 200C.2 160D.2 400答案 C2.(2020届某某某某一中第一次月考,8)中国有十二生肖,又叫十二属相,每一个人的出生年份对应了十二种动物(鼠、牛、虎、兔、龙、蛇、马、羊、猴、鸡、狗、猪)中的一种,现有十二生肖的吉祥物各一个,甲、乙、丙三位同学依次选一个作为礼物,甲同学喜欢牛和马,乙同学喜欢牛、兔、狗和羊,丙同学哪个吉祥物都喜欢,如果让三位同学选取礼物都满意,那么不同的选法有( )A.50种B.60种C.70种D.90种答案 C3.(2020届某某某某七中第二次月考,4)7个人排成一排准备照一X合影,其中甲、乙要求相邻,丙、丁要求分开,则不同的排法有( )A.480种B.720种C.960种D.1 200种答案 C4.(2020届某某洪湖二中月考,9)“学习强国”学习平台是由中宣部主管,以深入学习宣传新时代中国特色社会主义思想为主要内容,立足全党员、面向全社会的优质平台,现日益成为老百姓了解国家动态、紧跟时代脉搏的热门APP.该款软件主要设有“阅读文章”“视听学习”两个学习版块和“每日答题”“每周答题”“专项答题”“挑战答题”四个答题版块.某人在学习过程中,“阅读文章”与“视听学习”两个学习版块之间最多间隔一个答题版块的学习方法有( )A.192种B.240种C.432种D.528种答案 C5.(2018全国百所名校冲刺卷(四),8)航天员进行的一项太空实验中,要先后实施6个程序,其中程序A只能出现在第一或最后一步,程序B和C在实施时必须相邻,则实验顺序的编排方法共有( )A.34种B.48种C.96种D.144种答案 C6.(2019某某金卷先享题二,8)在高三下学期初,某校开展教师对学生的家庭学习问卷调查活动,已知现有3名教师对4名学生家庭进行问卷调查,若这3名教师每位至少到一名学生家中问卷调查,又这4名学生的家庭都能且只能得到一名教师的问卷调查,那么不同的问卷调查方案的种数为( )A.36B.72C.24D.48答案 A7.(2019某某某某一模)如图所示的几何体由三棱锥P-ABC与三棱柱ABC-A1B1C1组合而成,现用3种不同颜色对这个几何体的表面涂色(底面A1B1C1不涂色),要求相邻的面均不同色,则不同的涂色方案共有( )A.6种B.9种C.12种D.36种答案 C8.(2018某某哈六中二模,9)从5名学生中选出4名分别参加数学,物理,化学,生物四科竞赛,其中甲不能参加生物竞赛,则不同的参赛方案种数为( )A.48B.72C.90D.96答案 D9.(2019某某某某模拟,8)已知三棱锥的6条棱代表6种不同的化工产品,有公共顶点的两条棱代表的化工产品放在同一仓库是安全的,没有公共顶点的两条棱代表的化工产品放在同一仓库是危险的.现用编号为1,2,3的三个仓库存放这6种化工产品,每个仓库放2种,那么安全存放的不同方法种数为( )A.12B.24C.36D.48答案 D二、多项选择题(共5分)10.(改编题)下列说法正确的是( )A.5个不同的球,放入8个不同的盒子中,每个盒子里至多放一个球,不同的放法有A85种B.5个不同的球,放入8个不同的盒子中,每个盒子放球数量不限,不同的放法有85种C.5个相同的球,放入8个不同的盒子中,每个盒子里至多放一个球,则不同的放法有C85种D.8个相同的小球,放入5个不同的盒子中,每盒不空的放法有C84种答案ABC三、填空题(每题5分,共15分)11.(2020届某某夏季高考模拟,13)某元宵灯谜竞猜节目,有6名守擂选手和6名复活选手,从复活选手中挑选1名选手为攻擂者,从守擂选手中挑选1名选手为守擂者,则攻擂者、守擂者的不同构成方式共有种.答案3612.(2020届某某寿光现代中学10月月考,14)某工厂将甲、乙等五名新招聘员工分配到三个不同的车间.每个车间至少分配一名员工,甲、乙两名员工必须分到同一个车间,则不同分法的种数为.答案3613.(2019某某某某中学第一次摸底考试,15)由数字0,1组成的一串数字代码,其中恰好有7个1,3个0,则这样的不同数字代码共有个.答案12014.(2020届某某东阳中学10月月考,14)安排甲、乙、丙、丁、戊5名大学生去某某、某某、某某三个城市进行暑期社会实践,每个城市至少安排一人,则不同的安排方式共有种;其中学生甲被单独安排去某某的概率是.答案150;775。
高二数学测试题高考数学第一轮章节复习考试题(附答案和解释)

高二数学测试题2021届高考数学第一轮章节复习考试题(附答案和解释)第6章第4节一、选择题1.等差数列{an}的前n项和为Sn,若S2=2,S4=10,则S6等于()A.12B.18C.24D.42[答案] C[解析] 由题意设Sn=An2+Bn,又∵S2=2,S4=10,∴4A+2B=2,16A+4B=10,解得A=34,B=-12,∴S6=36×34-3=24.2.数列{an}的前n项和为Sn,若an=1?n+1??n+2?,则S8等于()A.25B.130C.730D.56[答案] A[解析] ∵an=1?n+1??n+2?=1n+1-1n+2,而Sn=a1+a2+…+an=12-13+13-14+…+1n-1n+1+1n+1-1n+2=12-1n+2=n2?n+2?,∴S8=82×?8+2?=25.3.数列1×12,2×14,3×18,4×116,…的前n项和为()A.2-12n-n2n+1B.2-12n-1-n2nC.12(n2+n+2)-12nD.12n(n+1)+1-12n-1[答案] B[解析]S=1×12+2×14+3×18+4×116+…+n×12n=1×121+2×122+ 3×123+…+n×12n,①则12S=1×122+2×123+3×124+…+(n-1)×12n+n×12n+1,②①-②得12S=12+122+123+…+12n-n×12n+1=121-12n1-12-n2n+1=1-12n-n2n+1.∴S=2-12n-1-n2n.4.122-1+132-1+142-1+…+1?n+1?2-1的值为()A.n+12?n+2?B.34-n+12?n+2?C.34-121n+1+1n+2D.32-1n+1+1n+2[答案] C[解析] ∵1?n+1?2-1=1n2+2n=1n?n+2?=121n-1n+2.∴Sn=121-13+12-14+13-15+…+1n-1n+2=1232-1n+1-1n+2=3 4-121n+1+1n+2.5.(2021?汕头模拟)已知an=log(n+1)(n+2)(n∈N*),若称使乘积a1?a2?a3?…?an为整数的数n为劣数,则在区间(1,2021)内所有的劣数的和为()A.2026B.2046C.1024D.1022[答案] A[解析]∵a1?a2?a2?…?an=lg3lg2?lg4lg3?…?lg?n+2?lg?n+1?=lg ?n+2?lg2=log2(n+2)=k,则n=2k-2(k∈Z).令12021,得k=2,3,4, (10)∴所有劣数的和为4?1-29?1-2-18=211-22=2026.6.(2021?威海模拟)已知数列{an}的前n项和Sn=n2-4n+2,则|a1|+|a2|+…+|a10|=()A.66B.65C.61D.56[答案] A[解析] 当n≥2时,an=Sn-Sn-1=2n-5;当n=1时,a1=S1=-1,不符合上式,∴an=-1,n=1,2n-5,n≥2,∴{|an|}从第3项起构成等差数列,首项|a3|=1,末项|a10|=15.∴|a1|+|a2|+…+|a10|=1+1+?1+15?×82=66.7.(文)(20XX?江西)公差不为零的等差数列{an}的前n项和为Sn,若a4是a3与a7的等比中项,S8=32,则S10等于()A.18B.24C.60D.90[答案] C[解析] 由题意可知a42=a3×a7S8=32,∴?a1+3d?2=?a1+2d??a1+6d?8a1+8×72×d=32,∴a1=-3d=2,∴S10=10×(-3)+10×92×2=60,选C.(理)(20XX?重庆)设{an}是公差不为0的等差数列,a1=2且a1,a3,a6成等比数列,则{an}的前n项和Sn=()A.n24+7n4B.n23+5n3C.n22+3n4D.n2+n[答案] A[解析] 设等差数列公差为d,∵a1=2,∴a3=2+2d,a6=2+5d.又∵a1,a3,a6成等比数列,∴a32=a1a6,即(2+2d)2=2(2+5d),整理得2d2-d=0.∵d≠0,∴d=12,∴Sn=na1+n?n-1?2d=n24+74n.故选A. 8.在等比数列{an}中,a1=2,前n项和为Sn,若数列{an+1}也是等比数列,则Sn等于()A.2n+1-2B.3nC.2nD.3n-1[答案] C[解析] 解法1:由{an}为等比数列可得an+1=an?q,an+2=an?q2由{an+1}为等比数列可得(an+1+1)2=(an+1)(an+2+1),故(an?q+1)2=(an+1)(an?q2+1),化简上式可得q2-2q+1=0,解得q=1,故an为常数列,且an=a1=2,故Sn=n?a1=2n,故选C.解法2:设等比数列{an}的公比为q,则有a2=2q且a3=2q2,由题设知(2q+1)2=3?(2q2+1),解得q=1,以下同解法1.二、填空题9.设f(x)=12x+2,则f(-9)+f(-8)+…+f(0)+…+f(9)+f(10)的值为________.[答案] 52[解析]∵f(-n)+f(n+1)=12-n+2+12n+1+2=2n1+2n?2+12n+1+2=2n?2 +12n+1+2=22,∴f(-9)+f(-8)+…+f(0)+…+f(9)+f(10)=52.10.(2021?启东模拟)对于数列{an},定义数列{an+1-an}为数列{an}的“差数列”,若a1=2,{an}的“差数列”的通项为2n,则数列{an}的前n项和Sn=________.[答案] 2n+1-2[解析] ∵an+1-an=2n,∴an=(an-an-1)+(an-1-an-2)+…+(a2-a1)+a1=2n-1+2n-2+…+22+2+2=2-2n1-2+2=2n-2+2=2n,∴Sn=2-2n+11-2=2n+1-2.11.(2021?江门模拟)有限数列A={a1,a2,…,an},Sn为其前n项的和,定义S1+S2+…+Snn为A的“凯森和”;如果有99项的数列{a1,a2,…,a99}的“凯森和”为1000,则有100项的数列{1,a1,a2,…,a99}的“凯森和”为________.[答案] 991[解析] ∵{a1,a2,…,a99}的“凯森和”为S1+S2+…+S9999=1000,∴S1+S2+…S99=1000×99,数列{1,a1,a2,…,a99}的“凯森和”为:1+?S1+1?+?S2+1?+…+?S99+1?100=100+S1+S2+…+S99100=991.三、解答题12.(2021?重庆文)已知{an }是首项为19,公差为-2的等差数列,Sn为{an}的前n项和.(1)求通项an及Sn;(2)设{bn-an}是首项为1,公比为3的等比数列,求数列{bn}的通项公式及其前n项和Tn.[解析] 本题主要考查等差数列的基本性质,以及通项公式的求法,前n项和的求法,同时也考查了学生的基本运算能力.(1)因为{an}为首项a1=19,公差d=-2的等差数列,所以an=19-2(n-1)=-2n+21,Sn=19n+n?n-1?2(-2)=-n2+20n.(2)由题意知bn-an=3n-1,所以bn=3n-1-2n+21Tn=b1+b2+…+bn=(1+3+…+3n-1)+Sn=-n2+20n+3n-12.13.已知数列{an}的前n项和Sn=2n2-3n.(1)求证:数列{an}是等差数列;(2)若bn=an?2n,求数列{bn}的前n项和Tn.[解析] (1)证明:a1=S1=-1,当n≥2时,an=Sn-Sn-1=2n2-3n-2(n-1)2+3(n-1)=4n-5. 又a1适合上式,故an=4n-5(n∈N*).当n≥2时,an-an-1=4n-5-4(n-1)+5=4,所以{an}是等差数列且d=4,a1=-1.(2)bn=(4n-5)?2n,∴Tn=-21+3?22+…+(4n-5)?2n,①2Tn=-22+…+(4n-9)?2n+(4n-5)?2n+1,②①-②得-Tn=-21+4?22+…+4?2n-(4n-5)?2n+1=-2+4?4?1-2n-1?1-2-(4n-5)?2n+1=-18-(4n-9)?2n+1,∴Tn=18+(4n-9)?2n+1.14.设数列{an}的前n项和为Sn,已知a1=1,且an+2SnSn-1=0(n≥2),(1)求数列{Sn}的通项公式;(2)设Sn=1f?n?,bn=f(12n)+1.记Pn=S1S2+S2S3+…+SnSn+1,Tn=b1b2+b2b3+…+bnbn+1,试求Tn,并证明Pn12.[解析] (1)解:∵an+2SnSn-1=0(n≥2),∴Sn-Sn-1+2SnSn-1=0.∴1Sn-1Sn-1=2.又∵a=1,∴Sn=12n-1(n∈N+).(2)证明:∵Sn=1f?n?,∴f(n)=2n-1.∴bn=2(12n)-1+1=(12)n-1.Tn=(12)0?(12)1+(12)1?(12)2+…+(12)n-1?(12)n=(12)1+( 12)3+(12)5+…+(12)2n-1=23[1-(14)n].∵Sn=12n-1(n∈N+)∴Pn=11×3+13×5+…+1?2n-1??2n+1?=121-12n+112.15.(2021?山东理)已知等差数列{an}满足:a3=7,a5+a7=26,{an}的前n项和为Sn.(1)求an及Sn;(2)令bn=1an2-1(n∈N*),求数列{bn}的前n项和Tn.[解析] 本题考查等差数列的通项公式与前n项和公式的应用、裂项法求数列的和,熟练掌握数列的基础知识是解答好本类题目的关键.对(1)可直接根据定义求解,(2)问采用裂项求和即可解决.(1)设等差数列{an}的公差为d,因为a3=7,a5+a7=26,所以有a1+2d=72a1+10d=26,解得a1=3,d=2,所以an=3+2(n-1)=2n+1;Sn=3n+n?n-1?2×2=n2+2n.(2)由(1)知an=2n+1,所以bn=1an2-1=1?2n+1?2-1=14?1n?n+1?=14?1n-1n+1,所以Tn=14?1-12+12-13+…+1n-1n+1=14?1-1n+1=n4?n+1?,即数列{bn}的前n项和Tn=n4?n+1?.[点评] 数列在高考中主要考查等差、等比数列的定义、性质以及数列求和,解决此类题目要注意合理选择公式,对于数列求和应掌握经常使用的方法,如:裂项、叠加、累积.本题应用了裂项求和.。
2023年新高考数学一轮复习7-2 等差数列及其前n项和(真题测试)解析版

专题7.2 等差数列及其前n 项和(真题测试)一、单选题1.(2022·全国·高考真题)图1是中国古代建筑中的举架结构,,,,AA BB CC DD ''''是桁,相邻桁的水平距离称为步,垂直距离称为举,图2是某古代建筑屋顶截面的示意图.其中1111,,,DD CC BB AA 是举,1111,,,OD DC CB BA 是相等的步,相邻桁的举步之比分别为11111231111,0.5,,DD CC BB AAk k k OD DC CB BA ====.已知123,,k k k 成公差为0.1的等差数列,且直线OA 的斜率为0.725,则3k =( )A .0.75B .0.8C .0.85D .0.9【答案】D 【解析】 【分析】设11111OD DC CB BA ====,则可得关于3k 的方程,求出其解后可得正确的选项. 【详解】设11111OD DC CB BA ====,则111213,,CC k BB k AA k ===, 依题意,有31320.2,0.1k k k k -=-=,且111111110.725DD CC BB AA OD DC CB BA +++=+++,所以30.530.30.7254k +-=,故30.9k =,故选:D2.(2021·北京·高考真题)《中国共产党党旗党徽制作和使用的若干规定》指出,中国共产党党旗为旗面缀有金黄色党徽图案的红旗,通用规格有五种.这五种规格党旗的长12345,,,,a a a a a (单位:cm)成等差数列,对应的宽为12345,,,,b b b b b (单位: cm),且长与宽之比都相等,已知1288a =,596=a ,1192b =,则3b =A .64 B .96C .128D .160【答案】C 【解析】 【分析】设等差数列{}n a 公差为d ,求得48d =-,得到3192a =,结合党旗长与宽之比都相等和1192b =,列出方程,即可求解. 【详解】由题意,五种规格党旗的长12345,,,,a a a a a (单位:cm)成等差数列,设公差为d , 因为1288a =,596=a ,可得519628848513a a d --===--, 可得3288(31)(48)192a =+-⨯-=, 又由长与宽之比都相等,且1192b =,可得3113a ab b =,所以3131192192=128288a b b a ⋅⨯==. 故选:C.3.(2020·全国·高考真题(理))北京天坛的圜丘坛为古代祭天的场所,分上、中、下三层,上层中心有一块圆形石板(称为天心石),环绕天心石砌9块扇面形石板构成第一环,向外每环依次增加9块,下一层的第一环比上一层的最后一环多9块,向外每环依次也增加9块,已知每层环数相同,且下层比中层多729块,则三层共有扇面形石板(不含天心石)( )A .3699块B .3474块C .3402块D .3339块 【答案】C 【解析】 【分析】第n 环天石心块数为n a ,第一层共有n 环,则{}n a 是以9为首项,9为公差的等差数列,设n S 为{}n a 的前n 项和,由题意可得322729n n n n S S S S -=-+,解方程即可得到n ,进一步得到3n S . 【详解】设第n 环天石心块数为n a ,第一层共有n 环,则{}n a 是以9为首项,9为公差的等差数列,9(1)99n a n n =+-⨯=, 设n S 为{}n a 的前n 项和,则第一层、第二层、第三层的块数分 别为232,,n n n n n S S S S S --,因为下层比中层多729块, 所以322729n n n n S S S S -=-+, 即3(927)2(918)2(918)(99)7292222n n n n n n n n ++++-=-+ 即29729n =,解得9n =, 所以32727(9927)34022n S S +⨯===.故选:C4.(2022·吉林·东北师大附中模拟预测(理))数列{}n a 为等差数列,前n 项的和为n S ,若10110a <,101110120a a +>,则当0n S <时,n 的最大值为( )A .1011B .1012C .2021D .2022【答案】C 【解析】 【分析】分析数列{}n a 的单调性,计算2021S 、2022S ,即可得出结论. 【详解】因为10110a <,101110120a a +>,则10120a >,故数列{}n a 为递增数列, 因为()12021202110112021202102a a S a +==<,()()120222022101110122022101102a a S a a +==+>,且当1012n ≥时,10120n a a ≥>,所以,当2022n ≥时,20220n S S ≥>, 所以,满足当0n S <时,n 的最大值为2021.故选:C.5.(2022·北京·高考真题)设{}n a 是公差不为0的无穷等差数列,则“{}n a 为递增数列”是“存在正整数0N ,当0n N >时,0n a >”的( ) A .充分而不必要条件 B .必要而不充分条件 C .充分必要条件 D .既不充分也不必要条件【答案】C 【解析】 【分析】设等差数列{}n a 的公差为d ,则0d ≠,利用等差数列的通项公式结合充分条件、必要条件的定义判断可得出结论. 【详解】设等差数列{}n a 的公差为d ,则0d ≠,记[]x 为不超过x 的最大整数. 若{}n a 为单调递增数列,则0d >,若10a ≥,则当2n ≥时,10n a a >≥;若10a <,则()11n a a n d +-=, 由()110n a a n d =+->可得11a n d >-,取1011a N d ⎡⎤=-+⎢⎥⎣⎦,则当0n N >时,0n a >, 所以,“{}n a 是递增数列”⇒“存在正整数0N ,当0n N >时,0n a >”; 若存在正整数0N ,当0n N >时,0n a >,取N k *∈且0k N >,0k a >, 假设0d <,令()0n k a a n k d =+-<可得k a n k d >-,且k ak k d->, 当1k a n k d ⎡⎤>-+⎢⎥⎣⎦时,0n a <,与题设矛盾,假设不成立,则0d >,即数列{}n a 是递增数列.所以,“{}n a 是递增数列”⇐“存在正整数0N ,当0n N >时,0n a >”.所以,“{}n a 是递增数列”是“存在正整数0N ,当0n N >时,0n a >”的充分必要条件. 故选:C.6.(2021·北京·高考真题)已知{}n a 是各项均为整数的递增数列,且13a ≥,若12100n a a a ++⋅⋅⋅+=,则n 的最大值为( ) A .9B .10C .11D .12【答案】C 【解析】【分析】使数列首项、递增幅度均最小,结合等差数列的通项及求和公式求得n 可能的最大值,然后构造数列满足条件,即得到n 的最大值. 【详解】若要使n 尽可能的大,则,递增幅度要尽可能小, 不妨设数列是首项为3,公差为1的等差数列,其前n 项和为,则,,所以11n ≤. 对于,,取数列各项为(1,2,10)n =⋯,1125a =,则1211100a a a ++⋅⋅⋅+=, 所以n 的最大值为11. 故选:C .7.(2022·海南海口·二模)设公差不为0的等差数列{}n a 的前n 项和为n S ,已知()9353m S a a a =++,则m =( ) A .9 B .8C .7D .6【答案】C 【解析】 【分析】根据等差数列的前n 项和的性质及等差数列通项公式化简可得. 【详解】因为()9353m S a a a =++,又959S a =, 所以()53593m a a a a =++,所以3553m a a a a ++=,即352m a a a +=,设等差数列{}n a 的公差为d ,则1112(1)2(4)a d a m d a d +++-=+, 所以(+1)8m d d =,又0d ≠,所以18m +=, 所以7m =. 故选:C.8.(2023·全国·高三专题练习)等差数列{}n a 的首项为正数,其前n 项和为n S .现有下列命题,其中是假命题的有( )A .若n S 有最大值,则数列{}n a 的公差小于0B .若6130a a +=,则使0n S >的最大的n 为18C .若90a >,9100a a +<,则{}n S 中9S 最大D .若90a >,9100a a +<,则数列{}n a 中的最小项是第9项 【答案】B 【解析】 【分析】由n S 有最大值可判断A ;由6139100a a a a +=+=,可得90a >,100a <,利用91018182+=⨯a a S 可判断BC ; 90a >,9100a a +<得90a >,991010a a a a =<-=,可判断D. 【详解】对于选项A ,∵n S 有最大值,∴ 等差数列{}n a 一定有负数项, ∴等差数列{}n a 为递减数列,故公差小于0,故选项A 正确; 对于选项B ,∵6139100a a a a +=+=,且10a >, ∴90a >,100a <, ∴179=170S a >,910181802a a S +=⨯=, 则使0n S >的最大的n 为17,故选项B 错误;对于选项C ,∵90a >,9100a a +<,∴90a >,100a <, 故{}n S 中9S 最大,故选项C 正确;对于选项D ,∵90a >,9100a a +<, ∴90a >,991010a a a a =<-=,故数列{}n a 中的最小项是第9项,故选项D 正确. 故选:B. 二、多选题9.(2023·全国·高三专题练习)已知等差数列{an }的公差为d ,前n 项和为Sn ,且91011S S S =<,则( ) A .d <0 B .a 10=0 C .S 18<0 D .S 8<S 9【答案】BC 【解析】 【分析】由91011S S S =<,得100,0d a >= ,判断出A,B 选项,再结合90a <,11818118910918()9()9()92a a S a a a a a +==+=+=判断C 选项,再根据等式性质判断D 选项 【详解】910S S = ,101090a S S ∴=-= ,所以B 正确又1011S S < ,111110100a S S a d ∴=-=+> ,0d ∴> ,所以A 错误 1090,0,0a d a =>∴<11818118910918()9()9()902a a S a a a a a +==+=+=<,故C 正确 9989890,,a S S a S S <=+∴> ,故D 错误故选:BC10.(2022·江苏·南京市宁海中学模拟预测)定义11222n nn a a a H n-+++=为数列{}n a 的“优值”.已知某数列{}n a 的“优值”2nn H =,前n 项和为n S ,下列关于数列{}n a 的描述正确的有( )A .数列{}n a 为等差数列B .数列{}n a 为递增数列C .2022202520222S = D .2S ,4S ,6S 成等差数列 【答案】ABC 【解析】【分析】由新定义可得112222n n n a a a n -++⋯+=⋅,利用该递推关系求出数列{}n a 的通项公式,然后逐一核对四个选项得答案. 【详解】 由已知可得112222n n nn a a a H n-+++==,所以112222n n n a a a n -+++=⋅,①所以2n ≥时,()211212212n n n a a a n ---+++=-⋅,②得2n ≥时,()()111221212n n n n n a n n n ---=⋅--⋅=+⋅,即2n ≥时,1n a n =+,当1n =时,由①知12a =,满足1n a n =+.所以数列{}n a 是首项为2,公差为1的等差数列,故A 正确,B 正确, 所以()32n n n S +=,所以32n S n n +=故2022202520222S =,故C 正确. 25S =,414S =,627S =,2S ,4S ,6S 不是等差数列,故D 错误,故选:ABC .11.(2022·江苏·南京市江宁高级中学模拟预测)已知两个等差数列{}n a 和{}n b ,其公差分别为1d 和2d ,其前n 项和分别为n S 和n T ,则下列说法正确的是( )A .若为等差数列,则112d a =B .若{}n n S T +为等差数列,则120d d +=C .若{}n n a b 为等差数列,则120d d ==D .若*n b N ∈,则{}n b a 也为等差数列,且公差为12d d 【答案】ABD 【解析】 【分析】对于A ,利用对于B ,利用()2211332S T S T S T +=+++化简可得答案; 对于C ,利用2211332a b a b a b =+化简可得答案;对于D ,根据112n n b b a a d d +-=可得答案. 【详解】对于A ,因为为等差数列,所以即 化简得()21120d a -=,所以112d a =,故A 正确;对于B ,因为{}n n S T +为等差数列,所以()2211332S T S T S T +=+++, 所以()11121111122223333a d b d a b a d b d +++=+++++, 所以120d d +=,故B 正确;对于C ,因为{}n n a b 为等差数列,所以2211332a b a b a b =+, 所以11121111122()()(2)(2)a d b d a b a d b d ++=+++, 化简得120d d =,所以10d =或20d =,故C 不正确;对于D ,因为11(1)n a a n d =+-,且*n b N ∈,所以11(1)n b n a a b d =+-()112111a b n d d =++--⎡⎤⎣⎦,所以()()1111211n b a a b d n d d =+-+-,所以()()()11111211112111n n b b a a a b d nd d a b d n d d +-=+-+-----12d d =, 所以{}n b a 也为等差数列,且公差为12d d ,故D 正确. 故选:ABD12.(2022·福建南平·三模)如图,在平面直角坐标系中的一系列格点(),i i i A x y ,其中1,2,3,,,i n =⋅⋅⋅⋅⋅⋅且,i i x y ∈Z .记n n n a x y =+,如()11,0A 记为11a =,()21,1A -记为20a =,()30,1A -记为31,a =-⋅⋅⋅,以此类推;设数列{}n a 的前n 项和为n S .则( )A .202242a =B .202287S =-C .82n a n =D .()245312n n n n S ++=【答案】ABD 【解析】 【分析】由图观察可知第n 圈的8n 个点对应的这8n 项的和为0,则2440n n S +=,同时第n 圈的最后一个点对应坐标为(),n n ,设2022a 在第k 圈,则k 圈共有()41k k +个数,可判断前22圈共有2024个数,2024a 所在点的坐标为()22,22,向前推导,则可判断A ,B 选项;当2n =时,16a 所在点的坐标为()2,2--,即可判断C 选项;借助2440n n S +=与图可知22222244144245454544n n n n n nn n n n n n S S S a a a++++++++=-=+++,即n 项之和,对应点的坐标为()1,+n n ,()1,1n n +-,…,()1,1n +,即可求解判断D 选项.【详解】由题,第一圈从点()1,0到点()1,1共8个点,由对称性可知81280S a a a =+++=;第二圈从点()2,1到点()2,2共16个点,由对称性可知248910240S S a a a -=+++=,即 240S =,以此类推,可得第n 圈的8n 个点对应的这8n 项的和为0,即()214482n nn n SS ++⨯==,设2022a 在第k 圈,则()()888168412k k k kk ++++==+,由此可知前22圈共有2024个数,故20240S =,则()2022202420242023S S a a =-+,2024a 所在点的坐标为()22,22,则2024222244a =+=,2023a 所在点的坐标为()21,22,则2023212243a =+=,2022a 所在点的坐标为()20,22,则2022202242a =+=,故A 正确;()()20222024202420230444387S S a a =-+=-+=-,故B 正确;8a 所在点的坐标为()1,1,则8112a =+=,16a 所在点的坐标为()2,2--,则16224a =--=-,故C 错误;22222244144245454544n n n n n nn n n n n n S S S aaa++++++++=-=+++,对应点的坐标为()1,+n n ,()1,1n n +-,…,()1,1n +,所以()()()()()245111112122n n S n n n n n n n n +=+++++-++++=+++++()()2123122n n n n n ++++==,故D 正确.故选:ABD 三、填空题13.(2019·全国·高考真题(理))记Sn 为等差数列{an }的前n 项和,12103a a a =≠,,则105S S =___________. 【答案】4. 【解析】 【分析】根据已知求出1a 和d 的关系,再结合等差数列前n 项和公式求得结果. 【详解】因213a a =,所以113a d a +=,即12a d =,所以105S S =11111091010024542552a d a a a d ⨯+==⨯+. 14.(2019·江苏·高考真题)已知数列*{}()n a n ∈N 是等差数列,n S 是其前n 项和.若25890,27a a a S +==,则8S 的值是_____.【答案】16. 【解析】 【分析】由题意首先求得首项和公差,然后求解前8项和即可.【详解】由题意可得:()()()25811191470989272a a a a d a d a d S a d ⎧+=++++=⎪⎨⨯=+=⎪⎩, 解得:152a d =-⎧⎨=⎩,则8187840282162S a d ⨯=+=-+⨯=. 15.(2021·福建省华安县第一中学高三期中)已知数列{}n a 的前n 项和为n S ,11a =,121n n a a n +=++(*n ∈N ),则99a 的值为________,99S 的值为________. 【答案】 99 4950 【解析】 【分析】利用数列的递推关系可知数列{}n a 的奇数项是首项为1,公差为2的等差数列,偶数项是首项为2,公差为2的等差数列,利用等差数列的通项公式和前n 项和公式即可求解. 【详解】将1n =代入121n n a a n +=++得2312a =-=, 由121n n a a n +=++①得123n n a a n +++=+2②, ②-①得22n n a a +-=,所以数列{}n a 的奇数项、偶数项都是以2为公差的等差数列,()991501299a =+-⨯=, ()()991359924698S a a a a a a a a =+++++++++ 5049494815022492495022⨯⨯=⨯+⨯+⨯+⨯=, 故答案为:99 ; 4950.16.(2020·海南·高考真题)将数列{2n –1}与{3n –2}的公共项从小到大排列得到数列{an },则{an }的前n 项和为________. 【答案】232n n - 【解析】 【分析】首先判断出数列{}21n -与{}32n -项的特征,从而判断出两个数列公共项所构成新数列的首项以及公差,利用等差数列的求和公式求得结果. 【详解】因为数列{}21n -是以1为首项,以2为公差的等差数列, 数列{}32n -是以1首项,以3为公差的等差数列,所以这两个数列的公共项所构成的新数列{}n a 是以1为首项,以6为公差的等差数列,所以{}n a 的前n 项和为2(1)16322n n n n n -⋅+⋅=-, 故答案为:232n n -. 四、解答题17.(2023·全国·高三专题练习)已知数列{}n a 中,11a =,当2n ≥时,11n n n n a a a a ---=⋅.求证:数列1{}na 是等差数列.【答案】证明见解析 【解析】 【分析】利用定义法证明出数列1{}na 是等差数列.【详解】当2n ≥时,11n n n n a a a a ---=⋅,因11a =,显然0n a ≠,否则10n a -=,由此可得10a =,矛盾, 两边同时除以1n n a a -⋅,得1111n n a a --=,而11a =1, 所以数列1{}na 是以1为首项,1为公差的等差数列.18.(2019·北京·高考真题(文))设{n a }是等差数列,a 1=–10,且a 2+10,a 3+8,a 4+6成等比数列.(Ⅰ)求{na }的通项公式;(Ⅱ)记{na }的前n 项和为Sn ,求Sn 的最小值.【答案】(Ⅰ)212n a n =-;(Ⅱ)30-. 【解析】 【分析】(Ⅰ)由题意首先求得数列的公差,然后利用等差数列通项公式可得{}n a 的通项公式;(Ⅱ)首先求得n S 的表达式,然后结合二次函数的性质可得其最小值. 【详解】(Ⅰ)设等差数列{}n a 的公差为d ,因为234+10+8+6a a a ,,成等比数列,所以2324(+8)(+10)(+6)a a a =,即2(22)(34)d d d -=-,解得2d =,所以102(1)212n a n n =-+-=-.(Ⅱ)由(Ⅰ)知212n a n =-, 所以22102121112111()224n n S n n n n -+-=⨯=-=--;当5n =或者6n =时,n S 取到最小值30-.19.(2016·全国·高考真题(文))等差数列{n a }中,34574,6a a a a +=+=. (Ⅰ)求{n a }的通项公式;(Ⅱ) 设[]n n b a =,求数列{}n b 的前10项和,其中[]x 表示不超过x 的最大整数,如[0.9]=0,[2.6]=2. 【答案】(Ⅰ)235n n a +=;(Ⅱ)24. 【解析】 【详解】试题分析:(Ⅰ) 根据等差数列的通项公式及已知条件求1a ,d ,从而求得n a ;(Ⅱ)由(Ⅰ)求n b ,再求数列{}n b 的前10项和.试题解析:(Ⅰ)设数列{}n a 的公差为d ,由题意有112+54,+53a d a d ==. 解得121,5a d ==.所以{}n a 的通项公式为235n n a +=. (Ⅱ)由(Ⅰ)知235n n b +⎡⎤=⎢⎥⎣⎦. 当n=1,2,3时,2312,15n n b +≤<=; 当n=4,5时,2323,25n n b +≤<=; 当n=6,7,8时,2334,35n n b +≤<=;当n=9,10时,2345,45n n b +≤<=. 所以数列{}n b 的前10项和为1322334224⨯+⨯+⨯+⨯=.20.(2022·全国·高考真题)记n S 为数列{}n a 的前n 项和,已知11,n n S a a ⎧⎫=⎨⎬⎩⎭是公差为13的等差数列.(1)求{}n a 的通项公式; (2)证明:121112na a a +++<.【答案】(1)()12n n n a +=(2)见解析 【解析】 【分析】(1)利用等差数列的通项公式求得()121133n n S n n a +=+-=,得到()23n n n a S +=,利用和与项的关系得到当2n ≥时,()()112133n n n n n n a n a a S S --++=-=-,进而得:111n n a n a n -+=-,利用累乘法求得()12n n n a +=,检验对于1n =也成立,得到{}n a 的通项公式()12n n n a +=; (2)由(1)的结论,利用裂项求和法得到121111211n a a a n ⎛⎫+++=- ⎪+⎝⎭,进而证得.(1)∵11a =,∴111S a ==,∴111S a =, 又∵n n S a ⎧⎫⎨⎬⎩⎭是公差为13的等差数列,∴()121133n n S n n a +=+-=,∴()23n n n a S +=, ∴当2n ≥时,()1113n n n a S --+=,∴()()112133n n n n n n a n a a S S --++=-=-,整理得:()()111n n n a n a --=+, 即111n n a n a n -+=-, ∴31211221n n n n n a a a a a a a a a a ---=⨯⨯⨯⋯⨯⨯()1341112212n n n n n n ++=⨯⨯⨯⋯⨯⨯=--,显然对于1n =也成立, ∴{}n a 的通项公式()12n n n a +=; (2)()12112,11n a n n n n ⎛⎫==- ⎪++⎝⎭∴12111na a a +++1111112121222311n n n ⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫=-+-+-=-< ⎪ ⎪ ⎪ ⎪⎢⎥++⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦ 21.(2022·安徽·合肥一中模拟预测(文))已知()f x =数列{}na 的前n 项和为n S ,点11,+⎛⎫- ⎪⎝⎭n n n P a a 在曲线()y f x =上(n N +∈)且11a =,0n a >.(1)求数列{}n a 的通项公式;(2)数列{}n b 的前n 项和为n T ,且满足212211683++=+--n nn n T Tn n a a ,确定1b 的值使得数列{}n b 是等差数列.【答案】(1)*N =∈n a n (2)1 【解析】 【分析】(1)根据点11,+⎛⎫- ⎪⎝⎭n n n P a a 在曲线()y f x =上(n N +∈),得到11+n a 212141+-=n n a a ,利用等差数列的定义求解; (2)由(1)化简得到114143+-=+-n n T Tn n ,利用等差数列的定义得到()()1431=-+-n T n T n ,再利用数列通项与前n 项和的关系求解. (1)解:因为()f x =11,+⎛⎫- ⎪⎝⎭n n n P a a 在曲线()y f x =上(n N +∈),所以11+=n a 212141+-=n n a a ,所以21n a ⎧⎫⎨⎬⎩⎭是以1为首项,以4为公差的等差数列,所以()2114143=+-=-n n n a,即*N =∈n a n ; (2)由(1)知:212211683++=+--n nn n T Tn n a a ,即为()()()()143414341+-=++-+n n n T n T n n ,整理得:114143+-=+-n n T Tn n , 所以数列43⎧⎫⎨⎬-⎩⎭n T n 是以1T 为首项,以1为公差的等差数列, 则1143=+--nT T n n ,即()()1431=-+-n T n T n , 当2n ≥时,114811-=-=+-n n n b T T b n , 若{}n b 是等差数列,则1b 适合上式, 令1n =,得1143=-b b ,解得11b =.22.(2021·全国·高考真题)已知数列{}n a 满足11a =,11,,2,.n n na n a a n ++⎧=⎨+⎩为奇数为偶数 (1)记2n n b a =,写出1b ,2b ,并求数列{}n b 的通项公式; (2)求{}n a 的前20项和.【答案】(1)122,5,31n b b b n ===-;(2)300. 【解析】 【分析】(1)方法一:由题意结合递推关系式确定数列{}n b 的特征,然后求和其通项公式即可; (2)方法二:分组求和,结合等差数列前n 项和公式即可求得数列的前20项和. 【详解】解:(1)[方法一]【最优解】:显然2n 为偶数,则21222212,1n n n n a a a a +++=+=+, 所以2223n n a a +=+,即13n n b b +=+,且121+12b a a ===, 所以{}n b 是以2为首项,3为公差的等差数列, 于是122,5,31n b b b n ===-.[方法二]:奇偶分类讨论由题意知1231,2,4a a a ===,所以122432,15b a b a a ====+=. 由11n n a a +-=(n 为奇数)及12n n a a +-=(n 为偶数)可知, 数列从第一项起,若n 为奇数,则其后一项减去该项的差为1, 若n 为偶数,则其后一项减去该项的差为2.所以*23()n n a a n N +-=∈,则()11331n b b n n =+-⨯=-.[方法三]:累加法由题意知数列{}n a 满足*113(1)1,()22nn n a a a n +-==++∈N . 所以11213(1)11222b a a -==++=+=, 322433223(1)3(1)11212352222b a a a a a --==++=+=+++=++=+=,则222121222111()()()121221+n n n n n n b a a a a a a a a a ---==-+-+-+=+++++++12(1)131n n n =+-+=-⨯.所以122,5b b ==,数列{}n b 的通项公式31n b n =-. (2)[方法一]:奇偶分类讨论 20123201351924620++++++++()()S a a a a a a a a a a a a =+=+++1231012310(1111)b b b b b b b b =-+-+-++-+++++110()102103002b b +⨯=⨯-=. [方法二]:分组求和由题意知数列{}n a 满足12212121,1,2n n n n a a a a a -+==+=+, 所以2122123n n n a a a +-=+=+.所以数列{}n a 的奇数项是以1为首项,3为公差的等差数列;同理,由2221213n n n a a a ++=+=+知数列{}n a 的偶数项是以2为首项,3为公差的等差数列. 从而数列{}n a 的前20项和为: 201351924260()()S a a a a a a a a =+++++++++1091091013102330022⨯⨯=⨯+⨯+⨯+⨯=.【整体点评】 (1)方法一:由题意讨论{}n b 的性质为最一般的思路和最优的解法;方法二:利用递推关系式分类讨论奇偶两种情况,然后利用递推关系式确定数列的性质; 方法三:写出数列{}n a 的通项公式,然后累加求数列{}n b 的通项公式,是一种更加灵活的思路. (2)方法一:由通项公式分奇偶的情况求解前n 项和是一种常规的方法;方法二:分组求和是常见的数列求和的一种方法,结合等差数列前n 项和公式和分组的方法进行求和是一种不错的选择.。
2020肥城一中高三一轮复习验收模拟测试数学试题(3)

肥城一中2017级高三一轮复习验收模拟测试3数学科试题(卷) 2020.03.30-03.31(考试时间:120分钟 试卷满分:150分)一、选择题:(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.给定集合A ,B ,定义{},,A B x x m n m A n B *==-∈∈,若{}4,5,6A =,{}1,2,3B =,则集合A B *中的所有元素之和为( ) A .15B .14C .27D .14-2.设复数2,z ai =+若z z = ,则实数a = ( ) A.0B.2C.1-D.2-3.设命题p :存在3,3,aa R a ∈>则p ⌝ 为( ) A.存在3,3aa R a ∈≤ B. 不存在3,3a a R a ∈>C.对任意3,3aa R a ∈≤D. 对任意3,3aa R a ∉≤4.222cos ()cos ()105ππθθ--+-= ( )A.12C.15.科赫曲线是一种外形像雪花的几何曲线,一段科赫曲线可以通过下列操作步骤构造得到。
任意画一条线段,然后把它分成三等分,以中间一段为边向外作正三角形,并把中间一段去掉,这样,原来的一条线段就变成了4条小线段构成的折线,称为“一次构造”,用同样的方法把每条小线段重复上述步骤得到16条更小的线段构成的折线称为“二次构造”, …,如此进行“n 次构造”,就可以得到一条科赫曲线。
若要在构造过程中使得到的折线的长度达到初始线段的1000倍,则至少需要通过构造的次数是(取lg30.4771,lg 20.3010≈≈)( )A.16B.17C.24D.256.已知直线10ax y +-=将圆22:(1)(2)4C x y -++=平分,则圆C 中以点(,)33a a -为中点的弦的弦长为( )A.2B.C.D.47.已知ABC ∆的内角A ,B ,C 的对边分别是a ,b ,c ,且()()222cos cos a b ca Bb A abc +-⋅+=,若ABC ∆的外接圆半径为23,则ABC ∆的周长的取值范围为( ) A .(]2,4B .(]4,6C .()4,6D .(]2,68.已知抛物线C :22x py =的焦点为F ,定点()23,0M ,若直线FM 与抛物线C 相交于A ,B 两点(点B 在F ,M 中间),且与抛物线C 的准线交于点N ,若7BN BF =,则AF 的长为( ) A .78B .1C .76D .3二、多项选择题:本题共4小题,每小题5分,共20分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2014文科数学课时作业复习资料第一章 集合与逻辑用语第1讲 集合的含义与基本关系1.(2011年江西)若全集U ={1,2,3,4,5,6},M ={2,3},N ={1,4},则集合{5,6}等于( )A .M ∪NB .M ∩NC .(∁U M )∪(∁U N )D .(∁U M )∩(∁U N )2.(2011年湖南)设全集U =M ∪N ={1,2,3,4,5},M ∩∁U N ={2,4},则N =( ) A .{1,2,3} B .{1,3,5} C .{1,4,5} D .{2,3,4}3.已知集合A ={1,2a},B ={a ,b },若A ∩B =⎩⎨⎧⎭⎬⎫12,则A ∪B 为( )4.已知全集U =R ,集合M ={x |-2≤x -1≤2}和N ={x |x =2k -1,k =1,2,…}的关系的韦恩(Venn)图如图K1-1-1所示,则阴影部分所示的集合的元素共有( )图K1-1-1A .3个B .2个C .1个D .无穷多个5.(2011年广东)已知集合A ={(x ,y )|x ,y 为实数,且x 2+y 2=1},B ={(x ,y )|x 、y 为实数,且y =x },则A ∩B 的元素个数为( )A .0B .1C .2D .36.(2011年湖北)已知U ={y |y =log 2x ,x >1},P =⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫y ⎪⎪⎪y =1x ,x >2,则∁UP =( )∪⎣⎢⎡⎭⎪⎫12,+∞7.(2011年上海)若全集U =R ,集合A ={x |x ≥1}∪{x |x ≤0},则∁U A =________________.8.(2011年北京)已知集合P ={x |x 2≤1},M ={a }.若P ∪M =P ,则a 的取值范围是____________.9.(2011年安徽合肥一模)A ={1,2,3},B ={x ∈R |x 2-ax +b =0,a ∈A ,b ∈A },求A ∩B =B 的概率.10.(2011届江西赣州联考)已知函数y =ln(2-x )[x -(3m +1)]的定义域为集合A ,集合B =⎩⎨⎧⎭⎬⎫x |x -m 2+1x -m <0.(1)当m =3时,求A ∩B ;(2)求使B ⊆A 的实数m 的取值范围.第2讲 命题及其关系、充分条件与必要条件1.(2011年湖南)设集合M ={1,2},N ={a 2},则“a =1”是“N ⊆M ”的( ) A .充分不必要条件 B .必要不充分条件 C .充分必要条件 D .既不充分又不必要条件2.(2010年陕西)“a >0”是“|a |>0”的( ) A .充分不必要条件 B.必要不充分条件 C .充要条件 D .既不充分也不必要条件3.a 、b 为非零向量,“a ⊥b”是“函数f (x )=(a x +b )·(x b -a )为一次函数”的( ) A .充分而不必要条件 B .必要不充分条件 C .充分必要条件 D .既不充分也不必要条件4.(2010年广东)“m <14”是“一元二次方程x 2+x +m =0”有实数解的( )A .充分非必要条件B .充分必要条件C .必要非充分条件D .非充分必要条件 5.对任意实数a ,b ,c ,给出下列命题: ①“a =b ”是“ac =bc ”的充要条件;②“a +5是无理数”是“a 是无理数”的充要条件; ③“a >b ”是“a 2>b 2”的充分条件; ④“a <5”是“a <3”的必要条件. 其中真命题的个数是( ) A .1 B .2 C .3 D .46.(2011年山东)已知a ,b ,c ∈R ,命题“若a +b +c =3,则a 2+b 2+c 2≥3”的否命题是( )A .若a +b +c ≠3,则a 2+b 2+c 2<3 B .若a +b +c =3,则a 2+b 2+c 2<3 C .若a +b +c ≠3,则a 2+b 2+c 2≥3 D .若a 2+b 2+c 2≥3,则a +b +c =37.(2010年上海)“x =2k π+π4(k ∈Z )”是“tan x =1”成立的( )A .充分不必要条件B .必要不充分条件C .充分条件D .既不充分也不必要条件 8.给定下列命题:①若k >0,则方程x 2+2x -k =0有实数根; ②“若a >b ,则a +c >b +c ”的否命题; ③“矩形的对角线相等”的逆命题;④“若xy =0,则x ,y 中至少有一个为0”的否命题. 其中真命题的序号是________.9.已知p:|x-4|≤6,q:x2-2x+1-m2≤0(m>0),且綈p是綈q的必要不充分条件,求实数m的取值范围.10.已知函数f(x)是(-∞,+∞)上的增函数,a,b∈R,对命题“若a+b≥0,则f(a)+f(b)≥f(-a)+f(-b)”.(1)写出逆命题,判断其真假,并证明你的结论;(2)写出逆否命题,判断其真假,并证明你的结论.第3讲 简单的逻辑联结词、全称量词与存在量词1.(2011年北京)若p 是真命题,q 是假命题,则( ) A .p ∧q 是真命题 B .p ∨q 是假命题 C .綈p 是真命题 D .綈q 是真命题2.(2010年湖南)下列命题中的假命题是( ) A .∃x ∈R ,lg x =0 B .∃x ∈R ,tan x =1 C .∀x ∈R ,x 3>0 D .∀x ∈R,2x>0 3.下列四个命题中的真命题为( ) A .若sin A =sin B ,则∠A =∠BB .若lg x 2=0,则x =1 C .若a >b ,且ab >0,则1a <1bD .若b 2=ac ,则a ,b ,c 成等比数列4.若函数f (x )=x 2+ax (a ∈R ),则下列结论正确的是( ) A .∃a ∈R ,f (x )是偶函数 B .∃a ∈R ,f (x )是奇函数C .∀a ∈R ,f (x )在(0,+∞)上是增函数D .∀a ∈R ,f (x )在(0,+∞)上是减函数5.(2011年广东揭阳市二模)已知命题p :∃x ∈R ,cos x =54;命题q :∀x ∈R ,x 2-x +1>0.则下列结论正确的是( )A .命题p ∧q 是真命题B .命题p ∧綈q 是真命题C .命题綈p ∧q 是真命题D .命题綈p ∧綈q 是假命题6.(2011届广东汕头水平测试)命题“∀x >0,都有x 2-x ≤0”的否定是( ) A .∃x >0,使得x 2-x ≤0 B .∃x >0,使得x 2-x >0 C .∀x >0,都有x 2-x >0 D .∀x ≤0,都有x 2-x >07.如果命题P :∅∈{∅},命题Q :∅⊆{∅},那么下列结论不正确的是( ) A .“P 或Q ”为真 B .“P 且Q ”为假 C .“非P ”为假 D .“非Q ”为假8.(2010年四川)设S 为实数集R 的非空子集.若对任意x ,y ∈S ,都有x +y ,x -y ,xy ∈S ,则称S 为封闭集.下列命题:①集合S ={a +b 3|a ,b 为整数}为封闭集; ②若S 为封闭集,则一定有0∈S ; ③封闭集一定是无限集;④若S 为封闭集,则满足S ⊆T ⊆R 的任意集合T 也是封闭集. 其中的真命题是________(写出所有真命题的序号).9.设函数f (x )=x 2-2x +m .(1)若∀x ∈[0,3],f (x )≥0恒成立,求m 的取值范围; (2)若∃x ∈[0,3],f (x )≥0成立,求m 的取值范围.10.已知m ∈R ,设命题P :|m -5|≤3;命题Q :函数f (x )=3x 2+2mx +m +43有两个不同的零点.求使命题“P 或Q ”为真命题的实数的取值范围.第二章 函数第1讲 函数与映射的概念1.下列函数中,与函数y =1x有相同定义域的是( )A .f (x )=ln xB .f (x )=1xC .f (x )=|x |D .f (x )=e x2.(2010年重庆)函数y =16-4x的值域是( ) A .[0,+∞) B .[0,4] C .[0,4) D .(0,4)3.(2010年广东)函数f (x )=lg(x -1)的定义域是( ) A .(2,+∞) B .(1,+∞) C .[1,+∞) D .[2,+∞)4.给定集合P ={x |0≤x ≤2},Q ={y |0≤y ≤4},下列从P 到Q 的对应关系f 中,不是映射的为( )A .f :x →y =2xB .f :x →y =x 2C .f :x →y =52x D .f :x →y =2x5.若函数y =f (x )的定义域是[0,2],则函数g (x )=f 2xx -1的定义域是( ) A .[0,1] B .[0,1) C .[0,1)∪(1,4] D .(0,1)6.若函数y =f (x )的值域是[1,3],则函数F (x )=1-2f (x +3)的值域是__________. 7.已知函数f (x ),g (x )分别由下表给出:x 1 2 3 f (x )131x 1 2 3 g (x )321则f [g (1)]的值为________;满足f [g (x )]>g [f (x )]的x 的值是________.8.(2011年广东广州综合测试二)将正整数12分解成两个正整数的乘积有1×12,2×6,3×4三种,其中3×4是这三种分解中,两数差的绝对值最小的,我们称3×4为12的最佳分解.当p ×q (p ≤q 且p ,q ∈N *)是正整数n 的最佳分解时,我们规定函数f (n )=p q ,例如f (12)=34.关于函数f (n )有下列叙述: ①f (7)=17;②f (24)=38;③f (28)=47;④f (144)=916.其中正确的序号为________(填入所有正确的序号).9.(1)求函数f (x )=lgx 2-2x9-x2的定义域; (2)已知函数f (2x)的定义域是[-1,1],求f (log 2x )的定义域.10.等腰梯形ABCD 的两底分别为AD =2a ,BC =a ,∠BAD =45°,作直线MN ⊥AD 交AD 于M ,交折线ABCD 于N ,记AM =x ,试将梯形ABCD 位于直线MN 左侧的面积y 表示为x 的函数,并写出函数的定义域.第2讲 函数的表示法1.设f (x +2)=2x +3,则f (x )=( ) A .2x +1 B .2x -1C .2x -3D .2x +72.(2011年浙江)已知f (x )=⎩⎪⎨⎪⎧x 2x >0,fx +1x ≤0,则f (2)+f (-2)的值为( )A .6B .5C .4D .23.设f ,g 都是由A 到A 的映射,其对应关系如下表(从上到下):映射f 的对应关系 原象 1 2 3 4 象3421原象 1 2 3 4 象4312则与f [g (1)]值相同的是A .g [f (1)] B .g [f (2)] C .g [f (3)] D .f [f (4)]4.(2010届广州海珠区第一次测试)直角梯形ABCD 如图K2-2-1(1),动点P 从点B 出发,由B →C →D →A 沿边运动,设点P 运动的路程为x ,△ABP 的面积为f (x ).如果函数y =f (x )的图象如图(2),则△ABC 的面积为( )(1) (2)图K2-2-1A .10B .32C .18D .165.(2011年福建)已知函数f (x )=⎩⎪⎨⎪⎧2x x >0,x +1 x ≤0,f (a )+f (1)=0,则实数a 的值等于( )A .-3B .-1C .1D .3 6.已知f (x )=x +1x -1(x ≠±1),则( ) A .f (x )·f (-x )=1 B .f (-x )+f (x )=0 C .f (x )·f (-x )=-1 D .f (-x )+f (x )=17.(2010年陕西)已知函数f (x )=⎩⎪⎨⎪⎧3x +2x <1,x 2+axx ≥1,若f [f (0)]=4a ,则实数a =________.8.(2011年广东广州调研)设函数f (x )=⎩⎪⎨⎪⎧2-x,x ∈-∞,1,x 2,x ∈[1,+∞.若f (x )>4,则x的取值范围是____________.9.二次函数f(x)满足f(x+1)-f(x)=2x+3,且f(0)=2.(1)求f(x)的解析式;(2)求f(x)在[-3,4]上的值域;(3)若函数f(x+m)为偶函数,求f[f(m)]的值;(4)求f(x)在[m,m+2]上的最小值.10.定义:如果函数y=f(x)在定义域内给定区间[a,b]上存在x0(a<x0<b),满足f(x0)=f b-f ab-a,则称函数y=f(x)是[a,b]上的“平均值函数”,x0是它的一个均值点.如y=x4是[-1,1]上的平均值函数,0就是它的均值点.(1)判断函数f(x)=-x2+4x在区间[0,9]上是否为平均值函数若是,求出它的均值点;若不是,请说明理由;(2)若函数f(x)=-x2+mx+1是区间[-1,1]上的平均值函数,试确定实数m的取值范围.第3讲 函数的奇偶性与周期性1.已知函数f (x )=ax 2+bx +3a +b 是定义域为[a -1,2a ]的偶函数,则a +b 的值是( )A .0 C .1 D .-12.(2010年重庆)函数f (x )=4x+12x 的图象( )A .关于原点对称B .关于直线y =x 对称C .关于x 轴对称D .关于y 轴对称3.(2011年广东)设函数f (x )和g (x )分别是R 上的偶函数和奇函数,则下列结论恒成立的是( )A .f (x )+|g (x )|是偶函数B .f (x )-|g (x )|是奇函数C .|f (x )|+g (x )是偶函数D .|f (x )|-g (x )是奇函数4.(2011年湖北)若定义在R上的偶函数f(x)和奇函数g(x)满足f(x)+g(x)=e x,则g(x)=( )A.e x-e-x5.(2010年山东)设f(x)为定义在R上的奇函数,当x≥0时,f(x)=2x+2x+b(b为常数),则f(-1)=( )A.-3 B.-1 C.1 D.36.(2011年辽宁)若函数f(x)=x2x+1x-a为奇函数,则a=( )D.17.(2011年湖南)已知f(x)为奇函数,g(x)=f(x)+9,g(-2)=3,则f(2)=________.8.函数f(x)对于任意实数x满足条件f(x+2)f(x)=1,若f(1)=-5,则f(-5)=________.9.已知函数f(x),当x>0时,f(x)=x2-2x-1.(1)若f(x)为R上的奇函数,求f(x)的解析式;(2)若f(x)为R上的偶函数,能确定f(x)的解析式吗请说明理由.10.已知定义在R 上的函数f (x )=-2x+a2x +1+b (a ,b 为实常数).(1)当a =b =1时,证明:f (x )不是奇函数; (2)设f (x )是奇函数,求a 与b 的值;(3)当f (x )是奇函数时,证明对任何实数x ,c 都有f (x )<c 2-3c +3成立.第4讲 函数的单调性与最值1.(2011年全国)下列函数中,既是偶函数又在(0,+∞)单调递增的函数是( ) A .y =x 3B .y =|x |+1C .y =-x 2+1 D .y =2-|x |2.(2011届广东惠州调研)已知定义域为(-1,1)的奇函数y =f (x )又是减函数,且f (a -3)+f (9-a 2)<0.则a 的取值范围是( )A .(3,10)B .(2 2,3)C .(2 2,4)D .(-2,3)3.设奇函数f (x )在(0,+∞)上为增函数,且f (1)=0,则不等式f x -f -xx<0的解集为( )A .(-1,0)∪(1,+∞)B .(-∞,1)∪(0,1)C .(-∞,-1)∪(1,+∞)D .(-1,0)∪(0,1)4.(2010年北京)给定函数①y =x 12;②y =log 12(x +1);③y =|x -1|;④y =2x +1,其中在区间(0,1)上单调递减的函数序号是( )A .①②B .②③C .③④D .①④5.(2011届上海十三校联考)设函数y =f (x )在R 内有定义,对于给定的正数k ,定义函数f k (x )=⎩⎪⎨⎪⎧f x f x ≤k ,kf x >k .取函数f (x )=log 2|x |.当k =12时,函数f k (x )的单调递增区间为________.6.(2011年江苏)函数f (x )=log 5(2x +1)的单调增区间是__________.7.(2011年上海)设g (x )是定义在R 上、以1为周期的函数,若f (x )=x +g (x )在[3,4]上的值域为[-2,5],则f (x )在区间[-10,10]上的值域为____________.8.(2011年北京)已知函数f (x )=⎩⎪⎨⎪⎧2xx ≥2,x -13 x <2,若关于x 的方程f (x )=k有两个不同的实根,则数k 的取值范围是________.9.已知函数f (x )=x 2+ax +4x(x ≠0).(1)若f (x )为奇函数,求a 的值;(2)若f (x )在[3,+∞)上恒大于0,求a 的取值范围.10.(2011年广东广州综合测试)已知函数f (x )=ax 2+bx +c (a ≠0)满足f (0)=0,对于任意x ∈R 都有f (x )≥x ,且f ⎝ ⎛⎭⎪⎫-12+x =f ⎝ ⎛⎭⎪⎫-12-x ,令g (x )=f (x )-|λx -1|(λ>0). (1)求函数f (x )的表达式; (2)求函数g (x )的单调区间.第三章 基本初等函数(Ⅰ)第1讲 指数式与指数函数1.(2011年山东)若点(a,9)在函数y =3x的图象上,则tan a π6的值为( )A .0 C .12.函数y =(a 2-3a +3)a x是指数函数,则a 的值为( ) A .1或2 B .1 C .2 D .a >0且a ≠1的所有实数 3.下列函数中值域为正实数的是( ) A .y =-5xB .y =⎝ ⎛⎭⎪⎫131-xC .y =⎝ ⎛⎭⎪⎫12x -2 D .y =1-2x4.若函数f (x )=a x+b -1(a >0且a ≠1)的图象经过第二、三、四象限,则一定有( ) A .0<a <1且b >1 B .a >1且b >0 C .0<a <1且b <0 D .a >1且b <05.设函数f (x )=1221(0), (>0)x x x x -⎧-≤⎪⎨⎪⎩若f (x 0)>1,则x 0的取值范围是( )A .(-1,1)B .(-1,+∞)C .(-∞,-2)∪(0,+∞)D .(-∞,-1)∪(1,+∞)6.已知命题p :关于x 的函数y =x 2-3ax +4在[1,+∞)上是增函数,命题q :函数y =(2a -1)x为减函数,若p ∧q 为真命题,则实数m 的取值范围是( )A .a ≤23B .0<a <12 <a ≤23 <a <17.方程2x +x 2=3实数解的个数为______.8.关于x 的不等式2·32x-3x +a 2-a -3>0,当0≤x ≤1时恒成立,则实数a 的取值范围为________________________________________________________________________.9.已知函数f (x )=2x-12x +1.(1)求f (x )的定义域; (2)求f (x )的值域;(3)证明f (x )在(-∞,+∞)上是增函数.10.已知函数f (x )是定义在R 上的偶函数,且x ≥0时,f (x )=⎝ ⎛⎭⎪⎫12x.(1)求f (-1)的值; (2)求函数f (x )的值域A ;(3)设函数g (x )=-x 2+a -1x +a 的定义域为集合B ,若A ⊆B ,求实数a 的取值范围.第2讲 对数式与对数函数1.(2010年浙江)已知函数f (x )=log 2(x +1),若f (a )=1,a =( )A .0B .1C .2D .32.(2011年北京)如果12log x <12log y <0,那么( )A .y <x <1B .x <y <1C .1<x <yD .1<y <x3.(2010年山东)函数f (x )=log 2(3x+1)的值域为( )A .(0,+∞)B .[0,+∞)C .(1,+∞)D .[1,+∞)4.已知A ={x |2≤x ≤π},定义在A 上的函数y =log a x (a >0且a ≠1)的最大值比最小值大1,则底数a 的值为( )C .π-2 或2π5.(2011年天津)已知a =,b =,c =,则( ) A .a >b >c B .a >c >b C .b >a >c D .c >a >b6.(2011年广东佛山质量检测)已知函数f (x )=⎩⎪⎨⎪⎧2xx ≤0,log 2x x >0,则f [f (-1)]=( )A .-2B .-1C .1D .27.(2011年辽宁)设函数f (x )=⎩⎪⎨⎪⎧21-xx ≤1,1-log 2x x >1,则满足f (x )≤2的x 的取值范围是( )A .[-1,2]B .[0,2]C .[1,+∞)D .[0,+∞)8.(2011年湖北)里氏震级M 的计算公式为:M =lg A -lg A 0,其中A 是测震仪记录的地震曲线的最大振幅,A 0是相应的标准地震的振幅,假设在一次地震中,测震仪记录的最大振幅是1 000,此时标准地震的振幅为,则此次地震的震级为________级.9级地震的最大振幅是5级地震最大振幅的______倍.9.已知函数f (x )=lg(ax 2+2x +1). (1)若f (x )的定义域为R ,求实数a 的范围;(2)若f(x)的值域为R,求实数a的范围.10.若方程lg(-x2+3x-m)=lg(3-x)在x∈(0,3)内有唯一解,求实数m的取值范围.第3讲 一次函数、反比例函数及二次函数1.设二次函数f (x )=ax 2+bx +c (a ≠0),如果f (x 1)=f (x 2)(其中x 1≠x 2),则f ⎝ ⎛⎭⎪⎫x 1+x 22等于( )A .-b 2aB .-baC .c2.已知二次函数f (x )的图象如图K3-3-1所示,则其导函数f ′(x )的图象大致形状是( )图K3-3-13.若f (x )=-x 2+2ax 与g (x )=ax +1在区间[1,2]上都是减函数,则a 的取值范围是( )A .(-1,0)∪(0,1)B .(-1,0)∪(0,1]C .(0,1)D .(0,1]4.设b >0,二次函数y =ax 2+bx +a 2-1的图象为图K3-3-2所示四个图中的一个,则a 的值为( )图K3-3-2A .1 B.-15.函数y =x -2x -1的图象是( )6.已知函数f(x)是R上的增函数,A(0,-1),B(3,1)是其图象上的两点,那么|f(x +1)|<1的解集是( )A.(1,4) B.(-1,2) C.(-∞,1)∪[4,+∞) D.(-∞,-1)∪[2,+∞)7.若函数f(x)=(x+a)(bx+2a)(常数a,b∈R)是偶函数,且它的值域为(-∞,4],则该函数的解析式f(x)=__________.8.设函数y=x2+(a+2)x+3,x∈[a,b]的图象关于直线x=1对称,则b=______.9.已知函数f(x)=x2+2ax+2,x∈[-5,5].(1)当a=-1时,求f(x)的最大值和最小值;(2)求实数a的取值范围,使y=f(x)在区间[-5,5]上是单调函数.10.定义:已知函数f(x)在[m,n](m<n)上的最小值为t,若t≤m恒成立,则称函数f(x)在[m,n](m<n)上具有“DK”性质.(1)判断函数f(x)=x2-2x+2在[1,2]上是否具有“DK”性质,说明理由;(2)若f(x)=x2-ax+2在[a,a+1]上具有“DK”性质,求a的取值范围.第4讲 幂函数1.下列结论中正确的个数有( )①幂函数的图象不可能过第四象限; ②幂函数的图象过定点(0,1)和(1,1);③幂函数y =x α,当α>0时,幂函数是增函数;当α<0时,幂函数是减函数; ④当α=0时,y =x α的图象是一条直线. A .0个 B .1个 C .2个 D .3个2.设α∈⎩⎨⎧⎭⎬⎫-1,1,12,3,则使函数y =x α的定义域为R 且为奇函数的所有α的值为( )A .1,3B .-1,1C .-1,3D .-1,1,33.在同一坐标系内,函数y =x a(a ≠0)和y =ax -1a的图象可能是( )4.给出命题:若函数y =f (x )是幂函数,则函数y =f (x )的图象不过第四象限.在它的逆命题、否命题、逆否命题三个命题中,真命题的个数是( )A .3B .2C .1D .05.已知函数f (x )=a x,g (x )=x a,h (x )=log a x (a >0且a ≠1),在同一直角坐标系中画出其中两个函数在第一象限内的图象,其中正确的是( )6.(2010年安徽)设a =⎝ ⎛⎭⎪⎫3525,b =⎝ ⎛⎭⎪⎫2535,c =⎝ ⎛⎭⎪⎫2525,则a ,b ,c 的大小关系是( ) A .a >c >b B .a >b >c C .c >a >b D .b >c >a7.(2011年广东揭阳一模)已知α∈⎩⎨⎧⎭⎬⎫-1,12,1,2,则使函数y =x α在[0,+∞)上单调递增的所有α值为_______________________________________________.8.请把图K3-4-1所示幂函数图象的代号填入表格内.图K3-4-1①y=x 23;②y=x-2;③y=x12;④y=x-1;⑤y=x 13;⑥y=x43;⑦y=x12;⑧y=x53.9.将下列各数从小到大排列起来:⎝ ⎛⎭⎪⎫2313-,⎝ ⎛⎭⎪⎫3512,323,⎝ ⎛⎭⎪⎫2512, ⎝ ⎛⎭⎪⎫3223,⎝ ⎛⎭⎪⎫560,(-2)3,⎝ ⎛⎭⎪⎫5313-.10.已知函数f (x )=(m 2-m -1)x -5m -3,m 为何值时,f (x )是: (1)幂函数;(2)幂函数,且是(0,+∞)上的增函数; (3)正比例函数; (4)反比例函数; (5)二次函数.第5讲函数的图象1.(2011年安徽)若点(a,b)在y=lg x图象上,a≠1,则下列点也在此图象上的是( ) B.(10a,1-b) D.(a2,2b)2.下列四个函数中,图象如图K3-5-1所示的只能是( )图K3-5-1A.y=x+lg x B.y=x-lg xC.y=-x+lg x D.y=-x-lg x3.(2011年陕西)方程|x|=cos x在(-∞,+∞)内( )A .没有根B .有且仅有一个根C .有且仅有两个根D .有无穷多个根 4.与函数y =(2x -1)的图象相同的函数是( )A .y =2x -1⎝ ⎛⎭⎪⎫x >12B .y =12x -1C .y =12x -1⎝ ⎛⎭⎪⎫x >12D .y =⎪⎪⎪⎪⎪⎪12x -15.(2011年陕西)设函数f (x )(x ∈R )满足f (-x )=f (x ),f (x +2)=f (x ),则函数y =f (x )的图象是( )A BC D 6.方程lg x =sin x 的实根的个数为( ) A .1个 B .2个 C .3个 D .4个7.在平面直角坐标系中,横坐标、纵坐标均为整数的点称为整点,如果函数f (x )的图象恰好通过n (n ∈N *)个整点,则称函数f (x )为n 阶整点函数.有下列函数:①f (x )=sin2x ;②g (x )=x 3;③h (x )=⎝ ⎛⎭⎪⎫13x ;④φ(x )=ln x .其中是一阶整点函数的是( ) A .①②③④ B .①③④ C .①④ D .④8.关于x 的方程|x 2-4x +3|-a =0有三个不相等的实数根,则实数a 的值是____.9.(2011年陕西3月模拟)已知函数f (x )=⎩⎪⎨⎪⎧⎝ ⎛⎭⎪⎫12x -2 x ≤-1,x -2|x |-1 x >-1,如果方程f (x )=a 有四个不同的实数根,求实数a 的取值范围.10.设a 为实数,函数f (x )=x 3-x 2-x +a . (1)求f (x )的极值;(2)当a 在什么范围内取值时,曲线y =f (x )与x 轴仅有一个交点.第6讲 函数与方程1.(2011年浙江)设函数f (x )=⎩⎪⎨⎪⎧ -x x ≤0,x 2 x >0.若f (a )=4,则实数a =( )A .-4或-2B .-4或2C .-2或4D .-2或22.由下表知f (x )=g (x )有实数解的区间是( ) x -1 0 1 2 3f (x ) -g (x ) -A.(-3.设函数f (x )=x 3-4x +3+ln x (x >0),则y =f (x )( )A .在区间⎝ ⎛⎭⎪⎫0,12,⎝ ⎛⎭⎪⎫12,2内均无零点B .在区间⎝ ⎛⎭⎪⎫0,12,⎝ ⎛⎭⎪⎫12,2内均有零点C .在区间⎝ ⎛⎭⎪⎫0,12内无零点,在区间⎝ ⎛⎭⎪⎫12,2内有零点D .在区间⎝ ⎛⎭⎪⎫0,12内有零点,在区间⎝ ⎛⎭⎪⎫12,2内无零点4.(2011年陕西)函数f (x )=x -cos x 在[0,+∞)内( )A .没有零点B .有且仅有一个零点C.有且仅有两个零点D.有无穷多个零点5.若关于x的方程x2+2kx-1=0的两根x1,x2满足-1≤x1<0<x2<2,则k的取值范围是( )6.(2011年陕西)设n∈N*,一元二次方程x2-4x+n=0有整数根的充要条件是n=______.7.函数f(x)=ln(x+2)-2x的零点所在区间是(n,n+1),则正整数n=____.8.下面是用区间二分法求方程2sin x+x-1=0在[0,1]内的一个近似解(误差不超过的算法框图,如图K3-6-1所示,则判断框内空白处应填入____________,才能得到需要的解.图K3-6-19.已知关于x的二次方程x2+2mx+2m+1=0.(1)若方程有两根,其中一根在区间(-1,0)内,另一根在区间(1,2)内,求m的范围;(2)若方程两根均在区间(0,1)内,求m的范围.10.已知函数f(x)=e x+2x2-3x.(1)求证:函数f(x)在区间[0,1]上存在唯一的极值点,并用二分法求函数取得极值时相应x的近似值(误差不超过;(2)当x≥1时,若关于x的不等式f(x)≥ax恒成立,试求实数a的取值范围(参考数据e≈,e≈,≈.第7讲 抽象函数1.(2010年陕西)下列四类函数中,有性质“对任意的x >0,y >0,函数f (x )满足f (x +y )=f (x )f (y )”的是( )A .幂函数B .对数函数C .指数函数D .余弦函数2.设f (x )是定义在R 上的偶函数,且在(-∞,0)上是增函数,已知x 1>0,x 2<0,且f (x 1)<f (x 2),那么一定有( )A .x 1+x 2<0B .x 1+x 2>0C .f (-x 1)>f (-x 2)D .f (-x 1)·f (-x 1)<03.已知函数f (x )是定义在R 上的函数且满足f ⎝ ⎛⎭⎪⎫x +32=-f (x ),若x ∈(0,3)时,f (x )=log 2(3x +1),则f (2 011)=( )A .4B .-2C .2D .log 274.已知定义域为R 的偶函数f (x )的一个单调递增区间是(2,6),那么x 的函数f (2-x )有( )A .对称轴为x =-2,一个递减区间是(4,8)B .对称轴为x =-2,一个递减区间是(0,4)C .对称轴为x =2,一个递增区间是(4,8)D .对称轴为x =2,一个递增区间是(0,4)5.若定义在R 上的函数f (x )满足:对任意x 1,x 2∈R ,有f (x 1+x 2)=f (x 1)+f (x 2)+1,则下列说法一定正确的是( )A .f (x )为奇函数B .f (x )为偶函数C .f (x )+1为奇函数D .f (x +1)为偶函数6.已知定义在R 上的奇函数f (x ),满足f (x -4)=-f (x ),且在区间[0,2]上是增函数,则( )A .f (-25)<f (11)<f (80)B .f (80)<f (11)<f (-25)C .f (11)<f (80)<f (-25)D .f (-25)<f (80)<f (11)7.对于函数f (x )定义域中任意的x 1,x 2(x 1≠x 2),有如下结论:①f (x 1+x 2)=f (x 1)·f (x 2);②f (x 1·x 2)=f (x 1)+f (x 2); ③f x 1-f x 2x 1-x 2>0; ④f x 1-1x 1<0(x 1≠0); ⑤f (-x 1)=1f x 1. 当f (x )=2x 时,上述结论中正确结论的序号是________.8.已知y =f (x )是定义在R 上的奇函数,且y =f ⎝⎛⎭⎪⎫x +π2为偶函数,对于函数y =f (x )有下列几种描述:①y =f (x )是周期函数;②x =π是它的一条对称轴;③(-π,0)是它图象的一个对称中心;④当x =π2时,它一定取最大值.其中描述正确的是____________.9.设函数y =f (x )是定义在(0,+∞)上的减函数,并且同时满足下面两个条件:①对正数x ,y 都有f (xy )=f (x )+f (y );②f ⎝ ⎛⎭⎪⎫12=1. (1)求f (1)和f (4)的值;(2)求满足f (x )+f (5-x )>-2的x 的取值范围.10.函数f (x )对任意的a ,b ∈R ,都有f (a +b )=f (a )+f (b )-1,并且当x >0时,f (x )>1.(1)求证:f (x )是R 上的增函数;(2)若f (4)=5,解不等式f (3m 2-m -2)<3.第8讲 函数模型及其应用1.在一定范围内,某种产品的购买量y 吨与单价x 元之间满足一次函数关系.如果购买1 000吨,每吨为800元;购买2 000吨,每吨为700元.一客户购买400吨,单价应该是( )A .820元B .840元C .860元D .880元2.用长度为24的材料围一矩形场地,中间加两道隔墙,要使矩形的面积最大,则隔墙的长度为( )A .3B .4C .6D .123.(2011届山东聊城调研)已知某驾驶员喝了m 升酒后,血液中酒精的含量f (x )(毫克/毫升)随时间x (小时)变化的规律近似满足表达式f (x )=⎩⎪⎨⎪⎧5x -2 0≤x ≤1,35·⎝ ⎛⎭⎪⎫13x x >1,《酒后驾车与醉酒驾车的标准及相应的处罚》规定:驾驶员血液中酒精含量不超过毫克/毫升,此驾驶员至少要过( )小时后才能开车(精确到1小时).( )A .2B .3C .4D .54.进货单价为80元的商品400个,按90元一个可以全部卖出,已知这种商品每涨价1元,其销售量就减少20个,问售价( )元时获得的利润最大( )A .85B .90C .95D .1005.某产品的总成本y(万元)与产量x(台)之间的函数关系式是y=3 000+20x-,x∈(0,240).若每台产品的售价为25万元,则生产者不亏本时(销售收入不小于总成本)的最低产量为______台.6.(2010年浙江)某商家一月份至五月份累计销售额达3 860万元,预测六月份销售额为500万元,七月份销售额比六月份递增x%,八月份销售额比七月份递增x%,九、十月份销售总额与七、八月份销售总额相等.若一月至十月份销售总额至少达7 000万元,则x的最小值是______.7.某商场宣传在节假日对顾客购物实行一定的优惠,商场规定:①如一次购物不超过200元,不予以折扣;②如一次购物超过200元,但不超过500元,按标价予以九折优惠;③如一次购物超过500元的,其中500元给予九折优惠,超过500元的给予八五折优惠;某人两次去购物,分别付款176元和432元,如果他只去一次购买同样的商品,则应付款______元.8.(2011届海淀区统测)如图K3-8-1(1)是反映某条公共汽车线路收支差额(即营运所得票价收入与付出成本的差)y与乘客量x之间关系的图象.由于目前该条公交线路亏损,公司有关人员提出了两种调整的建议,如图K3-8-1(2)(3)所示.图K3-8-1给出以下说法:(1)图(2)的建议是:提高成本,并提高票价;(2)图(2)的建议是:降低成本,并保持票价不变;(3)图(3)的建议是:提高票价,并保持成本不变;。
