平行四边形矩形菱形正方形
平行四边形、矩形、菱形、正方形定义 性质和判定归纳表
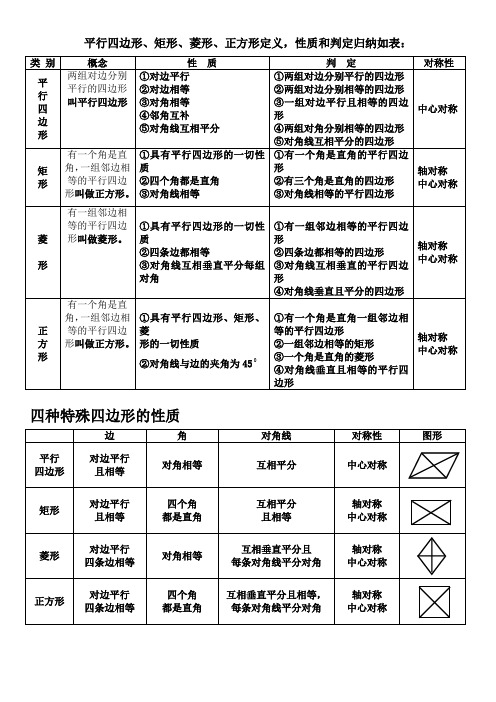
平行四边形、矩形、菱形、正方形定义,性质和判定归纳如表:类别概念性质判定对称性平行四边形两组对边分别平行的四边形叫平行四边形①对边平行②对边相等③对角相等④邻角互补⑤对角线互相平分①两组对边分别平行的四边形②两组对边分别相等的四边形③一组对边平行且相等的四边形④两组对角分别相等的四边形⑤对角线互相平分的四边形中心对称矩形有一个角是直角,一组邻边相等的平行四边形叫做正方形。
①具有平行四边形的一切性质②四个角都是直角③对角线相等①有一个角是直角的平行四边形②有三个角是直角的四边形③对角线相等的平行四边形轴对称中心对称菱形有一组邻边相等的平行四边形叫做菱形。
①具有平行四边形的一切性质②四条边都相等③对角线互相垂直平分每组对角①有一组邻边相等的平行四边形②四条边都相等的四边形③对角线互相垂直的平行四边形④对角线垂直且平分的四边形轴对称中心对称正方形有一个角是直角,一组邻边相等的平行四边形叫做正方形。
①具有平行四边形、矩形、菱形的一切性质②对角线与边的夹角为450①有一个角是直角一组邻边相等的平行四边形②一组邻边相等的矩形③一个角是直角的菱形④对角线垂直且相等的平行四边形轴对称中心对称四种特殊四边形的性质边角对角线对称性图形平行四边形对边平行且相等对角相等互相平分中心对称矩形对边平行且相等四个角都是直角互相平分且相等轴对称中心对称菱形对边平行四条边相等对角相等互相垂直平分且每条对角线平分对角轴对称中心对称正方形对边平行四条边相等四个角都是直角互相垂直平分且相等,每条对角线平分对角轴对称中心对称。
初中平行四边形、矩形、菱形、正方形知识点总结(精)

平行四边形、矩形、菱形、正方形知识点总结1.平行四边形、矩形、菱形、正方形的性质:平行四边形矩形菱形正方形图形性质边对边平行且相等对边平行且相等对边平行,四边相等对边平行,四边相等角对角相等,邻角互补四个角都是直角对角相等四个角都是直角对角线互相平分互相平分且相等互相垂直平分,且每条对角线平分一组对角互相垂直平分且相等,每条对角线平分一组对角对称性只是中心对称图形既是轴对称图形,又是中心对称图形面积ah=S ab=S2121S dd=(注:d1,d2为菱形两条对角线的长度。
)2S a=2. 判定方法小结:(1) 平行四边形:①两组对边分别平行的四边形是平行四边形;②两组对边分别相等的四边形是平行四边形;③两组对角分别相等的四边形是平行四边形;④对角线互相平分的四边形是平行四边形;⑤一组对边平行且相等的四边形是平行四边形。
(2)矩形:有一个角是直角的平行四边形叫做矩形。
①有一个角是直角的平行四边形是矩形;②对角线相等的平行四边形是矩形;③有三个角是直角的四边形是矩形;④对角线相等且互相平分的四边形是矩形。
(3) 菱形:有一组邻边相等的平行四边形叫做菱形.①有一组邻边相等的平行四边形是菱形;②对角线互相垂直的平行四边形是菱形;③四边都相等的四边形是菱形;④对角线互相垂直平分的四边形是菱形(4) 正方形:有一组邻边相等且有一个角是直角的平行四边形叫做正方形。
①有一组邻边相等且有一个角是直角的平行四边形是正方形;②对角线互相垂直且相等的平行四边形是正方形;③有一组邻边相等的矩形是正方形;④对角线互相垂直的矩形是正方形;⑤有一个角是直角的菱形是正方形;⑥对角线相等的菱形是正方形;⑦对角线互相垂直平分且相等的四边形是正方形。
2023年八年级数学平行四边形矩形菱形正方形知识点总结

平行四边形、矩形、菱形、正方形知识点总结平行四边形:性质:①边:对边平行且相等;②角:对角相等、邻角互补;③对角线:对角线互相平分;鉴定:①定义:两组对边分别平行旳四边形②措施1:两组对角分别相等旳四边形③措施2:两组对边分别相等旳四边形④措施3:对角线互相平分旳四边形⑤措施4:一组平行且相等旳四边形矩形:性质:①边:对边平行且相等;②角:对角相等、邻角互补;③对角线:对角线互相平分且相等;鉴定:①有一种角是直角旳平行四边形;②对角线相等旳平行四边形;③四个角都相等菱形:性质:①边:四条边都相等;②角:对角相等、邻角互补;③对角线:对角线互相垂直平分且每条对角线平分每组对角;④面积:则S菱形=底×高=ah;或者S菱形=12ab(对角线乘积旳二分之一).鉴定:①有一组邻边相等旳平行四边形;②对角线互相垂直旳平行四边形;③四条边都相等.正方形:性质:①边:四条边都相等;②角:四角相等;③对角线:对角线互相垂直平分且相等,对角线与边旳夹角为450;鉴定:①有一组邻边相等且有一种直角旳平行四边形②有一组邻边相等旳矩形;③对角线互相垂直旳矩形.④有一种角是直角旳菱形⑤对角线相等旳菱形;几种特殊四边形旳常用说理措施与解题思绪分析(1)识别矩形旳常用措施①先阐明四边形ABCD为平行四边形,再阐明平行四边形ABCD旳任意一种角为直角.②先阐明四边形ABCD为平行四边形,再阐明平行四边形ABCD旳对角线相等.③阐明四边形ABCD旳三个角是直角.(2)识别菱形旳常用措施①先阐明四边形ABCD为平行四边形,再阐明平行四边形ABCD旳任一组邻边相等.②先阐明四边形ABCD为平行四边形,再阐明对角线互相垂直.③阐明四边形ABCD旳四条相等.(3)识别正方形旳常用措施①先阐明四边形ABCD为平行四边形,再阐明平行四边形ABCD旳一种角为直角且有一组邻边相等.②先阐明四边形ABCD为平行四边形,再阐明对角线互相垂直且相等.③先阐明四边形ABCD为矩形,再阐明矩形旳一组邻边相等.④先阐明四边形ABCD为菱形,再阐明菱形ABCD旳一种角为直角.。
1.3平行四边形,矩形,菱形,正方形的性质和判定

第三节 平行四边形,矩形,菱形,正方形的性质和判定(一)平行四边形的性质和判定 一.教学重难点:重点:平行四边形的性质证明. 难点:分析、综合思考的方法.二.知识点和考点:1.平行四边形的定义2.平行四边形的性质,面积3.平行四边形的判定4.三角形的中位线及其性质三.知识点讲解考点一: 平行四边形的定义考点二:平行四边形的性质(1)平行四边形的对边相等注:在证明题时使用格式是:∵四边形ABCD 是平行四边形,定义:有两组对边分别平行的四边形叫做平行四边形。
记做例1:如图:在中,如果E F ∥AD ,GH ∥CD ,EF 与GH 相交于点O ,那么图中的平行四边形一共有 ( ) A .4个 B 、5个 C 、8个 D 、9个例2:如图,E 、F 分别是边AD 、BC 上的点,并且AF ∥CE ,求证:∠AFB=∠DEC 。
∴AB=DC,AD=BC例1、如图,在平行四边形ABCD中,AE=CF,求证:AF=CE。
例2.平行四边形的周长等于56cm,两邻边长的比为3:1,那么这个平行四边形较长的边长为(2).平行四边形的对角相等注:在证明题时使用格式是:∵四边形ABCD是平行四边形∴∠A=∠C,∠B=∠D例1.已知中,E、F是对角线AC上的两点,且AE=CF。
求证:∠ADF=∠CBE。
例2、在中,∠A、∠B的度数之比为5:4,则∠C等于()A、 B、 C、 D、(3)、平行四边形的对角线互相平分注:在证明题时使用格式是:∵四边形ABCD是平行四边形∴OA=OC,OB=OD例3.如图,,过其对角线交点O,引一直线交BC于E,交AD于F,若AB=2.4cm,BC=4cm,OE=1.1cm,求四边形ABEF的周长。
例4.如图,已知:中,AC、BD相交于O点,OE⊥AD于E,OF⊥BC于F,求证:OE=OF。
例5.如图,如果的周长之差为8,而AB:AD=3:2,那么的周长为多少?例6.如图,已知的周长为60cm,对角线AC、BD相交于点O,的周长长8cm,求这个四边形各边长.(4)平行四边形的面积如图(1),,也就是边长×高=ah(2)、同底(等底)同高(等高)的平行四边形面积相等。
矩形正方形菱形平行四边形的关系

矩形正方形菱形平行四边形的关系矩形、正方形、菱形和平行四边形都是几何学中常见的图形,它们之间存在着一定的关系。
本文将介绍这四种图形之间的关系,并分别阐述它们的特点和性质。
一、矩形矩形是一种具有特殊性质的四边形,它的四个内角都是直角(即90度)。
此外,矩形的对角线相等且垂直相交,对边平行且相等。
矩形的特点使得它在日常生活和工程设计中得到广泛应用。
例如,书桌、建筑物的窗户、墙壁等都常见到矩形的形状。
二、正方形正方形是矩形的特殊形式,它的四个边长相等且内角都是直角。
由于正方形具有对边平行且相等的性质,因此它也是平行四边形。
正方形的特点使得它在几何学中具有重要的地位,在城市规划、图案设计等领域中也被广泛应用。
三、菱形菱形是一种具有特殊性质的四边形,它的对边平行且相等。
此外,菱形的对角线相等且垂直相交,内角不是直角。
菱形的特点使得它在几何学中具有独特的地位,例如,菱形的形状常常被用于设计钻石、纹身等。
四、平行四边形平行四边形是一种具有特殊性质的四边形,它的对边平行且相等。
平行四边形的特点使得它在几何学中也是一个重要的图形。
平行四边形的对角线不相等,内角之和为360度。
平行四边形的形状常常出现在建筑物的立面、道路的标线等。
矩形、正方形、菱形和平行四边形之间的关系可以总结如下:1. 矩形是一种特殊的平行四边形,它的对边平行且相等。
2. 正方形是一种特殊的矩形和平行四边形,它的四个边长相等且内角都是直角。
3. 菱形是一种特殊的平行四边形,它的对边平行且相等,但内角不是直角。
4. 平行四边形是一种具有对边平行且相等的特性的四边形,它包括了矩形和菱形。
矩形、正方形、菱形和平行四边形之间存在着紧密的关系。
它们都是具有特殊性质的四边形,但在某些方面又有所不同。
矩形和正方形具有直角和对边相等的特点,而菱形则具有对边平行且相等的特点,平行四边形则是包含了矩形和菱形的更广义的概念。
这些图形在数学和几何学中具有重要的地位,在日常生活和工程设计中也得到了广泛的应用。
数学平行四边形、菱形、矩形、正方形的定理、性质、判定

平行四边形性质定理1 平行四边形的对角相等平行四边形性质定理2 平行四边形的对边相等且平行平行四边形性质定理3 平行四边形的对角线互相平分平行四边形判定定理1 两组对角分别相等的四边形是平行四边形平行四边形判定定理2 两组对边分别相等的四边形是平行四边形平行四边形判定定理3 对角线互相平分的四边形是平行四边形平行四边形判定定理4 一组对边平行相等的四边形是平行四边形平行四边形判定定理5 两组那边分别平行的四边形是平行四边形矩形性质定理1 矩形的四个角都是直角矩形性质定理2 矩形的对角线相等矩形判定定理1 有一个角是直角的平行四边形是矩形矩形判定定理2 对角线相等的平行四边形是矩形正方形性质定理1正方形的四个角都是直角,四条边都相等正方形性质定理2正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角菱形性质定理1 菱形的四条边都相等菱形性质定理2 菱形的对角线互相垂直菱形面积=对角线乘积的一半,即S=(a×b)÷2菱形判定定理1 四边都相等的四边形是菱形菱形判定定理2 对角线互相垂直的平行四边形是菱形菱形判定定理3是对称轴图形的平行四边形是菱形梯形及特殊梯形的定义梯形:一组对边平行而另一组对边不平行的四边形叫做梯形.(一组对边平行且不相等的四边形叫做梯形.)等腰梯形:两腰相等的梯形叫做等腰梯形.直角梯形:一腰垂直于底的梯形叫做直角梯形.等腰梯形的性质1、等腰梯形两腰相等、两底平行;2、等腰梯形在同一底上的两个角相等;3、等腰梯形的对角线相等;4、等腰梯形是轴对称图形,它只有一条对称轴,一底的垂直平分线是它的对称轴.等腰梯形的判定1、两腰相等的梯形是等腰梯形;2、在同一底上的两个角相等的梯形是等腰梯形;3、对角线相等的梯形是等腰梯形.。
数学平行四边形、菱形、矩形、正方形的定理、性质、判定

1. 定义: 两组对边分别平行的四边形叫做平行四边形。
2.性质:⑴如果一个四边形是平行四边形,那么这个四边形的两组对边分别相等。
(简述为“平行四边形的对边相等”)⑵如果一个四边形是平行四边形,那么这个四边形的两组对角分别相等。
(简述为“平行四边形的对角相等”)⑶夹在两条平行线间的平行线段相等。
⑷如果一个四边形是平行四边形,那么这个四边形的两条对角线互相平分。
(简述为“平行四边形的两条对角线互相平分”)⑸平行四边形是中心对称图形,对称中心是两条对角线的交点。
3.判定:(1)如果一个四边形的两组对边分别相等,那么这个四边形是平行四边形。
(简述为“两组对边分别相等的四边形是平行四边形”)(2)如果一个四边形的一组对边平行且相等,那么这个四边形是平行四边形。
(简述为“一组对边平行且相等的四边形是平行四边形”)(3)如果一个四边形的两条对角线互相平分,那么这个四边形是平行四边形。
(简述为“对角线互相平分的四边形是平行四边形”)(4)如果一个四边形的两组对角分别相等,那么这个四边形是平行四边形。
(简述为“两组对角分别相等的四边形是平行四边形”(5)如果一个四边形的两组对边分别平行,那么这个四边形是平行四边形。
(简述为“两组对边分别平行的四边形是平行四边形”)矩形的性质和判定定义:有一个角是直角的平行四边形叫做矩形.性质:①矩形的四个角都是直角;②矩形的对角线相等 .注意:矩形具有平行四边形的一切性质 .判定:①有一个角是直角的平行四边形是矩形;②有三个角是直角的四边形是矩形;③对角线相等的平行四边形是矩形 .菱形的性质和判定定义:有一组邻边相等的平行四边形叫做菱形.性质:①菱形的四条边都相等;②菱形的对角线互相垂直,并且每一条对角线平分一组对角 .注意:菱形也具有平行四边形的一切性质 .判定:①有一组邻边相等的平行四边形是菱形;②四条边都相等的四边形是菱形;③对角线互相垂直的平行四边形是菱形(4).有一条对角线平分一组对角的平行四边形是菱形正方形的性质和判定定义:有一组邻边相等并且有一角是直角的平行四边形叫做正方形.性质:①正方形的四个角都是直角,四条边都相等;②正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角 .判定:因为正方形具有平行四边形、矩形、菱形的一切性质,所以我们判定正方形有三个途径①四条边都相等的平行四边形是正方形②有一组临边相等的矩形是正方形③有一个角是直角的菱形是正方形梯形及特殊梯形的定义梯形:一组对边平行而另一组对边不平行的四边形叫做梯形.(一组对边平行且不相等的四边形叫做梯形.)等腰梯形:两腰相等的梯形叫做等腰梯形. 直角梯形:一腰垂直于底的梯形叫做直角梯形.等腰梯形的性质1、等腰梯形两腰相等、两底平行;2、等腰梯形在同一底上的两个角相等;3、等腰梯形的对角线相等;4、等腰梯形是轴对称图形,它只有一条对称轴,一底的垂直平分线是它的对称轴. 等腰梯形的判定1、两腰相等的梯形是等腰梯形;2、在同一底上的两个角相等的梯形是等腰梯形;3、对角线相等的梯形是等腰梯形.平行四边形性质定理1 平行四边形的对角相等平行四边形性质定理2 平行四边形的对边相等且平行平行四边形性质定理3 平行四边形的对角线互相平分平行四边形判定定理1 两组对角分别相等的四边形是平行四边形平行四边形判定定理2 两组对边分别相等的四边形是平行四边形平行四边形判定定理3 对角线互相平分的四边形是平行四边形平行四边形判定定理4 一组对边平行相等的四边形是平行四边形矩形性质定理1 矩形的四个角都是直角矩形性质定理2 矩形的对角线相等矩形判定定理1 有一个角是直角的平行四边形是矩形矩形判定定理2 对角线相等的平行四边形是矩形正方形性质定理1正方形的四个角都是直角,四条边都相等正方形性质定理2正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角菱形性质定理1 菱形的四条边都相等菱形性质定理2 菱形的对角线互相垂直菱形面积=对角线乘积的一半,即S=(a×b)÷2菱形判定定理1 四边都相等的四边形是菱形菱形判定定理2 对角线互相垂直的平行四边形是菱形菱形判定定理3是对称轴图形的平行四边形是菱形。
精华总结:平行四边形、矩形、菱形、正方形知识点
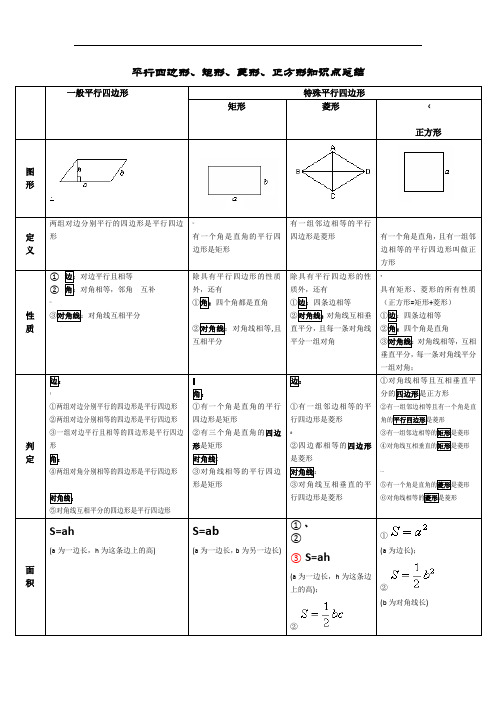
平行四边形、矩形、菱形、正方形知识点总结一般平行四边形特殊平行四边形矩形菱形(正方形图形·定义两组对边分别平行的四边形是平行四边形~有一个角是直角的平行四边形是矩形有一组邻边相等的平行四边形是菱形有一个角是直角,且有一组邻边相等的平行四边形叫做正方形性质①边:对边平行且相等②角:对角相等,邻角互补~③对角线:对角线互相平分除具有平行四边形的性质外,还有①角:四个角都是直角②对角线:对角线相等,且互相平分除具有平行四边形的性质外,还有①边:四条边相等②对角线:对角线互相垂直平分,且每一条对角线平分一组对角*具有矩形、菱形的所有性质(正方形=矩形+菱形)①边:四条边相等②角:四个角是直角③对角线:对角线相等,互相垂直平分,每一条对角线平分一组对角;判定边:!①两组对边分别平行的四边形是平行四边形②两组对边分别相等的四边形是平行四边形③一组对边平行且相等的四边形是平行四边形角:④两组对角分别相等的四边形是平行四边形对角线:⑤对角线互相平分的四边形是平行四边形;角:①有一个角是直角的平行四边形是矩形②有三个角是直角的四边形是矩形对角线:③对角线相等的平行四边形是矩形边:①有一组邻边相等的平行四边形是菱形#②四边都相等的四边形是菱形对角线:③对角线互相垂直的平行四边形是菱形①对角线相等且互相垂直平分的四边形是正方形②有一组邻边相等且有一个角是直角的平行四边形是菱形③有一组邻边相等的矩形是菱形④对角线互相垂直的矩形是菱形…⑤有一个角是直角的菱形是菱形⑥对角线相等的菱形是菱形面积S=ah(a为一边长,h为这条边上的高)S=ab(a为一边长,b为另一边长)①~②③S=ah(a为一边长,h为这条边上的高);②①(a为边长);②(b为对角线长)。
正方形、矩形、菱形和平行四边形四者知识点详细总结汇总
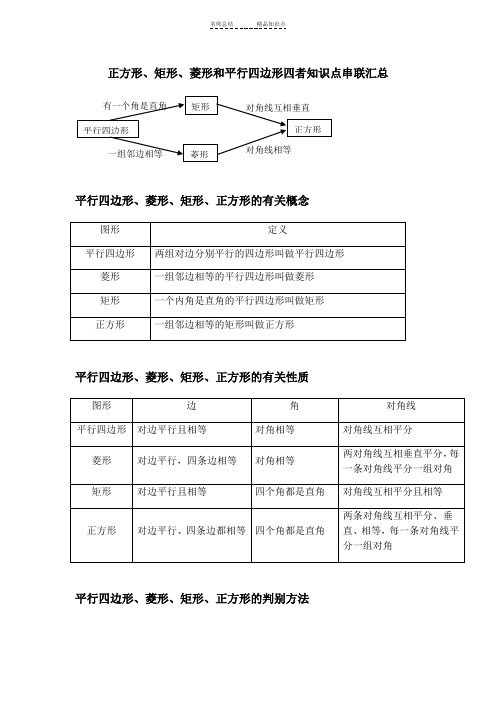
正方形、矩形、菱形和平行四边形四者知识点串联汇总平行四边形、菱形、矩形、正方形的有关概念图形 定义平行四边形 两组对边分别平行的四边形叫做平行四边形 菱形 一组邻边相等的平行四边形叫做菱形 矩形 一个内角是直角的平行四边形叫做矩形 正方形 一组邻边相等的矩形叫做正方形平行四边形、菱形、矩形、正方形的有关性质图形边角对角线平行四边形 对边平行且相等 对角相等 对角线互相平分菱形 对边平行,四条边相等 对角相等 两对角线互相垂直平分,每一条对角线平分一组对角 矩形对边平行且相等四个角都是直角对角线互相平分且相等 正方形 对边平行、四条边都相等 四个角都是直角两条对角线互相平分、垂直、相等,每一条对角线平分一组对角平行四边形、菱形、矩形、正方形的判别方法对角线相等对角线互相垂直有一个角是直角 一组邻边相等平行四边形矩形菱形正方形图形 判别方法平行四边形 两组对边分别平行的四边形是平行四边形 一组对边平行且相等的四边形是平行四边形两组对边分别相等的四边形是平行四边形 两组对角分别相等的四边形是平行四边形 对角线互相平分的四边形是平行四边形菱形 一组邻边相等的平行四边形是菱形四条边都相等的四边形是菱形 对角线互相垂直的平行四边形是菱形 矩形一个内角是直角的平行四边形是矩形对角线相等的平行四边形是矩形 正方形一组邻边相等的矩形是正方形 对角线互相垂直的矩形是正方形有一个角是直角的菱形是正方形 对角线相等的菱形是正方形二、梯形常见的辅助线 1.延长两腰交于一点作用:使梯形问题转化为三角形问题。
若是等腰梯形则得到等腰三角形。
2.平移一腰作用:使梯形问题转化为平行四边形及三角形问题。
3.作高作用:使梯形问题转化为直角三角形及矩形问题。
4.平移一条对角线作用:(1)得到平行四边形ACED,使CE=AD,BE等于上、下底的和=S△DBE(2)S梯形ABCD5.当有一腰中点时,连结一个顶点与一腰中点并延长交一个底的延长线。
平行四边形、矩形、菱形、正方形定义 性质和判定归纳表

平行四边形、矩形、菱形、正方形定义,性质和判定归纳如表:类别概念性质判定对称性平行四边形两组对边分别平行的四边形叫平行四边形①对边平行②对边相等③对角相等④邻角互补⑤对角线互相平分①两组对边分别平行的四边形②两组对边分别相等的四边形③一组对边平行且相等的四边形④两组对角分别相等的四边形⑤对角线互相平分的四边形中心对称矩形有一个角是直角,一组邻边相等的平行四边形叫做正方形。
①具有平行四边形的一切性质②四个角都是直角③对角线相等①有一个角是直角的平行四边形②有三个角是直角的四边形③对角线相等的平行四边形轴对称中心对称菱形有一组邻边相等的平行四边形叫做菱形。
①具有平行四边形的一切性质②四条边都相等③对角线互相垂直平分每组对角①有一组邻边相等的平行四边形②四条边都相等的四边形③对角线互相垂直的平行四边形④对角线垂直且平分的四边形轴对称中心对称正方形有一个角是直角,一组邻边相等的平行四边形叫做正方形。
①具有平行四边形、矩形、菱形的一切性质②对角线与边的夹角为450①有一个角是直角一组邻边相等的平行四边形②一组邻边相等的矩形③一个角是直角的菱形④对角线垂直且相等的平行四边形轴对称中心对称四种特殊四边形的性质边角对角线对称性图形平行四边形对边平行且相等对角相等互相平分中心对称矩形对边平行且相等四个角都是直角互相平分且相等轴对称中心对称菱形对边平行四条边相等对角相等互相垂直平分且每条对角线平分对角轴对称中心对称正方形对边平行四条边相等四个角都是直角互相垂直平分且相等,每条对角线平分对角轴对称中心对称。
平行四边形、矩形、菱形、正方形的定义、性质、判定

平行四边形定义:两组对边分别平行的四边形叫做平行四边形
平行四边形性质:对边平行且相等,对角相等,对角线互相平分
平行四边形判定:1、有一组对边平行且相等的四边形是平行四边形
2、两组对边分别平行的四边形是平行四边形
3、两组对边分别相等的四边形是平行四边形
4、对角线互相平分的四边形是平行四边形
矩形定义:有一个角是90°的平行四边形叫做矩形
矩形性质:1、四个角都是90°2、对角线相等
矩形判定:1、有一个角是90°的平行四边形是矩形
2、三个角都是90°的角是矩形
3、对角线相等的平行四边形是矩形
菱形定义:有一组邻边相等的平行四边形叫做菱形
菱形性质:1、四边相等2、对角线互相垂直
菱形判定:1、有一组邻边相等的平行四边形是菱形
2、四条边都相等的四边形是菱形
3、对脚线互相垂直的平行四边形是菱形
正方形定义:有一组邻边相等且有一个角是直角的平行四边形叫做正方形
正方形性质:具有平行四边形、菱形、矩形的所有性质
正方形判定:1、有一组邻边相等且有一个角是直角的平行四边形是正方形
2、有一组邻边相等的矩形是正方形
3、有一个角是直角的菱形是正方形。
平行四边形、菱形、矩形、正方形性质和判定归纳如表
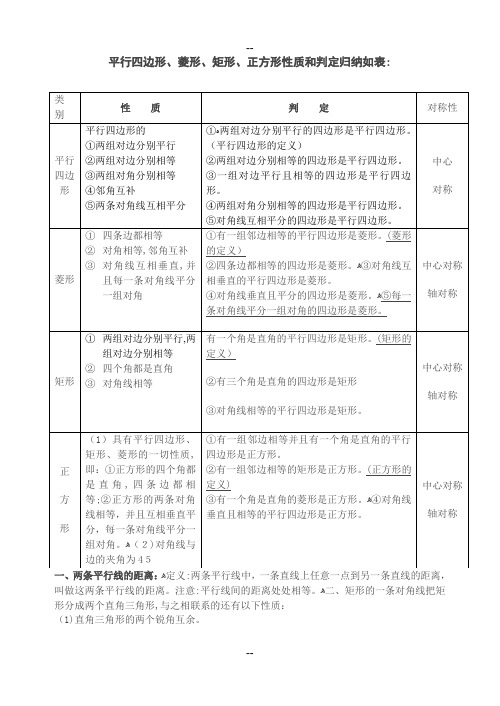
平行四边形、菱形、矩形、正方形性质和判定归纳如表:
一、两条平行线的距离:ﻫ定义:两条平行线中,一条直线上任意一点到另一条直线的距离,叫做这两条平行线的距离。
注意:平行线间的距离处处相等。
ﻫ二、矩形的一条对角线把矩形分成两个直角三角形,与之相联系的还有以下性质:
(1)直角三角形的两个锐角互余。
--
--
(2)直角三角形两直角边的平方和等于斜边的平方。
(即勾股定理) (3)直角三角形斜边上的中线等于斜边的一半。
(4)直角三角形中30 角所对的直角边等于斜边的一半。
四种特殊四边形的性质
四种特殊四边形常用的判定方法:
一组邻一个内角
一组邻。
平行四边形菱形矩形正方形的性质及判定归纳

平行四边形菱形矩形正方形的性质及判定归纳性质:1、边:平行四边形的对边平行且相等。
2、角:平行四边形的邻角互补,对角相等。
3、对角线:平行四边形的对角线互相平分。
4、中心对称图形,对称中心是对角线的交点。
5、夹在两条平行线间的平行线段相等。
6、若一直线过平行四边形两对角线的交点,则这直线被一组对边截下的线段以对角线的交点为中点,且这条直线平分分四边形的面积。
判定:1、边:①两组对边分别平行的四边形是平行四边形。
②两组对边分别相等的四边形是平行四边形。
③一组对边平行且相等的四边形是平行四边形。
2、角:两组对角分别相等的四边形是平行四边形。
3、对角线:对角线互相平分的四边形是平行四边形。
菱形性质1.边:四条边相等。
2.对角线:对角线互相垂直,并且每一条对角线平分一组对角。
3.菱形是轴对称、中心对称图形。
4.面积:①菱形面积=底×高=对角线乘积的一半。
②菱形的周长=棱长乘以4。
③S菱形=1/2×ab(a、b为两条对角线)。
判定1.一组邻边相等的平行四边形是菱形。
2.对角线互相垂直的平行四边形是菱形。
3.四条边相等的四边形是菱形。
4.对角线互相垂直平分的四边形是菱形。
〖注意〗1.对角线互相垂直的四边形不一定是菱形,必须加上平行四边形这个条件它才是菱形.2.利用菱形的性质及判定可以证明线段相等及倍分、角相等及倍分、直线平行、垂直,以及证明一个四边形是菱形和有关计算.矩形性质1:矩形的四个角都是直角.2:矩形的对角线相等.3.直角三角形斜边上的中线等于斜边的一半.判定:1、有一个角是直角的平行四边形。
用定义判定一个四边形是矩形,必须同时满足两个条件:一是有一个角是直角;二是平行四边形.也就是说有一角是直角的四边形,不一定是矩形,必须加上平行四边形这个条件,它才是矩形.2、对角线相等的平行四边形是矩形.用定理2证明一个四边形是矩形,也必须满足两个条件:一是对角线相等;二是平行四边形.也就说明:两条对角线相等的四边形不一定是矩形,必须加上平行四边形这个条件,它才是矩形.3、有三个角是直角的四边形是矩形.判定一个四边形是矩形,知道三个角是直角,条件就够了.因为由四边形内角和可知,这时第四个角一定是直角.正方形性质1、边:对边平行,四边相等;2、角:四个角都是直角;3、对角线:对角线相等,互相垂直平分,每条对角线平分一组对角.4、正方形是轴对称图形,有4条对称轴.5、正方形的一条对角线把正方形分成两个全等的等腰直角三角形,两条对角线把正方形分成四个小的全等的等腰直角三角形.6、正方形的面积:若正方形的边长为,对角线长为,则.判定一个四边形为正方形主要根据定义,途径有两种:①先证它是矩形,再证它有一组邻边相等.②先证它是菱形,再证它有一个角为直角.2.判定正方形的一般顺序:①先证明它是平行四边形;②再证明它是菱形(或矩形);③最后证明它是矩形(或菱形)。
平行四边形、矩形、菱形、正方形性质和判定归纳表
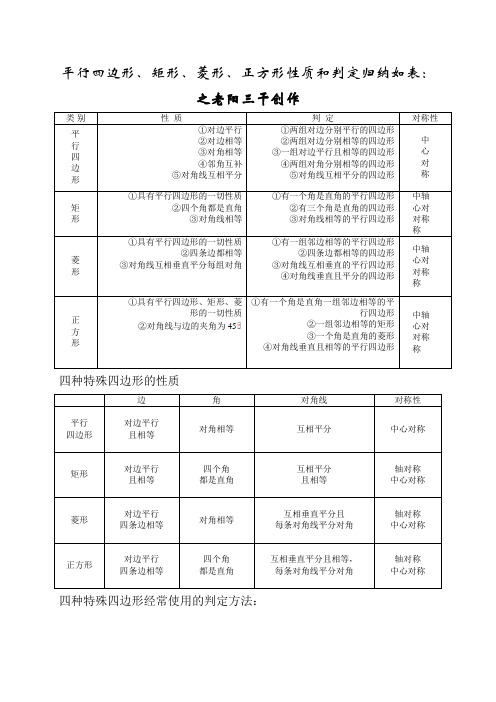
平行四边形、矩形、菱形、正方形性质和判定归纳如表:之老阳三干创作类别性质判定对称性平行四边形①对边平行②对边相等③对角相等④邻角互补⑤对角线互相平分①两组对边分别平行的四边形②两组对边分别相等的四边形③一组对边平行且相等的四边形④两组对角分别相等的四边形⑤对角线互相平分的四边形中心对称矩形①具有平行四边形的一切性质②四个角都是直角③对角线相等①有一个角是直角的平行四边形②有三个角是直角的四边形③对角线相等的平行四边形中轴心对对称称菱形①具有平行四边形的一切性质②四条边都相等③对角线互相垂直平分每组对角①有一组邻边相等的平行四边形②四条边都相等的四边形③对角线互相垂直的平行四边形④对角线垂直且平分的四边形中轴心对对称称正方形①具有平行四边形、矩形、菱形的一切性质45对角线与边的夹角为②①有一个角是直角一组邻边相等的平行四边形②一组邻边相等的矩形③一个角是直角的菱形④对角线垂直且相等的平行四边形中轴心对对称称四种特殊四边形的性质边角对角线对称性平行四边形对边平行且相等对角相等互相平分中心对称矩形对边平行且相等四个角都是直角互相平分且相等轴对称中心对称菱形对边平行四条边相等对角相等互相垂直平分且每条对角线平分对角轴对称中心对称正方形对边平行四条边相等四个角都是直角互相垂直平分且相等,每条对角线平分对角轴对称中心对称四种特殊四边形经常使用的判定方法:。
平行四边形、菱形、矩形、正方形性质和判定归纳如表
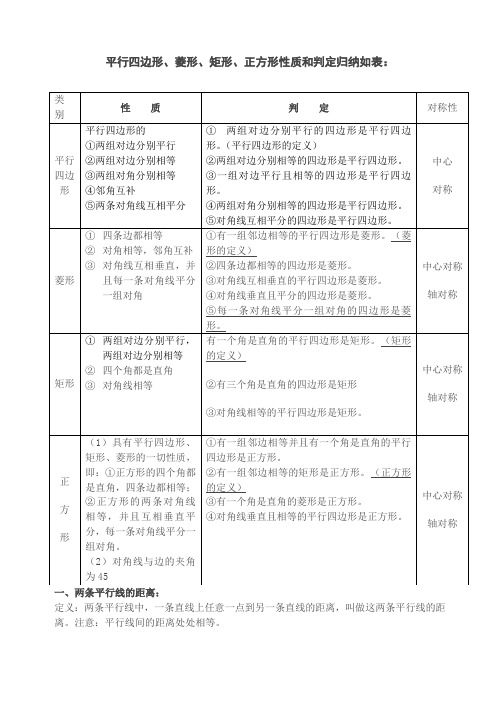
平行四边形、菱形、矩形、正方形性质和判定归纳如表:
定义:两条平行线中,一条直线上任意一点到另一条直线的距离,叫做这两条平行线的距离。
注意:平行线间的距离处处相等。
二、矩形的一条对角线把矩形分成两个直角三角形,与之相联系的还有以下性质:(1)直角三角形的两个锐角互余。
(2)直角三角形两直角边的平方和等于斜边的平方。
(即勾股定理)
(3)直角三角形斜边上的中线等于斜边的一半。
(4)直角三角形中30 角所对的直角边等于斜边的一半。
四种特殊四边形的性质
四种特殊四边形常用的判定方法:
一组邻
一组邻
边相等
对角线相
对角线
垂直
对角线
相等
对角线垂
直。
平行四边形菱形矩形正方形的易错点

平行四边形菱形矩形正方形的易错点平行四边形、菱形、矩形、正方形这些几何概念在初中数学中是非常重要的基础知识点。
然而,由于其相似的外观和特性,学生们常常容易混淆它们之间的区别和性质。
在这篇文章中,我们将介绍这些图形的易错点,以帮助学生们更好地理解它们。
首先,我们来看平行四边形。
平行四边形是一个具有两对平行边的四边形。
它的特点是对边平行且长度相等,相邻角的和为180°。
学生们常常容易将平行四边形和其他四边形混淆,例如矩形和菱形。
其次,菱形是一个特殊的平行四边形,具有以下特点:所有边都相等,对角线相互垂直且相等,对角线的交点称为菱心。
很多学生容易错误地认为菱形必定是矩形或正方形,这是一个常见的误解。
接下来,我们谈谈矩形。
矩形是一个具有四个直角的平行四边形,它的特点是所有角都是90°。
同样,学生们常常错把矩形当作正方形,因为它们都具备直角。
最后,我们来讨论正方形。
正方形是一个特殊的矩形,它具有以下特点:所有边相等,所有角都是90°,对角线相等且相互垂直。
尽管正方形的定义相对简单,但学生们在判断平行四边形、矩形和正方形时仍然容易出现困惑。
为了帮助学生们更好地区分这些图形,这里提供一些指导意义。
首先,要注意图形的边长和角度特征。
学生们可以通过测量边长和角度来判断一个图形到底是平行四边形、菱形、矩形还是正方形。
其次,要以图形的特征为准,而不是只凭直觉。
例如,如果一个图形具有所有边和角都相等的特点,那它就是一个正方形,而不是矩形或其他形状。
最后,多加练习和思考。
通过做一些练习题,学生们可以更好地理解和记忆这些图形的特性,避免出现混淆的情况。
总之,平行四边形、菱形、矩形和正方形是初中数学中非常基础的几何图形。
要正确理解和应用它们,学生们需要仔细观察它们的特点,并加以思考和实践。
希望这篇文章能帮助学生们更好地理解这些图形,并避免常见的易错点。
平行四边形 矩形 菱形正方形

平行四边形矩形菱形正方形一、考点梳理1.平行四边形、矩形、菱形、正方形的性质:平行四边形矩形菱形正方形图形性质1.对边且;2.对角;邻角;3.对角线;1.对边且;2.对角且四个角都是;3.对角线;1.对边且四条边都;2.对角;3.对角线且每条对角线;1.对边且四条边都;2.对角且四个角都是;3.对角线且每条对角线;面积2. 识别方法小结:(1) 识别平行四边形的方法:①两组对边的四边形是平行四边形;②两组相等的四边形是平行四边形;③对角线的四边形是平行四边形;④一组对边的四边形是平行四边形。
(2) 识别矩形的方法:①有一个角是的平行四边形是矩形;②对角线的平行四边形是矩形;③有三个角的四边形是矩形;④对角线且的四边形是矩形。
(3) 识别菱形的方法:①有一组邻边的是菱形;②对角线的平行四边形是菱形;③四边都相等的是菱形;④对角线的四边形是菱形。
(4) 识别正方形的方法:①有一组邻边相等且有一个角是直角的是正方形;②对角线的平行四边形是正方形;③有一组邻边相等的是正方形;④对角线互相垂直的是正方形;⑤有一个角是直角的是正方形;⑥对角线相等的是正方形;⑦对角线互相垂直平分且相等的是正方形。
二、例题精讲考点1 平行四边形的性质.例题1.如图,□ABCD的对角线交于点O,且AB=5,△OCD的周长为23,则□ABCD的两条对角线的和是()A.18 B.28 C.36 D.46例题2.如图,点E是□ABCD的边CD的中点,AD、BE的延长线相交于点F,DF=3,DE=2,则□ABCD的周长是()A.5 B.7 C.10 D.14例题3.如图,在△ABC中,AB=AC,D、E、F分别是AC、BC、BA延长线上的点,求证:AD =BF考点2 平行四边形的判定例题4.四边形ABCD 中,对角线AC ,BD 相交于点O ,给出下列四个条件:AD ∥BC ;②AD =BC ;③OA =OC ;④OB =OD ;从中任选两个条件,能使四边形ABCD 为平行四边形的选法有( ).A .3种B .4种C .5D .6种例题5.如图,已知:AB ∥CD ,BE ⊥AD ,垂足为点E ,CF ⊥AD ,垂足为点F ,并且AE =DF .求证:四边形BECF 是平行四边形.例题6.如图,在□ABCD 中,F 是AD 的中点,延长BC 到点E ,使CE=21BC ,连结DE ,CF 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
平行四边形
一、选择题 1.已知四边形ABCD ,有以下四个条件:①//AB CD ; ②AB CD =;③//BC AD ;④B C A D =.从这四个条件中任选两个,能使四边形ABCD 成为平行四边形的选法种数共有( )
(A )6种 (B )5种 (C )4种 (D )3种 2.四边形ABCD 中,对角线AC 、BD 相交于点O ,给出下列四组条件:①AB ∥CD ,AD ∥BC ;②AB =CD ,AD =BC ; ③AO =CO ,BO =DO ;④AB ∥CD ,AD =BC .其中一定能判定四边形是平行四边形的条件有( ) A .1组 B .2组 C .3组 D .4组 3.如图,D 是△ABC 内一点,BD ⊥CD , AD =6,BD =4,CD =3,E 、F 、G 、H 分别 是AB 、AC 、CD 、BD 的中点,则四边 形EFGH 的周长是( ) A .7 B .9 C .10 D .11
4.下面图形都是由同样大小的平行四边形按一定的规律组成,其中,第①个图形一共有1个平行四边形,第②个图形一共有5个平行四边形,第③个图形一共有11个平行四边形,……,则第⑥个图形中平行四边形的个数为
( )
……
图① 图② 图③ 图④ A .55 B .42 C .41 D .29
二、填空题
5.如图,在□ABCD 中,AB =3,AD =4,∠ABC =60°,过BC 的中点E 作EF ⊥AB ,垂足为点F ,与DC 的延长线相交于点H ,则△DEF 的面积是
6.如图,□ ABCD 中,E 是BA 延长线上一点,AB =AE ,连结CE 交AD 于点F ,若CF 平分∠BCD ,AB =3,则BC 的长为 .
菱形
一、选择题
1.菱形具有而矩形不一定具有的性质是( ) A .对角线互相垂直 B .对角线相等 C .对角线互相平分 D .对角互补
2.如图,E 、F 、G 、H 分别是BD 、BC 、AC 、AD 的中点,且AB=CD .下列结论:①EG ⊥FH , ②四边形EFGH 是矩形,③HF 平分∠EHG , ④EG=
2
1
(BC ﹣AD ),⑤四边形EFGH 是菱形. 其中正确的个数是( ) A 、1 B 、2 C 、3 D 、4
3.依次连接菱形的各边中点,得到的四边形是( ) A .矩形 B .菱形 C .正方形 D .梯形
4. 若顺次连接四边形ABCD 各边的中点所得四边形是菱形,则四边形ABCD 一定是( ) A .菱形 B .对角线互相垂直的四边形 C .矩形 D .对角线相等的四边形
5.如图,在平面直角坐标系中,菱形MNPO 的顶点P 的坐标是(3,4),则顶点M 、N 的坐标分别是( ) A 、M (5,0),N (8,4) B 、M (4,0),N (8,4) C 、M (5,0),N (7,4) D 、M (4,0),N (7,4)
二、填空题
6.菱形的两条对角线长分别是6cm 和8cm , 则菱形的 周长是_______cm .
7.如图,菱形ABCD 的边长 是2c m ,E 是AB 的中点,且DE 丄AB ,则菱形ABCD 的面积为
8.如图,菱形ABCD 的对角线AC 、BD 相交于点O ,且AC =8,BD =6,过点O 作OH 丄AB ,垂足为H ,则点O 到边AB 的距离
9.如图,菱形ABCD 周长8cm . ∠BAD =60°,则AC = cm .
10.已知菱形ABCD 的边长是8,点E 在直线AD 上,若DE =3,连接BE 与对角线AC 相交于点M ,则
MC
AM
的值是 .
11.已知正方形ABCD ,以CD 为边作等边△CDE ,则∠AED 的度数是
12.如图,依次连结第一个矩形各边的中点得到一个菱形,再依次连结菱形各边的中点得到第二个矩形,按照此方法继续下去.已知第一个矩形的面积为1,则第n 个矩形的面积为 .
三、解答题
13.如图,四边形
ABCD 为菱形,已知A (0,4), B (﹣3
,0).
(1)求点D 的坐标; (2)求经过点C 的
反比例函数解析式.
14.
如图,在平行四边形
ABCD
中,∠DAB =60°,AB =2AD ,点 E 、F 分别是CD 的中点,过点A 作AG
∥BD ,交CB 的延长线于点G .
(1)求证:四边形DEBF 是菱形;
(2)请判断四边形AGBD 是什么特殊四边形? 并加以证明.
矩形、正方形
1.如图,将正方形纸片ABCD 折叠,使边AB 、CB 均落在对角线BD 上,得折痕BE 、BF ,则∠EBF 的大小为( ) A 、15° B 、30° C 、45° D 、60°
2.如图,在正方形ABCD 中,点O 为对角线AC 的中点,过点O 作射线OM 、ON 分别交AB 、BC 于点E 、F ,且∠EOF =90°,BO 、EF 交于点P .则下列结论中: (1)图形中全等的三角形只有两对;
(2)正方形ABCD 面积=四边形
OEBF 面积的4倍;
(3)BE+BF =2OA ;
(4)AE 2+CF 2=EF 2,
正确的结论有( )个.
A 、1
B 、2
C 、3
D 、4
3.如图,在正方形纸片ABCD 中,E ,F 分别是AD ,BC 的中点,沿过点B 的直线折叠,使点C 落在EF 上,落点为N ,折痕交CD 边于点M ,BM 与EF 交于点P ,再展开.则下列结论中:①CM=DM ;②∠ABN =30°;
③AB 2=3CM 2;④△PMN 是等边三角形.正确的有( ) A 、1个 B 、2个 C 、3个 D 、4个
4.如图,平面内4条直线l 1、l 2、 l 3、 l 4是一组平行线,相邻2条平行线的距离都是1个单位长度,正方形ABCD 的4个顶点A 、B 、C 、D 都在这些平行线上,其中点A 、C 分别在直线l 1、
l 4上,该正方形的面积是 平方单位。
5.如图,正方形ABCD 中,点E 、F 分别在边BC 、CD 上,且AE =EF =FA .下列结论: ①△ABE ≌△ADF ;②CE =CF ;③∠AEB =75°;④BE+DF =EF ;⑤S △ABE +S △ADF =S △CEF ,其中正确的是 (只填序号).
6.两个全等的直角三角形重叠放在直线l 上,如图⑴,AB=6cm ,BC=8cm ,∠ABC=90°,将Rt △ABC 在直线l 上左右平移,如图⑵所示.
⑴ 求证:四边形ACFD 是平行四边形;
⑵ 怎样移动Rt △ABC ,使得四边形ACFD 为菱形; ⑶ 将Rt △ABC 向左平移cm 4,求四边形DHCF 面积.
… D l
(2)
F
E
C B A H
7.在△ABC中,AB =2,AC=4,BC=2,以AB为边
向△ABC外作△ABD,使△ABD为等腰直角三角形,求线段CD的长.
8.(1)如图①,在正方形ABCD中,△AEF的顶点E,F分别在BC,CD边上,高AG与正方形的边长相等,求∠EAF的度数.
(2)如图②,在Rt△ABD中,∠BAD=90°,AB=AD,点M,N是BD边上的任意两点,且∠MAN=45°,将△ABM绕点A逆时针旋转90°至△ADH位置,连接NH,试判断MN,ND,DH之间的数量关系,并说明理由.(3)在图①中,连接BD分别交AE,AF于点M,N,若EG=4,GF=6,BM=3求AG,MN的长.
9.以四边形ABCD的边AB.BC.CD.
DA为斜边分别向外侧作等腰直角三角形,直角顶点分别为E.F.G.H,顺次连接这四个点,得四边形EFGH.(1)如图1,当四边形ABCD为正方形时,我们发现四边形EFGH是正方形;如图2,当四边形ABCD为矩形时,请判断:四边形EFGH的形状(不证明);(2)如图3,当四边形ABCD为一般平行四边形时,设∠ADC=α(0°<α<90°),
①试用含α的代数式表示∠HAE;
②求证:HE=HG;
③四边形EFGH是什么四边形?并说明理由.。
