20014-2015电信概率试卷A卷答案
(完整word版)2014-2015概率论与数理统计A卷答案 (1)

系部 专业班级 学号 姓名 密封线 答题留空不够时,可写到纸的背面 注意保持装订完整,试卷折开无效 装订线二.填空题(每题2分,共10分)1.已知().P A =06, ()|.P B A =03, 则()P A B ⋂= ___0.18_______;2.甲、乙、丙3人独立地译出一种密码,他们能译出的概率分别为1/5,1/3,1/4,则能译出这种密码的概率为35; 3.一种动物的体重X 是一随机变量,设()(),E X D X ==334,10个这种动物的平均体重记作Y ,则()D Y =__ 0.4 _;4. 已知,36)(,25)(==Y D X D X 与Y 的相关系数为4.0=XY ρ,则)(Y X D -= 37 ;5. 设12,,,n X X X 是取自总体),(2σμN 的样本,则统计量2211()nii Xμσ=-∑服从2()n χ分布.三.计算下列各题(共80分)1.(10分)例 1.某电子设备制造厂所用的元件是由三家元件制造厂提供的,根据以往的记录三家厂的次品率分别为0.02,0.01,0.03,三家厂所提供的份额分别为0.15,0.80,0.05。
设这三家厂的产品在仓库中是均匀混合的,且无区别的标志.(1)在仓库中随机取一只元件,求它是次品的概率;(2)在仓库中随机取一只元件,若已知取到的是次品,求出此次品由第一家工厂生产的概率是多少?解:设A 表示“取到的是一只次品”,(i=1,2,3)表示“所取到的产品是由第i 家工厂提供的”,则P()=0.15 P()=0.80 P()=0.05P(=0.02 P(=0.01 P(=0.03 (3分)1>.由全概率公式()112233(|)()(|)()(|) ?()A B B A B B B A A B =++P P P P P P P 0.0125= (5分) 2>.由贝叶斯公式P() = = = 0.24 (10分)桂林理工大学考试试卷 (2014--2015 学年度第 一 学期)课 程 名 称:概率统计 A 卷 命 题:基础数学教研室 题 号 一二三总 分得 分一. 单项选择题(每小题2分,共10分)1.如果 1)()(>+B P A P ,则 事件A 与B 必定( C ))(A 独立 )(B 不独立 )(C 相容 )(D 不相容2.设随机变量X 服从二项分布(,)B n p ,且()()2.1 1.47==E X D X ,则二项分布的参数,n p 的值为( A ) ()70.3==A n p ()30.7==B n p ()210.1==C n p ()40.6==D n p3.设随机变量X 服从)1,0(N 分布,12+=X Y ,则~Y ( B ) ()(0,1)()(1,4)()(1,2)()(0,4)A N B N C N D N4. 已知X 服从泊松分布,则()D X 与()E X 的关系为( C ) )(A ()()D X E X > )(B ()()D X E X < )(C ()()D X E X = )(D 以上都不是5. 设321,,X X X 是取自N (,)μ1的样本,以下μ的四个估计量中最有效的是( D ))(A 32112110351ˆX X X ++=μ)(B 3212949231ˆX X X ++=μ)(C 3213216131ˆX X X ++=μ)(D 32141254131ˆX X X ++=μX-1-1 0.12将联合分布表每行相加得-10.6将联合分布表每列相加得-10.30,1,;0θ<<!!n e X , (4分)()1ln !!!n X X θ- n ,令ln 0,d d θ=得1n θ= (10000,0.005b49.75, ()2.84Φ-Φ。
2015中国电信考试试题

2015中国电信考试试题2015中国电信校园招聘各省自主安排考试,考试分为和。
考试内容为行测,部分省份会考查专业知识。
1、我国要求局用程控交换机的系统中断时间为平均每年不超过( )。
A、1小时B、3分钟C、24小时D、一周2、我国常用的用户信号音如拨号音、忙音、回铃音均采用( )A、540HZB、450HZC、双频D、1980HZ3、国标规定接入网的维护管理接口应符合( ) 接口标准A、ZB、DTE/DCEC、Q3D、2B1Q4、国标规定交换机中具备CID功能的用户电路的配置比例暂定为( ) 。
A、5%~10%B、10%~20%C、10%~30%D、10%~40%5、长途自动接续中对信号音的发送地点有统一规定,对于忙音的发送地点为( )。
A、长途局B、本地汇接局C 、发端本地局D、终端本地局6、下列能提供E1接口的路由器是(D)A、CISCO 2501;B、Quidway 2501;C、CISCO 2522;D、CISCO 45007、我们移动通信的体制规定,公众移动电话网的移动用户与市话、长话用户通话时,移动通信网内音频带内的信噪比大于或等于( ) dB。
A、12B、24C、29D、328、省信令网管理中心中的信令网管理系统最终应通过( ) 传送对LSTP和C3信令链路的管理信息A、PSDNB、数据通信网C、信令网D、N-ISDN(D通道)9、国标规定SDH设备在光缆线路出现下列情况下应即倒换( )A、链路故障B、帧丢失(LOF)C、传输出现告警D、其他10、当机房处在相对湿度较低的地区环境时,特别是当相对湿度处在( )以下时,应采用抗静电地面,加强抗静电措施。
A、10%B、20%C 、30% D、40%参考答案:1、B2、B3、C4、C5、C6、D7、C8、B9、B10、B。
2014年概率参考答案

2014年历年概率汇编 答案20.湖北卷解:(1)依题意,p 1=P (40<X <80)=1050=0.2,p 2=P (80≤X ≤120)=3550=0.7,p 3=P (X >120)=550=0.1.由二项分布得,在未来4年中至多有1年的年入流量超过120的概率为p =C 04(1-p 3)4+C 14(1-p 3)3p 3=0.94+4×0.93×0.1=0.947 7. (2)记水电站年总利润为Y (单位:万元). ①安装1台发电机的情形.由于水库年入流量总大于40,故一台发电机运行的概率为1,对应的年利润Y =5000,E (Y )=5000×1=5000.②安装2台发电机的情形.依题意,当40<X <80时,一台发电机运行,此时Y =5000-800=4200,因此P (Y =4200)=P (40<X <80)=p 1=0.2;当X ≥80时,两台发电机运行,此时Y =5000×2=10 000,因此P (Y =10 000)=P (X ≥80)= p 2+p 3=0.8.由此得Y 的分布列如下:所以,E (Y )=4200×0.2+10 000×③安装3台发电机的情形. 依题意,当40<X <80时,一台发电机运行,此时Y =5000-1600=3400,因此P (Y =3400)=P (40<X <80)=p 1=0.2;当80≤X ≤120时,两台发电机运行,此时Y =5000×2-800=9200,因此P (Y =9200)=P (80≤X ≤120)=p 2=0.7;当X >120时,三台发电机运行,此时Y =5000×3=15 000,因此P (Y =15 000)=P (X >120)=p 3=0.1.由此得Y所以,E (Y )=3400×0.2+9200综上,欲使水电站年总利润的均值达到最大,应安装发电机2台.四川卷17.解:(1)X 可能的取值为10,20,100,-200. 根据题意,有P (X =10)=C 13×⎝⎛⎭⎫121×⎝⎛⎭⎫1-122=38,P (X =20)=C 23×⎝⎛⎭⎫122×⎝⎛⎭⎫1-121=38, P (X =100)=C 33×⎝⎛⎭⎫123×⎝⎛⎭⎫1-120=18, P (X =-200)=C 03×⎝⎛⎭⎫120×⎝⎛⎭⎫1-123=18. 所以X 的分布列为:(2)设“第i 盘游戏没有出现音乐”为事件A i (i =1,2,3),则 P (A 1)=P (A 2)=P (A 3)=P (X =-200)=18.所以“三盘游戏中至少有一盘出现音乐”的概率为1-P (A 1A 2A 3)=1-⎝⎛⎭⎫183=1-1512=511512.因此,玩三盘游戏至少有一盘出现音乐的概率是511512.(3)由(1)知,X 的数学期望为EX =10×38+20×38+100×18-200×18=-54.这表明,获得分数X 的均值为负.因此,多次游戏之后分数减少的可能性更大. 18.福建卷解:(1)设顾客所获的奖励额为X .(i)依题意,得P (X =60)=C 11C 13C 24=12.即顾客所获的奖励额为60元的概率为12,(ii)依题意,得X 的所有可能取值为20,60. P (X =60)=12,P (X =20)=C 23C 24=12,即X 的分布列为所以顾客所获的奖励额的期望为E (X )=20×0.5+60×0.5=40(元).(2)根据商场的预算,每个顾客的平均奖励额为60元.所以,先寻找期望为60元的可能方案.对于面值由10元和50元组成的情况,如果选择(10,10,10,50)的方案,因为60元是面值之和的最大值,所以期望不可能为60元;如果选择(50,50,50,10)的方案,因为60元是面值之和的最小值,所以期望也不可能为60元,因此可能的方案是(10,10,50,50),记为方案1.对于面值由20元和40元组成的情况,同理可排除(20,20,20,40)和(40,40,40,20)的方案,所以可能的方案是(20,20,40,40),记为方案2.以下是对两个方案的分析:对于方案1,即方案(10,10,,则X 1的分布列为X 1的期望为E (X 1)=20×16+60×23+100×16=60,X 1的方差为D (X 1)=(20-60)2×16+(60-60)2×23+(100-60)2×16=16003.对于方案2,即方案(20,20,40,40),设顾客所获的奖励额为X 2,则X 2的分布列为X 2的期望为E (X 2)=40×16+60×23+80×16=60,X 2的方差为D (X 2)=(40-60)2×16+(60-60)2×23+(80-60)2×16=4003.由于两种方案的奖励额的期望都符合要求,但方案2奖励额的方差比方案1的小,所以应该选择方案2.16天津卷.解:(1)设“选出的3名同学是来自互不相同的学院”为事件A ,则P (A )=C 13·C 27+C 03·C 37C 310=4960, 所以选出的3名同学是来自互不相同学院的概率为4960.(2)随机变量X 的所有可能值为0,1,2,3.P (X =k )=C k 4·C 3-k6C 310(k =0,1,2,3), 所以随机变量X 的分布列是随机变量X 的数学期望E (X )=0×16+1×12+2×310+3×130=65.18.重庆卷解:(1)由古典概型中的概率计算公式知所求概率为P =C 34+C 33C 39=584.(2)X 的所有可能值为1,2,3,且P (X =1)=C 24C 15+C 34C 39=1742,P (X =2)=C 13C 14C 12+C 23C 16+C 33C 39=4384,P (X =3)=C 22C 17C 39=112,故X 的分布列为从而E (X )=1×1742+2×4384+3×112=4728.17.湖南卷解:记E ={甲组研发新产品成功},F ={乙组研发新产品成功},由题设知P (E )=23,P (E )=13,P (F )=35,P (F )=25,且事件E 与F ,E 与F ,E 与F ,E 与F 都相互独立.(1)记H ={至少有一种新产品研发成功},则H =E F ,于是P (H )=P (E )P (F )=13×25=215,故所求的概率为P (H )=1-P (H )=1-215=1315.(2)设企业可获利润为X (万元),则X 的可能取值为0,100,120,220.因为P (X =0)=P (E F )=13×25=215,P (X =100)=P (E F )=13×35=15,P (X =120)=P (E F )=23×25=415,P (X =220)=P (EF )=23×35=25,故所求的分布列为数学期望为E (X )=0×215+100×15+120×415+220×25=300+480+132015=210015=140.17.安徽卷解: 用A 表示“甲在4局以内(含4局)赢得比赛”,A k 表示“第k 局甲获胜”,B k 表示“第k 局乙获胜”,则P (A k )=23,P (B k )=13,k =1,2,3,4,5.(1)P (A )=P (A 1A 2)+P (B 1A 2A 3)+P (A 1B 2A 3A 4) =P (A 1)P (A 2)+P (B 1)P (A 2)P (A 3)+P (A 1)P (B 2)P (A 3)P (A 4)=⎝⎛⎭⎫232+13×⎝⎛⎭⎫232+23×13×⎝⎛⎭⎫232=5681. (2)X 的可能取值为2,3,4,5.P (X =2)=P (A 1A 2)+P (B 1B 2)=P (A 1)P (A 2)+P (B 1)P (B 2)=59,P (X =3)=P (B 1A 2A 3)+P (A 1B 2B 3)= P (B 1)P (A 2)P (A 3)+P (A 1)P (B 2)P (B 3)=29,P (X =4)=P (A 1B 2A 3A 4)+P (B 1A 2B 3B 4)=P (A 1)P (B 2)P (A 3)P (A 4)+P (B 1)P (A 2)P (B 3)·P (B 4)=1081,P (X =5)=1-P (X =2)-P (X =3)-P (X =4)=881.故X 的分布列为EX =2×59+3×29+4×1081+5×881=22481.16.北京卷解:(1)根据投篮统计数据,在10场比赛中,李明投篮命中率超过0.6的有5场,分别是主场2,主场3,主场5,客场2,客场4.所以在随机选择的一场比赛中,李明的投篮命中率超过0.6的概率是0.5.(2)设事件A 为“在随机选择的一场主场比赛中,李明的投篮命中率超过0.6”,事件B 为“在随机选择的一场客场比赛中,李明的投篮命中率超过0.6”,事件C 为“在随机选择的一个主场和一个客场中,李明的投篮命中率一场超过0.6,一场不超过0.6”.则C =AB ∪AB ,A ,B 相互独立.根据投篮统计数据,P (A )=35,P (B )=25.故P (C )=P (AB )+P (AB ) =35×35+25×25 =1325. 所以,在随机选择的一个主场和一个客场中,李明的投篮命中率一场超过0.6,一场不超过0.6的概率为1325.(3)EX =x -.21.江西卷解:(1)当n =3时,ξ的所有可能取值为2,3,4,5.将6个正整数平均分成A ,B 两组,不同的分组方法共有C 36=20(种),所以ξ的分布列为:E ξ=2×15+3×310+4×310+5×15=72.(2)ξ和η恰好相等的所有可能取值为n -1,n ,n +1,…,2n -2.又ξ和η恰好相等且等于n -1时,不同的分组方法有2种; ξ和η恰好相等且等于n 时,不同的分组方法有2种;ξ和η恰好相等且等于n +k (k =1,2,…,n -2)(n ≥3)时,不同的分组方法有2C k 2k 种. 所以当n =2时,P (C )=46=23,当n ≥3时,P (C )=2⎝⎛⎭⎫2+∑n -2k =1C k 2k C n 2n.(3)由(2)得,当n =2时,P (C )=13,因此P (C )>P (C ).而当n ≥3时,P (C )<P (C ).理由如下:P (C )<P (C )等价于4(2+∑n -2k =1C k 2k )<C n2n ,①用数学归纳法来证明:(i)当n =3时,①式左边=4(2+C 12)=4(2+2)=16,①式右边=C 36=20,所以①式成立. (ii)假设n =m (m ≥3)时①式成立,即4⎝⎛⎭⎫2+∑m -2k =1C k 2k <C m 2m 成立,那么,当n =m +1时, 左边=4⎝⎛⎭⎫2+∑m +1-2k =1C k 2k=4⎝⎛⎭⎫2+∑m -2k =1C k 2k +4C m -12(m -1)<C m 2m +4Cm -12(m -1)=(2m )!m !m !+4·(2m -2)!(m -1)!(m -1)!=(m +1)2(2m )(2m -2)!(4m -1)(m +1)!(m +1)!<(m +1)2(2m )(2m -2)!(4m )(m +1)!(m +1)!=C m +12(m +1)· 2(m +1)m (2m +1)(2m -1)<C m +12(m +1)=右边, 即当n =m +1时,①式也成立.综合(i)(ii)得,对于n ≥3的所有正整数,都有P (C )<P (C )成立.18.辽宁卷解:(1)设A 1表示事件“日销售量不低于100个”,A 2表示事件“日销售量低于50个”,B 表示事件“在未来连续3天里有连续2天日销售量不低于100个且另1天销售量低于50个”.因此P (A 1)=(0.006+0.004+0.002)×50=0.6,P (A 2)=0.003×50=0.15,P (B )=0.6×0.6×0.15×2=0.108.(2)X 可能取的值为0,1,2,3,相应的概率分别为P (X =0)=C 03·(1-0.6)3=0.064, P (X =1)=C 13·0.6(1-0.6)2=0.288,P (X =2)=C 23·0.62(1-0.6)=0.432,P (X =3)=C 33·0.63=0.216.X 的分布列为因为X ~B (3,0.6)(1-0.6)=0.72. 20.全国卷解:记A 1表示事件:同一工作日乙、丙中恰有i 人需使用设备,i =0,1,2. B 表示事件:甲需使用设备. C 表示事件:丁需使用设备.D 表示事件:同一工作日至少3人需使用设备.(1)因为P (B )=0.6,P (C )=0.4,P (A i )=C i 2×0.52,i =0,1,2, 所以P (D )=P (A 1·B ·C +A 2·B +A 2·B ·C )= P (A 1·B ·C )+P (A 2·B )+P (A 2·B ·C )=P (A 1)P (B )P (C )+P (A 2)P (B )+P (A 2)P (B )P (C )= 0.31.(2)X 的可能取值为0,1,2,3,4,其分布列为 P (X =0)=P (B ·A 0·C ) =P (B )P (A 0)P (C )=(1-0.6)×0.52×(1-0.4) =0.06,P (X =1)=P (B ·A 0·C +B ·A 0·C +B ·A 1·C )=P (B )P (A 0)P (C )+P (B )P (A 0)P (C )+P (B )P (A 1)P (C )=0.6×0.52×(1-0.4)+(1-0.6)×0.52×0.4+(1-0.6)×2×0.52×(1-0.4)=0.25,P (X =4)=P (A 2·B ·C )=P (A 2)P (B )P (C )=0.52×0.6×0.4=0.06, P (X =3)=P (D )-P (X =4)=0.25,P (X =2)=1-P (X =0)-P (X =1)-P (X =3)-P (X =4)=1-0.06-0.25-0.25-0.06=0.38,所以 EX =0×P (X =0)+1×P (X =1)+2×P (X =2)+3×P (X =3)+4×P (X =4)=0.25+2×0.38+3×0.25+4×0.06=2.18.山东卷解:(1)记A i 为事件“小明对落点在A 上的来球回球的得分为i 分”(i =0,1,3),则P (A 3)=12,P (A 1)=13,P (A 0)=1-12-13=16;记B i 为事件“小明对落点在B 上的来球回球的得分为i 分”(i =0,1,3), 则P (B 3)=15,P (B 1)=35,P (B 0)=1-15-35=15.记D 为事件“小明两次回球的落点中恰有1次的落点在乙上”.由题意,D =A 3B 0+A 1B 0+A 0B 1+A 0B 3, 由事件的独立性和互斥性,P (D )=P (A 3B 0+A 1B 0+A 0B 1+A 0B 3) =P (A 3B 0)+P (A 1B 0)+P (A 0B 1)+P (A 0B 3)=P (A 3)P (B 0)+P (A 1)P (B 0)+P (A 0)·P (B 1)+P (A 0)P (B 3) =12×15+13×15+16×35+16×15 =310, 所以小明两次回球的落点中恰有1次的落点在乙上的概率为310.由题意,随机变量ξ可能的取值为0,1,2,3,4,6. (2)由事件的独立性和互斥性,得 P (ξ=0)=P (A 0B 0)=16×15=130,P (ξ=1)=P (A 1B 0+A 0B 1)=P (A 1B 0)+P (A 0B 1)=13×15+16×35=16,P (ξ=2)=P (A 1B 1)=13×35=15,P (ξ=3)=P (A 3B 0+A 0B 3)=P (A 3B 0)+P (A 0B 3)=12×15+16×15=215,P (ξ=4)=P (A 3B 1+A 1B 3)=P (A 3B 1)+P (A 1B 3)=12×35+13×15=1130,P (ξ=6)=P (A 3B 3)=12×15=110.可得随机变量ξ所以数学期望E ξ=0×130+1×16+2×15+3×215+4×1130+6×110=9130.19.陕西卷解:(1)设A 表示事件“作物产量为300 kg ”,B 表示事件“作物市场价格为6元/kg ”, 由题设知P (A )=0.5,P (B )=0.4, ∵利润=产量×市场价格-成本, ∴X 所有可能的取值为500×10-1000=4000,500×6-1000=2000, 300×10-1000=2000,300×6-1000=800.P (X =4000)=P (A )P (B )=(1-0.5)×(1-0.4)=0.3,P (X =2000)=P (A )P (B )+P (A )P (B )=(1-0.5)×0.4+0.5×(1-0.4)=0.5, P (X =800)=P (A )P (B )=0.5×0.4=0.2, 所以X 的分布列为(2)设C i 表示事件“第i 季利润不少于2000元”(i =1,2,3), 由题意知C 1,C 2,C 3相互独立,由(1)知,P (C i )=P (X =4000)+P (X =2000)=0.3+0.5=0.8(i =1,2,3), 3季的利润均不少于2000元的概率为P (C 1C 2C 3)=P (C 1)P (C 2)P (C 3)=0.83=0.512; 3季中有2季利润不少于2000元的概率为P(C1C2C3)+P(C1C2C3)+P(C1C2C3)=3×0.82×0.2=0.384,所以,这3季中至少有2季的利润不少于2000元的概率为0.512+0.384=0.896.20.全国卷解:记A1表示事件:同一工作日乙、丙中恰有i人需使用设备,i=0,1,2.B表示事件:甲需使用设备.C表示事件:丁需使用设备.D表示事件:同一工作日至少3人需使用设备.(1)因为P(B)=0.6,P(C)=0.4,P(A i)=C i2×0.52,i=0,1,2,所以P(D)=P(A1·B·C+A2·B+A2·B·C)=P(A1·B·C)+P(A2·B)+P(A2·B·C)=P(A1)P(B)P(C)+P(A2)P(B)+P(A2)P(B)P(C)=0.31.(2)X的可能取值为0,1,2,3,4,其分布列为P(X=0)=P(B·A0·C)=P(B)P(A0)P(C)=(1-0.6)×0.52×(1-0.4)=0.06,P(X=1)=P(B·A0·C+B·A0·C+B·A1·C)=P(B)P(A0)P(C)+P(B)P(A0)P(C)+P(B)P(A1)P(C)=0.6×0.52×(1-0.4)+(1-0.6)×0.52×0.4+(1-0.6)×2×0.52×(1-0.4)=0.25,P(X=4)=P(A2·B·C)=P(A2)P(B)P(C)=0.52×0.6×0.4=0.06,P(X=3)=P(D)-P(X=4)=0.25,P(X=2)=1-P(X=0)-P(X=1)-P(X=3)-P(X=4)=1-0.06-0.25-0.25-0.06=0.38,所以EX=0×P(X=0)+1×P(X=1)+2×P(X=2)+3×P(X=3)+4×P(X=4)=0.25+2×0.38+3×0.25+4×0.06=2.。
20014-2015八上期中

2014-2015上学期期中学业水平测试年级试卷(满分:时间:分钟)答题须知:本试卷分A卷B卷C卷三个部分,A卷为容易题(70分)、B卷为中等题(20分)、C卷为较难题(10分)。
请同学们注意审题,由易到难先后答卷。
A卷(共80分)一.单项选择(每题1分,共25分)( ) 1. We saw ______ elephant in the zoo. ______ elephant was from India.A. a; TheB. the; AnC. an; TheD. the; A( ) 2. How much does an Iphone 4s _________ ?A. spendB. costC. payD. take( ) 3. Can you give me ______ on how to surf on the Internet?A. some adviceB. some advicesC. advicesD. an advice( ) 4. —Do you know Lin Shuhao?—Yes, he is famous________ playing basketball ________a basketball star.A. for; asB. as; forC. to; atD. at; to( ) 5. Mr. Wang is an _____man. He is_____ in telling jokes.A. interesting , interestedB. interested, interestingC. interesting , interestingD. interested, interested( ) 6. —What did you do last Sunday?—We went for a picnic_______ Danny, because he was ill.A.besideB. besidesC. exceptD. except for( ) 7. Tom ______ Sam in the match and ______ the prize.A. won; beatB. won; gotC. beat; wonD. bit; won( ) 8. They stayed in Hangzhou______ visit the West Lake.A. so thatB. in order that C . in order to D. such that( ) 9. – Is this coat yours? I found it on the playground.–Yes. Thank you . And I must ________ my things well.A. look afterB. look forC. look atD. look like( ) 10. I’m 1.70 meters. Yao Ming is 2.27 meters. I am ______ Yao Ming.A. as tall asB. taller thanC. not as tall asD. so tall as( ) 11.______ students couldn’t go to school and stayed at home ______ the serious earthquake.A. Thousands of ,becauseB. Thousand of , because ofC. Thousand, because ofD. Thousands of , because of( ) 12.—______would you like to go?—Sorry. I’m too tired. I want to have a rest.A. Where elseB. Where otherC. Else whereD. Other where( ) 13. Wang Fang is______ of the five basketball players, but she plays very well.A. thinnerB. thinnestC. the thinnestD. very thin( ) 14. He tries to spend as much time as he can ____ Chinese well.A to studyB studiesC studyingD study( ) 15. Listen! Can you hear the boy ______ in the next room?A. to singB. singsC. sangD. singing( ) 16. It’s ______ cheaper and ______ enjoyable to travel by train than by plane.A. much; moreB. very; very muchC. more; moreD. more; much( ) 17. Who listens______, Tom, Jack or Bill?A. the most carefullyB. more carefullyC. the most carefulD. more careful ( ) 18. Beijing is bigger than _____in Jiangsu.A. any other cityB. any cityC. any other citiesD. other cities( ) 19. Remember ______ this book to the library tomorrow.A. returningB. to borrowC. to returnD. borrowing( ) 20. How about for a walk.A. wentB. goC. goingD. to go( ) 21. - _____have you been at this school?– Since I finished primary school.A. How longB. How soonC. WhenD. How many times( ) 22.I go to school _____ bus every morning.A .in B. on C. at D. by( ) 23.The man tried several times to start the car, and he succeeded _______.A. in the pastB. in the endC. at firstD. at once( )24.-Would you like _______ a movie with us tonight?- Sorry, I have to help my mother do some chores.A. seeB. to seeC. seeingD. saw( )25 . Don’t forget _______ the door when you leave.A.CloseB. closingC. to closeD. closed二.完形填空(每题1.5分,共15分)Some English words have some __26___ behind them. The word ―sandwich‖ is very __27__ in England . Do you know the story behind it?You must know something about an Englishman __28___ Sandwich. He lived in the __29___ century.Sandwich was rich, and he __30___ cards for money. He often played cards for 24 hours and he didn’t ___31__ to have his meals. He asked his men __32__ him some meat between two pieces of bread __33__ his left hand when he was playing with his right hand.People liked his idea and began to eat bread and meat __34___.From the name of Sandwich, we __35___ the word ―sandwich‖ today.( )26. A. stories B. words C. history D. experience( )27. A. interesting B. popular C. beautiful D. different( )28. A. names B. about C. called D. of( )29. A. eighteenth B. eight C. last D. twenty-first( )30. A. enjoys playing B. enjoyed to play C. enjoyed playing D. enjoys to play ( )31. A. come B. start C. begin D. stop( )32. A. to bring B. to take C. to put D. to show( )33. A. in B. on C. to D. by( )34. A. by this way B. in this way C. in same way D. on this way( )35. A. call B. know C. take D. have三.阅读理解(每题2分,共30分)AIn China, more and more middle school students are getting shorter sleeping time than before. Most students sleep less than nine hours every night, because they have much homework to do. Some homework is given by their teachers, and some by their parents. Also , some students don’t know how to save time. They are not careful enough while they do their homework, so it takes them a lot of time. Some students have to get up early every morning on weekdays to get to school on time by bus, by bike or on foot. It can be a long way from home to school.Schools and parents should cut down some of the homework so that our children can enjoy more than nine hours of sleep every night for their health. For children, they should make best use of their time. When they have enough time for sleeping, they will find it much better for both their study and health.( )36. What makes most students sleep less than nine hours every night?A .Watching TV. B. Playing computer games.C. Doing their homework.D. Doing housework.( )37 Who else give children some homework to do except their teachers?A. Their parents B .Other students C. The children themselves D Nobody else ( )38. How do the students go to school on weekdays ?A. by busB. by bikeC. on footD. A.B and C( )39.How many hours of sleep is good for students’ health?A .Less than 9 hours.B .Over 9 hours. C. Only 9 hours. D. 8 hours. ( )40. Which of the following is not true?A . Some students are so careless that they spend lots of time on their homework.B. All the students stay up late for their homework.C . Children should be given less homework.D .Schools and parents should take care of children.BA man has a cat. He likes her very much. At mealtime the cat sits at the table with him. The man eats with a knife and a fork, but the cat eats from her plate. Sometimes, when she finishes her dish,her master will give her a bit of his food. He shares his meal with her. One day the cat is not at the table at mealtime.―Ah! Where is my cat?‖ asks the man..His wife says, ―Can’t you eat without her?‖So the meal begins without the cat. Before lunch is over, the cat rushes into the room and jumps into the chair quickly. She has two mice in her mouth, and before anyone can stop her, she drops(扔下) one into her own plate, and the other into her master’s plate.―Dear me!‖ cries the woman, ―A mouse is in your plate!‖―Hush(安静)!‖ says her husband. ―This show s that she is a nice cat. She knows what friendship(友谊) is. She wishes me to share her dinner as I often share mine with her.根据短文内容,判断正误,正确(T),错误(F)。
2014电信笔试题目及答案

2014电信笔试题目及答案电信(telecommunication 缩写:CT):指利用电子技术在不同的地点之间传递信息。
电信包括不同种类的远距离通讯方式,例如:无线电,电报,电视,电话,数据通讯以及计算机网络通讯等。
电信是信息化社会的重要支柱。
无论是在人类的社会、经济活动中,还是在人们日常生活的方方面面,都离不开电信这个高效、可靠的手段。
2014电信笔试题目及答案41.软交换网络体系采用( )的传送平台A.基于电路 B.基于分组 C.基于数据报 D.基于网关【答案】B42.NGN的网络体系架构中控制层可为( )。
A.媒体网关B.软交换设备C.应用服务器D.媒体网关控制器【答案】BD43.NGN传送层可以采用( )实现。
A.软交换设备 B.ATM网 C.IP分组网D.ISDN网【答案】BC44.NGN的网络体系架构分为( )。
A.接入层 B.传送层 C.控制层 D.业务应用层【答案】ABCD45.在NGN中,所有媒体网关属于( )。
A.应用层 B.控制层 C.传送层 D.接入层【答案】D46.中国电信广东公司的软交换网络智能化改造是NGN的具体应用。
上述表述是否正确?【答案】表述正确光纤最大的优点是( )。
A.频带宽、信息容量大B.损耗低、传输距离长C.抗干扰能力强D.材料资源丰富【答案】ABCD47.光纤中影响传输中继距离的因素主要有( )。
A.损耗 B.漂移 C.抖动 D.色散【答案】AD48.SDH的中文含义是( )。
A.准同步系列 B.同步系列 C.同步数字系列 D.同步复用数字系列【答案】C49.属于无线接入网的是( )。
A.固定无线接入网 B.移动接入网 C.HFC D.HDSL【答案】AB50.IP地址的组成包括( )。
A.用户地址 B.网络地址 C.主机地址 D.逻辑地址【答案】BC51.在Internet接入服务中,AAA的中文含义是( )。
A.互通 B.授权 C.计费D.认证【答案】BCD52.宽带城域网是以( )为基础的高带宽、多功能、多业务接入的多媒体通信网络。
14本二《概统》AB答案

河北科技大学2014-2015学年第一学期《 概率论与数理统计》试卷答案及评分标准班级一.单选题(每小题3分,共24分)A 卷 DBC AD A B C B 卷 B A D B C D C A7. 2111111()()()()()2(,)244X X D X D D X X D X D X Cov X X n σ+⎡⎤=<=+=++⎣⎦ 211111111123()()2(,)()()(,)444n i i n D X D X Cov X X D X D X Cov X X n n n σ=+⎡⎤⎡⎤=++=++=⎢⎥⎢⎥⎣⎦⎣⎦∑二.填空题(每小题3分,共24分)A 卷 1. 0.7 2. 1 3.1e - 4.49 5.(1,6)N - 6. 137. (7.51,8.49) 8./2(1)t n α⎫≥-⎬⎭ B 卷 1. 0.62 2. 1 3.22e - 4.29 5.(2,9)N 6. 21 7. (8.51,9.49)8./2z α⎫≥⎬⎭三. 计算题(共52分)1.(10分)设A 为“接收站收到信息0”,B 为事件“原发信息是0”,已知21(),(),()0.98,()0.0133P B P B P A B P A B ==== …………………………2分(1)21197()()()(|)()0.980.0133300P A P A B P B P A B P B =+=⨯+⨯=;……………4分(2) 1971963101.03298.03298.0)()()()(=⨯+⨯⨯==A P B A P B P A B P . ………………………4分 2.(10分)(1) 已知001()()2x x f x dx A e dx e dx A +∞+∞--∞-∞==+=⎰⎰⎰所以 A =12.………4分(2) 当0x <时,11()()22xx t x F x f t dt e dt e -∞-∞===⎰⎰;………………………………2分当0x ≥时,00111()1222x t t x F x e dt e dt e ---∞=+=-⎰⎰.……………………………… 2分故X 的分布函数1,0;2()11,02xx e x F x e x -⎧<⎪⎪=⎨⎪-≥⎪⎩(3) {}111122x P X e dx e+∞->==⎰. ………………………………………………… 2分10101/401/4101/20-X Y3.(10分)(1)(X ,Y )有六对可能值(-1,0),(-1,1),(0,0),(0,1),(1,0),(1,1), ……………1分 由已知{0}1P XY ==,得{0}0P XY ≠=,即 {1,1}{1,1}0P X Y P X Y =-===== …………………………………………2分又由X 和Y 的边缘分布律,得1{1,0}4P X Y =-== ………………………………1分1{1,0}4P X Y === ………………………………………………………………1分1{0,1}2P X Y === ………………………………………………………………1分{0,0}0P X Y === ………………………………………………………………1分 于是,X 和Y 的联合分布律为(2)由于111{0,0}{0}{0}224P X Y P X P Y ==≠===⨯=,所以X 与Y 不相互独立.3分4.(10分) (1) 2033,01()(,)0x X xdy x x f x f x y dy +∞-∞⎧⎪=<<==⎨⎪⎩⎰⎰,其它, ………… 3分1233(1),01()(,)20y Y xdx y y f y f x y dx +∞-∞⎧⎪=-<<==⎨⎪⎩⎰⎰其它; ……………………………3分 (2)1121112215(1)(,)3(63)8x x x y P X Y f x y dxdy dx xdy x x dx -+≥+≥===-=⎰⎰⎰⎰⎰. …………4分5.(12分)已知()X E X =,而1101()(;)(1)2E X xf x dx x dx θθθθθ+∞+-∞+==+=+⎰⎰,…4分 令12X θθ+=+,解得21ˆ1X X θ-=-,于是未知参数θ的矩估计量为21ˆ1X X θ-=-;…… 2分 对于总体X 的样本值n x x x Λ,,21,似然函数为121()(;)(1)(),01,1,2,,nn i n i i L f x x x x x i n θθθθ===+<<=∏L L ……… 2分对数似然函数为 1ln ()ln(1)ln ,01,1,2,,ni i i L n x x i n θθθ==++<<=∑L …… 1分对θ求导数,并令1ln ()ln 01ni i d L nx d θθθ==+=+∑,…………………………… 2分解得1ˆ1ln nii nxθ==--∑,于是未知参数θ的最大似然估计量为1ˆ1ln nii nxθ==--∑. …1分。
2013-2015概率统计试题及解答

(2) 设 Y 为 150h 内烧坏的电子管数,则 Y ~ B(3, p) , p = P{X < 150} = F (150) = 1 。(3 分)
3
所求为 P{Y ≥ 2} = C32 (1 3)2 (2 3) + (1 3)3 = 7 27 。(2 分)
∫ ∫ ∫ ∫ ∫ 三、1. (1) 由
姓名:
2014~2015 学年 第一学期试卷 课程名称:概率统计 考试形式:闭卷 试卷: A
题号
一 二 三 四 总分
标准分 24 16 30 30
得分
注 请填写清楚左侧装订线内的所有信息,并在交卷时保持三页试卷装订完好。
A 一、填空题和选择题 (每题 3 分,共 24 分)
1. 已知 P(A) = 0.5 , P(B) = 0.6 , P ( B A) = 0.8 ,则 P ( A ∪ B) =
⎪⎩ 0,
其它.
cov( X ,Y ), ρXY , D( X − Y ) 。
姓名:
学号: 线
专业班级: 订
专业班级: 全校工科、经管、理科各专业 [该项由出卷人填写]
装
第( 2 )页共( 3 )页
姓名:
2014~2015 学年 第一学期试卷 课程名称:概率统计 考试形式:闭卷 试卷: A
A 四、计算下列各题 (共 30 分) 1. (7 分) 某单位设置一电话总机,共有 100 架电话分机。设每个电话分机是否使用外线通话 是相互独立的,且每时刻每个分机有 10%的概率要使用外线通话。问总机需要多少外线才能
36
6
36
∫ ∫ ∫ ∫ E(XY ) =
+∞
+∞
xyf (x, y)dxdy =
2015级《概率论与数理统计》A卷及解答(精品文档)_共4页

x
s n
t
(n
1)
56.93
0.93 20
1.729
56.570
第4页共4页
步骤)
1.试卷中有一道选择题,共有 4 个答案可供选择,其中只有 1 个答案是正确的.任一考生如
果会解这道题,则一定能选出正确答案;如果不会解这道题,则不妨任选 1 个答案。设考
生会解这道题的概率是 0.8。
(1)求考生选出正确答案的概率;
(2)已知某考生所选答案是正确的,求他确实会解这道题的概率。
(2)设考试成绩至少高于 m 分, PX m 0.3333
因为 PX m 1 m 75 0.3333 , m 75 0.6667
15
15
于是 m 75 0.431 , m 81.465 15
故考试成绩至少高于 81 分能排名前 33.33%。
2
4
4.设(X,Y)为二维随机变量,且 D (X)>0,D (Y)>0,则下列等式成立的是
(A) (B)
(A) E( XY ) E( X ) E(Y ) (C) D( X Y ) D( X ) D(Y )
(B) Cov(X,Y) XY D( X ) D(Y ) (D) Cov(2X ,2Y ) 2Cov( X ,Y )
=0.09(i=1,2,…),则
lim
P
n
i 1
X
i-
0.1n
0.6
=
n
n
2
1
t2
e 2 dt (2)
2
5.设总体
概率统计答案(详解)

第一章 随机事件与概率1. 用集合的形式写出下列随机试验的样本空间与随机事件A :(1) 抛一枚硬币两次,观察出现的面,事件{=A 两次出现的面相同};(2) 记录某电话总机一分钟内接到的呼叫次数,事件{=A 一分钟内呼叫次数不超过3次};(3) 从一批灯泡中随机抽取一只,测试其寿命,事件{=A 寿命在2000到2500小时之间}。
解 (1) 用+表示出现正面,-表示出现反面。
)},(),,(),,(),,{(--+--+++=Ω, )},(),,{(--++=A . (2) 012{,,,,}kΩωωωω=,0123{,,,}A ωωωω=.其中k ω 表示1分钟内接到k 次呼唤,0,1,2,k =(3) 记x 为抽到的灯泡的寿命(单位:小时),则{|0}x x Ω=≥, {|20005000}A x x =≤≤.2. 在区间]2,0[上任取一数,记⎭⎬⎫⎩⎨⎧≤<=121x x A ,⎭⎬⎫⎩⎨⎧≤≤=2341x x B ,求下列事件的表达式:(1)B A ;(2)B A ;(3)B A ;(4)B A . 解 (1) 1342AB x x B ⎧⎫=≤≤=⎨⎬⎩⎭; (2) 10122AB x x x B ⎧⎫=≤≤<≤⎨⎬⎩⎭或1131422x x x x ⎧⎫⎧⎫=≤≤<≤⎨⎬⎨⎬⎩⎭⎩⎭; (3) 因为B A ⊂,所以ΦAB =;(4)130242AB A x x x ⎧⎫=≤<<≤⎨⎬⎩⎭或=⎭⎬⎫⎩⎨⎧≤<≤<<≤223121410x x x x 或或 3. 用事件C B A ,,的运算关系式表示下列事件:(1) A 出现,C B ,都不出现(记为1E ); (2) B A ,都出现,C 不出现(记为2E ); (3) 所有三个事件都出现(记为3E ); (4) 三个事件中至少有一个出现(记为4E ); (5) 三个事件都不出现(记为5E ); (6) 不多于一个事件出现(记为6E );(7) 不多于两个事件出现(记为7E ); (8) 三个事件中至少有两个出现(记为8E )。
西安邮电学院2008-2009年第一学期电子专业《概率论与随机过程》期末考试及答案A卷

(4)因为其一步转移概率矩阵
P
0.9 0.1
0.1 0.9
无零元,所以此链具有遍历性。
………… (12 分)
3.解 因为
说明:用本模板出题,请将插入方式换成改写方式,除填空题、图解及特殊要求外,一般不留答题空间;装订试卷、考生答卷纸不得拆开或在框外留有任何标记,否则按零分计
共 3 页 第 页 总印 1200
t1)
CX
(t1,
t2
)
RX
(t1, t2 )
X
(t1 ) X
(t2
)
RX
(t1,
t2
)
a2 2
cos (t2
t1)
……(10 分)
1
P{Y k} C3k pk (1 p)3k , k 0,1, 2, 3,其中p 1 e3.
…………… (10 分)
说明:用本模板出题,请将插入方式换成改写方式,除填空题、图解及特殊要求外,一般不留答题空间;装订试卷、考生答卷纸不得拆开或在框外留有任何标记,否则按零分计
1.设随机变量 (X ,Y ) 的联合密度函数为
1 f (x, y)
,
x2 y2 1,
0, x2 y2 1.
(1)求 XY ,判定 X和Y 是否是不相关的,为什么?(2) X和Y 是否相互独立,为什么?
4.某保险公司多年的统计资料表明,在索赔户中被盗索赔户占 20%,以 X 表示在随机抽查的 100 个索
线
学号(8 位)
线
共 3 页 第 页 总印 1200
份 (附卷纸
2 页)
200 年 月 日 考试用
西安邮电学院课程考试试题(A 卷)
(2008——2009 学年度第 一 学期)
中国电信山西分公司2015年校园招聘考试试题

中国电信山西分公司2015年校园招聘考试试题(附参考答案)考试时限为120分钟,满分100分。
第一部分常识判断下面题目中只有一个正确答案,请将正确答案的序号填入题内括号内1.“苟利国家生死以,岂因祸福避趋之”。
这句话反映的我国爱国主义优良传统是( A )。
A. 热爱祖国,矢志不渝B.天下兴亡,匹夫有责C.维护统一,反对分裂D.同仇敌忾,抵御外强2.在工业化过程中,随着农村富余劳动力向非农产业的逐步转移,农村富余劳动力将逐渐减少。
面对这一趋势,企业应该( D )。
A. 勇于承担社会责任,完善失业保险制度B.不断提高劳动生产率,提高企业竞争力C.与员工协商薪酬,不断提高劳动者待遇D.完善就业机制,加强员工职业技能培训3.国家“十二五”规划纲要提出,我国要实现经济(),国内生产总值年均增长( D )。
A. 持续稳定发展7%B.持续稳定发展8%C.平稳较快发展7.5%D.平稳较快发展7%4.从古代的“把酒问青天”、“嫦娥奔月”,到今天的“神舟”号系列对太空的探索,再到“天宫一号”的发射,我们对太空的了解越来越深入,这说明( B )。
①追求真理是一个永无止境的过程②人类对自然界的认识是一帆风顺的③实践锻炼并提高了人的认识能力④实践决定认识,认识是实践的目的A. ①②B.①③C.②④D.③④5.当前世界上最大的区域性贸易集团是( A )。
A. 欧洲联盟B.世界贸易组织C.石油输出国组织D.东南亚国家联盟6.下列有关“通告”的表述中,错误的是( C )。
A.发布在一定范围内应当遵守的事项B.通告发布机关的级别一般比公告发布者低C.告知的范围比公告宽泛D.通告的文字具有强制力和严肃性7.世界大河中,与长江流向大致相同的是:( C )A.尼罗河B.印度河C.亚马逊河D.伏尔加河8.下列音乐作品与创作作者对应不正确的是:( A )A..《蓝色多瑙河》——巴赫B.《安魂曲》——莫扎特C.《天鹅湖》——柴可夫斯基D.《命运交响曲》——贝多芬9.根据以下素材拟写的公文标题,符合规范的是( B )。
2015年最新我国电信招聘笔试试题和答案解析

绝密2015年中国电信招聘综合素质能力测试祝各位考生发挥出自己的最佳水平!说明:请仔细阅读以下的注意事项,这对你顺利通过考试非常重要:监考老师宣布考试开始时,你才可以开始答题。
请用2B铅笔在答题卡上作答,写在本题册上的答案无效,请勿折叠答题卡。
答题卡“试卷类型”必填,“工号”栏填准考证号,如有遗漏,视作废卷。
请勿在本题册上书写、涂改或留下任何标记,题册最后两页是空白草稿纸,可拆下来正反使用,如果需要增加,请举手示意监考老师。
在考试结束时,请留在座位上,等监考老师收取答题卡、考卷和草稿纸。
不得将这些物品带出考场。
如需提前交卷,请先举手示意监考老师收取。
第一部分常识判断(共8题,参考时限5分钟)请开始答题:1. 古人云:“天下事有难易乎?为之,则难者亦易矣;不为,则易者亦难矣。
人之为学有难易乎?学之,则难者亦易矣;不学,则易者亦难矣。
”这句话反映了()。
A.世界上一切事物都是相对运动的B.时间与空间是事物的存在方式C.矛盾是对立统一的D.物质和运动是不可分的2. 《国家“十二五”规划纲要》提出积极构建有利于转变经济发展方式的财税体制。
下列表述不属于加快财税体制改革的是()。
A.完善转移支付制度,增加一般性特别是均衡性转移支付规模和比例B.在完善社会保险基金预算基础上研究编制社会保障预算C.继续推进费改税,全面推进资源税和耕地占用税改革D.稳步推进利率市场化改革,加强金融市场基准利率体系建设3. 下列关于我国司法系统的说法,正确的是()。
A.国务院是最高国家审判机关和最高法律监督机关B.司法机关在审理案件中独立行使职权的同时,必须依法行事,不得滥用权利C.人民检察院可与人民法院在法律允许的范围类协商合作,依照法律行使自己的职权D.国家司法权只能由国家各级审判机关独立行使,任何其他机关和团体均无权行使此权力4. 军衔是区别军人等级的称号,一般分为将官、校官、尉官、士官和士兵5等,每级再细分数级,部分国家设元帅和准尉。
2015年高考数学—概率(解答+答案)
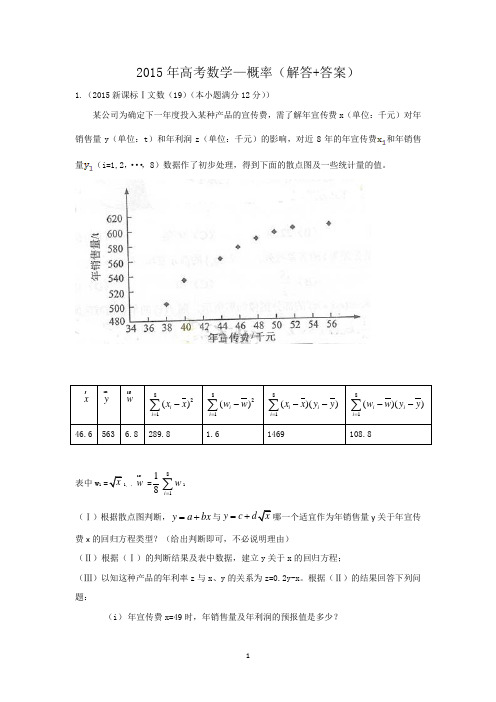
2015年高考数学—概率(解答+答案)1.(2015新课标Ⅰ文数(19)(本小题满分12分))某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费x (单位:千元)对年销售量y (单位:t )和年利润z (单位:千元)的影响,对近8年的年宣传费和年销售量(i=1,2,···,8)数据作了初步处理,得到下面的散点图及一些统计量的值。
x ry u r w u r821()ii x x =-∑821()ii w w =-∑81()()iii x x y y =--∑ 81()()iii w w y y =--∑46.6 563 6.8 289.8 1.6 1469 108.8表中w 1 x 1, ,w u r =1881i w =∑1(Ⅰ)根据散点图判断,y a bx =+与y c x =+哪一个适宜作为年销售量y 关于年宣传费x 的回归方程类型?(给出判断即可,不必说明理由)(Ⅱ)根据(Ⅰ)的判断结果及表中数据,建立y 关于x 的回归方程;(Ⅲ)以知这种产品的年利率z 与x 、y 的关系为z=0.2y-x 。
根据(Ⅱ)的结果回答下列问题:(i ) 年宣传费x=49时,年销售量及年利润的预报值是多少?(ii)年宣传费x为何值时,年利率的预报值最大?+u的斜率和附:对于一组数据(u1 v1),(u2 v2)…….. (u n v n),其回归线v=αβ截距的最小二乘估计分别为:2.(2015新课标II文数18.(本小题满分12分))某公司为了解用户对其产品的满意度,从A,B两地区分别随机调查了40个用户,根据用户对产品的满意度评分,得到A地区用户满意度评分的频率分布直方图和B地区用户满意度评分的频数分布表。
A地区用户满意度评分的频率分布直方图B 地区用户满意度评分的频数分布表(1)在答题卡上作出B 地区用户满意度评分的频率分布直方图,并通过直方图比较两地区满意度评分的平均值及分散程度(不要求计算出具体值,给出结论即可);B 地区用户满意度评分的频率分布直方图(2)根据用户满意度评分,将用户的满意度从低到高分为三个等级:估计哪个地区的满意度等级为不满意的概率大?说明理由频率/5060708090100 满意度评分405060708090满意度评分100 频率/3.(2015安徽文数17.(本小题满分12分))某企业为了解下属某部门对本企业职工的服务情况,随机访问50名职工,根据这50名职工对该部门的评分,绘制频率分布直方图(如图所示),其中样本数据分组区间为[40,50),[50,60),...,[80,90),[90,100](Ⅰ)求频率分布图中a的值;(Ⅱ)估计该企业的职工对该部门评分不低于80的概率;(Ⅲ)从评分在[40,60)的受访职工中,随机抽取2人,求此2人评分都在[40,50)的概率.4.(2015北京文数(17)(本小题13分))某超市随机选取1000位顾客,记录了他们购买甲、乙、丙、丁四种商品的情况,整理成如下统计表,其中“√”表示购买,“×”表示未购买。
电信概率复习

2012-2013学期概率论与数理统计复习重点第一章:概率的性质(尤其两个事件的和,差公式和对立事件公式,独立和互不相容的关系),全概率公式和贝叶斯公式(大题),独立性。
第二章:离散型随机变量的分布律的性质,连续性随机变量的概率密度的性质, 分布函数的性质,随机变量的函数的分布(大题)。
第三章:给定联合概率密度求未知参数,求边缘概率密度,判断独立性,求落在某区域内的概率(大题)。
独立的正态分布的线性组合仍然服从正态分布。
第四章:期望的性质,方差的性质,协方差和相关系数的性质,独立不相关的关系,六个基本分布的期望方差,切比雪夫不等式做估计,离散型二维分布求相关系数(大题)。
第五章:中心极限定理近似计算(Laplace 中心极限定理)(大题) 第六章:三个抽样分布的构造,正态总体均值和方差的分布 第七章:点估计(尤其矩估计)(大题),单个正态总体均值的区间估计(大题),估计量的评选标准(无偏性,有效性)第八章:区分第一类、第二类错误,单个正态总体均值的假设检验(大题)。
一、概念B A ,互斥(互不相容):φ=AB相互独立:)()()(B P A P AB P =条件概率:)()()|(A P AB P A B P =X 的分布函数:}{)(x X P x F ≤=(1)R ∈∀x ,1)(0≤≤x F . (2))(x F 为单调不减函数.(3)0)(lim =-∞→x F x ,1)(lim =+∞→x F x 。
(4))(x F 为右连续函数性质(1)0≥k p (2)11=∑∞=k kp. X 数学期望:∑=kk k p x EX连续型X 的概率密度函数)(t ϕ:若⎰∞-=xdt t x F )()(ϕ性质(1)0)(≥t ϕ (2) 1)(=⎰+∞∞-dt t ϕ. X 数学期望:=EX ⎰+∞∞-dx x x )(ϕ.二维连续型),(Y X 的概率密度函数),(y x ϕ:若⎰⎰∞-∞-=x ydudv v u y x F ),(),(ϕ边缘分布:⎰+∞∞-=dy y x x X ),()(ϕϕ , ⎰+∞∞-=dx y x y Y ),()(ϕϕX 与Y 相互独立⇔)()(),(y x y x Y X ϕϕϕ=X 的方差:2)(EX X E DX -=. 22)(EX EX DX -=X 与Y 的协方差:))((),cov(EY Y EX X E Y X --=. EY EX XY E Y X ⋅-=)(),cov( X 与Y 的相关系数:DYDX Y X XY ),cov(=ρ.契比雪夫不等式:2}|{|εεDXEX X P ≤≥- 或 21}|{|εεDXEX X P -≥<-.2()n χ分布:22212n X X X +++ ,样本),,,(21n X X X 来自总体)1,0(N()t n, )1,0(~N X ,)(~2n Y χ独立 12(,)F n n 分布:12//X n Y n , )(~12n X χ,)(~22n Y χ独立 样本均值:∑==ni i X n X 11.样本方差:212)(11X X n S ni i --=∑=. 二、公式B A AB A B A =-=-若B A ⊂,则)()()(A P B P A B P -=-.()1()P A P A =-)()()()(AB P B P A P B A P -+= )|()()(A B P A P AB P =全概率公式:∑=iiiA B P A P B P )|()()(.贝叶斯公式:∑=kk k i i i A B P A P A B P A P B A P )|()()|()()|(.)()(}{a F b F b X a P -=≤<),(~2σμN X ,则⎪⎭⎫⎝⎛-Φ-⎪⎭⎫ ⎝⎛-Φ=≤<σμσμa b b X a P }{.()[()]|()|Y X y h y h y ϕϕ'=,βα<<y .∑∑===mi i i mi i i EX c X c E 11)(EY EX XY E ⋅=)(,若X 与Y 独立.22)(EX EX DX -=DY b DX a bY aX D 22)(+=±,若X 与Y 独立.),cov(2)(Y X DY DX Y X D ±+=± ),cov(),cov(X Y Y X =.),cov(),cov(Y X kl lY kX =,l k ,为常数. ),cov(),cov(),cov(Z X Y X Z Y X ±=±. EY EX XY E Y X ⋅-=)(),cov(∑==kk k p x f X Ef EY )()(. )(X Ef EY =⎰+∞∞-=dx x x f )()(ϕ.∑==ji ij j i p y x f Y X Ef EZ ,),(),(. ),(Y X Ef EZ =⎰⎰+∞∞-+∞∞-=dxdy y x y x f ),(),(ϕ.中心极限定理近似计算),(~p n B Y n: {}n P a Y b ⎛⎫⎛⎫<≤≈Φ-Φ)1,0(~/N nX σμ-.)1(~/--n t nS X μ.)1(~)1(222--n S n χσ.三、常用分布:两点分布(01;)p -:1(1)kkk p p p -=-. EX p =,(1)DX p p =-二项分布),(p n B :kn k kn k p p C p --=)1(. np EX =,)1(p np DX -=泊松分布) (λP :λλ-=e k p kk !. λ=EX ,λ=DX均匀分布],[b a U :⎪⎩⎪⎨⎧≤≤-=. ,0,1)(其他,b t a a b t ϕ . 2b a EX +=,12)(2a b DX -=指数分布) (λExp : ⎩⎨⎧≤>=-.0 ,0,0 )(t t e t t ,λλϕ. λ/1=EX ,2/1λ=DX正态分布),(2σμN :222)(21)(σμσπϕ--=t e t . μ=EX ,2σ=DX四、例1、设A,B,C 为三个事件,试将下列事件用A,B,C 表示出来: (1) 三个事件都发生; ABC(2) 三个事件都不发生;C B A(3) 三个事件至少有一个发生; C B A (4) A 发生,B,C 不发生; C B A(5) A,B 都发生,C 不发生;C AB(6) 三个事件中至少有两个发生;CA BC AB (7) 不多于一个事件发生;CA BC AB(8) 不多于两个事件发生。
2015年春季学期电信信息技术与业务期末习题与参考答案

邮电大学网络学院《电信信息技术与业务》试题库(含答案)一、填空题1. 是使用有线、无线、光或其他电磁系统,传输、发射或者接收符号、信号、文字、图像、声音等性质的信息的系统。
答:电信2.2000年颁布了《中华人民国电信条例》。
(什么机构)答:国务院3.电信系统的基本组成包括、、信道、噪声源、反变换器及信宿。
答:信源、变换器4.是指电信服务企业利用电信技术和电信基础设施为不同用户提供的各种信息发送、传输和接收等服务项目的总称。
答:电信业务5.电信业务包括和两大类。
答:基础电信业务;增值电信业务ICT。
7.中国联通的“智慧沃家”业务的基本业务一般包括宽带、和通信业务。
答:移动;固定(固定;移动)9.固定通信的主要特征是终端的性或性。
答:不可移动;有限移动10.用户拨打本地网固定不加,直接拨打被叫。
答:长途区号11.本地业务包括:本地网营业区业务和本地网业务。
答:营业区间12.是指一个用户装设的、供部互相通话,并通过市话中继线经本地局与市其他用户通话的设备。
答:用户交换机13.是利用电信网和数据库技术,集信息采集、加工、存储、传播和服务于一体,通过向社会提供综合性、全方位、多层次的信息咨询的服务业务。
答:信息服务14.是指在国不同的“长途编号”区,即不同的本地网之间提供的业务。
(写文字)答:国长途业务16.泛指利用IP网络协议,通过IP网络提供或通过网络和IP网络共同提供的。
答:IP业务17.在我国,电信运营商提供的IP业务,其接入号均使用“××”的形式。
答:17918.计账卡呼叫业务允许用户在任何一部机上呼叫而不必立刻支付费,而是将话费计在专属19.业务是指用户利用公共网的用户网络和交换设备等资源构成一个能在一个用户群进行相互通信联系的逻辑上的专用网络。
答:虚拟专用网VPN20.全部由受话人付费的业务是“”业务。
答:80021.移动通信是指通信双方,至少有一方在进行信息交换的通信方式。
2015年江西电信招聘考试试题及参考答案

中国电信江西分公司2015年校园招聘考试试题(附参考答案)注意事项1.本次考试是对考生综合能力的测试。
请仔细资料,按要求作答。
2.本试题考试时限为120分钟,满分100分。
3.答题前,考生应用黑色签字笔或钢笔将自己的姓名、准考证号填写清楚,用2B铅笔将准考证号所选项涂黑。
用黑色签字笔或钢笔在答题卡规定答题区域内作答,超出答题区域的作答无效。
4.监考人员宣布考试结束时,考生应立即停止作答,将试题本、答题卡和草稿纸都留在桌上,待监考人员允许后,方可离开。
第一部分常识判断本部分包括两种类型的题目,请根据题目要求做出正确选择。
请开始答题:1.万物皆备于我是( C )A.形而上学B.辩证法C.主观唯心主义D.客观唯心主义2.甲.乙两企业签订销售合同,甲按约给付乙方4万元定金后,乙企业违约.甲企业依法有权要求乙企业给付( A ).A.8万元B.2万元C.4 万元D.6万元3.“审计风暴”显示,由于企业会计核算和纳税申报不实,导致税收严重流失。
对此,国家税务总局对存在违规涉税问题的企业进行了税务专项稽查,这是因为( A )。
①市场经济具有自发性②税收是国家实现经济监督的重要手段③税收是国家组织财政收入的基本形式④在商品服务市场上,市场主体必须遵守平等原则A.①②③B.①③C.①③④D.③④4.质量互变规律揭示了事物发展的( A ).A.形式和状态B.源泉和动力C.方向和途径D.内因和外因5.“北美自由贸易区”是(B )三国于1992年8月12日宣布成立的,是发达国家和发展中国家共同参与的经济一体化组织.A.美国.加拿大.智利B.美国.加拿大.墨西哥C.美国.智利.秘鲁D.美国.阿根廷.巴西6.艾滋病被称为“20世纪的瘟疫”,艾滋病病毒以人体内的(C)作为攻击目标.A.红细胞B.血红蛋白C.淋巴细胞D.神经系统7.我国是一个统一的多民族国家,其中少数民族占全国人口的8%左右.请问下列少数民族中,人口最少的是.( A)A.高山族B.苗族C.回族D.壮族8.要从战略上调整国民经济布局,对关系国民经济命脉的重要行业和关键领域,国有经济必须占据支配地位,在其他领域,可以通过资产重组的结构调整,提高国有资产的整体质量。
