如何巧记并运用 阿伏伽德罗定律的推论
阿伏伽德罗定律
=
同温、同体积下,气与物质的量成正比体的压强成正比
T、p、m相同
=
同温、同压下,相同质量的气体的体积与摩尔质体的密度与摩尔质量成正比
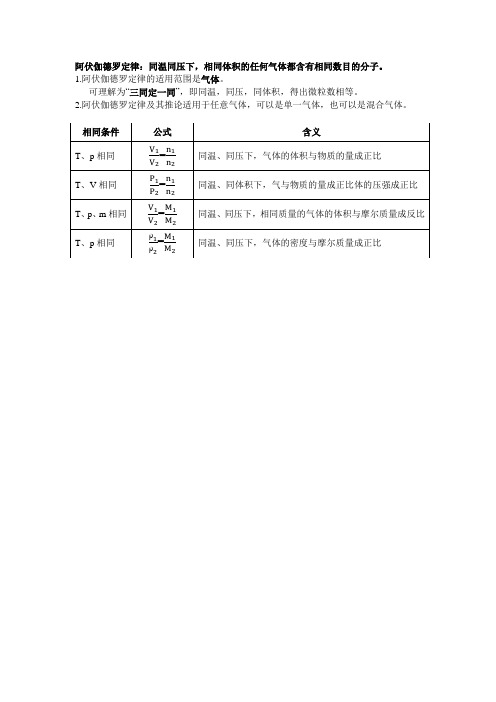
阿伏伽德罗定律:同温同压下,相同体积的任何气体都含有相同数目的分子。
1.阿伏伽德罗定律的适用范围是气体。
可理解为“三同定一同”,即同温,同压,同体积,得出微粒数相等。
2.阿伏伽德罗定律及其推论适用于任意气体,可以是单一气体,也可以是混合气体。
相同条件
公式
含义
T、p相同
=
同温、同压下,气体的体积与物质的量成正比
阿伏伽德罗定律及其推论

A.3∶2
B.1∶3
C.2∶3
D.1∶2
【规范解答】选A。1 mol H2含氢原子2 mol,1 mol NH3含 氢原子3 mol,若H2和NH3所含氢原子数相等,则H2和NH3 的物质的量之比为3∶2,同温同压下气体的体积比等于
其物质的量之比,两个容器的体积比是3∶2。
精品课件
【互动探究】(1)若改为A容器中H2与B容器中 NH3所含原子数相等,则两个容器的体积之比为 ________。
气体摩尔体积(二)
阿伏加德罗定律及其推论
精品课件
气体摩尔体积 定义:单位物质的量的 气体所占的体积 Vm=V/n 单位:L/mol
精品课件
[注意]
★ 气体摩尔体积的数值不是固定不变的,它与 温度和压强有关
★ 气体摩尔体积只适用于气态物质,对于固态 物质和液态物质来讲,都是不适用的。
★ 标准状况下气体摩尔体积约为22.4L/mol (标准状况:T=0 ℃,P=101KPa)
物质的量分数)
精品课件
例题讲析
已知氮气和氨气的混合气体在标准状况 下的密度为1g/L,求混合气体的平均相 对分子质量。
解析:混合气体的平均摩尔质量为: 1g/L×22.4L/mol=22.4g/mol
故混合气体的平均相对分子质量为22.
精品课件
【练习4】
标准状况下
CO和CO2的混和气体 5g 所占体积为 3. 36L。 求CO的质量、CO2的体积及混和气体的平均式量。
精品课件
5. 气体的相对分子质量(M)的计算
(1)已知标准状M=况ρ下标气体. 2密2度.4ρ标
(2)已知两种气体的相对密度D
M(A)=D . M(B)
(3)混合气体的平均相对分子质量(M)
阿伏加德罗定律

定义:在相同的温度和压强下,相同体积的任何气体都含有相同数目的分子。所以又叫四同定律,也叫五同定律或克拉贝隆方程(五同指同温、同压、同体积、同分子个数、同物质的量)。
适用范围:理想气体(即气体分子无体积,各分子间无作用力。P.S:在高温高压下,许多气体都接近于理想气体),可以是单一气体,也可以是混合气体。可以是单质气体,也可以是化合物气体。以A、B两种气体 Nhomakorabea进行讨论。
(1)在相同T、P、V时:根据①式:nA=nB(即阿伏加德罗定律),分子量一定,摩尔质量之比=密度之比=相对密度。若mA=mB则MA=MB。
(2)在相同T、P、m时:体积之比=摩尔质量的反比;两气体的物质的量之比=摩尔质量的反比。
物质的量之比=气体密度的反比;两气体的体积之比=气体密度的反比。
(3)在相同T·V时:两气体的压强之比=气体分子量的正比=摩尔质量的反比。
定律推论:我们可以利用阿伏加德罗定律以及物质的量与分子数目、摩尔质量之间的关系得到以下有用的推论:
(1)同温同压时:①V1:V2=n1:n2=N1:N2②ρ1:ρ2=M1:M2③同质量时:V1:V2=M2:M1
(2)同温同体积时:④P1:P2=n1:n2=N1:N2⑤同质量时:P1:P2=M2:M1
克拉佩龙方程通常用下式表示:PV=nRT……①
P表示压强、V表示气体体积、n表示物质的量、T表示绝对温度、R表示气体常数。所有气体R值均相同。如果压强、温度和体积都采用国际单位(SI),R=8.31帕·米3/摩尔·开。如果压强为大气压,体积为升,则R=0.082大气压·升/摩尔·度。
阿伏加德罗定律及推论

答:8.5g氨在标准状况时的体积是11.2L。
2.利用气体摩尔体积,进行有关 式量的计算
【例题2】在标准状况时,0.2L的容器里所含一氧化碳 的质量为0.25g,计算一氧化碳的式量。
分析:M=m/n
【解】
n=V/Vm
答:一氧化碳的式量是28。
练一练
1.同温同压下,等质量的二氧化硫和二氧化 AD 碳相比较,下列叙述中,正确的是( ) (A)密度比为16:11 (B)密度比为11:16 (C)体积比为1:1 (D)体积比为11:16 2.在相同温度和压强下,下列气体密度最小的 是( B ) A. CO2 B.H2 C.O2 D.Cl2
小结: 根据克拉泊龙方程导出阿伏加德罗定律的推 论:
练一练
1.同温同压下,相同体积的下列气体中, 质量最大的是(A ) (A)氯气 (B)氢气 (C)氧气 (D)氮气 2.同温同压下,同物质的量的CH4气体 与CO体积比是(B) (A)3:1 (B)1:1 (C)1:3 (D)2:3
理想气体的状态方程: PV=nRT
气体Ⅰ 气体Ⅱ P1V1 P2V2 = P1V1=n1RT1 P2V2=n2RT2 n1RT1 n2RT2
V1=V2
同温同体积: T1=T2
P 1 n1 同 T、V: = P2 n2
推论2:同温、同体积,气体的压强之比等于分
子数之比
T、V相同
P1 n1 —— = — P2 n2
练一练
1. 同温同体积下,相同压强的氢气和甲烷 的原子个数之比是(A ) A.2:5 B.1:1 C.1:5 D.1:8 2. 一个密闭容器中盛有11gCO2时,压强为 1×104Pa.如果在相同温度下,把更多的CO2充 入容器中,使容器内压强增至5×104Pa,这时容 器内气体的分子数约为( C) A.3.3×1025 C. 7.5×1023 B. 3.3×1024 D. 7.5×1022
阿伏加德罗定律及其推论

推论3:同温、同体积,气体的压强之比等于分
子数之比
T、V相同
P1 n1 —— = — P2 n2
【例】. 在标准状况下,一个密闭容器中盛有11gCO2.如 果在相同温度下,把更多的CO2充入容器中,使容器内
压强增至5×105Pa,这时容器内气体的分子数约为(C )
A.3.3×1025 B. 3.3×1024
推论2:同温同压下,任何气体的密度之比等于 摩尔质量之比(即相对分子质量之比)
1 M1 2 = M2
【08年海南】在两个密闭容器中,分别充有质量相同的 甲、乙两种气体,若两容器的温度和压强均相同 ,且甲 的密度大于乙的密度,则下列说法正确的是( B) A.甲的分子数比乙的分子数多 B.甲的物质的量比乙的物质的量少 C.甲的摩尔体积比乙的摩尔体积小 D.甲的相对分子质量比乙的相对分子质量小
C. 7.5×1023
D. 7.5×1022
根据克拉泊ห้องสมุดไป่ตู้方程导出阿伏加德罗定律的推论:
1 求某气体相对分子质量的方法
① 根据化学式和相对原子质量直接求。
② 根据气体在标准状况下的密度来求。
M = ρ×Vm
ρ =m / v
③ 还可以由某气体对特定气体的相对密度来求。
ρ 1 M1 D ρ 2 M2
(D 为相对密度)
2 求混合气体的平均摩尔质量 ① 混合气体的总质量除以混合气体总的物质的量。
m总 m1 m 2 m3 M n总 n1 n 2 n3
__
② 混合气体中各组份气体的摩尔质量与其所占的物 质的量分数的乘积之和。
M
___
=MA×a%+MB×b%+MC×c%+……
二、阿伏加德罗定律的几个推论
8阿伏伽德罗定律以及推论

阿伏伽德罗定律以及推论【知识整合】一、阿伏加德罗定律在相同温度和压强下,相同体积.............的任何气体都含有相同数目的分子数。
注意:在该定律中有“四同”:同温、同压、同体积、同分子数目,有“三同”就可定“一同”。
二、阿伏加德罗定律的推论根据阿伏加德罗定律及气态方程(pV =nRT )限定不同的条件,便可得到阿伏加德罗定律的多种形式, ○1T 、p 相同21N N =21V V 同温同压下,气体的分子数与其体积成正比○2T 、V 相同21p p =21N N 温度、体积相同的气体,压强与其分子数成正比○3n 、p 相同21V V =21T T 分子数相等、压强相同的气体,体积与其温度成正比○4n 、T 相同21p p =12V V 分子数相等、温度相同的气体,压强与其体积成反比○5○6○7T 、p 、m 相同21MM =12V V 同温同压下,等质量的气体相对分子质量与其体积成反比【典例分析】例1、 同温同压下,质量相等的O 2与CO 2,密度比为_______,体积比为_______;同温同压下,体积相等的O 2与CO 2,密度之比为_______,质量之比为_________。
例2、 同温同压下,某瓶充满O 2,质量为116g ,充满CO 2质量为122g ,充满气体X ,质量为114g ,则X 的相对分子质量为( )A .28B .60C .32D .44例3、体积相同的容器,一个盛有一氧化氮,另一个盛有氮气和氧气,在同温同压下两容器内的气体一定具有相同的( ) A. 原子总数 B. 质子总数 C. 分子总数 D. 质量例4、某非金属单质A 和氧气发生化合反应生成B 。
B 为气体,其体积是反应掉氧气体积的两倍(同温同压)。
以下对B 分子组成的推测一定正确的是()A. 有1个氧原子B. 有2个氧原子C. 有1个A 原子D. 有2个A 原子例5、在150℃时,(NH 4)2CO 3分解的方程式为:(NH 4)2CO 3=====△2NH 3↑+H 2O↑+CO 2↑,若完全分解,产生的气态混合物的密度是相同条件下氢气密度的( ) A .96倍 B .48倍 C .12倍 D .10倍【测评反馈】1.同温、同压下,下列有关比较等质量的二氧化硫气体和二氧化碳气体的叙述中正确的是( )A .密度比为16:11B .密度比为11:16C .体积比为1:1D .体积比为11:162.下列各组中,两种气体的分子数一定相等是( )A .温度相同、体积相同的O 2和2NB .质量相等、密度不等的2N 和42HC C .体积相等、密度相等的CO 和42H CD .压强相同、体积相同的2N 和2O3.在一定条件下,气体A 可发生如下反应:,若知所得混合气体对氢气的相对密度为4.25,则A 的相对分子质量可能为( ) A .34 B .8.5C .17 D .16 4.在一定温度和压强下,1体积2X (气)和3体积2Y (气)化合生成2体积Z (气),则Z 的分子式是( )A .3XYB .XYC .Y X 3D .32Y X5.在标准状况下,如果25.0LO 含有m 个2O 分子,则阿伏加德罗常数可表示为( ) A .m/22.4 B .44.8mC .22.4m D .m/326.在同温、同压下,有同质量的气体X 和Y 。
阿伏加德罗定律

阿伏加德罗定律
阿伏伽德罗定律(Avogadro's Law)是化学和物理学中的一个基本定律,由意大利化学家阿伏伽德罗(Amedeo Avogadro)于1811年提出。
该定律表明,在相同的温度和压力条件下,等体积的气体中包含的分子数相等。
具体来说,阿伏伽德罗定律可以表示为:相同条件下,等
压下不同气体的体积与该气体包含的粒子数成正比。
这意
味着,如果将两种不同的气体分别放置在相同的温度和压
力下,它们的体积与其中所包含的分子数成正比关系。
阿伏伽德罗定律的数学表达式可以写为 V = k * n,其中V
代表气体的体积,n代表气体中的分子数,k为比例常数。
根据这个定律,当气体的分子数增加时,其体积也会增加,反之亦然。
阿伏伽德罗定律对于研究气体的性质和气体化学反应等方面具有重要的应用价值,为化学和物理学领域的研究提供了基础理论支持。
阿伏加德罗定律及其推论

阿伏加德罗定律及其推论1.理想气体状态方程我们设定:T .温度;p .气体夺强;n .物质的量;V .气体的体积;m .气体的质量;M .气体的摩尔质量; .气体的密度N .气体的分子数。
理想气体状态方程为:(1)111T V p =222T V p ;(2)pV =nRT =RT Mm (R 为常数)。
对(2)若p 的单位为大气压(atm ),V 为升(L ),T 为绝对温度时,R =0.082。
若p 为帕斯卡(Pa ),V 为立方米(m 3),T 为绝对温度时,R =8.31。
2.阿伏加德罗定律在相同温度和压强下,相同体积.............的任何气体都含有相同数目的分子数。
这是意大利科学家阿伏加德罗最早提出的,因此称为“阿伏加德罗定律”。
理解时注意:在该定律中有“四同”:同温、同压、同体积、同分子数目,有“三同”就可定“一同”。
如,同温同压下,同体积的两种气体必含有相同数目的分子;同温同压下,同分子数目的两种气体必然同体积;再如,在同温下,两种气体同体积又同分子数目,则必然同压。
3.阿伏加德罗定律的推论根据阿伏加德罗定律及气态方程(pV =nRT )限定不同的条件,便可得到阿伏加德罗定律的多种形式,熟练并掌握了它们,解答有关问题时,可达到事半功倍的效果。
条件结论语言叙述T 、p 相同 21N N =21V V 同温同压下,气体的分子数与其体积成正比 T 、V 相同21p p =21N N 温度、体积相同的气体,压强与其分子数成正比 n 、p 相同21V V =21T T 分子数相等、压强相同的气体,体积与其温度成正比 n 、T 相同21p p =12V V 分子数相等、温度相同的气体,压强与其体积成反比 T 、p 、m 相同21M M =12V V 同温同压下,等质量的气体相对分子质量与其体积成反比。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
“气体摩尔体积” 在讲 时, 必定要学习阿伏伽德罗定律 , 将其加以引申就会出现阿伏伽德罗定律的推论 . 如果要完 全记住是非常困难的 , 所以需要一定的技巧 . 下面介绍一种记忆方法 . 公式: pV = nRT. ① p: 表示气体的压强, V: 表示气体的体积, n: 表示气体的 R: 表示一个常数, T: 表示气体的温度. 物质的量, 推论 1 : 同温同压下, 气体的体ቤተ መጻሕፍቲ ባይዱ之比等于其物质的量 之比. V1 n1 = . V2 n2 推论 2 : 同温同体积下, 气体的压强之比等于其物质的 量之比. p1 n1 = . p2 n2 推论 3 : 同温同物质的量的气体 , 压强比等于其体积的 反比. p1 V2 = . p2 V1 上述推论都可以用公式 ① 得到. 由于 R 是常量, 其他四 个量有两个量是相同的 , 则另两个量就成一定的比例 . 另外, 将公式①变形, 可得: pV = m RT . M
同样, 可以得出两个变量的比例关系 . 推论 4 : 同温同压下, 相同体积的任何气体的质量之比 等于摩尔质量之比. m1 M 1 = . m2 M 2 推论 5 : 同温同压下, 同质量的气体体积与其摩尔质量 成反比. V1 M 2 = . V2 M 1 推论 6 : 同温同体积下, 同质量的两种气体, 其压强与摩 尔质量成反比. p1 M 2 = . p2 M 1 将公式②变形, 可得: pM = ρRT. 推论 7 : 同温同压下,任何气体的密度之比等于其摩尔 质量之比.
p1 M 1 = . p2 M 2 推论 8 : 同温同密度下, 摩尔质量与压强成反比 . p1 M 2 = . p2 M 1 这样, 推理记忆就比较方便. 利用上述推论解决一些问题就比较容易 . 例1 H2 、 O2 三种气 在三个密闭容器中分别充入 Ne、 ). 体, 当它们的温度和密度都相同时 , 这三种气体的压强 ( p ) 从大到小的顺序是( A. p( Ne) ﹥ p( H2 ) ﹥ p( O2 ) B. p( O2 ) ﹥ p( Ne) ﹥ p( H2 ) C. p( H2 ) ﹥ p( O2 ) ﹥ p( Ne) D. p( H2 ) ﹥ p( Ne) ﹥ p( O2 ) 分析: 根据推论 8 可知, 当它们的温度和密度相同时 , 因 为摩尔质量与压强成反比 , 所以摩尔质量由小到大的顺序 为 H2 ﹤ Ne ﹤ O2 . 所以 p( H2 ) > p( Ne) > p( O2 ) . 答案为 D. 例2 在两个密闭容器中, 分别充有质量相同的甲 、 乙 ). 两种气体, 若两容器的温度和压强均相同 , 且甲的密度大于 乙的密度, 则下列说法正确的是( A. 甲的分子数比乙的分子数多 B. 甲的物质的量比乙的物质的量少 C. 甲的摩尔体积比乙的摩尔体积小 D. 甲的相对分子质量比乙的相对分子质量小 分析: 根据推论 7 得, 同温同压下,任何气体的密度之 比等于其摩尔质量之比 . 由于甲的密度大于乙的密度 , 而两 者质量相等, 所以甲的物质的量比乙的物质的量少 , 甲的分 子数比乙少. 由于它们的外界条件相同 , 所以它们的摩尔体 积相同. 答案为 B.
