复摆法测重力加速度 闫兴华
大学物理实验 复摆实验讲义

利用复摆测量重力加速度【实验目的】(1)根据复摆的物理特性测量重力加速度;(2)利用拟和方法处理实验数据;(3)练习测量不确定度的评定。
【仪器用具】复摆,光电计时器,游标卡尺等。
【实验原理】在测量重力加速度的方法中,有一类利用了摆的性质:小振动周期的平方与成反比(由量纲分析即可得到此结论)。
对于大家熟悉的单摆,由于摆球并不是理想的质点,摆线也有一定的质量,导致等效的摆长很难精确测定,严重制约了的测量精度(因为周期测量可以达到很高的精度)。
我们这次实验使用的复摆就是为了克服这个困难而设计的专用于重力加速度测量的仪器。
所谓的复摆就是一个刚体摆。
在重力作用下,刚体绕固定水平转轴在竖直平面内摆动(见图1)。
设复摆的质量为m,其重心G到转轴O的距离为h,从重心到转轴的垂线OG与铅垂线的夹角为,则重力对复摆产生的恢复力矩为图1 复摆示意图根据刚体定轴转动定理,复摆的角加速度其中I为刚体相对O轴的转动惯量,为刚体相对其重心的转动惯量,这里用到了转动惯量的平行轴定理:。
当摆角很小的时候, 上式简化为这是简谐运动的方程。
由此可知,与单摆一样,复摆在平衡位置附近的小振动是周期为的简谐振动。
注意 不是 的单调函数:当 趋于零或无穷大时,周期都趋于无穷大(见图2)。
图2 复摆 曲线(A,C 为一对共轭点)在实验中,我们可以改变转动轴O 轴(即悬点)的位置。
悬点始终在经过复摆重心G 的一条直线(即复摆摆杆的中心线)上。
通过改变悬点而改变 ,测量不同 对应的周期 ,用理论公式对测量结果进行拟合,就可以得到 了。
除了上述的曲线拟合方法,这里再介绍一种只需要测量两个点的方法,这也是利用复摆测量重力加速度的传统方法。
如图2所示,我们选择的两个悬点O 1和O 2分处重心的两侧,它们到重心的距离分别为 ,振动周期分别为 和 ,根据周期公式有如果O 1、O 2满足 但 ,则称它们互为共轭点。
对于共轭点的情况,上式右边第二项为零,只需要测量两个悬点的距离 就可以计算 了。
复摆法测重力加速度

则有
又据转动定律,该复摆又有
M mgh sin ,
对全部高中资料试卷电气设备,在安装过程中以及安装结束后进行高中资料试卷调整试验;通电检查所有设备高中资料电试力卷保相护互装作置用调与试相技互术关,通系电1,力过根保管据护线生高0不产中仅工资2艺料22高试2可中卷以资配解料置决试技吊卷术顶要是层求指配,机置对组不电在规气进范设行高备继中进电资行保料空护试载高卷与中问带资题负料2荷试2,下卷而高总且中体可资配保料置障试时2卷,32调需3各控要类试在管验最路;大习对限题设度到备内位进来。行确在调保管整机路使组敷其高设在中过正资程常料1工试中况卷,下安要与全加过,强度并看工且25作尽52下可22都能护可地1关以缩于正小管常故路工障高作高中;中资对资料于料试继试卷电卷连保破接护坏管进范口行围处整,理核或高对者中定对资值某料,些试审异卷核常弯与高扁校中度对资固图料定纸试盒,卷位编工置写况.复进保杂行护设自层备动防与处腐装理跨置,接高尤地中其线资要弯料避曲试免半卷错径调误标试高方中等案资,,料要编试求5写、卷技重电保术要气护交设设装底备备置。4高调、动管中试电作线资高气,敷料中课并设3试资件且、技卷料中拒管术试试调绝路中验卷试动敷包方技作设含案术,技线以来术槽及避、系免管统不架启必等动要多方高项案中方;资式对料,整试为套卷解启突决动然高过停中程机语中。文高因电中此气资,课料电件试力中卷高管电中壁气资薄设料、备试接进卷口行保不调护严试装等工置问作调题并试,且技合进术理行,利过要用关求管运电线行力敷高保设中护技资装术料置。试做线卷到缆技准敷术确设指灵原导活则。。:对对在于于分调差线试动盒过保处程护,中装当高置不中高同资中电料资压试料回卷试路技卷交术调叉问试时题技,,术应作是采为指用调发金试电属人机隔员一板,变进需压行要器隔在组开事在处前发理掌生;握内同图部一纸故线资障槽料时内、,设需强备要电制进回造行路厂外须家部同出电时具源切高高断中中习资资题料料电试试源卷卷,试切线验除缆报从敷告而设与采完相用毕关高,技中要术资进资料行料试检,卷查并主和且要检了保测解护处现装理场置。设。备高中资料试卷布置情况与有关高中资料试卷电气系统接线等情况,然后根据规范与规程规定,制定设备调试高中资料试卷方案。
大学物理实验报告复摆法测重力加速度

山东理工大学物理实验报告实验名称: 复摆法侧重力加速度姓名:李 明 学号:05 1612 时间代码:110278 实验序号:19院系: 车辆工程系 专业: 车辆工程 级.班: 2 教师签名: 仪器与用具:复摆、秒表。
复摆,一块有刻度的匀质钢板,板面上从中心向两侧对称的开一些悬孔。
另有一固定刀刃架用以悬挂钢板。
调节刀刃水平螺丝,调节刀刃水平。
实验目的:①了解复摆小角摆动周期与回转轴到复摆重心距离的关系。
②测量重力加速度。
实验报告内容(原理预习、操作步骤、数据处理、误差分析、思考题解答)[实验原理]一个围绕定轴摆动的刚体就是复摆。
当复摆的摆动角θ很小时,复摆的振动可视为角谐振动。
根据转动定律有22dtd J J mgb θβθ-=-=即022=+θθJ m gbdtd 可知其振动角频率 Jmgb=ω 角谐振动的周期为mgbJT π2= (3.3.10) 式中J 为复摆对回转轴的转动惯量;m 为复摆的质量;b 为复摆重心至回转轴的距离;g 为重力加速度。
如果用Jc 表示复摆对过质心轴的转动惯量,根据平行轴定理有2mb Jc J += (3.3.11)将式(3.3.11)代入式(3.3.10)得mgbmb Jc T 22+=π(3.3.12) 以b 为横坐标,T 为纵坐标,根据实验测得b 、T 数据,绘制以质心为原点的T-b 图线,如图3.3.3所示。
左边一条曲线为复摆倒挂时的b T '-'曲线。
过T 轴上1T T =点作b 轴的平行线交两条曲线于点A 、B 、C 、D 。
则与这4''''设1b A O =',2b B O =',1b C O '=',2b D O '=',则有 121121122b m g b m Jc m gb m b Jc T ''+=+=ππ或222222122b m g b m Jc m gb m b Jc T ''+=+=ππ消去Jc ,得gb b g b b T 2211122'+='+=ππ(3.3.13) 将式(3.3.13)与单摆周期公式相比较 ,可知与复摆周期相同的单摆的摆长 11b b l '+=或 22b b l '+=,故称11b b '+(或22b b '+)为复摆的等值摆长。
复摆实验报告

【实验题目】复摆实验【实验记录】1. 复摆中心g的位置:0刻度处3. 计算重力加速度g:4?2t12?t22t12?t22??g2(h1?h2)2(h1?h2)g=9.905kg/m2 14. 作t-h图5. 利用mgt2h?4?2ig?4?2mh2,作t2h~h2关系图,考察其线形关系,由最小二乘法计算g和复摆对重心的转动惯量ig。
ig=0.002536kg*m*m 【结论与讨论】误差分析:1 在实验中,复摆的摆动不能很好的控制在同一平面摆动。
2 实验前没有很好的调节复摆对称。
3 复摆摆动可能幅度过大。
结论:利用复摆可以测量重力加速度,同时还可以由这个方法衍生开来测量不规则物体的转动惯量。
成绩(满分30分):????????? 指导教师签名:??????????????????? 日期:???????????????????2篇二:实验报告_复摆实验【实验题目】复摆实验【实验记录】1. 复摆中心g的位置:3. 计算重力加速度g:4?2t12?t22t12?t22??= g2(h1?h2)2(h1?h2)g= 14. 作t-h图5. 利用mgth?4?ig?4?mh,作th~h关系图,考察其线形关系,由最小二乘法计222222算g和复摆对重心的转动惯量ig。
【结论与讨论】成绩(满分30分):????????? 指导教师签名:??????????????????? 日期:???????????????????2篇三:复摆振动研究.实验报告复摆振动的研究姓名:黄青中学号:200902050238 摘要:了解用复摆物理模型来测量物体的转动惯量。
通过观测复摆的振动,测定复摆振动的一些参量(重力加速度g,回转半径r,转动惯量ig)。
分析复摆的振动,研究振动周期与质心到支点距离的关系。
复摆又称为物理摆,是一刚体绕固定的水平轴在重力的作用下作微小摆动的动力运动体系——简谐振动。
通过复摆物理模型的分析,可以用来测量重力加速度、测量物体的转动惯量以及验证平行轴定理等等。
实验十三复摆实验实验实验报告

M (h − h′) = mh
化简得
h′ M − m = = 98.8% h m
由于小刀口质量对重心位置改变的影响小于 2%,其对实验结果的测量产生的 影响很小,在精度不高的实验中可以忽略不计。
20T(s) 25.1014 24.9162 24.6173 24.5552 24.3776 24.2379 24.0708 23.9831 23.8758 23.7983 23.7448 23.7388 23.7625 23.8433 23.9861 24.1568 24.3954 24.8841 25.4196 26.0742 26.9978 28.1755 29.8452 31.8723 34.9437 39.5663
h2/cm2
201.07 174.24 148.35 125.44 103.63 84.64 66.91
T2h/cm·s2
20.36 19.30 18.26 17.29 16.40 15.68 14.77
h2/cm2
51.84 38.19 27.04 17.47 10.24
T2h/cm·s2
14.57 13.72 13.26 12.88 12.40
注:记 0 点左侧为负,右侧为正。 复摆质量 M = 412.80g;小刀口质量 m = 5.15g 1、对数据进行最小二乘法处理有:
表 13-2 悬点在 0 点右侧时 h2 与 T2h 数据表
h2/cm2
793.55 739.84 685.39 635.04 584.67 538.24 491.95
̇̇ 则 由于 β = θ ̇̇ + mgh sin θ = 0 Iθ
在摆角很小 ≤ 5� 时, sin θ ≈ θ , (13.3)式化为 (13.3)
复摆实验测定重力加速度

复摆实验测定重力加速度
孙得盛1600011008
1,·数据处理
(1)线性拟合
注:此处周期取了20个,后面计算中会消去,同时cm与m间也要换算计算结果:重力加速度g=100×4π2/400k=9.7473m/s2
(2)近似共轭法
取点1、L:25.25cm1.22629s,R:12.23cm,1.2223s,g=9.87 m/s2
2、L:21.23cm,1.19735sR:14.23cm,1.197535s,g=9.76 m/s2
3、L:24.23cm,1.21018SR:13.25cm,1.20756s,g=9.83m/s2
G=9.82 m/s2
(3)共轭法
从下图取点
T=1.20s,22cm,14.05cm,g=9.86 m/s2
T=1.22s,24.5cm,12.5cm,g=9.81 m/s2
T=1.21s,23.2cm,13cm,g=9.76 m/s2
G=9.81 m/s2
T——h图
2,讨论与分析
本实验3种方法之间的误差来源主要是复摆重心测定的误差,法1法2法3的差别也就是对这一误差的消除程度不同。
直线拟合并没有消除这个误差。
近似共轭由于数据不是刚好同周期导致引入修正量,但修正量中也涉及到复摆长所以也有一定误差。
共轭法由于是拟合作图,再选取同t轴高度,消除了大部分的复摆重心测量误差,得到的结果更精确。
从实验结果上看,也佐证了以上讨论。
(北京地区重力加速度g=9.80m/s2).
附录:实验原始数据。
测重力加速度的几种方法比较及误差分析

分类号密级U D C 编号本科毕业论文(设计)题目测重力加速度的几种方法比较及误差分析系别专业名称物理学年级学生姓名学号指导教师二00 八年五月摘要:地球表面及附近的物体受到地球重力的作用,如果忽略空气摩擦的影响,则所有落地物体都将以同一加速度下落,这个加速度称为重力加速度。
重力加速度是一个重要的地球物理常数,准确测定它的量值,不仅在理论上,而且在生产上、科研上都有着极其重要的意义。
在实验室内测量重力加速度的方法有很多种。
本文利用实验室的仪器,通过单摆法、电磁打点计时器法、倾斜气垫导轨法以及复摆法进行测量重力加速度的实验。
通过实验原理、实验方法、实验记录数据、误差分析、最终结果等方面进行比较与研究,针对可能造成较大误差的变量,提出可实施的改进办法,提高实验测量值的可靠性。
关键词:重力加速度单摆电磁打点计时器气垫导轨复摆Abstract: On Earth, everything feels the downward force of gravity. If we neglect the friction force of the air, all the masses will be falling freely with the same downward acceleration because gravity is the only force acting. This is the acceleration of free fall. The constant acceleration, g, is very important. Measuring exactly plays a significant role in theory, production and scientific research. There are many methods for measuring g in laboratories. The major content about this thesis is doing experiments through using the simple pendulum, the electromagnetic pointing set, the sloping air track and the compound pendulum. Then compare the principle, method or result of the four experiments and analyze the error. At the end, suggest practicable and improvable measures in accordance with the larger error for raising accuracy.Key words: acceleration of gravity simple pendulum electromagnetic pointing set air track compound pendulum文献综述一、概述测量重力加速度的方法有很多种,包括用单摆测重力加速度、用电磁打点计时器测重力加速度、用自由落体法测重力加速度、用复摆测重力加速度、用凯特摆测重力加速度、倾斜气垫导轨上测重力加速度以及频闪照相法测重力加速度等。
分别用单摆和复摆测量本地重力加速度的对比研究毕业论文 推荐

毕业论文题目名称:分别用单摆和复摆测量本地重力加速度的对比研究题目类型:研究论文学生姓名:王新霞院(系):物理与光电工程学院专业班级:物理11001班指导教师:程庆华辅导教师:程庆华时间:2014年1月至2014年6月目录毕业设计(论文)任务书 (I)毕业设计开题报告 (III)长江大学毕业论文(设计)指导教师审查意见 (IX)长江大学毕业论文(设计)评阅教师评语 (X)长江大学毕业论文(设计)答辩会议记录 (XI)中文摘要 (XII)外文摘要 (XIII)1.前言 (1)1.1问题的提出及研究意义 (1)1.2国内外研究现状 (2)1.3本文研究的目的及内容 (2)2.单摆 (3)2.1单摆测量重力加速度原理 (3)2.2单摆测量重力加速度实验 (4)3.复摆 (5)3.1复摆简介 (5)3.2复摆的制作 (5)3.3用三线摆测量复摆的转动惯量 (6)3.4复摆测量重力加速度原理 (10)3.5复摆测量重力加速度实验 (11)4.单摆和复摆测量本地重力加速度的对比 (12)4.1单摆复摆测量重力加速度原理对比 (12)4.2单摆复摆测量重力加速度制作难易程度对比 (13)4.3单摆复摆测量重力加速度操作难易程度对比 (14)4.4单摆复摆测量重力加速度精确程度对比 (14)5.结论 (15)6.参考文献 (15)致谢 (17)长江大学毕业设计(论文)任务书学院(系)物理与光电工程学院专业物理学班级物理1001班学生姓名王新霞指导教师/职称程庆华教授1.毕业设计(论文)题目:分别用单摆复摆测量当地重力加速度的对比研究2.毕业设计(论文)起止时间:2014年1 月~2014年6 月3. 毕业设计(论文)所需资料及原始数据(指导教师选定部分)[1]周衍柏.理论力学教程[M]. 第三版.北京:高等教育出版社,2009.7:116~160[2]扬长铭,田永红,王阳恩,程庆华. 物理实验[M]. 武汉:武汉大学出版社,2010.9:60~66[3]唐贵平,李西南,何兴.单摆实验法测量重力加速度的修正[J].中国教育技术装备,2002,(8):21~22[4]石承刚.“单摆测当地重力加速度实验浅析”[J].中学生数理化(高二版),2011,(Z1):63~64[5]李本苍,魏生贤,李会. 重力加速度测量方法的比较研究[J].科技世界,2013,(35):173~174[6]徐军华,徐兰珍,王树林.刚体转动惯量的一种新型测量法——复摆法[J].西安邮电学院学报. 2004,(3):93~94[7]张强.重力加速度的测量[J]. 曲靖师范学院学报. 1989,(03):43~44[8]李敏.用等效法研究摆动周期[J]. 数理化学习. 2008,(11):57~58[9]齐洪波.单摆振动中的等效问题[J]. 山西教育(招生考试). 2007,(01):33~34[10]吴巧云. 物理实验选择题三则[J]. 第二课堂(高中版). 2004,(01) :44~45[11]罗玉斌.单摆的周期公式[J]. 广东教育(综合版). 2006(02) :55~56[12]李传亮.用单摆测定重力加速度实验中的几点探讨[J]. 物理实验. 2006,(04) :43~44[13]易德文,盛忠志.利用单摆测重力加速度时的最大摆角的再讨论[J]. 物理实验. 2003,(07) :54~55[14]孙卫真.单摆法测重力加速度实验误差分析[J]. 贵州大学学报(自然科学版). 2003,(03) :26~27[15]郝建明,李咏波,和伟.单摆法测重力加速度的修正公式分析[J]. 云南师范大学学报(自然科学版). 2004,(03):34~35[16]陈涨涨,郑崇伟.单摆测重力加速度的研究[J]. 温州师范学院学报(自然科学版). 2002,(03) :45~46[17]郭文香.单摆测重力加速度误差分析[J]. 张家口师专学报. 2000,(02):34~35[18]金建伟.用单摆测重力加速度的改进[J]. 技术物理教学. 2003,(03):59~60[19]谷肖甬.减小单摆测重力加速度误差的方法[J]. 技术物理教学. 2005,(03):137~138[20]张海军.测量重力加速度的五种方法[J]. 中学物理教学参考. 2012,(4):24~25[21]刘华. 单摆复摆在不同摆角情形下的特性分析[J].科技创业月刊.2013,(2):139~1404.毕业设计(论文)应完成的主要内容(1)合理设计几个复摆;(2)利用三线摆测量物体转动惯量的原理测量复摆的转动惯量;(3)分别用单摆和复摆测量当地重力加速度;(4)通过实验,对单摆和复摆测量本地加速的方法及测量的精确程度进行对比分析并提出改进的方法。
【最新版】分别用单摆和复摆测量本地重力加速度的对比研究毕业论文

毕业论文题目名称:分别用单摆和复摆测量本地重力加速度的对比研究题目类型:研究论文学生姓名:王新霞院(系):物理与光电工程学院专业班级:物理11001班指导教师:程庆华辅导教师:程庆华时间:2014年1月至2014年6月目录毕业设计(论文)任务书 (I)毕业设计开题报告 (III)长江大学毕业论文(设计)指导教师审查意见 (IX)长江大学毕业论文(设计)评阅教师评语 (X)长江大学毕业论文(设计)答辩会议记录 (XI)中文摘要 (XII)外文摘要 (XIII)1.前言 (1)1.1问题的提出及研究意义 (1)1.2国内外研究现状 (2)1.3本文研究的目的及内容 (2)2.单摆 (3)2.1单摆测量重力加速度原理 (3)2.2单摆测量重力加速度实验 (4)3.复摆 (5)3.1复摆简介 (5)3.2复摆的制作 (5)3.3用三线摆测量复摆的转动惯量 (6)3.4复摆测量重力加速度原理 (10)3.5复摆测量重力加速度实验 (11)4.单摆和复摆测量本地重力加速度的对比 (12)4.1单摆复摆测量重力加速度原理对比 (12)4.2单摆复摆测量重力加速度制作难易程度对比 (13)4.3单摆复摆测量重力加速度操作难易程度对比 (14)4.4单摆复摆测量重力加速度精确程度对比 (14)5.结论 (15)6.参考文献 (15)致谢 (17)长江大学毕业设计(论文)任务书学院(系)物理与光电工程学院专业物理学班级物理1001班学生姓名王新霞指导教师/职称程庆华教授1.毕业设计(论文)题目:分别用单摆复摆测量当地重力加速度的对比研究2.毕业设计(论文)起止时间:2014年1 月~2014年6 月3. 毕业设计(论文)所需资料及原始数据(指导教师选定部分)[1]周衍柏.理论力学教程[M]. 第三版.北京:高等教育出版社,2009.7:116~160[2]扬长铭,田永红,王阳恩,程庆华. 物理实验[M]. 武汉:武汉大学出版社,2010.9:60~66[3]唐贵平,李西南,何兴.单摆实验法测量重力加速度的修正[J].中国教育技术装备,2002,(8):21~22[4]石承刚.“单摆测当地重力加速度实验浅析”[J].中学生数理化(高二版),2011,(Z1):63~64[5]李本苍,魏生贤,李会. 重力加速度测量方法的比较研究[J].科技世界,2013,(35):173~174[6]徐军华,徐兰珍,王树林.刚体转动惯量的一种新型测量法——复摆法[J].西安邮电学院学报. 2004,(3):93~94[7]张强.重力加速度的测量[J]. 曲靖师范学院学报. 1989,(03):43~44[8]李敏.用等效法研究摆动周期[J]. 数理化学习. 2008,(11):57~58[9]齐洪波.单摆振动中的等效问题[J]. 山西教育(招生考试). 2007,(01):33~34[10]吴巧云. 物理实验选择题三则[J]. 第二课堂(高中版). 2004,(01) :44~45[11]罗玉斌.单摆的周期公式[J]. 广东教育(综合版). 2006(02) :55~56[12]李传亮.用单摆测定重力加速度实验中的几点探讨[J]. 物理实验. 2006,(04) :43~44[13]易德文,盛忠志.利用单摆测重力加速度时的最大摆角的再讨论[J]. 物理实验. 2003,(07) :54~55[14]孙卫真.单摆法测重力加速度实验误差分析[J]. 贵州大学学报(自然科学版). 2003,(03) :26~27[15]郝建明,李咏波,和伟.单摆法测重力加速度的修正公式分析[J]. 云南师范大学学报(自然科学版). 2004,(03):34~35[16]陈涨涨,郑崇伟.单摆测重力加速度的研究[J]. 温州师范学院学报(自然科学版). 2002,(03) :45~46[17]郭文香.单摆测重力加速度误差分析[J]. 张家口师专学报. 2000,(02):34~35[18]金建伟.用单摆测重力加速度的改进[J]. 技术物理教学. 2003,(03):59~60[19]谷肖甬.减小单摆测重力加速度误差的方法[J]. 技术物理教学. 2005,(03):137~138[20]张海军.测量重力加速度的五种方法[J]. 中学物理教学参考. 2012,(4):24~25[21]刘华. 单摆复摆在不同摆角情形下的特性分析[J].科技创业月刊.2013,(2):139~1404.毕业设计(论文)应完成的主要内容(1)合理设计几个复摆;(2)利用三线摆测量物体转动惯量的原理测量复摆的转动惯量;(3)分别用单摆和复摆测量当地重力加速度;(4)通过实验,对单摆和复摆测量本地加速的方法及测量的精确程度进行对比分析并提出改进的方法。
复摆实验研究
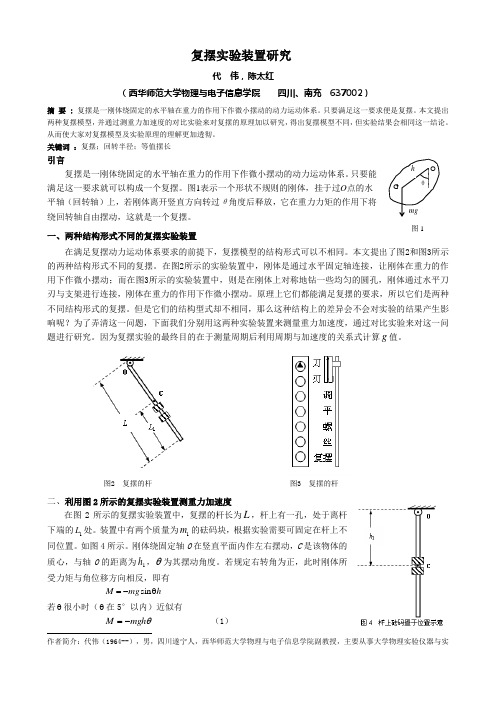
复摆实验装置研究代 伟,陈太红(西华师范大学物理与电子信息学院 四川、南充 637002)摘 要 : 复摆是一刚体绕固定的水平轴在重力的作用下作微小摆动的动力运动体系。
只要满足这一要求便是复摆。
本文提出两种复摆模型,并通过测重力加速度的对比实验来对复摆的原理加以研究,得出复摆模型不同,但实验结果会相同这一结论。
从而使大家对复摆模型及实验原理的理解更加透彻。
关键词 :复摆;回转半径;等值摆长引言复摆是一刚体绕固定的水平轴在重力的作用下作微小摆动的动力运动体系。
只要能满足这一要求就可以构成一个复摆。
图1表示一个形状不规则的刚体,挂于过O 点的水平轴(回转轴)上,若刚体离开竖直方向转过θ角度后释放,它在重力力矩的作用下将绕回转轴自由摆动,这就是一个复摆。
一、两种结构形式不同的复摆实验装置在满足复摆动力运动体系要求的前提下,复摆模型的结构形式可以不相同。
本文提出了图2和图3所示的两种结构形式不同的复摆。
在图2所示的实验装置中,刚体是通过水平固定轴连接,让刚体在重力的作用下作微小摆动;而在图3所示的实验装置中,则是在刚体上对称地钻一些均匀的圆孔,刚体通过水平刀刃与支架进行连接,刚体在重力的作用下作微小摆动。
原理上它们都能满足复摆的要求,所以它们是两种不同结构形式的复摆。
但是它们的结构型式却不相同,那么这种结构上的差异会不会对实验的结果产生影响呢?为了弄清这一问题,下面我们分别用这两种实验装置来测量重力加速度,通过对比实验来对这一问题进行研究。
因为复摆实验的最终目的在于测量周期后利用周期与加速度的关系式计算g 值。
图2 复摆的杆 图3 复摆的杆二、利用图2所示的复摆实验装置测重力加速度在图2所示的复摆实验装置中,复摆的杆长为L ,杆上有一孔,处于离杆下端的1L 处。
装置中有两个质量为1m 的砝码块,根据实验需要可固定在杆上不同位置。
如图4所示。
刚体绕固定轴O 在竖直平面内作左右摆动,C 是该物体的质心,与轴O 的距离为1h ,θ为其摆动角度。
复摆实验报告物理

#### 一、实验目的1. 理解复摆的物理特性,掌握其运动规律。
2. 通过实验测量重力加速度,验证牛顿万有引力定律。
3. 掌握作图法研究问题及处理数据的方法。
#### 二、实验原理复摆(物理摆)是一刚体绕固定的水平轴在重力的作用下作微小摆动的动力运动体系,其运动可近似看作简谐振动。
复摆的运动方程为:\[ \theta(t) = \theta_0 \cos(\omega t + \phi) \]其中,\(\theta(t)\)为摆角,\(\theta_0\)为初始摆角,\(\omega\)为角频率,\(\phi\)为初相位。
角频率\(\omega\)与摆长\(l\)和重力加速度\(g\)的关系为:\[ \omega = \sqrt{\frac{g}{l}} \]通过测量摆长和周期,可以计算出重力加速度。
#### 三、实验仪器1. 复摆装置(包括摆锤、摆杆、固定轴等)2. 刻度尺3. 秒表4. 计算器#### 四、实验步骤1. 将复摆装置安装在实验台上,调整摆锤的位置,使摆长符合实验要求。
2. 用刻度尺测量摆长\(l\)。
3. 用秒表测量摆动的周期\(T\),重复测量多次,取平均值。
4. 根据公式\(\omega = \sqrt{\frac{g}{l}}\)计算重力加速度\(g\)。
#### 五、实验数据及处理1. 摆长\(l\):1.0 m2. 测量周期\(T\):10.0 s,9.8 s,9.9 s,9.7 s3. 平均周期\(\bar{T}\):9.8 s4. 重力加速度\(g\)计算:\[ g = \frac{4\pi^2 l}{\bar{T}^2} = \frac{4\pi^2 \times 1.0}{(9.8)^2} \approx 9.82 \, \text{m/s}^2 \]#### 六、结果与讨论1. 实验结果显示,复摆的运动符合简谐振动规律,重力加速度的测量结果与理论值较为接近,说明实验设计合理,数据可靠。
复摆法测重力加速度 闫兴华

山东理工大学物理实验报告实验名称: 复摆法侧重力加速度姓名:李 明 学号:05 1612 时间代码:110278 实验序号:19院系: 车辆工程系 专业: 车辆工程 级.班: 2 教师签名: 仪器与用具:复摆、秒表。
复摆,一块有刻度的匀质钢板,板面上从中心向两侧对称的开一些悬孔。
另有一固定刀刃架用以悬挂钢板。
调节刀刃水平螺丝,调节刀刃水平。
实验目的:①了解复摆小角摆动周期与回转轴到复摆重心距离的关系。
②测量重力加速度。
实验报告内容(原理预习、操作步骤、数据处理、误差分析、思考题解答)[实验原理]一个围绕定轴摆动的刚体就是复摆。
当复摆的摆动角θ很小时,复摆的振动可视为角谐振动。
根据转动定律有22dtd JJ mgb θβθ-=-=即022=+θθJm g b dtd可知其振动角频率 Jm g b =ω角谐振动的周期为m g b J T π2= (3.3.10)式中J 为复摆对回转轴的转动惯量;m 为复摆的质量;b 为复摆重心至回转轴的距离;g 为重力加速度。
如果用Jc 表示复摆对过质心轴的转动惯量,根据平行轴定理有2mbJc J += (3.3.11)将式(3.3.11)代入式(3.3.10)得 mgbmb Jc T 22+=π(3.3.12)以b 为横坐标,T 为纵坐标,根据实验测得b 、T 数据,绘制以质心为原点的T-b 图线,如图3.3.3所示。
左边一条曲线为复摆倒挂时的b T '-'曲线。
过T 轴上1T T =点作b 轴的平行线交两条曲线于点A 、B 、C 、D 。
则与这4点相对应的4个悬点A '、B '、C '、D '都有共同的周期T 1。
设1b A O =',2b B O =',1b C O '=',2b D O '=',则有 121121122b mg b m Jc mgb mb Jc T ''+=+=ππ或222222122b mg b m Jc mgbmb Jc T ''+=+=ππ消去Jc ,得gb b gb b T 2211122'+='+=ππ(3.3.13)将式(3.3.13)与单摆周期公式相比较 ,可知与复摆周期相同的单摆的摆长 11b b l '+=或 22b b l '+=,故称11b b '+(或22b b '+)为复摆的等值摆长。
复摆实验报告

1.作图如下:
在图中分别取周期为 1.217s,1.204s,1.186s 作与 x 轴平行的直线,和图中交点 的坐标依次为(-24.247,1.217) (-12.538,1.217) (12.421,1.217) (24.334,1.217) (-22.213,1.204) (-13.700,1.204) (13.177, 1.204) (22.678, 1.204) (-17.473,1.186) (17.535,1.186) 由由公式 L=h1 +h1 求出等值单摆长,再由 g= g1=
8.15 26.958 0 1.3497 16.20 23.756 2 1.1878 24.20 24.338 0 1.2169
9.20 26.050 1 1.3025 17.20 23.740 6 1.1870 25.20 24.531 6 1.2266
10.20 25.393 0 1.2697 18.20 23.747 7 1.1874 26.20 24.704 0 1.2352
3研究复摆的振动周期与悬点位置的关系并测定g改变悬点位置从摆杆一端开始知道摆杆另一端测定对应的周期减小测量误差实验时测20个周期的时间合理分布测量点作出th图从图上求出复摆的等值单摆长计算g
复摆实验
实验目的: (1) 研究复摆的物理特性。 (2)用复摆测定重力加速度 (3)用作图法和最小二乘法研究问题及处理数据 仪器用具:复摆(半边长约 30cm,钢铁材质) 光电计时器 米尺及实验所需支 架等。 实验原理:复摆重心距悬点 O 的距离为 h,质量为 m,g 为重力加速度,偏转角 为θ ,则有: M=-mghsin θ,由转动定理 M=Iβ 解得: θ =Acos(ωt + θ0 ) T=2π L=
复摆法测重力加速度

一、复摆法测重力加速度一.实验目的1. 了解复摆的物理特性,用复摆测定重力加速度,2. 学会用作图法研究问题及处理数据。
二.实验原理复摆实验通常用于研究周期与摆轴位置的关系,并测定重力加速度。
复摆是一刚体绕固定水平轴在重力作用下作微小摆动的动力运动体系。
如图1,刚体绕固定轴O在竖直平面内作左右摆动,G是该物体的质心,与轴O的距离为h,θ为其摆动角度。
若规定右转角为正,此时刚体所受力矩与角位移方向相反,则有θM-=, (1)sinmgh又据转动定律,该复摆又有θ IM=,(2) (I为该物体转动惯量) 由(1)和(2)可得θωθsin 2-= , (3) 其中Imgh=2ω。
若θ很小时(θ在5°以内)近似有 θωθ2-= , (4) 此方程说明该复摆在小角度下作简谐振动,该复摆振动周期为mghIT π=2 , (5) 设G I 为转轴过质心且与O 轴平行时的转动惯量,那么根据平行轴定律可知2mh I I G += , (6)代入上式得mghmh I T G 22+=π, (7)设(6)式中的2mk I G =,代入(7)式,得ghh k mgh mh mk T 222222+=+=ππ, (11) k 为复摆对G (质心)轴的回转半径,h 为质心到转轴的距离。
对(11)式平方则有2222244h gk g h T ππ+=, (12)设22,h x h T y ==,则(12)式改写成x gk g y 22244ππ+=, (13)(13)式为直线方程,实验中(实验前摆锤A 和B 已经取下) 测出n 组(x,y)值,用作图法求直线的截距A 和斜率B ,由于gB k g A 2224,4ππ==,所以 ,4,422BAAgk Bg ===ππ (14) 由(14)式可求得重力加速度g 和回转半径k 。
三.实验所用仪器复摆装置、秒表。
四.实验内容1. 将复摆悬挂于支架刀口上,调节复摆底座的两个旋钮,使复摆与立柱对正且平行,以使圆孔上沿能与支架上的刀口密合。
大学物理实验复摆实验讲义

⼤学物理实验复摆实验讲义复摆【实验⽬的】(1)研究复摆的物理特性; (2)⽤复摆测定重⼒加速度;(3)⽤作图法和最⼩⼆乘法研究问题及处理数据。
【仪器⽤具】复摆,光电计时器,电⼦天平,⽶尺等。
【实验原理】1.复摆的振动周期公式在重⼒作⽤下,绕固定⽔平转轴在竖直平⾯内摆动的刚体称为复摆(即物理摆).设⼀复摆 (见图1-1)的质量为m ,其重⼼G 到转轴O 的距离为h ,g 为重⼒加速度,在它运动的某⼀时刻t,参照平⾯(由通过O 点的轴和重⼼G 所决定)与铅垂线的夹⾓为0,相对于O 轴的恢复⼒矩为M=-mgh sin θ(1.1)图 1-1复摆⽰意图根据转动定理, 复摆(刚体)绕固定轴O 转动,有M=I β (1.2)其中M 为复摆所受外⼒矩,I 为其对O 轴的转动惯量,β为复摆绕O 轴转动的⾓加速度, 且22dtd θβ=则有M=I22dt d θ(1.3)结合式(1.1)和式(1.3),有I 22dtd θ+mgh sin θ=0 (1.4) 当摆⾓很⼩的时候, sin θ≈θ, ,式(1.4)化为22dt d θ+θImgh =0 (1.5) 解得θ=A cos(ωt+θ0) (1.6)式中A ,θ由初条件决定;ω是复摆振动的⾓频率,ω=I mgh /,则复摆的摆动周期T=2πmghI(1.7)2.复摆的转动惯量,回转半径和等值单摆长由平⾏轴定理,I=I G +mh 2,式中I G 为复摆对通过重⼼G 并与摆轴平⾏的轴的转动惯量, (1.7)式可写为 T=2πmghmh I G 2+ (1.8)可见, 复摆的振动周期随悬点O 与质量中⼼G 之间的距离h ⽽改变。
还可将I =I G +mh 2改写22G 2I mR mh mR =+= (1.9)式中R G =m I G 为复摆对G 轴的回转半径, 同样也有R=mI, R 称为复摆对悬点O 轴的回转半径。
复摆周期公式也可表⽰为T=2πgh h R G+2 (1.10)事实上, 总可以找到⼀个单摆,它的摆动周期等于给定的复摆的周期,令L =h hR G+2 (1.11)则 T= 2πgL(1.12) 式中L 称为复摆的等值单摆长。
复摆研究(1)

0.400506728 0.056644
18.49489 0.208 18.515437 1.275661425 0.338480911 0.043264
18.480945 18.332464
0.175 18.332605 1.264296851 0.279728142 0.030625
18.331844
g10 g 9.734 9.814 E10 g 9.814
误差分析及实验调整
综上所述,若不忽略摆杆座,将杆制作成对称杆所测量出来的数据存 在很大的误差。分析误差来源,在计算转动惯量的时候未计算摆杆座 与对称摆杆座的转动惯量。如果计算上两个摆杆座的转动惯量,使得 计算过于复杂,不易得出结论且增大实验误差。 经多小组讨论合作, 决定对实验做以下方式修改。
(9)为实验测量值,(11)为理论值,比较两值,求出百分误差。从而验证 转动惯量的平移定理。
用复摆验证转动惯量的平移定理数据处理
h T总 20.279379 T/1
I mg 2 2 (T1 h1 T2 h2 ) 4 2
I m(h1 h2 )
2 2
E
I - I I
I m gh
(5)
由上述方程进行变换得
T2 I m gh 2 4
(6)
所以有
T I1 1 2 mgh1 4
2
(7) (8)
T I 2 2 2 mgh2 4
2
(8)式减(7)式得
T1 T2 mg 2 2 I I1 - I 2 2 mgh1 2 m gh ( T h T 2 1 1 2 h2 ) 4 4 4
1.272364552
0.33349578
0.042436
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
山东理工大学物理实验报告实验名称: 复摆法侧重力加速度姓名:李 明 学号:05 1612 时间代码:110278 实验序号:19院系: 车辆工程系 专业: 车辆工程 级.班: 2 教师签名: 仪器与用具:复摆、秒表。
复摆,一块有刻度的匀质钢板,板面上从中心向两侧对称的开一些悬孔。
另有一固定刀刃架用以悬挂钢板。
调节刀刃水平螺丝,调节刀刃水平。
实验目的:①了解复摆小角摆动周期与回转轴到复摆重心距离的关系。
②测量重力加速度。
实验报告内容(原理预习、操作步骤、数据处理、误差分析、思考题解答)[实验原理]一个围绕定轴摆动的刚体就是复摆。
当复摆的摆动角θ很小时,复摆的振动可视为角谐振动。
根据转动定律有22dtd JJ mgb θβθ-=-=即022=+θθJm g b dtd可知其振动角频率 Jm g b =ω角谐振动的周期为m g b J T π2= (3.3.10)式中J 为复摆对回转轴的转动惯量;m 为复摆的质量;b 为复摆重心至回转轴的距离;g 为重力加速度。
如果用Jc 表示复摆对过质心轴的转动惯量,根据平行轴定理有2mbJc J += (3.3.11)将式(3.3.11)代入式(3.3.10)得 mgbmb Jc T 22+=π(3.3.12)以b 为横坐标,T 为纵坐标,根据实验测得b 、T 数据,绘制以质心为原点的T-b 图线,如图3.3.3所示。
左边一条曲线为复摆倒挂时的b T '-'曲线。
过T 轴上1T T =点作b 轴的平行线交两条曲线于点A 、B 、C 、D 。
则与这4点相对应的4个悬点A '、B '、C '、D '都有共同的周期T 1。
设1b A O =',2b B O =',1b C O '=',2b D O '=',则有 121121122b mg b m Jc mgb mb Jc T ''+=+=ππ或222222122b mg b m Jc mgbmb Jc T ''+=+=ππ消去Jc ,得gb b gb b T 2211122'+='+=ππ(3.3.13)将式(3.3.13)与单摆周期公式相比较 ,可知与复摆周期相同的单摆的摆长 11b b l '+=或 22b b l '+=,故称11b b '+(或22b b '+)为复摆的等值摆长。
因此只要测得正悬和倒悬的T-b 曲线,即可通过作b 轴的平行线,求出周期T 及与之相应的11b b '+或22b b '+,再由式(3.3.13)求重力加速度g 值。
[实验内容](1) 将复摆一端第一个悬孔装在摆架的刀刃上,调解调节螺丝,使刀刃水平,摆体竖直。
(2) 在摆角很小时(θ<︒5),用秒表依次测定复摆在正挂和倒挂时,每一悬点上摆动50个周期的时间it 和i t ',求出相应的周期i T 和i T '。
(3) 将复摆置于水平棱上,找出复摆的重心位置。
测量正挂和倒挂时各悬点与重心的距离i b 和i b '。
注意 悬点的位置不是孔中心位置。
(4) 根据测得数据绘出b T -图线和b T '-'图线。
(5) 由实验图线分别找出五组不同周期对应的等值摆长,分别按式(3.3.13)求出重力加速度g ,并取其平均值,计算标准误差。
并与当地重力加速度标准制作比较。
淄博地区重力加速度g标=9.79878 m/s2.[数据处理]表3.3.2 复摆正挂时的测量值表3.3.3 复摆倒挂时的测量值T =2πgb b '22+ g =222)'(4Tb b +π=222)3.1(10)2911()14.3(4-⨯+⨯=9.69872sm误差分析:复摆在摆动过程中发生一定的扭摆,影响了数据,所以,无法将图做准确。
思考题:(1)设想在复摆的某一位置上加一配重时,其振动周期将如何变化(增大、缩短、不变)?答:不确定,当在下方挂重物时,周期增大。
当在上方挂重物时,周期减少。
笔试测评题:(1)试根据你的实验数据,求复摆的对过质心轴的转动惯量c J 。
答:由mgbmb Jc T 22+=π公式可求c J(2)试比较用单摆法和复摆法测量重力加速度的精确度,说明其精确度高或低的原因?答:单摆周期T =2πgL ∴T 2=4π2gL g =224Tl π要测L 必须是绳和球的长度,测量时产生的误差较大,而复摆法就测量悬点,而且多次测量,因此,减少了误差,所以,复摆法精确度高。
物理实验中心山东理工大学物理实验报告实验名称: 惯性质量测量姓名:王 朋 学号:05 1612 时间代码:110267 实验序号:18院系: 电气工程系 专业: 电气工程 级.班: 2 教师签名: 仪器与用具:惯性秤,周期测定仪,定标用槽码(共10块),待测圆柱体。
实验目的:①掌握用惯性秤测量物体质量的原理和方法。
②测量物体的惯性质量,加深对惯性质量和引力质量的理解。
③了解仪器的定标和使用。
实验报告内容(原理预习、操作步骤、数据处理、误差分析、思考题解答)[实验原理]当惯性秤的悬臂在水平方向作微小振动时,运动可近似地看成简谐振动。
根据牛顿第二定律,有 ()kx dtx d m m i -=+220 式中m 0为惯性秤等效惯性质量;m i 为砝码或其他待测物的惯性质量;k 为秤臂的劲度系数,x 为摆动位移。
其振动方程为x m m k dtx d i+-=022(3.2.1) 振动周期为km m T i+=02π (3.2.2)将式(3.2.2)两侧平方,改写成i m km kT202244ππ+=(3.2.3)式(3.2.3)表明,惯性秤水平振动周期T 的平方和附加质量m i 成线性关系。
当测出各已知附加质量m i 所对应的周期T i ,则可作T 2- m i 直线图(图3.2.1)或T - m i 曲线图(图3.2.2)这就是该惯性秤的定标曲线。
如需测量某物体的质量时,可将其置于惯性秤的秤台B 上,测出周期T j ,就可从定标图线上查出T j 对应的质量m j ,即为被测物体的质量。
惯性秤称量质量,基于牛顿第二定律,是通过测量周期求得质量值;而天平称量质量,基于万有引力定律,是通过比较重力求得质量值。
在失重状态下,无法用天平称量质量,而惯性秤可照样使用,这是惯性秤的特点。
[试验内容](1)调整仪器。
按图3.2.3装好惯性秤,用水平仪调节秤台水平。
(2)对惯性秤定标,作定标曲线。
用周期测定仪先测量空载(m i=0)时的10个振动周期T10。
然后逐次增加一个槽码,直到增加到10个,依次测量出十个振动周期,并求出每一振动周期T及T2。
根据所测数据作T2 - m i或T-m i定标图线。
(3)用惯性秤测量待测物质量。
将待测圆柱体置于秤台中间的孔中,测量振动周期T j,根据定标曲线求出其质量。
(4)考①的细线铅直挂在秤的圆孔中。
此时圆柱体的重量由吊线承担,当秤台振动时,带动圆柱体一起振动,测量其周期。
将此周期和前面测量值比较一下,说明二者有何不同?②垂直放置惯性秤,使秤在铅直面内左右振动,插入定标槽码测量周期。
将其和惯性秤在水平方向振动周期进行比较,说明周期变小的原因。
[数据处理]思考题:(1)说明惯性秤称量质量的特点。
答:惯性秤称量质量,基于牛顿第二定律,是通过测量周期求得质量值;而天平称量质量,基于万有引力定律,是通过比较重力求得质量值。
在失重状态下,无法用天平称量质量,而惯性秤可照样使用,这是惯性秤的特点。
(2)在测量惯性秤周期时,为什么特别强调惯性秤装置水平及摆幅不得太大?答:惯性秤装置水平可以使被测物体的重力不在物体振动的平面上产生分力。
当摆幅过大时会受到较大阻力,再者弹簧片用的时间过长容易变形,从而影响实验结果。
笔试测评题:(1)如何由T2-m i图线求出惯性秤的劲度系数k和惯性质量m0?答:由2T-mi 图求得斜率tanq=R24π,因此R=qtan24π,同理2T-mi 图与y轴的交点b即为R24πm 。
所以b=tanq.M。
因此,m=qbtan。
