2012届高考数学课时复习题35
2012年高考真题汇编——理科数学(解析版)5:三角函数
2012高考真题分类汇编:三角函数一、选择题1.【2012高考真题重庆理5】设tan ,tan αβ是方程2320x x -+=的两个根,则tan()αβ+的值为(A )-3 (B )-1 (C )1 (D )3 【答案】A【解析】因为βαtan ,tan 是方程2320x x -+=的两个根,所以3tan tan =+βα,2tan tan =βα,所以3213tan tan 1tan tan )tan(-=-=-+=+βαβαβα,选A.2.【2012高考真题浙江理4】把函数y=cos2x+1的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),然后向左平移1个单位长度,再向下平移 1个单位长度,得到的图像是【答案】A【解析】根据题设条件得到变化后的函数为)1cos(+=x y ,结合函数图象可知选项A 符合要求。
故选A.3.【2012高考真题新课标理9】已知0ω>,函数()sin()4f x x πω=+在(,)2ππ上单调递减.则ω的取值范围是( )()A 15[,]24 ()B 13[,]24()C 1(0,]2 ()D (0,2]【答案】A【解析】函数)4sin()(πω+=x x f 的导数为)4c o s ()('πωω+=x x f ,要使函数)4sin()(πω+=x x f 在),2(ππ上单调递减,则有0)4cos()('≤+=πωωx x f 恒成立, 则πππωππk x k 223422+≤+≤+,即ππωππk x k 24524+≤≤+,所以Z k k x k ∈+≤≤+,ωπωπωπωπ2424,当0=k 时,ωπωπ454≤≤x ,又ππ<<x 2,所以有πωππωπ≥≤45,24,解得45,21≤≥ωω,即4521≤≤ω,选A. 4.【2012高考真题四川理4】如图,正方形ABCD 的边长为1,延长BA 至E ,使1AE =,连接EC 、ED 则sin CED ∠=( )ABCD【答案】B【解析】2EB EA AB =+=,EC =3424EDC EDA ADC πππ∠=∠+∠=+=,由正弦定理得sin sin 5CED DC EDC CE ∠===∠,所以3sin sin sin 4CED EDC π∠=∠==5.【2012高考真题陕西理9】在ABC ∆中,角,,A B C 所对边长分别为,,a b c ,若2222a b c +=,则cos C 的最小值为( )A.2B. 2C. 12D. 12-【答案】C.【解析】由余弦定理知214242)(212cos 222222222=≥+=+-+=-+=ab ab ab b a ab b a b a ab c b a C ,故选C.6.【2012高考真题山东理7】若42ππθ⎡⎤∈⎢⎥⎣⎦,,sin 2θ,则sin θ=(A )35 (B )45 (C )4(D )34 【答案】D【解析】因为]2,4[ππθ∈,所以],2[2ππθ∈,02cos <θ,所以812s i n 12c o s 2-=--=θθ,又81s i n 212c o s 2-=-=θθ,所以169sin 2=θ,43sin =θ,选D.7.【2012高考真题辽宁理7】已知sin cos αα-=,α∈(0,π),则tan α=(A) -1 (B) - (C) (D) 1 【答案】A【解析一】sin cos )sin()144ππαααα-=-=∴-=3(0),,tan 14παπαα∈∴=∴=- ,,故选A【解析二】2sin cos (sin cos )2,sin 21,ααααα-=∴-=∴=-33(0,),2(0,2),2,,tan 124ππαπαπααα∈∴∈∴=∴=∴=- ,故选A 【点评】本题主要考查三角函数中的和差公式、倍角公式、三角函数的性质以及转化思想和运算求解能力,难度适中。
2012届高考数学第一轮专题复习测试卷第九讲 指数与指数函数 学生

指数与指数函数一、选择题:(本大题共6小题,每小题6分,共36分,将正确答案的代号填在题后的括号内.)1.下列结论中正确的个数是( )①当a <0时,(a 2)32=a 3;②n a n =|a |;③函数y =(x -2)12-(3x -7)0的定义域是(2,+∞);④若100a =5,10b =2,则2a +b =1.A .0B .1C .2D .3 2.(36a 9)4·(63a 9)4(a ≥0)的化简结果是( ) A .a 16 B .a 8C .a 4D .a 23.若函数y =(a 2-5a +5)·a x 是指数函数,则有( )A .a =1或a =4B .a =1C .a =4D .a >0,且a ≠14.在平面直角坐标系中,函数f (x )=2x +1与g (x )=21-x 图象关于( )A .原点对称B .x 轴对称C .y 轴对称D .直线y =x 对称5.若函数f (x )=a |2x -4|(a >0,a ≠1),满足f (1)=19,则f (x )的单调递减区间是( ) A .(-∞,2] B .[2,+∞)C .[-2,+∞)D .(-∞,-2]6.已知函数f (x )=⎝⎛⎭⎫13x -log 2x ,实数a 、b 、c 满足f (a )f (b )f (c )<0(0<a <b <c ),若实数x 0是方程f (x )=0的一个解,那么下列不等式中,不可能成立的是( )A .x 0<aB .x 0>bC .x 0<cD .x 0>c二、填空题:(本大题共4小题,每小题6分,共24分,把正确答案填在题后的横线上.)7.已知不论a 为何正实数,y =a x +1-2的图象恒过定点,则这个定点的坐标是________.8.函数y =(13)x -3x 在区间[-1,1]上的最大值为________. 9.定义:区间[x 1,x 2](x 1<x 2)的长度为x 2-x 1.已知函数y =2|x |的定义域为[a ,b ],值域为[1,2],则区间[a ,b ]的长度的最大值与最小值的差为________.10.设f (x )=e x +e -x 2,g (x )=e x -e -x2,计算f (1)g (3)+g (1)f (3)-g (4)=________,f (3)g (2)+g (3)f (2)-g (5)=________,并由此概括出关于函数f (x )和g (x )的一个等式,使上面的两个等式是你写出的等式的特例,这个等式是________.三、解答题:(本大题共3小题,11、12题13分,13题14分,写出证明过程或推演步骤.)11.已知函数f (x )=b ·a x(其中a ,b 为常量且a >0,a ≠1)的图象经过点A (1,6),B (3,24).(1)试确定f (x );(2)若不等式⎝⎛⎭⎫1a x +⎝⎛⎭⎫1b x -m ≥0在x ∈(-∞,1]时恒成立,求实数m 的取值范围.12.已知函数f (x )=⎝⎛⎭⎫13ax 2-4x +3.(1)若a =-1,求f (x )的单调区间;(2)若f (x )有最大值3,求a 的值.(3)若f (x )的值域是(0,+∞),求a 的取值范围.13.已知函数f (x )=2x -12|x |(1)若f (x )=2,求x 的值;(2)若2t f (2t )+mf (t )≥0对于t ∈[1,2]恒成立,求实数m 的取值范围.。
2012 年全国各地高考数学试题及解答汇编大全
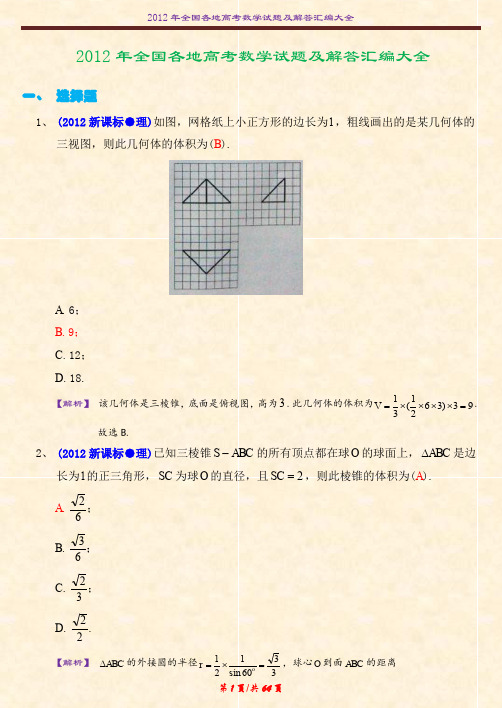
3、 (2012 全国卷大纲版●理)将字母 a,a,b,b,c,c 排成三行两列, 要求每行的字母 互不相同,每列的字母也互不相同,则不同的排列方法共有(A). A. 12 种; B. 18 种; C. 24 种; D. 36 种. 4、 (2012 全国卷大纲版●理)正方形 ABCD 的边长为 1,点 E 在边 AB 上,点 F 在边 BC 上, AE BF
2、 (2012 新课标●理)已知三棱锥 S ABC 的所有顶点都在球 O 的球面上, ABC 是边 长为 1 的正三角形, SC 为球 O 的直径,且 SC 2 ,则此棱锥的体积为(A). A. B. C. D.
2 ; 6
3 ; 6 2 ; 3
2 . 2
【解析】 ABC 的外接圆的半径 r 1 1 o 3 ,球心 O 到面 ABC 的距离 2 sin 60 3 第 1 页/共 64 页
1 1 1 1 f ( y),即 y f 1 ( x) g ( x) 知, y f (2 x) 的 2 2 2
反函数是 y 1 g ( x) ,故函数 y f (2 x) 与 y 1 g ( x) 的图像也关于直线 y x 对称;正 2 2 确. ③ f ( x) f (2 x) f ( x 2) f [2 ( x 2)] f (4 x) f ( x 4) .故 f ( x) 是周期为 4 的函数. 故选 C.
由对称性知, y x,y 1 , ( x 1) 2 ( y 1) 2 1 围成的面积与 x
1 y x,y , ( x 1)2 ( y 1)2 1 围成的面积相等. x
故 A B 所表示的平面图形的面积为 y x , ( x 1)2 ( y 1)2 1 围成的面积
2012年高考数学试题分类汇编--立体几何

2012年高考真题理科数学解析汇编:立体几何一、选择题错误!未指定书签。
.(2012年高考(新课标理))已知三棱锥S ABC -的所有顶点都在球O 的求面上,ABC ∆是边长为1的正三角形,SC 为球O 的直径,且2SC =;则此棱锥的体积为( )ABC.D.2错误!未指定书签。
.(2012年高考(新课标理))如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则此几何体的体积为A .6B .9C .12 D .18错误!未指定书签。
.(2012年高考(浙江理))已知矩形ABCD ,AB =1,BC将∆ABD 沿矩形的对角线BD 所在的直线进行翻着,在翻着过程中, ( )A .存在某个位置,使得直线AC 与直线BD 垂直B .存在某个位置,使得直线AB 与直线CD 垂直C .存在某个位置,使得直线AD 与直线BC 垂直D .对任意位置,三直线“AC 与BD ”,“AB 与CD ”,“AD 与BC ”均不垂直错误!未指定书签。
.(2012年高考(重庆理))设四面体的六条棱的长分别为和a ,且长为a ,则a 的取值范围是 ( )A .B .C .D .错误!未指定书签。
.(2012年高考(四川理))如图,半径为R 的半球O 的底面圆O 在平面α内,过点O 作平面α的垂线交半球面于点A ,过圆O 的直径CD 作平面α成45角的平面与半球面相交,所得交线上到平面α的距离最大的点为B ,该交线上的一点P 满足60BOP ∠=,则A 、P 两点间的球面距离为( )A .RB .4R πC .RD .3R π错误!未指定书签。
.(2012年高考(四川理))下列命题正确的是( )A .若两条直线和同一个平面所成的角相等,则这两条直线平行B .若一个平面内有三个点到另一个平面的距离相等,则这两个平面平行C .若一条直线平行于两个相交平面,则这条直线与这两个平面的交线平行D .若两个平面都垂直于第三个平面,则这两个平面平行 错误!未指定书签。
2012年全国各地高考数学试题及解答分类汇编大全(01 集合)

2012年全国各地高考数学试题及解答分类汇编大全(01集合)一、选择题:1.(2012安徽文)设集合{3213}A x x =-≤-≤,集合B 是函数lg(1)y x =-的定义域;则A B =( )A.(1,2)B. [1,2]C. [,)12 D .(,]12【解析】选D{3213}[1,2]A x x =-≤-≤=-,(1,)(1,2]B A B =+∞⇒=2.(2012北京文、理)已知集合A={x ∈R|3x+2>0} B={x ∈R|(x+1)(x-3)>0} 则A ∩B=( ) A .(-∞,-1) B .(-1,-23) C .(-23,3) D . (3,+∞) 【解析】和往年一样,依然的集合(交集)运算,本次考查的是一次和二次不等式的解法。
因为32}023|{->⇒>+∈=x x R x A ,利用二次不等式可得1|{-<=x x B 或}3>x 画出数轴易得:}3|{>=x x B A .故选D .【答案】D3. (2012福建文)已知集合M={1,2,3,4},N={-2,2},下列结论成立的是( ) A.N ⊆M B.M ∪N=M C.M ∩N=N D.M ∩N={2}4. (2012广东文) 设集合{1,2,3,4,5,6}U =,{1,3,5}M =,则U M =ð( ) A. {2,4,6} B. {1,3,5} C. {1,2,4} D. U 4. A. U M =ð{2,4,6}.5.(2012广东理)设集合}6,5,4,3,2,1{=U ,}4,2,1{=M ,则M C U =( )A .UB .}5,3,1{C .}6,5,3{D .}6,4,2{ 解析:(C ).6.(2012湖北文) 已知集合A{x| 2x -3x +2=0,x ∈R } , B={x|0<x <5,x ∈N },则满足 条件A ⊆C ⊆B 的集合C 的个数为( ) A 1 B 2 C 3 D 4 6.D 【解析】求解一元二次方程,得{}()(){}2|320,|120,A x x x x x x x x =-+=∈=--=∈R R{}1,2=,易知{}{}|05,1,2,3,4=<<∈=N B x x x .因为⊆⊆A C B ,所以根据子集的定义,集合C 必须含有元素1,2,且可能含有元素3,4,原题即求集合{}3,4的子集个数,即有224=个.故选D.【点评】本题考查子集的概念,不等式,解一元二次方程.本题在求集合个数时,也可采用列举法.列出集合C 的所有可能情况,再数个数即可.来年要注意集合的交集运算,考查频度极高.7. (2012湖南文)设集合M={-1,0,1},N={x|x 2=x},则M ∩N=( )A.{-1,0,1}B.{0,1}C.{1}D.{0} 【答案】B 【解析】{}0,1N = M={-1,0,1} ∴M ∩N={0,1}【点评】本题考查了集合的基本运算,较简单,易得分.先求出{}0,1N =,再利用交集定义得出M ∩N.8 (2012湖南理) 设集合M={-1,0,1},N={x|x 2≤x},则M ∩N=( )A.{0}B.{0,1}C.{-1,1}D.{-1,0,0}【答案】B 【解析】{}0,1N = M={-1,0,1} ∴M ∩N={0,1}.【点评】本题考查了集合的基本运算,较简单,易得分. 先求出{}0,1N =,再利用交集定义得出M ∩N.9. (2012江西文) 若全集U={x ∈R |x 2≤4} A={x ∈R ||x+1|≤1}的补集CuA 为( ) A |x ∈R |0<x <2| B |x ∈R |0≤x <2| C |x ∈R |0<x≤2| D |x ∈R |0≤x≤2|【答案】C【解析】考查集合的基本运算{|22}U x x =-≤≤,{|20}A x x =-≤≤,则{|02}U C A x x =<≤. 10、(2012江西理) 若集合{1,1}A =-,{0,2}B =,则集合{|,,}z z x y x A y B =+∈∈中的元素的个数为( )A .5 B.4 C .3 D.210.C 【解析】本题考查集合的概念及元素的个数.容易看出x y +只能取-1,1,3等3个数值.故共有3个元素.【点评】集合有三种表示方法:列举法,图像法,解析式法.集合有三大特性:确定性,互异性,无序性.本题考查了列举法与互异性.来年需要注意集合的交集等运算,Venn 图的考查等.12. (2012辽宁文、理)已知全集U={0,1,2,3,4,5,6,7,8,9},集合A={0,1,3,5,8},集合B={2,4,5,6,8},则)()(B C A C U U 为( )(A){5,8} (B){7,9} (C){0,1,3} (D){2,4,6} 【答案】B【解析一】因为全集U={0,1,2,3,4,5,6,7,8,9},集合A={0,1,3,5,8},集合B={2,4,5,6,8},所以{}{}9,7,3,1,0,9,7,6,4,2==B C A C U U ,所以)()(B C A C U U 为{7,9}。
2012届高考数学第一轮复习精品试题:函数-学生版

2012届高考数学第一轮复习精品试题:函数§2.1.1 函数的概念和图象经典例题:设函数f (x )的定义域为[0,1],求下列函数的定义域: (1)H (x )=f (x2+1);(2)G (x )=f (x+m )+f (x -m )(m >0).当堂练习:1. 下列四组函数中,表示同一函数的是( ) A.(),()f x x g x ==B.2(),()f x x g x ==C .21(),()11x f x g x x x -==+- D.()()f x g x ==2函数()y f x =的图象与直线x a =交点的个数为( )A .必有一个B .1个或2个C .至多一个D .可能2个以上3.已知函数1()1f x x =+,则函数[()]f f x 的定义域是( )A .{}1x x ≠ B .{}2x x ≠- C .{}1,2xx ≠-- D .{}1,2x x ≠-4.函数1()1(1)f x x x =--的值域是( )A .5[,)4+∞B .5(,]4-∞C . 4[,)3+∞D .4(,3-∞ 5.对某种产品市场产销量情况如图所示,其中:1l 表示产品各年年产量的变化规律;2l 表示产品各年的销售情况.下列叙述: ( )(1)产品产量、销售量均以直线上升,仍可按原生产计划进行下去;(2)产品已经出现了供大于求的情况,价格将趋跌;(3)产品的库存积压将越来越严重,应压缩产量或扩大销售量;(4)产品的产、销情况均以一定的年增长率递增.你认为较合理的是( ) A .(1),(2),(3) B .(1),(3),(4) C .(2),(4) D .(2),(3)6.在对应法则,,,x y y x b x R y R→=+∈∈中,若25→,则2-→ , →6.7.函数()f x 对任何x R +∈恒有1212()()()f x x f x f x ⋅=+,已知(8)3f =,则f = .8.规定记号“∆”表示一种运算,即a b a b a b R+∆++∈,、. 若13k ∆=,则函数()fx k x=∆的值域是___________.9.已知二次函数f(x)同时满足条件: (1) 对称轴是x=1; (2) f(x)的最大值为15;(3) f(x)的两根立方和等于17.则f(x)的解析式是 .10.函数2522y x x =-+的值域是 .11. 求下列函数的定义域 : (1)()121x f x x =-- (2)(1)()x f x x x+=-12.求函数y x =13.已知f(x)=x2+4x+3,求f(x)在区间[t,t+1]上的最小值g(t)和最大值h(t).14.在边长为2的正方形ABCD 的边上有动点M ,从点B 开始,沿折线BCDA 向A 点运动,设M 点运动的距离为x ,△ABM 的面积为S . (1)求函数S=的解析式、定义域和值域; (2)求f[f(3)]的值.§2.1.2 函数的简单性质经典例题:定义在区间(-∞,+∞)上的奇函数f (x )为增函数,偶函数g (x )在[0,+∞ )上图象与f (x )的图象重合.设a >b >0,给出下列不等式,其中成立的是 f (b )-f (-a )>g (a )-g (-b ) ②f (b )-f (-a )<g (a )-g (-b )③f (a )-f (-b )>g (b )-g (-a ) ④f (a )-f (-b )<g (b )-g (-a ) A .①④ B .②③ C .①③ D .②④ 当堂练习:1.已知函数f(x)=2x2-mx+3,当()2,x ∈-+∞时是增函数,当(),2x ∈-∞-时是减函数,则f(1)等于 ( )A .-3B .13C .7D .含有m 的变量2.函数1()x f x -=是( )A . 非奇非偶函数B .既不是奇函数,又不是偶函数奇函数C . 偶函数D . 奇函数3.已知函数(1)()11f x x x =++-,(2)()f x =2()33f x x x =+(4)0()()1()R x Q f x x C Q ∈=∈⎧⎨⎩,其中是偶函数的有( )个 A .1 B .2 C .3 D .44.奇函数y=f (x )(x ≠0),当x ∈(0,+∞)时,f (x )=x -1,则函数f (x -1)的图象为( )5.已知映射f:A →B,其中集合A={-3,-2,-1,1,2,3,4},集合B 中的元素都是A 中元素在映射f 下的象,且对任意的A a ∈,在B 中和它对应的元素是a,则集合B 中元素的个数是( )A .4B .5C .6D .76.函数2()24f x x tx t =-++在区间[0, 1]上的最大值g(t)是 .7. 已知函数f(x)在区间(0,)+∞上是减函数,则2(1)f x x ++与()34f 的大小关系是 .8.已知f(x)是定义域为R 的偶函数,当x<0时, f(x)是增函数,若x1<0,x2>0,且12x x <,则1()f x 和2()f x 的大小关系是 .9.如果函数y=f(x+1)是偶函数,那么函数y=f(x)的图象关于_________对称.10.点(x,y)在映射f作用下的对应点是(,)22y x +-,若点A 在f 作用下的对应点是B(2,0),则点A 坐标是 .13. 已知函数2122()x x f x x++=,其中[1,)x ∈+∞,(1)试判断它的单调性;(2)试求它的最小值.14.已知函数2211()a f x aa x+=-,常数0>a 。
(理科)(大纲版)2012年全国统一高考数学试卷答案与解析

2012年全国统一高考数学试卷(理科)(大纲版)参考答案与试题解析一、选择题(共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.(5分)(2014•大庆二模)复数=()的分子分母都乘以分母的共轭复数,得=或.C D.轴上,且椭圆的方程为4.(5分)已知正四棱柱ABCD﹣A 1B1C1D1中,AB=2,,E为CC1的中点,则直线AC1与平面BED的C DEC=×××BD=2BE=DE==2×=2×h=5.(5分)(2014•重庆三模)已知等差数列{a n}的前n项和为S n,a5=5,S5=15,则数列的前100项和为.C D.=∴==6.(5分)△ABC中,AB边的高为CD,若=,=,•=0,||=1,||=2,则=().C D.,进而可求,从而可求与解:∵•=0∵||=1||=2AB=∴∴∴7.(5分)(2014•宜春模拟)已知α为第二象限角,,则cos2α=()D.=,两边平方得:=﹣,)×8.(5分)(2014•闸北区三模)已知F1、F2为双曲线C:x2﹣y2=2的左、右焦点,点P在C上,|PF1|=2|PF2|,则cos∠F1PF2=.C D.,==9.(5分)(2014•湖北)已知x=lnπ,y=log52,,则(),>,即可得到答案.5=,=>,即(311.(5分)将字母a,a,b,b,c,c排成三行两列,要求每行的字母互不相同,每列的字母也互不相同,则不同12.(5分)正方形ABCD的边长为1,点E在边AB上,点F在边BC上,,动点P从E出发沿直线向F运动,每当碰到正方形的边时反弹,反弹时反射角等于入射角,当点P第一次碰到E时,P与正方形的边碰撞的CG=DH=二、填空题:本大题共4小题,每小题5分,共20分,把答案填在题中横线上.(注意:在试题卷上作答无效)13.(5分)若x,y满足约束条件则z=3x﹣y的最小值为﹣1.解:作出不等式组14.(5分)(2014•武汉模拟)当函数y=sinx﹣cosx(0≤x<2π)取得最大值时,x=.﹣cosx cosx=2sinx cosx﹣﹣<,=,x=.故答案为:)15.(5分)若的展开式中第3项与第7项的二项式系数相等,则该展开式中的系数为56.解:由题意可得,此时系数为16.(5分)三棱柱ABC﹣A1B1C1中,底面边长和侧棱长都相等,∠BAA1=∠CAA1=60°,则异面直线AB1与BC1所成角的余弦值为.=,,,∵∴()﹣++=|==|===<,=所成角的余弦值为三.解答题:本大题共6小题,共70分,解答应写出文字说明,证明过程或演算步骤.17.(10分)△ABC的内角A、B、C的对边分别为a、b、c,已知cos(A﹣C)+cosB=1,a=2c,求C.,sinAsinC=①sinC=18.(12分)如图,四棱锥P﹣ABCD中,底面ABCD为菱形,PA⊥底面ABCD,,PA=2,E是PC上的一点,PE=2EC.(Ⅰ)证明:PC⊥平面BED;(Ⅱ)设二面角A﹣PB﹣C为90°,求PD与平面PBC所成角的大小.,(2),﹣∴2,(,()∴=﹣=0•=0),(的法向量为,则,=,则,﹣),∴•﹣b=∴,,(﹣,﹣<,==19.(12分)乒乓球比赛规则规定:一局比赛,双方比分在10平前,一方连续发球2次后,对方再连续发球2次,依次轮换.每次发球,胜方得1分,负方得0分.设在甲、乙的比赛中,每次发球,发球方得1分的概率为0.6,各次发球的胜负结果相互独立.甲、乙的一局比赛中,甲先发球.(Ⅰ)求开始第4次发球时,甲、乙的比分为1比2的概率;(Ⅱ)ξ表示开始第4次发球时乙的得分,求ξ的期望.1,根据120.(12分)设函数f(x)=ax+cosx,x∈[0,π].(Ⅰ)讨论f(x)的单调性;(Ⅱ)设f(x)≤1+sinx,求a的取值范围.,构造函数)x;②≤﹣时,∵,即x时,有时,,当时,≤≤21.(12分)已知抛物线C:y=(x+1)2与圆(r>0)有一个公共点A,且在A处两曲线的切线为同一直线l.(Ⅰ)求r;(Ⅱ)设m,n是异于l且与C及M都相切的两条直线,m,n的交点为D,求D到l的距离.,到该切线的距离为,建立方程,求得,的斜率×=r=|MA|=到该切线的距离为∴﹣﹣﹣的距离为22.(12分)函数f(x)=x2﹣2x﹣3,定义数列{ x n}如下:x1=2,x n+1是过两点P(4,5),Q n(x n,f(x n))的直线PQ n与x轴交点的横坐标.(Ⅰ)证明:2≤x n<x n+1<3;(Ⅱ)求数列{ x n}的通项公式.的方程为时,可得,可得,可得是以﹣为首项,的方程为时,∴的方程为时,∴,∴,可得,∴∴∴是以﹣为首项,∴∴∴。
2012届江苏高考数学二轮复习:教案+学案+课后训练(含完整答案)整套word稿-课时答案

专题一集合、简单逻辑用语、函数、不等式、导数及应用第1讲集合与简单逻辑用语1. x<0,有x2≤02. (2,3)解析:M=(-∞,3),N=(2,+∞),∴ M∩N=(2,3).3. (-∞,-1)∪(3,+∞)解析:不等式对应的二次函数开口向上,则Δ=(a-1)2-4>0.4. [-1,1]解析:集合A=[-1,1],B=(-∞,1],∴ A∩B=A.5.215解析:⎩⎪⎨⎪⎧0≤a,a+45≤10≤a≤15,⎩⎪⎨⎪⎧b-13≥0,b≤113≤b≤1,利用数轴,分类讨论可得集合A∩B的“长度”的最小值为13-15=215.6. ⎣⎡⎦⎤-12,13解析:p:x2+x-6<0为真,则不等式的解集为A=(-3,2),由q:mx +1>0得m=0时,解集为B=R,m>0时,解集为B=⎝⎛⎭⎫-1m,+∞,m<0时,解集为B=⎝⎛⎭⎫-∞,-1m,m=0时,A B成立;m>0时,-1m≤-3,0<m≤13;m<0时,-1m≥2,-12≤m<0,综上m∈⎣⎡⎦⎤-12,13.7. 12解析:这是一个典型的用韦恩图来求解的问题,如图.设两者都喜欢的人数为x,则只喜爱篮球的有15-x,只喜爱乒乓球的有10-x,由此可得(15-x)+(10-x)+x+8=30,解得x=3,所以15-x=12,即所求人数为12.8. (-∞,-4)∪(42,+∞)解析:两集合分别表示半圆和直线,画图利用几何性质可得答案.9. 解:(1) 2-x+3x+1≥02x+2-(x+3)x+1≥0x-1x+1≥0(x-1)(x+1)≥0且x≠-1x≥1或x<-1.∴集合A={x|x≥1或x<-1}.(2) (x-a-1)(2a-x)>0(a<1)(x-a-1)(x-2a)<0.∵a<1,∴2a<a+1.∴2a<x<a +1.∴不等式的解为2a<x<a+1.∴集合B={x|2a<x<a+1}.∵B A,∴2a≥1或a +1≤-1,∴ a≥12或a≤-2.又a<1,则实数a的取值范围是(-∞,-2]∪⎣⎡⎭⎫12,1.10. 解:若命题p为真,则⎩⎪⎨⎪⎧m2-4>0,-m<0m>2.若命题q为真,Δ=16(m-2)2-16<0,1<m<3.p或q为真,p且q为假,所以若命题p为真,命题q为假,则m≥3;若命题p 为假,命题q为真,则1<m≤2,综上,则实数m的取值范围是{m|1<m≤2或m≥3}.第2讲函数、图象及性质1. f(x)=(x-2)2解析:函数满足f(x)=f(x+2),函数周期为2.则x∈[2,3],x-2∈[0,1],f(x)=f(x -2)=(x -2)2.2. (0,1] 解析:y =x x -m =1+m x -m,由反比例函数性质可得到0<m ≤1;也可以用导数求得.3. 12 解析:f(-x)=12-x -1+a =2x 1-2x+a ,f(-x)=-f(x) 2x 1-2x +a =-⎝⎛⎭⎫12x -1+a 2a =11-2x -2x 1-2x=1,故a =12;也可用特殊值代入,但要检验.4. 1<a <2 解析:函数为奇函数,在(-1,1)上单调递减,f(1-a)+f(1-a 2)>0,得f(1-a)>f(a 2-1).∴ ⎩⎪⎨⎪⎧-1<1-a <1,-1<1-a 2<11-a <a 2-1,1<a < 2.5. [3,+∞) 解析:⎩⎪⎨⎪⎧|x -2|-1≥0,x -1>0,x -1≠1⎩⎪⎨⎪⎧x -2≥1或x -2≤-1,x >1,x ≠2x ≥3.6. 2 解析:函数满足f(x +2)=1f (x ),故f(x +4)=1f (x +2)=f(x),函数周期为4,f(2 012)=f(0),又f(2)=1f (0),∴ f(0)=2.7. 3 解析:画图可知a +(-1)2=1,a =3,也可利用f(0)=f(2)求得,但要检验.8. 1 解析:由y =|x 2-2x -t|得y =|(x -1)2-1-t|,函数最大值只能在y(0),y(1),y(3)中取得,讨论可得只有t =1时成立.9. 解:(1) ∵ f(a +2)=18,f(x)=3x ,∴ 3a +2=183a =2, ∴ g(x)=(3a )x -4x =2x -4x ,x ∈[-1,1].(2) g(x)=-(2x )2+2x =-⎝⎛⎭⎫2x -122+14,当x ∈[-1,1]时,2x ∈⎣⎡⎦⎤12,2,令t =2x ,∴ y =-t 2+t =-⎝⎛⎭⎫t -122+14,由二次函数单调性知当t ∈⎣⎡⎦⎤12,2时y 是减函数,又t =2x 在[-1,1]上是增函数,∴ 函数g(x)在[-1,1]上是减函数.(也可用导数的方法证明)(3) 由(2)知t =2x,2x ∈⎣⎡⎦⎤12,2,则方程g(x)=m 有解m =2x -4x在[-1,1]内有解m =t -t 2=-⎝⎛⎭⎫t -122+14,t ∈⎣⎡⎦⎤12,2, ∴ m 的取值范围是⎣⎡⎦⎤-2,14. 10. (1) 证明:取x =y =0,f(0)=f(0)+f(0),∴ f(0)=0,取y =-x ,则f(0)=f(x)+f(-x),∴ f(-x)=-f(x),故f(x)是奇函数.(2)解: 任取x 2>x 1,则x 2-x 1>0,∴ f(x 2-x 1)<0,又f(x 2-x 1)=f(x 2)+f(-x 1)=f(x 2)-f(x 1)<0,∴ f(x 2)<f(x 1),f(x)在[-3,3]上单调递减,f(-3)=-f(3)=-3f(1)=6,∴ f(x)在[-3,3]上的最大值f(-3)=6,最小值f(3)=-6.第3讲 基本初等函数1. 2 解析:lg 22+lg2lg5+lg50=lg2(lg2+lg5)+lg5+lg10=lg2lg(2·5)+lg5+1=2.2. a ∈(1,2) 解析:y =log a (2-ax)是[0,1]上关于x 的减函数,∴ ⎩⎪⎨⎪⎧a >1,2-a >01<a <2.3. [-3,1] 解析:2x 2+2x -4≤122x 2+2x -4≤2-1x 2+2x -4≤-1x 2+2x -3≤0-3≤x ≤-1.4. (2,2)5. a ≥2 解析: 二次函数f(x)=-x 2+2ax -1+a 2开口向下,对称轴x =-2a-2=a ,则a ≥2.6. ⎣⎡⎦⎤1,3127 解析:f(x)为偶函数,则b =0,又a -1+2a =0,∴ a =13,f(x)=13x 2+1在⎣⎡⎦⎤-23,23上的值域为⎣⎡⎦⎤1,3127.7. f(-25)<f(80)<f(11) 解析:∵ f(x -4)=-f(x),∴ f(x -4)=f(x +4),∴ 函数周期T =8.∵ f(x)为奇函数,在区间[0,2]上是增函数,∴ f(x)在[-2,2]上是增函数.则f(-25)=f(-1),f(11)=f(3)=-f(-1)=f(1),f(80)=f(0).∵ f(-1)<f(0)<f(1),∴ f(-25)<f(80)<f(11).8. 4 解析:函数图象恒过定点(1,1),从而m +n =1,又mn >0,∴ 1m +1n =m +n m +m +nn=2+n m +m n ≥4,当且仅当m =n 时取等号,1m +1n的最小值为4.9. 解:f(x)=12p x 2-x +3=12p (x -p)2+3-p 2.① p ≤-1时,f(x)在[-1,2]上递减,M =f(-1)=12p +4,m =f(2)=2p +1,由2M +m =3,得p =-12(舍).② -1<p <0,M =f(p)=3-p 2,m =f(2)=2p +1,由2M +m =3,得p =2-6,p =2+6(舍).③ 0<p <12,M =f(2),m =f(p),由2M +m =3,得p =2±23(舍).④ 12≤p ≤2,M =f(-1),m =f(p)由2M +m =3,得p =8±66(舍). ⑤ p >2,M =f(-1),m =f(2)由2M +m =3,得p =-12(舍).综上,当p =2-6时,2M +m =3成立.10. 解:(1) 设P(x 0,y 0)是y =f(x)图象上的点,Q(x ,y)是y =g(x)图象上的点,则⎩⎪⎨⎪⎧ x =x 0-2a ,y =-y 0.∴ ⎩⎪⎨⎪⎧x 0=x +2a ,y 0=-y.又y 0=log a (x 0-3a),∴ -y =log a (x +2a -3a ),∴ y =log a1x -a (x >a),即y =g(x)=log a 1x -a(x >a). (2) ∵ ⎩⎪⎨⎪⎧x -3a >0,x -a >0,∴ x >3a ,∵ f(x)与g(x)在x ∈[a +2,a +3]上有意义,∴ 3a <a +2,0<a <1,∵ |f(x)-g(x)|≤1恒成立,∴ |log a (x -3a)(x -a)|≤1恒成立.∴⎩⎪⎨⎪⎧-1≤log a [(x -2a )2-a 2]≤1,0<a <1a ≤(x -2a)2-a 2≤1a.对x ∈[a +2,a +3]时恒成立,令h(x)=(x -2a)2-a 2,其对称轴x =2a,2a <2,而2<a +2,∴ 当x ∈[a +2,a +3]时,h(x)min =h(a +2),h(x)max =h(a +3).∴ ⎩⎪⎨⎪⎧a ≤h (x )min ,1a ≥h (x )max⎩⎪⎨⎪⎧a ≤4-4a ,1a ≥9-6a0<a ≤9-5712.第4讲 函数的实际应用1. log 32 解析:本题主要考查分段函数和简单的已知函数值求x 的值.由⎩⎪⎨⎪⎧x ≤1,3x=2x =log 32或⎩⎪⎨⎪⎧x >1,-x =2无解,故应填log 32.2. 20% 解析:设该产品初始成本为a ,每年平均降低百分比为p ,则a(1-p)2=0.64a ,∴ p =0.2.3. m ∈(1,2) 解析:令f(x)=x 2-2mx +m 2-1,则⎩⎪⎨⎪⎧f (0)>0,f (1)<0,f (2)<0,f (3)>0.解得1<m <2.4. a >1 解析:设函数y =a x (a >0,且a ≠1)和函数y =x +a ,则函数f(x)=a x -x -a(a>0且a ≠1)有两个零点, 就是函数y =a x (a >0且a ≠1)与函数y =x +a 有两个交点,由图象可知当0<a <1时两函数只有一个交点,不符合要求,当a >1时,因为函数y =a x (a >1)的图象过点(0,1),而直线y =x +a 所过的点一定在点(0,1)的上方,所以一定有两个交点.所以实数a 的取值范围是a >1.5. 14 解析:设每个销售定价为x 元,此时销售量为100-10(x -10),则利润y =(x -8)[100-10(x -10)]=10(x -8)(20-x)≤10⎝⎛⎭⎫x -8+20-x 22=360,当且仅当x =14时取等号.6. ⎝⎛⎭⎫-1,-13 解析:由题意得f(1)·f(-1)<0,即(3a +1)(a +1)<0,-1<a <-13. 7. 6 解析:⎩⎨⎧-a +22=1,a +b2=1b =6.8. ①③④ 解析:函数f(x)=-|x|x 2+bx 2+c 为偶函数,当x ≥0时,f(x)=-x 3+bx 2+c ,b <0,∴ f ′(x)=-3x ⎝⎛⎭⎫x -2b3≤0对x ∈[0,+∞)恒成立,∴ x =0时,f(x)在R 上有最大值,f(0)=c ;由于f(x)为偶函数,②不正确;取b =3,c =-2③正确;若b <0,取a =0,若b ≥0,取a =2b3,故一定存在实数a ,使f(x)在[a ,+∞)上单调减.9. (1)证明:由条件知f(2)=4a +2b +c ≥2恒成立.又∵ x =2时,f(2)=4a +2b +c ≤18(2+2)2=2恒成立,∴ f(2)=2.(2)解: ∵ ⎩⎪⎨⎪⎧4a +2b +c =2,4a -2b +c =0,∴ 4a +c =2b =1,∴ b =12,c =1-4a.又f(x)≥x 恒成立,即ax 2+(b -1)x +c ≥0恒成立. ∴ a >0,Δ=⎝⎛⎭⎫12-12-4a(1-4a)≤0,∴(8a -1)2≤0. 解得:a =18,b =12,c =12,∴ f(x)=18x 2+12x +12.(3)解:(解法1) 由分析条件知道,只要f(x)图象(在y 轴右侧部分,包含与y 轴交点)总在直线y =m 2x +14上方即可,也就是直线的斜率m2小于直线与抛物线相切时的斜率,∴⎩⎨⎧y =18x 2+12x +12,y =m 2x +14,解得 m ∈⎝⎛⎭⎫-∞,1+22. (解法2)g(x)=18x 2+⎝⎛⎭⎫12-m 2x +12>14在x ∈[0,+∞)必须恒成立, 即x 2+4(1-m)x +2>0在x ∈[0,+∞)恒成立. ① Δ<0,即[4(1-m)]2-8<0,解得:1-22<m <1+22; ② ⎩⎪⎨⎪⎧Δ≥0,-2(1-m )≤0,f (0)=2>0,解得:m ≤1-22. 综上,m ∈⎝⎛⎭⎫-∞,1+22. 10. (1)证明: 当x ≥7时,f(x +1)-f(x)=0.4(x -3)(x -4),而当x ≥7时,函数y =(x -3)(x -4)单调递增,且(x -3)(x -4)>0, 故f(x +1)-f(x)单调递减,∴ 当x ≥7时,掌握程度的增长量f(x +1)-f(x)总是下降.(2)解: 由题意可知0.1+15ln a a -6=0.85,整理得aa -6=e 0.05,解得a =e 0.05e 0.05-1·6=20.50×6=123.0,123.0∈(121,127],由此可知,该学科是乙学科.第5讲 不等式及其应用1. (-∞,-2)∪(3,+∞)2. (-1,2) 解析:由已知得a <0,b =-a ,ax -b x -2>0即为ax +a x -2>0,得x +1x -2<0,得-1<x <2.3. -6 解析:作出可行域,求出凸点坐标分别为(3,-3),(4,-5),(5,-1),(6,-3),则最优解为(4,-5);或让直线t =x +2y 平行移动,当直线过点(4,-5)时,目标函数取最小值.4.116 解析:∵ x ,y ∈R +,∴ 1=x +4y ≥2x·4y ,∴ xy ≤116,当且仅当x =4y ,即x =12,y =18时取等号. 5. 9 解析:∵ x >0,y >0,1x +4y =1,∴ x +y =(x +y)⎝⎛⎭⎫1x +4y =5+y x +4xy ≥5+2y x ·4x y=9,当且仅当y x =4xy,即x =3,y =6时取等号.6. m ≤-5 解析:x 2+mx +4<0,x ∈(1,2)可得m <-⎝⎛⎭⎫x +4x ,而函数y =-⎝⎛⎭⎫x +4x 在(1,2)上单调增,∴ m ≤-5.7. ⎣⎡⎦⎤95,6 解析:变量x ,y 满足约束条件构成的区域是以(1,3),(1,6),⎝⎛⎭⎫52,92三点为顶点的三角形区域(含边界),y x 表示区域内的点与原点连线的斜率,∴ y x ∈⎣⎡⎦⎤95,6 8. x ≥1 解析:n n +1=1-1n +1<1,当n 无限变大时,nn +1的值趋近于1,不等式要恒成立,显然x >12,2x -1|x|>n n +1等价于2x -1x ≥1且x >12,故x ≥1.9. 解:(1) y =2 150+10×55+⎝⎛⎭⎫a 6x 2+13x (55-1)x =2 700x +9ax +18.(0<x ≤20,12≤a ≤1).(2) 当34≤a ≤1时,y ≥22 700x·9ax +18=1803a +18. 当且仅当2 700x =9ax ,即x =300a时取等号. 即当x =300a时,y min =1803a +18; 当12≤a <34时,y ′=-2 700x 2+9a <0,故y =f(x)在(0,20]上是减函数, 故当x =20时,y min =2 70020+180a +18=153+180a. 答:若12≤a <34,则当车队速度为20 m/s 时,通过隧道所用时间最少;若34≤a ≤1时,则当车队速度为300am/s 时,通过隧道所用时间最少.10. 解:(1) ⎩⎪⎨⎪⎧f (0)=0,f (-2)=0⎩⎪⎨⎪⎧b =6,c =0,∴ f(x)=3x 2+6x ; (2) g(x)=3⎣⎡⎦⎤x +⎝⎛⎭⎫1+m 62-2-3×⎝⎛⎭⎫1+m 62,-⎝⎛⎭⎫1+m 6≤2,m ≥-18; (3) f(x)+n ≤3即n ≤-3x 2-6x +3,而x ∈[-2,2]时,函数y =-3x 2-6x +3的最小值为-21,∴ n ≤-21,实数n 的最大值为-21.第6讲 导数及其应用1. f(x)=x 2+2x +12. 98 解析:f ′(2)=4.5-4=-98,切线方程为y =-98x +92,∴ f(2)=94. 3. y =x -1 解析:y ′=3x 2-2,k =y ′x =1=1,则切线方程y -0=1·(x -1), ∴ x -y -1=0.4. ⎣⎡⎭⎫0,π2∪⎣⎡⎭⎫2π3,π 解析:y ′=3x 2-3≥-3,∴ tanα≥-3,0≤α<π且α≠π2,结合正切函数图象可得答案.5. a ≥-4 解析:x ∈(0,+∞),f ′(x)=1x +4x +a ≥0恒成立,由基本不等式1x +4x+a ≥4+a ,当且仅当x =12时取等号,∴ a +4≥0,∴ a ≥-4.6. 32 解析:f(x)=x 3-12x +8,f ′(x)=3(x -2)(x +2),则f(x)的单调增区间是[-3,-2]∪[2,3],减区间是[-2,2],f(-3)=17,f(2)=-8,f(3)=-1,f(-2)=24,∴ M =24,m =-8.7. (-2,2) 解析:设f(x)=x 3-3x +a ,f ′(x)=3(x +1)(x -1),f(x)在x =-1取极大值,在x =1时取极小值,⎩⎪⎨⎪⎧f (-1)>0,f (1)<0⎩⎪⎨⎪⎧a +2>0,a -2<0-2<a <2.8. 4 解析:若x =0,则不论a 取何值,f(x)≥0显然成立;当x >0即x ∈(0,1]时,f(x)=ax 3-3x +1≥0可化为,a ≥3x 2-1x3,设g(x)=3x 2-1x 3,则g ′(x)=3(1-2x )x 4,所以g(x)在区间⎝⎛⎦⎤0,12上单调递增,在区间⎣⎡⎭⎫12,1上单调递减,因此g(x)max =g ⎝⎛⎭⎫12=4,从而a ≥4;当x <0即x ∈[-1,0)时,f(x)=ax 3-3x +1≥0可化为a ≤3x 2-1x 3,设g(x)=3x 2-1x 3,则g ′(x)=3(1-2x )x 4>0,显然g(x)在区间[-1,0)上单调递增,因此g(x)min =g(-1)=4,从而a ≤4,综上,a =4.9. 解:(1) 因为函数f(x),g(x)的图象都过点(t,0),所以f(t)=0,即t 3+at =0.因为t ≠0,所以a =-t 2.g(t)=0,即bt 2+c =0,所以c =ab.又因为f(x),g(x)在点(t,0)处有相同的切线,所以f ′(t)=g ′(t)而f ′(x)=3x 2+a ,g ′(x)=2bx ,所以3t 2+a =2bt.将a =-t 2代入上式得b =t.因此c =ab =-t 3.故a =-t 2,b =t ,c =-t 3.(2) y =f(x)-g(x)=x 3-t 2x -tx 2+t 3,y ′=3x 2-2tx -t 2=(3x +t)(x -t),因为函数y =f(x)-g(x)在(-1,3)上单调递减,所以⎩⎪⎨⎪⎧ y ′x =-1≤0,y ′x =3≤0.即⎩⎪⎨⎪⎧(-3+t )(-1-t )≤0,(9+t )(3-t )≤0,解得t ≤-9或t ≥3.所以t 的取值范围为(-∞,-9]∪[3,+∞).10. 解:(1) ∵ f(x)=x 3+ax ,g(x)=x 2+bx ,∴ f ′(x)=3x 2+a ,g ′(x)=2x +b.x ∈[-1,+∞),f ′(x)g ′(x)≥0,即x ∈[-1,+∞),(3x 2+a)(2x +b)≥0,∵ a >0,∴3x 2+a >0,∴ x ∈[-1,+∞),2x +b ≥0,即∴ x ∈[-1,+∞),b ≥-2x ,∴ b ≥2,则所求实数b 的取值范围是[2,+∞).(2) b 的最小值为2,h(x)=x 3-x 2+ax -2x ,h ′(x)=3x 2-2x +a -2=3⎝⎛⎭⎫x -132+a -73.当a ≥73时,h ′(x)=3x 2-2x +a -2≥0对x ∈[-1,+∞)恒成立,h(x)在[-1,+∞)上单调增,当0<a <73时,由h ′(x)=3x 2-2x +a -2=0得,x =1±7-3a 3>-1,∴h(x)在⎣⎢⎡⎦⎥⎤-1,1-7-3a 3上单调增,在⎣⎢⎡⎦⎥⎤1-7-3a 3,1+7-3a 3上单调减,在⎣⎢⎡⎭⎪⎫1+7-3a 3,+∞上单调增.滚动练习(一)1.24 解析:f(x)=x α,f(4)=12,α=-12,f(x)=x -12,f(8)=24. 2. x ∈R ,都有x 2+2x +5≠03. (-∞,0] 解析:x <-1时,不等式可化为x +(x +1)(-x -1+1)≤1,-x 2≤1,∴ x <-1;x ≥-1时,不等式可化为x +x +1≤1,x ≤0,∴ -1≤x ≤0,综上x ≤0.4. 12 解析:考虑x >0时,f(x)=x x +1=1x +1x ≤12,当且仅当x =1时取等号. 5. [-4,0)∪(0,1) 解析:⎩⎪⎨⎪⎧x 2-3x +2≥0,-x 2-3x +4≥0,x ≠0.上面式中等号不能同时成立.6. 2 解析:在同一个直角坐标系中作出函数y =⎝⎛⎭⎫12x,y =3-x 2的图象,两个函数图象有两个交点.7. (-∞,-1)∪(3,+∞) 解析:x 2+ax >4x +a -3可化为(x -1)a +x 2-4x +3>0对a ∈[0,4]恒成立,设f(a)=(x -1)a +x 2-4x +3,∴ ⎩⎪⎨⎪⎧f (0)>0,f (4)>0.解得x <-1或x >3.8. -1或-2564 解析: 设过(1,0)的直线与y =x 3相切于点(x 0,x 30),所以切线方程为y -x 30=3x 20(x -x 0),即y =3x 20x -2x 30,又(1,0)在切线上,则x 0=0或x 0=32,当x 0=0时,由直线y =0与抛物线y =ax 2+154x -9相切可得a =-2564,当x 0=32时,由直线y =274x -274与曲线y =ax 2+154x -9相切可得a =-1.9. 2 008 解析:令3x =t ,则x =log 3t ,则f(2)+f(4)+f(8)+…+f(28)=4log 23(log 321+2+…+8)+233×8=2 008.10. a ≥2 解析:由log a x +log a y =3,得y =a 3x ,函数y =a 3x 在x ∈[a,2a]上单调递减,得其值域为⎣⎡⎦⎤a 32a ,a 3a ,由题知⎣⎡⎦⎤a 32a ,a3a [a ,a 2],∴ a ≥2. 11. 解:p 为真,则|x -4|≤6的解集为A =[-2,10],q 为真,x 2-2x +1-m 2≤0(m >0)的解集为B =[1-m,1+m],∵ p 是q 的必要而不充分条件,∴ p 是q 的充分而不必要条件,∴ A =[-2,10]B =[1-m,1+m],∴⎩⎪⎨⎪⎧1+m ≥10,1-m ≤-2.两式中等号不能同时成立,又m >0,∴ m ≥9. 12. 解:(1) 令g(x)=f(x)-x =x 2+(a -1)x +a ,则由题意可得⎩⎪⎨⎪⎧Δ>0,<1-a 2<1,g (1)>0,g (0)>0⎩⎪⎨⎪⎧a >0,-1<a <1,a <3-22或a >3+220<a <3-2 2.故所求实数a 的取值范围是(0,3-22).(2) f(0)·f(1)-f(0)=2a 2,令h(a)=2a 2.∵ 当a >0时h(a)单调递增,∴ 当0<a <3-22时,0<h(a)<h(3-22)=2(3-22)2=2(17-122)=217+122<116,即f(0)·f(1)-f(0)<116.13. 解:(1) ① 当0<t ≤10时,V(t)=(-t 2+14t -40)e 14t +50<50,化简得t 2-14t +40>0,解得t <4或t >10,又0<t ≤10,故0<t <4.② 当10<t ≤12时,V(t)=4(t -10)(3t -41)+50<50,化简得(t -10)(3t -41)<0,解得10<t <413,又10<t ≤12,故10<t ≤12.综合得0<t <4或10<t ≤12;故知枯水期为1月,2月,3月,11月,12月共5个月.(2)由(1)知:V(t)的最大值只能在(4,10)内达到.由V ′(t)=e 14t ⎝⎛⎭⎫-14t 2+32t +4=-14e 14t(t +2)(t -8),令V ′(t)=0,解得t =8(t =-2舍去). 当t 变化时,V ′(t) 与V (t)的变化情况如下表:t (4,8) 8 (8,10) V ′(t) + 0 - V(t)极大值由上表,V(t)在t =8时取得最大值V(8)=8e +50=108.32(亿立方米).故知一年内该水库的最大蓄水量是108.32亿立方米.14. 解:(1) 当x ∈[-2,-1)时,f(x)=x +1x 在[-2,-1)上是增函数(用导数判断),此时f(x)∈⎣⎡⎭⎫-52,-2,当x ∈⎣⎡⎭⎫-1,12时,f(x)=-2,当x ∈⎣⎡⎦⎤12,2时,f(x)=x -1x 在⎣⎡⎦⎤12,2上是增函数,此时f(x)∈⎣⎡⎦⎤-32,32,∴ f(x)的值域为⎣⎡⎦⎤-52,-2∪⎣⎡⎦⎤-32,32. (2) ① 若a =0,g(x)=-2,对于任意x 1∈[-2,2],f(x 1)∈⎣⎡⎦⎤-52,-2∪⎣⎡⎦⎤-32,32,不存在x 0∈[-2,2]使得g(x 0)=f(x 1)都成立.② 若当a >0时,g(x)=ax -2在[-2,2]是增函数,g(x)∈[-2a -2,2a -2],任给x 1∈[-2,2],f(x 1)∈⎣⎡⎦⎤-52,-2∪⎣⎡⎦⎤-32,32,若存在x 0∈[-2,2],使得g(x 0)=f(x 1)成立,则⎣⎡⎦⎤-52,-2∪⎣⎡⎦⎤-32,32[-2a -2,2a -2],∴有⎩⎨⎧-2a -2≤-52,2a -2≥32,解得 a ≥74.③ 若a <0,g(x)=ax -2在[-2,2]上是减函数,g(x)∈[2a -2, -2a -2],任给x 1∈[-2,2],f(x 1)∈⎣⎡⎦⎤-52,-2∪⎣⎡⎦⎤-32,32, 若存在x 0∈[-2,2]使得g(x 0)=f(x 1)成立, 则⎣⎡⎦⎤-52,-2∪⎣⎡⎦⎤-32,32[2a -2,-2a -2]⎩⎨⎧2a -2≤-52,-2a -2≥32,解得 a ≤-74.综上,实数a 的取值范围是⎝⎛⎦⎤-∞,-74∪⎣⎡⎭⎫74,+∞.专题二 三角函数与平面向量 第7讲 三角函数的图象与性质1. y =sin ⎝⎛⎭⎫2x +π3,x ∈R 2. 103. 1 解析:f(x)=f ⎝⎛⎭⎫π4cosx +sinx ,f ′(x)=-f ′⎝⎛⎭⎫π4sinx +cosx ,f ′⎝⎛⎭⎫π4=-22f ′⎝⎛⎭⎫π4+22,f ′⎝⎛⎭⎫π4=2-1,f(x)=(2-1)cosx +sinx ,f ⎝⎛⎭⎫π4=(2-1)×22+22=1. 4. 6 解析:平移后f(x)=cos ⎝⎛⎭⎫ωx -ωπ3,与原来函数图象重合,则ωπ3=2kπ,k ∈Z ,∵ ω>0,∴ ωmin =6.5. ⎣⎡⎦⎤-54,1 解析:a =cos 2x -cosx -1=⎝⎛⎭⎫cosx -122-54,转化为函数的值域问题. 6. 2+22 解析:f(x)=2sin πx4,周期为8,f(1)+f(2)+f(3)+…+f(2 012)=f(1)+f(2)+f(3)+f(4)=2+2 2.7. 2 解析:T =2ππ2=4,对任意x ∈R ,都有f(x 1)≤f(x)≤f(x 2)成立,f(x)min =f(x 1),f(x)max=f(x 2),于是|x 1-x 2|min =T2=2.8. 23 解析:考查三角函数的图象、数形结合思想.线段P 1P 2的长即为sinx 的值,且其中的x 满足6cosx =5tanx ,解得sinx =23.线段P 1P 2的长为23.9. 解:f(x)=-2asin ⎝⎛⎭⎫2x +π6+2a +b ,sin ⎝⎛⎭⎫2x +π6∈⎣⎡⎦⎤-12,1, 当a >0时,-2a +2a +b =-5,-2a ×⎝⎛⎭⎫-12+2a +b =1,∴ a =2,b =-5; 当a <0时,-2a +2a +b =1,-2a ×⎝⎛⎭⎫-12+2a +b =-5,∴ a =-2,b =1; a =0,不存在.综上,a =2,b =-5或a =-2,b =1.10. 解:(1) 由最低点为M ⎝⎛⎭⎫2π3,-2得A =2,由T =π得ω=2πT =2ππ=2, 由点M ⎝⎛⎭⎫2π3,-2在图象上得2sin ⎝⎛⎭⎫4π3+φ=-2,即sin ⎝⎛⎭⎫4π3+φ=-1, 所以4π3+φ=2kπ-π2,故φ=2kπ-11π6(k ∈Z ).又φ∈⎝⎛⎭⎫0,π2,所以φ=π6,所以f(x)=2sin ⎝⎛⎭⎫2x +π6. (2) 因为x ∈⎣⎡⎦⎤0,π12,2x +π6∈⎣⎡⎦⎤π6,π3,所以当2x +π6=π6时,即x =0时,f(x)取得最小值1;当2x +π6=π3,即x =π12时,f(x)取得最大值 3.第8讲 三角变换与解三角形1. 3 解析:∵ sin 2α+cos2α=14,∴ sin 2α+1-2sin 2α=14,∴ sin 2α=34,∵ α∈⎝⎛⎭⎫0,π2,∴ s inα=32,∴ α=π3,tanα= 3. 2. 523 解析:由正弦定理a sinA =b sinB ,得 a =bsinAsinB =5·1322=523.3. 5 解析:12arcsinB =2,c =42,由余弦定理可求得b.4. 1 解析:由sin 2α+sinαcosα-2cos 2α=0,得tan 2α+tanα-2=0,tanα=1或tanα=-2(舍),sin2α=2sinαcosα=2tanα1+tan 2α=21+1=1. 5. 4 解析:由余弦定理得b a +ab =6cosC ,a 2+b 2ab =6×a 2+b 2-c 22ab ,a 2+b 2=32c 2,tanC tanA +tanC tanB =sinC cosC ⎝⎛⎭⎫cosA sinA +cosB sinB =1cosC ⎝⎛⎭⎫sin 2C sinAsinB =2ab a 2+b 2-c 2⎝⎛⎭⎫c 2ab =2c 2a 2+b 2-c 2,将a2+b 2=32c 2代入上式即可.注:(1) 在用正、余弦定理处理三角形中的问题时,要么把所有关系转化为边的关系,要么把所有的关系都转化为角的关系;(2) 本题也可以转化为角的关系来处理.6.724 解析:tanα=-34,tanβ=-12,tan2β=-43. 7. -17 解析:由余弦定理得c =a 2+b 2-2abcosC =3,故最大角为角B.8.817 解析:12bcsinA =-(b 2+c 2-a 2)+2bc ,12bcsinA =-2bccosA +2bc , 2-12sinA =2cosA ,⎝⎛⎭⎫2-12sinA 2=(2cosA)2=4(1-sin 2A),sinA =817. 9. 解:(1) ∵ c 2=a 2+b 2-2abcosC =1+4-4×14=4,∴ c =2,∴ △ABC 的周长为a +b +c =1+2+2=5. (2) ∵ cosC =14,∴ sinC =1-cos 2C =1-⎝⎛⎭⎫142=154, ∴ sinA =asinC c =1542=158.∵ a <c ,∴ A <C ,故A 为锐角,∴ cosA =1-sin 2A =1-⎝⎛⎭⎫1582=78,∴ cos(A -C)=cosAcosC +sinAsinC =78×14+158×154=1116.10. 解:(1) sin 2B +C 2+cos2A =1-cos (B +C )2+cos2A =1+cosA 2+2cos 2A -1=5950.(2) ∵ cosA =45,∴ sinA =35,∴ S △ABC =12bcsinA =310bc ,∵ a =2,由余弦定理得:a 2=b 2+c 2-2bccosA =4,∴ 85bc +4=b 2+c 2≥2bc ,bc ≤10,∴ S △ABC =12×bcsinA =310bc ≤3,当且仅当b =c 时,取得最大值,所以当b =c 时,△ABC 的面积S 的最大值为3.第9讲 平面向量及其应用1. ⎝⎛⎭⎫45,-35或⎝⎛⎭⎫-45,352.10 解析:|α|=1,|β|=2,α⊥(α-2β),得α·(α-2β)=0,α·β=12,|2α+β|=4α2+4α·β+β2=10.3. π3 解析:∵ (a +2b )·(a -b )=-6,∴ |a|2-2|b|2+a·b =-6,∴ a·b =1,cos 〈a ,b 〉=a·b |a|·|b|=12. 4. 4 解析:设BC 边中点为D ,则AO →=23AD →,AD →=12(AB →+AC →),∴ AO →·AC →=13(AB →+AC →)·AC →=13(3×2×cos60°+32)=4.5. (-3,1)或(-1,1) 解析:设a =(x ,y),∴ a +b =(x +2,y -1),∴ ⎩⎪⎨⎪⎧ y -1=0,(x +2)2+(y -1)2=1,∴ ⎩⎪⎨⎪⎧ x =-1,y =1或⎩⎪⎨⎪⎧x =-3,y =1. 6. -14 解析:AD →·BE →=12(AB →+AC →)·⎝⎛⎭⎫23AC →-AB → =12⎝⎛⎭⎫-1+23-13×12=-14. 7. 1-2 解析:设a +b =2d ,则d 为单位向量. (a -c )·(b -c )=1-(a +b )·c =1-2d·c =1-2cos 〈d ,c 〉.8. 2 解析:取O 为坐标原点,OA 所在直线为x 轴,建立直角坐标系,则A(1,0),B ⎝⎛⎭⎫-12,32,设∠COA =θ,则θ∈⎣⎡⎦⎤0,2π3,C(cosθ,sinθ),∴ (cosθ,sinθ)=x(1,0)+y ⎝⎛⎭⎫-12,32,x +y =3sinθ+cosθ=2sin ⎝⎛⎭⎫θ+π6,θ=π3时取最大值2. 9. 解:(1) 由m·n =0得-cosA +3sinA =0,tanA =33,A ∈(0,π), ∴ A =π6.(2)1+sin2B cos 2B -sin 2B =-3,∴ sinB +cosBcosB -sinB=-3,∴ tanB =2,∴ tanC =tan ⎝⎛⎭⎫π-π6-B =-tan π6+tanB 1-tan π6tanB=8+5 3. 10. 解:(1) 在Rt △ADC 中,AD =8,CD =6, 则AC =10,cos ∠CAD =45,sin ∠CAD =35.又∵ AB →·AC →=50,AB =13,∴ cos ∠BAC =AB →·AC →|AB →||AC →|=513.∵ 0<∠BAC <π,∴ sin ∠BAC =1213.∴ sin ∠BAD =sin(∠BAC +∠CAD)=6365.(2) S △BAD =12AB·AD·sin ∠BAD =2525,S △BAC =12AB·AC·sin ∠BAC =60,S △ACD =24,则S △BCD =S △ABC +S △ACD -S △BAD =1685,∴ S △ABD S △BCD =32.滚动练习(二)1. {-1,0,1} 解析:M ={-2,-1,0,1},N ={-1,0,1,2,3},则M ∩N ={-1,0,1}.2. 0 解析:f(1)=-f(-1)=-(-3+2+1)=0.3. 2 解析:cos10°+3sin10°1-cos80°=2sin40°2sin 240°= 2.4. (-3,2) 解析:6-x -x 2>0,∴ x 2+x -6<0,∴ -3<x <2.5. 2 解析:f ′(x)=3x 2-6x =3x(x -2),则函数的增区间是(-∞,0)∪(2,+∞),减区间是(0,2),所以函数在x =2处取极小值.6. 1 解析:a -2b =(3,3)与c 共线,则3·3=3k ,∴ k =1.7. 6 解析:A*B ={0,2,4}.8. 充要 解析:f(x)=x 2+mx +1的图象关于直线x =1对称-m2=1m =-2.9. (-∞,2ln2-2] 解析:f ′(x)=e x -2,x ∈(-∞,ln2),f ′(x)<0,x ∈(ln2,+∞),f ′(x)>0,x =ln2时,f(x)取极小值即为最小值2-2ln2+a ≤0,a ≤2ln2-2;本题也可转化为a =-e x +2x ,求函数g(x)=-e x +2x 值域即可.10. ②④ 解析:函数为偶函数,在⎣⎡⎦⎤0,π2上单调增,画图即可. 11. 点拨:本题考查函数的概念和性质,对分段函数在讨论其性质时要整体考虑.对二次函数要能用数形结合的思想来研究它的单调性与最值等问题.解:(1) 函数f(x)为奇函数,f(-x)+f(x)=0对x ∈R 恒成立,m =2;(2) 由f(x)=⎩⎪⎨⎪⎧-x 2+2x ,x >00,x =0,x 2+2x ,x <0,知f(x)在[-1,1]上单调递增,∴ ⎩⎪⎨⎪⎧a -2>-1,a -2≤1,得1<a ≤3,即实数a 的取值范围是(1,3]. 12. 点拨:本小题主要考察综合运用三角函数公式、三角函数的性质进行运算、变形、转换和求解的能力.解:(1)∵ f(x)=sin(π-ωx)cosωx +cos 2ωx ,∴ f(x)=sinωxcosωx +1+cos2ωx 2=12sin2ωx +12cos2ωx +12=22sin ⎝⎛⎭⎫2ωx +π4+12,由ω>0得2π2ω=π,∴ ω=1. (2) 由(1)知f(x)=22sin ⎝⎛⎭⎫2x +π4+12, ∴ g(x)=f(2x)=22sin ⎝⎛⎭⎫4x +π4+12,当0≤x ≤π16时,π4≤4x +π4≤π2,∴ 22≤sin ⎝⎛⎭⎫4x +π4≤1. 因此1≤g(x)≤1+22,故x =0时,g(x)在此区间内取最小值为1.13. 点拨:本题考查同角三角函数的基本关系,三角形面积公式,向量的数量积,利用余弦定理解三角形以及运算求解能力.解:由cosA =1213,得sinA =1-⎝⎛⎭⎫12132=513.又12bcsinA =30,∴ bc =156. (1) AB →·AC →=bccosA =156×1213=144.(2) a 2=b 2+c 2-2bccosA =(c -b)2+2bc(1-cosA)=1+2×156×⎝⎛⎭⎫1-1213=25,∴ a =5. 14. 点拨:应用题是高考必考题型,解决应用题的关键要学会审题,根据条件,选择合适的变量,建立数学模型,选择适当的方法解题,结论要符合题意.解:∵ △ABC 是直角三角形,AB =2,BC =1,∴ ∠A =30°.设∠FEC =α,则α∈⎝⎛⎭⎫0,π2,∠EFC =90°-α,∠AFD =180°-60°-(90°-α)=30°+α,∴ ∠ADF =180°-30°-(30°+α)=120°-α,再设CF =x ,则AF =3-x ,在△ADF 中有DFsin30°=3-x sin (120°-α),由于x =EF·sinα=DF·sinα, ∴DF sin30°=3-DF·sinαsin (120°-α),化简得DF =32sinα+3cosα≥37=217, ∴ △DEF 边长的最小值为217.专题三 数 列第10讲 等差数列与等比数列1. 13 解析:a 3=7,a 5=a 2+6,∴ 3d =6,∴ a 6=a 3+3d =13.2. 13 解析:6S 5-5S 3=5,∴ 6(5a 1+10d)-5(3a 1+3d)=5,得a 1+3d =13. 3. 20 解析:a n =41-2n ,a 20>0,a 21<0.4.152 解析:a 2=1,a n +2+a n +1=6a n ,∴ q 2+q =6(q >0),∴ q =2,则S 4=152. 5. 15 解析:S 4a 4=a 1(1-q 4)1-q a 1q 3=1-q 4(1-q )q 3=15.6. 4 解析:设公差为d ,则⎩⎨⎧4a 1+4×32d ≥10,5a 1+5×42d ≤15.即⎩⎪⎨⎪⎧2a 1+3d ≥5,a 1+2d ≤3.又a 4=a 1+3d ,由线性规划可知a 1=1,d =1时,a 4取最大值4.7.212解析:a n =(a n -a n -1)+(a n -1-a n -2)+…+(a 2-a 1)+a 1=33+2(1+2+…+(n -1))=n 2-n +33,a n n =n +33n -1,数列⎩⎨⎧⎭⎬⎫a n n 在1≤n ≤6,n ∈N *时单调减,在n ≥7,n ∈N *时单调增,∴ n =6时,a nn取最小值.8. 4 解析:⎩⎨⎧k (k +4)⎝⎛⎭⎫23k≥(k -1)(k +3)⎝⎛⎭⎫23k -1,k (k +4)⎝⎛⎭⎫23k≥(k +1)(k +5)⎝⎛⎭⎫23k +1,10≤k ≤1+10,k ∈N *,∴ k =4.9. 解:(1) 设公差为d ,则⎩⎪⎨⎪⎧(a 1+2d )(a 1+5d )=55,2a 1+7d =16,解得⎩⎪⎨⎪⎧ a 1=1,d =2.或⎩⎪⎨⎪⎧a 1=15,d =-2.(舍去) ∴ a n =2n -1(n ∈N *).(2) n =1时,a 1=b 12,a 1=1,∴ b 1=2,n ≥2时,a n -1=b 12+b 222+…+b n -12n -1,2=a n -a n -1=b n 2n (n ≥2),b n =2n +1(n ≥2),∴ b n =⎩⎪⎨⎪⎧2(n =1),2n +1(n ≥2,n ∈N *),S n =2n +2-6(n ∈N *). 10. (解法1)(1)证明:由b n +1b n =q ,有a n +1a n +2a n a n +1=a n +2a n=q ,∴ a n +2=a n q 2(n ∈N *). (2)证明:∵ a n =a n -2q 2(n ≥3,n ∈N *),∴ a 2n -1=a 2n -3q 2=…=a 1q 2n -2,a 2n =a 2n -2q 2=…=a 2q 2n -2,∴ c n =a 2n -1+2a 2n =a 1q 2n -2+2a 2q 2n -2=(a 1+2a 2)q 2n -2=5q 2n -2. ∴ {c n }是首项为5,以q 2为公比的等比数列.(3) 解:由(2)得1a 2n -1=1a 1q 2-2n ,1a 2n =1a 2q 2-2n ,于是1a 1+1a 2+…+1a 2n =⎝⎛⎭⎫1a 1+1a 3+…+1a 2n -1+⎝⎛⎭⎫1a 2+1a 4+…+1a 2n =1a 1⎝⎛⎭⎫1+1q 2+1q 4+…+1q 2n -2+1a 2⎝⎛⎭⎫1+1q 2+1q 4+…+1q 2n -2=32⎝⎛⎭⎫1+1q 2+1q 4+…+1q 2n -2. 当q =1时,1a 1+1a 2+…+1a 2n =32⎝⎛⎭⎫1+1q 2+1q 4+…+1q 2n -2=32n.当q ≠1时,1a 1+1a 2+…+1a 2n =32⎝⎛⎭⎫1+1q 2+1q 4+…+1q 2n -2=32⎝ ⎛⎭⎪⎫1-q -2n 1-q -2=32⎣⎢⎡⎦⎥⎤q 2n -1q 2n -2(q 2-1). 故1a 1+1a 2+…+1a 2n=⎩⎨⎧32n ,q =1,32⎣⎢⎡⎦⎥⎤q 2n -1q 2n -2(q 2-1),q ≠1.(解法2)(1) 证明:同解法1(1).(2) 证明:c n +1c n =a 2n +1+2a 2n +2a 2n -1+2a 2n =q 2a 2n -1+2q 2a 2na 2n -1+2a 2n=q 2(n ∈N *),又c 1=a 1+2a 2=5,∴ {c n }是首项为5,以q 2为公比的等比数列.(3) 解:由(2)的类似方法得a 2n -1+a 2n =(a 1+a 2)q 2n -2=3q 2n -2,1a 1+1a 2+…+1a 2n =a 1+a 2a 1a 2+a 3+a 4a 3a 4+…+a 2n -1+a 2n a 2n -1a 2n ,∵ a 2k -1+a 2k a 2k -1a 2k =3q 2k -22q 4k -4=32q -2k +2,k =1,2,…,n.∴1a 1+1a 2+…+1a 2k =32(1+q 2+…+q -2n +2).下同解法1.第11讲 数列求和及其综合应用1. 2n +1-n -2 解析:a n =2n -1,1+(1+2)+(1+2+4)+…+(1+2+…+2n -1)=(2+22+23+…+2n )-n =2(2n -1)-n =2n +1-n -22. 2+lnn 解析:累加可得.3. T 8T 4 T 12T 84. -p -q 解析:由求和公式知q =pa 1+p (p -1)2d ,p =qa 1+q (q -1)2d ,因为p ≠q ,两式相减得到-1=a 1+p +q -12d ,两边同时乘以p +q ,则-(p +q)=(p +q)a 1+(p +q )(p +q -1)2d ,即S p +q =-(p +q).5. 2n +1 解析:由条件得b n +1=a n +1+2a n +1-1=2a n +1+22a n +1-1=2a n +2a n -1=2b n 且b 1=4,所以数列{b n }是首项为4,公比为2的等比数列,则b n =4·2n -1=2n +1.6. 11 解析:(a 1+1)2+(a 2+1)2+…+(a 50+1)2=107,则(a 21+a 22+…+a 250)+2(a 1+a 2+…+a 50)+50=107,∴ a 21+a 22+…+a 250=39,故a 1,a 2,…,a 50中数字0的个数为50-39=11.7. [24,36] 解析:a n =6n -(9+a),由题知5.5≤9+a6≤7.5,∴ 24≤a ≤36.8. 470 解析:由于⎩⎨⎧⎭⎬⎫cos 2nπ3-sin 2nπ3以3 为周期,故S 30=⎝⎛⎭⎫-12+222+32+⎝⎛⎭⎫-42+522+62+…+⎝⎛⎭⎫-282+2922+302 =∑k =110⎣⎡⎦⎤-(3k -2)2+(3k -1)22+(3k )2=∑k =110 ⎣⎡⎦⎤9k -52=9×10×112-25=470,分组求和是解决本题的关键.9. 解:(1) 由S n =(1+λ)-λa n S n -1=(1+λ)-λa n -1(n ≥2).相减得:a n =-λa n +λa n -1,∴ a n a n -1=λ1+λ(n ≥2),∴ 数列{a n }是等比数列.(2) f(λ)=λ1+λ,∴ b n =b n -11+b n -11b n =1b n -1+1,∴ ⎩⎨⎧⎭⎬⎫1b n 是首项为1b 1=2,公差为1的等差数列,∴ 1b n =2+(n -1)=n +1.∴ b n =1n +1.(n ∈N *) (3) λ=1时,a n =⎝⎛⎭⎫12n -1,∴ c n =a n⎝⎛⎭⎫1b n-1=⎝⎛⎭⎫12n -1n , ∴ T n =1+2⎝⎛⎭⎫12+3⎝⎛⎭⎫122+…+n ⎝⎛⎭⎫12n -1, ①12T n =⎝⎛⎭⎫12+2⎝⎛⎭⎫122+3⎝⎛⎭⎫123+…+n ⎝⎛⎭⎫12n , ② ①-②得:12T n =1+⎝⎛⎭⎫12+⎝⎛⎭⎫122+⎝⎛⎭⎫123+…+⎝⎛⎭⎫12n -1-n ⎝⎛⎭⎫12n ∴ 12T n =1+⎝⎛⎭⎫12+⎝⎛⎭⎫122+⎝⎛⎭⎫123+…+⎝⎛⎭⎫12n -1-n ⎝⎛⎭⎫12n = 2⎣⎡⎦⎤1-⎝⎛⎭⎫12n -n ⎝⎛⎭⎫12n , 所以:T n =4-⎝⎛⎭⎫12n -2-2n ⎝⎛⎭⎫12n =4-n +22n -1. 10. 解:(1) n =1时,由S 2=tS 1+a ,解得a 2=at ,当n ≥2时,S n =tS n -1+a ,所以S n +1-S n =t(S n -S n -1),即a n +1=a n t , 当n =1时,由S 2=tS 1+a 得a 2=ta 1,又因为a 1=a ≠0,综上,有a n +1a n=t(n ∈N *),所以{a n }是首项为a ,公比为t 的等比数列,所以a n =at n -1.(2) 当t =1时,S n =na ,b n =na +1,b n +1-b n =[(n +1)a +1]-[na +1]=a , 此时{b n }为等差数列;当a >0时,{b n }为单调递增数列,且对任意n ∈N *,a n >0恒成立,不合题意;当a <0时,{b n }为单调递减数列,由题意知b 4>0,b 6<0,且有⎩⎪⎨⎪⎧b 4≥|b 5|,-b 6≥|b 5|,即⎩⎪⎨⎪⎧|5a +1|≤4a +1,|5a +1|≤-6a -1,解得-29≤a ≤-211.综上,a 的取值范围是⎣⎡⎦⎤-29,-211. (3) 因为t ≠1,b n =1+a 1-t -at n 1-t ,所以c n =2+⎝⎛⎭⎫1+a 1-t n -a 1-t (t +t 2+…+t n)=2+⎝⎛⎭⎫1+a 1-t n -a (t -t n +1)(1-t )2=2-at (1-t )2+1-t +a 1-t ·n +at n +1(1-t )2,由题设知{c n }是等比数列,所以有⎩⎪⎨⎪⎧2-at (1-t )2=0,1-t +a 1-t =0,解得⎩⎪⎨⎪⎧a =1,t =2,即满足条件的数对是(1,2).(或通过{c n }的前3项成等比数列先求出数对(a ,t),再进行证明)滚动练习(三)1. {4,5} 解析:A ∪B ={1,2,3}.2. π4 解析:由正弦定理a sinA =c sinC ,∴ sinA =cosA ,∴ tanA =1,∵ 0<A <π, ∴ A =π4.3. 12 解析:由a 1+3a 8+a 15=60得5a 1+35d =60,a 8=12,2a 9-a 10=a 8=12.4. 12 解析:周期是4π,∴ ω=2π4π=12. 5. [0,4) 解析:mx 2+mx +1≠0对x ∈R 恒成立.当m =0时,成立;当m ≠0时,Δ=m 2-4m <0,∴ 0<m <4.综上,0≤m <4.6. 6 解析:本题考查线性规划内容.7. ⎝⎛⎭⎫7π6,11π6 解析:y ′=1+2sinx <0,∴ sinx <-12,∴ 7π6<x <11π6. 8. π3 解析:∵ m ⊥n ,∴ (a +c)(a -c)+b(b -a)=0,∴ a 2+b 2-c 22ab =12, ∴ cosC =12,∴ C =π3.9. (-∞,-1)∪(2,+∞) 解析:画出符合题意的草图,则x -2<-3或x -2>0.10. 4 解析:本题其实是关于最小正周期问题.a 2=a 1-t ,a 3=t +2-a 1+t =2t +2-a 1,a 4=a 3-t =t +2-a 1,a 5=t +2-a 4=a 1,故实数k 的最小值是4.11. 解:(1) f(x)=12sin2x +3cos 2x =12sin2x +32(1+cos2x)=sin ⎝⎛⎭⎫2x +π3+32,∴ f(x)的最小正周期为T =2π2=π. (2) 依题意得g(x)=f ⎝⎛⎭⎫x -π4+32=sin ⎣⎡⎦⎤2⎝⎛⎭⎫x -π4+π3+32+32=sin ⎝⎛⎭⎫2x -π6+3,当x ∈⎣⎡⎦⎤0,π4时,2x -π6∈⎣⎡⎦⎤-π6,π3,∴ -12≤sin ⎝⎛⎭⎫2x -π6≤32,∴ 23-12≤g(x)≤332,∴ g(x)在⎣⎡⎦⎤0,π4的最大值为332. 12. 解:(1) 当n ≤6时,数列{a n }是首项为120,公差为-10的等差数列.a n =120-10(n -1)=130-10n ;当n ≥7时,数列{a n }是以a 6为首项,公比为34的等比数列,又a 6=70,所以a n =70×⎝⎛⎭⎫34n-6,因此,第n 年初,M 的价值a n 的表达式为a n =⎩⎪⎨⎪⎧130-10n ,n ≤6,n ∈N *,70×⎝⎛⎭⎫34n -6,n ≥7,n ∈N *. (2) 设S n 表示数列{a n }的前n 项和,由等差及等比数列的求和公式得当1≤n ≤6时,S n =120n -5n(n -1),A n =120-5(n -1)=125-5n >80;当n ≥7时,S n =S 6+(a 7+a 8+…+a n )=570+70×34×4×⎣⎡⎦⎤1-⎝⎛⎭⎫34n -6=780-210×⎝⎛⎭⎫34n-6,A n =780-210×⎝⎛⎭⎫34n -6n.因为{a n }是递减数列,所以{A n }是递减数列,又A 8=780-210×⎝⎛⎭⎫348-68=824764>80,A 9=780-210×⎝⎛⎭⎫349-69=767996<80,所以须在第9年初对M进行更新.13. 解:(1) f ′(x)=3x 2+2ax +b.由题意得⎩⎪⎨⎪⎧f ′⎝⎛⎭⎫23=3×⎝⎛⎭⎫232+2a ×23+b =0,f ′(1)=3×12+2a ×1+b =3.解得⎩⎪⎨⎪⎧a =2,b =-4.设切线l 的方程为y =3x +m(m>0),由原点到切线l 的距离为1010, 有|m|32+1=1010,解得m =1.∵ 切线l 不过第四象限,∴ m =1,m =-1(舍),∴ 切线l 的方程为y =3x +1,由于切点的横坐标为x =1,∴ 切点坐标为(1,4),∵ f(1)=1+a +b +c =4,∴ c =5.(2) 由(1)知f(x)=x 3+2x 2-4x +5,所以f ′(x)=3x 2+4x -4=(x +2)(3x -2),令f ′(x)=0,得x 1=-2,x 2=23.x -4 (-4,-2)-2 ⎝⎛⎭⎫-2,2323 ⎝⎛⎭⎫23,1 1 f ′(x) +0 -0 +f(x)极大值 极小值函数值-11139527414. 解:(1) ∵ -1,S n ,a n +1成等差数列,∴ 2S n =a n +1-1, ① 当n ≥2时,2S n -1=a n -1, ②①-②得:2(S n -S n -1)=a n +1-a n ,∴ 3a n =a n +1,∵ a 1=1≠0,∴ a n ≠0, ∴ a n +1a n=3.当n =1时,由①得∴ 2S 1=2a 1=a 2-1,又a 1=1,∴ a 2=3, ∴a 2a 1=3,∴ {a n }是以3为公比的等比数列,∴ a n =3n -1. (2) ∵ f(x)=log 3x ,∴ f(a n )=log 33n -1=n -1,b n =1(n +3)[f (a n )+2]=1(n +1)(n +3)=12⎝⎛⎭⎫1n +1-1n +3,∴ T n =1212-14+13-15+14-16+15-17+…+1n -1n +2+1n +1-1n +3=1212+13-1n +2-1n +3=512-2n +52(n +2)(n +3),比较T n 与512-2n +5312的大小,只需比较2(n +2)(n +3)与312的大小即可.又2(n +2)(n +3)-312=2(n 2+5n +6-156)=2(n 2+5n -150)=2(n +15)(n -10),∵ n ∈N *,∴ 当1≤n ≤9时n ∈N *,2(n +2)(n +3)<312,即T n <512-2n +5312;∴ 当n=10时,2(n +2)(n +3)=312,即T n =512-2n +5312;当n >10且n ∈N *时,2(n +2)(n +3)>312,即T n >512-2n +5312;当n =10时,2(n +2)(n +3)=312,即T n =512-2n +5312;当n>10且n ∈N *时,2(n +2)(n +3)>312,即T n >512-2n +5312.。
2012各省市高考高考题数学题含答案

注息事项: 1.本试卷分第Ⅰ卷选择题和第Ⅱ卷非选择题两部分。
答卷前考生务必将自己的姓名、准考证号填写在本试卷和答题卡相应位置上。
2.问答第Ⅰ卷时。
选出每小题答案后用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动.用橡皮擦干净后再选涂其它答案标号。
写在本试卷上无效. 3.回答第Ⅱ卷时。
将答案写在答题卡上.写在本试卷上无效· 4.考试结束后.将本试卷和答且卡一并交回。
第一卷一选择题本大题共12小题每小题5分在每小题给同的四个选项中只有一项是符合题目要求的。
1已知集合12345ABxyxAyAxyA 则B中所含元素的个数为A3 B6 C D 2将2名教师4名学生分成2个小组分别安排到甲、乙两地参加社会实践活动每个小组由1名教师和2名学生组成不同的安排方案共有A12种B10种C种D种3下面是关于复数21zi的四个命题其中的真命题为1:2pz 22:2pzi 3:pz的共轭复数为1i 4:pz的虚部为1 A23pp B 12pp Cpp Dpp 4设12FF是椭圆2222:10xyEabab的左、右焦点P为直线32ax上一点21FPF是底角为30的等腰三角形则E的离心率为A12 B 23 C D 5已知na为等比数列472aa568aa则110aa A7 B 5 C D 6如果执行右边的程序框图输入正整数2NN和实数12...naaa输出AB则AAB为12...naaa的和B2AB为12...naaa的算术平均数CA和B分别是12...naaa中最大的数和最小的数DA和B分别是12...naaa中最小的数和最大的数7如图网格纸上小正方形的边长为1粗线画出的是某几何体的三视图则此几何体的体积为A6 B 9 C D 8等轴双曲线C的中心在原点焦点在x轴上C与抛物线xy162的准线交于AB 两点43AB则C的实轴长为A2 B 22 C D 9已知0函数sin4fxx在2上单调递减。
则的取值范围是A1524 B 1324 C 102 D02 10 已知函数1ln1fxxx则yfx的图像大致为11已知三棱锥SABC的所有顶点都在球O的求面上ABC是边长为1的正三角形SC为球O的直径且2SC则此棱锥的体积为A26 B 36 C 23 D22 12设点P在曲线12xye上点Q在曲线ln2yx上则PQ最小值为第Ⅱ卷本卷包括必考题和选考题两部分。
2012年高考数学一轮复习全册课时训练及各单元检测试卷[全套]
![2012年高考数学一轮复习全册课时训练及各单元检测试卷[全套]](https://img.taocdn.com/s3/m/dcfac24dcf84b9d528ea7aed.png)
解析 A={x|-a≤x≤a},根据题意可知 1≤a<2. 10.设集合 A={-1,0,1},集合 B={0,1,2,3},定义 A*B={(x,y)|x∈A∩B,y∈A∪B}, 则 A*B 中元素的个数为________. 答案 10 解析 由题知,A∩B={0,1},A∪B{-1,0,1,2,3},所以满足题意的实数对有(0,-1),
[精品]2012 年高考数学一轮复习全册课时训练及各单元检测试卷解析版[全套]
(0,0),(0,1),(0,2),(0,3),(1,-1),(1,0),(1,1),(1,2),(1,3),共 10 个,即 A*B 中的元素 有 10 个. 11.设集合 A、B 都是 U={1,2,3,4}的子集,已知(∁UA)∩(∁UB)={2},(∁UA)∩B={1}, 且 A∩B=∅,则 A=________. 答案 {3,4}
2x-1>0 2x-1<0 或 1-|x|<0 1-|x|>0
)
1 B.x>1 或-1<x< 2 1 D.x<-1 或 x> 2
1 1 x>2 x<2 ∴ 或 x>1或x<-1 -1<x<1 1 ∴x>1 或-1<x< ,故选 B. 2 7.(2011· 徐州质检)已知集合 M={x|x2-2008x-2009>0},N={x|x2+ax+b≤0},若 M ∪N=R,M∩N=(2009,2010],则( A.a=2009,b=-2010 C.a=2009,b=2010 答案 D 解析 化简得 M={x|x<-1 或 x>2009}, 由 M∪N=R,M∩N=(2009,2010]可知 N={x|-1≤x≤2010},即-1,2010 是方程 x2+ ax+b=0 的两个根. 所以 b=-1×2010=-2010,-a=-1+2010,即 a=-2009. 8.已知不等式 ax2+bx+2>0 的解集为{x|-1<x<2},则不等式 2x2+bx+a<0 的解集为 ( ) 1 A.{x|-1<x< } 2 C.{x|-2<x<1} 答案 A 解析 由题意知 x=-1,x=2 是方程 ax2+bx+2=0 的根. 1 B.{x|x<-1 或 x> } 2 D.{x|x<-2 或 x>1} ) B.a=-2009,b=2010 D.a=-2009,b=-2010
2012年全国新课标高考文科数学真题及答案(Word版)

绝密*启用前2012年普通高等学校招生全国统一考试 文科数学 注息事项:1. 本试卷分第I 卷(选择题)和第n 卷 号填写在本试卷和答题卡相应位置上。
2. 问答第I 卷时。
选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动 擦干净后,再选涂其它答案标号。
写在本试卷上无效3.回答第n 卷时。
将答案写在答题卡上 .写在本试卷上无效•4. 考试结束后.将本试卷和答且卡一并交回。
1y i ) (i=1,2,…,n)都在直线y=2x+1上,则这组样本数据的样本相关系数为x 2 y 2 3aF 2是椭圆E :耸+ y^= 1(a>b>0)的左、右焦点,P 为直线x=3a 上一点,△ F 1PF 2是底角为30°a b 2 的等腰三角形,则 E 的离心率为()(A) 1 ( B ) 2 (C ) 4( D ) 4 5、已知正三角形 ABC 的顶点A(1,1),B(1,3),顶点C 在第一象限,若点(x ,丫)在厶ABC 内部,贝U z= —x+y 的取值范围是 (A ) (1 — 3, 2) ( B ) (0, 2)( C ) ( 3— 1, 2)( D ) (0,1+ 3)(6)如果执行右边的程序框图,输入正整数 N(N >2)和实数a 1,a 2,…,a N ,输出A,B ,则(A)A+B 为 a 1,a 2,…,a N 的和 A + B(B)—2 —为a1,a 2,…,a N 的算术平均数(A )— 1(B) 0 (D) 1(非选择题)两部分。
答卷前,考生务必将自己的姓名、准考证.用橡皮 、选择题: 本大题共 12小题, 每小题5分,在每小题给同的四个选项中,只有一项是符合题目要求的。
1、已知集合 A={ x|x 2— x — 2<0}, B={ x|— 1<x<1},(A) A B(B ) B A (C ) A=B(D ) A n B=(2)复数 z =—的共轭复数是2+i(A) 2+i( B ) 2 — i(C )— 1+i (D )— 1— i3、在一组样本数据(X 1, y 1), (x 2, y 2),…,(x n .y n ) ( n > 2, X 1,x 2,…,X n 不全相等)的散点图中,若所有样本点(X i ,(4)设 F 1、(C) A和B分别是a i,a2,…,a N中最大的数和最小的数(D) A和B分别是a i,a2,…,a N中最小的数和最大的数(7) 如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则此几何体的体积为(A) 6(B) 9(C) 12(D)18(8) 平面a截球0的球面所得圆的半径为1球心O到平面a的距离为,2,则此球的体积为(A) 6n ( B) 4 3n (C) 4 6n (D) 6 3n(9) 已知3>0, 0< o <n直线x=4和x=5^函数f(x)=sin( ®x+妨图像的两条相邻的对称轴,贝Un n n 3 n(A ) 4 (B) 3 ( C) 2 ( D) G(10) 等轴双曲线C的中心在原点,焦点在x轴上,C与抛物线y2=l6x的准线交于A , B两点, 则C的实轴长为(A ) 2 (B) 2 2 (C) 4 ( D) 8(11) 当0<x< 2时,4x<|og a x,贝y a的取值范围是(A ) (0,子) (B)(今,1) (C) (1 , 2) ( D) (.2, 2)(12) 数列{a n}满足a n+1 + (- 1)n a n = 2n- 1,则{a n}的前60项和为(A) 3690 ( B) 3660 (C) 1845 ( D) 1830本卷包括必考题和选考题两部分。
2012年高考数学试题分类汇编--立体几何

2012年高考真题理科数学解析汇编:立体几何一、选择题1 .(2012年高考(新课标理))已知三棱锥S ABC -的所有顶点都在球O 的求面上,ABC∆是边长为1的正三角形,SC 为球O 的直径,且2SC =;则此棱锥的体积为 ( )A.6B.6C.3 D22 .(2012年高考(新课标理))如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则此几何体的体积为A .6B .9C .12D .183 .(2012年高考(浙江理))已知矩形ABCD ,AB =1,BC将∆ABD 沿矩形的对角线BD 所在的直线进行翻着,在翻着过程中, A .存在某个位置,使得直线AC 与直线BD 垂直 B .存在某个位置,使得直线AB 与直线CD 垂直 C .存在某个位置,使得直线AD 与直线BC 垂直D .对任意位置,三直线“AC 与BD ”,“AB 与CD ”,“AD 与BC ”均不垂直4 .(2012年高考(重庆理))设四面体的六条棱的长分别为a ,且长为a 的,则a 的取值范围是 ( )A .B .C .D .5 .(2012年高考(四川理))如图,半径为R 的半球O 的底面圆O在平面α内,过点O 作平面α的垂线交半球面于点A ,过圆O 的直径CD 作平面α成45角的平面与半球面相交,所得交线上到平面α的距离最大的点为B ,该交线上的一点P 满足60BOP ∠=,则A 、P 两点间的球面距离为( )A .RB .4R πC .RD .3R π6 .(2012年高考(四川理))下列命题正确的是( )A .若两条直线和同一个平面所成的角相等,则这两条直线平行B .若一个平面内有三个点到另一个平面的距离相等,则这两个平面平行C .若一条直线平行于两个相交平面,则这条直线与这两个平面的交线平行D .若两个平面都垂直于第三个平面,则这两个平面平行7 .(2012年高考(上海春))已知空间三条直线.l m n 、、若l 与m 异面,且l 与n 异面,则 [答] ( )A .m 与n 异面.B .m 与n 相交.C .m 与n 平行.D .m 与n 异面、相交、平行均有可能.8 .(2012年高考(陕西理))如图,在空间直角坐标系中有直三棱柱111ABC A B C -,12CA CC CB ==,则直线1BC 与直线1AB 夹角的余弦值为 ( )ABCD .359 .(2012年高考(江西理))如图,已知正四棱锥S-ABCD 所有棱长都为1,点E 是侧棱SC上一动点,过点E 垂直于SC 的截面将正四棱锥分成上、下两部分.记SE=x(0<x<1),截面下面部分的体积为V(x),则函数y=V(x)的图像大致为10.(2012年高考(湖南理))某几何体的正视图和侧视图均如图1所示,则该几何体的俯视图不可能是11.(2012年高考(湖北理))我国古代数学名著《九章算术》中“开立圆术”曰:置积尺数,以十六乘之,九而一,所得开立方除之,即立圆径. “开立圆术”相当于给出了已知球的体积V ,求其直径d的一个近似公式d ≈. 人们还用过一些类似的近似公式. 根据π =3.14159判断,下列近似公式中最精确的一个是( )A.d B.d C.d ≈D .(一)必考题(11—14题)12.(2012年高考(湖北理))已知某几何体的三视图如图所示,何体的体积为A 图1BC D侧视图正视图俯视图A .8π3B .3πC .10π3D .6π13.(2012年高考(广东理))(立体几何)某几何体的三视图如图1所示,它的体积为 ( )A .12πB .45πC .57πD .81π14.(2012年高考(福建理))一个几何体的三视图形状都相同、大小均相等,那么这个几何体不可以是 ( )A .球B .三棱柱C .正方形D .圆柱15.(2012年高考(大纲理))已知正四棱柱1111ABCD A BC D -中,12,AB CC E ==为1CC 的中点,则直线1AC 与平面BED 的距离为 ( ) A .2BCD .116.(2012年高考(北京理))某三棱锥的三视图如图所示,该三棱锥的表面积是 ( )A.28+ B.30+ C.56+D.60+17.(2012年高考(安徽理))设平面α与平面β相交于直线m ,直线a 在平面α内,直线b在平面β内,且b m ⊥,则“αβ⊥”是“a b ⊥”的 ( )A .充分不必要条件B .必要不充分条件C .充要条件D .即不充分不必要条件二、填空题18.(2012年高考(天津理))―个几何体的三视图如图所示(单位:m ),则该几何体的体积为______3m .19.(2012年高考(浙江理))已知某三棱锥的三视图(单位:cm)如图所示,则该三棱锥的体积等于___________cm 3.20.( 2012年高考(四川理))如图,在正方体1111ABCD A BC D -中,M 、N 分别是CD 、1CC 的中点,则异面直线1A M 与DN 所成角的大小是____________.21.(2012年高考(上海理))如图,AD 与BC 是四面体ABCD 中互相垂直的棱,BC=2。
河南省_2012年_高考新课标全国卷数学真题(理科数学)(附答案)_历年历届试题(详解)

绝密*启用前2012年普通高等学校招生全国统一考试(新课标)理科数学注息事项:1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
答卷前,考生务必将自己的姓名、准考证号填写在本试卷和答题卡相应位置上。
2.问答第Ⅰ卷时。
选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动.用橡皮擦干净后,再选涂其它答案标号。
写在本试卷上无效.3.回答第Ⅱ卷时。
将答案写在答题卡上.写在本试卷上无效·4.考试结束后.将本试卷和答且卡一并交回。
第一卷一. 选择题:本大题共12小题,每小题5分,在每小题给同的四个选项中,只有一项是符合题目要求的。
(1)已知集合{1,2,3,4,5}A =,{(,),,}B x y x A y A x y A =∈∈-∈;,则B 中所含元素的个数为( )()A 3 ()B 6()C 8 ()D 10(2)将2名教师,4名学生分成2个小组,分别安排到甲、乙两地参加社会实践活动,每个小组由1名教师和2名学生组成,不同的安排方案共有( )()A 12种 ()B 10种()C 9种 ()D 8种(3)下面是关于复数21z i=-+的四个命题:其中的真命题为( ) 1:2p z = 22:2p z i = 3:p z 的共轭复数为1i + 4:p z 的虚部为1- ()A 23,p p ()B 12,p p ()C ,p p 24 ()D ,p p 34(4)设12F F 是椭圆2222:1(0)x y E a b a b +=>>的左、右焦点,P 为直线32ax =上一点,∆21F PF 是底角为30 的等腰三角形,则E 的离心率为( )()A 12 ()B 23 ()C 34()D 45(5)已知{}n a 为等比数列,472a a +=,568a a =-,则110a a +=( )()A 7 ()B 5 ()C -5()D -7(6)如果执行右边的程序框图,输入正整数(2)N N ≥和实数12,,...,n a a a ,输出,A B ,则( )()A A B +为12,,...,n a a a 的和 ()B 2A B+为12,,...,n a a a 的算术平均数 ()C A 和B 分别是12,,...,n a a a 中最大的数和最小的数 ()D A 和B 分别是12,,...,n a a a 中最小的数和最大的数(7)如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则此几何体的体积为( ) ()A 6 ()B 9 ()C 12 ()D 18(8)等轴双曲线C 的中心在原点,焦点在x 轴上,C 与抛物线x y 162=的准线交于,A B两点,AB =C 的实轴长为( )()A ()B ()C 4 ()D 8(9)已知0ω>,函数()sin()4f x x πω=+在(,)2ππ上单调递减。
苏州大学2012届高考数学考前指导题组

19-3.在直角坐标平面上有一点列P1(x1,y1),P2(x2,y2),…,Pn(xn,yn),…,对一切正整数n, 13 5 点Pn位于函数y=3x+ 4 的图象上,且Pn的横坐标构成以-2为首项,-1 为公差的等差数列{xn}. (1)求点 Pn 的坐标; (2)设抛物线列 c1,c2,c3,…,cn,…中的每一条的对称轴都垂直于 x 轴,第 n 条抛物线 cn 的顶点为 Pn,且过点 Dn(0,n2+1),设与抛物线 cn 相切于 Dn 的直线的斜率为 kn. 1 1 1 求:k k +k k +…+ ; k - 1 2 2 3 n 1kn * (3)设S={x|x=2xn,n∈N },T={y|y=4yn,n∈N*},等差数列{an}的任一项an∈S∩T,其中 a1 是S∩T中的最大数,-265<a10<-125,求{an}的通项公式.
y P
F1 A
O
F2
B
x
18-3.设 F1 , F2 是椭圆 C :
x2 y 2 1 (a b 0) 的左、右 a 2 b2 焦点,A, B 分别为其左顶点和上顶点,BF1 F2 是面积为 3
A
y
B
O
N
M
的正三角形. (1)求椭圆 C 的方程; (2)过右焦点 F2 的直线 l 交椭圆 C 于 M , N 两点,直线
A
A
F D C E 图(1) B
F
D
C
E 图(2)
B
18 - 1 .如图,已知椭圆
x2 y 2 1 (a b 0) 的左,右焦点为 a 2 b2 F1 , F2 ,点 P 为椭圆上动点,弦 PA,PB 分别过点 F1 , F2 . 24 (1) 若 F1 (3,0) , 当 PF1 F1 F2 时, 点 O 到 PF2 的距离为 , 17 求椭圆的方程; (2)设 PF1 1 F1 A , PF2 2 F2 B, 1 , 2 R ,求证: 1 2 为定值.
2012届高考数学综合复习检测试题

第十七章综合检测一.选择题: (以下题目从4项答案中选出一项,每小题5分,共40分) 1. 集合P ={1, 4, 9, 16…},若a ∈P , b ∈P 则a ⊕b ∈P ,则运算⊕可能是 A .加法 B .减法 C .除法 D .乘法[解析] D.2. 若平面四边形ABCD 满足0AB CD +=,()0AB AD AC -⋅=,则该四边形一定是 A .直角梯形 B .矩形 C .正方形 D .菱形 [解析] D.[AB//CD,BD ⊥AC]3. (2008·珠海市高三教学质量检测)给出下面类比推理命题(其中Q 为有理数集,R 为实数集,C 为复数集): ①“若a,b b a b a R =⇒=-∈0,则”类比推出“若a,b b a b a C =⇒=-∈0,则”;②“若a,b,c,d d b c a di c bi a R ==⇒+=+∈,,则复数”类比推出“若a,b,c,d ,Q ∈则d b c a d c b a ==⇒+=+,22”;③“若a,b b a b a R >⇒>-∈0,则” 类比推出“若a,b b a b a C >⇒>-∈0,则”;其中类比结论正确的个数是 ( ) (A).0 (B).1 (C).2 (D).3[解析] B.[正确命题①]4. (09深圳九校)平面向量也叫二维向量,二维向量的坐标表示及其运算可以推广到(3)n n ≥维向量,n 维向量可用123(,,,,)n x x x x 表示.设123(,,,,)n a a a a a =,123(,,,,)n b b b b b =,规定向量a 与b 夹角θ的余弦为∑∑∑====n i ni i i ni ii b a ba 11221))((cos θ.当(1,1,1,1)a =,(1,1,1,1)b =--时,cos θ=A .nn 1- B .nn 3- C .nn 2- D .nn 4- [解析]n n 2- [=⋅-=nn n 2cos θn n 2-]5. 下列函数中,在区间02π⎛⎫⎪⎝⎭,上为增函数且以π为周期的函数是A .sin2xy = B . sin y x = C . tan y x =- D . cos 2y x =-[解析] D6. 若一系列函数的解析式相同、值域相同,但其定义域不同,则称这些函数为“同族函数”,那么函数解析式为y =x 2、值域为{0,4}的“同族函数”共有( )个. A. 2 B. 3 C. 4 D.无数[解析]3. [定义域可以是以下3种情况:{0,2}、{0,-2}、{0,2,-2}]7.(08南昌调研)对于使22x x M -+≤成立的所有常数M 中,我们把M 的最小值1叫做22x x -+的上确界,若,,1a b R a b +∈+=且,则122a b --的上确界为A .92B .92-C .41 D .4-[解析] B122a b--29)2225()221)((-≤++-=++-=b a a b b a b a ,29-≥∴M ,122a b --的上确界为92-8. (2008深圳二模)如图,圆周上按顺时针方向标有1,2,3,4,5五个点。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(时间60分钟,满分80分)
一、选择题(共6个小题,每小题5分,满分30分)
1.不等式(x -2y +1)(x +y -3)≤0在坐标平面内表示的区域(用阴影部分表示)应是
( )
解析:(x -2y +1)(x +y -3)≤0
⇔⎩⎪⎨⎪⎧ x -2y +1≥0,x +y -3≤0或⎩⎪⎨⎪⎧
x -2y +1≤0,x +y -3≥0.
结合图形可知选C. 答案:C
2.设D 是由⎩
⎪⎨⎪⎧
(x -y )(x +y )≥0,y ≥0所确定的平面区域,记D 被夹在直线x =-1和x =t (t
∈[-1,1])间的部分的面积为S ,则函数S =f (t )的大致图象为( )
解析:如图,由不等式组画出平面区域.根据题意,由函数S =f (t )的单调递增情况易选出答案B.
答案:B
3.设变量x ,y 满足约束条件⎩⎪⎨⎪
⎧
x ≥0,x -y +1≥0,
x +y -3≤0,则z =2x +y 的最大值为( )
A .-2
B .4
C .6
D .8
解析:在坐标平面内画出题中的不等式组表示的平面区域及直线2x +y =0,平移该直线,当该直线经过该平面区域内的点(3,0)时,相应直线在x 轴上的截距最大,此时z =2x +y 取得最大值,最大值是z =2x +y =2×3+0=6.
答案:C
4.不等式组⎩⎪⎨⎪
⎧
x -y +5≥0y ≥a 0≤x ≤3表示的平面区域是一个三角形,则a 的范围是( )
A .a <5
B .a ≥8
C .5≤a <8
D .a <5或a ≥8
解析:如图所示,⎩⎪⎨⎪⎧
x -y +5=0
x =0的交点为(0,5),
⎩
⎪⎨⎪⎧
x -y +5=0
x =3的交点为(3,8),∴5≤a <8.
答案:C
5.已知约束条件⎩⎪⎨⎪
⎧
x -3y +4≥0x +2y -1≥0
3x +y -8≤0,若目标函数z =x +ay (a ≥0)恰好在点(2,2)处取得最
大值,则a 的取值范围为( )
A .0<a <1
3
B .a ≥1
3
C .a >1
3
D .0<a <1
2
解析:画出已知约束条件的可行域为△ABC 内部(包括边界),
如图,易知当a =0时,不符合题意;当a >0时,由目标函数z =x
+ay 得y =-1
a x +z a
,
则由题意得-3=k AC <-1
a <0, 故a >13.综上所述,a >13.
答案:C
6.设不等式组⎩⎪⎨⎪
⎧
x +y -11≥03x -y +3≥0
5x -3y +9≤0
表示的平面区域为D .若指数函数y =a x 的图象上存在
区域D 上的点,则a 的取值范围是( )
A .(1,3]
B .[2,3]
C .(1,2]
D .[3,+∞)
解析:画出不等式组表示的平面区域如图中阴影部分所示(包括边界).当a >1时才能够使函数y =a x 的图象上存在区域D 上的点,由图可知当函数y =a x 的图象经过点A 时a 取得最大值,
由方程组
⎩⎪⎨⎪⎧
x +y -11=0,
3x -y +3=0,
解得x =2,y =9,即点A (2,9), 代入函数解析式得9=a 2, 即a =3,故1<a ≤3. 答案:A
二、填空题(共3个小题,每小题5分,满分15分) 7.如果点P 在平面区域⎩⎪⎨⎪⎧
x ≥1y ≤2
x -y ≤0上,点M 的坐标为(3,0),那么|PM |的最小值是
________.
解析:点P 所在的可行域如图中阴影部分(包括边界)所示,点M 到A (1,1),
B (2,2)的距离分别为5,5,
又点M (3,0)到直线x -y =0的距离为322,故|PM |的最小值为32
2.
答案:
32
2
8.不等式组⎩⎪⎨⎪
⎧
x -2≤0,y +2≥0,
x -y +1≥0
表示的区域为D ,z =x +y 是定义在D 上的目标函数,则
区域D 的面积为________;z 的最大值为________.
解析:图象的三个顶点分别为(-3,-2)、(2,-2)、(2,3),所以面积为
25
2
,因为目标函数的最值在顶点处取得,把它们分别代入z =x +y 得,x =2,y =3时,有z max =5.
答案:
252
5 9.设z =x +y ,其中x ,y 满足⎩⎪⎨⎪
⎧
x +2y ≥0x -y ≤0
0≤y ≤k
,若z 的最大值为6,则z 的最小值为________.
解析:如图,x +y =6过点A (k ,k ),k =3,z =x +y 在点B 处取得最小值,B 点在直
线x +2y =0上,
B (-6,3),
∴z min =-6+3=-3. 答案:-3
三、解答题(共3个小题,满分35分) 10.画出不等式组⎩⎪⎨⎪
⎧
x -y +5≥0,x +y ≥0,
x ≤3表示的平面区域,并回答下列问题:
(1)指出x 、y 的取值范围; (2)平面区域内有多少个整点?
解:(1)不等式x -y +5≥0表示直线x -y +5=0上及其右下方的点的集合,x +y ≥0表示直线x +y =0上及其右上方的点的集合,x ≤3表示直线x =3上及其左方的点的集合.
所以,不等式组⎩⎪⎨⎪
⎧
x -y +5≥0,x +y ≥0,
x ≤3
表示的平面区域如图所示.
结合图中可行域得x ∈⎣⎡⎦⎤-5
2,3,y ∈[-3,8]. (2)由图形及不等式组知
⎩⎪⎨⎪⎧
-x ≤y ≤x +5,-52
≤x ≤3,且x ∈Z , 当x =3时,-3≤y ≤8,有12个整点; 当x =2时,-2≤y ≤7,有10个整点; 当x =1时,-1≤y ≤6,有8个整点; 当x =0时,0≤y ≤5,有6个整点; 当x =-1时,1≤y ≤4,有4个整点; 当x =-2时,2≤y ≤3,有2个整点; ∴平面区域内的整点共有 2+4+6+8+10+12=42(个).
11.某班计划用少于100元的钱购买单价分别为2元和1元的大小彩球装点联欢晚会的会场,根据需要,大球数不少于10个,小球数不少于20个,请你给出几种不同的购买方案?
解:设可购买大球x 个,小球y 个.
依题意有⎩⎪⎨⎪⎧
2x +y <100
x ≥10y ≥20
x ∈N *
y ∈N
*
,
其整数解为⎩⎪⎨⎪⎧ x =10y =20,⎩⎪⎨⎪⎧ x =20y =30,⎩⎪⎨⎪⎧ x =30y =30,⎩
⎪⎨⎪
⎧
x =35y =29,…,
都符合题目要求(满足2x +y -100<0即可).
12.某营养师要为某个儿童预订午餐和晚餐.已知一个单位的午餐含12个单位的碳水化合物,6个单位的蛋白质和6个单位的维生素C ;一个单位的晚餐含8个单位的碳水化合物,6个单位的蛋白质和10个单位的维生素C.另外,该儿童这两餐需要的营养中至少含64个单位的碳水化合物,42个单位的蛋白质和54个单位的维生素C.如果一个单位的午餐、晚餐的费用分别是2.5元和4元.那么要满足上述的营养要求,并且花费最少,应当为该儿童分别预订多少个单位的午餐和晚餐?
解:法一:设需要预订满足要求的午餐和晚餐分别为x 个单位和y 个单位,所花的费用为z 元,则依题意得:
z =2.5x +4y ,且x ,y 满足
⎩⎪⎨⎪⎧
x ≥0,y ≥0,12x +8y ≥64,6x +6y ≥42,6x +10y ≥54.
即⎩⎪⎨⎪⎧
x ≥0,y ≥0,
3x +2y ≥16,x +y ≥7,3x +5y ≥27.
z 在可行域的四个顶点A (9,0),B (4,3),C (2,5),D (0,8)处的值分别是 z A =2.5×9+4×0=22.5, z B =2.5×4+4×3=22, z C =2.5×2+4×5=25, z D =2.5×0+4×8=32.
比较之,z B 最小,因此,应当为该儿童预订4个单位的午餐和3个单位的晚餐,就可满足要求.
法二:设需要预订满足要求的午餐和晚餐分别为x 个单位和y 个单位,所花的费用为z 元,则依题意得:z =2.5x +4y ,且x ,y 满足
⎩⎪⎨⎪⎧
x ≥0,y ≥0,
12x +8y ≥64,6x +6y ≥42,6x +10y ≥54.
即⎩⎪⎨⎪⎧
x ≥0,y ≥0,
3x +2y ≥16,x +y ≥7,3x +5y ≥27.
让目标函数表示的直线2.5x +4y =z 在可行域上平移, 由此可知z =2.5x +4y 在B (4,3)处取得最小值.
因此,应当为该儿童预订4个单位的午餐和3个单位的晚餐,就可满足要求.。
