一次函数
一次函数

y=2x过点A,当2x<kx+b<0时,x的取值范围是( )
A. B. C. D.
第4题图
第5题图
第6题图
7. 如图,直线y=kx+b交坐标轴于A(-3,0)、B(0,5)两点,当-
3<x<0时,y的取值 范围是
.
8. 如图,已知函数和的图象交点为,则不等式的解集为
.
9. 如图,已知函数和的图像交于点,则根据图像可得不等式的解集是
C.(1,-1)
D.(1,1)
5. 如图,已知直线y=kx+b经过第一、二、四象限,则直线y=bx-k过(
)
A.第一、二、四象限 B.第二、三、四象限 C.第一、三、四象限 D.第一、二、三象限 6. 在同一平面直角坐标系中,一次函数与正比例函数
(是常数,
且)
的图象只可能是( )
D 0 x
0 A y x 0 C x 0 B x y y y
是x的正比例函数.所以,正比例函数是一次函数的特例.
3、会画一次函数的图像,掌握当k和b取不同的值时一次函数图像所
经过的象限。 4、掌握一次函数的性质以及其在实际问题中的应用。 5、会解决一次函数与几何问题的综合问题。 【知识结构】 1、一次函数的概念与一般形式:y=kx+b(k、b为常数,k ≠ 0)。 2、一次函数的图像。 3、一次函数的性质。 4、一次函数与实际 问题的结合。 【重点知识解析】
到达点B,最后走下坡路到达工作单位,所用的时间与路程的关
系如图所示.下班后,如果他沿原路返回,且走平路、上坡路、
下坡路的速度分别保持和去上班时一致,那么他从单位到家门口
需要的时间是( )
A.12分钟 B.15分钟 C.25分钟
一次函数的定义和性质

一次函数的定义和性质一次函数是指形如y=ax+b的函数,其中a和b为常数,且a不等于零。
它也被称为线性函数,因为它的图像是一条直线。
一次函数是数学中的基础概念之一,具有一些重要的性质和应用。
一. 定义一次函数是指以x为自变量,以y为因变量的函数,其表达式为y=ax+b,其中a和b为实数,且a不等于零。
其中,a称为一次项的系数,b称为常数项。
当x取不同的值时,y的取值也相应地发生变化,这种对应关系可以通过一条直线来表示。
二. 图像特征1. 直线特征:一次函数的图像总是一条直线,因此它具有线性特征;2. 斜率特征:一次函数的斜率表示为常数a,描述了图像在x轴正方向上的倾斜程度。
斜率为正时,表示图像向上倾斜;斜率为负时,表示图像向下倾斜;3. 截距特征:一次函数的截距表示为常数b,描述了图像与y轴的交点位置。
截距为正时,表示图像与y轴正半轴交于正值点;截距为负时,表示图像与y轴负半轴交于负值点。
三. 性质1. 单调性:一次函数的单调性由斜率的正负决定。
当a大于零时,函数单调递增;当a小于零时,函数单调递减;2. 定义域和值域:一次函数的定义域为所有实数;值域为所有实数,即函数的取值范围没有限制;3. 零点:一次函数的零点即为函数的根,表示当x取某个值时,函数的值等于零。
对于一次函数,当且仅当x=-b/a时,函数的值为零;4. 最值:一次函数没有最大值和最小值,因为它的图像是一条直线;5. 平移:通过给定一次函数的表达式,可以进行平移操作来得到新的函数。
平移操作可以在x轴和y轴上分别进行,通过改变常数a和b的值,可以使图像在平面上发生移动。
四. 应用一次函数在现实生活中有着广泛的应用,例如:1. 财务收入:一些经济指标和统计数据的变化趋势可以通过一次函数来表示,如年度收入的增长率;2. 运动模型:一次函数可以表示一些常见的运动模型,如匀速运动的位移和速度关系;3. 经济学模型:在经济学中,一次函数可以用来表示供求关系、成本和收益关系等;4. 工程预测:一次函数可以用来进行工程测量、预测物理量的变化趋势等。
一次函数

一次函数知识点聚焦一、函数的概念定义:在某一变化过程中,可以取不同数值的量,叫做变量,例如x 和y ,对于x 的每一个值,y 都有惟一..的值与之对应,我们就说x 是自变量,y 是因变量,此时也称y 是x 的函数. 二、一次函数概念:1.一次函数的概念:一般地,如果y =kx +b(k 、b 是常数,k ≠0),那么y 叫做x 的一次函数.特别地,当b =0时,一次函数y =kx +b 就成为y =kx(k 是常数,k ≠0),这时,y 叫做x 的正比例函数.由定义知:y 是x 的一次函数⇔它的解析式是y =kx +b ,其中k 、b 是常数,且k ≠0.2.一次函数解析式y =kx +b(k ≠0)的结构特征:(1)k ≠0;(2)x 的次数是1;(3)常数项b 可为任意实数.3.正比例函数解析式y =kx(k ≠0)的结构特征:(1)k ≠0;(2)x 的次数是1;(3)没有常数项或者说常数项为0.4. 正比例函数是一次函数,但一次函数y =kx +b(k ≠0)不一定是正比例函数,只有当b=0时才是正比例函数。
三、一次函数的图像1.一次函数y =kx +b(k≠0)的图象是经过点(0,b)和(-b k,0)的一条直线.2.正比例函数y =kx(k ≠0)的图象是经过点(0,0)和(1,k)的一条直线.注意:画一次函数的图像,只需要过图像上两点作直线即可,一般取(0,b )、(-b k,0)两点。
四、一次函数图像的性质1. 一次函数y =kx +b ,当k >0时,y 随x 的增大而增大,图象一定经过第一、三象限;当k <0时,y 随x 的增大而减小,图象一定经过第二、四象限.b>0时,直线交y 轴正半轴,b<0时,直线交y 轴负半轴。
2.一次函数y=kx+b(k ≠0)的图象是经过点(0,b)且平行于直线y=kx (k ≠0)的一条直线3. 平移规律在原有函数的基础上“k 值正右移,负左移;b 值正上移,负下移”。
一次函数
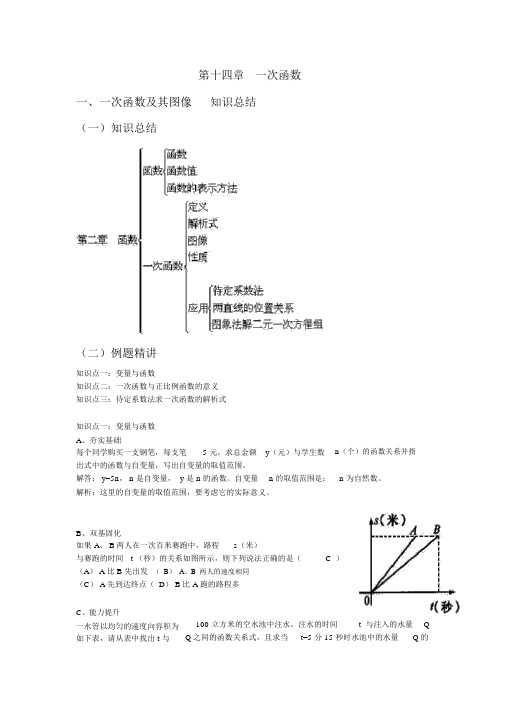
第十四章一次函数一、一次函数及其图像知识总结(一)知识总结(二)例题精讲知识点一:变量与函数知识点二:一次函数与正比例函数的意义知识点三:待定系数法求一次函数的解析式知识点一:变量与函数A、夯实基础每个同学购买一支钢笔,每支笔 5 元,求总金额y(元)与学生数出式中的函数与自变量,写出自变量的取值范围。
解答: y=5n, n 是自变量, y 是 n 的函数。
自变量n 的取值范围是:解析:这里的自变量的取值范围,要考虑它的实际意义。
n(个)的函数关系并指n 为自然数。
B、双基固化如果 A、 B两人在一次百米赛跑中,路程s(米)与赛跑的时间t (秒)的关系如图所示,则下列说法正确的是((A) A 比 B 先出发(B)A、B两人的速度相同(C) A 先到达终点( D) B 比 A 跑的路程多C )C、能力提升一水管以均匀的速度向容积为如下表,请从表中找出 t 与100 立方米的空水池中注水,注水的时间t 与注入的水量Q Q之间的函数关系式,且求当t=5 分 15 秒时水池中的水量Q的值.T(分钟)2468...Q(立方米)481216...解答:∵水管是匀速流出水于池中,速度是(4 ÷ 2)=2 ,即每分钟Q=2t,自变量 t 为非负数 .又∵水池容积为100 立方米,时间不能超过100÷2=50( 分钟 ) ,∴0≤ t ≤ 50.2 立方米,函数解析式为当t=5 分 15 秒时, Q=2× 5.25=10.5( 立方米 )即当 t 为 5 分 15 秒时,水量为10.5立方米.知识点二:一次函数与正比例函数的意义A、夯实基础下列函数中 , 哪些是一次函数(1)Y = -3X+7是一次函数.(2)Y = 6X2-3X不是一次函数.(3)Y = 8X是一次函数, 也是正比例函数(4)Y = 1+9X是一次函数(5)Y =6不是一次函数XB、双基固化列出下列函数关系式,判别其中哪些为一次函数、正比例函数.(1)正方形周长 p 和一边的长 a.解答 :(1)∵p=4a.自变量 a 为一次且其系数为4( 不为零 ) .∴p为 a 的一次函数.又∵不含常数项∴也是正比例函数.(2) 长 a 一定时矩形面积y 与宽 x.解答:∵ y=ax,自变量x 为一次且系数 a 为长度 ( 不为零 ) .∴y是 x 的一次函数.∵不含常数项.∴y也是 x 的正比例函数.(3)定期存 100 元本金,月利率 1.8 %,本息和 y 与所存月数 x.解答 : ∵ y=100+100× 1.8%x,自变量 x 的次数为一次,又含有常数项.∴ y 是 x 的一次函数但不是正比例函数.(4) 水库原存水Q立方米,现以每小时 a 立方米的流量开闸放水,同时上游以每小时 b 立方米的流量向水库注水,求这时水库的蓄水量M与时间 t 的函数关系.解答 : ∵ M=Q+(b-a)t ,因为自变量 t 的次数为一次,当 a≠ b 时, M是 t 的一次函数.若 Q=0 时,M是 t 的正比例函数;若 a=b 时, M是常量函数,不是 t 的一次函数.C、能力提升已知 y = -(m2+2m)xm2+m-1 ,当 m是什么数值时,为正比例函数?解答:设正比例函数为y = kx (k≠ 0),∵正比例函数k≠ 0,x 的指数为1.∴m2+2m≠ 0,解得 m1≠ 0, m2≠-2 ,且m2+m-1 = 1 ,解得 m3 = -2 ,m4 = 1 .∴当 m = 1 时,为正比例函数.知识点三:待定系数法求一次函数的解析式B、双基固化已知一次函数y=kx+b 在 x=-4 时的值为9,在 x=6 时的值为 3,求k 与 b解:由已知得:9 = - 4k + b3 = 6k + b解得 k=- 0.6, b = 6.6C、能力提升一次函数的图象经过点(0,2)和点( 4, 6)。
一次函数课件ppt

奇偶性
一次函数既不是奇函数也不是偶函数 ,因为它们的图像不关于原点或 y 轴 对称。
02 一次函数的表达式与系数
一次函数的表达式
01
一次函数的一般表达式为 $y = ax + b$,其中 $a$ 和 $b$ 是常 数,且 $a neq 0$。
02
当 $a > 0$ 时,函数为增函数; 当 $a < 0$ 时,函数为减函数。
已知函数与$x$轴和$y$轴的截距,使用截 距式$y = frac{x}{a} + frac{b}{a}$求函数解 析式。
一次函数的解题技巧
数形结合
利用函数图像直观理解 函数性质,如增减性、
最值等。
整体代入
在求解过程中,将表达 式整体代入,简化计算
。
分类讨论
根据不同情况分类讨论 ,得出不同情况下的函
斜率与图像
斜率决定了图像的倾斜程 度,当 a > 0 时,图像向 右倾斜;当 a < 0 时,图 像向左倾斜。
一次函数的性质
单调性
无界性
一次函数的单调性由斜率决定,当 a > 0 时,函数单调递增;当 a < 0 时 ,函数单调递减。
一次函数的值域是全体实数,即对于 任意实数 x,y = ax + b 总有一个对 应的值。
一次函数的系数
一次函数的斜率为 $a$,表示函数图 像的倾斜程度。
当 $a > 0$ 时,函数图像从左下到右 上倾斜;当 $a < 0$ 时,函数图像从 左上到右下倾斜。
一次函数的应用
一次函数在数学、物理、工程等领域都有广泛应用。
在实际生活中,一次函数可以用来描述一些简单的问题,如速度与时间的关系、 价格与数量的关系等。
一次函数基本概念

一次函数基本概念篇一:一次函数是一种基本的数学函数,表示输入一次变量的值,就可以得到输出变量的值。
一次函数通常用于描述简单的数学计算,如求和、加减、乘除等。
在一元一次函数中,输入的变量只可能是一个整数,输出的变量也只会是一个整数。
例如,y = 2x + 1是一次函数,因为输入的变量x为2,输出的变量y为3。
在二元一次函数中,输入的变量可以是两个整数,输出的变量也可以是两个整数。
例如,z = 2x + 3和y = 4x + 2是一次函数,因为输入的变量x为2,输出的变量y为6,输入的变量z为3,输出的变量z为9。
一次函数的解析式通常可以用一次方程表示,例如y = 2x + 1。
一次方程是一个二元一次方程,它的解可以用一个整数来表示,例如x = 2,y = 3。
在实际应用中,我们可以使用代数方法来求解一次方程,例如消元、代入等方法。
除了基本的一次函数,还有很多其他的数学函数,例如二次函数、指数函数、对数函数等。
这些函数都有不同的输入和输出变量,但它们的共同点是都可以描述一些复杂的数学问题。
在数学研究中,我们可以使用这些函数来解决一些复杂的问题,例如几何、微积分等。
篇二:一次函数是一种基本的数学函数,描述了一个变量随着另一个变量的变化而变化的函数。
在数学中,一次函数通常用字母f(x) 表示,其中 x 是自变量,f(x) 是因变量。
一次函数可以写成这样的形式:f(x) = c,其中 c 是常数,通常被称为函数的“导数”。
这个表达式表示,当自变量 x 变化时,因变量 f(x) 的变化率等于常数 c。
一次函数具有一些特殊的性质,例如它的图像是一条直线、它的导数等于函数本身等。
这些性质使得一次函数在许多领域中都有广泛的应用,例如物理学、工程学、经济学等。
除了上面的基本概念外,一次函数还有一些更深入的拓展。
例如,一次函数可以表示为两个变量的线性关系,即 f(x) =k1x1 + k2x2,其中 k1 和 k2 是常数。
一次函数公式

一次函数公式
一次函数公式是数学中常用的一种函数公式,它是一类函数的代表,它的特点是它的函数图像只有一个拐点,而且拐点处的斜率是一恒定的值。
一次函数公式的形式为:y=ax+b,其中a和b是常数,x是变量,y是函数值。
一次函数公式的应用非常广泛,它可以用来解决许多数学问题,例如求解抛物线的顶点、求解一元二次方程的根、求解正弦函数的最大值等。
同时,一次函数公式还可以用来解决实际问题,例如求解经济学中的供求曲线、求解物理学中的势能曲线、求解化学中的反应速率曲线等。
一次函数公式的研究和应用,可以帮助我们更好地理解自然界的规律,也可以为我们解决实际问题提供有效的帮助。
一次函数最值问题

一次函数最值问题
一次函数一般形式为 y = kx + b,其中 k 和 b 是常数,且k ≠ 0。
对于一次函数,其斜率为 k。
1. 当 k > 0 时,函数 y = kx + b 是增函数,即随着 x 的增加,y 也增加。
因此,函数的最大值出现在 x 的正无穷大处,此时 y 的值为正无穷大。
函数的最小值出现在 x = -b/k 处,此时 y 的值为 -b。
2. 当 k < 0 时,函数 y = kx + b 是减函数,即随着 x 的增加,y 减小。
因此,函数的最大值出现在 x 的负无穷大处,此时 y 的值为正无穷大。
函数的最小值出现在 x = -b/k 处,此时 y 的值为 -b。
需要注意的是,由于一次函数的定义域是全体实数,因此其最值是相对于定义域而言的。
在实际情况中,我们可能需要考虑函数的定义域和值域,以及函数的实际应用背景来求解最值问题。
一次函数详解

一次函数
一次函数的定义
一般地,形如y=kx+b(k,b是常数,且k≠0)
的函数,叫做一次函数,其中x是自变量。当b=0 时,一次函数y=kx(k≠0),又叫做正比例函数 (正比例函数是一次函数的特例,一次函数包括 正比例函数)。
析式
形式是y=kx+b,判断一个函数是否是一次函数, 就是判断是否能化成这种形式。 注:一次函数一般形式 y=kx+b (k不为零) ① k不为零 ②x指数为1 ③ b取任意实数
图像
一次函数y=kx+b在直角坐标系中 的图像是一条直线。k是斜率(反 映直线对x轴的倾斜度)。
k>0时,图像从左到右上升,y随x 的增大而增大,经过的象限如图:
k<0时,图像从左到右下降,y 随x的增大而减小,经过的象限 如图:
性质
在一次函数上的任意一点P(x,y),都满足 等式:y=kx+b(k≠0)。
一次函数与y轴交点的坐标总是(0,b),与x轴 总是交于(-b/k,0),正比例函数的图像都是过 原点的。
最值
一般情况,一次函数没有最大值或最小值,但 是当自变量的取值范围有限制时,在端点可以 取到最大值或最小值。在应用题中要特别注意 自变量的取值范围。
过定点
正比例函数y=kx,过(0,0),(1,k) 一次函数y=kx+b,过(0,b),(-b/k,0) 例如直线y=kx-k,此时b=-k,套用(-b/k,0),可知y=kx-k 过定点(1,0)。 这种题也可以这样理解,对于y=kx-k,当x确定时y与k值有 关,所以y不确定,想过定点(x1,y1),需要使y与k无关。 由于参数k是字母,可以把它当作关于k的方程,即y=(x-1)k。 该方程有无数个解(无论k取何值,(x1,y1)都满足这个方程)
一次函数专题

一次函数【知识点】1、一次函数的定义一般地,形如y kx b =+(k ,b 是常数,且0k ≠)的函数,叫做一次函数,其中x 是自变量。
当0b =时,一次函数y kx =,又叫做正比例函数。
⑴一次函数的解析式的形式是y kx b =+,要判断一个函数是否是一次函数,就是判断是否能化成以上形式.⑵当0b =,0k ≠时,y kx =仍是一次函数.⑶当0b =,0k =时,它不是一次函数.⑷正比例函数是一次函数的特例,一次函数包括正比例函数.2、正比例函数及性质一般地,形如y=kx (k 是常数,k≠0)的函数叫做正比例函数,其中k 叫做比例系数.(1)解析式:y=kx(k 是常数,k≠0)(2)必过点:(0,0)、(1,k)(3)走向:k>0时,图像经过一、三象限;k<0时, 图像经过二、四象限(4)增减性:k>0,y 随x 的增大而增大;k<0,y 随x 增大而减小(5)倾斜度:|k|越大,越接近y 轴;|k|越小,越接近x 轴3、一次函数及性质一般地,形如y=kx +b(k,b 是常数,k≠0),那么y 叫做x 的一次函数.当b=0时,y=kx +b 即y=kx ,所以说正比例函数是一种特殊的一次函数.注:一次函数一般形式y=kx+b (k 不为零)①k 不为零②x 指数为1③b 取任意实数一次函数y=kx+b 的图象是经过(0,b)和(-kb,0)两点的一条直线,我们称它为直线y=kx+b,它可以看作由直线y=kx 平移|b|个单位长度得到.(当b>0时,向上平移;当b<0时,向下平移)(1)解析式:y=kx+b(k、b 是常数,k ≠0)(2)必过点:(0,b)和(-kb,0)(3)走向:k>0,图象经过第一、三象限;k<0,图象经过第二、四象限b>0,图象经过第一、二象限;b<0,图象经过第三、四象限⇔⎩⎨⎧>>0b k 直线经过第一、二、三象限⇔⎩⎨⎧<>0b k 直线经过第一、三、四象限⇔⎩⎨⎧><00b k 直线经过第一、二、四象限⇔⎩⎨⎧<<00b k 直线经过第二、三、四象限(4)增减性:k>0,y 随x 的增大而增大;k<0,y 随x 增大而减小.(5)倾斜度:|k|越大,图象越接近于y 轴;|k|越小,图象越接近于x 轴.(6)图像的平移:当b>0时,将直线y=kx 的图象向上平移b 个单位;当b<0时,将直线y=kx 的图象向下平移b 个单位.4、一次函数y=kx +b 的图象的画法.根据几何知识:经过两点能画出一条直线,并且只能画出一条直线,即两点确定一条直线,所以画一次函数的图象时,只要先描出两点,再连成直线即可.一般情况下:是先选取它与两坐标轴的交点:(0,b ),.即横坐标或纵坐标为0的点.b>0b<0b=0k>0经过第一、二、三象限经过第一、三、四象限经过第一、三象限图象从左到右上升,y 随x 的增大而增大k<0经过第一、二、四象限经过第二、三、四象限经过第二、四象限图象从左到右下降,y 随x 的增大而减小5、正比例函数与一次函数之间的关系一次函数y=kx +b 的图象是一条直线,它可以看作是由直线y=kx 平移|b|个单位长度而得到(当b>0时,向上平移;当b<0时,向下平移)考点例析考点1认识一次函数1.下列函数关系式:①y=-2x,②y=-2x,③y=-2x2,④y=3x,⑤y=2x-1.其中是一次函数的有()A.①⑤B.①④⑤C.②⑤D.②④⑤2.若一次函数y=kx+b,当x=-2时,y=7;当x=1时,y=-11,则k、b的值为()A.k=6,b=5B.k=-1,b=-5C.k=-6,b=-5D.k=1,b=53.据调查,某地铁自行车存放处在某星期天的存车量为4000辆次,其中变速车存车费是每辆一次0.30元,普通自行车存车费是每辆一次0.20元,若普通自行车存车数为x辆,存车费总收入为y元,则y关于x的函数关系式为()A.y=0.10x+800(0≤x≤4000)B.y=0.10x+1200(0≤x≤4000)C.y=-0.10x+800(0≤x≤4000)D.y=-0.10x+1200(0≤x≤4000)4.若函数y=(n+2)x+(n2-4)是一次函数,则n__________;若函数y=(n+2)x+(n2-4)是正比例函数,则n__________.5.已知y=(m+1)x2-|m|+n+4.(1)当m,n取何值时,y是x的一次函数?(2)当m,n取何值时,y是x的正比例函数?6.函数y=(m-2)x n-1+n是一次函数,则m、n应满足的条件是()A.m≠2且n=0B.m=2且n=2C.m≠2且n=2D.m=2且n=07.若3y-4与2x-5成正比例,则y是x的()A.正比例函数B.一次函数C.没有函数关系D.以上均不正确8.如图,在△ABC中,∠ABC与∠ACB的平分线交于点P,设∠A=x,∠BPC=y,当∠A变化时,求y与x之间的函数关系式,并判断y是不是x的一次函数,指出自变量的取值范围.9.+(b-2)2=0,则函数y=(b+3)x-a+1-2ab+b2是什么函数?当x=-12时,函数值y是多少?10.已知y=y1+y2,y1与x成正比例,y2与x-2成正比例,当x=1时,y=0;当x=-3时,y=4.(1)求y与x的函数关系式,并说明此函数是什么函数;(2)当x=3时,求y的值.考点2一次函数的图象与性质1.(2014·东营)直线y=-x+1经过的象限是()A.第一、二、三象限B.第一、二、四象限C.第二、三、四象限D.第一、三、四象限2.(2014·资阳)一次函数y=-2x+1的图象不经过的象限是()A.第一象限B.第二象限C.第三象限D.第四象限3.(2014·温州)一次函数y=2x+4的图象与y轴交点的坐标是()A.(0,-4)B.(0,4)C.(2,0)D.(-2,0)4.若一次函数y=(2-m)x-2的函数值y随x的增大而减小,则m的取值范围是()A.m<0B.m>0C.m<2D.m>25.如果一次函数y=k x+b的图象经过第一、三、四象限,那么()A.k>0,b>0B.k>0,b<0C.k<0,b>0D.k<0,b<06.(2014·邵阳)已知点M(1,a)和点N(2,b)是一次函数y=-2x+1图象上的两点,则a与b的大小关系是()A.a>bB.a=bC.a<bD.以上都不对7.已知一次函数y=(a+8)x+(6-b),求:(1)a、b为何值时,y随x的增大而增大?(2)a、b为何值时,函数与y轴交点在x轴上方?(3)a、b为何值时,图象过原点?10.(2014·河北)如图,直线l经过第二、三、四象限,l的解析式是y=(m-2)x+n,则m的取值范围在数轴上表示为()11.(2014·达州)直线y=kx+b不经过第四象限,则()A.k>0,b>0B.k<0,b>0C.k>0,b≥0D.k<0,b≥012.(2014·娄底)一次函数y=kx-k(k<0)的图象大致是()13.(2014·巴中)已知直线y=mx+n,其中m、n是常数,且满足:m+n=6,mn=8,那么该直线经过()A.第二、三、四象限B.第一、二、三象限C.第一、三、四象限D.第一、二、四象限14.(2014·鞍山)在一次函数y=kx+2中,若y随x的增大而增大,则它的图象不经过第__________象限.15.(2014·嘉兴)点A(-1,y1),B(3,y2)是直线y=kx+b(k<0)的两点,则y1-y2__________0.(填“>”或“<”)16.如图是一个正比例函数的图象,把该图象向左平移1个单位长度,得到的函数图象的解析式为__________.17.已知一次函数y=kx-4,当x=2时,y=-3.(1)求一次函数的解析式;(2)将该函数的图象向上平移6个单位,求平移后的图象与x轴交点的坐标.18.作出一次函数y=2x-1的图象,根据图象回答问题:(1)y的值随x的变化怎样变化?(2)当x取何值时,y>0,y=0,y<0?(3)指出图象与两坐标轴的交点坐标.19.已知函数y=(2m+1)x+m-3.(1)若函数图象经过原点,求m的值;(2)若函数的图象平行直线y=3x-3,求m的值;(3)若这个函数是一次函数,且y随着x的增大而减小,求m的取值范围.挑战自我20.如图,点B是直线y=-x+8在第一象限的一动点,A(6,0),设△AOB的面积为S.(1)写出S与x之间的函数关系式,并求出x的取值范围;(2)画出S与x之间函数关系式的图象;。
一次函数知识点总结

一次函数知识点总结一次函数(也称线性函数)在数学中是一种基本的函数类型,具有简单直观的图像和重要的应用。
下面将对一次函数的相关知识点进行总结。
1. 定义和表达式一次函数是指具有形如 y = kx + b 的函数,其中 k 和 b 是常数,且k ≠ 0。
其中 k 表示斜率,b 表示截距。
一次函数的图像是一条直线。
2. 斜率的意义斜率是一次函数最重要的特征之一,它表示了函数图像在平面上的倾斜程度。
具体而言,斜率 k 表示单位自变量变化时,因变量相应的变化量。
斜率可以正负,正斜率表示函数图像从左下到右上逐渐升高,负斜率表示函数图像从左上到右下逐渐降低。
3. 截距的意义截距是一次函数图像与 y 轴交点的纵坐标,也就是当 x = 0 时,对应的 y 值。
截距 b 表示了函数图像与 y 轴的相对位置关系,它是一次函数图像上的常数项。
4. 图像特征和性质一次函数的图像是一条直线,根据斜率和截距的不同取值,可以分为四种情况:正斜率正截距、正斜率负截距、负斜率正截距和负斜率负截距。
根据斜率的大小可以判断函数图像的陡峭程度,斜率越大,函数图像越陡峭。
5. 函数的性质一次函数的性质非常重要,有助于解决实际问题和理解其他函数类型。
一次函数是一个线性函数,它的图像是直线,因此具有以下性质:- 一次函数上的任意两个点可以唯一确定一条直线。
- 一次函数的函数值随自变量的变化是线性变化的。
- 一次函数图像关于 y 轴对称。
- 一次函数图像不存在极值和拐点。
6. 直线方程与一次函数的关系一次函数可以通过直线方程 y = ax + b 来表示,其中 a 是斜率,b 是截距。
直线方程是一种常见的形式,可以更直观地表示函数图像的性质和特点。
7. 一次函数的应用举例一次函数在实际问题中有广泛的应用。
例如,在经济学中,一次函数可以用来描述成本和收入的关系;在物理学中,一次函数可以用来表示速度和位移的关系;在统计学中,一次函数可以用来进行线性回归等。
一次函数的概念说

斜率的概念与计算方法
斜率是一次函数的重要特征之一,它表示函数图像的斜率或倾斜程度。 斜率的计算方法包括利用直线上的两个点的坐标、借助方程的系数以及使用图像上的特征点等。 斜率在数学和物理等学科中广泛应用,帮助我们理解和解决各种实际问题。
截距的概念与计算方法
截距是一次函数图像与坐标轴的交点位置,它在函数的定义中起到重要的作用。 截距的计算方法包括利用函数的定义和图像上的特征点等。 截距的概念和计算方法对于理解和应用一次函数都具有重要意义。
一次函数的概念说
一次函数是数学中的基本函数之一。它具有许多重要的定义、特征和性质, 是解决各种实际问题的有力工具。
一次函数的定义及特征
一次函数是指函数的最高次数为1的多项式函数。它的一般形式可以表示为y = kx + b,其中k表示斜率,b表示截距。 一次函数具有线性关系、单一的倾斜方向,以及与坐标系的关系等特征。 一次函数的定义和特征对于理解和应用其他类型的函数都至关重要。
一次函数的变形与操作规律
一次函数可以通过改变斜率和截距的值进行变形和操作。 常见的一次函数变形包括水平平移、垂直平移、水平伸缩和垂直伸缩等。 对一次函数进行变形和操作可以改变其图像和性质,从而更好地适应实际问 题的需求。
点斜式方程的推导与应用
点斜式方程是一种表示一次函数的方程形式。 通过已知一次函数上的一点和斜率,可以推导出该函数的点斜式方程。 点斜式方程在几何和物理等学科中有广泛的应用,帮助我们分析和解决各种 实际问题。
线性方程与一次函数的关系
线性方程是一次方程的一种特殊形式。一次函数可以通过线性方程来表示。
通过解线性方程,我们可以确定一次函数的斜率和截距,从而得到该函数的 图像和性质。
线性方程和一次函数之间的关系是数学中的基本概念之一,也被广泛应用于 科一条直线。它在坐标系中呈现出特定的形状和方向。 一次函数的图像具有直线的特点,如斜率、截距以及与坐标轴的交点。 通过分析一次函数的图像,我们可以了解其特点和行为,从而更好地理解和应用一次函数。
一次函数

知识要点一、一次函数的概念(一)一次函数概念1、一般地,解析式形如y kx b =+(其中k 、b 是常数,且k ≠0)的函数叫做一次函数 定义域是一切实数2、正比例函数是一次函数的特例3、常值函数:一般地,我们把函数y c =(c 为常数)叫做常值函数(二)待定系数法求一次函数1、待定系数法:先设出待求函数的关系式,再根据条件求出未知系数,从而得到所求结果的方法,叫做待定系数法2、用待定系数法确定一次函数关系式的一般步骤:① 设函数关系式为y kx b =+(其中k 、b 为待定系数);② 将已知点的坐标代入函数关系式,解方程(组)③ 求出k 与b 的值,得到函数关系式二、一次函数的图像1、一次函数y kx b =+(其中k 、b 是常数,且k ≠0)的图像是一条直线。
一次函数y kx b =+的图像也称为直线y kx b =+2、一次函数图像的画法画一次函数的图像可通过“列表、描点、连线”获得。
也可由“两点确定一条直线”的知识,只需描出两个点,然后过这两点作一条直线一次函数与x 轴、y 轴的交点分别为,0b k ⎛⎫- ⎪⎝⎭、()0,b ,在画一次函数时,只需取者两点就可以了3、直线的截距一条直线与y 轴的交点的纵坐标叫做这条直线在y 轴上的截距,简称直线的截距 截距与距离是两个完全不一样的概念,截距可以是任意实数,而距离总是非负数4、一般地,一次函数y kx b =+(b ≠0)的图像可由正比例函数y kx =的图像平移得到。
当0b >时,向上平移b 个单位;当0b <时,向下平移b 个单位5、如果12b b ≠,那么直线1y kx b =+于直线2y kx b =+平行;反过来,如果直线12y k x b =+与直星之韵---睿思理科 2014 春季 一 次 函 数线22y k x b =+平行,那么12k k =,12b b ≠三、一次函数的性质0,0 0,0 0,0 0,0 k b y kx b k b y kx b k b y kx b k b y kx b >>=+⎧⎪><=+⎪⎨<>=+⎪⎪<<=+⎩直线经过第一、二、三象限直线经过第一、三、四象限直线经过第一、二、四象限直线经过第二、三、四象限题型1:一次函数的概念☆☆(一)选择题1、下列函数中,是y 关于x 的一次函数的是 ( )A. 2125y x =+ B. 2y =- C. 2、下列函数解析式中,属于一次函数的是( )① ()()20y a x a =+≠ ② ()10y ax a a=-≠ ③()()11y a x a =-+≠- ④ ()0a y a x a x =+≠ A ① B ①②③ C ①③ D 全部都是3、已知函数32y x =+,当x a =时的函数值为1,则a 的值为( ) A. 13 B. -1 C. -13D. 1 4、下列四个命题中,错误的是( )A. 正比例函数一定是一次函数B. 反比例函数不是一次函数C. 若1y -和x 成正比例,则y 是x 的一次函数D. 若1y -和x 成反比例,则y 是x 的一次函数5、下列函数:①()()50y m x m =-≠; ②()10y ax a a=+≠ ③()()33y k x k =-+≠- ④k y kx x =+()0k ≠ 其中是一次函数的有( )A. ①②③④B. ①C. ①②③D. ①③(二)填空题1、 已知常值函数()3f x =-,则()1f =____________2、 已知函数()52y m x b =+-+,当___________时,此函数是一次函数;当____________时,此函数是正比例函数。
一次函数总结

主要结论➢一次函数四种表达方式:1)斜截式:y=kx+b(k≠0)2)点斜式:(y−y0)=k(x−x0)(k≠0)3)两点式:y−y1y2−y1=x−x1x2−x14)方程式表达:Ax+By+C=0 (A,B≠0)➢点与点距离(弦长公式):d=√(1+k2)×|x1−x2|=√(1+1k2)×|y1−y2|➢点到直线距离:00√A2+B200√k2+1➢直线到直线距离:d=12√(A2+B2)2一、一次函数形式:1、斜截式:y=kx+b(k≠0)备注:也是直线常规表达方式,y轴交点为(0,b),2、点斜式:需知道斜率k,已知点(x0,y0)(y−y0)=k(x−x0)(k≠0)3、两点式:需知道直线上任意两点(x1,y1),(x2,y2)y−y1 y2−y1=x−x1 x2−x14、方程式表达:Ax+By+C=0 (A,B≠0)二、点与点距离(弦长公式):已知直角坐标系两点E(x1,y1),F(x2,y2),求EF线段长度三、点与直线关系:1、点到直线距离:1)已知直线L为Ax+By+C=0,直线外点P(x0,y0),则点P到直线距离为:|Ax+By+C|√A2+B22)已知直接L为y=kx+b,直线外点P(x0,y0),则点P到直线距离为:|kx−y+b|√k2+12、点关于直线的对称点:1)特殊情况:点P(x1,y1)关于x轴,y轴平行线对称2)特殊情况:点P(x1,y1)关于直线y=±x+c对称以上图y=x+c为例,将P点y1带入直线y1=x+c,求得的x即为对称点的x2;对应x1带如求得y2。
3)一般情况:点P(x1,y1)关于直线Ax+By+C=0对称本例题因为选择题,不用求解对称点,可用y 2−y 1x 2−x 1=−1k=−12,选出垂线上的点,如果有多选,可以用(x 1+x 22,y 1+y 22)过直线L 来筛选。
四、直线与直线关系设两条直线方程为Ax+By+C1=0Ax+By+C2=0则其距离公式为d=12222。
一次函数的性质及应用

一次函数的性质及应用一次函数,又称为线性函数,是数学中常见且重要的函数类型。
它的一般形式可以表示为y = ax + b,其中a和b为常数,x为自变量,y 为因变量。
本文将探讨一次函数的性质以及其在实际问题中的应用。
一、一次函数的性质1. 斜率:一次函数的斜率可以通过系数a来确定,斜率的正负表示函数的上升或下降趋势,斜率越大越陡峭。
斜率为正表示函数递增,斜率为负表示函数递减,斜率为零表示函数为水平线。
2. 截距:一次函数的截距可以通过常数b来确定,截距表示函数与坐标轴的交点位置。
当x为零时,对应的y值即为函数的纵轴截距;当y为零时,对应的x值即为函数的横轴截距。
3. 函数图像:一次函数的图像为一条直线。
根据斜率和截距的不同取值,函数的图像可能是上升的直线、下降的直线或者水平线。
二、一次函数的应用1. 表示一种关系:一次函数常用于描述两个变量之间的线性关系。
例如,经济学中的供需关系、物理学中的速度与时间关系等都可以用一次函数来表示。
2. 预测与推理:通过确定一次函数的斜率和截距,可以进行数据的预测与推理。
例如,通过已知的数据点(x1,y1)、(x2,y2)可以利用一次函数来预测其他数据点的值。
3. 优化问题:一次函数在优化问题中也有广泛应用。
例如,生产成本与产量之间的关系、投资与回报之间的关系等,都可以用一次函数来描述,并通过计算斜率和截距来实现最优化。
三、实例分析为了更好地理解一次函数的性质及应用,我们来看一个实例分析。
假设小明每天步行去上学,他发现他步行的时间与距离之间存在一种线性关系。
他记录了以下数据:距离(公里)时间(分钟)1 102 203 30通过这些数据点,我们可以得到一次函数的图像并进一步分析其性质和应用。
首先,根据给定的数据点,我们可以利用最小二乘法确定一次函数的表达式为y = 10x。
其中斜率为10,表示小明步行速度为每分钟10米;截距为0,表示小明在出发时不需要额外的时间。
通过这个函数表达式,我们可以回答一些问题。
一次函数知识点整理

一次函数知识点整理一次函数知识点总结一、定义与定义式:自变量x和因变量y有如下关系:y=kx+b则此时称y是x的一次函数。
特别地,当b=0时,y是x的正比例函数。
即:y=kx (k为常数,k≠0)二、一次函数的性质:1.y的变化值与对应的x的变化值成正比例,比值为k 即:y=kx+b (k为任意不为零的实数 b取任何实数)2.当x=0时,b为函数在y轴上的截距。
三、一次函数的图像及性质:1.作法与图形:通过如下3个步骤(1)列表;(2)描点;(3)连线,可以作出一次函数的图像——一条直线。
因此,作一次函数的图像只需知道2点,并连成直线即可。
(通常找函数图像与x轴和y轴的交点)2.性质:(1)在一次函数上的任意一点P(x,y),都满足等式:y=kx+b。
(2)一次函数与y轴交点的坐标总是(0,b),与x轴总是交于(-b/k,0)正比例函数的图像总是过原点。
3.k,b与函数图像所在象限:当k0时,直线必通过一、三象限,y随x的增大而增大;当k0时,直线必通过二、四象限,y随x的增大而减小。
当b0时,直线必通过一、二象限;当b=0时,直线通过原点当b0时,直线必通过三、四象限。
特别地,当b=O时,直线通过原点O(0,0)表示的是正比例函数的图像。
这时,当k0时,直线只通过一、三象限;当k0时,直线只通过二、四象限。
四、确定一次函数的表达式:已知点A(x1,y1);B(x2,y2),请确定过点A、B的一次函数的表达式。
(1)设一次函数的表达式(也叫解析式)为y=kx+b。
(2)因为在一次函数上的任意一点P(x,y),都满足等式y=kx+b。
所以可以列出2个方程:y1=kx1+b ……①和 y2=kx2+b ……②(3)解这个二元一次方程,得到k,b的值。
(4)最后得到一次函数的表达式。
五、一次函数在生活中的应用:1.当时间t一定,距离s是速度v的一次函数。
s=vt。
2.当水池抽水速度f一定,水池中水量g是抽水时间t的一次函数。
一次函数知识点

DOCS
DOCS SMART CREATE
一次函数知识点详解
01
一次函数的概念与形式
一次函数的定义与性质
一次函数的定义
• 形式:y = kx + b • 定义:函数中只含有一个未知数x,且x的指数为1
一次函数的性质
• 性质1:y的值随着x的值增大而增大 • 性质2:y的值随着x的值减小而减小 • 性质3:一次函数图像是一条直线
03
一次函数的方程与不等式
一次函数的方程表示与求解
一次函数的方程表示
• 形式:y = kx + b • 其中,k为斜率,b为截距
一次函数的方程求解
• 求解方法:将已知条件代入方程,解出x或y的值
一次函数的不等式表示与求解
一次函数的不等式表示
• 形式:kx + b < y 或 kx + b > y • 其中,k为斜率,b为截距
一次函数的截距
• 定义:直线与y轴的交点 • 计算:截距b = y - kx
一次函数的单调性与最值
一次函数的单调性
• 单调递增:当k > 0时,y随x的增大而增大 • 单调递减:当k < 0时,y随x的增大而减小
一次函数的最值
• 最小值:当x = -b / k时,y取得最小值 • 最大值:当x = -b / k时,y取得最大值
伸缩变换的应用
• 应用1:求解直线在x轴上的伸缩比例 • 应用2:求解直线与y轴的交点
05
一次函数的综合问题与解题技巧
一次函数的最大值与最小值问题
最大值问题
• 解题方法:利用一次函数的单调性,求出最大值点
最小值问题
一次函数的解法

一次函数的解法一次函数,也被称为线性函数,是数学中常见且重要的一种函数形式。
它的一般形式为f(x) = ax + b,其中a和b为常数,x为自变量。
本文将介绍一次函数的解法,帮助读者更好地理解和应用这一函数形式。
一、一次函数的定义及性质一次函数是指次数为1的多项式函数。
它具有以下几个重要的性质:1. 一次函数的图像是一条直线;2. 当a≠0时,一次函数的斜率为a;3. 一次函数的图像在直角坐标系中的斜率表示直线的倾斜程度。
二、一次函数的解法要解一次函数,主要就是找到函数中的未知数x的值。
以下介绍两种常见的解法。
1. 直接解法直接解法是将已知的函数方程f(x) = ax + b中的x代入,然后求出f(x)的值。
具体步骤如下:1) 将已知函数方程中的x值代入,得到f(x)的值;2) 判断f(x)的值是否等于0;3) 若f(x)的值等于0,则代表找到了一次函数的解,即该x的值满足方程ax + b = 0;4) 若f(x)的值不等于0,则代表未找到解。
通过直接解法,我们可以迅速得到一次函数的解,从而对函数的性质和图像有更深入的理解。
2. 斜率截距法斜率截距法是一种常用的解一次函数的方法,它将函数方程f(x) =ax + b转化为y = ax + b的形式,并利用直线的斜率和截距来解析函数性质和解。
具体步骤如下:1) 将已知函数方程f(x) = ax + b转化为y = ax + b的形式;2) 利用斜率a和截距b来分析函数的性质和解;3) 斜率a表示直线的倾斜程度,正值表示直线向上倾斜,负值表示直线向下倾斜。
当a>0时,函数图像向右上方倾斜,a<0时,函数图像向右下方倾斜;4) 截距b表示直线与y轴的交点,也即当x=0时,函数的值。
因此,解一次函数的关键是求出截距b的值;5) 通过计算斜率和截距,我们可以得到一次函数图像的一些基本特征,如斜率和截距对应的坐标点,从而更直观地理解和应用一次函数。
一次函数解释

一次函数解释一次函数是函数中的一种,它反映了变量之间的一种线性关系。
本文将从定义域、函数表达式、图像特征、斜率、与坐标轴的交点、单调性以及函数性质等方面,对一次函数进行详细的解释。
1.定义域定义域是一次函数的基本属性,它表示自变量x的取值范围。
对于任何一个一次函数,定义域都是整个实数集R。
在函数表达式中,x表示自变量,而y是因变量,定义域就是x可以取到的所有值的集合。
2.函数表达式一次函数的函数表达式为y=kx+b,其中k和b是常数,k≠0。
k 称为斜率,b是y轴上的截距。
这个表达式表明,函数的图像是一条直线,直线的斜率是k,它在y轴上的截距是b。
3.图像特征一次函数的图像是一条直线,它的形状由斜率k确定。
当k>0时,直线从左下方向右上方倾斜;当k<0时,直线从左上方向右下方倾斜。
截距b决定了直线在y轴上的位置。
4.斜率斜率是一次函数的重要属性,它反映了函数图像的倾斜程度。
斜率的计算公式为k=(y2-y1)/(x2-x1),其中(x1,y1)和(x2,y2)是函数图像上任意两点的坐标。
5.与坐标轴的交点一次函数与坐标轴的交点是函数图像与x轴或y轴的交点。
当y=0时,一次函数与x轴的交点为(b/k,0);当x=0时,一次函数与y 轴的交点为(0,b)。
这些交点对于理解函数的性质以及解决某些问题非常重要。
6.单调性一次函数在某个区间内的单调性与其斜率密切相关。
当k>0时,函数在(-∞,+∞)上单调递增;当k<0时,函数在(-∞,+∞)上单调递减。
单调性可以帮助我们了解函数值随自变量变化的趋势。
7.函数性质一次函数具有以下性质:(1)定义域为R;(2)值域为R;(3)图像是一条直线;(4)斜率是常数;(5)与坐标轴的交点是有限的;(6)在一定区间内具有单调性;(7)是连续的但不一定是有界的。
总之,一次函数作为一种基本的函数类型,具有丰富的定义域、表达式、图像、斜率、与坐标轴交点、单调性和函数性质。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
课题
函数图象信息题——中考第25题的解法策略
学科
数学
教者
xxx
学校
xxx学校
时间
2012、5、17
教
学
目
标
知识与技能
1、深刻理解一次函数图象的意义,培养学生从读图、读题的过程中获取信息的能力。
2、通过操作,演示、等活动,合作探究等方法,师生共同探讨,剖析寻找此类问题的解决方法及策略。
3、通过分析与解答,培养学生运用知识解决实际问题的能力,发展学生逻辑思维能力,体会数形结合的思想
过程与方法
情感态度
与价值观
课程资源的开发与利用
多媒体课件及对中考第25题题型的搜选
学情分析
重点
弄清题意,读懂图象,获取必要信息
难点
数形结合,获取信息,建模解题。
教学过程与实施策略
师生行为及设计意图
预设
时间
15’
活动3:巩固训练,深化目标
教师用多媒体出示练习,学生合作完成。真正让学生当家做主。
6’
活动4:小结与回顾
学生总结,教师补充。
师生共同总结,点睛知识、深化目标。
2’
板书设计:函数图象信息题之行程问题
——中考第25题专项训练
解题策略:1)、2)、3)
教学反思:
活动1:中考链接
1)考察内容
2)考察的数学思想
学生总结,回答
2’
活动2:初探解题策略
学生根据以往对此类题型的解答,总结此类题型的解题策略。
2’
活动2:问
教师操作课件、演示情境,引导、启发,学生观察思考、合作交流、共同探究。使学生在愉快的氛围中获取信息提高解题能力,感受数形结合思想。
