2012届高三数学选填练习(五)(带答案)
2012江苏数学高考模拟试卷5

22.【必做题】本题满分10分.解答时应写出文字说明、证明过程或演算步骤.
某射击运动员向一目标射击,该目标分为3个不同部分,第一、二、三部分面积之比为1∶3∶6.击中目标时,击中任何一部分的概率与其面积成正比.
(1)若射击4次,每次击中目标的概率为 且相互独立.设 表示目标被击中的次数,求 的分布列和数学期望 ;
19.解:(1)由 ,得 .
由于 , ,且等号不能同时取得,所以 .
从而 恒成立, .………………………………………4分
设 .求导,得 .………………6分
, ,
从而 , 在 上为增函数.
所以 ,所以 .…………………………………………………8分
(2) 设 为曲线 上的任意一点.
假设曲线 上存在一点 ,使∠POQ为钝角,
22.解:(1)依题意知 , 的分布列
ξ
0
1
2
3
4
数学期望 = (或 = ).
………………………………………………………………………………………………5分
(2)设 表示事件“第一次击中目标时,击中第 部分”, ,
表示事件“第二次击中目标时,击中第 部分”, .
依题意,知 , ,
,…………………………………………………………7分
B.解:矩阵M的特征多项式为 ……………………3分
令 ,从而求得对应的一个特征向量分别为
.………………………………………………………………………5分
令 所以求得 .………………………………………………7分
.…………………………………………………………10分
C.解: ,圆心 ,半径 ,
,圆心 ,半径 .……………………………3分
2012高考数学模拟试题及答案(五)

16.[2011·安徽卷]设f(x)=asin2x+bcos2x,其中a,b∈R,ab≠0.若f(x)≤ 对一切x∈R恒成立,则
①f =0;
② < ;
③f(x)既不是奇函数也不是偶函数;
④f(x)的单调递增区间是 (k∈Z);
(1)当实数 为何值时,数列 是等比数列?
(2)在(1)的结论下,设 , 是数列 的前 项和,求 的值.
21.(理)(本小题满分12分)
已知可行域 的外接圆C与x轴交于点A1、A2,椭圆C1以线段A1A2为长轴,离心率 .
(1)求圆C及椭圆C1的方程;
(2)设椭圆C1的右焦点为F,点P为圆C上异于A1、A2的动点,过原点O作直线PF的垂线交直线 于点Q,判断直线PQ与圆C的位置关系,并给出证明.
(1)求证:EF⊥平面DCE;
(2)当AB的长为何值时,二面角A-EF-C的大小为60°.
20.(本小题满分12分)(理)[2011·山东青岛一模]已知数列 满足 ,且 , 为 的前 项和.
(1)求证:数列 是等比数列,并求 的通项公式;
(2)如果对任意 ,不等式 恒成立,求实数 的取值范围.
(文)[2011·山东青岛一模]数列 的前 项和记为 , ,点 在直线 上, .
A.(x-1)2+(y-3)2= B.(x-3)2+(y-1)2=( )2
C.(x-2)2+(y- )2=9D.(x- )2+(y- )2=9
8.[2011·陕西卷]设集合M={y|y=|cos2x-sin2x|,x∈R},N= ,则M∩N为()
A.(0,1)B.(0,1]C.[0,1)D.[0,1]
2012.5 高三数学(理科)答案

2012年福州市高中毕业班综合练习 理科数学试卷参考答案及评分参考一、选择题(本大题共10小题,每小题5分,共50分)1.B2.A3.C4.D5.B6.D7. C8. B9.D 10. D 二、填空题(本大题共5小题,每小题4分,共20分) 11. 2 12. 12 13. (1,)+∞ 14. 5- 15. ①④三、解答题(本大题共6小题,共80分) 16.(本小题满分13分) 解:(Ⅰ)记事件“小强试用的3个岗位中恰有2个在甲部门的概率”为A ,则()21443837C C P A C ⋅==. ···································································· 6分 (Ⅱ)22000.424000.326000.228000.12400E =⨯+⨯+⨯+⨯=甲(元), ··············· 7分 20000.424000.328000.232000.12400E =⨯+⨯+⨯+⨯=乙(元). ·························· 8分()()()()()2222220024000.4240024000.3260024000.2280024000.1D X =-⨯+-⨯+-⨯+-⨯甲 40000=, ········································································································ 9分 ()()()()()2222200024000.4240024000.3280024000.2320024000.1D X =-⨯+-⨯+-⨯+-⨯乙 160000=. ····································································································· 10分 选择甲部门:因为()()X X D X D X =<甲乙甲乙,,说明甲部门各岗位的工资待遇波动比乙部门小,竞争压力没有乙部门大,比较安稳. ··························································· 13分选择乙部门:因为()()X X D X D X =<甲乙甲乙,,说明乙部门各岗位的工资待遇波动比甲部门大,岗位工资拉的比较开,工作比较有挑战性,能更好地体现工作价值. ······ 13分17.(本小题满分13分)解:依题意,可建立如图所示的空间直角坐标系A xyz -,设1AA h =,则 ()()()()112,0,0,0,6,0,2,0,,0,0,,0,6,,0,3,32h h B C D A h C h E ⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭.2分(Ⅰ)证明:由1AA ⊥平面ABC 可知()10,0,1n =为平面ABC 的一个法向量.∴ ()12,3,0,0,1066h h DE n ⎛⎫⋅=-⋅=≠ ⎪⎝⎭. ························· 3分∴ 直线DE 与平面ABC 不平行. ···························· 4分(Ⅱ)设平面1ADC 的法向量为()2,,n x y z =,则 ()()()221,,2,0,2033,,0,6,60h h n AD x y z x z n AC x y z h y hz ⎧⎛⎫⋅=⋅=+= ⎪⎪⎝⎭⎨⎪⋅=⋅=+=⎩, ··············· 5分 取6z =-,则x y h ==,故()2,,6n h h =-. ·············· 6分∴121212cos cos ,1n n n n n n θ⋅=<>==⨯=, ············································ 7分解得h =.∴ 1AA = ········································································································· 8分 (Ⅲ)在平面11BCC B 内,分别延长1CB C D 、,交于点F ,连结AF ,则直线AF 为平面1ADC 与平面ABC 的交线. ··························································································· 9分∵ 1//BD CC ,1111==33BD BB CC ,∴113BF BD FC CC ==. ∴ 12BF CB =,∴ ()()()112,0,02,6,03,3,022AF AB BF AB CB =+=+=+-=-. ························ 11分由(Ⅱ)知,h =,故(2,3,6h DE ⎛⎫=-=- ⎪⎝⎭,∴ cos ,3AF DE AF DE AF DE⋅<>===. ··············································· 12分 ∴ 直线l 与DE 所成的角的余弦值为= ········································· 13分 18.(本小题满分13分)解:(Ⅰ)设圆C 的半径为r (0r >),依题意,圆心坐标为(,2)r . ····················· 1分∵ 3MN =∴ 222322r ⎛⎫=+ ⎪⎝⎭,解得2254r =. ·········································································· 3分∴ 圆C 的方程为()22525224x y ⎛⎫-+-= ⎪⎝⎭. ···························································· 5分(Ⅱ)把0y =代入方程()22525224x y ⎛⎫-+-= ⎪⎝⎭,解得1x =,或4x =,即点()1,0M ,()4,0N . ···························································································· 6分 (1)当AB x ⊥轴时,由椭圆对称性可知ANM BNM ∠=∠. ································· 7分 (2)当AB 与x 轴不垂直时,可设直线AB 的方程为()1y k x =-.联立方程()22128y k x x y ⎧=-⎨+=⎩,消去y 得,()22222280k x k x k +-+-=. ······················· 8分 设直线AB 交椭圆Γ于()()1122,,A x y B x y 、两点,则212222k x x k +=+,212282k x x k -⋅=+. ············································································· 9分 ∵ ()()11222,2y k x y k x =-=-, ∴ ()()12121212114444AN BN k x k x y y k k x x x x --+=+=+---- ()()()()()()122112141444k x x k x x x x --+--=--.····································································· 10分∵()()()()()()221221121222281014142588022k k x x x x x x x x k k ---+--=-++=-+=++, ··································································································································· 11分 ∴ 0AN BN k k +=,ANM BNM ∠=∠. ·································································· 12分 综上所述,ANM BNM ∠=∠. ················································································ 13分19.(本小题满分13分)解:(Ⅰ)当2a =时,2()ln(1)1xf x x x =+++, ∴22123()1(1)(1)x f x x x x +'=+=+++, ·········································································· 1分 ∴ (0)3f '=,所以所求的切线的斜率为3. ····························································· 2分 又∵()00f =,所以切点为()0,0. ·········································································· 3分 故所求的切线方程为:3y x =. ··············································································· 4分(Ⅱ)∵()ln(1)1axf x x x =+++(1)x >-, ∴221(1)1()1(1)(1)a x ax x a f x x x x +-++'=+=+++. ································································· 5分 ①当0a ≥时,∵1x >-,∴()0f x '>; ···································································· 6分 ②当0a <时,由()01f x x '<⎧⎨>-⎩,得11x a -<<--;由()01f x x '>⎧⎨>-⎩,得1x a >--; ····························· 7分综上,当0a ≥时,函数()f x 在(1,)-+∞单调递增;当0a <时,函数()f x 在(1,1)a ---单调递减,在(1,)a --+∞上单调递增. ········· 8分 (Ⅲ)方法一:由(Ⅱ)可知,当1a =-时,()()ln 11xf x x x =+-+在()0,+∞上单调递增. ························································· 9分 ∴ 当0x >时,()()00f x f >=,即()ln 11xx x +>+. ······································· 10分 令1x n =(*n ∈N ),则111ln 111n n n n ⎛⎫+>= ⎪+⎝⎭+. ··················································· 11分另一方面,∵()2111n n n <+,即21111n n n-<+,∴21111n n n>-+. ································································································· 12分 ∴ 2111ln 1n n n ⎛⎫+>- ⎪⎝⎭(*n ∈N ). ········································································· 13分方法二:构造函数2()ln(1)F x x x x =+-+,(01)x ≤≤ ········································· 9分 ∴1(21)'()1211x x F x x x x +=-+=++, ··································································· 10分∴当01x <≤时,'()0F x >;∴函数()F x 在(0,1]单调递增. ·············································································· 11分 ∴函数()(0)F x F > ,即()0F x >∴(0,1]x ∀∈,2ln(1)0x x x +-+>,即2ln(1)x x x +>- ··································· 12分 令1x n =(*n ∈N ),则有2111ln 1n n n ⎛⎫+>- ⎪⎝⎭. ························································ 13分20.(本小题满分14分)解:(Ⅰ)已知α是锐角,根据三角函数的定义,得3sin 5α=,4cos 5α=,·············· 1分 又5cos 13β=,且β是锐角,所以12sin 13β=. ························································· 2分 所以4531216cos()cos cos sin sin 51351365αβαβαβ+=-=⨯-⨯=-. ··························· 4分(Ⅱ)证明:依题意得,sin MA α=,sin NB β=,sin()PC αβ=+ 因为0παβ⎛⎫∈ ⎪⎝⎭,,2,所以cos (0,1)α∈,cos (0,1)β∈,于是有sin()sin cos cos sin sin sin αβαβαβαβ+=+<+,① ·············································· 6分又∵()0,,1cos()1αβπαβ∈∴-<<++,sin sin(())sin()cos cos()sin sin()sin ααββαββαββαββ=+-=+⋅-+⋅<++,②··········································································································································· 7分同理,sin sin()sin βαβα<++,③ 由①,②,③可得,线段MA 、NB 、PC 能构成一个三角形. ································································· 8分 (III )第(Ⅱ)小题中的三角形的外接圆面积是定值,且定值为4π. 不妨设A B C '''∆的边长分别为()sin sin sin αβαβ+、、,其中角A '、B '、C '的对边分别为()sin sin sin αββα+、、.则由余弦定理,得: 222sin sin sin ()cos 2sin sin A αβαβαβ+-+'=⋅ ···································································· 9分222222sin sin sin cos cos sin 2sin cos cos sin 2sin sin αβαβαβαβαβαβ+---=⋅ 2222sin sin sin sin 2sin cos cos sin 2sin sin αββααβαβαβ⋅+-=⋅ sin sin cos cos αβαβ=⋅-cos()αβ=-+ ································································································· 11分因为0παβ⎛⎫∈ ⎪⎝⎭,,2,所以(0,)αβπ+∈,所以sin sin()A αβ'=+,······················· 12分设A B C '''∆的外接圆半径为R ,由正弦定理,得sin()21sin sin()B C R A αβαβ''+==='+,∴12R =, ······································· 13分 所以A B C '''∆的外接圆的面积为4π. ········································································ 14分 21.(1)(本小题满分7分)选修4-2:矩阵与变换 解:(Ⅰ)由条件得矩阵1002M ⎛⎫=⎪⎝⎭. ·································································· 2分 (Ⅱ)因为矩阵1002M ⎛⎫=⎪⎝⎭的特征多项式为10()(1)(2)02f λλλλλ-==---, 令()0f λ=,解得特征值为11λ=,22λ=,····························································· 4分 设属于特征值1λ的矩阵M 的一个特征向量为1x e y ⎛⎫= ⎪⎝⎭,则12x x M e y y ⎛⎫⎛⎫== ⎪ ⎪⎝⎭⎝⎭,解得0y =,取1x =,得110e ⎛⎫= ⎪⎝⎭, ··························································································· 5分同理,对于特征值2λ,解得0x =,取1y =,得201e ⎛⎫= ⎪⎝⎭, ····································· 6分所以110e ⎛⎫= ⎪⎝⎭是矩阵M 属于特征值11λ=的一个特征向量,201e ⎛⎫= ⎪⎝⎭是矩阵M 属于特征值22λ= 的一个特征向量. ······························································································ 7分(2)(本小题满分7分) 选修4—4:极坐标与参数方程解:(Ⅰ)∵点A 、B 的极坐标分别为(1,)3π、2(3,)3π, ∴点A 、B的直角坐标分别为1(,2、3(,2-, ······································· 2分 ∴直线AB的直角坐标方程为40y +-=. ············································ 4分(Ⅱ)由曲线C 的参数方程cos ,(sin x r y r ααα=⎧⎨=⎩为参数)化为普通方程为222x y r +=,5分 ∵直线AB 和曲线C 只有一个交点,∴半径r == ······································································ 7分 (3)(本小题满分7分) 选修4—5:不等式选讲解:(Ⅰ)∵关于xm 对于任意的[1,2]x ∈-恒成立max m ⇔> ·························································································· 1分根据柯西不等式,有222222(11[11]]6=≤+⋅+=12x =时等号成立,故m > ···················· 3分 (Ⅱ)由(Ⅰ)得20m ->,则()221111(2)(2)2(2)22(2)f m m m m m m =+=-+-++-- ∴()22f m ≥ ············································ 5分 当且仅当211(2)2(2)m m -=-,即2m > ································ 6分 所以函数()21(2)f m m m =+-2. ··············································· 7分。
2012届高考数学填空题专练

2012届高考数学填空题专练俯视图侧视图正视图3342012届高三数学填空题专练(1)1.在复平面内,复数1+i2009(1-i)2 对应的点位于____________。
2.已知cos 0()(1)10xx f x f x x π->⎧⎪=⎨++≤⎪⎩,则)34()34(-+f f 的值等于____________。
3.设函数()f x a b =•,其中向量(2cos ,1),(cos ,3sin 2)a x b x x ==,则函数f(x)的最小正周期是____________。
4.已知函数=-'-'+=)31(,)31(2)(2f x f x x f 则____________。
5.)1,2(),3,(-==b x a ,若a 与b 的夹角为锐角,则x 的范围是____________。
6.当0a >且1a ≠时,函数()log (1)1af x x =-+的图像恒过点A ,若点A 在直线0mx y n -+=上,则42m n+的最小值为_ _ __。
7.若一个底面为正三角形、侧棱与底面垂直的棱柱的三视图如下图所示,则这个棱柱的体积为____________。
8.已知向量1(3,1),(2,),2a b ==-直线l 过点(1,2)A 且与向量2a b+垂直,则直线l 的一般方程是____________。
9.在公差为正数的等差数列{a n }中,a 10+a 11<0且a 10a 11<0,S n 是其前n 项和,则使S n 取 最小值的n 是____________。
10. 函数)24sin(3x y -=π图象是将函数x y 2sin 3-=的图象经过怎样的平移而得_ _。
11.已知函数f(x)是偶函数,并且对于定义域内任意的x, 满足f(x+2)= -)(1x f , 当3<x<4时,f(x)=x, 则f(2008.5)= 。
2012高考数学试题及答案

2012高考数学试题及答案2012年高考数学试题一、选择题(本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有一项是符合题目要求的,把所选选项前的字母填在题后的括号内。
)1. 若集合A={1, 2, 3},B={2, 3, 4},则A∪B的元素个数是()。
A. 3B. 4C. 5D. 62. 函数f(x) = x^2 + 2x - 3的对称轴方程是()。
A. x = -1B. x = 1C. x = -2D. x = 23. 若等差数列的首项为a,公差为d,且a1 + a2 + a3 = 3,a2 + a3 + a4 = 7,则a的值为()。
A. 1B. 3C. 5D. 74. 已知三角形ABC中,∠A=90°-∠B,若AB=5,AC=12,则BC的长度为()。
A. 13B. 9C. 7D. 35. 已知球面上两点P和Q,球的半径为r,PQ=r/2,那么P和Q两点所在的大圆的圆心角的弧度数是()。
A. π/3B. π/2C. πD. 2π/36. 若复数z满足|z - 1| = |z + 1|,则z在复平面上对应的点位于()。
A. x轴B. y轴C. 直线y=xD. 直线y=-x7. 已知函数g(x) = x^3 - 3x^2 + 2x + 1,若g(x)在区间[-1, 2]上单调递减,则实数a的取值范围是()。
A. a ≥ 5B. a ≤ -5C. a ≥ -2D. a ≤ 28. 一个圆的周长为20π,则该圆的面积是()。
A. 25πB. 50πC. 100πD. 200π9. 在直角坐标系中,点A(2, 3)关于直线y=x的对称点坐标是()。
A. (3, 2)B. (2, 2)C. (3, 4)D. (4, 3)10. 若a, b, c是等比数列,且abc = 8,a + b + c = 6,则b的值为()。
A. 2B. 2√2C. 4D. 4√2二、填空题(本大题共5小题,每小题5分,共25分。
2012年高考理科数学(全国卷)含答案及解析

2012年普通高等学校招生全国统一考试理科数学(必修+选修II )一、 选择题(1)、复数131i i-++= A. 2 B. 2 C. 12 D. 12i i i i +-+- 【考点】复数的计算【难度】容易【答案】C 【解析】13(13)(1)24121(1)(1)2i i i i i i i i -+-+-+===+++-. 【点评】本题考查复数的计算。
在高二数学(理)强化提高班下学期,第四章《复数》中有详细讲解,其中第02节中有完全相同类型题目的计算。
在高考精品班数学(理)强化提高班中有对复数相关知识的总结讲解。
(2)、已知集合A ={1.3. m },B ={1,m } ,A B =A , 则m =A. 0或3B. 0或3C. 1或3D. 1或3【考点】集合【难度】容易【答案】B【解析】(1,3,),(1,)30,1()3A B A B A A m B m m A m m m m m m ⋃=∴⊆==∴∈∴==∴===或舍去.【点评】本题考查集合之间的运算关系,及集合元素的性质。
在高一数学强化提高班下学期课程讲座1,第一章《集合》中有详细讲解,其中第02讲中有完全相同类型题目的计算。
在高考精品班数学(理)强化提高班中有对集合相关知识及综合题目的总结讲解。
(3) 椭圆的中心在原点,焦距为4, 一条准线为x =﹣4 ,则该椭圆的方程为 A. 216x +212y =1 B. 212x +28y =1 C. 28x +24y =1 D. 212x +24y =1 【考点】椭圆的基本方程【难度】容易【答案】C【解析】椭圆的一条准线为x =﹣4,∴2a =4c 且焦点在x 轴上,∵2c =4∴c =2,a =22∴椭圆的方程为22=184x y + 【点评】本题考查椭圆的基本方程,根据准线方程及焦距推出椭圆的方程。
在高二数学(理)强化提高班,第六章《圆锥曲线与方程》中有详细讲解,其中在第02讲有相似题目的详细讲解。
2012年高考数学试题及答案

2012年高考数学试题及答案一、选择题(本题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
)1. 若函数f(x) = 2x^2 - 4x + 3,求f(1)的值。
A. 1B. 3C. 5D. 7答案:B2. 已知等差数列{a_n}的前三项为1, 3, 5,求该数列的公差d。
A. 1B. 2C. 3D. 4答案:B3. 圆的方程为(x-2)^2 + (y-3)^2 = 9,求圆心坐标。
A. (2, 3)B. (-2, 3)C. (2, -3)D. (-2, -3)答案:A4. 已知直线方程为y = 2x + 1,求该直线与x轴的交点坐标。
A. (-1/2, 0)B. (1/2, 0)C. (-1, 0)D. (1, 0)答案:B5. 已知复数z = 3 + 4i,求其共轭复数。
A. 3 - 4iB. -3 + 4iC. 3 + 4iD. -3 - 4i答案:A6. 若函数f(x) = x^3 - 6x^2 + 11x - 6,求f'(x)。
A. 3x^2 - 12x + 11B. 3x^2 - 12x + 10C. 3x^2 - 6x + 11D. 3x^2 - 6x + 10答案:A7. 已知向量a = (1, 2),b = (3, 4),求向量a与b的点积。
A. 11B. 14C. 10D. 12答案:B8. 已知集合A = {1, 2, 3},B = {2, 3, 4},求A∩B。
A. {1, 2, 3}B. {2, 3}C. {1, 2, 4}D. {1, 3, 4}答案:B9. 已知函数f(x) = sin(x),求f'(x)。
A. cos(x)B. -sin(x)C. sin(x)D. -cos(x)答案:A10. 已知等比数列{a_n}的前三项为2, 4, 8,求该数列的公比q。
A. 1B. 2C. 3D. 4答案:B二、填空题(本题共5小题,每小题5分,共25分。
2012高考数学(理)专题练习:五 空间几何体
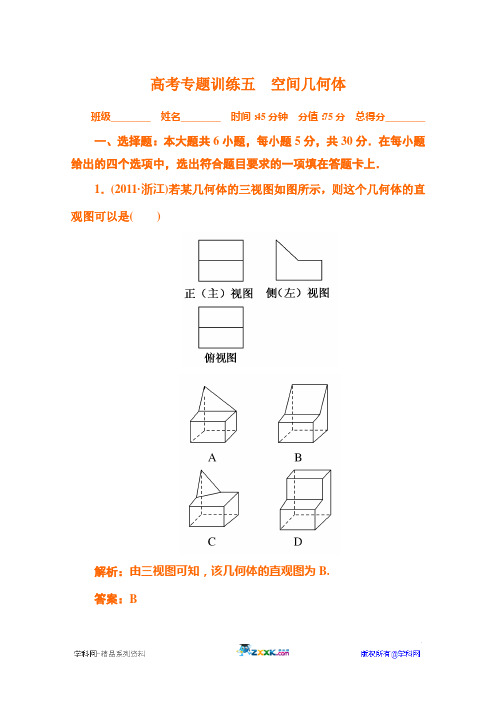
高考专题训练五空间几何体班级________姓名________时间:45分钟分值:75分总得分________一、选择题:本大题共6小题,每小题5分,共30分.在每小题给出的四个选项中,选出符合题目要求的一项填在答题卡上.1.(2011·浙江)若某几何体的三视图如图所示,则这个几何体的直观图可以是()解析:由三视图可知,该几何体的直观图为B.答案:B2.(2011·辽宁)一个正三棱柱的侧棱长和底面边长相等,体积为23,它的三视图中的俯视图如图所示,侧(左)视图是一个矩形,则这个矩形的面积是( )A .4B .2 3C .2D. 3解析:设该正三棱柱侧棱长和底面边长为a , 则34a 2·a =23, ∴a 3=8,∴a =2,由俯视图知,该正三棱柱如图ABC -A 1B 1C 1, 其侧(左)视图即为矩形CDD 1C 1, 其面积为3×2=2 3. 答案:B3.(2011·山师大附中高三模拟)已知某一几何体的正(主)视图与侧(左)视图如图所示,则下列图形中,可以是该几何体的俯视图的图形有()A.①②③⑤B.②③④⑤C.①②④⑤D.①②③④解析:根据给出的正(主)视图和侧(左)视图可知,该组合体由上、中、下三个几何体组合而成,由于正(主)视图和侧(左)视图中三层均为矩形,所以这些几何体可能是一些长方体、底面为直角三角形的直三棱柱以及圆柱组合而成的.而第⑤个俯视图中,有两处与已知不符,一是上层几何体的俯视图不正确,由于上层几何体的正(主)视图与侧(左)视图为两个相同的矩形,所以其俯视图中矩形的两边长应该相等;二是下层几何体的俯视图不正确,如果下层几何体的底面为俯视图所示的三角形,则在正(主)视图中底层的矩形应有一条中位线,这与已知不符合,所以⑤不可能,故选D.[来源:学科网]答案:D4.(2011·湖北)设球的体积为V1,它的内接正方体的体积为V2,下列说法中最合适的是()A.V1比V2大约多一半B.V1比V2大约多两倍半C.V1比V2大约多一倍D.V1比V2大约多一倍半解析:设球的内接正方体的边长为a , 球的半径为R ,∴2R =3a ,∴R =32a .∴V 1=43πR 3=43π·338a 3=32πa 3,V 2=a 3,∴V 1=32πV 2≈2.5V 2,∴V 1-V 2≈1.5V 2.[来源:学科网] 答案:D5.(2011·北京卷)某四棱锥的三视图如图所示,该四棱锥的表面积是( )A .32B .16+16 2C .48D .16+32 2解析:由三视图可知,该四棱锥为正四棱锥 S 底=4×4=16,S 侧=4×12×4×22=16 2∴S 表面积=S 底+S 侧=16+16 2.6.(2011·辽宁)已知球的直径SC =4,A ,B 是该球球面上的两点,AB =2,∠ASC =∠BSC =45°,则棱锥S -ABC 的体积为( )[来源:学科网ZXXK]A.33B.233C.433D.533解析:如图所示.∠ASC =∠BSC =45° 且OS =OB =OA =OC =2,∴△SOB ,△SOA 为全等的等腰直角三角形, 且SC ⊥OB ,SC ⊥OA ,又OA ∩OB =O ,∴SC ⊥平面AOB 又∵AB =OB =OA =2, ∴△AOB 为等边三角形∴V S -ABC =V S -AOB +V C -AOB =13·S △AOB ·SC =13×3×4=433.二、填空题:本大题共4小题,每小题5分,共20分,把答案填在题中横线上.[来源:学科网]7.(2011·全国新课标版)已知两个圆锥有公共底面,且两圆锥的顶点和底面的圆周都在同一个球面上.若圆锥底面面积是这个球面面积的316,则这两个圆锥中,体积较小者的高与体积较大者的高的比值为________.解析:令球心为O ,圆锥底面圆圆心为O ′,球半径为R ,圆锥底面圆半径为r ,则316·4πR 2=πr 2,∴r =32R ,在Rt △AOO ′中, OO ′=AO 2-AO ′2=R 2.故h H =R -R 2R +R 2=13. 答案:138.(2011·洛阳市高三模拟)图2中的实线围成的部分是长方体(图1)的平面展开图,其中四边形ABCD 是边长为1的正方形.若向虚线围成的矩形内任意抛掷一质点,它落在长方体的平面展形图内的概率是14,则此长方体的体积是________.解析:设长方体的高为h ,则图2中虚线围成的矩形长为2+2h ,宽为1+2h ,面积为(2+2h )(1+2h ),展开图的面积为2+4h ;由几何概型的概率公式知2+4h (2+2h )(1+2h )=14,得h =3,所以长方体的体积是V =1×3=3.答案:39.(2011·北京市海淀区高三第二学期练习)如图,在正方体ABCD -A 1B 1C 1D 1中,点P 是上底面A 1B 1C 1D 1内一动点,则三棱锥P -ABC 的正(主)视图与侧(左)视图的面积的比值为________.[来源:]解析:依题意得三棱锥P-ABC的正(主)视图与侧(左)视图分别是一个三角形,且这两个三角形的底边长都等于正方体的棱长,底边上的高也都相等,因此三棱锥P-ABC的正视图与侧视图的面积之比等于1.答案:110.一个几何体的三视图如图所示,已知正(主)视图是底边长为1的平行四边形,侧(左)视图是一个长为3,宽为1的矩形,俯视图为两个边长为1的正方形拼成的矩形,则该几何体的体积V是________.是边长为1的正方形,高为 3.所以V=1×1×3= 3.答案: 3三、解答题:本大题共2小题,共25分.解答应写出文字说明、证明过程或演算步骤.[来源:学*科*网Z*X*X*K]所示(其中M,N分别是AF,BC的中点).(1)求证:MN ∥平面CDEF ; (2)求二面角A -CF -B 的余弦值; (3)求多面体A -CDEF 的体积. 解:由三视图知,该多面体是底面为直角三角形的直三棱柱ADE -BCF ,且AB =BC =BF =4,DE =CF =42,∠CBF =π2.(1)证明:连接BE ,易知BE 通过点M ,连接CE .则EM =BM ,CN =BN ,∴MN ∥CE ,又CE ⊂平面CDEF ,MN⊄平面CDEF ,∴MN ∥平面CDEF .(2)作BQ ⊥CF 于Q ,连接AQ ,∵平面BFC ⊥平面ABFE ,平面ABFE ∩平面BCF =BF ,AB ⊂平面ABFE ,AB ⊥BF ,∴AB ⊥平面BCF ,又CF ⊂平面BCF ,∴AB ⊥CF ,又BQ ⊥CF ,AB ∩BQ =B ,∴CF ⊥平面ABQ ,∵AQ ⊂平面ABQ ,∴AQ ⊥CF ,故∠AQB 为所求二面角的平面角.在Rt △ABQ 中,tan ∠AQB =AB BQ =422=2,则 cos ∠AQB =33,故所求二面角的余弦值为33.[来源:学|科|网Z|X|X|K](3)多面体A -CDEF 的体积V =2×V A -CEF =2×V C -ABF =2×13S △ABF ·BC =643.12.(13分)(广东卷)某高速公路收费站入口处的安全标识墩如下图(1)所示.墩的上半部分是正四棱锥P -EFGH ,下半部分是长方体ABCD -EFGH .图(2)、(3)分别是该标识墩的正视图和俯视图.(1)请画出该安全标识墩的侧视图;(2)求该安全标识墩的体积;(3)证明:直线BD⊥平面PEG.分析:(1)根据正(主)视图和俯视图可以知道其侧(左)视图和正(主)视图是完全相同的;(2)根据两个视图给出的标记,这个安全墩的下半部分是一个底面边长为40 cm、高为20 cm的长方体,上半部分四棱锥的高为60 cm,根据公式计算即可;(3)根据正四棱锥的性质进行证明.解:(1)该安全标识墩侧(左)视图如右图所示.[来源:学科网](2)该安全标识墩的体积V =V P -EFGH +V ABCD -EFGH=13402×60+402×20=32000+32000=64000(cm 3). (3)证明:如右图所示,连接HF 、EG .由题设知四边形ABCD 和四边形EFGH 均为正方形,∴FH ⊥EG ,又∵ABCD -EFGH 为长方体,∴BD ∥FH .设点O 是EFGH 的对称中心,连接PO .∵P -EFGH 是正四棱锥,[来源:学&科&网Z&X&X&K]∴PO ⊥平面EFGH ,而FH ⊂平面EFGH ,∴PO ⊥FH .∵FH ⊥PO ,FH ⊥EG ,PO ∩EG =O ,PO ⊂平面PEG ,EG ⊂平面PEG ,∴FH ⊥平面PEG .而BD ∥FH ,故BD ⊥平面PEG .[来源:学科网ZXXK]点评:解这类给出了直观图和三视图中的两个图形的题目,只要根据直观图得出另一个视图的形状,再根据给出的两个视图上标注的几何量,在第三个视图上标注上几何量即可..精品资料。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2012届高三数学选填练习(五)
一、选择题
1.若集合},1{2m A =,}4,2{=B ,则“2=m ”是“}4{=⋂B A ”的( )
A .充分不必要条件
B .必要不充分条件
C .充要条件
D .既不充分也不必要条件
2.已知函数x
x x f +-=11lg
)(,若b a f =)(,则=-)(a f ( ) A .b B .b - C .b 1 D .b 1- 3.在等差数列}{n a 中,若882=+a a ,则其前9项和=9S ( ) A.2516 B.25
12 C.36 D9. 4.函数x a y =在]1,0[上的最大值与最小值的和为3,则=a ( )
A .21
B .2
C .4
D .4
1 5.已知x x f lg )(5=,则=)2(f ( )
A .2lg
B .32lg
C .32
1lg D .2lg 51 6.设)sin ,(cos θθ=,)4,3(=则⋅的最小值为( )
A .3-
B .4-
C .5-
D .0
7.函数x
e x
f x
1)(-=零点所在区间为( ) A .)21,0( B .)1,21( C .)23,1( D .)2,23( 8.数列}{n a 中,若211=
a ,111--=n n a a },2(N n n ∈≥,则2011a 的值为( ) A .1- B .
2
1 C .1 D .
2 二、填空题 9.设)(x f 是定义在R 上的奇函数,若当0≥x 时,)1(log )(3x x f +=,则=-)2(f _____-1
10.不等式2)
1(52≥-+x x 的解集为_______________ ]3,1()1,21[⋃- 11.当]2,1[-∈x 时,m x x x <--22
123恒成立,则实数m 的取值范围是________ 2>m 12.函数||sin |sin |x x y +=值域为_______________ ]2,0[
13.设)(x f 是偶函数,若曲线)(x f y =在点))1(,1(f 处的切线的斜率为1,则该曲线在点))1(,1(--f 处的斜率为___________ 1-
14.已知定义在R 上的函数)(x f 满足:①)()4(,x f x f R x =+∈∀;②2021≤<≤∀x x ,有)()(21x f x f <;③)2(+=x f y 是偶函数.将)5(f 、)5.6(f 、)5.15(f 从小到大排序为________________________ )5.15(f <)5(f <)5.6(f。
