2016年小升初数论知识汇总
小升初数学-数论-基础篇-整数专题解析必考知识点总结

小升初数学-数论-基础篇-整数专题解析必考知识点总结整数的认识1. 自然数整数02. 计数单位数位位数3. 数级4. 读法写法5. 改写省略四舍五入保留几位小数6. 近似数准确数7. 连续自然数8. 和积关系一自然数整数0自然数:定义:个数,极限:基本单位:意义:整数:定义:个数,极限:分类:0:作用:归类:例1. 判断:-3,-1,0,2,5都是自然数。
1. 判断:-6,-3,0,8,19都是整数。
()0既是自然数,也是整数。
()整数就是自然数。
()例2. 最小的自然数是(),最大的自然数是()自然数的基本单位是()1 . 最小的整数是(),最大的整数是(),整数有()个例3. 下列选项中的数是序数的是()A. 6只鸡B. 5支铅笔C. 2幢楼D. 第6节课例4. 判断:7067中的0表示百位上一个计数单位都没有。
二计数单位数位位数计数单位:数位:位数:最小的1位数是:最大的1位数是:最小的两位数是:最大的两位数是:最小的三位数是:最大的三位数是:数位:1. 从个位起,第六位是()位,第九位是()位,第七位是()位。
2. 与万位相邻的数位是()和()。
3.判断: 整数的最高位是千亿位。
()计数单位:1. 与百万相邻的计数单位是()和()。
位数:1. 60606000是一个()位数,最高位是(),从左往右数第二个6在()位上,第三个6表示6个()2. 一个数,它的最高位是十亿位,这个数是()位数。
3. 最小的一位数是(),最小的三位数是(),最小的四位数是(),最大的五位数是(),最大的两位数是()4. 最大的四位数与最小的三位数差(),最大的三位数比最小的三位数大(),比最小的六位数少1的数是()。
5.判断:最小的四位数缩小到它的1/10 是最小的三位数。
()6. 用最小的三位数与最大的两位数之差去乘最大的三位数与最小的四位数之和,积为()三数级个级数位:计数单位:表示:万级数位:计数单位:表示:亿级数位:计数单位:表示:1. 个级的计数单位有()2. 万级的数位有()3. 亿级的计数单位有()个,表示()四读法写法读法:写法:读法,写法:例1. 二百零三亿四千五百万六千写作()1. 二百零四亿零六十万零二十写作()例2. 128226200 ,读作()1. 6060076440,读作()例3. 一个数由5个亿,6个千万,3个万,9个百,4个一组成,这个数写作(),读作()1.你知道全国小学生的人数吗?这个数是由1个亿,2个千万,8个百万,9个十万,5个千组成的,这个数写作()例4.一个数,十位和百位上的数字都是5,这个数写作()1.写出一个最小的十位数,要使每个数位上的数字都不相同,这个数是()2. 一个九位数,最高位上是9,百万位上是2,万位上是4,千位上是6,其余各位上都是0,这个数写作()读作()3.一个数,千万位上的数字是最小的质数,十万位上的数字是最大的一位合数,个位上的数字是0.5的倒数,其余各位上都是最小的自然数,这个数写作(),读作()4.一个数,十万位上是最大的一位数,万位上是最小的合数,百位上是最小的质数,其余各位上都是0,这个数写作()读作()例5.一个多位数,第九位上的数是1,第五位上的数是5,其余各位上的数都是0,这个数写作()读作()1. 一个数,亿级上是78,个级上是78,这个数是()读作()2. 一个多位数,第八位上的数是1,第五位上的数是6,其余各位上的数都是0,这个数写作()读零:1. 90000604001读作()2. 下面各数不需要读出零的是()A. 3006210B. 6210300C.1206003.下面三个数中,两个0都读出来的是()A. 33030B. 33003C.303034.下面各数中,三个0都读出来的是()A. 60504032B. 60540320C.650403025.用两个0和三个8组成五位数,其中只读出一个0的数是()两个0都读出来的数是()两个0都不读出来的数是()6.用3个0和3个6组成一个六位数只读一个零的有(),读两个零的有(),一个零也不读的有()其中最大的一个数是(),最小的一个数是()两数相差()7.用5,7,8和四个0组成的七位数中,一个零也读不出来的最大数是()只读出一个零的最小数是()读出两个零的最大数是()读出两个零的最小数是()五改写,省略,四舍五入,保留几位小数改写改写的方法:1.改写成用“万”作单位的数改写成用“亿”作单位的数20345006000 ()()94063506000 ()()128226200 ()()320000500 ()()1950703000 ()()2.把0.42亿改写成用“万”作单位的数是()省略尾数省略尾数的方法:1. 省略万位后面的尾数约是省略亿位后面的尾数约是140900002 ()()94063506000 ()()700700070 ()()174500000 ()()1950703000 ()()四舍五入1. 四舍五入到万位约是四舍五入到亿位约是四舍五入法精确到万位约是四舍五入法精确到亿位约是85473870 ()()84001000 ()()700700070 ()()保留几位小数:1.3720600000改写成用“亿”作单位的数是()亿保留两位小数是()亿980064000 改写成用“亿”作单位的数是()亿保留两位小数是()128226200 保留一位小数是()亿1370000000 保留一位小数记作()亿六近似数,准确数例1.在下面的()中填上适当的数字,使第一个数最接近50亿,第二个数最接近15万。
(完整版)数论知识点总结

(完整版)数论知识点总结1. 整数与整除性质整数是数的基本单位,整除是整数相除所得到的商是整数的关系。
- 整数运算:加法、减法、乘法、除法。
- 整数性质:正整数、负整数、零。
- 整数除法:被除数、除数、商、余数。
2. 质数和合数质数是只能被1和自身整除的正整数,合数是除了1和本身外还能被其他正整数整除的正整数。
- 判断质数:试除法、素数筛法。
- 质因数分解:将一个合数分解成质因数的乘积。
3. 最大公约数和最小公倍数最大公约数是一组数的最大公因数,最小公倍数是一组数的最小公倍数。
- 欧几里得算法:用辗转相除法求最大公约数。
- 求最小公倍数:将数分解成质因数,再取每个质因数的最高次幂相乘。
4. 同余定理同余定理是描述整数之间关系的定理。
- 同余关系:如果两个整数对于同一个模数的除法所得的余数相等,则它们对于这个模数是同余的。
- 同余定理:如果a与b对于模数m同余,那么它们的和、差、积也对于模数m同余。
5. 欧拉函数欧拉函数是比给定正整数小且与它互质的正整数的个数。
- 欧拉函数公式:对于正整数n,欧拉函数的值等于n与所有小于n且与n互质的正整数的个数。
6. 莫比乌斯函数莫比乌斯函数是一个常用于数论的函数。
- 莫比乌斯函数的定义:对于任何正整数n,莫比乌斯函数的值分为三种情况,分别是μ(n) = 1,μ(n) = -1,μ(n) = 0。
7. 勒让德符号勒让德符号是用来判断一个整数是否是二次剩余的符号。
- 勒让德符号的定义:对于正整数a和奇素数p,勒让德符号的值是一个取值为-1、0或1的函数。
- 勒让德判别定理:如果勒让德符号等于1,则a是模p的二次剩余;如果勒让德符号等于-1,则a不是模p的二次剩余。
8. 素数定理和费马小定理素数定理和费马小定理是数论中的重要定理。
- 素数定理:对于足够大的正整数n,小于等于n的素数的个数约为n/(ln(n)-1)。
- 费马小定理:如果p是素数,a是不是p的倍数的正整数,则a^(p-1)与模p同余。
小升初数论必考知识点归纳

小升初数论必考知识点归纳数论是数学中研究整数性质的分支,对于小升初的学生来说,掌握数论的基础知识是非常重要的。
以下是一些小升初数论的必考知识点归纳:1. 整数和自然数:理解整数包括正整数、负整数和0,自然数则是从1开始的正整数。
2. 奇数和偶数:能够识别奇数(不能被2整除的整数)和偶数(能被2整除的整数)。
3. 质数和合数:质数是指只有1和它本身两个因数的大于1的自然数,合数则是有其他因数的自然数。
4. 最大公约数和最小公倍数:理解最大公约数(两个或多个整数共有约数中最大的一个)和最小公倍数(能够被几个整数整除的最小正整数)的概念,并掌握求法。
5. 因数和倍数:理解一个数的因数是能够整除该数的所有整数,倍数则是该数的整数倍。
6. 数的整除性:掌握整除的概念,即如果一个整数a除以另一个整数b(b≠0),得到的商是整数且没有余数,我们就说a能被b整除,或b能整除a。
7. 分解质因数:将一个合数写成几个质数相乘的形式,这个过程称为分解质因数。
8. 完全平方数:如果一个数可以表示为某个整数的平方,那么这个数就是完全平方数。
9. 数位和位数:理解数位是指数字在数中的位置,位数是指一个数包含的数位的个数。
10. 带余除法:掌握带余除法的概念,即除法运算中除不尽时的余数。
11. 同余:如果两个整数除以同一个数得到的余数相同,那么这两个整数是同余的。
12. 等差数列:理解等差数列的概念,即每一项与前一项的差是一个常数。
13. 奇偶性规律:掌握一些基本的奇偶性规律,如奇数加奇数等于偶数,偶数加偶数等于偶数,奇数乘以奇数等于奇数等。
14. 数的进位制:了解不同进位制的基本概念,例如十进制、二进制等。
15. 约数个数的计算:掌握如何根据一个数的质因数分解来计算它的约数个数。
通过这些知识点的学习,学生可以更好地理解整数的性质,为进一步学习数学打下坚实的基础。
在实际的学习过程中,不仅要理解这些概念,还要通过大量的练习来加深理解并提高解题能力。
小升初数论专项必刷题数论(1)---数的整除、数的奇偶、质数和合数

第十七讲数论(1)---数的整除、数的奇偶、质数和合数小升初考点直击数的整除:1.熟悉并掌握2、3、5、9的倍数的特征。
2.一个数的末两位数能被4或25整除,这个数就一定能被4或25整除。
(4×25=100)。
3.一个数的末三位数能被8或125整除。
那么这个数就能被8或25整除。
(8×125=1000。
)4.一个数的末三位数与末三位以前的数字组成的数的差分别能被7、11、13整除,这个数就能被7、11、13整除。
另外,一个数奇数位上的数字和与偶数位上的数字和的差(差等于0比较常见)能被11整除,这个数就能被11整除。
(很常用,请牢记。
)(7×11×13=1001。
)5.如果两个数都能被同一个数整除,那么这两个数的和或差也能被这个数整除。
即如果c︱a,c ︱b,则c︱(a+b)或c︱(a-b)。
6.如果一个数能被另一个数整除,那么这个数的整倍数也一定能被另一个数整除。
即如果c︱a,b是整数,则c︱ab。
7.如果一个数能被第二个数整除,第二个数又能被第三个数整除,那么,第一个数也能被第三个数整除。
即如果a︱b,b︱c,则a︱c。
8.如果一个数能同时被另外两个数整除,而且这两个数互质,那么这一个数一寂能被另外两个数的积整除。
即如果a︱c,b︱c,且a、b互质,则ab︱c。
奇数和偶数:1.两个奇偶性相同的数的和(或差)一定是偶数;两个奇偶性不同的数的和(或差)一定是奇数。
反过来,两个数的和(或差)是偶数,这两个数奇偶性相同;两个数的和(或差)是奇数,这两个数肯定是一奇一偶。
2.奇数个奇数的和(或差)是奇数;偶数个奇数的和(或差)是偶数。
任意多个偶数的和(或差)是偶数。
3.若干个数相乘,如果其中有一个因数是偶数,那么积必是偶数;如果所有因数都是奇数,那么积就是奇数。
反过来,如果若干个数的积是偶数,那么因数中至少有一个是偶数;如果若干个数的积是奇数,那么所有的因数都是奇数。
小升初数学知识点之数论

千里之行,始于足下。
小升初数学学问点之数论数论是数学中的一个分支,主要争辩整数的性质和关系,涉及到整数的整除性、素数性质、同余关系等内容。
在小升初数学中,数论也是一个重要的学问点,以下是数学学问点之数论的主要内容。
一、整数的整除性1. 整数的定义及性质:整数是指正整数、0和负整数的统称。
整数有加法、减法、乘法运算,但并非全部整数都可以进行除法运算。
2. 整除与倍数:整数a除以整数b得到整数c,可以表示为a能整除b,记作a|b;假如b能整除a,也就是存在整数c,使得b=ac,则称a是b的倍数,b是a的约数。
3. 因数与倍数的关系:一个数的因数是指能整除这个数的整数,而这个数称为这些因数的倍数。
二、素数与合数1. 素数的定义:素数是大于1且只能被1和自身整除的整数。
2. 基本性质:素数只有两个因数,即1和自身;除了2之外的素数都是奇数。
3. 求解素数的方法:试除法、素数筛法等。
4. 合数的定义:合数是指除了1和本身之外还有其他因数的整数。
三、最大公约数与最小公倍数1. 公约数的定义:假如a和b都能被c整除,则称c是a和b的公约数。
2. 最大公约数的定义:最大公约数是指a和b的公约数中最大的那个数,记作gcd(a,b)。
3. 求解最大公约数的方法:辗转相除法、质因数分解法等。
4. 公倍数的定义:假如a和b都能被c整除,则称c是a和b的公倍数。
第1页/共2页锲而不舍,金石可镂。
5. 最小公倍数的定义:最小公倍数是指a和b的公倍数中最小的那个数,记作lcm(a,b)。
6. 最大公约数与最小公倍数的关系:对于任意两个整数a和b,有gcd(a,b) * lcm(a,b) = a * b。
四、同余关系1. 同余关系的定义:设a、b、n为整数,假如n能整除a-b,则称a和b 对模n同余,记作a ≡ b (mod n)。
2. 同余定理:若a≡b (mod n),c≡d (mod n),则有a±c≡b±d (mod n),ac≡bd (mod n)。
小升初数论基础知识点总结

小升初数论基础知识点总结一、质数1. 定义:质数是指只有1和本身两个因数的自然数。
2. 常见质数表:2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, ...3. 判断方法:一个自然数a是否是质数,可以试除从2到sqrt(a)的所有素数,如果a都不能被整除,那么a就是质数。
二、最大公约数1. 定义:两个不全为0的整数a和b的公共因数中最大的那一个就是a和b的最大公约数。
2. 求解方法:欧几里得算法是一种求最大公约数的有效方法,可以通过连续做辗转相除,得到最终的最大公约数。
三、最小公倍数1. 定义:两个不全为0的整数a和b的公共倍数中最小的那一个就是a和b的最小公倍数。
2. 求解方法:最小公倍数可以通过最大公约数求得,即两个数的乘积除以它们的最大公约数就是它们的最小公倍数。
四、整除与余数1. 定义:当a能被b整除时,a称为b的倍数,b称为a的约数。
如果a不能被b整除,那么a除以b的余数称为a对b的余数。
2. 性质:若a能被b整除,零是任何整数的公约数和公倍数。
3. 算法:整除运算可以通过乘法和减法的结合进行模拟,即a能否被b整除可以通过a-b 的连续减法得到结果。
五、除法定理和带余除法1. 定理:对于任意整数a和b,b不等于0,存在一对整数q和r,使得a = bq + r,其中q是商,r是余数。
2. 带余除法:将除数b不断增加倍数,直到超过被除数a,那么最后一次减法运算得到的余数就是带余除法的结果。
六、素数的判定与分解1. 判定方法:通过试除法可以判定一个数是不是素数,若一个数不能被2到sqrt(n)之间的素数整除,那么它就是素数。
2. 分解方法:每个正整数都可以分解成若干个素数的乘积,这就是素数分解定理,通过连续除素数得到的结果就是素数的分解。
七、互质数1. 定义:两个数的最大公约数为1时,这两个数就称为互质数。
2. 性质:互质数的乘积等于它们的最小公倍数,即互质数的最小公倍数就是它们的乘积。
小升初数学-数论-奥数篇-整除专题解析 必考知识点
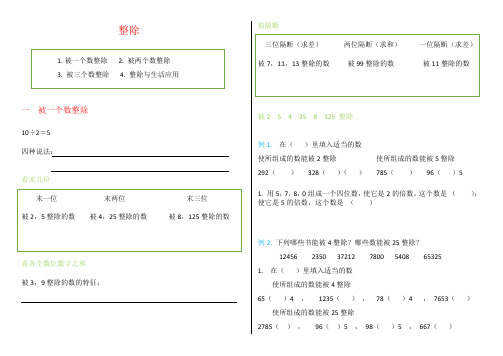
整除1.被一个数整除2. 被两个数整除3. 被三个数整除4. 整除与生活应用一被一个数整除10÷2=5四种说法:看末几位末一位末两位末三位被2,5整除的数被4,25整除的数被8,125整除的数看各个数位数字之和被3,9整除的数的特征:取隔断三位隔断(求差)两位隔断(求和)一位隔断(求差)被7,11,13整除的数被99整除的数被11整除的数被2 5 4 25 8 125 整除例1.在()里填入适当的数使所组成的数能被2整除使所组成的数能被5整除292()328()()785()96()51. 用5,7,8,0组成一个四位数,使它是2的倍数,这个数是();使它是5的倍数,这个数是()例2. 下列哪些书能被4整除?哪些数能被25整除?12456 2350 37212 7800 5408 653251. 在()里填入适当的数使所组成的数能被4整除65()4 ,1235(),78()4 ,7653()使所组成的数能被25整除2785(),96()5 ,98()5 ,667()例3.在()里填入适当的数使所组成的数能被8整除2210(),427()6 ,23()6使所组成的数能被125整除662(),887()0 ,4525()(),6673()()被3 9 整除例1.下面12个自然数,哪些能被3整除,哪些能被9整除?864 650 432 3675 9064 22125 5748 3108 96311125 2950 72901. 在89 121 135 480 157 483 中,是3的倍数的有()个。
2. 有一个四位数7AA1 是9的倍数,那么A是()3. 1024至少减去()就是3的倍数,1708至少加上()就是5的倍数。
4. 判断:个位上是3,6,9的数都是3的倍数。
()对于两个不相等的自然数,它们的和、差、积中必有一个是3的倍数。
()5. 已知x+2y(其中x y都是正整数)能被9整除,则2(5x-8y-4)被9除的余数为()被7 11 13 整除例1. 下面5个自然数中:128114 94146 64152 6139 4913678哪些能被7整除?哪些能被11整除?哪些能被13整除?1. 小月写了一个两位数59,冬冬写了一个两位数89 ,他们让小白写一个一位数放在59和89之间组成一个五位数59()89,使这个五位数能被7整除,小白写的数字是多少?被99 整除例1.2007a12b2既是9的倍数,又是11的倍数,那么这个数是多少?1. 已知七位数92AB427能被99整除,那么AB=2. 若1A219B7能被99整除,那么两位数A+B=()3. 六位数()2008()能同时被9和11整除。
2016小升初数学重点知识梳理

2016小升初数学重点知识梳理
知识体系:
约数倍数:
(1)最大公约最小公倍数(2)约数个数决定法则(小升初常考内容)
质数合数:
(1)质数、合数的概念和判断(2)分解质因数(重点)
余数问题:
(1)带余除式的理解和运用;(2)同余的性质和运用;(3)中国剩余定理奇偶问题:(1)奇偶与四则运算;(2)奇偶性质在实际解题过程中的应用完全平方数:(1)完全平方数的判断和性质(2)完全平方数的运用整数及分数的分解与分拆(重点、难点)
整除问题:
(1)数的整除的特征和性质(小升初分班常考内容)
(2)位值原理的应用(用字母和数字混合表示多位数)
这四个问题我们需要掌握到什么样的程度?
由于以上的四个问题,学生容易入门,但不易熟练,时常犯错误,因此成为近年来重点中学考试的热点,据了解,重点中学近年来的这几大问题的考题占据全部了80%左右,对这些问题的考察也十分偏重,而数论和行程问题的考察更是重中之重,往往占到一张试卷的50%,建议备战小升初数学的考生一定要引起足够的重视。
小升初二轮复习全攻略|小学期末考试(上册)试卷汇编
小学1—6年级语数英知识要点归纳|中外名著读后感大全
精心整理,仅供学习参考。
数论基础知识点总结

数论基础知识点总结1. 整数的性质整数是我们熟悉的数学概念,包括正整数、负整数和零。
整数有许多基本性质,比如加法、减法和乘法的封闭性、交换律、结合律和分配律等。
这些性质在数论中都有重要的应用,例如在证明整数的性质、定理及推论时经常用到。
2. 素数素数是指只能被1和自身整除的正整数,例如2、3、5、7、11等。
素数具有许多重要的性质,比如任何一个大于1的整数都可以被唯一地分解为若干个素数的乘积。
这就是著名的素因数分解定理。
素数在密码学中有着重要的应用,比如RSA加密算法就是基于素数的乘积难以分解的特性来实现的。
3. 同余同余是数论中一种重要的概念,表示两个数的差能被某个数整除。
例如,对于整数a、b和n,如果a-b能够被n整除,即(a-b) mod n=0,则称a与b关于模n同余,记作a≡b(mod n)。
同余在数论中有着广泛的应用,比如判断整数的奇偶性、最大公约数等问题。
4. 求模运算求模运算是数论中常见的一种运算,它指的是对一个整数进行取余操作。
例如,对于整数a和n,a mod n表示a除以n的余数。
求模运算在数论中有着重要的应用,比如判断奇偶性、判断整数是否能被某个数整除等问题。
5. 费马小定理费马小定理是数论中的一个重要定理,它描述了在模p意义下的幂的性质。
具体来说,费马小定理说明,如果p是素数,且a是p的倍数,那么a^p与a模p同余。
费马小定理在密码学中有着重要的应用,比如用来生成加密密钥、生成大素数等。
6. 欧拉定理欧拉定理是数论中的一个重要定理,它描述了模n意义下幂的性质。
具体来说,欧拉定理说明,如果n是大于1的整数,a和n互质(即它们的最大公约数是1),那么a的φ(n)次方与a模n同余,其中φ(n)表示小于n且与n互质的正整数的个数。
欧拉定理有着广泛的应用,比如RSA加密算法就是基于欧拉定理来实现的。
7. 等差数列等差数列是数学中常见的一种数列,它的每一项与前一项之差都相等。
例如,1,3,5,7,9就是一个公差为2的等差数列。
小升初数论部分知识点总结

数论数的整除一、整除性质性质1 如果数a和数b都能被数c整除,那么它们的和或差也能被c整除.即如果c︱a,c︱b,那么c︱(a±b).性质2 如果数a能被数b整除,b又能被数c整除,那么a也能被c整除.即如果b∣a,c∣b,那么c∣a.性质3 如果数a能被数b与数c的积整除,那么a也能被b或c整除.即如果bc∣a,那么b∣a,c∣a.性质4 如果数a能被数b整除,也能被数c整除,且数b和数c互质,那么a一定能被b与c的乘积整除.即如果b∣a,c∣a,且(b,c)=1,那么bc∣a.例:如果3∣12,4∣12,且(3,4)=1,那么(3×4) ∣12.性质5 如果数a能被数b整除,那么am也能被bm整除.如果b|a,那么bm|am(m为非0整数);性质6 如果数a能被数b整除,且数c能被数d整除,那么ac 也能被bd整除.如果b|a ,且d|c,那么bd|ac;二、常见数字的整除特征1. 一个数的末位能被2或5整除,这个数就能被2或5整除;一个数的末两位能被4或25整除,这个数就能被4或25整除;一个数的末三位能被8或125整除,这个数就能被8或125整除;2. 一个位数数字和能被3整除,这个数就能被3整除;一个数各位数数字和能被9整除,这个数就能被9整除;3. 如果一个整数的奇数位上的数字之和与偶数位上的数字之和的差能被11整除,那么这个数能被11整除.4. 如果一个整数的末三位与末三位以前的数字组成的数之差能被7、11或13整除,那么这个数能被7、11或13整除.约数倍数一、约数倍数中的重要公式:1. 约数个数计算公式对于一个数a可以分解质因数:a=a1的r1次方乘以a2的r2次方乘以a3的r3次方乘以……则a的约数的个数就是(r1+1)(r2+1)(r3+1)……其中,a1,a2,a3……都是a的质因数。
r1,r2,r3……是a1,a2,a3……的指数。
用一句话概括就是指数加一连乘2. 约数之和计算公式如果一个合数分解质因数后是a m×b n×c p×……(a,b,c……均为质数,m,n,p……均为自然数),那么,这个合数的全部约数之和为:(a0+a1+a2+……+a m)×(b0+b1+b2+……+b n)×(c0+c1+c2+……+c p)×……3. 约数乘积计算方法一个数的约数乘积就是它本身的约数个数一半的次方二、约数的概念与最大公因数0被排除在约数与倍数之外1.求最大公约数的方法①分解质因数法:先分解质因数,然后把相同的因数连乘起来.例如:,,所以;②短除法:先找出所有共有的因数,然后相乘.例如:,所以;③辗转相除法:每一次都用除数和余数相除,能够整除的那个余数,就是所求的最大公因数.用辗转相除法求两个数的最大公因数的步骤如下:先用小的一个数除大的一个数,得第一个余数;再用第一个余数除小的一个数,得第二个余数;又用第二个余数除第一个余数,得第三个余数;这样逐次用后一个余数去除前一个余数,直到余数是0为止.那么,最后一个除数就是所求的最大公因数.(如果最后的除数是1,那么原来的两个数是互质的).例如,求600和1515的最大公因数:;;;;;所以1515和600的最大公因数是15.2.最大公因数的性质①几个数都除以它们的最大公因数,所得的几个商是互质数;②几个数的公因数,都是这几个数的最大公因数的因数;③几个数都乘以一个自然数,所得的积的最大公因数等于这几个数的最大公因数乘以.3.求一组分数的最大公因数先把带分数化成假分数,其他分数不变;求出各个分数的分母的最小公倍数a;求出各个分数的分子的最大公因数b;即为所求.三、倍数的概念与最小公倍数1. 求最小公倍数的方法①分解质因数的方法;例如:,,所以;②短除法求最小公倍数;例如:,所以;③.2. 最小公倍数的性质①两个数的任意公倍数都是它们最小公倍数的倍数.②两个互质的数的最小公倍数是这两个数的乘积.③两个数具有倍数关系,则它们的最大公因数是其中较小的数,最小公倍数是较大的数.3. 求一组分数的最小公倍数方法步骤先将各个分数化为假分数;求出各个分数分子的最小公倍数;求出各个分数分母的最大公因数;即为所求.例如:注意:两个最简分数的最大公因数不能是整数,最小公倍数可以是整数.例如:四、最大公因数与最小公倍数的常用性质1.两个自然数分别除以它们的最大公因数,所得的商互质。
小升初数论知识点汇总总结

小升初数论知识点汇总总结数论是数学的一个分支,研究整数的性质和关系。
在小学升初中阶段,数论是数学教学中的一个重要知识点,同时也是很多数学竞赛和考试中的重点内容之一。
因此,了解数论的基本知识,对学生提高数学水平是非常有帮助的。
本文将对小升初数论知识点进行汇总总结,希望能够帮助学生更好地掌握数论知识。
一、整数的性质1. 整数的分类:整数可分为正整数、负整数和零三种类型。
2. 整数的大小比较:在同一类型的整数中,绝对值越大的整数,它的值越大。
3. 整数的运算性质:整数的四则运算规则与正整数类似,要注意加法和乘法的封闭性、交换律、结合律、分配律。
4. 整数的倍数与约数:若一个整数能被另一个整数整除,那么这个整数就是另一个整数的倍数;而可以整除的整数就是这个整数的约数。
一个数的约数是所有可以整除这个数的整数。
5. 整数的质数与合数:整数中除了1和本身外,没有其他正约数的整数称为质数,否则为合数。
例如,2、3、5、7、11、13等都是质数。
6. 整数的互质与最大公约数:两个整数如果最大公约数为1,则这两个整数互质。
最大公约数是两个或多个整数共有约数中最大的一个,通常记为gcd(a, b)。
二、质数与素数1. 质数的性质:除了1和本身外,没有其他正约数的自然数即为质数。
2. 素数的判定:判断一个数是不是素数,可以使用试除法或者埃氏筛法,试除法即从2到这个数的平方根之间的所有整数去除这个数,如果都不能整除,那么这个数就是素数。
3. 质因数分解:一个合数可以分解为若干个质数的乘积,这种分解式称为质因数分解。
4. 最小公倍数和最大公约数:两个或多个整数公有的倍数中最小的一个数称为这几个数的最小公倍数,两个或多个整数公有的约数中最大的一个数称为这几个数的最大公约数。
5. 素数的应用:素数在密码学、密码学、计算机科学等领域有着广泛的应用,如RSA加密算法就是基于素数特性实现安全的加密通信。
三、常见定理与公式1. 勾股定理:直角三角形的两条直角边的平方和等于斜边的平方,即a² + b² = c²。
小升初数学-数论-基-小数专题解析 必考知识点总结

千里之行,始于足下。
小升初数学-数论-基-小数专题解析必考学问点总结小升初数学中,数论是一个重要的考点。
而基-小数专题是数论中的一个重要分支,包括基本概念、性质、运算规章等内容。
下面是关于基-小数专题的必考学问点总结。
一、基本概念1. 整数:正整数、负整数、零。
2. 有理数:整数、分数。
3. 小数:有限小数、无限循环小数、无限不循环小数。
二、进制与位权1. 进制:二进制、八进制、十进制、十六进制等。
2. 位权:十进制中,各位上数字的位权依次是个位、十位、百位等。
其他进制下也有类似概念。
三、位权运算1. 加法:同进制下的数相加,按位相加,留意进位。
2. 减法:同进制下的数相减,按位相减,留意借位。
3. 乘法:同进制下的数相乘,按位相乘,留意进位。
4. 除法:同进制下的数相除,按位相除,留意进位和余数的计算。
四、小数的运算1. 加法:小数的十进制数相加,按位相加,留意进位。
2. 减法:小数的十进制数相减,按位相减,留意借位。
3. 乘法:小数的十进制数相乘,按位相乘,留意进位。
4. 除法:小数的十进制数相除,按位相除,留意进位和余数的计算。
第1页/共2页锲而不舍,金石可镂。
五、小数与分数的关系1. 有限小数可以表示为有限小数,例如 0.75=3/4。
2. 无限循环小数可以表示为无限不循环小数,例如0.999 (1)3. 无限不循环小数可以近似表示为分数,例如π≈22/7。
六、题型与解法1. 进制转换题:例如二进制转换为十进制。
2. 位权运算题:例如十进制数相加、相乘等。
3. 小数与分数的相互转换题:例如小数化分数、分数化小数。
4. 小数的四则运算题:例如小数的加减乘除。
5. 近似表示题:例如求一个无限不循环小数的近似分数。
以上是小升初数学数论基-小数专题的必考学问点总结。
这些学问点在小升初数学考试中经常消灭,把握好这些学问点,可以挂念我们在考试中取得好成果,同时也对我们今后的学习有很大的挂念。
所以,我们要认真学习并把握这些学问点,做好相应的习题,加深理解,提高解题力量。
小升初数论高级知识点总结

小升初数论高级知识点总结一、质数与因数1.1 质数质数是指除了1和自身以外,没有其他约数的正整数,如2、3、5、7、11等都是质数。
小升初学生在学习质数时需要掌握的内容包括:如何判断一个数是否为质数、寻找质数的方法、质数的性质等。
1.2 因数一个数如果可以被除了1和它本身以外的数整除,那么这个数就有因数。
小升初学生需要学习如何分解因数、因数分解的方法和应用、最大公因数和最小公倍数的相关知识。
二、最大公因数和最小公倍数2.1 最大公因数最大公因数(简称最大公约数)指的是两个或多个整数公有的最大约数。
小升初数学中需要学生掌握最大公因数的求解方法,以及最大公因数在分数化简、整数的性质和公式运用等方面的应用。
2.2 最小公倍数最小公倍数是指若干个数公有的最小的倍数。
小升初学生需要掌握最小公倍数的求解方法,以及最小公倍数在分数化简、整数的性质和公式运用等方面的应用。
三、整数的奇偶性3.1 整数的奇偶性规律小升初学生需要掌握整数的奇偶性,包括偶数的特征和性质、奇数的特征和性质、偶数和奇数的运算规律等内容。
3.2 整数的奇偶性应用学生需要了解整数奇偶性在分数化简、整数性质推导、方程式解法等方面的应用。
四、约数与倍数4.1 约数约数是指整数a能被整数b整除,那么b就是a的约数。
小升初学生需要掌握约数的判定和求解方法、约数在分数化简、整数性质推导等方面的应用。
4.2 倍数整数b是a的倍数,指的是a能被b整除。
小升初学生需要掌握倍数的判定和求解方法、倍数在分数化简、整数性质推导等方面的应用。
五、同余定理同余定理是数论中一个重要的概念,它描述了同一性质的整数在某个数的作用下的相等情况。
小升初学生需要了解同余定理的表达和应用,同时能够运用同余定理解决一些整数的性质问题。
六、费马小定理费马小定理是数论中的一个重要定理,它描述了质数性质中的一个重要规律。
小升初学生需要了解费马小定理的具体表达和应用,同时能够用费马小定理解决一些整数问题。
数论综合(小升初)

小升初数论综合知识概要一、奇数与偶数:1、判断一个多位数奇数还是偶数,只要看这个数的个位,个位是奇数,这个数就是奇数,个位是偶数,这个数就是偶数。
2、加减法结果的奇偶性判断方法:只看算式中奇数的个数,个数是奇数,结果就是奇数;个数是偶数,结果就是偶数。
(奇数个奇数的和或差还是奇数)3、乘法结果的奇偶性判断方法:只看有没有偶数,有偶数,结果就是偶数;无偶数,结果就是奇数。
(有偶则偶,无偶为奇)4、数列与奇偶数个数结合时,利用周期问题的知识解决。
二、因数与倍数:(一)最大公约数与最小公倍数如果一个自然数a 能被自然数b (不为零)整除,则称a 是b 的倍数,b 是a 的约数。
1、 几个自然数公有的约数,叫做这几个自然数的公约数。
公约数中最大的一个公约数,称为这几个自然数的最大公约数。
一般用符号()a b ,表示a 、b 的最大公约数。
公约数只有1的两个数,这两个数互质。
2、 几个自然数公有的倍数,叫做这几个自然数的公倍数。
公倍数中最小的一个大于零的公倍数,叫做这几个数的最小公倍数。
一般用符号[]a b ,表示a 、b 的最小公倍数。
3、最大公约数和最小公倍数之间的关系设a 、b 为两个正整数,则()a b ,和[]a b ,有如下关系(,)[,][,]=(,)ab ab a b a b a b a b =⨯或 4、求最大公约数和最小公倍数常用的方法:(1)分解质因数法;(2)短除法;(3)辗转相除法。
(二)最大公约数与最小公倍数的常用性质两个自然数分别除以它们的最大公约数,所得的商互质。
如果m 为A 、B 的最大公约数,且A ma =,B mb =,那么a b 、互质,所以A 、B 的最小公倍数为mab ,所以最大公约数与最小公倍数有如下一些基本关系:①A B ma mb m mab ⨯=⨯=⨯,这两个数的积等于两个数的最大公约数与最小公倍数之积;②两个数的和等于最大公约数乘这两个数独有因数的和③两个数的差等于最大公约数乘这两个数独有因数的差;④两个数的最小公倍数除以最大公约数等于两个数独有因数的乘积;⑤两个数的最小公倍数等于两个数的最大公约数乘两个数的独有因数。
小升初数论高频考点汇总与方法总结(上)

小升初数论高频考点汇总与方法总结(上) 小升初数论高频考点汇总与方法总结(上)本讲重点:1.数论专题系统梳理2.数论专题综合性题目选讲模块一:数论专题系统梳理一、整除性质1.如果自然数a为M的倍数,则ka为M的倍数。
(k为正整数)2.如果自然数a、b均为M的倍数,则a+b、a-b均为M的倍数。
3.如果a为M的倍数,p为M的约数,则a为p的倍数。
4.如果a为M的倍数,且a为N的倍数,则a为[M,N]的倍数。
二、整除特征1.末位系列:(2,5)末位,(4,25)末两位,(8,125)末三位。
2.数段和系列:3、9各位数字之和。
3.任意分段原则(无敌乱切法):33,99两位截断法,偶数位任意分段原则。
4.数段差系列:11整除判断-奇和与偶和之差,余数判断-奇和-偶和(不够减补十一,直到够减为止)。
5.7、11、13-三位截断法:从右往左,三位一隔,整除判断-奇段和与偶段和之差,余数判断-奇段和-偶段和(不够减则补,直到够减)。
三、整除技巧:1.除数分拆:(互质分拆,要有特征)2.除数合并:(结合试除,或有特征)3.试除技巧:(末尾未知,除数较大)4.同余划删:(从前往后,剩的纯粹)5.断位技巧:(两不得罪,最小公倍)四、约数三定律1.约数个数定律:(指数+1)再连乘。
2.约数和定律:(每个质因子不同次幂相加)再连乘。
3.约数积定律:自身n(n=约数个数÷2)。
五、完全平方数1.末位。
1、4、5、6、9.2.特征:÷3余或1余数,÷4余或1余数。
3.奇数个约数=完全平方数=偶指性。
六、短除模型七、质数明星:2=奇偶性,5=个位。
八、分解质因数1.质数:快速判断。
2.唯一分解定律。
3.见积就拆-大质因子分析。
九、余数定律1.利用整除性质求余数。
2.利用余数性质求余数。
3.利用除数分拆求余数。
十、带余除式代数思想=数论方程=去余化乘,找倍试约。
十一、同余问题1.同余定理:如果a与b除以m余数相同,则a、b之差为m的倍数。
小升初数学专题复习-专题一 数论 通用版

专题一数论考点扫描数论知识包括数的奇偶性、质数、合数、数的整除、余数的性质、数位的含义、平均数、分解因数、平方数、倍数与因数。
1.数的奇偶性奇数+奇数=偶数奇数+偶数=奇数偶数+偶数=偶数奇数×奇数=奇数偶数×偶数=偶数奇数×偶数=偶数奇数个奇数相加=奇数偶数个奇数相加=偶数(只要式子中含有偶数,那么相乘结果就是偶数)2.数的整除,常见的数的整除特征(1)2:个位是偶数;(2)3:各个数位之和是3的倍数;(3)5:个位是 0或5;(4)4、25:后两位可以被4(25)整除;(5)8、125:后三位可以被8(125)整除;(6)9:各个数位之和是9的倍数;(7)7:一个整数的个位数字截去,再从余下的数中,减去个位数的2倍,差是7的倍数。
例如,判断133是否7的倍数的过程如下:13-3×2=7,所以133是7的倍数;又例如判断6139是否7的倍数的过程如下:613-9×2=595 , 59-5×2=49,所以6139是7的倍数;(8)11:奇数位上的数字之和与偶数位上的数字之和的差(以大减小)是11的倍数;(9)13:一个多位数的末三位数与末三位以前的数字所组成的数之差,可以被13整除即可被13整除;(10)17:若一个整数的个位数字截去,再从余下的数中,减去个位数的5倍,如果差是17的倍数,则原数能被17整除。
3.余数的性质(1)余数的可加性:和的余数等于余数的和;(2)余数的可减性:差的余数等于余数的差;(3)余数的可乘性:积得余数等于余数的积;(4)同余的性质:对于同一个余数,如果有两个整数余数相同,那么它们的差就一定能被这个除数整除;对于同一个除数,如果有两个整数余数相同,那么它们的乘方就一定能被这个除数整数。
抛砖引玉【例1】下列各数中,()同时是3和5的倍数.A.18 B.102 C.45【解析】同时是3和5的倍数必须满足:末尾是0或5,并且各个数位上的和能被3整除;进而得出结论.18个位上是8,不是5的倍数,102个位上是2,不是5的倍数,45是5的倍数,4+5=9,是3的倍数。
小升初民办初中必考知识点之数论

小升初民办初中必考知识点之数论一、数论1.奇偶性问题奇±奇=偶奇×奇=奇奇±偶=奇奇×偶=偶偶±偶=偶偶×偶=偶2.位值原则形如:abc=100a+10b+c4.整除性质①如果c|a、c|b,那么c|(a±b)。
②如果bc|a,那么b|a,c|a。
③如果b|a,c|a,且(b,c)=1,那么bc|a。
④如果c|b,b|a,那么c|a.⑤a个连续自然数中必恰有一个数能被a整除。
5.带余除法一般地,如果a是整数,b是整数(b≠0),那么一定有另外两个整数q和r,0≤r<b,使得a=b×q+r当r=0时,我们称a能被b整除。
当r≠0时,我们称a不能被b整除,r为a除以b的余数,q为a除以b的不完全商(亦简称为商)。
用带余数除式又可以表示为a÷b=q……r, 0≤r<b a=b×q+r6. 唯一分解定理任何一个大于1的自然数n都可以写成质数的连乘积,即n= p11a× p22a×...×p k ak7.约数个数与约数和定理设自然数n的质因子分解式如n= p11a× p22a×...×p k ak那么:n的约数个数:d(n)=(a1+1)(a2+1)....(ak+1)n的所有约数和:(1+P1+P12+…p11a)(1+P2+P22+…p22a)…(1+Pk+Pk2+…pk ak)8.同余定理①同余定义:若两个整数a,b被自然数m除有相同的余数,那么称a,b对于模m同余,用式子表示为a≡b(mod m)②若两个数a,b除以同一个数c得到的余数相同,则a,b的差一定能被c整除。
③两数的和除以m的余数等于这两个数分别除以m的余数和。
④两数的差除以m的余数等于这两个数分别除以m的余数差。
⑤两数的积除以m的余数等于这两个数分别除以m的余数积。
9.完全平方数性质①平方差: A2-B2=(A+B)(A-B),其中我们还得注意A+B, A-B同奇偶性。
数论知识点归纳

数论知识点归纳整数a除以整数b(b≠0),除得的商正好是整数而没有余数,我们就说a能被b整除(也可以说b能整除a)。
数的整除的特征1.能被2(或5)整除的数:一个数个位上的数能被2(或5)整除,这个数就能被2(或5)整除。
2.能被4(或25)整除的数:一个数末两位数能被4(或25)整除,这个数就能被4(或25)整除。
3.能被8(或125}整除的数:一个数末三位数能被8(或125)整除,这个数就能被8(或125)整除。
4.能被3(或9)整除的数:若一个整数的各位上数字的和能被3(或9)整除,则这个数就能被3或9整除。
5.能被11整除的数;若一个整数的奇位数字之和与偶位数字之和的差能被11整除,则这个数就能被11整除。
6.能被7(11或13)整除的数:一个整数的末三位数与末三位以前的数字所组成的数之差(以大减小)能被7(11或13)整除,则这个数就能被7、11或13整除。
整除的性质A,b,c都是自然数(a>b),且a能被c整除,b也能被c整除,那么a+b能被c整除.a-b也能被c整除。
:因数和倍数(1)因数和倍数只限于在自然数范围内研究,不适用于其他数(如小数、分数)。
我们不能说“3.5是7的约数”,也不能说“7是3.5的倍数”,只能说“7能被3.5除尽”。
(2)因数和倍数是两个自然数在具有整除关系的前提下相互依存的。
因数是对倍数而言,倍数是对因数而言的,离开任何一方,另一方就不能成立,所以不能孤立地说某数是因数(或倍数),而应说某数是某数的因数(或倍数)。
以下四种情况可直接判断两数互质。
类型举例相邻的两个自然数如18与19相邻的两个奇数如31和33两个不同质数如53和711与任何自然数如1与12此外,两个数中一个是合数,另一个是质数,这个合数又不是这个质数的倍数,这样的两个数一定是互质数,如19与35。
如果一个质数是某个数的因数,那么就说这个质数是这个数的质因数。
把一个合数用质因数相乘的形式表示出来,叫做分解质因数。
小升初数论知识点总结

小升初数论知识点总结一、正整数和负整数1、正整数:大于0的整数,用正号表示。
2、负整数:小于0的整数,用负号表示。
二、整数的大小比较1、绝对值的大小比较:绝对值越大,数值越大。
2、同号比较:绝对值相等时,正数大于负数。
3、异号比较:正数大于负数。
4、零的比较:0大于任何负数,小于任何正数。
三、整数的加减运算1、同号:绝对值相加,符号不变。
2、异号:绝对值相减,符号取绝对值较大的数。
3、加法的逆运算:减法。
4、减法的逆运算:加法。
5、加减法的规律:交换律、结合律。
四、整数的乘法1、同号乘积为正,异号乘积为负。
2、乘法的逆运算:除法。
五、整数的除法1、除数不为零。
2、同号相除商为正,异号相除商为负。
3、商的符号由绝对值相除后得出。
六、公约数和最大公约数1、约数:整数a能被b整除,则b为a的约数。
2、公约数:两个数公有的约数。
3、最大公约数:公约数中最大的那个。
七、互质数和最小公倍数1、互质数:最大公约数为1的两个数。
2、最小公倍数:是两个数的公倍数中最小的那个。
八、素数和合数1、素数:只有1和自身作为约数的正整数。
2、合数:除了1和自身还有其他约数的正整数。
九、质因数分解1、任何一个大于1的自然数都能唯一地被素数分解。
2、将一个自然数素数乘积的形式叫做它的质因数分解式。
十、余数和整除性质1、整除:a能被b整除,a/b为整数。
2、余数:a除以b余c,c为余数。
3、整除性质:a能被b整除,b能被c整除,则a能被c整除。
十一、同余式1、同余式:a ≡ b (mod m),表示a与b相差m的倍数。
以上就是小升初数学数论的知识点总结。
希望对你有所帮助。
2016六年级数学小升初知识点

2016六年级数学小升初知识点(一)分解质因数在数的整除性这部分知识中,既是整除、约数、质数等基础知识的综合运用,也是后面学习最大公约数和最小公倍数的前提和准备,所以,在数的整除中,它具有承上启下的作用。
把一个合数分解质因数,就是把这个合数用质因数相乘的形式表示出来。
或者说,把一个合数写成几个质数的连乘积。
譬如36是合数,把36分解成因数相乘,会有以下几种情况:(1)36=1×36 (2)36=2×18(3)36=4×9 (4)36=3×12(5)36=6×6在上面五种分解中,只有(2)式的2和(4)式的3是质数,其他都不是。
要分解质因数就要把不是质数的数(1不是质数,也不是合数,排除在外),再分解成质数连乘的形式。
如(3)式中的4和9都是合数,4可以分解为:2×2; 9可以分解为:3 × 3。
这样,把 36分解质因数,36=2×2×3×3。
事实上,除(l)式外,(2)(4)(5)式继续分解,其最后结果也是同样的。
把一个合数分解质因数,具体过程可采用短除法。
例如:把420分解质因数。
(从最小的质因数开始)420有2、2、5、3、7五个质因数,420分解质因数的结果是:420=2×2×5×3×7。
在进行分解质因数时,最后的书写格式要特别注意,一定要把所要分解的合数写在等号的左边,如:24=2×2×2×3,105=3×5×7等,而不能写在等号的右边,如:2× 2×2×3= 24,这样就与乘法算式相混淆,而不是分解质因数了。
2016六年级数学小升初知识点(二)一、圆柱的特征:1、圆柱的两个圆面叫做底面,周围的面叫做侧面,底面是平面,侧面是曲面,。
2、圆柱的高:圆柱两个底面之间的距离叫做高。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
在小学阶段小升初考试是一次重要的考试,需要家长和小朋友们格外重视。
为此查字典数学网小升初频道为大家提供2016年小升初数论知识汇总,希望能够真正的帮助到家长和小学生们!1.奇偶性问题奇奇=偶奇×奇=奇奇偶=奇奇×偶=偶偶偶=偶偶×偶=偶2.位值原则形如:=100a+10b+c3.数的整除特征4.整除性质①如果c|a、c|b,那么c|(ab)。
②如果bc|a,那么b|a,c|a.③如果b|a,c|a,且(b,c)=1,那么bc|a.④如果c|b,b|a,那么c|a.⑤a个连续自然数中必恰有一个数能被a整除。
5.带余除法一般地,如果a是整数,b是整数(b≠0),那么一定有另外两个整数q和r,0≢rb,使得a=b×q+r p=当r=0时,我们称a能被b整除。
当r≠0时,我们称a不能被b整除,r为a除以b的余数,q为a除以b的不完全商(亦简称为商)。
用带余数除式又可以表示为a÷b=q……r,0≢rba=b×q+r p=6.唯一分解定理任何一个大于1的自然数n都可以写成质数的连乘积,即n=p1×p2×……×pk7.约数个数与约数和定理设自然数n的质因子分解式如n=p1×p2×……×pk那么:n的约数个数:d(n)=(a1+1)(a2+1)……(ak+1)n的所有约数和:(1+P1+P1+…p1)(1+P2+P2+…p2)…(1+Pk+Pk+…pk)8.同余定理①同余定义:若两个整数a,b被自然数m除有相同的余数,那么称a,b对于模m同余,用式子表示为a≡b(modm)②若两个数a,b除以同一个数c得到的余数相同,则a,b的差一定能被c整除。
③两数的和除以m的余数等于这两个数分别除以m 的余数和。
④两数的差除以m的余数等于这两个数分别除以m的余数差。
⑤两数的积除以m 的余数等于这两个数分别除以m的余数积。
9.完全平方数性质①平方差:A-B=(A+B)(A-B),其中我们还得注意A+B,A-B同奇偶性。
②约数:约数个数为奇数个的是完全平方数。
约数个数为3的是质数的平方。
③质因数分解:把数字分解,使他满足积是平方数。
④平方和。
10.孙子定理(中国剩余定理)11.辗转相除法12.数论解题的常用方法枚举、归纳、反证、构造、配对、估计希望我们准备的小升初数论知识符合大家的实际需求,愿大家都以优异的成绩考入理想的重点初中院校!。
