建筑力学:静定结构内力分析
合集下载
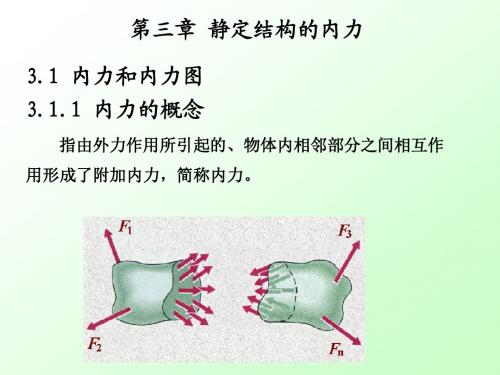
建筑力学第三章静定结构内力计算

01
02
03
04
排架是由两个单层刚架组成的 结构,其内力可以通过整体法
和分离法进行计算。
整体法是将两个单层刚架作为 一个整体进行分析,从而求得
整个排架的内力。
分离法是将排架拆分成两个单 层刚架进行分析,然后分别求
得每个单层刚架的内力。
在计算过程中,需要考虑到排 架的自重、外力以及支座反力
的影响。
组合结构的内力计算实例
03 静定结构的内力计算方法
截面法
总结词
通过在指定截面上截取隔离体,然后对隔离体进行受力分析,计算出内力的方法。
详细描述
截面法是静定结构内力计算的基本方法之一。在截面法中,我们首先在结构中选择一个或多个截面, 然后将这些截面处的杆件暂时断开,并分析这些杆件的内力。通过这种方法,我们可以确定每个杆件 的内力大小和方向。
组合结构是由两种或多种结构组成的 结构,其内力可以通过叠加法进行计 算。
在计算过程中,需要考虑到组合结构 是将每种结构的内力分别计算 出来,然后根据结构的特点进行叠加, 从而求得整个组合结构的内力。
05 静定结构内力计算的注意 事项
材料强度的考虑
材料强度
在计算静定结构内力时,必须考虑材 料的强度。不同的材料有不同的抗拉 、抗压、抗剪强度,应确保结构中的 应力不超过材料的容许应力。
节点法
总结词
通过分析节点处的平衡状态,计算出节点所受内力的方法。
详细描述
节点法是一种基于力的平衡原理的计算方法。在节点法中,我们首先确定节点 的位置和数量,然后分析每个节点处的平衡状态。通过这种方法,我们可以计 算出每个节点所受的内力大小和方向。
弯矩图法
总结词
通过绘制弯矩图,直观地表示出结构的弯矩 分布情况,进而计算出结构的内力。
建筑力学之 静定结构的内力分析知识详解

第二个脚标表示该截面所属杆件的另一端。例如 则表M示BA AB杆B端截面的弯矩。
表M示AB AB杆A端截面的弯矩,
❖ (3)内力图绘制
❖ 静定刚架内力图有弯矩图、剪力图、轴力图。刚架的内力图由各杆的内力图组合 而成,而各杆的内力图,只需求出杆端截面的内力后,即可按照梁内力图的绘制 方法画出。
❖ 6.平面刚架计算步骤
第十一章 静定结构的内力分析
❖ 第一节 楼梯斜梁和多跨静定梁 ❖ 1. 楼梯斜梁 ❖ 楼梯斜梁承受的荷载主要有两种,一种是沿
斜梁水平投影长度分布的荷载,如楼梯上人群 的重量等;另一种是沿倾斜的梁轴方向分布的 竖向荷载,如梁的自重等。 ❖ 一般在计算时,为计算简便可将沿梁轴方 向分布的竖向荷载按等值转换为沿水平方向分 布的竖向荷载,如图11-1 (a),沿梁轴线方向分 布 则的 由荷 于载 是等′值转转换换为,沿所水q 以平有方:向分布的荷q 载 ,
❖ (2)杆端内力的表示:如:FNAB 、 、 、 FNBA FQAB FQBA 、M AB 、M BA 等。 ❖ 注意:刚结点处不同方向有不同的杆端内力。
❖ 为了明确表示刚架上不同截面的内力,特别是为了区别汇交于同一结点的不同杆
端截面的内力,在内力符号右下角采用两个脚标;第一个脚标表示内力所属截面,
❖ 详解见教材
图11-21
❖ (6)结点法与截面法的联合应用 ❖ 欲求图11-23所示a杆的内力,如果只用结点法计算,不论取哪个结
点为隔离体,都有三个以上的未知力无法直接求解;如果只用截面法 计算,也需要解联立方程。 ❖ 为简化计算,可以先作Ⅰ-Ⅰ截面,如图所示,取右半部分为隔离 体,由于被截的四杆中,有三杆平行,故可先求1B杆的内力,然后以 B结点为隔离体,可较方便地求出3B杆的内力,再以3结点为隔离体, 即可求得a杆的内力。
建筑力学静定结构内力计算

工业建筑及大跨度民用建筑中的屋架、托 架、檩条等常常采用桁架结构。
上弦杆 斜杆 竖杆
节间距离
下弦杆 跨度
桁架的计算简图常常采用下列假定: (1) 联结杆件的各结点,是无任何摩擦的理想铰。 (2) 各杆件的轴线都是直线,都在同一平面内,并且 都通过铰的中心。 (3) 荷载和支座反力都作用在结点上,并位于桁架平 面内。
Nc=33.3 kN (拉力)
求Nb:取Na与Nc的交点O为矩心, 如图 (c)所示,并将Nb在1结点处分 解为Vb、Hb,则: ∑MO=0: ∑MO=VAx+Vb(x+4)-10x-
20(x+2)=0 根据相似三角形的比例关系有: x=6m 将x=6代入∑MO 40×6+Vb×10-60-20×(6+2)=0 Vb=-2 kN 根据力Nb与其竖向分量Vb的比
也就是说,当杆件变形达到一定限度,点之间出 现开裂现象。当截面上的内力都达到了极限,所有点 之间都出现了裂缝,则意味着杆件发生断裂破坏了。
具体的定量表达将在后面介绍的强度条件中描述。
2、截面法
确定杆件某一截面中的内力,假想将杆件沿需求内力的 截面截开,使杆件分为两部分,取其中任一部分作为研究对 象。用作用于截面上的内力,代替舍去部分对留下部分的作 用力。 再由静力平衡条件求出此内力的方法,称为截面法。 截面法可归纳为两个步骤:
在桁架中,有时会出现轴力为零的杆件,它 们被称为零杆。在计算之前先断定出哪些杆件为 零杆,哪些杆件内力相等,可以使后续的计算大 大简化。在判别时,可以依照下列规律进行。
(1) 对于两杆结点,当没有外力作 用于该结点上时,则两杆均为零杆, 如图 (a)所示;当外力沿其中一杆的 方向作用时,该杆内力与外力相等, 另一杆为零杆,如图 (b)所示。 (2) 对于三杆结点,若其中两杆共 线,当无外力作用时,则第三杆为零 杆,其余两杆内力相等,且内力性质 相同(均为拉力或压力)。如图 (c) 所示。 (3) 对于四杆结点,当杆件两两共 线,且无外力作用时,则共线的各杆 内力相等,且性质相同。如图 (d)所
上弦杆 斜杆 竖杆
节间距离
下弦杆 跨度
桁架的计算简图常常采用下列假定: (1) 联结杆件的各结点,是无任何摩擦的理想铰。 (2) 各杆件的轴线都是直线,都在同一平面内,并且 都通过铰的中心。 (3) 荷载和支座反力都作用在结点上,并位于桁架平 面内。
Nc=33.3 kN (拉力)
求Nb:取Na与Nc的交点O为矩心, 如图 (c)所示,并将Nb在1结点处分 解为Vb、Hb,则: ∑MO=0: ∑MO=VAx+Vb(x+4)-10x-
20(x+2)=0 根据相似三角形的比例关系有: x=6m 将x=6代入∑MO 40×6+Vb×10-60-20×(6+2)=0 Vb=-2 kN 根据力Nb与其竖向分量Vb的比
也就是说,当杆件变形达到一定限度,点之间出 现开裂现象。当截面上的内力都达到了极限,所有点 之间都出现了裂缝,则意味着杆件发生断裂破坏了。
具体的定量表达将在后面介绍的强度条件中描述。
2、截面法
确定杆件某一截面中的内力,假想将杆件沿需求内力的 截面截开,使杆件分为两部分,取其中任一部分作为研究对 象。用作用于截面上的内力,代替舍去部分对留下部分的作 用力。 再由静力平衡条件求出此内力的方法,称为截面法。 截面法可归纳为两个步骤:
在桁架中,有时会出现轴力为零的杆件,它 们被称为零杆。在计算之前先断定出哪些杆件为 零杆,哪些杆件内力相等,可以使后续的计算大 大简化。在判别时,可以依照下列规律进行。
(1) 对于两杆结点,当没有外力作 用于该结点上时,则两杆均为零杆, 如图 (a)所示;当外力沿其中一杆的 方向作用时,该杆内力与外力相等, 另一杆为零杆,如图 (b)所示。 (2) 对于三杆结点,若其中两杆共 线,当无外力作用时,则第三杆为零 杆,其余两杆内力相等,且内力性质 相同(均为拉力或压力)。如图 (c) 所示。 (3) 对于四杆结点,当杆件两两共 线,且无外力作用时,则共线的各杆 内力相等,且性质相同。如图 (d)所
第六章--静定结构的内力计算-建筑力学

120kN
40kN/m
C
A
120kN D
B
C
40kN/m
D
60kN
A B
60kN
145kN
145
FS图 +
(kN )
M图 (kN m)
320
235kN
60
-
+
-
60
175
120
180
§6-6 三铰拱
q
C
FAx = FH A
FA y
l 2
l 4
l
q
A
C
FA0y
F
f
B
l
FB x
4 FB y
F
B
FB0y
dx l l y2 = 3m
FA y
81.5m =12m
FB y
100kN
A
20kN/m
C
B
M 2 = M 20 - FH y2 = 67.5kN m
FSL2 = FSL20 c os - FH sin
= 41.6kN
FSR2 = FSR20 c os - FH sin
FA0y tg2 = 0.667
0.5m
FA = 19kN
D
1.5m
8kN
A
FNAC
FxAD
19kN
FyAD
FNAD
FyAD = 11kN FxAD = 33kN
FNAD = 34.8kN FNAC = -33kN
P
P+P'
无外载时的内力: P
有外载时的内力: P+P'
ΔP=P+P'-P=P' —(附加)内力 研究的是外力所产生的附加内力, 简称内力
建筑力学与结构第三章
M 0 x a V ( x ) R A l AC段 : M ( x) R x Mx 0 x a A l
M /l
V
Mb / l
M
Ma / l
讨论:集中力偶M作用点C处:
M V ( x) RB l a x l CB段 : M ( x) RB l x M l x a x l l
4、判断各段V、M图形状:
3.8 2.2 CA和DB段:
q=0,V图为水平线, M图为斜直线。
AD段:q<0, V 图为向下斜直线,
1.41
M图为下凸抛物线。
按叠加原理作弯矩图(AB=2a,力P作用在梁AB的中点处)。 P A P A V B + M B x
Pa qa2 + 2 2
+ x
= +
V B
V=12KN/m
根据2-2截面右侧的外力计算V2 、 M2 V2 =+(V· 1.5)-RB =12· 1.5-29 =-11KN M2 =-(V· 1.5)· 1.5/2+RB· 1.5 =-(12· 1.5)· 1.5/2+29· 1.5 = +30 KN· m
M2 V2Βιβλιοθήκη RB第三章 静定结构的内力
MDC=30×2=-60KNM(左拉)
NDE=30KN(压力) VDE=40KN MDE= 30×2=-60KNM(上拉)
VBE=30KN
MBE= 0
60
180
30
40
30 80
M图(KNM)
30 40
V图(KN)
80
N图(KN)
三、三铰刚架弯矩图
M /l
V
Mb / l
M
Ma / l
讨论:集中力偶M作用点C处:
M V ( x) RB l a x l CB段 : M ( x) RB l x M l x a x l l
4、判断各段V、M图形状:
3.8 2.2 CA和DB段:
q=0,V图为水平线, M图为斜直线。
AD段:q<0, V 图为向下斜直线,
1.41
M图为下凸抛物线。
按叠加原理作弯矩图(AB=2a,力P作用在梁AB的中点处)。 P A P A V B + M B x
Pa qa2 + 2 2
+ x
= +
V B
V=12KN/m
根据2-2截面右侧的外力计算V2 、 M2 V2 =+(V· 1.5)-RB =12· 1.5-29 =-11KN M2 =-(V· 1.5)· 1.5/2+RB· 1.5 =-(12· 1.5)· 1.5/2+29· 1.5 = +30 KN· m
M2 V2Βιβλιοθήκη RB第三章 静定结构的内力
MDC=30×2=-60KNM(左拉)
NDE=30KN(压力) VDE=40KN MDE= 30×2=-60KNM(上拉)
VBE=30KN
MBE= 0
60
180
30
40
30 80
M图(KNM)
30 40
V图(KN)
80
N图(KN)
三、三铰刚架弯矩图
静定结构的内力—结点法求静定平面桁架内力(建筑力学)

20kN
FyDC FNDC
C
30 5
D A
FNDF
2m
F
FxDF
4m
FyDF
FNDF
51
2
Fy 0,
FyDC 30 20 FyDF 0
(FyDF 10kN )
FyDC 30 20 10 20kN
FNDC FyDC (l / l y ) 20( 5 / 1) 44.72kN (压)
FAy= FBy= 30kN (↑) FAx= 0KN
2)判断零杆: 见图中标注。 3)求各杆轴力:
20kN
D 0
0
AE
20kN
C
20kN
G
1m
0
1m
F
H
B
30kN 2m 2m 2m 2m 30kN
取结点隔离体的顺序为:A、E、D、C。
由于结构对称,荷载对称,只需计算半边结构。
结点A: Fy 0,
4) 运用比例关系:
FN Fx 。Fy l lx ly
结点受力的特殊情况:
1)
FN1
0。
90
0
FN2
s
结点上无荷载,则FN1=FN2=0。
由∑FS=0,可得FN2=0,故FN1=0。
2)
FN1
FN2
Fy 0, FN 3 0;
0
FN3
Fx 0,
FN 1
FN
。
2
3) FN1
FN4 FN3
结点C:
Fy 0,
FNCF 20 40 0, FNCF 20kN(拉)。
20 5
20k N
C
20 5
FNCF
20kN
建筑力学 第九章(最终)

图9-7
② 求各杆杆端的内力。 考虑结点 D 的平衡: 由
求得
由 求得
由
求得 考虑结点 E 的平衡: 由
求得
由 求得
由 求得
M D 0, M DE 18 0
M DE 18 kN m
Fx 0, FNDE 3 0
FNDE 3 kN
Fy 0, FQDE 4.5 0
FQDE 4.5 kN
截取横梁 CF 为研究对象,根据 FN 图、FQ 图 和 M 图,画出其受力图如图9-6e 所示。
MC 24 20 20 2 12 5 36 4 0 Fx 10 10 0
Fy 36 4 20 12 0
可见横梁 CF 满足平衡条件,表明所求作的内 力图正确。
图9-6
【例9-4】试作出图9-7a 所示三铰刚架的内力图。 解:① 计算支座反力。
图9-3
由本例可见,求作多跨静定梁内力图的关键是 要分清梁的组成层次,作出层次图,以及如何将梁 拆开来计算其支座反力。梁的支座反力一旦求出, 求作多跨静定梁内力图的问题就归结为求作各单跨 静定梁内力图的问题,而单跨静定梁的内力图绘制 已是熟悉的求作问题。所以,求作多跨静定梁内力 图只不过是在单跨静定梁的内力图绘制基础上所做 的一种引伸,而并非新的计算问题。
12 110
2
4
kN
由
Fy 0, FBy FAy 20 12 0
求得
FBy 20 12 FAy 20 12 4 36 kN
② 求各杆的杆端弯矩,作 M 图。
杆AC: M AC 0, MCA 22 4 8 4 2 24kN m
用区段叠加法绘出杆 AC 段弯矩图。应用虚线连接杆端弯 矩 MAC 和 MCA,再叠加该杆段为简支梁在均布荷载作用下的弯 矩图。
第五章 静定结构的内力分析

1 a) A 1 B
MB
2 2
MC
C
解:1.计算外力偶矩
M A 9549
m T 1592N· 637N· m
b) T c)
M B 9549
x
637N· m
x
2.求各段扭矩 AB段:T1= MA=1592N· m BC段:T2= MA- MB=1592-955=637N· m
30 955N m 300 20 M C 9549 637N m 300
压缩与弯曲的组合
弯曲与扭转的组合
在进行结构设计时,为保证结构安全正常工
作,要求各构件必须具有足够的强度和刚度。解
决构件的强度和刚度问题,首先需要确定危险截
面的内力,内力计算是结构设计的基础。
5—1 轴向拉压杆
沿杆件轴线作用一对相反的外力,杆件将发生沿轴线方向
的伸长或缩短,这种变形称为轴向拉伸或压缩。
建筑力学
第5章 静定结构的内力分析
杆件结构——由杆件组成的结构。
杆件——长度远大于其横截面的宽度和高度的构件。
几何特点:横截面是与杆件长度方向垂直的截面,而轴线 是各横截面形心的连线。细而长,即l>>h,l>>b。
杆件结构
杆又可分为直杆和曲杆。
受外力作用后,其几何形状和尺寸一般都要发生改 变,这种改变称为变形。作用在构件上的荷载是各种 各样的,因此,杆件的变形形式就呈现出多样性,并 且有时比较复杂,但分解来看,变形的基本形式却只 有四种:
3.求截面2-2的内力
Fy 0 : FAy F FQ 2 0, 5 1 得FQ 2 FAy F F F F 4 4 M 2 0 : 2Fl M 2 0,
MB
2 2
MC
C
解:1.计算外力偶矩
M A 9549
m T 1592N· 637N· m
b) T c)
M B 9549
x
637N· m
x
2.求各段扭矩 AB段:T1= MA=1592N· m BC段:T2= MA- MB=1592-955=637N· m
30 955N m 300 20 M C 9549 637N m 300
压缩与弯曲的组合
弯曲与扭转的组合
在进行结构设计时,为保证结构安全正常工
作,要求各构件必须具有足够的强度和刚度。解
决构件的强度和刚度问题,首先需要确定危险截
面的内力,内力计算是结构设计的基础。
5—1 轴向拉压杆
沿杆件轴线作用一对相反的外力,杆件将发生沿轴线方向
的伸长或缩短,这种变形称为轴向拉伸或压缩。
建筑力学
第5章 静定结构的内力分析
杆件结构——由杆件组成的结构。
杆件——长度远大于其横截面的宽度和高度的构件。
几何特点:横截面是与杆件长度方向垂直的截面,而轴线 是各横截面形心的连线。细而长,即l>>h,l>>b。
杆件结构
杆又可分为直杆和曲杆。
受外力作用后,其几何形状和尺寸一般都要发生改 变,这种改变称为变形。作用在构件上的荷载是各种 各样的,因此,杆件的变形形式就呈现出多样性,并 且有时比较复杂,但分解来看,变形的基本形式却只 有四种:
3.求截面2-2的内力
Fy 0 : FAy F FQ 2 0, 5 1 得FQ 2 FAy F F F F 4 4 M 2 0 : 2Fl M 2 0,
