层次分析法在旅游地点选择中的应用

合集下载

层次分析法在旅游综合决策中的应用我的

层次分析法在旅游综合决策中的应用摘要：层次分析法是一种定性与定量分析相结合的多目标决策分析方法，将决策者的经验判断给予量化，对目标(因素)结构复杂而且缺乏必要的数据情况下，采用此方法较为实用，是常用的一种系统分析方法。

本文通过一个旅游问题的实例来说明其在分析决策中的应用，这种分析的方法可以推而广之，解决其他决策问题，是决策应用的通行思路。

关键词：层次分析法旅游决策一：背景在日常生活中，我们会遇到许多决策问题。

例如选择旅游景点，选择升学志愿，选择职业，选择科研课题等等。

人们在决策时，要考虑涉及到经济、社会、人文等方方面面的因素：选择旅游景点经常会考虑景色、费用和居住、饮食、交通等条件是否舒适和方便；要选择升学志愿，必然要考虑到你本人的兴趣爱好、学习基础、专业前途以及收费标准等因素；选择职业一般依据工作环境、工资待遇、发展前途、住房条件等因素；选择科研课题一般依据课题的可行性、应用价值、理论价值、被培养人才等因素。

当我们面临各种各样的方案，在对这些因素作比较、判断、评价、决策时，常常无法量化这些因素的重要性、影响力或者优先程度，人的主观选择会起到作用，因此，应用常规的数学方法解决这一问题带来本质上的困难。

美国运筹学家托马斯·沙旦(T.L.Saaty)等人在20 世纪70 年代提出了一种能有效处理这类问题的实用方法，即层次分析法（Analytic Hierarchy Process，AHP）。

层次分析法这是一种定性和定量相结合的、系统化的、层次化的分析方法。

过去研究自然和社会现象主要有机理分析法和统计分析法两种方法，前者用经典的数学工具分析现象的因果关系，后者以随机数学为工具，通过大量的观察数据寻求统计规律。

近年发展的系统分析是又一种方法，而层次分析法是系统分析的数学工具之一，它把一个复杂问题分解成组成因素，并按支配关系形成层次结构，然后应用两两比较的方法确定决策方案的相对重要性。

由于层次分析法在处理复杂的决策问题上的实用性和有效性，目前，层次分析法在经济计划和管理、能源政策和分配、行为科学、军事指挥、运输、农业、教育、人才、医疗、环境保护、冲突求解及决策预报等领域得到了广泛的应用。

层次分析法在旅游综合体规划中的应用

层次分析法在旅游综合体规划中的应用一、概况规划地块位于浙江省诸暨市枫桥镇枫江一侧。

该地区属于夏热冬冷地区，春末夏初为梅雨季节，夏秋偶受热带风暴和台风袭击。

该地块位于山体与水体附近，地势平坦，即使在汛期也有南面山体相挡，北面山体有两个较大山谷，有一定山洪危险。

地块土壤较为结实，植被覆盖良好，山清水秀，环境优美。

该地块附近有高速路，增加了该地块项目的可达性。

该地块得天独厚的地理位置和丰富的动植物资源以及良好的水质条件为该地块开发旅游事业带来了诸多有利条件。

二、建立层次结构模型根据该次规划的目标“达到最高综合效益”，将其作为层次分析的目标层（G）；将决定经济效益的环境条件、经济条件、“硬件”条件和“软件”条件作为层次分析法的准则层（C）；以景观、气候、政策、服务等16种主要影响因子作为层次分析法的方案层（P）。

以此建立旅游综合体规划层次结构模型（如下图）。

三、层次结构模型因素说明从环境层面来看，优美的自然景观作为优越的旅游资源无疑是旅游项目最重要的因素之一，宜居的气候又促进了旅游房地产的发展。

安全的环境以及便利的交通更是会增加游客量带动经济。

另外，宁静的声学环境也是人们向往的。

环境，也可以说是氛围，如果有一种独特的氛围很吸引人，必定能使经济效益大幅体现。

从经济层面看，政府部门的支持会大力推动旅游业的快速发展，客源量也是拉动经济的直观数据。

同时，区域经济发展水平也决定了该地块的建设规模质量与服务能力。

对于资金回报的快慢，影响到度假与房地产的相互协调。

从硬件条件来看，旅游综合体的功能（如康体娱乐、休憩等）以及游玩项目的类型、建筑的类型等如果丰富多彩，将增加有趣性。

旅游项目的高含金量，地产项目的过硬质量（靠得住的质量，实惠的购买单价，舒适的户型，怡人的装修……谁会不心动呢？），综合体较高的整体质量，都将为其带来丰厚的回报。

项目的成片以及产业的集聚会带来集群效应，完整的配套设施会给房主带来便利，配套的服务设施（如门票、停车、住宿、餐饮等）不仅会吸引游客，同时在这些相关产业中增加收益。

层次分析法对旅游地的选择

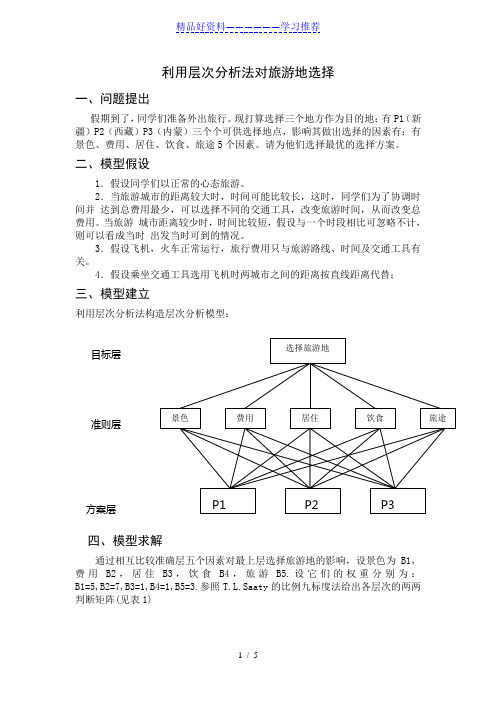
利用层次分析法对旅游地选择一、问题提出假期到了，同学们准备外出旅行。

现打算选择三个地方作为目的地：有P1（新疆）P2（西藏）P3（内蒙）三个个可供选择地点，影响其做出选择的因素有：有景色、费用、居住、饮食、旅途5个因素。

请为他们选择最优的选择方案。

二、模型假设1．假设同学们以正常的心态旅游。

2．当旅游城市的距离较大时，时间可能比较长，这时，同学们为了协调时间并达到总费用最少，可以选择不同的交通工具，改变旅游时间，从而改变总费用。

当旅游城市距离较少时，时间比较短，假设与一个时段相比可忽略不计，则可以看成当时出发当时可到的情况。

3．假设飞机，火车正常运行，旅行费用只与旅游路线、时间及交通工具有关。

4．假设乘坐交通工具选用飞机时两城市之间的距离按直线距离代替；三、模型建立利用层次分析法构造层次分析模型：四、模型求解通过相互比较准确层五个因素对最上层选择旅游地的影响，设景色为B1，费用B2，居住B3，饮食B4，旅游B5.设它们的权重分别为：B1=5,B2=7,B3=1,B4=1,B5=3.参照T.L.Saaty的比例九标度法给出各层次的两两判断矩阵(见表1)表1 同学们对准则层各因素相对重要性的两两比较判断矩阵B1 B2 B3 B4 B5 权重系数B1 1 5/7 5/3 3 5/3 0.364B2 7/5 1 7/1 7/1 7/3 0.374B3 1/5 1/7 1 1 1/3 0.183B4 1/5 1/7 1 1 1/3 0.481B5 3/5 3/7 3 3 1 0.237 λ=0.3006 CI=0.003 CR=0.001同学们对给出方案层的判断矩阵相同，都是如下结果（见表2，表3，表4）表2 同学们就提出的三个方案在景色上面的两两判断矩阵P1 P2 P3 权重系数P1 1 1 1/2 0.237P2 3 1 3/2 0.362P3 2 2/3 1 0.311 λ=0.3012 CI=0.004 CR=0.010表3就同学们提出的三个方案在费用上的两两判断矩阵P1 P2 P3 权重系数P1 1 2/3 2 0.492P2 3/2 1 3 0.124P3 1/2 2/3 1 0.271 λ=3.0007 CI=0.003 CR= 0.005 表4同学们就提出的三个方案在住宿方面的两两判断矩P1 P2 P3 权重系数P1 1 2/3 2 0.643P2 3/2 1 3 0.124P3 1/2 2/3 1 0.431 λ=3.013 CI=0.0065 CR=0.011P1 P2 P3 权重系数P1 1 1/2 2 0.265P2 2 1 5 0.606P3 1/2 1/5 1 0.129 = 3.023 CI=0.004 CR=0.007P1 P2 P3 权重系数P1 1 4 6 0.691P2 1/4 1 2 0.204P3 1/6 1/2 1 0.105 =3.013 CI=0.0065 CR=0.011五、模型分析层次单排序及一致性检验根据层次分析法的计算步骤，必须对以上的六个表的两两判断矩阵进行层次单排序，计算各自的权重系数，并对它们逐个进行一致性检验。

基于层次分析法的旅游景点选择应用(1)

基于层次分析法的旅游景点选择应用层次分析法（AHP）是一种多准则决策方法，可以帮助旅游者选择最适合他们的旅游景点。

该方法可以帮助旅游者根据他们的偏好和需要对不同的景点进行比较和评估，以便做出最佳的选择。

下面我们将介绍如何使用AHP来选择旅游景点。

1.确定标准首先，旅游者需要确定选择旅游景点的标准。

例如，您希望景点具有美丽的风景、历史文化遗产和娱乐设施等等。

您应该根据您的优先级制定一个清晰的标准列表，以便稍后进行比较。

2.创建层次结构接下来，您需要创建一个包含标准和景点的层次结构。

这个层次结构应该先从最高级别开始，然后逐步细化到次级别。

例如：第一层：选择标准第二层：美丽的风景、历史文化遗产、娱乐设施第三层：旅游景点1、旅游景点2、旅游景点33.建立判断矩阵判断矩阵是用来比较标准和景点之间的重要性的。

您需要为每个标准和景点创建一个权重，这个权重是一个百分比，表示该标准或景点在您的选择中的重要性。

例如：您认为美丽的风景比历史文化遗产和娱乐设施更重要，应该赋予它更高的权重。

美丽的风景：0.5历史文化遗产：0.3娱乐设施：0.24.计算一致性比率在AHP中，一致性是一个很重要的概念，因为它可以帮助您检查您的权重是否合理。

为了计算一致性比率，您需要对比每个标准和景点的一对判断，然后计算它们的一致性指数。

接下来，您需要把这些指数加起来，得出一个总体一致性指数CAL。

例如，如果您认为美丽的风景比历史文化遗产更重要，则比较这两个标准的一致性指数如下：美丽的风景比历史文化遗产更重要：1历史文化遗产比美丽的风景更重要：3然后您必须计算这两个一致性指数的比率，以了解它们之间的一致性。

如果这个比率超过0.1，则意味着您的权重是不一致的。

您需要重新调整它们的权重，直到比率小于0.1。

5.计算最终权重一旦您确定了每个标准和景点的权重，并检查了它们之间的一致性，您就可以计算出每个景点的最终权重。

计算公式为：最终权重=标准权重×景点权重。

基于层次分析法的旅游景点选择应用

基于层次分析法的旅游景点选择应用在旅游出行中，选择合适的旅游景点是至关重要的。

然而，很多时候旅游者会困惑于众多景点之间的选择。

为了帮助旅游者更好地选择旅游景点，我们可以利用层次分析法进行决策分析。

层次分析法是一种经典的多准则决策方法，被广泛应用于各种决策分析问题中。

它的核心思想是将决策问题分解为多个层次，将复杂的决策问题简化成易于理解的层次结构，然后通过对各层次之间的比较来确定最终的决策结果。

在旅游景点的选择问题中，我们可以将决策问题分解为三个层次：目标层、准则层和方案层。

在目标层，我们需要确定自己旅游的目标，比如休闲度假、文化探险、自然风光观赏等等。

在准则层，我们需要确定影响景点选择的各种因素，比如交通便利性、景点知名度、景点口碑等等。

在方案层，我们需要列出各种旅游景点方案。

接下来，我们需要对每个层次进行权重分析，以确定各个准则和方案的重要程度。

可以采用问卷调查、专家咨询等多种方法进行权重分析。

例如，在准则层中，我们可以邀请一些旅游专家或者常常旅游的人士，询问他们对各种准则的看法和评价，并根据他们的意见，确定各个准则的相对重要程度。

在确定了各个层次的权重之后，我们可以利用层次分析法的计算方法，对各个方案进行比较。

具体来说，我们可以采用层次分析法的征求意见矩阵法，将各个方案与准则的比较结果输入到一个矩阵中，通过计算矩阵的特征向量来确定最终权重，进而确定最优的旅游方案。

在结果评价方面，我们可以利用一些数据分析方法，比如聚类分析、主成分分析等等，对各个方案的优劣进行评价和比较。

此外，我们还可以采用一些可视化工具，比如地图、图表等等，为旅游者提供更直观、易懂的决策支持。

总之，基于层次分析法的旅游景点选择应用，可以帮助旅游者更加科学、合理地选择旅游景点，提高旅游的质量和效果。

虽然该方法需要一定的专业知识和数据分析技能，但只要认真学习掌握，就可轻松应对各种旅游决策问题。

层次分析法对旅游景点选择的研究

摘要：旅游是人们离开家门，求新、求知、求乐的一种社会活动，也是假日休闲的首选，因此旅游对于景色、居住、饮食等都要有详细的了解，然而最重要的就是确定最终要出行的地点。

文章主要是写影响旅游地点的因素，建立了基于AHP的选择目的地的评价模型，为此对旅游地点的确定提供了一个有效的方法。

关键词：旅游；层次分析法；一致性检验；目的地0引言旅游是人的天性，是人才的摇篮，只有在旅途中，人类的天才智慧才能得到淋漓尽致的发挥，这是旅游的特殊意义。

然而，想有个好的旅途心情，对它的景色、居住、饮食等有足够的了解，才能对旅途的心情有所保障。

目前我国的旅游业也发展的挺有前景，因此对一些附带的产业有很好的提升，带动了周边的发展。

在选择旅游景点的时候我们不能单一的看某方面，应该全面的考察一下该景点的多种因素，旅游本身就是让我们高兴放松身心的的事情，不要因为考察的不全面为我们的旅途带来不必要的情绪。

鉴于此，本文结合旅游景点因素的分析，利用层次分析法，建立一套能够完全了解景点的综合的评价指标体系，以定量的方法帮我们进行科学的决策。

1.景点选择影响因素的分析根据题目妖气，选择旅游景点应从旅游路线，费用，时间等因素来考虑，归纳如下几点：（1）景点：主要是指旅游地点有哪些可以玩的，有纪念意义的地方，有些是自然形成的，有些是人工建成的。

（2）费用：旅途中所有的费用不要太多，能在个人接受的范围内即可（3）居住：我们对居住没有太大的要求只要干净舒服，价钱合适即可（4）饮食：对于吃的可口即可（5）旅途路线：沿途中有美好的风景（6）时间：旅行的总耗时总之，旅游地点的选择应综合考虑各方面的因素进行，既要考虑经济层面,又要考虑舒适层面。

每个景点的因素虽然不是完全相同，不过但部分的模式还都是固定的，我们不能通过一些方法来确定它的好坏优劣，所以需要一种定性和定量分析相结合的评价方法——AHP 方法来辅助选择旅游地点。

2.层次分析法概述层次分析法（简记AHP）是美国学者T. L. Saaty在20世纪70年代末提出的一种定性与定量分析相结合的多准则决策方法。

层次分析法在商洛市旅游景点选择中的应用

２１０２年８月
决策问题提供了有效的方法，广泛应用于经济、军事、农业等领域。用ＡＰ法对商洛旅游景点运Ｈ．
基金项目：陕西省社会科学界重大理论与现实问题研究项目（０２０９；商洛学院科研基金项目（０Ｋ０８２１Ｃ３）１ＳＹ１０；
ｌＳＯＫＹ０２２）
作者筒介：岳毅蒙，，男陕西富平人，硕士，商洛学院数学与计算科学系助教
商洛学院学报
最为看重费用，次是其他条件。要解决这类问其
题，次分析法提供了一定的理论基础。它针对层
自然资源丰富，山水风景秀丽，史文化悠久，历全市共有国家级森林公园４家，国家３以上旅游Ａ景区３家，以金丝峡、背粱、牛天竺山等为代表的
ｃｌｕａｅａｅｎｊｄｎｅｍａｉｏｓｔｃｓａｄａｅｎｔｅｔｒｔｔａｔｎｖｌａｅ，ｈｎａｌｔｄｂｓｏｇｇｔｔｘｃｎｉｅｙｔｔｔｒａｉｕｓａｒｃｉｓｉｅａｕｔｄｔｅｃｄｕｉｈｒｓｎｅｌｎｖｏｉｔｏｓ
摘要：商洛市三个旅游景点的最优选择进行了研究，据旅游者的不同要求，用层对根采次分析法构建各层因子间的判断矩阵，在对判断矩阵进行一致性检验的基础上计算出各因
Байду номын сангаас
子的权重，以此为模型对可供选择的景点进行评价，到了各旅游者在景点选择上的最优并得

基于层次分析法的旅游景点选择应用

基于层次分析法的旅游景点选择应用本文从网络收集而来，上传到平台为了帮到更多的人，如果您需要使用本文档，请点击下载按钮下载本文档（有偿下载），另外祝您生活愉快，工作顺利，万事如意！1.概念层次分析法是对一些较为繁琐问题作出决策的简易方法，它尤其适用于那些不易完全定量分析的问题，是一种层次化的、定性和定量相结合的分析方法。

近年发展起来的系统分析是一种新方法，而层次分析法是其数学工具之一。

它是美国运筹学家教授于上世纪70年代初期提出的一种简便而又实用的多准则决策方法。

2.层次分析法的原理与步骤建立层次结构模型。

应用层次分析法处理决策问题时，首先要把问题层次化，构造出一个有层次的结构模型。

在模型中，复杂问题被分解为因素的组成部分。

这些因素又按其属性及关系形成几个层次。

上一层次的因素对下一层次有关因素起支配作用。

这些层次可分为三类：最高层：这一层次中通常只有一个因素，一般它是分析问题的设定目标或最终结果，因此也称为目标层。

中间层：这一层次中包含了为实现目标所涉及的中间环节，它可以由若干个层次组成，包括所需考虑的准则、子准则，因此也称为准则层。

最底层：这一层次包括了为实现目标可供选择的各种措施、决策方案等，因此也称为措施层或方案层。

在层次分类及因素选取时，我们要注意三点：1）上层对下层有支配作用；2）同一层因素不存在支配关系；3）每层因素一般不要超过9个。

构造成对比较阵。

面对的决策问题：要比较n个因素x1、x2…xn对目标z的影响。

我们要确定它们在C中所占的比重，即这n个因素对目标C的相对重要性。

我们用两两比较的方法将各因素的重要性量化。

每次取两个因素xi和xj，用正数aij表示与aij=SX1aijSX），aij>0，i，j=1，…，n的重要性之比。

全部比较结果得到的矩阵A=n*n称为成对比较阵。

显然有如何选取aij呢？萨迪提出了一种方法：用数字1，2，…，9及其倒数1/2，1/3，…，1/9作为标度，其意义是在每两个级别之间有一个中间状态，可分别取值2，4，…，8。

层次分析法对旅游地的选择

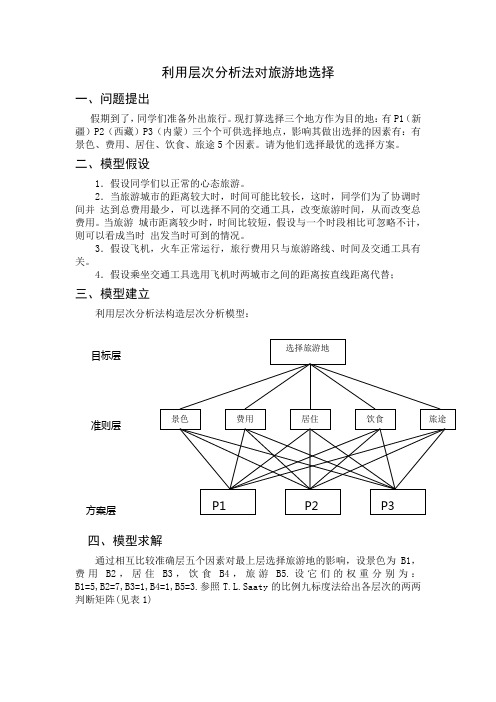
利用层次分析法对旅游地选择一、问题提出假期到了，同学们准备外出旅行。

请为他们选择最优的选择方案。

二、模型假设1．假设同学们以正常的心态旅游。

当旅游城市距离较少时，时间比较短，假设与一个时段相比可忽略不计，则可以看成当时出发当时可到的情况。

3．假设飞机，火车正常运行，旅行费用只与旅游路线、时间及交通工具有关。

4．假设乘坐交通工具选用飞机时两城市之间的距离按直线距离代替；三、模型建立利用层次分析法构造层次分析模型：四、模型求解通过相互比较准确层五个因素对最上层选择旅游地的影响，设景色为B1，费用B2，居住B3，饮食B4，旅游B5.设它们的权重分别为：B1=5,B2=7,B3=1,B4=1,B5=3.参照T.L.Saaty的比例九标度法给出各层次的两两判断矩阵(见表1)表1 同学们对准则层各因素相对重要性的两两比较判断矩阵B1 B2 B3 B4 B5 权重系数B1 1 5/7 5/3 3 5/3 0.364B2 7/5 1 7/1 7/1 7/3 0.374B3 1/5 1/7 1 1 1/3 0.183B4 1/5 1/7 1 1 1/3 0.481B5 3/5 3/7 3 3 1 0.237 λ=0.3006 CI=0.003 CR=0.001同学们对给出方案层的判断矩阵相同，都是如下结果（见表2，表3，表4）表2 同学们就提出的三个方案在景色上面的两两判断矩阵P1 P2 P3 权重系数P1 1 1 1/2 0.237P2 3 1 3/2 0.362P3 2 2/3 1 0.311 λ=0.3012 CI=0.004 CR=0.010表3 就同学们提出的三个方案在费用上的两两判断矩阵P1 P2 P3 权重系数P1 1 2/3 2 0.492P2 3/2 1 3 0.124P3 1/2 2/3 1 0.271 λ=3.0007 CI=0.003 CR= 0.005 表4 同学们就提出的三个方案在住宿方面的两两判断矩P1 P2 P3 权重系数P1 1 2/3 2 0.643P2 3/2 1 3 0.124P3 1/2 2/3 1 0.431λ=3.013 CI=0.0065 CR=0.011 表5 同学们就提出的三个方案在饮食方面的两两判断矩P1 P2 P3 权重系数P1 1 1/2 2 0.265P2 2 1 5 0.606P3 1/2 1/5 1 0.129λ= 3.023 CI=0.004 CR=0.007表6 同学们就提出的三个方案在旅途方面的两两判断矩P1 P2 P3 权重系数P1 1 4 6 0.691P2 1/4 1 2 0.204P3 1/6 1/2 1 0.105 λ=3.013 CI=0.0065 CR=0.011五、模型分析层次单排序及一致性检验根据层次分析法的计算步骤，必须对以上的六个表的两两判断矩阵进行层次单排序，计算各自的权重系数，并对它们逐个进行一致性检验。

基于层次分析法的旅游景点选择应用

基于层次分析法的旅游景点选择应用【摘要】本文探讨了基于层次分析法的旅游景点选择应用。

首先介绍了层次分析法的原理，该方法通过比较不同因素之间的重要性来进行决策。

然后探讨了旅游景点选择的重要性，指出了选择合适的景点对旅行体验的影响。

接着通过应用案例分析，说明了如何利用层次分析法进行景点选择。

同时也探讨了该方法的优势和局限性，以及决策者在选择景点时需要考虑的因素。

最后总结了基于层次分析法的旅游景点选择的有效性，并展望了未来发展的潜力。

通过本文的分析，可以帮助旅行者更科学地选择旅游景点，提升旅行体验。

【关键词】层次分析法、旅游景点选择、应用案例、优势、局限性、决策者、有效性、未来发展1. 引言1.1 基于层次分析法的旅游景点选择应用基于层次分析法的旅游景点选择应用是一种结构化的决策方法，通过分层的方式对不同因素进行比较和评估，从而帮助决策者更加科学地确定最适合的旅游景点。

随着旅游业的快速发展，游客对于旅游景点的选择变得越来越重要，因此利用层次分析法来帮助做出更加准确的决策具有重要意义。

通过层次分析法，决策者可以将各个景点的各项因素进行量化和比较，包括景点的交通便利程度、风景质量、服务水平、文化内涵等方面。

在这个过程中，决策者会更加清晰地了解各个因素之间的关系和重要性，从而有针对性地选择最适合自己需求的旅游景点。

基于层次分析法的旅游景点选择应用可以有效帮助决策者更加客观地进行决策，避免主观偏见和随意选择的情况发生，提高选择的准确性和满意度。

这种决策方法在旅游业中具有广泛的应用前景，并将为旅游者提供更好的旅游体验。

2. 正文2.1 层次分析法的原理层次分析法是一种定性与定量相结合的决策方法，用于解决复杂多层次问题。

其原理是将一个复杂的问题层层分解成若干个层次，然后通过比较不同层次之间的相对重要性，最终确定最优解决方案。

层次分析法的原理包括构建层次结构、建立判断矩阵、计算权重、一致性检验等步骤。

决策问题被分解成若干个层次，从总目标到具体措施逐级细化。

旅游行业中的目的地选择模型

旅游行业中的目的地选择模型随着人们生活水平的提高和旅游意识的增强，旅游行业发展迅猛，市场竞争激烈。

在众多旅游目的地中，游客如何选择适合自己的目的地成为一个重要问题。

为了解决这个问题，旅游行业中出现了一些目的地选择模型，帮助游客合理、科学地做出选择。

本文将介绍几种常见的旅游目的地选择模型。

1. 层次分析法（AHP）层次分析法是一种经典的目的地选择模型，它将各种选择因素按照重要性进行排序。

首先，需要明确旅游目的，比如休闲度假、文化体验等。

然后，选择几个重要的因素，比如交通便利程度、自然风景、旅游设施等，并给这些因素分配权重。

接下来，将选择的旅游目的地与这些因素进行比较，得出最适合的目的地。

层次分析法在旅游行业中应用广泛，它能够帮助游客根据自己的需求和偏好，选择最符合的目的地。

2. 旅游意向模型旅游意向模型是一种基于心理学和行为学原理的目的地选择模型。

根据游客的个性、态度和态度等方面的差异，将游客划分为不同的类别，然后根据不同类别的游客的旅游意向来选择目的地。

比如，有些人喜欢寻求刺激和冒险，他们更倾向于选择自然风景优美、具有挑战性的目的地；而有些人则偏向于享受安逸和放松，他们更愿意选择能够提供高品质服务的目的地。

通过分析游客的意向，旅游行业可以更加精准地为游客推荐目的地，提高满意度。

3. 聚类分析模型聚类分析模型是一种将游客按照相似性进行分组的目的地选择模型。

通过对游客的个人特征、偏好和行为进行分析，将游客分成若干个类别。

然后，根据不同类别的游客选择的目的地进行统计和分析，找出共同特征较大的游客类别，为这些类别的游客推荐相似的目的地。

聚类分析模型能够帮助游客找到与自己兴趣相同的游客，分享旅游经验和目的地选择建议，提高旅游的互动性和乐趣。

4. 网络推荐系统随着互联网的发展，网络推荐系统在旅游行业中得到了广泛应用。

网络推荐系统通过分析用户的历史行为和偏好，在众多目的地中为用户推荐最适合的目的地。

通过用户的点击、浏览和购买等行为数据，系统能够了解用户的兴趣和需求，并根据用户的特点为其个性化推荐。

基于层次分析法的旅游景点选择应用

基于层次分析法的旅游景点选择应用
随着旅游业的发展，人们对旅游景点的选择要求越来越高，而
使用基于层次分析法的旅游景点选择应用则成为了一种有效的方法。

该方法是一种多层次结构分析法，它可以将一个决策问题拆分成多
个层级，每个层级对应一个决策因素，然后通过比较这些因素的重
要性，确定最终的决策。

首先，我们需要明确旅游景点选择的目标和要素，例如旅游目的、地理位置、历史文化、自然风光、交通便利度、旅游设施等。

然后，我们可以将这些因素划分成不同的层级，从而建立起层次结构。

例如，我们可以将旅游目的、自然风光和历史文化划分为第一
层级，将地理位置、交通便利度和旅游设施划分为第二层级。

最后，根据这些因素的重要性比较，确定最终的决策。

使用基于层次分析法的旅游景点选择应用需要注意以下几点：
1. 精细划分层级结构：划分层级结构时，需要根据实际情况进
行精细化划分，避免因过于笼统或过于细致所导致的评价偏差。

2. 充分确定因素权重：在确定因素权重时，可以采用专家评价、广泛调查和数据统计等方法，以确保权重的准确性和可信度。

3. 合理折算标准化指标：由于每个因素都有不同的度量单位和
量性质，所以需要对这些指标进行标准化处理，以方便进行比较。

4. 综合评价得出最终选择：根据各因素的权重和标准化指标，
计算出每个景点的评价得分，最终将所有景点进行综合评价，选择
评价得分最高的景点作为最终决策。

通过使用基于层次分析法的旅游景点选择应用，可以减少选择
的主观性和随意性，提高选择的客观性和科学性。

但同时需要结合
实际情况进行综合考虑和决策。

层次分析法在旅游资源评价中的应用

第一步, 确定目标层(A) 。

根据本文主题将其定为旅游资源最佳。

第二步, 确定样本层(C) 。

通常称之为方案层。

根据目标层, 峨眉山、黄山、庐山、泰山、华山理当成为样本层。

第三步, 确定准则层(B) 。

它就是用来衡量与判断方案层实现目标优劣的依据, 就是层次分析法的关键。

它要求所选择的因子准确、全面, 同时又互不相关。

这就必须选择那些主要的, 对旅游资源整体开发价值与重要程度有重大影响的因素作为评价因子。

为尽量简化评估工作, 本文选择自然景观, 人文景观与景区容量三项指标构建准则层。

据此, 依计算顺序, 形成如下结构图设准则层B 1 对目标层A 的权重为: W i (i =1 , ……, 3) : 样本层: C j (j = 1 , ⋯, 5) , 对准则层Bi 的权重为aij (i = 1 , ……3 ; j = 1 , ……, 5) , 则样本层Cj 对目标层的最终权重为:A=∑∑∑∑∑=====⋅⋅=⋅⋅=⋅5131313151)()(j i i i j aij wi Cj Cj ij a wi Bi wi由此得任一样本C j 对目标A 的权重值为:∑=⋅31i aij wi。

该权重的大小也就表明了样本CJ 对目标层A 的意义或影响程度。

层次分析法设计者将线性代数处理转化为建立在实验心理学基础上的判断表格, 并进而形成判断矩阵, 通过矩阵的特征值与特征向量, 求出近似值以完成权重的最后求取。

相对重要性标度*①计算矩阵各行各元素乘积i m =∏=ni ij a 1②计算n 次方根i w =n im③对向量T n w w w w ),,(21⋅⋅⋅=，进行规范化∑==nj jii ww w1ˆj=1,2,…,n得到T n w w ww)ˆ,ˆ,ˆ(ˆ21，⋯=,为所求特征向量近似值,即各因素权重。

④计算矩阵的最大特征值λmax ;∑==n i ii w wA n 1)ˆ(1max λ其中,i wA )ˆ(为向量wA ˆ的第i 个元素。

基于层次分析法的旅游目的地选择分析研究

基于层次分析法的旅游目的地选择分析研究旅游是人们日常生活中的重要组成部分，不仅可以放松身心，丰富自己的生活体验，还可以拓展人们的视野和认知。

在旅游时，选择适宜的目的地尤为重要，因为旅游的成功与否很大程度上取决于目的地的选择。

近年来，基于层次分析法（Analytic Hierarchy Process，简称AHP）的旅游目的地选择分析研究备受重视。

本文将深入探讨AHP在旅游目的地选择方面的应用，并提供一些有关旅游目的地选择的实用建议。

一、AHP理论介绍层次分析法是一种定量分析方法，它可以定量地分析并解决问题。

AHP通常由目标层次、准则层次和方案层次三个层次构成，用于评估各备选方案实现目标的程度。

AHP理论认为，对于一个复杂的决策问题，可以将其分解成多个相互关联的层次，从而使决策问题变得更加具体和明确。

在这种情况下，评估者需要考虑多个方面，包括选定目的地的交通、住宿、餐饮、景点、费用和时间等因素。

然后，评估者应使用AHP模型对这些因素进行定量分析，最终确定一个最有可能的目的地，这个目的地可以满足评估者的各类需求和期望。

二、AHP在旅游目的地选择方面的应用在旅游目的地的选择中，AHP理论构建了一个包含几个方面的层次，每个方面按照其重要性进行排序，最终，这些方面会被加权。

在层次分析中，不仅要考虑每个方面的重要性，还要考虑它们之间的相互关系。

例如，对于一个旅游目的地，评估者可能会考虑以下几个因素：1.景点这个方面包括目的地是否拥有丰富的人文历史或自然景观，景点是否受欢迎等等。

2.住宿这个方面包括是否有多种住宿选择，价格合理，清洁卫生等等。

3.交通这个方面包括交通是否方便，是否有公共交通，是否有租车等。

4.餐饮这个方面包括当地的特色餐饮是否多样化，价格是否合理，卫生是否有保证等等。

5.费用这个方面包括旅行成本如何，是否有各种折扣等等。

6.时间这个方面考虑旅行时间长度是否合适，旅行时间是否在预算内等等。

一旦选择了这些因素，评估者就可以将给这些因素赋予相对权重，并根据这些权重进行分析，最终得出一个最适宜的旅游目的地。

层次分析法对旅游景点选择的研究

文章主要是写影响旅游地点的因素，建立了基于AHP的选择目的地的评价模型，为此对旅游地点的确定提供了一个有效的方法。

然而，想有个好的旅途心情，对它的景色、居住、饮食等有足够的了解，才能对旅途的心情有所保障。

目前我国的旅游业也发展的挺有前景，因此对一些附带的产业有很好的提升，带动了周边的发展。

鉴于此，本文结合旅游景点因素的分析，利用层次分析法，建立一套能够完全了解景点的综合的评价指标体系，以定量的方法帮我们进行科学的决策。

2.层次分析法概述层次分析法（简记AHP）是美国学者T. L. Saaty在20世纪70年代末提出的一种定性与定量分析相结合的多准则决策方法。

层次分析法在泰山、杭州和承德三处旅游景点选择上运用

一致性检验。可用其归一化特征向量作为权向量，否则要重新构造成对比较矩阵A，对 aij 加以调整。
19
（2）对准则层对目标层的判断矩阵A进行运算并进行一致性检验
对判断矩阵A进行运算（使用matlab软件），得到权向量
(特征向量)w =(0.263,0.475,0.055,0.090,0.110)T
6
中间层：即准则层。表示采取的方案所涉及的中间环节——
景点的景色、居住的环境、饮食的特色、交通便利和旅游的费用。最低层：即方案层。表示决策时的备选方案——泰山、杭州和承德。
7
每层有若干元素，层间元素的关系用相连直线表示。
Z
A1
A1 , A2 , A3 , A4 , A5
分别分别表示景色、费用、居住、饮食、交通。
4
二、层次分析法的步骤和方法
运用层次分析法构造系统模型时，大体可以分为以下四个步骤：
1. 建立层次结构模型
2. 构造判断(成对比较)矩阵
3. 层次单排序及其一致性检验
4. 层次总排序及其一致性检验
5
三、研究过程
1.建立层次结构模型
将决策问题分为3个层次最高层：即目标层。表示决策的目的、要解决问题，即层次分析要达到的总目标——选择哪个旅游地。
20
判断矩阵A的最大特征根=5.073 一致性指标
CI 5.073 5 0.018 5 1
随机一致性指标 RI=1.12 (查表)
一致性比率CR=0.018/1.12=0.016<0.1
通过一致性检验
21
（3）对判断矩阵B1、B2、B3、B4、B5 求层次单排序的权向量并进行一致性检验，结果如下：
25
四、结论

层次分析法在旅游产品选择中的应用研究

层次分析法在旅游产品选择中的应用研究作者：丁烨来源：《商情》2015年第27期[摘要]：旅游产品的选择受到多种因素的影响和制约，综合考虑制约因素选择满意的旅游产品是众多旅游者关心的问题。

从景点的景色、居住的环境、饮食的特色、交通便利和旅游的费用等五个方面构建旅游产品选择的层次结构模型，构造各个旅游地的判断矩阵并计算权重，进行层次排序和一致性检验，利用层次分析法选择旅游目的地。

[关键词]：旅游产品选择层次分析法1 引言随着社会的进步、经济的发展以及人们对高质量生活期望的提高，人们的旅游需求旺盛，旅游业越来越受到重视。

人们对于旅行方式的选择也随着科技的进步变得多样化，很多人已经厌倦了老套死板的跟团游，他们更加渴望追寻符合自己需求的旅游产品。

游客在选择旅游产品时经常考虑旅游目的地的食、宿、行、游、购等，如何综合考虑这些因素选择一个比较满意的旅游产品是一项织的研究的课题，本文将层次分析法引入到旅游产品的选择中具有一定的实用价值。

2 层次分析法层次分析法（Analytic Hierarchy Process，简称AHP）是将与决策总是有关的元素分解成目标、准则、方案等层次，在此基础之上进行定性和定量分析的决策方法。

该方法是美国运筹学家匹茨堡大学教授萨蒂于20世纪70年代初，在为美国国防部研究"根据各个工业部门对国家福利的贡献大小而进行电力分配"课题时，应用网络系统理论和多目标综合评价方法，提出的一种层次权重决策分析方法。

层次分析法的特点是在对复杂的决策问题的本质、影响因素及其内在关系等进行深入分析的基础上，利用较少的定量信息使决策的思维过程数学化，从而为多目标、多准则或无结构特性的复杂决策问题提供简便的决策方法。

尤其适合于对决策结果难于直接准确计量的场合。

层次分析法是将决策问题按总目标、各层子目标、评价准则直至具体的备投方案的顺序分解为不同的层次结构，然后得用求解判断矩阵特征向量的办法，求得每一层次的各元素对上一层次某元素的优先权重，最后再加权和的方法递阶归并各备择方案对总目标的最终权重，此最终权重最大者即为最优方案。

层次分析法在旅游目的地决策中的应用

层次分析法在旅游目的地决策中的应用作者：王晨哲来源：《读与写·教育教学版》2018年第04期摘要：随着社会发展，旅游成为人们假日休闲的首选，但是在众多的旅游景点中如何选择满意的目的地成为旅游的一个首要问题。

本文应用层次分析法来对比影响旅游的各项因素并进行决策，通过旅游目的地选择的实例来说明其在分析决策中的应用，认为这种分析方法可推而广之，借以解决其他决策问题，是决策应用的通行思路。

关键词：层次分析法旅游考虑因素一致性检验目的地决策中图分类号：G642 文献标识码：A 文章编号：1672-1578（2018）04-0042-011 问题背景为保证拥有较好的出行体验，人们需要经过考虑多个因素来确定自己的目的地。

根据以往的旅游体会和网上关于旅游反馈的调查报告，从以下几个因素考虑：（1）景色：指旅游地点的可观赏风景和游玩项目，包括自然风光与人文景观的差异等。

（2）费用：花销需要符合实际的消费水平和合理的消费预期。

（3）食宿：希望品尝当地特色美食，且好的居住条件可以满足旅游者良好的精神状态。

（4）交通：既影响了旅游行程的时间，也体现了到达目的地是否具有较好的便利性与安全保障。

以上因素较难用具体数字量化，不同的人的要求不同。

拟利用层次分析法，建立一套能够多方位了解景点的综合的评价指标体系，以定量的方法对备选目的地进行全面分析比较后，得到一个最优的旅游目的地决策。

根据旅游网站上的国内当季热门旅游点，本文选择了厦门、桂林、上海和吐鲁番四地。

在旅游目的地的选择中旅游者进行思维判断过程，在判断各个准则重要性时考虑个人主观因数。

2 研究方法：层次分析法（AHP）2.1方法概述层次分析法是20世纪70年代末被提出的一种定性与定量分析相结合的多准则决策方法。

它把人的思维过程层次化、数量化，并用数字为分析、决策、预报或控制提供定量的依据[1]。

该方法提高了决策者进行决策的有效性、可靠性和可行性，将经验判断给予量化，对目标结构复杂而且缺乏必要的数据情况下，此方法较为实用。