初中数学人教版八年级上册平行线与三角形内角和的综合应用(习题及答案)
八年级数学平行线与三角形内角和过程训练(内角和)(人教版)(含答案)

学生做题前请先回答以下问题问题1:三角形的内角和等于_______;直角三角形两锐角_______.问题2:要求一个角的度数,我们可以怎么考虑?平行线与三角形内角和过程训练(内角和)(人教版)一、单选题(共8道,每道12分)1.已知:如图,在△ABC中,∠A=60°,∠B=50°.求∠C的度数.解:如图,在△ABC中,∠A=60°,∠B=50°(已知)∴∠C=180°-∠A-∠B=180°-60°-50°=________(____________)①60°;②70°;③三角形的内角和等于180°;④平角的定义.以上空缺处依次所填正确的是( )A.①③B.②③C.①④D.②④答案:B解题思路:试题难度:三颗星知识点:三角形内角和定理2.如图,在△ABC中,∠B=40°,AD平分∠BAC,且∠BAD=30°,求∠C的度数.解:如图,∵AD平分∠BAC(已知)∴∠BAC=2∠BAD(________________)∵∠BAD=30°(已知)∴∠BAC=2×30°=60°(等量代换)在△ABC中,∠BAC=60°,∠B=40°(已知)∴∠C=180°-____-∠B=180°-60°-40°=80°(________________)①角平分线的定义;②∠BAD;③∠BAC;④平角的定义;⑤三角形的内角和等于180°.以上空缺处依次所填正确的是( )A.②③⑤B.①③⑤C.①③④D.②③④答案:B解题思路:试题难度:三颗星知识点:角平分线3.已知:如图,AB∥CD,AD和BC相交于点O,∠A=20°,∠COD=100°.求∠C的度数.解:如图,∵AB∥CD(已知)∴∠A=______(两直线平行,内错角相等)∵∠A=20°(已知)∴∠D=20°(等量代换)在△COD中,∠D=20°,∠COD=100°∴∠C=180°-∠D-∠COD=180°-20°-100°=60°(____________________)①∠D;②∠C;③三角形的内角和等于180°;④平角的定义.以上空缺处依次所填正确的是( )A.①③B.②③C.①④D.②④答案:A解题思路:试题难度:三颗星知识点:三角形内角和定理4.已知:如图,点D,E分别在△ABC的边AB,AC上,且DE∥BC,∠B=60°,∠AED=40°,求∠A的度数.解:如图,∵DE∥BC(已知)∴______=∠C(____________________)∵∠AED=40°(已知)∴∠C=40°(等量代换)在△ABC中,∠B=60°,∠C=40°=180°-60°-40°=80°(三角形的内角和等于180°)①∠AED;②∠E;③∠ADE;④两直线平行,同位角相等;⑤同位角相等,两直线平行.以上空缺处依次所填正确的是( )A.②⑤B.③⑤C.①④D.③④答案:C解题思路:试题难度:三颗星知识点:三角形内角和定理5.已知:如图,BE交CD于点F,∠B=125°,∠D=45°,∠E=80°.求证:AB∥CD.证明:如图,在△DEF中,∠D=45°,∠E=80°(已知)=180°-45°-80°=55°(____________________)∵∠BFC=∠DFE(____________________)∴∠BFC=55°(等量代换)∵∠B=125°(已知)∴∠BFC+∠B=55°+125°=180°(等式性质)∴AB∥CD(____________________)①平角的定义;②三角形的内角和等于180°;③对顶角相等;④两直线平行,同旁内角互补;⑤同旁内角互补,两直线平行.以上空缺处依次所填正确的是( )A.②③④B.②③⑤C.①③④D.①③⑤答案:B解题思路:试题难度:三颗星知识点:三角形内角和定理6.已知:如图,直线AB∥DE,∠1=55°,∠2=65°,求∠3的度数.解:如图,∵∠1=∠CDE(对顶角相等)∠1=55°(已知)∴_________(等量代换)∵AB∥DE(已知)∴∠2=∠CED(____________________)∵∠2=65°(已知)∴∠CED=65°(等量代换)在△CDE中,∠CDE=55°,∠CED=65°∴∠3=180°-∠CDE-∠CED=180°-55°-65°=60°(____________________)①∠D=55°;②∠CDE=55°;③内错角相等,两直线平行;④两直线平行,内错角相等;⑤平角的定义;⑥三角形的内角和等于180°.以上空缺处依次所填正确的是( )A.①④⑤B.②④⑤C.①③⑤D.②④⑥答案:D解题思路:试题难度:三颗星知识点:三角形内角和定理7.已知:如图,将Rt△ABC的直角顶点C放在直线a上,∠1=50°,∠2=60°,∠3=70°.求证:a∥b.证明:如图,在△ACD中,∠1=50°,∠2=60°∴∠ADC=180°-∠1-∠2=180°-50°-60°=70°(____________________)∵∠ADC=∠4(对顶角相等)∴∠4=70°(等量代换)∵∠3=70°(已知)∴__________(等量代换)∴a∥b(____________________)①三角形的内角和等于180°;②平角的定义;③∠3=∠4;④∠3=∠D;⑤同位角相等,两直线平行;⑥两直线平行,同位角相等.以上空缺处依次所填正确的是( )A.①③⑤B.①④⑤C.②④⑥D.②③⑥答案:A解题思路:试题难度:三颗星知识点:三角形内角和定理8.已知:如图,AB∥CD,∠B=120°,CE⊥BF,垂足为E.求∠ECF的度数.解:如图,∵AB∥CD(已知)∴∠B+______=180°(____________________)∵∠B=120°(已知)∴∠BFC=60°(等式性质)∵CE⊥BF(已知)∴∠CEF=90°(垂直的定义)∴∠C=90°-∠BFC=90°-60°=30°(____________________)①∠BFC;②∠F;③两直线平行,同旁内角互补;④同旁内角互补,两直线平行;⑤直角三角形两锐角互余;⑥三角形的内角和等于180°.以上空缺处依次所填正确的是( )A.①④⑤B.①③⑤C.②④⑥D.②③⑥答案:B解题思路:试题难度:三颗星知识点:直角三角形两锐角互余。
八年级数学上册平行线与三角形内角和的综合应用(习题及答案)(人教版)
)
在△ ACD中,∠ 1=30°,∠ ACB=85°
∴∠ EDP=180°- ∠1- ∠ACB
=180°- 30°- 85°
=65°
( __________________________)_
∵PE⊥ AD
( __________________________)_
∴∠ EPD=90°
( __________________________)_
证自明的“基本事实” ,可以当做已知的大前提来进行使用.而其中的三条,
是我们在几何证明中不经意间多次用到的,下面对它们来进行简单的解释.
当我们证明时,会遇到如下的推理:
∵a=b,b=c
∴a=c
在这个推理过程中,我们很容易就理解它的正确性,但往往不知道它的依据
是什么.其实,它的依据就是欧几里得公理体系中 5 条公理中的第一条:“(1)
∴∠ A+∠ C=90°(等量代换)
这里推理的依据就是第一条公理, 我们把它简记为 “等量代换”.“等量代换”
第5页 共7页
A
D
B
C
第3页 共7页
6. 已知:如图, AB∥CD,∠ BAE=∠DCE=45°. 求证:∠ E=90°.
A
B
1 E
Байду номын сангаас
2
C
D
7. 已知:如图, EF⊥BC, DE⊥AB,∠ B=∠ADE. 求证: AD∥EF. A
E
B
F
D
C
第4页 共7页
思考小结
1. 在证明过程中: (1)由平行可以想 ________相等、 __________相等、 ________互补;
=180°- 30°- 85°
平行线与三角形内角和的综合应用(讲义)
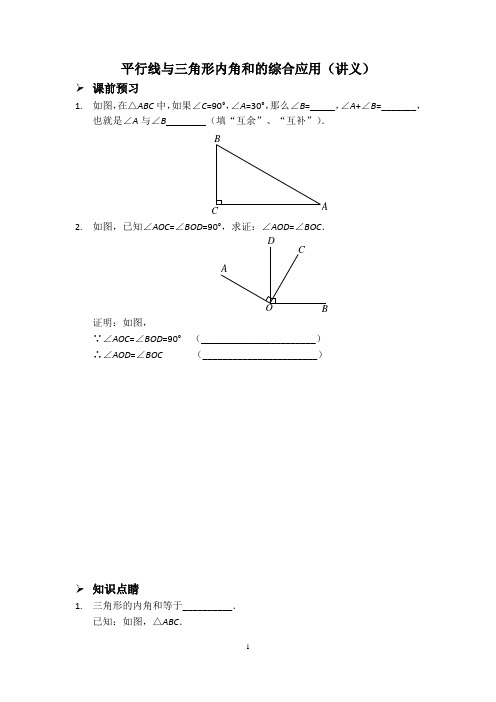
平行线与三角形内角和的综合应用(讲义)➢ 课前预习1. 如图,在△ABC 中,如果∠C =90°,∠A =30°,那么∠B =_____,∠A +∠B =_______,也就是∠A 与∠B ________(填“互余”、“互补”).ABC2. 如图,已知∠AOC =∠BOD =90°,求证:∠AOD =∠BOC .DCB OA证明:如图,∵∠AOC =∠BOD =90° (_______________________) ∴∠AOD =∠BOC (_______________________)➢ 知识点睛1. 三角形的内角和等于__________.已知:如图,△ABC .求证:∠BAC +∠B +∠C =180°.A MBC12N证明:_______,___________________________. ∵MN ∥BC ( 已作 ) ∴∠B =∠1,∠C =∠2(_______________________)∵∠BAC+∠1+∠2=180°(_______________________) ∴∠BAC +∠B +∠C =180°(_______________________)2. 直角三角形两锐角___________.➢ 精讲精练1. 如图,在△ABC 中,∠A =50°,∠C =72°,BD 是△ABC 的一条角平分线,则∠ABD=__________.DAC FED C BA第1题图 第2题图2. 如图,在△ABC 中,∠B =∠C ,E 是AC 上一点,ED ⊥BC ,DF ⊥AB ,垂足分别为D ,F .若∠AED =140°,则∠C =_____,∠BDF =______,∠A =______.3. 如图,AE ∥BD ,∠1=110°,∠2=30°,则∠C =______.21EDCB A FDAEB第3题图 第4题图4. 如图,AD ∥BC ,AB ∥CD ,E 在CB 的延长线上,EF 经过点A ,∠C =50°,∠FAD =60°,则∠EAB =_______.5. 如图,在△ABC 中,CD 平分∠ACB 交AB 于点D ,过点D 作DE ∥BC 交AC 于点E .若∠A =75°,∠ADE =35°,则 ∠EDC =_________.6. 如图,在△ABC 中,∠B =40°,∠BAC =68°,AD ⊥BC 于点D ,求∠DAC 的度数.解:如图,在△ABC 中,∠B =40°,∠BAC =68°(已知) ∴∠C =180°-______-______ =180°-_____-_____=______(_______________________) ∵AD ⊥BC (已知)∴∠ADC =90°(垂直的定义) ∴∠C +_____=90°(直角三角形两锐角互余)∴∠DAC =90°-______=90°-______=______(_______________________)7. 如图,在Rt △ABC 中,∠ACB =90°,CD ⊥AB ,垂足为D .求证:∠A =∠BCD .证明:如图, ∵∠ACB =90°(已知)∴∠A +_____=90°(直角三角形两锐角互余) ∵CD ⊥AB (已知)ABDABCDEDCBA∴∠CDB =90°(垂直的定义)∴_____+∠B =90°(______________________) ∴∠A =∠BCD (______________________)8. 如图,在△ABC 中,∠C =90°,点D 是边AC 上一点,DE ∥BC ,∠1=60°,求∠A 的度数.ADE1BC9. 如图,BD ∥AE 交△ABC 的边AC 于点F ,∠CAE =95°,∠CBD =30°,求∠C 的度数.AB CDEF10.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,AF平分∠CAB交CD于点E,交BC于点F.求证:∠1=∠2.【参考答案】➢课前预习1.60°,90°,互余2.已知,同角的余角相等➢知识点睛1.180°如图,过点A作MN∥BC两直线平行,内错角相等平角的定义等量代换2.互余➢精讲精练1.29°21FEDCB A2.50°,40°,80°3.40°4.70°5.35°6.解:如图,在△ABC中,∠B=40°,∠BAC=68°(已知)∴∠C=180°-∠B-∠BAC=180°-40°-68°=72°(三角形的内角和等于180°)∵AD⊥BC(已知)∴∠ADC=90°(垂直的定义)∴∠C+∠DAC=90°(直角三角形两锐角互余)∴∠DAC=90°-∠C=90°-72°=18°(等式的性质)7.证明:如图,∵∠ACB=90°(已知)∴∠A+∠B=90°(直角三角形两锐角互余)∵CD⊥AB(已知)∴∠CDB=90°(垂直的定义)∴∠BCD+∠B=90°(直角三角形两锐角互余)∴∠A=∠BCD(同角的余角相等)8.解:如图,∵DE∥BC(已知)∴∠1=∠B(两直线平行,同位角相等)∵∠1=60°(已知)∴∠B=60°(等量代换)∵∠C=90°(已知)∴∠A+∠B=90°(直角三角形两锐角互余)∴∠A=90°-∠B=90°-60°=30°(等式的性质)9.解:如图,∵BD∥AE(已知)∴∠CFD=∠CAE(两直线平行,同位角相等)∵∠CAE=95°(已知)∴∠CFD=95°(等量代换)∴∠CFB =180°-∠CFD=180°-95°=85°(平角的定义)在△CBF 中,∠CBD =30°,∠CFB =85°(已知) ∴∠C =180°-∠CBD -∠CFB =180°-30°-85°=65°(三角形的内角和等于180°) 10. 证明:如图,∵∠ACB =90°(已知)∴∠CAF +∠2=90°(直角三角形两锐角互余) ∵CD ⊥AB (已知)∴∠EDA =90°(垂直的定义)∴∠DAE +∠AED =90°(直角三角形两锐角互余) ∵AF 平分∠CAB (已知)∴∠CAF =∠DAE (角平分线的定义) ∴∠2=∠AED (等角的余角相等) ∵∠1=∠AED (对顶角相等) ∴∠1=∠2(等量代换)平行线与三角形内角和的综合应用(随堂测试)1. 已知:如图,AB ∥CD ,∠ABF =120°,CE ⊥BF ,垂足为E ,则∠ECF =___________.ABC D EF2. 已知:如图,在△ABC 中,∠B =40°,AD 平分∠BAC 交BC 于点D ,DE ∥BA 交AC 于点E ,∠ADE =40°,求∠C 的度数.EDC BA【参考答案】1.30°2.解:如图,∵DE∥BA(已知)∴∠BAD=∠ADE(两直线平行,内错角相等)∵∠ADE=40°(已知)∴∠BAD=40°(等量代换)∵AD平分∠BAC(已知)∴∠BAC=2∠BAD=2×40°=80°(角平分线的定义)在△ABC中,∠B=40°,∠BAC=80°(已知)∴∠C=180°-∠B-∠BAC=180°-40°-80°=60°(三角形的内角和等于180°)。
人教版_部编版八年级数学上册第十一章第二节三角形的内角试题(含答案) (87)

人教版_部编版八年级数学上册第十一章第二节三角形的内角试题(含答案)如图,ABC ∆的两条外角平分线交于点P ,50A ∠=︒,三角形的内角和为180︒,求P ∠的度数.【答案】65P ∠=︒.【解析】【分析】先由三角形的内角和定理求出130ACB ABC ∠+∠=︒,然后再根据补角及角平分线的性质求出PCB CBP ∠+∠,最后再根据三角形的内角和定理求出∠P 即可.【详解】解:50A ∠=︒130ACB ABC ∴∠+∠=︒ CP 平分ECB ∠,BP 平分DBC ∠3601301152PCB CBP ︒-︒∴∠+∠==︒ 18011565P ∴∠=︒-︒=︒【点睛】本题主要考查了三角形的内角和定理、角平分线的性质及补角的性质,熟练掌握三角形的内角和定理是解题的关键.62.如图,已知线OX OY ⊥,A ,B 为OX ,OY 上两动点,A ∠平分线与B 的外角平分线交于C ,试问:C ∠的度数是否随A ,B 运动而发生变化?【答案】C ∠的度数不随点A 、B 的运动而发生变化.【解析】【分析】 根据角平分线和垂线的性质,可求得12BAC BAO ∠=∠,1452OBC BAO ∠=︒+∠,然后再根据三角形的内角和定理求得90ABO BAO =︒-∠,再利用代入法和三角形内角和定理求得∠C 即可.【详解】解:OX OY ⊥90AOB ∠=︒∴∵A ∠的平分线与B 的外角平分线交于点C12BAC BAO ∴∠=∠ 90145222AOB A A OBC BAO ∠+∠︒+∠∠===︒+∠ ∵180ABO AOB BAO ∠+∠+∠=︒90ABO BAO ∴∠=︒-∠180C ABC BAC ∠+∠+∠=︒且ABC OBC ABO ∠=∠+∠∴∠C+45°+12∠BAO+90°-∠BAO+12∠BAO=180°, 45C ∴∠=︒C ∴∠是个定值,C ∠的度数不随点A 、B 的运动而发生变化,45C ∠=︒.【点睛】本题主要考查了角平分线、垂线的性质及三角形的内角和定理,熟练掌握数学基础知识是解题的关键.63.如图,直线m 与直线n 互相垂直,垂足为O 、A 、B 两点同时从点O 出发,点A 沿直线m 向左运动,点B 沿直线n 向上运动.(1)若∠BAO 和∠ABO 的平分线相交于点Q ,在点A ,B 的运动过程中,∠AQB 的大小是否会发生变化?若不发生变化,请求出其值,若发生变化,请说明理由.(2)若AP 是∠BAO 的邻补角的平分线,BP 是∠ABO 的邻补角的平分线,AP 、BP 相交于点P ,AQ 的延长线交PB 的延长线于点C ,在点A ,B 的运动过程中,∠P 和∠C 的大小是否会发生变化?若不发生变化,请求出∠P 和∠C 的度数;若发生变化,请说明理由.【答案】(1)∠AQB 的大小不发生变化,∠AQB =135°;(2)∠P 和∠C 的大小不变,∠P=45°,∠C=45°.【解析】【分析】第(1)题因垂直可求出∠ABO 与∠BAO 的和,由角平分线和角的和差可求出∠BAQ 与∠ABQ 的和,最后在△ABQ 中,根据三角形的内角各定理可求∠AQB的大小.第(2)题求∠P的大小,用邻补角、角平分线、平角、直角和三角形内角和定理等知识求解.【详解】解:(1)∠AQB的大小不发生变化,如图1所示,其原因如下:∵m⊥n,∴∠AOB=90°,∵在△ABO中,∠AOB+∠ABO+∠BAO=180°,∴∠ABO+∠BAO=90°,又∵AQ、BQ分别是∠BAO和∠ABO的角平分线,∴∠BAQ=12∠BAC,∠ABQ=12∠ABO,∴∠BAQ+∠ABQ=12(∠ABO+∠BAO)=12×90∘=45∘又∵在△ABQ中,∠BAQ+∠ABQ+∠AQB=180°,∴∠AQB=180°﹣45°=135°.(2)如图2所示:①∠P的大小不发生变化,其原因如下:∵∠ABF+∠ABO=180°,∠EAB+∠BAO=180°∠BAQ+∠ABQ=90°,∴∠ABF+∠EAB=360°﹣90°=270°,又∵AP、BP分别是∠BAE和∠ABP的角平分线,∴∠PAB=12∠EAB,∠PBA=12∠ABF,∴∠PAB+∠PBA=12(∠EAB+∠ABF)=12×270°=135°,又∵在△PAB中,∠P+∠PAB+∠PBA=180°,∴∠P=180°﹣135°=45°.②∠C的大小不变,其原因如下:∵∠AQB=135°,∠AQB+∠BQC=180°,∴∠BQC=180°﹣135°,又∵∠FBO=∠OBQ+∠QBA+∠ABP+∠PBF=180°∠ABQ=∠QBO=12∠ABO,∠PBA=∠PBF=∠ABF,∴∠PBQ=∠ABQ+∠PBA=90°,又∵∠PBC=∠PBQ+∠CBQ=180°,∴∠QBC=180°﹣90°=90°.又∵∠QBC+∠C+∠BQC=180°,∴∠C=180°﹣90°﹣45°=45°【点睛】本题考查三角形内角和定理,垂直,角平分线,平角,直角和角的和差等知识点,同时,也是一个以静求动的一个点型题目,有益于培养学生的思维几何综合题.64.已知:如图1,线段AB、CD相交于点O,连接AD、CB,如图2,在图1的条件下,∠DAB和∠BCD的平分线AP和CP相交于点P,并且与CD、AB分别相交于M、N,试解答下列问题:(1)在图1中,请直接写出∠A、∠B、∠C、∠D之间的数量关系:_____________________;(2)在图2中,若∠D=40°,∠B=30°,试求∠P的度数(写出解答过程);(3)如果图2中,∠D和∠B为任意角,其他条件不变,试写出∠P与∠D、∠B之间的数量关系(直接写出结论即可).【答案】(1)∠A+∠D=∠B+∠C;(2)35°;(3)2∠P=∠B+∠D【解析】【分析】(1)根据三角形的内角和等于180°,易得∠A+∠D=∠B+∠C;(2)仔细观察图2,得到两个关系式∠1+∠D=∠3+∠P,∠2+∠P=∠4+∠B,再由角平分线的性质得∠1=∠2,∠3=∠4,两式相减,即可得结论.(3)参照(2)的解题思路.【详解】解:(1)∠A+∠D=∠B+∠C ;(2)由(1)得,∠1+∠D=∠3+∠P ,∠2+∠P=∠4+∠B ,∴∠1-∠3=∠P-∠D ,∠2-∠4=∠B-∠P ,又∵AP 、CP 分别平分∠DAB 和∠BCD ,∴∠1=∠2,∠3=∠4,∴∠P-∠D=∠B-∠P ,即2∠P=∠B+∠D ,∴∠P=(40°+30°)÷2=35°.(3)由(2)的解题步骤可知,∠P 与∠D 、∠B 之间的数量关系为:2∠P=∠B+∠D .【点睛】考查三角形内角和定理, 角平分线的定义,掌握三角形的内角和定理是解题的关键.65.如图,在ABC 中,90BAC ∠=,AB AC =,点D 在BC 上,且BD BA =,点E 在BC 的延长线上,且CE CA =.求DAE ∠的度数.【答案】45【解析】根据等腰直角三角形的性质求出∠B=∠ACB=45°,根据等边对等角的性质求出∠BAD=∠BDA ,∠E=∠CAE ,再根据三角形的一个外角等于和它不相邻的两个内角的和即可求出∠DAE 的度数.【详解】解:∵603024x -=,AB AC =,∴45B ACB ∠=∠=,∵BD BA =, ∴()11804567.52BAD BDA ∠=∠=-=, ∵CE CA =, ∴14522.52E CAE ∠=∠=⨯=, ∴DAE BDA E ∠=∠-∠67.522.5=-,45=.【点睛】考查了等边对等角的性质和三角形的外角性质,解题关键熟练并灵活利用等边对等角的性质和三角形的外角性质.三、填空题66.在△ABC 中,36,2A B C B ∠-∠=∠=∠,则B ∠=______.【答案】36°【解析】根据角度的关系与三角形的内角和即可求解.【详解】由36,2A B C B ∠-∠=∠=∠,又∠A+∠B+∠C=180°,则∠A+3∠B=180°,解得∠A=72°,∠B=36°,【点睛】此题主要考察三角形的角度计算,解题的关键是熟知三角形的内角和为180°.67.在△ABC 中,若∠B=∠C=2∠A,则∠A=_____【答案】36°【解析】【分析】设∠A =x ,则∠B =∠C =2x .根据三角形内角和定理解答即可.【详解】设∠A =x ,则∠B =∠C =2x .∵∠A +∠B +∠C =180°,∴x +2x +2x =180°,解得:x =36°,∴∠A =36°.故答案为:36°.【点睛】本题考查了三角形内角和定理.熟练掌握三角形内角和定理是解答本题的关键.68.如图,在ABC △中,90ACB ∠=︒,将ABC △沿CD 折叠,使点B 恰好落在AC 边上的点E 处,若20A ∠=︒,则ADE ∠的度数是________.【答案】50︒【解析】【分析】首先根据题意,可得:∠CED=∠B ,然后根据三角形的内角和定理,求出∠B 的度数,即可求出∠ADE 的度数是多少.【详解】∵将△ABC 沿CD 折叠,使点B 恰好落在AC 边上的点E 处,∴∠CED=∠B ,∵∠ACB=90°,∠A=20°,∴∠B=180°-90°-20°=70°,∴∠CED=70°,∵∠CED=∠ADE+∠A ,∴∠ADE=70°-20°=50°.故答案是:50°.【点睛】考查了三角形的内角和定理,要熟练掌握,解答此题的关键是要明确:三角形的内角和是180°.69.如果直角三角形的一个内角为40°,则这个直角三角形的另一个锐角为_____.【答案】50°【解析】【分析】根据直角三角形两锐角互余进行求解即可.【详解】∠直角三角形的一个内角为40°,∠这个直角三角形的另一个锐角=90°﹣40°=50°,故答案为50°.【点睛】本题考查了直角三角形两锐角互余的性质,熟练掌握是解题的关键.70.如果三角形的三个内角的比是3:4:7,那么这个三角形是_________三角形(按角分类);【答案】直角【解析】【分析】设三个角分别为:3x,4x,7x.根据三角形的内角和定理得3x+4x+7x=180°,可得到x的值,即可得到7x的值,于是可判断三角形的形状.【详解】设三个角分别为:3x,4x,7x.∵3x+4x+7x=180°,∴x=907o,∴7x=90°,所以此三角形为直角三角形.故答案是:直角.【点睛】考查了三角形的内角和定理:三角形的三个内角的和为180°.同时考查了三角形的分类.。
平行线与三角形内角和的综合应用作业及答案
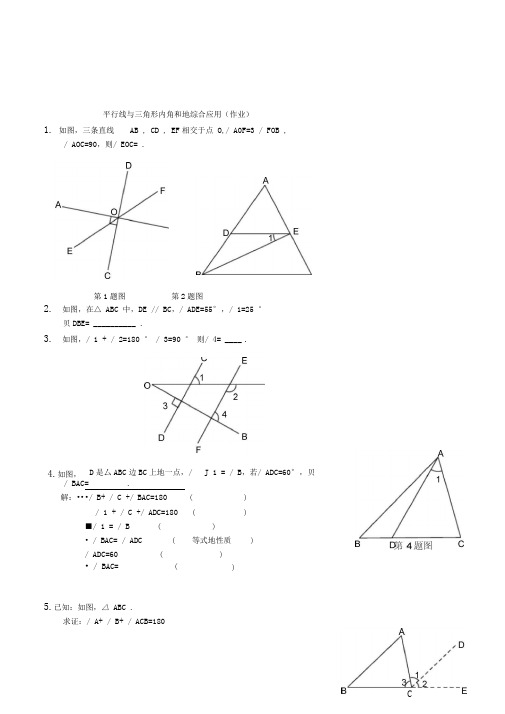
平行线与三角形内角和地综合应用(作业)1. 如图,三条直线 AB , CD , EF 相交于点 O ,/ A0F=3 / FOB ,/ AOC=90,则/ EOC= .2. 如图,在△ ABC 中,DE // BC ,/ ADE=55°,/ 1=25 °贝DBE= __________ .3. 如图,/ 1 + / 2=180 ° / 3=90 ° 则/ 4= ____ .5.已知:如图,△ ABC .求证:/ A+ / B+ / ACB=180C 第2题图4.如图, D 是厶ABC 边BC 上地一点,/ J 1 = / B ,若/ ADC=60°,贝U / BAC= .解:•• •/ B+ / C +/ BAC=180 ()/ 1 + / C +/ ADC=180 ()■/ 1 = / B ( )• / BAC= / ADC ( 等式地性质 )/ ADC=60 ( )• / BAC= ( )第1题图证明:作 BC 地延长线 CE ,过点C 作CD // AB ,•/ CD // AB•••/ A= / 1 / B= / 2 •••/ 1 + Z 2+ / 3=180° •••/ A+ / B+ / ACB=180 ( ( )(( ))) 第5题6.已知 如图, AB // CD ,/ BAE= / DCE=45° ./ E=90° . •/ AB // CD ( )+ =180 ( )•••/ BAE= 7 D C E=45 ( )• 7 1+45°+ 7 2+45° =即7 1 + 7 2= ( )•••/ E=180° - (/ 1+ / 2)=180 °-90 °=90 ° ( )7.已知:如图,/ 1 = / ACB ,/ 2=7 3.求证:CD // HF.证明:•••7 1= 7 ACB ( )• // ( )• 7 2=• 7 2=7 3 ( )'• 7 3= ( )•• // ( )【参考答案】1. 45°2. 30°3. 90°4. 60 °三角形三个内角地和是 180。
2022-2022八年级数学上册 综合训练 平行线与三角形内角和过程训练(二)天天练(新版)新人教版

平行线与三角形内角和过程训练综合测试〔二〕一、单项选择题(共6道,每道16分)1.请根据过程示范完成下题.例题::如图,直线AB,CD被直线EF所截,AB∥CD,∠2=50°,求∠1的度数.过程示范如下:解:如图,∵AB∥CD〔〕∴∠1=∠2〔两直线平行,同位角相等〕∵∠2=50°〔〕∴∠1=50°〔等量代换〕问题::如图,在△ABC中,点D,E分别在AB,AC边上,DE∥BC,∠1=60°,求∠B的度数.解:如图,∵_____________〔〕∴_____________〔________________〕∵∠1=60°〔〕∴_____________〔________________〕①DE∥BC;②∠1=∠B;③∠AED=∠C;④同位角相等,两直线平行;⑤两直线平行,同位角相等;⑥等量代换;⑦同位角相等;⑧∠B=60°.以上空缺处依次所填正确的选项是( )A.①②⑤⑧⑥B.①③⑤⑧⑦C.①②④⑧⑦D.②③⑤⑧⑥2.请根据过程示范,完成下题.例题::如图,在△ABC中,∠A=30°,∠C=100°,求∠B的度数.解:如图,在△ABC中,∠A=30°,∠C=100°〔〕∴∠B=180°-∠A-∠C=180°-30°-100°=50°〔三角形的内角和等于180°〕问题::如图,AB与CD交于点E,连接BC,∠1=75°,∠C=50°,求∠B的度数.解:如图,∵∠1=75°〔〕∠CEB=∠1〔对顶角相等〕∴∠CEB=75°〔等量代换〕_____________________________横线处应填写的过程恰当的是( )A.在△ECB中,∠1=75°,∠C=50°〔〕∴∠B=180°-∠1-∠C=180°-75°-50°=55°〔三角形的内角和等于180°〕B.在△ECB中,∠CEB=75°,∠C=50°〔〕∴∠B=180°-∠CEB-∠C=180°-75°-50°=55°〔三角形的内角和等于180°〕C.∵∠1是△ECB的一个外角〔外角的定义〕∴∠B=∠1-∠C=75°-50°=25°〔三角形的一个外角等于和它不相邻的两个内角的和〕D.∵三角形的内角和等于180°∴∠B=180°-∠CEB-∠C=180°-75°-50°=55°〔三角形的内角和等于180°〕3.:如图,在△ABC中,AD平分∠BAC,∠B=67°,∠C=33°,求∠CAD的度数.解:如图,_______________________∵AD平分∠BAC〔〕横线处应填写的过程恰当的是( )A.∵∠BAC=180°-∠B-∠C=180°-67°-33°=80°〔三角形的内角和等于180°〕B.∵三角形的内角和等于180°∴∠BAC=180°-∠B-∠C=180°-67°-33°=80°〔三角形的内角和等于180°〕C.在△ABC中,∠B=67°,∠C=33°〔〕∴∠BAC=180°-∠B-∠C=180°-67°-33°=80°〔三角形的内角和等于180°〕D.∵△ABC∴∠BAC=180°-∠B-∠C=180°-67°-33°=80°〔三角形的内角和等于180°〕4.:如图,∠ABC=∠ADC,BE平分∠ABC,DF平分∠ADC,∠1=∠2.求证:AD∥BC.证明:如图,∵BE平分∠ABC〔〕∴∠3=∠ABC〔角平分线的定义〕∵DF平分∠ADC〔〕∴∠1=∠ADC〔_____________________〕∵∠ABC=∠ADC〔〕∴_________〔等式的性质〕∵∠1=∠2〔〕∴∠2=∠3〔等量代换〕∴AD∥BC〔_____________________〕①;②角平分线的定义;③∠1=∠3;④∠2=∠3;⑤内错角相等,两直线平行;⑥两直线平行,内错角相等.以上空缺处依次所填正确的选项是( )A.①③⑥B.②③⑤C.①④⑤D.②③⑥5.:如图,直线AB∥CD,且OD与AC相交于点O.假设∠BAC=140°,∠ODC=30°,求∠COD的度数.解:如图,∵AB∥CD〔〕∴∠BAC+∠ACD=180°〔___________〕_________________________________在△OCD中,∠ACD=40°,∠ODC=30°〔〕∴∠COD=180°-∠ACD-∠ODC=180°-40°-30°=110°〔三角形的内角和等于180°〕①平角的定义②两直线平行,同旁内角互补③∴∠ACD=40°④∴∠ACD=180°-∠BAC=180°-140°=40°〔等式的性质〕⑤∵∠BAC=140°〔〕∴∠ACD=180°-∠BAC=180°-140°=40°〔等式的性质〕横线处应填写的过程最恰当的是( )A.①⑤B.②③C.②⑤D.②④6.:如图,AB∥CD,点E在AC上.求证:∠A=∠CED+∠D.那么以下证明过程错误的选项是( )A.证明:如图,∵∠A+∠C=180°〔两直线平行,同旁内角互补〕∴∠A=180°-∠C〔等式的性质〕∵∠C+∠CED+∠D=180°〔三角形的内角和等于180°〕∴∠CED+∠D=180°-∠C〔等式的性质〕∴∠A=∠CED+∠D〔等量代换〕B.证明:如图,∵∠C+∠CED+∠D=180°〔三角形的内角和等于180°〕∴∠CED+∠D=180°-∠C〔等式的性质〕∵AB∥CD〔〕∴∠A+∠C=180°〔两直线平行,同旁内角互补〕∴∠A=180°-∠C〔等式的性质〕∴∠A=∠CED+∠D〔等量代换〕C.证明:如图,∵AB∥CD〔〕∴∠A+∠C=180°〔两直线平行,同旁内角互补〕∵∠CED+∠D+∠C=180°〔三角形的内角和等于180°〕∴∠A+∠C=∠CED+∠D+∠C〔等量代换〕∴∠A=∠CED+∠D〔等式的性质〕D.证明:如图,∵AB∥CD〔〕∴∠A+∠C=180°〔两直线平行,同旁内角互补〕∴∠A=180°-∠C〔等式的性质〕∵∠C+∠CED+∠D=180°〔三角形的内角和等于180°〕∴∠CED+∠D=180°-∠C〔等式的性质〕∴∠A=∠CED+∠D〔等量代换〕。
人教版八年级数学上册第一单元《三角形的内角和》同步练习2(含参考答案)

人教版八年级数学上册第一单元《三角形的内角和》同步练习2(含参考答案)一.选择题1.已知在Rt△ABC中,∠B=90°,∠C=35°,则∠A等于()A.35°B.45°C.55°D.65°2.如右图,已知AB⊥BD,AC⊥CD,∠A=40°,则∠D的度数为()A.40°B.50°C.60°D.70°3.如右图,Rt△ABC中,∠ACB=90°,CD⊥AB于点D,则下列结论不一定成立的是()A.∠1+∠2=90°B.∠2=∠3 C.∠1=∠4 D.∠1=30°4.直角三角形两个锐角平分线相交所成的钝角的度数为()A.90°B.135°C.120°D.45°或135°5.如右图△ABC中,∠BAC=90°,AD⊥BC,AE平分∠BAC,∠B=2∠C,∠DAE的度数是()A.45°B.20°C.30°D.15°二.填空题6.若直角三角形的一个锐角为15°,则另一个锐角等于.7.如右图,直线a∥b,在Rt△ABC中,点C在直线a上,若∠1=54°,∠2=24°,则∠B的度数为.8.在直角三角形中,两个锐角的度数比为2:3,那么较小锐角的度数是.9.如右图,在△ABC中,∠ACB=90°,AD平分∠CAB,交边BC于点D,过点D作DE⊥AB,垂足为E.若∠CAD=20°,则∠EDB的度数是.10.将两张矩形纸片如图所示摆放,使其中一张矩形纸片的一个顶点恰好落在另一张矩形纸片的一条边上,则∠1+∠2=.三.解答题11.AD、BE为△ABC的高,AD、BE相交于H点,∠C=50°,求∠BHD.12.解方程组:.参考答案一.选择题1.已知在Rt△ABC中,∠B=90°,∠C=35°,则∠A等于()A.35°B.45°C.55°D.65°【分析】根据直角三角形的两锐角互余计算即可.【解答】解:在Rt△ABC中,∠B=90°,∠C=35°,则∠A=90°﹣35°=55°,故选:C.【点评】本题考查的是直角三角形的性质,掌握直角三角形的两锐角互余是解题的关键.2.如图,已知AB⊥BD,AC⊥CD,∠A=40°,则∠D的度数为()A.40°B.50°C.60°D.70°【分析】根据直角三角形的性质求出∠AEB的度数,根据对顶角相等求出∠DEC,根据直角三角形的两个锐角互余计算即可.【解答】解:∵AB⊥BD,∠A=40°,∴∠AEB=50°,∴∠DEC=50°,又AC⊥CD,∴∠D=40°,故选:A.【点评】本题考查的是直角三角形的性质,掌握直角三角形的两个锐角互余是解题的关键.3.如图,Rt△ABC中,∠ACB=90°,CD⊥AB于点D,则下列结论不一定成立的是()A.∠1+∠2=90°B.∠2=∠3C.∠1=∠4D.∠1=30°【分析】根据垂直得出∠ADC=∠BDC=90°,再根据直角三角形的性质逐个判断即可.【解答】解:A.∵∠ACB=90°,∴∠1+∠2=90°,故本选项不符合题意;B.∵CD⊥AB,∴∠ADC=90°,∴∠1+∠3=90°,∵∠1+∠2=90°,∴∠2=∠3,故本选项不符合题意;C.∵CD⊥AB,∴∠BDC=90°,∴∠2+∠4=90°,∵∠1+∠2=90°,∴∠1=∠4,故本选项不符合题意;D.根据已知条件不能推出∠1=30°,故本选项符合题意;故选:D.【点评】本题考查了垂直定义和直角三角形的性质,注意:直角三角形的两锐角互余.4.直角三角形两个锐角平分线相交所成的钝角的度数为()A.90°B.135°C.120°D.45°或135°【分析】本题可根据直角三角形内角的性质和三角形内角和为180°进行求解.【解答】解:如图:∵AE、BD是直角三角形中两锐角平分线,∴∠OAB+∠OBA=90°÷2=45°,两角平分线组成的角有两个:∠BOE与∠EOD这两个角互补,根据三角形外角和定理,∠BOE=∠OAB+∠OBA=45°,∴∠EOD=180°﹣45°=135°,故选:B.【点评】本题考查的是直角三角形的性质,熟知直角三角形的性质是解答此题的关键.5.△ABC中,∠BAC=90°,AD⊥BC,AE平分∠BAC,∠B=2∠C,∠DAE的度数是()A.45°B.20°C.30°D.15°【分析】根据三角形的内角和∠B=60°,根据角平分线的定义得出∠BAE=45°,根据直角三角形的两锐角互余得出∠BAD=30°,即可根据角的和差得解.【解答】解:∵∠BAC=90°,∠B=2∠C,∴∠B=60°,∵AD⊥BC,AE平分∠BAC,∴∠ADB=90°,∠BAE=∠BAC=45°,∴∠BAD=90°﹣60°=30°,∴∠DAE=45°﹣30°=15°.故选:D.【点评】此题考查了直角三角形的性质,熟记直角三角形的两锐角互余是解题的关键.二.填空题6.若直角三角形的一个锐角为15°,则另一个锐角等于75°.【分析】根据直角三角形的两锐角互余列式计算即可.【解答】解:∵直角三角形的一个锐角为15°,∴另一个锐角=90°﹣15°=75°,故答案为:75°.【点评】本题考查的是直角三角形的性质,掌握直角三角形的两锐角互余是解题的关键.7.如图,直线a∥b,在Rt△ABC中,点C在直线a上,若∠1=54°,∠2=24°,则∠B的度数为60°.【分析】利用平行线的性质,三角形的外角的性质求出∠A即可解决问题.【解答】解:如图,∵a∥b,∴∠1=∠3=54°,∵∠3=∠2+∠A,∴∠A=54°﹣24°=30°,∵∠ACB=90°,∴∠B=90°﹣30°=60°,故答案为60°.【点评】本题考查平行线的性质,三角形的外角的性质,三角形的内角和定理等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.8.在直角三角形中,两个锐角的度数比为2:3,那么较小锐角的度数是36°.【分析】根据比例设两锐角分别为2k、3k,然后利用直角三角形两锐角互余列方程求解即可.【解答】解:设两锐角分别为2k、3k,由题意得2k+3k=90°,解得k=18°,所以较小锐角的度数为18×2=36°.故答案为:36°.【点评】本题考查了直角三角形的性质,解题时注意:在直角三角形中,两个锐角互余.9.如图,在△ABC中,∠ACB=90°,AD平分∠CAB,交边BC于点D,过点D作DE⊥AB,垂足为E.若∠CAD=20°,则∠EDB的度数是40°.【分析】根据角平分线的定义得∠CAB=40°,由直角三角形的性质计算即可得解.【解答】解:∵AD平分∠CAB,∠CAD=20°,∴∠CAB=2∠CAD=40°,∵∠ACB=90°,∴∠B=90°﹣40°=50°,∵DE⊥AB,∴∠DEB=90°,∴∠EDB=90°﹣50°=40°,故答案为:40°.【点评】本题考查了角平分线的定义和直角三角形的性质,熟记性质是解题的关键.10.将两张矩形纸片如图所示摆放,使其中一张矩形纸片的一个顶点恰好落在另一张矩形纸片的一条边上,则∠1+∠2=90°.【分析】如图,连接两交点,根据两直线平行,同旁内角互补和直角三角形两锐角互余的性质解答.【解答】解:如图,连接两交点,根据矩形两边平行,得∠1+∠2+∠3+∠4=180°,又矩形的角等于90°,∴∠3+∠4=90°,∴∠1+∠2=180°﹣90°=90°.故答案为:90.【点评】本题主要考查平行线的性质和直角三角形两锐角互余的性质.三.解答题11.AD、BE为△ABC的高,AD、BE相交于H点,∠C=50°,求∠BHD.【分析】根据同角的余角相等求出∠BHD=∠C,从而得解.【解答】解:∵AD是△ABC的高,∴∠BHD+∠HBD=90°,∵BE是△ABC的高,∴∠HBD+∠C=90°,∴∠BHD=∠C,∵∠C=50°,∴∠BHD=50°.【点评】本题考查了直角三角形两锐角互余的性质,同角的余角相等的性质,熟记性质并准确识图是解题的关键.12.解方程组:.【分析】运用加减消元解答即可.【解答】解:,②﹣①得,4y=8,解得y=2,把y=2代入①得,x﹣2=1,解得x=3,故原方程组的解为.【点评】此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.。
八年级数学上册 综合训练 平行线与三角形内角和过程训练(一)天天练(新版)新人教版

平行线与三角形内角和过程训练综合测试〔一〕一、单项选择题(共8道,每道12分)1.:如图,AB⊥BC,BC⊥CD,垂足分别为B,C,∠1=∠2.证明:BE∥CF.证明:如图,∵AB⊥BC〔〕∴∠1+∠EBC=90°〔垂直的定义〕∵BC⊥CD〔〕∴∠2+∠BCF=90°〔垂直的定义〕∵∠1=∠2〔〕∴∠EBC=∠BCF〔____________________〕∴BE∥CF〔____________________〕①等角的余角相等;②等角的补角相等;③两直线平行,内错角相等;④内错角相等;⑤内错角相等,两直线平行.以上空缺处依次所填正确的选项是( )A.①⑤B.①④C.②⑤D.②③2.:如图,AB∥CD,EF分别交AB,CD于点M,N,∠EMB=40°,MG平分∠BMN交CD于点G,求∠1的度数.解:如图,∵∠EMB=40°〔〕∴∠BMN=140°〔__________________〕∵MG平分∠BMN〔〕∵AB∥CD〔〕∴∠1=______〔__________________〕∴∠1=70°〔等量代换〕①平角的定义;②三角形的内角和等于180°;③∠2;④∠BME;⑤内错角相等,两直线平行;⑥两直线平行,内错角相等.以上空缺处依次所填正确的选项是( )A.②④⑥B.①③⑥C.①③⑤D.②④⑤3.如图,AB∥CD,∠BAE=40°,∠DCE=50°,求∠E的度数.解:如图,∵AB∥CD〔〕∴∠BAC+______=180°〔_____________________〕即∠BAE+∠1+∠2+∠DCE=180°∵∠BAE=40°,∠DCE=50°〔〕∴∠1+∠2=180°-∠BAE-∠DCE=180°-40°-50°=90°〔等式的性质〕在△ACE中,________________∴∠E=180°-〔∠1+∠2〕=180°-90°=90°〔_____________________〕①∠C;②∠ACD;③两直线平行,同旁内角互补;④同旁内角互补,两直线平行;⑤∠1+∠2=90°;⑥∠1=50°,∠2=40°;⑦平角的定义;⑧三角形的内角和等于180°.以上空缺处依次所填正确的选项是( )A.②③⑤⑧B.①③⑥⑧C.①④⑤⑦D.②③⑥⑧4.如图,在△ABC中,AD⊥BC,垂足为D,E是AC边上一点,BE与AD交于点F.假设∠ABC=45°,∠BAC=75°,∠BFD=60°,那么∠BEC的度数为( )解:如图,∵AD⊥BC〔〕∴∠FDB=90°〔垂直的定义〕∵∠BFD=60°〔〕∴∠1=90°-∠BFD=90°-60°=30°〔____________________〕在△ABC中,∠ABC=45°,∠BAC=75°∴∠C=180°-∠ABC-∠BAC=180°-45°-75°=60°〔____________________〕在△BEC中,∠1=30°,∠C=60°∴∠BEC=180°-∠1-∠C=180°-30°-60°=90°〔三角形的内角和等于180°〕①等式的性质;②垂直的定义;③三角形的内角和等于180°;④直角三角形两锐角互余.以上空缺处依次所填正确的选项是( )A.①③B.②③C.④②D.④③5.:如图,直线AB∥CD,EF分别交AB,CD于点G,M,射线GH,MN分别平分∠BGM,∠DMF.求证:GH∥MN.证明:如图,∵AB∥CD〔〕∴∠BGM=∠DMF〔__________________〕∵GH平分∠BGM〔〕∴〔角平分线的定义〕∵MN平分∠DMF〔〕∴〔角平分线的定义〕∴____________〔等式的性质〕∴GH∥MN〔__________________〕①∠2=∠4;②∠1=∠3;③两直线平行,同位角相等;④等量代换;⑤同位角相等,两直线平行;⑥同旁内角互补,两直线平行;⑦内错角相等,两直线平行.以上空缺处依次所填正确的选项是( )A.③②⑦B.④②⑤C.③①⑤D.③①⑦6.:如图,BD⊥AC,EF⊥AC,垂足分别为D,F,G是AB上一点,且∠l=∠2.求证:GD∥BC.证明:如图,∵BD⊥AC〔〕∴∠BDC=90°〔垂直的定义〕∵EF⊥AC〔〕∴∠EFC=90°〔垂直的定义〕∴∠BDC=∠EFC〔等量代换〕∴BD∥EF〔_________________〕∴∠2=∠3〔_________________〕∵∠l=∠2〔〕∴_______〔等量代换〕∴GD∥BC〔内错角相等,两直线平行〕①同位角相等,两直线平行;②两直线平行,同位角相等;③两直线平行,内错角相等;④内错角相等,两直线平行;⑤∠l=∠3;⑥∠2=∠3.以上空缺处依次所填正确的选项是( )A.①③⑥B.②①⑤C.④②⑥D.①②⑤7.如图,在△ABC中,∠B=∠C,FD⊥BC,DE⊥AB,垂足分别为D,E,∠AFD=140°,求∠EDF的度数.证明:如图,∵∠AFD=140°〔〕∴∠2=40°〔平角的定义〕∵FD⊥BC〔〕∴∠FDC=90°〔垂直的定义〕∴∠2+∠C=90°〔____________________〕∵DE⊥AB〔〕∴∠BED=90°〔垂直的定义〕∴___________〔直角三角形两锐角互余〕∵∠B=∠C〔〕∴∠1=∠2〔____________________〕∴∠1=40°〔等量代换〕∴∠EDF=180°-∠FDC-∠1=180°-90°-40°=50°〔____________________〕①垂直的定义;②直角三角形两锐角互余;③等角的余角相等;④∠1+∠B=90°;⑤∠1+∠EDF=90°;⑥平角的定义;⑦三角形的内角和等于180°.以上空缺处依次所填正确的选项是( )A.①⑤②⑦B.③④②⑦C.②④③⑥D.②⑤③⑦8.:如图,BF∥DG,AD∥EF,∠ACF=70°,∠G=30°.求∠EFG的度数.证明:如图,∵BF∥DG〔〕∴∠ACF=______〔两直线平行,同位角相等〕∵AD∥EF〔〕∴∠D=______〔两直线平行,同位角相等〕∴∠ACF=∠1〔等量代换〕∵∠ACF=70°〔〕∴∠1=70°〔等量代换〕在△FEG中,∠1=70°,∠G=30°∴∠EFG=180°-∠1-∠G=180°-70°-30°=80°〔____________________〕①∠CFE;②∠D;③∠1;④∠ACF;⑤平角的定义;⑥三角形的内角和等于180°.以上空缺处依次所填正确的选项是( )A.①③⑤B.①④⑥C.②③⑥D.②④⑤如有侵权请联系告知删除,感谢你们的配合!。
2020年秋人教版八年级数学上册第11章三角形综合应用(讲义、随堂练习、习题及答案)

人教版八年级数学上册第11章 三角形综合应用(讲义)➢ 知识点睛在三角形背景下处理问题的思考方向: 1. 三角形中的隐含条件是:边:_______________________________________________. 角:①______________________________________________;②_____________________________________________.2. 角平分线出现时,为了计算方便,通常采用__________解决问题.3. 高线出现时考虑__________或__________.➢ 精讲精练1. 现有3cm ,4cm ,7cm ,9cm 长的四根木棒,任取其中三根组成一个三角形,那么可以组成的三角形的个数是() A .1个B .2个C .3个D .4个2. 如图,用四个螺丝将四条不可弯曲的木条围成一个木框,中相邻两螺丝的距离依次为2,3,4,6A .5 B .6 C .7 D .10 3. 下列五种说法:①三角形的三个内角中至少有两个锐角;②三角形的三个内角中至少有一个钝角;③一个三角形中,至少有一个角不小于60°;④钝角三角形中,任意两个内角的和必大于90°;⑤直角三角形中两锐角互余.其中正确的说法有__________________(填序号). 4. 如图,在三角形纸片ABC 中,∠A =60°,∠B =55°.将纸片一角折叠使点C 落在△ABC 内,则∠1+∠2=_________.C 21AABCDE第4题图第5题图5. 如图,一个五角星的五个角的和是________.6. 如图,∠A +∠B +∠C +∠D +∠E +∠F =________.第2题图FEBA7. 如图1,线段AB ,CD 相交于点O ,连接AD ,BC ,我们把形如图1的图形称之为“X 型”.如图2,在图1的条件下,∠DAB 和∠BCD 的平分线AP 和CP 相交于点P ,并且与CD ,AB 分别相交于M ,N ,试解答下列问题: (1)在图1中,请直接写出∠A ,∠B ,∠C ,∠D 之间的数量关系:_____________________________; (2)在图2中,共有______个“X 型”;(3)在图2中,若∠D =40°,∠B =30°,则∠APC =_______; (4)在图2中,若∠D =α,∠B =β,则∠APC =__________.图2图1P NMABCDOO DCBA8. 探究:(1)如图1,在△ABC 中,BP 平分∠ABC ,CP 平分∠ACB ,猜想∠P 和∠A 有何数量关系?(2)如图2,在△ABC 中,BP 平分∠ABC ,CP 平分外角∠ACE ,猜想∠P 和∠A 有何数量关系?(3)如图3,BP 平分∠CBF ,CP 平分∠BCE ,猜想∠P 和∠A 有何数量关系?E C AB FPA PP A CE图1 图2 图39. 如图,在△ABC 中,三个内角的角平分线交于点O ,OE ⊥BC 于点E .(1)∠ABO +∠BCO +∠CAO =____________;(2)∠BOD 和∠COE 的数量关系是________________.O D ECM ANB DA第9题图第10题图10. 如图,在Rt △ABC 中,∠BAC =90°,AD ⊥BC 于点D .(1)若AB =6,AC =8,BC =10,则AD =____________;(2)若AB =2,BC =3,则AC :AD =____________.11. 如图,在△ABC 中,若AB =2cm ,AC =3cm ,BC =4cm ,AD ,BF ,CE为△ABC 的三条高,则这三条高的比AD :BF :CE =____________________.C EAF 12. 如图,在△ABC 中,AB =AC ,P 是BC 边上任意一点,PD ⊥AB 于点D ,PE ⊥AC 于点E .(1)若AB =8,△ABC 的面积为14,则PD +PE 的值是多少?(2)过点B 作BF ⊥AC 于点F ,求证:PD +PE =BF .D PCEFA【参考答案】➢ 知识点睛1. 三角形两边之和大于第三边,两边之差小于第三边;三角形内角和等于180°;三角形的一个外角等于和它不相邻的两个内角的和. 2. 设元 3. 互余,面积➢精讲精练1. B2. C3.①③⑤4.130°5.180°6.360°7.(1)∠A+∠D=∠B+∠C;(2)3;(3)35°;(4)12(α+β)8.(1)∠P=90°+12∠A;(2)∠P=12∠A;(3)∠P=90° 12∠A9.(1)90°(2)∠BOD=∠COE10.(1)245(2)3:211.3:4:612.(1)72(2)证明略三角形综合应用(讲义)➢知识点睛在三角形背景下处理问题的思考方向:4.三角形中的隐含条件是:边:_______________________________________________.角:①______________________________________________;②_____________________________________________.5.角平分线出现时,为了计算方便,通常采用__________解决问题.6.高线出现时考虑__________或__________.➢精讲精练13.现有3cm,4cm,7cm,9cm长的四根木棒,任取其中三根组成一个三角形,那么可以组成的三角形的个数是()A.1个B.2个C.3个D.4个14.如图,用四个螺丝将四条不可弯曲的木条围成一个木框,中相邻两螺丝的距离依次为2,3,4,6A.5 B.6 C.7 D.10第2题图15. 下列五种说法:①三角形的三个内角中至少有两个锐角;②三角形的三个内角中至少有一个钝角;③一个三角形中,至少有一个角不小于60°;④钝角三角形中,任意两个内角的和必大于90°;⑤直角三角形中两锐角互余.其中正确的说法有__________________(填序号). 16. 如图,在三角形纸片ABC 中,∠A =60°,∠B =55°.将纸片一角折叠使点C 落在△ABC 内,则∠1+∠2=_________.BC 21AABCDE第4题图第5题图17. 如图,一个五角星的五个角的和是________. 18. 如图,∠A +∠B +∠C +∠D +∠E +∠F =________.FEBA19. 如图1,线段AB ,CD 相交于点O ,连接AD ,BC ,我们把形如图1的图形称之为“X 型”.如图2,在图1的条件下,∠DAB 和∠BCD 的平分线AP 和CP 相交于点P ,并且与CD ,AB 分别相交于M ,N ,试解答下列问题: (1)在图1中,请直接写出∠A ,∠B ,∠C ,∠D 之间的数量关系:_____________________________; (2)在图2中,共有______个“X 型”;(3)在图2中,若∠D =40°,∠B =30°,则∠APC =_______; (4)在图2中,若∠D =α,∠B =β,则∠APC =__________.图2图1P NMABCDOO DCBA20. 探究:(1)如图1,在△ABC 中,BP 平分∠ABC ,CP 平分∠ACB ,猜想∠P 和∠A 有何数量关系?(2)如图2,在△ABC 中,BP 平分∠ABC ,CP 平分外角∠ACE ,猜想∠P 和∠A 有何数量关系?(3)如图3,BP 平分∠CBF ,CP 平分∠BCE ,猜想∠P 和∠A 有何数量关系?E C AB FA PP A CE图1 图2 图321. 如图,在△ABC 中,三个内角的角平分线交于点O ,OE ⊥BC 于点E .(1)∠ABO +∠BCO +∠CAO =____________;(2)∠BOD 和∠COE 的数量关系是________________.O D ECM ANB DC B A第9题图第10题图22. 如图,在Rt △ABC 中,∠BAC =90°,AD ⊥BC 于点D .(1)若AB =6,AC =8,BC =10,则AD =____________;(2)若AB =2,BC =3,则AC :AD =____________.23. 如图,在△ABC 中,若AB =2cm ,AC =3cm ,BC =4cm ,AD ,BF ,CE为△ABC 的三条高,则这三条高的比AD :BF :CE =____________________.C DEAF B 24. 如图,在△ABC 中,AB =AC ,P 是BC 边上任意一点,PD ⊥AB 于点D ,PE ⊥AC 于点E .(1)若AB =8,△ABC 的面积为14,则PD +PE 的值是多少?(2)过点B 作BF ⊥AC 于点F ,求证:PD +PE =BF .D BPCEFA【参考答案】➢ 知识点睛4. 三角形两边之和大于第三边,两边之差小于第三边;三角形内角和等于180°;三角形的一个外角等于和它不相邻的两个内角的和. 5. 设元 6. 互余,面积➢ 精讲精练 13. B 14. C15. ①③⑤ 16. 130° 17. 180° 18. 360°19. (1)∠A +∠D =∠B +∠C ;(2)3; (3)35°;(4)12(α+β)20. (1)∠P =90°+12∠A ; (2)∠P =12∠A ;(3)∠P =90° 12∠A21. (1)90° (2)∠BOD =∠COE22. (1)245(2)3:223. 3:4:624. (1)72(2)证明略三角形综合应用(随堂测试)1. 现有2cm ,3cm ,4cm ,5cm 长的四根木棒,任取其中三根组成一个三角形,那么可以组成的三角形的个数是() A .1个B .2个C .3个D .4个2. 如图,∠A +∠B +∠C +∠D +∠E =___________.3. 如图,点E ,D 分别在△ABC 的边BA ,CA 的延长线上,CF ,EF 分别平分∠ACB 和∠AED ,若∠B =65°,∠D =45°,则∠F 的度数为________.【参考答案】1. C2. 180°3. 55°E DCBAE DCBA三角形综合应用(习题)➢ 例题示范例1:如图,BD ,CD 分别平分∠ABC ,∠ACB ,CE ⊥BD 交BD 的延长线于点E . 求证:∠DCE =∠CAD .【思路分析】①看到条件BD ,CD 平分∠ABC ,可知AD 也平分∠BAC ,得到:,,;②根据CE ⊥BD ,得,所以;③题目所求为∠DCE =∠CAD ,若能够说明即可; ④根据三角形的内角和定理得:,所以,再根据三角形的外角定理可知,所以,证明成立. 【过程书写】 证明:如图,∵BD ,CD 分别平分∠ABC ,∠ACB∴,,在△ABC 中,∴ ∵∠EDC 是△BCD 的一个外角 ∴ ∴ ∵CE ⊥BE ∴ ∴ ∴∠DCE =∠CAD➢ 巩固练习1. 现有2cm ,4cm ,6cm ,8cm 长的四根木棒,任意选取三根组成一个三角形,DECBA12DAC BAC ∠=∠12DBC ABC ∠=∠12DCB ACB ∠=∠90DEC ∠=︒90DCE EDC ∠+∠=︒90CAD EDC ∠+∠=︒180BAC ABC ACB ∠+∠+∠=︒90CAD DBC DCB ∠+∠+∠=︒EDC DBC DCB ∠=∠+∠90CAD EDC ∠+∠=︒12DAC BAC ∠=∠12DBC ABC ∠=∠12DCB ACB ∠=∠180BAC ABC ACB ∠+∠+∠=︒90CAD DBC DCB ∠+∠+∠=︒EDC DBC DCB ∠=∠+∠90CAD EDC ∠+∠=︒90DEC ∠=︒90DCE EDC ∠+∠=︒DECBA那么可以组成三角形的个数为() A .1个B .2个C .3个D .4个2. 满足下列条件的△ABC 中,不是直角三角形的是()A .∠B +∠A =∠C B .∠A :∠B :∠C =2:3:5 C .∠A =2∠B =3∠CD .一个外角等于和它相邻的一个内角3. 如图,一个直角三角形纸片,剪去直角后,得到一个四边形,则∠1+∠2=___________.4. 如图,∠A +∠B +∠C +∠D +∠E +∠F =________.第4题图第5题图5. 如图,在Rt △ABC 中,∠C =90°,若∠CAB 与∠CBA 的平分线相交于点O ,则∠AOB =__________.6. 如图,在△ABC 中,∠ABC 的平分线BD 与外角平分线CE 的反向延长线交于点D ,若∠A =30°,则∠D =________.7. 如图,在△ABC 中,AD 平分∠BAC ,点F 在DA 的延长线上,FE ⊥BC 于E ,若∠B =40°,∠C =70°,则∠D F E =________.第2题图12F ECBAOC FECBA第7题图第8题图8. 如图,在△ABC 中,∠1=∠2,G 为AD 的中点,延长BG 交AC 于点E ,且满足BE ⊥AC ,F 为AB 上一点,且CF ⊥AD 于点H .下列结论:①线段AG 是△ABE 的角平分线;②BE 是△ABC 的中线;③线段AE 是△ABG 的边BG 上的高;④△ABG 与△DBG 的面积相等.其中正确的结论有________(填序号). 9. 如图,在△ABC 中,若AB =2cm ,BC =4cm ,则△ABC 的高AD 与CE 的比是__________. 10. 如图,在△ABC 中,AD 是高,AE ,BF 是角平分线,它们相交于点O ,∠BAC =50°,∠C =60°,求∠CAD 及∠AOB 的度数.➢ 思考小结F E CAG H FE DCA 21OFE D CAE D C B A(1)“X 型”:(2)“角平分线模型”1902P A ∠=︒+∠12P A ∠=∠1902P A∠=︒-∠【参考答案】➢ 巩固练习 1. A 2. C 3. 270° 4. 360° 5. 135° 6.15°E7.15°8.①③④9.1:210.∠CAD=30°,∠AOB=120°➢思考小结1.大于,小于,180°,和它不相邻的两个内角的和2.略。
八年级平行线、三角形内角和答案

B EAC F平行线、三角形内角和定理一、基本知识1.平行线性质:两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补。
平行线判定:同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行。
3.三角形内角和定理:三角形三个内角的和等于180°。
直角三角形两锐角互余;四边形的内角和等于360°。
三角形的一个外角等于和它不相邻的两个内角的和;三角形的外角大于和它不相邻的任何一个内角。
二、训练题1.下列说话正确的是( B )A 、互补的两个角一定是邻补角B 、同一平面内,b // a, c // a,则b//cC 、同一平面内,,,.a c b c a b ⊥⊥⊥则D 相等的角一定是对顶角。
2.如图1,∠1=∠2,则有( A )A 、 EB//CF,B 、 AB//CF,C 、 EB//CD,D 、 AB//CD,3.如图2,已知∠1=80°, m//n, 则∠4=( A ) A 、100°, B 、70° C 、80°, D 、60°,4.如图3,AB//EF,BC//DE, ∠B=40°,则∠E=( C )A 、90°,B 、120°C 、140°,D 、360°,5.如图4,点E 在AC 的延长线上,下列条件中能判断AB//CD 的是( A ) A 、∠1=∠2, B 、∠3=∠4 C 、∠D=∠DCE D ∠D+∠ACD=180°6.如图5,AB//CD//EF, ∠ABE=38°,∠ECD=100°,则∠BEC=( A ) A 、42°, B 、32° C 、62°, D 、38°,7.如图6,AE//CD, DE 平分∠ADC ,∠EAD=50°则∠DEA= 65° 。
八年级数学上册三角形综合应用(习题及答案)

第1页共4页三角形综合应用(习题)
例题示范
例1:如图,BD ,CD 分别平分∠ABC ,∠ACB ,CE ⊥BD 交BD 的延长线于点E .求证:∠DCE=∠CAD .
D
E
C
B A
【思路分析】
①看到条件BD ,CD 平分∠ABC ,可知AD 也平分∠BAC ,得到:1
2DAC BAC ,
12DBC ABC ,1
2DCB ACB ;
②根据CE ⊥BD ,得90DEC ,所以90DCE EDC ;
③题目所求为∠DCE=∠CAD ,若能够说明90CAD EDC 即可;④根据三角形的内角和定理得:180BAC ABC ACB ,所以
90CAD DBC DCB ,再根据三角形的外角定理可知
EDC DBC DCB ,所以90CAD EDC ,证明成立.
【过程书写】
证明:如图,
∵BD ,CD 分别平分∠ABC ,∠ACB
∴12DAC BAC ,1
2DBC ABC ,1
2DCB ACB
在△ABC 中,180
BAC ABC ACB ∴90CAD DBC DCB ∵∠EDC 是△BCD 的一个外角∴EDC DBC DCB
∴90CAD EDC ∵CE ⊥BE ∴90
DEC ∴90
DCE EDC ∴∠DCE=∠CAD
巩固练习
1.现有2 cm ,4 cm ,6 cm ,8 cm 长的四根木棒,任意选取三根组成一个三角形,
那么可以组成三角形的个数为()
A .1个
B .2个
C .3个
D .4个
D
E
C
B A。
平行线与三角形内角和计算(人教版)(含答案)

学生做题前请先回答以下问题问题1:看到平行,想什么?为什么这么想?问题2:三角形的内角和等于_______.问题3:直角三角形两锐角_______.平行线与三角形内角和计算(人教版)一、单选题(共8道,每道12分)1.如图,在△ABC中,AD平分∠BAC,且与BC相交于点D,∠B=40°,∠BAD=30°,则∠C 的度数为( )A.80°B.90°C.100°D.110°答案:A解题思路:如图,由AD平分∠BAC,∠BAD=30°,可得∠BAC=2∠BAD=2×30°=60°,在△ABC中,∠B=40°,由三角形的内角和等于180°,可得∠C=180°-∠B-∠BAC=180°-40°-60°=80°.故选A.试题难度:三颗星知识点:三角形内角和定理2.已知在△ABC中,∠B是∠A的2倍,∠C比∠A大20°,则∠A的度数为( )A.30°B.40°C.60°D.80°答案:B解题思路:由题意可知∠B和∠C都与∠A有关,因此可设∠A=α,则∠B=2α,∠C=α+20°,由三角形的内角和等于180°,可得α+2α+(α+20°)=180°,解得,α=40°,即∠A=40°.故选B.试题难度:三颗星知识点:三角形内角和定理3.如图,在△ABC中,∠B=∠C,FD⊥BC,DE⊥AB,垂足分别为D,E.若∠AFD=158°,则∠EDF=( )A.42°B.44°C.68°D.79°答案:C解题思路:如图,由FD⊥BC,DE⊥AB可知,∠FDC=∠DEB=90°,因为∠AFD=158°,由平角的定义,可得∠2=180°-158°=22°,再由直角三角形两锐角互余,可得∠C=68°.因为∠B=∠C,可得∠B=68°;由直角三角形两锐角互余,可得∠1+∠B=90°;又因为FD⊥BC,所以∠1+∠EDF=90°,由同角的余角相等,可得∠EDF=∠B=68°.故选C.试题难度:三颗星知识点:互余4.如图,在△ABC中,AE平分∠BAC,AD⊥BC,垂足为D,若∠BAC=128°,∠C=36°,则∠DAE的度数为( )A.10°B.12°C.15°D.18°答案:A解题思路:如图,因为AE平分∠BAC,且∠BAC=128°,所以,因为AD⊥BC,∠C=36°,根据直角三角形两锐角互余,可得∠DAC=90°-∠C=90°-36°=54°,因此∠DAE=∠CAE-∠DAC=64°-54°=10°.故选A.试题难度:三颗星知识点:互余5.如图,在△ABC中,∠BAC=4∠1,∠C=∠1,BD⊥CA于点D,则∠DBA=( )A.20°B.60°C.45°D.30°答案:D解题思路:在△ABC中,由三角形的内角和等于180°,可得∠BAC+∠1+∠C=180°,由∠BAC=4∠1,∠C=∠1,得4∠1+∠1+∠1=180°,解得∠1=30°,所以∠C=30°,∠BAC=120°.由平角的定义,可得∠BAD=180°-∠BAC=180°-120°=60°.因为BD⊥CA于点D,则∠D=90°,在Rt△ABD中,根据直角三角形两锐角互余,可得∠DBA=90°-∠BAD=90°-60°=30°.故选D.试题难度:三颗星知识点:互余6.如图,在四边形ABCD中,点E在BC上,AB∥DE,∠B=78°,∠C=60°,则∠EDC的度数为( )A.42°B.60°C.78°D.80°答案:A解题思路:如图,因为AB∥DE,根据两直线平行,同位角相等,可得∠DEC=∠B.已知∠B=78°,则∠DEC=78°.在△DEC中,∠C=60°,∠DEC=78°,由三角形的内角和等于180°,可得∠EDC=180°-∠C-∠DEC=180°-60°-78°=42°.故选A.试题难度:三颗星知识点:三角形内角和定理7.如图,直线BD∥EF,AE与BD交于点C,若∠B=30°,∠A=75°,则∠CEF的度数为( )A.60°B.75°C.90°D.105°答案:D解题思路:如图,在△ABC中,∠B=30°,∠A=75°,由三角形的内角和等于180°,可得∠ACB=180°-∠B-∠A=180°-30°-75°=75°.根据对顶角相等,可得∠DCE=∠ACB=75°.已知BD∥EF,根据两直线平行,同旁内角互补,可得∠CEF=180°-∠DCE=180°-75°=105°.故选D.试题难度:三颗星知识点:三角形内角和定理8.如图,直线AB∥CD,∠EFA=28°,∠EHC=50°,则∠E=( )A.28°B.22°C.32°D.38°答案:B解题思路:如图,因为AB∥CD,∠EHC=50°,根据两直线平行,同旁内角互补,可得∠AGH=180°-∠EHC=180°-50°=130°,根据对顶角相等,可得∠EGF=∠AGH=130°,在△EGF中,∠EFA=28°,∠EGF=130°,由三角形的内角和等于180°,可得∠E=180°-∠EFA-∠EGF=180°-28°-130°=22°.故选B.试题难度:三颗星知识点:三角形内角和定理。
平行线与三角形内角和过程训练(综合)(二)(人教版)(含答案)
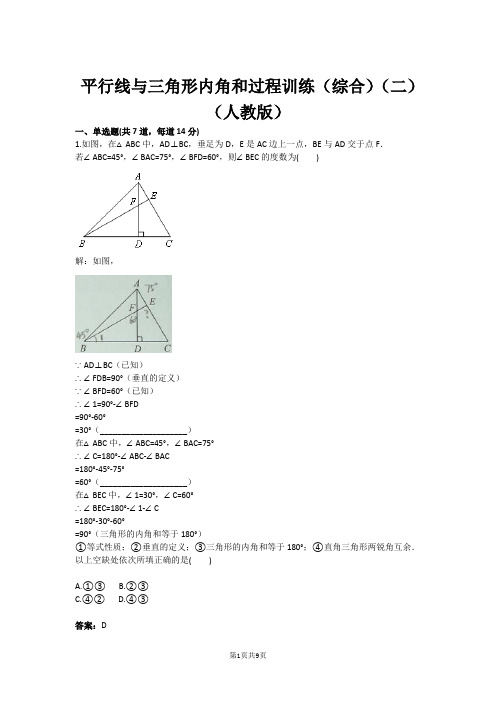
平行线与三角形内角和过程训练(综合)(二)(人教版)一、单选题(共7道,每道14分)1.如图,在△ABC中,AD⊥BC,垂足为D,E是AC边上一点,BE与AD交于点F.若∠ABC=45°,∠BAC=75°,∠BFD=60°,则∠BEC的度数为( )解:如图,∵AD⊥BC(已知)∴∠FDB=90°(垂直的定义)∵∠BFD=60°(已知)∴∠1=90°-∠BFD=90°-60°=30°(____________________)在△ABC中,∠ABC=45°,∠BAC=75°∴∠C=180°-∠ABC-∠BAC=180°-45°-75°=60°(____________________)在△BEC中,∠1=30°,∠C=60°∴∠BEC=180°-∠1-∠C=180°-30°-60°=90°(三角形的内角和等于180°)①等式性质;②垂直的定义;③三角形的内角和等于180°;④直角三角形两锐角互余.以上空缺处依次所填正确的是( )A.①③B.②③C.④②D.④③答案:D解题思路:要求∠BEC的度数,考虑放在△BCE中利用三角形的内角和等于180°来求解,只要求出三角形的另外两个角就可以了.如图,在Rt△BFD中,∠BFD=60°,由直角三角形两锐角互余,可得∠1=30°(因此第一个空选④).在△ABC中,∠ABC=45°,∠BAC=75°,由三角形的内角和等于180°,可得∠C=60°(因此第二个空选③).最后在△BCE中利用三角形的内角和等于180°,求出∠BEC=180°-∠1-∠C=90°.故选D.试题难度:三颗星知识点:三角形的内角和2.如图,AB∥CD,∠BAE=40°,∠DCE=50°,求∠E的度数.解:如图,∵AB∥CD(已知)∴∠BAC+______=180°(_____________________)即∠BAE+∠1+∠2+∠DCE=180°∵∠BAE=40°,∠DCE=50°(已知)∴∠1+∠2=180°-∠BAE-∠DCE=180°-40°-50°=90°(等式性质)在△ACE中,________________∴∠E=180°-(∠1+∠2)=180°-90°=90°(_____________________)①∠C;②∠ACD;③两直线平行,同旁内角互补;④同旁内角互补,两直线平行;⑤∠1+∠2=90°;⑥∠1=50°,∠2=40°;⑦平角的定义;⑧三角形的内角和等于180°.以上空缺处依次所填正确的是( )A.②③⑤⑧B.①③⑥⑧C.①④⑤⑦D.②③⑥⑧答案:A解题思路:要求∠E的度数,考虑放在△ACE中利用三角形的内角和等于180°来求解,只要求出∠1+∠2的度数即可.由AB∥CD,利用两直线平行,同旁内角互补,得∠BAC+∠ACD=180°(因此第一个空选②,第二个空选③).由∠BAE=40°,∠DCE=50°,利用等式性质,得∠1+∠2=90°.在△ACE中,∠1+∠2=90°,利用三角形的内角和等于180°,得∠E=90°(因此第三个空选⑤,第四个空选⑧).故选A.试题难度:三颗星知识点:三角形内角和定理3.已知:如图,BF∥DG,AD∥EF,∠ACF=70°,∠G=30°.求∠EFG的度数.证明:如图,∵BF∥DG(已知)∴∠ACF=______(两直线平行,同位角相等)∵AD∥EF(已知)∴∠D=______(两直线平行,同位角相等)∴∠ACF=∠1(等量代换)∵∠ACF=70°(已知)∴∠1=70°(等量代换)在△FEG中,∠1=70°,∠G=30°∴∠EFG=180°-∠1-∠G=180°-70°-30°=80°(____________________)①∠CFE;②∠D;③∠1;④∠ACF;⑤平角的定义;⑥三角形的内角和等于180°.以上空缺处依次所填正确的是( )A.①③⑤B.①④⑥C.②③⑥D.②④⑤答案:C解题思路:要求∠EFG的度数,考虑放在△EFG中利用三角形的内角和等于180°来求解,已知∠G=30°,只要求出∠1的度数即可,已知∠ACF=70°,因此利用平行线的性质转移角.由BF∥DG,利用两直线平行,同位角相等,得∠ACF=∠D(因此第一个空选②).由AD∥EF,利用两直线平行,同位角相等,得∠D=∠1(因此第二个空选③).已知∠ACF=70°,利用等量代换,得∠1=70°,在△EFG中,∠1=70°,∠G=30°,利用三角形的内角和等于180°,得∠EFG=80°(因此第三个空选⑥).故选C.试题难度:三颗星知识点:三角形内角和定理4.已知:如图,∠ABC=∠ADC,BE平分∠ABC,DF平分∠ADC,∠1=∠2.求证:AD∥BC.证明:如图,∵BE平分∠ABC(已知)∴∠3=∠ABC(角平分线的定义)∵DF平分∠ADC(已知)∴∠1=∠ADC(_____________________)∵∠ABC=∠ADC(已知)∴_________(等式性质)∵∠1=∠2(已知)∴∠2=∠3(等量代换)∴AD∥BC(_____________________)①已知;②角平分线的定义;③∠1=∠3;④∠2=∠3;⑤内错角相等,两直线平行;⑥两直线平行,内错角相等.以上空缺处依次所填正确的是( )A.①③⑥B.②③⑤C.①④⑤D.②③⑥答案:B解题思路:要证AD∥BC,考虑同位角,内错角,同旁内角,观察题目中的已知条件,本题利用内错角相等,两直线平行.由角平分线的定义,得,(因此第一个空选②).又因为∠ABC=∠ADC,利用等式性质,即∠1=∠3(因此第二个空选③).已知∠1=∠2,利用等量代换,得∠2=∠3,利用内错角相等,两直线平行,得AD∥BC(因此第三个空选⑤).故选B.试题难度:三颗星知识点:角平分线5.已知:如图,在△ABC中,D为BC边上一点,DF⊥AB,垂足为F,DE∥AC,∠A=∠B.求证:∠1=∠2.证明:如图,∵DE∥AC(已知)∴∠A=______(两直线平行,同位角相等)∵∠A=∠B(已知)∴∠B=∠3(等量代换)∵DF⊥AB(已知)∴∠DFE=∠DFB=90°(垂直的定义)∴∠3+∠1=90°,∠B+∠2=90°(____________________)∴∠1=∠2(____________________)①∠1;②∠3;③垂直的性质;④直角三角形两锐角互余;⑤等角的补角相等;⑥等角的余角相等.以上空缺处依次所填正确的是( )A.①③⑥B.②④⑥C.①③⑤D.②④⑤答案:B解题思路:要证∠1=∠2,题目中有平行,考虑利用平行线的性质转移角.由DE∥AC,利用两直线平行,同位角相等,得∠A=∠3(因此第一个空选②).结合已知条件∠A=∠B,利用等量代换,得∠B=∠3,由DF⊥AB,利用垂直的定义,得∠DFE=∠DFB=90°,利用直角三角形两锐角互余,得∠3+∠1=90°,∠B+∠2=90°(因此第二个空选④).进而利用等角的余角相等,得∠1=∠2(因此第三个空选⑥).故选B.试题难度:三颗星知识点:余角定理6.已知:如图,AD⊥BC,EF⊥BC,垂足分别为D,F,∠1=∠2.求证:AB∥DG.证明:如图,∵EF⊥BC(已知)∴∠EFB=90°(垂直的定义)∴∠B+∠1=90°(____________________)∵AD⊥BC(已知)∴∠2+∠3=90°(垂直的定义)∵∠1=∠2(已知)∴∠B=∠3(____________________)∴____________(同位角相等,两直线平行)①直角三角形两锐角互余;②垂直的定义;③等角的余角相等;④等角的补角相等;⑤等量代换;⑥EF∥AD;⑦AB∥DG.以上空缺处依次所填正确的是( )A.②④⑦B.②③⑥C.⑤③⑦D.①③⑦答案:D解题思路:要证AB∥DG,考虑同位角,内错角,同旁内角,结合已知条件本题利用同位角相等,两直线平行.由已知EF⊥BC,AD⊥BC,利用垂直的定义,∠EFB=90°,∠2+∠3=90°,利用直角三角形两锐角互余,得∠B+∠1=90°(因此第一个空选①).结合已知∠l=∠2,利用等角的余角相等,得∠B=∠3(因此第二个空选③).再利用同位角相等,两直线平行,得AB∥DG(因此第三个空选⑦).故选D.试题难度:三颗星知识点:余角定理7.已知:如图,在△ABC中,AD⊥BC,垂足为D.E是CA延长线上一点,EG⊥BC,垂足为G,∠E=∠1.求证:AD平分∠BAC.证明:如图,∵AD⊥BC(已知)∴∠ADC=90°(垂直的定义)∵EG⊥BC(已知)∴∠EGC=90°(垂直的定义)∴∠ADC=∠EGC(等量代换)∴EG∥AD(____________________)∴∠E=______(两直线平行,同位角相等)∠1=______(两直线平行,内错角相等)∵∠E=∠1(已知)∴∠2=∠3(等量代换)∴AD平分∠BAC(角平分线的定义)①两直线平行,同位角相等;②同位角相等,两直线平行;③∠2;④∠3.以上空缺处依次所填正确的是( )A.②④③B.②③④C.①④③D.①③④答案:A解题思路:如图,要证AD平分∠BAC,根据角平分线的定义,只需证明∠2=∠3即可.由已知AD⊥BC,EG⊥BC,利用垂直的定义,∠ADC=90°,∠EGC=90°,利用等量代换,得∠ADC=∠EGC,利用同位角相等,两直线平行,得EG∥AD(因此第一个空选②).进而利用两直线平行,同位角相等,得∠E=∠3(因此第二个空选④);利用两直线平行,内错角相等,得∠1=∠2(因此第三个空选③).又因为∠E=∠1,利用等量代换,得∠2=∠3,由角平分线的定义,得AD平分∠BAC.故选A.想一想:1.由平行可以想什么?2.要证平行,怎么想?3.要求一个角的度数,我们可以怎么考虑?参考答案:1.由平行可以想同位角相等、内错角相等、同旁内角互补.2.要证平行,找同位角、内错角、同旁内角,因为同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行.3、首先观察图形,结合已知条件,看它可以看成什么角,然后设计方案求解.如果看成三角形的内角,可以考虑通过三角形的内角和等于180°求解;如果有平行,可以考虑通过平行转移角,等等.试题难度:三颗星知识点:平行线的性质、判定。
人教版八年级数学上学期同步练习与三角形有关的角(含答案解析)

11.2与三角形有关的角专题一利用三角形的内角和求角度1.如图,在^ ABGK /ABC的平分线与/ACB的外角平分线相交于D 点,/ A=50° ,则0=( )A. 15B. 20C. 25D. 302.如图,已知:在直角△ ABC, / C=90 BD平分/ABC且交AC于D.若AP平分/BAC且交BD于P,求/BPA的度数.B 03.已知:如图1,线段AB、CD相交于点O,连接AD、CB ,如图2,在图1的条件下,ZDAB和ZBCD的平分线AP和CP相交于点P, 并且与CD、AB分别相交于M、N.试解答下列问题:(1)在图1中,请直接写出/A、ZB、/C、/D之间的数量关系:__________ ;(2)在图2中,若/ D=40° , / B=30° ,试P的度数;(写出解答过程)(3)如果图2中/D和/B为任意角,其他条件不变,试写出/ P与/ D、/B 之间的数量关系.(直接写出结论即可)专题二利用三角形外角的性质解决问题4.如图,ABD, ZACD的角平分线交于点P,若/ A=50° /D=10 , 则/P的度数为(A. 15B. 20C. 25D. 305.如图,△ AB的,CD是dCB的角平分线,CE是AB边上的高, 若/ A=40 , / B=72 .(1)求/DCE的度数;(2)试写出/DCE与小、ZB的之间的关系式.(不必证明)6.如图:(1)求证:/BDC=zA+zB+zC;(2)如果点D与点A分别在线段BC的两侧,猜想/BDC、小、/ ABD、/ACD这4个角之间有怎样的关系,并证明你的结论.状元笔记【知识要点】1.三角形内角和定理三角形三个内角的和等于180 .2.直角三角形的性质及判定性质:直角三角形的两个锐角互余.判定:有两个角互余的三角形是直角三角形.3.三角形的外角及性质外角:三角形的一边与另一边的延长线组成的角,叫做三角形的外角.性质:三角形的外角等于与它不相邻的两个内角的和.【温馨提示】1.三角形的外角是一边与另一边的延长线组成的角,而不是两边延长线组成的角.2.三角形的外角的性质中的内角一定是与外角不相邻的内角.【方法技巧】1.在直角三角形中已知一个锐角求另一个锐角时,可直接使用“直角三角形的两个锐角互余”.2.由三角形的外角的性质可得出:三角形的外角大于任何一个与它不相邻的内角.参考答案:1. C 解析::ABC的平分线与/ACB的外角平分线相交于点D,/1=1zACE, Z2=1zABC ,又.\D=/1—Z2, zA= zACE —/ABC , 2 2 ZD=1/A=25° .故置. 23 C E2.解:(法1) 因为/ C=90° ,所以BAC + /ABC=90 , 1所以1 (zBAC + / ABC)=45 .因为BD平分/ABC, AP平分/BAC ,zBAP= 1 zBAC , ZABP= 1 zABC , 2 2即/BAP + / ABP=45 ,所以 / APB=180 — 45 =135 .(法2)因为/ C=90 ,所以BAC + /ABC=90 ,所以 1 (zBAC + / ABC)=45° ,因为BD平分/ABC , AP平分/BAC ,zDBC= 1 ZABC , zPAC= 1 zBAC , 2 2所以/DBC + / PAD=45 .所以ZAPB= 2PDA + ZPAD = zDBC + ZC+ /PAD= zDBC + ZPAD + Z C =45 + 90 =135 .3.解:(1) zA+zD=zB+/C;(2)由(1)得,/1 + zD=z3+zP, Z2+zP=z4+zB, /.1-Z3=zP-zD, z2-z4=zB-zP,又〈AP、CP分别平分/DAB和/BCD,「.1=2 /3=4/.P-zD=zB-ZP,即2zP= zB+zD,・•・P= (40 +30 ) + 2=35 .(3) 2zP= zB+zD.4. B解析:延长DC,与AB交于点E.根据三角形的外角等于不相邻的两内角和,可得/ ACD=50 +/AEC=50 +/ABD+10整理得/ACD —/ABD=60 .设AC 与BP 相交于点O,则“OB=/POC,「. /P+1 "CD= "+1 ZABD ,即 / P=50 」(ZACD-ZABD) =20 .故 2 2 2选B.5.解:(1) .「/ A=40 , / B=72 ,・•. / ACB=68 ..CD 平分ZACB, 1・•・DCB= 1 / ACB=34 . 2 ..CE是AB边上的高,・•./ECB=90 — / B=90 — 72 =18 ・•./ DCE=34 — 18 =16 .,、,一 1 ,一,、(2) ZDCE= 1 (ZB—小).6.(1)证明:延长BD交AC于点E, ・. BEC是△ ABE的外角,・•.BEC= zA+zB.vBDC是4CED的外角,・•. BDC= ZC+ zDEC= ZC+ ZA+ zB.⑵ 猜想:/BDC+/ACD+zA+ZABD=360证明:/BDC+zACD+zA+zABD= z3+ N+/6+/5+ z4+Z1=(Z3+/2+ Z1) + (/6+Z5+ z4)=180 +180 =360 .。
平行线与三角形综合练习

平行线与三角形综合练习一、选择题(共8小题;共40分)1. 如图,将一副三角板和一张对边平行的纸条按下列方式摆放,两个三角板的一直角边重合,含30∘角的直角三角板的斜边与纸条一边重合,含45∘角的三角板的一个顶点在纸条的另一边上,则∠1的度数是 ( )A. 30∘B. 20∘C. 15∘D. 14∘2. 下列命题是真命题的有( )①相等的角是对顶角;②三角形两个内角的和一定大于60∘;③三角形的外角都比内角大;④如果x3>0,那么x>0;⑤同位角相等,两直线平行.A. 1个B. 2个C. 3个D. 4个3. 如图,在△ABC中,AB=AC,∠A=30∘,E为BC延长线上一点,∠ABC与∠ACE的平分线相交于点D,则∠D的度数为 ( )A. 15∘B. 17.5∘C. 20∘D. 22.5∘4. 如图,AD∥CB,∠D=43∘,∠B=25∘,则∠DEB的度数为 ( )A. 72∘B. 68∘C. 63∘D. 18∘5. 如图,已知点A(−1,0)和点B(1,2),在坐标轴上确定点P,使得△ABP为直角三角形,则满足这样条件的点P共有 ( )A. 2个B. 4个C. 6个D. 7个6. 如图,m∥n,直线l分别交m,n于点A、点B,AC⊥AB,AC交直线n于点C,若∠1=35∘,则∠2等于 ( )A. 35∘B. 45∘C. 55∘D. 65∘7. 如图,直角三角板的直角顶点落在直尺边上,若∠1=56∘,则∠2的度数为 ( )A. 56∘B. 44∘C. 34∘D. 28∘8. 如图,在△ABC中,∠C=90∘,点D在AC边上,DE∥AB,若∠ADE=46∘,则∠B的度数是 ( )A. 34∘B. 44∘C. 46∘D. 54∘二、填空题(共6小题;共30分)9. 如图,在△ABC中,∠1=∠2,∠3=∠4,∠BAC=60∘,则∠DAC=∘.10. 如图,已知AB∥CD,∠A=56∘,∠C=27∘,则∠E的度数为.11. 已知△ABC中,∠A=60∘,∠ABC,∠ACB的平分线交于点O,则∠BOC的度数为.12. 如图,将一副三角尺叠放在一起,使直角的顶点重合于点O,则∠AOC+∠BOD=.13. 如图,直线m∥n,Rt△ABC的顶点A在直线n上,∠C=90∘.若∠1=25∘,∠2=70∘,则∠B=∘.14. 如图,有一块含有60∘角的直角三角板的两个顶点放在矩形的对边上.如果∠1=15∘,那么∠2的度数是.三、解答题(共10小题;共130分)15. 如图,在Rt△ABC中,∠ACB=90∘,D是AB上一点,且∠ACD=∠B.求证:CD⊥AB.16. 如图,在△ABC中,GD⊥AC于点D,∠AFE=∠ABC,∠1+∠2=180∘,∠AEF=65∘.求:∠1的度数.17. 解答题:(1)如图①,△ABC的内角∠ABC的平分线与外角∠ACD的平分线相交于P点,∠A=40∘,求∠P的度数.(2)如图,四边形ABCD中,设∠A=α,∠D=β,∠P为四边形ABCD的内角∠ABC与外角∠DCE的平分线所在直线相交而形成的锐角.①如图②,若α+β>180∘,求∠P的度数.(用α,β的代数式表示)(1)请你计算出图①中∠ABC的度数.(2)图②中AE∥BC,请你计算出∠AFD的度数.22. 如图,在△ACB中,∠ACB=90∘,CD⊥AB于点D.(1)试说明:∠ACD=∠B.(2)若AF平分∠CAB分别交CD,BC于点E,F,试说明:∠CEF=∠CFE.23.(1)问题:如图1,在△ABC中,BE平分∠ABC,CE平分∠ACB.若∠A=80∘,则∠BEC=;若∠A=n∘,则∠BEC=.(2)探究:(i)如图2,在△ABC中,BD,BE三等分∠ABC,CD,CE三等分∠ACB.若∠A=n∘,则∠BEC=;(ii)如图3,在△ABC中,BE平分∠ABC,CE平分外角∠ACM.若∠A=n∘,则∠BEC=;(iii)如图4,在△ABC中,BE平分外角∠CBM,CE平分外角∠BCN.若∠A=n∘,则∠BEC=.24. 如图所示,已知∠MON=120∘,点A,B分别在射线OM,ON上移动,∠OAB的平分线与∠OBA的外角平分线所在的直线相交于点C,随着A,B两点的移动,∠ACB的度数是否发生变化?证明你的结论.答案第一部分1. C2. B3. A4. B5. C6. C7. C8. B第二部分9. 2010. 29∘11. 120∘12. 180∘13. 4514. 15∘第三部分15. ∵∠ACB=90∘,∴∠A+∠B=90∘.∵∠ACD=∠B,∴∠A+∠ACD=90∘.∴∠ADC=90∘.∴CD⊥AB.16. ∵∠AFE=∠ABC,∴EF∥BC,∴∠1=∠EBG,∵∠1+∠2=180∘,∴∠EBG+∠2=180∘,∴EB∥DG∴∠GDE=∠BEA,∵GD⊥AC于点D,∴∠GDE=90∘,∴∠BEA=∠GDE=90∘,∴∠1=∠BEA−∠AEF=90∘−65∘=25∘.17. (1)∵△ABC的一个内角∠ABC的平分线和一个外角∠ACD的平分线相交于点P,∴∠PCD=12∠ACD,∠PBD=12∠ABD∴∠P=∠PCD−∠PBD=12(∠ACD−∠ABD)=12∠A=12×40∘=20∘(2)①延长BA,CD交于点F.∠FAD=180∘−α,∠FDA=180∘−β,∠F=180∘−(180∘−α+180∘−β)=α+β−180∘,∴∠P=α2+β2−90∘② ∠P=90º−α2−β218. (1)如图,过点P作AC的平行线PO,∵AC∥PO,∴∠β=∠CPO.∵AC∥BD,∴PO∥BD,∴∠α=∠DPO,∴∠α+∠β=∠γ.(2)当点P在MB上运动时(如图),∵l1∥l2,∴∠β=∠CFD.∵∠CFD是△DFP的外角,∴∠CFD=∠α+∠γ.∴∠β=∠γ+∠α.同理可得,当点P在AN上运动时,∠α=∠γ+∠β.19. 设∠DAC=x∘.∵∠BAC=63∘,∴∠1=63∘−x∘.∵∠1=∠2,∴∠3=2(63∘−x∘)=∠4,∴x+2(63∘−x∘)+2(63∘−x∘)=180∘.∴∠DAC=24∘.20. ① 当△ABC为锐角三角形时,如图所示:因为BD,CE是△ABC的高,所以∠A+∠2=90∘,∠1+∠2=90∘.所以∠A=∠1=50∘,即∠BAC=50∘.② 当△ABC为钝角三角形时,如图所示:因为BD,CE是△ABC的高,所以∠1+∠2=90∘,∠O+∠2=90∘.所以∠1=∠O=50∘.所以∠BAC=180∘−50∘=130∘.综上可得,∠BAC为50∘或130∘.21. (1)因为∠F=30∘,∠EAC=45∘,所以∠ABF=∠EAC−∠F=45∘−30∘=15∘.因为∠FBC=90∘,所以∠ABC=∠FBC−∠ABF=90∘−15∘=75∘.(2)因为∠B=60∘,∠BAC=90∘,所以∠C=30∘.因为AE∥BC,所以∠CAE=∠C=30∘.所以∠AFD=∠CAE+∠E=30∘+45∘=75∘.22. (1)因为∠ACB=90∘,CD⊥AB于点D,所以∠ACD+∠BCD=90∘,∠B+∠BCD=90∘,所以∠ACD=∠B.(2)在Rt△AFC中,∠CFA=90∘−∠CAE,同理在Rt△AED中,∠AED=90∘−∠DAE,因为AF平分∠CAB,所以∠CAF=∠DAE,所以∠AED=∠CFE.因为∠CEF=∠AED,所以∠CEF=∠CFE.23. (1)130∘;90∘+12n∘(2)(i)60∘+23n∘;(ii)12n∘.(iii)90∘−12n∘.24. ∠ACB的度数不变.证明如下:因为AC平分∠OAB,所以∠OAB=2∠BAC.因为BD平分∠ABN,所以∠ABN=2∠ABD.又因为∠ABD=∠ACB+∠BAC,所以12∠ABN=∠ACB+12∠OAB,即∠ACB=12∠ABN−12∠OAB=12(∠ABN−∠OAB)=12∠MON.因为∠MON=120∘,所以∠ACB=12×120∘=60∘.所以随着A,B两点的移动,∠ACB的度数恒为60∘.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
初中数学人教版八年级上册实用资料
平行线与三角形内角和的综合应用(习题)
➢ 例题示范
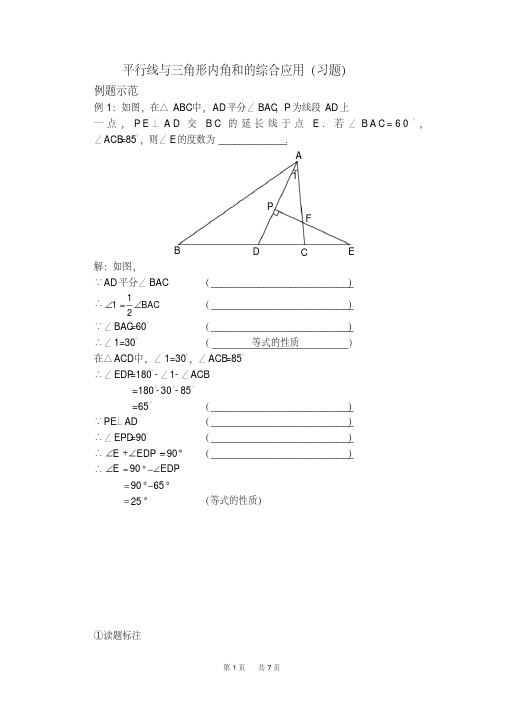
例1:如图,在△ABC 中,AD 平分∠BAC ,P 为线段AD 上
一点,P E ⊥A D 交B C 的延长线于点E .若∠B A C =60°, ∠ACB =85°,则∠E 的度数为_____________.
A D C
E
F
P
1
解:如图, ∵AD 平分∠BAC
(___________________________) ∴1
12
BAC ∠=∠
(___________________________) ∵∠BAC =60° (___________________________) ∴∠1=30°
( 等式的性质 )
在△ACD 中,∠1=30°,∠ACB =85° ∴∠EDP =180°-∠1-∠ACB
=180°-30°-85° =65°
(___________________________) ∵PE ⊥AD (___________________________) ∴∠EPD =90°
(___________________________) ∴90E EDP ∠+∠=︒ (___________________________)
∴90E EDP ∠=︒-∠
9065=︒-︒ 25=︒ (等式的性质)
①读题标注
85°30°30°1P
F
E
C
D
B A
②梳理思路
要求∠E 的度数,可以将∠E 放在Rt △PDE 中,利用直角三角形两锐角互余求解,由PE ⊥AD ,则∠EPD =90°,所以需要求出∠ADC 的度数.结合已知条件,把∠ADC 放在△ADC 中利用三角形的内角和等于180°求解. ③过程书写 解:如图, ∵AD 平分∠BAC
(已知)
∴1
12
BAC ∠=∠
(角平分线的定义) ∵∠BAC =60° (已知) ∴∠1=30°
(等式的性质)
在△ACD 中,∠1=30°,∠ACB =85° ∴∠EDP =180°-∠1-∠ACB
=180°-30°-85° =65°
(三角形的内角和等于180°) ∵PE ⊥AD (已知) ∴∠EPD =90°
(垂直的定义)
∴90E EDP ∠+∠=︒(直角三角形两锐角互余) ∴90E EDP ∠=︒-∠
9065=︒-︒ 25=︒
(等式的性质)
➢ 巩固练习
1. 在△ABC 中,123A B C =∠:∠:∠::,则A =∠___,B =∠___.
2. 将一副直角三角板如图放置,使含30°角的三角板的短直角边和含45°角的三
角板的一条直角边重合,则图中∠1的度数为___________.
1
3. 如图,直线m ∥n ,在△ABC 中,∠C =90°.若∠1=25°,∠2=70°,则∠
B =____________.
n
m
2
1
C
B
A
4. 已知:如图,AD 与BC 交于点O ,∠C =35°,∠A =∠B =90°,求∠D 的度数.
O
D
C A
B
解:如图,
∵∠A =∠B =90°(已知) ∴__________________,
__________________(直角三角形两锐角互余) ∵∠AOC =∠BOD (对顶角相等)
∴_____________(____________________) ∵∠C =35°(已知)
∴_____________(等量代换)
5. 已知:如图,在△ABC 中,CD 平分∠ACB ,∠B =34°,
∠ACD =50°,求∠A 的度数.
A
B D
C
6.已知:如图,AB∥CD,∠BAE=∠DCE=45°.
求证:∠E=90°.
21
E
D
C
B A
7.已知:如图,EF⊥BC,DE⊥AB,∠B=∠ADE.
求证:AD∥EF.
F E
D
B C A
➢ 思考小结
1. 在证明过程中:
(1)由平行可以想________相等、__________相等、________互补; (2)要证平行,找_______角、_______角、_______角;
(3)要求一个角的度数,如果看成三角形的内角,可以考虑__________________________. 2. 阅读材料
等量代换与等式的性质
在欧几里得公理体系中提到过5条公理.这5条公理是我们公认为正确的不证自明的“基本事实”,可以当做已知的大前提来进行使用.而其中的三条,是我们在几何证明中不经意间多次用到的,下面对它们来进行简单的解释. 当我们证明时,会遇到如下的推理: ∵a =b ,b =c ∴a =c
在这个推理过程中,我们很容易就理解它的正确性,但往往不知道它的依据是什么.其实,它的依据就是欧几里得公理体系中5条公理中的第一条:“(1)
跟同一件东西相等的一些东西,它们彼此也是相等的.”这句话比较的生涩难懂,我们不妨来翻译一下,直观的意思就是“与同一个量相等的所有量都相等”,这就是我们在几何推理中经常用到的“等量代换”.
例如,我们经常这么写:
①∵a=b,b=5(已知)
∴a=5(等量代换)
②∵∠A+∠B=90°,∠B=∠C
∴∠A+∠C=90°(等量代换)
这里推理的依据就是第一条公理,我们把它简记为“等量代换”.“等量代换”
还可以解释为把相等的量换掉.
与“等量代换”一样,经常用到的还有“等式的性质”.
公理中第(2)(3)条的内容如下:
(2)等量加等量,总量仍相等.
(3)等量减等量,余量仍相等.
它们组合起来使用,就叫做“等式的性质”,我们可以找一些例子来看一下.例如:
∵a+b=10,c=5
∴a+b-c=10-5=5(等式性质)
再如:
∵∠A+∠B+∠C=180°,∠A+2∠1=90°
∴∠B+∠C=90°+2∠1(等式的性质)
上述过程中的推理依据都是“等式的性质”.一般地,我们利用代数运算进行推理时,其依据基本都是“等式的性质”.
【参考答案】
➢巩固练习
1.30°,60°
2.105°
3.45°
4.解:如图,
∵∠A=∠B=90°(已知)
∴∠C+∠AOC=90°,
∠D+∠BOD =90°(直角三角形两锐角互余)∵∠AOC=∠BOD(对顶角相等)
∴∠C=∠D(等角的余角相等)
∵∠C=35°(已知)
∴∠D=35°(等量代换)
5.解:如图,
CD平分∠ACB(已知)
∴∠ACB=2∠ACD(角平分线的定义)
∵∠ACD=50°(已知)
∴∠ACB=2×50°=100°(等量代换)
在△ABC中,∠B=34°,∠ACB=100°(已知)
∴∠A=180°-∠B-∠ACB
=180°-34°-100°
=46°(三角形的内角和等于180°)
6.证明:如图,
∵AB∥CD(已知)
∴∠BAC+∠ACD =180°(两直线平行,同旁内角互补)∵∠BAE=∠DCE=45°(已知)
∴∠1+∠2=180°-∠BAE-∠DCE
=180°-45°-45°
=90°(等式的性质)
∴∠E=180°-(∠1+∠2)
=180°-90°
=90°(三角形的内角和等于180°)
7.证明:如图,
∵EF⊥BC(已知)
∴∠EFB=90°(垂直的定义)
∴∠BEF+∠B=90°(直角三角形两锐角互余)
∵DE⊥AB(已知)
∴∠AED=90°(垂直的定义)
∴∠BAD+∠ADE=90°(直角三角形两锐角互余)
∵∠B=∠ADE(已知)
∴∠BEF=∠BAD(等角的余角相等)
∴AD∥EF(同位角相等,两直线平行)
➢思考小结
1.(1)同位角,内错角,同旁内角;
(2)同位,内错,同旁内;
(3)三角形的内角和等于180°.。
