【期末试卷】贵州省黔南州2015-2016学年高一下学期期末考试数学试题 Word版(含答案)

合集下载

贵州省黔东南州2015_2016学年高一数学下学期期末文化水平测试试题(扫描版)

贵州省黔东南州2015-2016学年高一数学下学期期末文化水平测试试题（扫描版）黔东南州2015—2016学年度第二学期期末文化水平测试高一数学参考答案一、选择题二、填空题13、5 14、1 15、⎩⎨⎧∈≥-==*),2(12)1(3N n n n n a n 16、36三、计算题17、解：（1）因为直线AB 的斜率为23=AB k ，直线AC 的斜率为32-=AC k 1-=∙AC AB k k∴ 直线AB 与AC互相垂直，因此，ABC ∆为直角三角形。

（2）解方程组⎩⎨⎧=--=-+012301832y x y x ，得⎩⎨⎧==43y x ，即)4,3(A设点A 到直线BC 的距离为d ，则52543443322m md -=+-⨯+⨯=由题意知1=d ，即1525=-m ，即3020或=m 。

18、解：（1）由2222cos b a c ac B =+-⋅， 3a =，b =，3π=B 得2320c c -+=，12c ∴=或（2）由二倍角公式得11(A)2cos222f A A +- 1(A)sin(2A )62f π∴=+-，当6A π=时，()f A 最大值为12，此时ABC ∆为直角三角形，此时ABC ∆的外接圆半径72127sin 21=⨯=⨯=Aa r 。

19、证明：（1）因为E D ,是AC PC ,中点，∴PA =DEDEF PA DEF DE 面，且面⊄⊂∴//PA 平面DEF（2）因为,,D E F 分别为棱,,PC AC AB 的中点，∴PA =DE 2， FE BC 2=5,8,6===DF BC PA5,4,3===∴DF EF DE ，222DF EF DE =+∴ EF DE ⊥∴，中点为PC D AD PD ,= DC AD =∴ 中点为AC E AC DE ⊥∴由ABC ABC DE ABC ,面面面⊥⇒⎪⎪⎪⎭⎪⎪⎪⎬⎫⊄⊂=⋂⊥⊥DE EF AC E EF AC AC DE EFDE ， ABC DEF DEF DE 面面面⊥∴⊂, 。

2015-2016学年高一下学期期末考试数学试题带答案

2015—2016学年度高一下学期期末考试数学试题命题人：陈文科考试时间：120分钟分值：150分一、选择题（本大题共12个小题，每小题5分，共60分，在每小题所给出的四个选项中，只有一项是符合题目要求的）1．等差数列{}n a 中，若464=+a a ,则132a a -的值为（）A ．1B ．2C ．3D ．4 2．设βα,为不重合的两个平面，n m ,为不重合的两条直线，则下列判断正确的是 ( ) A ．若α⊥β，α∩β＝n ，m ⊥n ，则m ⊥α B ．若m ⊂α，n ⊂β，m ∥n ，则α∥βC ．若m ∥α，n ∥β，m ⊥n ，则α⊥βD ．若n ⊥α，n ⊥β，m ⊥β，则m ⊥α 3．若两直线0343=++y x 与016=++my x 平行，则它们之间的距离为（）A ．21B ．25 C ．52 D ．552 4．在如图所示的长方体1111D C B A ABCD -中，21==AB AA ，1=AD ,G F E ,,分别是11,,CC AB DD 的中点，则异面直线E A 1与FG 所成角的余弦值是 ( )A ．515B ．22 C ．510D ．05．已知点(2,3),(3,2)A B --，若直线l 过点(1,1)P 与线段AB 相交，则直线l 的斜率k 的取值范围是（）A ．34k ≥ B ．324k ≤≤ C ．324k k ≥≤或 D ．2k ≤ 6．在空间直角坐标系中，点)2,3,2(),2,3,1(--B A ，则B A ,两点间的距离为（） A ．14B ．5C ．31D ．257．在ABC ∆中，角C B A ,,所对的边分别为c b a ,,，已知4,6π==A b ，若三角形有两解，则边a 的取值范围为（）A ．)6,0(B ．)6,1(C ．)6,3(D ．),3(+∞8．半径为1，圆心角为π32的扇形卷成一个圆锥，则它的体积为 ( ) A ．8122πB ．2722πC ．27π D ．3π 9．过点)2,4(P 作圆222=+y x 的两条切线，切点分别为B A ,，点O 为坐标原点，则AOB ∆的外接圆方程是（） A ．()5)1(222=+++y xB ．()20)2(422=+++y xC ．()5)1(222=-+-y xD ．()20)2(422=-+-y x10．一个几何体是由一个三棱柱截去一个四棱锥而成，它的三视图如图所示，则这个几何体的体积是 ( ) A ．1 B ．2 C ．3 D ．4 11．已知圆4:22=+y x O 上到直线m y x l =+:的距离为1的点有且仅有2个，则m 的取值范围是（） A ．(),2()2,+∞-∞- B ．)23,2()2,23( -- C ．)23,23(- D ． )2,2(-12．已知圆1)1(:22=+-y x M ，设)25(),6,0(),,0(-≤≤-+t t B t A ，若圆M 是ABC ∆的内切圆，则ABC ∆面积的最大值为（） A ．215B ．429C ．7D ．427 二、填空题（本大题共4小题，每小题5分，共20分，把答案填在答题卡中的横线上） 13．经过直线01:,05:21=--=-+y x l y x l 的交点且垂直于直线032=-+y x 的直线方程为 .正视图侧视图14．已知y x ,满足条件020x y x x y k ≥⎧⎪≤⎨⎪++≤⎩(0≤k )，若目标函数3z x y =+的最大值为8，则k 的值为 .15．已知点)2,4(),6,2(),2,2(----C B A ，点P 在圆422=+y x 上运动，则222PC PB PA ++的最大值为 .16．已知正方体D C B A ABCD ''''-的棱长为1，下列说法：①对角线C A '被平面BD A '和平面D C B ''三等分；②以正方体的顶点为顶点的四面体的体积都是61； ③正方体的内切球，与各条棱相切的球，外接球的表面积之比为3:2:1；④正方体与以A 为球心，1为半径的球的公共部分的体积为3π；则正确的是 . （写出所有正确的序号）三、解答题（本大题共6小题，满分70分，解答应写出文字说明、证明过程或演算步骤） 17．（10分）设直线l 的方程为R a a y x a ∈=-+++,02)1(；（Ⅰ）若直线l 不经过第二象限，求实数a 的取值范围；（Ⅱ）若直线l 与坐标轴围成三角形的面积为2，求实数a 的值.18．（12分）在ABC ∆中，角,,A B C 的对边分别为54cos ,4,,,=π=B A c b a ．（Ⅰ）求C cos 的值；（Ⅱ）若2=c ，求ABC ∆的面积．19．（12分）如图1所示，在边长为1的等边三角形ABC 中，E D ,分别是AC AB ,边上的点，AE AD =，F 是BC 的中点，AF 与DE 交于点G ，将ABC ∆沿AF 折叠，得到如图2所示的三棱锥BCF A -，其中22=BC；（Ⅰ）证明：//DE 平面BCF ；（Ⅱ）证明：⊥CF 平面ABF ；（III ）当32=AD 时，求三棱锥DEG F -的体积．20．（12分）甲、乙两地相距1000km ，货车从甲地匀速行驶到乙地，速度不得超过80km/h ，已知货车每小时的运输成本（单位：元）由可变成本和固定成本组成，可变成本是速度平方的14倍，固定成本为a 元；（Ⅰ）将全程运输成本y （元）表示为速度v （km/h ）的函数，并指出这个函数的定义域；（Ⅱ）若400=a ，为了使全程运输成本最小，货车应以多大的速度行驶？21．（12分）已知点))(,(*N n b a P n n n ∈都在直线22:+=x y l 上，1P 为直线l 与x 轴的交点，数列{}n a 成等差数列，公差为1；（Ⅰ）求数列{}n a ，{}n b 的通项公式；（Ⅱ）若)(n f =⎩⎨⎧)(b )(n 为偶数为奇数n n a n 问是否存在*N k ∈,使得2)(2)5(-=+k f k f 成立；若存在，求出k 的值，若不存在，说明理由；（III ）求证：*21231221,2,52111N n n P P P P P P n∈≥<+⋅⋅⋅++.22．（12分）已知⎩⎨⎧+-≥≤+--+501810222a x y y x y xR y x ∈,，若由不等式组围成的区域为P ，设两曲线的交点为B A ,，)5,(a C 且P C ∈；（Ⅰ）求实数a 的取值范围；（Ⅱ）若0=a ，求ABC ∆的面积；（III ）求ABC ∆的面积的最大值.2015—2016学年度高一下学期期末考试数学答案一、选择题1~5 BDADC 6~10 BCACD 11~12 BA 二、填空题13. 012=+-y x 14. 88 15. 6- 16. ①③ 三、解答题17. 解：（Ⅰ）由题意知：⎩⎨⎧≤-≥+-020)1(a a ∴1-≤a（Ⅱ）由题意知：1-≠a 令2,0-==a y x 令12,0+-==a a y y ∴212221=+--=a a a S ∴0=a ，或8=a 18.（Ⅰ）53sin ,054cos =∴>=B B )4c o s ()]4(cos[cos B B C +-=+-=πππ10254225322)sin 4sincos 4(cos-=⋅-⋅=--=B B ππ（Ⅱ）由（Ⅰ）知1027sin =C 由正弦定理知：C c A a sin sin = ∴ 725=a∴7353272521sin 21=⋅⋅⋅==B ac S19.（Ⅰ）在等边三角形ABC 中，AD ＝AE ，∴AD DB ＝AEEC .在折叠后的三棱锥A -BCF 中也成立，∴DE ∥BC . ∵DE 平面BCF ，BC ⊂平面BCF ，∴DE ∥平面BCF . （Ⅱ）在等边三角形ABC 中，F 是BC 的中点， ∴AF ⊥FC ，BF ＝CF ＝12.∵在三棱锥A -BCF 中，BC ＝22， ∴BC 2＝BF 2＋CF 2，∴CF ⊥BF . ∵BF ∩AF ＝F ，∴CF ⊥平面ABF .（III ）由(1)可知GE ∥CF ，结合(2)可得GE ⊥平面DFG .∴V F -DEG ＝V E -DFG ＝13×12×DG ×FG ×GE ＝13×12×13×⎝⎛⎭⎫13×32×13＝3324. 20.（Ⅰ）可变成本为241v ，固定成本为a 元，所用时间为v1000 ∴⎪⎭⎫ ⎝⎛+=a v v y 2411000，即⎪⎭⎫ ⎝⎛+=v a v y 411000。

2015-2016学年高一下学期期末考试数学试题带答案

2016年春季学期高一期末考试数学试卷(本试卷共三大题,满分150分,考试时间为120分钟)一、选择题（12道题，每题5分，共60分）1、若集合A ＝{0,1,2,3}，B ＝{1,2,4}，则集合A ∪B 等于( )A ．{0,1,2,3,4}B ．{1,2,3,4}C ．{1,2}D ．{0} 2.若θ是第二象限的角,且4sin 5θ=,则cos θ=( )A. 15B. 15- C. 35D. 35-3. 设=-=-=(1,3),(2,4),(0,5)a b c 则-+3a b c =（）A. (3,-8)B.(-2,3)C.(2,3)D.(3,8) 4若已知=(4,2), =(6,x),且∥,则x=( )A.3B. 5C.1D.-1 5.－400°角的终边所在的象限是( )A ．第一象限B ．第二象限C ．第三象限D ．第四象限6. 函数y=sin(3x+3π)+2的最小正周期为（）A. 2πB. 3πC. 3πD.23π7. 若向量a ＝(3,3)，b ＝(－3,2)，则|a ＋2b|＝( )8已知角α的终边过点P （－1-,2）,tan α的值为 ( )A ．－55 B ．2 C D ．129已知向量1(2BA =uu v ,1),2BC =uu u v 则∠ABC=（）(A)300 (B) 450 (C) 600 (D)120010若A 是第三象限的角,1cos()3A p -=,求2sin()A p+=（）A.13-B.23C.23-D. 1311在ABC △中，A B 边上的高等于13BC ,则cos B = （）（A （B （C （D ）-12设函数f (x )＝A sin(ωx ＋φ)(A ，ω，φ是常数，A >0，ω>0)．若f (x )在区间⎣⎢⎡⎦⎥⎤π6，π2上具有单调性，且f ⎝ ⎛⎭⎪⎫π2＝f ⎝ ⎛⎭⎪⎫2π3＝－f ⎝ ⎛⎭⎪⎫π6，则f (x )的最小正周期为（）A. 2πB. πC.23pD.2p二、填空题（4道题，每题5分，共20分）13.=(4,2), =(6,x)若与相互垂直，则X= 14. sin 810°= 15.若tanA=12,求4c si os n 2s in o s c A A AA -+=16.函数的图像可由函数的图像得到。

15—16高一第二学期期末考试卷含答案

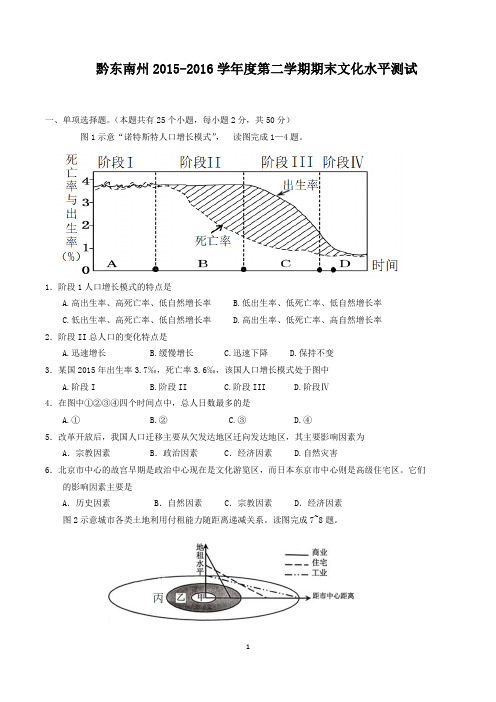
黔东南州2015-2016学年度第二学期期末文化水平测试一、单项选择题。

（本题共有25个小题，每小题2分，共50分）图1示意“诺特斯特人口增长模式”，读图完成1—4题。

1．阶段1人口增长模式的特点是A.高出生率、高死亡率、低自然增长率B.低出生率、低死亡率、低自然增长率C.低出生率、高死亡率、低自然增长率D.高出生率、低死亡率、高自然增长率2．阶段II总人口的变化特点是A.迅速增长B.缓慢增长C.迅速下降D.保持不变3．某国2015年出生率3.7‰，死亡率3.6‰，该国人口增长模式处于图中A.阶段IB.阶段IIC.阶段IIID.阶段Ⅳ4．在图中①②③④四个时间点中，总人日数最多的是A.①B.②C.③D.④5．改革开放后，我国人口迁移主要从欠发达地区迁向发达地区，其主要影响因素为A．宗教因素B．政治因素 C．经济因素 D.自然灾害6．北京市中心的故宫早期是政治中心现在是文化游览区，而日本东京市中心则是高级住宅区。

它们的影响因素主要是A．历史因素 B．自然因素 C．宗教因素 D．经济因素图2示意城市各类土地利用付租能力随距离递减关系。

读图完成7~8题。

7．甲、乙、丙依次对应的城市功能区为A．工业区、住宅区、商业区B．住宅区、工业区、商业区C．商业区、工业区、住宅区D．商业区、住宅区、工业区8．城市中甲功能区形成的原因有A．环境污染严重 B．地租最便宜 C．交通运输便捷 D．人口流量低为缓解停车难问题，北京市朝阳区采取“错峰停车”措施，鼓励各社会单位将停车位夜间或双休日向周边社区市民开放。

右图示意“朝阳区某功能．区不同时段人口流动状况”。

完成9—11题。

9．该功能区属于A．商业区 B．住宅区C．工业区 D．行政区10.“错峰停车”主要利用了该功能区与相邻功能区A．地租水平的差异 B．人口密度的差异C．汽车拥有量的差异 D．人口流动状况的差异11. 2016年春节期间，北京的大街小巷再也不像工作时间那么堵车的原因是A．人们不愿上街购物B．北京外来人口较多C．汽车数量大幅减少D．街上活动多，出行少开车12.右图示意中心地等级体系，与乙、丙等级城市相比较，对甲等级城市叙述正确的有A．分布数量最多 B．服务范围最小C．服务功能最全 D．城市级别最低随着铁路和离速公路的相继开通，某城市的交通条件大为改善，城市规模也迅速扩大。

2015-2016学年高一第二学期期末考试数学试题带答案

2015～2016学年度第二学期期末考试高一数学试题(考试时间：120分钟总分：160分)注意事项：所有试题的答案均填写在答题纸上，答案写在试卷上的无效．参考公式：棱锥的体积公式：V棱锥13sh =，其中s 为棱锥的底面积，h 为高. 一、填空题：（本大题共14小题，每小题5分，共70分．请将答案填入答题纸填空题的相应答题线上．）1．已知(1,1)A ，(2,2)B ，则直线AB 的斜率为． 2．在公差为2的等差数列}{n a 中，若21a =，则5a 的值是．3．若ABC ∆满足：60A =︒，75C =︒，BC =AC 的长度为． 4．已知π4αβ+=，且tan 2α=，则tan β的值是． 5．如图，在直三棱柱111ABC A B C -中， 3 cm AB =， 4 cm BC =， 5 cm CA =，1 6 cm AA =，则四棱锥111A B BCC -的体积为 3cm ．6．在平面直角坐标系x O y 中，直线210x a y +-=和直线(21)10a x y --+=互相垂直，则实数a 的值是．7．已知正实数,a b 满足24a b +=，则ab 的最大值是．8．在平面直角坐标系x O y 中，(1,3)A ，(4,2)B ，若直线20ax y a --=与线段AB 有公共点，则实数a 的取值范围是．9．已知实数,x y 满足：11x y -≤+≤，11x y -≤-≤，则2x y +的最小值是． 10．如图，对于正方体1111ABCD A B C D -，给出下列四个结论：①直线// AC 平面1111A B C D ②直线1// AC 直线1A B ③直线AC ⊥平面11DD B B ④直线1AC ⊥直线BD 其中正确结论的序号为．11．在ABC ∆中，角A ，B ，C 的对边分别为a ，b ，c ，已知πsin()62bC a+=，则角A 的值是．12．在平面直角坐标系xOy 中，圆C 的方程为22(2)(3)9x y -+-=，若过点(0,3)M 的直线与圆C 交于,P Q 两点（其中点P 在第二象限），且2PMO PQO ∠=∠，则点Q 的横坐标为．13．已知各项均为正数的数列{}n a 满足11(2)(1)0n n n n a a a a ++--=()n N *∈，且120a a =，则1a 的最大值是．14．如图，边长为1a b ++（0,0a b >>）的正方形被剖分为9个矩形，这些矩形的面积如图所示，则3572468152S S S S S S S S S +++++的最小值是．二、解答题（本大题共6小题，共90分．解答应写出文字说明、证明过程或演算步骤．） 15．（本题满分14分）在平面直角坐标系xOy 中，直线:30l x by b ++=．（1）若直线l 与直线20x y -+=平行，求实数b 的值；（2）若1b =，(0,1)A ，点B 在直线l 上，已知AB 的中点在x 轴上，求点B 的坐标． 16．（本题满分14分）在ABC ∆中，角A 、B 、C 的对边分别为a 、b 、c （a b c <<），已知2cos 2cos a C c A a c +=+．（1）若35c a =，求sin sin AB的值；（2）若2sin 0c A =，且8c a -=，求ABC ∆的面积S ．17．（本题满分14分）如图，在三棱锥P ABC -中，平面PAC ⊥平面ABC ，PA PC ⊥，AB BC =，点M ，N 分别为PC ，AC 的中点．求证：（1）直线 //PA 平面BMN ；（2）平面PBC ⊥平面BMN ．18．（本题满分16分）如图，某隧道的截面图由矩形ABCD 和抛物线型拱顶DEC 组成（E 为拱顶DEC 的最高点），以AB 所在直线为x 轴，以AB 的中点为坐标原点，建立平面直角坐标系xOy ，已知拱顶DEC 的方程为2164y x =-+(44)x -≤≤．（1）求tan AEB ∠的值；（2）现欲在拱顶上某点P 处安装一个交通信息采集装置，为了获得最佳采集效果，需要点P 对隧道底AB 的张角APB ∠最大，求此时点P 到AB 的距离．19．（本题满分16分）在平面直角坐标系xOy 中，圆C 的方程为22(4)1x y -+=，且圆C 与x 轴交于M ，N 两点，设直线l 的方程为 (0)y kx k =>．（1）当直线l 与圆C 相切时，求直线l 的方程；（2）已知直线l 与圆C 相交于A ，B 两点．（ⅰ）若AB ≤，求实数k 的取值范围；（ⅱ）直线AM 与直线BN 相交于点P ，直线AM ，直线BN ，直线OP 的斜率分别为1k ，2k ，3k ，是否存在常数a ，使得123k k ak +=恒成立？若存在，求出a 的值；若不存在，说明理由．20．（本题满分16分）已知数列}{n a 的首项10a >，前n 项和为n S ．数列n S n ⎧⎫⎨⎬⎭⎩是公差为12a的等差数列．（1）求62a a 的值；（2）数列}{nb 满足：1(1)2n a pn n n b b ++-=，其中,N*n p ∈．（ⅰ）若11p a ==，求数列}{n b 的前4k 项的和，N*k ∈；（ⅱ）当2p =时，对所有的正整数n ，都有1n n b b +>，证明：1112111222a a a b ---<<．2015～2016学年度第二学期期末考试高一数学参考答案一、填空题1．1； 2．7； 3 4．13-； 5．24； 6．23； 7．2； 8．(,3][1,)-∞-+∞ ； 9． 2-； 10．①③④； 11．π6； 12．1； 13．512 ； 14．2. 二、解答题15. 解：（1）∵直线l 与直线20x y -+=平行， ∴1(1)10b ⨯--⨯=，∴1b =-，经检验知，满足题意． ………………７分（2）由题意可知：:30l x y ++=，设00(,3)B x x --，则AB 的中点为002(,)22x x --， ………………１０分 ∵AB 的中点在x 轴上，∴02x =-，∴(2,1)B --． ………………１４分 16. 解：（1）∵2cos 2cos a C c A a c +=+由正弦定理：2sin cos 2sin cos sin sin A C C A A C+=+∴sin sin 2sin()2sin(π)2sin A C A C B B +=+=-= ………………２分 ∵35c a =由正弦定理：3sin 5sin C A =， ………………４分∴82sin sin sin sin 3B A C A =+=，∴sin 3sin 4A B =． ………………7分（2）由2sin 0c A =得：sin C =，∵(0,π)C ∈，∴π3C =或2π3C = 当π3C =时， ∵a b c <<，∴A B C <<，此时πA B C ++<，舍去， ∴23C π=， ………………9分由（1）可知：2a c b +=，又∵8c a -=， ∴4,8b a c a =+=+，∴2222(8)(4)2(4)cos3a a a a a π+=++-⋅+， ∴6a =或4a =-（舍） ………………12分所以11sin 61022S ab C ==⨯⨯= ………………14分 17.（1）证明：∵点M ，N 分别为PC ，AC 的中点，∴//MN PA ， ………………2分又∵PA ⊄平面BMN ，MN ⊂平面BMN ，∴直线 //PA 平面BMN ． ………………6分（2）证明：∵AB BC =，点N 为AC 中点， ∴BN AC ⊥，∵平面PAC ⊥平面ABC ，平面PAC 平面ABC AC =，BN ⊂平面ABC ，BN AC ⊥， ∴BN ⊥平面PAC ， ………………9分 ∵PC ⊂平面PAC ，∴PC BN ⊥，由（1）可知：//MN PA ， ∵PA PC ⊥，∴PC MN ⊥，∵PC BN ⊥，PC MN ⊥，BN MN N = ，,BN MN 在平面BMN 内，∴PC ⊥平面BMN ， ………………12分 ∵PC ⊂平面PAC ，∴平面PBC ⊥平面BMN ． ………………14分18. （1）解：由题意：(0,6)E ，(4,0)B ， ∴2tan 3BO BEO EO ∠==， ∴222123tan tan 2251()3AEB BEO ⨯∠=∠==-， ………………5分（2）（法1）设00(,)P x y ，026y ≤≤，过P 作PH AB ⊥于H ，设,APH BPH αβ∠=∠=，则000044tan ,tan x x y y αβ+-==， ………………8分 ∴00222000088tan tan()1648y y APB y x y y αβ∠=+==---+00828()4y y =≤=+- ………………12分∵026y ≤≤，∴当且仅当0y =tan APB ∠最大，即APB ∠最大．答：位置P 对隧道底AB 的张角最大时P 到AB的距离为 ………………14分（法2）设00(,)P x y ，026y ≤≤，∴22200000000(4,)(4,)1648PA PB x y x y x y y y ⋅=---⋅--=-+=-+ ，∴200||||cos 48PA PB AFB y y ⋅∠=-+ ，∴20048cos y y AFB PA PB-+∠=⋅ ………………8分∵011||||sin 822AFB S PA PB APB y ∆=⋅∠=⋅⋅ ，∴08sin y APB PA PB∠=⋅∴0200008sin 8tan 28cos 48()4y APB APB APB y y y y ∠∠====≤=∠-++- ………12分∵026y ≤≤，∴当且仅当0y =tan APB ∠最大，即APB ∠最大．答：位置P 对隧道底AB 的张角最大时P 到AB的距离为 ………………14分 19．（1）解：由题意，0k >，∴圆心C 到直线l的距离d =， ………………2分∵直线l 与圆C相切，∴1d ==，∴k =，∴直线:l y ． ………………4分（2）解：由题意得：0AB <=≤，1d ≤<， ………………６分由（1）可知：d =，1<，∴14k ≤<． ………………９分（3）证明：1:(3)AM l y k x =-，与圆C 22:(4)1x y -+=联立，得：2211(3)[(1)(35)]0x k x k -+-+=， ∴3M x =，2121351A k x k +=+，∴2112211352(,)11k k A k k +++，同理可得：2222222532(,)11k k B k k +-++， ………………12分 ∵OA OB k k =，∴122212221222122211355311k k k k k k k k -++=++++，即1212(1)(35)0k k k k ++=， ∵121k k ≠-，∴2135k k =-， ………………14分设00(,)P x y ，∴010020(3)(5)y k x y k x =-⎧⎨=-⎩， ∴1201212012352k k x k k k k y k k -⎧=⎪-⎪⎨-⎪=⎪-⎩，∴12121212352(,)k k k k P k k k k ----，即1315(,)44kP ，∴1313141554k k k ==， ∴1213225k k k k +==，∴存在常数2a =，使得1232k k k +=恒成立． ………………16分 20. （1）解：由题意，1111(1)122n S S a n n a n +=+-⋅=， ∴1(1)2n n n S a +=，当2n ≥时，1111(1)(1)22n n n n n n n a S S a a na -+-=-=-=，当1n =时，上式也成立，∴1n a na =，*n N ∈， ∵10a > ∴6121632a a a a ==． ………………3分（2）（ⅰ）由题意：1(1)2n n n n b b ++-=，当N*k ∈时，4342432k k k b b ----=，4241422k k k b b ---+=，414412k k k b b ---=， ∴4243434341222k k k k k b b -----+=-=，4142424242232k k k k k b b ----+=+=⋅，∴43434241472k k k k k b b b b ----+++=⨯， ………………6分 ∴前4k 项的和4123456784342414()()()k k k k k T b b b b b b b b b b b b ---=++++++++++++154314(161)72727215k k --=⨯+⨯++⨯=． ………………8分（ⅱ）证明：由题意得：1112(2)na a n n n b b ++==，令12a t =，(1,)t ∈+∞， ∴11()(1)(1)n n nn nb b t ++-=----， ∴112211112211()()()(1)(1)(1)(1)(1)(1)(1)(1)n n n n n n n n n n b b b b b b b b ------=-+-++-+-------- 12111()[()()()]()11nn t t t t t b b t t--=--+-++--=-+-+ ，∴1()(1)11n nn t t b b t t=--+++， ………………11分 ∵1n n b b +>,N*n ∈，∴11111()(1)()(1)1111n n n nn n t t t t b b b b t t t t +++-=--+----++++ 12()(1)(1)011n nt t b t t t=---+->++，∴1(1)()(1)12(1)n nt t t b t t --->++，N*n ∈， ①当n 为偶数时，1(1)2(1)1n t t tb t t->+++，∵(1,)t ∈+∞，2(1)(1)(2)2(1)12(1)12n t t t t t t t t t t t t ---+≤+=++++，∴1(2)2t t b ->， ………………13分 ②当n 为奇数时，1(1)2(1)1n t t tb t t-<+++，∵(1,)t ∈+∞，1(1)(1)2(1)12(1)12n t t t t t t tt t t t --+≥+=++++， ∴12tb <， ………………15分高一数学试题第 11 页共 11 页综上：1(2)22t t t b -<<，即1112111222a a a b ---<<． ………………16分。

2015—2016学年度下期期末高一数学参考答案.doc

2015—2016学年度下期期末高一数学参考答案一、选择题BCBBB CAACB CB二、填空题 13. 13 14. 231- 15. [1,1]- 16. 1[1,)2- 三、解答题17．解 (Ⅰ)∵c ∥a ，∴设c ＝λa ，则c ＝(λ，2λ)．…………2分又|c |＝25，∴λ＝±2，∴c ＝(2,4)或(－2，－4)．……………5分(Ⅱ)∵()a ＋2b ⊥(2a －b )，∴(a ＋2b )·(2a －b )＝0. ……………7分∵|a |＝5，|b |＝52，∴a·b ＝－52. ∴cos θ＝a·b |a||b |＝－1，∴θ＝180°. ……………10分 18.解:( Ⅰ)设回归直线方程为ˆy =ˆbx+ˆa . ∵72i i 1x =∑=280,72i i 1y =∑=45 309,7i 1=∑x i y i =3 487,x =6,y =5597, ……………2分 ∴ˆb =5593487767280736-⨯⨯-⨯=13328=4.75, ……………4分 ˆa =5597-6×4.75≈51.36, ∴回归直线方程为ˆy =4.75x+51.36. ……………6分(Ⅱ)当x=20时,ˆy =4.75×20+51.36≈146.故某天的销售量为20件时,估计这天可获纯利大约为146元. ……………12分19.解:(Ⅰ)由题设可知,第3组的频率为0.06×5=0.3,第4组的频率为0.04×5=0.2,第5组的频率为0.02×5=0.1. ……………3分(Ⅱ)第3组的人数为0.3×100=30,第4组的人数为0.2×100=20,第5组的人数为0.1×100=10. ……………5分因为第3、4、5组共有60名学生,所以利用分层抽样在60名学生中抽取6名学生,每组抽取的人数分别为第3组:3060×6=3, 第4组:2060×6=2, 第5组:1060×6=1. 所以第3、4、5组分别抽取3人,2人,1人. ……………7分(Ⅲ)设第3组的3位同学为A 1,A 2,A 3,第4组的2位同学为B 1,B 2,第5组的1位同学为C 1.则从六位同学中抽两位同学有(A 1,A 2),(A 1,A 3),(A 1,B 1),(A 1,B 2),(A 1,C 1),(A 2,A 3),(A 2,B 1),(A 2,B 2),(A 2,C 1),(A 3,B 1),(A 3,B 2),(A 3,C 1),(B 1,B 2),(B 1,C 1),(B 2,C 1),共15种可能. ……………9分其中第4组的2位同学为B 1,B 2至少有一位同学入选的有(A 1,B 1),(A 1,B 2),(A 2,B 1),(A 2,B 2).(A 3,B 1),(B 1,B 2),(A 3,B 2),(B 1,C 1),(B 2,C 1),共9种可能.所以第4组至少有一名学生被甲考官面试的概率为915=35.……………12分 20.解 (Ⅰ)如图所示建立直角坐标系，设角(0)2πϕϕ-<<是以Ox 为始边，0OP 为终边的角,则.6πϕ=-……………2分OP 每秒钟内所转过的角为52.606ππ⨯=……………4分由OP 在时间()t s 内所转过的角为52().606t t ππ⨯= 由题意可知水轮逆时针转动，故所求的函数关系式为4sin() 2.66z t ππ=-+……………6分 (Ⅱ)令4sin()26,66z t ππ=-+=……………9分得sin()1,66t ππ-= ,4,662t t πππ-==令得故点p 第一次到达最高点大约需要4s . ……………12分 21．解：（Ⅰ）sin θ因为，θcos 为方程21204x bx -+=的两根，则有： 220(1)sin cos (2)21sin cos (382)b b θθθθ⋯⎧⎪∆=-≥⎪⎪+=⎨⋯⎪⋯=⋯⋯⎪⎪⎩分由（2）、（3）有：21144b =+，解得：b =520∆=->，……………4分又sin cos )04πθθθ+=+>，b ∴=……………6分（Ⅱ）sin 1cos 1sin cos 1cos sin 1sin cos θθθθθθθθ+++==-+-因为……………8分且sin cos )04πθθθ-=->，sin cos 2θθ∴-=……………10分sin 1cos 1sin cos 21cos sin 1sin cos θθθθθθθθ+++∴+=⋅=-+-.……………12分1cos(2)1cos 2322.:()()221[cos(2)cos 2]2313(2cos 2)222)23x x f x x x x x x πωωπωωωωπω+--=-=-+=+=+解Ⅰ………………………………………………………2分 2,(),0,,12f x ππωπωω>∴==由题意可知的最小正周期为且即())3()122f x x f ππ∴=+∴=………………………………………………………………………………5分 ()|()|1,()1()1f x m f x m f x -≤-≤≤+Ⅱ即min max 7[,0]|()|1,12()1()1,x f x m m f x m f x π∃∈--≤≥-≤+因为使得成立所以且 ………………………………………………………………………………7分max min 750,2126331sin(2)33)343(),()42x x x x f x f x ππππππ-≤≤-≤+≤-≤+≤≤+≤==-因为所以所以所以即 …………………………………………………………………10分7147[1,].24m m -≤≤--即的取值范围是 ………………………………………………………………………………12分。

贵州省黔南布依族苗族自治州数学高一下学期理数期末考试试卷

贵州省黔南布依族苗族自治州数学高一下学期理数期末考试试卷姓名:________ 班级:________ 成绩:________一、选择题 (共12题；共24分)1. （2分）下列两个程序（1）和（2）的运行的结果i分别是（）A . 7，7B . 7，6C . 6，7D . 6，62. （2分）已知角α的终边上一点P的坐标为（sin， cos），则角α的最小正角为（）A .B .C .D .3. （2分） 2012年学期末，某学校对100间学生公寓进行综合评比，依考核分数分为A,B,C,D四种等级，其中分数在为D等级，有15间；分数在为C等级，有40间；分数在为B等级，有20间；分数在为D等级，有25间. 考核评估后，得其频率直方图如图所示，估计这100间学生公寓评估得分的中位数是（）A . 78.65B . 78.75C . 78.80D . 78.854. （2分） (2016高二上·桓台期中) 直线l过点A（3，4）且与点B（﹣3，2）的距离最远，那么l的方程为（）A . 3x﹣y﹣13=0B . 3x﹣y+13=0C . 3x+y﹣13=0D . 3x+y+13=05. （2分） (2017高一下·珠海期末) 一支田径运动队有男运动员56人，女运动员42人．现用分层抽样的方法抽取若干人，若男运动员抽取了8人，则女运动员抽取的人数为（）A . 5B . 6C . 7D . 86. （2分） (2015高三上·广州期末) 在二项式的展开式中，前三项的系数成等差数列，把展开式中所有的项重新排成一列，则有理项都不相邻的概率为（）A .B .C .D .7. （2分）(2017·广东模拟) 某程序框图如图所示，该程序运行后若输出S的值是2，则判断框内可填写（）A . i≤2015？B . i≤2016？C . i≤2017？D . i≤2018？8. （2分）如图，平行四边形ABCD中，，点M在AB边上，且,则等于（）A .B .C . -1D . 19. （2分）函数（其中）的图象如图所示，为了得到的图象，则只要将f(x)的图象（）A . 向右平移个单位长度B . 向右平移个单位长度C . 向左平移个单位长度D . 向左平移个单位长度10. （2分）已知三点A（1，﹣1），B（a，3），C（4，5）在同一直线上，则实数a的值是（）A . 1B . 4C . 3D . 不确定11. （2分） (2019高一上·柳州月考) 函数，若，则的值为（）A .B . 5C .D .12. （2分）(2019·湖州模拟) 已知向量，的夹角为，且，则的最小值为（）A .B .C . 5D .二、填空题 (共4题；共4分)13. （1分）(2020·重庆模拟) 已知，则 ________.14. （1分）将1440°化为弧度，结果是________15. （1分） (2016高二下·黑龙江开学考) 向量 =（m﹣2，m+3）， =（2m+1，m﹣2），若与的夹角为锐角，则m的取值范围是________．16. （1分） (2019高一上·会宁期中) 如果函数满足对任意的，都有成立，那么实数的取值范围是________．三、解答题 (共6题；共45分)17. （5分） (2016高一下·赣州期中) 已知△ABC的三个内角A，B，C所对的边分别为a，b，c. ，，且．（Ⅰ）求A的大小；（Ⅱ）若a=1，．求S△ABC ．18. （5分）(2018·河北模拟) 某市政府为了引导居民合理用水，决定全面实施阶梯水价，阶梯水价原则上以住宅（一套住宅为一户）的月用水量为基准定价：若用水量不超过12吨时，按4元/吨计算水费；若用水量超过12吨且不超过14吨时，超过12吨部分按6.60元/吨计算水费；若用水量超过14吨时，超过14吨部分按7.8元/吨计算水费．为了了解全市居民月用水量的分布情况，通过抽样，获得了100户居民的月用水量（单位：吨），将数据按照分成8组，制成了如图1所示的频率分布直方图．（Ⅰ）假设用抽到的100户居民月用水量作为样本估计全市的居民用水情况．（ⅰ）现从全市居民中依次随机抽取5户，求这5户居民恰好3户居民的月用水量都超过12吨的概率；（ⅱ）试估计全市居民用水价格的期望（精确到0.01）；（Ⅱ）如图2是该市居民李某2016年1～6月份的月用水费（元）与月份的散点图，其拟合的线性回归方程是．若李某2016年1～7月份水费总支出为294.6元，试估计李某7月份的用水吨数．19. （10分） (2015高一下·嘉兴开学考) 已知．（1）λ何值时，最小？此时与的位置关系如何？（2）λ何值时，与的夹角的余弦值最大？此时与的位置关系如何？20. （5分）用随机模拟的方法估算边长是2的正方形内切圆的面积(如图所示),并估计π的近似值.21. （10分） (2019高一上·鹤岗期末) 已知函数（，）为奇函数，且相邻两对称轴间的距离为 .（1）当时，求的单调递减区间；（2）将函数的图象沿轴方向向右平移个单位长度，再把横坐标缩短到原来的（纵坐标不变），得到函数的图象.当时，求函数的值域.22. （10分） (2016高一上·启东期末) 已知函数f（x）= sinxcosx+sin2x﹣．（1）求f（x）的最小正周期及其对称轴方程；（2）设函数g（x）=f（ + ），其中常数ω＞0，|φ|＜．（i）当ω=4，φ= 时，函数y=g（x）﹣4λf（x）在[ ， ]上的最大值为，求λ的值；（ii）若函数g（x）的一个单调减区间内有一个零点﹣，且其图象过点A（，1），记函数g（x）的最小正周期为T，试求T取最大值时函数g（x）的解析式．参考答案一、选择题 (共12题；共24分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、二、填空题 (共4题；共4分)13-1、14-1、15-1、16-1、三、解答题 (共6题；共45分)17-1、18-1、19-1、19-2、20-1、21-1、21-2、22-1、22-2、。

2015-2016学年贵州省黔南州高一下学期期末考试数学试题(扫描版)

学年度第二学期期末联考高一数学参考答案一、选择题．1.D2.A3.B4.C5.D6.B7.D8.C9.D 10.A 11.A 12.C二、填空题．13.3- 14.6 15.3π 16. n 三、解答题．17.解：（1）∵62115=+-+=AB k ，（2分） ∴AB 边上的高线所在的直线方程：)4(613--=-x y （4分）即0226=-+y x （5分）（2）直线AB 的方程：0116=+-y x （6分） ∵37)15()21(22=+++-=AB （7分）点C 到直线AB 的距离3732)1(61132422=-++-=h （9分） ∴1637323721=⋅⋅=∆ABC S （10分） 18.解：（1）⎩⎨⎧=+=+⇒⎩⎨⎧==64288736471184d a d a S a （3分）解得2,11==d a （5分）12211-=⋅-+=n n a n )(（6分）（2）设数列{}n b 的前n 项的和为n T .)121121(21)12)(12(1+--=+-=n n n n b n （8分） ⎥⎦⎤⎢⎣⎡-++-+-=)(...)()(20111991513131121100T （10分） 2011002011121=-=)(（12分） 19.（1）证明：连接C A 1交1AC 于点E ，连接DE∵斜三棱柱中，C C AA 11是平行四边形.∴E 是C A 1的中点.又∵D 是BC 的中点，∴B A DE 1//（3分）又∵⊂DE 平面1ADC⊄B A 1平面1ADC (5分)∴//1B A 平面1ADC (6分)（2）∵ABC ∆中，D AC AB ,=为BC 的中点.∴BC AD ⊥(8分)又∵平面⊥ABC 平面11B BCC ，交线为BC⊂AD 平面ABC⊥∴AD 面11B BCC (10分)∵⊂1DC 平面11B BCC1DC AD ⊥∴(12分)20.解：(1)∵π<<=A A 0,43tan ∴54cos ,53sin ==A A (2分) 由余弦定理及c b 5=，可得A bc c b a cos 2222-+==218c ，即c a 23=(4分) 由正弦定理可得102sin sin ==a A c C (6分) （2）由C B B ac S sin sin 6sin 21==，得526=ac (9分) 又c a 23=，解得556=a (12分) 21.（1）证明：∵AB 为圆O 的直径，D 为圆周上一点.BD AD ⊥∴(1分)∵⊥PB 平面ABDAD PB ⊥∴(2分)又∵B PB BD =⋂⊥∴AD 平面PBD (3分)∵⊂BF 平面PBDBF AD ⊥∴又∵D PD AD PD BF =⋂⊥,⊥∴BF 平面PAD (4分)（2）解：∵⊥PB 平面ABDPDB ∠∴是直线PD 与平面ABD 所成的角.2tan =∠∴PDB (5分)在PBD Rt ∆中，可得2=DB在ABD Rt ∆中，o 90=∠ADB ，2=AB ，2=BD 可得12221,2=⨯⨯=∴=∆ADB S AD (6分)∵PA BE BP AB ⊥==,2∴E 是PA 的中点.∵⊥PB 平面ABD∴三棱锥ABD E -的高121==PB h ∴11111333E ABD ABD V S h -∆==⨯⨯= (8分)（3）连接EF 并延长交AD 的延长线于点G ，连接BG ，则BG 为平面BEF 与ABD 的交线。

贵阳市普通高中2015-2016高一(下)贵阳市期末

贵阳市普通中学2015-2016学年度第二学期期末监测考试试卷第1页，共2页………………○………………内………………○………………装………………○………………订………………○………………线………………○………………… 学校：______________姓名：_____________班级：_______________考号：______________________绝密★启用前贵阳市普通中学2015-2016学年度第二学期期末监测考试试卷高一数学试卷试卷满分：100分考试时长：120分钟考生须知：1．本试卷分为第I 卷（选择题）和第II 卷（非选择题）两部分。

2. 答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。

3. 考生答题时，将答案写在专用答题卡上。

选择题答案请用2B 铅笔将答题卡上对应题目的答案涂黑；非选择题答案请用直径0.5毫米黑色墨水签字笔在答题卡上各题的答题区域内规范作答，凡是答题不规范一律无效。

4. 测试范围：必修2，必修5。

5. 考试结束后，将答题卡交回，并保存好试卷。

第I 卷（选择题）一、选择题（本题10小题，每小题4分，共40分。

） 1．过点()1,2A 且斜率为1的直线方程是（） A.01=--y x B.03=--y x C.03=-+y xD.01=-+y x2．观察下列数列的特点：Λ,4,4,4,4,3,3,3,2,2,1其中第20项是（） A ．5B ．6C ．7D ．103．在空间直角坐标系中，点()4,1,2关于xoy 平面对称点的坐标为（） A ．()4,1,2-- B ．()4,1,2-- C ．()4,1,2-D ．()4,1,2--4．下列命题中正确的是（） A.若b a >，则22bc ac > B.若b a >，则22b a >C.若d c b a >>,，则bd ac >D.若d c b a <>,，则d b c a ->-5．如图，网格纸上小正方形的边长为1，粗实线画出的是某多面体的三视图，则该多面体的体积为（） A ．1B ．2C ．3D ．66．在ABC ∆中，角C B A ,,所对的边分别为c b a ,,，24,34,60===b a A ο，则B 等于（）A.ο30B.ο45C.ο60D.ο1357．某工厂近5年内生产总值从a 元开始以每年比上年产值增加%10，则这个厂近5年内的总产值为（） A ．a 41.1B ．a 51.1C ．()11.1106-aD ．()11.1105-a8．设0,0>>b a ，若3是a 3与b3的等比中项，则ba 11+的最小值为（） A ．4B ．6C ．32D ．4329．已知n m ,是两条不同直线，γβα,,是三个不同平面，下列命题中正确的是（） A ．若αα//,//n m ，则n m // B ．若γβγα⊥⊥,，则βα// C ．若αα//,//m m ，则βα//D ．若αα⊥⊥n m ,，则n m //10．设R m ∈，过定点A 的动直线0=+my x 和过定点B 的动直线03=+--m y mx 交于点()y x P ,，则PB PA ⋅的最大值为（）A.4B.5C.6D.8二、填空题（本题5小题，每小题4分，共20分。

贵州黔南州15-16学年高一下期末考试--数学(WORD版)

角的大小、
22、（本小题满分12分）
已知数列的前n项和Sn满足且
（I）求证：数列为等比数列
（II）记，求数列的前n项和Tn
2015—2016学年度第二学期期末联考
高一数学参考答案
一、选择题．
1.D 2.A 3.B 4.C 5.D 6.B 7.D 8.C 9.D 10.A 11.A 12.C
在中，，，
可得 (6分)
∵ ∴ 是的中点.
∵ 平面
三棱锥的高
∴ (8分)
（3）连接并延长交的延长线于点，连接，则为平面与的交线。（9分）
在中，
在中，
∴
∵ 面 .∴
在中，可求得 .∴ .
又∵ ∴
∴ ∴ (10分)
又∵ ∴
又∵ 面
∴
∴ 面
∴
∴ 是平面与平面所成锐二面角的平面角(11分)
21、（本小题满分12分）
如图1，AB为圆O的直径，D为圆周上异于A，B的点，PB垂直于圆O所在的平面，BE⊥PA，
BF⊥PD，垂足分别为E，F。已知AB＝BP＝2，直线PD与平面ABD所成角的正切值为、
（I）求证：BF⊥平面PAD
（II）求三棱锥E－ABD的体积
（III）在图2中，作出平面BEF与平面ABD的交线，并求平面BEF与平面ABD所成锐二面
如图，已知斜三棱柱ABC－A1B1C1中，AB＝AC，D为线段BC的中点、
（I）求证院A1B∥平面ADC1
（II）若平面ABC⊥平面BCC1B1，求证:AD⊥DC1
20、（本小题满分12分）
在△ABC中，角A，B，C的对边分别为a，b，c，已知
（I）求sinC的值
（II）若△ABC的面积S＝6sinBsinC，求a的值、

贵州省黔南州2015-2016学年高一下学期期末考试数学试题含解析

贵州省黔南州2015-2016学年高一下学期期末考试数学试题第Ⅰ卷（共60分）一、选择题：本大题共12个小题,每小题5分,共60分。

在每小题给出的四个选项中,只有一项是符合题目要求的。

1.【题文】直线3x ＋3y ＋1＝0的倾斜角是（ )A 、30°B 、60°C 、120°D 、150°【答案】D【解析】试题分析：由直线方程可知斜率33tan 15033k θθ=-∴=-∴= 考点:直线斜率和倾斜角【结束】2.【题文】不等式－x 2－x ＋2＜0的解集为（）A 、 {x ｜x ＜－2或 x ＞1 }B 、 {x ｜－2＜x ＜1 ｝C 、 {x ｜x ＜－1 或x ＞2 }D 、｛x|－1＜x ＜2 }【答案】A【解析】试题分析：不等式变形为()()22021012x x x x x x +->∴+->∴><-或,所以不等式解集为｛x|x ＜－2或 x ＞1 ｝考点：一元二次不等式解法【结束】3.【题文】一个几何体的三视图如图所示,则该几何体可以是(）A 、圆柱B 、圆台C 、棱柱D 、棱台【答案】B【解析】试题分析：由俯视图可知该几何体底面为两个圆，因此该几何体为圆台考点：几何体三视图【结束】4.【题文】△ABC 中,A ＝6π，BC ＝3 ，则△ABC 的外接圆面积为( ） A 、π B 、2π C 、3π D 、4π 【答案】C【解析】试题分析：由正弦定理可得外接圆半径满足23223331sin 2BC R R S R A ππ===∴=∴== 考点：正弦定理解三角形【结束】5.【题文】两直线3x+y-3=0 与6x+my+1=0 平行，则它们之间的距离为（）A 、 4【答案】D【解析】试题分析：由两直线平行可得2m =直线3x+y —3=0变形为6x+2y —6=0，所以距离为22167102062d +==+ 考点:两直线间的距离【结束】6。

2015-2016学年贵州省黔西南州望谟民族中学高一(下)期末数学试卷(解析版)

2015-2016学年贵州省黔西南州望谟民族中学高一（下）期末数学试卷一、选择题（共12个小题，每小题5分，共60分）1．（5分）等差数列{a n}满足a3﹣a1=2，a5=5，则前4项和S4=（）A．6 B．8 C．10 D．122．（5分）下列命题正确的是（）A．经过三点确定一个平面．B．两两相交且不共点的三条直线确定一个平面．C．经过一条直线和一个点确定一个平面．D．四边形确定一个平面．3．（5分）已知cosα=，则cos2α=（）A．B．C．1 D．4．（5分）在正方体ABCD﹣A1B1C1D1中，E是A1D1的中点，则直线AE与直线CC1所成角的正切值是（）A．B．2 C．D．5．（5分）用斜二测画法画一个水平放置的平面图形的直观图为如图所示的一个正方形，则原来的图形是（）A．B．C．D．6．（5分）表面积为3π的圆锥，它的侧面展开图是一个半圆，则该圆锥的底面直径为（）A．1 B．2 C．D．7．（5分）不等式x2＞x的解集是（）A．（﹣∞，0）B．（0，1） C．（1，+∞）D．（﹣∞，0）∪（1，+∞）8．（5分）如图，已知半径为2的半圆中，BC为直径，O为圆心，点A在半圆弧上，且AB=AC，则图中阴影部分绕直线BC旋转一周所形成的几何体的体积为（）A．B．C．16πD．32π9．（5分）若直线a与平面α不平行，则下列结论成立的是（）A．平面α内任意直线都与直线a异面B．平面α内不存在与直线a平行的直线C．平面α内的直线都与直线a相交D．直线a与平面α一定有公共点10．（5分）已知tanα=，tanβ=，则tan（α﹣β）=（）A．﹣1 B．C．1 D．11．（5分）已知等差数列{a n}满足a1=5，a3=1，前n项和为S n，则下列说法正确的是（）A．{a n}的前n项和中S3最大B．{a n}是递增数列C．{a n}中存在值为0的项D．S4＜S512．（5分）望谟民族中学在迎接“申示二评”期间成功展示了大型竹鼓操，得到各位专家的好评．已知高一（1）班同学按身高由低到高站队，且前10位同学身高呈等比数列，若第四位同学身高为1.5米，第十位同学身高为1.62米，则第七位同学身高为（）A．米B．米C．米D．米二、填空题（共4个小题，每小题5分，共20分）13．（5分）设0＜α＜π，且sin=，则sinα=．14．（5分）如图是某几何体的三视图，则该几何体的体积为．15．（5分）设的最小值是．16．（5分）若变量x，y满足约束条件，则z=3x﹣y的最小值为．三、解答题（共6小题，第17题10分，其余每题12分，共70分.）17．（10分）设0＜α＜，0＜β＜，且sinα=，cosβ=，求sin（α+β）的值．18．（12分）在△ABC中，a=3，b=2，∠B=2∠A．（1）求cosA的值；（2）求AB边长．19．（12分）（1）解不等式：≤2；（2）已知不等式x2﹣2x+k2﹣1＞0对一切实数x恒成立，求实数k的取值范围．20．（12分）如图，三棱柱ABC﹣A1B1C1中，CA=CB，AB=AA1，∠BAA1=60°（Ⅰ）证明：AB⊥A1C；（Ⅱ）若AB=CB=2，A1C=，求三棱柱ABC﹣A1B1C1的体积．21．（12分）等差数列{a n}中，a7=4，a19=2a9，（Ⅰ）求{a n}的通项公式；（Ⅱ）设b n=，求数列{b n}的前n项和S n．22．（12分）如图，直四棱柱ABCD﹣A1B1C1D1中，AB∥CD，AD⊥AB，AB=AD=CD=1．点P为线段C1D1的中点．（Ⅰ）求证：AP∥平面BDC1；（Ⅱ）求证：平面BCC1⊥平面BDC1．2015-2016学年贵州省黔西南州望谟民族中学高一（下）期末数学试卷参考答案与试题解析一、选择题（共12个小题，每小题5分，共60分）1．（5分）等差数列{a n}满足a3﹣a1=2，a5=5，则前4项和S4=（）A．6 B．8 C．10 D．12【解答】解：在等差数列{a n}中，由a3﹣a1=2，得2d=2，d=1，又a5=5，∴a1=a5﹣4d=5﹣4×1=1，∴．故选：C．2．（5分）下列命题正确的是（）A．经过三点确定一个平面．B．两两相交且不共点的三条直线确定一个平面．C．经过一条直线和一个点确定一个平面．D．四边形确定一个平面．【解答】解：对A，当三点共线时，平面不确定，故A错误；对B，∵两条相交直线确定一个平面α，第三条直线与这两条直线分别相交且交点不重合，则第三条直线也在α内，∴两两相交且不共点的三条直线确定一个平面，故B正确；对C，当点在直线上时，不能确定平面，故C错误；对D，∵空间四边形不在一个平面内，故D错误．故选：B．3．（5分）已知cosα=，则cos2α=（）A．B．C．1 D．【解答】解：cosα=，则cos2α=2cos2α﹣1=2×﹣1=﹣．故选：D．4．（5分）在正方体ABCD﹣A1B1C1D1中，E是A1D1的中点，则直线AE与直线CC1所成角的正切值是（）A．B．2 C．D．【解答】解：如图所示由正方体的性质可得：AA1∥CC1，∴∠A1AE为异面直线AE与直线CC1所成角．在Rt△AA1E中，tan∠A1AE==．故选：A．5．（5分）用斜二测画法画一个水平放置的平面图形的直观图为如图所示的一个正方形，则原来的图形是（）A．B．C．D．【解答】解：根据斜二测画法知，平行于x轴的线段长度不变，平行于y的线段变为原来的，∵O′C′=1，O′A′=，∴OC=O′C′=1，OA=2O′A′=2；由此得出原来的图形是A．故选：A．6．（5分）表面积为3π的圆锥，它的侧面展开图是一个半圆，则该圆锥的底面直径为（）A．1 B．2 C．D．【解答】解：设圆锥的底面的半径为r，圆锥的母线为l，则由πl=2πr得l=2r，而S=πr2+πr•2r=3πr2=3π故r2=1解得r=1，所以直径为：2．故选：B．7．（5分）不等式x2＞x的解集是（）A．（﹣∞，0）B．（0，1） C．（1，+∞）D．（﹣∞，0）∪（1，+∞）【解答】解：∵不等式x2＞x，∴x2﹣x＞0，∴x（x﹣1）＞0，解得x＞1或x＜0，故选：D．8．（5分）如图，已知半径为2的半圆中，BC为直径，O为圆心，点A在半圆弧上，且AB=AC，则图中阴影部分绕直线BC旋转一周所形成的几何体的体积为（）A．B．C．16πD．32π【解答】解：半圆绕BC旋转一周所得球体的体积V==．球三角形ABC绕BC旋转一周所得几何体体积V′==．﹣V′=．∴阴影部分绕BC旋转一周所得几何体体积V=V球故选：A．9．（5分）若直线a与平面α不平行，则下列结论成立的是（）A．平面α内任意直线都与直线a异面B．平面α内不存在与直线a平行的直线C．平面α内的直线都与直线a相交D．直线a与平面α一定有公共点【解答】解：若直线a不平行于平面α，则直线a与平面α相交或在平面内对于A，α内的所有直线与直线a异面，也可能相交，故不成立；对于B，α内不存在与a平行的直线，当a在平面α内就存在与a平行的直线，故不成立；对于C，α内的直线均与a相交，也可能异面；故不成立；对于D，直线a与平面α有公共点，当直线a与平面α相交与在平面内都有公共点，故成立．故选：D．10．（5分）已知tanα=，tanβ=，则tan（α﹣β）=（）A．﹣1 B．C．1 D．【解答】解：tanα=，tanβ=，则tan（α﹣β）===．故选：B．11．（5分）已知等差数列{a n}满足a1=5，a3=1，前n项和为S n，则下列说法正确的是（）A．{a n}的前n项和中S3最大B．{a n}是递增数列C．{a n}中存在值为0的项D．S4＜S5【解答】解：设等差数列{a n}的公差为d，∵a1=5，a3=1，∴5+2d=1，解得d=﹣2．∴a n=5﹣2（n﹣1）=7﹣2n，由a n≥0，即7﹣2n≥0，解得n，∴{a n}的前n项和中S3最大，{a n}是单调递减数列，不存在值为0的项，S4＞S5．故选：A．12．（5分）望谟民族中学在迎接“申示二评”期间成功展示了大型竹鼓操，得到各位专家的好评．已知高一（1）班同学按身高由低到高站队，且前10位同学身高呈等比数列，若第四位同学身高为1.5米，第十位同学身高为1.62米，则第七位同学身高为（）A．米B．米C．米D．米【解答】解：依题意得：a4=1.5，a10=1.62，则a72=a4•a10=1.5×1.62=2.43．又因为该数列属于正数数列，所以a7=．故选：C．二、填空题（共4个小题，每小题5分，共20分）13．（5分）设0＜α＜π，且sin=，则sinα=．【解答】解：0＜α＜π，且sin=，可得cos==．sinα=2sin cos=2×=．故答案为：．14．（5分）如图是某几何体的三视图，则该几何体的体积为．【解答】解：由三视图可知：该几何体为一个四棱锥，其中一条侧棱与底面垂直．∴该几何体的体积==10．故答案为：10．15．（5分）设的最小值是2．【解答】解：∵a＞0，b＞0，a+b=2∴=（）（a+b）=1+（）≥2当且仅当即a=b=1时取等号∴的最小值为2故答案为：216．（5分）若变量x，y满足约束条件，则z=3x﹣y的最小值为﹣7．【解答】解：x，y满足约束条件对应的平面区域如图：当直线y=3x﹣z经过C时使得z最小，解得，所以C（﹣2，1），所以z=3x﹣y的最小值为﹣2×3﹣1=﹣7；故答案为：﹣7．三、解答题（共6小题，第17题10分，其余每题12分，共70分.）17．（10分）设0＜α＜，0＜β＜，且sinα=，cosβ=，求sin（α+β）的值．【解答】解：∵0＜α＜，0＜β＜，且sinα=，cosβ=，∴，，∴．18．（12分）在△ABC中，a=3，b=2，∠B=2∠A．（1）求cosA的值；（2）求AB边长．【解答】解：（1）因为∠B=2∠A，所以由正弦定理有，得．（2）由余弦定理a2=b2+c2﹣2bccosA得c2﹣8c+15=0解得c=3或c=5，因为∠B=2∠A，所以，经验证AB=3不符合题意，所以AB=5．19．（12分）（1）解不等式：≤2；（2）已知不等式x2﹣2x+k2﹣1＞0对一切实数x恒成立，求实数k的取值范围．【解答】解：（1）由题意，得到，所以，所以x＜﹣4，或x；所以不等式的解集为（﹣∞，﹣4）∪[，+∞）；（2）因为不等式x2﹣2x+k2﹣1＞0对一切实数x恒成立，所以△=4﹣4（k2﹣1）＜0，所以k＞，或者k＜．20．（12分）如图，三棱柱ABC﹣A1B1C1中，CA=CB，AB=AA1，∠BAA1=60°（Ⅰ）证明：AB⊥A1C；（Ⅱ）若AB=CB=2，A1C=，求三棱柱ABC﹣A1B1C1的体积．【解答】（Ⅰ）证明：如图，取AB的中点O，连结OC，OA1，A1B．因为CA=CB，所以OC⊥AB．由于AB=AA1，，故△AA1B为等边三角形，所以OA1⊥AB．因为OC∩OA1=O，所以AB⊥平面OA1C．又A1C⊂平面OA1C，故AB⊥A1C；（Ⅱ）解：由题设知△ABC与△AA1B都是边长为2的等边三角形，所以．又，则，故OA 1⊥OC．因为OC∩AB=O，所以OA1⊥平面ABC，OA1为三棱柱ABC﹣A1B1C1的高．B1C1的体积又△ABC的面积，故三棱柱ABC﹣A．21．（12分）等差数列{a n}中，a7=4，a19=2a9，（Ⅰ）求{a n}的通项公式；（Ⅱ）设b n=，求数列{b n}的前n项和S n．【解答】解：（I）设等差数列{a n}的公差为d∵a7=4，a19=2a9，∴解得，a1=1，d=∴=（II）∵==∴s n===22．（12分）如图，直四棱柱ABCD﹣A1B1C1D1中，AB∥CD，AD⊥AB，AB=AD=CD=1．点P为线段C1D1的中点．（Ⅰ）求证：AP∥平面BDC1；（Ⅱ）求证：平面BCC1⊥平面BDC1．【解答】证明：（Ⅰ）∵点P是线段C1D1的中点，∴PC1=，由题意PC 1∥DC，∴PC1，又AB，∴PC 1AB，∴四边形ABC1P为平行四边形，∴AP∥BC1，又∵AP⊄平面BDC1，BC1⊂平面BDC1，∴AP∥平面BDC1．（Ⅱ）在底面ABCD中，∵AB∥CD，AD⊥AB，AB=AD=，∴BD=BC=，在△BCD中，BD2+BC2=CD2，∴BD⊥BC，由已知CC1⊥底面ABCD，∴CC1⊥BD，又BC∩CC1=C，∴BD⊥平面BCC1．又∵BD⊂平面BDC1，∴平面BCC1⊥平面BDC1．。

2015-2016学年贵州省黔东南州锦屏县三江中学高一(下)期末数学试卷与解析word

2015-2016学年贵州省黔东南州锦屏县三江中学高一（下）期末数学试卷一、选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项符合题目要求1．（5分）若数列{a n}的通项公式为a n=2n+1，则a6=（）A．13 B．14 C．15 D．162．（5分）圆x2+y2+2x﹣4y﹣6=0的圆心和半径分别是（）A．（﹣1，﹣2），11 B．（﹣1，2），11 C．（﹣1，﹣2），D．（﹣1，2），3．（5分）如果直线ax+2y+2=0与直线3x﹣y﹣2=0平行，则a=（）A．﹣3 B．﹣ C．﹣6 D．4．（5分）不等式x（2﹣x）≤0的解集为（）A．{x|0≤x≤2}B．{x|x≤0，或x≥2}C．{x|x≤2}D．{x|x≥0}5．（5分）经过两点A（4，2y+1），B（2，﹣3）的直线的倾斜角为，则y=（）A．﹣1 B．﹣3 C．0 D．26．（5分）在△ABC中，A=60°，AB=1，AC=2，则S△ABC的值为（）A．B．C．D．27．（5分）设l是直线，α，β是两个不同的平面，则下列说法正确的是（）A．若l∥α，l∥β，则α∥βB．若l∥α，l⊥β，则α⊥βC．若α⊥β，l⊥α，则l∥βD．若α⊥β，l∥α，则l⊥β8．（5分）已知某三棱锥的三视图（单位：cm）如图所示，则该三棱锥的体积是（）A．1 m3B．2 cm3C．3 cm3D．6 cm39．（5分）已知等差数列{a n}中，a7+a9=16，则a8的值是（）A．16 B．8 C．7 D．410．（5分）一个正四棱柱的各个顶点都在一个半径为2cm的球面上，如果正四棱柱的底面边长为2cm，那么该棱柱的表面积为（）A．（2+4）cm2B．（4+8）cm2C．（8+16）cm2D．（16+32）cm2 11．（5分）若x＞0，y＞0且x+2y=1，则xy的最大值为（）A．B．C．D．12．（5分）正方体ABCD﹣A1B1C1D1中，E、F分别是AA1、AB的中点，则EF与对角面A1C1CA所成角的度数是（）A．30°B．45°C．60°D．150°二、填空题：本大题共4小题，每题5分，共20分．13．（5分）若直线y=ax﹣2与y=（a+2）x+1相互垂直，则a=．14．（5分）不等式组所表示的平面区域的面积等于．15．（5分）在等比数列{a n}中，已知a3=8，a7=2，则a5的值为．16．（5分）在△ABC中，角A、B、C所对的边为a、b、c，若a2=b2+c2﹣bc，则角A=．三、解答题：本大题共6小题，共70分，解答应写出文字说明，证明过程或演算步骤．17．（10分）已知直线l经过点P（﹣2，5），且斜率为﹣（1）求直线l的方程；（2）若直线m与l平行，且点P到直线m的距离为3，求直线m的方程．18．（12分）在等差数列{a n}中，前n项和为S n，若a10=18，S5=﹣15．（1）求数列{a n}的通项公式；（2）求S3﹣S4的值．19．（12分）已知圆C1：x2+y2﹣3x﹣3y+3=0，圆C2：x2+y2﹣2x﹣2y=0，求两圆的公共弦所在的直线方程及弦长．20．（12分）如图，在四棱锥P﹣ABCD中，平面PAD⊥平面ABCD，AB=AD，∠BAD=60°，E、F分别是AP、AD的中点，求证：（1）直线EF∥平面PCD；（2）平面BEF⊥平面PAD．21．（12分）在△ABC中，内角A，B，C的对边分别为a，b，c．已知．（1）求的值；（2）若cosB=，△ABC的周长为5，求b的长．22．（12分）已知数列{a n}的前n项和为S n，a1=2，S n=n2+n．（1）求数列{a n}的通项公式；（2）设{}的前n项和为T n，求证T n＜1．2015-2016学年贵州省黔东南州锦屏县三江中学高一（下）期末数学试卷参考答案与试题解析一、选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项符合题目要求1．（5分）若数列{a n}的通项公式为a n=2n+1，则a6=（）A．13 B．14 C．15 D．16【解答】解：∵通项公式是a n=2n+1，∴a6=2×6+1=13，故选：A．2．（5分）圆x2+y2+2x﹣4y﹣6=0的圆心和半径分别是（）A．（﹣1，﹣2），11 B．（﹣1，2），11 C．（﹣1，﹣2），D．（﹣1，2），【解答】解：将圆x2+y2+2x﹣4y﹣6=0化成标准方程，得（x+1）2+（y﹣2）2=11，∴圆心的坐标是（﹣1，2），半径r=．故选：D．3．（5分）如果直线ax+2y+2=0与直线3x﹣y﹣2=0平行，则a=（）A．﹣3 B．﹣ C．﹣6 D．【解答】解：由于直线ax+2y+2=0与直线3x﹣y﹣2=0平行，故它们的斜率相等，故有﹣=3，解得a=﹣6，故选：C．4．（5分）不等式x（2﹣x）≤0的解集为（）A．{x|0≤x≤2}B．{x|x≤0，或x≥2}C．{x|x≤2}D．{x|x≥0}【解答】解：不等式x（2﹣x）≤0可化为x（x﹣2）≥0，∴x≥2，或x≤0．∴不等式x（2﹣x）≤0的解集为{x|x≥2或x≤0}．故选：B．5．（5分）经过两点A（4，2y+1），B（2，﹣3）的直线的倾斜角为，则y=（）A．﹣1 B．﹣3 C．0 D．2【解答】解：因为直线经过两点A（4，2y+1），B（2，﹣3）所以直线AB的斜率k==y+2又因为直线的倾斜角为，所以k=﹣1，所以y=﹣3．故选：B．6．（5分）在△ABC中，A=60°，AB=1，AC=2，则S△ABC的值为（）A．B．C．D．2【解答】解：S=•AB•AC•sinA=×1×2×=，△ABC故选：B．7．（5分）设l是直线，α，β是两个不同的平面，则下列说法正确的是（）A．若l∥α，l∥β，则α∥βB．若l∥α，l⊥β，则α⊥βC．若α⊥β，l⊥α，则l∥βD．若α⊥β，l∥α，则l⊥β【解答】解：对于A．若l∥α，l∥β，则α∥β或α，β相交，故A错；对于B．若l∥α，l⊥β，则由线面平行的性质定理，得过l的平面γ∩α=m，即有m∥l，m⊥β，再由面面垂直的判定定理，得α⊥β，故B对；对于C．若α⊥β，l⊥α，则l∥β或l⊂β，故C错；对于D．若α⊥β，l∥α，若l平行于α，β的交线，则l∥β，故D错．故选：B．8．（5分）已知某三棱锥的三视图（单位：cm）如图所示，则该三棱锥的体积是（）A．1 m3B．2 cm3C．3 cm3D．6 cm3【解答】解：由三视图知，几何体是一个三棱锥，底面是直角边长为1cm和2cm 的直角三角形，面积是×1×2=1cm2，三棱锥的一条侧棱与底面垂直，且长度是3cm，这是三棱锥的高，∴三棱锥的体积是×1×3=1cm3，故选：A．9．（5分）已知等差数列{a n}中，a7+a9=16，则a8的值是（）A．16 B．8 C．7 D．4【解答】解：由等差数列的性质可知，a7+a9=2a8=16∴a8=8故选：B．10．（5分）一个正四棱柱的各个顶点都在一个半径为2cm的球面上，如果正四棱柱的底面边长为2cm，那么该棱柱的表面积为（）A．（2+4）cm2B．（4+8）cm2C．（8+16）cm2D．（16+32）cm2【解答】解：∵一个正四棱柱的各个顶点都在一个半径为2cm的球面上，正四棱柱的底面边长为2cm，球的直径为正四棱柱的体对角线∴正四棱柱的体对角线为4，正四棱柱的底面对角线长为2，∴正四棱柱的高为=，∴该棱柱的表面积为2×22+4×2×=8+16，故选：C．11．（5分）若x＞0，y＞0且x+2y=1，则xy的最大值为（）A．B．C．D．【解答】解：∵x＞0，y＞0且x+2y=1，∴1，化为：xy≤，当且仅当x=2y=时取等号．则xy的最大值为．故选：B．12．（5分）正方体ABCD﹣A1B1C1D1中，E、F分别是AA1、AB的中点，则EF与对角面A1C1CA所成角的度数是（）A．30°B．45°C．60°D．150°【解答】解：∵E、F分别是AA1、AB的中点，∴EF∥A1B，则EF与对角面A1C1CA所成角等于A1B对角面A1C1CA所成角连接BD交AC于O由正方体的几何特征可得BD⊥平面A1C1CA即∠BA1O即为EF与对角面A1C1CA所成角在Rt△BA1O中，∵BA1=2BO∴∠BA1O=30°故选：A．二、填空题：本大题共4小题，每题5分，共20分．13．（5分）若直线y=ax﹣2与y=（a+2）x+1相互垂直，则a=﹣1．【解答】解：∵直线y=ax﹣2与y=（a+2）x+1相互垂直，∴a（a+2）=﹣1，即a2+2a+1=0，∴a=﹣1；故答案为：﹣114．（5分）不等式组所表示的平面区域的面积等于．【解答】解：由题意可知：可行域如图：所以平面区域的面积为：．故答案为：．15．（5分）在等比数列{a n}中，已知a3=8，a7=2，则a5的值为4．【解答】解：∵在等比数列{a n}中，a3=8，a7=2，∴，∴a1＞0，∴，=16，∴a5=4．故答案为：4．16．（5分）在△ABC中，角A、B、C所对的边为a、b、c，若a2=b2+c2﹣bc，则角A=600．【解答】解：∵在△ABC中，a2=b2+c2﹣bc，即b2+c2﹣a2=bc，∴由余弦定理得：cosA==，则A=60°．故答案为：60°三、解答题：本大题共6小题，共70分，解答应写出文字说明，证明过程或演算步骤．17．（10分）已知直线l经过点P（﹣2，5），且斜率为﹣（1）求直线l的方程；（2）若直线m与l平行，且点P到直线m的距离为3，求直线m的方程．【解答】解：（1）由点斜式写出直线l的方程为y﹣5=﹣（x+2），化简为3x+4y ﹣14=0．（2）由直线m与直线l平行，可设直线m的方程为3x+4y+c=0，由点到直线的距离公式，得，即，解得c=1或c=﹣29，故所求直线方程3x+4y+1=0，或3x+4y﹣29=0．18．（12分）在等差数列{a n}中，前n项和为S n，若a10=18，S5=﹣15．（1）求数列{a n}的通项公式；（2）求S3﹣S4的值．【解答】解：（1）设{a n}的首项，公差分别为a1，d．则解得a1=﹣9，d=3，∴a n=3n﹣12．（2）∵，∴S3=﹣18，S4=﹣18，∴S3﹣S4=0．19．（12分）已知圆C1：x2+y2﹣3x﹣3y+3=0，圆C2：x2+y2﹣2x﹣2y=0，求两圆的公共弦所在的直线方程及弦长．【解答】解：把圆C1：x2+y2﹣3x﹣3y+3=0和圆C2：x2+y2﹣2x﹣2y=0的方程相减，可得两圆的公共弦所在的直线方程为x+y﹣3=0．由于圆C2：x2+y2﹣2x﹣2y=0，即圆C2：（x﹣1）2+（y﹣1）2 =2，故C2（1，1），半径r2=，求得点C2到公共弦所在的直线的距离d==，故公共弦的长为2=2=．20．（12分）如图，在四棱锥P﹣ABCD中，平面PAD⊥平面ABCD，AB=AD，∠BAD=60°，E、F分别是AP、AD的中点，求证：（1）直线EF∥平面PCD；（2）平面BEF⊥平面PAD．【解答】证明：（1）在△PAD中，∵E，F分别为AP，AD的中点，∴EF∥PD．又∵EF不在平面PCD中，PD⊂平面PCD∴直线EF∥平面PCD．（2）连接BD．在△ABD中，∵AB=AD，∠BAD=60°．即两底角相等并且等于60°，∴△ABD为正三角形．∵F是AD的中点，∴BF⊥AD．∵平面PAD⊥平面ABCD，BF⊂平面ABCD，平面PAD∩平面ABCD=AD，∴BF⊥平面PAD．又∵BF⊂平面EBF，∴平面BEF⊥平面PAD．21．（12分）在△ABC中，内角A，B，C的对边分别为a，b，c．已知．（1）求的值；（2）若cosB=，△ABC的周长为5，求b的长．【解答】解：（1）因为所以即：cosAsinB﹣2sinBcosC=2sinCcosB﹣cosBsinA所以sin（A+B）=2sin（B+C），即sinC=2sinA所以=2（2）由（1）可知c=2a…①a+b+c=5…②b2=a2+c2﹣2accosB…③cosB=…④解①②③④可得a=1，b=c=2；所以b=222．（12分）已知数列{a n}的前n项和为S n，a1=2，S n=n2+n．（1）求数列{a n}的通项公式；（2）设{}的前n项和为T n，求证T n＜1．【解答】解：（1）当n≥2时，a n=S n﹣S n﹣1=n2+n﹣[（n﹣1）2+（n﹣1）]=2n．∵n=1时，a1=2×1=2，也适合∴数列{a n}的通项公式是a n=2n．（2）==﹣∴{}的前n项和为T n=（1﹣）+（﹣）+（﹣）+…+（﹣）=1﹣=∵0＜＜1∴1﹣∈（0，1），即T n＜1对于一切正整数n均成立．赠送初中数学几何模型【模型五】垂直弦模型：图形特征：运用举例：1.已知A、B、C、D是⊙O上的四个点.(1)如图1，若∠ADC＝∠BCD＝90°，AD＝CD，求证AC⊥BD；(2)如图2，若AC⊥BD，垂足为E，AB＝2，DC＝4，求⊙O的半径.2.如图，已知四边形ABCD 内接于⊙O ，对角线AC ⊥BD 于P ，设⊙O 的半径是2。

2015-2016高一下学期期末教学水平监测数学试题(解析版)7

高一下学期期末教学水平监测数学试题一、选择题1．计算sin 43cos13cos 43sin13- 的结果等于（）A.122【答案】A 【解析】略2．下列各组平面向量中，可以作为基底的是A.B.C. D.【答案】B【解析】能做基底的两个向量必须不共线，所以A 选项中有零向量，不符。

C 选项中，不符。

D 选项中，不符。

B 选项中,两向量不平行。

所以选B.3．n S 为等差数列{}n a 的前n 项和， 286a a +=，则9S ＝ A.272B. 54C. 27D. 108 【答案】B【解析】试题分析：由等差中项得，,所以．故选B ．【考点】等差数列的性质． 4．设，，则下列不等式成立的是A. B. C. D.【答案】D【解析】A 选项中，令， =0不符。

A 错。

B 选项中，只有正数满足同向相乘，所以B 错。

C 选项中，令，不符，C 错。

D选项利用不等式性质同向相加，D 对。

选D.5．在中，已知D 是AB 边上一点，若，，则＝A. B. C. D.【答案】D【解析】因为A,D，B三点共线，所以。

选D.【点睛】若P在直线AB外，若C在直线AB上，则。

若P在直线AB外，若，则C在直线AB上。

6．在中，则B等于A. B. C. D.【答案】C【解析】由正弦定理因为所以，所以.选C.7．某几何体的三视图如图所示，则该几何体的表面积为A. 180B. 200C. 220D. 240【答案】D【解析】由三视图可知：该几何体是一个横放的直四棱柱，高为10；其底面是一个等腰梯形，上下边分别为2，8，高为4．∴S表面积=2××（2+8）×4+2×5×10+2×10+8×10=240．故选D．8．设1e 、2e 是夹角为60的两个单位向量， 12122,32a e e b e e =+=-+ ，则向量a 与b的夹角为（）A. 30B. 60C. 120D. 150【答案】C 【解析】略9．如图，设A ，B 两点在涪江的两岸，一测量者在A 的同侧所在的江岸边选定一点C ，测出AC 的距离为50 m ，∠ACB ＝45°，∠CAB ＝105°. 则A ，B 两点间的距离为A.m B. m C. m D. m【答案】A【解析】由正弦定理，选A.10．已知等差数列{a n }的前n 项和为，，，则使得取最大值时n 的值为A. 11或12B. 12C. 13D. 12或13 【答案】D【解析】由题意可得，，，所以最大。

2015-2016高一下期末考试

黔东南州2015—2016学年度第二学期期末考试高一数学试卷一、选择题（60分）1、设集合2{|560},M x x x U R =-->=，则U C M =A.[2,3]B.(,2][3,)-∞+∞C.[1,6]-D.[6,1]-2、在各项均为正数的等比数列{}n a 中，若379a a ⋅=，则343536log log log a a a ++=A.1B.2C.3D.43、设点B 为点(3,4,5)A -关于xoz 面的对称点，则||AB =A.6B.8C.10D.4、过点(2,5)-且垂直于直线24150x y -+=的直线方程为A.210x y +-=B. 250x y +-=C. 250x y +-=D. 270x y -+=5、已知实数,x y 满足：11y x x y y ≤⎧⎪+≤⎨⎪≥-⎩，则2z x y =+的最大值为 A.2 B.32C. 3-D.3 6、如果方程2242410x y x y k +++++=表示圆，那么k 的取值范围是A.(,)-∞+∞B.(,1)-∞C.(,1]-∞D.[1,)+∞7、直线L 的方程为0Ax By C --+=，若直线L 过原点和一、三象限，则A.0,0C B =>B.0,0,0A B C >>=C.0,0AB C <=D.0,0,C AB =>8、已知某几何体的正视图，侧视图和俯视图均为边长为1的正方形（如图），若该几何体的顶点都在同一个球面上，则此球的表面积为A.4πB.3πC.2πD.π9、已知{}n a 是公差为1 的等差数列，n S 为{}n a 的前n 项和，若844S S =，则10a = A.172 B.12 C.10 D.19210、如图，在四面体ABCD 中，截面PQMN 是正方形，则在下列命题中，错误的为A.AC BD =B.//AC 截面PQMNC.异面直线PM 与BD 所成的角为45D.AC BD ⊥11、已知直线,m n 与平面,αβ，下列命题正确的是A.,//m n αβ⊥且αβ⊥，则m n ⊥.B.,m n αβ⊥⊥且αβ⊥，则m n ⊥.C.,m n m αβ=⊥且αβ⊥，则n α⊥.D. //,//m n αβ且//αβ，则//m n .12、在ABC 中，,4B BC π=边上的高等于13BC ，则cos A =D. 二、填空题（20分） 13、当3x >时，函数13y x x =+-的最小值为_______________________________ 14、若直线(1)20x m y m +++-=与24160mx y ++=没有公共点，则m 的值为______________15、在数列{}n a 中，若21232()n a a a a n n N *+++⋅⋅⋅+=+∈，则n a =_________________________16、在直三棱柱111ABC A B C -中，1,AB BC AB BC AA ⊥==，,E F 分别为1,AC CC 的中点，则直线EF 与平面1A AB 所成角的余弦值为_________________三、解答题（70分）17、（10分）在ABC 中，直线AB 的方程为3210x y --=，直线AC 的方程为23180x y +-=，直线BC 的方程为340(25)x y m m +-=≠.（1）、求证：ABC 为直角三角形；（2）、当ABC 的BC 边上的高为1时，求m 的值.18、（12分）在ABC 中，,,a b c 分别为角,,A B C 所对的边，3B π=.（1）、若3,a b ==，求c 的值；（2）、若()sin sin ),f A A A A a =-()f A 的最大值及此时ABC 的外接圆的半径.19、（12分）如图在三棱锥P ABC -中，,,D E F 分别为棱,,PC AC AB 的中点，已知,6,AD PD PA ==8,5BC DF ==.求证：（1）、直线//PA 平面DEF ；（2）、平面DEF ⊥平面ABC .20、（12分）已知{}n a 是各项均为正数的数列，{}n b 是等差数列，且11521,37a b a b ==-=,2112(2)0()n n n n a a a a n N *+++--=∈.（1）、求{}n a 和{}n b 的通项公式；（2）、设,n n n c a b n N *=∈，求数列{}n c 的前项和.21、（12）已知圆心为C 的圆: 22()()8x a y b -+-=（,a b 为正整数）过点(0,1)A 且与直线30y --=相切.（1）、求圆C 的方程；（2）、若过点(4,1)M -的直线l 与圆C 相交于,E F 两点，且0CE CF ⋅=，求直线l 的方程.22、（12分）设矩形()ABCD AB CD >的周长为24，把ABC 沿AC 向ADC 折叠，AB 折过去后交DC 于点P ，设AB x =，求ADP 的最大面积及相应x 的值.。

2015-2016学年贵州省贵阳市高一(下)期末数学试卷

2015-2016学年贵州省贵阳市高一（下）期末数学试卷一、选择题（本题共10小题，每小题4分，满分40分，每小题有四个选项，其中只有一个选项正确，请将你认为正确的选项填在答题卷相应的位置上）1．（4分）过点A（2，1）且斜率为1的直线方程是（）A．x﹣y﹣1=0 B．x﹣y﹣3=0 C．x+y﹣3=0 D．x+y﹣1=02．（4分）观察下列数列的特点：1，2，2，3，3，3，4，4，4，4，…，其中第20项是（）A．5 B．6 C．7 D．103．（4分）在空间直角坐标系中，点（2，1，4）关于xOy平面对称点的坐标为（）A．（﹣2，﹣1，4） B．（﹣2，1，﹣4） C．（2，1，﹣4）D．（2，﹣1，﹣4）4．（4分）下列命题中正确的是（）A．若a＞b，则ac2＞bc2B．若a＞b，则a2＞b2C．若a＞b，c＞d，则ac＞bd D．若a＞b，c＜d，则a﹣c＞b﹣d5．（4分）如图，网格纸上小正方形的边长为1，粗实线画出的是某多面体的三视图，则该多面体的体积为（）A．1 B．2 C．3 D．66．（4分）在△ABC中，角A，B，C所对的边分别为a，b，c，A=60°，a=4，b=4，则B等于（）A．30°B．45°C．60°D．135°7．（4分）某工厂近5年内生产总值从a元开始以每年比上年产值增加10%，则这个厂近5年内的总产值为（）A．1.14a B．1.15a C．10a（1.16﹣1）D．10a（1.15﹣1）8．（4分）设a＞0，b＞0．若是3a与3b 的等比中项，则+的最小值为（）A．4 B．6 C．2 D．29．（4分）已知m，n是两条不同直线，α，β，γ是三个不同平面，下列命题中正确的是（）A．若m∥α，n∥α，则m∥n B．若α⊥γ，β⊥γ，则α∥βC．若m∥α，m∥β，则α∥βD．若m⊥α，n⊥α，则m∥n10．（4分）设m∈R，过定点A的动直线x+my=0和过定点B的动直线mx﹣y﹣m+3=0交于点P（x，y），则|PA|•|PB|的最大值是（）A．4 B．5 C．6 D．8二、填空题（本大题共5小题，每小题4分，满分20分）11．（4分）不等式x2+x﹣2＜0的解集为．12．（4分）一个棱长为2cm的正方体的顶点都在球面上，则该球的表面积是．13．（4分）已知公差不为0的等差数列{a n}满足：a1=2，且a1、a2、a5成等比数列，则数列{a n}的通项公式是．14．（4分）已知直线l经过点（1，3），且与圆x2+y2=1相切，直线l的方程为．15．（4分）将正方形ABCD沿对角线BD折成直二面角A﹣BD﹣C，有如下四个结论：①AC⊥BD；②△ACD是等边三角形；③AB与平面BCD成60°的角；④AB与CD所成的角为60°；其中正确结论是（写出所有正确结论的序号）三、解答题（本大题共5小题，每小题8分，满分40分，解答应写出文字说明，证明过程或演算步骤）16．（8分）已知在等差数列{a n}中，a4=7，a2+a7=16．（1）求数列{a n}的通项公式；（2）设b n=+n，求数列{b n}的前n项和T n的表达式．17．（8分）在锐角△ABC中，a，b，c分别为角A，B，C 所对的边，且c=2asinC，（1）求角A；（2）若a=2，且△ABC 的面积等于，求b，c．18．（8分）一个化肥厂生产甲、乙两种混合肥料，生产1车皮甲、乙两种肥料所需要的主要原料磷酸盐、硝酸盐如表，已知现库存磷酸盐10t、硝酸盐66t，在此基础上生产这两种混合肥料，设x，y分别为计划生产甲、乙两种混合肥料的车皮数．磷酸盐（t）硝酸盐（t）生产1车皮甲种肥料418生产1车皮乙种肥料115（1）列出满足生产条件的数学关系式，并画出相应的平面区域；（2）若生产1车皮甲种肥料，产生的利润为1万元；生产1车皮乙种肥料，产生的利润为0.5万，那么分别生产甲、乙两种肥料各多少车皮，能够产生最大的利润？最大利润是多少？19．（8分）如图，在四棱锥P﹣ABCD中，底图ABCD是正方形，PD⊥平面ABCD，E是PC的中点（1）证明：PA∥平面BDE；（2）若PD=DC=2，求三棱锥P﹣EDB的体积．20．（8分）在平面直角坐标系xOy中，已知圆心在x轴上、半径为2的圆C位于y轴右侧，且与直线相切．（1）求圆C的方程；（2）在圆C上，是否存在点M（m，n），使得直线l：mx+ny=1与圆O：x2+y2=1相交于不同的两点A，B，且△OAB的面积最大？若存在，求出点M的坐标及对应的△OAB的面积；若不存在，请说明理由．2015-2016学年贵州省贵阳市高一（下）期末数学试卷参考答案与试题解析一、选择题（本题共10小题，每小题4分，满分40分，每小题有四个选项，其中只有一个选项正确，请将你认为正确的选项填在答题卷相应的位置上）1．（4分）过点A（2，1）且斜率为1的直线方程是（）A．x﹣y﹣1=0 B．x﹣y﹣3=0 C．x+y﹣3=0 D．x+y﹣1=0【解答】解：过点（2，1）且斜率为1的直线方程为：y﹣1=x﹣2，整理，得x﹣y﹣1=0，故选：A．2．（4分）观察下列数列的特点：1，2，2，3，3，3，4，4，4，4，…，其中第20项是（）A．5 B．6 C．7 D．10【解答】解：数列1，2，2，3，3，3，4，4，4，4，…，的特点是1有1个，2有2个，3有3个，…n 有n个则数列一共有项，＜20，解得n≤5当n=5时，数列一共有15项，而当n=6时，有6项，则第20项为6，故选：B．3．（4分）在空间直角坐标系中，点（2，1，4）关于xOy平面对称点的坐标为（）A．（﹣2，﹣1，4） B．（﹣2，1，﹣4） C．（2，1，﹣4）D．（2，﹣1，﹣4）【解答】解：点关于xOy平面对称点的坐标满足x，y不变，z相反，即点（2，1，4）关于xOy平面对称点的坐标为（2，1，﹣4），故选：C．4．（4分）下列命题中正确的是（）A．若a＞b，则ac2＞bc2B．若a＞b，则a2＞b2C．若a＞b，c＞d，则ac＞bd D．若a＞b，c＜d，则a﹣c＞b﹣d【解答】解：对与A，当c=0时，不成立，对于B：当a=1，b=﹣2时不成立，对于C：当a＞0，b，c，d＜0时，不成立，对于D：若a＞b，c＜d，则﹣c＞﹣d，则a﹣c＞b﹣d，故成立，故选：D．5．（4分）如图，网格纸上小正方形的边长为1，粗实线画出的是某多面体的三视图，则该多面体的体积为（）A．1 B．2 C．3 D．6【解答】解：根据三视图可知几何体是以左视图为底面，高为3的直三棱柱，∴该多面体的体积为=3，故选：C．6．（4分）在△ABC中，角A，B，C所对的边分别为a，b，c，A=60°，a=4，b=4，则B等于（）A．30°B．45°C．60°D．135°【解答】解：由正弦定理可得：=，解得sinB=，∵b＜a，∴B为锐角，∴B=45°．故选：B．7．（4分）某工厂近5年内生产总值从a元开始以每年比上年产值增加10%，则这个厂近5年内的总产值为（）A．1.14a B．1.15a C．10a（1.16﹣1）D．10a（1.15﹣1）【解答】解：∵某工厂近5年内生产总值从a元开始以每年比上年产值增加10%，∴这个厂近5年内年产值构成一个首项为a，公比为1.1的等比数列，∴这个厂近5年内的总产值为：S==10a（1.15﹣1）．故选：D．8．（4分）设a＞0，b＞0．若是3a与3b 的等比中项，则+的最小值为（）A．4 B．6 C．2 D．2【解答】解：a＞0，b＞0，是3a与3b的等比中项，∴3=3a•3b=3a+b，∴a+b=1，∴+=（+）（a+b）=2++≥2+2=4，当且仅当=即a=b=时取等号，故选：A．9．（4分）已知m，n是两条不同直线，α，β，γ是三个不同平面，下列命题中正确的是（）A．若m∥α，n∥α，则m∥n B．若α⊥γ，β⊥γ，则α∥βC．若m∥α，m∥β，则α∥βD．若m⊥α，n⊥α，则m∥n【解答】解：A、m，n平行于同一个平面，故m，n可能相交，可能平行，也可能是异面直线，故A错误；B、α，β 垂直于同一个平面γ，故α，β 可能相交，可能平行，故B错误；C、α，β平行与同一条直线m，故α，β 可能相交，可能平行，故C错误；D、垂直于同一个平面的两条直线平行，故D正确．故选：D．10．（4分）设m∈R，过定点A的动直线x+my=0和过定点B的动直线mx﹣y﹣m+3=0交于点P（x，y），则|PA|•|PB|的最大值是（）A．4 B．5 C．6 D．8【解答】解：由题意可知，动直线x+my=0经过定点A（0，0），动直线mx﹣y﹣m+3=0即m（x﹣1）﹣y+3=0，经过点定点B（1，3），注意到动直线x+my=0和动直线mx﹣y﹣m+3=0始终垂直，P又是两条直线的交点，则有PA⊥PB，∴|PA|2+|PB|2=|AB|2=10．故|PA|•|PB|≤=5（当且仅当|PA|=|PB|=时取“=”）故选：B．二、填空题（本大题共5小题，每小题4分，满分20分）11．（4分）不等式x2+x﹣2＜0的解集为（﹣2，1）．【解答】解：方程x2+x﹣2=0的两根为﹣2，1，且函数y=x2+x﹣2的图象开口向上，所以不等式x2+x﹣2＜0的解集为（﹣2，1）．故答案为：（﹣2，1）．12．（4分）一个棱长为2cm的正方体的顶点都在球面上，则该球的表面积是12πcm2．【解答】解：正方体的棱长为：2cm，正方体的体对角线的长为：2cm，就是球的直径，∴球的表面积为：S2=4π（）2=12πcm2．故答案为：12πcm2．13．（4分）已知公差不为0的等差数列{a n}满足：a1=2，且a1、a2、a5成等比数列，则数列{a n}的通项公式是a n=4n﹣2．【解答】解：设等差数列{a n}的公差为d≠0，∵a1=2，且a1、a2、a5成等比数列，则=a1a5，∴（2+d）2=2（2+4d），解得d=4．∴a n=2+4（n﹣1）=4n﹣2．故答案为：a n=4n﹣2．14．（4分）已知直线l 经过点（1，3），且与圆x2+y2=1相切，直线l的方程为x=1或4x﹣3y+5=0．【解答】解：设切线方程为y﹣3=k（x﹣1），即kx﹣y+3﹣k=0．由于直线与圆相切，故圆心到直线的距离等于半径，即=1，解得k=，其方程为4x﹣3y+5=0．又当斜率不存在时，切线方程为x=1，综上所述，直线l的方程为x=1或4x﹣3y+5=0．故答案为：x=1或4x﹣3y+5=0．15．（4分）将正方形ABCD沿对角线BD折成直二面角A﹣BD﹣C，有如下四个结论：①AC⊥BD；②△ACD是等边三角形；③AB与平面BCD成60°的角；④AB与CD所成的角为60°；其中正确结论是①②④（写出所有正确结论的序号）【解答】解：作出如图的图象，其中A﹣BD﹣C=90°，E是BD的中点，可以证明出∠AED=90°即为此直二面角的平面角对于命题①，由于BD⊥面AEC，故AC⊥BD，此命题正确；对于命题②，在等腰直角三角形AEC中可以解出AC等于正方形的边长，故△ACD是等边三角形，此命题正确；对于命题③AB与平面BCD所成的线面角的平面角是∠ABE=45°，故AB与平面BCD成60°的角不正确；对于命题④可取AD中点F，AC的中点H，连接EF，EH，FH，由于EF，FH是中位线，可证得其长度为正方形边长的一半，而EH是直角三角形的中线，其长度是AC的一半即正方形边长的一半，故△EFH是等边三角形，由此即可证得AB与CD所成的角为60°；综上知①②④是正确的故答案为①②④三、解答题（本大题共5小题，每小题8分，满分40分，解答应写出文字说明，证明过程或演算步骤）16．（8分）已知在等差数列{a n}中，a4=7，a2+a7=16．（1）求数列{a n}的通项公式；（2）设b n=+n，求数列{b n}的前n项和T n的表达式．【解答】解：（1）设等差数列{a n}的首项为a1，公差为d，由a4=7，a2+a7=16得，得a1=1，d=2，则a n=1+2（n﹣1）=2n﹣1．（2）b n=+n=22n﹣1+n，则数列{b n}的前n项和T n=（21+23+…+22n﹣1）+（1+2+…+n）=+=（4n﹣1）+．17．（8分）在锐角△ABC中，a，b，c分别为角A，B，C 所对的边，且c=2asinC，（1）求角A；（2）若a=2，且△ABC 的面积等于，求b，c．【解答】（本题满分为12分）解：（1）在△ABC 中，∵c=2asinC．∴由正弦定理可得：sinC=2sinAsinC，…（3分）又∵sinC≠0，∴sinA=，∵A为锐角，可得A=，…（6分）（2）∵由余弦定理a2=b2+c2﹣2bccosA，又a=2，A=，可得：4=b2+c2﹣bc=（b+c）2﹣3bc，①又∵△ABC 的面积=bcsinA=bc，解得：bc=4，②∴由①②可解得：b=c=2．…（12分）18．（8分）一个化肥厂生产甲、乙两种混合肥料，生产1车皮甲、乙两种肥料所需要的主要原料磷酸盐、硝酸盐如表，已知现库存磷酸盐10t、硝酸盐66t，在此基础上生产这两种混合肥料，设x，y分别为计划生产甲、乙两种混合肥料的车皮数．磷酸盐（t）硝酸盐（t）生产1车皮甲种肥料418生产1车皮乙种肥料115（1）列出满足生产条件的数学关系式，并画出相应的平面区域；（2）若生产1车皮甲种肥料，产生的利润为1万元；生产1车皮乙种肥料，产生的利润为0.5万，那么分别生产甲、乙两种肥料各多少车皮，能够产生最大的利润？最大利润是多少？【解答】解：（1）x，y 满足的线性约束条件为，可行域如图．（2）设生产甲肥料x车皮，乙种肥料y车皮，能够产生最大的利润，则目标函数为z=x +y，即y=﹣2x+2z．平移直线y=﹣2x+2z．由图可知当直线y=﹣2x+2z经过可行域上的点M时，截距z最大，解方程组，此时z=2+×2=2+1=3，所以z mx=3．答：分别生产甲、乙两种肥料各2车皮，能够产生最大的利润，最大的利润为3万元．19．（8分）如图，在四棱锥P﹣ABCD中，底图ABCD是正方形，PD⊥平面ABCD，E是PC的中点（1）证明：PA∥平面BDE；（2）若PD=DC=2，求三棱锥P﹣EDB的体积．【解答】证明：（1）连接AC，设AC，BD的交点为O，连OE，由O，E分别为AC，CP中点，∴OE∥PA又OE⊂平面EDB，PA⊄平面EDB，∴PA∥平面EDB．（2）∵PD⊥平面ABCD，CD⊂平面平面ABCD，∴PD⊥DC，∵E是PC的中点，且PD=DC=2，∴S△PDE =S△PDC=，∵PD⊥平面ABCD，AD⊂平面平面ABCD，∴PD⊥AD，∵AD⊥CD，PD∩CD=D，∴AD⊥平面PDC，∵BC∥AD．∴BC⊥平面PDC，则V P﹣EDB=V B﹣PDE =S△PDE|BC|==．20．（8分）在平面直角坐标系xOy中，已知圆心在x轴上、半径为2的圆C位于y轴右侧，且与直线相切．（1）求圆C的方程；（2）在圆C上，是否存在点M（m，n），使得直线l：mx+ny=1与圆O：x2+y2=1相交于不同的两点A，B，且△OAB的面积最大？若存在，求出点M的坐标及对应的△OAB的面积；若不存在，请说明理由．【解答】解：（1）设圆心是（x0，0）（x0＞0），它到直线的距离是，解得x0=2或x0=﹣6（舍去）…（3分）∴所求圆C的方程是（x﹣2）2+y2=4…（4分）（2）∵点M（m，n）在圆C上∴（m﹣2）2+n2=4，n2=4﹣（m﹣2）2=4m﹣m2且0≤m≤4…（6分）又∵原点到直线l：mx+ny=1的距离…（8分）解得…（10分）而∴…（11分）∵…（12分）∴当，即时取得最大值，此时点M 的坐标是与，面积的最大值是．。

贵州省黔南布依族苗族自治州高一下学期数学期末调研考试试卷

贵州省黔南布依族苗族自治州高一下学期数学期末调研考试试卷姓名:________ 班级:________ 成绩:________一、单选题 (共10题；共20分)1. （2分） (2016高一上·金华期中) 设全集U={（x，y）|x，y∈R}，集合M={（x，y）| =1}，N={（x，y）|y=x+1}，则N∩（∁UM）等于（）A . ∅B . {（2，3）}C . （2，3）D . {（x，y）|y=x+1}2. （2分） (2018高二上·长寿月考) 过点P（4，－1）且与直线3x－4y＋6＝0垂直的直线方程是（）A . 4x＋3y－13＝0B . 4x－3y－19＝0C . 3x－4y－16＝0D . 3x＋4y－8＝03. （2分）(2017·福建模拟) 设f（x）是定义在R上的函数，它的图象关于点（1，0）对称，当x≤1时，f（x）=2xe﹣x（e为自然对数的底数），则f（2+3ln2）的值为（）A . 48ln2B . 40ln2C . 32ln2D . 24ln24. （2分） (2019高一上·遵义期中) 设，，，则，，的大小关系是（）A .B .C .D .5. （2分）要得到函数y=sin（4x﹣）的图象，只需将函数y=sin4x的图象（）A . 向左平移单位B . 向右平移单位C . 向左平移单位D . 向右平移单位6. （2分）不等式组，表示的平面区域的面积是（）A .B .C .D . 37. （2分） (2017高二下·深圳月考) 在数列1，2，2，3，3，3，4，4，4，4，……中，第2018项为（）A . 2018B . 63C . 64D . 658. （2分）抛物线y2=4x的焦点为F，点A,B在抛物线上，且，弦AB中点M在准线l上的射影为M'，则的最大值为（）A .B .C .D .9. （2分） (2019高一上·阜新月考) （）A .B .C .D .10. （2分）设点M是线段BC的中点，点A在直线BC外，，则=（）A . 2B . 4C . 6D . 8二、双空题 (共4题；共4分)11. （1分） (2019高二上·辽宁月考) 直线过定点________；过此定点倾斜角为的直线方程为________．12. （1分）已知角的终边过点P（﹣1，2），则cosα的值为________．13. （1分） (2016高一上·长春期中) 设f（x）是R上的奇函数，当x≥0时，f（x）=2x+3x﹣b（b为常数），则f（﹣2）=________14. （1分） (2017高一下·河北期末) 对于数列{an}，定义Hn= 为{an}的“优值”，现在已知某数列{an}的“优值”Hn=2n+1 ，记数列{an﹣kn}的前n项和为Sn ，若Sn≤S5对任意的n（n∈N*）恒成立，则实数k的取值范围为________．三、填空题 (共3题；共3分)15. （1分） (2018高一上·海安月考) 已知为非零实数，，且同时满足：① ，② ，则的值等于________．16. （1分） (2018高二下·双鸭山月考) 设，若，则的最小值为________.17. （1分）已知函数，若|f（x）|≥ax，则a的取值范围是________四、解答题 (共5题；共25分)18. （5分） (2016高一下·桐乡期中) 已知函数f（x）=2sinxcosx+2cos（x+ ）cos（x﹣）．（1）求f（x）的单调递减区间；（2）设α∈（0，π），f（）= ，求sinα的值．19. （5分） (2018高二上·镇江期中) 在某海礁A处有一风暴中心，距离风暴中心A正东方向200km的B处有一艘轮船，正以北偏西a（a为锐角）角方向航行，速度为40km/h．已知距离风暴中心180km以内的水域受其影响．（1）若轮船不被风暴影响，求角α的正切值的最大值？（2）若轮船航行方向为北偏西45°，求轮船被风暴影响持续多少时间？20. （5分） (2018高一上·海安月考) 如图，在海岸A处，发现南偏东45°方向距A为(2 －2)海里的B 处有一艘走私船，在A处正北方向，距A为海里的C处的缉私船立即奉命以10 海里/时的速度追截走私船．（1）刚发现走私船时，求两船的距离；（2）若走私船正以10 海里/时的速度从B处向南偏东75°方向逃窜，问缉私船沿什么方向能最快追上走私船？并求出所需要的时间(精确到分钟，参考数据：≈1.4，≈2.5)．21. （5分） (2019高一上·宁波期中) 已知二次函数满足且 .（1）求函数的解析式；（2）若且在上的最大值为8，求实数的值.22. （5分） (2016高一下·芦溪期末) 已知等差数列{an}首项a1=1，公差为d，且数列是公比为4的等比数列，（1）求d；（2）求数列{an}的通项公式an及前n项和Sn；（3）求数列的前n项和Tn．参考答案一、单选题 (共10题；共20分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、二、双空题 (共4题；共4分)11-1、12-1、13-1、14-1、三、填空题 (共3题；共3分)15-1、16-1、17-1、四、解答题 (共5题；共25分) 18-1、18-2、19-1、19-2、20-1、20-2、21-1、21-2、22-1、22-2、22-3、。

【期末试卷】贵州省黔南州2015-2016学年高一下学期期末考试数学试题 Word版(含答案)

贵州省黔东南州2015_2016学年高一数学下学期期末文化水平测试试题(扫描版)

2015-2016学年高一下学期期末考试数学试题带答案

2015-2016学年高一下学期期末考试数学试题带答案

15—16高一第二学期期末考试卷含答案

2015-2016学年高一第二学期期末考试数学试题带答案

2015—2016学年度下期期末高一数学参考答案.doc

贵州省黔南布依族苗族自治州数学高一下学期理数期末考试试卷

2015-2016学年贵州省黔南州高一下学期期末考试数学试题(扫描版)

贵阳市普通高中2015-2016高一(下)贵阳市期末

贵州黔南州15-16学年高一下期末考试--数学(WORD版)

贵州省黔南州2015-2016学年高一下学期期末考试数学试题 含解析

2015-2016学年贵州省黔西南州望谟民族中学高一(下)期末数学试卷(解析版)

2015-2016学年贵州省黔东南州锦屏县三江中学高一(下)期末数学试卷与解析word

2015-2016高一下学期期末教学水平监测数学试题(解析版)7

2015-2016高一下期末考试

2015-2016学年贵州省贵阳市高一(下)期末数学试卷

贵州省黔南布依族苗族自治州高一下学期数学期末调研考试试卷

贵州省黔南州2015-2016学年高一下学期期末考试数学试题含解析