遗传算法matlab
用MATLAB实现遗传算法程序

用MATLAB实现遗传算法程序一、本文概述遗传算法(Genetic Algorithms,GA)是一种模拟自然界生物进化过程的优化搜索算法,它通过模拟自然选择和遗传学机制,如选择、交叉、变异等,来寻找问题的最优解。
由于其全局搜索能力强、鲁棒性好以及易于实现并行化等优点,遗传算法在多个领域得到了广泛的应用,包括函数优化、机器学习、神经网络训练、组合优化等。
本文旨在介绍如何使用MATLAB实现遗传算法程序。
MATLAB作为一种强大的数学计算和编程工具,具有直观易用的图形界面和丰富的函数库,非常适合用于遗传算法的实现。
我们将从基本的遗传算法原理出发,逐步介绍如何在MATLAB中编写遗传算法程序,包括如何定义问题、编码、初始化种群、选择操作、交叉操作和变异操作等。
通过本文的学习,读者将能够掌握遗传算法的基本原理和MATLAB编程技巧,学会如何使用MATLAB实现遗传算法程序,并能够在实际问题中应用遗传算法求解最优解。
二、遗传算法基础遗传算法(Genetic Algorithm,GA)是一种模拟自然选择和遗传学机制的优化搜索算法。
它借鉴了生物进化中的遗传、交叉、变异等机制,通过模拟这些自然过程来寻找问题的最优解。
遗传算法的核心思想是将问题的解表示为“染色体”,即一组编码,然后通过模拟自然选择、交叉和变异等过程,逐步迭代搜索出最优解。
在遗传算法中,通常将问题的解表示为一个二进制字符串,每个字符串代表一个个体(Individual)。
每个个体都有一定的适应度(Fitness),适应度越高的个体在下一代中生存下来的概率越大。
通过选择(Selection)、交叉(Crossover)和变异(Mutation)等操作,生成新一代的个体,并重复这一过程,直到找到满足条件的最优解或达到预定的迭代次数。
选择操作是根据个体的适应度,选择出适应度较高的个体作为父母,参与下一代的生成。
常见的选择算法有轮盘赌选择(Roulette Wheel Selection)、锦标赛选择(Tournament Selection)等。
matlab中的遗传算法

matlab中的遗传算法【原创版】目录一、引言二、遗传算法的基本原理1.种群概念2.适应度函数3.选择操作4.交叉操作5.变异操作三、MATLAB 中遗传算法的实现1.准备工作2.遗传算法的实现四、遗传算法的应用案例1.旅行商问题2.装载问题五、遗传算法的优缺点六、结论正文一、引言遗传算法(Genetic Algorithm,GA)是一种模拟自然界生物进化过程的优化算法,其主要思想是将进化过程中的自然选择、交叉和变异等遗传操作应用到问题的求解过程中,从而实现对问题的优化求解。
遗传算法在解决复杂问题、非线性问题以及大规模问题等方面具有较强的优势,因此在各个领域得到了广泛的应用。
本文将介绍遗传算法的基本原理以及在MATLAB 中的实现。
二、遗传算法的基本原理1.种群概念遗传算法以一个种群作为优化过程的载体。
种群中的个体代表问题的解,每个个体由一组参数表示。
在优化过程中,种群会不断进化,最终收敛到问题的最优解。
2.适应度函数适应度函数是遗传算法的核心部分,用于评价种群中个体的优劣。
适应度函数的取值范围为 [0, 1],其中 1 表示最优解,0 表示最劣解。
在遗传算法的优化过程中,适应度函数用于选择优秀的个体,从而指导种群的进化。
3.选择操作选择操作是基于适应度函数的一种选择策略,用于选择下一代的父代个体。
常见的选择方法有轮盘赌选择、锦标赛选择等。
4.交叉操作交叉操作是遗传算法中产生新个体的主要方式,通过将选中的优秀个体进行交叉操作,产生具有更好适应度的新个体。
常见的交叉方法有单点交叉、多点交叉、均匀交叉等。
5.变异操作变异操作是在遗传算法中引入随机性的一种方式,通过随机改变某些基因的值,使新个体在进化过程中具有一定的多样性。
变异操作的强度由变异概率控制。
三、MATLAB 中遗传算法的实现1.准备工作在 MATLAB 中实现遗传算法,首先需要定义适应度函数、选择操作、交叉操作和变异操作等。
此外,还需要设置遗传算法的参数,如迭代次数、种群大小、交叉概率、变异概率等。
matlab遗传算法实例

matlab遗传算法实例Matlab遗传算法实例引言:遗传算法是一种模拟自然界生物遗传与进化过程的算法,它通过模拟自然选择、交叉、变异等操作来搜索最优解。
Matlab作为一种强大的数值计算软件,提供了丰富的工具箱来实现遗传算法。
本文将介绍一个基于Matlab的遗传算法实例,以帮助读者更好地理解遗传算法的原理和应用。
一、遗传算法基本原理遗传算法主要包括个体编码、适应度评价、选择、交叉和变异等基本操作。
个体编码是将问题的解表示为染色体,通常使用二进制编码。
适应度评价是根据问题的目标函数对个体进行评估,以确定其适应度值。
选择操作通过一定的策略选择适应度较高的个体作为下一代的父代。
交叉操作将选定的父代个体通过染色体交叉产生新的子代个体。
变异操作以一定的概率对个体的染色体进行变异,以增加种群的多样性。
通过迭代上述操作,逐步优化种群,最终找到问题的最优解。
二、遗传算法实例假设我们要解决一个简单的函数优化问题,即求解函数f(x) = x^2 + 8x + 16的最小值。
我们可以使用遗传算法来搜索函数的最优解。
1. 初始化种群我们需要初始化一个包含N个个体的种群。
每个个体都表示问题的一个解,即一个实数x。
这里,我们将种群大小设置为50,取值范围为[-10, 10]之间的随机数。
2. 适应度评价对于每个个体,我们计算其适应度值,即函数f(x)的值。
根据函数的性质,我们知道函数的最小值为-4,在x=-4时取得。
因此,我们可以将适应度值定义为f(x)与-4之间的差的倒数。
3. 选择操作选择操作决定了哪些个体将成为下一代的父代。
通常采用轮盘赌选择算法,即根据个体的适应度值来确定其被选中的概率。
适应度值较高的个体被选中的概率较大。
4. 交叉操作在选择出的父代个体中,通过染色体交叉操作来产生新的子代个体。
我们可以选择单点交叉或多点交叉。
例如,我们可以随机选择两个个体,将它们的染色体在一个随机位置进行交叉,得到两个新的子代个体。
遗传算法matlab程序代码

遗传算法matlab程序代码遗传算法是一种优化算法,用于在给定的搜索空间中寻找最优解。
在Matlab中,可以通过以下代码编写一个基本的遗传算法:% 初始种群大小Npop = 100;% 搜索空间维度ndim = 2;% 最大迭代次数imax = 100;% 初始化种群pop = rand(Npop, ndim);% 最小化目标函数fun = @(x) sum(x.^2);for i = 1:imax% 计算适应度函数fit = 1./fun(pop);% 选择操作[fitSort, fitIndex] = sort(fit, 'descend');pop = pop(fitIndex(1:Npop), :);% 染色体交叉操作popNew = zeros(Npop, ndim);for j = 1:Npopparent1Index = randi([1, Npop]);parent2Index = randi([1, Npop]);parent1 = pop(parent1Index, :);parent2 = pop(parent2Index, :);crossIndex = randi([1, ndim-1]);popNew(j,:) = [parent1(1:crossIndex),parent2(crossIndex+1:end)];end% 染色体突变操作for j = 1:NpopmutIndex = randi([1, ndim]);mutScale = randn();popNew(j, mutIndex) = popNew(j, mutIndex) + mutScale;end% 更新种群pop = [pop; popNew];end% 返回最优解[resultFit, resultIndex] = max(fit);result = pop(resultIndex, :);以上代码实现了一个简单的遗传算法,用于最小化目标函数x1^2 + x2^2。
matlab遗传算法工具箱关于离散变量优化算例

1. 引言遗传算法是一种模拟自然选择与遗传机制的优化算法,被广泛应用于离散变量优化问题的求解。
在Matlab软件中,有专门的工具箱可以支持遗传算法的实现与应用,极大地方便了工程技术人员进行离散变量优化问题的研究与应用。
本文将介绍Matlab遗传算法工具箱在离散变量优化算例中的应用,并通过具体案例来展示其实际求解效果。
2. Matlab遗传算法工具箱介绍Matlab遗传算法工具箱是Matlab软件的一个重要工具箱,它提供了丰富的遗传算法函数和工具,方便用户进行遗传算法的实现和应用。
在离散变量优化问题的求解中,用户可以利用工具箱提供的函数对问题进行建模、参数设置、运行算法等操作,从而快速高效地求解问题。
3. 离散变量优化算例为了更好地展示Matlab遗传算法工具箱在离散变量优化中的应用效果,我们选取了一个经典的离散变量优化问题作为算例,具体问题描述如下:设有一组零件需要进行装配,零件的形状和尺寸有多种选择。
每种零件的装配工艺和成本不同,需要选择最佳的零件组合方案来满足装配要求并使总成本最低。
假设可供选择的零件种类有n种,每种零件有m个备选方案,且装配每种零件的成本已知。
问应选择哪些零件及其具体方案才能使得总装配成本最低?4. Matlab遗传算法工具箱的应用为了利用Matlab遗传算法工具箱求解上述离散变量优化问题,我们可以按照以下步骤进行操作:1) 利用Matlab的数据处理工具,将零件的备选方案数据以矩阵的形式导入Matlab环境;2) 利用工具箱提供的函数对遗传算法的参数进行设置,例如选择交叉方式、变异方式、群体大小、迭代次数等;3) 利用工具箱提供的函数对离散变量优化问题进行编码和解码,以便算法能够对离散变量进行操作;4) 利用工具箱提供的函数编写适应度函数,用于评价每个个体的适应度;5) 利用工具箱提供的主函数运行遗传算法,获取最优解及其对应的总装配成本。
5. 案例求解结果分析通过上述步骤,我们在Matlab环境中成功应用遗传算法工具箱求解了离散变量优化问题。
遗传算法精英保留策略 matlab

遗传算法精英保留策略 matlab在遗传算法中,精英保留策略是指在每一代进化过程中,保留上一代中表现最优秀的个体,以保证优秀基因的传递和保留。
实现精英保留策略的MATLAB代码如下:```function [newPopulation] = elitePreservation(oldPopulation, eliteIndividuals)% 输入参数:% oldPopulation:上一代的种群% eliteIndividuals:精英个体的数量% 根据适应度对种群进行排序oldPopulation = sortPopulation(oldPopulation);% 选择精英个体elite = oldPopulation(1:eliteIndividuals);% 根据适应度从高到低排序,删除多余个体elite = sortPopulation(elite, 'descend');elite = elite(1:eliteIndividuals);% 将精英个体和其余个体合并为新一代种群newPopulation = [elite;oldPopulation(eliteIndividuals+1:end)];endfunction [sortedPopulation] = sortPopulation(population, sortDirection)% 输入参数:% population:待排序的种群% sortDirection:排序方向,'ascend'表示适应度从低到高排序,'descend'表示适应度从高到低排序(可选参数,默认为'ascend') if nargin < 2sortDirection = 'ascend';end% 计算种群的适应度fitness = calculateFitness(population);% 根据适应度进行排序[~, sortIndex] = sort(fitness, sortDirection);% 根据排序索引重新排序种群sortedPopulation = population(sortIndex, :);endfunction [fitness] = calculateFitness(population)% 输入参数:% population:待计算适应度的种群% 根据具体问题计算个体的适应度,此处假设fitness函数已经实现fitness = fitness(population);end```在代码中,通过调用`elitePreservation`函数即可实现精英保留策略。
遗传算法 matlab

遗传算法 Matlab什么是遗传算法?遗传算法是一种模拟生物进化过程的优化算法。
它模拟了自然界中的遗传、突变和选择等过程,利用这些操作来搜索和优化问题的解空间。
遗传算法具有以下几个关键步骤:1.初始化种群:通过生成一组随机解来初始化初始种群。
每个解被编码为一个染色体,染色体通常由二进制字符串表示。
2.评价适应度:使用适应度函数评估每个个体的适应度。
适应度函数通常通过衡量个体在解空间中的性能来定义。
3.选择操作:选择操作基于个体的适应度进行,通过概率选择操作来确定哪些个体应该参与繁殖下一代。
适应度较高的个体有更大的概率被选中。
4.交叉操作:选择的个体进行交叉操作,生成下一代的染色体。
交叉操作通过交换个体染色体中的信息来生成新的个体。
5.变异操作:为了保持种群的多样性,变异操作在染色体中进行随机的变异。
这个过程通过随机改变染色体中的部分基因来进行。
6.替换操作:根据新生成的染色体替换当前种群中某些个体,以此来形成新的种群。
7.重复上述步骤:重复执行上述步骤直到满足终止条件(例如达到最大迭代次数或找到满意的解)。
如何在 Matlab 中实现遗传算法?在 Matlab 中,可以使用遗传算法和优化工具箱来实现遗传算法。
以下是实现遗传算法的一般步骤:1.定义适应度函数:根据具体问题定义适应度函数,该函数衡量每个个体在解空间中的性能。
适应度函数的设计将影响到最终结果。
2.初始化种群:使用内置函数或自定义函数来生成初始种群。
每个个体都应该表示为染色体形式的解。
3.设置遗传算法参数:根据具体问题设置遗传算法的参数,如种群大小、迭代次数、选择操作和交叉操作的概率等。
4.编写遗传算法主循环:在主循环中,使用选择操作、交叉操作和变异操作来生成新的染色体,并计算每个个体的适应度。
5.选择操作:使用选择函数根据适应度值选择染色体。
具体的选择函数可以根据问题的特点进行调整。
6.交叉操作:使用交叉函数对染色体进行交叉操作,生成下一代的染色体。
遗传算法在matlab中的实现

遗传算法是一种模拟自然选择与遗传机制的优化算法,它模拟了生物进化的过程,通过优化个体的基因型来达到解决问题的目的。
在工程和科学领域,遗传算法被广泛应用于求解优化问题、寻找最优解、参数优化等领域。
而MATLAB作为一款强大的科学计算软件,拥有丰富的工具箱和编程接口,为实现遗传算法提供了便利。
下面将通过以下步骤介绍如何在MATLAB中实现遗传算法:1. 引入遗传算法工具箱需要在MATLAB环境中引入遗传算法工具箱。
在MATLAB命令窗口输入"ver",可以查看当前已安装的工具箱。
如果遗传算法工具箱未安装,可以使用MATLAB提供的工具箱管理界面进行安装。
2. 定义优化问题在实现遗传算法前,需要清楚地定义优化问题:包括问题的目标函数、约束条件等。
在MATLAB中,可以通过定义一个函数来表示目标函数,并且可以采用匿名函数的形式来灵活定义。
对于约束条件,也需要进行明确定义,以便在遗传算法中进行约束处理。
3. 设置遗传算法参数在实现遗传算法时,需要对遗传算法的参数进行设置,包括种群大小、交叉概率、变异概率、迭代次数等。
这些参数的设置将会直接影响遗传算法的收敛速度和优化效果。
在MATLAB中,可以通过设置遗传算法工具箱中的相关函数来完成参数的设置。
4. 编写遗传算法主程序编写遗传算法的主程序,主要包括对适应度函数的计算、选择、交叉、变异等操作。
在MATLAB中,可以利用遗传算法工具箱提供的相关函数来实现这些操作,简化了遗传算法的实现过程。
5. 运行遗传算法将编写好的遗传算法主程序在MATLAB环境中运行,并观察优化结果。
在运行过程中,可以对结果进行实时监测和分析,以便对遗传算法的参数进行调整和优化。
通过以上步骤,可以在MATLAB中实现遗传算法,并应用于实际的优化问题与工程应用中。
遗传算法的实现将大大提高问题的求解效率与精度,为工程领域带来更多的便利与可能性。
总结:遗传算法在MATLAB中的实现涉及到了引入遗传算法工具箱、定义优化问题、设置算法参数、编写主程序和运行算法等步骤。
遗传算法介绍并附上Matlab代码
1、遗传算法介绍遗传算法,模拟达尔文进化论的自然选择和遗产学机理的生物进化构成的计算模型,一种不断选择优良个体的算法。
谈到遗传,想想自然界动物遗传是怎么来的,自然主要过程包括染色体的选择,交叉,变异(不明白这个的可以去看看生物学),这些操作后,保证了以后的个基本上是最优的,那么以后再继续这样下去,就可以一直最优了。
2、解决的问题先说说自己要解决的问题吧,遗传算法很有名,自然能解决的问题很多了,在原理上不变的情况下,只要改变模型的应用环境和形式,基本上都可以。
但是遗传算法主要还是解决优化类问题,尤其是那种不能直接解出来的很复杂的问题,而实际情况通常也是这样的。
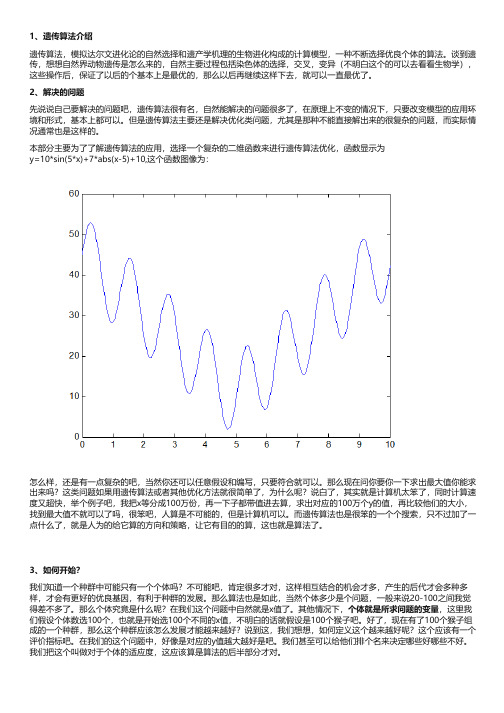
本部分主要为了了解遗传算法的应用,选择一个复杂的二维函数来进行遗传算法优化,函数显示为y=10*sin(5*x)+7*abs(x-5)+10,这个函数图像为:怎么样,还是有一点复杂的吧,当然你还可以任意假设和编写,只要符合就可以。
那么现在问你要你一下求出最大值你能求出来吗?这类问题如果用遗传算法或者其他优化方法就很简单了,为什么呢?说白了,其实就是计算机太笨了,同时计算速度又超快,举个例子吧,我把x等分成100万份,再一下子都带值进去算,求出对应的100万个y的值,再比较他们的大小,找到最大值不就可以了吗,很笨吧,人算是不可能的,但是计算机可以。
而遗传算法也是很笨的一个个搜索,只不过加了一点什么了,就是人为的给它算的方向和策略,让它有目的的算,这也就是算法了。
3、如何开始?我们知道一个种群中可能只有一个个体吗?不可能吧,肯定很多才对,这样相互结合的机会才多,产生的后代才会多种多样,才会有更好的优良基因,有利于种群的发展。
那么算法也是如此,当然个体多少是个问题,一般来说20-100之间我觉得差不多了。
那么个体究竟是什么呢?在我们这个问题中自然就是x值了。
其他情况下,个体就是所求问题的变量,这里我们假设个体数选100个,也就是开始选100个不同的x值,不明白的话就假设是100个猴子吧。
遗传算法matlab代码

遗传算法matlab代码以下是一个简单的遗传算法的MATLAB 代码示例:matlab复制代码% 遗传算法参数设置pop_size = 50; % 种群大小num_vars = 10; % 变量数目num_generations = 100; % 进化的代数mutation_rate = 0.01; % 变异率crossover_rate = 0.8; % 交叉率% 初始化种群population = rand(pop_size, num_vars);% 开始进化for i = 1:num_generations% 计算适应度fitness = evaluate_fitness(population);% 选择操作selected_population = selection(population, fitness);% 交叉操作offspring_population = crossover(selected_population,crossover_rate);% 变异操作mutated_population = mutation(offspring_population,mutation_rate);% 生成新种群population = [selected_population; mutated_population];end% 选择最优解best_solution = population(find(fitness == max(fitness)), :);% 适应度函数function f = evaluate_fitness(population)f = zeros(size(population));for i = 1:size(population, 1)f(i) = sum(population(i, :));endend% 选择函数function selected_population = selection(population, fitness)% 轮盘赌选择total_fitness = sum(fitness);probabilities = fitness / total_fitness;selected_indices = zeros(pop_size, 1);for i = 1:pop_sizer = rand();cumulative_probabilities = cumsum(probabilities);for j = 1:pop_sizeif r <= cumulative_probabilities(j)selected_indices(i) = j;break;endendendselected_population = population(selected_indices, :);end% 交叉函数function offspring_population = crossover(parental_population, crossover_rate)offspring_population = zeros(size(parental_population));num_crossovers = ceil(size(parental_population, 1) *crossover_rate);crossover_indices = randperm(size(parental_population, 1),num_crossovers);以下是另一个一个简单的遗传算法的MATLAB 代码示例:matlab复制代码% 初始化种群population = rand(nPopulation, nGenes);% 进化迭代for iGeneration = 1:nGeneration% 计算适应度fitness = evaluateFitness(population);% 选择父代parentIdx = selection(fitness);parent = population(parentIdx, :);% 交叉产生子代child = crossover(parent);% 变异子代child = mutation(child);% 更新种群population = [parent; child];end% 评估最优解bestFitness = -Inf;for i = 1:nPopulationf = evaluateFitness(population(i, :));if f > bestFitnessbestFitness = f;bestIndividual = population(i, :);endend% 可视化结果plotFitness(fitness);其中,nPopulation和nGenes分别是种群大小和基因数;nGeneration是迭代次数;evaluateFitness函数用于计算个体的适应度;selection函数用于选择父代;crossover函数用于交叉产生子代;mutation函数用于变异子代。
遗传算法 matlab

遗传算法 matlab遗传算法(GeneticAlgorithm,GA)是一种基于自然进化规律的算法,用于解决多变量多目标问题,在搜索全局最优解的过程中,被广泛应用在工业界、社会科学研究中。
由于它的复杂性和强大的优化性能,广泛被认为是一种有效的解决搜索问题的工具。
Matlab是一种面向科学和工程的数学软件,在求解很多复杂问题时,可以使用Matlab来设计并实现遗传算法,以解决一些复杂的搜索问题。
这篇文章将详细介绍Matlab的遗传算法的基本原理,以及如何使用Matlab来设计并实现遗传算法,以解决一些复杂的搜索问题。
首先,需要熟悉一下遗传算法的基本原理,具体来说,遗传算法是利用模拟自然界中进化规律来求解优化问题,由一个种群组合五个进化策略和一系列的操作构成的,每个策略都可以根据问题的要求来进行重新设计和定义,从而更好的解决搜索问题。
由于遗传算法本身具有复杂性,所以往往需要借助软件来实现,比如Matlab。
Matlab作为一种强大的软件,可以帮助我们设计并实现自定义的遗传算法,从而帮助我们解决复杂的搜索问题。
Matlab可以帮助我们设计种子算子,这些种子算子可以用来替代遗传算法中的遗传运算,从而提高算法的效率和性能。
例如交叉算子,变异算子和选择算子等,可以根据问题的要求相应地修改和定义,从而有效的提高搜索效率。
此外,Matlab还可以帮助我们设计一系列算法模型,通过这些模型,可以有效的应用遗传算法来求解复杂的搜索问题,最常用的模型有穷举法、贪婪法、粒子群算法、模拟退火算法和遗传算法等。
最后,Matlab还可以帮助我们实现一些自定义的功能,从而有效的改进算法的性能,比如增加种群的大小,增大迭代次数,改变染色体的结构,增加交叉率,改变选择策略和变异策略等,都能够较好的改进算法的性能。
综上所述,Matlab是一种非常有效的解决搜索问题的工具,它可以为我们设计并实现自定义的遗传算法,帮助我们解决复杂的搜索问题,并且,Matlab还可以帮助我们实现一些自定义的功能,从而有效的改进算法的性能,由此可见,使用Matlab对于搜索问题有着重要的意义。
MATLAB中的遗传算法及其应用示例

MATLAB中的遗传算法及其应用示例引言:遗传算法是一种基于自然进化规律的优化方法,适用于求解复杂的问题。
作为MATLAB的重要工具之一,遗传算法在各个领域的优化问题中被广泛应用。
本文将介绍MATLAB中的遗传算法的原理及其应用示例。
一、遗传算法的原理遗传算法(Genetic Algorithm, GA)是一种基于进化的搜索算法,源于对达尔文进化论的模拟。
它模拟了自然界中生物个体基因遗传和自然选择的过程,通过优胜劣汰和进化操作寻找问题的最优解。
遗传算法的基本步骤包括:初始化种群、适应度评估、选择、交叉、变异和进化终止准则。
在初始化阶段,种群中的个体由一组基因表示,基因可以是二进制、实数或其他形式。
适应度评估阶段根据问题的特定要求对每个个体进行评估。
选择操作通过适应度大小选择出较优的个体,形成下一代种群。
交叉操作模拟自然界中的基因交换过程,将不同个体的基因进行组合。
变异操作引入新的基因,增加种群的多样性。
经过多次迭代后,算法会逐渐收敛,并得到一个近似的最优解。
二、遗传算法的应用示例:函数优化遗传算法在函数优化问题中有广泛应用。
以一个简单的函数优化问题为例,假设我们要求解以下函数的最小值:f(x) = x^2 + 5sin(x)首先,我们需要定义适应度函数,即f(x)在给定范围内的取值。
接下来,我们需要设置参数,例如种群数量、交叉概率和变异概率等。
然后,我们可以利用MATLAB中的遗传算法工具箱,通过以下步骤实现函数的最小化求解:1. 初始化种群:随机生成一组个体,每个个体表示参数x的一个取值。
2. 适应度评估:计算每个个体在函数中的取值,得到适应度。
3. 选择:根据适应度大小选择优秀的个体。
4. 交叉:随机选择两个个体进行基因交叉。
5. 变异:对个体的基因进行变异操作,引入新的基因。
6. 迭代:重复步骤2至步骤5,直到达到迭代终止条件。
通过上述步骤,我们可以较快地找到给定函数的最小值。
在MATLAB中,我们可以使用遗传算法工具箱的相关函数来实现遗传算法的迭代过程,如'ga'函数。
matlab 遗传算法 参数

matlab 遗传算法参数摘要:1.MATLAB 简介2.遗传算法简介3.MATLAB 中遗传算法的应用实例4.参数设置对遗传算法性能的影响5.如何在MATLAB 中调整遗传算法参数正文:一、MATLAB 简介MATLAB(Matrix Laboratory)是一款广泛应用于科学计算、数据分析、可视化等领域的商业数学软件。
MATLAB 语言具有高效的矩阵计算能力,丰富的函数库和工具箱,方便用户进行各种复杂数学运算和模拟。
二、遗传算法简介遗传算法(Genetic Algorithm, GA)是一种模拟自然界生物进化过程的优化算法。
遗传算法通过模拟自然选择、交叉和变异等遗传操作,逐步搜索问题空间中的最优解。
遗传算法具有全局搜索能力,适用于解决复杂非线性、非凸优化问题。
三、MATLAB 中遗传算法的应用实例在MATLAB 中,遗传算法工具箱(Genetic Algorithm Toolbox)提供了丰富的函数和应用程序接口(API),方便用户实现遗传算法。
以下是一个简单的遗传算法应用实例:```matlab% 定义问题f = @(x) -sum(x.*sin(x)); % 目标函数:f(x) = -x*sin(x)lb = [-5 -5]; % 种群范围ub = [5 5]; % 适应度函数定义域% 设置遗传算法参数pop_size = 50; % 种群规模um_generations = 100; % 进化代数crossover_rate = 0.8; % 交叉率mutation_rate = 0.1; % 变异率% 运行遗传算法[best_fit, best_solution] = genetic(f, [], [], pop_size,num_generations, crossover_rate, mutation_rate, lb, ub);```四、参数设置对遗传算法性能的影响遗传算法的性能受到多种参数的影响,包括种群规模、进化代数、交叉率、变异率等。
遗传算法MATLAB完整代码

遗传算法解决简单问题%主程序:用遗传算法求解y=200*exp*x).*sin(x)在区间[-2,2]上的最大值clc;clear all;close all;global BitLengthglobal boundsbeginglobal boundsendbounds=[-2,2];precision=;boundsbegin=bounds(:,1);boundsend=bounds(:,2);%计算如果满足求解精度至少需要多长的染色体BitLength=ceil(log2((boundsend-boundsbegin)'./precision));popsize=50; %初始种群大小Generationmax=12; %最大代数pcrossover=; %交配概率pmutation=; %变异概率%产生初始种群population=round(rand(popsize,BitLength));%计算适应度,返回适应度Fitvalue和累计概率cumsump [Fitvalue,cumsump]=fitnessfun(population);Generation=1;while Generation<Generationmax+1for j=1:2:popsize%选择操作seln=selection(population,cumsump);%交叉操作scro=crossover(population,seln,pcrossover);scnew(j,:)=scro(1,:);scnew(j+1,:)=scro(2,:);%变异操作smnew(j,:)=mutation(scnew(j,:),pmutation);smnew(j+1,:)=mutation(scnew(j+1,:),pmutation);endpopulation=scnew; %产生了新的种群%计算新种群的适应度[Fitvalue,cumsump]=fitnessfun(population);%记录当前代最好的适应度和平均适应度[fmax,nmax]=max(Fitvalue);fmean=mean(Fitvalue);ymax(Generation)=fmax;ymean(Generation)=fmean;%记录当前代的最佳染色体个体x=transform2to10(population(nmax,:));%自变量取值范围是[-2,2],需要把经过遗传运算的最佳染色体整合到[-2,2]区间xx=boundsbegin+x*(boundsend-boundsbegin)/(power((boundsend),BitLength)-1);xmax(Generation)=xx;Generation=Generation+1;endGeneration=Generation-1;Bestpopulation=xx;Besttargetfunvalue=targetfun(xx);%绘制经过遗传运算后的适应度曲线。
matlab智能算法代码

matlab智能算法代码MATLAB是一种功能强大的数值计算和科学编程软件,它提供了许多智能算法的实现。
下面是一些常见的智能算法及其在MATLAB中的代码示例:1. 遗传算法(Genetic Algorithm):MATLAB中有一个专门的工具箱,称为Global Optimization Toolbox,其中包含了遗传算法的实现。
以下是一个简单的遗传算法示例代码:matlab.% 定义目标函数。
fitness = @(x) x^2;% 设置遗传算法参数。
options = gaoptimset('Display', 'iter','PopulationSize', 50);% 运行遗传算法。
[x, fval] = ga(fitness, 1, options);2. 粒子群优化算法(Particle Swarm Optimization):MATLAB中也有一个工具箱,称为Global Optimization Toolbox,其中包含了粒子群优化算法的实现。
以下是一个简单的粒子群优化算法示例代码:matlab.% 定义目标函数。
fitness = @(x) x^2;% 设置粒子群优化算法参数。
options = optimoptions('particleswarm', 'Display','iter', 'SwarmSize', 50);% 运行粒子群优化算法。
[x, fval] = particleswarm(fitness, 1, [], [], options);3. 支持向量机(Support Vector Machine):MATLAB中有一个机器学习工具箱,称为Statistics and Machine Learning Toolbox,其中包含了支持向量机的实现。
matlab遗传算法ga工具箱调用gpu运算

matlab遗传算法ga工具箱调用gpu运算全文共四篇示例,供读者参考第一篇示例:Matlab是一个强大的科学计算工具,而遗传算法(Genetic Algorithm,GA)被广泛应用于优化问题的求解。
在大规模优化问题中,GA的求解速度往往是一个瓶颈,为了加速GA的求解过程,可以利用GPU进行并行计算。
在Matlab中,可以通过GPU进行加速的工具箱,称为Parallel Computing Toolbox。
本文将介绍如何利用Matlab的Parallel Computing Toolbox和GA工具箱结合起来,实现GPU加速GA的求解过程。
我们需要在Matlab中安装Parallel Computing Toolbox和GA 工具箱。
在安装完成后,就可以开始编写适用于GPU加速的GA程序了。
在编写程序时,需要注意以下几点:1. 设定GA参数:一般来说,可以设置GA的种群大小、迭代次数、交叉概率、变异概率等参数。
这些参数的设定将直接影响到GA的求解效果和速度。
2. 定义适应度函数:在GA中,适应度函数决定了个体的适应程度,从而影响被选择的几率。
在编写适用于GPU加速的适应度函数时,要注意将计算过程向量化,以便GPU并行计算。
3. 设置GPU运算环境:在Matlab中,可以通过parallel.gpu.GPUDevice函数获取当前可用的GPU设备列表,并选择一个合适的设备进行计算。
在进行GPU计算时,需要将待处理的数据转换为GPU数组,以便GPU并行计算。
4. 调用GA函数并启用GPU加速:在进行GA求解过程中,可以通过设置options参数启用GPU加速。
在调用GA函数时,可以通过设定eParallel参数为true,来启用GPU加速。
下面,我们来看一个简单的例子,演示如何利用Parallel Computing Toolbox和GA工具箱结合GPU加速GA的求解过程。
假设我们要求解一个简单的函数f(x) = x^2 + 5,在区间[-10, 10]内的最小值。
第9讲 MATLAB遗传算法

s3’’=11011(27), s4’’=10000(16)
变异
设变异率pm=0.001。
这样,群体S1中共有
5×4×0.001=0.02
位基因可以变异。 0.02位显然不足 1位,所以本轮遗传操作不 做变异。
● 选择-复制(selection-reproduction)
● 交叉(crossover,亦称交换、交配或杂交)
● 变异(mutation,亦称突变)
选择 - 复制
通常做法是:对于一个规模为 N
的种群 S, 按每个染色体 xi∈S 的选择概率 P(xi) 所决
定的选中机会 , 分 N 次从 S 中随机选定 N 个染色体 ,
(3) 计算各代种群中的各个体的适应度 , 并
对其染色体进行遗传操作,直到适应度最高的个
体(即31(11111))出现为止。
首先计算种群S1中各个体 s1= 13(01101), s2= 24(11000) s3= 8(01000), s4= 19(10011) 的适应度f (si) 。 容易求得 f (s1) = f(13) = 132 = 169 f (s2) = f(24) = 242 = 576 f (s3) = f(8) = 82 = 64 f (s4) = f(19) = 192 = 361
于是,得到第二代种群S2:
s1=11001(25), s2=01100(12)
s3=11011(27), s4=10000(16)
第二代种群S2中各染色体的情况 染色体 s1=11001 s2=01100 s3=11011 适应度 625 144 729 选择概率 0.36 0.08 0.41 积累概率 0.36 0.44 0.85 估计的 选中次数 1 0 2
matlab遗传算法设计

matlab遗传算法设计在MATLAB中设计遗传算法需要遵循以下步骤:1.定义问题参数:首先,你需要定义问题的参数,包括适应度函数、种群大小、交叉概率、变异概率和迭代次数等。
2.初始化种群:根据问题的参数,初始化一个种群,通常可以使用随机数生成器来生成初始解。
3.评估适应度:对于每个个体,计算其适应度值,这通常是通过将个体作为输入参数传递给适应度函数来完成的。
4.选择操作:根据适应度值,选择出适应度较高的个体,用于下一代种群的生成。
5.交叉操作:随机选择两个个体进行交叉操作,生成新的个体。
6.变异操作:对新的个体进行变异操作,以增加种群的多样性。
7.迭代更新:重复上述步骤,直到达到预设的迭代次数或满足终止条件。
8.输出结果:输出最终的种群中最优的个体作为问题的解。
下面是一个简单的MATLAB遗传算法示例代码:matlab复制代码% 遗传算法参数设置popSize = 100; % 种群大小crossoverRate = 0.8; % 交叉概率mutationRate = 0.01; % 变异概率maxGeneration = 100; % 最大迭代次数% 初始化种群pop = round(rand(popSize,1)); % 生成初始种群% 适应度函数(这里假设我们要最小化的目标函数是 x^2)fitnessFunction = @(x) x.^2;% 迭代更新种群for generation = 1:maxGeneration% 评估适应度fitness = fitnessFunction(pop);% 选择操作[newPop,~] = rouletteWheelSelection(pop,fitness);% 交叉操作newPop = crossover(newPop, crossoverRate);% 变异操作newPop = mutation(newPop, mutationRate);% 更新种群pop = newPop;end% 输出最优解[~, bestIndex] = min(fitness);bestSolution = pop(bestIndex);fprintf('最优解:%d\n', bestSolution);在这个示例中,我们使用了轮盘赌选择、均匀交叉和均匀变异等遗传算法的操作。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
%轮盘选择
for i=1:1:popsize
p(i)=f(i)/F;
end
F=0;
for i=2:1:popsize
p(i)=p(i)+p(i-1);
end
for i=1:1:popsize
r(i)=rand(1,1);
if r(i)<=p(1)
Pt(i,:)=Pt(1,:);
else
for j=1:1:L-1
if p(j)<r(i)&r(i)<=p(j+1)
Pt(i,:)=Pt(j+1,:);
break;
end
end
end
end
t=t+1;
end
max=f(1);
for i=2:1:popsize
if f(i)>max
max=f(i);
x1a=x1(i);
x2a=x2(i);
end
end
x1a,x2a,max
%解码
for i=1:1:popsize
for j=1:1:L1
dec=dec+Pt(i,j)*2^(L1-j);
end
x1(i)=a1+dec*(b1-a1)/(2^L1-1);
dec=0;
for j=L1+1:1:L
dec=dec+Pt(i,j)*2^(L-j);
end
x2(i)=a2+dec*(b2-a2)/(2^L2-1);
popsize=100;L=39;L1=21;L2=18;F=0;dec=0;dec1=0;
f=0;p=0;r=0;x1=0;x2=0;
m=0;n=0;cut=0;t=1;max=0;
a1=-3.0;b1=12.1;a2=4.1;b2=5.8;pc=0.25;pm=0.01;
Pt=round(rand(popsize,L));
dec=0;
dec1=0;
for j=L1+1:1:L
dec=dec+Pt(m,j)*2^(L-j);
dec1=dec1+Pt(n,j)*2^(L-j);
end
x2(m)=a2+dec*(b2-a2)/(2^L2-1);
x2(n)=a2+dec1*(b2-a2)/(2^L2-1);
dec=0;
dec1=0;
for i=1:1:popsize/2
r(i)=rand(1,1);
if pc>=r(i)
m=0;n=0;
while m==n
m=randint(1,1,[1 popsize]);
n=randint(1,1,[1 popsize]);
end
cut=randint(1,1,L);
%m,n
for j=cut+1:1:L
dec=0;
%求适应度值
f(i)=21.5+x1(i)*sin(4*pi*x1(i))+x2(i)*sin(20*pi*x2(i));
F=F+f(i);
end
%轮盘选择
for i=1:1:popsize
p(i)=f(i)/F;end NhomakorabeaF=0;
for i=2:1:popsize
p(i)=p(i)+p(i-1);
%求适应度值
f(m)=21.5+x1(m)*sin(4*pi*x1(m))+x2(m)*sin(20*pi*x2(m));
f(n)=21.5+x1(n)*sin(4*pi*x1(n))+x2(n)*sin(20*pi*x2(n));
end
end
%变异
for i=1:1:popsize
r(i)=rand(1,1);
dec=0;
for j=L1+1:1:L
dec=dec+Pt(i,j)*2^(L-j);
end
x2(i)=a2+dec*(b2-a2)/(2^L2-1);
dec=0;
%求适应度值
f(i)=21.5+x1(i)*sin(4*pi*x1(i))+x2(i)*sin(20*pi*x2(i));
F=F+f(i);
Pt(m,j)=Pt(n,j);
Pt(n,j)=Pt(m,j);
end
for j=1:1:L1
dec=dec+Pt(m,j)*2^(L1-j);
dec1=dec1+Pt(n,j)*2^(L1-j);
end
x1(m)=a1+dec*(b1-a1)/(2^L1-1);
x1(n)=a1+dec1*(b1-a1)/(2^L1-1);
end
for i=1:1:popsize
r(i)=rand(1,1);
if r(i)<=p(1)
Pt(i,:)=Pt(1,:);
else
for j=1:1:L-1
if p(j)<r(i)&r(i)<=p(j+1)
Pt(i,:)=Pt(j+1,:);
break;
end
end
end
end
%交叉
while t<=1000
if pm>=r(i)
pos=randint(1,1,[1 L-1]);
Pt(i,pos)=1-Pt(i,pos);
end
end
for i=1:1:popsize
for j=1:1:L1
dec=dec+Pt(i,j)*2^(L1-j);
end
x1(i)=a1+dec*(b1-a1)/(2^L1-1);
较好的一次运行结果:x1a=10.1416 x2a=5.7231 max=37.1035
