5安培环路定理
13-5 安培环路定理

bc
B dl
cd
B dl
da
B dl
Bl 0 Bl 0 2 Bl 0 jl
1 B 0 j 2
B 与
j 符合右手关系。
习题13-8 已知 1.0 105 m2 的裸铜线允许通过50A电 流而不致过热,电流在导线横截面上均匀分布。求: (1)导线内,外磁感强度的分布;(2)导线表面的 磁感强度。 解:电流均匀分布,电流密度为
I j S
R
磁场分布轴对称,取圆形回路,由安培 环路定理得 Bdl 0 I
l
rrLeabharlann I当 rR时,
B1 2 r 0 j r 2
0 Ir 1 1 I B1 0 jr 0 r 2 2 S 2S
方向符合右 手关系
当rR时
B2 2 r 0 I
例2 求载流螺绕环内的磁场
l B d l 2π RB 0 NI 0 NI B 2π R
令
当
2)选回路 .
d
R
L 2 πR
B 0 NI L
2R d 时,螺绕环内可视为均匀场 .
例13-4 无限大均匀载流平面的磁场。
设电流在无限大平面里均匀分布,单位宽度里的 电流为j,试求平面两侧任一点的磁感强度B.
当rR时
0 I B2 方向符合右手关系 2 r 0 I BR 5.6 103 T 2 R
习题13-9 一根很长的同轴电缆,由一半径为 R1 的圆柱形直导体和同轴导体圆筒组成。导体圆筒的内 半径为 R2 ,外半径为 R3 ,圆柱形直导体和同轴 导体圆筒中的电流大小均为I,方向相反,导体的磁性 可不考虑。试计算以下各处的磁感强度:(1)r R1;
简述安培环路定理

简述安培环路定理安培环路定理是由华乐士安培(GeorgeOhm)于1827年发现的一个物理规律,它被认为是电路理论的基础。
它描述了在一个环路中,电流与电阻之间的依赖关系:流过环路的电流量与环路中所有电阻值的乘积总和(称为电动势)之间的绝对值是一定的。
此外,安培环路定理还指出,任何环路均可通过计算环路的总阻抗及电动势的差来确定电流的方向及大小。
安培环路定理的数学表达式为:V=I×R,其中,V表示电动势,I表示电流和R表示环路中的总阻抗。
在安培环路定理中,电流的方向是从电动势高的一端流向低的一端。
安培环路定理可以让我们更加清楚地了解电路中电流的变化规律。
它有助于我们在分析电路中发生的物理过程、计算电路参数与解决电路问题方面取得进展。
由于安培环路定理可以深入地探究电路的内部机制,因此它也被广泛应用于电路的设计和分析。
安培环路定理在实际应用中可以用来计算电路中的电流或电压。
例如,当给定一个电路的构成以及电阻值后,可以根据安培环路定理计算电流的大小及方向。
此外,安培环路定理还可以用来计算环路中的其他参数,例如比较电阻值之间的差异,根据两个电压之间的差异求出电阻,以及计算某一电阻下的电流值等。
安培环路定理的本质是电路的经验定律,因此在其定义中并没有出现物理概念,但其实安培环路定理是建立在一定的假设之上的。
其一,指出环路中电流的数量只依赖于环路中电阻的总和,即环路中所有电源的电动势,不受它们之间的接线方式所影响;其二,安培环路定理只适用于线性的电路,即电阻的值不会随着电流的变化而有所变化。
安培环路定理是电路理论的重要组成部分,其简洁的数学表达式和有效的计算方法的实用性,使它成为不可或缺的物理定律之一。
它的发现也为进一步探索电路设计问题提供了帮助,因此,它在电路设计中有着深远的影响。
安培环路定理

安培环路定理
安培环路定理,又称为安培定理或安培第二定理,是电磁学中的一条重要定理,描述了由电流所产生的磁场的性质。
它是由法国物理学家安德烈-玛丽·安培在19世纪初提出的。
安培环路定理是基于麦克斯韦方程组中的一个方程,可以用来计算磁场的强度。
根据该定理,通过电流所形成的磁场的磁感应强度H,沿着任意封闭曲线所围成的面积S的总磁通量Φ,与该封闭曲线所围成的电流之间的关系为:
∮H·dl = ∫∫S B·dS = Φ
其中,H是磁场的强度,dl是沿着闭合曲线的微元路径元素,B是磁感应强度,dS是平面面元素,Φ是通过该曲线所围成的面积的磁通量。
安培环路定理本质上是一个积分方程,可以通过对曲线的路径和曲面的选择来灵活地应用。
根据闭合曲线的选择不同,可以得到更方便的计算磁场的方法。
通常情况下,选择封闭曲线为简单的几何形状,例如圆形、矩形或直线,可以大大简化计算的过程。
安培环路定理的应用广泛,可以用于解决与电流所产生的磁场相关的问题。
例如,在电磁铁中,可以利用安培环路定理计算铁芯的磁场分布;在电感器中,可以通过该定理计算电感量。
此外,还可以利用安培环路定理推导出其他电磁学中的重要定理,如磁场的叠加定理和比奥-萨伐尔定律等。
综上所述,安培环路定理是电磁学中的一条基本定理,描述了电流所产生的磁场的性质。
通过应用安培环路定理,可以方便地计算出磁场的强度和分布,解决各种与电流和磁场相关的问题,为电磁学的研究和应用提供了重要的理论基础。
大学物理 5.4 磁场的安培环路定理
l
B
例2 载流长直螺线管磁场分布
如图,均匀密绕无限长直
螺线管通有电流为I,单位
长度匝数为n)
I
解:对称性分析—— 管内垂轴
b
Ba
平面上任意一点与 B轴平行
cd b c d a
(3)磁场是有旋场 —— 电流是磁场涡旋的轴心
B dl —— 不代表磁场力的功,仅是磁场与电流的关系
L
(4)安培环路定理只适用于闭合的载流导线,对于任 意设想的一段载流导线不成立
2. 安培环路定理的应用
在静电场中,当带电体具有一定对称性时 可以利用高斯定理很方便的计算其电场分布。 在恒定磁场中,如果电流分布具有某种对称性, 也可以利用安培环路定理计算电流磁场的分布。
由 于 这 时 I 内 =0 , 所 以 有 B=0 (在螺线环外)
l2
l1
可见,螺线环的磁场集中在
环内,环外无磁场。
对载流长直密绕螺线管,若线圈中通有电流强度为I的电
流,沿管长方向单位长度上的匝数为n,则由安培环路定理容
易求得:管内: B onI
说明
(1)积分回路绕行方向与电流方向呈右螺旋
关系
满足右螺旋关系时 Ii 0 反之 Ii 0
I
1
I
I
3
2l
I I
l
l B dl o ( I1 I2 ) l B dl o ( 2I I) oI
(2)公式中的 B 是环路上的磁感应强度,使
空间所有电流共同激发的。
L
B
LB
dr
安培环路定理

(1)管内:取L矩形回路 abcda
边在轴上,两边与轴平行,另
aP b
两个边垂直于轴。
LB dl Bab ab Bcd cd Bab ab
e
Q
f
0I 0nI ab
d
c
∞
B内 onI 其方向与电流满足右手螺旋.
(2)管外 :
取回路efbae同理可证,无限长直螺线管外任一点的磁场为
A(rQ )
0I 2
ln
r Q
r P
A(rP )
A(rQ
)
0I 2
ln
r Q
r
-I
r P
P
两式相加,得:
A(rP )
A(rQ )
0I 2
ln
rQ rP
rP rQ
0I 2
ln
rP rP
A(rP )
A(rQ )
0I 2
ln
r P
r P
若选Q点的矢势为零,则
A(rP )
0I 2
ln
r P
r P
例2.一无限长载流圆柱导体,半径为R, 电流I均匀分布
ldr
0I 2
l
ln
rQ r
A(rP ) A(rQ )
0I 2
ln
rQ rP
+I
Q
若选Q点的矢势为零,则
A(rp
)
0I 2
ln
rQ rP
r P
注意:若选Q点在无穷远处或导线
上,磁矢势将无意义.
讨论:两根平行的载流直导线,电流大 小相等方向相反,求磁矢势.
选Q点在两直线电流之间垂线的中点处.
A(rP )
B dS 0
安培环路定理表达式 -回复

安培环路定理表达式 -回复
安培环路定理的表达式是:对任意闭合路径,线积分∫B·dl=μ0I。
在此公式中,B表示环路中的磁感应强度,dl表示线元,I表示通过闭合路径环绕的电流总和,μ0表示真空中的磁导率。
实际上该公式说明了电流产生磁场的本质规律,是磁场理论中的重要公式之一。
安培环路定理的应用广泛,例如在计算无限长直导线的磁场、螺线管磁场等问题中有着重要作用。
公式中的线积分∫B·dl可以理解为沿着闭合路径的磁感线密度的积累,而μ0I则代表了通过该闭合路径的净电流。
此外,安培环路定理的形式相当通用,可以适用于电流密度不随时间变化的情况,也可以适用于时变电场中的情况。
安培环路定理的适用性由电磁场的洛伦兹力公式保证。
在实际应用中,安培环路定理一般结合对称性进一步简化计算。
例如在无限长直导线的磁场计算中,由于磁场对于离线的距离具有对称性,因此我们可以选择一个以导线为圆心的环路进行计算,进而得到磁场与离线距离的函数关系。
同理,在计算螺线管磁场时,也可以选择一个以螺线管轴线为中心的矩形环路进行计算,以简化问题。
总得来说,安培环路定理是电磁学中的一大重要工具,说明了磁场源于电流这一基本观点,对于我们理解和研究电磁现象有着重要意义。
5安培环路定理(大学物理 - 磁场部分)

安培环路定理
一、定理表述
磁感应强度沿闭合回路的线积分, ( B 的环流),等于环路所包围的电流 代数和乘以 0。
L B dl 0 I
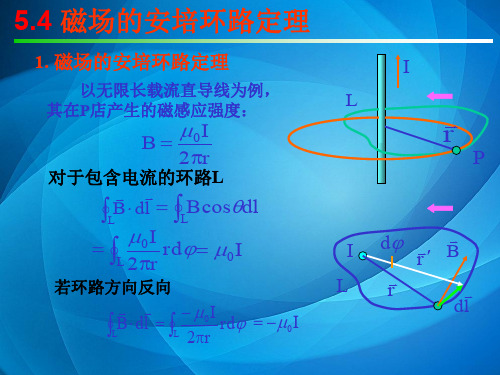
二、定理证明 特例:以无限长载流直导线为例。
§5.安培环路定理 / 一、表述。二、证明
长直导线周围的 B 线为一系列的同 心圆,选取路径方 向与 B 相同;
B 0nI
§5.安培环路定理 / 六、举例
例3:一环形载流 螺线管,匝数为 N ,内径为 R1 , 外径为 R2 ,通有 电流 I ,求管内磁 感应强度。
解:在管内作环路 半径为 r , 环路内电流代数和为
I NI
§5.安培环路定理 / 六、举例
o R1 rR
2
L B dl 0 I
r < R 区域
§5.安培环路定理 / 六、举例
I
R
选取半径为 r 的环路, 环路内电流代数和为: 2 r I 2 I r I 2 2 R R
Bdl cos 0 I
I
R
由于环路上各点 B 大小 相等,方向 B // dl 0 , cos 1
§5.安培环路定理 / 六、举例
B2r 0 NI
0 NI B 2r 当 r >> ( R2 – R1) 时
N n 2r
o R1 rR
2
为沿轴向线圈密度;
B 0nI 与直螺管的结论一致。
§5.安培环路定理 / 六、举例
例4:圆柱形载流导 体半径为 R ,通有 电流为 I ,电流在 导体横载面上均匀 分布,求圆柱体内、 外的磁感应强度的 分布。 解:1.圆柱体内部
解:理想密绕螺线 管,管内的磁场是 均匀的,管外的磁 场为 0 ;
安培环路定理的原理及应用

安培环路定理的原理及应用1. 安培环路定理的原理安培环路定理是电磁学中的基本定理之一,它描述了电流通过一个封闭路径的总和等于该路径上环绕的总磁场的空间积分。
安培环路定理是麦克斯韦方程组中的一部分,对于理解和分析电路中的电磁现象非常重要。
根据安培环路定理,一个封闭路径上的环绕磁场的空间积分等于该路径上的电流的总和乘以真空中的磁导率常数,即:$$\\oint \\vec{B} \\cdot \\vec{dl} = \\mu_0 \\cdot I_{\\text{enc}}$$其中, - $\\vec{B}$ 表示磁场的矢量 - $\\vec{dl}$ 表示路径上的无穷小位移矢量 - $\\mu_0$ 是真空中的磁导率常数 - $I_{\\text{enc}}$ 表示通过封闭路径所包围的电流的总和2. 安培环路定理的应用2.1 电磁铁电磁铁是利用安培环路定理工作的重要装置之一。
在电磁铁中,通电线圈产生的磁场可以吸引或排斥物体,从而实现各种实际应用。
根据安培环路定理,我们可以通过改变通电线圈中的电流大小来控制磁场的强度,进而达到对物体的吸引或排斥。
2.2 变压器变压器也是应用安培环路定理的重要设备。
变压器是一种用于改变交流电压的装置,它由两个共用一个磁路的线圈构成。
输入线圈(原线圈)中的交流电流通过变压器的磁场感应出感应电动势,进而产生在输出线圈上的输出电压。
安培环路定理被用于分析和计算变压器中的磁场和电流之间的关系。
2.3 电感与电感耦合安培环路定理在电感和电感耦合的研究和应用中也起到了重要作用。
电感是一种储存电能的元件,当电流通过电感时,会在其周围产生磁场。
根据安培环路定理,我们可以得到电感中的磁场与电流的关系,从而进一步分析和设计电感相关的电路。
而电感耦合是指通过电感的互相感应,将两个或多个电路联系起来。
在电感耦合的应用中,安培环路定理可用于计算和描述各个电路之间的电磁相互作用,以及电感耦合的性能与参数之间的关系。
安培环路定理的三个公式

安培环路定理的三个公式安培环路定理是电磁学中的一个重要定理,它描述了磁场的环流与电流之间的关系。
在这个定理中,有三个常用的公式,下面咱们就来好好唠唠这三个公式。
咱们先来说说第一个公式,这个公式表述为:在真空中,磁感应强度 B 沿任何闭合回路的线积分,等于穿过该回路所包围面积的电流的代数和乘以真空磁导率μ₀。
这听起来可能有点绕,咱举个例子啊。
就比如说,你想象有一个环形的电线,电流在里面流动。
咱们把这个环形电线想象成一个跑道,而磁场呢,就像是在跑道上奔跑的运动员。
这个运动员沿着跑道跑一圈,他跑的路程就是磁感应强度 B 的线积分。
而跑道里面的电流,就决定了这个运动员跑得有多快、跑的路程有多长。
再来讲讲第二个公式。
这个公式在有介质存在的情况下适用。
啥是介质呢?简单说,就是除了真空以外的其他物质。
这时候,磁感应强度 B 沿闭合回路的线积分,等于穿过回路所包围面积的传导电流和磁化电流的代数和乘以真空磁导率μ₀。
咱还是举个例子。
假设你有一块磁铁,周围有一些铁粉。
这些铁粉会被磁铁吸引,形成特定的分布。
这个分布就相当于一种介质。
在这种情况下,磁场的环流就不仅仅取决于传导电流,还和磁化电流有关。
最后说说第三个公式。
这个公式是在时变电磁场中的情况。
它可就更复杂一点啦,磁感应强度 B 沿闭合回路的线积分,等于穿过回路所包围面积的全电流的代数和乘以真空磁导率μ₀。
这里的全电流包括传导电流、位移电流。
那啥是位移电流呢?想象一下,有一个电容器正在充电,虽然没有电荷在电容器极板之间流动,但是电场在变化,就好像有电流在流动一样,这就是位移电流。
我记得之前给学生们讲这部分内容的时候,有个小家伙瞪着大眼睛一脸懵地问我:“老师,这也太抽象了,到底有啥用啊?”我笑着跟他说:“孩子,你想想咱们家里用的电器,比如电灯泡能亮、风扇能转,这里面可都离不开这些知识呢。
”那孩子似懂非懂地点点头。
其实啊,安培环路定理的这三个公式虽然看起来复杂,但在实际的电磁学应用中可是非常重要的。
磁场的安培环路定理公式

磁场的安培环路定理公式安培环路定理(Ampere's Circuital Law)是电磁学中的一个重要定理,描述了电流所产生的磁场的性质。
该定理是由法国科学家安德烈·玛丽·安培于1826年提出的。
安培环路定理公式可以用来计算闭合曲线上的磁场和电流之间的关系。
安培环路定理可以表述如下:在真空中,闭合曲线上的磁场的环流等于通过该闭合曲线所围成的面内的电流的代数和的N倍,即B·l=μ0·N·I。
其中,B表示磁场强度,单位为特斯拉(T);l表示闭合曲线的长度,单位为米(m);μ0表示真空中的磁导率(磁场的常量),约等于4π×10^-7N/A^2;N表示闭合曲线所围成的面内的匝数;I表示通过该闭合曲线所围成的面内的电流,单位为安培(A)。
这个公式表明了闭合曲线上的磁场强度与该闭合曲线所围成的面内电流的代数和成正比。
当电流的方向与闭合曲线所围成的面的法线方向相同时,为正;而当电流的方向与闭合曲线所围成的面的法线方向相反时,为负。
安培环路定理的应用非常广泛。
通过安培环路定理,我们可以计算出闭合曲线上的磁场强度,从而了解电流所产生的磁场的强度和分布情况。
此外,我们还可以通过安培环路定理来计算导线上的磁场,从而提前预测电流的影响范围和磁场的强度。
安培环路定理的一个重要应用是计算长直导线产生的磁场。
对于一根长度为l的直导线,安培环路定理公式可以简化为B=μ0·I/2πr,其中r为距离导线的垂直距离。
另一个应用是计算无限长薄直导线产生的磁场。
在这种情况下,合理的选择闭合曲线为无限大的圆形曲线,通过计算可以得到B=μ0·I/2r,其中r为距离导线的垂直距离。
安培环路定理还可以应用于计算线圈产生的磁场。
对于一个具有N匝的螺线管,安培环路定理的公式可以表示为B·2πr=μ0·N·I,其中B 为螺线管中心处的磁场强度,r为距离螺线管中心的距离。
简述安培环路定理

简述安培环路定理
安培环路定理,又称电流定律,是电子技术中重要的基本定理。
它是1745年由安培发现的。
它指出,任何完整封闭环路中,由电源或电容器提供的电势差总称为电势差V。
电流I在环路中以电导率γ流通,所以电流I可以用以下公式来表示:V=I x。
安培环路定理是一组电路定理,主要涉及电流、电压、电阻以及电势。
它是建立在电流流向定律(也称作Kirchhoff定律)的基础上的。
它是基于物理和电路学的几个事实和原理,由电流定律(也称作Kirchhoff定律)定义的。
安培环路定理中假定所有元件都是线性元件。
安培环路定理以及电流定律可以用于确定任何给定环路中穿过
它的电流及电压,从而形成电路的基本模型。
它可以用来解决复杂的电路,如多节点电路、三极管电路、反馈电路、脉冲电路、放大器等,它是电子技术中最重要的基本定理之一。
安培环路定理的另外一个重要的应用就是确定电路的性能参数。
比如,可以用它来确定电路的电阻、电容、电感以及参数等。
如果把它们结合起来,可以很快地计算出电路的稳定性、增益以及频率响应特性。
安培环路定理可以应用于不同理论,以及不同技术领域,比如电子技术、电路技术、数学理论等。
安培环路定理是电子技术中一个重要的基础,几乎所有的电子设计都会用到它。
总之,安培环路定理是一个重要的电子理论,它可以用于设计现
代电子设备。
它可以用来解决复杂的电路,并且可以确定电路的性能参数。
它也被广泛用于不同的理论和技术领域,所以它在现代电子技术中起到了重要的作用。
8-5 安培环路定理

dl dl dl //
L
dl
0 I l B dl 2π Rdl B dl 0 I
l
L I dl dl // dl
B dl
L
L
B dl //
I
2π R 2 I B 0 2π r
0 I
2π R
B
0 r 2π rB 2 I R
2
0 Ir B 2π R 2
R
o R
r
例3 无限长载流圆柱面的磁场
L1
r
R
I
L2
解:
0 I 2π R
B
r
o R r
0 r R, B d l 0 B 0 l 0 I r R, B d l 0 I B
l
I2
I3
l
结论:在真空的稳恒磁场中,
磁感强度 B 沿任一闭合路径的 积分(即 B 的环流) 的值,等于
说明 1.表达式中的 B是闭合回路上的 磁感强度, I i指闭合回路内所 包围的电流强度的代数和. 当 I i 与L的绕行方向呈右手螺旋关 系, I i 0 ,反之 I i 0 ;不穿 过L 的电流对 B 的环流无贡献。 讨论:
磁感强度 B B dS 0
S
B dl 0
I
i
场性质
有源场,电场线始于正 无源场(涡旋场),磁感 电荷、终于负电荷,保 线无始无终,非保守场 守场(有电势能) (无磁势能)
二、安培环路定理的应用举例 解题思路和方法 1) 对称性分析;
安培环路定理

安培环路定理什么是安培环路定理?安培环路定理(Ampere’s Circuital Law),简称「安培定理」,是电磁学中的一个重要定理。
它描述了在电流通过的闭合回路周围所产生的磁场的性质。
安培环路定理是电磁学理论中的基础之一,为理解和推导电磁现象提供了重要的工具。
安培环路定理的表述安培环路定理可以用以下的数学表达方式来描述:∮ B · dl = μ₀ · I其中,左边是磁场强度(B)沿闭合回路的环路积分,右边是穿过该闭合回路的电流(I)乘以真空磁导率(μ₀)。
安培环路定理的原理安培环路定理的原理是基于磁场的环流与通过该闭合回路的电流之间的关系。
根据安培环路定理,磁场强度沿一个闭合回路的环路积分等于穿过该闭合回路的总电流。
这个原理可以通过法拉第定律和电流的产生方式来理解。
根据法拉第定律,变化的磁场会产生电流。
当通过一个闭合回路的电流发生变化时,它会产生一个变化的磁场。
根据安培环路定理,通过这个闭合回路的环流与产生的磁场有直接关系。
通过积分环路上的磁场求和,我们可以得到与通过闭合回路的总电流相等的结果。
安培环路定理的应用安培环路定理在电磁学中的应用非常广泛。
它可以用于解决许多关于磁场和电流之间相互作用的问题。
1. 计算特定位置的磁场强度通过安培环路定理,我们可以计算在给定位置的磁场强度。
通过选择一个合适的闭合回路,并测量通过该回路的电流,可以通过安培环路定理计算出该位置的磁场强度。
2. 推导磁场分布通过运用安培环路定理和其他相关定理,我们可以推导出复杂电流分布下的磁场分布。
这对于设计和分析电磁装置,如电机和电感器,非常重要。
3. 求解电流分布在某些情况下,已知磁场分布和闭合回路上的磁场强度分布,我们可以使用安培环路定理求解闭合回路上的电流分布。
结论安培环路定理是电磁学中的一个基本定理,描述了闭合回路周围产生的磁场与通过该回路的电流之间的关系。
它广泛应用于计算特定位置的磁场强度、推导磁场分布和求解电流分布等领域。
安培环路定理的推导与应用

安培环路定理的推导与应用安培环路定理是电磁学中的重要定律之一,它描述了电流在闭合回路中所围成的磁通量与电路中的总电流的关系。
本文将对安培环路定理的推导进行讲解,并介绍一些其在实际应用中的例子。
一、安培环路定理的推导安培环路定理是由法国物理学家安培在19世纪初提出的。
它的数学表达形式是:∮B·dl = μ0·I其中,∮B·dl表示磁场B在闭合回路上的环路积分,μ0为真空中的磁导率,I为该回路中的总电流。
推导安培环路定理的基本思路是利用法拉第电磁感应定律和高斯定理。
我们知道,根据法拉第电磁感应定律,磁感应强度B的变化率与电场强度E的闭合回路积分之比等于贯穿该回路的总电流I:∮(B·dl)/(dt) = -∫E·ds = -dΦE/dt其中,ΦE表示电场的通量。
再根据高斯定理,可以将闭合回路上的磁场积分转化为磁通量的二重积分:∮B·dl = ∬(∇×B)·dS结合以上两个式子,可得到安培环路定理的数学表达式:∬(∇×B)·dS = -μ0·dΦE/dt = -μ0·d/dt(∬E·dS)经过进一步的推导和化简,可以得到安培环路定理的最终形式。
二、安培环路定理的应用安培环路定理可以应用于各种电磁场问题的求解中,下面将介绍几个实际应用的例子。
1. 电磁铁电磁铁是一种利用电流通过线圈时产生的磁场吸引铁磁物质的装置。
根据安培环路定理,可以计算电磁铁中磁场的分布情况,从而设计合适的线圈参数,使得电磁铁的吸引力能够满足实际需求。
2. 变压器变压器是一种利用电磁感应原理来改变电压的装置。
在变压器的设计和工作过程中,安培环路定理可以用来分析和计算铁芯中的磁场分布情况,从而确定绕组的布置和匝数比。
3. 电感电感是电路中常见的一种元件,它的基本单位是亨利(Henry)。
利用安培环路定理,可以计算电感器中的磁场分布情况,从而更好地理解和分析电感元件的特性。
05-安培环路定理

IB U V1 V2 k d 1 k RH nq
霍耳效应的应用
UH
1 IB nq b
1、确定半导体的类型 n型半导体载流子为电子 p型半导体载流子为带正电的空穴 2、根据霍耳系数的大小的测定, 可以确定载流子的浓度
3、测定磁场 霍耳效应已在测量技术、电子技术、计算 技术等各个领域中得到越来越普遍的应用。
磁流体发电 在导电流体中同样会产生霍耳效应
导电气体
B q q 发电通道
电极
磁流体发电原理图
使高温等离子体(导电流体)以1000ms-1的高速进 入发电通道(发电通道上下两面有磁极),由于洛仑 兹力作用,结果在发电通道两侧的电极上产生电势差 。不断提供高温高速的等离子体,便能在电极上连续 输出电能。
B
f 0
v v0
粒子做直线运动
× × × × × × × × × × × × ×
f qvB
v qvB m R
2
mv R qB
×f ×
q
×
×B
v ×
× × × × ×
× ×
× × × × ×
2R 2m T v qB
粒子做匀速圆周运动
( 3) v与B 成角
为垂直于B的方向向上。即从 上往下俯视,线圈是逆时针转动
B
60 0
B n
俯视图
4
带电粒子在电场和磁场中的运动
一、若电场和磁场同时存在:
F Fe Fm qE qv B
洛伦兹 力
二、 带电粒子在磁场中的运动
f qv B
安培环路定理知识点

安培环路定理知识点安培环路定理(Kirchhoff's loop rule),又称为基尔霍夫环路定律,是电路分析中的重要基本原理。
它描述了在闭合电路中电流的流动规律,从而帮助我们理解和解决各种电路问题。
本文将介绍安培环路定理的定义、原理和应用。
一、安培环路定理的定义安培环路定理是基于电荷守恒定律和电场的环路定理推导而来的。
根据安培环路定理,在任何一个闭合电路中,电流的代数和必须等于零,即电流在电路中经过各分支的代数和等于电流离开电路的代数和。
二、安培环路定理的原理1. 闭合电路的特性安培环路定理适用于闭合电路,即电流可以通过一条回路从一个点流向另一个点。
闭合电路是电流分析的基本前提,只有满足闭合条件,安培环路定理才能有效地应用。
2. 电流的代数和为零根据安培环路定理,电流的代数和在闭合电路中必须等于零。
这是因为电流在电路中没有被消耗或产生,而是通过各分支流动,因此电流的代数和保持平衡。
3. 方向与正负号在应用安培环路定理时,我们需要为电路中的每个分支选择一个参考方向,并赋予正负号。
一般来说,沿着参考方向流动的电流取正号,相反方向流动的电流取负号。
4. 电阻和电动势根据欧姆定律,电阻中的电流与电压成正比。
在安培环路定理中,我们可以使用电阻和电动势(如电池或电源)来描述电路中的元件。
电动势提供了驱动电流流动的能量。
三、安培环路定理的应用1. 电路分析安培环路定理是电路分析中常用的工具,特别适用于复杂电路的分析。
通过将电路划分为多个闭合回路,并应用安培环路定理,我们可以解析电流和电压的分布,找到各个分支中的电流大小和方向。
2. 电源电流计算在电路中,电源提供了电流的驱动力。
应用安培环路定理,我们可以通过计算各个分支中的电流来确定电源的输出电流。
这对于设计电路和选择合适的电源非常重要。
3. 电感和电容的分析除了电阻和电源外,安培环路定理也适用于电感和电容。
在交流电路中,电感和电容的特性可以通过安培环路定理来分析,并计算它们在电路中的作用。
安培环路定理

结论
所以有: 从载流直导线中心O出发,可以作许多条射线,将环路分割成许多成对的线元,磁感强度对每对线元的标量 积之和,都有上式的结果,故即环路不包围电流时,B的环流值为零。 安培环路定理反映了磁场的基本规律。和静电场的环路定理相比较,稳恒磁场中B的环流,说明稳恒磁场的 性质和静电场不同,静电场是保守场,稳恒磁场是非保守场。
微分形式
根据开尔文-斯托克斯定理,这方程也可以写为微分形式。只有当电场不含时间的时候,也就是说,当电场 对于时间的偏微分等于零的时候,这方程才成立。采用国际单位制,这方程表示为
。 磁场的旋度等于(产生该磁场的)传导电流密度。
缺点
缺点
原版安培定律只适用于静磁学。在电动力学里,当物理量含时间,有些细节必须仔细检查。思考安培方程, ;
简介
积分形式
微分形式
ห้องสมุดไป่ตู้分形式
电流I在一个曲面上的通量,等于B场沿着的边缘闭合回路的路径积分。采用国际单位制,原版安培定律的积 分形式可以写为:
。
请注意到这方程有些模糊之处,需要特别澄清: 第一,边界曲线的正向与曲面的侧符合右手规则。 第二,(固定 )定理之成立与以为边界的的选择无关。
安培定律可由毕奥-萨伐尔定律和磁场的叠加性证明(请参阅毕奥-萨伐尔定律)。在静磁学中,安培定律的 角色与高斯定律在静电学的角色类似。当系统组态具有适当的对称性时,我们可以利用这对称性,使用安培定律 来便利地计算磁场。例如,当计算一条直线的载流导线或一个无限长螺线管的磁场时,可以采用圆柱坐标系来匹 配系统的圆柱对称性。
证明方法
对称环路 任意环路
不包围电流 结论
对称环路
在垂直于长直载流导线的平面内,以载流导线为圆心作一条半径为r的圆形环路l, 则在这圆周上任一点的磁感强度H的大小为 其方向与圆周相切.取环路的绕行方向为逆时针方向,取线元矢量dl,则H与dl间的夹角,H沿这一环路 l 的环流为 式中积分是环路的周长。 于是上式可写成为 从上式看到,H沿此圆形环路的环流只与闭合环路所包围的电流I有关,而与环路的大小、形状无关。
安培环路定理的表述和证明

安培环路定理的表述和证明磁感应线是套连载闭合载流回路上的闭合线。
若取磁感应强线的环路积分,则因B与dL的夹角θ=0,cosθ=1,故在每条线上,从而。
安培环路定理就是反映磁感应这一特点的。
安培环路定理:磁感应强度沿任何闭合环路L的线积分,等于穿过这环路全部电流强度的代数和的μ0倍。
用公式表示有: 。
其中电流I的正负规定如下:当穿过回路L的电流方向与回路L的环绕方向听从右手法则时,I0,反之,I0。
假如电流不穿过回路L,则它对上式右端无贡献。
安培环路定理的证明,如图:dL是L上的线元,dL'代表载流回路L'上的线元。
根据毕奥-萨伐尔定律:其中代表dS对场点P所张的立体角dω,沿L'的积分代表整个载流回路作位移-dl时扫过的带状面对P点所张的立体角ω。
所以。
假设以L'为边界作一曲面S',S'对P点也张有肯定的立体角Ω。
当L'平移时,Ω随之转变。
如上图L2'和L1'分别是L'沿-dl平移前后的新、旧位置,令S2'和S1'代表S'的相应位置,Ω2和Ω1代表相应的立体角。
因S2'和S1'和带状面组成闭合曲面,它对于外边的P点所张的总立体角Ω2-Ω1+ω=0,所以:由于dl是任意的,从而,即磁场正比于载流线圈对场点所张立体角的梯度。
假设场点P沿闭合的安培环路L移动一周,则环路积分将正比于立体角Ω在此过程中的总转变量ΔΩ。
假如L不与L'套连,则ΔΩ=0,于是: 但是,当L与L'套连时,ΔΩ=4π。
因此:。
所以安培环路定理得证。
留意:该定理表达式中各物理量的意义。
I只包括穿过闭合回路L的电流。
B代表空间全部电流产生的磁场强度的矢量和,其中也包括那些不穿过L的电流产生的磁场,只不过后者的磁场沿闭合环路积分后的总效果为0。
I只包括穿过闭合回路L的电流。
安培环路定理物理含义

安培环路定理是物理中的一个重要定律,它表示了能量传递和守恒。
通过这个定律,我们可以对许多现象进行很好的解释:例如,为什么光能够沿直线传播?为什么两物体之间会有引力作用?这些都与能量守恒定律有关。
1:安培环路定理的由来安培环路定理是一个基本的物理定理,它描述了电流环闭合时电荷守恒。
根据这一定理,我们可以得出结论:如果电流不能够完全通过导线,那么电流就不能穿过这条线路。
为了证明这个定理,物理学家们利用了一个简单得多的例子来说明其作用:假设有一条电路板上连接着两台电脑,其中一台装有电子数据处理软件。
当两条电线接入该电路板中的两根导线时会出现问题,因为此时电流无法顺利流过这条路。
但是,如果在另一根导线的两端接上电阻器或电容器之后,情况则会大不相同。
2:安培环路定理物理含义安培环路定理是一个数学概念,用来表示直线上两点之间的距离等于这两点间的总距离。
它可以简单地理解为:在一条射线PA上有一点E′,而在另一条射线PB上也有同样数量的点C′,根据“E”-PA定律,如果我们将这条射线从C点到D点画一条弧线,那么经过这条弧线PA到D点的垂足长度就等于它们的距离比,这个比值叫做安培环路系数<s56>Jacquency Fraction<s0>。
通过使用安培环路定理,人们能够很容易计算出任意两点之间的距离。
要想运用这个定理,需要知道其中两个点的坐标。
例如,如果我们要测量地球上某一点至其北极点或南极点之间的距离,只需找到该处并画出一条直线即可。
然而,要精确测量两点之间的距离,需要精确测量每段路程中所有可能经过的点。
3:如何运用安培环路定理如何运用安培环路定理是一个非常重要的问题。
它可以帮助我们理解许多物理现象,比如电场和磁场。
安培环路定理表明:两个运动物体之间会产生一种相互作用——互相吸引、相互排斥或者“推拉”。
这就是为什么在同一个封闭空间里存在着大小相等而方向相反的力。
这个定律也被应用于能量守恒和动量守恒定律中。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
L
B ∫ dl = B 2 π r = µ0 ∑ I 2 r B 2πr = µ0 2 I R
I
µ0I B = r ∝r 2 2π R
2.圆柱体外一点 圆柱体外一点 r > R 区域 在圆柱体外作一环路, 在圆柱体外作一环路,
§5.安培环路定理 / 六、举例 安培环路定理
L L
r R r
环路内电流代数和为: 环路内电流代数和为:
§5.安培环路定理 / 六、举例 安培环路定理
例4:圆柱形载流导 : 体半径为 R ,通有 电流为 I ,电流在 导体横载面上均匀 分布,求圆柱体内、 分布,求圆柱体内、 外的磁感应强度的 分布。 分布。 解:1.圆柱体内部 圆柱体内部 r < R 区域
§5.安培环路定理 / 六、举例 安培环路定理
§5.安培环路定理 / 二、定理证明 安培环路定理
µ0I 2π r = µ 0 I 左边= 左边 B ∫ dl = 2π r L
右边= µ0 ∑ I = µ0 I 右边 I L
∴ 左边 右边 定理成立。 左边=右边 定理成立。 推广到任意路径都成立,证毕。 推广到任意路径都成立,证毕。 三、明确几点 ∫L B ⋅ dl = µ0 ∑ I
∑ I =I ∫ Bdl cos θ = µ 0 ∑ I
I
由于环路上各点 B 大小 相等, 相等,方向 B // d l , θ = 0 , cosθ = 1
B ∫ dl = B 2 π r = µ0 I
R
r
L
µ0I 1 B = ∝ 2π r r
§5.安培环路定理 / 六、举例 安培环路定理
分布曲线 B
§5.安培环路定理 / 四、选取环路原则 安培环路定理
或 B⊥dl ,
cosθ = 0
3.环路要经过所研究的场点。 环路要经过所研究的场点。 环路要经过所研究的场点
§5.安培环路定理 / 四、选取环路原则 安培环路定理
五、解题方法 场对称性分析; 1.场对称性分析; 场对称性分析 2.选取环路; 选取环路; 选取环路 3.确定环路内电流的代数和 ∑ I ; 确定环路内电流的代数和 4.应用环路定理列方程求解。 应用环路定理列方程求解。 应用环路定理列方程求解 应用环路定理求 B 要比毕萨定律简 但只适用于具有高度对称的场。 单,但只适用于具有高度对称的场。
§5.安培环路定理 / 三、明确几点 安培环路定理
环路定理对有限电流不适用。 环路定理对有限电流不适用。 例如:将环路定理用到有限电流。 例如:将环路定理用到有限电流。 沿磁力线作半径为 r 的环路 ∫ B ⋅ dl = B ∫ dl =µ0 I r B ⋅ 2πr = µ0 I L µ0 I B= 2πr 矛盾, 与无限电流磁感应强度相同 ,矛盾,对有 限电流不适用。 限电流不适用。
第五节 安培环路定理
一、定理表述 磁感应强度沿闭合回路的线积分, 磁感应强度沿闭合回路的线积分, 的环流), ),等于环路所包围的电流 ( B 的环流),等于环路所包围的电流 代数和乘以 µ0。
∫L B ⋅ dl = µ0 ∑ I
二、定理证明 特例:以无限长载流直导线为例。 特例:以无限长载流直导线为例。
Q B⊥dl , cosθ = 0
b
d c
∫ B ⋅ dl = 0
...............
a
b
B
Q 螺线管外B =0; 螺线 ∴ ∫ B ⋅ dl = ∫ B ⋅ dl
a b
d
c
= B ab = µ0 ∑ I = µ0nabI
B = µ0nI
§5.安培环路定理 / 六、举例 安培环路定理
例3:一环形载流 : 螺线管, 螺线管,匝数为 N ,内径为 R1 , 外径为 R2 ,通有 电流 I ,求管内磁 感应强度。 感应强度。 解:在管内作环路 半径为 r , 环路内电流代数和为
§5.安培环路定理 / 三、明确几点 安培环路定理
四、选取环路原则 1.利用安培环路定理计算磁场 B ,要求磁 利用安培环路定理计算磁场 要求磁 场具有高度的对称性 ; 2.目的是将 目的是将: 目的是将 写成
∫L B ⋅ dl = µ0 ∑ I
∫L Bdl cosθ =B ∫ dl = µ0 ∑ I µ0 ∑ I B= ∫ dl 大小相等, 要求环路上各点 B 大小相等,B 的方向 与环路方向一致, 与环路方向一致, B // dl, cosθ = 1
例2:密绕载流螺 : 线管通有电流为 I, 线圈密度为 n,求 , 管内一点的 B 。 解:理想密绕螺线 管,管内的磁场是 均匀的, 均匀的,管外的磁 场为 0 ;
§5.安培环路定理 / 六、举例 安培环路定理
...............B
作闭合环路 abcda, 环路内的电流代数 和为: 和为:
§5.安培环路定理 / 五、解题方法 安培环路定理
六、举例 例1:如图所示,求环路 的环流 ∫ B ⋅ dl 。 :如图所示,求环路L的环流 解:由环路定理
I1 I2
I3
∫L B ⋅ dl = µ0 ∑ I
= µ 0 ( −2 I 1 + I 2 )
L
§5.安培环路定理 / 六、举例 安培环路定理
1.电流正负规定 电流正负规定 电流方向与环路方向满足右手定则电 取正;反之取负。 流 I 取正;反之取负。
§5.安培环路定理 / 三、明确几点 安培环路定理
2. ∑ I 为环路内的电流代数和。 为环路内的电流代数和。 3.环流 ∫ B ⋅ dl 只与环路内的电流有关, 环流 只与环路内的电流有关, 而与环路外电流无关。 而与环路外电流无关。 4. B为环路上一点的磁感应强度,不是任 为环路上一点的磁感应强度, 为环路上一点的磁感应强度 意点的,它与环路内外电流都有关。 意点的,它与环路内外电流都有关。 5.若 ∫ B ⋅ dl = 0 并不一定说明环路上各点 若 的 B 都为 0。 6.若 ∫ B ⋅ dl = 0 环路内并不一定无电流。 环路内并不一定无电流。 若 7.环路定理只适用于闭合电流或无限电流, 环路定理只适用于闭合电流或无限电流, 环路定理只适用于闭合电流或无限电流
...............
a
b
B B外 = 0
∑ I = nabI
B 的环流为: 的环流为:
b c d c a
c aBiblioteka dca∫ B ⋅ dl = ∫ B ⋅ dl + ∫ B ⋅ dl + ∫ B ⋅ dl + ∫ B ⋅ dl
b d
∫ B ⋅ dl = ∫ B ⋅ dl = 0,
d
§5.安培环路定理 / 六、举例 安培环路定理
表述。 §5.安培环路定理 / 一、表述。二、证明 安培环路定理
长直导线周围的 B 线为一系列的同 心圆, 心圆,选取路径方 相同; 向与 B 相同; 左边= ∫L B ⋅ dl 左边
I B L
= ∫L Bdl cosθ
由于环路上各点的 B 大 小相等; 小相等;且 B // dl ;
θ = 0, cosθ = 1
µ0 I 2πR B ∝ r
o
R
1 B∝ r
r
§5.安培环路定理 / 六、举例 安培环路定理
I
R
的环路, 选取半径为 r 的环路, 环路内电流代数和为: 环路内电流代数和为: 2 r I 2 πr = 2 I ∑ I = 2 R πR
∫ Bdl cos θ = µ 0 ∑ I
I
R
r
由于环路上各点 B 大小 相等, 相等,方向 B // d l θ = 0 , cosθ = 1
§5.安培环路定理 / 六、举例 安培环路定理
∑ I = NI
§5.安培环路定理 / 六、举例 安培环路定理
o R1 rR
2
∫L B ⋅ dl = µ0 ∑ I
B2πr = µ0 NI
µ0 NI B= 2πr
当 r >> ( R2 – R1) 时
o R1 rR
2
N =n 2πr
为沿轴向线圈密度; 为沿轴向线圈密度;
B = µ0nI 与直螺管的结论一致。 与直螺管的结论一致。
