第16次课第3章 数值运算及运算器
操作方法PPT课件
原码乘法及实现(2)
Ⅱ.用硬件乘法器和除法器实现。 硬件上:设置有并行加法器、移位器和若干循环、计数控制逻辑电路搭成的串行乘除法器。 指令系统:具有乘除法指令。 实现:乘除运算通过微程序一级(硬件+微程序)来实现。 算法:在微程序中依据串行乘除运算算法,循环累加、右移指令→乘法,循环减、左移指令→除法。 运算速度:有所提高,但硬件设计也相对复杂。 适用场合:低性能CPU。
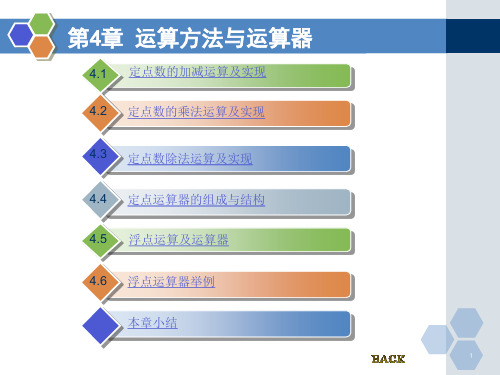
4.1 定点数的加减运算及实现
补码加减运算与运算器
机器数的移位运算
移码加减运算与判溢
十进制加法运算
一
二
三
四
药掇游二梨册惊衰房跃群刺靛勉平坪毋慧缎掘奠慰氧枚生吮荧雷肘寞笆联第3章操作方法第4章 运算方法与运算器
一、补码加减运算与运算器
补码加减运算方法
补码加减运算的溢出判断
二
袄涟孩急疵撩哉位魂狙率氨加路赁渭碑爬恋陌姆哼周侗淌裁接轮脊义浓退第3章操作方法第4章 运算方法与运算器
4.2 定点数的乘法运算及实现
原码乘法及实现
补码乘法及实现
阵列乘法器
一
二
三
金哄逊盟逐丸锻芳嚏戈远是重痉糯赏壬奈撒布伏装峰赞团券辑乾否胃庸甄第3章操作方法第4章 运算方法与运算器
原码乘法及实现(1)
1.0011
0.0011
栽横嫂毡孕搁姬锌蝴结猪沙漂菇谈偿乞碴价厌烩担慢彝矢败炸全驭次臆逻第3章操作方法第4章 运算方法与运算器
补码加减运算举例
例:已知X=+1011,Y=-0100,用补码计算X+Y和X-Y。 写出补码: [X]补 =0,1011 [Y]补 =1,1100 [-Y]补 =0,0100 计算:
第3章(09.2)

4.加1指令(5条) INC INC INC INC INC A Rn direct @Ri DPTR
指令功能:使操作数所指定的单元的内容加1 例:已知A=12H,R0=33H,(21H)=32H,(34H)=22H, DPTR=1234H,连续执行下面的指令。 说明:除了“INC A”影响奇偶标志位外,其余操作均 INC A 不影响PSW;“INC DPTR”是一条16位加1指令,这条 INC R0 指令在加1过程中,若低8位有进位可直接向高8位进位, INC 21H 不需要通过进位位Cy传送。 INC @R0 INC DPTR
4.清0与取反指令(2条) 取反: CPL A 5.循环移位指令(4条) RL A RR A RLC A RRC A 清零: C0
A.0 A.7 A.7 A.0 A.0
CY
CY
后两条指令,影响P标志和CY。
综合举例: 例1:把累加器A中的低4位状态,通过P1口的高4 位输出, P1口的低4位状态不变。 ANL A,#0FH ;屏蔽A的高4位 SWAP A ANL P1,#0FH ;清P1口高4位 ORL P1,A ;P1口高4位输出A的低4位; 例2:编制程序将存放在片外RAM的30H单元中某 数的低4位取反,高2位置1,其余2位清0。 例3:编制程序求片内RAM的20H,21H,22H单元 中的数的补码,并将结果仍放回到20H,21H, 22H中。
(40H)= (41H)=
H H
(50H) = (51H)=
H H
A= R0=
H H
5.减1指令(4条) DEC DEC DEC DEC A Rn direct @Ri
指令功能:使操作数所指定的单元的内容减1
说明:减1指令中没有DPTR减1指令.
第三章 运算方法

第三章运算方法一名词解释(1)溢出——在运算过程中如出现数据超过这个数表示范围的现象,称溢出。
(2)运算器——运算器是一个用于信息加工的部件,又称执行部件。
它对数据进行算术运算和逻辑运算。
(3)并行加法器——全加器的位数与操作数的位数的加法器称并行加法器。
(4)进位链——进位信号的产生与传递的逻辑结构称为进位链。
(5)进位产生函数——当xi与yi都为1时,Ci=1,即有进位信号产生,所以将xiyi称为进位产生函数,以Gi表示。
(6)进位传递函数——当xi⊕yi=1、Ci-1=1时,则Ci=1。
这种情况可看作是当xi⊕yi=1时,第i-1位的进位信号Ci-1可以通过本位向高位传送。
因此把xi⊕yi称为进位传递函数,以Pi表示。
(7)桶形移位器——在选择电路的控制下可以实现左移、右移、直送操作的具有移位功能的电路。
一.选择题1.大部分计算机内的减法是用_____实现。
A.将被减数加到减数中B.从被减数中减去减数C.补码数的相加 D.补码数的相减2.原码加减法是_____。
A.操作数用原码表示,连符号位直接相加减B.操作数用原码表示,尾数直接相加减,符号位单独处理C.操作数用原码表示,根据两数符号决定实际操作,符号位单独处理D.操作数取绝对值,直接相加减,符号位单独处理3.补码加减法是指______。
A.操作数用补码表示,两尾数加减,符号位单独处理,减法用加法代替B.操作数用补码表示,符号位和尾数一起参加运算,结果的符号与加减相同C.操作数用补码表示,连符号位直接相加减,减某数用加负某数的补码代替,结果的符号在运算中形成D.操作数用补码表示,由数符决定两尾数的操作,符号位单独处理4.在原码加减交替除法中,符号位单独处理,参加操作的数是_____。
A.原码 B.绝对值C.绝对值的补码 D.补码5.两补码相加,采用1位符号位,则当_____时,表示结果溢出。
A.最高位有进位 B.最高位进位和次高位进位异或结果为0C.最高位为1 D.最高位进位和次高位进位异或结果为16.在下列有关不恢复余数法何时需恢复余数的说法中,正确的是_____。
北师大版七年级数学上第三章全部课件

例1 列代数式,并求值.
门票: 成人10元/人; 学生5元/人.
(1)一个旅游团有成人x人、学生y人,请 你根据上图确定该旅游团应付多少门票费?
(2)如果该旅游团有37个成人,15个学生, 那么门票费是多少呢? 解:(1)该旅游团应付的门票费是
(10x+5y)元.
(2)把x=37,y=15代入代数式得
积为 a
搭一搭,填一填:
` (1)我们按如图的摆法搭一行正方形。记录你所搭
的正方形的个数和所用的火柴棒的根数,并填表
正方形个数 1 火柴根数 4
23 4 7 10 13
X… …
探讨 按这样的方法搭建10个正方形
要多少根火柴呢?
• 要求 • 一:列出算式。 • 二:尽量找出多种计算方法。
……
方法一
2、在求代数式的值时,可先合并同 类项将代数式化简,然后再代入数值计算, 这样往往会简化运算过程。
整式的加减(二)
复习回顾:
1、什么叫同类项?合并同类项的法 则是什么?
2、下面各题中的两项是不是同类项
(1) a 2b3与 1 b3a 2
(2)
1
2
ya4与
1
a4 y
5
5
(3)3a 2b与3ab3
(5)一条高为4的三角形的面积为2L,其中的L表示
_三_角_形_的_ 底_. (6)底面积是50的长方体的体积为100x,其中的x表示 _高_的_一_半.
创设情景
你能结合生活中的实例表示下列式字吗?
1. 3a
2. m-3
探究 用牙签按下图方式搭三角形
三角形个数 牙签根数
123
357
45
9 11
照这样的规律搭下去,搭n个这样 的三角形需要多少根牙签?
微型计算机原理及应用第三版课后答案

微型计算机原理及应用第三版课后答案【篇一:《微型计算机原理及应用》课后习题答案】=txt>第一章1.1 解释题(1) 微处理器【解答】由大规模集成电路芯片构成的中央处理器(cpu),叫做微处理器。
(2) 微型计算机【解答】以微处理器为基础,配以内存储器、输入输出接口电路、总线以及相应的辅助电路而构成的计算机裸机,叫做微型计算机。
(3) 微型计算机系统【解答】微型计算机系统由硬件系统和软件系统组成。
即由微型计算机、配以相应的外部设备(如打印机、显示器、键盘、磁盘机等),再配以足够的软件而构成的系统。
(4) 单板机【解答】将微处理器、ram、rom以及i/o接口电路,再配上相应的外设(如小键盘、led显示器等)和固化在rom中的监控程序等,安装在一块印刷电路板上构成的微型计算机系统称为单板机。
(5) 运算器【解答】运算器是直接完成各种算术运算、逻辑运算的部件,主要由alu(arithmetic and logic unit,算术逻辑部件)、通用寄存器、标志寄存器等组成。
(6) 地址总线【解答】地址总线是cpu对内存或外设进行寻址时,传送内存及外设端口地址的一组信号线。
地址总线的条数多少决定了cpu的寻址能力。
(7) 数据总线【解答】数据总线是cpu与内存或外设进行信息交换时,所用的一组数据信号线。
它决定了cpu一次并行传送二进制信息的位数,反映出cpu的“字长”这个重要性能指标。
(8) 控制总线【解答】控制总线是在cpu与外部部件之间传送控制信息(如读/写命令、中断请求命令等)的一组信号线。
1-2 单片机应包括哪些基本部件?其主要应用于哪些领域?【解答】一般单片机芯片中包括微处理器、ram、rom、i/o接口电路、定时器/计数器,有的还包括a/d、d/a转换器等。
其主要应用于智能化仪器仪表及工业控制领域。
1-3 按图1-11和图1-12,写出取第二条指令操作码和执行第二条指令的过程。
【解答】1) ip的值(002h)送入地址寄存器ar;2) ip的内容自动加1,变为003h;3) ar将地址码通过地址总线送到存储器的地址译码器,经译码后选中002h单元;4) 微处理器给出读命令;5) 所选中的002h单元内容04h送上数据总线db;6) 数据总线db上的数据04h送到数据寄存器dr;7) 因是取指操作,取出的是指令操作码04h,即由dr送入指令寄存器ir;8) ir中的操作码经指令译码器id译码后,通过pla发出执行该指令的有关控制命令。
第3章计算机基础知识、计算机中数据的表示

日
三
省
吾
我知
身
进步
❖大一:大学计算机基础 ❖大二:VB、C、Athorware、
Access、Photoshop
课程定位
基本技能
中英文录入(50字/分) 计算机基础知识 Windows XP 网络应用 Word 2019 文字处理软件 Excel 2019 电子表格处理软件 PowerPoint 2019 演示软件
【方法】除基逆取余
【例】将十进制数253转换成二进制数
十进制数(D)
余数
2 253
└2 126 └2 63 └2 31 └2 15 └2 7 └2 3 └2 1 └0
1
转换结果的最低位
0
1
1
1
1
1
1
转换结果的最高位
转换结果: (253)10=(11111101)2
【例】将十进制数253转换成八进制数转换结果的最低位
集成电路
Integrated
大规模集成电路
Large Scale Integration
计算机各个发展阶段的比较
发展对象
比较 特点 对象
第一代
第二代
(1946~1957) (1958~1964)
第三代 (1965~1970)
第四代 (1971至今)
电子器件
电子管
晶体管
中、小规模集成电 路
主存储器
磁芯、磁鼓
6 0 3.2 5
6×102 3×100
2×10-1
5×10-2
计算机中常用的几种计数制
十进制 二进制 八进制
数码
0~9
0,1
0~7
基数
10
1632位微机原理汇编语言及接口技术课后习题答案

第一章1.1 解:五代,详细见书1.2 解:微型计算机:以大规模、超大规模集成电路为主要部件,以集成了计算机主要部件——控制器和运算器的微处理器为核心,所构造出的计算机系统。
PC机:PC(Personal Computer)机就是面向个人单独使用的一类微机。
单片机:用于控制的微处理器芯片,内部除CPU外还集成了计算机的其他一些主要部件,如:ROM、RAM、定时器、并行接口、串行接口,有的芯片还集成了A/D、D/A转换电路等。
数字信号处理器DSP:主要面向大流量数字信号的实时处理,在宿主系统中充当数据处理中心,在网络通信、多媒体应用等领域正得到越来越多的应用1.3 解:微机主要有存储器、I/O设备和I/O接口、CPU、系统总线、操作系统和应用软件组成,各部分功能如下:CPU:统一协调和控制系统中的各个部件系统总线:传送信息存储器:存放程序和数据I/O设备:实现微机的输入输出功能I/O接口:I/O设备与CPU的桥梁操作系统:管理系统所有的软硬件资源1.4 解:系统总线:传递信息的一组公用导线,CPU通过它们与存储器和I/O设备进行信息交换。
好处:组态灵活、扩展方便三组信号线:数据总线、地址总线和控制总线。
其使用特点是:在某一时刻,只能由一个总线主控设备来控制系统总线,只能有一个发送者向总线发送信号;但可以有多个设备从总线上同时获得信号。
1.5解:(1)用于数值计算、数据处理及信息管理方向。
采用通用微机,要求有较快的工作速度、较高的运算精度、较大的内存容量和较完备的输入输出设备,为用户提供方便友好的操作界面和简便快捷的维护、扩充手段。
(2)用于过程控制及嵌人应用方向。
采用控制类微机,要求能抵抗各种干扰、适应现场的恶劣环境、确保长时间稳定地工作,要求其实时性要好、强调其体积要小、便携式应用强调其省电。
1.6 解:1.7 解:I/O通道:位于CPU和设备控制器之间,其目的是承担一些原来由CPU处理的I/O任务,从而把CPU从繁杂的I/O任务中解脱出来。
大学计算机基础简明教程(第3版)教学课件3

R进制数用 r个基本符号(0,1,2,…,r-1) 表示数码
R进制数N 展开式可表示为:
N=an-1×rn-1+an-2×rn-2+…+a0×r0+a-1×r-1+…+a-m×r-m
n 1
ai r i
im
6
二进制位权表示:
不足补零
问题:
1 101 101 110.110 101(B)= 1556.65(O) 已知456.78(D)
15 5 6 6 5
如何快速地转换成
11 0110 1110.1101 01(B)=36F.D4(H) 二、八、十六进制?
36 F D4
10
二进制、八进制、十六进制数间的关系
八进制 对应二进制
输出设备
内存
各种处理
二/十进制转换
数值
西文字形码
西文
汉字字形码
汉字
数/模转换
声音、图像
3
3.1数制与转换
4
3.1.1进位计数制
十进制数的表示,如678.34的位权展开式 678.34=6×102+7×101+8×100 +3×10-1+4×10-2
数码
基数
权
问题: 七进制数4532.1的位权展开式?
职称编码
教师 科研 工程
教授 011 研究员 061 教授级高工 081
副教授 012 副研 062 高工
082
讲师 013 助研 063 助教 014 见习 064 未定职 019 未定职 069
工程师 助工 未定职
083 084 089
2020-2021学年五年级数学上册第三章小数除法人教新课标版(含解析)

2020-2021学年五年级数学上册暑假预习与检测衔接讲义第三章小数除法【知识点归纳】1、小数除以整数的计算方法:小数除以整数,按整数除法的方法去除,商的小数点要和被除数的小数点对齐。
整数部分不够除,商0,点上小数点。
如果有余数,要添0再除。
2、除数是小数的除法的计算方法:先将除数和被除数扩大相同的倍数(把小数点向右移动相同的位数),使除数变成整数,再按“除数是整数的小数除法”的法则进行计算。
注意:向右移动小数点时,如果被除数的位数不够,在被除数的末尾用0补足。
3、除法中的变化规律:①商不变性质:被除数和除数同时乘或除以同一个数(0除外),商不变。
②除数不变,被除数乘或除以几,商随着乘或除以几。
③被除数不变,除数乘或除以几,商就除以或乘几。
④被除数大于除数,商就大于1;被除数小于除数,商就小于1。
⑤一个非0的数除以大于1的数,商就小于被除数;一个非0的数除以小于1的数,商就大于被除数。
⑥积不变性质:一个因数乘一个数,另一个除以同一个数(0除外),积不变。
⑦一个因数不变,另一个数乘几,积就乘几。
⑧一个因数不变,另一个因数除以几,积就除以几。
4、求商时有时也需要求近似数。
方法三种。
取商的近似数时,保留到哪一位,一定要除到那一位的下一位,然后用四舍五入的方法取近似数。
没有要求时,除不尽的一般保留两位小数。
5、一个数的小数部分,从某一位起,一个数字或者几个数字依次不断重复出现,这样的小数叫做循环小数。
一个循环小数的小数部分,依次不断重复出现的数字,叫循环节。
如6.3232……的循环节是32,注意不是23一定要是第一次重复出现的数字是3在前2在后重复出现!6、循环小数的记法:(1)用省略号表示。
写出两个完整的循环节,加省略号。
如:3.55…, 2.0321321…(2)简便记法。
在循环节的首位和末位上加小圆点。
如0.36,2.587循环小数是无限小数,无限小数不一定是循环小数。
7、小数部分的位数是有限的小数,叫做有限小数。
Matlab详细学习讲义

Matlab详细学习讲义《MA TLAB软件应⽤》讲义[第2 / 16次课]第1章基础准备及⼊门⼀点名⼆作业讲评三复习提问MATLAB界⾯由⼏⼤组件组成?MATLAB的搜索路径主要有什么应⽤途径?四上机练习内容启动MATLAB。
在D盘根⽬录下,以“学号_姓名”的格式创建⽂件夹,并在Matlab中将该⽬录设置为Current Folder。
(利⽤MA TLAB Toolbar 中Current Folder组合框后的按钮)。
以下为本章教学必须掌握的知识点。
在MA TLAB的Command Window中练习以下代码,并观察系统输出,并逐⾏进⾏注释。
本次课结束后将代码⽂件上传。
在MA TLAB程序界⾯中进⾏以下操作:1 上机实习内容提⽰及要求启动MATLAB后,依次练习MA TLAB的菜单项、⼯具栏和Command Window、Current Folder、Command History、Workspace等主要组件的基本功能,按指定内容在MA TLAB程序界⾯下进⾏操作练习。
2 上机实习内容在MATLAB程序界⾯中进⾏以下操作:1) Command Window指令窗⼝在集成窗体和独⽴窗体之间切换(Undock/Dock按钮)2) 在Command Window中运⾏以下指令,掌握换⾏符(...)的使⽤>> (12+2*(7-4))/3^2>> S=1-1/2+1/3-1/4+1/5-1/6+1/7-1/8>> S=1-1/2+1/3-1/4+…+1/5-1/6+1/7-1/83)在Command Window中分别输⼊以下数值,并按回车,观察MA TLAB的输出(数值如3, -99, 0.001, 9.456, 1.3e-3, 4.5e33, eps, 等)4)以下实例涉及变量的定义规则,在Command Window中分别输⼊并按回车,观察MA TLAB的输出结果.输出结果为错误提⽰时,分析出现错误的原因.>> xyz_4=32.75>> var1=3.09e-5*1028>> 4xyz=32.75>> 4*xyz=198.28>>4,xyz=198.285) 在Command Window中输⼊下列数学常数,并按回车:eps, i, j, Inf, inf, intmax, NaN, nan, pi, realmax, realmin,观察并分析系统的输出。
七年级数学第三章 字母表示数 第一、二、三节北师大版知识精讲

初一数学第三章字母表示数第一、二、三节北师大版【本讲教育信息】一. 教学内容:第三章:字母表示数第一节:字母能表示什么第二节:代数式第三节:代数式求值二. 教学目标知识与能力1、探索规律并用代数式表示规律的过程,能用代数式表示运算律和计算公式。
2、理解字母表示数的意义,能求出代数式的值。
3、会求代数式的值,感受代数式求值,可以理解一个转化过程或某种算法。
三. 重点及难点1. 重点:(1)用含有字母的式子表示规律及计算公式、运算律。
(2)代数式的含义(3)代数式的实际含义2. 难点:(1)探索规律的过程及用代数式表示规律的方法(2)解释不同代数式的意义(3)根据代数式求值推断代数式所反映的规律四. 课堂教学[知识要点](一)字母能表示什么搭1个正方形需要4根木棒(1)搭两个正方形需要(7 )根木棒,搭3个正方形需要(10 )根木棒(2)搭10个这样的正方形需要(31 )根木棒(3)搭100个这样的正方形需要(301 )根木棒(4)如果用x表示所搭正方形的个数,那么搭x个这样的正方形需要多少根木棒?分析:第一种方法:第一个正方形用4根,每增加一个正方形增加3根,那么搭x个正方形就需要木棒4+3(x-1)第二种方法:上面的一排和下面的一排各用了x根木棒,竖直方向用了(x+1)根木棒,共用了[x+x+(x+1)]根木棒。
(5)利用分析的方法记算,搭200个这样的正方形需要()根木棒4+3(x-1)=4+3(200-1)=601我们可以用字母表示以前学过的公式和法则用字母表示运算律:如果用a、b表示两个数,那么加法交换律可以表示成a+b=b+a乘法交换律可以表示成ab=ba注意:字母之间的乘法省略×号我们还可以计算一些图形的周长和面积长方形的周长和面积分别为:2(m+n)、mn,其中m表示长方形的长,n表示长方形的宽。
圆的周长和面积分别为:2πr,πr²,其中r表示圆的半径。
长方形的体积为:abc,其中a、b、c分别表示长方形的长、宽、高。
C程序设计作业集

C程序设计作业集第一章C语言概述一.填空题1.C程序是由构成的,一个C程序中至少包含因此,是C程序的基本单位。
2.C程序注释是由和所界定的文字信息组成的。
3.C语言是一个用途广泛,功能强大的程序语言,它具有的主要特点是:(1),(2),(3),(4),(5),(6),(7),(8)4.在C程序开发过程中,遵循如下所示的开发步骤,请填空。
()()()()有错?有错?有错?结束有有有程序代码错误设计算法错误5.函数体一般包括和二.判断题1.一个C程序的执行总是从该程序的main函数开始,在main函数最后结束。
【】2.main函数必须写在一个C程序的最前面。
【】3.一个C程序可以包含若干的函数。
【】4.C程序的注释部分可以出现在程序的任何位置,它对程序的编译和运行不起任何作用。
但是可以增加程序的可读性。
【】5.C程序的注释只能是一行。
【】6.C程序的注释不能是中文文字信息。
【】7.判断下列各个程序中的程序注释是否正确。
#in/某包含某/clued#includemain()main/某某/(/某主函数某/){【】{【】}}#include#includemain()main(){【】{int某=10;【】int某/某初始化某/=10;/某打印某/某某=10某/的值某/}}8.可以使用TurboC来编译和连接一个C程序。
【】开始9.可以使用TurboC来运行一个C程序。
【】10.可以使用TurboC来实时调试(即动态调试)一个C程序。
【】三.简答题1.写出一个C程序的基本结构。
2.简要叙述使用TurboC2.0编译和运行一个程序的步骤。
四.编程题1.提高题:参照课本例1.1,试编写一个C程序,输出如下信息。
(提示:使用键盘上的一些符号)。
2.提高题:试编写一个C程序,输出如下信息。
试试看,可以输出其他组合图案吗?第二章程序的灵魂——算法一.填空题1.是程序设计的灵魂。
2.一个计算机程序应包括和的内容。
高考总复习一轮数学精品课件 第3章 函数与基本初等函数 第6节 指数与对数运算

3
1.(-3) =
3
-3 =
6
2
(-3) .( × )
2.log2a2=2log2|a|.(
)
3.若MN>0,则loga(MN)=logaM+logaN(a>0,a≠1).( × )
1
2 4
1
4
2
4.(m ) = ( ) .( × )
题组二 回源教材
1
2
1
2
-
5.(人教A版必修第一册习题4.1第8题改编)已知 + =3 ,则a+a-1=______,
于底数的右上角
个
正整数指数幂 an=···…·(n∈N*)
指 有理指数幂 零指数幂 a0=1(a≠0)
数 的分类
-n 1
负整数指数幂 a = (a≠0,n∈N*)
幂
0 的正分数指数幂等于 0,0 的负分数指数幂没有意义
aman=am+n(a>0,m,n∈Q)
有理指数幂 m n mn
(a ) =a (a>0,m,n∈Q)
5
a-3b 25
,所以 4 = ,故选
3
9
C.
9.(2021·全国甲,文6)青少年视力是社会普遍关注的问题,视力情况可借助
视力表测量.通常用五分记录法和小数记录法记录视力数据,五分记录法的
数据L和小数记录法的数据V满足L=5+lg V.已知某同学视力的五分记录法
的数据为4.9,则其视力的小数记录法的数据约为(
1
5+
(4)(2024·辽宁沈阳模拟)若log32=m,则log296=________(用含m的式子表示).
解析 由
第三章基本数值计算方法一

1.0000 0 0 -1.6757 1.0676
U0
0 1.0000
0
-1.8378
-1.2162
,
0 0 1.0000 0.9820 0.3018
0
0
0
0
0
这个最简行阶梯形式说明原 来的方程组是欠定的。
欠定方程组解的特点
它等价于下列方程组:
x1
-1.6757 x4 = 1.0676
1
0
3
0
0
(柠檬酸)x1
1 1
,(小苏打)x2
8 6
(, 碳酸钠)x3
0 6
,
(水)x4
2 0
,
(二氧化碳)x5
0 1
,
3
8
7
1
2
• 按四种元素左右平衡列出四个方程,得:
1 0 3 0 0 0
1
1
x1
8
6
x2
0 6
x3
2 0
x4
0 1
x5
0 0
Ax
=
b
=
0
3
8
7
1
2
0
化学方程配平程序
X4 = 8.66
为什么要提出这种新的计算方法?
把上例中第四个方程改为:
4x1 + 2x2 + 7x3 -778/222 x4 877 / 222
,求其解。
解:输入新参数
A=[6,1,6,-6;1,-1,9,9;-2,4,0,4;4,2,7,-778/222];
b=[7;5;-7;877/222]; 键入U=rref([A,b]),得到
4x1 + 2x2 + 7x3 -5x4 9
第三章 线性方程组解法

§3.3 高斯-塞德尔迭代
x ik 1a 1 ii(b iij 1 1a ijxk j 1j n i 1a ijxk j),i 1 ,2 ...,n
大家好
21
§3.1 问题的提出
由原方程
8x1 x2 4 x1 10 x2
2x3 12 x3 21
3x1 2x2 5x3 16
构造
xx12((kk11))
2.5x2(k) 0.25x3(k) 1.5x1(k) 2.5x3(k)
5.25 8.0
(2) (3)
x3(k1) 4x1(k) 0.5x2(k) 6.0
§3.1 问题的提出
是方程组的精确解,用有限次运算得不到精 确解。迭代法是牛顿最先提出来的,1940年 经司威尔提出的松弛法也是一种迭代法,共 轭梯度法则是另一种迭代法,是弗莱彻等人 于20世纪60年代提出来的。
大家好
16
§3.1 问题的提出
例3.1
5x 2y 8 3x 20 y 26
5) 给出估计误差和迭代停止判据。
大家好
25
§3.1 问题的提出
❖ 定义:在n维空间中给定一个向量序
列 x k ,xk (x1 k,x2 k,...xn k)T ,如果对每一个分
量
x
k i
,当
k
时都有极限xi,
即
lim
k
xik
沪科版八年级下册数学教学课件 第16章 二次根式 16-2 二次根式的运算 第16章 小结与复习

当 a 2 时,
原式
2 2 1 2
2.
考点五 本章解题思想方法
分类讨论思想 例8 已知a是实数,求 a 22 a 12 的值. 解: a 22 a 12 a 2 a 1 , 分三种情况讨论: 当a≤-2时,原式=(-a-2)-[-(a-1)]
=-a-2+a-1=-3; 当-2<a≤1时,原式=(a+2)+(a-1)= 2a+1; 当a>1时,原式=(a+2)-(a-1)=3.
8. 计算:
(1) 24 1 4 1 (1 2)0; (2) 3( 2 3) 24 | 6 3 | .
3
8
解:(1)原式
24 1 4 2 1 2 2
3
4
2
2.
(2)原式 6 3 2 6 3 6 6.
9. 交警为了估计肇事汽车在出事前的速度,总结出 经验公式 v 16 df ,其中v是车速(单位:千米每 小时),d是汽车刹车后车轮滑动的距离(单位: 米),f是摩擦系数.在某次交通事故调查中,测得 d=20米,f=1.2,请你帮交警计算一下肇事汽车在出 事前的速度.
(1)7;
(2)x2 1;
解:(1)7
2
7.
(3) 1 . 11
2
(2)x2 1= x2 1 .
2
(3)
1 11
=
1
11
.
考点三 二次根式的运算及应用
例4 计算:
(1) 8 12 2;
2
(3) 6 5 ;
(2)5 15
3 5
15;
(4) 5 6 2 5 6 2 .
第16章
八年级数学下(HK) 教学课件
二次根式
计算机组成原理第4章

数据开关 (11000001)
C1H
打开三 态门 SW_G=0
-1 0 +1 定点小数
器允许的表示范围(溢出)。
补码 纯小数:0≤X<1
总线1 总线2
通用 寄存器
ALU
特殊 寄存器
总线 旁路器
总线3
16
4.9 运算器的基本组成与实例
4.9.2 ALU举例 1. ALU电路
ALU即算术逻辑单元,它是既能完成算术运 算又能完成逻辑运算的部件。前面已经讨论过, 无论是加、减、乘、除运算,最终都能归结为加 法运算。因此,ALU的核心首先应当是一个并行 加法器,同时也能执行像“与”、“或”、 “非”、“异或”这样的逻辑运算。由于ALU能 完成多种功能,所以ALU又称多功能函数发生器。
C1=G1+P1C0 C2=G2+P2C1=G2+P2G1+P2P1C0
C3=G3+P3G2+P3P2G1+P3P2P1C0 C4=G4+P4G3+P4P3G2+P4P3P2G1+P4P3P2P1C0
6
C1=G1+P1C0 C2=G2+P2C1 C3=G3+P3G2+P3P2G1+P3P2P1C0 C4=G4+P4G3+P4P3G2+P4P3P2G1+P4P3P2P1C0
…
…
第三章导数及其应用3-1导数的概念及运算

重点难点
重点:导数的概念、公式及运算法则,导数 的应用
难点:①导数的定义 ②复合函数的导数及积商的导数公式
知识归纳 一、导数及有关概念
(2)瞬时速度 设物体运动路程与时间的关系是 s=f(t),当 Δt 趋近 于 0 时,函数 f(t)在 t0 到 t0+Δt 这段时间内的平均变化率 ΔΔst=ft0+ΔΔtt-ft0趋近于常数,我们把这个常数称为 t0 时刻的瞬时速度.
3.导数 设函数 y=f(x)在 x0 处及其附近有定义,当自变量在 x=x0 附近改变量为 Δx 时,函数值相应地改变量 Δy=f(x0 +Δx)-f(x0).如果当 Δx 趋近于 0 时,平均变化率ΔΔyx= fx0+ΔΔxx-fx0趋近于一个常数 l,那么常数 l 称为函数 f(x) 在点 x0 处的瞬时变化率.函数在点 x0 处的瞬时变化率通 常称为 f(x)在 x=x0 处的导数,又称函数 f(x)在 x=x0 处可 导.
分析:本例所给的函数是100个因式的积, 对于这种结构形式的函数,直接求导比较困 难,可通过两边取对数后再求导,就可以使 问题简化. 但必须注意取对数时真数应为正 实数.
解析:两边取对数得 lny=ln(x-1)+ln(x-2)+…+ln(x-100). 两边对 x 求导:y′y =x-1 1+x-1 2+…+x-1100. ∴y′=x-1 1+x-1 2+…+x-1100·(x-1)(x-2)·…·(x -100).
2.深刻理解“函数在一点处的导数”、 “导函数”、“导数”的区别与联系
(1)函数在一点处的导数f ′(x0)是一个常数, 不是变量.
(2)函数的导数,是针对某一区间内任意点x 而言的.函数f(x)在区间(a,b)内每一点都 可导,是指对于区间(a,b)内的每一个确定 的值x0,都对应着一个确定的导数f ′(x0).根 据函数的定义,在开区间(a,b)内就构成了 一个新的函数,就是函数f(x)的导函数f ′(x).
新编16 32位微型计算机原理及应用答案(第五版)_第三章参考答案

第三章 8086/8088微处理器及其系统 教材习题3.1-3.70参考答案3.1 为什么要研究8086/8088微处理器及其系统?这比直接研究32位微处理器及其系统有何优缺点?解:尽管8086/8088后续的80286、80386、80486以及Pentium系列CPU结构和功能已发生很大变化,但从基本概念与结构以及指令格式上来讲,他们仍然是经典的8086/8088CPU的延续与提升。
3.2 8086 CPU有多少根数据线和地址线?它能寻址多少内存地址单元和I/O端口?8088CPU又有多少根数据线和地址线?为什么要设计8088CPU?解:8086 CPU有16根数据线和20根地址线,可寻址1MB存储单元和64KB的I/O端口。
8088 CPU 有16位内部数据线和8条外部数据总线,20根地址线。
8088 CPU 是8086 CPU的向下兼容版,这样设计主要为了与INTEL原有的8位外围接口芯片直接兼容。
3.3 8086 CPU内部按功能可分为哪两大部分?他们各自的主要功能是什么?解:从功能上讲,8086可分为两个部分,即总线接口单元(bus interface unit,BIU)和执行单元(execution unit ,EU)。
总线接口单元(BIU)的功能是负责CPU与存储器或I/O设备之间的数据传送。
EU的功能只是负责执行指令;执行的指令从BIU的指令队列缓冲器中取得,执行指令的结果或执行指令所需要的数据,都由EU向BIU发出请求,再由BIU经总线控制电路对存储器或外设存取。
3.4 8086 CPU内部的总线接口单元BIU由哪些功能部件组成?他们的基本操作原理是什么?解:BIU内有4个16位的段地址寄存器CS、DS、SS和ES,16位指令指针IP,6字节指令队列缓冲器,20位地址加法器和总线控制电路。
基本操作原理是BIU要从内存取指令送到指令队列缓冲器;CPU执行指令时,总线接口单元要配合执行单元从指定的内存单元或者外设端口中取数据,将数据传送给执行单元,或者把执行单元的操作结果传送到指定的内存单元或外设端口中。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
• 全加和Σ 全加和Σ
∑i= AiBiCi
i
的逻辑表达式: 及进位 Ci+1 的逻辑表达式:
+ AiBiCi + AiBiCi + AiBiCi Ci+1= AiBiCi + AiBiCi + AiBiCi + AiBiCi
第二部分: 第二部分:第3章 数值运算及运算器
一、基本算术运算的实现 1、加法器 全加器( (1)全加器(续) 根据上述真值表和式子, 根据上述真值表和式子,可得到全加器的逻 辑表达式为: 辑表达式为: Si=Ai⊕Bi⊕Ci-1 Ci=AiBi+(Ai⊕Bi)Ci-1
一、基本算术运算的实现 计算机中最基本的算术运算是加法运算, 计算机中最基本的算术运算是加法运算 , 不论加、 不论加 、 减 、 乘 、 除运算最终都可以归结为加 法运算。所以在此讨论最基本的运算部件—— 法运算。 所以在此讨论最基本的运算部件 加法器,以及并行加法器的进位问题。 加法器,以及并行加法器的进位问题。
第二部分: 第二部分:第3章 数值运算及运算器
一、基本算术运算的实现 2、进位的产生和传递 (2)对进位公式的分析
设相加的两个n位操作数为: 设相加的两个 位操作数为: 位操作数为 A=AnAn-1…Ai..A1 B=BnBn-1…Bi..B1
Ci = AiBi + (Ai⊕Bi) Ci-1 —— 进位逻辑表达式 进位产生函数(Carry Generate Function) 设:Gi = AiBi —— 进位产生函数 Pi = Ai⊕Bi —— 进位传递函数 进位传递函数(Carry Propagate Function) 则每一位的进位表达式为: 则每一位的进位表达式为:Ci=Gi+PiCi-1
ty
8 6 4 2
C16
C12
C8
C4
C1 C0
Ci
16位单级先行进位时间图 图7 16位单级先行进位时间图
第二部分: 第二部分:第3章 数值运算及运算器
一、基本算术运算的实现 3、分组并行进位方式
(2)多级先行进位方式(组内并行、组间并行) 多级先行进位方式(组内并行、组间并行) 仍以字长为16位的加法器作为例子 位的加法器作为例子, 仍以字长为 位的加法器作为例子,分析两级先行 进位加法器的设计方法。 第一小组的进位输出C 进位加法器的设计方法 。 第一小组的进位输出 4 可以 变成两个与项相或: 变成两个与项相或: C4=G4+P4G3+P4P3G2+P4P3P2G1+P4P3P2P1C0 =G1*+P1*C0 其中: 其中:G1*=G4+P4G3+P4P3G2+P4P3P2G1 P1*=P4P3P2P1 Gi*称为组进位产生函数 Pi*称为组进位传递函数
C1 = G1 + P1C0 =A1B1+(A1 ⊕ B1)C0 C2 = G2 + P2C1=A2B2+(A2 ⊕ B2)C1 C3 = G3 + P3C2=A3B3+(A3⊕ B3)C2 … Cn = Gn + PnCn-1=AnBn+(An ⊕ Bn)Cn-1
第二部分: 第二部分:第3章 数值运算及运算器
一、基本算术运算的实现 1、加法器 (2)串行加法器与并行加法器 加法器有串行和并行之分。 加法器有串行和并行之分 。 在串行加法器 位字长的加法器仅有一位全加器, 中 n位字长的加法器仅有一位全加器 , 使用移 位字长的加法器仅有一位全加器 位寄存器从低位到高位串行地提供操作数, 位寄存器从低位到高位串行地提供操作数 , 分 n步进行相加。 步进行相加。 步进行相加 并行加法器则由多个全加器组成, 并行加法器则由多个全加器组成,其位数的 多少取决于机器的字长,数据的各位同时求和。 多少取决于机器的字长 , 数据的各位同时求和 。
第二部分: 第二部分:第3章 数值运算及运算器
┇
全部进位输出信号仅由进位产生函数 Gi,进位传递函 决定,与低位进位无关。 数 Pi 以及最低位进位 C0 决定,与低位进位无关。
C4
C3
C2
C1
+
+
+
+
C0
G3 P3
G2
P2
G1 P1
G0 P0
图5 四位并行进位链线路 每位进位延迟时间为 每位进位延迟时间为4T 进位延迟时间为
第二部分: 第二部分:第3章 数值运算及运算器
一、基本算术运算的实现 2、进位的产生和传递 串行进位( (3)串行进位(续) 串行进位的并行加法器的总延迟时间与字 长成正比,字长越长,总延迟时间就越长。 长成正比,字长越长,总延迟时间就越长。假 将一级“与门” 或门” 定,将一级“与门”、“或门”的延迟时间定 为t,从上述公式中可看出,每一级全加器的进 ,从上述公式中可看出, 位延迟时间为2t。在字长为n位的情况下 位的情况下, 位延迟时间为 。在字长为 位的情况下,若不 考虑G 的形成时间, 考虑 i、Pi的形成时间,从C0→Cn的最长延迟 为加法器最低位的进位输入, 时间为2nt( 时间为 (设C0为加法器最低位的进位输入, Cn为加法器最高位的进位输出)。 为加法器最高位的进位输出)。
第二部分: 第二部分:第3章 数值运算及运算器
一、基本算术运算的实现 1、加法器 (1)全加器 全加器( 全加器 ( FA) 是最基本的加法单元 , 它有 ) 是最基本的加法单元, 三个输入量: 操作数A 三个输入量 : 操作数 i 和 Bi 、 低位传来的进位 Ci-1,两个输出量:本位和 i、向高位的进位 i 两个输出量:本位和S 向高位的进位C Si 。
第二部分: 第二部分:第3章 数值运算及运算器
一、基本算术运算的实现 3、分组并行进位方式
(1)单级先行进位方式(组内并行、组间串行)(续) 单级先行进位方式(组内并行、组间串行)(续 )(
S16~S13 C16 C12 S12~S9 C8 S8~S5 C4 S4~S1 C0
4位CLA 加法器
4位CLA 加法器
第二部分: 第二部分:第3章 数值运算及运算器
一、基本算术运算的实现 2、进位的产生和传递 (1)并行加法器的进位结构 并行加法器中传递进位信号的逻辑线路称为进 并行加法器中传递进位信号的逻辑线路称为进 位链。 位链。 进位线路结构分为:串行进位;并行进位; 进位线路结构分为:串行进位;并行进位;将 分为 整个加法器分组(分级)、对组内、组间( )、对组内 整个加法器分组(分级)、对组内、组间(级 分别采用串行或并行进位。 间)分别采用串行或并行进位。
4位CLA 加法器 A8~A5 B8~B5
4位CLA 加法器 A4~A1 B4~B1
A16~A13 A12~A9 B16~B13 B12~B9
图6
16位单级先行进位加法器 16位单级先行进位加法器
第二部分: 第二部分:第3章 数值运算及运算器
一、基本算术运算的实现 3、分组并行进位方式
(1)单级先行进位方式(组内并行、组间串行)(续) 单级先行进位方式(组内并行、组间串行)(续 )(
一、基本算术运算的实现 2、进位的产生和传递 并行进位( (4)并行进位(续) 这种进位方式是快速的,若不考虑 这种进位方式是快速的,若不考虑Gi、Pi的 形成时间, 的最长延迟时间仅为2t, 形成时间,从C0→Cn的最长延迟时间仅为 ,而 与字长无关。但是随着加法器位数的增加, 与字长无关。但是随着加法器位数的增加,Ci的 逻辑表达式会变得越来越长,输入变量会越来越 逻辑表达式会变得越来越长, 这会使电路结构变得很复杂, 多,这会使电路结构变得很复杂,所以完全采用 并行进位是不现实的。 并行进位是不现实的。
第二部分: 第二部分:第3章 数值运算及运算器
一、基本算术运算的实现 3、分组并行进位方式
(1)单级先行进位方式(组内并行、组间串行) 单级先行进位方式(组内并行、组间串行)
位加法器为例, 以16位加法器为例,可分为 组,每组 位。 位加法器为例 可分为4组 每组4位 第一小组组内的进位逻辑函数C 第一小组组内的进位逻辑函数 1、C2、C3、C4 的表达式与前述相同,它们是同时产生的, 的表达式与前述相同,它们是同时产生的,实现 上述进位逻辑函数的电路称之为4位先行进位电 上述进位逻辑函数的电路称之为 位先行进位电 路(CLA),其延迟时间是 。 ) 其延迟时间是2t。 利用这种4位的 位的CLA电路以及进位产生 传递 电路以及进位产生/传递 利用这种 位的 电路以及进位产生 电路和求和电路可以构成4位的 位的CLA加法器。用4 加法器。 电路和求和电路可以构成 位的 加法器 个这样的CLA加法器,很容易构成 位的单级先 加法器, 个这样的 加法器 很容易构成16位的单级先 行进位加法器。 行进位加法器。
第二部分: 第二部分:第3章 数值运算及运算器
一、基本算术运算的实现 1、加法器 串行加法器与并行加法器( (2)串行加法器与并行加法器(续)
