展开图与折叠问题-勾股定理
关于勾股定理的八大应用

关于勾股定理的八大应用
对于勾股定理的八大应用,具体如下:
1)判断是否超速:利用勾股定理可以判断司机是否超速。
2)求旗杆高度:利用勾股定理可以求旗杆高度。
3)折叠问题:利用勾股定理可以解决折叠问题,例如折叠矩形
纸张的问题。
4)求树高:利用勾股定理可以求树的高度。
5)求梯子最省力的位置:利用勾股定理可以求梯子最省力的位
置。
6)求面积问题:利用勾股定理可以解决一些求面积的问题。
7)求台风问题:利用勾股定理可以解决台风问题,例如台风眼
里是否有平地的问题。
8)九章算术问题:利用勾股定理可以解决九章算术中的一些问
题。
勾股定理应用中的翻折问题
3 x 2
C
2
1 1 3 (4 x ) 5 x 2 2 3 12 3 x 5 x x 2
3
A x
3
x
E5
3 B
G
4
4-x
训练1:
长方形ABCD如图折叠,使点D落在BC边上的点F处, 已知AB=8,BC=10,求折痕AE的长。
42 (8 x)2 x 2
解: H
x2+32=(9-x)2
x=4 9-x=5
D
3 A 9-x
E
5 5 10 9-x
C 3
4 x 9 F 1 G
B
1、如图,在△ABC中,AB=AC=17, BC=16,求△ABC的面积。
(2)求腰AC上的高。
A
17 8
17 15 B 8 D 16
C
2、如图6,在锐角△ABC中,AD⊥BC, AB=15 , AD=12 , AC=13 ,求△ ABC 的 周长和面积。
B
D x
如图,∠B=∠C=∠D=∠E=90°,且AB=CD=3, BC=4,DE=EF=2,则求AF的长。 A 3 B 3 2 4 C 3 D
10 E 2 2 F
4
2
如图,一条河同一侧的两村庄A、B,其中A、B 到河岸最短距离分别为AC=1km,BD=2km, CD=4cm,现欲在河岸上建一个水泵站向A、B 两村送水,当建在河岸上何处时,使到A、B两 村铺设水管总长度最短,并求出最短距离。 B A 1 C 1 A′ P 4 4 5 2 D 1 E
A 15 B 9 12 13 C
D 5
如图,将一根25cm长的细木棍放入长,宽 高分别为8cm、6cm、和 10 3 cm的长方体 无盖盒子中,求细木棍露在外面的最短长 度是多少? 25
勾股定理中的折叠问题(分类整理版)

勾股定理中的折叠问题
1、如图,在Rt△ABC中,AB=9,BC=6,∠B=90°,将△ABC折叠,使A点与BC的中点D重合,折痕为MN,求
线段BN的长.
2、在一张直角三角形纸片中,两条直角边BC等于6,AC等于8,将三角形ABC按如图所示的方式折叠,使点A 和点B重合,折痕为DE,求CD的长
3、如图所示,在△ABC中,AB=20,AC=12,BC=16,把△ABC折叠,使AB落在直线AC上,求重叠部分(阴影部分)
的面积.
变式:如图,有一块直角三角形纸片,两直角边AC=6cm,BC=8cm,现将直角边AC沿直线AD折叠,使AC恰好落在
斜边AB上,且点C与点E重合,求CD的长。
4、如图所示,折叠长方形的一边AD,使点D落在BC边上的点F处,已知AB=8cm,BC=10CM,求DE的长
5、在长方形ABCD中,AB=6,BC=8,将长方形ABCD沿CE折叠后,点D恰好在对角线AC上的点F处、求EF的长。
6、如图,矩形纸片ABCD的边AB=10cm,BC=6cm,E为BC上一点,将矩形纸片沿AE折叠,点B恰好落
在CD边上的点G处,求BE的长.
7、如图,在长方形ABCD中,将△ABC沿AC对折至△AEC位置,CE与AD交于点F.
(1)试说明:AF=FC;
(2)如果AB=3,BC=4,求AF的长.。
利用勾股定理解决折叠问题及答案

小专题(二) 利用勾股定理解决折叠与展开问题类型1 利用勾股定理解决平面图形的折叠问题 1.如图,有一张直角三角形纸片,两直角边AC =5 cm ,BC =10 cm ,将△ABC 折叠,使点B 与点A 重合,折痕为DE ,则CD 的长为( )A.252 cmB.152 cmC.254 cm D.154cm2.如图所示,有一块直角三角形纸片,∠C =90°,AC =4 cm ,BC =3 cm ,将斜边AB 翻折,使点B 落在直角边AC 的延长线上的点E 处,折痕为AD ,则CE 的长为( )A .1 cmB .1.5 cmC .2 cmD .3 cm3.(青岛中考)如图,将长方形ABCD 沿EF 折叠,使顶点C 恰好落在AB 边的中点C ′上,若AB =6,BC =9,则BF 的长为( )A .4B .3 2C .4.5D .54.如图,长方形纸片ABCD 中,已知AD =8,折叠纸片使AB 边与对角线AC 重合,点B 落在点F 处,折痕为AE ,且EF =3,则AB 的长为( )A .3B .4C .5D .65.(铜仁中考)如图,在长方形ABCD 中,BC =6,CD =3,将△BCD 沿对角线BD 翻折,点C 落在点C ′处,BC ′交AD 于点E ,则线段DE 的长为( )A .3 B.154 C .5 D.1526.如图,在长方形ABCD中,AB=4,AD=6,E是AB边的中点,F是线段BC上的动点,将△EBF沿EF所在直线折叠得到△EB′F,连接B′D,则B′D的最小值是( )A.210-2B.6C.213-2D.47.如图所示,在△ABC中,∠B=90°,AB=3,AC=5,将△ABC折叠,使点C与点A重合,折痕为DE,则△ABE 的周长为________.8.如图,在Rt△ABC中,∠C=90°,BC=6 cm,AC=8 cm,按图中所示方法将△BCD沿BD折叠,使点C落在AB 边的C′点,那么△ADC′的面积是________.9.如图,已知Rt△ABC中,∠C=90°,AC=6,BC=8,将它的锐角A翻折,使得点A落在BC边的中点D处,折痕交AC边于点E,交AB边于点F,则DE的值为________.10.如图,在Rt△ABC中,∠B=90°,AB=3,BC=4,将△ABC折叠,使点B恰好落在边AC上,与点B′重合,AE为折痕,则EB′=________.11.为了向建国六十六周年献礼,某校各班都在开展丰富多彩的庆祝活动,八年级(1)班开展了手工制作竞赛,每个同学都在规定时间内完成一件手工作品.陈莉同学在制作手工作品的第一、二个步骤是:①先裁下了一张长BC=20 cm,宽AB=16 cm的长方形纸片ABCD,②将纸片沿着直线AE折叠,点D恰好落在BC边上的F处,请你根据①②步骤解答下列问题:计算EC,FC的长.类型2 利用勾股定理解决立体图形的展开问题1.如图,一圆柱体的底面周长为24 cm,高AB为5 cm,BC是直径,一只蚂蚁从点A出发沿着圆柱体的表面爬行到点C的最短路程是( )A.6 cm B.12 cmC.13 cm D.16 cm2.如图,圆柱形玻璃杯,高为12 cm,底面周长为18 cm,在杯内离杯底4 cm的点C处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿4 cm与蜂蜜相对的点A处,则蚂蚁到达蜂蜜的最短距离为________cm.3.如图,在一个长为2 m,宽为1 m的长方形草地上,放着一根长方体的木块,它的棱和场地宽AD平行且棱长大于AD,木块从正面看是边长为0.2 m的正方形,一只蚂蚁从点A处到达C处需要走的最短路程是________m(精确到0.01 m).4.一位同学要用彩带装饰一个长方体礼盒.长方体高6 cm,底面是边长为4 cm的正方形,从顶点A到顶点C′如何贴彩带用的彩带最短?最短长度是多少?5.如图,一个长方体形状的木柜放在墙角处(与墙面和地面均没有缝隙),有一只蚂蚁从柜角A处沿着木柜表面爬到柜角C1处.(1)请你画出蚂蚁能够最快到达目的地的可能路径;(2)当AB=4,BC=4,CC1=5时,求蚂蚁爬过的最短路径的长.参考答案类型11.D 2.A 3.A 4.D 5.B 6.A 7.7 8.6 cm29.13310.1.511.因为△ADE与△AFE关于AE对称,所以△ADE≌△AFE.所以DE=FE,AD=AF.因为BC=20 cm,AB=16 cm,所以CD=16 cm,AD=AF=20 cm.在Rt△ABF中,由勾股定理,得BF=12 cm.所以CF=20-12=8(cm).因为四边形ABCD是长方形,所以∠C=90°.设CE=x,则DE=EF=16-x,在Rt△CEF中,由勾股定理,得(16-x)2=64+x2.解得:x=6.所以EC=6 cm.答:EC=6 cm,CF=8 cm.类型21.C 2.15 3.2.604.把长方体的面DCC′D′沿棱C′D′展开至面ABCD上,如图.构成矩形ABC′D′,则A到C′的最短距离为AC′的长度,连接AC′交DC于O,易证△AOD≌△C′OC.∴OD=OC.即O为DC的中点,由勾股定理,得AC′2=AD′2+D′C′2=82+62=100,∴AC′=10 cm.即从顶点A沿直线到DC中点O,再沿直线到顶点C′,贴的彩带最短,最短长度为10 cm.5.(1)如图,木柜的表面展开图是两个矩形ABC′1D1和ACC1A1.蚂蚁能够最快到达目的地的可能路径有如图所示的AC′1和AC1两种.(2)蚂蚁沿着木柜表面经线段A1B1到C′1,爬过的路径的长l1=42+(4+5)2=97.蚂蚁沿着木柜表面经线段BB1到C1,爬过的路径的长l2=(4+4)2+52=89.∵l1>l2,∴最短路径的长是89.。
勾股定理之“图形折叠”模型-2023年新八年级数学核心知识点与常见题型(北师大版)(解析版)

重难点:勾股定理之“图形折叠”模型【知识梳理】图形折叠一定要注意折叠前后的边角对应关系,计算时联想到利用勾股定理对新形成的直角三角形进行求解.翻折变换(折叠问题)1、翻折变换(折叠问题)实质上就是轴对称变换.2、折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.3、在解决实际问题时,对于折叠较为复杂的问题可以实际操作图形的折叠,这样便于找到图形间的关系.首先清楚折叠和轴对称能够提供给我们隐含的并且可利用的条件.解题时,我们常常设要求的线段长为x,x的代数式表示其他线段的长度,选择适当的直角三角形,运用勾股定理列出方程求出答案.我们运用方程解决时,应认真审题,设出正确的未知数.【考点剖析】一.选择题(共9小题)1.如图,已知矩形ABCD沿着直线BD折叠,使点C落在C′处,BC′交AD于E,AD=8,AB=4,则DE的长为()A.3B.4C.5D.6【分析】根据折叠前后角相等可知△ABE≌△C′ED,利用勾股定理可求出.【解答】解:设DE=x,则AE=8﹣x,AB=4,在直角三角形ABE中,x2=(8﹣x)2+16,解之得,x=5.故选:C.【点评】本题考查图形的翻折变换,解题过程中应注意折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,如本题中折叠前后角相等.2.矩形纸片ABCD的边长AB=4,AD=2.将矩形纸片沿EF折叠,使点A与点C重合,折叠后在其一面着色(如图),则着色部分的面积为()A.8B.C.4D.【分析】着色部分的面积等于原来矩形的面积减去△ECF的面积,应先利用勾股定理求得FC的长,进而求得相关线段,代入求值即可.【解答】解:在Rt△GFC中,有FC2﹣CG2=FG2,∴FC2﹣22=(4﹣FC)2,解得,FC=2.5,∴阴影部分面积为:AB•AD﹣FC•AD=,故选:B.【点评】折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,本题中没有着色的部分为△ECF,利用了矩形和三角形的面积公式,勾股定理求解.3.直角三角形纸片的两直角边长分别为6,8,现将△ABC如图折叠,使点A与点B重合,则折痕DE的长是()A.B.C.D.【分析】先通过勾股数得到AB=10,再根据折叠的性质得到AD=DB=5,AE=BE,∠ADE=90°,设AE=x,则BE=x,CE=8﹣x,在Rt△CBE中利用勾股定理可计算出x,然后在Rt△BDE中利用勾股定理即可计算得到DE的长.【解答】解:∵直角三角形纸片的两直角边长分别为6,8,∴AB=10,又∵折叠,∴AD=DB=5,AE=BE,∠ADE=90°,设AE=x,则BE=x,CE=8﹣x,在Rt△CBE中,BE2=BC2+CE2,即x2=62+(8﹣x)2,解得x=,在Rt△BDE中,DE==故选:D.【点评】本题考查了折叠的性质:折叠前后两图形全等,即对应角相等,对应线段相等.也考查了勾股定理.4.如图所示,在长方形纸片ABCD中,AB=32cm,把长方形纸片沿AC折叠,点B落在点E处,AE交DC 于点F,AF=25cm,则AD的长为()A.16cm B.20cm C.24cm D.28cm【分析】首先根据平行线的性质以及折叠的性质证明∠EAC=∠DCA,根据等角对等边证明FC=AF,则DF即可求得,然后在直角△ADF中利用勾股定理求解.【解答】解:∵长方形ABCD中,AB∥CD,∴∠BAC=∠DCA,又∵∠BAC=∠EAC,∴∠EAC=∠DCA,∴FC=AF=25cm,又∵长方形ABCD中,DC=AB=32cm,∴DF=DC﹣FC=32﹣25=7cm,在直角△ADF中,AD===24(cm).故选:C.【点评】本题考查了折叠的性质以及勾股定理,在折叠的过程中注意到相等的角以及相等的线段是关键.5.如图,矩形ABCD沿直线BD折叠,使点C落在点C处,BC交AD于点E,AD=8,AB=4,则BE的长为()A.3B.4C.5D.2【分析】由矩形的性质和折叠的性质得出∠C′BD=∠DBC=∠BDA,可得DE=BE,设BE=DE=x,则AE=8﹣x.根据勾股定理得出方程,解方程即可.【解答】解:∵四边形ABCD是矩形,∴AD∥BC,∴∠DBC=∠BDA,由折叠的性质得:∠C′BD=∠DBC,∴∠C′BD=∠BDA,∴DE=BE,设BE=DE=x,则AE=8﹣x.在△ABE中,由勾股定理得:x2=42+(8﹣x)2.解得:x=5,∴BE=5.故选:C.【点评】此题考查了矩形的性质、翻折变换的性质、等腰三角形的判定、勾股定理;熟练掌握矩形和翻折变换的性质,由勾股定理得出方程是解决问题的关键.6.直角三角形纸片的两直角边长分别为6,8,现将△ABC如图那样折叠,使点A与点B重合,折痕为DE,则的值是()A.B.C.D.【分析】先设CE=x,再根据图形翻折变换的性质得出AE=BE=8﹣x,再根据勾股定理求出x的值,进而可得出的值.【解答】解:设CE=x,则AE=8﹣x,∵△BDE是△ADE翻折而成,∴AE=BE=8﹣x,在Rt△BCE中,BE2=BC2+CE2,即(8﹣x)2=62+x2,解得x=,∴==.故选:C.【点评】本题考查的是图形翻折变换的性质及勾股定理,熟知“折叠是一种对称变换,它属于轴对称,折叠7.将正方形ABCD折叠,使顶点A与CD边上的点M重合,折痕交AD于E,交BC于F,边AB折叠后与BC边交于点G(如图).如果DM:MC=3:2,则DE:DM:EM=()A.7:24:25B.3:4:5C.5:12:13D.8:15:17【分析】先根据折叠的性质得EM=EA,再根据勾股定理得ME的长,从而求比值.【解答】解:由折叠知,EM=EA,设CD=AD=5a,∴DE=5a﹣EM,DM=3a,MC=2a,在Rt△EDM中,EM2=DE2+DM2,即ME2=(5a﹣ME)2+(3a)2,解得ME=a∴ED=a∴DE:DM:EM=a:3a:a=8:15:17.故选:D.【点评】本题利用了:1、折叠的性质:折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等;2、通过设适当的参数,利用正方形的性质,勾股定理求解.8.如图,矩形纸片ABCD中,AB=18cm,把矩形纸片沿直线AC折叠,点B落在点E处,AE交DC于点F,若AF=13,则AD的长为()A.5cm B.6cm C.10cm D.12cm=FC,在直角三角形ADF中,运用勾股定理求解.【解答】解:根据折叠前后角相等可知△ADF≌△CEF,设DA=x,又AF=13,DF=18﹣13=5,在直角三角形ADF中,x2+52=132,解之得,x=12cm.故选:D.【点评】本题考查图形的翻折变换,解题过程中应注意折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,如本题中折叠前后角相等.9.如图,将一个边长分别为4,8的长方形纸片ABCD折叠,使C点与A点重合,则折痕EF的长是()A.B.C.D.【分析】根据轴对称的性质,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等和勾股定理求解.【解答】解:根据折叠的性质知,四边形AFEB与四边形CEFD全等,有EC=AF=AE,由勾股定理得,AB2+BE2=AE2即42+(8﹣AE)2=AE2,解得,AE=AF=5,BE=3,作EG⊥AF于点G,则四边形AGEB是矩形,有AG=3,GF=2,GE=AB=4,由勾股定理得EF=.故选:D.【点评】本题利用了:1、折叠的性质;2、矩形的性质.二.填空题(共1小题)10.已知,矩形ABCD中,AB=3cm,AD=9cm,将此长方形折叠,使点B与点D重合,折痕为EF,则△ABE的面积为A.6cm2B.8cm2C.10cm212cm2.【分析】根据折叠的条件可得:BE=DE,在直角△ABE中,利用勾股定理就可以求解.【解答】解:将此长方形折叠,使点B与点D重合,∴BE=ED.∵AD=9cm=AE+DE=AE+BE.∴BE=9﹣AE,根据勾股定理可知:AB2+AE2=BE2.解得AE=4.∴△ABE的面积为3×4÷2=6.故选A.【点评】本题考查了利用勾股定理解直角三角形的能力,即:直角三角形两直角边的平方和等于斜边的平方.三.解答题(共1小题)11.如图所示,折叠长方形一边AD,点D落在BC边的点F处,已知BC=10厘米,AB=8厘米,求BF与FC的长.【分析】由图形翻折变换的性质可知,AD=AF,设BF=x,则FC=10﹣x,在Rt△ABF中利用勾股定理即可求解BF,再由BC=12厘米可得出FC的长度.【解答】解:∵△AEF是△AED沿直线AE折叠而成,AB=8cm,BC=10cm,∴AD=AF=10cm,设BF=x,则FC=10﹣x,在Rt△ABF中,AF2=AB2+BF2,即102=82+x2,解得x=6,即BF=6厘米.∴FC=BC﹣BF=10﹣6=4cm.综上可得BF的长为6厘米、FC的长为4厘米.BF,AF的长度,在△ABF中利用勾股定理,难度一般.【过关检测】一.选择题(共11小题)1.(2022秋•大东区校级期末)如图,已知矩形ABCD沿着直线BD折叠,使点C落在C′处,BC′交AD 于E,AD=8,AB=4,则DE的长为()A.3B.4C.5D.6【分析】先根据翻折变换的性质得出CD=C′D,∠C=∠C′=90°,再设DE=x,则AE=8﹣x,由全等三角形的判定定理得出Rt△ABE≌Rt△C′DE,可得出BE=DE=x,在Rt△ABE中利用勾股定理即可求出x的值,进而得出DE的长.【解答】解:∵Rt△DC′B由Rt△DBC翻折而成,∴CD=C′D=AB=8,∠C=∠C′=90°,设DE=x,则AE=8﹣x,∵∠A=∠C′=90°,∠AEB=∠DEC′,∴∠ABE=∠C′DE,在Rt△ABE与Rt△C′DE中,,∴Rt△ABE≌Rt△C′DE(ASA),∴BE=DE=x,在Rt△ABE中,AB2+AE2=BE2,∴42+(8﹣x)2=x2,解得:x=5,∴DE的长为5.故选:C.【点评】本题考查的是翻折变换的性质及勾股定理,熟知折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等的知识是解答此题的关键.2.(2021秋•镇海区校级期中)如图,将矩形ABCD的四个角向内折起,恰好拼成一个无缝隙无重叠的四边形EFGH,若EH=5厘米,EF=12厘米,则边HF的长是()A.12厘米B.13厘米C.14厘米D.15厘米【分析】利用折叠的性质得出∠HEF=90°,再利用勾股定理即可求解.【解答】解:∵△AEH折叠得到△MEH,△BEF折叠得到△MEF,∴∠AEH=∠MEH,∠BEF=∠MEF,∴∠HEF=∠MEH+∠MEF=(∠AEM+∠BEM)=90°,∴△HEF为直角三角形,在Rt△HEF中,EH2+EF2=HF2,∵EH=5厘米,EF=12厘米,∴HF==13厘米,故选:B.【点评】本题考查折叠的性质,勾股定理,解题的关键是利用折叠性质得到∠HEF=90°.3.(2022春•杭锦后旗期中)如图是一张直角三角形的纸片,两直角边AC=6cm、BC=8cm,现将△ABC折叠,使点B与点A重合,折痕为DE,则CD的长为()A.cm B.cm C.cm D.无法确定【分析】设CD=xcm,则BD=BC﹣CD=(8﹣x)cm,再根据折叠的性质得AD=BD=8﹣x,然后在△ACD 中根据勾股定理得到(8﹣x)2=62+x2,再解方程即可.【解答】解:设CD=xcm,则BD=BC﹣CD=(8﹣x)cm,∵△ABC折叠,使点B与点A重合,折痕为DE,∴AD=BD=8﹣x,在△ACD中,∠C=90°,∴AD2=AC2+CD2,∴(8﹣x)2=62+x2,解得x=,即CD的长为cm.故选:C.【点评】本题考查了折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.也考查了勾股定理.4.(2021春•永嘉县校级期末)如图,将边长为8cm正方形纸片ABCD折叠,使点D落在BC边的中点E 处,点A落在点F处,折痕为MN,则线段CN的长是()A.6cm B.5cm C.4cm D.3cm【分析】根据折叠的性质,只要求出DN就可以求出NE,在直角△CEN中,若设CN=x,则DN=NE=8﹣x,CE=4cm,根据勾股定理就可以列出方程,从而解出CN的长.【解答】解:由题意设CN=x cm,则EN=(8﹣x)cm,又∵CE=DC=4cm,∴在Rt△ECN中,EN2=EC2+CN2,即(8﹣x)2=42+x2,解得:x=3,即CN=3cm.故选:D.【点评】本题考查翻折变换的问题,折叠问题其实质是轴对称,对应线段相等,对应角相等,找到相应的直角三角形利用勾股定理求解是解决本题的关键.5.(2021秋•裕华区校级期末)如图是一张直角三角形的纸片.两直角边AC=6cm,BC=8cm将△ABC折叠,使点B与点A DE,则AD的长为()A.cm B.10cm C.cm D.5cm【分析】首先设AD=xcm,由折叠的性质得:BD=AD=xcm,又由BC=8cm,可得CD=8﹣x(cm),然后在Rt△ACD中,利用勾股定理即可求得方程,解方程即可求得答案.【解答】解:设AD=xcm,由折叠的性质得:BD=AD=xcm,∵在Rt△ABC中,AC=6cm,BC=8cm,∴CD=BC﹣BD=8﹣x(cm),在Rt△ACD中,AC2+CD2=AD2,即:62+(8﹣x)2=x2,解得:x=,∴AD=cm.故选:A.【点评】此题考查了折叠的性质与勾股定理的知识.此题难度适中,注意掌握数形结合思想与方程思想的应用,注意掌握折叠前后图形的对应关系.6.(2021春•漳平市期中)如图,在长方形ABCD中,AB=3cm,AD=9cm,将此长方形折叠,使点B与点D重合,折痕为EF,则△ABE的面积为()A.6cm2B.8cm2C.10cm2D.12cm2【分析】首先根据翻折的性质得到ED=BE,再设出未知数,分别表示出线段AE,ED,BE的长度,然后在Rt △ABE中利用勾股定理求出AE AE的长度,就可以利用面积公式求得△ABE的面积了.【解答】解:∵长方形折叠,使点B与点D重合,∴ED=BE,设AE=xcm,则ED=BE=(9﹣x)cm,在Rt△ABE中,AB2+AE2=BE2,∴32+x2=(9﹣x)2,解得:x=4,∴△ABE的面积为:3×4×=6(cm2).故选:A.【点评】此题主要考查了图形的翻折变换和学生的空间想象能力,解题过程中应注意折叠后哪些线段是重合的,相等的,如果想象不出哪些线段相等,可以动手折叠一下即可.7.(2020•饶平县校级模拟)如图,将边长为8cm的正方形纸片ABCD折叠,使点D落在AB边中点E处,点C落在点Q处,折痕为FH,则线段AF的长是()A.3cm B.4cm C.5cm D.6cm【分析】根据△AEF是直角三角形利用勾股定理求解即可.【解答】解:由折叠可得DF=EF,设AF=x,则EF=8﹣x,∵AF2+AE2=EF2,∴x2+42=(8﹣x)2,解得x=3.故选:A.【点评】本题考查折叠问题;找到相应的直角三角形利用勾股定理求解是解决本题的关键.8.(2021春•环翠区校级期中)如图:长方形纸片ABCD中,AD=4cm,AB=10cm,按如图的方式折叠,使点B与点D重合.折痕为DE长为()A.4.8cm B.5cm C.5.8cm D.6cm【分析】在折叠的过程中,BE=DE,从而设BE=DE=x,即可表示AE,在直角三角形ADE中,根据勾股定理列方程即可求解.【解答】解:设DE=xcm,则BE=DE=x,AE=AB﹣BE=10﹣x,在Rt△ADE中,DE2=AE2+AD2,即x2=(10﹣x)2+16.解得:x=5.8.故选:C.【点评】此题主要考查了翻折变换的问题,解答本题的关键是掌握翻折前后对应线段相等,另外要熟练运用勾股定理解直角三角形.9.(2021秋•开福区校级期末)如图,将矩形ABCD沿EF折叠,使顶点C恰好落在AB边的中点C′上.若AB=6,BC=9,则BF的长为()A.4B.3C.4.5D.5【分析】先求出BC′,再由图形折叠特性知,C′F=CF=BC﹣BF=9﹣BF,在Rt△C′BF中,运用勾股定理BF2+BC′2=C′F2求解.【解答】解:∵点C′是AB边的中点,AB=6,∴BC′=3,由图形折叠特性知,C′F=CF=BF=9﹣BF,在Rt△C′BF中,BF2+BC′2=C′F2,∴BF2+9=(9﹣BF)2,解得,BF=4,故选:A.【点评】本题考查了折叠问题及勾股定理的应用,综合能力要求较高.同时也考查了列方程求解的能力.解题的关键是找出线段的关系.10.(2021春•宁明县期中)如图,矩形纸片ABCD中,AB=8cm,把矩形纸片沿直线AC折叠,点B落在点E处,AE交DC于点F,若AF=cm,则AD的长为()A.4cm B.5cm C.6cm D.7cm【分析】由折叠的性质可证AF=FC.在Rt△ADF中,由勾股定理求AD的长.【解答】解:由折叠的性质知,AE=AB=CD,CE=BC=AD,∴△ADC≌△CEA,∠EAC=∠DCA∴AF=CF=cm,DF=CD﹣CF=在Rt△ADF中,由勾股定理得,AD=6cm.故选:C.【点评】本题利用了:①折叠的性质:折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等;②全等三角形的判定和性质,勾股定理求解.11.(2021秋•东平县期末)如图,在平面直角坐标系中,点A的坐标是(﹣3,0),点B的坐标是(0,4),点M是OB上一点,将△ABM沿AM折叠,点B恰好落在x轴上的点B'处,则点M的坐标为()A.(,0)B.(0,)C.(,0)D.(0,)【分析】设沿直线AM将△ABM B正好落在x轴上的B'点,则有AB=AB',而AB的长度根据已知可以求出,所以B'点的坐标由此求出;又由于折叠得到B'M=BM,在直角△B'MO中根据勾股定理可以求出OM,也就求出M的坐标.【解答】解:∵将△ABM沿AM折叠,∴AB=AB',又A(﹣3,0),B(0,4),∴AB=5=AB',∴点B'的坐标为:(2,0),设M点坐标为(0,b),则B'M=BM=4﹣b,∵B'M2=B'O2+OM2,∴(4﹣b)2=22+b2,∴b=,∴M(0,),故选:B.【点评】本题考查了一次函数图象上点的坐标特征,也考查了翻折变换,题中利用折叠知识与直线的关系以及直角三角形等知识求出线段的长是解题的关键.二.填空题(共6小题)12.(2022秋•江北区期末)如图,有一张直角三角形的纸片,∠ACB=90°,AB=5,AC=3.现将三角形折叠,使得边AC与AB重合,折痕为AE,则CE长为.【分析】解法一:先根据勾股定理求得BC的长,再根据折叠的性质得到CE=DE,AC=AD,∠C=∠EDA=90°,则BD=AB﹣AD,∠EDB=90°,设CE=DE=x,在Rt△BDE中根据勾股定理列出方程,求解即可.解法二:先根据勾股定理求得BC的长,再根据折叠的性质可推出∠EDB=90°,以此可得△BDE∽△BCA,设CE=DE=x,根据相似三角形的性质即可解答.【解答】解:解法一:在Rt△ABC中,由勾股定理得BC==4,根据折叠的性质可知CE=DE,AC=AD=3,∠C=∠EDA=90°,∴∠EDB=90°,BD=AB﹣AD=5﹣3=2,设CE=DE=x,则BE=4﹣x,Rt△BDE中,DE2+BD2=BE2,即x2+22=(4﹣x)2,解得:,∴CE=.故答案为:.解法二:在Rt△ABC中,由勾股定理得BC==4,根据折叠的性质可知CE=DE,∠C=∠EDA=90°,∴∠EDB=∠C=90°,∵∠B为公共角,∴△BDE∽△BCA,∴,设CE=DE=x,则BE=4﹣x,∴,∴x=,∴CE=.故答案为:.【点评】本题主要考查翻折变换、勾股定理、相似三角形的判定与性质,解题时,我们常常设要求的线段长为x,然后根据折叠和轴对称的性质用含x的代数式表示其他线段的长度,选择适当的直角三角形,运用勾股定理列出方程求出答案13.(2022中,AB=5,BC=12,点E是边AD上的一个动点,把△BAE沿BE折叠,点A落在A'处,当△A'DE是直角三角形时,DE的长为.【分析】当△A'DE是直角三角形时,可分两种情况进行讨论:①当∠EA′D=90°时,此时A′在BD上,由勾股定理可得BD=13,根据折叠的性质可得AE=A′E,AB=A′B=5,A′D=8,设AE=A′E=x,则DE=12﹣x,最后根据勾股定理即可解答;②当∠A′ED=90°时,根据折叠的性质可得∠AEB=∠AEB,以此可推出△ABE为等腰直角三角形,AB=AE=5,再根据DE=AD﹣AE即可求解.【解答】解:①当∠EA′D=90°时,如图,∵四边形ABCD为矩形,∴∠A=90°,BC=AD=12,AB=5,∴BD=,根据折叠的性质可得,AE=A′E,AB=A′B=5,∴A′D=BD﹣A′B=8,设AE=A′E=x,则DE=12﹣x,在Rt△A'DE中,根据勾股定理得AE2+A′D2=DE2,∴x2+82=(12﹣x)2,解得:,∴AE=,;②当∠A′ED=90°时,如图,∴∠AEA=90°,根据折叠的性质可得,∠AEB=∠AEB,∵∠AEB+∠AEB=90°,∴∠AEB=∠AEB=45°,∴△ABE为等腰直角三角形,AB=AE=5,∴DE=AD﹣AE=12﹣5=7;综上,DE=或7.故答案为:或7.【点评】本题主要考查勾股定理、矩形的性质、折叠的性质,据折叠和轴对称的性质用含x的代数式表示其他线段的长度,选择适当的直角三角形,运用勾股定理列出方程求出答案是解题关键.14.(2021秋•鼓楼区校级期末)如图,在△ABC中,∠C=90°,AB的垂直平分线交AB、AC于点D、E,若AC=8,BD=5,则CE的长度是.【分析】连接BE,根据线段垂直平分线的性质得出BE=AE,BD=AD=5,根据勾股定理求出BC,设CE=x,再根据勾股定理得出方程62+(8﹣x)2=x2,求出x,即可得到CE的长.【解答】解:如图所示,连接BE,∵AB的垂直平分线交AB、AC于点D、E,BD=5,∴BE=AE,AD=BD=5,∴AB=5+5=10,在Rt△ABC中,由勾股定理得:BC===6,设CE=x,则BE=AE=8﹣x,在Rt△CBE中,由勾股定理得:BC2+CE2=BE2,∴62+x2=(8﹣x)2,解得:x=,∴CE=,故答案为:.【点评】本题考查了线段垂直平分线性质和勾股定理等知识点,能熟记线段垂直平分线上的点到线段两个端点的距离相等是解此题的关键.15.(2022秋•南关区校级期末)如图,透明的圆柱形玻璃容器(容器厚度忽略不计)的高为20cm,在容器内壁离容器底部4cm的点B处有一滴蜂蜜,此时一只蚂蚁正好在容器外壁,位于离容器上沿4cm的点A 处,若蚂蚁吃到蜂蜜需爬行的最短路径为25cm,则该圆柱底面周长为.【分析】将容器的侧面展开,建立点A关于CE的对称点A′,根据两点之间线段最短可知A′B的长度即为所求.【解答】解:将圆柱的侧面展开,EC为上底面圆周长的一半,作点A关于CE的对称点A′,连接A′B交EC于点F,则蚂蚁吃到蜂蜜需爬行的最短路径为AF+BF,即AF+BF=A′F+BF=A′B=25m,延长BC,过A′作A′D⊥BC于点D,∵AE=A′E=DC=4cm,∴BD=20cm,Rt△A′BD中,由勾股定理可得A′D===15cm,则该圆柱底面周长为30cm.故答案为:30cm.【点评】本题考查了平面展开﹣最短路径问题,将图形展开,利用轴对称的性质和勾股定理进行计算是解题关键.16.(2022秋•鼓楼区期中)如图,矩形ABCD中,AB=5,BC=3,将矩形沿BE折叠,使顶点A落在CD 上的点F处,其中E在AD上,连接AF,则AE=.【分析】首先利用勾股定理求出FC的长,设AE=EF=x,在Rt△DEF中,利用勾股定理构建方程即可解决问题;【解答】解:∵四边形ABCD是矩形,∴∠D=∠C=90°,在Rt△BCF中,BF=AB=5,BC=AD=3,∴CF==4,∴DF=CD﹣CF=1,设AE=EF=x,在Rt△DEF中,∵EF2=DE2+DF2,∴x2=(3﹣x)2+12,∴x=,∴AE=.故答案为:.【点评】本题考查四边形综合题、矩形的性质和判定、全等三角形的判定和性质、勾股定理等知识,解题的关键是学会利用勾股定理构建方程解决问题.17.(2022秋•下城区校级期中)在△ABC中,∠C=90°,AC=6,BC=8,将它的一个锐角翻折,使该锐角顶点落在其对边的中点D处,折痕交另一直角边于点E,交斜边于点F,则DE的长为.【分析】根据题意设DE=x求出CE的长,然后在Rt△ECD中利用勾股定理列方程求解即可.【解答】解:分两种情况:①如图1所示:∵D是BC的中点,∴CD=BC=4,由折叠的性质得:DE=AE,设DE=x,则CE=6﹣x,在Rt△ECD中,DE2=EC2+CD2,即x2=(6﹣x)2+16,解得x=,即DE=.②如图1所示:∵D是BC的中点,∴CD=AC=3,由折叠的性质得:DE=BE,设DE=x,则CE=8﹣x,在Rt△ECD中,DE2=EC2+CD2,即x2=(8﹣x)2+9,解得x=,即DE=;故答案为:或.【点评】本题考查了翻折变换的性质以及勾股定理等知识;熟练掌握翻折变换和勾股定理是解题的关键.三.解答题(共4小题)18.(2022秋•西湖区校级期中)如图,在等边△ABC中,点D,E分别是AB,AC上的点,将△ADE沿DE 所在直线对折,点A落在BC边上的点A′处,且DA′⊥BC.(1)求∠AED的度数.(2)若AD=,求线段AB和CE的值.【分析】(1)根据等边三角形的性质得∠A=∠B=∠C=60°,根据折叠的性质得∠A=∠DA′E=60°,∠AED=∠A′ED,进而求得∠EA′C=30°,由三角形的外角性质得∠AEA′=∠EA′C+∠C=2∠AED,以此即可求解;(2)根据折叠的性质可得AD=A′D,根据含30度角的直角三角形性质可A′B=x,则BD=2x,根据勾股定理列出方程解得x=1,则AB=BC=2,由(1)可知∠EA′C=30°,最后根据30度角所对的直角边等于斜边的一半即可求解.【解答】解:(1)∵△ABC为等边三角形,∴∠A=∠B=∠C=60°,根据折叠可知,∠A=∠DA′E=60°,∠AED=∠A′ED,∵∠DA′⊥BC,∴∠DA′C=90°,∴∠EA′C=∠DA′C﹣∠DA′E=90°﹣60°=30°,∴∠AEA′=∠EA′C+∠C=2∠AED=30°+60°=90°,∴∠AED=90°÷2=45°;(2)根据折叠可知,AD=A′D,∵AD=,∴A′D=AD=,由(1)可知,∠B=60°,∠DA′B=90°,∴∠A′DB=30°,∴BD=2A′B,设A′B=x,则BD=2x,在Rt△A′BD中,由勾股定理得A′B2+A′D2=BD2,即,解得:x=1或﹣1(舍去),∴A′B=1,BD=2,∴AB=AD+BD=2,∵△ABC为等边三角形,∴BC=AB=2,∴A′C=BC﹣A′B=,由(1)知,∠EA′C=30°,∴∠A′EC=180°﹣∠EA′C﹣∠C=90°,在Rt△A′EC中,∠EA′C=30°,∴CE==.综上,线段AB=2,CE=.【点评】本题主要考查折叠的性质、等边三角形的性质、三角形的外角性质、勾股定理,熟记30度角所对的直角边等于斜边的一半是解题关键.19.(2022秋•和平区期末)在△ABC中,AB=25,,AP垂直直线BC于点P.(1)当BC=25时,求AP的长;(2)当AP=20时,①求BC的长;②将△ACP沿直线AC翻折后得到△ACQ,连接BQ,请直接写出△BCQ的周长为.【分析】(1)设PC=x,则BP=25﹣x,根据勾股定理列出方程求解即可;(2)①分两种情况:Ⅰ.当△ABC为锐角三角形,根据勾股定理求出CP、BP,则BC=CP+BP;Ⅱ.当△ABC为钝角三角形,根据勾股定理求出PC、PB,则BC=PB﹣PC;②分两种情况:Ⅰ.当△ABC为锐角三角形,连接PQ,交AC于点E,过Q作QD⊥BC交BC反向延长线于点D,根据折叠的性质可得CP=CQ=10,PE=QE=,且PQ⊥AC,根据等面积法求出PE=,则PQ =2PE=,设CD=a,则DP=10+a,根据勾股定理可得QD2=CQ2﹣CD2=100﹣a2,QD2=PQ2﹣DP2=320﹣(10+a)2,以此列出方程,求解得CD=6,QD=8,则BD=CD+BC=31,根据勾股定理求出BQ,以此即可求解;Ⅱ.当△ABC为锐角三角形,连接PQ,交AC于点E,过Q作QD⊥BC交BC反向延长线于点D,根据折叠的性质可得CP=CQ=10,PE=QE=,且PQ⊥AC,根据等面积法求出PE=,则PQ=2PE=,设BD=m,则CD=5+m,PD=15+m,根据勾股定理可得QD2=CQ2﹣CD2=100﹣(5+m)2,QD2=PQ2﹣PD2=320﹣(15+m)2,以此列出方程,求解得BD=1,QD=8,根据勾股定理求出BQ,以此即可求解.【解答】解:(1)如图,设PC=x,则BP=25﹣x,∵AP⊥BC,∴∠APC=∠APB=90°,在Rt△ACP中,由勾股定理得AP2AC2﹣PC2=500﹣x2在Rt△ABP中,由勾股定理得AP2=AB2﹣BP2=625﹣(25﹣x)2,∴500﹣x2=625﹣(25﹣x)2,解得:x=10,∴AP==20;(2)①Ⅰ.当△ABC为锐角三角形,如图,∵AP⊥BC,∴∠APC=∠APB=90°,在Rt△ACP中,AC=,由勾股定理得=10,在Rt△ABP中,AB=25,由勾股定理得BP==15,∴BC=CP+BP=25;Ⅱ.当△ABC为钝角三角形,如图,∵AP⊥BC,∴∠APB=90°,在Rt△APC中,由勾股定理得PC==10,在Rt△APB中,由勾股定理得PB==15,∴BC=PB﹣PC=5;综上,BC的长为25或5;②Ⅰ.当△ABC为锐角三角形,连接PQ,交AC于点E,过Q作QD⊥BC交BC反向延长线于点D,如图,由(2)①Ⅰ知,CP=10,PB=15,BC=25,由折叠的性质可知,CP=CQ=10,PE=QE=,且PQ⊥AC,∵,即,∴PE=,∴PQ=2PE=,设CD=a,则DP=10+a,在Rt△QDC中,由勾股定理得QD2=CQ2﹣CD2=100﹣a2,在Rt△QDP中,由勾股定理得QD2=PQ2﹣DP2=320﹣(10+a)2,∴100﹣a2=320﹣(10+a)2,解得:a=6,∴CD=6,QD==8,∴BD=CD+BC=31,在Rt△QDB中,由勾股定理得=,∴△BCQ的周长为CQ+PC+PB+BQ=10+10+15+=35+;Ⅱ.当△ABC为锐角三角形,连接PQ,交AC于点E,过Q作QD⊥BC交BC反向延长线于点D,如图,由(2)①Ⅱ知,CP=10,PB=15=5,由折叠的性质可知,CP=CQ=10,PE=QE=,且PQ⊥AC,∵,即,∴PE=,∴PQ=2PE=,设BD=m,则CD=5+m,PD=15+m,在Rt△QDC中,由勾股定理可得QD2=CQ2﹣CD2=100﹣(5+m)2,在Rt△QDP中,由勾股定理得QD2=PQ2﹣PD2=320﹣(15+m)2,∴100﹣(5+m)2=320﹣(15+m)2,解得:m=1,在Rt△QDB中,由勾股定理得BQ=,∴△BCQ的周长为BC+BQ+CQ=5++10=15+.综上,△BCQ的周长为35+或15+.故答案为:35+或15+.【点评】本题主要考查勾股定理、折叠的性质、等面积法求三角形的高,解题关键在于根据题意正确画出图形,利用数形结合思想解决问题.20.(2022秋•武侯区校级期中)在四边形ABCD中,∠A=∠B=∠C=∠D=90°,AB=CD=10,BC=AD =6,P为射线BC上一点,将△ABP沿直线AP翻折至△AEP的位置,使点B落在点E处.(1)若P为BC上一点.①如图1,当点E落在边CD上时,求CE的长;②如图2,连接CE,若CE∥AP,则BP与BC有何数量关系?请说明理由;(2)如果点P在BC的延长线上,当△PEC为直角三角形时,求PB的长.【分析】(1)①以点A为圆心,AB为半径交CD于点E,利用勾股定理求出DE的长即可;②根据平行线的性质和翻折的性质可证EP=CP,BP=PE,从而BP=PC;(2)由△PEC是直角三角形,当∠EPC=90°时,则四边形ABPE是正方形,得PB=AB=10;当∠ECP=90°时,设BP=x,则PC=x﹣6,在Rt△ECP中,利用勾股定理列方程即可求解,当∠PEC=90°时,点P在线段BC上,不符合题意,舍去.【解答】解:(1)①如图:以点A为圆心,AB为半径交CD于点E,∵AE=AB=10,AD=6,∠D=90°,∴CE=DC﹣DE=10﹣8=2;②BC=2BP,理由如下:∵将△ABP沿直线AP翻折至△AEP的位置,∴∠APB=∠APE,PE=BP,∵CE∥AP,∴∠CEP=∠APE,∠ECP=∠APB,∴∠PEC=∠ECP,∴EP=CP,∴BP=BC,∴BC=2BP;(2)∵△PEC是直角三角形,当∠EPC=90°时,∵∠EPC=∠AEP=∠B=90°,且=BP,∴四边形ABPE是正方形,∴PB=AB=10;当∠ECP=90°时,则∠ECP=∠B=90°,∴EC∥AB,∵DC∥AB,∴点E、D、C三点共线,由翻折知AE=AB=10,根据勾股定理得DE=8,∴EC=18,设BP=x,则PC=x﹣6,在Rt△ECP中,由勾股定理得:182+(x﹣6)2=x2,解得x=30,∴PB=30;当∠PEC=90°时,点P在线段BC上,不符合题意,舍去,综上:BP=10或30.【点评】本题属于几何变换综合题,考查了矩形的性质,翻折变换,勾股定理等知识,解题的关键是学会利用参数构建方程解决问题,学会利用分类讨论的思想思考问题,属于中考压轴题.21.(2022秋•绥德县期中)如图所示,折叠长方形一边AD,点D落在BC边的点F处,已知BC=10厘米,AB=8厘米.(1)求BF与FC的长.(2)求EC的长.【分析】(1)由图形翻折变换的性质可知,AD=AF=10,在Rt△ABF中利用勾股定理即可求解BF,再由BC =12厘米可得出FC的长度;(2)将CE的长设为x,得出DE=10﹣x=EF,在Rt△CEF中,根据勾股定理列出方程求解即可.【解答】解:(1)∵△ADE折叠后的图形是△AFE,∴AD=AF,∠D=∠AFE,DE=EF.∵AD=BC=10cm,∴AF=AD=10cm.又∵AB=8cm,在Rt△ABF AB2+BF2=AF2∴82+BF2=102,∴BF=6cm,∴FC=BC﹣BF=10﹣6=4cm.(2)设EC的长为xcm,则DE=(8﹣x)cm.在Rt△EFC中,根据勾股定理,得:FC2+EC2=EF2,∴42+x2=(8﹣x)2,即16+x2=64﹣16x+x2,化简,得16x=48,∴x=3,故EC的长为3cm.【点评】本题主要考查了勾股定理的应用,解题时常设要求的线段长为x,然后根据折叠和轴对称的性质用含x的代数式表示其他线段的长度,选择适当的直角三角形,运用勾股定理列出方程求出答案.。
勾股定理折叠问题六种模型

勾股定理折叠问题六种模型首先,我们来先了解勾股定理折叠问题。
勾股定理告诉我们:任意一个直角三角形,其斜边的平方等于它的两个直角边的平方之和。
例如a²+b²=c²,其中a和b分别代表两条直角边,而c是斜边。
勾股定理折叠问题是由米彻斯把勾股定理转化为一个寻找三角形元素来组成一个功能性三角形的解决方案。
它需要一个有序的折叠和解释来完成。
一、利用三角形抽象模型利用三角形抽象模型是以好的方式实现勾股定理折叠问题的一种方法,这种方法基于三角形的内在几何结构,从而找出完美的三角形。
实用性非常强,可以帮助设计各种不同的形状的三角形,而且阻止结构受到外部环境的影响,使三角形保持其准确性,用于各种应用场景。
二、基本折叠模型基本折叠模型是一种利用简单形状折叠和拼接两个等边三角形成直角三角形的方法。
可以使用画线和折线绘制出三角形,也可以通过纸张折叠,压入特定几何形状实现最简单的直角三角形。
三、网线折叠模型网线折叠是一种快速折叠和拼接两个等边三角形的方法,它可以使用网格布线,或用具有相同数目的线段绘制几何图形,而不需要画太多细节,使折叠过程变得更简单快捷。
四、极限折叠模型极限折叠是利用特殊的几何形状(如螺旋状线条)来构建等边三角形的方法。
如果可以使用螺旋状线条,就可以节省大量长度,同时保持精确度,成功实现三角形拼接。
五、纯几何折叠模型纯几何折叠模型是一种利用几何图形功能来折叠和连接两个等边三角形的技术,这种方法使用精确的几何图形,考虑物理原理和几何角度,从而精确折叠出正确形状,使得三角形完美体现。
六、超级折叠模型超级折叠模型是一种将分层折叠和几何折叠结合到一起的方法,该方法在折叠时考虑多个因素,利用几何图形折叠和正确的分层折叠,最终得到准确的直角三角形。
它非常可靠,除了得到准确的直角三角形外,还可以用于构建其他复杂的几何模型,以满足设计需求。
立体几何中的折叠与展开问题
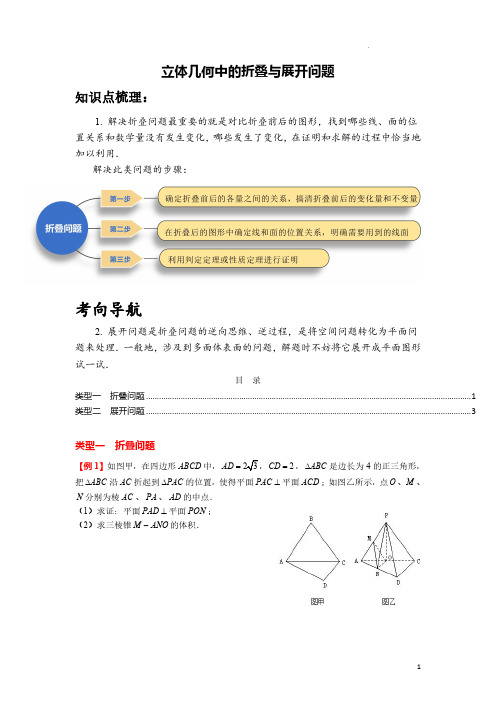
立体几何中的折叠与展开问题知识点梳理:1.解决折叠问题最重要的就是对比折叠前后的图形,找到哪些线、面的位置关系和数学量没有发生变化,哪些发生了变化,在证明和求解的过程中恰当地加以利用.解决此类问题的步骤:考向导航2.展开问题是折叠问题的逆向思维、逆过程,是将空间问题转化为平面问题来处理.一般地,涉及到多面体表面的问题,解题时不妨将它展开成平面图形试一试.目录类型一折叠问题 (1)类型二展开问题 (3)类型一折叠问题【例1】如图甲,在四边形ABCD中,23AD=2∆是边长为4的正三角形,CD=,ABC把ABC∆的位置,使得平面PAC⊥平面ACD;如图乙所示,点O、M、∆沿AC折起到PACN分别为棱AC、PA、AD的中点.(1)求证:平面PAD⊥平面PON;(2)求三棱锥M ANO-的体积.【例2】如图,在平面图形PABCD 中,ABCD 为菱形,60DAB ∠=︒,2PA PD ==,M 为CD 的中点,将PAD ∆沿直线AD 向上折起,使BD PM ⊥.(1)求证:平面PAD ⊥平面ABCD ;(2)若直线PM 与平面ABCD 所成的角为30︒,求四棱锥P ABCD -的体积.【变式1-1】如图甲的平面五边形PABCD 中,PD PA =,5AC CD BD ===,1AB =,2AD =,PD PA ⊥,现将图甲中的三角形PAD 沿AD 边折起,使平面PAD ⊥平面ABCD 得图乙的四棱锥P ABCD -.在图乙中(1)求证:PD ⊥平面PAB ;(2)求二面角A PB C --的大小;(3)在棱PA 上是否存在点M 使得BM 与平面PCB 所成的角的正弦值为13?并说明理由.类型二展开问题【例1】如图,已知正三棱柱111ABC A B C -的底面边长为2cm ,高为5cm ,则一质点自点A 出发,沿着三棱柱的侧面绕行两周到达点1A 的最短路线的长为()A .5cm B .12cm C .13cm D .25cm【例2】如图,正三棱锥S ABC -中,40BSC ∠=︒,2SB =,一质点自点B 出发,沿着三棱锥的侧面绕行一周回到点B 的最短路线的长为()A .2B .3C .3D .33【变式2-1】如图,在直三棱柱111ABC A B C -中,1AB =,2BC =,13BB =,90ABC ∠=︒,点D 为侧棱1BB 上的动点.(1)求此直三棱柱111ABC A B C -的表面积;(2)当1AD DC +最小时,三棱锥1D ABC -的体积.巩固训练1.把如图的平面图形分别沿AB 、BC 、AC 翻折,已知1D 、2D 、3D 三点始终可以重合于点D 得到三棱锥D ABC -,那么当该三棱锥体积最大时,其外接球的表面积为.2、如图,AB 是圆O 的直径,点C 是圆O 上异于A ,B 的点,PO 垂直于圆O 所在的平面,且1PO OB ==,(Ⅰ)若D 为线段AC 的中点,求证:AC ⊥平面PDO ;(Ⅱ)求三棱锥P ABC -体积的最大值;(Ⅲ)若2BC =E 在线段PB 上,求CE OE +的最小值.3.请从下面三个条件中任选一个,补充在下面的横线上,并作答.①()0BA PA PD ⋅+= ;②7PC =;③点P 在平面ABCD 的射影在直线AD 上.如图,平面五边形PABCD 中,PAD ∆是边长为2的等边三角形,//AD BC ,22AB BC ==,AB BC ⊥,将PAD ∆沿AD 翻折成四棱锥P ABCD -,E 是棱PD 上的动点(端点除外),F ,M 分别是AB ,CE 的中点,且____.(1)求证://FM 平面PAD ;(2)当EF 与平面PAD 所成角最大时,求平面ACE 与平面ABCD 所成的锐二面角的余弦值.4.如图,在矩形ABCD 中,2,23AB AD ==,ABPCDFEE ,F 分别为AD ,BC 的中点,以DF 为折痕把CDF ∆折起,点C 到达点P 的位置,使1PE =.(1)证明:平面PEF ⊥平面ABFD ;(2)求二面角P DF E --的正弦值.参考答案类型一折叠问题【例1】【分析】(1)证明PO ⊥平面ACD 可得PO AD ⊥,根据中位线定理和勾股定理可证AD ON ⊥,故而AD ⊥平面PON ,于是平面PAD ⊥平面PON ;(2)分别计算AON ∆的面积和M 到平面ACD 的距离,代入体积公式计算.【解答】(1)证明:PA PC = ,O 是AC 的中点,PO AC ∴⊥,又平面PAC ⊥平面ACD ,平面PAC ⋂平面ACD AC =,PO ∴⊥平面ACD ,又AD ⊂平面ACD ,PO AD ∴⊥,23AD = ,2CD =,4AC =,222AD CD AC ∴+=,AD CD ∴⊥,ON 是ACD ∆的中位线,//ON CD ∴,AD ON ∴⊥,又ON PO O = ,AD ∴⊥平面PON ,又AD ⊂平面PAD ,∴平面PAD ⊥平面PON .(2)PAC ∆ 是边长为4的等边三角形,3PO ∴=M ∴到平面ACD 的距离132d PO ==,ON 是ACD ∆的中位线,1113324422AON ACD S S ∆∆∴==⨯=,11131332322M ANO AON V S PO -∆∴==⨯⨯ .【点评】本题考查了面面垂直的判定,棱锥的体积计算,属于中档题.【例2】【分析】(1)取AD 中点E ,连接PE ,EM ,AC ,可得PE AD ⊥,然后证明BD PE ⊥,可得PE ⊥平面ABCD ,进一步得到平面PAD ⊥平面ABCD ;(2)由(1)知,PE ⊥平面ABCD ,连接EM ,可得30PME ∠=︒,求解三角形可得1PE =,再求出四边形ABCD 的面积,代入棱锥体积公式求解.【解答】(1)证明:取AD 中点E ,连接PE ,EM ,AC ,PA PD = ,得PE AD ⊥,由底面ABCD 为菱形,得BD AC ⊥,E ,M 分别为AD ,CD 的中点,//EM AC ∴,则BD EM ⊥,又BD PM ⊥,BD ∴⊥平面PEM ,则BD PE ⊥,PE ∴⊥平面ABCD ,而PE ⊂平面PAD ,∴平面PAD ⊥平面ABCD ;(2)解:由(1)知,PE ⊥平面ABCD ,连接EM ,可得30PME ∠=︒,设AB a =,则224a PE =-,322AC EM ==,故tan tan 30PE PME EM ∠=︒=,即2234332a a -=,解得2a =.故1PE =,3ABCD S =四边形.故23133P ABCD ABCD V S PE -=⋅⋅=四边形.【点评】本题考查平面与平面垂直的判定,考查空间想象能力与思维能力,训练了多面体体积的求法,是中档题.【变式1-1】【分析】(1)推导出AB AD ⊥,AB ⊥平面PAD ,AB PD ⊥,PD PA ⊥,由此能证明PD ⊥平面PAB .(2)取AD 的中点O ,连结OP ,OC ,由AC CD =知OC OA ⊥,以O 为坐标原点,OC 所在的直线为x 轴,OA 所在的直线为y 轴建立空间直角坐标系,利用向量法能求出二面角A PB C --的大小.(3)假设点M 存在,其坐标为(x ,y ,)z ,BM 与平面PBC 所成的角为α,则存在(0,1)λ∈,有AM AP λ= ,利用向量法能求出在棱PA 上满足题意的点M 存在.【解答】证明:(1)1AB = ,2AD =,5BD =222AB AD BD ∴+=,AB AD ∴⊥,平面PAD ⊥平面ABCD ,平面PAD ⋂平面ABCD AD =,AB ∴⊥平面PAD ,又PD ⊂ 平面PAD ,AB PD ∴⊥,又PD PA ⊥ ,PA AB A= PD ∴⊥平面PAB .解:(2)取AD 的中点O ,连结OP ,OC ,由平面PAD ⊥平面ABCD 知PO ⊥平面ABCD ,由AC CD =知OC OA ⊥,以O 为坐标原点,OC 所在的直线为x 轴,OA 所在的直线为y 轴建立空间直角坐标系如图示,则(2C ,0,0),(0P ,0,1),(0D ,1-,0),(0A ,1,0),(1B ,1,0)∴(1,1,1)PB =- ,(2,0,1)PC =- ,(0,1,1)PD =-- ,设平面PBC 的法向量为(,,)m a b c = ,由00m PB m PC ⎧⋅=⎪⎨⋅=⎪⎩ ,得020a b c a c +-=⎧⎨-=⎩,令1a =得1b =,2c =,∴(1,1,2)m = ,PD ⊥ 平面PAB ,∴(0DP = ,1,1)是平面PAB 的法向量,设二面角A PB C --大小为θ,则123cos 2||||62m DP m DP θ⋅==⋅⋅ ,0θπ ,∴二面角A PB C --的大小6πθ=.(3)假设点M 存在,其坐标为(x ,y ,)z ,BM 与平面PBC 所成的角为α,则存在(0,1)λ∈,有AM AP λ= ,即(x ,1y -,)(0z λ=,1-,1),(0M ,1λ-,)λ,则(1,,)BM λλ=-- ,从而211sin ||3||||612m BM m BM αλ⋅==⋅⋅+ ,[0λ∈ ,1],103λ∴=-,∴在棱PA 上满足题意的点M 存在.【点评】本题考查线面垂直的证明,考查二面角的求法,考查满足线面角的正弦值点是否存在的判断与求法,考查空间中线线、线面、面面间的位置关系等基础知识,考查运算求解能力,是中档题.类型二展开问题【例1】【分析】将三棱柱展开两次如图,不难发现最短距离是六个矩形对角线的连线,正好相当于绕三棱柱转两次的最短路径.【解答】解:将正三棱柱111ABC A B C -沿侧棱展开,再拼接一次,其侧面展开图如图所示,在展开图中,最短距离是六个矩形对角线的连线的长度,也即为三棱柱的侧面上所求距离的最小值.由已知求得矩形的长等于6212⨯=,宽等于5,由勾股定理2212513d =+=.故选:C .【点评】本题考查棱柱的结构特征,考查空间想象能力和思维能力,考查数学转化思想方法,是中档题.【例2】【分析】画出解答几何体的部分侧面展开图,利用三角形的边的关系容易解得边长的值,从而得出其中的最小值.【解答】解:将三棱锥S ABC -沿侧棱SB 展开,其侧面展开图如图所示,由图中红色路线可得结论.根据余弦定理得,沿着三棱锥的侧面绕行一周回到点B 的最短路线的长为:14422232++⨯⨯⨯=故选:C .【点评】本题考查多面体和旋转体表面上的最短距离问题,空间想象能力,几何体的展开与折叠,是基础题.【变式2-1】【分析】(1)直三棱柱111ABC A B C -的表面积:1111112ABC ABB A BCC B ACC A S S S S S ∆=+++矩形矩形矩形.(2)将直三棱柱111ABC A B C -展开成矩形11ACC A ,如图,连结1AC ,交1BB 于D ,此时1AD DC +最小,当1AD DC +最小时,1BD =,此时三棱锥1D ABC -的体积:11D ABC C ABD V V --=,由此能求出结果.【解答】解:(1) 在直三棱柱111ABC A B C -中,1AB =,2BC =,13BB =,90ABC ∠=︒,∴此直三棱柱111ABC A B C -的表面积:1111112ABC ABB A BCC B ACC A S S S S S ∆=+++矩形矩形矩形121213231432=⨯⨯⨯+⨯+⨯++1135=+(2)将直三棱柱111ABC A B C -展开成矩形11ACC A ,如图,连结1AC ,交1BB 于D ,此时1AD DC +最小,1AB = ,2BC =,13BB =,90ABC ∠=︒,点D 为侧棱1BB 上的动点,∴当1AD DC +最小时,1BD =,此时三棱锥1D ABC -的体积:11D ABC C ABDV V --=1113ABD S B C ∆=⨯111132AB BD B C =⨯⨯⨯⨯1111232=⨯⨯⨯⨯13=.∴当1AD DC +最小时,三棱锥1D ABC -的体积为13.【点评】本题考查几何体的表面积、体积的求法,考查空间中线线、线面、面面的位置关系等基础知识,考查推理论证能力、运算求解能力、空间思维能力,考查数数结合思想、函数与方程思想、化归与转化思想,是中档题.巩固练习1.【分析】在三棱锥D ABC -中,当且仅当DA ⊥平面ABC 时,三棱锥的体积达到最大,然后根据三棱锥的性质求出外接球的半径,进而可以求解.【解答】解:在三棱锥D ABC -中,当且仅当DA ⊥平面ABC 时,三棱锥的体积达到最大,此时,设外接球的半径为R ,球心为O ,球心O 到平面ABC 的投影点为F ,则有2222R OA OF AF ==+,又1522OF AD ==,1522AF AC ==,所以2225525()()222R =+=,所以球的表面积为22544502S R πππ==⨯=,故答案为:50π.【点评】本题考查了三棱锥的外接球的表面积问题,考查了学生的空间想象能力以及运算能力,属于中档题.2、【分析】(Ⅰ)由题意可证AC DO ⊥,又PO AC ⊥,即可证明AC ⊥平面PDO .(Ⅱ)当CO AB ⊥时,C 到AB 的距离最大且最大值为1,又2AB =,即可求ABC ∆面积的最大值,又三棱锥P ABC -的高1PO =,即可求得三棱锥P ABC -体积的最大值.(Ⅲ)可求22112PB PC +==,即有PB PC BC ==,由OP OB =,C P C B '=',可证E 为PB 中点,从而可求2626OC OE EC +'=+'=,从而得解.【解答】解:(Ⅰ)在AOC ∆中,因为OA OC =,D 为AC 的中点,所以AC DO ⊥,又PO 垂直于圆O 所在的平面,所以PO AC ⊥,因为DO PO O = ,所以AC ⊥平面PDO .(Ⅱ)因为点C 在圆O 上,所以当CO AB ⊥时,C 到AB 的距离最大,且最大值为1,又2AB =,所以ABC ∆面积的最大值为12112⨯⨯=,又因为三棱锥P ABC -的高1PO =,故三棱锥P ABC -体积的最大值为:111133⨯⨯=.(Ⅲ)在POB ∆中,1PO OB ==,90POB ∠=︒,所以22112PB =+=同理2PC =,所以PB PC BC ==,在三棱锥P ABC -中,将侧面BCP 绕PB 旋转至平面BC P ',使之与平面ABP 共面,如图所示,当O ,E ,C '共线时,CE OE +取得最小值,又因为OP OB =,C P C B '=',所以OC '垂直平分PB ,即E 为PB 中点.从而2626222OC OE EC '=+'=+=.亦即CE OE +的最小值为:262.【点评】本题主要考查了直线与直线、直线与平面的位置关系、锥体的体积的求法等基础知识,考查了空间想象能力、推理论证能力、运算求解能力,考查了数形结合思想、化归与转化思想,属于中档题.3.【分析】(1)取CD 中点为G ,连接MG ,FG ,//GM PD ,//FG AD ,进而可证平面//MFG 平面PAD ,可证//FM 平面PAD ;(2)根据条件选择①:由已知可证BA ⊥平面PAD ,PO ⊥平面ABCD ,以点O 为坐标原点,以OC 为x 轴,OD 为y 轴,OP 为z 轴,建立如图所示的空间直角坐标系,利用向量法平面ACE 与平面PAD 所成的锐二面角的余弦值.同理选择②,③可求平面ACE 与平面ABCD 所成的锐二面角的余弦值.【解答】(1)证明:取CD 中点为G ,连接MG ,FG ,则MG ,FG 分别为三角形CDE ,梯形ABCD 的中位线,//GM PD ∴,//FG AD ,MG FG G = ,∴平面//MFG 平面PAD ,FM ⊂ 平面MGF ,//FM ∴平面PAD ,(2)解:取AD 为O ,连接PO ,FG ,EG .选择①:因为()0BA PA PD ⋅+= ,2PA PD PO += ,所以0BA PO ⋅= ,即BA PO ⊥.又BA AD ⊥,AD PO O = ,所以BA ⊥平面PAD .连接AE ,EF ,所以AEF ∠即为EF 与平面PAD 所成的角.因为1tan AF AEF AE AE∠==,所以当AE 最小时,AEF ∠最大,所以当AE PD ⊥,即E 为PD 的中点,AE 最小.下面求二面角余弦值法一:BA ⊂ 平面ABCD ,∴平面ABCD ⊥平面PAD ,平面ABCD ⊥平面PAD ,平面ABCD ⋂平面PAD AD =,PO AD ⊥ ,PO ∴⊥平面ABCD ,以点O 为坐标原点,以OC 为x 轴,OD 为y 轴,OP 为z 轴,建立如图所示的空间直角坐标系,则(0A ,1-,0),1(0,2E ,(2C ,0,0).所以3(0,2AE = ,(2,1,0)AC = .设平面CAE 的法向量为111(,,)m x y z =,则111130,220y x y ⎧+=⎪⎨⎪+=⎩,令1z =,得1(,2m =- .由题意可知:平面ABCD 的法向量为(0,0,1)n = ,所以cos ,||||17m n m n m n ⋅〈〉==⋅ ,所以平面ACE 与平面PAD 所成的锐二面角的余弦值为25117.法二:在平面PAD 内,作ER AD ⊥,垂足为R ,则ER ⊥平面ABCD ,过R 作RK AC ⊥,连接EK ,由三垂线定理及逆定理知EKR ∠为平面ACE 与平面ABCD 所成的锐二面角的平面角,在EKR RT ∆中,易得2ER =,RK =,则EK =所以251cos 17RK EKR EK ∠==,所以平面ACE 与平面PAD.选择②:连接OC ,则2OC AB ==,OP =,因为PC =,222PC OP OC =+,所以BA PO ⊥.又BA AD ⊥,AD PO O = ,所以BA ⊥平面PAD .连接AE ,EF ,所以AEF ∠即为EF 与平面PAD 所成的角.因为1tan AF AEF AE AE∠==,所以当AE 最小时,AEF ∠最大,所以当AE PD ⊥,即E 为PD 的中点,AE 最小.下面求二面角余弦值,法一:BA ⊂ 平面ABCD ,∴平面ABCD ⊥平面PAD ,平面ABCD ⊥平面PAD ,平面ABCD ⋂平面PAD AD =,PO AD ⊥ ,PO ∴⊥平面ABCD ,以点O 为坐标原点,以OC 为x 轴,OD 为y 轴,OP 为z 轴,建立如图所示的空间直角坐标系,于是(0A ,1-,0),1(0,2E ,(2C ,0,0).所以3(0,2AE = ,(2,1,0)AC = .设平面CAE 的法向量为111(,,)m x y z = ,则111130,220y x y ⎧+=⎪⎨⎪+=⎩,令1z =,得1(,2m =- .由题意可知:平面ABCD 的法向量为(0,0,1)n = ,所以cos ,||||m n m n m n ⋅〈〉==⋅ ,所以平面ACE 与平面PAD.法二:在平面PAD 内,作ER AD ⊥,垂足为R ,则ER ⊥平面ABCD ,过R 作RK AC ⊥,连接EK ,由三垂线定理及逆定理知EKR ∠为平面ACE 与平面ABCD 所成的锐二面角的平面角,在EKR RT ∆中,易得ER =RK =,则EK =所以cos 17RK EKR EK ∠==,选择③:因为点P 在平面ABCD 的射影在直线AD 上,所以平面PAD ⊥平面ABCD .因为平面PAD ⋂平面ABCD CD =,OP ⊂平面PAD ,AD PO ⊥,所以OP ⊥平面ABCD ,所以BA PO ⊥.又BA AD ⊥,AD PO O = ,所以BA ⊥平面PAD .连接AE ,EF ,所以AEF ∠即为EF 与平面PAD 所成的角.因为1tan AF AEF AE AE∠==,所以当AE 最小时,AEF ∠最大,所以当AE PD ⊥,即E 为PD 中点,AE 最小.下面求二面角余弦值,法一:BA ⊂ 平面ABCD ⊥,∴平面ABCD ⊥平面PAD ,平面ABCD ⋂平面PAD ,平面ABCD ⋂平面PAD AD =,PO AD ⊥ ,PO ∴⊥平面ABCD ,以点O 为坐标原点,以OC 为x 轴,OD 为y 轴,OP 为z 轴,建立如图所示的空间直角坐标系,于是(0A ,1-,0),1(0,2E ,(2C ,0,0).所以3(0,2AE = ,(2,1,0)AC = .设平面CAE 的法向量为111(,,)m x y z = ,则1111330,2220y z x y ⎧+=⎪⎨⎪+=⎩,令1z =,得1(,2m =- .由题意可知:平面ABCD 的法向量为(0,0,1)n = ,所以cos ,||||m n m n m n ⋅〈〉==⋅ ,所以平面ACE 与平面PAD所成的锐二面角的余弦值为17.法二:在平面PAD 内,作ER AD ⊥,垂足为R ,则ER ⊥平面ABCD ,过R 作RK AC ⊥,连接EK ,由三垂线定理及逆定理知EKR ∠为平面ACE 与平面ABCD 所成的锐二面角的平面角,在EKR RT ∆中,易得ER =RK =,则EK =所以cos 17RK EKR EK ∠==,【点评】本题考查线面平行的证明,以及面面角的求法,属中档题.4.【分析】(1)推导出//EF AB 且3DE =,AD EF ⊥,DE PE ⊥,AD PE ⊥,由此能证明AD ⊥平面PEF ,从而平面PEF ⊥平面ABFD .(2)过点P 作PH EF ⊥交EF 于H ,由平面垂直性质定理得PH ⊥平面ABFD ,过点P 作PO DF ⊥交DF 于O ,连结OH ,则OH DF ⊥,从而POH ∠为二面角P DF E --的平面角,由此能求出二面角P DF E --的正弦值.【解答】证明:(1)E 、F 分别为AD ,BC 的中点,//EF AB ∴且3DE =,在矩形ABCD 中,AD AB ⊥,AD EF ∴⊥,由翻折的不变性,2,3PD PF CF DE ===,7DF =又1PE =,有222PD PE DE =+,DE PE ∴⊥,即AD PE ⊥,又PE EF E = ,PE ,EF ⊂平面PEF ,AD ∴⊥平面PEF ,AD ⊂ 平面ABFD ,∴平面PEF ⊥平面ABFD .解:(2)过点P 作PH EF ⊥交EF 于H ,由平面垂直性质定理得PH ⊥平面ABFD ,过点P 作PO DF ⊥交DF 于O ,连结OH ,则OH DF ⊥,POH ∴∠为二面角P DF E --的平面角.222PE PF EF += ,90EPF ∴∠=︒,由等面积法求得322127PH PO ==.在直角POH ∆中,7sin 4PH POH PO ∠==,即二面角P DF E --的正弦值为74.【点评】本题考查面面垂直的证明,考查二面角的正弦值的求法,考查运算求解能力,考查函数与方程思想,考查化归与转化思想,是中档题.。
勾股定理翻折问题12种类型例题

勾股定理翻折问题12种类型例题勾股定理翻折问题12种类型例题引言在数学领域中,勾股定理是一个非常基础但又十分重要的定理。
它主要描述了直角三角形中三条边之间的关系,这一定理在几何学中应用广泛。
而勾股定理的翻折问题则是对勾股定理的一种延伸和拓展,涉及到更多的变数和复杂的计算。
今天,我将以深度和广度兼具的方式来探讨这一问题,并给出12种类型的例题,希望能够给大家带来一些启发和帮助。
1. 直角三角形的性质我们来回顾一下直角三角形的性质。
在一个直角三角形ABC中,有一个直角,记作∠C=90°。
根据勾股定理,我们知道a^2 + b^2 = c^2,其中a和b分别代表三角形中的两条短边,c代表斜边。
这是我们解决翻折问题的基础。
2. 翻折问题的定义接下来,我们需要了解翻折问题的定义。
翻折问题是指在平面直角坐标系上,已知一个单一的点A(x,y),通过某种方法,将该点按照直角三角形的勾股定理进行“翻折”,得到一个点B,使得点B满足勾股定理的条件。
3. 常见类型的例题现在,让我们来看一下翻折问题中的一些常见类型的例题,以便更好地理解这一概念。
第一种类型:已知直角三角形的斜边长度c,求翻折后的点B的坐标。
在这种类型的例题中,我们已知直角三角形的斜边长度c,需要求出点B的坐标。
这需要我们运用勾股定理来解决问题,具体的计算过程可能会涉及到一些代数运算和方程求解。
第二种类型:已知直角三角形的两条短边a和b,求翻折后的点B的坐标。
这种类型的例题相较于第一种类型来说更为简单,因为我们已知直角三角形的两条短边a和b,可以直接套用勾股定理来求解点B的坐标。
第三种类型:已知点A的坐标(x,y),求其翻折后的点B的坐标。
在这种类型的例题中,我们已知点A的坐标(x,y),需要根据这一坐标来求解点B的坐标。
这个过程需要我们巧妙地运用勾股定理和坐标的计算方式,是一个比较灵活和有趣的问题。
第四种类型:已知点A的坐标(x,y)和直角三角形的斜边长度c,求翻折后的点B的坐标。
第11讲勾股定理折叠问题

第十一讲勾股定理折叠问题一、知识梳理初中数学中,有关折叠的问题也是相对比较难的问题,主要涉及求角的度数、求线段的长度、求周长、面积等,其中求线段的长度的问题必然用到勾股定理.图形折叠问题核心实质是轴对称性质,即先找出对称轴,再观察元素不变量与变量,然后运用所学知识合理、有序、全面解决问题。
图形折叠对象主要是三角形、矩形、梯形等,考查问题涉及点坐标、角度、线段、周长、面积、图形规律、最值、三角函数、比例、解析式等等,折叠问题中,“折”是过程,“叠”是结果,此题型灵活多变,能考查学生的自主探索能力与空间想象能力以及推理能力,解决折叠问题,首先要对图形折叠有一定准确定位,把握折叠实质,从点、线、面三个方面发现图形中的位置关系和数量关系,抓住图形的变量和不变量,其次探索折叠变化规律,充分挖掘图形隐含的几何性质,运用所学知识合理、有序、全面解决问题。
折叠性质:①对应线段相等(能够重合的线段)②对应角相等(能够重合的角)性质记忆:折叠必有角相等、边相等。
处理策略:求什么设什么,找直角三角形,用勾股定理二、典型例题(1)折叠与角度问题例1、如图,在Rt△ABC中,∠ACB=90°,点D在AB边上,将△CBD沿CD折叠,使点B恰好落在AC边上的点E处.若∠A=25°,则∠CDE=__________.解:∵将△CBD沿CD折叠,使点B恰好落在AC边上的点E处,∠ACB=90°,∴∠BCD=∠ECD=45°,∠B=∠CED,∵∠A=25°,∴∠B=90°-25°=65°,∴∠CED=65°,∴∠CDE=180°-45°-65°=70°,故答案为:70°.例2、如图,在△ABC 中,∠ACB=90°,将∠A 折叠,使点A 落在边CB 上的点A′处,折痕为CD ;若∠A′DC=84°,则∠B=________°.解:∵△CDA′与△CDA 关于CD 成轴对称,∴∠ADC=∠A′DC=84°,∵∠ACB=90°,∴∠DCA=∠DCB=45°,∵∠CDA=∠B+∠DCB ,∴∠B=84°-45°=39°故答案为:39.(2)折叠与线段长度例3、如图,有一张直角三角形纸片,90ACB ∠=︒,5cm AB =,3cm AC =,现将ABC ∆折叠,使边AC 与AB 重合,折痕为AE ,则CE 的长为()A .1cmB .2cmC .3cm2D .5cm 2【解析】∵90ACB ∠=︒,5cm AB =,3cm AC =∴4BC ===由折叠可知CE=DE,AC=AD ,90ADE ACE ∠=∠=︒设CE x =,则4,2,BE x BD AB AD =-=-=在Rt BDE 中∵222DE BD BE +=∴2222(4)x x +=-解得32x =故选C例4、如图,在矩形ABCD 中,6,8AB AD ==,点E 是边A D 上一动点,将ABE △沿直线BE 对折,点A 的落点为A ',当A DE ' 为直角三角形时,线段AE 的长为()A .3B .4C .6或3D .3或4【答案】C 【分析】当A DE ' 为直角三角形时,有两种情况:①当点A '在矩形内部时,如图1所示,先利用勾股定理求出BD =10,根据折叠的性质得90BA E DA E ''∠=∠=︒,设AE =x ,则A E x '=,DE =8-x ,然后在Rt A DE ' 中运用勾股定理计算出x 的值即可;②当点A '落在边BC 上时,如图2所示,此时四边形ABA E '是正方形,得出AE =AB =6.【详解】解:∵四边形ABCD 是矩形∴∠A =∠C =90°,AB =6,AD =8∴10BD ===当A DE ' 为直角三角形时,有两种情况:①当点A '在矩形内部时,如图1所示,由折叠的性质得,AE A E '=,6A B AB '==设AE x =,则A E x '=,8DE x =-∴1064DA BD A B ''=-=-=在Rt A DE ' 中,222A E DA DE ''+=∴2224(8)x x +=-解得,x =3∴AE =3;②当点A '落在边BC 上时,如图2所示,此时四边形ABA E '是正方形,∴AE =AB =6故选:C .例5、如图,在Rt ABC 的纸片中,90C ∠=︒,5AC =,13AB =.点D 在边BC 上,以A D 为折痕将ADB △折叠得到AD B ' ,A B '与边BC 交于点E .若D EB ' 为直角三角形,则BD 的长是_______.【答案】7或263【分析】由勾股定理可以求出BC 的长,由折叠可知对应边相等,对应角相等,当△DEB′为直角三角形时,可以分为两种情况进行考虑,分别利用勾股定理可求出BD 的长.【详解】解:在Rt ABC 中,12BC ===,(1)当90ED B ∠'=︒时,如图1,过点B ′作B F AC '⊥,交AC 的延长线于点F ,由折叠得:13AB AB ='=,BD B D C F ='=,设BD x =,则B D CF x '==,12B F CD x '==-,在Rt AFB' 中,由勾股定理得:222(5)(12)13x x ++-=,即:270x x -=,解得:10x =(舍去),27x =,因此,7BD =.(2)当90D EB ∠'=︒时,如图2,此时点E 与点C 重合,由折叠得:13AB AB ='=,则1358B C '=-=,设BD x =,则B D x '=,12CD x =-,在Rt △B CD ¢中,由勾股定理得:222(12)8x x -+=,解得:263x =,因此263BD =.故答案为:7或263.例6、如图,在Rt △ABC 中,∠ACB=90°,AC=6,BC=8,将边AC A 沿CE 翻折,使点A 落在AB 上的点D 处;再将边BC 沿CF 翻折,使点B 落在CD 的延长线上的点B'处,两条折痕与斜边AB 分别交于点E 、F ,则△B'FC 的面积为______________.【答案】9625【分析】由题意可得AB=10,根据面积可得CE=4.8,根据勾股定理可求BE=6.4,由折叠可求∠ECF=45°,可得EC=EF=4.8,即可求BF 的长,可求面积.【详解】解:∵Rt △ABC 中,∠ACB=90°,AC=6,BC=8,∴BA==10,∵将边AC 沿CE 翻折,使点A 落在AB 上的点D 处,∴∠AEC=∠CED ,∠ACE=∠DCE ,∵∠AED=180°,∴∠CED=90°,即CE ⊥AB ,∵S △ABC =12AB×EC=12AC×BC ,∴EC=4.8,在Rt △BCE 中,=6.4,∵将边BC 沿CF 翻折,使点B 落在CD 的延长线上的点B′处,∴BF=B'F ,∠BCF=∠B'CF ,∵∠BCF+∠B'CF+∠ACE+∠DCE=∠ACB=90°,∴ECF=45°,又CE ⊥AB ,∴∠EFC=∠ECF=45°,∴CE=EF=4.8,∵BF=BE-EF=6.4-4.8=1.6,∴△BFC 的面积为:12FB×EC=18249625525⨯⨯=,由翻折可知,△B'FC 的面积=△BFC 的面积=9625故答案为9625.【点睛】本题考查了折叠问题,勾股定理,根据折叠的性质求∠ECF=45°是本题的关键.(2)折叠与最值问题例7、如图,在ABC 中,,904C AC ︒∠==cm ,3BC =cm ,点D 、E 分别在AC 、BC上,现将DCE 沿DE 翻折,使点C 落在点'C 处,连接AC ',则AC '长度的最小值()A .不存在B .等于1cmC .等于2cmD .等于2.5cm【解析】当C′落在AB 上,点B 与E 重合时,AC'长度的值最小,∵∠C=90°,AC=4cm ,BC=3cm ,∴AB=5cm ,由折叠的性质知,BC′=BC=3cm ,∴AC′=AB-BC′=2cm .故选:C .例8、如图,矩形纸片ABCD,3AD=,折叠纸片,使点A落在BC边上的E处,AB=,5折痕为PQ,当点E在BC边上移动时,折痕的端点P、Q也随之移动,若限定点P、Q分别在AB、A D边上移动,则点E在BC边上可移动的最大距离为()A.1B.2C.4D.5【答案】B【分析】根据翻折变换,当点Q与点D重合时,点E到达最左边,当点P与点B重合时,点E到达最右边,所以点E就在这两个点之间移动,分别求出这两个位置时EB的长度,然后两数相减就是最大距离.【详解】解:如图1,当点D与点Q重合时,根据翻折对称性可得ED=AD=5,在Rt△ECD中,ED2=EC2+CD2,即52=(5-EB)2+32,解得EB=1,例9、如图2,当点P与点B重合时,根据翻折对称性可得EB=AB=3,∵3-1=2,∴点E在BC边上可移动的最大距离为2.故选:B .例10、如图,在矩形ABCD 中,10AB =,12AD =,点E 是AB 的中点,点F 是A D 边上的动点,将AEF ∆沿EF 翻折,得到A EF '∆,则A C '的最小值是()A .6B .7C .8D .9【答案】C 【分析】求A C '的最小值,先求出EC 的大小,再根据EA A C EC ''+≥,求出A C '的范围即可.【详解】解析:连接E C 在△A CE '中,可得EA A C EC ''+≥.在Rt EBC ∆中,由勾股定理,得13EC ==.由折叠可知,5EA EA '==,∴8A C '≥故选C .【点睛】本题主要考查了三角形三边的大小关系及勾股定理,正确掌握三角形三边的大小关系及勾股定理是解题的关键.例11、如图在三角形纸片ABC 中,已知∠ABC =90º,AC =5,BC=4,过点A 作直线l 平行于BC ,折叠三角形纸片ABC ,使直角顶点B 落在直线l 上的点P 处,折痕为MN ,当点P 在直线l 上移动时,折痕的端点M 、N 也随之移动,若限定端点M 、N 分别在AB 、BC 边上(包括端点)移动,则线段AP 长度的最大值与最小值的差为________________.【答案】1【分析】分别找到两个极端,当M 与A 重合时,AP 取最大值,当点N 与C 重合时,AP 取最小,即可求出线段AP 长度的最大值与最小值之差【详解】如图所示,当M 与A 重合时,AP 取最大值,此时标记为P 1,由折叠的性质易得四边形AP 1NB是正方形,在Rt △ABC 中,,∴AP 的最大值为A P 1=AB=3如图所示,当点N 与C 重合时,AP 取最小,过C 点作CD ⊥直线l 于点D ,可得矩形ABCD ,∴CD=AB=3,AD=BC=4,由折叠的性质有PC=BC=4,在Rt △PCD 中,∴AP 的最小值为AD PD=4-线段AP 长度的最大值与最小值之差为(1AP AP=341----故答案为1例12、如图,在△ABC 中,∠C =90°,∠ABC =45°,D 是BC 边上的一点,BD =2,将△ACD 沿直线AD 翻折,点C 刚好落在AB 边上的点E 处.若P 是直线AD 上的动点,则△PEB 的周长的最小值是________.【答案】2【分析】连接CE,交AD于M,根据折叠和等腰三角形性质得出当P和D重合时,PE+BP的值最小,此时△BPE的周长最小,最小值是BE+PE+PB=BE+CD+DB=BC+BE,先求出BC和BE 长,代入求出即可.【详解】如图,连接CE,交AD于M,∵沿AD折叠C和E重合,∴∠ACD=∠AED=90°,AC=AE,∠CAD=∠EAD,∴AD垂直平分CE,即C和E关于AD对称,BD=2,∴,∴当P和D重合时,PE+BP的值最小,即此时△BPE的周长最小,最小值是BE+PE+PB=BE+CD+DB=BC+BE,∵∠DEA=90°,∴∠DEB=90°,∵∠ABC=45°,∴∠B=45°,∵,∴,即,∴△PEB 的周长的最小值是.故答案为.【点睛】本题考查了折叠性质,等腰三角形性质,轴对称-最短路线问题,勾股定理,含30度角的直角三角形性质的应用,关键是求出P 点的位置.三、课堂练习1.如图所示,将长方形ABCD 沿DE 折叠,使点C 恰好落在BA 边上,得到点C′,若∠C′EB=40°,求∠EDC′的度数.2.在Rt △ACB 中,∠ACB =90°,点D 在边AB 上,连接CD ,将△ADC 沿直线CD 翻折,点A 恰好落在BC 边上的点E 处,若AC =3,BE =1,则DE 的长是_____.【答案】157【分析】过点D 作DHAC ⊥于H ,DF BC ⊥于F ,由折叠的性质可得3AC CE ==,45ACD BCD ∠=∠=︒,由勾股定理可求5AB =,由面积法可求D F 的长,由勾股定理可求D E 的长.【详解】解:如图,过点D 作DHAC ⊥于H ,DF BC ⊥于F ,将ADC ∆沿直线CD 翻折,3AC CE ∴==,45ACD BCD ∠=∠=︒,4BC ∴=,D H AC ⊥ ,DF BC ⊥,45ACD BCD ∠=∠=︒,DF DH ∴=,45DCF FDC ∠=∠=︒,DF CF ∴=,22291625AB AC BC =+=+= ,5AB ∴=,111222ABC S AC BC AC DH BC DF ∆=⨯⨯=⨯⨯+⨯⨯ ,127DF ∴=,127DF ∴=,127DF CF ∴==,97EF =,157DE ∴===,故答案为:157.3.如图,矩形ABCD 中,AB=8,BC=4,把矩形ABCD 沿过点A 的直线AE 折叠,点D 落在矩形ABCD 内部的点D′处,则CD′的最小值是()A .4B .C .4-D .4+【答案】C 【解析】【分析】根据翻折的性质和当点D'在对角线AC 上时CD′最小解答即可.【详解】解:当点D'在对角线AC 上时CD′最小,∵矩形ABCD中,AB=4,BC=2,把矩形ABCD沿过点A的直线AE折叠点D落在矩形ABCD内部的点D处,∴AD=AD'=BC=2,在Rt△ABC中,=4∴,故选:C.4.如图,在长方形ABCD的边CD上适当选定一点E,沿直线AE把△ADE折叠,使点D恰好落在边BC上的点F处.已知AB=6cm,△ABF的面积是24cm2.(1)求BF的长;(2)求AD的长;(3)求点E与点C的距离.【答案】(1)8cm;(2)10cm;(3)83 cm【分析】(1)由在长方形ABCD中,AB=6cm,△ABF的面积是24cm2,即可求得BF的长;(2)由(1),易得AD=AF,DE=EF,即可求得AF的长,然后得出AD的长;(3)首先设EC=xcm,则EF=DE=(6﹣x)cm.由勾股定理得:CE2+CF2=EF2求出x 的值即可得出答案.【详解】(1)∵ABCD是长方形,∴△ABF是直角三角形,∵△ABF面积是24cm2,∴12AB•BF=24.∵AB=6cm,∴BF=8cm;(2)由题意知,△ADE和△AFE重合,则△ADE≌△AFE,则AD=AF,DE=EF.在Rt△ABF中,由勾股定理得10AF===(cm).则AD=10cm;(3)∵BC=AD=10cm,∴CF=BC﹣BF=2cm.设EC =xcm ,则EF =DE =(6﹣x )cm .由勾股定理得:CE 2+CF 2=EF 2,∴x 2+22=(6﹣x )2,解得:83x =,∴点E 与点C 间的距离是83cm.【点睛】此题考查长方形的性质、勾股定理、折叠的性质,(3)是此题的难点,根据(2)求出CF ,由折叠得到EF =DE ,设EC =xcm ,因此利用勾股定理列得关于x 的关系式解出x 的值,由此解答此题.5.在矩形纸片ABCD 中,3AB =,5AD =.如图所示,折叠纸片,使点A 落在BC 边上的'A 处,折痕为PQ ,当点'A 在BC 边上移动时,折痕的端点P ,Q 也随之移动,若限定点P 、Q 分别在线段AB 、A D 边上移动,则点'A 在BC 边上可移动的最大距离为()A .1B .2C .3D .4【答案】B 【分析】根据翻折变换,当点Q 与点D 重合时,点A′到达最左边,当点P 与点B 重合时,点A′到达最右边,所以点A′就在这两个点之间移动,分别求出这两个位置时A′B 的长度,然后两数相减就是最大距离.【详解】解:如图1,当点D 与点Q 重合时,根据翻折对称性可得A’D=AD=5,在Rt △A’CD 中,A’D 2=A’C 2+CD 2,即52=(5-A’B)2+32,解得A’B=1;如图2,当点P与点B重合时,根据翻折对称性可得A’B=AB=3,∵3-1=2,∴点A’在BC边上可移动的最大距离为2.故选B.6.矩形ABCD中,AB=4,BC=6,点E是AB的中点,点F是BC上任意一点,把△EBF沿直线EF翻折,点B落在点P处,则PC的最小值是_______________.【答案】2【详解】连接CE,当点P在CE上时,CP的值最小.CE===∴=-=.CP CE EP2故答案为:2.7.如图,在长方形纸片ABCD 中,3AB =,9AD =,折叠纸片ABCD ,使顶点C 落在边A D 的点G 处,折痕分别交边A D 、BC 于点E 、F .(1)求证:GEF △是等腰三角形(2)求GEF △面积的最大值.【答案】(1)见解析;(2)152【分析】(1)根据翻折的性质得到EFC EFG ∠=∠,根据//AD BC 得到EFC GEF ∠=∠,从而得到EFG GEF ∠=∠,问题得证;(2)根据GEF △高为AB=3,得到当点G 与点A 重合时,GEF △的面积最大.根据勾股定理求出AF=5,进而得到GE=5,即可求出GEF △的面积.【详解】(1)由翻折得:EFC EFG ∠=∠.∵//AD BC ,∴EFC GEF ∠=∠,∴EFG GEF ∠=∠,∴GE=GF ,∴GEF △是等腰三角形.(2)如图,∵GEF △高为AB=3,∴当GE 最大时GEF △的面积最大,∴当点G 与点A 重合时,GEF △的面积最大.在Rt ABF 中,222AF AB BF =+,∴()22239AF AF =+-,解得:5AF =,∴5GE AF ==,∴GEF △的面积最大值=1155322=⨯⨯=.四、举一反三1.如图,EF 是正方形两对边中点的连线段,将∠A 沿DK 折叠,使它的顶点A落在EF 上的G 点,求∠DKG 的度数.2.如图,在Rt ABC 中,90,A AB AC ∠=︒==,点,E F 分别是边,AB BC 上的动点,沿EF 所在直线折叠B Ð,使点B 的对应点B ′始终落在边AC 上,若FB C ' 为直角三角形,则BF 的长为__________.【解析】90,A AB AC ∠=︒==,∴∠C=45°,2BC ==,折叠后,要使FB C ' 为直角三角形,则有:FB C ' 也为等腰直角三角形,①当90B FC '∠=︒时,∴45C FB C '∠=∠=︒,此时点B '与点C 重合,∴E 、F 分别是AB 、BC 的中点,∴112BF BC ==,②当90FB C'∠=︒时,∴45C B FC '∠=∠=︒,∴BF FB B C ''==,在Rt B FC '△中,FC F '=,BC=BF+FC ,∴)12BC BF BF =+=+=,解得:2BF =-;故答案为2-或1.3.如图,Rt △ABC 中,AB =18,BC =12,∠B =90°,将△ABC 折叠,使点A 与BC 的中点D 重合,折痕为MN ,则线段BN 的长为()A .8B .6C .4D .104.如图,长方形纸片ABCD ,10AB =,8BC =,点P 在BC 边上,将CDP 沿DP 折叠,点C 落在E 处,PE ,D E 分别交AB 于点O ,F ,且OP OF =,则A F 长为______.【答案】103【分析】根据折叠的性质可得出DC=DE 、CP=EP ,由“AAS”可证△OEF ≌△OBP ,可得出OE=OB 、EF=BP ,设EF=x ,则BP=x 、DF=10-x 、BF=PC=8-x ,进而可得出AF=2+x ,在Rt △DAF 中,利用勾股定理可求出x 的值,即可得AF 的长.【详解】解:∵将△CDP 沿DP 折叠,点C 落在点E 处,∴DC=DE=10,CP=EP .在△OEF 和△OBP 中,90EOF BOP E B OF OP ∠=∠⎧⎪∠=∠=︒⎨⎪=⎩∴△OEF ≌△OBP (AAS ),∴OE=OB ,EF=BP .设EF=x ,则BP=x ,DF=DE -EF=10-x ,又∵BF=OB+OF=OE+OP=PE=PC ,PC=BC-BP=8-x ,∴AF=AB -BF=2+x .在Rt △DAF 中,AF 2+AD 2=DF 2,∴(2+x )2+82=(10-x )2,∴43x =;∴410233AF =+=.故答案为:103.5.如图,在矩形ABCD 中,AB=3,AD=4,点E 是AD 边上一动点,将△ABE 沿BE 折叠,使点A 的对应点A′恰好落在矩形ABCD 的对角线上,则AE 的长为_______.答案:3924or 6.如图,已知等腰△ABC 中,AB =AC =5,BC =8,E 是BC 上的一个动点,将△ABE 沿着AE 折叠到△ADE 处,再将边AC 折叠到与AD 重合,折痕为AF ,当△DEF 是等腰三角形时,BE 的长是___________.【答案】52或258或74.【分析】分三种情况讨论:DE=DF ,DE=EF ,EF=DF .利用等腰三角形的性质和全等三角形解题.【详解】解:由折叠可知,BE=DE ,DF=CF ,AD=AB=AC=5,当DE=DF 时,如图1,此时DE=DF=BE=CF ,∵AB=AC ,∴∠B=∠C ,在△ABE 和△ACF 中,AB AC B C BE CF =⎧⎪=⎨⎪=⎩∠∠∴△ABE ≌△ACF ,∴AE=AF ,∴AD 垂直平分EF ,∴EH=FH ,142BH CH BC ===,∴3AH ===,∴532HD =-=,设BE DE x ==,则4EH x =-,则在直角△DHE 中,()22242x x -+=,解得52x =,当DE=EF 时,如图2,作AH ⊥BC 于H ,连接BD ,延长AE 交BD 于N ,可知BE=DE=EF ,∵AH ⊥BC ,AB=AC ,BC=8∴BH=CH=4,∴3AH ===,设EH m =,则4BE EF m ==-,∴()8242CF m m =--=,即2DF m=∵AB=AD ,∠BAN=∠DAN ,∴AN ⊥BD ,BN=DN ,∴12EN DF m ==,∴EN EH=在△AHE 和△BNE 中,90AHE BNE EH ENAEH BEN ==︒⎧⎪=⎨⎪=⎩∠∠∠∠∴△AHE ≌△BNE ,∴AE=BE ,设BE AE x ==,则4EH x =-,在直角△AEH 中,()22243x x -+=,解得258x =,当DF=EF 时,如图3,过A 作AH ⊥BC 于H ,延长AF 交DC 于M,同理258 EF CF==∴252578884 BE=--=故答案为:52或258或74.【点睛】本题考查了折叠问题,全等三角形的判定和性质,等腰三角形的性质,注意分类讨论是解题的关键.7.如图,等腰△ABC中,AB=AC=10,BC=12,AD平分B A C∠,且AD=8,P,Q分别是AB、AD上的动点,连接BP,PQ,则BP+PQ的最小值为___.【答案】9.6【分析】过C作CQ⊥AB于Q,交AD于P,得到CQ=BP+PQ的最小值,由勾股定理不求得AD=8,再利用等面积法即可求得其值.【详解】∵AB=AC,AD是角平分线,∴AD⊥BC,BD=CD,∴B点,C点关于AD对称,如图,过C作CQ⊥AB于Q,交AD于P,则CQ=BP+PQ的最小值,根据勾股定理得,AD=8,利用等面积法得:AB•CQ=BC•AD,∴CQ=12310BC ADAB⨯==9.6故答案为:9.6.8.如图,在△ABC中,∠BAC=90°,AB=3,AC=4,点D是BC的中点,将△ABD沿AD翻折得到△AED,联结CE.(1)求证:AD∥CE;(2)求CE的长.【答案】(1)见解析;(2)75【分析】(1)由折叠的性质可得DE=BD ,AE=AB ,可证EF=BF ,AD ⊥BE ,由等腰三角形的性质可求∠DBE =∠DEB ,∠DEC =∠DCE ,由三角形的内角和定理可求CE ⊥BE ,可得结论;(2)由三角形的面积公式可求BF 的长,由勾股定理可求CE 的长.【详解】证明:(1)∵∠BAC =90°,AB =3,AC =4,∴BC 5==,∵点D 是BC 的中点,∴AD =BD =DE =52,∵将△ABD 沿AD 翻折得到△AED ,∴DE =BD ,AE =AB ,∴AD 垂直平分BE ,∴EF =BF ,AD ⊥BE ,∵DE =DB =CD ,∴∠DBE =∠DEB ,∠DEC =∠DCE ,∵∠DBE +∠DEB +∠DEC +∠DCE =180°,∴∠DEB +∠DEC =90°,∴∠BEC =90°,∴CE ⊥BE ,∴AD ∥CE ;(2)∵S △ABC =12×AC ×AB =12×3×4=6,且CD =BD ,∴S △ADB =12S △ABC =3,∴12AD ×FB =3,∴FB =125,∴BE =245,∴CE 75==.【点睛】本题考查了翻折变换,直角三角形的性质,平行线的判定,三角形的面积公式,勾股定理等知识,灵活运用这些性质解决问题是本题的关键.五、课后练习一、选择题1.如图,在△ABC 中,AB =10,AC =6,BC =8,将△ABC 折叠,使点C 落在AB 边上的点E 处,AD 是折痕,则△BDE 的周长为()A .6B .8C .12D .14【解析】在Rt △ABC 中,∵AC =6,BC =8,∠C =90°,∴AB ==10,由翻折的性质可知:AE =AC =6,CD =DE ,∴BE =4,∴△BDE 的周长=DE +BD +BE =CD +BD +E =BC +BE =8+4=12.故选:C .2.如图,将等腰直角三角形ABC (90ABC ∠=︒)沿EF 折叠,使点A 落在BC 边的中点1A 处,6BC =,那么线段AE 的长度为()A .5B .4C .4.25D .154【解析】由折叠的性质可得AE=A 1E ,∵△ABC 为等腰直角三角形,BC=6,∴AB=6,∵A 1为BC 的中点,∴A 1B=3,设AE=A 1E=x ,则BE=6-x ,在Rt △A 1BE 中,由勾股定理可得32+(6-x )2=x 2,解得x=154,故选:D .3.如图,矩形ABCD ,AB =3,BC =4,点E 是AD 上一点,连接BE ,将△ABE 沿BE 折叠,点A 恰好落在BD 上的点G 处,则AE 的长为()A .2B .52C .32D .3【解析】在Rt △ABD 中,AB=3,AD=BC=4,∴BD=5由折叠得,∠BGE=∠A=90°,BG=AB=3,EG=AE ,∴DG=BD-BG=2,DE=AD-AE=4-AE ,在Rt △DEG 中,EG 2+DG 2=DE 2,∴AE 2+4=(4-AE )2,∴AE=32.故选:C .4.如图,在四边形ABCD 中,∠A =∠B =90°,∠C =60°,BC =CD =8,将四边形ABCD 折叠,使点C 与点A 重合,折痕为EF ,则BE 的长为()A .1B .2CD .2【解析】作DG ⊥BC ,连接AE ,在Rt △CDG ,∠DCG=60°,得出CG=4,∴DG=4AB=,设BE=x ,则CE=8-x ,根据折叠得AE=CE=8-x ,在Rt △ABE 中,AE 2=AB 2+BE 2,即(8-x)2)2+x 2解得x=1,故选A.5.如图,有一块直角三角形纸片,两直角边6AC cm =,8BC cm =,现将直角边AC 沿直线AD折叠,使它落在斜边AB上且与AE重合,则CD等于()A.2cm B.3cm C.4cm D.5cm【解析】在RT△ABC中,∵AC=6,BC=8,∴AB=10,△ADE是由△ACD翻折,∴AC=AE=6,EB=AB−AE=10−6=4,设CD=DE=x,在RT△DEB中,∵DE2+EB2=DB2,∴x2+42=(8−x)2∴x=3,∴CD=3.故选:B.6.如图,将矩形ABCD沿EF折叠,使顶点C恰好落在AB边的中点C′上.若AB=6,BC =9,则BF的长为()A.4B.C.4.5D.5【解析】∵点C′是AB边的中点,AB=6,∴BC′=3,由图形折叠特性知,C′F=CF=BC﹣BF=9﹣BF,在Rt△C′BF中,BF2+BC′2=C′F2,∴BF2+9=(9﹣BF)2,解得,BF=4,故选:A.二、填空题7.如图,在矩形ABCD 中,AB =5,BC =6,P 为AD 上一动点,把△ABP 沿BP 翻折,使点A 落在点F 处,连接CF ,若BF =CF ,则AP 的长为_____.【答案】53【分析】过点F 作EN ∥DC 交BC 于点N ,交AD 于点E ,设AP =x ,则PF =x ,得出(3﹣x )2+12=x 2,解方程即可得解.【详解】解:过点F 作EN ∥DC 交BC 于点N ,交AD 于点E ,∵四边形ABCD 是矩形,∴∠A =∠D =∠DCB =90°,∴FN ⊥BC ,FE ⊥AD ,∵BF =CF ,BC =6,∴CN =BN =3,由折叠的性质可知,AB =BF =5,AP =PF ,∴4FN ==,∴EF =EN ﹣FN =5﹣4=1,设AP =x ,则PF =x ,∵PE 2+EF 2=PF 2,∴(3﹣x )2+12=x 2,解得,53x =,故答案为:53.【点睛】本题主要考查了折叠变换的性质、等腰三角形的性质、矩形的性质、勾股定理的综合运用;熟练掌握折叠变换的性质、勾股定理是关键.8.如图,三角形纸片ABC 中,∠ACB =90 ,BC =6,AB =10.在AC 边上取一点E ,以BE 为折痕,使AB 的一部分与BC 重合,A 与BC 延长线上的点D 重合,则CE 的长为________.【答案】3【分析】根据折叠得,BD=AB=10,EA=ED,求出CD=4,在直角三角形CDE中,设未知数,利用勾股定理列方程求解即可.【详解】∵∠ACB=90 ,BC=6,AB=10∴8=由折叠得,BD=AB=10,EA=ED,设CE=x,则EA=ED=8−x,在Rt△DCE中,CD=10−6=4,由勾股定理得,x2+42=(8−x)2,解得,x=3故填:3.9.如图,在四边形ABCD中,AD∥BC,AB⊥BC,点E在射线BC上运动,AD=AB=1,则△ADE的周长最小值为______.【答案】1+【分析】作D点关于BC的对称点D’,连接AD’与BC的交点即为E点,此时△ADE的周长为AD+AE+DE=AD+AD’,故可求解.【详解】作D点关于BC的对称点D’,连接AD’与BC的交点即为E点,此时△ADE的周长最小,即△ADE的周长AD+AE+DE=AD+AD’,∵在四边形ABCD中,AD∥BC,AB⊥BC,AD=AB=1∴四边形ABFD为正方形,∴AD+AD’=1+1+1+.10.如图,矩形ABCD中,AB=1,BC=2,点E是BC边上一点,连接AE,把∠B沿AE 折叠,使点B落在点B′处.当△CEB′为直角三角形时,BE的长为___________.【答案】12-或1.【分析】当△CEB′为直角三角形时,有两种情况:①当点B′落在矩形内部时,如答图1所示.连结AC,先利用勾股定理计算出据折叠的性质得∠AB′E=∠B=90°,而当△CEB′为直角三角形时,只能得到∠EB′C=90°,所以点A、B′、C共线,即∠B沿AE折叠,使点B落在对角线AC上的点B′处,则EB=EB′,AB=AB′=1,可计算出-1,设BE=x,则EB′=x,CE=2-x,然后在Rt△CEB′中运用勾股定理可计算出x.②当点B′落在AD边上时,如答图2所示.此时ABEB′为正方形.【详解】解:当△CEB′为直角三角形时,有两种情况:①当点B′落在矩形内部时,如图1所示.连结AC,在Rt△ABC中,AB=1,BC=2,∴=∵∠B沿AE折叠,使点B落在点B′处,∴∠AB′E=∠B=90°,当△CEB′为直角三角形时,只能得到∠EB′C=90°,∴点A、B′、C共线,即∠B沿AE折叠,使点B落在对角线AC上的点B′处,∴EB=EB′,AB=AB′=1,∴CB′=1-,设BE=x,则EB′=x,CE=2-x,在Rt△CEB′中,∵EB′2+CB′2=CE2,∴x2+1-)2=(2-x)2,解得x=51 2-,∴BE=1 2;②当点B′落在AD边上时,如图2所示.此时ABEB′为正方形,∴BE=AB=1.故答案为:12-或1.11.如图,在Rt△ABC中,∠C=90°,∠BAC=30°,点D是BC边上的点,AB=18,将△ABC沿直线AD翻折,使点C落在AB边上的点E处,若点P是直线AD上的动点,则BP+EP的最小值是____.【答案】9【分析】根据翻折变换的性质可得点C、E关于AD对称,再根据轴对称确定最短路线问题,BC与AD的交点D即为使PB+PE的最小值的点P的位置,然后根据直角三角形两锐角互余求出∠BAC=60°,再求出∠CAD=30°,然后解直角三角形求解即可.【详解】∵将△ACD沿直线AD翻折,点C落在AB边上的点E处,∴点C、E关于AD对称,∴点D即为使PB+PE的最小值的点P的位置,PB+PE=BC,∵∠C=90°,∠BAC=30°,∴BC=12AB,∴BC=9.∴PB+PE的最小值为9.故答案为9.12.如图,在Rt△ABC中,∠C=90°,AC=6,∠A=60°,点F在边AC上,并且CF=2,点E为边BC上的动点,将△CEF沿直线EF翻折,点C落在点P处,则点P到边AB距离的最小值是_________.【答案】.【分析】延长FP交AB于M,当FP⊥AB时,点P到AB的距离最小.运用勾股定理求解.【详解】解:如图,延长FP交AB于M,当FP⊥AB时,点P到AB的距离最小.∵AC=6,CF=2,∴AF=AC-CF=4,∵∠A=60°,∠AMF=90°,∴∠AFM=30°,∴AM=12AF=2,∴,∵FP=FC=2,∴-2,∴点P到边AB距离的最小值是-2.故答案为:.【点睛】本题考查了翻折变换,涉及到的知识点有直角三角形两锐角互余、勾股定理等,解题的关键是确定出点P 的位置.12.如图,折叠矩形纸片ABCD ,使B 点落在A D 上一点E 处,折痕FG 的两端点分别在AB BC 、上(含端点),且6,10AB BC ==.则AE 的最大值是_____,最小值是_______.【答案】6;2.【分析】点G 在AB 边上,点F 在BC 边上.分别利用当点F 与点C 重合时,以及当点G 与点A 重合时,求出AE 的极值进而得出答案:【详解】解:如图,设AE 的长度为,x 当点F 与点C 重合时,根据翻折对称性可得10,EC BC ==在Rt CDE ∆中,222,CE CD ED =+即()22210106AE =-+,解得2,AE =即2,x =如图,当点G 与点A 重合时,根据翻折对称性可得6,AE AB ==即6x =;所以AE 的最大值是6,最小值为2.故答案是:6,2.三、解答题13.如图,在矩形ABCD 中,AB=8,BC=10,E 为CD 边上一点,将△ADE 沿AE 折叠,使点D 落在BC 边上的点F 处.(1)求BF 的长;(2)求CE的长.【答案】(1)BF长为6;(2)CE长为3,详细过程见解析.【分析】(1)由矩形的性质及翻折可知,∠B=90°,AF=AD=10,且AB=8,在Rt△ABF中,可由勾股定理求出BF的长;(2)设CE=x,根据翻折可知,EF=DE=8-x,由(1)可知BF=6,则CF=4,在Rt△CEF中,可由勾股定理求出CE的长.【详解】解:(1)∵四边形ABCD为矩形,∴∠B=90°,且AD=BC=10,又∵ AFE是由 ADE沿AE翻折得到的,∴AF=AD=10,又∵AB=8,在Rt△ABF中,由勾股定理得:,故BF的长为6.(2)设CE=x,∵四边形ABCD为矩形,∴CD=AB=8,∠C=90°,DE=CD-CE=8-x,又∵△AFE是由△ADE沿AE翻折得到的,∴FE=DE=8-x,由(1)知:BF=6,故CF=BC-BF=10-6=4,CF+CE=EF,在Rt△CEF中,由勾股定理得:2224+x=(8-x),解得:x=3,∴222故CE的长为3.14.如图,在△ABC中,∠C=90°,把△ABC沿直线DE折叠,使△ADE与△BDE重合.(1)若∠A=35°,则∠CBD的度数为________;(2)若AC=8,BC=6,求AD的长;(3)当AB=m(m>0),△ABC的面积为m+1时,求△BCD的周长.(用含m的代数式表示)【答案】(1)∠CBD=20°;(2)AD=164;(3)△BCD 的周长为m+2【分析】(1)根据折叠可得∠1=∠A=35°,根据三角形内角和定理可以计算出∠ABC=55°,进而得到∠CBD=20°;(2)根据折叠可得AD=DB ,设CD=x ,则AD=BD=8-x ,再在Rt △CDB 中利用勾股定理可得x 2+62=(8-x )2,再解方程可得x 的值,进而得到AD 的长;(3)根据三角形ACB 的面积可得112AC CB m =+ ,进而得到AC•BC=2m+2,再在Rt △CAB 中,CA 2+CB 2=BA 2,再把左边配成完全平方可得CA+CB 的长,进而得到△BCD 的周长.【详解】(1)∵把△ABC 沿直线DE 折叠,使△ADE 与△BDE 重合,∴∠1=∠A=35°,∵∠C=90°,∴∠ABC=180°-90°-35°=55°,∴∠2=55°-35°=20°,即∠CBD=20°;(2)∵把△ABC 沿直线DE 折叠,使△ADE 与△BDE 重合,∴AD=DB ,设CD=x ,则AD=BD=8-x ,在Rt △CDB 中,CD 2+CB 2=BD 2,x 2+62=(8-x )2,解得:x=74,AD=8-74=164;(3)∵△ABC的面积为m+1,∴12AC•BC=m+1,∴AC•BC=2m+2,∵在Rt△CAB中,CA2+CB2=BA2,∴CA2+CB2+2AC•BC=BA2+2AC•BC,∴(CA+BC)2=m2+4m+4=(m+2)2,∴CA+CB=m+2,∵AD=DB,∴CD+DB+BC=m+2.即△BCD的周长为m+2.15.如图,长方形ABCD中,AB=8,BC=10,在边CD上取一点E,将△ADE折叠后点D恰好落在BC边上的点F处(1)求CE的长;(2)在(1)的条件下,BC边上是否存在一点P,使得PA+PE值最小?若存在,请求出最小值:若不存在,请说明理由.【答案】(1)3;(2.【分析】(1)先判断出AF=AD=8,进而利用勾股定理求出BF=6,最后在Rt△ECF,利用勾股定理,即可得出结论;(2)先作出点E关于BC的对称点E,进而求出DE',再利用勾股定理即可得出结论.【详解】解:(1)长方形ABCD中,AB=8,BC=10,∴∠B=∠BCD=90°,CD=AB=8,AD=BC=10,由折叠知,EF=DE,AF=AD=8,在Rt△ABF中,根据勾股定理得,BF6,∴CF=BC﹣BF=4,设CE=x,则EF=DE=CD﹣CE=8﹣x,在Rt△ECF中,根据勾股定理得,CF2+CE2=EF2,∴16+x2=(8﹣x)2,∴x=3,∴CE=3;(2)如图,延长EC 至E '使CE '=CE =3,连接AE '交BC 于P ,此时,PA +PE 最小,最小值为AE ',∵CD =8,∴DE '=CD +CE '=8+3=11,在Rt △ADE '中,根据勾股定理得,AE '.16.如图,在矩形ABCD 中,2,AB AD m ==,动点P 从点D 出发,沿射线DA 以每秒1个单位的速度向点A 方向运动,连接CP ,把PDC △沿PC 翻折,得到PEC V .设点P 的运动时间为()t s .(1)若3m =,当P E B 、、三点在同一直线上时,求t 的值;(2)若点E 到直线BC 的距离等于1,求t 的值;(3)若AE 的最小值为1,直接写出m 的值.【答案】(1)t=3(2)t=;(3)m=【分析】(1)如图1中,设PD=t .则PA=3-t .首先证明BP=BC=6,在Rt △ABP 中利用勾股定理即可解决问题;(2)通过添加辅助线,构造直角三角形再解决问题;(3)当点A,点E ,点C 在同一条直线上时,AE 最短,利用勾股定理求值即可.【详解】解:(1)如图1中,设PD=t .则PA=3-t∵P 、B 、E 共线,∴∠BPC=∠DPC ,∵AD ∥BC ,∴∠DPC=∠PCB ,∴∠BPC=∠PCB ,∴BP=BC=3,在Rt △ABP 中,∵AB 2+AP 2=BP 2,∴22+(3-t )2=32,∴t=3(舍去)或∴当t=3P E B 、、三点在同一直线上.(2)过点E 作MN ⊥BC ,交AD 于点M∵四边形ABCD 是矩形,MN ⊥BC∴MN ⊥AD∵点E 到直线BC 的距离等于1∴EN=1∵MN=AB=2,EC=CD=2,∴EN=MN-EN=2-1=1∴在Rt △ENC 中,∴MD=∵由题意得:-t,ME=MN-EN=2-1=1,EP=PD=t∴在Rt △MPE 中,222=ME MP PE +即:)2221=t +,解得:(3)如图,当点A,点E ,点C 在同一条直线上时,AE 最短.由题意得:AE=1,EC=CD=AB=2∴在Rt△ABC中,BC=∴.【点睛】本题考查四边形综合题、矩形的性质、勾股定理,学会构造图形思考问题是解答此题的关键,属于中考压轴题.。
(完整版)勾股定理中的折叠问题

C E勾股定理中的折叠问题例1:如图,小红用一张长方形纸片ABCD 进行折纸,已知该纸片宽AB 为8cm ,•长BC•为10cm .当小红折叠时,顶点D 落在BC 边上的点F:处(折痕为AE )(1)求BF 的长; (2)求EC 的长。
BC ,使点B 落在AD 边的F 处,已知:AB=3,BC=5,例2:已知,如图长方形ABCD 中,AB=3cm ,AD=9cm ,将此长方形折叠,使点B 与点D 重合,折痕为EF ,则△ABE 的面积为( )A 、6cm 2B 、8cm 2C 、10cm 2D 、12cm 2对应练习:1、如图2-2,把一张长方形纸片ABCD 折叠起来,使其对角顶点A 、C 重合,•若其长BC 为a ,宽AB 为b ,则折叠后不重合部分的面积是多少?第11题图AE BCDF2、如图2-3,把矩形ABCD 沿直线BD 向上折叠,使点C 落在C ′的位置上,已知AB=•3,BC=7,求重合部分△EBD 的面积例3:有一个直角三角形纸片,两直角边AC=6cm,BC=8cm,现将直角边AC 沿∠CAB 的角平分 线AD 折叠,使它落在斜边AB 上,且与AE 重合,你能求出CD 的长吗?对应练习:1、如图,在△ABC 中,∠B= 90,AB=BC=6,把△ABC 进行折叠,使点A 与点D 重合,BD:DC=1:2,折痕为EF ,点E 在AB 上,点F 在AC 上,求EC 的长。
AECDB ADBCE F例4:如图,一块直角三角形的纸片,两直角边AC=6㎝,BC=8㎝。
现将直角边AC 沿直线AD 折叠,使它落在斜边AB 上,恰与AE 重合,求CD对应练习:1、如图,四边形ABCD 是矩形,AB =3,BC =4,把矩形沿直线AC 折叠,点B 落在点F 处,连接DF ,CF 与AD 相交于点E ,求DE 的长和△ACE 的面积.2、如图,折叠矩形纸片ABCD ,先折出折痕(对角线)BD ,再折叠,使AD 落在对角线BD 上,得折痕DG ,若AB = 2,BC = 1,求AG .ACD BEG A BC'EDCB A 总结:一、 三角形中的折叠基本图形二、矩形FEDCBA EA(B)图1ACBDC ´ABCD E FA ′B ′。
《勾股定理》典型例题折叠问题

《勾股定理》典型例题折叠问题1、如图,有一张直角三角形纸片,两直角边A C=6,BC=8,将△AB C折叠,使点B 与点A 重合,折痕为DE,则CD 等于( )A. 425B. 322C. 47D . 352、如图所示,已知△A BC中,∠C=90°,AB 的垂直平分线交BC •于M,交AB 于N,若AC =4,MB=2M C,求AB 的长.3、折叠矩形AB CD 的一边AD,点D 落在BC 边上的点F 处,已知A B=8CM,BC=10C M,求C F 和EC 。
4、如图,在长方形ABCD 中,DC=5,在DC 边上存在一点E,沿直线A E把△ABC 折叠,使点D 恰好在BC 边上,设此点为F ,若△ABF 的面积为30,求折叠的△AE D的面积B CEDDCBAF E5、如图,矩形纸片ABCD 的长AD =9㎝,宽AB=3㎝,将其折叠,使点D与点B重合,那么折叠后DE 的长是多少?6、如图,在长方形AB CD中,将∆ABC 沿AC 对折至∆AEC 位置,C E与AD 交于点F 。
(1)试说明:AF=FC ;(2)如果AB=3,B C=4,求A F的长7、如图2所示,将长方形ABCD 沿直线A E折叠,顶点D正好落在B C边上F点处,已知CE=3cm ,AB =8cm,则图中阴影部分面积为_______.8、如图2-3,把矩形ABCD沿直线BD向上折叠,使点C落在C′的位置上,已知AB=•3,BC=7,重合部分△EBD的面积为________.9、如图5,将正方形ABCD折叠,使顶点A与CD边上的点M重合,折痕交AD于E,交BC于F,边AB折叠后与BC边交于点G。
如果M为CD边的中点,求证:DE:DM:EM=3:4:5。
10、如图2-5,长方形ABCD中,AB=3,BC=4,若将该矩形折叠,使C点与A点重合,•则折叠后痕迹EF的长为( )A.3.74 B.3.75 C.3.76 D.3.772-511、如图1-3-11,有一块塑料矩形模板ABCD,长为10cm,宽为4cm,将你手中足够大的直角三角板PHF的直角顶点P落在AD边上(不与A、D重合),在AD上适当移动三角板顶点P:①能否使你的三角板两直角边分别通过点B与点C?若能,请你求出这时AP 的长;若不能,请说明理由.②再次移动三角板位置,使三角板顶点P在AD上移动,直角边PH 始终通过点B,另一直角边PF与DC的延长线交于点Q,与BC交于点E,能否使CE=2cm?若能,请你求出这时AP 的长;若不能,请你说明理由.12、如图所示,△ABC是等腰直角三角形,AB=AC,D是斜边BC的中点,E、F分别是AB、AC边上的点,且DE⊥DF,若BE=12,CF=5.求线段EF的长。
方法归纳 利用勾股定理解决折叠问题
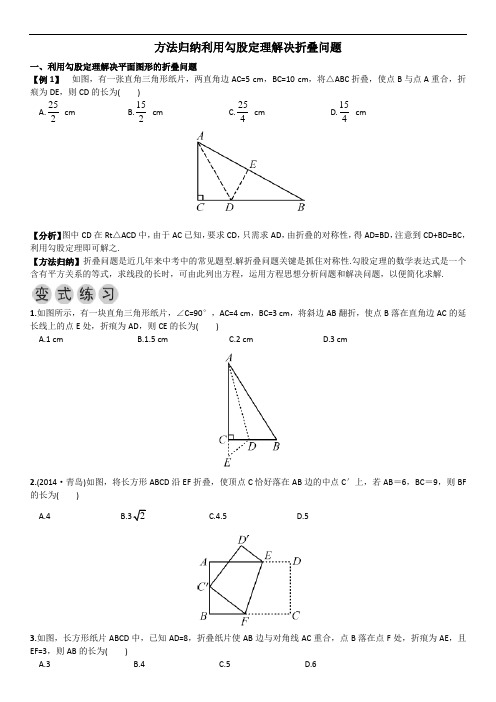
方法归纳利用勾股定理解决折叠问题一、利用勾股定理解决平面图形的折叠问题【例1】如图,有一张直角三角形纸片,两直角边AC=5 cm,BC=10 cm,将△ABC折叠,使点B与点A重合,折痕为DE,则CD的长为( )A.252cm B.152cm C.254cm D.154cm【分析】图中CD在Rt△ACD中,由于AC已知,要求CD,只需求AD,由折叠的对称性,得AD=BD,注意到CD+BD=BC,利用勾股定理即可解之.【方法归纳】折叠问题是近几年来中考中的常见题型.解折叠问题关键是抓住对称性.勾股定理的数学表达式是一个含有平方关系的等式,求线段的长时,可由此列出方程,运用方程思想分析问题和解决问题,以便简化求解.1.如图所示,有一块直角三角形纸片,∠C=90°,AC=4 cm,BC=3 cm,将斜边AB翻折,使点B落在直角边AC的延长线上的点E处,折痕为AD,则CE的长为( )A.1 cmB.1.5 cmC.2 cmD.3 cm2.(2014·青岛)如图,将长方形ABCD沿EF折叠,使顶点C恰好落在AB边的中点C′上,若AB=6,BC=9,则BF 的长为( )A.4 C.4.5 D.53.如图,长方形纸片ABCD中,已知AD=8,折叠纸片使AB边与对角线AC重合,点B落在点F处,折痕为AE,且EF=3,则AB的长为( )A.3B.4C.5D.64.如图,长方形ABCD的边AD沿折痕AE折叠,使点D落在BC上的F处,已知AB=6,△ABF的面积是24,则FC 等于( )A.1B.2C.3D.45.如图,四边形ABCD是边长为9的正方形纸片,将其沿MN折叠,使点B落在CD边上的B′处,点A对应点为A′,且B′C=3,则AM的长为( )A.1.5B.2C.2.25D.2.56.如图所示,在△ABC中,∠B=90°,AB=3,AC=5,将△ABC折叠,使点C与点A重合,折痕为DE,则△ABE的周长为__________.7.如图,在Rt△ABC中,∠C=90°,BC=6 cm,AC=8 cm,按图中所示方法将△BCD沿BD折叠,使点C落在AB边的C′点,那么△ADC′的面积是__________.8.如图,已知Rt△ABC中,∠C=90°,AC=6,BC=8,将它的锐角A翻折,使得点A落在BC边的中点D处,折痕交AC边于点E,交AB边于点F,则DE的值为__________.二、利用勾股定理解决立体图形的展开问题【例2】如图,圆柱形玻璃杯,高为12 cm,底面周长为18 cm,在杯内离杯底4 cm的点C处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿4 cm与蜂蜜相对的点A处,则蚂蚁到达蜂蜜的最短距离为__________cm.【分析】将圆柱形平面展开,将A、C两点放在同一平面内,然后利用勾股定理进行计算.【方法归纳】在曲面上求两点之间的最短距离,根据“两点之间线段最短”和“化曲面为平面”两种思想,利用勾股定理解决.解决本题时要注意展开后有一直角边长是9 cm而不是18 cm.9.如图,一圆柱体的底面周长为24 cm,高AB为5 cm,BC是直径,一只蚂蚁从点A出发沿着圆柱体的表面爬行到点C的最短路程是( )A.6 cmB.12 cmC.13 cmD.16 cm10.如图,在一个长为2 m,宽为1 m的长方形草地上,放着一根长方体的木块,它的棱和场地宽AD平行且棱长大于AD,木块从正面看是边长为0.2 m的正方形,一只蚂蚁从点A处到达C处需要走的最短路程是__________m(精确到0.01 m).11.一位同学要用彩带装饰一个长方体礼盒.长方体高6 cm,底面是边长为4 cm的正方形,从顶点A到顶点C′如何贴彩带用的彩带最短?最短长度是多少?12.如图,一个长方体形状的木柜放在墙角处(与墙面和地面均没有缝隙),有一只蚂蚁从柜角A处沿着木柜表面爬到柜角C1处.(1)请你画出蚂蚁能够最快到达目的地的可能路径;(2)当AB=4,BC=4,CC1=5时,求蚂蚁爬过的最短路径的长.参考答案例1要使A,B两点重合,则折痕DE必为AB的垂直平分线.设CD=x,则AD=BD=10-x.在Rt△ACD中,由勾股定理,得x2+52=(10-x)2.解得x=15 4.故应选D. 变式练习1.A2.A3.D4.B5.B6.77.6 cm28.13 3例2如图,圆柱形玻璃杯展开(沿点A竖直剖开)后,侧面是一个长18 cm,宽12 cm的长方形,作点A关于杯上沿MN的对称点B,连接BC交MN于点P,连接BM,过点C作AB的垂线交剖开线MA于点D.由轴对称的性质和三角形三边关系知AP+PC为蚂蚁到达蜂蜜的最短距离,且AP=BP.由已知和长方形的性质,得DC=9,BD=12.在Rt△BCD中,由勾股定理得∴AP+PC=BP+PC=BC=15.即蚂蚁到达蜂蜜的最短距离为15 cm.变式练习9.C 10.2.6011.把长方体的面DCC′D′沿棱C′D′展开至面ABCD上,如图.构成矩形ABC′D′,则A到C′的最短距离为AC′的长度,连接AC′交DC于O,易证△AOD≌△C′OC.∴OD=OC.即O为DC的中点,由勾股定理得AC′2=AD′2+D′C′2=82+62=100,∴AC′=10 cm.即从顶点A沿直线到DC中点O,再沿直线到顶点C′,贴的彩带最短,最短长度为10 cm.12.(1)如图,木柜的表面展开图是两个矩形ABC1′D1和ACC1A1.蚂蚁能够最快到达目的地的可能路径有如图所示的AC1′和AC1两种.(2)蚂蚁沿着木柜表面经线段A1B1到C1′,爬过的路径的长l1.蚂蚁沿着木柜表面经线段BB1到C1,爬过的路径的长l2∵l1>l2,鱼儿,在水中串上串下,吐着顽皮的泡泡;鸟儿从荷叶上空飞过,想亲吻荷花姑娘的芳泽。
勾股定理的展开与折叠问题

01 勾股定理的应用——展开图
杜登尼(Dudeney,1857-1930年)是19世 纪英国知名的谜题创作者.“蜘蛛和 苍蝇”问题最早出现在1903年的英国 报纸上,它是杜登尼最有名的谜题之 一.它对全世界难题爱好者的挑战, 长达四分之三个世纪.
A
B
如图,有一棱长为4m的立方体房间,一只 蜘蛛在A处. ⑴若一只苍蝇在B处,蜘蛛去抓苍蝇需要爬 行的最短路程是多少? ⑵若苍蝇在C处,则最短路程是多少?
例1、如图,一块直角三角形的纸片,两 直角边AC=6㎝,BC=8㎝。现将直角边 AC沿直线AD折叠,使它落在斜边AB上, 且与AE重合,求CD的长.
A
E
C
D D
B
例2、如图,小颍同学折叠一个直角三角形 的纸片,使A与B重合,折痕为DE,若已知 AC=10cm,BC=6cm,你能求出CE的长吗?
D
C
C
4m
4m 上 B
C
4m 左 前 后
右
下 A
如图,一圆柱体木块的底面周长为24cm,
高AB为4cm ,BC是直径,一只蚂蚁从点
A出发沿着圆柱体的表面爬行到点C的最短
路程大约是(
)
A.6cm B.12cm C.13cm D.16cm
B
C
ABCຫໍສະໝຸດ BCB1沿AB剪开
A
A
A1
∵ 底面圆的周长为24cm ∴BB1=24cm 又∵点C 是BB1 的中点 ∴BC=12cm 而∵AB=4cm ∴ 在Rt△ABC中,根据勾股定理得: AC2=AB2+BC2
如图是一个三级台阶,它的每一级的长宽和高分别为20dm、 3dm、2dm,A和B是这个台阶两个相对的端点, A点有一只蚂蚁,想到B点去吃可口的食物,则蚂蚁沿 着台阶面爬到B点最短路程是多少?
