(完整版)初中数学证明题汇总(含参考答案),推荐文档
初中数学几何证明经典试题(含答案)
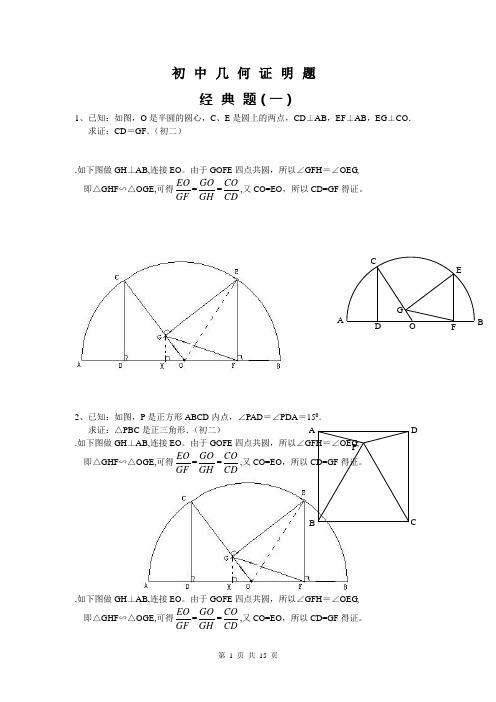
初中几何证明题经典题(一)1、已知:如图,O是半圆的圆心,C、E是圆上的两点,CD⊥AB,EF⊥AB,EG⊥CO.求证:CD=GF.(初二).如下图做GH⊥AB,连接EO。
由于GOFE四点共圆,所以∠GFH=∠OEG,即△GHF∽△OGE,可得EOGF=GOGH=COCD,又CO=EO,所以CD=GF得证。
2、已知:如图,P是正方形ABCD内点,∠PAD=∠PDA=150.求证:△PBC是正三角形.(初二).如下图做GH⊥AB,连接EO。
由于GOFE四点共圆,所以∠GFH=∠OEG,即△GHF∽△OGE,可得EOGF=GOGH=COCD,又CO=EO,所以CD=GF得证。
.如下图做GH⊥AB,连接EO。
由于GOFE四点共圆,所以∠GFH=∠OEG,即△GHF∽△OGE,可得EOGF=GOGH=COCD,又CO=EO,所以CD=GF得证。
APCDBAFGCEBOD3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二)4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC的延长线交MN 于E 、F .求证:∠DEN =∠F .经典题(二)1、已知:△ABC 中,H 为垂心(各边高线的交点),O 为外心,且OM ⊥BC 于M . (1)求证:AH =2OM ; (2)若∠BAC =600,求证:AH =AO .(初二)D 2 C 2B 2 A 2D 1 C 1 B 1 C B DA A 1 A N FE CDMB · A HEOF2、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A 引圆的两条直线,交圆于B 、C 及D 、E ,直线EB 及CD 分别交MN 于P 、Q . 求证:AP =AQ .(初二)3、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN 于P 、Q . 求证:AP =AQ .(初二)4、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P 是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.经典题(三)1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F .求证:CE =CF .(初二)2、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .(初二)3、设P 是正方形ABCD 一边求证:PA =PF .(初二)4、如图,PC 切圆O 于C ,AC 为圆的直径,PEFB 、D .求证:AB =DC ,BC =AD.(初三)经典1、已知:△ABC 是正三角形,P 是三角形内一点,PA =3,PB =4,求:∠APB 的度数.(初二)2、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA . 求证:∠PAB =∠PCB .(初二)3、设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =AC ·BD .(初三)4、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .(初二)经典难题(五)1、 设P 是边长为1的正△ABC 内任一点,L =PA +PB +PC ,求证:≤L <2.2、已知:P 是边长为1的正方形ABCD 内的一点,求PA +PB +PC 的最小值.3、P 为正方形ABCD 内的一点,并且PA =a ,PB =2a ,PC =3a ,求正方形的边长.C BD A F PD E CB A APCBACPDA CBPD4、如图,△ABC中,∠ABC=∠ACB=800,D、E分别是AB、AC上的点,∠DCA=300,∠EBA=200,求∠BED的度数.经典题(一)1.如下图做GH⊥AB,连接EO。
初中数学几何证明经典题(含答案)

初中数学几何证明经典题(含答案)初中几何证明题经典题(一)1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO .求证:CD =GF .(初二).如下图做GH ⊥AB,连接EO 。
由于GOFE 四点共圆,所以∠GFH =∠OEG , 即△GHF ∽△OGE,可得EOGF=GO GH=CO CD,又CO=EO ,所以CD=GF 得证。
APDA F G C EB O D3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二)4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC 的延长线交MN 于E 、F .求证:∠DEN =∠F .D 2 C 2B 2 A 2 D 1C 1B 1CD A A1A N F EC DM B经典题(二)1、已知:△ABC 中,H 为垂心(各边高线的交点),O 为外心,且OM ⊥BC 于M . (1)求证:AH =2OM ;(2)若∠BAC =600,求证:AH =AO .(初二)2、设MN 是圆O外一直线,过O · AD HE M C B O于A,自A引圆的两条直线,交圆于B、C及D、E,直线EB及CD分别交MN于P、Q.求证:AP=AQ.(初二)3、如果上题把直线MN由圆外平移至圆内,则由此可得以下命题:设MN是圆O的弦,过MN的中点A 任作两弦BC、DE,设CD、EB分别交MN于P、Q.求证:AP=AQ.(初二)·OQPB DECN M ·AP CG F B Q A D E4、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P 是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.(初二)经典题(三)1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F . 求证:CE =CF .(初二)AFD ECB2、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F . 求证:AE =AF .(初二)3、设P 是正方形ABCD 一边BC 上的任一点,PF ⊥AP ,CF 平分∠DCE . 求证:PA =PF .(初二)4、如图,PC 切圆O 于C DED A CBFFEP C BA为圆的割线,AE 、AF 与直线PO 相交于B 、D .求证:AB =DC ,BC =AD .(初三)经典题(四)1、已知:△ABC 是正三角形,P 是三角形内一点,PA =3,PB =4,PC =5.求:∠APB 的度数.(初二)2、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA .求证:∠PAB =∠PCB .(初二)APC B PA DCB3、设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =AC ·BD .(初三)4、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .(初二)CBD AFP DE CB A经典难题(五)1、 设P 是边长为1的正△内任一点,L=PA +PB +PC , 求证:≤L <2.2、已知:P 是边长为1的正方形ABCD 内的一点,求PA +PB +PC 的最小值.3、P 为正方形ABCD 内的一点,并且PA =a ,PB =2a ,PC =3a ,求正方形的边长.4、如图,△ABC 中,∠ABC =∠ACB =0、AP CB ACBP D ACBPDE分别是AB、AC上的点,∠DCA=300,∠EBA =200,求∠BED的度数.经典题(一)1.如下图做GH⊥AB,连接EO。
初二证明题考试题及答案

初二证明题考试题及答案一、选择题1. 已知在△ABC中,AB=AC,点D在BC上,且BD=DC,那么下列说法正确的是:A. AD是△ABC的中线B. AD是△ABC的角平分线C. AD是△ABC的高线D. AD是△ABC的中线、角平分线和高线答案:D2. 在等腰三角形中,如果顶角的角平分线也是底边的高线,那么这个三角形是:A. 等边三角形B. 等腰三角形C. 直角三角形D. 不能确定答案:A二、填空题1. 在平行四边形ABCD中,若∠A=60°,则∠B的度数为______。
答案:120°2. 已知等腰三角形的底边长为6cm,腰长为5cm,那么它的高线长度为______。
答案:4cm三、解答题1. 已知在△ABC中,AB=AC,点D在BC上,且BD=DC,求证:AD是△ABC的中线、角平分线和高线。
证明:因为AB=AC,所以△ABC是等腰三角形。
又因为BD=DC,所以D是BC的中点,故AD是△ABC的中线。
在△ABD和△ACD中,有AB=AC,BD=DC,AD=AD,根据SSS(边边边)全等条件,可得△ABD≌△ACD。
因此,∠BAD=∠CAD,所以AD是△ABC的角平分线。
又因为△ABD≌△ACD,所以∠ADB=∠ADC,即AD是△ABC的高线。
综上所述,AD是△ABC的中线、角平分线和高线。
2. 在等腰三角形ABC中,AB=AC,点D是底边BC上的一点,使得AD 是底边BC的高线,求证:BD=DC。
证明:因为AB=AC,所以△ABC是等腰三角形。
又因为AD是底边BC的高线,根据等腰三角形的性质,底边的高线也是底边的中线,所以BD=DC。
因此,BD=DC得证。
(完整版)初中几何证明题五大经典(含答案)
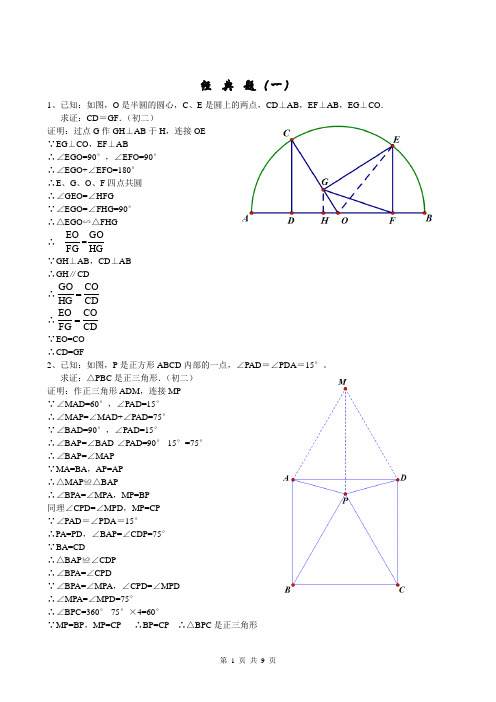
经典题(一)1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .(初二)证明:过点G 作GH ⊥AB 于H ,连接OE ∵EG ⊥CO ,EF ⊥AB∴∠EGO=90°,∠EFO=90° ∴∠EGO+∠EFO=180° ∴E 、G 、O 、F 四点共圆 ∴∠GEO=∠HFG∵∠EGO=∠FHG=90° ∴△EGO ∽△FHG ∴FG EO =HGGO∵GH ⊥AB ,CD ⊥AB ∴GH ∥CD∴CD COHG GO =∴CDCO FG EO = ∵EO=CO ∴CD=GF2、已知:如图,P 是正方形ABCD 内部的一点,∠PAD =∠PDA =15°。
求证:△PBC 是正三角形.(初二) 证明:作正三角形ADM ,连接MP ∵∠MAD=60°,∠PAD=15° ∴∠MAP=∠MAD+∠PAD=75° ∵∠BAD=90°,∠PAD=15°∴∠BAP=∠BAD-∠PAD=90°-15°=75° ∴∠BAP=∠MAP ∵MA=BA ,AP=AP ∴△MAP ≌△BAP∴∠BPA=∠MPA ,MP=BP 同理∠CPD=∠MPD ,MP=CP ∵∠PAD =∠PDA =15°∴PA=PD ,∠BAP=∠CDP=75° ∵BA=CD∴△BAP ≌∠CDP ∴∠BPA=∠CPD∵∠BPA=∠MPA ,∠CPD=∠MPD ∴∠MPA=∠MPD=75°∴∠BPC=360°-75°×4=60°∵MP=BP ,MP=CP ∴BP=CP ∴△BPC 是正三角形3、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC 的延长线交MN于E 、F .求证:∠DEN =∠F .证明:连接AC ,取AC 的中点G ,连接NG 、MG ∵CN=DN ,CG=DG ∴GN ∥AD ,GN=21AD ∴∠DEN=∠GNM ∵AM=BM ,AG=CG ∴GM ∥BC ,GM=21BC ∴∠F=∠GMN ∵AD=BC ∴GN=GM∴∠GMN=∠GNM ∴∠DEN=∠F经典题(二)1、已知:△ABC 中,H 为垂心(各边高线的交点),O 为外心,且OM ⊥BC 于M . (1)求证:AH =2OM ;(2)若∠BAC =600,求证:AH =AO .(初二) 证明:(1)延长AD 交圆于F ,连接BF ,过点O 作OG ⊥AD 于G ∵OG ⊥AF ∴AG=FG ∵AB⌒ =AB ⌒ ∴∠F=∠ACB又AD ⊥BC ,BE ⊥AC ∴∠BHD+∠DBH=90° ∠ACB+∠DBH=90° ∴∠ACB=∠BHD ∴∠F=∠BHD∴BH=BF 又AD ⊥BC ∴DH=DF∴AH=AG+GH=FG+GH=GH+DH+DF+GH=2GH+2DH=2(GH+DH )=2GD 又AD ⊥BC ,OM ⊥BC ,OG ⊥AD ∴四边形OMDG 是矩形 ∴OM=GD ∴AH=2OM (2)连接OB 、OC∵∠BAC=60∴∠BOC=120° ∵OB=OC ,OM ⊥BC ∴∠BOM=21∠BOC=60°∴∠OBM=30° ∴BO=2OM由(1)知AH=2OM ∴AH=BO=AO2、设MN 是圆O 外一条直线,过O 作OA ⊥MN 于A ,自A 引圆的两条割线交圆O 于B 、C 及D 、E ,连接CD 并延长交MN 于Q ,连接EB 并延长交MN 于P. 求证:AP =AQ .证明:作点E 关于AG 的对称点F ,连接AF 、CF 、QF ∵AG ⊥PQ ∴∠PAG=∠QAG=90°又∠GAE=∠GAF ∴∠PAG+∠GAE=∠QAG+∠GAF 即∠PAE=∠QAF∵E 、F 、C 、D 四点共圆 ∴∠AEF+∠FCQ=180° ∵EF ⊥AG ,PQ ⊥AG ∴EF ∥PQ∴∠PAF=∠AFE ∵AF=AE∴∠AFE=∠AEF ∴∠AEF=∠PAF ∵∠PAF+∠QAF=180° ∴∠FCQ=∠QAF ∴F 、C 、A 、Q 四点共圆 ∴∠AFQ=∠ACQ 又∠AEP=∠ACQ ∴∠AFQ=∠AEP3、设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN 于P 、Q . 求证:AP =AQ .(初二)证明:作OF ⊥CD 于F ,OG ⊥BE 于G ,连接OP 、OQ 、OA 、AF 、AG ∵C 、D 、B 、E 四点共圆 ∴∠B=∠D ,∠E=∠C ∴△ABE ∽△ADC ∴DFBGFD 2BG 2DC BE AD AB === ∴△ABG ∽△ADF ∴∠AGB=∠AFD ∴∠AGE=∠AFC ∵AM=AN , ∴OA ⊥MN 又OG ⊥BE ,∴∠OAQ+∠OGQ=180° ∴O 、A 、Q 、E 四点共圆 ∴∠AOQ=∠AGE 同理∠AOP=∠AFC ∴∠AOQ=∠AOP又∠OAQ=∠OAP=90°,OA=OA ∴△OAQ ≌△OAP ∴AP=AQ 在△AEP 和△AFQ 中 ∠AFQ=∠AEP AF=AE ∠QAF=∠PAE ∴△AEP ≌△AFQ ∴AP=AQ4、如图,分别以△ABC 的AB 和AC 为一边,在△ABC 的外侧作正方形ABFG 和正方形ACDE ,点O 是DF 的中点,OP ⊥BC求证:BC=2OP (初二)证明:分别过F 、A 、D 作直线BC 的垂线,垂足分别是L 、M 、N ∵OF=OD ,DN ∥OP ∥FL ∴PN=PL∴OP 是梯形DFLN 的中位线 ∴DN+FL=2OP ∵ABFG 是正方形∴∠ABM+∠FBL=90° 又∠BFL+∠FBL=90° ∴∠ABM=∠BFL又∠FLB=∠BMA=90°,BF=AB ∴△BFL ≌△ABM ∴FL=BM同理△AMC ≌△CND ∴CM=DN∴BM+CN=FL+DN ∴BC=FL+DN=2OP经典题(三)1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F . 求证:CE =CF .(初二)证明:连接BD 交AC 于O 。
初中数学几何证明题含答案

初中数学几何证明题含答案Newly compiled on November 23, 2020初中几何证明题 经典题(一)1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO .求证:CD =GF .(初二).如下图做GH ⊥AB,连接EO 。
由于GOFE 四点共圆,所以∠GFH =∠OEG, 即△GHF ∽△OGE,可得EO GF =GO GH =COCD,又CO=EO ,所以CD=GF 得证。
2、已知:如图,P 是正方形ABCD 内点,∠PAD =∠PDA =150. 求证:△PBC 是正三角形.(初二).如下图做GH ⊥AB,连接EO 。
由于GOFE 四点共圆,所以∠GFH =∠OEG, 即△GHF ∽△OGE,可得EO GF =GO GH =COCD,又CO=EO ,所以CD=GF得证。
.如下图做GH ⊥AB,连接EO 。
由于GOFE 四点共圆,所以∠GFH =∠OEG, 即△GHF∽△OGE,可得EO GF =GO GH =COCD,又CO=EO ,所以CD=GF 得证。
3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二)4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 点,AD 、BC 的延长线交MN 于E 、F .APCDB CDAFG CEBOD求证:∠DEN=∠F.经典题(二)1、已知:△ABC中,H为垂心(各边高线的交点),O为外心,且OM⊥BC 于M.(1)求证:AH=2OM;(2)若∠BAC=600,求证:AH=AO.(初二)2、设MN是圆O外一直线,过O作OA⊥MN于A,自圆于B、C及D、E,直线EB及CD分别交MN于P、求证:AP=AQ.(初二)3、如果上题把直线MN设MN是圆O的弦,过MN的中点A任作两弦分别交MN于P、Q.求证:AP=AQ.(初二)4、如图,分别以△ABC的AC和BC为一边,在△ABC 和正方形CBFG,点P是EF的中点.求证:点P到边AB1、如图,四边形ABCD求证:CE=CF2、如图,四边形ABCD长线于F.求证:AE=AF3、设P 是正方形ABCD 一边BC 上的任一点,PF ⊥AP ,CF 平分∠DCE . 求证:PA =PF .(初二)4、如图,PC 切圆O 于C ,AC 为圆的直径,PEF 为圆的割线,AE 、AF 与直线PO 相交于B 、D .求证:AB =DC ,BC =AD .(初三)经典题(四)1、已知:△ABC 是正三角形,P 是三角形内一点,PA =3,PB =4,PC =5.求:∠APB 的度数.(初二)2、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA . 求证:∠PAB =∠PCB .(初二)3、设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =AC ·BD .(初三)4、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且AE =CF .求证:∠DPA =∠DPC .(初二)经典难题(五)1、 设P 是边长为1的正△ABC 内任一点,L =PA +PB +PC , 求证:≤L <2.2、已知:P 是边长为1的正方形ABCD 内的一点,求PA +PB PC的最小值. 3、P 为正方形ABCD 内的一点,并且PA =a ,PB =2a PC =3a ,求正方形的边长.DFEP C BAO D B FAEC PAPCB P ADCB C B DAF P DE CBAAPCBAP D AC BP D4、如图,△ABC 中,∠ABC =∠ACB =800,D 、E 分别是AB 、AC 上的点,∠DCA =300,∠EBA =200,求∠BED 的度数.经典题(一)1.如下图做GH ⊥AB,连接EO 。
初中数学几何证明经典试题(含答案)
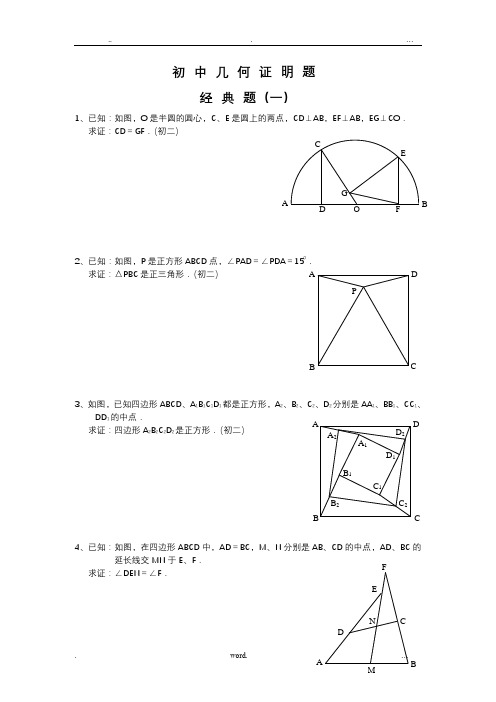
初中几何证明题经典题(一)1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .(初二)2、已知:如图,P 是正方形ABCD 点,∠PAD =∠PDA =150. 求证:△PBC 是正三角形.(初二)3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二)4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC 的延长线交MN 于E 、F .求证:∠DEN =∠F .A P C DB A FG CE B O D D 2 C 2B 2 A 2 D 1C 1 B 1C B DA A 1F 经典题(二)1、已知:△ABC 中,H 为垂心(各边高线的交点),O(1)求证:AH =2OM ; (2)若∠BAC =600,求证:AH =AO .(初二)2、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A 引圆的两条直线,交圆于B 、C 及D 、E ,直线EB及CD 分别交MN 于P 、Q . 求证:AP =AQ .(初二)3、如果上题把直线MN 由圆外平移至圆,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE P 、Q . 求证:AP =AQ .(初二)4、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P 是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.经典题(三)1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F .求证:CE =CF .(初二)2、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .(初二)3、设P 是正方形ABCD 一边BC求证:PA =PF .(初二)4、如图,PC 切圆O 于C ,AC 为圆的直径,PEF 为圆的割线,D .求证:AB =DC ,BC =AD .(初三)经典题(四)1、已知:△ABC 是正三角形,P 是三角形一点,PA =3,PB =4,PC求:∠APB 的度数.(初二)2、设P 是平行四边形ABCD 部的一点,且∠PBA =∠PDA .求证:∠PAB =∠PCB .(初二)3、设ABCD 为圆接凸四边形,求证:AB ·CD +AD ·BC =AC·BD .(初三)4、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .(初二)经典难题(五)1、 设P 是边长为1的正△ABC 任一点,L =PA +PB +PC , 求证:≤L <2.2、已知:P 是边长为1的正方形ABCD 的一点,求PA +PB +PC 的最小值.3、P 为正方形ABCD 的一点,并且PA =a ,PB =2a ,PC =3a ,求正方形的边长.4、如图,△ABC 中,∠ABC =∠ACB =800,D 、E 分别是AB 、AC 上的点,∠DCA =300,∠EBA =200,求∠BED 的度数.APCBACBPDACBPD经典题(一)1.如下图做GH⊥AB,连接EO。
初中数学证明题汇总(含参考答案)

(B)
40°
(C)50°
(D)
9.如图4,
AB
AC BC,图中与ZCAB互余的角
有(
60°
(B)等腰直角三角形
5.在厶ABC中,
ZA,ZB的外角分别是
(A
(B
6.如图1,11/
12,
Z仁50°,则Z2的度数是
(A
(B)
7.如图2所示,
不能推出
AD//
(A)ZDAB
ZABC
180o
(B)Z2
(C)Z1
Z
(D)等边三角形
(C)直角三角形
BC的是(
(D)Z
(C)50°
8.如图3,
a
a,Z1
130o,则Z2等于(
(C)两条直线被第三条直线所截,内错角相等
学号评价等级
(B)对顶角相等
(D)两点确定一条直线
(B)两锐角对应相等的两个直角三角形全等
(D)面积相等的两个三角形全等
锐角三角形中最大的角一定大于或等于60°
(D)矩形的对角线相等且互相平分
4.△ABC中,ZAZB 120o,/C/A,
则△ABC是(
)•
(A)钝角三角形
证明(一)
班级姓名
一、选择题
1.下列句子中,不是命题的是()
(A)三角形的内角和等于180度
(C)过一点ห้องสมุดไป่ตู้已知直线的平行线
2.下列说法中正确的是()
(A)两腰对应相等的两个等腰三角形全等
(C)两角及其夹边对应相等的两个三角形全等
3.下列命题是假命题的是()
(A)如果a//b,b//c,那么a//c(B
初中数学几何证明经典题(含答案)

初中几何证明题经典题(一)1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .(初二).如下图做GH ⊥AB,连接EO 。
由于GOFE 四点共圆,所以∠GFH =∠OEG ,即△GHF ∽△OGE,可得EO GF =GO GH =COCD,又CO=EO ,所以CD=GF 得证。
APDAFGCEBOD2、已知:如图,P是正方形ABCD内点,∠PAD=∠PDA=150.求证:△PBC是正三角形.(初二).如下图做GH⊥AB,连接EO。
由于GOFE四点共圆,所以∠GFH=∠OEG,即△GHF∽△OGE,可得EOGF =GOGH=COCD,又CO=EO,所以CD=GF得证。
.如下图做GH⊥AB,连接EO。
由于GOFE四点共圆,所以∠GFH=∠OEG,即△GHF∽△OGE,可得EOGF =GOGH=COCD,又CO=EO,所以CD=GF得证。
3、如图,已知四边形ABCD、A1B1C1D1都是正方形,A2、B2、C2、D2分别是AA1、BB1、CC1、DD1的中点.求证:四边形A2B2C2D2是正方形.(初二)4、已知:如图,在四边形ABCD中,AD=、CD的中点,AD、BC的延长线交求证:∠DEN=∠F.D2C2B2A2D1C1B1C BD AA1经典题(二)1、已知:△ABC中,H为垂心(各边高线的交点),O为外心,且OM⊥BC于M.(2)若∠BAC=600,求证:AH=AO.F2、设MN 是圆O 外一直线,过O 作OA ⊥MN 于条直线,交圆于B 、C 及D 、E ,直线EB 及Q .求证:AP =AQ .(初二)3、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A CD 、EB 分别交MN 于P 、Q .求证:AP =AQ .(初二)4、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P 是EF 的中点. 求证:点P 到边AB 的距离等于AB经典题(三)1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F .求证:CE =CF .(初二)2、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F . 求证:AE =AF .3、设P是正方形ABCD一边BC上的任一点,PF⊥AP,CF平分∠DCE.求证:PA=PF.(初二)4、如图,PC切圆O于C,ACAF与直线PO相交于B、D经典题(四)1、已知:△ABC 是正三角形,P 是三角形内一点,PC =5.求:∠APB的度数.(初二)2、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA. 求证:∠PAB =∠PCB .(初二)3、设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =AC ·BD .(初三)4、平行四边形ABCD中,设E、F分别是BC、AB上的一点,AE与CF相交于P,且AE=CF.求证:∠DPA=∠DPC.(初二)经典难题(五)1、设P是边长为1的正△ABC内任一点,L求证:≤L<2.2、已知:P 是边长为1的正方形ABCD的最小值.3、P 为正方形ABCD 内的一点,并且PA =a ,PB =正方形的边长.4、如图,△ABC 中,∠ABC =∠ACB =800,D 、E上的点,∠DCA=300,∠EBA=200,求∠BED的度数.经典题(一)1.如下图做GH⊥AB,连接EO。
初中数学几何证明经典试题(含答案)
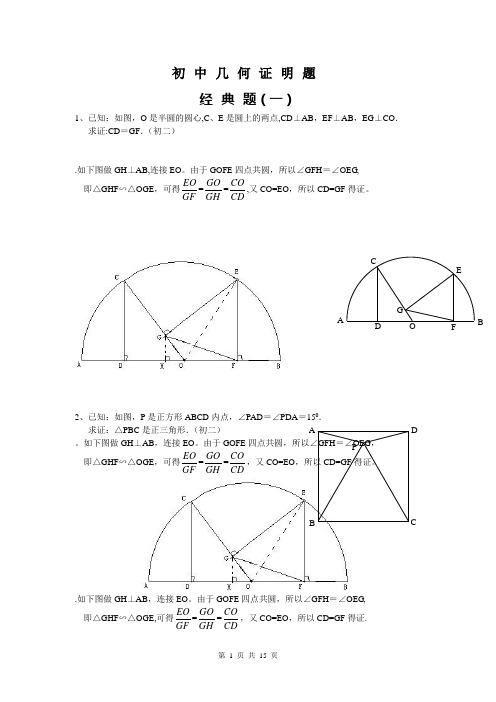
初中几何证明题经典题(一)1、已知:如图,O是半圆的圆心,C、E是圆上的两点,CD⊥AB,EF⊥AB,EG⊥CO.求证:CD=GF.(初二).如下图做GH⊥AB,连接EO。
由于GOFE四点共圆,所以∠GFH=∠OEG,即△GHF∽△OGE ,可得EOGF=GOGH=COCD,又CO=EO,所以CD=GF得证。
2、已知:如图,P是正方形ABCD内点,∠PAD=∠PDA=150.求证:△PBC是正三角形.(初二)。
如下图做GH⊥AB,连接EO。
由于GOFE四点共圆,所以∠GFH=∠OEG,即△GHF∽△OGE,可得EOGF=GOGH=COCD,又CO=EO,所以CD=GF得证。
.如下图做GH⊥AB,连接EO。
由于GOFE四点共圆,所以∠GFH=∠OEG,即△GHF∽△OGE,可得EOGF=GOGH=COCD,又CO=EO,所以CD=GF得证.APCDBAFGCEBOD3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二)4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC 的延长线交MN 于E 、F .求证:∠DEN =∠F .经典题(二)1、已知:△ABC 中,H 为垂心(各边高线的交点),O 为外心,且OM ⊥BC 于M . (1)求证:AH =2OM ; (2)若∠BAC =600,求证:AH =AO .(初二)D 2 C 2B 2 A 2D 1 C 1 B 1 C B DA A 1 A N FE CDMB · A HEOF 2、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A,自A 引圆的两条直线,交圆于B 、C 及D 、E ,直线EB 及CD 分别交MN 于P 、Q . 求证:AP =AQ .(初二)3、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN 于P 、Q . 求证:AP =AQ .(初二)4、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P 是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.经典题(三)1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F .求证:CE =CF .(初二)2、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .(初二)3、设P 是正方形ABCD 一边求证:PA =PF .(初二)4、如图,PC 切圆O 于C ,AC 为圆的直径,PEFB 、D .求证:AB =DC,BC =AD .(初三)经典 1、已知:△ABC 是正三角形,P是三角形内一点,PA =3,PB =4,求:∠APB 的度数.(初二)2、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA . 求证:∠PAB =∠PCB .(初二)3、设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =AC ·BD .(初三)4、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .(初二)经典难题(五)1、 设P 是边长为1的正△ABC 内任一点,L =PA +PB +PC ,求证:≤L <2.2、已知:P 是边长为1的正方形ABCD 内的一点,求PA +PB +PC 的最小值.3、P 为正方形ABCD 内的一点,并且PA =a ,PB =2a ,PC =3a ,求正方形的边长.C BD A F PD E CB A APCBACPDA CBPD4、如图,△ABC中,∠ABC=∠ACB=800,D、E分别是AB、AC上的点,∠DCA=300,∠EBA=200,求∠BED的度数.经典题(一)1.如下图做GH⊥AB,连接EO。
初中数学几何证明经典试题(含答案)
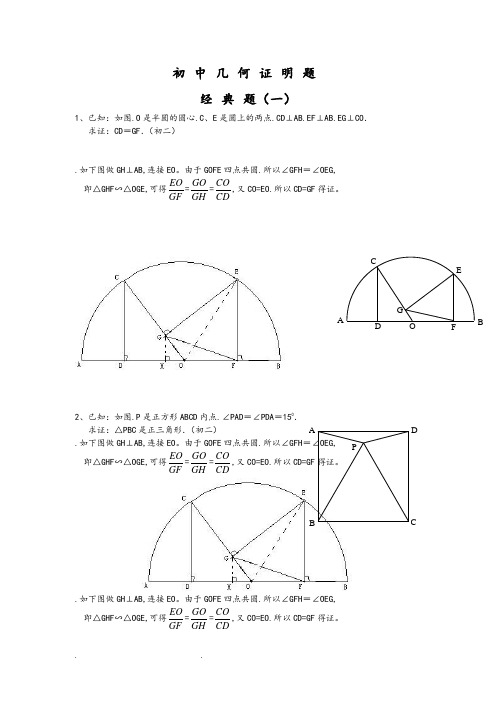
初中几何证明题经典题(一)1、已知:如图.O是半圆的圆心.C、E是圆上的两点.CD⊥AB.EF⊥AB.EG⊥CO.求证:CD=GF.(初二).如下图做GH⊥AB,连接EO。
由于GOFE四点共圆.所以∠GFH=∠OEG,即△GHF∽△OGE,可得EOGF=GOGH=COCD,又CO=EO.所以CD=GF得证。
2、已知:如图.P是正方形ABCD内点.∠PAD=∠PDA=150.求证:△PBC是正三角形.(初二).如下图做GH⊥AB,连接EO。
由于GOFE四点共圆.所以∠GFH =∠OEG,即△GHF∽△OGE,可得EOGF=GOGH=COCD,又CO=EO.所以CD=GF得证。
.如下图做GH⊥AB,连接EO。
由于GOFE四点共圆.所以∠GFH=∠OEG,即△GHF∽△OGE,可得EOGF=GOGH=COCD,又CO=EO.所以CD=GF得证。
APCDBAFGCEBOD3、如图.已知四边形ABCD 、A 1B 1C 1D 1都是正方形.A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二)4、已知:如图.在四边形ABCD 中.AD =BC.M 、N 分别是AB 、CD 的中点.AD 、BC 的延长线交MN 于E 、F .求证:∠DEN =∠F .经典题(二)1、已知:△ABC 中.H 为垂心(各边高线的交点).O 为外心.且(1)求证:AH =2OM ;(2)若∠BAC =600.求证:AH =AO .(初二)D 2 C 2B 2 A 2D 1 C 1 B 1 C B DA A 1 BF2、设MN 是圆O 外一直线.过O 作OA ⊥MN 于A.自A 引圆的两条直线.交圆于B 、C 及D 、E.直线EB 及CD 分别交MN 于P 、Q . 求证:AP =AQ .(初二)3、如果上题把直线MN 由圆外平移至圆内.则由此可得以下命题:设MN 是圆O 的弦.过MN 的中点A 任作两弦BC 、DE.设CD 、EB 分别交MN 于P 、Q .求证:AP =AQ .(初二)4、如图.分别以△ABC 的AC 和BC 为一边.在△ABC 的外侧作正方形是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.经典题(三)1、如图.四边形ABCD 为正方形.DE ∥AC.AE =AC.AE 与CD 相交于F .求证:CE =CF .(初二)2、如图.四边形ABCD 为正方形.DE ∥AC.且CE =CA.直线EC 交DA 延长线于F .求证:AE =AF .(初二)3、设P 是正方形ABCD 一边BC求证:PA =PF .(初二)4、如图.PC 切圆O 于C.AC 为圆的直径.PEF 为圆的割线.AE 、证:AB =DC.BC =AD .(初三)经典1、已知:△ABC 是正三角形.P 是三角形内一点.PA =3.PB =4.PC =5.求:∠APB 的度数.(初二)2、设P 是平行四边形ABCD 内部的一点.且∠PBA =∠PDA . 求证:∠PAB =∠PCB .(初二)3、设ABCD 为圆内接凸四边形.求证:AB ·CD +AD ·BC =AC ·BD .(初三)4、平行四边形ABCD 中.设E 、F 分别是BC 、AB 上的一点.AE 与CF 相交于P.且 AE =CF .求证:∠DPA =∠DPC .(初二)经典难题(五)1、 设P 是边长为1的正△ABC 内任一点.L =PA +PB +PC.求证:≤L <2.2、已知:P 是边长为1的正方形ABCD 内的一点.求PA +PB +PC 的最小值.3、P 为正方形ABCD 内的一点.并且PA =a.PB =2a.PC =3a.求正方形的边长.4、如图.△ABC中.∠ABC=∠ACB=800.D、E分别是AB、AC上的点.∠DCA=300.∠EBA=200.求∠BED的度数.经典题(一)1.如下图做GH⊥AB,连接EO。
初中数学几何证明经典题含答案

初中几何证明题经典题(一)1、已知:如图,O是半圆的圆心,C、E是圆上的两点,CD⊥AB,EF⊥AB,EG⊥CO.求证:CD=GF.(初二).如下图做GH⊥AB,连接EO。
由于GOFE四点共圆,所以∠GFH=∠OEG,即△GHF∽△OGE,可得EOGF=GOGH=COCD,又CO=EO,所以CD=GF得证。
2、已知:如图,P是正方形ABCD内点,∠PAD=∠PDA=150.求证:△PBC是正三角形.(初二).如下图做GH⊥AB,连接EO。
由于GOFE四点共圆,所以∠GFH=∠OEG,即△GHF∽△OGE,可得EOGF=GOGH=COCD,又CO=EO,所以CD=GF得证。
.如下图做GH⊥AB,连接EO。
由于GOFE四点共圆,所以∠GFH=∠OEG,即△GHF∽△OGE,可得EOGF=GOGH=COCD,又CO=EO,所以CD=GF得证。
APCDBAFGCEBOD3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二)4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC的延长线交MN 于E 、F .求证:∠DEN =∠F .经典题(二)1、已知:△ABC 中,H 为垂心(各边高线的交点),O(1)求证:AH =2OM ;(2)若∠BAC =600,求证:AH =AO .(初二)D 2 C 2B 2 A 2D 1 C 1 B 1 C B DA A 1 BF2、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A 引圆的两条直线,交圆于B 、C 及D 、E ,直线EB 及CD 分别交MN 于P 、Q . 求证:AP =AQ .(初二)3、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN于P 、Q .求证:AP =AQ .(初二)4、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P 是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.经典题(三)1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F .求证:CE =CF .(初二)2、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .(初二)3、设P 是正方形ABCD 一边求证:PA =PF .(初二)4、如图,PC 切圆O 于C ,AC 为圆的直径,PEFB 、D .求证:AB =DC ,BC =AD.(初三)经典1、已知:△ABC 是正三角形,P 是三角形内一点,PA =3,PB =4,求:∠APB 的度数.(初二)2、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA . 求证:∠PAB =∠PCB .(初二)3、设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =AC ·BD .(初三)4、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .(初二)经典难题(五)1、 设P 是边长为1的正△ABC 内任一点,L =PA +PB +PC ,求证:≤L <2.2、已知:P 是边长为1的正方形ABCD 内的一点,求PA +PB +PC 的最小值.3、P 为正方形ABCD 内的一点,并且PA =a ,PB =2a ,PC =3a ,求正方形的边长.4、如图,△ABC中,∠ABC=∠ACB=800,D、E分别是AB、AC上的点,∠DCA=300,∠EBA=200,求∠BED的度数.经典题(一)1.如下图做GH⊥AB,连接EO。
初中数学几何证明经典题(含答案)
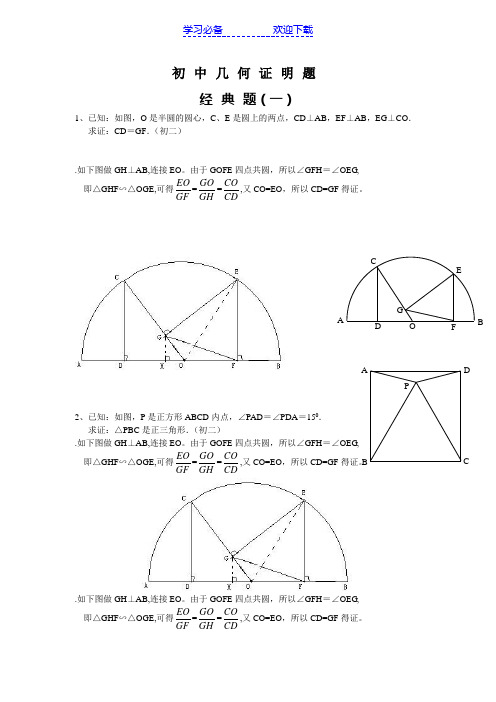
初中几何证明题经典题(一)1、已知:如图,O是半圆的圆心,C、E是圆上的两点,CD⊥AB,EF⊥AB,EG⊥CO.求证:CD=GF.(初二).如下图做GH⊥AB,连接EO。
由于GOFE四点共圆,所以∠GFH=∠OEG,即△GHF∽△OGE,可得EOGF=GOGH=COCD,又CO=EO,所以CD=GF得证。
2、已知:如图,P是正方形ABCD内点,∠PAD=∠PDA=150.求证:△PBC是正三角形.(初二).如下图做GH⊥AB,连接EO。
由于GOFE四点共圆,所以∠GFH=∠OEG,即△GHF∽△OGE,可得EOGF=GOGH=COCD,又CO=EO,所以CD=GF得证。
.如下图做GH⊥AB,连接EO。
由于GOFE四点共圆,所以∠GFH=∠OEG,即△GHF∽△OGE,可得EOGF=GOGH=COCD,又CO=EO,所以CD=GF得证。
APCDBAFGCEBOD3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二)4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC的延长线交MN 于E 、F .求证:∠DEN =∠F .经典题(二)1、已知:△ABC 中,H 为垂心(各边高线的交点),O(1)求证:AH =2OM ;(2)若∠BAC =600,求证:AH =AO .(初二)D 2 C 2B 2 A 2D 1 C 1 B 1 C B DA A 1 BF2、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A 引圆的两条直线,交圆于B 、C 及D 、E ,直线EB 及CD 分别交MN 于P 、Q . 求证:AP =AQ .(初二)3、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN于P 、Q .求证:AP =AQ .(初二)4、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P 是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.经典题(三)1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F .求证:CE =CF .(初二)2、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .(初二)3、设P 是正方形ABCD 一边求证:PA =PF .(初二)4、如图,PC 切圆O 于C ,AC 为圆的直径,PEFB 、D .求证:AB =DC ,BC =AD.(初三)经典1、已知:△ABC 是正三角形,P 是三角形内一点,PA =3,PB =4,求:∠APB 的度数.(初二)2、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA . 求证:∠PAB =∠PCB .(初二)3、设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =AC ·BD .(初三)4、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .(初二)经典难题(五)1、 设P 是边长为1的正△ABC 内任一点,L =PA +PB +PC ,求证:≤L <2.2、已知:P 是边长为1的正方形ABCD 内的一点,求PA +PB +PC 的最小值.3、P 为正方形ABCD 内的一点,并且PA =a ,PB =2a ,PC =3a ,求正方形的边长.4、如图,△ABC中,∠ABC=∠ACB=800,D、E分别是AB、AC上的点,∠DCA=300,∠EBA=200,求∠BED的度数.经典题(一)1.如下图做GH⊥AB,连接EO。
(完整版)初中数学几何证明经典试题(卷)[含答案解析],推荐文档
![(完整版)初中数学几何证明经典试题(卷)[含答案解析],推荐文档](https://img.taocdn.com/s3/m/7dc1e43981c758f5f61f67ed.png)
求证:AE=AF.(初二)
F
A
D
B
C
3、设 P 是正方形 ABCD 一边 BC 上的任一点,PF⊥AP,CF 平分∠DCE.
E
求证:PA=PF.(初二)
A
D
F
B
P
C
E
4、如图,PC 切圆 O 于 C,AC 为圆的直径,PEF 为圆的割线,AE、AF 与直线 PO 相交于 B、D.求证:AB=DC,BC=AD.(初三)
C
D P
C
A D
B
C
4、平行四边形 ABCD 中,设 E、F 分别是 BC、AB 上的一点,AE 与 CF 相交于 P,且 AE=CF.求证:∠DPA=∠DPC.(初二)
A
D
F
B
经 典 难 题(五)
1 设 P 是边长为 1 的正△ABC 内任一点,L=PA➡PB➡PC, 求证: ≤L<2.
B
P EC
C
O·
B
D
MP
A
QN
3、如果上题把直线 MN 由圆外平移至圆内,则由此可得以下命题:
设 MN 是圆 O 的弦,过 MN 的中点 A 任作两弦 BC、DE,设 CD、EB 分别交 MN 于
P、Q. 求证:AP=AQ.(初二)
C MP
E
A
Q
·
N
·O
B
D
4、如图,分别以△ABC 的 AC 和 BC 为一边,在△ABC 的外侧作正方形 ACDE 和正方形
初中几何证明题 经 典 题(一)
1、已知:如图,O 是半圆的圆心,C、E 是圆上的两点,CD⊥AB,EF⊥AB,EG⊥CO. 求证:CD=GF.(初二)
.如下图做 GH⊥AB,连接 EO。由于 GOFE 四点共圆,所以∠GFH=∠OEG,
初中数学几何证明经典题(含答案)
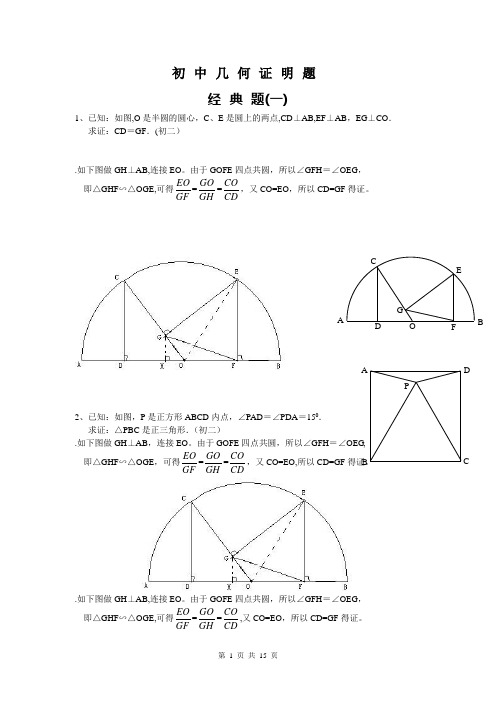
初中几何证明题经典题(一)1、已知:如图,O是半圆的圆心,C、E是圆上的两点,CD⊥AB,EF⊥AB,EG⊥CO.求证:CD=GF.(初二).如下图做GH⊥AB,连接EO。
由于GOFE四点共圆,所以∠GFH=∠OEG,即△GHF∽△OGE,可得EOGF=GOGH=COCD,又CO=EO,所以CD=GF得证。
2、已知:如图,P是正方形ABCD内点,∠PAD=∠PDA=150.求证:△PBC是正三角形.(初二).如下图做GH⊥AB,连接EO。
由于GOFE四点共圆,所以∠GFH=∠OEG,即△GHF∽△OGE,可得EOGF=GOGH=COCD,又CO=EO,所以CD=GF得证。
.如下图做GH⊥AB,连接EO。
由于GOFE四点共圆,所以∠GFH=∠OEG,即△GHF∽△OGE,可得EOGF=GOGH=COCD,又CO=EO,所以CD=GF得证。
APCDBAFGCEBOD3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二)4、已知:如图,在四边形ABCD 中,AD =BC,M 、N 分别是AB 、CD 的中点,AD 、BC 的延长线交MN 于E 、F .求证:∠DEN =∠F .经典题(二)1、已知:△ABC 中,H 为垂心(各边高线的交点),O 为外心,且OM ⊥BC 于M . (1)求证:AH =2OM; (2)若∠BAC =600,求证:AH =AO .(初二)D 2 C 2B 2 A 2D 1 C 1 B 1 C B DA A 1 AN FE CDMB· A HEOF2、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A,自A 引圆的两条直线,交圆于B 、C 及D 、E ,直线EB 及CD 分别交MN 于P 、Q . 求证:AP =AQ .(初二)3、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN 于P 、Q . 求证:AP =AQ .(初二)4、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P 是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.经典题(三)1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F .求证:CE =CF .(初二)2、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA,直线EC 交DA 延长线于F .求证:AE =AF .(初二)3、设P 是正方形ABCD 一边求证:PA =PF .(初二)4、如图,PC 切圆O 于C,AC 为圆的直径,PEF 为圆的割线,AE 、证:AB =DC,BC =AD .(初三)经典1、已知:△ABC 是正三角形,P 是三角形内一点,PA =3,PB =4,PC =5求:∠APB 的度数.(初二)2、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA . 求证:∠PAB =∠PCB .(初二)3、设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =AC ·BD .(初三)4、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P,且 AE =CF .求证:∠DPA =∠DPC .(初二)经典难题(五)1、 设P 是边长为1的正△ABC 内任一点,L =PA +PB +PC,求证:≤L <2.2、已知:P 是边长为1的正方形ABCD 内的一点,求PA +PB +PC 的最小值.3、P 为正方形ABCD 内的一点,并且PA =a ,PB =2a,PC =3a ,求正方形的边长.C BD A F PD E CB A APCBACPDA CBPD4、如图,△ABC中,∠ABC=∠ACB=800,D、E分别是AB、AC上的点,∠DCA=300,∠EBA=200,求∠BED的度数.经典题(一)1。
(完整版)精选初中数学几何证明经典试题(含答案)
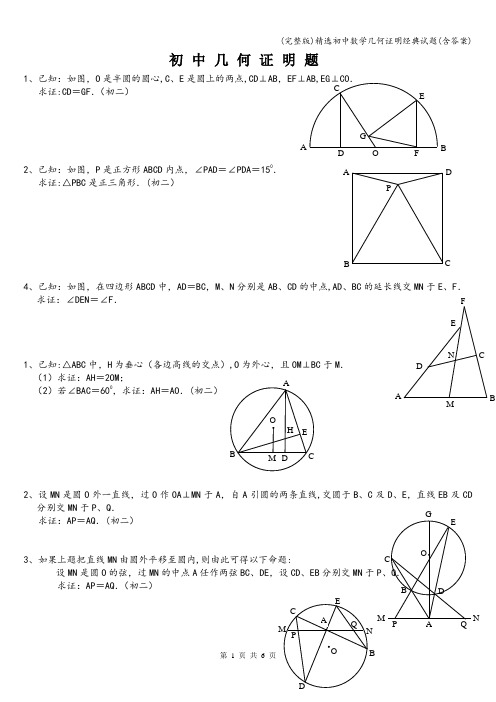
初中几何证明题1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB,EG ⊥CO .求证:CD =GF .(初二)2、已知:如图,P 是正方形ABCD 内点,∠PAD =∠PDA =150. 求证:△PBC 是正三角形.(初二)4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC 的延长线交MN 于E 、F . 求证:∠DEN =∠F .1、已知:△ABC 中,H 为垂心(各边高线的交点),O 为外心,且OM ⊥BC 于M . (1)求证:AH =2OM ;(2)若∠BAC =600,求证:AH =AO .(初二)2、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A 引圆的两条直线,交圆于B 、C 及D 、E ,直线EB 及CD 分别交MN 于P 、Q .求证:AP =AQ .(初二)3、如果上题把直线MN 由圆外平移至圆内,设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE 求证:AP =AQ .(初二)APCDB AFGCEB O D NF 4、如图,分别以△ABC 的AC 和BC 为一边,在△ABC ,点P 是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.经典题(三)1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F .求证:CE =CF .(初二)2、如图,四边形ABCD 为正方形,DE ∥AC,且CE =CA,直线EC求证:AE =AF .(初二)3、设P 是正方形ABCD 一边BC 上的任一点,PF ⊥AP ,CF 求证:PA =PF .(初二)4、如图,PC 切圆O于C ,AC 为圆的直径,PEF 为圆的割线,AE 、AF 与直线PO 相交于B 、D .求证:AB =DC ,BC =AD .(初三)经典题(四)1、已知:△ABC 是正三角形,P 是三角形内一点,PA =3,PB =求:∠APB 的度数.(初二)2、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA .求证:∠PAB =∠PCB .(初二)4、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .(初二)D经典题(一)1。
(完整版)八年级几何证明题集锦及解答值得收藏

(完整版)八年级几何证明题集锦及解答值得收藏八年级几何全等证明题归纳1.如图,梯形ABCD中,AD∥BC,∠DCB=45°,BD⊥CD.过点C作CE⊥AB 于E,交对角线BD于F,点G为BC中点,连接EG、AF.求证:CF=AB+AF.证明:在线段CF上截取CH=BA,连接DH,∵BD⊥CD,BE⊥CE,∴∠EBF+∠EFB=90°,∠DFC+∠DCF=90°,∵∠EFB=∠DFC,∴∠EBF=∠DCF,∵DB=CD,BA=CH,∴△ABD≌△HCD,∴AD=DH,∠ADB=∠HDC,∵AD∥BC,∴∠ADB=∠DBC=45°,∴∠HDC=45°,∴∠HDB=∠BDC—∠HDC=45°,∴∠ADB=∠HDB,∵AD=HD,DF=DF,∴△ADF≌△HDF,∴AF=HF,∴CF=CH+HF=AB+AF,∴CF=AB+AF.2.如图,ABCD为正方形,E为BC边上一点,且AE=DE,AE与对角线BD交于点F,连接CF,交ED于点G.判断CF与ED的位置关系,并说明理由.解:垂直.理由:∵四边形ABCD为正方形,∴∠ABD=∠CBD,AB=BC,∵BF=BF,∴△ABF≌△CBF,∴∠BAF=∠BCF,∵在RT△ABE和△DCE中,AE=DE,AB=DC,∴RT△ABE≌△DCE,∴∠BAE=∠CDE,∴∠BCF=∠CDE,∵∠CDE+∠DEC=90°,∴∠BCF+∠DEC=90°,∴DE⊥CF.3.如图,在直角梯形ABCD中,AD∥BC,∠A=90o,AB=AD,DE⊥CD交AB于E,DF平分∠CDE交BC于F,连接EF.证DA明:CF=EF解:EB F C过D作DG⊥BC于G.由已知可得四边形ABGD为正方形,∵DE⊥DC∴∠ADE+∠EDG=90°=∠GDC+∠EDG,∴∠ADE=∠GDC.又∵∠A=∠DGC且AD=GD,∴△ADE≌△GDC,∴DE=DC且AE=GC.在△EDF和△CDF中∠EDF=∠CDF,DE=DC,DF为公共边,∴△EDF ≌△CDF,∴EF=CF4.已知:在⊿ABC中,∠A=900,AB=AC,D是AC的中点,AE⊥BD,AE延长线交BC于F,求证:∠ADB=∠FDC。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
证明(一)一、选择题1. 下列句子中,不是命题的是()(A )三角形的内角和等于180度 (B )对顶角相等(C )过一点作已知直线的平行线 (D )两点确定一条直线2. 下列说法中正确的是()(A )两腰对应相等的两个等腰三角形全等 (B )两锐角对应相等的两个直角三角形全等(C )两角及其夹边对应相等的两个三角形全等 (D )面积相等的两个三角形全等3. 下列命题是假命题的是()(A )如果,,那么 (B )锐角三角形中最大的角一定大于或等于a b ∥b c ∥a c ∥60°(C )两条直线被第三条直线所截,内错角相等 (D )矩形的对角线相等且互相平分4. 中,,,则是( ).ABC △120A B += ∠∠C A =∠∠ABC △(A )钝角三角形(B )等腰直角三角形(C )直角三角形(D )等边三角形5. 在中,,的外角分别是120°、150°,则( ).ABC △A ∠B ∠C =∠(A )120°(B )150°(C )60°(D )90°6.如图1,l 1∥l 2,∠1=50°, 则∠2的度数是( )(A )135°(B )130°(C )50°(D )40°7.如图2所示,不能推出的是( )AD BC ∥(A ) (B )180DAB ABC += ∠∠24=∠∠(C ) (D )13=∠∠CBE DAE=∠∠8. 如图3,,,,则等于( )a b ∥c a ⊥1130=∠2∠(A )30°(B )40°(C )50°(D )60°9. 如图4,,,图中与互余的角AB CD ∥AC BC ⊥CAB ∠1有( )(A )1个(B )2个(C )3个(D )4个10.若三角形的一个外角等于和它相邻的内角,则这个三角形是( )(A )锐角三角形(B )直角三角形(C )钝角三角形 (D )都有可能二、填空题11.将命题“对顶角相等”改写成“如果……,那么……”的形式:如果 ,那么 .12.如图5所示,如果平分,补上BD ABC ∠一个条件 作为已知,就能推出.AB CD ∥13.如图6,,交、于,平分,,AB CD ∥AF AB CD A C ,CE DCF ∠1120=∠则 .2∠=14.如图7,一个顶角为40°的等腰三角形纸片,剪去顶角后,得到一个四边形,则 .12+=∠∠15. 若一个三角形的三个内角之比为4∶3∶2,则这个三角形的最大内角的外角为 .三、解答题16. 如图8,直线AB 、CD 相交与点O ,∠AOD =70º,OE 平分∠BOC ,求∠DOE的度数。
CB17.已知:如图9,,.BE DF ∥=B D ∠∠求证:.AD BC ∥18.如图10,,若,,,求,//AC DE 70ABC =∠50E =∠75D =∠A ∠的度数.ABD ∠19.如图11,已知AE ⊥BC ,FD ⊥BC ,∠1=∠2,求证:AB ∥CD 。
A F B31 HG2C DE图2ABGP20.小明到工厂去进行社会实践活动时,发现工人生产了一种如图12所示的零件,工人师傅告诉他:,,,小明马上运用已学的数学知识得出了AB CD ∥40A =∠70AEC =∠的度数,聪明的你一定知道的度数.C ∠C ∠证明(二)一、选择题1.如图1,某同学把一块三角形的玻璃打碎成三片,现在他要到玻璃店去配一块形状完全一样的玻璃.那么最省事的办法是带( )去配. (A ) ① (B ) ② (C ) ③(D ) ①和②2.如图2,P 在AB 上,AE =AG ,BE =BG ,则图中全等三角形的对数有( )(A )1(B )2(C )3(D )43.直角三角形斜边上的中线把直角三角形分成的两个三角形的关系是()(A )形状相同 (B ) 周长相等 (C ) 面积相等 (D ) 全等4.等腰三角形一腰上的高等于这腰的一半,则这个等腰三角形的顶角等于( )(A )30°(B )60°(C )30°或150°(D )60°或120°5.△ABC 中,∠A :∠B :∠C =1:2:3,最小边BC =4cm ,最长边AB 的长是( )(A )5cm(B )6cm(C )cm(D )8cm56.如图3,P 是∠BAC 的平分线AP 上一点,PE ⊥AB 于E ,PF ⊥AC 于F ,下列结论中不正确的是( )(A) (B ) PE PF =AE AF =(C )△APE ≌△APF (D )AP PE PF=+7.一个三角形的两边长为4和5,要使三角形为直角三角形,则第三边的长为( )(A )3(B )(C )3或 (D )3或4131418.如图4,已知MB =ND ,∠MBA =∠NDC ,下列哪个条件不能判定△ABM ≌△CDN ( )(A )∠M =∠N(B )AB =CD(C )AM =CN(D )AM ∥CN9.下列命题中真命题是()(A )两边分别对应相等且有一角为30º的两个等腰三角形全等(B )两边和其中一边的对角分别对应相等的两个三角形全等(C )两个锐角分别对应相等的两个直角三角形全等(D )两角和一边分别对应相等的两个三角形全等10.有一块边长为24米的正方形绿地,如图5所示,在绿地旁边处B 有健身器材,由于居住在处的居民践踏了绿地,小明想在处树A A 立一个标牌“少走▇米,踏之何忍?”请你计算后帮小明在标牌的“▇”填上适当的数字是( ).(A )23米(B )24米(C )25米(D )26米二、填空题11.等腰三角形的一个底角是50°,则其顶角为 .12.在△ABC 中,已知∠A =80°,则∠B 、∠C 的角平分线相交所成的钝角为 .13.边长为2cm 的等边三角形的面积为 cm 214.如图6, △ABC 中, ∠C =90°,AB 的垂直平分线DE 交BC 于D ,若∠CAD =20°,则AP CB EF 图3图4∠B = .15.如图7,有一腰长为5cm ,底边长为4cm 的等腰三角形纸片,沿着底边上的中线将纸片剪开,得到两个全等的直角三角形纸片,用这两个直角三角形纸片拼成的平面图形中有 ____个不同的四边形.三、解答题16.如图8,△ABC ,AB =AC ,点M、N分别在BC 所在直线上,且AM =AN 。
求证:BM =CN17.已知,如图9,延长的各边,使得,,顺次连接ABC △BF AC =AE CD AB ==,得到为等边三角形.D E F ,,DEF △求证:(1);AEFCDE △≌△(2)为等边三角形.ABC △18.如图10,在△AFD 和△CEB 中,点A 、E 、F 、C 在同一条直线上,有下面四个结断:①AD =CB ;②AE =CF ;③∠B =∠D ;④AD ∥BC .请用其中三个作为条件,余下的一个作为结论编一道数学题,并证明结论成立.CAEB D图6图7BCMNA图8图9E19.求证:有两条高相等的三角形是等腰三角形(先画出图,再写出已知、求证和证明)20.如图11,,OM 平分,将直角三角板直角的顶点P 在射线OM 090AOB ∠=AOB ∠上移动,两直角边分别与OA 、OB 相交于点C 、D ,问PC 与PD 相等吗?试说明理由.C图11证明(三)一、选择题1.对角线互相垂直平分的四边形是( )(A )平行四边形、菱形(B )矩形、菱形 (C )矩形、正方形 (D )菱形、正方形2.顺次连结任意四边形各边中点所得到的四边形一定是( )(A )平行四边形 (B )矩形 (C )菱形 (D )正方形3.下列四边形中,两条对角线一定不相等的是( )(A )正方形 (B )矩形 (C )等腰梯形 (D )直角梯形4.正方形具有而菱形不一定具有的性质是( )(A )对角线相等(B )对角线互相垂直平分(C )对角线平分一组对角 (D )四条边相等5.菱形的两条对角线长分别为6、8,则它的面积为( ).cm cm 2cm(A )6 (B )12 (C )24 (D )486.如图1,在□ABCD 中, ∠B =110°,延长AD 至F ,延长CD 至E ,连接EF ,则∠E +∠F 的值为( )(A)110°(B)30°(C)50°(D)70°7.如图2,在平行四边形ABCD 中,∠ABD =90°,若AB =3,BC =5,则平行四边形ABCD 的面积为( )(A )6 (B )10 (C )12 (D )158.如图3,把菱形ABCD 沿着对角线AC 的方向移动到菱形A ′B ′C ′D ′的位置,它们的重叠部分(图中阴影部分)的面积是菱形ABCD 的面积的.若AC ,菱形移动的12距离AA ′是( )(A )(B )(C )1(D 121图99.如图4,等腰梯形ABCD 中,AD ∥BC ,AE ∥DC ,∠B =60º,BC =3,△ABE 的周长为6,则等腰梯形的周长是( )(A )8 (B )10 (C )12 (D )1610.如图5,在矩形ABCD 中,R ,P 分别是DC ,BC 上的点,E ,F 分别是AP ,RP 的中点,当点P 在BC 上从B 向C 移动而R 不动时,那么下列结论成立的是( )(A )线段EF 的长逐渐增大 (B )线段EF 的长逐渐减少(C )线段EF的长不变(D )线段EF 的长不能确定二、填空题11.如图6, , 要使四边形是平行四边形,还需补充//AB DC ABCD 一个条件是.12.已知菱形的两条对角线长分别为8cm 、10cm ,则它的边长为 cm .13.在直线上依次摆放着七个正方形(如图7所示)。
已知斜放置的三个正方形的面积分l别是1. 2. 3,正放置的四个正方形的面积依次是S 1. S 2. S 3. S 4,则S 1+S 2+S 3+S 4=_______.14.如图8,菱形ABCD 的对角线的长分别为2和5,P 是对角线AC 上任一点(点P 不与点A 、C 重合),且PE ∥BC 交AB 于E ,PF ∥CD 交AD 于F _____.15.如图9,等边△ABC 中,D 、E 、F 分别是AB 、BC 、CA 边上的中点,那么图中有_________个等边三角形,有_________个菱形.三、解答题16.如图10,平行四边形ABCD 中,AE ⊥BD ,CF ⊥BD ,垂足分别为E 、F ,求证:∠BAE =∠DCF 。
