一次函数和二次函数的结合求三角形面积

合集下载

中考数学复习考点知识与题型专题讲义15---二次函数的最值(基础篇)

中考数学复习考点知识与题型专题讲义15 二次函数的最值（基础）1．已知二次函数y1＝ax2+4x+b与y2＝bx2+4x+a都有最小值，记y1、y2的最小值分别为m、n．（1）若m+n＝0，求证：对任意的实数x，都有y1+y2≥0；（2）若m，n均大于0，且mn＝2，记M为m，n中的最大者，求M的最小值．【分析】（1）根据题意可以用用含a，b的代数式表示m、n，然后根据m+n＝0，可以解答本题；（2）根据题意可以用用含a，b的代数式表示m、n，然后根据mn＝2，记M为m，n中的最大者，可以求得M的最小值．【解答】解：（1）∵二次函数y1＝ax2+4x+b与y2＝bx2+4x+a都有最小值，y1、y2的最小值分别为m、n，∴y1+y2≥m+n，∵m+n＝0，∴y1+y2≥0；（2））∵y1＝ax2+4x+b＝a（x+2a）2+ab−4a，∴m=ab−4 a，∵y2＝bx2+4x+a＝b（x+2b）2+ab−4b，∴n=ab−4 b，∵mn＝2，m，n均大于0，∴ab−4a•ab−4b=2，解得，ab＝2（舍去）或ab＝8，∴{m =4a n =4b ， ∴m =4a ，n =a 2，∵M 为m ，n 中的最大者，∴当0＜a ＜2√2时，M =4a ＞√2，当a ＝2√2时，M =√2，当a ＞2√2时，M =a 2由上可得，M 的最小值是√2．【点评】本题考查二次函数的最值，解题的关键是明确题意，可以将函数的一般式化为顶点式，利用分类讨论的数学思想和数形结合的思想解答问题．2．若一次函数y ＝（a +1）x +a 的图象过第一、三、四象限，则二次函数y ＝ax 2﹣ax 有最大值还是最小值，并求出其最值．【分析】先根据一次函数的性质得到a +1＞0且a ＜0，则﹣1＜a ＜0，再利用配方法得到y ＝ax 2﹣ax ＝a （x −12）2−14a ，然后利用二次函数的性质解决问题．【解答】解：∵一次函数y ＝（a +1）x +a 的图象过第一、三、四象限，∴a +1＞0且a ＜0，∴﹣1＜a ＜0，∵y ＝ax 2﹣ax ＝a （x 2﹣x ）＝a （x 2﹣x +14−14）＝a （x −12）2−14a ，而a ＜0，∴二次函数有最大值，最大值为−14a ．【点评】本题考查了二次函数的最值：确定一个二次函数的最值，首先看自变量的取值范围，当自变量取全体实数时，其最值为抛物线顶点坐标的纵坐标；当自变量取某个范围时，要分别求出顶点和函数端点处的函数值，比较这些函数值，从而获得最值．也考查了一次函数的性质．3．若函数f(x)=−12x 2+133当a ≤x ≤b 时的最小值为2a ，最大值为2b ，求a 、b 的值．【分析】根据二次函数的增减性以及当a ＜b ≤0时，当a ≤0＜b 时，若0＜a ＜b 时分别得出a ，b 的值即可．【解答】解：函数f(x)=−12x 2+133的顶点是（0，133），对称轴是y 轴，最大值为133，如右图，（1）当a ＜b ≤0时，x ＝a 时有最小值2a ，x ＝b 时有最大值2b ，于是−12a 2+133=2a ， −12b 2+133=2b ，可知a 、b 是方程−12x 2+133=2x 的两个根，即3x 2+12x ﹣26＝0，由于△＞0，x 1x 2=−263，此方程有一正一负两个根，这与a ＜b ≤0矛盾，故此情况舍去；（2）当a ≤0＜b 时，x ＝0时有最大值133=2b ，解得b =136，x ＝b 时有最小值2a ，即−12×（136）2+133=14372＞0，而2a ≤0，矛盾，所以只能是x ＝a 时取最小值，（−12）a 2+133=2a ， 3a 2+12a ﹣26＝0 a =−6−√1143＜0，符合条件，（3）若0＜a ＜b ，显然有（−12）a 2+133=2b ①，−12b 2+133=2a ②，①﹣②得：（−12）（a ﹣b ）（a +b ）＝2（b ﹣a ），则a+b＝4，b＝4﹣a，代入①得：（−12）a2+133=2（4﹣a），3a2﹣12a+22＝0，∵△＜0，∴此方程无实数根，故此情况舍去．故有一组解符合要求：a=−6−√1143，b=136．【点评】此题主要考查了二次函数的最值求法，根据自变量的取值范围分别将a，b代入求出是解题关键．4．已知二次函数y＝ax2+bx+c的图象经过点（1，2），且当x＝﹣1时，y有最小值y＝﹣2．（1）求这个函数的关系式；（2）试判断点（3，14）是否在此函数图象上．【分析】二次函数得最小值出现于对称轴处．因此本题利用二次函数得基本性质便可解题．【解答】解：（1）由题意得，对称轴x=−b2a=−1，代入函数得y＝a﹣b+c＝﹣2将点（1，2）代入函数得a+b+c＝2，解得a＝1，b＝2，c＝﹣1 ∴解析式为y＝x2+2x﹣1（2）当x＝3时，y＝14∴（3，14）在此函数图象上【点评】本题主要考察二次函数得基本性质，熟练掌握二次函数是本题得关键5．如图，在Rt△ABC中，∠A＝90°．AB＝8cm，AC＝6cm，若动点D从B出发，沿线段BA运动到点A为止（不考虑D与B，A重合的情况），运动速度为2cm/s，过点D作DE∥BC交AC于点E，连接BE，设动点D运动的时间为x（s），AE的长为y（cm）．（1）求y关于x的函数表达式，并写出自变量x的取值范围；（2）当x为何值时，△BDE的面积S有最大值？最大值为多少？【分析】（1）由平行线得△ABC∽△ADE，根据相似形的性质得关系式；（2）由S=12•BD•AE；得到函数解析式，然后运用函数性质求解．【解答】解：（1）动点D运动x秒后，BD＝2x．又∵AB＝8，∴AD＝8﹣2x．∵DE∥BC，∴ADAB=AEAC，∴AE=6(8−2x)8=6−32x，∴y关于x的函数关系式为y=−32x+6（0＜x＜4）．（2）解：S△BDE=12⋅BD⋅AE=12×2x(−32x+6)=−32x2+6x（0＜x＜4）．当x=−62×(−32)=2时，S△BDE最大，最大值为6cm2．【点评】本题主要考查相似三角形的判定、三角形的面积及涉及到二次函数的最值问题，找到等量比是解题的关键．6．已知二次函数y＝一x2+4x+6．（1）当x 为何值时，y 有最值？是多少？（2）当一2≤x ≤1时，求函数的最值．（3）当x ≥4时．求函数的最值．【分析】（1）将函数解析式配方成顶点式后，根据二次函数的性质即可得；（2）由x ＜2时，y 随x 的增大而增大，结合x 的范围求解可得；（3）由x ＞2时，y 随x 的增大而减小，结合x 的范围求解可得．【解答】解：（1）∵y ＝﹣x 2+4x +6＝﹣（x 2﹣4x +4﹣4）+6＝﹣（x ﹣2）2+10，∴当x ＝2时，y 有最大值，最大值为10；（2）∵当x ＜2时，y 随x 的增大而增大，∴由﹣2≤x ≤1知，当x ＝﹣2时，y 取得最小值，最小值y ＝﹣4﹣8+6＝﹣6，当x ＝1时，y 取得最大值，最大值y ＝﹣1+4+6＝9；（3）∵当x ＞2时，y 随x 的增大而减小，∴在x ≥4范围内，当x ＝4时，函数取得最大值，最大值y ＝﹣16+16+6＝6，无最小值．【点评】本题主要考查二次函数的最值，解题的关键是熟练将二次函数的一般式配方成顶点式及二次函数的性质．7．对于二次函数f （x ）＝ax 2﹣bx +c ，当a ＞0时，只有最小值为4ac−b 24a ，这个结论一定正确吗？【分析】直接利用配方法求出二次函数的顶点式，即可求得出二次函数的顶点坐标，根据二次函数的性质求得出二次函数的最小值．【解答】解：对于二次函数f （x ）＝ax 2﹣bx +c ，当a ＞0时，只有最小值为4ac−b 24a ，这个结论一定正确；∵二次函数f （x ）＝ax 2﹣bx +c＝a （x −b 2a ）2+4ac−b 24a ； ∴图象的顶点坐标为：（b 2a ，4ac−b 24a ）， ∵a ＞0，∴函数的最小值为：4ac−b 24a ．【点评】此题主要考查了求二次函数的最值，熟练掌握二次函数的性质是解题关键．8．求函数y =3x 2+x+2x 2+2x+1的最小值．【分析】将函数整理成关于x 的一元二次方程，然后利用根的判别式列出不等式求解即可．【解答】解：∵y =3x 2+x+2x 2+2x+1， ∴y （x 2+2x +1）＝3x 2+x +2，整理得，（y ﹣3）x 2+（2y ﹣1）x +（y ﹣2）＝0，∵关于x 的一元二次方程有解，∴△＝b 2﹣4ac ＝（2y ﹣1）2﹣4（y ﹣3）（y ﹣2）≥0，整理得，16y ﹣24≥0，解得y ≤32，所以，函数的最小值为32．【点评】本题考查了二次函数的最值，题目难度较大，将函数整理成关于x 的一元二次方程并考虑利用根的判别式求解是解题的关键．9．已知：二次函数y ＝﹣x 2+2（α+1）x +1，其中a 为常数．（1）若y 的最大值为2，求a 的值；（2）求y ＝﹣x 2+2（a +1）x +1在0≤x ≤|a |时的最小值；（3）若方程|﹣x 2+2（a +1）x +1|＝2﹣x 的正实数根只有一个，求a 的取值范围．【分析】（1）把y＝﹣x2+2（α+1）x+1配方即可得到结论；（2）根据二次函数的性质即可得到结论；（3）根据题意得到即该方程的一次项的系数为0，判别式△≥0且二次项的系数与常数项的符号相反．解方程即可得到结论．【解答】解：（1）∵二次函数y＝﹣x2+2（α+1）x+1＝﹣[x﹣（a+1）]2+a2+2a+2，∵y的最大值为2，∴a2+2a+2＝2解得：a＝0或a＝﹣2即y的最大值为2时，a的值为0或﹣2；（2）∵二次函数y＝﹣x2+2（α+1）x+1＝﹣[x﹣（a+1）]2+（a+1）2+1的图象开口向下，对称轴x ＝a+1，当|a|≤a+1时，解得a≥−1 2当a＞−12时，0≤x≤|a|时，函数值随x的增大而增大，故：函数y＝﹣x2+2（a+1）x+1的最小值为：y min═﹣[0﹣（a+1）]2+（a+1）2+1＝1，当a＜−12时，0≤x≤|a|时，函数值随x的增大而减小，x＝|a|时，有最小值，最小值＝﹣a2﹣2a（a+1）+1＝﹣3a2﹣2a+1．（3）∵方程|﹣x2+2（a+1）x+1|＝2﹣x的正实数根只有一个，判别式△≥0且二次项的系数与常数项的符号相反．∴当方程﹣x2+2（a+1）x+1＝2﹣x时，有：x2﹣（2a+3）x+1＝0，而此时二次项的系数与常数项的符号相同，不符合题意，舍去．∴当方程为：﹣x 2+2（a +1）x +1＝x ﹣2时，化简整理得：x 2﹣（2a +1）x ﹣3＝0，∵△＝[﹣（2a +1）]2﹣4×（﹣3）＝4a 2+4a +13＝（2a +1）2+12＞0，∴a 的取值范围为任意实数．【点评】本题考查了二次函数的最值，二次方程的判别式，正确的理解题意是解题的关键．10．已知函数y =k 2x k 2﹣2是关于x 的二次函数（1）求满足条件的k 的值；（2）k 为何值时，函数有最大值？最大值为多少？当x 为何值时，y 随x 的增大而减小？【分析】（1）根据二次函数的指数是二，可得方程，根据解方程，可得答案；（2）根据函数有最大值，可得二次项系数是负数，根据顶点坐标是函数的最值，可得答案；根据a ＜0时，对称轴的右侧y 随x 的增大而减小，可得答案．【解答】解：（1）函数y =k 2x k 2﹣2是关于x 的二次函数，得{k 2−2=2k 2≠0，解得k ＝2或k ＝﹣2；（2）当k ＝﹣2时，函数y ＝﹣x 2有最大值，最大值是0；∴此时函数y =k 2x k 2﹣2是开口向下的，对称轴为x ＝0；∴当x ＞0时，y 随x 的增大而减小．【点评】本题考查了二次函数的定义，利用二次函数的定义得出k 值是解题关键，又利用了二次函数的性质．11．如图．抛物线y ＝ax 2+bx +52与直线AB 交于点A （﹣1，0），B （4，52），点D 是抛物线上位于直线AB 上方的一点（不与点A ，B 重合），连接AD ，BD ．（1）求抛物线的解析；（2）设△ADB 的面为S ，求出当S 取最大值时的点D 的坐标．【分析】（1）把A 、B 两点坐标代入抛物线解析式即可．（2）设点D 坐标为（m ，−12m 2+2m +52），直线DC ⊥x 轴，与AB 交于点C ，根据S △ABD ＝S △ACD +S △BCD 构建二次函数，利用二次函数的最值问题解决．【解答】解：（1）∵抛物线y ＝ax 2+bx +52经过点A （﹣1，0），B （4，52），∴{a −b +52=016a +4b +52=52解得{a =−12b =2， ∴抛物线解析式为y =−12x 2+2x +52．（2）设点D 坐标为（m ，−12m 2+2m +52），直线DC ⊥x 轴，与AB 交于点C ， ∵直线AB 解析式为y =12x +12，∴点C 坐标（m ，12m +12）， ∵S △ABD ＝S △ACD +S △BCD =12（−12m 2+2m +52−12m −12）×（4+1）=−54（m 2﹣3m ﹣4）=−54（m −32）2+12516，∴当m =32时，△ADB 面积最大，此时点D 坐标（32，358）．【点评】本题考查二次函数的最值、一次函数等知识，解题的关键是掌握待定系数法确定函数解析式，学会构建二次函数，利用二次函数的性质解决问题，属于中考常考题型．12．如图，四边形ABCD的两条对角线AC，BD互相垂直，AC+BD＝12，当AC，BD的长分别是多少时，四边形ABCD的面积最大？【分析】直接利用对角线互相垂直的四边形面积求法得出S=12AC•BD，再利用配方法求出二次函数最值．【解答】解：设AC＝x，四边形ABCD面积为S，则BD＝12﹣x，则：S=12AC•BD=12x（12﹣x）=−12（x﹣6）2+18，当x＝6时，S最大＝18；所以AC＝BD＝6时，四边形ABCD的面积最大．【点评】此题主要考查了二次函数最值以及四边形面积求法，正确掌握对角线互相垂直的四边形面积求法是解题关键．13．如图，点E、F分别是正方形ABCD的边BC、CD上两点，且CE＝CF，AB＝4．（1）设CE＝x，△AEF的面积为y，求y关于x的函数关系式；（2）当x取何值时，△AEF面积最大？求出此时△AEF的面积．【分析】（1）由已知可得，AB＝BC＝CD＝AD＝4，CE＝x，由图形得出y＝S正方形ABCD﹣S△ABE﹣S △ADF﹣S△CEF，便可求出x与y的关系式．（2）化成顶点式即可求得结论．【解答】解：（1）∵BC＝DC，CE＝CF，∴BE＝DF＝x，∴y＝S正方形ABCD﹣S△ABE﹣S△ADF﹣S△CEF，∴y＝42−12×4×（4﹣x）−12×4×（4﹣x）−12⋅x2∴y=−12x2+4x（0≤x≤4）．（2）∵y=−12x2+4x=−12（x﹣4）2+8，∴当x＝4时，△AEF的面积最大，此时△AEF的面积是8．【点评】本题考查了二次函数的最值，正方形的性质，三角形的面积，正确求得函数的解析式是解题的关键．14．如图（1）放置两个全等的含有30°角的直角三角板ABC与DEF（∠B＝∠E＝30°），若将三角板ABC向右以每秒1个单位长度的速度移动（点C与点E重合时移动终止），移动过程中始终保持点B、F、C、E在同一条直线上，如图（2），AB与DF、DE分别交于点P、M，AC与DE交于点Q，其中AC＝DF=√3，设三角板ABC移动时间为x秒．（1）在移动过程中，试用含x的代数式表示△AMQ的面积；（2）计算x等于多少时，两个三角板重叠部分的面积有最大值？最大值是多少？【分析】（1）解直角三角形ABC求得EF＝BC＝3，由题意可知CF＝x，可求AQ=√33x，MN=12x，根据三角形面积公式即可求出结论；（2）根据“S重叠＝S△ABC﹣S△AMQ﹣S△BPF”列出函数关系式，通过配方求解即可．【解答】解：（1）解：因为Rt△ABC中∠B＝30°，∴∠A＝60°，∵∠E＝30°，∴∠EQC＝∠AQM＝60°，∴△AMQ为等边三角形，过点M作MN⊥AQ，垂足为点N．在Rt△ABC中，AC=√3，BC=AC⋅tanA=3，∴EF＝BC＝3，根据题意可知CF＝x，∴CE＝EF﹣CF＝3﹣x，CQ=CE⋅tanE=√33(3−x)，∴AQ=AC−CQ=√3−√33(3−x)=√33x，∴AM =AQ =√33x ，而MN =AM ⋅sinA =12x ，∴S △MAQ =12AQ ⋅MN =12×√33x ⋅12x =√312x 2，（2）由（1）知BF ＝CE ＝3﹣x ，PF =BF ⋅tanB =√33(3−x)，∴S 重叠=S △ABC −S △AMQ −S △BPF =12AC ⋅BC −12AQ ⋅MN −12BF ⋅PF=12×3×√3−√312x 2−12（3﹣x ）×√33（3﹣x ） =−√34x 2+√3x =−√34(x −2)2+√3，所以当x ＝2时，重叠部分面积最大，最大面积是√3．【点评】本题属于几何变换综合题，考查了平移变换，等边三角形的性质和判定，解直角三角形，二次函数的性质等知识，解题的关键是灵活运用所学知识解决问题，学会用分类讨论的思想思考问题，属于中考压轴题．15．如图，函数y ＝﹣x 2+12x +c （﹣2020≤x ≤1）的图象记为L 1，最大值为M 1；函数y ＝﹣x 2+2cx +1（1≤x ≤2020）的图象记为L 2，最大值为M 2．L 1的右端点为A ，L 2的左端点为B ，L 1，L 2合起来的图形记为L ．（1）当c ＝1时，求M 1，M 2的值；（2）若把横、纵坐标都是整数的点称为“美点”，当点A ，B 重合时，求L 上“美点”的个数；（3）若M 1，M 2的差为4716，直接写出c 的值．【分析】（1）当c ＝1时，把函数的解析式化成顶点式即可求得M 1，M 2的值；（2）由已知可得点A，B重合时，c−12=2c，c=−12，L1上有1011个“美点”，L2上有2020个“美点”．则L上“美点”的个数是1011+2020﹣1＝3030；（3）当x=14时，M1=116+c，由于L2的对称轴为x＝c，分两种情况求解：当c≥1时，M2＝c2+1；当c＜1时，M2＝2c；再由已知列出等式即可求c的值．【解答】解：（1）当c＝1时，函数y＝﹣x2+12x+c＝﹣x2+12x+1＝﹣（x−14）2+1716．又∵﹣2020≤x≤1，∴M1=17 16，y＝﹣x2+2cx+1＝﹣x2+2x+1＝﹣（x﹣1）2+2．又∵1≤x≤2020，∴M2＝2；（2）当x＝1时，y＝﹣x2+12x+c＝c−12；y＝﹣x2+2cx+1＝2c．若点A，B重合，则c−12=2c，c=−12，∴L1：y＝﹣x2+12x−12（﹣2020≤x≤1）；L2：y＝﹣x2﹣x+1（1≤x≤2020）．在L1上，x为奇数的点是“美点”，则L1上有1011个“美点”；在L2上，x为整数的点是“美点”，则L2上有2020个“美点”．又点A，B重合，则L上“美点”的个数是1011+2020﹣1＝3030．（3）y＝﹣x2+12x+c（﹣2020≤x≤1）上时，当x=14时，M1=116+c，y＝﹣x2+2cx+1（1≤x≤2020），对称轴为x＝c，当c≥1时，M2＝c2+1，∴|116+c ﹣c 2﹣1|=4716， ∴c ＝﹣1（舍去）或c ＝2；当c ＜1时，M 2＝2c ，∴|2c −116−c |=4716， ∴c ＝3（舍去）或c =−238；∴c =−238或2．【点评】本题考查二次函数的图象及性质；能够根据函数所给的取值范围，通过适当的分类讨论，正确的求函数的最大值是解题的关键．16．在矩形ABCD 中，点E 、F 、G 、H 分别在边AB 、BC 、CD 、DA 上，且AE ＝AH ＝CF ＝CG ，已知AB ＝a ，BC ＝b ．（1）若b 3≤a ≤3b 时，求四边形EFGH 的面积的最大值；（2）若a ＝4，b ＝16，求四边形EFGH 的面积的最大值．【分析】（1）由已知可证明△AEH ≌△CGF （SAS ），△BEF ≌△DGH （SAS ），则S 四EFGH ＝S 矩ABCD ﹣2S △AEH ﹣2S △BEF ＝﹣2x 2+（a +b ）x ，由二次函数的性质即可求面积最大值；（2）将a ＝4，b ＝16代入（1）所得的式子即可．【解答】解：（1）设AE ＝x ，∵AE ＝AH ＝CF ＝CG ，∴△AEH ≌△CGF （SAS ），∵AB ＝CD ，AD ＝BC ，∴BE＝DG，HD＝BF，∴△BEF≌△DGH（SAS），∴S四EFGH＝S矩ABCD﹣2S△AEH﹣2S△BEF＝ab﹣2×12x2﹣2×12（a﹣x）（b﹣x）＝ab﹣x2﹣（ab﹣ax﹣bx+x2）＝﹣2x2+（a+b）x，当x=a+b4时，S四EFGH有最大值，最大值为(a+b)28；（2）当a＝4，b＝16时，四边形EFGH的面积＝﹣2x2+20x，∴当x＝4时，四边形EFGH的面积的最大值为48．【点评】本题考查矩形的性质；熟练掌握矩形的性质，通过三角形全等求面积，再由二次函数求面积的最大值是解题的关键．17．如图，在△ABC中，∠B＝90°，AB＝6cm，BC＝8cm，点P从A点开始沿AB边向点B以1cm/秒的速度移动，同时点Q从B点开始沿BC边向点C以2cm/秒的速度移动，且当其中一点到达终点时，另一个点随之停止移动．（1）P，Q两点出发几秒后，可使△PBQ的面积为8cm2．（2）设P，Q两点同时出发移动的时间为t秒，△PBQ的面积为Scm2，请写出S与t的函数关系式，并求出△PBQ面积的最大值．【分析】（1）由题意，可设P、Q经过t秒，使△PBQ的面积为8cm2，则PB＝6﹣t，BQ＝2t，根据三角形面积的计算公式，S△PBQ=12BP×BQ，列出表达式，解答出即可；（2）利用三角形面积公式表示S=12×（6﹣t）×2t＝﹣t2+6t＝﹣（t﹣3）2+9，利用二次函数的性质解题．【解答】解：（1）设经过t秒后，△PBQ的面积等于8cm2．12×（6﹣t）×2t＝8，解得：t1＝2，t2＝4，答：经过2或4秒后，△PBQ的面积等于8cm2．（2）依题意，得S=12×PB×BQ=12×（6﹣t）×2t＝﹣t2+6t＝﹣（t﹣3）2+9，∴在移动过程中，△PBQ的最大面积是9cm2．【点评】本题考查了二次函数的运用．关键是根据题意，列出相应的函数关系式，运用二次函数的性质解题．18．如图，在Rt△ABC中，∠C＝90°，AC＝12cm，BC＝6cm，点P从点C开始沿CB向点B以1cm/s 的速度移动，点Q从A开始沿AC向点C以2cm/s的速度移动，如果点P，Q同时从点C，A出发，试问：（1）出发多少时间时，点P，Q之间的距离等于2√17cm？（2）出发多少时间时，△PQC的面积为6cm2？（3）△PQC面积的是否有最大值？若有是多少？此时时间是多少？【分析】（1）可设出发xs时间时，点P，Q之间的距离等于2√17cm，根据勾股定理列出方程求解即可；（2）可设出发ys时间时，△PQC的面积为6cm2，根据三角形的面积公式列出方程求解即可；（3）根据题意得到△PQC面积和时间t的关系式，根据关系式即可得到结论．【解答】解：（1）设出发xs时间时，点P，Q之间的距离等于2√17cm，依题意有x2+（12﹣2x）2＝（2√17）2，解得x1＝2，x2＝7.6（不合题意舍去）．答：出发2s时间时，点P，Q之间的距离等于2√17cm；（2）设出发ys时间时，△PQC的面积为6cm2，依题意有12y（12﹣2y）＝6，解得y1＝3−√3，y2＝3+√3．答：出发（3−√3）s或（3+√3）s时间时，△PQC的面积为6cm2；（3）依题意有S△PQC=12t（12﹣2t）＝﹣（t﹣3）2+9，∵﹣1＜0，∴△PQC面积的有最大值9，此时时间是3．【点评】此题主要考查了二次函数的最值，一元二次方程的应用，熟练掌握二次函数的性质是解题关键．19．如图，已知点A（0，2），B（2，2），C（﹣1，﹣2），抛物线F：y＝x2﹣2mx+m2﹣2与直线x＝﹣2交于点P．（1）当抛物线F经过点C时，求它的表达式；（2）设点P的纵坐标为y p，求y p的最小值，此时抛物线F上有两点（x1，y1），（x2，y2），且x1＜x2≤﹣2，比较y1与y2的大小．【分析】（1）根据待定系数法即可求得；（2）把x＝﹣2代入解析式得到P点的纵坐标y P＝4+4m+m2﹣2＝（m+2）2﹣2，即可得到当m＝﹣2时，y P的最小值＝﹣2，然后根据二次函数的性质即可判断y1与y2的大小．【解答】解：（1）∵抛物线F经过点C（﹣1，﹣2），∴﹣2＝1+2m+m2﹣2，∴m＝﹣1，∴抛物线F的表达式是y＝x2+2x﹣1．（2）当x＝﹣2时，y P＝4+4m+m2﹣2＝（m+2）2﹣2，∴当m＝﹣2时，y P的最小值＝﹣2．此时抛物线F的表达式是y＝（x+2）2﹣2，∴当x≤﹣2时，y随x的增大而减小．∵x1＜x2≤﹣2，∴y1＞y2．【点评】本题考查了待定系数法求二次函数的解析式，二次函数的性质，二次函数图象上点的坐标特征，熟练掌握二次函数的性质是解题的关键．20．如图，在平面直角坐标系中，点A，B是一次函数y＝x图象上两点，它们的横坐标分别为a，a+3，其中a＞0，过点A，B分别作y轴的平行线，交抛物线y＝x2﹣4x+8于点C，D．（1）若AD＝BC，求a的值；（2）点E是抛物线上的一点，求△ABE面积的最小值．【分析】（1）将已知点的坐标代入相应的函数解析式，再结合AD＝BC，可得关于a的方程，解得a的值即可；（2）设点E（m，m2﹣4m+8），过E作EM垂直于x轴交AB于点M，作BF⊥EM，AG⊥EM，垂足分别为F，G，由题意可得M（m，m），从而可用含m的式子表示出EM的长，根据二次函数的性质及三角形的面积公式可得答案．【解答】解：（1）∵点A，B是一次函数y＝x图象上两点，它们的横坐标分别为a，a+3，∴A（a，a），B（a+3，a+3）．y＝x2﹣4x+8＝（x﹣2）2+4，将x＝a，代入得：y＝（a﹣2）2+4；将x＝a+3，代入得：y＝（a+1）2+4．∴D（a，（a﹣2）2+4），C（a+3，（a+1）2+4），∴AD＝（a﹣2）2+4﹣a，CB＝（a+1）2+4﹣（a+3）．由AD＝BC得：（a﹣2）2+4﹣a＝（a+1）2+4﹣（a+3），∴a＝1．（2）设点E（m，m2﹣4m+8），过E作EM垂直于x轴交AB于点M，作BF⊥EM，AG⊥EM，垂足分别为F，G，由题意得：M（m，m），∴EM＝m2﹣4m+8﹣m＝m2﹣5m+8=(m−52)2+74，∴S△ABE＝S△AEM+S△EMB=12EM⋅AG+12EM⋅BF=12EM(AG+BF)=32(m−52)2+218，由32＞0，得S△ABE有最小值．∴当m=52时，S△ABE的最小值为218．【点评】本题考查了二次函数的最值、一次函数与二次函数图象上的点与坐标的关系及三角形的面积计算等知识点，熟练掌握相关性质及定理并数形结合是解题的关键．。

一次函数与二次函数疑难解析

一次函数和二次函数新知全解：1．一次函数（1）一次函数的概念函数叫做一次函数，它的定义域是R，值域为R一次函数的图象是，其中叫做该直线的，b叫做该直线在y 轴上的．一次函数又叫．（2）一次函数的性质①函数的改变量Δy＝与自变量改变量Δ＝__________的比值等于，的大小表示直线与轴的．②当>0时，一次函数是；当<0时，一次函数是．③当b＝0时，一次函数为，是；当b≠0时，它．④直线y＝＋b与轴的交点为，与y轴的交点为。

2．二次函数（1）函数y＝a2＋b＋ca≠0叫做，它的定义域为R（2）二次函数的性质与图象a ＜0 值域a>0 a<0 24[,)4ac b y a -∈+∞ 24(,]4ac b y a -∈-∞ 奇偶性 b=0时为偶函数，b≠0时既非奇函数也非偶函数单调性 a>0 a<0(,],2b x a∈-∞-时递增 [,)2b x a ∈-+∞时递减图象特点 ()()241:;2:(,)224b b ac b x a a a-=--对称轴顶点最值抛物线有最低点，当2b x a =-时，y 有最小值2min 44ac b y a -= 抛物线有最高点，当2b x a =-时，y 有最大值2max 44ac b y a-= 3配方法将二次函数y ＝a 2＋b ＋c 配成顶点式y ＝a －h 2＋来求抛物线的顶点和函数y 的最值问题．配方法是研究二次函数的主要方法，熟练地掌握配方法是掌握二次函数性质的关键，对一个具体的二次函数，通过配方就能知道这个二次函数的主要性质．(,],2b x a ∈-∞-时递减[,)2b x a ∈-+∞时递增（4）二次函数解析式的三种形式①一般式：f （）=a 2bca≠0②顶点式：f=f=a-h 2a≠0，，h 为顶点坐标．③两根式：f=a-1-2a≠0，1、2为两实根．3．待定系数法一般地，在求一个函数时，如果知道这个函数的一般形式，可先把所求函数写为一般形式，其中系数待定，然后再根据题设条件求出这些待定系数这种通过求待定系数来确定变量之间关系式的方法叫做待定系数法。

2023届山东省济宁市市中学区九年级数学第一学期期末质量检测试题含解析

2022-2023学年九上数学期末模拟试卷考生须知：1．全卷分选择题和非选择题两部分，全部在答题纸上作答。

选择题必须用2B 铅笔填涂；非选择题的答案必须用黑色字迹的钢笔或答字笔写在“答题纸”相应位置上。

2．请用黑色字迹的钢笔或答字笔在“答题纸”上先填写姓名和准考证号。

3．保持卡面清洁，不要折叠，不要弄破、弄皱，在草稿纸、试题卷上答题无效。

一、选择题(每小题3分,共30分)1．如图，在矩形ABCD 中，DE ⊥AC 垂足为F ，交BC 于点E ，BE=2EC ，连接AE ．则tan ∠CAE 的值为（）A ．24B ．13C ．39D ．142．若反比例函数3k y x -=的图象在每一条曲线上y 都随x 的增大而减小，则k 的取值范围是（） A ．3k > B ．3k < C ．03k << D ．3k ≤3．下面是投影屏上出示的抢答题，需要回答横线上符号代表的内容则回答正确的是（）A ．◎代表B ．@代表同位角C ．▲代表D ．※代表4．抛物线y ＝（x ﹣2）2+3的顶点坐标是（）A ．(2，3)B ．(﹣2，3)C ．(2，﹣3)D ．(﹣2，﹣3)5．同学们喜欢足球吗？足球一般是用黑白两种颜色的皮块缝制而成的，如图所示，黑色皮块是正五边形，白色皮块是正六边形．若一个球上共有黑白皮块32块，请你计算一下，黑色皮块和白色皮块的块数依次为（）A ．16块，16块B ．8块，24块C ．20块，12块D ．12块，20块6．如图，P 1、P 2、P 3是双曲线上的三点，过这三点分别作y 轴的垂线，得到三个三角形，它们分别是△P 1A 1O 、△P 2A 2O 、△P 3A 30，设它们的面积分别是S 1、S 2、S 3，则（）A ．S 1＜S 2＜S 3B ．S 2＜S 1＜S 3C ．S 3＜S 1＜S 2D ．S1＝S 2 ＝S 37．一个布袋里装有2个红球、3个黄球和5个白球，除颜色外其它都相同．搅匀后任意摸出一个球，是黄球的概率为( )A ．12B ．310C ．15D ．7108．抛物线y=-2（x+3）2-4的顶点坐标是：A ．（3，-4）B ．（-3，4）C ．（-3，-4）D ．（-4，3） 9．已知35x y =，那么下列等式中，不一定正确的是（） A ．53x y = B ．8x y += C ．85x y y += D ．35x x y y +=+ 10．常胜村2017年的人均收入为12000元，2019年的人均收入为15000元，求人均收入的年增长率．若设人均收入的年增长率为x ，根据题意列方程为（）A ．()212000115000x +=B ．()120001215000x +=C ．()215000112000x -=D ．()212000115000x += 二、填空题(每小题3分,共24分)11．计算211a a a ---的结果是_______. 12．用一块圆心角为120°的扇形铁皮，围成一个底面直径为10cm 的圆锥形工件的侧面，那么这个圆锥的高是_____cm ．13．已知二次函数222y x x -=-，当-1≤x≤4时，函数的最小值是__________．14．如图，小明同学用自制的直角三角形纸板DEF 测量树AB 的高度，他调整自己的位置，使斜边DF 保持水平，并且边DE 与点B 在同一直线上．已知纸板的两条直角边DE ＝40cm ，EF ＝20cm ，测得边DF 离地面的高度AC ＝1.5m ，CD ＝10m ，则AB ＝_____m ．15．如图，在⊙O 的内接四边形ABCD 中，∠A=70°，∠OBC=60°，则∠ODC=__________．16．抛物线y ＝12（x ﹣2）2的顶点坐标是_____． 17．请写出一个开口向下，且与y 轴的交点坐标为（0，4）的抛物线的表达式_____．18．一个多边形的内角和为900°，这个多边形的边数是____．三、解答题(共66分)19．（10分）如图,已知直线y=-2x+3与抛物线y=x 2相交于A,B 两点,O 为坐标原点.(1)求点A 和B 的坐标；(2)连结OA,OB,求△OAB 的面积.20．（6分）化简：23()5()()2(2)+-+-+-m n m n m n m m n ．21．（6分）阅读下面材料，完成（1）﹣（3）题数学课上，老师出示了这样一道题：如图，四边形ABCD ，AD ∥BC ，AB =AD ，E 为对角线AC 上一点，∠BEC =∠BAD =2∠DEC ，探究AB 与BC 的数量关系．某学习小组的同学经过思考，交流了自己的想法：小柏：“通过观察和度量，发现∠ACB=∠ABE”；小源：“通过观察和度量，AE和BE存在一定的数量关系”；小亮：“通过构造三角形全等，再经过进一步推理，就可以得到线段AB与BC的数量关系”．……老师：“保留原题条件，如图2，AC上存在点F，使DF=CF=k AE，连接DF并延长交BC于点G，求ABFG的值”．（1）求证：∠ACB=∠ABE；（2）探究线段AB与BC的数量关系，并证明；（3）若DF=CF=k AE，求ABFG的值（用含k的代数式表示）．22．（8分）（1）解方程：x（x﹣3）＝x﹣3；（2）用配方法解方程：x2﹣10x+6＝023．（8分）如图，在△ABC和△ADE中，AB BC ACAD DE AE==，点B、D、E在一条直线上，求证：△ABD∽△ACE．24．（8分）如图，一次函数y1＝mx+n与反比例函数y2＝kx（x＞0）的图象分别交于点A（a，4）和点B（8，1），与坐标轴分别交于点C和点D．（1）求一次函数与反比例函数的解析式；（2）观察图象，当x＞0时，直接写出y1>y2的解集；（3）若点P是x轴上一动点，当△COD与△ADP相似时，求点P的坐标．25．（10分）解方程（1）2x 2﹣7x +3=1；（2）x 2﹣3x =1．26．（10分）已知反比例函数k y x=的图象与一次函数y kx m =+的图象相交于点（2，1）．（1）分别求出这两个函数的解析式；（2）试判断点P （－1，5）关于x 轴的对称点P '是否在一次函数y kx m =+图象上．参考答案一、选择题(每小题3分,共30分)1、C【分析】证明△AFD ∽△CFE ，得出3AF DF AD CF EF CE===，由△CFE ∽△DFC ，得出2233CF DF EF m m m =⨯=⋅=，设EF=x ，则DE=3x ，再由三角函数定义即可得出答案．【详解】解：设EC=x ，∵BE=2EC=2x ，∴BC=BE+CE=3x ，∵四边形ABCD 是矩形，∴AD=BC=3x ，AD ∥EC ，∴△AFD ∽△CFE ， ∴3AF DF AD CF EF CE=== ，，设CF=n ，设EF=m ，∴DF=3EF=3m ，AF=3CF=3n ，∵△ECD 是直角三角形，DE AC ⊥，∴△CFE ∽△DFC ， ∴CF EF DF CF=， ∴2233CF DF EF m m m =⨯=⋅=，即223n m =，∴n =，∵3AF n ==，∴tan ∠CAE=EF AF == 故选：C ．【点睛】本题考查了相似三角形的判定和性质，矩形的性质，三角函数等知识；熟练掌握矩形的性质，证明三角形相似是解题的关键．2、A【分析】根据反比例函数的图象和性质，当反比例函数y 3k x -=的图象的每一条曲线上，y 都随x 的增大而减小，可知，k ﹣1＞0，进而求出k ＞1．【详解】∵反比例函数y 3k x -=的图象的每一条曲线上，y 都随x 的增大而减小， ∴k ﹣1＞0，∴k ＞1．故选：A ．【点睛】本题考查了反比例函数的图象和性质，对于反比例函数y k x=，当k ＞0时，在每个象限内，y 随x 的增大而减小；当k ＜0时，在每个象限内，y 随x 的增大而增大．3、C【解析】根据图形可知※代表CD ，即可判断D ；根据三角形外角的性质可得◎代表∠EFC ，即可判断A ；利用等量代换得出▲代表∠EFC ，即可判断C ；根据图形已经内错角定义可知@代表内错角．【详解】延长BE 交CD 于点F ，则∠BEC =∠EFC +∠C （三角形的外角等于与它不相邻两个内角之和）．又∠BEC =∠B +∠C ，得∠B =∠EFC ．故AB ∥CD （内错角相等，两直线平行）．故选C ．【点睛】本题考查了平行线的判定，三角形外角的性质，比较简单．4、A【分析】根据抛物线的顶点式可直接得到顶点坐标.【详解】解：y ＝（x ﹣2）2+3是抛物线的顶点式方程，根据顶点式的坐标特点可知，顶点坐标为（2，3）．故选：A ．【点睛】本题考查了二次函数的顶点式与顶点坐标，顶点式y=（x-h ）2+k ，顶点坐标为（h ，k ），对称轴为直线x=h ，难度不大.5、D【解析】试题分析：根据题意可知：本题中的等量关系是“黑白皮块32块”和因为每块白皮有3条边与黑边连在一起，所以黑皮只有3y 块，而黑皮共有边数为5x 块，依此列方程组求解即可．解：设黑色皮块和白色皮块的块数依次为x ，y ．则，解得，即黑色皮块和白色皮块的块数依次为12块、20块．故选D ．6、D【分析】由于P 1、P 2、P 3是同一反比例图像上的点，则围成的三角形虽然形状不同，但面积均为1||2k ．【详解】根据反比例函数的k 的几何意义，△P 1A 1O 、△P 2A 2O 、△P 3A 3O 的面积相同，均为1||2k ，所以S1=S2=S3，故选D ．【点睛】本题考查反比例函数系数k 的几何意义，过同一反比例上的任意一点分别向两条坐标轴作垂线，与坐标轴围成的矩形面积就等于|k|，而围成的三角形的面积为1||2k ，本知识点是中考的重要考点，应高度关注． 7、B【分析】用黄色小球的个数除以总个数可得．【详解】解：搅匀后任意摸出一个球，是黄球的概率为3323510=++ 故答案为B ．【点睛】本题考查了概率公式,解答的关键在于确定发生事件的总发生数和所求事件发生数.8、C【解析】试题分析：抛物线22(3)4y x =-+-的顶点坐标是（-3，-4）．故选C ．考点：二次函数的性质．9、B【分析】根据比例的性质作答．【详解】A 、由比例的性质得到3y=5x ，故本选项不符合题意．B 、根据比例的性质得到x+y=8k （k 是正整数），故本选项符合题意．C 、根据合比性质得到85x y y +=，故本选项不符合题意． D 、根据等比性质得到35x x y y +=+，故本选项不符合题意．故选：B ．【点睛】此题考查了比例的性质，解题关键在于需要掌握内项之积等于外项之积、合比性质和等比性质．10、D【分析】根据“每年的人均收入=上一年的人均收入⨯（1+年增长率）”即可得．【详解】由题意得：2018年的人均收入为12000(1)x +元2019年的人均收入为212000(1)(1)12000(1)x x x ++=+元则212000(1)15000x +=故选：D ．【点睛】本题考查了列一元二次方程，理解题意，正确找出等式关系是解题关键．二、填空题(每小题3分,共24分)11、11a - 【分析】根据分式的加减运算法则，先通分，再加减.【详解】解：原式=()211a a a -+- =()()21111a a a a a -+--- =2211a a a -+-=11a -. 故答案为：11a -. 【点睛】本题考查了分式的加减运算，解题的关键是掌握运算法则和运算顺序.12、【分析】求得圆锥的母线的长利用勾股定理求得圆锥的高即可．【详解】设圆锥的母线长为l ，则1201180π＝10π，解得：l ＝15，＝，故答案为：.【点睛】考查了圆锥的计算，解题的关键是了解圆锥的底面周长等于圆锥的侧面扇形的弧长，难度不大．13、-1【分析】根据题意和二次函数的性质可以求得当−1≤x ≤4时，函数的最小值．【详解】解：∵二次函数222y x x -=-，∴该函数的对称轴是直线x ＝1，当x ＞1时，y 随x 的增大而增大，当x ＜1时，y 随x 的增大而减小，∵−1≤x≤4，∴当x ＝1时，y 取得最小值，此时y ＝-1，故答案为：-1．【点睛】本题考查二次函数的性质、二次函数的最值，解答本题的关键是明确题意，利用二次函数的性质解答．14、6.5【分析】利用直角三角形DEF 和直角三角形BCD 相似求得BC 的长后加上AC 的长即可求得树AB 的高．【详解】∵∠DEF ＝∠BCD ＝90°，∠D ＝∠D ，∴△DEF ∽△DCB ， ∴BC DC EF DE =， ∵DE ＝40cm ＝0.4m ，EF ＝20cm ＝0.2m ，CD ＝10m ， ∴100.20.4BC =，解得：BC ＝5（m ），∵AC=1.5m ，∴AB ＝AC+BC ＝1.5+5＝6.5（m ），故答案为：6.5【点睛】本题考查相似三角形的应用，如果两个三角形的两个角与另一个三角形的两个角对应相等，那么这两个三角形相似；熟练掌握相似三角形的判定定理是解题关键．15、50°．【详解】解：∵∠A=70°，∴∠C=180°﹣∠A=110°，∴∠BOD=2∠A=140°，∵∠OBC=60°，∴∠ODC=360°﹣110°﹣140°﹣60°=50°，故答案为50°．考点：圆内接四边形的性质．16、（2，0）．【分析】已知条件的解析式是抛物线的顶点式，根据顶点式的坐标特点，直接写出顶点坐标.【详解】解：∵抛物线解析式为y ＝12（x ﹣2）2， ∴二次函数图象的顶点坐标是（2，0）．故答案为（2，0）．【点睛】本题的考点是二次函数的性质.方法是根据顶点式的坐标特点写出答案.17、y=﹣x 2+4.【解析】试题解析：开口向下，则0.a <y 轴的交点坐标为()04,，4.c = 这个抛物线可以是2 4.y x =-+故答案为2 4.y x =-+18、1【分析】根据多边形内角和定理：（n ﹣2）×180°，列方程解答出即可．【详解】设这个多边形的边数为n ，根据多边形内角和定理得：（n ﹣2）×180°＝900°，解得n ＝1．故答案为：1【点睛】本题主要考查了多边形内角和定理的应用，熟记多边形内角和公式并准确计算是解题的关键．三、解答题(共66分)19、（1）A(1,1) ，B(-3,9)；（2）6.【分析】（1）将直线与抛物线联立解方程组，即可求出交点坐标；（2）过点A 与点B 分别作AA 1、BB 1垂直于x 轴，由图形可得△OAB 的面积可用梯形AA 1B 1B 的面积减去△OBB 1的面积，再减去△OAA 1得到.【详解】（1）∵直线y=-2x+3与抛物线y=x 2相交，∴将直线与抛物线联立得223y x y x=-+⎧⎨=⎩，解得11x y =⎧⎨=⎩或39x y =-⎧⎨=⎩， ∴A （1，1），B （-3，9）；（2）过点A 与点B 分别作AA 1、BB 1垂直于x 轴，如下图所示，由A 、B 的坐标可知AA 1=1，BB 1=9，OB 1=3，OA 1=1，A 1B 1=4，梯形AA 1B 1B 的面积=()()1111111942022+⋅=⨯+⨯=AA BB A B ， △OBB 1的面积=11113913.522⋅=⨯⨯=OB BB ， △OAA 1的面积=1111110.522⋅=⨯⨯=OA AA ， ∴△OAB 的面积=2013.50.56--=.故答案为6.【点睛】本题考查了求一次函数与二次函数的交点和坐标系中三角形的面积计算，求函数图像交点，就是将两个函数联立解方程组，坐标系中不规则图形的面积通常采用割补法计算.20、228mn n +【分析】根据完全平方公式和平方差公式,先算整式乘法,再算加减.【详解】解：原式=222223(2)5()24m mn n m n m mn ++--+-=222223635524m mn n m n m mn ++-++-=228mn n +【点睛】考核知识点：整式乘法.熟记乘法公式是关键.21、（1）见解析；（2）CB=2AB ；（3）AB FG =【分析】（1）利用平行线的性质以及角的等量代换求证即可；（2）在BE 边上取点H ，使BH=AE ，可证明△ABH ≌△DAE ，△ABE ∽△ACB ，利用相似三角形的性质从而得出结论；（3）连接BD 交AC 于点Q ，过点A 作AK ⊥BD 于点K ，得出12AD DK CB DB ==，通过证明△ADK ∽△DBC 得出∠BDC=∠AKD=90°，再证DF=FQ ，设AD=a ，因此有DF=FC=QF=ka ，再利用相似三角形的性质得出AC=3ka ，AB =，1122FG DF ka ==，从而得出答案．【详解】解：（1）∵∠BAD=∠BEC∠BAD=∠BAE+∠EAD∠BEC=∠ABE+BAE∴∠EAD=∠ABE∵AD ∥BC∴∠EAD=∠ACB∴∠ACB=∠ABE（2）在BE 边上取点H ，使BH=AE∵AB=AD∴△ABH≌△DAE∴∠AHB=∠AED∵∠AHB+∠AHE=180°∠AED+∠DEC=180°∴∠AHE=∠DEC∵∠BEC=2∠DEC∠BEC=∠HAE+∠AHE ∴∠AHE=∠HAE∴AE=EH∴BE=2AE∵∠ABE=∠ACB∠BAE=∠CAB∴△ABE∽△ACB∴EB AE CB AB=∴CB=2AB；（3）连接BD交AC于点Q，过点A作AK⊥BD于点K ∵AD=AB∴12 DK BD=∠AKD=90°∵12AB AD BC == ∴12AD DK CB DB == ∵AD ∥BC∴∠ADK=∠DBC∴△ADK ∽△DBC∴∠BDC=∠AKD=90°∵DF=FC∴∠FDC=∠DFC∵∠BDC=90°∴∠FDC+∠QDF=90°∠DQF+∠DCF=90°∴DF=FQ设AD=a∴DF=FC=QF=ka∵AD ∥BC∴∠DAQ=∠QCB∠ADQ=∠QBC∴△AQD ∽△CQB ∴12AD QA BC CQ== ∴AQ=ka=QF=CF∴AC=3ka∵△ABE ∽△ACB ∴AE AB AB AC=∴AB =同理△AFD ∽△CFG12DF AF FG FC ==∴1122 FG DF ka ==ABFG=．【点睛】本题是一道关于相似的综合题目，难度较大，根据题目作出合适的辅助线是解此题的关键，解决此题还需要较强的数形结合的能力以及较强的计算能力．22、（1）x＝3或x＝1；（2）x＝5【分析】（1）利用因式分解法求解可得；（2）利用配方法求解可得．【详解】解：（1）∵x（x﹣3）＝x﹣3，∴x（x﹣3）﹣（x﹣3）＝0，则（x﹣3）（x﹣1）＝0，∴x﹣3＝0或x﹣1＝0，解得x＝3或x＝1；（2）∵x2﹣10x+6＝0，∴x2﹣10x＝﹣6，则x2﹣10x+25＝﹣6+25，即（x﹣5）2＝19，∴x﹣5则x＝5【点睛】本题主要考查解一元二次方程的能力，熟练掌握解一元二次方程的几种常用方法：直接开平方法、因式分解法、公式法、配方法，结合方程的特点选择合适、简便的方法是解题的关键．23、证明见解析；【分析】根据三边对应成比例的两个三角形相似可判定△ABC∽△ADE，根据相似三角形的性质可得∠BAC=∠DAE，即可得∠BAD=∠CAE，再由AB ACAD AE=可得AB ADAC AE=，根据两边对应成比例且夹角相等的两个三角形相似即可判定△ABD∽△ACE．【详解】∵在△ABC和△ADE中，AB BC AC AD DE AE==,∴△ABC∽△ADE，∴∠BAC=∠DAE ，∴∠BAD=∠CAE ， ∵AB AC AD AE=， ∴AB AD AC AE =， ∴△ABD ∽△ACE ．【点睛】本题考查了相似三角形的判定与性质，熟知相似三角形的判定方法是解决本题的关键．24、（1）y 1＝﹣12x+5， y 2=8x；（2）2＜x ＜1；（3）点P 的坐标为（2，0）或（0，0）时，△COD 与△ADP 相似．【分析】（1）先将点B 代入反比例函数解析式中求出反比例函数的解析式，然后进一步求出A 的坐标，再将A,B 代入一次函数中求一次函数解析式即可；（2）根据图象和两函数的交点即可写出y 1>y 2的解集；（3）先求出C,D 的坐标，从而求出CD,AD,OD 的长度，然后分两种情况：当COD APD ∠=∠时，△COD ∽△APD ；当COD PAD ∠=∠时，△COD ∽△PAD ，分别利用相似三角形的性质进行讨论即可．【详解】解：（1）把B （1，1）代入反比例函数2k y x =中，则18k =，解得8k ∴反比例函数的关系式为 28y x =， ∵点 A （a ，4）在28y x =图象上， ∴ a ＝84＝2，即A （2，4）把A （2，4），B （1，1）两点代入y 1＝mx+n 中得42m 18n m n +⎧⎨=+⎩＝解得：125m n ⎧=-⎪⎨⎪=⎩，所以直线AB 的解析式为：y 1＝﹣12x+5；反比例函数的关系式为y 2=8x，（2）由图象可得，当x ＞0时，y 1>y 2的解集为2＜x ＜1．（3）由（1）得直线AB 的解析式为y 1＝﹣12x+5，当x ＝0时，y ＝5，∴ C （0，5），∴ OC ＝5，当y＝0时，x＝10，∴D点坐标为（10，0）∴ OD＝10，∴ CD＝22OC OD+＝55∵A（2，4），∴ AD＝22(102)4-+＝45设P点坐标为（a，0），由题可知，点P在点D左侧，则PD＝10﹣a 由∠CDO＝∠ADP可得①当COD APD∠=∠时，COD APD，如图1此时AD PD CD OD=，451010 55a-=，解得a＝2，故点P坐标为（2，0）②当COD PAD∠=∠时，COD PAD，如图2当时，AD PD OD CD=，4555=a＝0，即点P的坐标为（0，0）因此，点P的坐标为（2，0）或（0，0）时，△COD与△ADP相似．【点睛】本题主要考查反比例函数与一次函数的综合，相似三角形的判定与性质，掌握待定系数法和相似三角形的判定及性质是解题的关键．25、（1）x1=2，x212=；（2）x1 =1或x2 =2．【分析】（1）先分解因式，即可得出两个一元一次方程，求出方程的解即可；(2)提取公因式x后，求出方程的解即可；【详解】解：（1）2x2﹣7x+2=1，(x﹣2)(2x﹣1)=1，∴x﹣2=1或2x﹣1=1，∴x1=2，x212 =；（2）x2﹣2x=1，x(x﹣2)=1，x1 =1 或，x2 =2．【点睛】本题主要考查了解一元二次方程，掌握解一元二次方程是解题的关键.26、（1）2yx=，23y x=-；（1）P'在一次函数y kx m=+图象上．【分析】（1）把点的坐标代入反比例函数和一次函数的一般式即可求出函数解析式．（1）首先根据关于x 轴对称点的坐标特点：横坐标不变，纵坐标互为相反数，求出点P （-1，5）关于x 轴的对称点P′的坐标，再代入一次函数解析式，看看是否满足解析式，满足则在一次函数y=kx+m 的图象上，反之则不在．【详解】解：（1）∵k y x =经过点（1，1）， ∴k =1．∵一次函数2y x m =+的图象经过（1，1），∴1=1×1+m ∴m =－3， ∴反比例函数解析式为2y x=，一次函数解析式为23y x =-．（1）∵P （-1，5）关于x 轴的对称点P '坐标为（-1，-5），∴把x =－1代入23y x =-，得：y =－5，∴P '在一次函数y kx m =+图象上．【点睛】此题主要考查了待定系数法求反比例函数解析式以及待定系数法求一次函数解析式，关键是把握住凡是图象经过的点都能满足解析式．。

中考数学频考点突破--二次函数与一次函数综合

中考数学频考点突破--二次函数与一次函数综合1．如图，在直角坐标平面内，直线y=－x+5与轴和轴分别交于A、B两点，二次函数y= x2+bx+c的图象经过点A、B，且顶点为C．（1）求这个二次函数的解析式；（2）求sin∠OCA的值；（3）若P是这个二次函数图象上位于x轴下方的一点，且ABP的面积为10，求点P的坐标．2．如图，已知二次函数y＝12x2－x－32的图象与x轴交于A、B两点，与y轴交于C 点．（1）求A、B、C三点的坐标；（2）求直线BC的函数表达式；（3）若D是线段OB上一个动点，过D作x轴的垂线交直线BC于E点，交抛物线于F点，求线段EF的最大值．3．如图二次函数的图象经过A（－1，0）和B（3，0）两点，且交y 轴于点C．（1）试确定、的值；（2）若点M为此抛物线的顶点，求∠MBC的面积．4．设a，b是任意两个实数，用min{a，b}表示a，b两数中较小者，例如：min{﹣1，﹣1}＝﹣1，min{1，2}＝1，min{4，﹣3}＝﹣3，参照上面的材料，解答下列问题：（1）min{﹣3，2}＝，min{﹣1，﹣2}＝；（2）若min{3x+1，﹣x+2}＝﹣x+2，求x的取值范围；（3）求函数y＝﹣x2﹣2x+4与y＝﹣x﹣2的图象的交点坐标，函数y＝﹣x2﹣2x+4的图象如图所示，请你在图中作出直线y＝﹣x﹣2，并根据图象直接写出min{﹣x2﹣2x+4，﹣x﹣2}的最大值.5．已知，二次三项式﹣x2+2x+3.（1）关于x的一元二次方程﹣x2+2x+3＝﹣mx2+mx+2（m为整数）的根为有理数，求m的值；（2）在平面直角坐标系中，直线y＝﹣2x+n分别交x，y轴于点A，B，若函数y＝﹣x2+2|x|+3的图象与线段AB只有一个交点，求n的取值范围.6．如图，二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A，B两点，与y轴交于点C(0,3)，且二次函数图象的顶点坐标为(−1,4)，点C，D是抛物线上的一对对称点，一次函数的图象过点B，D.（1）求A，B两点的坐标.（2）根据图象直接写出使一次函数值大于二次函数值的x的取值范围.7．小明根据华师版八年级下册教材P37学习内容，对函数y= 12x2的图象和性质进行了探究，试将如下尚不完整的过程补充完整．（1）自变量x的取值范围是全体实数，x与y的几组对应数值如表：x…﹣4n﹣2﹣101234…y…8 4.520.500.52 4.58…；（2）如图，在平面直角三角形坐标系xOy中，已描出了以上表中的部分数值为坐标的点，根据描出的点，画出该函数的大致图象．（3）根据画出的函数图象，小明观察发现：该函数有最小值，没有最大值；当函数值取最小时，自变量x的值为．（4）进一步探究函数的图象发现：①若点A（x a，y a），点B（x b，y b）在函数y= 12x2的图象上；当x a＜x b＜0时，y a与y b的大小关系是；当0＜x a＜x b时，y a与y b的大小关系是；②直线y1恰好经过函数的图象上的点（﹣2，2）与（1，0.5）；当y＜y1时，x的取值范围是．8．如图所示，将抛物线y＝12x2沿x轴向右平移2个单位长度，再向下平移1个单位长度，得到新的抛物线．（1）直接写出新抛物线的解析式为；（2）设新抛物线交x轴于A、B两点，交y轴于C，顶点为D，作CE∠CD交抛物线于E，如图所示，探究如下问题：①求点E的坐标；②若一次函数y＝kx+1的图象与抛物线存在唯一交点且交对称轴交于点F，连接DE，猜测直线DE与对称轴的夹角和一次函数y＝kx+1的图象与对称轴的夹角之间的大小关系，并证明．9．某超市准备销售一种儿童玩具，进货价格为每件40元，并且每件的售价不低于进货价．经过市场调查，每月的销售量y（件）与每件的售价x（元）之间满足如图所示的函数关系．（1）求每月的销售量y（件）与每件的售价x（元）之间的函数关系式；（不必写出自变量的取值范围）（2）物价部门规定，该儿童玩具每件的利润不允许高于进货价的60%．设销售这种儿童玩具每月的总利润为w（元），那么每件售价定为多少元可获得最大利润？最大利润是多少？10．已知二次函数y＝x2－2x－3的图象为抛物线C．（1）写出抛物线C的开口方向、对称轴和顶点坐标；（2）当2≤x≤4时，求该二次函数的函数值y的取值范围；（3）将抛物线C先向右平移2个单位长度，得到抛物线C1；再将抛物线C1向下平移1个单位长度，得到抛物线C2，请直接写出抛物线C1，C2对应的函数解析式．11．如图，在平面直角坐标系xOy中，直线y=x+3交x轴于A点，交y轴于B点，过A、B两点的抛物线y=-x2+bx+c交x轴于另一点C，点D是抛物线的顶点．（1）求此抛物线的解析式；（2）点P是直线AB上方的抛物线上一点，（不与点A、B重合），过点P作x轴的垂线交x轴于点H，交直线AB于点F，作PG∠AB于点G．求出∠PFG的周长最大值；（3）在抛物线y=-x2+bx+c上是否存在除点D以外的点M，使得∠ABM与∠ABD 的面积相等？若存在，请求出此时点M的坐标；若不存在，请说明理由．12．如图，顶点M在y轴上的抛物线与直线y=x+1相交于A、B两点，且点A在x轴上，点B的横坐标为2.（1）求抛物线的函数关系式；（2）把抛物线与直线y=x的交点称为抛物线的不动点.若将（1）中抛物线平移，使其顶点为（m，2m），当m满足什么条件时，平移后的抛物线总有不动点.13．如图1，在平面直角坐标系中，直线l与x轴、y轴分别交于点B（4，0）、C （0，3），点A为x轴负半轴上一点，AM∠BC于点M交y轴于点N，满足4CN=5ON．已知抛物线y=ax2+bx+c经过点A、B、C．（1）求抛物线的函数关系式；（2）连接AC，点D在线段BC上方的抛物线上，连接DC、DB，若∠BCD和∠ABC面积满足S∠BCD= 35S∠ABC，求点D的坐标；（3）如图2，E为OB中点，设F为线段BC上一点（不含端点），连接EF．一动点P从E出发，沿线段EF以每秒1个单位的速度运动到F，再沿着线段FC以每秒5 3个单位的速度运动到C后停止．若点P在整个运动过程中用时最少，请直接写出最少时间和此时点F的坐标．14．如图，二次函数y=-x²-2x+3的图象交x轴于点A，B（点A在点B的左侧），交y 轴于点C。

13 三角形面积求最大值问题——铅垂法-【初中数学】120个题型大招!冲刺满分秘籍!

铅垂法求三角形面积最值问题求三角形的面积是几何题中常见问题之一，可用的方法也比较多，比如面积公式、割补、等积变形、三角函数甚至海伦公式，本文介绍的方法是在二次函数问题中常用的一种求面积的方法——铅垂法．【问题描述】在平面直角坐标系中，已知()1,1A 、()7,3B 、()4,7C ，求△ABC 的面积．【分析】显然对于这样一个位置的三角形，面积公式并不太好用，割补倒是可以一试，比如这样：构造矩形ADEF ，用矩形面积减去三个三角形面积即可得△ABC 面积．这是在“补”，同样可以采用“割”：()111222ABC ACD BCD S S S CD AE CD BF CD AE BF =+=⋅+⋅=+ 此处AE +AF 即为A 、B 两点之间的水平距离．由题意得：AE +BF =6．下求CD ：根据A 、B 两点坐标求得直线AB 解析式为：1233y x =+由点C 坐标（4,7）可得D 点横坐标为4，将4代入直线AB 解析式得D 点纵坐标为2，故D 点坐标为（4,2），CD =5,165152ABC S =⨯⨯= ．【方法总结】作以下定义：A 、B 两点之间的水平距离称为“水平宽”；过点C 作x 轴的垂线与AB 交点为D ，线段CD 即为AB 边的“铅垂高”．如图可得：=2ABC S ⨯ 水平宽铅垂高【解题步骤】（1）求A 、B 两点水平距离，即水平宽；（2）过点C 作x 轴垂线与AB 交于点D ，可得点D 横坐标同点C ；（3）求直线AB 解析式并代入点D 横坐标，得点D 纵坐标；（4）根据C 、D 坐标求得铅垂高；（5）利用公式求得三角形面积．【思考】如果第3个点的位置不像上图一般在两定点之间，如何求面积？铅垂法其实就是在割补，重点不在三个点位置，而是取两个点作水平宽之后，能求出其对应的铅垂高！因此，动点若不在两定点之间，方法类似：【铅垂法大全】（1）取AB 作水平宽，过点C 作铅垂高CD ．（2）取AC 作水平宽，过点B 作BD ⊥x 轴交直线AC 于点D ，BD 即对应的铅垂高，=2ABC ABD BCD S S S ⨯-= 水平宽铅垂高（3）取BC 作水平宽，过点A 作铅垂高AD ．甚至，还可以横竖互换，在竖直方向作水平宽，在水平方向作铅垂高．（4）取BC作水平宽，过点A作铅垂高AD．（5）取AC作水平宽，过点B作铅垂高BD．（6）取AB作水平宽，过点C作铅垂高CD．方法突破例一、如图，已知抛物线25y ax bx =++经过(5,0)A -，(4,3)B --两点，与x 轴的另一个交点为C ．（1）求该抛物线的表达式；（2）点P 为该抛物线上一动点（与点B 、C 不重合），设点P 的横坐标为m ．当点P 在直线BC 的下方运动时，求PBC ∆的面积的最大值．【分析】（1）265y x x =++，（2）取BC 两点之间的水平距离为水平宽，过点P 作PQ ⊥x 轴交直线BC 于点Q ，则PQ 即为铅垂高．根据B 、C 两点坐标得B 、C 水平距离为4，根据B 、C 两点坐标得直线BC 解析式：y =x +1，设P 点坐标为（m ，m ²+6m +5），则点Q （m ，m +1），得PQ =-m ²-5m -4，考虑到水平宽是定值，故铅垂高最大面积就最大．当52-时，△BCP 面积最大，最大值为278．【小结】选两个定点作水平宽，设另外一个动点坐标来表示铅垂高．例二、在平面直角坐标系中，将二次函数2(0)y ax a =>的图像向右平移1个单位，再向下平移2个单位，得到如图所示的抛物线，该抛物线与x 轴交于点A 、B （点A 在点B 的左侧），1OA =，经过点A 的一次函数(0)y kx b k =+≠的图像与y 轴正半轴交于点C ，且与抛物线的另一个交点为D ，ABD ∆的面积为5．（1）求抛物线和一次函数的解析式；（2）抛物线上的动点E 在一次函数的图像下方，求ACE ∆面积的最大值，并求出此时点E 的坐标．【分析】（1）抛物线解析式：21322y x x =--；一次函数解析式：1122y x =+．（2）显然，当△ACE 面积最大时，点E 并不在AC 之间．已知A （-1,0）、10,2C ⎛⎫ ⎪⎝⎭，设点E 坐标为213,22m m m ⎛⎫-- ⎪⎝⎭，过点E 作EF ⊥x 轴交直线AD 于F 点，F 点横坐标为m ，代入一次函数解析式得11,22m m ⎛⎫+ ⎪⎝⎭可得213222EF m m =-++考虑到水平宽是定值，故铅垂高最大面积最大．既然都是固定的算法，那就可以总结一点小小的结论了，对坐标系中已知三点()11,A x y 、()22,B x y 、()33,C x y ，按铅垂法思路，可得：12233121321312ABC S x y x y x y x y x y x y =++--- 如果能记住也不要直接用，可以当做是检验的方法咯．【总结】铅垂法是求三角形面积的一种常用方法，尤其适用于二次函数大题中的三角形面积最值问题，弄明白方法原理，熟练方法步骤，加以练习，面积最值问题轻轻松松．专项训练1．已知二次函数2y x bx c =-++和一次函数y mx n =+的图象都经过点(3,0)A -，且二次函数2y x bx c =-++的图象经过点(0,3)B ，一次函数y mx n =+的图象经过点(0,1)C -．（1）分别求m 、n 和b 、c 的值；（2）点P 是二次函数2y x bx c =-++的图象上一动点，且点P 在x 轴上方，写出ACP ∆的面积S 关于点P 的横坐标x 的函数表达式，并求S 的最大值．【分析】（1）把直线和曲线经过的点代入得到方程组，求解即可得到答案；（2）分两种情况：①当点P 在y 轴左侧时，过点P 作//PD y 轴交AC 于点D ，②当点P 在y 轴右侧时，过点P 作//PD y 轴交AC 的延长线于点D ，分别根据三角形面积公式得到关系式，利用函数式表示三角形PAC 的面积，配方可得答案．【解答】解：（1）二次函数2y x bx c =-++和一次函数y mx n =+的图象都经过点(3,0)A -，一次函数y mx n =+的图象经过点(0,1)C -，∴301m n n -+=⎧⎨=-⎩，∴131m n ⎧=-⎪⎨⎪=-⎩，二次函数2y x bx c =-++和一次函数y mx n =+的图象都经过点(3,0)A -，二次函数2y x bx c =-++的图象经过点(0,3)B ，∴9303b c c --+=⎧⎨=⎩，∴23b c =-⎧⎨=⎩．（2）由（1）知一次函数与二次函数的解析式分别为：113y x =--或223y x x =--+，①当点P 在y 轴左侧时，过点P 作//PD y 轴交AC 于点D ，则13|3|22PAC S PD PD ∆=⨯⨯-=，②当点P 在y 轴右侧时，过点P 作//PD y 轴交AC 的延长线于点D，则13|3|22PAC S PD x x PD ∆=⨯⨯+-=，点P 在抛物线上，设2(,23)P x x x --+，则1(,1)3D x x --，2215231433PD x x x x x ∴=--+++=--+，233535169(4)(2232624PAC S PD x x x ∆∴==-++=-++，即当56x =-时，PAC S ∆最大16924=．【点评】本题考查的是二次函数综合运用，涉及一次函数、图形面积的计算等，掌握其性质及运算是解决此题关键，2．如图，抛物线经过(2,0)A -，(4,0)B ，(0,3)C -三点．（1）求抛物线的解析式；（2）在直线BC 下方的抛物线上有一动点P ，使得PBC ∆的面积最大，求点P 的坐标；（3）点M 为x 轴上一动点，在抛物线上是否存在一点N ，使以A ，C ，M ，N 四点构成的四边形为平行四边形？若存在，求出点N的坐标；若不存在，请说明理由．【分析】（1）将点A 、B 、C 的坐标代入抛物线表达式，即可求解；（2）由PBC ∆的面积PHB PHC S S ∆∆=+，即可求解；（3）分AC 是边、AC 是对角线两种情况，利用平移的性质和中点公式即可求解．【解答】解：（1）将点A 、B 、C 的坐标代入抛物线表达式得42016403a b c a b c c -+=⎧⎪++=⎨⎪=-⎩，解得38343a b c ⎧=⎪⎪⎪=-⎨⎪=-⎪⎪⎩，故抛物线的表达式为233384y x x =--；（2）设直线BC 的表达式为y mx n =+，则043m n n =+⎧⎨=-⎩，解得343m n ⎧=⎪⎨⎪=-⎩，故直线BC 的表达式为334y x =-，过点P 作y 轴的平行线交BC 于点H ，设点P 的坐标为233(,3)84x x x --，则点3(,3)4H x x -，则PBC ∆的面积221133334(33)3224844PHB PHC S S PH OB x x x x x ∆∆=+=⋅=⨯⨯--++=-+，304-< ，故该抛物线开口向下，PBC ∆的面积存在最大值，此时2x =，则点P 的坐标为(2,3)-；（3）存在，理由：设点N 的坐标为(,)m n ，则233384n m m =--①，①当AC 是边时，点A 向下平移3个单位得到点C ，则点()M N 向下平移3个单位得到点()N M ，则03n -=或03n +=②，联立①②并解得23m n =⎧⎨=-⎩或13m n ⎧=-⎪⎨=⎪⎩（不合题意的值已舍去）；②当AC 是对角线时，则由中点公式得：11(03)(0)22n -=+③，联立①③并解得23m n =⎧⎨=-⎩（不合题意的值已舍去）；综上，点N 的坐标为(2,3)-或(1-3)或(1--3)．【点评】本题是二次函数综合题，主要考查了一次函数的性质、平行四边形的性质、面积的计算等，其中（3），要注意分类求解，避免遗漏．3．综合与探究：如图，在平面直角坐标系中，二次函数的图象交坐标轴于(1,0)A -，(3,0)B ，(0,4)C -三点，点(,)P m n 是直线BC 下方抛物线上的一个动点．（1）求这个二次函数的解析式；（2）动点P 运动到什么位置时，PBC ∆的面积最大，求出此时P 点坐标及PBC ∆面积的最大值；（3）在y 轴上是否存在点Q ，使以O ，B ，Q 为顶点的三角形与AOC ∆相似？若存在，请直接写出点Q 的坐标；若不存在，请说明理由．【分析】（1）将A 、B 、C 坐标代入即可求解析式；（2）设P 坐标，表示出PBC ∆的面积，再求出最大面积和面积最大时P 的坐标；（3）两个直角顶点是对应点，而AOC ∆两直角边的比为14，只需BOQ ∆两直角边比也为14，两个三角形就相似，分两种情况列出比例式即可．【解答】解：（1）设二次函数的解析式为12()()y a x x x x =--，二次函数的图象交坐标轴于(1,0)A -，(3,0)B ，(0,4)C -，11x ∴=-，23x =，124()()a x x x x -=--，解得11x =-，23x =，43a =，∴二次函数的解析式为2448(1)(3)4333y x x x x =+-=--，故答案为：2448(1)(3)4333y x x x x =+-=--；（2）设直线BC 解析式为y kx b =+，将(3,0)B ，(0,4)C -代入得034k b b =+⎧⎨-=⎩，解得43b =，4c =-，BC ∴解析式是443y x =-，如答图1，过P 作//PD y 轴，交BC 于D ，点(,)P m n 是直线BC 下方抛物线上的一个动点，03m ∴<<，248433n m m =--，4(,4)3D m m -，224484(4)(4)43333PD m m m m m ∴=----=-+，22211439()(4)(30)262()22322PBC B C S PD x x m m m m m ∆∴=⋅-=-+⋅-=-+=--+，3032<< ，32m ∴=时，PBC S ∆最大为92，此时224843834()45333232n m m =--=⨯-⨯-=-，3(2P ∴，5)-，故答案为：3(2P ，5)-，PBC S ∆最大为92；(3(1,0)A - ，(0,4)C -，(3,0)B ，∴14OA OC =，3OB =，点Q 在y 轴上，90BOQ AOC ∴∠=∠=︒，若以O ，B ，Q 为顶点的三角形与AOC ∆相似，则BOQ ∠与AOC ∠对应，分两种情况：①如答图2，AOC QOB∆∆∽，则14OQ OAOB OC==即134OQ=，解得34OQ=，13(0,4Q∴或23 (0,)4Q-；②AOC BOQ∆∆∽，则14OB OAOQ OC==即314OQ=，解得12OQ=，3(0,12)Q∴或4(0,12)Q-，综上所述，存在y轴上的点Q，使以O，B，Q为顶点的三角形与AOC∆相似，这样的点一共4个：13 (0, 4Q或23 (0,)4Q-，3(0,12)Q或4(0,12)Q-，故答案为：存在这样的点Q，坐标分别是：13 (0, 4Q或23 (0,)4Q-，3(0,12)Q或4(0,12)Q-，【点评】本题是二次函数、相似三角形、面积等问题的综合题，主要考查坐标、线段的转化，面积的表示，涉及方程思想，分类思想等，难度适中．4．如图1，抛物线2y x bx c=-++与x轴交于A、B两点，与y轴交于点C，已知点B坐标为(3,0)，点C 坐标为(0,3)．（1）求抛物线的表达式；（2）点P 为直线BC 上方抛物线上的一个动点，当PBC ∆的面积最大时，求点P 的坐标；（3）如图2，点M 为该抛物线的顶点，直线MD x ⊥轴于点D ，在直线MD 上是否存在点N ，使点N 到直线MC 的距离等于点N 到点A 的距离？若存在，求出点N 的坐标；若不存在，请说明理由．【分析】（1）利用待定系数法可求解析式；（2）过点P 作PH x ⊥轴于H ，交BC 于点G ，先求出BC 的解析式，设点2(,23)P m m m -++，则点(,3)G m m -+，由三角形面积公式可得221133273(3)()22228PBC S PG OB m m m ∆=⨯⨯=⨯⨯-+=--+，由二次函数的性质可求解；（3）设直线MC 与x 轴交于点E ，过点N 作NQ MC ⊥于Q ，先求出点A ，点M 坐标，可求MC 解析式，可得4DE MD ==，由等腰直角三角形的性质可得MQ NQ ==，由两点距离公式可列222(|4|)42n n -=+，即可求解．【解答】解：（1）点(3,0)B ，点(0,3)C 在抛物线2y x bx c =-++图象上，∴9303b c c -++=⎧⎨=⎩，解得：23b c =⎧⎨=⎩，∴抛物线解析式为：223y x x =-++；（2）点(3,0)B ，点(0,3)C ，∴直线BC 解析式为：3y x =-+，如图，过点P 作PH x ⊥轴于H ，交BC 于点G ，设点2(,23)P m m m -++，则点(,3)G m m -+，22(23)(3)3PG m m m m m ∴=-++--+=-+，221133273(3)()22228PBC S PG OB m m m ∆=⨯⨯=⨯⨯-+=--+ ，∴当32m =时，PBC S ∆有最大值，∴点3(2P ，154；（3）存在N 满足条件，理由如下：抛物线223y x x =-++与x 轴交于A 、B 两点，∴点(1,0)A -，2223(1)4y x x x =-++=--+ ，∴顶点M 为(1,4)，点M 为(1,4)，点(0,3)C ，∴直线MC 的解析式为：3y x =+，如图，设直线MC 与x 轴交于点E ，过点N 作NQ MC ⊥于Q ，∴点(3,0)E -，4DE MD ∴==，45NMQ ∴∠=︒，NQ MC ⊥ ，45NMQ MNQ ∴∠=∠=︒，MQ NQ ∴=，22MQ NQ ∴==，设点(1,)N n ，点N 到直线MC 的距离等于点N 到点A 的距离，NQ AN ∴=，22NQ AN ∴=，222()2MN AN ∴=，222(|4|)42n n ∴-=+，2880n n ∴+-=，46n ∴=-±，∴存在点N 满足要求，点N 坐标为(1,426)-+或(1,426)--．【点评】本题是二次函数综合题，考查了待定系数法求解析式，二次函数的性质，一次函数的性质，两点距离公式，等腰直角三角形的性质等知识，利用参数列方程是本题的关键．5．如图，抛物线过点(0,1)A 和C ，顶点为D ，直线AC 与抛物线的对称轴BD 的交点为B ，0)，平行于y 轴的直线EF 与抛物线交于点E ，与直线AC 交于点F ，点F 的横坐标为3，四边形BDEF 为平行四边形．（1）求点F 的坐标及抛物线的解析式；（2）若点P 为抛物线上的动点，且在直线AC 上方，当PAB ∆面积最大时，求点P 的坐标及PAB ∆面积的最大值；（3）在抛物线的对称轴上取一点Q ，同时在抛物线上取一点R ，使以AC 为一边且以A ，C ，Q ，R 为顶点的四边形为平行四边形，求点Q 和点R 的坐标．【分析】（1）由待定系数法求出直线AB 的解析式为13y x =-+，求出F 点的坐标，由平行四边形的性质得出1613181(33a a a -+=-+--，求出a 的值，则可得出答案；（2）设2(,1)P n n -++，作PP x '⊥轴交AC 于点P '，则(,1)P n '+，得出2PP n '=-+，由二次函数的性质可得出答案；（3）联立直线AC 和抛物线解析式求出C ，4)3-，设Q ，)m ，分两种情况：①当AQ 为对角线时，②当AR 为对角线时，分别求出点Q 和R 的坐标即可．【解答】解：（1）设抛物线的解析式为2(0)y ax bx c a =++≠，(0,1)A ，B ，0)，设直线AB 的解析式为y kx m =+，∴01m m +==⎪⎩，解得31k m ⎧=⎪⎨⎪=⎩，∴直线AB的解析式为13y x =+，点FF ∴点纵坐标为113=-，F ∴点的坐标为，1)3-，又点A 在抛物线上，1c ∴=，对称轴为：2b x a=-=，b ∴=-，∴解析式化为：21y ax =-+，四边形DBFE 为平行四边形．BD EF ∴=，1613181(33a a a ∴-+=-+--，解得1a =-，∴抛物线的解析式为21y x =-++；（2）设2(,1)P n n -++，作PP x '⊥轴交AC 于点P '，则3(,1)3P n '+，2733PP n n '∴=-+，2213737493)32222624ABP S OB PP n n ∆'==-+=--+ ，∴当736n =ABP ∆49324，此时7(36P 47)12．（3） 231231y y x x ⎧=+⎪⎨⎪=-++⎩，0x ∴=或733x =7(33C ∴，43-，设(3Q ，)m ，①当AQ 为对角线时，47(3,)33R m ∴+，R 在抛物线2(3)4y x =--+上，274(33)433m ∴+=--+，解得443m =-，44(3,3Q ∴-，437(3,33R -；②当AR 为对角线时，107(3,33R m ∴-，R 在抛物线2(4y x =--+上，2743m ∴-=--+，解得10m =-，Q ∴10)-，37)3R -．综上所述，443Q -，37(3R -；或Q ，10)-，37)3R -．【点评】本题是二次函数综合题，考查了待定系数法，二次函数的性质，二次函数图象上点的坐标特征，平行四边形的性质等知识，熟练掌握二次函数的性质及方程思想，分类讨论思想是解题的关键．6．在平面直角坐标系xOy 中，等腰直角ABC ∆的直角顶点C 在y 轴上，另两个顶点A ，B 在x 轴上，且4AB =，抛物线经过A ，B ，C 三点，如图1所示．（1）求抛物线所表示的二次函数表达式．（2）过原点任作直线l 交抛物线于M ，N 两点，如图2所示．①求CMN ∆面积的最小值．②已知3(1,2Q -是抛物线上一定点，问抛物线上是否存在点P ，使得点P 与点Q 关于直线l 对称，若存在，求出点P 的坐标及直线l 的一次函数表达式；若不存在，请说明理由．【分析】（1）先根据等腰直角三角形的性质求得OA 、OB 、OC ，进而得A 、B 、C 三点的坐标，再用待定系数法求得抛物线的解析式；（2）①设直线l 的解析式为y kx =，1(M x ，1)y ，2(N x ，2)y ，联立方程组求得12||x x -，再由三角形的面积公式求得结果；②假设抛物线上存在点21(,2)2P m m -，使得点P 与点Q 关于直线l 对称，由OP OQ =列出方程求得m 的值，再根据题意舍去不合题意的m 值，再求得PQ 的中点坐标，便可求得直线l 的解析式．【解答】解：（1）设抛物线的解析式为2(0)y ax bx c a =++≠，在等腰Rt ABC ∆中，OC 垂直平分AB ，且4AB =，2OA OB OC ∴===，(2,0)A ∴-，(2,0)B ，(0,2)C -，∴4204202a b c a b c c ++=⎧⎪-+=⎨⎪=-⎩，解得，1202a b c ⎧=⎪⎪=⎨⎪=-⎪⎩，∴抛物线的解析式为2122y x =-；（2）①设直线l 的解析式为y kx =，1(M x ，1)y ，2(N x ，2)y ，由2122y x y kx ⎧=-⎪⎨⎪=⎩，可得21202x kx --=，122x x k ∴+=，124x x =- ，∴222121212()()4416x x x x x x k -=+-=+，∴12||x x -=∴121||2CMN S OC x x ∆=-= ，∴当0k =时取最小值为4．CMN ∴∆面积的最小值为4．②假设抛物线上存在点21(,2)2P m m -，使得点P 与点Q 关于直线l 对称，OP OQ ∴==解得，1m 2m =，31m =，41m =-，31m = ，41m =-不合题意，舍去，当1m =1)2P -，线段PQ 的中点为1)-，∴1=-，∴1k =，∴直线l 的表达式为：(1y x =-，当2m =时，点(P 1)2-，线段PQ 的中点为，1)-，∴1=-，∴1k =，∴直线l 的解析式为(1y x =+．综上，点P ，1)2-，直线l 的解析式为(1y x =-或点(P ，1)2-，直线l 的解析式为(1y x =+．【点评】本题是二次函数的综合题，主要考查了二次函数的图象与性质，一次函数的图象与性质，待定系数法，轴对称的性质，第（2）①题关键是求得M 、N 两点的横坐标之差，第（2）②小题关键是根据轴对称性质列出m 的方程，以及求得PQ 的中点坐标．。

一次函数和二次函数相交的问题

类型一：已知一次函数和二次函数解析式求交点坐标并比较大小1如图，已知直线y=x与抛物线y=-x2交于A、B两点.21 (2)记一次函数y=x的函数值为y i,二次函数y=^x2 若y i>y2,求x的取值范围.类型二：已知相关点的坐标求解一次函数和二次函数的解析式并比较大小如图，二次函数y (x-2) 2+m的图象与y轴交于点C,点B是点C关于该二次函数图象的对称轴对称的点.已知一次函数y=kx+b的图象经过该二次函数图象上点 A (1, 0)及点B.(1) 求一次函数与二次函数的解析式；(2) 根据图象，写出满足kx+b>(x-2) 2+m的x的取值范围.练习1:如图所示，二次函数的图象与x轴相交于A、B两点，与y轴相交于点C,点C、D 是二次函数图象上的一对对称点，一次函数的图象过点B、D. (1)求D点的坐标和一次函数、二次函数的解析式；(2)根据图象写出使一次函数值大于二次函数值的x的取值范围.练习2:在同一直角坐标系，开口向上的抛物线与坐标轴分别交于 A (-1, 0), B (3, 0), C (0, -3), 一次函数图象与二次函数图象交于B、C两点.(1)求一次函数和二次函数的解析式.(2) 当自变量x为何值时，两函数的函数值都随x的增大而增大?(3) 当自变量x为何值时，一次函数值大于二次函数值.(4) 当自变量x为何值时，两函数的函数值的积小于0.类型三：与一次函数和二次函数的交点有关的面积类问题1如图，一次函数y=x- 1与x轴交点A恰好是二次函数与x的其中一个交点，已知二次函数图2象的对称轴为x=1，并与y轴的交点为(0，1).( 1)求二次函数的解析式；(2)设该二次函数与一次函数的另一个交点为C点，连接BC,求三角形ABC的面积. 瑞练习1：如图，A (-1，0)、B (2，-3)两点在一次函数y i=-x+m与二次函数y2=a«+bx-3的图象上.(1 )求m的值和二次函数的解析式.(2) 二次函数交y轴于。

一次函数与二次函数的面积问题

一次函数与二次函数的面积问题一、引言在高中数学中，我们学习了一次函数和二次函数，它们是数学中非常重要的概念。

本文将探讨一次函数与二次函数的面积问题，通过几个具体的例子，帮助读者理解并解决这类问题。

二、一次函数的面积一次函数又称为线性函数，其代数表达式为$y=ax+b$。

为了计算一次函数在特定区间上的面积，我们可以使用定积分的方法。

2.1一次函数的几何图像一次函数的几何图像是一条直线，其斜率决定了直线的倾斜程度，截距决定了直线与$y$轴的交点。

2.2一次函数的面积计算我们考虑一次函数$y=ax+b$在区间$[x_1,x_2]$上的面积。

首先，我们需要确定该函数在该区间上的单调性。

如果$a>0$，则函数是递增的，如果$a<0$，则函数是递减的。

接下来，我们使用定积分的定义来计算面积。

一次函数的面积可以表示为$$S=\i nt_{x_1}^{x_2}(a x+b)dx$$根据定积分的性质，我们可以求解出这个积分。

2.3一次函数面积的例子让我们通过一个具体的例子来解决一次函数的面积问题。

例子：计算函数$y=2x+1$在区间$[1,3]$上的面积。

解：首先，确定函数是递增的，因为斜率$a=2$是正数。

然后，我们计算积分：$$S=\i nt_{1}^{3}(2x+1)dx$$将积分求解出来，得到$S=8$。

因此，函数$y=2x+1$在区间$[1,3]$上的面积为8。

三、二次函数的面积二次函数的代数表达式为$y=a x^2+bx+c$。

与一次函数类似，我们也可以使用定积分的方法计算二次函数在特定区间上的面积。

3.1二次函数的几何图像二次函数的几何图像是一条抛物线，其开口方向由二次系数$a$的正负决定，顶点决定了抛物线的最低（或最高）点。

3.2二次函数的面积计算我们考虑二次函数$y=ax^2+b x+c$在区间$[x_1,x_2]$上的面积。

与一次函数类似，我们先确定函数在该区间上的单调性。

接着，我们使用定积分的定义来计算面积。

中考数学频考点突破--二次函数与一次函数

中考数学频考点突破--二次函数与一次函数1．某超市对进货价为10元/千克的某种苹果的销售情况进行统计，发现每天销售量y （千克）与销售价x（元/千克）存在一次函数关系，如图所示．（1）求y关于x的函数关系式（不要求写出x的取值范围）；（2）应怎样确定销售价，使该品种苹果的每天销售利润最大？最大利润是多少？2．已知抛物线C：y1=a（x﹣h）2﹣1，直线L：y2=kx﹣kh﹣1（1）试说明：抛物线C的顶点D总在直线y2=kx﹣kh﹣1上；（2）当a=﹣1，m≤x≤2时，y1≥x﹣3恒成立，求m的最小值；（3）当0＜a≤2，k＞0时，若在直线L下方的抛物线C上至少存在两个横坐标为正整数的点，求k的取值范围．3．某商场以每千克40元的价格购进某种海鱼，计划以每千克60元的价格销售.为了让顾客得到更大的实惠，现决定降价销售，已知这种海鱼销售量y（kg）与每千克降价x （元）（0＜x＜20）之间满足一次函数关系，其图象如图所示.（1）求y关于x的函数表达式；（2）商场在销售这种海鱼中要想获利2090元，则这种海鱼每千克应降价多少元？共销售了多少千克这种海鱼？4．如图，已知二次函数y=ax2+2x+c的图象经过点C(0,3)，与x轴交于点A，B，直线BC的解析式是y=x+b.（1）求二次函数图象的顶点坐标.（2）求不等式ax2+2x+c⩽x+b的解.5．在平面直角坐标系中，设二次函数y=ax2+bx+2（a，b是常数，a≠0）.（1）若a=1，当x=−1时，y=4.求y的函数表达式.（2）写出一题a，b的值，使函数y=ax2+bx+2的图象与x轴只有一个公共点，并求此函数的顶点坐标.（3）已知，二次函数y=ax2+bx+2的图象和直线y=ax+4b都经过点（2，m），求证a2+b2≥12.6．已知，如图：直线AB过x轴上的点A(2，0)，且与抛物线y=ax2相交于B，C两点，点B的坐标为(1，1)．（1）求直线AB和抛物线的函数解析式；（2）如果抛物线上有一点D，使得S△AOD=S△BCO，求点D的坐标．7．（1）化简：4aa2−1+a−1 a+1；（2）已知二次函数y=ax2+43(a≠0)与正比例函数y=4x的图象只有一个交点，求a的值．8．已知，如图，抛物线与x轴交点坐标为A（1，0），C（-3，0），（1）若已知顶点坐标D为（-1，4）或B点（0，3），选择适当方式求抛物线的解析式.（2）若直线DH为抛物线的对称轴，在（1）的基础上，求线段DK的长度，并求△DBC的面积．（3）将图（2）中的对称轴向左移动，交x轴于点p（m，0）(－3<m<－1)，与线段BC、抛物线的交点分别为点K、Q，用含m的代数式表示QK的长度，并求出当m 为何值时，△BCQ的面积最大？9．定义：在平面直角坐标系中，图形G上点P（x，y）的纵坐标y与其横坐标x的差y﹣x称为点P的“坐标差”，而图形G上所有点的“坐标差”中的最大值称为图形G的“特征值”．（1）求点A（2，1）的“坐标差”和抛物线y＝﹣x2+3x+4的“特征值”．（2）某二次函数＝﹣x2+bx+c（c≠0）的“特征值”为﹣1，点B与点C分别是此二次函数的图象与x轴和y轴的交点，且点B与点C的“坐标差”相等，求此二次函数的解析式．（3）如图所示，二次函数y＝﹣x2+px+q的图象顶点在“坐标差”为2的一次函数的图象上，四边形DEFO是矩形，点E的坐标为（7，3），点O为坐标原点，点D在x 轴上，当二次函数y＝﹣x2+px+q的图象与矩形的边有四个交点时，求p的取值范围．10．如图，直线l：y=−3x+3与x轴、y轴分别相交于A、B两点，抛物线y= ax2−2ax+a+4(a<0)经过点B．（1）求该抛物线的函数表达式：（2）已知点M是抛物线上的一个动点，并且点M在第一象限内，连接AM、BM，设点M的横坐标为m，△ABM的面积为S，求S与m的函数表达式，并求出S的最大值．11．抛物线y=x2与直线y=x+2交于A,B两点，点A在第二象限，求（1）A、B两点的坐标；（2）△AOB的面积12．某化工材料经销公司购进一种化工材料若干千克，价格为每千克40元，物价部门规定其销售单价不高于每千克70元，不低于每千克40元．经市场调查发现，日销量y(千克)是销售单价x(元)的一次函数，且当x＝70时，y＝80；x＝60时，y＝100．在销售过程中，每天还要支付其他费用350元．（1）求y与x的函数关系式，并写出自变量x的取值范围；（2）求该公司销售该原料日获利w(元)与销售单价x(元)之间的函数关系式；（3）当销售单价为多少元时，该公司日获利最大？最大利润是多少元？13．如图，抛物线y=x2+mx与直线y=−x+b交于点A(2，0)和点B.（1）求m和b的值；（2）求点B的坐标，并结合图象写出不等式x2+mx>−x+b的解集；（3）点M是直线AB上的一个动点，将点M向左平移3个单位长度得到点N，若线段MN与抛物线只有一个公共点，直接写出点M的横坐标x M的取值范围.14．如图，二次函数的图象与x轴交于A（-3，0）和B（1，0）两点，交y轴于点C （0，3），点C、D是二次函数图象上的一对对称点，一次函数的图象过点B、D．（1）请直接写出D点的坐标；（2）求一次函数和二次函数的解析式；（3）根据图象直接写出使一次函数值大于二次函数值的x的取值范围．15．为迎接中国森博会，某商家计划从厂家采购A，B两种产品共20件，产品的采购单价（元/件）是采购数量（件）的一次函数，下表提供了部分采购数据．采购数量（件）12…A产品单价（元/件）14801460…B产品单价（元/件）12901280…1y1与x的关系式；（2）经商家与厂家协商，采购A产品的数量不少于B产品数量的119，且A产品采购单价不低于1200元，求该商家共有几种进货方案；（3）该商家分别以1760元/件和1700元/件的销售单价售出A，B两种产品，且全部售完，在（2）的条件下，求采购A种产品多少件时总利润最大，并求最大利润．16．如图，已知二次函数y1=ax2+bx+c的图象过点A（1，0），B（﹣3，0），C（0，﹣3）（1）求此二次函数的解析式和顶点坐标；（2）直线y2=kx+b过B、C两点，请直接写出当y1＞y2时，自变量x的取值范围．答案解析部分1．【答案】（1）解：设y=kx+b ，由图象可知，{20k +b =2030k +b =0，解之，得： {k =−2b =60 ，∴y=﹣2x+60（2）解：p=（x ﹣10）y =（x ﹣10）（﹣2x+60） =﹣2x 2+80x ﹣600， ∵a=﹣2＜0， ∴p 有最大值，当x=﹣ 80−2×2=20时，p 最大值=200．即当销售单价为20元/千克时，每天可获得最大利润200元【知识点】二次函数与一次函数的综合应用【解析】【分析】（1）由待定系数法求一次函数解析式。

(完整版)一次函数和二次函数相交的问题

一次函数和二次函数相交的问题类型一：已知一次函数和二次函数解析式求交点坐标并比较大小如图，已知直线y=x 与抛物线y=21x 2交于A 、B 两点．（1）求交点A 、B 的坐标；（2）记一次函数y=x 的函数值为y 1，二次函数y=21x 2的函数值为y 2．若y 1＞y 2，求x 的取值范围．类型二：已知相关点的坐标求解一次函数和二次函数的解析式并比较大小如图，二次函数y=（x-2）2+m 的图象与y 轴交于点C ，点B 是点C 关于该二次函数图象的对称轴对称的点．已知一次函数y=kx+b 的图象经过该二次函数图象上点A （1，0）及点B ．（1）求一次函数与二次函数的解析式；（2）根据图象，写出满足kx+b≥（x-2）2+m 的x 的取值范围．练习1：如图所示，二次函数的图象与x 轴相交于A 、B 两点，与y 轴相交于点C ，点C 、D 是二次函数图象上的一对对称点，一次函数的图象过点B 、D ．（1）求D 点的坐标和一次函数、二次函数的解析式；（2）根据图象写出使一次函数值大于二次函数值的x 的取值范围．练习2：在同一直角坐标系，开口向上的抛物线与坐标轴分别交于A （-1，0），B （3，0），C （0，-3），一次函数图象与二次函数图象交于B 、C 两点．（1）求一次函数和二次函数的解析式．（2）当自变量x 为何值时，两函数的函数值都随x 的增大而增大？（3）当自变量x 为何值时，一次函数值大于二次函数值．（4）当自变量x 为何值时，两函数的函数值的积小于0．ABC Oxy练习3：一次函数y=2x+3与二次函数y=ax 2+bx+c 的图象交于A （m ，5）和B （3，n ）两点，且点B 是抛物线的顶点．（1）求一次函数和二次函数的表达式；（2）在同一坐标系中画出两个函数的图象；（3）从图象上观察，x 为何值时，两个函数的值都随x 的增大而增大，当x 为何值时，二次函数的值大于一次函数的值？类型三：与一次函数和二次函数的交点有关的面积类问题。

高三数学一次函数与二次函数试题答案及解析

高三数学一次函数与二次函数试题答案及解析1.已知中心在原点，焦点在轴上的椭圆的离心率为，椭圆上异于长轴顶点的任意点与左右两焦点、构成的三角形中面积的最大值为.（1）求椭圆的标准方程；（2）已知点，连接与椭圆的另一交点记为，若与椭圆相切时、不重合，连接与椭圆的另一交点记为，求的取值范围.【答案】（1）；（2）.【解析】（1）先利用已知条件列举出有关、、的方程组，结合三者之间满足的勾股关系求出、、的值，从而确定椭圆的方程；（2）设直线与的方程分别为以及，将两条直线方程与椭圆方程联立，结合韦达定理得到点与点之间的关系（关于轴对称），从而得到两点坐标之间的关系，最后将利用点的坐标进行表示，注意到坐标的取值范围，然后利用二次函数求出的取值范围.（1）由题可知：，，解得：，，，故椭圆的方程为：；（2）不妨设、、，由题意可知直线的斜率是存在的，故设直线的斜率为，直线的斜率为的方程为：代入椭圆方程，得，，将，代入解得：，的方程为：代入椭圆方程，得，，将，，代入解得：，，又、不重合，，，.【考点】1.椭圆的方程；2.直线与椭圆的位置关系；3.二次函数；4.向量的数量积2.设函数f(x)＝ax2＋(b－2)x＋3(a≠0)，若不等式f(x)＞0的解集为(－1,3)．(1)求a，b的值；(2)若函数f(x)在x∈[m,1]上的最小值为1，求实数m的值．【答案】（1）a＝－1，b＝4 （2）1－【解析】(1)由条件得，解得：a＝－1，b＝4.(2)f(x)＝－x2＋2x＋3，对称轴方程为x＝1，∴f(x)在x∈[m,1]上单调递增．∴x＝m时，f(x)＝－m2＋2m＋3＝1，min解得m＝1±.∵m＜1，∴m＝1－.3.已知函数在区间（）上的最大值为4，最小值为3，则实数m的取值范围是( )A．B．C．D．【答案】A【解析】作出函数的图象如下图所示，从图可以看出当时，函数在区间（）上的最大值为4，最小值为3.故选A.【考点】二次函数.4.设二次函数满足条件：①；②函数的图像与直线相切．（1）求函数的解析式；（2）若不等式在时恒成立，求实数的取值范围．【答案】（1）；（2）．【解析】由的图象的对称轴方程是，于是有，依题意，方程组有且只有一解，利用即可求得与，从而得函数的解析式；（2）利用指数函数的单调性质，知在时恒成立，构造函数，由即可求得答案．试题解析：（1）由①可知，二次函数图像对称轴方程是，；又因为函数的图像与直线相切，所以方程组有且只有一解，即方程有两个相等的实根，，所以，函数的解析式是．（2），等价于，即不等式在时恒成立，问题等价于一次函数在时恒成立，即，解得：或，故所求实数的取值范围是．【考点】1、函数恒成立问题；2、二次函数的性质．5.椭圆c：（a>b>0）的离心率为，过其右焦点F与长轴垂直的弦长为1，（1）求椭圆C的方程；（2）设椭圆C的左右顶点分别为A，B，点P是直线x=1上的动点，直线PA与椭圆的另一个交点为M，直线PB与椭圆的另一个交点为N，求证：直线MN经过一定点.【答案】（1）；（2）证明详见解析【解析】（1）由已知可得，＝１，解出a，b即可.（2）设Ｐ（１，ｔ）,则直线，联立直线PA方程和椭圆方程可得，同理得到，由椭圆的对称性可知这样的定点在轴，不妨设这个定点为Ｑ，由，求得m的存在即可.试题解析：（1）依题意过焦点Ｆ与长轴垂直的直线ｘ＝ｃ与椭圆联立解答弦长为＝１， 2分所以椭圆的方程. 4分（2）设Ｐ（１，ｔ），直线，联立得：即，可知所以，则 6分同理得到 8分由椭圆的对称性可知这样的定点在轴，不妨设这个定点为Ｑ， 10分又，，，，. 12分【考点】1.椭圆方程的性质；2.点共线的证法.6.设二次函数f(x)=ax2+bx+c,如果f(x1)=f(x2)(x1≠x2),则f(x1+x2)等于()A．-B．-C．c D．【答案】C【解析】∵f(x1)=f(x2),∴f(x)的对称轴为x=-=,得f(x1+x2)=f-=a×+b×+c=c,故选C.7.函数的图象和函数的图象的交点个数是。

04(解答题(二))-2021年中考数学专题(湖南长沙卷)(解析版)

2021年中考数学冲刺挑战压轴题专题汇编（湖南长沙卷）04挑战压轴题（解答题（二））1. （2020年长沙中考第24题）我们不妨约定：若某函数图像上至少存在不同的两点关于原点对称，则把该函数称之为“H 函数”，其图像上关于原点对称的两点叫做一对“H 点”。

根据该约定，完成下列各题。

（1）在下列关于x 的函数中，是“H 函数”的，请在相应题目后面的括号内打“√”，不是“H 函数”的打“×”。

① x y 2= （） ② ）（0≠=m xmy （） ③ 13-=x y （）（2）若点A （1，m ）与点B （n ，-4）是关于x 的“H 函数”）（02≠++=a c bx ax y 的一对“H 点”，且该函数的对称轴始终位于直线x=2的右侧，求a 、b 、c 的值或取值范围。

（3）若关于x 的“H 函数”是常数），，（c b a c bx ax y 322++=同时满足下列两个条件：① 0=++c b a ， ② 0322<++•-+）（）（a b c a b c ，求该“H 函数”截x 轴得到的线段长度的取值范围。

【答案】（1）√、√、× （2）-1<a<0，b=4，0<c<1 （3）72221<-<x x【解析】（1）根据题意，易知“H 函数”图像上存在关于原点对称的点。

①、②图像均关于原点对称，故为“H 函数”；对于函数③，变形为：31=+x y ，令xy x y -+-=+33，无解，故不是“H 函数”。

（2）∵若点A （1，m ）与点B （n ，-4）是关于x 的“H 函数”）（02≠++=a c bx ax y 的一对“H 点”∴m=4，n=-1 ∴A （1，4） B （-1，-4）代入c bx ax y ++=2中，得:⎩⎨⎧-=+-=++44c b a c b a 解得：⎩⎨⎧==+40b c a∵函数的对称轴始终位于直线x=2的右侧 ∴22->ab∴224>-a解得：01<<-a ∵100<<∴=+c c a∴-1<a<0，b=4，0<c<1（3）c bx ax y 322++=∵是H 函数，∴至少存在不同的两点关于原点对称的“H 点” 设H 点坐标分别为（m ，n ）；（-m ，-n ），则:⎪⎩⎪⎨⎧-=+-=++nc bm am n c bm am 323222∴n bm c am ==+2032因为002<∴>ac c a m 异号，即、∵c a b c b a -=∴=++0∵0322<++•-+）（）（a b c a b c ∴0)32)(2(<+-----a c a c a c a c∴0)2)(2(<+-a c a c 即：224a c <∴22<∴<a cac ∴02<<-ac 令02<<-∴=t act设函数与x 轴的两个交点分别为)0(1，x 、)0(2，x ，则21x x 、是方程0322=++c bx ax 的两根 ∴a ca c a a c ab a ac b x x 12)(4124124a 2222221-+=-=-=∆=-)1(412)21(412))(21(4222+-=-++=•-+•+=t t t t t aca c a c 43)21(22+-=t ∵时02<<-t 函数递减，所以当t=-2时取最大值，当t=0时取最小值∴72221<-<x x2.（2019年长沙中考第25题）已知抛物线)2020()2(22-+-+-=c x b x y (b ，c 为常数)．（1）若抛物线的顶点坐标为(1，1)，求b ，c 的值；（2）若抛物线上始终存在不重合的两点关于原点对称，求c 的取值范围；（3）在（1）的条件下，存在正实数m ，n ( m<n )，当n x m ≤≤时，恰好有122112+≤+≤+n ny m m ，求m ，n 的值．【解析】（1）由题可设()1122+--=x y去括号得：1422-+-=x x y⎩⎨⎧-=-=-∴1202042c b20196==∴c b ，（2）设抛物线上关于远点对称且不重合的两点坐标分别为()()0000--y x y x ，、，代入解析式可得：⎪⎩⎪⎨⎧-+---=--+-+-=)2020()2(2)2020()2(202000200c x b x y c x b x y∴两式相加可得：0)2020(24-20=-+c x20202020220≥∴+=∴c x c（3）由（1）可知抛物线为()11214222+--=-+-=x x x y ，∴1≤y12211210+≤+≤+≤≤<<n ny m m n x m m 时，恰好有，当nm m mm y n <≤∴≥≤∴≤≤∴111111，即 ∵抛物线对称轴x =1，开口向下 ∴当n x m ≤≤时，y 随x 增大而减小∴当x =m 时，1422max -+-=m m y当x =n 时，1422min -+-=n n y又∵my n 11≤≤ ⎪⎪⎩⎪⎪⎨⎧=-+=-+∴）（）（21142-11142-22m m m n n n将（1）式整理得：014223=++-n n n变形得：()()01232223=----n n n n 即：()()()0112122=-+--n n n n()()012212=---∴n n n1>n01222=--∴n n（舍去），2311-=∴n 2312+=n 同理整理（2）式得：()()012212=---m m mn m <≤1.2312311321（舍去）（舍去），，+=-==∴m m m ∴综上所示：m =1，n =231+ 3.（2018年长沙中考第25题）如图，在平面直角坐标系xOy 中，函数xmy =（m 为常数，m ＞1，x ＞0）的图象经过点P （m ，1）和Q （1，m ），直线PQ 与x 轴，y 轴分别交于C ，D 两点，点M （x ，y ）是该函数图象上的一个动点，过点M 分别作x 轴和y 轴的垂线，垂足分别为A ，B ．（1）求∠OCD 的度数；（2）当m =3，1＜x ＜3时，存在点M 使得△OPM ∽△OCP ，求此时点M 的坐标；（3）当m =5时，矩形OAMB 与△OPQ 的重叠部分的面积能否等于4.1？请说明你的理由．【分析】（1）想办法证明OC =OD 即可解决问题；（2）设M （a ，a 3），由△OPM ∽△OCP ，推出CPPMOP OM OC OP ==，由此构建方程求出a ，再分类求解即可解决问题；（3）不存在分三种情形说明：①当1＜x ＜5时，如图1中；②当x ≤1时，如图2中；③当x ≥5时，如图3中；【解答】解：（1）设直线PQ 的解析式为y =kx +b ，则有⎩⎨⎧=+=+m b k b km 1，解得⎩⎨⎧+=-=11m b k ，∴y =﹣x +m +!，令x =0，得到y =m +1，∴D （0，m +1），令y +0，得到x =m +1，∴C （m +1，0），∴OC =OD ，∵∠COD =90°， ∴∠OCD =45°．（2）设M （a ，a 3），∵△OPM ∽△OCP ，∴CPPM OP OM OC OP ==，∴OP 2=OC •OM ，当m =3时，P （3，1），C （4，0），OP 2=32+12=10，OC =4，OM =229a a +，∴410=OC OP ，∴10=4229a a +， ∴4a 4﹣25a 2+36=0，（4a 2﹣9）（a 2﹣4）=0， ∴a =±23，a =±2， ∵1＜a ＜3， ∴a =23或2，当a =23时，M （23，2）， PM =213，CP =2， 4102213≠=CM PM （舍弃），当a =2时，M （2，23），PM =25，CP =2，∴410225==CP PM ，成立，∴M （2，23）．（3）不存在．理由如下：当m =5时，P （5，1），Q （1，5），设M （x ，x5）， OP 的解析式为：y =51x ，OQ 的解析式为y =5x ， ①当1＜x ＜5时，如图1中，E∴E （x 1，x 5），F （x ，51x ）， S =S 矩形OAMB ﹣S △OAF ﹣S △OBE =5﹣21•x •51x ﹣21•x 1•x5=4.1，化简得到：x 4﹣9x 2+25=0，△＜O ， ∴没有实数根． ②当x ≤1时，如图2中，S=S△OGH＜S△OAM=2.5，∴不存在，③当x≥5时，如图3中，S=S△OTS＜S△OBM=2.5，∴不存在，综上所述，不存在．1．（2021·湖南长沙市·九年级一模）如图1，我们将经过抛物线顶点的所有非竖直的直线，叫做该抛物线的“风车线”，若抛物线的顶点为P(a，b)，则它的所有“风车线”可以统一表示为：y＝k（x﹣a）＋b，即当x＝a时，y始终等于b．（1）若抛物线y＝﹣2（x＋1）2＋3与y轴交于点A，求该抛物线经过点A的“风车线”的解析式；（2）若抛物线可以通过y＝﹣x2平移得到，且它的“风车线”可以统一表示为y＝kx＋3k﹣2，求该抛物线的解析式；（3）如图2，直线m：y＝x＋3与直线n：y＝﹣2x＋9交于点A，抛物线y＝﹣2（x﹣2）2＋1的“风车线”与直线m、n分别交于B、C两点，若△ABC的面积为12，求满足条件的“风车线”的解析式．【答案】（1）y=-2x+1；（2）y=-（x+3）2-2；（3）y= -x+3或y=1．【分析】（1）先求出点A的坐标，再确定P的坐标为（-1,3），然后将A点坐标代入求解即可；（2）y=kx+3k-2=k（x+3）-2，确定点P的坐标为（-3，-2），然后求出解析式即可；（3）由△ABC的面积=S△APB+S△APC=12，求出x C-x B=6，则点x B（t,t+3），x C（t+6，-2t-3），将点B、C的坐标分别代入y=k（x-2）+1求解即可．【详解】解：（1）∵y=-2（x+1）2+3，∴令x=0，则y=1，∴点A的坐标为（0,1），顶点P的坐标为（-1,3），∴风车线的表达式为y=k（x+1）+3，将点A的坐标代入并求解得：k=-2∴“风车线”的解析式为y=-2（x+1）+3=-2x+1；（2）∵y=kx+3k-2=k（x+3）-2∴点P的坐标为（-3，-2），∴平移后的抛物线表达式为y=-（x+3）2-2；（3）∵y=-2（x-2）2+1，∴点P（2，1），即“风车线”的表达式为y=k（x-2）+1，联立329y xy x=+⎧⎨=-+⎩，解得25xy=⎧⎨=⎩，故点A（2，5），∴AP=5-1=4，∴△ABC的面积=S△APB+S△APC=12×4×（x C-x B）=12，解得：x C-x B=6，设点B的横坐标为t，则点C的横坐标为t+6，∵点B在直线m上，∴点B（t，t+3），同理：点C（t+6，-2t-3），将点B、C的坐标分别代入y=k（x-2）+1，得：3(2)123(62)1t k tt k t+=-+⎧⎨--=+-+⎩解得1tk=⎧⎨=-⎩或2tk=⎧⎨=-⎩∴“风车线”的表达式为y=k（x-2）+1=-（x-2）+1=-x+3或y=1．【点睛】本题属于二次函数综合题，主要考查了一次函数的性质、面积的计算等知识点，灵活应用所学知识成为解答本题的关键．2．（2021·湖南长沙市·九年级一模）我们不妨约定，过坐标平面内任意两点（例如A ，B 两点）作x 轴的垂线，两个垂足之间的距离叫做这两点在x 轴上的“垂足距”，记作____AB ．根据该约定，完成下列各题（1）若点A （1x ，4），B （2x ，8-）．当点A 、B 在函数4y x =的图象上时，____AB = ；当点A ，B 在函数16y x=-的图象上时，____AB = ．（2）若一次函数()30y kx k =+≠的图象上有两点A （1x ，k ），B （2x ，222k -），当____AB k =时，求k的值．（3）若抛物线2y ax bx c =++与直线()230y bx c b =--≠在同一坐标平面内交于点A （1x ，1y ），B （2x ，2y ），且同时满足下列两个条件：①a b c >>；②抛物线经过点（1，0），试求____AB 的范围、【答案】（1）3，6；（2）k =2或1；（3____AB 【分析】（1）先把点A 和点B 坐标代入4y x =和16y x=-分别得出 1x 和2x 的值，由“垂足距”的定义即可得出答案（2）根据“垂足距”的定义得出k 的方程，解方程即可；（3）由2=23++--ax bx c bx c 得出1x ，2x 是方程234=0++ax bx c 的两根，根据根与系数的关系可得1x +2x 和1x 2x 的值，再结合抛物线经过点（1，0）得出22____b b 9+16+16a a ⎛⎫⎛⎫⎛⎫= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭AB ，再根据a b c >>和二次函数的增减性得出答案；【详解】解：（1）∵点A （1x ，4），B （1x ，8-）在函数4y x =的图象上，∴1=1x ，2=-2x ，∴()____=1--2=3AB ，∵点A （1x ，4），B （2x ，8-）在函数16y x=-的图象上 ∴1=-4x ，2=2x ，∴()____=2--4=6AB ，（2）∵A （1x ，k ），B （2x ，222k -）在()30y kx k =+≠的图象， ∴1k-3=k x ，222k -5=kx ， ∵____AB k = ∴22k -5k-3-=k k k， ∴222--2=k k k当22--20＞k k 时，2--2=0k k ，解得：k =2或-1，当22--20＜k k 时，23--2=0k k ，解得：k =2-3或1， ∵k ＞0，∴k =2或1；（3）∵2=23++--ax bx c bx c ()0b ≠∴234=0++ax bx c∴1x ，2x 是方程234=0++ax bx c 的两根，∴1x +23b =-a x ，1x 24c =a x ； ∴()()22221212___122_9b -16ac =x -x =x +x -4x x =a ⎛⎫ ⎪⎝⎭AB ， ∵抛物线经过点（1，0），∴=0a b c ++，∴=--c a b ， ∴____22229b -16ac b b =9+16+16a a a ⎛⎫⎛⎫⎛⎫= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭AB ， ∵a b c >>，∴b -a-b >， ∴1b -a 2>， ∴1a -a 2>， ∴a 0>， ∴1b -12a＜＜， ∵22____b b 9+16+16a a ⎛⎫⎛⎫⎛⎫= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭AB ， ∴对称轴为b 81=--a 92＜， ∴当1b -12a ＜＜时，_2___⎛⎫ ⎪⎝⎭AB 随b a 的增大而增大， ∴当b =1a时， ____AB ，∴当b 1=-a 2时， ____AB∴____AB 的范围为____2AB ；【点睛】本题是二次函数和一次函数的综合题，解题的关键是理解题意，利用“垂足距”的定义解决问题，属于压轴题． 3．（2021·湖南长沙市·九年级专题练习）我们约定：图象关于y 轴对称的函数称为偶函数．（1）下列函数是偶函数的有（填序号）；①y ＝x +1；②y ＝﹣2020x 2+5；③y ＝|2018x|；④y ＝2021x 2﹣2020x +2018．（2）已知二次函数y ＝（k +1）x 2+（k 2﹣1）x +1（k 为常数）是偶函数，将此偶函数进行平移得到新的二次函数y ＝ax 2+bx +c ，新函数的图象与x 轴交于A ，B 两点（A 在B 的左侧），与y 轴交于点C ，若AB ＝2，且以AB 为直径的圆恰好经过点C ，求平移后新函数的解析式；（3）如图，已知偶函数y ＝ax 2+bx +c （a ≠0）经过（1，2），（2，5），过点E （0，2）的一次函数的图象与二次函数的图象交于A ，B 两点（A 在B 的左侧），过点AB 分别作AC ⊥x 轴于点C ，BD ⊥x 轴于点D ，分别用S 1，S 2，S 3表示△ACE ，△ECD ，△EDB 的面积，问：是否存在实数m ，使S 22＝m S 1S 3都成立？若成立，求出m 的值，若不存在，说明理由．【答案】（1）②③；（2）y ＝2x 2﹣4x 或y ＝2x 2+4x 或y ＝2x 2﹣12-或y ＝2x 2x ﹣12；（3）存在，m ＝4【分析】(1)根据每个函数是否关于y 轴对称进行判断； (2)根据偶函数的概念可得：k 2﹣1＝0且k +1≠0，即可求得抛物线解析式，再依据平移的性质可知a ＝2，设A （x 1，0），B （x 2，0）（x 1＜x 2），利用根与系数关系及乘法公式可得：b 2﹣8c ＝16，再根据圆的性质和勾股定理得：b 2+16c 2＝16，从而求得b 、c ，即可得到新函数的解析式；(3)由偶函数性质可知b ＝0，再利用待定系数法即可得函数解析式，设过点E （0，2）的一次函数解析式为：y ＝kx +2，设A （x 1，y 1），B （x 2，y 2），则x 1+x 2＝k ，x 1x 2＝﹣1，根据题意建立方程求解即可．【详解】解：(1)①y ＝x +1的图像经过第一、三象限，y 轴不是其对称轴，所以y ＝x +1不是偶函数；②y ＝﹣2020x 2+5的图像抛物线是轴对称图形，且对称轴是y 轴，是偶函数；③y ＝|2018x|是关于y 轴对称的，是偶函数； ④y ＝2021x 2﹣2020x +2018的图像抛物线是轴对称图形，对称轴是直线x ＝10102021，不是偶函数；故答案为：②③；(2)∵二次函数y ＝（k +1）x 2+（k 2﹣1）x +1（k 为常数）是偶函数，∴21010k k ⎧-=⎨+≠⎩，解得：k ＝1，∴该二次函数解析式为：y ＝2x 2+1，∵平移抛物线时，开口方向和形状都不变，即a 的值不变，∴平移得到新的二次函数为y ＝2x 2+bx +c ，由题意知，新函数的图象与x 轴交于A ，B 两点（A 在B 的左侧），与y 轴交于点C ，设A （x 1，0），B （x 2，0）（x 1＜x 2），令x ＝0，得y ＝c ，∴C （0，c ），∵AB ＝2，∴x 2﹣x 1＝2，由根与系数关系可知：x 1+x 2＝﹣2b ，x 1x 2＝2c ， ∵（x 1+x 2）2﹣4x 1x 2＝（x 2﹣x 1）2，∴（﹣2b ）2﹣4×2c ＝22，即b 2﹣8c ＝16， ∵以AB 为直径的圆恰好经过点C ，∴该圆的圆心为F （122x x +，0），即F （﹣4b ，0）， ∴CF ＝1，即（﹣4b ）2+c 2＝1，整理，得：b 2+16c 2＝16，联立方程组：2228161616b c b c ⎧-=⎨+=⎩，解得：1140b c =-⎧⎨=⎩，2240b c =⎧⎨=⎩，3312b c ⎧=-⎪⎨=-⎪⎩，4412b c ⎧=⎪⎨=-⎪⎩； ∴平移后新函数的解析式为：y ＝2x 2﹣4x 或y ＝2x 2+4x 或y ＝2x 2﹣x 12-或y ＝2x 2﹣12； (3)∵偶函数y ＝ax 2+bx +c （a ≠0）经过（1，2），（2，5），∴b ＝0，即y ＝ax 2+c ，∴245a ca c+=⎧⎨+=⎩，解得：11ac=⎧⎨=⎩，∴y＝x2+1，设过点E（0，2）的一次函数解析式为：y＝kx+2，将y＝x2+1代入，得：x2+1＝kx+2，即x2﹣kx﹣1＝0，设A（x1，y1），B（x2，y2），则x1+x2＝k，x1x2＝﹣1，∴y1y2＝（kx1+2）（kx2+2）＝k2•x1x2+2k（x1+x2）+4＝k2+4，∵用S1，S2，S3表示△ACE，△ECD，△EDB的面积，∴S1＝12AC•（﹣x1）＝12y1•（﹣x1）＝﹣12x1y1，S2＝12CD•OE＝12（x2﹣x1）×2＝x2﹣x1，S3＝12BD•x2＝12x2y2，∴S22＝（x2﹣x1）2＝（x1+x2）2﹣4x1x2＝k2﹣4×（﹣1）＝k2+4，S1S3＝﹣12x1y1•12x2y2＝﹣14（x1x2）（y1y2）＝﹣14×（﹣1）×（k2+4）＝14（k2+4），∵S22＝m S1S3，∴k2+4＝m•14（k2+4），∴m＝4．【点睛】本题考查了待定系数法，一次函数和二次函数交点，根与系数关系，三角形面积，圆的性质等，是一道综合性强，涉及知识点多的中考压轴题型；解题关键是灵活运用根与系数关系和乘法公式．4．（2021·湖南长沙市·九年级专题练习）在平面直角坐标系中，A(0，a)，B(b，0)，D(c，0)c2﹣4c＋4＝0，b为最大的负整数，DE⊥x轴且∠BED＝∠ABD，BE交y轴于点C，AE交x轴于点F．（1）求A，B，D的坐标；（2）在y轴上是否存在点G使得GF＋GE有最小值？如果存在，求出GF＋GE的最小值；如果不存在，请说明理由；（3）如图，过P(0，﹣1)作x轴的平行线，在平行线上有一点Q（点Q在P的右侧）使∠QEM＝45°，QE交x轴于N，ME交y轴正半轴于M，求AM MQPQ-的值．【答案】（1）A(0，3)，B(﹣1，0)，D(2，0)；（2；（3）1．【分析】（1）由非负数的性质可求得a、c的值，可求得A、B、D的坐标；（2）由条件可证明△ABO≌△BED，可求得DE和BD的长，可求得E点坐标，再求得直线AE的解析式，可求得F点坐标；如图1，作点F关于y轴的对称点F'(﹣3，0)，连接EF'，交AO于G，则GF＋GE最小值为EF'，由勾股定理可求解；（3）过E作EG⊥OA于点G，EH⊥PQ于点H，可证明四边形GEHP为正方形，在GA上截GI＝QH，可证明△IGE≌△QHE，可证得∠IEM＝∠MEQ＝45°，可证明△EIM≌△EQM，可得到IM＝MQ，再结合条件可求得AI＝PQ，可求得答案．【详解】解：（1）＋c2﹣4 c＋4＝0，＋（c﹣2）2＝0，∴a＝3，c＝2，∵b为最大的负整数，∴b＝﹣1，∴A(0，3)，B(﹣1，0)，D(2，0)；（2）∵A(0，3)，B(﹣1，0)，D(2，0)，∴OB＝1，OD＝2，OA＝3，∴AO＝BD，在△ABO和△BED中，90ABOBED AOBBDE AO BD ，∴△ABO ≌△BED （AAS ），∴DE ＝BO ＝1，∴E (2，1)，设直线AE 解析式为y ＝kx ＋b ，把A 、E 坐标代入可得312b k b ，解得13k b =-⎧⎨=⎩，∴直线AE 的解析式为y ＝﹣x ＋3，令y ＝0，可解得x ＝3，∴F (3，0)，如图1，作点F 关于y 轴的对称点F '(﹣3，0)，连接EF '，交AO 于G ，则GF ＋GE 最小值为EF '，∴EF ' ，∴GF ＋GE（3）过E 作EG ⊥OA ，EH ⊥PQ ，垂足分别为G 、H ，在GA 上截取GI ＝QH ，如图2，∵E (2，1)，P (﹣1，0)，∴GE ＝GP ＝EH ＝PH ＝2，∴四边形GEHP 为正方形，∴∠IGE ＝∠EHQ ＝90°，在Rt △IGE 和Rt △QHE 中，{GE HEIGE EHQ IG QH=∠=∠=∴△IGE ≌△QHE （SAS ），∴IE ＝EQ ，∠1＝∠2，∵∠QEM ＝45°，∴∠2＋∠3＝45°，∴∠1＋∠3＝45°，∴∠IEM ＝∠QEM ，在△EIM 和△EQM 中，IE QEIEM QEMME ME，∴△EIM≌△EQM（SAS），∴IM＝MQ，∴AM﹣MQ＝AM﹣IM＝AI，由（2）可知OA＝OF＝3，∠AOF＝90°，∴∠A＝∠AEG＝45°，∴PH＝GE＝GA＝IG＋AI，∴AI＝GA﹣IG＝PH﹣QH＝PQ，∴AM MQ AIPQ PQ-=＝1．【点睛】本题是三角形综合题，涉及知识点有非负数的性质，全等三角形的判定和性质，待定系数法，正方形的判定和性质等知识，熟悉相关性质是解题的关键．5．（2021·湖南长沙市·九年级专题练习）如图1，已知抛物线F1：y＝ax2﹣36a（a＞0）与x轴交于A，B两点（A在B的左侧），与y轴交于点C，直线l：y＝kx+b经过点B，与y轴负半轴交于点D．（1）若D（0，﹣8）为△ABC的外心，求a的值；（2）如图2，若D为△ABC的内心且△ABC的内切圆半径为3，点P为线段BC的中点，求经过点P的反比例函数的解析式；（3）如图3，点E是抛物线F1与直线l的另一个交点，已知OC＝2OD，△BCE的面积为6，点E在双曲线F2：y＝1cx+上，若当m≤x≤n（其中mn＜0）时，二次函数y＝﹣x2+2x+c的函数值的取值范围恰好是2m≤y≤2n，求m +n 的值．【答案】（1）a ＝12；（2）y ＝﹣6x 或y ＝﹣18x；（3）m +n ＝3【分析】（1）在y ＝ax 2﹣36a 中，令y ＝0，可求得点A ，B 的坐标，根据D （0，﹣8）为△ABC 的外心，可得DA ＝DB ＝DC ，再运用勾股定理即可求得a 的值；（2）根据勾股定理可求得AC ＝BC ，可得S △ABC ＝12AB •OC ＝216a ，再根据D 为△ABC 的内心且△ABC 的内切圆半径为3，亦可得S △ABC ＝12×（AB +BC +AC ）×3，建立方程即可求得a 的值，从而可得点C 坐标，再利用中点坐标公式可得点P 坐标，即可求得结论；（3）先运用待定系数法求得直线l 解析式，再联立方程组求得点E 坐标，利用△BCE 的面积建立方程求a 的值，通过点E 坐标求得c 的值，从而得到抛物线解析式，再结合二次函数增减性和最值进行分类讨论求得m ，n 的值即可得到答案．【详解】解：（1）在y ＝ax 2﹣36a 中，令y ＝0，得：ax 2﹣36a ＝0，解得：x 1＝﹣6，x 2＝6，∴A （﹣6，0），B （6，0），∵D（0，﹣8）为△ABC的外心，∴DA＝DB＝DC，∵抛物线F1：y＝ax2﹣36a（a＞0）与y轴交于点C，∴C（0，﹣36a），∴DC＝﹣8﹣（﹣36a）＝36a﹣8，在Rt△BOD中，DB＝10，∴36a﹣8＝10，∴a＝12；（2）由（1）知：AB＝6﹣（﹣6）＝12，OC＝36a，由勾股定理得：AC＝BC，∵D为△ABC的内心且△ABC的内切圆半径为3，∴S△ABC＝12×（AB+BC+AC）×3，∵S△ABC＝12AB•OC＝12×12×36a＝216a，∴12×（AB+BC+AC）×3＝216a，即12×（×3＝216a，解得：a1＝19，a2＝13，∴C（0，﹣4）或C（0，﹣12），∵点P为线段BC的中点，∴P（3，﹣2）或P（3，﹣6），设经过点P的反比例函数的解析式为y＝kx，将P（3，﹣2）或P（3，﹣6）分别代入，得：k＝﹣6或﹣18，∴经过点P的反比例函数的解析式为y＝﹣6x或y＝﹣18x；（3）由（1）知：B（6，0），C（0，﹣36a），∵OC＝2OD，∴D（0，﹣18a），∵直线l：y＝kx+b经过点B，与y轴负半轴交于点D，∴6018k bb a+=⎧⎨=-⎩，解得：318k ab a=⎧⎨=-⎩，∴直线l解析式为：y＝3ax﹣18a，∵点E是抛物线F1与直线l的另一个交点，∴236318y ax a y ax a ⎧=-⎨=-⎩，解得：116 0x y =⎧⎨=⎩（舍去）22327xy a=-⎧⎨=-⎩，∴E（﹣3，﹣27a），∴S△BCE＝12×DC×（3+6）＝12×[﹣18a﹣（﹣36a）]×9＝81a，∵△BCE的面积为6，∴81a＝6，解得：a＝2 27，∴E（﹣3，﹣2），∵点E在双曲线F2：y＝1cx上，∴c+1＝6，∴c＝5，∵当m≤x≤n（其中mn＜0）时，二次函数y＝﹣x2+2x+c的函数值的取值范围恰好是2m≤y≤2n，∴二次函数y＝﹣x2+2x+5，当m≤x≤n（其中mn＜0）时，2m≤y≤2n，且m＜0，由y＝﹣x2+2x+5＝﹣（x﹣1）2+6，可知：抛物线对称轴为直线x＝1，顶点（1，6），①当n≤1时，y随x增大而增大，又x＝m时，y＝2m，x＝n时，y＝2n，∴2m＝﹣m2+2m+5或2n＝﹣n2+2n+5，解得：m n∵m＜0，0＜n≤1，∴m，n＝；②当n＞1时，则2n＝6，解得n＝3，若﹣1＜m＜0，则最小值在x＝3处取得，即2m＝﹣32+2×3+5＝2，解得：m＝1＞0，不符合题意，舍去；若m≤﹣1，最小值在x＝m处取得，即2m＝﹣m2+2m+5，解得：m1m2，∴m，n＝3，综上所述，m，n＝3；∴m+n＝3【点睛】本题考查了二次函数的性质，待定系数法，一次函数与二次函数交点，三角形内心、外心，三角形面积，中点坐标，反比例函数等；是一道综合性较强的压轴题，解题时务必要认真审题，理清思路，能够将相关知识点结合起来；充分利用题目中的信息，运用方程思想，分类讨论思想是解题关键．6．（2020·湖南广益实验中学九年级月考）已知点M为关于x的二次函数y＝ax2﹣2amx+am2﹣2m+2（a≠0，m为常数）的顶点．（1）若此二次函数与x轴只有一个交点，试确定m的值；（2）已知以坐标原点O为圆心的圆半径是45，试判断点M与⊙O的位置关系，若能确定，请说明理由，若不能确定，也请分类讨论之；（3）对于任意实数m，点M都是直线l上一点，直线l与该二次函数相交于A、B两点，a是以3、4、5为边长的三角形内切圆的半径长，点A、B在以O为圆心的圆上．①求⊙O的半径；②求该二次函数的解析式．【答案】（1）1；（2）点M在⊙O外，理由见解析；（3）①4；②21634 525y x x=-+【分析】（1）由二次函数与x轴只有一个交点，可得△＝0，从而得出关于m的方程，解方程即可确定m的值；（2）写出点M的坐标，用含m的式子表示出OM2，从而可得关于m的二次函数，将其写成顶点式，根据二次函数的性质可得OM2的最小值，求其算术平方根，可得OM的最小值，从而可判断点M与⊙O的位置关系；（3）①由切线长定理求得a的值，将其代入抛物线的解析式，写出直线l的解析式，由抛物线的解析式与直线l的解析式可得关于x的方程，解方程，从而用含m的式子表示出点A和点B的坐标，由勾股定理或两点距离公式可得⊙O的半径；②将a和m的值代入抛物线y＝ax2﹣2amx+am2﹣2m+2计算即可得出答案．【详解】解:（1）∵二次函数与x轴只有一个交点，∴△＝(﹣2am)2﹣4a(am2﹣2m+2)＝0，∴8am﹣8a＝8a(m﹣1)＝0，∵a≠0，∴m﹣1＝0，∴m＝1；（2）∵点M为关于x的二次函数y＝ax2﹣2amx+am2﹣2m+2的顶点，∴M(m，﹣2m+2)，∵原点O的坐标为(0，0)，∴OM2＝m2+(﹣2m+2)2＝5m 2﹣8m +4 ＝2445()55m -+， ∴当m ＝45时，OM 2有最小值45，455=>， ∴点M 在⊙O 外；（3）①作出以3、4、5为边长的三角形，F ，G ，H 是三角形与⊙O 的切点，连接OF ，OG ，如图所示:由勾股定理可知该三角形是直角三角形，则∠E ＝90°，由切线的性质可知，OF ⊥DE ，OG ⊥CE ，∴∠OFE ＝90°，∠OGE ＝90°，∴四边形OFEG 是矩形，∵OF ＝OG ＝a ，∴四边形OFEG 是正方形，∴FE ＝EG ＝a ，∵CH ＝CG ，DH ＝DF ，∴2a ＝3+4﹣5，∴a ＝1，∴y ＝x 2﹣2mx +m 2﹣2m +2，∵对于任意实数m ，点M 都是直线l 上一点，且M (m ，﹣2m +2)，∴直线l 的解析式为y ＝﹣2x +2，令﹣2x +2＝x 2﹣2mx +m 2﹣2m +2，解得x 1＝m ，x 2＝m ﹣2，∴A (m ，﹣2m +2)，B (m ﹣2，﹣2m +6)，∵点A 、B 在以O 为圆心的圆上，∴m 2+(﹣2m +2)2＝(m ﹣2)2+(﹣2m +6)2，解得m ＝85，∴⊙O 4==． ②将a ＝1，m ＝85代入抛物线y ＝ax 2﹣2amx +am 2﹣2m +2得21634525y x x =-+． ∴该二次函数的解析式为21634525y x x =-+．【点睛】本题属于二次函数综合题，考查了抛物线与x 轴的交点、利用二次函数的性质求最值、点与圆的位置关系、切线长定理、直线与抛物线的交点及解一元二次方程等知识点，综合性较强，需要熟练掌握相关性质及定理并正确运算．7．（2021·长沙市湘郡培粹实验中学九年级期末）对于一个函数给出如下定义；对于函数y ，若当a x b ≤≤，函数值y 满足m y n ≤≤，且满足()n m k b a -=-，则称此函数为“k 属合函数”．例如：正比例函数2y x =-，当13x ≤≤时，62y -≤≤-，则()()2631k ---=-，求得：2k =，所以函数2y x =-为“2属合函数”．（1）一次函数10,13()y ax a x =-<≤≤为“1属合函数”，求a 的值．（2）反比例函数(0,k y k a x b x=>≤≤，且0a b <<）是“k 属合函数”，且a b +=，请求出22a b +的值；（3）已知二次函数22362y x ax a a =-+++，当11x -≤≤时，y 是“k 属合函数”，求k 的取值范围．【答案】（1）a =-1；（2）2019；（3）k ≥32．【分析】（1）利用“k 属合函数”的定义即可得出结论；（2）先判断出函数的增减性，利用“k 属合函数”的定义得出ab =1，最后利用完全平方公式即可得出结论；（3）分四种情况，各自确定出最大值和最小值，最后利用“k 属合函数”的定义即可得出结论．【详解】解：（1）当a ＜0时，一次函数的y 随着x 的增大而减小，∵1≤x ≤3，∴3a -1≤y ≤a -1，∵一次函数y =ax -1（a ＜0，1≤x ≤3）为“1属合函数”，∴（a -1）-（3a -1）=1×（3-1），∴a =-1；（2）∵反比例函数y =k x，k ＞0， ∴在第一象限内，y 随x 的增大而减小，当a ≤x ≤b 且0＜a ＜b 是“k 属合函数”， ∴()k k k b a a b-=-， ∴ab =1，∵a+b∴a2+b2=（a+b）2-2ab=2021-2=2019；（3）∵二次函数y=-3x2+6ax+a2+2a的对称轴是：直线62(3)ax a =-=⨯-，∴当-1≤x≤1时，y是“k属合函数”，∴当x=-1时，y=a2-4a-3，当x=1时，y=a2+8a-3，当x=a时，y=4a2+2a，①如图1，当a≤-1时，当x=-1时，有y max=a2-4a-3，当x=1时，有y min=a2+8a-3，∴（a2-4a-3）-（a2+8a-3）=2k，∴k=-6a，∴k≥6；②如图2，当-1＜a≤0时，当x =a 时，有y max =4a 2+2a ，当x =1时，有y min =a 2+8a -3，∴（4a 2+2a ）-（a 2+8a -3）=2k ， ∴23(1)2k a =-， ∴362k ≤<； ③如图3，当0＜a ≤1时，当x =a 时，有y max =4a 2+2a ，当x =-1时，有y min =a 2-4a -3∴（4a 2+2a ）-（a 2-4a -3）=2k ， ∴23(1)2k a =+， ∴362k <≤； ④如图4，当a ＞1时，当x =1时，有y max =a 2+8a -3，当x =-1时，有y min =a 2-4a -3，∴（a 2+8a -3）-（a 2-4a -3）=2k ，∴k =6a ，∴k ＞6；综上，k 的取值范围为k ≥32．【点睛】此题是二次函数，一次函数，反比例函数的综合题，主要考查了新定义的理解和应用，反比例函数的性质，二次函数的性质，一次函数的性质，利用分类讨论的思想解决问题是解本题的关键．8．（2021·湖南长沙市·九年级专题练习）一般地，在画一个图形关于某点的中心对称图形时，首先找到对称中心，将关键点与对称中心相连，并延长至等长，最后将所得的对应点连接即可得到对称图形．若将函数C 1的图象沿某一点旋转180度，与函数C 2的图象重合，则称函数C 1与C 2关于这个点互为“中心对称函数”，这个点叫作函数C 1、C 2的“对称中心”，如：求函数y x =的关于（1，0）的中心对称函数，可以在函数上取（0，0）和（1，1），两个点关于（1，0）中心对称点分别是（2，0）和（1，1-），这样我们就可以得到函数y x =关于（1，0）中心对称函数2y x =-．（1）求函数32y x =+关于（1，0）的中心对称函数；（2）若函数C 1：2y x b =+，对称中心是（0，b -），此时C 1的关于（0，b -）的中心对称函数C 2的图象与函数2y x=-的图象有且只有一个交点，求b 的值；（3）若函数C 1：211y x =+，对称中心是（1，10），当04x ≤≤时，此时函数C 1关于（1，10）的中心对称函数C 2的图象与函数3y kx k =+的图象始终有交点，求k 的取值范围．【答案】（1）y=3x-8；）（2）b=43±；（3）57≤k≤2．【分析】（1）由“中心对称函数”的概念解答即可；（2）在函数2y x b =+求出两个点关于（0，b -）的中心对称点，则得到函数2C 的解析式，再根据C 2的图象与函数2y x=-的图象有且只有一个交点，得△=0，求出b 即可；（3）求出函数C 1：211y x =+关于（1，10）的中心对称函数2C ，再根据C 2的图象与函数3y kx k =+的图象始终有交点，得△≥0，求出k ，再根据x 的取值范围对k 进行检验．【详解】解：（1）由题意得：可在32y x =+上取（0，2）和（-23，0），两个点关于（1，0）的中心对称点分别是（2，-2）和（8,03），则得到函数32y x =+关于（1，0）的中心对称函数y=3x-8；（2）可在函数1C ：y=2x+b 上取（0，b ）和（-b ,02），两个点关于（0，b -）的中心对称点分别是（0，-3b ）和（,22b b -），则得到函数y=2x+b 关于（0，b -）的中心对称函数2C ： y=2x-3b ，又∵函数C 2的图象与函数2y x=-的图象有且只有一个交点， ∴2x+b=-2x22320x bx -+=△=29b 160-=b=±43（3）在函数C 1：211y x =+上取（0，11）、（1，12），两个点关于（1，10）的中心对称点分别是（2，9）、（1，8），则得到函数2C 的解析式：y=-245x x ++，当x=4时，y=5，∴A(4，5)，∵函数C 2的图象与函数3y kx k =+的图象在0≤x≤4上始终有交点，∴-245x x ++=kx+3k∴-2(4)530x k x k +-+-=∵△=2(4)+4(53)k k -⨯-=0∴22036k k -+=0解得：122,18k k ==，把A(4，5)代入y=kx+3k 得k=57， ∴k 的取值范围为57≤k≤2．【点睛】本题考查了对“中心对称函数”的概念理解与运用和判别式的应用，掌握这些知识点是解题的关键． 9．（2021·湖南长沙市·九年级专题练习）规定：我们把一个函数关于某条直线或者某点作对称后形成的新函数，称之为原函数的“对称函数”．（1）已知一次函数y ＝﹣2x +3的图象，求关于直线y ＝﹣x 的对称函数的解析式；（2）已知二次函数y ＝ax 2+4ax +4a ﹣1的图象为C 1；①求C 1关于点R （1，0）的对称函数图象C 2的函数解析式；②若两抛物线与y 轴分别交于A 、B 两点，当AB ＝16时，求a 的值；（3）若直线y ＝﹣2x ﹣3关于原点的对称函数的图象上的存在点P ，不论m 取何值，抛物线y ＝mx 2+（m ﹣23）x ﹣（2m ﹣38）都不通过点P ，求符合条件的点P 坐标．【答案】（1）y =1322x - ，(2) ①28161y ax ax a =-+-+ ，②910或7-10 （3）（1，1），(-2，7). 【分析】（1）取y =-2x +3上两点（0，3），（32，0），求出这两点关于y =-x 对称点，代入y =k x +b ，求出k ，b 的值则可以得出解析式；（2）①设C 2上的点为（x ，y ），其关于（1，0）的对称点代入C 1上，则可以求出C 2 的解析式； ②C 1与y 轴交于（0，4a -1）， C 2与y 轴交于（0，-16a +1）根据AB =16，列方程求出a 的值，（3）求出y =-2x -3关于原点对称函数为y =-2x +3，根据抛物线不通过点P ：222323()(2)(2)3838y mx m x m x x x =+---=+--+ ，令220x x +-= ，得出x ，将x 的值代入y =-2x +3中，由于函数值得唯一性，得出点P 的坐标.【详解】（1）取y =-2x +3上两点（0，3），（32 ，0）两点关于y =-x 对称点为（-3，0），（0，-32）设y =x +b ，则0332k b b =-+⎧⎪⎨=-⎪⎩ ，解得1232k b ⎧=-⎪⎪⎨⎪=-⎪⎩ ，则1322y x =-- ，（2）①设C 2上的点为（x ，y ），其关于（1，0）的对称点为（2-x ，-y ），(2-x ，-y )在C 1上，则()()224241y a x a x a -=-+-+-C 2:28161y ax ax a =-+-+，②C 1关于y 轴交于（0，4a -1）， C 2关于y 轴交于（0，-16a +1），AB =｜(4a -1)-(-16a +1)｜=16，｜2a -2｜=16，解得a =910或-710 ，（3）y =-2x -3关于原点对称函数为y =-2x +3，抛物线:()222323223838y mx m x m x x m x ⎛⎫⎛⎫=+---=+--+ ⎪ ⎪⎝⎭⎝⎭ 令220x x +-= ，得x 1=1，x 2=-1，则抛物线经过（1，7-24 ），（-2，4124）令x =1，y =-2x -3=1，令x =-2，y =-2x +3=7，点（1，1）（-2，7）在y =-2x +3上由于函数值的唯一性，上述两点不可能在抛物线上，故P 为(1，1)或(-2，7)．【点睛】此题是一次函数，二次函数的综合，包含求函数的解析式，函数的对称性，一次函数的点的坐标特征，二次函数图像和性质，以及一次函数与一元一次方程结合，解题的关键是熟悉一次函数，二次函数的图像和性质．10．（2020·湖南长沙市·九年级月考）已知y 是关于x 的函数，若其图像经过点(,2)P t t ，则称点P 为函数图像上的“偏离点”．例如：直线3y x =-上存在“偏离点”(3,6)P --．（1）在双曲线1y x =上是否存在“偏离点”？若存在，请求出“偏离点”的坐标；若不存在，请说明理由．（2）若抛物线2212221239y x a x a a ⎛⎫=-++--+ ⎪⎝⎭上有“偏离点”，且“偏离点”为()11,A x y 和()22,B x y ，求22123ka w x x =+-的最小值（用含k 的式子表示）；（3）若函数21(2)24y x m t x n t =+-+++-的图像上存在唯一的一个“偏离点”，且当23m -≤≤时，n 的最小值为t ，求t 的值．【答案】（1）2P ⎛ ⎝和2P ⎛- ⎝；（2）2241632k k ++-；（2）4或1．【分析】（1）根据“偏离点”的坐标特征设出坐标，代入双曲线中，有解则有“偏离点”；（2）设抛物线“偏离点”的坐标为P （x ，2x ），代入抛物线的关系式中得到关于x 的一元二次方程，因为有两个偏离点，则这两个偏离点的横坐标就是这个一元二次方程的两个根，先由△的值确定a 的取值，再由根与系数的关系得：两根和与两根据积的式子，再将所求式子代入w=x 12+x 22-3ka 进行变形，得到w 关于a 的二次函数，求最小值即可；（3）设函数“偏离点”的坐标为P （x ，2x ），代入函数的关系式中得到关于x 的一元二次方程，因为有一个偏离点，则△=0，得到n=（m-t ）2-t+2，把它看成一个二次函数，对称轴m=t ，分三种情况讨论：①t ＜-2，列方程，方程无解，没有符合条件的t 值；②t ＞3，列方程，解出t 并取舍；③当-2≤t≤3，同理得t=1．【详解】（1）设存在这样的“偏离点”P ，坐标为(),2t t ，将点P 的坐标代入双曲线1y x=得： 12t t =，221t =，解得2t =±，故存在两个“偏离点”，坐标为2P ⎛ ⎝和2P ⎛- ⎝．（2）设抛物线“偏离点”的坐标为(),2P x x ，将点P 的坐标代入抛物线2212221239y x a x a a ⎛⎫=-++--+ ⎪⎝⎭中得 22122221239x x a x a a ⎛⎫=-++--+ ⎪⎝⎭， 2212210239x ax a a -+--+=， ∵“偏离点”为()11,A x y 和()22,B x y ， ∴1x 、2x 是方程2212210239x ax a a -+--+=的两个根， 22212410329a a a ⎛⎫⎛⎫⎛⎫∆=-⨯---+≥ ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭， 224221099a a a ⎛⎫∆=+--+≥ ⎪⎝⎭， 220a ∆=-+≥，∴1a ≤， ∵12243132a a x x +=-=-，2212214922192a a x x a a --+⋅==+--，()2221212122244222393233a ka a a ka ka w x x x x x x ⎛⎫=+-=+-⎛⎫=-+-- ⎪ ⎪⎝⎭⎝⎭-， 28(4)493k w a a =-++， ∵809>， ∴抛物线开口向上，且对称轴：4363391628kk a --+=-=⨯ ， ∴若36316k a +=≥1时，即36+3k≥16，则当a=1时，w 的最小值是：893k -；若36316k a +=＜1时，即36+3k ＜16，k ＜203-，则当36316k a +=时，则w 小=28449849(4)3k ⨯⨯-⨯+=21313242k k ---=2241632k k ++- ；（3）设函数“偏离点”的坐标为(),2P x x ，将点P 的坐标代入函数()21224y x m t x n t =+-+++-得 ()21224x x m t x n t =+-+++-， ()21204x m t x n t +-++-=， ∵存在唯一的一个“偏离点”，∴()()214204m t n t ∆=--⨯⨯+-=，()22n m t t =--+，这是一个n 关于m 的二次函数，图象为抛物线，开口向上，对称轴为m t =，对称轴左侧，n 随m 的增大而减小；对称轴右侧，n 随m 的增大而增大；①2t <-，当23m -≤≤时，在对称轴右侧递增，∴当2m =-时，n 有最小值为t ，即()222t t t ---+=，2260t t ++=， 44160∆=-⨯⨯<，方程无解，②3t >，当23m -≤≤时，在对称轴左侧递减，∴当3m =时，n 有最小值为t ，即()232t t t --+=，解得14t =243t =<（舍），③当23t -≤≤，当23m -≤≤时，n 有最小值为2t -+，∴2t t -+=，1t =．综上所述，t 的值为4+或1．【点睛】本题是一个阅读理解问题，考查了对函数“偏离点”的掌握和运用，还考查了反比例函数和二次函数的性质及一元二次方程的根与二次函数的关系；明确一元二次方程根据与系数的关系，方程的解与根的判别式的关系；尤其是二次函数的最值问题，在自变量的所有取值中：当a ＞0时，抛物线在对称轴左侧，y 随x 的增大而减少；在对称轴右侧，y 随x 的增大而增大，函数有最小值，当a ＜0时，抛物线在对称轴左侧，y 随x 的增大而增大；在对称轴右侧，y 随x 的增大而减少，函数有最大值；如果在规定的取值中，要看图象和增减性来判断．。

二次函数压轴题专题突破练专题04 二次函数背景下的图形面积的探究(学生版)

备战2019年中考数学压轴题之二次函数专题04 二次函数背景下的图形面积的探究【方法综述】面积问题中，以三角形的面积的情况居多，通常三角形的面积探究方法如下：方法一：应用相似三角形性质，面积比等于相似比平方处理面积；方法二：同底等高类的三角形面积：当两个三角形同底（高）等高（底）时，两个三角形的面积相等，同底（高）且高（底）不等的两个三角形面积之比等于高（底）之比方法三：割补法，一些情况下，三角形和四边形的面积可以采用割补法解决；坐标系中的三角形面积可以采用平行线相切法例如：求抛物线在直线AC 上方一点，使得△PAC 面积最大，当把直线AC 向上平移时，与抛物线的切点即为满足条件的P 点，因此，若直线AC 斜率为k ，则可以设一条直线解析式为y=kx+b ，该直线与抛物线联立的方程有两个相等实数根时，可求得b ，进而求得P 点坐标。

另外，用铅垂高法解决面积最值问题基本模型如下：S △PAB ＝12·PQ·||x B －x A .根据二次函数解析式设出点P 的坐标，结合一次函数解析式从而得到点Q 的坐标，从而转化为S 与点P 横坐标之间的二次函数解析式，再根据二次函数增减性求最值.一般情况下，当铅P垂线段PQ最大时，S△PAB取得最大值，此时点Q为线段AB的中点.【典例示范】类型一实际问题的面积探究例1：用一段长32m的篱笆和长8m的墙，围成一个矩形的菜园．（1）如图1，如果矩形菜园的一边靠墙AB，另三边由篱笆CDEF围成①设DE等于xm，直接写出菜园面积y与x之间的函数关系式，并写出自变量的取值范围；②菜园的面积能不能等于110m2？若能，求出此时x的值；若不能，请说明理由；（2）如图2，如果矩形菜园的一边由墙AB和一节篱笆BF构成，另三边由篱笆ADEF围成，求菜园面积的最大值．针对训练1.如图，用一段长为60m的篱笆围成一个一边靠墙（墙的长度不限）的长方形菜园ABCD，设与墙平行的篱笆AB的长为xm，菜园的面积为ym2．（1）试写出y与x之间的关系式；（2）当AB的长为10m，菜园的面积是多少？2.问题情境:有一堵长为的墙，利用这堵墙和长为的篱笆围成一个矩形养鸡场，怎样围面积最大？最大面积是多少？题意理解:根据题意，有两种设计方案：一边靠墙（如图①）和一边“包含”墙（如图②）．特例分析:（1）当时，若按图①的方案设计，则该方案中养鸡场的最大面积是；若按图②的方案设计，则该方案中养鸡场的最大面积是．（2）当时，解决“问题情境”中的问题．解决问题:（3）直接写出“问题情境”中的问题的答案．3晨光中学课外活动小组准备围建一个矩形生物苗圃园，其中一边靠墙，另外三边用长为30米的篱笆围成．已知墙长为18米（如图所示），设这个苗圃园垂直于墙的一边的长为x米．(1)若平行于墙的一边长为y米，直接写出y与x的函数关系式及其自变量x的取值范围；(2)设这个苗圃园的面积为S，求S与x之间的函数关系．4.2018年，汶上县县委、县政府启动创建全国卫生县城和全国文明县城工作，各单位都积极投身创城工作某单位为进一步美化我县环境，在临街的围墙外靠墙摆设一长方形花圃景观，花圃一边靠墙，墙长18m，外围用40m的栅栏围成，如图所示，若设花圃的BC边长为x(m)，花圃的面积为y(m2)．(1)求出y与x之间的函数关系式，并写出自变量x的取值范围；(2)利用所学知识试着求出花圃的最大面积．5．某小区业主委员会决定把一块长50m，宽30m的矩形空地建成健身广场，设计方案如图所示，阴影区域为绿化区（四块绿化区为全等的矩形），空白区域为活动区，且四周的4个出口宽度相同，其宽度不小于14m，不大于26m，设绿化区较长边为xm，活动区的面积为ym2（1）直接写出：①用x的式子表示出口的宽度为；②y与x的函数关系式及x的取值范围；（2）求活动区的面积y的最大面积；（3）预计活动区造价为50元/m2，绿化区造价为40元/m2，如果业主委员会投资不得超过72000元来参与建造，当x为整数时，共有几种建造方案？类型二面积计算例2．已知直线l：y＝kx＋1与抛物线y＝x2－4x.(1)求证：直线l与该抛物线总有两个交点；(2)设直线l与该抛物线的两交点为A，B，O为原点，当k＝－2时，求△OAB的面积．针对训练1.如图，直线与轴交于点，与轴交于点,抛物线经过点.(1)求抛物线的解析式，(2)已知点是抛物线上的一个动点，并且点在第二象限内，过动点作轴于点，交线段于点.①如图1，过作轴于点，交抛物线于两点(点位于点的左侧)，连接，当线段的长度最短时，求点的坐标，②如图2，连接，若以为顶点的三角形与相似，求的面积.2.如图，已知抛物线与轴、轴分别相交于点A（－1，0）和B（0，3），其顶点为D．（1）求这条抛物线的解析式；（2）若抛物线与轴的另一个交点为E，求△ODE的面积；（3）抛物线的对称轴上是否存在点P使得△PAB的周长最短．若存在请求出点P的坐标，若不存在说明理由．3.如图1，在平面直角坐标系xOy中，抛物线W的函数表达式为y=﹣x2+x+4．抛物线W与x轴交于A，B两点（点B在点A的右侧，与y轴交于点C，它的对称轴与x轴交于点D，直线l经过C、D两点．(1)求A、B两点的坐标及直线l的函数表达式．(2)将抛物线W沿x轴向右平移得到抛物线W′，设抛物线W′的对称轴与直线l交于点F，当△ACF为直角三角形时，求点F的坐标，并直接写出此时抛物线W′的函数表达式．(3)如图2，连接AC，CB，将△ACD沿x轴向右平移m个单位（0＜m≤5），得到△A′C′D′．设A′C交直线l 于点M，C′D′交CB于点N，连接CC′，MN．求四边形CMNC′的面积（用含m的代数式表示）．4.抛物线经过点A(3,0) 和点B（0,3）,且这个抛物线的对称轴为直线l，顶点为C.（1）求抛物线的解析式；（2）连接AB、AC、BC，求△ABC的面积.5.如图1，抛物线的顶点A的坐标为（1，4），抛物线与x轴相交于B、C两点，与y轴交于点E（0，3）．（1）求抛物线的表达式；（2）已知点F（0，﹣3），在抛物线的对称轴上是否存在一点G，使得EG+FG最小，如果存在，求出点G 的坐标；如果不存在，请说明理由．（3）如图2，连接AB，若点P是线段OE上的一动点，过点P作线段AB的垂线，分别与线段AB、抛物线相交于点M、N（点M、N都在抛物线对称轴的右侧），当MN最大时，求△PON的面积．6．已知：m，n是方程x2﹣6x+5＝0的两个实数根，且m＜n，抛物线y＝﹣x2+bx+c的图象经过点A（m，0），B（0，n）．（1）求这个抛物线的解析式；（2）设（1）中的抛物线与x轴的另一交点为C，抛物线的顶点为D，试求出点C，D的坐标和△BCD的面积．7.已知二次函数y＝﹣x2+bx+c（b，c均为常数）的图象经过两点A（2，0），B（0，﹣6）．（1）求这个二次函数的解析式；（2）若点C（m，0）（m＞2）在这个二次函数的图象上，连接AB，BC，求△ABC的面积．9.如图，二次函数与一次函数交于顶点和点两点，一次函数与轴交于点.（1）求二次函数和一次函数的解析式；（2）轴上存在点使的面积为9，求点的坐标.类型三三角形面积的最值问题例3．如图，在平面直角坐标系中，平行四边形ABOC如图放置，将此平行四边形绕点O顺时针旋转90°得到平行四边形A′B′OC′．抛物线y＝﹣x2+2x+3经过点A、C、A′三点．（1）求A、A′、C三点的坐标；（2）求平行四边形ABOC和平行四边形A′B′OC′重叠部分△C′OD的面积；（3）点M是第一象限内抛物线上的一动点，问点M在何处时，△AMA′的面积最大？最大面积是多少？并写出此时M的坐标．针对训练1.如图，已知抛物线y＝﹣x2+bx+c与一直线相交于A（1，0）、C（﹣2，3）两点，与y轴交于点N，其顶点为D．（1）求抛物线及直线AC的函数关系式；（2）若P是抛物线上位于直线AC上方的一个动点，求△APC的面积的最大值及此时点P的坐标；（3）在对称轴上是否存在一点M，使△ANM的周长最小．若存在，请求出M点的坐标和△ANM周长的最小值；若不存在，请说明理由．2.如图1，已知抛物线y=ax2+bx+c（a≠0）与x轴交于A（-1，0）、B（4，0）两点，与y轴交于点C（0，2），点P是抛物线上的一个动点，过点P作PQ⊥x轴，垂足为Q，交直线BC于点D．（1）求该抛物线的函数表达式；（2）若以P、D、O、C为顶点的四边形是平行四边形，求点Q的坐标；（3）如图2，当点P位于直线BC上方的抛物线上时，过点P作PE⊥BC于点E，设△PDE的面积为S，求当S取得最大值时点P的坐标，并求S的最大值．3.已知：抛物线y＝ax2+bx+c与x轴交于A、B两点（点A在点B的左边），与y轴交于点C，直线y＝﹣x+3经过B、C两点（1）填空：b＝（用含有a的代数式表示）；（2）若a＝﹣1①点P为抛物线上一动点，过点P作PM∥y轴交直线y＝﹣x+3于点M，当点P在第一象限内时，是否存在一点P，使△PCB面积最大？若存在，求出点P的坐标；若不存在，请说明理由．②当m≤x≤m+3时，y的取值范围是2m≤y≤4，求m的值．4．如图，直线AB和抛物线的交点是A(0，﹣3)，B(5，9)，已知抛物线的顶点D的横坐标是2．(1)求抛物线的解析式及顶点坐标；(2)在x轴上是否存在一点C，与A，B组成等腰三角形？若存在，求出点C的坐标，若不在，请说明理由；(3)在直线AB的下方抛物线上找一点P，连接PA，PB使得△PAB的面积最大，并求出这个最大值．5.如图，已知，二次函数的图像交轴正半轴于点，顶点为，一次函数的图像交轴于点，交轴于点，的正切值为.（1）求二次函数的解析式与顶点坐标；（2）将二次函数图像向下平移个单位，设平移后抛物线顶点为，若，求的值.6.如图，已知抛物线的对称轴是直线x=3，且与x轴相交于A，B两点（B点在A点右侧）与y轴交于C点．（1）求抛物线的解析式和A、B两点的坐标；（2）若点P是抛物线上B、C两点之间的一个动点（不与B、C重合），则是否存在一点P，使△PBC的面积最大．若存在，请求出△PBC的最大面积；若不存在，试说明理由；（3）若M是抛物线上任意一点，过点M作y轴的平行线，交直线BC于点N，当MN=3时，求M点的坐标．7.在平面直角坐标系xOy中，抛物线y=-x2+bx+c经过点A、B、C，已知A（-1，0），C（0，3）．(1)求抛物线的表达式；(2)如图1，P为线段BC上一点，过点P作y轴平行线，交抛物线于点D，当△BCD的面积最大时，求点P 的坐标；(3)如图2，抛物线顶点为E，EF⊥x轴于F点，N是线段EF上一动点，M（m，0）是x轴上一动点，若∠MNC=90°，直接写出实数m的取值范围．8.已知抛物线y＝x2﹣2mx+m2﹣3（m是常数）．（1）证明：无论m取什么实数，该抛物线与x轴都有两个交点；（2）设抛物线的顶点为A，与x轴两个交点分别为B，D，B在D的右侧，与y轴的交点为C．①求证：当m取不同值时，△ABD都是等边三角形；②当|m|≤，m≠0时，△ABC的面积是否有最大值，如果有，请求出最大值，如果没有，请说明理由．9.如图，抛物线与x轴交与A(1,0),B(- 3，0)两点.⑴求该抛物线的解析式；⑵设⑴中的抛物线交y轴与C点，在该抛物线的对称轴上是否存在点Q，使得△QAC的周长最小？若存在，求出Q点的坐标；若不存在，请说明理由.⑶在抛物线上BC段是否存在点P，使得△PBC面积最大，若存在，求P点坐标；若不存在，说明理由.10.如图，在平面直角坐标系中，抛物线y＝ax2＋bx＋3与x轴交于A(－4，0)、B(－1，0)两点，与y轴交于点C，点D是第三象限的抛物线上一动点．(1)求抛物线的表达式；(2)设点D的横坐标为m，△ACD的面积为S，求出S与m的函数关系式，并确定m为何值时S有最大值，最大值是多少？11．如图，已知抛物线过点A（4，0），B（﹣2，0），C（0，﹣4）．（1）求抛物线的解析式；（2）如图，点M是抛物线AC段上的一个动点，当图中阴影部分的面积最小值时，求点M的坐标．类型四以面积为条件的问题计算例4：如图1，在平面直角坐标系中，抛物线y＝ax2+bx+3与直线y＝x﹣3交于点A（3，0）和点B（﹣2，n），与y轴交于点C．（1）求出抛物线的函数表达式；（2）在图1中，平移线段AC，点A、C的对应点分别为M、N，当N点落在线段AB上时，M点也恰好在抛物线上，求此时点M的坐标；（3）如图2，在（2）的条件下，在抛物线上是否存在点P（不与点A重合），使△PMC的面积与△AMC的面积相等？若存在，直接写出点P的坐标；若不存在，请说明理由．针对训练1.如图，抛物线与轴交于点、点，与轴交于点，顶点为，，求：抛物线的解析式；若抛物线上有一点，使得直线将的面积分成相等的两部分，求点的坐标．2.如图，在直角坐标系中，O是坐标原点，直线AB交x轴于点A（﹣4，0），交y轴于点B，抛物线y=ax2+2ax+3（a≠0）经过A，B两点．P是线段AO上的一动点，过点P作PC⊥x轴交直线AB于点C，交抛物线于点D．（1）求a及AB的长．（2）连结PB，若tan∠ABP=，求点P的坐标．（3）连结BD，以BD为边作正方形BDEF，是否存在点P使点E恰好落在抛物线的对称轴上？若存在，请求出点P的坐标；若不存在，请说明理由．（4）连结OC，若S△BDC：S△OBC=1：2，将线段BD绕点D按顺时针方向旋转，得到DB′．则在旋转的过程中，当点A，B到直线DB′的距离和最大时，请直接写出点B′的坐标．3.如图，对称轴为直线x＝﹣1的抛物线y＝ax2+bx+c（a≠0）与x轴相交于A、B两点，其中点A的坐标为（﹣3，0）．（1）求点B的坐标；（2）已知a＝1，C为抛物线与y轴的交点，若点P在抛物线上，且S△POC＝4S△BOC．求点P的坐标．4．在平面直角坐标系中，抛物线与轴的两个交点分别为A（-3，0）、B（1，0），与y轴交于点D(0，3)，过顶点C作CH⊥x轴于点H.（1）求抛物线的解析式和顶点C的坐标；（2）连结AD、CD，若点E为抛物线上一动点（点E与顶点C不重合），当△ADE与△ACD面积相等时，求点E的坐标；（3）若点P为抛物线上一动点（点P与顶点C不重合），过点P向CD所在的直线作垂线，垂足为点Q，以P、C、Q为顶点的三角形与△ACH相似时，求点P的坐标.5.如图，二次函数y=x2+bx+c的图象交x轴于A，D两点，并经过B点，对称轴交x轴于点C，连接BD，BC，已知A点坐标是（2，0），B点的坐标是（8，6）（1）求二次函数的解析式．（2）求该函数图象的顶点坐标及D点的坐标．（3）抛物线上有一个动点P，与A，D两点构成△ADP，是否存在S△ADP=S△BCD？若存在，直接写出所有符合条件的点P的坐标；若不存在．请说明理由．6.如图，已知二次函数的图象经过点A(4,0)，与y轴交于点B．在x轴上有一动点C(m,0)(0<m<4)，过点C作x轴的垂线交直线AB于点E，交该二次函数图象于点D．（1）求a的值和直线AB的解析式；（2）过点D作DF⊥AB于点F，设△ACE，△DEF的面积分别为S1，S2，若S1=4S2，求m的值；（3）点H是该二次函数图象上位于第一象限的动点，点G是线段AB上的动点，当四边形DEGH是平行四边形，且周长取最大值时，求点G的坐标．7.已知二次函数y=ax2+bx+c的图象对称轴为x=，图象交x轴于A，B，交y轴于C（0，-3），且AB=5，直线y=kx+b（k＞0）与二次函数图象交于M，N（M在N的右边），交y轴于P．（1）求二次函数图象的解析式；（2）若b=-5，且△CMN的面积为3，求k的值；（3）若b=-3k，直线AN交y轴于Q，求的值或取值范围．8.已知抛物线y＝﹣x2﹣（m+3）x+m2﹣12与x轴交于A（x1，0）、B（x2，0）两点，且x1＜0，x2＞0，抛物线与y轴交于点C，OB＝2OA．（1）求抛物线解析式；（2）已知直线y＝x+2与抛物线相交于M、N两点，分别过M、N作x轴的垂线，垂足为M1、N1，是否存在点P，同时满足如下两个条件：①P为抛物线上的点，且在直线MN上方；②:＝6：35若存在，则求点P横坐标t，若不存在，说明理由．9.如图，在直角坐标系中，抛物线经过点A（0，4），B（1，0），C（5，0）（1）求抛物线的解析式和对称轴；（2）在抛物线的对称轴上是否存在一点P，使△P AB的周长最小？若存在，请求出点P的坐标；若不存在，请说明理由；（3）该抛物线有一点D（x，y），使得S△ABC＝S△DBC，求点D的坐标．10.如图1，抛物线y＝﹣x2+bx+c经过点A（2，0），B（0，2），与x轴交于另一点C．（1）求抛物线的解析式及点C的坐标；（2）点P是抛物线y＝﹣x2+bx+c在第一象限上的点，过点P分别向x轴、y轴作垂线，垂足分别为D，E，求四边形ODPE的周长的最大值；（3）如图2，点P是抛物线y＝﹣x2+bx+c在第一象限上的点，过点P作PN⊥x轴，垂足为N，交AB于M，连接PB，P A．设点P的横坐标为t，当△ABP的面积等于△ABC面积的时，求t的值．。

二次函数和一次函数交点问题

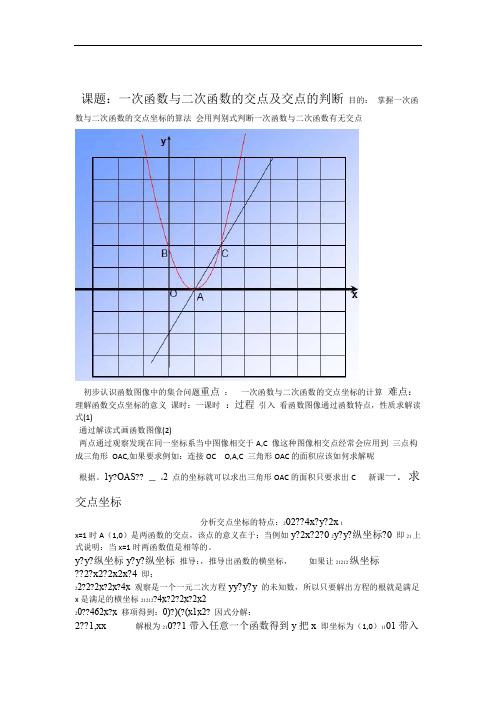
课题：一次函数与二次函数的交点及交点的判断目的：掌握一次函数与二次函数的交点坐标的算法会用判别式判断一次函数与二次函数有无交点初步认识函数图像中的集合问题重点：一次函数与二次函数的交点坐标的计算难点：理解函数交点坐标的意义课时：一课时：过程引入看函数图像通过函数特点，性质求解读式(1)通过解读式画函数图像(2)两点通过观察发现在同一坐标系当中图像相交于A,C 像这种图像相交点经常会应用到三点构成三角形OAC,如果要求例如：连接OC O,A,C 三角形OAC的面积应该如何求解呢根据。

1y?OAS??c2点的坐标就可以求出三角形OAC的面积只要求出C新课一．求交点坐标分析交点坐标的特点：202??4x?y?2x1x=1时A（1,0）是两函数的交点，该点的意义在于：当例如y?2x?2?02y?y?纵坐标?0即21上式说明：当x=1时两函数值是相等的。

y?y?纵坐标y?y?纵坐标推导：，推导出函数的横坐标，如果让21212纵坐标??2?x2?2x2x?4即：22?2?2x?2x?4x观察是一个一元二次方程yy?y?y的未知数，所以只要解出方程的根就是满足x是满足的横坐标21212?4x?2?2x?2x220??462x?x移项得到：0)?)(?(x1x2?因式分解：2??1,xx解根为210??1带入任意一个函数得到y把x即坐标为（1,0）1101带入任意一个函数得到y?把x?即坐标为（2,2）11由此得到交点坐标的方法：?>0（两个交点）1：令两函数值相等（解读式等）??=0（一个交点）：2?<0（无交点）3：解出等式的未知数x4：把未知数x的值带入两函数任意一个（一般是一次函数）5：写出交点坐标（x，y）二．练习121??2y?xx1y?x?12解：2y?y1??x?x2x?1令即212?x?x?1,解方程：211???2,y?x?1,x?2y带入上述函数的到把2211-1）（-2，1,2即交点坐标为（）练习22?3xx?4y?1y??x?1得交点求2解：2yy?1?4??xx?3x?即令21解方程：无解y?y也就是没有交点分析：无解说明没有x能满足21如何能在不计算的情况判断函数有无交点。

中考数学复习考点知识与题型专题讲义16--- 二次函数与不等式(组)(提高篇)

中考数学复习考点知识与题型专题讲义16 二次函数与不等式（组）（提高篇）1．关于x的二次函数y1＝kx2+（2k﹣1）x﹣2（k为常数）和一次函数y2＝x+2．（1）求证：函数y1＝kx2+（2k﹣1）x﹣2的图象与x轴有交点．（2）已知函数y1的图象与x轴的两个交点间的距离等于3，①试求此时k的值；②若y1＞y2，试求x的取值范围．【分析】（1）证明△＝b2﹣4ac≥0，便可得结论；（2）①函数y1的图象与x轴的两个交点间的距离等于3，根据根与系数的关系列出k的方程，便可求解；②分k＝1和k=−15两种情况，依据y1＞y2列出关于x的不等式，解之可得．【解答】解：（1）∵△＝（2k﹣1）2+8k＝4k2﹣4k+1+8k＝4k2+4k+1＝（2k+1）2≥0，∴函数y1＝kx2+（2k﹣1）x﹣2的图象与x轴有交点；（2）①设kx2+（2k﹣1）x﹣2＝0的两根为x1，x2，则x1+x2=−2k−1k，x1x2=−2k，∴(x1−x2)2=(x1+x2)2−4x1x2=(2k+1)2k2，∵函数y1的图象与x轴的两个交点间的距离等于3，∴|x1﹣x2|＝3，∴(2k+1)2k2=32，解得，k＝1或k=−1 5；②当k＝1时，y1＝（x+2）（x﹣1），y2＝x+2∵y1＞y2，∴（x+2）（x﹣1）＞x+2，即（x+2）（x﹣2）＞0，解得：x＜﹣2或x＞2；当k=−15时，∵y1＞y2，∴−15（x+2）（x+5）＞x+2，即（x+2）（x+10）＜0，解得：﹣10＜x＜﹣2．【点评】本题主要考查二次函数与不等式组及二次函数与x轴的交点，熟练掌握二次函数的图象和性质是解题的关键．2．已知二次函数y1=−12x2+bx+c（b，c是常数）与一次函数y2＝kx+c（k是常数，k≠0）．（1）若y1的图象与x轴只有一个交点（2，0），求b，c的值；（2）若y1的图象可由抛物线y＝ax2+2c（a是常数，a≠0）向左平移2个单位，向上平移1个单位得到，求出y1的函数关系式；（3）若k+b＝3，当x≥2时，y1＜y2恒成立，求k的取值范围．【分析】（1）抛物线的对称轴x=−b2a=b＝2，当x＝2时，y1＝0，即可求解；（2）由平移的性质即可求解；（3）两个函数交点的横坐标为2或2b﹣2k，当x≥2时，y1＜y2恒成立，即：2b﹣2k≥2，即可求解．【解答】解：（1）抛物线的对称轴x=−b2a=b＝2，当x＝2时，y1=−12x2+bx+c＝﹣2+4+c＝0，解得：c＝﹣2，故b＝2，c＝﹣2；（2）由题意得：a=−12，则y=−12（x+2）2+2c+1=−12x2﹣2x+2c﹣1=−12x2+bx+c，故2c﹣1＝c，解得：c＝1，故抛物线的表达式为：y=−12x2﹣2x+1；（3）联立两个函数的表达式并整理得：x2＝2b﹣2kx，解得：x＝0或2b﹣2k，又∵k+b＝3，故两个函数的交点的横坐标为0或6﹣4k，当6﹣4k≤0时，即k≥1.5时，恒有y1＜y2；当0＜k＜1.5时，6﹣4k≤2，即1≤k＜1.5；当k＜0时，6﹣4k≤2，解得k≥1，故无解；当k＝1时，b＝2，当x＝2时，有y1＝y2，综上，k＞1．【点评】本题考查的是二次函数综合运用，涉及到一次函数、图形的平移、解不等式等，有一定的综合性，难度适中．3．如图，抛物线y1＝ax2+c的顶点为M，且抛物线与直线y2＝kx+1相交于A、B两点，且点A在x 轴上，点B的坐标为（2，3），连结AM、BM．（1）a＝1，c＝﹣1，k＝1（直接写出结果）；（2）当y1＜y2时，则x的取值范围为﹣1＜x＜2（直接写出结果）；（3）在直线AB下方的抛物线上是否存在一点P，使得△ABP的面积最大？若存在，求出△ABP 的最大面积及点P坐标．【分析】（1）将点B的坐标（2，3）代入y2＝kx+1求得k值；再令y2＝0，可求得点A的坐标；将A（﹣1，0）、B（2，3）代入y1＝ax2+c，解方程组可求得a和c的值；（2）由A（﹣1，0）、B（2，3），结合函数图象可得答案；（3）如图，设平行于直线y2＝x+1的直线解析式为：y3＝x+b，则该直线与抛物线在第四象限相切时，△ABP的面积最大，由一元二次方程的根的判别式可求得b值，从而可得点P坐标及y3＝x+b 的解析式，从y3＝x+b与x轴的交点C向直线y2＝kx+1作垂线段CD，在等腰直角三角形△ACD 中，可求得CD的长；求得AB的长，利用三角形的面积公式，可得答案．【解答】解：（1）将点B的坐标（2，3）代入y2＝kx+1得：3＝2k+1解得：k＝1∴y2＝x+1令y2＝0得：0＝x+1解得：x＝﹣1∴A（﹣1，0）将A（﹣1，0）、B（2，3）代入y1＝ax2+c得：{0=a+c3=4a+c解得：a＝1，c＝﹣1故答案为：1，﹣1，1；（2）∵A （﹣1，0）、B （2，3）∴结合图象可得：当y 1＜y 2时，则x 的取值范围为﹣1＜x ＜2故答案为：﹣1＜x ＜2；（3）在直线AB 下方的抛物线上存在一点P ，使得△ABP 的面积最大．如图，设平行于直线y 2＝x +1的直线解析式为：y 3＝x +b由{y 2=x 2−1y 3=x +b得：x 2﹣1＝x +b ∴x 2﹣x ﹣1﹣b ＝0令△＝0得：1﹣4（﹣1﹣b ）＝0解得：b =−54∴y 3＝x −54，∴x 2﹣x ﹣1+54=0解得：x 1＝x 2=12∴P （12，−34） ∴当点P 坐标为（12，−34）时，△ABP 的面积最大设y 3＝x −54与x 轴交于点C ，则点C 坐标为：（54，0），过点C 作CD ⊥AB 由平行线间的距离处处相等，可知线段CD 的长度即为△ABP 的高的长度∵y 2＝x +1与x 轴所成锐角为45°∴△ACD 为等腰直角三角形∵AC =54−（﹣1）=94∴CD =√2=94√2=9√28 ∵A （﹣1，0）、B （2，3）∴AB =√(2+1)2+32=3√2∴△ABP 的面积为：12×3√2×9√28=278∴在直线AB 下方的抛物线上存在一点P ，使得△ABP 的面积最大；△ABP 的最大面积为278；点P坐标为（12，−34）．【点评】本题考查了求一次函数、二次函数的解析式中的相关字母、构成的三角形的面积最大值的动点的存在性、二次函数与不等式的关系、抛物线与直线的交点个数与一元二次方程的实数根的关系等知识点，具有一定的综合性与难度．4．已知在同一平面直角坐标系中有函数y 1＝ax 2﹣2ax +b ，y 2＝﹣ax +b ，其中ab ≠0．（1）求证：函数y 2的图象经过函数y 1的图象的顶点；（2）设函数y 2的图象与x 轴的交点为M ，若点M 关于y 轴的对称点M '在函数y 1图象上，求a ，b 满足的关系式；（3）当﹣1＜x ＜1时，比较y 1与y 2的大小．【分析】（1）将函数y 1的解析式配方，即可找出其顶点坐标，将顶点坐标代入函数y 2的解析式中，即可证得结论；（2）设函数y 2的图象与x 轴的交点M （m ，0），则点M 关于y 轴的对称点M '（﹣m ，0），根据图象上点的坐标特征得出{−am +b =0am 2+2am +b =0，解得b ＝﹣3a ；（3）两函数解析式做差，即可得出y 1﹣y 2＝ax （x ﹣1），根据x 的取值范围可得出x （x ﹣1）的符号，分a ＞0或a ＜0两种情况考虑，即可得出结论．【解答】解：（1）证明：∵y 1＝ax 2﹣2ax +b ＝a （x ﹣1）2﹣a +b ，∴函数y 1的顶点为（1，﹣a +b ），把x ＝1代入y 2＝﹣ax +b 得，y ＝﹣a +b ，∴函数y 2的图象经过函数y 1的图象的顶点；（2）设函数y 2的图象与x 轴的交点M （m ，0），则点M 关于y 轴的对称点M '（﹣m ，0），由题意可知{−am +b =0am 2+2am +b =0，解得b ＝﹣3a ；（3）∵y 1＝ax 2﹣2ax +b ，y 2＝﹣ax +b ，∴y 1﹣y 2＝ax （x ﹣1）．∵﹣1＜x ＜1，∴当﹣1＜x ＜0，x （x ﹣1）＞0．当0＜x ＜1，x （x ﹣1）＜0，当x ＝0，x （x ﹣1）＝0， ∴y 1＝y 2；当a ＞0且﹣1＜x ＜0时，ax （x ﹣1）＞0，y 1＞y 2；当a ＞0且0＜x ＜1时，ax （x ﹣1）＜0，y 1＜y 2；当a ＜0且﹣1＜x ＜0时，ax （x ﹣1）＜0，y 1＜y 2；当a ＜0且0＜x ＜1时，ax （x ﹣1）＞0，y 1＞y 2．【点评】本题考查了二次函数的图象上点的坐标特征，二次函数的性质，分类讨论是解题的关键．5．已知抛物线C ：y 1＝﹣x 2+bx +4．（1）如图，抛物线与x 轴相交于两点（1﹣m ，0）、（1+m ，0）．①求b 的值；②当n ≤x ≤n +1时，二次函数有最大值为3，求n 的值．（2）已知直线l ：y 2＝2x ﹣b +9，当x ≥0时，y 1≤y 2恒成立，求b 的取值范围．【分析】（1）﹣x2+bx+4＝0，x1+x2=b−1=1﹣m+1+m＝2，b＝2；（2）分n+1≤1即n≤0、n≤1≤n+1即0≤n≤1、iii：n≥1三种情况，分别求解即可；（3）①：△≤0，（2﹣b）2﹣4（5﹣b）≤0；②：△＞0，则b＞4或b＜﹣4，即可求解．【解答】解：（1）﹣x2+bx+4＝0x1+x2=b−1=1﹣m+1+m＝2，b＝2；（2）抛物线开口向下，对称轴左侧y随x的增大而增大；对称轴右侧，y随x的增大而减小．i：n+1≤1即n≤0，当x＝n+1时，y有最大值，﹣（n+1）2+2（n+1）+4＝3，n=±√2，又∵n≤0，∴n=−√2，ii：n≤1≤n+1即0≤n≤1，当x＝1时y有最大值，﹣12+2＜1+4＝3不成立，iii：n≥1时，当x＝n时，y有最大值，﹣n2+2n+4＝3，解得n＝1±√2，又∵n≥1，∴n=1+√2，综上所述：n=−√2或n=1+√2；（3）y1≤y2，﹣x2+bx+4≤2x﹣b+9，x2+（2﹣b）x+5﹣b≥0，①：△≤0，（2﹣b）2﹣4（5﹣b）≤0，﹣4≤b≤4；②：△＞0则b＞4或b＜﹣4，i：−2−b2＞0，不成立，ii：{−2−b2≤05−b≥0，b≤2，又∵b＞4或b＜﹣4，∴b＜﹣4，综上所述b≤4．【点评】本题考查的是抛物线与x轴的交点，主要考查函数图象上点的坐标特征，要求学生非常熟悉函数与坐标轴的交点、顶点等点坐标的求法，及这些点代表的意义及函数特征．6．如图，已知直线y1＝﹣x+3与x轴交于点B，与y轴交于点C，抛物y2＝ax2+bx+c经过点B，C并与x轴交于点A（﹣1，0）．（1）求抛物线解析式，并求出抛物线的顶点D坐标（1，4）；（2）当y2＜0时、请直接写出x的取值范围x＜﹣1或x＞3；（3）当y1＜y2时、请直接写出x的取值范围0＜x＜3；（4）将抛物线y2向下平移，使得顶点D落到直线BC上，求平移后的抛物线解析式y＝x2+2x+1．【分析】（1）列方程得到C（0，3），B（3，0），设抛物线解析式为y＝a（x+1）（x﹣3），列方程即可得到结论；（2）由图象即可得到结论；（3）由图象即可得到结论；（4）当根据平移的性质即可得到结论．【解答】解：（1）对于y1＝﹣x+3，当x＝0时，y＝3，∴C（0，3），当y＝0时，x＝3，∴B（3，0），∵抛物线与x轴交于A（﹣1，0）、B（3，0）两点，设抛物线解析式为y＝a（x+1）（x﹣3），抛物线过点C（0，3），∴3＝a（0+1）（0﹣3），解得：a＝1，∴y＝（x+1）（x﹣3）＝x+2x+3，∴顶点D（1，4）；（2）由图象知，当y2＜0时、x的取值范围为：x＜﹣1或x＞3；（3）由图象知当y1＜y2时、x的取值范围为：0＜x＜3；（4）当x＝1时，y＝﹣1+3＝2，∵抛物线向下平移2个单位，∴抛物线解析式为y＝﹣x2+2x+3﹣2＝﹣x2+2x+1．故答案为：（1）（1，4）；（2）x＜﹣1或x＞3；（3）0＜x＜3；（4）y＝﹣x2+2x+1．【点评】本题考查了二次函数的性质，待定系数法取函数的解析式，正确的理解题意是解题的关键．7．如图，已知抛物线y1＝ax2+k经过点（﹣2，﹣2）和（0，2）（1）求y1的解析式；（2）直接写出：抛物线y1向右平移一个单位，当y1＞y2时，自变量x的取值范围为x＜12．【分析】（1）依题意得：k＝2，将点（﹣2，﹣2）代入函数表达式得：﹣2＝4a+2，解得：a＝﹣1，即可求解；（2）y2＝﹣（x﹣1）2+2，联立①②并解得：x=12，即可求解．【解答】解：（1）依题意得：k＝2，将点（﹣2，﹣2）代入函数表达式得：﹣2＝4a+2，解得：a＝﹣1，故抛物线的表达式为：y1＝﹣x2+2…①；（2）y2＝﹣（x﹣1）2+2…②，联立①②并解得：x=1 2，从图象可以看出，当y1＞y2时，自变量x的取值范围为：x＜1 2；故答案为：x＜1 2．【点评】本题考查的是二次函数与不等式（组），主要要求学生通过观察函数图象的方式来求解不等式．8．已知二次函数y＝﹣x2+4x+m．（1）如果二次函数的图象与x轴有两个交点，求m的取值范围；（2）如图，二次函数的图象过点A（6，0），与y轴交于点B，点P是二次函数对称轴上的一个动点，当PB+P A的值最小时，求P的坐标；（3）在（2）的条件下，根据图象直接写出使一次函数值大于二次函数值的x的取值范围．【分析】（1）由抛物线与x轴有两个交点可知△＞0，从而得到关于m的不等式，然后求得不等式的解集即可；（2）连结AB，与对称轴交于点P，此时PB+P A最小．根据抛物线解析式求出B（0，12），利用待定系数法求出直线AB的解析式，于是得到结论；（3）根据图象即可求得使一次函数值大于二次函数值的x的取值范围．【解答】解：（1）∵二次函数的图象与x轴有两个交点，∴△＝42+4m＞0．解得：m＞﹣4．（2）连结AB，与对称轴交于点P，此时PB+P A最小．把（6，0）代入y ＝﹣x 2+4x +m ，得﹣62+4×6+m ＝0．解得m ＝12．故该抛物线解析式是y ＝﹣x 2+4x +12当x ＝0时，y ＝12，则B （0，12）．设直线AB 的解析式为y ＝mx +n ，∵A （6，0），B （0，12），∴{6m +n =0n =12，解得∴{m =−2n =12， ∴直线AB 的解析式为y ＝﹣2x +12，∵y ＝﹣x 2+4x +12＝﹣（x ﹣2）2+16，∴对称轴是直线x ＝2．把x ＝2代入y ＝﹣2x +12得，y ＝﹣4+12＝8，∴P （2，8）；（3）∵A （6，0），B （0，12），使一次函数值大于二次函数值的x 的取值范围是x ＜0或x ＞6．【点评】本题是二次函数综合题，其中涉及到二次函数与不等式，二次函数的性质，函数图象上点的坐标特征，轴对称﹣最短路线问题等知识，利用数形结合是解题的关键．9．如图，一次函数y ＝﹣2x +6的图象与y 轴交于A 点，与x 轴交于B 点，二次函数y ＝﹣x 2+bx +c 的图象经过A 、B 两点．（1）求二次函数的解析式；（2）根据图象直接写出当x 取何值时，﹣2x +6＞﹣x 2+bx +c ＞0；（3）点P 是抛物线在第一象限上的一个动点，是否存在点P ，使△ABP 面积最大，若存在，求出此时点P 坐标以及△ABP 面积，若不存在，请说明理由．【分析】（1）先求出一次函数y ＝﹣2x +6与y 轴、x 轴交点A 、B 的坐标，再用待定系数法求出二次函数的解析式；（2）观察图象直接得到答案；（3）过点P 作y 轴的平行线PQ 交AB 于点Q ，先利用图象上点的特征表示出P 、Q 两点的坐标，再求出PQ 的长，进而表示出△ABP 的面积，利用顶点坐标求最值．【解答】解：∵一次函数y ＝﹣2x +6的图象与y 轴交于A 点，与x 轴交于B 点，∴A （0，6），B （3，0），∵二次函数y ＝﹣x 2+bx +c 的图象经过A 、B 两点，∴{c =6−9+3b +c =0，解得：{b =1c =6， ∴二次函数的解析式的解析式为：y ＝﹣x 2+x +6；（2）当y ＝0时，﹣x 2+x +6＝0，解得x 1＝﹣2，x 2＝3，∴抛物线与x 轴交点坐标为（﹣2，0），（3，0），当﹣2＜x ＜0或x ＞3时，﹣2x +6＞﹣x 2+bx +c ，但只有当﹣2＜x ＜0时，﹣2x +6＞﹣x 2+bx +c ＞0，当﹣2＜x ＜0时，﹣2x +6＞﹣x 2+bx +c ＞0；（3）过点P 作y 轴的平行线PQ 交AB 于点Q ，由点P在y＝﹣x2+x+6的图象上，可设P（m，﹣m2+m+6）（0＜m＜3），则Q（m，﹣2m+6），则PQ＝﹣m2+m+6+2m﹣6＝﹣m2+3m，∴S△ABP=12OB×PQ=12×3×（﹣m2+3m）=−32（m−32）2+278，∵﹣2＜0，∴当m=32时，即P点坐标为（32，214）时，S△ABP取得最大值，最大值为278．【点评】本题考查了用待定系数法求二次函数解析式、二次函数与坐标轴的交点问题、二次函数与不等式组、二次函数的最值问题，观察图象、求出特殊点坐标是解题的关键．10．如图，二次函数y＝x2﹣4x+3与一次函数y＝x﹣1的图象交于点A及点B，与y轴交于点C．（1）求点A、B、C的坐标；（2）根据图象，直接写出满足x﹣1≥x2﹣4x+3的x的取值范围；（3）在抛物线的对称轴上是否存在一点P，使得P A+PC最小，求点P坐标及P A+PC的最小值．【分析】（1）根据题意解方程组即可得到结论；（2）根据函数图象点A以及点A右边的部分，点B以及点B左边的部分的自变量x的取值范围即为不等式的解集；（3）根据点B 是点C 关于该二次函数图象的对称轴对称的点，于是得到直线AB 与对称轴的交点即为点P ，P A +PC 最小值＝AB ，根据勾股定理得到AB ，把x ＝2代入y ＝x ﹣1即可得到结论．【解答】解：（1）在y ＝x 2﹣4x +3中，令x ＝0，得y ＝3，∴C （0，3），解{y =x 2−4x +3y =x −1得，{x =1y =0，{x =4y =3， ∴A （1，0），B （4，3）；（2）由图象可知，满足kx +b ≥x 2﹣4x +m 的x 的取值范围为：1≤x ≤4；（3）存在，∵点B 是点C 关于该二次函数图象的对称轴对称的点，∴直线AB 与对称轴的交点即为点P ，则P A +PC 最小值＝AB ，∴AB =√(4−1)2+(3)2=3√2，把x ＝2代入y ＝x ﹣1得，y ＝1，∴P （2，1），P A +PC 最小值＝3√2．【点评】本题考查了二次函数与不等式（组），待定系数法求二次函数解析式，待定系数法求一次函数解析式，轴对称的性质，难点在于求出点B 的坐标．11．直线y 1＝x +m 与抛物线y 2＝ax 2+bx +c 交于P 、Q （2，3）两点，其中P 在x 轴上，Q （2，3）是抛物线y 2的顶点．（1）求y 1与y 2的函数解析式；（2）求函数值y 1＜y 2时x 的取值范围．【分析】（1）先求出Q 点的坐标，再求出直线的解析式，再把Q 、P 的坐标代入二次函数的解析式求出a 的值即可；（2）根据函数的性质和交点坐标得出即可．【解答】解：（1）把点Q（2，3）代入y＝x+m，∴3＝2+m，∴m＝1，∴y1＝x+1，∴令y＝0，x+1＝0，∴x＝﹣1，∴P（﹣1，0），∴顶点为（2，3），∴设抛物线y＝a（x﹣2）2+3，把P（﹣1，0）代入得：0＝a（﹣1﹣2）2+3，解得：a=−1 3，∴y2=−13(x−3)2+3，即y=−13x2+43x+53；（2）∵直线y1＝x+1与抛物线y2=−13（x﹣3）2+3交于P（﹣1，0）、Q（2，3）两点，∴函数值y1＜y2时x的取值范围是﹣1＜x＜2．【点评】本题考查了一次函数与二次函数的交点问题，一次函数和二次函数的图象和性质，用待定系数法求一次函数与二次函数的解析式等知识点，能求出两函数的解析式是解此题的关键．12．已知抛物线y＝x2+（1﹣3m）x﹣3m，（−14＜m≤2）．直线l：y＝（k+1）x﹣3m+4．（1）若该抛物线与y轴交点的纵坐标为﹣4，求该抛物线的顶点坐标．（2）证明：该抛物线与直线l必有两个交点．（3）若该抛物线经过点（t，﹣4），且对任意实数x，不等式x2+（1﹣3m）x﹣3m≥﹣4都成立；当k﹣2≤x≤k时，该二次函数的最小值为﹣2k+1．求直线l的解析式．【分析】（1）依题意可知﹣3m＝﹣4，即可求解；（2）将y＝（k+1）x﹣3m+4代入y＝x2+（1﹣3m）x﹣3m，整理得：x2﹣（k+3m）x﹣4＝0，△＝[﹣（k+3m）]2﹣4×（﹣4）＝（k+3m）2+16＞0，即可求解；（3）分k＜1、1≤k≤3、k＞3三种情况，分别求解即可．【解答】解：（1）依题意可知﹣3m＝﹣4，解得：m=4 3，∴该抛物线对应的函数解析式为y=x2−3x−4=(x−32)2−254，∴该抛物线的顶点坐标为（32，−254）．（2）联立y＝（k+1）x﹣3m+4和y＝x2+（1﹣3m）x﹣3m并整理得：x2﹣（k+3m）x﹣4＝0，∵△＝[﹣（k+3m）] 2﹣4×（﹣4）＝（k+3m）2+16＞0，∴该抛物线与直线l必有两个交点．（3）∵由抛物线经过点（t，﹣4），且对任意实数x，不等式x2+（1﹣3m）x﹣3m≥﹣4都成立，∴抛物线y＝x2+（1﹣3m）x﹣3m的最小值为﹣4，∵y＝x2+（1﹣3m）x﹣3m=(x+1−3m2)2−3m−(1−3m2)2=(x+1−3m2)2−9m2+6m+14，∴−9m2+6m+14=−4，整理得3m2+2m﹣5＝0，解得m＝1或m=−53（−53＜−14，舍去），∴当m＝1时，抛物线的解析式为y＝x2﹣2x﹣3＝（x﹣1）2﹣4，①当k＜1时，函数值y随x的增大而减小，∴当x＝k时，y min＝k2﹣2k﹣3，∴k2﹣2k﹣3＝﹣2k+1，解得k＝﹣2或k＝2（舍去），∴直线l的解析式为y＝﹣x+1；②当k﹣2≤1≤k时，即1≤k≤3，当x＝1时，y min＝﹣4＝﹣2k+1，解得k=5 2，∴直线l的解析式为y=72x+1；③当k﹣2＞1时，函数值y随x的增大而增大，∴当x＝k﹣2时，y min＝（k﹣2）2﹣2（k﹣2）﹣3，∴（k﹣2）2﹣2（k﹣2）﹣3＝﹣2k+1，解得k1＝k2＝2（舍去），综上，直线l的解析式为y＝﹣x+1或y=72x+1．【点评】本题考查的是二次函数与不等式（组）和待定系数法求二次函数解析式，解题的关键是确定函数图象的交点，根据交点处图象之间的位置关系，确定不等式的解集．13．如图，二次函数y＝（x+2）2+m的图象与y轴交于点C，点B在抛物线上，且与点C关于抛物线的对称轴对称，已知一次函数y＝kx+b的图象经过该二次函数图象上的点A（﹣1，0）及点B．（1）求二次函数与一次函数的解析式；（2）根据图象，写出满足（x+2）2+m≥kx+b的x的取值范围．【分析】（1）将点A的坐标代入二次函数解析式求出m的值，再根据二次函数解析式求出点C的坐标，然后求出点B 的坐标，最后利用待定系数法求一次函数解析式求解即可；（2）根据函数图象点A 以及点A 右边的部分，点B 以及点B 左边的部分的自变量x 的取值范围即为不等式的解集．【解答】解：（1）∵抛物线y ＝（x +2）2+m 经过点A （﹣1，0），∴0＝1+m ，∴m ＝﹣1，∴抛物线解析式为y ＝（x +2）2﹣1＝x 2+4x +3，∴点C 坐标（0，3），∵对称轴x ＝﹣2，B 、C 关于对称轴对称，∴点B 坐标（﹣4，3），∵y ＝kx +b 经过点A 、B ，∴{−k +b =0−4k +b =3，解得{k =−1b =−1， ∴一次函数解析式为y ＝﹣x ﹣1；（2）由图象可知，满足（x +2）2+m ≥kx +b 的x 的取值范围为x ≤﹣4或x ≥﹣1．【点评】本题考查了二次函数与不等式，待定系数法求二次函数解析式，待定系数法求一次函数解析式，难点在于求出点B 的坐标．14．如图，一元二次方程x 2+2x ﹣3＝0的二根x 1，x 2（x 1＜x 2）是抛物线y ＝ax 2+bx +c 与x 轴的两个交点B ，C 的横坐标，且此抛物线过点A （3，6）．（1）求此二次函数的解析式；（2）写出不等式ax 2+bx +c ≥0的解集；（3）设此抛物线的顶点为P，对称轴与线段AC相交于点Q，求点P和点Q的坐标；（4）在x轴上有一动点M，当MQ+MA取得最小值时，求M点的坐标．【分析】（1）先求出一元二次方程的两个根，即可知与x轴的两个交点的坐标，进而即可求出二次函数的解析式；（2）根据B、C两点的坐标可求出二次函数的顶点坐标及对称轴，根据A、C两点坐标可求出直线AC的解析式，再联立两个方程即可求出Q点的坐标；（3）根据两点之间线段最短，当此三点在同一条直线上时MQ+MA取得最小值，作A点关于x轴的对称点进而求得M点的坐标．【解答】解：（1）一元二次方程x2+2x﹣3＝0的二根x1，x2（x1＜x2）为：x1＝﹣3，x2＝1．∴抛物线y＝ax2+bx+c与x轴的两个交点的坐标为B（1，0），C（﹣3，0）．设二次函数的解析式为y＝a（x+3）（x﹣1），∵抛物线过点A（3，6）．∴6＝a（3+3）（3﹣1），解得a=1 2．∴二次函数的解析式为y=12（x+3）（x﹣1）=12x2+x−32．（2）根据图象可知：不等式ax2+bx+c≥0的解集为：x≤﹣3或x≥1；（3）由y=12x2+x−32．∴抛物线的顶点坐标为P（﹣1，﹣2），对称轴方程为x＝﹣1．设直线AC解析式为y＝kx+b，将A（3，6），C（﹣3，0），代入解得：k＝1，b＝3，直线AC解析式为y＝x+3．将x＝﹣1代入，得y＝2．∴Q（﹣1，2）．（4）作点A关于x轴的对称点A′（3，﹣6），连接A′Q，A′Q与x轴交于点M即为所求的点．设直线A′Q的解析式为y＝kx+b，将A′（3，﹣6），Q（﹣1，2）代入解得：k＝﹣2，b＝0．∴直线A′C的解析式为y＝﹣2x．令x＝0，则y＝0．∴M（0，0）．【点评】本题考查了二次函数的综合知识，解决本题的关键是综合运用二次函数相关知识．15．如图，二次函数y＝ax2+bx+c的图象与x轴交于A，B两点，其中点A（﹣1，0），点C（0，5），点D（1，8）都在抛物线上，M为抛物线的顶点．（1）求抛物线的函数解析式；（2）求△MCB的面积；（3）根据图形直接写出使一次函数值大于二次函数值的x的取值范围．【分析】（1）把A点、C点和D点坐标代入y＝ax2+bx+c得到关于a、b、c的方程组，然后解方程求出a、b、c即可得到抛物线解析式；（2）连接OM，如图，先把（1）中解析式配成顶点式得到M（2，9），再利用对称性得到B（5，0），然后利用S△BCM＝S△OCM+S△BOM﹣S△OBC进行计算；（3）观察函数图象，写出一次函数图象在抛物线上方所对应的自变量的范围即可．【解答】解：（1）∵A（﹣1，0），C（0，5），D（1，8）三点在抛物线y＝ax2+bx+c上，∴{a−b+c=0c=5a+b+c=8解方程组得{a=−1b=4c=5，∴抛物线的解析式为y＝﹣x2+4x+5；（2）连接OM，如图，∵y＝﹣x2+4x+5＝﹣（x﹣2）2+9，∴M（2，9），∵抛物线的对称轴为直线x＝2，∴B（5，0），∴S△BCM＝S△OCM+S△BOM﹣S△OBC=12×5×2+12×5×9−12×5×5＝15；（3）x＜0或x＞2．【点评】本题考查了二次函数与不等式（组）：利用两个函数图象在直角坐标系中的上下位置关系求自变量的取值范围，可作图利用交点直观求解，也可把两个函数解析式列成不等式求解．也考查了待定系数法求抛物线解析式．16．如图，一次函数y＝kx+b的图象与二次函数y＝﹣x2+c的图象相交于A（﹣1，2），B（2，n）两点．（1）求一次函数和二次函数的解析式；（2）根据图象直接写出使二次函数的值大于一次函数的值的x的取值范围；（3）设二次函数y＝﹣x2+c的图象与y轴相交于点C，连接AC，BC，求△ABC的面积．【分析】（1）把A坐标代入二次函数解析式求出c的值，确定出二次函数解析式，把B坐标代入求出n 的值，把A 与B 坐标代入一次函数解析式求出k 与b 的值即可；（2）根据函数图象，确定出所求x 的范围即可；（3）连接AC ，BC ，设直线AB 与y 轴交于点D ，三角形ABC 面积等于三角形ACD 面积+三角形BCD 面积，求出即可．【解答】解：（1）把A （﹣1，2）代入y ＝﹣x 2+c 得：﹣1+c ＝2，解得：c ＝3，∴y ＝﹣x 2+3，把B （2，n ）代入y ＝﹣x 2+3得：n ＝﹣1，∴B （2，﹣1），把A （﹣1，2）、B （2，﹣1）分别代入y ＝kx +b 得{−k +b =22k +b =−1，解得：{k =−1b =1， ∴y ＝﹣x +1；（2）根据图象得：使二次函数的值大于一次函数的值的x 的取值范围是﹣1＜x ＜2；（3）连接AC 、BC ，设直线AB 交y 轴于点D ，把x ＝0代入y ＝﹣x 2+3得：y ＝3，∴C （0，3），把x ＝0代入y ＝﹣x +1得：y ＝1，∴D（0，1），∴CD＝3﹣1＝2，则S△ABC＝S△ACD+S△BCD=12×2×1+12×2×2＝1+2＝3．【点评】此题考查了二次函数与不等式，待定系数法求二次函数解析式，以及待定系数法求一次函数解析式，熟练掌握待定系数法是解本题的关键．17．如图，抛物线y1＝ax2+2ax+1与x轴有且仅有一个公共点A，经过点A的直线y2＝kx+b交该抛物线于点B，交y轴于点C，且点C是线段AB的中点．（1）求a的值；（2）求直线AB对应的函数解析式；（3）直接写出当y1≥y2时，x的取值范围．【分析】（1）根据判别式的意义得到△＝4a2﹣4a＝0，然后解方程和根据二次函数的定义可确定a 的值；（2）把抛物线的解析式配成顶点式得到A（﹣1，0），则把A点坐标代入y＝kx+b中得b＝k，所以一次函数解析式为可表示为y＝kx+k，则C（0，k），利用线段中点坐标公式得到B（1，2k），然后把B（1，2k）代入y＝x2+2x+1求出k即可得到直线AB的解析式；（3）利用函数图象，写出抛物线在直线AB上方所对应的自变量的范围即可．【解答】解：（1）∵抛物线y1＝ax2+2ax+1与x轴有且仅有一个公共点A，∴△＝4a 2﹣4a ＝0，而a ≠0，∴a ＝1；（2）抛物线的解析式为y ＝x 2+2x +1＝（x +1）2，∴A （﹣1，0），把A （﹣1，0）代入y ＝kx +b 得﹣k +b ＝0，解得b ＝k ，∴一次函数解析式为y ＝kx +k ，当x ＝0时，y ＝kx +k ＝k ，则C （0，k ），∵点C 是线段AB 的中点，∴B （1，2k ），把B （1，2k ）代入y ＝x 2+2x +1得2k ＝1+2+1，解得k ＝2，∴直线AB 的解析式为y ＝2x +2；（3）当x ≤﹣1或x ≥1时，y 1≥y 2．【点评】本题考查了二次函数与不等式（组）：利用两个函数图象在直角坐标系中的上下位置关系求自变量的取值范围，可作图利用交点直观求解，也可把两个函数解析式列成不等式求解．也考查了抛物线与x 轴的交点和二次函数的性质．18．如图，在平面直角坐标系中，已知抛物线C 1：y =32x 2+6x +2的顶点为M ，与y 轴相交于点N ，先将抛物线C 1沿x 轴翻折，再向右平移p 个单位长度后得到抛物线C 2：直线l ：y ＝kx +b 经过M ，N 两点．（1）结合图象，直接写出不等式32x 2+6x +2＜kx +b 的解集；（2）若抛物线C 2的顶点与点M 关于原点对称，求p 的值及抛物线C 2的解析式．【分析】（1）令抛物线C 1的解析式中x ＝0，求出y 值即可得出点N 的坐标，再利用配方法将抛物线C 1的解析式配方，即可得出顶点M 的坐标，结合函数图象的上下位置关系，即可得出不等式的解集；（2）找出点M 关于x 轴对称的对称点的坐标，找出点M 关于原点对称的对称点的坐标，二者横坐标做差即可得出p 的值，根据抛物线的开口大小没变，开口方向改变，再结合平移后的抛物线的顶点坐标即可得出抛物线C 2的解析式；【解答】解：（1）令y =32x 2+6x +2中x ＝0，则y ＝2，∴N （0，2）；∵y =32x 2+6x +2=32（x +2）2﹣4，∴M （﹣2，﹣4）．观察函数图象，发现：当﹣2＜x ＜0时，抛物线C 1在直线l 的下方，∴不等式32x 2+6x +2＜kx +b 的解集为﹣2＜x ＜0．（2）∵y =32x 2+6x +2抛物线C 1：的顶点为M （﹣2，﹣4），沿x 轴翻折后的对称点坐标为（﹣2，4）．∵抛物线C 2的顶点与点M 关于原点对称，∴抛物线C 2的顶点坐标为（2，4），∴p ＝2﹣（﹣2）＝4．∵抛物线C 2与C 1开口大小相同，开口方向相反，∴抛物线C 2的解析式为y =−32（x ﹣2）2+4=−32x 2+6x ﹣2．【点评】本题考查了二次函数的性质、二次函数图象上点的坐标特征、待定系数法求函数解析式以及根的判别式，解题的关键是：（1）求出M 、N 点的坐标；（2）根据点M 找出抛物线C 2的顶点坐标；19．已知二次函数y ＝ax 2+bx +c 的图象经过点（﹣2，0），且对一切实数x ，都有2x ≤ax 2+bx +c ≤12x 2+2成立．（1）当x ＝2时，求y 的值；（2）求此二次函数的表达式；（3）当x ＝t +m 时，二次函数y ＝ax 2+bx +c 的值为y 1，当x =t 2时，二次函数y ＝ax 2+bx +c 的值为y 2，若对一切﹣1≤t ≤1，都有y 1＜y 2，求实数m 的取值范围．【分析】（1）可令x ＝2，可得4≤4a +2b +c ≤4，即有4a +2b +c ＝4；（2）通过图象过一点点（﹣2，0）得到4a ﹣2b +c ＝0，由x ＝2得4a +2b +c ＝4，再将b 、c 都有a 表示．不等式2x ≤ax 2+bx +c ≤12x 2+2对一切实数x 都成立可转化成两个一元二次不等式即{ax 2−x +2−4a ⩾0(a −12)x 2+x −4a ⩽0恒成立，即可解得a =14；（3）当﹣1≤t ≤1时，y 1﹣y 2＜0，可得3t 2+（8+8m ）t +4m 2+16m ＜0 恒成立．设W ＝3t 2+（8+8m ）t +4m 2+16m ，则{3+(8+8m)+4m 2+16m ＜03−(8+8m)+4m 2+16m ＜0，由此求得t 的范围．【解答】解：（1）解：∵不等式2x ≤ax 2+bx +c ≤12x 2+2对一切实数x 都成立，∴当x ＝2时也成立，即4≤4a +2b +c ≤4，即有y ＝4；（2）根据二次函数y ＝ax 2+bx +c 的图象经过点（﹣2，0），可得4a ﹣2b +c ＝0 ①，又f （2）＝4，即4a +2b +c ＝4 ②．由①②求得 b ＝1，4a +c ＝2，∴y ＝ax 2+x +2﹣4a ，∴2x ≤ax 2+x +2﹣4a ≤12x 2+2，即{ax 2−x +2−4a ⩾0(a −12)x 2+x −4a ⩽0恒成立， ∴{ a ＞0△1=1−4a(2−4a)⩽0a −12＜0△2=1−4(a −12)⋅(−4a)⩽0，解得：a =14，∴c ＝2﹣4a ＝1，二次函数的表达式为y =14x 2+x +1．（3）∵当﹣1≤t ≤1时，y 1＜y 2，即：y 1﹣y 2＜0，即[14(t +m)2+(t +m)+1]−[14（t 2）2+t 2+1]＜0．整理得：3t 2+（8+8m ）t +4m 2+16m ＜0，∵当t ＝1或﹣1时均成立，∴{3+(8+8m)+4m 2+16m ＜03−(8+8m)+4m 2+16m ＜0，整理得：{4m 2+24m +11＜04m 2+8m −5＜0解得：{−112＜m ＜−12−52＜m ＜12，∴−52＜m＜−12【点评】本题考查了二次函数与不等式恒成立问题，以及二次函数的性质，赋值法（特殊值法）可以使问题变得比较明朗，它是解决这类问题比较常用的方法．20．二次函数y1＝ax2+2x过点A（﹣2，0）和点B，过点A，B作一次函数y2＝kx+b，若点B的横坐标为1．（1）求出二次函数与一次函数的解析式；（2）根据图象，当y2＞y1时，请直接写出x的取值范围；（3）若P点在抛物线y1上，且横坐标为﹣1，求△ABP的面积．【分析】（1）利用待定系数法求二次函数与一次函数的解析式；（2）根据图象直接写出y2＞y1时，﹣2＜x＜1；（3）过P作PQ∥y轴，交AB于Q，依据S△ABP＝S△APQ+S△BPQ进行计算即可．【解答】解：（1）如图1，把A（﹣2，0）代入y1═ax2+2x中得：4a+2×（﹣2）＝0，a＝1，∴二次函数的解析式y1═x2+2x，当x＝1时，y1＝1+2＝3，∴B（1，3），把A（﹣2，0）、B（1，3）代入y2＝kx+b中得：{−2k +b =0k +b =3，解得：{k =1b =2， ∴一次函数的解析式：y 2＝x +2；（2）由图象得：当﹣2＜x ＜1时，y 2＞y 1；（3）过P 作PQ ∥y 轴，交AB 于Q ，y 1═x 2+2x ，令x ＝﹣1，则y ＝﹣1，即P （﹣1，﹣1），y 2＝x +2，令x ＝﹣1，则y ＝1，即Q （﹣1，1），∴PQ ＝2，∴S △ABP ＝S △APQ +S △BPQ =12×2×（1+2）＝3．【点评】本题主要考查了利用待定系数法求二次函数与一次函数的解析式；采用数形结合的方式是解决第2小题的关键，第3问中需要运用割补法计算三角形的面积．。

二次函数与一次函数结合问题

二次函数与一次函数相结合的专题一、知识点1、二次函数的解析式求解：（待定系数法）①一般式法：设二次函数为)0(2≠++=a c bx ax y 利用这种方法求解时，往往题目会告诉我们二次函数经过几个点的坐标，到底需要几个点的坐标就能求出解析式呢就看c b a ,,不知道几个，3个系数都不知道就需要3个点的坐标，2个系数不知道就需要2个点的坐标，1个系数都不知道就需要1个点的坐标。

把坐标带入函数，然后求解方程组得到系数，就可以得到解析式；例：已知二次函数),,(2均为常数c b a c bx ax y ++=的图象经过三点A （2,0），B （0，-6），C （1，-2），求这个二次函数的解析式；解：把A （2,0），B （0，-6），C （1，-2）代入c bx ax y ++=2，得 ⎪⎩⎪⎨⎧-==-=⇒⎪⎩⎪⎨⎧-=++-==++65126024c b a c b a c c b a 所以二次函数的解析式为：652-+-=x x y②顶点式法：设二次函数为)0()(2≠+-=a k h x a y￥利用这种方法求解时，往往题目会告诉我们一个条件就是对称轴和顶点坐标，因为在所设的函数中，对称轴就是x=h ，所以顶点坐标是（h,k ）。

只要告诉我们二次函数的顶点坐标，那么就知道了h 和k 两个未知数（a,h,k ）的值，需要再告诉我们函数上一个点的坐标就可以求出a ，即求出了解析式；例：已知某二次函数的顶点坐标为（1,5），且该函数经过点A （），求这个二次函数的解析式；解：由题意，可设该二次函数为5)1(2+-=x a y ，又因为函数经过点A （0,7），把A （0,7）代入函数得 2,75)10(2=∴=+-a a所以二次函数的解析式为：742,5)1(222+-=+-=x x y x y 即③交点式法：设二次函数为)0)()((21≠--=a x x x x a y利用这种方法求解时，往往题目会告诉我们某二次函数与x 轴的两个交点的坐标，所以只需要再告诉我们函数上一个点的坐标就可以求出a ，即求出了解析式；例、已知某二次函数的图象与x 轴相交于两点A （3,0）和B （5,0），且该二次函数经过点C （6,6），求该二次函数的解析式；解：由题意，可设该二次函数的解析式为)5)(3(--=x x a y。

九年级数学上册28.3二次函数中的三角形面积问题说课稿

3.对二次函数与坐标轴围成的三角形面积最值问题感到困惑。
（三）学习动机
为了激发学生的学习兴趣和动机，我将采取以下策略或活动：
1.创设情境：以实际问题为背景，引发学生对二次函数与三角形面积问题的思考；
2.分组讨论：组织学生进行合作交流，让学生在讨论中相互启发，共同解决问题；
3.激励评价：对
3.合理安排课堂时间，关注学生的学习进度，对学习困难的学生给予个别辅导。
课后评估教学效果：
1.课后收集学生的作业和数学日记，分析他们的学习效果和困惑；
2.与学生进行交流，了解他们对课堂知识的掌握程度；
3.反思自己的教学过程，针对学生的反馈，调整教学策略。
具体反思和改进措施：
1.针对学生对知识点的掌握情况，调整教学内容和难度，确保学生能扎实掌握基础知识；
2.提高题：布置一些富有挑战性的题目，培养学生的解题能力和创新思维。
3.实践题：布置与实际生活相关的二次函数与三角形面积问题，让学生将所学知识应用于生活实践。
作业的目的在于：巩固所学知识，提高学生的应用能力；培养学生的独立思考和解决问题的能力；增强学生对数学学科的兴趣和信心。
五、板书设计与教学反思
（一）板书设计
2.问题驱动的教学：以实际问题为载体，引导学生运用所学知识解决问题，提高学生的知识运用和问题解决能力。
3.合作学习：组织学生进行分组讨论和合作交流，培养学生的团队协作能力和沟通能力，同时通过互相启发，提高学生的思维品质。
（二）媒体资源
我将使用以下教具、多媒体资源和技术工具来辅助教学：
1.教具：三角板、直尺、计算器等，用于直观演示和操作，帮助学生理解二次函数图像与三角形面积的关系。
（三）互动方式
为实现师生互动和生生互动，我计划采取以下措施：

二次函数与一次函数交点问题

二次函数与一次函数交点问题课题：一次函数与二次函数的交点及交点的判断目的：掌握一次函数与二次函数的交点坐标的算法，能够用判别式判断一次函数与二次函数有无交点，初步认识函数图像中的集合问题。

重点：一次函数与二次函数的交点坐标的计算。

难点：理解函数交点坐标的意义。

课时：1课时过程：引入1)通过观察函数图像的特点和性质求解析式。

2)通过解析式画出函数图像。

通过观察发现，在同一坐标系中，函数图像相交于A、C 两点。

这种图像相交点经常会应用到例如连接OCO、A、C三点构成的三角形OAC，如果要求三角形OAC的面积，应该如何求解呢？根据S=1/2×OA×y_c^2，只要求出C点的坐标就可以求出三角形OAC的面积。

新课一．求交点坐标分析交点坐标的特点：当两个函数的值相等时，它们的交点坐标即为满足该条件的坐标。

例如A（1,0）是两函数的交点，该点的意义在于当x=1时，y_1=y_2=0.即y_1=y_2=纵坐标。

因此，可以得到以下方程：2x-4x+2=2x-2=纵坐标。

观察2x-4x+2=2x-2，可以发现它是一个一元二次方程。

x 是满足y_1=y_2的未知数，所以只要解出方程的根就是满足y_1=y_2的横坐标。

2x^2-4x+2=2x-2，移项得到2x-6x+4=0，因式分解得到(x-1)(x-2)=0.解根为x_1=1，x_2=2.把x_1=1带入任意一个函数得到y_1=0，即坐标为（1,0）。

把x_2=2带入任意一个函数得到y_2=2，即坐标为（2,2）。

由此得到交点坐标的方法：1.令两函数值相等（解析式等）Δ>0（两个交点）。

2.Δ=0（一个交点）。

3.解出等式的未知数xΔ<0（无交点）。

4.把未知数x的值带入两函数任意一个（一般是一次函数）。

5.写出交点坐标（x，y）。

二．练练1：y_1=x^2+2x-1，y_2=x+1.解：令y_1=y_2，即x+2x-1=x+1.解方程得到x_1=1，x_2=-2.把x_1=1和x_2=-2带入上述函数得到y_1=2和y_2=-1，即交点坐标为（1,2）和（-2，-1）。

有关一次函数和二次函数相交问题的探究

单击添加大标题
练习3：一次函数y=2x+3与二次函数y=ax2+bx+c的图象交于A（m，5）和B（3，n）两点，且点B是抛物线的顶点．求一次函数和二次函数的表达式；在同一坐标系中画出两个函数的图象；从图象上观察，x为何值时，两个函数的值都随x的增大而增大，当x为何值时，二次函数的值大于一次函数的值？
单击此处添加大标题内容
练习2：在同一直角坐标系，开口向上的抛物线与坐标轴分别交于A（-1，0），B（3，0），C（0，-3），一次函数图象与二次函数图象交于B、C两点．求一次函数和二次函数的解析式．当自变量x为何值时，两函数的函数值都随x的增大而增大？当自变量x为何值时，一次函数值大于二次函数值．当自变量x为何值时，两函数的函数值的积小于0．
变式：已知一次函数y1=-x+m与二次函数y2=ax2+bx-3的图象交于两点A（-1，0）、 B（2，-3），且二次函数与y轴交于点C，P为抛物线顶点．求△ABP的面积．
练习2：如图，一次函数的图象与x轴交于点A，与y轴交于点B；二次函数y= 1/2x2+bx+c的图象与一次函数y=2x+1的图象交于B，C两点，与x轴交于D，E两点，且D点坐标为（1，0）．求二次函数的解析式；求线段BC的长及四边形BDEC的面积S；
如图，二次函数y=（x-2）2+m的图象与y轴交于点C，点B是点C关于该二次函数图象的对称轴对称的点．已知一次函数y=kx+b的图象经过该二次函数图象上点A（1，0）及点B．（1）求一次函数与二次函数的解析式；（2）根据图象，写出满足kx+b≥（x-2）2+m的x的取值范围．
A
B
C
O

一次函数与二次函数解题技巧

直线与二次函数解题方法闫萧寒博士提起中考倒数第二道大题——二次函数，很多同学可能就会觉得头疼。

二次函数大题一般二到三问，其中第一问送分题，计算一次函数解析式，或者计算点坐标；第二和第三问，考察学生知识的融合能力，以抛物线为几何载体的代数几何综合能力考察，涉及三角形、四边形的特殊图形动点问题，相似问题，图形判定以及面积计算等。

很多学生从第二问开始，有时候就是老虎吃天，无从下手，知识点，模型记了一大推，结果反而失去了自我思考自我总结的能力，题目稍微一新颖，稍微一灵活，稍微一难，他们不晓得该从哪个知识点下手了。

本文主要给正在上初三和即将升入初三的同学讲讲一条线的事儿，即直线在解决二次函数大题时的一些巧妙运用。

希望可以帮助大家，辨真去伪，直抓核心。

中考加油！【一条线的事儿·知识点篇】那些年，直线不可不知的秘密——精简核心版2.斜率和截距A.斜率定义：倾斜角不是90°的直线，它的倾斜角的正切叫做这条直线的斜率。

直线的斜率常用k表示。

斜率反映直线与轴的倾斜程度。

B. 斜率计算：① ()② 已知直线上任意两点11(,)A x y ，22(,)B x y ，则直线斜率为212121()AB y y k x x x x -=≠-③ 已知直线的一般式：0Ax By C ++=，则 3. 两条直线位置关系（仅仅研究特殊情况：垂直和平行）已知直线111:l y k x b =+和222:l y k x b =+ A ．若两直线垂直，则121k k =- B ．若两直线平行，则1212,k k b b =≠ 4. 直线平移（关键）已知直线:l y kx b =+则与他平行的直线方程可设为：':l y kx c =+5. 两点距离公式已知平面内任意两点11(,)A x y ，22(,)B x y，则AB d =6. 直线与二次函数交点和韦达定理2y kx m y ax bx c =+⎧⎨=++⎩联系化简得20Ax Bx C ++=，则韦达定理可知：1212B x x A C x x A⎧+=-⎪⎪⎨⎪=⎪⎩ 另外，① 方程组有两组不同的解时，直线与二次函数有两个交点; ② 方程组只有一组解时，直线与二次函数只有一个交点； ③ 方程组无解时，直线与二次函数没有交点7. 补充知识两个三角形面积相等：等底等高三角形面积最大：定底边，令高最大即可。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。