结构力学 第九章 矩阵位移法-董
结构力学课后习题解答:9矩阵位移法习题解答.docx

第9章矩阵位移法习题解答习题9.1是非判断题(1)矩阵位移法既可计算超静定结构,又可以计算静定结构。
()(2)矩阵位移法基本未知量的数目与位移法基本未知量的数目总是相等的。
()(3)单元刚度矩阵都具有对称性和奇异性。
()(4)在矩阵位移法中,整体分析的实质是建立各结点的平衡方程。
()(5)结构刚度矩阵与单元的编号方式有关。
()(6)原荷载与对应的等效结点荷载使结构产生相同的内力和变形。
()【解】(1)正确。
(2)错误。
位移法中某些不独立的杆端位移不计入基本未知量。
(3)错误。
不计结点线位移的连续梁单元的单刚不具奇异性。
(4)正确。
(5)错误。
结点位移分量统一编码会影响结构刚度矩阵,但单元或结点编码则不会。
(6)错误。
二者只产生相同的结点位移。
习题9.2填空题(1)矩阵位移法分析包含三个基本环节,其一是结构的,其二是分析,其三是分析。
(2)已知某单元的定位向量为[3 5 6 7 8 9]七则单元刚度系数炫应叠加到结构刚度矩阵的元素中去。
(3)将非结点荷载转换为等效结点荷载,等效的原则是。
(4)矩阵位移法中,在求解结点位移之前,主要工作是形成矩阵和_________________ 列阵。
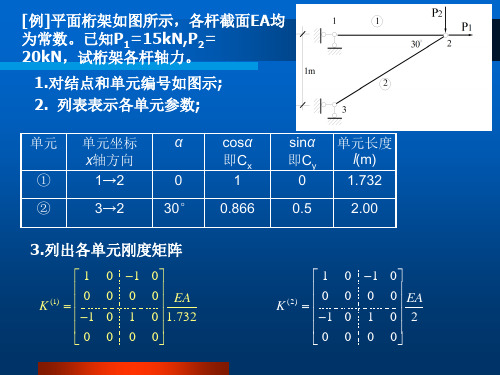
(5)用矩阵位移法求得某结构结点2的位移为4=[. V2 ft]T=[0.8 0.3 0.5]T,单元①的始、末端结点码为3、2,单元定位向量为尸>=[0 0 0 3 4 5]T ,设单元与x轴之间的夹角为a =买,则2 尹> =O(6 )用矩阵位移法求得平面刚架某单元在单元坐标系中的杆端力为F e =[7.5 -48 -70.9 -7.5 48 -121.09]T ,则该单元的轴力心=kN。
【解】(1)离散化,单元,整体;(2)灯8;(3)结点位移相等;(4)结构刚度,综合结点荷载;(5)[0 0 0 0.3 -0.8 0.5]。
(6)-7.5o离、空的值以及K ⑴中元素妍、愚、姒的值。
【解】各刚度系数的物理意义如习题解9.3图所示。
结构力学矩阵位移法

k jk 表示,k端弯矩用 k kk 表示,放在劲度矩阵第二列;
k(1)k(2)k(3) k kk jjj
k kk jk k 2 4ii
2i 4i
21
K1是 1 1自由度发生单1自 位由 转度 角引 在起的刚
位移法用结点的平衡
K1
1.位移法作结点位移引起的单位内力(弯矩、剪力) 图 矩阵位移法将结点位移引起的杆端力放在单元劲度 矩阵中。
2.位移法从结点位移引起的单位内力(弯矩、剪力) 图中取出结点作为脱离体,由脱离体的力平衡条件 求得附加约束反力,即整体劲度系数。
矩阵位移法由单元劲度矩阵集合成整体劲度矩阵。
10
位移法和矩阵位移法求自由项系数的方法有何不同?
11
背:位移法矩阵位移法整体结点位移正负号规定?
整体结点位移,矩阵位移法中与整体坐标方向一 致为正。位移法中角位移顺钟向为正,线位移无 规定。
12
第二专题: 只有转角未知量的连续梁的矩阵位移法
13
用位移法和矩阵位移法求图示连续梁的杆端弯矩
FP1 FP FP2 2FP ql FP
14
背:位移法和矩阵位移法的基本系-结点转角处附加刚臂
K21kk(2j) 2i
23
K12是2自由度发生单1自 位由 转度 角引 在起的刚
位移法用结点的平衡
K12的形成
矩阵位移法:与1和2自由度都 有关的单元单元只有(2)单 元,1自由度对应(2)单元的 j端,2自由度对应(2)单元 的k端,故:
K12k(j2k) 2i
24
K22是2自由度发生单2自 位由 转度 角引 在起的刚
5
背:为什么矩阵位移法比位移法可能有更多的独立的 结点线位移作为基本未知量?
结构力学基础矩阵位移法基本概念、计算程序和例题讲解

例形成图示刚架可动结点劲度矩阵,E,I ,A为常数。
解: 1.编号,如图(b) 2.确定单元杆端自由度序号。
3.计算 kmi 4.计算单元转换矩阵
5.形成单元在整体坐标系中的劲度矩阵
6.根据单元杆端自由度序号叠加
二、可动结点劲度矩阵性质
1.对称方阵
反力互等定理
2.非奇异矩阵 考虑了约束条件,排除了刚体位移
7.求杆端力Fmi
8.求支座反力 支座反力由下式
计算,得
9.内力图
例2 求图2-21(a)所示平面刚架的内力,已知各杆 I 0.005m4
A0.05m2,E2106kNmA2B杆、CD杆杆
返回
§9—3 可动结点劲度矩阵
一、形成可动结点劲度矩阵的步骤
步骤: 1.对结构进行结点编号、单元标号、自由度编号: 2.确定单元杆端自由度序号(考虑约束条件); 3.计算单元在局部坐标系中的劲度矩阵kmi 4.计算单元转换矩阵Ti 5.形成单元在整体坐标系中的劲度矩阵ki TiTkmiTi
6.按”对号入座”原则,将ki叠加到 k 中。
结构力学基础 矩阵位移法基本概念、计算程
序和例题讲解
§9-1 矩阵位移法基本概念 §9-2 单元劲度矩阵 §9-3 可动结点劲度矩阵 §9-4 可动结点等效荷载列阵 §9-5 单元杆端力和支座反力 §9-6 例题 §9-7 平面刚架计算程序
§9—1 矩阵位移法的基本概念
一、坐标系和符号规定 图示连续梁:
4.求 K
(1)计算机各单元的方向余弦和杆长:
(2)求 kmi
(3)求ki
单元(1):Cx=0 Cy=1
杆长:l 同理:
(4)求 按照“对号入座“原则,由ki形成k哪
例如: 同理:
结构力学应用-矩阵位移法

3、集成总刚
(6)定位向量法:对号入座,同号相加 定位向量法:对号入座,
4.综合结点荷载
综合结点荷载 {F}={FD}+{FE} }――直接结点荷载 ①{FD}――直接结点荷载 }――等效结点荷载 ②{FE}――等效结点荷载 (7-1)局部坐标系单元固端力 (7-2)整体坐标系单元固端力 (7-3)单元等效结点荷载。 单元等效结点荷载。
等效原则: 等效原则: ——两种荷载对基本体系产生相同的结点位移。 两种荷载对基本体系产生相同的结点位移 ——两种荷载对基本体系产生相同的结点位移。
矩阵位移法的计算步骤及示例
矩阵位移法计算平面刚架 计算机计算――程序化) 程序化) (计算机计算 程序化
1. 编码、整理原始数据 编码、
(1)整体与局部坐标系 ) (2)结点位移编码 ) 单元编码 (3)原始数据: )原始数据: E 、A i、I i、l i 定位向量{λ} 定位向量 e, αi([ T ]) ])
几点补充说明
1、结点位移分量编号,定位向量 、结点位移分量编号,
——引入支承条件:已知位移约束的方向,编码为零。 引入支承条件:已知位移约束的方向,编码为零。 引入支承条件
2、铰结点处理: 铰结点处理: 铰结点处理
铰结的各杆杆端的转角均为基本未知量 ——分别编码(统一单元,程序简单) 分别编码(统一单元,程序简单) 分别编码
矩阵位移法
矩阵位移法——基本原理与位移法相同 基本原理与位移法相同 矩阵位移法 *数学工具 —— 矩阵运算
1、矩阵知识 矩阵: (1)矩阵:A 方阵: 方阵: 阶方阵A相应的行列式 (2)行列式:n阶方阵 相应的行列式 )行列式: 阶方阵 相应的行列式D 若D=0,A为奇异矩阵 (3)矩阵运算 相等:加减:数乘: 相等:加减:数乘: l aik 乘法: 乘法:Cmn=Aml*Bln,则 cij =
结构力学 第九章 矩阵位移法-董 - 副本
Cx Cx
2
2
C xC y
C xC y 2 C y EA C xC y l 2 Cy
K
(2)
0 .75 0 .433 0 .75 0 .433
0 .433 0 .25 0 .433 0 .25
0 .75 0 .433 0 .75 0 .433
[例]
形成连续梁的整体刚度矩阵
(0) 1 (1)
2
(2)
3
(3)
4
(4)
5
(5)
i1
1 2
i2
3
i3
4
i4
5
i5
6
解:1)编号及建立坐标
2)单元刚度矩阵
(连续梁每个结点只一个位移)
0
4 i1 [k ] 2 i1
①
1
定位向量 ②
1
4 i2 [k ] 2 i2
2
定位向量
(2) 整体坐标系中的单元 刚 度矩阵 单元①: 0 , T I
0
k
(1)
k
1 0 0 0 0 0
(1)
90 0 , 单元②:
0 1 0 T 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 1 0 0 0 0 0 0 0 1
e
k (6×6);
e
转换成整体坐标系 k
e
;
(5)把单元定位向量标在整体坐标系的单元刚度矩阵边上, 并划去已知支座位移等于零的行和列; (6)按照定位向量号,“对号入座”集合成整体刚度矩阵。
例 求整体刚度矩阵[K]。已知各杆刚度系数为 5 4 2 : EA 6.6 10 kN , EI 1.2 10 kN .m 。
结构力学教学课件-09矩阵位移法

学习者可以通过实际的结构分析案例,将矩阵位移法应用于实际问题中,加深理解和掌 握。
THANKS
感谢观看
矢量与张量
在结构力学中,矢量与张量是描述结 构内力和位移的重要工具,矩阵位移 法中需要用到这些概念。
矩阵位移法的计算步骤
建立结构离散化模型
将结构划分为若干个离散的单元,每个单元 具有一定的自由度。
建立单元刚度方程
根据结构力学中的刚度原理,建立每个单元 的刚度方程。
集成整体刚度方程
将所有单元的刚度方程集成在一起,形成整 体刚度方程。
课程目标
掌握矩阵位移法的基本原理和步骤,理解如何应 用矩阵位移法解决实际工程问题。
学会使用相关软件进行结构分析,提高解决实际 问题的能力。
培养学生对结构力学学科的兴趣和热爱,为今后 从事土木工程领域的工作打下基础。
02
矩阵位移法基础
矩阵位移法概述
矩阵位移法是一种基于矩阵运算的数值分析方法,用 于解决结构力学中的位移问题。
结构力学教学课件-09矩阵位移法
目 录
• 引言 • 矩阵位移法基础 • 矩阵位移法的基本原理 • 矩阵位移法的应用实例 • 结论
01
引言
课程背景
01
结构力学是土木工程学科中的重 要基础课程,矩阵位移法是结构 力学中的一种重要分析方法,用 于解决结构的位移和内力问题。
02
随着计算机技术的发展,矩阵位 移法在结构分析中得到了广泛应 用,因此掌握矩阵位移法对于土 木工程师来说具有重要意义。
矩阵位移法的应用范围
矩阵位移法广泛应用于各种工程结构的分析,如桥梁、建筑、机械等 。
下一步学习建议
深入学习矩阵位移法的数学基础
为了更好地理解和应用矩阵位移法,建议学习者深入学习线性代数和数值分析等相关数 学基础。
第九节矩阵位移法

(2 =1)
0
6EI l2 2EI l
0
6EI
l2 4EI
l
e
…(9-4)
F e k ee
…(9-5)
即为一般单元的刚度方程。其中 k e 称为局部坐标系中的单
元刚度矩阵。
2、一般单元刚度矩阵的性质
(1)单元刚度系数的意义
单元刚度矩阵中的每个元素称为单元刚度系数 kij ,其物理
意义表示由于单位杆端位移引起的杆端力。
( v1e
v2e
)
Fye1
6EI l2
(1e
2e )
12EI l3
( v1e
v2e )
Fye2
6EI l2
(1e
e 2
)
12 l
EI
3
( v1e
v2e
)
Fx1 M1
1
v1
Fy1
u1
…(9-2)
e
1
M2
Fx2
2 Fy2
v2
u2
2
式(9-1) 、(9-2)即为局部坐标系下平面刚架一般单元的单元刚度方
ke T Tk eT
F e kee
即为单元e在整体坐标中的单元刚度方程 其中 k e为整体坐标系的单元刚度矩阵,和 k e 同阶,且具有类似的性质。
§9-4 结构的整体刚度矩阵
作用在结构上的荷载与结构的结点位移, 也存在一一对应的关系,即为结构的整体刚 度方程。结构的整体刚度方程反映了结点荷 载和结构位移之间的关系,其实质就是位移 法的基本方程。求解方法一种是传统位移法, 另一种是直接刚度法。
l
Fxe1
EA l
u1e
EA l
u2e
矩阵位移法

TT T T T T I
Fx1 F y1 M1 单元坐标 转换矩阵 F x2 Fy 2 M 2
e
Hale Waihona Puke eF e TF e
T 1 T T
单元坐标转换矩阵T是一正交矩阵。
EI 25 104 kN m l
0 300 0
5m
0 为了简洁,下面将矩阵 中各元素的单位略去。 12 30 0 12 30 30 100 0 30 50 4 EA 10 0 0 l 0 0 300 0 0 12 30 0 12 30 12 EI 6 EI [k11 ] 0 3 2 30 50 0 30 100 l l 6 EI 4 EI 第一列元素变符号即第四列,第二列元素变符号即第五列 0 ①: 2 ②求整体坐标系中的单刚, k l l 第一行元素变符号即第四行,第二行元素变符号即第五行
3、有限单元法的三个基本环节: ①单元划分:一根等截面直杆作为一个单元,单元间由结点相联。 ②单元分析:建立单元刚度方程,形成单元刚度矩阵(物理关系)。 ③整体分析:由单元刚度矩阵形成整体刚度矩阵,建立结构的 位移法基本方程(几何关系、平衡条件)。
§9-2 单元刚度矩阵(element stiffnessmatrix)(局部坐标系)
T11 T12 T T T 21 22
因此,(a)式的逆转换式为: 同理
F e T TF e
e T e
(b)
e T T e
整体坐标系中的单元刚度矩阵
F e TF e
(a)
e T e
(b)
单元刚度矩阵的性质 设局部坐标系中、整体坐标系中的单元刚度方程分别为: ①单元刚度矩阵是杆端力用杆端位移来表达的联系矩阵。 e e e F k Δ (c) ②其中每个元素称为单元刚度系数,表示由于单位杆端位移引起的杆端力。 ③单元刚度矩阵是对称矩阵。 F e k eΔe (d ) ④第k列元素分别表示当第k个杆端位移=1时引起的六个杆端力分量。 e e e e ⑤一般单元刚度矩阵是奇异矩阵。不存在逆矩阵。因此, 将式(a)、(b)代入式(c) k eT IF T T TTF ke T T 可由单元刚度方程,由杆端位移唯一确定杆端力;但由杆端力反推杆端位移时, 可能无解、可能解不唯一。 k e T T k eT
《结构力学》第9章矩阵位移法.

结构力学
第1章 结构的计算简图 第2章 平面体系的几何组成 第3章 静定结构的受力分析 第4章 静定结构的位移计算 第5章 力法 第6章 位移法 第7章 力矩分配法 第8章 影响线 第9章 矩阵位移法 第10章 结构动力计算基础
结构力学
9.1 概 述 9.2 结构离散化及位移、力的表示与编码 9.3 单元刚度方程和单元刚度矩阵 9.4 结构的整体刚度方程和整体刚度矩阵 9.5 非结点荷载的等效化 9.6 计算步骤和算例
2. 局部坐标系下的单元刚度方程和单元刚度矩阵
单元刚度方程,指单元杆端力与杆端位移之间的关系。
结构力学
局部坐标系下的单元刚度方程
可简记为
结构力学
局部坐标系下的单元刚度矩阵
结构力学
3.单元刚度矩阵的性质
(1)单元刚度系数的意义。 中的元素称为单元刚度矩阵的系 数,代表单元杆端位移与其所引起的杆端力的关系,数值上等 于单位杆端位移引起的杆端力的大小。通常用下标i,j分别表 示元素在矩阵中所处的行、列号。 (2)单元刚度系数仅与单元的横截面积A、惯性矩I、弹性模量E 和长度l有关。 (3) 是对称矩阵,它的对称性指其元素有关系:
图9.1
结构力学
2.位移、力的正方向规定
为了统一(如力的正、负号可直接代入平衡方程等),在矩阵 位移法中,对于所有的外力、结点位移、杆端力、杆端位移等矢 量,规定坐标系的正方向为它们的正方向。 本章采用左手坐标系,用oxy表示结构平面,z轴为截面惯性轴方 向。转角位移、力矩、弯矩以顺时针方向为正(即左手螺旋轴与z 相同为正。
结构力学
9.3 单元刚度方程和单元刚度矩阵
1. 单元局部坐标系
结构中每个杆件的位置、方向各不相同,为了便于讨论杆 件本身杆端力与杆端位移间的关系,对每个单元分别建立单元 局部坐标系。 在局部坐标系下,可表示出杆端力分量分别为轴向力、横向力、 弯矩,杆端位移分量分别对应轴向位移、横向位移、转角位移。
结构力学矩阵位移法

§9-1节 位移法概述
?
矩阵力法
?结构矩阵分析
一般刚度法
?
矩阵位移法
?
直接刚度法
?以直接刚度法的程序最为简单且通用性强,应 用最广。
?⑷矩阵位移法是有限元法的雏形,故杆件结构 的矩阵分析也称作杆件结构的限元法分析,具 体包括两部分内容:
§9-1节 位移法概述
第九章 矩阵位移法
仅限于求解杆系结构在静荷载作用下的位 移和内力。以位移法(附加约束法)为基础,从 有限单元法的角度讲解结构的静力分析。既适 用于静定结构,也适用于超静定结构,易于编 写通用的计算机程序,尤其对于大型复杂结构, 该法具有很大的优越性,可大大减少手算的工 作量,是面向计算机的计算方法。
§9-1节 位移法概述
⑴ 力法和位移法均为传统的结构力学的计算 方法,其相应的计算手段手算,因而只能解 决计算简图较粗略基本未知量数目不太多的 结构分析问题。
⑵计算机的出现和广泛应用,使结构力学的计 算发生了巨大变化,电算能够解决手算难以 解决的大型复杂问题。由此产生了适合电算 的分析方法 —— 结构矩阵分析。
6EI
Fy2 ? ? l 3 (v1 ? v2 ) ? l 2 (?1 ? ? 2 )
M1
?
6EI l2
(v1
?
v2 ) ?
4
EI l
?
1
?
2EI l
?
2
6EI
2EI 4EI
M2 ? l 2 (v1 ? v2 ) ? l ?1 ? l ? 2
§9-2节 单元刚度矩阵(局部坐标系)
一般单元的刚度方程
(a)单元分析:将结构离散成有限个两端固定杆件作为计 算单元,按照单元的力学性质(物理关系),建立单元 的杆端力和杆端位移的关系—单元的刚度方程,形成单元 刚度矩阵。
结构力学-矩阵位移法

以上杆端力和杆端线位移与相应的坐标轴正 方向一致为正,相反为负。
M1e,M 2e,1e,2e,M1e,M 2e,1e ,2e
以上杆端力矩和杆端转角均以顺时针方向为 正,逆时针方向为负。
10
3. 单元坐标转换矩阵
③
4
④
7
⑤
⑥
1
36
曲杆可用多段直杆近似代替(以直代曲)。
进行结点编号时,要尽量使单元两端结点编号 的差值最小。
4
三、单元杆端力和杆端位移的坐标变换
1.坐标系
结构整体分析 —整体坐标系xy
x
2
②
4
y
①③
④
单元分析—局部坐标系 x y 1
3
单元始端指向末端的方向就
是 x 轴的正方向
1
x
坐标轴遵循右手法则,即
Fx1e
M
e 1
1
M
e 1
e
y
x
2
y
x
单元杆端力
x
2
②
4
y
①③
④
1
3
y v1e 1
1
u1e
u1e
v1e
1e
1e
e
y
x
2
x
2
单元杆端位移
7
Fxe1 Fye1
uv11ee
F
e
MFxe12e
e
u12ee
Fye2
v2e
M
e 2
e 2
Fxe1 Fye1
uv11ee
点,单元与单元、单元与支座均通
结构力学——矩阵位移法

学习内容
有限单元法的基本概念,结构离散化。 平面杆系结构的单元分析:局部坐标系下的单元刚度矩
阵和整体坐标系下的单元刚度矩阵。 平面杆系结构的整体分析:结构整体刚度矩阵和结构整
体刚度方程。 边界条件的处理,单元内力计算。 利用对称性简化位移法计算。 矩阵位移法的计算步骤和应用举例。
2
学习目的和要求
2、局部坐标系中的单元刚度矩阵
k
e
EA l
1 1
1
1
kk1211
k12 k22
刚度系数的物理意义: • 单元刚度矩阵是杆端力与杆端位移之物理关系; • 矩阵的阶数与杆端位移分量数相等; • kij 表示 uj 1 引起的杆端力Fi 的大小。
15
第二节 单元分析(局部坐标系下的单元分析 )
5
第一节 矩阵位移法概述
结构力学传统方法与结构矩阵分析方法,二者同源而有别:
在原理上同源,在作法上有别
前者在“手算”的年代形成,后者则着眼于“电算”,计算手 段的不同,引起计算方法的差异。
与传统的力法、位移法相对应,在结构矩阵分析中也有矩阵力 法和矩阵位移过程程序化的优点而广为流传。
3、局部坐标系中的单元刚度矩阵性质
矩阵位移法的要点 :
化整为零
集零为整
(离散化、单元分析) (结点力平衡、位移协调)
9
第一节 矩阵位移法概述
2、单元划分
将一个在荷载作用下的连续结构剖分成若干个各自独立 的单元,原结构可以看成是由各单元在连接点(称结点) 连接而成的体系——化整为零
在杆件结构矩阵分析中,一般 是把杆件的转折点、汇交点、 边界点、突变点或集中荷载作 用点等列为结点,结点之间的 杆件部分作为单元。
3
第9章 矩阵位移法-结构矩阵分析基础

阵位移法的符号表示方法和正负号规定,则(d) 式中相应符号应做如下变换
M AB = M i
M BA = M j
FQAB = −FQi
§9-2 单元刚度阵
杆件结构的离散化 9.2.1 单元与结点的划分和编码
由若干根杆件组成的结构称为杆件结构。使用 矩阵位移法分析结构的第一步,是将结构“拆散” 为一根根独立的杆件,这一步骤称为离散化。为方 便起见,常将杆件结构中的等截面直杆作为矩阵位 移法的独立单元,这就必然导致结构中杆件的转折 点、汇交点、支承点、截面突变点、自由端、材料 改变点等成为连接各个单元的结点。只要确定了杆 件结构中的全部结点,结构中各结点间的所有单元 也就随之确定了。
3)单元杆端力和杆端位移
单元杆端截面的内力和位移分别称为单元杆端 力和杆端位移。
下图所示为平面刚架中的单元 e ,其始端为i, 末端为j。
13
§9-2 单元刚度阵
f 3 ( 3)
f1 ( 1)
i
e
f 2 ( 2)
j f 6 ( 6)
y
f 5 ( 5)
x
f4 ( 4)
(a) 单元坐标系下的广义分量
Mi ( i)
(b)
7
§9-2 单元刚度阵
9.2.2 两种直角坐标系
结构离散化后,杆件单元的方向千差万别。在 作整体分析时,需要在结点处建立平衡方程,为此 又需要一个统一的计算基准坐标系。因此,这里引 入两套直角坐标系来建立后续需要研究的力和位移 等物理量之间的关系。
(1)单元坐标系
单元坐标系(又称局部坐标系)是单元分析时 使用的坐标系,它只与具体某一单元相对应。对结 构中任意单元 e ,本章约定其坐标系用 x − y表示; 坐标系原点取为该单元一端的端结点i(称为始结 点或始端);由原点指向另一端结点j(称为末结 点或末端)的方向,为杆轴 x 坐标正向,记作x (e) ;
结构力学 矩阵位移法

§9-2节 单元刚度矩阵(局部坐标系)
一.一般单元的刚度方程和刚度矩阵
1.单元两端采用局部编码1、2
1
e
2.六个杆端位移组成杆端位移列向量。
v1
1
u1
EAI L
3.六个杆端力组成杆端力列向量。
y
2
2 vu22 x
e
1
2
e
u1 v1
e
3
1
F1
e
F2
e
F x1 Fy1
单元刚度矩阵中的每个元素都代表单元
杆端单位位移引起的杆端力称之为单元
刚度系数。其中
k
表示第j个杆端单位位移
ij
引起的第i个杆端力。
⑵单元刚度矩阵为对称矩阵。 kij k ji
⑶一般单元刚度矩阵为奇异矩阵 k e 0
三、特殊单元刚度方程和刚度矩阵
⑴连续梁中的受弯杆件单元 ⑵桁架结构中杆件单元
⑴连续梁中的受弯杆件单元
忽略轴变时单元的刚度矩阵
12EI
l3 6EI
k
e
l2
12E
l3 6EI
I
l2
6EI
l2 4EI
l 6EI
l2 2EI
l
12EI l3
6EI l2
12EI
l3 6EI l2
6EI
e
l2 2EI
l
6EI l2
4EI
l
§9-3节 单元刚度矩阵(整体坐标系)
一、单元坐标转换矩阵
⑶根据所选基本未知量的不同,结构矩阵分析 包括:
§9-1节 位移法概述
矩阵力法
结构矩阵分析
一般刚度法
矩阵位移法
直接刚度法
工程力学-结构力学课件-9矩阵位移法

结构离散化,单元分析,整体分析
1)离散,进行单元分析,建立单元杆端力和杆端位移的关系。 2)集合,进行整体分析,建立结点力与结点位移的关系。
单元 分析
整体 分析
任务
建立杆端力与杆端位移 间的刚度方程,形成单 元刚度矩阵
由变形条件和平衡条件 建立结点力与结点位移 间的刚度方程,形成整 体刚度矩阵
1
F1e
e 1
l, A, E e
e 2
2
F2e
单元杆端力和单元杆端位移的方向与局部坐标系一致为正。
F
e
FF12ee
----单元杆端力
F1e
1
e 1Leabharlann e12ee
----单元杆端位移
l, A, E e
F1e F2
EA/l EA/l
13 2
1(1,2)
57 6
3(5,6)
10 13 10(19,20)
11
9
12
14 15
16
17 9(17,18)
结点的选择:转折点、汇交点、支承点、 刚度变化、荷载作用点等
整体编码:单元编码、结点编码、 结点位移编码。
坐标系:整体(结构)坐标系; 局部(单元)坐标系.
曲杆结构:以直代曲.
6
5(13,14,15) 6(16,17,18)
i
j
i
e
i
Mi
Fxi
i
Fyi
j
x
j j
Fxj
Mj
Fyi
e [i i i j j j ]eT
y
----单元杆端位移
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
0 6 EI l2 2 EI l 0 6 EI l2 4 EI l
e u1 e v1 1 u2 v 2 2
矩阵表示: a11
a 21 an1 a12 a1n x1 b1 a22 a2 n x2 b2 an 2 ann xn bn
第九章
主要内容
§9-1 §9-2 §9-3 §9-4 §9-5 §9-6 §9-7 §9-8 §9-9 概述 局部坐标下的单元刚度矩阵 整体坐标下的单元刚度矩阵 连续梁的整体刚度矩阵 刚架的整体刚度矩阵 等效结点荷载 计算步骤及算例 忽略轴向变形时矩形刚架的整体分析 桁架及组合结构的整体分析
基本要求:
即 aij a ji
b2 b4 d2 d4
8. 矩阵分块
A B C D
A、B、C、D
均为子矩阵
9、逆矩阵 除法运算由矩阵求逆来完成。例如,若
AB =C
则
B=A 1 C
此处A-1 称为矩阵A的逆矩阵。 一个矩阵的逆矩阵由以下关系式定义:
A A 1 = A 1 A =I
方阵:
a11 a12 a1n a a22 a2 n aij 21 n n an1 an 2 ann a11 0 a22 0 ann a11 0 a a22 21 an1 an 2 ann
4i 2i 6i l 6i l
2i 4i 6i l 6i l
6i l 6i A l B 12i l2 12i 2 l
一端简支等截面直杆的刚度方程
3. 矩阵相等
4. 矩阵加减
A=B aij bij
m n m n
A B aij bij
m n
5. 矩阵相乘
ab c
m n n p
两者相等才可乘
m p矩阵ຫໍສະໝຸດ 乘:m n n p p q
两者相等才可乘
abc d
刚度方程:
l
M AB 3i A 3i
1 QAB QBA ( M AB M BA ) l 3i 3i QAB QBA A B 2 l l
写成矩阵的形式:
3i M AB 3i QAB Q l BA 3i l
2
Me
2
v2
X 2e
Y1e u1
u2
e Y2
首先,由两个杆端轴向位移 u1和u2 可推算出相应的杆端轴向力
X1 和X 2
X1 e
1
e
2
u1
EA u1 u2 l EA X2 u1 u2 l X1
u2
X 2e
其次,由杆端横向位移
v1 , v2和转角1 ,2 ,
(1) (2)
0 12EI l3 6EI l2 0
0 6EI l2 4EI l 0
k = (4)
(5) (6)
e
(3)
0
EA l 0 0
2EI l
0 -6EI l2 只与杆件本身物理性 质有关而与外荷载、 位移、位置等无关
0 0
-12EI -6EI l3 l2 6EI l2 2EI l
对角阵:
a11 a12 a1n a22 a2 n 上(下)三角阵: 0 ann
单位阵:
1 0 1 n n In 0 1
力法、位移法方程的 系数矩阵均为对称阵
对称阵:
AT=A
a1 a 3 c1 c3 a2 a4 c2 c4 b1 b3 d1 d3
6 1 4 7 5 3
a b d e g h
c f i
1 i 4 i 2 i 5 i
注意矩阵与行列式的区别:
1 4 1 4 2 5 与 2 5
2. 矩阵的简记
a11 a12 a1n a a22 a2 n A= aij 21 am1 am 2 amn
将上面六个方程合并,写成矩阵形式: X 1 EA e EA
l Y 1 0 M1 0 EA X2 l 0 Y2 0 M 2 0 0 l 0 12 EI l3 6 EI l2 0 12 EI l3 6 EI l2 6 EI l2 4 EI l 0 6 EI l2 2 EI l 0 0 EA l 0 0 12 EI l3 6 EI 2 l 0 12 EI l3 6 EI 2 l
阵删除与零杆端位移对应的行和列得到。
e
以连续 梁为例:
u1 0
FX EA 1 e l F Y1 0 M1 0 EA FX2 l 0 FY2 0
mq
6. 矩阵转置 规则:
m n
T T
A
行列互换
n m
T
A
T
ab b a
7. 矩阵种类 行矩阵(向量):
a a1 a2 an
b1 b T b 2 b1 b2 bn bn
列矩阵(向量):
1
1
v1 0
e
0 6 EI l2 4 EI l 0 6 EI l2 2 EI l EA l 0 0 EA l 0 0
2
2
u2 0 v2 0
0 12 EI l3 6 EI 2 l 0 12 EI l3 6 EI 2 l 0 6 EI l2 2 EI l 0 6 EI l2 4 EI l e u1 e v1 1 u2 v 2
可以用角变位移方程推导出相应的杆端横向力
Y1 , Y2 和杆端力矩M1 , M 2
M1 M2 Y1 Y2
e
e
e
e
4 EI 2 EI 6 EI 1 2 2 v1 v2 l l l 2 EI 4 EI 6 EI 1 2 2 v1 v2 l l l 6 EI 12 EI 2 1 2 3 v1 v2 l l 6 EI 12 EI 2 1 2 3 v1 v2 l l
简记:
AX=B
X = A-1B
解的表达式:
位移法回顾
位移法基本未知量:杆端节点位移。 位移法基本方程:节点位移对应的平衡方程.
k111 k12 2 k133 k1n n F1 p 0 k211 k22 2 k233 k2 n n F2 p 0 k311 k32 2 k333 k3n n F3 p 0 kn11 kn 2 2 kn 33 knn n Fnp 0
3i l 3i A l2 3i l2
§9-2
一般单元
单元刚度矩阵(局部坐标系)
在单元两端加上人为控制的附加约束,使基本杆单元的两端产生任意指 定的六个位移,然后根据这六个杆端位移来推导相应的六个杆端力。
1
e
e M1 1
2
v1
X1 e
上面的式子可以用矩阵符号记为 e e e F k
局部坐标系的单元刚度矩阵
(2) (3) (4) (5) u1 1 v1 1 1 1 u2 1 v2 1 EA l 0 0 -EA l EA l 0
(1)
(6) 2 1
e
0 12EI l3 6EI l2 0 12EI l3 -6EI l2 0 6EI l2
§9-1
概述
2)矩阵位移法 (1)结构离散化——划分单元; (2) 单元分析 ——建立单元的杆端力与杆端 位移间的关系,形成单元刚度矩阵;
(3) 整体分析 ——建立整个结构的结点位移 与结点荷载间的关系,形成结构刚度矩阵。
▲ 必要的矩阵与矩阵运算知识(复习) 1. 矩阵定义—— 实数或复数的集合排列成矩形的阵式称为矩阵。 例:
熟练掌握两种坐标系中的单元刚度矩阵、结构 的整体刚度矩阵、等效结点荷载的形成,已知 结点位移求单元杆端力的计算方法,整体刚度 矩阵和结构结点荷载的集成过程。 理解单元刚度矩阵中和整体刚度矩阵中的元素 的物理意义。 掌握不计轴向变形时矩形刚架的整体分析。
§9-1
概述
1、结构分析方法
1)传统方法——前面介绍的力法、位移法、
4EI l
二、单元刚度矩阵的性质
(1)单元刚度系数的意义
kij
e
—代表单元杆端第j个位移分量等于1时所引起的第i个杆端力分量。
e (2)单元刚度矩阵 k 是对称矩阵,即 kij k ji。 (3)一般单元的刚度矩阵 k 是奇异矩阵; e
特殊单元
单元的某个或某些杆端位移的值已知为零。如梁单元、 柱单元。 特殊单元的单元刚度矩阵,可由一般单元的单元刚度矩
刚度方程或叠加法求得各杆端内力。
等截面直杆的刚度方程
刚度方程:
l M BA 2i A 4i B 6i l 1 QAB QBA ( M AB M BA ) l 6i 6i 12i QAB QBA A B 2 l l l M AB 写成矩阵的形式: M BA QAB QBA M AB 4i A 2i B 6i
