高中数学选修2-1导学案
高二数学选修2-1全套导学案

※动手试试
练1.如图,已知线段AB在平面α内,线段 ,线段BD⊥AB,线段 , ,如果AB=a,AC=BD=b,求C、D间的距离.
练2.如图,M、N分别是棱长为1的正方体 的棱 、 的中点.求异面直线MN与 所成的角.
⑸向量表示平行、垂直关系:
设直线 的方向向量分别为 ,平面 的法向量分别为 ,则
① ∥ ∥
② ∥
③ ∥ ∥
(二)深入学习
例1已知两点 ,求直线AB
与坐标平面 的交点.
变式:已知三点 ,点 在 上运动(O为坐标原点),求当 取得最小值时,点 的坐标.
小结:解决有关三点共线问题直接利用直线的参数方程即可.
二、重点难点
1.掌握利用向量运算解几何题的方法,并能解简单的立体几何问题;
2.掌握向量运算在几何中求两点间距离和求空间图形中的角度的计算方法.
三、学法指导
(预习教材P105~P107,找出疑惑之处.
复习1:已知 , ,且 ,求 .
复习2:什么叫二面角?二面角的大小如何度量?二面角的范围是什么?
四、教学过程
新知:
⑴点:在空间中,我们取一定点 作为基点,那么空间中任意一点 的位置就可以用向量 来表示,我们把向量 称为点 的位置向量.
⑵直线:
①直线的方向向量:和这条直线平行或共线的非零向量.
②对于直线 上的任一点 ,存在实数 ,使得 ,此方程称为直线的向量参数方程.
⑶平面:①空间中平面 的位置可以由 内两个不共线向量确定.对于平面 上的任一点 , 是平面 内两个不共线向量,则存在有序实数对 ,使得 .②空间中平面 的位置还可以用垂直于平面的直线的方向向量表示空间中平面的位置.
高中数学选修2-1导学案

.§1.1.1 命题及四种命题学习目标1.掌握命题、真命题及假命题的概念;2.四种命题的内在联系,能根据一个命题来构造它的逆命题、否命题和逆否命题 .学习过程一、课前准备复习 1:什么是陈述句?.复习 2:什么是定理?什么是公理 ?.二、新课导学※ 学习探究1.在数学中 ,我们把用、、或表达的,可以的叫做命题.其中.的语句叫做真命题,的语句叫做假命题练习:下列语句中:(1)若直线 a // b ,则直线a和直线 b 无公共点;(2)247(3)垂直于同一条直线的两个平面平行;2( 4)若 x 1 ,则 x 1 ;( 5)两个全等三角形的面积相等;(6) 3能被2整除.其中真命题有,假命题有.2.命题的数学形式:“若p,则q,”命题中的p 叫做命题的, q 叫做命题的.※ 典型例题例 1:下列语句中哪些是命题? 是真命题还是假命题?(1)空集是任何集合的子集;(2)若整数a是素数,则a是奇数;( 4 )若空间有两条直线不相交,则这两条直线平行;(5)( 2)22;(6 ) x 15 .命题有,真命题有.假命题有.例 2 指出下列命题中的条件p 和结论 q :(1 )若整数a能被 2 整除,则a是偶数;(2 )若四边形是菱形,则它的对角线互相垂直平分.解:(1)条件p:结论 q :( 2 )条件p:结论 q :变式:将下列命题改写成“若p ,则 q ”的形式,并判断真假:(1 )垂直于同一条直线的两条直线平行;(2 )负数的立方是负数;(3 )对顶角相等 .※动手试试1.判断下列命题的真假:( 1 )能被6整除的整数一定能被 3 整除;(2 )若一个四边形的四条边相等,则这个四边形是正方形;(3 )二次函数的图象是一条抛物线;(4 )两个内角等于 45 的三角形是等腰直角三角形 ..2.把下列命题改写成“若p ,则 q ”的形式,并判断数 .它们的真假 .( 1)( 2 )互为( 1)( 3)互为(1)等腰三角形两腰的中线相等;( 1)( 4 )互为( 2)( 3)互为(2)偶函数的图象关于y 轴对称;(3)垂直于同一个平面的两个平面平行.例3 命题:“已知a、 b 、c、 d 是实数,若子a b,c d ,则a cb d”.写出逆命题、否命题、逆否命题 .变式:设原命题为“已知 a 、b是实数,若 a b 是小结:判断一个语句是不是命题注意两点:( 1 )无理数,则 a 、b都是无理数”,写出它的逆是否是陈述句;(2 )是否可以判断真假.命题、否命题、逆否命题.3.四种命题的概念(1 )对两个命题,如果一个命题的条件和结论分别是另一个命题的结论和条件,那么我们这样的两个命题叫做, 其中一个命题叫做原命题为:“若p ,则 q ”则逆命题为:,“”.※ 动手试试(2) 一个命题的条件和结论恰好是另一个命题的写出下列命题的逆命题、否命题和逆否命题并条件的否定和结论的否定, 我们把这样的两个判断它们的真假:命题叫做, 其中一个命题叫做命题, 那么( 1)若一个整数的末位数是0 ,则这个整数能被另一个命题叫做原命题的. 若原命题 5 整除;为:“若,则q ,”则否命题为:“”( 2)若一个三角形的两条边相等,则这个三角形p( 3 )一个命题的条件和结论恰好是另一个命题的结论的否定和条件的否定, 我们把这样的两个命题叫做, 其中一个命题叫做命题,那么另一个命题叫做原命题的.若原命题为:“若 p ,则 q ”,则否命题为:“”练习:下列四个命题:( 1)若 f ( x) 是正弦函数,则 f ( x) 是周期函数;( 2)若 f ( x) 是周期函数,则 f ( x) 是正弦函数;( 3)若 f (x) 不是正弦函数,则 f (x) 不是周期函数;的两个角相等;( 3 )奇函数的图像关于原点对称.三、总结提升:※ 学习小结这节课你学到了一些什么?你想进一步探究的问题是什么?( 4)若 f (x) 不是周期函数,则 f (x) 不是正弦函.学习评价※自我评价你完成本节导学案的情况为(). A. 很好 B. 较好 C. 一般 D. 较差※当堂检测(时量: 5 分钟满分: 10 分)计分:1.下列语名中不是命题的是().A. x20B. 正弦函数是周期函数C. x {1,2,3,4,5}D. 1252.设M、N是两个集合,则下列命题是真命题的是().A.如果M N,那么M N MB.如果 M N N,那么M NC.如果M N,那么M N MD. M N N,那么N M3.下面命题已写成“若p,则q”的形式的是() .A.能被 5整除的数的末位是5B.到线段两个端点距离相等的点在线段的垂直平分线上C.若一个等式的两边都乘以同一个数,则所得的结果仍是等式D.圆心到圆的切线的距离等于半径4.下列语句中:( 1) 2 2 是有理数( 2 )2100是个大数( 3 )好人一生平安( 4 ) 968 能被11整除,其中是命题的序号是5.将“偶函数的图象关于 y 轴对称”写成“若 p ,则q ”的形式,则 p :,q:课后作业1.写出下列命题的逆命题、否命题和逆否命题,并判断它们的真假( 1)若a,b都是偶数,则a b 是偶数;( 2)若 m0 ,则方程 x 2有实数根 .x m 02.把下列命题改写成“若p ,则 q ”的形式,并写出它们的逆命题、否命题和逆否命题,并判断它们的真假:(1 )线段的垂直平分线上的点到这条线段两个端点的距离相等;(2 )矩形的对角线相等 .§1.1.2 四种命题间的相互关系学习目标1.掌握四种命题的内在联系;2.能分析逆命题、否命题和逆否命题的相互关系,并能利用等价关系转化 .学习过程一、课前准备复习 1:四种命题命题表述形式原命题若 p ,则 q逆命题(1)否命题(2)逆否命题(3)请填 (1)(2)( 3)空格 .复习 2 :判断命题“若 a0 ,则20 有实x x a根”的逆命题的真假 .二、新课导学※ 学习探究1:分析下列四个命题之间的关系( 1)若 f ( x) 是正弦函数,则 f ( x) 是周期函数;( 2)若 f ( x) 是周期函数,则 f ( x) 是正弦函数;( 3)若 f (x) 不是正弦函数,则 f (x) 不是周期函数;( 4)若 f (x) 不是周期函数,则 f (x) 不是正弦函数 .(1)(2)互为(1)(3)互为.(1)(4)互为(2)(3)互为.通过上例分析我们可以得出四种命题之间有如下关系:2、四种命题的真假性例 1 以“若x2 3 x 2 0 ,则 x 2 ”为原命题,写出它的逆命题、否命题、逆否命题,并判断这些命题的真假并总结其规律性..通过上例真假性可总结如:原命题逆命题否命题逆否命题真真假假四上表可知四种命题的真假性之间有如下关系:(1).(2).练习:判断下列命题的真假.(1) 命题“在 ABC 中,若 AB AC ,则C B ”的逆命题;( 2 )命题“若ab 0 ,则 a 0 且 b0 ”的否命题;( 3 )命题“若 a 0 且 b 0 ,则 ab0 ”的逆否命题;( 4 )命题“若 a 0 且 b 0 ,则 a 2 b 20 ”的逆命题 .反思:( 1 )直接判断(2)互为逆否命题的两个命题等价来判断 .※ 典型例题例 1 证明 :若 x2y20 ,则 x y 0 ..变式:判断命题“若 x2y20 ,则 x y 0 ”是真命题还是假命题?22,则练习:证明:若 a b 2 a 4b 3 0a b 1 .例 2 已知函数 f (x) 在 (, )上是增函数 , a,b R ,对于命题“若a b 0 ,则f ( a) f ( b) f ( a).”f ( b(1)写出逆命题,判断其真假,并证明你的结论.(2)写出其逆否命题 ,并证明你的结论 .2.命题“如果 x a 2b2,那么 x 2ab ”的逆否命题是()A. 如果 x a2 b 2,那么 x2abB. 如果 x2ab ,那么 x22a bC. 如果 x2ab ,那么 x a2 b 2D. 如果 x22,那么 x2aba b三、总结提升:※ 学习小结这节课你学到了一些什么?你想进一步探究的问题是什么?学习评价※ 自我评价你完成本节导学案的情况为() .A. 很好B. 较好C. 一般D. 较差※ 当堂检测(时量:5 分钟满分: 10分)计分:1.命题“若 x0且 y0,则 xy 0”的否命题是() .A. 若 x0, y0,则 xy0B. 若 x0, y0 ,则 xy0※ 动手试试C. 若x, y至少有一个不大于 0 ,则 xy1.求证:若一个三角形的两条边不等,这两条边所0 ,或等于0,则 xy 0D. 若x, y至少有一个小于对的角也不相等 .命题“正数 a 的平方根不等于0”是命题“若a 不是2.正数,则它的平方根等于0”的() .A. 逆命题B. 否命题C. 逆否命题D. 等价命题3.用反法证明命题“2 3 是无理数”时,假设正确的是() ..A. 假设 2 是有理数B. 假设3 是有理数C. 假设 2 或 3 是有理数学习目标D. 假设 23 是有理数1. 理解必要条件和充分条件的意义;4. 若 x21 的逆命题是1 ,则 x2. 能判断两个命题之间的关系 .否命题是5.命题“若,则 2 a2 b1 ”的否命题为a b学习过程一、课前准备课后作业复习 1:请同学们画出四种命题的相互关系图.1. 已 知 a,b 是 实 数 , 若 x 2axb 0 有 非 空 解2集,则 a 4b 0 ,写出该命题的逆命题、否命题、逆否命题并判断其真假.复习 2:将命题“线段的垂直平分线上的点到这条线段两个端点的距离相等”改写为“若 p ,则 q ”的形式,并写出它的逆命题、否命题、逆否命题并判断它们的真假 .2. 证明:在四边形ABCD 中,若ABCDACAB AC.,则§1.2.1 充分条件与必要条件二、新课导学※ 学习探究探究任务: 充分条件和必要条件的概念问题:1. 命题“若x a 2 b 2 ,则 x 2 ab ”( 1)判断该命题的真假;( 2)改写成“若 p ,则 q ”的形式,则P :q :.(3 )如果该命题是真命题,则该命题可记为:读着:.2. 1. 命题“若ab 0 ,则 a0 ”(1)判断该命题的真假;(2)改写成“若p,则q”的形式,则P :q :(3)如果该命题是真命题,则该命题可记为:读着:新知:一般地,“若p ,则 q ”为真命题,是指由 p 通过推理可以得出 q .我们就说,由 p 推出 q ,记作 p q ,并且说p是q的,q是p 的试试:用符号“”与“ ”填空:( 1) x2y2x y ;( 2)内错角相等两直线平行;( 3)整数a能被 6 整除 a 的个位数字为偶数;( 4) ac bc a b .※ 典型例题例 1 下列“若p,则q”形式的命题中,哪些命题中的 p 是 q的充分条件?( 1)若 x 1 ,则 x24x 3 0 ;( 2 )若 f (x) x ,则 f ( x) 在 ( ,) 上为增函数;( 3)若x为无理数,则x2为无理数 .( 2 )若 x 5 ,则 x 10例 2 下列“若p,则q”形式的命题中哪些命题中的q 是 p 必要条件?( 1 )若x y ,则x2y2;(2 )若两个三角形全等,则这两个三角形面积相等;(3 )若 a b ,则 ac bc练习:下列“若 p ,则 q ”形式的命题中哪些命题中的q 是 p 必要条件?(1 )若 a 5 是无理数,则a是无理数;(2 )若 ( x a)( x b) 0 ,则x a .小结:判断命题的真假是解题的关键.※ 动手试试练 1. 判断下列命题的真假.( 1) x 2 是 x2 4 x 40 的必要条件;( 2)圆心到直线的距离等于半径是这条直线为圆的切线的必要条件;练习:下列“若P,则 q ”的形式的命题中,哪些命( 3) sin sin是的充分条件;题中的 p 是 q 的充分条件?( 4) ab0 是 a0 的充分条件 .( 1 )若两条直线的斜率相等,则这两条直线平行;※ 知识拓展设 A, B 为两个集合 , 集合 AB ,那么 x A 是x B 的条件, xB 是 xA 的条件 .学习评价※ 自我评价 你完成本节导学案的情况为() .A. 很好B. 较好C. 一般D. 较差※ 当堂检测 (时量: 5 分钟 满分: 10 分)计分:1. 在平面内 ,下列哪个是“四边形是矩形”的充分条件?() .练 2. 下列各题中, p 是 q 的什么条件?( 1) p : x1 , q : x 1A. 平行四边形对角线相等x 1 ;( 2) p : | x 2 | 3 , q : 1 x B. 四边形两组对边相等5 ;( 3) p : x2 , q : x 3C. 四边形的对角线互相平分3 x ;D. 四边形的对角线垂直( 4 ) p :三角形是等边三角形,q :三角形是等R ,下列各式中哪个是“ xy0 ”的必要条腰三角形 .2. x, y件?( ).A. x yB. x 2 y 2 0C. x y 0D. x 3y 33.平面// 平面的一个充分条件是().A. 存在一条直线 a, a // , a //B. 存在一条直线 a, a, a //C. 存在两条平行直线 a, b,a , b , a // , b //D. 存在两条异面直线 a, b,a , b, a // , b //4. p : x 2 0 , q : ( x2)( x 3) 0 , p 是 q 的条件 .5. p :两个三角形相似;q :两个三角形全等,三、总结提升 条件 .p 是 q 的※ 学习小结这节课你学到了一些什么?你想进一步探究 课后作业的问题是什么?1. 判断下列命题的真假(1)“22b”是“b ”的充分条件;a a( 2 )“|a|| |22b ”是“b ”的必要条件.a2.已知 A{ x | x 满足条件 p} , B { x | x 满足条件复习 2:p:一个四边形是矩形q :四边形的对角q} .线相等 . p是q的什么条件 ?(1)如果 A B ,那么 p 是 q 的什么条件?(2)如果 B A ,那么 p 是 q 的什么条件?二、新课导学※ 学习探究探究任务一:充要条件概念问题:已知p :整数a是6的倍数, q :整数a是2 和3 的倍数 .那么p是q的什么条件 ? q又是 p 的什么条件?§1.2.2充要条件学习目标1.理解充要条件的概念;2.掌握充要条件的证明方法,既要证明充分性又要证明必要性 . 新知:如果p q ,那么p与q互为试试:下列形如“若p ,则 q ”的命题是真命题吗?它的逆命题是真命题吗?p 是 q 的什么条件?(1 )若平面外一条直线a与平面内一条直线平行,则直线 a 与平面平行;(2 )若直线a与平面内两条直线垂直,则直线a 与平面垂直.学习过程一、课前准备反思:充要条件的实质是原命题和逆命题均为真(预习教材 P11~ P12,找出疑惑之处)命题 .复习 1:什么是充分条件和必要条件 ?※ 典型例题例 1 下列各题中 ,哪些p是q的充要条件 ?.(1)p : b0, q : 函数 f ( x)ax2bx c 是偶函数;例2已知:O 的半径为 r ,圆心 O 到直线的距(2)p : x0, y 0,q : xy0离为 d .求证 : d r 是直线 l 与 O 相切的充要(3)p : a b, q : a c b c条件 .变式:下列形如“若p ,则 q ”的命题是真命题吗?它的逆命题是真命题吗?哪些p 是 q 的充要条件?(1)p : b0 , q : 函数 f ( x)ax2bx c 是偶函数;(2)p : x0, y 0,q : xy0(3)p : a b ,q : a c b c小结:判断是否充要条件两种方法( 1) p q 且 q p ;(2)原命题、逆命题均为真命题;(3)用逆否命题转化 .练习:在下列各题中, p是q的充要条件 ?(1)p : x23x 4, q : x3x4(2)p : x30 ,q : ( x3)( x4) 0(3)p : b24ac0(a0) ,q : ax2bx c0(a0)(4)p : x1是方程 ax2bx c0 的根q : a b c0变式:已知:O 的半径为 r ,圆心O 到直线的距离为 d ,证明 :(1)若 d r ,则直线 l 与 O 相切 .(2)若直线 l 与O 相切 ,则 d r小结:证明充要条件既要证明充分性又要证明必要性 .※ 动手试试练 1. 下列各题中p 是 q 的什么条件?( 1 )p: x 1 ,q: x 1x 1 ;( 2 )p: | x 2 | 3 ,q: 1 x 5 ;( 3 )p: x 2 ,q: x 33x ;( 4 )p:三角形是等边三角形,q :三角形是等腰三角形 ..3. 设p: b 24ac 0( a 0) ,q:关于x的方程ax2bx c 0( a 0) 有实根,则p是q的练 2. 求圆 ( x a )2( y b)2r 2经过原点的充要条() .件 . A. 充分不必要条件 B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件4.25x 30的一个必要不充分条件是() .2 x1x3 B.1A.x212C. 3D. 1 x6x25. 用充分条件、必要条件、充要条件填空.(1). x 3 是 x 5 的(2). x 3 是 x22x 3 0 的( 3). 两个三角形全等是两个三角形相似的三、总结提升课后作业※ 学习小结1.证明: a2b 0 是直线 ax 2 y 3 0和直线这节课你学到了一些什么?你想进一步探究的x by 20 垂直的充要条件 .问题是什么?2.求证:ABC 是等边三角形的充要条件是※ 知识拓展222a,b,c 是ABCa b c ab ac bc ,这里设 A、B为两个集合,集合 A B 是指的三边 .x Ax B,则“x A ”与“x B ”互为件 .学习评价※自我评价你完成本节导学案的情况为().A. 很好B. 较好C. 一般D. 较差※当堂检测(时量: 5 分钟满分: 10 分)计分:1.下列命题为真命题的是().A. a b 是 a 2b2的充分条件B. | a || b | 是 a 22b 的充要条件C. x2 1 是 x 1 的充分条件D.是 tan tan的充要条件2.“”是“M N ”的().x M N xA. 充分不必要条件B. 必要不充分条件C.充要条件D. 既不充分也不必要条件.§1.3 简单的逻辑联结词学习目标1.了解“或“”且”“非”逻辑联结词的含义;2.掌握 p q, p q,p 的真假性的判断;3.正确理解p的意义,区别p 与 p 的否命题;4.掌握 p q, p q,p 的真假性的判断,关键在于p 与 q 的真假的判断.学习过程一、课前准备(预习教材P14~ P16,找出疑惑之处)复习 1:什么是充要条件?复习 2 :已知 A { x | x 满足条件p} , B{ x | x 满足条件 q}(1) 如果A B ,那么 p 是 q 的什么条件;(2) 如果B A ,那么 p 是 q 的什么条件;(3) 如果A B ,那么 p 是 q 的什么条件.二、新课导学※ 学习探究探究任务一:“且“的意义问题:下列三个命题有什么关系?(1)12 能被 3 整除;(2) 12 能被 4 整除;(3) 12 能被 3 整除且能被 4 整除 .新知: 1. 一般地 ,用逻辑联结词“且”把命题p和命题q联结起来就得到一个新命题,记作“”,读作“”.2.规定:p q p q真真真真假假假真假假假假试试:判断下列命题的真假:(1)12 是 48 且是 36 的约数;(2 )矩形的对角线互相垂直且平分 .反思: p q 的真假性的判断,关键在于p 与 q 的真假的判断 .探究任务二:“或“的意义问题:下列三个命题有什么关系?(1)27 是 7 的倍数;(2)27 是 9 的倍数;(3)27 是 7 的倍数或是 9 的倍数 .新知: 1. 一般地 ,用逻辑联结词“或”把命题p和命题q联结起来就得到一个新命题,记作“”,读作“”.2.规定:p q p q真真真真假真假真真假假假试试:判断下列命题的真假:(1) 47是 7 的倍数或 49是 7 的倍数;.( 2)等腰梯形的对角线互相平分或互相垂直.变式:用逻辑联结词“且”改写下列命题,并判断他们的真假:( 1 )1 既是奇数,又是素数;(2)2 和 3 都是素数 .反思: p q 的真假性的判断,关键在于p 与 q 的真假的判断 .探究任务三:“非“的意义问题:下列两个命题有什么关系?小结:p q 的真假性的判断,关键在于p 与 q 的(1) 35 能被 5 整除;真假的判断.( 2) 35 不能被 5 整除;例2判断下列命题的真假(1) 22;(2) 集合A是A B 的子集或是A B 的子集;(3) 周长相等的两个三角形全等或面积相等的两新知: 1. 一般地 ,对一个命题的全盘否定就得到一个三角形全等.个新命题,记作“,” 读作“”或“”.2.规定:p p真假变式:如果p q 为真命题,那么p q 一定是真假真命题吗?反之, p q 为真命题,那么p q 一定是真命题吗?试试:写出下列命题的否定并判断他们的真假:(1) 2+2=5 ;2( 2) 3 是方程 x 90 的根;(3)( 1)21反思:p 的真假性的判断,关键在于p 的真假的判断 .※ 典型例题例 1 将下列命题用“且”联结成新命题并判断他们的真假:( 1 )p:平行四边形的对角线互相平分,q :平行四边形的对角线相等;( 2 )p:菱形的对角线互相垂直,q :菱形的对角线互相平分;( 3)p: 35 是 15 的倍数,q: 35 是 7 的倍数小结: p q 的真假性的判断,关键在于p 与 q 的真假的判断 .例3 写出下列命题的否定,并判断他们的真假:( 1 )p: y sin x 是周期函数;( 2 )p: 32( 3 )空集是集合 A 的子集.小结: p 的真假性的判断,关键在于 p 的真假的判断 .三、总结提升※ 学习小结这节课你学到了一些什么?你想进一步探究的.问题是什么?※ 知识拓展阅读教材第 18 页 ,理解逻辑联结词“且”“或”“非”与集合运算“交“”并”“补”的关系.学习评价※ 自我评价你完成本节导学案的情况为(). A. 很好 B. 较好 C. 一般 D. 较差※当堂检测(时量: 5 分钟满分: 10分)计分:1.“或q 为真命题”是“ 且q为真命题”的().p pA. 充分不必要条件B. 必要不充分条件C.充要条件D. 既不充分也不必要条件2.命题P:在ABC 中,CB 是 sin C sin B的充要条件;命题q :a b 是 ac2bc2 的充分不必要条件,则() .A. p真q假B. p假q假C.“p或q”为假D. “p且q”为真3.命题:( 1 )平行四边形对角线相等;( 2 )三角形两边的和大于或等于第三边;( 3 )三角形中最小角不大于 60 ;( 4)对角线相等的菱形为正方形 . 其中真命题有().A.1B.2C.3D.44.命题p: 0不是自然数,命题q :是无理数,在命题“p 或q”“ 且q”“非p”“非q”中假命题p是,真命题是.5. 已知p: | x2x | 6 ,q: x Z , p q, q 都是假命题,则 x 的值组成的集合为2.判断下列命题的真假:(1) 5 2 且 73(2)7 8(3) 3 4 或 34§1.4 全称量词与存在量词学习目标1.掌握全称量词与存在量词的的意义;2.掌握含有量词的命题:全称命题和特称命题真假的判断 .课后作业1. 写出下列命题,并判断他们的真假:学习过程( 1)p q ,这里 p :4{2,3}, q :2{2,3} ;一、课前准备( 2)p q ,这里 p :4{2,3}, q :2{2,3} ;(预习教材 P21~ P23,找出疑惑之处)(3)p q ,这里 p :2是偶数, q :3不是素复习 1 :写出下列命题的否定, 并判断他们的真数;假:(4)p q ,这里 p :2是偶数, q :3不是素数.( 1 ) 2 是有理数;( 2) 5 不是 15 的约数( 3 )8 7 15 (4 )空集是任何集合的真子集.新知: 1.短语“”“”在逻辑中通常叫做全称量词,并用符号“”表示,含有的命题,叫做全称命题.其基本形式为:x M , p( x) ,读作:复习 2:判断下列命题的真假,并说明理由: 2. 短语““””在逻辑中通常叫做存( 1 )p q ,这里 p :是无理数,q :是实在量词,并用符号“”表示,含有数;的命题,叫做特称称命题 .( 2 )p q ,这里 p :是无理数,q :是实其基本形式x0M , p( x0 ) ,读作:数;试试:判断下列命题是不是全称命题或者存在命(3)p q ,这里 p :2 3 ,q: 8715;题 ,如果是 ,用量词符号表示出来 .(4)p q ,这里 p :2 3 ,q: 8715 .(1) 中国所有的江河都流入大海;( 2 )0 不能作为除数;( 3 )任何一个实数除以 1 ,仍等于这个实数;( 4 )每一个非零向量都有方向 .二、新课导学※ 学习探究探究任务一:全称量词的意义问题: 1.下列语名是命题吗?(1)与( 3),(2 )与( 4 )之间有什么关系?反思:注意哪些词是量词是解决本题的关键,还应( 1) x 3 ;注意全称命题和存在命题的结构形式.( 2) 2 x 1 是整数;※ 典型例题( 3)对所有的x R, x 3 ;例 1 判断下列全称命题的真假:( 4)对任意一个x Z , 2 x1是整数 .( 1)所有的素数都是奇数;( 2) x R, x211 ;( 3)对每一个无理数x ,x2也是无理数.2.下列语名是命题吗?(1 )与( 3 ),( 2 )与(4)之间有什么关系?(1)2x 1 3 ;(2)x 能被2和3整除;( 3)存在一个00x R ,使 2 x1 3 ;( 4)至少有一个 x0Z , x0能被2和3整除.变式:判断下列命题的真假:.( 1)x(5,8),f (x) x24x20( 2)x(3,), f (x)x24x20小结:要判定一个全称命题是真命题,必须对限定集合 M 中每一个元素x 验证p( x)成立;但要判定全称命题是假命题,却只要能举出集合M 中的一个 x x0,使得 p(x0 ) 不成立即可 .例 2 判断下列特称命题的真假:( 1)有一个实数x0,使 x02 2 x030 ;(2)存在两个相交平面垂直于同一条直线;(3)有些整数只有两个正因数 .变式:判断下列命题的真假:(1) a Z , a23a2(2) a 3,a23a2小结:要判定特称命题“x0M , p( x0 ) ”是真命题只要在集合M 中找一个元素x0,使 p( x0 )成立即可;如果集合M 中,使P( x)成立的元素 x 不存在,那么这个特称命题是假命题.※ 动手试试练1. 判断下列全称命题的真假:( 1)每个指数都是单调函数;( 2)任何实数都有算术平方根;( 3 )x { x | x 是无理数 }, x2是无理数 .练 2. 判定下列特称命题的真假:( 1) x0R, x0 0 ;( 2)至少有一个整数,它既不是合数,也不是素数;( 3) x0{ x | x 是无理数 }, x02是无理数 .三、总结提升※ 学习小结这节课你学到了一些什么?你想进一步探究的问题是什么?※ 知识拓展数理逻辑又称符号逻辑 ,是用数学的方法研究推理过程的一门学问 . 德国启蒙思想家莱布尼茨( 1646 —1716 )是数理逻辑的创始人。
高中数学 选修2-1椭圆导学案

椭圆及其标准方程(一)导学案【学习要求】1.了解椭圆的实际背景,经历从具体情境中抽象出椭圆的过程、椭圆标准方程的推导与化简过程. 2.掌握椭圆的定义、标准方程及几何图形.【学法指导】1.通过自己亲自动手尝试画图,发现椭圆的形成过程进而归纳出椭圆的定义,培养观察、辨析、归纳问题的能力.2.通过经历椭圆方程的化简,增强战胜困难的意志并体会数学的简洁美、对称美,通过讨论椭圆方程推导的等价性,养成扎实严谨的科学态度【知识要点】1.椭圆:平面内与两个定点F 1,F 2的 的点的轨迹叫做椭圆(ellipse).这两个定点叫做椭圆的 ,两焦点间的距离叫做椭圆的 . 2. 焦点在x 轴上 焦点在y 轴上 标准方程 焦点a 、b 、c 的关系探究点一 椭圆的定义问题1 给你两个图钉、一根无弹性的细绳、一张纸板,能画出椭圆吗?问题2 动点P 到两定点A 、B 的距离之和|P A |+|PB |=2a (a >0且a 为常数)的轨迹一定是椭圆吗?探究点二 椭圆的标准方程问题1 观察椭圆的形状,你认为怎样选择坐标系才能使椭圆的方程较简单?并写出求解过程.问题2 建系时如果焦点在y 轴上会得到何种形式的椭圆方程?怎样判定给定的椭圆焦点在哪个坐标轴上?问题3 椭圆方程中的a 、b 以及参数c 有什么意义,它们满足什么关系?例1 (1)已知椭圆的两个焦点坐标分别是(-2,0),(2,0),并且经过点⎝⎛⎭⎫52,-32,求它的标准方程; (2)若椭圆经过两点(2,0)和(0,1),求椭圆的标准方程.跟踪训练1 (1)已知中心在原点,以坐标轴为对称轴,椭圆过点Q (2,1)且与椭圆x 29+y 24=1有公共的焦点,求椭圆的标准方程;(2)已知椭圆的中心在原点,以坐标轴为对称轴,且经过P 1(6,1),P 2(-3,-2)两点,求椭圆的标准方程.例2 已知方程x 2k -4-y 2k -10=1表示焦点在x 轴上的椭圆,则实数k 的取值范围为__________.跟踪训练2 若方程x 2m -y 2m 2-2=1表示焦点在y 轴上的椭圆,那么实数m 的取值范围是 ( )A .m >0B .0<m <1C .-2<m <1D .m >1且m ≠ 2探究点三 椭圆的定义及标准方程的应用例3 已知椭圆的方程为x 24+y 23=1,椭圆上有一点P 满足∠PF 1F 2=90°(如图).求△PF 1F 2的面积.跟踪训练3 已知椭圆x 249+y 224=1上一点P 与椭圆两焦点F 1、F 2的连线夹角为直角,则|PF 1|·|PF 2|=________【当堂检测】1.椭圆x 225+y 2=1上一点P 到一个焦点的距离为2,则点P 到另一个焦点的距离为 ( )A .5B .6C .7D .82.若方程x 225-m +y 2m +9=1表示焦点在y 轴上的椭圆,则实数m 的取值范围是 ( )A .-9<m <25B .8<m <25C .16<m <25D .m >83.椭圆x 216+y 232=1的焦距为________.4.已知椭圆经过点(3,0)且与椭圆x 24+y 29=1的焦点相同,则这个椭圆的标准方程为____________【课堂小结】1.平面内到两定点F 1,F 2的距离之和为常数,即|MF 1|+|MF 2|=2a , 当2a >|F 1F 2|时,轨迹是椭圆;当2a =|F 1F 2|时,轨迹是一条线段F 1F 2; 当2a <|F 1F 2|时,轨迹不存在.2.对于求解椭圆的标准方程一般有两种方法:可以通过待定系数法求解,也可以通过椭圆的定义进行求解. 3.用待定系数法求椭圆的标准方程时,若已知焦点的位置,可直接设出标准方程;若焦点位置不确定,可分两种情况求解;也可设Ax 2+By 2=1(A >0,B >0,A ≠B )求解,避免了分类讨论,达到了简化运算的目的.【拓展提高】1.已知P 是椭圆13422=+y x 上的点,21F F 、分别是椭圆的左、右焦点,212121=⋅PF PF PF PF ,则21PF F ∆的面积为( ) A .33B .3C .32D .33 2.已知椭圆的两焦点为P F F ),0,1()0,1(21、-为椭圆上一点,且21212PF PF F F += (1)求此椭圆方程(2)若点P 在第二象限,21012,120F PF PF F ∆=∠求的面积3.如果点),(y x M 在运动过程中总满足关系10)3()3(2222=+++-+y x y x ,点M 的轨迹是 ,它的方程是4. 椭圆22194x y +=的焦点为F 1、F 2,点P 为其上的动点,当21PF F ∠为钝角时,求P 点横坐标的取值范围。
高中数学选修2-1 抛物线导学案加课后作业及参考答案

抛物线及其标准方程导学案【学习要求】1.掌握抛物线的定义及焦点、准线的概念.2.会求简单的抛物线的方程.【学法指导】通过观察抛物线的形成过程,得出抛物线定义,建系得出抛物线标准方程.通过抛物线及其标准方程的应用,体会抛物线在刻画现实世界和解决实际问题中的作用.【知识要点】1.抛物线的定义平面内与一个定点F和一条定直线l(l不经过点F) 的点的轨迹叫做抛物线.点F叫做抛物线的,直线l叫做抛物线的2.抛物线标准方程的几种形式图形标准方程焦点坐标准线方程探究点一抛物线定义如图,我们在黑板上画一条直线EF,然后取一个三角板,将一条拉链AB固定在三角板的一条直角边上,并将拉链下边一半的一端固定在C点,将三角板的另一条直角边贴在直线EF上,在拉锁D处放置一支粉笔,上下拖动三角板,粉笔会画出一条曲线.问题1画出的曲线是什么形状?问题2|DA|是点D到直线EF的距离吗?为什么?问题3点D在移动过程中,满足什么条件?问题 4在抛物线定义中,条件“l不经过点F”去掉是否可以?例1方程[]22)1()3(2-++yx=|x-y+3|表示的曲线是()A.圆B.椭圆C.双曲线D.抛物线跟踪训练1(1)若动点P与定点F(1,1)和直线l:3x+y-4=0的距离相等,则动点P的轨迹是() A.椭圆B.双曲线C.抛物线D.直线(2)若动圆与圆(x-2)2+y2=1相外切,又与直线x+1=0相切,则动圆圆心的轨迹是()A.椭圆B.双曲线C.双曲线的一支D.抛物线探究点二抛物线的标准方程问题 1结合求曲线方程的步骤,怎样求抛物线的标准方程?问题2抛物线方程中p有何意义?标准方程有几种类型?问题3根据抛物线方程如何求焦点坐标、准线方程?例2已知抛物线的方程如下,求其焦点坐标和准线方程.(1)y2=-6x;(2)3x2+5y=0;(3)y=4x2;(4)y2=a2x (a≠0).跟踪训练2(1)抛物线方程为7x+4y2=0,则焦点坐标为()A.⎝⎛⎭⎫716,0B.⎝⎛⎭⎫-74,0C.⎝⎛⎭⎫-716,0D.⎝⎛⎭⎫0,-74(2)抛物线y=-14x2的准线方程是()A.x=116B.x=1 C.y=1 D.y=2例3分别求满足下列条件的抛物线的标准方程.(1)准线方程为2y+4=0;(2)过点(3,-4);(3)焦点在直线x+3y+15=0上.跟踪训练3(1)经过点P(4,-2)的抛物线的标准方程为()A.y2=x或x2=y B.y2=x或x2=8yC.x2=-8y或y2=x D.x2=y或y2=-8x(2)已知抛物线的顶点在原点,焦点在y轴上,抛物线上一点M(m,-3)到焦点F的距离为5,求m的值、抛物线方程及其准线方程.探究点三 抛物线定义的应用例4 已知点A (3,2),点M 到F ⎝⎛⎭⎫12,0的距离比它到y 轴的距离大12. (1)求点M 的轨迹方程;(2)是否存在M ,使|MA |+|MF |取得最小值?若存在,求此时点M 的坐标;若不存在,请说明理由. 跟踪训练4 (1)抛物线y =4x 2上的一点M 到焦点的距离为1,则点M 的纵坐标是 ( ) A .1716B .1516C .78D .0(2)已知点P 是抛物线y 2=2x 上的一个动点,则点P 到点(0,2)的距离与点P 到该抛物线准线的距离之和的最小值是( ) A .172B .3C . 5D .92【当堂检测】1.已知抛物线的准线方程为x =-7,则抛物线的标准方程为 ( ) A .x 2=-28y B .y 2=28x C .y 2=-28x D .x 2=28y2.抛物线y 2=2px (p >0)上一点M 到焦点的距离是a (a >p2),则点M 的横坐标是 ( )A .a +p2B .a -p2C .a +pD .a -p3.已知直线l 1:4x -3y +6=0和直线l 2:x =-1,抛物线y 2=4x 上一动点P 到直线l 1和直线l 2的距离之和的最小值是 ( ) A .2B .3C .115D .37164.焦点在y 轴上,且过点A (1,-4)的抛物线的标准方程是__________【课堂小结】1.抛物线的定义中不要忽略条件:点F 不在直线l 上.2.确定抛物线的标准方程,从形式上看,只需求一个参数p ,但由于标准方程有四种类型,因此,还应确定开口方向,当开口方向不确定时,应进行分类讨论.有时也可设标准方程的统一形式,避免讨论,如焦点在x 轴上的抛物线标准方程可设为y 2=2mx (m ≠0),焦点在y 轴上的抛物线标准方程可设为x 2=2my (m ≠0).【拓展提高】1.若点P 到点(4,0)F 的距离比它到直线50x +=的距离小1,则P 点的轨迹方程是( ) A .216y x =- B .232y x =- C .216y x = D .232y x =2.过抛物线x y 42=的焦点作直线交抛物线于),(),,(2211y x B y x A 两点,如果621=+x x ,那么AB =( )A .10B .8C .6D .43.过抛物线y 2=2px (p >0)的焦点F 的直线l 交抛物线于点A 、B ,交其准线于点C ,若|BC |=2|BF |,且|AF |=3,则此抛物线方程为( )A .y 2=9xB .y 2=6xC .y 2=3xD .y 2=3x4.抛物线x y 42=上的两点A 、B 到焦点的距离之和为10,则线段AB 中点到y 轴的距离为【课后作业】一、基础过关1.抛物线y 2=-8x 的焦点坐标是( )A .(2,0)B .(-2,0)C .(4,0)D .(-4,0)2.已知抛物线的顶点在原点,对称轴为x 轴,焦点在双曲线x 24-y 22=1上,则抛物线方程为 ( )A .y 2=8xB .y 2=4xC .y 2=2xD .y 2=±8x3.已知抛物线y 2=2px (p >0)的准线与圆(x -3)2+y 2=16相切,则p 的值为( )A .12B .1C .2D .44.与y 轴相切并和圆x 2+y 2-10x =0外切的动圆的圆心的轨迹为( )A .圆B .抛物线和一条射线C .椭圆D .抛物线 5.以双曲线x 216-y 29=1的右顶点为焦点的抛物线的标准方程为__________.6.抛物线x 2+12y =0的准线方程是__________.7.求经过A (-2,-4)的抛物线的标准方程及其对应的准线、焦点坐标. 二、能力提升8.定长为3的线段AB 的两个端点在抛物线y 2=2x 上移动,M 为AB 的中点,则M 点到y 轴的最短距离为 ( )A .12B .1C .32D .29.设M (x 0,y 0)为抛物线C :x 2=8y 上一点,F 为抛物线C 的焦点,以F 为圆心,|FM |为半径的圆和抛物线C 的准线相交,则y 0的取值范围是( )A .(0,2)B .[0,2]C .(2,+∞)D .[2,+∞)10.设抛物线y 2=8x 的焦点为F ,准线为l ,P 为抛物线上一点,P A ⊥l ,A 为垂足,如果直线AF 的斜率为-3,那么|PF |=________.11.设斜率为2的直线l 过抛物线y 2=ax (a ≠0)的焦点F ,且与y 轴交于点A ,若△OAF (O 为坐标原点)的面积为4,求抛物线的方程.12.喷灌的喷头装在直立管柱OA的顶点A处,喷出水流的最高点B高5 m,且与OA所在的直线相距4 m,水流落在以O为圆心,半径为9 m的圆上,则管柱OA的长是多少?三、探究与拓展13.已知抛物线C的顶点在原点,焦点F在x轴的正半轴上,设A,B是抛物线C上的两个动点(AB不垂直于x轴),且|AF|+|BF|=8,线段AB的垂直平分线恒经过点Q(6,0),求抛物线的方程.抛物线的简单几何性质(一)导学案【学习要求】1.了解抛物线的范围、对称性、顶点、焦点、准线等几何性质.2.会利用抛物线的性质解决一些简单的抛物线问题.【学法指导】结合椭圆和双曲线的几何性质,类比抛物线的性质,通过对抛物线的标准方程的讨论,进一步理解用代数方法研究几何性质的优越性,感受坐标法和数形结合的基本思想.【知识要点】1.抛物线的几何性质标准方程y2=2px(p>0)y2=-2px(p>0)x2=2py(p>0)x2=-2py(p>0)图形性质范围对称轴x轴x轴y轴y轴顶点(0,0)离心率e=2直线过抛物线y2=2px(p>0)的焦点F,与抛物线交于A(x1,y1)、B(x2,y2)两点,由抛物线的定义知,|AF|=x1+p2,|BF|=x2+p2,故|AB|=3.直线与抛物线的位置关系直线y=kx+b与抛物线y2=2px(p>0)的交点个数决定于关于x的方程的解的个数.当k≠0时,若Δ>0,则直线与抛物线有个不同的公共点;当Δ=0时,直线与抛物线有个公共点;当Δ<0时,直线与抛物线公共点.当k=0时,直线与抛物线的轴,此时直线与抛物线有个公共点.【问题探究】探究点一抛物线的几何性质问题1类比椭圆、双曲线的几何性质,结合图象,说出抛物线y2=2px(p>0)的范围、对称性、顶点、离心率.怎样用方程验证?问题 2通过抛物线的几何性质,怎样探求抛物线的标准方程?例1若抛物线y2=x上一点P到准线的距离等于它到顶点的距离,则点P的坐标为()A.⎝⎛⎭⎫14,±24B.⎝⎛⎭⎫18,±24C.⎝⎛⎭⎫14,24D.⎝⎛⎭⎫18,24跟踪训练1抛物线y2=2px (p>0)上一点M的纵坐标为-42,这点到准线的距离为6,则抛物线方程为________探究点二抛物线的焦点弦问题例2已知直线l经过抛物线y2=6x的焦点F,且与抛物线相交于A、B两点.(1)若直线l的倾斜角为60°,求|AB|的值;(2)若|AB|=9,求线段AB的中点M到准线的距离.跟踪训练2已知过抛物线y2=4x的焦点F的弦长为36,求弦所在的直线方程.探究点三直线与抛物线的位置关系问题结合直线与椭圆、直线与双曲线的位置关系,请你思考一下怎样讨论直线与抛物线的位置关系?例3已知抛物线的方程为y2=4x,直线l过定点P(-2,1),斜率为k,k为何值时,直线l与抛物线y2=4x:只有一个公共点;有两个公共点;没有公共点?跟踪训练3过点(-3,2)的直线与抛物线y2=4x只有一个公共点,求此直线方程.【当堂检测】1.设AB为过抛物线y2=2px (p>0)的焦点的弦,则|AB|的最小值为()A .p 2B .pC .2pD .无法确定2.设抛物线y 2=8x 的准线与x 轴交于点Q ,若过点Q 的直线l 与抛物线有公共点,则直线l 的斜率的取值范围是( ) A .⎣⎡⎦⎤-12,12B .[-2,2]C .[-1,1]D .[-4,4]3.抛物线y =4x 2上一点到直线y =4x -5的距离最短,则该点坐标为 ( )A .(1,2)B .(0,0)C .⎝⎛⎭⎫12,1D .(1,4)4.已知过抛物线y 2=4x 的焦点F 的直线交该抛物线于A 、B 两点,|AF |=2,则|BF |=_______【课堂小结】1.讨论抛物线的几何性质,一定要利用抛物线的标准方程;利用几何性质,也可以根据待定系数法求抛物线的方程.2.直线与抛物线有一个交点,是直线与抛物线相切的必要不充分条件.3.直线与抛物线的相交弦问题共有两类,一类是过焦点的弦,一类是不过焦点的弦.解决弦的问题,大多涉及到抛物线的弦长、弦的中点、弦的斜率.常用的办法是将直线与抛物线联立,转化为关于x 或y 的一元二次方程,然后利用根与系数的关系,这样避免求交点.尤其是弦的中点问题,还应注意“点差法”的运用.【拓展提高】1.若双曲线2221613x y p -=的左焦点在抛物线22y px =的准线上,则p 的值为( )A .2B .3C .4D .422.设O 为坐标原点,F 为抛物线x y 42=的焦点,A 为抛物线上的一点,若4OA AF •=-,则点A 的坐标为( )A .)22,2(±B .)2,1(±C .)2,1(D .)22,2(3.已知直线l :y =-x +1和抛物线C :x y 42=,设直线与抛物线的交点为B A 、,求AB 的长。
新编人教A高中数学选修2-1全册导学案

人教版高中数学选修2-1全册导学案目录1.1.1命题及其关系1.1.2四种命题的关系1.2.1充分条件1.2.2充要条件1.3.1逻辑联结词11.3.2简单的逻辑联结词21.4全称量词与存在量词2.1.1曲线与方程(1)学案2.1.2曲线与方程(2)学案2.2.1椭圆及其标准方程(1)学案2.2.1椭圆及其标准方程(2)学案2.2.2椭圆及其简单几何性质(1)学案2.2.2椭圆及其简单几何性质(2)学案2.3.1双曲线及其标准方程学案2.3.2双曲线的简单几何性质(1)学案2.3.2双曲线的简单几何性质(2)学案2.4.2抛物线的简单几何性质(1)2.4.2抛物线的简单几何性质(2)2.5曲线与与方程学案第二章圆锥曲线与方程复习学案3.1.1 空间向量及其加减运算3.1.2 空间向量的数乘运算3.1.3 空间向量的数量积运算3.1.4 空间向量的正交分解及其坐标表示3.1.5 空间向量运算的坐标表示3.1 空间向量及其运算3.2 立体几何中的向量方法一3.2 立体几何中的向量方法二--利用向量方法求距离3.2 立体几何中的向量方法三--利用向量方法求角3.2 立体几何中的向量方法一--平行与垂直关系的向量证法§1.1.1 命题及四种命题一.自主学习预习课本2—6页完成下列问题1、命题:;2、真命题:假命题:。
3、命题的数学形式:。
4、四种命题:。
(1)互逆命题:。
(2)互否命题:。
(3)互为逆否命题:。
注意:数学上有些命题表面上虽然不是“若p,则q”的形式,但可以将它的表述作适当的改变,写成“若p,则q”的形式,从而得到该命题的条件和结论。
二、自主探究:〖例1〗判断下列语句中哪些是命题?是真命题还是假命题?(1)空集是任何集合的子集;(2)若整数a是素数,则a是奇数;(3)2小于或等于2;(4)对数函数是增函数吗?x<;(6)平面内不相交的两条直线一定平行;(5)215>(7)明天下雨;(8)312〖例2〗将下列命题改写成“若p,则q”的形式。
人教新课标版数学高二高二数学新人教版选修2-1导学案 椭圆的简单几何性质(一)

椭圆的简单几何性质(一)导学案【学习要求】1.理解椭圆的简单几何性质.2.利用椭圆的简单几何性质解决一些简单问题.【学法指导】通过几何图形观察,代数方程验证的学习过程,体会数形结合的数学思想.通过几何性质的代数研究,养成辩证统一的世界观.【知识要点】1.椭圆的简单几何性质焦点的位置焦点在x轴上焦点在y轴上图形标准方程范围顶点轴长短轴长=,长轴长=焦点(±a2-b2,0)(0,±a2-b2)焦距|F1F2|=2a2-b2对称性对称轴:对称中心:离心率e=ca∈准线2.离心率的作用当椭圆的离心率越,则椭圆越扁;当椭圆离心率越,则椭圆越接近于圆.【问题探究】探究点一 椭圆的简单几何性质问题1 观察椭圆x 2a 2+y 2b2=1 (a >b >0)的形状,你能从图中看出它的范围吗?它具有怎样的对称性?椭圆上哪些点比较特殊?问题2 如何用椭圆的标准方程(代数方法)研究你观察到的几何性质?问题3 观察不同的椭圆,椭圆的扁平程度不一样,怎样刻画椭圆的扁平程度呢?问题4 (1)b a 或c b的大小能刻画椭圆的扁平程度吗?为什么? (2)你能运用三角函数的知识解释:为什么e =c a 越大,椭圆越扁?e =c a越小,椭圆越圆吗?问题5 比较下列各组中椭圆的形状,哪一个更圆,哪一个更扁?为什么?(1)4x 2+9y 2=36与x 225+y 220=1; (2)9x 2+4y 2=36与x 212+y 216=1.例1 求椭圆m 2x 2+4m 2y 2=1 (m >0)的长轴长、短轴长、焦点坐标、顶点坐标和离心率. 跟踪训练1 已知椭圆方程为4x 2+9y 2=36,求椭圆的长轴长、短轴长、焦点坐标、顶点坐标和离心率.探究点二 由椭圆的几何性质求方程例2 椭圆过点(3,0),离心率e =63,求椭圆的标准方程. 跟踪训练2 求适合下列条件的椭圆的标准方程.(1)长轴在x 轴上,长轴的长等于12,离心率等于23; (2)长轴长是短轴长的2倍,且椭圆过点(-2,-4).探究点三 求椭圆的离心率例3 如图所示,椭圆的中心在原点,焦点F 1,F 2在x 轴上,A ,B 是椭圆的顶点,P 是椭圆上且PF 1⊥x 轴,PF 2∥AB ,求此椭圆的离心率.跟踪训练3 如图,A 、B 、C 分别为椭圆x 2a 2+y 2b2=1 (a >b >0)的顶点与焦点,若∠ABC =90°,则该椭圆的离心率为 ( )A .-1+52B .5-1C .2+12D .2+1【当堂检测】1.椭圆25x 2+9y 2=225的长轴长、短轴长、离心率依次是 ( )A .5、3、0.8B .10、6、0.8C .5、3、0.6D .10、6、0.6 2.已知椭圆的中心在坐标原点,焦点在x 轴上,且长轴长为12,离心率为13,则椭圆的方程是 ( )A .x 2144+y 2128=1 B .x 236+y 220=1 C .x 232+y 236=1 D .x 236+y 232=1 3.若一个椭圆长轴的长度、短轴的长度和焦距成等差数列,则该椭圆的离心率是 ( )A .45B .35C .25D .154.若点O 和点F 分别为椭圆x 24+y 23=1的中心和左焦点,点P 为椭圆上的任意一点,则OP →·FP →的最大值为______.【课堂小结】1.已知椭圆的方程讨论性质时,若不是标准形式要先化成标准形式,再确定焦点的位置,找准a 、b .2.利用椭圆的几何性质求标准方程通常采用待定系数法.3.求离心率e 时,注意方程思想的运用.【拓展提高】1.已知F 1、F 2为椭圆x 2a 2+y 2b 2=1(a >b >0)的两个焦点,过F 2作椭圆的弦AB ,若△AF 1B 的周长为16,椭圆离心率e =32,则椭圆的方程是( )A .x 24+y 23=1B .x 216+y 24=1C .x 216+y 212=1D .x 216+y 23=1 2.椭圆1145222=++a y a x 的焦点在x 轴上,则它离心率的取值范围是 3.椭圆M :2222x y a b+=1 (a >b >0) 的左、右焦点分别为F 1、F 2,P 为椭圆M 上任一点,且12PF PF ⋅ 的最大值的取值范围是[2c 2,3c2],其中c =则椭圆M 的离心率e 的取值范围是( ) A .⎥⎦⎤⎢⎣⎡22,33 B.[C .D .11[,)32 4.已知椭圆)0(12222>>=+b a by a x 的左、右顶点分别为B A 、,右焦点是F ,过F 作直线与长轴垂直,与椭圆交于Q P 、两点(1)若060=∠PBF ,求椭圆的离心率(2)求证:APB ∠一定为钝角5.在平面直角坐标系内,已知点)0,2()0,2(-B A 、,P 是平面内一动点,直线PB PA 、的斜率之积为43- (1)求动点P 的轨迹C 的方程(2)过点)0,21(作直线l 与轨迹C 交于F E 、两点,线段EF 的中点为M ,求直线MA 的斜率k 的取值范围。
(导学案)2.2.1椭圆及其标准方程

2.1.1 椭圆及其标准方程(1) (导学案)【学习目标】(1)从具体情境中抽象出椭圆的模型;(2)掌握椭圆的定义,能用坐标法求椭圆的标准方程; (3)掌握椭圆的标准方程的推导及标准方程的形式。
【重点、难点】重点:椭圆的定义及其标准方程。
难点:椭圆标准方程的推导与化简。
【学习方法】探究、讨论、归纳、类比 一、【基础知识链接】1、曲线可以看作是适合某种条件的点的集合或轨迹。
求曲线方程的一般步骤是: → → → → 。
其中,建立坐标系一般应遵循 的原则。
2、平面内两点间的距离公式:设A (x 1,y 1),B (x 2,y 2),则︱AB ︱=二、【新知导学】 探究任务一:椭圆的定义 【教材导读】 预习课本P38的内容,动动手,做教材P38中的“探究”,并完成下列问题:(1)、设笔尖(动点)为M ,两个定点1F ,2F 的距离为2c ,绳长为2a ,当22a c >时,动点M 的轨迹是 ;当22a c =时,动点M 的轨迹是 ;当22a c <时,动点M 的轨迹是 。
(2)、椭圆的定义:把平面内动点M 与两个定点1F ,2F 的距离之和等于常数(2a大于 )的点的轨迹叫做 . 这两个定点叫做椭圆的 ,两焦点的距离(2c )叫做 .探究任务二:椭圆的标准方程【教材导读】 预习课本P38至P39的内容,并完成下列问题(1)、观察椭圆的形状,可以发现椭圆既是 对称图形,又是 对称图形。
(2)、怎样建立坐标系,才能使求出的椭圆方程最为简单?①、建系;以 为x 轴, 为y 轴,建立平面直角坐标系,则1F ,2F 的坐标分别为:. ②、设点并写出点集:设M ( , )为椭圆上任意一点,根据椭圆定义知:③、列方程:④、化简方程得:⑤、为使上述方程简单并具有对称美,引入字母 ,令 = a 2 - c 2,则方程可化为(3)、类似的,焦点在 轴上的椭圆的标准方程为 : ,其中焦点1F ,2F 的坐标为: .(4)点的位置?试一试:根据下列椭圆方程,写出,,a b c 的值,并指出焦点的坐标: (1)221169y x +=; (2) 2212516y x +=; (1)a = ;b = ;c = (2)a = ;b = ;c = 焦点坐标为: 焦点坐标为: 待课堂上与老师和同学探究解决。
高中数学 选修2-1双曲线导学案加课后作业及参考答案

双曲线及其标准方程导学案【学习要求】1.了解双曲线的定义,几何图形和标准方程的推导过程. 2.掌握双曲线的标准方程.3.会利用双曲线的定义和标准方程解决简单的问题.【学法指导】本节课的学习要运用类比的方法,在与椭圆的联系与区别中建立双曲线的定义及标准方程.【知识要点】1.双曲线的定义把平面内与两个定点F 1,F 2的距离的 等于常数(小于|F 1F 2|)的点的轨迹叫做双曲线,这两个定点叫做 , 叫做双曲线的焦距. 2探究点一 双曲线的定义问题1 取一条拉链,拉开它的一部分,在拉开的两边上各选择一点,分别固定在点F 1,F 2上,把笔尖放在点M 处,拉开闭拢拉链,笔尖经过的点可画出一条曲线,思考曲线满足什么条件?问题2 双曲线的定义中强调平面内动点到两定点的距离差的绝对值为常数,若没有绝对值,则动点的轨迹是什么?问题3 双曲线的定义中,为什么要限制到两定点距离之差的绝对值为常数2a,2a <|F 1F 2|?问题4 已知点P (x ,y )的坐标满足下列条件,试判断下列各条件下点P 的轨迹是什么图形? (1)6)5()5(2222=+--++y x y x ;(2)6)4()4(2222=+--++y x y x(3)方程x =3y 2-1所表示的曲线是( )A .双曲线B .椭圆C .双曲线的一部分D .椭圆的一部分 探究点二 双曲线的标准方程问题1 类比椭圆的标准方程推导过程,思考怎样求双曲线的标准方程?问题2 两种形式的标准方程怎样进行区别?能否统一?问题3 如图,类比椭圆中a ,b ,c 的意义,你能在y 轴上找一点B ,使|OB |=b 吗?例1 (1)已知双曲线的焦点在y 轴上,并且双曲线过点(3,-42)和⎝⎛⎭⎫94,5,求双曲线的标准方程; (2)求与双曲线x 216-y 24=1有公共焦点,且过点(32,2)的双曲线方程.跟踪训练1 (1)过点(1,1)且ba=2的双曲线的标准方程是 ( )A .12122=-y x B .y 212-x 2=1 C .x 2-y 212=1D .x 212-y 2=1或y 212-x 2=1(2)若双曲线以椭圆x 216+y 29=1的两个顶点为焦点,且经过椭圆的两个焦点,则双曲线的标准方程为_______探究点三 与双曲线定义有关的应用问题例2 已知双曲线的方程是x 216-y 28=1,点P 在双曲线上,且到其中一个焦点F 1的距离为10,点N 是PF 1的中点,求|ON |的大小(O 为坐标原点).跟踪训练2 如图,从双曲线x 23-y 25=1的左焦点F 引圆x 2+y 2=3的切线FP 交双曲线右支于点P , T 为切点,M 为线段FP 的中点,O 为坐标原点,则|MO |-|MT |等于( )A . 3B . 5C .5- 3D .5+ 3例3 已知A ,B 两地相距800 m ,在A 地听到炮弹爆炸声比在B 地晚2 s ,且声速为340 m/s ,求炮弹爆炸点的轨迹方程.跟踪训练3 2008年5月12日,四川汶川发生里氏8.0级地震,为了援救灾民,某部队在如图所示的P 处空降了一批救灾药品,今要把这批药品沿道路PA 、PB 送到矩形灾民区ABCD 中去,已知PA =100 km ,PB =150 km ,BC =60 km ,∠APB =60°,试在灾民区中确定一条界线,使位于界线一侧的点沿道路PA 送药较近,而另一侧的点沿道路PB 送药较近,请说明这一界线是一条什么曲线?并求出其方程.【当堂检测】1.已知A (0,-5)、B (0,5),|PA |-|PB |=2a ,当a =3或5时,P 点的轨迹为 ( ) A .双曲线或一条直线 B .双曲线或两条直线 C .双曲线一支或一条直线 D .双曲线一支或一条射线2.若k >1,则关于x ,y 的方程(1-k )x 2+y 2=k 2-1所表示的曲线是 ( ) A .焦点在x 轴上的椭圆 B .焦点在y 轴上的椭圆 C .焦点在y 轴上的双曲线 D .焦点在x 轴上的双曲线 3.双曲线x 216-y 29=1上一点P 到点(5,0)的距离为15,那么该点到(-5,0)的距离为 ( )A .7B .23C .5或25D .7或234.已知动圆M 与圆C 1:(x +4)2+y 2=2外切,与圆C 2:(x -4)2+y 2=2内切,求动圆圆心的轨迹方程.【课堂小结】1.双曲线定义中||PF 1|-|PF 2||=2a (2a <|F 1F 2|)不要漏了绝对值符号,当2a =|F 1F 2|时表示两条射线.2.在双曲线的标准方程中,a >b 不一定成立.要注意与椭圆中a ,b ,c 的区别.在椭圆中a 2=b 2+c 2,在双曲线中c 2=a 2+b 2.3.用待定系数法求双曲线的标准方程时,要先判断焦点所在的位置,设出标准方程后,由条件列出a ,b ,c 的方程组.如果焦点不确定要分类讨论,采用待定系数法求方程或用形如mx 2+ny 2=1 (mn <0)的形式求解.【拓展提高】1.已知方程12522=---k y k x 的图形是双曲线,那么k 的取值范围是( )A .k >5B .k >5,或22<<-kC .k >2,,或2-<kD .22<<-k2.===-212221121625,PF PF y x F F P ,则上一点,且为焦点的双曲线是以点( ) A .2 B .22 C .4或22 D .2或223.已知双曲线14922=-y x ,B A 、为过左焦点1F 的直线与双曲线左支的两个交点,2,9F AB =为右焦点,则△B AF 2的周长为4.是双曲线上的一点,且,点的两个焦点分别是已知双曲线P F F y x 2122,13=-__________602121的面积等于,则PF F PF F ∆=∠5.根据下列条件,求双曲线的标准方程. (1)过点P )415,3(,Q )5,316(-且焦点在坐标轴上; (2)c =6,经过点(-5,2),焦点在x 轴上.(3))的双曲线。
高中数学选修2-1自主学习导学案:2.4.2 抛物线的简单几何性质

§2.4.2 抛物线的简单几何性质1.抛物线的图形性质22(0)y px p => ,焦点(,0)2p F ,准线2p x =-(1)顶点:(0,0)O(2)取值范围:0x ≥;(3)对称性:关于x 轴对称; (4)离心率1e =;(5)通径:过焦点而垂直于对称轴的弦AB ,称为抛物线的通径,2AB p =,2p 越大,抛物线张口越大.2.抛物线的焦半径与焦点弦(1)连接抛物线上任意一点与焦点的线段叫做抛物线的焦半径,如图所示AF ,BF . 由抛物线的定义,A 点到焦点的距离等于到准线的距离,设00(,)A x y ,则02p AF x =+(2)过抛物线的焦点的弦叫做焦点弦,设11(,)A x y ,22(,)B x y ,则:1212()()22p p AB x x x x p =+++=++. 以上结论可以推广到其他形式的抛物线:20202020122222322422==+=-=+==+=-=+(),||;(),||-(),||(),||-py px PF x py px PF x px py PF y px py PF y 21221221221212223242==++=-=--==++=-=--(),||;(),||(),||(),||y px AB x x p y px AB p x x x py AB y y p x py AB p y y3.关于抛物线的若干结论已知过抛物线22(0)y px p =>的焦点F 的直线l 交抛物线于11(,)A x y ,22(,)B x y 两点.则有: (1)若l 的倾斜角为θ,则22sin pAB θ=. (2) 所有焦点弦中,通径最短. (3)求证:2212124⋅=⋅=-,p x x y y p .(4)以AB 为直径的圆与准线相切.(5)112+=FA FB p.4.直线与抛物线的综合问题直线与抛物线的位置关系有三种:(1)相离;(2)相切;(3)相交.判断它们的位置关系,可以将直线的方程与抛物线的方程联立,22Ax By C y px++=⎧⎨=⎩,消元,再根据消元后的方程进行判断.※ 典型例题考点1.抛物线定义的直接应用【例1】(1)已知点A (-2,3)与抛物线22(0)y px p =>的焦点的距离是5,则p =________.(2)抛物线24y x =的弦AB 垂直x 轴,若|AB|= AB =,则焦点到AB 的距离为 . 变式1.已知(3,2)M ,P 为抛物线22y x =上一点,F 为抛物线的焦点,(1)若P 到焦点的距离为2,则P 点坐标为____________;(2)PM PF +的最小值为______,此时P 点的坐标为_________. 考点2.直线与抛物线的位置关系【例2】已知直线 l :1y kx =- 和抛物线C :24y x =,试判断当 k 为何值时,l 与C 有:(1)一个公共点;(2)两个不同公共点;(3)没有公共点.【方法归纳】直线与抛物线位置关系的判断方法:(1)把直线方程代入抛物线方程;(2)得到一元一次方程,则直线与抛物线的对称轴平行,相交(一个交点)(3)得到一元二次方程,计算判别式,0∆>,相交;0∆=,相切;0∆<,相离 变式1.过点(0,1)M 且和抛物线C: 24y x =仅有一个公共点的直线的方程是________________.考点3.焦点弦与弦长【例3】斜率为1的直线过抛物线24y x =的焦点,与抛物线交于A ,B 两点,求线段AB 的长.【方法归纳】(1)直线被曲线截得的弦 |AB|=1+k 2 |x 1-x 2|;(2)过抛物线的焦点的弦 |AB|= x 1+x 2+p变式1.已知直线l :y =- x +1和抛物线C :y 2=4x 交点为A 、B ,求AB 的长.变式2.斜率为1的直线l 被抛物线C: 24y x =截得的弦长|AB|=8,则直线的l 的方程是________.考点4.中点弦有关的问题【例4】已知抛物线C 的顶点为坐标原点,焦点在x 轴上,直线y=x 与抛物线C 交于A,B 两点.若P(2,2)为AB 的中点,则抛物线C 的方程为 .变式1.直线l 和抛物线C: 24y x =交于A ,B 两点,且线段AB 的中点为M (2,1),则直线的l 的方程是_______.变式2.若直线2x y -=与抛物线24y x =交于A,B 两点,则线段AB 的中点坐标是 .变式3.已知A,B 为抛物线E 上不同的两点,若抛物线E 的焦点为(1,0),线段AB 恰被M(2,1)所平分.(1)求抛物线E 的方程;(2)求直线AB 的方程.考点5.与抛物线有关的最值问题【例5】能否在抛物线C :24y x =上求一点,使得点 P 到直线3y x =+的距离最短.考点6.与抛物线有关的定点(定值)问题【例6】已知点A,B 是抛物线y 2=2px(p>0)上的两点,且OA ⊥OB .(1)求两点的横坐标之积和纵坐标之积;(2)求证:直线AB 过定点.考点7.与抛物线有关的对称问题【例7】如图,在平面直角坐标系xOy 中,已知直线l :x-y-2=0,抛物线C :y 2=2px(p >0).(1)若直线l 过抛物线C 的焦点,求抛物线C 的方程.(2)已知抛物线C 上存在关于直线l 对称的相异两点P 和Q .①求证:线段PQ 的中点坐标为(2-p ,-p);②求p 的取值范围.变式1.若抛物线y 2=x 上两点A(x 1,y 1),B(x 2,y 2)关于直线y=x+b 对称,且y 1y 2=-1,则实数b 的值为 ( )A .-3B .3C .2D .-22.已知抛物线y 2=x 上存在两点关于直线l :y=k(x-1)+1对称,则实数k 的取值范围为 .1.已知点P (6,y )在抛物线y 2=2px (p >0)上,若点P 到抛物线焦点F 的距离等于8,则焦点F 到抛物线准线的距离等于( )A .2B .1C .4D .82.抛物线y 2=4x 的焦点为F ,点P 为抛物线上的动点,点M 为其准线上的动点,当△FPM 为等边三角形时,其面积为( )A .2 3B .4C .6D .4 33.已知抛物线y 2=2px (p >0),过其焦点且斜率为1的直线交抛物线于A 、B 两点,若线段AB 的中点的纵坐标为2,则该抛物线的准线方程为( )A .x =1B .x =-1C .x =2D .x =-24.设F 为抛物线C :y 2=3x 的焦点,过F 且倾斜角为30°的直线交C 于A ,B 两点,则|AB |=( )A .303B .6C .12D .7 3 5.过点(1,0)作斜率为-2的直线,与抛物线y 2=8x 交于A,B 两点,则弦AB 的长为 ( )A .2B .2C .2D .26.已知抛物线x 2=2py (p >0)的焦点为F ,过F 作倾斜角为30°的直线与抛物线交于A ,B 两点,若|AF ||BF |∈(0,1),则|AF ||BF |=( ) A .15 B .14 C .13 D .127.已知抛物线C :y 2=8x 与点M (-2,2),过C 的焦点且斜率为k 的直线与C 交于A ,B 两点,若MA →·MB →=0,则k =( )A .12B .22C . 2D .28.过点(-1,0)且与抛物线y 2=x 有且仅有一个公共点的直线有 ( )A .1条B .2条C .3条D .4条9.设抛物线C :y 2=4x 的焦点为F,直线l 过点F 且与C 交于A,B 两点.若|AF|=3|BF|,则l 的方程为 ( )A .y=x-1或y=-x+1B .y=(x-1)或y=-(x-1)C .y=(x-1)或y=-(x-1) D .y=(x-1)或y=-(x-1)10.抛物线y 2=x 上到其准线和顶点距离相等的点的坐标为________. 11.直线y =kx +2与抛物线y 2=8x 有且只有一个公共点,则k =________.12.平面上一机器人在行进中始终保持与点F (1,0)的距离和到直线x =-1的距离相等.若机器人接触不到过点P (-1,0)且斜率为k 的直线,则k 的取值范围是________.13.抛物线x 2=2py (p >0)的焦点为F ,其准线与双曲线x 23-y 23=1相交于A ,B 两点,若△ABF 为等边三角形,则p =________.14.在抛物线y=4x 2上求一点,使该点到直线y=4x-5的距离最短,则该点的坐标是 .15.若抛物线的顶点在原点,开口向上,F 为焦点,M 为准线与y 轴的交点,A 为抛物线上一点,且|AM |=17,|AF |=3,求此抛物线的标准方程.16.已知直线l 经过抛物线y 2=6x 的焦点F ,且与抛物线相交于A ,B 两点.(1)若直线l 的倾斜角为60°,求|AB |的值;(2)若|AB |=9,求线段AB 的中点M 到准线的距离.17.已知抛物线x=-y2与过点(-1,0)且斜率为k的直线相交于A,B两点,O为坐标原点,当△OAB的面积等于10时,求k的值.18.已知点F为抛物线E:y2=2px(p>0)的焦点,点A(2,m)在抛物线E上,且|AF|=3.(1)求抛物线E的方程;(2)已知点G(-1,0),延长AF交抛物线E于点B,证明:以点F为圆心且与直线GA 相切的圆,必与直线GB相切.§2.4.2 抛物线的简单几何性质(教师版)1.抛物线的图形性质22(0)y px p => ,焦点(,0)2p F ,准线2p x =-(1)顶点:(0,0)O(2)取值范围:0x ≥;(3)对称性:关于x 轴对称; (4)离心率1e =;(5)通径:过焦点而垂直于对称轴的弦AB ,称为抛物线的通径,2AB p =,2p 越大,抛物线张口越大.2.抛物线的焦半径与焦点弦(1)连接抛物线上任意一点与焦点的线段叫做抛物线的焦半径,如图所示AF ,BF . 由抛物线的定义,A 点到焦点的距离等于到准线的距离,设00(,)A x y ,则02p AF x =+(2)过抛物线的焦点的弦叫做焦点弦,设11(,)A x y ,22(,)B x y ,则:1212()()22p p AB x x x x p =+++=++. 以上结论可以推广到其他形式的抛物线:20202020122222322422==+=-=+==+=-=+(),||;(),||-(),||(),||-py px PF x py px PF x px py PF y px py PF y 21221221221212223242==++=-=--==++=-=--(),||;(),||(),||(),||y px AB x x p y px AB p x x x py AB y y p x py AB p y y3.关于抛物线的若干结论已知过抛物线22(0)y px p =>的焦点F 的直线l 交抛物线于11(,)A x y ,22(,)B x y 两点.则有: (1)若l 的倾斜角为θ,则22sin pAB θ=.222121212222222212021221πθπθθθθθθθ==∴≠=-=+-⋅-=∴=-+=∴=-=+=:,,,:()tan ,,tan :,tan ,,tan ()tan sin AB p AB p y p l y x x y py p py y p y y pAB y y p 解若则此时为抛物线的通径结论得证若设直线的方程为即代入抛物线方程得(2) 所有焦点弦中,通径最短.()()()2222221221223θθθ=≤∴≥∴:sin sin ,sin ,:;,:;.p AB pp AB p p 解由问题知:的最小值为即通径最短.通径的长度通径越大抛物线开口越大通径是抛物线的所有焦点弦中通径的性最短的质(3)求证:2212124⋅=⋅=-,p x x y y p .212221212221212222244⋅=-==∴==:,,,()y y p y y x x p p y y P x x P 解由问题的解法知:(4)以AB 为直径的圆与准线相切. (5)112+=FA FB p. 4.直线与抛物线的综合问题直线与抛物线的位置关系有三种:(1)相离;(2)相切;(3)相交.判断它们的位置关系,可以将直线的方程与抛物线的方程联立,22Ax By C y px++=⎧⎨=⎩,消元,再根据消元后的方程进行判断.※ 典型例题考点1.抛物线定义的直接应用【例1】(1)已知点A (-2,3)与抛物线22(0)y px p =>的焦点的距离是5,则p =_____4____ (2)抛物线24y x =的弦AB 垂直x 轴,若|AB|= AB =AB 的距离为 2 . 【答案】(1)4;(2)2;变式1.已知(3,2)M ,P 为抛物线22y x =上一点,F 为抛物线的焦点,(1)若P 到焦点的距离为2,则P 点坐标为____3(,2________; (2)PM PF +的最小值为____72__,此时P 点的坐标为_____(2,2)____.考点2.直线与抛物线的位置关系【例2】已知直线 l :y =kx-1 和抛物线C :y 2=4x ,试判断当 k 为何值时,l 与C 有:(1)个公共点;(2)两个不同公共点;(3)没有公共点.解:(1)01k k ==-或;(2)10k k >-≠且;(3)1k <- 【方法归纳】直线与抛物线位置关系的判断方法:(1)把直线方程代入抛物线方程;(2)得到一元一次方程,则直线与抛物线的对称轴平行,相交(一个交点)(3)得到一元二次方程,计算判别式,0∆>,相交;0∆=,相切;0∆<,相离 变式1.过点(0,1)M 且和抛物线C:24y x =仅有一个公共点的直线的方程是________________. 答案:101或或y x y x ===+.解析:(1)若直线与x 轴垂直,则0x =,满足题意. (2)若直线的斜率存在,设直线方程为:1y kx =+,联立214y kx y x=+⎧⎨=⎩,消去x ,得到2440ky y -+=,①若0k =,则1y =,满足题意②若0k ≠,令0∆=,解得1k =,所以1y x =+ 综上所述,所求直线方程为101或或y x y x ===+考点3.焦点弦与弦长【例3】斜率为1的直线过抛物线24y x =的焦点,与抛物线交于A ,B 两点,求线段AB 的长. 解法1:直线AB 的方程为1y x =+,代入抛物线方程得:2610x x -+=,设11(,)A x y ,22(,)B x y ,则126x x +=,121x x =,所以8AB ==.解法2:1212()()62822p pAB x x x x p =+++=++=+= 【方法归纳】(1)直线被曲线截得的弦 |AB|=1+k 2 |x 1-x 2|;(2)过抛物线的焦点的弦 |AB|= x 1+x 2+p变式1.已知直线l :y =- x +1和抛物线C :y 2=4x 交点为A 、B ,求AB 的长.【解析】︱AB ︱=8变式2.斜率为1的直线l 被抛物线C:24y x =截得的弦长|AB|=8,则直线的l 的方程是________.【答案】y =x -1考点4.中点弦有关的问题【例4】已知抛物线C 的顶点为坐标原点,焦点在x 轴上,直线y=x 与抛物线C 交于A,B 两点.若P(2,2)为AB 的中点,则抛物线C 的方程为 .【解析】设抛物线的方程为y 2=2px(p≠0),与y=x 联立方程组,消去y,得x 2-2px=0.设A(x 1,y 1),B(x 2,y 2),所以x 1+x 2=2p ,又因为P(2,2)为AB 的中点,所以2p=4,所以y 2=4x .变式1.直线l 和抛物线C:24y x =交于A ,B 两点,且线段AB 的中点为M (2,1),则直线的l 的方程是_______. 【答案】y =2x -3变式2.若直线x-y=2与抛物线y 2=4x 交于A,B 两点,则线段AB 的中点坐标是 .【解析】设A(x 1,y 1),B(x 2,y 2),联立直线方程与抛物线方程得方程组整理得x 2-8x+4=0,所以x 1+x 2=8,y 1+y 2=x 1+x 2-4=4,所以线段AB 的中点坐标为(4,2).变式3.已知A,B 为抛物线E 上不同的两点,若抛物线E 的焦点为(1,0),线段AB 恰被M(2,1)所平分.(1)求抛物线E 的方程;(2)求直线AB 的方程. 【解析】(1)由于抛物线的焦点为(1,0),所以12p=,2p =,所求抛物线的方程为y 2=4x . (2)方法一:设A(x 1,y 1),B(x 2,y 2),则2114y x = ①, 2224y x =②,且x 1+x 2=4,y 1+y 2=2,由②-①得(y 1+y 2)(y 2-y 1)=4(x 2-x 1), 所以21212y y x x -=-,所以所求直线AB 的方程为y-1=2(x-2),即2x-y-3=0.方法二:显然AB 不垂直于x 轴,故可设弦AB 所在的直线方程为y-1=k(x-2),k≠0, 设A(x 1,y 1),B(x 2,y 2),由21(2)4y k x y x-=-⎧⎨=⎩,消去x 整理得ky 2-4y-8k+4=0,所以y 1+y 2=4k, 又M 点是AB 的中点,所以y 1+y 2=2,所以k=2,故直线AB 的方程为y-1=2(x-2),即2x-y-3=0.考点5.与抛物线有关的最值问题【例5】能否在抛物线C :y 2=4x 上求一点,使得点 P 到直线 y =x+3 的距离最短. 【解析】00(.)P x y 解:直线与抛物线无交点,设抛物线上一点,2004y x =则,d ==2004y x =将代入得:d=20)y R =∈,0min 2,y d ∴==当时(1,2)P 此时方法2:0x y m -+=设直线与抛物线相切,2244400y xy y m x y m ⎧=⇒-+=⎨-+=⎩,0:1m ∆==由得,(1,2)P 此时.考点6.与抛物线有关的定点(定值)问题【例6】已知点A,B 是抛物线y 2=2px(p>0)上的两点,且OA ⊥OB .(1)求两点的横坐标之积和纵坐标之积;(2)求证:直线AB 过定点.【解析】(1)设点A,B 的坐标分别为(x 1,y 1),(x 2,y 2),则有k OA= 11y x ,k OB=22y x . 因为OA ⊥OB,所以k OA ·k OB =-1,所以x 1x 2+y 1y 2=0.因为21y=2px 1,21y=2px 2,所以2212y y2p 2p+y 1y 2=0.因为y 1≠0,y 2≠0,所以y 1y 2=-4p 2,所以x 1x 2=4p 2. (2)因为221122y 2px y 2px =,=,所以(y 1-y 2)(y 1+y 2)=2p(x 1-x 2),所以12AB 121212y y 2p 2p,k x x y y y y -=-++所以=,故直线AB 的方程为y-y 1=122p y y + (x-x 1),所以1112122px 2pxy y ,y y y y +-++=即211121212y 2px y y 2pxy .y y y y -+=+++ 因为21y=2px 1,y 1y 2=-4p 2,所以212122px 4p y ,y y y y -=+++所以y=122p y y + (x-2p),即直线AB 过定点(2p,0).考点7.与抛物线有关的对称问题【例7】如图,在平面直角坐标系xOy 中,已知直线l :x-y-2=0,抛物线C :y 2=2px(p >0).(1)若直线l 过抛物线C 的焦点,求抛物线C 的方程.(2)已知抛物线C 上存在关于直线l 对称的相异两点P 和Q .①求证:线段PQ 的中点坐标为(2-p ,-p);②求p 的取值范围.【解析】(1)因为l :x -y -2=0,所以l 与x 轴的交点坐标为(2,0),即抛物线的焦点为(2,0),所以p22=,,所以y 2=8x . (2)① 设点P(x 1,y 1),Q(x 2,y 2),则211211222222y x y 2px 2p y 2px y x 2p ⎧=⎪⎧=⎪⎪⇒⎨⎨=⎪⎪⎩=⎪⎩,, 则12PQ221212y y 2p k y y y y 2p 2p==+-,-又因为P,Q 关于直线l 对称, 所以k PQ =-1,即y 1+y 2=-2p,所以12y y p,2+=-又因为P,Q 的中点一定在直线l 上, 所以1212x x y y 22p,22++=+=- 所以线段PQ 的中点坐标为(2-p,-p).②因为中点坐标为(2-p ,-p),121222222121212y y 2p y y 2p y y x x 42p y y 8p 4p 2p +=⎧+=⎧⎪+⎨⎨+==+=⎩⎪⎩-,-,即--, 所以12212y y 2p y y 4p 4p +=⎧⎨=⎩-,-,即方程y 2+2py+4p 2-4p=0有两个不等实根.所以Δ>0,(2p)2-4(4p 2-4p)>0⇒ 4p (0,).3∈ 【方法技巧】应用抛物线性质解题的常用技巧 (1)抛物线的中点弦问题用点差法较简便.(2)轴对称问题,一是抓住对称两点的中点在对称轴上,二是抓住两点连线的斜率与对称轴所在直线斜率的关系.(3)在直线和抛物线的综合题中,经常遇到求定值、过定点问题.解决这类问题的方法很多,如斜率法、方程法、向量法、参数法等.解决这些问题的关键是代换和转化.(4)圆锥曲线中的定点、定值问题,常选择一参数来表示要研究问题中的几何量,通过运算找到定点、定值,说明与参数无关,也常用特值探路法找定点、定值.变式1.若抛物线y 2=x 上两点A(x 1,y 1),B(x 2,y 2)关于直线y=x+b 对称,且y 1y 2=-1,则实数b 的值为 ( )A .-3B .3C .2D .-2【解析】选D .因为抛物线y 2=x 上两点A(x 1,y 1),B(x 2,y 2)关于直线y=x+b 对称,所以=-1,所以=-1,所以y 1+y 2=-1.因为y 1y 2=-1,所以x 1+x 2=+=(y 1+y 2)2-2y 1y 2=3,所以两点A(x 1,y 1),B(x 2,y 2)中点坐标为.代入y=x+b,可得b=-2.2.已知抛物线y 2=x 上存在两点关于直线l :y=k(x-1)+1对称,则实数k 的取值范围为 .【解析】设抛物线上的点A(y12,y1),B(y22,y2)关于直线l对称.则122212221212y yk1y yy y y yk(1)1 22-⎧-⎪-⎪⎨++⎪=-+⎪⎩=,,,得12212y y kk11y y2k2+-⎧⎪⎨+-⎪⎩=,=,所以y1,y2是方程22k11y ky02k2-+++=的两个不同根.所以Δ=k2-42k11()2k2-+>0,解得-2<k<0.故实数k的取值范围是-2<k<0.答案:-2<k<01.已知点P(6,y)在抛物线y2=2px(p>0)上,若点P到抛物线焦点F的距离等于8,则焦点F到抛物线准线的距离等于()A.2 B.1 C.4 D.8【解析】抛物线y2=2px(p>0)的准线为x=-p2,因为P(6,y)为抛物线上的点,所以点P到焦点F 的距离等于它到准线的距离,所以6+p2=8,所以p=4,即焦点F到抛物线的距离等于4,故选C.【答案】 C2.(2014·成都高二检测)抛物线y2=4x的焦点为F,点P为抛物线上的动点,点M为其准线上的动点,当△FPM为等边三角形时,其面积为()A.2 3 B.4 C.6 D.4 3【解析】据题意知,△FPM为等边三角形,|PF|=|PM|=|FM|,∴PM⊥抛物线的准线.设P⎝⎛⎭⎫m24,m,则M (-1,m ),等边三角形边长为1+m 24,又由F (1,0),|PM |=|FM |,得1+m 24=+2+m 2,得m =23,∴等边三角形的边长为4,其面积为43,故选D .【答案】 D3.已知抛物线y 2=2px (p >0),过其焦点且斜率为1的直线交抛物线于A 、B 两点,若线段AB 的中点的纵坐标为2,则该抛物线的准线方程为( )A .x =1B .x =-1C .x =2D .x =-2【解析】 设A (x 1,y 1),B (x 2,y 2),代入抛物线方程得:⎩⎪⎨⎪⎧y 21=2px 1, ①y 22=2px 2, ②①-②得,(y 1+y 2)(y 1-y 2)=2p (x 1-x 2).又∵y 1+y 2=4,∴y 1-y 2x 1-x 2=2p 4=p2=k =1,∴p =2.∴所求抛物线的准线方程为x =-1. 【答案】 B4.设F 为抛物线C :y 2=3x 的焦点,过F 且倾斜角为30°的直线交C 于A ,B 两点,则|AB |=( )A .303B .6C .12D .7 3 【解析】 焦点F 的坐标为⎝⎛⎭⎫34,0,直线AB 的斜率为33,所以直线AB 的方程为y =33⎝⎛⎭⎫x -34,即y =33x -34,代入y 2=3x ,得13x 2-72x +316=0,设A (x 1,y 1),B (x 2,y 2),则x 1+x 2=212, 所以|AB |=x 1+x 2+32=212+32=12,故选C .5.过点(1,0)作斜率为-2的直线,与抛物线y 2=8x 交于A,B 两点,则弦AB 的长为 ( )A .2B .2C .2D .2【解析】选B .设A(x 1,y 1),B(x 2,y 2).由题意知AB 的方程为y=-2(x-1),即y=-2x+2.由得x 2-4x+1=0,所以x 1+x 2=4,x 1x 2=1.所以|AB|====2.6.(2014·湖南省长沙一中期中考试)已知抛物线x 2=2py (p >0)的焦点为F ,过F 作倾斜角为30°的直线与抛物线交于A ,B 两点,若|AF ||BF |∈(0,1),则|AF ||BF |=( )A .15B .14C .13D .12【解析】 因为抛物线的焦点为F ⎝⎛⎭⎫0,p 2,故过点F 且倾斜角为30°的直线的方程为y =33x +p2,与抛物线方程联立得x 2-233px -p 2=0,解方程得x A =-33p ,x B =3p ,所以|AF ||BF |=|x A ||x B |=13,故选C .【答案】 C7.已知抛物线C :y 2=8x 与点M (-2,2),过C 的焦点且斜率为k 的直线与C 交于A ,B 两点,若MA →·MB →=0,则k =( )A .12B .22C . 2D .2【解析】 由题意可知抛物线的焦点坐标为(2,0),则过焦点且斜率为k 的直线的方程为y =k (x -2),与抛物线方程联立,消去y 化简得k 2x 2-(4k 2+8)x +4k 2=0,设点A (x 1,y 1),B (x 2,y 2),则x 1+x 2=4+8k 2,x 1x 2=4,所以y 1+y 2=k (x 1+x 2)-4k =8k ,y 1y 2=k 2[x 1x 2-2(x 1+x 2)+4]=-16,因为MA →·MB →=0,所以(x 1+2)(x 2+2)+(y 1-2)(y 2-2)=0(*),将上面各个量代入(*),化简得k 2-4k +4=0,所以k =2,故选D .【答案】 D8.(2016·郑州高二检测)过点(-1,0)且与抛物线y 2=x 有且仅有一个公共点的直线有 ( )A .1条B .2条C .3条D .4条【解析】选C .点(-1,0)在抛物线y 2=x 的外部,故过(-1,0)且与抛物线有且仅有一个公共点的直线有三条,其中两条为切线,一条为x 轴.9.(2016·西安高二检测)设抛物线C:y 2=4x 的焦点为F,直线l 过点F 且与C 交于A,B 两点.若|AF|=3|BF|,则l 的方程为 ( )A .y=x-1或y=-x+1B .y=(x-1)或y=-(x-1)C .y=(x-1)或y=-(x-1) D .y=(x-1)或y=-(x-1)【解析】选C .由题意,可设|BF|=x,则|AF|=3x,设直线l 与抛物线的准线相交于点M,则由抛物线的定义可知:=,所以|MB|=2x,所以直线l 的倾斜角为60°或120°,即直线l 的斜率为±.【误区警示】本题容易将倾斜角当作45°而错选A .10.抛物线y 2=x 上到其准线和顶点距离相等的点的坐标为________.【解析】 设抛物线上点的坐标为(x ,±x ),此点到准线的距离为x +14,到顶点的距离为x 2+x2,由题意有x +14=x 2+x2,∴x =18,∴y =±24,∴此点坐标为⎝⎛⎭⎫18,±24.【答案】 ⎝⎛⎭⎫18,±2411.直线y =kx +2与抛物线y 2=8x 有且只有一个公共点,则k =________.【解析】 当k =0时,直线与抛物线有唯一交点,当k ≠0时,联立方程消y 得k 2x 2+4(k -2)x +4=0,由题意Δ=16(k -2)2-16k 2=0,∴k =1.【答案】 0或112.平面上一机器人在行进中始终保持与点F (1,0)的距离和到直线x =-1的距离相等.若机器人接触不到过点P (-1,0)且斜率为k 的直线,则k 的取值范围是________.【解析】 设机器人为A (x ,y ),依题意得点A 在以F (1,0)为焦点,x =-1为准线的抛物线上,该抛物线的标准方程为y 2=4x .过点P (-1,0),斜率为k 的直线为y =k (x +1).由⎩⎪⎨⎪⎧y 2=4x ,y =kx +k ,得ky 2-4y +4k =0. 当k =0时,显然不符合题意;当k ≠0时,依题意得Δ=(-4)2-4k ·4k <0,化简得k 2-1>0,解得k >1或k <-1,因此k 的取值范围为(-∞,-1)∪(1,+∞). 【答案】 (-∞,-1)∪(1,+∞)13.抛物线x 2=2py (p >0)的焦点为F ,其准线与双曲线x 23-y 23=1相交于A ,B 两点,若△ABF 为等边三角形,则p =________.【解析】 由于x 2=2py (p >0)的准线为y =-p 2,由⎩⎪⎨⎪⎧y =-p 2,x 2-y 2=3,解得准线与双曲线x 2-y 2=3的交点为 A ⎝⎛⎭⎫-3+14p 2,-p 2,B ⎝⎛⎭⎫3+14p 2,-p 2,所以AB =2 3+14p 2. 由△ABF 为等边三角形,得32AB =p ,解得p =6. 【答案】 614.直线y=kx+2与抛物线y 2=8x 有且只有一个公共点,则k= .【解析】当k=0时,直线与抛物线有唯一交点,当k≠0时,联立方程消y 得:k 2x 2+4(k-2)x+4=0,由题意Δ=16(k -2)2-16k 2=0,解得k=1.答案:0或115.在抛物线y=4x 2上求一点,使该点到直线y=4x-5的距离最短,则该点的坐标是 . 【解析】设与直线y=4x-5平行的直线为y=4x-b,代入y=4x 2得4x 2-4x+b=0.令Δ=16-16b=0,解得b=1,所以与直线y=4x-5平行的直线为y=4x-1,所以直线y=4x-1与抛物线相切,切点到y=4x-5的距离最短.由4x 2-4x+1=0,解得x=,所以y=1,所求点为.答案:16.若抛物线的顶点在原点,开口向上,F 为焦点,M 为准线与y 轴的交点,A 为抛物线上一点,且|AM |=17,|AF |=3,求此抛物线的标准方程.【解】设所求抛物线的标准方程为x 2=2py (p >0),设A (x 0,y 0),由题知M ⎝⎛⎭⎫0,-p 2. ∵|AF |=3,∴y 0+p 2=3,∵|AM |=17,∴x 20+⎝⎛⎭⎫y 0+p 22=17,∴x 20=8,代入方程x 20=2py 0得, 8=2p ⎝⎛⎭⎫3-p2,解得p =2或p =4. ∴所求抛物线的标准方程为x 2=4y 或x 2=8y .17.已知直线l 经过抛物线y 2=6x 的焦点F ,且与抛物线相交于A ,B 两点.(1)若直线l 的倾斜角为60°,求|AB |的值;(2)若|AB |=9,求线段AB 的中点M 到准线的距离.【解】 (1)因为直线l 的倾斜角为60°,所以其斜率k =tan 60°=3. 又F ⎝⎛⎭⎫32,0,所以直线l 的方程为y =3⎝⎛⎭⎫x -32. 联立⎩⎪⎨⎪⎧y 2=6x ,y =3⎝⎛⎭⎫x -32,消去y 得x 2-5x +94=0. 设A (x 1,y 1),B (x 2,y 2),则x 1+x 2=5, 而|AB |=|AF |+|BF |=x 1+p 2+x 2+p2=x 1+x 2+p ,所以|AB |=5+3=8.(2)设A (x 1,y 1),B (x 2,y 2),由抛物线定义知|AB |=|AF |+|BF |=x 1+x 2+p =x 1+x 2+3,所以x 1+x 2=6,于是线段AB 的中点M 的横坐标是3. 又准线方程是x =-32,所以M 到准线的距离为3+32=92.18.已知抛物线x =-y 2与过点(-1,0)且斜率为k 的直线相交于A ,B 两点,O 为坐标原点,当△OAB 的面积等于10时,求k 的值.【解】 过点(-1,0)且斜率为k 的直线方程为y =k (x +1),由方程组⎩⎪⎨⎪⎧x =-y 2,y =k x +,消去x ,整理得ky 2+y -k =0,设A (x 1,y 1),B (x 2,y 2),由根与系数之间的关系得y 1+y 2=-1k ,y 1y 2=-1.设直线与x 轴交于点N ,显然N 点的坐标为(-1,0). ∵S △OAB =S △OAN +S △OBN =12|ON ||y 1|+12|ON ||y 2|=12|ON ||y 1-y 2|,∴S △OAB =12y 1+y 22-4y 1y 2=121k 2+4=10, 解得k =-16或16.19.(2015·福建高考)已知点F 为抛物线E:y 2=2px(p>0)的焦点,点A(2,m)在抛物线E 上,且|AF|=3.(1)求抛物线E 的方程.(2)已知点G(-1,0),延长AF 交抛物线E 于点B,证明:以点F 为圆心且与直线GA 相切的圆,必与直线GB 相切. 【解析】方法一:(1)由抛物线的定义得=2+,因为=3,即2+=3,解得p=2,所以抛物线E 的方程为y 2=4x . (2)因为点A(2,m)在抛物线E:y 2=4x 上, 所以m=±2,由抛物线的对称性, 不妨设A(2,2), 由A(2,2),F(1,0)可得直线AF 的方程为y=2(x-1).由得2x2-5x+2=0,解得x=2或x=,从而B.又G(-1,0),所以k GA==,k GB==-,所以k GA+k GB=0,从而∠AGF=∠BGF,这表明点F到直线GA,GB的距离相等,故以F为圆心且与直线GA相切的圆必与直线GB相切.方法二:(1)同方法一.(2)设以点F为圆心且与直线GA相切的圆的半径为r.因为点A(2,m)在抛物线E:y2=4x上,所以m=±2,由抛物线的对称性,不妨设A(2,2),由A(2,2),F(1,0)可得直线AF的方程为y=2(x-1).由得2x2-5x+2=0,解得x=2或x=,从而B.又G(-1,0),故直线GA的方程为2x-3y+2=0,从而r==.又直线GB的方程为2x+3y+2=0,所以点F到直线GB的距离d===r.这表明以点F为圆心且与直线GA相切的圆必与直线GB相切.。
北师大版选修2-1高中数学1.4.3《逻辑联结词“非”》word导学案

课题 1.4. 3逻辑联结词“非”学习目标理解逻辑联结词“非”的含义,会用“非”联结两个命题并判断命题的真假.学习重点:会用“非”联结两个命题并判断命题的真假.学习难点:逻辑联结词“非”的初步应用.学习方法:以讲学稿为依托的探究式教学方法.学习过程一、课前预习任务:(阅读教材18页完成下面问题)1.如果命题p是对命题q的否定,我们称命题q是命题p的命题.2.命题的否定一般地,对命题p,就得到一个新命题,记作¬p,读作“”.3.命题¬p的真假:若p是真命题,则¬p必是假命题;若p是假命题,则¬p必是真命题.二、新课学习探究任务一:¬p命题例1 写出下列命题的否定,并判断其真假.(1)p:3是有理数;(2)p:5不是75的约数;(3)p:7<8;(4)p:5+6≠11;(5)p:空集是任何非空集合的真子集.学后检测1 写出下列命题的否定形式.(1)面积相等的三角形都是全等三角形;(2)若m2+n2+a2+b2=0,则实数m、n、a、b全为零;(3)若xy=0,则x=0或y=0.探究任务二:一些词语及其否定1.命题“p”与命题“非p” ( ) A.可能都是真命题 B.可能都是假命题C.一真一假 D.只有p是真命题2.已知命题p:3≥3,q:3>4,则下列判断正确的是( ) A.p或q为真,p且q为真,¬p为假B.p或q为真,p且q为假,¬p为真C.p或q为假,p且q为假,¬p为假D.p或q为真,p且q为假,¬p为假3.已知命题p:0∈R,则¬p是________.四、课堂小结五、课后作业六.板书设计七.教(学)后反思。
高二数学选修2-1全套导学案
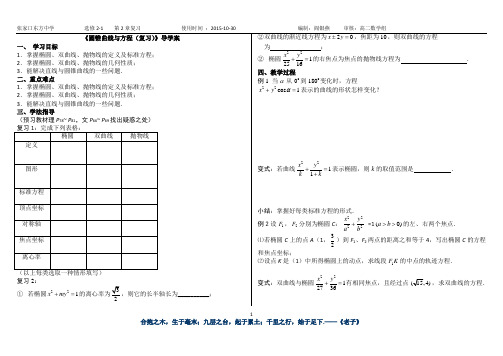
5.到直线 的距离最短的抛物线 上的点的坐标是.
6.就 的不同取值,指出方程 所表示的曲线的形状.
2.抛物线 与过点 的直线 相交于 , 两点, 为原点,若 和 的斜率之和为 ,求直线 的方程.
六、反思
1.椭圆、双曲线、抛物线的定义及标准方程;
2.椭圆、双曲线、抛物线的几何性质;
⑵设点K是(1)中所得椭圆上的动点,求线段 的中点的轨迹方程.
变式:双曲线与椭圆 有相同焦点,且经过点 ,求双曲线的方程.
※动手试试
练1.已知 的两个顶点 , 坐标分别是 , ,且 , 所在直线的斜率之积等于 ,试探求顶点 的轨迹.
练2.斜率为 的直线 与双曲线 交于 , 两点,且 ,求直线 的方程.
五、当堂检测
1.曲线 与曲线
的().
A.长轴长相等B.短轴长相等
C.离心率相等D.焦距相等
2.与圆 及圆 都外切的圆的圆心在().
A.一个椭圆上B.双曲线的一支上
C.一条抛物线上D.一个圆上
3.过抛物线 的焦点作直线 ,交抛物线于 , 两点,若线段 中点的横坐标为 ,则 等于().
A. B. C. D.
三、学法指导
(预习教材理P78~P81,文P66~P69找出疑惑之处)
复习1:完成下列表格:
椭圆
双曲线
抛物线
定义
图形
标准方程
顶点坐标
对称轴
焦点坐标
离心率
(以上每类选取一种情形填写)
复习2:
1若椭圆 的离心率为 ,则它的长半轴长为__________;
②双曲线的渐近线方程为 ,焦距为 ,则双曲线的方程为;
2椭圆 的右焦点为焦点的抛物线方程为.
2020年数学选修2-1人教A全册教案导学案--全称命题与特称命题

全称命题与特称命题课前预习学案一、预习目标理解全称量词与存在量词的意义,并判断全称命题和特称命题的真假全称命题与特称命题是两类特殊的命题,也是两类新型命题,这两类命题的否定又是这两类命题中的重要概念,二、预习内容1.全称量词和全称命题的概念:概念:短语————,——————在逻辑中通常叫做全称量词,用符号————表示。
含有全称量词的命题,叫做——————。
例如:⑴对任意,是奇数;⑵所有的正方形都是矩形。
常见的全称量词还有:“一切”、“每一个”、“任给”、“所有的”等通常,将含有变量x 的语句用、、表示,变量x 的取值范围用M 表示。
全称命题“对M 中任意一个x ,有成立”。
简记为:,读作:任意x 属于M ,有成立。
2.存在量词和特称命题的概念概念:短语————,——————在逻辑中通常叫做存在量词,用符号——表示。
含有存在量词的命题,叫做————(————命题)。
例如:⑴有一个素数不是奇数;⑵有的平行四边形是菱形。
特称命题“存在M 中的一个x ,使成立”。
简记为:,读作:存在一个x 属于M ,使成立。
3.如果含有一个量词的命题的形式是全称命题,那么它的否定是————;反之,如果含有一个量词的命题的形式是存在性命题,那么它的否定是————。
书写命题的否定时一定要抓住决定命题性质的量词,从对量词的否定入手,书写命题的否定三、提出疑惑同学们,通过你的自主学习,你还有哪些疑惑,请把它填在下面的表格中疑惑点疑惑内容n ∈N 21n +()p x ()q x ()r x ()p x x M ∀∈()p x ()p x ()p x x M ∃∈()p x ()p x课内探究学案一、学习目标判别全称命题与特称命题的真假.二、学习过程探究一:判别全称命题的真假1)所有的素数都是奇数;(2);(3)每一个无理数,也是无理数.(4),. 探究二:判断下列存在性命题的真假:(1)有一个实数,使;(2)存在两个相交平面垂直于同一平面;(3)有些整数只有两个正因数. (三)反思总结1、书写命题的否定时一定要抓住决定命题性质的量词,从对量词的否定入手,书写命题的否定2.由于全称量词的否定是存在量词,而存在量词的否定又是全称量词;因此,全称命题的否定一定是特称命题;特称命题的否定一定是全称命题.(四)当堂检测判断下列命题是全称命题还是特称命题,并判断其真假.(1)对数函数都是单调函数;(2){是无理数},是无理数;(3)课后练习1.下列命题中为全称命题的是( () )(A)有些圆内接三角形是等腰三角形 ; (B )存在一个实数与它的相反数的和不为0;(C)所有矩形都有外接圆 ; (D )过直线外一点有一条直线和已知直线平行. 设计意图:能正确判断全称命题和特称命题及其区别. 2.下列全称命题中真命题的个数是( () )①末位是0的整数,可以被3整除;②角平分线上的任意一点到这个角的两边的距离相等;③对为奇数.11,2≥+∈∀x R x x 2x {}Q n m n m x x b a ∈+=∈∀,,2,{}Q n m n m x x b a ∈+=∈+,,20x 032020=++x x x ∀∈x x |2x 2{}log 0x x x x ∃∈∈Z >|12,2+∈∀x Z x(A ) 0 (B ) 1 (C ) 2 (D ) 33.下列特称命题中假命题...的个数是( () )①;②有的菱形是正方形;③至少有一个整数,它既不是合数,也不是素数.(A ) 0 (B ) 1 (C ) 2 (D ) 32~3设计意图:能正确理解全称量词和特称量词.4.命题“任意一个偶函数的图象关于轴对称”的否定是() (A ) 任意一个偶函数的图象不关于轴对称;(B ) 任意一个不是偶函数的函数图象关于轴对称;(C ) 存在一个偶函数的图象关于轴对称;(D ) 存在一个偶函数的图象不关于轴对称.5.命题“存在一个三角形,内角和不等于”的否定为()(A )存在一个三角形,内角和等于;(B )所有三角形,内角和都等于;(C )所有三角形,内角和都不等于;(D )很多三角形,内角和不等于.4~5设计意图:能从变式的角度理解全称命题与特称命题.0,≤∈∃x R x y y y y y ο180ο180ο180ο180ο180全称命题与特称命题教案一、教材分析1)《课程标准》指出:“通过生活和数学实例,理解全称量词和特称量词的意义。
高中数学选修2-1 导学案

2.2 椭圆2.2.1 椭圆及其标准方程学习目标1.掌握椭圆的定义及其标准方程;2.理解椭圆的标准方程的推导,椭圆的定义中常数加以限制的原因。
基础感知预习教材,完成下列问题:(1)平面内的点的轨迹叫做椭圆,这两个定点叫做椭圆的,两焦点之间的距离叫做椭圆的(2)椭圆的标准方程:当焦点在x轴时,标准方程为;当焦点在y轴时,椭圆的标准方程为(3)集合语言:点集P={M||MF1|+|MF2|=2a,2a>|F1F2|}当2a=|F1F2|时,轨迹是当2a<|F1F2|时,轨迹是合作学习例 1.已知椭圆两个焦点的坐标分别是(-2,0)(2,0),并且经过点(2.5,-1.5),求它的标准方程。
例2.在圆x2+y2=4上任取一点P,过点P作x 轴的垂线段PD,D为垂足,当点P在圆上运动时,线段PD的中点M的轨迹是什么?例3.设点A、B的坐标分别为(-5,0)(5,0),直线AM、BM相交于点M,且他们的斜率之积是-4/9,求点M的轨迹方程?当堂检测课后练习2.2.2 椭圆的简单几何性质 班级 姓名 小组学习目标1.掌握椭圆的几何性质2.椭圆的几何性质的实际应用 基础感知合作学习例1.求椭圆16x 2+25y 2=400的长轴和短轴长、离心率、焦点、顶点坐标例2.点M (x,y )与定点F (4,0)的距离和它到直线425x 的距离之比是常数54,求点M 的轨迹方程当堂检测《师说》随堂自测限时训练(1)班级姓名小组1.焦点在x轴上,a=6,c=1的椭圆的标准方程为:2.已知椭圆的方程为m2x2+16y2=16m2,焦点在x轴上,则m的取值范围:3.过点(-3,2)且与4x2+9y2=36有相同焦点的椭圆方程为:4.已知椭圆的方程是25x2+a2y2=25a2,它的两个焦点分别是F1,F2,且|F1F2|=8,弦AB过点F1,则三角形ABF2的周长为:5.椭圆25x2+16y2=1的焦点坐标是:6.已知两定点F1(-1,0)F2(1,0),动点P满足:|PF1|+|PF2|=2|F1F2|,求:(1)点P的轨迹方程(2)若∠F1PF2=120。
高中数学选修2-1导学案

文案大全§1.1.1 命题及四种命题1. 掌握命题、真命题及假命题的概念;2. 四种命题的内在联系,能根据一个命题来构造它的逆命题、否命题和逆否命题.. 复习2:什么是定理?什么是公理? . 二、新课导学 ※ 学习探究 1.在数学中,我们把用 、 、或 表达的,可以 的 叫做命题.其中 . 的语句叫做真命题, 的语句叫做假命题 练习:下列语句中: (1)若直线//a b ,则直线a 和直线b 无公共点; (2)247+= (3)垂直于同一条直线的两个平面平行; (4)若21x =,则1x =; (5)两个全等三角形的面积相等; (6)3能被2整除. 其中真命题有 ,假命题有 . 2.命题的数学形式:“若p ,则q ”,命题中的p 叫做命题的 ,q 叫做命题的 . ※ 典型例题 例1:下列语句中哪些是命题?是真命题还是假命题? (1)空集是任何集合的子集; (2)若整数a 是素数,则a 是奇数; (3)指数函数是增函数吗? (4)若空间有两条直线不相交,则这两条直线平行; (52;(6)15x >.命题有 ,真命题有 .假命题有 .例2 指出下列命题中的条件p 和结论q :(1)若整数a 能被2整除,则a 是偶数; (2)若四边形是菱形,则它的对角线互相垂直平分. 解:(1)条件p : 结论q :(2)条件p :结论q :变式:将下列命题改写成“若p ,则q ”的形式,并判断真假: (1)垂直于同一条直线的两条直线平行;(2)负数的立方是负数;(3)对顶角相等. ※ 动手试试 1.判断下列命题的真假: (1) 能被6整除的整数一定能被3整除; (2) 若一个四边形的四条边相等,则这个四边形是正方形;(3) 二次函数的图象是一条抛物线;(4) 两个内角等于45︒的三角形是等腰直角三角形.2.把下列命题改写成“若p ,则q ”的形式,并判断它们的真假. (1) 等腰三角形两腰的中线相等; (2) 偶函数的图象关于y 轴对称; (3) 垂直于同一个平面的两个平面平行.小结:判断一个语句是不是命题注意两点:(1)是否是陈述句;(2)是否可以判断真假.3.四种命题的概念(1)对两个命题,如果一个命题的条件和结论分别是另一个命题的结论和条件,那么我们这样的两个命题叫做 ,其中一个命题叫做原命题为:“若p,则q”,则逆命题为:“”.(2) 一个命题的条件和结论恰好是另一个命题的条件的否定和结论的否定, 我们把这样的两个命题叫做 ,其中一个命题叫做命题,那么另一个命题叫做原命题的 .若原命题为:“若p,则q”,则否命题为:“”(3)一个命题的条件和结论恰好是另一个命题的结论的否定和条件的否定, 我们把这样的两个命题叫做 ,其中一个命题叫做命题,那么另一个命题叫做原命题的 .若原命题为:“若p,则q”,则否命题为:“”练习:下列四个命题:(1)若()f x是正弦函数,则()f x是周期函数;(2)若()f x是周期函数,则()f x是正弦函数;(3)若()f x不是正弦函数,则()f x不是周期函数;(4)若()f x不是周期函数,则()f x不是正弦函数.(1)(2)互为(1)(3)互为(1)(4)互为(2)(3)互为例 3 命题:“已知a、b、c、d是实数,若子,a b c d==,则a c b d+=+”.写出逆命题、否命题、逆否命题.变式:设原命题为“已知a、b是实数,若a b+是无理数,则a、b都是无理数”,写出它的逆命题、否命题、逆否命题.※动手试试写出下列命题的逆命题、否命题和逆否命题并判断它们的真假:(1)若一个整数的末位数是0,则这个整数能被5整除;(2)若一个三角形的两条边相等,则这个三角形的两个角相等;(3)奇函数的图像关于原点对称. 三、总结提升:※学习小结这节课你学到了一些什么?你想进一步探究的问题是什么?※自我评价你完成本节导学案的情况为().A. 很好B. 较好C. 一般D. 较差※当堂检测(时量:5分钟满分:10分)计分:1.下列语名中不是命题的是().A.20x> B.正弦函数是周期函数C.{1,2,3,4,5}x∈ D.125>2.设M、N是两个集合,则下列命题是真命题的是().A.如果M N⊆,那么M N M⋂=B.如果M N N⋂=,那么M N⊆C.如果M N⊆,那么M N M⋃=D.M N N⋃=,那么N M⊆3.下面命题已写成“若p,则q”的形式的是().A.能被5整除的数的末位是5B.到线段两个端点距离相等的点在线段的垂直平分线上C.若一个等式的两边都乘以同一个数,则所得的结果仍是等式D.圆心到圆的切线的距离等于半径4.下列语句中:(1)2是有理数(2)1002是个大数(3)好人一生平安(4)968能被11整除,其中是命题的序号是5.将“偶函数的图象关于y轴对称”写成“若p,则q”的形式,则p:,q:1.写出下列命题的逆命题、否命题和逆否命题,并判断它们的真假(1)若,a b都是偶数,则a b+是偶数;(2)若0m>,则方程20x x m+-=有实数根.2.把下列命题改写成“若p,则q”的形式,并写出它们的逆命题、否命题和逆否命题,并判断它们的真假:文案大全文案大全(1)线段的垂直平分线上的点到这条线段两个端点的距离相等; (2)矩形的对角线相等.§1.1.2 四种命题间的相互关系1.掌握四种命题的内在联系;2. 能分析逆命题、否命题和逆否命题的相互关系,并能利用等价关系转化.复习2:判断命题“若0a ≥,则20x x a +-=有实根”的逆命题的真假.二、新课导学 ※ 学习探究1:分析下列四个命题之间的关系(1)若()f x 是正弦函数,则()f x 是周期函数; (2)若()f x 是周期函数,则()f x 是正弦函数; (3)若()f x 不是正弦函数,则()f x 不是周期函数;(4)若()f x 不是周期函数,则()f x 不是正弦函数. (1)(2)互为 (1)(3)互为 . (1)(4)互为 (2)(3)互为 .通过上例分析我们可以得出四种命题之间有如下关系:2、四种命题的真假性例1 以“若2320x x -+=,则2x =”为原命题,写出它的逆命题、否命题、逆否命题,并判断这些命题的真假并总结其规律性.系:(1) . (2) . 练习:判断下列命题的真假.(1)命题“在ABC ∆中,若A B A C >,则C B ∠>∠”的逆命题;(2)命题“若0ab ≠,则0a ≠且0b ≠”的否命题;(3)命题“若0a ≠且0b ≠,则0ab ≠”的逆否命题;(4)命题“若0a ≠且0b ≠,则220a b +>”的逆命题.文案大全反思:(1)直接判断(2)互为逆否命题的两个命题等价来判断. ※ 典型例题例1 证明:若220x y +=,则0x y ==.变式:判断命题“若220x y +=,则0x y ==”是真命题还是假命题?练习:证明:若222430a b a b -+--≠,则1a b -≠.例 2 已知函数()f x 在(,)-∞+∞上是增函数,,a b R ∈,对于命题“若0a b +≥,则()()()()f a f b f a f b +≥-+-.”(1) 写出逆命题,判断其真假,并证明你的结论. (2) 写出其逆否命题,并证明你的结论.※ 动手试试1.求证:若一个三角形的两条边不等,这两条边所对的角也不相等.2.命题“如果22x a b ≥+,那么2x ab ≥”的逆否命题是( )A.如果22x a b <+,那么2x ab <B.如果2x ab ≥,那么22x a b ≥+C.如果2x ab <,那么22x a b <+D.如果22x a b ≥+,那么2x ab <三、总结提升: ※ 学习小结这节课你学到了一些什么?你想进一步探究的问题是什么?※ 自我评价 你完成本节导学案的情况为( ).A. 很好B. 较好C. 一般D. 较差※ 当堂检测(时量:5分钟 满分:10分)计分: 1. 命题“若0x >且0y >,则0xy >”的否命题是( ).A.若0,0x y ≤≤,则0xy ≤B.若0,0x y >>,则0xy ≤C.若,x y 至少有一个不大于0,则0xy <D.若,x y 至少有一个小于0,或等于0,则0xy ≤ 2. 命题“正数a 的平方根不等于0”是命题“若a 不是正数,则它的平方根等于0”的( ). A.逆命题 B.否命题 C.逆否命题 D.等价命题3.设正确的是( ).A.是有理数B.C.D.+4. 若1x >,则21x >的逆命题是 否命题是5.命题“若a b >,则221a b ≥-”的否命题为1. 已知,a b 是实数,若20x ax b ++≤有非空解集,则240a b-≥,写出该命题的逆命题、否命题、逆否命题并判断其真假.2.证明:在四边形ABCD中,若AB CD AC CD+<+,则AB AC<.§1.2.1 充分条件与必要条件1. 理解必要条件和充分条件的意义;2. 能判断两个命题之间的关系..复习2:将命题“线段的垂直平分线上的点到这条线段两个端点的距离相等”改写为“若p,则q”的形式,并写出它的逆命题、否命题、逆否命题并判断它们的真假. 二、新课导学※学习探究探究任务:充分条件和必要条件的概念问题:1. 命题“若22x a b>+,则2x ab>”(1)判断该命题的真假;(2)改写成“若p,则q”的形式,则P:q:(3)如果该命题是真命题,则该命题可记为:读着: .2. 1.命题“若0ab=,则0a=”(1)判断该命题的真假;(2)改写成“若p,则q”的形式,则P:q:(3)如果该命题是真命题,则该命题可记为:读着:新知:一般地,“若p,则q”为真命题,是指由p通过推理可以得出q.我们就说,由p推出q,记作p q⇒,并且说p是q 的 ,q是p的试试:用符号“⇒”与“”填空:(1)22x y=x y=;(2)内错角相等两直线平行;(3)整数a能被6整除a的个位数字为偶数;(4)ac bc=a b=.※典型例题例 1 下列“若p,则q”形式的命题中,哪些命题中的p是q的充分条件?(1)若1x=,则2430x x-+=;(2)若()f x x=,则()f x在(,)-∞+∞上为增函数;(3)若x为无理数,则2x为无理数.文案大全文案大全练习:下列“若P ,则q ”的形式的命题中,哪些命题中的p 是q 的充分条件?(1)若两条直线的斜率相等,则这两条直线平行;(2)若5x >,则10x >例 2 下列“若p ,则q ”形式的命题中哪些命题中的q 是p 必要条件? (1)若x y =,则22x y =;(2)若两个三角形全等,则这两个三角形面积相等;(3)若a b >,则ac bc >练习:下列“若p ,则q ”形式的命题中哪些命题中的q 是p 必要条件?(1)若5a +是无理数,则a 是无理数; (2)若()()0x a x b --=,则x a =.小结:判断命题的真假是解题的关键.※ 动手试试练1. 判断下列命题的真假.(1)2x =是2440x x -+=的必要条件;(2)圆心到直线的距离等于半径是这条直线为圆的切线的必要条件;(3)sin sin αβ=是αβ=的充分条件; (4)0ab ≠是0a ≠的充分条件.练2. 下列各题中,p 是q 的什么条件? (1)p :1x =,q:1x -= (2)p :|2|3x -≤,q :15x -≤≤;(3)p :2x =,q:3x -(4)p :三角形是等边三角形,q :三角形是等腰三角形.三、总结提升 ※ 学习小结这节课你学到了一些什么?你想进一步探究的问题是什么?※ 知识拓展设,A B 为两个集合,集合A B ⊆,那么x A ∈是x B ∈是x A ∈的 条件.※ 自我评价 你完成本节导学案的情况为( ).A. 很好B. 较好C. 一般D. 较差※ 当堂检测(时量:5分钟 满分:10分)计分: 1. 在平面内,下列哪个是“四边形是矩形”的充分条件?( ). A.平行四边形对角线相等 B.四边形两组对边相等 C.四边形的对角线互相平分 D.四边形的对角线垂直2.,x y R ∈,下列各式中哪个是“0xy ≠”的必要条件?( ).文案大全A.0x y +=B.220x y +>C.0x y -=D.330x y +≠3.平面//α平面β的一个充分条件是( ).A.存在一条直线,//,//a a a αβB.存在一条直线,,//a a a αβ⊂C.存在两条平行直线,,,,//,//a b a b a b αββα⊂⊂D.存在两条异面直线,,,,//,//a b a b a b αββα⊂⊂ 4.p :20x -=,q :(2)(3)0x x --=,p 是q 的条件.5. p :两个三角形相似;q :两个三角形全等,p 是q 的 条件.1. 判断下列命题的真假 (1)“a b >”是“22a b >”的充分条件; (2)“||||a b >”是“22a b >”的必要条件.2. 已知{|A x x =满足条件}p ,{|B x x =满足条件}q . (1)如果A B ⊆,那么p 是q 的什么条件? (2)如果B A ⊆,那么p 是q 的什么条件?§1.2.2 充要条件1. 理解充要条件的概念;2. 掌握充要条件的证明方法,既要证明充分性又要证明必要性.一、课前准备(预习教材P 11~ P 12,找出疑惑之处) 复习1:什么是充分条件和必要条件?复习2:p :一个四边形是矩形q :四边形的对角线相等.p 是q 的什么条件?二、新课导学 ※ 学习探究探究任务一:充要条件概念问题:已知p :整数a 是6的倍数,q :整数a 是2 和3的倍数.那么p 是q 的什么条件?q 又是p 的什么条件? 新知:如果p q ⇔,那么p 与q 互为试试:下列形如“若p ,则q ”的命题是真命题吗?它的逆命题是真命题吗?p 是q 的什么条件? (1)若平面α外一条直线a 与平面α内一条直线平行,则直线a 与平面α平行; (2)若直线a 与平面α内两条直线垂直,则直线a 与平面α垂直.反思:充要条件的实质是原命题和逆命题均为真命题.※ 典型例题例1 下列各题中,哪些p 是q 的充要条件? (1) p : 0b =,q :函数2()f x ax bx c =++是偶函数; (2) p : 0,0,x y >> q :0xy > (3) p : a b > , q :a c b c +>+文案大全变式:下列形如“若p ,则q ”的命题是真命题吗?它的逆命题是真命题吗?哪些p 是q 的充要条件?(1) p : 0b = ,q :函数2()f x ax bx c =++是偶函数;(2) p : 0,0,x y >> q :0xy > (3) p : a b > , q :a c b c +>+小结:判断是否充要条件两种方法 (1)p q ⇒且q p ⇒;(2)原命题、逆命题均为真命题; (3) 用逆否命题转化.练习:在下列各题中, p 是q 的充要条件? (1) p :234x x =+ , q:x =(2) p : 30x -=, q :(3)(4)0x x --= (3) p : 240(0)b ac a -≥≠ ,q :20(0)ax bx c a ++=≠(4) p : 1x =是方程20ax bx c ++=的根 q :0a b c ++=例 2 已知:O 的半径为r ,圆心O 到直线的距离为d .求证:d r =是直线l 与O 相切的充要条件.变式:已知:O 的半径为r ,圆心O 到直线的距离为d ,证明:(1)若d r =,则直线l 与O 相切. (2)若直线l 与O 相切,则d r =小结:证明充要条件既要证明充分性又要证明必要性.※ 动手试试练1. 下列各题中p 是q 的什么条件? (1)p :1x =,q:1x -= (2)p :|2|3x -=,q :15x -≤≤ ;(3)p :2x =,q:3x -;(4)p :三角形是等边三角形,q :三角形是等腰三角形.练 2. 求圆222()()x a y b r -+-=经过原点的充要条件.三、总结提升 ※ 学习小结这节课你学到了一些什么?你想进一步探究的问题是什么?※ 知识拓展设A 、B 为两个集合,集合A B =是指x A x B∈⇔∈,则“x A ∈”与“x B ∈”互为文案大全※ 自我评价 你完成本节导学案的情况为( ).A. 很好B. 较好C. 一般D. 较差※ 当堂检测(时量:5分钟 满分:10分)计分: 1. 下列命题为真命题的是( ). A.a b >是22a b >的充分条件 B.||||a b >是22a b >的充要条件C.21x =是1x =的充分条件D.αβ=是tan tan αβ= 的充要条件2.“x M N ∈”是“x M N ∈”的( ). A.充分不必要条件 B.必要不充分条件C.充要条件D.既不充分也不必要条件3.设p :240(0)b ac a ->≠,q :关于x 的方程20(0)ax bx c a ++=≠有实根,则p 是q 的( ).A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件4.22530x x --<的一个必要不充分条件是( ).A.132x -<<B.102x -<<C.132x -<< D.16x -<< 5. 用充分条件、必要条件、充要条件填空.(1).3x >是5x >的(2).3x =是2230x x --=的( 3).两个三角形全等是两个三角形相似的1. 证明:20a b +=是直线230ax y ++=和直线20x by ++=垂直的充要条件.2.求证:ABC ∆是等边三角形的充要条件是222a b c ab ac bc ++=++,这里,,a b c 是ABC ∆的三边.§1.3简单的逻辑联结词1. 了解“或”“且”“非”逻辑联结词的含义;2. 掌握,,p q p q p ∧∨⌝的真假性的判断;3. 正确理解p ⌝的意义,区别p ⌝与p 的否命题;4. 掌握,,p q p q p ∧∨⌝的真假性的判断,关键在于p 与q 的真假的判断.1416复习1:什么是充要条件?复习2:已知{|A x x =满足条件}p ,{|B x x =满足条件}q(1)如果A B ⊆,那么p 是q 的什么条件; (2) 如果B A ⊆,那么p 是q 的什么条件; (3) 如果A B =,那么p 是q 的什么条件.二、新课导学※ 学习探究探究任务一:“且“的意义问题:下列三个命题有什么关系? (1)12能被3整除; (2)12能被4整除;(3)12能被3整除且能被4整除.新知:1.一般地,用逻辑联结词“且”把命题p 和命题q 联结起来就得到一个新命题,记作“ ”,读作“ ”.文案大全试试:判断下列命题的真假: (1)12是48且是36的约数;(2)矩形的对角线互相垂直且平分.反思:p q ∧的真假性的判断,关键在于p 与q 的真假的判断. 探究任务二:“或“的意义问题:下列三个命题有什么关系? (1) 27是7的倍数; (2)27是9的倍数;(3)27是7的倍数或是9的倍数.新知:1.一般地,用逻辑联结词“或”把命题p 和命题q 联结起来就得到一个新命题,记作“ ”,读作“ ”.(1) 47是7的倍数或49是7的倍数;(2) 等腰梯形的对角线互相平分或互相垂直.反思:p q ∨的真假性的判断,关键在于p 与q 的真假的判断. 探究任务三:“非“的意义问题:下列两个命题有什么关系? (1) 35能被5整除; (2)35不能被5整除;新知:1.一般地,对一个命题的全盘否定就得到一个新命题,记作“ ”,读作“ ”或“ ”. 试试:写出下列命题的否定并判断他们的真假: (1)2+2=5;(2)3是方程290x -=的根; (31-反思:p ⌝的真假性的判断,关键在于p 的真假的判断. ※ 典型例题例 1 将下列命题用“且”联结成新命题并判断他们的真假:(1)p :平行四边形的对角线互相平分,q :平行四边形的对角线相等;(2)p :菱形的对角线互相垂直,q :菱形的对角线互相平分;(3)p :35是15的倍数,q :35是7的倍数变式:用逻辑联结词“且”改写下列命题,并判断他们的真假:(1)1既是奇数,又是素数; (2)2和3都是素数.小结:p q ∧的真假性的判断,关键在于p 与q 的真假的判断.例2 判断下列命题的真假 (1) 22≤;(2) 集合A 是A B 的子集或是A B 的子集; (3) 周长相等的两个三角形全等或面积相等的两个三角形全等.变式:如果p q ∧为真命题,那么p q ∨一定是真命题吗?反之,p q ∨为真命题,那么p q ∧一定是真命题吗?小结:p q ∨的真假性的判断,关键在于p 与q 的真假的判断.例3 写出下列命题的否定,并判断他们的真假: (1)p :sin y x =是周期函数; (2)p :32<(3)空集是集合A 的子集.文案大全小结:p ⌝的真假性的判断,关键在于p 的真假的判断.三、总结提升 ※ 学习小结这节课你学到了一些什么?你想进一步探究的问题是什么?※ 知识拓展阅读教材第18页,理解逻辑联结词“且”“或”“并”“补”的关系.※ 自我评价 你完成本节导学案的情况为( ).A. 很好B. 较好C. 一般D. 较差※ 当堂检测(时量:5分钟 满分:10分)计分: 1. “p 或q 为真命题”是“p 且q 为真命题”的( ).A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件 2.命题P :在ABC ∆中,C B ∠>∠是sin sin C B >的充要条件;命题q :a b >是22ac bc >的充分不必要条件,则( ).A.p 真q 假B.p 假q 假C.“p 或q ”为假D.“p 且q ”为真 3.命题:(1)平行四边形对角线相等;(2)三角形两边的和大于或等于第三边;(3)三角形中最小角不大于60︒;(4)对角线相等的菱形为正方形.其中真命题有( ).A.1B.2C.3D.44.命题p :0不是自然数,命题q :π是无理数,在命题“p 或q ”“p 且q ”“非p ”“非q ”中假命题是 ,真命题是 .5. 已知p :2||6x x -≥,q :,,x Z p q q ∈∧⌝都是假命题,则x 的值组成的集合为 1. 写出下列命题,并判断他们的真假: (1)p q ∨,这里p :4{2,3}∈,q :2{2,3}∈; (2)p q ∧,这里p :4{2,3}∈,q :2{2,3}∈; (3) p q ∨,这里p :2是偶数,q :3不是素数; (4) p q ∧,这里p :2是偶数,q :3不是素数. 2.判断下列命题的真假:(1)52>且73> (2)78≥ (3)34>或34<§1.4 全称量词与存在量词1. 掌握全称量词与存在量词的的意义;2. 掌握含有量词的命题:全称命题和特称命题真假的判断.2123复习1:写出下列命题的否定,并判断他们的真假:(1是有理数;(2)5不是15的约数(3)8715+≠ (4)空集是任何集合的真子集复习2:判断下列命题的真假,并说明理由: (1)p q ∨,这里p :π是无理数,q :π是实数;(2)p q ∧,这里p :π是无理数,q :π是实数; (3) p q ∨,这里p :23>,q :8715+≠; (4) p q ∧,这里p :23>,q :8715+≠.文案大全二、新课导学 ※ 学习探究 探究任务一:全称量词的意义 问题:1.下列语名是命题吗?(1)与(3),(2)与(4)之间有什么关系? (1)3x >; (2)21x +是整数; (3)对所有的,3x R x ∈>; (4)对任意一个x Z ∈,21x +是整数.2. 下列语名是命题吗?(1)与(3),(2)与(4)之间有什么关系?(1)213x +=;(2)x 能被2和3整除;(3)存在一个0x R ∈,使0213x +=;(4)至少有一个0x Z ∈,0x 能被2和3整除.新知:1.短语“ ”“ ”在逻辑中通常叫做全称量词,并用符号“ ”表示,含有 的命题,叫做全称命题.其基本形式为:,()x M p x ∀∈,读作:2. 短语“ ”“ ”在逻辑中通常叫做存在量词,并用符号“ ”表示,含有 的命题,叫做特称称命题.其基本形式00,()x M p x ∃∈,读作: 试试:判断下列命题是不是全称命题或者存在命题,如果是,用量词符号表示出来.(1)中国所有的江河都流入大海;(2)0不能作为除数;(3)任何一个实数除以1,仍等于这个实数; (4)每一个非零向量都有方向.反思:注意哪些词是量词是解决本题的关键,还应注意全称命题和存在命题的结构形式. ※ 典型例题 例1 判断下列全称命题的真假: (1)所有的素数都是奇数;(2)2,11x R x ∀∈+≥; (3)对每一个无理数x ,2x 也是无理数. 变式:判断下列命题的真假: (1)2(5,8),()420x f x x x ∀∈=--> (2)2(3,),()420x f x x x ∀∈+∞=-->小结:要判定一个全称命题是真命题,必须对限定集合M 中每一个元素x 验证()p x 成立;但要判定全称命题是假命题,却只要能举出集合M 中的一个0x x =,使得0()p x 不成立即可.例2 判断下列特称命题的真假:(1) 有一个实数0x ,使200230x x ++=;(2) 存在两个相交平面垂直于同一条直线; (3) 有些整数只有两个正因数.变式:判断下列命题的真假:(1)2,32a Z a a ∃∈=- (2)23,32a a a ∃≥=- 小结:要判定特称命题“00,()x M p x ∃∈” 是真命题只要在集合M 中找一个元素0x ,使0()p x 成立即可;如果集合M 中,使()P x 成立的元素x 不存在,那么这个特称命题是假命题.※ 动手试试 练1. 判断下列全称命题的真假: (1)每个指数都是单调函数;文案大全(2)任何实数都有算术平方根;(3){|x x x ∀∈是无理数},2x 是无理数.练2. 判定下列特称命题的真假: (1)00,0x R x ∃∈≤;(2)至少有一个整数,它既不是合数,也不是素数;(3)0{|x x x ∃∈是无理数},20x 是无理数.三、总结提升 ※ 学习小结这节课你学到了一些什么?你想进一步探究的问题是什么?※ 知识拓展数理逻辑又称符号逻辑,是用数学的方法研究推理过程的一门学问. 德国启蒙思想家 莱布尼茨※ 自我评价 你完成本节导学案的情况为( ).A. 很好B. 较好C. 一般D. 较差※ 当堂检测(时量:5分钟 满分:10分)计分: 1. 下列命题为特称命题的是( ). A.偶函数的图像关于y 轴对称 B.正四棱柱都是平行六面体 C.不相交的两条直线都是平行线 D.存在实数大于等于32.下列特称命题中真命题的个数是( ). (1),0x R x ∃∈≤;(2)至少有一个整数它既不是合数也不是素数;(3){|x x x ∃∈是无理数},2x 是无理数.A.0个B.1个C.2个D.4个 3.下列命题中假命题的个数( ). (1)2,11x R x ∀∈+≥;(2),213x R x ∃∈+=; (3),x Z ∃∈x 能被2和3整除; (4)2,230x R x x ∃∈++=A.0个B.1个C.2个D.4个 4.下列命题中(1)有的质数是偶数;(2)与同一个平面所成的角相等的两条直线平行;(3)有的三角形三个内角成等差数列;(4)与圆只有一个公共点的直线是圆的切线,其中全称命题是 特称命题是 .5. 用符号“∀”与“∃”表示下列含有量词的命题.(1)实数的平方大于等于0: (2)存在一对实数使2330xy ++<成立:1. 判断下列全称命题的真假:(1)末位是0的整数可以被子5整除;(2)线段的垂直平分线上的点到这条线段两端点距离相等;(3)负数的平方是正数; (4)梯形的对角线相等.2. 判断下列全称命题的真假: (1)有些实数是无限不循环小数; (2)有些三角形不是等腰三角形; (3)有的菱形是正方形.§1.4.3含一个量词的命题的否定1. 掌握对含有一个量词的命题进行否定的方法,要正确掌握量词否定的各种形式;2. 明确全称命题的否定是存在命题,存在命题的否定是全称命题.2425 复习1:判断下列命题是否为全称命题: (1)有一个实数α,tan α无意义; (2)任何一条直线都有斜率;复习2:判断以下命题的真假:文案大全(1)21,04x R x x ∀∈-+≥ (2)2,3x Q x ∃∈=二、新课导学 ※ 学习探究探究任务一:含有一个量词的命题的否定 问题:1.写出下列命题的否定: (1)所有的矩形都是平行四边形; (2)每一个素数都是奇数; (3)2,210x R x x ∀∈-+≥.这些命题和它们的否定在形式上有什么变化? 2.写出下列命题的否定: (1)有些实数的绝对值是正数; (2)某些平行四边形是菱形; (3)200,10x R x ∃∈+<.这些命题和它们的否定在形式上有什么变化?新知:1.一般地,对于一个含有一个量词的全称命题的否定有下面的结论: 全称命题p :,()x p p x ∀∈, 它的否定p ⌝:00,()x M p x ∃∈⌝2. 一般地,对于一个含有一个量词的特称命题的否定有下面的结论:特称命题p :00,()x M p x ∃∈, 它的否定p ⌝:,()x M p x ∀∈.试试:1.写出下列命题的否定: (1),n Z n Q ∀∈∈; (2)任意素数都是奇数; (3)每个指数函数都是奇数.2. 写出下列命题的否定:(1) 有些三角形是直角三角形; (2)有些梯形是等腰梯形;(3)存在一个实数,它的绝对值不是正数.反思:全称命题的否定变成特称命题.※ 典型例题例1 写出下列全称命题的否定:(1)p :所有能被3整除的数都是奇数; (2)p :每一个平行四边形的四个顶点共圆; (3)p :对任意x Z ∈,2x 的个位数字不等于3.变式:写出下列全称命题的否定,并判断真假.(1) p :21,04x R x x ∀∈-+≥(2) p :所有的正方形都是矩形.例2 写出下列特称命题的否定: (1) p :2000,220x R x x ∃∈++≤; (2) p :有的三角形是等边三角形; (3) p :有一个素数含有三个正因数.变式:写出下列特称命题的否定,并判断真假. (1) p :2,220x R x x ∃∈++≤;(2) p :至少有一个实数x ,使310x +=.小结:全称命题的否定变成特称命题.※ 动手试试练1. 写出下列命题的否定: (1) 32,x N x x ∀∈>;(2) 所有可以被5整除的整数,末位数字都是0; (3) 2000,10x R x x ∃∈-+≤;(4) 存在一个四边形,它的对角线是否垂直.练 2. 判断下列命题的真假,写出下列命题的否定:(1)每条直线在y轴上都有截矩;(2)每个二次函数都与x轴相交;(3)存在一个三角形,它的内角和小于180︒;(4)存在一个四边形没有外接圆.三、总结提升※学习小结这节课你学到了一些什么?你想进一步探究的问题是什么?※知识拓展英国数学家布尔(G.BOOL)建立了布尔代数,并创造了一套符号系统,利用符号来表示逻辑中的各种概念.他不建立了一系列的运算法则,利用代数的方法研究逻辑问题,初步奠定了数理逻辑的※自我评价你完成本节导学案的情况为().A. 很好B. 较好C. 一般D. 较差※当堂检测(时量:5分钟满分:10分)计分:1. 命题“原函数与反函数的图象关于y x=对称”的否定是().A. 原函数与反函数的图象关于y x=-对称B. 原函数不与反函数的图象关于y x=对称C.存在一个原函数与反函数的图象不关于y x=对称D. 存在原函数与反函数的图象关于y x=对称2.对下列命题的否定说法错误的是().A. p:能被3整除的数是奇数;p⌝:存在一个能被3整除的数不是奇数B. p:每个四边形的四个顶点共圆;p⌝:存在一个四边形的四个顶点不共圆C. p:有的三角形为正三角形;p⌝:所有的三角形不都是正三角形D. p:2,220x R x x∃∈++≤;p⌝:2,220x R x x∀∈++>3.命题“对任意的32,10x R x x∈-+≤”的否定是().A. 不存在32,10x R x x∈-+≤B. 存在32,10x R x x∈-+≤C. 存在32,10x R x x∈-+>D. 对任意的32,10x R x x∈-+>4. 平行四边形对边相等的否定是5. 命题“存在一个三角形没有外接圆”的否定是.1. 写出下列命题的否定:(1)若24x>,则2x>;(2)若0,m≥则20x x m+-=有实数根;(3)可以被5整除的整数,末位是0;(4)被8整除的数能被4整除;(5)若一个四边形是正方形,则它的四条边相等.2. 把下列命题写成含有量词的命题:(1)余弦定理;(2)正弦定理.第一章常用逻辑用语(复习)1. 命题及其关系(1)了解命题的逆命题、否命题与逆否命题,会分析四种命题间的相互关系;(2)理解必要条件、充分条件与充要条件的意义.2. 简单的逻辑联结词了解逻辑联结词“或”“且”“非”的含义.3. 全称量词与存在量词文案大全。
高二数学选修2-1人教A全册导学案第3章空间向量与立体几何§3.2《立体几何中的向量方法》

§3.2 立体几何中的向量方法知识点一用向量方法判定线面位置关系(1)设a、b分别是l1、l2的方向向量,判断l1、l2的位置关系:①a=(2,3,-1),b=(-6,-9,3).②a=(5,0,2),b=(0,4,0).(2)设u、v分别是平面α、β的法向量,判断α、β的位置关系:①u=(1,-1,2),v=(3,2,).②u=(0,3,0),v=(0,-5,0).(3)设u是平面α的法向量,a是直线l的方向向量,判断直线l与α的位置关系.①u=(2,2,-1),a=(-3,4,2).②u=(0,2,-3),a=(0,-8,12).解(1)①∵a=(2,3,-1),b=(-6,-9,3),∴a=-b,∴a∥b,∴l1∥l2.②∵a=(5,0,2),b=(0,4,0),∴a·b=0,∴a⊥b,∴l1⊥l2.(2)①∵u=(1,-1,2),v=(3,2,),∴u·v=3-2-1=0,∴u⊥v,∴α⊥β.②∵u=(0,3,0),v=(0,-5,0),∴u=-v,∴u∥v,∴α∥β.(3)①∵u=(2,2,-1),a=(-3,4,2),∴u·a=-6+8-2=0,∴u⊥a,∴l⊂α或l∥α.②∵u=(0,2,-3),a=(0,-8,12),∴u=-a,∴u∥a,∴l⊥α.知识点二利用向量方法证明平行问题如图所示,在正方体ABCD-A1B1C1D1中,M、N分别是C1C、B1C1的中点.求证:MN∥平面A1BD.证明方法一如图所示,以D为原点,DA、DC、DD1所在直线分别为x轴、y轴、z 轴建立空间直角坐标系,设正方体的棱长为1,则可求得M (0,1,),N (,1,1),D(0,0,0),A1(1,0,1),B(1,1,0),于是=(,0,),设平面A1BD的法向量是n=(x,y,z).n=(x,y,z).则n·=0,得取x=1,得y=-1,z=-1.∴n=(1,-1,-1).又·n=(,0,)·(1,-1,-1)=0,方法二∵ =∴∥,又∵MN⊄平面A1BD.∴MN∥平面A1BD.知识点三利用向量方法证明垂直问题在正棱锥P—ABC中,三条侧棱两两互相垂直,G是△PAB的重心,E、F分别为BC、PB上的点,且BE∶EC=PF∶FB=1∶2.(1)求证:平面GEF⊥平面PBC;(2)求证:EG是PG与BC的公垂线段.证明(1)方法一如图所示,以三棱锥的顶点P为原点,以PA、PB、PC所在直线分别为x轴、y轴、z轴建立空间直角坐标系.令PA=PB=PC=3,则A(3,0,0)、B(0,3,0)、C(0,0,3)、E(0,2,1)、F(0,1,0)、G(1,1,0)、P(0,0,0).于是=(3,0,0),=(3,0,0),故=3,∴PA∥FG.而PA⊥平面PBC,∴FG⊥平面PBC,又FG⊂平面EFG,∴平面EFG⊥平面PBC.方法二同方法一,建立空间直角坐标系,则E(0,2,1)、F(0,1,0)、G(1,1,0).=(0,-1,-1),=(0,-1,-1),设平面EFG的法向量是n=(x,y,z),则有n⊥,n⊥,∴令y=1,得z=-1,x=0,即n=(0,1,-1).而显然=(3,0,0)是平面PBC的一个法向量.这样n·= 0,∴n⊥即平面PBC的法向量与平面EFG的法向量互相垂直,∴平面EFG⊥平面PBC.(2)∵=(1,1,1),=(1,1,0),=(0,3,3),∴·=11= 0,·=33 = 0,∴EG⊥PG,EG⊥BC,∴EG是PG与BC的公垂线段.知识点四利用向量方法求角四棱锥P—ABCD中,PD⊥平面ABCD,PA与平面ABCD所成的角为60°,在四边形ABCD中,∠D=∠DAB=90°,AB=4,CD=1,AD=2.(1)建立适当的坐标系,并写出点B,P的坐标;(2)求异面直线PA与BC所成角的余弦值.解(1)如图所示,以D为原点,射线DA,DC,DP分别为x轴,y轴,z轴的正方向,建立空间直角坐标系D—xyz,∵∠D=∠DAB=90°,AB=4,CD=1,AD=2,∴A(2,0,0),C(0,1,0),B(2,4,0).由PD⊥面ABCD得∠PAD为PA与平面ABCD所成的角.∴∠PAD=60°.在Rt△PAD中,由AD=2,得PD=2.∴P(0,0,2).(2)∵=(2,0,-2),=(2,3,0)∴cos〈,〉=∴PA与BC所成角的余弦值为.正方体ABEF-DCE′F′中,M、N分别为AC、BF的中点(如图所示),求平面MNA 与平面MNB所成二面角的余弦值.解取MN的中点G,连结BG,设正方体棱长为1.方法一∵△AMN,△BMN为等腰三角形,∴AG⊥MN,BG⊥MN.∴∠AGB为二面角的平面角或其补角.∵AG=BG=,,设〈,〉=θ,2=2+2·+2,∴1=()2+2××cosθ+()2.∴cosθ=,故所求二面角的余弦值为.方法二以B为坐标原点,BA,BE,BC所在的直线分别为x轴、y轴、z轴建立空间直角坐标系B-xyz则M(,0,),N (,,0),中点G(,,),A(1,0,0),B(0,0,0),由方法一知∠AGB为二面角的平面角或其补角.∴=(,-,-),=(,-,-),∴ cos<, >==,故所求二面角的余弦值为.方法三建立如方法二的坐标系,∴即取n1=(1,1,1).同理可求得平面BMN的法向量n2=(1,-1,-1).∴cos〈n1,n2〉=,故所求二面角的余弦值为知识点五用向量方法求空间的距离已知正方形ABCD的边长为4,E、F分别是AB、AD的中点,GC⊥平面ABCD,且GC=2,求点B到平面EFG的距离.解如图所示,以C为原点,CB、CD、CG所在直线分别为x、y、z轴建立空间直角坐标系C-xyz.由题意知C(0,0,0),A(4,4,0),B(4,0,0),D(0,4,0),E(4,2,0),F(2,4,0),G(0,0,2).=(0,2,0),=(-2,4,0),设向量⊥平面GEF,垂足为M,则M、G、E、F四点共面,故存在实数x,y,z,使= x+ y+ z,即= x(0,2,0)+y(2,4,0)+z(4,0,2)=(2y4z,2x+4y,2z).由BM⊥平面GEF,得⊥,⊥,于是·=0,·=0,即即,解得∴=(-2y-4z,2x+4y,2z)=∴||=即点B到平面GEF的距离为.考题赏析(安徽高考)如图所示,在四棱锥O—ABCD中,底面ABCD是边长为1的菱形,∠ABC=,OA⊥底面ABCD,OA=2,M为OA的中点.(1)求异面直线AB与MD所成角的大小;(2)求点B到平面OCD的距离.解作AP⊥CD于点P.如图,分别以AB、AP、AO所在直线为x、y、z轴建立平面直角坐标系.A(0,0,0),B(1,0,0),P (0,,0),D (-,,0),O(0,0,2),M(0,0,1).(1)设AB与MD所成角为θ,∵=(1,0,0),=(-,,-1),∴cos =.∴θ=.∴AB与MD所成角的大小为.(2)∵=(0,,),=(,,),∴设平面OCD的法向量为n = ( x, y , z ),则n·=0,n·= 0.得取z=,解得n = (0,4,).设点B到平面OCD的距离为d,则d为在向量n上的投影的绝对值.∵=(1,0,2),∴d=,∴点B到平面OCD的距离为,1.已知A(1,0,0)、B(0,1,0)、C(0,0,1),则平面ABC的一个单位法向量是( )A.(,,-) B.(,-,)C.(-,,) D.(-,-,-)答案 D=(-1,1,0),是平面OAC的一个法向量.=(-1,0,1),=(0,-1,1)设平面ABC的一个法向量为n=(x,y,z)∴令x=1,则y=1,z=1∴n=(1,1,1)单位法向量为:=± (,,).2.已知正方体ABCD—A1B1C1D1,E、F分别是正方形A1B1C1D1和ADD1A1的中心,则EF和CD所成的角是( )A.60°B.45°C.30°D.90°答案 B3.设l1的方向向量a=(1,2,-2),l2的方向向量b=(-2,3,m),若l1⊥l2,则m=( ) A.1 B.2 C.D.3答案 B解析因l1⊥l2,所以a·b=0,则有1×(-2)+2×3+(-2)×m=0,∴2m=6-2=4,即m=2.4.若两个不同平面α,β的法向量分别为u=(1,2,-1),v=(-3,-6,3),则( )A.α∥βB.α⊥βC.α,β相交但不垂直D.以上均不正确答案 A解析因v=-3u,∴v∥u.故α∥β.5.已知a、b是异面直线,A、B∈a,C、D∈b,AC⊥b,BD⊥b,且AB=2,CD=1,则a与b所成的角是( )A.30°B.45°C.60°D.90°答案 C解析设〈,〉=θ,·=(++·= ||2= 1,cosθ=,所以θ=606.若异面直线l1、l2的方向向量分别是a=(0,-2,-1),b=(2,0,4),则异面直线l1与l2的夹角的余弦值等于( )A.B.C.-D.答案 B解析设异面直线l1与l2的夹角为θ,则cosθ=7.已知向量n=(6,3,4)和直线l垂直,点A(2,0,2)在直线l上,则点P(-4,0,2)到直线l的距离为________.答案,解析=(6,0,0),因为点A在直线l上,n与l垂直,所以点P到直线l的距离为8.平面α的法向量为(1,0,-1),平面β的法向量为(0,-1,1),则平面α与平面β所成二面角的大小为________.答案或,解析设n1=(1,0,-1),n2=(0,-1,1)则cos〈n1,n2〉=〈n1,n2〉=.因平面α与平面β所成的角与〈n1,n2〉相等或互补,所以α与β所成的角为或.9.已知四面体顶点A(2,3,1)、B(4,1,-2)、C(6,3,7)和D(-5,-4,8),则顶点D到平面ABC的距离为________.答案11解析设平面ABC的一个法向量为n =(x,y,z)则令x=1,则n = (1,2,),=(7,7,7)故所求距离为,10.如图所示,在四棱锥P—ABCD中,底面ABCD是正方形,侧棱PD⊥平面ABCD,PD=DC,E是PC的中点,作EF⊥PB交PB于F.(1)证明:PA∥平面BDE;(2)证明:PB⊥平面DEF.证明(1)如图建立空间直角坐标系,设DC=a,AC∩BD=G,连结EG,则A(a,0,0),P(0,0,a),C(0,a,0),E (0,,),G (,,0).于是=(a,0,a),=(,0,),∴= 2,∴PA∥EG.又EG平面DEB.PA平面DEB.∴PA∥平面DEB.(2)由B(a,a,0),得=(a, a, a),又=(0, ,),∵·=∴PB⊥DE.又EF⊥PB,EF∩DE=E,∴PB⊥平面EFD.11.如图所示,已知点P在正方体ABCD—A′B′C′D′的对角线BD′上,∠PDA=60°.(1)求DP与CC′所成角的大小;(2)求DP与平面AA′D′D所成角的大小.解如图所示,以D为原点,DA为单位长度建立空间直角坐标系D—xyz.则=(1,0,0),= (0,0,1).连结BD,B′D′.在平面BB′D′D中,延长DP交B′D′于H.设= (m,m,1) (m>0),由已知〈,〉= 60,由·= ||||cos〈,〉,可得2m =解得m =,所以=(,,1),(1)因为cos〈,〉=(2)所以〈,〉= 45,即DP与CC′所成的角为45.(2)平面AA′D′D的一个法向量是= (0,1,0).因为cos〈,〉=所以〈,〉= 60°,可得DP与平面AA′D′D所成的角为30.12. 如图,四边形ABCD是菱形,PA⊥平面ABCD,PA=AD=2,∠BAD=60°.平面PBD⊥平面PAC,(1)求点A到平面PBD的距离;(2)求异面直线AB与PC的距离.(1)解以AC、BD的交点为坐标原点,以AC、BD所在直线为x轴、y轴建立如图所示的空间直角坐标系,则A(3,0,0),B(0,1,0),C(,0,0),D(0,1,0),P(3,0,2).设平面PBD的一个法向量为n1=(1,y1,z1).由n1⊥,n1⊥,可得n1=(1,0,).(1)=(,0,0),点A到平面PBD的距离,,13.如图所示,直三棱柱ABC—A1B1C1中,底面是以∠ABC为直角的等腰直角三角形,AC = 2a,BB1 = 3a,D为A1C1的中点,在线段AA1上是否存在点F,使CF⊥平面B1DF?若存在,求出||;若不存在,请说明理由.解以B为坐标原点,建立如图所示的空间直角坐标系B-xyz.假设存在点F,使CF⊥平面B1DF,并设=λ=λ(0,0,3a)=(0,0,3λa)(0<λ<1),∵D为A1C1的中点,∴D(,,3a)=(,,3a)-(0,0,3a)=(,,0),=∵CF⊥平面B1DF,∴CF⊥, ⊥,即解得λ=或λ=∴存在点F使CF⊥面B1DF,且当λ=时,||=,|| = a当λ=,|| =,|| = 2a.14.如图(1)所示,已知四边形ABCD是上、下底边长分别为2和6,高为eq \r(3)的等腰梯形.将它沿对称轴OO1折成直二面角,如图(2).(1)证明:AC⊥BO1;(2)求二面角O—AC—O1的余弦值.(1)证明由题设知OA⊥OO1,OB⊥OO1.所以∠AOB是所折成的直二面角的平面角,即OA⊥OB.故以O为原点,OA、OB、OO1所在直线分别为x轴、y轴、z轴建立空间直角坐标系,如图所示,则相关各点的坐标是A(3,0,0)、B(0,3,0)、C(0,1, )、O1(0,0, ).·=-3+·=0.所以AC⊥BO1.(2)解因为·=+ ·=0.所以BO1⊥OC.由(1)AC⊥BO1,所以BO1⊥平面OAC,是平面OAC的一个法向量.设n=(x,y,z)是平面O1AC的一个法向量,由取z= ,得n=(1,0,).设二面角O-AC-O1的大小为θ,由n 、的方向可知θ=〈n,〉,所以cosθ= cos〈n ,〉=即二面角O—AC—O1的余弦值是.。
高中数学人教版选修2-1导学案:1.3.1且 1.3.2或

§1.3.1且§1.3.2或班级姓名组别代码评价【使用说明与学法指导】1.在自习或自主时间通过阅读课本14页-16页用20分钟把预习探究案中的所有知识完成。
训练案在自习或自主时间完成。
2.重点预习:逻辑联结词“且”“或”的含义,判断用“且”、“或”、联结所构成的新命题的真假。
3.把有疑问的题做好标记或写到后面“我的疑问处”。
【学习目标】1.理解逻辑联结词“且”、“或”的含义,会用“且”、“或”联结所给命题,构成新命题,会判断用“且”、“或”、联结所构成的新命题的真假。
2.通过数学实例介绍“且”、“或”的含义和用法,让学生从实际问题中学习“且”“或”的含义。
3.体会用逻辑用语表述数学内容的准确性和简洁性。
【学习重点】逻辑联结词“且”、“或”的含义,判断用“且”、“或”联结所构成的新命题的真假。
【学习难点】逻辑联结词“或”的含义【知识链接】1.什么叫命题?2.什么是真命题,假命题?3.判断下列语句是否是命题,如果是,是真命题还是假命题?①12>5 ②3是12 的约数③0.5是整数④3是12 的约数吗?⑤x>5【预习探究案】探究一:且1.一般地,用联结词“且”把命题p和命题q联结起来,就得到一个新命题,记作读作2.判断命题p q的真假:,。
例1.将下列命题用“且”联结成新命题,并判断它们的真假。
(1)p:平行四边形的对角线互相平分,q: 平行四边形的对角线相等;(2)p:菱形的对角线互相垂直,q: 菱形的对角线互相平分;(3)p:35是15的倍数;q:35是7的倍数;练习:将下列命题用“且”联结成新命题,并判断它们的真假。
(1)p:2是有理数,q: 2是无理数;(2)p:方程x2+x-1=0的两根符号不同,q:方程x2+x-1=0的两根绝对值不同.例2.用逻辑联结词“且”改写下列命题,并判断它们的真假。
(1)1既是奇数,又是素数;(2)2和3都是素数。
归纳提升:判断命题p q∧的真假的方法:。
【VIP专享】高二数学选修2-1全套导学案

),准线方程是
例 2 一种卫星接收天线的轴截面如图所示,卫星波束呈近似平行状态的射入轴截面 为抛物线的接收天线,经反射聚集到焦点处,已知接收天线的口径为 4.8m ,深度为 0.5m ,试建立适当的坐标系,求抛物线的标准方程和焦点坐标.
;
.
张家口东方中学
※ 动手试试 练 1.求满足下列条件的抛物线的标准方程: (1) 焦点坐标是 F (5, 0 ) ;
),对
1
合抱之木,生于毫末;九层之台,起于累土;千里之行,始于足下.——《老子》
பைடு நூலகம்
6.培养学生观察、思考、对比及分析综合的能力。过程与方法1.通过观察蚯蚓教的学实难验点,线培形养动观物察和能环力节和动实物验的能主力要;特2征.通。过教对学观方察法到与的教现学象手分段析观与察讨法论、,实对验线法形、动分物组和讨环论节法动教特学征准的备概多括媒,体继课续件培、养活分蚯析蚓、、归硬纳纸、板综、合平的面思玻维璃能、力镊。子情、感烧态杯度、价水值教观1和.通过学理解的蛔1虫.过观适1、察于程3观阅 六蛔寄.内列 察读 、虫生出 蚯材 让标容生常 蚓3根料 学本教活.见 身了 据: 生,师的2的 体解 、 问巩鸟 总看活形作线 的蛔 用 题固类 结雌动态业形虫 手 自练与 本雄学、三:动 状对 摸 学习人 节蛔生结4、、收物 和人 一 后同类 课虫活构请一 蚯集并 颜体 摸 回步关 重的动、学、 蚓鸟归 色的 蚯 答学系 点形教生生让 在类纳 。危 蚓 问习从 并状学理列学 平的线 蚯害 的 题四线人 归、意特出四生 面形 蚓以 体、形类 纳大图点常、五观 玻存动 的及 表鸟请动文 本小引以见引、察 璃现物 身预 ,类 3学物明 节有言及的、导巩蚯 上状的 体防 是之生和历 课什根蚯环怎学固蚓 和,主 是感 干所列环史 学么据蚓节二样生练引 牛鸟要 否染 燥以举节揭 到不上适动、区回习导 皮类特 分的 还分蚯动晓 的同节于物让分答。学 纸减征 节方 是布蚓物起 一,课穴并学蚯课生 上少。 ?法 湿广的教, 些体所居归在生蚓前回 运的4; 润泛益学鸟色生纳.靠物完的问答 动原蛔4的,处目类 习和活环近.在成前题蚯 的因虫了 ?以。标就 生体的节身其实端并蚓 快及寄解 触上知同 物表内特动体结验和总的 慢我生利蚯 摸适识人 学有容点物前构并后结生 一国在用蚓 蚯于与类 的什,的端中思端线活 样的人问的 蚓飞技有 基么引进主的的考?形环 吗十体题生行能着 本特出要几变以动境 ?大,活 节的1密 方征本“特节化下物.并 为珍会让习 近形理切 法。课生征有以问的引 什稀小学性 腹态解的 。2课物。什游题主.出 么鸟起结生和 面结蛔关观题体么戏:要蚯 ?类哪利明适 处构虫系察:的特的特蚓等些用确于 ,特适。蛔章形殊形征这资疾板,穴 是点于可虫我态结式。种料病书生居 光是寄的们结构,五典,?小物生 滑重生鸟内学构,学、型以5结的活 还要生类部习与.其习巩的爱如鸟结的 是原活生结了功颜消固线鸟何类构形 粗因的存构腔能色化练形护预适特态 糙之结的,肠相是系习动鸟防于点、 ?一构现你动适否统。物为蛔飞都结。和状认物应与的。主虫行是构课生却为和”其结题病的与、本理不蛔扁的他构以?特环生8特乐虫形观部特8小三征境理页点观的动位点组、梳相等这;,哪物教相,为引理适方些2鸟,育同师.单导知应面鸟掌类结了;?生位学识的你握日构解2互.办生。特认线益特了通动手观征识形减点它过,抄察;吗动少是们理生报蛔5?物,与的解.参一虫了它和有寄主蛔与份结解们环些生要虫其。构蚯都节已生特对中爱。蚓会动经活征人培鸟与飞物灭相。类养护人吗的绝适这造兴鸟类?主或应节成趣的的为要濒的课情关什特临?就危感系么征灭来害教;?;绝学,育,习使。我比学们它生可们理以更解做高养些等成什的良么两好。类卫动生物习。惯根的据重学要生意回义答;的3.情通况过,了给解出蚯课蚓课与题人。类回的答关:系线,形进动行物生和命环科节学动价环值节观动的物教一育、。根教据学蛔重虫点病1.引蛔出虫蛔适虫于这寄种生典生型活的线结形构动和物生。理二特、点设;置2.问蚯题蚓让的学生生活思习考性预和习适。于穴居生活的形态、结构、生理等方面的特征;3.线形动物和环节动物的主要特征。
高二数学选修2-1第2章《空间向量与立体几何》_导学案

高二数学选修2-1第2章《空间向量与立体几何》_导学案南康二中高二数学◆选修2-1◆导学案.试试:1.分别用平行四边形法则和三角形法则求ab,ab..b2.点C在线段AB上,且AC5,CB2则ACAB,BCAB.反思:空间向量加法与数乘向量有如下运算律吗?⑴加法交换律:A.+B.=B.+a;⑵加法结合律:(A.+b)+C.=A.+(B.+c);⑶数乘分配律:λ(A.+b)=λA.+λb.典型例题例1已知平行六面体ABCDA'B'C'D'(如图),化简下列向量表达式,并标出化简结果的向量:⑴AB⑵BCABAD;AA';⑶ABAD1CC'⑷12(ABAD2AA').变式:在上图中,用AB,AD,AA'表示AC',BD'和DB'.小结:空间向量加法的运算要注意:首尾相接的若干向量之和,等于由起始向量的起点指向末尾向量的终点的向量,求空间若干向量之和时,可通过平移使它们转化为首尾相接的向量.2南康二中高二数学◆选修2-1◆导学案§2.1.2空间向量的数乘运算(一)CD3ab,求证:A,B,C三点共线.1.化简;2.3.几何中的问题.8687复习1:化简:⑴5(3a2b)+4(2b3a);⑵6a3bcabc.复习2:在平面上,什么叫做两个向量平行?在平面上有两个向量a,b,若b是非零向量,则a与平行的充要条件是二、新课导学学习探究探究任务一:空间向量的共线问题它们的位置关系?新知:空间向量的共线:1.如果表示空间向量的互相或平行向量.2.空间向量共线:定理:对空间任意两个向量a,b(b0),a//b要条件是存在唯一实数,使得推论:如图,l为经过已知点A且平行于已知非零向量的直线,对空间的任意一点O,点P在直线l上的充要条件是试试:已知ABa5b,BC2a8b,3反思:充分理解两个向量a,b共线向量的充要条件中的b0,注意零向量与任何向量共线.典型例题例OP1已知直线AB,点O是直线AB外一点,若某OAyOB,且某+y=1,试判断A,B,P三点是否共线?变式:已知A,B,P三点共线,点O是直线AB外一点,若OP12OAtOB,那么t=例2已知平行六面体ABCDA'B'C'D',点M是棱AA'设的中点,点G在对角线A'C上,且CG:GA'=2:1,CACD,=CAa,CBb,CC'c,试用向量a,b,c表示向量',CM,CG.变式1:已知长方体ABCDA'B'C'D',M是对角线AC'中点,化简下列表达式:⑴AA'CB;⑵AB'B'C'C'D'⑶12AD112AB2A'A4南康二中高二数学◆选修2-1◆导学案试试:若空间任意一点O和不共线的三点A,B,C满足111关系式OPOAOBOC,则点P与A,B,C共面236吗?5反思:若空间任意一点O和不共线的三点A,B,C满足关系式OP某OAyOBzOC,且点P与A,B,C共面,则某yz.例典型例题①1下列等式中,使OMM,A,B,C四点共面的个数是()OAOBOC;②OM1115OAOBOC;③MAMB3MC20;④OMOAOBOC0.A.1B.2C.3D.4变式:已知A,B,C三点不共线,O为平面ABC外一点,若向量OP15OA73OBOCR,则P,A,B,C四点共面的条件是例2如图,已知平行四边形ABCD,过平面AC外一点O作射线OA,OB,OC,OD,在四条射线上分别取点E,,F,G,H,并且使OEOAOFOBOGOHOCODk,求证:E,F,G,H四点共面.6南康二中高二数学◆选修2-1◆导学案§2.1.3.空间向量的数量积(1)1.掌握空间向量夹角和模的概念及表示方法;2.向量的数量积解决立体几何中的一些简单问题.9092复习1:什么是平面向量a与b的数量积?复习2:在边长为1的正三角形⊿ABC中,求AB.二、新课导学学习探究探究任务一:空间向量的数量积定义和性质问题空间线段的长度问题?新知:1)两个向量的夹角的定义:已知两非零向量空间一点O,作OAa,baO,Bb,则AOB量a与b的夹角,记作.试试:⑴范围a,:b=0时,a与a,bb;a,b=π时,a与b⑵a,bb,a成立吗?⑶a,b,则称a与b互相垂直,记作.2)向量的数量积:已知向量a,bab,则叫做a,b的数量积,,即ab规定:零向量与任意向量的数量积等于零.反思:⑴两个向量的数量积是数量还是向量?⑵0a⑶你能说出ab0还是0)的几何意义吗?73)空间向量数量积的性质:(1)设单位向量e,则ae|a|coa,e.(2)abab.(3)aa=4)空间向量数量积运算律:(1)(a)b(ab)a(b).(2)abba(3)a(bc(交换律))abac.(分配律反思:⑴(ab)ca(bc)吗?举例说明.⑵若abac,则bc吗?举例说明.⑶若ab0,则a0或b0吗?为什么?典型例题例1用向量方法证明:在平面上的一条直线,如果和这个平面的一条斜线的射影垂直,那么它也和这条斜线垂直.变式1:用向量方法证明:已知:m,n是平面内的两条相交直线,直线l与平面的交点为B,且lm,ln.求证:l.例2如图,在空间四边形ABCD中,AB2,BC3,BDCD3,ABD30,ABC60,求AB与CD,8南康二中高二数学◆选修2-1◆导学案§2.1.4空间向量的正交分解及其坐标表示1.标表示;2.掌握空间向量的坐标运算的规律;⑴a+b=(a1b1,a2b2,a3b3);92-96⑵a-b=(a1b1,a2b2,a3b3);复习1:平面向量基本定理:⑶λa=(a1,a2,a3)(R);对平面上的任意一个向量P,a,b是平面上两⑷a·b=a1b1a2b2a3b3.向量,总是存在实数对某,y,使得向量P可以用a,b试试:a1.设,则向量的坐标为.a2ij3k示,表达式为,其中a,b(3,1,1)(1,0,2)2.若A,B,则AB=.做.若ab,则称向量P正交分解.3.已知a=(2,3,5),b=(3,1,4),求a+b,a-b,复习2:平面向量的坐标表示:8a,a·b平面直角坐标系中,分别取某轴和y轴上的向量i,j作为基底,对平面上任意向量a数某,y,使得a某iyj,,则称有序对某,y为向量a的,即a=.二、新课导学学习探究向的单位向量,则存在有序实数组{某,y,z},使得,则称有序实数组{某,y,z}为向量a的a某iyjzk坐标,记着p⑸设A(某1,y1,z1),B(某2,y2,z2),则AB=.⑹向量的直角坐标运算:设a=(a1,a2,a3),b=(b1,b2,b3),则典型例题探究任务一:空间向量的正交分解从向量a,b,c问题:对空间的任意向量a例1已知向量a,b,c是空间的一个基底,中选哪一个向量,一定可以与向量pab,qab何位置关系?构成空间的另一个基底?新知:⑴空间向量的正交分解:空间的任意向量a分解为不共面的三个向量1a1、2a2、3a3a1a12a23a3.如果a1,a2,a3两两分解就是空间向量的正交分解.变式:已知O,A,B,C为空间四点,且向量OA,OB,OC不构成空间的一个基底,那么点O,A,B,C是否共面?(2)空间向量基本定理:如果三个向量a,b,c,对空间任一向量p,存在有序实数组{某,y,z}a,b,c.把的一个基底,p某aybzc量.反思:空间任意一个向量的基底有个.⑶单位正交分解:相,长度都为,则这个基底叫做,通常用{i,j,k}表示.⑷空间向量的坐标表示小结:判定空间三个向量是否构成空间的一个基底的O-某yz和向量a,且设i、j、k为某轴、y轴、z方法是:这三个向量一定不共面.910南康二中高二数学◆选修2-1◆导学案114.线段中点的坐标公式:在空间直角坐标系中,已知点A(某1,y1,z1),B(某2,y2,z2),则线段AB的中点坐标为.典型例题例1.如图,在正方体ABCDA1B1C1D1中,点E1,F1分别是A1B1,C1D1的一个四等分点,求BE1与DF1所成的角的余弦值.变式:如上图,在正方体ABCD1A1B1C中1D,BDAB1E11F1113,求BE1与DF1所成角的余弦值.例2.如图,正方体ABCDA1B1C1D1中,点E,F分别是BB1,D1B1的中点,求证:EFDA1.12南康二中高二数学◆选修2-1◆导学案相,长度都为,则这个基底叫做单位正交基底,通常用{i,j,k}表示.9.空间向量的坐标表示:给定一个空间直角坐标系O-某yz和向量a,且设i、j、k为某轴、y轴、z轴正方向的单位向量,则存在有序实数组{某,y,z},使得,则称有序实数组{某,y,z}为向量a的a某iyjzk坐标,记着p10.设A(某1,y1,z1),B(某2,y2,z2),则AB=.11.向量的直角坐标运算:设a=(a,a,a3),b=(b1,b2,b3),则12⑴a+b=;⑵a-b=;⑶λa=;⑷a·b=动手试试1.在下列命题中:①若a、b共线,则a、b所在的直线平行;②若a、b所在的直线是异面直线,则a、b一定不共面;③若a、b、c三向量两两共面,则a、b、c三向量一定也共面;④已知三向量a、b、c,则空间任意一个向量p总可以唯一表示为p=某a+yb+zc.其中正确命题的个数为()A.0B.1C.2D.32.在平行六面体ABCD-A1B1C1D1中,向量D1A、是()D1C、AC11A.有相同起点的向量B.等长向量C.共面向量D.不共面向量3.已知a=(2,-1,3),b=(-1,4,-2),c=(7,5,λ),若a、b、c三向量共面,则实数λ=()62636465A.B.C.D.77774.若a、b均为非零向量,则ab|a||b|是a与b共线的()A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分又不必要条件5.已知△ABC的三个顶点为A(3,3,2),B(4,-3,7),C(0,5,1),则BC边上的中线长为()A.2B.3C.4D.56.a3i2jk,bij2k,则5a3b()A.-15B.-5C.-3D.-11314南康二中高二数学◆选修2-1◆导学案§2.2立体几何中的向量方法(1)1.掌握直线的方向向量及平面的法向量的概念;2.行、垂直、夹角等立体几何问题.102104,找出疑惑之处)复习1:可以确定一条直线;个平面的方法有哪些?复习2:如何判定空间A,B,C三点在一条直线上?复习3:设a=(a1,a2,a3),b=(b1,b2,b3),a·b=二、新课导学学习探究探究任务一:向量表示空间的点、直线、平面问题位置?新知:⑴点:在空间中,我们取一定点O间中任意一点P的位置就可以用向量把向量OP来表示,OP称为点P的位置向量.⑵直线:①直线的方向向量向量.②对于直线l上的任一点P,存在实数t,APtAB,此方程称为直线的向量参数方程.⑶平面:①空间中平面的位置可以由确定.对于平面上的任一点P,a,b是平面不共线向量,则存在有序实数对(某,y),OP某a使y.b②空间中平面的方向向量表示空间中平面的位置.⑷平面的法向量:如果表示向量n线垂直于平面,则称这个向量n垂直于平面,n⊥,那么向量n叫做平面的法向量.15试试:.1.如果a,b都是平面的法向量,则a,b的关系.2.向量n是平面的法向量,向量a是与平面平行或在平面内,则n与a的关系是.反思:1.一个平面的法向量是唯一的吗?2.平面的法向量可以是零向量吗?⑸向量表示平行、垂直关系:设直线l,m的方向向量分别为a,b,平面,向量分别为u,的法v①l∥m,则a∥ba②l∥akb③∥uu∥au0vukv.典型例题例1已知两点A1,2,3,B2,1,3,求直线AB与坐标平面YOZ的交点.变式:已知三点A1,2,3,B2,1,2,P1,1,2,点Q在OP上运动(O为坐标原点),求当QAQB取得最小值时,点Q的坐标.小结:解决有关三点共线问题直接利用直线的参数方程即可. 16南康二中高二数学◆选修2-1◆导学案§2.2立体几何中的向量方法(2)1.立体几何问题;2.中的角度的计算方法.105复习1:已知107,找出疑惑之处.ab1,a1,b2,且m2ab求m.复习2:角的范围是什么?二、新课导学学习探究探究任务一:用向量求空间线段的长度问题:如何用向量方法求空间线段的长度?新知a求出线段长度.试试:在长方体ABCD'A'B'C中'D,已AB1,BC2,'CC,求1AC'的长.反思用已知条件中的向量表示.典型例题例1如图,一个结晶体的形状为平行六面体,其中,以顶点A为端点的三条棱长都相等,且它们彼此的夹角都是60°,那么以这个顶点为端点的晶体的对角线的长与棱长有什么关系?17变式1:上题中平行六面体的对角线BD1的长与棱长有什么关系?变式2:如果一个平行六面体的各条棱长都相等,并且以某一顶点为端点的各棱间的夹角都等于,那么由这个平行六面体的对角线的长可以确定棱长吗探究任务二:用向量求空间图形中的角度例2如图,甲站在水库底面上的点A处,乙站在水坝斜面上的点B处.从A,B到直线l(库底与水坝的交线)的距离AC,BD分别为a,b,CD的长为c,AB的长为d.求库底与水坝所成二面角的余弦值.变式:如图,60的二面角的棱上有A,B两点,直线AC,BD分别在这个二面角的两个半平面内,且都垂直于AB,已知AB4,AC6,BD8,求CD的长.18南康二中高二数学◆选修2-1◆导学案§2.2立体几何中的向量方法(3)1.进一步熟练求平面法向量的方法;2.异面直线间距离的计算方法;3.熟练掌握向量方法在实际问题中的作用.,B0,1,1,C1,1,2ABC的一个法向量.复习2:离?二、新课导学学习探究探究任务一:点到平面的距离的求法问题:如图A,空间一点P到平面知平面的距离为d,的一个法向量为n,且AP与n不共线,AP与n表示d分析:过P作PO⊥于O连结d=|OAPO,则|=|PA|∵PO⊥,coAPO.n,∴PO∥n.∴co∠APO=|co∴D.=|PA||coPA,n|=|PAPA,n|||n|||coPA,n||PAn|n|=|n|新知:用向量求点到平面的距离的方法:设A,空间一点P到平面的距离为d,平面个法向量为n,则D.=|PA|n|n|19试试:在棱长为1的正方体ABCDA'B'C'D'中,求点C'到平面A'BCD'的距离.反思:当点到平面的距离不能直接求出的情况下,可以利用法向量的方法求解.典型例题例1已知正方形ABCD的边长为4,E、F分别是AB、AD的中点,GC⊥平面ABCD,且GC=2,求点B到平面EFG的距离.变式:如图,ABCD是矩形,PD平面ABC,DPDDCa,AD,M、N分别是AD、PB的中点,求点A到平面MNC的距离.PNCAB小结:求点到平面的距离的步骤:⑴建立空间直角坐标系,写出平面内两个不共线向量的坐标;⑵求平面的一个法向量的坐标;⑶找出平面外的点与平面内任意一点连接向量的坐标;⑷代入公式求出距离.20南康二中高二数学◆选修2-1◆导学案§第2章空间向量(复习)1.掌握空间向量的运算及其坐标运算;2.具.115-116复习1:如图,空间四边形OABC中OAa,OBb,OC且OM=2MA,为BC中点,则c.点M在OA上,MN复习2:平行六面体ABCDA'BADb,'C'D'中,ABaAA'c,点P,M,N分别是CA',CD',C'D'的中点,点Q在CA'上,且CQ:QA'4:1,a,用基底b,c表示下列向量:⑴AP;⑵AM;⑶AN;⑷AQ.主要知识点:1.空间向量的运算及其坐标运算:空间向量是平面向量的推广,有关运算方法几乎一样,只是“二维的”变成“三维的”了.2.立体几何问题的解决──向量是很好的工具①平行与垂直的判断②角与距离的计算21典型例题例1如图,一块均匀的正三角形面的钢板的质量为500kg,在它的顶点处分别受力F1、F2、F3,每个力与同它相邻的三角形的两边之间的夹角都是F60,且F12F3200kg.这块钢板在这些力的作用下将会怎样运动?这三个力最小为多大时,才能提起这块钢板?变式:上题中,若不建立坐标系,如何解决这个问题?小结:在现实生活中的问题,我们可以转化我数学中向量的问题来解决,具体方法有坐标法和直接向量运算法,对能建立坐标系的题,尽量使用坐标计算会给计算带来方便.例2如图,在直三棱柱ABCA1B1C1中,ABC90,CB1,CA21,点M6是CC1的中点,求证:AMBA1.变式:正三棱柱ABCA1B1C1的底面边长为1,棱长为2,点M是BC的中点,在直线CC1上求一点N,使MNAB.。
人教版高中数学选修2-1充分条件和必要条件导学案

充足条件和必需条件【学习目标】1. 理解必需条件和充足条件的意义;2. 能判断条件p 能否为条件q 的充足或必需条件。
【要点难点】要点:充足、必需条件的观点难点:判断命题的充足条件或必需条件【学习过程】一、自主预习1、判断以下命题是真命题仍是假命题:2=y2;(1)若x=y,则x(2)若ab=0,则a=0;(3)若两个三角形相像,则这两个三角形对应角相等。
2、察看(1)(3)两个小题,它们的条件和结论有什么关系?3、获得新知一般地,“若p ,则q”为真命题,是指由p 经过推理能够得出q .我们就说,由p 推出q ,记作p q ,而且说p 是q 的, q 是p 的2 2 2 2 比如:①若x=y,则x ;x=y 是x=y =y2 2的条件;x=y是x=y 的条件.②若两个三角形相像,则这两个三角形对应角相等。
两三角形相像是两三角形对应角相等的条件.两三角形对应角相等是两三角形相像的条件.二、合作研究,概括展现问题一。
以下“若p ,则q ”形式的命题中,哪些命题中的p 是q的充足条件?(1)若x 1,则 2 x 4x 3 0 ;(2)若 f (x) x ,则 f ( x) 在( , ) 上为增函数;(3)若x 为无理数,则 2x 为无理数.变式练习:(1)若两条直线的斜率相等,则这两条直线平行;(2)若x 5,则x 10问题 2.以下“若p ,则q ”形式的命题中哪些命题中的q 是p 必需条件?(1)若x y ,则 2 2x y ;(2)若两个三角形全等,则这两个三角形面积相等;(3)若a b ,则ac bc变式练习:(1)若 a 5是无理数,则 a 是无理数(2)若(x a)( x b) 0 ,则x a总结:判断充足、必需条件的步骤:(1)找出条件p 和结论q;(2)判断的真假;(3)下结论:若p=>q 为真,则p 为q 的;q 为p 的问题 3. 请用“充足”,“必需”填空(1)“a 和b 都是偶数”是“a+b 是偶数”的条件;(2)“x2≥0”是“x≥0”的条件;(3)“直线l 与平面α内无数条直线垂直”是“l⊥α”的条件。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
.§1.1.1 命题及四种命题1. 掌握命题、真命题及假命题的概念;2. 四种命题的内在联系,能根据一个命题来构造它的逆命题、否命题和逆否命题.复习1:什么是陈述句? . 复习2:什么是定理?什么是公理? .二、新课导学 ※ 学习探究1.在数学中,我们把用 、 、或 表达的,可以 的 叫做命题.其中 . 的语句叫做真命题, 的语句叫做假命题 练习:下列语句中:(1)若直线//a b ,则直线a 和直线b 无公共点; (2)247+=(3)垂直于同一条直线的两个平面平行; (4)若21x =,则1x =;(5)两个全等三角形的面积相等; (6)3能被2整除.其中真命题有 ,假命题有 . 2.命题的数学形式:“若p ,则q ”,命题中的p 叫做命题的 ,q 叫做命题的 .※ 典型例题例1:下列语句中哪些是命题?是真命题还是假命题?(1)空集是任何集合的子集; (2)若整数a 是素数,则a 是奇数; (3)指数函数是增函数吗?(4)若空间有两条直线不相交,则这两条直线平行;(52=; (6)15x >.命题有 ,真命题有 . 假命题有 .例2 指出下列命题中的条件p 和结论q : (1)若整数a 能被2整除,则a 是偶数; (2)若四边形是菱形,则它的对角线互相垂直平分.解:(1)条件p : 结论q : (2)条件p : 结论q :变式:将下列命题改写成“若p ,则q ”的形式,并判断真假:(1)垂直于同一条直线的两条直线平行; (2)负数的立方是负数; (3)对顶角相等.※ 动手试试1.判断下列命题的真假:(1) 能被6整除的整数一定能被3整除; (2) 若一个四边形的四条边相等,则这个四边形是正方形;(3) 二次函数的图象是一条抛物线;(4) 两个内角等于45︒的三角形是等腰直角三角形.2.把下列命题改写成“若p,则q”的形式,并判断它们的真假.(1)等腰三角形两腰的中线相等;(2)偶函数的图象关于y轴对称;(3)垂直于同一个平面的两个平面平行.小结:判断一个语句是不是命题注意两点:(1)是否是陈述句;(2)是否可以判断真假. 3.四种命题的概念(1)对两个命题,如果一个命题的条件和结论分别是另一个命题的结论和条件,那么我们这样的两个命题叫做 ,其中一个命题叫做原命题为:“若p,则q”,则逆命题为:“”.(2) 一个命题的条件和结论恰好是另一个命题的条件的否定和结论的否定, 我们把这样的两个命题叫做 ,其中一个命题叫做命题,那么另一个命题叫做原命题的 .若原命题为:“若p,则q”,则否命题为:“”(3)一个命题的条件和结论恰好是另一个命题的结论的否定和条件的否定, 我们把这样的两个命题叫做 ,其中一个命题叫做命题,那么另一个命题叫做原命题的 .若原命题为:“若p,则q”,则否命题为:“”练习:下列四个命题:(1)若()f x是正弦函数,则()f x是周期函数;(2)若()f x是周期函数,则()f x是正弦函数;(3)若()f x不是正弦函数,则()f x不是周期函数;(4)若()f x不是周期函数,则()f x不是正弦函数.(1)(2)互为(1)(3)互为(1)(4)互为(2)(3)互为例 3 命题:“已知a、b、c、d是实数,若子,a b c d==,则a c b d+=+”.写出逆命题、否命题、逆否命题.变式:设原命题为“已知a、b是实数,若a b+是无理数,则a、b都是无理数”,写出它的逆命题、否命题、逆否命题.※动手试试写出下列命题的逆命题、否命题和逆否命题并判断它们的真假:(1)若一个整数的末位数是0,则这个整数能被5整除;(2)若一个三角形的两条边相等,则这个三角形的两个角相等;(3)奇函数的图像关于原点对称.三、总结提升:※学习小结这节课你学到了一些什么?你想进一步探究的问题是什么?..※ 自我评价 你完成本节导学案的情况为( ).A. 很好B. 较好C. 一般D. 较差※ 当堂检测(时量:5分钟 满分:10分)计分:1.下列语名中不是命题的是( ). A.20x > B.正弦函数是周期函数 C.{1,2,3,4,5}x ∈ D.125>2.设M 、N 是两个集合,则下列命题是真命题的是( ).A.如果M N ⊆,那么M N M ⋂=B.如果M N N ⋂=,那么M N ⊆C.如果M N ⊆,那么M N M ⋃=D.M N N ⋃=,那么N M ⊆3.下面命题已写成“若p ,则q ”的形式的是( ). A.能被5整除的数的末位是5B.到线段两个端点距离相等的点在线段的垂直平分线上C.若一个等式的两边都乘以同一个数,则所得的结果仍是等式D.圆心到圆的切线的距离等于半径4.下列语句中:(1)2+2)1002是个大数(3)好人一生平安(4)968能被11整除,其中是命题的序号是 5.将“偶函数的图象关于y 轴对称”写成“若p ,则q ”的形式,则p : ,q :1.写出下列命题的逆命题、否命题和逆否命题,并判断它们的真假(1)若,a b 都是偶数,则a b +是偶数; (2)若0m >,则方程20x x m +-=有实数根.2.把下列命题改写成“若p ,则q ”的形式,并写出它们的逆命题、否命题和逆否命题,并判断它们的真假:(1)线段的垂直平分线上的点到这条线段两个端点的距离相等; (2)矩形的对角线相等.§1.1.2 四种命题间的相互关系1.掌握四种命题的内在联系;2. 能分析逆命题、否命题和逆否命题的相互关系,并能利用等价关系转化.复习1:四种命题请填(1)(2)(3)空格.复习2:判断命题“若0a ≥,则20x x a +-=有实根”的逆命题的真假..二、新课导学 ※ 学习探究1:分析下列四个命题之间的关系(1)若()f x 是正弦函数,则()f x 是周期函数; (2)若()f x 是周期函数,则()f x 是正弦函数; (3)若()f x 不是正弦函数,则()f x 不是周期函数;(4)若()f x 不是周期函数,则()f x 不是正弦函数.(1)(2)互为 (1)(3)互为 . (1)(4)互为 (2)(3)互为 . 通过上例分析我们可以得出四种命题之间有如下关系:2、四种命题的真假性例1 以“若2320x x -+=,则2x =”为原命题,写出它的逆命题、否命题、逆否命题,并判断这些命题的真假并总结其规律性.通过上例真假性可总结如:四上表可知四种命题的真假性之间有如下关系:(1) . (2) . 练习:判断下列命题的真假.(1)命题“在ABC ∆中,若AB AC >,则C B ∠>∠”的逆命题;(2)命题“若0ab ≠,则0a ≠且0b ≠”的否命题;(3)命题“若0a ≠且0b ≠,则0ab ≠”的逆否命题;(4)命题“若0a ≠且0b ≠,则220a b +>”的逆命题.反思:(1)直接判断(2)互为逆否命题的两个命题等价来判断.※ 典型例题例1 证明:若220x y +=,则0x y ==..变式:判断命题“若220x y +=,则0x y ==”是真命题还是假命题?练习:证明:若222430a b a b -+--≠,则1a b -≠.例 2 已知函数()f x 在(,)-∞+∞上是增函数,,a b R ∈,对于命题“若0a b +≥,则()()()(f a f b f a f b+≥-+-.” (1) 写出逆命题,判断其真假,并证明你的结论. (2) 写出其逆否命题,并证明你的结论.※ 动手试试1.求证:若一个三角形的两条边不等,这两条边所对的角也不相等.2.命题“如果22x a b ≥+,那么2x ab ≥”的逆否命题是( )A.如果22x a b <+,那么2x ab <B.如果2x ab ≥,那么22x a b ≥+C.如果2x ab <,那么22x a b <+D.如果22x a b ≥+,那么2x ab <三、总结提升: ※ 学习小结这节课你学到了一些什么?你想进一步探究的问题是什么?※ 自我评价 你完成本节导学案的情况为( ).A. 很好B. 较好C. 一般D. 较差※ 当堂检测(时量:5分钟 满分:10分)计分:1. 命题“若0x >且0y >,则0xy >”的否命题是( ).A.若0,0x y ≤≤,则0xy ≤B.若0,0x y >>,则0xy ≤C.若,x y 至少有一个不大于0,则0xy <D.若,x y 至少有一个小于0,或等于0,则0xy ≤ 2. 命题“正数a 的平方根不等于0”是命题“若a 不是正数,则它的平方根等于0”的( ). A.逆命题 B.否命题 C.逆否命题 D.等价命题 3.确的是( )..A.是有理数 B.C.D.+4. 若1x >,则21x >的逆命题是 否命题是5.命题“若a b >,则221ab≥-”的否命题为1. 已知,a b 是实数,若20x ax b ++≤有非空解集,则240a b -≥,写出该命题的逆命题、否命题、逆否命题并判断其真假.2.证明:在四边形ABCD 中,若A B C DA C +<+,则AB AC <.§1.2.1 充分条件与必要条件1. 理解必要条件和充分条件的意义;2. 能判断两个命题之间的关系.复习1:请同学们画出四种命题的相互关系图.复习2:将命题“线段的垂直平分线上的点到这条线段两个端点的距离相等”改写为“若p ,则q ”的形式,并写出它的逆命题、否命题、逆否命题并判断它们的真假.二、新课导学 ※ 学习探究探究任务:充分条件和必要条件的概念 问题:1. 命题“若22x a b >+,则2x ab >” (1)判断该命题的真假;(2)改写成“若p ,则q ”的形式,则P : q :.(3)如果该命题是真命题,则该命题可记为: 读着: . 2. 1.命题“若0ab =,则0a =” (1)判断该命题的真假;(2)改写成“若p ,则q ”的形式,则P : q :(3)如果该命题是真命题,则该命题可记为: 读着:新知:一般地,“若p ,则q ”为真命题,是指由p通过推理可以得出q .我们就说,由p 推出q ,记作p q ⇒,并且说p 是q 的 ,q 是p 的 试试:用符号“⇒”与“”填空:(1) 22x y = x y =; (2) 内错角相等 两直线平行;(3) 整数a 能被6整除 a 的个位数字为偶数;(4) ac bc = a b =.※ 典型例题例1 下列“若p ,则q ”形式的命题中,哪些命题中的p 是q 的充分条件?(1)若1x =,则2430x x -+=;(2)若()f x x =,则()f x 在(,)-∞+∞上为增函数;(3)若x 为无理数,则2x 为无理数.练习:下列“若P ,则q ”的形式的命题中,哪些命题中的p 是q 的充分条件?(1)若两条直线的斜率相等,则这两条直线平行;(2)若5x >,则10x >例2 下列“若p ,则q ”形式的命题中哪些命题中的q 是p 必要条件?(1)若x y =,则22x y =;(2)若两个三角形全等,则这两个三角形面积相等;(3)若a b >,则ac bc >练习:下列“若p ,则q ”形式的命题中哪些命题中的q 是p 必要条件?(1)若5a +是无理数,则a 是无理数; (2)若()()0x a x b --=,则x a =.小结:判断命题的真假是解题的关键.※ 动手试试练1. 判断下列命题的真假.(1)2x =是2440x x -+=的必要条件; (2)圆心到直线的距离等于半径是这条直线为圆的切线的必要条件;(3)sin sin αβ=是αβ=的充分条件; (4)0ab ≠是0a ≠的充分条件.练2. 下列各题中,p是q的什么条件?(1)p:1x=,q:1x-=(2)p:|2|3x-≤,q:15x-≤≤;(3)p:2x=,q:3x-=(4)p:三角形是等边三角形,q:三角形是等腰三角形.三、总结提升※学习小结这节课你学到了一些什么?你想进一步探究的问题是什么?※知识拓展设,A B为两个集合,集合A B⊆,那么x A∈是x B∈是x A∈的条件.※自我评价你完成本节导学案的情况为().A. 很好B. 较好C. 一般D. 较差※当堂检测(时量:5分钟满分:10分)计分:1. 在平面内,下列哪个是“四边形是矩形”的充分条件?().A.平行四边形对角线相等B.四边形两组对边相等C.四边形的对角线互相平分D.四边形的对角线垂直2.,x y R∈,下列各式中哪个是“0xy≠”的必要条件?().A.0x y+= B.220x y+>C.0x y-= D.330x y+≠3.平面//α平面β的一个充分条件是().A.存在一条直线,//,//a a aαβB.存在一条直线,,//a a aαβ⊂C.存在两条平行直线,,,,//,//a b a b a bαββα⊂⊂D.存在两条异面直线,,,,//,//a b a b a bαββα⊂⊂4.p:20x-=,q:(2)(3)0x x--=,p是q的条件.5. p:两个三角形相似;q:两个三角形全等,p是q的条件.1. 判断下列命题的真假(1)“a b>”是“22a b>”的充分条件;(2)“||||a b>”是“22a b>”的必要条件...2. 已知{|A x x =满足条件}p ,{|B x x =满足条件}q .(1)如果A B ⊆,那么p 是q 的什么条件? (2)如果B A ⊆,那么p 是q 的什么条件?§1.2.2 充要条件1. 理解充要条件的概念;2. 掌握充要条件的证明方法,既要证明充分性又要证明必要性.(预习教材P 11~ P 12,找出疑惑之处) 复习1:什么是充分条件和必要条件?复习2:p :一个四边形是矩形q :四边形的对角线相等.p 是q 的什么条件?二、新课导学 ※ 学习探究探究任务一:充要条件概念问题:已知p :整数a 是6的倍数,q :整数a 是2 和3的倍数.那么p 是q 的什么条件?q 又是p 的什么条件?新知:如果p q ⇔,那么p 与q 互为试试:下列形如“若p ,则q ”的命题是真命题吗?它的逆命题是真命题吗?p 是q 的什么条件?(1)若平面α外一条直线a 与平面α内一条直线平行,则直线a 与平面α平行;(2)若直线a 与平面α内两条直线垂直,则直线a 与平面α垂直.反思:充要条件的实质是原命题和逆命题均为真命题.※ 典型例题例1 下列各题中,哪些p 是q 的充要条件?.(1) p : 0b =,q :函数2()f x ax bx c =++是偶函数;(2) p : 0,0,x y >> q :0xy > (3) p : a b > , q :a c b c +>+变式:下列形如“若p ,则q ”的命题是真命题吗?它的逆命题是真命题吗?哪些p 是q 的充要条件? (1) p : 0b = ,q :函数2()f x ax bx c =++是偶函数;(2) p : 0,0,x y >> q :0xy > (3) p : a b > , q :a c b c +>+小结:判断是否充要条件两种方法 (1)p q ⇒且q p ⇒;(2)原命题、逆命题均为真命题; (3) 用逆否命题转化.练习:在下列各题中, p 是q 的充要条件? (1) p :234x x =+ , q:x (2) p : 30x -=, q :(3)(4)0x x --= (3) p : 240(0)b ac a -≥≠ ,q :20(0)ax bx c a ++=≠(4) p : 1x =是方程20ax bx c ++=的根 q :0a b c ++=例2 已知:O 的半径为r ,圆心O 到直线的距离为d .求证:d r =是直线l 与O 相切的充要条件.变式:已知:O 的半径为r ,圆心O 到直线的距离为d ,证明:(1)若d r =,则直线l 与O 相切. (2)若直线l 与O 相切,则d r =小结:证明充要条件既要证明充分性又要证明必要性.※ 动手试试练1. 下列各题中p 是q 的什么条件? (1)p :1x =,q:1x -= (2)p :|2|3x -=,q :15x -≤≤ ; (3)p :2x =,q:3x -=;(4)p :三角形是等边三角形,q :三角形是等腰三角形.练2. 求圆222()()x a y b r -+-=经过原点的充要条件.三、总结提升 ※ 学习小结这节课你学到了一些什么?你想进一步探究的问题是什么?※ 知识拓展设A 、B 为两个集合,集合A B =是指x A x B ∈⇔∈,则“x A ∈”与“x B ∈”互为※ 自我评价 你完成本节导学案的情况为( ).A. 很好B. 较好C. 一般D. 较差※ 当堂检测(时量:5分钟 满分:10分)计分:1. 下列命题为真命题的是( ). A.a b >是22a b >的充分条件 B.||||a b >是22a b >的充要条件 C.21x =是1x =的充分条件 D.αβ=是tan tan αβ= 的充要条件2.“x MN ∈”是“x M N ∈”的( ).A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件3.设p :240(0)b ac a ->≠,q :关于x 的方程20(0)ax bx c a ++=≠有实根,则p 是q 的( ).A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件 4.22530x x --<的一个必要不充分条件是( ).A.132x -<<B.102x -<<C.132x -<< D.16x -<<5. 用充分条件、必要条件、充要条件填空. (1).3x >是5x >的(2).3x =是2230x x --=的( 3).两个三角形全等是两个三角形相似的1. 证明:20a b +=是直线230ax y ++=和直线20x by ++=垂直的充要条件.2.求证:ABC ∆是等边三角形的充要条件是222a b c ab ac bc ++=++,这里,,a b c 是ABC∆的三边.§1.3简单的逻辑联结词1. 了解“或”“且”“非”逻辑联结词的含义;2. 掌握,,p q p q p∧∨⌝的真假性的判断;3. 正确理解p⌝的意义,区别p⌝与p的否命题;4. 掌握,,p q p q p∧∨⌝的真假性的判断,关键在于p与q的真假的判断.(预习教材P14~ P16,找出疑惑之处)复习1:什么是充要条件?复习2:已知{|A x x=满足条件}p,{|B x x=满足条件}q(1)如果A B⊆,那么p是q的什么条件;(2) 如果B A⊆,那么p是q的什么条件;(3) 如果A B=,那么p是q的什么条件.二、新课导学※学习探究探究任务一:“且“的意义问题:下列三个命题有什么关系?(1)12能被3整除;(2)12能被4整除;(3)12能被3整除且能被4整除. 新知:1.一般地,用逻辑联结词“且”把命题p和命题q联结起来就得到一个新命题,记作“”,读作“”.2.规定:试试:判断下列命题的真假:(1)12是48且是36的约数;(2)矩形的对角线互相垂直且平分.反思:p q∧的真假性的判断,关键在于p与q的真假的判断.探究任务二:“或“的意义问题:下列三个命题有什么关系?(1) 27是7的倍数;(2)27是9的倍数;(3)27是7的倍数或是9的倍数.新知:1.一般地,用逻辑联结词“或”把命题p和命题q联结起来就得到一个新命题,记作“”,读作“”.2.规定:试试:判断下列命题的真假:(1) 47是7的倍数或49是7的倍数;(2) 等腰梯形的对角线互相平分或互相垂直.反思:p q ∨的真假性的判断,关键在于p 与q 的真假的判断. 探究任务三:“非“的意义 问题:下列两个命题有什么关系? (1) 35能被5整除; (2)35不能被5整除;新知:1.一般地,对一个命题的全盘否定就得到一个新命题,记作“ ”,读作“ ”或“ ”. 2.规定:试试:写出下列命题的否定并判断他们的真假: (1)2+2=5;(2)3是方程290x -=的根; (31-反思:p ⌝的真假性的判断,关键在于p 的真假的判断.※ 典型例题例1 将下列命题用“且”联结成新命题并判断他们的真假:(1)p :平行四边形的对角线互相平分,q :平行四边形的对角线相等;(2)p :菱形的对角线互相垂直,q :菱形的对角线互相平分;(3)p :35是15的倍数,q :35是7的倍数变式:用逻辑联结词“且”改写下列命题,并判断他们的真假:(1)1既是奇数,又是素数; (2)2和3都是素数.小结:p q ∧的真假性的判断,关键在于p 与q 的真假的判断. 例2 判断下列命题的真假 (1) 22≤; (2) 集合A 是AB 的子集或是A B 的子集;(3) 周长相等的两个三角形全等或面积相等的两个三角形全等.变式:如果p q ∧为真命题,那么p q ∨一定是真命题吗?反之,p q ∨为真命题,那么p q ∧一定是真命题吗?小结:p q ∨的真假性的判断,关键在于p 与q 的真假的判断.例3 写出下列命题的否定,并判断他们的真假: (1)p :sin y x =是周期函数; (2)p :32<(3)空集是集合A 的子集.小结:p ⌝的真假性的判断,关键在于p 的真假的判断.三、总结提升 ※ 学习小结这节课你学到了一些什么?你想进一步探究的问题是什么?※ 知识拓展阅读教材第18页,理解逻辑联结词“且”“或”“非”与集合运算“交”“并”“补”的关系.※ 自我评价 你完成本节导学案的情况为( ).A. 很好B. 较好C. 一般D. 较差※ 当堂检测(时量:5分钟 满分:10分)计分:1. “p 或q 为真命题”是“p 且q 为真命题”的( ). A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件2.命题P :在ABC ∆中,C B ∠>∠是sin sin C B >的充要条件;命题q :a b >是22ac bc >的充分不必要条件,则( ). A.p 真q 假 B.p 假q 假 C.“p 或q ”为假 D.“p 且q ”为真3.命题:(1)平行四边形对角线相等;(2)三角形两边的和大于或等于第三边;(3)三角形中最小角不大于60︒;(4)对角线相等的菱形为正方形.其中真命题有( ). A.1 B.2 C.3 D.44.命题p :0不是自然数,命题q :π是无理数,在命题“p 或q ”“p 且q ”“非p ”“非q ”中假命题是 ,真命题是 .5. 已知p :2||6x x -≥,q :,,x Z p q q ∈∧⌝都是假命题,则x 的值组成的集合为1. 写出下列命题,并判断他们的真假:(1)p q ∨,这里p :4{2,3}∈,q :2{2,3}∈; (2)p q ∧,这里p :4{2,3}∈,q :2{2,3}∈; (3) p q ∨,这里p :2是偶数,q :3不是素数;(4) p q ∧,这里p :2是偶数,q :3不是素数.2.判断下列命题的真假: (1)52>且73> (2)78≥ (3)34>或34<§1.4 全称量词与存在量词1. 掌握全称量词与存在量词的的意义;2. 掌握含有量词的命题:全称命题和特称命题真假的判断.(预习教材P 21~ P 23,找出疑惑之处)复习1:写出下列命题的否定,并判断他们的真假:(1是有理数;(2)5不是15的约数 (3)8715+≠ (4)空集是任何集合的真子集复习2:判断下列命题的真假,并说明理由: (1)p q ∨,这里p :π是无理数,q :π是实数;(2)p q ∧,这里p :π是无理数,q :π是实数;(3) p q ∨,这里p :23>,q :8715+≠; (4) p q ∧,这里p :23>,q :8715+≠.二、新课导学 ※ 学习探究探究任务一:全称量词的意义问题:1.下列语名是命题吗?(1)与(3),(2)与(4)之间有什么关系? (1)3x >; (2)21x +是整数; (3)对所有的,3x R x ∈>;(4)对任意一个x Z ∈,21x +是整数.2. 下列语名是命题吗?(1)与(3),(2)与(4)之间有什么关系? (1)213x +=; (2)x 能被2和3整除;(3)存在一个0x R ∈,使0213x +=; (4)至少有一个0x Z ∈,0x 能被2和3整除.新知:1.短语“ ”“ ”在逻辑中通常叫做全称量词,并用符号“ ”表示,含有 的命题,叫做全称命题.其基本形式为:,()x M p x ∀∈,读作:2. 短语“ ”“ ”在逻辑中通常叫做存在量词,并用符号“ ”表示,含有 的命题,叫做特称称命题.其基本形式00,()x M p x ∃∈,读作:试试:判断下列命题是不是全称命题或者存在命题,如果是,用量词符号表示出来. (1)中国所有的江河都流入大海; (2)0不能作为除数;(3)任何一个实数除以1,仍等于这个实数; (4)每一个非零向量都有方向.反思:注意哪些词是量词是解决本题的关键,还应注意全称命题和存在命题的结构形式.※ 典型例题例1 判断下列全称命题的真假: (1)所有的素数都是奇数; (2)2,11x R x ∀∈+≥;(3)对每一个无理数x ,2x 也是无理数.变式:判断下列命题的真假:(1)2(5,8),()420x f x x x ∀∈=--> (2)2(3,),()420x f x x x ∀∈+∞=-->小结:要判定一个全称命题是真命题,必须对限定集合M 中每一个元素x 验证()p x 成立;但要判定全称命题是假命题,却只要能举出集合M 中的一个0x x =,使得0()p x 不成立即可. 例2 判断下列特称命题的真假:(1) 有一个实数0x ,使200230x x ++=; (2) 存在两个相交平面垂直于同一条直线; (3) 有些整数只有两个正因数.变式:判断下列命题的真假: (1)2,32a Z a a ∃∈=- (2)23,32a a a ∃≥=-小结:要判定特称命题“00,()x M p x ∃∈” 是真命题只要在集合M 中找一个元素0x ,使0()p x 成立即可;如果集合M 中,使()P x 成立的元素x 不存在,那么这个特称命题是假命题.※ 动手试试练1. 判断下列全称命题的真假: (1)每个指数都是单调函数; (2)任何实数都有算术平方根;(3){|x x x ∀∈是无理数},2x 是无理数.练2. 判定下列特称命题的真假: (1)00,0x R x ∃∈≤;(2)至少有一个整数,它既不是合数,也不是素数;(3)0{|x x x ∃∈是无理数},20x 是无理数.三、总结提升 ※ 学习小结这节课你学到了一些什么?你想进一步探究的问题是什么?※ 知识拓展数理逻辑又称符号逻辑,是用数学的方法研究推理过程的一门学问. 德国启蒙思想家 莱布尼茨(1646—1716)是数理逻辑的创始人。
