19 2008年北京市西城区中考数学一模试卷
2019届北京市西城区九年级下学期第一次中考模拟测验数学试卷【含答案及解析】

2019届北京市西城区九年级下学期第一次中考模拟测验数学试卷【含答案及解析】————————————————————————————————作者:————————————————————————————————日期:2019届北京市西城区九年级下学期第一次中考模拟考试数学试卷【含答案及解析】姓名___________ 班级____________ 分数__________题号一二三四总分得分一、选择题1. 64的立方根是()A. ±8B. ±4C. 8D. 42. 2014年11月北京主办了第二十二届APEC(亚太经合组织)领导人会议,“亚太经合组织”联通太平洋两岸,从地理概念上逐渐变成了一个拥有280000000人口的经济合作体,把“280000000”用科学记数法表示正确的是()A. B. C. D.3. 如右图是由四个相同的小正方体组成的立体图形,它的俯视图为()4. 一名射击爱好者5次射击的中靶环数依次为:6,7,9,8,9,这5个数据的中位数是()A.6 B.7 C.8 D.95. 下列图形中,是中心对称图形的是()6. 在函数中,自变量x的取值范围是()A. B. C. D.7. 一个不透明的口袋中,装有4个红球,3个黄球,1个白球,这些球除颜色外其余都相同,从口袋中随机摸一个球,则摸到红球的概率为()A. B. C. D.8. 如图,⊙的半径为5,为⊙的弦,⊥于点.若,则弦的长为()A.4 B.6 C.8 D.109. 若正多边形的一个外角为60º,则这个正多边形的中心角的度数是()A.30° B.60° C.90° D.120°10. 如图,菱形ABCD的对角线AC,BD相交于点O,AC=6,BD=8,动点P从点B出发,沿着B-A-D在菱形ABCD的边上运动,运动到点D停止,点是点P关于BD的对称点,交BD于点M,若BM=x,的面积为y,则y与x之间的函数图象大致为()二、填空题11. 若则.12. 质量检测部门对甲、乙两工厂生产的同样产品抽样调查,计算出甲厂的样本方差为0.99,乙厂的样本方差为1.22.由此可以推断出生产此类产品,质量比较稳定的是厂.13. 在综合实践课上,小明同学设计了如图测河塘宽AB的方案:在河塘外选一点O,连结AO,BO,测得m,m,延长AO,BO分别到D,C两点,使m,m,又测得m,则河塘宽AB= m.14. 写出一个当自变量时,y随x的增大而增大的反比例函数表达式_____.15. 居民用电计费实行“一户一表”政策,以年为周期执行阶梯电价,即:一户居民全年不超过2880度的电量,执行第一档电价标准为0.48元/度;全年用电量在2880度到4800度之间(含4800),超过2880度的部分,执行第二档电价标准为0.53元/度;全年用电量超过4800度,超过4800度的部分,执行第三档电价标准为0.78元/度.小敏家2014年用电量为3000度,则2014年小敏家电费为元.16. 规定:在平面直角坐标系xOy中,“把某一图形先沿x轴翻折,再沿y轴翻折”为一次变化.如图,已知正方形ABCD,顶点A(1,3),C(3,1).若正方形ABCD经过一次上述变化,则点A变化后的坐标为,如此这样,对正方形ABCD连续做2015次这样的变化,则点D变化后的坐标为.三、计算题17. 计算:.18. 解不等式组:四、解答题19. 如图,C,D为线段AB上两点,且AC=BD,AE∥BF.AE=BF.求证:∠E=∠F.20. 已知,求代数式的值.21. 已知关于的一元二次方程有两个不相等的实数根.(1)、求k的取值范围;(2)、若k为小于2的整数,且方程的根都是整数,求k的值.22. 列方程或方程组解应用题:在练习100米跑步时,小丽为了帮助好朋友小云提高成绩,让小云先跑7.5秒后自己再跑,结果两人同时到达终点,这次练习中小丽的平均速度是小云的1.6倍,求小云这次练习中跑100米所用的时间.23. 如图,平行四边形ABCD中,点E是AD边上一点,且CE⊥BD于点F,将△DEC沿从D 到A的方向平移,使点D与点A重合,点E平移后的点记为G.(1)、画出△DEC平移后的三角形;(2)、若BC=,BD=6,CE=3,求AG的长.24. 为了提倡“绿色”出行,顺义区启动了公租自行车项目,为了解我区居民公租自行车的使用情况,某校的社团把使用情况分为A(经常租用)、B(偶尔租用)、C(不使用)三种情况.先后在2015年1月底和3月底做了两次调查,并根据调查结果绘制成了如下两幅不完整的统计图:根据以上信息解答下列问题:(1)在扇形统计图中,A(经常租用)所占的百分比是;(2)求两次共抽样调查了多少人;并补全折线统计图;(3)根据调查的结果,请你谈谈从2015年1月底到2015年3月底,我区居民使用公租自行车的变化情况.25. 如图,是⊙的直径,是⊙上一点,是的中点,过点D作⊙O的切线,与AB,AC的延长线分别交于点E,F,连结AD.(1)求证:AF⊥EF;(2)若,AB=5,求线段BE的长.26. 阅读、操作与探究:小亮发现一种方法,可以借助某些直角三角形画矩形,使矩形邻边比的最简形式(如4:6的最简形式为2:3)为两个连续自然数的比,具体操作如下:如图1,Rt△ABC中,BC,AC,AB的长分别为3,4,5,先以点B为圆心,线段BA的长为半径画弧,交CB的延长线于点D,再过D,A两点分别作AC,CD的平行线,交于点E.得到矩形ACDE,则矩形ACDE的邻边比为.请仿照小亮的方法解决下列问题:(1)如图2,已知Rt△FGH中,GH:GF:FH= 5:12:13,请你在图2中画一个矩形,使所画矩形邻边比的最简形式为两个连续自然数的比,并写出这个比值;(2)若已知直角三角形的三边比为(n为正整数),则所画矩形(邻边比的最简形式为两个连续自然数的比)的邻边比为.27. 在平面直角坐标系xOy中,抛物线与y轴交于C点,与x轴交于A,B两点(点A在点B左侧),且点A的横坐标为-1.(1)求a的值;(2)设抛物线的顶点P关于原点的对称点为,求点的坐标;(3)将抛物线在A,B两点之间的部分(包括A, B两点),先向下平移3个单位,再向左平移m()个单位,平移后的图象记为图象G,若图象G与直线无交点,求m 的取值范围.28. 如图,△ABC中,AB=AC,点P是三角形右外一点,且∠APB=∠ABC.(1)如图1,若∠BAC=60°,点P恰巧在∠ABC的平分线上,PA=2,求PB的长;(2)如图2,若∠BAC=60°,探究PA,PB,PC的数量关系,并证明;(3)如图3,若∠BAC=120°,请直接写出PA,PB,PC的数量关系.29. 已知:如图1,抛物线的顶点为M,平行于x轴的直线与该抛物线交于点A,B(点A 在点B左侧),根据对称性△AMB恒为等腰三角形,我们规定:当△AMB为直角三角形时,就称△AMB为该抛物线的“完美三角形”.(1)①如图2,求出抛物线的“完美三角形”斜边AB的长;②抛物线与的“完美三角形”的斜边长的数量关系是;(2)若抛物线的“完美三角形”的斜边长为4,求a的值;(3)若抛物线的“完美三角形”斜边长为n,且的最大值为-1,求m,n的值.参考答案及解析第1题【答案】第2题【答案】第3题【答案】第4题【答案】第5题【答案】第6题【答案】第7题【答案】第8题【答案】第9题【答案】第10题【答案】第11题【答案】第12题【答案】第13题【答案】第14题【答案】第15题【答案】第16题【答案】第17题【答案】第18题【答案】第19题【答案】第20题【答案】第21题【答案】第22题【答案】第23题【答案】第24题【答案】第25题【答案】第26题【答案】第27题【答案】第28题【答案】第29题【答案】。
北京市西城区2007—2008学年第一学期期末测试初三数学试卷

A BC DP O2008年北京市西城区初三数学抽样测试(120分钟,满分120分)学校 ______________ 班级 _________ 姓名_________第I 卷(机读卷 共32分)一、选择题(共8个小题,每小题4分,共32分)1.在直角坐标系中,点A( 2,-3)关于原点对称的点在( ).(A)第一象限 (B) 第二象限 (C) 第三象限 (D)第四象限 2.如果两圆的半径分别是3和5,圆心距是8,那么这两圆的位置关系是( ). (A)相离 (B)外切 (C)相交 (D)内切3.已知ABC DEF ∆∆,若对应边AB:DE=1:2,则它们的周长比等于(). (A)1:2 (B)1:4 (C)2:1 (D)4:14. 1.将抛物线22y x =向左平移1个单位,再向上平移3个单位得到的抛物线表达式是( ). (A) 22(1)3y x =-- (B)22(1)3y x =++ (C) 22(1)3y x =-+ (D) 22(1)3y x =+-5.同时投掷两枚硬币每次出现反面都向上的概率为( ). (A)14 (B)13 ( C)12 (D) 346.抛物线2(0)y x x p p =++≠与x 轴相交,其中一个交点的横坐标是p.那么该抛物线的顶点的坐标是( ). (A) (0,-2) (B) 19(,)24- (C) 19(,)24-(D)19(,)24--) 7. 如图,AB 是圆O 的直径,弦AD ,BC 相交于点P ,60DPB BC ︒∠=AC,D 是的中点,则的值是()AB(A )12 (B )2 (C (D )38.如图,二次函数2(0)y ax bx c a =++≠的图象经过点(-1,2),与y 轴交于(0,2)点, 且与x 轴交点的横坐标分别为12,x x ,其中1221,01x x -<<-<< 下列结论①4a-2b+c<0,②2a-b <0 ③a<-1 ④284b a ac +> 其中正确的有( ).(A )1个 (B )2个 (C )3个 (D )4个A B C DE F AD 第II 卷(非机读卷 共88分)二、填空题(共4个小题,每小题4分,共16分)9.如果2210y y ++,那么xy 的值等于 .10.在平面直角坐标系内,已知A(6,3),B(6,0)两点,以坐标原点O 为位似中心,相似比为13,把线段AB 缩小后得到线段''A B ,则''A B 、的坐标分别是 .11.已知圆锥的侧面积为10π平方厘米,底面半径为2厘米,则圆锥的母线长为 。
2019北京市西城区初三一模数学试题及答案
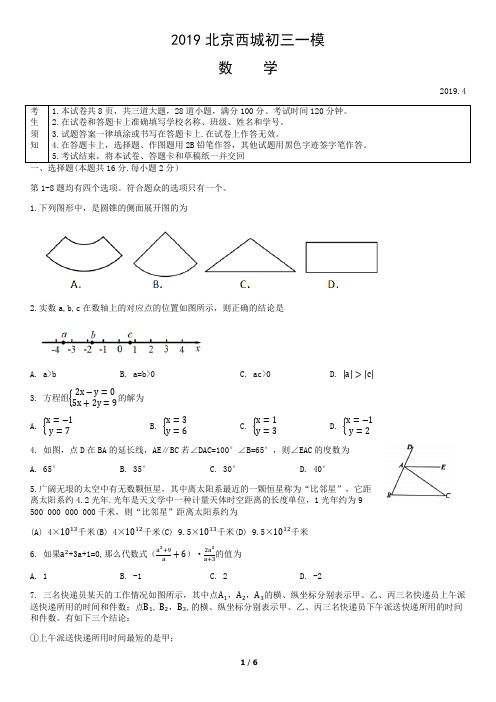
2019北京西城初三一模数 学2019.4考生须知1.本试卷共8页,共三道大题,28道小题,满分100分。
考试时间120分钟。
2.在试卷和答题卡上准确填写学校名称、班级、姓名和学号。
3.试题答案一律填涂或书写在答题卡上.在试卷上作答无效。
4.在答题卡上,选择题、作图题用2B 铅笔作答,其他试题用黑色字迹签字笔作答。
5.考试结束,将本试卷、答题卡和草稿纸一并交回 第1-8题均有四个选项。
符合题众的选项只有一个。
1.下列图形中,是圆锥的侧面展开图的为2.实数a,b,c 在数轴上的对应点的位置如图所示,则正确的结论是A. a>bB. a=b>0C. ac>0D. |a |>|c |3. 方程组{2x −y =05x +2y =9的解为A. {x =−1y =7B. {x =3y =6C. {x =1y =3D. {x =−1y =24. 如图,点D 在BA 的延长线,AE ∥BC 若∠DAC=100°∠B=65°,则∠EAC 的度数为 A. 65°B. 35°C. 30°D. 40°5.广阔无垠的太空中有无数颗恒星,其中离太阳系最近的一颗恒星称为“比邻星”,它距离太阳系约4.2光年.光年是天文学中一种计量天体时空距离的长度单位,1光年约为9 500 000 000 000千米,则“比邻星”距离太阳系约为(A) 4×1013千米(B) 4×1012千米(C) 9.5×1013千米(D) 9.5×1012千米 6. 如果a 2+3a+1=0,那么代数式(a 2+9a+6)·2a 2a+3的值为 A. 1B. -1C. 2D. -27. 三名快递员某天的工作情况如图所示,其中点A 1,A 2,A 3的横、纵坐标分别表示甲、乙、丙三名快递员上午派送快递所用的时间和件数;点B 1, B 2,B 3,的横、纵坐标分别表示甲、乙、丙三名快递员下午派送快递所用的时间和件数。
2008年北京市中考数学试题与答案

解:(1)重叠三角形 的面积为;
(2)用含 的代数式表示重叠三角形 的面积为; 的取值范围为.
七、解答题(本题满分7分)
23.已知:关于 的一元二次方程 .
可得 .
.
四边形 是菱形,
.
.
.
, .
.
即 .
, ,
, .
.6分
(3) .8分
六、解答题(共2道小题,共9分)
21.解:设这次试车时,由北京到天津的平均速度是每小时 千米,则由天津返回北京的平均速度是每小时 千米.1分
依题意,得 .3分
解得 .4分
答:这次试车时,由北京到天津的平均速度是每小时200千米.5分
22.解:(1)重叠三角形 的面积为 .1分
(2)用含 的代数式表示重叠三角形 的面积为 ;2分
的取值范围为 .4分
七、解答题(本题满分7分)
23.(1)证明: 是关于 的一元二次方程,
.
当 时, ,即 .
方程有两个不相等的实数根.2分
(2)解:由求根公式,得 .或 .3分,源自.,, .4分
.
即 为所求.5分
(3)解:在同一平面直角坐标系中分别画出
与 的图象.
6分
由图象可得,当 时, .7分
八、解答题(本题满分7分)
第Ⅰ卷(机读卷共32分)
考
生
须
知:
1.第Ⅰ卷从第1页到第2页,共2页,共一道大题,8道小题.
2.考生须将所选选项按要求填涂在答题卡上,在试卷上作答无效.
一、选择题(共8道小题,每小题4分,共32分)
2008年北京市中考模拟数学分类汇编(四)——函数

08年北京市中考模拟分类汇编⑷函数一、函数基本知识1.(海淀一模)函数y =x 的取值范围是 . 2.(朝阳一模)函数y =中,自变量x 的取值范围是( ) A.2x ≥-且0x ≠ B.2x ≥- C.2x >-且0x ≠ D.2x >- 3. (朝阳一模)如图,抛物线2y ax bx c =++,OA OC =,下列关系中正确的是( )A.1ac b +=B.1ab c +=C.1bc a +=D.1ac b +=4.(大兴一模)函数y =自变量 x 的取值范围是( )A.1x < .1B x > .1C x ≤ .1D x ≤-5. (大兴一模)若反比例函数2y x=-的图象上有两点1(1)A y ,,2(2)B y ,,则1y _____2y (填“>”或“=”或“<”). 6. (丰台一模)写出一个图像在第二、第四象限的反比例函数的解析式 .7. (宣武一模)已知一次函数y kx b =+(k ,b 是常数,且0k ≠),x 与y 的部分对应值如表所示,那么m 的值等于( ). (A )1- (B ) 0 (C )12(D )2 8. (宣武一模)如图,二次函数2y ax bx c =++的图象开口向上,图象经过点(1,2)-和(1,0),且与y 轴相交于负半轴,给出四个结论:①0a >;②0b >;③0c >;④0a b c ++=.其中正确的序号是 .9. (石景山二模)如图所示:边长分别为1和2的两个正方形,其一边在同一水平线上,小正方形沿该水平线自左向右匀速穿过大正方形.设穿过的时间为t ,大正方形内除去小正方形部分的面积为S (阴影部分),那么S 与t 的大致()10. (昌平二模)如果反比例函数ky x=的图象经过点(12)-,,那么k 的值是( ) A.2-B.2C.12-D.12二、函数综合1. (大兴一模)如图2,是一次函数y kx b =+与反比例函数2y x=的图象,则关于x 的方程2kx b x+=的解为( ) A .121,2x x == B .122,1x x =-=- C .121,2x x ==- D .122,1x x ==-2. (海淀一模)已知一次函数332y x =-+的图象与y 轴,x 轴分别交于,A B ,直线y kx b =+经过OA 上的三分之一点D ,且交x 轴的负半轴于点C ,如果AOB DOC S S ∆∆=,求直线y kx b =+的解析式. 3. (宣武一模)如图,反比例函数ky x=的图象与一次函数y mx b =+的图象交于A (1,3)、B (n ,1-)两点.⑴ 求反比例函数与一次函数的解析式;⑵ 根据图象回答:当x 取何值时,反比例函数的值大于一次函数的值? 4. (朝阳一模)已知a 、b 是关于x 的一元二次方程()22330kx k x k +-++=的两个实数根,其中k 为非负整数,点(A a ,)b 是一次函数(2)y k x m =-+与反比例函数ny x=图象的交点,且m 、n 为常数. ⑴ 求k 的值;⑵ 求一次函数与反比例函数的解析式.5. (丰台一模)一次函数y kx k =+的图象经过点(1,4),且分别与x 轴、y 轴交于点A 、B . 点P (,0)a 在x 轴正半轴上运动,点Q (0,)b 在y 轴正半轴上运动,且PQ AB ⊥. ⑴ 求k 的值,并在给出的平面直角坐标系中画出该一次函数的图象; ⑵ 求a 与b 满足的等量关系式.6. (朝阳一模)如图,在矩形ABCD 中,8cm AD =,6cm AB =,点A 处有一动点E 以1cm/s 的速度由A 向BE运动,同时点C 处也有一动点F 以2cm/s 的速度由C 向D 运动,设运动的时间为()x s ,四边形EBFD 的面积为2(cm )y ,求y 与x 的函数关系式及自变量x 的取值范围. 7. (朝阳一模)已知抛物线2y ax bx c =++的图象与x 轴交于A 、B 两点(点A 在点B 的左边),与y 轴交于点(0C ,3),过点C 作x 轴的平行线与抛物线交于点D ,抛物线的顶点为M ,直线5y x =+经过D 、M 两点.⑴ 求此抛物线的解析式;⑵ 连接AM 、AC 、BC ,试比较MAB ∠和ACB ∠的大小,并说明你的理由. 8. (昌平二模)抛物线()20y ax bx c a =++≠交x 轴于A 、B 两点,交y 轴于点C ,已知抛物线的对称轴为直线x = -1,B(1,0),C(0,-3). ⑴ 求二次函数()20y ax bx c a =++≠的解析式;⑵ 在抛物线对称轴上是否存在一点P ,使点P 到A 、C 两点距离之差最大?若存在,求出点P 坐标;若不存在,请说明理由. 9. (大兴一模)已知二次函数2y ax bx c =++的图象和点A ,与y 轴的交点为B (0,4),且ac b =.⑴ 求该二次函数的解析表达式;⑵ 将一次函数y =3-x 为L ,图象L 与抛物线的另一个交点为C ,求△10. 【(宣武一模)已知:直线6y x =+交x 轴、y 轴于A 两点的抛物线2(0)y ax bx a =+<的顶点B 在直线AC ⑴ 求A C 、两点坐标;⑵ 求出该抛物线的函数关系式; ⑶ 以B 点为圆心,以AB 为半径作B ,将B 沿x 试判断直线AC 与D 的位置关系,并说明理由; ⑷ 若E 为B 优弧 ACO 上一动点,联结AE OE 、,问在抛物线上是否存在一点M ,使:2:3M O A A E O ∠∠=,若存在,试求出点M的坐标;若不存在,试说明理由.三、函数与应用1.根据以上表格所提供的信息回答:⑴ 当烤制的风味肠的质量为2.5千克时,需要烤制时间是多少? ⑵ 当烤制的风味肠的质量为a 千克时,需要烤制时间是多少分钟?2. 【 (丰台一模)某公司专销产品A ,第一批产品A 上市40天内全部售完.该公司对第一批产品A 上市后的市场销售情况进行了跟踪调查,调查结果如图(1)和图(2)所天)1()图示,其中图(1)中的折线表示的是市场日销售量y (万件)与上市时间t (天)的关系,图(2)中的折线表示的是每件产品A 的日销售利润ω(元)与上市时间t (天)的关系.⑴ 试写出第一批产品A 的市场日销售量y (万件)与上市时间t (天)的关系式; ⑵ 第一批产品A 上市后,哪一天这家公司市场日销售利润最大?最大利润是多少万元?3. (丰台一模)有一座抛物线型拱桥,其水面宽AB 为18米,拱顶O 离水面AB 的距离OM 为8米,货船在水面上的部分的横断面是矩形CDEF ,如图建立平面直角坐标系.⑴ 求此抛物线的解析式,并写出自变量的取值范围; ⑵ 如果限定CD 的长为9米,DE 不能超过多少米,才能使船通过拱桥? ⑶ 若设EF a =,请将矩形CDEF 的面积S 用含a 的代数式表示,并指出a 的取值范围. 4. (昌平二模)在正常情况下,一个人在运动时所能承受的每分钟心跳的最高次数S (次/分)是这个人年龄n (岁)的一次函数. 已知在正常情况下,年龄15岁和45岁的人在运动时所能承受的最高心跳次数分别为164次/分和114次/分. ⑴ 根据以上信息,求在正常情况下,S 关于n 的函数关系式;⑵ 若一位63岁的人在跑步,医生在途中给他测得10秒心跳为26次,问:他是否有危险?为什么?5. (昌平二模)五一期间,某区一中、二中组织100名优秀教师去某景区旅游,(其中一中教师多于二中教师),景区门票价格规定如下表:若两校都以校为单位一次性够票,则两校一共需付4725元,求两校各有多少名优秀教师参加这次旅游?若两校联合起来,作为一个团体够票,能节约多少钱?。
2019年北京市西城区中考一模数学试卷 (word版含答案)

(A) (B) (C) (D)
3.如图,AB∥CD,DA⊥CE于点A.若∠EAB=55°,则∠D的度数为
(A)25°(B)35°
(C)45°(D)55°
4.右图是某几何体的三视图,该几何体是
(A)三棱柱(B)长方体
表1甲种种植技术种出的西瓜质量统计表
编号
1
2
3
4
5
6
7
8
9
10
西瓜质量.(单位:kg)
3.5
4.8
5.4
4.9
4.2
5.0
4.9
4.8
5.8
4.8
编号
11
12
13
14
15
16
17
18
19
20
西瓜质量.(单位:kg)
5.0
4.8
5.2
4.9
5.1
5.0
4.8
6.0
5.7
5.0
表2乙种种植技术种出的西瓜质量统计表
16.下面是“经过已知直线外一点作这条直线的平行线”的尺规作图过程.
已知:如图1,直线l和直线l外一点P.
求作:直线l的平行直线,使它经过点P.
作法:如图2.
(1)过点P作直线m与直线l交于点O;
(2) 在直线m上取一点A(OA<OP),以点O为圆心,OA长为半径画弧,与直线l交于点B;
(3) 以点P为圆心,OA长为半径画弧,交直线m于点C,以点C为圆心,AB长为半径画弧,两弧交于点D;
优等品西瓜个数
平均数
方差
甲种种植技术种出的西瓜质量
08年北京市中考模拟分类汇编(1)数与式

08年北京市中考模拟分类汇编⑴数与式1.相反数、绝对值、科学记数法、平方根1. (海淀一模)一个数的相反数是8-,则这个数是( )A.8 B -8 1C.8 1D.-8 【答案】A.2. (朝阳一模)4-的倒数是( )A.4B.4- 1C.4 1D.4- 【答案】D3. (大兴一模) –3的绝对值是( )A. 31B.31-C. 3D. 3-【答案】 C4. -3的相反数是 ( )A.-3 B.3 C.13 D.-13【答案】 B5. (石景山二模)一个数的倒数是-2,则这个数是 ( )A .-2 B. 21-C. 2D.21【答案】 B6. (昌平二模)4的算术平方根是( ) A.16 B.2 C.-2 D.±2 【答案】 B7. (大兴一模) –据统计,2006“超级女声”短信投票的总票数约327 000 000张,将这个数写成科学数法是( ) A .63.2710⨯ B .7107.32⨯ C .83.2710⨯ D .93.2710⨯ 【答案】 C8. (朝阳一模)人体中红细胞的直径约为0.0000077m ,将0.0000077用科学记数法表示为( ) 5A.7.710-⨯ 6B.7.710-⨯ 7C.7710-⨯ 5D.0.7710-⨯ 【答案】 B9. (丰台一模)光年是天文学中的距离单位,1光年大约是95000000万千米.将95000000用科学记数法表示为( )A.9.5×107 B.95×106 C.9.5×106 D.0.95×108 【答案】 A10. (海淀一模)中国国家大剧院位于人民大会堂西侧,西长安街以南,由国家大剧院主体建筑及南北两侧的水下长廊、地下停车场、人工湖、绿地等组成,其中人工湖面积约为35500平方米,将数据35500用科学记数法表示为 . 【答案】43.5510⨯11. (宣武一模)5的算术平方根是( ).(A )25 (B )5± (C )5 (D )5-【答案】C12. (石景山二模)1天24小时共有86400秒,用科学记数法可表示为(保留两个有效数字) ( )A .4106.8⨯秒B .4107.8⨯秒C . 3106.8⨯秒D .3107.8⨯秒 【答案】 A2.因式分解1. (海淀一模)把代数式32816x x x -+分解因式,下列分解结果正确的是( )A.2(4)x x +B.2(4)x x -C.34(24)x x x --D.2(8)16x x x -+【答案】 B .2. (石景山二模)分解因式:x x 93-=______________________.【答案】)3)(3(-+x x x3. (大兴一模)分解因式:228x -【答案】:22282(4)x x -=-=2(2)(2)x x +-4. (朝阳一模)因式分解21025ax ax a -+=____________________.【答案】 2(5)a x -【答案】 (丰台一模)分解因式:x x 43-.【答案】原式=)4(2-x x …………………………………2分=)2)(2(-+x x x .………………………………4分5. (宣武一模)现给出三个多项式,1212-+x x ,13212++x x ,xx -221,请你选择其中两个进行加法运算,并把结果因式分解.【答案】22211(1)(31)422x x x x x x+-+++=+…………………………… 2分(4)x x =+ ………………………………………… 5分其他情况如下:)1)(1(1)21()121(222-+=-=-+-+x x x x x x x ; 2222)1(12)21()1321(+=++=-+++x x x x x x x .3..分式1. (海淀一模)先化简,再求值.2121114x x x x --⋅++-,其中3x =.【答案】15.2. (海淀一模)当分式53x x -+的值为零时,x 的值是( ) A.3x = B.3x ≠ C.5x = D.5x ≠ 【答案】 选C.3. (朝阳一模)已知 210a a --=,求代数式111a a --的值.【答案】 ∵210a a --=,∴21a a -=. ………………………………………………………………1分 ()11111a a a a a a ---=--…………………………………………………………3分()11a a =--………………………………………………………4分21a a =--1.=-……………………………………………………………… 5分4. (大兴一模) –已知022=-x ,求代数式11)1(222++--x x x x 的值. 【答案】1=原式.5. (石景山二模)x x x x 4)2121(2-⋅+-- 【答案】x 46. (昌平二模)有这样一道题:“先化简,再求值:22241244x x x x x -⎛⎫+÷ ⎪+--⎝⎭,其中x =”小玲做题时把“x =x =,但她的计算结果也是正确的,请你解释这是怎么回事?【答案】22241244x x x x x -⎛⎫+÷ ⎪+--⎝⎭ 222444(4)4x x x x x -++=⨯-- 24x =+ ……………………4分因为x =x =2x 的值均为3,原式的计算结果都为7.所以把“x =x =,计算结果也是正确的.……………………5分4..综合运算1. (朝阳一模)下列各式计算正确的是( A ) A.321x x -=235B.()x x =34C.x x x ⋅=22D.()()a b b a a b +-=-【答案】C2. (石景山二模)下列计算正确的是 ( )A .a 2·a 3=a 5B .(a 2)3=a 5C .a 10÷a 2=a 5D .2a 5-a 5=2【答案】 A3. (海淀一模)计算2021((3.14)()2sin305π-+--+︒【答案】 -184. (朝阳一模)计算 1024sin 60(-+︒-.【答案】 原式1412=+-…………………………………………………4分12=-.…………………………………………………………………5分5. (大兴一模) –计算:12160sin 42327-⎪⎭⎫⎝⎛-︒--+ 【答案】原式24=-⨯-26. (丰台一模)计算:01()12π---+.【答案】原式=1112+……………………………4分=122++=525分7. (石景山二模)计算:|2|)215(60cos 201-+--︒+-【答案】2.8. (昌平二模)计算:()012007-+【答案】原式21-+……………………4分= 1 ……………………5分9. (昌平二模)化简:()()234226123x x x x -+-÷【答案】原式=22424x x x +-……………………3分=2x ……………………4分。
2019年北京市西城初三数学一模试卷 2019.4

西 城 区 九 年 级 统 一 测 试2019.4一、选择题(本题共16分,每小题2分)第1—8题均有四个选项,符合题意的选项只有..一个. 1.下列图形中,是圆锥的侧面展开图的为2.实数a ,b ,c 在数轴上的对应点的位置如图所示,则正确的结论是(A )a b >(B )0a b +>(C )0ac > (D )a c >3.方程组20,529x y x y -=⎧⎨+=⎩的解为(A )1,7x y =-⎧⎨=⎩ (B )3,6x y =⎧⎨=⎩(C )1,2x y =⎧⎨=⎩(D )1,2x y =-⎧⎨=⎩4.如图,点D 在BA 的延长线上,AE ∥BC .若∠DAC =100°,∠B =65°,则∠EAC 的度数为 (A )65° (B )35°(C )30° (D )40°5.广阔无垠的太空中有无数颗恒星,其中离太阳系最近的一颗恒星称为“比邻星”,它距离太阳系约4.2光年.光年是天文学中一种计量天体时空距离的长度单位,1光年约为9 500 000 000 000千米,则“比邻星”距离太阳系约 (A )4×1013千米 (B )4×1012千米(C )9.5×1013千米 (D )9.5×1012千米6.如果2310a a ++=,那么代数式229263a a a a ⎛⎫++⋅⎪+⎝⎭的值为 (A )1(B )1- (C )2 (D ) 2-7.三名快递员某天的工作情况如图所示,其中点A 1,A 2,A 3的横、纵坐标分别表示甲、乙、丙三名快递员上午派送快递所用的时间和件数;点B 1,B 2,B 3的横、纵坐标分别表示甲、乙、丙三名快递员下午派送快递所用的时间和件数. 有如下三个结论:①上午派送快递所用时间最短的是甲; ②下午派送快递件数最多的是丙; ③在这一天中派送快递总件数最多的是乙. 上述结论中,所有正确结论的序号是 (A )①② (B )①③ (C )② (D )②③8.中国科学技术馆有“圆与非圆”展品,涉及了“等宽曲线”的知识.因为圆的任何一对平行切线的距离总是相等的,所以圆是“等宽曲线”.除了圆以外,还有一些几何图形也是“等宽曲线”,如勒洛三角形(图1).它是分别以等边三角形的每个顶点为圆心,以边长为半径,在另两个顶点间画一段圆弧,三段圆弧围成的曲边三角形.图2是等宽的勒洛三角形和圆.下列说法中错误的是(A ) 勒洛三角形是轴对称图形 (B )图1中,点A 到BC 上任意一点的距离都相等(C ) 图2中,勒洛三角形上任意一点到等边三角形DEF 的中心O 1的距离都相等 (D ) 图2中,等宽的勒洛三角形和圆,它们的周长相等二、填空题(本题共16分,每小题2分)9.如图,在线段AD ,AE ,AF 中,△ABC 的高是线段________.10在实数范围内有意义,则实数x 的取值范围是__________.11.分解因式:225ab a -= .12.如图,点O ,A ,B 都在正方形网格的格点上,将△OAB绕点O 顺时针旋转后得到△OA ′B ′,点A ,B 的对应点 A ′,B ′也在格点上,则旋转角α(0180α<<)的度数 为_________°.13.用一组a ,b 的值说明命题“对于非零实数a ,b ,若a b <,则11a b>”是错误的,这组值可以是a = ,b = .14.如图,在矩形ABCD 中,点E 在边CD 上,将矩形ABCD沿AE 所在直线折叠,点D 恰好落在边BC 上的点F 处. 若DE =5,FC =4,则AB 的长为________.15.小芸一家计划去某城市旅行,需要做自由行的攻略,父母给她分配了一项任务:借助网络评价选取该城市的一家餐厅用餐.小芸根据家人的喜好,选择了甲、乙、丙三家餐厅,对每家餐厅随机选取了1000条网络评价,统计如下:(说明:网上对于餐厅的综合评价从高到低,依次为五星、四星、三星、二星和一星.) 小芸选择在 (填“甲”、“乙”或“丙”)餐厅用餐,能获得良好用餐体验(即评价不低于四星)的可能性最大.16.高速公路某收费站出城方向有编号为A ,B ,C ,D ,E 的五个小客车收费出口,假定各收费出口每20分钟通过小客车的数量分别都是不变的.同时开放其中的某两个收费出口,这两个出口20分钟一共通过的小客车数量记录如下:在A ,B ,C ,D ,E 五个收费出口中,每20分钟通过小客车数量最多的收费出口的编号三、解答题(本题共68分,第17﹣22题,每小题5分,第23﹣26题,每小题6分,第27,28题,每小题7分)解答应写出文字说明、演算步骤或证明过程. 17.计算:052sin 60(2019)-+︒--π.18.解不等式组4(21)31,385x x x x -<+⎧⎪-⎨<⎪⎩.19.下面是小东设计的“作圆的一个内接矩形,并使其对角线的夹角为60°”的尺规作图过程. 已知:⊙O .求作:矩形ABCD ,使得矩形ABCD 内接于⊙O ,且其对角线AC ,BD 的夹角为60°. 作法:如图,①作⊙O 的直径AC ;②以点A 为圆心,AO 长为半径画弧,交直线AC 上方的圆弧于点B ;③连接BO 并延长交⊙O 于点D ; ④连接AB ,BC ,CD ,DA .所以四边形ABCD 就是所求作的矩形.根据小东设计的尺规作图过程,(1)使用直尺和圆规,补全图形(保留作图痕迹); (2)完成下面的证明.证明:∵点A ,C 都在⊙O 上, ∴OA = OC .同理OB =OD .∴四边形ABCD 是平行四边形. ∵AC 是⊙O 的直径,∴∠ABC =90°(__________)(填推理的依据).∴四边形ABCD 是矩形.∵AB =______ =BO , ∴∠AOB =60°.∴四边形ABCD 是所求作的矩形.20.已知关于x 的一元二次方程20x bx c ++=.(1)当2c b =-时,利用根的判别式判断方程根的情况;(2)若方程有两个相等的非零实数根,写出一组满足条件的b ,c 的值,并求此时方程的根.21.如图,在△ABC中,AC=BC,D,E,F分别是AB,AC,BC的中点,连接DE,DF.(1)求证:四边形DFCE是菱形;(2)若∠A=75°,AC=4,求菱形DFCE的面积.22.在平面直角坐标系xOy中,直线l:y x b=+与x轴交于点A(2-,0),与y轴交于点B.双曲线kyx=与直线l交于P,Q两点,其中点P的纵坐标大于点Q的纵坐标.(1)求点B的坐标;(2)当点P的横坐标为2时,求k的值;(3)连接PO,记△POB的面积为S,若112S<<,直接写出k的取值范围.23.如图,AB是⊙O的直径,CB与⊙O相切于点B.点D在⊙O上,且BC=BD,连接CD 交⊙O于点E.过点E作EF⊥AB于点H,交BD于点M,交⊙O于点F.(1)求证:∠MED=∠MDE;(2)连接BE,若ME=3,MB=2,求BE的长.小腾根据学习函数的经验,分别对函数1y ,2y 随自变量x 的变化而变化的规律进行了探究.下面是小腾的探究过程,请补充完整:(1)按照下表中自变量x 的值进行取点、画图、测量,分别得到了1y ,2y 与x 的几组对应值;(2)在同一平面直角坐标系xOy 中,描出补全后的表中各组数值所对应的点(x ,1y ),(x ,2y ),并画出函数1y ,2y 的图象;(3)结合函数图象,解决问题:连接BC ,当△BCD 是以CD 为腰的等腰三角形时, DA 的长度约为___________cm .25.某公司的午餐采用自助的形式,并倡导员工“适度取餐,减少浪费”.该公司共有10个部门,且各部门的人数相同.为了解午餐的浪费情况,公司从这10个部门中随机抽取了A ,B 两个部门,进行了连续四周(20个工作日)的调查,得到这两个部门每天午餐浪费饭菜的重量,以下简称“每日餐余重量”(单位:千克),并对这些数据进行了整理、描述和分析.下面给出了部分信息.a . A 部门每日餐余重量的频数分布直方图如下(数据分成6组:0≤x <2,2≤x <4,4≤x <6,6≤x <8,8≤x <10,10≤x ≤12):b . A 部门每日餐余重量在6≤x <8这一组的是: 6.1 6.6 7.0 7.0 7.0 7.8c . B 部门每日餐余重量如下:1.42.8 6.9 7.8 1.9 9.73.14.6 6.9 10.86.9 2.67.5 6.9 9.5 7.88.4 8.39.4 8.8d .根据以上信息,回答下列问题: (1)写出表中m ,n 的值; (2)在A ,B 这两个部门中,“适度取餐,减少浪费”做得较好的部门是 (填“A ”或“B ”),理由是 ; (3)结合A ,B 这两个部门每日餐余重量的数据,估计该公司(10个部门)一年(按240个工作日计算)的餐余总重量.26.在平面直角坐标系xOy 中,已知抛物线2y x mx n =-+. (1)当2m =时,①求抛物线的对称轴,并用含n 的式子表示顶点的纵坐标;②若点A (2-,1y ),B (2x ,2y )都在抛物线上,且21y y >,则2x 的取值范围 是_____;(2)已知点P (1-,2),将点P 向右平移4个单位长度,得到点Q .当3n =时,若抛物线与线段PQ 恰有一个公共点,结合函数图象,求m 的取值范围.27.如图,在△ABC 中,∠ABC =90°,BA =BC .将线段AB 绕点A 逆时针旋转90°得到线段AD ,E 是边BC 上的一动点,连接DE 交AC 于点F ,连接BF .(1)求证:FB =FD ;(2)点H 在边BC 上,且BH =CE ,连接AH 交BF 于点N .①判断AH 与BF 的位置关系,并证明你的结论;②连接CN .若AB =2,请直接写出线段CN 长度的最小值.28.在平面直角坐标系xOy 中,对于两个点P ,Q 和图形W ,如果在图形W 上存在点M ,N(M ,N 可以重合)使得PM =QN ,那么称点P 与点Q 是图形W 的一对平衡点.(1)如图1,已知点A (0,3),B (2,3).①设点O 与线段AB 上一点的距离为d ,则d 的最小值 是________,最大值是______;②在13(,0)2P ,2(1,4)P ,3(3,0)P -这三个点中,与点O 是线段AB 的一对平衡点的是_________;(2)如图2,已知⊙O 的半径为1,点D 的坐标为(5,0).若点E (x ,2)在第一象限,且点D 与点E 是⊙O 的一对平衡点,求x 的取值范围;(3)如图3,已知点H (3-,0),以点O 为圆心,OH 长为半径画弧交x 轴的正半轴于点K .点C (a ,b )(其中b ≥0)是坐标平面内一个动点,且OC =5,⊙C 是以点C 为圆心,半径为2的圆.若HK 上的任意两个点都是⊙C 的一对平衡点,直接写出b 的取值范围.。
2019年北京市西城初三一模数学考试试卷+答案

5
y1/cm
5
4.9
4
3
0
y2/cm
4
3.32 2.47
1.4
0
3
(2)在同一平面直角坐标系 xOy 中,描出补全后的表中各组数值所对应的点 (x,y1),(x,y2),并画出函数 y1,y2 的图象;
8
北京新东方优能中学&优能 1 对 1 联合出品
(3)结合函数图象,解决问题:连接 BC,当△BCD 是以 CD 为腰的等腰三角形
描述和分析.下面给出了部分信息
a. A 部门每日餐余重量的频数分布直方图如下(数据分成 6 组: 0 x 2 ,
2 x 4 , 4 x 6 , 6 x 8,8 x 10 ,10 x 12 ):
b. A 部门每日餐余重量在 6 x 8这一组的是:
6.1 6.6 7.0 7.0 7.0 7.8
c. B 部门每日餐余重量如下:
A
C
O
所以四边形 ABCD 就是所求作的矩形.Βιβλιοθήκη 根据小东设计的尺规作图过程,
(1)使用直尺和圆规,补全图形(保留作图痕迹);
(2)完成下面的证明
证明:∵点 A , C 都在⊙O 上,
∴OA=OC.
同理 OB=OD.
∴四边形 ABCD 是平行四边形
5
北京新东方优能中学&优能 1 对 1 联合出品
∵AC 是⊙O 的直径,
星.)
小芸选择在
(填“甲”、“乙”或“丙”)餐厅用餐,能获得良好用餐体验(即评价
不低于四星)的可能性最大.
16. 高速公路某收费站出城方向有编号为 A,B,C,D,E 的五个小客车收费出口,
假定各收费出口每 20 分钟通过小客车的数量分别都是不变的.同时开放其中的某两个
2008年北京市中考数学试题和答案(WORD版)

2008年北京市高级中等学校招生考试数 学 试 卷一、选择题(共8道小题,每小题4分,共32分) 1.6-的绝对值等于( ) A .6B .16C .16-D .6-2.截止到2008年5月19日,已有21 600名中外记者成为北京奥运会的注册记者,创历届奥运会之最.将21 600用科学记数法表示应为( ) A .50.21610⨯B .321.610⨯C .32.1610⨯D .42.1610⨯3.若两圆的半径分别是1cm 和5cm ,圆心距为6cm ,则这两圆的位置关系是( ) A .内切B .相交C .外切D .外离4.众志成城,抗震救灾.某小组7名同学积极捐出自己的零花钱支援灾区,他们捐款的数额分别是(单位:元):50,20,50,30,50,25,135.这组数据的众数和中位数分别是( ) A .50,20B .50,30C .50,50D .135,505.若一个多边形的内角和等于720,则这个多边形的边数是( ) A .5B .6C .7D .86.如图,有5张形状、大小、质地均相同的卡片,正面分别印有北京奥运会的会徽、吉祥物(福娃)、火炬和奖牌等四种不同的图案,背面完全相同.现将这5张卡片洗匀后正面向下放在桌子上,从中随机抽取一张,抽出的卡片正面图案恰好是吉祥物(福娃)的概率是( )A .15B .25C .12D .357.若230x y ++-=,则xy 的值为( )A .8-B .6-C .5D .68.已知O 为圆锥的顶点,M 为圆锥底面上一点,点P 在OM 上.一只蜗牛从P 点出发,绕圆锥侧面爬行,回到P 点时所爬过的最短路线的痕迹如右图所示.若沿OM 将圆锥侧面剪开并展开,所得侧面展开图是( )二、填空题(共4道小题,每小题4分,共16分) 9.在函数121y x =-中,自变量x 的取值范围是 . 10.分解因式:32a ab -= .11.如图,在ABC △中,D E ,分别是AB AC ,的中点, 若2cm DE =,则BC = cm .12.一组按规律排列的式子:2b a -,53b a ,83b a -,114b a,…(0ab ≠),其中第7个式子是 ,第n 个式子是 (n 为正整数). 三、解答题(共5道小题,共25分) 13.(本小题满分5分)计算:1182sin 45(2)3-⎛⎫-+-π- ⎪⎝⎭.解:14.(本小题满分5分)解不等式5122(43)x x --≤,并把它的解集在数轴上表示出来. 解:CA E D B1 2 30 1- 2- 3- OPM OM 'M PA .OM 'M PB .OM 'M PC .OM 'M PD .15.(本小题满分5分)已知:如图,C 为BE 上一点,点A D ,分别在BE 两侧.AB ED ∥,AB CE =,BC ED =. 求证:AC CD =. 证明:16.(本小题满分5分)如图,已知直线3y kx =-经过点M ,求此直线与x 轴,y 轴的交点坐标. 解:17.(本小题满分5分) 已知30x y -=,求222()2x yx y x xy y+--+的值. 解:ACEDB3y kx =- yxOM11 2-四、解答题(共2道小题,共10分) 18.(本小题满分5分)如图,在梯形ABCD 中,AD BC ∥,AB AC ⊥,45B ∠=,2AD =,42BC =,求DC 的长. 解:19.(本小题满分5分)已知:如图,在Rt ABC △中,90C ∠=,点O 在AB 上,以O 为圆心,OA 长为半径的圆与AC AB ,分别交于点D E ,,且CBD A ∠=∠. (1)判断直线BD 与O 的位置关系,并证明你的结论;(2)若:8:5AD AO =,2BC =,求BD 的长. 解:(1) (2)ABCDDCOABE五、解答题(本题满分6分)20.为减少环境污染,自2008年6月1日起,全国的商品零售场所开始实行“塑料购物袋有偿使用制度”(以下简称“限塑令”).某班同学于6月上旬的一天,在某超市门口采用问卷调查的方式,随机调查了“限塑令”实施前后,顾客在该超市用购物袋的情况,以下是根据100位顾客的100份有效答卷画出的统计图表的一部分:“限塑令”实施后,塑料购物袋使用后的处理方式统计表处理方式 直接丢弃直接做垃圾袋再次购物使用其它选该项的人数占总人数的百分比5%35%49%11%请你根据以上信息解答下列问题:(1)补全图1,“限塑令”实施前,如果每天约有2 000人次到该超市购物.根据这100位顾客平均一次购物使用塑料购物袋的平均数,估计这个超市每天需要为顾客提供多少个塑料购物袋?(2)补全图2,并根据统计图和统计表说明...........,购物时怎样选用购物袋,塑料购物袋使用后怎样处理,能对环境保护带来积极的影响. 解:(1) (2)40 35 30 25 2015 10 5 0 图1 1 2 3 4 5 6 7 4 3 11 26 379 塑料袋数/个 人数/位 “限塑令”实施前,平均一次购物使用不同数量塑料..购物袋的人数统计图 “限塑令”实施后,使用各种购物袋的人数分布统计图 其它 5% 收费塑料购物袋 _______% 自备袋 46%押金式环保袋24% 图2六、解答题(共2道小题,共9分)21.(本小题满分5分)列方程或方程组解应用题:京津城际铁路将于2008年8月1日开通运营,预计高速列车在北京、天津间单程直达运行时间为半小时.某次试车时,试验列车由北京到天津的行驶时间比预计时间多用了6分钟,由天津返回北京的行驶时间与预计时间相同.如果这次试车时,由天津返回北京比去天津时平均每小时多行驶40千米,那么这次试车时由北京到天津的平均速度是每小时多少千米? 解:22.(本小题满分4分)已知等边三角形纸片ABC 的边长为8,D 为AB 边上的点,过点D 作DG BC ∥交AC 于点G .DE BC ⊥于点E ,过点G 作GF BC ⊥于点F ,把三角形纸片ABC 分别沿DG DE GF ,,按图1所示方式折叠,点A B C ,,分别落在点A ',B ',C '处.若点A ',B ',C '在矩形DEFG 内或其边上,且互不重合,此时我们称A B C '''△(即图中阴影部分)为“重叠三角形”.AGCF B ' C 'E BDA ' 图1AGCFB 'C ' E BDA '图2(1)若把三角形纸片ABC 放在等边三角形网格中(图中每个小三角形都是边长为1的等边三角形),点A B C D ,,,恰好落在网格图中的格点上.如图2所示,请直接写出此时重叠三角形A B C '''的面积;(2)实验探究:设AD 的长为m ,若重叠三角形A B C '''存在.试用含m 的代数式表示重叠三角形A B C '''的面积,并写出m 的取值范围(直接写出结果,备用图供实验,探究使用).解:(1)重叠三角形A B C '''的面积为 ;(2)用含m 的代数式表示重叠三角形A B C '''的面积为 ;m 的取值范围为 . 七、解答题(本题满分7分)23.已知:关于x 的一元二次方程2(32)220(0)mx m x m m -+++=>. (1)求证:方程有两个不相等的实数根;(2)设方程的两个实数根分别为1x ,2x (其中12x x <).若y 是关于m 的函数,且212y x x =-,求这个函数的解析式;(3)在(2)的条件下,结合函数的图象回答:当自变量m 的取值范围满足什么条件时,2y m ≤.A CB备用图ACB备用图(1)证明:(2)解:(3)解:1 2 3 44 3 2 1xy O -1 -2 -3 -4 -4-3 -2 -124.在平面直角坐标系xOy 中,抛物线2y x bx c =++与x 轴交于A B ,两点(点A 在点B 的左侧),与y 轴交于点C ,点B 的坐标为(30),,将直线y kx =沿y 轴向上平移3个单位长度后恰好经过B C ,两点. (1)求直线BC 及抛物线的解析式;(2)设抛物线的顶点为D ,点P 在抛物线的对称轴上,且APD ACB ∠=∠,求点P 的坐标;(3)连结CD ,求OCA ∠与OCD ∠两角和的度数.解:(1) (2) (3)1 Oy x2 3 44 32 1 -1 -2 -2-125.请阅读下列材料:问题:如图1,在菱形ABCD 和菱形BEFG 中,点A B E ,,在同一条直线上,P 是线段DF 的中点,连结PG PC ,.若60ABC BEF ∠=∠=,探究PG 与PC 的位置关系及PGPC的值.小聪同学的思路是:延长GP 交DC 于点H ,构造全等三角形,经过推理使问题得到解决.请你参考小聪同学的思路,探究并解决下列问题: (1)写出上面问题中线段PG 与PC 的位置关系及PGPC的值; (2)将图1中的菱形BEFG 绕点B 顺时针旋转,使菱形BEFG 的对角线BF 恰好与菱形ABCD 的边AB 在同一条直线上,原问题中的其他条件不变(如图2).你在(1)中得到的两个结论是否发生变化?写出你的猜想并加以证明.(3)若图1中2(090)ABC BEF αα∠=∠=<<,将菱形BEFG 绕点B 顺时针旋转任意角度,原问题中的其他条件不变,请你直接写出PGPC 的值(用含α的式子表示). 解:(1)线段PG 与PC 的位置关系是 ;PGPC= . (2)DAB EF CPG 图1DCG PAB EF图22008年北京市高级中等学校招生考试数学试卷答案及评分参考阅卷须知:1.一律用红钢笔或红圆珠笔批阅,按要求签名.2.第Ⅰ卷是选择题,机读阅卷.3.第Ⅱ卷包括填空题和解答题.为了阅卷方便,解答题中的推导步骤写得较为详细,考生只要写明主要过程即可.若考生的解法与本解法不同,正确者可参照评分参考给分.解答右端所注分数,表示考生正确做到这一步应得的累加分数.第Ⅰ卷(机读卷共32分)一、选择题(共8道小题,每小题4分,共32分)题号 1 2 3 4 5 6 7 8答案 A D C C B B B D第Ⅱ卷(非机读卷共88分)二、填空题(共4道小题,每小题4分,共16分)题号9 10 11 12答案12x≠()()a ab a b+- 4207ba-31(1)nnnba--三、解答题(共5道小题,共25分)13.(本小题满分5分)解:11 82sin45(2π)3-⎛⎫-+-- ⎪⎝⎭2222132=-⨯+-····················································································4分22=-.···································································································5分解:去括号,得51286x x --≤. ···································································· 1分 移项,得58612x x --+≤. ··········································································· 2分 合并,得36x -≤. ······················································································· 3分 系数化为1,得2x -≥. ················································································· 4分 不等式的解集在数轴上表示如下:··················································································································· 5分 15.(本小题满分5分) 证明:AB ED ∥,B E ∴∠=∠. ······························································································· 2分 在ABC △和CED △中,AB CE B E BC ED =⎧⎪∠=∠⎨⎪=⎩,,, ABC CED ∴△≌△. ···················································································· 4分 AC CD ∴=. ······························································································· 5分 16.(本小题满分5分)解:由图象可知,点(21)M -,在直线3y kx =-上, ·············································· 1分231k ∴--=.解得2k =-.································································································ 2分∴直线的解析式为23y x =--. ······································································· 3分令0y =,可得32x =-. ∴直线与x 轴的交点坐标为302⎛⎫- ⎪⎝⎭,. ······························································· 4分令0x =,可得3y =-.∴直线与y 轴的交点坐标为(03)-,. ································································· 5分1 2 30 1- 2- 3-解:222()2x yx y x xy y +--+22()()x yx y x y +=-- ························································································· 2分 2x yx y+=-. ··································································································· 3分 当30x y -=时,3x y =. ·············································································· 4分原式677322y y y y y y +===-. ··············································································· 5分四、解答题(共2道小题,共10分) 18.(本小题满分5分)解法一:如图1,分别过点A D ,作AE BC ⊥于点E , DF BC ⊥于点F . ····································· 1分 ∴AE DF ∥.又AD BC ∥,∴四边形AEFD 是矩形.2EF AD ∴==. ····································· 2分AB AC ⊥,45B ∠=,42BC =, AB AC ∴=. 1222AE EC BC ∴===. 22DF AE ∴==,2CF EC EF =-= ····················································································· 4分在Rt DFC △中,90DFC ∠=,2222(22)(2)10DC DF CF ∴=+=+=. ············································· 5分解法二:如图2,过点D 作DF AB ∥,分别交AC BC ,于点E F ,. ···················· 1分AB AC ⊥,ABCDFE 图190AED BAC ∴∠=∠=. AD BC ∥,18045DAE B BAC ∴∠=-∠-∠=.在Rt ABC △中,90BAC ∠=,45B ∠=,42BC =,2sin 454242AC BC ∴==⨯= ································································· 2分 在Rt ADE △中,90AED ∠=,45DAE ∠=,2AD =,1DE AE ∴==.3CE AC AE ∴=-=. ·················································································· 4分 在Rt DEC △中,90CED ∠=,22221310DC DE CE ∴=+=+=. ························································· 5分 19. (本小题满分5分) 解:(1)直线BD 与O 相切. ········································································ 1分 证明:如图1,连结OD .OA OD =, A ADO ∴∠=∠.90C ∠=, 90CBD CDB ∴∠+∠=.又CBD A ∠=∠,90ADO CDB ∴∠+∠=. 90ODB ∴∠=.∴直线BD 与O 相切. ················································································· 2分(2)解法一:如图1,连结DE .AE 是O 的直径, 90ADE ∴∠=. :8:5AD AO =, 4cos 5AD A AE ∴==. ······················································································ 3分 90C ∠=,CBD A ∠=∠,DCOABE 图1ABCDFE图24cos 5BC CBD BD ∴∠==. ··············································································· 4分 2BC =, 52BD ∴=. ······································································ 5分 解法二:如图2,过点O 作OH AD ⊥于点H . 12AH DH AD ∴==.:8:5AD AO =, 4cos 5AH A AO ∴==. ··················· 3分 90C ∠=,CBD A ∠=∠,4cos 5BC CBD BD ∴∠==. ································· 4分 2BC =, 52BD ∴=. ································································································· 5分 五、解答题(本题满分6分)解:(1)补全图1见下图. ·············································································· 1分9137226311410546373003100100⨯+⨯+⨯+⨯+⨯+⨯+⨯==(个). 这100位顾客平均一次购物使用塑料购物袋的平均数为3个. ································· 3分200036000⨯=.估计这个超市每天需要为顾客提供6000个塑料购物袋. ········································· 4分 (2)图2中,使用收费塑料购物袋的人数所占百分比为25%. ······························· 5分 根据图表回答正确给1分,例如:由图2和统计表可知,购物时应尽量使用自备袋和押金式环保袋,少用塑料购物袋;塑料购物袋应尽量循环使用,以便减少塑料购物袋的使用量,为DCO ABH图240 35 30 25 20 15 10 5 0图1123 4 567 4 311 26379 塑料袋数/个人数/位 “限塑令”实施前,平均一次购物使用不同数量塑料..购物袋的人数统计图 10环保做贡献. ································································································· 6分 六、解答题(共2道小题,共9分)21.解:设这次试车时,由北京到天津的平均速度是每小时x 千米,则由天津返回北京的平均速度是每小时(40)x +千米. ········································································· 1分 依题意,得3061(40)602x x +=+. ···································································· 3分 解得200x =. ······························································································ 4分 答:这次试车时,由北京到天津的平均速度是每小时200千米. ······························ 5分 22.解:(1)重叠三角形A B C '''的面积为3. ··················································· 1分(2)用含m 的代数式表示重叠三角形A B C '''的面积为23(4)m -; ······················· 2分m 的取值范围为843m <≤. ··········································································· 4分七、解答题(本题满分7分) 23.(1)证明:2(32)220mx m x m -+++=是关于x 的一元二次方程,222[(32)]4(22)44(2)m m m m m m ∴∆=-+-+=++=+.当0m >时,2(2)0m +>,即0∆>.∴方程有两个不相等的实数根. ········································································ 2分(2)解:由求根公式,得(32)(2)2m m x m+±+=.22m x m+∴=或1x =. ·················································································· 3分 0m >, 222(1)1m m m m++∴=>. 12x x <,11x ∴=,222m x m +=. ················································································ 4分 21222221m y x x m m+∴=-=-⨯=.即2(0)y m m =>为所求. ······················· 5分(3)解:在同一平面直角坐标系中分别画出4 3 2 1xy2(0)y m m=> 2(0)y m m =>。
北京西城区2019中考一模试卷-数学

3下面各题均有四个选项,其中只有一个..是符合题意的、 1、计算:2()A 、-1B 、-3C 、3D 、52、我市深入实施环境污染整治,某经济开发区的40家化工企业中已关停、整改32家,每年排放的污水减少了167000吨、将167000用科学记数法表示为() A 、316710⨯ B 、416.710⨯ C 、51.6710⨯ D 、60.16710⨯ 3、,如图,AD 与BC 相交于点O ,AB ∥CD ,如果∠B =20°,∠D =40°,那么∠BOD 为() A 、40° B 、50° C 、60° D 、70°4、因式分解()219x --的结果是()A 、()()24x x +- B 、()()81x x ++C 、()()24x x -+ D 、()()108x x -+5、如图,是由一些相同的小正方体搭成的几何体的三视图,搭成这个几何体的小正方体的个数有()A 、2个B 、3个C 、4个D 、6个6、抛一枚均匀硬币正面朝上的概率为12,以下说法正确的选项是()A 、连续抛一枚均匀硬币2次必有1次正面朝上B 、连续抛一枚均匀硬币10次都可能正面朝上C 、大量反复抛一枚均匀硬币,平均每100次出现下面朝上50次D 、通过抛一枚均匀硬币确定谁先发球的比赛规那么是公平的 7、如图,AB 是⊙O 的直径,AB =4,AC 是弦,AC =AOC 为()A 、120°B 、130°C 、140°D 、150°8、如图,在△ABC 中,∠ACB =90°,AC=BC =2、E 、F 分别是射线AC 、CB 上的动点,且AE =BF ,EF 与AB 交于点G ,EH ⊥AB 于点H ,设AE =x ,GH =y ,下面能够反映y 与x 之间函数关系的图象是()ACBOCACE DCBA【二】填空题(此题共16分,每题4分)9、函数y =__________、 10、如图,点P 在双曲线(0)k y k x =≠上,点(12)P ',与点P 关于y 轴对称,那么此双曲线的解析式为、11、如图,在平面直角坐标系中,等边三角形ABC 的顶点B ,C,0),过坐标原点O 的一条直线分别与边AB ,AC 交于点M ,N ,假设OM =MN ,那么点M 的坐标为______________、12、如图,点A 1,A 2,A 3,A 4,…,A n 在射线OA 上,点B 1,B 2,B 3,…,B n ―1在射线OB 上,且A 1B 1∥A 2B 2∥A 3B 3∥…∥A n ―1B n ―1,A 2B 1∥A 3B 2∥A 4B 3∥…∥A n B n ―1,△A 1A 2B 1,△A 2A 3B 2,…,△A n ―1A n B n ―1为阴影三角形,假设△A 2B 1B 2,△A 3B 2B 3的面积分别为1、4,那么△A 1A 2B 1的面积为__________;面积小于2017的阴影三角形共有__________个、2),【三】解答题(此题共30分,每题5分) 13、计算:1024sin 60(-︒-、14、〔1〕解不等式:112x x >+; 〔2〕解方程组20328x y x y -=⎧⎨+=⎩15、:如图,A 点坐标为302⎛⎫- ⎪⎝⎭,,B点坐标为()03,、 〔1〕求过A B ,两点的直线解析式;〔2〕过B 点作直线BP 与x 轴交于点P ,且使2OP OA =,求ABP ∆的面积、x16、如图,分别以Rt △ABC 的直角边AC 及斜边AB 向外作等边△ACD 、等边△ABE 、∠BAC =30º,EF ⊥AB ,垂足为F ,连结DF 、 〔1〕求证:AC =EF ;〔2〕求证:四边形ADFE 是平行四边形、17、先化简:2313(1)2349223x x x x ÷⋅++--;假设结果等于23,求出相应x 的值、18、在某市举办的“读好书,讲礼仪”活动中,东华学校积极行动,各班图书角的新书、好书不断增多,除学校购买外,还有师生捐献的图书、下面是七年级〔1〕班全体同学捐献图书的情况统计图:请你根据以上统计图中的信息,解答以下问题: 〔1〕该班有学生多少人? 〔2〕补全条形统计图;〔3〕七〔1〕班全体同学所捐献图书的中位数和众数分别是多少?O1 23 4 5 A B DEF【四】解答题(此题共20分,每题5分)19、某批发商以每件50元的价格购进800件T 恤、第一个月以单价80元销售,售出了200件;第二个月如果单价不变,预计仍可售出200件,批发商为增加销售量,决定降价销售,根据市场调查,单价每降低1元,可多售出10件,但最低单位应高于购进的价格;第二个月结束后,批发商将对剩余的T 恤一次性清仓销售,清仓时单价为40元、设第二个月单价降低x 元、 〔1〕填表(不需要化简)时间 第一个月 第二个月 清仓时 单价(元) 80 ▲ 40 销售量(件)200 ▲ ▲〔2〕如果批发商希望通过销售这批T 恤获利9000元,那么第二个月的单价应是多少元? 20、如图,等腰梯形ABCD 中,AD ∥BC ,AD =AB =CD =2,∠C =60°,M 是BC 的中点、 〔1〕求证:△MDC 是等边三角形;〔2〕将△MDC 绕点M 旋转,当MD (即MD ′)与AB 交于一点E ,MC (即MC ′)同时与AD 交于一点F 时,点E ,F 和点A 构成△AEF 、试探究△AEF 的周长是否存在最小值、如果不存在,请说明理由;如果存在,请计算出△AEF 周长的最小值、C'CBM21、如图,ABC △,以BC 为直径,O 为圆心的半圆交AC 于点F ,点E 为弧CF 的中点,连接BE 交AC 于点M ,AD 为△ABC 的角平分线,且AD BE ⊥,垂足为点H 、 〔1〕求证:AB 是半圆O 的切线; 〔2〕假设3AB =,4BC =,求BE 的长、22、:如图1,矩形ABCD 中,AB =6,BC =8,E 、F 、G 、H 分别是AB 、BC 、CD 、DA 四条边上的点(且不与各边顶点重合),设m =AB +BC +CD +DA ,探索m 的取值范围、 〔1〕如图2,当E 、F 、G 、H 分别是AB 、BC 、CD 、DA 四边中点时,m =________、〔2〕为了解决这个问题,小贝同学采用轴对称的方法,如图3,将整个图形以CD 为对称轴翻折,接着再连续翻折两次,从而找到解决问题的途径,求得m 的取值范围、 ①请在图1中补全小贝同学翻折后的图形; ②m 的取值范围是____________、H GF EC DBA 图1图2HGF E C D BA 图3A BDCE FGH【五】解答题(此题共22分,第23题7分,第24题7分,第25题8分) 23、一元二次方程x 2+ax +a -2=0、〔1〕求证:不论a 为何实数,此方程总有两个不相等的实数根;〔2〕设a <0,当二次函数y =x 2+ax +a -2的图象与x出此二次函数的解析式;〔3〕在〔2〕的条件下,假设此二次函数图象与x 轴交于A 、B 两点,在函数图象上是否存在点P ,使得△PAB,假设存在求出P 点坐标,假设不存在请说明理由、 24、如图,在△ABC 中,点D 是BC 上一点,∠B =∠DAC =45°、〔1〕如图1,当∠C =45°时,请写出图中一对相等的线段;_________________ 〔2〕如图2,假设BD =2,BAAD 的长及△ACD 的面积、图1CD BA图2ABD C25、巳知二次函数y =a (x 2-6x +8)(a >0)的图象与x 轴分别交于点A 、B ,与y 轴交于点C 、点D 是抛物线的顶点、〔1〕如图①、连接AC ,将△OAC 沿直线AC 翻折,假设点O 的对应点0'恰好落在该抛物线的对称轴上,求实数a 的值;〔2〕如图②,在正方形EFGH 中,点E 、F 的坐标分别是(4,4)、(4,3),边HG 位于边EFA A A的右侧、小林同学经过探索后发现了一个正确的命题:“假设点P 是边EH 或边HG 上的任意一点,那么四条线段PA 、PB 、PC 、PD 不能与任何一个平行四边形的四条边对应相等(即这四条线段不能构成平行四边形)、“假设点P 是边EF 或边FG 上的任意一点,刚才的结论是否也成立?请你积极探索,并写出探索过程;〔3〕如图②,当点P 在抛物线对称轴上时,设点P 的纵坐标l 是大于3的常数,试问:是否存在一个正数a ,使得四条线段PA 、PB 、PC 、PD 与一个平行四边形的四条边对应相等(即这四条线段能构成平行四边形)?请说明理由、2018年北京市西城区初三一模试卷参考答案1、A 、2、C 、3、C 、4、A 、5、C 、6、A 、7、A 、8、C 、9、x ≥3、 10、2y x -=、11、(54,34) 12、12;6、13、解:原式=1412+=12-、 14、〔1〕解:112x x ->,112x >,所以2x >、 〔2〕21x y =⎧⎨=⎩15、〔1〕23y x =+;〔2〕设P 点坐标为()0x ,,依题意得3x =±,所以P 点坐标分别为()()123030P P -,,,、1132733224ABP S ∆⎛⎫=⨯+⨯= ⎪⎝⎭,213933224ABP S ∆⎛⎫=⨯-⨯=⎪⎝⎭,所以ABP ∆的面积为274或94、 16、略、17、原式=(23)(23)1233)233223x x x x x x +--+⋅⋅⋅+-=23x ;由23x =23,可,解得x18、解:〔1〕因为捐2本的人数是15人,占30%,所以该班人数为1530%=50〔2〕根据题意知,捐4本的人数为:50-(10+15+7+5)=13、(如图)〔3〕七〔1〕班全体同学所捐献图书的中位数是242+=3(本),众数是2本、19、〔1〕80-x ,200+10x ,800-200-(200+10x );〔2〕根据题意,得80×200+(80-x )(200+10x )+40[800-200-(200+10x )]-50×800=9000、整理,得x 2-20x +100=0,解这个方程得x 1=x 2=10, 当x =10时,80-x =70>50、 答:第二个月的单价应是70元、 20、解:〔1〕证明:过点D 作DP ⊥BC ,于点P ,过点A 作AQ ⊥BC 于点Q ,PQCMB∵∠C =∠B =60°∴CP =BQ =12AB ,CP +BQ =AB ,又∵ADPQ 是矩形,AD =PQ , 故BC =2AD ,由,点M 是BC 的中点, BM =CM =AD =AB =CD ,即△MDC 中,CM =CD ,∠C =60°, 故△MDC 是等边三角形、〔2〕解:△AEF 的周长存在最小值,理由如下:连接AM ,由〔1〕平行四边形ABMD 是菱形, △MAB ,△MAD 和△MC ′D ′是等边三角形,∠BMA =∠BME +∠AME =60°,∠EMF =∠AMF +∠AME =60°, ∴∠BME =∠AMF ,在△BME 与△AMF 中,BM =AM ,∠EBM =∠FAM =60°, ∴△BME ≌△AMF (ASA ),∴BE =AF ,ME =MF ,AE +AF =AE +BE =AB ,∵∠EMF =∠DMC =60°,故△EMF 是等边三角形,EF =MF , ∵MF 的最小值为点M 到ADEF△AEF 的周长=AE +AF +EF =AB +EF , △AEF 的周长的最小值为2答:存在,△AEF 的周长的最小值为2、 21、〔1〕连结CE ,过程略;〔2〕∵3AB =,4BC =、由〔1〕知,90ABC ∠=,∴5AC =、在ABM △中,AD BM ⊥于H ,AD 平分BAC ∠, ∴3AM AB ==,∴2CM =、 由CME △∽BCE △,得12EC MC EB CB ==、∴2EB EC =,∴BE = 22、〔1〕20;〔2〕如下图(虚线可以不画),20≤m <28、H GFE CDBA23、解:〔1〕因为△=a 2-4(a -2)=(a -2)2+4>0,所以不论a 为何实数,此方程总有两个不相等的实数根、〔2〕设x 1、x 2是y =x 2+ax +a -2=0的两个根,那么x 1+x 2=-a ,x 1•x 2=a -2,因两,所以|x 1-x 2|、即:(x 1-x 2)2=13变形为:(x 1+x 2)2-4x 1•x 2=13所以:(-a )2-4(a -2)=13 整理得:(a -5)(a +1)=0解方程得:a =5或-1 又因为:a <0,所以:a =-1所以:此二次函数的解析式为y =x 2-x -3、〔3〕设点P 的坐标为(x 0,y 0),因为函数图象与x, 所以:ABS △PAB =12AB •|y 0|即:|y 0|=3,那么y 0=±3当y 0=3时,x 02-x 0-3=3,即(x 0-3)(x 0+2)=0 解此方程得:x 0=-2或3当y 0=-2时,x 02-x 0-3=-3,即x 0(x 0-1)=0 解此方程得:x 0=0或1综上所述,所以存在这样的P 点,P 点坐标是(-2,3),(3,3),(0,-3)或(1,-3)、 24、〔1〕AB =AC 或AD =BD =CD ; 〔2〕AD1,S △ACD提示:过点A 作AE ⊥BC ,可以求出AD 的长、过D 作平行线或过C 作垂线,可以利用两次相似求面积、ECDBAFABDCGCDB A25、解:〔1〕令y =0,由2(68)0a x x -+=解得122,4x x ==;令x =0,解得y =8A 、∴点A 、B 、C 的坐标分别是(2,0)、(4,0)、(0,8a ), 该抛物线对称轴为直线x =3、 ∴OA =2、如图①,设抛物线对称轴与x 轴交点为M ,那么AM =1、 由题意得:2O A OA '==、 ∴2O A AM '=,∴∠O ′AM =60°、∴OC AO ==,即8a =、∴a =、 〔2〕假设点P 是边EF 或边FG 上的任意一点,结论同样成立、(Ⅰ)如图②,设点P 是边EF 上的任意一点(不与点E 重合),连接PM 、 ∵点E (4,4)、F (4,3)与点B (4,0)在一直线上,点C 在y 轴上, ∴PB <4,PC ≥4,∴PC >PB 、 又PD >PM >PB ,PA >PM >PB , ∴PB ≠PA ,PB ≠PC ,PB ≠PD 、∴此时线段PA 、PB 、PC 、PD 不能构成平行四边形、 (Ⅱ)设P 是边FG 上的任意一点(不与点G 重合), ∵点F 的坐标是(4,3),点G 的坐标是(5,3)、 ∴FB =3,GB =3≤PB∵PC ≥4,∴PC >PB 、图①〔3〕存在一个正数a ,使得线段PA 、PB 、PC 能构成一个平行四边形、 如图③,∵点A 、B 时抛物线与x 轴交点,点P 在抛物线对称轴上, ∴PA =PB 、∴当PC =PD 时,线段PA 、PB 、PC 能构成一个平行四边形、 ∵点C 的坐标是(0,8a ),点D 的坐标是(3,-a )、 点P 的坐标是(3,t ),∴PC 2=32+(t -8a )2,PD 2=(t +a )2、 整理得7a 2-2ta +1=0,∴Δ=4t 2-28、 ∵t 是一个常数且t >3,∴Δ=4t 2-28>0∴方程7a 2-2ta +1=0有两个不相等的实数根a ==、(图②)(图③)显然0a =>,满足题意、∵当t 是一个大于3的常数,存在一个正数7t a +=,使得线段PA 、PB 、PC 能构成一个平行四边形、。
2008年北京市西城区中考数学一模试卷

2008年北京市西城区中考数学一模试卷第Ⅰ卷(机读卷 共32分)一、选择题(共8个小题,每小题4分,共32分) 1.2的相反数是( ) A .-2B .2C .0D .-21 2.长城总长约为6700000米,用科学记数法表示是( ) A .67×105米 B .6.7×106米 C .0.67×109米 D .6.7×108米 3.如图,l 1∥l 2,∠1=120°,∠2=100°,则∠3=( )第3题图A .20°B .40°C .50°D .60° 4.若实数x 、y 满足(x +y +2)(x +y -1)=0,则x +y 的值为( ) A .1 B .-2 C .2或-1 D .-2或15.在一次射击练习中,王明的射击成绩(单位:环)分别是9,8,9,10,9.下列关于这组数据的说法中错误的是( ) A .平均数是9 B .中位数是9 C .众数是9 D .方差是96.如图,在△ABC 中,AB =AC ,∠A =36°,BD 平分∠ABC ,DE ∥BC ,在图中与△ABC 相似的三角形(不包括△ABC )的个数为( )个第6题图A .0B .1C .2D .37.正方体骰子的六个面上分别刻有1到6的点数,抛掷二枚相同的正方体骰子并掷得点数和为8,且这两个点数均为奇数的概率是( ) A .21 B .365 C .181 D .53 8.如图,若正方形OABC 、ADEF 的顶点A 、D 、C 在坐标轴上,点F 在AB 上,点B 、E 在函数xy 1(x >0)的图象上,则点E 的坐标是( )第8题图A .⎪⎪⎭⎫⎝⎛-+215,215 B .⎪⎪⎭⎫⎝⎛+-215,215 C .⎪⎪⎭⎫⎝⎛+-253,253D .⎪⎪⎭⎫⎝⎛-+253,253第Ⅱ卷(非机读卷 共88分)二、填空题(共4个小题,每小题4分,共16分)9.某种商品的价格为a 元,该商品经过两次降价后,它的价格降低到原来价格的36%,若平均每次降低的百分率相同,设为x ,则x =________.(用百分数表示)10.如图,在Rt △ABC 中,∠BAC =90°,AB =AC =2,若以AB 为直径的圆交BC 于点D ,则阴影部分的面积是________.第10题图11.为了估计湖中有多少条鱼,先从湖中捕捉50条鱼并做上记号,然后放回湖里,经过一段时间,等带记号的鱼完全混于鱼群中之后,再第二次捕捞鱼共200条,有10条做了记号,则估计湖里有________条鱼.12.如图所示,将一张矩形纸片对折,可得到一条折痕(图中的虚线),连续对折,对折时每次折痕与上次折痕保持平行,连续操作三次可以得到7条折痕,那么对折n 次可得到折痕的条数是________.…第12题图三、解答题(共13个小题,共75分)13.(5分)计算:ο60tan )7π(273102+--+⎪⎭⎫⎝⎛-.14.(5分)解方程组⎩⎨⎧=+=+②①.832,723y x y x15.(5分)先化简再求值:1112421222-÷+--+-⋅m m m m m m ,其中3=m .16.(5分)已知:如图,△ABC 是等腰直角三角形,D 为AB 边上的一点,∠ACB =∠DCE=90°,DC =EC . 求证:∠B =∠EAC .第16题图17.(5分)已知关于x 的一元二次方程x 2-2(m +1)x +m 2-2m -3=0的两个不相等的实根中,有一个根是0,求m 的值.18.(5分)如图,四边形ABCD 中,一组对边AB =DC =4,另一组对边AD ≠BC ,对角线BD 与边DC 互相垂直,M 、N 、H 分别是AD 、BC 、BD 的中点,且∠ABD =30°. 求:(1)MH 的长; (2)MN 的长.第18题图19.(5分)如图,⊙O 的直径AB =6,C 为圆周上的一点,BC =3.过C 点作⊙O 的切线GE ,作AD ⊥GE 于点D ,交⊙O 于点F .(1)求证:∠ACG=∠B.(2)计算线段AF的长.第19题图20.(4分)平面直角坐标系xOy中,点A的坐标是(6,0),点P满足AP=OP=6.(1)直接写出点P的坐标;(2)若点P在直线y=-x+m上,求m的值.21.(5分)如图,梯形纸片ABCD中,AD∥BC,AB≠DC.设AD=a,BC=b.过AD的中点和BC的中点的直线可将梯形纸片ABCD分成面积相等的两部分.请你再设计一种方法,只须用剪刀剪一次就将梯形纸片ABCD分割成面积相等的两部分.画出设计的图形并简要说明你的分割方法.第21题图22.(6分)某区组织文艺汇演,甲、乙两校共92人(其中甲校人数多于乙校人数,且甲校人购买服装的套数1套至45套46套至90套91套及以上每套服装的价格60元50元40元如果两所学校分别单独购买服装,一共应付5000元.(1)如果甲、乙两校联合起来购买服装,那么比各自购买服装共可以节省多少钱?(2)甲、乙两校各有多少学生准备参加演出?(3)如果甲校有9名同学抽调去参加书法比赛而不能参加演出,请你设计一种两校联合购买服装最省钱的方案(直接写出购买方案,不必说明理由).23.(7分)如图,四边形ABCD的对角线AC、BD交于点P,过点P作直线交AD于点E,交BC于点F.若PE=PF,且AP+AE=CP+CF.(1)求证:P A=PC.(2)若AD=12,AB=15,∠DAB=60°,求四边形ABCD的面积.第23题图24.(7分)已知抛物线C1:y=ax2-2amx+am2+2m+1(a>0,m>1)的顶点为A,抛物线C2的对称轴是y轴,顶点为点B,且抛物线C1和C2关于点P(1,3)成中心对称.(1)用含m的代数式表示抛物线C1的顶点坐标;(2)求m的值和抛物线C2的解析式;(3)设抛物线C2与x轴正半轴的交点是C,当△ABC为等腰三角形时,求a的值.第24题图25.(8分)如图,正六边形ABCDEF中,点M在AB边上,∠FMH=120°,MH与六边形外角的平分线BQ交于点H.(1)当点M不与点A、B重合时,求证:∠AFM=∠BMH.(2)当点M在正六边形ABCDEF一边AB上运动(点M不与点B重合)时,猜想FM与MH的数量关系,并对猜想的结果加以证明.第25题图答 案19.2008年北京市西城区中考数学一模试卷一、选择题1.A 2.B 3.B 4.D 5.D 6.C 7.C 8.A 二、填空题9.40% 10.1 11.1000 12.2n -1 三、解答题13.解:3483133960tan )7π(273102+=+-+=+--+⎪⎭⎫⎝⎛-ο.14.解:①×2-②×3,得y =2.将y =2代入方程②,得x =1.所以⎩⎨⎧==2,1y x 是原方程组的解.15.解:-+--++-=-÷+--+-⋅⋅⋅⋅m m m m m m m m m m m m m ()1()1()2)(2(21111242122221)=(m -2)(m +1)=m 2-m -2.将m =3代入上式,得(3)2-3-2=1-3. 16.证明:∵△ABC 是等腰直角三角形,∠ACB =90°,第16题答图∴AC =CB .∵∠ACB =∠DCE =90°,∴∠ACE =90°-∠ACD =∠DCB .在△ACE 和△BCD 中,⎪⎩⎪⎨⎧=∠=∠=,,,DC EC BCD ACE CB AC∴△ACE ≌△BCD . ∴∠B =∠EAC .17.解:∵x =0是原方程的根,∴m 2-2m -3=0.解得m 1=3,m 2=-1.又b 2-4ac =[-2(m +1)]2-4(m 2-2m -3)=16m +16.∵方程有两个不等的实根,∴b 2-4ac >0,得16m +16>0,得m >-1. 故应舍去m =-1,得m =3为所求. 18.解:(1)∵M 、H 分别是AD ,BD 的中点,∴MH ∥AB ,AB MH 21=.∵AB=4,∴MH=2.(2)连结HN,作HQ⊥MN,交MN于点Q.同(1)可知,HN∥DC,HN=2.∴△MHN是等腰三角形.∵∠ABD=30°,∠BDC=90°,∴∠MHN=120°.∵HQ⊥MN,∴HQ平分∠MHN,NQ=QM.∵MH=2,∠MHQ=60°,∴MQ=HM·sin60°=3,∴MN=2MQ=23.第18题答图19.(1)证明:连结OC,BF.∵GE是过点C的⊙O的切线,∴OC⊥GE,即∠ACG+∠OCA=90°.∵AB是⊙O的直径,AO=OC,C为圆周上的一点,∴∠ACB=90°,∠BAC=∠OCA.∵∠B+∠CAB=90°,∴∠B=∠ACG.(2)解:∵Rt△ACB中,AB=6,BC=3,∴∠CAB=30°.∵∠B=∠ACG,AD⊥GE,∴∠CAD=30°.∴∠CAD+∠CAB=60°∵AB是⊙O的直径,∴∠AFB=90°∵AB=6,∴AF=AB.cos60°=3.第19题答图20.解:(1)P1(3,33),P2(3,-33).(2)将P1(3,33)代入y=-x+m中,得m=3+33.将P2(3,-33)代入y=-x+m中,得m=3-33.21.方法一:如图①,取)(21b a BM +=,连结AM .AM 把梯形纸片ABCD 分成面积相等的两部分.方法二(如图②):(1)取DC 的中点G ,过G 作EF ∥AB ,交BC 于点F ,交AD 的延长线于点E .(2)连结AF ,BE ,相交于点O .(3)过O 任作直线MN ,分别与AD ,BC 相交于点N 、M ,沿MN 剪一刀即把梯形纸片ABCD 分成面积相等的两部分.第21题答图①第21题答图②22.解:(1)如果甲、乙两校联合起来购买服装需40×92=3680(元).比各自购买服装共可以节省:5000-3680=1320(元).(2)设甲校有学生x 人(依题意,46<x <90),则乙校有学生(92-x )人.依题意,50x +60×(92-x )=5000.解得x =52,有92-x =40. 故甲校有52人,乙校有40人.(3)按每套服装40元一次购买91套服装最省钱. (理由如下:如果甲校有9名同学抽调去参加书法比赛而不能参加演出,则甲校有43人,乙校有40人.依题意,50×(43+40)=4150(元).依题意,若联合买91套服装,需40×91=3640(元). 因为4150>3640,所以联合购买91套服装最省钱)23.(1)证明:在P A 和PC 的延长线上分别取点M 、N ,使AM =AE ,CN =CF .第23题答图∵AP +AE =CP +CF , ∴PN =PM . ∵PE =PF ,∴四边形EMFN 是平行四边形. ∴ME =FN ,∠EMA =∠CNF .又∵∠AME =∠AEM ,∠CNF =∠CFN ,∴△EAM ≌△FCN .∴AM =CN .∵PM =PN ,∴P A =PC . (2)解:∵P A =PC ,EP =PF , ∴四边形AFCE 为平行四边形. ∴AE ∥CF .∵∠PED =∠PFB ,∠EPD =∠FPB ,EP =PF , ∴△PED ≌△PFB .∴DP =PB .由(1)知P A =PC , ∴四边形ABCD 为平行四边形.∵AB =15,AD =12,∠DAB =60°, ∴四边形ABCD 的面积为903.24.解:(1)因为y =ax 2-2amx +am 2+2m +1=a (x -m )2+2m +1,所以抛物线C 1的顶点为A (m ,2m +1).(2)如图,因为点A 、B 关于点P (1,3)成中心对称,作PE ⊥y 轴于点E ,作AF ⊥y 轴于点F ,可知△BPE ∽△BAF .所以AF =2PE ,即m =2.又P (1,3),A (2,5),设直线AP 的解析式为y =kx +b ,把A 、P 的坐标代入得⎩⎨⎧+=+=.3,25b k b k所以k =2,b =1.故直线AB 的解析式是y =2x +1,得抛物线C 2的顶点的坐标是B (0,1).因为C 1、C 2关于点P 成中心对称,所以抛物线的开口大小相同,方向相反,得C 2的解析式是y =-ax 2+1.(3)在Rt △ABF 中,因为AB =2242+=25<5,所以不存在AB =AC 的情况.当△ABC 为等腰三角形时,只有以下两种情况:第24题答图①第24题答图②第24题答图③①如图②,设C (x ,0),若BC =AB =25,则1922=-=OB BC OC ,得C (19,0).又C (19,0)在抛物线y =-ax 2+1上,则191=a . ②如图③,若AC =BC ,设C (x ,0),作AD ⊥x 轴于点D . 在Rt △OBC 中,BC 2=x 2+1.在Rt △ADC 中,AC 2=(x -2)2+25. 由x 2+1=(x -2)2+25,解得x =7.因为C (7,0)在抛物线y =-ax 2+1上,所以491=a . 综上,使△ABC 是等腰三角形的a 的值有两个:1911=a ,4912=a .25.(1)证明:∵六边形ABCDEF 为正六边形,∴每个内角均为120°.∵∠FMH =120°,A 、M 、B 在一条直线上,∴∠AFM +∠FMA =∠FMA +∠BMH =60°∴∠AFM =∠BMH .第25题答图①(2)解:猜想:FM =MH .证明:①当点M 与点A 重合时,∠FMB =120°,MB 与BQ 的交点H 与点B 重合,有FM =MH .②当点M 与点A 不重合时,证法一:如图①,连结FB 并延长到G ,使BG =BH ,连结MG . ∵∠BAF =120°,AF =AB ,∴∠AFB =∠FBA =30°.⎪⎩⎪⎨⎧=∠=∠=,,,MB MB MBG MBH BG BH Θ ∴△MBH ≌△MBG . ∴∠MHB =∠MGB ,MH =MG .∵∠AFM =∠BMH ,∠HMB +∠MHB =30°, ∴∠AFM +∠MGB =30°. ∵∠AFM +∠MFB =30°,∴∠MFB =∠MGB .∴FM =MG =MH .证法二:如图②,在AF 上截取FP =MB ,连结PM . ∵AF =AB ,FP =MB ,∴P A =AM∵∠A =120°, ∴οοο30)120180(21=-⨯=∠APM , 有∠FPM =150°.∵BQ 平分∠CBN ,∴∠MBQ =120°+30°=150°, 有∠FPM =∠MBH .由(1)知∠PFM =∠HMB , ∴△FPM ≌△MBH .∴FM =MH .第25题答图②。
8年北京市中考数学试卷(含答案)

一、选择题(共 8 道小题,每小题 4 分,共 32 分)
1. 6 的绝对值等于(
)A. 6
B. 1
6
C. 1
6
D. 6
【2者【.解解,析析截A创】.】止历AD0到.2届16h奥欢2t01t运0p0迎58:会/ 访/年b之l问o5最gB月...si将n12a91..6c日o21m,103.已6c0n有0/ b用e2i1j科Cin.6学g0s20记.t1u6名数d1y中法03 外表记示者应成为D.为(2北.16京1奥04运)会的注册记
依题意,得 30
6 x
1 (x
40) . · ··········
3分
60
2
解得 x 200 . ················· 4 分
答:这次试车时,由北京到天津的平均速度是每小时 200 千米. 5 分
2已点按2知图.G(等.本1D边E小所三题示B角C满方形于分式纸点折片4E叠,分,过A)hB欢点点Ct t的p迎G:A/边作,访/ b长BG,l问oF为Cg.分s8Bi,别Cna于落.Dc点o为在m点FA.cB,n边把A/ b,上三ei的角jBin,点形gs,纸Ct u过片处dy点.AB若CD点分作别ADG沿,∥BDBGC,,交DCEA在,CG矩于F
据这
1 100
位2 顾3客图平41均一5 次6购物7 使塑用料塑袋料数购/物袋的平均数,图估2计这个超市每天需要
为顾客提供多少个塑料购物袋? (2)补全图 2,并根.据.统.计.图.和.统.计.表.说.明. ,购物时怎样选用购物袋,塑料购物
袋使用后怎样处理,能对环境保护带来积极的影响.
【解析】 ⑴ 补全图 1 见下图. 1 分
【解析】 ⑴ 直线 BD 与 e O 相切. 1 分
5西城区抽样测试 (一模)

北京市西城区2008年抽样测试 2008.5初三数学第Ⅰ卷 (机读卷 共32分)一、选择题(共8个小题,每小题4分,共32分) 1.2的相反数是( ).A.-2B.2C.0D.12-2.长城总长约为6700000米,用科学记数法表示是( ). A. 51067⨯米 B. 66.710⨯米 C. 0.67910⨯米 D.86.710⨯米 3.如图,12//l l ,1120︒∠=,2100︒∠=,则3∠=( ). A. 20︒B. 40︒C.50︒D.60︒4.若实数x 、y 满足(x+y+2)(x+y -1)=0,则x+y 的值为( ). A.1 B. -2 C.2或-1 D.-2或15.在一次射击练习中,王明的射击的成绩(单位:环)分别是9,8,9,10,9.下列关于这组数据的说法中错误的是( ).A.平均数是9B.中位数是9C. 众数是9D.方差是96.如图,在△ABC 中,AB=AC,36A ︒∠=,BD 平分ABC ∠,DE//BC,在图中与△ABC 相似的三角形(不包括△ABC )的个数有( )个.A.0B.1C.2D.37.正方体骰子的六个面上分别刻有1到6的点数,抛掷二枚相同的正方体骰子并掷得点数和为8,且这两个点数均为奇数的概率是( ). A. 12 B. 536C. 181D.3512l 2l 13AB CDEx8.如图,若正方形OABC,ADEF 的顶点A 、D 、C 在坐标轴上,点F 在AB上,点B 、E 在函数1y x=(0x >)的图象上,则点E 的坐标是(). A.11(,)22B. 11(,)22C.D.第Ⅱ卷 (非机读卷 共88分)二、填空题(共4个小题,每小题4分,共16分)9.某种商品价格a 元,该商品经过两次降价后它的价格降低到原来价格的36%,若平均每次降低的百分率相同,设为x,则x= .10.如图,在Rt ABC ∆中,90BAC ︒∠=,AB=AC=2,若以AB 为直径的圆交BC 于点D,则阴影部分的面积是 . 11.为了估计湖中有多少条鱼,先从湖中捕捉50条鱼做记号,然后放回湖里,经过一段时间,等带记号的鱼完全混于鱼群中之后,再捕捞第二次鱼共200条,有10条做了记号,则估计湖里有 条鱼.12.如图所示,将一张矩形纸片对折,可得到一条折痕(图中的虚线),连续对折,对折时每次折痕与上次折痕保持平行,连续操作三次可以得到7条折痕,那么对折n 次可得到折痕的条数是 .三、解答题(共5个小题,共25分) 13.(本题满分5分) 计算:︒-+--+60tan )7(27)31(02π.14.(本题满分5分) 解方程组:327,238.x y x y +=⎧⎨+=⎩15.(本题满分5分)先化简再求值:2221412211m m m m m m --⋅÷+-+-,其中m . 16.(本题满分5分)已知:如图,ABC ∆是等腰直角三角形,D 为AB 边上的一点,90ACB DCE ︒∠=∠=,DC=EC.求证:B EAC ∠=∠. 17.(本题满分5分)已知关于x 的一元二次方程222(1)230x m x m m -++--=的两个不相等的实根中,有一个根是0,求m 的值.BADCE18.(本题满分5分) 如图,四边形ABCD 中,一组对边AB=DC=4,另一组对边AD ≠BC ,对角线BD 与边DC 互相垂直, M 、N 、H 分别是AD 、BC 、BD 的中点,且30ABD ︒∠=.求(1)MH 的长; (2)MN 的长. 19.(本题满分5分)如图,⊙O 的直径AB=6,C 为圆周上的一点,BC=3.过点C 作⊙O的切线GE ,作AD ⊥GE 于点D ,交⊙O 于点F. (1)求证:∠ACG=∠B (2)计算线段AF 的长.DBCA HMNA B CD 20.(本题满分4分)平面直角坐标系xOy 中,点A 的坐标是(6,0),点P 满足AP=OP=6. (1)直接写出点P 的坐标;(2)若点P 在直线y x m =-+上,求m 的值.21.(本题满分5分)如图,梯形纸片ABCD 中,AD ∥BC 且AB ≠DC.设AD=a,BC=b.过AD 中点和BC 的中点的直线可将梯形纸片ABCD 面积分成面积相等的两部分. 请你再设计一种方法: 只须用剪子剪一次将梯形纸片ABCD 分割成面积相等的二部分, 画出设计的图形并简要说明你的分割方法.六.解答题22.(本题满分6分)某区组织文艺汇演,甲、乙两校共92人(其中甲校人数多于乙校人数,且甲校人数不够90人)准备统一购买服装参加演出,下面是服装厂给出的演出服装的价格表:如果两所学校分别单独购买服装,一共应付5000元.(1)如果甲、乙两校联合起来购买服装,那么比各自购买服装共可以节省多少钱?(2)甲、乙两校各有多少学生准备参加演出?(3)如果甲校有9名同学抽调去参加书法比赛不能参加演出,请你设计一种两校联合购买服装最省钱的方案(直接写出购买方案,不必说明理由).七.解答题(本题满分7分) 23.(本题满分7分)如图,四边形ABCD 的对角线AC 、BD 交于点P ,过点P 作直线 交AD 于点E ,交BC 于点F. 若PE=PF ,且AP+AE=CP+CF. (1)求证:PA=PC ;(2)若AD=12,AB=15,60DAB ︒∠=,求四边形ABCD 的面积.ABCD PEF八.解答题(本题满分7分)24.已知抛物线1C :22221y ax amx am m =-+++(0,1)a m >>的顶点为A ,抛物线2C 的对称轴是y 轴,顶点为点B ,且抛物线1C 和2C 关于P (1,3)成中心对称. (1)用m 的代数式表示抛物线1C 的顶点坐标; (2)求m 的值和抛物线2C 的解析式;(3)设抛物线2C 与x 轴正半轴的交点是C ,当ABC ∆为等腰三角形时,求a 的值.九.解答题(本题满分8分) 25.如图,正六边形ABCDEF,点M 在AB 边上,120FMH ︒∠=, MH 与六边形ABC ∠外角的平分线BQ 交于H 点.(1)当点M 不与点A 、B 重合时,求证:∠AFM=∠BMH;(2)当点M 在正六边形ABCDEF 一边AB 上运动(点M 不与点B 重合)时,猜想FM 与MH 的数量关系,并对猜想的结果加以证明.E DF ACBNHQ北京市西城2008年抽样测试 2008.5 数学评分标准和参考答案二、填空题(共4个小题,每小题4分,共16分) 9.40%; 10. 1; 11.1000; 12.21n-. 三.解答题 13.(本题满分5分) 计算:︒-+--+60tan )7(27)31(02π.解:︒-+--+60tan )7(27)31(02π=9+31+-------------------4分. =8+34.----------------------------5分. 14.(本题满分5分) 解方程组: 327(1)238(2)x y x y +=-----⎧⎨+=-----⎩解: (1)2(2)3⨯-⨯,得y=2.--------------------3分. 将y=2代入方程(1),得x=1.---------------------4分. 所以1,2.x y =⎧⎨=⎩是原方程组的解.--------------------5分.15.(本题满分5分)先化简再求值:2221412211m m m m m m --⋅÷+-+-,其中m . 解: 2221412211m m m m m m --⋅÷+-+- =21(2)(2)(1)(1)2(1)m m m m m m m -+-⋅⋅+-+--------------------------2分. =(2)(1)m m -+=22m m --.--------------------------------------------------------------4分.将m 代入上式,得3123)3(2-=-------------------5分.A BDMNHQ16.证明:ABC ∆是等腰直角三角形, 90ACB ︒∠=∴AC=CB.-----------------------1分.90ACB DCE ︒∠=∠=,90ACE ACD DCB ︒∴∠=-∠=∠.---------3分. ACE BCD ∆∆在和中⎪⎩⎪⎨⎧=∠=∠=.,,DC EC BCD ACE CB AC ∴ACE BCD ∆≅∆.--------------------------------4分. ∴B EAC ∠=∠.-------------------------------------5分.17.解:x=0是原方程的根, ∴2230m m --=.解得 123,1m m ==-.------------------------2分.又[]22242(1)4(23)b ac m m m -=-+---=16m +16.------------3分.方程有两个不等的实根,∴240b ac ->,得16160,m +>得 1.m >-------------4分. 故应舍去1m =-,得3m =为所求.--------------------5分. 四.解答题18.解(1)M 、H 分别是AD ,BD 的中点,1//2MH AB MH AB ∴=,.---------------------1分. 4AB =, 2MH ∴=.-------------------------------------------2分.(2)连接HN ,作HQ ⊥MN 交MN 于点Q.--------------3分.同理(1)可知,HN//DC,HN=2.3090ABD BDC ︒︒∠=∠=,,∴MHN ∆是等腰三角形,120MHN ︒∠=.HQ MN ⊥,HQ MHN ∴∠平分,NQ=QM.--------------------------------4分.MH=2,60MHQ ︒∠=,MQHM ∴=sin 60︒2MN MQ ∴==分.BADCEABCDEFGOABCDMAB CDEFG O MN19. 证明: 连结OC,BF.-------------------------1分. (1)GE 是过点C 的⊙O 切线,OC GE ∴⊥,即︒=∠+∠90OCA ACG .AB 是⊙O 的直径,AO=OC,C 为圆周上的一点,∴90,ACB BAC OCA ︒∠=∠=∠.90,B CAB ︒∠+∠=∴B ACG ∠=∠.-------------------------3分.(2)RtACB ∆中,AB=6,BC=3,30CAB ︒∴∠=.B ACG ∠=∠,AD GE ⊥,∴30CAD ︒∠=.----------------------------------4分.︒=∠+∠∴60CAB CAD ..AB 是⊙O 的直径,90AFB ︒∴∠=. 6=AB ,cos60AF AB ︒∴=⋅=3.---------------------------5分.五. 解答题(共2个题,共9分) 20.(本题满分4分)解:(1)12(3,P P -.--------------2分.(2)将1P 代入yx m =-+中,得3m =+ 将2(3,P -代入yx m =-+,得3m =-分. 21. (本题满分5分) 方法1:取BM=1()2a b +,连结AM.AM 把梯形ABCD 分成面积 相等的两部分.方法2: (1)取DC 的中点G,过G 作EF//AB,交BC 于点F,交AD 的 延长线于点E.(2)连结AF,BE 相交于点O.(3)过O 任作直线MN 与AD,BC 相交于点M 、N,沿MN 剪一刀 即把梯形ABCD 分成面积相等的两部分. 说明: (1)用其他方法正确分割且说明方法的给满分.(2)仅画图正确未说明方法的给3分. 六. 解答题(本题满分6分)A BC DE F MNP 22.解:(1) 如果甲、乙两校联合起来购买服装需40⨯92=3680(元).比各自购买服装共可以节省:5000-3680=1320(元).-------------------------2分. (2)设甲校有学生x 人(依题意46<x<90),则乙校有学生(92-x)人.----------3分. 依题意 50x+60⨯ (92-x)=5000. ---------------------------------------------4分. 解出 x=52, 有92-x=40.答:甲校有52人,乙校有40人.---------------------------------------------------5分.(3)按40元一次购买91套服装最省钱.------------------------------------------------------------6分. ( 理由如下: 如果甲校有9名同学抽调去参加书法比赛不能参加演出,则甲校有43人,乙校有40人.依题意 50⨯ (43+40)=4150(元).依题意若联合买91套服装需40⨯91=3640(元). 因为4150>3640,所以选择购买91套服装最省钱).七.解答题(本题满分7分) 23.(本题满分7分)(1)在PA 和PC 的延长线上分别取点M 、N 使AM=AE , CN=CF ,-------------------------------------------------------1分. AP+AE=CP+CF, ∴PN=PM. PE=PF,∴四边形EMFN 是平行四边形.--------------------------2分.∴ME=FN,EMA CNF ∠=∠. AME AEM ∠=∠,CNF CFN ∠=∠,∴EAM FCN ∆≅∆. ∴AM=CN. PM=PN,∴PA=PC.---------------------------------------------------------------4分. (2)PA=PC,EP=PF,∴四边形AFCE 为平行四边形. ∴AE//CF.PED PFB ∠=∠,FPB EPD ∠=∠,EP=PF , PED PFB ∴∆≅∆.有DP=PB,由(1)知PA=PC.∴四边形ABCD 为平行四边形.------------------------------6分. AB=15,AD=12,60DAB ︒∠=,∴四边形ABCD的面积为.-----------------------------7分.24.(1)因为12)(122222++-=+++-=m m x a m am amx ax y , 所以,抛物线1C 的顶点A (m ,2m+1).------------------------2分.(2) 如图,因为点A 、B 关于点P (1,3)成中心对称,作PE ⊥y 轴于点E , 作AF ⊥y 轴于点F ,可知.∽BPE ∆BAF∆所以,AF=2PE,即m=2.--------3分.又P (1,3),A (2,5)设直线AP 的解析式为y=kx+b,把A 、P 的坐标代入得21,3.m km b k b +=+⎧⎨=+⎩所以k=2,b=1.故直线AB 的解析式是y=2x+1,得抛物线2C 的顶点的坐标是B(0,1).-------4分.因为12C C 、关于点P 成中心对称,所以,抛物线的开口大小相同,方向相反, 得2C 的解式是12+-=ax y(3)在Rt ABF ∆中,因为5=<,当ABC ∆为等腰三角形时,只有以下两种情况:①如图1,设C(x,0),若BC=AB=则得又 在21y ax =-+上,则119a =②如图2,若AC=BC ,设C (x ,0),作AD ⊥x 轴于点D , 在RtOBC ∆中,221BC x =+; 在Rt ADC ∆中,22(2)25.AC x =-+ 由221(2)25x x +=-+,解得x=7.因为C(7,0)在21y ax =-+上,所以a=149.综上,满足使ABC ∆是等腰三角形的a 的值有两个:1211,1949a a ==.------------7分.25.(1)六边形ABCDEF 为正六边形,∴每个内角均为120︒.120,FMH ︒∠=A 、M 、B 在一条直线上,∴60AFM FMA FMA BMH ︒∠+∠=∠+∠=.∴∠AFM=∠BMH.-----------------------------------------------2(2)猜想:FM=MH.--------------------------------------------------3分.①当点M 与点A 重合时,︒=∠120FMB ,MB 与BQ 交点H 与点B 重合,有FM=MH .----4分. ②当点M 与点A 不重合时,连结FB 并延长到G 使BG=BH,连结MG .-----------5分.120BAF ︒∠=,AF=AB,图1图230AFB FBA ︒∴∠=∠=.⎪⎩⎪⎨⎧=∠=∠=.,,MB MB MBG MBH BG BH MBH MBG ∴∆≅∆.MHB MGB ∴∠=∠,MH=MG .-------------------------7分.AFM BMH ∠=∠, 30HMB MHB ︒∠+∠=,︒=∠+∠∴30MGB GMB . 30AFM MFB ︒∠+∠=, MFB MGB ∴∠=∠.∴FM=MG=MH.--------------------------------------------------8分.关于②当点M 与点A 不重合时的证法2在AF 上截取FP=MB,连结PM.--------------5分.MB FP AB AF ==, ,∴PA=AM. ︒=∠120A ,︒︒︒=-=∠∴30)120180(21APM ,有︒=∠150FPM . CBN BQ ∠平分 ,︒︒︒=+=∠∴15030120MBQ ,有MBH FPM ∠=∠.----------6分.由(1)知,HMB PFM ∠=∠,MBH FPM ∆∆∴≌.------------------------------7分. MH FM =∴.----------------------------------------8分.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
19 2008年北京市西城区中考数学一模试卷第Ⅰ卷(机读卷 共32分)一、选择题(共8个小题,每小题4分,共32分) 1.2的相反数是( ) A .-2B .2C .0D .-212.长城总长约为6700000米,用科学记数法表示是( )A .67×105米B .6.7×106米 C .0.67×109米D .6.7×108米3.如图,l 1∥l 2,∠1=120°,∠2=100°,则∠3=( )第3题图A .20°B .40°C .50°D .60°4.若实数x 、y 满足(x +y +2)(x +y -1)=0,则x +y 的值为( ) A .1 B .-2 C .2或-1 D .-2或15.在一次射击练习中,王明的射击成绩(单位:环)分别是9,8,9,10,9.下列关于这组数据的说法中错误的是( ) A .平均数是9B .中位数是9C .众数是9D .方差是96.如图,在△ABC 中,AB =AC ,∠A =36°,BD 平分∠ABC ,DE ∥BC ,在图中与△ABC 相似的三角形(不包括△ABC )的个数为( )个第6题图A .0B .1C .2D .37.正方体骰子的六个面上分别刻有1到6的点数,抛掷二枚相同的正方体骰子并掷得点数和为8,且这两个点数均为奇数的概率是( ) A .21 B .365 C .181 D .538.如图,若正方形OABC 、ADEF 的顶点A 、D 、C 在坐标轴上,点F 在AB 上,点B 、E 在函数xy 1(x >0)的图象上,则点E 的坐标是( )第8题图A .⎪⎪⎭⎫⎝⎛-+215,215 B .⎪⎪⎭⎫⎝⎛+-215,215 C .⎪⎪⎭⎫⎝⎛+-253,253 D .⎪⎪⎭⎫⎝⎛-+253,253 第Ⅱ卷(非机读卷 共88分)二、填空题(共4个小题,每小题4分,共16分)9.某种商品的价格为a 元,该商品经过两次降价后,它的价格降低到原来价格的36%,若平均每次降低的百分率相同,设为x ,则x =________.(用百分数表示) 10.如图,在Rt △ABC 中,∠BAC =90°,AB =AC =2,若以AB 为直径的圆交BC 于点D ,则阴影部分的面积是________.第10题图11.为了估计湖中有多少条鱼,先从湖中捕捉50条鱼并做上记号,然后放回湖里,经过一段时间,等带记号的鱼完全混于鱼群中之后,再第二次捕捞鱼共200条,有10条做了记号,则估计湖里有________条鱼. 12.如图所示,将一张矩形纸片对折,可得到一条折痕(图中的虚线),连续对折,对折时每次折痕与上次折痕保持平行,连续操作三次可以得到7条折痕,那么对折n 次可得到折痕的条数是________.…第12题图三、解答题(共13个小题,共75分) 13.(5分)计算:60tan )7π(273102+--+⎪⎭⎫ ⎝⎛-.14.(5分)解方程组⎩⎨⎧=+=+②①.832,723y x y x15.(5分)先化简再求值:1112421222-÷+--+-⋅m m m m m m ,其中3=m .16.(5分)已知:如图,△ABC 是等腰直角三角形,D 为AB 边上的一点,∠ACB =∠DCE=90°,DC =EC .求证:∠B =∠EAC .第16题图17.(5分)已知关于x 的一元二次方程x 2-2(m +1)x +m 2-2m -3=0的两个不相等的实根中,有一个根是0,求m 的值.18.(5分)如图,四边形ABCD 中,一组对边AB =DC =4,另一组对边AD ≠BC ,对角线BD 与边DC 互相垂直,M 、N 、H 分别是AD 、BC 、BD 的中点,且∠ABD =30°. 求:(1)MH 的长; (2)MN 的长.第18题图19.(5分)如图,⊙O 的直径AB =6,C 为圆周上的一点,BC =3.过C 点作⊙O 的切线GE ,作AD ⊥GE 于点D ,交⊙O 于点F .(1)求证:∠ACG=∠B.(2)计算线段AF的长.第19题图20.(4分)平面直角坐标系xOy中,点A的坐标是(6,0),点P满足AP=OP=6.(1)直接写出点P的坐标;(2)若点P在直线y=-x+m上,求m的值.21.(5分)如图,梯形纸片ABCD中,AD∥BC,AB≠DC.设AD=a,BC=b.过AD的中点和BC的中点的直线可将梯形纸片ABCD分成面积相等的两部分.请你再设计一种方法,只须用剪刀剪一次就将梯形纸片ABCD分割成面积相等的两部分.画出设计的图形并简要说明你的分割方法.第21题图22.(6分)某区组织文艺汇演,甲、乙两校共92人(其中甲校人数多于乙校人数,且甲校人数不够90人),准备统一购买服装参加演出,下面是服装厂给出的演出服装的价格表.如果两所学校分别单独购买服装,一共应付5000元.(1)如果甲、乙两校联合起来购买服装,那么比各自购买服装共可以节省多少钱?(2)甲、乙两校各有多少学生准备参加演出?(3)如果甲校有9名同学抽调去参加书法比赛而不能参加演出,请你设计一种两校联合购买服装最省钱的方案(直接写出购买方案,不必说明理由).23.(7分)如图,四边形ABCD的对角线AC、BD交于点P,过点P作直线交AD于点E,交BC于点F.若PE=PF,且AP+AE=CP+CF.(1)求证:PA=PC.(2)若AD=12,AB=15,∠DAB=60°,求四边形ABCD的面积.第23题图24.(7分)已知抛物线C1:y=ax2-2amx+am2+2m+1(a>0,m>1)的顶点为A,抛物线C2的对称轴是y轴,顶点为点B,且抛物线C1和C2关于点P(1,3)成中心对称.(1)用含m的代数式表示抛物线C1的顶点坐标;(2)求m的值和抛物线C2的解析式;(3)设抛物线C2与x轴正半轴的交点是C,当△ABC为等腰三角形时,求a的值.第24题图25.(8分)如图,正六边形ABCDEF中,点M在AB边上,∠FMH=120°,MH与六边形外角的平分线BQ交于点H.(1)当点M不与点A、B重合时,求证:∠AFM=∠BMH.(2)当点M在正六边形ABCDEF一边AB上运动(点M不与点B重合)时,猜想FM与MH的数量关系,并对猜想的结果加以证明.第25题图答 案19.2008年北京市西城区中考数学一模试卷一、选择题1.A 2.B 3.B 4.D 5.D 6.C 7.C 8.A 二、填空题9.40% 10.1 11.1000 12.2n -1 三、解答题 13.解:3483133960tan )7π(273102+=+-+=+--+⎪⎭⎫⎝⎛-.14.解:①×2-②×3,得y =2.将y =2代入方程②,得x =1.所以⎩⎨⎧==2,1y x 是原方程组的解.15.解:-+--++-=-÷+--+-⋅⋅⋅⋅m m m m m m m m m m m m m ()1()1()2)(2(21111242122221)=(m -2)(m +1)=m 2-m -2.将m =3代入上式,得(3)2-3-2=1-3. 16.证明:∵△ABC 是等腰直角三角形,∠ACB =90°,第16题答图∴AC =CB .∵∠ACB =∠DCE =90°,∴∠ACE =90°-∠ACD =∠DCB . 在△ACE 和△BCD 中,⎪⎩⎪⎨⎧=∠=∠=,,,DC EC BCD ACE CB AC∴△ACE ≌△BCD . ∴∠B =∠EAC .17.解:∵x =0是原方程的根,∴m 2-2m -3=0.解得m 1=3,m 2=-1.又b 2-4ac =[-2(m +1)]2-4(m 2-2m -3)=16m +16.∵方程有两个不等的实根,∴b 2-4ac >0,得16m +16>0,得m >-1. 故应舍去m =-1,得m =3为所求. 18.解:(1)∵M 、H 分别是AD ,BD 的中点,∴MH ∥AB ,AB MH 21=.∵AB=4,∴MH=2.(2)连结HN,作HQ⊥MN,交MN于点Q.同(1)可知,HN∥DC,HN=2.∴△MHN是等腰三角形.∵∠ABD=30°,∠BDC=90°,∴∠MHN=120°.∵HQ⊥MN,∴HQ平分∠MHN,NQ=QM.∵MH=2,∠MHQ=60°,∴MQ=HM·sin60°=3,∴MN=2MQ=23.第18题答图19.(1)证明:连结OC,BF.∵GE是过点C的⊙O的切线,∴OC⊥GE,即∠ACG+∠OCA=90°.∵AB是⊙O的直径,AO=OC,C为圆周上的一点,∴∠ACB=90°,∠BAC=∠OCA.∵∠B+∠CAB=90°,∴∠B=∠ACG.(2)解:∵Rt△ACB中,AB=6,BC=3,∴∠CAB=30°.∵∠B=∠ACG,AD⊥GE,∴∠CAD=30°.∴∠CAD+∠CAB=60°∵AB是⊙O的直径,∴∠AFB=90°∵AB=6,∴AF=AB.cos60°=3.第19题答图20.解:(1)P1(3,33),P2(3,-33).(2)将P1(3,33)代入y=-x+m中,得m=3+33.将P2(3,-33)代入y=-x+m中,得m=3-33.21.方法一:如图①,取)(21b a BM +=,连结AM .AM 把梯形纸片ABCD 分成面积相等的两部分.方法二(如图②):(1)取DC 的中点G ,过G 作EF ∥AB ,交BC 于点F ,交AD 的延长线于点E .(2)连结AF ,BE ,相交于点O .(3)过O 任作直线MN ,分别与AD ,BC 相交于点N 、M ,沿MN 剪一刀即把梯形纸片ABCD 分成面积相等的两部分.第21题答图①第21题答图②22.解:(1)如果甲、乙两校联合起来购买服装需40×92=3680(元).比各自购买服装共可以节省:5000-3680=1320(元).(2)设甲校有学生x 人(依题意,46<x <90),则乙校有学生(92-x )人.依题意,50x +60×(92-x )=5000.解得x =52,有92-x =40.故甲校有52人,乙校有40人.(3)按每套服装40元一次购买91套服装最省钱.(理由如下:如果甲校有9名同学抽调去参加书法比赛而不能参加演出,则甲校有43人,乙校有40人.依题意,50×(43+40)=4150(元).依题意,若联合买91套服装,需40×91=3640(元). 因为4150>3640,所以联合购买91套服装最省钱)23.(1)证明:在P A 和PC 的延长线上分别取点M 、N ,使AM =AE ,CN =CF .第23题答图∵AP +AE =CP +CF , ∴PN =PM .∵PE =PF ,∴四边形EMFN 是平行四边形. ∴ME =FN ,∠EMA =∠CNF .又∵∠AME =∠AEM ,∠CNF =∠CFN ,∴△EAM ≌△FCN .∴AM =CN .∵PM =PN ,∴P A =PC . (2)解:∵PA =PC ,EP =PF , ∴四边形AFCE 为平行四边形. ∴AE ∥CF .∵∠PED =∠PFB ,∠EPD =∠FPB ,EP =PF , ∴△PED ≌△PFB .∴DP =PB .由(1)知PA =PC , ∴四边形ABCD 为平行四边形. ∵AB =15,AD =12,∠DAB =60°, ∴四边形ABCD 的面积为903.24.解:(1)因为y =ax 2-2amx +am 2+2m +1=a (x -m )2+2m +1,所以抛物线C 1的顶点为A (m ,2m +1).(2)如图,因为点A 、B 关于点P (1,3)成中心对称,作PE ⊥y 轴于点E ,作AF ⊥y 轴于点F ,可知△BPE ∽△BAF .所以AF =2PE ,即m =2.又P (1,3),A (2,5),设直线AP 的解析式为y =kx +b ,把A 、P 的坐标代入得⎩⎨⎧+=+=.3,25b k b k所以k =2,b =1.故直线AB 的解析式是y =2x +1,得抛物线C 2的顶点的坐标是B (0,1).因为C 1、C 2关于点P 成中心对称,所以抛物线的开口大小相同,方向相反,得C 2的解析式是y =-ax 2+1.(3)在Rt △ABF 中,因为AB =2242+=25<5,所以不存在AB =AC 的情况.当△ABC 为等腰三角形时,只有以下两种情况:第24题答图①第24题答图②第24题答图③①如图②,设C (x ,0),若BC =AB =25,则1922=-=OBBC OC ,得C (19,0).又C (19,0)在抛物线y =-ax 2+1上,则191=a .②如图③,若AC =BC ,设C (x ,0),作AD ⊥x 轴于点D . 在Rt △OBC 中,BC 2=x 2+1. 在Rt △ADC 中,AC 2=(x -2)2+25.由x 2+1=(x -2)2+25,解得x =7.因为C (7,0)在抛物线y =-ax 2+1上,所以491=a .综上,使△ABC 是等腰三角形的a 的值有两个:1911=a ,4912=a .25.(1)证明:∵六边形ABCDEF 为正六边形,∴每个内角均为120°.∵∠FMH =120°,A 、M 、B 在一条直线上,∴∠AFM +∠FMA =∠FMA +∠BMH =60°∴∠AFM =∠BMH .第25题答图①(2)解:猜想:FM =MH .证明:①当点M 与点A 重合时,∠FMB =120°,MB 与BQ 的交点H 与点B 重合,有FM =MH .②当点M 与点A 不重合时,证法一:如图①,连结FB 并延长到G ,使BG =BH ,连结MG . ∵∠BAF =120°,AF =AB ,∴∠AFB =∠FBA =30°. ⎪⎩⎪⎨⎧=∠=∠=,,,MB MB MBG MBH BG BH ∴△MBH ≌△MBG . ∴∠MHB =∠MGB ,MH =MG .∵∠AFM =∠BMH ,∠HMB +∠MHB =30°, ∴∠AFM +∠MGB =30°. ∵∠AFM +∠MFB =30°,网址:www ∴∠MFB =∠MGB .∴FM =MG =MH .证法二:如图②,在AF 上截取FP =MB ,连结PM .∵AF =AB ,FP =MB ,∴PA =AM∵∠A =120°, ∴30)120180(21=-⨯=∠APM , 有∠FPM =150°.∵BQ 平分∠CBN ,∴∠MBQ =120°+30°=150°,有∠FPM =∠MBH .由(1)知∠PFM =∠HMB ,∴△FPM ≌△MBH .∴FM =MH .第25题答图②。
