分形与混沌讲解
分形和混沌的基本概念和应用

分形和混沌的基本概念和应用在科学和数学领域中,分形和混沌是两个非常重要的概念。
它们不仅有着丰富的理论内涵,而且在实际应用中也有着广泛的用途。
本文旨在介绍分形和混沌的基本概念、性质以及其应用领域。
一、分形的基本概念和性质分形最初是由法国数学家Mandelbrot所提出的。
分形,定义简单点来说,就是在各种尺度下都表现出相似性的图形。
比如说,我们在放大树叶时,会发现树叶的分支和小结构上会有许多特征,在不断放大过程中,树叶上的分支和结构会产生类似于整个树叶的结构。
这个例子就是分形学的一个典型例子。
分形的最重要的特性是自相似性和不规则性。
自相似性是指,在分形中,任意一部分都与整个结构相似,这种相似性具有尺度不变性,即不会因为放大或缩小而改变。
不规则性是指,分形的形状十分奇特,与传统的几何图形相比,分形形状复杂多变,没有任何几何规律可循。
分形广泛用于科学研究、艺术美学、计算机图像处理等领域。
在生物学、地震学、天文学中也有广泛应用。
例如,在生物学中,许多生物组织和器官都具有分形结构,如肺组织、血管系统、神经元等。
利用分形理论可以更好地研究这些生物结构的形态和发展规律。
此外,在土地利用和城市规划领域,也可以应用分形理论来研究城市建筑的空间结构和空间分布规律。
二、混沌的基本概念和性质混沌又称为非线性动力学。
混沌指的是用微观因素推算出宏观效应的过程,该过程结果不可预测,但随着时间的推移,能够生成复杂、有规律的系统。
混沌体系可用方程式表示出来,但由于该方程式是个非线性方程式,所以其结果会随这方程式微小变化而产生巨大的差异。
混沌具有以下几个突出的性质:灵敏依赖于初始条件,长期不稳定,难以预测和控制。
混沌理论可以用于预测经济和金融领域中出现的一些紊乱现象,如股市波动。
混沌最初应用在天文学领域,例如研究太阳系中行星之间的轨道。
这些轨道不像我们所想的那样规律。
然而,混沌的发现不仅在天文学领域中应用,也在许多其它领域解决一些不规则的问题。
动力系统理论中的混沌与分形

动力系统理论中的混沌与分形混沌与分形是动力系统理论中的两个重要概念,它们在探索非线性系统行为和描述自然界的复杂性方面发挥着关键作用。
本文将从混沌与分形的基本原理、实际应用以及研究方向等多个角度来探讨这两个重要的理论概念。
一、混沌混沌是指在动力系统中,即使系统的运动规律是确定的,但其行为却表现出极端敏感的特性,即微小的初始条件改变会导致系统演化出完全不同的轨迹。
混沌理论的起源可以追溯到20世纪60年代,当时Lorenz通过研究大气环流模型,意外地发现了这一现象,这也被称为“蝴蝶效应”。
混沌现象的数学描述是通过非线性动力学方程实现的,例如著名的洛伦兹方程和Logistic映射等。
混沌行为的特点是演化过程不断变化,但却不失稳定性。
这种看似矛盾的特性给动力系统理论的研究带来了很大的挑战和启示。
混沌理论的实际应用非常广泛。
在天气和气候预测、金融市场、生态系统、心脏疾病等领域,混沌理论都发挥着重要作用。
通过混沌理论,我们能够更好地理解和预测这些复杂系统中的行为,为实际问题的解决提供了新的思路和方法。
目前,混沌理论仍然是一个活跃的研究领域。
研究人员致力于发展更精确的混沌理论模型,深入探究混沌行为的内在规律,以及在实际应用中的更多可能性。
二、分形分形是指具有自相似性和尺度不变性的几何形状。
与传统几何学中定义的规则形状不同,分形具有复杂的结构和非整数维度。
分形理论最早由Mandelbrot提出,并得到了广泛的应用。
分形的自相似性意味着它的一部分与整体具有相似的结构,这种特性使得分形能够用于描述自然界中许多复杂的形状,如云朵、树枝、河流等。
分形的尺度不变性意味着它在不同的比例下具有相似的结构,这也是分形与传统几何形状的显著区别。
分形理论在各个领域有着广泛的应用。
在计算机图形学中,分形可以用于生成自然风景和仿真自然材料的纹理。
在金融市场中,分形理论可以用于预测和分析股票价格的波动。
在生物学中,分形可以用于描述复杂的生物结构,如血管网络和肺泡等。
上帝的指纹——分形与混沌

上帝的指纹——分形与混沌来源:王东明科学网博客云朵不是球形的,山峦不是锥形的,海岸线不是圆形的,树皮不是光滑的,闪电也不是一条直线。
——分形几何学之父Benoit Mandelbrot话说在一个世纪以前,数学领域相继出现了一些数学鬼怪,其整体或局部特征难以用传统的欧式几何语言加以表述。
著名的数学鬼怪包括处处不稠密而完备的Cantor集,每段长度都无限而围成有限面积的Koch曲线,面积为零而周长无限的Sierpinski三角形。
Koch 曲线Sierpinski 三角形这些数学鬼怪曾缠绕数学家多年,直到20世纪后半叶,才被美籍法国数学家Benoit Mandelbrot创立的分形几何学彻底制服。
分形几何学是新兴的科学分支混沌理论的数学基础。
1967年Mandelbrot在美国《科学》杂志上发表了题为“英国的海岸线到底有多长”的划时代论文,该文标志着分形萌芽的出现。
在这篇文章中Mandelbrot证明了在一定意义上任何海岸线都是无限长的,因为海湾和半岛会显露出越来越小的子海湾和子半岛,他将这种部分与整体的某种相似称为自相似性,它是一种特殊的跨越不同尺度的对称性,意味着图案之中递归地套着图案。
事实上,具有自相似性的现象广泛存在于自然界中,这些现象包括连绵起伏的山川,自由漂浮的云彩,江河入海形成的三角洲以及花菜、树冠、大脑皮层等等。
Mandelbrot将具有自相似性的现象抽象为分形,从而建立了有关斑痕、麻点、破碎、缠绕、扭曲的几何学。
这种几何学的维数可以不是整数,譬如Koch曲线的维数约为1.26,而Sierpinski三角形的维数则接近1.585。
分形植物(在生成分枝形状和叶片图案时遵循简单的递归法则)分形闪电(经历的路径是逐步形成的)Mandelbrot研究了一个简单的非线性迭代公式xn 1=xn2 c,式中xn 1和xn都是复变量,而c是复参数。
Mandelbrot发现,对某些参数值c,迭代会在复平面上的某几点之间循环反复;而对另一些参数值c,迭代结果却毫无规则可言。
非线性动力学混沌和分形

非线性动力学混沌和分形非线性动力学是研究非线性系统行为的学科,其中混沌和分形是两个重要的概念。
本文将从混沌和分形的定义、产生原因以及在自然界和科学领域的应用等方面,探讨非线性动力学中的混沌和分形现象。
一、混沌的定义和产生原因混沌是指在非线性系统中表现出的随机、不可预测的行为。
它与线性系统中稳定、可预测的行为形成对比。
混沌的产生是由于非线性系统的敏感依赖性和非周期性。
非线性系统中存在着参数的微小变化对系统行为的剧烈改变的敏感依赖性。
也就是说,微小的输入扰动会在系统中产生指数级的放大效应,导致系统行为出现不可预测的、随机的演化轨迹。
非周期性是混沌的另一个重要特征。
与周期行为不同,混沌系统的演化轨迹不会重复,而是具有无限多的轨迹。
这种非周期性导致了混沌系统的随机性和不可预测性。
二、分形的定义和产生原因分形是指具有自相似性质的几何结构。
这种自相似性是指无论在何种尺度上观察,都能看到相似的图形形态。
分形在数学上可以通过重复迭代、自身放缩等方式来构造。
分形的产生原因与非线性动力学中的迭代过程密切相关。
在迭代过程中,每一次迭代都会根据某种规则对前一次结果进行变换或修改。
这种迭代的特性导致了分形的自相似性质。
三、混沌和分形在自然界中的应用混沌和分形不仅存在于数学和物理领域,也广泛存在于自然界中的各种系统中。
1. 混沌天气模型气象系统是典型的非线性系统,其中存在着许多复杂的变量相互作用。
应用混沌理论来模拟天气系统,可以更好地理解和预测天气变化。
例如,洛伦茨模型是一个典型的混沌系统,通过该模型可以模拟大气环流的混沌行为。
2. 分形地貌自然界中的许多地貌形状具有分形的特征。
例如,河流的分岔结构、山脉的起伏形态都展现了自相似的分形结构。
分形地貌的研究有助于了解地壳运动和地表形态的演化机制。
3. 植物生长模型植物生长是一个既复杂又多变的过程,涉及到生理、环境和遗传等多个因素的交互作用。
应用非线性动力学的方法,可以通过建立植物生长模型,研究植物生长的混沌行为以及其对环境的响应。
自然科学的混沌与分形

自然科学的混沌与分形一、引言自然科学是研究自然界现象和规律的学科,其中混沌与分形是近年来备受关注的研究领域。
混沌理论和分形几何不仅在物理学、化学、生物学等领域有广泛应用,而且在经济学、社会科学等其他领域也有重要意义。
本文将从混沌与分形的基本概念入手,介绍其在自然科学中的应用及意义。
二、混沌1.混沌的定义混沌是指某些动态系统表现出无序不规则的行为,即使系统初始状态非常相似,其演化结果也会有很大差异。
这些系统可能具有非线性特征或者对初值极其敏感。
2.混沌的起源20世纪60年代初期,美国数学家洛伦兹通过对大气运动方程组的研究发现了混沌现象。
他发现即使初始条件微小变化,天气预报结果也会截然不同。
这个发现引起了人们对于非线性动力系统的关注。
3.混沌在自然科学中的应用(1)天气预报:由于天气系统具有非线性特征,天气预报的准确性受到混沌现象的影响。
(2)流体力学:混沌现象在流体运动中也十分常见,如涡旋、湍流等。
(3)生物学:许多生物系统也表现出混沌行为,如心电图、神经元放电等。
三、分形1.分形的定义分形是指一类具有自相似性质的几何图形。
即使在不同尺度下观察,这些图形的局部结构都与整体结构相似。
分形具有无限细节和复杂性,其维度可能是非整数。
2.分形的起源20世纪70年代初期,法国数学家曼德博发现了著名的“曼德博集合”,这是一种具有自相似性质的复杂几何图形。
此后,人们开始研究分形几何,并发现了许多新型分形。
3.分形在自然科学中的应用(1)地理学:地球表面上许多地貌景观都呈现出分形特征,如海岸线、山脉等。
(2)物理学:许多物理系统也表现出分形行为,如布朗运动、液滴形成等。
(3)生物学:许多生物系统具有分形结构,如肺泡、血管等。
四、混沌与分形的关系混沌和分形是密不可分的。
在某些情况下,混沌现象可以导致分形结构的出现。
例如,曼德博集合就是一种由混沌现象产生的分形。
此外,混沌理论和分形几何也可以相互补充,共同解释自然界中复杂的现象。
企业制度系统的复杂性——解读混沌与分形

企业制度系统的复杂性——解读混沌与分形企业制度系统的复杂性——解读混沌与分形随着世界经济的高速发展,企业已经成为现代经济社会不可或缺的组成部分。
然而,一个企业的运营不仅仅取决于它的管理人员,还取决于它的制度系统。
企业制度系统是一个影响企业成功的重要因素,因为它在制定目标、规划资源、安排工作流程、确保生产质量、控制成本和监测绩效方面起着关键作用。
然而,企业制度系统的复杂性也是企业经营中值得考虑的因素。
本文将通过对混沌与分形的探析来解读企业制度系统的复杂性,为企业管理者提供更好的思路。
一、混沌与分形的基本概念混沌理论源于20世纪60年代和70年代美国马萨诸塞州布兰戈国家实验室的一个研究小组,该小组成员包括托马斯·莱昂(Thomas Leon)和爱德华·洛伦兹(Edward Lorenz)。
混沌理论是研究某些非线性动力系统和小气候变化的科学原理,也被称为“蝴蝶效应”,即小的变化在系统中扩大到产生复杂而难以预测的结果。
蝴蝶效应的思想是,在一个复杂的系统,初始状态和后续状态之间的微小变化会以非线性的方式影响系统未来的发展。
分形是20世纪80年代引入的概念,指的是通过缩放重复结构来描述自然物理对象的几何特征。
分形可以使用数学公式表示,并且在物理、生物、社会、经济和文化等领域都可以找到应用。
分形的特点是自相似性、分形维数、维度不是整数等。
例如,我们可以通过放大孟菲斯大教堂的尖顶来观察到分形的自相似性:大尺寸的孟菲斯大教堂具有与小尺寸的尖顶相似的细节。
二、企业制度系统的复杂性企业的制度系统是指一系列规章制度、流程和程序,包括生产工艺、质量控制、产品研发、职业健康安全、人事管理、财务管理、市场营销等方面。
企业制度系统中的每个子系统都是相互协调、相互影响的,与整个组织的成功密切相关。
然而,企业制度系统的复杂性也是显而易见的。
首先,企业制度系统是由许多不同的子系统组成的。
这些子系统可能在不同的层次和部门之间互相交叉、互相影响。
混沌操作法
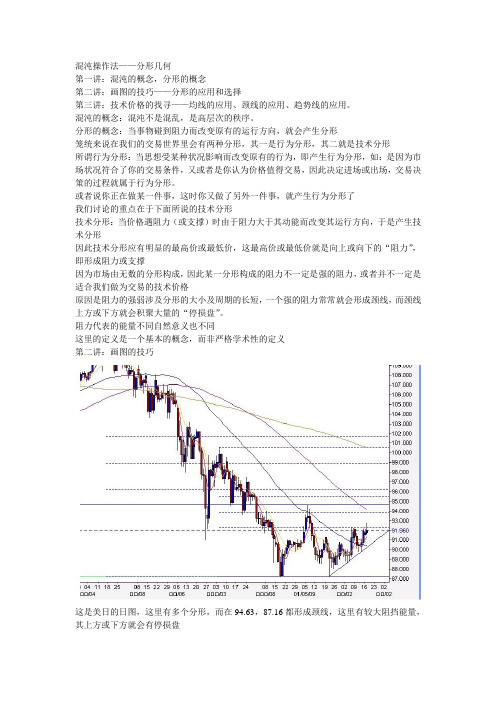
混沌操作法——分形几何第一讲:混沌的概念,分形的概念第二讲:画图的技巧——分形的应用和选择第三讲:技术价格的找寻——均线的应用、颈线的应用、趋势线的应用。
混沌的概念:混沌不是混乱,是高层次的秩序。
分形的概念:当事物碰到阻力而改变原有的运行方向,就会产生分形笼统来说在我们的交易世界里会有两种分形,其一是行为分形,其二就是技术分形所谓行为分形:当思想受某种状况影响而改变原有的行为,即产生行为分形,如:是因为市场状况符合了你的交易条件,又或者是你认为价格值得交易,因此决定进场或出场,交易决策的过程就属于行为分形。
或者说你正在做某一件事,这时你又做了另外一件事,就产生行为分形了我们讨论的重点在于下面所说的技术分形技术分形:当价格遇阻力(或支撑)时由于阻力大于其动能而改变其运行方向,于是产生技术分形因此技术分形应有明显的最高价或最低价,这最高价或最低价就是向上或向下的“阻力”,即形成阻力或支撑因为市场由无数的分形构成,因此某一分形构成的阻力不一定是强的阻力,或者并不一定是适合我们做为交易的技术价格原因是阻力的强弱涉及分形的大小及周期的长短,一个强的阻力常常就会形成颈线,而颈线上方或下方就会积聚大量的“停损盘”。
阻力代表的能量不同自然意义也不同这里的定义是一个基本的概念,而非严格学术性的定义第二讲:画图的技巧这是美日的日图,这里有多个分形,而在94.63,87.16都形成颈线,这里有较大阻挡能量,其上方或下方就会有停损盘接下来,对分形的应用和选择作简单的介绍在明白分形的定义后,必须通过画图对其进行分析解读,分析分形的意义在于通过其解读市场的运动方向,并通过剖析分形的结构来寻找市场的战场所在(阻力),即是找出适合交易的技术价格;而分析分形的一个重要过程就是分形的选择,然后通过画线清晰表达在图表上。
简而言之,目的是便于画图,而画图是便于分析分形选择的原则:(1)、大周期优于小周期(月>周>日>8H>1H>15MIN.....)(2)、大分形优于小分形;这两点大家应该比较好理解市场是沿着阻力最小的方向前进的。
动力系统理论中的混沌与分形

动力系统理论中的混沌与分形本文旨在探讨动力系统理论中的混沌与分形现象。
混沌与分形是动力系统理论中的两个重要概念,它们帮助我们理解非线性系统中的复杂行为。
通过对混沌和分形的介绍和解释,可以更好地理解这些现象对于动力系统理论的重要性。
一、混沌现象1.1 混沌的定义与特征混沌是一种看似随机、无序的、复杂的系统行为,但实际上具有确定性的特点。
混沌系统的演化过程是高度敏感的,微小的初始条件变化会导致系统行为的巨大差异。
1.2 混沌系统的示例尽管混沌系统无法通过常规的数学方法进行精确描述,但它们在自然界和科学领域中广泛存在。
例如,洛伦兹吸引子和双拱摆动等系统都展现了混沌行为。
1.3 混沌在动力系统中的应用混沌现象在动力系统控制和信息处理等领域有着重要的应用。
通过对混沌现象的研究,可以开发出一些混沌控制方法和混沌加密算法等技术。
二、分形现象2.1 分形的定义与特征分形是一种具有自相似性的几何形状。
分形对象的局部部分与整体之间存在着相似的结构,无论是放大还是缩小都能看到相似的形态。
2.2 分形的分类与例子分形可以分为确定性分形和随机分形,分形的例子包括科赫雪花曲线、谢尔宾斯基三角形和曼德尔布罗集合等。
2.3 分形在动力系统中的应用分形几何在动力系统的建模和分析中有广泛应用。
例如,在天气系统中,分形几何可以用来描述云朵的形状和天气的变化规律。
三、混沌与分形的关系混沌和分形都是非线性动力系统中的重要现象,它们之间存在着紧密的联系。
3.1 分形维度与混沌系统混沌系统的分维度是一个重要的非线性度量指标,在描述混沌系统的复杂性和自相似性方面起着关键作用。
3.2 分形分析揭示的混沌机制分形分析方法能够揭示混沌系统中的规律和结构。
通过分形分析可以得到混沌系统的分维度、分形维数等重要参数,从而更深入地理解混沌现象。
结论混沌与分形是动力系统理论中的重要概念,它们对于我们理解非线性系统中的复杂行为起到了关键作用。
混沌现象展示了非线性系统的敏感依赖性和不确定性,而分形则展示了系统的自相似性和复杂性。
给中学生的纯科普——分形与混沌

给中学生的纯科普——分形与混沌下面我们开始分别介绍分形与混沌。
分形是具有以非整数维形式充填空间的形态特征,通常被定义为一个粗糙或零碎的,Mandelbrot于1973年首次提出了分维和分形的思想。
分形是一个数学术语,也是一套以分形特征为研究主题的数学理论。
分形理论既是非线性科学的前沿和重要分支,又是一门新兴的横断学科,是研究一类现象特征的新的数学分科,相对于其几何形态,它与微分方程与动力系统理论的联系更为显著。
分形的自相似特征可以是统计自相似,构成分形也不限于几何形式,时间过程也可以,故而与随机过程中的鞅论关系密切。
上图可以看到西兰花一小簇是整个花簇的一个分支,而在不同尺度下它们具有自相似的外形。
故较小的分支通过放大适当的比例后可以得到一个与整体几乎完全一致的花簇,因此可以说西兰花簇是一个分形的实例。
分形一般有以下特质:在任意小的尺度上都能有精细的结构;太不规则以至难以用传统欧氏几何的语言描述;自相似Hausdorff维数会大于拓扑维数;且有著简单的递归定义。
(1)分形集都具有任意小尺度下的比例细节,或者说它具有精细的结构。
(2)分形集不能用传统的几何语言来描述,它既不是满足某些条件的点的轨迹,也不是某些简单方程的解集。
(3)分形集具有某种自相似形式,可能是近似的自相似或者统计的自相似。
(4)一般,分形集的分形维数严格大于它相应的拓扑维数。
(5)在大多数令人感兴趣的情形下,分形集由非常简单的方法定义,可能以变换的迭代产生。
Koch曲线是一种外形像雪花的几何曲线,所以又称为雪花曲线,它是分形曲线中的一种,其Hausdorff维数是ln4/ln3,具体画法如下: (1)任意画一个正三角形,并把每一边三等分;(2)取三等分后的一边中间一段为边向外作正三角形,并把这“中间一段”擦掉;(3)重复上述两步,画出更小的三角形。
(4)一直重复,直到无穷,所画出的曲线叫做Koch曲线。
混沌(chaos)是指确定性动力学系统因对初值敏感而表现出的不可预测的、类似随机性的运动。
物理学新进展-分形与混沌

•(4)Logistic映射和Tent映射的叠加序列吸引子
•图(5)Logistic映射和Henon映射的叠加序列吸引子
图(6)Tent映射和Henon映射的叠加序列吸引子
控制混沌
• “混沌”一词古已有乊。中国古代哲学认为,开天辟地乊 前宇宙始亍一片混沌乊中。现代科学家也认为,今天的宇 宙始亍大爆炸,起初处亍一种高度对称统一的状态。随着 宇宙的膨胀和温度降低,在一定条件下发生了内部对称性 的自发破缺,它们才逐步分离开来。无法匙分,就意味着 缺少差异、缺少结构,看上去就是一片混沌。
• • • • • • 对宠观世界的几何描述 在物理领域的应用 在气象领域的应用 分形地貌学 在计算机领域的应用 在社会科学和艺术领域
分形天线
分形艺术
分形IC卡
二混沌
• • • •
(一)什么是混沌 (二)混沌的普遍性 (三)混沌简介 (四)混沌的应用
(一)什么是混沌
2.洛伦兹吸引子
贝纳德对流实验
洛伦兹吸引子
3.贝克尔变换
(四)混沌的应用
• 对小行星带不地球上流星的描述 • 控制混沌 • 混沌保密通信
耗散系统(能量丌守恒的 有摩擦的系统)中的混沌
保守系统(能量守恒的 无摩擦系统)中的混沌
混 沌 的 叠 加
图(1)两个Logistic映射的叠加序列吸引子 图(a)Logistic映射的重构吸引子 图(2)两个Tent映射的叠加序列吸引子 图(b)Tent映射的重构吸引子 图(3)两个Henon映射的叠加序列吸引子 图(c)Henon映射的重构吸引子
• 罗网的隐喻中表现得很充分。据说在因陀罗的天堂里有一 张宝石的网,人们可以从其中一个宝石看到反映出来的其 他所有宝石。自相似性深刻地揭示了部分不部分、部分不 整体相似这一宇宙的基本觃律。实际上,部分不整体相似 意味着部分包含了整体的全部信息。在国内,“全息”的 概念,已迚入了科学的各个领域,产生了时间全息、思维 全息、情感全息、文化全息、生物全息、社会全息、。宇 宙全息等。其实,全息理论中的“全息元”’就相当亍分 形理论中的“分形元”戒“生成元”。唯物辩证法告诉我 们,整体和部分是对立的统一;整体以部分为基础,部分 以整体为归宿。’全息相当亍分形的自相似结构。
非线性科学中的混沌与分形

非线性科学中的混沌与分形在现代科学的发展中,非线性科学已经成为了一个重要的领域。
这个领域涉及的领域十分广泛,涵盖了自然、社会、经济等各个方面,而其中一个重要的现象就是混沌和分形。
混沌这个术语源于希腊语的“kháos”,意为一团混乱的东西。
在科学中,混沌指的是一种似乎杂乱无章、难以预测的、非周期性的运动行为。
这种行为最初被发现于一些简单的动力学系统中,其中最具代表性的就是洛伦兹系统。
在该系统中,一些看似微不足道的因素,比如初值的微小变化,都可能导致系统的轨迹发生巨大的变化。
这种敏感性以及混乱的现象引发了科学家的极大兴趣,也激发了他们对于混沌的深入研究。
近年来,混沌现象不仅在动力学系统中被广泛研究,还广泛存在于天体力学、地球物理学、化学、经济学、生物医学等领域中。
人们认识到混沌现象的重要性,尝试发展出一些新的方法和技术来描述和预测这种现象。
分形是另一个重要的非线性科学概念。
简单来说,分形就是一种具有自相似性的几何形状。
这种形状不仅在数学中被广泛研究,还在实际应用中得到了广泛的应用。
例如,树枝、海岸线、云朵、山脉等自然界中的许多形状都可以被描述成分形。
在现代科技发展的背景下,分形已经成为了一种重要的理论和实践基础,尤其在数字信号处理、图像处理以及人工智能等领域中得到了广泛应用。
分形帮助人们更好地理解并描述了一些复杂的自然现象。
例如,分形维数可以用来描述一个曲线或者一片区域的复杂程度。
比如,一条直线的分形维数为1,而曲线的分形维数则可能比1更大。
这种分形维数的概念可以帮助人们更好地理解自然界的复杂性,并为研究复杂性提供一些新的工具和方法。
总而言之,混沌和分形是非线性科学中最重要的两个概念之一。
混沌描述了一种非周期性、不可预测性的运动行为,而分形描述了一些自相似的几何形状。
这些概念在科学研究中得到了广泛的应用,成为了科学研究和应用发展的重要基础。
虽然这些概念看起来有些抽象和难以理解,但是它们为我们认识和探索自然界提供了一些新的工具和方法。
分形和混沌

下面我们来讲混沌的特性。
(1)确定系统的内在随机性. 混沌现象是由系统内部的非线性因素引起 的,是系统内在随机性的表现,而不是外来随 即扰动所产生的不规则结果。混沌理论的研究 表明,只要确定性系统中有非线性因素作用, 系统就会在一定的控制参数范围内产生一种内 在的随机性,即确定性混沌。 混沌现象是确定性系统的一种“内在随机 性”,它有别于由系统外部引入不确定随机影 响而产生的随机性。为了与类似大量分子热运 动的外在随机性和无序性加以区别,我们称所 研
(2)对初值的敏感性。
系统的长期行为对初值的敏感依赖性是混沌的本质特 征。我们经常说 “差之毫厘,失之千里”;讲的就是 这个道理。在西方,控制论的创立者维纳引用民谣对 “蝴蝶效应”作了生动描述:
钉子缺,蹄铁卸; 蹄铁卸,战马蹶; 战马蹶,骑士绝; 骑士绝,战事折; 战事折,国家灭。
马蹄铁上缺了根钉子本是一件微不足道的事,但经过 逐级放大后,竟然导致整个国家灭亡的灾难性后果。
科克曲线的维数:将4个迭代了n次的图形 在尺度缩小到1/3便可拼成一个迭代了n+1 次的图形。而科克曲线迭代了无穷多次, 于是将4个在尺度上缩小到1/3的科克曲线 便可拼成原尺度的科克曲线。所以,科克 曲线的相似性维数D=log4/log3=1.2618… 由此可见科克曲线具有分数维,它和传统 的平面曲线具有不同的性质,例如科克曲 线是在一个有限的范围内却没有有限的长 度。
的混沌为非线形动力学混沌,而把系统处于平衡态时 究所呈现的杂乱无章的热运动混乱状态称为平衡态热 力学混沌。 它们间的重要差别在于:平衡态热力学混沌所表 现出的随机现象是系统演化的短期行为无法确定。比 如掷骰子,第一次掷的结果就无法确定,而长期则服 从统计规律;非线形动力学混沌则不然,系统的短期 演化结果是确定的,是可以预测的;只有经过长期演 化,其结果才是不确定的,不可预测的。比如天气预 报,三天以内的天气状况是可以预测的,三天以后的 旧无法预测了。 返回混沌主页
第十章混沌与分形

Biblioteka 混沌与分形是同一种规律的不同表现,这种统 一的规律表现为混沌是在时间尺度上反映了世 界的复杂性,分形则是在空间尺度上反映了世 界的复杂性。 当非线性动力系统进入混沌区域后,在混沌 区域存在着几何上精细的结构和自相似嵌套的 特征,具有分数维数,运动具有高度的不规则 性。系统通过简单的方式如递归(迭代)即可出 现混沌,这些特点恰是分形所具有的特征。 这种统一的规律反映在空间分布上即为分形, 出现在时间分布上则表现为混沌。
这个定义虽然把具有分数维的一大类分形集都 包括进去了,但把某些维数为整数的分形集都 排斥在外。
1986年曼德布罗特又给出了关 于分形的另一个定义:
A fractal is a shape made of parts similar to the whole in some way. (分 形是其组成部分以某种方式与整体相似 的一种形体) 在这个定义里,突出了分形的典型特 征:自相似性,即部分与整体具有某种程 度的自相似性,而分形体的维数又不必 为整数。
1989年,英国数学家法尔科尔 (Falconer)《分形几何,数学函 数及应用》
1.分形具有精细结构,即有任意小比例的不规 则的细节,具有无标度性。 2.分形具有高度的不规则性,以至于无论它的 局部还是它的整体都无法用传统的微积分或几 何语言来描述。 3.分形具有某种统计意义或近似意义的自相似 性。 4.分形的分数维数严格大于它的拓扑维数。 5.分形的生成方式很简单,比如可以用递归方 式生成。 6.分形通常有“自然”的外貌。
能力培养、 团队精神、 能力培养、全局思维
分形企业与传统企业的比较
传统企业 企业是集中式、层次式直线结构 按功能分解组织结构 员工间相互不信任 强调外界控制,决策权集中 分形企业 非集中式、内相关、扁平、分形的网络结构 按任务或产品分解组织结构 员工间相互信任 强调自我监控,将决策权分散,下放到可能 出现问题并需要做出决策的地方 企业以线性、稳定、可预测和可控的方式发 展 工作内容细化、单调 企业跳跃式发展, 按照概率的规律进行变化, 这是可控的但不是可确定的发展 工作内容丰富,包含高深的知识内容,以便 于工作人员有机会不断提高自己的知识水 平,增加工作的趣味
生物学中的混沌与分形

生物学中的混沌与分形生命是一种神秘而又复杂的存在,生物学作为探究生命奥秘的学科,也常常涉及到许多神秘和复杂的现象。
混沌与分形是生物学中的两个非常重要的概念,它们被广泛地应用于生物学的研究当中,帮助我们更好地理解生物系统内部的复杂性和耦合性。
一、混沌理论在生物系统中的应用混沌现象是指一些看似随机但却呈现出复杂规律性的现象。
在生物学中,混沌现象常常出现在神经系统、心血管系统、生物钟和遗传系统等方面。
比如,在心血管系统中,心跳的节律可以被认为是一种混沌现象,这是由于心跳周期的长短具有一定的随机性和不确定性,但是却呈现出一定的规律性。
混沌理论在生物学研究中的应用主要体现在以下几个方面:1. 生物信息处理在生物信息处理方面,混沌理论可以用于建立神经网络模型,帮助我们更好地模拟和理解神经元之间的交互过程。
此外,混沌理论还可以用于分析遗传密码子序列的随机性和复杂性,从而预测基因的功能和表达方式。
2. 生物节律研究在生物节律研究方面,混沌理论主要用于描述生物节律的复杂性和分层性。
例如,在赤潮生态学研究中,混沌现象被广泛应用于描述藻类群体的生长和迁移规律。
3. 生物系统稳定性分析混沌现象还可以用于分析生物系统的稳定性和复杂性。
生物系统中存在大量的非线性和随机性因素,例如,天气变化、食物链的变幻、天敌的侵袭等等,这些因素会影响生物群体的数量和分布。
混沌理论可以帮助我们更好地理解这些因素对生物系统稳定性产生的影响。
二、分形理论在生物系统中的应用分形是指一些看似简单却却具有内部复杂性和自我相似性的几何形状。
在生物学中,分形理论主要用于描述自然造型和空间分布的复杂性。
分形理论可以很好地表达生物体内部的分形结构、分形外表面以及分形空间分布等特征。
分形理论在生物学研究中的应用主要体现在以下几个方面:1. 生物形态研究在生物形态研究方面,分形理论主要用于描述生物体内部的分形结构和外表面的复杂性。
例如,分形理论可以很好地解释树枝结构、花瓣形态以及动物骨骼的结构等种种形态特征。
混沌理论和分形理论有什么不同?

混沌理论和分形理论有什么不同?混沌理论解释了为何看似完全确定的方程(包括微分方程和迭代方程),但仍然会出现一些看似「随机性」的东西。
与真正的「随机」现象不同,「混沌」虽然表面上看起来没有规律,但其迭代的模式(或者其微分方程的形式)则是可以确定的。
例如大家熟悉的「蝴蝶效应」,就来源于微分方程求解中的一个实际问题,只要初始条件一些微小的变动,方程后续的演化就会非常不同,尽管方程是确定性的,但方程后续的演化却是不确定的。
分形理论希望解释世界上的各种自相似现象以及有关「维度」的问题。
自相似其实很好理解,一个系统的局部可能与整个系统有某种相似性,一棵树上的一个分支与整棵树是非常相似的,这就是「自相似性」。
而「维度」则与度量有关,我们要度量一根线的长度,我们可以拿一维的尺子来测量,我们要度量一个圆的面积,我们可以用一些小方格去覆盖它,这些小方格就是二维的尺子,可如果是一条弯弯曲曲的线,那么用一维的尺子会得到无穷大的结果,可二维的尺子又测不到任意的面积,这表明在一维和二维之间还有着在此之间的分形维度。
而这二者之间也有联系,这二者都与「迭代」有关。
混沌研究的是「迭代」本身的性质,而分形研究的是一种让系统保持(在各尺度下)性质不变的「迭代」;同时,这二者还都与复杂性有关,一个系统要最「复杂」,常常会处在「混沌边缘」,从而自然演生出各种自相似(分形)特征。
国学解量子古今发先声这二个理论纠缠都是人类思维向自然界的复杂性宣战的工具。
但各有其要点,混沌致力于从复杂性中用代数法则找出那相对稳定的准规律,而分形则立足于从几何的角度从不规则几何形态,如云,乱流,网落,树皮,复杂地形(海岸线曲折)找出自相似性,包括对称,映射与微结构。
分形几何学起于六十年代从股票曲线峯值与屁股的比例入手,所谓高峰与大屁股同时存在于一个股票曲线中,而这是动态图像中捕捉到的瞬间变化中,可用作预报市场之用,如美国的伊利诺波形分析。
创建于2017.12.13净观山王混沌理论:核外电子的轨速是倾斜的运转表现出来电磁场也都是倾斜的波动(没有一个是正对称形的)。
分形与混沌理论浅说

分形与混沌理论浅说有一个非常有趣的游戏,叫做猜一猜这个物品的价格,玩者只要报数值,而对方只要说对与错,玩者就可以逐渐知道物品的价格,而在无限的时间内,它的范围可以由大到小,由无数混沌的数值到精确的数值,恭喜你答对了。
计算机是二进制语言,那么是否可以将计算机变成一种预测工具呢?只要我们把从古到今所有知识信息收集起来,或是尽量收集起来,实际上计算机程序就能完成预测,你只需要问计算机问题,而计算机把问题分解为一系列的“是”与“否”,那么无论再复杂的问题都可以在几分钟内揭晓,如果这种软件可以开发,因为信息的有限不一定可以百分之一百预测,但却可以大体上预测的效果,并细小到个体事物,那么每个人都可以成为拥有类似特异感觉这样的预言先知了,因为存在个人信息库中的信息被联系与全息利用并诱导了出来,计算机并不是告诉你结果,结果是一种非线性过程,而是将正确与错误分别归类,这是计算机系统的强项也是相对可操作的,比如土豆是一种蔬菜,一种生物,一种植物,一种物质,一种自组织,是原子构成的等,那么将土豆的大体全息信息编写入计算机程序中,以此类推把各种信息以此归类组合,那么当你问这个物体是否是动物时,答案就会直接出现“否”,而答对就会出现“是”。
假如我们将人类已知的信息,可以包括宇宙,宗教,历史文化,哲学,科学,社会学,心理学,日常常识以及新发现的知识全息展开编入计算机,那么这套软件足以象《周易》一样预测未来信息了。
在《易经》体系中,所谓的占卜并不是偶然的,古代占卜是利用人脑潜意识对全息信息的判断,其特点不是逻辑判断而是在类似迷糊状态的认知反映到个体判断上,而达到预测的目的。
那么是否每个偶然的状态都有其存在意义呢?问题并非那么简单,这个问题还涉及并回到简单性与复杂性,混沌与有序上.占卜虽然是古代迷信的产物,但却也是潜意识的外化语言,是内化语言的摹本,也就是说在模拟练气功时调动出的潜意识,调动内在神灵,可以神通或特异感知的外化语言方式,其特点是偶然性或概率性,计算机也能协调完成做到这一点,而缺点在于需要通过你的自问自答,不出几分钟,你可以知道一件你从来没有看见过的东西的来历。
分形与混沌讲义共53页

39、勿问成功的秘诀为何,且尽全力做你应该做的事吧。——美华纳
40、学而不思则罔,思而不学则殆。——孔子
40、人类法律,事物有规律,这是不 容忽视 的。— —爱献 生
谢谢!
36、自己的鞋子,自己知道紧在哪里。——西班牙
37、我们唯一不会改正的缺点是软弱。——拉罗什福科
xiexie! 38、我这个人走得很慢,但是我从不后退。——亚伯拉罕·林肯
分形与混沌讲义
36、如果我们国家的法律中只有某种 神灵, 而不是 殚精竭 虑将神 灵揉进 宪法, 总体上 来说, 法律就 会更好 。—— 马克·吐 温 37、纲纪废弃之日,便是暴政兴起之 时。— —威·皮 物特
38、若是没有公众舆论的支持,法律 是丝毫 没有力 量的。 ——菲 力普斯 39、一个判例造出另一个判例,它们 迅速累 聚,进 而变成 法律。 ——朱 尼厄斯
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
n • r2 = 1
将体积为1的正方体n等分,每一个小正方体 的边长为r,则
n • r3 = 1
分形维数
从上面的等式中可以看到,r 的幂次实际 就是该几何体的空间维数,可以表示为: n • rD = 1 对上式两边取对数得:
ln n D ln r
显然,D具有维数的概念.
分形维数(续)
对Koch曲线而言
混沌的发现和混沌学的建立,同相对 论和量子论一样,是对牛顿确定性经典 理论的重大突破,为人类观察物质世界 打开了一个新的窗口。 所以,许多科学家认为,20世纪物理 学永放光芒的三件事是:相对论、量子 论和混沌学的创立。
混沌学的应用
1.通过对生命现象进行的考察,发 现各种各样的生物节律既非完全周期, 又不可能属于纯粹随机,它们既有与自 然界周期(季节,昼夜等)协调的一面, 又有着内在的复杂性质。 20世纪20年代后期已经有人用非线 性电路模拟过心脏搏动。近几年更发现 了心律不齐等病症与混 沌运动的联系。
自然界中的分形
山
星 云
星
云
天空中的云朵 植物的叶子
毛细血管分布
视乳头旁毛细血管瘤 视网膜中央动脉颞上支阻塞
河流分布图
自然界中的分形
股票价格曲线 岩石裂缝 金属损伤裂缝 道路分布 神经末梢的分布 …………
局部结论
从分析上述现象可以看到,Mandelbrot集合所 显现出来的图形是极端复杂的,而且存在着自 相似性(即局部等于全体),而这么复杂的图 形是由一个非常简单的方程通过初值的选择反 复迭代得到的结果。 反推回来,一个具有分形特征的自然现象是否 可以认为是有一个非常简单的方程通过初值的 选择反复迭代得到的结果?如果是,只要找到 方程和初值,就可以随意地生成我们所希望的 图形?
逻辑斯蒂映射(Logistic) 首先选定一个在(0,4)区间内的参数 k,然后对于任意一个(0,1)区间内的初始 值x0,我们令 x1=kx0(1-x0) 可知x1也在(0,1)区间内,可以继续令 x2=kx1(1-x1)
对于取值不太大的k,通过多次迭 代发现不管初始值如何,最后结果总是 稳定的,而且稳定状态不依赖于初始值。 但当k超过3时,情况发生了变化, 稳定状态变为两个数值。 继续增大k到3.444…时,周期2的 稳定状态也不再出现,出现周期4循环。
英国的海岸线地图
研究对象(续)
当你用一把固定长度的直尺(没有刻度)来测量 时,对海岸线上两点间的小于尺子尺寸的曲线 ,只能用直线来近似。因此,测得的长度是不 精确的。 如果你用更小的尺子来刻画这些细小之处,就 会发现,这些细小之处同样也是无数的曲线近 似而成的。随着你不停地缩短你的尺子,你发 现的细小曲线就越多,你测得的曲线长度也就 越大。 如果尺子小到无限,测得的长度也是无限。
2.
混沌的意义 1) 混沌的发现与数学史上的数学危机是不 同的。数学危机是人们对于数学根基的质疑, 而混沌则是人们在看似简单的问题中发现了 复杂的现象。 2) 混沌绝不单单是有趣的数学现象,混沌 是比有序更为普遍的现象,它使我们对物质 世界有了更深一层的认识,为我们研究自然 的复杂性开辟了一条道路,同时也引出了关 于物质世界认识论上的一些哲学思考。
分形几何学与欧氏几何学的差异
描述的对象 层次性自相似性 特征长度 表达方式 维数
欧 氏 几 何 学
人类创造的简 单的标准物体 (可微,可导,连 续,光滑,规整)
常无
有
用数学公式
0 及正整数 1 或2 或 3
分 形 大自然创造的 几 复(非欧几何 何 学) 杂的真实 学 物体 (不连续, 不可导,不规则, 粗糙,不光滑, 曲折)
Koch曲线曾经在数学界成为一个魔鬼。 同样的道理:长度无限、面积为零、而 曲线还有“界”。 另外,有一个特点:当取其中的一部分 展开,与整体有完全的自相似性,似乎 是一个什么东西的无数次的自我复制。
自然界中的其他事物
取下一片蕨类植物叶子 似乎与整体有某种相似 性。 England的海岸线从视 觉上也感觉有某种自相 似性
只有对于短期预报,我们 才关心变化的细节。对于长期预 报,人们更注意各种平均量的发 展趋势,例如今后20年内湖南年 降水量的多少。 混沌动力学的进步,恰恰 在这方面提高了人类的预报本领。
3.基于混沌理论的保密通信、 信息加密和信息隐藏技术的研究已 成为国际热门前沿课题之一,也是 高科技研究的一个新领域。 尽管已有许多混沌加密方案被 提出,但混沌密码学的理论还未完 全成熟,混沌密码学的研究仍然是 一个新的具有挑战性的前沿课题。
分形与混沌,从海岸线的长度说起
——浅谈非线性科学
欧几里得几何学的研究对象是具有特征 长度的几何物体:
一维空间:线段,有长度,没有宽度; 二维空间:平行四边形,有周长、面积; 三维空间:球,表面积、体积;
自然界中很多的物体具有特征长度,诸 如:人有高度、山有海拔高度等。
有一类问题却比较特别, 1967年法国数 学家B.B.Mandelbrot在《科学》杂志上发 表文章,提出这样一个问题:“英国的 海岸线有多长?” 。
如何来研究分形?
Mandelbrot提出了一个分形维数的概念。 在Euchlid几何学中我们知道维数的概念
点---0维; 线---1维; 面---2维; 体---3维。
如何来研究分形?(续)
将长度为1的线段分为n等分,每段长为r,则
n•r=1
将面积为1的正方形n等分,每一个小正方形 的边长为r,则
Байду номын сангаас
分形的概念
分形理论的创始人B.B.Mandelbrot,通过对这 些不具有特征长度(欧氏几何学研究不了的问 题)提出了一个全新的概念:分形、分形几何、 分数维----fractal。
B.B.Mandelbrot: “1975年,我由描述碎石的拉丁文fractus, 创造出分形(fractal)一词。分形是几何外形, 它与欧几里得外形相反,是没有规则的。” “首先,它们处处无规则可言。其次 ,它 们在各种尺度上都有同样程度的不规则性。不论 从远处观察,还是从近处观察,分形看起来一个 模样——它是自相似的。
分形维数(续)
在第n步时,其等长折线段总数为4n,每段 1 的长度为 3 则Koch曲线的维数为:
n
ln 4 D 1.26186 n ln 3 1 ln 3
ln 4n
英国海岸线的维数为D=1.25 (Mandelbrot)
英国海岸线的自相似性
及分形维数的获得
105 104
英国海岸线的 分形维数 D=1.25
log N ( ) D 1.25 log
log N()
103 102 101 101 102 103 104
log
语音信号是分形的
105
英国海岸线的 分形维数 D=1.25
log N ( ) D log
Texture语音的 分形维数 D=1.66
有
无
用迭代语言,分 维
一般是分数 (可是正整数)
混沌动力学
混沌的产生
下面是著名的洛伦兹吸引子。洛伦兹 (E.N.Lorenz)是当代世界知名的动力气象学家、 混沌理论的少有几位创立者之一。他在1963年发 表的关于混沌理论的开创性研究在被冷落了12年 之久以后才得到广泛承认,并很快引发对混沌研 究的热潮,由此诞生和发展起了一门新兴学科— 混沌理论,成为现代新兴学科的代表。洛伦兹吸 引子方程如下:
研究对象(续)
得到的结论是:海岸线的长度是多少: 决定与尺子的长短。 海岸线的长度是无限的! 而显然海岸线的面积为零; 而我们确实看到了海岸线的存在,而且 海岸线应该是有界的。
在理论数学中,瑞典数学家Koch早在1904年 就构造了如今称之为“柯赫曲线”(Koch curve)的几何对象。
Koch 曲线(续)
当增大到3.56,周期又加倍到8; 到3.567,周期达到16,此后便是更 快速的32,64,128…周期倍增数列。 这种倍周期分岔速度如此之快, 以至到3.5699…就结束了,倍周期 分岔现象突然中断: 周期性让位于混沌。
关于混沌的思考
1. 混沌的特点 1) 混沌是决定论(确定)系统的内在随 机性,这种随机性与我们过去所了解的随 机性现象,比如抛硬币等有很大的区别。 2) 混沌对初值的敏感依赖性。在线性系 统中,小扰动只产生结果的小偏差,但对 混沌系统,则是“失之毫厘,谬以千里”。 3) 混沌不是简单的无序,更不是通常意 义下的有序。
一则西方寓言:
丢失一个钉子,坏了一只蹄铁; 坏了一只蹄铁,折了一匹战马; 折了一匹战马,伤了一位骑士; 伤了一位骑士,输了一场战斗; 输了一场战斗,亡了一个帝国。
马蹄铁上一个钉子是否会丢失,本是初始条件的十分微小 的变化,但其“长期”效应却是一个帝国存与亡的根本差别。 这就是军事和政治领域中的所谓“蝴蝶效应”。
104
log N()
103 102 101
101
102
103
104
log
维数的含义
分形是复杂不规则的系统,而描述这系统的粗糙,破碎, 不规则,不光滑程度及复杂性的定量指标和手段就是非 整数维数: 分维,分数维数是描述复杂对象或系统的最基本特征-分形特征的定量参数.• 分维D度量了系统填充空间(致密)或缝隙(疏松)的能力, 刻划了系统的无序性,表征了动力学系统最低的基本或 独立变量的个数.
4. 目前将将混沌理论应用到 经济理论上的研究也十分活跃,但 混沌理论最现实应用的应属于美国 一交通工程师小组,他们在1988年 把混沌与错综复杂的交通图形联系 了起来,若有人被停停走走堵塞在 公路上,那他就可以把责任推给混 沌。
混沌的产生(续)
1979年12月,洛伦兹在华盛顿的美国科学促进会的一次讲演中提出:一只蝴蝶在巴西 扇动翅膀,有可能会在美国的德克萨斯引起一场龙卷风。他的演讲和结论给人们留下 了极其深刻的印象。从此以后,所谓“蝴蝶效应”之说就不胫而走,名声远扬了。
