单筋矩形截面梁截面设计
单筋梁截面承载力计算

基本构件计算:单筋矩形梁正截面承载力计算一、计算简图二、基本公式1.公式法的三个基本公式:单筋矩形梁正截面受弯承载力计算的三个基本公式:s y c A f bx f =1α⎪⎭⎫ ⎝⎛-=≤201x h bx f M M c u α⎪⎭⎫ ⎝⎛-=≤20x h A f M M s y u式中 M —— 弯矩设计值;M u —— 受弯承载力设计值,即破坏弯矩设计值;c f 1α—— 混凝土等效矩形应力图的应力值; y f —— 钢筋抗拉强度设计值; s A —— 受拉钢筋截面面积; b —— 梁截面宽度; x —— 混凝土受压区高度;h 0 —— 截面有效高度,即截面受压边缘到受拉钢筋合力点的距离,h 0=h-a ; a —— 受拉钢筋合力点到梁受拉边缘的距离,当受拉钢筋为一排时,a =c+d/2; c —— 混凝土保护层厚度; d —— 受拉钢筋直径。
2.系数法的基本公式(1)系数的公式).(s ξ-ξ=α501(4-21)s αξ211--= (4-25)ξ-=α-+=γ5012211.ss (4-26)(2)基本公式 21201)5.01(bh f bh f M c s c ααξξα=-=0h A f M s s y γ=三、基本公式的适用条件1)防止超筋破坏b ξξ≤ 或 b ρρ≤ 或 0h x b ξ≤2)防止少筋破坏bh A A s s min min ,ρ=≥四、计算方法1.截面选择(设计题)按已知的荷载设计值作用下的弯矩M 设计截面时,常遇到下列两种情形: 情形1 : 已知:M 、混凝土强度等级及钢筋等级;构件截面尺寸b 及h 。
求:所需的受拉钢筋截面面积A s 。
[解](1)确定基本数据c f ;y f ;a h h -=0(2)计算有关系数21bh f Mc s αα=s αξ211--=ξ-=α-+=γ5012211.ss(3)计算受拉钢筋 0h f MA s y s γ=或 01bh f f A ycs αξ=(4)根据求得的受拉钢筋A s ,按照有关构造要求从附表20中选用钢筋直径和根数 (5)验算适用条件1)适用条件:b ξ≤ξ;2)若b ξ>ξ:需加大截面,或提高混凝土强度等级,或改用双筋矩形截面 3)验算bh A A m in m in ,s s ρ=≥。
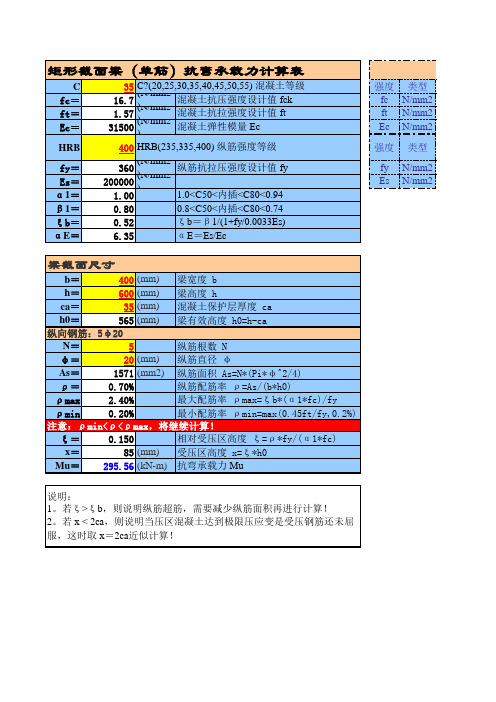
矩形截面梁(单筋)抗弯承载力计算表
0.70%
纵筋配筋率 ρ=As/(b*h0)
ρmax
2.40%
最大配筋率 ρmax=ξb*(α1*fc)/fy
ρmin
0.20%
最小配筋率 ρmin=max(0.45ft/fy,0.2%)
注意:ρmin<ρ<ρmax,将继续计算!
ξ=
0.150
相对受压区高度 ξ=ρ*fy/(α1*fc)
x= Mu=
25500
C25 11.9 1.27 28000
C30 14.3 1.43 30000
C35 16.7 1.57 31500
C40 19.1 1.71 32500
C45 21.1 1.8 33500
HPB23 HRB33 HRB40
5
5
0
210 300 360
210000 200000 200000
C50 23.1 1.89 34500
C55 25.3 1.96 3表
C fc= ft= Ec=
35 C?(20,25,30,35,40,45,50,55) 混凝土等级
16.7 (N/mm2
1.57 )(N/mm2
31500
)(N/mm2 )
混凝土抗压强度设计值 fck 混凝土抗拉强度设计值 ft 混凝土弹性模量 Ec
HRB
400 HRB(235,335,400) 纵筋强度等级
强度 类型
fy N/mm2 Es N/mm2
梁截面尺寸
b=
400 (mm)
h=
600 (mm)
ca=
35 (mm)
h0=
565 (mm)
纵向钢筋:5φ20
梁宽度 b 梁高度 h 混凝土保护层厚度 ca 梁有效高度 h0=h-ca
6单筋矩形截面

2某教学楼钢筋混凝土矩形截面简支梁,安全等级为二级,截面尺寸 b×h=250×550mm,承受恒载标准值10kN/m(不包括梁的自重),活荷载标准 值12kN/m,计算跨度=6m,采用C20级混凝土,HRB335级钢筋。试确定纵向 受力钢筋的数量。
3. 计算x,并判断是否属超筋梁
2M 2 148.165106 2 x h0 h 510 510 1 f c b 1.0 9.6 250
2)复核己知截面的承载力 己知:构件截面尺寸b×h,钢筋截面面积As,混凝土强度等级fc,钢筋级别 fy ,弯矩设计值M 。 求:复核截面是否安全 、弯矩承载力Mu= ?
计算步骤如下:
①确定截面有效高度h0 ②判断梁的类型 As f y
x
1 f c b
若As minbh,且x b h0 为适筋梁;
若x b h0 为超筋梁;若As minbh 为少筋梁。
③计算截面受弯承载力Mu
适筋梁 M u As f y h0 x 2
2 超筋梁 M M f bh u u, max 1 c 0 b (1 0.5b )
对少筋梁,应将其受弯承载力降低使用(已建成工程)或修改设计。 ④判断截面是否安全 若M ≤Mu ,则截面安全。
防止少筋的条件:
x xb b h0
min
AS AS ,min minbh
取x =ξbh0 ,即得到单筋矩形截面所能承受的最大弯矩的表达式:
2 M u,max 1 f c bh0 b (1 0.5 b )
混凝土受压区高度计算式: x h0
2M h 1 f c b
③ 少筋梁
配筋率小于最小配筋率的梁为少筋梁。 破坏特征:梁破坏时, 裂缝往往集中出现一条, 不但开展宽度大,而且 沿梁高延伸较高。一旦 出现裂缝,钢筋的应力 就会迅速增大并超过屈 服强度而进入强化阶段, 甚至被拉断。属于“脆 性破坏”
钢筋混凝土受弯构件正截面承载力计算—单筋矩形截面梁计算

受压混凝土的应力-应变关系
计算原则
2)等效矩形应力图
简化原则:受压区混凝土的合力大小不变;受压区混凝土的合力作用点不变。
等效矩形应力图形的混凝土受压区高度 x 1xn ,等效矩形应力图形的应力值 为 1 fc, 1、1 的值见下表。
表 1、1 值
混凝土强 度等级
≤C50
C55
C60
C65
C70
C75
(2)求跨中截面的最大弯矩设计值。
因仅有一个可变荷载,故弯矩设计值应有取下列两者中的较大值:
M 1 1.2g 1.4q l 2
8
1 1.2 5 1.4 10 5.02 62.5
8
M 1 1.35g 1.4 0.7q l 2
8
1 1.35 5 1.4 0.7 10 5.02 51.7
需要加固、补强
计算原则
1)基本假定
01 平截面假定。
02
钢筋的应力 s 等于钢筋应变 s 与其弹性模量 Es 的乘积,但不得大
于其强度设计值 fy,即
s sEs fv
03 不考虑截面受拉区混凝土的抗拉强度。
计算原则
04
受压混凝土采用理想化的应力-应变关系,当混凝土强度等级为
C50及以下时,混凝土极限压应变 cu=0.0033。
(1)受拉钢筋为4 25,As=1964 mm2; (2)受拉钢筋为3 18,As=763 mm²。
单筋矩形截面梁计算
解 查表得:
fc 9.6N/mm2
ft 1.10N/mm2
f y 300N/mm2 c 1.0
b 0.550
c 30mm
单筋矩形截面梁计算
(1)
d
25
h0 h c 2 450 30 2 408
单筋矩形截面梁、板正截面受弯承载力计算教学课件.

0.96
0.76
0.95
0.73
0.94
0.74
水工混凝土结构
1.3 相对受压区计算高度
相对受压区计算高度是等效矩形混凝土受压区计算高度x
与截面有效高度h0的比值,用ξ= x/h0表示。 当梁发生界限破坏时,即受拉钢筋屈服的同时,受压区
混凝土也达到极限压应变εcu。这时混凝土受压区计算高度xb
与截面有效高度h0的比值,称为相对界限受压区计算高度ξb, ξb= xb/h0。这一临界破坏状态,就是适筋梁与超筋梁的界限。
HPB235
≤C50 HRB335 HRB400 RRB400
0.614
0.550 0.518
0.425
0.399 0.384
0.522
0.468 0.440
0.386
0.358 0.343
水工混凝土结构
1.4 受拉钢筋配筋率 受拉钢筋的配筋率ρ是指受拉钢筋截面面积As与截面有效 截面面积bh0比值的百分率,即ρ =As /(bh0 )×100﹪。 通常用ρmax表示受拉钢筋的最大配筋率; 用ρmin表示受拉钢筋的最小配筋率。 当ρ>ρmax时,将发生超筋破坏; 当ρ<ρmin时,将发生少筋破坏; 当ρmin≤ρ≤ρmax时,将发生适筋破坏。 为避免发生超筋破坏与少筋破坏,截面设计时,应控制 受拉纵筋的配筋率ρ在ρmin~ρmax范围内。
水工混凝土结构
2015.03
钢筋混凝土梁板设计
单筋矩形截面梁、板正截面承载力计算
1 正截面承载力计算的一般规定
1.1 计算方法的基本假定
(1) 截面应变保持为平面:
c
x
c
y
c
单筋梁截面承载力计算

单筋梁截面承载力计算单筋梁是一种常见的钢结构梁,在计算其承载力时,需要考虑两种极限状态,即弯曲极限状态和局部破坏极限状态。
首先,我们来看弯曲极限状态的计算。
单筋梁在弯曲时,主要靠材料的受拉能力来承载荷载。
弯曲截面的受拉区域称为筋部,受压区域称为翼缘或者是受拉钢筋的折减后的面积。
在计算弯曲承载力时,需要考虑以下几个参数:1.混凝土的强度:一般使用混凝土的抗压强度来计算,在计算承载力时,一般假定混凝土为强度等级为C30的材料。
2.钢筋的强度:钢筋的强度也需要考虑,在计算承载力时,一般假定钢筋的强度等级为HRB3353.截面形状:单筋梁的截面形状可以是矩形、T形或者是箱形等,根据不同截面形状,计算方法也会有所不同。
4.截面尺寸:截面尺寸包括截面的宽度和高度,需要根据实际情况进行测量或者计算。
在计算弯曲承载力时,一般采用以下公式:M = αβfc*b*h^2/6其中,M为截面所受弯矩,α为混凝土强度参数,取值范围为0.5-0.95,β为形状系数,根据不同截面形状取不同值,fc为混凝土的抗压强度,b为截面的宽度,h为截面的高度。
下面我们来看局部破坏极限状态的计算。
局部破坏主要发生在梁的支座区域。
梁的支座区域受到的压力较大,容易出现局部压力过大而破坏的情况。
在计算局部破坏承载力时1.支座宽度:支座宽度是一个重要参数,在计算局部破坏时需要考虑。
2.支座深度:支座深度也是一个重要参数,需要根据实际情况进行测量或者计算。
3.材料强度:在计算局部破坏承载力时,需要考虑材料的强度,包括混凝土和钢筋的强度。
计算局部破坏承载力时,一般采用以下公式:N = γfcb*bhd其中,N为局部破坏时截面所受力的分力,γ为混凝土局部破坏的形状参数,取值范围为0.25-0.8,fcb为混凝土的抗压强度,b为支座宽度,h为支座深度,d为混凝土的有效高度。
综上所述,单筋梁截面承载力的计算涉及到材料的强度、截面形状及尺寸等参数。
通过以上的公式及参数计算,可以评估单筋梁的承载能力,为工程设计提供依据。
矩形截面设计

=
f y As α1 fcbh0
(
x
=
ξ h0 )
2. 判别:判别ξ 与ξb
a) 如果ξ ≥ ξb , Mu = α1 fcbh02ξb (1− 0.5ξb ) ;
b) 如果ξ < ξb , Mu = α1 fcbh02ξ (1− 0.5ξ ) ;。
1. 比较: M > Mu ,不安全; M ≤ Mu ,安全。
⎛
⎜
( ) ( ) ⎜
另法:
x
=
h0
⎜1 ⎜
−
⎡ 2 ⎢M 1− ⎢⎣
− α1 fc
b'f − b h'f α1 fcbh02
⎛ ⎜⎜⎝
h0
−
h'f 2
⎞⎤ ⎟⎟⎠⎥⎥⎦
⎞ ⎟ ⎟ ⎟ ⎟
,
x
≤
xb
时,
As
= α1 fcbx + α1 fc fy
b'f − b h'f
⎜⎜⎝
⎟⎟⎠
x > xb 时,截面超筋,应加大截面或提高混凝土强度等级。
2.
比较
M1
与
M
:
M1
=
α1
fcbxb
⎛ ⎜⎝
h0
−
xb 2
⎞ ⎟⎠
a) 如果 M1 ≥ M ,只需配单筋;
b) 如果 M1 < M ,应配双筋。
3.
求
As1
=
α1
fcbxb fy
ቤተ መጻሕፍቲ ባይዱ
4. 求 M 2 、 As' 、 As2
M2 = M − M1
( ) As'
=
f
建筑工程中单筋矩形截面正截面承载力计算

度设计值 一混凝土轴心抗压强度设计值, 一 矩形截面宽度 , ——受拉区纵 向受力钢筋的截面面积 : b
矩形 应力 图 的应 力 ( 根据 GB5 0 0 2 0 混 凝土 结构 设 计规 范 》根 据 混凝土 强 度 等级 的 不同 分别 取 09 M . O 1- 0 2《 4 0)
程 中数 量最多≮ 用面积最 广的 一类构件 。 ≯ ◆ 使 -_ 0 l l l l l l l_ 0 _ 1 l ≯ _ 一
关 键痢 筋癯 土 _筋粱 应 分 钢 凝 梁 连 力 布图 混 土 构 等袅 化 平 面 定 钢筋 凝 结 简 假
所 谓 单筋截 面是 指只在 截面 的受 拉区 配有纵 向受 力钢筋 的矩 形截 面 。
码:一 一 一 一 一 一 主亨 一 一0-752—) 一01. 一 一 _ 一 一 一 一 一 一  ̄:— . — 一 —01- — 一 2 一 一 一 07一 4 ( 1 一 02-一 1 — 0—一 一— —— O 0 0
摘要: 钢筋混凝土结构 的基本计算原理是先 把构件截面上 的应力分 通过适 寒 等 布j 挟 效戚力学上的应l分布自_, 力 形I 然
这些条件主要包括( 材 1 料应力的基本假定o2 区混凝土应力分布的等教简 ) l (受压 ) 化 (葆馥适筋梁 3 ) 的条件 构件曩 受弯
指 面 通 声 矩 力 用 轴 忽 不 的 件车 . 中 分 每 截 l 常 : 舜 共 作 而 力 以 略 计 构 筑 簪 誉 毒 受 l ∞ ≥ 王 上 事 向 可 工 件 走 寺 构
面 相对 受压 区 高度 善 与截 面配 筋率 p 之 间存 在 对应 关 系 。 由 可求 出适 筋 受弯 构 件截 面 最 大配 筋率 的计算 公 式 :
・ .
矩形截面梁配筋

矩形截面单筋梁配筋理解的几个关键点
1.受压区混凝土对受拉区钢筋取距,得到用混凝土受力表示的弯矩: 10()2
c x M f bx h α=- (1.1) 将0x h ξ=
对上式进行变形,
210110()(10.5)(10.5)2c c c x x x M f bx h f b hh f bh h h αααξξ=-=-=- (1.2) 此时,令
(10.5)s ξξα-= (1.3) 给s α一个名字,截面抵抗矩系数,将s α看成一个常数,那么这就是一个关于ξ的
一元二次方程,即
2220s ξξα-+= (1.4) 用求根公式解得(注意01x h ξ=
<),
1ξ=(1.5)
2.当已知弯矩设计值时,首先通过式(1.2)得到s α,然后根据式(1.5)得到相对受压区高度ξ。
3.求出ξ之后,要与b ξ进行比较。
如果b ξξ>,说明混凝土受压范围过大,导致钢筋无法屈服,即混凝土破坏时,钢筋并未失效,为超筋梁,造成了浪费且无延性。
此时需要增大截面尺寸,或提高混凝土的强度等级。
如果b ξξ<,则继续进行。
4.当b ξξ<时(即适筋梁),根据下式即可求出钢筋面积。
00()(10.5)2y S y S x M f A h f A h ξ=-=- (1.6)
5.当计算出S A 后,结合截面尺寸,选取钢筋直径和对应根数。
这里,实际配筋与就算配筋相差在±5%,亦即不一定要比计算钢筋截面积大,稍微小一点点也是可以允许的。
水工钢筋混凝土矩形单筋截面受弯构件配筋计算设计——按新规范SL/T191—96

式 中 : 为荷 载 作用 下 的弯 矩 设 计 值 ( 载 效 应 ) 系 由 各 荷 肘 荷 , 载标 准值 乘 以相 应 的荷 载 分 项 系 数 后 所 产 生 的效 应 总 和 并 再乘 以结构 重 要性 系 数 7 及 设 计状 况 系数 后 的值 。 为 。 受 弯构 件极 限承载 力 ( 力 )计 算 值 。 值 就 是 由受 压 区 混 抗 凝土 应力 的合 力 与 受 拉 区全 部 受拉 钢 筋 应 力 的合 力 所 组 成 的一 对 力偶 。 我们 可 以绘 制 简化 等 效矩 形 应 力 图形 及 构 件 图 形 。 受拉 区钢 筋应 力 合力 距 混凝 土 构件 边 缘 的距 离 为 a。 由水 平 方 向力 的平 衡 条件 , 以得 到 : 可
水工钢筋混凝土矩形单筋截面受弯构件配筋计算设计按新规范slt19196水 利 科 技 H i n j n c n ea d T c n lg f tr o sra c e o gi g S i c n e h ooy o e nev y l a e Wa C n
赵 丽梅 , 德 强 , 景 弘 黄 于
( 龙 江 省 水 利 水 电 勘 测 设 计 研 究 院 , 龙 江 啥 尔 滨 10 8 ) 黑 黑 5 00
摘 要 简要 说明水 工 混凝 土结 构设计 必 须充 分 考虑 的有关 内容 , 对钢 筋 混凝 土矩 形单 筋截 面受 弯 构件 设 汁汁茆 做 J 分析 , 导 了 推
77 ( c , o a ) R( , 0 7 7 Q , a) () 1 式 中 : ( )为 荷 载 效 应 函 数 ; ・ S ・ R( )为 结 构 构 件 抗 力 函 数 。 为永 久荷 载标 准 值 ; 为可 变荷 载 标准 值 。 。为永 久荷 载 分 Q 7 项 系数 ; 载分 项 系数 按 《 工建 筑 物荷 载设 计 规 范 》取 用 。 荷 水 参 考 值 为 10 ; 。 可变 荷 载分 项 系数 。 考 值 为 12 。 为 .5 7 为 参 .0 材 料 强度 设计 值 。 为 结构 构 件几 何 参 数 的标 准 值 。 。为结 a 7 构 重 要 性 系 数 , 结 构 安 全 级 别 为 I、 、 级 的 结 构 及 构 对 Ⅱ Ⅲ 件 , 别 取 11 10 O 9 为 设 计 状 况 系 数 , 应 于 持 久 状 分 .、 . 、 . ; 对 况 、 暂 状况 、 然 状况 , 别取 10 0 9 、 .5 7 短 偶 分 . 、 .5 0 8 ; j为 结 构 系 数 , 水 工钢 筋 混凝 土结 构取 12 对 于 偶 然 组 合 , 然 荷 载 对 .。 偶 分 项 系数取 为 10; 与组 合 的 某 些 可 变 荷 载 , 适 当折 减 ; . 参 作 仍取 12 .。 正 常 使 用 极 限 状 态 验 算 规 定按 荷 载 效应 采 用 下列 设 计 表 达式 : 对 于短 期组 合 , 计 表 达式 为 设 y S( o Q , , a )≤ c l () 2
第三章 第四节 单筋矩形截面受弯构件正截面承载力计算
Mu
xc
C
Z
x 0 T C
xt
h0
Tc T s
M 0
M u TZ CZ
设AS—钢筋的面积;fy—钢筋的屈服强度,T= ASfy 。 Z和C与压区高度及压区应力分布有关。
第四节
单筋矩形截面受弯构件正截面承载力计算
b x h
一、计算基本公式及适用条件
基本公式 h0 受弯构件正截面承载能力计算,应满足作用 在结构上的荷载在结构截面中产生的弯矩设计 值M不超过按材料的强度设计值计算得到的受 as 弯构件承载能力设计值Mu, 即:M ≤ Mu
h0——截面有效高度, h0=h-as h——截面高度 as ——受拉钢筋合力点至混凝土受拉边缘的距离,初步计算时,对 于C25~C45等级的混凝土,可按35mm(单排受拉筋)、60mm(双排受拉 筋)、20mm(平板)取值。
第四节 单筋矩形截面受弯构件正截面承载力计算 一、计算基本公式及适用条件
◆ 例题3-1
解:查表得: fc=9.6N/mm2 ,; fy=300N/mm2 ; ξb=0.55;截面有效 高度 h。=500-40=460mm ;纵向受拉钢筋按一排放置,则梁的有效 高度h0=500—40=460mm。 1.计算受压区高度x
f y As 300 804 x 125.6mm b h0 0.55 460 253mm 1 f cb 1.0 9.6 200
第四节 单筋矩形截面受弯构件正截面承载力计算 一、计算基本公式及适用条件
第四节 单筋矩形截面受弯构件正截面承载力计算 一、计算基本公式及适用条件
单筋矩形截面 仅在受拉区布置纵向受力钢筋的矩形截面 双筋矩形截面 同时在受拉区和受压区布置纵向受力钢筋的矩形截面
单筋矩形截面计算例题

单筋矩形截面计算例题例题1:某矩形截面梁,截面b×h =300×500,混凝土为C30,该截面承担弯矩为200kNm,配置HRB335级钢筋,请计算该截面所需配置的最小钢筋面积。
ΣM=0 M=а1f c bx(h0-x/2)由于混凝土强度等级为C30,不超过C50,所以а1取为1.0,可以查相应的材料表格,f c=14.3 N/mm2;对于HRB335级钢筋,f y=300 N/mm2。
设受拉区钢筋配置为梁底单排,因此有:h0=h-35=500-35=465mm因此有:200×106 = 14.3×300 × x(465-x/2)解得x=112mm对于计算结果x,进行校核x,防止出现大于x b的情况而超筋。
x b=ξb h0对于C30混凝土与HRB335级钢筋,ξb=0.55。
x b=ξb h0=0.55×465=255.75mm > x,结果满足适筋梁要求。
因此A s =а1f c bx/f y= 14.3×300×112/300=1601.6mm2截面配筋率:ρ=A s/bh0=1601.6/300×465=1.15%>ρmin查钢筋表,对于HRB 335(20MnSi)钢筋,选择4Φ20+2Φ16,A S= 1256+402=1658 mm2>1601.6 mm2,可以满足要求。
通过本例题可以看出,求解方程组必须校核其结果x,只有x< x b才可以作进一步的设计,截面配筋率也必须大于最小配筋率。
同时在解方程时也要注意,由于ΣM=0:M=а1f c bx(h0-x/2)为一个一元二次方程,可能出现两个方程根,根据截面的尺度状况,可以自然约减下去一个根。
例题2:某矩形截面梁,截面b×h =400×600,混凝土为C30,该截面梁底配有双排HRB335级钢筋4Φ25+4Φ20,求该截面能够承担的最大弯矩。
