找中点构造三角形中位线解题(教师)
八年级数学下册《三角形的中位线》教案、教学设计
4.学生在小组内分享解题思路，教师巡回指导，解答学生的疑问。
（四）课堂练习，500字
1.教师出示一组练习题，要求学生独立完成，运用中位线定理解决问题。
2.学生完成练习题后，教师选取部分题目进行讲解，强调解题方法和技巧。
引导学生思考中位线定理在生活中的应用，激发他们的创新意识。同时，鼓励学生探索其他几何图形的中位线性质，提高他们的几何图形识别和分析能力。
6.总结反馈，情感交流
在课堂结束时，教师组织学生总结本节课的学习内容，分享学习心得。同时，关注学生的情感态度，鼓励他们积极面对学习中的困难，培养自信、坚韧的品质。
7.课后作业，延伸学习
三、教学重难点和教学设想
（一）教学重难点
1.理解并掌握三角形的中位线定理及其证明，这是本章节的核心内容，也是学生学习的重点和难点。学生对中位线定理的理解程度，直接影响到后续几何知识的学习。
2.能够运用中位线定理解决实际问题，培养学生将理论知识应用于实际情境的能力。
3.提高学生的几何证明和逻辑推理能力，使他们能够熟练运用几何知识分析和解决问题。
4.教师详细讲解中位线定理的证明过程，强调证明方法及逻辑推理的重要性。
5.针对学生的疑问，进行个别辅导，确保他们掌握中位线定理。
（三）学生小组讨论，500字
1.教师将学生分成小组，每组发放一张三角形图形，要求学生在图中找出中位线，并讨论中位线的性质。
2.各小组汇报讨论成果，教师点评并总结中位线的认识和运用有了更深入的理解。
5.教师布置适量的课后作业，巩固课堂所学知识，并鼓励学生利用课余时间探索几何知识。
五、作业布置
为了巩固学生对三角形中位线知识的掌握，提高他们的几何图形识别、分析和解决问题的能力，特布置以下作业：
专题11 利用中点构造全等三角形(解析版)
七年级数学下册解法技巧思维培优专题11 利用中点构造全等三角形题型一 倍长中线法的运用【典例1】已知：如图，AD 是△ABC 中BC 边上的中线，延长AD 到E ，使DE ＝AD ．（1）求证：AB ＝EC ；（2）试说明AB +AC ＞2AD 的理由；（3）当AB ＝6，AC ＝4时，中线AD 的取值范围为 1＜AD ＜5 ．【点睛】（1）根据三角形中线的定义可得BD ＝CD ，然后利用“边角边”证明△ABD 和△ECD 全等，根据全等三角形对应边相等可得AB ＝EC ；（2）根据三角形的任意两边之和大于第三边可得EC +AC ＞AE ，然后等量代换即可得证；（3）根据三角形的任意两边之和大于第三边，任意两边之差小于第三边求出AE 的取值范围，再除以2即可．【详解】（1）证明：∵AD 是△ABC 中BC 边上的中线，∴BD ＝CD ，在△ABD 和△ECD 中，{DE =AD∠ADB =∠EDC BD =CD，∴△ABD ≌△ECD （SAS ），∴AB ＝EC ；（2）解：由三角形的三边关系得，EC +AC ＞AE ，∵DE ＝AD ，∴AE ＝2AD ，又∵AB ＝EC ，∴AB+AC＞2AD；（3）解：∵AB＝6，∴EC＝6，又∵AC＝4，∴6﹣4＜AE＜6+4，即2＜AE＜10，∵AE＝2AD，∴1＜AD＜5．故答案为：1＜AD＜5．【典例2】（2019•海安月考）数学兴趣小组在活动时，老师提出了这样一个问题：如图1，在△ABC中，AB＝8，AC＝6，D是BC的中点，求BC边上的中线AD的取值范围．小明在组内经过合作交流，得到了如下的解决方法：延长AD到E，使DE＝AD，再证明“△ADC≌△EDB”．（1）探究得出AD的取值范围是1＜AD＜7；（2）【问题解决】如图2，△ABC中，∠B＝90°，AB＝2，AD是△ABC的中线，CE⊥BC，CE＝4，且∠ADE＝90°，求AE的长．【点睛】（1）根据全等三角形的性质、三角形的三边关系计算；（2）延长AD交EC的延长线于F，证明△ABD≌△FCD，根据全等三角形的性质解答．【详解】解：（1）AD的取值范围是1＜AD＜7；故答案为：1＜AD＜7（2）延长AD 交EC 的延长线于F ，∵AB ⊥BC ，EF ⊥BC ，∴∠ABD ＝∠FCD ，在△ABD 和△FCD 中，{∠ABD =∠FCD BD =CD ∠ADB =∠FDC，∴△ABD ≌△FCD （ASA ）∴CF ＝AB ＝2，AD ＝DF ，∵∠ADE ＝90°，∴AE ＝EF ，∵EF ＝CE +CF ＝CE +AB ＝4+2＝6，∴AE ＝6． 【典例3】（2019•恩平市校级月考）如图，AD 是△ABC 的中线，点E 在BC 的延长线上，CE ＝AB ，∠BAC＝∠BCA ，求证：AE ＝2AD ．【点睛】首先延长AD 至M ，使DM ＝AD ，先证明△ABD ≌△MCD ，进而得出MC ＝AB ，∠B ＝∠MCD ，即可得出∠ACM ＝∠ACE ，再证明△ACM ≌△ACE ，即可得出答案．【详解】证明：延长AD 至M ，使DM ＝AD ，∵AD是△ABC的中线，∴DB＝CD，且∠ADB＝∠MDC，AD＝DM∴△ABD≌△MCD（SAS），∴MC＝AB，∠B＝∠MCD，∵AB＝CE，∴CM＝CE，∵∠BAC＝∠BCA，∴∠B+∠BAC＝∠ACB+∠MCD，即∠ACM＝∠ACE，且AC＝AC，CM＝CE，∴△ACM≌△ACE（SAS）．∴AE＝AM，∵AM＝2AD，∴AE＝2AD．题型二作垂线法的运用4．如图，△ABC中，D为BC的中点，（1）在图中作出CM⊥AD，BN⊥AD，垂足分别为M、N；（2）求证：DM＝DN；（3）求AD＝3，求AM+AN的值．【点睛】（1）根据条件作出图形，即可解答；（2）证明△BND≌△CMD，即可得到DN＝DM．（3）由△BND ≌△CMD ，得到DM ＝DN ，利用线段的和与差得到AM ＝AD +DM ，AN ＝AD ﹣ND ，所以AM +AN ＝AD +DM +AD ﹣ND ＝2AD ＝6．【详解】解：（1）如图，（2）∵D 为BC 的中点，∴BD ＝CD ，∵CM ⊥AD ，BN ⊥AD ，∴∠BND ＝∠CMD ＝90°，在△BND 和△CMD 中，{∠BND =∠CMD ∠BDN =∠CDM BD =CD∴△BND ≌△CMD ，∴DN ＝DM ．（3）∵△BND ≌△CMD ，∴DM ＝DN ，∵AM ＝AD +DM ，AN ＝AD ﹣ND ，∴AM +AN ＝AD +DM +AD ﹣ND ，∵DM ＝DN ，∴AM +AN ＝2AD ＝6．5．已知如图，在△ABC 中，∠BAC ＝90°，AB ＝AC ，M 是AC 边的中点，AD ⊥BM 交BC 于D ，交BM 于E ，CF ⊥AC ，证明：（1）△ABM ≌△CAF ；（2）∠AMB ＝∠DMC ．【点睛】（1）由三角形ABC 为等腰直角三角形，利用等腰直角三角形的性质得到AB ＝AC ，且∠ABC ＝∠ACB ＝45°，利用同角的余角相等得到一对角相等，再由一对直角相等，且AB ＝AC ，利用AAS 得到三角形ABM 与三角形CAF 全等；（2）由全等三角形的对应边相等得到AM ＝CF ，由M 为AC 中点，得到AM ＝CM ，等量代换得到CM ＝CF ，由公共边CD ＝CD ，且夹角相等得到三角形CMD 与三角形CFD 全等，利用全等三角形对应角相等得到∠DMC ＝∠F ，等量代换即可得证．【详解】证明：（1）∵在△ABC 中，∠BAC ＝90°，AB ＝AC ，∴∠ABC ＝∠ACB ＝45°，∵∠F +∠CAF ＝90°，∠CAF +∠AMB ＝90°，∴∠F ＝∠AMB ，在△ABM 和△CAF 中，{∠BAM =∠ACF ∠AMB =∠F AB =CA，∴△ABM ≌△CAF （AAS ）；（2）∵∠MCD ＝45°，∴∠FCD ＝90°﹣∠MCD ＝45°，∵M 为AC 的中点，∴AM ＝CM ，∵△ABM ≌△CAF ，∴AM ＝CF ，∴CM ＝CF ，在△CMD 和△CFD 中，{CM =CF ∠MCD =∠FCD CD =CD，∴△CMD ≌△CFD （SAS ），∴∠DMC ＝∠F ，则∠AMB ＝∠DMC ．6．如图．∠C ＝90°，BE ⊥AB 且BE ＝AB ，BD ⊥BC 且BD ＝BC ，CB 的延长线交DE 于F（1）求证：点F 是ED 的中点；（2）求证：S △ABC ＝2S △BEF ．【点睛】（1）过点E 作EM ⊥CF 交CF 的延长线于M ，根据同角的余角相等求出∠EBM ＝∠A ，然后利用“角角边”证明△ABC 和△BEM 全等，根据全等三角形对应边相等可得BC ＝EM ，再求出BD ＝EM ，然后利用“角角边”证明△EMF 和△DBF 全等，根据全等三角形对应边相等可得EF ＝DF ，从而得证；（2）根据全等三角形的面积相等和等底等高的三角形的面积相等进行证明．【详解】证明：（1）如图，过点E 作EM ⊥CF 交CF 的延长线于M ，∵BE ⊥AB ，∴∠EBM +∠ABC ＝180°﹣90°＝90°，∵∠C ＝90°，∴∠A +∠ABC ＝180°﹣90°＝90°，在△ABC 和△BEM 中，{∠EBM =∠A∠C =∠M =90°BE =AB，∴△ABC ≌△BEM （AAS ），∴BC ＝EM ，∵BD ＝BC ，∴BD ＝EM ，在△EMF和△DBF中，{∠M=∠DBF=90°∠EFM=∠DFBBD=EM，∴△EMF≌△DBF（AAS），∴EF＝DF，∴点F是ED的中点；（2）∵△ABC≌△BEM，△EMF≌△DBF，∴S△ABC＝S△BEM，S△EMF＝S△DBF，∵点F是ED的中点，∴S△BEF＝S△DBF=12S△BEM=12S△ABC，∴S△ABC＝2S△BEF．巩固练习1．如图，四边形ABCD中，AC⊥BD，求证：BC+AD＞AB+CD．【点睛】在OD上截取OB'＝OB，在OC上截取OC'＝OA，连接C'B'，DC'，CB'，设CB'，DC'交于点E，易证△ABO≌△C'B'O可得AB＝B'C'，易证△DOA≌△DOC'可得AD＝DC'，易证△COB≌△COB'可得BC＝B'C，根据三角形三边关系即可求得CB'+DC'＞AB+CD即可解题．【详解】解：在OD上截取OB'＝OB，在OC上截取OC'＝OA，连接C'B'，DC'，CB'，设CB'，DC'交于点E（如图），在△ABO 和△C 'B 'O 中，{OC′=OA ∠AOB =∠C′OB′OB′=OB，∴△ABO ≌△C 'B 'O （SAS ），∴AB ＝B 'C '，在△DOA 和△DOC '中，{OA =OC′∠AOD =∠C′OD OD =OD，∴△DOA ≌△DOC '（SAS ），∴AD ＝DC '，在△COB 和△COB '中，{BO =B′O ∠BOC =∠B′OC CO =CO，∴△COB ≌△COB '（SAS ），∴BC ＝B 'C ，∵在△B 'C 'E 中，B 'E +C 'E ＞B 'C '，①在△CDE 中，CE +DE ＞CD ，②①+②得：CE +C 'E +DE +B 'E ＞B 'C '+CD ，∴CB '+DC '＞AB +CD ，∴BC +AD ＞AB +CD ．2．（2019•德城区期末）如图，Rt △ACB 中，∠ACB ＝90°，△ABC 的角平分线AD 、BE 相交于点P ，过P作PF ⊥AD 交BC 的延长线于点F ，交AC 于点H（1）求∠APB 度数；（2）求证：△ABP ≌△FBP ；（3）求证：AH +BD ＝AB ．【点睛】（1）根据角平分线性质可得∠P AB +∠PBA ＝45°，即可解题；（2）易得∠DPB ＝45°，可得∠BPF ＝135°，即可证明△ABP ≌△FBP ；（3）由（2）结论可得∠F ＝∠BAD ，AP ＝PF ，AB ＝BF ，即可求得∠F ＝∠CAD ，即可证明△APH ≌△FPD ，可得AH ＝DF ，即可解题．【详解】解：（1）∵AD 平分∠BAC ，BE 平分∠ABC ，∴∠P AB +∠PBA =12（∠ABC +∠BAC ）＝45°，∴∠APB ＝180°﹣45°＝135°；（2）∵∠APB ＝135°，∴∠DPB ＝45°，∵PF ⊥AD ，∴∠BPF ＝135°，在△ABP 和△FBP 中，{∠BPF =∠APB =135°BP =BP ∠ABP =∠FBP，∴△ABP ≌△FBP （ASA ）；（3）∵△ABP ≌△FBP ，∴∠F ＝∠BAD ，AP ＝PF ，AB ＝BF ，∵∠BAD ＝∠CAD ，∴∠F ＝∠CAD ，在△APH 和△FPD 中，{∠F =∠CAD AP =PF ∠APH =∠FPD =90°，∴△APH ≌△FPD （ASA ），∴AH ＝DF ，∵BF ＝DF +BD ，∴AB ＝AH +BD ．3．（2019•鄂州期末）如图，在Rt △ABC 中，∠ACB ＝90°，AC ＝BC ，∠ABC ＝45°，点D 为BC 的中点，CE ⊥AD 于点E ，其延长线交AB 于点F ，连接DF ．求证：∠ADC ＝∠BDF ．【点睛】作BG ⊥CB ，交CF 的延长线于点G ，由ASA 证明△ACD ≌△CBG ，得出CD ＝BG ，∠CDA ＝∠CGB ，证出BG ＝BD ，∠FBD ＝∠GBF =12∠CBG ，再由SAS 证明△BFG ≌△BFD ，得出∠FGB ＝∠FDB ，即可得出结论．【详解】证明：作BG ⊥CB ，交CF 的延长线于点G ，如图所示：∵∠CBG ＝90°，CF ⊥AD ，∴∠CAD +∠ADC ＝∠BCG +∠ADC ＝90°，∴∠CAD ＝∠BCG ，在△ACD 和△CBG 中，{∠CAD =∠BCG AC =BC ∠ACD =∠CBG =90°，∴△ACD ≌△CBG （ASA ），∴CD ＝BG ，∠CDA ＝∠CGB ，∵CD ＝BD ，∴BG ＝BD ，∵∠ABC ＝45°，∴∠FBD ＝∠GBF =12∠CBG ，在△BFG 和△BFD 中，{BG =BD ∠FBD =∠GBF BF =BF，∴△BFG ≌△BFD （SAS ），∴∠FGB ＝∠FDB ，∴∠ADC ＝∠BDF ．4．（2019•嘉祥期末）如图，BE ，AD 是△ABC 的高且相交于点P ，点Q 是BE 延长线上的一点．（1）试说明：∠1＝∠2；（2）若AP ＝BC ，BQ ＝AC ，线段CP 与CQ 会相等吗？请说明理由．【点睛】（1）由余角的性质可得∠1＝∠2；（2）由“SAS ”可证△APC ≌△BCQ ，可得CP ＝CQ ．【详解】证明：（1）∵BE ，AD 是△ABC 的高∴∠1+∠BCA ＝90°，∠2+BCA ＝90°，∴∠1＝∠2，（2）∵AP ＝BC ，∠1＝∠2，BQ ＝AC ，∴△APC ≌△BCQ （SAS ）∴CP ＝CQ ．5．（2019•高邑期末）问题原型：如图①，在锐角△ABC 中，∠ABC ＝45°，AD ⊥BC 于点D ，在AD 上取点E ，使DE ＝CD ，连结BE ．求证：BE ＝AC ．问题拓展：如图②，在问题原型的条件下，F为BC的中点，连结EF并延长至点M，使FM＝EF，连结CM．（1）判断线段AC与CM的大小关系，并说明理由．（2）若AC=√5，直接写出A、M两点之间的距离．【点睛】问题原型：由AD⊥BC可得∠ADB＝∠ADC＝90°，又∠ABC＝45°易得∠ABC＝∠BAD，可得AD＝BD，由SAS定理可得△BDE≌△ADC；问题拓展：（1）利用SAS判断出△BEF≌△CMF，得出BE＝CM，即可得出结论；（2）借助问题原型与问题延伸的结论判断出△ACM是等腰直角三角形，即可得出结论．【详解】解：问题原型：∵AD⊥BC，∴∠ADB＝∠ADC＝90°，∵∠ABC＝45°，∴∠BAD＝45°，∴∠ABC＝∠BAD，∴AD＝BD，在△BDE和△ADC中，∵{BD=AD∠EDB=∠CDA DE=DC，∴△BDE≌△ADC（SAS），∴BE＝AC，问题拓展：（1）AC＝CM，理由：∵点F是BC中点，∴BF＝CF，在△BEF和△CMF中，∵{BF=CF∠BFE=∠CFM EF=MF，∴△BEF≌△CMF（SAS），∴BE＝CM，由（1）知，BE＝AC，∴AC＝CM；（2）如图②，连接AM，由（1）知，△BDE≌△ADC，∴∠BED＝∠ACD，由（2）知，△BEF≌△CMF，∴∠EBF＝∠BCM，∴∠ACM＝∠ACD+∠BCM＝∠BED+∠EBF＝90°，∵AC＝CM，∴AM=√2AC=√10．。
中点辅助线.中位线(2013_2014)_教师版
2014年中考解决方案构造中位线学生姓名：×××上课时间：2013.××.××知识点一中点一、与中点有关的概念三角形中线的定义：三角形顶点和对边中点的连线三角形中线的相关定理：直角三角形斜边的中线等于斜边的一半等腰三角形底边的中线三线合一(底边的中线、顶角的角平分线、底边的高重合)三角形中位线定义：连结三角形两边中点的线段叫做三角形的中位线．三角形中位线定理：三角形的中位线平行于第三边并且等于它的一半．中位线判定定理：经过三角形一边中点且平行于另一边的直线必平分第三边．直角三角形斜边中线：直角三角形斜边中线等于斜边一半斜边中线判定：若三角性一边上的中线等于该边的一半，则这个三角形是直角三角形二、与中点有关的辅助线秘籍一：倍长中线解读：凡是出现中线或类似中线的线段，都可以考虑倍长中线，倍长中线的目的可以旋转等长度的线段，从而达到将条件进行转化的目的。
秘籍二：构造中位线解读：凡是出现中点，或多个中点，都可以考虑取另一边中点，或延长三角形一边，从而达到构造三角形中位线的目的。
秘籍三：构造三线合一自检自查必考点解读：只要出现等腰三角形，或共顶点等线段，就需要考虑构造三线合一，从而找到突破口其他位置的也要能看出秘籍四：构造斜边中线解读：只要出现直角三角形，或直角，则考虑连接斜边中线段，第一可以出现三条等线段，第二可以出现两个等腰三角形，从而转化线段关系。
他位置的也要能看出一、构造三角形中位线☞考点说明：①凡是出现中点，或多个中点，都可以考虑取四边形对角线中点、等腰三角形底边中点、直角三角形斜边中点或其他线段中点，②延长三角形一边，从而达到构造三角形中位线的目的。
“题中有中点，莫忘中位线”．与此很相近的几何思想是“题中有中线，莫忘加倍延”，这两个是常用几何思想，但注意倍长中线的主要目的是通过构造三角形全等将分散的条件集中起来．平移也有类似功效．【例1】 已知：AD 是ABC △的中线，AE 是ABD △的中线，且AB BD =，求证：2AC AE =．【答案】取AC 的中点F ，连结DF ，易得12DF AB =∥，ADF BAD ADF ==∠∠∠，而1122DE BD AB ==，故DF DE =．再证ADE ADF △≌△，得AE AF =．【练1】如右下图，在ABC ∆中，若2B C ∠=∠，AD BC ⊥，E 为BC 边的中点．求证：2AB DE =．【答案】如右下图，则取AC 边中点F ，连结EF 、DF ．由中位线可得，12EF AB =且B CEF ∠=∠．DF 为Rt ADC ∆斜边上的中线，∴DF CF =．∴CDF C ∠=∠，又∵DFE FDE CEF ∠+∠=∠，即2C DFE C ∠+∠=∠，∴DFE EDF ∠=∠，∴12DE EF AB ==，∴2AB DE =．【练2】在ABC △中，CD 、AE 分别为AB 、BC 边上的高，60B =︒∠，求证：12DE AC =．【考点】三角形的中位线，30°所对的直角边等于斜边的一半【答案】取AB 、BC 的中点，连结MN ，∵60B =︒∠，∴30BAE BCD ==︒∠∠．从而得12BE BM AB ==，12BD BN BC ==，BDE BNM △≌△，MN DE =．中考满分必做题又因12MN AC =，故12DE AC =．【练3】在ABC ∆中，90ACB ∠=︒，12AC BC =，以BC 为底作等腰直角BCD ∆，E 是CD 的中点，求证：AE EB ⊥且AE BE =．【答案】过E 作EF BC ∥交BD 于F135ACE ACB BCE ∠=∠+∠=︒ ∵45DFE DBC ∠=∠=︒∴135EFB ∠=︒又∵EF BC ∥，12EF BC =，12AC BC = ∴EF AC =，CE FB =∴EFB ACE ∆∆≌ ∴CEA DBE ∠=∠ 又∵90DBE DEB ∠+∠=︒ ∴90DEB CEA ∠+∠=︒ 故90AEB ∠=︒∴AE EB ⊥且AE BE =．【例2】 已知四边形ABCD 的对角线AC BD =，E 、F 分别是AD 、BC 的中点，连结EF 分别交AC 、BD于M 、N ，求证：AMN BNM =∠∠．【答案】设AB 的中点为G ，连结GE 、GF ，容易证得12GE BD =∥，12GF AC =∥，从而GF GE =，GEF GFE =∠∠，所以 AMN BNM =∠∠．【练1】已知四边形ABCD 中，AC BD <，E F 、分别是AD BC 、的中点，EF 交AC 于M ；EF 交BD 于N ，AC 和BD 交于G 点．求证：GMN GNM ∠>∠．GBCDEFM N A【答案】取AB 中点H ，连接EH FH 、．∵AE =ED AH =BH ，∴12EH BD EH =BD ∥，,∴GNM HEF ∠=∠ ∵AH =BH BF =CF ，HGNM E DA∴12FH AC FH =AC ∥， ∴GMN HFE ∠=∠ ∵AC <BD ∴FH <EH∴<HEF HFE ∠∠ ∴GMN GNM ∠>∠【练2】已知：在ABC ∆中，BC AC >，动点D 绕ABC ∆的顶点A 逆时针旋转，且AD BC =，连结DC ．过AB 、DC 的中点E 、F 作直线，直线EF 与直线AD 、BC 分别相交于点M 、N ．（1）如图1，当点D 旋转到BC 的延长线上时，点N 恰好与点F 重合，取AC 的中点H ，连结HE 、HF ，求证： AMF BNE ∠=∠（2）当点D 旋转到图2中的位置时，AMF ∠与BNE ∠有何数量关系？请证明．MN AB EF DC(N )M F EDCBA【答案】取AC 的中点H ，连结HE 、HF∵F 是DC 的中点，H 是AC 的中点 ∴HF AD ∥，12HF AD = ∴AMF HFE ∠=∠同理，HE CB ∥，12HE CB =∴ENB HEF ∠=∠∵AD BC = ∴HF HE =， ∴HEF HFE ∠=∠ ∴ENB AMF ∠=∠【例3】 如图，在五边形ABCDE 中，90ABC AED ∠=∠=︒，BAC EAD ∠=∠，F 为CD 的中点．求证：BF EF =．【答案】取AC 中点M ，AD 中点N ．连结MF 、NF 、MB 、NE ，则根据直角三角形斜边中线的性质及中位线的性质有12MF AD NE ==，12NF AC MB ==，MF AD ∥，NF AC ∥，∴DNF CAD CMF ∠=∠=∠，∵BM AM =，∴MBA CAB ∠=∠．∴2BMC MBA CAB CAB ∠=∠+∠=∠．同理可证2DNE DAE ∠=∠． ∵BAC EAD ∠=∠，∴BMC END ∠=∠． ∴BMC CMF FND DNE ∠+∠=∠+∠，即BMF ENF ∠=∠，∴MBF NFE ∆∆≌，∴BF EF =．【练1】如图所示，在ABC ∆中，D 为AB 的中点，分别延长CA 、CB 到点E 、F ，使DE DF =．过E 、F 分别作直线CA 、CB 的垂线，相交于点P ，设线段PA 、PB 的中点分别为M 、N ．求证：（1）DEM FDN ∆∆≌； （2）PAE PBF ∠=∠．【答案】（1）如图所示，根据题意可知DM BN ∥且DM BN =，DN AM ∥且DN AM =，所以AMD APB DNB ∠=∠=∠．而M 、N 分别是直角三角形AEP ∆、BFP ∆的斜边的中点， 所以EM AM DN ==，FN BN DM ==， 又已知DE DF =， 从而DEM FDN ∆∆≌． （2）由(1)可知EMD DNF ∠=∠，则由AMD DNB ∠=∠可得AME BNF ∠=∠． 而AME ∆、BNF ∆均为等腰三角形， 所以PAE PBF ∠=∠．【练2】已知：在ABC ∆中，分别以AB 、AC 为斜边作等腰直角三角形ABM ，和CAN ，P 是边BC 的中点．求证：PM PN =PNMCBA【答案】取AB 中点Q AC ，中点R连结PQ PR MQ NR ，，， 12PQ AC PQ AC NR ==∥， PR AB PR MQ ∥，＝ PQM PRN ∠∠＝ (两边分别垂直)∴PQM NRP PM PN ∆∆≌， ＝【练3】如图所示，已知ABD ∆和ACE ∆都是直角三角形，且90ABD ACE ∠=∠=︒，连接DE ，设M 为DE的中点．（1）求证MB MC =．（2）设BAD CAE ∠=∠，固定Rt ABD ∆，让Rt ACE ∆移至图示位置，此时MB MC =是否成立？请证明你的结论．EMDCBA EM DCBA【答案】（1）如图所示，延长BM 交CE 于N ．因为DM EM =，CE BD ∥， 故DBM ENM ∆∆≌， 则BM NM =， 从而12MC BN MB ==．（2）结论是肯定的．取AD 、AE 的中点F 、G ， 连接FB 、FM 、MG 、GC ．由BF 、CG 是Rt ABD ∆、Rt ACE ∆斜边上的中线 可得12BF AD =，12CG AE =， 从而MF CG =，MG BF =．又因为22CGE CAE BAD BFD ∠=∠=∠=∠， MFD DAE MGE ∠=∠=∠，故BFM MGC ∠=∠，NEMDCA MGFEDCBAPNMQRCBA从而BFM MGC ∆∆≌， 故MB MC =．【例4】 以ABC ∆的两边AB 、AC 为腰分别向外作等腰Rt ABD ∆和等腰Rt ACE ∆，90BAD CAE ∠=∠=︒.连接DE ，M 、N 分别是BC 、DE 的中点．探究：AM 与DE 的位置关系及数量关系．（1）如图① 当ABC ∆为直角三角形时，AM 与DE 的位置关系是________；线段AM 与DE 的数量关系是________；（2）将图①中的等腰Rt ABD ∆绕点A 沿逆时针方向旋转θ︒(090θ<<)后，如图②所示，（1）问中得到的两个结论是否发生改变？并说明理由．图①NM EDCB A图②NM EDCBA【答案】（1）AM DE ⊥，12AM DE =; （2）结论仍然成立。
初中数学-三角形中的中线的用法教师版
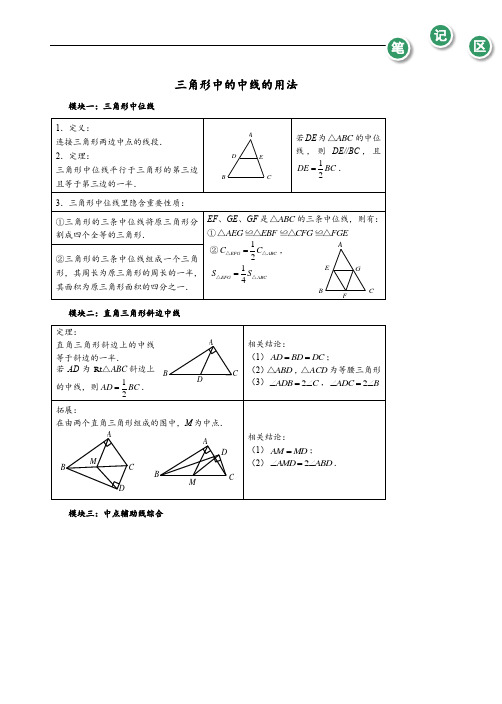
三角形中的中线的用法模块一：三角形中位线 1．定义：连接三角形两边中点的线段． 2．定理：三角形中位线平行于三角形的第三边且等于第三边的一半．若DE 为ABC △的中位线，则DE//BC ，且12DE BC =．3．三角形中位线里隐含重要性质： ①三角形的三条中位线将原三角形分割成四个全等的三角形．EF 、GE 、GF 是ABC △的三条中位线，则有：①AEG EBF CFG FGE △△△△≌≌≌②12EFG ABC C C =△△，14EFG ABC S S =△△②三角形的三条中位线组成一个三角形，其周长为原三角形的周长的一半，其面积为原三角形面积的四分之一． 模块二：直角三角形斜边中线 定理：直角三角形斜边上的中线等于斜边的一半．若AD 为Rt ABC △斜边上的中线，则12AD BC =．相关结论：（1）AD BD DC ==； （2）ABD △，ACD △为等腰三角形 （3）2ADB C ∠=∠，2ADC B ∠=∠拓展：在由两个直角三角形组成的图中，M 为中点．相关结论：（1）AM MD =；（2）2AMD ABD ∠=∠． 模块三：中点辅助线综合E DCB AMMABCDA BCDDCBAFA B CE G（1）如图1-1，在ABC△中，D，E，F分别是AB，BC，AC的中点，若ABC△的周长为20cm，则DEF△的周长为__________．（2）如图1-2，在Rt ABC△中，30A∠=︒，1BC=，点D，E分别是直角边BC，AC的中点，则DE的长为__________．图1-1 图1-2（3）如图1-3，ABC△中，6AB AC==，8BC=，AE平分BAC∠交BC于点E，点D为AB的中点，连接DE，则BDE△的周长是__________．（4）如图1-4，在四边形ABCD中，E、F分别为AB、CD的中点．求证：1()2EF AC BD<+．图1-3 图1-4【解析】（1）10cm．（2）1．（3）10．（4）证明：取AD的中点M，连结EM和FM．∵E、F是AB、CD中点，∴12EM BD=，12FM AC=．又∵EF EM FM<+，∴1()2EF AC BD<+．【教师备课提示】考察中位线产生的线段长度关系．第（4）题利用中位线构造出长为12AC，12BD的线段并将线段集中；也可以求证1()2EF AD BC<+，方法是取AC 或BD的中点．FEDCBA模块一三角形中位线例题1MAB CDEF（1）如图2-1，在四边形ABCD 中，P 是对角线BD 的中点，E ，F 分别是AB ，CD 的中点，AD BC =，18PEF ∠=︒，则PFE ∠的度数是__________度．（2）如图2-2，已知四边形ABCD 的对角线AC BD =，E 、F 分别是AD 、BC 的中点，连结EF 分别交AC 、BD 于M 、N ，求证：AMN BNM =∠∠．（3）已知，如图2-3四边形ABCD 中，AD BC =，E 、F 分别是AB 和CD 的中点，AD 、EF 、BC 的延长线分别交于M 、N 两点．求证：AME BNE ∠=∠．图2-1 图2-2 图2-3【解析】（1）18．（2）设AB 的中点为G ，连结GE 、GF ，容易证得：GE //BD ，12EG BD =，GF //AC ，12EF AC =，从而GF GE =，GEF GFE ∠=∠， ∴AMN BNM =∠∠．（构造中位线来利用对角线相等的条件，也可以取AC 或BD 的中点．） （3）连接AC ，取AC 中点H ，连接FH 、EH ．∵DF CF =，AH CH =，∴FH//AD ，12FH AD =，同理，12EH BC =，EH//BC ， ∵AD BC =，∴EH FH =，∴HFE HEF ∠=∠， ∵FH//AM ，EH//BC ， ∴AM E HFE ∠=∠，HEF BNE ∠=∠， ∴AME BNE ∠=∠．【教师备课提示】考察中位线的性质，学会通过构造中位线去利用已知的条件．CM FEND B AA CDM FE NB例题2CM FE G NDB AA H C D MF E NB如图，在ABC △中，D 、G 分别为AB 、AC 上的点，且BD CG =，M 、N 分别是BG 、CD 的中点，过MN 的直线交AB 于点P ，交AC 于点Q ，求证：AP AQ =．【解析】连DG ，找DG 的中点E ，连ME 、NE ，∵M 、N 分别是BG 与CD 的中点．∴ME//AB ，12ME BD =，NE//AC ，12NE GC =．∴APQ EMN ∠=∠，AQP ENM ∠=∠．∵BD GC =，∴EM EN =， ∴EMN ENM ∠=∠，∴APQ AQP ∠=∠，∴AP AQ =． 【教师备课提示】还可以取BC 中点．总结：已知四边形对角线中点，则取一边中点，可出两条中位线，学会构造出中位线去利用题目中给出的等量关系．已知：在ABC △中，90ABC ∠=︒，点E 在直线AB 上，ED 与直线AC 垂直，垂足为D ，且点M 为EC 中点，连接BM 、DM ．（1）如图4-1，若点E 在线段AB 上，探究线段BM 与DM 及BM D ∠与BCD ∠所满足的数量关系，并直接写出你得到的结论；（2）如图4-2，若点E 在BA 延长线上，你（1）中的结论是否发生变化？写出你的猜想并证明．图4-1 图4-2【解析】（1）BM DM =，2BMD BCD ∠=∠；（2）结论不变，由题意知MB MC MD ==，∴2BME BCM ∠=∠，2DME DCM ∠=∠，两式相减，得2BMD BCD ∠=∠．NM PQG D C BAEA BC DG Q PM N 图2图1BEM CDAMEDCBA例题3模块二直角三角形斜边中线例题4如图，90MON∠=︒，ABC△中，90BAC∠=︒，2AB=，1AC=，AB在MON∠上滑动，求OC的最大值．【解析】取AB的中点D，连结OD、DC，则1OD=，2DC=，可得12OC≤+，即OC的最大值为12+（O、D、C三点共线时）．在Rt ABC△中，90BAC∠=︒，AD BC⊥，E、F、G分别是AB、AC、BC的中点，M 是DG的中点，求证：ME MF=．【解析】连结DF、EG，可证DF GE=，MDF MGE∠=∠，MD MG=，则MDF MGE△≌△，得证．例题5模块三中点辅助线综合例题6如图，在五边形ABCDE 中，90ABC AED ∠=∠=︒，BAC EAD ∠=∠，F 为CD 的中点．求证：BF EF =．【解析】方法一：如图1，取AC 中点M ，取AD 中点N ，连BM ，MF ，NF ，EN ． ∵90ABC AED ∠=∠=︒，1122BM AC FN EN AD MF ====，，∴BMF FNE △≌△，∴BF EF =，方法二：如图2，延长CB 到M ，使得MB BC =， 延长DE 到N ，使得NE DE =， 连接AM ，AN ，MD ，CN ． 由90ABC AED ∠=∠=°，AMC △，ADN △是等腰三角形，F 是CD 中点，则BF //MD ，12BF MD =，EF//CN ，12EF CN =，MAD CAN △≌△，MD CN =，∴BF EF =，此题的两种解法中综合了中点的三个基本用法：等腰三角形三线合一；直角三角形斜边中线；中位线，即以下三个模型：图2图1MNN MACBDEF F EDB CA例题7FEDB C A（1）如图1-1，在ABC△中，点D是BC中点，AE平分∠BAC，BE⊥AE于E，延长BE 交AC于F．若AB=10厘米，AC=16厘米，则DE的长度为__________．（2）如图1-2，已知，在四边形ABCD中，AD BC=，P是对角线BD的中点，N是DC 的中点，M是AB的中点，30DBC∠=︒，70ADB∠=︒．求MNP∠度数．图1-1 图1-2【解析】（1）3厘米；（2）∵在四边形ABCD中，P是对角线BD的中点，M、N分别是AB、CD的中点，∴NP，PM分别是CDB△与DAB△的中位线，∴12PN BC=，12PM AD=，PN//BC，PM//AD，∴30NPD DBC∠=∠=︒，70MPB ADB∠=∠=︒，∴110DPM∠=︒；∴140NPM∠=︒，∵AD BC=；∴PN PM=，故NMP△是等腰三角形．∵140NPM∠=︒，∴20PMN PNM∠=∠=︒．复习巩固模块一三角形中位线演练1（1）如图2-1,ABC △中，过点A 分别作ABC ∠、ACB ∠的外角平分线．．．．．的垂线．．AD 、AE ，垂足为D 、E ．求证：①//ED BC ；②1()2ED AB AC BC =++．（2）（四川省中考题）如图2-2,已知：AD 是ABC △的中线，AE 是ABD △的中线，且AB BD =，求证：2AC AE =．图2-1 图2-2【解析】（1）①分别延长AD 、AE 与直线BC 交于点F 、G ，∵BD ⊥AD ，且BD 为ABF ∠的角平分线∴AD FD =，且AB BF =（等腰三角形的三线合一） 同理可得AE GE =，AC GC =， ∴DE 为AFG △的中位线，∴ED //BC ，且12DE FG =．②由（1）知12DE FG =，且AB BF =，AC GC =，∴111()()222ED FG=FB BC CG AB BC AC =++=++．（2）取AC 的中点F ，连结DF ，易得DF//AB ，12DF AB =，ADF BAD ∠=∠，而1122DE BD AB ==，故DF DE =．再证ADE ADF △≌△，∴AE AF =，∴2AC AE =．C ED BA演练2CF E D B A（1）如图3-1，四边形ABCD 中，90ADC ∠=︒，取AC 中点O ，BC 中点E ，连接OD 、OE 、DE ，20CAD CAB ∠=∠=︒，则DOE ∠=__________．（2）如图3-2所示，ABC △中，AH BC ⊥于H ，点E 、D 、F 分别是AB 、BC 、AC 的中点，10cm HF =，则ED 的长度是__________．图3-1 图3-2【解析】（1）60︒．（2）10cm ．（1）如图4-1，在ABC △中，2B C ∠=∠，M 是BC 中点，AD BC ⊥于D ．求证：12DM AB =．（2）如图4-2，已知：ABD △和ACE △都是直角三角形，且90ABD ACE ∠=∠=︒，BAD CAE ∠=∠．连接DE ，设M 为DE 的中点．求证：MB MC =．【解析】（1）法一：取AB 中点G ，连结GD 、GM ，则12GD AB =，GM AC ∥．则GMD C ∠=∠． 而GD GB B GDB GMD DGM =⇒∠=∠=∠+∠ C DGM =∠+∠，由于2B C ∠=∠，所以DGM C GMD ∠=∠=∠．∴12MD GD AB ==． OEDC B AMEDCBA模块二直角三角形斜边中线演练3模块三中点辅助线综合演练4CAB GNDMC AB D M法二：同理可以取AC的中点N，连接DN，MN．（2）如图，分别取AD、AE的中点P、Q，连接PB、PM、QC、QM，由P、M、Q分别是AD、DE、AE的中点，∴PM//AE，12PM AE=，QM//AD，12QM AD=，∵ABD△、ACE△是直角三角形，∴12PB AD=，12CQ AE=，∴PB QM=，PM QC=，∵BAD CAE∠=∠，∴ADB AEC∠=∠，∴DPB CQE∠=∠，由AD//QM，AE//PM，∴APM AQM∠=∠，∴BPM MQC∠=∠，∴BPM MQC△≌△，∴MB MC=．QPAB CDE M图3。
如何构造三角形中位线
如何构造三角形中位线作者：***来源：《中学生数理化·八年级数学人教版》2020年第04期三角形的中位线定理，是一个很有价值的定理，解题时若遇到中点，它是必须被联想到的定理之一.但是，在题目中往往只知道一个中点，而另一个中点未知，需要同学们根据题目的特点去寻找.下面，就向大家介绍几种构造中位线的方法，供参考.一、连接两点构造中位线例1 如图1.已知△ABC.分别以AB，AC为边向外作两个等边三角形ABM和ACN.D，E，F分别是MB.BC，CN的中点，连接DE、EF。
求证：DE=EF证明：连接CM，BN，如图2.△ABM和△ACN是等边三角形，易证△MAC≌△BAN（边角边）.∴MC=BN.∵D，E，F分别是MB，BC，CN的中点，∴DE=1/2MC，EF=1/2BN，从而DE=EF.二、用“角平分线+垂直”构造中位线例2 已知M为△ABC的边BC的中点.AB=12，AC=18.BD⊥AD于D，连接MD.（1）如图3，若AD为∠BAC的平分线，求MD的长：（2）如图4，若AD为△ABC的外角的平分线，求MD的长，解：（）如图5.延长BD交AC于E.∵AD为∠BAC的平分线，BD⊥AD，∴BD=DE，AE=AB=12.∴CE=AC-AE=18-12=6.又∵M为BC的中点，∴MD是△BCE的中位线，MD=3.（2）延长BD，CA交于E，如图6.仿（1），CE=AC+AE=AC+AB=30，∴MD=CE2=15.三、倍长法构造中位线例3 如图7.在△ABC中，∠ABC=90°，BA=BC.△BEF为等腰直角三角形，如何构造三角形中位线吉林省长春市解放大路学校王翰琛三角形的中位线定理，是一个很有价值的定理，解题時若遇到中点，它是必须被联想到的定理之一.但是，在题目中往往只知道一个中点，而另一个中点未知，需要同学们根据题目的特点去寻找.下面，就向大家介绍几种构造中位线的方法，供参考.一、连接两点构造中位线例1 如图1.已知△ABC.分别以AB，AC为边向外作两个等边三角形ABM和ACN.D，E，F分别是MB.BC，CN的中点，连接DE、EF。
构造三角形的中位线定理使用条件解题例析
构造三角形的中位线定理使用条件解题例析作者：孙中淼来源：《教育周报·教研版》2018年第22期三角形的中位线定理揭示了三角形中两条线段的位置关系和数量关系，利用它来解决几何证明题是行之有效的方法。
在解答与中点有关的几何题时，若能根据题意巧妙构造中位线定理使用条件，就会有出奇制胜的效果。
下面通过几道题说明之，以供参考。
一、没有第三边，添加第三边【例1】如图，点E、F、G、H分别是CD、BC、AB、DA的中点.求证：四边形EFGH是平行四边形.证明：连接BD，∵E、F、分别是CD、BC的中点，∴EF∥BD，，又∵G、H分别是AB、DA的中点，∴GH∥BD，，∴，∴四边形EFGH是平行四边形.二、没有中位线，作出中位线【例2】已知，如图在，在□ABCD中，E是CD的中点，F是AE的中点，FC与BE交于G.求证：GF=GC.证明：取BE的中点H，连接FH、CH，∵F是AE的中点，H是BE的中点，∴FH是三角形ABE的中位线，∴FH∥AB且，又∵点E是DC的中点，∴，又∵，∴.∴四边形EFHC 是平行四边形，∴GF=GC.三、同时作出中位线和第三边【例3】如图，同底边BC的△ABC与△DBC中，E、F、G、H分别是AB、AC、DB、DC的中点，求证：EH与FG互相平分.证明：连接EG、GH、FH、EF，∵点E、F、G、H分别是AB、CD、AC、BD的中点，∴EF、GH分别是△ABC与△DBC的中位线，∴，，∴.∴四边形EGFH为平行四边形.∴EF 与GH互相平分.四、两边中有一边不全，补全两边【例4】如图，已知在△ABC中，E是AB的中点，CD平分∠ACB，AD⊥CD，求证：（1）DE∥BC；（2）证明：延长AD交BC于F.（1）∵AD⊥CD，∴∠ADC=∠FDC=90°.∵CD平分∠ACB，∴∠ACD=∠FCD.在△ACD 与△FCD中，∠ADC=∠FDC， DC=DC，∠ACD=∠FCD，∴△ACD≌△FCD.∴AC=FC，AD=DF.又∵E为AB的中点，∴DE∥BF，即DE∥BC.（2）由（1）知AC=FC，，∴.总之，三角形的中位线定理是一个非常有价值的定理.它是一个遇到中点，必须联想到的重要定理，但是在解题时，往往只知道它的一部分，因此就需要同学们根据题目的特点自己去寻找，补全中位线定理的基本图形，解决问题，从而达到学习的目的.。
专题05 三角形中位线(知识点串讲)(解析版)
专题05 三角形中位线重难突破三角形中位线1．三角形中位线：连接三角形两边中点的线段叫做三角形的中位线.2．三角形中位线定理：三角形的中位线平行于三角形的第三边，并且等于第三边的一半.3．相关结论：顺次连接任意四边形中点所得到的四边形是平行四边形.（连接原四边形一条对角线，由中位线定理可证）4．拓展：①梯形的中位线等于上底加下底和的一半. （连接梯形一条对角线，由中位线定理可证）②过三角形一边的中点作另一边的平行线，与第三边交于一点，则这两点之间的线段为三角形的中位线. 如图，过△ABC的边AB的中点作平行于边BC的直线，交边AC于点E，则DE为△ABC的中位线.典例1．（2018春•定兴县期末）如图所示，已知P、R分别是四边形ABCD的边BC、CD上的点，E、F分别是PA、PR的中点，点P在BC上从B向C移动，点R不动，那么EF的长（）A．逐渐增大B．逐渐变小C．不变D．先增大，后变小【答案】C【解析】解：∵E、F分别是PA、PR的中点，∴EF AR，∴EF的长不变，故选：C．【点睛】根据三角形中位线定理得到EF AR，判断即可．本题考查的是三角形中位线定理，掌握三角形的中位线平行于第三边，且等于第三边的一半是解题的关键．典例2．（2018春•柳州期末）在Rt△ABC中，∠ACB＝90°，AE，BD是角平分线，CM⊥BD于M，CN ⊥AE于N，若AC＝6，BC＝8，则MN＝___．【答案】2【解析】解：延长CM交AB于G，延长CN交AB于H，∵∠ACB＝90°，AC＝6，BC＝8，∴AB＝10，在△BMC和△BMG中，，∴△BMC≌△BMG，∴BG＝BC＝8，CM＝MG，∴AG＝2，同理，AH＝AC＝6，CN＝NH，∴GH＝4，∴MN GH＝2，故答案为：2．【点睛】延长CM交AB于G，延长CN交AB于H，证明△BMC≌△BMG，得到BG＝BC＝8，CM＝MG，同理得到AH＝AC＝6，CN＝NH，根据三角形中位线定理计算即可．典例3．（2018春•成都期末）已知：如图，AD、BE分别是△ABC的中线和角平分线，AD⊥BE，AD＝BE ＝2，则AC的长等于______．【答案】见解析【解析】解：过D点作DF∥BE，∵AD是△ABC的中线，AD⊥BE，∴F为EC中点，AD⊥DF，∵AD＝BE＝2，则DF＝1，AF，∵BE是△ABC的角平分线，AD⊥BE，∴△ABG≌△DBG，∴G为AD中点，∴E为AF中点，∴AE＝EF＝CF，∴AC AF．故答案为：．【点睛】过D点作DF∥BE，则DF BE＝1，F为EC中点，在Rt△ADF中求出AF的长度，根据已知条件易知G为AD中点，因此E为AF中点，则AC AF．典例4．（2018春•吉州区期末）如图，在△ABC中，已知AB＝6，AC＝10，AD平分∠BAC，BD⊥AD于点D，E为BC中点．求DE的长．【答案】见解析【解析】解：如图，延长BD与AC相交于点F，∵AD平分∠BAC，BD⊥AD，∴∠DAB＝∠DAF，AD＝AD，∠ADB＝∠ADF，∴△ADB≌△ADF，∴AF＝AB，BD＝DF，∵AB＝6，AC＝10，∴CF＝AC﹣AF＝AC﹣AB＝10﹣6＝4，∵E为BC中点，∴DE是△BCF的中位线，∴DE CF4＝2．【点睛】延长BD与AC相交于点F，根据等腰三角形的性质可得BD＝DF，再利用三角形的中位线平行于第三边并且等于第三边的一半可得DE CF，然后求解即可．典例5．（2018春•濮阳期末）已知等边三角形ABC的边长为a分别以这个三角形的三边中点为顶点作一个三角形，记为△A1B1C1，再以△A1B1C1各边中点为顶点做三角形记为△A2B2C2，…依次做下去，求△A5B5C5的周长．【答案】见解析【解析】解：等边△ABC的边长为a，∴等边△ABC的周长为3a．∵A2、B2分别是边A1B1、B1C1的中点，∴A2B2是△A1B1C1的中位线，∴A2B2A1B1．同理，A2C2A1C1，C2B2C1B1．∴△A2B2C2的周长等边△A1B1C1的周长．同理，△A3B3C3的周长△A2B2C2的周长等边△A1B1C1的周长．…，∴△A n B n∁n的周长△A1B1C1的周长．∴△A5B5C5的周长．【点睛】据三角形中位线定理知，△A2B2C2的各边的边长是△A1B1C1的各边边长的，△A3B3C3是△A2B2C2的各边的边长的，找出规律即可得出结论．本题考查了等边三角形的性质、三角形中位线定理．三角形中位线的性质，即三角形的中位线平行于第三边且等于第三边的一半．典例6．（2018春•南山区期末）如图，△ABC中，AB＞AC，AD，AE分别是其角平分线和中线，过点C作CG⊥AD于点F，交AB于点G，连接EF，则①EF∥AB；②∠BCG（∠ACB﹣∠ABC）；③EF （AB﹣AC）；④（AB﹣AC）＜AE（AB+AC）．其中正确的是（）A．①②③④B．①②C．②③④D．①③④【答案】A【解析】解：∵AD平分∠BAC，∴∠GAF＝∠CAF，∵CG⊥AD，∴∠AFG＝∠AFC＝90°，在△AFG和△AFC中∴△AFG≌△AFC（ASA），∴GF＝CF，∵AE为△ABC的中线，∴BE＝CE，∴EF∥AB，故①正确；∵△AFG≌△AFC，∴∠AGC＝∠ACB，∵∠AGC＝∠B+∠BCG，∴∠ACG＝∠B+∠BCG，∴∠BCG＝∠ACB﹣∠ACG＝∠ACB﹣（∠B+∠BCG），∴2∠BCG＝∠ACB﹣∠B，∴∠BCG（∠ACB﹣∠B），故②正确；∵△AFG≌△AFC，∴AC＝AG，∴BG＝AB﹣AG＝AB﹣AC，∵F、E分别是CG、BC的中点，∴EF BG，∴EF（AB﹣AC），故③正确；∵∠AFG＝90°，∴∠EAF＜90°，∵∠AFE＝∠AFG+∠EFG＞90°，∴∠AFE＞∠EAF，∴AE＞EF，∵EF（AB﹣AC），∴（AB﹣AC）＜AE，延长AE到M，使AE＝EM，连接BM，∵在△ACE和△MBE中∴△ACE≌△MBE（SAS），∴AC＝BM，在△ABM中，AM＜AB+AC，∵AE＝EM，∴2AE＜AB+AC，∴AE（AB+AC），即（AB﹣AC）＜AE（AB+AC），故④正确；故选：A．【点睛】求出F为CG中点，根据三角形的中位线性质即可判断①，求出∠ACG＝∠AGC＝∠B+∠BCG，即可判断②；根据三角形中位线性质即可判断③，求出2AE＜AB+BC和AE＞EF，即可判断④．巩固练习1．（2018春•坪山区期末）如图，在△ABC中，AB＝5，BC＝6，AC＝7，点D，E，F分别是△ABC三边的中点，则△DEF的周长为（）A．12 B．11 C．10 D．9【答案】D【解析】解：∵点D，E分别AB、BC的中点，∴DE AC＝3.5，同理，DF BC＝3，EF AB＝2.5，∴△DEF的周长＝DE+EF+DF＝9，故选：D．2．（2018春•抚顺期末）如图，在四边形ABCD中，P是对角线BD的中点，E，F分别是AB，CD的中点，AD＝BC，∠PEF＝25°，则∠EPF的度数是（）A．100°B．120°C．130°D．150°【答案】C【解析】解：∵P是对角线BD的中点，E，F分别是AB，CD的中点，∴PE AD，PF BC，∵AD＝BC，∴PE＝PF，∴∠PFE＝∠PEF＝25°，∴∠EPF＝130°，故选：C．3．（2018春•颍东区期末）如图在△ABC中，M是BC中点，AP是∠A平分线，BP⊥AP于P，AB＝12，AC＝22，则MP长为（）A．3 B．4 C．5 D．6【答案】C【解析】解：延长BP交AC于N.∵AP是∠BAC的角平分线，BP⊥AP于P，∴∠BAP＝∠NAP，∠APB＝∠APN＝90°，∴△ABP≌△ANP（ASA），∴AN＝AB＝12，BP＝PN，∴CN＝AC﹣AN＝22﹣12＝10，∵BP＝PN，BM＝CM，∴PM是△BNC的中位线，∴PM CN＝5．故选：C．4．（2018春•开江县期末）如图，将腰长为4的等腰直角三角形放在直角坐标系中，顺次连接各边中点得到第1个三角形，再顺次连接各边中点得到第2个三角形，……如此操作下去，那么第5个三角形直角顶点的坐标为（）A．（，）B．（）C．（）D．（）【答案】B【解析】解：由题意：第1个三角形的直角顶点坐标：（﹣2，2）；第2个三角形的直角顶点坐标：（﹣1，1）；第3个三角形的第1个三角形的直角顶点坐标：（，）；第4个三角形的直角顶点坐标：（，）；第5个三角形的直角顶点坐标：（，）；故选：B．5．（2017秋•洪雅县期末）如图，在△ABC中，AB＝5，AC＝3，AD是角平分线，AE是中线，过点C作CG⊥AD于点F，交AB于点G，连接EF，则线段EF的长为___．【答案】1【解析】解：∵AD是其角平分线，CG⊥AD于F，∴△AGC是等腰三角形，∴AG＝AC＝3，GF＝CF，∵AB＝5，AC＝3，∴BG＝2，∵AE是中线，∴BE＝CE，∴EF为△CBG的中位线，∴EF BG＝1 故答案为：1.。
部编数学八年级下册专题18构造三角形中位线的常用技巧(解析版)含答案
专题18 构造三角形中位线的常用技巧（解析版）专题典例剖析及针对训练类型一 连接两中点构造中位线典例1如图，在△ABC 中，AB ＝AC ＝5，BC ＝6，D 、E 分别是AB 、AC 的中点，F 、G 为BC 上的两点，FG ＝3，线段DG ，EF 的交点为O ，当线段FG 在线段BC 上移动时，三角形FGO 的面积与四边ADOE 的面积之和恒为定值，则这个定值是（ ）A ．15B ．12C ．9D ．6思路指引：连接DE ，过A 作AH ⊥BC 于H ．由于DE 是AB 、AC 的中点，利用三角形中位线定理可得DE ∥BC ，并且可知△ADE 的高等于12AH ，再结合等腰三角形三线合一性质，以及勾股定理可求AH ，那么△ADE 的面积就可求．而所求S △FOG +S 四边形ADOE ＝S △ADE +S △DOE +S △FOG ，又因为△DOE 和△FOG 的底相等，高之和等于AH 的一半，故它们的面积和可求，从而可以得到S △FOG +S 四边形ADOE 的面积．解：如图：连接DE ，过A 向BC 作垂线，H 为垂足，∵△ABC 中，D 、E 分别是AB 、AC 的中点，∴DE ，AH 分别是△ABC 的中位线和高，BH ＝CH =12BC =12×6＝3，∵AB ＝AC ＝5，BC ＝6，由勾股定理得AH ==4，∴S △ADE =12BC •AH 2=12×3×42=3，设△DOE 的高为a ，△FOG 的高为b ，则a +b =AH 2=2，∴S △DOE +S △FOG =12DE •a +12FG •b =12×3（a +b ）=12×3×2＝3，∴三角形FGO 的面积与四边ADOE 的面积之和恒为定值，则这个定值是S △ADE +S △DOE +S △FOG ＝3+3＝6．故选：D ．方法点睛：本题属中等难度题目，涉及到三角形中位线定理，解答此类题目时一般只要知道中点要作中位线，已知等腰三角形要作高线，利用勾股定理解答．针对训练1．如图，△ABC 的中线BD ，CE 相交于点0，F ，G 分别是BO ，CO 的中点，求证：EF ∥DG 且EF ＝DG ．解：连接ED ，FG .证四边形DEFG 是平行四边形，∴EF ∥DG 且EF ＝DG ．类型二 连接第三边构造中位线典例2（2022秋•泰山区校级期末）如图，在菱形ABCD 中，E ，F 分别是边CD ，BC 上的动点，连接AE ，EF ，G ，H 分别为AE ，EF 的中点，连接GH ．若∠B ＝45°，BC ＝GH 的最小值为（ ）ABC DGF E DC B AABDE F G思路指引：连接AF，利用三角形中位线定理，可知GH=12AF，求出AF的最小值即可解决问题．解：连接AF，如图所示：∵四边形ABCD是菱形，∴AB=BC=∵G，H分别为AE，EF的中点，∴GH是△AEF的中位线，∴GH=12 AF，当AF⊥BC时，AF最小，GH得到最小值，则∠AFB＝90°，∵∠B＝45°，∴△ABF是等腰直角三角形，∴AF==∴GH=即GH故选：D．方法点睛：本题考查了菱形的性质、三角形的中位线定理、等腰直角三角形的判定与性质、垂线段最短等知识，解题的关键是学会添加常用辅助线，属于中考常考题型．针对训练1．（2021秋•孟津县期末）如图所示，已知四边形ABCD，R、P分别是DC、BC上的点，点E、F分别是AP、RP的中点，当点P在边BC上从点B向点C移动，且点R从点D向点C移动时，那么下列结论成立的是（ ）A ．线段EF 的长逐渐增大B ．线段EF 的长逐渐减少C ．线段EF 的长不变D ．△ABP 和△CRP 的面积和不变思路指引：连接AR ，根据三角形的中位线定理可得EF =12AR ，根据AR 的变化情况即可判断．解：连接AR ，∵E ，F 分别是AP ，RP 的中点，∴EF =12AR ，∵当点P 在BC 上从点C 向点B 移动，点R 从点D 向点C 移动时，AR 的长度逐渐增大，∴线段EF 的长逐渐增大．S △ABP +S △CRP =12BC •（AB +CR ）．∵CR 随着点R 的运动而减小，∴△ABP 和△CRP 的面积和逐渐减小．观察选项，只有选项A 符合题意．故选：A ．方法点睛：此题考查的是三角形中位线的性质，即三角形的中位线平行于第三边且等于第三边的一半． 典例3 如图，点B 为AC 上一点，分别以AB ，BC 为边在AC 同侧作等边△ABD 和等边△BCE ，点P ，M ，N 分别为AC ，AD ，CE 的中点．（1）求证：PM ＝PN ；（2）求∠MPN 的度数．思路指引：（1）连接DC和AE，AE交CD于点M，证明△ABE≌△DBC，得到AE＝DC，利用中位线的性质证明PM＝PN；（2）根据中位线的性质把∠MPA+∠NPC转化成∠MCA+∠MAC，根据∠DMA＝∠MCA+∠MAC可知求出∠DMA度数即可．解：（1）连接DC和AE，AE交CD于点M，在△ABE和△DBC中，AB=BD∠ABE=∠DBCBE=BC∴△ABE≌△DBC（SAS）．∴AE＝DC．∵P为AC中点，N为EC中点，AE．∴PN=12DC．同理可得PM=12所以PM＝PN．（2）∵P为AC中点，N为EC中点，∴PN∥AE．∴∠NPC＝∠EAC．同理可得∠MPA＝∠DCA∴∠MPA+∠NPC＝∠EAC+∠DCA．又∠DQA＝∠EAC+∠DCA，∴∠MPA+∠NPC＝∠DQA．∵△ABE ≌△DBC ，∴∠QDB ＝∠BAQ ．∴∠DQA ＝∠DBA ＝60°．∴∠MPA +∠NPC ＝60°．∴∠MPN ＝180°﹣60°＝120°．方法点睛：本题主要考查全等三角形的判定和性质、中位线的性质、等边三角形的性质，解题的关键是找到“手拉手”全等模型．针对训练1.如图，分别以△ABC 的边AB ，AC 同时向外作等腰直角三角形，其中AB ＝AE ，AC ＝AD ，∠BAE ＝∠CAD ＝90°，点G 为BC 的中点，点F 为BE 的中点，点H 为CD 的中点．探索GF 与GH 的数量关系及位置关系，并说明理由．解：连接BD ，CE ，易证△ABD ≌△AEC ，∴BD ＝ CE ，易证BD ⊥CE .由中位线性质可得GF ＝GH ，GF ⊥GH .类型三 取中点构造中位线（1）直接取一边中点典例4（2022春•武昌区期中）如图，在△ABC 中，∠A ＝60°，BD 为AC 边上的高，E 为BC 边的中点，点F 在AB 边上，∠EDF ＝60°，若AF ＝2，BF =103，则BC 边的长为（ ）HG FEDCB AAB CDEFG HA ．163BCD 思路指引：过点D 作DM ⊥AB ，垂足为M ，取AB 的中点H ，连接EH ，DH ，根据已知可求出AB =163，先在Rt △ABD 中求出AD ，AH 的长，从而可得△ADH 是等边三角形，进而可得AD ＝DH ，∠ADH ＝∠AHD ＝60°，然后利用利用等腰三角形的三线合一性质求出AM 的长，从而求出DM ，DF 的长，最后证明手拉手模型﹣旋转型全等△ADF ≌△HDE ，从而利用全等三角形的性质可得DE ＝DF 进而利用直角三角形斜边上的中线，即可解答．解：过点D 作DM ⊥AB ，垂足为M ，取AB 的中点H ，连接EH ，DH ，∵AF ＝2，BF =103，∴AB ＝AF +BF =163，∵BD ⊥AC ，∴∠ADB ＝∠CDB ＝90°，∵∠A ＝60°，∴∠ABD ＝90°﹣∠A ＝30°，∴AD =12AB =83，∵点H 是AB 的中点，∴AH ＝BH =12AB =83，∴AD ＝AH ，∴△ADH 是等边三角形，∴AD ＝DH ，∠ADH ＝∠AHD ＝60°，∴AM＝MH=12AH=43，∴DM=∵AF＝2，∴MF＝AF﹣AM＝2―43=23，∴DF∵点H是AB的中点，点E是BC的中点，∴EH是△ABC的中位线，∴EH∥AC，∴∠DHE＝∠ADH＝60°，∴∠ADH＝∠A＝60°，∵∠EDF＝∠ADH＝60°，∴∠ADH﹣∠FDH＝∠EDF﹣∠FDH，∴∠ADF＝∠HDE，∴△ADF≌△HDE（ASA），∴DE＝DF=∵∠CDB＝90°，∴BC＝2DE=故选：D．方法点睛：本题考查了等边三角形的判定与性质，直角三角形斜边上的中线，三角形的中位线定理，全等三角形的判定与性质，含30度角的直角三角形，根据题目的已知条件并结合图形添加适当的辅助线是解题的关键．针对训练1．（2022•长春一模）如图，菱形ABCD的对角线AC与BD相交于点O，AC＝8，BD＝12，点E是CD的中点，点F是OA的中点，连结EF，则线段EF的长为 ．思路指引：取AD的中点M，连接FM，EM，构造三角形中位线，利用三角形中位线定理分别求得FM、EM的长度；然后利用勾股定理求得EF的长度．解：如图，取AD的中点M，连接FM，EM，∵点E是CD的中点，∴EM是△ACD的中位线．∴EM∥AC，EM=12AC＝4．同理，FM∥BD，FM=12OD=14BD＝3．在菱形ABCD中，AC⊥BD，则FM⊥ME．故在直角△EFM中，由勾股定理得到：EF5．故答案是：5．方法点睛：本题主要考查了菱形的性质和三角形中位线定理，解题过程中，巧妙地作出辅助线，利用三角形中位线定理求得直角三角形的两直角边的长度．（2）连接对角线，再取对角线中点典例5（2021秋•龙岗区校级期末）如图，四边形ABCD中，E，F分别是边AB，CD的中点，则AD，BC 和EF的关系是（ ）A．AD+BC＞2EF B．AD+BC≥2EF C．AD+BC＜2EF D．AD+BC≤2EF思路指引：连接AC，取AC的中点G，连接EF，EG，GF，根据三角形中位线定理求出EG=12BC，GF=12AD ，再利用三角形三边关系：两边之和大于第三边，即可得出AD ，BC 和EF 的关系．解：如图，取AC 的中点G ，连接EF ，EG ，GF ，∵E ，F 分别是边AB ，CD 的中点，∴EG ，GF 分别是△ABC 和△ACD 的中位线，∴EG =12BC ，GF =12AD ，在△EGF 中，由三角形三边关系得EG +GF ＞EF ，即12BC +12AD ＞EF ，∴AD +BC ＞2EF ，当AD ∥BC 时，点E 、F 、G 在同一条直线上，∴AD +BC ＝2EF ，所以四边形ABCD 中，E ，F 分别是边AB ，CD 的中点，则AD ，BC 和EF 的关系是AD +BC ≥2EF ．故选：B ．方法点睛：此题主要考查学生对三角形中位线定理和三角形三边关系的灵活运用，熟练掌握三角形的中位线定理是解题的关键．针对训练1．如图，在□ABCD 中，E 是CD 中点，F 是AE 的中点，FC 交BE 于点G（1）求证：GF ＝GC（2）求证：BG ＝3EG解：（1）取BE 的中点M ，∵FM ＝21AB ，∴FM //EC ，∴四边形 FMCE 为平行四边形，∴GF ＝GC（2）易证EG ＝MG ，∴EM ＝MB ，∴BG ＝3EG类型四 延长一边构造中位线典例6（2022秋•江北区校级期末）如图，在正方形ABCD 中，点E ，G 分别在AD ，BC 边上，且AE ＝3DE ，BG ＝CG ，连接BE 、CE ，EF 平分∠BEC ，过点C 作CF ⊥EF 于点F ，连接GF ，若正方形的边长为4，则GF 的长度是（ ）A B ．2C D 思路指引：延长CF 交BE 于H ，利用已知条件证明△HEF ≌△CEF （ASA ），然后利用全等三角形的性质证明GF =12BH ，最后利用勾股定理即可求解．解：延长CF 交BE 于H ，∵EF 平分∠BEC ，∴∠HEF ＝∠CEF ，∵CF ⊥EF ，∴∠HFE ＝∠CFE ，在△HEF 和△CEF 中，∠HEF =∠CEF EF =EF ∠HFE =∠CFE，∴△HEF ≌△CEF （ASA ），∴HF ＝CF ，EH ＝EC ，而BG ＝CG ，∴GF =12BH ，∵AE ＝3DE ，正方形的边长为4，∴AE ＝3，AB ＝CD ＝4，DE ＝1，在Rt △ABE 中，BE =5，在Rt △CDE 中，CE ＝HE ==∴BH ＝BE ﹣HE ＝5―∴GF =12BH 故选：C ．方法点睛：此题主要考查了全等三角形的性质与判定，也利用了正方形的性质，三角形的中位线的性质，有一定的综合性，对于学生的能力要求比较高．针对训练1．（2022•合肥一模）如图，△ABC 中，AD 平分∠BAC ，E 是BC 中点，AD ⊥BD ，AC ＝7，AB ＝4，则DE 的值为（ ）A ．1B ．2C ．12D ．32思路指引：延长BD 交AC 于H ，证明△ADB ≌△ADH ，根据全等三角形的性质得到AH ＝AB ＝4，BD ＝DH ，根据三角形中位线定理计算即可．解：延长BD 交AC 于H ，在△ADB 和△ADH 中，∠BAD =∠HAD AD =AD ∠ADB =∠ADH，∴△ADB ≌△ADH （ASA ）．∴AH ＝AB ＝4，BD ＝DH ，∴HC ＝AC ﹣AH ＝3，∵BD ＝DH ，BE ＝EC ，∴DE =12HC =32，故选：D ．方法点睛：本题考查的是三角形中位线定理、全等三角形的判定和性质，掌握三角形的中位线平行于第三边，且等于第三边的一半是解题的关键．类型五 延长两边构造中位线典例7（2022秋•封丘县校级期末）如图，在△ABC 中，AE 平分∠BAC ，D 是BC 的中点AE ⊥BE ，AB ＝5，AC ＝3，则DE 的长为（ ）A ．1B ．32C ．2D ．52思路指引：连接BE 并延长交AC 的延长线于点F ，易证明△ABF 是等腰三角形，则得AF 的长，点E 是BF 的中点，求得CF 的长，从而DE 是中位线，即可求得DE 的长．解：连接BE 并延长交AC 的延长线于点F ，如图，∵AE ⊥BE ，∴∠AEB ＝∠AEF ＝90°，∵AE 平分∠BAC ，∴∠BAE ＝∠FAE ，∴∠ABE ＝∠AFE ，∴△ABF 是等腰三角形，∴AF ＝AB ＝5，点E 是BF 的中点，∴CF ＝AF ﹣AC ＝5﹣3＝2，DE 是△BCF 的中位线，∴DE =12CF =1．故选：A ．方法点睛：本题考查了等腰三角形的判定与性质，三角形中位线的性质定理，关键是作辅助线得到等腰三角形．针对训练1．如图，AD 为△ABC 的外角平分线，且AD ⊥BD 、M 为BC 的中点，若AB ＝12，AC ＝18，求MD 的长8．延长BD ，CA 交于点E ，易证AE ＝AB ，BD ＝ED ，∵BM ＝CM ，∴DM ＝21CE ＝21(AB ＋AC )＝15.类型六作平行线或倍长中线先构造8字全等再构造中位线典例7（2021秋•宛城区期中）如图，在△ABC中，∠A＝90°，AC＞AB＞4，点D、E分别在边AB、AC上，BD＝4，CE＝3，取DE、BC的中点M、N，线段MN的长为（ ）A．2.5B．3C．4D．5思路指引：如图，作CH∥AB，连接DN，延长DN交CH于H，连接EH，首先证明CH＝BD，∠ECH＝90°，解直角三角形求出EH，利用三角形中位线定理即可解决问题．解：作CH∥AB，连接DN并延长交CH于H，连接EH，∵BD∥CH，∴∠B＝∠NCH，∠ECH+∠A＝180°，∵∠A＝90°，∴∠ECH＝∠A＝90°，在△DNB和△HNC中，∠B=∠NCHBN=CN，∠DNB=∠HNC∴△DNB≌△HNC（ASA），∴CH＝BD＝4，DN＝NH，在Rt△CEH中，CH＝4，CE＝3，∴EH=5，∵DM＝ME，DN＝NH，EH＝2.5，∴MN=12故选：A．方法点睛：本题考查全等三角形的判定和性质，三角形的中位线定理，勾股定理等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题．针对训练：如图，AB＝BC，DC＝DE，∠ABC＝∠CDE＝90°，D、B、C在一条直线上，F为AE的中点．（1）求证：BF∥CE；（2）若AB＝2，DE＝5，求BF的长．思路指引：（1）延长AB交CE于G，求出△ACG是等腰直角三角形，再根据等腰直角三角形的性质求出AB＝BG，然后根据三角形的中位线平行于第三边并且等于第三边的一半证明；（2）根据等腰直角三角形的性质求出CE、CG，再求出GE，然后求解即可．（1）证明：如图，延长AB交CE于G，∵AB＝BC，DC＝DE，∠ABC＝∠CDE＝90°，∴△ABC和△CDE都是等腰直角三角形，∴△ACG也是等腰直角三角形，∵∠ABC＝90°，∴BC⊥AG，∴AB＝BG，∵点F是AE的中点，∴BF是△AGE的中位线，∴BF∥CE；（2）解：∵AB ＝2，DE ＝5，∴CG ＝AC =＝CE =＝∴GE ＝CE ﹣CG ＝=∵BF 是△AGE 的中位线，∴BF =12GE方法点睛：本题考查了三角形的中位线平行于第三边并且等于第三边的一半，等腰直角三角形的判定与性质，熟记性质与定理并作辅助线构造出以BF 为中位线的三角形是解题的关键。
三角形中位线定理的运用例谈(Word版-含解析、点评和练习设计)
2017-2018下学期八数专题复习 二：三角形中位线定理的运用例谈 第 1页（共 8页） 第 2页 （共 8页）2017—2018下学期八年级数学专题复习 二:三角形中位线定理的运用例谈赵化中学 郑宗平三角形的中位线定理在平面几何中比较特殊，它既反映三角形的中位线与三角形边的位置关系，又有与三角形边的数量关系的规律性结论；在一些所谓的几何难题中常见它的身影，而三角形的中位线往往能起牵线搭桥甚至是关键性的作用;下面我精选一部分“含"三角形的中位线的几何解答题，让我们共同来探究、解析、训练.知识要点:三角形的中位线平行于三角形第三边,并且等于第三边的一半.1。
三角形三条中位线围成的三角形与原三角形在某些数量上的关系⑴.周长关系如图点D E F 、、分别是⊿ABC 的三边BC CA AB 、、的中点，请探究⊿DEF 的周长 ⊿ABC 的周长的关系？分析: 点D E F 、、分别是⊿ABC 的三边BC CA AB 、、,,,111EF BC DE AB DF AC 222=== ∴()12EF DE DF BC AC AB ++=++所以三角形的三条中位线围成的三角形的周长是原三角形的周长的一半。
追踪练习：以上面的图为例，若⊿DEF 的周长为23cm ，则⊿ABC 的周长为 . ⑵。
面积关系如图点D E F 、、分别是⊿ABC 的三边BC CA AB 、、的中点，请探究⊿DEF 的面积与⊿ABC 的面积关系？ 略析：根据三角形中位线定理可以得出,,,,111EF BC DF AC DE AB EF BC DF AC DE AB 222===；,再利用线段中点的定义、平行线性质、平行四边形的性质等可以进一步推出DEF 、AFE 、FBD 、DEC是全等的，故它们的面积是相等的,则S ⊿ABC =4S ⊿DEF .所以三角形的三条中位线围成的三角形的面积是原三角形的面积的14. 说明：今后我们学习了相似三角形的性质后，这个结论的推导就简单多了。
2020年山西中考重点专题讲解——几何“中点问题”六大模型(教师版)
2020年山西中考重点专题讲解——几何“中点问题”六大模型很多同学遇到几何题就头疼，很大的原因是没有掌握一些解题模型，也就是套路。
今天就给大家梳理下几何中的中点问题怎么解，这七大模型一定要记好哦！ 模型一 一般三角形遇中点模型分析1：在一般三角形中，当遇见中线或中点时，利用三角形中线等分三角形面积，得到三角形中线分成的两个三角形面积相等.已知：如图，在△ABC 中，AD 是△ABC 的中线.1.在△ABC 中，点D ，E ，F 分别为BC ，AD ，CE 的中点，且S △ABC =16.则S △DEF =（ ）A.2B.8C.4D.1 2.如图，在边长为a 的正方形ABCD 中，点E 是AB 432模型分析2：在一般三角形中，当遇见中线或者与中点有关的线段的时候，可以尝试倍长中线或类中线，构造全等三Ⅰ.已知：如图①，在△ABC 中，AD 是△ABC 的中线. 构造：延长 AD 至点 E 使得 DE=AD ，连接 BE. 得到：△ADC≌△EDB （SAS ）；图①Ⅱ.已知：如图②，在△ABC 中，D 是 BC 中点. 构造：延长 FD 至点 E 使得DE=FD ，连接 CE. 得到：△FDB ≌△EDC（SAS ）.图②3.如图，△ABC 中，AB=7，AC=5，点D 为BC 的中点，则AD 的取值范围为________.4.如图，已知在△ABC 中，AD 是 BC 边上的中线，E 是 AD 上一点，连接 BE 并延长交 AC 于点F ，AF=EF.求证：AC=BE.变式：已知AC=BE ，求证：AF=EF.5.（相似法/坐标法/倍长中线法）如图，在正方形 ABCD 中，E 为 AB 边的中点，G 、F 分别为 AD ，BC 边上的点，若 AG=2，BF=4，∠GEF=90°，求 GF 的长.模型二 等腰三角形遇中点模型分析：等腰三角形中遇到有底边中点时,常作底边上的中线,利用等腰三角形“三线合一”（等腰三角形底边中线，高，顶角平分线三线合一）可得到线段/角间的数量关系（∠BAD=∠CAD,AD ⊥BC,BD=CD ）来解题。
三角形中位线定理的几种证明方法及教学中需要说明的地方
三角形中位线定理的证明及其教学说明以下内容作者为：青岛第四中学杨瀚书老师一、 三角形中位线定理的几种证明方法法1： 如图所示，延长中位线DE 至F ，使，连结CF ，则，有ADFC ，所以FCBD ，则四边形BCFD 是平行四边形，DF BC 。
因为 ，所以DEBC 21．法2C 作交DE 的延长线于F ，则，有FCAD ，那么FCBD ，则四边形BCFD 为平行四边形，DFBC 。
因为 ，所以DEBC 21．法3：如图所示，延长DE 至F ，使 ，连接CF 、DC 、AF ，则四边形ADCF 为平行四边形，有ADCF ，所以FCBD ，那么四边形BCFD 为平行四边形，DF BC 。
因为 ，所以DEBC 21．法4：如图所示，过点E 作MN ∥AB ，过点A 作AM ∥BC ，则四边形ABNM 为平行四边形，易证CEN AEM ∆≅∆，从而点E 是MN 的中点，易证四边形ADEM 和BDEN 都为平行四边形，所以DE=AM=NC=BN ，DE ∥BC ，即DEBC 21。
法5：如图所示，过三个顶点分别向中位线作垂线．二、教学说明1、三角形中位线定理的另外一种猜想过程：“二维”转化为“一维”在引导学生探索三角形中位线定理时，由于学生画出中位线后，就不难直观地发现平行关系，难的是发现数量关系，我联想到在此之前认识线段中点时的一道典型例题，挖掘它与原有知识的内在联系，从而作如下探索引导。
⑴如图，A为线段BC(或线段BC的延长线)上的任意一点，D、E分别是AB、AC 的中点，线段DE与BC有什么关系？AB C图⑴：⑵如果点A不在直线BC上，图形如何变化？上述结论仍然成立吗?C图⑵：说明：学生观察（几何画板制作的）课件演示：当△ABC的顶点A运动到直线B C上时,中位线DE也运动到BC上，这样由“二维”转化为“一维”，学生就不难猜想性质的两方面，特别是数量关系，而想到去度量、验证和猜想，水到渠成.如果教师直接叫学生去度量角度和长度，是强扭的瓜不甜.2、教学重点：本课重点是掌握和运用三角形中位线定理。
八年级数学下找中点构造中位线解题知识点分析人教版
找中点构造中位线解题三角形的中位线定理，是一个非常有价值的定理。
它是一个遇到中点，必须联想到的重要定理之一。
但是，在解题时，往往只知道一个中点，而另一个中点就需要同学们，根据题目的特点，自己去寻找。
本文就向同学们介绍三种在不同条件下寻找中点的方法，供同学们学习时参考。
一、知识回顾1、三角形中位线定理：三角形的中位线平行于第三边，并且等于它的一半。
2、应用时注意的几个细节：①定理的使用前提：三角形。
②定理使用时，满足的具体条件：两条边的中点，且连接这两点，成一条线段。
③定理的结论：位置上：与第三边是平行的；大小上：等于第三边的一半。
在应用时，要灵活选择结论。
二、应用举例1、直接找线段的中点，应用中位线定理例1、如图1所示，在三角形ABC 中，∠B=2∠C ，AD 是三角形的高，点M 是边BC 的中点，求证：DM=21AB 。
分析：看到结论的表达形式，我们就想到，三角形的中位线定理，有这样的特点，因此，我们就可以构造AB 上的中位线，再证明这条中位线与DM 是相等的。
证明：如图2所示，取边AC 的中点E ，连接ME ，则ME ∥AB ，ME=21AB ， 因为，ME ∥AB ，所以，∠B=∠EMC ，因为，∠B=2∠C ，所以，∠EMC=2∠C ，∠EMC 是三角形DME 的一个外角，所以，∠EMC=∠MDE+∠MED ，所以，2∠C=∠MDE+∠MED ，因为，AD 是三角形的高，所以，∠ADC 是直角，所以，DE 是直角三角形ADC 斜边上的中线，所以，DE=EC ，所以，∠MDE=∠C ，所以，2∠C=∠C +∠MED ，所以，∠MED=∠C ，所以，∠MDE=∠MED ，所以，DM=ME ，所以，DM=21AB 。
2、利用等腰三角形的三线合一找中点，应用中位线定理例2、如图3所示，在三角形ABC 中，AD 是三角形ABC ∠BAC 的角平分线，BD ⊥AD ，点D 是垂足，点E 是边BC 的中点，如果AB=6,AC=14，则DE 的长为 。
专训2--常用构造中位线的五种方法-(2)
方法 2 已知角平分线和垂直构造中位线
2．如图，在△ABC中，点M为BC的中点，AD为△ABC 的外角平分线，且AD⊥BD，若AB＝12，AC＝18， 求DM的长．
解：如图，延长BD，CA交于N.
由题易知∠NAD＝∠BAD，∠ADN＝∠ADB＝
90°.又AD＝AD，
∴△AND≌△ABD.
∴DN＝DB，AN＝AB.
习题课 阶段方法技巧训练（一）
专训2 常用构造中位线的 五种方法
三角形的中位线具有两方面的性质：一是位置 上的平行关系，二是数量上的倍分关系．因此，当 题目中给出三角形两边的中点时，可以直接连出中 位线；当题目中给出一边的中点时，往往需要找另 一边的中点，作出三角形的中位线．
方法 1 连接两点构造三角形的中位线
1．如图，点B为AC上一点，分别以AB，BC为边在AC 同侧作等边三角形ABD和等边三角形BCE，点P，M， N分别为AC，AD，CE的中点． (1)求证：PM＝PN； (2)求∠MPN的度数．
证明：(1)如图，连接CD，AE.
由三角形中位线定理可得
PM
＝∥
1 2
CD，PN
＝∥
1 2
AE.
∵△ABD和△BCE是等边三角形，
又∵∠FBA＋∠CBF＝90°，
∴∠CBF＝∠ABN.
BF BN ,
在△BCF和△BAN中，CBF ABN ,
BC BA, ∴△BCF≌△BAN.∴CF＝AN.∴ME＝
1 2
AN＝
1 2
CF.
方法 4 已知一边中点，取另一边中点构造三角形的中位线
5．如图，在△ABC中，∠C＝90°，CA＝CB，E，F分 别为CA，CB上一点，CE＝CF，M，N分别为AF， BE的中点，求证：AE＝ 2 MN.
中考数学专题复习学案 三角形中位线 (含答案)
中考复习之三角形中位线定义：：连结三角形两边中点的线段叫做三角形的中位线一、与中点有关的概念三角形中线的定义：三角形顶点和对边中点的连线三角形中线的相关定理：直角三角形斜边的中线等于斜边的一半等腰三角形底边的中线三线合一(底边的中线、顶角的角平分线、底边的高重合)三角形中位线定义：连结三角形两边中点的线段叫做三角形的中位线．三角形中位线定理：三角形的中位线平行于第三边并且等于它的一半．中位线判定定理：经过三角形一边中点且平行于另一边的直线必平分第三边．直角三角形斜边中线：直角三角形斜边中线等于斜边一半二、常见的题型题型一:求线段的长例1、已知：如图，E、D、F分别为AB、BC、CA的中点.（1）若AC=10cm，则DE= 5 cm. （2）若EF=6cm，则CB= 12 cm.（3）若AB=10，AC=12，BC=8，则△DEF的周长 15练习：1.已知△ABC的周长为50cm，中位线DE=8cm，中位线EF=10cm，则另一条中位线DF的长是（）A.5cmB. 7cmC. 9cmD. 10cm【答案】B3.如图，在△ABC中，点D，E分别是AB，AC的中点，∠A=50°，∠ADE=60°，则∠C的度数为（）A.50°B. 60°C. 70°D. 80°【答案】C3.如图，在△ABC中，E，D，F分别是AB、BC、CA的中点，AB=6，AC=4，则四边形AEDF的周长是（）A. 10B. 20C. 30D. 40【答案】B4.如图，在△ABC中，D，E，F分别为BC，AC，AB边的中点，AH⊥BC于H，FD=8，则HE等于（）A. 20B. 16C. 12D. 8 【答案】D题型二：证明线段的倍分问题例1.如图,△ABC 中,AB=AC,AD 是中线,BE=CF.(1)求证: △BDE ≌△CDF;(2)当∠B=60°时,G 、H 分别是AB 、AD 的中点,求证:GH=14AB证明：(1)∵AB=AC ∴∠ B=∠ C ∵AD 为中线，∴BD=CD 又∵EB=FC ∴△BDE ≌△CDF(2)∵AB=AC ∴△ABC 为等腰三角形，又∵∠B=60°，∴△ABC 为等边三角形 ∴BC=AB ∵G 、H 分别是AB 、AD 的中点 ∴GH=21BD=14BC 又∵BC=AB 所以GH=41AB. 练习：如图,在△ABC 中,AB=AC,延长AB 到D,使BD=AB,E 为AB 中点,连结CE 、CD ， 求证：CD=2EC证明：延长CE 使EF=CE=1/2CF 即 CF=2CE ∵∠AEC=∠BEF E 是AB 中点，即AE=BE CE=EF∴△ACE ≌△BFE(SAS) ∴BF=AC ∠FBE=∠A ∵AB=AC ∴∠ABC=∠ACB∵∠FBC=∠FBE+∠ABC=∠A+∠ABC ∠DBC=∠A+∠ACB ∴∠FBC=∠DBC∵BD=BA∴BF=BD∵BC=BC∠FBC=∠DBC∴△BCF≌△BCD(SAS)∴CF=CD∴CD=2CE题型三：常规辅助线的添加一：利用角平分线+垂直，构造等腰三角形如图，M是△ABC的边BC的中点，AN平分∠BAC，BN⊥AN于点N，延长BN交AC于点D，已知AB=10，BC=15，MN=3（1）求证：BN=DN；（2）求△ABC的周长．【解析】1）证明：在△ABN和△ADN中，∵12AN ANANB AND ∠=∠⎧⎪=⎨⎪∠=∠⎩，∴△ABN≌△ADN，∴BN=DN．（2）解：∵△ABN≌△ADN，∴AD=AB=10，DN=NB，又∵点M是BC中点，∴MN是△BDC的中位线，∴CD=2MN=6，故△ABC的周长=AB+BC+CD+AD=10+15+6+10=41．1.如图所示，M是△ABC的边BC的中点，AN平分∠BAC，BN⊥AN于点N，且AB=8，MN=3，则AC的长是（）A．12 B．14 C．16 D．18【答案】B2.如图，在△ABC中，AB=8，AC=6，AD、AE分别是其角平分线和中线，过点C作CG⊥AD于F，交AB于G，连接EF，则线段EF的长为（）A．1 B．2 C． 3 D．7【答案】A3.如图，△ABC中，BD平分∠ABC，且AD⊥BD，E为AC的中点，AD=6cm，BD=8cm，BC=16cm，则DE的长为（）cm．【答案】3如图，△ABC中，AB=8cm，AC=5cm，AD平分∠BAC，且AD⊥CD，E为BC中点，则DE=（）A.3 B.5 C.2.5 D.1.5【答案】D二：取中点构造中位线如图，在四边形ABCD 中，AD=BC ，20,110,,,CBD BDA E F P ∠=︒∠=︒分别是AB 、CD 、BD 的中点，探索PF 与EF 的数量关系.证明：连接PE ，20,11090CBD BDA EPF ∠=︒∠=︒⇒∠=︒，易得EF =.三：借助平行四边形的性质1. 如图，平行四边形ABCD 的对角线AC ，BD 相交于点O ，点E ，F 分别是线段AO ，BO 的中点．若AC+BD=24cm ，△OAB 的周长是18cm ，则EF 的长为________cm ．【答案】∵四边形ABCD 是平行四边形，∴OA=OC，OB=OD，又∵AC+BD=24厘米，∴OA+OB=12厘米，∵△OAB的周长是18厘米，∴AB=6厘米，∵点E，F分别是线段AO，BO的中点，∴EF是△OAB的中位线，∴EF=1/2AB=3厘米．题型三借助平行四边形的性质边AB、BC的中点，G、H为AC的两个三等分点，连接EG、例3.如图，（1）E,F为ABCFH，并延长交于D，连接AD、CD.求证：四边形ABCD是平行四边形.【答案】如图，E、F分别为△ABC的边AB、BC的中点，G、H是AC上的三等分点。
人教版初中数学八下 小专题(六) 构造三角形的中位线的常用方法
方法四 直接倍长线段、构造中位线 4.如图，P为△ABC的边BC的中点，分别以AB，AC为斜边作Rt△ABD和Rt△ACE，且
∠BAD＝∠CAE.求证：PD＝PE. 证明：延长BD至点M，使DM＝DB，延长CE至点 N，使EN＝EC，连接CM，BN，AM，AN.易证 △ABN≌△AMC，得BN＝CM.
（1）求证：GF＝GC；
（2）求证：BG＝3EG.
∵四边形ABCD是平行四边形，∴AB ∥ CD.
证明：（2）易证EG＝MG. ∵EM＝MB，∴BG＝3EG.
方法三 已知双中点，另取一中点构造双中位线 3.如图，在四边形ABCD中，BC，AD不平行，且∠BAD＋∠ADC＝270°，AB2＋CD2
小专题（六） 构造三角形的中位 线的常用方法
方法一 已知两中点，连中点构造中位线 1.如图，△ABC和△DCE都是等腰直角三角形，∠ACB＝∠DCE＝90°，点D，C，B在
同一条直线上，F，G，M分别为AD，BE，AB的中点. （1）求∠FGM的度数；
方法二 已知单中点，另取一中点构造单中位线 2.如图，在▱ABCD中，E是CD的中点，F是AE的中点，FC交BE于点G.
（2）若AB＝5，BC＝8，求EF的长.
＝64，E，F分别是AD，BC的中点，求EF的长. 解：连接BD，取BD的中点G，连接EG并延长交BC于点M.连接GF. ∵E，F分别是AD，BC的中点，
∴∠ABC＝∠EMF，∠C＝∠GFM. ∵∠BAD＋∠ADC＝270°，∴∠ABC＋∠C＝90°， ∴∠EMF＋∠GFM＝90°，∴∠EGF＝90°，∴EF2＝GE2＋GF2. ∵AB2＋CD2＝64，∴（2GE）2＋（2GF）2＝64， ∴EF2＝16，∴EF＝4.
方法五 已知角平分线或垂线构造中位线 5.如图，在△ABC中，D，E分别为AB，AC的中点，点F在DE上，且AF⊥BF.
构造三角形中位线解题例析
‘ ． ．
△ ＡＤＭ △ ＰＣＭ （ ＡＡＳ ） ，
ＡＭ ＝ ＰＭ 。 ＡＤ — ＰＣ ，
别是如何正确添 加辅 助线 构造 三角形 的中位线 对 每一
个 学生来 说是一个重点也是一个 难点． 要求 学生要 善于
．
又 ‘ ． ‘ ＡＢ— ＡＤ＋ ＢＣ，
． ．
觉察图形 的有关 定理的基本 图形． 涉及 中点问题联 想到
： ． ＰＮ Ｍ ＝ ＝ Ｏ Ｅ｝ ，
的 中 点 ， 求 证 ： Ｄ Ｍ 一 吉 Ａ Ｂ ． Ｂ Ｄ Ｍ Ｃ
解析 ： 取 ＡＣ的 中点 Ｅ，连接 ＭＥ ，由三角形 中位 线
又 ． 。 ＡＣ＝ ＢＤ ，
．
定理可知 ＭＥ ／ ／ ＡＢ，
１
ＰＭ — ＰＮ ，
有关定理 ， 就很容易解决问题 ， 从而达到学习的 目的． （ 责任编辑 黄春香）
ＡＢ— ＰＣ＋ ＢＣ— ＰＢ，
所以Ａ Ｍ上Ｂ Ｍ（ ￣ Ｉ Ｊ 用 三角形的“ 三线合一” ） ． 【 例３ 】 四边形 Ａ Ｂ Ｃ Ｄ的对角线相交于点 （ ） ， 且 ＡＣ
＝
Ｂ Ｄ， Ｍ， Ｎ 分 别是 ＡＢ， Ｃ Ｄ的中点， ＭＮ 分 别 交 Ｂ Ｄ，
ＡＡＢ Ｃ中 ， Ｂ一 ２ Ｃ，ＡＤ
Ｐ Ｍ 是 ＡＡ Ｂ Ｃ的中位线 ，
１
‘
．
．
Ｐ Ｍ ／ ／ Ａ Ｃ 且Ｐ Ｍ＝ ＠Ａ Ｃ ，
ＰＭ Ｎ 一 ｏＦＥ．
Ｐ Ｃ
．
同理 可 证 ， ＰＮ∥ Ｂ Ｄ，Ｐ Ｎ一
１
图４
是 三角形 的高 ， 点 Ｍ 是边 Ｂ Ｃ
＿ 去 － ＢＤ，
Ｚ ＨＯＮ ＧＸ ＵＥ Ｊ Ｉ Ａ ＯＸ ＵＥ ＣＡ ＮＫＡＯ
构造中位线
构造中位线“遇中点找中点，联想中位线”是一个解题突破口，但在一般问题中，要应用中位线的性质时，往往需要作辅助线.下面介绍几种如何构造中位线的方法，供大家参考.一、连中点，构造三角形的中位线例1如图1，D、E、F分别是等边三角形ABC的边AB、BC、AC的中点，P为BC上任意一点，△DPM是等边三角形.连接FM.那么EP与FM相等吗？为什么？分析：由D、E、F是中点，想到连接中点，得到中位线DE、DF.这样就可以把EP、FM放到△DPE、△DMF中，进而推出它们全等使问题得以解决.解：连接DF、DE.因为D、E、F分别是等边三角形ABC的边AB、BC、AC的中点，所以DF∥BC，DF=12BC；DE∥AC,DE=12AC.所以四边形DECF是平行四边形. 所以∠C=∠EDF=60°.因为△ABC、△DPM是等边三角形，所以BC＝AC，DP＝DM，∠PDM＝60°.所以DF＝DE.因为∠EDP＝60°－∠PDF，∠FDM＝60°－∠PDF，所以∠EDP＝∠FDM.所以△DEP≌△DFM.所以EP＝FM.跟踪训练1如图2，四边形ABCD中，AC=BD，AC、BD相交于点O，M、N分别是边AB、CD的中点，MN交BD于点E、交AC于点F.OE与EF相等吗？为什么？二、找中点，构造三角形的中位线例2如图3，在四边形ABCD中，AB＝CD，M、N分别是BC、AD边的中点，延长BA、MN交于点F，延长CD交MF于点E.请说明∠1与∠2相等.分析：因为M、Ｎ分别是BC、AD的中点，若连接BD，取其中点G，再连接NG、MG,则NG∥AB，NG＝12AB，MG∥CD，MG＝12CD.这样把∠1与∠2通过中位线移到同一个等腰三角形ＧMＮ中，从而使问题得以解决.解：连接BD，取BD的中点G，连接NG、MG，则NG∥AB，NG＝12AB，MG∥CD，MG＝12CD.所以∠1＝∠GNM，∠2＝∠GMN.因为AB＝CD，所以NG＝MG.所以∠GNM＝∠GMN.所以∠1=∠2.跟踪训练2如图4，△ABC的一个外角平分线AE与过点C的直线互相垂直，垂足为点E，D为BC的中点，试说明：DE∥AB，且DE=12（AB+AC）答案1.解：取AD的中点Ｇ，连接GM、GN，得GM∥BD，GN∥AC，且GM＝12BD，GN＝12AC，因为AC＝BD，故GM＝GN，所以∠GMN＝∠GNM，又∠OEF＝∠GMN，∠OFE＝∠GNM，所以∠OEF＝∠OFE，所以OE＝OF．2.解：延长BA、CE相交于点F，由AE⊥CF，AE平分∠CAF，得EF＝EC，AF＝AC，又D是BC的中点，所以DE是△BCF的中位线，故有DE∥AB，且DE=12BF=12（AB+AC）．。
专题18构造三角形中位线的常用技巧(原卷版)
专题18 构造三角形中位线的常用技巧（原卷版）专题典例剖析及针对训练类型一 连接两中点构造中位线典例1如图，在△ABC 中，AB ＝AC ＝5，BC ＝6，D 、E 分别是AB 、AC 的中点，F 、G 为BC 上的两点，FG ＝3，线段DG ，EF 的交点为O ，当线段FG 在线段BC 上移动时，三角形FGO 的面积与四边ADOE 的面积之和恒为定值，则这个定值是（ ）A ．15B ．12C ．9D ．6针对训练1．如图，△ABC 的中线BD ，CE 相交于点0，F ，G 分别是BO ，CO 的中点，求证：EF △DG 且EF ＝DG ．类型二 连接第三边构造中位线典例2（2022秋•泰山区校级期末）如图，在菱形ABCD 中，E ，F 分别是边CD ，BC 上的动点，连接AE ，EF ，G ，H 分别为AE ，EF 的中点，连接GH ．若∠B ＝45°，BC ＝2√3，则GH 的最小值为（ ）A ．√3B ．√22C ．√6D ．√62针对训练1．如图所示，已知四边形ABCD ，R 、P 分别是DC 、BC 上的点，点E 、F 分别是AP 、RP 的中点，当点P 在边BC 上从点B 向点C 移动，且点R 从点D 向点C 移动时，那么下列结论成立的是（ ）A ．线段EF 的长逐渐增大B ．线段EF 的长逐渐减少C ．线段EF 的长不变D ．△ABP 和△CRP 的面积和不变典例3 如图，点B 为AC 上一点，分别以AB ，BC 为边在AC 同侧作等边△ABD 和等边△BCE ，点P ，M ，N GF E DBA分别为AC ，AD ，CE 的中点．（1）求证：PM ＝PN ；（2）求△MPN 的度数．针对训练1.如图，分别以△ABC 的边AB ，AC 同时向外作等腰直角三角形，其中AB ＝AE ，AC ＝AD ，△BAE ＝△CAD ＝90°，点G 为BC 的中点，点F 为BE 的中点，点H 为CD 的中点．探索GF 与GH 的数量关系及位置关系，并说明理由．类型三 取中点构造中位线（1）直接取一边中点典例4（2022春•武昌区期中）如图，在△ABC 中，∠A ＝60°，BD 为AC 边上的高，E 为BC 边的中点，点F 在AB 边上，∠EDF ＝60°，若AF ＝2，BF =103，则BC 边的长为（ ）A ．163B ．83√3C ．23√13D ．43√13针对训练1．（2022•长春一模）如图，菱形ABCD 的对角线AC 与BD 相交于点O ，AC ＝8，BD ＝12，点E 是CD 的中点，点F 是OA 的中点，连结EF ，则线段EF 的长为 ．（2）连接对角线，再取对角线中点HG FEDCBA典例5（2021秋•龙岗区校级期末）如图，四边形ABCD 中，E ，F 分别是边AB ，CD 的中点，则AD ，BC和EF 的关系是（ ）A ．AD +BC ＞2EFB ．AD +BC ≥2EF C ．AD +BC ＜2EF D ．AD +BC ≤2EF针对训练1．如图，在□ABCD 中，E 是CD 中点，F 是AE 的中点，FC 交BE 于点G（1）求证：GF ＝GC（2）求证：BG ＝3EG类型四 延长一边构造中位线典例6（2022秋•江北区校级期末）如图，在正方形ABCD 中，点E ，G 分别在AD ，BC 边上，且AE ＝3DE ，BG ＝CG ，连接BE 、CE ，EF 平分∠BEC ，过点C 作CF ⊥EF 于点F ，连接GF ，若正方形的边长为4，则GF 的长度是（ ）A ．5−√32B ．5−√152C ．5−√172D ．√17−32针对训练1．如图，AD 为△ABC 的外角平分线，且AD △BD 、M 为BC 的中点，若AB ＝12，AC ＝18，求MD 的长类型六作平行线或倍长中线先构造8字全等再构造中位线典例7（2021秋•宛城区期中）如图，在△ABC中，△A＝90°，AC＞AB＞4，点D、E分别在边AB、AC上，BD＝4，CE＝3，取DE、BC的中点M、N，线段MN的长为（）A．2.5B．3C．4D．5针对训练：如图，AB＝BC，DC＝DE，∠ABC＝∠CDE＝90°，D、B、C在一条直线上，F为AE的中点．（1）求证：BF∥CE；（2）若AB＝2，DE＝5，求BF的长．。
例析构造三角形中位线策略
例析构造三角形中位线策略作者：***来源：《中学教学参考·理科版》2023年第11期［摘要］三角形中位线是一条重要的线段，在解题过程中构造三角形中位线将事半功倍，能使问题获得突破。
文章结合几个例题，探讨构造三角形中位线的策略，给学生一些启示。
［关键词］构造；三角形；中位线；初中数学［中图分类号］ G633.6 ［文献标识码］ A ［文章编号］ 1674-6058（2023）32-0020-03三角形中位线是一条重要的线段，三角形中位线定理是初中阶段学习的重要定理。
在解题过程中，构造三角形中位线，将事半功倍，能使问题获得突破。
本文结合几个例题，探讨构造三角形中位线的策略，给学生一些启示。
一、直接连接两边中点，构造三角形中位线如果图形中有两个及以上的线段中点，此时，应考虑使用三角形中位线，辅助线作法为直接连接两边的中点，找出这两边所在的三角形，利用三角形中位线定理解决问题。
［例1］如图1所示，在边长为4的等边[△ABC]中，[D]、[E]分别为[AB]、[BC]的中点，[EF⊥AC]于点[F]，[G]为[EF]的中点，连接[DG]；（1）求[EF]的长；（2）求[DG]的长。
分析：（1）如图2所示，连接[DE]，利用三角形中位线定理得[DE=2]，且[DE]∥[AC]，再解直角三角形[EFC]求得[EF]的长；（2）在直角三角形[DEG]中，利用勾股定理求得[DG]的长。
解：（1）如图2所示，连接[DE]，∵在边长为4的等边[△ABC]中，[D]、[E]分别为[AB]、[BC]的中点，∴[DE]是[△ABC]的中位线，∴[DE=2]，且[DE]∥[AC]，[BD=BE=EC=2]，∵[EF⊥AC]于点[F]，[∠C=60°]，∴[∠FEC=30°]，[∠DEF=∠EFC=90°]，∴[FC=12EC=1]，故[EF=22−12=3]。
（2）∵[G]为[EF]的中点，∴[EG=32]，∴[DG=DE2+EG2=22+322=192]。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
找中点构造三角形中位线解题
三角形的中位线定理，是一个非常有价值的定理。
它是一个在三角形中遇到中点，必须联想到的重要定理之一。
但是，在解题时，往往只知道一个中点，而另一个中点就需要同学们，根据题目的特点，自己去寻找。
现介绍几种在不同条件下寻找中点的方法，供同学们学习时参考。
一、三角形中位线定理：
三角形的中位线平行于第三边，并且等于它的一半。
二、应用时注意的几个细节： ①定理的使用前提：三角形。
②定理使用时，满足的具体条件：两条边的中点，且连接这两点，成一条线段。
③定理的结论：
位置上：与第三边是平行的，利用此定理可证明线段平行，从而可证明两角相等； 大小上：等于第三边的一半。
利用此定理可证明两条线段之间的倍分关系； 三、应用举例
1、如果已知三角形两边中点，就直接连接构成三角形的中位线
例1、如图，在四边形ABCD 中，AB=CD ，E 、F 、G 分别是AD 、BC 、BD 的中点，H 是EF 的中点，试说明线段GH 与线段EF 的位置关系；
简析：在△ABC 中，E 、G 分别是AD 、BD 的中点，可连接EG ，则
有AB EG 2
1
=；在△BCD 中，G 、F 分别是BD 、BC 的中点，可
连接GF ，则有CD FG 2
1
=, 而AB=CD ，所以EG FG =,即△
EFG 是等腰三角形，又H 是底边EF 的中点，由等腰三角形的三线合一定理可知GH ⊥EF. 2、如果已知三角形一边中点，则可以取另一边的中点连接起来构成三角形的中位线 例2、如图1所示，在三角形ABC 中，∠B=2∠C ，AD 是三角形的高，点M 是边BC 的中点，求证：DM=
2
1
AB 。
分析：看到结论的表达形式，我们就想到，三角形的中位线
定理，有这样的特点，因此，我们就可以构造AB 上的中位线，再证明这条中位线与DM 是相等的。
H
G
F
E
D
C
B A
3、利用等腰三角形的三线合一找中点，应用中位线定理
例3如图，自△ABC 的顶点A ，向∠B 和∠C 的平分线作垂线，重足分别为D 、E 。
求证：DE ∥BC
分析：欲证ED//BC 我们可想到有关平行的判定，但要找到有关角的关系很难，这时只要通过延长AD 、AE ，交BC 与CB 的延长线于G 与H ，通过证明△ABD 与△GBD 全等易证D 是AG 中点，同理E 为AH 的中点，故，ED 是△AEG 的中位线，当然有DE ∥BC 。
小结：由此题我们可以知道证明直线或线段平行除了平行判定等，还可以用中位线定理来证明直线或线段平行。
例4、如图3所示，在三角形ABC 中，AD 是三角形ABC ∠BAC 的角平分线，BD ⊥AD ，点D 是垂足，点E 是边BC 的中点，如果AB=6,AC=14，则DE 的长为 。
分析：因为，点E 是BC 的中点，如果点D 也是某一边的中点，
我们就可以利用三角形的中位线定理，来求得DE 的长度。
循着这条思路，我们不妨延长BD ，交AC 于点F ，只要证明点D 是BF 的中点就可以了。
4、利用平行四边形对角线的交点找中点，应用中位线定理
例5、如图5所示，AB ∥CD ，BC ∥AD ，DE ⊥BE ，DF=EF ，甲从B 出发，沿着BA 、AD 、DF 的方向运动，乙B 出发，沿着BC 、CE 、EF 的方向运动，如果两人的速度是相同的，且同时从B 出发，则谁先到达？
分析：要想知道谁先到达，因为，他们的速度相等，所以，谁走的路程短，就是谁先到达，
所以，关键是比较BA+AD+DF 与BC+CE+EF 的大小。
四、训练题
1、如图1，△ABC 中，BM 平分∠ABC ，AM ⊥BM ，垂足为M ，点N 为AC 的中点，设AB ＝10，BC ＝6，求MN 的长度.
21G
H
D
E
C
B
A
2、如图，同底边BC 的△ABC 与△DBC 中，E 、F 、G 、H 分别是AB 、AC 、DB 、DC 的中点，求证：EH 与FG 互相平分。
3、如图，已知平行四边形ABCD 中，BD 为对角线，点E 、F 分别是AB 、CD 的中点，连线EF ，交BD 于M 点。
求证：（1）BM=1
4
BD （2）ME=MF ；
4、如图所示，在梯形ABCD 中， AD ∥BC ，AD+BC=8，且AD ：BC=3:7,E , F 分别是BD ，AC 的中点，求EF 的长。
5、 如图5，在△ABC 中，AD 平分∠BAC ，AD=AB ，CM ⊥AD 于M . 求证：AB+AC=2AM
H
G
F E
D
C
B
A
M F
E
D
C
B
A
H
C
6、如图，四边形ABCD 中，G 、H 分别是AD 、BC 的中点，AB=CD.BA 、CD 的延长线交HG 的延长线于E 、F. 求证：∠BEH=∠CFH.
7．如图1，D 、E 、F 分别是等边△ABC 的边AB 、BC 、AC 的中点，P 为BC 上任意一点，△DPM 为等边三角形，求证：EP=FM
8. 如图，在△ABC 中，D 、E 是AB 、AC 上的点，且BD=CE ，M 、N 分别是BE 、CD 的中点，直线MN 分别交AB 、AC 于P 、Q . 求证：AP=AQ
E。