金融随机分析全套课件184p
合集下载
专题课件数据金融金融大数据调研分析报告PPT课件

PPT的内容输入完成之后,在“动画 ”菜单 栏中, 可以根 据需要 对不同 的内容 设置动 画效果F HX+LHJ。
调研报告综合概述
请此输入标题
请在此输入您需要的文字内容感谢您
感谢您使用我们的PPT模板,请在此输入您需要的文字内容,感谢 您使用我们的PPT模板,请在此输入您需要的文字内容。感谢您使
PPT的内容输入完成之后,在“动画 ”菜单 栏中, 可以根 据需要 对不同 的内容 设置动 画效果F HX+LHJ。
PPT的内容输入完成之后,在“动画 ”菜单 栏中, 可以根 据需要 对不同 的内容 设置动 画效果F HX+LHJ。
PPT的内容输入完成之后,在“动画 ”菜单 栏中, 可以根 据需要 对不同 的内容 设置动 画效果F HX+LHJ。
PPT的内容输入完成之后,在“动画 ”菜单 栏中, 可以根 据需要 对不同 的内容 设置动 画效果F HX+LHJ。
调研报告综合概述
PPT的内容输入完成之后,在“动画 ”菜单 栏中, 可以根 据需要 对不同 的内容 设置动 画效果F HX+LHJ。
01
标题
PPT的内容输入完成之后,在“动画 ”菜单 栏中, 可以根 据需要 对不同 的内容 设置动 画效果F HX+LHJ。
输入标题文本
点击输入您的文字内容或复制粘贴具体文本、用简 明扼要的文字说明此项内容。
输入标题文本
点击输入您的文字内容或复制粘贴具体文本、用简 明扼要的文字说明此项内容。
输入标题文本
点击输入您的文字内容或复制粘贴具体文本、用简 明扼要的文字说明此项内容。
投资市场评估报告
PPT的内容输入完成之后,在“动画 ”菜单 栏中, 可以根 据需要 对不同 的内容 设置动 画效果F HX+LHJ。
金融数据分析汇报PPT模板

2019
演讲完毕 谢谢您的观看
工作总结 数据报告 教育教学 项目策划
单击此处添加标题
您的内容打在这里,或者通过 复制您的文本后,在此框中选 择粘贴,并选择只保留文字。 在此录入上述图表的综合描述 说明,在此录入上述图表的综 合描述说明,在此录入上述图 表的综合描述说明。
单击此处添加标题
您的内容打在这里,或者通过 复制您的文本后,在此框中选 择粘贴,并选择只保留文字。 在此录入上述图表的综合描述 说明,在此录入上述图表的综 合描述说明,在此录入上述图 表的综合描述说明。
认真做好一件事
知道如何做好一件事,比对很多事情都懂一点皮毛要 强得多。
单击添加标题
为自己树立一个工作目标是发挥自己潜能、提升自己 工作能力的重要途径。
单击添加标题
把目标变成行动,把行动变成结果,没有任何借口保 质保量完成工作。
02
工作完成情况
CLICK TO ADD UP YOUR TITLE HERE
标题文本预设
此部分内容作为文字排版占位显示 (建议使用主题字体)
40%
20% 15%
40%
标题文本预设
此部分内容作为文字排版占位显示 (建议使用主题字体)
标题文本预设
此部分内容作为文字排版占位显示 (建议使用主题字体)
成功项目展示
标题文字添加
您的文字添加到这里,也可以通 过复制粘贴到此处
标题文字添加
添加标题 添加标题
添加标题
您的内容打在这里您的内容打在这里,或者通过复制您的文本后,在此 框中选择粘贴,并选择只保留文字。您的内容打在这里您的内容打在这 里,或者通过复制您的文本后,在此框中选择粘贴,并选择只保留文字。
添加标题
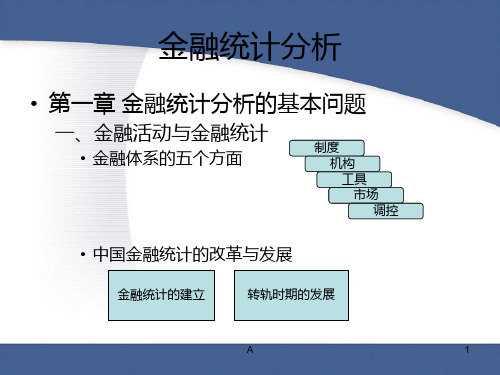
《金融统计分析》PPT课件
款
1536 1126 -410 -2
门债权
58232 70690 12458 72
3.对中央银行
6.对非货币金
的负债
14210 14003 -207 -1
融机构债权
776 2224 1448 8
4.对非货币金
融机构负债
579 1501 922
5
5.债券
288 287
-1
0
6.所有者权益 A 7.其它(净)
A
19
第三章 证券市场统计分析
第二节 债券估价理论
• 2.债券理论评估一般模型分析
• 债券价格与预期现金流大小成反比,与贴现率高低成反 比,与期限也成反比。
• 评估价格分为发行价和转让价 • 期限指有效期限、待偿期限、持有期限三种。 • 讨论:上述三种期限有何区别? • 计算发行价,应使用有效期限;计算转让价时应使用待
A
14
第二章 货币与银行统计分析
第四节货币需求与货币供给统计分析
货币供给分析实例 :(一)货币当局的资产操作与基础货币的创造
1996 1997
比上 年增 加
增量 结构
%
1996
1997
比上 年增 加
增量 结构%
资产
26467 31413 4946 100 负债
26467 31413 4946 100
(1)活期存 18765 23810 5045 29 款
(2)库存现 金
633
803 170 1
(2)定期存 款
5042 6739 1697 10
3.中央银行债
券
0
98 98 1
(3)储蓄存
款
36373 43635 7262 42
金融随机分析

1 设商场一天内的顾客到达人数N是参数为的泊松随机变量,每个顾客在该商场的消费是相互独立的,其消费金额(元)都服从[0,a ]上的均匀分布,求商场一天的平均营业额。
2 设随机过程,其中(j=1,2,…,n)是相互独立的随机
变量,且P{=1}=p, P{=0}=1-p=q ,求{}的均值函数和协方差函数。
3 设{}是具有参数的泊松过程,令表示t时刻事件A发生的次数,,,……分别表示第一次,第二次,……事件A发生的时间,表示从第n-1次事件A发生到第n次事件A发生的时间间隔,证明:
(1)(n=1,2,……)是独立同分布的均值为1/的指数分布(2)服从参数为n与的分布,其概率密度函数为
(3) 设在[0,t]内事件A已经发生n 次,其0<s<t ,对于0<k<n ,
求P{}
4 设{}是强度为的泊松过程,{(k=1,2,…)}是一列独立
同分布随机变量,且与{}独立,令, t o ,若
E,求E[]及Var[]。
《随机分析》课件

随机过程的数字特征
01
数字特征
数字特征是描述随机过程的一些 具体数值,如样本均值、样本方
差等。
03
样本方差
样本方差是随机过程的另一个具 体数值,表示随机过程的波动程
度。
02
样本均值
样本均值是随机过程的一个具体 数值,表示随机过程的平均水平
。
04
其他数字特征
除了样本均值和样本方差外,还 有其他一些数字特征可以用来描 述随机过程,如偏度、峰度等。
根据转移概率的性质,可以将状态分为吸收 态、周期态、正常返态和非周期态等。
马尔科夫链的极限定理与平稳分布
要点一
极限定理
要点二
平稳分布
描述马尔科夫链在长时间运行后趋于稳定状态的性质。
在极限状态下,马尔科夫链的状态分布趋于一个稳定的分 布,称为平稳分布。
马尔科夫链的应用
01
02
03
排队论
马尔科夫链用于描述排队 系统中的顾客行为和等待 时间。
生物信息学
马尔科夫链用于描述基因 序列的进化模型和蛋白质 序列的预测。
金融工程
马尔科夫链用于描述股票 价格的变化和风险评估。
05
随机分析的应用
在金融领域的应用
风险评估
随机分析用于评估投资风险,通过模拟未来 市场走势和价格波动,为投资者提供决策依 据。
金融衍生品定价
随机分析在金融衍生品定价中发挥关键作用,如期 权、期货等金融工具的定价模型基于随机分析理论 。
随机动力学
03
随机分析用于描述系统中的随机扰动对动力学行为的影响,如
混沌理论中的随机扰动。
在社会科学中的应用
经济学
在经济学中,随机分析用于研究经济现象中的不确定性,如市场 供需、价格波动等。
财务金融数据分析PPT模板cbtp.pptx

点击此处输入文字点击此处输入文字点击此处输入文字点击此处输入文字点击此处输入文字点击此处输入文字
点击此处输入文字点击此处输入文字点击此处输入文字点击此处输入文字点击此处输入文字点击此处输入文字
点击此处输入文字点击此处输入文字点击此处输入文字点击此处输入文字点击此处输入文字点击此处输入文字
明 年 工 作 计 划
项 目 成 果 展 示
添加标题内容
添加标题内容
添加标题内容
添加标题内容
单击此处添加简短说明,添加简短文字,具体文字添加此处。
单击此处添加简短说明,添加简短文字,具体文字添加此处。
单击此处添加简短说明,添加简短文字,具体文字添加此处。
单击此处添加简短说明,添加简短文字,具体文字添加此处。
添加标题内容
此处添加标题
点击输入简要文字内容,文字内容需概括精炼,不用多余的文字修饰,
此处添加标题
点击输入简要文字内容,文字内容需概括精炼,不用多余的文字修饰,言简意赅的说明
项 目 成 果 展 示
添加标题内容
添加标题内容
添加标题内容
添加标题内容
添加标题内容
添加文本内容添加文本内容添加文本内容添加文本内容添加文本内容添加文本内容添加文本内容添加文本内容添加文本内容添加文本内容添加文本内容添加文本内容添加文本内容添加文本内容添加文本内容添加文本内容添加文本内容
工 作 完 成 情 况
标题
文字
文字
文字
文字
项目成果展示
此处添加文本内容此处添加文本内容此处添加文本内容
项 目 成 果 展 示
点击输入简要文字内容,文字内容需概括精炼,不用多余的文字修饰,言简意赅的说明分项内容……点击输入简要文字内容,文字内容需概括精炼,不用多余的文字修饰,言简意赅的说明分项内容……
点击此处输入文字点击此处输入文字点击此处输入文字点击此处输入文字点击此处输入文字点击此处输入文字
点击此处输入文字点击此处输入文字点击此处输入文字点击此处输入文字点击此处输入文字点击此处输入文字
明 年 工 作 计 划
项 目 成 果 展 示
添加标题内容
添加标题内容
添加标题内容
添加标题内容
单击此处添加简短说明,添加简短文字,具体文字添加此处。
单击此处添加简短说明,添加简短文字,具体文字添加此处。
单击此处添加简短说明,添加简短文字,具体文字添加此处。
单击此处添加简短说明,添加简短文字,具体文字添加此处。
添加标题内容
此处添加标题
点击输入简要文字内容,文字内容需概括精炼,不用多余的文字修饰,
此处添加标题
点击输入简要文字内容,文字内容需概括精炼,不用多余的文字修饰,言简意赅的说明
项 目 成 果 展 示
添加标题内容
添加标题内容
添加标题内容
添加标题内容
添加标题内容
添加文本内容添加文本内容添加文本内容添加文本内容添加文本内容添加文本内容添加文本内容添加文本内容添加文本内容添加文本内容添加文本内容添加文本内容添加文本内容添加文本内容添加文本内容添加文本内容添加文本内容
工 作 完 成 情 况
标题
文字
文字
文字
文字
项目成果展示
此处添加文本内容此处添加文本内容此处添加文本内容
项 目 成 果 展 示
点击输入简要文字内容,文字内容需概括精炼,不用多余的文字修饰,言简意赅的说明分项内容……点击输入简要文字内容,文字内容需概括精炼,不用多余的文字修饰,言简意赅的说明分项内容……
金融类经济数据分析ppt模板

02
平台联合20w+顶尖设计师、创意工作室以及国内外图库平台,汇集1500w+优质原 创内容。
感谢您下载XXX网平台上提供的PPT作品,为了您和XXX网以及原创作者的利益,请勿复制、传播、销售,否则将承担法律责任!XXX网将对作品进行维权,按照传播下载次数进行十倍的索取赔偿!
XXX.XXX
感谢您下载XXX网平台上提供的PPT作品,为了您和XXX网以及原创作者的利益,请勿复制、传播、销售,否则将承担法律责任!XXX网将对作品进行维权,按照传播下载次数进行十倍的索取赔偿!
各业输出正版的图片、视频、音频、源文件素
科技标题
材。截止2018年12月,内容累积下载量超过4亿
次。
02
平台联合20w+顶尖设计师、创意工作室以及国内外图库平 台,汇集1500w+优质原创内容,为各行各业输出正版的图 感谢您下载XXX网平台上提供的PPT作品,为了您和XXX网以及原创作者的利益,请勿复制、传播、销售,否则将承担法律责任!XXX网将对作品进行维权,按照传播下载次数进行十倍的索取赔偿!
XXX.XXX
感谢您下载XXX网平台上提供的PPT作品,为了您和XXX网以及原创作者的利益,请勿复制、传播、销售,否则将承担法律责任!XXX网将对作品进行维权,按照传播下载次数进行十倍的索取赔偿!
XXX.XXX
02
平台联合20w+顶尖设计师、创意工作室以及国内 感谢您下载XXX网平台上提供的PPT作品,为了您和XXX网以及原创作者的利益,请勿复制、传播、销售,否则将承担法律责任!XXX网将对作品进行维权,按照传播下载次数进行十倍的索取赔偿! XXX.XXX
外图库平台,汇集1500w+优质原创内容,为各行
第2章-金融工程的分析方法wxpPPT课件

6
24/10/11
金融产品的巨大价格波动性
1999年 5月31日至6月28日美元兑日元汇率走势图
7
24/10/11
无套利定价的思想
无套利定价的原理与应用
2.1 无套利定价法
8
24/10/11
无套利定价的思想套利:是在某项金融资产的交易过程中,交易者可以在不需要期初投资支出的条件下获取无风险报酬。比如同一资产在两个不同的市场上进行交易,但交易价格不同。交易者就可以在一个市场上低价买进,然后立即在另一市场上高价卖出。因此,套利可概括为利用一个或多个市场存在的价格差异,在不冒任何损失风险且无需自有资金的情况下获取利润的行为。严格套利的三大特征:无风险/复制/零投资
2.1 无套利定价法
20
24/10/11
无套利定价方法的主要特征
解读1:无套利定价原则首先要求套利活动在无风险的状态下进行。 ——但在实际交易活动中,纯粹零风险的套利活动比较少见。因此,实际的交易者在套利时往往不要求零风险,实际套利活动有相当大一部分是风险套利。
21
24/10/11
无套利定价方法的主要特征
未来每年现金流-EBIT的1%1%×320万元=3.2万元1%×(EBIT-320万元) 0
有套利机会的存在,说明B公司股票的价格被低估,套利活动将推动其股价上升,但上升过高比如110元时,会引起相反的套利活动。
2.1 无套利定价法
18
24/10/11
3
24/10/11
金融产品的特点
金融产品供给的特殊性 金融产品需求的特殊性
4
24/10/11
金融产品供给和需求的特殊性
普通产品 金融产品主要成本 原材料,资本, 智力,生产过程 劳动力 几乎无成本制造时间 必要的劳动时间 几乎可以瞬间产生供应量 有限 如果允许卖空且保 证金允许,供应量 几乎可达到无限大需求的影响 与人的生活生产 脱离人的基本需求,因素 密切相关 容易受个人影响需求量 短时间变化 短时间内变化幅度 幅度小 可能很大功能 消费或生产 投资或投机
金融统计分析及案例ppt课件

沪铜与LME三月期铜价格 散点图
LME三月期铜价格与美元 指数散点图
精品课件
二、一元线性回归
2、相关系数的计算
相关系数是在直线相关的条件下,说明两个变量之间的相关关系密切程度的 统计分析指标。相关系数也称为相关量,是用来描述变量之间变化方向和密 切程度的数字特征量,样本间相关一般用r表示,总体间相关一般用ρ表示。
金融统计分析及案例
中期研究院 常务副院长 王红英
精品课件
目录
1 统计分析对金融投资分析的意义
2
一元线性回归
3
多元线性回归
精品课件
一、统计分析对金融投资分析的意义
1、统计分析对金融投资分析的重要性
1952年马克维茨发表了资产组合理论,开启了金融问题定量研究的先河。 他利用概率论和数理统计的相关理论,构造了分析证券价格的模型框架。 马克维茨资产组合理论的产生和发展显示了统计分析在金融投资领域应用 的强大生命力。
时间序列法
根据历史数据去找出事物随时间发展的轨迹,并预测未来发展状况的定量分析方法。时间 序列研究方法主要集中于研究趋势变动和周期变动。
精品课件
二、一元线性回归
1、如何理解相关关系?
相关关系是指变量之间的不确定的依存关系。 在经济领域,社会和经济变量受随机因素的 影响很大,它们之间的关系主要表现为相关 关系。
2009-3-20
33,100
31,960
2009-3-27
35,250
33,650
……
……
……
SUMMARY OUTPUT
回归统计
Multiple R
0.997317133
R Square
0.994641464
Adjusted R Square 标准误差
LME三月期铜价格与美元 指数散点图
精品课件
二、一元线性回归
2、相关系数的计算
相关系数是在直线相关的条件下,说明两个变量之间的相关关系密切程度的 统计分析指标。相关系数也称为相关量,是用来描述变量之间变化方向和密 切程度的数字特征量,样本间相关一般用r表示,总体间相关一般用ρ表示。
金融统计分析及案例
中期研究院 常务副院长 王红英
精品课件
目录
1 统计分析对金融投资分析的意义
2
一元线性回归
3
多元线性回归
精品课件
一、统计分析对金融投资分析的意义
1、统计分析对金融投资分析的重要性
1952年马克维茨发表了资产组合理论,开启了金融问题定量研究的先河。 他利用概率论和数理统计的相关理论,构造了分析证券价格的模型框架。 马克维茨资产组合理论的产生和发展显示了统计分析在金融投资领域应用 的强大生命力。
时间序列法
根据历史数据去找出事物随时间发展的轨迹,并预测未来发展状况的定量分析方法。时间 序列研究方法主要集中于研究趋势变动和周期变动。
精品课件
二、一元线性回归
1、如何理解相关关系?
相关关系是指变量之间的不确定的依存关系。 在经济领域,社会和经济变量受随机因素的 影响很大,它们之间的关系主要表现为相关 关系。
2009-3-20
33,100
31,960
2009-3-27
35,250
33,650
……
……
……
SUMMARY OUTPUT
回归统计
Multiple R
0.997317133
R Square
0.994641464
Adjusted R Square 标准误差
《随机分析》课件

02
概率空间与随机变量
概率空间
01
02
03
样本空间
定义为一个包含所有可能 结果的集合,表示试验的 所有可能结果。
事件
样本空间中的某些子集, 表示试验中可能出现的结 果。
概率
用于描述事件发生的可能 性大小的数值,满足非负 性、规范性、可加性等性 质。
随机变量的定义与性质
定义
随机变量是定义在样本空间上的一个 实值函数,表示试验结果的数值特征 。
随机过程的独立性与平稳性
独立性
如果两个随机过程相互独立,则一个随 机过程的输出不会影响另一个随机过程 的输出。
VS
平稳性
如果一个随机过程的统计特性不随时间推 移而改变,则称该随机过程是平稳的。
04
马尔科夫链பைடு நூலகம்
马尔科夫链的定义与性质
定义
马尔科夫链是一个随机过程,其中每个状态只依赖于前一个状态,具有记忆性。
计算方法
极限分布可以通过求解转移概率矩阵的特征 向量得到,也可以通过迭代法或直接计算法 进行计算。在某些特殊情况下,如齐次马尔 科夫链,极限分布可以通过简单公式求解。
05
随机分析的应用实例
蒙特卡洛模拟
蒙特卡洛模拟是一种基于概率统计的数值模拟方法,通过随机抽样和统 计方法来求解数学、物理、工程等领域的问题。
随机分析的基本概念
随机变量
可以取不同值的变量,其取值 具有不确定性。
期望值
随机变量的平均值,用于描述 随机变量的中心趋势。
概率
描述随机事件发生的可能性, 通常用实数表示。
分布函数
描述随机变量取值的概率分布 情况,通常用概率密度函数或 累积分布函数表示。
方差
金融统计分析(ppt 99页)

贷方记录对外获得收入的工程,它反映国际 交往中国内实际资源减少或金融资产的减少 或负债增加。
国际收支记帐规那么
借方
贷方
商品进口支付
商品出口收入
劳务及其他支付
劳务、投资及其他收入
经常转移支付(国内转出) 经常转移收入(国外转入)
本国常住者获得的外国资产 外国常住者获得的本国资产或对
(资产增加)
本国的投资(负债增加)
四、国际收支统计与其它统计的关系
〔一〕国际收支统计与国民经济核算体系的 关系
国民经济核算体系是收集、报告一经济体 的经济统计资料的全面系统的体系,其国 际标准是国民账户体系〔SNA〕,它包括 交易、其他流量、存量以及影响记录期转 变中的资产负债的变化。
国际收支和国民账户体系存在密切的关系
具体表现:
广义的国际收支----不需外汇支付和无实 际外汇收支的活动出现〔无偿捐助、捐赠、
租赁、易货贸易等〕
第一节 国际收支统计
一、国际收支的概念
〔二〕概念
国际收支是一特定时期的统计报表,它系统地总结一个 经济体与世界其它经济体之间的经济交易。它反映的 是:
1、一个经济实体与世界上其它经济实体之间的商品、 劳务和收益交易(常住单位与非常住单位之间的交易);
2、时间上:
国际收支统计是以所有权转移为记录的时 间。外汇收支统计那么是在收支行为发生
第二节 国际收支统计的根底 一、国际收支统计的根本核算原那么 〔一〕复式记账法
它是根据资金平衡的原理,在反映每一项业 务活动时按其内容都以相等的金额同时在贷 方和借方进行登记。
国际收支统计中以借贷为记账符号,借方工 程为负号工程,贷方工程为正方工程;以 “有借必有贷,借贷必相等〞为记账规那么。
国际收支记帐规那么
借方
贷方
商品进口支付
商品出口收入
劳务及其他支付
劳务、投资及其他收入
经常转移支付(国内转出) 经常转移收入(国外转入)
本国常住者获得的外国资产 外国常住者获得的本国资产或对
(资产增加)
本国的投资(负债增加)
四、国际收支统计与其它统计的关系
〔一〕国际收支统计与国民经济核算体系的 关系
国民经济核算体系是收集、报告一经济体 的经济统计资料的全面系统的体系,其国 际标准是国民账户体系〔SNA〕,它包括 交易、其他流量、存量以及影响记录期转 变中的资产负债的变化。
国际收支和国民账户体系存在密切的关系
具体表现:
广义的国际收支----不需外汇支付和无实 际外汇收支的活动出现〔无偿捐助、捐赠、
租赁、易货贸易等〕
第一节 国际收支统计
一、国际收支的概念
〔二〕概念
国际收支是一特定时期的统计报表,它系统地总结一个 经济体与世界其它经济体之间的经济交易。它反映的 是:
1、一个经济实体与世界上其它经济实体之间的商品、 劳务和收益交易(常住单位与非常住单位之间的交易);
2、时间上:
国际收支统计是以所有权转移为记录的时 间。外汇收支统计那么是在收支行为发生
第二节 国际收支统计的根底 一、国际收支统计的根本核算原那么 〔一〕复式记账法
它是根据资金平衡的原理,在反映每一项业 务活动时按其内容都以相等的金额同时在贷 方和借方进行登记。
国际收支统计中以借贷为记账符号,借方工 程为负号工程,贷方工程为正方工程;以 “有借必有贷,借贷必相等〞为记账规那么。
金融统学分析-PPT精品

方
法和相关数据来描述和分析影响现实金融问题的影响因素,揭示其
基本的数量关系。为制定决策提供可供操作的政策上的数量界限。
回总目录 回本章目录
二.金融统计的内容
金融统计的内容包括金融工具统计和金融市
场统计,其中,金融统计指标是金融统计分析的基
础。
从金融统计体系的内容来看,包括货币供
应量统计、信贷收支统计、现金收支统计、对外金
融统计、保险统计、资金流量统计等。
回总目录 回本章目录
三.金融统计的研究方法
(一)金融风险计量方法研究
• Markowits的方差类风险计量方法
• Sharpe的β值风险计量方法
• 下偏矩风险计量方法
• 基于Hurst指数的风险计量方法
• VaR风险计量方法
• 连接函数计量方法
虽然这些方法都存在不同的缺陷,但它们的出现对风险的
回总目录 回本章目录
下偏矩风险计量方法
风险的下偏矩计量方法将损失作为风险的计量因 子,反映了投资者对风险的真实心理感受,符合行为科 学的原理。而且从资源配置效率看,该计量方法优于方 差方法。尽管下偏矩计量方法比较好,但是也有它的不 足,该方法考虑的只是风险的某些侧面,是一种事前风 险的事后估计方法,而且对下方风险的刻画并不精细。 此外,与方差方法相比,它的计算要复杂得多。
市场体系所进行的政策性调节的机制。
一般由三部分内容构成:
(1) 决策执行机构,这是调控得以落实的组织保证
多数国家是由中央银行来承担。
(2) 长期起作用的金融法令法规,这是实施调控的
制度性内容。
(3) 货币政策,这是针对调节任务所进行的政策设
金融统计分析精讲课件

于对商业银行的资产负债表进行评估和评级方面,实质性的金融 监管权一直都掌握在日本政府手中(1998年之前由大藏省负责, 现在由1998年成立的金融监督厅负责)。 – 在英国,1997年成立了金融服务局(Financial Services Authority,FSA),将银行监管的职能从英格兰银行中分离出来, 与其他金融监管机构合并,负责对各领域内的金融活动进行监管。 – 在德国(两德统一前为联邦德国),德意志联邦银行也不具有对 银行业的监督权,而是由联邦财政部的联邦银行监督局负责。 – 韩国(1998)、澳大利亚(1998)和卢森堡(1999)等国 也是 如此
货币供应量统计的相关问题
• 货币发行方面
– 不少国家的财政部介入辅币的发行,如美国。银行券(Federal Reserve Notes)由12家联邦储备银行发行,按成本价向美国财政 部(U.S. Treasury)下属的Bureau of Engraving and Pringting购 买美元现钞;至于硬币(coins),由12家联邦储备银行向美国财 政部下属的Bureau of the Mint按照面值购买。其差异表现为银行 券的铸币税收入归12家联邦储备银行所有,硬币的铸币税归财政 部所有。
邮政储汇局、财务公司。 – 其他金融性公司包括:保险公司和养老基金(企业年
金)、信托投资公司、金融租赁公司、资产管理公司、 汽车金融服务公司、金融担保公司、证券公司、投资 基金、证券交易所和其他金融辅助机构 – 货币当局资产负债表与其他存款性公司资产负债表合 并,编制出存款性公司概览,广义货币为存款性公司 概览中的货币和准货币
货币供应量统计的相关问题
• 货币政策的制定与执行方面
– 在有的国家,货币政策的最终目标并不是中央银行来制定,如新 西兰储备银行、英格兰银行等国家的中央银行。最早实行通胀目 标制的国家——新西兰,就是由其财政部和新西兰储备银行共同 确定货币政策的最终目标,然后赋予新西兰储备银行相应的独立 性来实现这一目标。
货币供应量统计的相关问题
• 货币发行方面
– 不少国家的财政部介入辅币的发行,如美国。银行券(Federal Reserve Notes)由12家联邦储备银行发行,按成本价向美国财政 部(U.S. Treasury)下属的Bureau of Engraving and Pringting购 买美元现钞;至于硬币(coins),由12家联邦储备银行向美国财 政部下属的Bureau of the Mint按照面值购买。其差异表现为银行 券的铸币税收入归12家联邦储备银行所有,硬币的铸币税归财政 部所有。
邮政储汇局、财务公司。 – 其他金融性公司包括:保险公司和养老基金(企业年
金)、信托投资公司、金融租赁公司、资产管理公司、 汽车金融服务公司、金融担保公司、证券公司、投资 基金、证券交易所和其他金融辅助机构 – 货币当局资产负债表与其他存款性公司资产负债表合 并,编制出存款性公司概览,广义货币为存款性公司 概览中的货币和准货币
货币供应量统计的相关问题
• 货币政策的制定与执行方面
– 在有的国家,货币政策的最终目标并不是中央银行来制定,如新 西兰储备银行、英格兰银行等国家的中央银行。最早实行通胀目 标制的国家——新西兰,就是由其财政部和新西兰储备银行共同 确定货币政策的最终目标,然后赋予新西兰储备银行相应的独立 性来实现这一目标。
第一章_基本概率 《金融数据统计分析》ppt课件

领域都非常重要的概率分布。
若随机变量 X 服从一个位置参数为 、标准差为 的概率分布,记为: X ~ N(, 2)
则其概率密度函数为
f (x)
1
e
(
x )2 2 2
2
标准差 的平方 2 称为方差。
正态分布概率密度图
试验相互独立,这种试验在统计学上称为伯努利试验。二项分布即重 复次的伯努利试验。 如果事件发生的概率是 p ,则不发生的概率 q 1 p ,N 次独立重复试验 中发生 k 次的概率是:
p(X k) Cnk pk (1 p)nk
正态分布
正态分布(normal distribution)是一个在数学、物理、工程及金融等
多个事件的概率运算
互斥事件:不可能同时发生的事件。
对可数个两两互斥事件 Ai iN,有:
P(Ai ) P Ai 。
i1
i1
广义加法公式
对于任意两个事件A 和 B,计算A 或 B 发生的概率如图所示。
计算公式为: P(A B) P(A) P(B) P(A B)
条件概率
条件概率(conditional probability)就是事件A 在另外一个事件B 已
•如果是连续复利,则 EAR er 1 。
投资与随机变量
几乎在所有的投资决策中,都会用到随机变量,例如股票收益率和每股 收益都是常见的随机变量的例子。
二项期权定价模型:一种期权定价模型,主要用于计算美式期权的价值
罗伊第一安全比率准则
在投资组合中,超亏风险是指资产组合的价值低于某个可以接受的 最低值的风险。
➢ 第三,资产收益率的高低反映了企业经营管理水平高低和经济责 任制的落实情况。
收益率的类型
必要收益率 (Required Rate of Return)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1. (W) 1 2. If A1, A2, is a sequence of disjoint sets in , then
Ak (Ak ) k1 k1
(W, , P) is called a probability triple; a measurable subset of W is called an event.
6
Example 1.1.3
W HHH , HHT , HTH , HTT , THH , THT , TTH , TTT
1 , W, HHH , HHT , HTH , HTT , THH ,THT ,TTH ,TTT
Hale Waihona Puke H on the first toss AH
3. k1 Ak , Ak
A pair (W, ) is called a measurable space. An element of is called a measurable subset of W
• A s-algebra contains , so does W,
0 , W : trivial s-algebra
5
Probability measure
Definition 1.1.2: A probability measure is a function mapping into [0, 1] with the following properties:
Stochastic calculus for finance
1 Probablity theory
1
参考书: [1]Steven E Severve,Stochastic calculus for finance 2,Springer,2008
[2] Bernt ksendal ,Stochastic differential equations, An introduction with applications
Definition 1.1.4: A filtration is an increasing sequence of s-algebras w.r.t time s.t.
0 1 2 k
(W, , {k }, P) is called a filtered space, where 0 1
s AHH , AHT , ATH , ATT
0 1 2
7
• 0 contains no information • 1 contains the information up to time 1 (the first toss) • 2 contains the information up to time 2 (the first two tosses)
8
1.2 Random variable,distribution
Definition 1.2.1: Given (W, , P), a function f : W is called measurable if
f 1(B) W f B
4
1.1 Probability and measure theory
Definition1.1.1: A s-algebra is a collection of subsets of W with
the following three properties: 1. 1. If A, then its complement Ac
1 Probablity theory
1.1 Probability and measure theory 1.2 Random variable,distribution 1.3. Integration using general probability
measure 1.4 conditional Expectation 1.5 Stochastic process 1.6 martingales 1.7 Markov Processes
T on the first toss AT
2 , W, HHH , HHT , HTH , HTT , THH ,THT , TTH ,TTT ,
AHH
AHT
ATH
ATT
and all sets which can be build by taking unions of these }
Springer, 2000
2
Introduction
PROBLEM Consider the simple stock price model
dS t t S t , S 0 x (1.1)
dt
Where S(t) is the stock price at time t, and μ(t) is the relative rate of growth at time t. It might happen that μ(t) is not completely known, but subject to some random environmental effects, so that we have
(t) r(t) "noise"
Where we do not know the exact behaviour of the noise term, only its probability distribution. the function r(t)is assumed to be nonrandom. How do we solve (1.1)in this case?
Ak (Ak ) k1 k1
(W, , P) is called a probability triple; a measurable subset of W is called an event.
6
Example 1.1.3
W HHH , HHT , HTH , HTT , THH , THT , TTH , TTT
1 , W, HHH , HHT , HTH , HTT , THH ,THT ,TTH ,TTT
Hale Waihona Puke H on the first toss AH
3. k1 Ak , Ak
A pair (W, ) is called a measurable space. An element of is called a measurable subset of W
• A s-algebra contains , so does W,
0 , W : trivial s-algebra
5
Probability measure
Definition 1.1.2: A probability measure is a function mapping into [0, 1] with the following properties:
Stochastic calculus for finance
1 Probablity theory
1
参考书: [1]Steven E Severve,Stochastic calculus for finance 2,Springer,2008
[2] Bernt ksendal ,Stochastic differential equations, An introduction with applications
Definition 1.1.4: A filtration is an increasing sequence of s-algebras w.r.t time s.t.
0 1 2 k
(W, , {k }, P) is called a filtered space, where 0 1
s AHH , AHT , ATH , ATT
0 1 2
7
• 0 contains no information • 1 contains the information up to time 1 (the first toss) • 2 contains the information up to time 2 (the first two tosses)
8
1.2 Random variable,distribution
Definition 1.2.1: Given (W, , P), a function f : W is called measurable if
f 1(B) W f B
4
1.1 Probability and measure theory
Definition1.1.1: A s-algebra is a collection of subsets of W with
the following three properties: 1. 1. If A, then its complement Ac
1 Probablity theory
1.1 Probability and measure theory 1.2 Random variable,distribution 1.3. Integration using general probability
measure 1.4 conditional Expectation 1.5 Stochastic process 1.6 martingales 1.7 Markov Processes
T on the first toss AT
2 , W, HHH , HHT , HTH , HTT , THH ,THT , TTH ,TTT ,
AHH
AHT
ATH
ATT
and all sets which can be build by taking unions of these }
Springer, 2000
2
Introduction
PROBLEM Consider the simple stock price model
dS t t S t , S 0 x (1.1)
dt
Where S(t) is the stock price at time t, and μ(t) is the relative rate of growth at time t. It might happen that μ(t) is not completely known, but subject to some random environmental effects, so that we have
(t) r(t) "noise"
Where we do not know the exact behaviour of the noise term, only its probability distribution. the function r(t)is assumed to be nonrandom. How do we solve (1.1)in this case?
