2.2.2-2.2.3 双曲线的参数方程 抛物线的参数方程 课件(人教A选修4-4)
合集下载
高中数学 2.2.2双曲线的参数方程 新人教A版选修4-4

链 接
= 3.
即点 M0 到双曲线的最小距离为 3.
整理课件
►变式训练
2.已知圆 O1:x2+(y-2)2=1 上一点 P 与双曲线 x2-y2=1 上一
点 Q,求 P,Q 两点间距离的最小值.
栏
点拨:先求圆心
O1
与点
Q
的距离的最小值,再利用圆的性质得目
链
出 PQ 的最小值.
接
解析:设 Q(sec θ,tan θ),
【解题策略】利用双曲线的参数方程可以求目标函数的最值,这
是常见的方法和题型,一定要熟练掌握.
整理课件
析疑难
提
能
力栏 目 ≥|O1Q|. |O1Q|2=sec2θ+(tan θ-2)2
整理课件
=(tan2 θ+1)+(tan2 θ-4tan θ+4)
=2tan2 θ-4tan θ+5
=2(tan θ-1)2+3,
栏 目
链
当 tan θ=1 时,|O1Q|2 取得最小值为 3,
接
此时有|O1Q|min= 3,|PQ|min= 3-1.
2.2.2 双曲线的参数方程
整理课件
栏 目 链 接
整理课件
1.理解双曲线参数方程的概念. 2.能选取适当的参数,求简单曲线的参数方程. 3.掌握参数方程化为普通方程几种基本方法. 4.利用双曲线的参数方程求最值和有关点的轨迹问 题.
整理课件
栏 目 链 接
整理课件
题型一 双曲线参数方程的 理解
例 1 写出圆锥曲线 x2-y2=4 的参数方程.
栏
解析:x2-y2=4 变形为:x42-y42=1.
目 链
接
∴参数方程为x=2sec y=2tan
高中数学 2.2.2双曲线的参数方程课件 新人教A版选修4-4

答案;60°
完整版ppt
6
题型二 双曲线参数方程应用
例 2 求点 M0(0,2)到双曲线 x2-y2=1 的最小距离(即双曲线上
任一点 M 与点 M0 距离的最小值).
栏
分析:点 M0 与双曲线上任一点 M 距离可转化为一个函数关系式目链
接
来进一步研究求解.
解析:把双曲线方程化为参数方程x=sec y=tan
由题意知|O1P|+|PQ|≥|O1Q|. |O1Q|2=sec2θ+(tan θ-2)2
完整版ppt
9
析疑难
提
能
力栏 目 链
接
完整版ppt
10
θ, θ (θ 为参数),
设双曲线上动点为 M(sec θ,tan θ),则
|M0M|2=sec2θ+(tan θ-2)2
完整版பைடு நூலகம்pt
7
=(tan2θ+1)+(tan2θ-4tan θ+4)
=2tan2θ-4tan θ+5
=2(tan θ-1)2+3,
栏
目
当 tan θ-1=0,即 θ=π4 时,|M0M|2 取最小值 3,此时有|M0M|
链 接
= 3.
即点 M0 到双曲线的最小距离为 3.
完整版ppt
8
►变式训练
2.已知圆 O1:x2+(y-2)2=1 上一点 P 与双曲线 x2-y2=1 上一
点 Q,求 P,Q 两点间距离的最小值.
栏
点拨:先求圆心
O1
与点
Q
的距离的最小值,再利用圆的性质得目
链
出 PQ 的最小值.
接
解析:设 Q(sec θ,tan θ),
2.2.2 双曲线的参数方程
二双曲线的参数方程课件

详细描述
在物理学中,二双曲线参数方程可以用于描述振动、波动等现象;在工程学中,可以用于分析机械振 动、控制系统等;在天文学中,可以用于研究行星轨道、卫星运动等。此外,二双曲线参数方程还在 信号处理、图像处理等领域有广泛应用。
02
二双曲线参数方程的推导
参数方程的推导过程
参数方程的基本形式
参数方程通常由两个方程组成,分别表示位 置和时间的关系。在二双曲线的参数方程中 ,位置由直角坐标或极坐标表示,时间则由 参数t表示。
在工程学中的应用
航天工程
在航天工程中,二双曲线的参数方程 可以用来描述卫星轨道和航天器的运 动轨迹。
机械工程
在机械工程中,二双曲线的参数方程 可以用来描述机械运动和机构的设计 。
在数学建模中的应用
微分方程求解
在求解某些微分方程时,二双曲线的参数方程可以作为解的 一种表达方式。
数值分析
在数值分析中,二双曲线的参数方程可以用来描述数值方法 的迭代过程和收敛性分析。
参数方程的推导方法
通过将二双曲线的标准方程进行适当的变换 和整理,可以得到其参数方程。变换过程通 常涉及消去方程中的平方项,并引入参数t来 表示时间或角度。
参数方程的求解步骤
求解参数方程的过程包括对方程进行整理、 代入已知条件、解出参数t等步骤。求解过程 中需要注意方程的解是否合理,并排除无效 解。
参数方程在实际生活中有广泛的应用,学 习参数方程可以帮助学生更好地理解数学 与现实世界的联系,增强数学应用意识。
感谢您的观看
THANKS
等相关的物理问题。
03
几何解释的局限性
需要注意的是,参数方程的几何解释仅适用于特定的问题和情境,不能
盲目套用。此外,对于复杂的几何图形,参数方程的求解可能会变得非
在物理学中,二双曲线参数方程可以用于描述振动、波动等现象;在工程学中,可以用于分析机械振 动、控制系统等;在天文学中,可以用于研究行星轨道、卫星运动等。此外,二双曲线参数方程还在 信号处理、图像处理等领域有广泛应用。
02
二双曲线参数方程的推导
参数方程的推导过程
参数方程的基本形式
参数方程通常由两个方程组成,分别表示位 置和时间的关系。在二双曲线的参数方程中 ,位置由直角坐标或极坐标表示,时间则由 参数t表示。
在工程学中的应用
航天工程
在航天工程中,二双曲线的参数方程 可以用来描述卫星轨道和航天器的运 动轨迹。
机械工程
在机械工程中,二双曲线的参数方程 可以用来描述机械运动和机构的设计 。
在数学建模中的应用
微分方程求解
在求解某些微分方程时,二双曲线的参数方程可以作为解的 一种表达方式。
数值分析
在数值分析中,二双曲线的参数方程可以用来描述数值方法 的迭代过程和收敛性分析。
参数方程的推导方法
通过将二双曲线的标准方程进行适当的变换 和整理,可以得到其参数方程。变换过程通 常涉及消去方程中的平方项,并引入参数t来 表示时间或角度。
参数方程的求解步骤
求解参数方程的过程包括对方程进行整理、 代入已知条件、解出参数t等步骤。求解过程 中需要注意方程的解是否合理,并排除无效 解。
参数方程在实际生活中有广泛的应用,学 习参数方程可以帮助学生更好地理解数学 与现实世界的联系,增强数学应用意识。
感谢您的观看
THANKS
等相关的物理问题。
03
几何解释的局限性
需要注意的是,参数方程的几何解释仅适用于特定的问题和情境,不能
盲目套用。此外,对于复杂的几何图形,参数方程的求解可能会变得非
高中数学 第二讲 二 圆锥曲线的参数方程 2-3 双曲线的参数方程 抛物线的参数方程课件 新人教A版
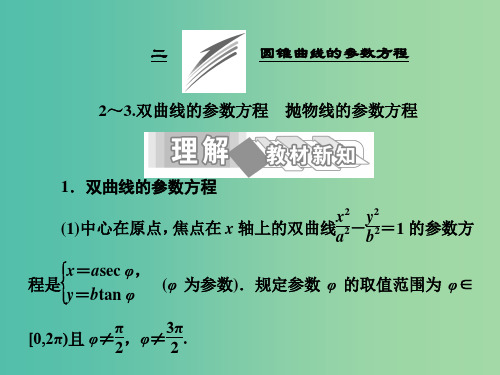
方程是xy==abstaecn
φ, φ
(φ 为参数).
2.抛物线的参数方程
(1)抛物线 y2参数). (2)参数 t 的几何意义是抛物线上除顶点外的任意一点与
原点连线的斜率的倒数.
双曲线、抛物线参数方程的基本问题
[例 1] (1)双曲线xy==62se3ctαan α, (α 为参数)的焦点坐标是
=(sec2 θ+2 2sec θ+2+tan2θ)(sec2 θ-2 2sec θ+2+tan2θ) =( 2sec θ+1)2( 2sec θ-1)2 =(2sec2 θ-1)2. 又|OP|2=sec2 θ+tan2θ=2sec2 θ-1, 由此得|F1P|·|F2P|=|OP|2.
感谢亲观看此幻灯片,此课件部分内容来源于网络, 如有侵权请及时联系我们删除,谢谢配合!
_______.
x=tan t,
(2)将方程y=11- +ccooss
2t 2t
(t 为参数)化为普通方程是_______.
[思路点拨] (1)可先将方程化为普通方程求解;
(2)利用代入法消去 t.
[解析] (1)将xy==62se3ctαan α, 化为3y62 -1x22=1, 可知双曲线焦点在 y 轴,且 c= 36+12=4 3, 故焦点坐标是(0,±4 3). (2)由 y=11-+ccooss 22tt=22csions22tt=tan2t, 将 tan t=x 代入上式,得 y=x2,即为所求方程. [答案] (1)(0,±4 3);(2)y=x2
的距离是8,那么P到它的左焦点距离是________.
解析:由双曲线参数方程可知a=1,
故P到它左焦点的距离|PF|=10或|PF|=6.
答案:10或6
2.2.2-2.2.3 双曲线的参数方程 抛物线的参数方程 课件(人教A选修4-4)

提示:参数 α 表示抛物线上除顶点外的任意一点 M,以射线 OM 为终边的角.
[研一题] [例 1] 距离为 2. 在双曲线 x2-y2=1 上求一点 P, P 到直线 y=x 的 使
[精讲详析]
本题考查双曲线的参数方程的应用,解答本题
需要先求出双曲线的参数方程, 设出 P 点的坐标, 建立方程求解. 设 P 的坐标为(secφ, φ), P 到直线 x-y=0 的距离为 2 tan 由 |secφ-tan φ| 得 = 2 2 1 sin φ 得|cos φ-cos φ|=2,|1-sin φ|=2|cos φ|
证明:设双曲线为 x2-y2=a2,取顶点 A(a,0), 弦 B′B∥Ox,B(asecα,atan α),则 B′(-asecα,atan α). atan α atan α ∵kB′A= ,kBA= , -asecα-a asecα-a ∴kB′A·BA=-1. k ∴以 BB′为直径的圆过双曲线的顶点.
[读教材· 填要点] 1.双曲线的参数方程 x2 y2 (1)中心在原点, 焦点在 x 轴上的双曲线a2-b2=1 的参数方程是 x=asecφ π 3π φ∈[0,2π)且 φ≠2,φ≠ 2 y=btan φ 规定参数 φ 的取值范围为 y2 x2 (2)中心在原点, 焦点在 y 轴上的双曲线a2-b2=1 的参数方程是 x=btan φ y=asecφ .
x2 y2 设椭圆a2+b2=1,∴a=5,c=4,b=3. x2 y2 ∴方程为25+ 9 =1. 设椭圆上一点 P(5cos θ,3sin θ), 双曲线一渐近线为 3x-4y=0, |3×5cos θ-12sin θ| ∴点 P 到直线的距离 d= 5 3| 41sin θ-φ| 5 = (tan φ=4). 5 3 41 ∴dmax= 5 .
人教A版高中数学选修4-4课件 抛物线的参数方程课件2

解:由于M1
,
M
两点对应的参数方程分
2
别是t1和t
2,则可得点M1和M
的坐标分别为
2
M1(2 pt12 , 2 pt1 ), M2 (2 pt22 , 2 pt2 )
kM1M 2
2 pt1 2 pt12
2 pt2 2 pt22
t1
1 t2
例2.设M为抛物线y2 2 x上的动点, 给 定点M0 (1, 0),点P为线段M0 M的中点, 求点P的轨迹方程。
例3.如图O是直角坐标原点, A, B是抛物线
y2 2 px( p 0)上异于顶点的两动点,且 OA OB,OM AB并于AB相交于点M, 求点M的轨迹方程。
yA
M
o
x
B
解 : 根据条件,设点M , A, B的坐标分别为( x, y),
(2
pt12 ,
2
pt1 ), )(t1
x
y
2p
tan2
2p
tan
(为参数)
这就是抛物线(5)(不包括顶点)的参数方程
( , )
22
如果令t 1 , t (, 0) (0, ),则有
tan
x
2
pt
2
(t为参数)
y 2 pt
当t 0时,由参数方程表示的点正好就是抛物线
的顶点(0, 0)因此当t (, )时,参数方程就表
《抛物线的参数方程》课件2
y
M(x,y)
( , )
22
o
x
设抛物线的普通方程为 y2 2 px...........(5)
因为点M 在的终边上,根据三角函数的
定义可得 y tan ..................................(6)
2.2 2~3双曲线的参数方程 抛物线的参数方程 课件(人教A选修4-4)

[答案] (1)(0,± 3);(2)y=x2. 4
返回
(1)解决此类问题要熟练掌握双曲线与抛物线的参
数方程,特别是将参数方程化为普通方程,还要明确参 数的意义. (2)对双曲线的参数方程,如果x对应的参数形式是 sec φ,则焦点在x轴上;如果y对应的参数形式是sec φ, 则焦点在y轴上.
返回
返回
4.如图所示,O是直角坐标原点,A,B是 抛物线y2=2px(p>0)上异于顶点的两动
点,且OA⊥OB,OM⊥AB于点M,求
点M的轨迹方程.
返回
解: 根据条件, 设点 M, B 的坐标分别为(x, (2pt2, A, y), 1 2pt1),(2pt2,2pt2)(t1≠t2,且 t1· ≠0),则 t2
返回
返回
则:(|F1P|· 2P|)2 |F =[(sec θ+ 2)2+tan2θ]· [(sec θ- 2)2+tan2θ] =(sec2 θ+2 2sec θ+2+tan2θ)(sec2 θ-2 2sec θ+2+tan2θ) =( 2sec θ+1)2( 2sec θ-1)2 =(2sec2 θ-1)2. 又|OP|2=sec2 θ+tan2θ=2sec2 θ-1, 由此得|F1P|· 2P|=|OP|2. |F
x=btan φ, 数方程是 y=asec φ.
返回
2.抛物线的参数方程 (1)抛物线 y2=2px
x=2pt2, 的参数方程为 y=2pt
t∈R.
(2)参数 t 的几何意义是抛物线上除顶点外的任意一点与 原点连线的斜率的倒数.
返回
[例 1]
x=2 3tan (1)双曲线 y=6sec α
返回
返回
1.双曲线的参数方程 x2 y2 (1)中心在原点,焦点在 x 轴上的双曲线 2- 2=1 的参 a b
返回
(1)解决此类问题要熟练掌握双曲线与抛物线的参
数方程,特别是将参数方程化为普通方程,还要明确参 数的意义. (2)对双曲线的参数方程,如果x对应的参数形式是 sec φ,则焦点在x轴上;如果y对应的参数形式是sec φ, 则焦点在y轴上.
返回
返回
4.如图所示,O是直角坐标原点,A,B是 抛物线y2=2px(p>0)上异于顶点的两动
点,且OA⊥OB,OM⊥AB于点M,求
点M的轨迹方程.
返回
解: 根据条件, 设点 M, B 的坐标分别为(x, (2pt2, A, y), 1 2pt1),(2pt2,2pt2)(t1≠t2,且 t1· ≠0),则 t2
返回
返回
则:(|F1P|· 2P|)2 |F =[(sec θ+ 2)2+tan2θ]· [(sec θ- 2)2+tan2θ] =(sec2 θ+2 2sec θ+2+tan2θ)(sec2 θ-2 2sec θ+2+tan2θ) =( 2sec θ+1)2( 2sec θ-1)2 =(2sec2 θ-1)2. 又|OP|2=sec2 θ+tan2θ=2sec2 θ-1, 由此得|F1P|· 2P|=|OP|2. |F
x=btan φ, 数方程是 y=asec φ.
返回
2.抛物线的参数方程 (1)抛物线 y2=2px
x=2pt2, 的参数方程为 y=2pt
t∈R.
(2)参数 t 的几何意义是抛物线上除顶点外的任意一点与 原点连线的斜率的倒数.
返回
[例 1]
x=2 3tan (1)双曲线 y=6sec α
返回
返回
1.双曲线的参数方程 x2 y2 (1)中心在原点,焦点在 x 轴上的双曲线 2- 2=1 的参 a b
高二数学双曲线与抛物线的参数方程PPT教学课件

参数t表示抛物线上除顶点外的任意一点 与原点连线的斜率的倒数.
思考5:设点M为抛物线y2=2px(p>0)上
任意一点,若以点M到抛物线准线的距离 t为参数,则该抛物线的参数方程是什么?
x
t
p 2
或
y 2 pt p 2
yt M
O
x
x
y
t
p 2 2 pt
p2
(t为参数)
例1 设点M为双曲线
复习提问:椭圆的参数方程
1、对于椭圆方程
x2 a2
y2 b2
1(ab0)
由此得到椭圆的参数方程是什么?
x a cos
y
bsin
(φ为参数)
2、类似地,椭圆
y2 a2
x2 b2
1(ab0)
的参数方程是什么?
x
y
b cos a sin
(φ为参数)
3、参数φ几何意义是什么?范围?
探究(一):双曲线的参数方程
x b tan
y
a
sec
(φ为参数)
探究(二):抛物线的参数方程
思考1:对于抛物线y2=2px(p>0),设 点M(x,y)为抛物线上除顶点外的任意一 点,以Ox为始边,OM为终边的角为α, 则x,y,α三者关系是什么?
yM
y tan
x
α
O
x
思考2:联立y2=2px和y=xtanα,可得 x,y分别等于什么?
思考1:由 1 sin2
cos2
1,得
cos12tan21
记 1 sec ,则 sec2tan21
cos
类比建立椭圆参数方程的方法,双曲线
a x2 2b y2 2
1(a0,b0)的参数方程是什么?
2.2.2-2.2.3 双曲线的参数方程 抛物线的参数方程 课件(人教A选修4-4)

提示:参数 α 表示抛物线上除顶点外的任意一点 M,以射线 OM 为终边的角.
[研一题] [例 1] 距离为 2. 在双曲线 x2-y2=1 上求一点 P, P 到直线 y=x 的 使
[精讲详析]
本题考查双曲线的参数方程的应用,解答本题
需要先求出双曲线的参数方程, 设出 P 点的坐标, 建立方程求解. 设 P 的坐标为(secφ, φ), P 到直线 x-y=0 的距离为 2 tan 由 |secφ-tan φ| 得 = 2 2 1 sin φ 得|cos φ-cos φ|=2,|1-sin φ|=2|cos φ|
[悟一法] 参数方程是用一个参数表示曲线上点的横纵坐标的,因而曲 线的参数方程具有消元的作用,利用它可以简化某些问题的求解 过程,特别是涉及到最值、定值等问题的计算时,用参数方程可 将代数问题转化为三角问题,然后利用三角知识处理.
[通一类] 1.求证:等轴双曲线平行于实轴的弦为直径的圆过双曲线的顶 点.
证明:设双曲线为 x2-y2=a2,取顶点 A(a,0), 弦 B′B∥Ox,B(asecα,atan α),则 B′(-asecα,atan α). atan α atan α ∵kB′A= ,kBA= , -asecα-a asecα-a ∴kB′A·BA=-1. k ∴以 BB′为直径的圆过双曲线的顶点.
2.抛物线的参数方程 (1)抛物线 y2=2px 的参数方程为
x=2pt2 y=2pt
,t∈ R .
(2)参数 t 的几何意义是抛物线上除顶点外的任意一点与原点 连线的 斜率的倒数 .
[小问题·大思维]
1.在双曲线的参数方程中,φ的几何意义是什么? 提示:参数φ是点M所对应的圆的半径OA的旋转角(称为点 M的离心角),而不是OM的旋转角.
高中数学 第二讲 参数方程 2-2-2 双曲线与抛物线的参数方程课件 新人教A版选修4-4

5.过抛物线 y2=4ax(a>0)的顶点,引互相垂直的两条射线 OA、OB,求顶点 O 在 AB 上的射影 H 的轨迹方程.
解析 设抛物线上动点A、B的坐标为(at12,2at1)和(at22, 2at2)(t1,t2≠0),则AB的方程为2x-(t1+t2)y+2at1t2=0.
∵OA⊥OB,∴2aat1t21·2aat2t22=-1即t1t2=-4. ∴AB的方程为2x-(t1+t2)y-8a=0.① 过点O与AB垂直的直线OP的方程为 (t1+t2)x+2y=0.② 由①②消去t1,t2,得x2+y2-4ax=0. 故所求轨迹为圆心为(2a,0),半径为2|a|的圆.
π 当tanθ-1=0即θ= 4 时,|M0M|2取最小值3,此时有|M0M|
= 3,即M0点到双曲线的最小距离为 3.
思考题2 设P为等轴双曲线x2-y2=1上的一点,F1,F2
为两个焦点,证明:|F1P|·|F2P|=|OP|2. 【解析】 如图所示,设双曲线上的动点为P(x,y),焦点
F1(- 2,0),F2( 2,0),
课时学案
题型一 写出圆锥曲线的参数方程 例1 写出下列圆锥曲线的参数方程: (1)x2-y2=4; (2)y2=4x. 【解析】 根据圆锥曲线参数方程的写法可直接写出. (1)xy= =22staencθθ,(θ∈[0,2π)且θ≠π2 ,θ≠3π 2 );
x=4t2, (2)y=4t.
思考题1 写出下列圆锥曲线的参数方程:
(1)x42-y92=1; (2)x2=4y.
x=2secθ,
π
【答案】 (1)y=3tanθ (θ为参数,θ∈[0,2π)且θ≠ 2 ,
ቤተ መጻሕፍቲ ባይዱ
3π θ≠ 2 )
双曲线的参数方程、抛物线的参数方程 课件

[解题过程]
根据题意,设点A,B的坐标分别为A(2pt
2 1
,
2pt1),B(2pt22,2pt2)(t1≠t2,且t1t2≠0),
则|OA|= 2pt212+2pt12=2p|t1| t21+1,
|OB|= 2pt222+2pt22=2p|t2| t22+1.
因为OA⊥OB,所以O→A ·O→B =0,
即2pt21·2pt22+2pt1·2pt2=0,
所以t1·t2=-1.
△AOB的面积为
S△AOB=12|OA|·|OB|=12·2p|t1| t12+1·2p|t2| t22+1
=2p2|t1t2| t21+1t22+1
=2p2 t21+t22+2=2p2 ≥2p2 2+2=4p2.
t12+t121+2
抛物线的参数方程
如图所示,O是直角坐标系的原点,A, B是抛物线y2=2px(p>0)上异于顶点的两 动点,且OA⊥OB,A,B在什么位置时, △AOB的面积最小?最小值是多少?
[思路点拨] 利用抛物线的参数方程设出A,B点坐标. 设参数 表―示―A→,B 求|OA|,|OB| 求―面 ―→积 求最值
[解题过程]
双曲线x2-y2=1的参数方程为xy= =staenc
θ, θ,
则Q(sec θ,tan θ),又圆心C(0,2),
则|CQ|2=sec2θ+(tan θ-2)2
=(tan2θ+1)+(tan θ-2)2
=2(tan θ-1)2+3,
当tan θ=1,即tan θ=π4时, |CQ|2取最小值3, 此时有|CQ|min= 3. 又因为|PC|=1, 所以|PQ|min= 3-1.
[规律方法] (1)抛物线Y2=2PX(P>0)的参数方程为
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
设 M(x、y)为抛物线上的动点,P(x0,y0)在抛物线的延长 线上, M 为线段 OP 且
x=2t, 的中点, 抛物线的参数方程为 y=2t2,
x0=4t, 由中点坐标公式得 y0=4t2,
1 2 变形为 y0=4x0,即 x2=4y. 表示的为抛物线.
[悟一法] 在求曲线的轨迹和研究曲线及方程的相关问题时,常根据需 要引入一个中间变量即参数(将 x,y 表示成关于参数的函数),然 后消去参数得普通方程.这种方法是参数法,而涉及曲线上的点 的坐标时,可根据曲线的参数方程表示点的坐标.
[悟一法] 参数方程是用一个参数表示曲线上点的横纵坐标的,因而曲 线的参数方程具有消元的作用,利用它可以简化某些问题的求解 过程,特别是涉及到最值、定值等问题的计算时,用参数方程可 将代数问题转化为三角问题,然后利用三角知识处理.
[通一类] 1.求证:等轴双曲线平行于实轴的弦为直径的圆过双曲线的顶 点.
平方得 1-2sin φ+sin 2φ=4(1-sin 2φ), 即 5sin 2φ-2sin φ-3=0. 3 解得 sin φ=1 或 sin φ=-5. sin φ=1 时,cos φ=0(舍去). 3 4 sin φ=-5时,cos φ=± . 5 5 3 5 3 ∴P 的坐标为(4,-4)或(-4,4).
提示:参数 α 表示抛物线上除顶点外的任意一点 M,以射线 OM 为终边的角.
[研一题] [例 1] 距离为 2. 在双曲线 x2-y2=1 上求一点 P, P 到直线 y=x 的 使
[精讲详析]
本题考查双曲线的参数方程的应用,解答本题
需要先求出双曲线的参数方程, 设出 P 点的坐标, 建立方程求解. 设 P 的坐标为(secφ, φ), P 到直线 x-y=0 的距离为 2 tan 由 |secφ-tan φ| 得 = 2 2 1 sin φ 得|cos φ-cos φ|=2,|1-sin φ|=2|cos φ|
[悟一法] 对于同一个方程,确定的参数不同, 所表示的曲线就不同, 当题目条件中出现多个字母时,一定要注明什么是参数,什么是 常量,这一点尤其重要.
[通一类]
x= 5cos 3.(2011· 广东高考)已知两曲线参数方程分别为 y=sin θ
θ
5 x= t2 4 (0≤θ≤π)和 (t∈R), 它们的交点坐标为___________. y=t
[研一题] [ 例 3]
x=4secθ, y=3tan θ
如果椭圆右焦点和右顶点分别是双曲线 (θ 为参数)的右顶点和右焦点,求该椭圆上的点到双
曲线渐近线的最大距离.
[精讲详析]
本题考查椭圆及双曲线的参数方程, 解答本题需
要先将双曲线化为普通方程并求得渐近线方程,然后根据已知条 件求出椭圆的参数方程求解即可. x2 y2 ∵16- 9 =1,∴右焦点(5,0),右顶点(4,0).
2
2 5 又 y≥0,所以其交点坐标为(1, 5 ).
2 5 答案:(1, 5 )
本课时的考点是双曲线或抛物线的参数方程与普通方程的互 化.2012 年天津高考以抛物线的参数方程为载体考查抛物线定义 的应用,属低档题. [考题印证]
x=2pt2, (2012· 天津高考)已知抛物线的参数方程为 y=2pt,
[通一类] 2.已知抛物线
x=2t2 C: y=2t
(t 为参数),设 O 为坐标原点,点 M
在抛物线 C 上,且点 M 的纵坐标为 2,求点
,得 y2=2x,即抛物线的标准方程为 y2=2x.
又∵M 点的纵坐标为 2,∴M 点的横坐标也为 2. 即 M(2,2). 1 又∵抛物线的准线方程为 x=-2. 1 1 5 ∴由抛物线的定义知|MF|=2-(-2)=2+2=2. 5 即点 M 到抛物线焦点的距离为2.
(t 为参
数),其中 p>0,焦点为 F,准线为 l.过抛物线上一点 M 作 l 的垂 线, 垂足为 E.若|EF|=|MF|, M 的横坐标是 3, p=________. 点 则
[命题立意]
本题考查抛物线的参数方程与普通方程的互化
及抛物线定义的应用.
[解析]
由题意知,抛物线的普通方程为 y2=2px(p>0),焦点
p p F(2,0),准线 x=-2,设准线与 x 轴的交点为 A.由抛物线定义可 得|EM|=|MF|,所以△MEF 是正三角形,在 Rt△EFA 中,|EF| p =2|FA|,即 3+2=2p,得 p=2.
[答案] 2
点击进入 创新演练大冲关
[读教材· 填要点] 1.双曲线的参数方程 x2 y2 (1)中心在原点, 焦点在 x 轴上的双曲线a2-b2=1 的参数方程是 x=asecφ π 3π φ∈[0,2π)且 φ≠2,φ≠ 2 y=btan φ 规定参数 φ 的取值范围为 y2 x2 (2)中心在原点, 焦点在 y 轴上的双曲线a2-b2=1 的参数方程是 x=btan φ y=asecφ .
2.抛物线的参数方程 (1)抛物线 y2=2px 的参数方程为
x=2pt2 y=2pt
,t∈ R .
(2)参数 t 的几何意义是抛物线上除顶点外的任意一点与原点 连线的 斜率的倒数 .
[小问题·大思维]
1.在双曲线的参数方程中,φ的几何意义是什么? 提示:参数φ是点M所对应的圆的半径OA的旋转角(称为点 M的离心角),而不是OM的旋转角.
x= 5cos 解析:由 y=sin θ
θ
x2 2 (0≤θ≤π)得 5 +y =1(y≥0),
52 x= t 5 2 4 由 (t∈R)得 x=4y . y=t
2 x +y2=1, 5 联立方程可得 x=5y2 4
则 5y4+16y2-16=0,
4 5 2 2 解得 y =5或 y =-4(舍去),则 x=4y =1.
x2 y2 设椭圆a2+b2=1,∴a=5,c=4,b=3. x2 y2 ∴方程为25+ 9 =1. 设椭圆上一点 P(5cos θ,3sin θ), 双曲线一渐近线为 3x-4y=0, |3×5cos θ-12sin θ| ∴点 P 到直线的距离 d= 5 3| 41sin θ-φ| 5 = (tan φ=4). 5 3 41 ∴dmax= 5 .
2.如何由双曲线的参数方程判断焦点的位置?
提示:如果 x 对应的参数形式是 asecφ,则焦点在 x 轴上; 如果 y 对应的参数形式是 asecφ,则焦点在 y 轴上. 2p x=tan 2α, 3. 若抛物线的参数方程表示为 则参数 α 的几何意 y= 2p . tan α
义是什么?
证明:设双曲线为 x2-y2=a2,取顶点 A(a,0), 弦 B′B∥Ox,B(asecα,atan α),则 B′(-asecα,atan α). atan α atan α ∵kB′A= ,kBA= , -asecα-a asecα-a ∴kB′A·BA=-1. k ∴以 BB′为直径的圆过双曲线的顶点.
[研一题] [例 2] 连结原点 O 和抛物线 2y=x2 上的动点 M,延长 OM
到 P 点,使|OM|=|MP|,求 P 点的轨迹方程,并说明它是何曲线.
[精讲详析]
本题考查抛物线的参数方程的求法及其应用. 解
答本题需要先求出抛物线的参数方程并表示出 M、P 的坐标,然 后借助中点坐标公式求解.
