导学案322代数式2
北师大版数学七年级上册3.2 第1课时 代数式2教案与反思

3.2 代数式路漫漫其修远兮,吾将上下而求索。
屈原《离骚》江南学校李友峰第1课时代数式教学目标:1.进一步理解字母表示数的意义,能结合具体情景给字母赋于实际意义;理解代数式和代数式的值的意义,能解释一些简单代数式的实际背景或几何意义,在具体情景中能求出代数式的值. (重难点)2.通过创设实际背景和引用符号,经历观察、体验、验算、猜想、归纳等数学过程,体会数学与现实世界的联系,增强符号感,发展运用符号解决问题和数学探究意识.教法学法:教学方法:引导—探究—发现法.学习方法:自主探究与合作交流相结合.课前准备:多媒体课件、投影仪、电脑教学过程:一、创设情境,引入新课.欣赏视频,导入新课师:国庆六十周年大阅兵,同学们看了吗?首先请同学们来欣赏一段视频.(26秒.定格在胡锦涛主席乘坐红旗轿车阅兵的一个瞬间.)师:这是新中国成立以来,规模最大、装备最新、机械化程度最高的一次大阅兵.有谁知道胡主席乘坐的是什么品牌的车吗?生:国产红旗大轿车.师:对﹗国产红旗大轿车﹗这是我们民族的骄傲﹗提到造车,有一个人,功不可没,不能不提.同学们知道是谁吗?生:造车鼻祖—奚仲.(官桥镇所在地,是造车鼻祖—奚仲的故里,学生对此了解较多.)师:(多媒体展示一张奚仲造车的图片.)师:那我先来考考同学们:上面的图片中的一辆推车几个轮子?两辆推车几个轮子?x辆推车几个轮子?生:2个,4个,2x个.师:板书2x.设计意图:通过创设教学情境,激发学生的学习兴趣,使学生在注意力集中前提下顺利过渡到本节知识内容.引导学生体验把实际问题抽象成数学问题的一般方法,同时在解答问题中形成认知冲突.通过这一情境的引入,让学生感受到祖国的强大,增强爱国的热情,民族的自豪感.了解到学习这些知识的重要性,极大地调动了学生学习数学的积极性.同时滲透了把实际问题抽象成数学问题的一般思想方法.师: 上节课,我们学习了字母能表示什么,这节课我们继续学习§3.2代数式.(板书课题)下面请同学们快速完成导学案的第一题.二、自主探索,合作交流.1.温故而知新填空:⒈边长为a cm的正方形的周长是 cm,面积是cm2.2 . 钢笔每支2元,铅笔每支0.5元,m支钢笔和n支铅笔共____________元.⒊温度由2℃下降t℃后是℃.⒋小亮用t秒走了s米,他的速度是为米/秒生:(完成填空,如有疑难可在小组内交流、讨论.)生1:通过实物投影展示答案:4a , a2 , 2m +0.5n , t -2, t s 生2:第2、3题应该加上括号.师:板书正确答案.师:观察上面的这些式子有什么特点?生:(以小组为单位,进行组内交流、讨论.) 生1:含有数、字母、生2:含有运算符号.师:像2x,4a , a2 , 2m +0.5n , t -2,ts 等式子都是代数式(algebraic e x pression).单独一个数或一个字母也是代数式.师: 你还能举几个代数式的例子吗?生1:2,m,a ﹢b …生2: m-n,5, 2n …师:真棒.面再来考考你的眼力,请同学们快速完成导学案 : 自主探索,合作交流的第1题.2.考考你的眼力:师:下列各式中些是代数式?哪些不是?(1)m +5 (2)a +b =b +a (3)0(4) x 2+3x +4 (5)x +y >1(6)生: (1)、(3)、(4)、(6)是代数式, (2)、(5)不是.师:小结:(1)代数式中不含“=”,“>”,“<”,“≥”,“≤”,“≠”等符号.(2)单独的一个数或字母也是代数式.师:同学们回答的很好,那我们就来巩固一下吧.生:完成巩固练习:用代数式表示(1) f 的11倍再加上2可以表示为_____________.(2)数a 与它的的和可以表示为_________.(3)一个教室有2扇门和4扇窗户,n个这样的教室共有___________扇门和_________扇窗户.(4)小华、小明的速度分别为x米/秒,y米/秒,6分钟后它们一共走了米.生:(完成填空并回答,如有疑难可在小组内交流、讨论.)生1: 11f+2 ,a+a,2n,4n,6(x+y)生2:(4)小题也可以写成(6x+6y)生3:第(2)小题也可以写成1a,师: 1a通常写成a,带分数写成假分数.师:通过前面的练习,同学们想一想,说一说:代数式在书写时应该注意那些问题呢?生: 以小组为单位,进行组内交流、讨论后回答问题.( 同学们在充分交流的过程中,教师可参与其中,听听同学的想法,看看同学们在交流过程中的表现,积极引导不善交流的同学倾吐自己的想法,形成好的合作交流的气氛)生1:数与字母,字母与字母相乘,乘号可以省略,也可写成“.”;数字与数字相乘,乘号不能省略;数字要写在字母前面;生2:在含有字母的除法中,一般不用“÷”号,而写成分数的形式;式子后面有单位时,和差形式的代数式要在单位前把代数式括起来.生3:带分数一定要写成假分数.师:同学们回答的非常好,非常的全面.现在请同学们回过头来看一看,前面你所列的代数式符合要求吗?生:自我检查,同位之间互查.设计意图:让学生从实际问题中抽象出数学问题,学会列代数式,体验数学来源于生活,又为现实生活服务,极大地调动学生学习的主动性、积极性;规定代数式的书写要求,代数式求值的格式并用多媒体展示,目的在于让学生体会数学的规范性,严密性,进一步培养学生的数感和符号感.教学效果:本环节开始就有效地激发了学生的学习兴趣,调动了学生学习的积极性,学生主动学习和合作交流较为充分,学生成功的交流,使学生感受到数学结果的多样性,数学符号的美妙性,同时初步学会了列代数式的方法.师:我们知道了代数式,会列代数式,现在我们就来共同探究一下生活中的数学. 请同学们完成导学案的探究一.三、合作探究,拓展新知.内容:讨论教材上的例题.分析需要使用代数式表达信息的原因.通过解决具体问题,让学生感受代数式求值的含义.探究一:学习要求:请认真读题并完成题后的填空:1. (1)某公园的门票价格是:成人票每人10元,儿童票每人5元.一个旅游团有x名成人和y名儿童,用代数式表示这个旅游团应付的门票费.(分析:x名成人的门票费为;y名儿童的门票费为;解:这个旅游团应付的门票费为 .(2)如果这个旅游团有37名成人和15名儿童,那么应付门票费多少元?(分析:这个旅游团有37名成人即字母 =37;儿童15名即 =15;分别把它们代入(1)中的代数式,即可求出应付门票费)解: (学生口述)生: (先独立思考,再小组内交流后回答问题.)生: (通过实物投影展示答案.)生1:(1) x名成人的门票费为10x, y名儿童的门票费为5y,这个旅游团应付的门票费为,(10x+5y)元.生2:(2) 如果这个旅游团有37名成人和15名儿童,那么应付门票费445元. 师: 在回答(2)题时,我们要注意解题的格式.(板书解题过程,并加以强调.) 师:刚才我们解决了生活中的一个问题,下面我们再来探究一下生物世界的奥秘吧.请同学们快速完成导学案的探究二.探究二:1.请认真读题,参照1题的答题格式,完成下题的解答过程.----相信你能行!在某地,人们发现某种蟋蟀叫的次数与气温之间有如下的近似关系:用蟋蟀1分钟叫的次数除以7,然后加上3,就近似地得到该地当时的气温(℃).(1)用代数式表示该地当时的气温;(2)当蟋蟀1分钟叫的次数分别是80,100和120时,该地当时的气温大约是多少?(结果保留整数)生: 先独立思考,再小组内交流后回答问题.x生1: 口答1. 用x表示蟋蟀1分钟叫的次数,则该地当时的气温为(7+3) ℃.生2: 通过实物投影展示(2)小题答案.设计意图:这里首先展示出学生生活中非常熟悉的小动物――蟋蟀的图片,从而提出蟋蟀每分钟叫的次数与当时温度的关系的问题,目的是刺激学生的感官,引发学生的求知欲望.对第(1)中的蟋蟀1分所叫的次数探求或变式,目的在于帮助学生自设字母来表示有关的量,为学生列代数式铺平道路,同时让学生体会数学建模的思想.求x=80、100、120时,该地当时的温度,目的在于让学生进一步学会求代数式的值,加深对蟋蟀1分叫的次数与当时温度的关系的体会.教学效果:在这个环节中教师首先给出一个实际背景,一下子就引起了学生的注意力,接着通过师生循序渐进的分析,学生很自然地领悟了数学建模的方法,掌握了列代数式的新的方法――先设字母,再列式子,使课堂气氛显得格外轻松.同时在这里通过变式,增强了思维的灵活性,降低了学习的难度,调动了学生学习的积极性.师:同学们完成的非常棒.通过刚才的探究,我们深切体会到了:知识来源于生活,又运用于生活.小组讨论:代数式10x+5y还可以表示什么?想一想, 比一比!看谁说的既多又准!(要求学生在独立思考的基础之上,做小组交流,随后全班交流.)①如果用x(元)1支铅笔的价格,用y(元)1个练习本的价格,那么10x+5y 可以表示的总钱数②如果,那么生:(先完成①小题,然后仿照上题完成②小题.)生1:老师有 x张10元,有y 张5元的钱,则(10x+5y)元就表示老师有多少钱. 生2:一辆车以x千米/小时的速度行驶了10小时,然后又以y千米/小时的速度行驶了5小时,则 (10x+5y)千米表示这辆车所走的路程.生3:某种数学资料每本要10元,英语资料每本要5元,小明买了x本数学资料,y本英语资料,则( 10x+5y)元表示共用了多少钱.师:同学们真棒,举出这么多代数式10x+5y所表示的实际背景.设计意图:用多媒体将问题展示后,让学生充分地观察、思考,进而产生联想,针对“10x+5y”所表示的意义让学生各自发表自己观点,并在小组进行交流,通过交流,学生意识到了“10x+5y”可以表示很多不同的问题,接着让各小组长上台进行展示和师生对答案进行综合评价,最后教师又用多媒体展示部分准确答案,目的是帮助学生进一步体会符号表示的意义,同时也是为了拓宽学生的思维,发展学生联想、类比、归纳等能力.四、拓展延伸讨论回答下列问题:1.写出一个你最喜欢的一个两位数.2.一个两位数的个位数字是a,十位数字是2,请用代数式表示这个两位数;3.一个两位数的个位数字是a,十位数字是b,请用代数式表示这个两位数如何用代数式表示一个三位数?生:( 以小组为单位,进行组内交流、讨论后回答问题.)生1: 通过实物投影展示答案1.我喜欢362.这个两位数是20+a3.这个两位数是10b+a4.设这个三位数的个位数字是a,十位数字是b,百位数字是c,这个三位数是100c+10b+a.生2: 通过实物投影展示答案1.我喜欢96 ,第2,3题答案和上面的同学相同,第4题.设这个三位数的个位数字是x,十位数字是y,百位数字是z,这个三位数是100z+10y+x.师: 总结:两位数表示:10十位数字+个位数字三位数表示: 100百位数字+10十位数字+个位数字设计意图:为了检测学生的灵活应变能力,创新思维的能力,以满足不同层次的学生在数学发展方面的需要.选择题目的出发点在于帮助学生学会列代数式,进一步明确代数式的实际背景或几何意义,发展学生的符号感;让学生进一步把握本章的重点,明确学习的方向.教学效果:学生分层次独立完成,再由教师念答案学生自我评分,按不同的要求统计优秀成绩(基础差的同学做对第1,2,3题就是优秀),让每个学生都有了成就感,增强了学生学习数学的信心,真正做到了面向全体学生.五、小结回顾:师:请同学们谈一谈,通过本节课的学习,你有哪些收获?(生1、生2、生3自发站起来谈学习收获,教师作出点评、补充.)设计意图:鼓励学生结合本节课的学习谈自己的收获,学生交流,互相补充,完成本节知识的梳理.六、作业:1. P108 读一读“代数”的由来2. P109 第1题板书设计:教学反思:本节课采用导学案的方式,主要讲解代数式的基本知识,并在具体情景中讲解列代数式的方法和简单的求值.通过这些内容,让学生逐渐熟悉代数式的表示方法,并培养符号逻辑思维能力.以具体的事例引入代数式的概念,既形象又浅显易懂.通过两个探究题,使学生感受到数学与日常生活的密切联系.通过学生自己大胆的尝试,让学生在学习中得到乐趣,指导学生在变化中探索规律,培养团结合作精神.通过学生对知识和技能的总结,理清本节的知识结构,使知识系统化,提升分析问题、解决问题的能力,提升与人交往的能力.无论是教学环节设计,还是课外作业的安排上,我都重视知识的产生过程,关注人的发展,意到个体间的差异,让每一个学生在课堂上都有所感悟,都有着各自的数学体验,不同的人在数学上都得到不同的发展.当然本节课在教学过程中也有遗憾的地方,在今后的教学中,我将努力克服自己在教学中的不足之处,争取在今后的教学工作中做到更好.【素材积累】阿达尔切夫说过:“生活如同一根燃烧的火柴,当你四处巡视以确定自己的位置时,它已经燃完了。
四川省成都市七年级数学上册3.2代数式导学案2(无答案)(新版)北师大版

第二节 代数式(2)【学习目标】1.计算代数式的值的一般步骤。
2.求代数式的值应注意的问题。
3.用代数式求值推断反映的规律及意义。
【学习重难点】重点:求代数式的值。
难点:代数式的含义。
【学习方法】自主探究与合作交流相结合.【学习过程】模块一 预习反馈一.知识回顾1、用数值代替代数式中的字母,按照代数式中指明的运算,计算出的结果,叫做代数式的值一般来讲随着字母的取值的不同而有所变化。
二、自主学习(P 83——84)2、如图是一组“数值转换机”,请填写。
提示:在代入数字求值时,一定要注意符号的问题。
代数式求值下面是一对数值转换机,写出左图的输出结果;写出右图的运算过程。
×6x 输入-3x6输出x 输入??)(36 x ?输出归结:求代数式的值,关键是正确代入数值,遇到负数时,要合理地添加括号。
实践练习:判断:(1)一个代数式,只可能有一个值 ( )(2)当字母的取值不同,则同一个代数式的值就一定不同 ( )(3)当x=4时,代数式的值为0 ( )(4)当2x+y=3时,代数式(2x+y )2-(2x+y)+1的值是7。
( )【我的疑惑】探究一:(1)当m=2,n=时,求代数式 (2m-3n)(m+n) 的值.(2)已知a+b=3,求 (a+b)2 +a+b-10的值.分析:a+b是一个整体,注意整体代入。
探究二:已知:|a+5|+|b+3|=0.求代数式a2+3ab—2b3的值.模块三小结反思知识:1、求代数式的值,关键是正确代入数值,遇到负数时,要合理地添加括号。
模块四形成提升1.当x=7,y=3时,代数式的值是()A.B.C.D.2、已知:m= —2,求代数式m2—2(m+3)—5|m—5|的值.3.若a+b=10,ab=16,则代数式(a+b)2—ab=4、已知x+y=,xy= —,求代数式6x+5xy+6y的值.组长评价:你认为该成员这一节课的表现:(A)很棒 ( B)一般 (C) 没发挥出来 (D)还需努力.家长签名:。
新北师大代数式(2)导学案

课题:《代数式(2)》课时:第29课时主备人:汤虎审核人:沈自荣学生姓名:学习目标:1、使学生掌握代数式的值的概念,会求代数式的值.2、培养学生准确地运算能力,感受字母取值的变化与代数式的值变化之间的联系.学习重点:会求代数式的值.学习难点:感受字母取值的变化与代数式的值变化之间的联系.学习过程:一、自主学习:1.设教室里座位的行数是m,每行座位数比座位的行数多3,教室里总共有__________个座位?若甲班座位行数是6,该班总共有__________个座位?若乙班座位行数是7,该班有__________个座位?座位数在m=6或7时一样吗?m取不同的值时代数式m(m+3)的计算结果相同吗?2.为了开展体育活动,学校要添置一批排球,每班配2个,学校另外留10个,n个班总共需要__________个排球,若班数是15(即),则排球总数是:__________,若班数是20(即),则排球总数是__________。
我们说当n=30时,代数式的值是70;当n=40时,代数式的值是90.这就是今天我们要认识的代数式的值.二、合作探究:1、(1)当x=2,y=-3时,求代数式x(x-y)的值.(2)当a=2,b=-1,c=-3时,求代数式b2-4ac的值.讨论:由上面的求解过程,总结求代数式值的方法步骤?应该注意什么?点拨:求代数式的值的步骤:(1)代入,将字母所取的值代入代数式中;(2)计算,按照代数式指明的运算进行,计算出结果。
2、观察P83中图3-2的数值转换机,思考并填表.(1)的输出结果是;(2)的运算过程:3、讨论完成P84中的“议一议”。
5、当时,求代数式的值.三、训练巩固:1、填空:1).当 x=10时,求3x+1的值____ __ ;2).当 n=10时,求5n+2的值_____ _ ;3).当 BC=10,AD=8时,求△ABC的面积_ __ ;4).若x+1=5,则;5).若x+5y=4,则2x+10y+7=。
2019-2020学年七年级数学上册 3.2 代数式导学案2(新版)苏科版.doc

2019-2020学年七年级数学上册 3.2 代数式导学案2(新版)苏科版一:学习目标:1.理解单项式及单项式系数、次数的概念。
2.会准确迅速地确定一个单项式的系数和次数。
3.初步培养学生观察、分析、抽象、概括等思维能力和应用意识。
4.通过小组讨论、合作学习等方式,经历概念的形成过程,培养学生自主探索知识和合作交流能力。
二:学习重点:掌握单项式及单项式的系数、次数的概念,并会准确迅速地确定一个单项式的系数和次数。
三:学习难点:单项式概念的建立。
四:学习方法:分层次教学,讲授、练习相结合。
五:教学过程:(一)学前准备1、列代数式(1)若正方形的边长为a,则正方形的面积是;(2)若三角形一边长为a,并且这边上的高为h,则这个三角形的面积为;(3)若x表示正方形棱长,则正方形的体积是;(4)若m表示一个有理数,则它的相反数是;(5)小明从每月的零花钱中贮存x元钱捐给希望工程,一年下来小明捐款元。
2、请学生说出所列代数式的意义。
3、请学生观察所列代数式包含哪些运算,有何共同运算特征。
(二).探究理解学习研讨:1、概括:上面这些代数式都是由数与字母的乘积组成的,这样的代数式叫做单项式(monomial)。
例如,错误!嵌入对象无效。
、错误!嵌入对象无效。
、abc、-m都是单项式。
特别地,单独一个数或一个字母也是单项式。
单项式中的数字因数叫做这个单项式的系数(coefficient)。
例如,错误!嵌入对象无效。
的系数是错误!嵌入对象无效。
,错误!嵌入对象无效。
的系数是错误!嵌入对象无效。
,abc的系数是1,-m的系数是-1。
一个单项式中,所有字母的指数的和叫做这个单项式的次数(degree)。
例如,abc的次数是3,错误!嵌入对象无效。
的次数是4。
注意(1)圆周率错误!嵌入对象无效。
是常数;(2)当一个单项式的系数是1或-1时,“1”通常省略不写,如错误!嵌入对象无效。
,-abc;(3)单项式的系数是带分数时,通常写成假分数.如错误!嵌入对象无效。
七年级数学上册 3.2《代数式(2)》教案 (新版)苏科版

3.2代数式(2)
课型
新授课
用代数式表示简单问题的数量关系,解释一些简单代数式的实际背景或几何意义;
通过具体例子感受“同一个代数式可以表示不同的实际意义”,“理解符号所代表
的数量关系”.
教学重点、难点:代数式,单项式、单项式的系数和次数,多项式、多项式的次数,整
式的概念以及用代数式表示简单问题的数量关系.
对一些单项式中隐含的系数1和隐含的次数1强调说明.
例2要在长方形和环形地块中铺设草坪,长方形的长、宽分别为am、bm,环形的外圆、内圆的半径分别为Rm、rm,求共需草皮的面积.
几个单项式的和叫做多项式.例如,n-2、0.55a+0.35b、ab+πR2-πr2等都是多项式.
多项式中,每个单项式叫做多项式的一个项,次数最高项的次数,叫做这个多项式的次数.如πR2-πr2是πR2、-πr2两项的和,它的次数是2.
【感受代数式的意义】
1.苹果a元/kg,橘子b元/kg,买5kg苹果、6kg橘子应付元;
2.小明每步走am,小亮每步走bm,小明、小亮从小桥的两端相向而行,小明走5步,小亮走6步,两人相遇,小桥长
m;
3.a个五边形,b个六边形,共有
条边.
想一想:举例说明代数式2(x+y)可以表示哪些不同的实际意义.
单项式和多项式统称整式.
例3下列式子中哪些是代数式,哪些是整式,单项式和多项式?
,a-5, ,4a2b,-6,a2+3ab+b2,a,x=1,-x, > ,0
1.含有等号或不等号的式子一定不是代数式.
2.单独的一个数或字母也是单项式.
3.一般分母含有字母的式子不是整式.
例3为补充例题,它的设计是为了明晰概念.
2x+y呢?
七年级数学上册 3.2.2 代数式导学案(新版)苏科版

22b a 52xy π3a 22r π3.2.2 代数式一、【学习目标】1、了解单项式、单项式的系数和次数、多项式、多项式的项、多项式的次数、整式的概念。
2、能用代数式表示简单问题的数量关系。
3、能解释一些简单代数式的实际背景或几何意义。
二、【学习重难点】相关概念和代数式的实际意义三、【自主学习】1、自学课本P70到P72,完成练一练。
2、 叫做单项式, 也是单项式。
3、 叫做单项式的系数, 叫做单项式的次数。
4、 叫做多项式, 多项式的次数, 统称整式。
5、单项式- 的系数是 ,次数是 ; 单项式- 的系数是 ,次数是 多项式a2+b2c2-abc 是 次 项式。
四、【合作探究】1、自学例1,根据题意列出代数式。
像0.55a 、0.35b 、0.15m 、2a 、2a 2、0.8a 和 abc 都是数与字母的积,这样的代数式叫做单项式,单独一个数或一个字母也叫做单项式。
单项式前面的数字因数叫做它的系数。
单项式中所有字母的指数的和叫做它的次数。
单独一个数的系数是它本身,而次数是0,单独一个字母的系数是1,次数也是1。
练习:- 的系数是 ,次数是 ; 的系数是 ,次数是 。
2、自学例2,根据题意列出代数式。
几个单项式的和叫做多项式,多项式中每一个单项式叫做多项式的项,次数最高项的次数叫做多项式的次数。
例3、下列代数式是多项式吗?如果是多项式,说出它是几次几项式。
单项式与多项式统称为整式。
3、小组合作交流P70的“议一议”代数式(4a+5b )表示的实际意义可以是五、【达标巩固】1、把下列式子填入相应的空格内:⑴2.5,⑵-35,⑶2y,⑷x5,⑸2a+2b,⑹y x 3223 ,⑺2x>-3,⑻y=ax 2+bx+c,⑼kx+b.(填序号)代数式:_________________________.单项式:____________________.多项式:_________________________.整式:___________________ ___.2、 写出下列单项式的系数和次数① -2x y ② ab ③—0.52x y ④ -2y 3x3、 写出下列多项式是几次几项式?①ab —52a —72b ② -2x y +32x +2x 2y③32x —2x 2y +42x y ④ 3a —32a b +a 3b2. 用代数式表示:⑴比x 的3倍小2的数_______________.⑵一个两位数,十位上的数为x,个位上的数比十位上的数小1,这个两位数为______. ⑶x,y 两数的平方的差表示为__________.4.展开联想,从不同角度说出下列代数式的意义:(1)ab : ___________________________________________ (2)abc : ___________________________________________(3)2a+3b : ___________________________________________。
苏科版-数学-七年级上册-3.2代数式(2) 导学案

课题
主备 主 核 执教教师 课型 新授课 使用日期 学习
目标 1、知道代数式,单项式,单项式的系数、次数,多项式,多项式的项、次数,整式的概念并能说出某单项式的次数、系数、多项式、多项式的项、次数。
2、能用代数式表示简单问题的数量关系.
3、能解释一些简单代数式的实际背景或几何背景,通过具体例子感受“同一个代数式可以表示不同的实际意义”理解符号所表示的数量关系 重点难 点预测 重点
单项式的系数、次数,多项式的系数、次数。
难点 能解释一些简单代数式的实际背景或几何背景。
学生活动过程 教师导学过程
一、自主学习(独学)
任务1.阅读教材第70~72页
任务2.回答下列问题:
叫单项式,
也是单项式
叫单项式的系数, 叫单项式的次数
叫多项式的系数, 叫多项式的次数, 叫常数项,
叫整式
练习:
1、说出下列单项式的次数、系数
n 、-2 、
5
s 、0.8ab 、-5abc 、
2说出下列多项式中各项的系数和各多项式的次数.
43x x 2+-、 2n 3 +500、 2ab-2abc +2a 4
3.解释代数式300-2a ,3a+4b ,的实际意义.
4. 说说单项式,多项式,整式,代数式之间有什么联系与区别?。
3.2代数式(2)-苏科版七年级数学上册导学案

课题:3.2代数式(2)【学习目标】:1、会准确迅速地确定一个多项式的项数和次数。
2、会区别单项式和多项式。
【重点难点】:多项式和整式的有关概念【导学指导】:一、自主学习1.列代数式:(1)若长方形的长和宽分别为a、b,则长方形的周长是;(2若某班有男生x人,女生y人,则这个班的学生一共有人观察:它们与单项式有什么关系?2.多项式:;多项式的项:;*注意:多项式的每一项包括它____________.常数项:;多项式的次数:多项式中次数__的次数。
例如:3x2-2x+5 有____项,分别是_______________,常数项是____,其中最高次项是______,次数是______,因此3x2-2x+5是一个____次_____项式. 3.单项式与多项式统称_________.4.试一试:(1) a3-a2b+a3b2-b4的项有_____________________,次数是____,它是___次___项式,四次项系数是_______________.(2) x3-2x2y2+3y2的项有_____________________,次数是____,它是____次_____项式,其中最高次项是_______.(3) 的项是_______________,次数是____,它是___次___项式.(4) 下列代数式:① -34 x 2y;② x 2-1;③ 1x 2 +2x -4; ④1; ⑤2x 2-b 2; ⑥x+y 2; ⑦3a 2b -2a 3b 3+a 5⑧ ⑨其中单项式有______________ __;多项式有____________ _____;整式有_____________________(填序号)二、例题评析:1.多项式3x 2-2xy -4y 2+x -y+7的项是____________________ ;二次项是__________;一次项是_______ ;常数项是______ ;它是___次___项式。
七年级上北师大版数学3.2《代数式》导学案案

时间:2013.10. 设计:七二班数学老师审核:七年级数学老师代数式学习目标1、会判断一个式子是不是代数式2、能解释代数式的实际背景与几何意义;3、会列代数式,并会求代数式的值。
学习重点和难点重点:.会列代数式,并会求代数式的值。
难点:能解释代数式的实际背景与几何意义.学习过程一、提出问题1.在小学我们曾学过几种运算律?都是什么?如何用字母表示它们?(1)加法交换律(2)乘法交换律(3)加法结合律(4)乘法结合律(5)乘法分配律二、自主学习:(一)看课本P81,完成以下内容:1、叫代数式。
2、单独也叫代数式。
3、用,就可以求出代数式的值4、代数式的表示:(1)代数式中的数字与字母、字母与字母相乘时,×要省略,数字要写在字母的前面;(2)出现除法运算时,要写成的形式(3)带分数要化成(4)在实际问题中,需要带单位时,如果运算结果是和的形式,要把代数式括起来在带单位。
注:代数式中不能含有等号或不等号。
5、用代数式表示:(1)每包书有12册,n包书有册;(2)温度由t℃下降到2℃后是______℃;(3)棱长是a厘米的正方体的体积是______立方厘米;(4)产量由m千克增长10%,就达到______千克.6、判断下列各式是否代数式:a+b,3,a,a(b+c),a=15, b>c, abc, a2+b27、代数式10x+5y可以表示什么?举出两例。
8、若用s表示路程,t表示时间,v表示速度,你能用s与t表示v吗?9、(小黑板)一个正方形的边长是a厘米,则这个正方形的周长是面积是10、说出下列代数式的意义:(1)2a+3 (2) 2(a+3) (3)a2+b2 (4)(a+b)2以上内容为预习内容课堂检测:1.填空:(小黑板)(1)n箱苹果重p千克,每箱重__ ____千克;(2)甲身高a厘米,乙比甲矮b厘米,那么乙的身高为______厘米;(3)底为a,高为h的三角形面积是______;(4)全校学生总人数是x,其中女生占48%,则女生人数是______,男生人数是______.2.用代数式表示:(小黑板)(1)m与n的和除以10的商;(2)m与5n的差的平方;(3)x的2倍与y的和;(4)v的立方与t的3倍的积.3、从甲地到乙地的路程是15千米,步行要3小时,骑车要1小时,乘汽车要0.25小时,试问步行、骑车、乘汽车的速度分别是多少?4.用代数式表示:(1)x与y的和;(2)x的平方与y的立方的差;(3)a的60%与b的2倍的和;(4)a除以2的商与b除3的商的和.小结1.用字母表示数的意义是什么?2.什么叫代数式?作业:P83 知识技能第1题、第2题;问题解决第4题教师在学生回答上述问题的基础上,指出:①代数式实际上就是算式,字母像数字一样也可以进行运算;②在代数式和运算结果中,如有单位时,要正确地使用括号.六、作业:P83 知识技能第1题、第2题;问题解决第4题补充:1.一个三角形的三条边的长分别是a,b,c,求这个三角形的周长.2.张强比王华大3岁,当张强a岁时,王华的年龄是多少?3.a千克大米的售价是6元,1千克大米售多少元?4.圆的半径是P厘米,它的面积是多少?5.用代数式表示:(1)长为a,宽为b米的长方形的周长;(2)宽为b米,长是宽的2倍的长方形的周长;(3)宽为b米,长比宽多2米的长方形的周长.。
2018-2019年北师版七年级数学上册3.2.2代数式(二)导学案
3.2.2代数式(二)【学习目标】 知识与技能:能准确地按计算程序的步骤求值;过程与方法:通过设计程序求值培养学生良好的学习习惯和品质,提高运算能力与创新设计能力; 情感态度与价值观:通过字母取不同的值的变化来认识世界发展变化及全面的观点。
【学习重点】能准确地按计算程序的步骤求值。
【学习难点】按计算程序的步骤求值。
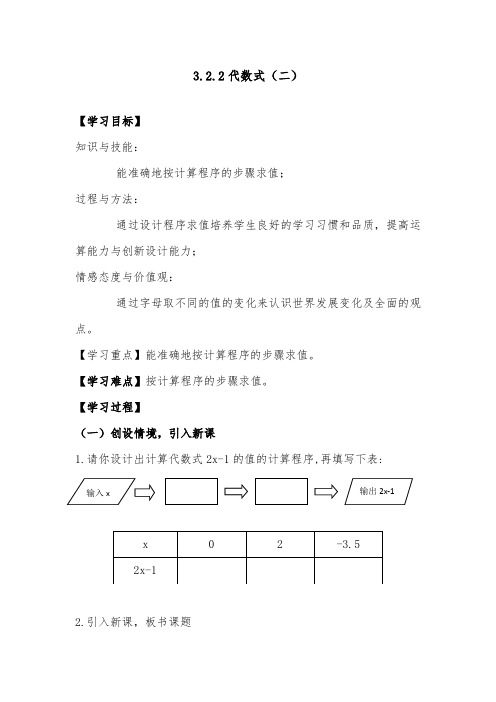
【学习过程】(一)创设情境,引入新课1.请你设计出计算代数式2x-1的值的计算程序,再填写下表:2.引入新课,板书课题(二)自主探究(1)如图是数值转换机的示意图,如果输入的数字用x表示,那么输出的数字可以用代数式_________表示;(2)下图是数值转换机的示意图,如果输入的数字用x表示,那么输出的数字用代数式-3x+5表示,请按照上题的样式,将数值转换机中的方框填上:(三)例题精讲例:填写下表,并回答有关问题:请认真观察你所填写的数字,看看有没有什么规律?然后猜想,如果x 1与x 2互为相反数,那么s 1与s 2的关系为___________.(四)练习设计 1.填表:2.小王利用计算机设计了一个计算程序,输入与输出的数据如下表:当输入数据8时,输出的数据是 ( ) A .618 B .638 C .658 D .678(五)课堂总结本节课你有什么收获?还有什么疑惑? (六)达标测评1.某同学在1月份栽了一棵树,每个月测量一交树的高度,得到下列表格:⑴按照表格的规律,6月份树的高度为________cm;⑵第x个月时,树的高度为_________cm;⑶在第_________月后,树的高度会超过185cm.。
3.2-2代数式导学案

如果你
能独立
完成,
说明你
很有天赋!
课后总结:(将发现的规律(生成)及疑惑记录下来,以备课下交流)
甲地的剩下人数=
乙地的剩下人数=
3、如果将“甲乙两地共抽调12人”改成“共抽调y人”其他条件不变,甲乙两地的剩余人数如何表示呢?请你认真思考,并与同学们交流。
甲地的剩下人数=
乙地的剩下人数=
如果忘记可查阅学过的教材或笔记。
阅读教材“一起探究”
认真阅读教材仔细完成表格
自主学习总结:(1、将自主学习内容进行归纳、记录;2、将不懂的问题记下来;3、将你发现的新问题,用文字写出来。)
(6)有一棵树苗,刚栽下去时,树高2.1米,以后每年长0.3米,则n年后的树高为(______)米.
2Hale Waihona Puke 选择题:(1)用代数式表示“比a的平方的2倍小1的数”为( )
A、2a2-1B、(2a)2-1C、2(a-1)2D、(2a-1)2
(2)小华每分钟走a米,小明每分钟走b米,2分钟后,他们一共走了()米。
我的课堂我做主,我的命运我把握
2014——2015学年度第一学期七年级数学学科导学卡
课题3.2--2代数式主编审核使用时间
学
习
目
标
1、能进一步理解代数式的定义及代数式的一些要求;
2、能说出问题中的数量关系。
3、能够运用代数式表示问题中的数量关系。
学
习
重
难
点
重点:1、、能说出问题中的数量关系。
七年级数学上册导学案:代数式(2)

35kg每位旅客免费携带20kg行李,超重部分每千克按飞机票价格的 1.5%付行李费。
④环形花坛铺草坪,大圆半径为Rm,小圆半径为rm,需要草皮多少平方米?2. 让学生先观察:30a 、 9b …你发现了什么?它们有什么公同的特征?(引导学生说出它们都是字母与数相乘)1)引入单项式定义:像0.9a,0.8b,2a,2a2,15×1.5%m等都是数与字母的积,这样的代数式叫单项式。
单独一个数或一个字母也是单项式。
2)单项式中的数字因数叫做这个单项式的系数。
3)单项式中所有字母的指数的和叫做它的次数。
二、多项式的相关概念1. 观察2ab+2bc +2ac,n – 2…(引入多项式)1)几个单项式的和叫做多项式。
其中的每个单项式叫做多项式的一个项。
2)次数最高项的次数叫做这个多项式的次数。
通过观察我们知道单项式和多项式都是代数式.单项式和多项式统称整式5.讨论总结:(1)单项式的特点;(2)单项式的次数如何确定,系数呢?(3)单项式与多项式的联系以及重要区别.二例题分析:例1、列代数式为提高电能利用效率,供电公司用“峰谷分时电价”引导居民合理安排用电时间,某地每天8:00到21:00为用电高峰段(简称“峰时”),峰时电价为0.55元/千瓦时;21:00到次日8:00为用电低谷时段(简称“谷时”),谷时电价为0.35/千瓦时.该地某用户上月峰时用电a千瓦时,谷时用电b千瓦时,该用户上月的峰时电费、谷时电费和总电费分别为多少?例2、列代数式如右图,要在长方形和环形地块中铺设草坪,长方形的长、宽分别为a 米、b 米,环形的外圆、内圆的半径分别为R 米、r米,求共需草皮的面积.例3.填空(1)苹果a元/kg,橘子b元/kg,买5kg苹果、8kg橘子应付元.(2)小明每步走a m,小亮每步走b m,小明、小亮从小桥的两端相向而行,小明走5步、小亮走6步两人相遇,小桥长 m.(3)a 个五边形、b个六边形共有条边.与同学交流列出的代数式,你有什么发现?代数式2(x+y)可以表示不同的实际意义,试举例说明.三、展示与交流1.用文字叙述下列代数式的意义。
苏科版七年级上册数学3-2代数式2导学案练习题

七年级数学学科第三章第2节3.2《代数式2》学讲预案一、自主先学1.在代数式)2、2x+(2yx+、y2y(mn中选择适当的填空:x+、2(yx+、2)mn、2)(1)x与y和的2倍是______________________;(2)x的2倍与y的和是____________________;(3)x、y的平方和是_______________________;(4)x、y和的平方是_______________________;(5)m与n的平方的积是____________________;(6)m与n积的平方是_______________________.二、合作助学2. 为提高电能利用效率,供电公司用“峰谷分时电价”引导居民合理安排用电时间.某地每天8:00到21:00为用电高峰段(简称“峰时”),峰时电价为0.55元/千瓦时;21:00时到次日8:00为用电低谷段(简称“谷时”),谷时电价为0.35元/千瓦时.该地某用户上月峰时用电a千瓦时,谷时用电b千瓦时,该用户上月的峰时电费、谷时电费和总电费分别为多少?3. 单项式定义:像0.9a ,0.8b ,2a ,2a 2,15×1.5%m 等都是数与字母的积,这样的代数式叫单项式.单独一个数或一个字母也是单项式.单项式中的数字因数叫做这个单项式的系数.单项式中所有字母的指数的和叫做它的次数. 如(1)50s的系数是________,次数是________; (2)abc 的系数是________,次数是________;(3) 212r 的系数是________,次数是________.4. 如图,要在长方形和环形地块中铺设草坪,长方形的长、 宽分别为a m 、b m ,环形的外圆、内圆的半径分别为Rm ,rm , 求共需草皮的面积.5. 多项式的定义:几个单项式的和叫做多项式.图3-4多项式中,每个单项式叫做多项式的项; 多项式里含有几项,就把这个多项式叫做几项式,其中次数最高项的次数叫做这个多项 式的次数,不含字母的项叫做常数项. 单项式和多项式统称整式(1)多项式2-n 是____项式,它的次数是____,其中2-是____项; (2)多项式22r R ab ππ-+是____项式,它的次数是____. 三、拓展导学 6. 填空:(1)苹果每千克a 元,橘子每千克b 元,买5千克苹果、6千克橘子应付_________元;(2)小明每步长a m ,小亮每步长b m ,小明、小亮从小桥的两端相向而行,小明走5步、小亮走6步两人相遇,小桥长___________m ;(3)a 个五边形、b 个六边形共有____________条边. 与同学交流列出的代数式,你有什么发现?7. 代数式)(2y x +可以表示不同的实际意义,试举例说明.8. 代数式-32ab 的系数是 ,x π-的系数是 .9. 单项式123-n y x 是关于x 、y 的五次单项式,则n = . 四、检测促学10. 若n 表示任意一个整数,试用含n 的代数式表示任意一个偶数、任意一个奇数.11. 用代数式表示:(1)比a 的2倍大5的数是___________; (2)与b 的和是100的数是___________;(3)自来水每立方米m 元,电每千瓦时n 元,小丽家本月用水8立方米、用电100千瓦时,应交水电费_____________元; (4)小明沿着一条直路跑3 km 后,再以4 km/h 的速度继续往前走了t h ,小明离起点_________km ; (5)一个两位数的个位数字是a ,十位数字是b ,这个两位数是________; (6)某商场推出7.5折优惠销售活动,现售价为y 元的商品的原价是__________元. 12. 说出下列多项式的次数和各项的系数:y x -,2332b a b a +-, ,3223b a +.五、反思悟学13. 解释代数式40-2n 的意义.专项训练二 概率初步一、选择题1.(徐州中考)下列事件中的不可能事件是( )A .通常加热到100℃时,水沸腾B .抛掷2枚正方体骰子,都是6点朝上32yx -C.经过有交通信号灯的路口,遇到红灯D.任意画一个三角形,其内角和是360°2.小张抛一枚质地均匀的硬币,出现正面朝上的可能性是( )A.25% B.50% C.75% D.85%3.(2016·贵阳中考)2016年5月,为保证“中国大数据产业峰会及中国电子商务创新发展峰会”在贵阳顺利召开,组委会决定从“神州专车”中抽调200辆车作为服务用车,其中帕萨特60辆、狮跑40辆、君越80辆、迈腾20辆,现随机从这200辆车中抽取1辆作为开幕式用车,则抽中帕萨特的概率是( )A.110B.15C.310D.254.(金华中考)小明和小华参加社会实践活动,随机选择“打扫社区卫生”和“参加社会调查”其中一项,那么两人同时选择“参加社会调查”的概率为( )A.14B.13C.12D.345.在一个不透明的袋中装着3个红球和1个黄球,它们只有颜色上的区别,随机从袋中摸出2个小球,两球恰好是一个黄球和一个红球的概率为( )A.12B.13C.14D.166.现有两枚质地均匀的正方体骰子,每枚骰子的六个面上都分别标有数字1、2、3、4、5、6.同时投掷这两枚骰子,以朝上一面所标的数字为掷得的结果,那么所得结果之和为9的概率是( )A.13B.16C.19D.1127.分别转动图中两个转盘一次,当转盘停止转动时,两个指针分别落在某个数所表示的区域,则两个数的和是2的倍数或3的倍数的概率等于( )A.316B.38C.58D.1316第7题图第8题图8.(2016·呼和浩特中考)如图,△ABC是一块绿化带,将阴影部分修建为花圃,已知AB=15,AC=9,BC=12,阴影部分是△ABC的内切圆,一只自由飞翔的小鸟将随机落在这块绿化带上,则小鸟落在花圃上的概率为( )A.16B.π6C.π8D.π5二、填空题9.已知四个点的坐标分别是(-1,1),(2,2),⎝ ⎛⎭⎪⎫23,32,⎝ ⎛⎭⎪⎫-5,-15,从中随机选取一个点,在反比例函数y =1x 图象上的概率是________.10.(黄石中考)如图所示,一只蚂蚁从A 点出发到D ,E ,F 处寻觅食物.假定蚂蚁在每个岔路口都可能随机选择一条向左下或右下的路径(比如A 岔路口可以向左下到达B 处,也可以向右下到达C 处,其中A ,B ,C 都是岔路口).那么,蚂蚁从A 出发到达E 处的概率是________.11.(贵阳中考)现有50张大小、质地及背面图案均相同的《西游记》任务卡片,正面朝下放置在桌面上,从中随机抽取一张并记下卡片正面所绘人物的名字后原样放回,洗匀后再抽.通过多次试验后,发现抽到绘有孙悟空这个人物卡片的频率约为0.3.估计这些卡片中绘有孙悟空这个人物的卡片张数约为________.12.(荆门中考)荆楚学校为了了解九年级学生“一分钟内跳绳次数”的情况,随机选取了3名女生和2名男生,则从这5名学生中,选取2名同时跳绳,恰好选中一男一女的概率是________.13.(重庆中考)点P 的坐标是(a ,b ),从-2,-1,0,1,2这五个数中任取一个数作为a 的值,再从余下的四个数中任取一个数作为b 的值,则点P (a ,b )在平面直角坐标系中第二象限内的概率是________.14.★从-1,1,2这三个数字中,随机抽取一个数记为a ,那么,使关于x 的一次函数y =2x +a 的图象与x 轴、y 轴围成的三角形的面积为14,且使关于x 的不等式组⎩⎪⎨⎪⎧x +2≤a ,1-x ≤2a 有解的概率为________.三、解答题15.(南昌中考)在一个不透明的袋子中装有仅颜色不同的10个小球,其中红球4个,黑球6个.(1)先从袋子中取出m (m >1)个红球,再从袋子中随机摸出1个球,将“摸出黑球”记为事件A ,请完成下列表格:(2)先从袋子中取出m 个红球,再放入m 个一样的黑球并摇匀,随机摸出1个黑球的概率等于45,求m 的值.16.(菏泽中考)锐锐参加我市电视台组织的“牡丹杯”智力竞答节目,答对最后两道单选题就顺利通关,第一道单选题有3个选项,第二道单选题有4个选项,这两道题锐锐都不会,不过锐锐还有两个“求助”可以用(使用“求助”一次可以让主持人去掉其中一题的一个错误选项).(1)如果锐锐两次“求助”都在第一道题中使用,那么锐锐通关的概率是________;(2)如果锐锐两次“求助”都在第二道题中使用,那么锐锐通关的概率是________;(3)如果锐锐将每道题各用一次“求助”,请用树状图或者列表来分析他顺利通关的概率.17.(丹东中考)甲、乙两人进行摸牌游戏.现有三张形状大小完全相同的牌,正面分别标有数字2,3,5.将三张牌背面朝上,洗匀后放在桌子上.(1)甲从中随机抽取一张牌,记录数字后放回洗匀,乙再随机抽取一张.请用列表法或画树状图的方法,求两人抽取相同数字的概率;(2)若两人抽取的数字之和为2的倍数,则甲获胜;若抽取的数字之和为5的倍数,则乙获胜.这个游戏公平吗?请用概率的知识加以解释.18.一只不透明的袋子中装有4个质地、大小均相同的小球,这些小球分别标有数字3,3,5,x,甲、乙两人每次同时从袋中各随机摸出1个球,并计算摸出的这2个球上数字之和,记录后将小球放回袋中搅匀,进行重复实验.实验数据如下表:(1)如果实验继续进行下去,根据上表数据,出现“和为8”的频率稳定在它的概率附近,估计出现“和为8”的概率是________;(2)如果摸出的这两个小球上数字之和为9的概率是13,那么x的值可以取4吗?请用列表法或画树状图法说明理由;如果x的值不可以取4,请写出一个符合要求的x的值.参考答案与解析1.D 2.B 3.C 4.A 5.A 6.C 7.C8.B 解析:∵AB =15,BC =12,AC =9,∴AB 2=BC 2+AC 2,∴△ABC 为直角三角形,∴△ABC 的内切圆半径为12+9-152=3,∴S △ABC =12AC ·BC =12×12×9=54,S 圆=9π,∴小鸟落在花圃上的概率为9π54=π6. 9.12 10.12 11.15 12.35 13.15 14.1315.解:(1)4 2或3(2)根据题意得6+m 10=45,解得m =2,所以m 的值为2. 16.解:(1)14 解析:第一道肯定能对,第二道对的概率为14,所以锐锐通关的概率为14; (2)16 解析:锐锐两次“求助”都在第二道题中使用,则第一道题对的概率为13,第二道题对的概率为12,所以锐锐能通关的概率为12×13=16; (3)锐锐将每道题各用一次“求助”,分别用A ,B 表示剩下的第一道单选题的2个选项,a ,b ,c 表示剩下的第二道单选题的3个选项,树状图如图所示.共有6种等可能的结果,锐锐顺利通关的只有1种情况,∴锐锐顺利通关的概率为16.17.解:(1)所有可能出现的结果如下表,从表格可以看出,总共有9种结果,每种结果出现的可能性相同,其中两人抽取相同数字的结果有3种,所以两人抽取相同数字的概率为13; (2)不公平.从表格可以看出,两人抽取数字之和为2的倍数有5种,两人抽取数字之和为5的倍数有3种,所以甲获胜的概率为59,乙获胜的概率为13.∵59>13,∴甲获胜的概率大,游戏不公平.2 3 5 22 23 2 5 2 32 3 3 3 5 3 52 53 5 5 518.解:(1)0.332 12=16≠13,所以x不能取4;当x=6时,摸出的两个小球上数字之和为9的概率是13.(2)当x为4时,数字和为9的概率为。
《3.2 代数式(2)》优质导学案

代数式(2)(预习导案)班级____姓名____________学号______【学习目标】1.会求代数式的值,感受代数式求值可以理解为一个转换过程或某种算法;2.会利用代数式求值推断代数式所反映的规律;3.能解释代数式值的实际意义. 【预习导航】 一.探索1.完成课本83P 和84P 有关数值转换机的相关内容(做在课本上).2.完成84P 页的议一议(做在课本上).跟踪练习:在课本上完成教材85页知识技能2、3.3.自学下面的例题,学习解题格式. 请仿照左边例题的格式完成课本85p 页知识技能1.例:求21=x 时,代数式122+-x x 的值. 解:当21=x 时,原式=121)21(22+-⨯=121412+-⨯=1 跟踪练习:⑴当a=-4,b=12时,代数式:a 2-ab的值为_______. ⑵完成84P 页随堂练习2(填表做在课本上,其它的做在下面空白处).二.生成4.学校的气象活动小组为了弄清气温随着高度变化而变化的情况, 在学校附近的一个小山上实地测量了一下不同高度的气温,测得的结果如下表: ⑴写出气温T 与高度h 之间的关系式.⑵计算350m 高度气温.【反思小结】通过预习你学到了哪些新知识和新收获,还有哪些疑难问题代数式(2)(个性超市)班级____姓名____________学号______【基础过关】正答率1.n 个球队进行单循环比赛,总的比赛数用代数式表示:2)1(-n n ,现有18个球队参加比 赛,总的比赛场数是( ).A 、76 B 、80 C 、153 D 、1262.一个学生由于粗心,在计算35+a 的值时,误将“+”看成“-”,结果是80,则35+a 的值应是________.3.若21)(x ++|y-3|=0,则2x 2-y 3=__________.4.在1、2、3、4、5中,使得代数式(x-2)(x-3)(x-4)的值为零的有( ). A 、1个 B 、2个 C 、3个 D 、4个5.224221,2b ab a b a +-=-=时,求代数式当的值.(1)写出用时间t 表示剩余汽油量Q 的代数式. (2)当t=22时,求剩余汽油量的值.【拓展提升】得分7.(4分)一物体从一高处由静止开始落下,它落下的高度h 与时间t 有下面关系:⑴写出计算物体落下的高度h 与时间t 的公式;答:___________. ⑵当t=5秒时,物体落下多少米【反思梳理】从知识、方法两方面反思所学及疑难.。
3.2《代数式(2)》导学案

七年级数学导学案课题:§3.2代数式(2)班级 姓名 学号主备人:学习目标:1、了解单项式、单项式的系数、次数,多项式、多项式的项、次数,整式概念;2、能用代数式表示简单问题的数量关系;3、能解释一些简单代数式的实际背景或几何背景。
学习重点:对代数式意义的理解,准确表述单项式、多项式相关概念。
学习难点:叙述代数式的意义。
学习过程:一、自学指导:(一)知识回顾:1、像a -1、30a 、9b 、b+2c +2ac 等这样的式子都称为 ;注意:单独一个数或一个字母也是代数式。
2、书写代数式规范要求:①字母与字母、字母与数字的和(差),并且后面带单位时,要加括号; ②出现除法运算时,要写成分数形式;③字母与数字积时,数字写在字母的前面,之间的乘号可以用“·”,也可以省略不写;字母与字母积时,之间的乘号可以用“·”,也可以省略不写;数字与数字积时,之间的乘号不能省略。
3、填空:(1)小明买了单价分别为10元和12元的两种共8本,其中单价为10元的书a 本,应付 元;(2)比a 的21大5的数是 ; (3)一个两位数的个位数字是a ,十位数字是b ,这个两位数是 ;(二)阅读课本P70-71,完成下列问题:1、自学课本例1,理解解题过程;2、像0.55a 、0.35b 、0.15m 、0.8a 2等都是数与字母的积,这样代数式叫做 ;注意:单独一个数或一个字母也是 ;3、单项式中的 叫做单项式的系数;单项式中所有 的指数和叫做单项式的次数;4、自学课本例2,理解解题过程;5、几个单项式的和叫做 。
多项式中,每一个单项式叫做多项式的一个 ;多项式里含有几项,就把这个多项式叫做几项式,其中次数最高项的次数,叫做这个多项式的 ;不含字母的项叫做 。
4、单项式和多项式统称 。
二、合作探究:1、如果—mxy |n –1 |是关于x 、y 的一个单项式,且系数是2,次数是3,则m= ,n= ;2、如果3a 3b -4ab k +25是五次多项式,那么k = ;3、完成下列填空:(1)苹果每千克a 元,橘子每千克b 元,买5千克苹果、6千克橘子,应付 元;(2)小明每步长a m ,小亮每步长b m ,小明、小亮从小桥的两端相向而行,小明5步、小亮6步两人相遇,小桥长 m ;(3)a 个五边形、b 个六边形共有 条边;4、从所列的代数式,你有咋样的发现?5、仿照上面的发现,用不同方式解释代数式2(x +y )所表示的实际意义。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
【学习目标】1.在代数式求值过程中,初步感受函数的对应思想;
2.感受字母取值的变化与代数式值的变化之间的联系,能利用代数式的值推断一些代数式所反映的规律。
预习学案
一、认真自学课本P83—P84,自主高效完成预习学案, 限时8分钟,对于疑问用红色笔做好标注
为了开展体育活动,容桂学校要添置一批篮球,每个班级配2个,学校另外留10个,学校有n 个班级,总共需要 个篮球 ;
思考:若班级数是18(即n =18),则篮球总数是:210_____________________n +==;若班级
数是56(即n =56),则篮球总数是:210_____________________n +==。
这说明n 取不同的值,代数式2 n +10的计算结果也不同。
探究学案
一、代数式求值的过程好比是一个工艺流程,当你从进料口放入原料(给定一个具体的数),经过事先设计好的工序(按运算顺序进行计算),最后就会得到所需的产品(代数式的值)
二、 填写下表,并观察下列两个代数式的值的变化情况:
(2) 估计一下,哪个代数式的值先超过20?先超过100?
三、完成课本P84,随堂练习第1,2题,做在课本上
训练学案
A组:1、当61
x y
==-
,时,代数式
1
(2)
3
x y
-+的值是( )
A.5
- B.4 C.
4
3
- D.
4
3
3、填表
B组、拓展提升
4、填写下表,并观察下列两个代数式的值的变化情况:
n 1 2 3 4 5 6 7 8
5
8+
-n
-
2
n
(1)
(2) 估计一下,哪个代数式的值小于—100?
本节课我的收获: . 还存在的疑惑: .
x 1 3 5 0.5
1
3
y0.5 2 2-2-3
23
x y
-
2
1
2
x y
-
()()
x y x y
+-。
