决战中考限时小卷(七)
2024届广东省茂名电白区七校联考中考冲刺卷语文试题含解析

2024届广东省茂名电白区七校联考中考冲刺卷语文试题注意事项:1.答卷前,考生务必将自己的姓名、准考证号、考场号和座位号填写在试题卷和答题卡上。
用2B铅笔将试卷类型(B)填涂在答题卡相应位置上。
将条形码粘贴在答题卡右上角"条形码粘贴处"。
2.作答选择题时,选出每小题答案后,用2B铅笔把答题卡上对应题目选项的答案信息点涂黑;如需改动,用橡皮擦干净后,再选涂其他答案。
答案不能答在试题卷上。
3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新答案;不准使用铅笔和涂改液。
不按以上要求作答无效。
4.考生必须保证答题卡的整洁。
考试结束后,请将本试卷和答题卡一并交回。
一、积累1.选出下列病句修改正确的一项。
A.这篇小说取材于真人真事,表现了当代大学生自立、自强的形象,给人以启示。
修改:将“表现”改为“体现”。
B.一个人之所以能够成为工匠的原因,就在于对产品品质的追求只有进行时,没有完成时。
修改:去掉“的原因”。
C.过去的一年,有利于工匠们诞生和成长的法律、制度等配套措施正在不断完善与健全。
修改:将“措施”改为“举措”。
D.市有关部门联合检查组发现在例行检查时,个别网吧接纳了未成年人。
修改:在“未成年人”后加“的现象”。
2.下列句子中加点成语使用恰当....的一项是()A.知识愈浅薄的人愈是侃侃而谈....,知识渊博的人则往往出言谨慎。
B.这两首诗有异曲同工....之妙,语言平白如话,情感直率奔放。
C.他的作文向来是文不加点....,不知该在什么地方断句,常常给人不知所云的感觉。
D.三年来,我们跟语文老师相处融洽,相敬如宾....,留下了许多美好的回忆。
3.下列各句中,没有语病的一项是()A.保持为政清廉,是关系到党和政府能否取得广大群众信任的重大问题。
B.从陈部长的讲话中,使我们明白办好人民满意的教育是十九大对教育工作的明确要求。
2024年中考语文考前押题密卷(天津卷)

2024年中考考前押题密卷(天津卷)语文(考试时间:150分钟试卷满分:120分)注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答第Ⅰ卷时,选出每小题答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
写在本试卷上无效。
3.回答第Ⅱ卷时,将答案写在答题卡上。
写在本试卷上无效。
4.考试结束后,将本试卷和答题卡一并交回。
第Ⅰ卷一、(本大题共11小题,共29分。
1~4小题,每题2分;5~11小题,每题3分)(一)积累与运用1.下面各组词语中加点字注音,完全正确..的一项是()A.荫.蔽(yīn)争执.(zhí)惩.戒(chēng)怪诞.不经(dàn)B.唠.叨(láo)秀颀.(qí)毋.宁(wú)摩肩接踵.(zhǒng)C.畸.形(qí)默契.(qì)两栖.(qī)鲜.为人知(xiǎn)D.龟.裂(jūn)修葺.(qì)笼.统(lóng)忧心忡.忡(chōng)2.依次填入下面一段文字横线处的词语,最恰当的一项是()所谓书卷气,是一种饱读诗书后形成的气质。
书卷气来自读书,在幽幽书香的之下,浊俗可以变为清雅,奢华可以变为淡泊,狭隘可以变为开阔,偏激可以变为。
捧起书来吧,你会发现里面的风景美不胜收!A.高雅熏陶平静B.高端陶冶平和C.高雅熏陶平和D.高端陶冶平静3.依次填入下面语段中方框内的标点符号,最恰当的一项是()奋力拼搏方能实现可贵的自我超越。
这种超越,是一种不惧挑战的勇毅,可谓“越是艰险越向前”;是一种战胜自我的奋起,可谓“不用扬鞭自奋蹄”;是一种不甘平庸的行进,可谓“苟日新,日同新,又日新”□马伟明坚持自主创新,带领团队破解科技难题、取得重大成果□景海鹏勇于自我加压,战胜生理心理的极限考验,书写□三度飞天□的传奇;苏炳添无惧伤痛,焕发精神与斗志,终在东京奥运会男子100米比赛中“飞”入决赛。
2022最新中考语文模拟卷及答案(七)

一、积累(20分)班级开展以“了解北京冬奥会,振奋民族精神”为主题开展综合性学习活动,请你完成以下任务。
【搜集冬奥会资料】“冬奥冰雪花丝如意”采用“燕京八绝”之一的花丝镶()qiàn技艺制作而成,其造型创意源于中国传统吉祥饰物如意,以北京冬奥会竞赛场馆“雪如意”为参考,如意头部边缘有22颗宝石。
既突显了非遗技艺的无穷()mèi力,又表现了中国如意文化的。
1、根据拼音写出汉字。
(2分)2、填入上文横线处的词语。
(2分)A内涵 B内含【吟唱冬奥会歌曲】《雪龙吟》是北京2022年冬奥会倒计时10天助力歌曲,由张杰演唱,二水作词,包胡尔查作曲,发行于2022年1月25日。
“我一声龙啸凌云志,热血燃冬扶摇起,看长城内外这天地,山河云开笑容里;我一声龙啸跨东西,踏雪而来创奇迹,来双奥之城感动你,神州铿锵亿万心;。
”我一声龙啸震天地,翩翩少年展雄姿,入九州大地威八方,祖国昌盛万民贺。
3、阅读上面语段,模仿《雪龙吟》示例,横线上补写一段振奋民族精神的内容。
(3分)【感受冬奥会文化】我国通过承办冬奥会,可以进一步振奋民族精神,宣传中华灿烂文明和优秀文化,展示大国实力和精神风貌,增强民族凝聚力和自豪感。
吟诵古诗文名篇,感受历代仁人志士的民族精神。
“商女不知亡国恨,_________,”表现了作者对国家命运的无比关怀和深切忧虑的情怀;“坐观垂钓者,_________,”是借此抒发自己的政治热情和希望;“先天下之忧而忧,_________,”是心忧天下的伟大抱负;“报君黄金台上意,_________,”引用典故写出将士誓死报效国家的决心。
“_________,化作春泥更护花。
”是作者对国家执著的忠诚。
“_________,西北望,射天狼”是作者希望能够承担卫国守边的重任。
4、将上面所引用名句填写完整。
(6分)【发扬冬奥会精神】新华社北京2月3日电(记者李典、岳冉冉)5日,北京冬奥会速度滑冰比赛将开赛。
专题七 动点在直角三角中的分类讨论问题 2020年中考数冲刺几何难点突破 动点问题(解析版)

2020年中考数冲刺几何难点突破动点问题专题七动点在直角三角中的分类讨论问题【专题说明】【精典例题】1、如图,在Rt△ABC中,△ACB=90°,△A=30°,点O为AB中点,点P为直线BC上的动点(不与点B、点C重合),连接OC、OP,将线段OP绕点P逆时针旋转60°,得到线段PQ,连接BQ.(1)如图△,当点P在线段BC上时,请直接写出线段BQ与CP的数量关系;(2)如图△,当点P在CB延长线上时,(1)中结论是否成立?若成立,请加以证明;若不成立,请说明理由;(3)如图△,当点P在BC延长线上时,若△BPO=45°,AC=6,请直接写出BQ的长.【答案】解:(1)CP =BQ; 【解法提示】如解图△,连接OQ ,图△由旋转可知,PQ =OP ,△OPQ =60°, △△POQ 是等边三角形, △OP =OQ ,△POQ =60°, 在Rt△ABC 中,O 是AB 中点, △OC =OA =OB ,△△BOC =2△A =60°=△POQ , △△COP =△BOQ ,在△COP 和△BOQ 中,⎩⎪⎨⎪⎧OC =OB △COP =△BOQ ,OP =OQ△△COP△△BOQ(SAS), △CP =BQ ; (2)成立,理由如下: 如解图△,连接OQ ,第3题解图△由旋转知PQ =OP ,△OPQ =60°,△△POQ 是等边三角形, △OP =OQ ,△POQ =60°, △在Rt△ABC 中,O 是AB 中点, △OC =OA =OB ,△△BOC =2△A =60°=△POQ ,△△COP =△BOQ , 在△COP 和△BOQ 中,⎩⎪⎨⎪⎧OC =OB △COP =△BOQ ,OP =OQ△△COP△△BOQ(SAS), △CP =BQ ; (3)BQ =6-22.【解法提示】在Rt△ABC 中,△A =30°,AC =6, △BC =AC·tanA =2,如解图△,过点O 作OH△BC 于点H ,第3题解图△△△OHB =90°=△BCA ,△OH△AC , △O 是AB 中点,△CH =12BC =22,OH =12AC =62, △△BPO =45°,△OHP =90°, △△BPO =△POH ,△PH =OH =62,-2mx-3mB(点A位于点B的左侧),与y轴交于点C(0,-3),点D在二次函数的图像上,CD//AB,联结AD.过点A 作射线AE交二次函数的图像于点E,AB平分△DAE.(1)用含m的式子表示a;(2)求证:ADAE为定值;(3)设该二次函数的图像的顶点为F.探索:在x轴的负半轴上是否存在点G,联结GF,以线段GF、AD、AE的长度为三边长的三角形是直角三角形?如果存在,只要找出一个满足要求的点G即可,并用含m 的代数式表示该点的横坐标;如果不存在,请说明理由.图1思路点拨1.不算不知道,一算真奇妙.通过二次函数解析式的变形,写出点A 、B 、F 的坐标后,点D 的坐标也可以写出来.点E 的纵坐标为定值是算出来的.2.在计算的过程中,第(1)题的结论21a m=及其变形21am =反复用到. 3.注意到点E 、D 、F 到x 轴的距离正好是一组常见的勾股数(5,3,4),因此过点F 作AD 的平行线与x 轴的交点,就是要求的点G . 满分解答(1)将C (0,-3)代入y =a (x 2-2mx -3m 2),得-3=-3am 2.因此21a m =. (2)由y =a (x 2-2mx -3m 2)=a (x +m )(x -3m )=a (x -m )2-4axm 2=a (x -m )2-4, 得A (-m , 0),B (3m , 0),F (m , -4),对称轴为直线x =m .所以点D 的坐标为(2m ,-3). 设点E 的坐标为(x , a (x +m )(x -3m )).如图2,过点D 、E 分别作x 轴的垂线,垂足分别为D ′、E ′. 由于△EAE ′=△DAD′,所以''''EE DD AE AD =.因此()(3)33a x m x m x m m +-=+. 所以am (x -3m )=1.结合21a m =,于是得到x =4m . 当x =4m 时,y =a (x +m )(x -3m )=5am 2=5.所以点E 的坐标为(4m , 5). 所以'3'5AD DD AE EE ==.图2 图33、如图1,抛物线2442y x x =--与x 轴交于A 、B 两点(点B 在点A 的右侧),与y 轴交于点C ,连结BC ,以BC 为一边,点O 为对称中心作菱形BDEC ,点P 是x 轴上的一个动点,设点P 的坐标为(m , 0),过点P 作x 轴的垂线l 交抛物线于点Q .(1)求点A 、B 、C 的坐标;(2)当点P 在线段OB 上运动时,直线l 分别交BD 、BC 于点M 、N .试探究m 为何值时,四边形CQMD 是平行四边形,此时,请判断四边形CQBM 的形状,并说明理由;(3)当点P 在线段EB 上运动时,是否存在点Q ,使△BDQ 为直角三角形,若存在,请直接写出点Q 的坐标;若不存在,请说明理由.图1思路点拨1.第(2)题先用含m的式子表示线段MQ的长,再根据MQ=DC列方程.2.第(2)题要判断四边形CQBM的形状,最直接的方法就是根据求得的m的值画一个准确的示意图,先得到结论.3.第(3)题△BDQ为直角三角形要分两种情况求解,一般过直角顶点作坐标轴的垂线可以构造相似三角形.满分解答(1)由21314(2)(8)424y x x x x=--=+-,得A(-2,0),B(8,0),C(0,-4).(2)直线DB的解析式为142y x=-+.由点P的坐标为(m, 0),可得1(,4)2M m m--,213(,4)42Q m m m--.所以MQ=221131(4)(4)82424m m m m m-+---=-++.当MQ=DC=8时,四边形CQMD是平行四边形.解方程21884m m-++=,得m=4,或m=0(舍去).此时点P是OB的中点,N是BC的中点,N(4,-2),Q(4,-6).所以MN=NQ=4.所以BC与MQ互相平分.所以四边形CQBM是平行四边形.图2 图3(3)存在两个符合题意的点Q ,分别是(-2,0),(6,-4). 考点伸展第(3)题可以这样解:设点Q 的坐标为1(,(2)(8))4x x x +-.△如图3,当△DBQ =90°时, 12QG BH GB HD ==.所以1(2)(8)1482x x x -+-=-.解得x =6.此时Q (6,-4).△如图4,当△BDQ =90°时, 2QG DH GD HB ==.所以14(2)(8)42x x x-+-=-. 解得x =-2.此时Q (-2,0).图3 图44、如图1,抛物线233384y x x =--+与x 轴交于A 、B 两点(点A 在点B 的左侧),与y 轴交于点C .(1)求点A 、B 的坐标;(2)设D 为已知抛物线的对称轴上的任意一点,当△ACD 的面积等于△ACB 的面积时,求点D 的坐标; (3)若直线l 过点E(4, 0),M 为直线l 上的动点,当以A 、B 、M 为顶点所作的直角三角形有且只有三个时,求直线l 的解析式.图1图2 图3(3)过点A 、B 分别作x 轴的垂线,这两条垂线与直线l 总是有交点的,即2个点M .以AB 为直径的△G 如果与直线l 相交,那么就有2个点M ;如果圆与直线l 相切,就只有1个点M 了. 联结GM ,那么GM △l .在R t △EGM 中,GM =3,GE =5,所以EM =4. 在R t △EM 1A 中,AE =8,113tan 4M A M EA AE ∠==,所以M 1A =6. 所以点M 1的坐标为(-4, 6),过M 1、E 的直线l 为334y x =-+.根据对称性,直线l 还可以是334y x =+. 5、在平面直角坐标系中,反比例函数与二次函数y =k (x 2+x -1)的图象交于点A (1,k )和点B(-1,-k ). (1)当k =-2时,求反比例函数的解析式;(2)要使反比例函数与二次函数都是y 随x 增大而增大,求k 应满足的条件以及x 的取值范围; (3)设二次函数的图象的顶点为Q ,当△ABQ 是以AB 为斜边的直角三角形时,求k 的值.(1)因为反比例函数的图象过点A (1,k ),所以反比例函数的解析式是k y x=. 当k =-2时,反比例函数的解析式是2y x=-. (2)在反比例函数k y x=中,如果y 随x 增大而增大,那么k <0. 当k <0时,抛物线的开口向下,在对称轴左侧,y 随x 增大而增大.抛物线y =k (x 2+x +1)=215()24k x k +-的对称轴是直线12x =-. 所以当k <0且12x <-时,反比例函数与二次函数都是y 随x 增大而增大. (3)抛物线的顶点Q 的坐标是15(,)24k --,A 、B 关于原点O 中心对称, 当OQ =OA =OB 时,△ABQ 是以AB 为直径的直角三角形. 由OQ 2=OA 2,得222215()()124k k -+-=+. 解得1233k =(如图2),2233k =-(如图3).图2 图36、在平面直角坐标系xOy 中,抛物线22153244m m y x x m m -=-++-+与x 轴的交点分别为原点O 和点A ,点B (2,n )在这条抛物线上.(1)求点B 的坐标;(2)点P 在线段OA 上,从点O 出发向点A 运动,过点P 作x 轴的垂线,与直线OB 交于点E ,延长PE 到点D ,使得ED =PE ,以PD 为斜边,在PD 右侧作等腰直角三角形PCD (当点P 运动时,点C 、D 也随之运动).△当等腰直角三角形PCD 的顶点C 落在此抛物线上时,求OP 的长;图1△若点P从点O出发向点A作匀速运动,速度为每秒1个单位,同时线段OA上另一个点Q从点A出发向点O作匀速运动,速度为每秒2个单位(当点Q到达点O时停止运动,点P也停止运动).过Q作x 轴的垂线,与直线AB交于点F,延长QF到点M,使得FM=QF,以QM为斜边,在QM的左侧作等腰直角三角形QMN(当点Q运动时,点M、N也随之运动).若点P运动到t秒时,两个等腰直角三角形分别有一条边恰好落在同一条直线上,求此刻t的值.图1图1 图2 图3考点伸展在本题情境下,如果以PD为直径的圆E与以QM为直径的圆F相切,求t的值.如图5,当P、Q重合时,两圆内切,103t=.如图6,当两圆外切时,30202t=-.图4 图5 图6。
中考历史7.主题七 解放战争
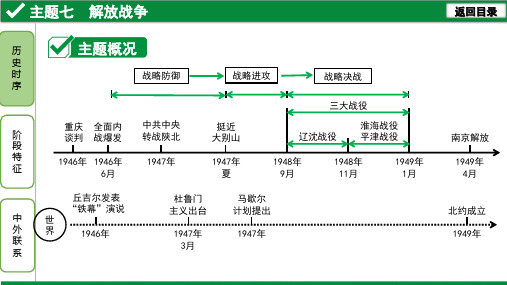
[2017年副题20(1)题4分]阅读下列材料,回答问题。 材料一
返回目录
(1)材料一图A革命斗争对象是什么?分析图A到图B革命斗争对象发生变化的原因。 指出图C所反映的事件对中国历史发展产生的重大影响。(4分) 对象:国民党反动派。(1分)原因:随着日本侵华加剧,中日民族矛盾上升为社会 主要矛盾;1937年日本全面侵华。(1分)影响:渡江战役的胜利,宣告国民党政权 覆灭;为中华人民共和国的成立打下了坚实的基础。(2分)
返回目录
考点 2 中共中央转战陕北 刘邓大军挺进大别山 三大战役 南京解放
2011版课标:了解中共中央转战陕北和刘邓大军挺进大别山的史实;知道辽沈、淮 海、平津三大战役和南京解放。
要素学考点
一、中共中央转战陕北
时间 1947年 (1)1946年6月,国民党军围攻中原解放区,发动全面内战 (2)解放区军民粉碎了国民党军的全面进攻
主题七 解放战争
返回目录
历
主题概况
史
时
战略防御
战略进攻
战略决战
序
三大战役
重庆 全面内 中共中央
挺近
阶
谈判 战爆发 转战陕北
大别山
段
辽沈战役
淮海战役 平津战役
南京解放
特 征
1946年 1946年 6月
1947年
1947年 夏
1948年 9月
1948年 11月
1949年 1月
1949年 4月
丘吉尔发表
“铁幕”演说
中世
外界 联
1946年
系
杜鲁门 主义出台
1947年 3月
马歇尔 计划提出
1947年
北约成立 1949年
(最新)2020版中考历史总复习 主题七 解放战争(备用题库)模拟试题

主题七解放战争题组一内战爆发1.(2018湖南衡阳,9,2分)解放战争时期,毛泽东非常形象地说:“蒋介石两个拳头(指陕北和山东)这么一伸,他的胸膛就露出来了。
所以,我们的战略就是要把这两个拳头紧紧地拖住,对准他的胸膛插上一刀。
”这里“插上一刀”是指( )A.千里挺进大别山B.辽沈战役C.中共中央转战陕北D.孟良崮战役答案 A 题干材料中“两个拳头(指陕北和山东)这么一伸”指的是蒋介石的重点进攻,“对准他的胸膛插上一刀”指的是刘邓大军千里挺进大别山,直接威胁到国民党的统治中心南京和武汉,故A项符合题意。
2.(2018新疆,2,2分)五四运动是新民主主义革命开始的标志。
下列发生在新民主主义革命时期的事件,按照时间先后排序正确的是( )①北伐战争②西安事变③黄埔军校建立④重庆谈判A.①②③④B.③①②④C.②③④①D.②①③④答案 B 本题主要考查对历史事件发生时间的掌握情况。
①北伐战争发生在1926—1928年,②西安事变发生在1936年12月12日,③黄埔军校建立是在1924年,④重庆谈判是在1945年。
按照时间顺序排序应该是③①②④,B项正确。
3.(2018山西,8,2分)“犹如一把钢刀,插入敌人心脏,严重威胁了国民党统治中心南京和湖北重镇武汉。
同时又能吸引国民党大量军队来援,减轻对华北解放区的压力。
”材料描述的军事行动是( )A.平型关大捷B.百团大战C.挺进大别山D.渡江战役答案 C 1947年夏刘伯承、邓小平率领晋冀鲁豫解放军主力挺进大别山,开辟了大别山根据地,严重威胁了国民党统治中心南京和湖北重镇武汉,揭开了人民解放军战略进攻的序幕。
故选C项。
A、B两项属于抗日战争时期八路军发动的主要战役,D项渡江战役直接推翻了南京国民政府,均与题目表述不符。
4.(2017河南,7,1分)刘邓大军以锐不可当之势,先后跨越重重障碍,经过20多天的艰苦跋涉和激烈战斗,完成了一次无后方依托,以长驱直入插进敌人战略纵深为特点的特殊形式的进攻行动。
语文(北京卷)(参考答案)

2023年中考语文第三次模拟考试(北京卷)语文·参考答案一、(共12分)1.(2分)【答案】B2.(2分)【答案】C3.(2分)【答案】示例:①跳动在二胡凄美的弓弦上②擂响在锣鼓铿锵的声音里4.(2分)【答案】A:④ B:②5.(2分)【答案】将“传承、保护并了解”改为“了解、保护并传承”。
6.(2分)【答案】难忘的镜头精彩的瞬间二、(共17分)(一)默写。
(共4分)【答案】7.波撼岳阳城 8.凭君传语报平安 9.①但愿人长久②千里共婵娟(二)(共6分)10.(2分)【答案】“三年羁旅客”写时间之长,漂泊异乡(或”抗击清兵,远走异乡”),“今日又南冠”说明现在已是第二次被捕。
(意思对即可)11.(4分)【答案】人去阴间,是为了为了“招旧部”“斩阎罗”,以此表达同敌人斗争到底的决心(或不屈不挠的战斗意志”);魂归人间,是为了看战旗在空中飘扬,以此表达壮志未酬的悲愤(或“表达对山河故乡的无限留恋”,或“表达对胜利的渴盼”)。
(三)(共7分)12.(3分)【答案】(1)“与”同“举”,推举;(2)女子出嫁;(3)由于,因为13.(2分)【答案】所以,君主的忧患,不是来自外面,而是常在自身。
14.(2分)【答案】D三、(5分)15.(3分)【答案】保尔是为了救护朱赫来,与匪兵搏斗。
简·爱则是长久遭受表哥的欺负,不让在阁楼看书,简爱·奋起反抗。
体现了他们的反抗精神。
16.(2分)【答案】鲁智深大闹野猪林,反抗是封建社会的黑暗腐朽、阶级制度的罪恶;孙悟空大闹天宫反抗权威、追求自由平。
他们都体现了对现实社会和命运不公的反抗,对生命的热爱及坚强不屈的精神,催人奋进。
四、(共26分)(一)(共9分)17.(2分)【答案】B18.(3分)【答案】示例1:选择B。
用问句的形式引人兴趣;同时给出了关键词“小伞卡”力求给人印象深刻;“也”字暗示他人已办,从而起到推广效果。
示例2:选择C。
指出了家电保修的核心要素,令人一目了然;用“一天不到1块钱”,让人觉得便宜,从而吸引人购买“小伞卡”。
2019年历史中考材料分析题专项训练七【两次世界大战及世界格局的演变】附答案解析

12019年历史中考材料分析题专项训练七【两次世界大战及世界格局的演变】1. 只有牢记战争,才能珍视和平。
阅读下列材料,回答问题。
只有牢记战争,才能珍视和平。
阅读下列材料,回答问题。
材料一“捷克斯洛伐克是在一战后,由战胜国一手制造出来的国家,这块土地应该纳入德意志第三帝国的疆土。
它一天尚存,一天就是帝国东部的威胁。
”——希特勒”——希特勒材料二“今天是我们大家最感到痛心的日子,但是没有一个人会比我更为痛心。
在我担任公职的一生中,我所信仰的一切,我所为之工作的一切,都已经毁于一旦。
”——张伯伦1939年9月3日在英国下院发表的演讲日在英国下院发表的演讲材料三1942年,美国总统罗斯福对他的儿子说:“如果没有中国,假如中国被打垮了,你想一想会有多少日本兵可以因此调到其他地方,他们可以占领澳门、打下印度……”日本兵可以因此调到其他地方,他们可以占领澳门、打下印度……”(1)根据材料一并结合所学,指出希特勒是怎样实现把捷克斯洛伐克纳入德意志疆土的美梦中的?这一事件产生了什么影响?事件产生了什么影响?(2)根据材料二并结合所学,指出张伯伦信仰的一切因为哪一事件毁于一旦?张伯伦所信仰的政策是什么?么?(3)根据材料三,指出罗斯福的话反映了中国的抗日战争和世界反法西斯战争有什么关系?结合所学知识,说说中国抗战胜利的因素有哪些?识,说说中国抗战胜利的因素有哪些?2. 当今世界,既充满希望又遍布危机。
回眸两次世界大战给人类带来了深刻的历史教训。
阅读下列材料,回答问题。
回答问题。
材料一由于帝国主义国家之间政治经济发展的不平衡,后起的帝国主义国家要求重新分割世界,与老牌帝2 国主义国家展开了激烈的争夺。
争夺霸权的结果,形成了两大敌对的帝国主义侵略集团,第一次世界大战一触即发。
——摘自张瑞德《第一次世界大战》一触即发。
——摘自张瑞德《第一次世界大战》材料二材料三英国首相丘吉尔在1940年对英国人民说:我们将战斗到底……我们绝不投降。
决战2020年中考数学压轴题综合提升训练:《四边形》(含答案)

决战2020中考数学压轴题综合提升训练:《四边形》1.如图①,在矩形ABCD中,已知BC=8cm,点G为BC边上一点,满足BG=AB=6cm,动点E以1cm/s的速度沿线段BG从点B移动到点G,连接AE,作EF⊥AE,交线段CD于点F.设点E移动的时间为t(s),CF的长度为y(cm),y与t的函数关系如图②所示.(1)图①中,CG= 2 cm,图②中,m= 2 ;(2)点F能否为线段CD的中点?若可能,求出此时t的值,若不可能,请说明理由;(3)在图①中,连接AF,AG,设AG与EF交于点H,若AG平分△AEF的面积,求此时t的值.解:(1)∵BC=8cm,BG=AB=6cm,∴CG=2cm,∵EF⊥AE,∴∠AEB+∠FEC=90°,且∠AEB+∠BAE=90°,∴∠BAE=∠FEC,且∠B=∠C=90°,∴△ABE∽△ECF,∴,∵t=6,∴BE=6cm,CE=2cm,∴∴CF=2cm,∴m=2,故答案为:2,2;(2)若点F是CD中点,∴CF=DF=3cm,∵△ABE∽△ECF,∴,∴∴EC2﹣8EC+18=0∵△=64﹣72=﹣8<0,∴点F不可能是CD中点;(3)如图①,过点H作HM⊥BC于点M,∵∠C=90°,HM⊥BC,∴HM∥CD,∴△EHM∽△EFC,∴∵AG平分△AEF的面积,∴EH=FH,∴EM=MC,∵BE=t,EC=8﹣t,∴EM=CM=4﹣t,∴MG=CM﹣CG=2﹣,∵,∴∴CF=∵EM=MC,EH=FH,∴MH=CF=∵AB=BG=6,∴∠AGB=45°,且HM⊥BC,∴∠HGM=∠GHM=45°,∴HM=GM,∴=2﹣,∴t=2或t=12,且t≤6,∴t=2.2.问题提出:(1)如图1,△ABC的边BC在直线n上,过顶点A作直线m∥n,在直线m上任取一点D,连接BD、CD,则△ABC的面积=△DBC的面积.问题探究:(2)如图2,在菱形ABCD和菱形BGFE中,BG=6,∠A=60°,求△DGE的面积;问题解决:(3)如图3,在矩形ABCD中,AB=12,BC=10,在矩形ABCD内(也可以在边上)存在一点P,使得△ABP的面积等于矩形ABCD的面积的,求△ABP周长的最小值.解:问题提出:(1)∵两条平行线间的距离一定,∴△ABC与△DBC同底等高,即△ABC的面积=△DBC的面积,故答案为:=;问题探究:(2)如图2,连接BD,∵四边形ABCD,四边形BGFE是菱形,∴AD∥BC,BC∥EF,AD=AB,BG=BE,∴∠A=∠CBE=60°,∴△ADB是等边三角形,△BGE是等边三角形,∴∠ABD=∠GBE=60°,∴BD∥GE,∴S△DGE=S△BGE=BG2=9;(3)如图3,过点P作PE∥AB,交AD于点E,∵△ABP的面积等于矩形ABCD的面积的,∴×12×AE=×12×10∴AE=8,作点A关于PE的对称点A',连接A'B交PE于点P,此时△ABP周长最小,∴A'E=AE=8,∴AA'=16,∴A'B===20,∴△ABP周长的最小值=AP+AB+PB=A'P+PB+AB=20+12=32.3.(1)方法感悟:如图①,在正方形ABCD中,点E、F分别为DC、BC边上的点,且满足∠EAF=45°,连接EF.将△ADE绕点A顺时针旋转90°得到△ABG,易证△GAF≌△EAF,从而得到结论:DE+BF=EF.根据这个结论,若CD=6,DE=2,求EF的长.(2)方法迁移:如图②,若在四边形ABCD中,AB=AD,∠B+∠D=180°,E、F分别是BC、CD上的点,且∠EAF=∠BAD,试猜想DE,BF,EF之间有何数量关系,证明你的结论.(3)问题拓展:如图③,在四边形ABCD中,AB=AD,∠B+∠ADC=180°,E、F 分别是边BC、CD延长线上的点,且∠EAF=∠BAD,试探究线段EF、BE、FD之间的数量关系,请直接写出你的猜想(不必说明理由).解:(1)方法感悟:∵将△ADE绕点A顺时针旋转90°得到△ABG,∴GB=DE=2,∵△GAF≌△EAF∴GF=EF,∵CD=6,DE=2∴CE=4,∵EF2=CF2+CE2,∴EF2=(8﹣EF)2+16,∴EF=5;(2)方法迁移:DE+BF=EF,理由如下:如图②,将△ADE绕点A顺时针旋转90°得到△ABH,由旋转可得,AH=AE,BH=DE,∠1=∠2,∠D=∠ABH,∵∠EAF=∠DAB,∴∠HAF=∠1+∠3=∠2+∠3=∠BAD,∴∠HAF=∠EAF,∵∠ABH+∠ABF=∠D+∠ABF=180°,∴点H、B、F三点共线,在△AEF和△AHF中,∴△AEF≌△AHF(SAS),∴EF=HF,∵HF=BH+BF,∴EF=DE+BF.(3)问题拓展:EF=BF﹣FD,理由如下:在BC上截取BH=DF,∵∠B+∠ADC=180°,∠ADC+∠ADF=180°,∴∠B=∠ADF,且AB=AD,BH=DF,∴△ABH≌△ADF(SAS)∴∠BAH=∠DAF,AH=AD,∵∠EAF=∠BAD,∴∠DAE+∠BAH=∠BAD,∴∠HAE=∠BAD=∠EAF,且AE=AE,AH=AD,∴△HAE≌△FAE(SAS)∴HE=EF,∴EF=HE=BE﹣BH=BE﹣DF.4.如图1,在▱ABCD中,AB=3cm,BC=5cm,AC⊥AB,△ACD沿AC的方向匀速平移得到△PNM,速度为1cm/s;同时,点Q从点C出发,沿CB方向匀速移动,速度为1cm/s,当△PNM停止平移时,点Q也停止移动,如图2,设移动时间为t(s)(0<<4),连结PQ,MQ,解答下列问题:(1)当t为何值时,PQ∥MN?(2)当t为何值时,∠CPQ=45°?(3)当t为何值时,PQ⊥MQ?解:(1)∵AB=3cm,BC=5cm,AC⊥AB,∴AC==4cm,∵MN∥AB,PQ∥MN,∴PQ∥AB,∴,∴,∴t=s(2)如图2,过点Q作QE⊥AC,则QE∥AB,∴,∴,∴CE=,QE=t,∵∠CPQ=45°,∴PE=QE=t,∴t+t+t=4,∴t=s(3)如图2,过点P作PF⊥BC于F点,过点M作MH⊥BC,交BC延长线于点H,∴四边形PMHF是矩形,∴PM=FH=5,∵∠A=∠PFC=90°,∠ACB=∠PCF,∴△ABC∽△FPC,∴,∴=∴PF=,CF=,∴QH=5﹣FQ=5﹣(CF﹣CQ)=,∵PQ⊥MQ,∴∠PQF+∠MQH=90°,且∠PQF+∠FPQ=90°,∴∠FPQ=∠MQH,且∠PFQ=∠H=90°,∴△PFQ∽△QHM,∴,∴∴t=s.5.问题背景:如图1,在正方形ABCD的内部,作∠DAE=∠ABF=∠BCG=∠CDH,根据三角形全等的条件,易得△DAE≌△ABF≌△BCG≌△CDH,从而得四边形EFGH是正方形.类比探究:如图2,在正△ABC的内部,作∠1=∠2=∠3,AD,BE,CF两两相交于D,E,F三点(D,E,F三点不重合).(1)△ABD,△BCE,△CAF是否全等?如果是,请选择其中一对进行证明;(2)△DEF是否为正三角形?请说明理由;(3)如图3,进一步探究发现,△ABD的三边存在一定的等量关系,设BD=a,AD=b,AB=c,请探索a,b,c满足的等量关系.(1)△ABD≌△BCE≌△CAF;理由如下:∵△ABC是正三角形,∴∠CAB=∠ABC=∠BCA=60°,AB=BC=AC,又∵∠1=∠2=∠3,∴∠ABD=∠BCE=∠CAF,在△ABD、△BCE和△CAF中,,∴△ABD≌△BCE≌△CAF(ASA);(2)△DEF是正三角形;理由如下:∵△ABD≌△BCE≌△CAF,∴∠ADB=∠BEC=∠CFA,∴∠FDE=∠DEF=∠EFD,∴△DEF是正三角形;(3)c2=a2+ab+b2.作AG⊥BD于G,如图所示:∵△DEF是正三角形,∴∠ADG=60°,在Rt△ADG中,DG=b,AG=b,在Rt△ABG中,c2=(a+b)2+(b)2,∴c2=a2+ab+b2.6.如图,在四边形ABCD中,AC是对角线,∠ABC=∠CDA=90°,BC=CD,延长BC交AD的延长线于点E.(1)求证:AB=AD;(2)若AE=BE+DE,求∠BAC的值;(3)过点E作ME∥AB,交AC的延长线于点M,过点M作MP⊥DC,交DC的延长线于点P,连接PB.设PB=a,点O是直线AE上的动点,当MO+PO的值最小时,点O与点E是否可能重合?若可能,请说明理由并求此时MO+PO的值(用含a的式子表示);若不可能,请说明理由.(1)证明:∵∠ABC=∠CDA=90°,∵BC=CD,AC=AC,∴Rt△ABC≌Rt△ADC(HL).∴AB=AD.(2)解:∵AE=BE+DE,又∵AE=AD+DE,∴AD=BE.∵AB=AD,∴AB=BE.∴∠BAD=∠BEA.∵∠ABC=90°,∴∠BAD═45°.∵由(1)得△ABC≌△ADC,∴∠BAC=∠DAC.∴∠BAC═22.5°.(3)解:当MO+PO的值最小时,点O与点E可以重合,理由如下:∵ME∥AB,∴∠ABC=∠MEC=90°,∠MAB=∠EMA.∵MP⊥DC,∴∠MPC=90°.∴∠MPC=∠ADC=90°.∴PM∥AD.∴∠EAM=∠PMA.由(1)得,Rt△ABC≌Rt△ADC,∴∠EAC=∠MAB,∴∠EMA=∠AMP.即MC平分∠PME.又∵MP⊥CP,ME⊥CE,∴PC=EC.如图,连接PB,连接PE,延长ME交PD的延长线于点Q.设∠EAM=α,则∠MAP=α.在Rt△ABE中,∠BEA=90°﹣2α.在Rt△CDE中,∠ECD=90°﹣∠BEA=2α.∵PC=EC,∴∠PEB=∠EPC=∠ECD=α.∴∠PED=∠BEA+∠PEB=90°﹣α.∵ME∥AB,∴∠QED=∠BAD=2α.当∠PED=∠QED时,∵∠PDE=∠QDE,DE=DE,∴△PDE≌△QDE(ASA).∴PD=DQ.即点P与点Q关于直线AE成轴对称,也即点M、点E、点P关于直线AE的对称点Q,这三点共线,也即MO+PO的值最小时,点O与点E重合.因为当∠PED=∠QED时,90°﹣α=2α,也即α=30°.所以,当∠ABD=60°时,MO+PO取最小值时的点O与点E重合.此时MO+PO的最小值即为ME+PE.∵PC=EC,∠PCB=∠ECD,CB=CD,∴△PCB≌△ECD(SAS).∴∠CBP=∠CDE=90°.∴∠CBP+∠ABC=180°.∴A,B,P三点共线.当∠ABD=60°时,在△PEA中,∠PAE=∠PEA=60°.∴∠EPA=60°.∴△PEA为等边三角形.∵EB⊥AP,∴AP=2AB=2a.∴EP=AE=2a.∵∠EMA=∠EAM=30°,∴EM=AE=2a.∴MO+PO的最小值为4a.7.已知:如图,在正方形ABCD中,点E在AD边上运动,从点A出发向点D运动,到达D点停止运动.作射线CE,并将射线CE绕着点C逆时针旋转45°,旋转后的射线与AB边交于点F,连接EF.(1)依题意补全图形;(2)猜想线段DE,EF,BF的数量关系并证明;(3)过点C作CG⊥EF,垂足为点G,若正方形ABCD的边长是4,请直接写出点G 运动的路线长.解:(1)补全图形如图1所示:(2)线段DE,EF,BF的数量关系为:EF=DE+BF.理由如下:延长AD到点H,使DH=BF,连接CH,如图2所示:∵四边形ABCD是正方形,∴∠BCD=∠ADC=∠B=90°,BC=DC,∴∠CDH=90°=∠B,在△CDH和△CBF中,,∴△CDH≌△CBF(SAS).∴CH=CF,∠DCH=∠BCF.∵∠ECF=45°,∴∠ECH=∠ECD+∠DCH=∠ECD+∠BCF=45°.∴∠ECH=∠ECF=45°.在△ECH和△ECF中,,∴△EC H≌△ECF(SAS).∴EH=EF.∵EH=DE+DH,∴EF=DE+BF;(3)由(2)得:△ECH≌△ECF(SAS),∴∠CEH=∠CEF,∵CD⊥AD,CG⊥EF,∴CD=CG=4,∴点G的运动轨迹是以C为圆心4为半径的弧DB,∴点G运动的路线长==2π.8.如图,在正方形ABCD中,P是边BC上的一动点(不与点B,C重合),点B关于直线AP的对称点为E,连接AE.连接DE并延长交射线AP于点F,连接BF.(1)若∠BAP=α,直接写出∠ADF的大小(用含α的式子表示);(2)求证:BF⊥DF;(3)连接CF,用等式表示线段AF,BF,CF之间的数量关系,并证明.(1)解:由轴对称的性质得:∠EAP=∠BAP=α,AE=AB,∵四边形ABCD是正方形,∴∠BAD=90°,AB=AD,∴∠DAE=90°﹣2α,AD=AE,∴∠ADF=∠AED=(180°﹣∠DAE)=(90°+2α)=45°+α;(2)证明:∵四边形ABCD是正方形,∴∠BAD=90°,AB=AD,∵点E与点B关于直线AP对称,∴∠AEF=∠ABF,AE=AB.∴AE=AD.∴∠ADE=∠AED.∵∠AED+∠AEF=180°,∴在四边形ABFD中,∠ADE+∠ABF=180°,∴∠BFD+∠BAD=180°,∴∠BFD=90°∴BF⊥DF;(3)解:线段AF,BF,CF之间的数量关系为AF=BF+CF,理由如下:过点B作BM⊥BF交AF于点M,如图所示:∵四边形ABCD是正方形,∴AB=CB,∠ABC=90°,∴∠ABM=∠CBF,∵点E与点B关于直线AP对称,∠BFD=90°,∴∠MFB=∠MFE=45°,∴△BMF是等腰直角三角形,∴BM=BF,FM=BF,在△AMB和△CFB中,,∴△AMB≌△CFB(SAS),∴AM=CF,∵AF=FM+AM,∴AF=BF+CF.9.如图1,已知等腰Rt△ABC中,E为边AC上一点,过E点作EF⊥AB于F点,以为边作正方形,且AC=3,EF=.(1)如图1,连接CF,求线段CF的长;(2)将等腰Rt△ABC绕点旋转至如图2的位置,连接BE,M点为BE的中点,连接MC,MF,求MC与MF关系.解:(1)如图1,∵△ABC是等腰直角三角形,AC=3,∴AB=3,过点C作CM⊥AB于M,连接CF,∴CM=AM=AB=,∵四边形AGEF是正方形,∴AF=EF=,∴MF=AM﹣AF=﹣,在Rt△CMF中,CF===;(2)CM=FM,CM⊥FM,理由:如图2,过点B作BH∥EF交FM的延长线于H,连接CF,CH,∴∠BHM=∠EFM,∵四边形AGEF是正方形,∴EF=AF∵点M是BE的中点,∴BM=EM,在△BMH和△EMF中,,∴△BMH≌△EMF(AAS),∴MH=MF,BH=EF=AF∵四边形AGEF是正方形,∴∠FAG=90°,EF∥AG,∵BH∥EF,∴BH∥AG,∴∠BAG+∠ABH=180°,∴∠CBH+∠ABC+∠BAC+∠CAG=180°.∵△ABC是等腰直角三角形,∴BC=AC,∠ABC=∠BAC=45°,∴∠CBH+∠CAG=90°,∵∠CAG+∠CAF=90°,∴∠CBH=∠CAF,在△BCH和△ACF中,,∴△BCH≌△ACF(SAS),∴CH=CF,∠BCH=∠ACF,∴∠HCF=∠BCH+∠BCF=∠ACF+∠BCF=90°,∴△FCH是等腰直角三角形,∵MH=MF,∴CM=FM,CM⊥FM;10.如图将正方形ABCD绕点A顺时针旋转角度α(0°<α<90°)得到正方形AB′C′D′.(1)如图1,B′C′与AC交于点M,C′D′与AD所在直线交于点N,若MN∥B′D′,求α;(2)如图2,C′B′与CD交于点Q,延长C′B′与BC交于点P,当α=30°时.①求∠DAQ的度数;②若AB=6,求PQ的长度.解:(1)如图1中,∵MN∥B′D′,∴∠C′MN=∠C′B′D′=45°,∠C′NM=∠C′D′B′=45°,∴∠C′MN=∠C′NM,∴C′M=C′N,∵C′B′=C′D′,'∴MB′=ND′,∵AB′=AD′,∠AB′M=∠AD′N=90°,∴△AB′M≌△AD′N(SAS),∴∠B′AM=∠D′AN,∵∠B′AD′=90°,∠MAN=45°,∴∠B′AM=∠D′AN=22.5°,∵∠BAC=45°,∴∠BAB′=22.5°,∴α=22.5°.(2)①如图2中,∵∠AB′Q=∠ADQ=90°,AQ=AQ,AB′=AD,∴Rt△AQB′≌Rt△AQD(HL),∴∠QAB′=∠QAD,∵∠BAB′=30°,∠BAD=90°,∴∠B′AD=30°,∴∠QAD=∠B′AD=30°.②如图2中,连接AP,在AB上取一点E,使得AE=EP,连接EP.设PB=a.∵∠ABP=∠AB′P=90°,AP=AP,AB=AB′,∴Rt△APB≌Rt△APB′(HL),∴∠BAP=∠PAB′=15°,∵EA=EP,∴∠EAP=∠EPA=15°,∴∠BEP=∠EAP+∠EPA=30°,∴PE=AE=2a,BE=a,∵AB=6,∴2a+a=6,∴a=6(2﹣).∴PB=6(2﹣),∴PC=BC﹣PB=6﹣6(2﹣)=6﹣6,∵∠CPQ+∠BPB′=180°,∠BAB′+∠BPB′=180°,∴∠CPQ=∠BAB′=30°,∴PQ===12﹣4.11.已知,如图1,在边长为2的正方形ABCD中,E是边AB的中点,点F在边AD上,过点A作AG⊥EF,分别交线段CD、EF于点G、H(点G不与线段CD的端点重合).(1)如图2,当G是边CD中点时,求AF的长;(2)设AF=x,四边形FHGD的面积是y,求y关于x的函数关系式,并写出x的取值范围;(3)联结ED,当∠FED=45°时,求AF的长.解:(1)∵E是AB的中点,AB=2,∴AE=AB=1,同理可得DG=1,∵AG⊥EF,∴∠AHF=∠HAF+∠AFH=90°,∵四边形ABCD是正方形,∴∠ADG=90°=∠DAG+∠AGD,∴∠AFH=∠AGD,∵∠EAF=∠ADG=90°,∴△EAF∽△ADG,∴,即,∴AF=;(2)如图1,由(1)知:△EAF∽△ADG,∴,即,∴DG=2x,∵∠HAF=∠DAG,∠AHF=∠ADG=90°,∴∠AHF∽△ADG,∴=,∴=,∴AH==,FH==,∴y=S△ADG﹣S△AFH,=,=2x﹣,如图2,当G与C重合时,∵EF⊥AG,∴∠AHE=90°,∵∠EAH=45°,∴∠AEH=45°,∴AF=AE=1,∴0<x<1;∴y关于x的函数关系式为:y=2x﹣(0<x<1);(3)如图3,过D作DM⊥AG,交BC于M,连接EM,延长EA至N,使AN=CM,连接DN,设CM=a,则AN=a,∵AD=CD,∠NAD=∠DCM=90°,∴△NAD≌△MCD(SAS),∴∠ADN=∠CDM,DN=DM,∵EF⊥AG,DM⊥AG,∴EF∥DM,∴∠EDM=∠FED=45°,∴∠ADE+∠CDM=∠EDM=45°,∴∠NDA+∠ADE=∠NDE=∠EDM,∵ED=ED,∴△NDE≌△MDE(SAS),∴EN=EM=a+1,∵BM=2﹣a,在Rt△EBM中,由勾股定理得:BE2+BM2=EM2,∴12+(2﹣a)2=(a+1)2,a=,∵∠AEF+∠EAG=∠EAG+∠DAG,∴∠AEF=∠DAG=∠CDM,∴tan∠AEF=tan∠CDM,∴,∴,∴AF=.12.如图1,对角线互相垂直的四边形叫做垂美四边形.(1)概念理解:如图2,在四边形ABCD中,AB=AD,CB=CD,问四边形ABCD 是垂美四边形吗?请说明理由;(2)性质探究:如图1,四边形ABCD的对角线AC、BD交于点O,AC⊥BD.试证明:AB2+CD2=AD2+BC2;(3)解决问题:如图3,△ACB中,∠ACB=90°,AC⊥AG且AC=AG,AB⊥AE 且AE=AB,连结CE、BG、GE.已知AC=4,AB=5,求GE的长.解:(1)四边形ABCD是垂美四边形,理由如下:连接AC,BD,∵AB=AD,∴点A在线段BD的垂直平分线上,∵CB=CD,∴点C在线段BD的垂直平分线上,∴AC是线段BD的垂直平分线,∴四边形ABCD是垂美四边形;(2)∵AC⊥BD,∴∠AOD=∠AOB=∠BOC=∠COD=90°,由勾股定理得,AD2+BC2=AO2+DO2+BO2+CO2,AB2+CD2=AO2+BO2+CO2+DO2,∴AD2+BC2=AB2+CD2;故答案为:AB2+CD2=AD2+BC2;(3)∵∠CAG=∠BAE=90°,∴∠CAG+∠BAC=∠BAE+∠BAC,即∠GAB=∠CAE,在△GAB和△CAE中,,∴△GAB≌△CAE(SAS),∴∠ABG=∠AEC,又∠AEC+∠AME=90°,∴∠ABG+∠AME=90°,即CE⊥BG,∴四边形CGEB是垂美四边形,由(2)得,CG2+BE2=CB2+GE2,∵AC=4,AB=5,∴BC=3,CG=4,BE=5,∴GE2=CG2+BE2﹣CB2=73,∴GE=.13.如图1,四边形ACEB,连接BC,∠ACB=∠BEC=90°,D在AB上,连接CD,∠ACD=∠ABC,BE=CD.(1)求证:四边形CDBE为矩形;(2)如图2,连接DE,DE交BC于点O,若tan∠A=2,在不添加任何辅助线和字母的情况下,请直接写出图中所有长度与AD的长度相等的线段.(1)证明:∵∠ACB=90°,∴∠A+∠ABC=90°,∵∠ACD=∠ABC,∴∠A+∠ACD=90°,∴∠ADC=90°,∴∠BDC=180°﹣90°=90°=∠BEC,在Rt△BCD和Rt△CBE中,,∴Rt△BCD≌Rt△CBE(HL),∴BD=CE,∵CD=BE,∴四边形CDBE是平行四边形,又∵∠BEC=90°,∴四边形CDBE为矩形;(2)解:图中所有长度与AD的长度相等的线段为AC=OC=OB=OD=OE=AD.理由如下:由(1)得:四边形CDBE为矩形,∠ADC=90°,∴BC=DE,OD=OE,OB=OC,∴OC=OB=OD=OE=BC,∵∠ADC=∠ACB=90°,∴tan∠A=2==,∴CD=2AD,BC=2AC,∴AC===AD,∴DE=BC=2AC,∴OC=OB=OD=OE=BC=AC=AD,∴AC=OC=OB=OD=OE=AD.14.如图在直角坐标系中,四边形ABCO为正方形,A点的坐标为(a,0),D点的坐标为(0,b),且a,b满足(a﹣3)2+|b﹣|=0.(1)求A点和D点的坐标;(2)若∠DAE=∠OAB,请猜想DE,OD和EB的数量关系,说明理由.(3)若∠OAD=30°,以AD为三角形的一边,坐标轴上是否存在点P,使得△PAD 为等腰三角形,若存在,直接写出有多少个点P,并写出P点的坐标,选择一种情况证明.解:(1)∵(a﹣3)2+|b﹣|=0,∴a=3,b=,∴D(0,),A(3,0);(2)DE=OD+EB;理由如下:如图1,在CO的延长线上找一点F,使OF=BE,连接AF,在△AOF和△ABE中,,∴△AOF≌△ABE(SAS),∴AF=AE,∠OAF=∠BAE,又∵∠OAB=90°,∠DAE=,∴∠BAE+∠DAO=45°,∴∠DAF=∠OAF+∠DAO=45°,∴∠DAF=∠EAD,在△AFD和△AED中,,∴△AFD≌△AED(SAS),∴DF=DE=OD+EB;(3)有3种情况共6个点:①当DA=DP时,如图2,Rt△ADO中,OD=,OA=3,∴AD===2,∴P 1(﹣3,0),P2(0,3),P3(0,﹣);②当AP4=DP4时,如图3,∴∠ADP4=∠DAP4=30°,∴∠OP4D=60°,Rt△ODP 4中,∠ODP4=30°,OD=,∴OP4=1,∴P4(1,0);③当AD=AP时,如图4,∴AD=AP 5=AP6=2,∴P 5(3+2,0),P6(3﹣2,0),综上,点P的坐标为:∴P(﹣3,0)或(0,3)或(0,﹣)或(1,0)或(3+2,0)或(3﹣2,0).证明:P 5(3+2,0),∵∠OAD=30°且△ADO是直角三角形,又∵AO=3,DO=,∴DA=2,而P 5A=|3+2﹣3|=2,∴P5A=DA,∴△P5AD是等腰三角形.15.已知,在四边形ABCD中,点M、N、P、Q分别为边AB、AD、CD、BC的中点,连接MN、NP、PQ、MQ.(1)如图1,求证:四边形MNPQ为平行四边形;(2)如图2,连接AC,AC分别交MN、PQ于点E、F,连接BD,BD分别交MQ、NP于点G、H,AC与BD交于点O,且AC⊥BD,若tan∠ADB=,在不添加任何辅助线的情况下,请直接写出图2中所有长度等于OD的线段.(1)证明:如图1,连接BD.∵Q,P分别是BC,CD的中点,所以PQ∥BD,PQ=BD.∵M,N分别是AB,AD的中点.∴MN∥BD,MN=BD.∴PQ∥MN,且PQ=MN.∴四边形MNPQ是平行四边形.(2)解:∵四边形MNPQ是平行四边形,AC⊥BD,∴四边形MNPQ是矩形,∴四边形NHOE和四边形EOGM都是矩形,∴NH=OE=MG=AE=,∵tan∠ADB=,∴,∴NH=OE=MG=AE=.即长度等于OD的线段有NH,OE,MG,AE.。
2019年决战中考物理复习题 声光热实验题 提高题含答案

决战中考——声光热实验题(提高)设计一个实验证明:水能够传声。
小明的主要实验步骤知下:、在学习演奏小提琴的过程中,小明和同学们发现弦乐器的琴弦发出声音的音调受很多因素的影响,他们决定对这种现象进行探究,经讨论后提出以下猜想:猜想一:琴弦发出声音的音调可能与琴弦的材料有关;猜想二:琴弦发出声音的音调可能与琴弦的长短有关;琴弦的横截面积D、估计待测液体的温度E、把温度计的玻璃泡全部浸入被测液体中。
F、把温度计的玻璃泡在液体中放一段时间,待示数稳定。
G.从液体中取出温度计;H.对温度计进行读数。
答:__________________________________________。
4、使用温度计时,先要观察它的量程和认清它的________。
小强在用温度计测量烧杯中液体温度时读取了四次数据,每次读数时温度计的位置如图所示,其中正确的是________。
图甲、乙所示的是用温度计分别测得的冰和水的温度,那么冰的温度是________℃,水的温度是________℃。
5、小光同学学习做饭的过程中,经常加热油和水,他猜想①油的沸点比水高;②油的比热容比水小。
(1)能够支持他的猜想①的事实是_____________。
A.同样情况下,油升温比水快B.油能把食物炸黄,而水不能C.油能漂在水面上D.油比水难蒸发(2)为了验证猜想②,小光向两个同样的烧杯里分别倒入_____________相同的水和油,并测量它们的初始温度,两温度计的示数相同,如图所示,它们的初始温度为_____________℃。
(3)在同样条件下加热相同时间后,水的温度达到25℃,油的温度达到30℃,由此可得油的比热容为____________J/(kg·℃)。
〔水的比热容为4.2×103J/(kg·℃)〕6、如图1是探究平面镜成像特点的实验装置图。
小鹭将一块玻璃板竖直架在一把刻度尺的上面,并保持玻璃板与刻度尺垂直。
2024学年辽宁省锦州市第七中学中考押题语文预测卷含解析

2024学年辽宁省锦州市第七中学中考押题语文预测卷考生请注意:1.答题前请将考场、试室号、座位号、考生号、姓名写在试卷密封线内,不得在试卷上作任何标记。
2.第一部分选择题每小题选出答案后,需将答案写在试卷指定的括号内,第二部分非选择题答案写在试卷题目指定的位置上。
3.考生必须保证答题卡的整洁。
考试结束后,请将本试卷和答题卡一并交回。
一、积累与运用1.把下列句子组合成语序合理、语意连贯的一段语,最恰当的一项是( )①而且这种现象越来越低龄化②但是互联网时代,汉字却陷入有声无形的窘境③汉字承载了中华民族的文明和智慧④专家学者认为:汉字对智力的开发有巨大作用;认识的汉字越多,联想就越丰富⑤其兼备象形和表意的特点及蕴含的思想和文化内涵是任何科技也无法模拟和取代的⑥现在越来越多的人出现提笔忘字的现象A.③⑥①⑤④②B.③⑤④②⑥①C.⑥①②③④⑤D.⑥②①④③⑤2.下列词语中,字形和加点字的注音完全正确的一项是( )A.澄.澈(chéng)哂.笑(shěn)戛.然而止(gā)B.诘.责(jié) 愧作.(zuò) 龙吟凤哕.(huì)C.取缔.(dì) 气氛.(fēn) 栩.栩如生(xǔ)D.威摄.(shè) 琐屑.(xiè) 如坐针毡.(zhān)3.下列各组词语中加点字的书写或注音有误的一项是()A.麾.下颦.蹙(pín)自出心.裁(xīn)屏.气凝神B.鹰隼.嗔.视(chēn)寻幽揽.胜(lǎn)如释.重负C.嫡.传褶.皱(zhě)莫名.其妙(míng)拈.轻怕重D.磕.绊葳蕤.(ruì)荒谬绝伦.(lún)不可思异.4.下列关于文学文化常识的说法正确的一项是()A.风骚,本指《诗经》里的《国风》和《楚辞》中的《离骚》,后来泛指文章辞藻;《乐府诗集》中的诗是配乐的歌词,按照所配乐曲的性质分为风、雅、颂三类,其中“颂”是祭祀乐歌,用于宫廷宗庙祭祀。
决战2020年中考数学压轴题综合提升训练《三角形》(含解析)

《三角形》1.已知,△ABC是等边三角形,过点C作CD∥AB,且CD=AB,连接BD交AC于点O.(1)如图1,求证:AC垂直平分BD;(2)如图2,点M在BC的延长线上,点N在线段CO上,且ND=NM,连接BN.求证:NB =NM.(1)证明:∵△ABC是等边三角形,∴∠ABC=∠ACB=∠CAB=60°,∵CD∥AB,且CD=AB,∴CD=CA=BC,∠ACD=∠ACB=60°,∴BO=DO,CO⊥BD,∴AC垂直平分BD;(2)由(1)知AC垂直平分BD,∴NB=ND,∵ND=NM,∴NB=NM.2.等腰Rt△ABC,点D为斜边AB上的中点,点E在线段BD上,连结CD,CE,作AH⊥CE,垂足为H,交CD于点G,AH的延长线交BC于点F.(1)求证:△ADG≌△CDE.(2)若点H恰好为CE的中点,求证:∠CGF=∠CFG.证明:(1)在等腰Rt△ABC中,∵点D为斜边AB上的中点,∴CD=AB,CD⊥AB,∵AD=AB,∴AD=CD,∵CD⊥AB,∴∠ADG=∠CDE=90°,∵AH⊥CE,∴∠CGH+∠GCH=90°,∵∠AGD+∠GAD=90°,又∵∠AGD=∠CGH,∴∠GAD=∠GCH,在△△ADG和△CDE中∵∠ADG=∠CDE=90°,AD=CD,∠GAD=∠GCH∴△ADG≌△CDE(ASA),(2)∵AH⊥CE,点H为CE的中点,∴AC=AE,∴∠CAH=∠EAH,∵∠CAH+∠AFC=90°,∠EAH+∠AGD=90°,∴∠AFC=∠AGD,∵∠AGD=∠CGH,∴∠AFC=∠CGH,即∠CGF=∠CFG.3.如图,在△ABC中,AD⊥BC且BD=DE,EF垂直平分AC,交AC于点F,交BC于点E.(1)若∠BAE=32°,求∠C的度数;(2)若AC=6cm,DC=5cm,求△ABC的周长.解:(1)∵AD⊥BC,BD=DE,EF垂直平分AC∴AB=AE=EC∴∠C=∠CAE,∵∠BAE=32°∴∠AED=(180°﹣32°)=74°;∴∠C=∠AED=37°;(2)由(1)知:AE=EC=AB,∵BD=DE,∴AB+BD=EC+DE=DC,∴△ABC的周长=AB+BC+AC,=AB+BD+DC+AC,=2DC+AC=2×5+6=16(cm).4.如图,在△ABC中,∠BAC和∠ABC的平分线相交于点O,过点O作EF∥AB交BC于F,交AC于E,过点O作OD⊥BC于D.(1)求证:∠AOB=90°+∠C;(2)求证:AE+BF=EF;(3)若OD=a,CE+CF=2b,请用含a,b的代数式表示△CEF的面积,S△CEF=ab(直接写出结果).证明:(1)∵OA,OB平分∠BAC和∠ABC,∴,,∴∠AOB=180°﹣∠OAB﹣∠OBA====(2)∵EF∥AB,∴∠OAB=∠AOE,∠ABO=∠BOF又∠OAB=∠EAO,∠OBA=∠OBF,∴∠AOE=∠EAO,∠BOF=∠OBF,∴AE=OE,BF=OF,∴EF=OE+OF=AE+BF;(3)∵点O在∠ACB的平分线上,∴点O到AC的距离等于OD,∴S△CEF=(CE+CF)•OD=•2b•a=ab,故答案为:ab.5.如图,在△ABC中,AB=AC,AD为BC边上的中线,DE⊥AB于点E.(1)求证:BD•AD=DE•AC.(2)若AB=13,BC=10,求线段DE的长.(3)在(2)的条件下,求cos∠BDE的值.证明:(1)∵AB=AC,BD=CD,∴AD⊥BC,∠B=∠C,∵DE⊥AB,∴∠DEB=∠ADC,∴△BDE∽△CAD.∴,∴BA•AD=DE•CA;(2)∵AB=AC,BD=CD,∴AD⊥BC,在Rt△ADB中,AD===12,∵•AD•BD=•AB•DE,∴DE=.(3)∵∠ADB=∠AED=90°,∴∠BDE=∠BAD,∴cos∠BDE=cos∠BAD=.6.如图,在△ABC中,AB=AC,以AB为直径作半圆O,交BC于点D,交AC于点E.(1)求证:BD=CD.(2)若弧DE=50°,求∠C的度数.(3)过点D作DF⊥AB于点F,若BC=8,AF=3BF,求弧BD的长.(1)证明:如图,连接AD.∵AB是圆O的直径,∴AD⊥BD.又∵AB=AC,∴BD=CD.(2)解:∵弧DE=50°,∴∠EOD=50°.∴∠DAE=∠DOE=25°.∵由(1)知,AD⊥BD,则∠ADB=90°,∴∠ABD=90°﹣25°=65°.∵AB=AC,∴∠C=∠ABD=65°.(3)∵BC=8,BD=CD,∴BD=4.设半径OD=x.则AB=2x.由AF=3BF可得AF=AB=x,BF=AB=x,∵AD⊥BD,DF⊥AB,∴BD2=BF•AB,即42=x•2x.解得x=4.∴OB=OD=BD=4,∴△OBD是等边三角形,∴∠BOD=60°.∴弧BD的长是:=.7.阅读下面材料:数学课上,老师给出了如下问题:如图,AD为△ABC中线,点E在AC上,BE交AD于点F,AE=EF.求证:AC=BF.经过讨论,同学们得到以下两种思路:思路一如图①,添加辅助线后依据SAS可证得△ADC≌△GDB,再利用AE=EF可以进一步证得∠G=∠FAE=∠AFE=∠BFG,从而证明结论.思路二如图②,添加辅助线后并利用AE=EF可证得∠G=∠BFG=∠AFE=∠FAE,再依据AAS可以进一步证得△ADC≌△GDB,从而证明结论.完成下面问题:(1)①思路一的辅助线的作法是:延长AD至点G,使DG=AD,连接BG;②思路二的辅助线的作法是:作BG=BF交AD的延长线于点G.(2)请你给出一种不同于以上两种思路的证明方法(要求:只写出辅助线的作法,并画出相应的图形,不需要写出证明过程).解:(1)①延长AD至点G,使DG=AD,连接BG,如图①,理由如下:∵AD为△ABC中线,∴BD=CD,在△ADC和△GDB中,,∴△ADC≌△GDB(SAS),∴AC=BG,∵AE=EF,∴∠CAD=∠EFA,∵∠BFG=∠G,∠G=∠CAD,∴∠G=∠BFG,∴BG=BF,∴AC=BF.故答案为:延长AD至点G,使DG=AD,连接BG;②作BG=BF交AD的延长线于点G,如图②.理由如下:∵BG=BF,∴∠G=∠BFG,∵AE=EF,∴∠EAF=∠EFA,∵∠EFA=∠BFG,∴∠G=∠EAF,在△ADC和△GDB中,,∴△A DC≌△GDB(AAS),∴AC=BG,∴AC=BF;故答案为:作BG=BF交AD的延长线于点G;(2)作BG∥AC交AD的延长线于G,如图③所示:则∠G=∠CAD,∵AD为△ABC中线,∴BD=CD,在△ADC和△GDB中,,∴△ADC≌△GDB(AAS),∴AC=BG,∵AE=EF,∴∠CAD=∠EFA,∵∠BFG=∠G,∠G=∠CAD,∴∠G=∠BFG,∴BG=BF,∴AC=BF.8.如图1,直线AB分别与x轴、y轴交于A、B两点,OC平分∠AOB交AB于点C,点D为线段AB上一点,过点D作DE∥OC交y轴于点E,已知AO=m,BO=n,且m、n满足n2﹣8n+16+|n﹣2m|=0.(1)求A、B两点的坐标;(2)若点D为AB中点,求OE的长;(3)如图2,若点P(x,﹣2x+4)为直线AB在x轴下方的一点,点E是y轴的正半轴上一动点,以E为直角顶点作等腰直角△PEF,使点F在第一象限,且F点的横、纵坐标始终相等,求点P的坐标.解:(1)∵n2﹣8n+16+|n﹣2m|=0,∴(n﹣4)2+|n﹣2m|=0,∵(n﹣4)2≥0,|n﹣2m|≥0,∴(n﹣4)2=0,|n﹣2m|=0,∴m=2,n=4,∴点A为(2,0),点B为(0,4);(2)延长DE交x轴于点F,延长FD到点G,使得DG=DF,连接BG,设OE=x,∵OC平分∠AOB,∴∠BOC=∠AOC=45°,∵DE∥OC,∴∠EFO=∠FEO=∠BEG=∠BOC=∠AOC=45°,∴OE=OF=x,在△ADF和△BDG中,,∴△ADF≌△BDG(SAS),∴BG=AF=2+x,∠G=∠AFE=45°,∴∠G=∠BEG=45°,∴BG=BE=4﹣x,∴4﹣x=2+x,解得:x=1,∴OE=1;(3)如图2,分别过点F、P作FM⊥y轴于点M,PN⊥y轴于点N,设点E为(0,m),∵点P的坐标为(x,﹣2x+4),∴PN=x,EN=m+2x﹣4,∵∠PEF=90°,∴∠PEN+∠FEM=90°,∵FM⊥y轴,∴∠MFE+∠FEM=90°,∴∠PEN=∠MFE,在△EFM和△PEN中,,∴△EFM≌△PEN(AAS),∴ME=NP=x,FM=EN=m+2x﹣4,∴点F为(m+2x﹣4,m+x),∵F点的横坐标与纵坐标相等,∴m+2x﹣4=m+x,解得:x=4,∴点P为(4,﹣4).9.在等边△ABC中,线段AM为BC边上的中线.动点D在直线AM上时,以CD为一边在CD 的下方作等边△CDE,连结BE.(1)若点D在线段AM上时(如图1),则AD=BE(填“>”、“<”或“=”),∠CAM =30 度;(2)设直线BE与直线AM的交点为O.①当动点D在线段AM的延长线上时(如图2),试判断AD与BE的数量关系,并说明理由;②当动点D在直线AM上时,试判断∠AOB是否为定值?若是,请直接写出∠AOB的度数;若不是,请说明理由.解:(1))∵△ABC与△DEC都是等边三角形∴AC=BC,CD=CE,∠ACB=∠DC E=60°∴∠ACD+∠DCB=∠DCB+∠BCE∴∠ACD=∠BCE.在△ADC和△BEC中,∴△ACD≌△BCE(SAS),∴AD=BE;∵△ABC是等边三角形,∴∠BAC=60°.∵线段AM为BC边上的中线∴∠CAM=∠BAC,∴∠CAM=30°.故答案为:=,30;(2)①AD=BE,理由如下:∵△ABC和△CDE都是等边三角形∴AB=BC,DC=EC,∠ACB=∠DCE=60°,∵∠ACD=∠ACB﹣∠DCB,∠BCE=∠DCE﹣∠DCB,∴∠ACD=∠BCE,∴△ACD≌△BCE(SAS)∴AD=BE.②∠AOB是定值,∠AOB=60°,理由如下:当点D在线段AM上时,如图1,由①知△ACD≌△BCE,则∠CBE=∠CAD=30°,又∠ABC=60°,∴∠CBE+∠ABC=60°+30°=90°,∵△ABC是等边三角形,线段AM为BC边上的中线∴AM平分∠BAC,即,∴∠BOA=90°﹣30°=60°.当点D在线段AM的延长线上时,如图2,∵△ABC与△DEC都是等边三角形∴AC=BC,CD=CE,∠ACB=∠DCE=60°∴∠ACB+∠DCB=∠DCB+∠DCE∴∠ACD=∠BCE在△ACD和△BCE中,∴△ACD≌△BCE(SAS)∴∠CBE=∠CAD=30°,同理可得:∠BAM=30°,∴∠BOA=90°﹣30°=60°.10.数学课上,王老师出示了如下框中的题目.小明与同桌小聪讨论后,进行了如下解答:(1)特殊情况•探索结论:在等边三角形ABC中,当点E为AB的中点时,点D在CB点延长线上,且ED=EC;如图1,确定线段AE与DB的大小关系.请你直接写出结论AE =DB;(2)特例启发,解答题目王老师给出的题目中,AE与DB的大小关系是:AE=DB.理由如下:如图2,过点E作EF∥BC,交AC于点F,(请你完成以下解答过程)(3)拓展结论,设计新题在△ABC中,AB=BC=AC=1;点E在AB的延长线上,AE=2;点D在CB的延长线上,ED =EC,如图3,请直接写CD的长1或3 .解:(1)如图1,过点E作EF∥BC,交AC于点F,∵△ABC为等边三角形,∴∠AFE=∠ACB=∠ABC=60°,△AEF为等边三角形,∴∠EFC=∠EBD=120°,EF=AE,∵ED=EC,∴∠EDB=∠ECB,∠ECB=∠FEC,∴∠EDB=∠FEC,在△BDE和△FEC中,,∴△BDE≌△FEC(AAS),∴BD=EF,∴AE=BD,故答案为:=;(2)解答过程如下:如图2,过点E作EF∥BC,交AC于点F,∵△ABC为等边三角形,∴∠AFE=∠ACB=∠ABC=60°,△AEF为等边三角形,∴∠EFC=∠EBD=120°,EF=AE,∵ED=EC,∴∠EDB=∠ECB,∠ECB=∠FEC,∴∠EDB=∠FEC,在△BDE和△FEC中,∴△BDE≌△FEC(AAS),∴BD=EF,∴AE=BD.故答案为:AE=DB.(3)解:分为四种情况:如图3,∵AB=AC=1,AE=2,∴B是AE的中点,∵△ABC是等边三角形,∴AB=AC=BC=1,△ACE是直角三角形(根据直角三角形斜边的中线等于斜边的一半),∴∠ACE=90°,∠AEC=30°,∴∠D=∠ECB=∠BEC=30°,∠DBE=∠ABC=60°,∴∠DEB=180°﹣30°﹣60°=90°,即△DEB是直角三角形.∴BD=2BE=2(30°所对的直角边等于斜边的一半),即CD=1+2=3.如图4,过A作AN⊥BC于N,过E作EM⊥CD于M,∵等边三角形ABC,EC=ED,∴BN=CN=BC=,CM=MD=CD,AN∥EM,∴△BAN∽△BEM,∴,∵△ABC边长是1,AE=2,∴,∴MN=1,∴CM=MN﹣CN=1﹣=,∴CD=2CM=1;如图5,∵∠ECD>∠EBC(∠EBC=120°),而∠ECD不能大于120°,否则△EDC不符合三角形内角和定理,∴此时不存在EC=ED;如图6,∵∠EDC<∠ABC,∠ECB>∠ACB,又∵∠ABC=∠ACB=60°,∴∠ECD>∠EDC,即此时ED≠EC,∴此时情况不存在,答:CD的长是3或1.故答案为:1或3.11.定义:如果一个三角形的一个内角等于另一个内角的两倍,则称这样的三角形为“倍角三角形”.(1)如图1,△ABC中,AB=AC,∠A=36°,求证:△ABC是倍角三角形;(2)若△ABC是倍角三角形,∠A>∠B>∠C,∠B=30°,AC=,求△ABC面积;(3)如图2,△ABC的外角平分线AD与CB的延长线相交于点D,延长CA到点E,使得AE=AB,若AB+AC=BD,请你找出图中的倍角三角形,并进行证明.(1)证明:∵AB=AC,∴∠B=∠C,∵∠A+∠B+∠C=180°,∠A=36°,∴∠B=∠C=72°,∴∠A=2∠C,即△ABC是倍角三角形,(2)解:∵∠A>∠B>∠C,∠B=30°,①当∠B=2∠C,得∠C=15°,过C作CH⊥直线AB,垂足为H,可得∠CAH=45°,∴AH=CH=AC=4.∴BH=,∴AB=BH﹣AH=﹣4,∴S=.②当∠A=2∠B或∠A=2∠C时,与∠A>∠B>∠C矛盾,故不存在.综上所述,△ABC面积为.(3)∵AD平分∠BAE,∴∠BAD=∠EAD,∵AB=AE,AD=AD,∴△ABD≌△AED(SAS),∴∠ADE=∠ADB,BD=DE.又∵AB+AC=BD,∴AE+AC=BD,即CE=BD.∴CE=DE.∴∠C=∠BDE=2∠ADC.∴△ADC是倍角三角形.12.如图,在平面直角坐标系中,OA=OB,AC=CD,已知两点A(4,0),C(0,7),点D 在第一象限内,∠DCA=90°,点B在线段OC上,AB的延长线与DC的延长线交于点M,AC与BD交于点N.(1)点B的坐标为:(0,4);(2)求点D的坐标;(3)求证:CM=CN.解:(1)∵A(4,0),∴OA=OB=4,∴B(0,4),故答案为:(0,4).(2)∵C(0,7),∴OC=7,过点D作DE⊥y轴,垂足为E,∴∠DEC=∠AOC=90°,∵∠DCA=90°,∴∠ECD+∠BCA=∠ECD+∠EDC=90°∴∠BCA=∠EDC,∴△DEC≌△COA(AAS),∴DE=OC=7,EC=OA=4,∴OE=OC+EC=11,∴D(7,11);(3)证明:∵BE=OE﹣OB=11﹣4=7 ∴BE=DE,∴△DBE是等腰直角三角形,∴∠DBE=45°,∵OA=OB,∴∠OBA=45°,∴∠DBA=90°,∴∠BAN+∠ANB=90°,∵∠DCA=90°,∴∠CDN+∠DNC=90°,∵∠DNC=∠ANB,∴∠CDN=∠BAN,∵∠DCA=90°,∴∠ACM=∠DCN=90°,∴△DCN≌△ACM(ASA),∴CM=CN.13.如图,在△ABC中,BD⊥AC,垂足为C,且∠A<∠C,点E是一动点,其在BC上移动,连接DE,并过点E作EF⊥DE,点F在AB的延长线上,连接DF交BC于点G.(1)请同学们根据以上提示,在上图基础上补全示意图.(2)当△ABD与△FDE全等,且AD=FE,∠A=30°,∠AFD=40°,求∠C的度数.解:(1)补全示意图如图所示,(2)∵DE⊥EF,BD⊥AC,∴∠DEF=∠ADB=90°.∵△ABD与△DEF全等,∴AB=DF,又∵AD=FE,∴∠ABD=∠FDE,∴BD=DE.在Rt△ABD中,∠ABD=90°﹣∠A=60°.∴∠FDE=60°.∵∠ABD=∠BDF+∠AFD,∵∠AFD=40°,∴∠BDF=20°.∴∠BDE=∠BDF+∠FDE=20°+60°=80°.∵BD=DE,∴∠DBE=∠BED=(180°﹣∠BDE)=50°.在Rt△BDC中,∠C=90°﹣∠DBE=90°﹣50°=40°.14.如图.CP是等边△ABC的外角∠ACE的平分线,点D在边BC上,以D为顶点,DA为一条边作∠ADF=60°,另一边交射线CP于F.(1)求证.AD=FD;(2)若AB=2,BD=x,DF=y,求y关于x的函数解析式;(3)联结AF,当△ADF的面积为时,求BD的长.证明:(1)如图1,连接AF,∵∠ACB=60°,∴∠ACE=120°,∵CP平分∠ACE,∴∠ACP=∠PCE=60°,∴∠ADF=∠ACP=60°,∴A、D、C、F四点共圆,∴∠AFD=∠ACB=60°,∴∠ADF=∠AFD=60°,∴∠DAF=60°,∴△ADF是等边三角形,∴AD=FD;(2)如图2,过点A作AH⊥BC,∵△ABC是等边三角形,AH⊥BC,AB=2,∴BH=1,AH=BH=,∴HD=BD﹣BH=x﹣1,∵DF==,∴y=(3)∵△ADF是等边三角形,且△ADF的面积为,∴DF2=,∴DF2==x2﹣2x+4∴x=∴BD=或15.如图,△ABC是等边三角形,D是BC边的中点,以D为顶点作一个120°的角,角的两边分别交直线AB、直线AC于M、N两点.以点D为中心旋转∠MDN(∠MDN的度数不变),当DM与AB垂直时(如图①所示),易证BM+CN=BD.(1)如图②,当DM与AB不垂直,点M在边AB上,点N在边AC上时,BM+CN=BD是否仍然成立?若成立,请给予证明;若不成立,请说明理由;(2)如图③,当DM与AB不垂直,点M在边AB上,点N在边AC的延长线上时,BM+CN =BD是否仍然成立?若不成立,请写出BM,CN,BD之间的数量关系,不用证明.解:(1)结论BM+CN=BD成立,理由如下:如图②,过点D作DE∥AC交AB于E,∵△ABC是等边三角形,∴∠A=∠B=∠C=60°,∵DE∥AC,∴∠BED=∠A=60°,∠BDE=∠C=60°,∴∠B=∠BED=∠BDE=60°,∴△BDE是等边三角形,∠EDC=120°,∴BD=BE=DE,∠EDN+∠CDN=120°,∵∠EDM+∠EDN=∠MDN=120°,∴∠CDN=∠EDM,∵D是BC边的中点,∴DE=BD=CD,在△CDN和△EDM中,,∴△CDN≌△EDM(ASA),∴CN=EM,∴BD=BE=BM+EM=BM+CN;(2)上述结论不成立,BM,CN,BD之间的数量关系为:BM﹣CN=BD;理由如下:如图③,过点D作DE∥AC交AB于E,∵△ABC是等边三角形,∴∠A=∠B=∠C=60°,∴∠NCD=120°,∵DE∥AC,∴∠BED=∠A=60°,∠BDE=∠C=60°,∴∠B=∠BED=∠BDE=60°,∴△BDE是等边三角形,∠MED=∠EDC=120°,∴BD=BE=DE,∠NCD=∠MED,∠EDM+∠CDM=120°,∵∠CDN+∠CDM=∠MDN=120°,∴∠CDN=∠EDM,∵D是BC边的中点,∴DE=BD=CD,在△CDN和△EDM中,,∴△CDN≌△EDM(ASA),∴CN=EM,∴BD=BE=BM﹣EM=BM﹣CN,∴BM﹣CN=BD.。
杭州专版中考英语决战中考限时许十精练本B本课件

D 1.Why is the writer of the passage interested in the book“How to make friends
with foreigners”? A.Because he wants to have some more close Chinese friends. B.Because he has greatly improved his Chinese language skills. C.Because no Chinese people would like to make friends with him. D.Because he wants to know about the Chinese writer's advice on this topic.
A.I take part in many after-school activities. B.I’m good at sports. C.I also do charity work when I have time. D.I do well at school. E.I always help other pupils. F.I also love music.
Friendship for a lot of foreigners is about spending time with someone whose company(陪伴) they really enjoy.So if there is any advice to give on making and keeping friendships with foreigners,I would say that it is this: Treat foreigners as people,not opportunities.Expect to make friendships step by step,over a period of time,not in a rush. ▲ If your only reason for becoming friends with a foreigner is to improve your English,then you will probably find that you don't have a foreign friend for long.
决战2012中考物理实验故障专题研讨

一、电学实验故障 二、光学实验故障 三、力学实验故障 四、热学实验故障
电学故障---中考链接
(2011黑龙江省哈尔滨)19.如图所示电路,电源电压为3V. 当开关S闭合时,却只有一只灯泡发光,且电压表示数为3V.由 这—现象可以判断电路的故障是( ) A.灯Ll短路 B.灯L2短路 C.灯Ll开路 D.灯L2开路 答案:B
答:结果不对,他没有注意游码刻度尺的分度 值为0.2g,正确读数应该是52.4g。读数应该注 意读游码的左端且注意分度值是多少!
7、小明测出石块的质量和体积如右图 ?试计算石块的密度是多少? 答:由图可知石块m=67g,V=10cm3 所以石块密度为6.7g/cm3。
8、小明实验后将天平等器材如图放置 ,他的失误是什么? 答:小明没有整理实验器材,他应该 将砝码放回盒内。
1
2 3
较缓
较陡 最陡
5.0
5.0 5.0
0.10
0.15 0.25
1.6
2.2
0.50
0.50 0.50
0.50
0.75 1.25
0.80
1.10
63%
68%
(1)如图第三次实验弹簧测力计示数为3.2 N, _ 机械效率约为 78% (精确到百分位)。 (2)小兰在对实验数据处理的过程中出现的错 误之处是:斜面的机械效率是变化的,不应计算平均值。 。 (3)改正错误后,对实验数据进行分析,你对斜 面机械效率问题可获得初步结论是 接触面粗糙程度 相同(或光滑程度相同)时,斜面越陡(或缓), 。
73
27
46
40
1.15
[一、实验仪器操作故障] 例:小明在测量石块密度实验中,使用了 天平和量筒两种测量仪器。 1、天平如图,小明把游码调到右图乙所 示位置,横梁平衡,则小馨的实验准备对 吗? 答:不对,实验前应调节平衡螺母使横梁 平衡。 2、小明的做法会使实验中测量的物质密 度如何,为什么? 答:会偏大,因为测量的质量偏大, 体积不变,所以测量的密度偏大。 3、小明应向哪个方向调节平衡螺母? 答:向右偏,右沉,应向左调平衡螺母。
决战2020年中考数学压轴题综合提升训练《圆的综合》(含解析)

《圆的综合》1.如图,四边形ABCD是⊙O的内接四边形,(1)求证:CD平分∠ACE;(2)若AC=8,CE=3,求CD的长.,AC为直径,DE⊥BC,垂足为E.(1)证明:∵四边形ABCD是⊙O内接四边形,∴∠BAD+∠BCD=180°,∵∠BCD+∠DCE=180°,∴∠DCE=∠BAD,∵,∴∠BAD=∠ACD,∴∠DCE=∠ACD,∴CD平分∠ACE;(2)解:∵AC为直径,∴∠AD C=90°,∵DE⊥BC,∴∠DEC=90°,∴∠DEC=∠ADC,∵∠DCE=∠ACD,∴△DCE∽△ACD,∴∴,即.,2.如图,AB为⊙O的直径,C、F为⊙O上两点,且点C为交AF的延长线于点E,交AB的延长线于点D.(1)求证:DE是⊙O的切线;的中点,过点C作AF的垂线,(2)当BD=2,sin D=时,求AE的长.(1)证明:连接OC,如图,∵点C为弧BF的中点,∴弧BC=弧CF.∴∠BAC=∠FAC,∵OA=OC,∴∠OCA=∠OAC.∴∠OCA=∠FAC,∴OC∥AE,∵AE⊥DE,∴OC⊥DE.∴DE是⊙O的切线;(2)∵sin D==,∴设OC=3x,OD=5x,则5x=3x+2,∴x=1,∴OC=3,OD=5,∴AD=8,∵sin D=∴AE==.=,3.如图,已知直线l切⊙O于点A,B为⊙O上一点,过点B作BC⊥l,垂足为点C,连接AB、OB.(1)求证:∠ABC=∠ABO;(2)若AB=,AC=1,求⊙O的半径.(1)证明:连接OA,∵OB=OA,∴∠OBA=∠OAB,∵AC切⊙O于A,∴OA⊥AC,∵BC⊥AC,∴OA∥BC,∴∠OBA=∠ABC,∴∠ABC=∠ABO;(2)解:过O作OD⊥BC于D,∵OD⊥BC,BC⊥AC,OA⊥AC,∴∠ODC=∠DCA=∠OAC=90°,∴OD=AC=1,在Rt△ACB中,AB=,AC=1,由勾股定理得:BC==3,∵OD⊥BC,OD过O,∴BD=DC=BC==1.5,在Rt△ODB中,由勾股定理得:OB==,即⊙O的半径是.4.如图,AB为⊙O的直径,C为⊙O上一点,经过点C的切线交AB的延长线于点E,AD⊥EC交EC的延长线于点D,连接AC.(1)求证:AC平分∠DAE;(2)若cos∠DAE=,BE=2,求⊙O的半径.(1)证明:连接OC,∵DE是⊙O的切线,∴OC⊥DE,∵AD⊥DE,∴OC∥AD,∴∠OCA=∠DAC,∵OA=OC,∴∠OCA=∠OAC,∴∠DAC=∠OAC,∴AC平分∠DAE;(2)解:设⊙O的半径为r,∵OC∥AD,∴∠DAE=∠COE,∴cos∠DAE=cos∠COE=,BE=2,∴=,解得:r=4,即⊙O的半径为4.5.如图a,AB为⊙O直径,AC为⊙O的为弦,PA为⊙O的切线,∠APC=2∠1.(1)求证:PC是⊙O的切线.(2)当∠1=30°,AB=4时,其他条件不变,求图b中阴影部分的面积.(1)证明:连结OC,在圆O中,OA=OC,∴∠BOC=2∠1=∠APC,∠BOC+∠AOC=180°,∴∠APC+∠AOC=180°,∵PA为⊙O的切线,∴∠OAP=90°又四边形内角和为360°,∴∠OCP=90°,OC为⊙O的半径,∴PC为⊙O的切线;(2)解:PA为⊙O的切线,PC为⊙O的切线.∴PA=PC,∵∠1=30°,∠APC=2∠1,∴∠APC=60°,∴△APC为等边三角形,连结OP,OC,∵S四边形AOCP =2××2×2=4,S扇形AOC=×π×4=π,∴S阴影部分的面积=4﹣π.6.如图,线段AB经过⊙O的圆心,交⊙O于A,C两点,BC=1,AD为⊙O的弦,连接BD,∠BAD=∠ABD=30°,连接DO并延长交⊙O于点E,连接BE交⊙O于点M.(1)求证:直线BD是⊙O的切线;(2)求切线BD的长;(3)求线段BM的长.(1)证明:∵∠BAD=∠ABD=30°,∴∠DOB=2∠BAD=60°,∴∠ODB=180°﹣30°﹣60°=90°,即OD⊥BD,∵OD过O,∴直线BD是⊙O的切线;(2)解:设OD=OC=r,在Rt△BDO中,sin30°==,解得:r=1,即OD=1,OB=1+1=2,由勾股定理得:BD==;(3)解:连接DM,∵DE是⊙O的直径,∴∠DME=90°,即∠DMB=∠BDE=90°,∵∠DBM=∠DBE,∴△BMD∽△BDE,∴∴,,解得:BM=.7.如图,四边形ABCD为⊙O的内接四边形,且AC为⊙O的直径,使得BE=AB,连接DE.(1)求证:AD=DE;(2)若DE为⊙O的切线,且DE=2,求的长度.=,延长BC到E,(1)证明:连接BD,∵=,∴∠ABD=∠DBE,∵AB=BE,BD=BD,∴△ABD≌△EBD(SAS),∴AD=DE;(2)解:连接OD,∵=,∴AD=CD,∵AD=DE,∴CD=DE,∵AC为⊙O的直径,∴∠B=∠ADC=90°,∵AD=CD,O为AC的中点,∴∠ODE=∠ADC=45°,∵DE为⊙O的切线,∴∠ODE=90,∴∠CDE=45°,∴∠ADE=90°+45°=135°,∵CD=DE,∴∠DCE=∠DEC=67.5°,∴∠BAD=67.5°,∵AD=CD,∠ADC=90°,∴∠DAC=45°,∴∠BAC=22.5°,∴AD=CD=2,∴AC=4,∴OC=2,∴的长度是=.8.如图,⊙O是△ABC的外接圆,AB是直径,OD⊥AC,垂足为D点,直线OD与⊙O相交于E,F两点,P是⊙O外一点,P在直线OD上,连接PA,PB,PC,且满足∠PCA=∠ABC (1)求证:PA=PC;(2)求证:PA是⊙O的切线;(3)若BC=8,,求DE的长.(1)证明∵OD⊥AC,∴AD =CD ,∴PD 是 AC 的垂直平分线,∴PA =PC ,(2)证明:由(1)知:PA =PC ,∴∠PAC =∠PCA .∵AB 是⊙O 的直径,∴∠ACB =90°,∴∠CAB +∠CBA =90°.又∵∠PCA =∠ABC ,∴∠PCA +∠CAB =90°,∴∠CAB +∠PAC =90°,即 AB ⊥PA ,∴PA 是⊙O 的切线;(3)解:∵AD =CD ,OA =OB ,∴OD ∥BC ,OD = BC ==4,∵= ,设 AB =3a ,DF =2a ,∵AB =EF ,∴DE =3a ﹣2a =a ,∴OD =4=﹣a ,a =8,∴DE =8.9.如图,C 是上的一定点,D 是弦 AB 上的一定点,P 是弦 CB 上的一动点,连接 DP ,将线段 PD 绕点 P 顺时针旋转 90°得到线段 PD ′,射线 PD ′与交于点 Q .已知 BC =6cm , 设 P ,C 两点间的距离为 xcm ,P ,D 两点间的距离为 y 1cm ,P ,Q 两点间的距离为 y 2cm .小石根据学习函数的经验,分别对函数 y 1,y 2 随自变量 x 的变化而变化的规律进行了探究,下面是小石的探究过程,请补充完整:(1)按照下表中自变量 x 的值进行取点、画图、测量,分别得到了 y 1,y 2 与 x 的几组对应值:x /cmy 1/cmy 2/cm4.290.88 13.332.84 23.57 31.654.04 41.224.17 51.503.20 62.240.98(2)在同一平面直角坐标系 xOy 中,描出补全后的表中各组数据所对应的点(x ,y 1), (x ,y 2),并画出函数 y 1,y 2 的图象;(3)结合函数图象,解决问题:连接 △D Q ,当DPQ 为等腰三角形时,PC 的长度约为 1.3或 5.7 cm .(结果保留一位小数)解:(1)观察图象发现规律可知:表格数据为:2.44;(2)如图所示:即为两个函数 y 1,y 2 的图象;(3)观察图象可知:两个图象的交点的横坐标即为△DPQ为等腰三角形时,PC的长度,两个交点的横坐标为1.3和5.7.故答案为:1.3或5.7.10.如图(1),某数学活动小组经探究发现:在⊙O中,直径AB与弦CD相交于点P,此时PA•PB=PC•PD(1)如图(2),若AB与CD相交于圆外一点P,上面的结论是否成立?请说明理由.(2)如图(3),将PD绕点P逆时针旋转至与⊙O相切于点C,直接写出PA、PB、PC之间的数量关系.(3)如图(3),直接利用(2)的结论,求当PC=,P A=1时,阴影部分的面积.解:(1)成立.理由如下:如图(2),连接AD、BC,则∠B=∠D∵∠P=∠P∴△PAD∽△PCB∴=∴PA•PB=PC•PD;(2)PC2=PA•PB理由如下:如图(3),连接BC,OC,∵PC与⊙O相切于点C,∴∠PCO=90°,∵AB是直径,∴∠ACB=90°∴∠PCA=∠OCB∵OC=OB∴∠OCB=∠OBC∴∠PCA=∠OBC∵∠P=∠P∴△PCA∽△PBC∴PC:PB=PA:PC∴PC2=PA•PB.(3)如图(3),连接OC,,PA=1∵PC2=PA•PB,PC=∴PB=3,AO=CO=1∴PO=2= ∵PC 与⊙O 相切于点 C ,∴△PCO 是直角三角形∴sin∠CPO ==∴∠CPO =30°,∠COP =60°∴△AOC 为等边三角形∴△S AOC=S 扇形 AOC ==∴S 阴影=S 扇形 AOC ﹣△S A OC=﹣ .11.在平面直角坐标系 xOy 中,已知点 A (0,2),点 B 在 x 轴上,以 AB 为直径作⊙C ,点 P在 y 轴上,且在点 A 上方,过点 P 作⊙C 的切线 PQ ,Q 为切点,如果点 Q 在第一象限,则称 Q 为点 P 的离点.例如,图 1 中的 Q 为点 P 的一个离点.(1)已知点 P (0,3),Q 为 P 的离点.①如图 2,若 B (0,0),则圆心 C 的坐标为(0,1) ,线段 PQ 的长为;②若 B (2,0),求线段 PQ 的长;(2)已知 1≤PA ≤2,直线 l : y =kx +k +3(k ≠0).①当 k =1 时,若直线 l 上存在 P 的离点 Q ,则点 Q 纵坐标 t 的最大值为6 ;②记直线 l :y =kx +k +3(k ≠0)在﹣1≤x ≤1 的部分为图形 G ,如果图形 G 上存在 P 的离点,直接写出 k 的取值范围.解:(1)①如图可知:C (0,1),在 Rt△PQC 中,CQ =1,PC =2,∴PQ = ,故答案为(0,1);;②如图,过C作CM⊥y轴于点M,连接CP,CQ.∵A(0,2),B(2,0),∴C(1,1).∴M(0,1).在Rt△ACM中,由勾股定理可得CA=∴CQ=.∵P(0,3),M(0,1),∴PM=2.在Rt△PCM中,由勾股定理可得PC=..在Rt△PCQ中,由勾股定理可得PQ=(2)①如图1:当k=1时,y=x+4,∴Q(t﹣2,t),∴CQ=,当t=2时,CQ最大,=.在Rt△CDQ中,CD=,CQ最大则DQ最大,∴Q(2,6),故答案为6;②∵﹣1≤x≤1,Q点的在端点(﹣1,3)和(1,2k+4)之间运动,当Q在(1,2k+4),P(0,4)时,直线PQ的解析式y=(2k﹣1)x+4,点C(1,1)到直线PQ的距离为∴0<k<4.时,可得k=0或k=4,12.已知AB为⊙O的直径.(1)如图a,点D为(2)如图b,点D为(3)如图c,点D为的中点,当弦BD=AC时,求∠A.的中点,当AB=6,点E为BD的中点时,求OE的长.上任意一点(不与A、C重合),若点C为的中点,探求BD、AD、CD之间的数量关系,直接写出你探求的结论,不要求证明.解:(1)如图1,连结OC,点D为∴=的中点,═,∵弦BD=AC,∴∴∴=═=,=═,即点C为的中点.∠A=∠COB=××180°=30°.(2)如图2,连结OD,BC,OD交AC于点F,AB为⊙O的直径,∴∠C=90o点D为的中点,半径OD所在的直线为⊙O的对称轴,则点A的对应点为C,∴OD⊥AC,OD平分AC,即:AF=CF,在△DEF和△BEC中,,∴△DEF≌△BEC(AAS),∴CE=EF,BC=DF,∵AO=BO,AF=CF,∴OF=BC=DF,又AB=6,∴OD=3∴OF=1,BC=DF=2.在Rt△ABC中,AB=6,BC=2,∴AC===4,∵点F为AC的中点,点E为FC的中点∴EF=,在Rt△OFE中,EF=∴OE==,OF=1,=.(3)BD、AD、CD之间的关系为:BD﹣AD=如图3,连接BC,OC,CD,∵AB为⊙O的直径,点C为的中点,∴∠ACB=90°,AC=BC,∴∠BAC=∠BDC=45°,过点C作CF⊥CD交BD于点F,∴△DCF是等腰直角三角形,∴,∵∠ACD=∠BCF=90°﹣∠ACF,又∵AC=BC,CD=CF∴△ACD≌△BCF(SAS),∴AD=BF,∵BD=BF+DF,∴BD=AD+即BD﹣AD=CD,CD.13.如图,在△ABC中,AB=AC,∠A=30°,AB=10,以AB为直径的⊙O交BC于点D,交AC于点E,连接DE,过点B作BP平行于DE,交⊙O于点P,连接CP、OP.(1)求证:点D为BC的中点;(2)求AP的长度;(3)求证:CP是⊙O的切线.解:(1)BD=DC.理由如下:如图1,连接AD,∵AB是直径,∴∠ADB=90°,∴AD⊥BC.(2)如图1,连接AP.∵AD是等腰△ABC底边上的中线,∴∠BAD=∠CAD,∴=,∴BD=DE.∴BD=DE=DC,∴∠DEC=∠DCE,△ABC中,AB=AC,∠A=30°,∴∠DCE=∠ABC=(180°﹣30°)=75°,∴∠DEC=75°,∴∠EDC=180°﹣75°﹣75°=30°,∵BP∥DE,∴∠PBC=∠EDC=30°,∴∠ABP=∠ABC﹣∠PBC=75°﹣30°=45°,∵OB=OP,∴∠OBP=∠OPB=45°,∴∠BOP=90°.∴△AOP是等腰直角三角形.∵AO=AB=5.∴AP=AO=5;(3)解法一:设OP交AC于点G,如图1,则∠AOG=∠BOP=90°,在Rt△AOG中,∠OAG=30°,∴又∵=,==,∴∴==,.又∵∠AGO=∠CGP,∴△AOG∽△CPG,∴∠GPC=∠AOG=90°,∴OP⊥PC,∴CP是⊙O的切线;解法二:如图2,作CM⊥AB于M,∵∠BOP=90°,∴CM∥OP,∵OP=AB,在Rt△AME中,∵∠BAC=30°,可∴CM=AC,∴CM=AB,∴CM=OP,∴四边形OPCM是矩形,∴∠CPO=90°,∴CP是圆O的切线.14.如图,⊙O的半径为,AB是⊙O的直径,F是⊙O上一点,连接FO、FB.C为劣弧的中点,过点C作CD⊥AB,垂足为D,CD交FB于点E,CG∥FB,交AB的延长线于点G.(1)求证:CG是⊙O的切线;(2)连接BC,若BC∥OF,如图2.①求CE的长;②图中阴影部分的面积等于2π.(1)证明:如图1,连接CO.∵C是的中点,∴∠BOC=∠FOC.又∵OF=OB,∴OC⊥BF.∵CG∥FB,∴OC⊥CG.∴CG是⊙O的切线.(2)①∵OF∥CB,∴∠AOF=∠OBC,∠COF=∠OCB.∵OC=OB,∴∠OCB=∠OBC.∴∠AOF=∠COF=∠BOC=60°.∴△OBC是等边三角形.∵CD⊥OB,OC⊥BF,∴点E是△OBC的重心.∴CE=2ED=CD.又∵⊙O的半径为,∴可求得:CD=OC•sin60°=2×=3,DE=1,∴CE=2;.②故答案是:2π.。
杭州专版2022中考英语决战中考限时许九精练本A本课件

A.The designers are proud of their work about Pepper.
B.Pepper has already been in use in the operation rooms.
C.Pepper's inner speech depends on its user's communication skills.
D.With or without inner speech,Pepper could complete a task equally well.
二、完形填空。(共15分) Pennsylvania is one of the oldest states in America,and it's full of
However,some people find the robot spends more time completing tasks when it talks to itself.The robot's inner speech is also limited to the knowledge that researchers gave it.Pepper's designers still say their work provides a framework(构架) to further explore how self-dialogue can help robots focus, plan,and learn.“In some ways,we are creating a generational(世代的) robot that likes to chat.From navigation apps and the camera on your phone to medical robots in the operation rooms,machines and computers alike can take advantage of this chatty feature,”says Chella.
浙江专版中考英语限时许六课件

Chase Burton,33,a deaf film-maker from Texas,US,has been testing out the suit for four years.He understands that a deaf person's experience with music is very different.“When I was a kid,I'd lie on the floor so I could feel the vibrations from my brother's music playing.”Burton told CNN.Now when he wears the vibrating suit,he says the sound hits different parts of his body. “Maybe it will shake me strongly in my knees first.And then I'll start to feel the vibrations in my back.And then I'll feel some pulsations.”Burton said.
“Well done,Tom!”said the teacher.“Now boys,let us give a good cheer for Tom and the snail on the wall.”The classroom rang with a great 15 . Everyone was glad that “Slow Tom” won the prize at last.
决战中考:初中化学浓硫酸的性质

决战中考:初中化学浓硫酸的性质决战2019中考:初中化学浓硫酸的性质(一)物理性质纯硫酸是一种无色油状液体。
常用的浓硫酸中H2SO4的质量分数为98.3%,其密度为1.84g?cm-3,其物质的量浓度为18.4mol?L-1。
硫酸是一种高沸点难挥发的强酸,易溶于水,能以任意比与水混溶。
浓硫酸溶解时放出大量的热,因此浓硫酸稀释时应该“酸入水,沿器壁,慢慢倒,不断搅。
”(二)特性1.吸水性将一瓶浓硫酸敞口放置在空气中,其质量将增加,密度将减小,浓度降低,体积变大,这是因为浓硫酸具有吸水性。
⑴就硫酸而言,吸水性是浓硫酸的性质,而不是稀硫酸的性质。
⑵浓硫酸的吸水作用,指的是浓硫酸分子跟水分子强烈结合,生成一系列稳定的水合物,并放出大量的热:H2SO4 + nH2O == H2SO4nH2O,故浓硫酸吸水的过程是化学变化的过程,吸水性是浓硫酸的化学性质。
⑶浓硫酸不仅能吸收一般的游离态水(如空气中的水),而且还能吸收某些结晶水合物(如CuSO4?5H2O、Na2CO3?10H2O)中的水。
2.脱水性⑴就硫酸而言,脱水性是浓硫酸的性质,而非稀硫酸的S + 2H2SO4(浓) === 3SO2↑ + 2H2O2P + 5H2SO4(浓) === 2H3PO4 + 5SO2↑ + 2H2O⑶跟其他还原性物质反应浓硫酸具有强氧化性,实验室制取H2S、HBr、HI等还原性气体不能选用浓硫酸。
H2S + H2SO4(浓) === S↓ + SO2↑ + 2H2O2HBr + H2SO4(浓) === Br2↑ + SO2↑ + 2H2O2HI + H2SO4(浓) === I2↑ + SO2↑ + 2H2O。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
决战中考限时小卷(七)(时间:45分钟分值:50分)一、完形填空。
(共15分)There was a time when I thought my dad didn't know how to be a good father. I couldn't 1 him ever saying the words “I love you”. It seems to me his only purpose in life was to say “No” to anywhere I wanted to go and anything I wanted to do,including getting a 2 . Some parents bought their kids cars when they got their driver's licenses. Not my dad— he said that I'd have to get a job and buy my own.So that is what I did. I got a job at a very nice restaurant and 3 every penny I could and when I had enough to buy my car,I did!The day I brought that car home,my dad was the first one I wanted to 4 it off to. “Look,Dad,a car of my own. If you ever want a ride,I'll only charge you five dollars. ” I offered with a smile. “I see” was all he said.One day,there was 5 wrong with my father's truck. So he needed a 6 to work. The sun wasn't even up when we left the house,7 it was already getting warm out. It was going to be a(n) 8 day. As I dropped my dad off. I watched him,dressed in his work clothes,getting his 9 from the trunk(车尾箱) of my car. Watching his sunweathered face,and even from a distance I could tell there were 10 lines than I ever remembered being there before. I realised how hard my dad works for the family. My father is a cement finisher(水泥修整工).In that instant,it occurred to me that he actually got down on his hands and knees to sweat over hot concrete(混凝土) to make a 11 for his family. And he did this day in and day out,however hot it got. Never,not once,had I heard him 12 about it. To him,we were“worth”it. And never once did he “charge” us for it.When he closed the trunk,his tools set off to the side,he walked over to my window to 13 me five dollars. I rolled down the window and said, “Goodbye,Dad. Keep your five dollars. It's my treat. Don't work too hard. I love you. ”His 14 met mine,then glanced away in the direction of his waiting tools,he 15 his throat(喉咙) and said, “Oh,and... me too. ”( B )1. A.like B.remember C.forget D.care( A )2. A.car B.friend C.job D.present( D )3. A.spent B.earned C.kept D.saved( D )4. A.kick B.take C.turn D.show( B )5. A.everything B.something C.nothing D.anything( A )6. A.ride B.leave C.trip D.hurry( C )7. A.as B.although C.but D.however( B )8. A.warm B.hot C.work D.special( A )9. A.tools B.clothes C.luggage D.bag( B )10. A.fewer B.more C.longer D.deeper( D )11. A.live B.alive C.lively D.living( B )12. A.talk B.complain C.ask D.speak( A )13. A.hand B.pass C.lend D.take( D )14. A.hands B.smile C.voice D.eyes( C )15. A.cleaned B.coughed C.cleared D.felt二、阅读理解。
(共10分)(2019温州市初中毕业适应性试卷)Researchers at Stanford University have developed a new material that can move heat out of buildings and into space. Theresearchers say the material can cool buildings even on hot days.The cooling material is a very thin board with many layers that could be placed on a roof like solar panels(板). However,instead of turning sunlight into energy as solar panels do,the material turns heat into radiation. Shanhui Fan is an electrical engineering professor at Stanford University. He says that the panels have a layer of material that is like sand and they act like a mirror,taking heat out of buildings and reflecting the light from the sun. He also says both the heat and sunlight are sent 100 kilometres into outer space. It's a structure that cools itself without electricity input,even in the sun. So,what it does is basically radiating(发散) heat to outer space and also reflecting the sunlight so it doesn't get heated up by the sun. Mr Fan says, “It is like having a window into space. The heat is sent directly into space without warming the air. ”He says buildings in developing countries that do not have electricity or air conditioning(空气调节) could use the panels. “In areas where electricity is out of reach for many people,there is a benefit for storing medicine or even food. In many of these situations,being able to reduce the temperature is important. And this would provide a way to do it. ”The Stanford researchers described their technology in the science publication Nature. The researchers say the main problem is creating actual cooling systems using the hightech panels. They say it may be possible to develop a cooling spray(喷涂) that could be used on present solid structures. They believe the cooling spray technology could be developed in the next three to five years. They say as much as 15 percent of the energy used in the United States is spent providing power to air conditioning systems.( D )16. The underlined word “reflecting” in Paragraph 2 probably means .A.turning off B.focusing onC.finding out D.throwing back( A )17. How does the new material work?A.It sends heat away right into space.B.It has a window to let out the heat.C.It takes in the heat and cools it down.D.It uses a mirror to cut off the sunlight.( D )18. What does the last paragraph mainly discuss?A.The various uses of cooling materials.B.The characteristics of cooling technology.C.The main problems with cooling technology.D.The future development of cooling technology.( B )19. Which of the following shows the structure of the whole text?三、词汇运用。
