结构的动力学计算
结构力学常用的3种计算方法

结构力学常用的3种计算方法
结构力学是研究物体在外力作用下的变形和破坏规律的学科。
在结构力学中,常用的计算方法有三种,分别是静力学方法、动力学方法和有限元方法。
静力学方法是结构力学中最基本的计算方法之一。
它是通过分析物体在静力平衡状态下的受力情况,来计算物体的变形和破坏情况。
静力学方法适用于简单的结构体系,如梁、柱、桥梁等。
在静力学方法中,常用的计算工具有受力分析、弹性力学、杆件理论等。
动力学方法是结构力学中另一种常用的计算方法。
它是通过分析物体在动力平衡状态下的受力情况,来计算物体的变形和破坏情况。
动力学方法适用于复杂的结构体系,如飞机、汽车、船舶等。
在动力学方法中,常用的计算工具有振动分析、动力学理论、有限元方法等。
有限元方法是结构力学中最常用的计算方法之一。
它是通过将物体分割成许多小的单元,然后对每个单元进行分析,最后将所有单元的分析结果综合起来,来计算物体的变形和破坏情况。
有限元方法适用于各种结构体系,无论是简单的还是复杂的。
在有限元方法中,常用的计算工具有有限元分析软件、数值计算方法、计算机模拟等。
结构力学中的三种计算方法各有优缺点,应根据具体情况选择合适的方法进行计算。
静力学方法适用于简单的结构体系,动力学方法
适用于复杂的结构体系,有限元方法则适用于各种结构体系。
在实际工程中,常常需要综合运用这三种方法,以得到更加准确的计算结果。
结构动力学

m ∆t2
+
c 2∆t
⎞⎠⎟ui+1
=
pi
−
⎛ ⎝⎜
k
−
2m ∆t2
⎞⎠⎟ui
−
⎛ ⎝⎜
m ∆t2
−
c 2∆t
⎟⎞⎠ui−1
中心差分法的数值稳定性证明
设体系为无阻尼,并设外荷载p=0 (算法的稳定性与外荷载无关),则 中心差逐步积分法的递推公式可以写成如下形式:
u&0
=
u1 − u−1 2∆t
u&&0
=
u1
−
2u0 + u−1 ∆t 2
u−1
=
u0
−
∆tu&0
+
∆t 2 2
u&&0
u&&0
=
1 m
(
p0
−
cu&0
−
ku0 )
⎛
5中.3心中差心分差法分计法算步骤:⎜⎝
m ∆t 2
+
c 2∆t
⎞ ⎟⎠
ui
+1
=
pi
−
⎛ ⎜⎝
k
−
2m ∆t 2
⎞ ⎟⎠
ui
−
⎛ ⎜⎝
u&(τ ) = A1 + (ωD A3 − ζωn A2 )e−ζωnτ cosωDτ − (ωD A2 + ζωn A3 )e−ζωnτ sin ωDτ
其中,
A0
=
pi k
− 2ζαi kωn
,
A1
=
αi
k
,
A2 = ui − A0,
结构动力学基础

m l/ 5
m l/ 5
m l/ 5
m l/ 5
0
1
2
3
4
5
l/5
0
l/5
1y = 1 1 φ1(x) 2
l/5
3
l/5
4
l/5
5
0
2 θ1 = 1 1 φ (x) 2
3
4
5
如图10-9a中,梁分为5个单元,取结点位移参数(挠度y 和转角θ)作为 广义坐标。在图10-9a中取中间四个结点的八个位移参数 y1、θ1,y2、θ2,y3、 θ3,y4、θ4 作广义坐标。
T
sin t
(10 3)
(10 4)
0 -y y T
t
y cos t
v v
y A
0
t
v
sin t
T t
0
A sin t
-A
3、结构的自振周期
由式
A
y (t ) A sin(t ) 及图,可见位移方程是一个周期函数。 2 y T 周 期: T
⑶ 是结构动力特性的重要数量标志。
泛美大厦,60层 钢结构,南北方向 的基本固有周期为 2.90秒,
大坝,400英尺高的混凝土重力坝的基 本固有周期由强迫振动试验测得在蓄水 为310英尺和345英尺十分别为0.288秒 和0.306秒,
金门大桥,金门大桥桥墩跨距1280.2米全桥总 长2737.4米的悬索桥,其横向振动的基本基本固 有周期为18.20秒,竖向振动的基本基本固有周期 为10.90秒,纵向振动的基本基本固有周期为3.81 秒,扭转振动的基本基本固有周期为4.43秒
结构力学-第十四章 结构动力学1

动的合成,为了便于研究合成运动,
令 (e)式改写成
y Asin,
v Acos
y(t) Asin( t )......... .......... ...( f )
它表示合成运动仍是一个简谐运动。其中A和可由下式确定
振幅
A
y2
v
2
.............................(g
由初始条件确定C1和C2;
设
y(0)
y(0)
y v
得 C1 y
C2
v
y r
y(t)
e t
( y
cos r t
v
r
y
sin rt)
21
y(t)
e t
(
y
cos r t
v
r
y
sin
rt
)
y(t) et Asin( rt )
2
其中
A
y2
v
y r
tg1 r y
v y
y
讨论(:a)衰减周期运动
m获得初位移y
m获得初速度 y
研究单自由度体系的自由振动重要性在于: 1、它代表了许多实际工程问题,如水塔、单层厂房等。 2、它是分析多自由度体系的基础,包含了许多基本概念。 自由振动反映了体系的固有动力特性。
要解决的问题包括:
建立运动方程、计算自振频率、周期和阻尼………. 9
一、运动微分方程的建立
(1)低阻尼情形 ( <1 )
1,2 i 1 2 , 令 r 1 2
y(t)
B e( ir )t 1
B e( ir )t 2
eix cos x i sin x
et (B1eirt B2eirt ) eix cos x i sin x
大规模结构动力学有限元并行计算

大规模结构动力学有限元并行计算1.引言大规模结构动力学有限元并行计算是在计算机技术不断进步的背景下,为了提高结构动力学有限元模拟的计算效率而诞生的技术手段。
随着计算机性能的不断提升,结构动力学有限元模拟的计算需求越来越强,对于传统的串行计算方式已经不能满足要求。
因此,并行计算成为大规模结构动力学有限元模拟的重要手段,对于提高计算效率,缩短计算时间、优化计算结果等方面都有着重要作用。
2.大规模结构动力学计算的特点大规模结构动力学有限元模拟计算其主要特点就是计算规模大、时间长,数据量大、数据处理复杂等方面的特点。
传统的串行计算方式将计算任务划分为多个小任务一步步完成,但是随着计算规模的不断扩大,计算时间变得越来越长,而且CPU处理的数据量也越来越大,数据复杂度也不断提高。
因此串行计算的效率日益降低,这时并行计算成为了必不可少的解决方式。
3.并行计算的优点并行计算使得多个CPU可以同时运行计算程序,计算任务可以分割为多个小任务分配给不同的CPU同时处理,以提高计算效率。
并行计算的另一个优点是,可以充分利用计算机内存,以最大化地提高计算机的计算能力。
并行计算的设计主要需要解决两个问题,第一个问题是如何将计算任务分割为多个小任务,第二个问题是如何有效地协调多个CPU之间的计算任务。
4.并行计算的应用大规模结构动力学有限元并行计算技术的应用领域非常广泛,主要适用于几何复杂、物理特性复杂的结构物动力学问题,是风洞试验、现场试验等一些实验手段无法解决的问题,如飞行器、高速列车、大型工程结构物等动态响应和破坏性分析等。
并行计算技术帮助用户可以通过一种虚拟试验的方式,不断调整和优化结构的设计,以提高结构的性能和安全性。
5.并行计算的挑战虽然并行计算的优点非常明显,但是并行计算的应用也存在着一些比较明显的挑战。
首先,分割任务分配给不同的CPU之后,需要考虑先后顺序和数据的传输,因此需要设计一些特殊的数据传输方式和计算协调方式;其次,并行计算的算法需要进行特殊优化以充分发挥计算机的性能;最后,并行计算的系统设计需要考虑大规模并发操作带来的瓶颈和性能损失。
结构动力学有限元混合分层并行计算方法

结构动力学有限元混合分层并行计算方法结构动力学是研究结构在外界载荷作用下的响应及其稳定性的一门学科。
有限元方法是结构动力学分析中广泛使用的一种数值方法。
为了提高计算效率和精度,混合分层并行计算方法应运而生。
混合分层并行计算方法是指将有限元方法与分层并行计算相结合的一种计算方法。
在结构动力学中,混合分层并行计算方法被广泛应用于解决大型结构的复杂动力学问题。
它通过将结构进行分层划分,将计算任务分配给不同的处理器进行并行计算,从而大幅提高计算速度和效率。
混合分层并行计算方法的基本思想是将结构分为多个子结构,并将每个子结构分配给一个处理器进行计算。
每个处理器独立地计算与其对应的子结构,然后通过通信机制将计算结果交换,并进行整体求解。
这种并行计算方法充分利用了计算机集群的计算能力,提高了计算效率。
在混合分层并行计算方法中,有限元方法被用于对每个子结构进行离散化,并建立相应的有限元模型。
有限元模型中的自由度数目较少,计算量相对较小,可以降低计算复杂度。
同时,分层并行计算策略使得计算任务可以被同时执行,加速了计算速度。
混合分层并行计算方法的应用范围广泛。
例如,在工程领域中,可以用于模拟大型桥梁、高层建筑等结构的动力学响应;在航空航天领域中,可以用于模拟飞机、卫星等复杂结构的动力学特性;在地震工程中,可以用于模拟地震对建筑物的影响等。
混合分层并行计算方法可以准确预测结构的振动特性、动态响应和破坏过程,为结构设计和分析提供了有力的工具。
总之,结构动力学有限元混合分层并行计算方法是一种高效、准确的计算方法。
它通过将结构进行划分和并行计算,充分利用计算机集群的计算能力,实现了大规模结构动力学分析的快速求解。
混合分层并行计算方法在工程领域中的应用潜力巨大,有着广阔的发展前景。
结构动力学习题解答

然后积分求初始速度
̇̇ d t = θ̇0 = θ 0
0+ 0+ 0+
∫
0
∫ hδ ( t ) d t = h ∫ δ ( t ) d t = h
0 0 0+
;
再积分求初位移
̇̇ d t == h )d t = 0 ; θ0 = θ 0
0+
∫
0
∫
0
̇̇ 、 θ̇ 和 θ 的瞬态响应 这样方程(6)的解就是系统对于初始条件 θ 0 0 0
1.6 求图 1-35 所示系统的固有频率。图中磙子半径为 R,质量为 M,作纯滚动。弹簧刚度 为K 。 解:磙子作平面运动, 其动能 T=T 平动 +T 转动 。
K R M 图 1-35 x
T平动 = T转动
1 ̇2; Mx 2 2 2 ̇ ⎞ 1 ⎛ MR 2 ⎞ ⎛ x ̇⎞ 1 ⎛x = I⎜ ⎟ = ⎜ ⎟⎜ ⎟ ; 2 ⎝R⎠ 2 ⎝ 2 ⎠⎝ R ⎠
U= r 2 1 1 1 1⎛ K A ϕ A 2 + K B ϕ B 2 = K Aϕ A 2 + K B ϕ B 2 = ⎜ K A + K B A 2 2 2 2 2⎜ rB ⎝
(
)
⎞ 2 ⎟ϕ ; ⎟ A ⎠
系统的机械能为
T +U = r 2 1 1⎛ ̇ A2 + ⎜ K A + K B A (m A + m B )rA 2ϕ 4 2⎜ rB 2 ⎝
d (T + U ) = 0 ,进一步得到系 dt
统的运动微分方程; (3) 求解该方程所对应的特征方程的特征根,得到该系统的固有频率。 1.2 叙述用衰减法求单自由度系统阻尼比的方法和步骤。 用衰减法求单自由度系统阻尼比的方法有两个:衰减曲线法和共振法。 方法一:衰减曲线法。 求解步骤: (1)利用试验测得单自由度系统的衰减振动曲线,并测得周期和相邻波峰和波谷 的幅值 Ai 、 Ai +1 。 (2)由对数衰减率定义 δ = ln(
结构动力学问题的有限元法

K Q
K Q
对于结构动力学问题,节点载荷阵还包括惯性力和阻尼力。
e e e K Q (M C ) e e 1 m
或改写为:
C K M Q
代入:
dV Q N u
T T T
M N N dV
dV N N
e T
e
e dV Q N u
e T T
N N dV C
其中:
M M C C
e
e
质量阵和阻尼阵的叠加方法与刚度阵的叠加方法相同,也 是对称稀疏阵。
三、动力方程的简化
M e N T N dV
称为一致质量矩阵,是稀疏带状阵。
如果将单元质量阵近似作为对角阵,则方程变成彼此独立,避免 联立,称为集中质量阵或团聚质量阵。 解耦 例如长度为L,截面积为A,密度为ρ的梁单元。 i
A,ρ
L
j
x
1 A L 0 集中质量阵: m 2 0 0
0 0 0 0
0 0 1 0
0 0 0 0
156 22L 22L 2 一致质量阵: 4 L AL m 13L 420 54 2 13 L 3 L
54 13L 13L 3L2 156 22L 2 22L 4 L
ˆ P K P K
T
在变换[K]和[M]的过程中,有时使用一次雅克比变换将一个 非对角线元素化为零以后,它在另一次变换中会重新变为非零 元素,但在素质上有所减小。这说明需要反复使用雅克比变换, 最终非对角线元素将趋于零。 在实际求解过程中,不必严格地把矩阵[K]和[M]所有的非对 角线元素变换为零,通常在完成一次变换后进行判断是否达到预 l 1 (l ) 设的精度:
结构动力学-3

代入方程,可得 P A m( 2 2 ) 通解为 P y(t ) c1 cos t c2 sin t sin t 2 2 m( )
若
y(0) 0, y(0) 0
c1 0
P c2 1 2 k
---频率比
l
P
EI
yst
/
P (t )
n n
cn e
int
1 cn TP
TP
0
P(t )e int dt
求简谐扰力
cn e int 的反应
2y 2 y eit / m y
n为奇数 n为偶数
2 P0 / n 1 a0 y (t ) [ sin nt ] 2 k 2 n 1、、 1 n 3 5
2 P0 / n 1 a0 y (t ) [ sin nt ] 2 k 2 n 1、、 1 n 3 5
n n /
1 应使频比增大.
减小结构自频. 减小刚度、增大质量.
0
0
P 1 y (t ) sin t P(t ) 2 2 m m
二.阻尼体系 运动方程及其解 m cy k11 y P sin t y P 2 y 2 y sin t 或 y m * 通解 y(t ) y (t ) y (t )
有阻尼时
1 a0 y (t ) n [an cos( nt n ) bn sin( nt n )] k 2 n 1
n
1
2 (1 n ) 2 ( 2n ) 2
tan n
2n 2 1 n
---谐波分析法(调和分析、频域分析)
结构动力学使用中心差分法计算单自由度体系动力反应的MATLAB程序

中心差分法计算单自由度体系动力反映的报告前言基于叠加原理的时域积分法与频域积分法一样,都假设结构在在全部反应过程中都是线性的。
而时域逐步积分法只是假设结构本构关系在一个微小的时间步距内是线性的,相当于分段直线来逼近实际的曲线。
时域逐步积分法是结构动力问题中研究并应用广泛的课题。
中心差分法是一种目前发展的一系列结构动力反应分析的时域逐步积分法的一种,时域逐步积分法还包括分段解析法、平均常加速度法、线性加速度法、Newmarket−β和Wilson−θ法等。
中心差分法(central difference method)原理中心差分法的基本思路将运动方程中的速度向量和加速度向量用位移的某种组合来表示,将微分方程组的求解问题转化为代数方程组的求解问题,并在时间区间内求得每个微小时间区间的递推公式,进而求得整个时程的反应。
中心差分法是一种显示的积分法,它基于用有限差分代替位移对时间的求导(即速度和加速度)。
如果采用等时间步长,∆t i=∆t(∆t为常数),则速度与加速度的中心差分近似为u i=u i+1+u i−12∆t(1)üi=u i+1−2u i+u i−1∆t2(2)用u表示位移,离散时间点的运动为:u i=u(t i),u i=u̇(t i),u i=ü(t i)(i=0,1,2…)体系的运动方程为mü(t)+cu̇(t)+ku(t)=P(t)(3)将速度和加速度的差分近似公式(1)和(2)代入(3)中得出在t i时刻的运动方程,将方程整理得到u i+1由u i 和u i−1表示的两步法的运动方程(4):(m ∆t2+c2∆t)u i+1=P i−(k−2m∆t2)u i−(m∆t2−c2∆t)u i−1(4)这样就可以根据t i及以前的时刻的运动求得t i+1时刻的运动。
中心差分法属于两步法,用两步法计算时存在起步问题,必须要给出相邻的两个时刻的位移值,才能逐步计算。
对于地震作用下结构的反应问题和一般的零初始条件下的动力问题,可以用(4)直接计算,因为总可以假设初始的两个时间点(一般取i=0,−1)的位移等于零。
结构动力学(无限自由度)

解:边界条件引入振幅曲线
左边: Y 0 0,Y0 0
得: C1 C3 0
振幅曲线简化为
Y x C2 sinh x C4 sin x 右边: Y l 0,Yl 0
C2 sinh l C4 sin l 0 C2 sinh l C4 sin l 0
令系数行列式=0
sinh l sin l
T t 2T t 0
Y IV x 4Y x 0
4 2m
EI
2 EI
m
两个方程的解分别为
T t asint
Y x C1 cosh x C2 sinh x C3 cosx C4 sin x
C1——C4由边界条件确定
则,振动方程的解为
yx,t Y xsint
例 14-5 试求等截面简支梁的自振频率和主振型。
1
Ep 2
EI
n i 1
aii
2
dx
2
2
m
n 1
aii
2
dx
令
kij EIi jdx,mij mi jdx
得
Ep
1 2
n i 1
n j 1
kij 2mij
aia j
应用驻值条件 Ep 0 ai
i 1,2, ,n
得
n
等截面梁弯曲时的静力平衡方程为
EI
d4 y dx4
q
在自由振动时,唯一的荷载就是惯性力,即
q
m
2 t
y
2
因此,等截面梁弯曲时的自由振动方程为
EI
4 y x4
m
2 y t 2
0
用分离变量法求解,令
yx,t Y xT t
代入振动方程,并整理得
结构动力学计算

变化,且作相位相同的同步运动,即它们在同一时刻均达极值;
➢ 由于在运动的任一瞬时质体都处于平衡状态,于是可在幅值
处建立运动方程,此时方程中将不含时间t,把微分方程转化为
代数方程,使计算得以简化。
例7. 求图示体系的自振频率
m1 m
B
EI C
m2
1 3
m
m l22kl2
A
0 .5 l
l
kD 0 .5 l
在质量上沿位移方向施加惯性力; 求外力(包括惯性力)引起的质量的位移; 令该位移等于体系的位移;
例2. 用柔度法建立体系的运动方程
m
l EI EI
l
O
y
my y
ym y
my 1 y 0
2l 3
11 3EI
my(t)32E l3Iy(t)0
P=1
图乘法
?
l
例3:用柔度法列运动方程
m y(t)
12 EI h3
6 EI h2
1
6 EI
k
h2
12 EI
h3
6 EI h2
k m
24EI mh3
T 2
练习3:计算图示结构水平振动和竖直振动时 的自振 频率,自重忽略不计。
m
EI常 数
l
l
l
Horizontal Vibration: -----Flexibility Method
Anti-symmetrical Load +symmetrical Structure
✓ 自振频率计算公式
k m
1
m
tan1
y
0 0
v
0
✓ 计算k或δ:静力学知识 l 3 1 8EI
10结构动力学概论

当 FP (t)为简谐荷载时,其解的形式为
第十章 结构动力学简介
y(t)
y0
cos ωt
ν0 ω
sin ωt
F
θ sin ωt
F
sin θt
m(ω2 θ 2 ) ω
m(ω2 θ 2 )
前两项为初始条件引起的自由振动;第三项为荷载(干扰力)引起的自由振 动,称为伴生自由振动。实际上,由于阻尼的存在,自由振动部分都很快 衰减掉。自由振动消失前的振动阶段称为过渡阶段。第四项为按荷载频率 进行的振动,此阶段为振动的平稳阶段,称为纯受迫振动或稳态振动。
2、平衡方程的建立
平衡方程的建立有两种方法:一是刚度法;一是柔度法。
my
y k
k
m
刚度法:根据达兰贝尔原理,沿位移正向,在质点上加上惯性力,列动态平 衡方程
ky my
k y ——总是与位移方向相反,指向平衡位置
平m衡y 方—程—与加速m度y方向相k反y 0
第十章 结构动力学简介
柔度法:在惯性力作用下,质点的位移等于实际位移
结构力学
STRUCTURAL MECHANICS
第十章 结构动力学简介
§10-1 概述
一、动力计算的内容
动力计算的内容:研究结构在动荷载作用下的动力反应的计算原理和方法。 涉及到内外两方面的因素: 1)确定动力荷载(外部因素,即干扰力); 2)确定结构的动力特性(内部因素,如结构的自振频率、周期、振型和 阻尼等等),类似静力学中的I、S等; 计算动位移及其幅值;计算动内力及其幅值。
纯受迫振动解的讨论请同学们课下自学完成!
第十章 结构动力学简介
三、阻尼对振动的影响
§10-3 单自由度体系的振动分析
结构力学的动力响应分析

结构力学的动力响应分析结构力学是研究物体在受力下产生变形和破坏的学科,而动力响应分析是结构力学的一个分支,专注于分析结构在动力载荷下的响应行为。
动力响应分析是工程领域中非常重要的研究内容之一,在设计和评估建筑物、桥梁、飞机等结构时起着关键作用。
本文将介绍结构力学的动力响应分析的基本原理和常用方法。
1. 动力响应分析的基本原理动力响应分析是基于动力学原理,通过建立结构的动力学方程,求解结构在动力载荷下的响应。
根据牛顿第二定律,结构的动力学方程可以描述为:m*a + c*v + k*u = F其中,m是结构的质量矩阵,a是结构的加速度,c是结构的阻尼矩阵,v是结构的速度,k是结构的刚度矩阵,u是结构的位移,F是结构的外力。
通过求解动力学方程,可以得到结构的加速度、速度和位移响应。
2. 动力响应分析的常用方法在实际应用中,有多种方法可以进行动力响应分析,下面介绍两种常用的方法:模态分析和时程分析。
2.1 模态分析模态分析是一种线性分析方法,通过求解结构的固有值和固有向量来描述结构的振动特性。
首先,通过求解结构的本征值问题,得到结构的固有值和固有向量。
然后,根据输入的外载荷,通过模态叠加的方法计算结构的动力响应。
模态分析适用于求解结构的频率响应和模态形态,对于周期性动力载荷较为有效。
2.2 时程分析时程分析是一种非线性分析方法,基于结构的动力学方程和具体的外载荷时程,通过数值积分的方法求解结构的动力响应。
时程分析可以模拟结构在任意形式的非线性动力载荷下的响应,适用于研究地震荷载、爆炸荷载等非周期性动力载荷。
3. 动力响应分析的应用动力响应分析在工程实践中有广泛的应用,下面列举几个常见的应用领域。
3.1 地震工程地震是一种非常具有破坏性的动力载荷,对结构的安全性和可靠性提出了极高的要求。
动力响应分析可以用于评估结构在地震荷载下的响应,进而指导地震设计和加固措施。
3.2 桥梁工程桥梁是承受交通载荷和风载等多种动力载荷的结构,其动力响应分析可以用于评估桥梁的振动稳定性、疲劳寿命等性能,指导桥梁的设计和检测。
结构力学应用-结构动力学

(小阻尼) 令
有阻尼的自振频率
1
2
y(t ) e
t
y0 y0 ( y0 cos t sin t )
*写成
y(t ) b e
2 0
t
sin(t )
(14-12)
y0 y0 2 其中 b y ( )
柔度法(力法)
MY KY 0 MY Y 0
10、按柔度法求解
振型方程: ([ ][ 2 [ 1 M ]){Y } 00} ([ I ] M ] ][ [ I ]){Y } { 2 频率(特征)方程
D [ ][ M ] [ I ] 0
y0 tg y0 y0
位移-时间曲线如图示:
阻尼比——阻尼的基本参数: a.阻尼对频率(周期)的影响
k
2m
1 2
T T 1 2 T
0.2
T T
b、阻尼对振幅的影响
be
t
——振幅随时间逐渐衰减
11m1
1
12 m2
(k )
0 0
(14 63)
{Y }
(k )
Y1 Y2
(k )
11m1 k 12 m2
12 m2
k2
(k=1、2)
结构的刚度和质量分布 ——对称 其主振型 ——对称、反对称 计算自振频率: ——分别就正、反对称情况 ——取半跨结构计算 ——两个单自由度问题计算 显然,振型分别为: [1 1]T、[1 -1]T
1
0.2,
yn ln 2 j yn j 相隔j个周期: 1
结构动力学多自由度

求解系数:由质量矩阵和刚度矩阵的正交性,阻尼矩阵的一般形式为:
不耦合的运动方程—有阻尼
同理:
故:
不耦合的运动方程—有阻尼
另一种方法:
不耦合的运动方程—有阻尼
体系的对角广义质量矩阵:
不耦合的运动方程—有阻尼
在上式中,每一振型对阻尼矩阵起的作用与振型的阻尼比成比例。因此,任何无阻尼的振型对阻尼矩阵不起作用。
对每一项乘一个未知的时间函数li(t),并且将这个乘积在时间间隔t1到t2积分:
由于变分为零:
令:
Lagrange运动方程可改写为:
规格化的主振型矩阵:
无阻尼多自由度结构体系自由振动方程:
第i 阶振型的特解:
这样的特解有n个!
振型的物理意义
将N个振型中的每一振型形式,用F表示N个振型所组成的方阵。
以上矩阵为结构的振型矩阵,为一N*N方阵。
各项前乘 ,可得:
即:
注意:即使质量矩阵和柔度矩阵都是对称的,它们的乘机也是不对称的!
几何约束条件:
Hamilton原理:
动能可以用广义坐标和它们的一次导数表示,位能可以单独用广义坐标表示。非保守力在广义坐标的一组任意变分所引起的虚位移上所做的虚功,可以表示为这些变分的线性函数。
代入Hamilton原理公式:
由分部积分公式:
由:
故:
Lagrange运动方程:
由算例:
此时:
Lagrange运动方程写为:
假定弯矩—位移关系:
上式中,第一项由保守力产生,第二项由非保守力产生。
非保守力所做的虚功:
假定非保守力仅限于横向分布荷载p(x,t),这些力的虚功为:
非保守力所做的总虚功为:
其中:
结构动力学-13直接积分法_OK
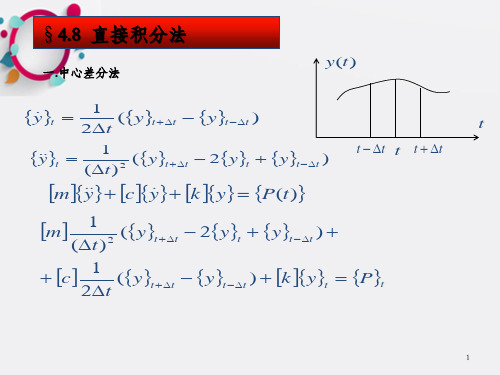
(1)计算 m, c, k
(2)确定 y0 , y0 , y0
(3)确定 ,并计t算
1
1
a0 (t )2 , a1 2t , a2 2a0
(4)计算
y t
(5)计算 m a0 m a1c
2.对每一时间分点t
(1)计算t时刻的
P t
(2)计算 时t 刻的位t移
m ytt P t
(3)根据需要计算t时刻的速度、加速度
( y tt
yt )
yt
yt
yt
2
2
yt
3 6t
( y tt
yt )
t
y tt
yt
tyt
1 2
t
(yt
t
yt
)
y(t t)
y(t)
t
t 令t tt,t 解出t
t yttt、ytt、ytt
y tt
yt
tyt
(t)2
6
( y tt
2yt
)
解出
y tt
6
(t)2
t
解出 y tt
R
Pt
( P tt
Pt
)
m(
6
(t
)2
yt
6
t
yt
2yt
)
c( 3
t
yt
2yt
2 t8yt
)
§4.3 威尔逊 - 法
y解 题 1y.(初t 始) 值计算
推导由t时刻的状态求 t t 时刻的状态的递推公式: 步骤y(t t)(1)求 k、m、c
对y解积t出y分ttyyyyyyt2(tytt.Rtt1对ty)ttttt每t计y一(ttyy算t3时(t6tt2t2(y间t)y2Pytyt分(ttttytt点yytt26ttt时y2t3(yttt刻(12)((Pt)的y6yyt)ttt拟tt)2(2(y荷tytaaat(yt3606载t3tt)yytP1(ytt2t确)t)63tttty/)2定/)2(y2t2,y),,ata2a(4ytm17)和)4ty确)a积((0ta3t定确k分/)t0t/t,2初定,步a,ya2a5令始拟长t8ytk值刚,2t(aa度并a12tttt、 2)/a矩计y解2t,y0t/y阵算06出t解m、 ty积出(ty、 yt分2tyt0a常、 1tyt数tyc)tt)0t
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
§8-1
动力计算概述
一、动力计算的特点、目的和内容
1、特点:静力荷载与动力荷载的特点及其效应。 “静力荷载”是指其大小、方向和作用位置不随时间而变化的荷载。这 类荷载对结构产生的惯性力可以忽略不计,由它所引起的内力和变形都是确定 的。 “动力荷载”是指其大小、方向和作用位置随时间而变化的荷载。这类
m
l
1 1 2 1 1 l 11 ( l l l l l l l l) EI 2 3 2 2 2 7 l3 12 EI
l
=1
11
l
=1
1 12 EI m 11 7ml 3
l
l/2
7ml 3 T 2 12 EI
15
2
例二.求图示体系的自振频率和周期.
共振时的振幅趋于无穷大。
共振时的振幅较大但为有限值。
事实上,由于非弹性力的存在,自由振动会衰减直到停止;共振时振幅也 不会无限增大,而是一个有限值。 非弹性力起着减小振幅的作用,使振动衰减,因此,为了进一步了解结构 的振动规律,就要研究阻尼。
20
关于阻尼,有两种定义或理解: 1)使振动衰减的作用; 2)使能量耗散。 2、在建筑物中产生阻尼、耗散能量的因素 1)结构在变形过程中材料内部有摩擦,称“内摩擦”,耗散能量; 2)建筑物基础的振动引起土壤发生振动,此振动以波的形式向周围扩散, 振动波在土壤中传播而耗散能量; 3)土体内摩擦、支座上的摩擦、结点上的摩擦和空气阻尼等等。 3、阻尼力的确定:总与质点速度反向;大小与质点速度有如下关系:
3EI l2
例1. 计算图示结构的频率和周期。 例2.计算图示结构的水平和竖向振动频率。 H 1 m EI m 1
V
l /2 1
l /2 A,E,I
E,I
E,A
l3 48EI m l3 T 2 3 48EI ml 48EI
例3.计算图示刚架的频率和周期。
m EI1= I I h
由式可知,位移是由初位移y引起的余弦运动和由初速度v引起的正弦 运动的合成,为了便于研究合成运动, 令 (e)式改写成
v
y ( 0 ) y (0) v y
sin t.......... ......(e)
y A sin ,
y(t ) Asin( t )......... .......... ...( f )
y ( x, t ) ak k ( x )
k 1
ak(t) ——称广义座标,为一组待定
参数,其个数即为自由度数,用此法可将
无限自由度体系简化为有限自由度体系。
x
n
y
7
四、动力计算的方法
动力平衡法(达朗伯尔原理)
m
(t ) P(t ) m y
P(t)
(t ) =I(t) m y
m
(t ) P(t ) m y
改写成 设其中
…………..运动方程
…………..平衡方程
(t ) 0 P(t ) m y
(t ) I (t ) m y
I(t)-惯性力,与加速度成正比,方向相反
虚功原理(拉格朗日方程) 哈米顿原理(变分方程)
都要用到抽象的虚位移概念
8
§8-2
m st T 2 2 k g
频率 1.只与结构的质量与刚度有关,与外界干扰无关; 和周 2.T与m的平方根成正比,与k成反比,据此可改变周期; 期的 14 讨论 3.是结构动力特性的重要数量标志。
三.自振频率和周期的计算 2.算例 例一.求图示体系的自振频率和周期. 解:
EI EI
厂房排架水平振 时的计算简图
m+αm柱
I 2I
单自由度体系
y2 y1
2个自由度 2个自由度
自由度与质量数不一定相等
5
ቤተ መጻሕፍቲ ባይዱ m1
m2
2个自由度
m3
4个自由度
v( t ) θ( t )
u(t)
水平振动时的计算体系
构架式基础顶板简化成刚性块
多自由度体系
6
m ( x)
无限自由度体系
x
y(x,t)
2、广义座标法: 如简支梁的变形曲线可用三角级数来表示
y ( x, t ) ak (t ) sin
k 1
n
kx l
x y(x,t)
用几条函数曲线来描述体系的振动曲 线就称它是几个自由度体系,其中
sin kx —— 是根据边界约束条件选取 l
1( x),2 ( x),........ .n ( x)
的函数,称为形状函数。
a1, a2,…….. an
m1 m
A l /2 l EI=
解:单自由度体系,
以表示位移参数的幅值,
B C k
1 m2 m 3
D l /2
各质点上所受的力为:
A1
. .
m1
B
k
C
m2
. .A
2
l I m1 A1 m 2 1 2 2 3 I 2 m2 A2 m l 3 2 1 m 2 l 2
二、动力荷载分类
P(t )
按起变化规律及其作用特点可分为:
1)周期荷载:随时间作周期性变化。(转动电机的偏心力) P
t 简谐荷载(按正余弦规律变化) 一般周期荷载
t
3
2)冲击荷载:短时内剧增或剧减。(如爆炸荷载)
P P tr t P(t )
P
tr t
3)随机荷载:(非确定性荷载) 荷载在将来任一时刻的数值无法事先确定。 (如地震荷载、风荷载)
13
-A
三、结构的自振周期和频率
由式
y(t ) Asin( t )
y A
及图可见位移方程是一个周期函数。
T t
0
-A
周期-T
2
,
工程频率- f
1 ( Hz ), T 2
园频率- 2f
2 T
计算频率和周期的几种形式
k 1 g g m m W st
荷载对结构产生的惯性力不能忽略,因动力荷载将使结构产生相当大的加速度,
由它所引起的内力和变形都是时间的函数。 与静力计算的对比:两者都是建立平衡方程,但动力计算,利用动静法,
建立的是形式上的平衡方程。力系中包含了惯性力,考虑的是瞬间平衡,荷 载、内力都是时间的函数。建立的平衡方程是微分方程。 2、目的和内容 计算结构的动力反应:内力、位移、速度与加速度,使结构在动内力与静
五、阻尼对振动的影响
1、阻尼的存在 实验证明,振动中的结构,不仅产生与变形成比例的弹性内力,还产生 非弹性的内力,非弹性力起阻尼作用。在不考虑阻尼的情况下所得出的某些 结论也反应了结构的振动规律,如: 忽略阻尼的振动规律 考虑阻尼的振动规律
结构的自振频率是结构的固有特性,与外因无关。 简谐荷载作用下有可能出现共振。 自由振动的振幅永不衰减。 自由振动的振幅逐渐衰减。
三、动力计算中体系的自由度
确定体系上全部质量位置所需独立参数的个数称为体系的振动自由度。 实际结构的质量都是连续分布的,严格地说来都是无限自由度体系。计算 困难,常作简化如下: 1、集中质量法 把连续分布的质量集中为几个质点,将一个无限自由度的问题简化成有限 自由度问题。
4
m m>>m梁 m +αm梁 I
它们的幅值产生于
sin(t ) 1 时,其值分别为:
y A
A 2 y
I mA 2
既然在运动的任一瞬时质体都处于平衡状态,在幅值出现时间也一样, 于是可在幅值处建立运动方程,此时方程中将不含时间t,结果把微分
方程转化为代数方程了,使计算得以简化。
18
例4. 计算图示体系的自振频率。
6 EI h2
l
1 H m H
1
6 EI h2
V
1 m V
由截面平衡
6 EI h2
12 EI h3
k
12 EI h3
k
24EI h3
k 24EI m m h3
6 EI h2
m h3 T 2 17 2 EI
四、简谐自由振动的特性
由式 可得,加速度为: 惯性力为:
9
一、运动微分方程的建立
方法:达朗伯尔原理 应用条件:微幅振动(线性微分方程) 力学模型 1、 刚度法:研究作用于被隔离的质量上的
力,建立平衡方程。
静平衡位置
重力
W
m 质量m在任一时刻的位移 y(t)=yj+yd
. y . .y
k
S(t)
m m
j d
.y
d
W
I(t)
+
弹性力 S (t ) ky(t ) k ( y j yd )
内力共同作用下满足强度和变形的要求。
2
动力计算的内容:研究结构在动荷载作用下的动力反应的计算原理和方法。 涉及到内外两方面的因素: 1)确定动力荷载(外部因素,即干扰力); 2)确定结构的动力特性(内部因素,如结构的自振频率、周期、振型和 阻尼等等),类似静力学中的I、S等; 计算动位移及其幅值;计算动内力及其幅值。
二、自由振动微分方程的解
I(t)
改写为
ky 0 m y k y 0 y m
.......... .......... .......... ......(b)
k y 0 其中 y m
2
2
它是二阶线性齐次微分方程,其一般解为:
y(t ) C1 sin t C2 cost
恒与位移反向
(t ) m( j d ) y y y 惯性力 I (t ) m
