鸡兔同笼的解题方法
鸡兔同笼问题的三种解法

鸡兔同笼问题的三种解法一、方法与技巧解决鸡兔同笼问题主要有三个解题方法:方程法、十字交叉法和假设法。
(1)方程法:通过一元一次方程或者二元一次方程组求解;(2)十字交叉图法:第一部分的平均值总数量的平均11则可得两部分的数量比为总量-第—部分的平均值兀总个数竿一翊八苹几抽第二部分的平均値—第一部分的平均值—床—即'纱、鸡兔同笼问题举例例:现有鸡兔同笼,已知鸡兔数头35,数脚94,求鸡和兔的个数。
(鸡兔同笼原型)方程法:设鸡的个数为x,则兔的个数为35-x,则有2x 4(35-x)=94,解得x=23。
故有鸡23只,兔12只。
第二却分的平均值h假设求法;十字交叉法:平均每个头对应澄只脚,根据十字交叉團法,有:所加兔的个数之比为:鸡1兔= ^<|| = 23J2,所以漏的个数为 廿冥」_“3,所以兔的个数为3%丄诂12+23 12+2^假设法:假设35只都罡馮 刑用公式解題;兔的只数=/.=12,则漓有4-2三、鸡兔同笼解题技巧的运用例:某地劳动部门租用甲、乙两个教室开展农村实用人才培训。
两教室均有5排座位,甲教室每排可坐10人,乙教室每排可坐9人。
两教室当月共举办该培训 27次,每次培训均 座无虚席,当月共培训 1290人次。
问甲教室当月共举办了多少次这项培训【答案】D【方程法】甲教室一次可坐 10X 5=50人,乙教室一次可坐 9X 5=45人,设甲教室举办 了 x 次培训,则有: 50x 45(27-x)=1290 ,解得 x=15。
故选 D【公式法】根据题意,甲教室一次可坐 10X 5=50人,乙教室一次可坐 9X 5=45人,则 由鸡兔同笼公式可知:甲教室举办的培训次数=94 3594 35463524 35实际垮训总人决-全部用乙載室的垮训人次 -1290 —= 15次召甲竅宣華应鬲曲人次-乙教童華次的培训人次50 -45"宀12QD 1^0人』根擔十字交夏厨E 有叶字交叉法】平均毎次培训対譬 三予田教室乙教室则甲、乙妲举办驱之比为罟:¥之4,故甲教室举办沁=15 次*故选肌27。
(奥数)鸡兔同笼问题五种解题思路

鸡兔同笼问题五种形式的解题思路(1)已知总头数和总脚数,求鸡、兔各多少:思路:假设全部都是鸡,总脚数减去鸡脚数后剩下的事兔子比鸡多的脚,ok 再除以脚的差,算出兔子数。
(总脚数-每只鸡的脚数×总头数)÷(每只兔的脚数-每只鸡的脚数)=兔数;总头数-兔数=鸡数。
或者是(每只兔脚数×总头数-总脚数)÷(每只兔脚数-每只鸡脚数)=鸡数;总头数-鸡数=兔数。
例如,“有鸡、兔共36只,它们共有脚100只,鸡、兔各是多少只?”解一(100-2×36)÷(4-2)=14(只)………兔;36-14=22(只)……………………………鸡。
解二(4×36-100)÷(4-2)=22(只)………鸡;36-22=14(只)…………………………兔。
(答略)(2)已知总头数和鸡兔脚数的差数,当鸡的总脚数比兔的总脚数多,求鸡和兔的数量思路:根据鸡兔脚数的差数,折算成鸡的数量,总头数减去相应的折算数量后,剩下的鸡和兔的脚一样多,如果鸡和兔的脚一样多,他们的头数比肯定为2:1,根据比例算出兔的个数。
(总头数-脚数之差/一只鸡的脚数)÷(2+1)=兔数;例:鸡兔同笼,鸡兔共40个头,鸡脚比兔脚共多32只,问鸡兔各多少只?兔:(40-32/2)÷(2+1)=8 只;鸡:40-8=3只(3)已知总数与鸡兔脚数的差数,当兔的总脚数比鸡的总脚数多思路:和上题目一样,根据鸡兔脚数的差数,折算成兔的数量,总头数减去相应的折算数量后,剩下的鸡和兔的脚一样多,如果鸡和兔的脚一样多,他们的头数比肯定为2:1,根据比例算出兔的个数。
(4) 已知鸡和兔的头数差以及脚数和例:鸡、兔共笼,鸡比兔多26只,足数共274只,问鸡、兔各几只?思路:总脚数减去多的动物的脚数后,除以两种动物的单个脚数为兔子的个数。
274-(26×2)÷(2+4)=37(只) 兔(5)鸡兔互换问题(已知总脚数及鸡兔互换后总脚数,求鸡兔各多少的问题),思路:根据互换前后的脚数相加除以(鸡的脚数加兔的脚数之和)为头数,再根据1求解。
鸡兔同笼五种解题方法

鸡兔同笼五种解题方法
鸡兔同笼,又称孰胜孰劣问题,是一个著名的古老问题,也可以用来考察学生的数学思维能力。
它被认为是一个古老又怪异的数学题目,有几种不同的解法,下面就详细介绍五种解题方法:
一、直接算法:
这是最常用的解题方法,即直接找出兔子与鸡的个数,用数学方法计算出来最精准的答案。
需要用到兔子加鸡等于总数,鸡的脚数也等于总数的概念。
二、迭代算法:
迭代算法是一种重复应用重复运算结果,以解决问题的解法,也就是说,先根据问题给出一个初始猜想,然后根据当前猜想推出下一个猜想,以此类推,直至找出最优解。
三、动态规划法:
动态规划法是根据问题求解步骤,它的特点是分析问题求解过程,建立模型,然后用模型解决问题,通过建立正确的递推关系,把复杂问题分解成一个个小问题,从而达到解决复杂问题的目的。
四、回溯法:
通过后向查找的方式,不断尝试可行的解决方案,通过回溯可以快速求出满足一定要求的解,但是这种方法如果不能提前给出限制条件,就会产生大量的岔路,影响解题效率。
五、枚举法:
枚举法的思想是将问题的所有可能情况一一枚举出来,然后判断
哪个解符合要求,从而找出最佳解。
枚举法的优点是简单易行,但是由于枚举出来的可能解太多,难以确定哪个解是最佳解,因此需要对可能的解进行优化,以节省解题时间。
鸡兔同笼13种解题方法

鸡兔同笼13种解题方法鸡兔同笼问题是一类经典的数学问题,常见于初中数学题目中。
这个问题的基本思路是通过解方程组来求解鸡和兔子的数量。
在本文中,将介绍13种不同的解题方法,包括逆向思维、代数法、图形法等多种方法,帮助读者更好地理解和掌握这一问题。
一、逆向思维法逆向思维法是一种比较简单易懂的方法,其基本思路是先确定总数量,再确定其中一个物品的数量,最后计算出另一个物品的数量。
1. 假设笼子里有13只动物,则鸡和兔子的总数量为13。
2. 假设有x只鸡,则有13-x只兔子。
3. 根据题目所给条件“总腿数为32”,得到方程式2x+4(13-x)=32。
4. 解方程得到x=6,则笼子里有6只鸡和7只兔子。
二、代数法代数法是一种常用的解题方法,其基本思路是通过设定未知量来建立方程组,并通过求解方程组来得到答案。
1. 设鸡和兔子的数量分别为x和y,则有方程组:x+y=132x+4y=322. 通过求解方程组得到x=6,y=7,则笼子里有6只鸡和7只兔子。
三、图形法图形法是一种直观易懂的方法,其基本思路是通过画图来解决问题。
1. 在平面直角坐标系中,设鸡和兔子的数量分别为x和y,则可以用一条直线表示鸡和兔子的总数量为13。
2. 根据题目所给条件“总腿数为32”,可以得到另一条直线表示鸡和兔子的总腿数为32。
3. 通过求解两条直线的交点,即可得到笼子里有6只鸡和7只兔子。
四、枚举法枚举法是一种简单易行的方法,其基本思路是通过列举所有可能情况来找到符合条件的答案。
1. 从1到12枚举鸡的数量x。
2. 根据题目所给条件“总腿数为32”,计算出相应的兔子数量y。
3. 如果x+y=13,则找到符合条件的答案。
五、分段函数法分段函数法是一种利用函数性质解题的方法,其基本思路是将问题拆分成多个部分,并建立相应的函数关系式来求解问题。
1. 假设笼子里有x只鸡,则有13-x只兔子。
2. 根据题目所给条件“总腿数为32”,可以得到下列函数关系式: f(x)=2x+4(13-x)3. 通过求解f(x)=32的解,即可得到笼子里有6只鸡和7只兔子。
鸡兔同笼的三种方法

鸡兔同笼的三种方法鸡兔同笼问题的原型是已知鸡和兔子这两类动物的头、脚的总数量,求鸡和兔子分别多少只。
在考试中,题干内容往往会有所变化。
鸡兔同笼解法方法一:普通方程法设邮递员派送平邮X件,则派送的EMS有(14-X)件,根据补助构建等量关系,可得:7X+10(14-X)=119,解得X=7,选择A选项。
普通方程法是最容易想到的方法,对于思维的要求度不高,只需要设出未知数,列好等式求解即可。
方法二:假设法假设邮递员当天派送的全部是EMS,则可得的补助为10×14=140元。
然而实际上邮递员的补助只有119元,差值为140-119=21元。
因此平邮有21÷(10-7)=7件。
假设法是解决鸡兔同笼问题最常用的方法,跳过了普通方程设未知数、列方程等步骤,直接进入计算求解阶段,解题效果最明显。
在假设时,要根据题干的问法选择合适的假设条件来求解。
方法三:不定方程法设平邮X件,EMS 有Y件,则7X+10Y=119,由于7和119都能被7整除,根据整除特性可知Y=7,因此X=7(也可以通过尾数法判断7X的尾数为9,因此X=7)。
不定方程法只用了题干中的部分条件,结合选项就能快速判断求解了。
运用此方法对题目选项以及具体数值的要求较高,特别是对不定方程的解法要非常熟练才能快速判断求解。
数学名题:鸡兔同笼大约在1500年前,《孙子算经》中就记载了这个有趣的问题。
书中是这样叙述的:今有雉兔同笼,上有三十五头,下有九十四足,问雉兔各几何?这四句话的意思是:有若干只鸡兔同在一个笼子里,从上面数,有35个头,从下面数,有94只脚。
问笼中各有多少只鸡和兔?这一问题的本质是一种二元方程。
如果教学方法得当,可以让小学生初步地理解未知数和方程等概念,并锻炼从应用问题中抽象出数的能力。
一般在小学四到六年级时,配合一元一次方程等内容教授。
同一本书中还有一道变题:今有兽,六首四足;禽,四首二足,上有七十六首,下有四十六足。
鸡兔同笼问题解题方法

鸡兔同笼问题解题方法
鸡兔同笼问题解法如下:
方法一、假设法
在解决“鸡兔同笼”问题时,最常见的方法就是假设法,而在孩子的学习过程中,也会喜欢使用这种简便而又快捷的方法。
常用的假设有:假设笼子里都是兔或者都是鸡,比如:笼子里有30只头,68只脚,兔多少?鸡多少?
解题方法是假设笼子里都是兔子,这样就可以得到鸡的只数(4×30-68)÷(4-2)=26(只),那么兔子就是30-26=4(只)
方法二、砍腿法
顾名思义,砍腿法就是把多余的腿给去掉,即把兔子的腿变为两条,那么笼子里还剩下的腿的数量应该是:30×2=60,而原来应该是有68只脚,那么这里应该减少了68-60=8(只)脚,当兔子去掉了2条腿,笼子里腿的数量就会减2,那么就是有8÷2=4(只)兔子,得出兔子的只数,鸡的数量也就可以得到了。
方法三、抬腿法
与砍腿法一样,抬腿法的方法也是与名字一样。
这个方法的步骤是让鸡抬起一只腿,兔子抬起两只腿,这样的话,笼子里腿的数量就会变成原来数量的一半,即68÷2=34。
然后让鸡和兔子抬起的腿落地,这样兔子的脚就会比兔子的数多1,而鸡的脚就是鸡的只数。
因此就可以推出,兔子的只数就是腿的数减去头的数,即34-30=4(只),而鸡的数量也就是30-4=26只。
鸡兔同笼的解题方法

鸡兔同笼的解题方法鸡兔同笼问题是一道经典的数学问题,是许多学生在初中数学中遇到的难题。
此问题描述了一个笼子里有鸡和兔子的总数量以及它们的脚的总数,我们需要通过解题方法求出鸡和兔子的数量。
本文将介绍几种解题方法。
方法一:方程法假设鸡的数量为x,兔子的数量为y,根据题目条件可得以下方程:(1) x + y = 总数量(2) 2x + 4y = 总脚数通过解以上方程组,可以求解出鸡和兔子的数量。
方法二:列举法列举可能的鸡和兔子的数量组合,逐一验证是否符合题目条件。
首先,确定鸡和兔子的数量的范围,通常根据题目给出的总数量来设定。
然后,通过列举不同数量组合,计算它们的脚的总数,与题目给出的总脚数进行对比,如果相等则满足条件。
方法三:逻辑推理法通过逻辑推理找到符合题目条件的限制条件,从而得到鸡和兔子的数量。
我们知道,每只鸡有2只脚,每只兔子有4只脚。
假设鸡的数量为a,兔子的数量为b,则a + b等于总数量,其中鸡的脚数为2a,兔子的脚数为4b。
根据题目条件,我们可以得到以下两个限制条件:2a ≤ 总脚数≤ 4b,以及a + b = 总数量。
基于以上限制条件,我们可以推理出以下三个不等式关系:1. 2a ≤ 总脚数:鸡的脚数不能超过总脚数。
2. 4b ≥ 总脚数:兔子的脚数至少等于总脚数。
3. a + b = 总数量:鸡和兔子的数量之和等于总数量。
通过逻辑推理,我们可以得到鸡和兔子数量的一个范围。
然后,结合列举法,我们可以进一步确定鸡和兔子的具体数量。
方法四:二进制法这是一种更加高效的解题方法。
我们可以通过二进制运算,通过计算出二进制位上数字的情况,进而得到鸡和兔子的数量。
首先,将总数量转化为二进制表示。
例如,总数量为n,可以表示为n = 2^k + r 的形式。
其中,k为非负整数,r为余数。
然后,对r进行判断,如果r小于等于2^k,则鸡的数量为k,兔子的数量为r;如果r大于2^k,则鸡的数量为k+1,兔子的数量为r-2^k。
鸡兔同笼解题总结

鸡兔同笼解题总结“鸡兔同笼”是我国古代著名的数学趣题之一,也是小学数学中经常会遇到的一类问题。
它虽然看似简单,但却能很好地锻炼我们的逻辑思维和数学运算能力。
接下来,咱们就一起来详细探讨一下鸡兔同笼问题的各种解题方法。
咱们先来看一个经典的鸡兔同笼问题:笼子里有若干只鸡和兔,从上面数有 35 个头,从下面数有 94 只脚,问鸡和兔各有多少只?方法一:假设法这是解决鸡兔同笼问题最常用的方法之一。
假设笼子里全是鸡,那么每只鸡有 2 只脚,35 只鸡就应该有 35×2= 70 只脚。
但实际上有 94 只脚,多出来的脚就是因为把兔子当成鸡来算了。
每只兔子有 4 只脚,我们当成鸡算了就少算了 4 2 = 2 只脚。
总共多出来 94 70 = 24 只脚,所以兔子的数量就是 24÷2 = 12 只。
鸡的数量就是 35 12 = 23 只。
反过来,咱们也可以假设笼子里全是兔子。
这样每只兔子 4 只脚,35 只兔子就应该有 35×4 = 140 只脚。
实际只有 94 只脚,少了 140 94 = 46 只脚。
这是因为把鸡当成兔子算了,每只鸡多算了 4 2 = 2 只脚,所以鸡的数量就是 46÷2 = 23 只,兔子就是 35 23 = 12 只。
方法二:方程法设鸡的数量为 x 只,兔的数量为 y 只。
因为头的总数是 35 个,所以 x + y = 35。
又因为鸡有 2 只脚,兔有 4 只脚,脚的总数是 94 只,所以 2x + 4y = 94。
然后联立这两个方程,通过解方程组来求解 x 和 y 的值。
首先由 x + y = 35 可得 x = 35 y ,将其代入 2x + 4y = 94 中,得到 2×(35 y) + 4y = 94 ,化简得到 70 2y + 4y = 94 ,2y = 24 ,y = 12 。
再把 y = 12 代入 x = 35 y ,得到 x = 23 。
鸡兔同笼的9种解法

鸡兔同笼是我国古代著名趣题之一,记载于《孙子算经》之中。
鸡兔同笼问题,是小学奥数的常见题型。
是指已知鸡与兔的总头数和总足数,求鸡和兔各是多少只的应用题。
1、列表法。
2、画图法,画图法也是低年级小朋友很好接受的一个方法,呵呵,画图还可以让数学变得形象化,而且经常画图还有助于创造力的培养!假设14只全部是鸡,先把鸡给画好。
3、金鸡独立法,让每只鸡都一只脚站立着,每只兔都用两只后脚站立着,那么地上的总脚数只是原来的一半,即19只脚。
鸡的脚数与头数相同,而兔的脚数是兔的头数的2倍。
4、吹哨法。
5、假设法,假设全部是鸡。
6、假设法,假设全部是兔子。
7、特异功能法,鸡有2条腿,比兔子少2条腿,这不公平,但是鸡有2只翅膀,兔子却没有。
假设鸡有特级功能,把两只翅膀变成2条腿,那么鸡也有4条腿。
8、特异功能法,假设每只鸡兔都具有“特异功能”,鸡飞起来,兔立起来,这时立在地上的脚全是兔的。
9、特异功能法,假设孙悟空变成兔子,说“变”,每只兔子又长出一个头来,然后对妖精说“将它劈开”,变成“一头两脚”的两只“半兔”,半兔与鸡都是两只脚。
10、砍足法,假如把每只砍掉1只脚、每只兔砍掉3只脚,则每只鸡就变成了“独角鸡”,每只兔就变成了“双脚兔”。
基本概念:鸡饭同笼问题又称为置换问题、假设问题,就是把假设错的那部分置换出来:基本思路:①假设,即假设某种现象存在(甲和乙一样或者乙和甲•样):②假设后,发生了和题目条件不同的差,找出这个差是多少:③每个事物造成的差是固定的,从而找出出现这个差的原因:④再根据这两个差作适当的调整,消去出现的差。
基本公式:①把所有鸡假设成兔子:鸡数=(兔脚数X总头数一总脚数)子(兔脚数一鸡脚数)②把所有兔子假设成鸡:兔数=(总脚数一鸡脚数X总头数)子(兔脚数一鸡脚数)关犍问题:找出总量的差与单位量的差。
解决鸡兔同笼一般用“假设法”来求解。
即假设全是鸡或是全是兔,然后根据出现的足数差,推算出鸡或兔的只数。
鸡兔同笼的五种解法

鸡兔同笼的五种解法鸡兔同笼问题是一个经典的数学问题。
在这个问题里,给定了笼子里的动物的总数和腿的总数,需要求出鸡和兔的数量。
这个问题可以用多种方法解决。
在这里,我们将介绍五种解题方法。
方法一:列方程假设鸡的数量是x,兔的数量是y,根据题意,我们可以得到以下方程组:x + y = 总数2x + 4y = 腿的总数根据这个方程组,我们可以解出x和y的值,从而得到鸡和兔的数量。
方法二:画图法我们可以画出一张鸡和兔的图,用数字表示每只鸡和兔的数量和腿的数量,然后用这张图来解题。
这种方法比较直观,适合孩子或初学者使用。
方法三:数学归纳法我们可以观察鸡兔同笼问题的特征,发现每增加一只动物,会增加两条腿。
因此,我们可以将问题转化为:有n 个动物,它们共有m条腿,求鸡和兔的数量。
然后使用数学归纳法来解决这个问题。
方法四:递归算法我们可以将问题分解为小问题,再利用递归算法来解决。
具体地,假设有n只动物,其中m只是鸡,n-m只是兔。
如果这些动物共有k条腿,我们可以先考虑只有一只动物的情况,然后逐步增加动物的数量,直到n只为止。
方法五:运用数学知识我们可以运用一些数学知识,如组合数学和二元一次方程等,来解决这个问题。
具体地,我们可以用组合数学的方法计算出在给定腿的数量下,鸡的数量和兔的数量的所有可能组合,然后用二元一次方程来验证哪种组合符合题意。
以上五种方法各有特点。
对于初学者来说,列方程和画图法比较易懂;对于高中学生或数学专业学生来说,数学归纳法和递归算法可能更加适合;而对于数学专业研究生或数学爱好者来说,运用数学知识的方法可能更为有趣和有挑战性。
不管采用哪种方法,解决鸡兔同笼问题都可以让人在玩乐中学习,锻炼数学思维能力。
鸡兔同笼的算法

鸡兔同笼的算法
鸡兔同笼的解法
(一)解法主要就是用方程解、假设法、列表法这三种。
(1)列表法、假设法是在学生还没有学习方程的情况下运用;
(2)用方程解,是在学生学习了方程后的解法。
至于其他方法,如:抬腿法、飞鸡法、绑腿法、松绑法……都是由“假设法”演变而来的。
其实方程方法就是假设法的提升。
(二)因为每个题目的已知条件、问题都有一定的差异性(特别是哪些“改头换面”题),所以在解题时一定要灵活运用上面介绍的方法。
鸡兔同笼公式
公式1:(兔的脚数×总只数-总脚数)÷(兔的脚数-鸡的脚数)=鸡的只数总只数-鸡的只数=兔的只数对应的二元方程操作:(s1*4-s2)/2
公式2:(总脚数-鸡的脚数×总只数)÷(兔的脚数-鸡的脚数)=兔的只数总只数-兔的只数=鸡的只数对应的二元方程操作:(s2-s1*2)/2以上两个公式与”本质解法“中用线性代数方法推算出来的公式完全相等。
公式3:总脚数÷鸡的脚数-总头数=兔的只数总只数-兔的只数=鸡的只数对应的二元方程操作:s2/2-s1公式4:兔脚数*X+鸡脚数(总数-X)=总脚数(X=兔,总数-X=鸡数。
也就
是鸡兔同笼一元方程的标准形式)。
所有预设公式都是将二元方程右边的值进行初等变换后的结果直接相加减得到的结果。
鸡兔同笼13种解题方法

鸡兔同笼13种解题方法1. 题目分析鸡兔同笼问题是一个经典的数学问题,常用于培养逻辑思维和解决实际问题的能力。
题目要求在已知鸡和兔的总数量以及总腿数的情况下,计算出鸡和兔的具体数量。
2. 解题思路根据题目要求,我们可以得到以下两个方程:•鸡 + 兔 = 总数量• 2 * 鸡 + 4 * 兔 = 总腿数通过解这个二元一次方程组,可以得到鸡和兔的具体数量。
3. 解题方法方法一:穷举法穷举法是最简单直观的解题方法之一。
我们可以从0开始依次尝试每种可能性,直到找到符合条件的答案为止。
def solve_chicken_rabbit(total_number, total_legs):for chicken in range(total_number + 1):rabbit = total_number - chickenif 2 * chicken + 4 * rabbit == total_legs:return chicken, rabbitreturn Nonetotal_number = 13total_legs = 32result = solve_chicken_rabbit(total_number, total_legs)if result:print("鸡的数量为", result[0])print("兔的数量为", result[1])else:print("无解")方法二:代数法代数法是通过代数运算解题的方法。
我们可以将鸡和兔的数量表示为变量,并根据已知条件列出方程,然后求解方程得到答案。
def solve_chicken_rabbit(total_number, total_legs):from sympy import symbols, Eq, solvechicken = symbols('chicken')rabbit = total_number - chickenequation1 = Eq(chicken + rabbit, total_number)equation2 = Eq(2 * chicken + 4 * rabbit, total_legs)result = solve((equation1, equation2), (chicken, rabbit))if result:return result[chicken], result[rabbit]else:return Nonetotal_number = 13total_legs = 32result = solve_chicken_rabbit(total_number, total_legs)if result:print("鸡的数量为", result[0])print("兔的数量为", result[1])else:print("无解")方法三:二分法二分法是一种高效的搜索算法,可以在有序列表中快速找到目标元素。
鸡兔同笼解题技巧全集

鸡兔同笼解题技巧全集鸡兔同笼问题是中国古代著名的数学趣题,也是小学数学中常见的一类应用题。
它具有一定的趣味性和挑战性,能够锻炼我们的逻辑思维和数学运算能力。
接下来,我将为您详细介绍鸡兔同笼问题的各种解题技巧。
一、假设法假设法是解决鸡兔同笼问题最常用的方法之一。
我们可以先假设笼子里全部都是鸡或者全部都是兔,然后根据实际的脚数与假设情况下的脚数差异来进行计算。
假设笼子里全部都是鸡,那么每只鸡有 2 只脚。
如果笼子里有 n 个头,那么脚的总数就是 2n 只。
但实际上的脚数比假设的要多,这是因为把兔当成鸡来计算时,每只兔少算了 2 只脚。
用实际脚数减去假设的脚数,再除以每只兔少算的 2 只脚,就可以得到兔的数量。
例如,笼子里有 35 个头,94 只脚。
假设全部都是鸡,那么脚的总数就是 35×2 = 70 只。
实际有 94 只脚,多出来的 94 70 = 24 只脚就是因为把兔当成鸡计算少算的。
每只兔少算 2 只脚,所以兔的数量就是 24÷2 = 12 只,鸡的数量就是 35 12 = 23 只。
同样,如果假设笼子里全部都是兔,那么每只兔有 4 只脚。
如果笼子里有 n 个头,脚的总数就是 4n 只。
实际脚数比假设的少,这是因为把鸡当成兔来计算时,每只鸡多算了 2 只脚。
用假设的脚数减去实际的脚数,再除以每只鸡多算的 2 只脚,就可以得到鸡的数量。
二、方程法方程法是一种比较直接和通用的方法。
我们可以设鸡的数量为x 只,兔的数量为 y 只。
根据题目中的条件,可以列出两个方程:方程一:x + y =头的总数方程二:2x + 4y =脚的总数然后通过解方程组来求出 x 和 y 的值。
比如,还是上面那个例子,有 35 个头,94 只脚。
设鸡有 x 只,兔有 y 只,可列出方程组:x + y = 35 (1)2x + 4y = 94 (2)由(1)式得 x = 35 y,将其代入(2)式:2×(35 y) + 4y = 9470 2y + 4y = 942y = 24y = 12将 y = 12 代入(1)式,可得 x = 23所以,鸡有 23 只,兔有 12 只。
鸡兔同笼四种方法

鸡兔同笼四种方法
鸡兔同笼问题是中国古代著名的趣题之一,通过研究解题方法可以提高我们的问题分析和解决能力。
下面介绍几种解鸡兔同笼问题的方法。
解法一:列表法。
这种方法通过列出表格,逐步尝试的方式来解决问题。
但是这种方法过程繁琐,不太符合大多数人的口味。
解法二:抬腿法。
这是古人解题的方法,即“金鸡独立”,兔两个后腿着地,前腿抬起。
这种方法可以得出公式:兔子的只数=总腿数÷2-总只数,鸡的只数=总只数-兔子的只数。
解法三:假设法。
这是鸡兔同笼类问题最常用的方法之一。
假设35个头都是兔子,腿数就应该是35×4=140,比94还多。
这时我们可以列式得出鸡的只数。
同样地,如果35个头都是鸡,腿数应该是35×2=70,比94还少。
这时我们可以列式得
出兔子的只数。
总结公式为:鸡的只数=(兔的脚数×总只数
-总腿数)÷(兔的腿数-鸡的腿数),兔的只数=(总脚数
-鸡的脚数×总只数)÷(兔的脚数-鸡的脚数)。
解法四:砍腿法。
这种方法比较暴力,即通过砍去一些腿,使得鸡兔数量满足条件。
但是这种方法不够科学,不太推荐使用。
通过研究这些方法,我们可以更加灵活地解决问题,提高我们的数学思维能力。
鸡兔同笼问题的三种解法

鸡兔同笼问题的三种解法
一、方法与技巧
解决鸡兔同笼问题主要有三个解题方法:方程法、十字交叉法和假设法。
(1)方程法:通过一元一次方程或者二元一次方程组求解;
(2)十字交叉图法:
二、鸡兔同笼问题举例
例:现有鸡兔同笼,已知鸡兔数头35,数脚94,求鸡和兔的个数。
(鸡兔同笼原型)方程法:设鸡的个数为x,则兔的个数为35-x,则有2x 4(35-x)=94,解得x=23。
故有鸡23只,兔12只。
1 / 2
三、鸡兔同笼解题技巧的运用
例:某地劳动部门租用甲、乙两个教室开展农村实用人才培训。
两教室均有5排座位,甲教室每排可坐10人,乙教室每排可坐9人。
两教室当月共举办该培训27次,每次培训均座无虚席,当月共培训1290人次。
问甲教室当月共举办了多少次这项培训?
A.8
B.10
C.12
D.15
【答案】D
【方程法】甲教室一次可坐10×5=50人,乙教室一次可坐9×5=45人,设甲教室举办了x次培训,则有: 50x 45(27-x)=1290,解得x=15。
故选D。
【公式法】根据题意,甲教室一次可坐10×5=50人,乙教室一次可坐9×5=45人,则由鸡兔同笼公式可知:甲教室举办的培训次数=
(注:文档可能无法思考全面,请浏览后下载,供参考。
可复制、编制,期待你的好评与关注)。
鸡兔同笼问题4种解题方法
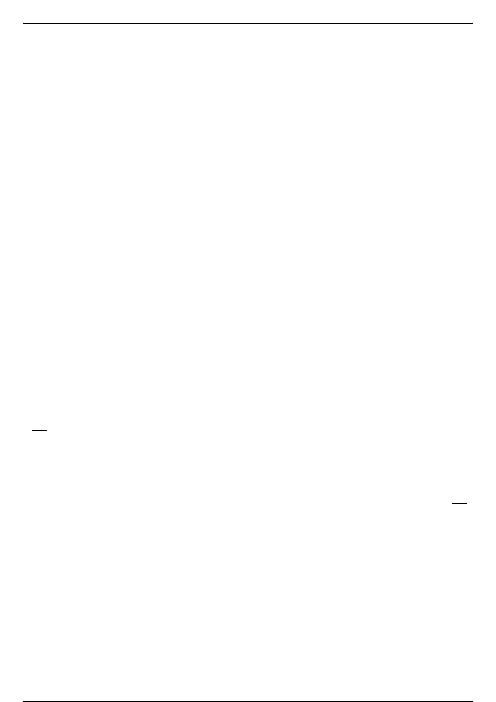
鸡兔同笼解题方法:1,假设法设全是鸡,则兔的只数为:(总头数×2--总脚数)÷2设全是兔,则鸡的只数为:(总头数x4--总脚数)÷2总只数--鸡只数=兔只数基本原理:总头数x2如果=总脚数,说明全是鸡,如果<总脚数,说明其中有兔,每少2只脚就有1只兔。
总头数×4=总脚数,说明全是兔,如果>总脚数,说明其中有鸡,每多2只就有1只鸡。
2,公式法:总脚数÷2--总头数=兔只数总只数--兔只数=鸡只数基本原理:原来的头总量是鸡头和兔头的总量,脚总量也是鸡脚和兔脚的总量。
用脚总数÷2是按全是鸡来计算的,如果商=总头数,说明全是鸡,如果商>总头数,说明其中有兔。
每多1个头就是1只兔。
因为1只兔有4只脚,前面÷的是2,1只兔就变成2个头,也就多了1个头,所以总脚数÷2--总头数的差是多少就有多少只兔。
3,排除法:(脚总量--总头数x2)÷2=兔只数:总只数--兔只数=鸡只数基本原理:先让每只鸡兔各抬起2只脚,这时鸡无剩下的脚,排除鸡后剩下的脚都是兔的。
前面 抬起2只脚,现在每只兔还剩下2只脚。
所以用总脚数--总头数×2的差再÷2就是兔的只数。
4,分组法(1)鸡兔共有100只,鸡脚比兔脚多20只,问鸡兔各有多少只?20÷2=10只100--10=90只兔:90÷(1+2)=30只100--30=70只验算:70×2--30×4=20(2)鸡兔共有90只,鸡的脚比兔的脚少60只,问有鸡兔各几只? 60÷4=15只90--15=75只免:75÷(1+2)=25只鸡:75--25=50 只验算:50×2=100(25+15)x4=160160--100=60 只5,方程法可用一元一次和二元一次方程直接解题。
等量关系:(1)设鸡为X,则兔为总头数--X2Ⅹ+4(总头数--X)=总脚数(2)X+y=总头数2X+4y=总脚数。
鸡兔同笼问题的几种解法

3、方程法
例题同上例。今有鸡、兔共居一笼,已知鸡头和兔头共35个,鸡 脚与兔脚共94只。问鸡、兔各有多少只?
①一元一次方程
• 解:设兔有x只,则鸡有(35-x)只。
4x+2(35-x)=94
2、抬脚法 就是让我们列出表格,采用依次列举,逐步尝试的方法来解决这个问题
例:鸡兔同笼共12个头,32条腿
2、分析与解:我们设想有一只“怪鸡”有1个头11只脚,一种“怪兔”有1个头19只脚,它们共有16个头,280只脚。
这只样不•, 过就这例将种买说。文法化,今用我品们有问理题解鸡转起换来、成更鸡容兔兔易同而共笼已问居题了一。 笼,已知鸡头和兔头共35个,鸡脚与兔
二、鸡兔同笼问题常用的解法 • 1、假设法 • 2、抬脚法 • 3、方程法 • 4、列表法
1、假设法
例。今有鸡、兔共居一笼,已知鸡头和兔头共35个,鸡脚与兔脚 共94只。问鸡、兔各有多少只?
解析:已知情况 鸡脚 2
鸡兔共35只
兔脚 4
鸡兔总脚数94只
①假设笼子里全是鸡:那么总脚数应为 35×2=70只 对比实际94 只的总脚数 假设的情况比实际情况少了 94-70=24只
解析: • 先用逐一列表的方式,计算出一只鸡11只兔的腿数,和2只鸡
10只兔的腿数,为第三步做准备。 • 通过第一、二步的计算,我们发现了兔子只数减少一只时,腿
=20(人)。
今但有是鸡 此、种头兔方共法数居过一程×笼太,过2已笨只知拙鸡、,头繁和琐(兔,头数3共字5越3×5大个越,2复鸡=杂脚7与0兔只脚共9)4只。由于鸡只有2只脚,所以笼子里
鸡兔同笼的五种方法

鸡兔同笼的五种方法介绍鸡兔同笼,顾名思义就是指将鸡和兔子放在同一个笼子中。
在这个任务中,我们将探讨解决鸡兔同笼问题的五种方法。
这个问题涉及到数学知识和逻辑思维,通过研究这些方法,我们可以提高自己的解题能力和思维灵活性。
方法一:暴力解法1.假设鸡的数量为x,兔子的数量为y,总共有z只动物。
2.使用两层循环,枚举所有可能的鸡和兔子的数量组合。
3.对于每一种组合,判断是否满足以下条件:x + y = z,2x + 4y = z。
如果满足条件,输出结果。
4.当找到一种满足条件的组合后,即可停止循环,得到问题的解。
方法二:二元一次方程求解1.由鸡和兔子的数量可得到两个方程:x + y = z,2x + 4y = z。
2.将第一个方程变形为x = z - y,代入第二个方程得到2(z - y) + 4y = z。
3.化简方程得到z = 2y,进一步代入得到x = z - y = 2y - y = y。
4.因此,鸡的数量等于兔子的数量,鸡兔同笼时,动物的数量应为偶数。
方法三:因数分解法1.设鸡的数量为x,兔子的数量为y,总共有z只动物。
2.将总数量z进行因数分解,得到两个因数a和b,满足z = a * b。
3.根据鸡和兔子的腿数算出总的腿数为2x + 4y。
4.将总腿数除以a,得到商c和余数d,即2x + 4y = a * c + d,其中d为0或2。
5.如果d = 0,那么总的腿数可以被a整除,将a代入方程可以得到x的值。
6.如果d = 2,那么总的腿数除以2得到的商再减去b,将得到的差代入方程可以得到x的值。
7.根据得到的x值,即可求得y的值。
方法四:二元一次方程的图像法1.将两个方程化为标准形式,即x + y = z和2x + 4y = z。
2.将方程右侧的常数项去掉,得到x + y = 0和2x + 4y = 0。
3.画出这两个方程所表示的直线的图像。
4.这两个直线的交点表示满足方程组的解。
如果交点在整数点上,则表示鸡和兔子的数量为整数。
多种方法解鸡兔同笼

多种方法解鸡兔同笼鸡兔同笼是一道经典的数学问题,在解题过程中可以运用多种方法。
下面将介绍一些常见的解题方法。
一、假设法假设鸡的数量为x,兔的数量为y。
根据题目条件,可以列出如下方程组:1.x+y=n(总数)2.2x+4y=m(腿的总数,2为鸡的腿数,4为兔的腿数)通过求解上述方程组,可以得到鸡和兔的数量。
二、矩阵法将鸡的数量表示为x,兔的数量表示为y。
根据题目条件,可以列出如下矩阵方程:11,,x,=,n24,,y,,m通过解矩阵方程,可以得到鸡和兔的数量。
三、图形法可以通过画图的方式解决鸡兔同笼问题。
1.以鸡的数量为横轴,以兔的数量为纵轴,画出一个平面直角坐标系。
2.根据题目条件,确定坐标系上的约束条件,以限制鸡和兔的数量。
3.找出约束条件所确定的区域,该区域即为可行解的范围。
4.根据题目给出的总数和腿数,确定具体的数值。
四、公式法有一个公式可以解决鸡兔同笼问题,称为“根号法”。
设鸡兔的总数为n,腿的总数为m,则可以使用如下公式计算鸡和兔的数量:鸡的数量=(4n-m)/2兔的数量=(m-2n)/2五、穷举法可以使用穷举法进行解题,在一定范围内逐个试探鸡和兔的数量,判断是否符合题目给定的总数和腿数。
这种方法比较直观,但是对于大规模的问题可能会比较耗时。
总结:以上是几种常见的解决鸡兔同笼问题的方法,每种方法都有其优缺点,具体使用哪种方法可以根据实际情况选择。
有时候可以结合多种方法进行验证,以确保解答的准确性。
鸡兔同笼问题虽然看起来简单,实际上涉及了数学推理和解方程的思维,对于培养思维能力和逻辑思维有很大的帮助。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
鸡兔同笼的解题方法
【鸡兔问题公式】
(1)已知总头数和总脚数,求鸡、兔各多少:
(总脚数-每只鸡的脚数×总头数)÷(每只兔的脚数-每只鸡的脚数)=兔数;
总头数-兔数=鸡数.
或者是(每只兔脚数×总头数-总脚数)÷(每只兔脚数-每只鸡脚数)=鸡数;
总头数-鸡数=兔数.
例如,“有鸡、兔共36只,它们共有脚100只,鸡、兔各是多少只?”
解一(100-2×36)÷(4-2)=14(只)………兔;
36-14=22(只)……………………………鸡.
解二(4×36-100)÷(4-2)=22(只)………鸡;
36-22=14(只)…………………………兔.
(答略)
(2)已知总头数和鸡兔脚数的差数,当鸡的总脚数比兔的总脚数多时,可用公式
(每只鸡脚数×总头数-脚数之差)÷(每只鸡的脚数+每只兔的脚数)=兔数;
总头数-兔数=鸡数
或(每只兔脚数×总头数+鸡兔脚数之差)÷(每只鸡的脚数+每只免的脚数)=鸡数;
总头数-鸡数=兔数.(例略)
(3)已知总数与鸡兔脚数的差数,当兔的总脚数比鸡的总脚数多时,可用公式.
(每只鸡的脚数×总头数+鸡兔脚数之差)÷(每只鸡的脚数+每只兔的脚数)=兔数;
总头数-兔数=鸡数.
或(每只兔的脚数×总头数-鸡兔脚数之差)÷(每只鸡的脚数+每只兔的脚数)=鸡数;
总头数-鸡数=兔数.(例略)
(4)得失问题(鸡兔问题的推广题)的解法,可以用下面的公式:
(1只合格品得分数×产品总数-实得总分数)÷(每只合格品得分数+每只不合格品扣分数)=不合格品数.或者是总产品数-(每只不合格品扣分数×总产品数+实得总分数)÷(每只合格品得分数+每只不合格品扣分数)=不合格品数.
例如,“灯泡厂生产灯泡的工人,按得分的多少给工资.每生产一个合格品记4分,每生产一个不合格品不仅不记分,还要扣除15分.某工人生产了1000只灯泡,共得3525分,问其中有多少个灯泡不合格?”
解一(4×1000-3525)÷(4+15)
=475÷19=25(个)
解二1000-(15×1000+3525)÷(4+15)
=1000-18525÷19
=1000-975=25(个)(答略)
(“得失问题”也称“运玻璃器皿问题”,运到完好无损者每只给运费××元,破损者不仅不给运费,还需要赔成本××元…….它的解法显然可套用上述公式.)(5)鸡兔互换问题(已知总脚数及鸡兔互换后总脚数,求鸡兔各多少的问题),可用下面的公式:
〔(两次总脚数之和)÷(每只鸡兔脚数和)+(两次总脚数之差)÷(每只鸡兔脚数之差)〕÷2=鸡数;
〔(两次总脚数之和)÷(每只鸡兔脚数之和)-(两次总脚数之差)÷(每只鸡兔脚数之差)〕÷2=兔数.
例如,“有一些鸡和兔,共有脚44只,若将鸡数与兔数互换,则共有脚52只.鸡兔各是多少只?”
解〔(52+44)÷(4+2)+(52-44)÷(4-2)〕÷2
=20÷2=10(只)……………………………鸡
〔(52+44)÷(4+2)-(52-44)÷(4-2)〕÷2
=12÷2=6(只)…………………………兔(答略)。
