第二章理想光学系统习题

合集下载

光学计算题最终版.

（1）该透镜第二面的曲率半径
（2）该齐明透镜的垂轴放大率
解：（1）物点位于第一个面的曲率中心，则经过第一个面的像点与物点重合，所以。此像点作为第二个面的物点，所以。由于第二面也满足齐名条件，但其物点既不在定点也不在曲率中心，因此需要满足第三类齐明点
所以第二面曲率半径
（2），所以齐明透镜放大率。
解：
（1）由于，平板上下表面反射都是从低折射率介质传输到高折射率介质，半波损失的情况一样，所以上、下表面反射光的光程差为
条纹中心对应折射角， ;
，光程差是波长的整数倍，所以中心是亮条纹。
（2）中心算第零个亮条纹，则第N个亮纹有，所以第10个亮条纹的角半径为，半径为
（3）条纹间距
22、用等厚条纹测量玻璃楔板的楔角时，在长达5cm的范围内共有15条亮条纹，玻璃楔板的折射率，所用光波波长，求楔角。
解：
，，
（1）求像方基点
利用正切计算法，假设一个高度为10mm的平行于光轴的光线入射，即，，
则
像方焦距
像方焦点到最后一个透镜的距离
像方主平面到最后一个透镜的距离
所以像方焦点在最后一个透镜前约35.51mm处，主平面在最后一个透镜后约0.72mm处。
（2）求物方基点
将三个透镜的排列顺序颠倒过来，按照相同的方法计算即可。
最后结果：
物方焦点在第一个透镜前约59.42mm处，物方主平面在第一个透镜前约23.19mm处。
12、白光经过顶角的色散棱镜，的色光处于最小偏向角。试求其最小偏向角的大小及的色光相对于的色光的夹角。
解：
（1）最小偏向角，根据和得
（2）时
时，，根据折射定律得
所以两种色光夹角

光学习题

一、填空题1. 小孔成像可用几何光学中的（）定律来解释。

2. 光学系统中物和像具有共轭关系的原因是（）。

3. 光学系统中像方顶焦距是（）。

4. 显微镜中的光学筒长指的是（ ` ）。

5. 光学系统的物方焦距和像方焦距之比等于 ( )之比。

6. 人眼的调节包含 ( ) 调节和 ( ) 调节。

7. 要使公共垂面内的光线方向改变60度，则双平面镜夹角应为( )。

8. 要求显微镜能分辨的最小间隔为0.5μm ，如果用波长555nm 的光成像，显微镜物镜的数值孔径至少为（）。

9.理想光学系统中，与像方焦点共轭的物点是（）。

10. 望远系统中物镜的相对孔径是（）。

11. 棱镜的转动定理是（）。

12. 设光从玻璃射入空气中，玻璃的折射率为1.52，则发生全反射的临界角为（）。

13. 一个人的眼睛的远点距为-500mm ，需带（）度数的眼镜，眼镜的焦距是（）。

14. 视场光阑是光学系统中对光束的（）起限制作用的光阑，其在系统像空间的共轭像称作（）。

15. 发生全反射现象的必要前提是（）。

16. 周视照相机可以拍摄大视场景物，其利用的是（）的性质。

17．在望远镜的视度调节中，为适应近视人群，应采取的是：（）A)使物镜远离目镜 B)使目镜远离物镜 C)使目镜靠近物镜 D)应同时调节物镜和目镜18. 棱镜系统中加入屋脊面，其作用是（）。

19. 光学系统中场镜的作用是（）A)改变成像光束的位置 B)减小目镜的尺寸 C)不改变像的成像性质 D)以上都正确 20. 理想光学系统中，与像方焦点共轭的物点是（）。

21.物镜和目镜焦距分别为mm f 2'=物和mm f 25'=目的显微镜，光学筒长△= 4mm ，则该显微镜的视放大率为（），物镜的垂轴放大率为（），目镜的视放大率为（）。

二、问答题1. 什么是理想光学系统？2. 对目视光学仪器的共同要求是什么？3. 如何计算眼睛的视度调节范围？如何校正常见非正常眼？4. 光学系统中可能有哪些光阑？5. 共轴光学系统的像差和色差主要有哪些？6. 显微镜的分辨率与哪些参数有关？通过什么途径可提高显微镜的分辨率？7. 复杂光学系统中设置场镜的目的是什么？8. 平面镜成像是否存在色差？9. 什么叫孔径光阑？它和入瞳和出瞳的关系是什么？10. 什么叫视场光阑？它和入窗和出窗的关系是什么？11. 几何像差主要包括哪几种？12. 什么叫远心光路？其光路特点是什么？13. 角放大倍率和视觉放大倍率的本质区别是什么？望远镜的角放大倍率和视觉放大倍率有何异同？14．场镜的作用是什么？若把一场镜（凸平）放置于望远物镜的像面上，场镜的垂轴放大倍率多大？场镜的初级球差多大？15. 目镜的作用是形成实像还是虚像？是倒立像还是正立像？是放大像还是缩小像？16. 为什么光楔有色散作用？当光楔顶角为θ时，光楔对F光和C光的角色散公式。

工程光学习题参考答案第二章理想光学系统

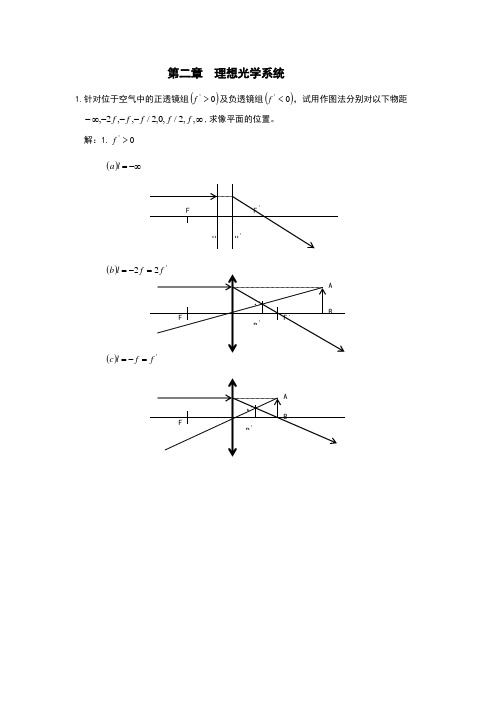
第二章理想光学系统1.针对位于空气中的正透镜组()0'>f 及负透镜组()0'<f ，试用作图法分别对以下物距 ∞---∞-,,2/,0,2/,,2,f f f f f ,求像平面的位置。

解：1.0'>f ()-∞=l a()'2f l b -=()f f l c =-=()/f l d -=()0=l e()/f l f =')(f f l g -=='22)(f f l h -==+∞=l i )(2.0'<f -∞=l a )(l b )(=l c =)(/)(f l d -=0 el(=)f=l2/ (f)()fg=l(=h)ll i)(+∞=2. 已知照相物镜的焦距f’＝75mm,被摄景物位于（以F 点为坐标原点）=x ,2,4,6,8,10,m m m m m -----∝-处，试求照相底片应分别放在离物镜的像方焦面多远的地方。

解：（1）x= -∝ ，xx ′=ff ′ 得到：x ′=0 （2）x ′= （3）x ′= （4）x ′= （5）x ′=（6）x ′=3.设一系统位于空气中，垂轴放大率*-=10β，由物面到像面的距离（共轭距离）为7200mm ，物镜两焦点间距离为1140mm 。

求该物镜焦距，并绘出基点位置图。

解:∵ 系统位于空气中，f f -='10''-===ll y y β 由已知条件：1140)('=+-+x f f7200)('=+-+x l l解得：mm f 600'= mm x 60-=4.已知一个透镜把物体放大*-3投影到屏幕上，当透镜向物体移近18mm 时，物体将被放大*-4，试求透镜的焦距，并用图解法校核之。

解：方法一：31'11-==l l β ⇒ ()183321'1--=-=l l l ①42'22-==l l β ⇒ 2'24l l -= ② 1821+-=-l l ⇒ 1821-=l l ③ '/1/1/11'1f l l =-'/1/1/12'2f l l =-将①②③代入④中得 mm l 2702-= mm l 1080'2-= ∴ mm f 216'=方法二： 311-=-=x fβ 422-=-=x fβ ⇒ mm f 216-= 1812=-x x方法三： 12)4)(3(21''=--==∆∆=ββαnn x x2161812'-=⨯=∆x''fx -=β143''''2'121=+-=∆=+-=-∴fx fx x ββ mm x f 216''=∆=∴5.一个薄透镜对某一物体成实像，放大率为⨯-1,今以另一个薄透镜紧贴在第一个透镜上，则见像向透镜方向移动，放大率为原先的3/4倍，求两块透镜的焦距为多少解：⇒ 2'21'1/1/1/1/1l l l l -=- ④6.有一正薄透镜对某一物成倒立的实像，像高为物高的一半，今将物面向物体移近100mm ，则所得像与物同大小，求该正透镜组的焦距。

工程光学基础教程习题答案(完整)

第一章几何光学基本定律1. 已知真空中的光速c ＝3810⨯m/s ，求光在水（n=1.333）、冕牌玻璃（n=1.51）、火石玻璃（n=1.65）、加拿大树胶（n=1.526）、金刚石（n=2.417）等介质中的光速。

解：则当光在水中，n=1.333时，v=2.25 m/s, 当光在冕牌玻璃中，n=1.51时，v=1.99 m/s, 当光在火石玻璃中，n ＝1.65时，v=1.82 m/s ，当光在加拿大树胶中，n=1.526时，v=1.97 m/s ，当光在金刚石中，n=2.417时，v=1.24 m/s 。

2. 一物体经针孔相机在屏上成一60mm 大小的像，若将屏拉远50mm ，则像的大小变为70mm,求屏到针孔的初始距离。

解：在同种均匀介质空间中光线直线传播，如果选定经过节点的光线则方向不变，令屏到针孔的初始距离为x ，则可以根据三角形相似得出：,所以x=300mm即屏到针孔的初始距离为300mm 。

3. 一厚度为200mm 的平行平板玻璃（设n =1.5），下面放一直径为1mm 的金属片。

若在玻璃板上盖一圆形的纸片，要求在玻璃板上方任何方向上都看不到该金属片，问纸片的最小直径应为多少？2211sin sin I n I n = 66666.01sin 22==n I745356.066666.01cos 22=-=I1mm I 1=90︒n 1 n 2200mmL I 2 x88.178745356.066666.0*200*2002===tgI xmm x L 77.35812=+=4.光纤芯的折射率为1n ，包层的折射率为2n ，光纤所在介质的折射率为0n ，求光纤的数值孔径（即10sin I n ，其中1I 为光在光纤内能以全反射方式传播时在入射端面的最大入射角）。

解：位于光纤入射端面，满足由空气入射到光纤芯中，应用折射定律则有： n 0sinI 1=n 2sinI 2 (1)而当光束由光纤芯入射到包层的时候满足全反射，使得光束可以在光纤内传播，则有：(2)由（1）式和（2）式联立得到n 0 .5. 一束平行细光束入射到一半径r=30mm 、折射率n=1.5的玻璃球上，求其会聚点的位置。

工程光学(知识讲座)

工程光学第二章理想光学系统1、一个折射率为1.52的双凸薄透镜，其中一个折射面的曲率半径是另一个折射面的2倍，且其焦距为5cm，则这两个折射面的曲率半径分别是〔7.8〕cm和〔-3.9〕cm。

2、一个薄透镜折射率为1.5，光焦度500D。

将它浸入某液体，光焦度变成-1.00D，则此液体的折射率为〔1.502〕。

3、反远距型光组由〔一个负透镜和一个正透镜〕组成，其特点是〔工作距大于组合焦距〕。

4、远摄型光组由一个〔正透镜〕和一个〔负透镜〕组成，其主要特点是〔焦距大于筒长〕，因此该组合系统常用在〔长焦距镜头〕的设计中。

第三章平面与平面系统1、反射棱镜在光学系统中的主要作用有〔折叠光路〕、〔转折光路〕和转像、倒像等，在光路中可等效为平行平板加〔平面反射镜〕。

2、某种波长的光入射到顶角为60°的折射棱镜，测得最小偏向角为42°15′，则该种玻璃对于入射波长的折射率为〔1.557〕。

3、唯一能完善成像的光学元器件是〔平面反射镜〕，利用其旋转特性可制作光学杠杆进行放大测量；利用双光楔也可以实现〔微小角度和微小位移〕的测量，主要有〔双光楔旋转测微〕和〔双光楔移动测微〕两种形式。

4、用于制作光学元件的光学材料包括光学玻璃，〔光学晶体〕和〔光学塑料〕三类。

选用光学玻璃时的两个重要参数是〔折射率〕和〔阿贝常数〕。

5、一个右手坐标的虚物，经一个直角屋脊棱镜反射后，成〔右手〕坐标的〔虚〕像。

第四章光学系统中的光束限制1、限制轴上物点成像光束宽度的光阑是〔孔径光阑〕，而〔渐晕光阑〕在其基础上进一步限制轴外物点的成像光束宽度。

2、为减少测量误差，测量仪器一般采用〔物方远心〕光路。

3、测量显微镜的孔径光阑放置在〔物镜后焦平面上〕，视场光阑放置在〔一次实像面处〕，如果用1/2″的CCD接收图像并用14″的监视器观察图像，要求系统放大倍率为140倍，则显微镜的放大倍率是〔5倍〕。

第五章光线的光路计算及像差理论1、实际像与〔理想像〕之间的差异称为像差，包括单色像差和色差两大类。

光学基础习题

第1章习题1. 举例说明光传播中几何光学各基本定律的现象和应用。

（略）2. 证明光线通过二表面平行的玻璃板时，出射光线与入射光线的方向平行。

（略）3. 光线由水中射向空气，求在界面处发生全反射时的临界角。

当光线由玻璃内部射向空气时，临界角又为多少？（n水=1.333，n玻璃=1.52）（略）4. 一根没有包外层的光纤折射率为1.3，一束光线以u1为入射角从光纤的一端射入，利用全反射通过光纤，求光线能够通过光纤的最大入射角u1max。

实际应用中，为了保护光纤，在光纤的外径处加一包层，设光纤的内芯折射率为1.7，外包层的折射率为1.52，问此时光纤的最大入射角u2max为多少？解：如图所示，n0sin u= n1sin i1，i1+i2=90°，恰能发生全反射时i2=arcsin(n2/n1)u=(1)没有外包层，即n2=n0=1，u1max=43.6°(2)有外包层，u2max=35.4°5. 在上一习题中，若光纤的长度为2m，直径为20μm，设光纤平直，问以最大入射角入射的光线从光纤的另一端射出时，经历了多少次反射？解：以有外包层时的情况计算，u2max=35.4°，i1=19.9°，l1=27.6μm 2m / (2*27.6μm) = 36231，经历了36231次反射6. 一个18mm高的物体位于折射球面前180mm处，球面半径r=30mm，n=1，n’=1.52，求像的位置、大小、正倒及虚实状况。

解：如图，可以按近轴光路计算，y=18mm，l=-180mm，r=30mm，n=1，n’=1.52根据折射球面的物像关系公式：n n n n l l r''--='，l ’=129.1mm 8.5mm l ry y l r'-'-==-+，倒立的实像7. 简化眼把人眼的成像归结为一个曲率半径为5.7mm ，介质折射率为1.333的单球面折射，求这种简化眼的焦点位置和光焦度。

光学教程第二版习题答案(一至七章)

∴ d1
=
h1 − h2 tan u1′
= 1.5 −1 0.015
= 33.33mm
tan u2 ′ = tan u2
+
h2 f 2′
= 0.015 +
1 = 0.011
− 250
∴d2
=
h2 − h3 tan u2 ′
1 − 0.9 =
0.011
= 9.091mm
2－13 一球形透镜，直径为 40mm，折射率为 1.5，求其焦距和主点位置。
= −200mm
lH
= dϕ2 ϕ
= 50 × 5 = −100mm − 2.5
2－11
有三个透镜，
f1′
= 100mm，
f2′
= 50mm，
f
′
3
=
−50mm，其间隔 d1
= 10mm，
d 2 = 10mm ，设该系统处于空气中，求组合系统的像方焦距。
解：设 h1 = 100mm， u1 = 0 ，则：
tan u3′
= tan u3 +
h3 f3′
= 2.8 +
62 − 50
= 1.56
∴组合系统的像方焦距为：
f
′=
h1 tan u3′
100 =
1.56
= 64.1mm
2－12
一个三片型望远镜系统，已知
f
′
1
= 100mm，
f
′
2
=
−250mm ，
f
′
3
= 800mm，入
射平行光在三个透镜上的高度分别为： h1 = 1.5mm， h2 = 1mm ， h3 = 0.9mm ，试求合成

2第二章理想光学系统(精通)

h1 r1
经过计算得 l 67.4907, u 0.121869,
焦距为 f h 82.055, tan u
主点位置l f 14.5644在最后折射面
左侧14.5644mm处
2020/6/15
14
3：物像关系
几何光学目的就是求像，（对于确定的光学系统，给定物体的位置、大小、方向，求像的位置、大小、正倒及虚实）。
2020/6/15
31
例题2
已知一个透镜把物体放大 -2倍，当透镜向物体移近20mm时，放大倍数为 -3倍，求一开始的物距以及透镜的焦距？
1
l l
1
1
f 1
l 2 l 1 (2)
3 (l 20) 1 (3)
l l f
l 180mm, f 2 (180) 120mm, 3
B
A
F
A’ F’
B’
注意：图像法只能求得像的大致位置，至于具体位置在哪，完全不清楚！因此需要一种可以定量求得像的位置的方法！！！
2020/6/15
24
解析法（牛顿公式以焦点为基准）
-x
A
FM
-f
H -y
x‘
M’ B’
f'
y’
H’ F’ A’
B
N
N’
-l
ABF MHF
MH
FH
l’
y
f
AB FA y x
二：选择主平面和焦点，在一定程度上决定了光学系统的成像特性，加上后面的解析公式可以更加方便的计算。
三：选择主平面的好处：将实际光学系统中多次折射反射等效于共轭光线的一次偏折代替。
2020/6/15
11

工程光学基础习题参考答案-第二章_02

3、设一系统位于空气中，设一系统位于空气中，垂轴放大率 β = −10 × ，由物面到像面的距离（共轭距）共轭距）为 7200mm，物镜两焦点间距离为 1140mm。求该物镜焦距，求该物镜焦距，并绘出基点位置图。并绘出基点位置图。解：由公式 β = − x' f = − （2-4）， f' x
f 2 ' = −240mm
8、一短焦距物镜一短焦距物镜，焦距物镜，已知其焦距为 35mm，筒长 L=65mm，工作距离 l k ' = 50mm ，按最简单结构的薄透镜系统考虑，最简单结构的薄透镜系统考虑，求系统结构。求系统结构。解：（仿照（仿照 P32 P32 例 2）利用正切计算法，设 h1 = 100mm ，有公式：
1 1 1 d （2-33） = + − f ' f1 ' f 2 ' f1 ' f 2 '
f1 ' f 2 ' nr1 r2 f ' = − f = − ∆ = ( n − 1)[n( r − r ) + ( n − 1)d ] 2 1 1 Φ = f ' − dr2 l ' = H n( r2 − r1 ) + ( n − 1)d − dr1 l = H n( r2 − r1 ) + ( n − 1)d
xx' = ff ' = − f ' 2 ∴ x' = − f2 x
代入数据得：
x = −∞, x' = 0.5625mm x = −10m, x' = 0.703mm x = −6m, x' = 0.9375mm x = −4m, x' = 1.406mm x = −2m, x' = 2.813mm

光学第2章_理想光学系统

透镜
(6)
空气中的薄透镜焦距
时为正透镜, 正透镜中心比边缘厚, 又称为凸透镜; f ′= f > 0 时为正透镜正透镜中心比边缘厚又称为凸透镜 f ′= f <0 时为负透镜,负透镜中心比边缘薄又称为凹透镜. 负透镜中心比边缘薄, 为负透镜负透镜中心比边缘薄又称为凹透镜
由( 3) 和(5)式, 得空气中的薄透镜成像公式:
按照这种设想,来自无穷远物点和焦点F的两条光线将既通过Q点亦通过Q'点.Q,Q'是一对共轭点,两个主平面是一对共轭面,且 β ≡ +1 总之,对于一个光学系统,找到其主平面(一对)和两个焦点F,F',其系统的基本结构模型就构成了,它们完全可以代表光学系统的成像性质.
第二节
理想光学系统的基点和基面
Q Q'
.
F
H
H'
.
f'
F'
-f
第二节
理想光学系统的基点和基面
自物方焦点入射的光线与其出射平行于光轴的光线的延长线的交点Q的垂点H称为主点,相应的垂直于光轴的平面称为物方主平面. 类似地,H'为像方主点,相应垂直于光轴的平面为像方主平面.
Q Q'
.
F
H
H'
.
f'
F'
-f
注意:图中,Q,Q'点并非实际光线的交点,而是实际光线延长线的交点.引入主平面的概念后,可大大简化成像过程的计算 .不妨就"认为"Q,Q'是实际光线的交点.
y' f l' β = = y f'l
f '= -f
l' β = l

工程光学习题1

(n 1)
习题1-8 如图1-6所示，光线芯的折射率为n1，包层的折射率为n2，光纤所在介质的折射率为n0，求光纤的数值孔径。
n2 sin I m n1 n0 sin I1 n1 cos I m n n
2 1 2 2
习题1-9 有一直角棱镜如图1-16所示，其折射率为n。问光线以多大的孔径角入射时，正好能够经其斜面全反射后出射。如果棱镜用冕牌玻璃K9制造，计算该孔径角的值。
• 2.已知真空中的光速，求光在水（n=1.333 ）、冕牌玻璃（n=1.51）、火石玻璃（ n=1.65）、加拿大树胶（n=1.526）、金刚石（n=2.417）等介质中的光速。 c 3 10 c v n • 答：根据 v ，分别代入数字得： n n m / s 3 10 v • （1）在水中（注意单位） 1.333 2.2510 m / s • （2）在冕牌玻璃中 • （3）在火石玻璃中 • （4）在加拿大树胶中 • （5）在金刚石中
L d lF
300m m d L lF f 3 lF
h1 f tanu h1 2 h2 tanu h2 2 lF h1 tanu1 f1 h h d tanu 1 1 2
1 1 2 l l r (1) 0, l l l , l 50m m

无限远轴上物点的共轭像点正好位于 r / 2处； (2) 0.1, l 550mm, l 55m m； (3) 0.2, l 300mm, l 60m m；
(1) l 时， 0； (2) l 1000mm时， 0.429 ； (3) l 100mm时， 1.5； (4) l 0时，l 0，物和像都位于折射球面的顶点， 0； (5) l 100mm时， 0.75； (6) l 150mm时， 0.667 ； (7) l 200mm时， 0.6；

应用光学习题第二章

该题中得到实像点时，采用的就是虚物成实像的形式（会聚光入射）
a.
正弯月单透镜r1
0，r2 r1 r2
0
r1 r2，所以第一个面对球心C1点在C2点的左边
i) 若透镜第二个面的球心C2恰好是第一个面的不晕点。
ii）那么过不晕点的共轭点S1的光线则过C2点
iii ）对于第二个面来说，过球心的光线保持方向不变，
答：根据不晕条件，物像点在透镜的同一侧，所以不晕透镜分两种情况，
一种是实物成虚像，一种是虚物成实像。
该题中 l =-60 mm<0 所以属于实物成虚像的情况。
(1) 如果是正弯月型透镜
1 2
n1l1 ' n1 ' l1
n2l2 ' n2 'l2
l1' nl2 ' l1' l2 ' 1 1 nl1 l2 l1 l2 1.5
正弯月单透镜构成不晕透镜C（2 S1，S2，S2）
n1 1
n2 1
S1
C1 C2
n
l2 l2
r1
l1
r2 l1
同心球面透镜构成不晕透镜C（2 C1，S1，S1，S2，S2）
n1 1
n2 1
C1
C2
n
r1
r2
l1 l1 l2 l2
编号 2_005 出处 P193_9
证明同心透镜的光焦度
y' nu n sin u
y n'u' n'sin u'
所以n'y' sin u' ny sin u满足正弦条件
编号 2_007 答：(接上一页）
（b）forl r,也就是说i' i 0，u u'，sinu sin u'

第二章理想光学系统

h －U A
－L
由三角关系： tgU h
6
L
当 L 即物点向无限远处左移时，由于任何光学系统口径有限，所以此时 U 0
h
－L
※ 无限远轴上物点发出的光线与光轴平行
7
（二）像方焦点、像方焦平面；像方主点、主平面；
像方焦距
像方
焦平
A
B
Q ’ E’
面
h
H’
像方主平面
U’
像方主点
f’
F’
像方焦点
F
（1）辅助物AB （2）由B作 BQ // 光轴（3）QQ’
（4）由Q’作直线过F ’ （5）BF （6）N ’M
（7）由B’作直线垂线于光轴交点即是A’
21
求AQ的出射光线：
F’ A
F’
R
R’
Q Q’
A’ H H’
（1）AQ N （2）辅助焦平面
（3）延长AQ到N （4）NR F （5）R’F ’
（3）平行平板，f ’为∞， Φ＝０，对光束不起会聚或发散作用。
14
第三节理想光学系统的物象关系
一、用作图法求光学系统的理想像 ※ 已知一个理想光学系统的主点和焦点的位置，利用光线通过它们后的性质，对物空间给定的点、线、面通过画图追踪典型光线求像，称为图解法求像。
这可是重点呦！
15
可供选择的典型光线和可供利用的性质有：
y f x
y
x
f
结论：光组焦距一定时，物在距焦点距离不同时，垂轴放大率也不同。
33
第二种表达方式：用主物距、主像距与焦距表达
在x ff x 的两边各加f '得
x f ' ff f ' f f x

工程光学习题解答

36.2( mm), l F
第二章理想光学系统
17、有三个薄透镜，其焦距分别为 f1 100mm, f 2 50mm, f 3 50mm, 其间隔 d1 10mm, d 2 10mm 求组合系统的基点。 h h1 100mm, tan U 2 tan U1 2 解：物方参数 f

lH f
l F l H f 1560mm, l F l H f 1360mm
第二章理想光学系统
10、解：
f f1f 2

100mm,
f1f 2 f
50mm
d f1 f 2 100mm lH f lH f d f2 d f1 100mm, l F l H f 0
A
OB 50 OB OB 30mm
A
A
n 6、解：0 sin I1 n1 sin I 2 I 2 90 I m
0
n1 sin I m n2 sin 90 sin I m n2 n1 n2 n1
2 2
0
cos I m 1
n0 sin I1 n1 1
H
lH
F2
F1
F
d
l F (lk )
L
f
第二章理想光学系统
9、已知一透镜 r1 200mm, r2 300mm, d 50mm, n 1.5 ，求其焦距、光焦度、基点位置。 nr1r2 解： f 1440mm 1.44m
( n 1)[ n( r2 r1 ) ( n 1)] 1 f 0.69 D n 1 n d1 120mm, l H f n 1 n d 2 80mm

理想光学系统习题

第二章理想光学系统一：选择题（可以有多选)1.有一个无限远物点，经某一理想光学系统成像，陈述正确的是（B ）A.其像点必在理想光学系统的像方焦点处。

B.其像点必在理想光学系统的像方焦平面上。

C.该物点与像点无穷远点共轭。

D.该物点与其像点可作为此理想光学系统的一对基点。

2.有一个置于空气中的理想光学系统，其垂轴放大率β>0,则（ AB ）A.物像位于系统的同侧。

B.角放大率γ>0。

C.像高大于物高。

D.光学系统的焦距为正。

3.一物体经理想光学系统后放大的实像。

当物体向光学系统方向移动一微小距离，则（ AC ）A.其像变大。

B.垂轴放大率β的绝对值变小。

C.角放大率γ的绝对值变小。

D.轴放大率α的绝对值变小。

4.理想光学系统的角放大率γ（ABD ）A.反映了理想光学系统能够把光束变宽或变窄的能力。

B.角放大率γ的大小取决于物像共轭位置。

C.改变理想光学系统物像方折射率的大小，角放大率γ值不变。

D.垂轴放大率β值越大，角放大率γ越小。

二、填空题1、一双凸透镜两球面的曲率半径都是12cm ，透镜玻璃的折射率为1.5，若将此透镜置于空气中，求透镜的焦距__12_ cm ______。

2、共轴理想光学系统的牛顿公式___ xx ’=ff ’______，高斯公式_1''=+lf l f ________。

3、一个折射率为1.52的双凸薄透镜，其中一个折射面的曲率半径是另一个折射面的2倍，且其焦距为5cm ，则这两个折射面的曲率半径分别为_ 7.8 _____cm 和__-3.9____cm 。

4、长60mm ，折射率为1.5的玻璃棒，在其两端磨成曲率半径为10mm 的凸球面，其焦距为____∞简答题1、共轴光学系统的成像性质有哪些？画出一对共轭面及两对共轭点已知情况下的物点和像点。

1、性质1 位于光轴上的物点对应的共轭像点也必然位于光轴上；位于过光轴的某一个截面内的物点对应的共轭像点必位于该平面的共轭像面内；同时，过光轴的任意截面成像性质都是相同的。