第六讲扩散与相变详解
第六章-扩散与固态相变全文编辑修改

关系式便可进行一些
扩散问题的计算。
间隙扩散 :当一个间隙 原子从一个间隙位置迁 移到另一个空的间隙位 置的过程,称为间隙扩
散,如图5-5所示。
在金属合金中,由于间隙 原子的半径较小,因此可 移动性强,间隙扩散比空 位扩散快得多。而且空的 间隙位置比空位数目多很 多,因此间隙原子移动的
可能性也比空位扩散大。
个微分方程式。
(1) 一维扩散
如图3所示,在扩散方向上取体积元 Ax, 和J x J分xx别表
示流入体积元及从体积元流出的扩散通量,则在Δt时间内, 体积元中扩散物质的积累量为
m (J x A J xx A)t
m
J x J xx
xAt
x
C J
t
x
C (D C ) t x x
如果扩散系数与浓度无关,则上式可写成
对于半无限固体其表面 浓度保持不变,例如对 于气体扩散问题,其表 面分压保持一定的情况 下,进行如下假设:
1)扩散前任何扩散 原子在体内的分布是均 匀的,此时的浓度设为C0
2)在表面的值设为 零且向固体内部为正方 向;
3)在扩散开始之前 的时刻确定为时间为零
Cx C0 1 erf x
Cs C0
图5-5 间隙扩散示意图
扩散前间隙原子 的位置
扩散后间隙原子 的位置
扩散系数
扩散系数是计算扩散问题的重要参数 ,目前普遍采用下式来求扩散系数,
即:D D0eQ / RT (5-5)
式中D0为扩散常数。Q为扩散激活能。对于 间隙扩散,Q表示每mol间隙原子跳跃时需越
过的势垒,Q表示NA个空位形成能加上每 1mol原子向空位跳动时需越过的势垒。
克肯达尔效应的实际意义续
Ni-Cu扩散偶经扩散后,在 原始分界面附近铜的横截面 由于丧失原子而缩小,在表 面形成凹陷,而镍的横截面 由于得到原子而膨胀,在表 面形成凸起。
材料科学基础基本第六章 扩散与固态相变

第一节 第二节 第三节 第四节 第五节 第六节 第七节 第八节
扩散定律及其应用 扩散机制 影响扩散的因素与扩散驱动力 几个特殊的有关扩散的实际问题 固态相变中的形核 固态相变的晶体成长 扩散型相变 无扩散相变
第一节 扩散定律及其应用
一. 扩散定律
(1)稳态扩散-菲克第 一定律 (Fick’s first law)
图5-6
ThemeGallery is a Design Digital Content & Contents mall developed by Guild Design Inc.
合金元素对碳在-Fe中的扩散的 影响
菲克第二定律
当扩散处于非稳态,即各点的浓度随时间 而改变时,利用式(1)不容易求出。但通 常的扩散过程大都是非稳态扩散,为便于求 出,还要从物质的平衡关系着手,建立第二
对于一定的扩散系统D0及Q为常数。某些 扩散系统的D0及Q见表6-2。由表中的数 据可以看到,置换扩散的Q值较高,这是
渗金属比渗碳慢得多的原因之一。
影响扩散 的因素
合金元素的影响
影响扩散的因素
1)温度:由(5-5)式可知D与温度成指数关系,可见温度对扩散速度影响很大。 例如从表6-2中可以看到,当温度从500℃升高到900℃时,Fe在-Fe中的扩散 系数从3.010-21增加到1.810-15m2/s,增加了近六个数量级。
对于半无限固体其表面 浓度保持不变,例如对 于气体扩散问题,其表 面分压保持一定的情况 下,进行如下假设:
1)扩散前任何扩散 原子在体内的分布是均 匀的,此时的浓度设为C0
2)在表面的值设为 零且向固体内部为正方 向;
3)在扩散开始之前 的时刻确定为时间为零
第六讲扩散与相变详解

概要
本章主要讨论固体材料中扩散的一般规律、扩散的影响因素和扩散机制等内
容
固体材料涉及金属、陶瓷和高分子化合物三类; 金属中的原子结合是以金属键方式; 陶瓷中的原子结合主要是以离子键结合方式为主; 而高分子化合物中的原子结合方式是共价键或氢键结合,并形成长链结构, 这就导致了三种类型固体中原子或分子扩散的方式不同,描述它们各自运动方式 的特征也是本章的主要目的之一。
1.两端成分不受扩散影响的扩散偶(diffusion couple)-焊接过程
解微分方程 → 引入中间变量和误差函数 → 求通解
A1 exp 2 d A2
0
x>0 则= 1
→ 边界条件 t=0 和初始条件
x= 则= 1 t=0 x=- 则= 2
x<0 则= 2
扩散的热力学分析
引起上坡扩散还可能有以下一些情况:
1.
弹性应力的作用。晶体中存在弹性应力梯度时,它促使较大半径的原子跑向 点阵伸长部分,较小半径原子跑向受压部分,造成固溶体中溶质原子的不均 匀分布。 晶界的内吸附。晶界能量比晶内高,原子规则排列较晶内差,如果溶质原子 位于晶界上可降低体系总能量,它们会优先向晶界扩散,富集于晶界上,此 时溶质在晶界上的浓度就高于在晶内的浓度。 大的电场或温度场也促使晶体中原子按一定方向扩散,造成扩散原子的不均 匀性。
x d 边界条件 t=, x=0, = 0 任意时刻 x ,t 0 dx 2 2 Dt x exp 正弦特解为 x, t 0 max 0 sin x 0 A sin
3.衰减薄膜源-表面沉积过程 初始条件 t=0, x=0, = x 0, =0 边界条件 t>0, x=, =0
扩散相变解答

材料的扩散与相变考试参考解答名词解释扩散激活能:在扩散过程中,原子从原始平衡位置跳动迁移到新的平衡位置,所必须越过的能垒值或称所必须增加的最低能量。
空位扩散:和空位相邻的原子比较容易进入空位位置而使其原来占据的位置变为空位,如此不断就可以实现原子迁移。
化学扩散:由于浓度梯度所引起的扩散。
扩散通量:单位时间内通过垂直于X 轴的单位平面的原子数量,单位为mol/cm 2s, 1/cm 2s, g/cm 2s 非均匀形核:新相优先在母相中存在的异质处形核,即依附于液相中的杂质或外表面形核。
反应扩散:由扩散造成的浓度分布以及由合金系统决定的不同相所对应的固溶度势必在扩散过程中产生中间相,这种通过扩散而形成新相的现象称为反应扩散。
惯析面:马氏体总是在母相的特定的晶面上析出,伴随着马氏体相变的切变,一般与此晶面平行,此晶面为基体与马氏体相所共有,称为惯析面。
TTT 图:过冷奥氏体等温转变动力学图,又称C 曲线。
溶质原子贫化区:由于空位的存在,促使溶质原子向晶界迁移的偏聚,辐射或加热时产生大量空位在冷却时向晶界迁移并消失,同时拖着溶质原子运动,溶质原子富集在晶界。
偏聚范围大,在晶界上形成一定宽度偏聚带,达几微米,偏聚带两侧有溶质原子贫化区。
解答题:(27分)1.在一维稳态扩散情况下,试推导出扩散物质的浓度与坐标的分布函数。
稳态扩散:220,0C C CD t t x∂∂∂===∂∂∂ 从而:,C(x)Ax+B Cconst A x∂===∂积分可得 设:得:211211121(),()C C C x C C C x B C A C x x C L C C L L---==⇒=⇒=+-2.将一根Fe-0.4%C-4%Si 合金棒与一根Fe-0.4%C 合金棒焊接在一起,经1015℃×10天扩散退火会产生什么现象?并说明产生这种现象的原因。
见上交材基3.公式2D P α=Γ的物理意义是什么?简述在间隙扩散与空位扩散机制中D 表达式的区别? D 表示单位梯度下的通量,即为扩散系数,单位为2/cm s 或2/m s 间隙扩散机制中D 的表达式:2**exp()exp()S H D a R RTαν∆∆=- 20*exp()S D a Rαν∆=为频率因子,*S ∆激活熵,*H ∆激活焓 空位扩散机制中D 的表达式:**2exp()exp()v vS S H H D a R RT αν∆+∆∆+∆=- *20exp()vS S D a Rαν∆+∆=频率因子可见,空位机制比间隙机制需要更大的扩散激活能。
扩散相变解答.

材料的扩散与相变考试参考解答名词解释扩散激活能:在扩散过程中,原子从原始平衡位置跳动迁移到新的平衡位置,所必须越过的能垒值或称所必须增加的最低能量。
空位扩散:和空位相邻的原子比较容易进入空位位置而使其原来占据的位置变为空位,如此不断就可以实现原子迁移。
化学扩散:由于浓度梯度所引起的扩散。
扩散通量:单位时间内通过垂直于X 轴的单位平面的原子数量,单位为mol/cm 2s, 1/cm 2s, g/cm 2s 非均匀形核:新相优先在母相中存在的异质处形核,即依附于液相中的杂质或外表面形核。
反应扩散:由扩散造成的浓度分布以及由合金系统决定的不同相所对应的固溶度势必在扩散过程中产生中间相,这种通过扩散而形成新相的现象称为反应扩散。
惯析面:马氏体总是在母相的特定的晶面上析出,伴随着马氏体相变的切变,一般与此晶面平行,此晶面为基体与马氏体相所共有,称为惯析面。
TTT 图:过冷奥氏体等温转变动力学图,又称C 曲线。
溶质原子贫化区:由于空位的存在,促使溶质原子向晶界迁移的偏聚,辐射或加热时产生大量空位在冷却时向晶界迁移并消失,同时拖着溶质原子运动,溶质原子富集在晶界。
偏聚范围大,在晶界上形成一定宽度偏聚带,达几微米,偏聚带两侧有溶质原子贫化区。
解答题:(27分)1.在一维稳态扩散情况下,试推导出扩散物质的浓度与坐标的分布函数。
稳态扩散:220,0C C CD t t x∂∂∂===∂∂∂ 从而:,C(x)Ax+B Cconst A x∂===∂积分可得 设:得:211211121(),()C C C x C C C x B C A C x x C L C C L L---==⇒=⇒=+-2.将一根Fe-0.4%C-4%Si 合金棒与一根Fe-0.4%C 合金棒焊接在一起,经1015℃×10天扩散退火会产生什么现象?并说明产生这种现象的原因。
见上交材基3.公式2D P α=Γ的物理意义是什么?简述在间隙扩散与空位扩散机制中D 表达式的区别? D 表示单位梯度下的通量,即为扩散系数,单位为2/cm s 或2/m s 间隙扩散机制中D 的表达式:2**exp()exp()S H D a R RTαν∆∆=- 20*exp()S D a Rαν∆=为频率因子,*S ∆激活熵,*H ∆激活焓 空位扩散机制中D 的表达式:**2exp()exp()v vS S H H D a R RT αν∆+∆∆+∆=- *20exp()vS S D a Rαν∆+∆=频率因子可见,空位机制比间隙机制需要更大的扩散激活能。
关于扩散与固态相变课件

3. 复合机制 在扩散过程中,当间隙原子和空位相遇时,二者
同时消失,这便是间隙原子与空位的复合机制,如 图。这种扩散一般是在存在费仑克尔缺陷的晶体中
进行。
4. 易位机制
相邻原子对调位置或是通过循环式的对调位置,从 而实现原子的迁移和扩散。这种扩散机制称为易位 式扩散机制。此种扩散机制要求相邻的两个原子或 更多的原子必须同时获得足够大的能量,以克服其 它原子的作用才能离开平衡位置实现易位,因而这 种过程必然会引起晶格较大的畸变,所以实现的可
一个在空位旁边的原子就有机会跳入空位之中,使 原来的位置变为空位,如图。另外的邻近原子也可 能占据这个新形成的空位,使空位继续运动。这就 是空位机制扩散。大多数元素固体的自扩散以空位 扩散为主。在离子化合物和氧化物中也常有这种扩 散。
2. 间隙机制 是原子在点阵的间隙位置间跃迁而导致的扩散,
如图。在间隙机制中,还有从间隙位置到格点位置 再到间隙位置的迁移过程,其特点是间隙原子取代 近邻格点上的原子,原来格点上的原子移到一个新 的位置。前种间隙机制主要存在于溶质原子较小的 间隙式固溶体中,而后种间隙机制主要存在于自扩 散晶体中。
即J=-D(dc/dx) 其中D:扩散系数,cm2/s,J:扩散通量,g/cm2·s
式中负号表明扩散通量的方向与浓度梯度方向相反。
可见,只要存在浓度梯度,就会引起原子的扩散,
一、扩散第一定律
Fick第一定律(Fick’ s first law)描述在稳态扩散(steady state diffusion)情况下 ,即各处浓度不随时间变化,只随距离 变化而变化. (一定时间内,浓度不随时间变化dc/dt=0)
置换式固溶体中,溶质、溶剂原子大 小相近,具有相近的迁移率,在扩散 中,溶质、溶剂原子同时扩散的现象。
第六讲扩散焊专题

a) 从经济角度考虑,应选择较低的压力; b) 通常扩散焊采用的压力在0.5~50MPa之间。 c) 对于异种金属扩散焊,较大的压力对减小或防止扩散孔洞
有良好作用。 d) 由于压力对扩散焊的第二、三阶段影响较小,在固态扩散
焊时可在后期将压力减小,以便减小工件的变形。
---精品---
---精品---
回顾上节 内 容
扩散焊特点 扩散焊分类 扩散连接原理及机制 扩散焊工艺 扩散焊设备 其他扩散焊方法
---精品---
扩散焊的特点
与常用压力焊的相同点:不同点。
扩散焊与熔焊、钎焊方法的比较 优缺点
---精品---
扩散焊的分类
---精品---
单晶硅和单晶硅扩散焊
不锈钢板和网
碳碳和铌合金
3、保温时间:与温度、压力、中间扩散层厚度和对接成分及组织 均匀化的要求密切相关,也受材料表面状态和中间层材料的影响。 扩散层深度或反应层厚度与扩散时间的平方根成正比。扩散连接 接头强度与保温时间的关系x=如k t下图所示。也存在一个临界保温时 间,接头强度、塑性、延伸率和冲击韧性与保温时间的关系均是 先增大到一定程度后趋于稳定
置换反应:活泼元素置换非活泼元素,如AlMg+SiO2,形成新相硅。
---精品---
扩散焊专题之二
---精品---
扩散焊工艺
工艺参数 主要包括温度、压力、时间、真空度以及焊件表面处理和中
间层材料的选择等,这些因素对扩散连接过程和接头质量有着极 其重要的影响。
1、温度:①对连接初期表面凸出部位塑性变形、扩散系数、表面 氧化物向母材内溶解及界面孔洞的消失过程等均产生影响;②也 决定了母材的相变、析出以及再结晶过程,从而直接或间接影响 到扩散连接过程及接头质量。温度越高,扩散系数越大;连接表 面达到紧密接触所需压力越小。但温度提高受到被焊材料冶金物 理特性方面的限制;提高加热温度还会造成母材软化及硬化
第六讲扩散焊专题

钟;
第三阶段是界面和孔洞消失,形成可靠接头阶段在接触部位形
成的结合层向体积方向发展,扩大牢固连接面消除界面孔洞,
形成可靠连接
三过程相互交叉进行,连接过程中可生成固溶体及共晶体,有
时形成金属间化合物,通过扩散、再结晶等过程形成
固态冶金结合,达到可靠连接
精选版课件ppt
11
图 扩散焊的三阶段模型
a) 凹凸不平的初始接触
(1)真空室: 真空室越大,要达到和保持一定的真空度,对所需真 空系统要求越高。真空室中应有由耐高温材料围成 的均匀加热区,以保持设定的温度;真空室外壳需 要冷却。
精选版课件ppt
33
(2)真空系统
一般由扩散泵和机械泵组成。机械泵只能达到 1.33×10-2 Pa的真空度,加扩散泵后可以达到
1.33×10-4 ~1.33×10-5 Pa的真空度,可以满足所
置换反应:活泼元素置换非活泼元素,如AlMg+SiO2,形成新相硅。
精选版课件ppt
15
扩散焊专题之二
精选版课件ppt
16
扩散焊工艺
工艺参数 主要包括温度、压力、时间、真空度以及焊件表面处理和中
间层材料的选择等,这些因素对扩散连接过程和接头质量有着极 其重要的影响。
1、温度:①对连接初期表面凸出部位塑性变形、扩散系数、表面 氧化物向母材内溶解及界面孔洞的消失过程等均产生影响;②也 决定了母材的相变、析出以及再结晶过程,从而直接或间接影响 到扩散连接过程及接头质量。温度越高,扩散系数越大;连接表 面达到紧密接触所需压力越小。但温度提高受到被焊材料冶金物 理特性方面的限制;提高加热温度还会造成母材软化及硬化
精选版课件ppt
35
加压只是使接触面产生微观的局部变形。扩散焊所施
第六章扩散(课件19)

图5-1-2是典型的扩散 问题。两根含有不同初 始浓度溶质原子的合金 棒焊接在一起,经高温 加热一段时间后,溶质 原子自浓度高的一侧流 向浓度低的一侧,使合 金棒沿纵向的浓度梯度 减小,溶质原子在合金 棒中分布趋于变得均匀
图5-1-2
典型的扩散举例
1.1 扩散的条件
扩散必需的三个基本条件: (1)扩散驱动力 使物质发生迁移(定向),一定存 在着某种力或场,如浓度梯度。 (2)温度 原子迁移所必需的基本条件,温度越高 ,扩散越容易。只有T足够高,才能使原子具有足 够的激活能,足以克服周围原子的束缚而发生迁 移。如Fe原子在500℃ 以上才能有效扩散,而C原 子在1000℃ 以上才能在Fe中扩散。 (3)时间 扩散是一个物质迁移的过程,而过程的 概念就体现在时间上。扩散原子在晶格中每一次 最多迁移0.3~0.5nm的距离,要扩散1㎜的距离, 必须迁移近亿次。
1.2 从不同的角度对扩散进行分类
(1)根据扩散过程中是否发生浓度变化分类: (2) 根据扩散方向是否与浓度梯度 (3)根据扩散过程中是否出现新相进行分类:
(1)
根据扩散过程中是否发生浓度变化分类:
•1.自扩散(Self—diffusion) :纯物质晶体中的扩散。 自扩散在扩散过程中不伴有浓度变化的扩散,与浓度梯度 (concentration gradientd)(dc/dx)无关,与热振动 有关。自扩散只发生在纯金属和均匀固溶体中。 例如:纯金属晶粒长大过程;均匀溶体的晶粒长大
例如:均匀化退火 、化学热处理
2.上坡扩散(uphill diffusion):沿浓度升高方向进 行的扩散,扩散使浓度发生两极分化。
例如:液态合金的共晶转变;固溶体的共析转变;固
溶体中新相析出及新相长大。
10材料科学基础课件-第六章扩散

• 若渗 件是低碳钢,成分为C0,则解为: 若渗C件是低碳钢,成分为 则解为: 件是低碳钢
x C(x, t) = Cs − (Cs −C0 )erf ( ) 2 Dt
返回
x C(x, t) = Cs − (Cs − C0 )erf ( ) 2 Dt
例2:含C量0.20%的低碳钢在927℃进行气体渗碳。假定 0.20%的低碳钢在927℃进行气体渗碳。 的低碳钢在927℃进行气体渗碳 表面C含量增加到0.9%,试求距表面0.5mm处 表面C含量增加到0.9%,试求距表面0.5mm处,C含 0.9% 0.5mm 量达0.4%所需的时间。已知D =1.28× 量达0.4%所需的时间。已知D927=1.28×10 0.4%所需的时间 解:已知C0 、Cs、C( x, t )、x、D代入式得: 代入式得: 已知 代入式得
返回
3、扩散偶问题
如图扩散偶,经时间t 如图扩散偶,经时间t 高温扩散后, 处的溶质浓 高温扩散后,x处的溶质浓 度为: 度为:
C1 + C2 C1 −C2 x C(x, t) = erf ( + ) 2 2 2 Dt
0 C C2 C2 J C2 > C1 C1
C1
x
返回
4、脱碳问题
C C0
含碳量为C0的碳钢在空气 量为C 中加热,经时间t 中加热,经时间t脱C浓度为: 浓度为:
61扩散的宏观规律及其应用62扩散的微观规律63上坡扩散与反应扩散64影响扩散的因素61扩散的宏观规律及其应用扩散偶实例其加热至高温并长时间保温后高浓度一端必然向低浓度端方向迁移沿长度方向浓度逐渐变缓最后趋于一致
第六章
扩散
物质中原子、分子的迁移现象 固体中物质传输的唯一方式
返回
扩散型相变和无扩散型相变名词解释

扩散型相变和无扩散型相变名词解释相变是物质在一定条件下从一种状态转变为另一种状态的过程。
在相变中,物质的性质和结构都会发生改变,因此相变是物质研究中的重要课题之一。
相变可以分为很多种类,其中扩散型相变和无扩散型相变是两种常见的相变类型。
扩散型相变是指物质在相变过程中需要通过扩散来完成。
扩散是指物质中的分子或离子在空间中的自由移动。
在扩散型相变中,物质的分子或离子需要通过扩散来完成相变过程。
扩散型相变的典型例子是固态金属的熔化。
在金属熔化的过程中,金属中的原子需要通过扩散来完成熔化过程。
此外,固态晶体的溶解、气体的液化和固态晶体的晶化等过程也属于扩散型相变。
无扩散型相变是指物质在相变过程中不需要通过扩散来完成。
在无扩散型相变中,物质的分子或离子不需要通过扩散来完成相变过程。
无扩散型相变的典型例子是液态水的沸腾。
在水的沸腾过程中,水分子不需要通过扩散来完成沸腾过程。
此外,气体的升华、液态晶体的相变和超导材料的相变等过程也属于无扩散型相变。
扩散型相变和无扩散型相变的区别在于相变过程中是否需要通过扩散来完成。
扩散型相变需要通过扩散来完成,而无扩散型相变不需要通过扩散来完成。
此外,扩散型相变和无扩散型相变的物理机制也不同。
扩散型相变的物理机制是分子或离子的扩散,而无扩散型相变的物理机制则是其他因素的影响,如温度、压力等。
总之,扩散型相变和无扩散型相变是物质相变中的两种常见类型。
它们的区别在于相变过程中是否需要通过扩散来完成。
了解这两种相变类型的特点和物理机制,有助于我们更好地理解物质的性质和结构,为物质研究提供更加深入的认识。
扩散与相变

扩散与相变铸锭均匀化的扩散机理1 基础理论众所周知,所有金属和合金凝固时都存在枝晶偏析,必须通过均匀化处理消除或减少晶内化学成分、组织的不均匀性和在铸锭快速冷却时所产生的内应力,改善铸锭的热塑性。
均匀化处理能改善合金的塑性,提高合金元素在基体中的固溶度,提高合金的强度。
均匀化过程越彻底,时效后合金的强度越高。
在工业生产中,液态合金经浇铸后(铸锭或铸件),冷却较快,一般是几分钟,最多是几小时就已凝固完毕,不可能达到平衡凝固。
由于非平衡凝固扩散进行不充分,铸锭或铸件的成分、组织、性能存在不均匀性。
主要体现在以下几个方面:铸锭存在成分偏析,如不消除会影响产品的性能的均匀性和降低耐蚀性。
铸锭中的低熔点组织在热加工过程中熔化,不利于加工。
(3)铸锭中存在较大的残余应力,在加工过程中可能导致铸锭开裂。
(4)铸锭中的硬脆相在加工过程中碎化,形成裂纹,降低合金的塑性。
鉴于以上问题,就需要对铸锭进行均匀化处理,以改善铸造合金的工艺性能,为后续冷、热加工和热处理创造条件,并且改善铸件的最终使用性能。
均匀化是一个在高温下进行的过程,需要一定时间才能完成,其微观机理是合金中一种或多种溶质原子在高温下在化学位梯度的作用下发生扩散,使合金的成分、组织不均匀性得以消除或者减少。
这是典型的扩散问题。
2 一个实际铸锭的枝晶偏析问题及其均匀化固溶体合金在非平衡结晶时,由于先后从液体中凝固出来的固相成分不同,加之冷却速度快,固相中均匀扩散来不及进行,结果使得晶粒内部化学成分不均匀。
往往会出现不同程度的枝晶偏析,从而损害合金的性能。
由于不平衡结晶,得到的固相晶粒内部先结晶区高熔点组元含量高,后结晶区低熔点组元含量高,这种在一个晶粒内部化学成分不均匀的现象就是晶内偏析。
由于固溶体晶体通常是树枝状,枝干和枝间的化学成分不同,因此又称为枝晶偏析。
如图Ni-Cu合金铸态组织,先凝固的晶体中心含Ni量高,后凝固的晶体部分含Cu量高,如图1所示。
材料物理(扩散与相变)
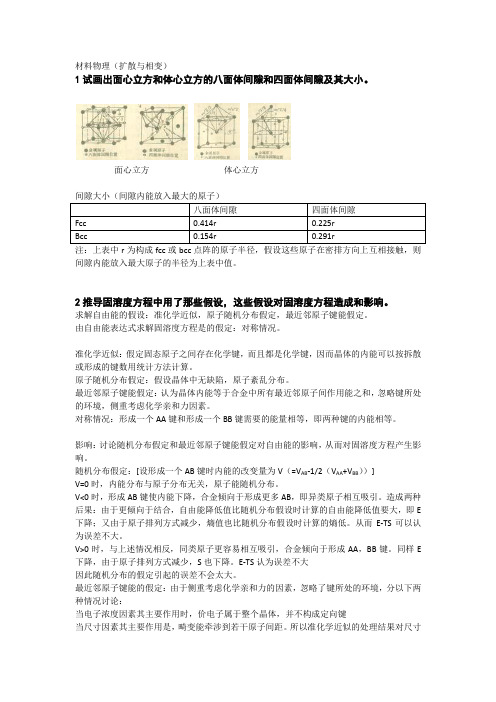
完全有序时,������������������ = 1,������ = 1;
完全无序时,������������������ = ������������,������ = 0;
短程序:只考虑最近邻的有序度。用短程序参数α1 表征。
������1
=
1
−
������������������ ���������∗���������
这要求临近的晶格格点上有空位。因此需要先形成空位,需要空位形成能Δ������������。同时形成空 位后,还要克服原子排列的能垒而迁移到空位位置,因此需克服能垒,即空位的迁移激活能
相变与位错及扩散.ppt

22
University Of Science and Technology Beijing
另一模式 “台阶”长大机制 AB、CD和EF是不易迁移的共格界面,BC、DE面是非共格的长大台
阶,台阶面上接纳原子比共格宽面上容易。原子加入台阶使台阶侧向移动。 界面覆盖后,沿法线方向推移了1个台阶厚度。继续长大需要出现新的台 阶。新台阶靠在宽面上以非均匀形核方式形成。台阶机制长大由共格宽面 上形核产生新台阶的过程所控制。
USTB
17
University Of Science and Technology Beijing
当新/母相成分相同时,长大只涉及界面的最近邻的原 子过程,称为界面过程控制长大。当新/母相成分不同时, 新相界面的推移除了需要上述的界面最邻近的原子过程外, 还可能要涉及原子的长程扩散过程。因而长大过程可能受 界面过程控制或受扩散过程控制,也可能同时受界面过程 和扩散过程控制。
相变的形核
固态相变形核过程的多样性: 可是扩散的或无扩散的;可同时完成晶体结构和成分的变化,也可使成分不 变仅使晶体结构改变(如块形相变)或使结构不变仅成分改变。 注意点:形核驱动力不同于相变总驱动力。 形核的驱动力和核心成分
驱动力 考察:成分为Xβ的少量物质 由α相移至β相的自由能变化
能量涨落 形成/阻力 形核驱动力
亚稳平衡过渡相的形成
从相变的总体看,相变应以转变成最稳定相告终,这是因为这个过程的总 吉布斯自由能降低是最多的。
右图却说明亚稳相析出的形核驱动力可能 更大。
在转变为平衡相之前的一种过渡性产物称 为过渡亚稳相。这种过渡亚稳相能够存在 多久,还要看相变的动力学条件。铁-碳合 金中的Fe3C相是亚稳定相的典型例子,石 墨是稳定相,但由于它形成十分缓慢,以 至我们常看到的是亚稳定的Fe3C相而不是 石墨。
扩散型相变名词解释

扩散型相变名词解释扩散型相变是指物质状态在内部不断扩散,引起物质状态变化而产生的一类热力学过程。
在这个过程中,物质因扩散而产生结构变化,这一变化可以跨越数量级,从微小到巨大。
这种物理现象的发现远古,不仅是科学家的兴趣,也是人们受关注的话题。
从古至今,扩散型相变已成为重要的学科,科学家为了更好地理解这种热力学过程,研究了大量的理论和实验,建立了多种模型以研究不同扩散现象和物质形式的变化。
扩散型相变一般包括一个或多个化合物或元素,比如组成水溶液的水分子和盐分子,组成合金的元素等,当这些物质在温度,压力,浓度等外部条件发生改变时,扩散型相变就会发生,使物质的结构由原来的晶态变为无序态,即相变发生。
扩散型相变的热力学状态方程由扩散系数,自发发生率和能量补偿项组成,是对统计力学原理的重要表述。
一般来说,当扩散系数增大,自发发生率增大,能量补偿项也增大时,相变发生率就会增大。
扩散型相变有许多类型,它们都具有一定的特点,最常见的主要有四种:(1)渗析变态,就是渗析剂从固体中渗入溶液中,变态的特征是溶质的渗入溶液的速度与渗析剂的浓度成正比,这种相变具有快速和显著的变化;(2)结晶变态,就是溶质从溶液中析出晶体的变态,这种过程的速度与当前的沉淀速度有关;(3)熔融变态,这是温度升高,溶液变为熔融物质的变态,当温度再次升高时,溶质又会发生变化;(4)混合变态,就是两种或多种物质混合,发生变态的特征之一就是混合物的热膨胀系数和它们分别的热膨胀系数不相等。
扩散型相变可以用于各种材料的加工,如熔融金属和非金属的合金,以及各种有机物的折射率和溶剂的选择等。
它甚至可以用作某些药物的制备和精细化工制备过程中的关键过程,如萃取、结晶、溶解和细化等。
扩散型相变是自然界中常见的热力学过程,关于这一过程的研究给人们提出了许多有趣的知识,受到了普遍的关注。
此外,扩散型相变也为科学家提供了解决多种问题的有益工具,如金属变态加工,萃取和结晶等,为社会发展奠定了坚实的基础。
第06章扩散与固态相变2011资料

称为扩散的驱动力,负号表示推动物质流向 化学位较低处
代替 Fick 第一定律的真实法则为:
扩散系数与化学位的关系
如果某组元的浓度提高反而可降低化学位(降低其吉 布斯自由能),则组元会进行上坡扩散。组元的集中降低 吉布斯自由能的原因和原子之间的键结合能来决定。所 以在分析扩散过程时,应该从化学位来分析,不能单从 浓度梯度来分析。 当然在很多情况下,当
(2) 组元浓度
间隙固溶体溶质的扩散系数随其浓度的增加而增 加。溶质浓度的增加使固溶体的晶格畸变加剧。
(3)第三组元的影响
影响扩散系数的因素
•晶体结构
1.原子排列越紧密,晶体结构的致密度越高,激活能 较大,扩散系数较小。
2.晶体结构的对称性差的材料中, 不同方向上扩散系数的差别也大, 常见金属材料的晶体结构,正确分析扩散规律, 必需用热力学来讨论扩散过程的实质,因为扩散的自发 进行方向也必然是系统吉布斯自由能下降。
驱动扩散的真实动力是自由能
化学位的定义,某溶质i的化学位为
平衡条件是各处的化学位相等。如果存在一化学位 梯度,表明物质迁移 dx 距离,系统的能量将变化了。 好象有一作用力推动它移动一样,设这个力为 F,所作
第六章 扩散与固态相变
第一节 扩散
• 概述 • 菲克定律 • 互扩散 • 扩散中的热力学 • 扩散的微观机制 • 影响扩散系数的因素 • 反应扩散
概述
扩散现象:大家已经在气体和液体 中知道,例如在房间的某处打开一瓶香 水,慢慢在其他地方可以闻到香味,在 清水中滴入一滴墨水,在静止的状态下 可以看到他慢慢的扩散。
程。若扩散系数D为常数,方程可写成:
三维情况,设在不同的方向扩散系数为相 等的常数,则扩散第二方程为:
扩散型相变

结论:过饱和蒸汽压差P-P0为凝聚相变过程的推动力
浓度条件:
对溶液:
C0 G RT ln C
若是电解质溶液,还要考虑电离度
C0 G RT ln C C ) RT 0 C G RT ln(1 C C C0 C C C 0 C0 C 0 C C0
u B[1 exp(
HT
RTT0
)]
—晶体生成速率
讨论
, G RT
H
RT0
2
u B (
HT
RTT0
) B
T
当过程离平衡很远时,即
T T0 , 则G RT
u B (1 0) B
此时晶体生长速率达到极限值10-5cm/s
C-C0即为这一相变过程的推动力
相变过程的推动力: 应为过冷度,过饱和浓度,过饱和蒸汽 压。即相变时系统温度、浓度和压力与相平 衡时温度、浓度和压力之差值。
三.晶核形成条件
当熔体冷却发生相变,由一相变为两相时,体系
G 在能量上出现两个变化: L S
G1 —系统中一部分原子(或离子)从高自由状态转 变为低自由能的另一态 G1 0
特点:
1 2
S1 S 2 V1 V2
C P1 C P 2 -热容
1 2 1 2
-等温压缩系数 如图8-2 - 等压膨胀系数
返回
二.按相变方式分类:
成核—长大型相变:由组成波动程度大、空间范围小 的浓度起伏开始发生的相变。初期起伏生成新相核 心,然后是新相核心长大。有均匀成核和非均匀成 核两类。 连续型相变:由组成波动程度小、空间波动范围广的 起伏引起的相变,即起伏连续地生长而形成新相。
扩散型相变名词解释

扩散型相变名词解释
扩散型相变是一种热力学状态,它指的是在多组分的合金中,当一种元素的晶体凝固时,由于温度、压力或添加元素等原因,其他元素也随之凝固。
扩散型相变通常发生在晶体内部,而不是在表面上。
它是由于物质内部态变而发生的,而表面没有显示任何变化。
扩散型相变是一种复杂的物理现象,由两个或多个元素的晶体结构的相互作用引起的。
在大多数情况下,这种相变只会发生在低温条件下,而在正常温度下是不可能发生的。
扩散型相变可以分为两种:一种是温度依赖型,另一种是压力依赖型。
温度依赖型扩散型相变是指在温度变化时,某些元素会渗入另一元素的晶体结构中,而压力依赖型扩散型相变指的是在压力变化时,某些元素会渗入另一元素的晶体结构中。
扩散型相变可以发生在金属、合金、金属氧化物、离子晶体和半导体等多种物质中。
在金属和合金中,扩散型相变往往伴随着晶体结构的形成和维持,它也会引起金属和合金的拉伸变形、弹性模量和热膨胀系数的变化。
扩散型相变在材料加工中也有着重要意义,它可以改变材料的组织和性能。
例如,在焊接过程中,会发生扩散
型相变,这使得熔接面组织更加紧密和结实,也使焊接面的抗拉强度和抗疲劳性能大大提高。
此外,当材料中元素的晶体结构发生变化时,也会发生扩散型相变。
这些变化可以影响材料的电学性能,特别是半导体材料的电学性能,因此在半导体器件的制造过程中,也会用到扩散型相变。
扩散型相变是一种复杂的物理现象,它也是材料性能改变的重要因素之一。
它可以用于改善材料的性能,如强度、硬度、抗磨损性能等,也可以用于改变材料的组织结构,从而改变材料的电学性能。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
结论: 1. 当lnr与呈直线关系时,D与碳浓度无关 2. 当lnr与为曲线关系时,D是碳浓度的函数
实测的lnr与关系
-lnr
d 稳态扩散 ( 0) dt
dx
(1>2) 1 2
d J D dx
J
J: D: :
d : dx
扩散通量(mass flux), kg/(m2 s) 扩散系数(diffusivity), m2/s 质量浓度,kg/m3
扩散方程的解-应用
第一定律—求解一阶微分方程
第 二 定 律 — 设 置 中 间 变 量 求 通 解 ( 高 斯 解 Gauss solution 、 误 差 函 数 解 error function solution、正玄解 sinusoidal solution) ,解微分方程初始条件,边界条 件求方程式。
应用:测定碳在-Fe中的扩散系数
2 r2
2r 2
l
1000C [C]
l>>r
2r1
平视方向
2r1
俯视方向
稳态时: 单位时间内通过半径为r(r2<r<r1) 的圆柱管壁的碳量为常数: q/t
q d J= D 径向通量: 2 rlt dr q d D 常数 由菲克第一定律得: 2 rlt d ln r
浓度梯度
若D与浓度无关,则:
D t x
2 2
对三维各向同性的情况:
D( ) t x y z
2 2 2 2 2 2
菲克定律描述了固体中存在浓度梯度时发生的扩散,称为化学扩散;当 扩散不依赖于浓度梯度,仅由热振动而引起时,则称为自扩散。
定义:自扩散系数
概要
本章主要讨论固体材料中扩散的一般规律、扩散的影响因素和扩散机制等内
容
固体材料涉及金属、陶瓷和高分子化合物三类; 金属中的原子结合是以金属键方式; 陶瓷中的原子结合主要是以离子键结合方式为主; 而高分子化合物中的原子结合方式是共价键或氢键结合,并形成长链结构, 这就导致了三种类型固体中原子或分子扩散的方式不同,描述它们各自运动方式 的特征也是本章的主要目的之一。
→ 求特解
x, t
1 2
2
1 2
2
x erf 2 Dt
x, t
2
x 1 erf 2 2 Dt
1=0
2.一端成分不受扩散影响的扩散体-表面热处理过程 初始条件 t=0, x0, =0 边界条件 t>0, x=0, =s x=, =0 求解方法同上,特解为
固体中原子及分子的运动
1.表象理论 2.扩散的热力学分析 6. 7.
影响扩散的因素 反应扩散
3.扩散的原子理论
4.扩散激活能 5.无规则行走与扩散距离
8.
9.
离子晶体中的扩散
高分子的分子运动
概要
物质的迁移可通过对流和扩散两种方式进行。在气体和液体中物质的迁移 一般是通过对流和扩散来实现的。但在固体中不发生对流,扩散是唯一的物质迁 移方式,其原子或分子由于热运动不断地从一个位置迁移到另一个位置。扩散是 固体材料中的一个重要现象,诸如金属铸件的凝固及均匀化退火,冷变形金属的 回复和再结晶,陶瓷或粉末冶金的烧结,材料的固态相变,高温蠕变,以及各种 表面处理等等,都与扩散密切相关。要深入地了解和控制这些过程,就必须先掌 握有关扩散的基本规律。研究扩散一般有两种方法: ①表象理论一根据所测量的参数描述物质传输的速率和数量等; ②原子理论一扩散过程中原子是如何迁移的。
(1) 对于同一扩散系统、扩散系数D与扩散时间t的乘积为一常数。 例题 1 :已知 Cu 在 Al 中扩散系数 D ,在 500℃和 600℃分别为 4.8×10-14m² s-1 和 5.3×10-13m² s-1,假如一个工件在600℃需要处理10h,若在500℃处理时,要达到同 样的效果,需要多少小时?(需110.4小时) (2) 对于钢铁材料进行渗碳处理时,x与t的关系是t x² 。 例题2:假设对-Wc=0.25%的钢件进行渗碳处理,要求渗层0.5㎜处的碳浓度为 0.8%,渗碳气体浓度为 Wc=1.2%,在950℃进行渗碳,需要7小时,如果将层深厚 度提高到1.0㎜,需要多长时间?(需要28小时)
x, t s 1 erf
Hale Waihona Puke x 2 Dt
x A Dt
x 2 BDt
工业生产中经常采用渗碳(Carburizing)的方法来提高钢铁零件的表面 硬度,所谓渗碳就是使碳原子由零件表面向内部扩散,以提高钢的含碳量。 含碳量越高,钢的硬度越高。 例题:p133 思考:若想将渗碳厚度增加一倍,需增加多少渗碳时间?
菲克第一定律
当固体中存在着成分差异时,原子将从浓度高处向浓度低处扩散。如何描 述原子的迁移速率,阿道夫 · 菲克( Adolf Fick )对此进行了研究,并在 1855年就得出:扩散中原子的通量与质量浓度梯度成正比,即
d J D dx
该方程称为菲克第一定律或扩散第一定律。式中,J为扩散通量,表示单 位时间内通 过 垂 直 于 扩 散 方 向 x 的单位面积的扩散物质质量 ,其单位为 kg/(m2· s);D为扩散系数,其单位为m2/s;而r是扩散物质的质量浓度,其 单位为kg/m3。式中的负号表示物质的扩散方向与质量浓度梯度。
扩散(diffusion): 在一个相内因分子或原子的热激活运动导致成分混合 或均匀化的分子动力学过程。
水
加入染料 部分混合
完全混合
时间
碳的扩散方向
Fe-C合金
高碳含量区域
低碳含量区域
概要
物质的传输方式
气体: 扩散+对流
固体: 扩散
离 子 键
液体: 扩散+对流
金属
陶瓷
高分子
扩散机制不同
表象理论
J Ds lim 0 x x
x1
x2
非稳态扩散d/dt0
推 导 过 程 : 菲 克 第 一 定 律 + 质 量 守 恒
A
质 量 浓 度
J1 dx
J2
扩散通量为J1的物质 经过体积元后的变化
浓度和距离的瞬时变化
通 量
J1
J2
x
通量和距离的瞬时关系
1.两端成分不受扩散影响的扩散偶(diffusion couple)-焊接过程
解微分方程 → 引入中间变量和误差函数 → 求通解
A1 exp 2 d A2
0
x>0 则= 1
→ 边界条件 t=0 和初始条件
x= 则= 1 t=0 x=- 则= 2
x<0 则= 2
