扩散与相变
第六章-扩散与固态相变全文编辑修改

关系式便可进行一些
扩散问题的计算。
间隙扩散 :当一个间隙 原子从一个间隙位置迁 移到另一个空的间隙位 置的过程,称为间隙扩
散,如图5-5所示。
在金属合金中,由于间隙 原子的半径较小,因此可 移动性强,间隙扩散比空 位扩散快得多。而且空的 间隙位置比空位数目多很 多,因此间隙原子移动的
可能性也比空位扩散大。
个微分方程式。
(1) 一维扩散
如图3所示,在扩散方向上取体积元 Ax, 和J x J分xx别表
示流入体积元及从体积元流出的扩散通量,则在Δt时间内, 体积元中扩散物质的积累量为
m (J x A J xx A)t
m
J x J xx
xAt
x
C J
t
x
C (D C ) t x x
如果扩散系数与浓度无关,则上式可写成
对于半无限固体其表面 浓度保持不变,例如对 于气体扩散问题,其表 面分压保持一定的情况 下,进行如下假设:
1)扩散前任何扩散 原子在体内的分布是均 匀的,此时的浓度设为C0
2)在表面的值设为 零且向固体内部为正方 向;
3)在扩散开始之前 的时刻确定为时间为零
Cx C0 1 erf x
Cs C0
图5-5 间隙扩散示意图
扩散前间隙原子 的位置
扩散后间隙原子 的位置
扩散系数
扩散系数是计算扩散问题的重要参数 ,目前普遍采用下式来求扩散系数,
即:D D0eQ / RT (5-5)
式中D0为扩散常数。Q为扩散激活能。对于 间隙扩散,Q表示每mol间隙原子跳跃时需越
过的势垒,Q表示NA个空位形成能加上每 1mol原子向空位跳动时需越过的势垒。
克肯达尔效应的实际意义续
Ni-Cu扩散偶经扩散后,在 原始分界面附近铜的横截面 由于丧失原子而缩小,在表 面形成凹陷,而镍的横截面 由于得到原子而膨胀,在表 面形成凸起。
9-2扩散型相变
对于成分在极小值与拐点之间的合金C 0’,如右图所示:由于G ”(C 0’)>0,自由能-成分曲线上凹,所以一旦出现成分起伏,体系自由能将由分解前的G(C 0’)升高到G 1。
但如果能分解成为成分为C a 的α1和成分为C b 的α2两相,系统自由能G2低于分解前的自由能G(C 0’)。
此时要靠形核方式分解,但是形核要满足成分条件和形核功。
所以过饱和固溶体的分解可以分为调幅分解和形核长大两种方式。
调幅分解时新相和旧相的成分连续变化,母相中溶质原在α中的溶解度如图所示。
A、脱溶系列(如Al-Cu合金)右图为几种不同成分的Al-Cu合金在130℃的时效硬化曲线。
由图可知:( A )随着Cu%的↗,时效硬化效果越明显,( B )硬度的峰值总是与θ”+θ’并存的组织相对应,一旦θ”消失,硬度将明显下降。
rβ2β扩散一旦发生,亚平衡I被打破,如右图b所示:(2)过饱和固溶体的脱溶③不连续脱溶过饱和固溶体的不连续脱溶也叫两相式脱溶,或者胞状式脱溶。
通常在母相晶界上形核,然后呈胞状向某一相邻晶粒内生长(与珠光体相类似)。
脱溶胞状物与母相有明显界面。
如图所示:不连续沉淀脱溶反应可以写成α’(C 0)→α(C α’)+β(C β) ,其中α’相是成分为C 0的过饱和固溶体;β是的晶体结构和成分都不同于α’的平衡析出相。
胞状脱溶物中的α与母相α’成分不同,但结构相同。
片状共析组织棒状共析组织共析转变指由单一的固态母相分解为两个结构和成分不同的新相的过程。
共析转变的反应式 :γ→α+β共析转变包括形核与长大两个过程。
但是由于共析转变在固态下进行,原子扩散速度缓慢,所以共析转变的形核与长大如图所示:(3)共析转变①共析转变的形核与长大共析体形核之后,靠原子的短程扩散,导致两相耦合。
原子的扩散主要沿着新旧两相的界面进行。
如右图所示:。
扩散相变解答.

材料的扩散与相变考试参考解答名词解释扩散激活能:在扩散过程中,原子从原始平衡位置跳动迁移到新的平衡位置,所必须越过的能垒值或称所必须增加的最低能量。
空位扩散:和空位相邻的原子比较容易进入空位位置而使其原来占据的位置变为空位,如此不断就可以实现原子迁移。
化学扩散:由于浓度梯度所引起的扩散。
扩散通量:单位时间内通过垂直于X 轴的单位平面的原子数量,单位为mol/cm 2s, 1/cm 2s, g/cm 2s 非均匀形核:新相优先在母相中存在的异质处形核,即依附于液相中的杂质或外表面形核。
反应扩散:由扩散造成的浓度分布以及由合金系统决定的不同相所对应的固溶度势必在扩散过程中产生中间相,这种通过扩散而形成新相的现象称为反应扩散。
惯析面:马氏体总是在母相的特定的晶面上析出,伴随着马氏体相变的切变,一般与此晶面平行,此晶面为基体与马氏体相所共有,称为惯析面。
TTT 图:过冷奥氏体等温转变动力学图,又称C 曲线。
溶质原子贫化区:由于空位的存在,促使溶质原子向晶界迁移的偏聚,辐射或加热时产生大量空位在冷却时向晶界迁移并消失,同时拖着溶质原子运动,溶质原子富集在晶界。
偏聚范围大,在晶界上形成一定宽度偏聚带,达几微米,偏聚带两侧有溶质原子贫化区。
解答题:(27分)1.在一维稳态扩散情况下,试推导出扩散物质的浓度与坐标的分布函数。
稳态扩散:220,0C C CD t t x∂∂∂===∂∂∂ 从而:,C(x)Ax+B Cconst A x∂===∂积分可得 设:得:211211121(),()C C C x C C C x B C A C x x C L C C L L---==⇒=⇒=+-2.将一根Fe-0.4%C-4%Si 合金棒与一根Fe-0.4%C 合金棒焊接在一起,经1015℃×10天扩散退火会产生什么现象?并说明产生这种现象的原因。
见上交材基3.公式2D P α=Γ的物理意义是什么?简述在间隙扩散与空位扩散机制中D 表达式的区别? D 表示单位梯度下的通量,即为扩散系数,单位为2/cm s 或2/m s 间隙扩散机制中D 的表达式:2**exp()exp()S H D a R RTαν∆∆=- 20*exp()S D a Rαν∆=为频率因子,*S ∆激活熵,*H ∆激活焓 空位扩散机制中D 的表达式:**2exp()exp()v vS S H H D a R RT αν∆+∆∆+∆=- *20exp()vS S D a Rαν∆+∆=频率因子可见,空位机制比间隙机制需要更大的扩散激活能。
材料固态相变与扩散 第4章_扩散性相变

(4)对式求极值得到r = 2 r ,dr/dt 为极大值。当 r >2
时的质点,其长大速度逐渐降低;
r (5)在长大过程中,当 增大时,所有粒子dr/dt
均降低;
(6)温度的影响是比较复杂。综合效果T↑,dr/dt ↑
r (7)体系过程刚开始时,稍大于 的质点长大速度小
于体系中粒子的平均长大速度,有可能在后期可能重新 被溶解。
讨论正沉淀增长情况。由于Gibbs-Thompson效应,析出相 顶端边缘附近基体中的平衡浓度要比原来没有效应时的平衡 浓度高,设为Cr 。作为近似处理,可设S为有效扩散距离, S=Kr ,其中K为常数,随析出相形状而改变,一般均取1。 设两相的摩尔体积相等,由Fick定律得:
dl D dC D C dt C C dx / C C Kr
dn 4R 2 D dC
dt
Vm
dR
此流量是提供给析出粒子长大的,析出粒子长大所需流量为:
n V 4 r 3
Vm 3 Vm
dn 4r 2
dr
Vm
dn 4r 2 dr
dt
Vm dt
根据质量平衡
dR D dC
R2
r 2 dr
dt
从粒子半径到距离R的最大值积分,设瞬时dr/dt是恒定的
(8)使析出相稳定的途径:低 σ ;D小;C0 要小。
扩散控制的析出相粒子 Ostwald长大规律
粒子体积分数对分散度的影响
根据能量最小原理,可以近似地假定
dr dr dt dt max
r
3
r03
8 9
D
VmC RT
()
t
考虑体积分数:
r
3
r03
扩散与相变计算题

金属中的扩散与相变2010硕士10班13.扩散习题课和复习34567891011121314151617例一:有一20钢齿轮气体渗碳,炉温为927℃,炉气氛使工件表面含碳量维持在0.9%C,这时碳在铁中的扩散系数为D=1.28x10-11m2s-1,试计算为使距表面0.5mm处含碳量达到0.4%C所需要的时间?解:可以用半无限长棒的扩散来解:18例二:上例中处理条件不变,把碳含量达到0.4%C处到表面的距离作为渗层深度,推出渗层深度与处理时间之间的关系,层深达到1.0mm则需多少时间?解:因为处理条件不变在温度相同时,扩散系数也相同,因此渗层深度与处理时间之间的关系:因为x2/x1= 2,所以t2/t1= 4,这时的时间为34268s = 9.52hr1920例1:含0.20%碳的碳钢在927 ℃进行气体渗碳。
假定表面C 含量增加到0.9%,试求距表面0.5mm 处的C 含量达0.4%所需的时间。
已知D 972=1.28 ×10-11m 2/s 解:已知c s ,x ,c 0,D ,c x 代入式得erf ()=0.7143查表得erf (0.8)=0.7421,erf (0.75)=0.7112,用内差法可得β=0.755因此,t=8567s=2.38h21例2:渗碳用钢及渗碳温度同上,求渗碳5h 后距表面0.5mm 处的c 含量。
解:已知c s ,x ,c 0,D ,t 代入式得(0.9% -c x )/0.7%=erf (0.521)=0.538c x =0.52%与例1比较可以看出,渗碳时间由2.38h 增加到5h ,含0.2%c 的碳钢表面0.5mm 处的c 含量仅由0.4%增加到0.52%。
2324252627考题一.名词解释二.简答题三.计算题四.叙述题28谢谢大家!29。
华南师范大学材料科学与工程教程第七章 扩散与固态相变(一)

25/11/2018
1
概述
扩散现象:气体和液体中,例如在房间的某处打开一瓶 香水,慢慢在其他地方可以闻到香味,在清水中滴入一滴墨 水,在静止的状态下可以看到他慢慢的扩散。 扩散:由构成物质的微粒 ( 离子、原子、分子 ) 的热运动 而产生的物质迁移现象称为扩散。扩散的宏观表现是物质的 定向输送。
25/11/2018
34268s = 9.52hr
27
例2 一铁棒中碳的原始浓度为0.20%。现在1273K的温度下对 其进行渗碳处理,试确定在距表面0.01cm处碳浓度达到 0.24%所需的时间。已知在渗碳气氛中,铁棒的表面碳浓度 维持在0.40%;碳在铁中的扩散系数与温度的关系为
D (2 105 m 2 / s){exp[(142000 J / mol) / RT ]}
dC J D dx
25/11/2018 18
2) 扩散第二方程
解决问题的关键:搞清问题的起始条件和边界条件,并假定任一时 刻t溶质的浓度是按怎样的规律分布。 对不同的实际问题,可采用不同的浓度分布形式来处理,如正态分 布、误差分布、正弦分布、指数分布等。
解析解通常有高斯解、误差函数解和正弦解等
一维无限长棒中扩 散方程误差函数解:
25/11/2018 30
water
25/11/2018
adding dye
partial mixing
homogenization
time
2
说明
在固体材料中也存在扩散,并且它是固体中物 质传输的唯一方式。因为固体不能象气体或液体那
样通过流动来进行物质传输。即使在纯金属中也同
样发生扩散,用掺入放射性同位素可以证明。 扩散在材料的生产和使用中的物理过程有密切 关系,例如:凝固、偏析、均匀化退火、冷变形后 的回复和再结晶、固态相变、化学热处理、烧结、
第五章 金属扩散及固态转变

⑷原子扩散的影响
对于扩散型相变,新旧两相的成分不同,相变通过 组元的扩散才能进行。在此种情况下,扩散就成为 相变的主要控制因素。但原子在固态中的扩散速度 远低于液态,两者的扩散系数相差几个数量级。 当过冷度增加到一定程度时,扩散成为决定性 因素,再增大过冷度会使转变速度减慢,甚至 原来的高温转变被抑制,在更低温度下发生无 扩散相变。 例如共析钢从高温奥氏体状态快速冷却下来,扩 散型的珠光体相变被抑制,在更低温度下发生无 扩散的马氏体相变,生成亚稳的马氏体组织。
a)
b)
c)
d)
e)
图5-14 共析转变的形核与生长示意图
1 共析转变的形核
⑴假定富含B组元的β为领 先相,γ相需源源不断提供 B组元才能保证β相的生长。 ⑵由于B组元不断降低,这 样为富含A组元的α相的形 核创造了条件,于是便在B 元的侧面形成了α相。 ⑶ α相 β相就这样不断地交 替生长,并向γ相纵深发展, 最后形成层片状的共析领域。
所有元素在α-Fe 的扩散系数>γ-Fe 中的扩散系数
例:900℃时,置换原子Ni在α -Fe中的扩散系数比在γ -Fe 中约大 1400 倍 ;527℃时 , 间隙原子 N 在 α -Fe 中的扩散系数 比在γ -Fe 中约大1500倍。
表明:致密度大,扩散系数小. 应用:渗氮温度尽量选在共析转变温度以下(590 ℃),可 以缩短工艺周期。
应用举例 铸造合金消除枝晶偏析的均匀化退火
钢在加热和冷却时的一些相变
变形金属的回复与再结晶
钢的化学热处理
金属加热过程中的氧化和脱碳
固态扩散的实验(柯肯达尔效应) • 把Cu、Ni棒对焊,在焊接面上镶嵌上钨丝作为界面 标志。加热到高温并保温,界面标志钨丝向纯Ni一 侧移动了一段距离.
材料名词解释

扩散:热激活的院子通过自身的热震动克服束缚而迁移它处的过程。
超结构:在某些合金“固溶体”中,当缓慢冷却达到一定温度时,原来呈无序分布的溶质原子将变为有序分布,即占据溶剂晶体点阵中一定的位置。
这种固溶体称为有序固溶体,其所形成的晶体点阵称为超结构。
随着超结构的形成,合金的性能发生突变,如硬度增高而电阻、塑性降低等。
自扩散:不依赖于浓度梯度,而仅由热振动而产生的扩散。
互扩散:在置换式固溶体中,两组元互相扩散。
间隙扩散:这是原子扩散的一种机制,对于间隙原子来说,由于其尺寸较小,处于晶格间隙中,在扩散时,间隙原子从一个间隙位置跳到相邻的另一个间隙位置,形成原子的移动。
反应扩散: 伴随有化学反应而形成新相的扩散称为反应扩散。
空位扩散:扩散原子从正常位置跳动到邻近的空位,即通过原子与空位交换位置而实现扩散。
每次跳迁须有空位迁移与之配合。
下坡扩散:组元从高浓度区向低浓度区迁移的扩散的过程称为下坡扩散。
上坡扩散:组元从低浓度区向高浓度区迁移的扩散的过程称为上坡扩散。
稳态扩散:扩散组元的浓度只随距离变化,而不随时间变化。
非稳态扩散: 扩散组元的浓度不仅随距离x 变化,也随时间变化的扩散称为非稳态扩散。
扩散系数:相当于质量浓度为一时,单位时间内的扩散通量。
互扩散系数:在互扩散当中,用来代替两种原子的方向相反的扩散系数D1、D2。
体扩散:物质在晶体内部的迁移过程。
表面扩散:是指原子、离子、分子以及原子团在固体表面沿表面方向的运动。
当固体表面存在化学势梯度场,扩散物质的浓度变化或样品表面的形貌变化时。
晶界扩散:是指原子沿着晶界渗入晶粒。
扩散退火:生产上常将铸件加热到固相线以下100-200℃长时间保温,以使原子充分扩散、成分均匀,消除枝晶偏析,这种热处理工艺称做扩散退火。
柯肯达尔效应: 反映了置换原子的扩散机制,两个纯组元构成扩散偶,在扩散的过程中,界面将向扩散速率快的组元一侧移动。
层错能:金属结构在堆垛时,没有严格的按照堆垛顺序,形成堆垛层错,层错是一种晶格缺陷它破坏了晶格的周期完整性,引起能量升高,通常把单位面积层错所增加的能量称为层错能。
材料的凝固-气相沉积扩散与固态相变

温度
温度越高,扩散系数越大,扩散速率越快。T与D成指数关系,对 扩散影响较大。
例:碳在γ-Fe中扩散时,D0=2×10-5m2/s,Q=140×103J/mol。 D1200=1.61×10-11m2/s; D1300=4.74×10-11m2/s。
晶体缺陷
晶界和表面处原子排列不紧密,不规则,能量较高,扩散激活 能低,即QL>Qgb>Qs,故扩散系数关系为Ds>Dgb>Dl。 晶界扩散与体扩散的相对贡献以 Dgb 衡量。
Z
exp(S
f
S m ) R
通常其值为5×10-6~5×10-4m2·s-1,故对扩散过程影响较小。
扩散激活能Q
扩散机制:间隙扩散 Q H;空位扩散 Q H f H m 。 晶体结构:结构不太紧密的晶体中,原子扩散容易。
原子结合力:结合键强,熔点高,激活能大,扩散不易。
合金成分: 间隙固溶体:溶质浓度高,扩散容易; 置换固溶体:使熔点降低的元素,合金D升高, 反之亦然。
J1
x
(D
C x
)
x
dx
(J1
J
2)
dx
x
(D
C x
)
适用于:非稳态扩散
c D 2 c
t
x2
浓度随时间的变化与浓度分布曲线在该点的二阶导数成正比。
c D 2 c
t
x2
扩散第二定律应用
➢ 钢的渗碳
钢棒在富含一定浓度的CH4气氛中进行渗碳处理。(零件被看作是 无限长的棒,并假定碳在奥氏体中的扩散系数为一常数)
➢ Al-Cu合金的淬火时效
选用Al-WCu4%合金,加热至550℃,Cu原子全部溶入α固溶体 中,冷却进行时效处理 。
材料科学基础名词解释(全)

材料科学基础名词解释(全)晶体:即内部质点在三维空间呈周期性重复排列的固体。
非晶体:原子没有长程的排列,无固定熔点、各向同性等。
晶体结构:指晶体中原子或分子的排列情况,由空间点阵和结构基元构成。
空间点整:指几何点在三维空间作周期性的规则排列所形成的三维阵列,是人为的对晶体结构的抽象。
晶面指数:结晶学中用来表示一组平行晶面的指数。
晶胞:从晶体结构中取出来的反映晶体周期性和对称性的重复单元。
晶胞参数:晶胞的形状和大小可用六个参数来表示,即晶胞参数。
离子晶体晶格能:1mol离子晶体中的正负离子,由相互远离的气态结合成离子晶体时所释放的能量。
原子半径:从原子核中心到核外电子的几率分布趋向于零的位置间的距离。
配位数:一个原子或离子周围同种原子或异号离子的数目。
极化:离子紧密堆积时,带电荷的离子所产生的电厂必然要对另一个离子的电子云产生吸引或排斥作用,使之发生变形,这种征象称为极化。
同质多晶:化学组成相同的物质在不同的热力学条件下形成结构不同的晶体的现象。
类质同晶:化学组成相似或相近的物质在相同的热力学条件下形成具有相同结构晶体的现象。
铁电体:指具有自发极化且在外电场作用下具有电滞回线的晶体。
正、反尖晶石:在尖晶石结构中,如果A离子占据四面体空隙,B离子占据八面体空隙,称为正尖晶石。
如果半数的B离子占据四面体空隙,A离子和另外半数的B离子占据八面体空隙则称为反尖晶石。
反萤石结构:正负离子位置刚好与萤石结构中的相反。
压电效应:由于晶体在外力作用下变形,正负电荷中心产生相对位移使晶体总电矩发生变化。
结构缺陷:通常把晶体点阵结构中周期性势场的畸变称为结构缺陷。
空位:指正常结点没有被质点占据,成为空结点。
间隙质点:质点进入正常晶格的间隙位置。
点缺陷:缺陷尺寸处于原子大小的数量级上,三维方向上的尺寸都很小。
线缺陷:指在一维方向上偏离理想晶体中的周期性、规则性排列而产生的缺陷。
面缺陷:是指在二维方向上偏离理想晶体中的周期性、规则性排列而产生的缺陷。
固态相变的主要类型及特点

固态相变的主要类型及特点
固态相变的主要类型和特点如下:
1. 扩散型相变:这类相变涉及原子或离子的扩散。
特点是需要较高的温度,原子或离子活动能力强,会使相的成分发生改变。
包括脱溶沉淀、调幅分解、共析转变等。
2. 非扩散型相变:这类相变中,原子或离子仅作有规则的迁移,使点阵发生改组。
其特点是迁移时相邻原子相对移动不超过原子间距,相邻原子的相对位置保持不变,可以在原子或离子不能扩散时发生。
例如马氏体转变。
3. 一级相变:自由能的一阶偏导数不相等,相变伴随着体积的膨胀或收缩,潜热的放出或吸收。
大多数相变为一级相变。
4. 二级相变:自由能的一阶偏导数相等,但自由能的二阶偏导数不相等。
其特点是材料无体积效应和热效应,如压缩系数、热膨胀系数、比定压热容突变。
大多数磁性转变和有序-无序转变为二级相变。
此外,还有调幅分解、有序化转变、块状转变等相变类型,具体可咨询专业人士获取更多信息。
扩散型相变和无扩散型相变名词解释

扩散型相变和无扩散型相变名词解释相变是物质在一定条件下从一种状态转变为另一种状态的过程。
在相变中,物质的性质和结构都会发生改变,因此相变是物质研究中的重要课题之一。
相变可以分为很多种类,其中扩散型相变和无扩散型相变是两种常见的相变类型。
扩散型相变是指物质在相变过程中需要通过扩散来完成。
扩散是指物质中的分子或离子在空间中的自由移动。
在扩散型相变中,物质的分子或离子需要通过扩散来完成相变过程。
扩散型相变的典型例子是固态金属的熔化。
在金属熔化的过程中,金属中的原子需要通过扩散来完成熔化过程。
此外,固态晶体的溶解、气体的液化和固态晶体的晶化等过程也属于扩散型相变。
无扩散型相变是指物质在相变过程中不需要通过扩散来完成。
在无扩散型相变中,物质的分子或离子不需要通过扩散来完成相变过程。
无扩散型相变的典型例子是液态水的沸腾。
在水的沸腾过程中,水分子不需要通过扩散来完成沸腾过程。
此外,气体的升华、液态晶体的相变和超导材料的相变等过程也属于无扩散型相变。
扩散型相变和无扩散型相变的区别在于相变过程中是否需要通过扩散来完成。
扩散型相变需要通过扩散来完成,而无扩散型相变不需要通过扩散来完成。
此外,扩散型相变和无扩散型相变的物理机制也不同。
扩散型相变的物理机制是分子或离子的扩散,而无扩散型相变的物理机制则是其他因素的影响,如温度、压力等。
总之,扩散型相变和无扩散型相变是物质相变中的两种常见类型。
它们的区别在于相变过程中是否需要通过扩散来完成。
了解这两种相变类型的特点和物理机制,有助于我们更好地理解物质的性质和结构,为物质研究提供更加深入的认识。
扩散与相变

扩散与相变铸锭均匀化的扩散机理1 基础理论众所周知,所有金属和合金凝固时都存在枝晶偏析,必须通过均匀化处理消除或减少晶内化学成分、组织的不均匀性和在铸锭快速冷却时所产生的内应力,改善铸锭的热塑性。
均匀化处理能改善合金的塑性,提高合金元素在基体中的固溶度,提高合金的强度。
均匀化过程越彻底,时效后合金的强度越高。
在工业生产中,液态合金经浇铸后(铸锭或铸件),冷却较快,一般是几分钟,最多是几小时就已凝固完毕,不可能达到平衡凝固。
由于非平衡凝固扩散进行不充分,铸锭或铸件的成分、组织、性能存在不均匀性。
主要体现在以下几个方面:铸锭存在成分偏析,如不消除会影响产品的性能的均匀性和降低耐蚀性。
铸锭中的低熔点组织在热加工过程中熔化,不利于加工。
(3)铸锭中存在较大的残余应力,在加工过程中可能导致铸锭开裂。
(4)铸锭中的硬脆相在加工过程中碎化,形成裂纹,降低合金的塑性。
鉴于以上问题,就需要对铸锭进行均匀化处理,以改善铸造合金的工艺性能,为后续冷、热加工和热处理创造条件,并且改善铸件的最终使用性能。
均匀化是一个在高温下进行的过程,需要一定时间才能完成,其微观机理是合金中一种或多种溶质原子在高温下在化学位梯度的作用下发生扩散,使合金的成分、组织不均匀性得以消除或者减少。
这是典型的扩散问题。
2 一个实际铸锭的枝晶偏析问题及其均匀化固溶体合金在非平衡结晶时,由于先后从液体中凝固出来的固相成分不同,加之冷却速度快,固相中均匀扩散来不及进行,结果使得晶粒内部化学成分不均匀。
往往会出现不同程度的枝晶偏析,从而损害合金的性能。
由于不平衡结晶,得到的固相晶粒内部先结晶区高熔点组元含量高,后结晶区低熔点组元含量高,这种在一个晶粒内部化学成分不均匀的现象就是晶内偏析。
由于固溶体晶体通常是树枝状,枝干和枝间的化学成分不同,因此又称为枝晶偏析。
如图Ni-Cu合金铸态组织,先凝固的晶体中心含Ni量高,后凝固的晶体部分含Cu量高,如图1所示。
扩散型相变和无扩散型相变名词解释

扩散型相变和无扩散型相变名词解释相变是物理学中一个重要的概念,指的是物质在特定温度下从一种状态转变为另一种状态的过程。
根据相变的性质和机制,可以将相变分为多种类型。
其中,扩散型相变和无扩散型相变是两种常见的相变类型。
扩散型相变是一种需要原子或分子间的扩散运动才能发生的相变。
在扩散型相变中,物质在温度或压力的变化下,原子或分子会发生定向的移动,从而使整个系统发生相变。
这种相变通常伴随着能量的释放或吸收,以及原子或分子的重新排列。
比如金属的熔化和凝固、冰的融化和冻结等都是扩散型相变的示例。
相比之下,无扩散型相变则不需要原子或分子间的扩散运动。
在无扩散型相变中,物质会在温度或压力的变化下,直接发生相变,而不需要原子或分子的扩散运动。
这种相变通常伴随着某种物理或化学机制的改变,比如晶体的相变、铁磁体的自旋转变等都是无扩散型相变的示例。
除了上述基本定义外,扩散型相变和无扩散型相变还有一些不同之处。
首先,扩散型相变通常需要较长的时间才能发生,因为原子或分子的扩散运动需要时间。
相比之下,无扩散型相变通常发生得更快,因为它不需要原子或分子的扩散运动。
其次,扩散型相变和无扩散型相变的热力学性质也有所不同。
扩散型相变通常伴随着能量的释放或吸收,以及物质的体积变化。
相比之下,无扩散型相变通常不伴随着能量的释放或吸收,也不会发生体积变化。
最后,扩散型相变和无扩散型相变的机制也有所不同。
扩散型相变通常涉及到原子或分子的扩散运动,而无扩散型相变则涉及到某种物理或化学机制的改变。
比如晶体相变的机制是晶格的重构,铁磁体相变的机制是自旋的重新排列。
总之,扩散型相变和无扩散型相变是两种常见的相变类型,它们的机制、热力学性质、时间尺度等各有不同。
了解这些基本概念,有助于我们更深入地理解物质的相变过程,也有助于我们在实际应用中更好地控制和利用相变现象。
材料物理(扩散与相变)
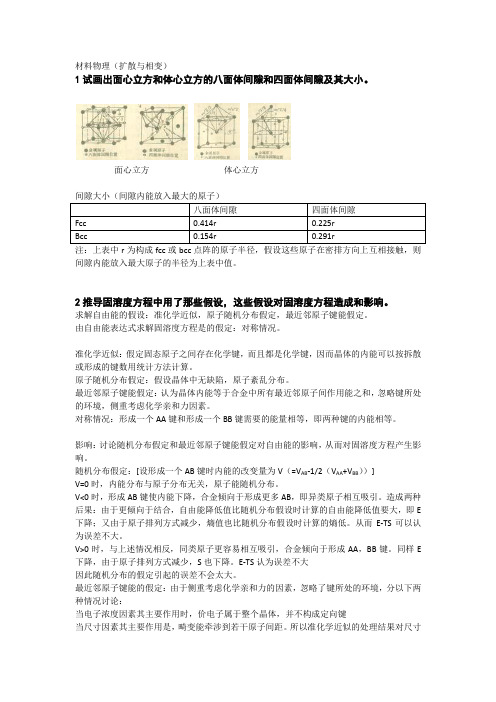
完全有序时,������������������ = 1,������ = 1;
完全无序时,������������������ = ������������,������ = 0;
短程序:只考虑最近邻的有序度。用短程序参数α1 表征。
������1
=
1
−
������������������ ���������∗���������
这要求临近的晶格格点上有空位。因此需要先形成空位,需要空位形成能Δ������������。同时形成空 位后,还要克服原子排列的能垒而迁移到空位位置,因此需克服能垒,即空位的迁移激活能
第七章扩散与固态相变

由于热或其他原因导致的原子运动,物质从系统 的一部分迁移至另一部分的现象,被称为扩散。 扩散是一种非常普遍的自然现象,对一些物理 及化学变化起着重要的作用。特别是在固体中, 由于不存在对流,扩散就成为物质传输的惟一 方式。在材料科学这门学科中和扩散有关的各 种问题很多,如扩散型相变、渗碳和渗氮工艺、 氧化过程、高温蠕变等都和扩散有关。
第二节 扩散机制
扩散机制:均匀固溶体中间隙机制和空位机制最主要。
1. 间隙机制 发生在间隙固溶体中,小尺寸溶质原子C、N、H、 B、O在间隙位臵。从一个间隙位臵跳到其临 近的另一个间隙位臵。
一、扩散方程
稳态扩散与非稳态扩散
1. 稳态扩散下的菲克第一定律(一定时间 内,浓度不随时间变化dc/dt=0) 单位时间内通过垂直于扩散方向的单 位截面积的扩散物质流量(扩散通量)与 该面积处的浓度梯度成正比 即J=-D(dc/dx) 其中D:扩散系数,m2/s,J:扩散通量, g/m2· s 式中负号表明扩散通量的方向与浓度梯度方 向相反。 可见,只要存在浓度梯度,就会引起原 子的扩散,
Fick第二定律 的解无限 大物体中 扩散应用
如一根长的 纯铁一端 放在碳浓 度Co不变 的气氛中, 铁棒端部 碳原子达 到Co后, 同时向右 经铁棒中 扩散的情 形
试验结果与计算 结果符合很
恒定源扩散
2、恒定源扩散
恒定源扩散特点是,表面浓度保持恒定,而物体 的长度大于 4 Dt 。对于金属表面的渗碳、渗氮处 理来说,金属外表面的气体浓度就是该温度下相 应气体在金属中的饱和溶解度C0,它是恒定不变 的;而对于真空除气来说,表面浓度为0,也是恒 定不变的。
t
c J 1 D( ) x x
(Fick第一定律)
固态扩散与相变书籍

固态扩散与相变书籍
固态扩散和相变是固态物理学中重要的研究领域,有许多相关的书籍可以供参考。
以下是一些关于固态扩散和相变的书籍推荐:
1. 《固体物理学》(作者,Charles Kittel)这本经典教材涵盖了固体物理学的各个方面,其中包括固态扩散和相变的基本原理和应用。
2. 《固体物理学导论》(作者,Ashcroft和Mermin)这本教材介绍了固态物理学的基本概念和原理,并包含了关于固态扩散和相变的内容。
3. 《固体物理学中的相变和相图》(作者,Rosenberg和Cohen)这本书详细介绍了相变和相图的理论和实验方法,包括固态扩散过程的描述和应用。
4. 《固体物理学中的扩散和反应》(作者,Mehrer和Krupp)这本书系统地介绍了固态扩散和反应的基本原理和数学模型,包括相变和相图的相关内容。
5. 《固体物理学中的相变和相变动力学》(作者,Pierre-Claude Zinn-Justin)这本书讨论了相变和相变动力学的理论和实验研究,包括固态扩散和相变的相关内容。
6. 《固体物理学中的相变和相变动力学》(作者,Sethna,Lubensky,O'Hern和Shah)这本书介绍了相变和相变动力学的基本概念和数学方法,包括固态扩散和相变的应用。
以上这些书籍涵盖了固态扩散和相变的基本原理、实验方法、数学模型和应用等方面的内容。
阅读这些书籍可以帮助你全面了解固态扩散和相变的知识,并深入理解相关的研究领域。
希望对你有帮助!。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
研究背景
3、枝晶偏析会造成合金在热处理后组织不 均,直接影响到合金的力学性能和抗腐蚀性 能 4、解决枝晶偏析问题的一般的方法就是通 过在热加工之前对合金铸锭进行均匀化热处 理,提高加工塑性
3、枝晶偏析会造成合金在热处理后组织不 均,直接影响到合金的力学性能和抗腐蚀性 能 4、解决枝晶偏析问题的一般的方法就是通 过在热加工之前对合金铸锭进行均匀化热处 理,提高加工塑性
相信大家都很熟悉
图(1)正弦模型浓度分布
图(2)高斯模型浓度分布
那么问题来了
?对于初始浓度分布不是呈源自弦分布的均匀化问题该怎么解决?
建立高斯解模型
图(1)正弦模型浓度分布
图(2)高斯模型浓度分布
材料扩散与相变研究 报告
(枝晶偏析均匀化扩散动力学研究)
小组成员:江树青 金亚军 冯士安 梁轩 胡斌
研究背景
1、枝晶偏析是两种或两种以上成分的金属 材料在凝固时先凝固的枝干和后凝固的枝干 间成分不均匀 2、枝晶偏析是一种非常普遍的现象,对枝 晶偏析溶质分布规律有众多研究,并根据凝 固的具体条件,建立了各种传质动力学模型, 但对枝晶偏析在铸造后的热加工过程中的扩 散传质问题则相对研究较少。且对物理冶金 过程所形成的枝晶偏析的扩散均匀化动力学 的研究一直未能有一个既有理论依据又和实 际吻合较好的传质数学模型
