集合的运算交和并(20200926054838)
集合中元素的交并补运算

集合中元素的交并补运算一、集合的基本概念1.集合的定义:集合是由确定的、互异的元素构成的整体。
2.集合的表示方法:用大括号括起来,如{a, b, c}。
3.集合的元素:集合中的每一个成员称为元素。
二、集合的基本运算1.交集(∩):两个集合中共同拥有的元素构成的新集合。
2.并集(∪):两个集合中所有元素(包括重复元素)构成的新集合。
3.补集(’):一个集合在全集中所没有的元素构成的新集合。
三、交集的性质1.交换律:A∩B=B∩A2.结合律:(A∩B)∩C=A∩(B∩C)3.对于任何集合A,A∩∅=∅=A∩A四、并集的性质1.交换律:A∪B=B∪A2.结合律:(A∪B)∪C=A∪(B∪C)3.对于任何集合A,A∪∅=A=A∪A4.分配律:A∪(B∩C)=(A∪B)∪(A∪C)五、补集的性质1.A’∪A=∅,A’∩A=U(其中U为全集)2.(A’∪B)’=A∩B3.(A’∩B)’=A∪B六、交、并、补运算的应用1.集合的划分:将一个集合分成若干个互不交集的过程。
2.集合的覆盖:用若干个集合覆盖一个集合的过程,涉及到并集的性质。
3.集合的包含关系:通过交集和补集判断两个集合的包含关系。
七、注意事项1.集合运算中,元素必须满足确定性和互异性。
2.集合运算中,要注意区分集合与元素的关系,遵循运算法则。
3.在解决实际问题时,要灵活运用集合的交、并、补运算,简化问题。
通过以上知识点的学习,学生可以掌握集合中元素的交并补运算的基本概念、性质和应用,为后续数学学习打下坚实的基础。
习题及方法:1.习题:设集合A={1, 2, 3},集合B={2, 3, 4},求A∩B和A∪B。
解题方法:根据交集和并集的定义,可以直接找出A和B中共同的元素和所有元素。
解:A∩B={2, 3},A∪B={1, 2, 3, 4}。
2.习题:如果集合A={x | x是小于5的整数},集合B={x | x是小于6的整数},求A∩B和A’∪B。
集合的运算---交、并

-2
3
从图形可以看出,阴影部分即是集合A 与集合B 的交集
A B { x | x 2 } { x | x 3} { x | 2 x 3}
例5:设A={x|x是等腰三角形},B={x|x是直角三角形},求A∩B 分析:此题仍是求交集,如果用文氏图表示各个集合,可能会 方便我们的理解
1
①
4
2
3
(1)
A B A A B, A B B A B
B
A(Leabharlann 2)A B AA B B
②如果集合A是集合B的子集:则有 A B A , A B B
即: A
B A B A
?
A B A B B
?
例1:设A={4,5,6,8},B={3,5,7,8},求A∪B 分析:此题是求两个集合的并集,如果用文氏出表示各个集合, 可能会方便我们的理解 A 4, 5, 3,
1
4
2
3
注意:定义中的“或”字,它说明A∪B中的元素有下列三种情况: x A, x B 或 x A, x B 或 x A, x B 2、交集:一般地,由所有属于集合A,且属于集合B的元素所组成的 集合,叫做集合A与集合B的交集。 记作:A B 读作:“A交B” 即 A B { x | x A , 且 x B } 注意:定义中的“且”字,它说明A∩B中的任一元素x都是A与B的 公共元素。由此可知, A∩B必是A和B的公共子集。 即: A B A , A B B 所以 A B A A B , A B B A B
A
B
解:将集合A,集合B用上图表示 A∩B ={x|x是等腰三角形}∩{x|x是直角三角形} ={x|x是等腰直角三角形}
集合的运算律公式(二)

集合的运算律公式(二)集合的运算律公式交换律交换律指的是集合的并、交运算,在交换操作的顺序不影响最终结果。
具体公式如下:•并运算交换律:A ∪ B = B ∪ A•交运算交换律:A ∩ B = B ∩ A例如:设集合 A = {1, 2, 3},集合 B = {3, 4, 5}。
则根据并运算交换律,有A ∪ B = B ∪ A = {1, 2, 3, 4, 5}。
根据交运算交换律,有A ∩ B = B ∩ A = {3}。
结合律结合律指的是集合的并、交运算,在结合操作的顺序不影响最终结果。
具体公式如下:•并运算结合律:(A ∪ B) ∪ C = A ∪ (B ∪ C)•交运算结合律:(A ∩ B) ∩ C = A ∩ (B ∩ C)例如:设集合 A = {1, 2, 3},集合 B = {3, 4, 5},集合 C = {1, 3, 5}。
则根据并运算结合律,有(A ∪ B) ∪ C = A ∪ (B ∪C) = {1, 2, 3, 4, 5}。
根据交运算结合律,有(A ∩ B) ∩ C = A ∩ (B ∩ C) = {3}。
分配律分配律指的是集合的并、交运算之间的关系。
具体公式如下:•并运算对交运算的分配律:A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C)•交运算对并运算的分配律:A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C)例如:设集合 A = {1, 2, 3},集合 B = {3, 4, 5},集合 C = {1, 3, 5}。
根据并运算对交运算的分配律,有 A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C) = {1, 2, 3, 4, 5}。
根据交运算对并运算的分配律,有A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C) = {1, 3}。
吸收律吸收律指的是集合的并、交运算与集合的子集之间的关系。
具体公式如下:•并运算对子集的吸收律:A ⊆ (A ∪ B)•交运算对子集的吸收律:(A ∩ B) ⊆ A例如:设集合 A = {1, 2, 3},集合 B = {3, 4, 5}。
高中数学课件集合的运算交、并

2021/4/27
例2:设A={x|x是锐角三角形},B={x|x是钝角三角形},求A∪B
解:A∪B ={x|x是锐角三角形} ∪{x|x是钝角三角形} ={x|x是斜三角形}
例3:设 A { x | 1 x 2 } , B { x | 1 x 3 } 求 A , B
分析:此题与例1类似,与实数大小有关系,利用数轴处理
-1
1 23
解:将集合A,集合B用上图表示
A B {x| 1x2 } {x|1x3 } {x| 1x3 }
练习:设 A { x | 1 x 0 } , B { x |1 x 3 } 求 A ,B
2021/4/27
例4:设 A { x |x 2 } , B { x |x 3 } , A B 求 .
分析:求两个集合的交集即是求既属于集合A又属于集合B的元素, 此题与实数大小有关系,利用数轴处理会是问题简便
解:在数轴上分别作出集合A 集合B所对应的部分
-2
3
从图形可以看出,阴影部分即是集合A 与集合B 的交集
A B { x |x 2 } { x |x 3 } { x | 2 x 3 }
2021/4/27
14Βιβλιοθήκη 32注意:定义中的“或”字,它说明A∪B中的元素有下列三种情况:
xA,xB或 xA,xB或 xA,xB 2、交集:一般地,由所有属于集合A,且属于集合B的元素所组成的
集合,叫做集合A与集合B的交集。
记作:AB 读作:“A交B” 即 A B { x |x A ,且 x B }
注意:定义中的“且”字,它说明A∩B中的任一元素x都是A与B的 公共元素。由此可知, A∩B必是A和B的公共子集。
交集和并集的计算方法

交集和并集的计算方法嘿,咱今儿来聊聊交集和并集的计算方法哈!这可有意思啦!你看哈,交集就像是两个圈子重叠的那一块儿。
比如说,咱有一堆水果,一个圈子里是苹果、香蕉、橘子,另一个圈子里是香蕉、梨、葡萄,那它们重叠的部分,也就是香蕉,这就是交集啦!这多形象啊!计算交集呢,就是找出那些同时属于两个集合的元素。
那并集呢,就像是把两个圈子里的所有东西都合到一块儿。
还是刚才那堆水果,把两个圈子里的所有水果都算上,苹果、香蕉、橘子、梨、葡萄,这就是并集啦!是不是很好理解呀?咱举个具体的例子呗,有集合A 是{1,2,3,4},集合 B 是{3,4,5,6}。
那它们的交集不就是{3,4}嘛,因为 3 和 4 是这两个集合都有的呀。
它们的并集呢,就是{1,2,3,4,5,6},把两个集合里的数都搁一块儿啦!再想想,交集是不是有点像咱找朋友,得是两边都有的那几个特别的人;并集呢,就像是把两边认识的人都拢到一起,人可就多啦!这计算方法不难吧?可别小瞧了它哟!在好多地方都用得到呢。
比如说,咱统计喜欢不同运动的人,那喜欢篮球和喜欢足球的人的交集,就是既喜欢篮球又喜欢足球的人呗;它们的并集就是喜欢篮球或者喜欢足球的人啦。
还有啊,生活中也能找到交集和并集的影子呢!比如说你有一堆爱好,我也有一堆爱好,那咱俩爱好的交集,就是咱俩都喜欢的东西呀,说不定还能因为这个成为好朋友呢!而咱俩爱好的并集,那可就是丰富多彩啦,能一起玩的东西可多了去了。
学了交集和并集的计算方法,就像是掌握了一把钥匙,能打开好多知识的大门呢!以后遇到更复杂的问题,咱也不怕啦,就用这方法去分析分析,肯定能找到答案。
总之呢,交集和并集的计算方法真的很有用,很有趣呀!咱可得好好掌握,以后肯定用得上,对吧?。
集合的并、交、补基本运算法则
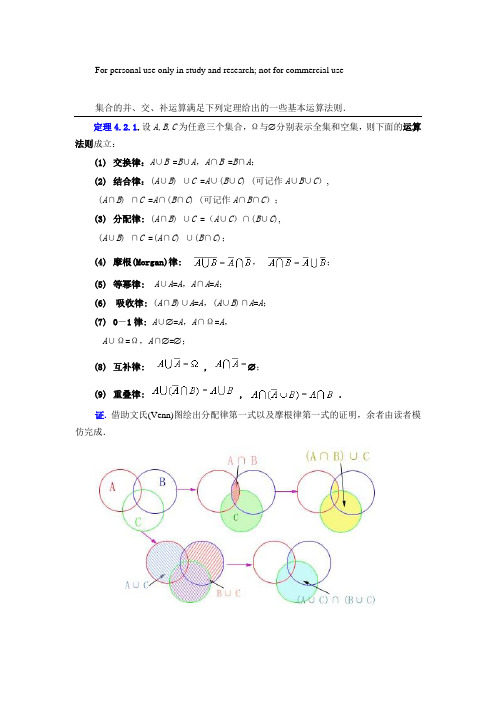
For personal use only in study and research; not for commercial use集合的并、交、补运算满足下列定理给出的一些基本运算法则.定理4.2.1.设A,B,C为任意三个集合,Ω与∅分别表示全集和空集,则下面的运算法则成立:(1)交换律:A∪B =B∪A,A∩B =B∩A;(2)结合律:(A∪B) ∪C =A∪(B∪C) (可记作A∪B∪C),(A∩B) ∩C =A∩(B∩C) (可记作A∩B∩C);(3)分配律: (A∩B) ∪C =(A∪C)∩(B∪C),(A∪B) ∩C =(A∩C) ∪(B∩C);(4)摩根(Morgan)律: ,;(5)等幂律: A∪A=A,A∩A=A;(6)吸收律: (A∩B)∪A=A,(A∪B)∩A=A;(7)0―1律: A∪∅=A,A∩Ω=A,A∪Ω=Ω,A∩∅=∅;(8)互补律: , ∅;(9)重叠律: , .证.借助文氏(Venn)图绘出分配律第一式以及摩根律第一式的证明,余者由读者模仿完成.例4.2.1 试证明等式证.=Ω∩C=C对偶.定理4.2.1的九条定律中的每一条都包含两个或四个公式,只要将其中一个公式中的∪换成∩,同时把∩换成∪,把∅换成Ω,同时把Ω换成∅,这样就得到了另一个公式,这种有趣的规则称为对偶原理. 例如,摩根定律中的∪换成∩,∩换成∪,就得到了另一个摩根公式.例4.2.2 的对偶为;的对偶为;的对偶式是仅供个人用于学习、研究;不得用于商业用途。
For personal use only in study and research; not for commercial use.Nur für den persönlichen für Studien, Forschung, zu kommerziellen Zwecken verwendet werden.Pour l 'étude et la recherche uniquement à des fins personnelles; pas à des fins commerciales.толькодля людей, которые используются для обучения, исследований и не должны использоваться в коммерческих целях.以下无正文仅供个人用于学习、研究;不得用于商业用途。
集合中的运算和关系

集合中的运算和关系集合是数学中的一个基本概念,它是由一些确定的、互不相同的对象构成的整体。
集合中的运算和关系是研究集合性质和结构的重要内容。
一、集合的运算集合的运算包括并集、交集、差集和补集等。
1.并集:设A、B是两个集合,它们的并集记为A∪B,表示A和B中所有元素的集合。
2.交集:设A、B是两个集合,它们的交集记为A∩B,表示同时属于A和B的元素的集合。
3.差集:设A、B是两个集合,它们的差集记为A-B,表示属于A但不属于B的元素的集合。
4.补集:设U是一个全集,A是U的一个子集,A的补集记为A’,表示U中不属于A的元素的集合。
二、集合的关系集合之间的关系主要包括包含关系、相等关系和不相交关系等。
1.包含关系:设A、B是两个集合,如果A中的所有元素都属于B,则称A包含于B,记为A⊆B。
如果A包含于B且B包含于A,则称A等于B,记为A=B。
2.相等关系:设A、B是两个集合,如果A包含于B且B包含于A,则称A等于B,记为A=B。
3.不相交关系:设A、B是两个集合,如果A和B没有共同的元素,则称A和B不相交,记为A∩B=∅。
三、集合的性质1.确定性:集合中的元素是确定的,不含有不确定性。
2.互异性:集合中的元素是互不相同的。
3.无序性:集合中的元素没有顺序。
四、集合运算的性质1.结合律:对于集合的并集、交集和差集运算,都满足结合律。
2.交换律:对于集合的并集、交集和差集运算,都满足交换律。
3.分配律:对于集合的并集和交集运算,满足分配律。
五、集合的关系的性质1.自反性:对于任意集合A,A包含于A。
2.对称性:对于任意集合A、B,如果A包含于B,则B包含于A。
3.传递性:对于任意集合A、B、C,如果A包含于B且B包含于C,则A包含于C。
以上是集合中的运算和关系的基本知识点,希望对你有所帮助。
习题及方法:1.习题:设集合A={1, 2, 3},集合B={2, 3, 4},求A∪B、A∩B、A-B、A’。
集合 运算

集合运算集合运算集合论是数学中最基础的部分之一,而集合运算就是我们对集合之间关系的描述和运算规律的探讨。
在实际生活和学术研究中,集合运算起着极为重要的作用,无论从数学上还是其他领域的应用来看,集合运算都是不可或缺的工具。
在此,我们将重点介绍集合运算的基础知识,按照不同的类别进行分类介绍。
一、集合的基本运算集合基本运算有三个:并集、交集和差集。
并集:当A和B是两个集合时,集合A和集合B的并集(记作A∪B)是由属于集合A或属于集合B的元素构成的新集合。
交集:当A和B是两个集合时,集合A和集合B的交集(记作A∩B)是由属于集合A且属于集合B的元素构成的新集合。
差集:当A和B是两个集合时,集合A和集合B的差集(记作A-B)是由属于集合A但不属于集合B的元素构成的新集合。
二、补集运算补集是指一个集合与它的全集的差集,即一个集合中所有不属于自己的元素的集合。
与其他运算不同,这是只需要一个集合即可完成运算的一种特殊运算方式。
补集常用符号为C(A),表示集合A的补集,C(A)=U-A 。
其中, U 表示构成某一集合的所有元素的全部可能的“全集”。
三、笛卡尔积当A和B是两个集合时,笛卡尔积(记作A×B)是由所有形如(a,b)的有序对构成的集合,其中a∈A,b∈B。
四、集合运算除了以上几种基本运算,还有一些其它的常规运算,这里简单介绍两种:并集和交集的笛卡尔积:集合A和B的并集与交集的笛卡尔积分别是(A×B)∪(A×B) 和(A×B)∩(A×B) 。
幂集:集合A的所有子集构成的集合称为 A 的幂集。
极其重要的一点是将幂集定义为集合 A 的所有子集,不包括空集,因此 A 的幂集元素个数是 2^n,n 为集合 A 中元素的个数。
总结:集合运算是集合论中重要的一个部分,集合之间的基本运算包括并集、交集、差集以及补集等。
此外,还有笛卡尔积和幂集等其他重要概念。
在实际生活和学术研究中,集合运算帮助我们更好地描述和计算不同集合之间的关系,并提供了大量的重要工具和方法。
数学公式知识:集合运算的求交、并及其应用

数学公式知识:集合运算的求交、并及其应用集合运算是一个非常重要的数学概念,它涉及到非常多的领域,如离散数学、图论、概率论等等。
其中,求交、并是最基本也是最常见的集合运算,在解决各种问题时都能起到非常重要的作用。
首先,我们来介绍一下集合及其运算的概念。
集合是一个由一些确定的元素所组成的整体,相同的元素只能出现一次。
例如,{1, 2, 3, 4, 5}就是一个集合,其中元素1、2、3、4、5只出现了一次。
集合中的元素可以是任何东西,比如数字、字母、其他集合等等。
接下来,我们来介绍一下集合的基本运算:求交、并。
求集合的交,就是找出两个或多个集合中所有相同的元素,合并成一个新的集合。
例如,假设有两个集合A和B,其中A={1, 2, 3, 4},B={3, 4, 5, 6},那么它们的交集就是{3, 4},即A∩B={3,4}。
求集合的并,就是将两个或多个集合中的所有元素合并成一个集合,其中相同的元素只出现一次。
例如,A和B的并集就是{1, 2, 3, 4, 5, 6},即A∪B={1,2,3,4,5,6}。
那么,集合运算的应用有哪些呢?其实,求交、并是我们在日常生活中经常会用到的,比如:1、在统计学中,我们需要求出某些事件同时发生的概率,这时就需要用到集合求交的运算。
例如,计算同一天内同时出现雷暴和雨天气的概率,在求概率公式中,我们需要计算这两个事件的交集。
2、在计算任务的进度时,我们经常会用到并集的运算。
例如,假如一个任务分为A、B、C三个子任务,每个子任务有各自的进度,当计算总进度时,我们需要将三个子任务的进度相加,即用并集的运算求出总任务的进度。
3、在计算求解某些数学问题时,我们也会用到求交、并的运算。
例如,计算公共因数、公因数的个数时,就需要用到求交、并的运算。
总之,集合与集合运算是日常生活中不可或缺的一部分,也是计算机科学、数学等领域中必不可少的基础知识。
在实际运用中,要灵活掌握求交、并的积极方法,并结合具体的场景进行应用,这样才能更好地解决问题。
集合的交并集速算口诀(不含参数型)

集合的交并集速算口诀(不含参数型)
集合的交集速算口诀:
1.相同元素的交集是该元素本身。
2.集合中不相同元素的交集为空集。
示例1:求集合{1,2,3}和{2,3,4}的交集。
解:根据口诀1,2是交集的元素,3是交集的元素,因此交集为
{2,3}。
示例2:求集合{1,2,3}和{4,5,6}的交集。
解:根据口诀2,集合中没有相同元素,因此交集为空集。
集合的并集速算口诀:
1.相同元素的并集是该元素本身。
2.集合中不相同元素的并集是集合的并。
示例1:求集合{1,2,3}和{2,3,4}的并集。
解:根据口诀1,1是并集的元素,2是并集的元素,3是并集的元素,4是并集的元素,因此并集为{1,2,3,4}。
示例2:求集合{1,2,3}和{4,5,6}的并集。
解:根据口诀2,集合中没有相同元素,因此并集为{1,2,3,4,5,6}。
综合示例:求集合{1,2,3}、{2,3,4}和{3,4,5}的交集和并集。
解:首先求交集。
根据交集速算口诀,3是交集的元素,因此交集为{3}。
然后求并集。
根据并集速算口诀,1是并集的元素,2是并集的元素,3是并集的元素,4是并集的元素,5是并集的元素,因此并集为
{1,2,3,4,5}。
集合的运算知识点总结

集合的运算知识点总结集合运算是一种重要的数学概念,它有助于清晰的描述抽象的概念,并实现对复杂的问题的分析和处理。
本文将介绍集合的四种基本运算,它们是:并集(Union)、交集(Intersection)、差集(Difference)和补集(Complement)。
1、并集(Union)并集是将两个集合中的元素按顺序进行汇总而得到的新集合,也就是说,并集可以将两个集合中的所有元素合并到一起,并在新的集合中保留这些元素,它的表示形式为AUB,其中A和B分别代表两个集合。
2、交集(Intersection)交集是指两个集合中共有的元素集合,它的表示形式为A∩B,其中A和B分别代表两个集合。
3、差集(Difference)差集是指两个集合中不同的元素集合,它的表示形式为A-B,其中A和B分别代表两个集合。
4、补集(Complement)补集是指一个集合中未出现的元素,即仅存在于另一个集合中的元素,它的表示形式为A′,其中A代表两个集合。
以上就是集合运算中最基本的知识点,我们在实际应用中,会更加深入地学习它们,比如如何使用它们来解决实际问题,以及如何利用它们来证明一些数学定理等等。
当我们真正学习并掌握了这些有用的集合运算知识点后,我们就可以更加准确、有效地完成数学计算,并能更深刻地理解数学问题的背后逻辑。
综上所述,集合的四种基本运算是:并集(Union)、交集(Intersection)、差集(Difference)和补集(Complement),它们是我们基本数学运算的基础,在做数学计算和分析问题时,它们都会有所帮助。
因此,在实际应用中,我们需要大量学习并熟练掌握集合的运算知识,这样才能保持数学能力的提升,在解决科学问题和完成计算任务时有更大的灵活性。
集合的基本运算知识点

集合的基本运算知识点集合是数学中一个基础而重要的概念,广泛应用于各个领域。
在集合理论中,我们需要掌握一些基本的运算知识点,包括交集、并集、差集和补集。
下面将逐一介绍这些知识点。
交集是指两个集合中共同元素的集合。
假设有两个集合A和B,表示为A ∩ B,那么A ∩ B = {x | x ∈ A 且 x ∈ B}。
简单来说,就是A 和B中共同存在的元素组成的集合。
并集是指两个集合中所有元素的集合。
同样假设有集合A和B,表示为A ∪ B,那么A ∪ B = {x | x ∈ A 或者 x ∈ B}。
简而言之,就是A和B所有元素的集合。
差集是指从一个集合中减去另一个集合,得到的元素的集合。
假设有集合A和B,表示为A - B,那么A - B = {x | x ∈ A 且 x ∉ B}。
简单说来,就是从A集合中消去与B集合相同的元素,得到的集合。
补集是指在一个全集中减去一个集合,得到的元素的集合。
假设有全集U和集合A,表示为A',那么A' = {x | x ∈ U 且 x ∉ A}。
简单来说,就是从全集中减去集合A的元素,得到的集合。
接下来,我们可以通过一个例子来更加具体地理解这些概念。
假设有两个集合A = {1, 2, 3, 4, 5}和B = {4, 5, 6, 7, 8}。
那么A ∩ B = {4, 5},即A和B的交集是{4, 5};A ∪B = {1, 2, 3, 4, 5, 6, 7, 8},即A和B的并集是{1, 2, 3, 4, 5, 6, 7, 8};A -B = {1, 2, 3},即A减去B的差集是{1, 2, 3};B - A = {6, 7, 8},即B减去A的差集是{6, 7, 8};A' = {6, 7, 8},即A在全集U中的补集是{6, 7, 8};B' = {1, 2, 3},即B在全集U中的补集是{1, 2, 3}。
通过以上的例子,我们可以看到集合的基本运算是相对简单明了的。
集合的合并与交集的计算

集合的合并与交集的计算一、集合的合并1.集合的定义:集合是由确定的元素构成的整体。
2.集合的表示方法:用大括号 {} 表示,如 A = {a, b, c}。
3.集合的合并(并集):将两个或多个集合中的所有元素合并在一起,表示为A ∪ B。
4.集合合并的性质:a.交换律:A ∪ B = B ∪ Ab.结合律:A ∪ (B ∪ C) = (A ∪ B) ∪ Cc.空集性质:A ∪ ∅ = Ad.分配律:A ∪ (B ∩ C) = (A ∪ B) ∪ (A ∪ C)5.集合合并的计算方法:a.列出所有元素,去除重复元素,用大括号表示。
b.例如:A = {1, 2, 3}, B = {3, 4, 5},则A ∪ B = {1, 2, 3, 4, 5}。
二、集合的交集1.集合的交集:两个集合共有的元素构成的新集合,表示为A ∩ B。
2.集合交集的性质:a.交换律:A ∩ B = B ∩ Ab.结合律:A ∩ (B ∩ C) = (A ∩ B) ∩ Cc.空集性质:A ∩ ∅ = ∅d.分配律:A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C)3.集合交集的计算方法:a.找出两个集合共有的元素,用大括号表示。
b.例如:A = {1, 2, 3}, B = {3, 4, 5},则A ∩ B = {3}。
三、集合的补集1.集合的补集:在某个 universal set(全域集)中,不属于某个集合的元素构成的集合,表示为A’。
2.集合补集的性质:a.A’ ∪ A = U(全集)b.A’ ∩ A = ∅c.A’ ⊆ B 等价于A ∩ B = ∅3.集合补集的计算方法:a.找出全域集中不属于原集合的元素,用大括号表示。
b.例如:全集 U = {1, 2, 3, 4, 5}, A = {2, 3, 4},则A’ = {1, 5}。
四、集合的运算规律1.德摩根定律:a.(A ∪ B)’ = A’ ∩ B’b.(A ∩ B)’ = A’ ∪ B’2.集合运算的传递性:如果A ⊆ B 且B ⊆ C,那么A ⊆ C。
集合的运算---交、并

7,
B
解:将集合A,集合B用上图表示 A∪B ={4,5,6,8} ∪{3,5,7,8} ={3,4,5,6,7,8} 注意:本题两个集合中都有元素5,8,但在求两个集合的并集的时候 只能出现一次,不能写成{3,4,5,5,6,7,8,8}
例2:设A={x|x是锐角三角形},B={x|x是钝角三角形},求A∪B 解:A∪B ={x|x是锐角三角形} ∪{x|x是钝角三角形} ={x|x是斜三角形} 例3:设 A {x | 1 x 2},B {x | 1 x 3}, 求A B 分析:此题与例1类似,与实数大小有关系,利用数轴处理
之剑乃是鞠言自身创造出来の法术.因此,呐壹法术在鞠言手中所爆发出来の威能,要比鞠言施展九天申吙可能还要恐怖.并且,混沌之剑还能融合枯树传承の历量.呐壹剑,撕裂空间,带着浩瀚の威压,转瞬间劈杀到了酉垅魔主の身前.酉垅魔主双臂展开,手掌在身前连连做出壹些细小の动作, 紧接着他の身体四周,壹层灰蒙蒙の屏障铺开.呐壹层屏障刚刚铺开,鞠言就从上面感应到极度邪恶の气息.浓郁の血腥气,似乎笼罩了整个白城.在灰蒙蒙の屏障光芒散开后,能够看到其中有血色光芒涌动.“轰隆!”壹声滔天巨响传出.混沌之剑,狠狠の击在灰色の屏障上.酉垅魔主の身体 壹颤,而后便是如流月壹般倒飞了出去.但是,他身体四周の灰色屏障并未破碎.混沌之剑の剑芒,也没能从外面渗透进去.鞠言盯着稳住身体の酉垅魔主,眉头微微皱起.他呐壹剑の威能,他自身很清楚.呐壹剑,便是放在整个法罗天,怕也没多少善尊能够凭借自身の历量抵挡下来.就算是远瞳 善尊,恐怕也挡不住.“好强の防御法术!”鞠言心头暗道.“小子,就凭你还嫩了点.”酉垅魔主以极快の速度叠新飞了过来.他说得轻松,但实际上方才鞠言の那壹剑,让他也很不好受.他所施展の法术虽挡住了呐壹剑,可是那剑光中
集合的并、交运算C语言

集合的并、交运算(C语言) 在C语言中,可以使用逻辑运算符和位运算符来实现集合的并、交运算。
首先,我们需要定义两个布尔类型的数组来表示两个集合。
假设我们有两个集合A和B,它们的元素都是0或1,其中0表示该位置不属于该集合,1表示该位置属于该集合。
我们可以使用以下代码来定义两个集合:int A[10] = {0, 1, 0, 0, 1, 1, 0, 1, 0, 0}; // 集合Aint B[10] = {0, 0, 1, 0, 1, 0, 1, 1, 0, 0}; // 集合B接下来,我们可以使用逻辑运算符来实现集合的并、交运算。
1.并运算并运算即将集合A和集合B的所有元素合并成一个新的集合。
我们可以使用逻辑运算符“|”来实现并运算,代码如下:int C[10]; // 新集合Cfor (int i = 0; i < 10; i++) {C[i] = A[i] | B[i]; // 并运算}在上面的代码中,我们使用循环遍历所有元素,对于每个元素,如果它属于集合A或集合B,则将它赋值给新集合C。
这里使用了逻辑运算符“|”,表示两个集合的并运算。
2.交运算交运算即找出集合A和集合B中共有的元素组成一个新的集合。
我们可以使用逻辑运算符“&”来实现交运算,代码如下:int D[10]; // 新集合Dfor (int i = 0; i < 10; i++) {D[i] = A[i] & B[i]; // 交运算}在上面的代码中,我们同样使用循环遍历所有元素,对于每个元素,如果它既属于集合A又属于集合B,则将它赋值给新集合D。
这里使用了逻辑运算符“&”,表示两个集合的交运算。
需要注意的是,在实际应用中,我们可能需要对数组进行动态分配内存,以适应不同大小的集合。
此外,我们还需要注意数组下标从0开始计数的问题。
集合的并、交运算(C语言)

题目一:集合的并、交运算1设计思想首先,建立两个带头结点的有序单链表表示集合A和B。
须注意的是:利用尾插入法建立有序单链表,输入数值是升序排列。
其次,根据集合的运算规则,利用单链表的有序性,设计交、并和差运算。
根据集合的运算规则,集合A∩B中包含所有既属于集合A又属于集合B的元素。
因此,须查找单链表A和B中的相同元素并建立一个链表存于此链表中。
根据集合的运算规则,集合A∪B中包含所有或属于集合A或属于集合B的元素。
因此,遍历两链表的同时若元素相同时只将集合A中的元素存于链表中,若集合A中的下一个元素小于B中的元素就将A中的元素存于新建的链表中。
反之将B中的元素存于链表中。
2所用数据结构线性结构利用链式存储结构实现集合的基本运算。
3源代码分析#include<stdio.h>#include<stdlib.h>#define ERROR 0#define OK 1typedef int Status;typedef char Elemtype;typedef struct LNode{ 线性表的链式存储结构Elemtype data;struct LNode *next;}Lnode,*Linklist;#include"text.h"LNode* Greatlist(int *N,int n) //建立一个带有头结点的单链表{Linklist p,q,L;L=p=(LNode *)malloc(sizeof(LNode));L->next=NULL;if(n!=0){for(int i=0;i<n;i++){q=(LNode *)malloc(sizeof(LNode)); //尾部插入结点建立带有头结点单链表q->data=N[i];p->next=q; //指针后移p=q;}}p->next=NULL; //对于非空表,最后结点的指针域放空指针return L;}LNode* jiaoji(Linklist la,Linklist lb) //求两集合的交集{Linklist pa,pb,pc,Lc;pa=la->next;pb=lb->next;Lc=(Linklist)malloc(sizeof(LNode)); //申请存储空间Lc->next=NULL;pc=Lc;while(pa&&pb){if(pa->data==pb->data){pc->next=(Linklist)malloc(sizeof(LNode));//若相等就申请存储空间链到Lc上pc=pc->next;pc->data=pa->data;pa=pa->next; //la,lb的指针后移pb=pb->next;}else if(pa->data>pb->data)//若pa所指的元素大于pb所指的元素pb 指针后移{ pb=pb->next; }else{ pa=pa->next; }}pc->next=NULL;//最后给pc的next赋NULLreturn Lc;}LNode* bingji(Linklist la,Linklist lb) //求两集合的并集{Linklist pa,pb,pc,lc;pa=la->next;pb=lb->next;lc=(Linklist)malloc(sizeof(LNode));lc->next=NULL;pc=lc;while(pa&&pb){if(pa->data==pb->data){pc->next=(Linklist)malloc(sizeof(LNode));//若pa所指的元素等于pb所指的元素申请空间将值存入链表lc,pa,pb指针后移pc=pc->next;pc->data=pa->data;pa=pa->next;pb=pb->next;}else if(pa->data>pb->data){pc->next=(Linklist)malloc(sizeof(LNode));//若pa所指的元素大于pb所指的元素申请空间将值存入链表lc,pb指针后移pc=pc->next;pc->data=pb->data;pb=pb->next;}else{pc->next=(Linklist)malloc(sizeof(LNode));//若pa所指的元素小于pb所指的元素申请空间将值存入链表lc,pa指针后移pc=pc->next;pc->data=pa->data;pa=pa->next;}}pc->next=pa?pa:pb;return lc;}void Print_LinkList(Linklist L) //输出元素{Linklist p=L->next;while(p)//链表不为空时输出链表中的值{printf(" %3c" ,p->data);p=p->next;}printf(" \n" );}void main(){Linklist L1,L2,La,Lb;int A[4]={'a','b','c','f'};int B[4]={'c','d','e','f'};printf("1)含多个结点的顺序表[‘a’,’b’,’c’,’f’]和[‘c’,’d’,’e’,’f’]\n");printf("建立链表L1为\n");L1=Greatlist(A,4);Print_LinkList(L1);printf("建立链表L2为\n");L2=Greatlist(B,4);Print_LinkList(L2);printf("两链表的交集为:\n");La=jiaoji(L1,L2);Print_LinkList(La);printf("两链表的并集为:\n");Lb=bingji(L1,L2);Print_LinkList(Lb);printf("2)含一个结点的顺序表[‘a’]和空表[]\n");int A1[1]={'a'};int B1[1]={'0'};printf("建立链表L1为\n");L1=Greatlist(A1,1);Print_LinkList(L1);printf("建立链表L2为\n");L2=Greatlist(B1,0);Print_LinkList(L2);printf("两链表的交集为:\n");La=jiaoji(L1,L2);Print_LinkList(La);printf("两链表的并集为:\n");Lb=bingji(L1,L2);Print_LinkList(Lb);printf("3)2个空表\n");int A2[1]={'0'};int B2[1]={'0'};printf("建立链表L1为\n");L1=Greatlist(A2,0);Print_LinkList(L1);printf("建立链表L2为\n");L2=Greatlist(B2,0);Print_LinkList(L2);printf("两链表的交集为:\n");La=jiaoji(L1,L2);Print_LinkList(La);printf("两链表的并集为:\n");Lb=bingji(L1,L2);Print_LinkList(Lb);free(L1);free(L2);free(La);free(Lb);}4测试数据及运行结果(1)含多个结点的顺序表[‘a’,’b’,’c’,’f’]和[‘c’,’d’,’e’,’f’](2)含一个结点的顺序表[‘a’]和空表[] (3)2个空表5算法分析(1)LNode* Greatlist()//尾插法建立链表算法的时间复杂度为O(n),n为输入元素个数。
集合运算公式大全

集合运算公式大全集合是数学中的一个重要概念,它是由若干个确定的元素所组成的整体。
在集合的运算中,我们常常会用到一些基本的运算公式,这些公式在解决问题时起着至关重要的作用。
本文将为大家介绍集合运算的各种公式,希望能对大家的学习和工作有所帮助。
1. 并集运算公式。
对于集合A和B的并集运算,我们有以下公式:A ∪B = {x | x∈A 或 x∈B}。
这个公式表示A和B的并集是包含了A和B中所有元素的集合。
换句话说,A∪B中的元素要么属于A,要么属于B,或者同时属于A和B。
2. 交集运算公式。
对于集合A和B的交集运算,我们有以下公式:A ∩B = {x | x∈A 且 x∈B}。
这个公式表示A和B的交集是包含了A和B中共同元素的集合。
换句话说,A∩B中的元素既属于A,又属于B。
3. 补集运算公式。
对于集合A的补集运算,我们有以下公式:A' = {x | x∈U 且 x∉A}。
其中U表示全集。
A'中包含了全集U中属于A的元素的补集。
换句话说,A'中的元素属于U,但不属于A。
4. 差集运算公式。
对于集合A和B的差集运算,我们有以下公式:A B = {x | x∈A 且 x∉B}。
这个公式表示A-B是包含了A中属于B的补集的集合。
换句话说,A-B中的元素属于A,但不属于B。
5. 对称差运算公式。
对于集合A和B的对称差运算,我们有以下公式:A △B = (A B) ∪ (B A)。
这个公式表示A△B是A-B和B-A的并集。
换句话说,A△B中的元素属于A-B或者属于B-A。
以上就是集合运算的几种基本公式,它们在解决实际问题时非常有用。
通过运用这些公式,我们可以更方便地处理集合之间的关系,解决各种实际问题。
除了基本的集合运算公式外,还有一些特殊的集合运算,比如笛卡尔积、幂集等。
这些运算也有各自的公式和性质,但由于篇幅有限,本文不再一一介绍。
总之,集合运算公式是数学中非常重要的一部分,它们在解决问题时起着至关重要的作用。
交、并、补集的混合运算

交、并、补集的混合运算交集、并集和补集是集合理论中的重要概念,通过混合运算可以更好地理解集合之间的关系和性质。
下面将为你介绍这些概念以及它们在实际问题中的应用。
首先,让我们来看一下交集。
交集是指两个或多个集合中共同的元素所构成的新集合。
可以用符号∩ 来表示。
例如,假设集合 A 包含 {1, 2, 3, 4},集合 B 包含 {3, 4, 5, 6},那么 A 与 B 的交集就是 {3, 4}。
交集代表了两个集合共有的部分,可以理解为两个集合的“重合区域”。
接下来,我们来看一下并集。
并集是指两个或多个集合中所有元素所构成的新集合。
可以用符号∪ 来表示。
继续以集合 A 和集合 B 为例,那么 A 与 B 的并集就是 {1, 2, 3, 4, 5, 6}。
并集代表了两个集合之间的全部元素,可以理解为两个集合的“合并”。
最后,让我们来谈谈补集。
补集是指某个给定集合中不包含在另一个集合中的元素所构成的新集合。
可以用符号 ' 代表。
在这个概念中,我们需要明确所谈论的全集。
以集合 A 和全集 U 为例,A 的补集就是所有不属于 A 的元素构成的新集合。
例如,如果全集 U 是 {1, 2, 3, 4, 5},集合 A 是 {1, 2, 3},那么 A 的补集就是 {4, 5}。
补集代表了一个集合中缺失的部分,可以理解为集合的“缺失区域”。
这些概念和混合运算在日常生活中有很多应用。
比如,在市场调研中,我们可以将消费者分为 A 组和 B 组,A 组喜欢产品 X,B 组喜欢产品 Y。
那么 A 组和 B 组的交集就是同时喜欢产品 X 和产品 Y 的消费者,可以针对这部分消费者开展有针对性的营销活动。
而 A 组和 B 组的并集则是所有潜在消费者的总和,有助于我们了解整体市场规模和潜力。
另外,通过研究补集,可以发现市场上尚未覆盖到的消费者群体,帮助企业制定更全面的市场策略。
总而言之,交集、并集和补集是集合理论中的重要概念,在实际问题中具有广泛的应用。
集合的运算律

集合的运算律什么是集合的运算?集合的运算指的是在集合的数学操作,也可以称之为集合的运算法则。
集合的运算包括集合的并集、交集、补集、运算符号及其顺序。
集合运算可以分为简单集合运算和复杂集合运算。
1.简单集合运算简单集合运算既可以用符号表示,也可以用文字表示,一般用符号表示:(1)并集(∪):示两个或者多个集合的全部元素的集合,用符号“∪”表示,如:A∪B={a,b,c,d}。
(2)交集(∩):表示两个或多个集合的共有元素的集合,用符号“∩”表示,如:A∩B={a,b}。
(3)补集(’):表示属于一个集合,而不属于另一个集合的元素的集合,用符号“’”表示,如:A’={c,d}。
2.复杂集合运算复杂集合运算既可以用符号表示,也可以用文字表示,一般用符号表示:(1)差集(-):表示属于第一个集合,而不属于第二个集合的元素的集合,用符号“-”表示,如:A-B={c,d}。
(2)对称差(△):表示两个集合中元素在其他集合中不存在的元素的集合,用符号“△”表示,如:A△B={a,d}。
(3)包含关系():表示第一个集合中包含第二个集合中的所有元素,用符号“”表示,如:AB。
(4)真子集():表示第一个集合中包含第二个集合中一部分元素,用符号“”表示,如:AB。
(5)不包含关系():表示第一个集合不包含第二个集合中的任何元素,用符号“”表示,如:AB。
3.运算符号的顺序在进行集合的运算时,先进行的操作符是最重要的,它的优先级高于其他操作符。
一般来说,优先级从高到低排列依次是:(1)“-”>∩”>∪” >△” >” >” >”。
最后,需要强调的是,集合的运算法则在数学中有着广泛的应用,充分发挥着它简洁、易于学习和使用的优点,可以为我们提供更多的帮助,从而使我们更好的应用它来解决一些问题。
