(完整版)北师大版七年级数学上册期末复习压轴题专题(带解析)
北师大版七年级数学上册:期末压轴题综合专题复习 (含答案)
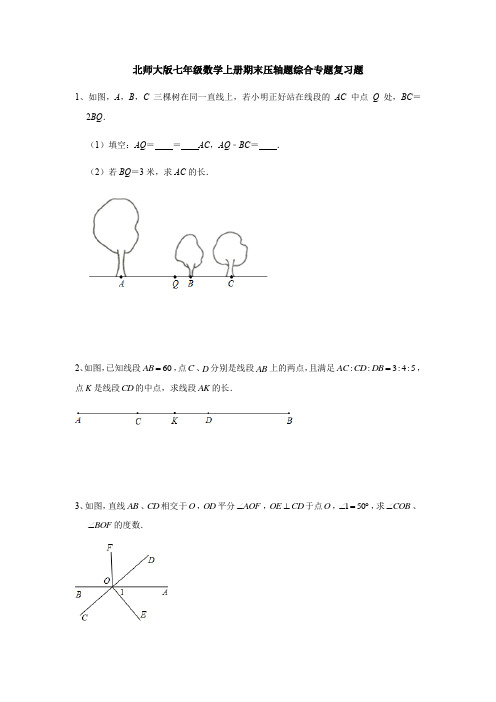
北师大版七年级数学上册期末压轴题综合专题复习题1、如图,A,B,C三棵树在同一直线上,若小明正好站在线段的AC中点Q处,BC=2BQ.(1)填空:AQ==AC,AQ﹣BC=.(2)若BQ=3米,求AC的长.2、如图,已知线段60AC CD DB=,AB=,点C、D分别是线段AB上的两点,且满足::3:4:5点K是线段CD的中点,求线段AK的长.3、如图,直线AB、CD相交于O,OD平分AOF∠、∠=︒,求COB⊥于点O,150∠,OE CD∠的度数.BOF4、如图,已知点C为AB上一点,15AC cm=,35CB AC=,D,E分别为AC,AB的中点,求DE的长.5、如图,已知射线OC在∠AOB内,OM和ON分别平分∠AOC和∠BOC.(1)若∠AOC=50°,∠BOC=30°,求∠MON的度数.(2)探究∠MON与∠AOB的数量关系.6、如图,点B、O、C在一条直线上,OA平分BOC∠,90DOE∠=︒,OF平分AOD∠,36AOE∠=︒.(1)求COD∠的度数;(2)求BOF∠的度数.7、已知:如图,120AOB ∠=︒,过点O 作射线OP ,若OM 平分AOP ∠,ON 平分BOP ∠, AOP α∠=.(1)如图1,补全图形,直接写出MON ∠= ° ; (2)如图2,若4BOM BON ∠=∠,求α的值.8、已知点A ,B ,C 在同一条直线上,点M ,N 分别是AC ,BC 的中点. (1)如图,若点C 在线段AB 上,6AC cm =,4CB cm =,求线段MN 的长; (2)若点C 在线段AB 上,且AC CB acm +=,试求MN 的长度,并说明理由;(3)若点C 在线段AB 的延长线上,且AC BC bcm -=,猜测MN 的长度,写出你的结论,画出图形并说明理由.BAOP图1BAOPMN图29、如图,已知点O 为直线AB 上一点,将一直角三角板MON 的直角顶点放在O 处. (1)如图1,将三角板的一边ON 与射线OB 重合,过点O 在三角板的内部做射线OC ,使2NOC MOC ∠=∠,求AOC ∠的度数;(2)如图2,将三角板绕点O 逆时针旋转一定角度到图2的位置,过点O 在三角板MON 的内部作射线OC 使得OC 恰好是MOB ∠的角的平分线,此时AOM ∠与NOC ∠满足怎样的关系?并说明理由.10、已知数轴上A ,B 两点对应的数分别为a 和b ,且a ,b 满足等式2(9)|7|0a b ++-=,p 为数轴上一动点,对应的数为x .(1)a = ,b = ,线段AB = .(2)数轴上是否存在点p ,使3PA PB =?若存在,求出x 的值;若不存在,请说明理由. (3)在(2)的条件下,若M ,N 分别是线段AB ,PB 的中点,试求线段MN 的长.11、如图1,点C 把线段AB 分成两条线段AC 和BC ,如果AC =2BC ,则称点C 是线段AB的内二倍分割点;如图2,如果BC =2AC ,则称点C 是线段BA 的内二倍分割点.图1 图2例如:如图3,数轴上,点A 、B 、C 、D 分别表示数-1、2、1、0,则点C 是线段AB 的内二倍分割点;点D 是线段BA 的内二倍分割点.图3(1)如图4,M 、N 为数轴上两点,点M所表示的数为-2,点N 所表示的数为7.图4(2)数轴上,点A 所表示的数为-30,点B 所表示的数为20.点P 从点B 出发,以2个单位每秒的速度沿数轴向左运动,设运动时间为t (t >0)秒. ②求当t 为何值时,P 、A 、B 三个点中恰有一个点为其余两点的内二倍分割点.12、已知A 、B 在数轴上对应的数分别用a 、b 表示,且21(100)|10|02ab a ++-=.P 是数轴的一动点.(1)在数轴上标出A 、B 的位置,并求出A 、B 之间的距离;(2)数轴上一点C 距A 点24个单位的长度,其对应的数c 满足||ac ac =-,当P 点满足2=时,求P点对应的数PB PC(3)动点M从原点开始第一次向左移动1个单位,第二次向右移动3个单位长度,第三次向左移动5个单位长度,第四次向右移动7个单位长度,⋯⋯点M能移动到与A或B重合的位置吗?若能,请探究第几次移动是重合;若不能,请说明理由.13、数轴上线段的长度可以用线段端点表示的数进行减法运算得到,例如:如图①,若点A,B在数轴上分别对应的数为a,()<,则AB的长度可以表示为AB b ab a b=-.请你用以上知识解决问题:如图②,一个点从数轴上的原点开始,先向左移动2个单位长度到达A点,再向右移动3个单位长度到达B点,然后向右移动5个单位长度到达C点.(1)请你在图②的数轴上表示出A,B,C三点的位置.(2)若点A以每秒1个单位长度的速度向左移动,同时,点B和点C分别以每秒2个单位长度和3个单位长度的速度向右移动,设移动时间为t秒.①当2t=时,求AB和AC的长度;②试探究:在移动过程中,34-的值是否随着时间t的变化而改变?若变化,请说明AC AB理由;若不变,请求其值.14、阅读理解:若A、B、C为数轴上三点,若点C到A的距离是点C到B的距离2倍,我们就称点C是【A,B】的好点.(1)如图1,点A表示的数为﹣1,点B表示的数为2.表示1的点C到点A的距离是2,到点B的距离是1,那么点C是【A,B】的好点;又如,表示0的点D到点A的距离是1,到点B的距离是2,那么点D【A,B】的好点,但点D【B,A】的好点.(请在横线上填是或不是)知识运用:(2)如图2,M、N为数轴上两点,点M所表示的数为4,点N所表示的数为﹣2.数所表示的点是【M,N】的好点;(3)如图3,A、B为数轴上两点,点A所表示的数为﹣20,点B所表示的数为40.现有一只电子蚂蚁P从点B出发,以4个单位每秒的速度向左运动,到达点A停止.当经过秒时,P、A和B中恰有一个点为其余两点的好点?15、对于数轴上的A,B,C三点,给出如下定义:若其中一个点到另外两个点的距离恰好满足n(n是大于1的整数)倍的数量关系,则称该点是另外两个点的“n倍和谐点”.例如:数轴上点A,B,C所表示的数分别为1,2,4,此时点B是点A,C的“2倍和谐点”;(1)若点A表示数是-1, 点C表示的数是5,点B1,B2,B3,依次表示-4,1,7各数,其2中是点A,C的“3倍和谐点”的是;(2)点A表示的数是-20,点C表示的数是40,点Q是数轴上一个动点.①若点Q是点A,C的“4倍和谐点”,求此时点Q表示的数;①若点Q在点A的右侧,且点Q是点A,C的“n倍和谐点”,用含有n的式子直接写出此时点Q所表示的数.参考答案1、如图,A,B,C三棵树在同一直线上,若小明正好站在线段的AC中点Q处,BC=2BQ.(1)填空:AQ=CQ=AC,AQ﹣BC=BQ.(2)若BQ=3米,求AC的长.【解答】解:(1)∵O是线段AC的中点,∴AQ=CQ=AC,AQ﹣BC=CQ﹣BC=QB,故答案为;(2)∵BQ=3米,BC=2BQ,∴BC=2BQ=6米,∴CQ=BC+BQ=6+3=9(米),∵Q是AC中点,∴AQ=QC=9(米),∴AC=AQ+QC=9+9=18(米),∴AC的长是18米.2、如图,已知线段60AB=,点C、D分别是线段AB上的两点,且满足::3:4:5AC CD DB=,点K是线段CD的中点,求线段AK的长.【解答】解:设3AC x =,则4CD x =,5DB x =, 60AB AC CD DB =++= 34560AB x x x ∴=++=.5x ∴=.点K 是线段CD 的中点. 1102KC CD ∴==.25AK KC AC ∴=+=.3、如图,直线AB 、CD 相交于O ,OD 平分AOF ∠,OE CD ⊥于点O ,150∠=︒,求COB ∠、BOF ∠的度数.【解答】解:OE CD ⊥于点O ,150∠=︒, 90140AOD ∴∠=︒-∠=︒, BOC ∠与AOD ∠是对顶角,40BOC AOD ∴∠=∠=︒. OD 平分AOF ∠, 40DOF AOD ∴∠=∠=︒, 180BOF BOC DOF ∴∠=︒-∠-∠1804040100=︒-︒-︒=︒.4、如图,已知点C 为AB 上一点,15AC cm =,35CB AC =,D ,E 分别为AC ,AB 的中点,求DE 的长.【解答】解:15AC cm =,35CB AC =, 31595CB cm ∴=⨯=,15924AB cm ∴=+=.D ,E 分别为AC ,AB 的中点,1122AE BE AB cm ∴===,17.52DC AD AC cm ===, 127.5 4.5DE AE AD cm ∴=-=-=.5、如图,已知射线OC 在∠AOB 内,OM 和ON 分别平分∠AOC 和∠BOC . (1)若∠AOC =50°,∠BOC =30°,求∠MON 的度数. (2)探究∠MON 与∠AOB 的数量关系.【解答】解:(1)∵OM ,ON 分别平分∠AOC 、∠BOC , ∴.∵∠AOC =50°,∠BOC =30°, ∴∠COM =25°,∠CON =15°,∴∠MON =∠COM +∠CON =25°+15°=40°. (2)∵OM 和ON 分别平分∠AOC 和∠BOC , ∴,∴=即:.6、如图,点B 、O 、C 在一条直线上,OA 平分BOC ∠,90DOE ∠=︒,OF 平分AOD ∠,36AOE ∠=︒.(1)求COD ∠的度数; (2)求BOF ∠的度数.【解答】解:(1)90DOE ∠=︒,36AOE ∠=︒, 903654AOD DOE AOE ∴∠=∠-∠=︒-︒=︒,点B 、O 、C 在一条直线上,OA 平分BOC ∠, 1180902AOB AOC ∴∠=∠=⨯︒=︒,5490144COD AOD AOC ∴∠=∠+∠=︒+︒=︒.(2)OF 平分AOD ∠, 154272AOF ∴∠=⨯︒=︒,90AOB ∠=︒,902763BOF AOB AOF ∴∠=∠-∠=︒-︒=︒.7、已知:如图,120AOB ∠=︒,过点O 作射线OP ,若OM 平分AOP ∠,ON 平分BOP ∠, AOP α∠=.(1)如图1,补全图形,直接写出MON ∠= ° ; (2)如图2,若4BOM BON ∠=∠,求α的值.解:(1)补全图形如图1所示,直接写出MON ∠= 60 ° ;BAOP图1BAOPMN图2(2)∵ OM 平分AOP ∠,AOP α∠=, ∴12AOM α∠=, ∵120AOB ∠=︒, ∴11202BOM α∠=︒- 120BOP α∠=-︒. ∵ON 平分BOP ∠,∴1202BON α-︒∠=∵ 4BOM BON ∠=∠, ∴11201204()22αα-︒︒-=⋅.解得144α=︒.8、已知点A ,B ,C 在同一条直线上,点M ,N 分别是AC ,BC 的中点. (1)如图,若点C 在线段AB 上,6AC cm =,4CB cm =,求线段MN 的长; (2)若点C 在线段AB 上,且AC CB acm +=,试求MN 的长度,并说明理由;(3)若点C 在线段AB 的延长线上,且AC BC bcm -=,猜测MN 的长度,写出你的结论,画出图形并说明理由.【解答】解:(1)6AC cm =,点M 是AC 的中点,0.53CM AC cm ∴==,4CB cm =,点N 是BC 的中点,0.52CN BC cm ∴==, 5MN CM CN cm ∴=+=,∴线段MN 的长度为5cm ,(2)12MN a =,当C 为线段AB 上一点,且M ,N 分别是AC ,BC 的中点,则存在12MN a =,(3)当点C 在线段AB 的延长线时,如图:则AC BC >,M 是AC 的中点,12CM AC ∴=, 点N 是BC 的中点, 12CN BC ∴=, 11()22MN CM CN AC BC b ∴=-=-=.9、如图,已知点O 为直线AB 上一点,将一直角三角板MON 的直角顶点放在O 处. (1)如图1,将三角板的一边ON 与射线OB 重合,过点O 在三角板的内部做射线OC ,使2NOC MOC ∠=∠,求AOC ∠的度数;(2)如图2,将三角板绕点O 逆时针旋转一定角度到图2的位置,过点O 在三角板MON 的内部作射线OC 使得OC 恰好是MOB ∠的角的平分线,此时AOM ∠与NOC ∠满足怎样的关系?并说明理由.【解答】解:(1)2NOC MOC ∠=∠, 1903021MOC ∴∠=︒⨯=︒+, 9030120AOC AOM MOC ∴∠=∠+∠=︒+︒=︒.(2)2AOM NOC ∠=∠,令NOC ∠为β,AOM ∠为γ,90MOC β∠=︒-, 180AOM MOC BOC ∠+∠+∠=︒,9090180γββ∴+︒-+︒-=︒, 20γβ∴-=,即2γβ=, 2AOM NOC ∴∠=∠.10、已知数轴上A ,B 两点对应的数分别为a 和b ,且a ,b 满足等式2(9)|7|0a b ++-=,p 为数轴上一动点,对应的数为x .(1)a = 9- ,b = ,线段AB = .(2)数轴上是否存在点p ,使3PA PB =?若存在,求出x 的值;若不存在,请说明理由. (3)在(2)的条件下,若M ,N 分别是线段AB ,PB 的中点,试求线段MN 的长.【解答】解:(1)由2(9)|7|0a b ++-=,得 90a +=,70b -=.解得9a =-,7b =.线段7(9)16AB b a =-=--=;(2)当P 在AB 上时,PA PB AB +=,即3PB PB AB +=, 即4PB =, 74x -=,解得3x =;当P 在线段AB 的延长线上时,PA PB AB -=, 3PB PB AB -=, 8PB =, 7815x =+=;(3)当P 在AB 上时,如图1;,点M 、点N 分别是线段AB ,PB 的中点,得 182MB AB ==,122BN PB ==. 由线段的和差,得826MN MB NB =-=-=;当P 在AB 的延长线上时,如图2;,点M 、点N 分别是线段AB ,PB 的中点,得 182MB AB ==,142BN PB ==. 由线段的和差,得8412MN MB NB =-=+=.综上所述:MN 的长为6或12. 故答案为:9-,7,16.11、如图1,点C 把线段AB 分成两条线段AC 和BC ,如果AC =2BC ,则称点C 是线段AB 的内二倍分割点;如图2,如果BC =2AC ,则称点C 是线段BA 的内二倍分割点.图1 图2例如:如图3,数轴上,点A 、B 、C 、D 分别表示数-1、2、1、0,则点C 是线段AB 的内二倍分割点;点D 是线段BA 的内二倍分割点.图3(1)如图4,M 、N 为数轴上两点,点M所表示的数为-2,点N 所表示的数为7.图4(2)数轴上,点A 所表示的数为-30,点B 所表示的数为20.点P 从点B 出发,以2个单位每秒的速度沿数轴向左运动,设运动时间为t (t >0)秒.②求当t为何值时,P、A、B三个点中恰有一个点为其余两点的内二倍分割点.【解答】(1(2)①则线段BP②当P在线段AB上时,有以下两种情况:如果P是AB的内二倍分割点时,则AP=2BP,所以50-2t = 2×2t,解得t=253;如果P是BA的内二倍分割点时,则BP=2AP,所以2t=2(50-2t),解得t=503;当P在点A左侧时,有以下两种情况:如果A是BP的内二倍分割点时,则BA=2PA,所以50=2(2t-50)解得t=752;如果A是PB的内二倍分割点时,则PA=2BA,所以2t-50=2×50,解得t=75;综上所述:当t 为253,503,752,75时,P 、A 、B 中恰有 一个点为其余两点的内二倍分割点。
北京师范大学附属中学七年级上册数学 压轴题 期末复习试卷(带答案)-百度文库

北京师范大学附属中学七年级上册数学压轴题期末复习试卷(带答案)-百度文库一、压轴题1.数轴上A、B两点对应的数分别是﹣4、12,线段CE在数轴上运动,点C在点E的左边,且CE=8,点F是AE的中点.(1)如图1,当线段CE运动到点C、E均在A、B之间时,若CF=1,则AB=,AC=,BE=;(2)当线段CE运动到点A在C、E之间时,①设AF长为x,用含x的代数式表示BE=(结果需化简.....);②求BE与CF的数量关系;(3)当点C运动到数轴上表示数﹣14的位置时,动点P从点E出发,以每秒3个单位长度的速度向右运动,抵达B后,立即以原来一半速度返回,同时点Q从A出发,以每秒2个单位长度的速度向终点B运动,设它们运动的时间为t秒(t≤8),求t为何值时,P、Q两点间的距离为1个单位长度.2.如图,已知数轴上点A表示的数为8,B是数轴上位于点A左侧一点,且AB=22,动点P从A点出发,以每秒5个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t>0)秒.(1)出数轴上点B表示的数;点P表示的数(用含t的代数式表示)(2)动点Q从点B出发,以每秒3个单位长度的速度沿数轴向右匀速运动,若点P、Q同时出发,问多少秒时P、Q之间的距离恰好等于2?(3)动点Q从点B出发,以每秒3个单位长度的速度沿数轴向左匀速运动,若点P、Q同时出发,问点P运动多少秒时追上点Q?(4)若M为AP的中点,N为BP的中点,在点P运动的过程中,线段MN的长度是否发生变化?若变化,请说明理由,若不变,请你画出图形,并求出线段MN的长.3.如图,从左到右依次在每个小方格中填入一个数,使得其中任意三个相邻方格中所填数之和都相等.6a b x-1-2...(1)可求得 x =______,第 2021 个格子中的数为______; (2)若前 k 个格子中所填数之和为 2019,求 k 的值; (3)如果m ,n为前三个格子中的任意两个数,那么所有的|m -n | 的和可以通过计算|6-a |+|6-b|+|a -b|+|a -6| +|b -6|+|b -a| 得到.若m ,n 为前8个格子中的任意两个数,求所有的|m-n|的和.4.观察下列等式:111122=-⨯,1112323=-⨯,1113434=-⨯,则以上三个等式两边分别相加得:1111111131122334223344++=-+-+-=⨯⨯⨯. ()1观察发现()1n n 1=+______;()1111122334n n 1+++⋯+=⨯⨯⨯+______. ()2拓展应用有一个圆,第一次用一条直径将圆周分成两个半圆(如图1),在每个分点标上质数m ,记2个数的和为1a ;第二次再将两个半圆周都分成14圆周(如图2),在新产生的分点标上相邻的已标的两数之和的12,记4个数的和为2a ;第三次将四个14圆周分成18圆周(如图3),在新产生的分点标上相邻的已标的两数之和的13,记8个数的和为3a ;第四次将八个18圆周分成116圆周,在新产生的分点标上相邻的已标的两个数的和的14,记16个数的和为4a ;⋯⋯如此进行了n 次.n a =①______(用含m 、n 的代数式表示);②当n a 6188=时,求123n1111a a a a +++⋯⋯+的值.5.如图,已知数轴上点A 表示的数为6,B 是数轴上在A 左侧的一点,且A ,B 两点间的距离为10.动点P 从点A 出发,以每秒5个单位长度的速度沿数轴向左匀速运动,动点Q 从点B 出发,以每秒3个单位长度的速度沿数轴向左匀速运动.(1)设运动时间为t (t >0)秒,数轴上点B 表示的数是 ,点P 表示的数是 (用含t 的代数式表示);(2)若点P 、Q 同时出发,求:①当点P 运动多少秒时,点P 与点Q 相遇?②当点P运动多少秒时,点P与点Q间的距离为8个单位长度?6.如图,在平面直角坐标系中,点M的坐标为(2,8),点N的坐标为(2,6),将线段MN向右平移4个单位长度得到线段PQ(点P和点Q分别是点M和点N的对应点),连接MP、NQ,点K是线段MP的中点.(1)求点K的坐标;(2)若长方形PMNQ以每秒1个单位长度的速度向正下方运动,(点A、B、C、D、E分别是点M、N、Q、P、K的对应点),当BC与x轴重合时停止运动,连接OA、OE,设运动时间为t秒,请用含t的式子表示三角形OAE的面积S(不要求写出t的取值范围);(3)在(2)的条件下,连接OB、OD,问是否存在某一时刻t,使三角形OBD的面积等于三角形OAE的面积?若存在,请求出t值;若不存在,请说明理由.7.我国著名数学家华罗庚曾经说过,“数形结合百般好,隔裂分家万事非.”数形结合的思想方法在数学中应用极为广泛.观察下列按照一定规律堆砌的钢管的横截面图:用含n的式子表示第n个图的钢管总数.(分析思路)图形规律中暗含数字规律,我们可以采用分步的方法,从图形排列中找规律;把图形看成几个部分的组合,并保持结构,找到每一部分对应的数字规律,进而找到整个图形对应的数字规律.如:要解决上面问题,我们不妨先从特例入手: (统一用S表示钢管总数)(解决问题)(1)如图,如果把每个图形按照它的行来分割观察,你发现了这些钢管的堆砌规律了吗?像n=1、n=2的情形那样,在所给横线上,请用数学算式表达你发现的规律.S=1+2 S=2+3+4 _____________ ______________(2)其实,对同一个图形,我们的分析眼光可以是不同的.请你像(1)那样保持结构的、对每一个所给图形添加分割线,提供与(1)不同的分割方式;并在所给横线上,请用数学算式表达你发现的规律:_______ ____________ _______________ _______________(3)用含n的式子列式,并计算第n个图的钢管总数.8.如图,P是定长线段AB上一点,C、D两点分别从P、B出发以1cm/s、2cm/s的速度沿直线AB向左运动(C在线段AP上,D在线段BP上)(1)若C、D运动到任一时刻时,总有PD=2AC,请说明P点在线段AB上的位置:(2)在(1)的条件下,Q是直线AB上一点,且AQ﹣BQ=PQ,求PQAB的值.(3)在(1)的条件下,若C、D运动5秒后,恰好有1CD AB2,此时C点停止运动,D点继续运动(D点在线段PB上),M、N分别是CD、PD的中点,下列结论:①PM﹣PN的值不变;②MNAB的值不变,可以说明,只有一个结论是正确的,请你找出正确的结论并求值.9.在数轴上,图中点A表示-36,点B表示44,动点P、Q分别从A、B两点同时出发,相向而行,动点P、Q的运动速度比之是3∶2(速度单位:1个单位长度/秒).12秒后,动点P到达原点O,动点Q到达点C,设运动的时间为t(t>0)秒.(1)求OC的长;(2)经过t秒钟,P、Q两点之间相距5个单位长度,求t的值;(3)若动点P到达B点后,以原速度立即返回,当P点运动至原点时,动点Q是否到达A点,若到达,求提前到达了多少时间,若未能到达,说明理由.10.数轴上线段的长度可以用线段端点表示的数进行减法运算得到,例如:如图①,若点A,B在数轴上分别对应的数为a,b(a<b),则AB的长度可以表示为AB=b-a.请你用以上知识解决问题:如图②,一个点从数轴上的原点开始,先向左移动2个单位长度到达A点,再向右移动3个单位长度到达B点,然后向右移动5个单位长度到达C点.(1)请你在图②的数轴上表示出A,B,C三点的位置.(2)若点A以每秒1个单位长度的速度向左移动,同时,点B和点C分别以每秒2个单位长度和3个单位长度的速度向右移动,设移动时间为t秒.①当t=2时,求AB和AC的长度;②试探究:在移动过程中,3AC-4AB的值是否随着时间t的变化而改变?若变化,请说明理由;若不变,请求其值.11.已知:A、O、B三点在同一条直线上,过O点作射线OC,使∠AOC:∠BOC=1:2,将一直角三角板的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.(1)将图1中的三角板绕点O按逆时针方向旋转至图2的位置,使得ON落在射线OB 上,此时三角板旋转的角度为度;(2)继续将图2中的三角板绕点O按逆时针方向旋转至图3的位置,使得ON在∠AOC的内部.试探究∠AOM与∠NOC之间满足什么等量关系,并说明理由;(3)将图1中的三角板绕点O按5°每秒的速度沿逆时针方向旋转一周的过程中,当直角三角板的直角边OM所在直线恰好平分∠BOC时,时间t的值为(直接写结果).12.如图,数轴上有A、B两点,且AB=12,点P从B点出发沿数轴以3个单位长度/s的速度向左运动,到达A点后立即按原速折返,回到B点后点P停止运动,点M始终为线段BP的中点(1)若AP=2时,PM=____;(2)若点A表示的数是-5,点P运动3秒时,在数轴上有一点F满足FM=2PM,请求出点F 表示的数;(3)若点P 从B 点出发时,点Q 同时从A 点出发沿数轴以2.5个单位长度/s 的速度一直..向右运动,当点Q 的运动时间为多少时,满足QM=2PM.13.如图,在数轴上从左往右依次有四个点,,,A B C D ,其中点,,A B C 表示的数分别是0,3,10,且2CD AB =.(1)点D 表示的数是 ;(直接写出结果)(2)线段AB 以每秒2个单位长度的速度沿数轴向右运动,同时线段CD 以每秒1个单位长度的速度沿数轴向左运动,设运动时间是t (秒),当两条线段重叠部分是2个单位长度时.①求t 的值;②线段AB 上是否存在一点P ,满足3BD PA PC -=?若存在,求出点P 表示的数x ;若不存在,请说明理由.14.(阅读理解)若A ,B ,C 为数轴上三点,若点C 到A 的距离是点C 到B 的距离的2倍,我们就称点C 是(A ,B )的优点.例如,如图①,点A 表示的数为﹣1,点B 表示的数为2.表示1的点C 到点A 的距离是2,到点B 的距离是1,那么点C 是(A ,B )的优点;又如,表示0的点D 到点A 的距离是1,到点B 的距离是2,那么点D 就不是(A ,B )的优点,但点D 是(B ,A )的优点. (知识运用)如图②,M 、N 为数轴上两点,点M 所表示的数为﹣2,点N 所表示的数为4.(1)数 所表示的点是(M ,N )的优点;(2)如图③,A 、B 为数轴上两点,点A 所表示的数为﹣20,点B 所表示的数为40.现有一只电子蚂蚁P 从点B 出发,以4个单位每秒的速度向左运动,到达点A 停止.当t 为何值时,P 、A 和B 中恰有一个点为其余两点的优点?15.问题一:如图1,已知A ,C 两点之间的距离为16 cm ,甲,乙两点分别从相距3cm 的A ,B 两点同时出发到C 点,若甲的速度为8 cm/s ,乙的速度为6 cm/s ,设乙运动时间为x (s ), 甲乙两点之间距离为y (cm ).(1)当甲追上乙时,x = .(2)请用含x 的代数式表示y .当甲追上乙前,y = ;当甲追上乙后,甲到达C 之前,y = ;当甲到达C 之后,乙到达C 之前,y = .问题二:如图2,若将上述线段AC 弯曲后视作钟表外围的一部分,线段AB 正好对应钟表上的弧AB (1小时的间隔),易知∠AOB=30°.(1)分针OD 指向圆周上的点的速度为每分钟转动 cm ;时针OE 指向圆周上的点的速度为每分钟转动 cm .(2)若从4:00起计时,求几分钟后分针与时针第一次重合.【参考答案】***试卷处理标记,请不要删除一、压轴题1.(1)16,6,2;(2)①162x -②2BE CF =;(3)t=1或3或487或527 【解析】【分析】(1)由数轴上A 、B 两点对应的数分別是-4、12,可得AB 的长;由CE =8,CF =1,可得EF 的长,由点F 是AE 的中点,可得AF 的长,用AB 的长减去2倍的EF 的长即为BE 的长;(2)设AF =FE =x ,则CF =8-x ,用含x 的式子表示出BE ,即可得出答案(3)分①当0<t ≤6时; ②当6<t ≤8时,两种情况讨论计算即可得解【详解】(1)数轴上A 、B 两点对应的数分别是-4、12,∴AB=16,∵CE=8,CF=1,∴EF=7,∵点F 是AE 的中点,∴AF=EF=7,,∴AC=AF ﹣CF=6,BE=AB ﹣AE=16﹣7×2=2,故答案为16,6,2;(2)∵点F 是AE 的中点,∴AF=EF ,设AF=EF=x,∴CF=8﹣x ,∴BE=16﹣2x=2(8﹣x ),∴BE=2CF.故答案为①162x -②2BE CF =;(3) ①当0<t ≤6时,P 对应数:-6+3t ,Q 对应数-4+2t ,=4t t =2t =1PQ ﹣+2﹣(﹣6+3)﹣,解得:t=1或3;②当6<t ≤8时,P 对应数()33126t 22t ---=21 , Q 对应数-4+2t , 37=4t =t 2=12t PQ -﹣+2﹣()25﹣21, 解得:48t=7或527; 故答案为t=1或3或487或527. 【点睛】 本题考查了一元一次方程在数轴上的动点问题中的应用,根据题意正确列式,是解题的关健2.(1)﹣14,8﹣5t ;(2)2.5或3秒时P 、Q 之间的距离恰好等于2;(3)点P 运动11秒时追上点Q ;(4)线段MN 的长度不发生变化,其值为11,见解析.【解析】【分析】(1)根据已知可得B 点表示的数为8﹣22;点P 表示的数为8﹣5t ;(2)设t 秒时P 、Q 之间的距离恰好等于2.分①点P 、Q 相遇之前和②点P 、Q 相遇之后两种情况求t 值即可;(3)设点P 运动x 秒时,在点C 处追上点Q ,则AC =5x ,BC =3x ,根据AC ﹣BC =AB ,列出方程求解即可;(3)分①当点P 在点A 、B 两点之间运动时,②当点P 运动到点B 的左侧时,利用中点的定义和线段的和差求出MN 的长即可.【详解】(1)∵点A 表示的数为8,B 在A 点左边,AB =22,∴点B 表示的数是8﹣22=﹣14,∵动点P 从点A 出发,以每秒5个单位长度的速度沿数轴向左匀速运动,设运动时间为t (t >0)秒,∴点P 表示的数是8﹣5t .故答案为:﹣14,8﹣5t ;(2)若点P 、Q 同时出发,设t 秒时P 、Q 之间的距离恰好等于2.分两种情况: ①点P 、Q 相遇之前,由题意得3t +2+5t =22,解得t =2.5;②点P、Q相遇之后,由题意得3t﹣2+5t=22,解得t=3.答:若点P、Q同时出发,2.5或3秒时P、Q之间的距离恰好等于2;(3)设点P运动x秒时,在点C处追上点Q,则AC=5x,BC=3x,∵AC﹣BC=AB,∴5x﹣3x=22,解得:x=11,∴点P运动11秒时追上点Q;(4)线段MN的长度不发生变化,都等于11;理由如下:①当点P在点A、B两点之间运动时:MN=MP+NP=12AP+12BP=12(AP+BP)=12AB=12×22=11;②当点P运动到点B的左侧时:MN=MP﹣NP=12AP﹣12BP=12(AP﹣BP)=12AB=11,∴线段MN的长度不发生变化,其值为11.【点睛】本题考查了数轴一元一次方程的应用,用到的知识点是数轴上两点之间的距离,关键是根据题意画出图形,注意分两种情况进行讨论.3.(1)6,-1;(2)2019或2014;(3)234【解析】【分析】(1)根据三个相邻格子的整数的和相等列式求出a、x的值,再根据第9个数是-2可得b=-2,然后找出格子中的数每3个为一个循环组依次循环,在用2021除以3,根据余数的情况确定与第几个数相同即可得解.(2)可先计算出这三个数的和,再照规律计算.(3)由于是三个数重复出现,因此可用前三个数的重复多次计算出结果.【详解】(1)∵任意三个相邻格子中所填整数之和都相等,∴6+a+b=a+b+x,解得x=6,a+b+x=b+x-1,∴a=-1,所以数据从左到右依次为6、-1、b、6、-1、b,第9个数与第三个数相同,即b=-2,所以每3个数“6、-1、-2”为一个循环组依次循环.∵2021÷3=673…2,∴第2021个格子中的整数与第2个格子中的数相同,为-1.故答案为:6,-1.(2)∵6+(-1)+(-2)=3,∴2019÷3=673.∵前k 个格子中所填数之和可能为2019,2019=673×3或2019=671×3+6,∴k 的值为:673×3=2019或671×3+1=2014.故答案为:2019或2014.(3)由于是三个数重复出现,那么前8个格子中,这三个数中,6和-1都出现了3次,-2出现了2次.故代入式子可得:(|6+2|×2+|6+1|×3)×3+(|-1-6|×3+|-1+2|×2)×3+(|-2-6|×3+|-2+1|×3)×2=234.【点睛】本题考查了列一元一次方程解实际问题的运用,规律推导的运用,此类题的关键是找出是按什么规律变化的,然后再按规律找出字母所代表的数,再进行进一步的计算.4.(1)11n n 1-+,n n 1+(2)①()()n 1n 2m 3++②75364 【解析】【分析】 ()1观察发现:先根据题中所给出的列子进行猜想,写出猜想结果即可;根据第一空中的猜想计算出结果;()2①由16a 2m m 3==,212a 4m m 3==,320a m 3=,430a 10m m 3==,找规律可得结论;②由()()n 1n 2m 22713173++=⨯⨯⨯⨯知()()m n 1n 22237131775152++=⨯⨯⨯⨯⨯=⨯⨯,据此可得m 7=,n 50=,再进一步求解可得.【详解】()1观察发现:()111n n 1n n 1=-++; ()1111122334n n 1+++⋯+⨯⨯⨯+, 1111111122334n n 1=-+-+-+⋯+-+, 11n 1=-+, n 11n 1+-=+, n n 1=+;故答案为11n n 1-+,n n 1+. ()2拓展应用16a 2m m 3①==,212a 4m m 3==,320a m 3=,430a 10m m 3==, ⋯⋯()()n n 1n 2a m 3++∴=, 故答案为()()n 1n 2m.3++ ()()n n 1n 2a m 61883②++==,且m 为质数,对6188分解质因数可知61882271317=⨯⨯⨯⨯,()()n 1n 2m 22713173++∴=⨯⨯⨯⨯, ()()m n 1n 22237131775152∴++=⨯⨯⨯⨯⨯=⨯⨯,m 7∴=,n 50=,()()n 7a n 1n 23∴=++, ()()n 131a 7n 1n 2=⋅++, 123n1111a a a a ∴+++⋯+ ()()33336m 12m 20m n 1n 2m =+++⋯+++()()311172334n 1n 2⎡⎤=++⋯+⎢⎥⨯⨯++⎢⎥⎣⎦31131172n 27252⎛⎫⎛⎫=-=- ⎪ ⎪+⎝⎭⎝⎭ 75364=. 【点睛】 本题主要考查数字的变化规律,解题的关键是掌握并熟练运用所得规律:()111n n 1n n 1=-++. 5.(1)﹣4,6﹣5t ;(2)①当点P 运动5秒时,点P 与点Q 相遇;②当点P 运动1或9秒时,点P与点Q间的距离为8个单位长度.【解析】【分析】(1)根据题意可先标出点A,然后根据B在A的左侧和它们之间的距离确定点B,由点P 从点A出发向左以每秒5个单位长度匀速运动,表示出点P即可;(2)①由于点P和Q都是向左运动,故当P追上Q时相遇,根据P比Q多走了10个单位长度列出等式,根据等式求出t的值即可得出答案;②要分两种情况计算:第一种是点P追上点Q之前,第二种是点P追上点Q之后.【详解】解:(1)∵数轴上点A表示的数为6,∴OA=6,则OB=AB﹣OA=4,点B在原点左边,∴数轴上点B所表示的数为﹣4;点P运动t秒的长度为5t,∵动点P从点A出发,以每秒5个单位长度的速度沿数轴向左匀速运动,∴P所表示的数为:6﹣5t,故答案为﹣4,6﹣5t;(2)①点P运动t秒时追上点Q,根据题意得5t=10+3t,解得t=5,答:当点P运动5秒时,点P与点Q相遇;②设当点P运动a秒时,点P与点Q间的距离为8个单位长度,当P不超过Q,则10+3a﹣5a=8,解得a=1;当P超过Q,则10+3a+8=5a,解得a=9;答:当点P运动1或9秒时,点P与点Q间的距离为8个单位长度.【点睛】在数轴上找出点的位置并标出,结合数轴求追赶和相遇问题是本题的考点,正确运用数形结合解决问题是解题的关键,注意不要漏解.6.(1)(4,8)(2)S△OAE=8﹣t(3)2秒或6秒【解析】【分析】(1)根据M和N的坐标和平移的性质可知:MN∥y轴∥PQ,根据K是PM的中点可得K 的坐标;(2)根据三角形面积公式可得三角形OAE的面积S;(3)存在两种情况:①如图2,当点B在OD上方时②如图3,当点B在OD上方时,过点B作BG⊥x轴于G,过D作DH⊥x轴于H,分别根据三角形OBD的面积等于三角形OAE的面积列方程可得结论.【详解】(1)由题意得:PM=4,∵K是PM的中点,∴MK=2,∵点M的坐标为(2,8),点N的坐标为(2,6),∴MN∥y轴,∴K(4,8);(2)如图1所示,延长DA交y轴于F,则OF⊥AE,F(0,8﹣t),∴OF=8﹣t,∴S△OAE=12OF•AE=12(8﹣t)×2=8﹣t;(3)存在,有两种情况:,①如图2,当点B在OD上方时,过点B作BG⊥x轴于G,过D作DH⊥x轴于H,则B(2,6﹣t),D(6,0),∴OG=2,GH=4,BG=6﹣t,DH=8﹣t,OH=6,S△OBD=S△OBG+S四边形DBGH+S△ODH,=12OG•BG+12(BG+DH)•GH﹣12OH•DH,=12×2(6-t)+12×4(6﹣t+8﹣t)﹣12×6(8﹣t),=10﹣2t,∵S △OBD =S △OAE ,∴10﹣2t =8﹣t ,t =2;②如图3,当点B 在OD 上方时,过点B 作BG ⊥x 轴于G ,过D 作DH ⊥x 轴于H ,则B (2,6﹣t ),D (6,8﹣t ),∴OG =2,GH =4,BG =6﹣t ,DH =8﹣t ,OH =6,S △OBD =S △ODH ﹣S 四边形DBGH ﹣S △OBG ,=12OH•DH ﹣12(BG+DH )•GH ﹣12O G•BG , =12×2(8-t )﹣12×4(6﹣t+8﹣t )﹣12×2(6﹣t ), =2t ﹣10,∵S △OBD =S △OAE ,∴2t ﹣10=8﹣t ,t =6;综上,t 的值是2秒或6秒.【点睛】本题考查四边形综合题、矩形的性质、三角形的面积、一元一次方程等知识,解题关键是灵活运用所学知识解决问题,学会用分类讨论的思想思考问题.7.(1)3456;45678S S =+++=++++ ;(2) 方法不唯一,见解析;(3)方法不唯一,见解析【解析】【分析】先找出前几项的钢管数,在推出第n 项的钢管数.【详解】(1)3456;45678S S =+++=++++(2)方法不唯一,例如:12S =+ 1233S =+++ 123444S =+++++ 12345555S =+++++++ (3)方法不唯一,例如:()()12.....2S n n n n =++++++()()()()=.....12.. (1112)n n n n n n n n +++++++=+++ ()312n n =+ 【点睛】此题主要考察代数式的规律探索及求和,需要仔细分析找到规律.8.(1)点P 在线段AB 上的13处;(2)13;(3)②MN AB 的值不变. 【解析】【分析】(1)根据C 、D 的运动速度知BD=2PC ,再由已知条件PD=2AC 求得PB=2AP ,所以点P 在线段AB 上的13处; (2)由题设画出图示,根据AQ-BQ=PQ 求得AQ=PQ+BQ ;然后求得AP=BQ ,从而求得PQ 与AB 的关系;(3)当点C 停止运动时,有CD =12AB ,从而求得CM 与AB 的数量关系;然后求得以AB 表示的PM 与PN 的值,所以MN =PN−PM =112AB . 【详解】解:(1)由题意:BD=2PC∵PD=2AC ,∴BD+PD=2(PC+AC ),即PB=2AP .∴点P 在线段AB 上的13处; (2)如图:∵AQ-BQ=PQ ,∴AQ=PQ+BQ,∵AQ=AP+PQ,∴AP=BQ,∴PQ=13 AB,∴13 PQ AB=(3)②MNAB的值不变.理由:如图,当点C停止运动时,有CD=12 AB,∴CM=14 AB,∴PM=CM-CP=14AB-5,∵PD=23AB-10,∴PN=1223(AB-10)=13AB-5,∴MN=PN-PM=112AB,当点C停止运动,D点继续运动时,MN的值不变,所以111212ABMNAB AB==.【点睛】本题考查了比较线段的长短.利用中点性质转化线段之间的倍分关系是解题的关键,在不同的情况下灵活选用它的不同表示方法,有利于解题的简洁性.同时,灵活运用线段的和、差、倍、分转化线段之间的数量关系也是十分关键的一点.9.(1)20;(2)t=15s或17s (3)4 3 s.【解析】【分析】(1)设P、Q速度分别为3m、2m,根据12秒后,动点P到达原点O列方程,求出P、Q 的速度,由此即可得到结论.(2)分两种情况讨论:①当A、B在相遇前且相距5个单位长度时;②当A、B在相遇后且相距5个单位长度时;列方程,求解即可.(3)算出P运动到B再到原点时,所用的时间,再算出Q从B到A所需的时间,比较即可得出结论.【详解】(1)设P、Q速度分别为3m、2m,根据题意得:12×3m=36,解得:m=1,∴P、Q速度分别为3、2,∴BC=12×2=24,∴OC=OB-BC=44-24=20.(2)当A、B在相遇前且相距5个单位长度时:3t+2t+5=44+36,5t=75,∴t=15(s);当A、B在相遇后且相距5个单位长度时:3t+2t-5=44+36,5t=85,∴t=17(s).综上所述:t=15s或17s.(3)P运动到原点时,t=3644443++=1243s,此时QB=2×1243=2483>44+38=80,∴Q点已到达A点,∴Q点已到达A点的时间为:3644804022+==(s),故提前的时间为:1243-40=43(s).【点睛】本题考查了一元一次方程的应用-行程问题以及数轴上的动点问题.解题的关键是找出等量关系,列出方程求解.10.(1)详见解析;(2)①16;②在移动过程中,3AC﹣4AB的值不变【解析】【分析】(1)根据点的移动规律在数轴上作出对应的点即可;(2)①当t=2时,先求出A、B、C点表示的数,然后利用定义求出AB、AC的长即可;②先求出A、B、C点表示的数,然后利用定义求出AB、AC的长,代入3AC-4AB即可得到结论.【详解】(1)A,B,C三点的位置如图所示:.(2)①当t=2时,A点表示的数为-4,B点表示的数为5,C点表示的数为12,∴AB=5-(-4)=9,AC=12-(-4)=16.②3AC-4AB的值不变.当移动时间为t秒时,A点表示的数为-t-2,B点表示的数为2t+1,C点表示的数为3t +6,则:AC=(3t+6)-(-t-2)=4t+8,AB=(2t+1)-(-t-2)=3t+3,∴3AC-4AB=3(4t+8)-4(3t+3)=12t+24-12t-12=12.即3AC﹣4AB的值为定值12,∴在移动过程中,3AC﹣4AB的值不变.【点睛】本题考查了数轴上的动点问题.表示出对应点所表示的数是解答本题的关键.11.(1)90°;(2)30°;(3)12秒或48秒.【解析】【分析】(1)依据图形可知旋转角=∠NOB,从而可得到问题的答案;(2)先求得∠AOC的度数,然后依据角的和差关系可得到∠NOC=60°-∠AON,∠AOM=90°-∠AON,然后求得∠AOM与∠NOC的差即可;(3)可分为当OM为∠BOC的平分线和当OM的反向延长为∠BOC的平分线两种情况,然后再求得旋转的角度,最后,依据旋转的时间=旋转的角度÷旋转的速度求解即可.【详解】(1)由旋转的定义可知:旋转角=∠NOB=90°.故答案为:90°(2)∠AOM﹣∠NOC=30°.理由:∵∠AOC:∠BOC=1:2,∠AOC+∠BOC=180°,∴∠AOC=60°.∴∠NOC=60°﹣∠AON.∵∠NOM=90°,∴∠AOM=90°﹣∠AON,∴∠AOM﹣∠NOC=(90°﹣∠AON)﹣(60°﹣∠AON)=30°.(3)如图1所示:当OM为∠BOC的平分线时,∵OM为∠BOC的平分线,∴∠BOM=∠BOC=60°,∴t=60°÷5°=12秒.如图2所示:当OM的反向延长为∠BOC的平分线时,∵ON为为∠BOC的平分线,∴∠BON=60°.∴旋转的角度=60°+180°=240°.∴t=240°÷5°=48秒.故答案为:12秒或48秒.【点睛】本题主要考查的是三角形的综合应用,解答本题主要应用了旋转的定义、直角三角形的定义以及角的和差计算,求得三角板旋转的角度是解题的关键. 12.(1)5 ;(2)点F 表示的数是11.5或者-6.5;(3)127t =或6t =. 【解析】【分析】(1)由AP=2可知PB=12-2=10,再由点M 是PB 中点可知PM 长度;(2)点P 运动3秒是9个单位长度,M 为PB 的中点,则可求解出点M 表示的数是2.5,再由FM=2PM 可求解出FM=9,此时点F 可能在M 点左侧,也可能在其右侧;(3)设Q 运动的时间为t 秒,由题可知t=4秒时,点P 到达点A ,再经过4秒点P 停止运动;则分04t ≤≤和48t <≤两种情况分别计算,由题可知即可QM=2PM=BP ,据此进行解答即可.【详解】(1)5 ;(2)∵点A 表示的数是5-∴点B 表示的数是7∵点P 运动3秒是9个单位长度,M 为PB 的中点 ∴PM=12PB=4.5,即点M 表示的数是2.5 ∵FM=2PM∴FM=9∴点F 表示的数是11.5或者-6.5(3)设Q 运动的时间为t 秒, 当04t ≤≤时,由题可知QM=2PM=BP ,故点Q 位于点P 左侧,则AB=AQ+QP+PB ,而QP=QM-PM=2PM-PM=12BP ,则可得12=2.5t+12⨯3t+3t=7t ,解得t=127; 当48t <≤时,由题可知QM=2PM=BP ,故点Q 位于点B 右侧,则PB=2QB ,则可得,()()123422.512t t --=-,整理得8t=48,解得6t =.【点睛】本题结合数轴上的动点问题考查了一元一次方程的应用,第3问要根据题干条件分情况进行讨论,作出图形更易理解.13.(1)16;(2)①t 的值为3或143秒;②存在,P 表示的数为314.【解析】【分析】(1)由数轴可知,AB=3,则CD=6,所以D 表示的数为16,(2)①当运动时间是t 秒时,在运动过程中,B 点表示的数为3+2t,A 点表示的数为2t, C 点表示的数为10-t ,D 点表示的数为16-t ,分情况讨论两条线段重叠部分是2个单位长度解答即可;②分情况讨论当t=3秒, t=143秒时,满足3BD PA PC -=的点P , 注意P 为线段AB 上的点对x 的值的限制.【详解】(1)16(2)①在运动过程中,B 点表示的数为3+2t,A 点表示的数为2t,C 点表示的数为10-t ,D 点表示的数为16-t.当BC =2,点B 在点C 的右边时,由题意得:32-10-2BC t t =+=(),解得:t =3,当AD=2,点A 在点D 的左边时,由题意得:16--22AD t t ==,解得:t =143. 综上,t 的值为3或143秒 ②存在,理由如下:当t=3时,A 点表示的数为6,B 点表示的数为9,C 点表示的数为7,D 点表示的数为13. 则13-94-6|-7|BD PA x PC x ====,,,-3BD PA PC =,()4--6|-7|x x ∴=, 解得:314x =或112, 又P 点在线段AB 上,则69x ≤≤314x ∴=. 当143t =时,A 点表示的数为283,B 点表示的数为373,C 点表示的数为163,D 点表示的数为343. 则37343816-1-|-|3333BD PA x PC x ====,,, -3BD PA PC =,∴ 28161--|-|33x x ⎛⎫= ⎪⎝⎭, 解得:7912x =或176, 又283733x ≤≤, x ∴无解综上,P 表示的数为314. 【点睛】本题考查了一元一次方程的应用以及数轴,解题的关键是:(1)由路程=速度×时间结合运动方向找出运动t 秒时点A 、B 、C 、D 所表示的数,(2)根据3BD PA PC -=列出关于t 的含绝对值符号的一元一次方程.14.(1)2或10;(2)当t 为5秒、10秒或7.5秒时,P 、A 和B 中恰有一个点为其余两点的优点.【解析】【分析】(1)设所求数为x ,根据优点的定义分优点在M 、N 之间和优点在点N 右边,列出方程解方程即可;(2)根据优点的定义可知分三种情况:①P 为(A ,B )的优点;②P 为(B ,A )的优点;③B 为(A ,P )的优点.设点P 表示的数为x ,根据优点的定义列出方程,进而得出t 的值.【详解】解:(1)设所求数为x ,当优点在M 、N 之间时,由题意得x ﹣(﹣2)=2(4﹣x ),解得x=2;当优点在点N 右边时,由题意得x ﹣(﹣2)=2(x ﹣4),解得:x=10;故答案为:2或10;(2)设点P 表示的数为x ,则PA=x+20,PB=40﹣x ,AB=40﹣(﹣20)=60,分三种情况:①P 为(A ,B )的优点.由题意,得PA=2PB ,即x ﹣(﹣20)=2(40﹣x ),解得x=20,∴t=(40﹣20)÷4=5(秒);②P 为(B ,A )的优点.由题意,得PB=2PA ,即40﹣x=2(x+20),解得x=0,∴t=(40﹣0)÷4=10(秒);③B 为(A ,P )的优点.由题意,得AB=2PA ,即60=2(x+20)解得x=10,此时,点P 为AB 的中点,即A 也为(B ,P )的优点,∴t=30÷4=7.5(秒);综上可知,当t 为5秒、10秒或7.5秒时,P 、A 和B 中恰有一个点为其余两点的优点.【点睛】本题考查了一元一次方程的应用及数轴,解题关键是要读懂题目的意思,理解优点的定义,找出合适的等量关系列出方程,再求解.15.问题一、(1)32;(2)3-2x ;2x -3;13-6x ;问题一、(1)35;120;24011. 【解析】【分析】问题一根据等量关系,路程=速度⨯时间,路程差=路程1-路程2,即可列出方程求解。
北师大版七年级数学上册期末数轴有关压轴题专题复习练习题(含答案)

北师大版七年级数学上册期末数轴有关压轴题专题复习练习题1、有理数a 、b 、c 在数轴上对应的点分别为A 、B 、C ,若a =-2,b =-3,c =,(1)填空:A ,B 之间的距离为,之间的距离为 ,A ,C 之间的距离为 ; (2)问在数轴上是否存在一点P ,使P 与A 的距离是P 与C 的距离的3倍,若存在,请求出P 点对应的有理数;若不存在,请说明理由.2、操作探究:已知在纸面上有一数轴(如图所示).操作一:(1)折叠纸面,使1表示的点与-1表示的点重合,则-3表示的点与________表示的点重合;操作二:(2)折叠纸面,使-1表示的点与3表示的点重合,回答以下问题: ①5表示的点与数________表示的点重合;②若数轴上A 、B 两点之间距离为11(A 在B 的左侧),且A 、B 两点经折叠后重合,求A 、B 两点表示的数是多少.3、结合数轴与绝对值的知识回答下列问题:(1)数轴上表示4和1的两点之间的距离是 ;表示﹣3和2两点之间的距离是 5 ;一般地,数轴上表示数m 和数n 的两点之间的距离等于|m ﹣n |.如果表示数a 和﹣2的两点之间的距离是3,那么a = ;(2)若数轴上表示数a 的点位于﹣4与2之间,求|a +4|+|a ﹣2|的值;(3)当a 取何值时,|a +5|+|a ﹣1|+|a ﹣4|的值最小,最小值是多少?请说明理由.4、数轴上从左到右的三个点A,B,C所对应的数分别为a,b,c.其中AB=2017,BC=1000,如图所示.(1)若以B为原点,写出点A,C所对应的数,并计算a+b+c的值.(2)若原点O在A,B两点之间,求|a|+|b|+|b﹣c|的值.(3)若O是原点,且OB=17,求a+b﹣c的值.5、如图,在一条不完整的数轴上从左到右有点A,B,C,其中AB=2BC,设点A,B,C所对应数的和是m.(1)若点C为原点,BC=1,则点A,B所对应的数分别为,,m的值为;(2)若点B为原点,AC=6,求m的值.(3)若原点O到点C的距离为8,且OC=AB,求m的值.6、如图所示,点A、B在数轴上分别表示有理数a、b,A、B两点之间距离表示为AB,在数轴上A、B两点之间的距离AB=|a﹣b|.回答下列问题:(1)若x表示一个有理数,|x﹣2019|+|x﹣2020|有最小值吗?若有,请求出最小值,若没有,写出理由.(2)求|x﹣1|+2|x﹣3|+3|x﹣4|的最小值.(3)已知(|x+1|+|x﹣2|)(|y﹣2|+|y+1|)(|z﹣3|+|z+1|)=36,求x+2y+3z的最大值和最小值.7、已知数轴上有A、B、C三个点对应的数分别是a、b、c,且满足|a+24|+|b+10|+(c﹣10)2=0;(1)求a、b、c的值;(2)动点P从A出发,以每秒1个单位的速度向终点C移动,设移动时间为t秒.若点P到A点距离是到B点距离的2倍,求点P的对应的数;(3)动点P从A出发向右运动,速度为每秒1个单位长度,同时动点Q从C出发向左运动,速度为每秒2个单位的速度.设移动时间为t秒.求t为何值时,P、Q两点之间的距离为8?8、已知A,B,C三点在数轴上的位置如图所示,它们表示的数分别是a,b,c.(1)填空:abc0,a+b0,ab﹣ac0;(填“>”,“=”或“<”)(2)若|a|=2且点B到点A,C的距离相等,①当b2=16时,求c的值;②P是数轴上B,C两点之间的一个动点,设点P表示的数为x,当P点在运动过程中,bx+cx+|x﹣c|﹣10|x+a|的值保持不变,求b的值.9、如图,在一张长方形纸条上画一条数轴.(1)若折叠纸条使数轴上表示﹣1的点与表示5的点重合,则折痕与数轴的交点表示的数是;(2)如果数轴上两点之间的距离为6+m2(m为常数),这两点经过(1)的折叠方式后折痕与数轴的交点与(1)中的交点相同,求左边这个点表示的数;(用含m的代数式表示)(3)如图2,若将此纸条沿A,B处剪开,将中间的一段纸条对折,使其左右两端重合,这样连续对折n次后,再将其展开,求最右端的折痕与数轴的交点表示的数.(用含n的代数式表示)10、数轴上两个质点A .B 所对应的数为﹣8、4,A .B 两点各自以一定的速度在数轴上运动,且A 点的运动速度为2个单位/秒.(1)点A .B 两点同时出发相向而行,在4秒后相遇,求B 点的运动速度;(2)A 、B 两点以(1)中的速度同时出发,向数轴正方向运动,几秒钟时两者相距6个单位长度;(3)A 、B 两点以(1)中的速度同时出发,向数轴负方向运动,与此同时,C 点从原点出发作同方向的运动,且在运动过程中,始终有CA =2CB ,若干秒钟后,C 停留在﹣10处,求此时B 点的位置?11、如图,在数轴上A 点表示数a ,B 点表示数b ,AB 表示A 点和B 点之间的距离,C 是AB的中点,且a 、b 满足|a+3|+(b+3a )2=0. (1)求点C 表示的数;(2)点P 从A 点以3个单位每秒向右运动,点Q 同时从B 点以2个单位每秒向左运动,若AP+BQ=2PQ ,求时间t ;(3)若点P 从A 向右运动,点M 为AP 中点,在P 点到达点B 之前:①的值不变;②2BM ﹣BP 的值不变,其中只有一个正确,请你找出正确的结论并求出其值.12、已知:a 是最大的负整数,且a 、b 、c 满足()052=++-b a c .(1)请求出a 、b 、c 的值; (2)所对应的点分别为A 、B 、C ,点P 为动点,其对应的数为x ,当点P 在B 到C之间运动时,化简:31--+x x ;(写出化简过程)(3)在(1)、(2)的条件下,点A 、B 、C 开始在数轴上运动,若点A 以每秒1个单位长度的速度向左运动,同时,点B 和点C 分别以每秒2个单位长度和5个单位长度的速度向右运动,假设秒钟过后,若点B 与点C 之间的距离表示为BC ,点A 与点B 之间的距离表示为AB .请问:BC-AB 的值是否随着时间t 的变化而改变?若变化,请说明理由;若不变,请求其值.13、如图,在数轴上点A表示的数是8,若动点P从原点O出发,以2个单位/秒的速度向左运动,同时另一动点Q从点A出发,以4个单位/秒的速度也向左运动,到达原点后立即以原来的速度返回,向右运动,设运动的时间为t(秒).(1)当t=0.5时,求点Q到原点O的距离;(2)当t=2.5时求点Q到原点O的距离;(3)当点Q到原点O的距离为4时,求点P到原点O的距离.14、已知,A,B在数轴上对应的数分别用a,b表示,且.(1)数轴上点A表示的数是,点B表示的数是(2)若点A与点C之间的距离表示为AC,点B与点C之间的距离表示为BC,当C点在数轴上且满足AC=3BC时,求C点对应的数.15、阅读理解:若A、B、C为数轴上三点,若点C到A的距离是点C到B的距离2倍,我们就称点C是【A,B】的好点.例如,如图1,点A表示的数为﹣1,点B表示的数为2.表示1的点C到点A的距离是2,到点B的距离是1,那么点C是【A,B】的好点.又如,表示0的点D到点A的距离是1,到点B的距离是2.那么点D就不是【A,B】的好点,但点D是【B,A】的好点:知识运用:51-b5a2=++)((1)如图1,点B是【D,C】的好点吗?是(填是或不是);(2)如图2,A、B为数轴上两点,点A所表示的数为﹣40,点B所表示的数为20.现有一只电子蚂蚁P从点B出发,以2个单位每秒的速度向左运动,到达点A停止当t为何值时,P、A和B中恰有一个点为其余两点的好点?16、如图,数轴上点A表示数a,点B表示数b,点C表示数c,b是最小的正整数,a、c满足|a+3|+(c﹣8)2=0,AB表示点A、B之间的距离,且AB=|a﹣b|.(1)a=,b=;(2)若将数轴折叠,使得A点与C点重合,则点B与数表示的点重合;(3)点A、B.、C在数轴上运动,若点A以每秒1个单位长度的速度向左运动,同时,点B和点C分别以每秒2个单位长度和4个单位长度的速度向右运动,假设t秒钟过后,若,点A与点C之间的距离表示为AC,点B与点C之间的距离表示为BC.则AC=,BC=.(用含t的代数式表示)(4)在(3)的条件下,请问:3BC﹣2AB的值是否随着时间t的变化而改变?若变化,请说明理由;若不变,请求其值.17、已知数轴上两点A、B对应的数分别是6,﹣8,M、N、P为数轴上三个动点,点M从A点出发,速度为每秒2个单位,点N从点B出发,速度为M点的3倍,点P从原点出发,速度为每秒1个单位.(1)若点M向右运动,同时点N向左运动,求多长时间点M与点N相距54个单位?(2)若点M、N、P同时都向右运动,求多长时间点P到点M,N的距离相等?(3)当时间t满足t1<t≤t2时,M、N两点之间,N、P两点之间,M、P两点之间分别有55个、44个、11个整数点,请直接写出t 1,t 2的值.参考答案:1、有理数a 、b 、c 在数轴上对应的点分别为A 、B 、C ,若a =-2,b =-3,c =, (1)填空:A ,B 之间的距离为,之间的距离为 ,A ,C 之间的距离为 ; (2)问在数轴上是否存在一点P ,使P 与A 的距离是P 与C 的距离的3倍,若存在,请求出P 点对应的有理数;若不存在,请说明理由.解:(1)1 ,311,38(2)存在.设P 点对应的有理数为x. ①当点P 在点A 的左边时,有-2-x=3(32-x ) 解之得:x=2 (不合条件,舍去) ②当点P 在点A 和点C 之间时,有x -(-2)= 3 (32-x) 解之得:x=0③当点P 在点C 的右边时,有x -(-2)= 3 (x -32) 解之得:x=2综上所述,满足条件的P 点对应的有理数为0或2.2、操作探究:已知在纸面上有一数轴(如图所示).操作一:(1)折叠纸面,使1表示的点与-1表示的点重合,则-3表示的点与________表示的点重合;操作二:(2)折叠纸面,使-1表示的点与3表示的点重合,回答以下问题: ①5表示的点与数________表示的点重合;②若数轴上A 、B 两点之间距离为11(A 在B 的左侧),且A 、B 两点经折叠后重合,求A 、B 两点表示的数是多少.解:(1)3 (2)①-3 ②由题意可得,A 、B 两点距离对称点的距离为11÷2=5.5.∵对称点是表示1的点,∴A 、B 两点表示的数分别是-4.5,6.5.、323、结合数轴与绝对值的知识回答下列问题:(1)数轴上表示4和1的两点之间的距离是 3 ;表示﹣3和2两点之间的距离是 5 ;一般地,数轴上表示数m和数n的两点之间的距离等于|m﹣n|.如果表示数a和﹣2的两点之间的距离是3,那么a=1或﹣5 ;(2)若数轴上表示数a的点位于﹣4与2之间,求|a+4|+|a﹣2|的值;(3)当a取何值时,|a+5|+|a﹣1|+|a﹣4|的值最小,最小值是多少?请说明理由.【解答】解:(1)3,5,1或﹣5;(2)因为|a+4|+|a﹣2|表示数轴上数a和﹣4,2之间距离的和.又因为数a位于﹣4与2之间,所以|a+4|+|a﹣2|=6;(3)根据|a+5|+|a﹣1|+|a﹣4|表示一点到﹣5,1,4三点的距离的和.所以当a=1时,式子的值最小,此时|a+5|+|a﹣1|+|a﹣4|的最小值是9.4、数轴上从左到右的三个点A,B,C所对应的数分别为a,b,c.其中AB=2017,BC=1000,如图所示.(1)若以B为原点,写出点A,C所对应的数,并计算a+b+c的值.(2)若原点O在A,B两点之间,求|a|+|b|+|b﹣c|的值.(3)若O是原点,且OB=17,求a+b﹣c的值.【答案】解:(1)∵点B为原点,AB=2017,BC=1000,∴点A表示的数为a=﹣2017,点C表示的数是c=1000,∴a+b+c=﹣2017+0+1000=﹣1017.(2)∵原点在A,B两点之间,∴|a|+|b|+|b﹣c|=AB+BC=2017+1000=3017.答:|a|+|b|+|b﹣c|的值为3017.(3)若原点O在点B的左边,则点A,B,C所对应数分别是a=﹣2000,b=17,c=1017,则a+b﹣c=﹣2000+17﹣1017=﹣3000;若原点O在点B的右边,则点A,B,C所对应数分别是a=﹣2034,b=﹣17,c=983,则a+b﹣c=﹣2034﹣17﹣983=﹣3034.5、如图,在一条不完整的数轴上从左到右有点A,B,C,其中AB=2BC,设点A,B,C所对应数的和是m.(1)若点C为原点,BC=1,则点A,B所对应的数分别为﹣3 ,﹣1 ,m的值为﹣4 ;(2)若点B为原点,AC=6,求m的值.(3)若原点O到点C的距离为8,且OC=AB,求m的值.【答案】解:(1)∵点C为原点,BC=1,∴B所对应的数为﹣1,∵AB=2BC,∴AB=2,∴点A所对应的数为﹣3,∴m=﹣3﹣1+0=﹣4;故答案为:﹣3,﹣1,﹣4;(2)∵点B为原点,AC=6,AB=2BC,∴点A所对应的数为﹣4,点C所对应的数为2,∴m=﹣4+2+0=﹣2;(3)∵原点O到点C的距离为8,∴点C所对应的数为±8,∵OC=AB,∴AB=8,当点C对应的数为8,∵AB=8,AB=2BC,∴BC=4,∴点B所对应的数为4,点A所对应的数为﹣4,∴m=4﹣4+8=8;当点C所对应的数为﹣8,∵AB=8,AB=2BC,∴BC=4,∴点B所对应的数为﹣12,点A所对应的数为﹣20,∴m=﹣20﹣12﹣8=﹣40综上所述m=8或﹣40.6、如图所示,点A、B在数轴上分别表示有理数a、b,A、B两点之间距离表示为AB,在数轴上A、B两点之间的距离AB=|a﹣b|.回答下列问题:(1)若x表示一个有理数,|x﹣2019|+|x﹣2020|有最小值吗?若有,请求出最小值,若没有,写出理由.(2)求|x﹣1|+2|x﹣3|+3|x﹣4|的最小值.(3)已知(|x+1|+|x﹣2|)(|y﹣2|+|y+1|)(|z﹣3|+|z+1|)=36,求x+2y+3z的最大值和最小值.解:(1)|x﹣2019|+|x﹣2020|表示数轴上表示x的点到表示2019、2020点的距离之和,要使距离之和最小,则2019≤x≤2020,∴|x﹣2019|+|x﹣2020|的最小值为2020﹣2019=1,答:|x﹣2019|+|x﹣2020|的最小值为1;(2)由(1)得,当x=3时,|x﹣1|+2|x﹣3|+3|x﹣4|的值最小,最小值为5.(3)当﹣1≤x≤2时,|x+1|+|x﹣2|的最小值为3,当﹣1≤y≤2时,|y﹣2|+|y+1|的最小值为3,当﹣1≤z≤3时,|z﹣3|+|z+1|的最小值为4,∵(|x+1|+|x﹣2|)(|y﹣2|+|y+1|)(|z﹣3|+|z+1|)=36,∴各自均取最小值,当x=﹣1、y=﹣1、z=﹣1时,x+2y+3z的值最小,x+2y+3z=﹣6,当x=2、y=2、z=3时,x+2y+3z的值最小,x+2y+3z=15,答:x+2y+3z的最大值为15,最小值为﹣6.7、已知数轴上有A、B、C三个点对应的数分别是a、b、c,且满足|a+24|+|b+10|+(c﹣10)2=0;(1)求a、b、c的值;(2)动点P从A出发,以每秒1个单位的速度向终点C移动,设移动时间为t秒.若点P到A点距离是到B点距离的2倍,求点P的对应的数;(3)动点P从A出发向右运动,速度为每秒1个单位长度,同时动点Q从C出发向左运动,速度为每秒2个单位的速度.设移动时间为t秒.求t为何值时,P、Q两点之间的距离为8?解:(1)∵|a+24|+|b+10|+(c﹣10)2=0,∴a+24=0,b+10=0,c﹣10=0,解得:a=﹣24,b=﹣10,c=10.(2)AB=﹣10﹣(﹣24)=14.①当点P在线段AB上时,t=2(14﹣t),解得:t=,∴点P的对应的数是﹣24+=﹣;②当点P在线段AB的延长线上时,t=2(t﹣14),解得:t=28,∴点P的对应的数是﹣24+28=4.综上所述,点P所对应的数是﹣或4.(3)点P、Q相遇前,t+2t+8=34,解得:t=;点P、Q相遇后,t+2t﹣8=34,解得:t=14.综上所述:当Q点开始运动后第秒或14秒时,P、Q两点之间的距离为8.8、已知A,B,C三点在数轴上的位置如图所示,它们表示的数分别是a,b,c.(1)填空:abc<0,a+b>0,ab﹣ac>0;(填“>”,“=”或“<”)(2)若|a|=2且点B到点A,C的距离相等,①当b2=16时,求c的值;②P是数轴上B,C两点之间的一个动点,设点P表示的数为x,当P点在运动过程中,bx+cx+|x﹣c|﹣10|x+a|的值保持不变,求b的值.【解答】解:(1)∵a<0<b<c,∴abc<0,a+b>0,ab﹣ac>0,故答案为:<,>,>;(2)①∵|a|=2 且a<0,∴a=﹣2,∵b2=16 且b>0,∴b=4,∵点B到点A,C的距离相等,∴|4﹣(﹣2)|=|c﹣4|,∴c=10;②依题意,得bx+cx+|x﹣c|﹣10|x+a|=bx+cx+c﹣x﹣10x﹣10a=(b+c﹣11)x﹣10a+c,∴原式=(b+c﹣11)x﹣10a+c∵当P点在运动过程中,原式的值保持不变,即原式的值与x无关,∴b+c﹣11=0,∵b+2=c﹣b,∴b=3.9、如图,在一张长方形纸条上画一条数轴.(1)若折叠纸条使数轴上表示﹣1的点与表示5的点重合,则折痕与数轴的交点表示的数是 2 ;(2)如果数轴上两点之间的距离为6+m2(m为常数),这两点经过(1)的折叠方式后折痕与数轴的交点与(1)中的交点相同,求左边这个点表示的数;(用含m的代数式表示)(3)如图2,若将此纸条沿A,B处剪开,将中间的一段纸条对折,使其左右两端重合,这样连续对折n次后,再将其展开,求最右端的折痕与数轴的交点表示的数.(用含n的代数式表示)【解答】解:(1)由折叠时,点﹣1与5是对称的,∴﹣1和5的中点为折痕与数轴的交点,∴交点为2,故答案为2;(2)设两个点左边的为x,右边的为y,∵两点之间的距离为6+m2,∴y﹣x=6+m2,由(1)知交点为2,∴x+y=4,∴x=﹣1﹣,∴左边的这个点表示的数是﹣1﹣.(3)对折n次后,每两条相邻折痕间的距离=,∴最右端的折痕与数轴的交点表示的数为4﹣.10、数轴上两个质点A.B所对应的数为﹣8、4,A.B两点各自以一定的速度在数轴上运动,且A点的运动速度为2个单位/秒.(1)点A.B两点同时出发相向而行,在4秒后相遇,求B点的运动速度;(2)A、B两点以(1)中的速度同时出发,向数轴正方向运动,几秒钟时两者相距6个单位长度;(3)A、B两点以(1)中的速度同时出发,向数轴负方向运动,与此同时,C点从原点出发作同方向的运动,且在运动过程中,始终有CA=2CB,若干秒钟后,C停留在﹣10处,求此时B点的位置?解(1)设B点的运动速度为x个单位/秒,A.B两点同时出发相向而行,他们的时间均为4秒,则有:(2+x)×4=12.解得x=1,所以B点的运动速度为1个单位/秒;(2)设经过时间为t.则B在A的前方,B点经过的路程﹣A点经过的路程=6,则2t﹣t=6,解得t=6.A在B的前方,A点经过的路程﹣B点经过的路程=6,则2t﹣t=12+6,解得t=18.(3)设点C的速度为y个单位/秒,运动时间为t,始终有CA=2CB,即:8+(2﹣y)t=2×[4+(y﹣1)t].解得y=.当C停留在﹣10处,所用时间为:秒.B的位置为.11、如图,在数轴上A点表示数a,B点表示数b,AB表示A点和B点之间的距离,C是AB的中点,且a 、b满足|a+3|+(b+3a)2=0.(1)求点C表示的数;(2)点P从A点以3个单位每秒向右运动,点Q同时从B点以2个单位每秒向左运动,若AP+BQ=2PQ,求时间t;(3)若点P从A向右运动,点M为AP中点,在P点到达点B之前:①的值不变;②2BM﹣BP的值不变,其中只有一个正确,请你找出正确的结论并求出其值.【解答】解:(1)∵|a+3|+(b+3a)2=0,∴a+3=0,b+3a=0,解得a=﹣3,b=9,∴=3,∴点C表示的数是3;(2)∵AB=9+3=12,点P从A点以3个单位每秒向右运动,点Q同时从B点以2个单位每秒向左运动,∴AP=3t,BQ=2t,PQ=12﹣5t.∵AP+BQ=2PQ,∴3t+2t=24﹣10t,解得t=;还有一种情况,当P运动到Q的左边时,PQ=5t﹣12,方程变为2t+3t=2(5t﹣12),求得t=24/5(6分)(3)∵PA+PB=AB为定值,PC先变小后变大,∴的值是变化的,∴①错误,②正确;∵BM=PB+,∴2BM=2PB+AP,∴2BM﹣BP=PB+AP=AB=12.12、已知:a 是最大的负整数,且a 、b 、c 满足()052=++-b a c . (1)请求出a 、b 、c 的值;(2)所对应的点分别为A 、B 、C ,点P 为动点,其对应的数为x ,当点P 在B 到C 之间运动时,化简:31--+x x ;(写出化简过程)(3)在(1)、(2)的条件下,点A 、B 、C 开始在数轴上运动,若点A 以每秒1个单位长度的速度向左运动,同时,点B 和点C 分别以每秒2个单位长度和5个单位长度的速度向右运动,假设秒钟过后,若点B 与点C 之间的距离表示为BC ,点A 与点B 之间的距离表示为AB .请问:BC-AB 的值是否随着时间t 的变化而改变?若变化,请说明理由;若不变,请求其值.解答:(1)依题意得,a=-1,c-5=0,a+b=0解得a=-1,b=1,c=5(2)当点P 在B 到C 之间运动时,1<x<5因此,当1<x ≤3时,x+1>0,x-3≤0,原式=x+1+x-3=2x-2;当3<x<5时, x+1>0,x-3>0,原式=x+1-(x-3)=4.(3)不变。
(完整版)北师大版七年级数学上册期末复习压轴题专题(带解析)

北师大版七年级上册期末压轴题压轴题选讲一选择题1.某企业今年1月份产值为x万元,2月份比1月份减少了10%,3月份比2月份增加了15%,则3月份的产值用代数式表示为( )A.(1﹣10%+15%)x万元 B.(1+10%﹣15%)x万元C.(x﹣10%)(x+15%)万元D.(1﹣10%)(1+15%)x万元2.有理数a、b在数轴上的位置如图所示,则化简|a﹣b|+|a+b|的结果为()A.﹣2a B.2a C.2b D.﹣2b3.如图,已知点A是射线BE上一点,过A作CA⊥BE交射线BF于点C,AD⊥BF交射线BF于点D,给出下列结论:①∠1是∠B的余角;②图中互余的角共有3对;③∠1的补角只有∠ACF;④与∠ADB互补的角共有3个.则上述结论正确的个数有( )A.1个B.2个C.3个D.4个4.如图是由一副三角尺拼成的图案,它们有公共顶点O,且有一部分重叠,已知∠BOD=40°,则∠AOC的度数是( )A.40°B.120°C.140°D.150°二填空题1.如图,线段AB=8,C是AB的中点,点D在直线CB上,DB=1.5,则线段CD的长等于.2.如图,在数轴上,点A表示1,现将点A沿x轴做如下移动,第一次点A向左移动2个单位长度到达点A1,第二次将点A1,向右移动4个单位长度到达点A2,第三次将点A2向左移动6个单位长度到达点A3,按照这种移动规律移动下去,第n次移动到点A n,如果点A n与原点的距离等于19,那么n的值是.3.如图所示,甲乙两人沿着边长为60cm的正方形,按A→B→C→D→A…的方向行走,甲从A点以60m/min的速度,乙从B点以69m/min的速度行走,两人同时出发,当乙第一次追上甲时,用了____________.4.将一些相同的“○”按如图所示的规律依次摆放,观察每个“龟图”中的“○”的个数,若第n 个“龟图”中有245个“○”,则n=______________.5.如图,长方形ABCD中,AB=6,第一次平移长方形ABCD沿AB的方向向右平移5个单位,得到长方形A1B1C1D1,第2次平移将长方形A1B1C1D1沿A1B1的方向向右平移5个单位,得到长方形A2B2C2D2…,第n次平移将长方形A n﹣1B n﹣1C n﹣1D n﹣1沿A n﹣1B n﹣1的方向平移5个单位,得到长方形A n B n C n D n(n>2),若AB n的长度为56,则n=.三、解答题1.如图,M是定长线段AB上一定点,点C在线段AM上,点D在线段BM上,点C、点D分别从点M、点B出发以1cm/s、2cm/s的速度沿直线BA向左运动,运动方向如箭头所示.(1)若AB=10cm,当点C、D运动了2s,求AC+MD的值;(2)若点C、D运动时,总有MD=2AC,直接填空:AM=AB;(3)在(2)的条件下,N是直线AB上一点,且AN﹣BN=MN,求的值.2.已知数轴上有A,B,C三点,分别表示数﹣24,﹣10,10.两只电子蚂蚁甲、乙分别从A,C两点同时相向而行,甲的速度为4个单位/秒,乙的速度为6个单位/秒.(1)问甲、乙在数轴上的哪个点相遇?(2)问多少秒后甲到A,B,C三点的距离之和为40个单位?若此时甲调头返回,问甲、乙还能在数轴上相遇吗?若能,求出相遇点;若不能,请说明理由.3.甲、乙两地相距720km,一列快车和一列慢车都从甲地驶往乙地,慢车先行驶1小时后,快车才开始行驶.已知快车的速度是120km/h,慢车的速度是80km/h,快车到达乙地后,停留了20min,由于有新的任务,于是立即按原速返回甲地.在快车从甲地出发到回到甲地的整个程中,与慢车相遇了两次,这两次相遇时间间隔是多少?4.(1)如图1,若CO⊥AB,垂足为O,OE、OF分别平分∠AOC与∠BOC.求∠EOF的度数;(2)如图2,若∠AOC=∠BOD=80°,OE、OF分别平分∠AOD与∠BOC.求∠EOF的度数;(3)若∠AOC=∠BOD=α,将∠BOD绕点O旋转,使得射线OC与射线OD的夹角为β,OE、OF分别平分∠AOD与∠BOC.若α+β≤180°,α>β,则∠EOC=.(用含α与β的代数式表示)5.如图,已知∠AOB=90°,以O为顶点、OB为一边画∠BOC,然后再分别画出∠AOC与∠BOC的平分线OM、ON.(1)在图1中,射线OC在∠AOB的内部.①若锐角∠BOC=30°,则∠MON=45°;②若锐角∠BOC=n°,则∠MON=45°.(2)在图2中,射线OC在∠AOB的外部,且∠BOC为任意锐角,求∠MON的度数.(3)在(2)中,“∠BOC为任意锐角”改为“∠BOC为任意钝角”,其余条件不变,(图3),求∠MON的度数.6.如图,∠AOB=120°,射线OC从OA开始,绕点O逆时针旋转,旋转的速度为每分钟20°;射线OD从OB开始,绕点O逆时针旋转,旋转的速度为每分钟5°,OC和OD同时旋转,设旋转的时间为t(0≤t≤15).(1)当t为何值时,射线OC与OD重合;(2)当t为何值时,射线OC⊥OD;(3)试探索:在射线OC与OD旋转的过程中,是否存在某个时刻,使得射线OC,OB与OD中的某一条射线是另两条射线所夹角的角平分线?若存在,请求出所有满足题意的t的取值,若不存在,请说明理由.7.如图,∠AOB的边OA上有一动点P,从距离O点18cm的点M处出发,沿线段MO,射线OB运动,速度为2cm/s;动点Q从点O出发,沿射线OB运动,速度为1cm/s.P、Q 同时出发,设运动时间是t(s).(1)当点P在MO上运动时,PO=cm (用含t的代数式表示);(2)当点P在MO上运动时,t为何值,能使OP=OQ?(3)若点Q运动到距离O点16cm的点N处停止,在点Q停止运动前,点P能否追上点Q?如果能,求出t的值;如果不能,请说出理由.8.如图,两个形状.大小完全相同的含有30゜、60゜的三角板如图放置,PA、PB与直线MN重合,且三角板PAC,三角板PBD均可以绕点P逆时针旋转.(1)试说明:∠DPC=90゜;(2)如图,若三角板PAC的边PA从PN处开始绕点P逆时针旋转一定角度,PF平分∠APD,PE平分∠CPD,求∠EPF;(3)如图,若三角板PAC的边PA从PN处开始绕点P逆时针旋转,转速为3゜/秒,同时三角板PBD的边PB从PM处开始绕点P逆时针旋转,转速为2゜/秒,在两个三角板旋转过程中(PC转到与PM重合时,两三角板都停止转动).设两个三角板旋转时间为t秒,则∠BPN=__________,∠CPD=________ (用含有t的代数式表示,并化简);以下两个结论:①为定值;②∠BPN+∠CPD为定值,正确的是___________(填写你认为正确结论的对应序号).压轴题选讲解析一选择题1.某企业今年1月份产值为x万元,2月份比1月份减少了10%,3月份比2月份增加了15%,则3月份的产值用代数式表示为( )A.(1﹣10%+15%)x万元 B.(1+10%﹣15%)x万元C.(x﹣10%)(x+15%)万元D.(1﹣10%)(1+15%)x万元【考点】列代数式.【分析】根据3月份、1月份与2月份的产值的百分比的关系列式计算即可得解.【解答】解:3月份的产值为:(1﹣10%)(1+15%)x万元.故选D.【点评】本题考查了列代数式,理解各月之间的百分比的关系是解题的关键.2.有理数a、b在数轴上的位置如图所示,则化简|a﹣b|+|a+b|的结果为()A.﹣2a B.2a C.2b D.﹣2b【考点】整式的加减;数轴;绝对值.【专题】计算题;整式.【分析】根据数轴上点的位置判断出绝对值里边式子的正负,利用绝对值的代数意义化简,合并即可得到结果.【解答】解:根据数轴上点的位置得:a<﹣1<0<b<1,∴a﹣b<0,a+b<0,则原式=b﹣a﹣a﹣b=﹣2a.故选A.【点评】此题考查了整式的加减,熟练掌握运算法则是解本题的关键.3.如图,已知点A是射线BE上一点,过A作CA⊥BE交射线BF于点C,AD⊥BF交射线BF于点D,给出下列结论:①∠1是∠B的余角;②图中互余的角共有3对;③∠1的补角只有∠ACF;④与∠ADB互补的角共有3个.则上述结论正确的个数有( )A.1个B.2个C.3个D.4个【考点】余角和补角.【分析】根据已知推出∠CAB=∠CAE=∠ADC=∠ADB=90°,再根据三角形内角和定理和三角形外角性质,互余、互补的定义逐个分析,即可得出答案.【解答】解:∵CA⊥AB,∴∠CAB=90°,∴∠1+∠B=90°,即∠1是∠B的余角,∴①正确;图中互余的角有∠1和∠B,∠1和∠DAC,∠DAC和∠BAD,共3对,∴②正确;∵CA⊥AB,AD⊥BC,∴∠CAB=∠ADC=90°,∵∠B+∠1=90°,∠1+∠DAC=90°,∴∠B=∠DAC,∵∠CAE=∠CAB=90°,∴∠B+∠CAB=∠DAC+∠CAE,∴∠ACF=∠DAE,∴∠1的补角有∠ACF和∠DAE两个,∴③错误;∵∠CAB=∠CAE=∠ADC=∠ADB=90°,∴与∠ADB互补的角共有3个,∴④正确;故选C.【点评】本题考查了互余、互补,三角形内角和定理,三角形的外角性质的应用,主要考查学生的推理能力和辨析能力,题目比较好,但是比较容易出错.4.如图是由一副三角尺拼成的图案,它们有公共顶点O,且有一部分重叠,已知∠BOD=40°,则∠AOC的度数是( )A.40°B.120°C.140°D.150°【考点】角的计算.【分析】根据同角的余角相等即可求解.【解答】解:∵∠AOB=∠COD=90°,∴∠AOD+∠BOD=∠BOC+∠BOD=90°,∴∠AOD=∠BOC=90°﹣∠BOD=50°,∴∠AOC=∠AOD+∠BOD+∠BOC=140°,故选C.【点评】此题主要考查了角的计算,余角的性质,熟记余角的性质是解题的关键二填空题1.如图,线段AB=8,C是AB的中点,点D在直线CB上,DB=1.5,则线段CD的长等于 2.5或5.5.【考点】两点间的距离.【分析】根据题意求出线段CB的长,分点D在线段CB的延长线上和点D在线段CB上两种情况、结合图形计算即可.【解答】解:∵线段AB=8,C是AB的中点,∴CB=AB=4,如图1,当点D在线段CB的延长线上时,CD=CB+BD=5.5,如图2,当点D在线段CB上时,CD=CB﹣BD=2.5.故答案为:2.5或5.5.【点评】本题考查的是两点间的距离的计算,掌握线段中点的定义、灵活运用数形结合思想和分情况讨论思想是解题的关键.2.如图,在数轴上,点A表示1,现将点A沿x轴做如下移动,第一次点A向左移动2个单位长度到达点A1,第二次将点A1,向右移动4个单位长度到达点A2,第三次将点A2向左移动6个单位长度到达点A3,按照这种移动规律移动下去,第n次移动到点A n,如果点A n与原点的距离等于19,那么n的值是18或19.【考点】数轴.【专题】推理填空题.【分析】根据题意可以分别写出点A移动的规律,当点A奇数次移动后对应数的都是负数,偶数次移动对应的数都是正数,从而可知A n与原点的距离等于19分两种情况,从而可以解答本题.【解答】解:由题意可得,第奇数次移动的点表示的数是:1+(﹣2)×,第偶数次移动的点表示的数是:1+2×,∵点A n与原点的距离等于19,∴当点n为奇数时,则﹣19=1+(﹣2)×,解得,n=19;当点n为偶数,则19=1+2×解得n=18.故答案为:18或19.【点评】本题考查数轴,解题的关键是明确题意,可以分别写出点A奇数次和偶数次移动的关系式.3.如图所示,甲乙两人沿着边长为60cm的正方形,按A→B→C→D→A…的方向行走,甲从A点以60m/min的速度,乙从B点以69m/min的速度行走,两人同时出发,当乙第一次追上甲时,用了20min.【考点】一元一次方程的应用.【专题】几何动点问题.【分析】设乙第一次追上甲用了x分钟,则有乙行走的路程等于甲行走的路程加上90×3,根据其相等关系列方程得69x=60x+60×3,解方程即可得出答案.【解答】解:设乙第一次追上甲用了x分钟,由题意得:69x=60x+60×3,解得:x=20.答:用了20min.故答案为:20【点评】本题考查了一元一次方程的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程,再求解.4.将一些相同的“○”按如图所示的规律依次摆放,观察每个“龟图”中的“○”的个数,若第n 个“龟图”中有245个“○”,则n=16.【考点】规律型:图形的变化类.【分析】由图可知:第1个图形中小圆的个数为5;第2个图形中小圆的个数为7;第3个图形中小圆的个数为11;第4个图形中小圆的个数为17;则知第n个图形中小圆的个数为n(n﹣1)+5.据此可以再求得“龟图”中有245个“○”是n的值.【解答】解:第一个图形有:5个○,第二个图形有:2×1+5=7个○,第三个图形有:3×2+5=11个○,第四个图形有:4×3+5=17个○,由此可得第n个图形有:[n(n﹣1)+5]个○,则可得方程:[n(n﹣1)+5]=245解得:n1=16,n2=﹣15(舍去).故答案为:16.【点评】此题主要考查了图形的规律以及数字规律,通过归纳与总结结合图形得出数字之间的规律是解决问题的关键,注意公式必须符合所有的图形.5.如图,长方形ABCD中,AB=6,第一次平移长方形ABCD沿AB的方向向右平移5个单位,得到长方形A1B1C1D1,第2次平移将长方形A1B1C1D1沿A1B1的方向向右平移5个单位,得到长方形A2B2C2D2…,第n次平移将长方形A n﹣1B n﹣1C n﹣1D n﹣1沿A n﹣1B n﹣1的方向平移5个单位,得到长方形A n B n C n D n(n>2),若AB n的长度为56,则n=10.【考点】平移的性质.【专题】规律型.【分析】根据平移的性质得出AA1=5,A1A2=5,A2B1=A1B1﹣A1A2=6﹣5=1,进而求出AB1和AB2的长,然后根据所求得出数字变化规律,进而得出AB n=(n+1)×5+1求出n即可.【解答】解:∵AB=6,第1次平移将矩形ABCD沿AB的方向向右平移5个单位,得到矩形A1B1C1D1,第2次平移将矩形A1B1C1D1沿A1B1的方向向右平移5个单位,得到矩形A2B2C2D2…,∴AA1=5,A1A2=5,A2B1=A1B1﹣A1A2=6﹣5=1,∴AB1=AA1+A1A2+A2B1=5+5+1=11,∴AB2的长为:5+5+6=16;∵AB1=2×5+1=11,AB2=3×5+1=16,∴AB n=(n+1)×5+1=56,解得:n=10.故答案为:10.【点评】此题主要考查了平移的性质以及一元一次方程的应用,根据平移的性质得出AA1=5,A1A2=5是解题关键.三、解答题1.如图,M是定长线段AB上一定点,点C在线段AM上,点D在线段BM上,点C、点D分别从点M、点B出发以1cm/s、2cm/s的速度沿直线BA向左运动,运动方向如箭头所示.(1)若AB=10cm,当点C、D运动了2s,求AC+MD的值;(2)若点C、D运动时,总有MD=2AC,直接填空:AM=AB;(3)在(2)的条件下,N是直线AB上一点,且AN﹣BN=MN,求的值.【考点】一元一次方程的应用;两点间的距离.【专题】几何动点问题.【分析】(1)计算出CM及BD的长,进而可得出答案;(2)根据C、D的运动速度知BD=2MC,再由已知条件MD=2AC求得MB=2AM,所以AM=AB;(3)分两种情况讨论,①当点N在线段AB上时,②当点N在线段AB的延长线上时,然后根据数量关系即可求解.【解答】解:(1)当点C、D运动了2s时,CM=2cm,BD=4cm,∵AB=10cm,CM=2cm,BD=4cm,∴AC+MD=AB﹣CM﹣BD=10﹣2﹣4=4cm;(2)根据C、D的运动速度知:BD=2MC,∵MD=2AC,∴BD+MD=2(MC+AC),即MB=2AM,∵AM+BM=AB,∴AM+2AM=AB,∴AM=AB.故答案为;(3)当点N在线段AB上时,如图.∵AN﹣BN=MN,又∵AN﹣AM=MN,∴BN=AM=AB,∴MN=AB,即=;当点N在线段AB的延长线上时,如图.∵AN﹣BN=MN,又∵AN﹣BN=AB,∴MN=AB,即=1.综上所述,=或1.【点评】本题考查了一元一次方程的应用,灵活运用线段的和、差、倍、分转化线段之间的数量关系是十分关键的一点.2.已知数轴上有A,B,C三点,分别表示数﹣24,﹣10,10.两只电子蚂蚁甲、乙分别从A,C两点同时相向而行,甲的速度为4个单位/秒,乙的速度为6个单位/秒.(1)问甲、乙在数轴上的哪个点相遇?(2)问多少秒后甲到A,B,C三点的距离之和为40个单位?若此时甲调头返回,问甲、乙还能在数轴上相遇吗?若能,求出相遇点;若不能,请说明理由.【考点】一元一次方程的应用;数轴.【分析】(1)可设x秒后甲与乙相遇,根据甲与乙的路程差为34,可列出方程求解即可;(2)设y秒后甲到A,B,C三点的距离之和为40个单位,分甲应为于AB或BC之间两种情况讨论即可求解.【解答】解:(1)设x秒后甲与乙相遇,则4x+6x=34,解得x=3.4,4×3.4=13.6,﹣24+13.6=﹣10.4.故甲、乙在数轴上的﹣10.4相遇;(2)设y秒后甲到A,B,C三点的距离之和为40个单位,B点距A,C两点的距离为14+20=34<40,A点距B、C两点的距离为14+34=48>40,C 点距A、B的距离为34+20=54>40,故甲应为于AB或BC之间.①AB之间时:4y+(14﹣4y)+(14﹣4y+20)=40解得y=2;②BC之间时:4y+(4y﹣14)+(34﹣4y)=40,解得y=5.①甲从A向右运动2秒时返回,设y秒后与乙相遇.此时甲、乙表示在数轴上为同一点,所表示的数相同.甲表示的数为:﹣24+4×2﹣4y;乙表示的数为:10﹣6×2﹣6y,依据题意得:﹣24+4×2﹣4y=10﹣6×2﹣6y,解得:y=7,相遇点表示的数为:﹣24+4×2﹣4y=﹣44(或:10﹣6×2﹣6y=﹣44),②甲从A向右运动5秒时返回,设y秒后与乙相遇.甲表示的数为:﹣24+4×5﹣4y;乙表示的数为:10﹣6×5﹣6y,依据题意得:﹣24+4×5﹣4y=10﹣6×5﹣6y,解得:y=﹣8(不合题意舍去),即甲从A向右运动2秒时返回,能在数轴上与乙相遇,相遇点表示的数为﹣44.【点评】考查了一元一次方程的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系列出方程,再求解.本题在解答第二问注意分类思想的运用.3.甲、乙两地相距720km,一列快车和一列慢车都从甲地驶往乙地,慢车先行驶1小时后,快车才开始行驶.已知快车的速度是120km/h,慢车的速度是80km/h,快车到达乙地后,停留了20min,由于有新的任务,于是立即按原速返回甲地.在快车从甲地出发到回到甲地的整个程中,与慢车相遇了两次,这两次相遇时间间隔是多少?【考点】一元一次方程的应用.【分析】在快车从甲地出发到回到甲地的整个程中,与慢车相遇了两次,第一次是从甲地驶往乙地时,快车追上慢车,根据追上时快车行驶的路程=慢车行驶的路程列方程求解;第二次是快车到达乙地后返回甲地时与慢车相遇,根据相遇时快车行驶的路程+慢车行驶的路程=甲、乙两地之间的路程×2列方程求解.【解答】解:设从甲地驶往乙地时,快车行驶x小时追上慢车,由题意得120x=80(x+1),解得x=2,则慢车行驶了3小时.设在整个程中,慢车行驶了y小时,则快车行驶了(y﹣1﹣)小时,由题意得120(y﹣1﹣)+80y=720×2,解得y=8,8﹣3=5(小时).答:在快车从甲地出发到回到甲地的整个程中,与慢车相遇了两次,这两次相遇时间间隔是5小时.【点评】本题考查了一元一次方程的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系列出方程,再求解.4.(1)如图1,若CO⊥AB,垂足为O,OE、OF分别平分∠AOC与∠BOC.求∠EOF的度数;(2)如图2,若∠AOC=∠BOD=80°,OE、OF分别平分∠AOD与∠BOC.求∠EOF的度数;(3)若∠AOC=∠BOD=α,将∠BOD绕点O旋转,使得射线OC与射线OD的夹角为β,OE、OF分别平分∠AOD与∠BOC.若α+β≤180°,α>β,则∠EOC=.(用含α与β的代数式表示)【考点】角的计算;角平分线的定义.【分析】(1)根据垂直的定义得到∠AOC=∠BOC=90°,根据角平分线的定义即可得到结论;(2)根据角平分线的定义得到∠EOD=∠AOD=×(80+β)=40+β,∠COF=∠BOC=×(80+β)=40+β,根据角的和差即可得到结论;(3)如图2由已知条件得到∠AOD=α+β,根据角平分线的定义得到∠DOE=(α+β),即可得到结论.【解答】解:(1)∵CO⊥AB,∴∠AOC=∠BOC=90°,∵OE平分∠AOC,∴∠EOC=∠AOC=×90°=45°,∵OF平分∠BOC,∴∠COF=∠BOC=×90°=45°,∠EOF=∠EOC+∠COF=45°+45°=90°;(2)∵OE平分∠AOD,∴∠EOD=∠AOD=×(80+β)=40+β,∵OF平分∠BOC,∴∠COF=∠BOC=×(80+β)=40+β,∠COE=∠EOD﹣∠COD=40+β﹣β=40﹣β;∠EOF=∠COE+∠COF=40﹣β+40+β=80°;(3)如图2,∵∠AOC=∠BOD=α,∠COD=β,∴∠AOD=α+β,∵OE平分∠AOD,∴∠DOE=(α+β),∴∠COE=∠DOE﹣∠COD==,如图3,∵∠AOC=∠BOD=α,∠COD=β,∴∠AOD=α+β,∵OE平分∠AOD,∴∠DOE=(α﹣β),∴∠COE=∠DOE+∠COD=.综上所述:,故答案为:.【点评】本题考查了角平分线的定义,角的计算,解题的关键是找出题中的等量关系列方程求解.5.如图,已知∠AOB=90°,以O为顶点、OB为一边画∠BOC,然后再分别画出∠AOC 与∠BOC的平分线OM、ON.(1)在图1中,射线OC在∠AOB的内部.①若锐角∠BOC=30°,则∠MON=45°;②若锐角∠BOC=n°,则∠MON=45°.(2)在图2中,射线OC在∠AOB的外部,且∠BOC为任意锐角,求∠MON的度数.(3)在(2)中,“∠BOC为任意锐角”改为“∠BOC为任意钝角”,其余条件不变,(图3),求∠MON的度数.【考点】角的计算;角平分线的定义.【分析】(1)①由角平分线的定义,计算出∠MOA和∠NOA的度数,然后将两个角相加即可;②由角平分线的定义,计算出∠MOA和∠NOA的度数,然后将两个角相加即可;(2)由角平分线的定义,计算出∠MOA和∠NOA的度数,然后将两个角相减即可;(3)由角平分线的定义,计算出∠MOA和∠NOA的度数,然后将两个角相加即可.【解答】解:(1)①∵∠AOB=90°,∠BOC=30°,∴∠AOC=60°,∵OM,ON分别平分∠AOC,∠BOC,∴∠COM=AOC,BOC,∴∠MON=∠COM+∠CON=∠AOB=45°,故答案为:45°,②∵∠AOB=90°,∠BOC=n°,∴∠AOC=(90﹣n)°,∵OM,ON分别平分∠AOC,∠BOC,∴∠COM=AOC=(90﹣n)°,BOC=n°,∴∠MON=∠COM+∠CON=∠AOB=45°,故答案为:45°;(2)∵∠AOB=90°,设∠BOC=α,∴∠AOC=90°+α,∵OM,ON分别平分∠AOC,∠BOC,∴∠COM=AOC,BOC,∴∠MON=∠COM﹣∠CON=∠AOB=45°,(3)∵OM,ON分别平分∠AOC,∠BOC,∴∠COM=AOC,BOC,∴∠MON=∠COM+∠CON=(∠AOC+∠BOC)=(360°﹣90°)=135°.【点评】本题考查了角平分线定义,角的有关计算的应用,解此题的关键是求出∠COM和∠CON的大小.6.如图,∠AOB=120°,射线OC从OA开始,绕点O逆时针旋转,旋转的速度为每分钟20°;射线OD从OB开始,绕点O逆时针旋转,旋转的速度为每分钟5°,OC和OD同时旋转,设旋转的时间为t(0≤t≤15).(1)当t为何值时,射线OC与OD重合;(2)当t为何值时,射线OC⊥OD;(3)试探索:在射线OC与OD旋转的过程中,是否存在某个时刻,使得射线OC,OB与OD中的某一条射线是另两条射线所夹角的角平分线?若存在,请求出所有满足题意的t的取值,若不存在,请说明理由.【考点】角的计算;角平分线的定义.【专题】探究型.【分析】(1)根据题意可得,射线OC与OD重合时,20t=5t+120,可得t的值;(2)根据题意可得,射线OC⊥OD时,20t+90=120+5t或20t﹣90=120+5t,可得t的值;(3)分三种情况,一种是以OB为角平分线,一种是以OC为角平分线,一种是以OD为角平分线,然后分别进行讨论即可解答本题.【解答】解:(1)由题意可得,20t=5t+120解得t=8,即t=8min时,射线OC与OD重合;(2)由题意得,20t+90=120+5t或20t﹣90=120+5t,解得,t=2或t=14即当t=2min或t=14min时,射线OC⊥OD;(3)存在,由题意得,120﹣20t=5t或20t﹣120=5t+120﹣20t或20t﹣120﹣5t=5t,解得t=4.8或t=或t=12,即当以OB为角平分线时,t的值为4.8min;当以OC为角平分线时,t的值为min,当以OD为角平分线时,t的值为12min.【点评】本题考查角的计算、角平分线的性质,解题的关键是明确题意,找出所求问题需要的条件.7.如图,∠AOB的边OA上有一动点P,从距离O点18cm的点M处出发,沿线段MO,射线OB运动,速度为2cm/s;动点Q从点O出发,沿射线OB运动,速度为1cm/s.P、Q 同时出发,设运动时间是t(s).(1)当点P在MO上运动时,PO=cm (用含t的代数式表示);(2)当点P在MO上运动时,t为何值,能使OP=OQ?(3)若点Q运动到距离O点16cm的点N处停止,在点Q停止运动前,点P能否追上点Q?如果能,求出t的值;如果不能,请说出理由.8.如图,两个形状.大小完全相同的含有30゜、60゜的三角板如图放置,PA、PB与直线MN重合,且三角板PAC,三角板PBD均可以绕点P逆时针旋转.(1)试说明:∠DPC=90゜;(2)如图,若三角板PAC的边PA从PN处开始绕点P逆时针旋转一定角度,PF平分∠APD,PE平分∠CPD,求∠EPF;(3)如图,若三角板PAC的边PA从PN处开始绕点P逆时针旋转,转速为3゜/秒,同时三角板PBD的边PB从PM处开始绕点P逆时针旋转,转速为2゜/秒,在两个三角板旋转过程中(PC转到与PM重合时,两三角板都停止转动).设两个三角板旋转时间为t秒,则∠BPN=180﹣2t,∠CPD=90﹣t (用含有t的代数式表示,并化简);以下两个结论:①为定值;②∠BPN+∠CPD为定值,正确的是①(填写你认为正确结论的对应序号).【考点】角的计算;角平分线的定义.【分析】(1)利用含有30゜、60゜的三角板得出∠DPC=180°﹣∠CPA﹣∠DPB,进而求出即可;(2)设∠CPE=∠DPE=x,∠CPF=y,则∠APF=∠DPF=2x+y,进而利用∠CPA=60゜求出即可;(3)首先得出①正确,设运动时间为t秒,则∠BPM=2t,表示出∠CPD和∠BPN的度数即可得出答案.【解答】解:(1)∵∠DPC=180°﹣∠CPA﹣∠DPB,∠CPA=60°,∠DPB=30°,∴∠DPC=180゜﹣30゜﹣60゜=90゜;(2)设∠CPE=∠DPE=x,∠CPF=y,则∠APF=∠DPF=2x+y,∵∠CPA=60゜,∴y+2x+y=60゜,∴x+y=30゜∴∠EPF=x+y=30゜(3)①正确.设运动时间为t秒,则∠BPM=2t,∴∠BPN=180﹣2t,∠DPM=30﹣2t,∠APN=3t.∴∠CPD=180﹣∠DPM﹣∠CPA﹣∠APN=90﹣t,∴==.②∠BPN+∠CPD=180﹣2t+90﹣t=270﹣3t,可以看出∠BPN+∠CPD随着时间在变化,不为定值,结论错误.故答案为:180﹣2t;90﹣t;①.【点评】此题主要考查了角的计算,利用数形结合得出等式是解题关键,还要理清角之间的关系.。
2023-2024学年北师大版七年级数学上册压轴题攻略 专题01 数轴的三种常见考法(解析版)

专题01数轴的三种常见考法【知识点精讲】1.数轴的概念1)数轴:用一条直线上的点表示数,这条直线叫作数轴2)三要素:①原点—参考点,正负数分界点;②方向—一般选取向右为正方向;③单位长度—同一条数轴上的单位长度应当一致2.数轴的读数与画法1)数轴的读数:在原点的左边,则为正数,在数轴的右边,则为负数。
2)画数轴步骤:a .直线b .确定原点c .选正方向(通常从原点向右或向上定位正方向)d .选取单位长度(选取适当长度为单位长度,直线上从原点向右,每隔一个单位长度取一个点,依次表示1,2,3,…;从原点向左,用类似方法依次表示-1,-2,-3,…)e .标数(用实心点标数).3.数轴上的点与有理数之间的关系(数形结合)1)数轴上的点并不是都是有理数2)正方向可以不按照常规方向选取3)a >0,与原点的距离是a ,在数轴上可以是±a (存在多解的情况)注:要确定在数轴上的具体位置,必须要距离+方向4.数轴与数的大小1)正方向上,离原点越远,数越大2)负方向上,离原点越近,数越大(负数数字越大,结果反而越小)注:数轴从负方向向正方向,数值逐渐增大。
类型一、利用数轴比较大小例.已知有理数a ,b 在数轴上的位置如图所示,则下列结论中正确的是()A .0a b +>B .0a b ->C .10a ->D .10+>b 【答案】B 【详解】解:根据图示知:101b a <-<<<,10b ∴+<,0a b +<,0a b ->,10a -<.故选:B .【点睛】本题考查了数轴的知识以及不等式的基本性质,解题的关键是利用数形结合的思想得出a ,b 与1,1-的大小关系.个结论:)个A .4B .3【答案】B A .0ab >B .0a b ->A .a b b a a b -<<<+【详解】(1)OA=__________cm,OB=__________cm(2)A点表示的数是4、B点表示的数是6、C点表示的数是(3)∵C点坐标是4-,【变式训练2】如图,在数轴上点A 表示的有理数为4-,点B 表示的有理数为6,点P 从点A 出发以每秒2个单位长度的速度在数轴上沿由A 到B 方向运动,当点P 到达点B 后立即返回,仍然以每秒2个单位长度的速度运动至点A 停止运动.设运动时间为t (单位:秒).(1)2t =时点P 表示的有理数为___________;(2)求点P 是AB 的中点时t 的值;(3)请直接写出点P 到点A 的距离(用含t 的代数式表示);(4)请直接写出点P 表示的有理数(用含t 的代数式表示).【答案】(1)0(2)2.5或7.5(3)2t 或(202)t -(4)162t-【分析】(1)当2t =时,点P 的路程与4-的和即为点表示的有理数;(2)求出AB 的长,分两种情况:由A 到B 方向运动时点P 是AB 的中点;由B 到A 方向运动时点P 是AB 的中点;(3)分两种情况:点P 由点A 到点B 的运动过程中,点P 到点A 的距离即点P 的运动路程;点P 由点B 到点A 的运动过程中,点P 到点A 的距离为2AB 与点P 运动路程的差;(4)分两种情况:点P 由点A 到点B 的运动过程中;点P 由点B 到点A 的运动过程中;由(3)的结果及两点间的距离即可求得点P 表示的有理数.【详解】(1)解:点P 表示的有理数为4220-+⨯=;故答案为:0;(2)解:6(4)10AB =--=,1025AP BP ∴==÷=,当由A 到B 方向运动时,52 2.5t =÷=,当由B 到A 方向运动时,(105)27.5t =+÷=.综上,点P 是AB 的中点时 2.5t =或7.5;(3)解:当点P 由点A 到点B 的运动过程中,点P 与点A 的距离AP 的长度为2t ;当点P 由点B 到点A 的运动过程中,点P 与点A 的距离为(202)t -;(4)解:在点P 由点A 到点B 的运动过程中,点P 表示的有理数是42t -+;在点P 由点B 到点A 的返回过程中,点P 表示的有理数是4(202)162t t -+-=-.【点睛】本题考查了数轴上动点问题,两点间距离,数轴上的点表示有理数等知识,注意数形结合.个单位长度,第依此规律跳下去,1.如图,有理数a ,b ,c ,d 在数轴上的对应点分别是A ,B ,C ,D ,若6b d +=,则a c +()A .b d+B .小于6C .等于6D .大于6【答案】D 【分析】由6b d +=,A 在D 的右边,C 在B 的右边,利用加数与和的关系可知a c +与6的大小关系.【详解】解:∵A 在D 的右边,C 在B 的右边,∴a d >,c b >,A .1-B .1A .向东行驶5个单位长度B .向西行驶单位长度D .向西行驶1个单位长度【答案】C A .a b >-B .0ab <,即可分析得出答案.A.1个B.2个【答案】<>【答案】2π1-【分析】由圆的周长为2π,再结合数轴上两点之间的距离可得答案.【答案】4或5或6【分析】由线段总长度及三条线段的长度之比,可得三条线段的长度,再分情况讨论即可.【详解】解:∵线段长为8,这三条线段的长度之比为1:1:。
北师大七年级上册期末数学压轴题总复习(一)(word解析版)

期末压轴题总复习(一)学校:___________姓名:___________班级:___________考号:___________一、解答题1.用长方形硬纸板做长方体盒子,底面为正方形.(1)每个长方形盒子有________个侧面,有________个底面;(2)长方形硬纸板以如图两种方法裁剪.A方法:剪3个侧面;B方法:剪2个侧面和2个底面.现有35张硬纸板,裁剪时x张用A方法,其余用B方法.①用含x的代数式分别表示裁剪出的侧面和底面的个数;②若裁剪出的侧面和底面恰好全部用完,问能做多少个盒子?2.如图,数轴上点A表示的数为﹣2,点B表示的数为8,点P从点A出发,以每秒3个单位长度的速度沿数轴向右匀速运动,同时点Q从点B出发,以每秒2个单位长度的速度向左匀速运动.设运动时间为t秒(t>0).(1)填空:①A、B两点间的距离AB=,线段AB的中点表示的数为;②用含t的代数式表示:t秒后,点P表示的数为;点Q表示的数为.(2)求当t为何值时,PQ=12AB;(3)当点P运动到点B的右侧时,PA的中点为M,N为PB的三等分点且靠近于P点,求PM﹣34BN的值.3.已知数轴上两点A、B对应的数分别是6,﹣8,M、N、P为数轴上三个动点,点M从A点出发速度为每秒1个单位长度,点N从点B出发速度为点M的3倍,点P从原点出发速度为每秒0.5个单位长度.(1)求A、B两点的距离为个单位长度.(2)若点M向右运动,同时点N向左运动,求经过多长时间点M与点N相距30个单位长度?(3)若点M、N同时向右运动,求经过多长时间点M、N相遇?并求出此时点N对应的数.(4)若点M、N、P同时都向右运动,当点M与点N相遇后,点M、P继续以原来的速度向右运动,点N改变运动方向,以原来的速度向左运动,求从开始运动后,经过多长时间点P到点M、N的距离相等?4.某超市第一次用3600元购进了甲、乙两种商品,其中甲种商品80件,乙种商品120件.已知乙种商品每件进价比甲种商品每件进价贵5元.甲种商品售价为20元/件,乙种商品售价为30元/件.(注:获利=售价﹣进价)(1)该超市第一次购进甲、乙两种商品每件各多少元?(2)该超市将第一次购进的甲、乙两种商品全部销售完后一共可获得多少利润?(3)该超市第二次又购进同样数量的甲、乙两种商品.其中甲种商品每件的进价不变,乙种商品进价每件少3元;甲种商品按原售价提价a%销售,乙种商品按原售价降价a%销售,如果第二次两种商品都销售完以后获得的总利润比第一次获得的总利润多260元,那么a的值是多少?5.某省公布的居民用电阶梯电价听证方案如下:第一档电量第二档电量第三档电量月用电量210度以下,每度价格0.52元月用电量210度至350度,每度比第一档提价0.05元月用电量350度以上,每度比第一档提价0.30元例:若某户月用电量400度,则需交电费为210×0.52+(350﹣210)×(0.52+0.05)+(400﹣350)×(0.52+0.30)=230(元)(1)以此方案请你回答:若小华家某月用电量是300度,则这个月的电费为元?(2)如果按此方案计算,小华家5月份的电费为138.84元,请你求出小华家5月份的用电量.6.某商场经销的甲、乙两种商品,甲种商品每件售价60元,利润率为50%;乙种商品每件进价50元,售价80元.(1)甲种商品每件进价为元,每件乙种商品利润率为.(2)若该商场同时购进甲、乙两种商品共60件,恰好总进价为2800元,求购进甲种商品多少件?(3)在国庆期间,该商场只对甲乙两种商品进行如下的优惠促销活动:打折前一次性购物总金额优惠措施少于等于450元不优惠超过450元,但不超过600元按售价的九折其中600元部分八点二折优惠,超过600元超过600元的部分打三折优惠.按上述优惠条件,若小华一次性购买乙种商品实际付款504元,求小华在该商场购买乙种商品多少件?7.点A、B、C在数轴上表示的数a、b、c满足2(3)|12|0++-=,且a是绝对值最小b c的有理数.(1)a的值为,b的值为,c的值为;(2)已知点P、点Q是数轴上的两个动点,点P从点B出发,以3个单位/秒的速度向右运动,点Q从点C出发,速度为2个单位/秒.①若在点P出发的同时点Q向左运动,几秒后点P和点Q在数轴上相遇?②若点P运动到点A处,动点Q再出发也向右运动,则P运动几秒后这两点之间的距离为2个单位?8.现象感知如图1,在数轴上,线段AB的中点为E,点E表示的数与点A、点B表示的数关系存在:482+=6;线段CD的中点为F,点F表示的数与点C、点D表示的数的关系也存在:512-+=﹣2归纳性质如图2,在数轴上,线段GH的中点为P.(1)如图2,在数轴上,点G、H、P表示的数分别为a,b,c,请猜想a,b,c的等量关系,请写出一等量关系式.小宇同学为了说明a,b,c的等量关系是正确的,采用了字母表示数的方法,设PG=PH=m,从而表示出G、H两点的数(含c和m).请完成小宇的说理过程.拓展应用(2)如图,点A,B,C在数轴上对应的数分别为﹣3,1,9,它们分别以每秒2个单位长度、1个单位长度和4个单位长度的速度在数轴上同时向左做匀速运动,设同时运动的时间为t秒.若A,B,C三点中,有一点恰为另外两点所连线段的中点,求t的值.9.为鼓励居民节约用电,某省试行阶段电价收费制,具体执行方案如表:档次每户每月用电量(度)执行电价(元/度)第一档小于等于2000.55第二档大于200小于4000.6第三档大于等于4000.85某户居民五、六月份共用电500度,缴电费290.5元.已知该用户六月份用电量大于五月份,且五、六月份的用电量均小于400度.问该户居民五、六月份各用电多少度?10.如图,一块长为5厘米,宽为2厘米的长方形纸板,一块长为4厘米,宽为1厘米的长方形纸板与一块边长为a厘米的正方形纸板以及另外两块长方形纸板,(1)用含a的式子表示图形左上角长方形的长AG= 厘米,宽AE= 厘米.(2)用含a的式子表示大图形边AD= 厘米,边AB= 厘米,若恰好拼成一个大正方形,问大正方形的面积是多少?参考答案1.(1)4,2;(2)①侧面(x +70)个,底面(70-2x )个②21个. 【分析】(1)根据长方体的性质求得答案; (2)①根据题意列出代数式即可;②根据题意列出一元一次方程,解方程求解即可. 【详解】(1)每个长方形盒子有4个侧面,有2个底面; 故答案为:4,2;(2)①A 方法剪3x 个侧面,B 方法剪()235x -个侧面和()235x -个底面32(35)70x x x +-=+,()235702x x -=-∴共有侧面()70x +个,底面()702x -个②根据已知条件可得7070242x x+-= 解得14x =1470=214+∴答:裁剪出的侧面和底面恰好全部用完,能做21个盒子. 【点睛】本题考查了一元一次方程的应用,正确的找出题中的等量关系是解题的关键. 2.(1(①10(3(②(2+3t(8(2t((2(t=1或3((3(5 【分析】(1((根据点A 表示的数为﹣2,点B 表示的数为8,即可得到A 、B 两点间的距离以及线段AB 的中点表示的数;(依据点P ,Q 的运动速度以及方向,即可得到结论; (2)由t 秒后,点P 表示的数﹣2+3t ,点Q 表示的数为8﹣2t ,于是得到PQ=|((2+3t(((8(2t(|=|5t(10|,列方程即可得到结论;(3)依据PA 的中点为M ,N 为PB 的三等分点且靠近于P 点,运用线段的和差关系进行计算,即可得到PM ﹣34BN 的值.【详解】解:(1(①8(((2(=10((2+12×10=3(②由题可得,点P表示的数为﹣2+3t,点Q表示的数为8(2t((2(∵t秒后,点P表示的数﹣2+3t,点Q表示的数为8(2t(∴PQ=|((2+3t(((8(2t(|=|5t(10|(又PQ=12AB=12×10=5(∴|5t(10|=5(解得:t=1或3(∴当t=1或3时,PQ=12AB((3(∵PA的中点为M(N为PB的三等分点且靠近于P点,∴MP=12AP=12×3t=32t(BN=23BP=23(AP(AB(=23×(3t(10(=2t(203(∴PM(34BN=32t(34(2t(203(=5(【点睛】本题考查了实数和数轴以及一元一次方程的应用应用,解题的关键是掌握点的移动与点所表示的数之间的关系,根据题目给出的条件,找出合适的等量关系列出方程求解.3.(1)14;(2)4;(3)7秒,此时N点对应的数是13;(4)23秒或7秒或403秒【分析】(1)由题意根据两点间的距离公式即可求出A、B两点的距离;(2)根据题意设经过x秒点M与点N相距30个单位,由点M从A点出发速度为每秒1个单位,点N从点B出发速度为M点的3倍,得出x+3x+14=30求解即可;(3)由题意根据追及问题即时间等于路程除以速度差求出点M、N相遇时间,进而代入时间得出点N对应的数;(4)根据题意设从开始运动后,相遇前经过t秒点P到点M、N的距离相等,或相遇后经过t秒点P到点M、N的距离相等,根据PM=PN列出方程,进而求解即可.【详解】解:(1)∵数轴上两点A、B对应的数分别是6,-8,∴A、B两点的距离为6-(-8)=14.故答案为:14;(2)设经过x秒点M与点N相距30个单位.依题意可列方程为:x+3x+14=30,解方程,得x=4.答:经过4秒点M与点N相距30个单位;;(3)点M与点N相遇的时间为14÷(3﹣1)=7秒,此时N点对应的数是﹣8 + 7×3=13;(4)点M与点N相遇的时间为14÷(3﹣1)=7秒,设从开始运动后,相遇前经过t秒点P到点M、N的距离相等.依题意可列方程为:0.5t-(-8+3t)=6+t-0.5t,解得t=23,设从开始运动后,相遇后经过t秒点P到点M、N的距离相等.依题意可列方程为:(t+6)-0.5t=0.5t-[13-3(t-7)],解得t=403.所以23秒或7秒或403秒,点P到点M、N的距离相等.【点睛】本题主要考查数轴上的动点问题和一元一次方程的应用,利用行程问题的基本数量关系,以及数轴直观解决问题即可.4.(1)该超市第一次购进甲种商品每件15元,乙种商品每件20元;(2)该超市将第一次购进的甲、乙两种商品全部销售完后一共可获得1600元的利润;(3)a的值是5.【分析】(1)设该超市第一次购进甲种商品每件x元,乙种商品每件(x+5)元,根据题意列出方程求解即可.(2)根据利润公式求出总利润即可.(3)根据题意列出方程求解即可.【详解】(1)设该超市第一次购进甲种商品每件x元,乙种商品每件(x+5)元.由题意得80x+120(x+5)=3600,解得:x=15,x+5=15+5=20.答:该超市第一次购进甲种商品每件15元,乙种商品每件20元.(2)该超市将第一次购进的甲、乙两种商品全部销售完后一共可获得的利润=80×(20﹣15)+120×(30﹣20)=1600元.答:该超市将第一次购进的甲、乙两种商品全部销售完后一共可获得1600元的利润.(3)由题意得80×[20(1+a%)﹣15]+120×[30(1﹣a%)﹣(20﹣3)]=1600+260,解得:a=5.答:a的值是5.【点睛】本题考查了一元一次方程的销售问题,掌握解一元一次方程的方法是解题的关键.5.(1)160.5;(2)小华家5月份的用电量为262度.【分析】(1)根据300度在第二档列式计算即可得解;(2)根据第二档的电费求法列方程计算即可得解.【详解】解:(1)小华家8月用电量为300度,需交电费210×0.52+(300-210)×(0.52+0.05)=160.5(元).故需交电费160.5元;故答案为:160.5;(2)月用电量为210度时,需交电费210×0.52=109.2(元)月用电量为350度时,需交电费210×0.52+(350-210)×(0.52+0.05)=189(元),所以小华家5月份的用电量在第二档.设小华家5月份的用电量为x度,则210×0.52+(x-210)×(0.52+0.05)=138.84,解得x=262.答:小华家5月份的用电量为262度.【点睛】本题考查了一元一次方程的应用,读懂题目信息,理解阶梯电价的收费方法和电费的计算方法是解题的关键.6.(1)40,60%;(2)20件;(3)7件或8件【分析】(1)设甲的进价为x元/件,根据甲的利润率为50%,求出x的值;(2)设购进甲种商品x件,则购进乙种商品(500−x)件,再由总进价是2800元,列出方程求解即可;(3)分两种情况讨论,①打折前购物金额超过450元,但不超过600元,②打折前购物金额超过600元,分别列方程求解即可.【详解】解:(1)设甲的进价为x元/件,则(60−x)=50%x,解得:x=40.故甲的进价为40元/件;乙商品的利润率为(80−50)÷50=60%.故答案是:40;60%;(2)设购进甲种商品x件,则购进乙种商品(500−x)件,由题意得,40x+50(60-x)=2800,解得:x=20.即购进甲商品20件.(3)设小华打折前应付款为y元,(若打折前购物金额超过450元,但不超过600元,由题意得0.9y=504,解得:y=560,560÷80=7(件),(若打折前购物金额超过600元,600×0.82+(y-600)×0.3=504,解得:y=640,640÷80=8(件),综上可得小华在该商场购买乙种商品件7件或8件.【点睛】本题考查了一元一次方程的应用,解答本题的关键是仔细审题,找到等量关系,利用方程思想求解.7.(1)0,-3,12;(2)①3秒;②11或15秒【分析】(1)根据非负数的性质即可求出bc 的值,根据a 是绝对值最小的有理数即可求出a 的值; (2)①设t s 后P 和Q 相遇,根据两人相遇一共走的路程即为BC 的长,即可得到答案; ②分P 在追上Q 前和P 在超过Q 后两种情况进行求解即可.【详解】解:(1)∵a 是绝对值最小的有理数,(a =0,∵()23120b c ++-=,()230b +≥,120c -≥,∴30b +=,120c -=,∴3b =-,12c =;故答案为:0,-3,12;(2)(设t s 后P 和Q 相遇,由题意得(3+2)t =12-(-3),解得t =3,∴3秒后点P 和点Q 在数轴上相遇(设P 点运动ts ,后这两点之间的距离为2个单位,∵B 表示的数是-3,A 表示的数是0,(AB =3,∴P 运动到A 的时间为1s ,即Q 在P 出发1s 后再出发,若P 在追上Q 前:3t +2=2(t -1)+12-(-3),解得t =11,若P 在超过Q 后:3t -2=2(t -1)+12-(-3),解得t =15,∴P 运动11秒或15后这两点之间的距离为2个单位.【点睛】本题主要考查了非负数的性质,绝对值的意义,数轴上的动点问题,解题的关键在于能够根据题意求出a 、b 、c 的值.8.(1)2a b c +=,见解析;(2)1秒或4秒或16秒 【分析】(1)用c m 、表示出点G H 、,然后求解即可;(2)分三种情况讨论求解即可,当点B 是线段AC 的中点、点C 是线段AB 的中点、点A 是线段BC 的中点时,分别求解即可.【详解】(1)2a b c +=;理由:H 点:b =c +m ,G 点:a =c -m , 2222a b c m c m c c +-++===,即2a b c +=. (2)运动t 秒后A 、B 、C 三点表示的数分别为A :-3-2t ,B :1-t ,C :9-4t ①当点B 是线段AC 的中点时:32941,12t t t t --+-=-= ②当点C 是线段AB 的中点时:32194,42t t t t --+-=-= ③当点A 是线段BC 的中点时:94132,162t t t t -+-=--= 综上所述,t 的值为1秒或4秒或16秒.【点睛】此题考查了数轴的有关应用,涉及了用数轴表示数,数轴上的动点问题,中点公式,解题的关键是掌握数轴的有关性质,正确求解.9.五月份用电190度,六月份用电310度.【分析】根据两个月份用电量共是500度,可知每个月用电量不可能都在第一档,根据题意用电量又都小于400度,且六月份用电量大于五月份用电量.分两种情况来讨论.(1)五月份用电量小于200度(2)五月份用电量大于200度,分别列出方程求解即可.【详解】设五月份用电量为x ,则六月份用电量为500-x ,且500-x >x .(1)当五月份用电量x <200时,六月份用电量500-x 一定大于200.根据题意可列方程:0.55x +0.6(500-x )=290.5解得x =190,所以五月份用电量为190度.所以六月份用电量为500-190=310度.(2)当五月份用电量x >200,且六月份用电量为500-x >200.根据题意可列方程:0.6x +0.6(500-x )=290.5方程无解,不符合题意.【点睛】本题考察了利用分类讨论的方法,列出一元一次方程来解决实际问题,总价=单价×数量是解决本题的关键.10.(1)(1+a),(5-a);(2)(9-a),(3+a),36平方厘米【分析】(1)根据图形可得AE=GH=NG-NH=BQ-NH=5-a,AG=EH=EF+FH=1+a;(2)根据图形可得AD=AE+ED=5-a+4=9-a,AB=AG+2=3+a,由AD=AB求出a的值,从而可得大正方形的面积.【详解】解:如图所示,∵四边形NMFH是正方形,∴NH=FH=a,又EF=1,∴AG=EH=EF+FH=1+a,AE=GH=NG-NH=BQ-NH=5-a,故答案为:(1+a),(5-a);(2)根据图形可得AD=AE+ED=5-a+4=9-a,AB=AG+2=3+a,∵AD=AB,∴9-a=3+a,解得,a=3,∴大正方形的边长为6厘米,∴大正方形的面积是6×6=36(平方厘米),答:大正方形的面积是36平方厘米.故答案为:(9-a),(3+a).【点睛】本题考查了一元一次方程的应用,找准等量关系,正确列出一元一次方程是解题的关键.。
2023—2024学年北师大版数学七年级上册期末复习题含参考答案

北师大版七年级上册数学期末复习题一、单选题
A.2b是小于1的正数
b a-<
C.0
A.文
7.已知:线段AB
若其中有一条线段的长度是另一条线段长度的两倍,则称点
A .51︒9.某项工程由甲单独做需们完成这项工程的时间是(
A .20A .37
B .38
C .39
D .40
二、填空题11.用“四舍五入法”将4.028精确到0.01,所得到的近似数为.
12.如果5x =时,代数式57ax bx +-的值为9,那么5x =-时,代数式
5a b x x +三、解答题
16.计算:
请你根据以上提供的信息,解答下列问题:
(1)补全上面的条形统计图和扇形统计图;
(2)若该校七年级共有960名学生,请你估算该年级学生中对数学学习
少人?
20.一个几何体由几个大小相同的小立方块搭成,从上面观察这个几何体,看到的形状如图1所示,其中小正方形中的数字表示在该位置的小立方块的个数.
21.足球是世界第一运动,2022年世界杯足球赛再一次点燃了人们对足球运动的热情世界杯期间光明区某文具店用14400元购进了甲、乙两款足球,一共
(1)当2t =时,点M 表示的数是(1)如图1,求AOE ∠的度数;
(2)如图2,射线OC 在EOB ∠内部,OF 平分AOC ∠,若求y 的值(用含n 的整式表示);
(3)如图3,在(2)的条件下,在BOC ∠的内部作射线OG 44COG FOE ∠+∠=︒,求COE ∠的度数.。
新北师大版七上数学压轴题训练专题09 :一元一次方程(学生版+解析版)

)
- A. 2006 2007
- B. 2007 2006
- c. 2007 1 003
- D. 1003 2007
5.若关于 x的方程(k-2013) x=2015-2014x的解,是整数,则整数k的值有( 〉
A. 4个
B. 8个
c. 12个
D. 16个
6. (2020秋·北仑区期末〉若不论 k 取什么实数, 关于x的方程坐土3 豆-ζ6�=1(。、 b 是常数〉的解总是
去分母得:2 (2x- I) - (3x+1) =6, 去括号得:4λ - 2 -3λ’ - )=6,
移项得 4x- 3x =6+2叫, 合并同类项得:x= 9:
(4) �r-21 =5, 去绝对值得:x-2=5或x-2=-5,
解得:x = 7或x= - 3.
).已知等式 3a=2b刊,则下列关于等式的变形不正确的是(
j刊[m]表示不大子m的最大整数,例如巳)=3’[2)=2, [ - 3.2)= - 4,如果整数x满足关系式z 3{巾2[λ]= 23,则 x=
10. (2020秋·辽阳瞅)小明解瓶子=子-3去分母时 , 方程右边的-3忘记乘6,因而求出的解为
x= 2 , 则原方程正确的解为一一一一-·
士 一一一 11.方程x +�+ 舌古+
布) 1=1,然后提取公囚式 , 酬, 合并同类项, 系数化为l 即可求解.
E解答过程1
解:
王+..:..+三…+一三一= 1,
3 15 35
2005×2007
x (-1 +-1 +-1 +…+ -)= I,
3 15 35
2005×2007
x[�
(
I-�) + -1
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
北师大版七年级上册期末压轴题压轴题选讲一选择题1.某企业今年1月份产值为x万元,2月份比1月份减少了10%,3月份比2月份增加了15%,则3月份的产值用代数式表示为( )A.(1﹣10%+15%)x万元 B.(1+10%﹣15%)x万元C.(x﹣10%)(x+15%)万元D.(1﹣10%)(1+15%)x万元2.有理数a、b在数轴上的位置如图所示,则化简|a﹣b|+|a+b|的结果为()A.﹣2a B.2a C.2b D.﹣2b3.如图,已知点A是射线BE上一点,过A作CA⊥BE交射线BF于点C,AD⊥BF交射线BF于点D,给出下列结论:①∠1是∠B的余角;②图中互余的角共有3对;③∠1的补角只有∠ACF;④与∠ADB互补的角共有3个.则上述结论正确的个数有( )A.1个B.2个C.3个D.4个4.如图是由一副三角尺拼成的图案,它们有公共顶点O,且有一部分重叠,已知∠BOD=40°,则∠AOC的度数是( )A.40°B.120°C.140°D.150°二填空题1.如图,线段AB=8,C是AB的中点,点D在直线CB上,DB=1.5,则线段CD的长等于.2.如图,在数轴上,点A表示1,现将点A沿x轴做如下移动,第一次点A向左移动2个单位长度到达点A1,第二次将点A1,向右移动4个单位长度到达点A2,第三次将点A2向左移动6个单位长度到达点A3,按照这种移动规律移动下去,第n次移动到点A n,如果点A n与原点的距离等于19,那么n的值是.3.如图所示,甲乙两人沿着边长为60cm的正方形,按A→B→C→D→A…的方向行走,甲从A点以60m/min的速度,乙从B点以69m/min的速度行走,两人同时出发,当乙第一次追上甲时,用了____________.4.将一些相同的“○”按如图所示的规律依次摆放,观察每个“龟图”中的“○”的个数,若第n 个“龟图”中有245个“○”,则n=______________.5.如图,长方形ABCD中,AB=6,第一次平移长方形ABCD沿AB的方向向右平移5个单位,得到长方形A1B1C1D1,第2次平移将长方形A1B1C1D1沿A1B1的方向向右平移5个单位,得到长方形A2B2C2D2…,第n次平移将长方形A n﹣1B n﹣1C n﹣1D n﹣1沿A n﹣1B n﹣1的方向平移5个单位,得到长方形A n B n C n D n(n>2),若AB n的长度为56,则n=.三、解答题1.如图,M是定长线段AB上一定点,点C在线段AM上,点D在线段BM上,点C、点D分别从点M、点B出发以1cm/s、2cm/s的速度沿直线BA向左运动,运动方向如箭头所示.(1)若AB=10cm,当点C、D运动了2s,求AC+MD的值;(2)若点C、D运动时,总有MD=2AC,直接填空:AM=AB;(3)在(2)的条件下,N是直线AB上一点,且AN﹣BN=MN,求的值.2.已知数轴上有A,B,C三点,分别表示数﹣24,﹣10,10.两只电子蚂蚁甲、乙分别从A,C两点同时相向而行,甲的速度为4个单位/秒,乙的速度为6个单位/秒.(1)问甲、乙在数轴上的哪个点相遇?(2)问多少秒后甲到A,B,C三点的距离之和为40个单位?若此时甲调头返回,问甲、乙还能在数轴上相遇吗?若能,求出相遇点;若不能,请说明理由.3.甲、乙两地相距720km,一列快车和一列慢车都从甲地驶往乙地,慢车先行驶1小时后,快车才开始行驶.已知快车的速度是120km/h,慢车的速度是80km/h,快车到达乙地后,停留了20min,由于有新的任务,于是立即按原速返回甲地.在快车从甲地出发到回到甲地的整个程中,与慢车相遇了两次,这两次相遇时间间隔是多少?4.(1)如图1,若CO⊥AB,垂足为O,OE、OF分别平分∠AOC与∠BOC.求∠EOF的度数;(2)如图2,若∠AOC=∠BOD=80°,OE、OF分别平分∠AOD与∠BOC.求∠EOF的度数;(3)若∠AOC=∠BOD=α,将∠BOD绕点O旋转,使得射线OC与射线OD的夹角为β,OE、OF分别平分∠AOD与∠BOC.若α+β≤180°,α>β,则∠EOC=.(用含α与β的代数式表示)5.如图,已知∠AOB=90°,以O为顶点、OB为一边画∠BOC,然后再分别画出∠AOC与∠BOC的平分线OM、ON.(1)在图1中,射线OC在∠AOB的内部.①若锐角∠BOC=30°,则∠MON=45°;②若锐角∠BOC=n°,则∠MON=45°.(2)在图2中,射线OC在∠AOB的外部,且∠BOC为任意锐角,求∠MON的度数.(3)在(2)中,“∠BOC为任意锐角”改为“∠BOC为任意钝角”,其余条件不变,(图3),求∠MON的度数.6.如图,∠AOB=120°,射线OC从OA开始,绕点O逆时针旋转,旋转的速度为每分钟20°;射线OD从OB开始,绕点O逆时针旋转,旋转的速度为每分钟5°,OC和OD同时旋转,设旋转的时间为t(0≤t≤15).(1)当t为何值时,射线OC与OD重合;(2)当t为何值时,射线OC⊥OD;(3)试探索:在射线OC与OD旋转的过程中,是否存在某个时刻,使得射线OC,OB与OD中的某一条射线是另两条射线所夹角的角平分线?若存在,请求出所有满足题意的t的取值,若不存在,请说明理由.7.如图,∠AOB的边OA上有一动点P,从距离O点18cm的点M处出发,沿线段MO,射线OB运动,速度为2cm/s;动点Q从点O出发,沿射线OB运动,速度为1cm/s.P、Q 同时出发,设运动时间是t(s).(1)当点P在MO上运动时,PO=cm (用含t的代数式表示);(2)当点P在MO上运动时,t为何值,能使OP=OQ?(3)若点Q运动到距离O点16cm的点N处停止,在点Q停止运动前,点P能否追上点Q?如果能,求出t的值;如果不能,请说出理由.8.如图,两个形状.大小完全相同的含有30゜、60゜的三角板如图放置,PA、PB与直线MN重合,且三角板PAC,三角板PBD均可以绕点P逆时针旋转.(1)试说明:∠DPC=90゜;(2)如图,若三角板PAC的边PA从PN处开始绕点P逆时针旋转一定角度,PF平分∠APD,PE平分∠CPD,求∠EPF;(3)如图,若三角板PAC的边PA从PN处开始绕点P逆时针旋转,转速为3゜/秒,同时三角板PBD的边PB从PM处开始绕点P逆时针旋转,转速为2゜/秒,在两个三角板旋转过程中(PC转到与PM重合时,两三角板都停止转动).设两个三角板旋转时间为t秒,则∠BPN=__________,∠CPD=________ (用含有t的代数式表示,并化简);以下两个结论:①为定值;②∠BPN+∠CPD为定值,正确的是___________(填写你认为正确结论的对应序号).压轴题选讲解析一选择题1.某企业今年1月份产值为x万元,2月份比1月份减少了10%,3月份比2月份增加了15%,则3月份的产值用代数式表示为( )A.(1﹣10%+15%)x万元 B.(1+10%﹣15%)x万元C.(x﹣10%)(x+15%)万元D.(1﹣10%)(1+15%)x万元【考点】列代数式.【分析】根据3月份、1月份与2月份的产值的百分比的关系列式计算即可得解.【解答】解:3月份的产值为:(1﹣10%)(1+15%)x万元.故选D.【点评】本题考查了列代数式,理解各月之间的百分比的关系是解题的关键.2.有理数a、b在数轴上的位置如图所示,则化简|a﹣b|+|a+b|的结果为()A.﹣2a B.2a C.2b D.﹣2b【考点】整式的加减;数轴;绝对值.【专题】计算题;整式.【分析】根据数轴上点的位置判断出绝对值里边式子的正负,利用绝对值的代数意义化简,合并即可得到结果.【解答】解:根据数轴上点的位置得:a<﹣1<0<b<1,∴a﹣b<0,a+b<0,则原式=b﹣a﹣a﹣b=﹣2a.故选A.【点评】此题考查了整式的加减,熟练掌握运算法则是解本题的关键.3.如图,已知点A是射线BE上一点,过A作CA⊥BE交射线BF于点C,AD⊥BF交射线BF于点D,给出下列结论:①∠1是∠B的余角;②图中互余的角共有3对;③∠1的补角只有∠ACF;④与∠ADB互补的角共有3个.则上述结论正确的个数有( )A.1个B.2个C.3个D.4个【考点】余角和补角.【分析】根据已知推出∠CAB=∠CAE=∠ADC=∠ADB=90°,再根据三角形内角和定理和三角形外角性质,互余、互补的定义逐个分析,即可得出答案.【解答】解:∵CA⊥AB,∴∠CAB=90°,∴∠1+∠B=90°,即∠1是∠B的余角,∴①正确;图中互余的角有∠1和∠B,∠1和∠DAC,∠DAC和∠BAD,共3对,∴②正确;∵CA⊥AB,AD⊥BC,∴∠CAB=∠ADC=90°,∵∠B+∠1=90°,∠1+∠DAC=90°,∴∠B=∠DAC,∵∠CAE=∠CAB=90°,∴∠B+∠CAB=∠DAC+∠CAE,∴∠ACF=∠DAE,∴∠1的补角有∠ACF和∠DAE两个,∴③错误;∵∠CAB=∠CAE=∠ADC=∠ADB=90°,∴与∠ADB互补的角共有3个,∴④正确;故选C.【点评】本题考查了互余、互补,三角形内角和定理,三角形的外角性质的应用,主要考查学生的推理能力和辨析能力,题目比较好,但是比较容易出错.4.如图是由一副三角尺拼成的图案,它们有公共顶点O,且有一部分重叠,已知∠BOD=40°,则∠AOC的度数是( )A.40°B.120°C.140°D.150°【考点】角的计算.【分析】根据同角的余角相等即可求解.【解答】解:∵∠AOB=∠COD=90°,∴∠AOD+∠BOD=∠BOC+∠BOD=90°,∴∠AOD=∠BOC=90°﹣∠BOD=50°,∴∠AOC=∠AOD+∠BOD+∠BOC=140°,故选C.【点评】此题主要考查了角的计算,余角的性质,熟记余角的性质是解题的关键二填空题1.如图,线段AB=8,C是AB的中点,点D在直线CB上,DB=1.5,则线段CD的长等于 2.5或5.5.【考点】两点间的距离.【分析】根据题意求出线段CB的长,分点D在线段CB的延长线上和点D在线段CB上两种情况、结合图形计算即可.【解答】解:∵线段AB=8,C是AB的中点,∴CB=AB=4,如图1,当点D在线段CB的延长线上时,CD=CB+BD=5.5,如图2,当点D在线段CB上时,CD=CB﹣BD=2.5.故答案为:2.5或5.5.【点评】本题考查的是两点间的距离的计算,掌握线段中点的定义、灵活运用数形结合思想和分情况讨论思想是解题的关键.2.如图,在数轴上,点A表示1,现将点A沿x轴做如下移动,第一次点A向左移动2个单位长度到达点A1,第二次将点A1,向右移动4个单位长度到达点A2,第三次将点A2向左移动6个单位长度到达点A3,按照这种移动规律移动下去,第n次移动到点A n,如果点A n与原点的距离等于19,那么n的值是18或19.【考点】数轴.【专题】推理填空题.【分析】根据题意可以分别写出点A移动的规律,当点A奇数次移动后对应数的都是负数,偶数次移动对应的数都是正数,从而可知A n与原点的距离等于19分两种情况,从而可以解答本题.【解答】解:由题意可得,第奇数次移动的点表示的数是:1+(﹣2)×,第偶数次移动的点表示的数是:1+2×,∵点A n与原点的距离等于19,∴当点n为奇数时,则﹣19=1+(﹣2)×,解得,n=19;当点n为偶数,则19=1+2×解得n=18.故答案为:18或19.【点评】本题考查数轴,解题的关键是明确题意,可以分别写出点A奇数次和偶数次移动的关系式.3.如图所示,甲乙两人沿着边长为60cm的正方形,按A→B→C→D→A…的方向行走,甲从A点以60m/min的速度,乙从B点以69m/min的速度行走,两人同时出发,当乙第一次追上甲时,用了20min.【考点】一元一次方程的应用.【专题】几何动点问题.【分析】设乙第一次追上甲用了x分钟,则有乙行走的路程等于甲行走的路程加上90×3,根据其相等关系列方程得69x=60x+60×3,解方程即可得出答案.【解答】解:设乙第一次追上甲用了x分钟,由题意得:69x=60x+60×3,解得:x=20.答:用了20min.故答案为:20【点评】本题考查了一元一次方程的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程,再求解.4.将一些相同的“○”按如图所示的规律依次摆放,观察每个“龟图”中的“○”的个数,若第n 个“龟图”中有245个“○”,则n=16.【考点】规律型:图形的变化类.【分析】由图可知:第1个图形中小圆的个数为5;第2个图形中小圆的个数为7;第3个图形中小圆的个数为11;第4个图形中小圆的个数为17;则知第n个图形中小圆的个数为n(n﹣1)+5.据此可以再求得“龟图”中有245个“○”是n的值.【解答】解:第一个图形有:5个○,第二个图形有:2×1+5=7个○,第三个图形有:3×2+5=11个○,第四个图形有:4×3+5=17个○,由此可得第n个图形有:[n(n﹣1)+5]个○,则可得方程:[n(n﹣1)+5]=245解得:n1=16,n2=﹣15(舍去).故答案为:16.【点评】此题主要考查了图形的规律以及数字规律,通过归纳与总结结合图形得出数字之间的规律是解决问题的关键,注意公式必须符合所有的图形.5.如图,长方形ABCD中,AB=6,第一次平移长方形ABCD沿AB的方向向右平移5个单位,得到长方形A1B1C1D1,第2次平移将长方形A1B1C1D1沿A1B1的方向向右平移5个单位,得到长方形A2B2C2D2…,第n次平移将长方形A n﹣1B n﹣1C n﹣1D n﹣1沿A n﹣1B n﹣1的方向平移5个单位,得到长方形A n B n C n D n(n>2),若AB n的长度为56,则n=10.【考点】平移的性质.【专题】规律型.【分析】根据平移的性质得出AA1=5,A1A2=5,A2B1=A1B1﹣A1A2=6﹣5=1,进而求出AB1和AB2的长,然后根据所求得出数字变化规律,进而得出AB n=(n+1)×5+1求出n即可.【解答】解:∵AB=6,第1次平移将矩形ABCD沿AB的方向向右平移5个单位,得到矩形A1B1C1D1,第2次平移将矩形A1B1C1D1沿A1B1的方向向右平移5个单位,得到矩形A2B2C2D2…,∴AA1=5,A1A2=5,A2B1=A1B1﹣A1A2=6﹣5=1,∴AB1=AA1+A1A2+A2B1=5+5+1=11,∴AB2的长为:5+5+6=16;∵AB1=2×5+1=11,AB2=3×5+1=16,∴AB n=(n+1)×5+1=56,解得:n=10.故答案为:10.【点评】此题主要考查了平移的性质以及一元一次方程的应用,根据平移的性质得出AA1=5,A1A2=5是解题关键.三、解答题1.如图,M是定长线段AB上一定点,点C在线段AM上,点D在线段BM上,点C、点D分别从点M、点B出发以1cm/s、2cm/s的速度沿直线BA向左运动,运动方向如箭头所示.(1)若AB=10cm,当点C、D运动了2s,求AC+MD的值;(2)若点C、D运动时,总有MD=2AC,直接填空:AM=AB;(3)在(2)的条件下,N是直线AB上一点,且AN﹣BN=MN,求的值.【考点】一元一次方程的应用;两点间的距离.【专题】几何动点问题.【分析】(1)计算出CM及BD的长,进而可得出答案;(2)根据C、D的运动速度知BD=2MC,再由已知条件MD=2AC求得MB=2AM,所以AM=AB;(3)分两种情况讨论,①当点N在线段AB上时,②当点N在线段AB的延长线上时,然后根据数量关系即可求解.【解答】解:(1)当点C、D运动了2s时,CM=2cm,BD=4cm,∵AB=10cm,CM=2cm,BD=4cm,∴AC+MD=AB﹣CM﹣BD=10﹣2﹣4=4cm;(2)根据C、D的运动速度知:BD=2MC,∵MD=2AC,∴BD+MD=2(MC+AC),即MB=2AM,∵AM+BM=AB,∴AM+2AM=AB,∴AM=AB.故答案为;(3)当点N在线段AB上时,如图.∵AN﹣BN=MN,又∵AN﹣AM=MN,∴BN=AM=AB,∴MN=AB,即=;当点N在线段AB的延长线上时,如图.∵AN﹣BN=MN,又∵AN﹣BN=AB,∴MN=AB,即=1.综上所述,=或1.【点评】本题考查了一元一次方程的应用,灵活运用线段的和、差、倍、分转化线段之间的数量关系是十分关键的一点.2.已知数轴上有A,B,C三点,分别表示数﹣24,﹣10,10.两只电子蚂蚁甲、乙分别从A,C两点同时相向而行,甲的速度为4个单位/秒,乙的速度为6个单位/秒.(1)问甲、乙在数轴上的哪个点相遇?(2)问多少秒后甲到A,B,C三点的距离之和为40个单位?若此时甲调头返回,问甲、乙还能在数轴上相遇吗?若能,求出相遇点;若不能,请说明理由.【考点】一元一次方程的应用;数轴.【分析】(1)可设x秒后甲与乙相遇,根据甲与乙的路程差为34,可列出方程求解即可;(2)设y秒后甲到A,B,C三点的距离之和为40个单位,分甲应为于AB或BC之间两种情况讨论即可求解.【解答】解:(1)设x秒后甲与乙相遇,则4x+6x=34,解得x=3.4,4×3.4=13.6,﹣24+13.6=﹣10.4.故甲、乙在数轴上的﹣10.4相遇;(2)设y秒后甲到A,B,C三点的距离之和为40个单位,B点距A,C两点的距离为14+20=34<40,A点距B、C两点的距离为14+34=48>40,C 点距A、B的距离为34+20=54>40,故甲应为于AB或BC之间.①AB之间时:4y+(14﹣4y)+(14﹣4y+20)=40解得y=2;②BC之间时:4y+(4y﹣14)+(34﹣4y)=40,解得y=5.①甲从A向右运动2秒时返回,设y秒后与乙相遇.此时甲、乙表示在数轴上为同一点,所表示的数相同.甲表示的数为:﹣24+4×2﹣4y;乙表示的数为:10﹣6×2﹣6y,依据题意得:﹣24+4×2﹣4y=10﹣6×2﹣6y,解得:y=7,相遇点表示的数为:﹣24+4×2﹣4y=﹣44(或:10﹣6×2﹣6y=﹣44),②甲从A向右运动5秒时返回,设y秒后与乙相遇.甲表示的数为:﹣24+4×5﹣4y;乙表示的数为:10﹣6×5﹣6y,依据题意得:﹣24+4×5﹣4y=10﹣6×5﹣6y,解得:y=﹣8(不合题意舍去),即甲从A向右运动2秒时返回,能在数轴上与乙相遇,相遇点表示的数为﹣44.【点评】考查了一元一次方程的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系列出方程,再求解.本题在解答第二问注意分类思想的运用.3.甲、乙两地相距720km,一列快车和一列慢车都从甲地驶往乙地,慢车先行驶1小时后,快车才开始行驶.已知快车的速度是120km/h,慢车的速度是80km/h,快车到达乙地后,停留了20min,由于有新的任务,于是立即按原速返回甲地.在快车从甲地出发到回到甲地的整个程中,与慢车相遇了两次,这两次相遇时间间隔是多少?【考点】一元一次方程的应用.【分析】在快车从甲地出发到回到甲地的整个程中,与慢车相遇了两次,第一次是从甲地驶往乙地时,快车追上慢车,根据追上时快车行驶的路程=慢车行驶的路程列方程求解;第二次是快车到达乙地后返回甲地时与慢车相遇,根据相遇时快车行驶的路程+慢车行驶的路程=甲、乙两地之间的路程×2列方程求解.【解答】解:设从甲地驶往乙地时,快车行驶x小时追上慢车,由题意得120x=80(x+1),解得x=2,则慢车行驶了3小时.设在整个程中,慢车行驶了y小时,则快车行驶了(y﹣1﹣)小时,由题意得120(y﹣1﹣)+80y=720×2,解得y=8,8﹣3=5(小时).答:在快车从甲地出发到回到甲地的整个程中,与慢车相遇了两次,这两次相遇时间间隔是5小时.【点评】本题考查了一元一次方程的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系列出方程,再求解.4.(1)如图1,若CO⊥AB,垂足为O,OE、OF分别平分∠AOC与∠BOC.求∠EOF的度数;(2)如图2,若∠AOC=∠BOD=80°,OE、OF分别平分∠AOD与∠BOC.求∠EOF的度数;(3)若∠AOC=∠BOD=α,将∠BOD绕点O旋转,使得射线OC与射线OD的夹角为β,OE、OF分别平分∠AOD与∠BOC.若α+β≤180°,α>β,则∠EOC=.(用含α与β的代数式表示)【考点】角的计算;角平分线的定义.【分析】(1)根据垂直的定义得到∠AOC=∠BOC=90°,根据角平分线的定义即可得到结论;(2)根据角平分线的定义得到∠EOD=∠AOD=×(80+β)=40+β,∠COF=∠BOC=×(80+β)=40+β,根据角的和差即可得到结论;(3)如图2由已知条件得到∠AOD=α+β,根据角平分线的定义得到∠DOE=(α+β),即可得到结论.【解答】解:(1)∵CO⊥AB,∴∠AOC=∠BOC=90°,∵OE平分∠AOC,∴∠EOC=∠AOC=×90°=45°,∵OF平分∠BOC,∴∠COF=∠BOC=×90°=45°,∠EOF=∠EOC+∠COF=45°+45°=90°;(2)∵OE平分∠AOD,∴∠EOD=∠AOD=×(80+β)=40+β,∵OF平分∠BOC,∴∠COF=∠BOC=×(80+β)=40+β,∠COE=∠EOD﹣∠COD=40+β﹣β=40﹣β;∠EOF=∠COE+∠COF=40﹣β+40+β=80°;(3)如图2,∵∠AOC=∠BOD=α,∠COD=β,∴∠AOD=α+β,∵OE平分∠AOD,∴∠DOE=(α+β),∴∠COE=∠DOE﹣∠COD==,如图3,∵∠AOC=∠BOD=α,∠COD=β,∴∠AOD=α+β,∵OE平分∠AOD,∴∠DOE=(α﹣β),∴∠COE=∠DOE+∠COD=.综上所述:,故答案为:.【点评】本题考查了角平分线的定义,角的计算,解题的关键是找出题中的等量关系列方程求解.5.如图,已知∠AOB=90°,以O为顶点、OB为一边画∠BOC,然后再分别画出∠AOC 与∠BOC的平分线OM、ON.(1)在图1中,射线OC在∠AOB的内部.①若锐角∠BOC=30°,则∠MON=45°;②若锐角∠BOC=n°,则∠MON=45°.(2)在图2中,射线OC在∠AOB的外部,且∠BOC为任意锐角,求∠MON的度数.(3)在(2)中,“∠BOC为任意锐角”改为“∠BOC为任意钝角”,其余条件不变,(图3),求∠MON的度数.【考点】角的计算;角平分线的定义.【分析】(1)①由角平分线的定义,计算出∠MOA和∠NOA的度数,然后将两个角相加即可;②由角平分线的定义,计算出∠MOA和∠NOA的度数,然后将两个角相加即可;(2)由角平分线的定义,计算出∠MOA和∠NOA的度数,然后将两个角相减即可;(3)由角平分线的定义,计算出∠MOA和∠NOA的度数,然后将两个角相加即可.【解答】解:(1)①∵∠AOB=90°,∠BOC=30°,∴∠AOC=60°,∵OM,ON分别平分∠AOC,∠BOC,∴∠COM=AOC,BOC,∴∠MON=∠COM+∠CON=∠AOB=45°,故答案为:45°,②∵∠AOB=90°,∠BOC=n°,∴∠AOC=(90﹣n)°,∵OM,ON分别平分∠AOC,∠BOC,∴∠COM=AOC=(90﹣n)°,BOC=n°,∴∠MON=∠COM+∠CON=∠AOB=45°,故答案为:45°;(2)∵∠AOB=90°,设∠BOC=α,∴∠AOC=90°+α,∵OM,ON分别平分∠AOC,∠BOC,∴∠COM=AOC,BOC,∴∠MON=∠COM﹣∠CON=∠AOB=45°,(3)∵OM,ON分别平分∠AOC,∠BOC,∴∠COM=AOC,BOC,∴∠MON=∠COM+∠CON=(∠AOC+∠BOC)=(360°﹣90°)=135°.【点评】本题考查了角平分线定义,角的有关计算的应用,解此题的关键是求出∠COM和∠CON的大小.6.如图,∠AOB=120°,射线OC从OA开始,绕点O逆时针旋转,旋转的速度为每分钟20°;射线OD从OB开始,绕点O逆时针旋转,旋转的速度为每分钟5°,OC和OD同时旋转,设旋转的时间为t(0≤t≤15).(1)当t为何值时,射线OC与OD重合;(2)当t为何值时,射线OC⊥OD;(3)试探索:在射线OC与OD旋转的过程中,是否存在某个时刻,使得射线OC,OB与OD中的某一条射线是另两条射线所夹角的角平分线?若存在,请求出所有满足题意的t的取值,若不存在,请说明理由.【考点】角的计算;角平分线的定义.【专题】探究型.【分析】(1)根据题意可得,射线OC与OD重合时,20t=5t+120,可得t的值;(2)根据题意可得,射线OC⊥OD时,20t+90=120+5t或20t﹣90=120+5t,可得t的值;(3)分三种情况,一种是以OB为角平分线,一种是以OC为角平分线,一种是以OD为角平分线,然后分别进行讨论即可解答本题.【解答】解:(1)由题意可得,20t=5t+120解得t=8,即t=8min时,射线OC与OD重合;(2)由题意得,20t+90=120+5t或20t﹣90=120+5t,解得,t=2或t=14即当t=2min或t=14min时,射线OC⊥OD;(3)存在,由题意得,120﹣20t=5t或20t﹣120=5t+120﹣20t或20t﹣120﹣5t=5t,解得t=4.8或t=或t=12,即当以OB为角平分线时,t的值为4.8min;当以OC为角平分线时,t的值为min,当以OD为角平分线时,t的值为12min.【点评】本题考查角的计算、角平分线的性质,解题的关键是明确题意,找出所求问题需要的条件.7.如图,∠AOB的边OA上有一动点P,从距离O点18cm的点M处出发,沿线段MO,射线OB运动,速度为2cm/s;动点Q从点O出发,沿射线OB运动,速度为1cm/s.P、Q 同时出发,设运动时间是t(s).(1)当点P在MO上运动时,PO=cm (用含t的代数式表示);(2)当点P在MO上运动时,t为何值,能使OP=OQ?(3)若点Q运动到距离O点16cm的点N处停止,在点Q停止运动前,点P能否追上点Q?如果能,求出t的值;如果不能,请说出理由.8.如图,两个形状.大小完全相同的含有30゜、60゜的三角板如图放置,PA、PB与直线MN重合,且三角板PAC,三角板PBD均可以绕点P逆时针旋转.(1)试说明:∠DPC=90゜;(2)如图,若三角板PAC的边PA从PN处开始绕点P逆时针旋转一定角度,PF平分∠APD,PE平分∠CPD,求∠EPF;(3)如图,若三角板PAC的边PA从PN处开始绕点P逆时针旋转,转速为3゜/秒,同时三角板PBD的边PB从PM处开始绕点P逆时针旋转,转速为2゜/秒,在两个三角板旋转过程中(PC转到与PM重合时,两三角板都停止转动).设两个三角板旋转时间为t秒,则∠BPN=180﹣2t,∠CPD=90﹣t (用含有t的代数式表示,并化简);以下两个结论:①为定值;②∠BPN+∠CPD为定值,正确的是①(填写你认为正确结论的对应序号).【考点】角的计算;角平分线的定义.【分析】(1)利用含有30゜、60゜的三角板得出∠DPC=180°﹣∠CPA﹣∠DPB,进而求出即可;(2)设∠CPE=∠DPE=x,∠CPF=y,则∠APF=∠DPF=2x+y,进而利用∠CPA=60゜求出即可;(3)首先得出①正确,设运动时间为t秒,则∠BPM=2t,表示出∠CPD和∠BPN的度数即可得出答案.【解答】解:(1)∵∠DPC=180°﹣∠CPA﹣∠DPB,∠CPA=60°,∠DPB=30°,∴∠DPC=180゜﹣30゜﹣60゜=90゜;(2)设∠CPE=∠DPE=x,∠CPF=y,则∠APF=∠DPF=2x+y,∵∠CPA=60゜,∴y+2x+y=60゜,∴x+y=30゜∴∠EPF=x+y=30゜(3)①正确.设运动时间为t秒,则∠BPM=2t,∴∠BPN=180﹣2t,∠DPM=30﹣2t,∠APN=3t.∴∠CPD=180﹣∠DPM﹣∠CPA﹣∠APN=90﹣t,∴==.②∠BPN+∠CPD=180﹣2t+90﹣t=270﹣3t,可以看出∠BPN+∠CPD随着时间在变化,不为定值,结论错误.故答案为:180﹣2t;90﹣t;①.【点评】此题主要考查了角的计算,利用数形结合得出等式是解题关键,还要理清角之间的关系.。
