流体力学第三章(7)动量方程及其应用及动量矩方程

合集下载

可压缩流体的动量方程和动量矩方程

一、概述可压缩流体是指密度随着压强和温度的变化而变化的流体。

在空气动力学和航天动力学中，可压缩流体动力学是一个重要的研究领域。

在研究可压缩流体运动时，动量方程和动量矩方程是非常重要的方程。

本文将从动量方程和动量矩方程入手，系统地阐述可压缩流体的动力学原理。

二、可压缩流体的动量方程动量方程描述了流体内部的动量变化。

对于可压缩流体，其动量方程可以通过Navier-Stokes方程推导得到。

Navier-Stokes方程是描述了流体运动的基本方程之一，其形式如下：∂(ρv)/∂t + ∇•(ρv⃗v⃗ ) = -∇p+ ∇•τ+ ρf⃗其中，ρ表示流体密度，v表示流体速度，t表示时间，p表示压强，τ表示应力张量，f⃗表示外力。

对于可压缩流体，动量方程还需要考虑压力和密度对流体速度的影响。

可以通过状态方程将压力和密度通联起来，从而得到包含压力-密度项的动量方程。

在一维情况下，动量方程可以表达为：∂(ρv)/∂t + ∂(ρv^2)/∂x = -∂p/∂x+ ρf在三维情况下，动量方程会更加复杂，需要同时考虑各个方向上的动量变化。

通过动量方程，我们可以清晰地了解流体内部的动量传递和转化过程，以及外力对流体动量的影响。

三、可压缩流体的动量矩方程动量矩方程描述了流体内部动量矩的变化。

对于可压缩流体，动量矩方程可以被用来分析流体内部旋转运动的特性。

动量矩方程可以通过Euler方程推导得到。

Euler方程是Navier-Stokes方程在无粘性流体情况下的特殊形式，其表达式如下：∂(ρv)/∂t + ∇•(ρv⃗v⃗ ) = -∇p+ ∇•τ+ ρf⃗在此基础上，再根据流体内部动量矩的性质，可以得到动量矩方程的表达式。

动量矩方程不仅包含了流体速度的变化，还考虑了流体内部的角动量变化。

对于可压缩流体，动量矩方程可以表达为：∂(ρv)/∂t + v•∇(ρv) +∇•(τ) = ρf⃗通过动量矩方程，我们可以研究流体内部旋转运动的特性，分析流体内部动量矩的传递和转化情况，为深入理解可压缩流体的运动提供重要的理论基础。

经典流体力学第三章 03

ω
V R
R V
解: 1)取半径为R的圆周为控制面, 则
2 ρ Q (VR cos θ − ω R ) = 0
2
V ∴ω = cos θ R
ω
V R
R V
2)
M = 2 ρ QVR cos θ
ω
V R
R V
M
习题
P206： 3-34，3-36，3-37
本章小结
一、几个基本概念 1）元流（Tube Flow）：充满在流管中的液流称为元流或微小流束。元流的极限是一条流线。无数元流之和就构成总流。 2）过水断面（Cross Section）：即水道（管道、明渠等）中垂直于水流流动方向的横断面，即与元流或总流的流线成正交的横断面称为过水断面。 3）点流速：流体流动中任一点的流速称为点流速，常用u表示。一般情况下过水断面上各点的点流速是不相等的。 4）平均流速：由通过过水断面的流量Q除以过水断面的面积A而得的流速称为断面平均流速，常用V表示，即
2 v12 v2 = 0+0+ 0+0+ 2g 2g 2 v12 v3 = 0+0+ 0+0+ 2g 2g 4Q ∴ v2 = v3 = v1 = v = 2 = 20m / s πd ∴v = v
y
d
x
1 Q,v 1
2
2
v2 θ
3
2y
3y
代入（1）可得：
Q1 = Q2 + Q3 = Q
Q2 = Q3 = Q 2
x
1 Q,v 1
2
d
2
v2 θ
3
1
θ
3 v3
P R
P2

流体力学第三章(7)动量方程及其应用及动量矩方程1

d ( mv ) F dt
作用在质点系上的总外力就不必通过分布压强的积分，而是通过求质点系动量变化率的办法计算出来，开辟了求解流体动力学问题的新途径。
F
d ( mv ) dt
由于各个质点速度不尽相同，似乎要计算质点系的动量变化率采用拉格朗日法比较适宜，由于运动的复杂性，很困难。质点系占据一定的空间，取这个空间为控制体，把拉格朗日法表示的动量变化率改换成用欧拉法表示，这样就容易求的作用在控制体内流体质点系上的外力。
vdV v(v dA) A t V
这就是用欧拉方法表示的动量方程式，这个方程式既适用于控制体固定的情况，也适用于控制体运动的情况。在运动时需将速度v换成相对速度，并在控制体上加上虚构的惯性力。动量方程式中，需注意 1. F 是作用在控制体内质点系上的所有外力的矢量和，既包括控制体外部流体及固体对控制体内流体的作用力（压力、摩擦力），也包括控制体内流体的重力。 2. 控制体内流体动量对时间的变化率，当流动为定常时，此项为零。是由于控制体内流体动量随时间变化而产生的一种力。
对于y方向同样得到
p1 A1 cos1 p2 A2 sin2 FRx qV v2 sin 2 v1 cos1 p1 A1 sin1 p2 A2 sin cos2 FRy qV v2 cos2 v1 sin 1
解方程组到
FRx p1 A1 cos 1 p2 A2 sin 2 qV (v1 cos 1 ) (v2 sin 2 ) FRy p2 A2 cos 2 p1 A1 sin 1 qV (v2 cos 2 ) (v1 sin 1 )
这是流体对任意变径弯管的作用力的计算公式，对其求合力得到

流体力学中的动量方程

流体力学中的动量方程动量方程是流体力学中描述流体运动的基本方程之一。

它描述了流体在运动过程中动量的变化，通过掌握动量方程，可以深入理解和分析流体的运动特性。

一、动量的定义与表达式根据牛顿第二定律，一个物体的动量等于其质量与速度的乘积。

对于流体来说，动量可以用密度、速度和体积来表达。

根据这个定义，流体的动量可以表示为：M = ρ * V其中，M为动量，ρ为流体的密度，V为流体的速度。

二、流体的动量守恒流体的动量守恒是指在一个封闭系统中，动量的总量在时刻保持不变。

这可以通过动量方程来表示。

对于流体的动量守恒方程，有两个基本形式：1.欧拉动量方程欧拉动量方程适用于描述非粘性流体的动量守恒。

其表达式为：∂(ρV)/∂t + ∇(ρV*V) = -∇P + ρg其中，ρ为流体的密度，V为流体的速度，t为时间，P为压力，g 为重力加速度。

2.纳维-斯托克斯动量方程纳维-斯托克斯动量方程适用于描述粘性流体的动量守恒。

其表达式为：∂(ρV)/∂t + ∇(ρV*V) = -∇P + μ∇²V + ρg其中，ρ为流体的密度，V为流体的速度，t为时间，P为压力，μ为流体的动力黏度，g为重力加速度。

三、动量方程的应用动量方程在流体力学的研究中有广泛的应用。

它可以用来解释和预测流体的运动特性，如流体的速度分布、流体中的压力和力的作用等。

1.速度分布根据动量方程，可以推导出流体在不同速度条件下的速度分布规律。

通过研究流体的速度分布，可以了解到流体的流动状态，从而更好地控制和管理流体运动。

2.压力分布动量方程中的压力项描述了流体中压力的变化规律。

通过分析动量方程中的压力项，可以获得流体的压力分布情况。

这对于设计和优化流体系统具有重要意义。

3.流体之间的相互作用在实际应用中，流体通常与其他物体或流体相互作用。

通过动量方程，可以分析流体与其他物体的相互作用力，并进行力学计算和设计。

四、总结动量方程是流体力学中重要的基本方程之一，通过它可以深入研究和理解流体的运动特性。

流体力学动量方程表达式

流体力学动量方程表达式
流体力学动量方程是描述流体运动的基本方程之一。

它以人类的视角，如同一位热血澎湃的足球运动员，在足球场上奔跑，用力踢球，为我们展现了流体的力学特性。

我们需要了解什么是动量。

动量是物体运动的基本属性，它与物体的质量和速度有关。

在流体力学中，动量方程描述了流体的动量变化与力的关系。

在足球场上，当我们踢球时，足球会受到力的作用而改变其速度和方向。

同样地，在流体中，流体微团也会受到外力的作用而改变其速度和方向。

动量方程告诉我们，流体微团的动量变化等于作用在它上面的力的总和。

动量方程的表达式如下：
动量变化 = 外力的作用 + 内力的作用
动量变化 = 外力的作用 + 压力的作用
外力的作用是指外部施加在流体微团上的力，例如重力、浮力等。

这些力会改变流体微团的动量。

内力的作用是指流体微团内部分子之间的相互作用力。

这些力同样会改变流体微团的动量。

而压力的作用是指流体微团受到外部压力的作用而产生的力。

压力
的作用同样会改变流体微团的动量。

通过动量方程，我们可以研究流体运动的各种现象。

例如，当水流经过狭窄的管道时，我们可以通过动量方程来分析水流的速度和压力的变化。

当风吹过一座桥时，我们也可以通过动量方程来分析桥面受到的力和压力的分布情况。

动量方程是研究流体运动的重要工具之一。

它以人类的视角，通过描述流体微团的动量变化与力的关系，为我们揭示了流体运动的奥秘。

无论是在足球场上还是在流体力学的研究中，动量方程都是我们的得力助手，帮助我们更好地理解和掌握流体运动的规律。

流体力学3_动量方程应用举例

动量方程应用举例：例：水在直径为cm 10的 60水平弯管中，以s m 5的速度流动。

弯管前端的压强为at 1.0。

不计损失，也不考虑重力作用，求水流对弯管1-2的作用力。

解：1、确定控制体。

取控制体为1-2断面间弯管占有的空间。

这样把受流体作用的弯管整个内表面包括在控制体内，又没有其他多余的固壁。

2、选择坐标系。

坐标系选择如图所示。

x 轴为弯管进口前管道的轴线，z 轴为垂直方向，y x -平面为水平面。

3、流出和流进控制体的动量差。

流出：2v Q ρ；流进：1v Q ρ。

动量差：()12v v Q -ρ。

由于断面积不变，s m v v v 521===。

若断面积变化，求未知流速时，通常要运用连续性方程。

4、控制体内流体受力分析。

由于不考虑重力作用，质量力为零。

表面力包括：断面1上：111A p P =，方向沿x 轴正向；断面2上：222A p P =，方向垂直于断面2，且指向控制体内；其余表面：R ——弯管内表面对流体的作用力。

由于R 的方向未知，应任意假设某方向。

不妨设R 在y x -平面上的投影方向与x 轴的夹角为α。

未知压强2p 应根据能量方程g v p Z g v p Z 2222222111++=++γγ求出。

由于21Z Z =，v v v ==21，故2219807m N p p p ===。

一般地，求某一未知压强总要用到能量方程。

5、联立动量方程并求解。

()()()()160cos 60cos cos 60cos 1cos 60cos 21211122211-=-=-=--=--=∑ Av v v A v v v Q R pA R A p A p F x x x ρρραα()() 60sin 060sin sin 60sin sin 60sin 221222Av v vA v v Q R pA R A p F y y y ρρραα=-=-=+-=+-=∑()z z z z v v Q R F 12-==∑ρ也即：()()()⎪⎩⎪⎨⎧-==+--=--z z zv v Q R Av R pA Av R pA 122260sin sin 60sin 160cos cos 60cos 1ρραρα 代入数据：()N pA 1.771.0498072=⨯⨯=π()()()()⎪⎪⎪⎩⎪⎪⎪⎨⎧=⨯⨯⨯⨯=+--⨯⨯⨯⨯=--⨯060sin 51.041000sin 60sin 1.77160cos 51.041000cos 60cos 11.772222z R R R παπα 联立求解，得：N R 272= 60=α6、分析。

流体力学的动量矩原理

流体力学的动量矩原理流体力学的动量矩原理是流体力学中最基本的原理之一。

它描述了流体的动量变化与力的关系，是研究流体运动的重要工具。

动量矩原理的基本思想是通过将流体分割为无限小的体积元，研究每个体积元的动量变化，然后统一求和得到整个流体的动量变化。

下面我将从基本概念、动量守恒定律、动量矩守恒定律以及应用四个方面详细介绍动量矩原理。

首先，我们来介绍一些流体力学中的基本概念。

流体是指那些没有一定形状，可以流动的物质。

在流体中，存在一种力称为剪切力，它是由于分子之间的相互作用而产生的。

同时，流体受到的外部力可以分为体力和面力。

体力是作用在流体体积上的力，如重力等。

而面力则是作用在流体表面上的力，如压力、粘性力等。

其次，动量守恒定律是流体力学的基本定律之一。

根据动量守恒定律，一个系统的总动量在没有外力作用时保持不变。

这意味着在一个封闭系统中，流体的总动量保持恒定。

动量守恒定律可以表示为以下方程式：\frac{\partial(\rho u)}{\partial t}+\nabla \cdot (\rho u u)=-\nabla p +\nabla \cdot \tau + \rho g其中，\rho表示流体的密度，u表示流体的速度，t表示时间，p表示压力，\tau 表示粘性应力，g表示重力加速度。

这个方程描述了流体的动量变化与各种力的作用之间的关系。

然后，我们来介绍动量矩守恒定律。

动量矩守恒定律是动量守恒定律在旋转参考系中的扩展。

它描述了流体运动过程中动量矩的变化与外部力矩的关系。

动量矩守恒定律可以表示为以下方程式：\frac{\partial(\rho u_i x_j)}{\partial t}+\frac{\partial(\rho u_i x_ju_k)}{\partial x_k}=-\left(\frac{\partial p}{\partial x_i}+\frac{\partial\tau_{ij}}{\partial x_k}\right) x_j+\rho g_i x_j其中，x_i表示坐标轴，x_j表示动量矩，u_i表示流体的速度分量，t表示时间，p表示压力，\tau_{ij}表示粘性应力张量，g_i表示重力加速度分量。

动量方程和动量矩方程

v1 v r1 ,

v 2 v r2
4 Q ( r1 r2 )
2
（5）代入动量矩方程，解得：

v ( r1 r2 ) r1 r2
2 2
4 Q ( r1 r2 )
d ( r1 r2 )
2 2 2
M Q ( v r1 v r2 )
d
t dV
r

S
V
n
( r v )d V
V

V
(r v )
( r v ) ( v n )d S M
而外力矩： M 于是有：
( r f )d V
V

S
( r p n )d S

V
(r v ) t
14
水流对喷嘴的作用力
已知：A1、 A2、 p1 - pa
求：水流给喷嘴的合力
图2.6.6 喷嘴
《流体力学》讲义 15
解: （1）取控制体：图中虚线所围部分；（2）设喷嘴壁面给水流控制体的合力为F，方向向左；（3）列动量方程(表压力)： 1
F ( p 1 p a ) A1 Q ( v 2 v1 ) F ( p 1 p a ) A1 Q ( v 2 v1 )
x
r
V
zu xv
S
y
z
《流体力学》讲义
5
动量积分方程和动量矩积分方程的应用
水流对弯管的作用力已知：A1、A2，θ，Q，不计重力。求：固定弯管所需的力F。

v ( v n ) ds
S

V

流体力学第三章伯努利方程及动量方程

渐缩管喉管渐扩管
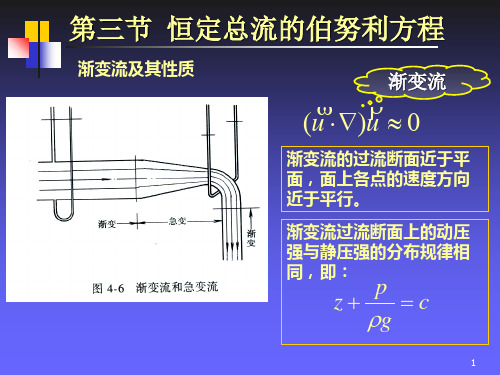
0 p1 v12 0 p2 v22
2g
2g
28
第三节恒定总流的伯努利方程
p1 p2 v22 v12 h
2g 2g
连续性方程
v1
4
d12
v2
4
d
2 2
v2 v1
d1 d2
Z1
dQ
p1
Z1
dQ
p1
Z1
Q
9
第三节恒定总流的伯努利方程
同理：
p2 Z2 dQ
p2
Z2
dQ
p2
Z2
dQ
p2
Z2
Q
10
第三节恒定总流的伯努利方程
二、动能积分 u2 dQ u3 dA u3dA
Q 2g
A 2g
2g A
表单位时间通过断面的流体动能
v
Q
udA
A
AA
u3dA u3dA
18
第三节恒定总流的伯努利方程
19
第三节恒定总流的伯努利方程
20
第三节恒定总流的伯努利方程
总水头线和测压管水头线
总水头=位置水头+压强水2g
H1 H2 hw 或 H2 H1 hw
v2 H H p 2g
水力坡度: J dH dhw dl dl
p1 (Z1 Z2 ) p2
Z1
p1
Z2
p2
4
第三节恒定总流的伯努利方程
Z1
p1
Z2
p2
均匀流过流断面上压强分布服从水静力学规律
Z p c
5
第三节恒定总流的伯努利方程
渐变流：非严格均匀流，接近于均匀流渐变流： 1）流线近似于平行直线。 2）惯性力忽略不计。 3）过流断面近似于平面。 4）过流断面上，压强分布可认为服从流体静力学规律。

工程流体力学第3章流体流动的基本方程

注意：空间点本身不具有密度、速度等物理参数，某一时刻占据该空间点的流体质点具有这些物理参数。流体的任意物理量可以表示为：
B F ( x, y, z, t )
比如，流体质点的速度场：
u F ( x, y, z, t )
第3章流体流动的基本方程
速度分布的分量可表示为：
u x F1 ( x, y , z , t ) u y F2 ( x, y , z , t ) u z F3 ( x, y , z , t )
u x 2 x 2 F1 (a, b, c, t ) ax 2 t t t 2 u y 2 y 2 F2 (a, b, c, t ) ay 2 t t t 2 u z 2 z 2 F3 (a, b, c, t ) az 2 t t t 2
教学内容
第0章绪论
第1章流体的主要物理性质
第2章流体静力学
第3章流体流动的基本方程
第4章势流理论
第5章相似理论与量纲分析
第6章粘性流体管内流动
第7章粘性流体绕物体的流动
第3章流体流动的基本方程
流体运动——满足质量守恒、牛顿第二定律、能量守恒… 推导——连续方程，动量方程，动量矩方程，能量方程…
第3章流体流动的基本方程
流体质点的速度和加速度
u ux i uy j uz k
x F1 (a, b, c, t ) ux t t y F2 (a, b, c, t ) uy t t z F3 (a, b, c, t ) uz t t
a ax i ay j az k
两边积分 ln x 2t C ，故 x c1e
' 1

大学课程《工程流体力学》PPT课件：第三章

§3.1 研究流体运动的方法
➢ 欧拉法时间导数的一般表达式
d (v ) dt t
d ：称为全导数，或随体导数。
dt
：称为当地导数。
t
v
：称为迁移导数。
例如，密度的导数可表示为： d (v )
dt t
§3.1 研究流体运动的方法
3.1.2 拉格朗日法
拉格朗日法的着眼点：特定的流体质点。
lim t0
(
dV
III
)
t
t
t
CS2 vndA
单位时间内流入控制体的物理量：
z
Ⅲ
Ⅱ’
Ⅰ
y
lim
t 0
(IdV )t t t CS1vndA
x
§3.3 雷诺输运方程
➢ 雷诺输运方程
dN dt
t
CV dV
CSvndA
雷诺输运方程说明，系统物理量 N 的时间变化率，等于控制体该种物理量的时间变化率加上单位时间内经过控制面的净通量。
d dt
V
dV
t
CV
dV
CS
vndA
0
因此，连续性方程的一般表达形式为：
t
CV
dV
CS
vndA
0
连续性方程是质量守恒定律在流体力学中的表现形式。
对定常流动，连续性方程简化为：
CS vndA 0
§3.4 连续性方程
对一维管流，取有效截面 A1 和 A2，及
v2
管壁 A3 组成的封闭空间为控制体：
ay
dv y dt
v y t
vx
v y x
vy
v y y
vz
v y z
az

流体力学7动量方程及其应用及动量矩方程

解方程组得到
FRx p1A1 cos1 p2 A2 sin2 qV (v1 cos1) (v2 sin2 )
F
d ( mv)
dt
fx
1
p x
[
2vx x 2
2vx y 2
2vx z 2
]
dvx dt
fy
1
p y
[
2vy x 2
2vy y 2
2vy z 2
]
dvபைடு நூலகம் dt
fz
1
p z
[
2vz x 2
2vz y 2
2vz z 2
]
dvz dt
作用在质点系上的总外力就不必通过分布压强的积分，而是通过求质点系动量变化率的办法计算出来，开辟了求解流体动力学问题的新途径。
，流量为
q
的流体对弯管的作用力
v
FRx，FRy
假定管道在水平平面内或者重力可以不加考虑，动量修正系数为1
取1-1、2-2断面及弯管内表面为流管控制体，作用在流体质点系的总外力包括
弯管对控制体内流体的作用力 FRx和 FRy , 过流断面上外界流体对控制体内流体的作用力P1A1, P2 A2
Fx qv (v2x v1x ) Fy qv (v2 y v1y ) Fz qv (v2z v1z )
p1A1 sin1 p2 A2 sin cos2 FRy qV v2 cos2 v1 sin1
p1A1 cos1 p2 A2 sin2 FRx qV v2 sin2 v1 cos1
p1A1 sin1 p2 A2 sin cos2 FRy qV v2 cos2 v1 sin1
本次课主要内容动量方程式及其应用
一、动量方程能解决运动流体中的什么问题

流体力学动量方程

流体力学动量方程
流体力学动量方程指的是：质量方程、动量方程（对于不可压缩牛顿流体来说是N-S方程）、能量方程。

方程式的写法有很多，微分形式的和积分形式的，用分量表示(工程类的教材居多)的或者张量形式(侧重于力学理论)的。

流体力学的动量方程中，为什么力和动量可以做加减法
力的量纲是N，动量是N*s，一般是不能做加减的。

但是流体力学里面有一种情况，在说动量的时候不使用质量去计算，而是用质量流量去计算，这样，动量的量纲就是N了，所以这个时候什么力都可以和动量加减。

至于系统动量改变等于受力，这个就是牛顿第二定律，牛顿最早表达他的第二定律的时候是这样写的F = d(m*v)/dt;而不是我们常说的F = m*a。

流体力学动量方程的实际应用
气象、水利的研究，船舶、飞行器、叶轮机械和核电站的设计及其运行，可燃气体或炸药的爆炸，汽车制造（联众集群），以及天体物理的若干问题等等，都广泛地用到流体力学知识。

许多现代科学技术所关心的问题既受流体力学的指导，同时也促进了它不断地发展。

流体力学动量守恒方程及各项含义

流体力学动量守恒方程及各项含义1. 动量守恒方程的基本概念1.1 什么是动量？大家都知道，动量就像是物体的“跑步速度”，它跟物体的质量和速度有关系。

想象一下，一个大象在慢慢走和一只小猫飞快冲过来，谁的动量大？当然是大象，尽管它速度慢，但那厚重的体型让它的动量不可小觑。

动量的公式很简单，就是质量乘以速度。

1.2 动量守恒是什么？动量守恒听起来有点高深，但其实很简单。

它的意思就是在一个孤立的系统里，动量总是守恒的，也就是说，系统内所有物体的动量加起来，永远不会变。

就像打乒乓球一样，球拍打到球，球的动量变了，但球拍的动量也相应改变，整体上动量没变。

这就是个天经地义的道理，哪怕你在打牌的时候也得记住，运气也是有保质期的。

2. 动量守恒方程的实际应用2.1 流体中的动量守恒在流体力学中，动量守恒方程就像是流动水的“守护神”。

想象一下水流过一个河口，水的动量会随着流动而变化。

如果你在河边打水漂，水在你手里的动量和在河里的动量是息息相关的。

这个方程帮我们理解流体如何在不同条件下运动，比如风在吹动水面时，水面上的波动和气流之间的关系。

2.2 工程中的应用在工程领域，动量守恒方程可是大显神威。

比如设计一座桥或者一栋摩天大楼，工程师们会仔细考虑风的力量、雨水的流动，甚至是周围建筑物对流体流动的影响。

想象一下，如果没有这套方程，那些高楼大厦可能就像一片“黄土”，随风而倒。

通过分析流体动量的变化，工程师们可以保证建筑的稳固，真是“稳如泰山”呀！3. 动量守恒方程的方程形式及意义3.1 方程形式动量守恒方程的表达式看起来有点复杂，但其实不难理解。

通常，它的形式是这样的：在某个控制体内，动量的变化率等于流入流出动量的差。

也就是说，如果有更多的动量流入，那这个控制体的动量就会增加；反之则会减少。

这就像一瓶水，水倒进来就满了，水倒出去就空了。

简单明了，谁都能懂。

3.2 各项的含义在这个方程中，涉及到几个关键的项，比如流动速度、密度和体积等。

稳定流的动量方程和动量矩方程的推导及应用

稳定流的动量方程和动量矩方程的推导及应用1 稳定流动量方程讨论运动流体与固体边界面上的相互作用力，例如：流体在弯曲管道内流动，弯管的受力情况；水力采矿时，高压水枪射流对水枪、对矿床的作用力；火箭飞行过程中，从火箭尾部喷射出的高温高压气体对火箭的反推力等等。

这类问题，需应用运动流体的动量方程来分析。

从物理学知，运动物体的动量为：图1流束动量变化根据质点系动量定理：用符号表示动量，即，则——流体作定常流动时的动量方程。

图示一弯管，其中的流体作定常流动，在总流中任意取一微小流束1－2，并取过水断面1－1、2－2间的流束段进行研究。

即对不可压缩流体，则微小流束的动量方程为：将上式推广到总流中去，则得：由定常流动总流的连续性方程，有：因为u在A上分布难以确定，所以用v代换u，有：式中、——动量修正系数，其实验值为1.02~1.05，工程计算上取＝＝1。

整理可得：——理想流体定常流动总流的动量方程。

其物理意义是：作用在所研究的流体上的外力矢量和等于单位时间内流出与流入的动量之差。

作用在流体上的外力：流束段1－2的重力，两过水断面1－1、2-2上的压力、，边界面上所受表面压力的总值。

上式也可写为：其分量式为：图2 流体作用于弯管上的力确定流体与固体边界之间的作用力，上述方程是一个重要方程。

2 动量方程的应用（1）流体作用于弯管上的力图示一弯管，沿x轴、y轴的动量方程为：所以则的方向为：流体对弯管的作用力，与是一对作用力和反作用力，大小与相等,方向与相反。

（2）射流作用在固定平面上的冲击力水射流清洗：船体、铸造清砂、矿车清扫流体从管嘴喷射出而形成射流。

如射流在同一大气压强之下，并忽略自身重力，则作用在流体上的力，只有固定平面对射流的阻力，它与射流对固定平面的冲击力构成一对作用力和反作用力。

图示固定平板与水平面成θ角，流体从喷嘴射出，射流的动量为：x轴方向的动量方程为：即射流对平板的冲击力：=-当θ＝900时如果平板不固定，沿射流方向以速度运动，则射流对移动平板的冲出力为：（3）射流的反推力烟花升空我们知道，火箭飞行的根本动力是火箭内部的燃料发生爆炸性燃烧，产生大量高温高压的气体，从尾部喷出形成射流，射流对火箭有一反推力，使火箭向前运动。

流体动量方程

流体动量方程流体动量方程是流体力学中一个重要的方程，它描述了流体的动量。

而言之，流体动量方程是一个描述物理系统的微分方程，它表示了任意一点的流体属性（如流速、密度或压力）是如何随着时间而变化的。

体动量方程可以用来研究多种类的流体从气体到液体，以及更加复杂的物质。

它可以用来模拟复杂的气体行为，探究不同流体类型之间的不同物理现象。

流体动量方程的公式表达式可以写作：ρU/t+/xj (ρUjUi)+/x(p+ρV2/2)=ρgj其中，ρ表示流体的密度，Ui表示流体的流速，p表示流体的压力，V表示流体的阻力，g表示重力加速度，t表示时间。

流体动量方程的核心思想是结合流体力学基本定律，即“流体总动量守恒定律”、“流体压力守恒定律”、“流体动量守恒定律”和“流体密度守恒定律”来推导出关于流体动量变化的微分方程。

也就是说，流体动量方程可以用来分析流体中流体动量单位时间的变化，从而解决流体动力学问题。

流体动量方程的应用非常广泛，它可以用来模拟流体的流速，从而推出其它的物理量，比如压力、密度和温度变化。

例如，它可以用来研究气体流动的特点，如气体传存量积分方程，以及时变气体紊流方程；它还可以用来计算液体流速的变化，比如计算水力学中流体的流速、压力和能量；它也可以用来模拟风力奇变的变化，比如计算风力的大小、方向和速度。

此外，流体动量方程在现代航空航天领域也有广泛的应用。

从信息传输到宇宙探测，流体动力学的关键概念及方程都发挥着重要的作用，可以帮助我们更好地研究太空物理现象，模拟航天器的飞行运动和研究宇宙中各种流体行为。

总之，流体动量方程是流体力学中一个重要的方程，它揭示了流体在时空变化中的动量变化规律，可以用来研究多种类的流体，而且在现代航空航天、气体动力学和宇宙探测等领域也有广泛的应用。