八年级下北师大版分式的加减法同步练习
【精品】数学八年级下北师大版5.3 分式加减法同步练习2

分式加减法一.选择题1.(2018年天津市静海县中考数学二模试卷) 计算的结果是( )A.B.C. D.12.(2018年黑龙江省哈尔滨市南岗区中考数学三模试卷)下列运算正确的是( ) A.a 0=0 B.(2-)(2+)=1C.-=D.+=3.(2017年山西省中考数学试卷)化简-的结果是( ) A.-x 2+2x B.-x 2+6x C.- D.2.11()xy xy+÷等于( )A .x +yB .22x y x y +C .1x y+ D .22x y x y +3.11(1)(1)x x+÷-等于( )A .11x x +-B .11x x -+ C .221x x - D .221x x -4.222x x x x x x--÷--等于( )A .0B .2xx - C .224(2)x x x -- D .22(2)x x -- 5.当a =-2时,222212212a a a a a a a --+-+--的值为( )A .-13B .-73C .1D .-536.已知271x x x =-+,则1x x+等于( ) A .87B .78C .6D .8 二.填空题 7.分式1x,1y ,1x y+的最简共分母为______________. 8.直接写出结果:(1)1111x x x ---=_______;(2)1a ba ab a b++÷--=_________. 9.计算234()22x x x x x x ---+=____________. 10.(2018年上海市奉贤区中考数学二模试卷)计算:=______.11.计算1a ab ba b-+-=-++________________. 12.把单价为每千克m 元的茶叶p 千克与单价为每千克n 元的茶叶q 千克混合起来卖出,要使卖出的钱数不变,则混合后茶叶的定价为___________元/千克. 三.解答题13.计算22226211962x x x x x x x x -++++÷-+--14.计算22[()]33x y x y x y x x y x x+----÷+15.已知yx m x y =-,y x n x y=+,求22m n -的值.16.工程队计划修建一条长1200米的公路,采取新的施工方式后,实际每天修建公路的长度比原计划增加15米,从而缩短了工期,设原计划每天修建公路x 米,那么 (1)原计划修建这段公路需要多少天?实际修建这段公路用了多少天? (2)实际修建这段公路的工期比原计划缩短了几天?17.(2018年河南省南阳市新野县中考数学二模试卷)先化简,再求值:(-)÷(-1),其中a 为不等式组的整数解.参考答案1.解:===1,故选:D.根据同分母分式的加法法则计算可得.本题主要考查分式的加减法,解题的关键是掌握同分母分式的加减运算法则.2.解:A.a0=1(a≠0),此选项错误;B.(2-)(2+)=4-3=1,此选项正确;C.-=2-,此选项错误;D.+=,此选项错误;故选:B.根据零指数幂.平方差公式.二次根式的减法及分式的加法计算可得.本题主要考查二次根式的混合运算,解题的关键是掌握零指数幂.平方差公式及二次根式的减法法则及分式的加法法则.3.解:原式=-==-故选(C)根据分式的运算法则即可求出答案.本题考查分式的运算,解题的关键是熟练运用分式的运算法则,本题属于基础题型.4.D5.D6.A7.xy(x +y)8.0 21a ab a b+++9.2x +8 10.解:原式=-=,故答案为:.首先通分,然后再根据同分母分式加减法法则:同分母的分式相加减,分母不变,把分子相加减.进行计算即可.此题主要考查了分式的加减,关键是掌握分式加减的计算法则. 11.aba b+ 12.mp nqp q++ 13.1 14.2xx y- 15.-416.解:(1)设原计划修建这段公路需要1200x天,实际修建这段公路用了120015x +天;(2)实际修建这段公路比原计划缩短了1200x-120015x +=1200(15)x x +(天)17.解:原式=[-]=•=,∵不等式组的解为<a<5,其整数解是2,3,4,a不能等于0,2,4,∴a=3,当a=3时,原式==1.。
北师大版初中数学八年级下册《5.3 分式的加减法》同步练习卷(3)

北师大新版八年级下学期《5.3 分式的加减法》同步练习卷一.解答题(共17小题)1.计算:4(x+)÷(2+﹣)2.计算:(﹣)÷.3.计算(m+2﹣)÷.4.化简:(x+1﹣)÷.5.计算题:(1)(2).6.计算:(1);(2).7.计算:.8.化简:÷(x+2﹣)﹣.9.计算:(1);(2).10.先化简,再求值:(+)÷,其中x从﹣2、﹣1、0、1四个数中适当选取一个数.11.先化简:,再选一个你喜欢的数代入并求值.12.先化简,后求值:÷(x﹣),其中x=3.13.先化简:,然后给a选择一个你喜欢的数代入求值.14.先化简,再求值:(+)÷,其中x=12.15.先化简,再求值:()•+1,其中x=﹣3,y=.16.计算(1)+.(2)+(3)﹣x+y;(4)﹣﹣.17.化简:.北师大新版八年级下学期《5.3 分式的加减法》2019年同步练习卷参考答案与试题解析一.解答题(共17小题)1.计算:4(x+)÷(2+﹣)【分析】利用平方差公式化为同分母的分式相加减,最后相除即可.【解答】解:4(x+)÷(2+﹣)=4×÷[+﹣],=4××,=2x.【点评】本题主要考查了分式的混合运算,解题的关键是正确的因式分解.2.计算:(﹣)÷.【分析】先算括号里面的,分解因式后约分,再根据分式的加减法则算减法,最后根据分式的乘除法则约分化成最简分式即可.【解答】解:原式=(﹣)•=•=.【点评】本题主要考查对通分、约分、最简公分母,最简分式,分式的加减、乘除法则等知识点的理解和掌握,能熟练地根据法则进行计算是解此题的关键.3.计算(m+2﹣)÷.【分析】根据分式混合运算顺序和运算法则计算可得.【解答】解:原式=(﹣)÷=•=2(m+3)=2m+6.【点评】本题主要考查分式的混合运算,解题的关键是掌握分式混合运算顺序和运算法则.4.化简:(x+1﹣)÷.【分析】利用分式的混合运算顺序计算即可.【解答】解:(x+1﹣)÷=×=.【点评】本题主要考查了分式的混合运算,解题的关键是分式的约分化简.5.计算题:(1)(2).【分析】(1)先因式分解,再约分求解即可;(2)利用通分求解即可.【解答】解:(1)=•=;(2)=﹣(a+1)=﹣=.【点评】本题主要考查了分式的混合运算,解题的关键是利用因式分解约分.6.计算:(1);(2).【分析】(1)首先通分,然后利用同分母的分式相加减的运算法则求解即可求得答案;(2)先将(xy﹣x2)分解因式,然后再利用分式的乘法运算法则求解即可求得答案.【解答】解:(1)﹣x﹣1=﹣(x+1)===;(2)(xy﹣x2)•=x(y﹣x)•=﹣x2y.【点评】本题主要考查分式的混合运算.注意通分、因式分解和约分是解答的关键.7.计算:.【分析】先将原式能因式分解的先因式分解,然后将除法转化为乘法,约分化简,然后再根据分式的加减进行计算即可.【解答】解:====2.【点评】本题考查分式的混合运算,解题的关键是明确分式混合运算的计算方法.8.化简:÷(x+2﹣)﹣.【分析】根据有括号先算括号内的,再算乘除,最后算加减,从而得出结果.【解答】解:÷(x+2﹣)﹣=÷﹣=×﹣=﹣==﹣1【点评】本题考查分式的加减乘除混合运算,同时其中还要异分母分式要先通分.9.计算:(1);(2).【分析】(1)根据异分母分式相加减法则,先通分,再分母不变,分子相加减即可;(2)先算括号里面的减法,再分解因式后约分即可求出答案.【解答】解:(1)原式=,=,=.(2)原式=•,=.【点评】本题主要考查对分式的加、减、乘、除法则,约分、通分,最简公分母,最简分式等知识点的理解和掌握,能熟练地运用性质进行计算是解此题的关键.10.先化简,再求值:(+)÷,其中x从﹣2、﹣1、0、1四个数中适当选取一个数.【分析】根据分式的混合运算法则把原式化简,根据分式有意义的条件选择适当的数代入计算即可.【解答】解:(+)÷=•x+•x=x﹣1+x﹣2=2x﹣3,当x=﹣1时,原式=2×(﹣1)﹣3=﹣5.【点评】本题考查的是分式的化简求值,掌握分式有意义的条件、分式的混合运算法则是解题的关键.11.先化简:,再选一个你喜欢的数代入并求值.【分析】首先先算括号里面的加法得到,再算乘法,分解因式后约分化成最简分式即可.【解答】解:原式=,∵x≠0,1,﹣1,∴x=2时,原式==.【点评】本题主要考查对分式的加减法,分式的乘除法,最简分式等知识点的理解和掌握,能熟练地进行分式的混合运算是解此题的关键.12.先化简,后求值:÷(x﹣),其中x=3.【分析】根据运算顺序先计算括号里的,应先把括号里的两项进行通分,使分母变为x,然后利用分母不变,只把分子相减,计算出结果,接着把除式的分子利用完全平方公式分解因式,然后利用除以一个数等于乘以这个数的倒数,把除法变为乘法运算,约分即可得到最简结果,最后把x的值代入化简的式子中,即可得到值.【解答】解:原式=÷(1分)=•(2分)=.(3分)当x=3,原式==.(4分)【点评】此题考查分式的化简求值运算,解答此题的关键是把分式化到最简,然后代值计算.化简时学生应通观全局,弄清运算顺序,利用法则、定律、公式及分解因式,来简化运算.13.先化简:,然后给a选择一个你喜欢的数代入求值.【分析】利用分式的混合运算法则把原式化简,根据分式有意义的条件确定a的取值范围,代入计算即可.【解答】解:原式=(﹣)×═(﹣)×=×=∵要使分式有意义,故a+1≠0且a﹣2≠0∴a≠﹣1且a≠2∴a=1时,原式==3.【点评】本题考查的是分式的化简求值,掌握分式的混合运算法则是解题的关键.14.先化简,再求值:(+)÷,其中x=12.【分析】先将括号内的分式进行通分后相加,再将除法化为乘法,然后将x的值代入即可解答本题.【解答】解:(+)÷,=[+]•,=,=,=,当x=12时,原式==.【点评】本题考查分式的运算,解题的关键是熟练运用分式的运算法则,本题属于基础题型.15.先化简,再求值:()•+1,其中x=﹣3,y=.【分析】分化简分式,再把x=﹣3,y=代入求解即可.【解答】解:()•+1=•+1,=﹣1++1,=,当x=﹣3,y=时原式=﹣.【点评】本题主要考查了分式的化简求值,解题的关键是正确的化简分式.16.计算(1)+.(2)+(3)﹣x+y;(4)﹣﹣.【分析】(1)利用分式混合运算的顺序求解即可.(2)利用分式混合运算的顺序求解即可.(3)利用分式混合运算的顺序求解即可.(4)利用分式混合运算的顺序求解即可.【解答】解:(1)+=.(2)+=﹣==2,(3)﹣x+y=﹣=;(4)﹣﹣=+﹣=.【点评】本题主要考查了分式的混合运算,解题的关键是熟记分式混合运算的顺序.17.化简:.【分析】变形后根据同分母分式相加减法则进行计算即可,注意结果化成最简分式.【解答】解:原式=﹣===x+y.【点评】本题考查了分式的加减法则的应用,能熟练地运用法则进行计算是解此题的关键.。
北师大版八年级数学下册分式的加减法练习试题及答案

3.3 分式的加减法(1)一、目标导航1.同分母的分式的加减法的运算法则及其应用;2.简单的异分母的分式相加减的运算.二、基础过关1.计算:(1)ab ab c ab c 743+-= ;(2)ab b b a a -+-= ; (3)=+-+3932a a a __________;(4)abcac ab 433265+-= . 2.下列计算正确的是( )A .m m m 312=-+B .1=---ab b b a a C .212122++=++-+y y y y y D .b a a b b b a a -=---1)()(22 3.分式25,34ca bc a 的最简公分母是_________. 4.计算:242+-x = . 5.计算213122x x x ---- 的结果是____________. 6.一项工程,甲单独做x 小时完成,乙单独做y 小时完成,则两人一起完成这项工程需要__________小时.7.计算:(1)ab a b 1+- (2) ab b a ab b a 22)2()2(+--(3)222)3(9)3(x y x y x ----- (4)22225421a a a a a a --+--8.先化简,再求值:))(())((2222a c b a b c c a b a b a ---+---,其中3=a ,2-=b ,1-=c .三、能力提升9.若222222M xy y x y x y x y x y--=+--+ ,则M=___________. 10.化简131224a a a -⎛⎫-÷ ⎪--⎝⎭ 的结果是___________. 11.化简11x y y x ⎛⎫⎛⎫-÷- ⎪ ⎪⎝⎭⎝⎭的结果是( ) A .1 B .x y C .y x D .-1 12.计算:(1)969392222++-+++x x x x x x x (2)23111x x x x -⎛⎫÷+- ⎪--⎝⎭13. 已知03461022=+--+b a b a ,求ab a b ab a ab b a b a b a -++⨯-÷⎪⎭⎫ ⎝⎛+-2222222的值.四、聚沙成塔已知x +y 1=z +x 1=1,求y +z 1的值.3.3分式的加减法(1)1.⑴abc -7,⑵1,⑶3-a ,⑷abc b c 129810+-;2.D ;3.15bc 2;4.22+x x ;5.2235--x x ;6.y x xy +;7.⑴a1-,⑵8-,⑶33-+x x ,⑷a a 2-;8.52;9.2x ;10.-2;11.B ;12.⑴2,⑵21+-x ;13.83;四.1.。
北师大版数学八年级下册第五章分式与分式方程5.3分式的加减法同步训练

北师大版数学八年级下册第五章分式与分式方程5.3分式的加减法同步训练学校:___________姓名:___________班级:___________考号:___________一、单选题1.若22z x y +M =229x y ,则M 为( ) A .229z x y - B .229z x y - C .9z xy - D .229z x y + 2.若a b =53,则222a a b -+22242ab b b a --+2222ab b a b--的值为( ) A .12 B .14 C .2 D .43.已知M =222(1)ab a a -- ,N =22(1)b a - ,若a ≠1,则M 与N 的大小关系为( ) A .M >N B .M <N C .M ≤N D .M ≥N4.化简2222a b ab b ab ab a----等于( ) A .b a B .a bC .﹣b aD .﹣a b 5.(2016内蒙古包头市)化简221111()()ab a b a b+÷-⋅,其结果是( ) A .22a b a b- B .22a b b a - C .1a b - D .1b a-二、填空题 6.化简:22x 4x 4x x 4x 2++-=-- . 7.若x 2-6x +9与|y -2|互为相反数,则22x xy y -+22y y xy -的值为__. 8.阅读下面题目的计算过程:22223223221111x x x x x x x x -----=-----① =x -3-2x +2②=-x -1.③(1)上面计算过程从哪一步开始出现错误?请写出该步骤的代号__;(2)错误原因是__________;(3)本题的正确结论是________.三、解答题9.计算:x y y x +-+y x y --2x y y x-- 10.计算:252x x ---2x x --12x x+- 11.先化简,再求值:(2122a a a ---)÷2212a a a -+-,其中a =3. 12.已知(x -3)2与2|y -2|互为相反数,试求232xy y x y --+223xy y x --+332x x y --的值. 13.已知A =22x x y -,B =22y y x -. (1)计算:A +B 和A -B ;(2)若已知A +B =2,A -B =-1,求x 、y 的值.参考答案1.B【解析】 ∵22z x y +M =229x y , ∴M =22222299z z x y x y x y --=. 故选B.2.B【解析】222a a b -+22242ab b b a --+2222ab b a b -- =222a a b --22242ab b a b --+2222ab b a b-- =22222422a ab b ab b a b -++-- =()()()2a b a b a b -+- =a b a b-+. ∵a b =53, ∴设a=5k ,b=3k,∴原式=a b 5k 3k a b 5k 3k --=++=14. 故选B.3.C【解析】∵M =()2221ab a a --,N =()221b a -,∴M -N =221ab a a ---21b a -=()()2222211ab a b a a ---- =()22221ab a b a --- =-()()221a b a --≤0,∴M ≤N .故选C.点睛:本题考查了利用作差法比较两个代数式的大小完全平方式的非负性,作差后整理化简,若差>0,则M>N ;若差=0,则M=N ;若差<0,则M<N.4.B【解析】试题分析:原式=22()()a b b a b ab a a b --+-=22a b b ab a -+=222a b b ab ab -+=2a ab =a b,故选B . 考点:分式的加减法.5.B【解析】()()222222221111a b b a a b b a ab ab ab a b a b ab b a ab b a b a ⎛⎫⎛⎫+-+⎛⎫⎛⎫⎛⎫⎛⎫+÷-⋅=÷⋅=⨯⋅ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪-+⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭=22a b b a- . 所以选B.6.2x 2-. 【解析】先将x 2﹣4分解为(x+2)(x ﹣2),然后通分,再进行计算:.7.52【解析】∵x 2-6x +9与|y -2|互为相反数,∴x 2-6x +9+|y -2|=0,∴(x -3)2+|y -2|=0,∴x +3=0,y -2=0,∴x =3,y =2, ∴22x xy y -+22y y xy- =2222x y xy y xy y --- =222x y xy y-- =()()()x y x y y x y +-- =x y y+ =322+ =52. 8.② 丢了分母 -11x - 【解析】 ∵22223223221111x x x x x x x x -----=-----∴从第②步开始出错;错误原因是:丢了分母;正确结论是: -11x -. 点睛:本题考查了同分母分式的加减运算,其运算法则是:同分母的分式相加减,分母不变,把分子相加减,然后化成最简分式或整式.9.1【解析】试题分析:根据分式加减的运算法则进行运算即可. 试题解析:原式22 1.x y y x y x y y x y y x y x y x y x y x y x+-+--+-=--===----- 10.x +2【解析】试题分析:根据分式加减的运算法则进行运算即可. 试题解析:原式()()2222251514 2.222222x x x x x x x x x x x x x x x x +--+--++-=-+====+------ 11.2【解析】试题分析:本题考查了分式的化简求值,先把括号里按照同分母分式的加减法化简,然后把除法转化为乘法,并把分子分母分解因式约分,最后代入求值即可.解:(2122a a a ---)÷2212a a a -+- =212a a --÷2212a a a -+- =()()a 1a 12a +--×()2a 21a -- =()()a 1a 12a +--×()2a 21a -- =a 11a +-, 当a =3时,原式=a 11a +-=3131+-=2. 12.65 【解析】试题分析:先根据相反数的意义及偶次方和绝对值的非负性,求出x 和y 的值,然后把所给代数式按照同分母分式的运算法则化简,然后再点入求值.解:∵(x -3)2与2|y -2|互为相反数,∴(x -3)2+2|y -2|=0,∴x -3=0,y -2=0,∴x =3,y =2, ∴232xy y x y --+223xy y x --+332x x y-- =232xy y x y ---232xy x y --+332x x y-- =22332xy y xy x x y--++--- =22332xy y xy x x y--++-- =132xy y x x y-+-- =623194-+-- =65 13.(1)11,x y x y +-;(2)1434x y ⎧=-⎪⎪⎨⎪=⎪⎩【解析】试题分析:(1)将A 与B 代入A +B 与A -B 中计算即可得到结果;(2)根据A +B =2,A -B =-1列出方程组,即可求出x 与y 的值. 解:(1) ∵A=22x x y -,B =22y y x -, ∴A +B =22x x y -+22y y x -=1x y+; A -B =22x x y --22y y x -==1x y-; (2)∵A +B =2,∴1x y+=2,∴x +y =,∵A-B=-1,∴1x y-=-1,∴x-y=-1,∴,∴1434 xy⎧=-⎪⎪⎨⎪=⎪⎩.点睛:此题考查了同分母分式的加减法,以及解二元一次方程组,熟练掌握同分母分式加减的运算法则及二元一次方程组的解法是解本题的关键.。
2022-2023学年北师大版八年级数学下册5

5.3 分式的加减法 同步练习题 2022-2023学年北师大版八年级数学下册一、选择题1.计算m 2m−1-2m−1m−1的结果是( )A.m +1B.m -1C.m -2D.-m -22.计算x x−1-y y−1的结果为( )A.−x+y (x−1)(y−1)B.x−y (x−1)(y−1)C.−x−y (x−1)(y−1)D.x+y (x−1)(y−1)3.若代数式(M +21−x )÷x−22x−2的化简结果为2x +2,则整式M 为( )A.-xB.xC.1-xD.x +1 4.如果x -y =4,那么代数式2x x 2−y 2-2y y 2−x 2的值是( )A.-2B.2C.12D.-12 5.粗心的小倩在放学回到家后,发现把数学练习册忘在教室了,担心教室关门,于是她跑步到学校取了练习册,再步行回到家(取书时间忽略不计).已知跑步速度为x ,步行速度为y ,则她往返一趟的平均速度是( )A.xB.yC.x+y 2 D.2xy x+y 6.如果m +n =1,那么代数式(2m+n m 2−mn +1m )·(m 2-n 2)的值为( )A.-3B.-1C.1D.3 7.设n =2x+3+23−x +2x+18x 2−9,若n 的值为整数,则整数x 可以取的值的个数是( )A .5 B.4 C.3 D.28.已知A =4x 2−4,B =1x+2+12−x ,其中x ≠±2,则A 与B 的关系是( )A.A =BB.A =-BC.A >BD.A <B 二、填空题9.计算:(a a+b +2b a+b )·a a+2b = .10.计算:m 2m+1+m+11+2m = .11.对于任意两个非零实数a 、b ,定义新运算“*”如下:a*b =1b -1a ,例如:3*4=14-13=-112.若x*y =2,则2 022xy x−y 的值为 .12.某单位全体员工在植树节义务植树240棵.原计划每小时植树m 棵,实际每小时植树的棵数比原计划每小时植树的棵数多10棵,那么实际比原计划提前了 小时完成任务.(用含m 的代数式表示)13.如果2x y +3y x =-5,那么4x 2+5xy+6y 22x 2+3y 2的值为 .14.若x 2-6x +9与|y -2|互为相反数,则x 2xy−y 2+y 2y 2−xy 的值为 .三、解答题15.通分:(1)x 6ab 2,y 9a 2bc ; (2)1x 2−16,12x−8; (3)1a 2−ab ,1a 2−b 2,1a 2−2ab+b 2.16.先化简,再求值:x 2x−y -y 2x−y ,其中x =1+2√3,y =1-2√3.17.化简:-5x x 2+2x ÷(1x−2−x−3x 2−4),再从-2,-1,0,1,2中选取一个合适的数作为x 的值代入求值.18.先化简,再求值:(a −1−2a−1a+1)÷a 2−4a+4a+1,其中a =2+√3.19.先化简,再求值:2a+1a+1+a 2−2a a 2−1÷(2a−1a−1−a −1),其中a =-32.20.先化简,再求值:a 3−6a2+9aa2+2a÷(5a+2−a+2),其中a为负整数且满足不等式3-a≤2(a+6).21.先化简,再求值:(a−4a )÷a−2a2,请从不等式组{a+1>0,4a−53≤1的整数解中选择一个合适的数代入求值.22.老师设计了接力游戏,用合作的方式完成分式化简,规则是每人只能看到前一人给的式子,并进行一步计算,再将结果传递给下一人,最后完成化简.过程如图所示:(1)接力中,自己负责的一步出现错误的同学是;(2)请你书写正确的化简过程,并在“-1,0,1”中选择一个合适的数作为x的值代入求值.23.阅读下面的材料,并解答问题.分式2x+8x+2(x≥0)的最大值是多少?解:2x+8x+2=2x+4+4x+2=2(x+2)x+2+4x+2=2+4x+2, 因为x ≥0,所以x +2的最小值是2, 所以4x+2的最大值是2, 所以2+4x+2的最大值是4, 即2x+8x+2(x ≥0)的最大值是4.根据上述方法,试求分式2x 2+5x 2+1的最大值.。
北师大版八年级数学下5.3《分式的加减法》同步练习含答案

5.3分式的加减法一、选择题:1.下列计算正确的是( )A .m m m 312=-+B .1=---ab b b a a C .212122++=++-+y y y y y D .b a a b b b a a -=---1)()(22 2.分式a-b +ba b +22的值为 ( ) A.ba b b a ++-22 B .a+bC.ba b a ++22D.以上都不对3.化简329122++-m m 的结果是( ) A.962-+m mB.32-mC.32+mD.9922-+m m 4.化简11x y y x ⎛⎫⎛⎫-÷- ⎪ ⎪⎝⎭⎝⎭的结果是( )A .1B .x yC .yx D .-1二、填空题 5.当x 时,分式32x x +-有意义. 6.=-+-ab bb a a .7.(0.5)2019÷201421⎪⎭⎫ ⎝⎛= .若6m ÷a =3m ,则a = . 8.设334=-x yx ,则yx = .9.分式25,34c abc a 的最简公分母是_________. 10.计算:242+-x = .11.计算213122xx x---- 的结果是____________. 12.一项工程,甲单独做x 小时完成,乙单独做y 小时完成,则两人一起完成这项工程需要__________小时.三、计算与解答题 13.计算.(1) abab ab 142--; (2)yx y y x x +-+22;(3) b a b a +--2121; (4)222222n m n m n m n m -+-+-.14.计算.(1) 221423----÷--x x x x x ;(2) ⎪⎭⎫⎝⎛-÷⎪⎭⎫ ⎝⎛+m n m n 11;(3) 2224124421x x xx x x x ---∙-+-+();(4) 2211111a a a a ⎛⎫⎛⎫-÷- ⎪ ⎪--+⎝⎭⎝⎭.15.先化简,再求值:923312-÷⎪⎭⎫ ⎝⎛+-+x xx x ,其中x =4.16.请你先将分式111222+++-+-a aa a a a 化简,再选取一个你喜欢且使原式有意义的数代入并求值.17. 某商店有一个不准确的天平(其臂长不等)和一个10克的砝码.一位顾客想购买20克化学药品,售货员先将砝码放在左盘上,放置药品于右盘,待平衡后交给顾客.然后又将砝码放在右盘上,放置药品于左盘,待平衡后交给顾客.请判断在这次买卖中,是商店吃亏还是顾客吃亏,并说明理由.18.计算:(1)969392222++-+++x x x x x x x (2)23111x x x x -⎛⎫÷+- ⎪--⎝⎭19. 已知03461022=+--+b a b a ,求ab a b ab a ab b a b a b a -++⨯-÷⎪⎭⎫⎝⎛+-2222222的值. 20.已知x +y1=z +x 1=1,求y +z 1的值.参考答案 1.D2.C[提示:原式=.221222222ba b a b a b b a b a b a b b a ++=+++-=++-]3.B 4 B5.≠26.17.21 2m 8.3 9.15bc 2;10.22+x x ;11.2235--x x;12.yx xy +;13.(1)ab3-. (2)x-y (3)2242b a b -. (4))(2n m n m ---.14.(1)2212(1)x x x +---. (2) n m n m --(3)x . (4)a a 2+. 15.解:2322(3)(3)13932x x x x x x x x x-+-⎛⎫+÷=∙ ⎪+-+⎝⎭=x -3.当x =4时,原式=4-3=1. 16.解:a a a a a a a a a a a a a a a a a 211)1()1(1)1(1)1(11122222+-=+-=+--=+++--=+++-+-.当a =2时,代入原式= -1+2×2=3.(答案不唯一)17.解:设天平的左臂长为a ,右臂长为b (a ≠b ),第一次交给顾客的药品为x 克,第二次交给顾客的药品为y 克,则有a ·10=bx ,ay =b ·10.所以x =10a b ,y =10ba而x+y -20=ab b a ab ab b a a b b a 222)(1020)(10201010-=-+=-+,且a >0,b >0,a ≠b ,所以abb a 2)(10->0,即x+y -20>0,所以x+y >20,故商店吃亏.18.⑴2,⑵21+-x ; 19.83;20.1.。
北师大八年级数学下册 5.3 分式的加减法(1) 同步练习题
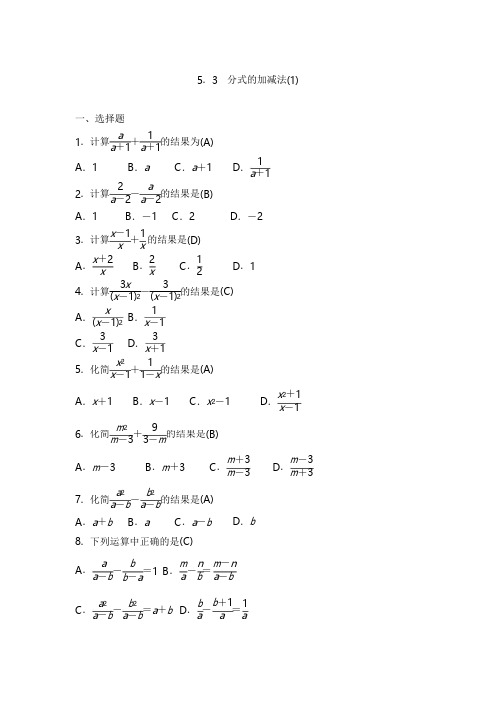
a+1a+1a-2a-2(x-1)2(x-1)2(x-1)2x-1x-1x+1x-11-x6.化简+的结果是(B) a-b a-bA.ab-aa-b5.3分式的加减法(1)一、选择题a11.计算+的结果为(A)A.1B.a C.a+1D.2a2.计算-的结果是(B)1 a+1A.1B.-1C.2x-113.计算x+x的结果是(D)D.-2x+22A.x B.x C.12D.13x34.计算-的结果是(C)x1A.B.33C.D.x215.化简+的结果是(A)A.x+1B.x-1C.x2-1m29m-33-m D.x2+1x-1A.m-3B.m+3C.m+3m-3D.m-3m+3a2b27.化简-的结果是(A)A.a+b B.a C.a-b D.b 8.下列运算中正确的是(C)b m n m-na-b-=1B.a-b=a-ba2b2b b+11 C.-a-b=a+b D.a-a=ax+1x+1x+1x+1x+111.计算:+=x+y.1×3132×4243×535+++…+(n≥3且n为整数),其结果为.13.化简:5a+3ba2-b2a2-b2a2-b2a2-b2(a+b)(a-b) (a+b)(a-b)a-b14.对于正数x,规定:f(x)=x.例如:f(1)=11+122+13=,f(2)==,f()==.+1(1)求值:f(3)+f()=1;f(4)+f()=1;2二、填空题9.化简:2x1-x+=1.x1x-110.计算-的结果为.x2y2x-y y-x12.观察下列各式:211=-;211=-;211=-;……请利用你所得结论,化简代数式:11113n2+5n 1×32×43×5n(n+2)4(n+1)(n+2)三、解答题2a-.解:5a+3b2a5a+3b-2a-=3(a+b)3==.x+111221121321314x +11 x +1 (3)求:f ( )+f ( )+…+f ( )+f (1)+f (2)+…+f (2 016)+f (2 017)的值. 解:原式=[f ( )+f (2017)]+[f ( )+f (2016)]+…+[f ( )+f (2)]+f (1)=2016x +1 1+x x +1 a +1 b +1 a +1 b +1 ∴M -N = aa +1b +1 a +1 b +1ab +a +b +1 ab +a +b +1 = - =0,2 1×2 2 6 2×3 2 3 12 3×4 3 4 20 4×5 4 5(1)由此可推导出 = - ;+ +…+ 的结 n +1 (x +1)(x +100)1(2)猜想:f (x )+f (x )=1,并证明你的结论:证明如下:∵f (x )=1 x,1∴f (x )= x 1 =, x +11 x 1x +1 ∴f (x )=f (x )= = = =1.1 1 12 017 2 016 2 1 1 12017 2016 2+0.5=2016.5.15.已知 a ,b 为实数,且 ab =1,M = a b 1 1+ ,N = + ,试确定 M 、N 的大小关系.解:∵ab =1,b 1 1 + -( + )ab +a +ab +b a +b +2 = -a +b +2 a +b +2ab +a +b +1 ab +a +b +1则 M =N .16.观察下列各式:1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 = =1- , = = - , = = - , = = - ,… 1 1 142 6 7(2)猜想出能表示上述特点的一般规律,用含字母 n 的等式表示出来(n 是正整数);(3)请用 (2)中的规律计算 1 1 1(x +1)(x +2) (x +2)(x +3) (x +99)(x +100)果.1 1 1 99解:(2)n (n +1)=n - ; (3)原式= .。
北师大版八年级(下) 中考题同步试卷:5.3 分式的加减法(09)

北师大版八年级(下)中考题同步试卷:5.3 分式的加减法(09)一、填空题(共3小题)1.若x+y=1,且x≠0,则(x+)÷的值为.2.已知a2+3ab+b2=0(a≠0,b≠0),则代数式+的值等于.3.如果实数x,y满足方程组,那么代数式(+2)÷的值为.二、解答题(共27小题)4.先化简,再求值:,其中,.5.先化简,再求值:,其中,a=1+,b=1﹣.6.先化简,再求值:(x﹣1)÷(﹣1),其中x为方程x2+3x+2=0的根.7.先化简,再求值:,其中x=3.8.先化简,再求值:,其中x=﹣1.9.先化简,再求值:,其中x=2013.10.(1)计算:﹣22++(3﹣π)0﹣|﹣3|(2)先化简()÷(1﹣),然后从﹣<x<范围内选取一个合适的整数作为x的值代入求值.11.(1)计算:;(2)先化简,再求代数式的值:,其中m=1.12.已知a2+a=0,先化简再求值:(+)÷.13.先化简,再求值:(﹣)•(x﹣1),其中x=2.14.化简求值:(﹣)÷,其中a=1﹣,b=1+.15.先化简,再求值:(1﹣)÷,其中a=.16.先化简,再求值:(1﹣)÷(x﹣),其中x=+3.17.先化简,再求值:•﹣3(x﹣1),其中x=2.18.先化简,再求值:÷﹣,其中x=﹣4.19.先化简,再求值:(﹣1)÷,其中a=+1,b=﹣1.20.先化简,再求值:(﹣)÷,其中a2+a﹣2=0.21.先化简,再求值:(﹣)÷,其中x=()﹣1﹣(π﹣1)0+.22.若|a|≠|b|,请你从三个代数式:①a2﹣2ab+b2,②3a﹣3b,③a2﹣b2中任意选两个代数式构造成分式,然后进行化简,并求当a=3,b=2时该分式的值.23.先化简,再求值:(1﹣)÷,其中x=(+1)0+()﹣1•tan60°.24.先化简,再求值:(+2)(x﹣2)+(x﹣1)2,其中x=.25.(1)解不等式组,并写出该不等式组的最小整数解.(2)先化简,再求值:÷(m﹣),其中m=﹣1,n=.26.先化简,再求值:b2﹣÷(a﹣),其中a=tan45°,b=2sin60°.27.先化简:(x﹣)÷,再任选一个你喜欢的数x代入求值.28.先简化,再求值:(1+)÷,其中x=3.29.先化简,再求值:(+)÷,其中x=﹣1.30.先化简,再求值:÷(a+2﹣),其中a2+3a﹣1=0.北师大版八年级(下)中考题同步试卷:5.3 分式的加减法(09)参考答案一、填空题(共3小题)1.1;2.﹣3;3.1;二、解答题(共27小题)4.;5.;6.;7.;8.;9.;10.;11.;12.;13.;14.;15.;16.;17.;18.;19.;20.;21.;22.;23.;24.;25.;26.;27.;28.;29.;30.;。
北师大版数学八年级下册 第五章 分式与分式方程 5.3.1 同分母的分式加减 同步练习

第五章 分式与分式方程 5.3.1 同分母的分式加减1.计算x +1x -1x 的结果为( ) A .1 B .x C .1x D .x +2x2.化简m 2m -n +n 2n -m的结果是( ) A .m +n B .n -m C .m -n D .-m -n3.下列计算正确的是( ) A .-b a +c a =-b +c a B .1a +2a =32aC.a -b a -a +b a =0 D .a a -b2-a b -a 2=0 4.化简x 2x -1+11-x的结果是( ) A .x +1 B .1x +1 C .x -1 D .x x -1 5.计算3x 2x +y +3xy x +y 的正确结果是( ) A.3x 2+3xy x +y B .3x C .3x 3y x +y D .6xy x +y6.若z x 2y 2+M =9x 2y2,则M 为( ) A.z -9x 2y 2 B .9-z x 2y 2 C .9-z xy D .z +5x 2y2 7.计算:3a +2b a 2-b 2-a a 2-b 2= . 8.化简:a +2b a -b +b b -a -2a a -b = .9.化简:x 2+4x +4x 2-4-x x -2= . 10. 小明用电脑录入汉字文稿的速度是他手抄汉字文稿速度的4倍,若小明手抄汉字文稿的速度为m 个字/小时.那么他用电脑录入4000字文稿比手抄少用 小时.11. 计算下列各题.(1)x 2x -3-9x -3;(2)32-3x -1+3x 2-3x;(3)x +y y -x +y x -y -2x -y y -x;(4)x 2-5x -2-x x -2-1+x 2-x.12. 先化简,再求值.(a +3a -1-1a -1)÷a 2+4a +4a 2-a,其中a =3.13.已知(x -3)2与2|y -2|互为相反数,试求2xy -y 3x -2y +xy -22y -3x +x -33x -2y 的值.14.阅读下面题目的计算过程:x -3x 2-1-2-2x 1-x 2=x -3x 2-1-2x -2x 2-1① =x -3-2x +2②=-x -1.③(1)上面计算过程从哪一步开始出现错误?请写出该步骤的代号 ;(2)错误原因是 ;(3)本题的正确结论是 .15.小明用电脑录入汉字文稿的速度是他手抄汉字文稿速度的4倍,若小明手抄汉字文稿的速度为m 字/小时,那么他用电脑录入4000字文稿比手抄少用多少小时?答案:1---8 AADAB B 7. 2a -b8. -19. 2x -210. 3000m 11. 解:(1)x +3;(2)1; (3)1;(4)x +2.12. 解:原式=a +2a -1·a a -1a +22=a a +2.把a =3代入,∴原式=33+2=35. 13. 解:根据题意,得:(x -3)2+2|y -2|=0,∴x=3,y =2,原式=2xy -y -xy +2+x -33x -2y =xy -y +x -13x -2y =3×2-2+3-13×3-2×2=65. 14. (1) ②(2) 丢了分母(3) -1x -115. 解:4000m -40004m =4000m -1000m =3000m小时.。
北师大版八年级下册第五章第三节分式的加减法同步练习(无答案)

a 2a
1
2a a 1
11.
计算:
x
x 2
1
1
x
1 1
12.化简:
.
13.先化简,再求值:
÷( ﹣x﹣2),其中 x=﹣2.
14.
化简求值: 9x4 y 2
3y6 2x2
y 3
,其中
y
x2
8/8
练习:
1.计算 ﹣ 的结果是( )
A.1
B.﹣1
2.化简 + 的结果是( )
C.2
D.﹣2
A.x+1
B.x﹣1
C.x2﹣1
D.
3.化简
﹣ 的结果是( )
A.﹣x2+2x
B.﹣x2+6x
C.﹣
D.
4.化简﹣
的结果为( )
A.﹣x+1
B.﹣x﹣1
C.﹣
D.
5
.
化简
a2 b2 ab
ab b2 ab a2
不要因为长期埋头科学,而失去对生活、对美、对待诗意的感受能力。——达尔文
题型一、同分母分式的加减
1.计算
的结果为( )
分式的加减法
A.1
B.a
C.a+1
D.
2.计算
﹣
的结果是( )
A.
B.
C.
D.
3.化简 + 的结果是( )
A.﹣x﹣y
B.y﹣x
4 .计算: x2 1 x 1 x 1
5.化简:
﹣
A.
B.
11. 化简 a b 的结果是(
)
ab ab
a2 b2 A. a2 b2
北师大版八年级数学下册同步训练课件第5章第36课时 分式的加减法

整理,得 (1-abc) (a+1)1(1+bc)+(b+1)1(1+ac)+(c+1)(11+ab)=0. ∵a,b,c 都是正数,∴1-abc=0,即 abc=1.
(2)x+1 1+x-1 1+x2-21x+1.
解
:
原
式
=
1 x+1
+
1 x-1
+
1 (x-1)2
=
(x-1)2 (x+1)(x-1)2
+
x2-1 (x+1)(x-1)2
+
x+1 (x+1)(x-1)2
=
x2-2x+1+x2-1+x+1 (x+1)(x-1)2
=(x2+x21-)(xx+-11)2.
乙两瓶中各取质量相等的盐水混合制成新盐水的含盐量
为( A ) A.a2+abb
B.a+abb
C.a1b
D.随所取盐水的质量而变化
2.(2019 秋·越秀区期末)分式2a33b2c与6aa-2bb4c的最简公 分母是__6_a_3b_4_c__.
3.通分: (1)a22-a 9与a2-63a+9; 解:a22-a 9=(a-2a3(a)2-(a+3) 3), a2-63a+9=(a-3(3a)+2(a3+) 3);
第五章 分式与分式方程
第五章 分式与分式方程
第五章 分式与分式方程
第五章 分式与分式方程
第五章 分式与分式方程
知识点二 异分母分式的加减法 ☞ 例 2 (教材 P121 习题 5.5 第 2 题)计算: (1)xy-xy-x2x+yy2; 解:原式=xxy2-xyy2 -x2+ xyy2=x2-y2-xyx2-y2=-x2yy2= -2xy;
(2)4a(xx+2)与6b(xy+2). 解:4a(xx+2)=12ab3(bxx+2), 6b(xy+2)=12ab2(axy+2).
北师大版八年级下册5.3分式的加减同步练习(word无答案)

5.3分式的加减同步练习一、选择题1.化简的结果为()A.B.a﹣1 C.a D.12.已知=3,则代数式的值是()A.B.C.D.3.下列式子,成立的是()A.B.C.D.=04.若(+)y=1(其中x≠±2),则y等于()A.x﹣2 B.x+2 C.﹣x﹣2 D.﹣x+25.已知:2+=22×;3+=32×;4+=42×;5+=52×…,若10+=102×符合前面式子的规律,则a+b=()A.99 B.109 C.100 D.1206.已知x+y=4,x﹣y=,则式子(x﹣y+)(x+y﹣)的值是()A.48 B.12C.16 D.127.若x+y=2,xy=﹣2,则+的值是()A.2 B.﹣2 C.4 D.﹣48.如果a﹣b=,那么代数式(a﹣)•的值是()A.﹣2 B.2 C.﹣D.二、填空题9.计算﹣的结果是.10.已知=+,则实数A=.11.若=A﹣,则A=.12.已知a2+1=3a,则代数式a+的值为.13.已知xy=1,则=.14.已知=+,则整式A﹣B=.三、解答题15.计算:(1)+﹣.(2)(m+2﹣)÷.(3)(﹣).(4)(1﹣)÷.16.先化简,再求值:(1)(x﹣2﹣)÷,其中x=.(2)﹣÷,其中x=﹣2.(3)÷x,其中x=.(4)(1+)•﹣,其中x=﹣2.(5)﹣÷,其中x=2.17.李老师在黑板上写了一道题目,计算:.小宇做得最快,立刻拿给李老师看,李老师看完摇了摇头,让小宇回去认真检查.请你仔细阅读小宇的计算过程,帮助小宇改正错误.=(A)=(B)=x﹣3﹣3(x+1)(C)=﹣2x﹣6(D)(1)上述计算过程中,哪一步开始出现错误?;(用字母表示)(2)从(B)到(C)是否正确?;若不正确,错误的原因是;(3)请你写出此题完整正确的解答过程.。
