BCJR译码算法的相关性研究
LS,MMSE,LMMSE,ML,MAP,LMS,AR,MSE误差等算法做一个比较清晰的介。。。

LS,MMSE,LMMSE,ML,MAP,LMS,AR,MSE误差等算法做⼀个⽐较清晰的介。
/s/blog_8afae2970101cz9d.htmlQ:是否有朋友能对LS,MMSE,LMMSE,ML,MAP,LMS,AR,MSE误差等算法做⼀个⽐较清晰的介绍呢S:谈谈我的理解,不当之处欢迎⼤家指正:这⼀系列算法都可以是基于接收数据来对⽬标数据进⾏估计,1。
LS⽤于接收到的数据块长度⼀定,并且数据、噪声(⼲扰)的统计特性未知或者⾮平稳的情况,其优化⽬标是使得基于该数据块的估计与⽬标数据块间加权的欧⼏⾥德距离最⼩,当有多个数据块可⽤时,可⽤其递归算法RLS减⼩计算量;2。
MMSE的优化⽬标是为了使基于接收数据的估计值和⽬标数据的均⽅误差最⼩化,LMMSE算是MMSE的特例,在这种情况下,基于接收数据的估计值是接收数据的线性变换,在数据统计特性已知的情况下,某些时候可以直接求解,⽐如维纳解;在数据统计特性未知但是平稳的时候,可以通过递归迭代的算法求解,诸如:LMS算法。
3。
ML和MAP顾名思义,前者是为了使似然概率最⼤后者是为了使得后验概率最⼤,具体说来就是,假设接收数据为rx,⽬标数据为tx,在已知rx的情况下,ML就是求使得p(rx|tx)最⼤的tx,MAP就是求使得p(tx|rx)最⼤的tx。
4。
AR(⾃回归),这是假设⽬标数据满⾜⾃回归模型,这时我们需要求解的就是相应的模型的系数了。
5。
MSE?如果是指均⽅误差,就可参见前⾯的叙述。
我记得有种算法是MOE,即最⼩化输出能量,结合⼀定的约束,它可以使得输出信号中⽬标信号成分不变,但是⼲扰最⼩化。
我先来谈谈ML(Maximum Likelihood,最⼤似然)和MAP(Maximum a posteriori Probability,最⼤后验概率)算法的区别在MAP算法中,后验概率由似然函数和先验概率组成。
由于引⼊了数据源的先验统计特性,理论上MAP算法⽐最⼤似然估计算法(ML)估计得要准确(如果输⼊的数据先验概率不等的话,如果先验概率相等的话性能是相当的)。
Turbo码原理简介
Turbo 码原理简介1993年C.Berrou 、A.Glavieux 和P.Thitimajshiwa 首先提出了称之为Turbo 码的并行级联编译码方案。
Turbo 码性能取决于码的距离特性。
线性码的距离分布同于重量分布,如果低重量的输入序列经编码得到的还是低重量的输出序列,则距离特性变坏。
该特性对于块码来说不存在问题;然而对于卷积码,则是个非常严重的问题。
因为卷积码的距离特性是影响误码率的一个非常重要的因素。
在Turbo 码中,利用递归系统卷积码(RSC)编码器作为成员码时,低重量的输入序列经过编码后可以得到高重量的输出序列。
同时交织器的使用,也能加大码字重量。
实际上,Turbo 码的目标不是追求高的最小距离,而是设计具有尽可能少的低重量码字的码。
Turbo 码由两个递归系统卷积码(RSC)并行级联而成。
译码采用特有的迭代译码算法。
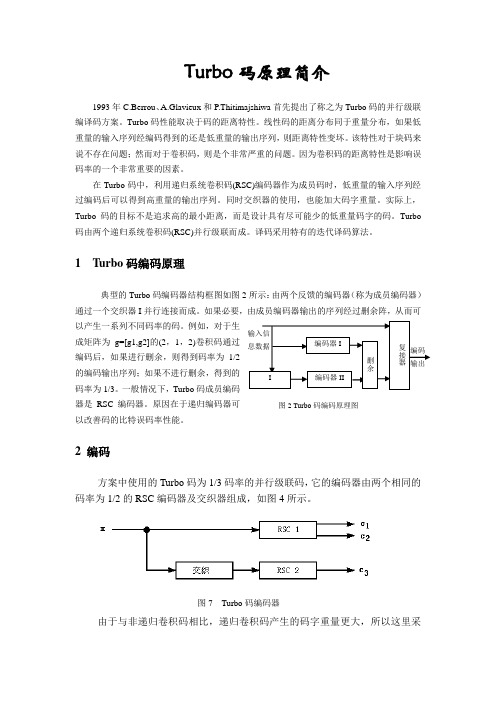
1 Turbo 码编码原理典型的Turbo 码编码器结构框图如图2所示:由两个反馈的编码器(称为成员编码器)通过一个交织器I 并行连接而成。
如果必要,由成员编码器输出的序列经过删余阵,从而可以产生一系列不同码率的码。
例如,对于生成矩阵为g=[g1,g2]的(2,1,2)卷积码通过编码后,如果进行删余,则得到码率为1/2的编码输出序列;如果不进行删余,得到的码率为1/3。
一般情况下,Turbo 码成员编码器是RSC 编码器。
原因在于递归编码器可以改善码的比特误码率性能。
2 编码方案中使用的Turbo 码为1/3码率的并行级联码,它的编码器由两个相同的码率为1/2的RSC 编码器及交织器组成,如图4所示。
由于与非递归卷积码相比,递归卷积码产生的码字重量更大,所以这里采图7 Turbo 码编码器输入信 息数据编码器II编码器II删余复接器编码 输出图2 Turbo 码编码原理图用了两个相同的系统递归卷积码(RSC)。
信息序列分成相同的两路,第一路经过RSC 编码器1,输出系统码1c 及校验码2c 。
基于SOVA与BCJR算法的CPM信号改进译码算法

基于SOVA与BCJR算法的CPM信号改进译码算法作者:傅蕾王雷王亮来源:《软件导刊》2017年第01期摘要摘要:BCJR算法是一种最优译码算法,但是计算量大、译码复杂;SOVA算法译码简单,但是性能稍差。
针对这两种算法的缺点,在连续相位调制信号系统中,提出一种基于减少搜索T-BCJR与SOVA算法的改进译码算法。
该算法能在减少迭代译码时的搜索路径数量、降低译码复杂度的同时达到比较好的译码性能。
经过实验仿真,验证了该算法的可行性与优越性。
关键词关键词:SOVA;T-BCJR;连续相位调制;迭代译码DOIDOI:10.11907/rjdk.162309中图分类号:TP312文献标识码:A文章编号文章编号:16727800(2017)001003503引言连续相位调制CPM(Continuous Phase Modulation)信号是一种恒包络且相位连续的调制信号,与其它调制方法相比,具有很高的频谱和功率利用率。
由于信号的包络恒定,对功放的非线性特性不敏感,可以使用C类(非线性)功率放大器。
另外,信号相位连续,带外辐射小,产生的邻道干扰也比较小。
因此,CPM调制技术近年来受到广泛关注。
G.Ungerboeck[1]提出了网格编码调制TCM (Trellis Coded Modulation)的设计方法,将线性调制技术与信道编码结合,很大程度上提高了系统的性能。
C.Berrou[2]提出了Turbo码,迭代解码的结构被应用到串行级联CPM系统的译码中。
孙锦华[3]提出了一种基于RSSD思想的减状态译码算法,降低了译码复杂度。
本文主要探讨连续相位调制信号在高斯白噪声信道下的译码算法,并提出一种基于Turbo 译码算法的改进结构,该算法结合了Turbo码译码的SOVA与BCJR算法的优点。
通过仿真实验,验证了该算法的可行性,可以在减少算法复杂度的同时改善系统的译码性能。
1基本概念1.1CPM概念与分解模型CPM信号的一般表达式为: S(t,α)=2ETcos(2πfct+φ(t,α)+φ0)(1)其中,fc是载波频率,φ0是载波的初始相位,T为码元周期,E是一个码元周期T内的信号能量,φ(t,α)是携带信息的相位,表示如下:φ(t,α)=2πh∑nk=-∞αkq(t-kT)nT≤t≤(n+1)T(2)其中,αk是M进制的信息符号,取值范围是αk∈{±1,±3,…,±(M-1)};h=K/P(K,P为互斥正整数)是调制指数;q(t)为相位响应函数,定义为脉冲函数g(t)的积分:q(t)=∫τ0g(τ)dτ(3)常见的脉冲函数有L-REC方波、L-RC升余弦和L-GMSK高斯成形脉冲。
BCH编码与译码简析

BCH编码自1950年汉明发表了纠正单个随机错误的码以来,几乎用了近十年的时间,才于1959年由霍昆格姆(Hocquenghem),1960年由博斯(Bose)和雷-查德胡里(Ray-Chaudhuri)分别提出了纠正多个随机错误的循环码——BCH码(Bose、Ray-Chaudhuri与Hocquenghem的首字母缩写)的构造方法。
BCH 码是用于校正多个随机错误模式的多级、循环、错误校正、变长数字编码,是迄今为止所发现的一类很好的线性纠错码类。
它的纠错能力很强,特别在短和中等码长下,其性能接近于理论值,并且构造方便,编码简单。
特别是它具有严格的代数结构,因此它在编码理论中起着重要的作用。
BCH码是迄今为止研究得最为详尽,分析得最为透彻,取得的成果也最多的码类之一。
1960年皮德逊(Peterson)从理论上解决了二进制BCH码的译码算法,奠定了BCH码译码的理论基础。
稍后,格林斯坦(Gorenstein)和齐勒尔把它推广到了多进制。
1966年伯利坎普(Berlekamp)利用迭代算法解BCH码,从而大大加快了译码速度,从实际上解决了BCH码的译码问题。
由于BCH码性能优良,结构简单,编译码设备也不太复杂,使得它在实际使用中受到工程技术人员的欢迎,是目前用得最为广泛的码类之一。
一、BCH码的构建BCH 码使用有限域上的域论与多项式。
为了检测错误可以构建一个检测多项式,这样接收端就可以检测是否有错误发生。
要构建一个能够检测、校正两个错误的BCH 码,我们要使用有限域GF(16) 或者Z2[x]/<x4 + x + 1>。
如果α是m1(x) = x4 + x + 1的一个根,那么m1就是α的极小多项式,这是因为m1(x) = (x -α)(x -α2)(x -α4)(x -α8)=x4 + x + 1。
如果要构建一个能够纠正一个错误的BCH码,那么就使用m1(x),这个代码就是所有满足:C(x)≡0(mod m1(x))且根为α,α2,α4,α8 的多项式C(x)。
第五章 卷积码的译码算法 for presention

011201, 120211, 120111)
图 5.4 DMC 信道下的 Viterbi 算法 每个状态上的数字表示幸存路径的度量,另一个路径就将被删除(绿 线部分) 。这样最后的码字(红线部分的输出)判决为:
ˆ (111,010,110,011,000,000,000) v
(5.8)
ˆ (11000) 。注意:网格图中最后的 m=2 个分 它对应的输入序列为 u
第五章 卷积码的译码算法
第五章 卷积码的译码算法
卷积编码器自身具有网格结构,基于此结构我们给出两种译码算法: Viterbi 译码算法和 BCJR 译码算法。基于某种准则,这两种算法都是最 优的。1967 年,Viterbi 提出了卷积码的 Viterbi 译码算法,后来 Omura 证明 Viterbi 译码算法等效于在加权图中寻找最优路径问题的一个动态规 划(Dynamic Programming)解决方案,随后,Forney 证明它实际上是 最大似然(ML,Maximum Likelihood)译码算法,即译码器选择输出的 码字通常使接收序列的条件概率最大化。BCJR 算法是 1974 年提出的, 它实际上是最大后验概率(MAP,Maximum A Posteriori probability)译 码算法。这两种算法的最优化目标略有不同:在 MAP 译码算法中,信息 比特错误概率是最小的,而在 ML 译码算法中,码字错误概率是最小的, 但两种译码算法的性能在本质上是相同的。 由于 Viterbi 算法实现更简单, 因此在实际应用比较广泛, 但在迭代译码应用中, 例如逼近 Shannon 限的 Turbo 码, 常使用 BCJR 算法。 另外, 在迭代译码应用中, 还有一种 Viterbi 算法的变种: 软输出 Viterbi 算法 (SOVA, Soft-Output Viterbi Algorithm) , 它是 Hagenauer 和 Hoeher 在 1989 年提出的。
文献综述

Adaptive Maximum Likelihood Sequence Detection for QPSK Coherent Optical Communication System
在本文中,主要研究了同时存在 LPN和NLPN时MLSD和自适 应MLSD的性能。仿真结果表明MLSD可以提供最优性能。 图 1 描述了单信道 QPSK 建模图。每 100km 光纤后有一个光放 大器用以补偿功率衰减,为了集中研究LPN和NLPN的影响,假设 CD和PMD可以用DSP和光学元件补偿。
图2 相位分集相干接收机
其中,R是平衡光电检测器的响应度。
Coherent Demodulation of Differential 8-Phase-Shift Keying with Optical Phase Diversity and Digital Signal Processing
激光相位噪声对8PSK信号性能的影响
图1 实验装置
Coherent Demodulation of Differential 8-Phase-Shift Keying with Optical Phase Diversity and Digital Signal Processing
信道编码原理及应用

信道编码原理及应用信道编码是指在通信系统中通过对信息进行编码和解码,以提高信号的可靠性和传输效率的技术手段。
信道编码的核心思想是利用冗余信息对原始信息进行编码,从而增强抗干扰能力,减小误码率,提高传输质量。
信道编码的原理主要包括三个方面:信息源编码、信道编码和信道解码。
1. 信息源编码:将原始信息进行压缩和转换,使得信息能够以更高的效率进行传输。
常见的信息源编码技术有Huffman编码、算术编码和Lempel-Ziv编码等。
2. 信道编码:将经过信息源编码的信号进行处理,引入冗余信息以增加信号的可靠性和抗干扰能力。
常用的信道编码技术有奇偶校验码、循环冗余检验码(CRC)、海明码(Hamming Code)和卷积码等。
其中,卷积码是一种常用的信道编码方法,通过引入冗余比特来控制干扰和噪声对信号传输的影响。
3. 信道解码:在接收端对编码后的信号进行解码,恢复原始信息。
信道解码的目标是最大程度地减小误码率,将错误的信号恢复为正确的原始信息。
常见的信道解码算法有最大似然译码、Viterbi译码和BCJR算法等。
Viterbi译码是一种基于动态规划思想的译码算法,适用于卷积码等线性块码的译码。
信道编码的应用广泛,主要体现在以下几个方面:1. 提高数据传输的可靠性:信道编码可以通过增加冗余信息来提高数据传输的可靠性,减小误码率。
在无线通信中,高效的信道编码技术可以有效抵抗信道噪声、多径衰落和干扰等,提高无线信号的抗干扰能力。
2. 数据加密和安全保障:信道编码可以用于数据加密和安全传输。
通过对数据进行编码,可以增加信息的随机性和复杂性,从而达到数据加密和保密传输的目的。
3. 提高频谱利用率:信道编码可以在一定程度上提高频谱的利用率。
通过在传输中引入编码冗余信息,可以减小信噪比要求,实现更高的信号传输速率。
4. 节省传输带宽和能耗:信道编码可以通过有效减小数据传输的冗余度,节省传输带宽和能耗。
在数据传输中,通过合理设计信道编码方案,可以有效降低信号的传输功耗,提高能源利用效率。
极化码:主要概念和实用译码算法汇总

极码:主要概念和实用译码算法摘要极码代表一类新兴的纠错码,他的功率接近一个离散无记忆信道的容量。
本文旨在说明其生成与解码技术的原则。
与传统能力编码策略不同,它试图让代码尽可能随机,极性代码遵循不同的原理,这也是由香农通过创建一个典型共同组提出的。
信道极化,一个概念的核心,就是极性代码,在数字世界中的马太效应之中被直观地阐述,对极性编码的构造方法进行了详细的概述。
极性码蝴蝶结构介绍中,源位相关,证明SC算法的使用为有效的解码。
从概念和实践的角度研究了供应链解码技术。
最先进的解码算法,如BP和一些广义的SC解码,也在一个广泛的框架下解释了。
仿真结果表明,极性码的级联与CRC码的性能优于Turbo码和LDPC码。
一些在实际情况下有前途的研究方向在最后也被讨论。
摘要 (1)引言 0通道极化 (1)编码和结构 (3)编码原则 (4)通道选择 (5)连续取消解码 (6)解码原理 (7)简单SC译码过程 (8)更有力的译码算法 (9)提高的SC译码过程 (9)CRC-AIDED解码 (11)置信传播解码 (11)ML或MAP解码 (11)优点和缺点 (12)极性码的缺点 (13)未来的研究方向 (14)结论 (15)附录 (15)引言在过去的六年中见证了数字通信编码理论的成功。
克劳德·香农著名的信道编码定理断言代码的存在,信息可以在可靠的噪声信道上传输速率信道容量。
三个基本想法背后的信道编码定理的证明是:(1).随机选择的代码(2).对于大型代码长度的联合渐近等分(AEP)之间的传输码字和接收序列。
(3).最优最大似然(ML)解码或次优联合典型的解码。
联合AEP在证明过程中扮演着重要的角色,在某种意义上,它保证接收到的序列与共同典型传输码字相似,并且共同典型解码错误的概率消失。
当然随机编码也很重要,但只是为了便于数学证明好的代码的存在。
逼近能力与实际编/解码复杂度是编码理论的一个主要挑战。
幸运的是,在过去的二十年里许多“turbo-like”代码家族,如涡轮码和低密度奇偶校验(LDPC)码,已经被发现实现这一目标。
bpsk调制信道卷积码的bcjr译码过程

BPSK调制信道卷积码的BCJR译码过程1. 引言在数字通信系统中,为了提高可靠性和传输效率,通常会采用调制和编码技术。
BPSK调制是一种常用的数字调制方式,而卷积码则是一种常用的编码方式。
BCJR (Bahl, Cocke, Jelinek, Raviv)算法是一种经典的软判决译码算法,广泛应用于卷积码的解码过程中。
本文将详细介绍BPSK调制信道卷积码的BCJR译码过程,包括相关理论背景、算法原理、步骤和实现方法等内容。
2. 背景知识2.1 BPSK调制BPSK(Binary Phase Shift Keying)是一种二进制相位调制方式,使用两个不同的相位表示二进制数据0和1。
具体而言,在BPSK调制中,将二进制数据0映射为相位为0°的载波信号,将二进制数据1映射为相位为180°(或π)的载波信号。
2.2 卷积码卷积码是一种线性时不变系统,在编码过程中利用一个或多个寄存器进行状态转移,并通过线性组合生成输出。
卷积码的编码过程是一种冗余度增加的操作,可以提高系统的抗干扰和纠错能力。
卷积码由三个参数表示:n、k和m。
其中,n表示每个码字的比特数,k表示信息比特数,m表示寄存器数。
通过这些参数,可以得到一个(n, k, m)卷积码。
2.3 BCJR算法BCJR算法是一种基于概率图模型的软判决译码算法,适用于线性时不变系统中的序列译码问题。
它利用前向和后向变量计算路径概率,并通过最大后验概率准则进行判决。
3. BCJR译码算法原理BCJR译码算法是一种迭代解码算法,主要包括前向过程、后向过程和路径更新三个步骤。
3.1 前向过程前向过程用于计算给定观测序列下每条路径的前向变量α。
首先,定义t时刻状态为s_i(i为状态索引),观测为o_t,则前向变量α在t时刻、状态s_i下的定义如下:α(t, s_i) = P(o_1, o_2, …, o_t, s_t = s_i)接着,根据递推关系计算前向变量α(t, s_i):α(t, s_i) = Σ[α(t-1, s_j) * a_ij * b_j(o_t)] (j为状态索引)其中,a_ij表示状态转移概率,b_j(o_t)表示观测到o_t时处于状态s_j的概率。
bcjr算法原理

bcjr算法原理
哎,兄弟,今儿咱来聊聊这个bcjr算法原理嘛。
虽然咱是四川人,但咱也得学点新鲜玩意儿,不是?这个bcjr算法啊,就像咱们贵州的酸汤鱼一样,味道独特,做法精细。
首先啊,你得明白这个算法是干啥子的。
说白了,它就是一种解码算法,就像咱陕西人吃的油泼面,面条筋道,调料得当,才能吃出那个味儿。
bcjr 算法就是用来解码卷积码的,把一堆乱码给咱整成能看懂的信息。
那它是咋工作的呢?这就好比咱北京炸酱面的制作过程,得一步步来,不能急。
首先,它得有个初始状态,就像炸酱面得准备好面条和酱一样。
然后,它就开始根据接收到的信号,一步步地进行解码。
这就像炸酱面开始烹饪,面条煮熟,酱也炒得喷香。
在这个过程中,bcjr算法会不断地计算路径度量,就像咱四川人做火锅,得掌握好各种调料的比例,才能让火锅味道恰到好处。
这些路径度量就是帮助算法判断哪条路径是最有可能的,从而找到正确的解码结果。
最后啊,这个算法就能给咱输出解码后的信息了,就像端上一碗香喷喷的炸酱面,咱就能大快朵颐了。
这就是bcjr算法原理的简要介绍,虽然咱说得有点土气,但道理是一样的,都是为了让大家能更容易理解。
所以说啊,学习这个bcjr算法原理,就像咱们学习各地的美食文化一样,得用心去感受,去体会其中的奥妙。
只有这样,咱才能真正掌握它,让它为咱的生活增添一份色彩。
5G无线通信系统物理层面临的挑战分析

5G无线通信系统物理层面临的挑战分析1、无线通信物理层技术基础物理层技术特别是调制、编码、多址、双工等技术,可以说是无线通信技术中的核心与灵魂,在学术界进行了广泛而深刻的研究。
随着移动通信的迅速发展和芯片技术进步带来的处理能力大幅提升,很多以前提出的技术在产业界得以实现,因而近二十年来无线通信应用技术迎来了爆发式的发展。
新技术应用带来了频谱效率和用户体验的大幅提升,速率从不足100kbit/s发展到了100Mbit/s以上。
然而,技术飞速发展繁荣的另一方面是,现有通信技术实现了自20世纪50年代以来无线通信原理上的大多技术储备,想要寻求突破性的物理层技术变革已非常困难。
可这也说明了现有技术在相当广阔的领域内已经达到原理上的极限,更重要的或许不再是突破极限而是更加灵活的应用。
由于场景多种多样,很难有一种技术适用于所有场景,因而如何将不同场景下的技术整合起来,采用灵活的物理接入技术将是物理层技术未来主要的发展方向之一。
2、LTE系统物理层技术分析现有LTE系统物理层技术中,编码采用Turbo码,调制采用QAM (QuadratureAmpli-tudeModulation,正交振幅调制)技术和MIMO技术,多址技术是OFDMA(OrthogonalFre-quencyDivisionMultipleAccess,正交频分多址)/SC-FDMA (Single-carrierFrequency-Di-visionMultipleAccess,单载波频分多址),双工则是FDD或TDD两种方式。
根据信息论中香农有噪信道传输定理,存在被称为信道容量的界,使得一切小于信道容量的速率都能无差错传输,而大于信道容量速率的传输都会出现差错。
而信源信道编码分离定理又表明,可以分别进行信源编码和信道编码而不损失信道容量,这使得现有通信技术在物理层传输时都不考虑信源编码,即假设信源编码是理想的,这时信道编码的输入便是独立等概率分布的0、1比特。
基于SOVA与BCJR算法的CPM信号改进译码算法

关键词 : S O VA; T—B C J R; 连续相位调制 ; 迭代译码
D OI : 1 0 . 1 1 9 0 7 / r j d k . 1 6 2 3 0 9
中图分类号 : TP 3 1 2
文献标识码 : A
文章编 号 : 1 6 7 2 — 7 8 0 0 ( 2 0 1 7 ) 0 0 1 - 0 0 3 5 — 0 3
C P M 信 号 的一 般 表 达 式 为 :
s( t , a)一
√ 筝 c o s ( 2  ̄ f , t ) )( 1 )
其中, / 是载波频率 , 。 是 载 波 的 初 始 相 位 ,丁 为码
元周期 , E 是 一个码 元周期 T 内的信号 能量 , ( , a ) 是 携带信息的相位 , 表示如下 :
GP S导 航 与 接 收 、 毫 米 波 导 引头 及 数 据 处 理 技 术 ; 王亮( 1 9 9 0 一) , 男, 江 苏泰 州人 , 南 京 理 工 大 学 电子 技 术 与 光 电 工 程 学 院
硕士研究生 , 研 究 方 向 为 通 信 与 信 息 系统 。
第1 6 卷 第1 期
2 0 l 7 年1 j
软 件 导 刊
S of t wa r e Gu i d e
Vo 1 .1 6 No.1
J a n.2 Ol 7
基于 S OVA 与 B C J R算 法 的 C P M 信 号 改 进 译 码 算 法
傅 蕾 , 王 雷 , 王 亮
q ( £ ) 一l g ( r ) r
( 3 )
常 见 的脉 冲 函数 有 L —R E C方 波 、 L —R C升 余 弦 和 L 。
关于bpsk调制信道卷积码的bcjr译码过程的文章

关于bpsk调制信道卷积码的bcjr译码过程的文章BCJR译码是一种常用的译码算法,用于解码卷积码。
在卷积编码中,信息位经过编码后变为冗余位,以增加信道的可靠性。
而BCJR译码则是通过对接收到的信号进行分析和计算,以恢复出原始的信息位。
在BPSK调制中,二进制相移键控(BPSK)是一种常见的调制方式。
它将数字信号转换为模拟信号,并通过改变信号的相位来表示不同的二进制值。
BPSK调制可以通过将1映射为正弦波,0映射为负弦波来实现。
BCJR译码过程可以分为三个主要步骤:前向计算、后向计算和路径回溯。
首先是前向计算。
在这一步骤中,我们需要计算每个时刻接收到的信号与每个可能状态之间的距离。
这个距离可以通过比较接收到的信号与每个可能状态下预期信号之间的差异来计算得出。
然后,我们需要根据这些距离值计算前向概率。
接下来是后向计算。
在这一步骤中,我们需要计算每个时刻接收到的信号与每个可能状态之间的距离,并根据这些距离值计算后向概率。
后向概率表示在给定接收到的信号的情况下,系统处于某个特定状态的概率。
最后是路径回溯。
在这一步骤中,我们需要根据前向和后向概率计算每个时刻的最优路径。
最优路径表示在给定接收到的信号的情况下,系统经过的状态序列中最有可能是真实状态序列的路径。
通过这三个步骤,我们可以得到译码器输出的最有可能的信息位序列。
BCJR译码算法通过对接收到的信号进行分析和计算,可以有效地恢复出原始的信息位。
总结起来,BCJR译码是一种常用于解码卷积码的算法。
它通过前向计算、后向计算和路径回溯三个步骤来恢复出原始信息位序列。
在BPSK调制中,BCJR译码可以帮助我们从接收到的信号中恢复出原始二进制信息。
这种译码算法在通信系统中具有重要意义,并被广泛应用于各种无线通信领域。
bcjr算法的分支概率

bcjr算法的分支概率BCJR算法是一种经典的推导算法,用于对线性块码进行译码。
它是由Bahl、Cocke、Jelinek和Raviv于1974年提出的,因此也被称为BCJR算法。
该算法主要用于实现硬判决译码和软判决译码。
它通过利用Viterbi译码和前向-后向算法,可以计算出译码器的输出和分支概率。
分支概率是指给定一条路径,根据当前输入和译码器状态,计算出跳转到下一个状态的概率。
在BCJR算法中,假设接收到的数据经过了加性高斯白噪声通道,译码器的输入是通过对接收数据进行采样得到的。
根据译码器的内部状态和输入数据,译码器会经过一个状态转移,并输出对应的译码结果。
在BCJR算法中,概率计算主要分为两个步骤:前向概率计算和后向概率计算。
前向概率计算是指根据当前状态和输入数据,计算从起始状态到当前状态的路径上的概率。
在计算前向概率时,需要利用当前输入数据的概率密度函数、状态转移概率和输出概率分布函数。
根据当前状态和输入数据,首先计算得到当前状态下的输出概率分布函数。
然后,根据前一个状态和输入数据计算得到前一个状态到当前状态的转移概率。
最后,通过将前一个状态的前向概率乘以转移概率和输出概率,得到当前状态的前向概率。
后向概率计算是指根据当前状态和输入数据,计算从当前状态到终止状态的路径上的概率。
在计算后向概率时,同样需要利用当前输入数据的概率密度函数、状态转移概率和输出概率分布函数。
根据当前状态和输入数据,首先计算得到当前状态下的输出概率分布函数。
然后,根据后一个状态和输入数据计算得到当前状态到后一个状态的转移概率。
最后,通过将后一个状态的后向概率乘以转移概率和输出概率,得到当前状态的后向概率。
利用前向概率和后向概率,可以计算出每个状态上的概率值。
根据每个状态上的概率值,可以计算出从每个状态到下一个状态的分支概率。
分支概率是指给定一条路径,根据当前输入和译码器状态,计算出跳转到下一个状态的概率。
分支概率是通过将前向概率和后向概率相乘,并除以译码器的输出概率,得到每个状态到下一个状态的概率。
bpsk调制信道卷积码的bcjr译码过程

标题:深入探讨BPSK调制信道卷积码的BCJR译码过程一、引言BPSK调制信道卷积码是现代通信领域中一种重要的调制和编码技术,其BCJR译码过程是保证通信系统中高可靠性和高错误纠正能力的关键环节。
本文将从BPSK调制信道卷积码的基本原理入手,逐步深入探讨其BCJR译码过程,旨在为读者提供全面、深刻的理解。
二、BPSK调制信道卷积码基本原理BPSK(二进制相移键控调制)是一种基本的数字调制方式,它将数字信号转换为模拟信号,并通过调制过程传输。
而信道卷积码则是一种纠错编码方式,通过引入冗余信息,提高信道传输的可靠性。
BPSK调制信道卷积码将这两种技术相结合,既能实现高效的数字调制,也能提高信道传输的可靠性和抗干扰能力。
三、BCJR译码过程概述BCJR译码是一种基于图论的译码算法,它能有效地对卷积码进行译码,并在有噪声的信道条件下实现可靠的译码性能。
其基本原理是利用图的搜索和路径求和,来寻找最大似然路径,从而实现对卷积码的译码。
BCJR译码过程涉及到前向和后向步骤,需要对信道条件、卷积码结构等多方面因素进行全面考虑和分析。
四、BPSK调制信道卷积码的BCJR译码过程详解1. 信道条件下的BPSK信号接收在BPSK调制信道卷积码的译码过程中,首先需要对接收到的BPSK信号进行处理,包括信号的采样、滤波等步骤,以便后续的译码过程能够准确进行。
2. 前向步骤前向步骤是BCJR译码过程的关键步骤之一,它需要根据接收到的信号和卷积编码器的结构,计算每一个时刻的状态度量和分支度量,并维护状态度量和分支度量的信息。
3. 后向步骤后向步骤是BCJR译码过程中的另一关键步骤,它需要根据前向步骤得到的状态度量和分支度量信息,利用递归关系计算每个时刻的后向度量,并根据后向度量和前向度量的关系,寻找最大似然路径。
5. 个人观点和总结在实际的通信系统中,BPSK调制信道卷积码的BCJR译码过程是非常复杂的,需要对信道、噪声、编码器结构等多方面因素进行综合考虑,以保证译码性能和系统可靠性。
基于BCJR网格的3×3核极化码简化连续消去译码算法

doi:10.3969/j.issn.1003-3114.2024.01.022引用格式:李逸飞,黄志亮,张莜燕,等.基于BCJR网格的3×3核极化码简化连续消去译码算法[J].无线电通信技术,2024,50(1):181-186.[LIYifei,HUANGZhiliang,ZHANGYouyan,etal.3×3PolarCodeSimplifiedSuccessiveCancellationDecodingAlgorithmBasedonBCJRTrellisConstruction[J].RadioCommunicationsTechnology,2024,50(1):181-186.]基于BCJR网格的3×3核极化码简化连续消去译码算法李逸飞,黄志亮,张莜燕,周水红(浙江师范大学物理与电子信息工程学院,浙江金华321004)摘 要:大核矩阵极化码的传统连续消去(SuccessiveCancellation,SC)译码算法有较高的计算复杂度,采用网格来降低大核矩阵极化码SC译码算法的复杂度。
发现了SC译码算法核内部运算和网格的联系,建立了相应的网格替代核内部运算,基于BCJR(Bahl,Cocke,Jelinek,Ravivconstruction)网格构造出SC核内部运算的最小网格。
有效降低了算法计算量。
仿真结果表明,3×3核的长度为243、码率为1/2的极化码,相比于直接计算式,运行时间减少了79.14%,节省了14.2%的计算成本。
关键词:极化码;大核矩阵;BCJR网格;连续消去译码中图分类号:TN919.23 文献标志码:A 开放科学(资源服务)标识码(OSID):文章编号:1003-3114(2024)01-0181-063×3PolarCodeSimplifiedSuccessiveCancellationDecodingAlgorithmBasedonBCJRTrellisConstructionLIYifei,HUANGZhiliang ,ZHANGYouyan,ZHOUShuihong(CollegeofPhysicsandElectronicInformationEngineering,ZhejiangNormalUniversity,Jinhua321004,China)Abstract:ThetraditionalSuccessiveCancellation(SC)decodingalgorithmforlargekernelmatrixpolarcodeshashighcomputationalcomplexity.ThispaperusesatrellistoreducethecomplexityoftheSCdecodingalgorithmforlargekernelmatrixpolarcodes.Firstly,thispaperestablishestheconnectionbetweentheinternaloperationsoftheSCdecodingalgorithmandthetrellis.Then,itestab lishesthecorrespondingtrellis basedreplacementsforinternaloperations.Finally,basedontheBCJR(Bahl,Cocke,Jelinek,Ravivcon struction)trellis,theminimumtrellisforinternaloperationsoftheSCkernelisconstructed.Thisapproacheffectivelyreducesthecom putationalloadofthealgorithm.Simulationresultsshowthatfor3×3kernelpolarcodeswithalengthof243andacoderateof1/2,thismethodreducestherunningtimeby79.14%comparedtodirectcalculation,savingsof14.2%incomputingcosts.Keywords:polarcode;largekernelmatrix;BCJRtrellis;SCdecoding收稿日期:2023-09-230 引言极化码最早由Arikan教授提出,是一种理论上证明在离散无记忆信道中可以达到信道容量的编码方案[1]。
降到最小-BCJR算法是利用最大后验概率准则(MAP)把

引言未来的无线通信系统必须能为用户提供高速率、高质量、实时的多媒体业务,然而无线信道,特别是移动无线信道是典型的随机时变信道,其在时间域、频率域以及空间角域均存在着随机性的扩散,这些扩散将造成接收信号在相对应的频率域、时间域以及空间域产生严重的衰落现象,衰落将严重地恶化无线通信系统的传输可靠性及频谱效率。
为了实现高效、可靠的无线数据传输,两种手段是必要的:①利用各种分集对抗衰落,②利用信道编码实现差错控制。
频率分集、时间分集、空间分集是主要的分集手段,充分利用这些分集方法将衰落信道尽可能地改造为AWGN信道,然后利用信道编码进行检错和纠错。
一般的信道编译码方案,难以在无线通信中以较低的信噪比达到数据业务的服务质量(QoS)(例如一般要求误比特率 BER≤10-6),即使在以前的无线移动通信系统中通常采用的RS码与卷积码串行级联的信道编码方案,与香农(C.E. Shannon)界有较大的差距,直到1993年出现的Turbo码的性能与香农界的差距仅为0.5dB。
他们发明的Turbo码的创新之处在于:用两个递归系统卷积成员码并行级联编码,这两个系统递归卷积成员码之间用一个伪随机交织器相连接,并且采用软入软出(SISO, Soft-In-Soft-Out)的迭代译码算法。
从此,Turbo 码就成为编码界的一个研究热点。
S. Ten Brink在[2]得到的Turbo码的性能与香农界的差距仅为0.1dB。
一、3G 移动通信系统的特点&Turbo 码的应用1.13G 移动通信系统的特点第三代移动通信系统的数据速率可从几kbps 到2 Mbps ;高速移动时为144 kbps ;慢速移动时为384 kbps ;静止时为2 Mbps 。
多媒体化:提供高质量的多媒体业务,如话音、可变速率数据、活动视频和高清晰图像等多种业务,实现多种信息一体化。
全球性:公用频段, 全球漫游, 大市场。
在设计上具有高度的通用性,该系统中的业务以及它与固定网之间的业务可以兼容,拥有足够的系统容量和强大的多种用户管理能力,能提供全球漫游。
