相对论的速度变换公式 质能关系共17页
相对论的速度变换

P =mv
E = mc
2
2
c v= P E
m0c
2 2
2
E = mc =
v 1− 2 c
=
m0c
2 4
1 c 2 1− 2 2 P c E
2 c 2 2 2 4 E 1 − 2 P = m0 c E
28
解得:
2 4 E 2= P 2 c 2 + m 0 c
或:
E = ( Pc) + E0
●按相对论,粒子间相互作用时,满足能量守 恒关系:
∑ E = ∑ (m c ) = const
2 i i i i
∑ m = const
i i
说明物质间相互作用时质量守恒。 如原子核反应中质量守恒:
∑m + ∑m = ∑m '+ ∑m
0 k 0
k
'
反应前后静质量和动质量可以相互转化。
23
例:氢弹核聚变反应引起的质能变化
1
2
1 v2 ≈ 1+ 2 2c
m0 2 2 ∴ EK = m0c + v − m0c 2
2
1 2 = m0v 2
●根据 EK = mc − m0 c
2 2
牛顿力学动能公式
=
m0 v 1− 2 c
2
c − m0c
2
2
17
得到粒子速率由动能表示的关系:
−2 E 2 2 v = c 1 − 1 + K 2 m0c
v v dt − dx 1 − u x dx − vdt u x − v c = c dt dx′ = dt dt ′ = = 2 2 1− β 2 1− β 2 1− β 1− β
《相对论的速度变换定律 质量和能量的关系》课件1

自主学习
名师解疑
分类例析
二、质量和速度的关系
m=
m0 1-vc22
(1)式中m0是物体静止时的质量(也称为静质量),m是物体以
速度v运动时的质量.这个关系式称为相对论质速关系.
(2)v≪c时,近似地m=m0.
自主学习
名师解疑
分类例析
(3) 微 观 粒 子 的 运 动 速 度 很 高 , 它 的 质 量 明 显 地 大 于 静 止 时 质 量.例如回旋加速器中被加速的粒子质量会变大,导致做圆周运 动的周期变大后,它的运动与加在D形盒上的交变电压不再同步, 回旋加速器的加速能量因此受到了限制. 特别提醒 (1)物体的质量会随速度的增大而增大. (2)物体运动的质量要大于静止质量.
自主学习
名师解疑
分类例析
【变式1】 若一宇宙飞船对地以速度v运动,宇航员在飞船内沿同方向 测得光速为c,问在地上的观察者看来,光速应为v+c吗? 解析 由相对论速度变换公式u=1u+′u+′c2vv,式中u′、v分别 为v和c.代入公式求得光对地速度u=1v++vcc2c=cvv+ +cc=c. 答案 在地面的观察者看来,光速是c不是v+c.
自主学习
名师解疑
分类例析
【变式3】 已知电子的静止能量为0.511
MeV,若电子的动能为0.25
MeV,则它所增加的质量Δm与静止质量m0的比值近似为 ( ).
A.0.1 B.0.2 C.0.5 D.0.9
自主学习
名师解疑
分类例析
解析 由题意E=m0c2 即m0c2=0.511×106×1.6×10-19 J① ΔE=Δmc2 即Δmc2=0.25×106×1.6×10-19 J② 由②①得Δmm0 =00..52151≈0.5,故只有C项正确. 答案 C
物理学中的质能转换

物理学中的质能转换质能转换是指质量和能量之间的转换关系。
在物理学中,能量和质量是等价的,它们可以相互转换。
这个关系由爱因斯坦的著名公式E=mc²给出,其中E表示能量,m表示质量,c表示光速。
此公式揭示了质量和能量之间的密切关系,推动了整个物理学的发展。
质能转换的基本原理在经典力学中,质量和能量是分离的观念。
而在相对论中,质量和能量是相互关联的。
当物体运动的速度趋近于光速时,质量会增加,而能量也会增加,两者是密切相关的。
当速度达到光速时,质量会达到无限大,此时只有能量存在,质量不存在。
这种质量和能量的相互转换关系被称为质能转换,其基本原理就是E=mc²。
生命中的质能转换质能转换不仅仅发生在自然界中的物理学,也发生在人类生活中。
例如,我们吃下食物后,身体会将其中的能量分解成糖分和脂肪,然后转换为体内所需的能量,用来维持身体正常的生理活动。
这也是质能转换的一种形式。
质能转换技术的应用质能转换技术在人类历史上具有重要的意义。
早在上世纪初期,科学家就尝试将物体中的原子核聚合起来,以产生巨大的能量,这就是核能。
核能的应用可以用于发电、医疗治疗以及制造核武器等方面。
此外,质能转换技术还可以应用在燃料电池中,将燃料(如氢气)通过氧化反应转换为电能。
这种技术不仅环保,还可以大幅降低能源消耗,对于人类的未来具有重大意义。
总结质能转换是物理学的核心概念之一,它揭示了质量和能量之间的密切关系,并具有广泛的应用价值。
无论是在自然界中的物理学,还是在人类生活和发展中,质能转换都扮演着重要的角色。
我们应该进一步研究和探索这个领域,为人类的发展和进步作出更大的贡献。
教科版选修3-4 第6章 第4节 相对论的速度变换公式 质能关系
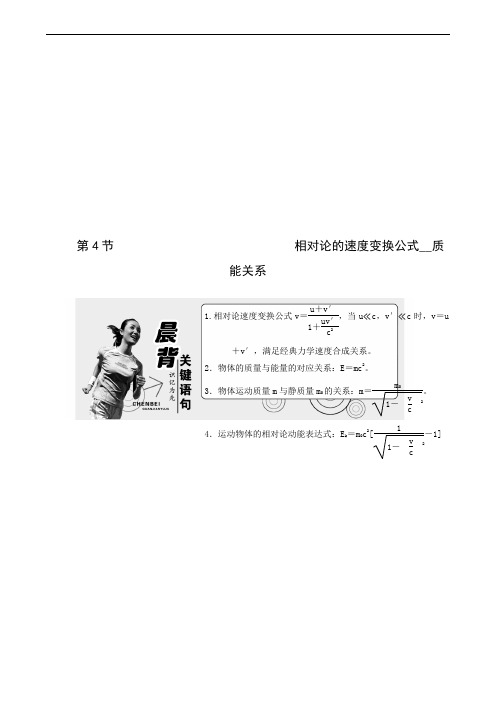
第4节相对论的速度变换公式__质能关系1.相对论速度变换公式v =u +v′1+uv′c2,当u ≪c ,v′≪c 时,v =u+v′,满足经典力学速度合成关系。
2.物体的质量与能量的对应关系:E =mc 2。
3.物体运动质量m 与静质量m 0的关系:m =m 01-v c 2。
4.运动物体的相对论动能表达式:E k =m 0c 2[11-v c2-1]v′沿着火车前进的方向相对火车运动,那么这个人相对地面的速度v 为v =u +v′1+uv′c2。
理解这个公式时请注意:(1)如果车上的人的运动方向与火车的运动方向相反,则v′取负值。
(2)如果u ≪c ,v′≪c ,这时v′uc 2可忽略不计,这时相对论的速度合成公式可近似变为v =v′+u 。
(3)如果v′与u 的方向垂直或成其他角度时,情况比较复杂,上式不适用。
[学后自检]┄┄┄┄┄┄┄┄┄┄┄┄┄┄(小试身手)在高速运动的火车上,设车对地面的速度为v ,车上的人以速度u′沿着火车前进的方向相对火车运动,那么他相对地面的速度u 与u′+v 的关系是( )A .u =u′+vB .u <u′+vC .u >u′+vD .以上均不正确解析:选B 按照经典的时空观,u =u′+v ,而实际上人对地面的速度按照相对论速度公式计算,u =u′+v1+u′v c2,因此u 比u′与v 之和要小,但只有在u′和v 的大小接近光速时才能观察此差别。
相对论质量和能量[自读教材·抓基础]1.质能关系式E =mc 2。
式中m 是物体的质量,E 是它具有的能量。
由此可见,物体质量越大,其蕴含的能量越大。
能量与质量成正比。
2.相对论质量 m =m 01-v 2c2(m 0指静质量); 与静质量对应的静能量为E 0=m 0c 2。
[跟随名师·解疑难]1.对质速关系m =m 01-v c2的理解(1)式中m 0是物体静止时的质量(也称为静质量),m 是物体以速度v 运动时的质量。
相对论的速度变换公式 质能关系

= 1.125×108 m/s
二、对相对论质量和质能方程的理解
1、相对论质量:物体的质量会随物体的速度的增大而增大,物体
以速度v运动时的质量m与静止时的质量m0之间的关系
m m0
(1)v≪c时,(
v c
1
v c
2
m为运动质量>m0为静止质量
)2=0此时有m=m0,也就是说:低速运动的物体
,可认为其质量与物体的运动状态无关.
☆如果车上人运动方向与火车运动方向相反,则u取负值。
一、对相对论的速度变换公式的理解
1.当物体运动方向与参考系相对地面的运动方向相反 时,公式中的u′取负值.
2.若物体运动方向与参考系运动方向不共线,此式不 可用.
3.由公式可知:u一定比u′+v小,但当u′和v都比c小 得多时,可认为u=u′+v,这就是低速下的近似,即经 典力学中的速度叠加.
(3)物体的能量变化ΔE与质量变化Δm的对应关系为:ΔE=Δmc2.
二、对相对论质量和质能方程的理解
例3、太阳由于向四面空间辐射能量,每秒损失了质量 4×109kg 。求太阳的辐射功率。
解:设太阳的辐射功率为P:
Pmc2 mc2 t 1
代入数据:P=4109(3108)2 =3.61026J/s =3.61026W
B
K系
中 国 航 天
中 国 航 天
A ux
。可知K′系相对K系是速度为
v = 2.0×108 m/s
飞船A 在K系中的速度为
ux = 2.5×108 m/s
飞船A 在K’系中的速度为
ux´=
u 1
x
v c
v ux
2
= 1
2.5×108 2.0×108
教科版高中物理选修3-4课件 6 相对论的速度变换定律 质量和能量的关系课件2

课堂互动讲练
长度的相对性问题 例1 如图6-3-2所示,假设一根10 m长的梭镖 以光速穿过一根10 m长的管子,它们的长度都是 在静止状态下测量的.以下叙述中哪项最好的描 述了梭镖穿过管子的情况( )
图6-3-2
A.梭镖收缩变短,因此在某些位置上,管子能完全 遮住它 B.管子收缩变短,因此在某些位置上,梭镖从管子 的两端伸出来 C.两者都收缩,且收缩量相等,因此在某个位置, 管子恰好遮住梭镖 D.所有这些都与观察者的运动情况有关
(4)由质能关系式可知 ΔE=Δmc2.
即时应用 (即时突破,小试牛刀)
3.一观察者测出电子质量为2m0,求电子速率是多 少?(m0为电子静止时的质量)
解析:m=2m0,代入质量公式 m=
m0 ,可得 1-vc2
2m0=m=
m0 ,解得 1-vc2
v=
23c=0.866c.
答案:0.866c
(2)质能方程
物体质量 m 与其蕴含的能量 E 之间的关系是:E =_m__c_2 _.
核心要点突破
一、对狭义相对论几个主要结论的理解 1.几个主要结论
在相对事件发生地或 物体静止的参考系中
观察
在相对事件发生地或物体运动的参考 系中观察
同时的 事件同时但不同地点
相对性
发生
事件不同时发生
时间间 隔的相
为 u=u′+v,与经典物理学的速度合成公式相同.
2.根据此式若u′=c,则u=c,那么c在惯性系中 都是相同的. 3.如果u′与v的方向不在一条直线上,(相互垂直 或成其他角度)时,情况比较复杂,上式不适用.
即时应用 (即时突破,小试牛刀) 2.地球上一观察者,看见一飞船A以速度2.5×108 m/s 从他身边飞过,另一飞船B以速度2.0×108 m/s跟随A 飞行.求: (1)A上的乘客看到B的速度是多少? (2)B上的乘客看到A的速度是多少? 解析:(1)A上的乘客看到地面的速度为u′=- 2.5×108 m/s,B相对于地面的速度为v=2.0×108 m/s,
高中物理 第六章 相对论 第4节 相对论的速度变换公式 质能关系课件 教科版选修3-4.ppt

7
活动三 相对论质量 物体的能量和质量之间存在
密切的联系,他们的关系是:
Emc2
这就是著名的爱因斯坦质能方程
8
具体推导过程如下:
Ek EE0 Emc2
E0 m0c2
v 1 c
Ek
m0c2 1 v 2
m0c2
c
1v2 11v2
判天地之美,析万物之理
物理学家费尔德曾指出: 当你领悟一个出色的公式时,你会得到
如同听巴哈的乐曲一样的感受。
1
4
相对论的速度变换公式 质能关系
2
活动一 相对论的速度变换
u
v
车对地的速度为v,人对车的速度为v′
地面上的人看到车上人相对 地面的速度为:
v
u v
1
uv c2
3
v
u v
1
uv c2
c
2c
Ek
m0c2
m0c2
1 2
m0c2
v
2
c
1
1
v
2
2c
1 2
m0v 2
9
Ek
1 2
m0v2
这就是我们过去熟悉的动能表达式,这也能让 我们看出,牛顿力学是相对论力学在低速情况下的 特例.
10
如果车上人运动方向与火车运动方向相反,则v′取负 值
4
活动二 相对论质量
物体的运动速度不能无限增加,那么物体的质量是否随 着速度而变化?
严格的论证表明,物体高速(与光速相比)运动时的质 量与它静止时的质量之间有下面的关系:
m
Hale Waihona Puke m01v2
质能方程推导质速关系

质能方程推导质速关系质能方程是相对论物理中的一个重要概念,它揭示了质量和能量之间的等价关系。
质能方程的推导涉及到相对论的基本原理和数学推导。
首先,我们从相对论的质量-能量关系开始推导。
根据相对论的能量-动量关系,我们知道能量E和动量p之间的关系可以表示为E² = (pc)² + (mc²)²,其中c是光速,m是物体的静止质量。
将动量p用质量m和速度v表示,得到E² = (mv)²c² +(mc²)²,然后可以进一步化简得到E² = m²c⁴ + m²v²c²。
接下来,我们利用经典力学中的动能公式K = 0.5mv²,将动能K代入上式,得到E² = m²c⁴ + 2mKc²。
再进一步化简,可以得到E² = m²c⁴(1 + 2K/(mc²))。
根据相对论的质量-能量关系,我们知道E = γmc²,其中γ是洛伦兹因子。
将E代入上式,得到(γmc²)² = m²c⁴(1 +2K/(mc²)),再进一步化简可以得到γ² = 1 + 2K/(mc²)。
最后,我们利用动能K与静止能量m₀c²之间的关系,即K =(γ 1)m₀c²,将K代入上式,可以得到γ = 1 / sqrt(1v²/c²)。
将γ代入E = γmc²中,最终可以得到著名的质能方程E = mc² / sqrt(1 v²/c²)。
因此,从相对论的能量-动量关系出发,经过数学推导和代换,我们最终得到了质能方程E = mc² / sqrt(1 v²/c²)。
这个推导过程涉及到相对论的基本原理和数学运算,揭示了质量和能量之间的等价关系。
6.4相对论的速度变换公式 质能关系

二、相对论的质量和能量
根据狭义相对论可得出:
E = mc
m= m0 v2 1− 2 c
2
E0 = m0c
2
在地面上空以u09c飞行的飞船向前发射一导弹导弹对飞船的速率二相对论的质量和能量根据狭义相对论可得出
6.4 相对论的速度变换公式
质能关系
一、相对论的速度变换
根据时空相对性,狭义相对论给出:在 以速率u相对于参考系S运动的参考系S'中, 一物体沿与u相同的方向以速率v' 运动时, 在参考系S中,它的速率为:
u + v′ v= uv′ 1+ 2 c
s
o
z
y
s'
o'
z'
y'r u Nhomakorabeax'
x
在地面上空以u=0.9c飞行的飞船, 向前发射一导弹,导弹对飞船的速率 为 v′ = 0.5c 。
按伽利略速率变换公式:
v = u + v′ = 1.4c
按相对论时空观:
u + v′ 0.9c + 0.5c v= = = 0.966c < c uv ′ 0.9c × 0.5c 1+ 2 1+ 2 c c
高中物理 6.4相对论的速度变换公式 质能关系课件 教科版选修3-4

【方法总结】
在两个惯性系中,虽然观察
到的结果并不相同,一个10 m/s,另一个30
m/s,但我们却应用了同样的运动定律和速
度合成法则.
第二节
狭义相对论的两个基本假设
狭义相对论提出的历史背景
19世纪后半叶,关于电磁场的研究不断深入, 人们认识到了光的电磁本质.我们已经知道,电 磁波是以巨大且有限的速度传播的,因此在电磁 场的研究中不断遇到一些矛盾,这些矛盾导致了 相对论的Βιβλιοθήκη 现.狭义相对论的两个基本假设
光速不变原理
在任何惯性系中,光在真空中的速度恒为c, 与光源的运动和观测者的运动无关
光速不变原理与伽利略速度叠加原理是针锋 相对的,具有观念上的革命性.
例.下列几种说法: ①所有惯性系统对物理基本规律都是等价的. ②在真空中,光的速度与光的频率、光源的运动状态无关.
③在任何惯性系中,光在真空中沿任何方向的传播速度都相
如果在车厢运动的速度远小于光速时, 在光到达车壁时间内,车厢运动的距 离观察不出来,所以经典时空观中的 同时的绝对性是在参考系低速运动的 情况下得出的结论。
例:如图所示,沿铁道排列的A、B两电杆正中央安装 一闪光装置C,光信号到达A电杆称为事件1,到达B电 杆称为事件2.则( D ) A.在地面观察者看来,事件1比事件2先发生;从车厢 中观察者看来,事件1、2同时发生 B.在地面观察者看来,事件1比事件2后发生;从车厢 中观察者看来,事件1、2同时发生 C.在地面观察者看来,事件1、2同时发生;从车厢中 观察者看来,事件2比事件1后发生 D.在地面观察者看来,事件1、2同时发生;从车厢中 观察者看来,事件2比事件1先发生
科学的旗手—爱因斯坦
1909—1914 进入大学工作
相对论质能关系

相对论质能关系
嘿,朋友们!今天咱来聊聊一个超级厉害的东西——相对论质能关系!
你想想看啊,我们平时看到的东西,比如一个苹果,一块石头,它们都有质量吧。
那质量和能量之间有啥神秘的联系呢?这就是相对论质能关系要告诉我们的啦!
爱因斯坦老爷子提出的这个相对论质能关系啊,简单来说就是质量和能量可以相互转换!哇塞,是不是很神奇?就好像魔法一样!你可以把质量变成能量,也可以把能量变成质量。
比如说,原子弹爆炸,那威力为啥那么大呀?就是因为里面发生了质量转变成能量的过程呀!一点点的质量消失了,却释放出了巨大无比的能量。
这就好比是一个小小的火种,却能引发一场超级大火一样。
再想想我们的太阳,它每天都在发光发热,这能量是从哪儿来的呢?就是太阳内部的氢在不断地发生核聚变,质量在减少,同时释放出了海量的能量。
这就像是一个无穷无尽的能量宝库,一直在为我们的地球提供着光和热。
那相对论质能关系对我们的生活有啥影响呢?可多啦!它让我们对世界的认识更深了一步呀。
它让我们知道,质量和能量可不是孤立存在的,它们之间有着紧密的联系。
而且,这还为我们未来的科技发展提供了巨大的想象空间呢!说不定哪天我们就能利用这个原理,创造出更强大的能源,或者实现一些以前想都不敢想的事情。
相对论质能关系,真的是太神奇啦!它让我们看到了一个不一样的世界,一个充满了无限可能的世界。
难道你不想更深入地了解它吗?我觉得呀,这绝对是值得我们每个人都去好好探索的领域呢!。
第六章 第4节 相对论的速度变换公式 质能关系

u′沿着火车前进的方向相对火车运动,那么他相对地面的速度
u 与 u′+v 的关系是
()
A.u=u′+v
B.u<u′+v
C.u>u′+v
D.以上均不正确
解析:按照经典的时空观,u=u′+v,而实际上人对地面的速度 按照相对论速度公式计算,u=1u+′u+′c2vv,因此 u 比 u′与 v 之和要 小,但只有在 u′和 v 的大小接近光速时才能观察此差别。
(2)如果 u ≪c,v′≪c,这时v′c2 u可忽略不计,这时相 对论的速度合成公式可近似变为 v=v′+u。
(3)如果 v′与 u 的方向垂直或成其他角度时,情况比较 复杂,上式不适用。
[学后自检]┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄(小试身手)
在高速运动的火车上,设车对地面的速度为 v,车上的人以速度
D.在相对论力学中,物体的质量随物体速度的增大而增大
解析:在牛顿力学中,物体的质量是保持不变的,故选项 A
正确,B 错误;在相对论力学中,由于物体的速度 v 不可能
达到光速 c,所以 v<c,1-(vc)2<1,根据 m=
m0 ,可判 1-vc2
断选项 C、D 均正确。
答案:ACD
3.设想有一艘飞船以 v=0.8c 的速度在地球上空飞行,如果这时
(2)对于一个以速率 v 运动的物体,其动能
Ek=m(3)物体的总能量 E 为动能与静质能之和,即 E=Ek+E0= mc2(m 为动质量)。
(4)由质能关系式可知 ΔE=Δmc2。
[学后自检]┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄(小试身手) 星际火箭以 0.8c 的速率飞行,其静止质量为运动质量的多少倍?
m/s=5.9×106
上述计算表明,加速后的电子还属于低速的,可以使用经典的
高中物理第六章相对论第4讲相对论的速度变换公式质能

二、广义相对论点滴(选学) 1.广义相对性原理和等效原理
(1)广义相对性原理 在__任__何__参__考__系__中物理规律都是_一__样___的. (2)等效原理 一个不受引力作用的加速度系统跟一个受引力作用的 _惯__性__系__统___是等效的. 2.支持广义相对论的几个观测结果 (1)光在引力场中传播时,将会发生__偏__折__,而不再是直线 传播. (2)引力作用使光波发生__频__移__.
第4讲 相对论的速度变换公式 质能关系
第5讲 广义相对论点滴(选学)
[目标定位] 1.知道相对论速度变换公式、相对论质量和质能 方程.2.了解广义相对论的基本原理.3.初步了解广义相对论的几 个主要观点以及主要观测证据.
一、相对论的速度变换公式 质能关系
1.相对论的速度变换
在以速率u相对于参考系S运动的参考系S′中,一物体沿与
(3)在引力场中时间也会__延__缓__,引力越强,时钟就走得越 __慢____. (4)水星绕太阳运动的轨道与根据牛顿万有引力定律计算所 得的不一致. (5)当两个天体相互绕转时,会向外界辐射出__引__力__波____. 3.宇宙的演化 (1)20世纪40年代末,物理学家伽莫夫把宇宙膨胀与粒子反 应理论结合起来,提出宇宙大爆炸假说. (2)宇宙大爆炸理论最大说服力的证据是宇宙背景辐射的发 现.
解析 已知 v=0.05c,ux′=0.8c. 由相对论速度叠加公式得 ux=1u+x′ux+c′2vv=cu2x+′u+x′vvc2, ux=c20+.8c0+.8c0×.050c.05c2c≈0.817c. 答案 0.817c
二、对相对论质量和质能方程的理解
1.相对论质量 物体的质量会随物体的速度增大而增大,物体以速度 v 运 动 时 的 质 量 m 与 静 止 时 的 质 量 m0 之 间 的 关 系 m = 1m-0 vc2.
6.4 相对论的速度变换公式 质能关系课件 教科版选修3-4课件

m/s。 上述计算表明,加速后的电子还属于低速的,可以使用经典的动7 J
0.02%
5.9×106 m/s
可以使
返回
用经典动能公式
[借题发挥 ] 相对论的质速关系 由相对论的质速关系 m= m0 v 2 1-( ) c 知,物体以速度 v
运动时的质量 m 大于静止时的质量 m0,且 v 越大, m 与 m0 相 差越大。微观粒子的运动速度很高,它的质量明显大于静止质 量,在粒子加速问题中注意考虑这一问题。
返回
[ 解析 ]
(1)由题意可知, v= 2.0×108 m/s, u=2.5× 108
u+ v′ m/s, v′为 B 相对于 A 的速度。由 v= 可得:v′=- uv′ 1+ 2 c 1.125× 108 m/s。 (2)由题意可知,v= 2.5× 108 m/s,u=2.0× 108 m/s,v′为 u+ v′ A 相对于 B 的速度,由 v= 可得: v′= 1.125×108 m/s。 uv′ 1+ 2 c
答案:0.6倍
返回
[例1]
地球上一观察者,看见一飞船A以速度
2.5×108 m/s从他身边飞过,另一飞船B以速度2.0×108 m/s跟随A飞行。求: (1)A上的乘客看到B的速度是多少?
(2)B上的乘客看到A的速度是多少?
[思路点拨] 解答本题时应注意以下两点:
(1)速度变换公式中各符号的含义; (2)所求解的速度相对的参考系。
[答案] (1)-1.125×108 m/s
(2)1.125×108 m/s
返回
1.一高能加速器沿相反方向射出两质点,速度均为0.6c,
它们的相对速度是多少?
v′+u 解析: 根据相对论的速度变换公式 v= , v′u 1+ 2 c v′+0.6c 可知- 0.6c= ,解得 v′≈-0.88c,即该质点相 0.6c×v′ 1+ c2 对于运动参考系 (另一质点 )的速度为- 0.88c。
教科版高中物理选修3-4课件 6 相对论的速度变换定律 质量和能量的关系课件3

再见
时,可认为v=u+v′,这就是低速下的近似,即经典力学 中的速度叠加. 4.当v′=u=c时,v=c,证明了光速是速度的极限,也反证 了光速不变原理.
课堂讲义
【例1】 一粒子以0.05c的速率相对实验室参考系运动.此粒 子衰变时发射一个电子,电子相对于粒子的速度为0.8c,电 子的衰变方向与粒子运动方向相同.求电子相对于实验室参 考系的速度. 解析 已知 v=0.05c,ux′=0.8c. 由相对论速度叠加公式得 ux=1u+x′ux+c′2vv=uc2x+′u+x′vvc2, ux=c20+.8c0+.8c0×.050c.05c2c=0.817c. 答案 0.817c
高中物理·选修3-4·教科版
相对论的速度变换公式 质能关系
[目标定位] 知道相对论速度变换公式,相对论质量和质能方 程.
预习导学
一、相对论的速度变换公式 质能关系 1.相对论的速度变换 在以速率u相对于参考系S运动的参考系S′中,一物体沿与u 相同的方向以速率v′运动时,在参考系S中,它的速率为 u+v′ v= 1+uvc2′.
课堂讲义
二、对相对论质量和质能方程的理解
1.相对论质量
物体的质量会随物体的速度的增大而增大,物体以速度 v 运
动时的质量 m 与静止时的v≪c 时,(vc)2=0 此时有 m=m0,也就是说:低速运动的
物体,可认为其质量与物体的运动状态无关.
课堂讲义
(2)物体的运动速率无限接近光速时,其相对论质量也将无限增 大,其惯性也将无限增大.其运动状态的改变也就越难,所以 超光速是不可能的.
课堂讲义
2.质能关系
(1)相对于一个惯性参考系,以速度 v 运动的物体其具有的相
对论能量
E=mc2=
