材料力学第10章_梁的应力(1)
材料力学第10章_梁的应力(1)

max
2 300 kNm
max
WZ
B
Wz
M
max
cm
3
B 1875
选择确定I字钢型号:INO50a
1875 1860 1875 100 % 0 .8 %
例 铸铁制作的悬臂梁,尺寸及受力如图示,图中F=20kN。梁的截面 为T字形,形心坐标yc=96.4mm。已知材料的拉伸许用应力和压缩许用应力 分别为[σ ]+=40MPa, [σ ]-=100MPa。试校核梁的强度是否安全。
Fa
Fb
C截面:
max
MC W zC
6
Fb
d 2
32
3
62 . 5 160 32
0 . 13
3
M
46 . 4 10 Pa 46 . 4 MPa
结论:轮轴安全
例 图示T形截面简支梁在中点承受集中力F=32kN,梁的长度L=2m。T形截 面的形心坐标yc=96.4mm,横截面对于z轴的惯性矩Iz=1.02×108mm4。求弯矩 最大截面上的最大拉应力和最大压应力。
y
(1)
(二)物理关系:
y
......
由纵向线应变的变化规律→正应力的分布规律。
在弹性范围内
d
E
O O1
E
Ey
...... (2)
A1
y
B1 x
E
Ey
1
为梁弯曲变形后的曲率
上式说明了横截面上正应力的分布规律,表明正应力沿截面高度
呈线性变化,距中性轴越远,应力值越大,在中性轴处正应力为零。
工程力学(静力学和材料力学)第2版课后习题答案 范钦珊主编 第10章 组合受力与变形杆件的强度计算

解:危险截面在 A 处,其上之内力分量为: 弯矩: M y = FP1 a , M z = FP2 H 扭矩: M x = FP2 a 轴力: FNx = FP1 在截面上垂直与 M 方向的垂直线 ab 与圆环截 求得 M y 与 M z 的矢量和 M 过截面中心, 面边界交于 a、b 两点,这两点分别受最大拉应力和最大压应力。但由于轴向压力的作用,最 大压应力值大于最大拉应力值,故 b 点为危险点,其应力状态如图所示。 10-7 试求图 a 和 b 中所示之二杆横截面上最大正应力及其比值。 解: (a)为拉弯组合
7
y
y
A
O
0.795
B
14.526
+13.73MPa
z
(a)
O O
+14.43MPa
(b)
C
y
A
C
B B
y
A
O O
B
z
12.6mm
14.1mm
zC
−15.32MPa
16.55MPa
zC
z
(c)
(d)
习题 10-9 解图
∴
+ σ max
= 14.526 − 0.795 = 13.73 MPa
− σ max = −14.526 − 0.795 = −15.32 MPa
Ebh
由此得
2 FP 6e
e=
10-9
ε1 − ε 2 h × ε1 + ε 2 6
图中所示为承受纵向荷载的人骨受力简图。试:
1.假定骨骼为实心圆截面,确定横截面 B-B 上的应力分布; 2.假定骨骼中心部分(其直径为骨骼外直径的一半)由海绵状骨质所组成,忽略海绵状承受 应力的能力,确定横截面 B-B 上的应力分布;
梁的应力计算公式全部解释

梁的应力计算公式全部解释应力是材料受力时产生的内部力,它是描述材料内部抵抗外部力的能力的物理量。
在工程领域中,计算材料的应力是非常重要的,可以帮助工程师设计和选择合适的材料,以确保结构的安全性和稳定性。
梁的应力计算公式是计算梁在受力时产生的应力的公式,它可以帮助工程师了解梁在不同条件下的应力情况,从而进行合理的设计和分析。
梁的应力计算公式是由弹性力学理论推导而来的,它可以根据梁的几何形状、受力情况和材料性质来计算梁的应力。
在工程实践中,梁的应力计算公式通常包括弯曲应力、剪切应力和轴向应力三种类型的应力。
下面将分别对这三种类型的应力计算公式进行详细解释。
1. 弯曲应力计算公式。
梁在受到外部力的作用时,会产生弯曲应力。
弯曲应力是由于梁在受力时产生的弯曲变形所引起的,它可以通过以下公式进行计算:σ = M c / I。
其中,σ表示梁的弯曲应力,单位为N/m^2;M表示梁的弯矩,单位为N·m;c表示梁截面内的距离,单位为m;I表示梁的惯性矩,单位为m^4。
弯曲应力计算公式可以帮助工程师了解梁在受力时产生的弯曲应力大小,从而进行合理的设计和分析。
在工程实践中,通常会根据梁的几何形状和受力情况选择合适的弯曲应力计算公式进行计算。
2. 剪切应力计算公式。
梁在受到外部力的作用时,会产生剪切应力。
剪切应力是由于梁在受力时产生的剪切变形所引起的,它可以通过以下公式进行计算:τ = V Q / (I b)。
其中,τ表示梁的剪切应力,单位为N/m^2;V表示梁的剪力,单位为N;Q 表示梁的截面偏心距,单位为m;I表示梁的惯性矩,单位为m^4;b表示梁的截面宽度,单位为m。
剪切应力计算公式可以帮助工程师了解梁在受力时产生的剪切应力大小,从而进行合理的设计和分析。
在工程实践中,通常会根据梁的几何形状和受力情况选择合适的剪切应力计算公式进行计算。
3. 轴向应力计算公式。
梁在受到外部力的作用时,会产生轴向应力。
轴向应力是由于梁在受力时产生的轴向变形所引起的,它可以通过以下公式进行计算:σ = N / A。
材料力学第10章(动载荷)

Kd 2
二、水平冲击 mg v
d
Fd d , Pst st
Pst mg 其中: mgl st EA
Fd
st
Pst
mv2 冲击前:动 T1 能 2
冲击后: 应变能Vε 2 Fd d 2
2 F 2 st mv d mg
h
P
h
解:
st
Pl 1.7 102 (mm) EA
2h K d 1 1 st
2 500 1 1 243 2 1.7 10
l
l
d 2 A 4
P 2 103 0.028(MPa) st 4 A 7.1 10 d Kd st
假设: (1)冲击物为刚体; (2)不计冲击过程中的声、光、热等能量损耗(能量守恒);
(3)冲击过程中被冲击物的变形为线弹性变形过程。(保守计算)
一、自由落体冲击
P
冲击前: T 0
V P(h d )
B
h
A
冲击后:
1 Vε d Fd d 2
A
Δd
能量守恒: T V Vd
B
2h st
l
4 Pl 3 22mm st 3 EI
K d 1 1 2 50 3.35 22
40 C 30
d Kd st
M max Pl 50(MPa) st W W
d Kd st 161 MPa) (
A
Δd
Fd
B
1 P (h d ) Fd d 2 Fd d P st
2 Fd 1 Fd P (h st ) st P 2 P
(完整版)材料力学各章重点内容总结

材料力学各章重点内容总结第一章 绪论一、材料力学中工程构件应满足的3方面要求是:强度要求、刚度要求和稳定性要求。
二、强度要求是指构件应有足够的抵抗破坏的能力;刚度要求是指构件应有足够的抵抗变形的能力;稳定性要求是指构件应有足够的保持原有平衡形态的能力。
三、材料力学中对可变形固体进行的3个的基本假设是:连续性假设、均匀性假设和各向同性假设。
第二章 轴向拉压一、轴力图:注意要标明轴力的大小、单位和正负号。
二、轴力正负号的规定:拉伸时的轴力为正,压缩时的轴力为负。
注意此规定只适用于轴力,轴力是内力,不适用于外力。
三、轴向拉压时横截面上正应力的计算公式:N F Aσ= 注意正应力有正负号,拉伸时的正应力为正,压缩时的正应力为负。
四、斜截面上的正应力及切应力的计算公式:2cos ασσα=,sin 22αστα=注意角度α是指斜截面与横截面的夹角。
五、轴向拉压时横截面上正应力的强度条件[],maxmax N F A σσ=≤六、利用正应力强度条件可解决的三种问题:1.强度校核[],maxmax N F A σσ=≤一定要有结论 2.设计截面[],maxN F A σ≥ 3.确定许可荷载[],max N F A σ≤七、线应变l l ε∆=没有量纲、泊松比'εμε=没有量纲且只与材料有关、 胡克定律的两种表达形式:E σε=,N F l l EA∆= 注意当杆件伸长时l ∆为正,缩短时l ∆为负。
八、低碳钢的轴向拉伸实验:会画过程的应力-应变曲线,知道四个阶段及相应的四个极限应力:弹性阶段(比例极限p σ,弹性极限e σ)、屈服阶段(屈服极限s σ)、强化阶段(强度极限b σ)和局部变形阶段。
会画低碳钢轴向压缩、铸铁轴向拉伸和压缩时的应力-应变曲线。
九、衡量材料塑性的两个指标:伸长率1100l l lδ-︒=⨯︒及断面收缩率1100A A Aϕ-︒=⨯︒,工程上把5δ︒≥︒的材料称为塑性材料。
十、卸载定律及冷作硬化:课本第23页。
材料力学第10章 组合变形

因此,截面O为危险截面。
危险截面上,由轴力引起的正应力均匀分布,其值
为
,由弯矩引起的正应力线性分布,其值为
。利用叠加原理,将拉伸及弯曲正应力叠加
后,危险截面上正应力沿截面高度的变化情况如图10.5
(e)所示,仍为线性分布。而且可以看出,最大拉应
力和最大压应力分别发生在O截面上、下边缘各点,其
值为
(10.4)
图10.5
依据上述分析,弯拉(压)组合变形时危险点处于单向应力状态,所以可将 截面上的σmax与材料的许用应力相比较建立其强度条件。对于拉压强度相等 的材料,强度条件为
对于抗拉与抗压性能不同的材料,强度条件为
下面举例说明弯拉(压)组合变形的强度计算。 例10.2如图10.6(a)所示的钢支架,已知载荷F=45 kN,尺寸如图。 (1)如材料为钢材,许用应力[σ]=160 MPa,试选择AC杆的工字钢型号。 (2)如材料为铸铁,许用拉应力[σt]=30 MPa,许用压应力[σc]=160 MPa,且AC杆截面形式和尺寸如图10.6(e)所示,A=15×10-3 m2,z0=75mm ,Iy=5.31×10-5 m4。试校核AC杆的强度。
其力矩矢量分别与y轴和z轴的正向一致(见图10.2(b))。 为了确定横截面上最大正应力点的位置,先求截面中性轴位置。记中性轴上 任一点的坐标为(y0,z0),由于中性轴上各点处的正应力均为零,所以由式 可得中性轴方程为
(10.2) 可见,中性轴是一条通过横截面形心的直线(见图10.2(c)),其与y轴的 夹角θ为
图10.3 例10.1如图10.4(a)所示,20a号工字钢悬臂梁承受均布载荷q和集中力
。已知钢的许用弯曲正应力[σ]=160 MPa,a=1 m。试求梁的许可 载荷集度[q]。 解由于梁所受到的横向力不在梁的两个纵向对称面内,此时可以将横向力向 两个纵向对称面分解(向y和z轴分解),从而将其看成是梁在其两个相互垂
第十章 材料力学压杆稳定

y
即 : 189.325.612.74(1.52a/2) 时合理
a4.32 cm
求临界力:
L 0.76
i Iz 2A1
0.76 396.610 212.74104
8
106.5
2 E 220010 9 p 99.3 6 P 20010
2 EI
(2l ) 2
=1
0.7
=0.5
=2
2l
l
例1钢质细长杆,两端铰支,长l=1.5m,横截面是矩形截面, h=50 mm,b=30 mm,材料是A3钢,弹性模量E=200GPa; 求临界力和临界应力。 解:
(1)由于杆截面是矩形,杆在不同方向发生弯曲的难易程度不同, 如下图
因为 Iy<Iz,所以在各个方向上发生弯曲时约束条件相同的情况下, 压杆最易在xz平面内发生弯曲;
三、其它支承情况下,压杆临界力的欧拉公式
2 EI min Pcr ( L) 2
压杆临界力欧拉公式的一般形式
—长度系数(或约束系数)。
1.一端固定一端自由的细长压杆,它相当于两端铰支长为2l的 压杆的挠曲线的一半部分;
2 EI 2 EI
4l
2
Pcr
2l
2
P l l
2.二端固定的细长压杆,其中间部分(0.5l) 相当于两端铰支长为 0.5l的压杆;
②挠曲线近似微分方程: M P y y EI EI P y y y k 2 y0 EI P 2 其中 :k EI
y
P x
M
P
③微分方程的解: ④确定积分常数:
y Asin xBcosx y(0) y( L)0
A0B0 即 : AsinkLBcoskL0
材料力学课后习题答案

材料力学课后习题答案材料力学课后习题答案欢迎大家来到聘才网小编搜集整理了材料力学课后习题答案供大家查阅希望大家喜欢1、解释下列名词1弹性比功:金属材料吸收弹性变形功的能力一般用金属开始塑性变形前单位体积吸收的最大弹性变形功表示2.滞弹性:金属材料在弹性范围内快速加载或卸载后随时间延长产生附加弹性应变的现象称为滞弹性也就是应变落后于应力的现象3.循环韧性:金属材料在交变载荷下吸收不可逆变形功的能力称为循环韧性4.包申格效应:金属材料经过预先加载产生少量塑性变形卸载后再同向加载规定残余伸长应力增加;反向加载规定残余伸长应力降低的现象5.解理刻面:这种大致以晶粒大小为单位的解理面称为解理刻面6.塑性:金属材料断裂前发生不可逆永久(塑性)变形的能力韧性:指金属材料断裂前吸收塑性变形功和断裂功的能力7.解理台阶:当解理裂纹与螺型位错相遇时便形成1个高度为b 的台阶8.河流花样:解理台阶沿裂纹前端滑动而相互汇合,同号台阶相互汇合长大,当汇合台阶高度足够大时,便成为河流花样是解理台阶的1种标志9.解理面:是金属材料在一定条件下当外加正应力达到一定数值后以极快速率沿一定晶体学平面产生的穿晶断裂因与大理石断裂类似故称此种晶体学平面为解理面10.穿晶断裂:穿晶断裂的裂纹穿过晶内可以是韧性断裂也可以是脆性断裂沿晶断裂:裂纹沿晶界扩展多数是脆性断裂11.韧脆转变:具有一定韧性的金属材料当低于某一温度点时冲击吸收功明显下降断裂方式由原来的韧性断裂变为脆性断裂这种现象称为韧脆转变12.弹性不完整性:理想的弹性体是不存在的多数工程材料弹性变形时可能出现加载线与卸载线不重合、应变滞后于应力变化等现象,称之为弹性不完整性弹性不完整性现象包括包申格效应、弹性后效、弹性滞后和循环韧性等决定金属屈服强度的因素有些?答:内在因素:金属本性及晶格类型、晶粒大小和亚结构、溶质元素、第二相外在因素:温度、应变速率和应力状态2、试述韧性断裂与脆性断裂的区别为什么脆性断裂最危险?答:韧性断裂是金属材料断裂前产生明显的宏观塑性变形的断裂这种断裂有1个缓慢的撕裂过程在裂纹扩展过程中不断地消耗能量;而脆性断裂是突然发生的断裂断裂前基本上不发生塑性变形没有明显征兆因而危害性很大3、剪切断裂与解理断裂都是穿晶断裂为什么断裂性质完全不同?答:剪切断裂是在切应力作用下沿滑移面分离而造成的滑移面分离一般是韧性断裂而解理断裂是在正应力作用以极快的速率沿一定晶体学平面产生的穿晶断裂解理断裂通常是脆性断裂4、何谓拉伸断口三要素?影响宏观拉伸断口性态的因素有些?答:宏观断口呈杯锥形由纤维区、放射区和剪切唇3个区域组成即所谓的断口特征三要素上述断口三区域的形态、大小和相对位置因试样形状、尺寸和金属材料的性能以及试验温度、加载速率和受力状态不同而变化5、论述格雷菲斯裂纹理论分析问题的思路推导格雷菲斯方程并指出该理论的局限性答:只适用于脆性固体,也就是只适用于那些裂纹尖端塑性变形可以忽略的情况第二章金属在其他静载荷下的力学性能一、解释下列名词:(1)应力状态软性系数材料或工件所承受的最大切应力τmax和最大正12应力σmax比值即:max(2)缺口效应绝大多数机件的横截面都不是均匀而无变化的光滑体往往存在截面的急剧变化如键槽、油孔、轴肩、螺纹、退刀槽及焊缝等这种截面变化的部分可视为“缺口”由于缺口的存在在载荷作用下缺口截面上的应力状态将发生变化产生所谓的缺口效应(3)缺口敏感度缺口试样的抗拉强度σbn的与等截面尺寸光滑试样的抗拉强度σb的比值称为缺口敏感度即:(4)布氏硬度用钢球或硬质合金球作为压头采用单位面积所承受的试验力计算而得的硬度(5)洛氏硬度采用金刚石圆锥体或小淬火钢球作压头以测量压痕深度所表示的硬度(6)维氏硬度以两相对面夹角为136的金刚石四棱锥作压头采用单位面积所承受的试验力计算而得的硬度(7)努氏硬度采用2个对面角不等的四棱锥金刚石压头由试验力除以压痕投影面积得到的硬度(8)肖氏硬度采动载荷试验法根据重锤回跳高度表证的金属硬度(9)里氏硬度采动载荷试验法根据重锤回跳速度表证的金属硬度二、说明下列力学性能指标的意义(1)σbc材料的抗压强度(2)σbb材料的抗弯强度(3)τs材料的扭转屈服点(4)τb材料的抗扭强度(5)σbn材料的抗拉强度(6)NSR材料的缺口敏感度(7)HBW压头为硬质合金球的材料的布氏硬度(8)HRA材料的洛氏硬度(9)HRB材料的洛氏硬度(10)HRC材料的洛氏硬度(11)HV材料的维氏硬度在弹性状态下的应力分布:薄板:在缺口根部处于单向拉应力状态在板中心部位处于两向拉伸平面应力状态厚板:在缺口根部处于两向拉应力状态缺口内侧处三向拉伸平面应变状态无论脆性材料或塑性材料都因机件上的缺口造成两向或三向应力状态和应力集中而产生脆性倾向降低了机件的使用安全性为了评定不同金属材料的缺口变脆倾向必须采用缺口试样进行静载力学性能试验八.今有如下零件和材料需要测定硬度试说明选择何种硬度实验方法为宜(1)渗碳层的硬度分布;(2)淬火钢;(3)灰铸铁;(4)鉴别钢中的隐晶马氏体和残余奥氏体;(5)仪表小黄铜齿轮;(6)龙门刨床导轨;(7)渗氮层;(8)高速钢刀具;(9)退火态低碳钢;(10)硬质合金(1)渗碳层的硬度分布HK或显微HV(2)淬火钢HRC(3)灰铸铁HB(4)鉴别钢中的隐晶马氏体和残余奥氏体显微HV或者HK(5)仪表小黄铜齿轮HV(6)龙门刨床导轨HS(肖氏硬度)或HL(里氏硬度)(7)渗氮层HV(8)高速钢刀具HRC(9)退火态低碳钢HB(10)硬质合金HRA第三章金属在冲击载荷下的力学性能冲击韧性:材料在冲击载荷作用下吸收塑性变形功和断裂功的能力【P57】冲击韧度::U形缺口冲击吸收功AKU除以冲击试样缺口底部截面积所得之商称为冲击韧度αku=Aku/S(J/cm2),反应了材料抵抗冲击载荷的能力,用aKU表示P57注释/P67冲击吸收功:缺口试样冲击弯曲试验中摆锤冲断试样失去的位能为mgH1mgH2此即为试样变形和断裂所消耗的功称为冲击吸收功以AK表示单位为JP57/P67低温脆性:体心立方晶体金属及合金或某些密排六方晶体金属及其合金特别是工程上常用的中、低强度结构钢(铁素体珠光体钢)在试验温度低于某一温度tk时会由韧性状态变为脆性状态冲击吸收功明显下降断裂机理由微孔聚集型变为穿晶解理型断口特征由纤维状变为结晶状这就是低温脆性韧性温度储备:材料使用温度和韧脆转变温度的差值保证材料的低温服役行为二、(1)AK:冲击吸收功含义见上面冲击吸收功不能真正代表材料的韧脆程度但由于它们对材料内部组织变化十分敏感而且冲击弯曲试验方法简便易行被广泛采用AKV(CVN):V型缺口试样冲击吸收功.AKU:U型缺口冲击吸收功.(2)FATT50:通常取结晶区面积占整个断口面积50%时的温度为tk 并记为50%FATT或FATT50%t50(或:结晶区占整个断口面积50%是的温度定义的韧脆转变温度.(3)NDT:以低阶能开始上升的温度定义的韧脆转变温度,称为无塑性或零塑性转变温度(4)FTE:以低阶能和高阶能平均值对应的温度定义tk记为FTE(5)FTP:以高阶能对应的温度为tk记为FTP四、试说明低温脆性的物理本质及其影响因素低温脆性的物理本质:宏观上对于那些有低温脆性现象的材料它们的屈服强度会随温度的降低急剧增加而断裂强度随温度的降低而变化不大当温度降低到某一温度时屈服强度增大到高于断裂强度时在这个温度以下材料的屈服强度比断裂强度大因此材料在受力时还未发生屈服便断裂了材料显示脆性从微观机制来看低温脆性与位错在晶体点阵中运动的阻力有关当温度降低时位错运动阻力增大原子热激活能力下降因此材料屈服强度增加影响材料低温脆性的因素有(P63P73):1.晶体结构:对称性低的体心立方以及密排六方金属、合金转变温度高材料脆性断裂趋势明显塑性差2.化学成分:能够使材料硬度强度提高的杂质或者合金元素都会引起材料塑性和韧性变差材料脆性提高3.显微组织:①晶粒大小细化晶粒可以同时提高材料的强度和塑韧性因为晶界是裂纹扩展的阻力晶粒细小晶界总面积增加晶界处塞积的位错数减少有利于降低应力集中;同时晶界上杂质浓度减少避免产生沿晶脆性断裂②金相组织:较低强度水平时强度相等而组织不同的钢冲击吸收功和韧脆转变温度以马氏体高温回火最佳贝氏体回火组织次之片状珠光体组织最差钢中夹杂物、碳化物等第二相质点对钢的脆性有重要影响当其尺寸增大时均使材料韧性下降韧脆转变温度升高五.试述焊接船舶比铆接船舶容易发生脆性破坏的原因焊接容易在焊缝处形成粗大金相组织气孔、夹渣、未熔合、未焊透、错边、咬边等缺陷增加裂纹敏感度增加材料的脆性容易发生脆性断裂七.试从宏观上和微观上解释为什么有些材料有明显的韧脆转变温度而另外一些材料则没有?宏观上体心立方中、低强度结构钢随温度的降低冲击功急剧下降具有明显的韧脆转变温度而高强度结构钢在很宽的温度范围内冲击功都很低没有明显的韧脆转变温度面心立方金属及其合金一般没有韧脆转变现象微观上体心立方金属中位错运动的阻力对温度变化非常敏感位错运动阻力随温度下降而增加在低温下该材料处于脆性状态而面心立方金属因位错宽度比较大对温度不敏感故一般不显示低温脆性体心立方金属的低温脆性还可能与迟屈服现象有关对低碳钢施加一高速到高于屈服强度时材料并不立即产生屈服而需要经过一段孕育期(称为迟屈时间)才开始塑性变形这种现象称为迟屈服现象由于材料在孕育期中只产生弹性变形没有塑性变形消耗能量所以有利于裂纹扩展往往表现为脆性破坏第四章金属的断裂韧度2.名词解释低应力脆断:高强度、超高强度钢的机件中低强度钢的大型、重型机件在屈服应力以下发生的断裂张开型(?型)裂纹:拉应力垂直作用于裂纹扩展面裂纹沿作用力方向张开沿裂纹面扩展的裂纹应力场强度因子K?:在裂纹尖端区域各点的应力分量除了决定于位置外尚与强度因子K?有关对于某一确定的点其应力分量由K?确定K?越大则应力场各点应力分量也越大这样K?即可表示应力场的强弱程度称K?为应力场强度因子“I”表示I型裂纹小范围屈服:塑性区的尺寸较裂纹尺寸及净截面尺寸为小时(小1个数量级以上)这就称为小范围屈服有效屈服应力:裂纹在发生屈服时的应力有效裂纹长度:因裂纹尖端应力的分布特性裂尖前沿产生有塑性屈服区屈服区内松弛的应力将叠加至屈服区之外从而使屈服区之外的应力增加其效果相当于因裂纹长度增加ry后对裂纹尖端应力场的影响经修正后的裂纹长度即为有效裂纹长度:a+ry裂纹扩展K判据:裂纹在受力时只要满足KI?KIC就会发生脆性断裂.反之即使存在裂纹若KI?KIC也不会断裂新P71:旧832、说明下列断裂韧度指标的意义及其相互关系K?C和KC答:临界或失稳状态的K?记作K?C或KCK?C为平面应变下的断裂韧度表示在平面应变条件下材料抵抗裂纹失稳扩展的能力KC为平面应力断裂韧度表示在平面应力条件下材料抵抗裂纹失稳扩展的能力它们都是?型裂纹的材料裂纹韧性指标但KC值与试样厚度有关当试样厚度增加使裂纹39材料力学性能课后习题答案材料力学课后习题答案尖端达到平面应变状态时断裂韧度趋于一稳定的最低值即为K?C 它与试样厚度无关而是真正的材料常数3、试述低应力脆断的原因及防止方法答:低应力脆断的原因:在材料的生产、机件的加工和使用过程中产生不可避免的宏观裂纹从而使机件在低于屈服应力的情况发生断裂预防措施:将断裂判据用于机件的设计上在给定裂纹尺寸的情况下确定机件允许的最大工作应力或者当机件的工作应力确定后根据断裂判据确定机件不发生脆性断裂时所允许的最大裂纹尺寸4、为什么研究裂纹扩展的力学条件时不用应力判据而用其它判据?答:由41可知裂纹前端的应力是1个变化复杂的多向应力如用它直接建立裂纹扩展的应力判据显得十分复杂和困难;而且当r→0时不论外加平均应力如何小裂纹尖端各应力分量均趋于无限大构件就失去了承载能力也就是说只要构件一有裂纹就会破坏这显然与实际情况不符这说明经典的强度理论单纯用应力大小来判断受载的裂纹体是否破坏是不正确的因此无法用应力判据处理这一问题因此只能用其它判据来解决这一问题5、试述应力场强度因子的意义及典型裂纹K?的表达式答:几种裂纹的K?表达式无限大板穿透裂纹:Ka;有限宽板穿透裂纹:aaK??1.2?a;有限宽板单边直裂纹:Kaf();Kaf()当b?a时bb 受弯单边裂纹梁:K??6Maf();无限大物体内部有椭圆片裂纹远处受3/2(b?a)b2均匀拉伸:Kaa2(sin??2cos2?)1/4;无限大物体表面有半椭圆裂纹远c1.1?a?处均受拉伸:A点的K??7、试述裂纹尖端塑性区产生的原因及其影响因素答:机件上由于存在裂纹在裂纹尖端处产生应力集中当σy趋于材料的屈服应力时在裂纹尖端处便开始屈服产生塑性变形从而形成塑性区影响塑性区大小的因素有:裂纹在厚板中所处的位置板中心处于平面应变状态塑性区较小;板表面处于平面应力状态塑性区较大但是无论平面应力或平面应变塑性区宽度总是与(KIC/σs)2成正比13、断裂韧度KIC与强度、塑性之间的关系:总的来说断裂韧度随强度的升高而降低15、影响KIC的冶金因素:内因:1、学成分的影响;2、集体相结构和晶粒大小的影响;3、杂质及第二相的影响;4、显微组织的影响外因:1、温度;2、应变速率16.有1大型板件材料的σ0.2=1200MPaKIc=115MPa*m1/2探伤发现有20mm长的横向穿透裂纹若在平均轴向拉应力900MPa下工作试计算KI及塑性区宽度R0并判断该件是否安全?解:由题意知穿透裂纹受到的应力为σ=900MPa根据σ/σ0.2的值确定裂纹断裂韧度KIC是否休要修正因为σ/σ0.2=900/1200=0.75>0.7所以裂纹断裂韧度KIC需要修正对于无限板的中心穿透裂纹修正后的KI为:a9000.01?KI168.1322)?0?0.177(0.75)(.177(?/?s)1?KI?塑性区宽度为:??R0比较K1与KIc:22s?因为K1=168.13(MPa*m1/2)KIc=115(MPa*m1/2)所以:K1>KIc裂纹会失稳扩展,所以该件不安全17.有一轴件平行轴向工作应力150MPa使用中发现横向疲劳脆性正断断口分析表明有25mm深度的表面半椭圆疲劳区根据裂纹a/c可以确定υ=1测试材料的σ0.2=720MPa试估算材料的断裂韧度KIC为多少?解:因为σ/σ0.2=150/720=0.208<0.7所以裂纹断裂韧度KIC不需要修正对于无限板的中心穿透裂纹修正后的KI为:KIC=Yσcac1/2对于表面半椭圆裂纹Y=1.1/υ=1.13?150?25?10所以KIC=Yσcac1/2=1.1=46.229(MPa*m1/2) 第五章金属的疲劳1.名词解释;应力幅σa:σa=1/2(σmaxσmin)p95/p108平均应力σm:σm=1/2(σmax+σmin)p95/p107应力比r:r=σmin/σmaxp95/p108疲劳源:是疲劳裂纹萌生的策源地一般在机件表面常和缺口裂纹刀痕蚀坑相连P96疲劳贝纹线:是疲劳区的最大特征一般认为它是由载荷变动引起的是裂纹前沿线留下的弧状台阶痕迹P97/p110疲劳条带:疲劳裂纹扩展的第二阶段的断口特征是具有略程弯曲并相互平行的沟槽花样称为疲劳条带(疲劳辉纹疲劳条纹)p113/p132 驻留滑移带:用电解抛光的方法很难将已产生的表面循环滑移带去除当对式样重新循环加载时则循环滑移带又会在原处再现这种永留或再现的循环滑移带称为驻留滑移带P111ΔK:材料的疲劳裂纹扩展速率不仅与应力水平有关而且与当时的裂纹尺寸有关ΔK是由应力范围Δσ和a复合为应力强度因子范围ΔK=KmaxKmin=Yσmax√aYσmin√a=YΔσ√a.p105/p120 da/dN:疲劳裂纹扩展速率即每循环一次裂纹扩展的距离P105 疲劳寿命:试样在交变循环应力或应变作用下直至发生破坏前所经受应力或应变的循环次数p102/p117过载损伤:金属在高于疲劳极限的应力水平下运转一定周次后其疲劳极限或疲劳寿命减小就造成了过载损伤P102/p1172.揭示下列疲劳性能指标的意义疲劳强度σ1σp,τ1,σ1N,P99,100,103/p114σ1:对称应力循环作用下的弯曲疲劳极限;σp:对称拉压疲劳极限;τ1:对称扭转疲劳极限;σ1N:缺口试样在对称应力循环作用下的疲劳极限疲劳缺口敏感度qfP103/p118金属材料在交变载荷作用下的缺口敏感性常用疲劳缺口敏感度来评定Qf=(Kf1)/(kt1).其中Kt为理论应力集中系数且大于一Kf为疲劳缺口系数Kf=(σ1)/(σ1N)过载损伤界P102,103/p117由实验测定测出不同过载应力水平和相应的开始降低疲劳寿命的应力循环周次得到不同试验点连接各点便得到过载损伤界疲劳门槛值ΔKthP105/p120在疲劳裂纹扩展速率曲线的Ⅰ区当ΔK≤ΔKth时da/aN=0,表示裂纹不扩展;只有当ΔK>ΔKth时da/dN>0,疲劳裂纹才开始扩展因此ΔKth是疲劳裂纹不扩展的ΔK临界值称为疲劳裂纹扩展门槛值4.试述疲劳宏观断口的特征及其形成过程(新书P96~98及PPT旧书P109~111)答:典型疲劳断口具有3个形貌不同的区域疲劳源、疲劳区及瞬断区(1)疲劳源是疲劳裂纹萌生的策源地疲劳源区的光亮度最大因为这里在整个裂纹亚稳扩展过程中断面不断摩擦挤压故显示光亮平滑另疲劳源的贝纹线细小(2)疲劳区的疲劳裂纹亚稳扩展所形成的断口区域是判断疲劳断裂的重要特征证据特征是:断口比较光滑并分布有贝纹线断口光滑是疲劳源区域的延续但其程度随裂纹向前扩展逐渐减弱贝纹线是由载荷变动引起的如机器运转时的开动与停歇偶然过载引起的载荷变动使裂纹前沿线留下了弧状台阶痕迹(3)瞬断区是裂纹最后失稳快速扩展所形成的断口区域其断口比疲劳区粗糙脆性材料为结晶状断口韧性材料为纤维状断口6.试述疲劳图的意义、建立及用途(新书P101~102旧书P115~117)答:定义:疲劳图是各种循环疲劳极限的集合图也是疲劳曲线的另1种表达形式意义:很多机件或构件是在不对称循环载荷下工作的因此还需要知道材料的不对称循环疲劳极限以适应这类机件的设计和选材的需要通常是用工程作图法由疲劳图求得各种不对称循环的疲劳极限1、?a?m疲劳图建立:这种图的纵坐标以?a表示横坐标以?m表示然后以不同应力比r条件下将?max表示的疲劳极限?r分解为?a和?m并在该坐标系中作ABC曲线即1?a(?max??min)1?r为?a??m疲劳图其几何关系为:tanm(?max??min)1?r2(用途):我们知道应力比r将其代入试中就可以求得tan?和?而后从坐标原点O引直线令其与横坐标的夹角等于?值该直线与曲线ABC 相交的交点B便是所求的点其纵、横坐标之和即为相应r的疲劳极限?rB?rB??aB??mB2、?max(?min)??m疲劳图建立:这种图的纵坐标以?max或?min表示横坐标以?m表示然后将不同应力比r下的疲劳极限分别以?max(?min)和?m表示于上述坐标系中就形成这种疲劳图几何关系为:tanmax2?max2m?max??min1?r (用途):我们只要知道应力比r,就可代入上试求得tan?和?而后从坐标原点O引一直线OH令其与横坐标的夹角等于?该直线与曲线AHC 相交的交点H的纵坐标即为疲劳极限8.试述影响疲劳裂纹扩展速率的主要因素(新书P107~109旧书P123~125)dac(?K)n答:1、应力比r(或平均应力?m)的影响:Forman提出:dN(1?r)Kc??K残余压应力因会减小r,使因会增大r使da降低和?Kth升高对疲劳寿命有利;而残余拉应力dNda升高和?Kth降低对疲劳寿命不利dN2、过载峰的影响:偶然过载进入过载损伤区内使材料受到损伤并降低疲劳寿命但若过载适当有时反而是有益的da3、材料组织的影响:①晶粒大小:晶粒越粗大其?Kth值越高越低对dN疲劳寿命越有利②组织:钢的含碳量越低铁素体含量越多时其?Kth值就越高当钢的淬火组织中存在一定量的残余奥氏体和贝氏体等韧性组织时可以提da高钢的?Kth降低③喷丸处理:喷丸强化也能提高?KthdN9.试述疲劳微观断口的主要特征答:断口特征是具有略呈弯曲并相互平行的沟槽花样称疲劳条带(疲劳条纹、疲劳辉纹)疲劳条带是疲劳断口最典型的微观特征滑移系多的面心立方金属其疲劳条带明显;滑移系少或组织复杂的金属其疲劳条带短窄而紊乱疲劳裂纹扩展的塑性钝化模型(Laird模型):图中(a),在交变应力为零时裂纹闭合图(b)受拉应力时裂纹张开在裂纹尖端沿最大切应力方向产生滑移图(c),裂纹张开至最大塑性变形区扩大裂纹尖端张开呈半圆形裂纹停止扩展由于塑性变形裂纹尖端的应力集中减小裂纹停止扩展的过程称为“塑性钝化”图(d)当应力变为压缩应力时滑移方向也改变了裂纹尖端被压弯成“耳状”切口图(e)到压缩应力为最大值时裂纹完全闭合裂纹尖端又由钝变锐形成一对尖角12.试述金属表面强化对疲劳强度的影响答:表面强化处理可在机件表面产生有利的残余压应力同时还能提高机件表面的强度和硬度这两方面的作用都能提高疲劳强度表面强化方法通常有表面喷丸、滚压、表面淬火及表面化学热处理等(1)表面喷丸及滚压喷丸是用压缩空气将坚硬的小弹丸高速喷打向机件表面使机件表面产生局部形变硬化;同时因塑变层周围的弹性约束又在塑变层内产生残余压应力表面滚压和喷丸的作用相似只是其压应力层深度较大很适于大工件;而且表面粗糙度低强化效果更好(2)表面热处理及化学热处理他们除能使机件获得表硬心韧的综合力学性能外还可以利用表面。
(仅供参考)《材料力学》第五版-刘鸿文第9-10章习题答案

湖北汽车工业学院 材料力学 主讲教师:马迅
9.16 10号工字梁的C端固定,A端铰支于空心钢管AB上。 钢管的内径和外径分别为30mm和40mm,B端亦为铰支。 当300N的重物落于梁的A端时,校核AB杆的稳定性。规 定稳定安全系数nst=2.5。
解: 包含一次静不定、冲击载荷 和屈曲三类问题。
解题思路: 利用变形协调条件求解静不定问
=
64 1× 2/cos30o 2
= 44.6N
2杆的许可载荷
[N2 ] =
Pcr n
=
44.6 N = 24.8N 1.8
P=12.4N
HAII MAXUN
1
2012-6-1
1/8
Printed with FinePrint - purchase at PDF created with pdfFactory trial version
Kd =1+
1+ 2×50=4 ∆ st
σ st max
=
M max W
= 37.5MPa
( yc )d = Kd ∆st = 0.05m (σ max )d = Kdσ max = 150MPa
HAII MAXUN
4
2012-6-1
4/8
Printed with FinePrint - purchase at PDF created with pdfFactory trial version
湖北汽车工业学院 材料力学 主讲教师:马迅
附加习题9-4:立柱CD为圆截面,材料的E=200Gpa, σp=200MPa。稳定安全系数nst=2,校核立柱的稳定性。
解:
λP =
π 2E = σPFra bibliotekπ 2 200 ×109 200 × 106
材料力学第六版答案第10章
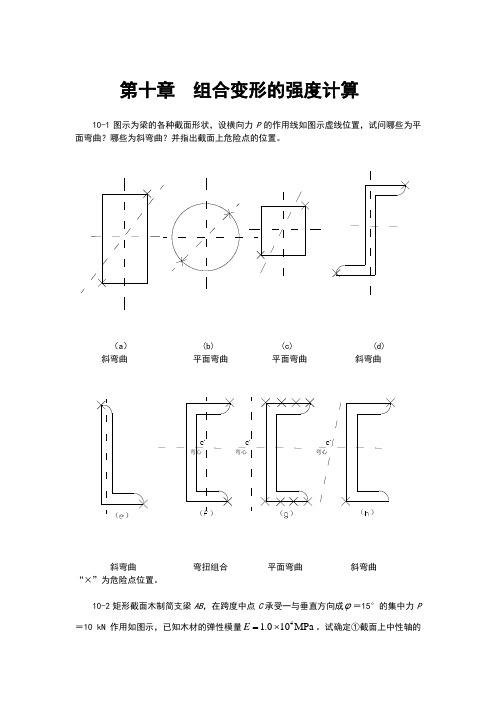
第十章 组合变形的强度计算10-1图示为梁的各种截面形状,设横向力P 的作用线如图示虚线位置,试问哪些为平面弯曲?哪些为斜弯曲?并指出截面上危险点的位置。
(a ) (b) (c) (d) 斜弯曲 平面弯曲 平面弯曲 斜弯曲弯心()()弯心弯心()()斜弯曲 弯扭组合 平面弯曲 斜弯曲“×”为危险点位置。
10-2矩形截面木制简支梁AB ,在跨度中点C 承受一与垂直方向成ϕ=15°的集中力P =10 kN 作用如图示,已知木材的弹性模量MPa 100.14⨯=E 。
试确定①截面上中性轴的位置;②危险截面上的最大正应力;③C 点的总挠度的大小和方向。
解:66.915cos 10cos =⨯==οϕP P y KN59.215sin 10sin =⨯==οϕP P z KN4310122015=⨯=z J 4cm 3310cm W z =335625121520cm J y =⨯=3750cm W y =25.74366.94max =⨯==l P M y z KN-M 94.14359.24m ax =⨯==l P M z y KN-MMPaW M W M yy z z 84.9107501094.110101025.763633maxmax max=⨯⨯+⨯⨯=+=--σ 中性轴:οο47.2515tan 562510tan tan tan 411=⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫⎝⎛-=--ϕαy z J J 2849333105434.0101010104831066.948--⨯=⨯⨯⨯⨯⨯⨯==z y y EJ l P f m28933310259.010562510104831059.248--⨯=⨯⨯⨯⨯⨯⨯==y z z EJ l P f m 602.0259.05434.022=+=f cm方向⊥中性轴:ο47.25=α10-3 矩形截面木材悬臂梁受力如图示,P 1=800 N ,P 2=1600 N 。
浙江工业大学材料力学第10章答案

浙江⼯业⼤学材料⼒学第10章答案10.1 ⼀端固定⼀端铰⽀的⼯字形截⾯细长压杆,已知弹性模量GPa 208=E ,截⾯尺⼨200mm×100mm ×7mm ,杆长m l10=,试确定压杆的临界压⼒。
解:4337.16796532121869312200100mm I x =?-?=4332.11719831271861210072mm I y =?+?=因为x y I I <,故y I I =()()kN N l EI F cr 1.49101.49100007.02.117198310208323222=?===πµπ10.2 两端固定的圆截⾯钢质压杆,直径为50mm ,受轴向压⼒F 作⽤。
已知GPa 210=E 和MPa 200=p σ,试确定能够使⽤欧拉公式的最短压杆长度l 。
解:8.10120010210505.044322=??==≥??===πσπλµµλp p E l d l i l可得:mm l 2545≥10.3 截⾯为矩形h b ?的压杆,两端⽤柱销联接(在y x -平⾯内弯曲时,可视为两端铰⽀;在zx -平⾯内弯曲时,可视为两端固定)。
已知GPa 200=E ,MPa 200=p σ,试求:(1)当mm 30=b ,mm50=h 时,压杆的临界压⼒;(2)若使压杆在两个平⾯(y x -和z x -⾯)内失稳的可能性相同时,求b 和h 的⽐值。
解:43331250012503012mm bh I z =?==,1=z µ,故()()kNN l EI F z z cr 1171011723001312500102003232221=?===πµπ43311250012305012mm hb I y =?==,5.0=y µ,故()()kN N l EI F y y cr 1681016823005.0112500102003232222=?===πµπ故kN F cr 117=。
材料力学 第10章 弯曲应力及强度

a
Φ14
30 工件
Fa x
10.4 弯曲强度条件
例10-5 梁的载荷及截面尺寸如图所示,材料的容许拉应力
[t]=40MPa、容许压应力[c] =100MPa,试校核该梁的强度。
q=10kN/m
F=20kN
AB 2m
CD 3m 1m
q=10kN/m
A
B
FB M
F=20kN
C
D
FD
10kN.m
x
157.5 200 30
10.3 横力弯曲时梁的切应力
三、其它形状截面
T型截面
圆形截面
环形截面
max
z
max
FSS
* z,m
ax
I zb1
z
max
z
max
max
4 3
FS A
max
2
FS A
10.3 横力弯曲时梁的切应力
21 560
例10-2 56a号工字钢制成的简支梁如图所示,F=150kN,求最大 切应力及最大切应力所在截面上K点处的切应力。
ad bc
a
d
b
c
σσ
M
ττ
10.2 纯弯曲时梁的正应力
3. 变形几何关系
o1o2 dx ρdθ
k1k2 (ρ y)dθ Δl=k1k2 k1k2 ( ρ y)dθ ρdθ ydθ
dx 中性层
y o1
o2
k1
k2
dx 变形前
o
d
o1
o2
k1
k 2
变形后
10.2 纯弯曲时梁的正应力
第10章 弯曲应力及弯曲强度
10.1 引言 10.2 纯弯曲时梁的正应力 10.3 横力弯曲时梁的切应力 10.4 弯曲强度条件 10.5 提高梁弯曲强度的措施
材料力学第十章

fC
1 EI
AC
M
(
x1
)
Fs
0
M ( x1 Fs
)
dx
)
f ( x) 1 EI
x 0
F
(l
x1
)(
x
x1
)dx1
Fx 2 6EI
(3l
x)
§10-4 卡氏第二定理
例10-5 图示悬臂梁AB,B端作用铅垂力F,梁的EI已知,
1)求梁的挠曲线方程;2)若在梁中截面再作用力F,求自
x2
F=F0
A
1)dx段应变能:
dU 1(A)( d
x
)
2
d
xA
FQ2dx
2
2G
2GA
dx dx
2)l段应变能:
U
l
0dU
0l
FQ2 dx 2GA
FQ—横截面剪力; A—横截面面积;
—截面系数
矩形:=6/5;实心圆:=10/9;薄圆环:=2;
3)注意:在一般细长梁中,远小于弯矩应变能的 剪力应变能,通常忽略不计。
若=0.3,h/l=0.1,比值为0.0312。长梁忽略剪切应变能。
3)求C点挠度:W
1 2
FfC
U弯
F 2l3 96EI
fC
Fl 3 48EI
§10-2 弹性应变能的计算
四、非线性固体的应变能
1.应变能
F 非线性
与比能:
U*
线性
非线性
u*
线性
2.余能与
F1
余比能:
U
d1
1 d
u
1
应变能:线弹性
F
由端挠度fB。
材料力学 第十章组合变形(1,2,3)

1.2m
解:求支反力,由平衡方程
FB B
FA
' FA
F ' A 0,
FA FB 5kN
A
1.6m 1.6m
m g f A
10kN C
m FAy
作折杆的受力图,折杆及 受力对称,只需分析一半 即杆AC 将FA分解, 得杆的轴力 FN、弯矩M (x)
B
FAx
FN FAx 3kN
3 10 8 10 t 81.1 2 3 c d / 4 d / 32 81.9
3 3
M W
[例10-2]圆截面杆的偏心压缩时不产生拉 力的载荷作用范围
P
y
P
y
Pa
a
z
z
CL11TU12
P
y
Pa
y
P
y
Pa
z
z
z
P
y y
Pa
y
P
z
Pa
z P
y y
z
Pa
y
P
CL11TU10
解: X A 3kN, A 4kN Y
任意横截面x上的内力:
FN X A 3kN FS YA 4kN M ( x) YA x 4 x
1 1截面上危险截面, 其上:FN 3kN,M 8kN m
FN A
M W
t FN M c A W
CL11TU5
y0 Iz tg tg z0 Iz
为中性轴与z轴夹角
3.强度计算:
1)危险截面:当x=0时 M Z , M y 同时取最大,固定端处为危险面 2)危险点:危险面上 D1 , D2点 3)最大应力
孙训方《材料力学》(第6版)笔记和课后习题(含考研真题)详解-弯曲问题的进一步研究(圣才出品)

cos
=
−
1 8
ql 2
cos
= − 1 2103 N/m(4.2 m)2 cos 20o 8
= −4144 N m
My
=
−M
sin
=
−
1 8
ql 2
sin
= − 1 2103 N/m(4.2 m)2 sin 20o 8
= −1508 N m
A、B 点坐标分别为:
yA=80mm,zA=(b-z0)=45mm,yB=-80mm,zB=-18mm
10.2 课后习题详解 10-1 截面为 16a 号槽钢的简支梁,跨长 l=4.2m,受集度为 q=2kN/m 的均布荷 载作用。梁放在 φ=20o 韵斜面上,如图 10-2-1 所示。若不考虑扭转的影响,试确定梁危 险截面上 A 点和 B 点处的弯曲正应力。
4 / 20
圣才电子书 十万种考研考证电子书、题库视频学习平台
A
=
−
1508 Ngm 73.310−8 m4
45 10−3
m
−
4144 Ngm 866.2 10−8 m4
80
10−3
m=
−131
MPa
点 B 处有最大拉应力
( ) ( ) B
=
−
1508 Ngm 73.310−8 m4
−1810−3 m
−
4144 Ngm 866.2 10−8 m4
−80 10−3 m
一、非对称纯弯曲梁的正应力 当梁不具有纵向对称面,或者梁虽具有纵向对称平面,但外力不作用在该平面时,梁将 发生非对称弯曲。非对称纯弯曲梁正应力计算公式见表 10-1-1。
表 10-1-1 非对称纯弯曲梁正应力计算公式
材料力学弯曲应力

材料力学弯曲应力材料力学是研究材料在外力作用下的变形和破坏规律的一门学科,而弯曲应力是材料在受到弯曲载荷时所产生的应力。
弯曲应力的研究对于工程结构设计和材料选用具有重要意义。
本文将从弯曲应力的概念、计算公式、影响因素等方面进行详细介绍。
弯曲应力是指在材料受到弯曲载荷作用下,横截面上的应力分布情况。
在弯曲过程中,材料上部受到压应力,下部受到拉应力,而中性面则不受应力影响。
根据梁的理论,弯曲应力与弯矩、截面形状以及材料性质有关。
在工程实践中,我们通常使用梁的弯曲应力公式来计算弯曲应力的大小。
梁的弯曲应力公式可以表示为:\[ \sigma = \frac{M \cdot c}{I} \]其中,σ为弯曲应力,M为弯矩,c为截面中性轴到受拉或受压纤维的距离,I为截面的惯性矩。
从公式中可以看出,弯曲应力与弯矩成正比,与截面形状和材料性质有关,截面越大,惯性矩越大,弯曲应力越小。
影响弯曲应力的因素有很多,主要包括载荷大小、截面形状、材料性质等。
首先是载荷大小,当外力作用在梁上时,产生的弯矩大小将直接影响弯曲应力的大小。
其次是截面形状,截面形状不同将导致截面惯性矩不同,进而影响弯曲应力的大小。
最后是材料性质,材料的弹性模量、屈服强度等参数也会对弯曲应力产生影响。
在工程实践中,我们需要根据具体的工程要求和材料性质来选择合适的截面形状和材料类型,以使得结构在受到弯曲载荷时能够满足强度和刚度的要求。
同时,还需要合理设计结构,减小弯曲应力集中的区域,避免出现应力集中而导致的破坏。
综上所述,弯曲应力是材料在受到弯曲载荷时产生的应力,其大小与弯矩、截面形状和材料性质有关。
在工程实践中,我们需要根据具体的工程要求和材料性质来计算和分析弯曲应力,以保证结构的安全可靠。
同时,合理设计结构和选择合适的材料也是降低弯曲应力的重要手段。
希望本文对于弯曲应力的理解和应用能够有所帮助。
材料力学第10章 动载荷

Kd = 1 + 1 + 2H
∆st
P
Pl 3 + P ∆st = 48EI 4C
σ st max = Pl / 4 = Pl
W
4W
MF
Pl/4
σd max = Kdσ st max ≤ [σ ] [H] =
∆st
2 σ st max
[(
[σ ]
−1) −1]
2
等截面刚架,重物P自高度 处自由下落。 、 、 自高度h处自由下落 例:等截面刚架,重物 自高度 处自由下落。 E、I、 W已知 。 试求截面的最大竖直位移和刚架内的最大 已知。 已知 冲击正应力( 刚架的质量可略去不计, 冲击正应力 ( 刚架的质量可略去不计 , 且不计轴力 对刚架变形的影响) 对刚架变形的影响)。
第十章 动载荷
§10.1 概述 §10.2 动静法的应用 §10.3 强迫振动的应力计算 §10.4 杆件受冲击时的应力和变形 §10.5 冲击韧性
§10.1 概述
1)动载荷问题的特点: )动载荷问题的特点: 静载荷问题:载荷平稳地增加, 静载荷问题:载荷平稳地增加,不引起构件 的加速度——准静态。 准静态。 的加速度 准静态 动载荷问题:载荷急剧变化, 动载荷问题:载荷急剧变化,构件速度发生 急剧变化。 急剧变化。
2FNd = qd (2R)
qd FNd FNd
qd
σd =
FNd = ρR2ω2 = ρv2 A
注意: 无关! 注意:与A无关! 无关
4)匀减速转动(飞轮刹车) )匀减速转动(飞轮刹车) 例 4 : 飞 轮 转 速 n=100r/min , 转 动 惯 量 为 Ix=0.5kNms2 , 轴 直 径 d=100mm , 10 秒停转,求最大动应力。 秒停转,求最大动应力。 解:角速度: ω0 = nπ 角速度: 30 角加速度: 角加速度:α = −ω0 / t
材料力学-学习指导及习题答案

材料力学-学习指导及习题答案第一章绪论1-1 图示圆截面杆,两端承受一对方向相反、力偶矩矢量沿轴线且大小均为M的力偶作用。
试问在杆件的任一横截面m-m上存在何种内力分量,并确定其大小。
解:从横截面m-m将杆切开,横截面上存在沿轴线的内力偶矩分量M x,即扭矩,其大小等于M。
1-2 如图所示,在杆件的斜截面m-m上,任一点A处的应力p=120 MPa,其方位角θ=20°,试求该点处的正应力ζ与切应力η。
解:应力p与斜截面m-m的法线的夹角α=10°,故ζ=p cosα=120×cos10°=118.2MPaη=p sinα=120×sin10°=20.8MPa1-3 图示矩形截面杆,横截面上的正应力沿截面高度线性分布,截面顶边各点处的正应力均为ζmax=100 MPa,底边各点处的正应力均为零。
试问杆件横截面上存在何种内力分量,并确定其大小。
图中之C点为截面形心。
解:将横截面上的正应力向截面形心C简化,得一合力和一合力偶,其力即为轴力F N=100×106×0.04×0.1/2=200×103 N =200 kN其力偶即为弯矩M z=200×(50-33.33)×10-3 =3.33 kN·m1-4 板件的变形如图中虚线所示。
试求棱边AB与AD的平均正应变及A点处直角BAD的切应变。
解:第二章轴向拉压应力2-1试计算图示各杆的轴力,并指出其最大值。
解:(a) F N AB=F, F N BC=0, F N,max=F(b) F N AB=F, F N BC=-F, F N,max=F(c) F N AB=-2 kN, F N2BC=1 kN, F N CD=3 kN, F N,max=3 kN(d) F N AB=1 kN, F N BC=-1 kN, F N,max=1 kN2-2 图示阶梯形截面杆AC,承受轴向载荷F1=200 kN与F2=100 kN,AB段的直径d1=40 mm。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
F l x l
150 kN
x 2m
2 x 2 . 667
200 kN 吊车
150 kN 吊车
2 x 2 . 667
2.确定I字钢型号
A B
C
F
l
辅助梁
x
M
max
A
200 l 2 . 667
266 . 6 kNm
FA
FB
M
max
B 150
F A 46 . 9 kN
31 . 9
查表
kN
28 . 1 3 . 75
15
N0 12.6工字钢 WZ=77.5cm3
kNm
13 . 16
例 简支梁如图所示,试求梁的最底层纤维的总伸长。 解 1、计算梁底层微段的伸长量
(x)
M (x) WZ
1
A
q
B
( x) E ( x)
x
考虑脱离体的平衡,须满足 下面三个平衡条件 (1)
z M
F
ix
0
dA 0
A
y A z σ
y
x
FN
dA
A
E
A
y
dA
E
ydA
A
E
Sz 0 Sz 0
(中性轴Z轴为形心轴)
(2)
M
y
M
iy
0
z
A
dA 0
dAz
最大正应力的确定
⑴ 截面关于中性轴对称
My IZ
max
t
My
max
IZ
c
WZ
IZ y max
z
max max
M Wz
Wz ——截面的抗弯截面系数
⑵ 截面关于中性轴不对称
max
t
My
t max
Iz
z
max
c
My
c max
Iz
几种常见截面的 IZ 和 WZ 圆截面 空心圆截面
a
c
b a o
A
d c o1
B
y
b
d
dx
d
A1 B 1 AB AB
A1 B 1 OO 1 OO 1
A1
O
O1
B1 x
( y )d d
d
y
y
A1 B 1 AB AB
A1 B 1 OO 1 OO 1
( y )d d
d
y
(1)
(二)物理关系:
y
......
由纵向线应变的变化规律→正应力的分布规律。
在弹性范围内
d
E
O O1
E
Ey
...... (2)
A1
y
B1 x
E
Ey
1
为梁弯曲变形后的曲率
上式说明了横截面上正应力的分布规律,表明正应力沿截面高度
呈线性变化,距中性轴越远,应力值越大,在中性轴处正应力为零。
Fa
Fb
C截面:
max
MC W zC
6
Fb
d 2
32
3
62 . 5 160 32
0 . 13
3
M
46 . 4 10 Pa 46 . 4 MPa
结论:轮轴安全
例 图示T形截面简支梁在中点承受集中力F=32kN,梁的长度L=2m。T形截 面的形心坐标yc=96.4mm,横截面对于z轴的惯性矩Iz=1.02×108mm4。求弯矩 最大截面上的最大拉应力和最大压应力。
y
150
F
A
96 . 4
A
M Ay l IZ
24 . 09 MPa
3
B
C 50
z
200
2F
1400 600
16 10 250 96 . 4 1 . 02 10
3
8
50
A
M Ay y IZ
12 kNm
A
A
E
y
zdA
E
A
yzdA
E
I yz 0
I
yz
0
z M
(y轴为对称轴,自然满足)
也就表明横截面的惯性积为零。 这就表示 y、z 轴是形心主轴。
y A z σ
y
E
x
(3)
M iz 0
y dA M 0
A
M
y dA
A
Z
E
A
y
ydA
h0
三、梁的正应力强度条件
max
材料的许用弯曲正应力
M
max
1、中性轴为横截面对称轴的等直梁
Wz
2、拉、压强度不相等的铸铁等脆性材料制成的梁
ycmax
t max [ t ]
O
ytmax
z y
c max [ c ]
为充分发挥材料的强度,最合理的设计为
tmax
200 kN 吊车 150 kN 吊车
1.确定F加在辅助梁的位置
A
B
M
M
A
0 0
F l x F B l F l x 0 l
Fx F A x F A l 0 l
C
辅助梁
x
B
FA
F
l
FB
令: F A
FB
Fx l
200 kN
x 2 . 667 m
200
C
z
IZ
50
例 长为2.5m的工字钢外伸梁,如图示,其外伸部分为0.5m,梁上承 受均布荷载,q=30kN/m,试选择工字钢型号。已知工字钢抗弯强度[σ] =215MPa。
q 30 kN m
解
B
A
0 .5 m
WZ
M
2m
F B 28 . 1kN
max
61 . 2 cm
3
线伸长区,中间必有一层纵向
无长度改变的过渡层------称 为中性层 。
中间层与横截面的交线 --中性轴
梁的弯曲变形实际上是各截面绕各自的中性轴转动 了一个角度,等高度的一层纤维的变形完全相同。
5、线应变的变化规律:
取dx长的微段梁进行研究 选中性层与横截面的交线为 z 轴,轴线方向为x 轴,与xz垂直 的为y 轴,取向下为正。 设中性层的曲率半径为 , 微段左右两截面的相对转角为 d , 因中性层长度不变,故有 dx d 因此距中性层为y处的线应变为
3、假设:
(1)弯曲平面假设: 梁变形前原为平面的横截面 变形后仍 为平面,且仍垂直于 变形后的轴线,只是各横截面绕 其上的某轴转动了一个角度。 (2)纵向纤维假设: 梁是由许多纵向纤维组成的, 且各纵向纤维之间无挤压。 突出一侧纤维伸长 凹入一侧纤维缩短
4、中性层与中性轴
根据变形的连续性可知, 梁弯曲时从其凹入一侧的纵向 线缩短区到其凸出一侧的纵向
Iz
c
1、强度校核
——
max ;
M Wz max 2、设计截面尺寸——
3、确定外荷载 —— Mmax Wz
;
例 试计算图示简支矩形截面木梁平放与竖放时的最大正应力, 并加以比较。
200
100
q 2 kN m
200
4m
100
qL 8
2
竖放
qL
2
max
IZ
d
64
4
WZ
d
32
3
d
IZ
D644源自(1 )4WZ
D
32
2
3
(1 )
4
d
D
矩形截面 空心矩形截面
IZ
bh 12
3
WZ
3 3
bh 6
h b
IZ
b0 h0 12
3
bh 12
WZ (
b0 h0 12
bh 12
3
) /( h 0 / 2 )
h
b b0
例 图示为机车轮轴的简图。试校核轮轴的强度。已知
材料的许用应力
60 MPa .
(1)计算简图 解: (2)绘弯矩图 (3)强度校核
B截面:
max
M
B
Fa
W zB
d1
32
6
3
62 . 5 267 32
0 . 16
3
41 . 5 10 Pa 41 . 5 MPa
M
M
max
y tmax
y cmax
Iz
max
[ t]
[ c]
y tmax y cmax
[ t] [ c]
cmax
Iz
弯曲正应力强度条件
max
M
max
max
Wz
M
max
t
