二次函数的图像与性质练习题及答案
二次函数的图像和性质练习题(含答案)

1.下列函数中是二次函数的为 A .y =3x -1B .y =3x 2-1C .y =(x +1)2-x2D .y =x 3+2x -32.抛物线y =2x 2+1的的对称轴是 A .直线x =14B .直线x =14-C .x 轴D .y 轴3.抛物线y =-(x -4)2-5的顶点坐标和开口方向分别是 A .(4,-5),开口向上B .(4,-5),开口向下C .(-4,-5),开口向上D .(-4,-5),开口向下4.抛物线y =-x 2不具有的性质是 A .对称轴是y 轴B .开口向下C .当x <0时,y 随x 的增大而减小D .顶点坐标是(0,0)5.已知点(-1,2)在二次函数y =ax 2的图象上,那么a 的值是 A .1B .2C .12D .-126.已知抛物线y =ax 2(a >0)过A (-2,y 1)、B (1,y 2)两点,则下列关系式一定正确的是 A .y 1>0>y 2B .y 2>0>y 1C .y 1>y 2>0D .y 2>y 1>07.当函数y =(x -1)2-2的函数值y 随着x 的增大而减小时,x 的取值范围是 A .x >0B .x <1C .x >1D .x 为任意实数8.对于二次函数2(3)4y x =--的图象,给出下列结论:①开口向上;②对称轴是直线3x =-;③顶点坐标是34--(,);④与x 轴有两个交点.其中正确的结论是 A .①②B .③④C .②③D .①④9.一种函数21(1)53m y m x x +=-+-是二次函数,则m =__________.10.把二次函数y =x 2-4x +3化成y =a (x -h )2+k 的形式是__________.11.将抛物线y =2(x -1)2+2向左平移3个单位,那么得到的抛物线的表达式为__________. 12.如图,抛物线y =ax 2-5ax +4a 与x 轴相交于点A ,B ,且过点C (5,4).(1)求a 的值和该抛物线顶点P 的坐标;(2)请你设计一种平移的方法,使平移后抛物线的顶点落在第二象限,并写出平移后抛物线的表达式.13.已知:抛物线2y x bx c =-++经过(30)B ,、(03)C ,两点,顶点为A . 求:(1)抛物线的表达式;(2)顶点A 的坐标.14.如图,已知二次函数y=ax2+bx+c的图象过A(2,0),B(0,-1)和C(4,5)三点.(1)求二次函数的解析式;(2)设二次函数的图象与x轴的另一个交点为D,求点D的坐标;(3)在同一坐标系中画出直线y=x+1,并写出当x在什么范围内时,一次函数的值大于二次函数的值.15.在平面直角坐标系中,将抛物线y=-12x2向下平移1个单位长度,再向左平移1个单位长度,得到的抛物线的解析式是A.y=-12x2-x-32B.y=-12x2+x-12C.y=-12x2+x-32D.y=-12x2-x-1216.二次函数y=ax2+bx+c的图象如图所示,那么一次函数y=bx+a的图象大致是A.B.C D.17.已知二次函数2(0)y ax bx c a =++≠的图象如图所示,有下列5个结论:①0abc >;②b a c <+;③420a b c ++>;④23c b <;⑤()(0)a b m am b m +>+≠,其中正确的结论有A .2个B .3个C .4个D .5个18.二次函数y =x 2-2x -3,当m -2≤x ≤m 时函数有最大值5,则m 的值可能为__________. 19.若直线y =ax -6与抛物线y =x 2-4x +3只有一个交点,则a 的值是__________.20.如图,已知二次函数y =ax 2+bx +8(a ≠0)的图象与x 轴交于点A (-2,0),B (4,0),与y 轴交于点C .(1)求抛物线的解析式及其顶点D 的坐标; (2)求△BCD 的面积;(3)若直线CD 交x 轴与点E ,过点B 作x 轴的垂线,交直线CD 与点F ,将抛物线沿其对称轴向上平移,使抛物线与线段EF 总有公共点.试探究抛物线最多可以向上平移多少个单位长度(直接写出结果,不写求解过程).21.(2018·四川成都)关于二次函数2241y x x =+-,下列说法正确的是A .图象与y 轴的交点坐标为(0,1)B .图象的对称轴在y 轴的右侧C .当0x <时,y 的值随x 值的增大而减小D .y 的最小值为-322.(2018·湖北黄冈)当a ≤x ≤a +1时,函数y =x 2-2x +1的最小值为1,则a 的值为A .-1B .2C .0或2D .-1或223.(2018·江苏连云港)已知学校航模组设计制作的火箭的升空高度h (m )与飞行时间t(s )满足函数表达式h =-t 2+24t +1.则下列说法中正确的是 A .点火后9 s 和点火后13 s 的升空高度相同 B .点火后24 s 火箭落于地面 C .点火后10 s 的升空高度为139 m D .火箭升空的最大高度为145 m24.(2018·山东德州)如图,函数221y ax x =-+和y ax a =-(a 是常数,且0a ≠)在同一平面直角坐标系的图象可能是A .B .C D .25.(2018·湖北恩施州)抛物线y =ax 2+bx +c 的对称轴为直线x =-1,部分图象如图所示,下列判断中:①abc >0;②b 2-4ac >0;③9a -3b +c =0;④若点(-0.5,y 1),(-2,y 2)均在抛物线上,则y 1>y 2;⑤5a -2b +c <0. 其中正确的个数有A.2 B.3 C.4 D.5 26.(2018·江苏淮安)将二次函数y=x2-1的图象向上平移3个单位长度,得到的图象所对应的函数表达式是__________.27.(2018·山东淄博)已知抛物线y=x2+2x-3与x轴交于A,B两点(点A在点B的左侧),将这条抛物线向右平移m(m>0)个单位长度,平移后的抛物线与x轴交于C,D两点(点C在点D的左侧),若B,C是线段AD的三等分点,则m的值为__________.1.【答案】B2.【答案】D【解析】∵抛物线y =2x 2+1中一次项系数为0,∴抛物线的对称轴是y 轴.故选D . 3.【答案】B【解析】∵抛物线的解析式为2(4)5y x =---, 10a =-<,∴抛物线的开口向下.抛物线2()y a x h k =-+的顶点坐标为(h ,k )∴抛物线2(4)5y x =---的顶点坐标为(4,-5).故选B . 4.【答案】C5.【答案】B【解析】∵点(-1,2)在二次函数2y ax =的图象上,∴2(1)2a ⋅-=,解得2a =.故选B . 6.【答案】C【解析】∵抛物线y =ax 2(a >0)的对称轴是y 轴,∴A (-2,y 1)关于对称轴的对称点的坐标为(2,y 1).又∵a >0,0<1<2,且当x =0时,y =0,∴0<y 2<y 1.故选C . 7.【答案】B【解析】对称轴是:x =1,且开口向上,如图所示,∴当x <1时,函数值y 随着x 的增大而减小.故选B . 8.【答案】D【解析】∵a =1>0,∴开口向上,①正确;∵x -3=0,∴对称轴为x =3,②错误;∵顶点坐标为:(3,-4),故③错误;∴在第四象限,所以与x 轴有两个交点,故④正确.故选D . 9.【答案】-1【解析】根据二次函数的二次项的次数是2,二次项的系数不等于零,可由21(1)53my m x x +=-+-是二次函数,得m 2+1=2且m −1≠0,解得m =-1,m =1(不符合题意要舍去).故答案为:-1. 10.【答案】y =(x -2)2-1【解析】y =x 2-4x +3=(x 2-4x +4)-4+3=(x -2)2-1,故答案为:y =(x -2)2-1. 11.【答案】y =2(x +2)2+2【解析】将抛物线y =2(x -1)2+2向左平移3个单位,那么得到的抛物线的表达式为y =2(x -1+3)2+2,即y =2(x +2)2+2.故答案为:y =2(x +2)2+2.13.【解析】(1)把(30)B ,、(03)C ,代入2y x bx c =-++,得9303b c c -++=⎧⎨=⎩,解得23b c =⎧⎨=⎩.故抛物线的解析式为223y x x =-++.(2)223y x x =-++=2(21)31x x --+++2(1)4x =--+, 所以顶点A 的坐标为(1,4).14.【解析】(1)∵二次函数y =ax 2+bx +c 的图象过A (2,0),B (0,-1)和C (4,5)三点,∴42011645a b c c a b c ++=⎧⎪=⎨⎪++=⎩, ∴a =12,b =-12,c =-1, ∴二次函数的解析式为y =12x 2-12x -1. (2)当y =0时,得12x 2-12x -1=0,解得x 1=2,x 2=-1, ∴点D 坐标为(-1,0). (3)图象如图,当一次函数的值大于二次函数的值时,x 的取值范围是-1<x <4. 15.【答案】A【解析】将抛物线y =-12x 2向下平移1个单位长度,得y =-12x 2-1,再向左平移1个单位长度,得到y =-12x +(1)2-1,即y =-12x 2-x -32.故选A .16.【答案】C【解析】∵二次函数图象开口向上,∴a >0,∵对称轴为直线x =-02ba,∴b <0,∴一次函数y =bx +a的图象经过一、二、四象限,故选C . 17.【答案】B18.【答案】0或4【解析】令y =5,可得x 2-2x -3=5,解得x =-2或x =4,所以m -2=-2或m =4,即m =0或4.故答案为:0或4. 19.【答案】2或-10【解析】由题意可知:x 2−4x +3=ax −6,整理得x 2−(4+a )x +9=0,∵只有一个交点,∴Δ=(4+a )2−4×1×9=0,解得a 1=2,a 2=−10.故答案为:2或-10.(3)如图,∵C(0,8),D(1,9),代入直线解析式y=kx+b,∴89bk b=⎧⎨+=⎩,解得18kb=⎧⎨=⎩,21.【答案】D【解析】∵y=2x2+4x-1=2(x+1)2-3,∴当x=0时,y=-1,故选项A错误;该函数的对称轴是直线x=-1,故选项B错误;当x<-1时,y随x的增大而减小,故选项C错误;当x=-1时,y取得最小值,此时y=-3,故选项D正确,故选D.22.【答案】D【解析】当y=1时,有x2-2x+1=1,解得:x1=0,x2=2.∵当a≤x≤a+1时,函数有最小值1,∴a=2或a+1=0,∴a=2或a=-1,故选D.23.【答案】D【解析】A、当t=9时,h=136;当t=13时,h=144;所以点火后9 s和点火后13 s的升空高度不相同,此选项错误;B、当t=24时h=1≠0,所以点火后24 s火箭离地面的高度为1 m,此选项错误;C、当t=10时h=141 m,此选项错误;D、由h=-t2+24t+1=-(t-12)2+145知火箭升空的最大高度为145 m,此选项正确.故选D.24.【答案】B【解析】A.由一次函数y=ax-a的图象可得:a<0,此时二次函数y=ax2-2x+1的图象应该开口向下.故选项错误;B.由一次函数y=ax-a的图象可得:a>0,此时二次函数y=ax2-2x+1的图象应该开口向上,对称轴x=-22a->0.故选项正确;C.由一次函数y=ax-a的图象可得:a>0,此时二次函数y=ax2-2x+1的图象应该开口向上,对称轴x=-22a->0,和x轴的正半轴相交.故选项错误;D.由一次函数y=ax-a的图象可得:a>0,此时二次函数y=ax2-2x+1的图象应该开口向上.故选项错误.故选B.25.【答案】B26.【答案】y=x2+2【解析】二次函数y=x2-1的顶点坐标为(0,-1),把点(0,-1)向上平移3个单位长度所得对应点的坐标为(0,2),所以平移后的抛物线解析式为y=x2+2.故答案为:y=x2+2.27.【答案】2【解析】如图,∵B,C是线段AD的三等分点,∴AC=BC=BD,由题意得:AC=BD=m,当y=0时,x2+2x-3=0,(x-1)(x+3)=0,x1=1,x2=-3,∴A(-3,0),B(1,0),∴AB=3+1=4,∴AC=BC=2,∴m=2,故答案为:2.。
二次函数图像和性质习题精选(含答案)
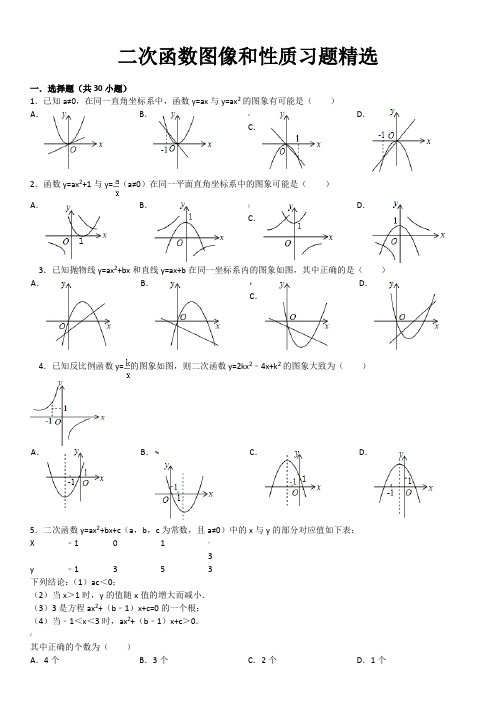
二次函数图像和性质习题精选一.选择题(共30小题)1.已知a≠0,在同一直角坐标系中,函数y=ax与y=ax2的图象有可能是()A.B.>D.C.2.函数y=ax2+1与y=(a≠0)在同一平面直角坐标系中的图象可能是()A.B.|D.C.3.已知抛物线y=ax2+bx和直线y=ax+b在同一坐标系内的图象如图,其中正确的是()A.B.#D.C.4.已知反比例函数y=的图象如图,则二次函数y=2kx2﹣4x+k2的图象大致为()C.D.A.B.%5.二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中的x与y的部分对应值如下表:X﹣101"3y﹣1353下列结论:(1)ac<0;(2)当x>1时,y的值随x值的增大而减小.(3)3是方程ax2+(b﹣1)x+c=0的一个根;(4)当﹣1<x<3时,ax2+(b﹣1)x+c>0./其中正确的个数为()A.4个B.3个C.2个D.1个6.二次函数y=ax2+bx+c(a≠0)的大致图象如图,关于该二次函数,下列说法错误的是()A.函数有最小值B.对称轴是直线x=` C.当x <,y随x的增大而减小D.当﹣1<x<2时,y>07.如图,平面直角坐标系中,点M是直线y=2与x轴之间的一个动点,且点M是抛物线y=x2+bx+c的顶点,则方程x2+bx+c=1的解的个数是()A.0或2B.:0或1C.1或2D.0,1或28.已知二次函数y=a(x﹣h)2+k(a>0),其图象过点A(0,2),B(8,3),则h的值可以是()A.6B.#5C.4D.39.二次函数y=ax2+bx+c图象上部分点的坐标满足下表:x…﹣3﹣2$﹣101…y…﹣3﹣2﹣3﹣6&﹣11…则该函数图象的顶点坐标为()A.(﹣3,﹣3)B.(﹣2,﹣2)C.(﹣1,﹣3)/D.(0,﹣6)10.已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列说法错误的是()A.图象关于直线x=1对称B.、函数y=ax2+bx+c(a≠0)的最小值是﹣4C.﹣1和3是方程ax2+bx+c=0(a≠0)的两个根D.当x<1时,y随x的增大而增大11.如图,二次函数的图象经过(﹣2,﹣1),(1,1)两点,则下列关于此二次函数的说法正确的是()?A.y的最大值小于0B.当x=0时,y的值大于1C.当x=﹣1时,y的值大于1D.@当x=﹣3时,y的值小于012.设二次函数y=x2+bx+c,当x≤1时,总有y≥0,当1≤x≤3时,总有y≤0,那么c的取值范围是()A.c=3B.c≥3C.1≤c≤3D.【c≤313.如图,直角坐标系中,两条抛物线有相同的对称轴,下列关系不正确的是()h>0,k>0A.h=m B.k=n C.k>n—D.14.已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下结论:①a>0;②该函数的图象关于直线x=1对称;③当x=﹣1或x=3时,函数y的值都等于0.其中正确结论的个数是()1D.0A.3B.2%C.15.二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论正确的是()A.a c<0当x=1时,y>0】B.C.方程ax2+bx+c=0(a≠0)有两个大于1的实数根D.存在一个大于1的实数x0,使得当x<x0时,y随x的增大而减小;当x>x0时,y随x的增大而增大*16.如图,抛物线y=ax2+bx+c(a>0)的对称轴是直线x=1,且经过点P(3,0),则a﹣b+c的值为()1D.2A.0B.﹣1!C.17.下列图中阴影部分的面积相等的是()②③C.③④D.①④A.①②)B.18.已知抛物线y=ax2+bx+c(a<0)的部分图象如图所示,当y>0时,x的取值范围是()A.…B.﹣4<x<2C.x<﹣2或x>2D.x<﹣4或x>2﹣2<x<219.已知:二次函数y=x2﹣4x﹣a,下列说法错误的是()A.@当x<1时,y随x的增大而减小B.若图象与x轴有交点,则a≤4C.当a=3时,不等式x2﹣4x+a<0的解集是1<x<3D.若将图象向上平移1个单位,再向左平移3个单位后过点(1,﹣2),则a=3$20.下列表格给出的是二次函数y=ax2+bx+c(a≠0)的几组对应值,那么方程ax2+bx+c=0的一个近似解可以是()xy﹣﹣~A.B.C.D.{21.已知二次函数y=ax2+bx+c的y与x的部分对应值如下表:则下列判断中正确的是()A.抛物线开口向上B.抛物线与y轴交于负半轴D.方程ax2+bx+c=0有两个相等实数根C.@当x=3时,y<022.已知二次函数y1=ax2+bx+c(a≠0)与一次函数y2=kx+m(k≠0)的图象相交于点A(﹣2,4),B(8,2)(如图所示),则能使y1<y2成立的x的取值范围是()A.x>2B.$C.x>0D.﹣2<x<8x<﹣223.在﹣3≤x≤0范围内,二次函数(a≠0)的图象如图所示.在这个范围内,有结论:①y1有最大值1、没有最小值;②y1有最大值1、最小值﹣3;③函数值y1随x的增大而增大;④方程ax2+bx+c=2无解;,⑤若y2=2x+4,则y1≤y2.其中正确的个数是()5A.2B.3C.4/D.24.抛物线y=﹣x2+bx+c上部分点的横坐标x,纵坐标y的对应值如下表:…x …﹣2﹣113.4y …04640…%根据上表判断下列四种说法:①抛物线的对称轴是x=1;②x>1时,y的值随着x的增大而减小:③抛物线有最高点:④抛物线的顶点、与x轴的两个交点三点为顶点的三角形的面积为36.其中正确说法的个数有()A.1B.2C.3D.4}25.如图,已知抛物线y=x2+bx+c的对称轴为x=2,点A,B均在抛物线上,且AB与x轴平行,其中点A的坐标为(0,3),则点B的坐标为()(4,3)A.(2,3)B.(3,2)C.(3,3)<D.26.如图为二次函数y=ax2+bx+c的图象,给出下列说法:①ab<0;②方程ax2+bx+c=0的根为x1=﹣1,x2=3;③a+b+c >0;④当x<1时,y随x值的增大而增大;⑤当y>0时,x<﹣1或x>3.其中,正确的说法有()①③⑤D.②④⑤A.①②④B.①②⑤~C.27.已知二次函数y=x2+2(a﹣1)x+2.如果x≤4时,y随x增大而减小,则常数a的取值范围是()C.a≥﹣3D.a≤﹣3A.a≥﹣5B.*a≤﹣528.如图,平行于y轴的直线l被抛物线y=+1,y=﹣1所截,当直线l向右平移3个单位时,直线l被两条抛物线所截得的线段扫过的图形面积为()平方单位.B.4C.6D.无法可求A.;329.已知直线经过点A(0,2),B(2,0),点C在抛物线y=x2的图象上,则使得S△ABC=2的点有()个.4B.3C.2D.1;A.30.如图,已知抛物线,直线y2=3x+3,当x任取一值时,x对应的函数值分别为y1,y2.若y1≠y2,取y1,y2中的较小值记为M;若y1=y2,记M=y1=y2.下列判断:①当x>0时,y1>y2;②使得M大于3的x值不存在;③当x<0时,x值越大,M值越小;④使得M=1的x 值是或.~其中正确的是()A.①③B.②④C.①④D.…②③二次函数图像和性质习题精选(含答案)参考答案与试题解析一.选择题(共30小题)1.(2014•宁夏)已知a≠0,在同一直角坐标系中,函数y=ax与y=ax2的图象有可能是()A.@B.C.D.考点:二次函数的图象;正比例函数的图象.'专题:数形结合.分析:本题可先由一次函数y=ax图象得到字母系数的正负,再与二次函数y=ax2的图象相比较看是否一致.(也可以先固定二次函数y=ax2图象中a的正负,再与一次函数比较.)解答:解:A、函数y=ax中,a>0,y=ax2中,a>0,但当x=1时,两函数图象有交点(1,a),故A错误;B、函数y=ax中,a<0,y=ax2中,a>0,故B错误;C、函数y=ax中,a<0,y=ax2中,a<0,但当x=1时,两函数图象有交点(1,a),故C正确;D、函数y=ax中,a>0,y=ax2中,a<0,故D错误.故选:C.'点评:函数中数形结合思想就是:由函数图象确定函数解析式各项系数的性质符号,由函数解析式各项系数的性质符号画出函数图象的大致形状.2.(2014•北海)函数y=ax2+1与y=(a≠0)在同一平面直角坐标系中的图象可能是()A.B.C.…D.考点:二次函数的图象;反比例函数的图象.分析:分a>0和a<0两种情况讨论二次函数和反比例函数图象所在的象限,然后选择答案即可.解答:解:a>0时,y=ax2+1开口向上,顶点坐标为(0,1),…y=位于第一、三象限,没有选项图象符合,a<0时,y=ax2+1开口向下,顶点坐标为(0,1),y=位于第二、四象限,B选项图象符合.故选:B.点评:本题考查了二次函数图象与反比例函数图象,熟练掌握系数与函数图象的关系是解题的关键.3.(2014•遵义)已知抛物线y=ax2+bx和直线y=ax+b在同一坐标系内的图象如图,其中正确的是()A.)B.C.D.考点:二次函数的图象;一次函数的图象.…分析:本题可先由二次函数图象得到字母系数的正负,再与一次函数和反比例函数的图象相比较看是否一致.逐一排除.解答:解:A、由二次函数的图象可知a<0,此时直线y=ax+b经过二、四象限,故A可排除;B、二次函数的图象可知a<0,对称轴在y轴的右侧,可知a、b异号,b>0,此时直线y=ax+b经过一、二、四象限,故B可排除;C、二次函数的图象可知a>0,此时直线y=ax+b经过一、三,故C可排除;正确的只有D.故选:D.点评:此题主要考查了一次函数图象与二次函数图象,应该识记一次函数y=kx+b在不同情况下所在的象限,以及熟练掌握二次函数的有关性质:开口方向、对称轴、顶点坐标等.@4.(2014•南昌)已知反比例函数y=的图象如图,则二次函数y=2kx2﹣4x+k2的图象大致为()A.B.C.}D.考点:二次函数的图象;反比例函数的图象.分析:本题可先由反比例函数的图象得到字母系数k<﹣1,再与二次函数的图象的开口方向和对称轴的位置相比较看是否一致,最终得到答案.解答:解:∵函数y=的图象经过二、四象限,∴k<0,由图知当x=﹣1时,y=﹣k>1,∴k<﹣1,、∴抛物线y=2kx2﹣4x+k2开口向下,对称为x=﹣=,﹣1<<0,∴对称轴在﹣1与0之间,故选:D.点评:此题主要考查了二次函数与反比例函数的图象与系数的综合应用,正确判断抛物线开口方向和对称轴位置是解题关键.属于基础题.5.(2014•泰安)二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中的x与y的部分对应值如下表:X﹣1-13y﹣1353下列结论:(1)ac<0;·(2)当x>1时,y的值随x值的增大而减小.(3)3是方程ax2+(b﹣1)x+c=0的一个根;(4)当﹣1<x<3时,ax2+(b﹣1)x+c>0.其中正确的个数为()A.4个B.3个C.:2个D.1个考点:二次函数的性质;二次函数图象与系数的关系;抛物线与x轴的交点;二次函数与不等式(组).专题:图表型.分析:根据表格数据求出二次函数的对称轴为直线x=,然后根据二次函数的性质对各小题分析判断即可得解.~解答:解:(1)由图表中数据可得出:x=1时,y=5,所以二次函数y=ax2+bx+c开口向下,a<0;又x=0时,y=3,所以c=3>0,所以ac<0,故(1)正确;(2)∵二次函数y=ax2+bx+c开口向下,且对称轴为x==,∴当x>时,y的值随x值的增大而减小,故(2)错误;(3)∵x=3时,y=3,∴9a+3b+c=3,∵c=3,∴9a+3b+3=3,∴9a+3b=0,∴3是方程ax2+(b﹣1)x+c=0的一个根,故(3)正确;(4)∵x=﹣1时,ax2+bx+c=﹣1,∴x=﹣1时,ax2+(b﹣1)x+c=0,∵x=3时,ax2+(b﹣1)x+c=0,且函数有最大值,∴当﹣1<x<3时,ax2+(b﹣1)x+c>0,故(4)正确.故选:B.点评:本题考查了二次函数的性质,二次函数图象与系数的关系,抛物线与x轴的交点,二次函数与不等式,有一定难度.熟练掌握二次函数图象的性质是解题的关键.6.(2014•广东)二次函数y=ax2+bx+c(a≠0)的大致图象如图,关于该二次函数,下列说法错误的是()'A.函数有最小值B.对称轴是直线x=C.当x <,y随x的增大而减小D.;当﹣1<x<2时,y>0考点:二次函数的性质.专题:数形结合.分析:根据抛物线的开口方向,利用二次函数的性质判断A;根据图形直接判断B;根据对称轴结合开口方向得出函数的增减性,进而判断C;!根据图象,当﹣1<x<2时,抛物线落在x轴的下方,则y<0,从而判断D.解答:解:A、由抛物线的开口向上,可知a>0,函数有最小值,正确,故A选项不符合题意;B、由图象可知,对称轴为x=,正确,故B选项不符合题意;C、因为a>0,所以,当x<时,y随x的增大而减小,正确,故C选项不符合题意;D、由图象可知,当﹣1<x<2时,y<0,错误,故D选项符合题意.故选:D.点评:本题考查了二次函数的图象和性质,解题的关键是利用数形结合思想解题.?7.(2014•盘锦)如图,平面直角坐标系中,点M是直线y=2与x轴之间的一个动点,且点M是抛物线y=x2+bx+c 的顶点,则方程x2+bx+c=1的解的个数是()A.0或2B.0或1C.1或2D.》0,1或2考点:二次函数的性质.专题:数形结合;分类讨论;方程思想.分析:分三种情况:点M的纵坐标小于1;点M的纵坐标等于1;点M的纵坐标大于1;进行讨论即可得到方程x2+bx+c=1的解的个数.解答:解:分三种情况:[点M的纵坐标小于1,方程x2+bx+c=1的解是2个不相等的实数根;点M的纵坐标等于1,方程x2+bx+c=1的解是2个相等的实数根;点M的纵坐标大于1,方程x2+bx+c=1的解的个数是0.故方程x2+bx+c=1的解的个数是0或1或2.故选:D.点评:考查了二次函数的性质,本题涉及分类思想和方程思想的应用.8.(2014•淄博)已知二次函数y=a(x﹣h)2+k(a>0),其图象过点A(0,2),B(8,3),则h的值可以是()6B.5C.4D.3<A.考点:@二次函数的性质.专题:计算题.分析:根据抛物线的顶点式得到抛物线的对称轴为直线x=h,由于所给数据都是正数,所以当对称轴在y轴的右侧时,比较点A和点B到对称轴的距离可得到h<4.解答:解:∵抛物线的对称轴为直线x=h,∴当对称轴在y轴的右侧时,A(0,2)到对称轴的距离比B(8,3)到对称轴的距离小,∴x=h<4.故选:D.'点评:本题考查了二次函数的性质:二次函数y=ax2+bx+c(a≠0)的顶点坐标为(﹣,),对称轴直线x=﹣,二次函数y=ax2+bx+c(a≠0)的图象具有如下性质:①当a>0时,抛物线y=ax2+bx+c(a≠0)的开口向上,x <﹣时,y随x的增大而减小;x >﹣时,y随x的增大而增大;x=﹣时,y取得最小值,即顶点是抛物线的最低点.②当a<0时,抛物线y=ax2+bx+c(a≠0)的开口向下,x <﹣时,y随x的增大而增大;x >﹣时,y随x的增大而减小;x=﹣时,y 取得最大值,即顶点是抛物线的最高点.9.(2013•徐州)二次函数y=ax2+bx+c图象上部分点的坐标满足下表:…x…﹣3﹣2﹣10。
苏科版九年级下册:5.2《二次函数的图像和性质》同步练习 含答案

5.2《二次函数的图像和性质》同步练习一.选择题1.二次函数y=x2+2x﹣5有()A.最大值﹣5B.最小值﹣5C.最大值﹣6D.最小值﹣62.在同一坐标系中,一次函数y=﹣mx+n2与二次函数y=x2+m的图象可能是()A.B.C.D.3.已知点A(1,y1),B(2,y2)在抛物线y=﹣(x+1)2+2上,则下列结论正确的是()A.2>y1>y2B.2>y2>y1C.y1>y2>2D.y2>y1>24.将抛物线y=x2﹣6x+21向左平移2个单位后,得到新抛物线的解析式为()A.y=(x﹣8)2+5B.y=(x﹣4)2+5C.y=(x﹣8)2+3D.y=(x﹣4)2+35.已知二次函数y=x2+(m﹣1)x+1,当x>1时,y随x的增大而增大,而m的取值范围是()A.m=﹣1B.m=3C.m≤﹣1D.m≥﹣16.如图是二次函数y=ax2+bx+c的图象,下列结论:①二次三项式ax2+bx+c的最大值为4;②4a+2b+c<0;③一元二次方程ax2+bx+c=1的两根之和为﹣1;④使y≤3成立的x的取值范围是x≥0.其中正确的个数有()A.1个B.2个C.3个D.4个7.对于二次函数y=﹣x2+x﹣4,下列说法正确的是()A.当x>0时,y随x的增大而增大B.当x=2时,y有最大值﹣3C.图象的顶点坐标为(﹣2,﹣7)D.图象与x轴有两个交点8.点P1(﹣1,y1),P2(3,y2),P3(5,y3)均在二次函数y=﹣x2+2x+c的图象上,则y1,y2,y3的大小关系是()A.y3>y2>y1B.y3>y1=y2C.y1>y2>y3D.y1=y2>y39.已知抛物线y=﹣x2+bx+4经过(﹣2,n)和(4,n)两点,则n的值为()A.﹣2B.﹣4C.2D.410.在平面直角坐标系中,把一条抛物线先向上平移3个单位长度,然后绕原点旋转180°得到抛物线y=x2+5x+6,则原抛物线的解析式是()A.y=﹣(x﹣)2﹣B.y=﹣(x+)2﹣C.y=﹣(x﹣)2﹣D.y=﹣(x+)2+11.把函数y=﹣x2的图象,经过怎样的平移变换以后,可以得到函数y=﹣(x﹣1)2+1的图象()A.向左平移1个单位,再向下平移1个单位B.向左平移1个单位,再向上平移1个单位C.向右平移1个单位,再向上平移1个单位D.向右平移1个单位,再向下平移1个单位12.将抛物线y=x2向左平移2个单位,再向下平移5个单位,平移后所得新抛物线的表达式为()A.y=(x+2)2﹣5B.y=(x+2)2+5C.y=(x﹣2)2﹣5D.y=(x﹣2)2+5 13.如图为二次函数y=ax2+bx+c(a≠0)的图象,则下列说法:①a>0 ②2a+b=0③a+b+c>0 ④当﹣1<x<3时,y>0其中正确的个数为()A.1B.2C.3D.414.函数y=与y=﹣kx2+k(k≠0)在同一直角坐标系中的图象可能是()A.B.C.D.15.如图,一次函数y1=x与二次函数y2=ax2+bx+c图象相交于P、Q两点,则函数y=ax2+(b﹣1)x+c的图象可能是()A.B.C.D.16.已知二次函数y=(x﹣h)2+1(h为常数),在自变量x的值满足1≤x≤3的情况下,与其对应的函数值y的最小值为5,则h的值为()A.1或﹣5B.﹣1或5C.1或﹣3D.1或317.如图,抛物线y=ax2+bx+c(a≠0)过点(﹣1,0)和点(0,﹣3),且顶点在第四象限,设P=a+b+c,则P的取值范围是()A.﹣3<P<﹣1B.﹣6<P<0C.﹣3<P<0D.﹣6<P<﹣3二.填空题18.抛物线y=ax2+bx+2经过点(﹣2,3),则3b﹣6a=.19.已知二次函数y=x2+2mx+2,当x>2时,y的值随x值的增大而增大,则实数m的取值范围是.20.已知点A(4,y1),B(,y2),C(﹣2,y3)都在二次函数y=(x﹣2)2﹣1的图象上,则y1、y2、y3的大小关系是.21.已知二次函数的图象经过点P(2,2),顶点为O(0,0)将该图象向右平移,当它再次经过点P时,所得抛物线的函数表达式为.22.矩形的周长等于40,则此矩形面积的最大值是.23.二次函数y=x2﹣4x+a在﹣2≤x≤3的范围内有最小值﹣3,则a=.24.已知四个二次函数的图象如图所示,那么a1,a2,a3,a4的大小关系是.(请用“>”连接排序)25.如图,抛物线y=ax2+bx+c的对称轴是x=﹣1.且过点(,0),有下列结论:①abc >0;②a﹣2b+4c=0;③25a﹣10b+4c=0;④3b+2c>0;⑤a﹣b≥m(am﹣b);其中所有正确的结论是.(填写正确结论的序号)三.解答题26.画出函数y=(x﹣2)2﹣1的图象.27.如图,抛物线y=﹣x2+x+c经过点(﹣2,2),求c的值及函数的最大值.28.已知抛物线y=﹣2x2﹣4x+1.(1)求这个抛物线的对称轴和顶点坐标;(2)将这个抛物线平移,使顶点移到点P(2,0)的位置,写出所得新抛物线的表达式和平移的过程.29.已知点(2,8)在函数y=ax2+b的图象上,当x=﹣1时,y=5.(1)求a,b的值.(2)如果点(12,m),(n,17)也在这个函数的图象上,求m与n的值.30.在平面直角坐标系xOy中,抛物线y=ax2+bx﹣与y轴交于点A,将点A向右平移2个单位长度,得到点B,点B在抛物线上.(1)求点B的坐标(用含a的式子表示);(2)求抛物线的对称轴;(3)已知点P(,﹣),Q(2,2).若抛物线与线段PQ恰有一个公共点,结合函数图象,求a的取值范围.31.下表给出一个二次函数的一些取值情况:x…01234…y…30﹣103…(1)请在直角坐标系中画出这个二次函数的图象;(2)根据图象说明:当x取何值时,y的值大于0?32.如图,已知点A(0,2),B(2,2),C(﹣1,﹣2),抛物线F:y=x2﹣2mx+m2﹣2与直线x=﹣2交于点P.(1)当抛物线F经过点C时,求它的表达式;(2)设点P的纵坐标为y P,求y P的最小值,此时抛物线F上有两点(x1,y1),(x2,y2),且x1<x2≤﹣2,比较y1与y2的大小;(3)当抛物线F与线段AB有公共点时,直接写出m的取值范围.参考答案一.选择题1.解:y=x2+2x﹣5=(x+1)2﹣6,∵a=1>0,∴当x=﹣1时,二次函数由最小值﹣6.故选:D.2.解:A、由直线与y轴的交点在y轴的负半轴上可知,n2<0,错误;B、由抛物线与y轴的交点在y轴的正半轴上可知,m>0,由直线可知,﹣m>0,错误;C、由抛物线y轴的交点在y轴的负半轴上可知,m<0,由直线可知,﹣m<0,错误;D、由抛物线y轴的交点在y轴的负半轴上可知,m<0,由直线可知,﹣m>0,正确,故选:D.3.解:当x=1时,y1=﹣(x+1)2+2=﹣(1+1)2+2=﹣2;当x=2时,y1=﹣(x+1)2+2=﹣(2+1)2+2=﹣7;所以2>y1>y2.故选:A.4.解:y=x2﹣6x+21=(x2﹣12x)+21=[(x﹣6)2﹣36]+21=(x﹣6)2+3,故y=(x﹣6)2+3,向左平移2个单位后,得到新抛物线的解析式为:y=(x﹣4)2+3.故选:D.5.解:抛物线的对称轴为直线x=﹣,∵当x>1时,y的值随x值的增大而增大,由图象可知:﹣≤1,解得m≥﹣1.故选:D.6.解:∵抛物线的顶点坐标为(﹣1,4),∴二次三项式ax2+bx+c的最大值为4,①正确;∵x=2时,y<0,∴4a+2b+c<0,②正确;根据抛物线的对称性可知,一元二次方程ax2+bx+c=1的两根之和为﹣2,③错误;使y≤3成立的x的取值范围是x≥0或x≤﹣2,④错误,故选:B.7.解:∵二次函数y=﹣+x﹣4可化为y=﹣(x﹣2)2﹣3,又∵a=﹣<0∴当x=2时,二次函数y=﹣x2+x﹣4的最大值为﹣3.故选:B.8.解:∵y=﹣x2+2x+c,∴对称轴为x=1,开口向下,P2(3,y2),P3(5,y3)在对称轴的右侧,y随x的增大而减小,∵3<5,∴y2>y3,根据二次函数图象的对称性可知,P1(﹣1,y1)与(3,y1)关于对称轴对称,故y1=y2>y3,故选:D.9.解:抛物线y=﹣x2+bx+4经过(﹣2,n)和(4,n)两点,可知函数的对称轴x=1,∴=1,∴b=2;∴y=﹣x2+2x+4,将点(﹣2,n)代入函数解析式,可得n=﹣4;故选:B.10.解:∵抛物线的解析式为:y=x2+5x+6,设原抛物线上有点(x0,y0),绕原点旋转180°后,变为(﹣x0,﹣y0),点(﹣x0,﹣y0)在抛物线y=x2+5x+6上,将(﹣x0,﹣y0)代入y=x2+5x+6得到新抛物线﹣y0=x02﹣5x0+6,所以原抛物线的方程为y0=﹣x02+5x0﹣6=﹣(x0﹣)2+,∴向下平移3个单位长度的解析式为y0=﹣(x0﹣)2+﹣3=﹣(x0﹣)2﹣.故选:A.11.解:抛物线y=﹣x2的顶点坐标是(0,0),抛物线线y=﹣(x﹣1)2+1的顶点坐标是(1,1),所以将顶点(0,0)向右平移1个单位,再向上平移1个单位得到顶点(1,1),即将函数y=﹣x2的图象向右平移1个单位,再向上平移1个单位得到函数y=﹣(x ﹣1)2+1的图象.故选:C.12.解:抛物线y=x2的顶点坐标为(0,0),先向左平移2个单位再向下平移5个单位后的抛物线的顶点坐标为(﹣2,﹣5),所以,平移后的抛物线的解析式为y=(x+2)2﹣5.故选:A.13.解:①图象开口向下,能得到a<0;②对称轴在y轴右侧,x==1,则有﹣=1,即2a+b=0;③当x=1时,y>0,则a+b+c>0;④由图可知,当﹣1<x<3时,y>0.故选:C.14.解:解法一:由解析式y=﹣kx2+k可得:抛物线对称轴x=0;A、由双曲线的两支分别位于二、四象限,可得k<0,则﹣k>0,抛物线开口方向向上、抛物线与y轴的交点为y轴的负半轴上;本图象与k的取值相矛盾,故A错误;B、由双曲线的两支分别位于一、三象限,可得k>0,则﹣k<0,抛物线开口方向向下、抛物线与y轴的交点在y轴的正半轴上,本图象符合题意,故B正确;C、由双曲线的两支分别位于一、三象限,可得k>0,则﹣k<0,抛物线开口方向向下、抛物线与y轴的交点在y轴的正半轴上,本图象与k的取值相矛盾,故C错误;D、由双曲线的两支分别位于一、三象限,可得k>0,则﹣k<0,抛物线开口方向向下、抛物线与y轴的交点在y轴的正半轴上,本图象与k的取值相矛盾,故D错误.解法二:①k>0,双曲线在一、三象限,﹣k<0,抛物线开口向下,顶点在y轴正半轴上,选项B符合题意;②K<0时,双曲线在二、四象限,﹣k>0,抛物线开口向上,顶点在y轴负半轴上,选项B符合题意;故选:B.15.解:点P在抛物线上,设点P(x,ax2+bx+c),又因点P在直线y=x上,∴x=ax2+bx+c,∴ax2+(b﹣1)x+c=0;由图象可知一次函数y=x与二次函数y=ax2+bx+c交于第一象限的P、Q两点,∴方程ax2+(b﹣1)x+c=0有两个正实数根.∴函数y=ax2+(b﹣1)x+c与x轴有两个交点,又∵﹣>0,a>0∴﹣=﹣+>0∴函数y=ax2+(b﹣1)x+c的对称轴x=﹣>0,∴A符合条件,故选:A.16.解:∵当x>h时,y随x的增大而增大,当x<h时,y随x的增大而减小,∴①若h<1≤x≤3,x=1时,y取得最小值5,可得:(1﹣h)2+1=5,解得:h=﹣1或h=3(舍);②若1≤x≤3<h,当x=3时,y取得最小值5,可得:(3﹣h)2+1=5,解得:h=5或h=1(舍);③若1≤h≤3时,当x=h时,y取得最小值为1,不是5,∴此种情况不符合题意,舍去.综上,h的值为﹣1或5,故选:B.17.解:∵抛物线y=ax2+bx+c(c≠0)过点(﹣1,0)和点(0,﹣3),∴0=a﹣b+c,﹣3=c,∴b=a﹣3,∵当x=1时,y=ax2+bx+c=a+b+c,∴P=a+b+c=a+a﹣3﹣3=2a﹣6,∵顶点在第四象限,a>0,∴b=a﹣3<0,∴a<3,∴0<a<3,∴﹣6<2a﹣6<0,即﹣6<P<0.故选:B.二.填空题18.解:把点(﹣2,3)代入y=ax2+bx+2得:4a﹣2b+2=3,2b﹣4a=﹣1,3b﹣6a=﹣,故答案为:﹣.19.解:抛物线的对称轴为直线x=﹣=﹣m,∵当x>2时,y的值随x值的增大而增大,∴﹣m≤2,解得m≥﹣2.故答案为:m≥﹣2.20.解:把A(4,y1),B(,y2),C(﹣2,y3)分别代入y=(x﹣2)2﹣1得:y1=(x﹣2)2﹣1=3,y2=(x﹣2)2﹣1=5﹣4,y3=(x﹣2)2﹣1=15,∵5﹣4<3<15,所以y3>y1>y2.故答案为y3>y1>y2.21.解:设原来的抛物线解析式为:y=ax2(a≠0).把P(2,2)代入,得2=4a,解得a=.故原来的抛物线解析式是:y=x2.设平移后的抛物线解析式为:y=(x﹣b)2.把P(2,2)代入,得2=(2﹣b)2.解得b=0(舍去)或b=4.所以平移后抛物线的解析式是:y=(x﹣4)2.故答案是:y=(x﹣4)2.22.解:设矩形的宽为x,则长为(20﹣x),S=x(20﹣x)=﹣x2+20x=﹣(x﹣10)2+100,当x=10时,S最大值为100.故答案为100.23.解:y=x2﹣4x+a=(x﹣2)2+a﹣4,当x=2时,函数有最小值a﹣4,∵二次函数y=x2﹣4x+a在﹣2≤x≤3的范围内有最小值﹣3,﹣2≤x≤3,y随x的增大而增大,∴a﹣4=﹣3,∴a=1,故答案为1.24.解:如图所示:①y=a1x2的开口小于②y=a2x2的开口,则a1>a2>0,③y=a3x2的开口大于④y=a4x2的开口,开口向下,则a4<a3<0,故a1>a2>a3>a4.故答案为;a1>a2>a3>a425.解:由抛物线的开口向下可得:a<0,根据抛物线的对称轴在y轴左边可得:a,b同号,所以b<0,根据抛物线与y轴的交点在正半轴可得:c>0,∴abc>0,故①正确;直线x=﹣1是抛物线y=ax2+bx+c(a≠0)的对称轴,所以﹣=﹣1,可得b=2a,a﹣2b+4c=a﹣4a+4c=﹣3a+4c,∵a<0,∴﹣3a>0,∴﹣3a+4c>0,即a﹣2b+4c>0,故②错误;∵抛物线y=ax2+bx+c的对称轴是x=﹣1.且过点(,0),∴抛物线与x轴的另一个交点坐标为(,0),当x=﹣时,y=0,即,整理得:25a﹣10b+4c=0,故③正确;∵b=2a,a+b+c<0,∴,即3b+2c<0,故④错误;假设结论正确可得:a﹣b+c≥m2a﹣mb+c∴am2﹣mb+b﹣a≤0,∵△=(b)2﹣4ab;b=2a∴△=4a2﹣4a(b﹣a)=0,∴关于y=am2﹣mb+b的图象与x轴有一个交点,又∵a<0,∴y=am2﹣mb+b﹣a有最大值ymax=0,所以⑤正确;故答案为:①③⑤.三.解答题26.解:列表得:x…01234…y…30﹣103…如图:27.解:把点(﹣2,2)代入y=﹣x2+x+c中得:﹣﹣+c=2解得c=,所以这个二次函数的关系式为y=﹣x2+x+.(2)∵y=﹣x2+x+=﹣(x﹣1)2+5,∴抛物线的开口向下,当x=1时,函数有最大值5.28.解:(1)y=﹣2x2﹣4x+1,=﹣2(x2+2x+1)+2+1,=﹣2(x+1)2+3,所以,对称轴是直线x=﹣1,顶点坐标为(﹣1,3);(2)∵新顶点P(2,0),∴y=﹣2(x﹣2)2,∵2﹣(﹣1)=2+1=3,0﹣3=﹣3,∴平移过程为:向右平移3个单位,向下平移3个单位.29.解(1)由题意可知:,解得.(2)将(12,m),(n,17)代入y=x2+4,得:m=144+4,17=n2+4,解得m=148,n=±.30.解:(1)A(0,﹣)点A向右平移2个单位长度,得到点B(2,﹣);(2)A与B关于对称轴x=1对称,∴抛物线对称轴x=1;(3)∵对称轴x=1,∴b=﹣2a,∴y=ax2﹣2ax﹣,①a>0时,当x=2时,y=﹣<2,当y=﹣时,x=0或x=2,∴函数与PQ无交点;②a<0时,当y=2时,ax2﹣2ax﹣=2,x=或x=当≤2时,a≤﹣;∴当a≤﹣时,抛物线与线段PQ恰有一个公共点;31.解:(1)描点、连线得:(2)由函数图象可知:当x<1或x>3时,y>0.32.解:(1)∵抛物线F经过点C(﹣1,﹣2),∴﹣2=(﹣1)2﹣2×m×(﹣1)+m2﹣2,解得,m=﹣1,∴抛物线F的表达式是:y=x2+2x﹣1;(2)当x=﹣2时,y p=4+4m+m2﹣2=(m+2)2﹣2,∴当m=﹣2时,y p取得最小值,最小值是﹣2,此时抛物线F的表达式是:y=x2+4x+2=(x+2)2﹣2,∴当x≤﹣2时,y随x的增大而减小,∵x1<x2≤﹣2,∴y1>y2;(3)m的取值范围是﹣2≤m≤0或2≤m≤4,理由:∵抛物线F与线段AB有公共点,点A(0,2),B(2,2),∴或或,解得,﹣2≤m≤0或2≤m≤4.。
人教版数学九年级上册_22.1《二次函数的图像和性质》测试题(含答案及解析)
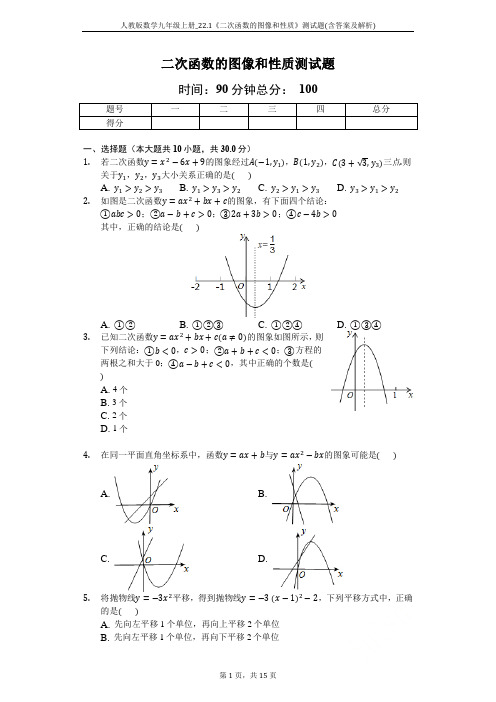
二次函数的图像和性质测试题时间:90分钟总分:100题号一二三四总分得分一、选择题(本大题共10小题,共30.0分)1.若二次函数y=x2−6x+9的图象经过A(−1,y1),B(1,y2),C(3+√3,y3)三点.则关于y1,y2,y3大小关系正确的是()A. y1>y2>y3B. y1>y3>y2C. y2>y1>y3D. y3>y1>y22.如图是二次函数y=ax2+bx+c的图象,有下面四个结论:①abc>0;②a−b+c>0;③2a+3b>0;④c−4b>0其中,正确的结论是()A. ①②B. ①②③C. ①②④D. ①③④3.已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:①b<0,c>0;②a+b+c<0;③方程的两根之和大于0;④a−b+c<0,其中正确的个数是()A. 4个B. 3个C. 2个D. 1个4.在同一平面直角坐标系中,函数y=ax+b与y=ax2−bx的图象可能是()A. B.C. D.5.将抛物线y=−3x2平移,得到抛物线y=−3(x−1)2−2,下列平移方式中,正确的是()A. 先向左平移1个单位,再向上平移2个单位C. 先向右平移1个单位,再向上平移2个单位D. 先向右平移1个单位,再向下平移2个单位6.已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,并且关于x的一元二次方程ax2+bx+c−m=0有两个不相等的实数根,下列结论:①b2−4ac<0;②abc>0;③a−b+c<0;④m>−2,其中,正确的个数有()A. 1B. 2C. 3D. 47.若抛物线y=x2−2x+3不动,将平面直角坐标系xOy先沿水平方向向右平移一个单位,再沿铅直方向向上平移三个单位,则原抛物线图象的解析式应变为()A. y=(x−2)2+3B. y=(x−2)2+5C. y=x2−1D. y=x2+48.二次函数y=2x2−3的图象是一条抛物线,下列关于该抛物线的说法,正确的是()A. 抛物线开口向下B. 抛物线经过点(2,3)C. 抛物线的对称轴是直线x=1D. 抛物线与x轴有两个交点9.在二次函数y=−x2+2x+1的图象中,若y随x的增大而减少,则x的取值范围是()A. x<1B. x>1C. x<−1D. x>−110.直线y=52x−2与抛物线y=x2−12x的交点个数是()A. 0个B. 1个C. 2个D. 互相重合的两个二、填空题(本大题共10小题,共30.0分)11.已知抛物线y=x2−(k+2)x+9的顶点在坐标轴上,则k的值为______.12.二次函数y=−x2+2x+2图象的顶点坐标是______.13.函数y=x2+mx−4,当x<2时,y随x的增大而减小,则m的取值范围是______ .14.抛物线y=ax2+bx+c经过点A(−5,4),且对称轴是直线x=−2,则a+b+c=______ .15.二次函数y=−2(x−1)2+5的图象的对称轴为______ ,顶点坐标为______ .16.如图,若抛物线y=ax2+bx+c上的P(4,0),Q两点关于它的对称轴x=1对称,则Q点的坐标为______ .17.如图,抛物线C1:y=12x2经过平移得到抛物线C2:y=12x2+2x,抛物线C2的对称轴与两段抛物线所围成的阴影部分的面积是______ .18.已知(−3,y1),(4,y2),(−1,y3)是二次函数y=x2−4x上的点,则y1,y2,y3从小到大用“<”排列是______.19.如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A、B两点,与y轴交于点C,对称轴是直线x=−1,点B的坐标为(1,0).下面的四个结论:①AB=4;②b2−4ac>0;③ab<0;④a−b+c<0,其中正确的结论是______ (填写序号).20.如图,抛物线y=ax2+bx+c过点(−1,0),且对称轴为直线x=1,有下列结论:①abc<0;②10a+3b+c>0;③抛物线经过点(4,y1)与点(−3,y2),则y1>y2;④无论a,b,c取,0);⑤am2+bm+何值,抛物线都经过同一个点(−caa≥0,其中所有正确的结论是______ .三、计算题(本大题共4小题,共24.0分)21.已知:二次函数图象的顶点坐标是(3,5),且抛物线经过点A(1,3).(1)求此抛物线的表达式;(2)如果点A关于该抛物线对称轴的对称点是B点,且抛物线与y轴的交点是C点,求△ABC的面积.22.已知二次函数y=(m−2)x2+(m+3)x+m+2的图象过点(0,5).(1)求m的值,并写出二次函数的解析式;(2)求出二次函数图象的顶点坐标和对称轴.23.已知函数y=−x2+(m−1)x+m(m为常数).(1)该函数的图象与x轴公共点的个数是______.A.0B.1C.2D.1或2(2)求证:不论m为何值,该函数的图象的顶点都在函数y=(x+1)2的图象上.(3)当−2≤m≤3时,求该函数的图象的顶点纵坐标的取值范围.24.如图,已知二次函数y=ax2+bx+c的图象过点A(−1,0)和点C(0,3),对称轴为直线x=1.(1)求该二次函数的关系式和顶点坐标;(2)结合图象,解答下列问题:①当−1<x<2时,求函数y的取值范围.②当y<3时,求x的取值范围.四、解答题(本大题共2小题,共16.0分)25.如图,已知抛物线y=−x2+bx+c与x轴交于点A(−1,0)和点B(3,0),与y轴交于点C,连接BC交抛物线的对称轴于点E,D是抛物线的顶点.(1)求此抛物线的解析式;(2)直接写出点C和点D的坐标;(3)若点P在第一象限内的抛物线上,且S△ABP=4S△COE,求P点坐标.注:二次函数y=ax2+bx+c(a≠0)的顶点坐标为(−b2a ,4ac−b24a)(m2+1)=0有实数根.26.已知关于x的一元二次方程x2−(m+1)x+12(1)求m的值;(m2+1)的图象关于x轴的对称图形,然后将所作图(2)先作y=x2−(m+1)x+12形向左平移3个单位长度,再向上平移2个单位长度,写出变化后图象的解析式;(3)在(2)的条件下,当直线y=2x+n(n≥m)与变化后的图象有公共点时,求n2−4n的最大值和最小值.答案和解析【答案】 1. A 2. C 3. B 4. C 5. D6. B7. C8. D 9. B 10. C11. 4,−8,−2 12. (1,3) 13. m ≤−4 14. 415. x =1;(1,5) 16. (−2,0) 17. 418. y 2<y 3<y 1 19. ①②④ 20. ②④⑤21. 解:(1)设抛物线的解析式为y =a(x −3)2+5, 将A(1,3)代入上式得3=a(1−3)2+5,解得a =−12, ∴抛物线的解析式为y =−12(x −3)2+5, (2)∵A(1,3)抛物线对称轴为:直线x =3 ∴B(5,3),令x =0,y =−12(x −3)2+5=12,则C(0,12), △ABC 的面积=12×(5−1)×(3−12)=5.22. 解:(1)把(0,5)代入y =(m −2)x 2+(m +3)x +m +2得m +2=5, 解得m =3所以二次函数解析式为y =x 2+6x +5; (2)因为y =x 2+6x +5=(x +3)2−4,所以此二次函数图象的顶点坐标为(−3,−4),对称轴为直线x =−3. 23. D24. 解:(1)根据题意得{a −b +c =0c =3−b2a =1,解得{a =−1b =2c =3, 所以二次函数关系式为y =−x 2+2x +3,因为y =−(x −1)2+4,所以抛物线的顶点坐标为(1,4);(2)①当x =−1时,y =0;x =2时,y =3; 而抛物线的顶点坐标为(1,4),且开口向下, 所以当−1<x <2时,0<y ≤4;②当y =3时,−x 2+2x +3=3,解得x =0或2, 所以当y <3时,x <0或x >2.25. 解:(1)由点A(−1,0)和点B(3,0)得{−9+3b +c =0−1−b+c=0,解得:{b=2,(2)令x =0,则y =3, ∴C(0,3),∵y =−x 2+2x +3=−(x −1)2+4, ∴D(1,4);(3)设P(x,y)(x >0,y >0),S △COE =12×1×3=32,S △ABP =12×4y =2y ,∵S △ABP =4S △COE ,∴2y =4×32, ∴y =3,∴−x 2+2x +3=3,解得:x 1=0(不合题意,舍去),x 2=2, ∴P(2,3).26. 解:(1)对于一元二次方程x 2−(m +1)x +12(m 2+1)=0,△=(m +1)2−2(m 2+1)=−m 2+2m −1=−(m −1)2, ∵方程有实数根, ∴−(m −1)2≥0, ∴m =1.(2)由(1)可知y =x 2−2x +1=(x −1)2, 图象如图所示:平移后的解析式为y =−(x +2)2+2=−x 2−4x −2.(3)由{y =2x +n y =−x 2−4x −2消去y 得到x 2+6x +n +2=0, 由题意∆≥0,∴36−4n −8≥0, ∴n ≤7,∵n ≥m ,m =1, ∴1≤n ≤7, 令,∴n =2时,y′的值最小,最小值为−4, n =7时,y′的值最大,最大值为21, ∴n 2−4n 的最大值为21,最小值为−4.1. 解:二次函数对称轴为直线x=−−62×1=3,3−(−1)=4,3−1=2,3+√3−3=√3,∵4>2>√3,∴y1>y2>y3.故选A.先求出二次函数的对称轴,再求出点A、B、C到对称轴的距离,然后根据二次函数增减性判断即可.本题考查了二次函数图象上点的坐标特征,主要利用了二次函数的对称性以及增减性,确定出各点到对称轴的距离的大小是解题的关键.2. 解:∵抛物线开口向上,∴a>0;∵抛物线的对称轴在y轴的右侧,∴x=−b2a>0,∴b<0;∵抛物线与y轴的交点在x轴下方,∴c<0,∴abc>0,所以①正确;∵x=−1时,y>0,∴a−b+c>0,所以②正确;∵x=−b2a =13,∴2a+3b=0,所以③错误;∵x=2时,y>0,∴4a+2b+c>0,把2a=−3b代入得−6b+2b+c>0,∴c−4b>0,所以④正确.故选:C.根据抛物线开口方向得到a>0;根据对称轴得到x=−b2a>0,则b<0;根据抛物线与y轴的交点在x轴下方得到c<0,则abc>0,可判断①正确;当自变量为−1时对应的函数图象在x轴上方,则a−b+c>0,可判断②正确;根据抛物线对称轴方程得到x=−b2a =13,则2a+3b=0,可判断③错误;当自变量为2时对应的函数图象在x轴上方,则4a+2b+c>0,把2a=−3b代入可对④进行判断.本题考查了二次函数的图象与系数的关系:二次函数y=ax2+bx+c(a≠0)的图象为抛物线,当a>0,抛物线开口向上;对称轴为直线x=--b2a;抛物线与y轴的交点坐标为(0,c).3. 解:∵抛物线开口向下,∴a<0,∵抛物线对称轴x>0,且抛物线与y轴交于正半轴,∴b>0,c>0,故①错误;>0,即x1+x2>0,故③正确;由对称轴x>0,可知x1+x22由可知抛物线与x轴的左侧交点的横坐标的取值范围为:−1<x<0,∴当x=−1时,y=a−b+c<0,故④正确.故选:B.由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点判断c与0的关系,然后根据对称轴及抛物线与x轴交点情况进行推理,进而对所得结论进行判断.本题主要考查二次函数图象与系数的关系,熟练掌握二次函数y=ax2+bx+c系数符号与抛物线开口方向、对称轴、与x轴、y轴的交点是关键.4. 解:A、对于直线y=ax+b来说,由图象可以判断,a>0,b>0;而对于抛物线>0,应在y轴的右侧,故不合题意,图形错误;y=ax2−bx来说,对称轴x=b2aB、对于直线y=ax+b来说,由图象可以判断,a<0,b>0;而对于抛物线y=ax2−bx<0,应在y轴的左侧,故不合题意,图形错误;来说,对称轴x=b2aC、对于直线y=ax+b来说,由图象可以判断,a>0,b>0;而对于抛物线y=ax2−bx>0,应在y轴的右侧,故符合题意;来说,图象开口向上,对称轴x=b2aD、对于直线y=ax+b来说,由图象可以判断,a>0,b>0;而对于抛物线y=ax2−bx 来说,图象开口向下,a<0,故不合题意,图形错误;故选:C.首先根据图形中给出的一次函数图象确定a、b的符号,进而运用二次函数的性质判断图形中给出的二次函数的图象是否符合题意,根据选项逐一讨论解析,即可解决问题.此主要考查了一次函数、二次函数图象的性质及其应用问题;解题的方法是首先根据其中一次函数图象确定a、b的符号,进而判断另一个函数的图象是否符合题意;解题的关键是灵活运用一次函数、二次函数图象的性质来分析、判断、解答.5. 解:∵y=−3x2的顶点坐标为(0,0),y=−3(x−1)2−2的顶点坐标为(1,−2),∴将抛物线y=−3x2向右平移1个单位,再向下平移2个单位,可得到抛物线y=−3(x−1)2−2.故选:D.找到两个抛物线的顶点,根据抛物线的顶点即可判断是如何平移得到.本题考查的是二次函数的图象与几何变换,熟知“上加下减,左加右减”的法则是解答此题的关键.6. 解:如图所示:图象与x轴有两个交点,则b2−4ac>0,故①错误;∵图象开口向上,∴a>0,∵对称轴在y轴右侧,∴a,b异号,∴b<0,∵图象与y轴交于x轴下方,∴c<0,∴abc>0,故②正确;当x=−1时,a−b+c>0,故此选项错误;∵二次函数y=ax2+bx+c的顶点坐标纵坐标为:−2,故二次函数y=ax2+bx+c向上平移小于2个单位,则平移后解析式y=ax2+bx+c−m与x轴有两个交点,此时关于x的一元二次方程ax2+bx+c−m=0有两个不相等的实数根,故④正确.故选:B.直接利用抛物线与x轴交点个数以及抛物线与方程之间的关系、函数图象与各系数之间关系分析得出答案.此题主要考查了二次函数图象与系数的关系,正确把握二次函数与方程之间的关系是解题关键.7. 解:将平面直角坐标系xOy先沿水平方向向右平移一个单位,再沿铅直方向向上平移三个单位,这个相当于把抛物线向左平移有关单位,再向下平移3个单位,∵y=(x−1)2+2,∴原抛物线图象的解析式应变为y=(x−1+1)2+2−3=x2−1,故答案为C.思想判定出抛物线的平移规律,根据左加右减,上加下减的规律即可解决问题.本题考查二次函数图象的平移,解题的关键是理解坐标系的平移和抛物线的平移是反方向的,记住左加右减,上加下减的规律,属于中考常考题型.8. 解:A、a=2,则抛物线y=2x2−3的开口向上,所以A选项错误;B、当x=2时,y=2×4−3=5,则抛物线不经过点(2,3),所以B选项错误;C、抛物线的对称轴为直线x=0,所以C选项错误;D、当y=0时,2x2−3=0,此方程有两个不相等的实数解,所以D选项正确.故选D.根据二次函数的性质对A、C进行判断;根据二次函数图象上点的坐标特征对B进行判断;利用方程2x2−3=0解的情况对D进行判断.本题考查了二次函数的性质:对于二次函数y=ax2+bx+c(a≠0),它的顶点坐标是(−b2a ,4ac−b24a),对称轴为直线x=−b2a,二次函数y=ax2+bx+c(a≠0)的图象具有如下性质:当a>0时,抛物线y=ax2+bx+c(a≠0)的开口向上,x<−b2a时,y随x的增大而减小;x>−b2a时,y随x的增大而增大;当a<0时,抛物线y=ax2+bx+c(a≠0)的开口向下,x<−b2a 时,y随x的增大而增大;x>−b2a时,y随x的增大而减小.9. 解:y=−x2+2x+1=−(x−1)2+2,抛物线的对称轴为直线x=1,∵a=−1<0,∴当x>1时,y随x的增大而减少.故选B.先配方得到抛物线的对称轴为直线x=1,然后根据二次函数的性质求解.本题考查了二次函数的性质:二次函数y=ax2+bx+c(a≠0)的顶点坐标是(−b2a ,4ac−b24a),对称轴直线x=−b2a,二次函数y=ax2+bx+c(a≠0)的图象具有如下性质:当a>0时,抛物线y=ax2+bx+c(a≠0)的开口向上,x<−b2a时,y随x的增大而减小;x>−b2a 时,y随x的增大而增大;x=−b2a时,y取得最小值4ac−b24a,对称即顶点是抛物线的最低点;当a<0时,抛物线y=ax2+bx+c(a≠0)的开口向下,x<−b2a 时,y随x的增大而增大;x>−b2a时,y随x的增大而减小;x=−b2a时,y取得最大值4ac−b24a,即顶点是抛物线的最高点.10. 解:直线y=52x−2与抛物线y=x2−12x的交点求法是:令52x−2=x2−12x,∴x2−3x+2=0,∴x1=1,x2=2,∴直线y=52x−2与抛物线y=x2−12x的个数是2个.故选C.根据直线与二次函数交点的求法得出一元二次方程的解,即可得出交点个数.此题主要考查了一元二次方程的性质,根据题意得出一元二次方程的解的个数是解决问题的关键.11. 解:当抛物线y=x2−(k+2)x+9的顶点在x轴上时,△=0,即△=(k+2)2−4×9=0,解得k=4或k=−8;当抛物线y=x2−(k+2)x+9的顶点在y轴上时,x=−b2a =k+22=0,解得k=−2.故答案为:4,−8,−2.由于抛物线的顶点在坐标轴上,故应分在x轴上与y轴上两种情况进行讨论.本题考查的是二次函数的性质,解答此题时要注意进行分类讨论,不要漏解.12. 解:∵y=−x2+2x+2=−(x2−2x+1)+3=−(x−1)2+3,故顶点的坐标是(1,3).故填空答案:(1,3).此题既可以利用y=ax2+bx+c的顶点坐标公式求得顶点坐标,也可以利用配方法求出其顶点的坐标.求抛物线的顶点坐标、对称轴的方法.13. 解:∵x<2时,y随x的增大而减小,∴−m2×1≥2,∴m≤−4.故答案为:m≤−4.根据二次函数的性质,二次函数的顶点的横坐标不小于2列式计算即可得解.本题考查了二次函数的性质,熟记性质,根据顶点的横坐标列出不等式是解题的关键.14. 解:∵对称轴方程为x=−2,∴−b2a=−2,整理可得b=4a,∵抛物线y=ax2+bx+c经过点A(−5,4),∴4=25a−5b+c,把b=4a代入可得,4=25a−20a+c,解得c=4−5a,∴抛物线解析式为y=ax2+4ax+4−5a,当x=1时,则有a+b+c=a+4a+4−5a=4,故答案为:4.把A点坐标代入抛物线解析式结合对称轴方程可用a分别表示出b和c,则可用a表示出抛物线解析式,再令x=1代入可求得y的值,即a+b+c的值.本题主要考查二次函数的解析式,分别用a表示出b和c,得出抛物线解析式是解题的关键.15. 解:∵y=−2(x−1)2+5,∴抛物线顶点坐标为(1,5),对称轴为x=1,故答案为:x=1,(1,5).由抛物线解析式可求得其顶点坐标及对称轴.本题主要考查二次函数的性质,掌握二次函数的顶点式是解题的关键,即在y=a(x−ℎ)2+k中,对称轴为x=ℎ,顶点坐标为(ℎ,k).16. 解:∵抛物线y=ax2+bx+c上的P(4,0),Q两点关于它的对称轴x=1对称,∴P,Q两点到对称轴x=1的距离相等,∴Q点的坐标为:(−2,0).故答案为:(−2,0).直接利用二次函数的对称性得出Q点坐标即可.此题主要考查了二次函数的性质,正确利用函数对称性得出答案是解题关键.17. 解:抛物线C1:y=12x2的顶点坐标为(0,0),∵y=12x2+2x=12(x+2)2−2,∴平移后抛物线的顶点坐标为(−2,2),对称轴为直线x=−2,当x=−2时,y=12×(−2)2=2,∴平移后阴影部分的面积等于如图三角形的面积为:12×(2+2)×2=4,故答案为:4.确定出抛物线y=12x2+2x的顶点坐标,然后求出抛物线的对称轴与原抛物线的交点坐标,从而判断出阴影部分的面积等于三角形的面积,再根据三角形的面积公式列式计算即可得解.本题考查了二次函数图象与几何变换,确定出与阴影部分面积相等的三角形是解题的关键.18. 解:y1=(−3)2+4×3=21,y2=42−4×4=0,y3=(−1)2+4×1=5,∴y2<y3<y1,故答案为:y2<y3<y1,可分别求出y1、y2、y3的值后,再进行比较大小.本题考查二次函数图象上的点的特征,解题的关键是求出各点的函数值,本题属于基础题型.19. 解:∵抛物线对称轴是直线x=−1,点B的坐标为(1,0),∴A(−3,0),∴AB=4,故选项①正确;∵抛物线与x轴有两个交点,∴b2−4ac>0,故选项②正确;∵抛物线开口向上,∴a>0,∵抛物线对称轴在y轴左侧,∴a,b同号,∴ab>0,故选项③错误;当x=−1时,y=a−b+c此时最小,为负数,故选项④正确;故答案为:①②④.利用二次函数对称性以及结合b2−4ac的符号与x轴交点个数关系,再利用数形结合分别分析得出答案.此题主要考查了二次函数图象与系数的关系,正确判断a−b+c的符号是解题关键.20. 解:由图象可知,抛物线开口向上,则a>0,顶点在y轴右侧,则b<0,抛物线与y轴交于负半轴,则c<0,∴abc>0,故①错误;∵抛物线y=ax2+bx+c过点(−1,0),且对称轴为直线x=1,∴抛物线y=ax2+bx+c过点(3,0),∴当x=3时,y=9a+3b+c=0,∵a>0,∴10a+3b+c>0,故②正确;∵对称轴为x=1,且开口向上,∴离对称轴水平距离越大,函数值越大,∴y1<y2,故③错误;当x=−ca 时,y=a⋅(−ca)2+b⋅(−ca)+c=c2−bc+aca=c(a−b+c)a,∵当x=−1时,y=a−b+c=0,∴当x=−ca 时,y=a⋅(−ca)2+b⋅(−ca)+c=0,即无论a,b,c取何值,抛物线都经过同一个点(−ca,0),故④正确;x=m对应的函数值为y=am2+bm+c,x=1对应的函数值为y=a+b+c,又∵x=1时函数取得最小值,∴am2+bm+c≥a+b+c,即am2+bm≥a+b,∵b=−2a,∴am2+bm+a≥0,故⑤正确;故答案为:②④⑤.由开口方向、对称轴及抛物线与y轴交点位置可判断①;由x=3时的函数值及a>0可判断②;由抛物线的增减性可判断③;由当x=−ca 时,y=a⋅(−ca)2+b⋅(−ca)+c=c(a−b+c)a且a−b+c=0可判断④;由x=1时函数y取得最小值及b=−2a可判断⑤.本题考查了二次函数图象与系数的关系.二次函数y=ax2+bx+c(a≠0)系数符号由抛物线开口方向、对称轴、抛物线与y轴的交点、抛物线与x轴交点的个数确定.21. (1)设顶点式y=a(x−3)2+5,然后把A点坐标代入求出a即可得到抛物线的解析式;(2)利用抛物线的对称性得到B(5,3),再确定出C点坐标,然后根据三角形面积公式求解.本题考查了待定系数法求二次函数的解析式:在利用待定系数法求二次函数关系式时,要根据题目给定的条件,选择恰当的方法设出关系式,从而代入数值求解.一般地,当已知抛物线上三点时,常选择一般式,用待定系数法列三元一次方程组来求解;当已知抛物线的顶点或对称轴时,常设其解析式为顶点式来求解;当已知抛物线与x 轴有两个交点时,可选择设其解析式为交点式来求解.22. (1)把已知点的坐标代入y =(m −2)x 2+(m +3)x +m +2可求出m 的值,从而得到抛物线解析式;(2)把(1)中的解析式配成顶点式,从而得到二次函数图象的顶点坐标和对称轴.本题考查了在利用待定系数法求二次函数关系式时,要根据题目给定的条件,选择恰当的方法设出关系式,从而代入数值求解.一般地,当已知抛物线上三点时,常选择一般式,用待定系数法列三元一次方程组来求解;当已知抛物线的顶点或对称轴时,常设其解析式为顶点式来求解;当已知抛物线与x 轴有两个交点时,可选择设其解析式为交点式来求解.也考查了二次函数的性质.23. 解:(1)∵函数y =−x 2+(m −1)x +m(m 为常数),∴△=(m −1)2+4m =(m +1)2≥0,则该函数图象与x 轴的公共点的个数是1或2,故选D ;(2)y =−x 2+(m −1)x +m =−(x −m−12)2+(m+1)24, 把x =m−12代入y =(x +1)2得:y =(m−12+1)2=(m+1)24, 则不论m 为何值,该函数的图象的顶点都在函数y =(x +1)2的图象上;(3)设函数z =(m+1)24,当m =−1时,z 有最小值为0;当m <−1时,z 随m 的增大而减小;当m >−1时,z 随m 的增大而增大,当m =−2时,z =14;当m =3时,z =4,则当−2≤m ≤3时,该函数图象的顶点坐标的取值范围是0≤z ≤4.(1)表示出根的判别式,判断其正负即可得到结果;(2)将二次函数解析式配方变形后,判断其顶点坐标是否在已知函数图象即可;(3)根据m 的范围确定出顶点纵坐标范围即可.此题考查了抛物线与x 轴的交点,以及二次函数的性质,熟练掌握二次函数的图象与性质是解本题的关键.24. (1)把A 点和C 点坐标代入y =ax 2+bx +c 得到两个方程,再加上对称轴方程即可得到三元方程组,然后解方程组求出a 、b 、c 即可得到抛物线解析式,再把解析式配成顶点式即可得到顶点坐标;(2)①先分别计算出x 为−1和2时的函数值,然后根据二次函数的性质写出对应的函数值的范围;②先计算出函数值为3所对应的自变量的值,然后根据二次函数的性质写出y <3时,x 的取值范围.本题考查了待定系数法求二次函数的解析式:在利用待定系数法求二次函数关系式时,要根据题目给定的条件,选择恰当的方法设出关系式,从而代入数值求解.一般地,当已知抛物线上三点时,常选择一般式,用待定系数法列三元一次方程组来求解;当已知抛物线的顶点或对称轴时,常设其解析式为顶点式来求解;当已知抛物线与x 轴有两个交点时,可选择设其解析式为交点式来求解.也考查了二次函数的性质.25. (1)将A 、B 的坐标代入抛物线的解析式中,即可求出待定系数b 、c 的值,进而可得到抛物线的对称轴方程;(2)令x =0,可得C 点坐标,将函数解析式配方即得抛物线的顶点C 的坐标;(3)设P(x,y)(x >0,y >0),根据题意列出方程即可求得y ,即得D 点坐标.此题主要考查了二次函数解析式的确定、抛物线的顶点坐标求法,图形面积的求法等知识,根据S△ABP=4S△COE列出方程是解决问题的关键.26. (1)由题意△≥0,列出不等式,解不等式即可;(2)画出翻折.平移后的图象,根据顶点坐标即可写出函数的解析式;(3)首先确定n的取值范围,利用二次函数的性质即可解决问题;本题考查抛物线与x轴的交点、待定系数法、翻折变换、平移变换、二次函数的最值问题等知识,解题的关键是理解题意,学会用转化的思想思考问题,属于中考常考题型.。
人教版九年级上册数学《二次函数的图像和性质》综合练习题【含答案】

《二次函数的图象和性质》同步练习题一、选择题(共10小题)1.下列函数中是二次函数的为 ()A .B .C .D .31y x =-231y x =-22(1)y x x =+-323y x x =+-2.二次函数与一次函数,它们在同一直角坐标系中的图象大致是2y ax bx c =++y ax c =+ ()A .B .C .D .3.已知一次函数的图象经过一、二、四象限,则二次函数的顶点y kx b =+2y kx bx k =+-在第 象限.()A .一B .二C .三D .四4.抛物线的顶点坐标是 22(3)2y x =-+()A .B .C .D .(3,2)-(3,2)(3,2)--(3,2)-5.已知,二次函数满足以下三个条件:①,②,③2y ax bx c =++24b c a >0a b c -+<,则它的图象可能是 b c <()A .B .C .D .6.把抛物线向下平移2个单位长度,再向右平移1个单位长度,所得抛物线是2(2)y x =+ ()A .B .C .D .2(2)2y x =++2(1)2y x =+-22y x =+22y x =-7.将抛物线平移得到抛物线,则这个平移过程正确的是 2y x =2(3)y x =+()A .向左平移3个单位B .向右平移3个单位C .向上平移3个单位D .向下平移3个单位8.二次函数的图象可能是 22y x x =-+()A .B .C .D .9.若点,,都在抛物线上,则下1(1,)M y -2(1,)N y 37(,)2P y 2241(0)y mx mx m m =-+++>列结论正确的是 ()A .B .C .D .123y y y <<132y y y <<312y y y <<213y y y <<10.二次函数与轴交点坐标为 23(2)5y x =--y ()A .B .C .D .(0,2)(0,5)-(0,7)(0,3)二、填空题(共4小题)11.请写出一个开口向上且与轴交点坐标为的抛物线的表达式: .y (0,1)12.若二次函数,当时,随的增大而减小,则的取值范围是 22()1y x k =-++2x - y x k .13.抛物线的对称轴是 .22247y x x =+-14.已知抛物线经过,,对于任意,点均不在抛2y ax bx c =++(0,2)A (4,2)B 0a >(,)P m n 物线上.若,则的取值范围是 .2n >m 三、解答题(共6小题)15.已知抛物线.2246y x x =--(1)请用配方法求出顶点的坐标;(2)如果该抛物线沿轴向左平移个单位后经过原点,求的值.x (0)m m >m 16.如图,在中,,,,动点从点开始沿边ABC ∆90B ∠=︒12AB mm =24BC mm =P A向以的速度移动(不与点重合),动点从点开始沿边向以AB B 2/mm s B Q B BC C 的速度移动(不与点重合).如果、分别从、同时出发,那么经过多少4/mm s C P Q A B 秒,四边形的面积最小.APQC17.已知二次函数.243(0)y ax ax b a =-++≠(1)求出二次函数图象的对称轴;(2)若该二次函数的图象经过点,且整数,满足,求二次函数的表(1,3)a b 4||9a b <+<达式;(3)对于该二次函数图象上的两点,,,,设,当时,1(A x 1)y 2(B x 2)y 11t x t + 25x 均有,请结合图象,直接写出的取值范围.12y y t 18.在平面直角坐标系中,抛物线经过点和.xOy 2(0)y ax bx c a =++>(0,3)A -(3,0)B (1)求的值及、满足的关系式;c a b(2)若抛物线在、两点间从左到右上升,求的取值范围;A B a (3)结合函数图象判断,抛物线能否同时经过点、?若能,写出(1,)M m n -+(4,)N m n -一个符合要求的抛物线的表达式和的值,若不能,请说明理由.n 19.小明利用函数与不等式的关系,对形如12()()()0n x x x x x x --⋯->为正整数)的不等式的解法进行了探究.(n (1)下面是小明的探究过程,请补充完整:①对于不等式,观察函数的图象可以得到如表格:30x ->3y x =-的范围x 3x >3x <的符号y +-由表格可知不等式的解集为.30x ->3x >②对于不等式,观察函数的图象可以得到如表表格:(3)(1)0x x -->(3)(1)y x x =--的范围x 3x >13x <<1x <的符号y +-+由表格可知不等式的解集为 .(3)(1)0x x -->③对于不等式,请根据已描出的点画出函数的(3)(1)(1)0x x x --+>(3)(1)(1)y x x x =--+图象;观察函数的图象补全下面的表格:(3)(1)(1)y x x x =--+的范围x 3x >13x <<11x -<<1x <-的符号y +- 由表格可知不等式的解集为 .(3)(1)(1)0x x x --+>⋯⋯小明将上述探究过程总结如下:对于解形如为正整数)的12()()()0(n x x x x x x n --⋯⋯->不等式,先将,,按从大到小的顺序排列,再划分的范围,然后通过列表格的1x 2x ⋯n x x 办法,可以发现表格中的符号呈现一定的规律,利用这个规律可以求这样的不等式的解y 集.(2)请你参考小明的方法,解决下列问题:①不等式的解集为 .(6)(4)(2)(2)0x x x x ---+>②不等式的解集为 .2(9)(8)(7)0x x x --->20.函数是二次函数.223y mx mx m =--(1)如果该二次函数的图象与轴的交点为,那么 ;y(0,3)m(2)在给定的坐标系中画出(1)中二次函数的图象.答案一、选择题(共10小题)1.解:、是一次函数,故错误;A 31y x =-A 、是二次函数,故正确;B 231y x =-B 、不含二次项,故错误;C 22(1)y x x =+-C 、是三次函数,故错误;D 323y x x =+-D 故选:.B 2.解:一次函数和二次函数都经过轴上的,y (0,)c 两个函数图象交于轴上的同一点,排除、;∴y B C 当时,二次函数开口向上,一次函数经过一、三象限,排除;0a >D 当时,二次函数开口向下,一次函数经过二、四象限,正确;0a <A 故选:.A 3.解:一次函数的图象经过一、二、四象限,y kx b =+,,0k ∴<0b >△,2224()40b k k b k =--=+>抛物线与轴有两个交点,∴x、异号,k b 抛物线的对称轴在轴右侧,∴y 二次函数的顶点在第一象限.∴2y kx bx k =+-故选:.A 4.解:抛物线的顶点坐标是,22(3)2y x =-+(3,2)故选:.B 5.解:二次函数满足以下三个条件:①,②,③, 2y ax bx c =++24b c a >0a b c -+<b c <由①可知当时,则抛物线与轴有两个交点,当时,∴0a >240b ac ->x 0a <240b ac -<则抛物线与轴无交点;x 由②可知:当时,,1x =-0y <由③可知:,0b c -+>,必须,0a b c -+< ∴0a <符合条件的有、,∴C D 由的图象可知,对称轴直线,,,抛物线交的负半轴,C 02b x a=->0a <0b ∴>y ,则,0c <b c >由的图象可知,对称轴直线,,,抛物线交的负半轴,D 02b x a=-<0a <0b ∴<y ,则有可能,0c <b c <故满足条件的图象可能是,D 故选:.D 6.解:抛物线的顶点坐标是,向下平移2个单位长度,再向右平移1个单2(2)y x =+(2,0)-位长度后抛物线的顶点坐标是,(1,2)--所以平移后抛物线的解析式为:2(1)2y x =+-故选:.B 7.解:抛物线的顶点坐标为,抛物线的顶点坐标为,2y x =(0,0)2(3)y x =+(3,0)-点向左平移3个单位可得到,(0,0)(3,0)-将抛物线向左平移3个单位得到抛物线.∴2y x =2(3)y x =+故选:.A 8.解:,,22y x x =-+ 0a <抛物线开口向下,、不正确,∴A C 又对称轴,而的对称轴是直线, 212x =-=-D 0x =只有符合要求.∴B 故选:.B 9.解:观察二次函数的图象可知:.132y y y <<故选:.B 10.解:23(2)5y x =-- 当时,,∴0x =7y =即二次函数与轴交点坐标为,23(2)5y x =--y (0,7)故选:.C 二、填空题(共4小题)11.解:抛物线开口方向向上,且与轴的交点坐标为,y (0,1)抛物线的解析式为.∴21y x =+故答案为.21y x =+12.解:,22()1y x k =-++对称轴为,∴x k =-,20a =-< 抛物线开口向下,∴在对称轴右侧随的增大而减小,∴y x 当时,随的增大而减小,2x - y x ,解得,2k ∴-- 2k 故.2k 13.解:抛物线的对称轴是:,22247y x x =+-24622x =-=-⨯故.6x =-14.解:依照题意,画出图形,如图所示.当时,或,2n >0m <4m >当时,若点均不在抛物线上,则.∴2n >(,)P m n 04m 故.04m三、解答题(共6小题)15.解:(1)2246y x x =--22(2)6x x =--,22(1)8x =--故该函数的顶点坐标为:;(1,8)-(2)当时,,0y =202(1)8x =--解得:,,11x =-23x =即图象与轴的交点坐标为:,,x (1,0)-(3,0)故该抛物线沿轴向左平移3个单位后经过原点,x 即.3m =16.解:设经过秒,四边形的面积最小x APQC 由题意得,,,2AP x =4BQ x =则,122PB x =-的面积PBQ ∆12BQ PB =⨯⨯1(122)42x x =⨯-⨯,24(3)36x =--+当时,的面积的最大值是,3x s =PBQ ∆236mm此时四边形的面积最小.APQC 17.解:(1)二次函数图象的对称轴是;422a x a-=-=(2)该二次函数的图象经过点,(1,3),433a a b ∴-++=,3b a ∴=把代入,3b a =4||9a b <+<得.43||9a a <+<当时,,则.0a >449a <<914a <<而为整数,a ,则,2a ∴=6b =二次函数的表达式为;∴2289y x x =-+当时,,则.0a <429a <-<922a -<<-而为整数,a 或,3a ∴=-4-则对应的或,9b =-12-二次函数的表达式为或;∴23126y x x =-+-24169y x x =-+-(3)当时,均有,25x 12y y 二次函数的对称轴是直线,243(0)y ax ax b a =-++≠2x =,12y y ①当时,有,即∴0a >12|2||2|x x -- 12|2|2x x -- ,212222x x x ∴--- ,2124x x x ∴- ,25x ,241x ∴-- 该二次函数图象上的两点,,,,1(A x 1)y 2(B x 2)y 设,当时,均有,11t x t + 25x 12y y ∴115t t -⎧⎨+⎩ .14t ∴- ②当时,,即0a <12|2||2|x x -- 12|2|2x x -- ,或,1222x x ∴-- 1222x x -- ,或12x x ∴ 124x x - ,25x ,241x ∴--该二次函数图象上的两点,,,,1(A x 1)y 2(B x 2)y 设,当时,均有,11t x t + 25x 12y y 比的最大值还大,或比的最小值还小,这是不存在的,t ∴2x 1t + 24x -故时,的值不存在,0a <t 综上,当时,.0a >14t - 18.解:(1)抛物线经过点和. 2(0)y ax bx c a =++>(0,3)A -(3,0)B ,∴3093c a b c-=⎧⎨=++⎩,.3c ∴=-310a b +-=(2)由1可得:,2(13)3y ax a x =+--对称轴为直线,132a x a -=-抛物线在、两点间从左到右上升,当时,对称轴在点左侧,如图: A B 0a >A即:,解得:,1302a a -- 13a.、两点间从左到右上升,103a ∴< A B 当时,抛物线在、两点间从左到右上升,∴103a < A B (3)抛物线不能同时经过点、.(1,)M m n -+(4,)N m n -理由如下:若抛物线同时经过点、.则对称轴为:,(1,)M m n -+(4,)N m n -(1)(4)322m m x -++-==由抛物线经过点可知抛物线经过,与抛物线经过相矛盾,A (3,3)-(3,0)B 故:抛物线不能同时经过点、(1,)M m n -+(4,)N m n -19.解:(1)②由表格可知不等式的解集为或,(3)(1)0x x -->3x >1x <故或;3x >1x <③图象如右图所示,当时,,当时,,11x -<<(3)(1)(1)0x x x --+>1x <-(3)(1)(1)0x x x --+<由表格可知不等式的解集为或,(3)(1)(1)0x x x --+>3x >11x -<<故,,或;+-3x >11x -<<(2)①不等式的解集为或或,(6)(4)(2)(2)0x x x x ---+>6x >24x <<2x <-故或或;6x >24x <<2x <-②不等式的解集为或且,2(9)(8)(7)0x x x --->9x >8x <7x ≠故或且9x >8x <7x ≠20.解:(1)该函数的图象与轴交于点, y (0,3)把,代入解析式得:,∴0x =3y =33m -=解得,1m =-故答案为;1-(2)由(1)可知函数的解析式为,223y x x =-++,2223(1)4y x x x =-++=--+ 顶点坐标为;∴(1,4)列表如下:x 2-1-01234y5-034305-描点;画图如下:。
二次函数的图像与性质经典练习题(11套)附带详细答案

练习一21.二次函数的图像开口向____,对称轴是____,顶点坐标是___yax_,图像有最___点,x___时,y随x的增大而增大,x___时,y随x的增大而减小。
12222.关于,yx,y3x的图像,下列说法中不正确的是()yx3A.顶点相同B.对称轴相同C.图像形状相同D.最低点相同223.两条抛物线yx与在同一坐标系内,下列说法中不正确的是()yxA.顶点相同B.对称轴相同C.开口方向相反D.都有最小值24.在抛物线上,当y<0时,x的取值范围应为()yxA.x>0B.x<0C.x≠0D.x≥0225.对于抛物线yx与yx下列命题中错误的是()xA.两条抛物线关于轴对称B.两条抛物线关于原点对称C.两条抛物线各自关于y轴对称D.两条抛物线没有公共点26.抛物线y=-bx+3的对称轴是___,顶点是___。
127.抛物线y=-(x2)-4的开口向___,顶点坐标___,对称轴___,x_2__时,y随x的增大而增大,x___时,y随x的增大而减小。
28.抛物线y2(x1)3的顶点坐标是()A.(1,3)B.(1,3)C.(1,3)D.(1,3)为()9.已知抛物线的顶点为(1,2),且通过达式(1,10),则这条抛物线的表22A.y=3(x1)-2B.y=3(x1)+222C.y=3-2D.y=-3-2(x1)(x1)210.二次函数的图像向左平移2个单位,向下平移3个单位,所得新函数表达yax式为()22A.y=a+3B.y=a-3(x2)(x2)22C.y=a(x2)+3D.y=a(x2)-324411.抛物线的顶点坐标是()yxxA.(2,0)B.(2,-2)C.(2,-8)D.(-2,-8)2212.对抛物线y=2(x2)-3与y=-2(x2)+4的说法不正确的是()A.抛物线的形状相同B.抛物线的顶点相同C.抛物线对称轴相同D.抛物线的开口方向相反213.函数y=a+c与y=ax+c(a≠0)在同一坐标系内的图像是图中的()x243243214.化yxx为y=xx为ya(x h)k的形式是____,图像的开口向____,顶点是____,对称轴是____。
二次函数的图像与性质-同步练习(含解析)
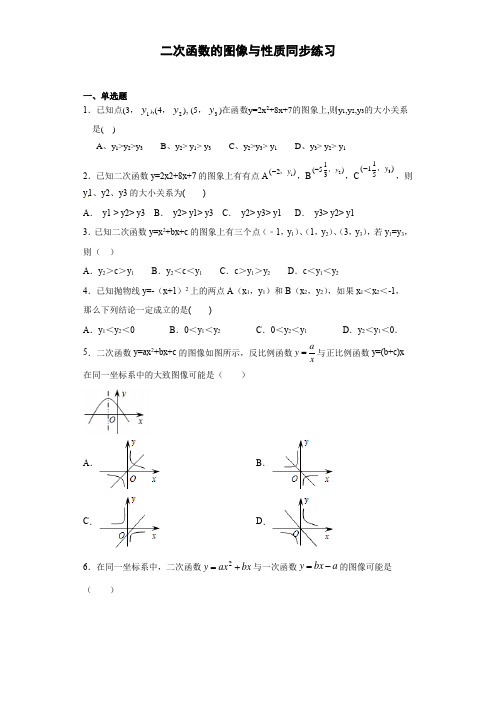
二次函数的图像与性质同步练习一、单选题1.已知点(3,1y ),(4,2y ), (5,3y )在函数y=2x 2+8x+7的图象上,则y 1,y 2,y 3的大小关系是( )A 、y 1>y 2>y 3B 、y 2> y 1> y 3C 、y 2>y 3> y 1D 、y 3> y 2> y 1 2.已知二次函数y=2x2+8x+7的图象上有有点A ,B ,C ,则y1、y2、y3的大小关系为( )A . y1 > y2> y3B . y2> y1> y3C . y2> y3> y1D . y3> y2> y13.已知二次函数y=x 2+bx+c 的图象上有三个点(﹣1,y 1)、(1,y 2)、(3,y 3),若y 1=y 3,则( )A .y 2>c >y 1B .y 2<c <y 1C .c >y 1>y 2D .c <y 1<y 24.已知抛物线y=-(x+1)2上的两点A (x 1,y 1)和B (x 2,y 2),如果x 1<x 2<-1,那么下列结论一定成立的是( ) A .y 1<y 2<0B .0<y 1<y 2C .0<y 2<y 1D .y 2<y 1<0.5.二次函数y=ax 2+bx+c 的图像如图所示,反比例函数ay x=与正比例函数y=(b+c)x 在同一坐标系中的大致图像可能是( )A .B .C .D .6.在同一坐标系中,二次函数2y ax bx =+与一次函数y bx a =-的图像可能是( )1(2)y -,21(5)3y -,31(1)5y -,A .B .C .D .7.反比例函数ky x=与一次函数()1y k x =-在同一坐标系中的图像可能是( ) A . B .C .D .8.在同一坐标系中,函数x k y =和3+=kx y 的图像可能是( )A .B .C .D . 9.如图,坐标系中抛物线是函数y=ax 2+bx +c 的图象,则下列式子能成立的是( )xxxxyyyyOOOO10.已知抛物线y=ax 2+bx+c (a≠0)在平面直角坐标系中的位置如图所示,对称轴是直线13x =.则下列结论中,正确的是( )A .a <0B .c <﹣1C .a ﹣b+c <0D .2a+3b=011.二次函数2y x bx c =++中(b ,c 是常数)的自变量x 与函数值y 的部分对应值如下表:下列结论正确的是:A .当2x =时,y 有最大值1B .当2x <时,y 随x 的增大而增大C .点(5,9)在该函数的图像上D .若1(,)A m y ,2(1,)B m y +两点都在该函数的图象上,则当32m >时,12y y <. 12.如图,四个二次函数的图象中,分别对应的是:①2y ax =;①2y bx =;①2y cx =;①2y dx =,则a b c d ,,,的大小关系为A .a b c d >>>B .a b d c >>>C .b a c d >>>D .b a d c >>>13.如图,抛物线的对称轴是直线x=1,且经过点P (3,0),则的值为( )A .0B .-1C .1D .214.若二次函数的x 与y 的部分对应值如下表,则当x 1=时,y 的值为( )A .5B .3-C .13-D .27-15.已知二次函数()2y ax bx c a 0=++≠,函数y 与自变量x 的部分对应值如下表所示下列说法错误的是( ) A .图象开口向下 B .抛物线的对称轴是直线x 2= C .2b 4ac 0-> D .当1x 3<<时,y 6<二、填空题16.已知抛物线2y x x =+-65经过点1()4a -,和1()a y -,,则y 1的值是_________. 17.将抛物线()2241y x =--先向左平移4个单位长度,再向上平移2个单位长度,平移后所得抛物线的解析式为__________.18.将抛物线y =-2x 2向上平移2个单位长度,再向右平移3个单位长度后,得到的抛物线的解析式为_____ 19.将抛物线的解析式y=向上平移3个单位长度,在向右平移1个单位长度后,得到的抛物线的解析式是 .20.如果二次函数y=(-2k+4)x 2-3x+1的图象开口向上,那么常数k 的取值范围是________三、解答题21.已知函数y=(k ﹣2)x k²﹣4k+5+2x 是关于x 的二次函数.求: (1)满足条件的k 的值;(2)当k 为何值时,抛物线有最高点?求出这个最高点,这时,x 为何值时,y 随x 的增大而增大?22.已知函数()242mm y m x +-=+是关于x 的二次函数.()1求m 的值.()2如果这个二次函数的图象经过点()18P -,求m 的值;()3对于()2中二次函数,函数有无最大值?若有,此时的x 为何值.23.求抛物线217322y x x =--+的对称轴、顶点坐标. 24.阅读下面文字:求代数式24x 7x -+的最值,我们可以这样做:()()2224x 74x 4323x x x -+=-++=-+,因为()22x -≥0,所以当x=2时,该代数式有最小值,最小值为3.仿照以上方法,求(1)28a 3a +-的最值.(2)222y y -++的最值.25.把函数y=3x 2+6x+10转化成y=a (x-h )2+k 的形式,然后指出它的图象开口方向,对称轴,顶点坐标和最值.26.如图,已知抛物线y=2x -+mx+3与x 轴交于A ,B 两点,与y 轴交于点C ,点B 的坐标为(3,0),(1)求m 的值及抛物线的顶点坐标.(2)点P 是抛物线对称轴l 上的一个动点,当PA+PC 的值最小时,求点P 的坐标.参考答案1.D【解析】解:抛物线的对称轴为2482-=-=-=a b x ,又02φ=a ,抛物线开口向上,在对称轴的右边y 随x 的增大而增大,345φφΘ,123y y y φφ∴,故选D 。
二次函数图像与性质练习题及参考答案

二次函数图像与性质练习题及参考答案二次函数是高中数学中一个重要的概念,在学习这一部分知识的过程中掌握二次函数的图像和性质是非常关键的。
本文将提供二次函数图像与性质的练习题及参考答案,帮助学生加深对这方面知识的理解和掌握。
第一题:给定函数 $f(x)=x^2+2x-3$,试回答下列问题:1. $f(x)$ 的自变量定义域是什么?2. $f(x)$ 的值域是什么?3. $f(x)$ 的对称轴方程是什么?4. $f(x)$ 的顶点坐标是什么?5. $f(x)$ 的图像是否有对称性?参考答案:1. 自变量定义域为实数。
2. 值域为 $y\ge -4$。
3. 对称轴方程为 $x=-1$。
4. 顶点坐标为 $(-1,-4)$。
5. 图像有对称轴对称性。
第二题:给定函数 $f(x)=-\frac{1}{2}x^2+4$,试回答下列问题:1. $f(x)$ 的自变量定义域是什么?2. $f(x)$ 的值域是什么?3. $f(x)$ 的对称轴方程是什么?4. $f(x)$ 的顶点坐标是什么?5. $f(x)$ 的图像是否有对称性?参考答案:1. 自变量定义域为实数。
2. 值域为 $y\le 4$。
3. 对称轴方程为 $x=0$。
4. 顶点坐标为 $(0,4)$。
5. 图像有对称轴对称性。
第三题:给定函数 $f(x)=3x^2-12x+7$,试回答下列问题:1. $f(x)$ 的自变量定义域是什么?2. $f(x)$ 的值域是什么?3. $f(x)$ 的对称轴方程是什么?4. $f(x)$ 的顶点坐标是什么?5. $f(x)$ 的图像是否有对称性?参考答案:1. 自变量定义域为实数。
2. 值域为 $y\ge -2$。
3. 对称轴方程为 $x=2$。
4. 顶点坐标为 $(2,-5)$。
5. 图像有对称轴对称性。
第四题:给定函数 $f(x)=-2x^2+8x+3$,试回答下列问题:1. $f(x)$ 的自变量定义域是什么?2. $f(x)$ 的值域是什么?3. $f(x)$ 的对称轴方程是什么?4. $f(x)$ 的顶点坐标是什么?5. $f(x)$ 的图像是否有对称性?参考答案:1. 自变量定义域为实数。
二次函数的图像和性质(内有经典例题和详细讲解)

二次函数的图象和性质一、选择题1. (2011湖北鄂州,15,3分)已知函数()()()()22113513x x y x x ⎧--⎪=⎨--⎪⎩≤>,则使y=k 成立的x 值恰好有三个,则k 的值为( ) A .0 B .1 C .2 D .3【答案】D2. (2011广东广州市,5,3分)下列函数中,当x >0时y 值随x 值增大而减小的是( ).A .y = x 2B .y = x -1C . y = 34xD .y = 1x【答案】D3. (2011山东滨州,7,3分)抛物线()223y x =+-可以由抛物线2y x =平移得到,则下列平移过程正确的是( )A.先向左平移2个单位,再向上平移3个单位B.先向左平移2个单位,再向下平移3个单位C.先向右平移2个单位,再向下平移3个单位D.先向右平移2个单位,再向上平移3个单位 【答案】B4. (2011山东德州6,3分)已知函数))((b x a x y --=(其中a b >)的图象 如下面右图所示,则函数b ax y +=的图象可能正确的是第6题图5. (2011山东菏泽,8,3分)如图为抛物线2y ax bx c =++的图像,A 、B 、C 为抛物线与坐标轴的交点,且OA =OC =1,则下列关系中正确的是A .a +b =-1B . a -b =-1C . b <2aD . ac <0【答案】B6. (2011山东泰安,20 ,3分)若二次函数y=ax 2+bx+c 的x 与y 的部分对应值如下表:X -7 -6 -5 -4 -3 -2 y-27-13-3353则当x =1时,y 的值为A.5B.-3C.-13D.-27 【答案】D7. (2011山东威海,7,3分)二次函数223y x x =--的图象如图所示.当y <0时,自变量x 的取值范围是( ). A .-1<x <3B .x <-1C . x >3D .x <-1或x >3【答案】A8. (2011山东烟台,10,4分)如图,平面直角坐标系中,两条抛物线有相同的对称轴,则下列关系正确的是( )A .m =n ,k >hB .m =n ,k <hC .m >n ,k =hD .m <n ,k =h【答案】A9. (2011浙江温州,9,4分)已知二次函数的图象(0≤x≤3)如图所示.关于该函数在所给自变量取值范围内,下列说法正确的是( )A.有最小值0,有最大值3 B.有最小值-1,有最大值0C.有最小值-1,有最大值3 D.有最小值-1,无最大值【答案】D10.(2011四川重庆,7,4分)已知抛物线y=ax2+bx+c(a≠0)在平面直角坐标系中的位置如图所示,则下列结论中正确的是( )A.a>0 B.b<0 C.c<0 D.a+b+c>0【答案】D11.(2011台湾台北,6)若下列有一图形为二次函数y=2x2-8x+6的图形,则此图为何?【答案】A12. (2011台湾台北,32)如图(十四),将二次函数228999931+-=x x y 的图形画在坐标平面上,判断方程式0899993122=+-x x 的两根,下列叙述何者正确?A .两根相异,且均为正根B .两根相异,且只有一个正根C .两根相同,且为正根D .两根相同,且为负根 【答案】A13. (2011台湾全区,28)图(十二)为坐标平面上二次函数c bx ax y ++=2的图形,且此图形通(-1 ,1)、(2 ,-1)两点.下列关于此二次函数的叙述,何者正确?A .y 的最大值小于0B .当x =0时,y 的值大于1C .当x =1时,y 的值大于1D .当x =3时,y 的值小于0 【答案】D14. (2011甘肃兰州,5,4分)抛物线221y x x =-+的顶点坐标是A .(1,0)B .(-1,0)C .(-2,1)D .(2,-1)【答案】A15. (2011甘肃兰州,9,4分)如图所示的二次函数2y ax bx c =++的图象中,刘星同学观察得出了下面四条信息:(1)240b ac ->;(2)c >1;(3)2a -b <0;(4)a +b +c <0。
人教版数学九年级上册《二次函数的图像和性质》综合练习(附答案)

22.1二次函数图像性质 综合练习题(附答案)1、函数()2h x a y -=的图象与性质1、抛物线()2321--=x y ,顶点坐标是 ,当x 时,y 随x 的增大而减小, 函数有最 值 。
2、试写出抛物线23x y =经过下列平移后得到的抛物线的解析式并写出对称轴和顶点坐标。
(1)右移2个单位;(2)左移32个单位;(3)先左移1个单位,再右移4个单位。
3、请你写出函数()21+=x y 和12+=x y 具有的共同性质(至少2个)。
4、二次函数()2h x a y -=的图象如图:已知21=a ,OA=OC ,试求该抛物线的解析式。
5、抛物线2)3(3-=x y 与x 轴交点为A ,与y 轴交点为B ,求A 、B 两点坐标及⊿AOB 的面积。
6、二次函数2)4(-=x a y ,当自变量x 由0增加到2时,函数值增加6。
求:(1)求出此函数关系式。
(2)说明函数值y 随x 值的变化情况。
7、已知抛物线9)2(2++-=x k x y 的顶点在坐标轴上,求k 的值。
2、()k h x a y +-=2的图象与性质 1、请写出一个以(2, 3)为顶点,且开口向上的二次函数: 。
2、二次函数 y =(x -1)2+2,当 x = 时,y 有最小值。
3、函数 y =12 (x -1)2+3,当 x 时,函数值 y 随 x 的增大而增大。
4、函数y=21(x+3)2-2的图象可由函数y=21x 2的图象向 平移3个单位,再向 平移2个单位得到。
5、已知抛物线的顶点坐标为()2,1,且抛物线过点()3,0,则抛物线的关系式是6、如图所示,抛物线顶点坐标是P (1,3),则函数y 随自变量x 的增大而减小的x 的取值范围是( )A 、x>3B 、x<3C 、x>1D 、x<17、已知函数()9232+--=x y 。
(1)确定下列抛物线的开口方向、对称轴和顶点坐标;(2)当x= 时,抛物线有最 值,是 。
(完整版)二次函数的图像与性质练习题及答案

二次函数的图像和性质练习题一、选择题1.下列函数是二次函数的有( )12)5(;)4();3()3(;2)2(;1)1(222+=++=-==-=x y c bx ax y x x y xy x y (6) y=2(x+3)2-2x 2A 、1个;B 、2个;C 、3个;D 、4个 2.关于213y x =,2y x =,23y x =的图像,下列说法中不正确的是( ) A .顶点相同 B .对称轴相同 C .图像形状相同 D .最低点相同 3.抛物线()12212++=x y 的顶点坐标是( ) A .(2,1) B .(-2,1) C .(2,-1) D .(-2,-1)4.已知二次函数)2(2-++=m m x mx y 的图象经过原点,则m 的值为 ( )A . 0或2B . 0C . 2D .无法确定 5.已知二次函数213x y -=、2231x y -=、2323x y =,它们的图像开口由小到大的顺序是( )A 、321y y y <<B 、123y y y <<C 、231y y y <<D 、132y y y <<6.两条抛物线2y x =与2y x =-在同一坐标系内,下列说法中不正确的是( )A .顶点相同B .对称轴相同C .开口方向相反D .都有最小值7.已知二次函数2y ax bx c =++(0a ≠)的图象如图所示,有下列结论:①0abc >;②a+b+c>0③a-b+c<0;A .1个B .2个C .3个D .4个8.已知抛物线的顶点为(-1,-2),且通过(1,10),则这条抛物线的表达式为( )A .y=32(1)x --2 B .y=32(1)x ++2 C .y=32(1)x +-2 D .y=-32)1(-x +29.抛物线23y x =向右平移1个单位,再向下平移2个单位,所得到的抛物线是( )A .23(1)2y x =-- B.23(1)2y x =+- C.23(1)2y x =++ D.23(1)2y x =-+10.抛物线244y x x =--的顶点坐标是( )A .(2,0)B .(2,-2)C .(2,-8)D .(-2,-8)11.与抛物线y=-12x 2+3x -5的形状、开口方向都相同,只有位置不同的抛物线是( )A. y = x 2+3x -5B. y=-12x 2xC. y =12x 2+3x -5D. y=12x 212.对抛物线y=22(2)x --3与y=-22(2)x -+4的说法不正确的是( )A .抛物线的形状相同B .抛物线的顶点相同C .抛物线对称轴相同D .抛物线的开口方向相反13.对于抛物线21(5)33y x =--+,下列说法正确的是( )A .开口向下,顶点坐标(53),B .开口向上,顶点坐标(53),C .开口向下,顶点坐标(53)-,D .开口向上,顶点坐标(53)-,14.抛物线y=222x mx m -++的顶点在第三象限,试确定m 的取值范围是( )A .m <-1或m >2B .m <0或m >-1C .-1<m <0D .m <-1 15.在同一直角坐标系中,函数y mx m =+和222y mx x =-++(m 是常数,且0m ≠)的图象可能..是( )16.函数y=12-2x +2x -5的图像的对称轴是( ) A .直线x=2 B .直线a=-2 C .直线y=2 D .直线x=4 17.二次函数y=221x x --+图像的顶点在( )A .第一象限B .第二象限C .第三象限D .第四象限 18.如果抛物线y=26x x c ++的顶点在x 轴上,那么c 的值为( )A .0B .6C .3D .9ABCD19.已知二次函数2y ax bx c =++,如果a >0,b <0,c <0,那么这个函数图像的顶点必在( )A .第一象限B .第二象限C .第三象限D .第四象限 20.已知正比例函数kx y =的图像如右图所示,则二次函数222k x kx y +-= 21.如图所示,满足a >0,b <0的函数y=2ax bx +的图像是( )22.若A (-4,y 1),B (-3,y 2),C (1,y 3)为二次函数y=x 2+4x-5的图象上的三点,则y 1,y 2,y 3的大小关系是( )A 、y 1<y 2<y 3B 、y 2<y 1<y 3C 、y 3<y 1<y 2D 、y 1<y 3<y 2二、填空题:23.二次函数2y ax =(0<a )的图像开口向____,对称轴是____,顶点坐标是____,图像有最___点,x ___时,y 随x 的增大而增大,x ___时,y 随x 的增大而减小。
初中数学二次函数图像性质练习题(附答案)

初中数学二次函数图像性质练习题(附答案)1、函数y=a(x-h)²的图像与性质:顶点坐标为(h,0),当x=h时,y有最小值。
2、抛物线y=3x²经过下列平移后得到的抛物线的解析式及对称轴和顶点坐标:1)y=3(x-2)²,对称轴为x=2,顶点坐标为(2,0);2)y=3(x+1)²,对称轴为x=-1,顶点坐标为(-1,0);3)y=3(x-3)²+1,对称轴为x=3,顶点坐标为(3,1)。
3、函数y=(x+1)²和y=x²+1具有的共同性质:对称轴都为x轴,顶点坐标都为(-1,1)。
4、已知a=1/2,OA=OC,抛物线的解析式为y=1/2(x-1)²。
5、抛物线y=3(x-3)²与x轴交点为(3,0),与y轴交点为(0,27),△AOB的面积为27.6、二次函数y=a(x-4)²,当自变量x由增加到2时,函数值y增加6.解得a=3/4,关系式为y=3/4(x-4)²,函数值y随x值的变化情况为随着x的减小而增加。
7、顶点在坐标轴上的抛物线y=x²-(k+2)x+9的顶点坐标为(1,k+6),由对称性可知对称轴为x=1,即k+2=2,解得k=0.22、y=a(x-h)²+k的图像与性质:顶点坐标为(h,k),开口方向由a的正负决定,当x=h时,y有最小值或最大值。
1、以(2,3)为顶点,开口向上的二次函数为y=a(x-2)²+3.2、二次函数y=(x-1)²+2,当x=1时,y有最小值为2.3、函数y=(x-1)²+3,当x增大时,y也随之增大。
4、函数y=(x+3)²-2的图像可由函数y=x²的图像向左平移3个单位,再向下平移2个单位得到。
5、已知抛物线顶点坐标为(2,1),过点(3,5),则抛物线的关系式为y=(1/2)(x-2)²+1.6、抛物线顶点坐标为P(1,3),函数y随自变量x的增大而减小的x的取值范围是x<1.7、函数y=-3(x-2)²+9的开口方向向下,对称轴为x=2,顶点坐标为(2,9);当x=2时,抛物线有最值9;当x增大时,y随之减小;当x减小时,y随之增大。
二次函数图像和性质习题精选(含答案)_百度文库

2
洛杉矶自由行,先看点评更安心
TripAdvisor猫途鹰,为您提供全球旅行者的,旅游点评。
下载
23. (2012•北辰区一模)在﹣ 3≤x≤0 范围内,二次函数 结论: ①y1 有最大值 1、没有最小值; ②y1 有最大值 1、最小值﹣3; y1 随 x 的增大而增大; ③函数值 2 ④方程 ax +bx+c=2 无解; ⑤若 y2=2x+4,则 y1≤y2. 其中正确的个数是( ) A. 2 B. 3 C. 4 D. 5
下一篇
搜索推荐
上海大闸蟹专卖店 生理学试题及答案 大闸蟹是发物吗 大闸蟹礼券 北京阳澄湖大闸蟹 螃蟹的做法 二次函数的解析式 阳澄湖大闸蟹礼券 上海阳澄湖大闸蟹 求二次函数最大值 小学生经典阅读 上海大闸蟹价格 习题及答案 二次函数的应用 qq头像带字的女生 二次函数知识点 小学阅读题及答案 根与系数的关系
人走茶蛋凉
新闻
网页
贴吧
知道
音乐
图片
视频地图百科加入VIP | 个人中心区
分类初中教育 数学教育精品机构合作VIP个人中心高考题库
二次函数图像和性质习题精选(含答案) kongziaaa 上传于 2016-07-22 | 暂无评价 |30 32人阅读 | 1次下载 | 暂无简介 | 举报文档 在手机打开 一.选择题(共 小题) 2 1. (2014•宁夏)已知 a≠0,在同一直角坐标系中,函数 y=ax 与 y=ax 的图象有可能是( A. B. C. D.
2
D.无法可求
29.已知直线经过点 A(0,2) ,B(2,0) ,点 C 在抛物线 y=x 的图象上,则使得 S△ ABC=2 的点有(
A.4
B.3
二次函数的图像和性质练习(含答案)

二次函数的图像和性质一、选择题(每题3分)1.下列四个函数中,一定是二次函数的是( )A .21y x x=+ B .y=ax 2+bx+c C .y=x 2﹣(x+7)2 D .y=(x+1)(2x ﹣1)【答案】D【解析】试题分析:因为形如y=ax 2+bx+c (0a ≠)的函数叫二次函数,所以选项A 、B 、C 错误,D 正确,故选:D .考点:二次函数的概念.2.若函数y=-2(x-1)2+(a-1)x 2为二次函数,则a 的取值范围为( ) A.a≠0 B.a≠1 C.a≠2 D.a≠3【答案】D .【解析】试题分析:根据二次函数的定义化成一般式为()2342y a x x =-+-, 则30a -≠3a ≠故选D .考点:二次函数的定义.3.下列函数中,不是二次函数的是( )A .y =1-x 2B .y =2(x -1)2+4C .y =(x -1)(x +4)D .y =(x -2)2-x 2【答案】D .【解析】试题分析:选项A ,y=1-x 2=-x 2+1,是二次函数,选项A 正确;选项B ,y=2(x-1)2+4=2x 2-4x+6,是二次函数,选项B 正确;选项C ,y=(x-1)(x+4)=x 2+x-2,是二次函数,选项C 正确;选项 D ,y=(x-2)2-x 2=-4x+4,是一次函数,选项D 错误.故答案选D .考点:二次函数的定义.二、填空题(每题3分)4.若函数y =(m -3)是二次函数,则m =______. 【答案】5.【解析】试题分析:已知函数y =(m -3)是二次函数,可得且m -3≠0,解得m=-5. 考点:二次函数的定义.5..一个圆柱的高等于底面半径,写出它的表面积S 与底面半径r 的函数关系式为_________.【答案】S=4π2r【解析】试题分析:根据题意可得h=2r ,则S=2πrh=4π2r .考点:二次函数的实际应用(时间:15分钟,满分25分)班级:___________姓名:___________得分:___________一、选择题(每题3分)1.下列函数中,不属于二次函数的是( )A .y=(x ﹣2)2B .y=﹣2(x+1)(x ﹣1)C .y=1﹣x ﹣x 2D .y=211x 【答案】D【解析】试题分析:整理一般形式后根据二次函数的定义判定即可:A 、整理为y=x 2﹣4x+4,是二次函数,不合题意;B 、整理为y=﹣2x 2+2,是二次函数,不合题意;C 、整理为y=﹣x 2﹣x+1,是二次函数,不合题意;D 、不是整式方程,符合题意.故选:D .考点:二次函数的定义2.下列函数中属于二次函数的是( )A .12-=x yB .12-=ax yC .222)1(2x x y --=D .)2)(1(π+-=x x y【答案】D .【解析】试题分析:A .12-=x y 是一次函数,故本选项错误;B .当0a =时,12-=ax y 不是二次函数,故本选项错误;C .222)1(2x x y --==42x -+是一次函数,故本选项错误;D )2)(1(π+-=x x y 是二次函数,故本选项正确.故选D .考点:二次函数的定义.3.若函数222(1)(1)y x a x =--+-为二次函数,则a 的取值范围为( )A .0a ≠B .1a ≠C .2a ≠D .3a ≠【答案】D .【解析】试题分析:由原函数解析式得到:222(1)(1)y x a x =--+-=2(3)42a x x -+-.∵函数 222(1)(1)y x a x =--+-为二次函数,∴30a -≠,解得3a ≠.故选D .考点:二次函数的定义.二、填空题(每题3分)4.在边长为16cm 的正方形铁皮上剪去一个圆,则剩下的铁皮的面积S (cm 2)与圆的半径r (cm )之间的函数表达式为 (不要求写自变量的取值范围).【答案】2256r S π-=【解析】试题分析:剩下的面积为:正方形的面积-圆的面积=162-πr 2=256-πr 2故答案为:2256r S π-=考点:函数的表达式.5..用长为8米的铝合金制成如图所示的窗框,若设窗框的宽为x 米,窗户的透光面积为S 平方米, 则S 关于x 的函数关系式 .【答案】S=x x 4232+-【解析】试题分析:设窗框的宽为x 米,则长为238x -米 ∴S=x x x x 4232382+-=⨯- 考点:实际问题抽象二次函数三、计算题(每题10分)6.已知,若函数2(1)3m y m x =-+是关于x 的一次函数.(1)求m 的值,并写出解析式;(2)若函数是关于x 的二次函数,求m 的值,.【答案】(1)1m =-;(2)m =.【解析】试题分析:(1)先根据一次函数的定义求出m 的值;(2)由22m =可得出m =试题解析:(1)∵函数2(1)3m y m x =-+是一次函数,∴21m =,解得1m =或1m =-,又∵10m -≠,∴1m ≠,∴1m =-,∴函数为:23y x =-+;m=可得出m=(2)由22考点:1.一次函数的定义;2.二次函数的定义.。
22.1:二次函数的图像和性质(选择题专练)(解析版)

22.1:二次函数的图像和性质(选择题专练)一、单选题1.已知抛物线24y x bx =++经过()2,n -和()4,n 两点,则n 的值为( )A .2-B .4-C .12D .4【答案】C 【解析】将(2)(4)n n -,,,分别代入抛物线24y x bx =++中,转化为解关于n 、b 的二元一次方程组,由代入消元法解题即可.【解答】将(2)(4)n n -,,,代入24y x bx =++中得, 4241644b n b n -+=⎧⎨++=⎩①② 把①代入②,解得2b =-,把2b =-代入①得12n =212b n =-⎧∴⎨=⎩ 故选:C .【点评】本题考查抛物线解析式的求法,其中涉及二元一次方程组的解法,是重要考点,难度较易,掌握相关知识是解题关键.2.若二次函数2()1y x m =--.当x ≤ 3时,y 随x 的增大而减小,则m 的取值范围是( ) A .m = 3B .m >3C .m ≥ 3D .m ≤ 3【答案】C【解析】由题知道二次函数对称轴为x m =,开口向上,根据二次函数图像的性质,当x 在对称轴左边的时候y 随x 的增大而减小,即可得解.【解答】解:由题知二次函数对称轴为x m =,开口向上,根据二次函数图像的性质:只需满足3x m ≤≤即可满足题意,故选C .【点评】本题考查了顶点式的二次函数图像的性质;掌握好二次函数图像的性质时本题的关键. 3.如果函数22(2)27m y m x x -=-+-是二次函数,则m 的取值范围是( ) A .2m =±B .2m =C .m =﹣2D .m 为全体实数【答案】C 【解析】根据二次函数定义可得m-2≠0,222m -=,再解即可.【解答】解:由题意得:m-2≠0,222m -=,解得:m=-2,故选:C .【点评】此题主要考查了二次函数定义,关键是掌握形如y=ax 2+bx+c (a 、b 、c 是常数,a≠0)的函数,叫做二次函数.4.把抛物线y=-2x 2向上平移1个单位,再向右平移1个单位,得到的抛物线是( )A .()2y 211x =-++B .()2y 211x =--+C .()2y 211x =---D .()2y 211x =-+- 【答案】B【解析】按“左加右减括号内,上加下减括号外”的规律平移即可得出所求函数的解析式.【解答】抛物线22y x =-向上平移1个单位,可得221y x =-+,再向右平移1个单位得到的抛物线是()2211y x =--+. 故选B .【点评】本题考查了二次函数图象的平移,其规律是:将二次函数解析式转化成顶点式y=a (x -h )2+k (a ,b ,c 为常数,a ≠0),确定其顶点坐标(h ,k ),在原有函数的基础上“h 值正右移,负左移; k 值正上移,负下移”. 5.二次函数y =ax 2+bx +c 与一次函数y =ax +c ,它们在同一直角坐标系中的图象大致是( ) A . B .C .D .【答案】A【解析】根据二次函数的开口方向,与y 轴的交点;一次函数经过的象限,与y 轴的交点可得相关图象.【解答】解:∵一次函数和二次函数都经过y 轴上的(0,c ),∴两个函数图象交于y 轴上的同一点,排除B 、C ;当a >0时,二次函数开口向上,一次函数经过一、三象限,排除D ;当a <0时,二次函数开口向下,一次函数经过二、四象限,A 正确;故选:A .【点评】本题考查二次函数及一次函数的图象的性质;用到的知识点为:二次函数和一次函数的常数项是图象与y 轴交点的纵坐标;一次函数的一次项系数大于0,图象经过一、三象限;小于0,经过二、四象限;二次函数的二次项系数大于0,图象开口向上;二次项系数小于0,图象开口向下.6.函数y=x 2+bx+c 与y=x 的图象如图所示,有以下结论:①b 2﹣4c >0;②b+c+1=0;③3b+c+6=0;④当1<x <3时,x 2+(b ﹣1)x+c <0.其中正确的个数为A .1B .2C .3D .4【答案】B 【解答】分析:∵函数y=x 2+bx+c 与x 轴无交点,∴b 2﹣4c <0;故①错误.当x=1时,y=1+b+c=1,故②错误.∵当x=3时,y=9+3b+c=3,∴3b+c+6=0.故③正确.∵当1<x <3时,二次函数值小于一次函数值,∴x 2+bx+c <x ,∴x 2+(b ﹣1)x+c <0.故④正确.综上所述,正确的结论有③④两个,故选B .7.关于抛物线:23(1)2y x =-++,下列说法正确的是( ).A .它的开口方向向上B .它的顶点坐标是(1,2)C .当1x <-时,y 随x 的增大而增大D .对称轴是直线1x =【答案】C【解析】根据题目中的抛物线和二次函数的性质,可以判断各个选项中的说法是否正确,从而可以解答本题.【解答】A 选项:∵30-<,∴抛物线23(1)2y x =-++的开口向下,故A 错误;B 选项:抛物线23(1)2y x =-++的顶点坐标是(-1,2),故B 错误;C 选项:对抛物线23(1)2y x =-++,当1x <-时,y 随x 增大而增大,故C 正确;D 选项:抛物线23(1)2y x =-++的对称轴是直线1x =-,故D 错误.故选C .【点评】本题考查二次函数的性质,解答本题的关键是明确题意,利用二次函数的性质解答.8.若二次函数y=mx 2-(m 2-3m )x+1-m 的图象关于y 轴对称,则m 的值为( )A .0B .3C .1D .0或3 【答案】B【解析】由于函数图象关于y 轴对称,则函数的解析式形式应该是y=ax 2+c 型,由此求得问题的答案.【解答】解:∵二次函数y=mx 2-(m 2-3m )x+1-m 的图象关于y 轴对称,∴函数的解析式形式应该是y=ax 2+c 型,∴-(m 2-3m )=0,解得:m=0或m=3,∵二次函数的二次项系数m 不能为0,∴m=3.故选:B .【点评】本题考查关于y 轴对称的抛物线的表达式是y=ax 2+c ,(a≠0,a 、c 为常数).熟练掌握此类型二次函数的性质是解答此题的关键.9.悬索桥,又名吊桥,指的是以通过索塔悬挂并锚固于两岸(或桥两端)的缆索(或钢链)作为上部结构主要承重构件的桥梁. 其缆索几何形状一般近似于抛物线.从缆索垂下许多吊杆(吊杆垂直于桥面),把桥面吊住.某悬索桥(如图1),是连接两个地区的重要通道.图2是该悬索桥的示意图.小明在游览该大桥时,被这座雄伟壮观的大桥所吸引.他通过查找资料了解到此桥的相关信息:这座桥的缆索(即图2中桥上方的曲线)的形状近似于抛物线,两端的索塔在桥面以上部分高度相同,即AB =CD ,两个索塔均与桥面垂直.主桥AC 的长为600m ,引桥CE 的长为124m .缆索最低处的吊杆MN 长为3m ,桥面上与点M 相距100m 处的吊杆PQ 长为13m .若将缆索的形状视为抛物线,请你根据小明获得的信息,建立适当的平面直角坐标系,求出索塔顶端D 与锚点E 的距离( ).A .150B .155C .160D .165【答案】B 【解析】先建立适当的平面直角坐标系,AC 所在直线为x 轴,MN 所在直线为y 轴,再由已知条件和抛物线的对称性确定出点坐标:(0,0)M ,(0,3)N ,(100,13)Q ,设抛物线的表达式为23y ax =+,将Q 的坐标带入,解得a 的值,就可得出抛物线的表达式,当300MC x ==时,带入抛物线的表达式,得出y 值就是CD 的长度,在Rt △DCE 中利用勾股定理得出DE 的长度,也就是塔顶端D 与锚点E 的距离.【解答】解:如图所示建立平面直角坐标系,依题意可知3MN =,13PQ =,100MP =,600AC =,124CE =,AB DC =,BA AC ⊥,DC AC ⊥,MN AC ⊥,PQ AC ⊥, 由抛物线的对称性可知,13002MC AC ==, 则得点坐标:(0,0)M ,(0,3)N ,(100,13)Q , 设抛物线的表达式为23y ax =+ ,∵抛物线经过点Q ,∴将点Q 的坐标带入得2131003a =+,解得11000a =得抛物线的表达式为2131000y x =+ , 当300x =时,得213003931000y =⨯+=, ∵DC AC ⊥,∴90DCE ∠=, ∴22222293124(331)(431)531155DE DC CE =+=+=⨯+⨯=⨯=,答:索塔顶端D 与锚点E 的距离为155米.【点评】本题考查了二次函数在实际生活中的运用,建立适当的坐标系,求出解析式,结合勾股定理,是解题的关键.10.在同一直角坐标系中,函数y mx m =+和222y mx x =-++的图象可能是( )A .B .C .D .【答案】D【解析】根据m 的符号,针对二次函数、一次函数的图象位置,开口方向,分类讨论,逐一判断即可.【解答】A :由函数y mx m =+的图像可知0m <,即函数222y mx x =-++开口应向上,与图像不符,故A 错误;B 、由函数y mx m =+的图像可知0m <,函数222y mx x =-++的对称轴21022b x a m m=-=-=<-,则对称轴应在y 轴的左侧与图像不符,故B 错误;C :由函数y mx m =+的图像可知0m >,即函数222y mx x =-++开口应向下,与图像不符,故C 错误;D :由函数y mx m =+的图像可知0m <,即函数222y mx x =-++开口向上,函数222y mx x =-++的对称轴21022b x a m m =-=-=<-,则对称轴应在y 轴的左侧与图像相符,故D 正确; 故选:D .【点评】本题主要考查了一次函数与二次函数图象,关键是熟练掌握一次函数y=kx+b 在不同情况下所在的象限,以及熟练掌握二次函数的有关性质:开口方向、对称轴、顶点坐标等.11.已知点P (m ,n )在抛物线y =a (x ﹣5)2+9(a≠0)上,当3<m <4时,总有n >1,当7<m <8时,总有n <1,则a 的值为( )A .1B .﹣1C .2D .﹣2【答案】D【解析】根据抛物线的解析式可以确定抛物线的顶点和增减性,再根据已知条件确定a 的符号和关于a 的不等式,从而得到a 的值.【解答】解:∵抛物线y =a (x ﹣5)2+9(a≠0),∴抛物线的顶点为(5,9),∵当7<m <8时,总有n <1,∴a 不可能大于0,则a <0,∴x <5时,y 随x 的增大而增大,x >5时,y 随x 的增大而减小,∵当3<m <4时,总有n >1,当7<m <8时,总有n <1,且x =3与x =7对称,∴m =3时,n≥1,m =7时,n≤1, ∴491491a a +≥⎧⎨+≤⎩, ∴4a+9=1,∴a =﹣2,故选:D .【点评】本题考查二次函数的图象与性质,熟练掌握二次函数的顶点坐标、增减性及其与图象的关系是解题关键.12.如果二次函数y =x 2﹣ax+1,当x≤﹣2时,y 随x 的增大而减小,且关于z 的分式方程1122az z z ----=2有正数解,则符合条件的整数a 的值有多少个( )A .3个B .4个C .5个D .6个 【答案】C【解析】先解分式方程求出z =22a-,关于z 的分式方程有正数解满足2﹣a >0利用二次函数y =x 2﹣a x+1,当x≤﹣2时,y 随x 的增大而减小,求出对称轴x =﹣-2a ≥﹣2,求出a 的范围﹣4≤a <2,且a ≠1即可. 【解答】解:∵11222az z z --=-- ∴1+1﹣a z =2(2﹣z )∴(2﹣a )z =2∴z =22a- 关于z 的分式方程有正数解 ∴22a->0 ∴2﹣a >0∴a <2但该分式方程当z =2时显然是增根,故当a =1时不符合题意,舍去.∵二次函数y =x 2﹣a x+1,当x≤﹣2时,y 随x 的增大而减小∴其对称轴x =﹣-2a ≥﹣2 ∴a ≥﹣4∴﹣4≤a <2,且a ≠1符合条件的整数a 的值有﹣4、﹣3、﹣2、﹣1、0,共5个故选择:C .【点评】本题考查分式方程的解法,抛物线的增减性,不等式的解法,掌握分式方程的解法,抛物线的性质,会求抛物线的对称轴,会利用分式方程的解为正数构造不等式,结合函数的增减性解决问题. 13.若二次的数2y ax bx c =++的x 与y 的部分对应值如下表:A .5B .3-C .13-D .27-【解析】首先观察表格可得二次函数2y ax bx c =++过点(4,3)-与(2,3)-,则可求得此抛物线的对称轴,然后由对称性求得答案. 【解答】解:二次函数2y ax bx c =++过点(4,3)-与(2,3)-,∴此抛物线的对称轴为:直线4(2)32x -+-==-, ∴横坐标为1x =的点的对称点的横坐标为7x =-,∴当1x =时,27y =-.故选:D .【点评】此题考查了二次函数的对称性,根据表格中的数据找到对称轴是解题的关键.14.从﹣3、﹣1、0、12、2、3这六个数中,随机抽取一个数记为a ,若数a 使关于x 的分式方程11ax x --﹣1=21x -有整数解,且使二次函数y =x 2﹣(a ﹣1)x +3,当x >12时,y 随x 的增大而增大,那么这六个数中满足所有条件的a 的值之和为( )A .﹣12B .12C .32D .52 【答案】D 【解析】求解分式方程12111ax x x--=--,利用使分式有意义和使分式有整数解的条件来判断符合的a 的值,再将这些数代入二次函数,根据二次函数的性质即可最后确定符合的a 的值,最后相加即可. 【解答】解分式方程12111ax x x--=--,得:21x a =-,且1x ≠. ∴1a ≠-.∴-3、-1、0、12、2、3这六个数中,使x 为整数的a 为:0、12、2、3;将上述满足条件的a (0、12、2、3)逐项代入二次函数表达式,根据二次函数的性质可知满足条件的a 为:0、12、2,∴其和为:52. 故选:D .【点评】本题考查二次函数的性质,解分式方程和使分式方程有意义的条件,掌握分式方程的解法和二次函数的性质是解答本题的关键.15.抛物线经过点(2,0),(1,0)A B -,且与y 轴交于点C .若2OC =,则该抛物线解析式为( ) A .2y x x 2=--B .22y x x =---或22y x x =++C .22y x x =-++D .2y x x 2=--或22y x x =-++【解析】抛物线和y 轴交点的为(0,2)或(0,-2),根据A 、B 两点坐标设出抛物线解析式为()()21y a x x =-+()0a ≠,代入C 点坐标即可求解.【解答】设抛物线的解析式为()()21y a x x =-+()0a ≠∵2OC =∴抛物线和y 轴交点的为(0,2)或(0,-2)①当抛物线和y 轴交点的为(0,2)时,得()()20201a =-+解得1a =-∴抛物线解析式为()()121y x x =--+,即22y x x =-++②当抛物线和y 轴交点的为(0,-2)时,()()20201a -=-+解得1a =∴抛物线解析式为()()y x 2x 1=-+,即2y x x 2=--故选D .【点评】本题考查了待定系数法求二次函数解析式,问题的关键是设出合适的解析式形式,本题选用两点式(又叫双根式)较为合适.16.已知二次函数2y ax bx c =+-的图像的对称轴为直线1x =,开口向下,且与x 轴的其中的一个交点是3,0,下列结论:①420a b c +->;②0a b c --<;③3c a =;④520a b c +->正确的个数是( )A .1个B .2个C .3个D .4个【答案】C 【解析】根据题意,由对称轴为直线1x =,开口向下,则0a <,抛物线与x 轴的另一个交点为()1,0-,当2x =时,0y >可判断①;当1x =-时,0y =可判断②;由12b a -=,0a b c --=可判断③;由3c a =,2b a =-代入计算,即可判断④;然后得到答案.【解答】解:根据题意,∵二次函数2y ax bx c =+-的图像的对称轴为直线1x =,开口向下,且与x 轴的其中的一个交点是()3,0, ∴0a <,抛物线与x 轴的另一个交点为()1,0-,12b x a=-=, 由图可知,当2x =时,函数图像在x 轴上方,则0y >,∴当2x =时,420y a b c =+->,故①正确;∵抛物线经过点()1,0-,∴当1x =-时,0y a b c =--=,故②错误; ∵12b a-=,0a b c --=, ∴2b a =-,∴(2)3c a b a a a =-=--=,故③正确;∵2b a =-,3c a =,∴5252233a b c a a a a +-=--⨯=-,∵0a <,则30a ,∴520a b c +->,故④正确;∴正确的选项有①③④,共3个;故选:C.【点评】本题考查了二次函数图象与系数的关系:对于二次函数y=ax 2+bx+c (a≠0),二次项系数a 决定抛物线的开口方向和大小.当a >0时,抛物线向上开口;当a <0时,抛物线向下开口;一次项系数b 和二次项系数a 共同决定对称轴的位置. 当a 与b 同号时(即ab >0),对称轴在y 轴左; 当a 与b 异号时(即ab <0),对称轴在y 轴右;常数项c 决定抛物线与y 轴交点位置:抛物线与y 轴交于(0,c ). 17.如图,正方形ABCD 边长为4,E 、F 、G 、H 分别是AB 、BC 、CD 、DA 上的点,且AE =BF =CG =DH .设A 、E 两点间的距离为x ,四边形EFGH 的面积为y ,则y 与x 的函数图象可能是( )A .B .C .D .【答案】A【解析】本题考查了动点的函数图象,先判定图中的四个小直角三角形全等,再用大正方形的面积减去四个直角三角形的面积,得函数y 的表达式,结合选项的图象可得答案.【解答】解:∵正方形ABCD 边长为4,AE =BF =CG =DH∴AH =BE =CF =DG ,∠A =∠B =∠C =∠D∴△AEH ≌△BFE ≌△CGF ≌△DHG∴y =4×4﹣12x (4﹣x )×4=16﹣8x+2x 2=2(x ﹣2)2+8∴y 是x 的二次函数,函数的顶点坐标为(2,8),开口向上,从4个选项来看,开口向上的只有A 和B ,C 和D 图象开口向下,不符合题意;但是B 的顶点在x 轴上,故B 不符合题意,只有A 符合题意.故选:A .【点评】本题考查了动点问题的函数图象,正确地写出函数解析式并数形结合分析是解题的关键. 18.如图,顶点坐标为(1,)n 的抛物线2y ax bx c =++经过点(1,0)A -,与y 轴的交点在(0,2),(0,3)之间(含端点),则下列结论:①30a b +>;②213a -≤≤-;③对于任意实数m ,()ab m am b +≥+总成立;④关于x 的方程21ax bxc n ++=-有两个不相等的实数根.其中结论正确的个数为( )A .1个B .2个C .3个D .4个【答案】C 【解析】利用抛物线开口方向得到a <0,再由抛物线的对称轴方程得到b =﹣2a ,则3a +b =a ,于是可对①进行判断;利用2≤c ≤3和c =﹣3a 可对②进行判断;利用二次函数的性质可对③进行判断;根据抛物线y =ax 2+bx +c 与直线y =n ﹣1有两个交点可对④进行判断.【解答】解:∵抛物线开口向下,∴a <0,而抛物线的对称轴为直线x =﹣2b a=1,即b =﹣2a , ∴3a +b =3a ﹣2a =a <0,所以①错误;∵2≤c ≤3,而c =﹣3a ,∴2≤﹣3a ≤3,∴﹣1≤a≤﹣23,所以②正确;∵抛物线的顶点坐标(1,n),∴x=1时,二次函数值有最大值n,∴a+b+c≥am2+bm+c,即a+b≥am2+bm,所以③正确;∵抛物线的顶点坐标(1,n),∴抛物线y=ax2+bx+c与直线y=n﹣1有两个交点,∴关于x的方程ax2+bx+c=n﹣1有两个不相等的实数根,所以④正确.故选:C.【点评】本题考查了二次函数图象与系数的关系:二次项系数a决定抛物线的开口方向和大小.当a>0时,抛物线向上开口;当a<0时,抛物线向下开口;一次项系数b和二次项系数a共同决定对称轴的位置:当a与b同号时,对称轴在y轴左;当a与b异号时,对称轴在y轴右.常数项c决定抛物线与y轴交点:抛物线与y轴交于(0,c).抛物线与x轴交点个数由判别式确定:b2﹣4ac>0时,抛物线与x轴有2个交点;b2﹣4ac=0时,抛物线与x轴有1个交点;b2﹣4ac<0时,抛物线与x轴没有交点.19.如图,若二次函数y=ax2+bx+c(a≠0)图象的对称轴为x=1,与y轴交于点C,与x轴交于点A、点B(﹣1,0),则①二次函数的最大值为a+b+c;②a﹣b+c<0;③b2﹣4ac<0;④当y>0时,﹣1<x<3,其中结论正确的有()A.①③B.①④C.①②D.①③④【答案】B【解析】由图象可知,当x=1时,y=a+b+c最大,故①正确;当x=﹣1时,y=a﹣b+c=0,故②错误;二次函数与x轴有两个不同交点,因此b2﹣4ac>0,故③错误;对称轴为x=1,B(﹣1,0),所以A(3,0),由图象可得,y>0时,﹣l<x<3,故④正确.【解答】解:①由图象可知,x=1时,y=a+b+c最大,因此二次函数的最大值为a+b+c,故①正确;②由图象可知,x=-1时,y=0,即a-b+c=0,因此a-b+c=0,故②错误;③由图象可知,函数图象与x轴有两个不同交点,因此b2﹣4ac>0,故③错误;④∵对称轴为x=1,B(-1,0),∴A(3,0),∴y >0时,-1<x <3,故④正确,则答案为:①④.故选:B .【点评】本题考查了二次函数图象与系数的关系.熟练掌握二次函数图象的性质是解题的关键. 20.关于二次函数245(0)y ax ax a =--≠的三个结论:①对任意实数m ,都有12x m =+与22x m =-对应的函数值相等;②若3≤x≤4,对应的y 的整数值有4个,则413a -<≤-或413a ≤<;③若抛物线与x 轴交于不同两点A ,B ,且AB≤6,则54a <-或1a ≥.其中正确的结论是( ) A .①②B .①③C .②③D .①②③【答案】D【解析】由题意可求次函数y=ax 2-4ax-5的对称轴为直线422a x a -=-=,由对称性可判断①;分a >0或a <0两种情况讨论,由题意列出不等式,可求解,可判断②;分a >0或a <0两种情况讨论,由题意列出不等式组,可求解,可判断③;即可求解.【解答】解:∵抛物线的对称轴为422a x a-=-=, ∴x 1=2+m 与x 2=2-m 关于直线x=2对称,∴对任意实数m ,都有x 1=2+m 与x 2=2-m 对应的函数值相等;故①正确;当x=3时,y=-3a-5,当x=4时,y=-5,若a >0时,当3≤x≤4时,-3a-5<y≤-5,∵当3≤x≤4时,对应的y 的整数值有4个, ∴413a ≤<, 若a <0时,当3≤x≤4时,-5≤y <-3a-5,∵当3≤x≤4时,对应的y 的整数值有4个, ∴413a -<≤-, 故②正确;若a >0,抛物线与x 轴交于不同两点A ,B ,且AB≤6,∴△>0,25a-20a-5≥0,∴216200550a a a ⎧+>⎨-≥⎩, ∴1a ≥;若a <0,抛物线与x 轴交于不同两点A ,B ,且AB≤6,∴△>0,25a-20a-5≤0,∴216200550a a a ⎧+>⎨-≤⎩∴a <54-, 综上所述:当a <54-或a≥1时,抛物线与x 轴交于不同两点A ,B ,且AB≤6. 故③正确;故选:D .【点评】本题考查了二次函数图象与系数的关系,二次函数图象上点的坐标特征,二次函数图象与x 轴的交点等知识,理解题意列出不等式(组)是本题的关键.21.在平面直角坐标系中,将抛物线y =x 2﹣(m ﹣1)x +m (m >1)沿y 轴向下平移3个单位.则平移后得到的抛物线的顶点一定在( )A .第一象限B .第二象限C .第三象限D .第四象限 【答案】D【解析】根据平移规律得到平移后抛物线的顶点坐标,然后结合m 的取值范围判断新抛物线的顶点所在的象限即可. 【解答】解:2221(1)(1)()24m m y x m x m x m --=--+=-+-, ∴该抛物线顶点坐标是1(2m -,2(1))4m m --, ∴将其沿y 轴向下平移3个单位后得到的抛物线的顶点坐标是1(2m -,2(1)3)4m m ---, 1m >,10m ∴->, ∴102m ->, 2222(1)4(21)12(3)4(3)3104444m m m m m m m ---+-------===--<, ∴点1(2m -,2(1)3)4m m ---在第四象限; 故选:D .【点评】本题考查了二次函数的图象与性质、平移的性质、抛物线的顶点坐标等知识;熟练掌握二次函数的图象和性质,求出抛物线的顶点坐标是解题的关键.22.已知二次函数2(0)y ax bx c a =++≠的图象如图所示,有下列4个结论:①0abc >;②b a c <+;③420a b c ++>;④(),(1)a b m am b m +>+≠;⑤23c b <其中正确的结论有( )A .2个B .3个C .4个D .5个【答案】B 【解析】由抛物线开口向下得到a <0;由抛物线的对称轴为直线x=2b a-=1得到b >0;由抛物线与y 轴的交点在x 轴的上方得到c >0,则abc <0;观察图象得到当x=-1时,y <0,即a-b+c <0;当x=2时,y >0,即4a+2b+c >0;根据二次函数的最值问题得到x=1时,y 有最大值a+b+c ,则a+b+c >am 2+bm+c (m≠1),变形得到a+b >m (am+b );当x=3时,得到y=9a+3b+c <0,根据对称轴得到a=2b -,代入,化简可得得2c <3b .【解答】解:①∵抛物线开口向下,∴a <0,∵抛物线的对称轴为直线x=2b a-=1, ∴b >0;∵抛物线与y 轴的交点在x 轴的上方,∴c >0,∴abc <0,所以①错误;②当x=-1时,y <0,即a-b+c <0,∴b >a+c ,所以②错误;③由图可知:当x=2时,y >0,即4a+2b+c >0,所以③正确;④∵抛物线的对称轴为直线x=1,∴x=1时,y 有最大值a+b+c ,∴a+b+c >am 2+bm+c (m≠1),∴a+b >m (am+b ),所以④正确;⑤当x=3时函数值小于0,y=9a+3b+c <0,且x=2b a -=1, 即a=2b -,代入得9(2b -)+3b+c <0,得2c <3b ,故⑤正确; 故选B .【点评】此题主要考查了图象与二次函数系数之间的关系,二次函数y=ax 2+bx+c 系数符号由抛物线开口方向、对称轴和抛物线与y 轴的交点、抛物线与x 轴交点的个数确定.23.已知:如图所示,抛物线y =ax 2+bx +c 的对称轴为x =﹣1,与x 轴交于A 、B 两点,交y 轴于点C ,且OB =OC ,则下列结论正确的个数是( )①b =2a ②a ﹣b +c >﹣1 ③0<b 2﹣4ac <4 ④ac +1=b .A .1个B .2个C .3个D .4个【答案】D 【解析】①根据抛物线y=ax 2+bx+c 的对称轴为x=﹣1,即﹣2b a=﹣1,整理后即可得到答案; ②根据图象法即可得到答案; ③观察图象知函数图象与x 轴有两个交点,从而得到b 2﹣4ac >0;然后根据表示出a ,b ,c 的值,根据不等式的性质,即可求得;④由抛物线与y 轴相交于点C ,就可知道C 点的坐标,然后代入函数式,即可得到答案.【解答】解:①∵抛物线y=ax 2+bx+c 的对称轴为x=﹣1,∴﹣2b a=﹣1, 整理得b=2a ,故①正确;④由抛物线与y 轴相交于点C ,就可知道C 点的坐标为(0,c ),又因OC=OB ,所以B (﹣c ,0),把它代入y=ax 2+bx+c ,即ac 2﹣bc+c=0,两边同时除以c ,即得到ac ﹣b+1=0,所以ac+1=b .故④正确;②∵抛物线过点B 、C ,且直线BC 与x 轴所夹锐角为45°,且抛物线只与直线BC 有两个交点B 、C , 设直线BC 与对称轴x=﹣1交于点D ,对称轴与x 轴交于点E ,易知DE <1,∴D 的纵坐标大于﹣1,而抛物线是光滑曲线与直线BC 相交于B 、C 后不会再与直线BC 相交,由此可知抛物线的顶点高于D 点,即:抛物线的顶点纵坐标大于﹣1,所以当x=﹣1时,a ﹣b+c >﹣1.故②正确;③∵函数图象与x 轴有两个交点,∴得到b 2﹣4ac >0,∵0<b 2<4,4ac >0,∴b 2﹣4ac <4,故③正确;故选:D .【点评】本题考查了二次函数的系数与图象的关系,根据抛物线与x 轴,y 轴的交点判断交点坐标,然后代入函数式,推理a ,b ,c 之间的关系.24.在平面直角坐标系中有两点()()2,4,2,4A B -,若二次函数()2230y ax ax a a =--≠的图像与线段AB 只有一个交点,则( )A .a 的值可以是43-B .a 的值可以是35C .a 的值不可能是-1.2D .a 的值不可能是-1 【答案】C【解析】先计算二次函数的对称轴,首先计算函数与直线AB 相交时a 的取值范围.然后分别计算函数与A ,B 相交时a 的值,并由此分别画出函数的大致图,根据大致图判断a 的取值范围.对上述 a 的取值范围综合分析即可得出a 的最终取值范围,最后依次对各选项进行判断即可. 【解答】由对称轴可知,212a x a-=-=是该函数的对称轴, 当函数与直线AB 相交时,2423ax ax a =--有解,整理得22(34)0ax ax a --+=,根据根的判别式2244(34)16160a a a a a ∆=++=+≥,解得0a ≥或1a ≤-,因为0a ≠,所以0a >或1a ≤-,且a=-1时,二次函数与AB 有唯一的交点(1,4).若函数与B 点相交时,将B (2,4)代入()2230y ax ax a a =--≠得4434a a a --= 解得43a =-,则此时如下图:函数恰好与线段AB 有两个交点,所以根据图象,当4434a a a -->时抛物线与线段AB 只有一个交点,解得43a <-; 若函数与A 点相交时,把A (−2,4)代入()2230y ax ax a a =--≠得4434a a a +-=,解得45a =,则此时如下图:函数恰好与线段有一个交点,根据图象当4434a a a +-≥时,抛物线与线段AB 也只有一个交点,解得45a . 综上所述43a <-或45a 或a=-1, A. a 的值不可以是43-,故A 错误; B. 3455<,a 的值不可以是35,B 错误; C. -1.2=6453->-,故a 的值不可能是-1.2,C 正确; D. a 的值可能是-1,故D 错误.故选C.【点评】本题考查二次函数图象与系数的关系,二次函数图象上点的坐标特征.本题中能分情况讨论,并能画出函数大致图,根据大致图去分析是解决此题的关键.在本题中还需注意函数的顶点正好在直线AB 上这种情况.。
二次函数图像和性质习题精选(含答案及解析)
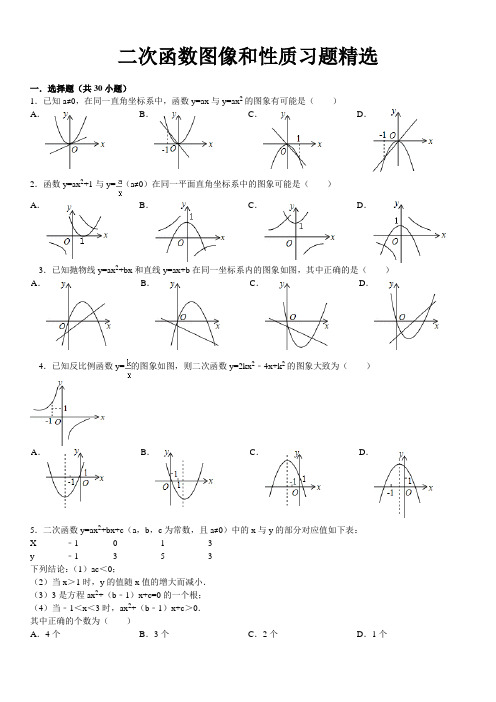
二次函数图像和性质习题精选一.选择题(共30小题)1.已知a≠0,在同一直角坐标系中,函数y=ax与y=ax2的图象有可能是()A.B.C.D.2.函数y=ax2+1与y=(a≠0)在同一平面直角坐标系中的图象可能是()A.B.C.D.3.已知抛物线y=ax2+bx和直线y=ax+b在同一坐标系内的图象如图,其中正确的是()A.B.C.D.4.已知反比例函数y=的图象如图,则二次函数y=2kx2﹣4x+k2的图象大致为()A.B.C.D.5.二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中的x与y的部分对应值如下表:X ﹣1 0 1 3y ﹣1 3 5 3下列结论:(1)ac<0;(2)当x>1时,y的值随x值的增大而减小.(3)3是方程ax2+(b﹣1)x+c=0的一个根;(4)当﹣1<x<3时,ax2+(b﹣1)x+c>0.其中正确的个数为()A.4个B.3个C.2个D.1个6.二次函数y=ax2+bx+c(a≠0)的大致图象如图,关于该二次函数,下列说法错误的是()A.函数有最小值B.对称轴是直线x=D.当﹣1<x<2时,y>0C.当x<,y随x的增大而减小7.如图,平面直角坐标系中,点M是直线y=2与x轴之间的一个动点,且点M是抛物线y=x2+bx+c的顶点,则方程x2+bx+c=1的解的个数是()A.0或2 B.0或1 C.1或2 D.0,1或28.已知二次函数y=a(x﹣h)2+k(a>0),其图象过点A(0,2),B(8,3),则h的值可以是()A.6B.5C.4D.39.二次函数y=ax2+bx+c图象上部分点的坐标满足下表:x …﹣3 ﹣2 ﹣1 0 1 …y …﹣3 ﹣2 ﹣3 ﹣6 ﹣11 …则该函数图象的顶点坐标为()A.(﹣3,﹣3)B.(﹣2,﹣2)C.(﹣1,﹣3)D.(0,﹣6)10.已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列说法错误的是()A.图象关于直线x=1对称B.函数y=ax2+bx+c(a≠0)的最小值是﹣4C.﹣1和3是方程ax2+bx+c=0(a≠0)的两个根D.当x<1时,y随x的增大而增大11.如图,二次函数的图象经过(﹣2,﹣1),(1,1)两点,则下列关于此二次函数的说法正确的是()A.y的最大值小于0 B.当x=0时,y的值大于1C.当x=﹣1时,y的值大于1 D.当x=﹣3时,y的值小于012.设二次函数y=x2+bx+c,当x≤1时,总有y≥0,当1≤x≤3时,总有y≤0,那么c的取值范围是()A.c=3 B.c≥3 C.1≤c≤3 D.c≤313.如图,直角坐标系中,两条抛物线有相同的对称轴,下列关系不正确的是()A.h=m B.k=n C.k>n D.h>0,k>014.已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下结论:①a>0;②该函数的图象关于直线x=1对称;③当x=﹣1或x=3时,函数y的值都等于0.其中正确结论的个数是()A.3B.2C.1D.015.二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论正确的是()A.a c<0B.当x=1时,y>0C.方程ax2+bx+c=0(a≠0)有两个大于1的实数根D.存在一个大于1的实数x0,使得当x<x0时,y随x的增大而减小;当x>x0时,y随x的增大而增大16.如图,抛物线y=ax2+bx+c(a>0)的对称轴是直线x=1,且经过点P(3,0),则a﹣b+c的值为()A.0B.﹣1 C.1D.217.下列图中阴影部分的面积相等的是()A.①②B.②③C.③④D.①④18.已知抛物线y=ax2+bx+c(a<0)的部分图象如图所示,当y>0时,x的取值范围是()A.﹣2<x<2 B.﹣4<x<2 C.x<﹣2或x>2 D.x<﹣4或x>219.已知:二次函数y=x2﹣4x﹣a,下列说法错误的是()A.当x<1时,y随x的增大而减小B.若图象与x轴有交点,则a≤4C.当a=3时,不等式x2﹣4x+a<0的解集是1<x<3D.若将图象向上平移1个单位,再向左平移3个单位后过点(1,﹣2),则a=320.下列表格给出的是二次函数y=ax2+bx+c(a≠0)的几组对应值,那么方程ax2+bx+c=0的一个近似解可以是()x 3.3 3.4 3.5 3.6y ﹣0.06 ﹣0.02 0.03 0.09A.3.25 B.3.35 C.3.45 D.3.5521.已知二次函数y=ax2+bx+c的y与x的部分对应值如下表:则下列判断中正确的是()A.抛物线开口向上B.抛物线与y轴交于负半轴C.当x=3时,y<0 D.方程ax2+bx+c=0有两个相等实数根A.x>2 B.x<﹣2 C.x>0 D.﹣2<x<823.在﹣3≤x≤0范围内,二次函数(a≠0)的图象如图所示.在这个范围内,有结论:①y1有最大值1、没有最小值;②y1有最大值1、最小值﹣3;③函数值y1随x的增大而增大;④方程ax2+bx+c=2无解;⑤若y2=2x+4,则y1≤y2.其中正确的个数是()A.2B.3C.4D.524.抛物线y=﹣x2+bx+c上部分点的横坐标x,纵坐标y的对应值如下表:x …﹣2 ﹣1 1 3 4 …y …0 4 6 4 0 …根据上表判断下列四种说法:①抛物线的对称轴是x=1;②x>1时,y的值随着x的增大而减小:③抛物线有最高点:④抛物线的顶点、与x轴的两个交点三点为顶点的三角形的面积为36.其中正确说法的个数有()A.1B.2C.3D.425.如图,已知抛物线y=x2+bx+c的对称轴为x=2,点A,B均在抛物线上,且AB与x轴平行,其中点A的坐标为(0,3),则点B的坐标为()A.(2,3)B.(3,2)C.(3,3)D.(4,3)26.如图为二次函数y=ax2+bx+c的图象,给出下列说法:①ab<0;②方程ax2+bx+c=0的根为x1=﹣1,x2=3;A.①②④B.①②⑤C.①③⑤D.②④⑤27.已知二次函数y=x2+2(a﹣1)x+2.如果x≤4时,y随x增大而减小,则常数a的取值范围是()A.a≥﹣5 B.a≤﹣5 C.a≥﹣3 D.a≤﹣328.如图,平行于y轴的直线l被抛物线y=0.5x2+1,y=0.5x2﹣1所截,当直线l向右平移3个单位时,直线l被两条抛物线所截得的线段扫过的图形面积为()平方单位.A.3B.4C.6D.无法可求29.已知直线经过点A(0,2),B(2,0),点C在抛物线y=x2的图象上,则使得S△ABC=2的点有()个.A.4B.3C.2D.130.如图,已知抛物线,直线y2=3x+3,当x任取一值时,x对应的函数值分别为y1,y2.若y1≠y2,取y1,y2中的较小值记为M;若y1=y2,记M=y1=y2.下列判断:①当x>0时,y1>y2;②使得M大于3的x值不存在;③当x<0时,x值越大,M值越小;④使得M=1的x 值是或.其中正确的是()A.①③B.②④C.①④D.②③二次函数图像和性质习题精选(含答案)参考答案与试题解析一.选择题(共30小题)1.(2014•宁夏)已知a≠0,在同一直角坐标系中,函数y=ax与y=ax2的图象有可能是()A.B.C.D.考点:二次函数的图象;正比例函数的图象.专题:数形结合.分析:本题可先由一次函数y=ax图象得到字母系数的正负,再与二次函数y=ax2的图象相比较看是否一致.(也可以先固定二次函数y=ax2图象中a 的正负,再与一次函数比较.)解答:解:A、函数y=ax中,a>0,y=ax2中,a>0,但当x=1时,两函数图象有交点(1,a),故A错误;B、函数y=ax中,a<0,y=ax2中,a>0,故B错误;C、函数y=ax中,a<0,y=ax2中,a<0,但当x=1时,两函数图象有交点(1,a),故C正确;D、函数y=ax中,a>0,y=ax2中,a<0,故D错误.故选:C.点评:函数中数形结合思想就是:由函数图象确定函数解析式各项系数的性质符号,由函数解析式各项系数的性质符号画出函数图象的大致形状.2.(2014•北海)函数y=ax2+1与y=(a≠0)在同一平面直角坐标系中的图象可能是()A.B.C.D.考点:二次函数的图象;反比例函数的图象.分析:分a>0和a<0两种情况讨论二次函数和反比例函数图象所在的象限,然后选择答案即可.解答:解:a>0时,y=ax2+1开口向上,顶点坐标为(0,1),y=位于第一、三象限,没有选项图象符合,a<0时,y=ax2+1开口向下,顶点坐标为(0,1),y=位于第二、四象限,B选项图象符合.故选:B.点评:本题考查了二次函数图象与反比例函数图象,熟练掌握系数与函数图象的关系是解题的关键.3.(2014•遵义)已知抛物线y=ax2+bx和直线y=ax+b在同一坐标系内的图象如图,其中正确的是()A.B.C.D.考点:二次函数的图象;一次函数的图象.分析:本题可先由二次函数图象得到字母系数的正负,再与一次函数和反比例函数的图象相比较看是否一致.逐一排除.解答:解:A、由二次函数的图象可知a<0,此时直线y=ax+b经过二、四象限,故A可排除;B、二次函数的图象可知a<0,对称轴在y轴的右侧,可知a、b异号,b>0,此时直线y=ax+b经过一、二、四象限,故B可排除;C、二次函数的图象可知a>0,此时直线y=ax+b经过一、三,故C可排除;正确的只有D.故选:D.点评:此题主要考查了一次函数图象与二次函数图象,应该识记一次函数y=kx+b 在不同情况下所在的象限,以及熟练掌握二次函数的有关性质:开口方向、对称轴、顶点坐标等.4.(2014•南昌)已知反比例函数y=的图象如图,则二次函数y=2kx2﹣4x+k2的图象大致为()A.B.C.D.考点:二次函数的图象;反比例函数的图象.分析:本题可先由反比例函数的图象得到字母系数k<﹣1,再与二次函数的图象的开口方向和对称轴的位置相比较看是否一致,最终得到答案.解答:解:∵函数y=的图象经过二、四象限,∴k<0,由图知当x=﹣1时,y=﹣k>1,∴k<﹣1,∴抛物线y=2kx2﹣4x+k2开口向下,对称为x=﹣=,﹣1<<0,∴对称轴在﹣1与0之间,故选:D.点评:此题主要考查了二次函数与反比例函数的图象与系数的综合应用,正确判断抛物线开口方向和对称轴位置5.(2014•泰安)二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中的x与y的部分对应值如下表:X ﹣1 0 1 3y ﹣1 3 5 3下列结论:(1)ac<0;(2)当x>1时,y的值随x值的增大而减小.(3)3是方程ax2+(b﹣1)x+c=0的一个根;(4)当﹣1<x<3时,ax2+(b﹣1)x+c>0.其中正确的个数为()A.4个B.3个C.2个D.1个考点:二次函数的性质;二次函数图象与系数的关系;抛物线与x轴的交点;二次函数与不等式(组).专题:图表型.分析:根据表格数据求出二次函数的对称轴为直线x=1.5,然后根据二次函数的性质对各小题分析判断即可得解.解答:解:(1)由图表中数据可得出:x=1时,y=5,所以二次函数y=ax2+bx+c开口向下,a<0;又x=0时,y=3,所以c=3>0,所以ac<0,故(1)正确;(2)∵二次函数y=ax2+bx+c开口向下,且对称轴为x==1.5,∴当x>1.5时,y的值随x值的增大而减小,故(2)错误;(3)∵x=3时,y=3,∴9a+3b+c=3,∵c=3,∴9a+3b+3=3,∴9a+3b=0,∴3是方程ax2+(b﹣1)x+c=0的一个根,故(3)正确;(4)∵x=﹣1时,ax2+bx+c=﹣1,∴x=﹣1时,ax2+(b﹣1)x+c=0,∵x=3时,ax2+(b﹣1)x+c=0,且函数有最大值,∴当﹣1<x<3时,ax2+(b﹣1)x+c>0,故(4)正确.故选:B.点评:本题考查了二次函数的性质,二次函数图象与系数的关系,抛物线与x轴的交点,二次函数与不等式,有一定难度.熟练掌握二次函数图象的性质是解题的关键.6.(2014•广东)二次函数y=ax2+bx+c(a≠0)的大致图象如图,关于该二次函数,下列说法错误的是()A.函数有最小值B.对称轴是直线x=C.D.当﹣1<x<2时,y>0当x<,y随x的增大而减小考点:二次函数的性质.专题:数形结合.分析:根据抛物线的开口方向,利用二次函数的性质判断A;根据图形直接判断B;根据对称轴结合开口方向得出函数的增减性,进而判断C;B、由图象可知,对称轴为x=,正确,故B选项不符合题意;C、因为a>0,所以,当x<时,y随x的增大而减小,正确,故C选项不符合题意;D、由图象可知,当﹣1<x<2时,y<0,错误,故D选项符合题意.故选:D.点评:本题考查了二次函数的图象和性质,解题的关键是利用数形结合思想解题.7.(2014•盘锦)如图,平面直角坐标系中,点M是直线y=2与x轴之间的一个动点,且点M是抛物线y=x2+bx+c 的顶点,则方程x2+bx+c=1的解的个数是()A.0或2 B.0或1 C.1或2 D.0,1或2考点:二次函数的性质.专题:数形结合;分类讨论;方程思想.分析:分三种情况:点M的纵坐标小于1;点M的纵坐标等于1;点M的纵坐标大于1;进行讨论即可得到方程x2+bx+c=1的解的个数.解答:解:分三种情况:点M的纵坐标小于1,方程x2+bx+c=1的解是2个不相等的实数根;点M的纵坐标等于1,方程x2+bx+c=1的解是2个相等的实数根;点M的纵坐标大于1,方程x2+bx+c=1的解的个数是0.故方程x2+bx+c=1的解的个数是0或1或2.故选:D.点评:考查了二次函数的性质,本题涉及分类思想和方程思想的应用.8.(2014•淄博)已知二次函数y=a(x﹣h)2+k(a>0),其图象过点A(0,2),B(8,3),则h的值可以是()A.6B.5C.4D.3考点:二次函数的性质.专题:计算题.分析:根据抛物线的顶点式得到抛物线的对称轴为直线x=h,由于所给数据都是正数,所以当对称轴在y轴的右侧时,比较点A和点B到对称轴的距离可得到h<4.解答:解:∵抛物线的对称轴为直线x=h,∴当对称轴在y轴的右侧时,A(0,2)到对称轴的距离比B(8,3)到对称轴的距离小,点评:本题考查了二次函数的性质:二次函数y=ax2+bx+c(a≠0)的顶点坐标为(﹣,),对称轴直线x=﹣,二次函数y=ax2+bx+c(a≠0)的图象具有如下性质:①当a>0时,抛物线y=ax2+bx+c(a≠0)的开口向上,x<﹣时,y随x的增大而减小;x>﹣时,y随x的增大而增大;x=﹣时,y取得最小值,即顶点是抛物线的最低点.②当a<0时,抛物线y=ax2+bx+c(a≠0)的开口向下,x<﹣时,y随x的增大而增大;x>﹣时,y随x的增大而减小;x=﹣时,y取得最大值,即顶点是抛物线的最高点.9.(2013•徐州)二次函数y=ax2+bx+c图象上部分点的坐标满足下表:x …﹣3 ﹣2 ﹣1 0 1 …y …﹣3 ﹣2 ﹣3 ﹣6 ﹣11 …则该函数图象的顶点坐标为()A.(﹣3,﹣3)B.(﹣2,﹣2)C.(﹣1,﹣3)D.(0,﹣6)考点:二次函数的性质.专题:压轴题.分析:根据二次函数的对称性确定出二次函数的对称轴,然后解答即可.解答:解:∵x=﹣3和﹣1时的函数值都是﹣3相等,∴二次函数的对称轴为直线x=﹣2,∴顶点坐标为(﹣2,﹣2).故选B.点评:本题考查了二次函数的性质,主要利用了二次函数的对称性,仔细观察表格数据确定出对称轴是解题的关键.10.(2013•南宁)已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列说法错误的是()A.图象关于直线x=1对称B.函数y=ax2+bx+c(a≠0)的最小值是﹣4C.﹣1和3是方程ax2+bx+c=0(a≠0)的两个根D.当x<1时,y随x的增大而增大考点:二次函数的性质.分析:根据对称轴及抛物线与x轴交点情况,结合二次函数的性质,即可对所得结论进行判断.解答:解:A、观察图象,可知抛物线的对称轴为直线x=1,则图象关于直线x=1对称,正确,故本选项不符合题意;B、观察图象,可知抛物线的顶点坐标为(1,﹣4),又抛物线开口向上,所以函数y=ax2+bx+c(a≠0)的最小值是﹣4,正确,故本选项不符合题意;C、由图象可知抛物线与x轴的一个交点为(﹣1,0),而对称轴为直线x=1,所以抛物线与x轴的另外一个交点为(3,0),则﹣1和3是方程ax2+bx+c=0(a≠0)的两个根,正确,故本选项不符合题意;D、由抛物线的对称轴为x=1,所以当x<1时,y随x的增大而减小,错误,故本选项符合题意.故选D.点评:此题考查了二次函数的性质和图象,解题的关键是利用数形结合思想解题.11.(2012•济南)如图,二次函数的图象经过(﹣2,﹣1),(1,1)两点,则下列关于此二次函数的说法正确的是()A.y的最大值小于0 B.当x=0时,y的值大于1C.当x=﹣1时,y的值大于1 D.当x=﹣3时,y的值小于0考点:二次函数的图象;二次函数的性质.专题:压轴题.分析:根据图象的对称轴的位置、增减性及开口方向直接回答.解答:解:A、由图象知,点(1,1)在图象的对称轴的左边,所以y的最大值大于1,不小于0;故本选项错误;B、由图象知,当x=0时,y的值就是函数图象与y轴的交点,而图象与y轴的交点在(1,1)点的左边,故y<1;故本选项错误;C、对称轴在(1,1)的右边,在对称轴的左边y随x的增大而增大,∵﹣1<1,∴x=﹣1时,y的值小于x=1时,y的值1,即当x=﹣1时,y的值小于1;故本选项错误;D、当x=﹣3时,函数图象上的点在点(﹣2,﹣1)的左边,所以y的值小于0;故本选项正确.故选D.点评:本题主要考查了二次函数图象上点的坐标特征.解答此题时,需熟悉二次函数图象的开口方向、对称轴、与x轴的交点等知识.12.(2012•德阳)设二次函数y=x2+bx+c,当x≤1时,总有y≥0,当1≤x≤3时,总有y≤0,那么c的取值范围是()A.c=3 B.c≥3 C.1≤c≤3 D.c≤3考点:二次函数的性质.专题:压轴题.分析:因为当x≤1时,总有y≥0,当1≤x≤3时,总有y≤0,所以函数图象过(1,0)点,即1+b+c=0①,由题意可知当x=3时,y=9+3b+c≤0②,所以①②联立即可求出c的取值范围.解答:解:∵当x≤1时,总有y≥0,当1≤x≤3时,总有y≤0,∴函数图象过(1,0)点,即1+b+c=0①,∵当1≤x≤3时,总有y≤0,∴当x=3时,y=9+3b+c≤0②,①②联立解得:c≥3,故选B.点评:本题考查了二次函数的增减性,解题的关键是由给出的条件得到抛物线过(1,0),再代入函数的解析式得到一次项系数和常数项的关系.13.(2009•新疆)如图,直角坐标系中,两条抛物线有相同的对称轴,下列关系不正确的是()A.h=m B.k=n C.k>n D.h>0,k>0考点:二次函数的图象.专题:压轴题.分析:借助图象找出顶点的位置,判断顶点横坐标、纵坐标大小关系.解答:解:根据二次函数解析式确定抛物线的顶点坐标分别为(h,k),(m,n),因为点(h,k)在点(m,n)的上方,所以k=n不正确.故选:B.点评:本题是抛物线的顶点式定义在图形中的应用.14.(2009•丽水)已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下结论:①a>0;②该函数的图象关于直线x=1对称;③当x=﹣1或x=3时,函数y的值都等于0.其中正确结论的个数是()A.3B.2C.1D.0考点:二次函数的性质.分析:根据抛物线的性质解题.解答:解:①抛物线开口向下,a<0,所以①错误;②抛物线是关于对称轴对称的轴对称图形,所以②该函数的图象关于直线x=1对称,正确;③当x=﹣1或x=3时,函数y的值都等于0,也正确.故选B.点评:本题考查了抛物线的开口方向,轴对称性和与x轴的交点等知识.15.(2009•南昌)二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论正确的是()A.a c<0B.当x=1时,y>0C.方程ax2+bx+c=0(a≠0)有两个大于1的实数根D.存在一个大于1的实数x0,使得当x<x0时,y随x的增大而减小;当x>x0时,y随x的增大而增大考点:二次函数的性质.专题:压轴题.分析:根据抛物线的形状与抛物线表达式系数的关系,逐一判断.解答:解:A、抛物线开口向上,a>0,抛物线与y轴交于正半轴,c>0,所以ac>0,错误;B、由图象可知,当x=1时,y<0,错误;C、方程ax2+bx+c=0(a≠0)有一个根小于1,一个根大于1,错误;D、存在一个大于1的实数x0,使得当x<x0时,y随x的增大而减小;当x>x0时,y随x的增大而增大,正确.故选D.点评:本题考查抛物线的形状与抛物线表达式系数的关系,涉及的知识面比较广.16.(2008•仙桃)如图,抛物线y=ax2+bx+c(a>0)的对称轴是直线x=1,且经过点P(3,0),则a﹣b+c的值为()A.0B.﹣1 C.1D.2考点:二次函数的图象.专题:压轴题.分析:由“对称轴是直线x=1,且经过点P(3,0)”可知抛物线与x轴的另一个交点是(﹣1,0),代入抛物线方程即可解得.解答:解:因为对称轴x=1且经过点P(3,0)所以抛物线与x轴的另一个交点是(﹣1,0)代入抛物线解析式y=ax2+bx+c中,得a﹣b+c=0.故选A.点评:巧妙利用了抛物线的对称性.17.(2007•烟台)下列图中阴影部分的面积相等的是()A.①②B.②③C.③④D.①④考点:二次函数的图象;一次函数的图象;反比例函数的图象.专题:压轴题.分析:根据坐标系的点的坐标特点,分别求出三角形的底和高,计算面积,再比较.解答:解:①与坐标轴的两个交点为(0,2)(2,0),阴影部分的面积为2×2÷2=2;②当x=1时,y=3,阴影部分的面积为1×3÷2=1.5;③与x轴的两个交点的横坐标为﹣1,1,两点间的距离为:1﹣(﹣1)=2,与y轴的交点为(0,﹣1).阴影部分的面积为2×1÷2=1;④当x=1时,y=4,阴影部分的面积为1×4÷2=2.①④面积相等.故选D.点评:解决本题的关键是根据各函数的特点得到相应的三角形的边以及边上的高.18.(2007•达州)已知抛物线y=ax2+bx+c(a<0)的部分图象如图所示,当y>0时,x的取值范围是()A.﹣2<x<2 B.﹣4<x<2 C.x<﹣2或x>2 D.x<﹣4或x>2考点:二次函数的图象.专题:压轴题.分析:先根据对称轴和抛物线与x轴的交点求出另一交点;再根据开口方向,结合图形,求出y>0时,x的取值范围.解答:解:因为抛物线过点(2,0),对称轴是x=﹣1,根据抛物线的对称性可知,抛物线必过另一点(﹣4,0),因为抛物线开口向下,y>0时,图象在x轴的上方,此时,﹣4<x<2.故选B.点评:解答本题,利用二次函数的对称性,关键是判断图象与x轴的交点,根据开口方向,形数结合,得出结论.19.(2007•泰州)已知:二次函数y=x2﹣4x﹣a,下列说法错误的是()A.当x<1时,y随x的增大而减小B.若图象与x轴有交点,则a≤4C.当a=3时,不等式x2﹣4x+a<0的解集是1<x<3D.若将图象向上平移1个单位,再向左平移3个单位后过点(1,﹣2),则a=3考点:二次函数的性质;二次函数图象与几何变换;抛物线与x轴的交点;二次函数与不等式(组).专题:压轴题.分析:A、当x<1时,在对称轴右侧,由此可以确定函数的单调性;B、若图象与x轴有交点,即△=16+4a≥0,利用此即可判断是否正确;C、当a=3时,不等式x2﹣4x+a<0的解集可以求出,然后就可以判断是否正确;D、根据平移规律可以求出a的值,然后判断是否正确.解答:解:二次函数为y=x2﹣4x﹣a,对称轴为x=2,图象开口向上.则:A、当x<1时,y随x的增大而减小,故选项正确;B、若图象与x轴有交点,即△=16+4a≥0则a≥﹣4,故选项错误;C、当a=3时,不等式x2﹣4x+a<0的解集是1<x<3,故选项正确;D、原式可化为y=(x﹣2)2﹣4﹣a,将图象向上平移1个单位,再向左平移3个单位后所得函数解析式是y=(x+1)2﹣3﹣a.函数过点(1,﹣2),代入解析式得到:a=3.故选项正确.故选B.点评:此题主要考查了二次函数的性质与一元二次方程之间的关系,以及图象的平移规律.这些性质和规律要求掌握.20.(2009•塘沽区一模)下列表格给出的是二次函数y=ax2+bx+c(a≠0)的几组对应值,那么方程ax2+bx+c=0的一个近似解可以是()x 3.3 3.4 3.5 3.6y ﹣0.06 ﹣0.02 0.03 0.09A.3.25 B.3.35 C.3.45 D.3.55考点:图象法求一元二次方程的近似根.分析:把三点代入解方程式,则代入y等于0时,x的值是多少即可.解答:解:代入各点坐标解得y=0.5x2﹣2.95x+4.23解得x=3.47左右则C最符合,故选C.点评:本题考查了一元二次方程的近似根,代入求近似值,再进行对比则最接近的即可.21.(2010•徐汇区一模)已知二次函数y=ax2+bx+c的y与x的部分对应值如下表:则下列判断中正确的是()A.抛物线开口向上B.抛物线与y轴交于负半轴C.当x=3时,y<0 D.方程ax2+bx+c=0有两个相等实数根考点:图象法求一元二次方程的近似根.专题:计算题.分析:结合图表可以得出当x=0或2时,y=1,可以求出此函数的对称轴是x=1,顶点坐标为(1,3),借助(0,1)两点可求出二次函数解析式,从而得出抛物线的性质.解答:解:∵由图表可以得出当x=0或2时,y=1,可以求出此函数的对称轴是x=1,顶点坐标为(1,3),∴二次函数解析式为:y=a(x﹣1)2+3,再将(0,1)点代入得:1=a(﹣1)2+3,解得:a=﹣2,∴y=﹣2(x﹣1)2+3,∵a<0∴A,抛物线开口向上错误,故:A错误;∵y=﹣2(x﹣1)2+3=﹣2x2+4x+1,与y轴交点坐标为(0,1),故与y轴交于正半轴,故:B错误;∵x=3时,y=﹣5<0,故:C正确;∵方程ax2+bx+c=0,△=16+4×2×1=22>0,此方程有两个不相等的实数根,故:D.方程有两个相等实数根错误;故选:C.点评:此题主要考查了二次函数解析式的求法,以及由解析式求函数与坐标轴的交点以及一元二次方程根的判别式的应用.22.(2013•沙湾区模拟)已知二次函数y1=ax2+bx+c(a≠0)与一次函数y2=kx+m(k≠0)的图象相交于点A(﹣2,4),B(8,2)(如图所示),则能使y1<y2成立的x的取值范围是()A.x>2 B.x<﹣2 C.x>0 D.﹣2<x<8考点:二次函数的性质.分析:根据两函数交点坐标得出,能使y1<y2成立的x的取值范围即是图象y2在图象y1上面是x的取值范围,即可得出答案.解答:解:∵二次函数y1=ax2+bx+c(a≠0)与一次函数y2=kx+m(k≠0)的图象相交于点A(﹣2,4),B(8,2),∵结合图象,∴能使y1<y2成立的x的取值范围是:﹣2<x<8,故选:D.点评:此题主要考查了利用函数图象判定两函数的大小关系,此题型是中考中考查重点也是难点,同学们应熟练掌握.23.(2012•北辰区一模)在﹣3≤x≤0范围内,二次函数(a≠0)的图象如图所示.在这个范围内,有结论:①y1有最大值1、没有最小值;②y1有最大值1、最小值﹣3;③函数值y1随x的增大而增大;④方程ax2+bx+c=2无解;⑤若y2=2x+4,则y1≤y2.其中正确的个数是()A.2B.3C.4D.5考点:二次函数的性质;二次函数的图象.专题:数形结合.分析:根据二次函数的性质,结合图象可判断①②③;根据二次函数与一元二次方程的关系可判断④;求出y2=2x+4与两坐标轴的交点画出直线y=2x+4,求出抛物线的解析式,根据y2﹣y1的符号即可判断出⑤.解答:解:由图象可知,在﹣3≤x≤0范围内,y1有最大值1、最小值﹣3,故①错误,②正确;由图象可知,当﹣3≤x<﹣1时,y1随x的增大而增大,当﹣1<x<0时,y1随x的增大而减小,故③错误;由于y1的最大值是1,所以y1=ax2+bx+c与y=2没有交点,即方程ax2+bx+c=2无解,故④正确;如图所示,由于y2=2x+4经过点(0,4),(﹣2,0),由图可知,二次函数(a≠0)中,当x=1时,y=﹣1;x=﹣2时,y=0,所以,解得,故此二次函数的解析式为y1=﹣x2﹣2x,所以y2﹣y1=2x+4+x2+2x=(x+2)2,因为=(x+2)2≥0,所以y1≤y2,故⑤正确.故选B.点评:本题考查的是二次函数的性质,能利用数形结合求出不等式的解集是解答此题的关键.24.(2011•苏州模拟)抛物线y=﹣x2+bx+c上部分点的横坐标x,纵坐标y的对应值如下表:x …﹣2 ﹣1 1 34…y …0 4 6 4 0 …根据上表判断下列四种说法:①抛物线的对称轴是x=1;②x>1时,y的值随着x的增大而减小:③抛物线有最高点:④抛物线的顶点、与x轴的两个交点三点为顶点的三角形的面积为36.其中正确说法的个数有()A.1B.2C.3D.4考点:二次函数的性质.专题:计算题.分析:根据抛物线的对称性,抛物线的顶点坐标为(1,6),且函数值6为最大值,由此判断.解答:解:观察表格可知,抛物线的顶点坐标为(1,6),且抛物线开口向下,故①②③正确;∵抛物线与x轴的两个交点为(﹣2,0),(4,0),顶点坐标为(1,6),∴抛物线的顶点、与x轴的两个交点三点为顶点的三角形的面积为×(4+2)×6=18,故④错误.其中正确说法是①②③.故选C.点评:本题考查了二次函数的性质.关键是由表格观察出抛物线的顶点坐标,开口方向及与x轴交点坐标.25.(2010•河北)如图,已知抛物线y=x2+bx+c的对称轴为x=2,点A,B均在抛物线上,且AB与x轴平行,其中点A的坐标为(0,3),则点B的坐标为()A.(2,3)B.(3,2)C.(3,3)D.(4,3)考点:二次函数的性质.专题:综合题;压轴题.分析:已知抛物线的对称轴为x=2,知道A的坐标为(0,3),由函数的对称性知B点坐标.解答:解:由题意可知抛物线的y=x2+bx+c的对称轴为x=2,∵点A的坐标为(0,3),且AB与x轴平行,可知A、B两点为对称点,∴B点坐标为(4,3)故选D.点评:本题主要考查二次函数的对称性.26.如图为二次函数y=ax2+bx+c的图象,给出下列说法:①ab<0;②方程ax2+bx+c=0的根为x1=﹣1,x2=3;③a+b+c>0;④当x<1时,y随x值的增大而增大;⑤当y>0时,x<﹣1或x>3.其中,正确的说法有()A.①②④B.①②⑤C.①③⑤D.②④⑤考点:二次函数的性质.专题:压轴题.分析:根据二次函数图象反映出的数量关系,逐一判断正确性.解答:解:根据图象可知:①对称轴﹣>0,故ab<0,正确;②方程ax2+bx+c=0的根为x1=﹣1,x2=3,正确;③x=1时,y=a+b+c<0,错误;④当x<1时,y随x值的增大而减小,错误;⑤当y>0时,x<﹣1或x>3,正确.正确的有①②⑤.故选B.点评:主要考查了二次函数的性质,会根据图象获取所需要的信息.掌握函数性质灵活运用.27.已知二次函数y=x2+2(a﹣1)x+2.如果x≤4时,y随x增大而减小,则常数a的取值范围是()A.a≥﹣5 B.a≤﹣5 C.a≥﹣3 D.a≤﹣3考点:二次函数的性质.分析:抛物线开口向上,由x≤4时,y随x增大而减小,可知对称轴x=1﹣a≥4,解不等式即可.解答:解:∵二次函数对称轴为直线x=1﹣a,开口向上,∴当x≤1﹣a时,y随x增大而减小,∴1﹣a≥4,解得a≤﹣3.故选D.点评:本题考查了二次函数的增减性.抛物线开口向上时,在对称轴左边,y随x的增大而减小,右边y随x的增大而增大;抛物线开口向下时,在对称轴左边,y随x的增大而增大,右边y随x的增大而减小.28.如图,平行于y轴的直线l被抛物线y=0.5x2+1,y=0.5x2﹣1所截,当直线l向右平移3个单位时,直线l被两条抛物线所截得的线段扫过的图形面积为()平方单位.A.3B.4C.6D.无法可求考点:二次函数的性质.分析:由于抛物线y=0.5x2+1是y=0.5x2﹣1向上平移2个单位长度得到的,平行于y轴的直线l与2个函数图象的交点纵坐标是个定值2,通过截补法可知阴影部分的面积是6个单位长度.解答:解:抛物线y=0.5x2+1是y=0.5x2﹣1向上平移2个单位长度得到的,即|y1﹣y2|=2.当直线l向右平移3个单位时,阴影部分的面积是:2×3=6.故选C.点评:主要考查了函数图象动态变化中的不变量,本题的关键点是能看出阴影部分的面积通过截补法是个平行四边形.29.已知直线经过点A(0,2),B(2,0),点C在抛物线y=x2的图象上,则使得S△ABC=2的点有()个.A.4B.3C.2D.1考点:二次函数的性质.专题:计算题;压轴题.分析:解:通过计算发现,当O与C重合时,S△ABC=2,据此据此推断出以AB为底边的三角形的高,从图上找到点C1、C2,再作CC3∥AB,使得C3与C到AB的距离相等,若求出C的坐标,则存在C3点,使得以AB为底的三角形面积为2.解答:解:∵S△ABC=×2×2=2,可见,当O与C重合时,S△ABC=2,作CD⊥AB,∵AO=BO=2,。
中考数学一轮复习《二次函数的图像与性质》练习题(含答案)

中考数学一轮复习《二次函数的图像与性质》练习题(含答案)课时1二次函数图象与性质、抛物线与系数a、b、c的关系(建议答题时间:20分钟)1. (2017长沙)抛物线y=2(x-3)2+4的顶点坐标是()A. (3,4)B. (-3,4)C. (3,-4)D. (2,4)2. (2017金华)对于二次函数y=-(x-1)2+2的图象与性质,下列说法正确的是()A. 对称轴是直线x=1,最小值是2B. 对称轴是直线x=1,最大值是2C. 对称轴是直线x=-1,最小值是2D. 对称轴是直线x=-1,最大值是23. (2017连云港)已知抛物线y=ax2(a>0)过A(-2,y1)、B(1,y2)两点,则下列关系式一定正确的是()A. y1>0>y2B. y2>0>y1C. y1>y2>0D. y2>y1>04. (人教九上41页第6题改编)对于二次函数y=-3x2-12x-3,下面说法错误的是()A. 抛物线的对称轴是x=-2B. x=-2时,函数存在最大值9C. 当x>-2时,y随x增大而减小D. 抛物线与x轴没有交点5. (2017眉山)若一次函数y=(a+1)x+a的图象过第一、三、四象限,则二次函数y=ax2-ax()A. 有最大值a4B. 有最大值-a4C. 有最小值a4D. 有最小值-a46. (2017广州)a≠0,函数y=ax与y=-ax2+a在同一直角坐标系中的大致图象可能是()7. (2017重庆巴蜀月考)已知二次函数y=a2x+bx+c(a≠0)的图象如图所示,对称轴为直线x=1,下列结论中正确的是()A. abc>0B. b=2aC. a+c>D. 4a+2b+c>0第7题图第9题图第11题图8. (2017乐山)已知二次函数y=x2-2mx(m为常数),当-1≤x≤2时,函数值y的最小值为-2,则m的值是()A. 32B. 2 C.32或 2 D. -32或 29. (2017日照)已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=2,与x轴的一个交点坐标为(4,0),其部分图象如图所示,下列结论:①抛物线过原点;②4a+b+c=0;③a-b+c<0;④抛物线的顶点坐标为(2,b);⑤当x<2时,y随x增大而增大.其中结论正确的是()A. ①②③B. ③④⑤C. ①②④D. ①④⑤10. (2017广州)当x=________时,二次函数y=x2-2x+6有最小值________.11. (2017兰州)如图,若抛物线y=ax2+bx+c上的P(4,0),Q两点关于它的对称轴x=1对称,则点Q的坐标为________.课时2 抛物线的平移、解析式的确定、与方程(不等式)的关系(建议答题时间:20分钟)1. (2017重庆南开模拟)将二次函数y =(x -1)2+2的图象向左平移2个单位,再向下平移3个单位,则新的二次函数解析式为( )A . y =(x -3)2-1B . y =(x +1)2+5C . y =(x +1)2-1D . y =(x -3)2+52. (2017徐州)若函数y =x 2-2x +b 的图象与坐标轴有三个交点,则b 的取值范围是( )A . b <1且b ≠0B . b >1C . 0<b <1D . b <13. (2017苏州)二次函数y =ax 2+1的图象经过点(-2,0),则关于x 的方程a (x -2)2+1=0的实数根为( )A . x 1=0,x 2=4B . x 1=-2,x 2=6C . x 1=32,x 2=52D . x 1=-4,x 2=04. (2017绵阳)将二次函数y =x 2的图象先向下平移1个单位,再向右平移3个单位,得到的图象与一次函数y =2x +b 的图象有公共点,则实数b 的取值范围是( )A . b >8B . b >-8C . b ≥8D . b ≥-85. (2017天津)已知抛物线y =x 2-4x +3与x 轴相交于点A ,B (点A 在点B 左侧),顶点为M ,平移该抛物线,使点M 平移后的对应点M ′落在x 轴上,点B 平移后的对应点B ′落在y 轴上,则平移后的抛物线解析式为( )A . y =x 2+2x +1B . y =x 2+2x -1C . y =x 2-2x +1D . y =x 2-2x -16. (2017随州)对于二次函数y =x 2-2mx -3,下列结论错误的是( )A . 它的图象与x 轴有两个交点B . 方程x 2-2mx =3的两根之积为-3C . 它的图象的对称轴在y 轴的右侧D . x <m 时,y 随x 的增大而减小7. (2018原创)在-2,-1,0,1,2五个数字中,任取一个作为a ,使不等式组⎩⎨⎧x +a ≥01-x >x +2无解,且函数y =ax 2+(a +2)x +12a +1的图象与x 轴只有一个交点,那么a 的值为( )A . 0B . 0或-2C . 2或-2D . 0,2或-28. (2017青岛)若抛物线y =x 2-6x +m 与x 轴没有交点,则m 的取值范围是________.9. 注重开放探究(2017上海)已知一个二次函数的图像开口向上,顶点坐标为(0,-1),那么这个二次函数的解析式可以是________.(只需写一个)10. (2017武汉)已知关于x 的二次函数y =ax 2+(a 2-1)x -a 的图象与x 轴的一个交点的坐标为(m ,0).若2<m <3,则a 的取值范围是________.11. (2017鄂州)已知正方形ABCD 中A (1,1)、B (1,2)、C (2,2)、D (2,1),有一抛物线y =(x +1)2向下平移m 个单位(m >0)与正方形ABCD 的边(包括四个顶点)有交点,则m 的取值范围是________.12. (2017杭州)在平面直角坐标系中,设二次函数y 1=(x +a )(x -a -1),其中a ≠0.(1)若函数y 1的图象经过点(1,-2),求函数y 1的表达式;(2)若一次函数y 2=ax +b 的图象与y 1的图象经过x 轴上同一点,探究实数a ,b 满足的关系式;(3)已知点P (x 0,m )和Q (1,n )在函数y 1的图象上.若m <n ,求x 0的取值范围.答案第1课时 二次函数图象与性质,抛物线与系数a 、b 、c 的关系1. A2. B3. C 【解析】画出抛物线y =ax 2(a >0)的草图如解图,根据图象可知,y 1>0,y 2>0,且y 1>y 2.第3题解图4. D 【解析】由y =-3x 2-12x -3=-3(x +2)2+9,可知对称轴是x =-2,选项A 正确;抛物线的开口向下,顶点坐标是(-2,9),当x =-2时,y 存在最大值9,选项B 正确;开口向下,当x >-2时,图象处于对称轴的右边,y 随x 增大而减小,选项C 正确;当y =0时,一元二次方程-3x 2-12x -3=0有实数解,所以抛物线与x 轴有交点,选项D 错误.5. B 【解析】∵一次函数y =(a +1)x +a 的图象过第一、三、四象限,∴⎩⎨⎧a +1>0a <0,解得-1<a <0,∵二次函数y =ax 2-ax =a (x -12)2-a 4,又∵-1<a <0,∴二次函数y =ax 2-ax 有最大值,且最大值为-a 4.6. D 【解析】如果a >0,则反比例函数y =a x 图象在第一、三象限,二次函数y=-ax 2+a 图象开口向下,排除A ;二次函数图象与y 轴交点(0,a )在y 轴正半轴,排除B ;如果a <0,则反比例函数y =a x图象在第二、四象限,二次函数y =-ax 2+a 图象开口向上,排除C ;故选D .7. D 【解析】观察函数图象,抛物线开口向下,则a <0.对称轴在y 轴右边,则a 、b 异号,∴b >0.抛物线与y 轴的交点在x 轴上方,则c >0,∴abc <0,选项A 错误;由抛物线的对称轴x =-b 2a =1,∴b =-2a ,选项B 错误;当x =-1时,y =a -b +c <0,∴a +c <b ,选项C 错误;根据对称性可知,当x =2时,y=4a +2b +c >0,选项D 正确.8. D 【解析】因为二次函数的对称轴为x =m ,所以对称轴不确定,因此需要讨论研究x 的范围与对称轴的位置关系,①当m ≥2时,此时-1≤x ≤2落在对称轴的左边,当x =2时y 取得最小值-2,即-2=22-2m ×2,解得m =32<2(舍);②当-1<m <2时,此时在对称轴x =m 处取得最小值-2,即-2=m 2-2m ·m ,解得m =-2或m =2,又-1<m <2,故m =2;③当m ≤-1时,此时-1≤x ≤2落在对称轴的右边,当x =-1时y 取得最小值-2,即-2=(-1)2-2m ×(-1),解得m =-32,综上所述,m =-32或 2.9. C 【解析】∵抛物线与x 轴交于(4,0),对称轴为x =2,∴抛物线与x 轴的另一个交点为(0,0).故①正确;∵抛物线经过原点,∴c =0.∵抛物线的对称轴为x =2,即-b 2a =2,∴4a +b =0,∴4a +b +c =0,故②正确;当x =-1时,抛物线的函数图象在x 轴上方,∴a (-1)2+(-1)b +c >0,即a -b +c >0,故③错误;∵c =0,4a +b =0,∴抛物线的解析式为y =-b 4x 2+bx =-b 4(x -2)2+b ,∴抛物线的顶点坐标为(2,b ),故④正确;由图象可知,抛物线开口向上,对称轴为x =2,当x <2时,y 随x 的增大而减小.故⑤错误.综上所述,①②④正确.10. 1,5 11.(-2,0)第2课时 抛物线的平移、解析式的确定、与方程(不等式)的关系1. C2. A3. A 【解析】∵二次函数y =ax 2+1的图象经过点(-2,0),∴代入得a (-2)2+1=0,解得a =-14,∴所求方程为-14(x -2)2+1=0,解方程得x 1=0,x 2=4.4. D 【解析】将二次函数y =x 2的图象先向下平移1个单位,再向右平移3个单位,得到的函数为y =(x -3)2-1,与一次函数联立得⎩⎨⎧y =(x -3)2-1y =2x +b ,整理得x 2-8x +8-b =0,∵两个函数图象有公共点,∴方程x 2-8x +8-b =0有解,则(-8)2-4(8-b )≥0,解得b ≥-8.5. A 【解析】∵抛物线与x 轴交于A 、B 两点,∴令y =0,即x 2-4x +3=0,解得,x 1=1,x 2=3,∴A (1,0),B (3,0),∵y =x 2-4x +3=(x -2)2-1,∴M (2,-1).∵要使平移后的抛物线的顶点在x 轴上,需将图象向上平移1个单位,要使点B 平移后的对应点落在y 轴上,需向左平移3个单位,∴M ′(-1,0),则平移后二次函数的解析式为y =(x +1)2,即y =x 2+2x +1.6. C 【解析】∵Δ=(-2m )2-4×1×(-3)=4m 2+12>0,∴图象与x 轴有两个交点,A 正确;令y =0得:x 2-2mx -3=0,方程的解即抛物线与x 轴交点的横坐标,由A 知图象与x 轴有两个交点,故方程有两个根,再根据一元二次方程根与系数的关系可得两根之积为c a =-31=-3,B 正确;根据抛物线对称轴公式可得对称轴为x =-b 2a =--2m 2=m ,∵m 的值不能确定,故对称轴是否在y 轴的右侧不能确定,C 错误;∵a =1>0,抛物线开口向上,∴对称轴的左侧的函数值y 随x 的增大而减小,由C 知抛物线对称轴为x =m ,∴当x <m 时,y 随x 的增大而减小,D 正确,故选C .7. B 【解析】解不等式x +a ≥0得x ≥-a ,解不等式1-x >x +2得x <-12,因为不等式组无解,故-a ≥-12,解得a ≤12;当a ≠0时,b 2-4ac =(a +2)2-4a (12a +1)=0,解得a =2或-2,当a =0时,函数是一次函数,图象与x 轴有一个交点,所以当a =0,2或-2时,图象与x 轴只有一个交点,但a ≤12,∴a =0或-2.8. m >9 9. y =x 2-1(答案不唯一)10. 13<a <12或3<a <-2 【解析】令y =0,即ax 2+(a 2-1)x -a =0,(ax -1)(x+a )=0,∴关于x 的二次函数y =ax 2+(a 2-1)x -a 的图象与x 轴的交点为(1a ,0)和(-a ,0),即m =1a 或m =-a ,又∵2<m <3,则13<a <12或-3<a <-2.11. 2≤m ≤8 【解析】∵将抛物线y =(x +1)2向下平移m 个单位,得到抛物线y =(x +1)2-m ,由平移后抛物线与正方形ABCD 的边有交点,则当点B 在抛物线上时,m 取最小值,此时(1+1)2-m =2,解得m =2,当点D 在抛物线上时,m 取最大值,此时(2+1)2-m =1,解得m =8,综上所述,m 的取值范围是2≤m ≤8.12. 解:(1)由题意知(1+a )(1-a -1)=-2,即a (a +1)=2,∵y 1=x 2-x -a (a +1),∴y1=x2-x-2;(2)由题意知,函数y1的图象与x轴交于点(-a,0)和(a+1,0),当y2的图象过点(-a,0)时,得-a2+b=0;当y2的图象过点(a+1,0)时,得a2+a+b=0;(3)由题意知,函数y1的图象的对称轴为直线x=12,所以点Q(1,n)与点(0,n)关于直线x=12对称.因为函数y1的图象开口向上,所以当m<n时,0<x0<1.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第1页,-共6页
二次函数的图像和性质 【2 】演习题
一.选择题
1.下列函数是二次函数的有( )
12)5(;)4();3()3(;2)2(;1)1(2
22+=++=-==
-=x y c bx ax y x x y x
y x y (6) y=2(x+3)2
-2x 2
A.1个;
B.2个;
C.3个;
D.4个
2.关于213
y x =,2y x =,2
3y x =的图像,下列说法中不准确的是( )
A .极点雷同
B .对称轴雷同
C .图像外形雷同
D .最低点雷同
3.抛物线()122
1
2++=
x y 的极点坐标是( ) A .(2,1) B .(-2,1) C .(2,-1) D .(-2,-1)
4.已知二次函数)2(2
-++=m m x mx y 的图象经由原点,则m 的值为
( )
A . 0或2
B . 0
C . 2
D .无法肯定
5.已知二次函数2
13x y -=.2231x y -=.232
3
x y =,它们的图像启齿由小到大的次序是( )
A.321y y y <<
B.123y y y <<
C.231y y y <<
D.132y y y <<
6.两条抛物线2
y x =与2
y x =-在统一坐标系内,下列说法中不准确的是
( )
A .极点雷同
B .对称轴雷同
C .启齿偏向相反
D .都有最小值
7.已知二次函数2y ax bx c =++(0a ≠)的图象如图所示,有下列结论:
①0abc >;②a+b+c>0③a-b+c<0;;
A .1个
B .2个
C .3个
D .4个
8.已知抛物线的极点为(-1,-2),且经由过程(1,10则这条抛物线的表达式为( ) A .y=32
(1)x --2 B .y=32
(1)x ++2
C .y=32(1)x +-2
D .y=-32
)1(-x +2
9.抛物线2
3y x =向右平移1个单位,再向下平移2个单位,所得到的抛物线是( )
A .
23(1)2y x =-- B.2
3(1)2y x =+- C.23(1)2y x =++ D.2
3(1)2y x =-+
10.抛物线2
44y x x =--的极点坐标是( )
A .(2,0)
B .(2,-2)
C .(2,-8)
D .(-2,-8)
11.与抛物线y=-12
x 2
+3x -5的外形.启齿偏向都雷同,只有地位不同的抛物线是( )
A. y = x 2+3x -5
B. y=-
12
x 2
x C. y =1x 2+3x -5 D. y=1
x 2
( )
A .抛物线的外形雷同
B .抛物线的极点雷同
C .抛物线对称轴雷同
D .抛物线的启齿偏向相反 13.对于抛物线2
1
(5)33
y x =--+,下列说法准确的是( ) A .启齿向下,极点坐标(53),B .启齿向上,极点坐标(53), C .启齿向下,极点坐标(53)-,D .启齿向上,极点坐标(53)-,
14.抛物线y=2
22x mx m -++的极点在第三象限,试肯定m 的取值规模是
( )
A .m <-1或m >2
B .m <0或m >-1
C .-1<m <0
D .m <-1 15.在统一向角坐标系中,函数y mx m =+和2
22y mx x =-++(m 是常数,且0m ≠)的图象可能..是( )
第3页,-共6页
16.函数y=12
-
2
x +2x -5的图像的对称轴是( ) A .直线x=2 B .直线a=-2 C .直线y=2 D .直线x=4
17.二次函数y=2
21x x --+图像的极点在( )
A .第一象限
B .第二象限
C .第三象限
D .第四象限
18.假如抛物线y=2
6x x c ++的极点在x 轴上,那么c 的值为( )
A .0
B .6
C .3
D .9
19.已知二次函数2
y ax bx c =++,假如a >0,b <0,c <0,那么这个函数图像的极点必在( )
A .第一象限
B .第二象限
C .第三象限
D .第四象限
20.已知正比例函数kx y =的图像如右图所示,则二次函数2
2
2k x kx y +-= 的图像大致为( )
21.如图所示,知足a >0,b <0的函数y=2
ax bx +的图像是( )
22.若A (-4,y 1),B (-3,y 2),C (1,y 3)为二次函数y=x 2
+4x-5的图象上的三点,则y 1,y 2,y 3的大小关系是( )
A.y 1<y 2<y 3
B.y 2<y 1<y 3
C.y 3<y 1<y 2
D.y 1<y 3<y 2
B .填空题:
23.二次函数2
()的图像启齿向____,对称轴是____,极点坐标是____,图像有最___点,x ___时,y 随x 的增大而增大,x
y
O x
O
x
y y
O x
y
O
x
y O x
第4页,-共6页
___时,y 随x 的增大而减小. 24.抛物线y=-
21
(2)2
x +-4的启齿向___,极点坐标___,对称轴___,x ___时,y 随x 的增大而增大,x ___时,y 随x 的增大而减小. 25.化2
43y x x =++为y =a 2
()x h -k +的情势是____,图像的启齿向____,极点是____,对称轴是____.
26.抛物线y=24x x +-1的极点是____,对称轴是____.
27.将抛物线y=3x 2向左平移6个单位,再向下平移7个单位所得新抛物线的解
析式为.
28.已知二次函数2
y ax bx c =++的图象如图
所示,则点()P a bc ,在第象限.
C .解答题
29.经由过程配方变形,说出函数2
288y x x =-+-的图像的启齿偏向,对称轴,极点坐标,这个函数有最大值照样最小值?这个值是若干?
30.(1)已知二次函数的图象以A (-1,4)为极点,且过点B (2,-5)
求该函数的关系式;
(2)抛物线过(-1,0),(3,0),(1,-5)三点,求二次函数的解析式;
31.已知二次函数y =ax 2
+bx +c ,当x =1时,y 有最大值为5,且它的图像经由点
(2,3),求这个函数的关系式.
32.已知二次函数y = -x 2
+bx +5,它的图像经由点(2,-3). (1)求这个函数关系式及它的图像的极点坐标.
(2)当x 为何值时,函数y 跟着x 的增大而增大?当为x 何值时,函数y 跟着
x 的增大而减小?
33.二次函数c bx ax y ++=2
的图像与
(2).求二次函数的图像的极点坐标;
参考答案
一.选择题
1.B2.C3.B 4.C 5.C
6.D 7.B 8.C 9 .A10.C
11.B 12.B 13.A 14.D 15.C 16.A 17.C 18.D 19.D 20.D
21.A 22.C
第6页,-共6页
4
)1(2++-=x y 24. 下 y 轴 (-2,-4) 直线x=-2 x<-2 x>-2; 25. 1)2(2
-+=x y 上 (-2,-1) 直线x=-1;
26. (-2,-5) 直线x=-2 ; 27.7)6(32
-+=x y 28.二 三.解答题
29.解法1:设y=a 2
(8)x -+9,将x=0,y=1代入上式得a=18
-
, ∴y=2
1(8)8x --+9=21218
x x -++
解法2:设y=2
ax bx c ++,由题意得2
1,8,
249,4c b a
ac b
a
⎧
⎪=⎪⎪-=⎨⎪⎪-=⎪
⎩解之1,82,1.a b c ⎧=-⎪⎪=⎨⎪=⎪⎩ ∴y=2
1218x x -
++
30.(1) (2)
31.5)1(22
+--=x y
32.(1)b=-2 522
+--=x x y (2) (-1,6) x<-1 x>-1
33.(1) 提醒:依据:OB OA OC ⋅=2,可求出OC=4,则C (0,4)
4
15
,25,45-
=-==c b a。
