分子量分解问题的参考解答
高中化学分子量的计算技巧详解

高中化学分子量的计算技巧详解化学是一门重要的自然科学,其中分子量的计算是化学学习中的基础知识之一。
掌握分子量的计算技巧对于高中化学学习至关重要。
本文将详细介绍高中化学分子量的计算技巧,并通过具体的题目举例,分析考点和解题思路,帮助高中学生及其父母更好地理解和掌握这一知识点。
一、分子量的概念和计算方法分子量是指化学物质中分子所含有的所有原子的质量之和。
通常用原子量单位来表示,即原子质量单位为g/mol。
要计算分子量,首先需要知道化学式中各个元素的原子量,然后根据化学式中各个元素的个数,将其与对应的原子量相乘,最后将所有元素的质量之和即为分子量。
例如,计算H2O的分子量。
根据元素周期表,H的原子量为1.008 g/mol,O的原子量为16.00 g/mol。
化学式H2O中,H的个数为2,O的个数为1。
因此,H2O的分子量为2×1.008 + 1×16.00 = 18.02 g/mol。
二、分子量计算中的常见考点和解题技巧1. 化学式中含有括号的情况有些化学式中含有括号,这时需要将括号内的化学式中的元素个数乘以括号后面的数字。
例如,计算Ca(OH)2的分子量。
根据元素周期表,Ca的原子量为40.08 g/mol,O的原子量为16.00 g/mol,H的原子量为1.008 g/mol。
化学式Ca(OH)2中,Ca的个数为1,O的个数为2,H的个数为2。
因此,Ca(OH)2的分子量为1×40.08 + 2×16.00 + 2×1.008 = 74.10 g/mol。
2. 化学式中含有水合物的情况有些化学式中含有水合物,即结合了水分子的化合物。
计算分子量时,需要将水合物中的水分子的质量也计算在内。
例如,计算CuSO4·5H2O的分子量。
根据元素周期表,Cu的原子量为63.55 g/mol,S的原子量为32.07 g/mol,O的原子量为16.00 g/mol,H的原子量为1.008 g/mol。
聚合物的分子量和分子量分布习题及解答
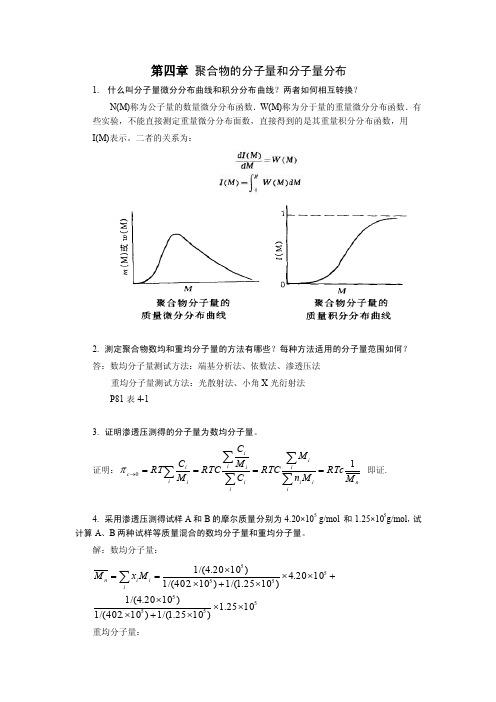
第四章 聚合物的分子量和分子量分布1. 什么叫分子量微分分布曲线和积分分布曲线?两者如何相互转换?N(M)称为公子量的数量微分分布函数.W(M)称为分于量的重量微分分布函数.有些实验,不能直接测定重量微分分布面数,直接得到的是其重量积分分布函数,用 I(M)表示。
二者的关系为:2. 测定聚合物数均和重均分子量的方法有哪些?每种方法适用的分子量范围如何? 答:数均分子量测试方法:端基分析法、依数法、渗透压法重均分子量测试方法:光散射法、小角X 光衍射法P81表4-13. 证明渗透压测得的分子量为数均分子量。
证明:n ii i i i i i i i i i ii c M RTc M n M RTC C M C RTC M C RT 10====∑∑∑∑∑→π 即证.4. 采用渗透压测得试样A 和B 的摩尔质量分别为4.20×105 g/mol 和1.25×105g/mol ,试计算A 、B 两种试样等质量混合的数均分子量和重均分子量。
解:数均分子量:555555551025.1)1025.1/(1)10.402/(1)1020.4/(11020.4)1025.1/(1)10.402/(1)1020.4/(1⨯⨯⨯+⨯⨯+⨯⨯⨯+⨯⨯==∑ii i n M x M重均分子量:55510725.21025.15.01020.45.0⨯=⨯⨯+⨯⨯==∑i ii M M ωω5.35℃时,,环已烷为聚苯乙烯(无规立构)的θ溶剂。
现将300mg 聚苯已烯(ρ=1.05 g/cm 3,n M =1.5×105)于 35℃溶于环己烷中,试计算:(1)第二维利系数A z ;(2)溶液的渗透压。
6.某聚苯乙烯试样经分级后得到5个级分。
用光散射法测定了各级分的重均分子量,用粘度法(22℃、二氯乙烷溶剂)测定了各级分的特性粘度,结果如下所示: 试计算Mark -Houwink 方程[η]=KM α中的两个参数K 和α。
高中化学气体的分子质量计算题解题技巧

高中化学气体的分子质量计算题解题技巧在高中化学学习中,气体的分子质量计算是一个重要的知识点。
掌握了这个技巧,不仅可以帮助我们解决各种与气体有关的计算题,还能帮助我们更好地理解气体分子的构成和性质。
本文将介绍一些解决气体分子质量计算题的技巧和方法。
首先,我们需要了解气体的分子质量是怎么计算的。
气体的分子质量是指一个气体分子中所有原子的质量之和。
例如,对于二氧化碳(CO2)这个分子来说,它由一个碳原子和两个氧原子组成。
碳的原子质量为12.01,氧的原子质量为16.00。
因此,CO2的分子质量可以通过计算12.01+16.00+16.00=44.01得到。
当我们遇到一个气体分子质量计算题时,首先要确定该气体的分子式。
分子式告诉我们一个气体分子中有多少个原子以及它们的种类。
例如,对于二氧化碳(CO2)这个分子来说,分子式告诉我们它由一个碳原子和两个氧原子组成。
接下来,我们需要查找每个原子的原子质量。
原子质量可以在元素周期表中找到。
例如,碳的原子质量为12.01,氧的原子质量为16.00。
然后,我们将每个原子的原子质量相加,得到气体分子的分子质量。
例如,对于二氧化碳(CO2)这个分子来说,我们将碳的原子质量12.01和氧的原子质量16.00相加,得到44.01。
在解决气体分子质量计算题时,有一些常见的考点需要我们特别注意。
首先是多原子分子的计算。
对于多原子分子来说,我们需要计算每个原子的原子质量,并将它们相加得到分子质量。
例如,硫酸(H2SO4)这个分子由两个氢原子、一个硫原子和四个氧原子组成。
我们需要计算氢、硫和氧的原子质量,并将它们相加得到硫酸的分子质量。
另一个考点是带有系数的分子式。
有时候,题目中给出的分子式前面会有一个系数。
这个系数表示该分子在化学反应中的个数。
我们在计算分子质量时,需要将该系数乘以每个原子的原子质量,并将它们相加得到分子质量。
例如,二氧化碳(CO2)这个分子的分子式中,氧的系数为2。
pm分子量问题回答

pm分子量
PM分子量是指聚合物中单个分子的平均质量。
它是衡量聚合物分子大小的重要指标,也是聚合物物理性质和化学性质的重要参数之一。
PM分子量的计算方法有多种,其中最常用的是凝胶渗透色谱法(GPC)。
该方法通过将聚合物样品溶解在适当的溶剂中,然后将其注入到一根特殊的柱子中,柱子内填充有一种特殊的凝胶。
当样品通过柱子时,由于分子大小的不同,聚合物分子会在凝胶中产生不同程度的阻力,从而分离出不同大小的分子。
通过检测分离出的分子的数量和大小,可以计算出聚合物的PM分子量。
PM分子量的大小对聚合物的性质有着重要的影响。
一般来说,PM分子量越大,聚合物的物理性质和化学性质就越好。
例如,高分子量的聚合物通常具有更高的强度、更好的耐热性和耐化学性,同时也更难降解。
因此,在聚合物材料的选择和设计中,PM分子量是一个非常重要的参数。
除了影响聚合物性质外,PM分子量还可以用于确定聚合物的合成方法和反应条件。
例如,在聚合物合成过程中,控制反应时间、温度和催化剂浓度等因素可以影响聚合物的PM分子量。
因此,通过对PM分子量的测定和分析,可以优化聚合物的合成过程,从而获得更好的聚
合物性质。
总之,PM分子量是衡量聚合物分子大小的重要指标,它对聚合物的物理性质、化学性质和合成方法都有着重要的影响。
因此,在聚合物材料的选择和设计中,PM分子量是一个不可忽视的参数。
《分子量分解问题》

分子量分解问题组号:第12小组程引 02 算法设计论文撰写刘静伟 04 C程序编程论文撰写李海欣 09 matlaB程序实现1问题提出生命蛋白质是由若干种氨基酸经不同的方式组合而成。
在实验中,为了分析某个生命蛋白质的分子组成,通常用质谱实验测定其分子量x (正整数),然后将分子量x分解为n个已知分子量a[i](i=1,2……n)氨基酸的和的形式。
某实验室所研究的问题中:n=18, x 1000a[i](i=1,2……18)分别为57, 71, 87, 97, 99, 101, 103, 113, 114, 115, 128, 129, 131, 137, 147, 156, 163, 186要求针对该实验室拥有或不拥有计算机的情况作出解答。
2问题分析#问题本身有一些不符合实际的情况如下:1)氨基酸组成蛋白质的时候会失去一分子的水,而且氨基酸组合方式不同形成不同形状的蛋白质如链形、环形等会失去不同个数的水分子;2)蛋白质水解的程度不同所得到的氨基酸分子的质量也不同;3)蛋白质中有些氨基酸是相互依存的,即,一种氨基酸的存在是以其他某一种或某几种氨基酸的存在为前提的;4)当给定的蛋白质重量增加时,所得到的解的个数可能成指数倍数上升,计算量庞大3模型假设针对2中对问题的分析,我们做一下假设:1)不考虑蛋白质水解时水分子的量,即,给定的蛋白质分子量就是几个已知分子量的和。
2)不考虑蛋白质水解程度的不同;3)被测定的蛋白质仅由给定分子量的氨基酸组成,而不含有其他物质或元素4)氨基酸组合成蛋白质的过程是任意排列组合的,一种氨基酸的存在不是以其他某一种或某几种氨基酸的存在为前提的;|4模型分析与建立给定蛋白质的分子量X 和各种氨基酸的分子量a(i),测定蛋白质的组成,即求解n 元线性方程X x a ni i =∑=1i 的所有整数解的问题。
当n=18时即为本题所要求解的问题 X x a i i =∑=181i ①i x 是非负整数(i=1,2,3……18) 再拥有和不拥有计算机的情况下可以使用不同的算法,,这里分别为“优化穷举法”和“矩阵”解法在拥有计算机的情况下求解——“优化穷举法”利用传统穷举法,我们可以先计算给定的蛋白质分子量X 包含ia 的最多的个数[X\i a ],即i x ∈{0,1,2…[X\i a ]},所以当全部结果都列举出来时,利用排列组合可以算出,要穷举的次数为]\[181i ∏=i a X ,当X=1000时将达到*10^17次,显然在实际计算中是不可行的。
分子量计算方法详解

分子量计算方法详解在化学中,分子量是指一个分子所含原子的总质量。
分子量的精确计算对于化学研究、实验以及工业应用都非常重要。
本文将详解分子量的计算方法。
1. 原子量首先要了解的是原子量。
原子量是元素中一个原子的相对质量。
相对质量是相对于碳-12原子的质量。
例如,氢的相对原子量为1.008,氧的相对原子量为15.999。
2. 分子式分子式是化学式的一种形式,用化学符号表示分子中化学元素的类型和个数。
例如,水的分子式为H2O,二氧化碳的分子式为CO2。
3. 分子量计算分子量是分子中所有原子对应原子量的总和。
可以使用以下公式来计算分子量:分子量= ∑(原子量 ×原子数量)以乙醇(C2H5OH)为例,可以计算出其分子量:C的原子量为12.01,出现2次H的原子量为1.008,出现6次O的原子量为15.999,出现1次因此,乙醇的分子量为:分子量 = (12.01 × 2) + (1.008 × 6) + (15.999 × 1) = 46.07这表明,乙醇的分子质量为46.07。
4. 相对分子质量相对分子质量是化合物分子质量相对于1/12碳-12原子质量的比值。
相对分子质量也可以表示为摩尔质量。
例如,乙醇的相对分子质量为46.07。
5. 摩尔质量分子量或相对分子质量可以转化为摩尔质量。
摩尔质量是指1摩尔物质的质量,其中1摩尔=6.02×1023个粒子(原子、分子或离子)。
可以使用以下公式将分子量转换为摩尔质量:摩尔质量 = 分子量 × 1g/mol以乙醇为例,它的分子量为46.07,因此其摩尔质量为:摩尔质量 = 46.07 × 1g/mol = 46.07g/mol6. 摩尔质量的应用摩尔质量在化学实验和化学工业中得到广泛应用。
它通常用于计算反应物和生成物的摩尔数,以便确定化学方程式中的量比。
例如,如果要制备1摩尔乙醇,将需要46.07克的乙醇。
高中化学分子质量计算题解题步骤

高中化学分子质量计算题解题步骤在高中化学学习中,分子质量计算是一个重要的知识点。
通过计算分子质量,我们可以了解化学物质的组成和性质。
本文将介绍解决分子质量计算题的步骤和技巧。
一、了解分子质量的概念分子质量是指一个分子中所有原子的质量之和。
在计算分子质量时,需要根据元素的相对原子质量(也称为相对分子质量或摩尔质量)来计算。
例如,对于化学式为H2O的水分子,H的相对原子质量为1,O的相对原子质量为16。
因此,水分子的分子质量为1×2+16=18。
二、分子质量计算题的解题步骤1. 确定化学式中各元素的相对原子质量。
首先,需要查找元素的相对原子质量。
这些数据通常可以在化学教科书或在线化学数据库中找到。
有时候,教师也会提供这些数据。
2. 计算各元素在化学式中的个数。
根据化学式中各元素的下标数字,计算各元素在化学式中的个数。
例如,对于化学式H2O,H的个数为2,O的个数为1。
3. 计算分子质量。
将各元素的相对原子质量与其在化学式中的个数相乘,然后求和,即可得到分子质量。
例如,对于化学式H2O,H的相对原子质量为1,个数为2;O的相对原子质量为16,个数为1。
因此,分子质量为1×2+16=18。
三、解题技巧和注意事项1. 注意化学式的写法化学式的写法应准确无误,特别是元素的下标数字。
一个错误的下标数字可能导致计算错误的分子质量。
2. 注意元素的相对原子质量在查找元素的相对原子质量时,应注意使用正确的数值。
不同的元素可能具有不同的相对原子质量。
3. 注意单位的转换在计算过程中,应注意单位的转换。
通常,相对原子质量的单位是g/mol,而分子质量的单位是g。
4. 多练习,熟悉常见化学式通过多做练习题,可以熟悉常见的化学式和它们的分子质量。
这样,在解决分子质量计算题时,就能更加快速和准确地计算。
举例说明:题目:计算化学式CaCO3的分子质量。
解题步骤:1. 查找元素的相对原子质量。
Ca的相对原子质量为40,C的相对原子质量为12,O的相对原子质量为16。
有关分子量的有机推断汇总

【例】(北京市模拟)已知: C 2H 5OH +HO —NO 2(硝酸)C 2H 5O —NO 2(硝酸乙酯)+H 2ORCH(OH)2 RCHO +H 2O现有只含C 、H 、O 的化合物A 、B、D、E ,其中A 为饱和多元醇,其它有关信息已注明在下图的方框内。
回答问题:(1) A 的分子式为 。
(2) 写出下列物质的结构简式D E 。
【随堂训练】已知: ①累积二烯烃(如:CH 2=C=CH 2)较不稳定,性质比较活泼。
化合物A 为烃,B~D 为烃的含氧衍生物,有关信息如下:则化合物A 的结构简式可能为例2.以某链烃A 为起始原料合成化合物G 的路径如下(图中Mr 表示相对分子质量): 又知:A 是不饱和链烃,没有甲基;NaOH 醇溶液可以和卤代烃发生消去反应产生不饱和碳不稳定,自动失水 浓硫酸原子;G 是有香味的物质,且可以使溴水褪色。
回答下列问题:(1)指出反应类型:B→C : ,E→F : 。
(2)写出下列物质的结构简式:A : ,F : 。
(3)写出下列反应的化学方程式:B → C : ;F → G : 。
3.[ 化学——选修有机化学基础](15分)(08年宁夏理综〃36)已知化合物A 中各元素的质量分数分别为C 37.5%,H 4.2%和O 58.3%。
请填空(1)0.01 molA 在空气中充分燃烧需消耗氧气 1.01 L (标准状况),则A 的分子式是 ;(2)实验表明:A 不能发生银镜反应。
1molA 与中量的碳酸氢钠溶液反应可以放出3 mol 二氧化碳。
在浓硫酸催化下,A 与乙酸可发生酯化反应。
核磁共振氢谱表明A 分子中有4个氢处于完全相同的化学环境。
则A 的结构简式是 ;(3)在浓硫酸催化和适宜的的反应条件下,A 与足量的乙醇反应生成B (C 12H 20O 7),B 只有两种官能团,其数目比为3∶1。
由A 生成B 的反应类型是 ,该反应的化学方程式是 ; (4)A 失去1分子水后形成化合物C ,写出C 的两种可能的结构简式及其官能团的名称① ,② 。
如何使用化学式进行物质的分子量计算

如何使用化学式进行物质的分子量计算化学式是描述物质组成的化学符号的组合。
通过化学式,我们可以知道一个物质中包含哪些元素以及元素的摩尔比例。
根据化学式,我们可以使用相应的计算公式来确定物质的分子量。
物质的分子量是指一个分子中所包含的所有原子的相对分子质量的总和。
它是计算化学反应中物质的摩尔量的重要指标。
下面以一些具体的案例来介绍如何使用化学式进行物质的分子量计算。
案例一:水(H2O)的分子量计算水是由氢元素和氧元素组成的,化学式为H2O。
氢元素(H)的相对原子质量为1,氧元素(O)的相对原子质量为16。
根据化学式,我们可以知道一个水分子中包含2个氢原子和1个氧原子。
因此,水的分子量计算公式为:分子量(H2O)= 2 * 相对原子质量(H)+ 相对原子质量(O)= 2* 1 + 16 = 18案例二:二氧化碳(CO2)的分子量计算二氧化碳是由碳元素和氧元素组成的,化学式为CO2。
碳元素(C)的相对原子质量为12,氧元素(O)的相对原子质量为16。
根据化学式,我们可以知道一个二氧化碳分子中包含1个碳原子和2个氧原子。
因此,二氧化碳的分子量计算公式为:分子量(CO2)= 相对原子质量(C)+ 2 * 相对原子质量(O)= 12 + 2 * 16 = 44案例三:硫酸(H2SO4)的分子量计算硫酸是由氢元素、硫元素和氧元素组成的,化学式为H2SO4。
氢元素(H)的相对原子质量为1,硫元素(S)的相对原子质量为32,氧元素(O)的相对原子质量为16。
根据化学式,我们可以知道一个硫酸分子中包含2个氢原子、1个硫原子和4个氧原子。
因此,硫酸的分子量计算公式为:分子量(H2SO4)= 2 * 相对原子质量(H)+ 相对原子质量(S)+ 4 * 相对原子质量(O)= 2 * 1 + 32 + 4 * 16 = 98通过上述案例,我们可以看出,使用化学式进行物质的分子量计算可以通过以下步骤进行:1. 根据化学式确定物质中包含的元素以及元素的摩尔比例;2. 查找元素的相对原子质量;3. 根据元素的摩尔比例,计算每个元素的摩尔量;4. 将每个元素的摩尔量相加,得到物质的分子量。
la分子量问题回答

la分子量
LA分子量是指五十二碳八胺酸(Leucine aminopeptidase,简称LA)这种酶在化学结构上的大小,常常用单位为千道尔顿(kDa)来表示。
LA分子量的大小对其在细胞生物学和生物化学中的作用至关重要。
LA 是一种脂溶性酶,主要参与蛋白质的降解和代谢,特别是在肠道消化
中具有重要的作用。
此外,LA还参与了许多与合成和分解氨基酸有关的生理过程,包括肝糖异生、肝脏代谢和酵素调节等。
LA分子量的研究也提供了一些重要的医学和生化信息。
例如,多种疾病,如癌症和感染性疾病,与LA酶的异常有关。
对LA分子量的进一步研究可以提高我们对这些疾病的诊断和治疗方面的理解。
总的来说,LA分子量作为一种生物化学参数,对于深入研究LA酶的
生物学功能和对各种疾病的诊断和治疗具有重要意义。
未来,我们可
以基于新技术和新理论,进一步探究LA分子量的作用,并将其应用于更广泛的生物和医学研究中。
高中化学分子量的计算方法

高中化学分子量的计算方法化学分子量是指化学物质分子中原子的质量总和。
在化学学习中,计算分子量是一个基础而重要的技巧。
本文将介绍高中化学中常见的分子量计算方法,并通过具体的例子进行说明,帮助读者掌握这一技巧。
一、元素的相对原子质量在计算分子量之前,我们首先需要了解元素的相对原子质量。
相对原子质量是指元素的原子质量与碳-12同位素的质量比值。
例如,氧的相对原子质量为16,即氧原子的质量是碳-12原子质量的16倍。
二、计算分子量的方法1. 单原子离子的分子量计算对于单原子离子,其分子量等于元素的相对原子质量。
例如,氧分子的分子量为16。
2. 多原子离子的分子量计算对于多原子离子,其分子量等于各原子的相对原子质量之和。
例如,硫酸根离子(SO4)的分子量为32+16*4=96。
3. 分子的分子量计算对于分子,其分子量等于各原子的相对原子质量之和。
例如,水分子(H2O)的分子量为1*2+16=18。
4. 化合物的分子量计算对于化合物,其分子量等于各元素的相对原子质量乘以相应的个数后相加。
例如,二氧化碳(CO2)的分子量为12+16*2=44。
三、举一反三:应用分子量计算分子量计算不仅可以用于单一化学物质的计算,还可以应用于化学方程式的计算以及实际问题的解答。
1. 化学方程式的计算在化学方程式中,反应物和生成物的分子量可以通过分子量计算得到。
例如,对于反应式2H2+O2→2H2O,反应物氢气(H2)的分子量为2*1=2,氧气(O2)的分子量为32,生成物水(H2O)的分子量为2*1+16=18。
2. 实际问题的解答分子量计算也可以应用于实际问题的解答。
例如,某种药物的化学式为C6H12O6,求其分子量。
根据分子量计算方法,可得分子量为6*12+12*1+6*16=180。
这样,我们就可以通过计算得到该药物的分子量。
总结起来,高中化学中分子量的计算方法包括单原子离子的计算、多原子离子的计算、分子的计算以及化合物的计算。
高中化学氧化还原反应的分子量计算技巧

高中化学氧化还原反应的分子量计算技巧在高中化学学习中,氧化还原反应是一个重要的内容,而其中的分子量计算是一个常见的考点。
本文将介绍一些分子量计算的技巧,帮助高中学生更好地理解和应用氧化还原反应中的分子量计算。
一、基本概念在进行分子量计算之前,我们需要了解一些基本概念。
分子量是指一个分子中各个原子的相对原子质量之和。
相对原子质量可以通过元素周期表查找得到,通常以g/mol为单位。
而化学方程式中的化合物,是由不同元素的原子组成的,因此可以通过分子量计算来确定化学方程式中各个物质的质量关系。
二、分子量计算的步骤1. 找到化学方程式中的各个物质的分子式。
2. 根据分子式,找到各个元素的相对原子质量。
3. 将各个元素的相对原子质量相加,得到该物质的分子量。
举例说明:假设有以下化学方程式:2HCl + Na2CO3 → 2NaCl + H2O + CO2我们需要计算Na2CO3的分子量。
1. 找到Na2CO3的分子式,即Na2CO3。
2. 根据元素周期表,我们可以得到Na的相对原子质量为23,C的相对原子质量为12,O的相对原子质量为16。
3. 将Na、C、O的相对原子质量相加:2×23 + 12 + 3×16 = 46 + 12 + 48 = 106。
因此,Na2CO3的分子量为106 g/mol。
三、分子量计算的注意事项1. 在计算分子量时,要注意化学方程式中的系数。
系数表示该物质的摩尔比例,需要乘以系数才能得到正确的分子量。
2. 若化学方程式中有括号,需要将括号内的分子式中各个元素的相对原子质量相加,再乘以括号外的系数。
3. 在计算分子量时,要注意元素的相对原子质量可能会有小数,需要进行四舍五入,保留合适的位数。
举一反三:除了上述的例子,还有其他类型的氧化还原反应需要进行分子量计算。
例如,当涉及到氧化剂和还原剂时,我们需要计算它们的分子量以确定摩尔比例。
另外,当涉及到酸碱中和反应时,我们也可以通过分子量计算来确定反应中各个物质的质量关系。
分子量与化学反应计算

分子量与化学反应计算化学是一门研究物质变化及其性质的科学,而计算则是运用数学方法来解决问题的过程。
分子量是化学中一个非常重要的概念,它与化学反应的计算密切相关。
在这篇文章中,我们将探讨分子量与化学反应计算之间的关系,并展示如何利用分子量来进行化学反应计算。
一、分子量的定义和意义分子量指的是一个分子中所有原子的质量之和。
它通常用原子质量单位(amu)来表示。
分子量的计算非常重要,因为它可以帮助我们确定化学物质的量,并进行化学反应的计算。
以水分子(H2O)为例,它由两个氢原子和一个氧原子组成。
氢的原子质量约为1.008 amu,氧的原子质量约为16.00 amu。
将它们相加,我们可以得到水分子的分子量为18.02 amu。
这意味着在一摩尔的水分子中,有18.02克的质量。
分子量的意义在于它可以帮助我们确定物质的量。
例如,如果我们知道了某个物质的质量是36.04克,而它的分子量是18.02 amu,那么我们可以计算出它的物质的量为2摩尔。
这对于化学反应计算非常重要。
二、化学反应计算的基本原理化学反应计算通常涉及到反应物的化学式和所需的比例关系。
这些比例关系是由化学方程式所决定的。
根据反应物和生成物的化学式,我们可以确定它们的分子量,从而计算出它们之间的物质的量比。
例如,考虑以下化学反应:2H2 + O2 → 2H2O在这个反应中,氢气和氧气是反应物,水是生成物。
氢气的分子量为2.02 amu,氧气的分子量为32.00 amu,水的分子量为18.02 amu。
根据化学方程式,我们可以得出反应比为2:1:2,即2摩尔的氢气和1摩尔的氧气反应产生2摩尔的水。
三、分子量在化学反应计算中的应用利用分子量,我们可以进行化学反应计算,以确定反应物和生成物之间的物质的量变化。
首先,我们需要将化学方程式平衡,确保反应物和生成物的物质的量比满足化学方程式的要求。
例如,考虑以下反应:CH4 + 2O2 → CO2 + 2H2O在这个反应中,甲烷和氧气反应生成二氧化碳和水。
初中化学分子量的计算方法及实际应用解析

初中化学分子量的计算方法及实际应用解析化学分子量是指化学物质中一个分子的质量。
它是化学计算中的重要概念,能够帮助我们了解和研究化学反应、物质的性质以及实际应用中的相关问题。
本文将介绍初中化学分子量的计算方法以及其在实际应用中的解析。
一、化学分子量的计算方法化学分子量的计算主要涉及到元素的相对原子质量,化学方程式以及化合物的化学式。
下面将分别介绍这几个方面的计算方法。
1. 相对原子质量相对原子质量是指一个元素相对于碳-12同位素的质量比值,在元素周期表上通常以一个带小数的数值标识。
例如,氧的相对原子质量为16.00。
2. 化学方程式化学方程式是化学反应过程的简化表示,由反应物和生成物的化学式组成。
在计算化学分子量时,需要通过化学方程式中的系数来确定各个物质的摩尔数。
3. 化合物的化学式化合物的化学式由元素符号和下标表示,可以表示物质中各个元素的种类和摩尔比。
例如,二氧化碳的化学式为CO2。
根据以上三个方面的计算方法,我们可以通过以下步骤计算出化学物质的分子量:步骤一:根据化学式确定化合物中各个元素的种类和数量。
步骤二:根据相对原子质量表,查找各个元素的相对原子质量。
步骤三:将各个元素的相对原子质量乘以其在化合物中的个数。
步骤四:将步骤三中的结果相加,得到化合物的分子量。
二、分子量的实际应用化学分子量在实际应用中具有广泛的用途,下面将对其中几个常见的应用进行解析。
1. 摩尔质量的计算摩尔质量是指物质的质量与其摩尔数之间的比值。
通过计算分子量,我们可以得到物质的摩尔质量。
摩尔质量在化学实验和计算中具有重要意义,可以帮助我们进行物质的定量计算。
例如,在实验室中,我们可以通过测量物质的质量,并利用分子量计算出物质的摩尔数。
2. 反应物计量关系的确定化学方程式中的系数可以告诉我们物质之间的摩尔比。
通过分子量的计算,我们可以确定反应物之间的质量比。
这对于确定反应物的量以及预测反应的进行过程具有重要意义。
例如,在化学合成反应中,我们可以利用分子量计算出所需的反应物质量,从而控制反应的进行。
有关平均分子量的计算

有关平均分⼦量的计算有关平均分⼦量的计算有关平均分⼦量的计算,本来在中学化学教学中就占有⽐较重要的地位。
虽然从形式上看,这只是⼀个有关算数平均值的简单讨论,但是如果没有注意到这类计算有多种类型、各类型还有各⾃的解题要点,教师的⼯作往往就是事倍功半的。
这⼀部分内容的教学,最好分为三个层次来进⾏。
⼀、平均分⼦量概念的引⼊学⽣在了解到空⽓的⼀些性质时,⼀般就会接触到平均分⼦量的概念。
学⽣对空⽓的平均分⼦量为什么是29,也会有浓厚的兴趣。
这时,实际上就可以引⼊平均分⼦量的概念。
例1,已知空⽓中的氮⽓占78%,氧⽓占21%,氩占1%。
求空⽓的平均分⼦量。
解,在给学⽣介绍清楚,这个百分数指的是反映分⼦个数的百分数后,学⽣是不难理解下⾯这个式⼦的。
当然,在介绍完物质的量概念,讨论了分⼦量的多种计算⽅法,知道了⽓体相对密度与分⼦量的关系,再进⾏平均分⼦量的计算,教师就更有底⽓了。
例2,爆鸣⽓是由2份氢⽓与1份氧⽓混合⽽成的。
求其平均分⼦量。
解,在知道,相同情况下⽓体的体积⽐就是分⼦个数⽐后,学⽣应该会列出下式,。
对这种简单的平均分⼦量的计算,教师可以给学⽣总结出如下的两个式⼦: (1)及, (2)在⼀定条件下,这个式⼦还可⽤于计算混合⽓体中某种分⼦的分⼦量,或者是计算其中某种分⼦的百分含量。
例3,已知某NO2与N2O4混合⽓体的平均分⼦量为69。
求其中NO2的百分含量。
例4,已知氧⽓与另⼀⽓态烃以5:2的体积⽐混合。
混合后的平均分⼦量为30.3。
求该⽓态烃的分⼦量。
这些都是学⽣应该掌握的,最为基本的计算题。
但是,⽤上⾯这些⽅法来解决某些问题时,会显得过于繁琐。
在适当的时候教师应该将这类题的解题思路及解题⽅法给予进⼀步的扩展。
⼆、分解反应进⾏完全时,⽓体产物平均分⼦量的计算与上述这些例⼦不同的是,还有⼀些题在本质上属于,利⽤化学⽅程式进⾏的计算。
也就是,要利⽤化学⽅程式来确定分⼦间的组成关系。
例5,在⼀定条件下加热NH4NO3,,其分解反应要按下式,NH4NO3=N2O+2H2O,来进⾏。
高分子计算与解答【可编辑范本】

计算题1.在搅拌下依次向装有四氢呋喃的反应釜中加入0。
2mol n—BuLi和20kO,然后继续反应。
假如g苯乙烯.当单体聚合了一半时,向体系中加入1.8g H2用水终止的和继续增长的聚苯乙烯的分子量分布指数均是1,试计算(1)水终止的聚合物的数均分子量;(2)单体完全聚合后体系中全部聚合物的数均分子量;(3)最后所得聚合物的分子量分布指数。
2。
有下列所示三成分组成的混合体系。
成分1:重量分数=0。
5,分子量=l×104成分2:重量分数=0.4,分子量=1 ×105.成分3:重量分数=0.1,分子量=1×106求:这个混合体系的数均分子量和重均分子量及分子量分布宽度指数。
3。
某一耐热性芳族聚酰胺其数均相对分子质量为24116。
聚合物经水解后,得39。
31%(质量百分数)•对苯二胺,59。
81%(质量百分数)•对苯二甲酸,0.88%苯甲酸(质量百分数).试写出聚合物结构式和其水解反应式?计算聚合物的数均相对分子质量?4。
等摩尔二元醇和二元酸缩聚,另加醋酸1。
5%,p=0.995或0。
999时聚酯的聚合度多少?5.等摩尔二元醇和二元酸缩聚,另加醋酸1。
5%,p=0。
995或0.999时聚酯的聚合度多少?6.AA、BB、A3混合体系进行缩聚,NA0=NB0=3。
0,A3中A基团数占混合物中A总数( )的10%,试求p=0。
970时的以及= 200时的p.7。
对苯二甲酸(1mol)和乙二醇(1mol)聚酯化反应体系中,共分出水18克,求产物的平均分子量和反应程度,设平衡常数K=4。
8.要求制备数均分子量为16000的聚酰胺66,若转化率为99。
5%时:(1)己二酸和己二胺的配比是多少?产物端基是什么?(2)如果是等摩尔的己二酸和己二胺进行聚合反应,当反应程度为99.5%时,聚合物的数均聚合度是多少?9.由1mol丁二醇和1mol己二酸合成数均分子量为5000的聚酯,(1)两基团数完全相等,忽略端基对数均分子量的影响,求终止缩聚的反应程度P;(2)假定原始混合物中羟基的总浓度为2mol,其中1。
新有机分子量的运用

分子量的运用1.某有机物完全燃烧只生成CO2和H2O,相对分子质量为128。
判断其分子式。
答案:C9H20;C10H8;C8H16O;C7H12O2;C6H8O3;C5H4O4。
要点:先按烃确定,然后注意两个转化:①C~12H;②O~CH42.C、H、O组成的物质,分子量不超过150,含O为50%,含C最多多少个?3.两种气态有机物按1:1混合,平均分子质量为23,完全燃烧只生成CO2和H2O。
确定组成。
提示:常见有机物分子量:甲烷—16;乙烷—30;乙烯—28;乙炔—26;甲醇—32;乙醇—46;甲醛—30;乙醛—44;甲酸—46;乙酸—60。
答案:必有甲烷,则另一种分子量为30的气态有机物,为乙烷或者甲醛。
3.某有机物可能含以下元素:C、H、O、F(原子量19)、S,其分子量为44。
确定其分子式。
提示:按S、F、O是否存在,存在的个数依次分析。
答案:CH≡CF;C2H4O。
(注意:CO2为无机物)。
4.某分子含C、H、O、N四种元素,分子量为60,写出其分子式。
答案:CO(NH2)2提示:C、H、O三元素组成的物质的分子量一定为偶数,C、H、O、N四种元素组成的物质,含N个数为奇数则分子量为奇数;含N个数为偶数则分子量为偶数。
所以该分子含N 原子为偶数,分析知:含N原子2个;进一步确定O、C原子。
5.A、B都是芳香族化合物,1 mol A水解得到1 mol B和1 mol醋酸A、B的分子量都不超过200,完全燃烧都只生成CO2和H2O。
且B分子中碳和氢元素总的质量百分含量为65.2%(即质量分数为0.652)。
A溶液具有酸性,不能使FeCl3溶液显色.(1)A、B分子量之差为_______________.(2)1个B分子中应该有_______________个氧原子.(3)A的分子式是_______________.(4)B可能的三种结构简式是:_______________、_______________、_______________.提示:依据反应,确定B的分子量不超过200+18-60=158,再依据百分含量确定B中氧原子个数最多为3个。
蛋白质分子的分解

蛋白质分子的分解上面我们从总体上讨论了蛋白质分子的结构——链的一般形状。
蛋白质分子结构的细节又是怎样的呢?例如,在某个给定的蛋白质分子中,每一种氨基酸各有多少个呢?我们可以把一个蛋白质分子分解成组成它的各种氨基酸(通过在酸中加热),然后测定混合液中每一种氨基酸有多少。
遗憾的是,有些氨基酸在化学性质上彼此非常相似,用普通的化学方法几乎不能把它们截然分开,而用色谱法能够把各种氨基酸分得清清楚楚(见第六章)。
1941年,英国生物化学家马丁和辛格首先把色谱法应用于这个方面。
他们采用的是用淀粉作为色柱里的填料。
1948年,美国生物化学家S.穆尔和斯坦把氨基酸的淀粉色谱法的效率提高到一个新水平,因此,他们分享了1972年的诺贝尔化学奖。
把各种氨基酸的混合液倒入淀粉柱里,待所有的氨基酸分子附着在淀粉颗粒上以后,再用新鲜的溶剂把氨基酸从柱中慢慢地淋洗下去。
每一种氨基酸都以自己特定的速率从柱中向下移动。
当每一种氨基酸从柱的底部分别流出时,那种氨基酸溶液的液滴就被收集在一个容器里;然后用一种能够使氨基酸呈色的化学药品,对每一个容器里的溶液进行处理。
颜色的强度表示溶液中某种氨基酸的含量。
这种颜色强度是用一种叫做分光光度计的仪器测量的。
分光光度计可以通过某一特定波长的光被吸收的量显示出颜色的强度)。
分光光度计。
光束被分为两部分,一部分通过要分析的标本,而另一部分直接到光电池。
因为通过标本的光束被减弱,在光电池中释放的电子比未被吸收的光束释放的少,所以这两部分光束在示波器上显示出电位差,这样就可以测量出标本的光的吸收量顺便说一下,分光光度计也可以用在其他的化学分析上。
如果让波长连续增加的光通过一种溶液,吸收的量就会平稳地改变,在某些波长时上升到最大值,而在另一些波长时下降到最小值。
结果形成一种吸收光谱。
每一种原子团都有自己特定的一个或几个吸收峰。
在刚刚进入20世纪的时候,美国物理学家柯布伦茨首先证明,在红外区域这种现象尤为明显。
分子交换法计算题

分子交换法计算题分子交换法,是一种计算分子量的方法,计算分子量的重要性主要在于分子量直接关系着化学物质的性质和实际的应用,是进行化学定量分析和合成设计的基础,因此掌握分子交换法计算题的方法非常重要。
本文将介绍分子交换法计算题的基本概念、计算方法和实例分析,希望对学习和掌握分子交换法计算有所帮助。
一、基本概念1. 分子量:表示分子中所有原子的质量总和,其单位是g/mol,可以用来确定化合物的相对分子质量。
2. 相对分子质量:是指一个分子的相对质量与1/12碳原子的质量相比的比值,通常用M来表示,相对分子质量的单位是g/mol。
3. 经验式:表示化合物中不同原子的数目比,而不考虑它们的原子量。
例如,化合物中含有2个碳原子和4个氢原子,可以用化学式C2H4表示。
4. 分子式:表示化合物分子中各原子的种类和数量,如H2O表示分子中含2个氢原子和1个氧原子。
分子式是描述化合物分子数量和结构的公式。
5. 化学计量数:表示一定量的物质中各原子的相对数量,可以用经验式或分子式表示。
二、计算方法分子交换法是利用化学计量关系计算分子量的一种方法。
化学计量关系是指在反应方程式中,各物质之间质量或摩尔之间的数量关系,包括化学反应定量关系、化学计量关系及化学量纲关系等三个方面。
在用分子交换法计算分子量时,需要遵循以下基本步骤:1. 化学式化简:将化学式用它们的化学计量数表示,便于进行计算。
2. 换组:将不同原子组合换到不同的分子中,即比例转移。
3. 比较:将换组后的各分子的质量比较,并计算它们的相对摩尔数。
4. 计算:根据摩尔比例计算相对分子量。
下面通过一个实例来说明分子交换法的计算方法。
实例:一种含碳、氢、氧三种元素的有机酸,它在水中的熔点为60°C,可溶于水,不溶于苯和正己烷。
10.02g该有机酸不完全燃烧生成13.55g CO2和4.41g H2O。
试推出该有机酸的分子式。
解题步骤:1. 确定该有机酸的分子式。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、分子量分解问题
1. 问题的提出
生命蛋白质是由若干种氨基酸经不同的方式组合而成。
在实验中,为了分析某个生命蛋白质的分子组成,通常用质谱实验测定其分子量x(正整数),然后将分子量x分解为n个已知分子量a[i](i=1,.......,n)氨基酸的和的形式。
某实验室所研究的问题中:
n=18, x≤1000
a[i](i=1,.......,18)分别为57, 71, 87, 97, 99, 101, 103, 113, 114, 115, 128, 129, 131, 137, 147, 156, 163, 186
要求针对该实验室拥有或不拥有计算机的情况作出解答。
2.问题的分析
上述问题就是要将任意给定的正整数表示为若干已知正整数的倍数
之和,亦即求解下列不定方程
∑==
n
i
x
i x
i
a
1
][
][
(1)
其中x是已知蛋白质的分子量,a[i]代表第i种氨基酸的分子量,x[i]代表该种蛋白质中所含第i种氨基酸的个数。
根据题意,我们作以下几点分析:
(A1)对一些给定的值x,不定方程(1)可能无解;但对实际问题,应有解,若出现无解,说明数值x有偏差,应重新测定。
(A2)以m表示(1)右端x的上界。
此时m=1000, n=18, 考虑用穷举法求出全部解,这时,每个m[i]的取值范围为0≤x[i]≤ [m/a[i]],所以穷举的次数要达到O(m n),实际为
故穷举法在实际上是不可行的。
(A3) 考虑分解x的一个反问题,将若干个分子量a[i](i=1,2,….,n)经组合,构成更大分子量的蛋白质,从中寻找具有分子量x的各种构成。
(A4) 若实验室没有计算机,我们事前仍可利用计算机求得一些便于查阅的工具或表格供实验室工作人员使用。
3 .模型的建立
(I)深度、广度搜索
先从穷举法着手,对给定的m,将其分解为a[i]的组合形式,具体过程可以分为深度搜索和广度搜索两种方式。
但这两种方式,一方面计算量随着m的增大而指数增加,另一方面,面对几万、几十万种组合,无法方便筛选。
(II)启发式搜索
考虑(A3)中的思想,对a[i](i=1,2,…..,n)不断求和。
看是否能达到x?由于在求和中只考虑和数小于m的范围,因此对每个a[i]的求和过程的计算工作量为O(m),整个求和过的计算工作量为O(mn),这比穷举法的计算量O(m n)要少得多。
为了实现上述方法,先引入下列定义:
Y={x|x≤m,x使(1)有解,x为正整数}
L(a[i])={0,a[i],2a[i],……..,[m/a[i]].a[i]}定义一种运算
其中U可为{1,2,…,m}的任何子集。
开始令Y=φ,然后对i=1,2,…,n用下列运算不断扩大集合Y:
Y:=Y])
a
⊕
L
(i
[
定义数组b[i](i=1,2,…,m),开始时一切b[x]=0,若在求和过程中得到一个x,则令b[x]=1,表示该x的不定方程(1)有解:定义另一种数组s[i](i=1,2,…,m),开始时一切s[x]=0, 以后在求和过程中每次得到一个x, 就令s[x]:= s[x]+1, 这样最终得到的s[x]相等于该x的不定方程(1)的解的个数.
然而, 我们不仅要得到解的个数, 还要求得所有的解, 因此在求和过程中还应记录更多的信息。
为此对不定方程(1)的解的构造作进一步的分析与提炼。
设(x[1],x[2],…x[n])为相应于x的(1)非负整数解,又设x[q]为
x[1],x[2],…,x[n]中最后一个非零项,即q∈[1,n]使x[q+1]=x[q+2]= …
=x[n]=0,q称为末项指标, 于是(1)可改写为
从而还可得到
q
x
a
q
+
+
x
=
-q
x
q
a
x
a
x
a
+
a
q
]1
-
[
[
[
](
)1
]
[
...
]1
[-
+
]2[
]
-
]1[
]2[
]1[
(2)
若记第q个分量为1的n维单位向量为e[q]. 如果(x[1],x[2],…,x[n])为相应于x的(1)的解,其末项指标为q,则(x[1],x[2],…,x[n])-e[q]为相应于x-a[q]的(1)的解,其末项指标为p≤q,考虑到多解的情况,q可能有多种选择,因此在求和过程Y:=Y⊕L(a[i])中还应记录末项可能的种数,记为v[x](v[x]≤n)及相应的末项指标q[x,1], q[x,2], …, q[x,v[x]].
有了一切v[x]及q[x,v[x]]后,我们可以利用(2)不断减少x来跟踪x 的所有解的情况。
为此将上述v[.]及q[.,.]记录为解的跟踪信息表。
下面给出了x≤186时的跟踪信息表,以示求解的过程。
表1 跟踪信息表的一部分
的两个解为
x=a[2]+a[5], x=a[1]+a[3]
又以表中未列出的x=284为例,有关的跟踪信息为
x=284, s[x]=6, v[x]=4, q[x,1]=9, q[x,2]=11, q[x3,]=15, q[x,4]=16 这些信息表明:解的总数s=6,末项指标有4种选择,分别为9、11、15、16,利用末项指标的信息,我们利用(2)得到
x-a[9]=170, x-a[11]=156, x-a[15]=137, x-a[16]=128
再对上述所得的4个数继续往前利用表1关于它们的跟踪信息,使末项指标不断下降,可得如下6个解:
x=a[2]+a[5]+a[9]; x=a[1]+a[8]+a[9]; x=a[1]+a[5]+a[11];
x=a[14]+a[15]; x=a[1]+a[2]+a[16]; x=a[11]+a[16] 上述跟踪方式的求解步骤,可描述为一棵树,可以据此编制出一个完整的程序。
对x≤1000, 解的个数最多可达几百个。
但对于没有计算机的实验室,我们可以给出x≤m(如x≤1000)的跟踪信息表用手算来实现跟踪也是可行的。
4 .进一步讨论
因算法的计算量为O(mn),故计算时间上是可行的。
由于存储解的跟踪信息表需一个m⨯n的矩阵q,所以空间需求为O(mn),当m与n 很大时,可以用压缩存放来发掘潜力。
其次,实验得到的蛋白质分子量x有偏差时的情况是有实际意义的。
如果偏差不超过3,则可对x、x±1、x±2、x±3分别求解,其结果供决策人员参考,因此,计算工作量还需随偏差量线性增加。
此外,当m与n相当大,且蛋白质分子量x相应的解数很多时,则为了减少计算以及缩小解的总数,还应增加其他求解条件,如通过实验验证某分子量为a[i]的氨基酸是否存在,某种氨基酸存在数量的上下限等,这样可使计算量大大减少。
